content
stringlengths 73
1.12M
| license
stringclasses 3
values | path
stringlengths 9
197
| repo_name
stringlengths 7
106
| chain_length
int64 1
144
|
|---|---|---|---|---|
<jupyter_start><jupyter_text># Popularity of Music Records<jupyter_code>import pandas as pd
import statsmodels.api as sm
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)<jupyter_output><empty_output><jupyter_text>## Problem 1.1 - Understanding the Data
How many observations (songs) are from the year 2010?<jupyter_code>songs = pd.read_csv('../data/songs.csv')
songs[songs['year']==2010].shape[0]<jupyter_output><empty_output><jupyter_text>## Problem 1.2 - Understanding the Data
How many songs does the dataset include for which the artist name is "Michael Jackson"?<jupyter_code>songs[songs['artistname']=='Michael Jackson'].shape[0]<jupyter_output><empty_output><jupyter_text>## Problem 1.3 - Understanding the Data
Which of these songs by Michael Jackson made it to the Top 10? *Select all that apply*.
- You Rock My World
- You Are Not Alone<jupyter_code>songs[
(songs['artistname']=='Michael Jackson')
& (songs['Top10']==1)
]['songtitle']<jupyter_output><empty_output><jupyter_text>## Problem 1.4 - Understanding the Data
The variable corresponding to the estimated time signature (timesignature) is discrete, meaning that it only takes integer values (0, 1, 2, 3, . . . ). What are the values of this variable that occur in our dataset? *Select all that apply*.
- 0
- 1
- 3
- 4
- 5
- 7
Which timesignature value is the most frequent among songs in our dataset?
- 4<jupyter_code>songs['timesignature'].value_counts().sort_index()<jupyter_output><empty_output><jupyter_text>## Problem 1.5 - Understanding the Data
Out of all of the songs in our dataset, the song with the highest tempo is one of the following songs. Which one is it?<jupyter_code>songs[songs['tempo']==songs['tempo'].max()]['songtitle']<jupyter_output><empty_output><jupyter_text>## Problem 2.1 - Creating Our Prediction Model
We wish to predict whether or not a song will make it to the Top 10. To do this, first split the data into a training set "SongsTrain" consisting of all the observations up to and including 2009 song releases, and a testing set "SongsTest", consisting of the 2010 song releases.
How many observations (songs) are in the training set?<jupyter_code>SongsTrain = songs[songs['year']<2010].copy()
SongsTest = songs[songs['year']>=2010].copy()
SongsTrain.shape[0]<jupyter_output><empty_output><jupyter_text>## Problem 2.2 - Creating our Prediction Model
In this problem, our outcome variable is "Top10" - we are trying to predict whether or not a song will make it to the Top 10 of the Billboard Hot 100 Chart. Since the outcome variable is binary, we will build a logistic regression model. We'll start by using all song attributes as our independent variables, which we'll call Model 1.
We will only use the variables in our dataset that describe the numerical attributes of the song in our logistic regression model. So we won't use the variables "year", "songtitle", "artistname", "songID" or "artistID".
Looking at the summary of your model, what is the value of the Akaike Information Criterion (AIC)?
- 4827.154102388615<jupyter_code>features = songs.columns[5:]
X_train1 = SongsTrain[features[:-1]].copy()
y_train1 = SongsTrain['Top10'].copy()
X_test1 = SongsTest[features[:-1]].copy()
y_test1 = SongsTest['Top10'].copy()
SongsLog1 = sm.Logit(y_train1, sm.add_constant(X_train1)).fit()
print(SongsLog1.aic)<jupyter_output>Optimization terminated successfully.
Current function value: 0.330451
Iterations 8
4827.154102388615
<jupyter_text>## Problem 2.3 - Creating Our Prediction Model
Let's now think about the variables in our dataset related to the confidence of the time signature, key and tempo (timesignature_confidence, key_confidence, and tempo_confidence). Our model seems to indicate that these confidence variables are significant (rather than the variables timesignature, key and tempo themselves). What does the model suggest?
- The higher our confidence about time signature, key and tempo, the more likely the song is to be in the Top 10 <jupyter_code>SongsLog1.params[:8]<jupyter_output><empty_output><jupyter_text>## Problem 2.4 - Creating Our Prediction Model
In general, if the confidence is low for the time signature, tempo, and key, then the song is more likely to be complex. What does Model 1 suggest in terms of complexity?
- Mainstream listeners tend to prefer less complex songs
## Problem 2.5 - Creating Our Prediction Model
Songs with heavier instrumentation tend to be louder (have higher values in the variable "loudness") and more energetic (have higher values in the variable "energy").
By inspecting the coefficient of the variable "loudness", what does Model 1 suggest?
- Mainstream listeners prefer songs with heavy instrumentation
By inspecting the coefficient of the variable "energy", do we draw the same conclusions as above?
- No<jupyter_code>print("Loudness:", SongsLog1.params.loc['loudness'])
print("Energy:", SongsLog1.params.loc['energy'])<jupyter_output>Loudness: 0.2998794034266897
Energy: -1.5021444680863525
<jupyter_text>## Problem 3.1 - Beware of Multicollinearity Issues!
What is the correlation between the variables "loudness" and "energy" in the training set?
- 0.7399067084558058
Given that these two variables are highly correlated, Model 1 suffers from multicollinearity. To avoid this issue, we will omit one of these two variables and rerun the logistic regression. In the rest of this problem, we'll build two variations of our original model: Model 2, in which we keep "energy" and omit "loudness", and Model 3, in which we keep "loudness" and omit "energy".<jupyter_code>X_train1[['loudness', 'energy']].corr().iloc[0, 1]<jupyter_output><empty_output><jupyter_text>## Problem 3.2 - Beware of Multicollinearity Issues!
Create Model 2, which is Model 1 without the independent variable "loudness".
Look at the summary of SongsLog2, and inspect the coefficient of the variable "energy". What do you observe?
- Model 2 suggests that songs with high energy levels tend to be more popular. This contradicts our observation in Model 1. <jupyter_code>X_train2 = X_train1.drop('loudness', axis=1)
X_test2 = X_test1.drop('loudness', axis=1)
SongsLog2 = sm.Logit(y_train1, sm.add_constant(X_train2)).fit()
SongsLog2.params.loc['energy']<jupyter_output>Optimization terminated successfully.
Current function value: 0.338276
Iterations 8
<jupyter_text>## Problem 3.3 - Beware of Multicollinearity Issues!
Now, create Model 3, which should be exactly like Model 1, but without the variable "energy".
Look at the summary of Model 3 and inspect the coefficient of the variable "loudness". Remembering that higher loudness and energy both occur in songs with heavier instrumentation, do we make the same observation about the popularity of heavy instrumentation as we did with Model 2?
- Yes<jupyter_code>X_train3 = X_train1.drop('energy', axis=1)
X_test3 = X_test1.drop('energy', axis=1)
SongsLog3 = sm.Logit(y_train1, sm.add_constant(X_train3)).fit()
SongsLog3.params.loc['loudness']<jupyter_output>Optimization terminated successfully.
Current function value: 0.332087
Iterations 8
<jupyter_text>## Problem 4.1 - Validating Our Model
Make predictions on the test set using Model 3. What is the accuracy of Model 3 on the test set, using a threshold of 0.45? (Compute the accuracy as a number between 0 and 1.)<jupyter_code>pred_3 = SongsLog3.predict(sm.add_constant(X_test3))
pred_3_bool = (pred_3 >= 0.45).astype(int)
(y_test1 == pred_3_bool).mean()<jupyter_output><empty_output><jupyter_text>## Problem 4.2 - Validating Our Model
Let's check if there's any incremental benefit in using Model 3 instead of a baseline model. Given the difficulty of guessing which song is going to be a hit, an easier model would be to pick the most frequent outcome (a song is not a Top 10 hit) for all songs. What would the accuracy of the baseline model be on the test set? (Give your answer as a number between 0 and 1.)<jupyter_code>1- y_test1.mean()<jupyter_output><empty_output><jupyter_text>## Problem 4.3 - Validating Our Model
It seems that Model 3 gives us a small improvement over the baseline model. Still, does it create an edge?
Let's view the two models from an investment perspective. A production company is interested in investing in songs that are highly likely to make it to the Top 10. The company's objective is to minimize its risk of financial losses attributed to investing in songs that end up unpopular.
A competitive edge can therefore be achieved if we can provide the production company a list of songs that are highly likely to end up in the Top 10. We note that the baseline model does not prove useful, as it simply does not label any song as a hit. Let us see what our model has to offer.
How many songs does Model 3 correctly predict as Top 10 hits in 2010 (remember that all songs in 2010 went into our test set), using a threshold of 0.45?<jupyter_code>test_pred = y_test1.to_frame()
test_pred['predicted'] = pred_3_bool
cfm = test_pred.value_counts().sort_index()
cfm<jupyter_output><empty_output><jupyter_text>## Problem 4.4 - Validating Our Model
What is the sensitivity of Model 3 on the test set, using a threshold of 0.45?
- 0.3220338983050847
What is the specificity of Model 3 on the test set, using a threshold of 0.45?
- 0.9840764331210191<jupyter_code>sensitivity = cfm.loc[1,1] / (cfm.loc[1,1] + cfm.loc[1,0])
specificity = cfm.loc[0,0] / (cfm.loc[0,0] + cfm.loc[0,1])
print("Sensitivity:", sensitivity)
print("Specificity:", specificity)<jupyter_output>Sensitivity: 0.3220338983050847
Specificity: 0.9840764331210191
|
no_license
|
/3_logistic_regression/popularity_of_music_records.ipynb
|
asgar0r/the_analytics_edge
| 17 |
<jupyter_start><jupyter_text>### Read images<jupyter_code>paths = [f for f in glob.glob('/home/shahbaz/proj/size_normed_images/**/*.jpg', recursive=True)
if f.endswith('.jpg')]
train, test = train_test_split(paths, test_size = 0.2)
train, valid = train_test_split(train, test_size = 0.2)
train_labels = [extract_class(l) for l in train]
#train_images = [Image.open(img) for img in train]
test_labels = [extract_class(l) for l in test]
#test_images = [Image.open(img) for img in test]
valid_labels = [extract_class(l) for l in valid]
Xtrain = np.zeros( (len(train), new_size[0] * new_size[1] * 3) )
for index, item in enumerate(train):
_img = Image.open(train[index])
Xtrain[index] = np.asarray(_img.resize((new_size[0],new_size[1]))).flatten()
_img.close()
Xtest = np.zeros( (len(test) , new_size[0] * new_size[1] * 3) )
for index, item in enumerate(test):
_img = Image.open(test[index])
Xtest[index] = np.asarray(_img.resize((new_size[0],new_size[1]))).flatten()
_img.close()
Xvalid = np.zeros( (len(valid) , new_size[0] * new_size[1] * 3) )
for index, item in enumerate(valid):
_img = Image.open(valid[index])
Xvalid[index] = np.asarray(_img.resize((new_size[0],new_size[1]))).flatten()
_img.close()
#?np.asarray(1,2,3).flatten()
Xtrain.shape
#len(train_labels)
confmat_labels = list(set(train_labels))
confmat_labels.sort()<jupyter_output><empty_output><jupyter_text>### Build a model<jupyter_code>"""
paramGrid = ParameterGrid({
'min_samples_leaf': [1,3,5,10,15,25,50,100,125,150,175,200],
'max_features': ['sqrt', 'log2', 0.4, 0.5, 0.6, 0.7],
'n_estimators': [60],
'n_jobs': [-1],
'random_state': [42]
})
best_model, best_score, all_models, all_scores = pf.bestFit(RandomForestClassifier, paramGrid,
Xtrain, np.array(train_labels), Xvalid, np.array(valid_labels),
metric=metrics.roc_auc_score, bestScore='max', scoreLabel='AUC')
print(best_model)
"""<jupyter_output><empty_output><jupyter_text>### Random Forest Optimized Model<jupyter_code>parameters = {
'min_samples_leaf': [1,3,5,10,15,25,50,100,125,150,175,200],
'max_features': ['sqrt', 'log2', 0.4, 0.5, 0.6, 0.7],
'n_estimators': [10, 30, 60, 90],
'n_jobs': [-1],
'random_state': [42]
}
random_forest_model = GridSearchCV(RandomForestClassifier(), parameters)
#random_forest_model = RandomForestClassifier()
%time random_forest_model.fit(Xtrain, np.array(train_labels))
best_model = random_forest_model
predictedTrain = random_forest_model.predict(X=Xtrain)
predictedTest = random_forest_model.predict(X=Xtest)
metrics.accuracy_score(np.array(test_labels), predictedTest)
confmat_train = metrics.confusion_matrix( predictedTrain, np.array(train_labels) )
confmat_test = metrics.confusion_matrix( predictedTest, np.array(test_labels) )
pd.DataFrame(confmat_test)
sn.heatmap(pd.DataFrame(confmat_test, confmat_labels, confmat_labels))
rf_probs = random_forest_model.predict_proba(Xtest)
metrics.log_loss(predictedTest, rf_probs)<jupyter_output><empty_output><jupyter_text>### SVM Optimized Model<jupyter_code>parameters = [{'kernel': ['rbf'], 'gamma': [1e-3, 1e-4], 'C': [1, 10, 100, 1000]},
{'kernel': ['linear'], 'C': [1, 10, 100, 1000]},
{'kernel': ['poly'], 'gamma': [1e-3, 1e-4], 'C': [1, 10, 100, 1000]},
{'kernel': ['sigmoid'], 'gamma': [1e-3, 1e-4], 'C': [1, 10, 100, 1000]}]
svm_model = GridSearchCV(estimator=SVC(probability=True), param_grid=parameters)
#svm_model = SVC()
%time svm_model.fit(Xtrain, np.array(train_labels))
svm_model.best_estimator_
best_model = svm_model
predictedTrain = svm_model.predict(X=Xtrain)
predictedTest = svm_model.predict(X=Xtest)
metrics.accuracy_score(np.array(test_labels), predictedTest)
confmat_train = metrics.confusion_matrix( predictedTrain, np.array(train_labels) )
#sn.heatmap(pd.DataFrame(confmat_train, train_labels, train_labels), annot=True)
confmat_test = metrics.confusion_matrix( predictedTest, np.array(test_labels) )
pd.DataFrame(confmat_test)
sn.heatmap(pd.DataFrame(confmat_test, confmat_labels, confmat_labels))
svm_probs = svm_model.predict_proba(Xtest)
metrics.log_loss(predictedTest, svm_probs)<jupyter_output><empty_output><jupyter_text>### Iterate through remaining models<jupyter_code>def run_classifier(train, test, train_labels, test_labels, classifier_class):
startt = time.time()
classifier_class.fit( train, train_labels )
probas = classifier_class.predict_proba(test)
results = classifier_class.predict( test)
log_loss = metrics.log_loss(test_labels, probas)
score = log_loss
#score = classifier_class.score( test, test_labels )
confmat = metrics.confusion_matrix(test_labels, results)
confmat = confmat.astype('float') / confmat.sum(axis=1)[:, np.newaxis] #normalize
duration = time.time() - startt
return (type(classifier_class).__name__, score, duration, confmat)
# Taken from http://scikit-learn.org/stable/auto_examples/classification/plot_classifier_comparison.html
classifiers = [
KNeighborsClassifier(3),
SVC(kernel="linear", C=0.025, probability=True),
SVC(gamma=2, C=1, probability=True),
#GaussianProcessClassifier(1.0 * RBF(1.0), warm_start=True),
DecisionTreeClassifier(max_depth=5),
RandomForestClassifier(max_depth=5, n_estimators=10, max_features=1),
MLPClassifier(alpha=1),
AdaBoostClassifier(),
GaussianNB(),
QuadraticDiscriminantAnalysis(),
LR(multi_class='ovr')]
#[(name, score, duration,confmat),(...),...]
classifier_rslt_all = [run_classifier(Xtrain, Xtest, train_labels, test_labels, classifier) for classifier in classifiers]
classifier_names = [e[0] for e in classifier_rslt_all]
confmats = [e[3] for e in classifier_rslt_all]
results = pd.DataFrame.from_records([ (e[0],e[1],e[2]) for e in classifier_rslt_all], columns=['Classifier', 'Score','Duration'])
results
#results.plot.scatter(x='Score', y='Duration')
ax = results.plot.scatter(x='Score', y='Duration', alpha=0.5)
for i, txt in enumerate(results.Classifier):
ax.annotate(txt, (results.Score.iat[i],results.Duration.iat[i]))
plt.show()
for confmat, classifier_name in zip(confmats, classifier_names):
plt.figure()
ax = plt.axes()
sn.heatmap(pd.DataFrame(confmat, labels, labels), annot=True)
ax.set_title(classifier_name)
<jupyter_output><empty_output>
|
no_license
|
/notebooks/End-to-end-NonNN.ipynb
|
jay-uChicago/yoga-image-classifier
| 5 |
<jupyter_start><jupyter_text># Example Plots
## Notebook with example interactions with the database for plotting data. <jupyter_code>import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import random
from database.db_setup import *
import database.config as config
erd = dj.ERD(epi_schema)
erd<jupyter_output><empty_output><jupyter_text># Multiple Eventplots### Check table contents: <jupyter_code>SpikeTimesDuringMovie()<jupyter_output><empty_output><jupyter_text>### Load in activity from the database:<jupyter_code>unit0 = get_spiking_activity(1, 1, 1)
unit1 = get_spiking_activity(2, 1, 1)
unit2 = get_spiking_activity(3, 1, 1)
unit3 = get_spiking_activity(3, 1, 20)<jupyter_output><empty_output><jupyter_text>### Plot activity <jupyter_code>fig, (ax1, ax2, ax3, ax4) = plt.subplots(4, 1, figsize=(20,15), sharex=True)
ax1.eventplot(unit0)
ax1.set_title("Mock Unit, 1")
ax1.spines['top'].set_visible(False)
ax1.spines['left'].set_visible(False)
ax1.spines['right'].set_visible(False)
ax1.set_yticks([])
ax2.eventplot(unit1)
ax2.set_title("Mock Unit, 2")
ax2.spines['top'].set_visible(False)
ax2.spines['left'].set_visible(False)
ax2.spines['right'].set_visible(False)
ax2.set_yticks([])
ax3.eventplot(unit2)
ax3.set_title("Mock Unit, 3")
ax3.spines['top'].set_visible(False)
ax3.spines['left'].set_visible(False)
ax3.spines['right'].set_visible(False)
ax3.set_yticks([])
ax4.eventplot(unit3)
ax4.set_title("Mock Unit, 4")
ax4.spines['top'].set_visible(False)
ax4.spines['left'].set_visible(False)
ax4.spines['right'].set_visible(False)
ax4.set_yticks([])
plt.xlabel("Time, msec")
plt.show()<jupyter_output><empty_output><jupyter_text># Highlight eventplot sections<jupyter_code>MovieSkips()
unit0 = get_spiking_activity(1, 1, 1)
values, start, stop = get_info_continuous_watch_segments(1, 1)
fig, ax1 = plt.subplots(1, 1, figsize=(20,5))
ax1.eventplot(unit0)
ax1.set_title("Unit")
ax1.spines['top'].set_visible(False)
ax1.spines['right'].set_visible(False)
ax1.spines['left'].set_visible(False)
ax1.set_yticks([])
ax1.set_xlabel("Time")
## add cont watch highlights
label = "Section 1"
for i in range(len(start)):
if i == (len(start) - 1):
ax1.axvspan(start[i], stop[i], edgecolor='dimgray', facecolor='gainsboro', alpha=0.5, label=label)
else:
ax1.axvspan(start[i], stop[i], edgecolor='dimgray', facecolor='gainsboro', alpha=0.5)
ax1.legend(loc='center left', bbox_to_anchor=(1,0.5), frameon=False)
<jupyter_output><empty_output>
|
non_permissive
|
/visualization/gallery.ipynb
|
a-darcher/epiphyte_dhv
| 5 |
<jupyter_start><jupyter_text>Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.# AutoML 03: Remote Execution using Batch AI
In this example we use the scikit-learn's [diabetes dataset](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_diabetes.html) to showcase how you can use AutoML for a simple classification problem.
Make sure you have executed the [00.configuration](00.configuration.ipynb) before running this notebook.
In this notebook you would see
1. Create an `Experiment` in an existing `Workspace`.
2. Attach an existing Batch AI compute to a workspace.
3. Configure AutoML using `AutoMLConfig`.
4. Train the model using Batch AI.
5. Explore the results.
6. Test the best fitted model.
In addition this notebook showcases the following features
- **Parallel** executions for iterations
- **Asynchronous** tracking of progress
- **Cancellation** of individual iterations or the entire run
- Retrieving models for any iteration or logged metric
- Specifying AutoML settings as `**kwargs`
## Create an Experiment
As part of the setup you have already created an Azure ML `Workspace` object. For AutoML you will need to create an `Experiment` object, which is a named object in a `Workspace` used to run experiments.<jupyter_code>import logging
import os
import random
from matplotlib import pyplot as plt
from matplotlib.pyplot import imshow
import numpy as np
import pandas as pd
from sklearn import datasets
import azureml.core
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
from azureml.train.automl import AutoMLConfig
from azureml.train.automl.run import AutoMLRun
ws = Workspace.from_config()
# Choose a name for the run history container in the workspace.
experiment_name = 'automl-remote-batchai'
project_folder = './sample_projects/automl-remote-batchai'
experiment = Experiment(ws, experiment_name)
output = {}
output['SDK version'] = azureml.core.VERSION
output['Subscription ID'] = ws.subscription_id
output['Workspace Name'] = ws.name
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Project Directory'] = project_folder
output['Experiment Name'] = experiment.name
pd.set_option('display.max_colwidth', -1)
pd.DataFrame(data = output, index = ['']).T<jupyter_output><empty_output><jupyter_text>## Diagnostics
Opt-in diagnostics for better experience, quality, and security of future releases.<jupyter_code>from azureml.telemetry import set_diagnostics_collection
set_diagnostics_collection(send_diagnostics = True)<jupyter_output><empty_output><jupyter_text>## Create Batch AI Cluster
The cluster is created as Machine Learning Compute and will appear under your workspace.
**Note:** The creation of the Batch AI cluster can take over 10 minutes, please be patient.
As with other Azure services, there are limits on certain resources (e.g. Batch AI cluster size) associated with the Azure Machine Learning service. Please read [this article](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-manage-quotas) on the default limits and how to request more quota.<jupyter_code>from azureml.core.compute import BatchAiCompute
from azureml.core.compute import ComputeTarget
# Choose a name for your cluster.
batchai_cluster_name = "mybatchai"
found = False
# Check if this compute target already exists in the workspace.
for ct_name, ct in ws.compute_targets().items():
print(ct.name, ct.type)
if (ct.name == batchai_cluster_name and ct.type == 'BatchAI'):
found = True
print('Found existing compute target.')
compute_target = ct
break
if not found:
print('Creating a new compute target...')
provisioning_config = BatchAiCompute.provisioning_configuration(vm_size = "STANDARD_D2_V2", # for GPU, use "STANDARD_NC6"
#vm_priority = 'lowpriority', # optional
autoscale_enabled = True,
cluster_min_nodes = 1,
cluster_max_nodes = 4)
# Create the cluster.
compute_target = ComputeTarget.create(ws, batchai_cluster_name, provisioning_config)
# Can poll for a minimum number of nodes and for a specific timeout.
# If no min_node_count is provided, it will use the scale settings for the cluster.
compute_target.wait_for_completion(show_output = True, min_node_count = None, timeout_in_minutes = 20)
# For a more detailed view of current Batch AI cluster status, use the 'status' property.<jupyter_output><empty_output><jupyter_text>## Create Get Data File
For remote executions you should author a `get_data.py` file containing a `get_data()` function. This file should be in the root directory of the project. You can encapsulate code to read data either from a blob storage or local disk in this file.
In this example, the `get_data()` function returns data from scikit-learn's [diabetes dataset](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_diabetes.html).<jupyter_code>if not os.path.exists(project_folder):
os.makedirs(project_folder)
%%writefile $project_folder/get_data.py
from sklearn import datasets
from scipy import sparse
import numpy as np
def get_data():
digits = datasets.load_digits()
X_train = digits.data
y_train = digits.target
return { "X" : X_train, "y" : y_train }<jupyter_output><empty_output><jupyter_text>## Instantiate AutoML
You can specify `automl_settings` as `**kwargs` as well. Also note that you can use a `get_data()` function for local excutions too.
**Note:** When using Batch AI, you can't pass Numpy arrays directly to the fit method.
|Property|Description|
|-|-|
|**primary_metric**|This is the metric that you want to optimize. Classification supports the following primary metrics: accuracyAUC_weightedbalanced_accuracyaverage_precision_score_weightedprecision_score_weighted|
|**max_time_sec**|Time limit in seconds for each iteration.|
|**iterations**|Number of iterations. In each iteration AutoML trains a specific pipeline with the data.|
|**n_cross_validations**|Number of cross validation splits.|
|**concurrent_iterations**|Maximum number of iterations that would be executed in parallel. This should be less than the number of cores on the DSVM.|<jupyter_code>automl_settings = {
"max_time_sec": 120,
"iterations": 20,
"n_cross_validations": 5,
"primary_metric": 'AUC_weighted',
"preprocess": False,
"concurrent_iterations": 5,
"verbosity": logging.INFO
}
automl_config = AutoMLConfig(task = 'classification',
debug_log = 'automl_errors.log',
path = project_folder,
compute_target = compute_target,
data_script = project_folder + "/get_data.py",
**automl_settings
)
<jupyter_output><empty_output><jupyter_text>## Train the Model
Call the `submit` method on the experiment object and pass the run configuration. For remote runs the execution is asynchronous, so you will see the iterations get populated as they complete. You can interact with the widgets and models even when the experiment is running to retrieve the best model up to that point. Once you are satisfied with the model, you can cancel a particular iteration or the whole run.
In this example, we specify `show_output = False` to suppress console output while the run is in progress.<jupyter_code>remote_run = experiment.submit(automl_config, show_output = False)<jupyter_output><empty_output><jupyter_text>## Explore the Results
#### Loading executed runs
In case you need to load a previously executed run, enable the cell below and replace the `run_id` value.<jupyter_code>remote_run = AutoMLRun(experiment = experiment, run_id = 'AutoML_5db13491-c92a-4f1d-b622-8ab8d973a058')<jupyter_output><empty_output><jupyter_text>#### Widget for Monitoring Runs
The widget will first report a "loading" status while running the first iteration. After completing the first iteration, an auto-updating graph and table will be shown. The widget will refresh once per minute, so you should see the graph update as child runs complete.
You can click on a pipeline to see run properties and output logs. Logs are also available on the DSVM under `/tmp/azureml_run/{iterationid}/azureml-logs`
**Note:** The widget displays a link at the bottom. Use this link to open a web interface to explore the individual run details.<jupyter_code>remote_run
from azureml.train.widgets import RunDetails
RunDetails(remote_run).show()
# Wait until the run finishes.
remote_run.wait_for_completion(show_output = True)<jupyter_output><empty_output><jupyter_text>
#### Retrieve All Child Runs
You can also use SDK methods to fetch all the child runs and see individual metrics that we log.<jupyter_code>children = list(remote_run.get_children())
metricslist = {}
for run in children:
properties = run.get_properties()
metrics = {k: v for k, v in run.get_metrics().items() if isinstance(v, float)}
metricslist[int(properties['iteration'])] = metrics
rundata = pd.DataFrame(metricslist).sort_index(1)
rundata<jupyter_output><empty_output><jupyter_text>## Cancelling runs
You can cancel ongoing remote runs using the `cancel` and `cancel_iteration` functions.<jupyter_code># Cancel the ongoing experiment and stop scheduling new iterations.
# remote_run.cancel()
# Cancel iteration 1 and move onto iteration 2.
# remote_run.cancel_iteration(1)<jupyter_output><empty_output><jupyter_text>### Retrieve the Best Model
Below we select the best pipeline from our iterations. The `get_output` method on `automl_classifier` returns the best run and the fitted model for the last invocation. Overloads on `get_output` allow you to retrieve the best run and fitted model for *any* logged metric or for a particular *iteration*.<jupyter_code>best_run, fitted_model = remote_run.get_output()
print(best_run)
print(fitted_model)<jupyter_output><empty_output><jupyter_text>#### Best Model Based on Any Other Metric
Show the run and the model which has the smallest `log_loss` value:<jupyter_code>lookup_metric = "log_loss"
best_run, fitted_model = remote_run.get_output(metric = lookup_metric)
print(best_run)
print(fitted_model)<jupyter_output><empty_output><jupyter_text>#### Model from a Specific Iteration
Show the run and the model from the third iteration:<jupyter_code>iteration = 3
third_run, third_model = remote_run.get_output(iteration=iteration)
print(third_run)
print(third_model)<jupyter_output><empty_output><jupyter_text>### Register the Fitted Model for Deployment<jupyter_code>description = 'AutoML Model'
tags = None
remote_run.register_model(description = description, tags = tags)
remote_run.model_id # Use this id to deploy the model as a web service in Azure.<jupyter_output><empty_output><jupyter_text>### Testing the Fitted Model
#### Load Test Data<jupyter_code>digits = datasets.load_digits()
X_test = digits.data[:10, :]
y_test = digits.target[:10]
images = digits.images[:10]<jupyter_output><empty_output><jupyter_text>#### Testing Our Best Pipeline<jupyter_code># Randomly select digits and test.
for index in np.random.choice(len(y_test), 2, replace = False):
print(index)
predicted = fitted_model.predict(X_test[index:index + 1])[0]
label = y_test[index]
title = "Label value = %d Predicted value = %d " % (label, predicted)
fig = plt.figure(1, figsize=(3,3))
ax1 = fig.add_axes((0,0,.8,.8))
ax1.set_title(title)
plt.imshow(images[index], cmap = plt.cm.gray_r, interpolation = 'nearest')
plt.show()<jupyter_output><empty_output>
|
permissive
|
/automl/03b.auto-ml-remote-batchai.ipynb
|
mohideensandhu/MachineLearningNotebooks
| 16 |
<jupyter_start><jupyter_text># Project. Life ExpectancyFor this project, the life expectancy dataset obtained from the website: https://www.kaggle.com/kumarajarshi/life-expectancy-who/version/1 was used. The data related to life expectancy and health factors were collected from the WHO website, and the corresponding economic data was collected from the United Nation website for the years 2000 to 2015.
This dataset was also used for a group project observing the linear relationship between of the life expectancy variable and other predictor variables in another class. However, during the statistical analysis process, we noticted that half of the dataset were missing information, which could lead to a miscalculation. To obtain a more accurate result for the analysis, I chose to perform missing-data imputations to clean the dataset so it could be analyzed as if there were no missing.
<jupyter_code>import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn import preprocessing
import math
from itertools import groupby<jupyter_output><empty_output><jupyter_text>## Goal of the projectThe main goal of this project is to handle missing data using a variety of methods learned in the class which are applications of the programming language Python, linear regression model, and advanced regression models in sklearn.## Data descriptionThere were 20 variables in the dataset which was collected for 193 countries during 16 years from 2000 to 2015. In total, we had 2938 observations.
Below are the list and description of all variables:
- Life expectancy Life expectancy (age) for a country in a particular year
- Year
- Status The status of country (Developed or Developing)
- Adult Mortality Probability of dying between 15 and 60 years per 1000 population
- Infant deaths Number of Infant Deaths per 1000 population
- Alcohol Alcohol, recorded per capita (15+) consumption (in litres)
- Percentage Expenditure Expenditure on health as a percentage of Gross Domestic Product per capita(%)
- Hepatitis B Hepatitis B immunization coverage among 1-year-olds (%)
- Measles Measles - number of reported cases per 1000 population
- BMI Average Body Mass Index of entire population
- Under-five deaths Number of under-five deaths per 1000 population
- Polio Polio immunization coverage among 1-year-olds (%)
- Total expenditure Government expenditure on health as a percentage of total government expenditure (%)
- Diphtheria Diphtheria tetanus toxoid and pertussis immunization coverage among 1-year-olds
- HIV/AIDS Deaths per 1000 live births HIV/AIDS (0-4 years)
- GDP Gross Domestic Product per capita (in USD)
- Population Population of the country
- Thinness 10-19 years Prevalence of thinness among children and adolescents for Age 10-19
- Thinness 5-9 year Prevalence of thinness among children for Age 5-9
- Income composition Human Development Index in terms of income of resources composition (from 0 to 1)
- Schooling Number of years of Schooling
<jupyter_code># Reading in data
Location = 'Life_Expectancy.csv'
df = pd.read_csv(Location)
df.head()<jupyter_output><empty_output><jupyter_text>Based on the counts in the below summary statistics table, we noticed that the following variables had missing data.
- Life expectancy: 10
- Adult mortality: 10
- Alcohol: 194
- Hepatitis B: 553
- BMI: 34
- Polio: 19
- Total expenditure: 226
- Diphtheria: 19
- GDP: 448
- Population: 652
- Thinness 10-19 years: 34
- Thinness 5-9 years: 34
- Income composition of resources: 167
- Schooling: 163<jupyter_code># Summary statistics
df.describe()<jupyter_output><empty_output><jupyter_text>We observed that the histogram plot of response variable life expectancy showed an approximately normal distribution.<jupyter_code># Plot histogram of the response variable life expectancy
plt.figure()
df['LE'].plot.hist()
plt.xlabel('Life Expectancy')
plt.title('Histogram of the response variable: Life Expectancy')
plt.show()<jupyter_output><empty_output><jupyter_text>Some of the scatter plots of the response variable life expectancy versus predictors showed a linear relationship which was a good signal to contrust a linear regression model to predict life expectancy.<jupyter_code>cols = [i for i in list(df.columns) if i not in ['Status','LE', 'Country']]
for col in cols:
fig, ax = plt.subplots(figsize=(12,8))
df.plot(kind='scatter', x=col, y='LE', ax=ax, s=10, alpha=0.5)
plt.show()
<jupyter_output><empty_output><jupyter_text>## Imputation for predictors
In a relevant project using the same dataset, we used the best subset techniques and a variety of tools to check the model validity to contruct various multiple linear regression models. Among those models, we decided the best model to predict life expectancy involving the following predictor variables: year, adult mortality, alcohol, percentage expenditure, BMI, HIV/AIDS, income composition of resources, schooling.
In this project, we chose these eight predictor variables in any linear regression used for missing data imputation methods.
However, five of those predictor variables had missing values as well.
- Adult mortality: 10 missing records
- Alcohol: 194 missing records
- BMI: 34 missing records
- Income composition of resources: 167 missing records
- Schooling: 163 missing records
Before handling the missing-data in response variable, we decided to replace missing values in predictors.
Adult MortalityThe variable adult mortality had 10 missing records which all came from less known countries in 2013. As noticed that there were no related information of those countries in the other years, the simple imputation methods such as mean imputation or last value carried forward could not be applied.
We observed that those countries had no information or just a few for population as well, therefore it was hard to find a similar country to do hot-deck imputation by learning the adult mortality ratio of population of a similar population density country. At last, we found that all those missing countries had zero value for infant deaths which gave some sense of replacing the missing values in adult mortality with zero.
<jupyter_code># Print missing-value records in Adult Mortality
missing1 = df['Adult_Mortality'].isnull()
print("\n\nBelow are 10 missing records:")
df.loc[missing1,:]
# Copy all values in Adult_Mortality to a new column Adult_Mortality_n
df['Adult_Mortality_n'] = df['Adult_Mortality']
# Replace missing values in Adult_Mortality_n with zero value
df.loc[missing1,'Adult_Mortality_n'] = 0
df.loc[missing1,:]<jupyter_output><empty_output><jupyter_text>Alcohol
There were 194 missing records in the variable alcohol. 176 of those were the alcohol consumption per capita for 176 countries for the year 2015; 16 were the information for the country South Sudan from 2000 to 2015; 1 missing-value record were of the country Montenegro in 2005; 1 were for Palau in 2013.
As most of missing records had the history data for previous years expect Montenegro, South Sudan and Palau; we decided to replace the missing alcohol assumption with the mean alcohol assumption of year 2000-2014 using the mean imputation method.<jupyter_code># Print missing-value records in Alcohol
missing2 = df['Alcohol'].isnull()
print("\n\nBelow are 194 missing records:")
df.loc[missing2,:]
# Copy all values in Alcohol to a new column Alcohol_n
df['Alcohol_n'] = df['Alcohol']
# Replace the missing-value records in Alcohol in 2015 with the grouped mean values of 2000-2014
df.loc[missing2, 'Alcohol_n'] = df.groupby('Country')['Alcohol'].transform('mean')<jupyter_output><empty_output><jupyter_text>For South Sudan and Palau whose alcohol variables had no values for all the years, I chose the zero value to replace for those missing records.<jupyter_code># Replace the missing-value records in Alcohol with 0 for South Sudan and Palau
df.loc[(df['Country']=='South Sudan'),['Alcohol_n']] = 0
df.loc[(df['Country']=='Palau'),['Alcohol_n']] = 0
# Print all missing alcohol with imputed data in column Alcohol_n
df.loc[missing2,:]<jupyter_output><empty_output><jupyter_text>BMI
The variable BMI had 34 missing-data records. 32 of those were missing values of Sudan and South Sudan in 16 years from 2000 to 2015; 1 were of the record for San Marino in 2013; and, 1 were for Monaco in 2013.
As there were no history data for those missing-value countries, we decided to replace those missing records with the mean of BMI of developing countries.<jupyter_code># Print missing-value records in BMI
missing3 = df['bmi'].isnull()
print("\n\nBelow are 34 missing records:")
df.loc[missing3,:]
# Copy all values in bmi to a new column bmi_n
df['bmi_n'] = df['bmi']
# Replace the missing-value records with the mean BMI of developing countries
df.loc[missing3, 'bmi_n'] = df.groupby('Status')['bmi'].transform('mean')
df.loc[missing3,:]<jupyter_output><empty_output><jupyter_text>Income composition of resources
There were 167 missing-value rows in the column Income_composition_of_resources. As the variable income composition of resources represented for the average income range of a country's population, the value of a developed country would be close to the other developed coutries, and this held true for developing countries as well.
We chose to replace those missing records with the mean of Income_composition_of_resources grouped by the country status.<jupyter_code># Print missing-value records
missing4 = df['Income_composition_of_resources'].isnull()
print("\n\nBelow are 167 missing records:")
df.loc[missing4,:]
# Copy all values in Income composition of resources to a new column income_n
df['income_n'] = df['Income_composition_of_resources']
# Replace the missing-value records with the mean grouped by Status
df.loc[missing4, 'income_n'] = df.groupby('Status')['Income_composition_of_resources'].transform('mean')
df.loc[missing4,:]<jupyter_output><empty_output><jupyter_text>Schooling
The variable Schooling had 163 missing-data records. Schooling recorded number of years of schooling. Common sense shows that there are similarity in terms of education between developed countries; therefore we decided to impute the missing data with the mean grouped by country statuses.<jupyter_code># Print missing-value records
missing5 = df['Schooling'].isnull()
print("\n\nBelow are 163 missing records:")
df.loc[missing5,:]
# Copy all values in Schooling to a new column schooling_n
df['schooling_n'] = df['Schooling']
# Replace the missing-value records with the mean grouped by Status
df.loc[missing5, 'schooling_n'] = df.groupby('Status')['Schooling'].transform('mean')
df.loc[missing5,:]<jupyter_output><empty_output><jupyter_text>After imputation for predictor variables, we created 5 new columns which contained the original and imputed data.
- Adult_Mortality_n
- Alcohol_n
- bmi_n
- income_n
- schooling_n
All those columns had no NaN values and would be used for imputing missing values in the response variable - life expectancy.<jupyter_code>df.describe()<jupyter_output><empty_output><jupyter_text>## Imputation for the response variable: life expectancy
We used three different methods including a linear regression model, a neural network regression model, and a kNN regression model to impute the missing data in the response variable - life expectancy (LE).
Linear Regression Model
The first step, we created a new data frame only including the variables which had significant effects on the response variable, life expectancy.<jupyter_code>df_new = df.loc[:,['Country','Year','LE','Adult_Mortality_n','Alcohol_n','percentage_expenditure','hiv_aids','bmi_n','income_n','schooling_n']]
df_new
# Summary of the new data frame
df_new.describe()<jupyter_output><empty_output><jupyter_text>We removed any rows with missing data (NaN), in order to fit the linear regression model.<jupyter_code>df_complete = df_new.dropna(axis=0, how='any')<jupyter_output><empty_output><jupyter_text>Then we divided that into features (X) and outcomes (y).<jupyter_code>X = df_complete.drop(['Country', 'LE'], axis = 1)
print("Here are the features (X):")
print(X.head())
print("\n\nHere is the outcome variable (y):")
y = df_complete['LE']
print(y)<jupyter_output>Here are the features (X):
Year Adult_Mortality_n Alcohol_n percentage_expenditure hiv_aids \
0 2015 263.0 0.01 71.279624 0.1
1 2014 271.0 0.01 73.523582 0.1
2 2013 268.0 0.01 73.219243 0.1
3 2012 272.0 0.01 78.184215 0.1
4 2011 275.0 0.01 7.097109 0.1
bmi_n income_n schooling_n
0 19.1 0.479 10.1
1 18.6 0.476 10.0
2 18.1 0.470 9.9
3 17.6 0.463 9.8
4 17.2 0.454 9.5
Here is the outcome variable (y):
0 65.0
1 59.9
2 59.9
3 59.5
4 59.2
5 58.8
6 58.6
7 58.1
8 57.5
9 57.3
10 57.3
11 57.0
12 56.7
13 56.2
14 55.3
15 54.8
16 77.8
17 77.5
18 77.2
19 76.9
20 76.6
21 7[...]<jupyter_text>We fited a linear regression model with the response variable y and the predictor variables X.<jupyter_code>lm = linear_model.LinearRegression()
lm.fit(X,y)
print ("Here are coefficients of the model:")
print(lm.coef_)
print ("\n\nHere is the intercept of the model:")
print(lm.intercept_)<jupyter_output>Here are coefficients of the model:
[-1.05675568e-02 -2.07583860e-02 6.84464674e-02 3.41383113e-04
-4.97830273e-01 5.53483375e-02 7.99574130e+00 8.90619017e-01]
Here is the intercept of the model:
76.2999575164769
<jupyter_text>Then we got predictions on the full dataset.<jupyter_code>X_all = df_new.drop(['Country', 'LE'], axis = 1)
preds = lm.predict(X_all)<jupyter_output><empty_output><jupyter_text>We copied all predictions to a new column LE1 to compare with the results of other methods.<jupyter_code>missing = df['LE'].isnull()
# Copy all predicted values to a new column LE1
df_new['LE1'] = preds
df_new.loc[missing,:]<jupyter_output><empty_output><jupyter_text>Neural Network Regression Model
As neural networks performs better when all the features are on roughly the same scale, we first scaled the variables X. <jupyter_code>X = pd.DataFrame(preprocessing.scale(X), columns = X.columns)
print("Here are the predictors (X):")
print(X.head())
print("\n\nHere is the outcome variable (y):")
print(y)<jupyter_output>Here are the predictors (X):
Year Adult_Mortality_n Alcohol_n percentage_expenditure hiv_aids \
0 1.626978 0.790238 -1.132904 -0.336102 -0.324055
1 1.410048 0.854614 -1.132904 -0.334975 -0.324055
2 1.193118 0.830473 -1.132904 -0.335128 -0.324055
3 0.976187 0.862660 -1.132904 -0.332633 -0.324055
4 0.759257 0.886801 -1.132904 -0.368345 -0.324055
bmi_n income_n schooling_n
0 -0.962510 -0.725476 -0.586852
1 -0.987700 -0.739948 -0.617215
2 -1.012890 -0.768893 -0.647577
3 -1.038081 -0.802663 -0.677939
4 -1.058233 -0.846080 -0.769026
Here is the outcome variable (y):
0 65.0
1 59.9
2 59.9
3 59.5
4 59.2
5 58.8
6 58.6
7 58.1
8 57.5
9 57.3
10 57.3
11 57.0
12 56.7
13 56.2
14 55.3
15 54.8
16 77.8
17 77.5
18 [...]<jupyter_text>Then we created an instance of the MLPRegressor class in sklearn which specified three hidden layers with sizes of 100, 100, and 50, respectively. After that, we fitted a neural network regression model (lm1).<jupyter_code>lm1 = MLPRegressor(hidden_layer_sizes=(100,100,50), solver='lbfgs', max_iter=500, random_state=1)
lm1.fit(X,y)<jupyter_output><empty_output><jupyter_text>Then we got predictions on the full dataset and copied all predictions to a new column LE2.<jupyter_code>X_all = pd.DataFrame(preprocessing.scale(X_all), columns=X_all.columns)
preds1 = lm1.predict(X_all)
# Copy all predicted values to a new column LE2
df_new['LE2'] = preds1
df_new.loc[missing,:]<jupyter_output><empty_output><jupyter_text>kNN Regression Model
Another method we examined in this project is kNN Regression Model using sklearn. We fitted a kNN regression model using 10 as k value.<jupyter_code>lm2 = KNeighborsRegressor(10)
lm2.fit(X,y)<jupyter_output><empty_output><jupyter_text>Then we got predictions on the full dataset and copied all predictions to a new column LE3.<jupyter_code>preds2 = lm2.predict(X_all)
df_new['LE3'] = preds2
df_new.loc[missing,:]<jupyter_output><empty_output><jupyter_text>## Evaluation
After imputation steps, we created three new columns in the dataset LE1, LE2, LE3 which contains predictions of the full dataset of three following techniques: linear regression model, neural network regression model, kNN regression model.
To evaluate which methods provided the most rational result, we compared the predicted and observed values of all non-missing-data observations.<jupyter_code>gs_LE = df_complete['LE']
preds_LE1 = df_new.loc[df_new['LE'].notnull(),'LE1']
preds_LE2 = df_new.loc[df_new['LE'].notnull(),'LE2']
preds_LE3 = df_new.loc[df_new['LE'].notnull(),'LE3']<jupyter_output><empty_output><jupyter_text>The scatter plot of predicted versus actual values of the neural network regression model showed the least differences in predictions and recorded data, which inferred that this method performed the most accurate results.<jupyter_code>plt.figure()
plt.scatter(preds_LE1, gs_LE)
plt.xlabel("Predicted Life Expectancy (Linear Regression Model)")
plt.ylabel("Actual Life Expectancy")
plt.show()
plt.figure()
plt.scatter(preds_LE2, gs_LE)
plt.xlabel("Predicted Life Expectancy (NN)")
plt.ylabel("Actual Life Expectancy")
plt.show()
plt.figure()
plt.scatter(preds_LE3, gs_LE)
plt.xlabel("Predicted Life Expectancy (kNN)")
plt.ylabel("Actual Life Expectancy")
plt.show()<jupyter_output><empty_output><jupyter_text>The mean-squared error (MSE) of MLP regressor was lowest which also showed that neural networks performed better than the other methods.<jupyter_code>mse1 = sum((gs_LE - preds_LE1)**2)/len(preds_LE1)
mse2 = sum((gs_LE - preds_LE2)**2)/len(preds_LE2)
mse3 = sum((gs_LE - preds_LE3)**2)/len(preds_LE3)
print("MSE with Linear Regression Model:", mse1)
print("MSE with MLP regressor:", mse2)
print("MSE with kNN regressor:", mse3)<jupyter_output>MSE with Linear Regression Model: 19.04402495053477
MSE with MLP regressor: 2.1928715620549233
MSE with kNN regressor: 5.602061577868857
<jupyter_text>## Conclusion
This project used the mean imputation method for filling missing values of predictor variables which are adult mortality, alcohol, BMI, Income composition of resources, and schooling. After that, the response variable life expectancy was replaced 10 missing values with predictions from three different methods: linear regression, neural network regression, and kNN regression. Comparing the predicted to the actual values of the subset of the data that was not missing showed the most accurate predictions from the neural network method. Therefore, we finally decided to replace 10 missing records of life expectancy with the predictions from neural network model. <jupyter_code>preds_missing = lm1.predict(X_all.loc[missing,:])
print(preds_missing)<jupyter_output>[66.47132079 73.39285682 79.22759044 72.16788389 68.48109618 66.95362586
73.93502337 74.17077723 70.63542556 79.09991754]
|
permissive
|
/python-mising-data-imputation-regression-knn-mpl.ipynb
|
mophan/Python-Missing-Data-Imputation-Regression-kNN-MPL
| 27 |
<jupyter_start><jupyter_text># Python tutorial #1본 페이지는 한림대학교 710231(딥러닝이해및응용) 수업에서 학생들의 Python 학습을 위해 만든 페이지입니다. ## Hello World !<jupyter_code>print('Hello World')
print('Hello World {} + {} = {}'.format(2, 3, 2+3))<jupyter_output>Hello World
Hello World 2 + 3 = 5
<jupyter_text>## Basic data types<jupyter_code>x = 3
print(type(x)) # Prints "<class 'int'>"
print(x) # Prints "3"
print(x + 1) # Addition; prints "4"
print(x - 1) # Subtraction; prints "2"
print(x * 2) # Multiplication; prints "6"
print(x ** 2) # Exponentiation; prints "9"<jupyter_output>4
2
6
9
<jupyter_text>## For statementrange: 영역을 설정<jupyter_code>A = range(5)
print(A)<jupyter_output>range(0, 5)
<jupyter_text>* A의 세번째 요소를 출력<jupyter_code>print(A[2])
for i in range(5):
#print(i, A[i])
print('{} ----- {}'.format(i, A[i]))
<jupyter_output>0 ----- 0
1 ----- 1
2 ----- 2
3 ----- 3
4 ----- 4
<jupyter_text>#### Excersise
구구단을 작성하시오 (아래 코드를 수정하시오)<jupyter_code>for i in range(9):
print('{} x {} = {}'.format(2, i, 2*i))<jupyter_output>2 x 0 = 0
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
2 x 8 = 16
<jupyter_text>## Operators<jupyter_code>print((1, 2, 3) * 3)
print([1, 2, 3] * 3)
print("Hello "*3)<jupyter_output>(1, 2, 3, 1, 2, 3, 1, 2, 3)
[1, 2, 3, 1, 2, 3, 1, 2, 3]
Hello Hello Hello
<jupyter_text>## Containers
Python includes several built-in container types: lists, dictionaries, sets, and tuples.### Tuple
A simple immutable (변경할 수 없는, 불변의) ordered sequence of items<jupyter_code># -*- coding: utf-8 -*-
# creating a tuple
months = ('January','February','March','April','May','June',\
'July','August','September','October','November','December')
print(months[0])
print("index of 7 ==> " , months[7])<jupyter_output>January
index of 7 ==> August
<jupyter_text>하나씩 출력하기<jupyter_code># iterate through them:
for item in months:
print (item)
t = ('john', 32, (2,3,4,5), 'hello')
print(t)
print(t[2])
print(t[2][1])
print(t[:2]) # index 포함 X
print(t[2:]) # index 포함 O
print(t[-1])
print(t[-2])<jupyter_output>('john', 32, (2, 3, 4, 5), 'hello')
(2, 3, 4, 5)
3
('john', 32)
((2, 3, 4, 5), 'hello')
hello
(2, 3, 4, 5)
<jupyter_text>### List
Mutable (바꿀수 있는, 변경가능한) ordered sequence of items of mixed types<jupyter_code>li = ['hallym', 1, 3.141572, 'hello']
print(li)
li[1] = 45
print(li)
li.append('September')
print(li)<jupyter_output>['hallym', 45, 3.141572, 'hello', 'September']
<jupyter_text>리스트에 새로운 것이 뒤에 붙은 것 (append)을 확인 가능* 비어있는 리스트 만들기<jupyter_code>v = []<jupyter_output><empty_output><jupyter_text>* 비어있는 리스트에 값 추가하기<jupyter_code>for i in range(0,3):
v.append(i*5)
print(i, v)<jupyter_output>0 [0]
1 [0, 5]
2 [0, 5, 10]
<jupyter_text>### + 연산자<jupyter_code>print((1, 2, 3) + (4, 5, 6))
print([1, 2, 3] + [4, 5, 6])
print("Hello" + " " + "World")<jupyter_output>(1, 2, 3, 4, 5, 6)
[1, 2, 3, 4, 5, 6]
Hello World
<jupyter_text>### * 연산자
The * operator produces a new tuple, list, or string that "repeats" the original content.<jupyter_code>y = 2.5
print(type(y)) # Prints "<class 'float'>"
print(y, y + 1, y * 2, y ** 2) # Prints "2.5 3.5 5.0 6.25"<jupyter_output><class 'float'>
2.5 3.5 5.0 6.25
<jupyter_text>### Enumeration (열거하기)<jupyter_code>for i, val in enumerate(v):
print('{} ---> {}'.format(i, val))
v2 = [ 'A', 'B', 'C', '0', '1', '2', '3']
print(v2)
for i, val in enumerate(v2):
print('{} ---> {}'.format(i, val))<jupyter_output>0 ---> A
1 ---> B
2 ---> C
3 ---> 0
4 ---> 1
5 ---> 2
6 ---> 3
<jupyter_text>### List comprehension (LC)
List comprehensions provide a concise way to create lists. <jupyter_code>squares = []
for x in range(10):
squares.append(x**2)
print(squares)<jupyter_output>[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
<jupyter_text>or, equivalently:<jupyter_code>squares = [x**2 for x in range(10)]
print(squares)
word = '메롱'
print([c * 2 for c in word])
A = [n for n in range(10) if n % 2 == 0]
print(A) # LC 에서 조건문을 통해 특정 값들을 필터링할 수 있다<jupyter_output>[0, 2, 4, 6, 8]
<jupyter_text>### Lambda
* 람다(lambda)는 익명함수를 지칭하는 용어
* lambda 인자리스트: 표현식
<jupyter_code>def jegob(x):
return x**2
g = lambda x: x**2
g(7)
print(g(8))
print(g(9))
f = lambda x, y: x + y
f(2, 3)<jupyter_output><empty_output>
|
no_license
|
/01_Python-basic/01-HelloPython.ipynb
|
hoznigo/Undergrad-DeepLearning-20Fall
| 17 |
<jupyter_start><jupyter_text> Big Data Systems - Assignment #2 # MongoDB (Estimated time: 4 hours)
The objective of this assignment is to introduce the use of sharding in MongoDB by studing the behavior of key and hash sharding.
We start by a guided study of the cluster configuration and the sharding process, by using the cities.txt dataset we used in lab #2. Later, the assignment requires you to apply what you learn in the guide by implementing a sharded cluster for a particular setting.
Notebook Layout (Table of Contents):
1. Environment Set-up
- Creating Virtual Machine
- Installing MongoDB
2. Studying Data Sharding using MongoDB
- Context
3. Guided tour on MongoDB sharding mechanisms
- Preparing a database
- Configuring a sharded cluster
- Sharding a database collection
- Balancing data across sharded cluster
4. Saharding in real-world application
1. Environment Set-up
For this assignment we will be using MongoDB on a virtual machine (VM) working on the Google Cloud. Please follow the instructions to set up the VM. You can always opt and install MongoDB on your own system. We don't recommend the latter.
1.1. Creating Virtual Machine
We will create a virtual machine with this configuration:
- **Name**: mongodbsvr
- **Zone**: us-central1-f
- **Machine Type**: 1vCPU with 3.75GB ram
- **Boot Disk**: Ubuntu 16.04LTS 10GB persistent Disk (you need to change this)
All the other parameters set to default. The estimated cost ir around $0.034 per hour. Your Cloud Compute VM creation screen should be similar to this:
1.2. Installing MongoDB
Once you have your machine, we will open an SSH terminal. Go to the VM list and click the SSH icon. We will be using several terminals for this assignment, so be ready to repeat this several times and to keep track of what we are doing with each terminal.

Once you are in the terminal first thing to do is to install MongoDB. We will be using version 2.6 for this assignment, which can be installed by using _apt_ on Ubuntu. So, run the following command:
sudo apt install --yes mongodb-server mongodb-clients
Once the program end you should get an output similar to the following, meaning the MongoDB server and client were installed successfully.
Adding system user `mongodb' (UID 113) ...
Adding new user `mongodb' (UID 113) with group `nogroup' ...
Not creating home directory `/var/lib/mongodb'.
Adding group `mongodb' (GID 117) ...
Done.
Adding user `mongodb' to group `mongodb' ...
Adding user mongodb to group mongodb
Done.
Processing triggers for libc-bin (2.23-0ubuntu10) ...
Processing triggers for systemd (229-4ubuntu21.1) ...
Processing triggers for ureadahead (0.100.0-19) ...
2. Studying Data Sharding using MongoDB
2.1. Context
NoSQL databases started gaining popularity in the 2000’s when companies began investing in distributed databases. An important aspect of NoSQL databases is that they have no predefined schema. Records can have different fields as necessary. NoSQL databases, apart from using an Application Programming Interface(API) or query language to access and modify data, may also use Map-Reduce which is used for performing a specific function on an entire dataset.
Sharding is a _method_ for storing a large collection of data across multiple servers called **shards** (cf. image below). This allows increased performance as each server handles different sets of data.

3. Guided tour on MongoDB sharding mechanisms
3.1. Preparing a database
MongoDB stores documents using its own binary format called BSON. This format is a binary version of the widely used JSON (JavaScript Object Notation) format and its name stands for Binary JSON. Although MongoDB uses BSON internally, the manipulation of documents in the MongoDB shell interface and client software is done using JSON due to its readability and open standard. In MongoDB databases are composed of collections of documents.
**For this exercise, first you have to (i) create a database and then (ii) create and populate a database collection.** We are going to use a data collection called cities.
3.1.1 Creating and populating a documents database
#### 3.1.1.1 Creating and populating a documents database
- Start a MongoDB instance:
mkdir -p ~/db/shard1 # Folder containing the DB files
mongod --shardsvr --dbpath ~/db/shard1 --port 27021
_Note:_ the instance will be used later as a shard server (option --shardsvr)#### 3.1.1.2 Creating a database and database collection
- Using a new shell, connect to the MongoDB instance:
mongo --host localhost:27021
- Create the database mydb and the database collection cities:
use mydb # Create the DB if not exists db.createCollection("cities")
- Verify the existence of the database (mydb) and the database collection (cities):
show dbs
show collection
#### 3.1.1.3 Populateing the database
- Using a new shell, import the content of the file cities.txt into mydb.cities collection. After that close the shell:
mongoimport --host localhost:27021 --db mydb --collection cities --file ~/cities.txt
**_Note:_** you need the file cities.txt. Review Lab #2 to get that file from the bucket.
- After the import is done, you can close that terminal.
- Using the other terminal check that the data was loaded correctly. You learned in Lab #2 how to do that.
3.2. Configuring a sharded cluster
As discussed in the course, MongoDB supports sharding through a sharded cluster. A sharded cluster is composed of the following components:
- Shards: store the data.
- Query routers: direct operations from clients to the appropriate shard(s) and return results to clients.
- Config servers: store cluster’s metadata. The query router uses this metadata to target operations to specific shards.
_Note:_ In a real-life scenario, each of these services we are going to be configuring and starting should reside in an individual server. However, in our case we will lunch all of them in this sole VM.
For the sake of simplicity you will configure with a simple sharded cluster (cf. image below) composed of:
- One config server
- One query router (mongos instance)
- One shard (mongod instance)
3.2.1. Starting a config server instance
- Using a **new shell**, start a config server (mongod instance):
mkdir -p ~/db/configdb
mongod --configsvr --dbpath ~/db/configdb --port 27020
3.2.2. Starting a query router instance
- Using a **new shell**, start a query router (mongos instance) connected to the config server instance in port 27020:
mongos --configdb localhost:27020 --port 27019
3.2.3. Adding a shard instance to the cluster
- Using a **new shell**, connect to the query router (mongos instance):
mongo --host localhost:27019
- Add to the cluster the mongo instance containing the **mydb** database:
use admin
db.runCommand( { addShard: "localhost:27021", name: "shard1" } )
- Verify the state of the cluster:
sh.status()
Question 1:
**What is an important information reported by this command?**<jupyter_code>--- Sharding Status ---
sharding version: {
"_id" : 1,
"version" : 4,
"minCompatibleVersion" : 4,
"currentVersion" : 5,
"clusterId" : ObjectId("5a9c93628e1c27c1fe6c0090")
}
shards:
{ "_id" : "shard1", "host" : "localhost:27021" }
databases:
{ "_id" : "admin", "partitioned" : false, "primary" : "config" }
{ "_id" : "mydb", "partitioned" : false, "primary" : "shard1" }
This command shows the cluster Id, the names and info of all current shards and the names and info of all current collections.<jupyter_output><empty_output><jupyter_text>
3.3. Sharding a database collection
Recall that sharding is enabled in MongoDB on a per-basis collection. When sharding is enabled on a collection, MongoDB partitions the data into the shards of a cluster using a **shard key**, an indexed field that exists in every document stored in the collection.
MongoDB divides the shard key values into **chunks** (of documents) and distributes the chunks evenly across shards. To divide the shard key values into chunks, MongoDB uses two kinds of partitioning strategies:
- **Range based partitioning:** data is partitioned into ranges [min, max] determined by the shard key. Each range represents a chunk.
- **Hash based partitioning:** data is partitioned into chunks using a hash function.
In what follows you will shard copies of the collection mydb.cities using range based and hash based partitioning.
3.3.1. Sharding a collection using range-based partition
- Using the **shell connected to the query router**(mongos instance), create the collection **cities1** in database **mydb**:
use mydb
db.createCollection("cities1")
show collections # Verify collection existence
- Enable sharding on the collection **mydb.cities1** using the attribute **state** as *shard key*:
sh.enableSharding("mydb")
sh.shardCollection("mydb.cities1", { "state": 1} )
- Verify the **number of chunks**:
sh.status()
Question 2:
a) **How many chunks did you create?**
b) **What are their associated ranges?**
Include a screenshot of the results of the command in your answer to support your answer.<jupyter_code>--- Sharding Status ---
sharding version: {
"_id" : 1,
"version" : 4,
"minCompatibleVersion" : 4,
"currentVersion" : 5,
"clusterId" : ObjectId("5a9c93628e1c27c1fe6c0090")
}
shards:
{ "_id" : "shard1", "host" : "localhost:27021" }
databases:
{ "_id" : "admin", "partitioned" : false, "primary" : "config" }
{ "_id" : "mydb", "partitioned" : true, "primary" : "shard1" }
mydb.cities1
shard key: { "state" : 1 }
chunks:
shard1 1
{ "state" : { "$minKey" : 1 } } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(1, 0)
a) This command created one chunk on the shard shard1
b) This chunk has a range of 1 to 1 since the min key is 1 and the max key is also 1<jupyter_output><empty_output><jupyter_text>- Populate the collection **cities1** using the content of the collection **mydb.cities** (we loaded that collection with _mongoimport_ tool before):
db.cities.find().forEach(
function(d) {
db.cities1.insert(d);
}
)
- Verify the **number of chunks** after population:
sh.status()
Question 3:
a) **How many chunks are there now?**
b) **What are their associated ranges?**
c) **What are the changes you can observe?**
Include a screenshot of the results of the command in your answer to support your answer.<jupyter_code>--- Sharding Status ---
sharding version: {
"_id" : 1,
"version" : 4,
"minCompatibleVersion" : 4,
"currentVersion" : 5,
"clusterId" : ObjectId("5a9c93628e1c27c1fe6c0090")
}
shards:
{ "_id" : "shard1", "host" : "localhost:27021" }
databases:
{ "_id" : "admin", "partitioned" : false, "primary" : "config" }
{ "_id" : "mydb", "partitioned" : true, "primary" : "shard1" }
mydb.cities1
shard key: { "state" : 1 }
chunks:
shard1 3
{ "state" : { "$minKey" : 1 } } -->> { "state" : "MA" } on : shard1 Timestamp(1, 1)
{ "state" : "MA" } -->> { "state" : "VT" } on : shard1 Timestamp(1, 3)
{ "state" : "VT" } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(1, 4)
a) There are now 3 chunks on shard1
b) chunk1 has range minKey 1 to MA, chunk 2 has range MA to VT, and chunk 3 has range VT to maxKey 1
c) This created 2 new chunks populated them and also gave the values an updated timestamp.<jupyter_output><empty_output><jupyter_text>
3.3.2. Sharding a collection using hash-based partition
Now let's study the sharding strategy using a hash function.
- Using the **shell connected to the query router**(mongos instance), create the collection **cities2** in database **mydb**:
use mydb
db.createCollection("cities2")
show collections # Verify collection existence
- Enable sharding on the collection **mydb.cities2**.The principle that we will adopt is to use the attribute **state** as shard key.
sh.enableSharding("mydb")
sh.shardCollection("mydb.cities2", { "state": "hashed"} )
**Note the difference between the command that shards by range and the one to shards by hash.**
- Verify the **number of chunks** before the population:
sh.status()
Question 4:
a) **How many chunks did you create?**
b) **What differences do you see with respect to the same task in the range sharding strategy?**
Include a screen copy of the results of the command in your answer to support your answer.<jupyter_code>--- Sharding Status ---
sharding version: {
"_id" : 1,
"version" : 4,
"minCompatibleVersion" : 4,
"currentVersion" : 5,
"clusterId" : ObjectId("5a9c93628e1c27c1fe6c0090")
}
shards:
{ "_id" : "shard1", "host" : "localhost:27021" }
databases:
{ "_id" : "admin", "partitioned" : false, "primary" : "config" }
{ "_id" : "mydb", "partitioned" : true, "primary" : "shard1" }
mydb.cities1
shard key: { "state" : 1 }
chunks:
shard1 3
{ "state" : { "$minKey" : 1 } } -->> { "state" : "MA" } on : shard1 Timestamp(1, 1)
{ "state" : "MA" } -->> { "state" : "VT" } on : shard1 Timestamp(1, 3)
{ "state" : "VT" } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(1, 4)
mydb.cities2
shard key: { "state" : "hashed" }
chub)nks:
shard1 2
{ "state" : { "$minKey" : 1 } } -->> { "state" : NumberLong(0) } on : shard1 Timestamp(1, 1)
{ "state" : NumberLong(0) } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(1, 2)
a) This opertation created 2 chunks.
b) This opertation created 2 chunks instead of 1 also the value of the key value pair is now a number instead of a string, and the state of the shard is hashed.<jupyter_output><empty_output><jupyter_text>
TO-DO:
a) **Populate the collection _cities2_**
Place your code below.<jupyter_code>db.cities.find().forEach(
function(d) {
db.cities2.insert(d);
}
)<jupyter_output><empty_output><jupyter_text>
Question 5:
a) **How many chunks are there now?**
b) **Compare the result with respect to the range sharding. Explain what you see different.**
Include a screen shot of the results of the command in your answer to support your answer.
<jupyter_code>--- Sharding Status ---
sharding version: {
"_id" : 1,
"version" : 4,
"minCompatibleVersion" : 4,
"currentVersion" : 5,
"clusterId" : ObjectId("5a9c93628e1c27c1fe6c0090")
}
shards:
{ "_id" : "shard1", "host" : "localhost:27021" }
databases:
{ "_id" : "admin", "partitioned" : false, "primary" : "config" }
{ "_id" : "mydb", "partitioned" : true, "primary" : "shard1" }
mydb.cities1
shard key: { "state" : 1 }
chunks:
shard1 3
{ "state" : { "$minKey" : 1 } } -->> { "state" : "MA" } on : shard1 Timestamp(1, 1)
{ "state" : "MA" } -->> { "state" : "VT" } on : shard1 Timestamp(1, 3)
{ "state" : "VT" } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(1, 4)
mydb.cities2
shard key: { "state" : "hashed" }
chunks:
shard1 3
{ "state" : { "$minKey" : 1 } } -->> { "state" : NumberLong(0) } on : shard1 Timestamp(1, 1)
{ "state" : NumberLong(0) } -->> { "state" : NumberLong("3630192931154748514") } on : shard1 Timestamp(1, 3)
{ "state" : NumberLong("3630192931154748514") } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(1, 4)
a) There are now 6 total chunks 3 range based and 3 hashed
b) The creation of addition chunks based one hash chunking created 1 addition chunk instead of 2 however they both have 3 total chunks due to having the same amount of data. The values for these chunks are longs instead of strings, but the min and max are both still minKey:1 and maxKey:1.<jupyter_output><empty_output><jupyter_text>
3.4. Balancing data across sharded cluster
Balancing is the process MongoDB uses to distribute data of a sharded collection evenly across a sharded cluster. When a shard has too many of a sharded collection’s chunks compared to other shards, MongoDB automatically balances the chunks across the shards.
MongoDB balancer supports **tagging** a range of shard key values. Using *tags* you can:
- Isolate specific subset of data on a specific set of shards.
- Ensure that relevant data reside on shards that are geographically close to the user.
For the final part of this exercise you will analyze the behavior of the *MongoDB balancing process* by adding *tagged shards* to your cluster.
3.4.1. Adding shards to a cluster
- Using a **new shell**, start *another* MongoDB instance:
mkdir -p ~/db/shard2
mongod --shardsvr --dbpath ~/db/shard2 --port 27022
- Using a **new shell **(mongos instance), add the new _mongo instance_ to the cluster:
use admin
db.runCommand( { addShard: "localhost:27022", name: "shard2" } )
- Wait a few seconds and check the status of the cluster:
sh.status()
Question 6:
**Draw the new configuration of the cluster and label each element (_router, config server and shards_) with its corresponding port as you defined in the previous tasks.**
_Note:_ you can present this as a table if it is easier than drawing, or you can insert an image.
<jupyter_code>--- Sharding Status ---
sharding version: {
"_id" : 1,
"version" : 4,
"minCompatibleVersion" : 4,
"currentVersion" : 5,
"clusterId" : ObjectId("5a9c93628e1c27c1fe6c0090")
}
shards:
{ "_id" : "shard1", "host" : "localhost:27021" }
{ "_id" : "shard2", "host" : "localhost:27022" }
databases:
{ "_id" : "admin", "partitioned" : false, "primary" : "config" }
{ "_id" : "mydb", "partitioned" : true, "primary" : "shard1" }
mydb.cities1
shard key: { "state" : 1 }
chunks:
shard2 1
shard1 2
{ "state" : { "$minKey" : 1 } } -->> { "state" : "MA" } on : shard2 Timestamp(2, 0)
{ "state" : "MA" } -->> { "state" : "VT" } on : shard1 Timestamp(2, 1)
{ "state" : "VT" } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(1, 4)
mydb.cities2
shard key: { "state" : "hashed" }
chunks:
shard2 1
shard1 2
{ "state" : { "$minKey" : 1 } } -->> { "state" : NumberLong(0) } on : shard2 Timestamp(2, 0)
{ "state" : NumberLong(0) } -->> { "state" : NumberLong("3630192931154748514") } on : shard1 Timestamp(2, 1)
{ "state" : NumberLong("3630192931154748514") } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(1, 4)
<jupyter_output><empty_output><jupyter_text>
3.4.2. Sharding using taged shards
- Using a **new shell**, start *another* MongoDB instance:
mkdir -p ~/db/shard3
mongod --shardsvr --dbpath ~/db/shard3 --port 27023
TO-DO:
- Using a **new shell **(mongos instance), add the new _mongo instance_ to the cluster:
Place your code bellow.<jupyter_code>use admin
db.runCommand( { addShard: "localhost:27023", name: "shard3" } )<jupyter_output><empty_output><jupyter_text>
- Using a **new shell **(mongos instance), associate tags to shard instances:
sh.addShardTag("shard1", "CA")
sh.addShardTag("shard2", "NY")
sh.addShardTag("shard3", "Others")
- Create, shard and populate a new collection named **cities3**:
use mydb;
db.createCollection("cities3")
sh.shardCollection("mydb.cities3", { "state": 1} )
db.cities.find().forEach(
function(d) {
db.cities3.insert(d);
}
)
- Associate **shard key ranges** to tagged shards:
sh.addTagRange("mydb.cities3", { state: MinKey }, { state: "CA" }, "Others")
sh.addTagRange("mydb.cities3", { state: "CA" }, { state: "CA_" }, "CA")
sh.addTagRange("mydb.cities3", { state: "CA_" }, { state: "NY" }, "Others")
sh.addTagRange("mydb.cities3", { state: "NY" }, { state: "NY_" }, "NY")
sh.addTagRange("mydb.cities3", { state: "NY_" }, { state: MaxKey }, "Others")
- Review the configuration of the cluster
sh.status()
Question 7:
**a)** Analyze the results and explain the logic behind this tagging strategy.
**b)** Connect to the shard that contains the data about California (the mongo server running that shard, e.g. shard2 server running on port 27022), and count the documents.
**c)** Do the same operation with the other shards.
**d)** Is the sharded data collection complete with respect to initial one?
**d)** Are shards orthogonal?
<jupyter_code>--- Sharding Status ---
sharding version: {
"_id" : 1,
"version" : 4,
"minCompatibleVersion" : 4,
"currentVersion" : 5,
"clusterId" : ObjectId("5a9c93628e1c27c1fe6c0090")
}
shards:
{ "_id" : "shard1", "host" : "localhost:27021", "tags" : [ "CA" ] }
{ "_id" : "shard2", "host" : "localhost:27022", "tags" : [ "NY" ] }
{ "_id" : "shard3", "host" : "localhost:27023", "tags" : [ "Others" ] }
databases:
{ "_id" : "admin", "partitioned" : false, "primary" : "config" }
{ "_id" : "mydb", "partitioned" : true, "primary" : "shard1" }
mydb.cities1
shard key: { "state" : 1 }
chunks:
shard2 1
shard3 1
shard1 1
{ "state" : { "$minKey" : 1 } } -->> { "state" : "MA" } on : shard2 Timestamp(2, 0)
{ "state" : "MA" } -->> { "state" : "VT" } on : shard3 Timestamp(3, 0)
{ "state" : "VT" } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(3, 1)
mydb.cities2
shard key: { "state" : "hashed" }
chunks:
shard2 1
shard3 1
shard1 1
{ "state" : { "$minKey" : 1 } } -->> { "state" : NumberLong(0) } on : shard2 Timestamp(2, 0)
{ "state" : NumberLong(0) } -->> { "state" : NumberLong("3630192931154748514") } on : shard3 Timestamp(3, 0)
{ "state" : NumberLong("3630192931154748514") } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(3, 1)
mydb.cities3
shard key: { "state" : 1 }
chunks:
shard2 3
shard3 1
shard1 1
{ "state" : { "$minKey" : 1 } } -->> { "state" : "CA" } on : shard2 Timestamp(3, 2)
{ "state" : "CA" } -->> { "state" : "CA_" } on : shard2 Timestamp(3, 4)
{ "state" : "CA_" } -->> { "state" : "MA" } on : shard2 Timestamp(3, 5)
{ "state" : "MA" } -->> { "state" : "VT" } on : shard3 Timestamp(3, 0)
{ "state" : "VT" } -->> { "state" : { "$maxKey" : 1 } } on : shard1 Timestamp(3, 1)
tag: Others { "state" : { "$minKey" : 1 } } -->> { "state" : "CA" }
tag: CA { "state" : "CA" } -->> { "state" : "CA_" }
tag: Others { "state" : "CA_" } -->> { "state" : "NY" }
tag: NY { "state" : "NY" } -->> { "state" : "NY_" }
tag: Others { "state" : "NY_" } -->> { "state" : { "$maxKey" : 1 } }
a) The idea behind this sharding strategy is to gather the states NY and CA onto their own shards to maximize comlumn level compression.
b) There are 1595 documents
c) On shard 1 there are 1516 documents, and on shard 3 there are 26242 documents.
d) Is the sharded data collection complete with respect to initial one? There are 29353 total records, 29353-26242-1516-1595 = 0 so we can see that all of the records are accounted for.
d) Yes all the documents exist and there are the exact amounts of documents in the shards as there are in the original collection and since the shards contain discrete documents that do not exist on other shards the shards must be orthogonal.<jupyter_output><empty_output><jupyter_text>
4. Sharding in real-world application
Considering the dataset from Amazon Kindle Stories Reviews (available [here](https://www.kaggle.com/bharadwaj6/kindle-reviews/downloads/kindle_reviews.json)), you should load the dataset into a mongo, and define a sharded cluster based on what we just implemented.
**Answer the following questions about your implementation. You can also use them as a guideline:**
1. Explain your reasons for choosing your sharding key. _Which are possible implications when querying data and when adding/deleting data?_
2. Implement a cluster with 3 shards and distribute the data across them according to your chosen key using **both the range and hash based strategies**.
3. Populate your sharded database using the data collection you downloaded.
4. **Compare the behavior of your sharding solution in the range-based strategy versus that of the hash-based strategy**:
1. Once you populate the sharded database, is the result balanced?
2. Give an example of query or a manipulation operation that can potentially benefit from your sharding strategy. Test your hypothesis and present the result of running the operation with and without sharding (include screenshots of the results).
3. In which cases your sharding is useless for scaling the management of the data collection? Give examples to support your arguments.
4. Define a criterion for defining critical documents and use the tagging strategy for isolating these data. Show evidence of the operation and results.<jupyter_code>====== Code for questions 2 and 3
== new shell ==
mkdir -p ~/db/configdb
mongod --configsvr --dbpath ~/db/configdb --port 27020
== new shell ==
mongos --configdb localhost:27020 --port 27019
======= Code ========
mkdir -p ~/db/shard1
mongod --shardsvr --dbpath ~/db/shard1 --port 27021
== new shell ==
mkdir -p ~/db/shard2
mongod --shardsvr --dbpath ~/db/shard2 --port 27022
== new shell ==
mkdir -p ~/db/shard3
mongod --shardsvr --dbpath ~/db/shard3 --port 27023
== new shell for hshard ==
mongoimport --host localhost:27021 --db mydb --collection kindle_reviews --file ~/kindle_reviews.json
mongo --host localhost:27019
use admin
db.runCommand( { addShard: "localhost:27021", name: "shard1" } )
db.runCommand( { addShard: "localhost:27022", name: "shard2" } )
db.runCommand( { addShard: "localhost:27023", name: "shard3" } )
use mydb
sh.enableSharding("mydb")
db.createCollection("kindle_reviews_hshard")
sh.shardCollection("mydb.kindle_reviews_hshard", { "reviewerID": "hashed"})
db.kindle_reviews.find().forEach(
function(d) {
db.kindle_reviews_hshard.insert(d);
}
)
== new shell for rshard ==
use mydb
sh.enableSharding("mydb")
db.createCollection("kindle_reviews_rshard")
sh.addShardTag("shard1", "<= 3")
sh.addShardTag("shard2", "4")
sh.addShardTag("shard3", "5")
sh.shardCollection("mydb.kindle_reviews_rshard", { overall: 1})
db.kindle_reviews.find().forEach(
function(d) {
db.kindle_reviews_rshard.insert(d);
}
)
sh.addTagRange("mydb.kindle_reviews_rshard", { overall: MinKey }, { overall: 3 }, "< 3")
sh.addTagRange("mydb.kindle_reviews_rshard", { overall: 3 }, { overall: 5 }, "4")
sh.addTagRange("mydb.kindle_reviews_rshard", { overall: 5 }, { state: MaxKey }, "5")
1) Explain your reasons for choosing your sharding key. Which are possible implications when querying data and when adding/deleting data?
For the hash based ranging implementation due to the nature of hashing the key choice was reviewerId, this decision was made because the value was unique so no 2 values would recieve the same hash. I chose not to focus on query optimization since the nature of hashing means any choice trying to force specific groupings would have no meaning.
For range based hashing I choose overall as my ranging key. This choice was based on the assumption that a large number of queries would be based on a users rating of a specific restraunt and those having them localized based on that value would be beneficial.
4) Compare the behavior of your sharding solution in the range-based strategy versus that of the hash-based strategy:
The hash based sharding strategy produced very evenly distributed results across all 3 shards with each of shard recieving roughly 1/3 of the records (328423, 325225, 328971) this can be seen below. AS stated in the mongo documentation hash based sharding optimizes data distribution at the cost of query slow down so there is no query that would benefit from except for the case of queries based on a single value for the hashed field such as shown below where the user with Id A1F6404F1VG29J is queried for. We can see that this query runs about 5 times faster with the hash based sharding. Hash based sharding could not be used for issolating critical documents.
The range based sharding strategy produced significantly less evenly distributed results, (575264, 23018, 384337). This was on purpose as I was attempting to isolate the values by there ratings. Over half of the ratings are 5 stars with the rest of the majority being 4 stars and only 23018 being 3 or less stars. Splitting the data like this provides a 33% speed up when querying for restraunts with 5 star ratings as can be seen below. This means that I achieved my desired goal of optemissing queries by rating by defining critical documents and using a range based tagging strategy to isolate the data by the range of the user rating.
=========== Output of sh.status for hash based ranging. =======================
mongos> sh.status(true)
--- Sharding Status ---
sharding version: {
"_id" : 1,
"version" : 4,
"minCompatibleVersion" : 4,
"currentVersion" : 5,
"clusterId" : ObjectId("5aa1f9a9782b5fa052f9b73e")
}
shards:
{ "_id" : "shard1", "host" : "localhost:27021" }
{ "_id" : "shard2", "host" : "localhost:27022" }
{ "_id" : "shard3", "host" : "localhost:27023" }
databases:
{ "_id" : "admin", "partitioned" : false, "primary" : "config" }
{ "_id" : "mydb", "partitioned" : true, "primary" : "shard1" }
mydb.kindle_reviews_hshard
shard key: { "reviewerID" : "hashed" }
chunks:
shard1 8
shard2 8
shard3 7
{ "reviewerID" : { "$minKey" : 1 } } -->> { "reviewerID" : NumberLong("-8467459023582830738") } on : shard1 Timestamp(3, 20)
{ "reviewerID" : NumberLong("-8467459023582830738") } -->> { "reviewerID" : NumberLong("-7716236592535699496") } on : shard1 Timestamp(3, 21)
{ "reviewerID" : NumberLong("-7716236592535699496") } -->> { "reviewerID" : NumberLong("-7063624095207653329") } on : shard1 Timestamp(3, 32)
{ "reviewerID" : NumberLong("-7063624095207653329") } -->> { "reviewerID" : NumberLong("-6148914691236517204") } on : shard1 Timestamp(3, 33)
{ "reviewerID" : NumberLong("-6148914691236517204") } -->> { "reviewerID" : NumberLong("-5431929121132567127") } on : shard1 Timestamp(3, 36)
{ "reviewerID" : NumberLong("-5431929121132567127") } -->> { "reviewerID" : NumberLong("-4771603862880028318") } on : shard1 Timestamp(3, 37)
{ "reviewerID" : NumberLong("-4771603862880028318") } -->> { "reviewerID" : NumberLong("-4099523846048513495") } on : shard1 Timestamp(3, 28)
{ "reviewerID" : NumberLong("-4099523846048513495") } -->> { "reviewerID" : NumberLong("-3074457345618258602") } on : shard1 Timestamp(3, 29)
{ "reviewerID" : NumberLong("-3074457345618258602") } -->> { "reviewerID" : NumberLong("-2357806851061618481") } on : shard2 Timestamp(3, 30)
{ "reviewerID" : NumberLong("-2357806851061618481") } -->> { "reviewerID" : NumberLong("-1591302812430778876") } on : shard2 Timestamp(3, 31)
{ "reviewerID" : NumberLong("-1591302812430778876") } -->> { "reviewerID" : NumberLong("-981932972817861657") } on : shard2 Timestamp(3, 34)
{ "reviewerID" : NumberLong("-981932972817861657") } -->> { "reviewerID" : NumberLong(0) } on : shard2 Timestamp(3, 35)
{ "reviewerID" : NumberLong(0) } -->> { "reviewerID" : NumberLong("556136071177553660") } on : shard2 Timestamp(3, 38)
{ "reviewerID" : NumberLong("556136071177553660") } -->> { "reviewerID" : NumberLong("1396956147964709185") } on : shard2 Timestamp(3, 39)
{ "reviewerID" : NumberLong("1396956147964709185") } -->> { "reviewerID" : NumberLong("2152230436667957450") } on : shard2 Timestamp(3, 26)
{ "reviewerID" : NumberLong("2152230436667957450") } -->> { "reviewerID" : NumberLong("3074457345618258602") } on : shard2 Timestamp(3, 27)
{ "reviewerID" : NumberLong("3074457345618258602") } -->> { "reviewerID" : NumberLong("3618467672757455414") } on : shard3 Timestamp(3, 40)
{ "reviewerID" : NumberLong("3618467672757455414") } -->> { "reviewerID" : NumberLong("4459449031503940523") } on : shard3 Timestamp(3, 41)
{ "reviewerID" : NumberLong("4459449031503940523") } -->> { "reviewerID" : NumberLong("5197357560686955676") } on : shard3 Timestamp(3, 24)
{ "reviewerID" : NumberLong("5197357560686955676") } -->> { "reviewerID" : NumberLong("6148914691236517204") } on : shard3 Timestamp(3, 25)
{ "reviewerID" : NumberLong("6148914691236517204") } -->> { "reviewerID" : NumberLong("7392717761316007936") } on : shard3 Timestamp(3, 18)
{ "reviewerID" : NumberLong("7392717761316007936") } -->> { "reviewerID" : NumberLong("8117740532216902925") } on : shard3 Timestamp(3, 22)
{ "reviewerID" : NumberLong("8117740532216902925") } -->> { "reviewerID" : { "$maxKey" : 1 } } on : shard3 Timestamp(3, 23)
================ Output of each server size. ====================
steezewizz@kindle-reviews-1:~$ mongo --host localhost:27021
MongoDB shell version: 2.6.10
connecting to: localhost:27021/test
> use mydb
switched to db mydb
> db.kindle_reviews_hshard.find().count()
328423
> exit
bye
steezewizz@kindle-reviews-1:~$ mongo --host localhost:27022
MongoDB shell version: 2.6.10
connecting to: localhost:27022/test
> use mydb
switched to db mydb
> db.kindle_reviews_hshard.find().count()
325225
> exit
bye
steezewizz@kindle-reviews-1:~$ mongo --host localhost:27023
MongoDB shell version: 2.6.10
connecting to: localhost:27023/test
> use mydb
switched to db mydb
> db.kindle_reviews_hshard.find().count()
328971
========== Ouput of Query. ================
mongos> db.kindle_reviews.find({"reviewerID" : "A1F6404F1VG29J"}).explain()
{
"cursor" : "BasicCursor",
"isMultiKey" : false,
"n" : 11,
"nscannedObjects" : 982619,
"nscanned" : 982619,
"nscannedObjectsAllPlans" : 982619,
"nscannedAllPlans" : 982619,
"scanAndOrder" : false,
"indexOnly" : false,
"nYields" : 7676,
"nChunkSkips" : 0,
"millis" : 598,
"server" : "kindle-reviews-1:27021",
"filterSet" : false,
"millis" : 598
}
mongos> db.kindle_reviews_hshard.find({"reviewerID" : "A1F6404F1VG29J"}).explain()
{
"clusteredType" : "ParallelSort",
"shards" : {
"localhost:27023" : [
{
"cursor" : "BtreeCursor reviewerID_hashed",
"isMultiKey" : false,
"n" : 11,
"nscannedObjects" : 11,
"nscanned" : 11,
"nscannedObjectsAllPlans" : 11,
"nscannedAllPlans" : 11,
"scanAndOrder" : false,
"indexOnly" : false,
"nYields" : 1,
"nChunkSkips" : 0,
"millis" : 90,
"indexBounds" : {
"reviewerID" : [
[
NumberLong("6639384163233327718"),
NumberLong("6639384163233327718")
]
]
},
"server" : "kindle-reviews-1:27023",
"filterSet" : false
}
]
},
"cursor" : "BtreeCursor reviewerID_hashed",
"n" : 11,
"nChunkSkips" : 0,
"nYields" : 1,
"nscanned" : 11,
"nscannedAllPlans" : 11,
"nscannedObjects" : 11,
"nscannedObjectsAllPlans" : 11,
"millisShardTotal" : 90,
"millisShardAvg" : 90,
"numQueries" : 1,
"numShards" : 1,
"indexBounds" : {
"reviewerID" : [
[
NumberLong("6639384163233327718"),
NumberLong("6639384163233327718")
]
]
},
"millis" : 91
}
=========== Output of sh.status for range based ranging. =======================
mongos> sh.status()
--- Sharding Status ---
sharding version: {
"_id" : 1,
"version" : 4,
"minCompatibleVersion" : 4,
"currentVersion" : 5,
"clusterId" : ObjectId("5aa4932f90b4a26b7689c44d")
}
shards:
{ "_id" : "shard1", "host" : "localhost:27021", "tags" : [ "<= 3" ] }
{ "_id" : "shard2", "host" : "localhost:27022", "tags" : [ "4" ] }
{ "_id" : "shard3", "host" : "localhost:27023", "tags" : [ "5" ] }
databases:
{ "_id" : "admin", "partitioned" : false, "primary" : "config" }
{ "_id" : "mydb", "partitioned" : true, "primary" : "shard1" }
mydb.kindle_reviews_rshard
shard key: { "overall" : 1 }
chunks:
shard2 1
shard3 3
shard1 1
{ "overall" : { "$minKey" : 1 } } -->> { "overall" : 2 } on : shard2 Timestamp(2, 0)
{ "overall" : 2 } -->> { "overall" : 3 } on : shard3 Timestamp(3, 2)
{ "overall" : 3 } -->> { "overall" : 4 } on : shard3 Timestamp(3, 4) jumbo
{ "overall" : 4 } -->> { "overall" : 5 } on : shard3 Timestamp(3, 5) jumbo
{ "overall" : 5 } -->> { "overall" : { "$maxKey" : 1 } } on : shard1 Timestamp(3, 1) jumbo
tag: <=3 { "overall" : { "$minKey" : 1 } } -->> { "overall" : 3 }
tag: 4 { "overall" : 3 } -->> { "overall" : 5 }
tag: 5 { "overall" : 5 } -->> { "state" : { "$maxKey" : 1 } }
================ Output of each server size. ====================
steezewizz@kindle-reviews-2:~$ mongo --host localhost:27021
MongoDB shell version: 2.6.10
connecting to: localhost:27021/test
> use mydb
switched to db mydb
> db.kindle_reviews_rshard.find().count()
575264
> exit
bye
steezewizz@kindle-reviews-2:~$ mongo --host localhost:27022
MongoDB shell version: 2.6.10
connecting to: localhost:27022/test
> use mydb
switched to db mydb
> db.kindle_reviews_rshard.find().count()
23018
> exit
bye
steezewizz@kindle-reviews-2:~$ mongo --host localhost:27023
MongoDB shell version: 2.6.10
connecting to: localhost:27023/test
> use mydb
switched to db mydb
> db.kindle_reviews_rshard.find().count()
384337
================= Query Results =============
mongos> db.kindle_reviews.find({overall : 5}).explain()
{
"cursor" : "BasicCursor",
"isMultiKey" : false,
"n" : 575264,
"nscannedObjects" : 982619,
"nscanned" : 982619,
"nscannedObjectsAllPlans" : 982619,
"nscannedAllPlans" : 982619,
"scanAndOrder" : false,
"indexOnly" : false,
"nYields" : 7676,
"nChunkSkips" : 0,
"millis" : 3011,
"server" : "kindle-reviews-2:27021",
"filterSet" : false,
"millis" : 3011
}
mongos> db.kindle_reviews_rshard.find({overall : 5}).explain()
{
"clusteredType" : "ParallelSort",
"shards" : {
"localhost:27021" : [
{
"cursor" : "BtreeCursor overall_1",
"isMultiKey" : false,
"n" : 575264,
"nscannedObjects" : 575264,
"nscanned" : 575264,
"nscannedObjectsAllPlans" : 575264,
"nscannedAllPlans" : 575264,
"scanAndOrder" : false,
"indexOnly" : false,
"nYields" : 4494,
"nChunkSkips" : 0,
"millis" : 2581,
"indexBounds" : {
"overall" : [
[
5,
5
]
]
},
"server" : "kindle-reviews-2:27021",
"filterSet" : false
}
]
},
"cursor" : "BtreeCursor overall_1",
"n" : 575264,
"nChunkSkips" : 0,
"nYields" : 4494,
"nscanned" : 575264,
"nscannedAllPlans" : 575264,
"nscannedObjects" : 575264,
"nscannedObjectsAllPlans" : 575264,
"millisShardTotal" : 2581,
"millisShardAvg" : 2581,
"numQueries" : 1,
"numShards" : 1,
"indexBounds" : {
"overall" : [
[
5,
5
]
]
},
"millis" : 2583
}
mongos> <jupyter_output><empty_output>
|
no_license
|
/Lab2/Assignment02/.ipynb_checkpoints/Assignment2-MongoDB-checkpoint.ipynb
|
sbachlet/bigdata
| 10 |
<jupyter_start><jupyter_text># 視覺化進出場策略 (Visualizing Strategies)## 看一下單一股票的進出場狀況<jupyter_code>import os
import sys
# 把我們自己寫的模組的位置,加入到模組搜尋路徑之中,不然會有 import error
module_dir = os.path.join(os.path.dirname(os.getcwd()), 'modules')
if not module_dir in sys.path:
sys.path.append(module_dir)
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from datetime import datetime
import crawler
import backtest<jupyter_output><empty_output><jupyter_text>## 讀取歷史股價<jupyter_code>start = datetime(2017,1,1)
end = datetime(2017,12,31)
# 讀取從指定日期之後的股價資訊
df = crawler.get_quotes("AMZN", start, end)<jupyter_output><empty_output><jupyter_text>## 訂定策略進出點的計算,可以參考:
https://www.quantstart.com/articles/Backtesting-a-Moving-Average-Crossover-in-Python-with-pandas<jupyter_code># 突破策略
def breakout(df):
# Donchian Channel
df['20d_high'] = pd.Series.rolling(df['Close'], window=20).max()
df['10d_low'] = pd.Series.rolling(df['Close'], window=10).min()
has_position = False
df['signals'] = 0
for t in range(2, df['signals'].size):
if df['Close'][t] > df['20d_high'][t-1]:
if not has_position:
df.loc[df.index[t], 'signals'] = 1
has_position = True
elif df['Close'][t] < df['10d_low'][t-1]:
if has_position:
df.loc[df.index[t], 'signals'] = -1
has_position = False
df['positions'] = df['signals'].cumsum().shift()
# 突破策略
def macross(df):
# 均線
df['20d'] = pd.Series.rolling(df['Close'], window=20).mean()
df['5d'] = pd.Series.rolling(df['Close'], window=5).mean()
has_position = False
df['signals'] = 0
for t in range(2, df['signals'].size):
if df['5d'][t] > df['20d'][t] and df['5d'][t-1] < df['20d'][t-1] and df['20d'][t] > df['20d'][t-1]:
if not has_position:
df.loc[df.index[t], 'signals'] = 1
has_position = True
elif df['Close'][t] < df['20d'][t] and df['Close'][t-1] < df['20d'][t-1]:
if has_position:
df.loc[df.index[t], 'signals'] = -1
has_position = False
df['positions'] = df['signals'].cumsum().shift()
def apply_strategy(strategy, df):
return strategy(df)
apply_strategy(macross, df)
# 底下這一行只是為了要在下面把 signals 跟 positions 畫出來做說明用
df[['signals', 'positions']].plot(subplots = True, ylim=(-1.1, 1.1), figsize = (10, 8))<jupyter_output><empty_output><jupyter_text>## 標出進出場點<jupyter_code>fig = plt.figure()
ax1 = fig.add_subplot(111, ylabel='Price in $')
df['Close'].plot(ax=ax1, color='gray', lw=1., figsize=(10,8))
df['5d'].plot(ax=ax1, color='r', lw=1.)
df['20d'].plot(ax=ax1, color='b', lw=1.)
# Plot the "buy" trades
ax1.plot(df.loc[df.signals == 1].index,df['Close'][df.signals == 1],'^', markersize=10, color='r')
# Plot the "sell" trades
ax1.plot(df.loc[df.signals == -1].index, df['Close'][df.signals == -1], 'v', markersize=10, color='k')<jupyter_output><empty_output><jupyter_text>## 計算Sharpe Ratio<jupyter_code>dailyRet = df['Close'].pct_change()
#假設無風險利率為 4%
#假設一年有252個交易日
excessRet = (dailyRet - 0.04/252)[df['positions']==1]
sharpeRatio = np.sqrt(252.0)*np.mean(excessRet)/np.std(excessRet)
sharpeRatio<jupyter_output><empty_output><jupyter_text>## 計算MaxDD跟MaxDDD<jupyter_code>df['Ret'] = np.where(df['positions']==1, dailyRet, 0)
cumRet = np.cumprod(1 + df['Ret'])
cumRet.plot(style='r-')
backtest.DrawDownAnalysis(cumRet)<jupyter_output><empty_output>
|
no_license
|
/03. strategies/視覺化進出場策略.ipynb
|
victorgau/KHPY20180901
| 6 |
<jupyter_start><jupyter_text>
Classification with Python
In this notebook we try to practice all the classification algorithms that we have learned in this course.
We load a dataset using Pandas library, and apply the following algorithms, and find the best one for this specific dataset by accuracy evaluation methods.
Let's first load required libraries:
<jupyter_code>import itertools
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import NullFormatter
import pandas as pd
import numpy as np
import matplotlib.ticker as ticker
from sklearn import preprocessing
%matplotlib inline<jupyter_output><empty_output><jupyter_text>### About dataset
This dataset is about past loans. The **Loan_train.csv** data set includes details of 346 customers whose loan are already paid off or defaulted. It includes following fields:
| Field | Description |
| -------------- | ------------------------------------------------------------------------------------- |
| Loan_status | Whether a loan is paid off on in collection |
| Principal | Basic principal loan amount at the |
| Terms | Origination terms which can be weekly (7 days), biweekly, and monthly payoff schedule |
| Effective_date | When the loan got originated and took effects |
| Due_date | Since it’s one-time payoff schedule, each loan has one single due date |
| Age | Age of applicant |
| Education | Education of applicant |
| Gender | The gender of applicant |
Let's download the dataset
### Load Data From CSV File
<jupyter_code>df = pd.read_csv('https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-ML0101EN-SkillsNetwork/labs/FinalModule_Coursera/data/loan_train.csv')
df.head()
df.shape<jupyter_output><empty_output><jupyter_text>### Convert to date time object
<jupyter_code>df['due_date'] = pd.to_datetime(df['due_date'])
df['effective_date'] = pd.to_datetime(df['effective_date'])
df.head()<jupyter_output><empty_output><jupyter_text># Data visualization and pre-processing
Let’s see how many of each class is in our data set
<jupyter_code>df['loan_status'].value_counts()<jupyter_output><empty_output><jupyter_text>260 people have paid off the loan on time while 86 have gone into collection
Let's plot some columns to underestand data better:
<jupyter_code>import seaborn as sns
bins = np.linspace(df.Principal.min(), df.Principal.max(), 10)
g = sns.FacetGrid(df, col="Gender", hue="loan_status", palette="Set1", col_wrap=2)
g.map(plt.hist, 'Principal', bins=bins, ec="k")
g.axes[-1].legend()
plt.show()
bins = np.linspace(df.age.min(), df.age.max(), 10)
g = sns.FacetGrid(df, col="Gender", hue="loan_status", palette="Set1", col_wrap=2)
g.map(plt.hist, 'age', bins=bins, ec="k")
g.axes[-1].legend()
plt.show()<jupyter_output><empty_output><jupyter_text># Pre-processing: Feature selection/extraction
### Let's look at the day of the week people get the loan
<jupyter_code>df['dayofweek'] = df['effective_date'].dt.dayofweek
bins = np.linspace(df.dayofweek.min(), df.dayofweek.max(), 10)
g = sns.FacetGrid(df, col="Gender", hue="loan_status", palette="Set1", col_wrap=2)
g.map(plt.hist, 'dayofweek', bins=bins, ec="k")
g.axes[-1].legend()
plt.show()
<jupyter_output><empty_output><jupyter_text>We see that people who get the loan at the end of the week don't pay it off, so let's use Feature binarization to set a threshold value less than day 4
<jupyter_code>df['weekend'] = df['dayofweek'].apply(lambda x: 1 if (x>3) else 0)
df.head()<jupyter_output><empty_output><jupyter_text>## Convert Categorical features to numerical values
Let's look at gender:
<jupyter_code>df.groupby(['Gender'])['loan_status'].value_counts(normalize=True)<jupyter_output><empty_output><jupyter_text>86 % of female pay there loans while only 73 % of males pay there loan
Let's convert male to 0 and female to 1:
<jupyter_code>df['Gender'].replace(to_replace=['male','female'], value=[0,1],inplace=True)
df.head()<jupyter_output><empty_output><jupyter_text>## One Hot Encoding
#### How about education?
<jupyter_code>df.groupby(['education'])['loan_status'].value_counts(normalize=True)<jupyter_output><empty_output><jupyter_text>#### Features before One Hot Encoding
<jupyter_code>df[['Principal','terms','age','Gender','education']].head()<jupyter_output><empty_output><jupyter_text>#### Use one hot encoding technique to conver categorical varables to binary variables and append them to the feature Data Frame
<jupyter_code>Feature = df[['Principal','terms','age','Gender','weekend']]
Feature = pd.concat([Feature,pd.get_dummies(df['education'])], axis=1)
Feature.drop(['Master or Above'], axis = 1,inplace=True)
Feature.head()
<jupyter_output><empty_output><jupyter_text>### Feature Selection
Let's define feature sets, X:
<jupyter_code>X = Feature
X<jupyter_output><empty_output><jupyter_text>What are our lables?
<jupyter_code>y = df['loan_status'].values
y[0:5]<jupyter_output><empty_output><jupyter_text>## Normalize Data
Data Standardization give data zero mean and unit variance (technically should be done after train test split)
<jupyter_code>X= preprocessing.StandardScaler().fit(X).transform(X)
X[0:5]<jupyter_output><empty_output><jupyter_text># Classification
Now, it is your turn, use the training set to build an accurate model. Then use the test set to report the accuracy of the model
You should use the following algorithm:
* K Nearest Neighbor(KNN)
* Decision Tree
* Support Vector Machine
* Logistic Regression
\__ Notice:\__
* You can go above and change the pre-processing, feature selection, feature-extraction, and so on, to make a better model.
* You should use either scikit-learn, Scipy or Numpy libraries for developing the classification algorithms.
* You should include the code of the algorithm in the following cells.
# K Nearest Neighbor(KNN)
Notice: You should find the best k to build the model with the best accuracy.\
**warning:** You should not use the **loan_test.csv** for finding the best k, however, you can split your train_loan.csv into train and test to find the best **k**.
<jupyter_code>from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.25, random_state=4)
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
Ks = 10
mean_acc = np.zeros((Ks-1))
std_acc = np.zeros((Ks-1))
for n in range(1,Ks):
#Train Model and Predict
neigh = KNeighborsClassifier(n_neighbors = n).fit(X_train,y_train)
yhat=neigh.predict(X_test)
mean_acc[n-1] = metrics.accuracy_score(y_test, yhat)
std_acc[n-1]=np.std(yhat==y_test)/np.sqrt(yhat.shape[0])
mean_acc
plt.plot(range(1,Ks),mean_acc,'g')
plt.fill_between(range(1,Ks),mean_acc - 1 * std_acc,mean_acc + 1 * std_acc, alpha=0.10)
plt.fill_between(range(1,Ks),mean_acc - 3 * std_acc,mean_acc + 3 * std_acc, alpha=0.10,color="green")
plt.legend(('Accuracy ', '+/- 1xstd','+/- 3xstd'))
plt.ylabel('Accuracy ')
plt.xlabel('Number of Neighbors (K)')
plt.tight_layout()
plt.show()
print( "The best accuracy was with", mean_acc.max(), "with k=", mean_acc.argmax()+1)
neigh = KNeighborsClassifier(n_neighbors = 5).fit(X_train,y_train)
<jupyter_output><empty_output><jupyter_text># Decision Tree
<jupyter_code>from sklearn.tree import DecisionTreeClassifier
Tree = DecisionTreeClassifier(criterion="entropy", max_depth = 6)
Tree.fit(X_train,y_train)
yhattree = Tree.predict(X_test)
print("DecisionTrees's Accuracy: ", metrics.accuracy_score(y_test, yhattree))<jupyter_output>DecisionTrees's Accuracy: 0.7471264367816092
<jupyter_text># Support Vector Machine
<jupyter_code>from sklearn import svm
clf = svm.SVC(kernel='poly')
clf.fit(X_train, y_train)
yhatSVM = clf.predict(X_test)
print("SVM's Accuracy: ", metrics.accuracy_score(y_test, yhatSVM))<jupyter_output>SVM's Accuracy: 0.7471264367816092
<jupyter_text># Logistic Regression
<jupyter_code>from sklearn.linear_model import LogisticRegression
LR = LogisticRegression(C=0.01, solver='liblinear').fit(X_train,y_train)
yhatLR = LR.predict(X_test)
print("Logistic Regression's Accuracy: ", metrics.accuracy_score(y_test, yhatLR))
<jupyter_output>Logistic Regression's Accuracy: 0.7126436781609196
<jupyter_text># Model Evaluation using Test set
<jupyter_code>from sklearn.metrics import jaccard_score
from sklearn.metrics import f1_score
from sklearn.metrics import log_loss
<jupyter_output><empty_output><jupyter_text>First, download and load the test set:
### Load Test set for evaluation
<jupyter_code>df = pd.read_csv('https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/ML0101ENv3/labs/loan_test.csv')
df.head()
df.shape
df['due_date'] = pd.to_datetime(df['due_date'])
df['effective_date'] = pd.to_datetime(df['effective_date'])
df['dayofweek'] = df['effective_date'].dt.dayofweek
df['weekend'] = df['dayofweek'].apply(lambda x: 1 if (x>3) else 0)
df['Gender'].replace(to_replace=['male','female'], value=[0,1],inplace=True)
Feature = df[['Principal','terms','age','Gender','weekend']]
Feature = pd.concat([Feature,pd.get_dummies(df['education'])], axis=1)
Feature.drop(['Master or Above'], axis = 1,inplace=True)
X = Feature
X_test= preprocessing.StandardScaler().fit(X).transform(X)
report=pd.DataFrame(columns = ['Algorithm' , 'Jaccard' , 'F1-score' , 'LogLoss'])
report['Algorithm'] = ['KNN' , 'Decision Tree' , 'SVM' , 'LogisticRegression']
yhatKNN = neigh.predict(X_test)
yhattree = Tree.predict(X_test)
yhatSVM = clf.predict(X_test)
yhatLR = LR.predict(X_test)
yhatprob = LR.predict_proba(X_test)
yhat = np.array([yhatKNN , yhattree , yhatSVM , yhatLR])
for i in range(0,4):
report['Jaccard'][i] = jaccard_score(df['loan_status'] , yhat[i , :] , pos_label= 'PAIDOFF')
report['F1-score'][i] = f1_score(df['loan_status'] , yhat[ i ,:] , average='weighted')
report['LogLoss'][3] = log_loss(df['loan_status'] , yhatprob )
report.head()
<jupyter_output><empty_output>
|
no_license
|
/Classification project.ipynb
|
matteolippolis/my_project
| 21 |
<jupyter_start><jupyter_text>Analyzing US Economic Data and Building a Dashboard
Description
Extracting essential data from a dataset and displaying it is a necessary part of data science; therefore individuals can make correct decisions based on the data. In this assignment, you will extract some essential economic indicators from some data, you will then display these economic indicators in a Dashboard. You can then share the dashboard via an URL.
Gross domestic product (GDP) is a measure of the market value of all the final goods and services produced in a period. GDP is an indicator of how well the economy is doing. A drop in GDP indicates the economy is producing less; similarly an increase in GDP suggests the economy is performing better. In this lab, you will examine how changes in GDP impact the unemployment rate. You will take screen shots of every step, you will share the notebook and the URL pointing to the dashboard.Table of Contents
Define a Function that Makes a Dashboard
Question 1: Create a dataframe that contains the GDP data and display it
Question 2: Create a dataframe that contains the unemployment data and display it
Question 3: Display a dataframe where unemployment was greater than 8.5%
Question 4: Use the function make_dashboard to make a dashboard
(Optional not marked) Save the dashboard on IBM cloud and display it
Estimated Time Needed: 180 min
Define Function that Makes a Dashboard We will import the following libraries.<jupyter_code>import pandas as pd
from bokeh.plotting import figure, output_file, show,output_notebook
output_notebook()<jupyter_output><empty_output><jupyter_text>In this section, we define the function make_dashboard.
You don't have to know how the function works, you should only care about the inputs. The function will produce a dashboard as well as an html file. You can then use this html file to share your dashboard. If you do not know what an html file is don't worry everything you need to know will be provided in the lab. <jupyter_code>def make_dashboard(x, gdp_change, unemployment, title, file_name):
output_file(file_name)
p = figure(title=title, x_axis_label='year', y_axis_label='%')
p.line(x.squeeze(), gdp_change.squeeze(), color="firebrick", line_width=4, legend="% GDP change")
p.line(x.squeeze(), unemployment.squeeze(), line_width=4, legend="% unemployed")
show(p)<jupyter_output><empty_output><jupyter_text>The dictionary links contain the CSV files with all the data. The value for the key GDP is the file that contains the GDP data. The value for the key unemployment contains the unemployment data.<jupyter_code>links={'GDP':'https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/projects/coursera_project/clean_gdp.csv',\
'unemployment':'https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/projects/coursera_project/clean_unemployment.csv'}<jupyter_output><empty_output><jupyter_text> Question 1: Create a dataframe that contains the GDP data and display the first five rows of the dataframe.Use the dictionary links and the function pd.read_csv to create a Pandas dataframes that contains the GDP data.Hint: links["GDP"] contains the path or name of the file.<jupyter_code>#csv_path1='https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/projects/coursera_project/clean_gdp.csv'
#df11=pd.read_csv(csv_path1)
#df11.head()
df1 = pd.read_csv(links["GDP"])<jupyter_output><empty_output><jupyter_text>Use the method head() to display the first five rows of the GDP data, then take a screen-shot.<jupyter_code>df1.head()<jupyter_output><empty_output><jupyter_text> Question 2: Create a dataframe that contains the unemployment data. Display the first five rows of the dataframe. Use the dictionary links and the function pd.read_csv to create a Pandas dataframes that contains the unemployment data.<jupyter_code>#csv_path2='https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/projects/coursera_project/clean_unemployment.csv'
#df22=pd.read_csv(csv_path2)
#df22.head()
df2 = pd.read_csv(links["unemployment"])<jupyter_output><empty_output><jupyter_text>Use the method head() to display the first five rows of the GDP data, then take a screen-shot.<jupyter_code>df2.head()<jupyter_output><empty_output><jupyter_text>Question 3: Display a dataframe where unemployment was greater than 8.5%. Take a screen-shot.<jupyter_code>df2 = pd.read_csv(links["unemployment"])
df21 = df2[df2.unemployment > 8.5]
df21
#df2['unemployment']>=8.5<jupyter_output><empty_output><jupyter_text>Question 4: Use the function make_dashboard to make a dashboardIn this section, you will call the function make_dashboard , to produce a dashboard. We will use the convention of giving each variable the same name as the function parameter.Create a new dataframe with the column 'date' called x from the dataframe that contains the GDP data.<jupyter_code>csv_path='https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/projects/coursera_project/clean_gdp.csv'
df1=pd.read_csv(csv_path)
#df1 = pd.read_csv(links['GDP'])
x=df1[['date']]
x<jupyter_output><empty_output><jupyter_text>Create a new dataframe with the column 'change-current' called gdp_change from the dataframe that contains the GDP data.<jupyter_code>#csv_path='https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/projects/coursera_project/clean_gdp.csv'
#df=pd.read_csv(csv_path)
#df1 = pd.read_csv(links['GDP'])
gdp_change = df1[['change-current']]
gdp_change<jupyter_output><empty_output><jupyter_text>Create a new dataframe with the column 'unemployment' called unemployment from the dataframe that contains the unemployment data.<jupyter_code>#csv_path='https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/projects/coursera_project/clean_unemployment.csv'
#df2=pd.read_csv(csv_path)
#df2 = pd.read_csv(links['unemployment'])
unemployment = df2[['unemployment']]
unemployment <jupyter_output><empty_output><jupyter_text>Give your dashboard a string title, and assign it to the variable title<jupyter_code>title = 'Analyzing US Economic Data'<jupyter_output><empty_output><jupyter_text>Finally, the function make_dashboard will output an .html in your direictory, just like a csv file. The name of the file is "index.html" and it will be stored in the varable file_name.<jupyter_code>file_name = "index.html"<jupyter_output><empty_output><jupyter_text>Call the function make_dashboard , to produce a dashboard. Assign the parameter values accordingly take a the , take a screen shot of the dashboard and submit it.<jupyter_code># Fill up the parameters in the following function:
# make_dashboard(x=, gdp_change=, unemployment=, title=, file_name=)
make_dashboard(x = x, gdp_change = gdp_change, unemployment = unemployment, title = title, file_name = file_name)<jupyter_output><empty_output><jupyter_text> (Optional not marked)Save the dashboard on IBM cloud and display it From the tutorial PROVISIONING AN OBJECT STORAGE INSTANCE ON IBM CLOUD copy the JSON object containing the credentials you created. You’ll want to store everything you see in a credentials variable like the one below (obviously, replace the placeholder values with your own). Take special note of your access_key_id and secret_access_key. Do not delete # @hidden_cell as this will not allow people to see your credentials when you share your notebook.
credentials = {
"apikey": "your-api-key",
"cos_hmac_keys": {
"access_key_id": "your-access-key-here",
"secret_access_key": "your-secret-access-key-here"
},
"endpoints": "your-endpoints",
"iam_apikey_description": "your-iam_apikey_description",
"iam_apikey_name": "your-iam_apikey_name",
"iam_role_crn": "your-iam_apikey_name",
"iam_serviceid_crn": "your-iam_serviceid_crn",
"resource_instance_id": "your-resource_instance_id"
}
<jupyter_code># The code was removed by Watson Studio for sharing.<jupyter_output><empty_output><jupyter_text>You will need the endpoint make sure the setting are the same as PROVISIONING AN OBJECT STORAGE INSTANCE ON IBM CLOUD assign the name of your bucket to the variable bucket_name <jupyter_code>endpoint = 'https://s3-api.us-geo.objectstorage.softlayer.net'<jupyter_output><empty_output><jupyter_text>From the tutorial PROVISIONING AN OBJECT STORAGE INSTANCE ON IBM CLOUD assign the name of your bucket to the variable bucket_name <jupyter_code>bucket_name = 'pythonbasicsfordatascienceproject-donotdelete-pr-uuc9blklvxhqgd'<jupyter_output><empty_output><jupyter_text>We can access IBM Cloud Object Storage with Python useing the boto3 library, which we’ll import below:<jupyter_code>import boto3<jupyter_output><empty_output><jupyter_text>We can interact with IBM Cloud Object Storage through a boto3 resource object.<jupyter_code>resource = boto3.resource(
's3',
aws_access_key_id = credentials["cos_hmac_keys"]['access_key_id'],
aws_secret_access_key = credentials["cos_hmac_keys"]["secret_access_key"],
endpoint_url = endpoint,
)<jupyter_output><empty_output><jupyter_text>We are going to use open to create a file object. To get the path of the file, you are going to concatenate the name of the file stored in the variable file_name. The directory stored in the variable directory using the + operator and assign it to the variable
html_path. We will use the function getcwd() to find current the working directory.<jupyter_code>import os
directory = os.getcwd()
html_path = directory + "/" + file_name<jupyter_output><empty_output><jupyter_text>Now you must read the html file, use the function f = open(html_path, mode) to create a file object and assign it to the variable f. The parameter file should be the variable html_path, the mode should be "r" for read. <jupyter_code>
# Type your code here
f = open (html_path, 'r')<jupyter_output><empty_output><jupyter_text>To load your dataset into the bucket we will use the method put_object, you must set the parameter name to the name of the bucket, the parameter Key should be the name of the HTML file and the value for the parameter Body should be set to f.read().<jupyter_code># Fill up the parameters in the following function:
# resource.Bucket(name=).put_object(Key=, Body=)
resource.Bucket(name=bucket_name).put_object(Key= file_name, Body= f.read())<jupyter_output><empty_output><jupyter_text>In the dictionary Params provide the bucket name as the value for the key 'Bucket'. Also for the value of the key 'Key' add the name of the html file, both values should be strings.<jupyter_code># Fill in the value for each key
# Params = {'Bucket': ,'Key': }
Params = {'Bucket': 'pythonbasicsfordatascienceproject-donotdelete-pr-uuc9blklvxhqgd','Key': file_name}<jupyter_output><empty_output><jupyter_text>The following lines of code will generate a URL to share your dashboard. The URL only last seven days, but don't worry you will get full marks if the URL is visible in your notebook. <jupyter_code>import sys
time = 7*24*60**2
client = boto3.client(
's3',
aws_access_key_id = credentials["cos_hmac_keys"]['access_key_id'],
aws_secret_access_key = credentials["cos_hmac_keys"]["secret_access_key"],
endpoint_url=endpoint,
)
url = client.generate_presigned_url('get_object',Params=Params,ExpiresIn=time)
print(url)<jupyter_output>https://s3-api.us-geo.objectstorage.softlayer.net/pythonbasicsfordatascienceproject-donotdelete-pr-uuc9blklvxhqgd/index.html?AWSAccessKeyId=7a9de9e3637c46ee9bb00da5ca5bed78&Signature=xDe5kKGZlopWLZKrAO4oFCgEtBk%3D&Expires=1593236290
|
no_license
|
/test_notebook_final.ipynb
|
pallavilanke/IBM-WATSON-STUDIO-NOTEBOOK
| 24 |
<jupyter_start><jupyter_text>## Data preprocessing
##### Copyright (C) Microsoft Corporation.
see license file for details<jupyter_code># Allow multiple displays per cell
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
# AZUREML_NATIVE_SHARE_DIRECTORY mapping to host dir is set by _nativeSharedDirectory_ in .compute file
import os
try:
amlWBSharedDir = os.environ['AZUREML_NATIVE_SHARE_DIRECTORY']
except:
amlWBSharedDir = ''
print('not using aml services?')
amlWBSharedDir
# # Use the Azure Machine Learning data collector to log various metrics
# from azureml.logging import get_azureml_logger
# logger = get_azureml_logger()
# Use Azure Machine Learning history magic to control history collection
# History is off by default, options are "on", "off", or "show"
# %azureml history on
# import utlity functions
import sys, os
paths_to_append = [os.path.join(os.getcwd(), os.path.join(*(['Code', 'src'])))]
def add_path_to_sys_path(path_to_append):
if not (any(path_to_append in paths for paths in sys.path)):
sys.path.append(path_to_append)
[add_path_to_sys_path(crt_path) for crt_path in paths_to_append]
import trvis_utils, image_featurization
#### Path variables
prj_consts = trvis_utils.trvis_consts()
data_base_input_dir=os.path.join(amlWBSharedDir, os.path.join(*(prj_consts.BASE_INPUT_DIR_list)))
data_dir = os.path.join(data_base_input_dir, os.path.join(*(['cats_and_dogs', 'train'])))
output_dir = os.path.join(data_base_input_dir, os.path.join(*(prj_consts.PROCESSED_DATA_DIR_list)))
pretrained_models_dir = os.path.join(data_base_input_dir, os.path.join(*(prj_consts.PRETRAINED_MODELS_DIR_list)))
os.makedirs(pretrained_models_dir, mode=0o777, exist_ok=True)
pretrained_models_dir
os.listdir(pretrained_models_dir)
os.makedirs(output_dir, mode=0o777, exist_ok=True)
output_dir
from keras.applications.resnet50 import ResNet50
from tqdm import tqdm
import numpy as np
import pandas as pd
from sklearn.manifold import TSNE
import random
from keras.layers import Dense
from keras.models import Model
from keras.models import load_model
from keras_contrib.applications.densenet import DenseNetImageNet121
from keras.layers import GlobalAveragePooling2D
import keras_contrib
RECOMPUTE=False
SAMPLE_DATA = False
# densenet layers
# name size connected_to
# dense_2_3_bn 1408 concatenate_311
# dense_2_8_bn 2048 concatenate_316
# dense_2_10_bn 2304 concatenate_318
# model_name_list = [ResNet50]
# model_layer_list = ['']
# model_name_list = [ResNet50, DenseNetImageNet121, DenseNetImageNet121, DenseNetImageNet121, DenseNetImageNet121]
# model_layer_list = ['','dense_2_3_bn', 'dense_2_8_bn', 'dense_2_10_bn', '']
# model_name_list = [DenseNetImageNet121, DenseNetImageNet121, DenseNetImageNet121]
# # model_layer_list = ['','concatenate_58', 'concatenate_56', 'concatenate_50']
# model_layer_list = ['activation_121','final_bn', 'dense_3_15_conv2D']
# model_name_list = [DenseNetImageNet121]
# model_layer_list = ['activation_121']
model_name_list = [ResNet50, DenseNetImageNet121]
model_layer_list = ['', 'activation_121']
sample_size = 400
saved_data_file_appendix = ''
if SAMPLE_DATA:
saved_data_file_appendix = '_sample'
%matplotlib inline
import matplotlib
matplotlib.use('agg')
import matplotlib.pyplot as plt
training_image_files = os.listdir(data_dir)
if SAMPLE_DATA:
training_image_files= random.sample(training_image_files, sample_size)
len(training_image_files)
training_image_files[:2]
image_file_names = list(os.path.join(data_dir, fname) for fname in training_image_files)
image_file_names[:2]
os.listdir(output_dir)
!ls ~/.keras/models/
class pretrained_model:
def set_model(self, DL_model, DL_model_name, base_model_dir = pretrained_models_dir):
self.name = DL_model_name
self.model = DL_model
self.base_model_dir = base_model_dir
def __init__(self, DL_architecture = None, intermediate_layer = '', base_model_dir = pretrained_models_dir):
if DL_architecture is None:
pass
else:
self.name = DL_architecture.__name__
base_model_file_name = os.path.join(base_model_dir, DL_architecture.__name__+'.h5')
if os.path.isfile( base_model_file_name ):
print(' - '+DL_architecture.__name__ + ' model: Base model ' + base_model_file_name + ' found!')
crt_base_model = load_model(base_model_file_name)
else:
crt_base_model = DL_architecture(input_shape=(224, 224, 3),
weights='imagenet',
include_top=False)
crt_base_model.save(base_model_file_name)
# print(crt_base_model.summary())
if not (intermediate_layer==''):
crt_model = Model(inputs=crt_base_model.input, outputs=crt_base_model.get_layer(intermediate_layer).output)
print(' - '+DL_architecture.__name__ + ' model: selected layer '+ intermediate_layer + '!')
else:
crt_model = crt_base_model
if DL_architecture.__name__.startswith('DenseNet'):
x = crt_model.output
tl_features = GlobalAveragePooling2D(name='GAP_pool')(x)
crt_model = Model(inputs=crt_model.input, outputs=tl_features)
print(' - '+DL_architecture.__name__ + ' model: added GAP layer')
print(crt_model.summary())
self.model = crt_model
def pretrained_models_generator(model_name_list):
"""Yield successive pretrained models."""
for crt_model_name in model_name_list:
yield pretrained_model(crt_model_name)
def get_keras_pretrained_model(architecture_name, last_layer_name, model_dir = pretrained_models_dir):
crt_model_file_name = os.path.join(model_dir, architecture_name.__name__+'_'+last_layer_name+'.h5')
if os.path.isfile( crt_model_file_name ):
print('Model ' + crt_model_file_name + ' found!')
crt_model = pretrained_model()
crt_model.set_model(load_model(crt_model_file_name), architecture_name.__name__)
else:
crt_model = pretrained_model(architecture_name, last_layer_name)
crt_model.model.save(crt_model_file_name)
return(crt_model)
# crt_pretrained_models = [pretrained_model(ResNet50), pretrained_model(DenseNetImageNet121)]
# print(crt_model.name for crt_model in crt_pretrained_models)
# models = dict([ (m.name, m.model) for m in crt_pretrained_models ])
somemodel = get_keras_pretrained_model(DenseNetImageNet121, '').model
somemodel.summary()
del somemodel
# model_layer_list = ['concatenate_290', 'concatenate_280', 'concatenate_260', 'concatenate_240']
# model_layer_list[0]
# crt_model1 = Model(inputs=somemodel.input, outputs=somemodel.get_layer(model_layer_list[0]).output)
def featurize_images_multiple_models(crt_image_file_names, output_dir, model_name_list, model_layer_list, batch_size=8):
for crt_model_name, crt_model_layer in zip(model_name_list, model_layer_list):
print('processing model ' + crt_model_name.__name__+' layer '+crt_model_layer)
features_filename = os.path.join(output_dir, 'features_' +\
crt_model_name.__name__+saved_data_file_appendix+\
crt_model_layer+'.npy')
if os.path.isfile(features_filename) and RECOMPUTE is False:
print("Features found!")
else:
print("Computing features")
# crt_model = pretrained_model(crt_model_name, crt_model_layer).model
crt_model = get_keras_pretrained_model(crt_model_name, crt_model_layer).model
features = image_featurization.featurize_images(crt_image_file_names, crt_model, batch_size)
print(features.shape)
np.save(features_filename, features)
del crt_model
del features
featurize_images_multiple_models(image_file_names, output_dir, model_name_list, model_layer_list)
# model_name_list = [DenseNetImageNet121]
def apply_tsne_to_multiple_features(output_dir, crt_model_name_list, model_layer_list):
for crt_model_name, crt_model_layer in zip(model_name_list, model_layer_list):
print('tsne processing for model ' + crt_model_name.__name__+' layer '+crt_model_layer)
tsne_features_filename = os.path.join(output_dir, 'features_' + \
crt_model_name.__name__+saved_data_file_appendix+\
crt_model_layer+'tsne.npy')
if os.path.isfile(tsne_features_filename) and RECOMPUTE is False:
print("tsne features found!")
else:
print("Computing tsne features")
original_features = np.load(os.path.join(output_dir, 'features_' + \
crt_model_name.__name__+saved_data_file_appendix+\
crt_model_layer+'.npy'))
print(original_features.shape)
original_features = original_features.reshape(original_features.shape[0], -1)
print(original_features.shape)
images_tsne = TSNE(n_components=2, random_state=0).fit_transform(original_features)
print(images_tsne.shape)
np.save(tsne_features_filename, images_tsne)
del images_tsne
del original_features
apply_tsne_to_multiple_features(output_dir, model_name_list, model_layer_list)
labels_filename = os.path.join(output_dir, 'labels_' + \
saved_data_file_appendix+\
'.npy')
if os.path.isfile(labels_filename) and RECOMPUTE is False:
print('Label file '+labels_filename+' found!')
y = np.load(labels_filename)
else:
y = pd.Series(training_image_files).str.contains('cat').astype(int).values
np.save(labels_filename, y)
print(y.shape)
print(y[y==0].shape)
print(y[y==1].shape)
cat_labels = y == 0
dog_labels = y == 1
def visualize_tsne_features(crt_model_name_list, model_layer_list):
for crt_model_name, crt_model_layer in zip(model_name_list, model_layer_list):
tsne_features_filename = os.path.join(output_dir, 'features_' + \
crt_model_name.__name__+saved_data_file_appendix+\
crt_model_layer+'tsne.npy')
tsne_features = np.load(tsne_features_filename)
plt.figure(figsize=(8, 8))
plt.scatter(x = tsne_features[:,0], y=tsne_features[:,1], marker=".", c=y, cmap=plt.cm.get_cmap('bwr'))
plt.show()
visualize_tsne_features(model_name_list, model_layer_list)
# jupyter nbconvert --to html .\Code\02_Model\020_visualize_class_separability.ipynb<jupyter_output><empty_output>
|
no_license
|
/Code/02_Model/020_visualize_class_separability.ipynb
|
georgeAccnt-GH/transfer_learning
| 1 |
<jupyter_start><jupyter_text>#US Baby Names Data Analysis<jupyter_code>%matplotlib inline
import warnings
warnings.filterwarnings("ignore", message="axes.color_cycle is deprecated")
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
import sqlite3
#%%sh
!pwd
!ls -ls /kaggle/input/*/
!ls ../input/
con = sqlite3.connect('../input/us-baby-names/database.sqlite')
cursor = con.cursor()
cursor.execute("SELECT name FROM sqlite_master WHERE type='table';")
print(cursor.fetchall())
# helper method to load the data
def load(what='NationalNames'):
assert what in ('NationalNames', 'StateNames')
cols = ['Name', 'Year', 'Gender', 'Count']
if what == 'StateNames':
cols.append('State')
df = pd.read_sql_query("SELECT {} from {}".format(','.join(cols), what), con)
return df
#National data
national = load(what='NationalNames')
national.head(5)
top_names = national.groupby(['Name','Gender'])['Count'].sum().reset_index().sort_values(by='Count',ascending=False)
top_names.head()<jupyter_output><empty_output><jupyter_text>## Top Male and Female Names<jupyter_code>top_names_male = top_names[top_names['Gender']=='M'].head(50)
top_names_female = top_names[top_names['Gender']=='F'].head(50)
#print(top_names_male.head())
#print(top_names_female.head())
import matplotlib.pyplot as plt
fig,ax=plt.subplots(1,2,figsize=(20,12))
sns.barplot(data=top_names_female,y='Name',x='Count',ax=ax[0], color='Red')
sns.barplot(data=top_names_male,y='Name',x='Count',ax=ax[1], color='Blue')
national['Decade'] = national['Year'].apply(lambda x: 10*(x//10))
import plotly.express as px
gender='M'
top_names_by_year = national[national['Gender']==gender].groupby(['Name','Decade'])['Count'].sum().reset_index().sort_values(by=['Decade','Count'],ascending=[True,False])
top_names_by_year.head()
fig = px.bar(top_names_by_year, x="Name", y="Count",
animation_frame="Decade", color='Count') #range_y=[0,4000000000]
fig.show()
# Is number of males increased over the year, compared to same of female?
tmp = national.groupby(['Year','Gender']).sum()
male = tmp.query("Gender=='M'").reset_index('Year').sort_index()
female = tmp.query("Gender=='F'").reset_index('Year').sort_index()
#print(male.head())
#print(female.head())
final = pd.merge(male, female, on = ['Year'], how = 'outer', suffixes = ['_m', '_f'])
final['male_extra'] = final['Count_m'] - final['Count_f']
final = final.set_index('Year').sort_index()
print(final.head())
final.plot()
name_year = national.groupby(['Name','Year']).sum().reset_index(['Name','Year'])
dr = name_year[name_year['Name']=='Michel']
dr['lag'] = (dr['Count'] - dr['Count'].shift(5))#/dr['Count']
print(dr['lag'].sum())
dr[['Year', 'Count', 'lag']].plot('Year')
name_year[name_year['Name']=='George'].plot('Year')<jupyter_output><empty_output>
|
no_license
|
/notebooks/kuberiitb/us-baby-names-analysis-and-yearly-animations.ipynb
|
Sayem-Mohammad-Imtiaz/kaggle-notebooks
| 2 |
<jupyter_start><jupyter_text># 資料準備<jupyter_code>import tensorflow as tf
import tensorflow.examples.tutorials.mnist.input_data as input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)<jupyter_output>Extracting MNIST_data/train-images-idx3-ubyte.gz
Extracting MNIST_data/train-labels-idx1-ubyte.gz
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz
<jupyter_text># 建立共用函數<jupyter_code>def weight(shape):
return tf.Variable(tf.truncated_normal(shape, stddev=0.1),
name ='W')
def bias(shape):
return tf.Variable(tf.constant(0.1, shape=shape)
, name = 'b')
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1,1,1,1],
padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1,2,2,1],
strides=[1,2,2,1],
padding='SAME')<jupyter_output><empty_output><jupyter_text># 輸入層 Input Layer<jupyter_code>with tf.name_scope('Input_Layer'):
x = tf.placeholder("float",shape=[None, 784]
,name="x")
x_image = tf.reshape(x, [-1, 28, 28, 1])<jupyter_output><empty_output><jupyter_text># Convolutional Layer 1<jupyter_code>with tf.name_scope('C1_Conv'):
W1 = weight([5,5,1,16])
b1 = bias([16])
Conv1=conv2d(x_image, W1)+ b1
C1_Conv = tf.nn.relu(Conv1 )
with tf.name_scope('C1_Pool'):
C1_Pool = max_pool_2x2(C1_Conv)<jupyter_output><empty_output><jupyter_text># Convolutional Layer 2<jupyter_code>with tf.name_scope('C2_Conv'):
W2 = weight([5,5,16,36])
b2 = bias([36])
Conv2=conv2d(C1_Pool, W2)+ b2
C2_Conv = tf.nn.relu(Conv2)
with tf.name_scope('C2_Pool'):
C2_Pool = max_pool_2x2(C2_Conv) <jupyter_output><empty_output><jupyter_text># Fully Connected Layer<jupyter_code>with tf.name_scope('D_Flat'):
D_Flat = tf.reshape(C2_Pool, [-1, 1764])
with tf.name_scope('D_Hidden_Layer'):
W3= weight([1764, 128])
b3= bias([128])
D_Hidden = tf.nn.relu(
tf.matmul(D_Flat, W3)+b3)
D_Hidden_Dropout= tf.nn.dropout(D_Hidden,
keep_prob=0.8)<jupyter_output><empty_output><jupyter_text># 輸出層Output<jupyter_code>with tf.name_scope('Output_Layer'):
W4 = weight([128,10])
b4 = bias([10])
y_predict= tf.nn.softmax(
tf.matmul(D_Hidden_Dropout,
W4)+b4)<jupyter_output><empty_output><jupyter_text># 設定訓練模型最佳化步驟<jupyter_code>with tf.name_scope("optimizer"):
y_label = tf.placeholder("float", shape=[None, 10],
name="y_label")
loss_function = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits
(logits=y_predict ,
labels=y_label))
optimizer = tf.train.AdamOptimizer(learning_rate=0.0001) \
.minimize(loss_function)<jupyter_output><empty_output><jupyter_text># 設定評估模型<jupyter_code>with tf.name_scope("evaluate_model"):
correct_prediction = tf.equal(tf.argmax(y_predict, 1),
tf.argmax(y_label, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))<jupyter_output><empty_output><jupyter_text># 訓練模型<jupyter_code>trainEpochs = 30
batchSize = 100
totalBatchs = int(mnist.train.num_examples/batchSize)
epoch_list=[];accuracy_list=[];loss_list=[];
from time import time
startTime=time()
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for epoch in range(trainEpochs):
for i in range(totalBatchs):
batch_x, batch_y = mnist.train.next_batch(batchSize)
sess.run(optimizer,feed_dict={x: batch_x,
y_label: batch_y})
loss,acc = sess.run([loss_function,accuracy],
feed_dict={x: mnist.validation.images,
y_label: mnist.validation.labels})
epoch_list.append(epoch)
loss_list.append(loss);accuracy_list.append(acc)
print("Train Epoch:", '%02d' % (epoch+1), \
"Loss=","{:.9f}".format(loss)," Accuracy=",acc)
duration =time()-startTime
print("Train Finished takes:",duration)
%matplotlib inline
import matplotlib.pyplot as plt
fig = plt.gcf()
fig.set_size_inches(4,2)
plt.plot(epoch_list, loss_list, label = 'loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['loss'], loc='upper left')
plt.plot(epoch_list, accuracy_list,label="accuracy" )
fig = plt.gcf()
fig.set_size_inches(4,2)
plt.ylim(0.8,1)
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend()
plt.show()
<jupyter_output><empty_output><jupyter_text># 評估模型準確率<jupyter_code>len(mnist.test.images)
print("Accuracy:",
sess.run(accuracy,feed_dict={x: mnist.test.images,
y_label: mnist.test.labels}))
print("Accuracy:",
sess.run(accuracy,feed_dict={x: mnist.test.images[:5000],
y_label: mnist.test.labels[:5000]}))
print("Accuracy:",
sess.run(accuracy,feed_dict={x: mnist.test.images[5000:],
y_label: mnist.test.labels[5000:]}))<jupyter_output>Accuracy: 0.9916
<jupyter_text># 預測機率<jupyter_code>y_predict=sess.run(y_predict,
feed_dict={x: mnist.test.images[:5000]})
y_predict[:5]<jupyter_output><empty_output><jupyter_text># 預測結果<jupyter_code>prediction_result=sess.run(tf.argmax(y_predict,1),
feed_dict={x: mnist.test.images ,
y_label: mnist.test.labels})
prediction_result[:10]
import numpy as np
def show_images_labels_predict(images,labels,prediction_result):
fig = plt.gcf()
fig.set_size_inches(8, 10)
for i in range(0, 10):
ax=plt.subplot(5,5, 1+i)
ax.imshow(np.reshape(images[i],(28, 28)),
cmap='binary')
ax.set_title("label=" +str(np.argmax(labels[i]))+
",predict="+str(prediction_result[i])
,fontsize=9)
plt.show()
show_images_labels_predict(mnist.test.images,mnist.test.labels,prediction_result)<jupyter_output><empty_output><jupyter_text># 找出預測錯誤<jupyter_code>for i in range(500):
if prediction_result[i]!=np.argmax(mnist.test.labels[i]):
print("i="+str(i)+
" label=",np.argmax(mnist.test.labels[i]),
"predict=",prediction_result[i])
def show_images_labels_predict_error(images,labels,prediction_result):
fig = plt.gcf()
fig.set_size_inches(8, 10)
i=0;j=0
while i<10:
if prediction_result[j]!=np.argmax(labels[j]):
ax=plt.subplot(5,5, 1+i)
ax.imshow(np.reshape(images[j],(28, 28)),
cmap='binary')
ax.set_title("j="+str(j)+
",l=" +str(np.argmax(labels[j]))+
",p="+str(prediction_result[j])
,fontsize=9)
i=i+1
j=j+1
plt.show()
show_images_labels_predict_error(mnist.test.images,mnist.test.labels,prediction_result)
saver = tf.train.Saver()
save_path = saver.save(sess, "saveModel/CNN_model1")
print("Model saved in file: %s" % save_path)
merged = tf.summary.merge_all()
train_writer = tf.summary.FileWriter('log/CNN',sess.graph)
#sess.close()<jupyter_output><empty_output>
|
no_license
|
/.ipynb_checkpoints/Tensorflow_Mnist_CNN-checkpoint.ipynb
|
LevineHuang/Book_Tensorflow-Keras
| 14 |
<jupyter_start><jupyter_text># Some More Python<jupyter_code>import numpy as np
import pandas as pd<jupyter_output><empty_output><jupyter_text># Strings### Arithmetic with Strings<jupyter_code>s = "spam"
e = "eggs"
s + e
s + " " + e
4 * (s + " ") + e
4 * (s + " ") + s + " and\n" + e<jupyter_output><empty_output><jupyter_text>### Watch out for variable types! <jupyter_code>n = 4
print("I would like " + n + " orders of spam")
print("I would like " + str(n) + " orders of spam")
m = '4'
1 + m
1 + int(m)<jupyter_output><empty_output><jupyter_text>### Use explicit formatting to avoid these errors<jupyter_code>A = 42
B = 123456789.987654321
C = 123.4567890987654321
D = 'Forty Two'<jupyter_output><empty_output><jupyter_text>d = Integer decimal g = Floating point format (Uses exponential format if exponent is less than -4)
f = Floating point decimal x = hex
s = String o = octal
e = Floating point exponential b = binary<jupyter_code>"I like the number {0:d}".format(A)
"I like the number {0:s}".format(D)
"The number {0:f} is fine, but not a cool as {1:d}".format(B,A)
"The number {0:.3f} is fine, but not a cool as {1:d}".format(B,A)
"The number {0:.3e} is fine, but not a cool as {1:d}".format(B,A)
"{0:g} and {1:g} are the same format but different results".format(B,C)
"Representation of the number {1:s} - int: {0:d}; hex: {0:x}; oct: {0:o}; bin: {0:b}".format(A,D)<jupyter_output><empty_output><jupyter_text>### You can compare strings<jupyter_code>"spam" == "good"
"spam" != "good"
"spam" == "spam"
"spam" < "eggs"
"sp" < "spam"<jupyter_output><empty_output><jupyter_text>### Strings are arrays of characters<jupyter_code>s,len(s),s[0],s[0:2]
s[::-1]<jupyter_output><empty_output><jupyter_text>### There are lots of `methods` that work on strings<jupyter_code>line = "My hovercraft is full of eels"<jupyter_output><empty_output><jupyter_text>#### Find and Replace<jupyter_code>line.replace('eels', 'wheels')<jupyter_output><empty_output><jupyter_text>#### Justification and Cleaning<jupyter_code>line.center(100)
line.ljust(100)
line.rjust(100, "*")
line2 = " My hovercraft is full of eels "
line2.strip()
line3 = "*$*$*$*$*$*$*$*$My hovercraft is full of eels*$*$*$*$"
line3.strip('*$')
line3.lstrip('*$'), line3.rstrip('*$')<jupyter_output><empty_output><jupyter_text>#### Splitting and Joining<jupyter_code>line.split()
'_'.join(line.split())
' '.join(line.split()[::-1])<jupyter_output><empty_output><jupyter_text>#### Formatting<jupyter_code>anotherline = "mY hoVErCRaft iS fUlL oF eEELS"
anotherline.upper()
anotherline.lower()
anotherline.title()
anotherline.capitalize()
anotherline.swapcase()<jupyter_output><empty_output><jupyter_text># Control Flow
Like all computer languages, Python supports the standard types of control flows including:
* IF statements
* WHILE loops
* FOR loops<jupyter_code>x = -1
if x > 0:
print("{O} is a positive number".format(x))
else:
print("{0} is not a positive number".format(x))
x = 0
if x > 0:
print("x is positive")
elif x == 0:
print("x is zero")
else:
print("x is negative")
y = 0
while y < 12:
print(s, end=" ") # specify what charater to print at the end of output
if y > 6:
print(e, end=" * ")
y += 1<jupyter_output><empty_output><jupyter_text>### `For loops` are a bit strange in python:<jupyter_code>T = pd.read_csv("Doctor.csv")
T
for i in T['Name']:
print(i)
for a,b in enumerate(T['Name']):
print(a,b)
for a,b in enumerate(T['Name']):
S = "Doctor number {0:d} was played by {1:s} who started when he was {2:d} years old.".format(a+1, b, T['Age'][a])
print(S)<jupyter_output><empty_output><jupyter_text>### Loops are slow in Python. Do not use them if you do not have to!<jupyter_code>BigZ = np.random.random(1000)
# This is slow!
for a,b in enumerate(BigZ):
if (b > 0.5):
BigZ[a] = 0
BigZ[-20:]
%%timeit -o
for a,b in enumerate(BigZ):
if (b > 0.5):
BigZ[a] = 0
# Masks are faster
mask = np.where(BigZ>0.5)
BigZ[mask] = 0
BigZ[-20:]
%%timeit -o
mask = np.where(BigZ>0.5)
BigZ[mask] = 0<jupyter_output><empty_output><jupyter_text>## Bonus Topic - Numerical Integration<jupyter_code>from scipy import integrate<jupyter_output><empty_output><jupyter_text>### $$ \int_0^3 x^2 dx = \frac{1}{3} (3)^3 - \frac{1}{3} (0)^3 = \frac{1}{3} 27 = 9$$<jupyter_code>def george(x):
return x ** 2<jupyter_output><empty_output><jupyter_text>### The function `itegrate.quad` returns the result and an error estimation<jupyter_code>results = integrate.quad(george, 0, 3)
results<jupyter_output><empty_output><jupyter_text>### For indefinite integrals use `np.inf` or `-np.inf`### $$ \int_0^{\infty} e^{-x} dx = 1$$<jupyter_code>def paul(x):
return np.exp(-x)
results = integrate.quad(paul, 0, np.inf)
results<jupyter_output><empty_output><jupyter_text>### $$ \int_0^{\infty} x\ dx = \infty$$<jupyter_code>def john(x):
return x
results = integrate.quad(john, 0, np.inf)
results<jupyter_output><empty_output><jupyter_text>## SymPy is a Python library for symbolic mathematics<jupyter_code>import sympy as sp
x = sp.symbols('x')<jupyter_output><empty_output><jupyter_text>### $$ \int \cos(x)\ dx = \sin(x)$$<jupyter_code>sp.integrate(sp.cos(x), x)<jupyter_output><empty_output><jupyter_text>### $$ \int \frac{1}{x}\ dx = \log(x)$$<jupyter_code>sp.integrate(1/x, x)<jupyter_output><empty_output><jupyter_text>### SyPy is slow### $$ \int_0^{\infty} e^{-x} dx = 1$$<jupyter_code>%%timeit -o
results = integrate.quad(paul, 0, np.inf)
%%timeit -o
X = sp.integrate(sp.exp(-x), (x, 0, sp.oo))<jupyter_output><empty_output>
|
no_license
|
/.working/Python_PartII.ipynb
|
acdurbin/Astro300
| 24 |
<jupyter_start><jupyter_text># fMRI data preprocessing[](https://colab.research.google.com/github/adasegroup/NEUROML2020/blob/seminar4/seminar-4/preprocessing.ipynb)fMRI scans are saved in dicom format. For scientific analysis of brain images the nifty format (.nii files) are often used.
The conversion from dicom to nifty can be done with [dcm2niix](https://www.nitrc.org/plugins/mwiki/index.php/dcm2nii:MainPage#Introduction)
Many file are generated during fMRI sessions. These can arranged in many ways, thus a standard is needed how to arrange them.
Commonly used standard is [Brain Imaging Data Structure (BIDS)](https://bids.neuroimaging.io/).
You can use [HeuDiConv](https://heudiconv.readthedocs.io/en/latest/) or [Dcm2Bids](https://cbedetti.github.io/Dcm2Bids/tutorial/) to automate the conversion from dicom to BIDS.
Let's download the data we will be working with.<jupyter_code>%%bash
datalad get -J 4 -d /data/ds000114 \
/data/ds000114/derivatives/fmriprep/sub-*/anat/*preproc.nii.gz \
/data/ds000114/sub-*/ses-test/func/*fingerfootlips*
from utils import list_files
# The data is already in BIDS format
# The subjects peformed 5 tasks. We will focus on fingerfootlips task
list_files('/data/ds000114/sub-01/ses-retest')
%%bash
cd /data/ds000114/
nib-ls derivatives/fmriprep/sub-01/*/*t1w_preproc.nii.gz sub-01/ses-test/f*/*fingerfootlips*.nii.gz<jupyter_output>derivatives/fmriprep/sub-01/anat/sub-01_t1w_preproc.nii.gz float32 [256, 156, 256] 1.00x1.30x1.00 sform
sub-01/ses-test/func/sub-01_ses-test_task-fingerfootlips_bold.nii.gz int16 [ 64, 64, 30, 184] 4.00x4.00x4.00x2.50 sform
<jupyter_text>With nibabel we can load a file and inspect its properties.<jupyter_code>import nibabel
from nilearn import plotting
import numpy as np
import warnings
warnings.filterwarnings('ignore')
anat = nibabel.load('/data/ds000114/derivatives/fmriprep/sub-01/anat/sub-01_t1w_preproc.nii.gz')
fmri = nibabel.load('/data/ds000114/sub-01/ses-test/func/sub-01_ses-test_task-fingerfootlips_bold.nii.gz')
print(anat.header)
print(f'Anatomical dimensionality is {anat.ndim} and fmri is {fmri.ndim}')
#The anatomical image have higher resolution then the fmri
print(f'Anatomical voxelization:{anat.shape} fMRI voxelization:{fmri.shape}')
#the data can be accessed as
data = np.array(anat.dataobj)
import json
#metadata is located in json files
with open('/data/ds000114/task-fingerfootlips_bold.json', 'rt') as fp:
task_info = json.load(fp)
task_info
len(task_info['SliceTiming'])<jupyter_output><empty_output><jupyter_text># Introduction Nipype**Why nipype?**
Nipype allows to build preprocessing pipelines from different softwares, and it is computationally efficient. There are some helpful ready to use pipleines written with Nipype like [fmriprep](https://fmriprep.org/en/stable/index.html). To use fmriprep the data have to be in valid BIDS format. The user have to supply only the path to the data setup the [parametars](https://fmriprep.org/en/stable/usage.html#command-line-arguments).
In Nipype, interfaces are python modules that allow you to use various external packages (e.g. FSL, SPM or FreeSurfer), even if they themselves are written in another programming language than python. Such an interface knows what sort of options an external program has and how to execute it.
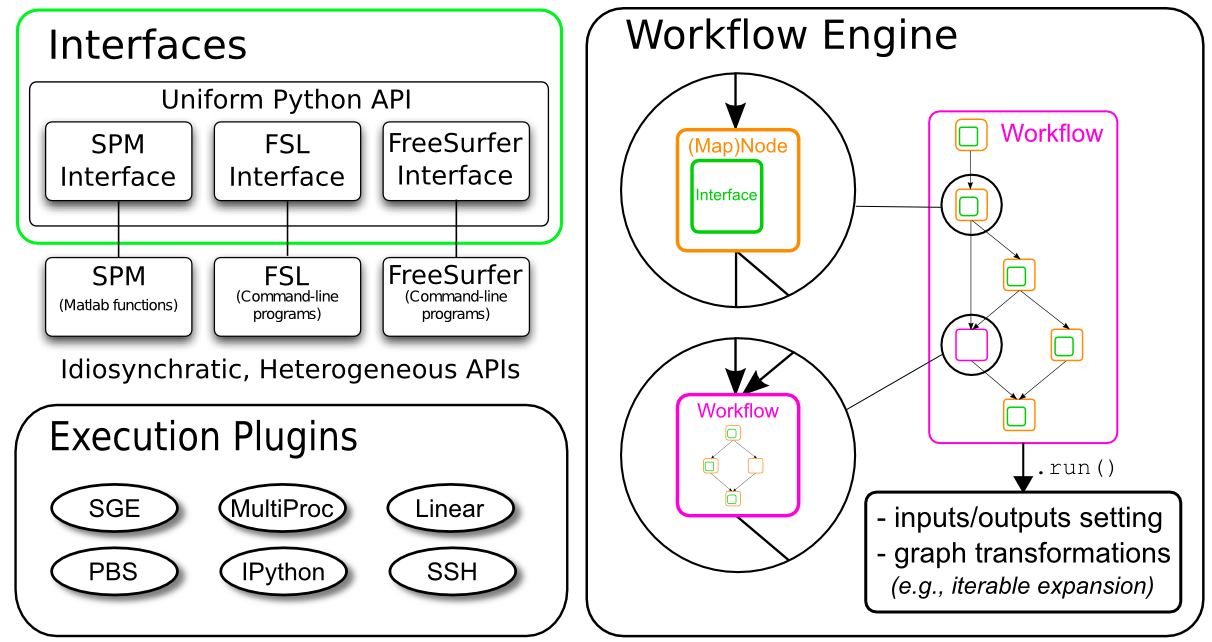
In Nipype, a node is an object that executes a certain function. This function can be anything from a Nipype interface to a user-specified function or an external script. Each node consists of a name, an interface category and at least one input field, and at least one output field.
Once you connect multiple nodes to each other, you create a directed graph. In Nipype we call such graphs either workflows or pipelines. Directed connections can only be established from an output field of a node to an input field of another node.<jupyter_code>from nipype import Node, Function, Workflow
from IPython.display import Image, clear_output
def multiply(a, b):
return a * b
#Create a Node that multiplies 2 numbers
mul = Node(Function(input_names=['a', 'b'],
output_names=['multiply_result'],
function=multiply),
name='a_x_b')
mul.inputs.a = 2
mul.inputs.b = 3
result = mul.run()
result.outputs
#Create a Node that adds 2 numbers
def add(a, b):
return a + b
adder = Node(Function(input_names=['a', 'b'],
output_names=['add'],
function=add),
name='a_plus_b')
adder.inputs.b = 10
#Create a workflow
wf = Workflow('hello')
# connect the nodes
wf.connect(mul, 'multiply_result', adder, 'a')
#visualize the graph
wf.write_graph(graph2use='flat', format='png', simple_form=True)
clear_output()
Image(filename='graph_detailed.png')
#run the graph
eg = wf.run()
clear_output()#don't print the pipeline steps during exection
#chek the results
eg = list(eg.nodes())
nodes_outputs = [node.result.outputs for node in eg]
nodes_outputs<jupyter_output><empty_output><jupyter_text># Preprocessing
In this workflow we will conduct the following steps:
**1. Coregistration of functional images to anatomical images (according to FSL's FEAT pipeline)**Co-registrationis the process of spatial alignment of 2 images. The target image is also called reference volume. The goodness of alignment is evaluated with a cost function.
We have to move the fmri series from fmri native space:<jupyter_code>_ = plotting.plot_anat(nibabel.nifti1.Nifti1Image(fmri.get_data()[:,:,:,1], affine=fmri.affine), cut_coords=(0,0,0), title='fmri slice')<jupyter_output><empty_output><jupyter_text> to native anatomical space:<jupyter_code>_ = plotting.plot_anat(anat, cut_coords=(0,0,0), title='Anatomical image')<jupyter_output><empty_output><jupyter_text>**2. Motion correction of functional images with FSL's MCFLIRT**
The images are aligned with rigid transformation - rotations, translations, reflections.
Then spatial interpolation is done, so as there was no movements.
 **3. Slice Timing correction**
The brain slices are not acquired at the same time. Therefore, interpolation is done between the nearest timepoints

[Slice timing corretion in python](https://matthew-brett.github.io/teaching/slice_timing.html)**4. Smoothing of coregistered functional images with FWHM set to 5/10 mm**
**5. Artifact Detection in functional images (to detect outlier volumes)****So, let's start!**## Imports
First, let's import all the modules we later will be needing.<jupyter_code>from nilearn import plotting
%matplotlib inline
from os.path import join as opj
import os
import json
from nipype.interfaces.fsl import (BET, ExtractROI, FAST, FLIRT, ImageMaths,
MCFLIRT, SliceTimer, Threshold)
from nipype.interfaces.spm import Smooth
from nipype.interfaces.utility import IdentityInterface
from nipype.interfaces.io import SelectFiles, DataSink
from nipype.algorithms.rapidart import ArtifactDetect
from nipype import Workflow, Node<jupyter_output><empty_output><jupyter_text>## Experiment parameters
It's always a good idea to specify all parameters that might change between experiments at the beginning of your script. We will use one functional image for fingerfootlips task for ten subjects.<jupyter_code>experiment_dir = '/output'
output_dir = 'datasink'
working_dir = 'workingdir'
# list of subject identifiers
subject_list = ['01', '02', '03', '04', '05', '06', '07', '08', '09', '10']
# list of session identifiers
task_list = ['fingerfootlips']
# Smoothing widths to apply
fwhm = [5, 10]
# TR of functional images(time from the application of an excitation pulse to the application of the next pulse)
with open('/data/ds000114/task-fingerfootlips_bold.json', 'rt') as fp:
task_info = json.load(fp)
TR = task_info['RepetitionTime']
# Isometric resample of functional images to voxel size (in mm)
iso_size = 4<jupyter_output><empty_output><jupyter_text>## Specify Nodes for the main workflow
Initiate all the different interfaces (represented as nodes) that you want to use in your workflow.<jupyter_code># ExtractROI - skip dummy scans
#t_min - Minimum index for t-dimension
#t_size - Size of ROI in t-dimension
extract = Node(ExtractROI(t_min=4, t_size=-1, output_type='NIFTI'),
name="extract")
#MCFLIRT - motion correction
#https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/MCFLIRT
#mean_vol- volumes are averaged to create a new template
#normcorr cost - https://www.fmrib.ox.ac.uk/datasets/techrep/tr02mj1/tr02mj1/node4.html
#sinc interpolation - https://math.stackexchange.com/questions/1372632/how-does-sinc-interpolation-work
mcflirt = Node(MCFLIRT(mean_vol=True,
save_plots=True,
output_type='NIFTI'),
name="mcflirt")
#SliceTimer - correct for slice wise acquisition
#https://poc.vl-e.nl/distribution/manual/fsl-3.2/slicetimer/index.html
#more on https://matthew-brett.github.io/teaching/slice_timing.html
#interleaved = -odd
#top to bottom = --down
#normcorr loss
slicetimer = Node(SliceTimer(index_dir=False,
interleaved=True,
output_type='NIFTI',
time_repetition=TR),
name="slicetimer")
#Smooth - image smoothing
#spm_smooth for 3D Gaussian smoothing
smooth = Node(Smooth(), name="smooth")
smooth.iterables = ("fwhm", fwhm)
# Artifact Detection - determines outliers in functional images via intensity and motion paramters
#http://web.mit.edu/swg/art/art.pdf
#norm_threshold - Threshold to use to detect motion-related outliers when composite motion is being used
#zintensity_threshold - Intensity Z-threshold use to detection images that deviate from the mean
#spm_global like calculation to determine the brain mask
#parameter_source - Source of movement parameters
#use_differences - Use differences between successive motion (first element) and
#intensity parameter (second element) estimates in order to determine outliers.
art = Node(ArtifactDetect(norm_threshold=2,
zintensity_threshold=3,
mask_type='spm_global',
parameter_source='FSL',
use_differences=[True, False],
plot_type='svg'),
name="art")<jupyter_output><empty_output><jupyter_text>## Coregistration Workflow
Initiate a workflow that coregistrates the functional images to the anatomical image (according to FSL's FEAT pipeline).<jupyter_code># BET - Skullstrip anatomical Image
#https://www.fmrib.ox.ac.uk/datasets/techrep/tr00ss2/tr00ss2.pdf
bet_anat = Node(BET(frac=0.5,
robust=True,
output_type='NIFTI_GZ'),
name="bet_anat")
# FAST - Image Segmentation
#https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FAST
#http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.200.3832&rep=rep1&type=pdf
segmentation = Node(FAST(output_type='NIFTI_GZ'),
name="segmentation", mem_gb=4)
# Select WM segmentation file from segmentation output
def get_wm(files):
return files[-1]
# Threshold - Threshold WM probability image
threshold = Node(Threshold(thresh=0.5,
args='-bin',
output_type='NIFTI_GZ'),
name="threshold")
# FLIRT - pre-alignment of functional images to anatomical images
#https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FLIRT
coreg_pre = Node(FLIRT(dof=6, output_type='NIFTI_GZ'),
name="coreg_pre")
# FLIRT - coregistration of functional images to anatomical images with BBR(uses the segmentation)
#https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FLIRT_BBR
coreg_bbr = Node(FLIRT(dof=6,
cost='bbr',
schedule=opj(os.getenv('FSLDIR'),
'etc/flirtsch/bbr.sch'),
output_type='NIFTI_GZ'),
name="coreg_bbr")
# Apply coregistration warp to functional images
#apply_isoxfm-apply transformation supplied by in_matrix_file
applywarp = Node(FLIRT(interp='spline',
apply_isoxfm=iso_size,
output_type='NIFTI'),
name="applywarp")
# Apply coregistration wrap to mean file
applywarp_mean = Node(FLIRT(interp='spline',
apply_isoxfm=iso_size,
output_type='NIFTI_GZ'),
name="applywarp_mean")
# Create a coregistration workflow
coregwf = Workflow(name='coregwf')
coregwf.base_dir = opj(experiment_dir, working_dir)
# Connect all components of the coregistration workflow
coregwf.connect([(bet_anat, segmentation, [('out_file', 'in_files')]),
(segmentation, threshold, [(('partial_volume_files', get_wm),
'in_file')]),
(bet_anat, coreg_pre, [('out_file', 'reference')]),
(threshold, coreg_bbr, [('out_file', 'wm_seg')]),
(coreg_pre, coreg_bbr, [('out_matrix_file', 'in_matrix_file')]),
(coreg_bbr, applywarp, [('out_matrix_file', 'in_matrix_file')]),
(bet_anat, applywarp, [('out_file', 'reference')]),
(coreg_bbr, applywarp_mean, [('out_matrix_file', 'in_matrix_file')]),
(bet_anat, applywarp_mean, [('out_file', 'reference')]),
])<jupyter_output><empty_output><jupyter_text>## Specify input & output stream
Specify where the input data can be found & where and how to save the output data.<jupyter_code># Infosource - a function free node to iterate over the list of subject names
infosource = Node(IdentityInterface(fields=['subject_id', 'task_name']),
name="infosource")
infosource.iterables = [('subject_id', subject_list),
('task_name', task_list)]
# SelectFiles - to grab the data
anat_file = opj('derivatives', 'fmriprep', 'sub-{subject_id}', 'anat', 'sub-{subject_id}_t1w_preproc.nii.gz')
func_file = opj('sub-{subject_id}', 'ses-test', 'func',
'sub-{subject_id}_ses-test_task-{task_name}_bold.nii.gz')
templates = {'anat': anat_file,
'func': func_file}
selectfiles = Node(SelectFiles(templates,
base_directory='/data/ds000114'),
name="selectfiles")
# Datasink - creates output folder for important outputs
datasink = Node(DataSink(base_directory=experiment_dir,
container=output_dir),
name="datasink")
## Use the following DataSink output substitutions
substitutions = [('_subject_id_', 'sub-'),
('_task_name_', '/task-'),
('_fwhm_', 'fwhm-'),
('_roi', ''),
('_mcf', ''),
('_st', ''),
('_flirt', ''),
('.nii_mean_reg', '_mean'),
('.nii.par', '.par'),
]
subjFolders = [('fwhm-%s/' % f, 'fwhm-%s_' % f) for f in fwhm]
substitutions.extend(subjFolders)
datasink.inputs.substitutions = substitutions<jupyter_output><empty_output><jupyter_text>## Specify Workflow
Create a workflow and connect the interface nodes and the I/O stream to each other.<jupyter_code># Create a preprocessing workflow
preproc = Workflow(name='preproc')
preproc.base_dir = opj(experiment_dir, working_dir)
# Connect all components of the preprocessing workflow
preproc.connect([(infosource, selectfiles, [('subject_id', 'subject_id'),
('task_name', 'task_name')]),
(selectfiles, extract, [('func', 'in_file')]),
(extract, mcflirt, [('roi_file', 'in_file')]),
(mcflirt, slicetimer, [('out_file', 'in_file')]),
(selectfiles, coregwf, [('anat', 'bet_anat.in_file'),
('anat', 'coreg_bbr.reference')]),
(mcflirt, coregwf, [('mean_img', 'coreg_pre.in_file'),
('mean_img', 'coreg_bbr.in_file'),
('mean_img', 'applywarp_mean.in_file')]),
(slicetimer, coregwf, [('slice_time_corrected_file', 'applywarp.in_file')]),
(coregwf, smooth, [('applywarp.out_file', 'in_files')]),
(mcflirt, datasink, [('par_file', 'preproc.@par')]),
(smooth, datasink, [('smoothed_files', 'preproc.@smooth')]),
(coregwf, datasink, [('applywarp_mean.out_file', 'preproc.@mean')]),
(coregwf, art, [('applywarp.out_file', 'realigned_files')]),
(mcflirt, art, [('par_file', 'realignment_parameters')]),
(coregwf, datasink, [('coreg_bbr.out_matrix_file', 'preproc.@mat_file'),
('bet_anat.out_file', 'preproc.@brain')]),
(art, datasink, [('outlier_files', 'preproc.@outlier_files'),
('plot_files', 'preproc.@plot_files')]),
])<jupyter_output><empty_output><jupyter_text>## Visualize the workflow
It always helps to visualize your workflow.<jupyter_code># Create preproc output graph
preproc.write_graph(graph2use='colored', format='png', simple_form=True)
# Visualize the graph
from IPython.display import Image
Image(filename=opj(preproc.base_dir, 'preproc', 'graph.png'))
# Visualize the detailed graph
preproc.write_graph(graph2use='flat', format='png', simple_form=True)
Image(filename=opj(preproc.base_dir, 'preproc', 'graph_detailed.png'))<jupyter_output>200921-08:13:47,944 nipype.workflow INFO:
Generated workflow graph: /output/workingdir/preproc/graph.png (graph2use=flat, simple_form=True).
<jupyter_text>## Run the Workflow
Now that everything is ready, we can run the preprocessing workflow. Change ``n_procs`` to the number of jobs/cores you want to use. **Note** that if you're using a Docker container and FLIRT fails to run without any good reason, you might need to change memory settings in the Docker preferences (6 GB should be enough for this workflow).<jupyter_code>preproc.run('MultiProc', plugin_args={'n_procs': 4})<jupyter_output>200921-08:13:48,38 nipype.workflow INFO:
Workflow preproc settings: ['check', 'execution', 'logging', 'monitoring']
200921-08:13:48,141 nipype.workflow INFO:
Running in parallel.
200921-08:13:48,149 nipype.workflow INFO:
[MultiProc] Running 0 tasks, and 10 jobs ready. Free memory (GB): 56.54/56.54, Free processors: 4/4.
200921-08:13:48,226 nipype.workflow INFO:
[Node] Setting-up "preproc.selectfiles" in "/output/workingdir/preproc/_subject_id_10_task_name_fingerfootlips/selectfiles".200921-08:13:48,227 nipype.workflow INFO:
[Node] Setting-up "preproc.selectfiles" in "/output/workingdir/preproc/_subject_id_09_task_name_fingerfootlips/selectfiles".
200921-08:13:48,228 nipype.workflow INFO:
[Node] Setting-up "preproc.selectfiles" in "/output/workingdir/preproc/_subject_id_08_task_name_fingerfootlips/selectfiles".
200921-08:13:48,236 nipype.workflow INFO:
[Node] Running "selectfiles" ("nipype.interfaces.io.SelectFiles")
200921-08:13:48,238 nipype.workflow INFO:
[Node] Runn[...]<jupyter_text>## Inspect output
Let's check the structure of the output folder, to see if we have everything we wanted to save.<jupyter_code>!tree /output/datasink/preproc/sub-01/task-fingerfootlips<jupyter_output>/output/datasink/preproc/sub-01/task-fingerfootlips
├── art.sub-01_ses-test_task-fingerfootlips_bold_outliers.txt
├── fwhm-10_ssub-01_ses-test_task-fingerfootlips_bold.nii
├── fwhm-5_ssub-01_ses-test_task-fingerfootlips_bold.nii
├── plot.sub-01_ses-test_task-fingerfootlips_bold.svg
├── sub-01_ses-test_task-fingerfootlips_bold_mean.mat
├── sub-01_ses-test_task-fingerfootlips_bold_mean.nii.gz
├── sub-01_ses-test_task-fingerfootlips_bold.par
└── sub-01_t1w_preproc_brain.nii.gz
0 directories, 8 files
<jupyter_text>## Visualize results
Let's check the effect of the different smoothing kernels.<jupyter_code>from nilearn import image, plotting
out_path = '/output/datasink/preproc/sub-01/task-fingerfootlips'
plotting.plot_epi(opj(out_path, 'sub-01_ses-test_task-fingerfootlips_bold_mean.nii.gz'),
title="fwhm = 0mm", display_mode='ortho', annotate=False, draw_cross=False, cmap='gray');
plotting.plot_epi(image.mean_img(opj(out_path, 'fwhm-5_ssub-01_ses-test_task-fingerfootlips_bold.nii')),
title="fwhm = 5mm", display_mode='ortho', annotate=False, draw_cross=False, cmap='gray');
plotting.plot_epi(image.mean_img(opj(out_path, 'fwhm-10_ssub-01_ses-test_task-fingerfootlips_bold.nii')),
title="fwhm = 10mm", display_mode='ortho', annotate=False, draw_cross=False, cmap='gray');<jupyter_output><empty_output><jupyter_text>Now, let's investigate the motion parameters. How much did the subject move and turn in the scanner?<jupyter_code>import numpy as np
import matplotlib.pyplot as plt
par = np.loadtxt('/output/datasink/preproc/sub-01/task-fingerfootlips/sub-01_ses-test_task-fingerfootlips_bold.par')
fig, axes = plt.subplots(2, 1, figsize=(15, 5))
axes[0].set_ylabel('rotation (radians)')
axes[0].plot(par[0:, :3])
axes[1].plot(par[0:, 3:])
axes[1].set_xlabel('time (TR)')
axes[1].set_ylabel('translation (mm)');<jupyter_output><empty_output><jupyter_text>There seems to be a rather drastic motion around volume 102. Let's check if the outliers detection algorithm was able to pick this up.<jupyter_code>import numpy as np
outlier_ids = np.loadtxt('/output/datasink/preproc/sub-01/task-fingerfootlips/art.sub-01_ses-test_task-fingerfootlips_bold_outliers.txt')
print('Outliers were detected at volumes: %s' % outlier_ids)
from IPython.display import SVG
SVG(filename='/output/datasink/preproc/sub-01/task-fingerfootlips/plot.sub-01_ses-test_task-fingerfootlips_bold.svg')<jupyter_output>Outliers were detected at volumes: [ 59. 102.]
|
no_license
|
/seminar4/preprocessing.ipynb
|
123rugby/NEUROML2020
| 17 |
<jupyter_start><jupyter_text># Least Squares
Natasha Watkins<jupyter_code>from scipy.linalg import norm
import numpy as np
import scipy
import matplotlib.pyplot as plt
import cmath<jupyter_output><empty_output><jupyter_text>### Problem 1<jupyter_code>def solve(A, b):
Q, R = scipy.linalg.qr(A, mode='economic')
n = R.shape[0]
y = Q.T @ b
x = scipy.linalg.solve_triangular(R, Q.T @ b)
return x
A = np.random.random((5, 5))
b = np.ones(5)
solve(A, b)
scipy.linalg.solve(A, b)<jupyter_output><empty_output><jupyter_text>### Problem 2<jupyter_code>housing = np.load('housing.npy')
b = housing[:, 1]
A = np.array([housing[:, 0], np.ones(len(housing))]).T
β = solve(A, b)
y = A @ β # Least squares line
x = housing[:, 0]
plt.scatter(x, housing[:, 1])
plt.scatter(x, y)
plt.show()<jupyter_output><empty_output><jupyter_text>### Problem 3<jupyter_code>def plot_p(degree, ax=None):
if ax == None:
fig, ax = plt.subplots()
A = np.vander(housing[:, 0], degree+1)
β = solve(A, b)
y = A @ β
ax.scatter(x, y)
ax.scatter(x, housing[:, 1])
ax.set(title=f'Polynomial of degree {degree}')
return ax
fig, axes = plt.subplots(2, 2, figsize=(13, 8))
for ax, d in zip(axes.flatten(), (3, 6, 9, 12)):
plot_p(d, ax=ax)
axes[0, 0].legend(['Polynomial fit', 'Original'])
plt.show()<jupyter_output><empty_output><jupyter_text>Using `np.polyfit()`<jupyter_code>def plot_poly(degree, ax=None):
if ax == None:
fig, ax = plt.subplots()
A = np.vander(housing[:, 0], degree+1)
β = np.polyfit(housing[:, 0], housing[:, 1], degree)
y = A @ β
ax.scatter(x, y)
ax.scatter(x, housing[:, 1])
ax.set(title=f'Polynomial of degree {degree}')
return ax
fig, axes = plt.subplots(2, 2, figsize=(13, 8))
for ax, d in zip(axes.flatten(), (3, 6, 9, 12)):
plot_poly(d, ax=ax)
axes[0, 0].legend(['Polynomial fit', 'Original'])
plt.show()<jupyter_output><empty_output><jupyter_text>### Problem 4<jupyter_code>ellipse = np.load('ellipse.npy')
x = ellipse[:, 0]
y = ellipse[:, 1]
A = np.array([x**2, x, x*y, y, y**2]).T
b = np.ones(len(A))
β = solve(A, b)
def plot_ellipse(a, b, c, d, e):
"""Plot an ellipse of the form ax^2 + bx + cxy + dy + ey^2 = 1."""
θ = np.linspace(0, 2*np.pi, 200)
cos_t, sin_t = np.cos(θ), np.sin(θ)
A = a * (cos_t**2) + c*cos_t*sin_t + e*(sin_t**2)
B = b * cos_t + d * sin_t
r = (-B + np.sqrt(B**2 + 4*A)) / (2 * A)
plt.plot(r * cos_t, r * sin_t, lw=2)
plt.gca().set_aspect("equal", "datalim")
plot_ellipse(*β)
plt.scatter(x, y)
plt.show()<jupyter_output><empty_output><jupyter_text>### Problem 5<jupyter_code>A = np.random.random((10, 10))
def power_method(A, max_iter=500, tol=1e-8):
m, n = A.shape
x = np.random.random(m)
x = x / norm(x)
k = 0
diff = 1e3
while (k < max_iter) & (diff > tol):
x_new = A @ x
x_new = x_new / norm(x_new)
diff = norm(x_new - x)
x = x_new
k = k + 1
return x.T @ A @ x, x
λ, x = power_method(A)
λ
A @ x
λ * x
np.max(scipy.linalg.eigvals(A))<jupyter_output><empty_output><jupyter_text>### Problem 6<jupyter_code>def qr_algorithm(A, N=1000, tol=1e-8):
m, n = A.shape
S = scipy.linalg.hessenberg(A)
for k in range(N-1):
Q, R = scipy.linalg.qr(S)
S = R @ Q
eigs = []
i = 0
while i < n:
if (S[i, i] == np.diag(S)[-1]):
eigs.append(S[i, i])
elif S[i+1, i] < tol:
eigs.append(S[i, i])
else:
a, b, c, d = S[i:i+2, i:i+2].flatten() # Get elements of block matrix
λ_1 = (a + d) + (cmath.sqrt((a + d)**2 - 4 * (a * d - b * c))) / 2
λ_2 = (a + d) - (cmath.sqrt((a + d)**2 - 4 * (a * d - b * c))) / 2
eigs.extend([λ_1, λ_2])
i = i + 1
i = i + 1
return eigs
A = np.random.random((10, 10))
qr_algorithm(A + A.T)
scipy.linalg.eigvals(A + A.T)<jupyter_output><empty_output>
|
no_license
|
/Probsets/Comp/Probset3/Least squares.ipynb
|
natashawatkins/BootCamp2018
| 8 |
<jupyter_start><jupyter_text>Visualizing Predictions <jupyter_code>model_conv = torchvision.models.vgg16(pretrained=True)
for param in model_conv.parameters():
param.requires_grad = False
print(model_conv.classifier.children)
model_conv.classifier = nn.Sequential(
nn.Linear(512 * 7 * 7, 4096),
nn.ReLU(True),
nn.Dropout(),
nn.Linear(4096, 4096),
nn.ReLU(True),
nn.Dropout(),
nn.Linear(4096, 2),
)
criterion = nn.CrossEntropyLoss()
model_conv.classifier.parameters()
optimizer_conv = optim.SGD(model_conv.classifier.parameters(), lr=0.001, momentum=0.9)
criterion
model_conv = train_model(model_conv, criterion, optimizer_conv,
exp_lr_scheduler, num_epochs=2)
def visualize_model(model, num_images=3):
images_so_far = 0
fig = plt.figure()
for i, data in enumerate(dataloader['val']):
inputs, labels = data['x'], data['y']
if use_gpu:
inputs,labels = Variable(inputs.cuda()), Variable(labels.cuda())
else:
inputs, labels = Variable(inputs), Variable(labels)
outputs = model(inputs)
_, preds = torch.max(outputs.data, 1)
print(inputs.size()[0])
for j in range(inputs.size()[0]):
images_so_far += 1
ax = plt.subplot(num_images//2, 2, images_so_far)
ax.axis('off')
ax.set_title('predicted: {}, label: {}'.format(preds[j],labels.cpu().data[j][0]))
# print(inputs.cpu().data[j].numpy().transpose(1,2,0).shape)
plt.imshow(inputs.cpu().data[j].numpy().transpose(1,2,0))
if images_so_far == num_images:
return
visualize_model(model_conv, num_images=6)
model_fcn = torchvision.models.vgg16(pretrained=True)
for param in model_fcn.parameters():
param.requires_grad = False
print(model_fcn.classifier.children)
model_conv.classifier = nn.Sequential(
nn.Conv2d(512, 4096, 7, stride=1, bias=False),
nn.ReLU(True),
nn.Dropout(),
nn.Conv2d(4096, 4096, 1),
nn.ReLU(True),
nn.Dropout(),
nn.Conv2d(4096, 2, 1),
)<jupyter_output><empty_output>
|
no_license
|
/FineTune_FCN_VGG.ipynb
|
romina72/faceDL
| 1 |
<jupyter_start><jupyter_text># 1 Matrix operations
## 1.1 Create a 4*4 identity matrix<jupyter_code>#This project is designed to get familiar with python list and linear algebra
#You cannot use import any library yourself, especially numpy
A = [[1,2,3],
[2,3,3],
[1,2,5]]
B = [[1,2,3,5],
[2,3,3,5],
[1,2,5,1]]
#TODO create a 4*4 identity matrix
I = [
[1,0,0,0],
[0,1,0,0],
[0,0,1,0],
[0,0,0,1]
]<jupyter_output><empty_output><jupyter_text>## 1.2 get the width and height of a matrix. <jupyter_code>#TODO Get the height and weight of a matrix.
def shape(M):
height = len(M)
weight = 0
if height > 0:
weight = len(M[0])
return height,weight
# run following code to test your shape function
%run -i -e test.py LinearRegressionTestCase.test_shape<jupyter_output>.
----------------------------------------------------------------------
Ran 1 test in 0.001s
OK
<jupyter_text>## 1.3 round all elements in M to certain decimal points<jupyter_code># TODO in-place operation, no return value
# TODO round all elements in M to decPts
def matxRound(M, decPts=4):
for row, rowList in enumerate(M):
for col, value in enumerate(rowList):
M[row][col] = round(value, decPts)
# run following code to test your matxRound function
%run -i -e test.py LinearRegressionTestCase.test_matxRound<jupyter_output>.
----------------------------------------------------------------------
Ran 1 test in 0.008s
OK
<jupyter_text>## 1.4 compute transpose of M<jupyter_code>#TODO compute transpose of M
def transpose(M):
return list(map(list, zip(*M)))
# run following code to test your transpose function
%run -i -e test.py LinearRegressionTestCase.test_transpose<jupyter_output>.
----------------------------------------------------------------------
Ran 1 test in 0.005s
OK
<jupyter_text>## 1.5 compute AB. return None if the dimensions don't match<jupyter_code>#TODO compute matrix multiplication AB, return None if the dimensions don't match
def matxMultiply(A, B):
height_A, weight_A = shape(A)
height_B, weight_B = shape(B)
DIMENSIONS_NOT_MATCH = "Matrix A's column number doesn't equal to Matrix b's row number"
if weight_A != height_B:
raise ValueError(DIMENSIONS_NOT_MATCH)
return [[sum((a*b) for a, b in zip(row, col)) for col in zip(*B)] for row in A]
# run following code to test your matxMultiply function
%run -i -e test.py LinearRegressionTestCase.test_matxMultiply<jupyter_output>.
----------------------------------------------------------------------
Ran 1 test in 0.033s
OK
<jupyter_text>---
# 2 Gaussian Jordan Elimination
## 2.1 Compute augmented Matrix
$ A = \begin{bmatrix}
a_{11} & a_{12} & ... & a_{1n}\\
a_{21} & a_{22} & ... & a_{2n}\\
a_{31} & a_{22} & ... & a_{3n}\\
... & ... & ... & ...\\
a_{n1} & a_{n2} & ... & a_{nn}\\
\end{bmatrix} , b = \begin{bmatrix}
b_{1} \\
b_{2} \\
b_{3} \\
... \\
b_{n} \\
\end{bmatrix}$
Return $ Ab = \begin{bmatrix}
a_{11} & a_{12} & ... & a_{1n} & b_{1}\\
a_{21} & a_{22} & ... & a_{2n} & b_{2}\\
a_{31} & a_{22} & ... & a_{3n} & b_{3}\\
... & ... & ... & ...& ...\\
a_{n1} & a_{n2} & ... & a_{nn} & b_{n} \end{bmatrix}$<jupyter_code>#TODO construct the augment matrix of matrix A and column vector b, assuming A and b have same number of rows
def augmentMatrix(A, b):
return [ra + rb for ra, rb in zip(A, b)]
# run following code to test your augmentMatrix function
%run -i -e test.py LinearRegressionTestCase.test_augmentMatrix<jupyter_output>.
----------------------------------------------------------------------
Ran 1 test in 0.003s
OK
<jupyter_text>## 2.2 Basic row operations
- exchange two rows
- scale a row
- add a scaled row to another<jupyter_code># TODO r1 <---> r2
# TODO in-place operation, no return value
def swapRows(M, r1, r2):
M[r1], M[r2] = M[r2], M[r1]
# run following code to test your swapRows function
%run -i -e test.py LinearRegressionTestCase.test_swapRows
# TODO r1 <--- r1 * scale
# TODO in-place operation, no return value
def scaleRow(M, r, scale):
if scale == 0:
raise ValueError
M[r] = [value * scale for value in M[r]]
# run following code to test your scaleRow function
%run -i -e test.py LinearRegressionTestCase.test_scaleRow
# TODO r1 <--- r1 + r2*scale
# TODO in-place operation, no return value
def addScaledRow(M, r1, r2, scale):
M[r1] = [e1 + e2 * scale for e1, e2 in zip(M[r1], M[r2])]
# run following code to test your addScaledRow function
%run -i -e test.py LinearRegressionTestCase.test_addScaledRow<jupyter_output>.
----------------------------------------------------------------------
Ran 1 test in 0.001s
OK
<jupyter_text>## 2.3 Gauss-jordan method to solve Ax = b
### Hint:
Step 1: Check if A and b have same number of rows
Step 2: Construct augmented matrix Ab
Step 3: Column by column, transform Ab to reduced row echelon form [wiki link](https://en.wikipedia.org/wiki/Row_echelon_form#Reduced_row_echelon_form)
for every column of Ab (except the last one)
column c is the current column
Find in column c, at diagonal and under diagonal (row c ~ N) the maximum absolute value
If the maximum absolute value is 0
then A is singular, return None (Prove this proposition in Question 2.4)
else
Apply row operation 1, swap the row of maximum with the row of diagonal element (row c)
Apply row operation 2, scale the diagonal element of column c to 1
Apply row operation 3 mutiple time, eliminate every other element in column c
Step 4: return the last column of Ab
### Remark:
We don't use the standard algorithm first transfering Ab to row echelon form and then to reduced row echelon form. Instead, we arrives directly at reduced row echelon form. If you are familiar with the stardard way, try prove to yourself that they are equivalent. <jupyter_code>#TODO implement gaussian jordan method to solve Ax = b
""" Gauss-jordan method to solve x such that Ax = b.
A: square matrix, list of lists
b: column vector, list of lists
decPts: degree of rounding, default value 4
epsilon: threshold for zero, default value 1.0e-16
return x such that Ax = b, list of lists
return None if A and b have same height
return None if A is (almost) singular
"""
def gj_Solve(A, b, decPts=4, epsilon = 1.0e-16):
height = len(A)
if height != len(b):
raise ValueError
B = augmentMatrix(A, b)
for col in range(height):
maxValue = 0
value = 0
maxRow = 0
for r in range(col, height):
if abs(B[r][col]) > maxValue:
maxValue = abs(B[r][col])
value = B[r][col]
maxRow = r
# singular
if maxValue < epsilon:
return None
if col != maxRow:
swapRows(B, col, maxRow)
if value != 1:
scaleRow(B, col, 1.0 / B[col][col])
else:
if value != 1:
scaleRow(B, col, 1.0 / B[col][col])
for num in range(0, height):
if num != col:
addScaledRow(B, num, col, -B[num][col])
result = []
for row in range(height):
result.append([])
result[row].append(round(B[row][-1], decPts))
return result
# run following code to test your addScaledRow function
%run -i -e test.py LinearRegressionTestCase.test_gj_Solve<jupyter_output>.
----------------------------------------------------------------------
Ran 1 test in 2.031s
OK
<jupyter_text>## 2.4 Prove the following proposition:
**If square matrix A can be divided into four parts: **
$ A = \begin{bmatrix}
I & X \\
Z & Y \\
\end{bmatrix} $, where I is the identity matrix, Z is all zero and the first column of Y is all zero,
**then A is singular.**
Hint: There are mutiple ways to prove this problem.
- consider the rank of Y and A
- consider the determinate of Y and A
- consider certain column is the linear combination of other columns# TODO Please use latex
### Proof:
Please see the proof.pdf---
# 3 Linear Regression:
## 3.1 Compute the gradient of loss function with respect to parameters
## (Choose one between two 3.1 questions)
We define loss funtion $E$ as
$$
E(m, b) = \sum_{i=1}^{n}{(y_i - mx_i - b)^2}
$$
and we define vertex $Y$, matrix $X$ and vertex $h$ :
$$
Y = \begin{bmatrix}
y_1 \\
y_2 \\
... \\
y_n
\end{bmatrix}
,
X = \begin{bmatrix}
x_1 & 1 \\
x_2 & 1\\
... & ...\\
x_n & 1 \\
\end{bmatrix},
h = \begin{bmatrix}
m \\
b \\
\end{bmatrix}
$$
Proves that
$$
\frac{\partial E}{\partial m} = \sum_{i=1}^{n}{-2x_i(y_i - mx_i - b)}
$$
$$
\frac{\partial E}{\partial b} = \sum_{i=1}^{n}{-2(y_i - mx_i - b)}
$$
$$
\begin{bmatrix}
\frac{\partial E}{\partial m} \\
\frac{\partial E}{\partial b}
\end{bmatrix} = 2X^TXh - 2X^TY
$$TODO Please use latex
### Proof:
Please see the proof.pdf## 3.1 Compute the gradient of loss function with respect to parameters
## (Choose one between two 3.1 questions)
We define loss funtion $E$ as
$$
E(m, b) = \sum_{i=1}^{n}{(y_i - mx_i - b)^2}
$$
and we define vertex $Y$, matrix $X$ and vertex $h$ :
$$
Y = \begin{bmatrix}
y_1 \\
y_2 \\
... \\
y_n
\end{bmatrix}
,
X = \begin{bmatrix}
x_1 & 1 \\
x_2 & 1\\
... & ...\\
x_n & 1 \\
\end{bmatrix},
h = \begin{bmatrix}
m \\
b \\
\end{bmatrix}
$$
Proves that
$$
E = Y^TY -2(Xh)^TY + (Xh)^TXh
$$
$$
\frac{\partial E}{\partial h} = 2X^TXh - 2X^TY
$$TODO Please use latex (refering to the latex in problem may help)
TODO Proof:## 3.2 Linear Regression
### Solve equation $X^TXh = X^TY $ to compute the best parameter for linear regression.<jupyter_code>#TODO implement linear regression
'''
points: list of (x,y) tuple
return m and b
'''
def linearRegression(points):
x = points[0]
y = points[1]
x_T = transpose(x)
x_T_x = matxMultiply(x_T, x)
x_T_y = matxMultiply(x_T, y)
result = gj_Solve(x_T_x, x_T_y)
m_compute, b_compute = result[0][0], result[1][0]
return m_compute, b_compute<jupyter_output><empty_output><jupyter_text>## 3.3 Test your linear regression implementation<jupyter_code>import random
%matplotlib inline
import matplotlib.pyplot as plt
#TODO Construct the linear function
m_truth = round(random.gauss(0, 10), 4)
b_truth = round(random.gauss(0, 10), 4)
#TODO Construct points with gaussian noise
x_data = []
x = []
y = []
for i in range(100):
x.append([])
x_value = round(random.gauss(0, 10), 4)
x[i].append(x_value)
x_data.append([])
x_data[i].append(x_value)
x[i].append(1)
y.append([])
y[i].append(m_truth * x[-1][0] + b_truth + random.gauss(0, 30))
p1 = plt.scatter(x_data, y)
#TODO Compute m and b and compare with ground truth
m_compute, b_compute = linearRegression((x, y))
y_predict = []
for i in range(100):
y_predict.append(x_data[i][0] * m_compute + b_compute)
p2 = plt.plot(x_data, y_predict, color='red')
plt.legend((p1, p2[0]), ("real", "predict"))
# if not (abs(m_compute - m_truth) / m_truth < 2e-2 and abs(b_compute - b_truth) / b_truth < 2e-2):
# raise ValueError("m_truth={}, b_truth={} but got m_compute={}, b_compute={}".format(m_truth, b_truth, m_compute, b_compute))
# print("OK")
print("m_truth={}, b_truth={}, m_compute={}, b_compute={}".format(m_truth, b_truth, m_compute, b_compute))<jupyter_output>m_truth=-21.6749, b_truth=-10.6706, m_compute=-21.6996, b_compute=-11.8987
|
no_license
|
/Basic/4-linear-algebra/linear_regression_project_en.ipynb
|
PhyA/Machine-Learning
| 10 |
<jupyter_start><jupyter_text># Lecture 2: Python Language Basics<jupyter_code>import numpy as np
np.random.seed(12345)
np.set_printoptions(precision=4, suppress=True)<jupyter_output><empty_output><jupyter_text>## Python Language Basics### Language Semantics#### Indentation, not braces
Example: Calculation of the Pythagorean Numbers
Generally, it is assumed that the Pythagorean theorem was discovered by Pythagoras that is why it has its name. But there is a debate whether the Pythagorean theorem might have been discovered earlier or by others independently. For the Pythagoreans, - a mystical movement, based on mathematics, religion and philosophy, - the integer numbers satisfying the theorem were special numbers, which had been sacred to them.
These days Pythagorean numbers are not mystical anymore. Though to some pupils at school or other people, who are not on good terms with mathematics, they may still appear so.
So the definition is very simple:
Three integers satisfying $a^2+b^2=c^2$ are called Pythagorean numbers.
The following program calculates all pythagorean numbers less than a maximal number.
Remark: We have to import the math module to be able to calculate the square root of a number```python
print('hello Data Curaion course!')
print('hello again, Data Curaion course!')
```<jupyter_code>from math import sqrt
n = input("Maximum Number? ")
n = int(n)+1
for a in range(1,n):
for b in range(a,n):
c_square = a**2 + b**2
c = int(sqrt(c_square))
if ((c_square - c**2) == 0):
print(a, b, c)<jupyter_output>Maximum Number? 10
3 4 5
6 8 10
<jupyter_text>#### Everything is an object<jupyter_code>type(n)
type(sqrt)
a = "hello world"
b = a
print(id(a))
print(id(b))
print(a is b)<jupyter_output>True
<jupyter_text>What does the id() function do? id() returns the actual memory location where the variable is stored. Since id(a) = id(b), we know that a and b both point to a single variable, that resides in a single memory location. This is what we mean by “multiple names bound to single object”.<jupyter_code>a = [1, 2, 3]
b = [1, 2, 3]
print(id(a))
print(id(b))
print(a is b)<jupyter_output>False
<jupyter_text>In this case, you can see that the objects that a and b point to occupy different places in memory. Why did Python behave differently in this example? The difference is that a string is *immutable*, but a list is *mutable*. The above lines of code created two separate lists. To have the two names point to the same object, you could write the following:<jupyter_code>a = [1, 2, 3]
b = a
print(b is a)<jupyter_output>True
<jupyter_text>An immutable variable cannot be changed after it is created. If you wish to change an immutable variable, such as a string, you must create a new instance and bind the variable to the new instance. A mutable variable can be changed in place.<jupyter_code>a.append(4)
print(a)
print(b is a)<jupyter_output>True
<jupyter_text>This is because the list is immutable but the the variable is still binded to the same object, so a is b can be considered as id(a) == id(b):<jupyter_code>print(id(a))
print(id(b))<jupyter_output>4552633992
4552633992
<jupyter_text>However, as string is immutable object, two string objects will be created and binded to different names:<jupyter_code>a = "hello world"
b = "hello world"
print(id(a))
print(id(b))
print(a == b)
print(a is b)<jupyter_output>False
<jupyter_text>**Exercises**
What is the output of the following code?
```python
a = 256
b = 256
print(a == b)
print(a is b)
```
Then waht is the output of the following code?
```python
a = 257
b = 257
print(a == b)
print(a is b)
```
Check the reason why this is the case at [wtfPython](https://github.com/satwikkansal/wtfPython?utm_source=mybridge&utm_medium=blog&utm_campaign=read_more#-is-is-not-what-it-is), does this contradict what you thought about?#### Comments
Any text preceded by the hash mark (pound sign) # is ignored by the Python interpreter.
This is often used to add comments to code. At times you may also want to
exclude certain blocks of code without deleting them.
Comments can also occur after a line of executed code. While some programmers
prefer comments to be placed in the line preceding a particular line of code, this can
be useful at times.<jupyter_code>results = []
for number in range(10):
# find the odd numbers
if number % 2 == 0:
results.append(number)
print(results) #list all odd numbers<jupyter_output>[0, 2, 4, 6, 8]
<jupyter_text>Comments that span multiple lines – used to explain things in more detail – are created by adding a delimiter (```“””```) on each end of the comment.<jupyter_code>"""
This would be a multiline comment
in Python that spans several lines and
describes your code, your day, or anything you want it to
"""
results = []
for number in range(10):
# find the odd numbers
if number % 2 == 0:
results.append(number)
print(results)
<jupyter_output>[0, 2, 4, 6, 8]
<jupyter_text>#### Function and object method callsYou call functions using parentheses and passing zero or more arguments, optionally
assigning the returned value to a variable:<jupyter_code>def add(a, b):
result = a + b
return result
result = add(10, 20)
print(result)<jupyter_output>30
<jupyter_text>**Exercises**
Write a function *square* with one argument of number to return the result of square. For example, square(5) = 25 #### Variables and argument passing
When assigning a variable (or name) in Python, you are creating a reference to the
object on the righthand side of the equals signIn practical terms, consider a list of
integers:<jupyter_code>a = [1, 2, 3]<jupyter_output><empty_output><jupyter_text>Suppose we assign a to a new variable b:In some languages, this assignment would cause the data [1, 2, 3] to be copied. In
Python, a and b actually now refer to the same object, the original list [1, 2, 3]<jupyter_code>b = a
a.append(4)
b<jupyter_output><empty_output><jupyter_text>When you pass objects as arguments to a function, new local variables are created referencing
the original objects without any copying. If you bind a new object to a variable
inside a function, that change will not be reflected in the parent scope. It is
therefore possible to alter the internals of a mutable argument. Suppose we had the
following function:<jupyter_code>def append_element(some_list, element):
some_list.append(element)
data = [1, 2, 3]
append_element(data, 4)
print(data)<jupyter_output>[1, 2, 3, 4]
<jupyter_text>#### Dynamic references, strong types
In contrast with many compiled languages, such as Java and C++, object references in
Python have no type associated with them. There is no problem with the following:<jupyter_code>a = 5
type(a)
a = 'foo'
type(a)<jupyter_output><empty_output><jupyter_text>Variables are names for objects within a particular namespace; the type information is
stored in the object itself. Some observers might hastily conclude that Python is not a
“typed language.”<jupyter_code>'5' + 5<jupyter_output><empty_output><jupyter_text>In some languages, such as Visual Basic, the string '5' might get implicitly converted
(or casted) to an integer, thus yielding 10. Yet in other languages, such as JavaScript,
the integer 5 might be casted to a string, yielding the concatenated string '55'. In this
regard Python is considered a strongly typed language, which means that every object
has a specific type (or class), and implicit conversions will occur only in certain obvious
circumstances, such as the following:<jupyter_code>a = 4.5
b = 2
# String formatting, to be visited later
print('a is {0}, b is {1}'.format(type(a), type(b)))
a / b<jupyter_output>a is <class 'float'>, b is <class 'int'>
<jupyter_text>Knowing the type of an object is important, and it’s useful to be able to write functions
that can handle many different kinds of input. You can check that an object is an
instance of a particular type using the isinstance function:<jupyter_code>a = 5
isinstance(a, int)<jupyter_output><empty_output><jupyter_text>isinstance can accept a tuple of types if you want to check that an object’s type is
among those present in the tuple:<jupyter_code>a = 5; b = 4.5
isinstance(a, (int, float))
isinstance(b, (int, float))<jupyter_output><empty_output><jupyter_text>**Exercises**
What is the output of the following code?
```python
a = True
print(a + 1)
print(type(a + 1))
```
What is the output of the following code?
```python
a = None
print(a + 1)
print(type(a + 1))
```#### Attributes and methods
Objects in Python typically have both attributes (other Python objects stored “inside”
the object) and methods (functions associated with an object that can have access to
the object’s internal data). Both of them are accessed via the syntax
obj.attribute_name:```python
In [1]: a = 'hello world'
In [2]: a.
a.capitalize a.format a.isupper a.rindex a.strip
a.center a.index a.join a.rjust a.swapcase
a.count a.isalnum a.ljust a.rpartition a.title
a.decode a.isalpha a.lower a.rsplit a.translate
a.encode a.isdigit a.lstrip a.rstrip a.upper
a.endswith a.islower a.partition a.split a.zfill
a.expandtabs a.isspace a.replace a.splitlines
a.find a.istitle a.rfind a.startswith
```<jupyter_code>a = 'hello world'<jupyter_output><empty_output><jupyter_text>Attributes and methods can also be accessed by name via the getattr function:<jupyter_code>getattr(a, 'split')
a.split()<jupyter_output><empty_output><jupyter_text>**Exercises**
Assign a to be string of 'hello data curation course', and then convert the first character in each word to Uppercase and remaining characters to Lowercase using method *title*, then try to make all characters in Uppercase#### Imports
In Python a module is simply a file with the .py extension containing Python code.<jupyter_code>import numpy
numpy.arange(10)<jupyter_output><empty_output><jupyter_text>If we wanted to access the variables and functions defined in some_module.py, from
another file in the same directory we could do:<jupyter_code>from numpy import arange
arange(10)<jupyter_output><empty_output><jupyter_text>By using the as keyword you can give imports different variable names:<jupyter_code>import numpy as np
np.arange(10)
#All of three ways can import arange from numpy module
import numpy
print(numpy.arange(10))
from numpy import arange
print(arange(10))
import numpy as np
print(np.arange(10))<jupyter_output>[0 1 2 3 4 5 6 7 8 9]
[0 1 2 3 4 5 6 7 8 9]
[0 1 2 3 4 5 6 7 8 9]
<jupyter_text>#### Import conventions
The Python community has adopted a number of naming conventions for commonly
used modules:<jupyter_code>import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import statsmodels as sm<jupyter_output><empty_output><jupyter_text>This means that when you see np.arange, this is a reference to the arange function in
NumPy. This is done because it’s considered bad practice in Python software development
to import everything (from numpy import *) from a large package like NumPy**Exercises**
import *math* module that has a lot of useful mathematical functions. Try to use the function *log* and *pow* to check which value is larger, $\log(1000000000)$ or $2^5$?
(Hint: try to use the *?function* to check the function declarations if you do not know it yet, e.g.:
```python
?math.log
```#### Binary operators and comparisons
Most of the binary math operations and comparisons are as you might expect:<jupyter_code>5 - 7
12 + 21.5
5 <= 2<jupyter_output><empty_output><jupyter_text>To check if two references refer to the same object, use the **is** keyword. **is not** is also
perfectly valid if you want to check that two objects are not the same:<jupyter_code>a = [1, 2, 3]
b = a
c = list(a)
a is b<jupyter_output><empty_output><jupyter_text>Since list always creates a new Python list (i.e., a copy), we can be sure that c is distinct
from a.<jupyter_code>a is not c<jupyter_output><empty_output><jupyter_text>Comparing with is is not the same as the == operator, because in this
case we have:<jupyter_code>a == c<jupyter_output><empty_output><jupyter_text>A very common use of is and is not is to check if a variable is None, since there is
only one instance of None:<jupyter_code>a = None
a is None<jupyter_output><empty_output><jupyter_text>**Exercises**
What is the output of the following code:
```python
print(10 > 0 and 5 < 10)
print(10 != 100 or 5 < 10)
print(not 5<10)
print(10!=100 and not 5<10)
```#### Assignment Operators
When programming, it is common to use compound assignment operators that perform an operation on a variable’s value and then assign the resulting new value to that variable. These compound operators combine an arithmetic operator with the *=* operator, so for addition we’ll combine *+* with *=* to get the compound operator *+=*:<jupyter_code>w = 10
w += 10
print(w)
w = 10
w *= 5
print(w)
w = 2
w **= 10
print(w)<jupyter_output>1024
<jupyter_text>#### Membership operators
**in** and **not in** are the membership operators in Python. They are used to test whether a value or variable is found in a sequence (string, list, tuple, set and dictionary)<jupyter_code>x = 'Hello data curation course'
print('H' in x)
print('hello' not in x)<jupyter_output>True
<jupyter_text>#### Mutable and immutable objects
Most objects in Python, such as lists, dicts, NumPy arrays, and most user-defined
types (classes), are mutable. This means that the object or values that they contain can
be modified:<jupyter_code>a_list = ['foo', 2, [4, 5]]
a_list[2] = (3, 4)
a_list<jupyter_output><empty_output><jupyter_text>Others, like strings and tuples, are immutable:<jupyter_code>a_tuple = (3, 5, (4, 5))
a_tuple[1] = 'four'<jupyter_output><empty_output><jupyter_text>Remember that just because you can mutate an object does not mean that you always
should. Such actions are known as side effects. For example, when writing a function,
any side effects should be explicitly communicated to the user in the function’s documentation
or comments. If possible, try to avoid side effects and
favor immutability, even though there may be mutable objects involved.#### Implications of passing mutable vs. immutable variables to functions …
<jupyter_code>def assign(param):
new_value = "new value"
value = "old value"
assign(value)
print(value)<jupyter_output>old value
<jupyter_text>It passes a string (which is an immutable type of object) into the function *assign*. Within the scope of the function *assign*, *param* has been bound to the same object that *value* has been bound to outside the scope of the function. Within the scope of the function *assign*, we modify "old value" to "new value" . But, as you’ll remember, strings are imutable, so *param* ends up pointing to a completely different object. Once we leave the scope of function *assign* , *param* is no longer in the name space, and the value that *value* refers to was never changed.
<jupyter_code>def assign(param):
param[2] = "nothing"
value = ['You', 'know', 'something', 'Jon', 'Snow']
assign(value)
print(value)<jupyter_output>['You', 'know', 'nothing', 'Jon', 'Snow']
<jupyter_text>### Scalar Types
Python along with its standard library has a small set of built-in types for handling
numerical data, strings, boolean (True or False) values, and dates and time. These
“single value” types are sometimes called scalar types#### Numeric types
The primary Python types for numbers are int and float. An int can store arbitrarily
large numbers:<jupyter_code>ival = 17239871
ival ** 6<jupyter_output><empty_output><jupyter_text>Floating-point numbers are represented with the Python float type. Under the hood
each one is a double-precision (64-bit) value. They can also be expressed with scientific
notation:<jupyter_code>fval = 7.243
fval2 = 6.78e-5<jupyter_output><empty_output><jupyter_text>Integer division not resulting in a whole number will always yield a floating-point
number:<jupyter_code>3 / 2<jupyter_output><empty_output><jupyter_text>To get C-style integer division (which drops the fractional part if the result is not a
whole number), use the floor division operator //:<jupyter_code>3 // 2<jupyter_output><empty_output><jupyter_text>**Exercises**
Write a function *remainder* to obtain the remainder of divisions between a and b, e.g.
```python
results = remainder(45, 8)
print(results) #results = 3
```#### Strings
Many people use Python for its powerful and flexible built-in string processing capabilities.
You can write string literals using either single quotes ' or double quotes ":<jupyter_code>a = 'one way of writing a string'
b = "another way"<jupyter_output><empty_output><jupyter_text>For multiline strings with line breaks, you can use triple quotes, either ''' or """:<jupyter_code>c = """
This is a longer string that
spans multiple lines
"""<jupyter_output><empty_output><jupyter_text>It may surprise you that this string c actually contains four lines of text; the line
breaks after """ and after lines are included in the string. We can count the new line
characters with the count method on c:<jupyter_code>c.count('\n')<jupyter_output><empty_output><jupyter_text>Python strings are immutable; you cannot modify a string:<jupyter_code>a = 'this is a string'
a[10] = 'f'<jupyter_output><empty_output><jupyter_text>Afer this operation, the variable a is unmodified:<jupyter_code>a
b = a.replace('string', 'longer string')
b<jupyter_output><empty_output><jupyter_text>Many Python objects can be converted to a string using the str function:<jupyter_code>a = 5.6
s = str(a)
print(s)<jupyter_output>5.6
<jupyter_text>Strings are a sequence of Unicode characters and therefore can be treated like other
sequences, such as lists and tuples (which we will explore in more detail in the next
chapter):<jupyter_code>s = 'python'
list(s)<jupyter_output><empty_output><jupyter_text>The syntax s[:3] is called slicing and is implemented for many kinds of Python
sequences.
Index starts from 0. Trying to access a character out of index range will raise an IndexError. The index must be an integer. We can't use float or other types, this will result into TypeError.<jupyter_code>s[:3]
s[10]<jupyter_output><empty_output><jupyter_text>The index of -1 refers to the last item, -2 to the second last item and so on. We can access a range of items in a string by using the slicing operator (colon).<jupyter_code>s[-2:-1]<jupyter_output><empty_output><jupyter_text>The backslash character \ is an escape character, meaning that it is used to specify
special characters like newline \n or Unicode characters. To write a string literal with
backslashes, you need to escape them:<jupyter_code>s = '12\\34'
print(s)<jupyter_output>12\34
<jupyter_text>If you have a string with a lot of backslashes and no special characters, you might find
this a bit annoying. Fortunately you can preface the leading quote of the string with r,
which means that the characters should be interpreted as is (The r stands for raw):<jupyter_code>s = r'this\has\no\special\characters'
s<jupyter_output><empty_output><jupyter_text>Adding two strings together concatenates them and produces a new string:<jupyter_code>a = 'this is the first half '
b = 'and this is the second half'
a + b<jupyter_output><empty_output><jupyter_text>String objects have a format method that
can be used to substitute formatted arguments into the string, producing a new
string:<jupyter_code>template = '{0:.2f} {1:s} are worth USD${2:d}'<jupyter_output><empty_output><jupyter_text>In this string,
* {0:.2f} means to format the first argument as a floating-point number with two
decimal places.
* {1:s} means to format the second argument as a string.
* {2:d} means to format the third argument as an exact integer.<jupyter_code>template.format(0.86, 'USD', 1)<jupyter_output><empty_output><jupyter_text>**Exercises**
Replace the word "Hello" from string "Hello, Data Curation Course!" to "Ola"
(Hint: you can either first split the string to the list of words and replace the word or use the ```replace``` method, check ?str.replace for more details)#### Bytes and Unicode
In modern Python (i.e., Python 3.0 and up), Unicode has become the first-class string
type to enable more consistent handling of ASCII and non-ASCII text. In older versions
of Python, strings were all bytes without any explicit Unicode encoding. You
could convert to Unicode assuming you knew the character encoding. Let’s look at an
example:<jupyter_code>val = "español"
val<jupyter_output><empty_output><jupyter_text>We can convert this Unicode string to its UTF-8 bytes representation using the
encode method:<jupyter_code>val_utf8 = val.encode('utf-8')
val_utf8
type(val_utf8)<jupyter_output><empty_output><jupyter_text>Assuming you know the Unicode encoding of a bytes object, you can go back using
the decode method:<jupyter_code>val_utf8.decode('utf-8')<jupyter_output><empty_output><jupyter_text>While it’s become preferred to use UTF-8 for any encoding, for historical reasons you
may encounter data in any number of different encodings:<jupyter_code>val.encode('latin1')
val.encode('utf-16')
val.encode('utf-16le')<jupyter_output><empty_output><jupyter_text>#### Booleans
The two boolean values in Python are written as True and False. Comparisons and
other conditional expressions evaluate to either True or False. Boolean values are
combined with the and and or keywords:<jupyter_code>True and True
False or True<jupyter_output><empty_output><jupyter_text>#### Type casting
The str, bool, int, and float types are also functions that can be used to cast values
to those types:<jupyter_code>s = '3.14159'
type(s)
fval = float(s)
type(fval)
int(fval)
bool(fval)
bool(0)<jupyter_output><empty_output><jupyter_text>**Exercises**
Case the course number 2489 into string and concatenate it with the string "Hello, Data Curation Course"#### None
None is the Python null value type. If a function does not explicitly return a value, it
implicitly returns None:<jupyter_code>a = None
a is None
b = 5
b is not None<jupyter_output><empty_output><jupyter_text>None is also a common default value for function arguments:<jupyter_code>def add_and_maybe_multiply(a, b, c=None):
result = a + b
if c is not None:
result = result * c
return result
add_and_maybe_multiply(2, 5)
add_and_maybe_multiply(2, 5, 8)<jupyter_output><empty_output><jupyter_text>None is not only a reserved keyword but also a unique instance of NoneType:<jupyter_code>type(None)<jupyter_output><empty_output><jupyter_text>#### Dates and times
The built-in Python datetime module provides datetime, date, and time types. The
datetime type, as you may imagine, combines the information stored in date and
time and is the most commonly used:<jupyter_code>from datetime import datetime, date, time
dt = datetime(2011, 10, 29, 20, 30, 21)
dt.day
dt.minute
dt.date()
dt.time()<jupyter_output><empty_output><jupyter_text>The strftime method formats a datetime as a string:<jupyter_code>dt.strftime('%m/%d/%Y %H:%M')<jupyter_output><empty_output><jupyter_text>Strings can be converted (parsed) into datetime objects with the strptime function:<jupyter_code>datetime.strptime('20091031', '%Y%m%d')<jupyter_output><empty_output><jupyter_text>When you are aggregating or otherwise grouping time series data, it will occasionally
be useful to replace time fields of a series of datetimes—for example, replacing the
minute and second fields with zero:<jupyter_code>dt.replace(minute=0, second=0)<jupyter_output><empty_output><jupyter_text>Since datetime.datetime is an immutable type, methods like these always produce
new objects.
The difference of two datetime objects produces a datetime.timedelta type:<jupyter_code>dt2 = datetime(2011, 11, 15, 22, 30)
delta = dt2 - dt
delta
type(delta)<jupyter_output><empty_output><jupyter_text>The output timedelta(17, 7179) indicates that the timedelta encodes an offset of 17
days and 7,179 seconds.<jupyter_code>dt<jupyter_output><empty_output><jupyter_text>Adding a timedelta to a datetime produces a new shifted datetime:<jupyter_code>dt + delta<jupyter_output><empty_output><jupyter_text>### Control Flow
Python has several built-in keywords for conditional logic, loops, and other standard
control flow concepts found in other programming languages.#### if, elif, and else
The if statement is one of the most well-known control flow statement types. It
checks a condition that, if True, evaluates the code in the block that follows:
```python
if x < 0:
print('It's negative')
```An if statement can be optionally followed by one or more elif blocks and a catchall
else block if all of the conditions are False:
```python
if x < 0:
print('It's negative')
elif x == 0:
print('Equal to zero')
elif 0 < x < 5:
print('Positive but smaller than 5')
else:
print('Positive and larger than or equal to 5')
```If any of the conditions is **True**, no further **elif** or **else** blocks will be reached. With
a compound condition using **and** or **or**, conditions are evaluated left to right and will
short-circuit:<jupyter_code>a = 5; b = 7
c = 8; d = 4
if a < b or c > d:
print('Made it')<jupyter_output>Made it
<jupyter_text>In this example, the comparison c > d never gets evaluated because the first comparison
was True.It is also possible to chain comparisons:<jupyter_code>4 > 3 > 2 > 1
a = True
if a == True:
print('a is True')
else:
print('a is False')
a = 0
if a == True:
print('a is True')
else:
print('a is False')<jupyter_output>a is False
<jupyter_text>**Exercises**
Input an integer number and check with the number is an odd/even number:
```python
number = input()
...
print("Number 35 is an odd number")
print("Number 42 is an even number")
```#### for loops**for** loops are for iterating over a collection (like a list or tuple) or an iterater. The
standard syntax for a for loop is:
```python
for value in collection:
# do something with value
```
You can advance a **for** loop to the next iteration, skipping the remainder of the block,
using the **continue** keyword. Consider this code, which sums up integers in a list and
skips None values:<jupyter_code>sequence = [1, 2, None, 4, None, 5]
total = 0
for value in sequence:
if value is None:
continue
total += value
print(total)<jupyter_output>12
<jupyter_text>A **for** loop can be exited altogether with the **break** keyword. This code sums elements
of the list until a 5 is reached:<jupyter_code>sequence = [1, 2, 0, 4, 6, 5, 2, 1]
total_until_5 = 0
for value in sequence:
if value == 5:
break
total_until_5 += value
print(total_until_5)<jupyter_output>13
<jupyter_text>The break keyword only terminates the innermost for loop; any outer for loops will
continue to run:<jupyter_code>for i in range(4):
for j in range(4):
if j > i:
break
print((i, j))<jupyter_output>(0, 0)
(1, 0)
(1, 1)
(2, 0)
(2, 1)
(2, 2)
(3, 0)
(3, 1)
(3, 2)
(3, 3)
<jupyter_text>**Exercises**
Print all odd numbers from 0 to 100
```python
print("Number 1 is an odd number")
print("Number 3 is an even number")
print("Number 99 is an even number")
```#### while loops
A **while** loop specifies a condition and a block of code that is to be executed until the
condition evaluates to **False** or the loop is explicitly ended with **break**:<jupyter_code>n = 100
# initialize sum and counter
sum = 0
i = 1
while i <= n:
sum = sum + i
i = i+1 # update counter
# print the sum
print("The sum is", sum)<jupyter_output>The sum is 5050
<jupyter_text>The **break** statement terminates the loop containing it. Control of the program flows to the statement immediately after the body of the loop.
If break statement is inside a nested loop (loop inside another loop), break will terminate the innermost loop.
<jupyter_code>x = 256
total = 0
while x > 0:
if total > 500:
break
total += x
x = x // 2
print(total)<jupyter_output>504
<jupyter_text>The **continue** statement is used to skip the rest of the code inside a loop for the current iteration only. Loop does not terminate but continues on with the next iteration.<jupyter_code># print the sum of all odd numbers small than 100
x = 0
total = 0
while x < 100:
if x % 2 == 0:
x += 1
continue
total += x
x += 1
print(total)<jupyter_output>2500
<jupyter_text>#### pass
**pass** is the “no-op” statement in Python. It can be used in blocks where no action is to
be taken (or as a placeholder for code not yet implemented); it is only required
because Python uses whitespace to delimit blocks:
```python
if x < 0:
print('negative!')
elif x == 0:
# TODO: put something smart here
pass
else:
print('positive!')
```** Exercises **
Loop through and print out all even numbers from the numbers list in the same order they are received. Don't print any numbers that come after 237 in the sequence.
```python
numbers = [
951, 402, 984, 651, 360, 69, 408, 319, 601, 485, 980, 507, 725, 547, 544,
615, 83, 165, 141, 501, 263, 617, 865, 575, 219, 390, 984, 592, 236, 105, 942, 941,
386, 462, 47, 418, 907, 344, 236, 375, 823, 566, 597, 978, 328, 615, 953, 345,
399, 162, 758, 219, 918, 237, 412, 566, 826, 248, 866, 950, 626, 949, 687, 217,
815, 67, 104, 58, 512, 24, 892, 894, 767, 553, 81, 379, 843, 831, 445, 742, 717,
958, 609, 842, 451, 688, 753, 854, 685, 93, 857, 440, 380, 126, 721, 328, 753, 470,
743, 527
]
```
#### range
The range function returns an iterator that yields a sequence of evenly spaced
integers:<jupyter_code>range(10)
list(range(10))<jupyter_output><empty_output><jupyter_text>Both a start, end, and step (which may be negative) can be given:<jupyter_code>list(range(0, 20, 2))
list(range(5, 0, -1))<jupyter_output><empty_output><jupyter_text>As you can see, range produces integers up to but not including the endpoint. A
common use of range is for iterating through sequences by index:<jupyter_code>seq = [1, 2, 3, 4]
for i in range(len(seq)):
val = seq[i]
print(val)<jupyter_output>1
2
3
4
<jupyter_text>While you can use functions like list to store all the integers generated by range in
some other data structure, often the default iterator form will be what you want. This
snippet sums all numbers from 0 to 99,999 that are multiples of 3 or 5:<jupyter_code>sum = 0
for i in range(100000):
# % is the modulo operator
if i % 3 == 0 or i % 5 == 0:
sum += i
print(sum)<jupyter_output>2333316668
<jupyter_text>#### Ternary expressions
A ternary expression in Python allows you to combine an if-else block that produces
a value into a single line or expression. The syntax for this in Python is:
```python
value = true-expr if condition else false-expr
```Here, true-expr and false-expr can be any Python expressions. It has the identical
effect as the more verbose:
```python
if condition:
value = true-expr
else:
value = false-expr
```<jupyter_code>x = 5
'Non-negative' if x >= 0 else 'Negative'<jupyter_output><empty_output>
|
permissive
|
/notebooks/lecture_2.ipynb
|
aadorian/data_curation_course
| 83 |
<jupyter_start><jupyter_text># 1. Vector data preparations
This script prepares the **Paavo zip code dataset** from the Statistics of Finland
for machine learning purposes.
It reads the original shapefile, scales all the numerical values, joins some auxiliary
data and encodes one text field for machine learning purposes. The result is saved as geopackage.<jupyter_code>import time
import geopandas as gpd
import pandas as pd
import os
from shapely.geometry import Point, MultiPolygon, Polygon
from sklearn.preprocessing import StandardScaler
from joblib import dump, load
import zipfile
from urllib.request import urlretrieve
import matplotlib.pyplot as plt<jupyter_output><empty_output><jupyter_text>### 1.1 Create directories if they do not already exist<jupyter_code>directories = ['../data']
for directory in directories:
if not os.path.exists(directory):
os.makedirs(directory)<jupyter_output><empty_output><jupyter_text>### 1.2 Download the Paavo data from Allas with urllib and unzip it to the data folder<jupyter_code>urlretrieve('https://a3s.fi/gis-courses/gis_ml/paavo.zip', '../data/paavo.zip')
with zipfile.ZipFile('../data/paavo.zip', 'r') as zip_file:
zip_file.extractall('../data')<jupyter_output><empty_output><jupyter_text>### 1.3 Define file paths<jupyter_code>zip_code_shapefile = '../data/paavo/pno_tilasto_2020.shp'
finnish_regions_shapefile = '../data/paavo/SuomenMaakuntajako_2020_10k.shp'
output_file_path = '../data/paavo/zip_code_data_after_preparation.gpkg'
scaler_path = '../data/paavo/zip_code_scaler.bin'<jupyter_output><empty_output><jupyter_text># 2. Reading and cleaning the data
Read the zip code dataset into a geopandas dataframe **original_gdf** and drop unnecessary rows and columns<jupyter_code>### Read the data from a shapefile to a geopandas dataframe
original_gdf = gpd.read_file(zip_code_shapefile, encoding='utf-8')
print(f"Original dataframe size: {len(original_gdf.index)} zip codes with {len(original_gdf.columns)} columns")
### Drop all rows that have missing values or where average income is -1 (=not known) or 0
original_gdf = original_gdf.dropna()
original_gdf = original_gdf[original_gdf["hr_mtu"]>0].reset_index(drop=True)
print(f"Dataframe size after dropping some rows: {len(original_gdf.index)} zip codes with {len(original_gdf.columns)} columns")
### Remove some columns that are strings (nanm, kunta = name of the municipality in Finnish and Swedish.
### or which might make the modeling too easy ('hr_mtu','hr_tuy','hr_pi_tul','hr_ke_tul','hr_hy_tul','hr_ovy')
columns_to_be_removed_completely = ['namn','kunta','hr_ktu','hr_tuy','hr_pi_tul','hr_ke_tul','hr_hy_tul','hr_ovy']
original_gdf = original_gdf.drop(columns_to_be_removed_completely,axis=1)
print(f"Dataframe size after dropping some columns: {len(original_gdf.index)} zip codes with {len(original_gdf.columns)} columns")
original_gdf.head()<jupyter_output><empty_output><jupyter_text>### 2.1 Plot the geodataframe
If plotting maps with matplotlib is not familiar. Here are some things you can play with
* figsize - different heigh, width
* column - try other zip code values
* cmap - this is the color map, here are the possibile options https://matplotlib.org/3.3.1/tutorials/colors/colormaps.html<jupyter_code>fig, ax = plt.subplots(figsize=(20, 10))
ax.set_title("Average income by zip code", fontsize=25)
ax.set_axis_off()
original_gdf.plot(column='hr_mtu', ax=ax, legend=True, cmap="magma")<jupyter_output><empty_output><jupyter_text># 3. Scale the numerical columns
Most machine learning algorithms benefit from feature scaling which means normalizing the dataset's variablity to values between e.g. 0-1
We do this for all numerical columns. Text (string) types of columns need different kind of treatment<jupyter_code>### Get list of all column headings
all_columns = list(original_gdf.columns)
### List the column names that we don't want to be scaled
col_names_no_scaling = ['postinumer','nimi','hr_mtu','geometry']
### List of column names we want to scale. (all columns minus those we don't want)
col_names_to_scaling = [column for column in all_columns if column not in col_names_no_scaling]
### Subset the data for only those to-be scaled
gdf = original_gdf[col_names_to_scaling]
### Apply a Scikit StandardScaler for all the columns left in gdf
scaler = StandardScaler()
scaled_values_array = scaler.fit_transform(gdf)
### You could save the scaler for later use with this
dump(scaler, scaler_path, compress=True)
### The scaled columns come back as a numpy ndarray, switch back to a geopandas dataframe again
gdf = pd.DataFrame(scaled_values_array)
gdf.columns = col_names_to_scaling
### Join the non-scaled columns back with the the scaled columns by index
scaled_gdf = original_gdf[col_names_no_scaling].join(gdf)
scaled_gdf.head()<jupyter_output><empty_output><jupyter_text># 4. Encode categorical (text) columns
As example for categorical value, add county names to post codes. The county for each post code area is retrieved from a spatial join with counties dataset (SuomenMaankuntajako_2020_10k.shp).
For text and categorical data we need different kind of pre-processing. In this excercise we use the most popular method of one-hot encoding (also called dummy variables) for categorical data.
More information on one-hot encoding
https://www.kaggle.com/dansbecker/using-categorical-data-with-one-hot-encoding
It might not always be the best option. See other options
https://towardsdatascience.com/stop-one-hot-encoding-your-categorical-variables-bbb0fba89809### 4.1 Spatially join the region information to the dataset <jupyter_code>### Read the regions shapefile and choose only the name of the region and its geometry
finnish_regions_gdf = gpd.read_file(finnish_regions_shapefile)
finnish_regions_gdf = finnish_regions_gdf[['NAMEFIN','geometry']]
### A function we use to return centroid point geometry from a zip code polygon
def returnPointGeometryFromXY(polygon_geometry):
## Calculate x and y of the centroid
centroid_x,centroid_y = polygon_geometry.centroid.x,polygon_geometry.centroid.y
## Create a shapely Point geometry of the x and y coords
point_geometry = Point(centroid_x,centroid_y)
return point_geometry
### Stash the polygon geometry to another column as we are going to overwrite the 'geometry' with centroid geometry
scaled_gdf['polygon_geometry'] = scaled_gdf['geometry']
### We will be joining the region name to zip codes according to the zip code centroid.
### This calls the function above and returns centroid to every row
scaled_gdf["geometry"] = scaled_gdf['geometry'].apply(returnPointGeometryFromXY)
### Spatially join the region name to the zip codes using the centroid of zip codes and region polygons
scaled_gdf = gpd.sjoin(scaled_gdf,finnish_regions_gdf,how='inner',op='intersects')<jupyter_output><empty_output><jupyter_text>### 4.2 One-hot encode the region name<jupyter_code>### Switch the polygon geometry back to the 'geometry' field and drop uselesss columns
scaled_gdf['geometry'] = scaled_gdf['polygon_geometry']
scaled_gdf.drop(['index_right','polygon_geometry'],axis=1, inplace=True)
### Encode the region name with the One-hot encoding (= in pandas, dummy encoding)
encoded_gdf = pd.get_dummies(scaled_gdf['NAMEFIN'])
### Join scaled gdf and encoded gdf together
scaled_and_encoded_gdf = scaled_gdf.join(encoded_gdf).drop('NAMEFIN',axis=1)
### The resulting dataframe has Polygon and Multipolygon geometries.
### This upcasts the polygons to multipolygon format so all of them have the same format
scaled_and_encoded_gdf["geometry"] = [MultiPolygon([feature]) if type(feature) == Polygon else feature for feature in scaled_and_encoded_gdf["geometry"]]
print("Dataframe size after adding region name: " + str(len(scaled_and_encoded_gdf.index))+ " zip codes with " + str(len(scaled_and_encoded_gdf.columns)) + " columns")
### Print the tail of the dataframe
scaled_and_encoded_gdf.tail()<jupyter_output><empty_output><jupyter_text># 5. Write the pre-processed zip code data to file as a Geopackage<jupyter_code>### Write the prepared zipcode dataset to a geopackage
scaled_and_encoded_gdf.to_file(output_file_path, driver="GPKG")<jupyter_output><empty_output>
|
no_license
|
/machineLearning/01_data_preparation/01_vectorDataPreparations.ipynb
|
VuokkoH/geocomputing
| 10 |
<jupyter_start><jupyter_text># Prepare Data
Plan - Acquire - **Prepare** - Explore - Model - Deliver
**Goal:** Prepare, tidy, and clean the data so that it is ready for exploration and analysis.
**Input:** 1 or more dataframes acquired through the "acquire" step.
**Output:** 1 dataset split into 3 samples in the form of dataframes: train, validate & test.
**Artifact:** prepare.py
## How?
1. Summarize our data:
- head(), describe(), info(), isnull(), value_counts(), shape, ...
- plt.hist(), plt.boxplot()
- document takeaways (nulls, datatypes to change, outliers, ideas for features, etc.)
2. Clean the data:
- missing values: drop columns with too many missing values, drop rows with too many missing values, fill with zero where it makes sense, and then make note of any columns you want to impute missing values in (you will need to do that on split data).
- outliers: ignore, drop rows, snap to a selected max/min value, create bins (cut, qcut)
- data errors: drop the rows/observations with the errors, correct them to what it was intended
- address text normalization issues...e.g. deck 'C' 'c'. (correct and standardize the text)
- tidy data: getting your data in the shape it needs to be for modeling and exploring. every row should be an observation and every column should be a feature/attribute/variable. You want 1 observation per row, and 1 row per observation. If you want to predict a customer churn, each row should be a customer and each customer should be on only 1 row. (address duplicates, aggregate, melt, reshape, ...)
- creating new variables out of existing variables (e.g. z = x - y)
- rename columns
- datatypes: need numeric data to be able to feed into model (dummy vars, factor vars, manual encoding)
- scale numeric data: so that continuous variables have the same weight, are on the same units, if algorithm will be used that will be affected by the differing weights, or if data needs to be scaled to a gaussian/normal distribution for statistical testing. (linear scalers and non-linear scalers) 3. Split the data:
- split our data into train, validate and test sample dataframes
- Why? overfitting: model is not generalizable. It fits the data you've trained it on "too well". 3 points does not necessarily mean a parabola.
- **train:** *in-sample*, explore, impute mean, scale numeric data (max() - min()...), fit our ml algorithms, test our models.
- **validate, test**: represents future, unseen data
- **validate**: confirm our top models have not overfit, test our top n models on unseen data. Using validate performance results, we pick the top **1** model.
- **test**: *out-of-sample*, how we expect our top model to perform in production, on unseen data in the future. **ONLY USED ON 1 MODEL.**
#### Should I do *this* on the full dataset or on the train sample?
1. Are you comparing, looking at the relationship or summary stats or visualizations with 2+ variables?
2. Are you using an sklearn method?
3. Are you moving into the explore stage of the pipeline?
If **ONE** or more of these is yes, then you should be doing it on your train sample.
If **ALL** are no, then the entire dataset is fine. ## Summarize Data<jupyter_code>import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.impute import SimpleImputer
import warnings
warnings.filterwarnings("ignore")
import acquire<jupyter_output><empty_output><jupyter_text>We'll use the funciton we defined in the last lesson to acquire our data:<jupyter_code>df = acquire.get_titanic_data()
# rows & columns
df.shape
# first n rows
df.head(5)
# information about the dataframe: column names, rows, datatypes, non-missing values
df.info()
# describe numeric columns
df.describe()
# plot distribution of numeric columns
# create a list of numeric column names
num_cols = df.select_dtypes(include = 'number').columns
num_cols
# loop through the list and plot a histogram for each numeric column
for col in num_cols:
plt.hist(df[col])
plt.title(col)
plt.show()
# describe object columns
obj_cols = df.select_dtypes(include = 'object').columns
for col in obj_cols:
print(df[col].value_counts())
print('\n')
print(df[col].value_counts(normalize=True, dropna = False))
print('---------------------------------\n')
# how many missing values we have in each column
df.isnull().sum()<jupyter_output><empty_output><jupyter_text>**Takeaways**
- embarked == embark_town, so remove embarked & keep embark_town
- class == pclass, so remove class & keep pclass (already numeric)
- drop deck...way too many missing values
- fill embark_town with most common value ('Southampton')
- drop age column
- encode or create dummy vars for sex & embark_town.
## Clean the Data<jupyter_code># drop duplicates rows...run just in case
df = df.drop_duplicates()
# drop columns deck, embarked, class and age
df = df.drop(columns = ['deck', 'embarked', 'class', 'age'])
df.head()
# check how many nulls are in each column
df.isnull().sum()
# look at value counts for embark_town
df.embark_town.value_counts()<jupyter_output><empty_output><jupyter_text>We could fill embark_town with most common value, 'Southampton', by hard-coding the value using the fillna() function, as below. Or we could use an imputer. We will demonstrate the imputer *after* the train-validate-test split. <jupyter_code>df['embark_town'] = df.embark_town.fillna(value='Southampton')
df.isnull().sum()<jupyter_output><empty_output><jupyter_text>### Encoding
- Encoding -- turning a string into a number
Two strategies:
- associate each unique value with a number -- label encoding
- one-hot encoding (get_dummies): turn each unique value into a separate column with either 1 or 0- Curse of dimensionality
- When to use one or the other?
- use the label encoder when the categories have an inherit order
- use one-hot encoding when there is no order Get dummy vars for sex and embark_town (aka one hot encoding)
- dummy_na: create a dummy var for na values, also?
- drop_first: drop first dummy var (since we know if they do not belong to any of the vars listed, then they must belong to the first one that is not listed). <jupyter_code># use pd.get_dummies. Returns a dataframe
df_dummy = pd.get_dummies(df[['sex', 'embark_town']], drop_first=[True, True])
df_dummy.head()
# append dummy df cols to the original df.
df= pd.concat([df, df_dummy], axis = 1)
df.head()<jupyter_output><empty_output><jupyter_text>Create a function to perform these steps when we need to reproduce our dataset. <jupyter_code>def clean_data(df):
'''
This function will drop any duplicate observations,
drop columns not needed, fill missing embarktown with 'Southampton'
and create dummy vars of sex and embark_town.
'''
df.drop_duplicates(inplace=True)
df.drop(columns=['deck', 'embarked', 'class', 'age'], inplace=True)
df.embark_town.fillna(value='Southampton', inplace=True)
dummy_df = pd.get_dummies(df[['sex', 'embark_town']], drop_first=True)
return pd.concat([df, dummy_df], axis=1)<jupyter_output><empty_output><jupyter_text>## Train Test Split
#### Sklearn has allows us to split our data easily:
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html<jupyter_code># 20% test, 80% train_validate
# then of the 80% train_validate: 25% validate, 75% train.
train, test = train_test_split(df, test_size = 0.2, random_state = 123, stratify = df.survived)
train, validate = train_test_split(train, test_size = 0.25, random_state = 123, stratify = train.survived)
train.shape, validate.shape, test.shape
def split_titanic_data(df):
"""
splits the data in train validate and test
"""
train, test = train_test_split(df, test_size = 0.2, random_state = 123, stratify = df.survived)
train, validate = train_test_split(train, test_size=.25, random_state=123, stratify=train.survived)
return train, validate, test<jupyter_output><empty_output><jupyter_text>## Option for Missing Values: Impute
Impute: Assign a value to something by inference
Strategies for imputing:
- fill with 0
- fill with the average
- fill with the median
- fill with subgroup mean
- fill with most frequent value
- build a model to predict missing values
We will use sklearn.imputer.SimpleImputer to do this.
1. Create the imputer object, selecting the strategy used to impute (mean, median or mode (strategy = 'most_frequent').
2. Fit to train. This means compute the mean, median, or most_frequent (i.e. mode) for each of the columns that will be imputed. Store that value in the imputer object.
3. Transform train: fill missing values in train dataset with that value identified
4. Transform test: fill missing values with that value identified<jupyter_code># Define the thing:
imputer = SimpleImputer(strategy='most_frequent')
imputer
# fit the thing
imputer = imputer.fit(train[['embark_town']])
imputer
# Use the thing (i.e transform)
train[['embark_town']] = imputer.transform(train[['embark_town']])
validate[['embark_town']] = imputer.transform(validate[['embark_town']])
test[['embark_town']] = imputer.transform(test[['embark_town']])<jupyter_output><empty_output><jupyter_text>Create a function that will run through all of these steps, when I provide a train and test dataframe, a strategy, and a list of columns. <jupyter_code>def impute_mode(train, validate, test):
'''
impute mode for embark_town
'''
imputer = SimpleImputer(strategy='most_frequent')
train[['embark_town']] = imputer.fit_transform(train[['embark_town']])
validate[['embark_town']] = imputer.transform(validate[['embark_town']])
test[['embark_town']] = imputer.transform(test[['embark_town']])
return train, validate, test<jupyter_output><empty_output><jupyter_text>#### Blend the clean, split and impute functions into a single prep_data() function. <jupyter_code># make a prep function:
def prep_titanic_data(df):
"""
takes in a data from titanic database, cleans the data, splits the data
in train validate test and imputes the missing values for embark_town.
Returns three dataframes train, validate and test.
"""
df = clean_data(df)
train, validate, test = split_titanic_data(df)
train, validate, test = impute_mode(train, validate, test)
return train, validate, test
# acquire data again
df = acquire.get_titanic_data()
df.head()
# make sure the above function works!
train, validate, test = prep_titanic_data(df)
train.info()<jupyter_output><class 'pandas.core.frame.DataFrame'>
Int64Index: 534 entries, 455 to 496
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 passenger_id 534 non-null int64
1 survived 534 non-null int64
2 pclass 534 non-null int64
3 sex 534 non-null object
4 sibsp 534 non-null int64
5 parch 534 non-null int64
6 fare 534 non-null float64
7 embark_town 534 non-null object
8 alone 534 non-null int64
9 sex_male 534 non-null uint8
10 embark_town_Queenstown 534 non-null uint8
11 embark_town_Southampton 534 non-null uint8
dtypes: float64(1), int64(6), object(2), uint8(3)
memory usage: 43.3+ KB
|
no_license
|
/prepare_lesson.ipynb
|
CurtisJohansen/classification-exercises
| 10 |
<jupyter_start><jupyter_text><jupyter_code>%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from skimage import color
from skimage.io import imread
#from skimage.data import shepp_logan_phantom
from skimage.transform import radon, rescale
from google.colab import files
uploaded = files.upload()
image_orig = mpimg.imread('abdo-ct-ped.jpg')
plt.imshow(image_orig)
print(image_orig.shape)
print(color.rgb2gray(image_orig).shape)
image_gray = color.rgb2gray(image_orig)
# Pad with zeros to get equal sizes.
image = np.zeros((max(image_orig.shape), max(image_orig.shape)))
c = ( int((image.shape[0]-image_orig.shape[0]) / 2), int((image.shape[1]-image_orig.shape[1]) / 2))
image[c[0]:c[0]+image_orig.shape[0], c[1]:c[1]+image_orig.shape[1]] = image_gray
plt.imshow(image, cmap=plt.cm.Greys_r)
print(image.shape)
#theta = np.linspace(0., 180., max(image.shape), endpoint=False)
theta = np.linspace(0., 180., 60, endpoint=False)
# I0 = 1e5
# sigma = np.sqrt(1e1)
# eps = sigma * 1e-2
#sinogram = radon(image, theta=theta, circle=True)
sinogram_orig = radon(image, theta=theta, circle=True)
# I = I0 * np.exp(-sinogram_orig)# + np.random.normal(scale=sigma, size=sinogram_orig.shape)
# # I[I <= eps] = eps
# # print(I.size)
# # print(I[I <= eps].size)
# #I[I >= eps] += np.random.poisson(I[I >= eps])
# I = np.random.poisson(I)
# sinogram = np.log(I0 / I)
#I[I <= eps] = 0
# I[I >= sigma] += np.random.poisson(I[I >= sigma])
# sinogram = np.log(I0 / I)
#sinogram = sinogram_orig + np.random.normal(scale=sigma, size=sinogram_orig.shape)
# sinogram[sinogram < sigma] = 0
# sinogram[sinogram >= sigma] += np.random.poisson(sinogram[sinogram >= sigma])
# sinogram = sinogram_poisson
# np.min(I[I >= sigma])
I0 = 1e5
sigma = 5e-2
I = I0 * np.exp(-sinogram_orig)
I += np.random.normal(scale=sigma * I)
print(I[I <= 0].size)
I[I <= 0] = 1e-4
sinogram = np.log(I0 / I)
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(12, 4.5))
ax1.set_title("Original")
ax1.imshow(image, cmap=plt.cm.Greys_r)
ax2.set_title("Noisy sinogram")
ax2.set_xlabel("Projection angle (deg)")
ax2.set_ylabel("Projection position (pixels)")
ax2.imshow(sinogram, cmap=plt.cm.Greys_r,
extent=(0, 180, 0, sinogram.shape[0]), aspect='auto')
ax3.set_title("Radon transform\n(Sinogram)")
ax3.set_xlabel("Projection angle (deg)")
ax3.set_ylabel("Projection position (pixels)")
ax3.imshow(sinogram_orig, cmap=plt.cm.Greys_r,
extent=(0, 180, 0, sinogram_orig.shape[0]), aspect='auto')
fig.tight_layout()
plt.show()
print(np.std(sinogram-sinogram_orig))<jupyter_output><empty_output><jupyter_text>Reconstruction with the Filtered Back Projection (FBP)
======================================================<jupyter_code>from skimage.transform import iradon
reconstruction_fbp = iradon(sinogram, theta=theta, circle=True)
error = reconstruction_fbp - image
print(f"FBP rms reconstruction error: {np.sqrt(np.mean(error**2)):.3g}")
imkwargs = dict(vmin=-0.2, vmax=0.2)
fig, (ax0, ax1, ax2) = plt.subplots(1, 3, figsize=(20, 24),
sharex=True, sharey=True)
ax0.set_title("Original picture downscaled")
ax0.imshow(image, cmap=plt.cm.Greys_r)
ax1.set_title("Reconstruction\nFiltered back projection")
ax1.imshow(reconstruction_fbp, cmap=plt.cm.Greys_r)
ax2.set_title("Reconstruction error\nFiltered back projection")
ax2.imshow(reconstruction_fbp - image, cmap=plt.cm.Greys_r, **imkwargs)
plt.show()<jupyter_output>FBP rms reconstruction error: 0.0453
<jupyter_text>Reconstruction with the Simultaneous Algebraic Reconstruction Technique
=======================================================================
<jupyter_code>from skimage.transform import iradon_sart
import math
relaxation = 0.6
nr_of_iterations = 4
is_momentum = False
alfa_momentum = 0.2
max_early_stopping = 2
reconstruction_sart = iradon_sart(sinogram, theta=theta, relaxation=relaxation)
error = reconstruction_sart - image
print("SART (1 iteration) rms reconstruction error: "
f"{np.sqrt(np.mean(error**2)):.3g}")
fig, axes = plt.subplots(3, 2, figsize=(20, 30), sharex=True, sharey=True)
ax = axes.ravel()
ax[0].set_title("Reconstruction\nSART")
ax[0].imshow(reconstruction_sart, cmap=plt.cm.Greys_r)
ax[1].set_title("Reconstruction error\nSART")
ax[1].imshow(reconstruction_sart - image, cmap=plt.cm.Greys_r, **imkwargs)
# Run a second iteration of SART by supplying the reconstruction
# from the first iteration as an initial estimate
reconstruction_sart2 = iradon_sart(sinogram, theta=theta,
image=reconstruction_sart, relaxation=relaxation)
error = reconstruction_sart2 - image
print("SART (2 iterations) rms reconstruction error: "
f"{np.sqrt(np.mean(error**2)):.3g}")
ax[2].set_title("Reconstruction\nSART, 2 iterations")
ax[2].imshow(reconstruction_sart2, cmap=plt.cm.Greys_r)
ax[3].set_title("Reconstruction error\nSART, 2 iterations")
ax[3].imshow(reconstruction_sart2 - image, cmap=plt.cm.Greys_r, **imkwargs)
nr_of_iterations = 4
iteration_sart = reconstruction_sart2.copy()
if is_momentum:
iteration_sart_previous = iteration_sart.copy()
previous_error = math.inf
early_stopping_counter = 0
for i in range(3, nr_of_iterations + 1):
if is_momentum == False:
iteration_sart = iradon_sart(sinogram, theta = theta, image=iteration_sart, relaxation=relaxation)
else:
previous_direction = iteration_sart - iteration_sart_previous
iteration_sart_previous = iteration_sart.copy()
iteration_sart = iradon_sart(sinogram, theta = theta,
image=iteration_sart + previous_direction * alfa_momentum,
relaxation=relaxation)
error = np.sqrt(np.mean((iteration_sart-image)**2))
print(f"SART ({i} iterations) rms reconstruction error: {error:.3g}")
if(previous_error < error):
early_stopping_counter += 1
if early_stopping_counter == max_early_stopping:
break
else: early_stopping_counter = 0
previous_error = error
reconstruction_sartX = iteration_sart
ax[4].set_title(f"Reconstruction\nSART, {nr_of_iterations} iterations")
ax[4].imshow(reconstruction_sartX, cmap=plt.cm.Greys_r)
ax[5].set_title("Reconstruction error\nSART, X iterations")
ax[5].imshow(reconstruction_sartX - image, cmap=plt.cm.Greys_r, **imkwargs)
plt.show()<jupyter_output>SART (1 iteration) rms reconstruction error: 0.0431
SART (2 iterations) rms reconstruction error: 0.0291
SART (3 iterations) rms reconstruction error: 0.0257
SART (4 iterations) rms reconstruction error: 0.0252
|
no_license
|
/NLTV_L1.ipynb
|
juhosattila/nn_tdk
| 3 |
<jupyter_start><jupyter_text># Q3 Crawling Chaos
## 問題URL:
http://ksnctf.sweetduet.info/q/3/unya.html## 概要
入力フォームと送信ボタンだけのシンプルなWebページが表示される。適当に入力・送信すると"No"が返ってくる。ブラウザのデベロッパツールでhtmlソースを覗いてみると"unya.html"内に以上に長い意味不明文字列が発見できる。(ᒧᆞωᆞ)=(/ᆞωᆞ/),(ᒧᆞωᆞ).ᒧうー=-!!(/ᆞωᆞ/).にゃー,(〳ᆞωᆞ)=(ᒧᆞωᆞ),(〳ᆞωᆞ).〳にゃー=- -!(ᒧᆞωᆞ).ᒧうー,(ᒧᆞωᆞ).ᒧうーー=(〳ᆞωᆞ).〳にゃー- -!(ᒧᆞωᆞ).ᒧうー,(〳ᆞωᆞ).〳にゃーー=(ᒧᆞωᆞ).ᒧうーー- -(〳ᆞωᆞ).〳にゃー,(ᒧᆞωᆞ).ᒧうーー=(〳ᆞωᆞ).〳にゃーー- -!(ᒧᆞωᆞ).ᒧうー,(〳ᆞωᆞ).〳にゃーー=(ᒧᆞωᆞ).ᒧうーー- -(〳ᆞωᆞ).〳にゃー,(ᒧᆞωᆞ).ᒧうーーー=(〳ᆞωᆞ).〳にゃーー- -!(ᒧᆞωᆞ).ᒧうー,(〳ᆞωᆞ).〳にゃーーー=(ᒧᆞωᆞ).ᒧうーーー- -(〳ᆞωᆞ).〳にゃー,(ᒧᆞωᆞ).ᒧうーーー=(〳ᆞωᆞ).〳にゃーーー- -!(ᒧᆞωᆞ).ᒧうー,(〳ᆞωᆞ).〳にゃーーー=(ᒧᆞωᆞ).ᒧうーーー- -(〳ᆞωᆞ).〳にゃー,ー='',(ᒧᆞωᆞ).ᒧうーーー=!(ᒧᆞωᆞ).ᒧうー+ー,(〳ᆞωᆞ).〳にゃーーー=!(〳ᆞωᆞ).〳にゃー+ー,(ᒧᆞωᆞ).ᒧうーーー={這いよれ:!(〳ᆞωᆞ).〳にゃー}+ー,(〳ᆞωᆞ).〳にゃーーー=(ᒧᆞωᆞ).ᒧニャル子さん+ー,(ᆞωᆞᒪ)=(コᆞωᆞ)=(ᒧᆞωᆞ).ᒧうー,(ᒧᆞωᆞ).ᒧうーーーー=(〳ᆞωᆞ).〳にゃーーー[(ᆞωᆞᒪ)- -(〳ᆞωᆞ).〳にゃー-(コᆞωᆞ)],(〳ᆞωᆞ).〳にゃーーーー=(ᒧᆞωᆞ).ᒧうーーー[(ᆞωᆞᒪ)- -(ᒧᆞωᆞ).ᒧうーー-(コᆞωᆞ)],(ᒧᆞωᆞ).ᒧうーーーー=(ᒧᆞωᆞ).ᒧうーーー[(ᆞωᆞᒪ)- -(〳ᆞωᆞ).〳にゃーー-(コᆞωᆞ)],(〳ᆞωᆞ).〳にゃーーーー=(〳ᆞωᆞ).〳にゃーーー[(ᆞωᆞᒪ)- -(ᒧᆞωᆞ).ᒧうーー-(コᆞωᆞ)],(ᒧᆞωᆞ).ᒧうーーーー=(ᒧᆞωᆞ).ᒧうーーー[(ᆞωᆞᒪ)- -(〳ᆞωᆞ).〳にゃーー-(コᆞωᆞ)],(〳ᆞωᆞ).〳にゃーーーー=(〳ᆞωᆞ).〳にゃーーー[(ᆞωᆞᒪ)-(コᆞωᆞ)],(ᒧᆞωᆞ).ᒧうーーーー=(〳ᆞωᆞ).〳にゃーーー[(ᆞωᆞᒪ)- -(〳ᆞωᆞ).〳にゃー-(コᆞωᆞ)],(〳ᆞωᆞ).〳にゃーーーー=(ᒧᆞωᆞ).ᒧうーーー[(ᆞωᆞᒪ)- -(〳ᆞωᆞ).〳にゃー-(コᆞωᆞ)],(ᒧᆞωᆞ).ᒧうーーーー=(ᒧᆞωᆞ).ᒧうーーー[(ᆞωᆞᒪ)- -(〳ᆞωᆞ).〳にゃー-(コᆞωᆞ)],(〳ᆞωᆞ).〳にゃーーーー=(〳ᆞωᆞ).〳にゃーーー[(ᆞωᆞᒪ)- -(〳ᆞωᆞ).〳にゃーー-(コᆞωᆞ)],(ᒧᆞωᆞ).ᒧうーーーー=(ᒧᆞωᆞ).ᒧうーーー[(ᆞωᆞᒪ)-(コᆞωᆞ)],(〳ᆞωᆞ).〳にゃーーーー=(〳ᆞωᆞ).〳にゃーーー[(ᆞωᆞᒪ)-(コᆞωᆞ)],(ᒧᆞωᆞ).ᒧうーーーー=/""ω""/+/\\ω\\/,(〳ᆞωᆞ).〳にゃーーーー=(ᒧᆞωᆞ).ᒧうーーーー[(ᆞωᆞᒪ)- -(〳ᆞωᆞ).〳にゃー-(コᆞωᆞ)],(ᒧᆞωᆞ).ᒧうーーーー=(ᒧᆞωᆞ).ᒧうーーーー[(ᆞωᆞᒪ)- -(〳ᆞωᆞ).〳にゃーーー-(コᆞωᆞ)],(〳ᆞωᆞ).〳にゃーーーー=(ᒧᆞωᆞ).ᒧうーーーー+(〳ᆞωᆞ).〳にゃーーーー,(ᒧᆞωᆞ).ᒧうーーーーー=(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうー,(〳ᆞωᆞ).〳にゃーーーーー =(ᒧᆞωᆞ).ᒧうーーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーー,(ᒧᆞωᆞ).ᒧうーーーーー=(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(ᒧᆞωᆞ).ᒧうー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(ᒧᆞωᆞ).ᒧうーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーーー+(〳ᆞωᆞ).〳にゃーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーーー+(〳ᆞωᆞ).〳にゃーーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(ᒧᆞωᆞ).ᒧうーー+(〳ᆞωᆞ).〳にゃーーー+(ᒧᆞωᆞ).ᒧうーーーーー+(〳ᆞωᆞ).〳にゃーー+(〳ᆞωᆞ).〳にゃーーーー+(〳ᆞωᆞ).〳にゃーーーー,(ᆞωᆞᒪ)=(コᆞωᆞ)=ー,(〳ᆞωᆞ).〳にゃーーーーー=(ᒧᆞωᆞ).ᒧうー[(ᆞωᆞᒪ)+(〳ᆞωᆞ).〳にゃーーーーー+(コᆞωᆞ)][(ᆞωᆞᒪ)+(〳ᆞωᆞ).〳にゃーーーーー+(コᆞωᆞ)],ᆞωᆞ=(ᒧᆞωᆞ).ᒧうー,(ᒧᆞωᆞ).ᒧうーーーーー=(〳ᆞωᆞ).〳にゃーーーーー(ᆞωᆞᒪ+(ᒧᆞωᆞ).ᒧうーーーーー+コᆞωᆞ)(ᆞωᆞ),(ᒧᆞωᆞ).ᒧうーーーーー=(〳ᆞωᆞ).〳にゃーーーーー(ᆞωᆞᒪ+(ᒧᆞωᆞ).ᒧうーーーーー+コᆞωᆞ)(ᆞωᆞ),(ᒧᆞωᆞ).ᒧうー=-!!(/ᆞωᆞ/).にゃー,(〳ᆞωᆞ).〳にゃー=- -!(ᒧᆞωᆞ).ᒧうー,(ᒧᆞωᆞ).ᒧうーー=(〳ᆞωᆞ).〳にゃー- -!(ᒧᆞωᆞ).ᒧうー,(〳ᆞωᆞ).〳にゃーー=(ᒧᆞωᆞ).ᒧうーー- -(〳ᆞωᆞ).〳にゃー,(ᒧᆞωᆞ).ᒧうーー=(〳ᆞωᆞ).〳にゃーー- -!(ᒧᆞωᆞ).ᒧうー,(〳ᆞωᆞ).〳にゃーー=(ᒧᆞωᆞ).ᒧうーー- -(〳ᆞωᆞ).〳にゃー,(ᒧᆞωᆞ).ᒧうーーー=(〳ᆞωᆞ).〳にゃーー- -!(ᒧᆞωᆞ).ᒧうー,(〳ᆞωᆞ).〳にゃーーー=(ᒧᆞωᆞ).ᒧうーーー- -(〳ᆞωᆞ).〳にゃー,(ᒧᆞωᆞ).ᒧうーーー=(〳ᆞωᆞ).〳にゃーーー- -!(ᒧᆞωᆞ).ᒧうー,(〳ᆞωᆞ).〳にゃーーー=(ᒧᆞωᆞ).ᒧうーーー- -(〳ᆞωᆞ).〳にゃー,(ᆞωᆞ)`` で囲まれているということは` (ᒧᆞωᆞ)=(/ᆞωᆞ/),(ᒧᆞωᆞ).ᒧうー=-!!(/ᆞωᆞ/).にゃー `は何かしらのスクリプトであると推察できる。デベロッパツールのconsoleで`console.log([上記うーにゃーのスクリプト])`として実行してみるとメッセージ欄にそれっぽいエラーコードがでるあるいは、`hoge.js`として保存して実行しても良い。#### メッセージ
/ᆞωᆞ/ -0 /ᆞωᆞ/ 1 2 3 4 5 6 7 8 9 "" "true" "false" "[object Object]" "undefined" -0 "a" "b" "c" "d" "e" "f" "n" "o" "r" "s" "t" "u" "/""ω""//\\ω\\/" """ "\" "\u" "\u00" "constructor" "return"\u0024\u0028\u0066\u0075\u006e\u0063\u0074\u0069\u006f\u006e\u0028\u0029\u007b\u0024\u0028\u0022\u0066\u006f\u0072\u006d\u0022\u0029\u002e\u0073\u0075\u0062\u006d\u0069\u0074\u0028\u0066\u0075\u006e\u0063\u0074\u0069\u006f\u006e\u0028\u0029\u007b\u0076\u0061\u0072\u0020\u0074\u003d\u0024\u0028\u0027\u0069\u006e\u0070\u0075\u0074\u005b\u0074\u0079\u0070\u0065\u003d\u0022\u0074\u0065\u0078\u0074\u0022\u005d\u0027\u0029\u002e\u0076\u0061\u006c\u0028\u0029\u003b\u0076\u0061\u0072\u0020\u0070\u003d\u0041\u0072\u0072\u0061\u0079\u0028\u0037\u0030\u002c\u0031\u0035\u0032\u002c\u0031\u0039\u0035\u002c\u0032\u0038\u0034\u002c\u0034\u0037\u0035\u002c\u0036\u0031\u0032\u002c\u0037\u0039\u0031\u002c\u0038\u0039\u0036\u002c\u0038\u0031\u0030\u002c\u0038\u0035\u0030\u002c\u0037\u0033\u0037\u002c\u0031\u0033\u0033\u0032\u002c\u0031\u0034\u0036\u0039\u002c\u0031\u0031\u0032\u0030\u002c\u0031\u0034\u0037\u0030\u002c\u0038\u0033\u0032\u002c\u0031\u0037\u0038\u0035\u002c\u0032\u0031\u0039\u0036\u002c\u0031\u0035\u0032\u0030\u002c\u0031\u0034\u0038\u0030\u002c\u0031\u0034\u0034\u0039\u0029\u003b\u0076\u0061\u0072\u0020\u0066\u003d\u0066\u0061\u006c\u0073\u0065\u003b\u0069\u0066\u0028\u0070\u002e\u006c\u0065\u006e\u0067\u0074\u0068\u003d\u003d\u0074\u002e\u006c\u0065\u006e\u0067\u0074\u0068\u0029\u007b\u0066\u003d\u0074\u0072\u0075\u0065\u003b\u0066\u006f\u0072\u0028\u0076\u0061\u0072\u0020\u0069\u003d\u0030\u003b\u0069\u003c\u0070\u002e\u006c\u0065\u006e\u0067\u0074\u0068\u003b\u0069\u002b\u002b\u0029\u0069\u0066\u0028\u0074\u002e\u0063\u0068\u0061\u0072\u0043\u006f\u0064\u0065\u0041\u0074\u0028\u0069\u0029\u002a\u0028\u0069\u002b\u0031\u0029\u0021\u003d\u0070\u005b\u0069\u005d\u0029\u0066\u003d\u0066\u0061\u006c\u0073\u0065\u003b\u0069\u0066\u0028\u0066\u0029\u0061\u006c\u0065\u0072\u0074\u0028\u0022\u0028\u300d\u30fb\u03c9\u30fb\u0029\u300d\u3046\u30fc\u0021\u0028\u002f\u30fb\u03c9\u30fb\u0029\u002f\u306b\u3083\u30fc\u0021\u0022\u0029\u003b\u007d\u0069\u0066\u0028\u0021\u0066\u0029\u0061\u006c\u0065\u0072\u0074\u0028\u0022\u004e\u006f\u0022\u0029\u003b\u0072\u0065\u0074\u0075\u0072\u006e\u0020\u0066\u0061\u006c\u0073\u0065\u003b\u007d\u0029\u003b\u007d\u0029\u003b"" "" ƒ Function() { [native code] } -0 "$(function(){$("form").submit(function(){var t=$('input[type="text"]').val();var p=Array(70,152,195,284,475,612,791,896,810,850,737,1332,1469,1120,1470,832,1785,2196,1520,1480,1449);var f=false;if(p.length==t.length){f=true;for(var i=0;i<p.length;i++)if(t.charCodeAt(i)*(i+1)!=p[i])f=false;if(f)alert("(」・ω・)」うー!(/・ω・)/にゃー!");}if(!f)alert("No");return false;});});" undefined -0 1 2 3 4 5 6 7 8 9 -0コードと思しき部分を整形すると以下のようになる
`
$(function(){
$("form").submit(function(){
var t=$('input[type="text"]').val();
var p=Array(70,152,195,284,475,612,791,896,810,850,737,1332,1469,1120,1470,832,1785,2196,1520,1480,1449);
var f=false;
if(p.length==t.length){
f=true;
for(var i=0;i<p.length;i++)
if(t.charCodeAt(i)*(i+1)!=p[i])
f=false;
if(f)
alert("(」・ω・)」うー!(/・ω・)/にゃー!");
}
if(!f)
alert("No");
return false;
}
);
});
`## スクリプト解析:何をしているのか
このコードは入力フォームで受け付けた文字列が正しい長さだった場合、
1. 配列 p を用いて正しい文字列であるかを判断し
1. 完全に正しい場合`(」・ω・)」うー!(/・ω・)/にゃー!` とポップアップを表示し
1. それ以外の場合には`No`を表示する
つまり、**配列pを用いて正解の文が生成可能である!**### フラグ取得スクリプト JavaScript 版
`
// javascript flag.js
var flag = "";
var o = '';
var p = Array(70, 152, 195, 284, 475, 612, 791, 896, 810, 850, 737, 1332, 1469, 1120, 1470, 832, 1785, 2196, 1520, 1480, 1449);
for (var i = 0; i < p.length; i++) {
//pの値から本来入力するべき値を逆算する
var o = p[i] / (i + 1);
//Strings.fromCode(o)でoの数値をUnicodeの文字に戻す
var flag = flag + String.fromCharCode(o);
};
console.log(flag);
`### フラグ取得スクリプト Python 版<jupyter_code>flag = ''
P = [70, 152, 195, 284, 475, 612, 791, 896, 810, 850, 737, 1332, 1469, 1120, 1470, 832, 1785, 2196, 1520, 1480, 1449]
for i, p in enumerate(P):
code = p//(i+1)
flag+=chr(code)
flag<jupyter_output><empty_output>
|
no_license
|
/ksnctf/KSNCTF/3/Q3_Crawling_Chaos.ipynb
|
adshidtadka/ctf
| 1 |
<jupyter_start><jupyter_text># Количество экземлпяров = 120, количество признаков = 12, из них информативных = 3, шум - случайное число в диапозоне 1-20### генерация выборк<jupyter_code>noiseRandom=random.randint(1,20)
noiseRandom
data, target, coef = datasets.make_regression(n_samples = 120, n_features = 12, n_informative = 3, n_targets = 1,
noise = noiseRandom, coef = True, random_state = 2)
<jupyter_output><empty_output><jupyter_text>### Вывод графиков зависимости target от всех признаков<jupyter_code>pyplot.figure(figsize(20, 20))
for plot_number in range(np.size(data,1)):
pyplot.subplot(4, 4, plot_number + 1)
pyplot.scatter(list(map(lambda x : x[plot_number], data)), target, color = 'b')
pyplot.title('feature ' + str(plot_number))
pyplot.xlabel(str(plot_number))
pyplot.ylabel('target')
<jupyter_output><empty_output><jupyter_text>### Обучение модели линейной регрессии на всей сгенерированной выборке
### Вывод в виде уранений<jupyter_code>regression_model = linear_model.LinearRegression()
regression_model.fit(data, target)
predictions = regression_model.predict(data)
print ("Learned regression model")
print ("y = {:.3f}*x1 + {:.3f}*x2 + {:.3f}*x3 + {:.3f}*x4 + {:.3f}*x5 + {:.3f}*x6 + {:.3f}*x7 + {:.3f}*x8 + {:.3f}*x9 + {:.3f}*x10 + {:.3f}*x11+ {:.3f}*x12 +{:.3f}\n"
.format(linear_regressor.coef_[0],
linear_regressor.coef_[1],
linear_regressor.coef_[2],
linear_regressor.coef_[3],
linear_regressor.coef_[4],
linear_regressor.coef_[5],
linear_regressor.coef_[6],
linear_regressor.coef_[7],
linear_regressor.coef_[8],
linear_regressor.coef_[9],
linear_regressor.coef_[10],
linear_regressor.coef_[11],
linear_regressor.intercept_))
print ("True regression model")
print ("y = {:.3f}*x1 + {:.3f}*x2 + {:.3f}*x3 + {:.3f}*x4 + {:.3f}*x5 + {:.3f}*x6 + {:.3f}*x7 + {:.3f}*x8 + {:.3f}*x9 + {:.3f}*x10 + {:.3f}*x11 + {:.3f}*x12\n "
.format(coef[0],
coef[1],
coef[2],
coef[3],
coef[4],
coef[5],
coef[6],
coef[7],
coef[8],
coef[9],
coef[10],
coef[11]))<jupyter_output>Learned regression model
y = -0.108*x1 + 0.046*x2 + 0.021*x3 + 2.687*x4 + -17.767*x5 + 3.810*x6 + 0.001*x7 + -1.476*x8 + 0.306*x9 + -0.012*x10 + -0.953*x11+ 0.009*x12 +36.459
True regression model
y = 0.000*x1 + 45.740*x2 + 10.578*x3 + 0.000*x4 + 0.000*x5 + 0.000*x6 + 0.000*x7 + 0.000*x8 + 17.355*x9 + 0.000*x10 + 0.000*x11 + 0.000*x12
<jupyter_text>### Подсчет RMSE на всей выборке<jupyter_code>from sklearn import metrics
mae = metrics.mean_absolute_error(target, predictions)
print ('MAE = ', mae)
mse = metrics.mean_squared_error(target, predictions)
print ('MSE = ', mse)<jupyter_output>MAE = 4.4825679482086604
MSE = 31.79798390714765
|
no_license
|
/Linear regression/Linear regression.ipynb
|
IlinykhYE/Data-mining
| 4 |
<jupyter_start><jupyter_text># US - Baby Names### Introduction:
We are going to use a subset of [US Baby Names](https://www.kaggle.com/kaggle/us-baby-names) from Kaggle.
In the file it will be names from 2004 until 2014
### Step 1. Import the necessary libraries<jupyter_code>import pandas as pd
import numpy as np<jupyter_output><empty_output><jupyter_text>### Step 2. Import the dataset from this [address](https://raw.githubusercontent.com/guipsamora/pandas_exercises/master/06_Stats/US_Baby_Names/US_Baby_Names_right.csv). ### Step 3. Assign it to a variable called baby_names.<jupyter_code>baby_names = pd.read_csv('https://raw.githubusercontent.com/guipsamora/pandas_exercises/master/06_Stats/US_Baby_Names/US_Baby_Names_right.csv', sep=',')<jupyter_output><empty_output><jupyter_text>### Step 4. See the first 10 entries<jupyter_code>baby_names.head()
baby_names.info()
baby_names.shape
# total number of names
baby_names.Name.count()
# how many unique names
baby_names.Name.nunique()
# how many times a name is repeated
baby_names.Name.value_counts()
# WE CAN CHECK FOR EACH NME HOW MANY TIMES REPEATED
(baby_names['Name'].values == 'Emily').sum()<jupyter_output><empty_output><jupyter_text>### Step 5. Delete the column 'Unnamed: 0' and 'Id'<jupyter_code>baby_names = baby_names.drop(labels = ['Unnamed: 0', 'Id'] , axis =1)
baby_names<jupyter_output><empty_output><jupyter_text>### Step 6. Is there more male or female names in the dataset?<jupyter_code>#different ways to calculate
# baby_names.Gender == 'M' # returns boolean value
baby_names.Gender.value_counts()
(baby_names['Gender'].values == 'M').sum()
(baby_names['Gender'].values == 'F').sum()
baby_names[baby_names.Gender == 'M'].value_counts()
baby_names[baby_names.Gender == 'F'].value_counts()<jupyter_output><empty_output><jupyter_text>### Step 7. Group the dataset by name and assign to names<jupyter_code># delete the year col
names = baby_names.drop(['Year'], axis=1)
names
# only cols with int values will be added
names=names.groupby(['Name']).sum()
names
names.shape<jupyter_output><empty_output><jupyter_text>### Step 8. How many different names exist in the dataset?<jupyter_code>baby_names.Name.nunique()
# as names df is gouped by Name alredy, so only unique names included
len(names)<jupyter_output><empty_output><jupyter_text>### Step 9. What is the name with most occurrences?<jupyter_code># idxmax() find the index of the maximum value along the index axis
names.Count.idxmax()
names.sort_values(by='Count', ascending=False)
names.Count.max()<jupyter_output><empty_output><jupyter_text>### Step 10. How many different names have the least occurrences?<jupyter_code>#different ways to do it
# we have to find how many of names have least occurances
names['Count'].value_counts()
# as we already know 5 is least occurent count
(names['Count'].values == 5).sum()
# we get df with names having least occurence
names[names['Count'] == names.Count.min()]<jupyter_output><empty_output><jupyter_text>### Step 11. What is the median name occurrence?<jupyter_code>names.median()
(names['Count'].values == 49).sum()
# To print df with names for count = 49
# names[names.Count == names.Count.median()]
names[names['Count'] == names.Count.median()]<jupyter_output><empty_output><jupyter_text>### Step 12. What is the standard deviation of names?<jupyter_code>names.std()<jupyter_output><empty_output><jupyter_text>### Step 13. Get a summary with the mean, min, max, std and quartiles.<jupyter_code>names.describe()<jupyter_output><empty_output>
|
no_license
|
/06_Stats/US_Baby_Names/Exercises.ipynb
|
prativadas/pandas_excercises
| 12 |
<jupyter_start><jupyter_text>## 1. Introduction
Version control repositories like CVS, Subversion or Git can be a real gold mine for software developers. They contain every change to the source code including the date (the "when"), the responsible developer (the "who"), as well as little message that describes the intention (the "what") of a change.
In this notebook, we will analyze the evolution of a very famous open-source project – the Linux kernel. The Linux kernel is the heart of some Linux distributions like Debian, Ubuntu or CentOS.
We get some first insights into the work of the development efforts by
identifying the TOP 10 contributors and
visualizing the commits over the years.
Linus Torvalds, the (spoiler alert!) main contributor to the Linux kernel (and also the creator of Git), created a mirror of the Linux repository on GitHub. It contains the complete history of kernel development for the last 13 years.
For our analysis, we will use a Git log file with the following content:<jupyter_code># Printing the content of git_log_excerpt.csv
!head datasets/git_log_excerpt.csv<jupyter_output>1502382966#Linus Torvalds
1501368308#Max Gurtovoy
1501625560#James Smart
1501625559#James Smart
1500568442#Martin Wilck
1502273719#Xin Long
1502278684#Nikolay Borisov
1502238384#Girish Moodalbail
1502228709#Florian Fainelli
1502223836#Jon Paul Maloy<jupyter_text>## 2. Reading in the dataset
The dataset was created by using the command git log --encoding=latin-1 --pretty="%at#%aN". The latin-1 encoded text output was saved in a header-less csv file. In this file, each row is a commit entry with the following information:
timestamp: the time of the commit as a UNIX timestamp in seconds since 1970-01-01 00:00:00 (Git log placeholder "%at")
author: the name of the author that performed the commit (Git log placeholder "%aN")
The columns are separated by the number sign #. The complete dataset is in the datasets/ directory. It is a gz-compressed csv file named git_log.gz.<jupyter_code># Loading in the pandas module
import pandas as pd
# Reading in the log file
git_log = pd.read_csv("datasets/git_log.gz", sep="#", encoding="latin-1", header=None, names=["timestamp", "author"])
# Printing out the first 5 rows
git_log.head()
<jupyter_output><empty_output><jupyter_text>## 3. Getting an overview
The dataset contains the information about every single code contribution (a "commit") to the Linux kernel over the last 13 years. We'll first take a look at the number of authors and their commits to the repository.<jupyter_code># calculating number of commits
number_of_commits = len(git_log)
# calculating number of authors
number_of_authors = git_log["author"].nunique()
# printing out the results
print("%s authors committed %s code changes." % (number_of_authors, number_of_commits))<jupyter_output>17385 authors committed 699071 code changes.
<jupyter_text>## 4. Finding the TOP 10 contributors
There are some very important people that changed the Linux kernel very often. To see if there are any bottlenecks, we take a look at the TOP 10 authors with the most commits.<jupyter_code># Identifying the top 10 authors
top_10_authors = git_log["author"].value_counts().nlargest(10)
# Listing contents of 'top_10_authors'
top_10_authors<jupyter_output><empty_output><jupyter_text>## 5. Wrangling the data
For our analysis, we want to visualize the contributions over time. For this, we use the information in the timestamp column to create a time series-based column.<jupyter_code># converting the timestamp column
#git_log["timestamp"] = pd.Timestamp(git_log["timestamp"], unit = "s")
git_log["timestamp"] = pd.to_datetime(git_log["timestamp"], unit = "s")
# summarizing the converted timestamp column
git_log.timestamp.describe()<jupyter_output><empty_output><jupyter_text>## 6. Treating wrong timestamps
As we can see from the results above, some contributors had their operating system's time incorrectly set when they committed to the repository. We'll clean up the timestamp column by dropping the rows with the incorrect timestamps.<jupyter_code># determining the first real commit timestamp
first_commit_timestamp = git_log.timestamp.iloc[-1]
# determining the last sensible commit timestamp
#last_commit_timestamp = pd.to_datetime("today")
last_commit_timestamp = pd.to_datetime("2017-10-03 12:57:00", format="%Y-%m-%d")
# filtering out wrong timestamps
corrected_log = git_log[(git_log["timestamp"] <= last_commit_timestamp) & (git_log["timestamp"] >= first_commit_timestamp)]
# summarizing the corrected timestamp column
corrected_log["timestamp"].describe()
<jupyter_output><empty_output><jupyter_text>## 7. Grouping commits per year
To find out how the development activity has increased over time, we'll group the commits by year and count them up.<jupyter_code># Counting the no. commits per year
commits_per_year = corrected_log.groupby(pd.Grouper(key = "timestamp", freq = "AS")).count()
# Listing the first rows
commits_per_year.head(5)<jupyter_output><empty_output><jupyter_text>## 8. Visualizing the history of Linux
Finally, we'll make a plot out of these counts to better see how the development effort on Linux has increased over the the last few years. <jupyter_code># Setting up plotting in Jupyter notebooks
%matplotlib inline
# plot the data
commits_per_year.plot(kind = "bar", title = "Annual Linux Commits", legend = False)<jupyter_output><empty_output><jupyter_text>## 9. Conclusion
Thanks to the solid foundation and caretaking of Linux Torvalds, many other developers are now able to contribute to the Linux kernel as well. There is no decrease of development activity at sight!<jupyter_code># calculating or setting the year with the most commits to Linux
year_with_most_commits = "2016"<jupyter_output><empty_output>
|
no_license
|
/Python--Exploring_the_evolution_of_Linux/notebook.ipynb
|
nlt-python/Datacamp_Projects
| 9 |
<jupyter_start><jupyter_text># Toronto - The City Of Neighborhoods The strength and vitality of the many neighbourhoods that make up Toronto, Ontario, Canada has earned the city its unofficial nickname of "the city of neighbourhoods. There are over 140 neighbourhoods officially recognized by the City of Toronto. The aim of this project is to explore, segment and clusterise Toronto according to its neighborhoods and find similarites and disimilarities using data science techniques.### Install Dependencies<jupyter_code>!pip3 install bs4
!pip3 install requests
!pip3 install html5lib<jupyter_output>Requirement already satisfied: bs4 in /opt/anaconda3/lib/python3.7/site-packages (0.0.1)
Requirement already satisfied: beautifulsoup4 in /opt/anaconda3/lib/python3.7/site-packages (from bs4) (4.8.2)
Requirement already satisfied: soupsieve>=1.2 in /opt/anaconda3/lib/python3.7/site-packages (from beautifulsoup4->bs4) (1.9.5)
Requirement already satisfied: requests in /opt/anaconda3/lib/python3.7/site-packages (2.22.0)
Requirement already satisfied: urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1 in /opt/anaconda3/lib/python3.7/site-packages (from requests) (1.25.8)
Requirement already satisfied: certifi>=2017.4.17 in /opt/anaconda3/lib/python3.7/site-packages (from requests) (2019.11.28)
Requirement already satisfied: chardet<3.1.0,>=3.0.2 in /opt/anaconda3/lib/python3.7/site-packages (from requests) (3.0.4)
Requirement already satisfied: idna<2.9,>=2.5 in /opt/anaconda3/lib/python3.7/site-packages (from requests) (2.8)
Requirement already satisfied: html5lib in /opt/anaconda3/lib/python3.7/si[...]<jupyter_text>### Import Dependencies
We import Beautifulsoup dependency for web scraping of wikipedia page, requests for making http calls, html5lib a type of beautifulsoup parser for html files and pandas for working with extracted data in the form of a dataframe
<jupyter_code>from bs4 import BeautifulSoup
import requests
import html5lib
import pandas as pd<jupyter_output><empty_output><jupyter_text>## Data Collection - Scrape Files<jupyter_code>scraping_url = "https://en.wikipedia.org/wiki/List_of_postal_codes_of_Canada:_M"
html_file = requests.get(scraping_url).text
soup = BeautifulSoup(html_file, "html5lib")
pd.set_option("display.max_columns", None)
<jupyter_output><empty_output><jupyter_text>## Data Preprocessing - Convert Files into DataFrame
The scraped html files will be conerted using pandas into a dataframe consisting on three columns postal code , borough and neighborhood<jupyter_code># Create a list of neighborhoods
neighborhoods = []
for row in soup.find("table").findAll("td"):
data = {}
if row.span.text == "Not assigned":
pass
else:
data["PostalCode"] = row.p.text[:3]
data["Borough"] = row.span.text.split("(")[0]
data["Neighborhood"] = (((row.span.text.split("(")[1]).strip(")")).replace("/",",").replace(')',' ')).strip(' ')
neighborhoods.append(data)
# create dataframe
df = pd.DataFrame(neighborhoods)
# replace outlying formats for boroughs
df['Borough']=df['Borough'].replace({
'Downtown TorontoStn A PO Boxes25 The Esplanade':'Downtown Toronto Stn A',
'East TorontoBusiness reply mail Processing Centre969 Eastern':'East Toronto Business',
'EtobicokeNorthwest':'Etobicoke Northwest',
'East YorkEast Toronto':'East York/East Toronto',
'MississaugaCanada Post Gateway Processing Centre':'Mississauga'})
# replace not assigned neighborhoods
not_assigned_neighborhoods = df[df["Neighborhood"]== "Not assigned"]
not_assigned_neighborhoods["Neighborhood"] = not_assigned_neighborhoods["Borough"]
df.sort_values(["PostalCode"],ascending=True, inplace=True)
df.reset_index(drop=True,inplace=True)
df.head(10)
print(df.shape)<jupyter_output>(103, 3)
<jupyter_text>### Get the Latitude and Longitude based on Postal Codes<jupyter_code>gc_df = pd.read_csv("Geospatial_Coordinates.csv")
gc_df.head()
df["Latitude"] = gc_df[df["PostalCode"] == gc_df["Postal Code"]]["Latitude"]
df["Longitude"] = gc_df[df["PostalCode"] == gc_df["Postal Code"]]["Longitude"]
df.head(5)<jupyter_output><empty_output><jupyter_text>## Exploring Neighborhoods
We want to explore the borough that has the large number of neighborhoods to find out similiarities amongst it neighbourhood Get the Borough with the maximum number of postal codes placement<jupyter_code>grouped_neighbourhood = df.groupby(["Borough"], axis=0).count()
grouped_neighbourhood.sort_values(["PostalCode"], ascending=False, inplace=True)
grouped_neighbourhood.reset_index(inplace=True)
grouped_neighbourhood.head(1)<jupyter_output><empty_output><jupyter_text>### Get the Borough with the maximum number of neighborhoods<jupyter_code>
# for each row get the number of neighbourhood in it
# first create a new data frame
new_neighborhoods = []
for index, row in df.iterrows():
data = {}
data["Borough"] = row["Borough"]
data["Neighborhood Count"] = row["Neighborhood"].count(",") + 1
new_neighborhoods.append(data)
neighborhoods_count = pd.DataFrame(new_neighborhoods)
grouped_neighbourhood = neighborhoods_count.groupby(["Borough"], axis=0).sum()
grouped_neighbourhood.sort_values(["Neighborhood Count"], ascending=False, inplace=True)
grouped_neighbourhood.reset_index(inplace=True)
grouped_neighbourhood.head(1)<jupyter_output><empty_output><jupyter_text>The results shows that while North York has the highest number of postal codes placements in the city of Toronto, Etobicoke has the highest numbr of neighborhoods. However because each postal code is attached to just a set of longitude and latitude, we will be using North York that has more postal codes instead of Etobicoke### Exploring North York NeighborhoodsWe install and import the neccessary packages for our exploration<jupyter_code>north_york_data = df[df["Borough"] == "North York"].reset_index(drop=True)
north_york_data.head()
from geopy.geocoders import Nominatim
from sklearn.cluster import KMeans
import json
import matplotlib.colors as colors
import matplotlib.cm as cm
import folium
geolocator = Nominatim(user_agent="ny_explorer")
location = geolocator.geocode("North York, Toronto")
latitude = location.latitude
longitude = location.longitude
print('The geograpical coordinate of North York, Toronto are {}, {}.'.format(latitude, longitude))<jupyter_output>The geograpical coordinate of North York, Toronto are 43.7543263, -79.44911696639593.
<jupyter_text>### Map of North York with its neighbourhoods superimposed on it.<jupyter_code>north_york_map = folium.Map(location=[latitude,longitude], zoom_start=10)
for lat, lng, label in zip(north_york_data['Latitude'], north_york_data['Longitude'], north_york_data['Neighborhood']):
label = folium.Popup(label, parse_html=True)
folium.CircleMarker(
[lat, lng],
radius=5,
popup=label,
color='blue',
fill=True,
fill_color='#3186cc',
fill_opacity=0.7,
parse_html=False).add_to(north_york_map)
north_york_map<jupyter_output><empty_output><jupyter_text>### Using Forsquare API
using foursquare api, we collect data about places nearby to a specific longitude and latitude<jupyter_code>CLIENT_ID = '*************************' # your Foursquare ID
CLIENT_SECRET = '*********************' # your Foursquare Secret
ACCESS_TOKEN = "***********************" # your FourSquare Access Token
VERSION = '20180605' # Foursquare API version
LIMIT = 100<jupyter_output><empty_output><jupyter_text>Let explore the neighbourhoods of north york by getting the top nearby venues for each neighbourhood in north york. <jupyter_code>
def getNearbyVenues(names, latitudes, longitudes, radius=500):
venues_list=[]
for name, lat, lng in zip(names, latitudes, longitudes):
# create the API request URL
url = 'https://api.foursquare.com/v2/venues/explore?&client_id={}&client_secret={}&v={}&ll={},{}&radius={}&limit={}'.format(
CLIENT_ID,
CLIENT_SECRET,
VERSION,
lat,
lng,
radius,
LIMIT)
# make the GET request
results = requests.get(url).json()["response"]['groups'][0]['items']
# return only relevant information for each nearby venue
venues_list.append([(
name,
lat,
lng,
venue['venue']['name'],
venue['venue']['location']['lat'],
venue['venue']['location']['lng'],
venue['venue']['categories'][0]['name']) for venue in results])
nearby_venues = pd.DataFrame([item for venue_list in venues_list for item in venue_list])
nearby_venues.columns = ['Neighborhood',
'Neighborhood Latitude',
'Neighborhood Longitude',
'Venue',
'Venue Latitude',
'Venue Longitude',
'Venue Category']
return(nearby_venues)
north_york_venues = getNearbyVenues(north_york_data["Neighborhood"], north_york_data["Latitude"], north_york_data["Longitude")
north_york_venues
print(north_york_venues.groupby("Neighborhood").count().shape)
north_york_venues.groupby("Neighborhood").count()
#
# one of the neighborhoods in north york have no nearby places with a 500m range<jupyter_output><empty_output><jupyter_text>## Analyzing North York Neighbourhoods
To be able to use this information for clustering we create dummy variables for each category<jupyter_code>
# add neighborhood column back to dataframe
north_york_dummies = pd.get_dummies(north_york_venues[['Venue Category']], prefix="", prefix_sep="")
north_york_dummies['Neighborhood'] = north_york_venues['Neighborhood']
# move neighborhood column to the first column
fixed_columns = [north_york_dummies.columns[-1]] + list(north_york_dummies.columns[:-1])
north_york_dummies = north_york_dummies[fixed_columns]
north_york_grouped = north_york_dummies.groupby("Neighborhood").mean().reset_index()
north_york_grouped
north_york_grouped.shape<jupyter_output><empty_output><jupyter_text>Lets print 10 top venues for each neighborhood<jupyter_code>import numpy as np
def return_most_common_venues(row, num_top_venues):
row_categories = row.iloc[1:]
row_categories_sorted = row_categories.sort_values(ascending=False)
return row_categories_sorted.index.values[0:num_top_venues]
num_top_venues = 10
indicators = ['st', 'nd', 'rd']
# create columns according to number of top venues
columns = ['Neighborhood']
for ind in np.arange(num_top_venues):
try:
columns.append('{}{} Most Common Venue'.format(ind+1, indicators[ind]))
except:
columns.append('{}th Most Common Venue'.format(ind+1))
# create a new dataframe
neighborhoods_venues_sorted = pd.DataFrame(columns=columns)
neighborhoods_venues_sorted['Neighborhood'] = north_york_grouped['Neighborhood']
for ind in np.arange(north_york_grouped.shape[0]):
neighborhoods_venues_sorted.iloc[ind, 1:] = return_most_common_venues(north_york_grouped.iloc[ind, :], num_top_venues)
neighborhoods_venues_sorted<jupyter_output><empty_output><jupyter_text>### Get Most Common Places in North York , Toronto<jupyter_code># get the unique list of most_common_places in all neigh
def get_most_common_place(neighborhoods_venues_sorted,val):
common_places_list = [venue for venues in neighborhoods_venues_sorted.iloc[:,val:].to_numpy() for venue in venues]
common_venues = pd.Series(np.array(common_places_list)).value_counts()
most_common_venues = common_venues.to_frame()
most_common_venues.reset_index(inplace =True)
most_common_venues.columns = ["Venues","Count"]
return most_common_venues
most_common_venues_in_north_york = get_most_common_place(neighborhoods_venues_sorted,1)
Ten_most_common_venues_in_north_york = most_common_venues_in_north_york .head(10)
Ten_most_common_venues_in_north_york<jupyter_output><empty_output><jupyter_text>The results show that while you are in any neighbourhood of North York Toronto, within a raduis of 500M of the neighborhood, you are most likely to see one of the following: miscellaneous shop, mobile phone shop, middle Eastern restaurant, movie theater, metro station, Coffee shop, Accessories store, park , lounge or pizza place## Clustering Neighborhoods in North YorkThere are 23 neighborhoods with nearby venues. We want to cluster them into four clusters to understand the similarities between this neighborhoods<jupyter_code>kclusters = 4
north_york_clustering_data = north_york_grouped.drop("Neighborhood", 1)
kmeans = KMeans(n_clusters=kclusters, random_state=0).fit(north_york_clustering_data)
kmeans.labels_
if 'Cluster Labels' in neighborhoods_venues_sorted.columns:
del neighborhoods_venues_sorted["Cluster Labels"]
neighborhoods_venues_sorted.insert(0, 'Cluster Labels', kmeans.labels_)
ny_merged = north_york_data
# merge manhattan_grouped with manhattan_data to add latitude/longitude for each neighborhood
ny_merged = ny_merged.join(neighborhoods_venues_sorted.set_index('Neighborhood'), on='Neighborhood')
# remove the neighborhood without any neraby values
ny_merged.dropna(inplace=True)
ny_merged["Cluster Labels"] = ny_merged["Cluster Labels"].astype(int)
ny_merged.reset_index(drop=True)
ny_merged.head()
map_clusters = folium.Map(location=[latitude, longitude], zoom_start=11)
# set color scheme for the clusters
x = np.arange(kclusters)
ys = [i + x + (i*x)**2 for i in range(kclusters)]
colors_array = cm.rainbow(np.linspace(0, 1, len(ys)))
rainbow = [colors.rgb2hex(i) for i in colors_array]
# add markers to the map
markers_colors = []
for lat, lon, poi, cluster in zip(ny_merged['Latitude'], ny_merged['Longitude'], ny_merged['Neighborhood'], ny_merged
['Cluster Labels']):
label = folium.Popup(str(poi) + ' Cluster ' + str(cluster), parse_html=True)
folium.CircleMarker(
[lat, lon],
radius=5,
popup=label,
color=rainbow[cluster-1],
fill=True,
fill_color=rainbow[cluster-1],
fill_opacity=0.7).add_to(map_clusters)
map_clusters
first_cluster =ny_merged.loc[ny_merged['Cluster Labels'] == 0, ny_merged.columns[[1] + list(range(5, ny_merged.shape[1]))]]
first_cluster
second_cluster =ny_merged.loc[ny_merged['Cluster Labels'] == 1, ny_merged.columns[[1] + list(range(5, ny_merged.shape[1]))]]
second_cluster
third_cluster =ny_merged.loc[ny_merged['Cluster Labels'] == 2, ny_merged.columns[[1] + list(range(5, ny_merged.shape[1]))]]
third_cluster
fourth_cluster =ny_merged.loc[ny_merged['Cluster Labels'] == 3, ny_merged.columns[[1] + list(range(5, ny_merged.shape[1]))]]
fourth_cluster
clusters = [first_cluster, second_cluster, third_cluster, fourth_cluster]
for cluster in clusters:
print(get_most_common_place(cluster, 2).head(10),"\n")<jupyter_output> Venues Count
0 Middle Eastern Restaurant 7
1 Mobile Phone Shop 7
2 Movie Theater 6
3 Miscellaneous Shop 6
4 Pizza Place 6
5 Coffee Shop 5
6 Accessories Store 4
7 Lounge 3
8 Bank 3
9 Pharmacy 3
Venues Count
0 Miscellaneous Shop 6
1 Coffee Shop 4
2 Middle Eastern Restaurant 4
3 Mobile Phone Shop 4
4 Movie Theater 3
5 Metro Station 3
6 Japanese Restaurant 3
7 Clothing Store 3
8 Gym 2
9 Restaurant 2
Venues Count
0 Middle Eastern Restaurant 4
1 Miscellaneous Shop 4
2 Mobile Phone Shop 4
3 Movie Theater 4
4 [...]
|
no_license
|
/capstone projects/city_of_neighbourhoods.ipynb
|
Cea-Learning/coursera
| 15 |
<jupyter_start><jupyter_text># Importing the dataset<jupyter_code>dataset = pd.read_csv(r"C:\Users\user\Downloads\WA_Fn-UseC_-HR-Employee-Attrition.csv")
print (dataset.head)
<jupyter_output><bound method NDFrame.head of Age Attrition BusinessTravel DailyRate Department \
0 41 Yes Travel_Rarely 1102 Sales
1 49 No Travel_Frequently 279 Research & Development
2 37 Yes Travel_Rarely 1373 Research & Development
3 33 No Travel_Frequently 1392 Research & Development
4 27 No Travel_Rarely 591 Research & Development
... ... ... ... ... ...
1465 36 No Travel_Frequently 884 Research & Development
1466 39 No Travel_Rarely 613 Research & Development
1467 27 No Travel_Rarely 155 Research & Development
1468 49 No Travel_Frequently 1023 Sales
1469 34 No Travel_Rarely 628 Research & Development
DistanceFromHome Education EducationFi[...]<jupyter_text># Information about the dataset<jupyter_code>dataset.head()
dataset['Attrition'].value_counts()
dataset.info()
<jupyter_output><class 'pandas.core.frame.DataFrame'>
RangeIndex: 1470 entries, 0 to 1469
Data columns (total 35 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Age 1470 non-null int64
1 Attrition 1470 non-null object
2 BusinessTravel 1470 non-null object
3 DailyRate 1470 non-null int64
4 Department 1470 non-null object
5 DistanceFromHome 1470 non-null int64
6 Education 1470 non-null int64
7 EducationField 1470 non-null object
8 EmployeeCount 1470 non-null int64
9 EmployeeNumber 1470 non-null int64
10 EnvironmentSatisfaction 1470 non-null int64
11 Gender 1470 non-null object
12 HourlyRate 1470 non-null int64
13 JobInvolvement 1470 non-null int64
14 JobLevel [...]<jupyter_text># Visualizing the data<jupyter_code>dataset.isnull().sum()
sns.set_style('darkgrid')
sns.countplot(x ='Attrition',data = dataset)
fig=plt.figure(figsize=(10,8))
sns.countplot(x='JobSatisfaction',hue='Attrition',data=dataset)
plt.show()
fig=plt.figure(figsize=(10,8))
sns.countplot(x='PerformanceRating',hue='Attrition',data=dataset)
plt.show()
fig=plt.figure(figsize=(10,8))
sns.countplot(x='TrainingTimesLastYear',hue='Attrition',data=dataset)
plt.show()
fig=plt.figure(figsize=(10,8))
sns.countplot(x='WorkLifeBalance',hue='Attrition',data=dataset)
plt.show()
fig=plt.figure(figsize=(10,8))
sns.countplot(x='YearsAtCompany',hue='Attrition',data=dataset)
plt.show()
fig=plt.figure(figsize=(10,8))
sns.countplot(x='YearsSinceLastPromotion',hue='Attrition',data=dataset)
plt.show()
f,ax=plt.subplots(figsize=(16,14))
corrmat=dataset.corr()
sns.heatmap(corrmat,annot=True,xticklabels=corrmat.columns.values,yticklabels=corrmat.columns.values)<jupyter_output><empty_output><jupyter_text># Preprocessing the data <jupyter_code>dataset.drop(['EmployeeCount','DailyRate','StandardHours','EmployeeNumber','Over18','HourlyRate','MonthlyRate','PerformanceRating','StockOptionLevel','TrainingTimesLastYear'],axis = 1, inplace = True)
dataset.shape
<jupyter_output><empty_output><jupyter_text># Input and Output data<jupyter_code>y = dataset.iloc[:, 1]
X = dataset
X.drop('Attrition', axis = 1, inplace = True)
<jupyter_output><empty_output><jupyter_text># Label Encoding<jupyter_code>from sklearn.preprocessing import LabelEncoder
lb = LabelEncoder()
y = lb.fit_transform(y)
X=pd.get_dummies(X)
print(X.shape)
print(y.shape)
<jupyter_output>(1470, 43)
(1470,)
<jupyter_text># Splitting data to training and testing<jupyter_code>from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size = 0.3, random_state = 10)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
<jupyter_output>(1029, 43)
(441, 43)
(1029,)
(441,)
<jupyter_text># Random Forest Classifier<jupyter_code>from sklearn.metrics import roc_auc_score
rf = RandomForestClassifier(n_estimators=300, max_depth= 4,max_features=0.3,min_samples_leaf=2)
rf.fit(X_train, y_train)
Y_pred_rf=rf.predict(X_test)
import sklearn.metrics
cols=['Model','ROC Score','Accuracy Score']
models_report=pd.DataFrame(columns=cols)
tmp1=pd.Series({'Model':"Random forest",'ROC Score':sklearn.metrics.roc_auc_score(y_test,Y_pred_rf),'Accuracy Score':sklearn.metrics.accuracy_score(y_test,Y_pred_rf)})
rf_report=models_report.append(tmp1,ignore_index=True)
rf_report
cfm=confusion_matrix(y_test,Y_pred_rf)
cfm
from sklearn.metrics import roc_curve
fpr,tpr,thresholds=roc_curve(y_test,Y_pred_rf)
roc_auc=auc(fpr,tpr)
roc_auc
plt.figure(figsize=(10,10))
plt.title('Receiver Operating Characteristic')
plt.plot(fpr,tpr,color='red',label='AUC=%0.2f'%roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],linestyle='--')
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')<jupyter_output><empty_output><jupyter_text># Logistic Regression<jupyter_code>from sklearn.linear_model import LogisticRegression
reg=LogisticRegression()
reg.fit(X_train,y_train)
y_pred_log=reg.predict(X_test)
import sklearn.metrics
cols=['Model','ROC Score','Accuracy Score']
models_report=pd.DataFrame(columns=cols)
tmp1=pd.Series({'Model':"Logistic Regression",'ROC Score':sklearn.metrics.roc_auc_score(y_test,y_pred_log),'Accuracy Score':sklearn.metrics.accuracy_score(y_test,y_pred_log)})
reg_report=models_report.append(tmp1,ignore_index=True)
reg_report
cfm=confusion_matrix(y_test,y_pred_log)
cfm
from sklearn.metrics import roc_curve
fpr,tpr,thresholds=roc_curve(y_test,y_pred_log)
roc_auc=auc(fpr,tpr)
roc_auc
plt.figure(figsize=(10,8))
plt.title('Receiver Operating Characteristic')
plt.plot(fpr,tpr,color='red',label='AUC=%0.2f'%roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],linestyle='--')
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
<jupyter_output><empty_output><jupyter_text># Models Comparison<jupyter_code>import sklearn.metrics
cols=['Model','ROC Score','Accuracy Score']
class_model=pd.DataFrame(columns=cols)
class_model=class_model.append([rf_report,reg_report])
class_model<jupyter_output><empty_output>
|
no_license
|
/industrialseminar.ipynb
|
shreshtha11/Projects
| 10 |
<jupyter_start><jupyter_text># Section 4 - Building an ANN<jupyter_code>import numpy as np
import matplotlib as plt
import pandas as pd
dataset = pd.read_csv('Churn_Modelling.csv')
X = dataset.iloc[:, 3:13].values
y = dataset.iloc[:, 13].values<jupyter_output><empty_output><jupyter_text>### Encode categorical features<jupyter_code>from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder()
X[:,1] = labelencoder_X_1.fit_transform(X[:,1])
labelencoder_X_2 = LabelEncoder()
X[:,2] = labelencoder_X_2.fit_transform(X[:,2])
onehotencoder = OneHotEncoder(categorical_features = [1])
X = onehotencoder.fit_transform(X).toarray()
X = X[:,1:]<jupyter_output><empty_output><jupyter_text>### Split the data set into train and test<jupyter_code>from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size = 0.2, random_state = 0)<jupyter_output><empty_output><jupyter_text>### Feature Scaling <jupyter_code>from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.fit_transform(X_test)<jupyter_output><empty_output><jupyter_text>### Import Keras library and packages <jupyter_code>import keras
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Dropout
from keras import regularizers<jupyter_output><empty_output><jupyter_text>### Initializing the ANN <jupyter_code>classifier_ann = Sequential()
# Adding the input layer and the 1st hidden layer
classifier_ann.add(Dense(units = 6, kernel_initializer = 'uniform', activation = 'relu', input_dim = 11))
# Adding the 2st hidden layer
classifier_ann.add(Dense(units = 6, kernel_initializer = 'uniform', activation = 'relu'))
# Adding the output layer
classifier_ann.add(Dense(units = 1, kernel_initializer = 'uniform', activation = 'sigmoid'))<jupyter_output><empty_output><jupyter_text>### Compiling the ANN<jupyter_code>classifier_ann.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])<jupyter_output><empty_output><jupyter_text>### Fit the ANN<jupyter_code>classifier_ann.fit(x = X_train, y = y_train, batch_size = 10, epochs = 100)
y_pred = (classifier_ann.predict(X_test) > 0.5)
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print('Accuracy is {}'.format(cm.diagonal().sum() / cm.sum()))
cm<jupyter_output>Accuracy is 0.843
<jupyter_text># Section 6 - Evaluating an ANN<jupyter_code>from keras.wrappers.scikit_learn import KerasClassifier
from sklearn.model_selection import KFold
skf = KFold(n_splits = 5)
accuracy_k = []
for train_index, test_index in skf.split(X, y):
#print('Train size is {} and test size is {}'.format(len(train_index),len(test_index)))
#print(sum(y[train_index]))
X_train, X_test = sc.fit_transform(X[train_index]), sc.fit_transform(X[test_index])
y_train, y_test = y[train_index], y[test_index]
classifier_ann.fit(x = X_train, y = y_train, batch_size = 10, epochs = 50)
y_pred = (classifier_ann.predict(X_test) > 0.5)
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
accuracy = cm.diagonal().sum() / cm.sum()
accuracy_k.append(accuracy)
print('Accuracy is {}'.format(accuracy))
print('Accuracy mean is {} and variance is {}'.format(np.mean(accuracy_k), np.var(accuracy_k)))<jupyter_output>Accuracy mean is 0.8356999999999999 and variance is 4.215999999999994e-05
|
no_license
|
/Part 1 - Artificial Neural Networks.ipynb
|
Efthymios-Stathakis/Deep-Learning-with-ANN
| 9 |
<jupyter_start><jupyter_text># EX 7<jupyter_code>from sklearn.datasets import make_moons
X, y = make_moons(n_samples=10000, noise=0.4, random_state=42)
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.model_selection import GridSearchCV
plt.scatter(X[:,0], X[:,1], c=y);
tree = DecisionTreeClassifier(random_state=42)
params = {
'max_depth': [2, 4, 8, 10, 12],
'min_samples_leaf': [1, 5, 10, 15],
'max_leaf_nodes': [None, 5, 10, 20, 25, 30, 35]
}
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
clf = GridSearchCV(tree, params, cv=5)
clf.fit(X_train, y_train)
clf.best_params_
y_pred = clf.best_estimator_.predict(X_test)
accuracy_score(y_test, y_pred)<jupyter_output><empty_output><jupyter_text># EX 8<jupyter_code>from sklearn.model_selection import ShuffleSplit
import numpy as np
rs = ShuffleSplit(n_splits=1000, test_size=.99, random_state=42)
acc = []
for train_index, test_index in rs.split(X_train):
tree_clf = DecisionTreeClassifier(**clf.best_params_)
tree_clf.fit(X_train[train_index], y_train[train_index])
y_pred = tree_clf_i.predict(X_test)
acc.append(accuracy_score(y_test, y_pred))
print(np.mean(acc))<jupyter_output>0.7943065
<jupyter_text>Реализуем модель случайного леса. Обучим 1000 классификаторов<jupyter_code>tree_clf = []
for train_index, test_index in rs.split(X_train):
one_clf = DecisionTreeClassifier(**clf.best_params_)
one_clf.fit(X_train[train_index], y_train[train_index])
tree_clf.append(one_clf)<jupyter_output><empty_output><jupyter_text>Оценим наш тестовый набор данных на каждом из классификаторов<jupyter_code>from scipy.stats import mode
y_pred_rf = []
for tree_num, tree in enumerate(tree_clf):
y_pred_rf.append(tree.predict(X_test))
y_pred_rf[:10]<jupyter_output><empty_output><jupyter_text>А затем выберем самый часто встречающийся прогноз, для каждого элемента тестовой выборки<jupyter_code>y_pred_majority_votes, n_votes = mode(y_pred_rf, axis=0)
y_pred_majority_votes[:10]<jupyter_output><empty_output><jupyter_text>Оценим итоговую точность<jupyter_code>accuracy_score(y_test, y_pred_majority_votes.reshape([-1]))<jupyter_output><empty_output>
|
permissive
|
/HW/6_Trees.ipynb
|
ss52/handson-ml2
| 6 |
<jupyter_start><jupyter_text># Linear Mixed Model Multi-Trait Example
In this tutorial we look at how to use linear mixed models to study genetic associations for multiple traits simultaneously. In some settings this can be a more powerful approach for analysis.## Setting up<jupyter_code># activate inline plotting
%matplotlib inline
from setup import *
if 0:
file_name = './../data/arab107/atwell_107.hdf5'
geno_reader = gr.genotype_reader_tables(file_name)
pheno_reader = phr.pheno_reader_tables(file_name)
#the data object allows to query specific genotype or phenotype data
dataset = data.QTLData(geno_reader=geno_reader,pheno_reader=pheno_reader)
if 1:
#the data used in this study have been pre-converted into an hdf5 file.
#to preprocess your own data, please use limix command line tool
file_name = './../data/BYxRM/BYxRM.hdf5'
geno_reader = gr.genotype_reader_tables(file_name)
pheno_reader = phr.pheno_reader_tables(file_name)
#the data object allows to query specific genotype or phenotype data
dataset = data.QTLData(geno_reader=geno_reader,pheno_reader=pheno_reader)
<jupyter_output><empty_output><jupyter_text>## Choose which phenotypes to model jointly
We look for correlated phenotypes.<jupyter_code>#choosing which phenotypes to model jointly ?
phenotypes,sample_idx = dataset.getPhenotypes(intersection=True)
phenotype_names = dataset.phenotype_ID
pl.figure(figsize=[20,20])
Ce= sp.cov(phenotypes.values.T)
pl.imshow(Ce,aspect='auto',interpolation='none')
pl.xticks(sp.arange(len(phenotype_names)),phenotype_names,rotation=90)
pl.yticks(sp.arange(len(phenotype_names)),phenotype_names,rotation=0)
pl.colorbar()
<jupyter_output><empty_output><jupyter_text>Now we select a subset of phenotypes to model. Which would you choose?<jupyter_code>#select subset of phenotypes
#flowering phenotypes (A. thaliana data)
phenotype_names = ['5_FT10','6_FT16','7_FT22']
#a larger set of correlated and anti correlated traits:
#phenotype_names = ['Ethanol','Congo_red','Galactose']
#YPD, different temperatures:
phenotype_names = ['YPD:37C','YPD:15C','YPD:4C']
phenotype_query = "(phenotype_ID in %s)" % str(phenotype_names)
data_subsample = dataset.subsample_phenotypes(phenotype_query=phenotype_query,
intersection=True)
sample_relatedness_unnormalized = data_subsample.getCovariance(normalize=True,center=True)
sample_relatedness = sample_relatedness_unnormalized/ \
sample_relatedness_unnormalized.diagonal().mean()
if 1:
#subsample for speed?
Is = sp.arange(dataset.geno_pos.shape[0])
#take every 10th SNP
Is = Is[::10]
data_subsample = data_subsample.subsample(cols_geno = Is)
#get variables we need from data
snps = data_subsample.getGenotypes(center=False,unit=False)
position = data_subsample.getPos()
position,chromBounds = data_util.estCumPos(position=position,offset=100000)
phenotypes,sample_idx = data_subsample.getPhenotypes(phenotype_query=phenotype_query,
intersection=True)
phenotype_std = preprocess.rankStandardizeNormal(phenotypes.values)
N = snps.shape[0]
S = snps.shape[1]
P = phenotypes.shape[1]
print "loaded %d samples, %d phenotypes, %s snps" % (N,P,S)<jupyter_output>loaded 804 samples, 3 phenotypes, 1163 snps
<jupyter_text>We transform the phenotypes using the Box-Cox procedure.<jupyter_code>#preprocess phenotypes using boxcox
if 0:
phenotype_vals_boxcox, maxlog = preprocess.boxcox(phenotypes.values)
phenotype_vals_boxcox -= phenotype_vals_boxcox.mean(axis=0)
phenotype_vals_boxcox /= phenotype_vals_boxcox.std(axis=0)
phenotypes.ix[:,:] = phenotype_vals_boxcox<jupyter_output><empty_output><jupyter_text># Correlation between phenotypes
* We start by examining the correlation between phenotypes<jupyter_code>#pairwise corrrelations of the first 3 traits
pl.figure(figsize=[15,5])
pl.subplot(1,3,1)
pl.plot(phenotypes[phenotype_names[0]].values,phenotypes[phenotype_names[1]].values,'.')
pl.xlabel(phenotype_names[0])
pl.ylabel(phenotype_names[1])
pl.subplot(1,3,2)
pl.plot(phenotypes[phenotype_names[1]].values,phenotypes[phenotype_names[2]].values,'.')
pl.xlabel(phenotype_names[1])
pl.ylabel(phenotype_names[2])
pl.subplot(1,3,3)
pl.plot(phenotypes[phenotype_names[0]].values,phenotypes[phenotype_names[2]].values,'.')
pl.xlabel(phenotype_names[0])
pl.ylabel(phenotype_names[2])
Ce = sp.corrcoef(phenotypes.T)
sample_relatedness = data_subsample.getCovariance()
#set parameters for the analysis
N, G = phenotypes.shape
# variance component model
vc = var.VarianceDecomposition(phenotypes.values)
vc.addFixedEffect()
vc.addRandomEffect(K=sample_relatedness,trait_covar_type='freeform')
vc.addRandomEffect(is_noise=True,trait_covar_type='freeform')
vc.optimize()
# retrieve geno and noise covariance matrix
Cg = vc.getTraitCovar(0)
Cn = vc.getTraitCovar(1)
pl.figure(figsize=[15,5])
pl.subplot(1,3,1)
pl.imshow(Ce,aspect='auto',interpolation='none',vmin=-1,vmax=1)
pl.xticks(sp.arange(len(phenotype_names)),phenotypes.columns)
pl.yticks(sp.arange(len(phenotype_names)),phenotypes.columns)
pl.title('empirical correlation')
pl.subplot(1,3,2)
pl.imshow(Cg,aspect='auto',interpolation='none',vmin=-1,vmax=1)
pl.xticks(sp.arange(len(phenotype_names)),phenotypes.columns)
pl.yticks(sp.arange(len(phenotype_names)),phenotypes.columns)
pl.title('genetic covariance')
pl.subplot(1,3,3)
pl.imshow(Cn,aspect='auto',interpolation='none',vmin=-1,vmax=1)
pl.xticks(sp.arange(len(phenotype_names)),phenotypes.columns)
pl.yticks(sp.arange(len(phenotype_names)),phenotypes.columns)
pl.title('noise covariance')
pl.colorbar()
#convert P-values to a DataFrame for nice output writing:
lmm = qtl.test_lmm(snps=snps[sample_idx],pheno=phenotypes.values,K=sample_relatedness)
#convert P-values to a DataFrame for nice output writing:
pvalues_lmm = pd.DataFrame(data=lmm.getPv().T,index=data_subsample.geno_ID,
columns=phenotype_names)
# Genome-wide manhatton plots for one phenotype:
for p_ID in phenotype_names:
pl.figure(figsize=[15,4])
plot_manhattan(posCum=position['pos_cum'],pv=pvalues_lmm[p_ID].values,chromBounds=chromBounds,thr_plotting=0.05)
pl.title(p_ID)<jupyter_output><empty_output><jupyter_text># Any-effect test<jupyter_code>P = phenotypes.values.shape[1]
covs = None #covariates
Acovs = None #the design matrix for the covariates
Asnps = sp.eye(P) #the design matrix for the SNPs
K1r = sample_relatedness #the first sample-sample covariance matrix (non-noise)
K2r = sp.eye(N) #the second sample-sample covariance matrix (noise)
K1c = None #the first phenotype-phenotype covariance matrix (non-noise)
K2c = None #the second phenotype-phenotype covariance matrix (noise)
covar_type = 'freeform' #the type of the trait/trait covariance to be estimated
searchDelta = False #specify if delta should be optimized for each SNP
test="lrt" #specify type of statistical test
# Running the analysis
# when cov are not set (None), LIMIX considers an intercept (covs=SP.ones((N,1)))
lmm, pvalues = qtl.test_lmm_kronecker(snps=snps[sample_idx],phenos=phenotypes.values,covs=covs,Acovs=Acovs,
Asnps=Asnps,K1r=K1r,trait_covar_type=covar_type)
#convert P-values to a DataFrame for nice output writing:
pvalues = pd.DataFrame(data=pvalues.T,index=data_subsample.geno_ID,columns=['multi_trait'])
pl.figure(figsize=[15,4])
thr = 0.1/snps.shape[1]
plot_manhattan(posCum=position['pos_cum'],thr=thr,pv=pvalues['multi_trait'].values,chromBounds=chromBounds,thr_plotting=0.05)
pl.title('Any effect test')
<jupyter_output><empty_output><jupyter_text># Testing for common effectsA common effect test is a 1 degree of freedom test and can be done by setting
\begin{equation}
\mathbf{A}_1^\text{(snp)} = \mathbf{1}_{1,P},\;\;\;
\mathbf{A}_0^\text{(snp)} = \mathbf{0}
\end{equation}<jupyter_code>P = phenotypes.values.shape[1]
covs = None #covariates
Acovs = None #the design matrix for the covariates
Asnps = sp.ones((1,P)) #the design matrix for the SNPs
K1r = sample_relatedness #the first sample-sample covariance matrix (non-noise)
K2r = sp.eye(N) #the second sample-sample covariance matrix (noise)
K1c = None #the first phenotype-phenotype covariance matrix (non-noise)
K2c = None #the second phenotype-phenotype covariance matrix (noise)
covar_type = 'freeform' #the type of the trait/trait covariance to be estimated
searchDelta = False #specify if delta should be optimized for each SNP
test="lrt" #specify type of statistical test
# Running the analysis
# when cov are not set (None), LIMIX considers an intercept (covs=SP.ones((N,1)))
lmm, pvalues_common = qtl.test_lmm_kronecker(snps=snps[sample_idx],phenos=phenotypes.values,covs=covs,Acovs=Acovs,
Asnps=Asnps,K1r=K1r,trait_covar_type=covar_type)
#convert P-values to a DataFrame for nice output writing:
pvalues_common = pd.DataFrame(data=pvalues_common.T,index=data_subsample.geno_ID,columns=['common'])
pl.figure(figsize=[15,4])
plot_manhattan(posCum=position['pos_cum'],pv=pvalues_common['common'].values,chromBounds=chromBounds,thr_plotting=0.1)
pl.title('common')<jupyter_output><empty_output><jupyter_text># Testing for GxE (specific effect test)For a specifc effect test for trait $p$
the alternative model is set to have both a common and a specific effect
for trait $p$ from the SNP while the null model has only a common effect.
It is a 1 degree of freedom test and,
in the particular case of $P=3$ traits and for $p=0$, it can be done by setting
\begin{equation}
\mathbf{A}_1^\text{(snp)} =
\begin{pmatrix}
1 & 0 & 0 \\
1 & 1 & 1
\end{pmatrix}
\;\;\;,
\mathbf{A}_0^\text{(snp)} = \mathbf{1}_{1,3}
\end{equation}<jupyter_code>Asnps0 = sp.ones((1,P)) #the null model design matrix for the SNPs
Asnps1 = sp.zeros((2,P)) #the alternative model design matrix for the SNPs
Asnps1[0,:] = 1.0
Asnps1[1,0] = 1.0
# Running the analysis
# when cov are not set (None), LIMIX considers an intercept (covs=SP.ones((N,1)))
pvalues_inter = qtl.test_interaction_lmm_kronecker(snps=snps[sample_idx],phenos=phenotypes.values,covs=covs,Acovs=Acovs,
Asnps0=Asnps0,Asnps1=Asnps1,K1r=K1r,trait_covar_type=covar_type)
print "Design(0): \n"+str(Asnps0)
print "Design(Alt): \n"+str(Asnps1)
#convert P-values to a DataFrame for nice output writing:
pvalues_inter = pd.DataFrame(data=sp.concatenate(pvalues_inter).T,index=data_subsample.geno_ID,
columns=["specific","null_common","alternative_any"])
pl.figure(figsize=[15,4])
plot_manhattan(posCum=position['pos_cum'],pv=pvalues_inter['specific'].values,chromBounds=chromBounds,thr_plotting=0.1)
pl.title('specific')
tests = ['Any effect test','Interaction effect test']
pl.figure(figsize=[15,10])
#lim = -1.2*sp.log10(SP.array([pvalues['alternative_any'].min(),
# pvalues_inter['null_common'].min(),pvalues_inter['specific'].min()]).min())
plt = pl.subplot(2,1,1)
plot_manhattan(position['pos_cum'],pvalues_inter['alternative_any'],
chromBounds,colorS='k',colorNS='k',alphaNS=0.05,labelS='any')
plot_manhattan(position['pos_cum'],pvalues_inter['null_common'],
chromBounds,colorS='y',colorNS='y',alphaNS=0.05,labelS='common')
plot_manhattan(position['pos_cum'],pvalues_inter['specific'],
chromBounds,colorS='r',colorNS='r',alphaNS=0.05,labelS='specific')
pl.legend(loc='upper left')
<jupyter_output><empty_output>
|
no_license
|
/LMM_multitrait/LMM_multitrait_example.ipynb
|
davismcc/embl_predocs_limix_tutorial_Nov2015
| 8 |
<jupyter_start><jupyter_text># Softmax Classification (with Cross-Entropy Loss)
In this exercise you will:
- Implement a fully-vectorized **loss function** for the Softmax classifier
- Implement the fully-vectorized expression for its **analytic gradient**
- **Check your implementation** with numerical gradient
- Use a validation set to **tune the learning rate and regularization** strength
- **Optimize** the loss function with **SGD**
- **Visualize** the final learned weights
<jupyter_code>import time
import random
import math
import numpy as np
from exercise_code.model_savers import save_softmax_classifier
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# for auto-reloading extenrnal modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2<jupyter_output><empty_output><jupyter_text>## CIFAR-10 Data Loading and Preprocessing
To your convenience, we have taken care of all the input handling. Nevertheless, you should go through the following code line by line so that you understand the general preprocessing pipeline.
The whole datasat is loaded, then subdivided into a training, validation and test dataset (the last one is different from the final evaluation dataset on our server!).
Before proceeding you should *always* take a look at some samples of your dataset, which is already implemented for you. This way you can make sure that the data input/preprocessing has worked as intended and you can get a feeling for the dataset.<jupyter_code>from exercise_code.data_utils import load_CIFAR10
# Load the raw CIFAR-10 data
cifar10_dir = 'datasets/'
X, y = load_CIFAR10(cifar10_dir)
# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y_hat, cls in enumerate(classes):
idxs = np.flatnonzero(y == y_hat)
idxs = np.random.choice(idxs, samples_per_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * num_classes + y_hat + 1
plt.subplot(samples_per_class, num_classes, plt_idx)
plt.imshow(X[idx].astype('uint8'))
plt.axis('off')
if i == 0:
plt.title(cls)
plt.show()
# Split the data into train, val, and test sets. In addition we will
# create a small development set as a subset of the data set;
# we can use this for development so our code runs faster.
num_training = 48000
num_validation = 1000
num_test = 1000
num_dev = 500
assert (num_training + num_validation + num_test) == 50000, 'You have not provided a valid data split.'
# Our training set will be the first num_train points from the original
# training set.
mask = range(num_training)
X_train = X[mask]
y_train = y[mask]
# Our validation set will be num_validation points from the original
# training set.
mask = range(num_training, num_training + num_validation)
X_val = X[mask]
y_val = y[mask]
# We use a small subset of the training set as our test set.
mask = range(num_training + num_validation, num_training + num_validation + num_test)
X_test = X[mask]
y_test = y[mask]
# We will also make a development set, which is a small subset of
# the training set. This way the development cycle is faster.
mask = np.random.choice(num_training, num_dev, replace=False)
X_dev = X_train[mask]
y_dev = y_train[mask]
# Preprocessing: reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_val = np.reshape(X_val, (X_val.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
X_dev = np.reshape(X_dev, (X_dev.shape[0], -1))
# As a sanity check, print out the shapes of the data
print('Training data shape: ', X_train.shape)
print('Validation data shape: ', X_val.shape)
print('Test data shape: ', X_test.shape)
print('dev data shape: ', X_dev.shape)
# Preprocessing: subtract the mean image
# first: compute the image mean based on the training data
mean_image = np.mean(X_train, axis=0)
print(mean_image[:10]) # print a few of the elements
plt.figure(figsize=(4,4))
plt.imshow(mean_image.reshape((32,32,3)).astype('uint8')) # visualize the mean image
plt.show()
# second: subtract the mean image from train and test data
X_train -= mean_image
X_val -= mean_image
X_test -= mean_image
X_dev -= mean_image
# third: append the bias dimension of ones (i.e. bias trick) so that our classifier
# only has to worry about optimizing a single weight matrix W.
X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))])
X_val = np.hstack([X_val, np.ones((X_val.shape[0], 1))])
X_test = np.hstack([X_test, np.ones((X_test.shape[0], 1))])
X_dev = np.hstack([X_dev, np.ones((X_dev.shape[0], 1))])
print(X_train.shape, X_val.shape, X_test.shape, X_dev.shape)<jupyter_output>(48000, 3073) (1000, 3073) (1000, 3073) (500, 3073)
<jupyter_text>## Softmax Classifier
In this section you will implement the essential elements of a softmax classifier. We will start with the cross-entropy loss and it's gradient with respect to the classifier's weights. We suggest that you first derive these expressions on paper.### Naive Implementation
First implement a naive cross-entropy loss function with nested loops. Open the file `exercise_code/classifiers/softmax.py` and implement the loss of the softmax classifier into the `cross_entropoy_loss_naive` function.
Running this method might take a while...<jupyter_code>from exercise_code.classifiers.softmax import cross_entropoy_loss_naive
# Generate a random weight matrix and use it to compute the loss.
W = np.random.randn(3073, 10) * 0.0001
loss, grad = cross_entropoy_loss_naive(W, X_dev, y_dev, 0.0)
# As a rough sanity check, our loss should be something close to -log(0.1).
print('loss: %f' % loss)
print('sanity check: %f' % (-np.log(0.1)))<jupyter_output>loss: 2.416855
sanity check: 2.302585
<jupyter_text>
Inline Question
Why do we expect our loss to be close to -log(0.1)? Explain briefly.
The number of classes is 10, due to random weight initialization, the probability
that a picture belongs to a certain class is 1/10.
Complete the implementation of the `cross_entropoy_loss_naive` function and implement a (naive) version of the gradient that uses nested loops. Use the following cell to check your results:<jupyter_code>from exercise_code.gradient_check import grad_check_sparse
# We take a smaller dev set since the naive implementation takes quite some while
X_dev_small, y_dev_small = X_dev[:10], y_dev[:10]
loss, grad = cross_entropoy_loss_naive(W, X_dev_small, y_dev_small, 0.0)
# We use numeric gradient checking as a debugging tool.
# The numeric gradient should be close to the analytic gradient.
f = lambda w: cross_entropoy_loss_naive(w, X_dev_small, y_dev_small, 0.0)[0]
grad_numerical = grad_check_sparse(f, W, grad, num_checks=3)
# Again, running this might take a while!
# Do another gradient check with regularization
loss, grad = cross_entropoy_loss_naive(W, X_dev_small, y_dev_small, 1e2)
f = lambda w: cross_entropoy_loss_naive(w, X_dev_small, y_dev_small, 1e2)[0]
grad_numerical = grad_check_sparse(f, W, grad, num_checks=3)<jupyter_output>numerical: -4.116960306932427 analytic: -4.1169603536852, relative error: 5.678069431982848e-09
numerical: -1.9947851302104522 analytic: -1.994785157159716, relative error: 6.754928919239908e-09
numerical: 6.491036001299299 analytic: 6.491036117742385, relative error: 8.969530073210708e-09
<jupyter_text>### Vectorized Implementation
Now that we have a naive implementation of the cross-entropy loss and its gradient, implement a vectorized version in `cross_entropoy_loss_vectorized`.
The two versions should compute the same results, but the vectorized version should be much faster.<jupyter_code>from exercise_code.classifiers.softmax import cross_entropoy_loss_vectorized
tic = time.time()
loss_naive, grad_naive = cross_entropoy_loss_naive(W, X_dev, y_dev, 0.00001)
toc = time.time()
print('naive loss: %e computed in %fs' % (loss_naive, toc - tic))
tic = time.time()
loss_vectorized, grad_vectorized = cross_entropoy_loss_vectorized(W, X_dev, y_dev, 0.00001)
toc = time.time()
print('vectorized loss: %e computed in %fs' % (loss_vectorized, toc - tic))
# We use the Frobenius norm to compare the two versions of the gradient.
grad_difference = np.linalg.norm(grad_naive - grad_vectorized, ord='fro')
print('Loss difference: %f' % np.abs(loss_naive - loss_vectorized))
print('Gradient difference: %f' % grad_difference)<jupyter_output>naive loss: 2.416855e+00 computed in 0.240100s
vectorized loss: 2.416855e+00 computed in 0.025755s
Loss difference: 0.000000
Gradient difference: 0.000000
<jupyter_text>
Inline Question
When you compute the softmax distribution, you are dividing by a sum of exponentials, i.e. potentially very large numbers, which can be numerically unstable. Do you see a way to avoid this problem?
(Hint: exploit properties of the exponential function to arrive at an expression that is mathematically the same, but numerically more stable)
Normalization by multiplying the top and bottom of the fraction by a constant C and push it into the sum:
$$\frac{e^{f_{y_i}}}{\sum_{j=1}e^{f_j}}= \frac{Ce^{f_{y_i}}}{C\sum_{j=1}e^{f_j}}=
\frac{e^{f_{y_i}+logC}}{\sum_{j=1}e^{f_j+logC}}
$$
This mathematically equivalent operation thus imporoves the numerical stability.
A commen choice for C is to set $logC= -max_j f_j$, which states that the values inside the vector f are shifted sotha t the highest value is zero.
### Stochastic Gradient Descent
We now have vectorized and efficient expressions for the loss, the gradient and our gradient matches the numerical gradient. We are therefore ready to usw SGD to minimize the loss. In the file `exercise_code/classifiers/linear_classifier.py`, implement SGD in the `LinearClassifier.train` method and test it with the code below.<jupyter_code>from exercise_code.classifiers.softmax import SoftmaxClassifier
# The SoftmaxClassifier class inherits from LinearClassifier
softmax = SoftmaxClassifier()
tic = time.time()
loss_hist = softmax.train(X_train, y_train, learning_rate=1e-7, reg=5e4,
num_iters=1500, verbose=True)
toc = time.time()
print('That took %fs' % (toc - tic))
# A useful debugging strategy is to plot the loss as a function of iterations:
plt.figure(figsize=(6,5))
plt.plot(loss_hist)
plt.xlabel('Iterations')
plt.ylabel('Loss value')
plt.show()<jupyter_output><empty_output><jupyter_text>Write the `LinearClassifier.predict` method and evaluate the performance on both the training and validation set:<jupyter_code>y_train_pred = softmax.predict(X_train)
print('training accuracy: %f' % (np.mean(y_train == y_train_pred), ))
y_val_pred = softmax.predict(X_val)
print('validation accuracy: %f' % (np.mean(y_val == y_val_pred), ))<jupyter_output>training accuracy: 0.331250
validation accuracy: 0.329000
<jupyter_text>### Training your Softmax Classifier
Use the validation set to tune hyperparameters (regularization strength and learning rate). You should experiment with different ranges for the learning rates and regularization strengths; if you are careful you should be able to get a classification accuracy of over 0.35 on the validation set. Implement the `softmax_hyperparameter_tuning` function in `exercise_code/classifiers/softmax.py`.<jupyter_code>from exercise_code.classifiers.softmax import SoftmaxClassifier, softmax_hyperparameter_tuning
best_softmax, results, all_classifiers = softmax_hyperparameter_tuning(X_train, y_train, X_val, y_val)
# Visualize the validation results
x_scatter = [math.log10(x[0]) for x in results]
y_scatter = [math.log10(x[1]) for x in results]
# plot training accuracy
marker_size = 100
colors = [results[x][0] for x in results]
plt.subplot(2, 1, 1)
plt.scatter(x_scatter, y_scatter, marker_size, c=colors)
plt.colorbar()
plt.xlabel('log learning rate')
plt.ylabel('log regularization strength')
plt.title('CIFAR-10 training accuracy')
# plot validation accuracy
colors = [results[x][1] for x in results] # default size of markers is 20
plt.subplot(2, 1, 2)
plt.scatter(x_scatter, y_scatter, marker_size, c=colors)
plt.colorbar()
plt.xlabel('log learning rate')
plt.ylabel('log regularization strength')
plt.title('CIFAR-10 validation accuracy')
plt.tight_layout()
plt.show()
# if you want to take a look at the other classifiers assign them to best_softmax here
sorted_classifiers = sorted(all_classifiers, key=lambda x : x[1])
best_softmax = sorted_classifiers[-1][0]
# evaluate on test set
# Evaluate the best softmax on test set
y_test_pred = best_softmax.predict(X_test)
test_accuracy = np.mean(y_test == y_test_pred)
print('softmax on raw pixels final test set accuracy: %f' % (test_accuracy, ))
# Visualize the learned weights for each class
#best_softmax = sorted_classifiers[idx][0]
w = best_softmax.W[:-1,:] # strip out the bias
w = w.reshape(32, 32, 3, 10)
w_min, w_max = np.min(w), np.max(w)
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
for i in range(10):
plt.subplot(2, 5, i + 1)
# Rescale the weights to be between 0 and 255
wimg = 255.0 * (w[:, :, :, i].squeeze() - w_min) / (w_max - w_min)
plt.imshow(wimg.astype('uint8'))
plt.axis('off')
plt.title(classes[i])<jupyter_output><empty_output><jupyter_text>
Inline Question
Describe what your visualized Softmax weights look like.
The visualized weight looks like the blurry versions of the original ones that they are “responsible” for classifying, whereas with faded shapes and the average background.
https://ml4a.github.io/ml4a/looking_inside_neural_nets/
The fact that we can tell the object from the weight images also hints that somethow overfitting this way (since it seems to "memorize" the training images)## Save the model
When you are satisfied with your training, save the model for submission. Your final score is computed by `accuracy * 100`. In order to pass this exercise, you have to achieve a score higher than __35__.
Warning
You might get an error like this:
PicklingError: Can't pickle ``: it's not the same object as exercise_code.classifiers.softmax.SoftmaxClassifier
The reason is that we are using autoreload and working on this class during the notebook session. If you get this error simply restart the kernel and rerun the whole script (Kernel -> Restart & Run All) or only the important cells for generating your model.
<jupyter_code>from exercise_code.model_savers import save_softmax_classifier
from exercise_code.classifiers.softmax import SoftmaxClassifier
save_softmax_classifier(best_softmax)<jupyter_output><empty_output>
|
no_license
|
/exercise_1/1_softmax.ipynb
|
Plan-T42/i2DL-Exercises
| 9 |
<jupyter_start><jupyter_text># Linear Regression model### Importing libraries<jupyter_code>import pandas as pd
import pickle
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split<jupyter_output><empty_output><jupyter_text>### Loding the dataset<jupyter_code>data = pd.read_csv('./dataset/weight-height.csv')<jupyter_output><empty_output><jupyter_text>### Preview of the data<jupyter_code>data.head()<jupyter_output><empty_output><jupyter_text>### Selecting x's and y's<jupyter_code>X = data[['Weight']].values
y = data[['Height']].values<jupyter_output><empty_output><jupyter_text>### Splitting the data to test and train<jupyter_code>X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=1/3)<jupyter_output><empty_output><jupyter_text>### Creating a LinearRegression object and fitting the data<jupyter_code>X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=1/3)
regressor = LinearRegression()
regressor.fit(X_train, y_train)<jupyter_output><empty_output><jupyter_text>### Testing the model<jupyter_code>heights = [161,187,195,156]
prediction = [regressor.predict([[height]]) for height in heights]
prediction = [round(float(weight[0][0]),2) for weight in prediction]
print("Predicted weights:",end='')
print(prediction)<jupyter_output>Predicted weights:[66.31, 69.18, 70.06, 65.76]
<jupyter_text>### Saving the model to a file<jupyter_code>try:
filename = 'model.pkl'
pickle.dump(regressor, open(filename, 'wb'))
print('Model saved as {}'.format(filename))
except Exception as e:
print("Something went wrong when writing to the file")
print(e)<jupyter_output>Model saved as model.pkl
|
permissive
|
/src/model/model_creator.ipynb
|
ashbin17/mldeploy
| 8 |
<jupyter_start><jupyter_text>Anatomia de un modulo
<jupyter_code>#Running
!java --module-path feeding --module zoo.animal.feeding/zoo.animal.feeding.Task
#Running (Short Form)
!java -p feeding -m zoo.animal.feeding/zoo.animal.feeding.Task
#Packaging
!jar -cvf mods/zoo.animal.feeding.jar -C feeding/ .<jupyter_output>added manifest
added module-info: module-info.class
adding: module-info.java(in = 34) (out= 36)(deflated -5%)
adding: zoo/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/feeding/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/feeding/Task.class(in = 429) (out= 301)(deflated 29%)
adding: zoo/animal/feeding/Task.java(in = 143) (out= 117)(deflated 18%)
<jupyter_text>Estructura del modulo y sus paquetes
The exports keyword is used to indicate that a module intends for those packages to be used by Java code outside the module. As you might expect, without an exports keyword, the module is only available to be run from the command line on its own. In the following example, we export one package:<jupyter_code>%%writefile feeding/module-info.java
module zoo.animal.feeding {
exports zoo.animal.feeding;
}
#Recompiling and repackaging
!javac -p mods -d feeding feeding/zoo/animal/feeding/*.java feeding/module-info.java
!jar -cvf mods/zoo.animal.feeding.jar -C feeding/ .<jupyter_output>added manifest
added module-info: module-info.class
adding: module-info.java(in = 62) (out= 45)(deflated 27%)
adding: zoo/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/feeding/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/feeding/Task.class(in = 429) (out= 301)(deflated 29%)
adding: zoo/animal/feeding/Task.java(in = 143) (out= 117)(deflated 18%)
<jupyter_text>Next, let’s create the **zoo.animal.care** module. This time, we are going to have **two** packages.
The **zoo.animal.care.medical** package will have the classes and methods that are intended for use by other modules.
The **zoo.animal.care.details** package is only going to be used by this module. It will not be exported from the module.
Think of it as healthcare privacy for the animals.
<jupyter_code>%%writefile care/module-info.java
module zoo.animal.care {
exports zoo.animal.care.medical;
requires zoo.animal.feeding;
}<jupyter_output>Overwriting care/module-info.java
<jupyter_text>#This time the module-info.java file specifies three things.
* Line 1 specifies the name of the module.
* Line 2 lists the package we are exporting so it can be used by other modules. So far, this is similar to the zoo.animal.feeding module.
* Line 3, we see a new keyword. The **requires** statement specifies that a module is needed. The zoo.animal.care module **depends on** the zoo.animal.feeding module.
<jupyter_code>#compiling care module
!javac -p mods -d care care/zoo/animal/care/details/*.java care/zoo/animal/care/medical/*.java care/module-info.java
#Note that order matters when compiling a module. A package must have at least one class in it in order to be exported
#create the module JAR
!jar -cvf mods/zoo.animal.care.jar -C care/ .<jupyter_output>added manifest
added module-info: module-info.class
adding: module-info.java(in = 95) (out= 69)(deflated 27%)
adding: zoo/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/care/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/care/details/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/care/details/HippoBirthday.class(in = 267) (out= 213)(deflated 20%)
adding: zoo/animal/care/details/HippoBirthday.java(in = 118) (out= 101)(deflated 14%)
adding: zoo/animal/care/medical/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/care/medical/Diet.class(in = 206) (out= 175)(deflated 15%)
adding: zoo/animal/care/medical/Diet.java(in = 57) (out= 59)(deflated -3%)
<jupyter_text>#CREATING THE TALKS MODULE
So far, we’ve used only one exports and requires statement in a module. Now you’ll learn how to handle **exporting multiple** packages or **requiring multiple** modules. Observe that the **zoo.animal.talks module** depends on two modules: **zoo.animal.feeding** and **zoo.animal.care**.
This means that there must be two requires statements in the module-info.java file.
We are going to export all three packages in this module.
First let’s look at the module-info.java file for zoo.animal.talks:
Line 1 shows the module name. Lines 2–4 allow other modules to reference all three packages. Lines 6–7 specify the two modules that this module depends on.<jupyter_code>%%writefile talks/module-info.java
module zoo.animal.talks {
exports zoo.animal.talks.content;
exports zoo.animal.talks.media;
exports zoo.animal.talks.schedule;
requires zoo.animal.feeding;
requires zoo.animal.care;
}
#compile and build the module talks
!javac -p mods -d talks talks/zoo/animal/talks/content/*.java talks/zoo/animal/talks/media/*.java talks/zoo/animal/talks/schedule/*.java talks/module-info.java
!jar -cvf mods/zoo.animal.talks.jar -C talks/ .<jupyter_output>added manifest
added module-info: module-info.class
adding: module-info.java(in = 200) (out= 91)(deflated 54%)
adding: zoo/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/content/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/content/ElephantScript.class(in = 227) (out= 186)(deflated 18%)
adding: zoo/animal/talks/content/ElephantScript.java(in = 67) (out= 68)(deflated -1%)
adding: zoo/animal/talks/content/SeaLionScript.class(in = 225) (out= 185)(deflated 17%)
adding: zoo/animal/talks/content/SeaLionScript.java(in = 66) (out= 68)(deflated -3%)
adding: zoo/animal/talks/media/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/media/Announcement.class(in = 464) (out= 318)(deflated 31%)
adding: zoo/animal/talks/media/Announcement.java(in = 170) (out= 134)(deflated 21%)
adding: zoo/animal/talks/media/Signage.class(in = 211) (out= 178)(deflated 15%)
adding: zoo/animal/talks/me[...]<jupyter_text>Our final module is zoo.staff. Figure 11.12 shows there is only one package inside. We will not be exposing this package outside the module:
<jupyter_code>%%writefile staff/module-info.java
module zoo.staff {
requires zoo.animal.feeding;
requires zoo.animal.care;
requires zoo.animal.talks;
}<jupyter_output>Overwriting staff/module-info.java
<jupyter_text>These represent the three modules that are required. Since no packages are to be exposed from zoo.staff, there are no exports statements:
<jupyter_code>#compile and build the module:
!javac -p mods -d staff staff/zoo/staff/*.java staff/module-info.java
!jar -cvf mods/zoo.staff.jar -C staff/ .<jupyter_output>added manifest
added module-info: module-info.class
adding: module-info.java(in = 112) (out= 66)(deflated 41%)
adding: zoo/(in = 0) (out= 0)(stored 0%)
adding: zoo/staff/(in = 0) (out= 0)(stored 0%)
adding: zoo/staff/Jobs.class(in = 192) (out= 165)(deflated 14%)
adding: zoo/staff/Jobs.java(in = 42) (out= 44)(deflated -4%)
<jupyter_text>EXPORTS
We’ve already seen how exports packageName exports a package to other modules. It’s also possible to export a package to a specific module. Suppose the zoo decides that only staff members should have access to the talks. We could update the module declaration as follows:<jupyter_code>%%writefile talks/module-info.java
module zoo.animal.talks {
exports zoo.animal.talks.content to zoo.staff;
exports zoo.animal.talks.media;
exports zoo.animal.talks.schedule;
requires zoo.animal.feeding;
requires zoo.animal.care;
}
#compile and build the talks module
!javac -p mods -d talks talks/zoo/animal/talks/content/*.java talks/zoo/animal/talks/media/*.java talks/zoo/animal/talks/schedule/*.java talks/module-info.java
!jar -cvf mods/zoo.animal.talks.jar -C talks/ .<jupyter_output>added manifest
added module-info: module-info.class
adding: module-info.java(in = 214) (out= 98)(deflated 54%)
adding: zoo/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/content/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/content/ElephantScript.class(in = 227) (out= 186)(deflated 18%)
adding: zoo/animal/talks/content/ElephantScript.java(in = 67) (out= 68)(deflated -1%)
adding: zoo/animal/talks/content/SeaLionScript.class(in = 225) (out= 185)(deflated 17%)
adding: zoo/animal/talks/content/SeaLionScript.java(in = 66) (out= 68)(deflated -3%)
adding: zoo/animal/talks/media/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/media/Announcement.class(in = 464) (out= 318)(deflated 31%)
adding: zoo/animal/talks/media/Announcement.java(in = 170) (out= 134)(deflated 21%)
adding: zoo/animal/talks/media/Signage.class(in = 211) (out= 178)(deflated 15%)
adding: zoo/animal/talks/me[...]<jupyter_text>From the zoo.staff module, nothing has changed. However, **no other modules would be allowed to access that package.**
You might have noticed that none of our other modules requires zoo.animal.talks in the first place. However, we don’t know what **other modules will exist in the future**. It is important to consider future use when designing modules. Since we want only the one module to have access, we only allow access for that module.The exports keyword essentially gives us more levels of access control. Table 11.3 lists the full access control options.
| Level | Within module code | Outside module code |
| :---: | :---: | :---: |
| private | Available only within class | No access |
| default (package-private) | Available only within package | No access |
| protected | Available only within package or to subclasses | Accessible to subclasses only if package is exported |
| public | Available to all classes | Accessible only if package is exported |REQUIRES TRANSITIVE
As you saw earlier in this chapter, **requires moduleName** specifies that the **current module depends on moduleName**. There’s also a **requires transitive moduleName**, which means that **any module** that requires **this module** will also **depend on moduleName**.Let’s look at an example. Figure shows the modules with dashed lines for the redundant relationships and solid lines for relationships specified in the module-info. This shows how the module relationships would look if we were to only use transitive dependencies.
For example, **zoo.animal.talks** depends on **zoo.animal.care**, which depends on **zoo.animal.feeding**. That means the **arrow between** **zoo.animal.talks** and **zoo.animal.feeding** **no longer appears** in Figure.Now let’s look at the four module-info files. The first module remains unchanged. We are exporting one package to any packages that use the module.
```java
module zoo.animal.feeding {
exports zoo.animal.feeding;
}
```The **zoo.animal.care** module is the first opportunity to improve things. Rather than **forcing all remaining modules** to **explicitly** specify **zoo.animal.feeding**, the code uses requires transitive.<jupyter_code>%%writefile care/module-info.java
module zoo.animal.care {
exports zoo.animal.care.medical;
requires transitive zoo.animal.feeding;
}
#compiling care module
!javac -p mods -d care care/zoo/animal/care/details/*.java care/zoo/animal/care/medical/*.java care/module-info.java
!jar -cvf mods/zoo.animal.care.jar -C care/ .<jupyter_output>added manifest
added module-info: module-info.class
adding: module-info.java(in = 106) (out= 79)(deflated 25%)
adding: zoo/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/care/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/care/details/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/care/details/HippoBirthday.class(in = 267) (out= 213)(deflated 20%)
adding: zoo/animal/care/details/HippoBirthday.java(in = 118) (out= 101)(deflated 14%)
adding: zoo/animal/care/medical/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/care/medical/Diet.class(in = 206) (out= 175)(deflated 15%)
adding: zoo/animal/care/medical/Diet.java(in = 57) (out= 59)(deflated -3%)
<jupyter_text>In the **zoo.animal.talks** module, we make a similar change and **don’t force** other modules to specify **zoo.animal.care**. We also **no longer need** to specify zoo.animal.feeding, so that line is commented out.<jupyter_code>%%writefile talks/module-info.java
module zoo.animal.talks {
exports zoo.animal.talks.content to zoo.staff;
exports zoo.animal.talks.media;
exports zoo.animal.talks.schedule;
// no longer needed requires zoo.animal.feeding;
// no longer needed requires zoo.animal.care;
requires transitive zoo.animal.care;
}
!javac -p mods -d talks talks/zoo/animal/talks/content/*.java talks/zoo/animal/talks/media/*.java talks/zoo/animal/talks/schedule/*.java talks/module-info.java
!jar -cvf mods/zoo.animal.talks.jar -C talks/ .<jupyter_output>added manifest
added module-info: module-info.class
adding: module-info.java(in = 293) (out= 122)(deflated 58%)
adding: zoo/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/content/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/content/ElephantScript.class(in = 227) (out= 186)(deflated 18%)
adding: zoo/animal/talks/content/ElephantScript.java(in = 67) (out= 68)(deflated -1%)
adding: zoo/animal/talks/content/SeaLionScript.class(in = 225) (out= 185)(deflated 17%)
adding: zoo/animal/talks/content/SeaLionScript.java(in = 66) (out= 68)(deflated -3%)
adding: zoo/animal/talks/media/(in = 0) (out= 0)(stored 0%)
adding: zoo/animal/talks/media/Announcement.class(in = 464) (out= 318)(deflated 31%)
adding: zoo/animal/talks/media/Announcement.java(in = 170) (out= 134)(deflated 21%)
adding: zoo/animal/talks/media/Signage.class(in = 211) (out= 178)(deflated 15%)
adding: zoo/animal/talks/m[...]<jupyter_text>Finally, in the **zoo.staff** module, we can **get rid** of two requires statements.<jupyter_code>%%writefile staff/module-info.java
module zoo.staff {
// no longer needed requires zoo.animal.feeding;
// no longer needed requires zoo.animal.care;
requires zoo.animal.talks;
}
#compile and build the staff module:
!javac -p mods -d staff staff/zoo/staff/*.java staff/module-info.java
!jar -cvf mods/zoo.staff.jar -C staff/ .<jupyter_output>added manifest
added module-info: module-info.class
adding: module-info.java(in = 152) (out= 84)(deflated 44%)
adding: zoo/(in = 0) (out= 0)(stored 0%)
adding: zoo/staff/(in = 0) (out= 0)(stored 0%)
adding: zoo/staff/Jobs.class(in = 192) (out= 165)(deflated 14%)
adding: zoo/staff/Jobs.java(in = 42) (out= 44)(deflated -4%)
<jupyter_text>The more modules you have, the more benefits of requires transitive compound. It is also more convenient for the caller. If you were trying to work with this zoo, you could just require zoo.staff and have the remaining dependencies automatically inferred.Effects of requires transitive
Given our newly updated module-info files and using Figure, **what is** the effect of **applying** the **transitive modifier** to the requires statement in our zoo.animal.care module? **Applying** the **transitive** modifiers has the following effect:
* Module zoo.animal.talks **can optionally declare** it requires the **zoo.animal.feeding** module, but it is not required.
* Module zoo.animal.care **cannot be compiled** or executed **without access** to the zoo.animal.feeding module.
* Module zoo.animal.talks **cannot be compiled **or executed **without access** to the zoo.animal.feeding module.
These **rules hold even** if the zoo.animal.care and zoo.animal.talks modules **do not explicitly reference any packages** in the zoo.animal.feeding module. On the other hand, **without the transitive modifier** in our module-info file of zoo.animal.care, **the other modules** would have to **explicitly use requires** in order to reference any packages in the zoo.animal.feeding module.PROVIDES, USES, AND OPENS
For the remaining three keywords (provides, uses, and opens), you only need to be aware they exist rather than understanding them in detail for the 1Z0-815 exam.
The **provides** keyword specifies that a class provides an implementation of a service. The topic of services is covered on the 1Z0-816 exam, so for now, you can just think of a service as a fancy interface. To use it, you supply the API and class name that implements the API:
```java
provides zoo.staff.ZooApi with zoo.staff.ZooImpl
```
The **uses** keyword specifies that a module is relying on a service. To code it, you supply the API you want to call:
```java
uses zoo.staff.ZooApi
```
The **opens**
Java allows callers to inspect and call code at runtime with a technique called reflection. This is a powerful approach that allows calling code that might not be available at compile time. It can even be used to subvert access control! **Don’t worry—you don’t need to know how to write code using reflection for the exam.**
Since reflection can be dangerous, **the module system requires developers to explicitly allow reflection** in the module-info if they want calling modules to be allowed to use it. Here are two examples:
```java
opens zoo.animal.talks.schedule;
opens zoo.animal.talks.media to zoo.staff;
```
The first example allows any module using this one to use reflection. The second example only gives that privilege to the zoo.staff package.<jupyter_code>#Describing a Module
!java -p mods -d zoo.animal.feeding
#alternate
!java -p mods --describe-module zoo.animal.feeding
%%writefile care/module-info.java
module zoo.animal.care {
exports zoo.animal.care.medical to zoo.staff;
requires transitive zoo.animal.feeding;
}
#compiling care module
!javac -p mods -d care care/zoo/animal/care/details/*.java care/zoo/animal/care/medical/*.java care/module-info.java
!jar -cvf mods/zoo.animal.care.jar -C care/ .
!java -p mods -d zoo.animal.care<jupyter_output>zoo.animal.care file:///home/jovyan/mods/zoo.animal.care.jar
requires java.base mandated
requires zoo.animal.feeding transitive
qualified exports zoo.animal.care.medical to zoo.staff
contains zoo.animal.care.details
<jupyter_text>The first line of the output is the absolute path of the module file.
The two requires lines should look familiar as well.
The first is in the module-info, and the other is added to all modules.
Next comes something new. The **qualified exports** is the full name of exporting to a **specific module**.
Finally, the **contains** means that there is a package in the module that is not exported at all.
This is true. Our module has two packages, and one is available only to code inside the module.<jupyter_code>#Listing Available Modules
!java --list-modules
#Let’s try again with the directory containing our zoo modules.
!java -p mods --list-modules
#Showing Module Resolution
!java --show-module-resolution -p feeding -m zoo.animal.feeding/zoo.animal.feeding.Task
#Like the java command, the jar command can describe a module. Both of these commands are equivalent:
!jar -f mods/zoo.animal.feeding.jar -d
!jar --file mods/zoo.animal.feeding.jar --describe-module
#The jdeps command gives you information about dependencies within a module
!jdeps -s mods/zoo.animal.feeding.jar
!echo "----"
!jdeps mods/zoo.animal.feeding.jar<jupyter_output>zoo.animal.feeding -> java.base
----
zoo.animal.feeding
[file:///home/jovyan/mods/zoo.animal.feeding.jar]
requires mandated java.base (@11.0.4)
zoo.animal.feeding -> java.base
zoo.animal.feeding -> java.io java.base
zoo.animal.feeding -> java.lang java.base
|
no_license
|
/modules/Modules.ipynb
|
mespinozah/LearnJava11Certification
| 13 |
<jupyter_start><jupyter_text>## Modules, Methods, Constants<jupyter_code>from sklearn import svm
from sklearn.decomposition import PCA
import numpy as np
import pandas as pd
import json
import re
import random as rd
nikkud = ['ֹ', 'ְ', 'ּ', 'ׁ', 'ׂ', 'ָ', 'ֵ', 'ַ', 'ֶ', 'ִ', 'ֻ', 'ֱ', 'ֲ', 'ֳ', 'ׇ']
alphabet = ['א','ב','ג','ד','ה','ו','ז','ח','ט','י','כ','ך','ל','מ','ם','נ','ן','ס','ע','פ','ף','צ','ץ','ק','ר','ש','ת']
punctuation = ['״', '׳']
characters = alphabet + nikkud + punctuation
def tok_to_vec(token, dim):
# print(token)
vec = [0]*dim
for i in range(len(token)):
vec[i * len(characters) + characters.index(token[i])] = 1
return vec
def clean(token):
return ''.join([c for c in token if c in characters])<jupyter_output><empty_output><jupyter_text>## Data<jupyter_code>with open('./data/vowelized_cal_texts/71667_each_training_data.json', encoding='utf-8') as f:
data = json.load(f)
data = [{'tag':d['tag'], 'word': clean(d['word'])} for d in data]
print('Aramaic words in corpus: ' + str(len([w for w in data if w['tag'] == 'A'])))
print('Hebrew words in corpus: ' + str(len([w for w in data if w['tag'] == 'R'])))
rd.shuffle(data)
train_data = data[:(len(data) * 3 // 4)]
test_data = data[(len(data) * 3 //4):]<jupyter_output><empty_output><jupyter_text>## Initial Basic Test<jupyter_code>train_size = 20000
test_size = 5000
train_labels = [d['tag'] for d in train_data]
test_labels = [d['tag'] for d in test_data]
dimension = max([len(d['word']) for d in data]) * len(characters)
print(dimension)
train_vecs = [tok_to_vec(d['word'], dimension) for d in train_data[:train_size]]
test_vecs = [tok_to_vec(d['word'], dimension) for d in test_data]
pc = dimension // 1
pca = PCA(pc).fit(train_vecs)
train_pcs = pca.transform(train_vecs)
test_pcs = pca.transform(test_vecs)
lang_clf = svm.SVC()#probability=True)
lang_clf.fit(train_pcs, train_labels[:train_size])
accuracy = sum(np.array(lang_clf.predict(test_pcs[:test_size])) == np.array(test_labels[:test_size])) / test_size
print(accuracy)<jupyter_output>0.9368
<jupyter_text>## Test on Talmud Data<jupyter_code># Nazir was not part of the training data
with open('./data/aligned_talmud/Nazir.json', encoding='utf-8') as f:
naz = json.load(f)
page = rd.randrange(len(naz))
chunk = rd.randrange(len(naz[page]['content']))
words = [word_forms[1] for word_forms in naz[page]['content'][chunk]['text']]
words
words_vecs = [tok_to_vec(word, dimension) for word in words]
words_pcs = pca.transform(words_vecs)
#naz_predictions = lang_clf.predict_proba(words_pcs)
naz_predictions = lang_clf.predict(words_pcs)
for i in range(len(words)):
print(words[i] + '\t' + str(naz_predictions[i]))<jupyter_output><empty_output><jupyter_text>## Testing Saved Model### Basic Test<jupyter_code>import joblib
rd.shuffle(data)
test_labels = [d['tag'] for d in data]
dimension = max([len(d['word']) for d in data]) * len(characters)
print(dimension)
test_vecs = [tok_to_vec(d['word'], dimension) for d in data]
lang_clf = joblib.load('./src/languagetagger/GemaraLanguageTagger.joblib')
accuracy = sum(np.array(lang_clf.predict(test_vecs[:500])) == np.array(test_labels[:500])) / 500
print(accuracy)<jupyter_output>0.964
<jupyter_text>### Real Masekhet Testing<jupyter_code>import joblib
lang_clf = joblib.load('./src/languagetagger/GemaraLanguageTagger.joblib')
with open('./data/aligned_talmud/Berakhot.json', encoding='utf-8') as f:
mas = json.load(f)
page = 0 #rd.randrange(len(mas))
chunk = 0 #rd.randrange(len(mas[page]['content']))
words = [word_forms[1] for word_forms in mas[page]['content'][chunk]['text']]
words
words_vecs = [tok_to_vec(word, dimension) for word in words]
mas_predictions = lang_clf.predict_proba(words_vecs)
print('\t' + 'Hebrew Aramaic')
for i in range(len(words)):
print(words[i] + '\t' + str(mas_predictions[i]))<jupyter_output> Hebrew Aramaic
מֵאֵימָתַי [0.08400024 0.91599976]
קוֹרִין [0.04981305 0.95018695]
אֶת [0.0498447 0.9501553]
שְׁמַע [0.96086188 0.03913812]
בָּעֲרָבִין [0.11935584 0.88064416]
מִשָּׁעָה [0.03898098 0.96101902]
שֶׁהַכֹּהֲנִים [0.02752469 0.97247531]
נִכְנָסִים [0.01633482 0.98366518]
לֶאֱכוֹל [0.10155507 0.89844493]
בִּתְרוּמָתָן [0.23402207 0.76597793]
עַד [0.04987237 0.95012763]
סוֹף [0.17321767 0.82678233]
הָאַשְׁמוּרָה [0.4110613 0.5889387]
הָרִאשׁוֹנָה [0.04981824 0.95018176]
דִּבְרֵי [0.04982186 0.95017814]
רַבִּי [0.04988215 0.95011785]
אֱלִיעֶזֶר [0.0213943 0.9786057]
|
no_license
|
/svm_language_classifier.ipynb
|
TalmudLab/talmud-word-translation
| 6 |
<jupyter_start><jupyter_text># Introduction to HTML
HyperText Markup Language (HTML), is the standard markup language used to create web pages.
* Used as markup language for basically every website on the internet.
* Developed by the World Wide Web Consortium (W3C).
* Current version: HTML5 is supported by most modern internet browsers.
## Resources
* w3schools: http://www.w3schools.com/html/default.asp
## A simple HTML documentThe Hello world version of an HTML document is:```html
This is a title
Hello world!
```Save this file as `index.html` and open it with your favorite web browser, e.g. `google-chome index.html`
## Syntax
* The HTML file consists of tags, denoted by ``
* Most HTML elements are marked by a tag pair (start tag and end tag): `content`
* Some HTML elements have no content (and hence no end tag): `` or ``
* A tag can have attributes, for example: ``## CommentsComments are enclosed the `` tag:```html
<!-- This is a multiline comment.
It will not be rendered. -->
```-------------------------------
## Formatting### Headings<jupyter_code>%%html
<h1>I am a header</h1>
<h2>I am a sub-header</h2><jupyter_output><empty_output><jupyter_text>----------------------------------------
## New linesThe HTML code for a newline is ``:<jupyter_code>%%html
Hello world<br>
This text is on the next line<jupyter_output><empty_output><jupyter_text>## Special charactersHTML uses special codes to encode special characters, for example for mathematical, technical and currency symbols.
A list
http://www.w3schools.com/html/html_symbols.aspExamples:
| Symbol | HTML entity |
| ------------- |:-------------:|
| Å | `Å` |
| å | `å` |
| Ø | `Ø` |
| ø | `ø` |
| Æ | `&Aelig;` |
| æ | `æ` |
| ' | `"` |
| " | `"` |
| & | `&` |<jupyter_code>%%html
<p>
Ås, Sør-Trøndelag
</p><jupyter_output><empty_output><jupyter_text># Paragraphs<jupyter_code>%%html
<p>
This is a paragraph.
</p>
<p>
This is another paragraph.
</p><jupyter_output><empty_output><jupyter_text>## Italic text, bold text and links<jupyter_code>%%html
<b>Bold text</b>
<br>
<i>Italic text</i>
<br>
<em>Emphasized text</em>
<br>
<a href="http://github.com">This is a link</a><jupyter_output><empty_output><jupyter_text>-------------------------------
## Tables<jupyter_code>%%html
<table>
<tr>
<th>Name</th>
<th>Course</th>
<th>Points</th>
</tr>
<tr>
<td>Peter</td>
<td>INF3331</td>
<td>50</td>
</tr>
<tr>
<td>George</td>
<td>INF4331</td>
<td>94</td>
</tr>
</table><jupyter_output><empty_output><jupyter_text>## Images<jupyter_code>%%html
<img src="Rhinoceros.png" alt="Dürer's Rhinoceros">Dürer's Rhinoceros<jupyter_output><empty_output><jupyter_text>## StylingEvery HTML document has a default style (background color white, text color black). The default style can be changed with the *style attribute*.
```html
```
Multiple properties can be set with:
```html
```
Some Valid property options:
* `width`
* `height`
* `color`
* `background-color`
* `font-family`
* `font-size`
* `text-align`
### Examples<jupyter_code>%%html
<img src="Rhinoceros.png" alt="Dürer's Rhinoceros" style="width:100px;">Dürer's Rhinoceros
%%html
<p style="color:blue; background-color:rgb(255,0,255);">
Some colorful text.
</p><jupyter_output><empty_output><jupyter_text>## RemarksWeb browsers are not very strict when it comes to handling erroneous HTML documents. You can check if your HTML page conforms to the W3C standard with the W3C validation service https://validator.w3.org<jupyter_code>%%html
<img src="Rhinoceros.png" alt="Dürer's Rhinoceros" style="width:100px;"></img>
<i>A Rhinoceros
<b>Hallo<jupyter_output><empty_output>
|
no_license
|
/notebooks/web/Introduction to HTML.ipynb
|
UiO-INF3331/code_snippets
| 9 |
<jupyter_start><jupyter_text>### Dictionaries for data science ###<jupyter_code>feature_names = ['CountryName', 'CountryCode', 'IndicatorName', 'IndicatorCode', 'Year', 'Value']
row_vals = ['Arab World', 'ARB', 'Adolescent fertility rate (births per 1,000 women ages 15-19)', 'SP.ADO.TFRT', '1960', '133.56090740552298']
# Zip lists: zipped_lists
zipped_lists = zip(feature_names, row_vals)
# Create a dictionary: rs_dict
rs_dict = dict(zipped_lists)
# Print the dictionary
print(rs_dict)<jupyter_output>{'CountryName': 'Arab World', 'CountryCode': 'ARB', 'IndicatorName': 'Adolescent fertility rate (births per 1,000 women ages 15-19)', 'IndicatorCode': 'SP.ADO.TFRT', 'Year': '1960', 'Value': '133.56090740552298'}
<jupyter_text>### Writing a function to help you ###<jupyter_code># Define lists2dict()
def lists2dict(list1, list2):
"""Return a dictionary where list1 provides
the keys and list2 provides the values."""
# Zip lists: zipped_lists
zipped_lists = zip(list1, list2)
# Create a dictionary: rs_dict
rs_dict = dict(zipped_lists)
# Return the dictionary
return rs_dict
# Call lists2dict: rs_fxn
rs_fxn = lists2dict(feature_names, row_vals)
# Print rs_fxn
print(rs_fxn)<jupyter_output>{'CountryName': 'Arab World', 'CountryCode': 'ARB', 'IndicatorName': 'Adolescent fertility rate (births per 1,000 women ages 15-19)', 'IndicatorCode': 'SP.ADO.TFRT', 'Year': '1960', 'Value': '133.56090740552298'}
<jupyter_text>### Using a list comprehension ###<jupyter_code>row_lists = [['Arab World', 'ARB', 'Adolescent fertility rate (births per 1,000 women ages 15-19)', 'SP.ADO.TFRT', '1960', '133.56090740552298'], ['Arab World', 'ARB', 'Age dependency ratio (% of working-age population)', 'SP.POP.DPND', '1960', '87.7976011532547'], ['Arab World', 'ARB', 'Age dependency ratio, old (% of working-age population)', 'SP.POP.DPND.OL', '1960', '6.634579191565161'], ['Arab World', 'ARB', 'Age dependency ratio, young (% of working-age population)', 'SP.POP.DPND.YG', '1960', '81.02332950839141'], ['Arab World', 'ARB', 'Arms exports (SIPRI trend indicator values)', 'MS.MIL.XPRT.KD', '1960', '3000000.0'], ['Arab World', 'ARB', 'Arms imports (SIPRI trend indicator values)', 'MS.MIL.MPRT.KD', '1960', '538000000.0'], ['Arab World', 'ARB', 'Birth rate, crude (per 1,000 people)', 'SP.DYN.CBRT.IN', '1960', '47.697888095096395'], ['Arab World', 'ARB', 'CO2 emissions (kt)', 'EN.ATM.CO2E.KT', '1960', '59563.9892169935'], ['Arab World', 'ARB', 'CO2 emissions (metric tons per capita)', 'EN.ATM.CO2E.PC', '1960', '0.6439635478877049'], ['Arab World', 'ARB', 'CO2 emissions from gaseous fuel consumption (% of total)', 'EN.ATM.CO2E.GF.ZS', '1960', '5.041291753975099'], ['Arab World', 'ARB', 'CO2 emissions from liquid fuel consumption (% of total)', 'EN.ATM.CO2E.LF.ZS', '1960', '84.8514729446567'], ['Arab World', 'ARB', 'CO2 emissions from liquid fuel consumption (kt)', 'EN.ATM.CO2E.LF.KT', '1960', '49541.707291032304'], ['Arab World', 'ARB', 'CO2 emissions from solid fuel consumption (% of total)', 'EN.ATM.CO2E.SF.ZS', '1960', '4.72698138789597'], ['Arab World', 'ARB', 'Death rate, crude (per 1,000 people)', 'SP.DYN.CDRT.IN', '1960', '19.7544519237187'], ['Arab World', 'ARB', 'Fertility rate, total (births per woman)', 'SP.DYN.TFRT.IN', '1960', '6.92402738655897'], ['Arab World', 'ARB', 'Fixed telephone subscriptions', 'IT.MLT.MAIN', '1960', '406833.0'], ['Arab World', 'ARB', 'Fixed telephone subscriptions (per 100 people)', 'IT.MLT.MAIN.P2', '1960', '0.6167005703199'], ['Arab World', 'ARB', 'Hospital beds (per 1,000 people)', 'SH.MED.BEDS.ZS', '1960', '1.9296220724398703'], ['Arab World', 'ARB', 'International migrant stock (% of population)', 'SM.POP.TOTL.ZS', '1960', '2.9906371279862403'], ['Arab World', 'ARB', 'International migrant stock, total', 'SM.POP.TOTL', '1960', '3324685.0']]
# Print the first two lists in row_lists
print(row_lists[0])
print(row_lists[1])
# Turn list of lists into list of dicts: list_of_dicts
list_of_dicts = [lists2dict(feature_names, sublist) for sublist in row_lists]
# Print the first two dictionaries in list_of_dicts
print(list_of_dicts[0])
print(list_of_dicts[1])<jupyter_output>['Arab World', 'ARB', 'Adolescent fertility rate (births per 1,000 women ages 15-19)', 'SP.ADO.TFRT', '1960', '133.56090740552298']
['Arab World', 'ARB', 'Age dependency ratio (% of working-age population)', 'SP.POP.DPND', '1960', '87.7976011532547']
{'CountryName': 'Arab World', 'CountryCode': 'ARB', 'IndicatorName': 'Adolescent fertility rate (births per 1,000 women ages 15-19)', 'IndicatorCode': 'SP.ADO.TFRT', 'Year': '1960', 'Value': '133.56090740552298'}
{'CountryName': 'Arab World', 'CountryCode': 'ARB', 'IndicatorName': 'Age dependency ratio (% of working-age population)', 'IndicatorCode': 'SP.POP.DPND', 'Year': '1960', 'Value': '87.7976011532547'}
<jupyter_text>### Turning this all into a DataFrame ###<jupyter_code># Import the pandas package
import pandas as pd
# Turn list of lists into list of dicts: list_of_dicts
list_of_dicts = [lists2dict(feature_names, sublist) for sublist in row_lists]
# Turn list of dicts into a DataFrame: df
df = pd.DataFrame(list_of_dicts)
# Print the head of the DataFrame
print(df.head())
<jupyter_output> CountryCode CountryName IndicatorCode \
0 ARB Arab World SP.ADO.TFRT
1 ARB Arab World SP.POP.DPND
2 ARB Arab World SP.POP.DPND.OL
3 ARB Arab World SP.POP.DPND.YG
4 ARB Arab World MS.MIL.XPRT.KD
IndicatorName Value Year
0 Adolescent fertility rate (births per 1,000 wo... 133.56090740552298 1960
1 Age dependency ratio (% of working-age populat... 87.7976011532547 1960
2 Age dependency ratio, old (% of working-age po... 6.634579191565161 1960
3 Age dependency ratio, young (% of working-age ... 81.02332950839141 1960
4 Arms exports (SIPRI trend indicator values) 3000000.0 1960
<jupyter_text>### Processing data in chunks (1) ###<jupyter_code># Open a connection to the file
with open('input/world_dev_ind.csv') as file:
# Skip the column names
file.readline()
# Initialize an empty dictionary: counts_dict
counts_dict = {}
# Process only the first 1000 rows
for j in range(0, 1000):
# Split the current line into a list: line
line = file.readline().split(',')
# Get the value for the first column: first_col
first_col = line[0]
# If the column value is in the dict, increment its value
if first_col in counts_dict.keys():
counts_dict[first_col] += 1
# Else, add to the dict and set value to 1
else:
counts_dict[first_col] = 1
# Print the resulting dictionary
print(counts_dict)
<jupyter_output>{'Arab World': 5, 'Caribbean small states': 5, 'Central Europe and the Baltics': 5, 'East Asia & Pacific (all income levels)': 5, 'East Asia & Pacific (developing only)': 5, 'Euro area': 5, 'Europe & Central Asia (all income levels)': 5, 'Europe & Central Asia (developing only)': 5, 'European Union': 5, 'Fragile and conflict affected situations': 5, 'Heavily indebted poor countries (HIPC)': 5, 'High income': 5, 'High income: nonOECD': 5, 'High income: OECD': 5, 'Latin America & Caribbean (all income levels)': 5, 'Latin America & Caribbean (developing only)': 5, 'Least developed countries: UN classification': 5, 'Low & middle income': 5, 'Low income': 5, 'Lower middle income': 5, 'Middle East & North Africa (all income levels)': 5, 'Middle East & North Africa (developing only)': 5, 'Middle income': 5, 'North America': 5, 'OECD members': 5, 'Other small states': 5, 'Pacific island small states': 5, 'Small states': 5, 'South Asia': 5, 'Sub-Saharan Africa (all income levels)': 5, 'Sub-Saha[...]
|
no_license
|
/4.Python-Data-Science-Toolbox(Part 2)/3.practice.ipynb
|
clghks/Data-Scientist-with-Python
| 5 |
<jupyter_start><jupyter_text># Convolutional Networks
So far we have worked with deep fully-connected networks, using them to explore different optimization strategies and network architectures. Fully-connected networks are a good testbed for experimentation because they are very computationally efficient, but in practice all state-of-the-art results use convolutional networks instead.
First you will implement several layer types that are used in convolutional networks. You will then use these layers to train a convolutional network on the CIFAR-10 dataset.<jupyter_code># As usual, a bit of setup
import numpy as np
import matplotlib.pyplot as plt
from cs231n.classifiers.cnn import *
from cs231n.data_utils import get_CIFAR10_data
from cs231n.gradient_check import eval_numerical_gradient_array, eval_numerical_gradient
from cs231n.layers import *
from cs231n.fast_layers import *
from cs231n.solver import Solver
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# for auto-reloading external modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
def rel_error(x, y):
""" returns relative error """
return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))
# Load the (preprocessed) CIFAR10 data.
data = get_CIFAR10_data()
for k, v in data.items():
print('%s: ' % k, v.shape)<jupyter_output>X_train: (49000, 3, 32, 32)
y_train: (49000,)
X_val: (1000, 3, 32, 32)
y_val: (1000,)
X_test: (1000, 3, 32, 32)
y_test: (1000,)
<jupyter_text># Convolution: Naive forward pass
The core of a convolutional network is the convolution operation. In the file `cs231n/layers.py`, implement the forward pass for the convolution layer in the function `conv_forward_naive`.
You don't have to worry too much about efficiency at this point; just write the code in whatever way you find most clear.
You can test your implementation by running the following:<jupyter_code>x_shape = (2, 3, 4, 4)
w_shape = (3, 3, 4, 4)
x = np.linspace(-0.1, 0.5, num=np.prod(x_shape)).reshape(x_shape)
w = np.linspace(-0.2, 0.3, num=np.prod(w_shape)).reshape(w_shape)
b = np.linspace(-0.1, 0.2, num=3)
conv_param = {'stride': 2, 'pad': 1}
out, _ = conv_forward_naive(x, w, b, conv_param)
correct_out = np.array([[[[-0.08759809, -0.10987781],
[-0.18387192, -0.2109216 ]],
[[ 0.21027089, 0.21661097],
[ 0.22847626, 0.23004637]],
[[ 0.50813986, 0.54309974],
[ 0.64082444, 0.67101435]]],
[[[-0.98053589, -1.03143541],
[-1.19128892, -1.24695841]],
[[ 0.69108355, 0.66880383],
[ 0.59480972, 0.56776003]],
[[ 2.36270298, 2.36904306],
[ 2.38090835, 2.38247847]]]])
# Compare your output to ours; difference should be around e-8
print('Testing conv_forward_naive')
print('difference: ', rel_error(out, correct_out))<jupyter_output>Testing conv_forward_naive
difference: 2.2121476417505994e-08
<jupyter_text># Aside: Image processing via convolutions
As fun way to both check your implementation and gain a better understanding of the type of operation that convolutional layers can perform, we will set up an input containing two images and manually set up filters that perform common image processing operations (grayscale conversion and edge detection). The convolution forward pass will apply these operations to each of the input images. We can then visualize the results as a sanity check.<jupyter_code>from imageio import imread
from PIL import Image
kitten = imread('notebook_images/kitten.jpg')
puppy = imread('notebook_images/puppy.jpg')
# kitten is wide, and puppy is already square
d = kitten.shape[1] - kitten.shape[0]
kitten_cropped = kitten[:, d//2:-d//2, :]
img_size = 200 # Make this smaller if it runs too slow
resized_puppy = np.array(Image.fromarray(puppy).resize((img_size, img_size)))
resized_kitten = np.array(Image.fromarray(kitten_cropped).resize((img_size, img_size)))
x = np.zeros((2, 3, img_size, img_size))
x[0, :, :, :] = resized_puppy.transpose((2, 0, 1))
x[1, :, :, :] = resized_kitten.transpose((2, 0, 1))
# Set up a convolutional weights holding 2 filters, each 3x3
w = np.zeros((2, 3, 3, 3))
# The first filter converts the image to grayscale.
# Set up the red, green, and blue channels of the filter.
w[0, 0, :, :] = [[0, 0, 0], [0, 0.3, 0], [0, 0, 0]]
w[0, 1, :, :] = [[0, 0, 0], [0, 0.6, 0], [0, 0, 0]]
w[0, 2, :, :] = [[0, 0, 0], [0, 0.1, 0], [0, 0, 0]]
# Second filter detects horizontal edges in the blue channel.
w[1, 2, :, :] = [[1, 2, 1], [0, 0, 0], [-1, -2, -1]]
# Vector of biases. We don't need any bias for the grayscale
# filter, but for the edge detection filter we want to add 128
# to each output so that nothing is negative.
b = np.array([0, 128])
# Compute the result of convolving each input in x with each filter in w,
# offsetting by b, and storing the results in out.
out, _ = conv_forward_naive(x, w, b, {'stride': 1, 'pad': 1})
def imshow_no_ax(img, normalize=True):
""" Tiny helper to show images as uint8 and remove axis labels """
if normalize:
img_max, img_min = np.max(img), np.min(img)
img = 255.0 * (img - img_min) / (img_max - img_min)
plt.imshow(img.astype('uint8'))
plt.gca().axis('off')
# Show the original images and the results of the conv operation
plt.subplot(2, 3, 1)
imshow_no_ax(puppy, normalize=False)
plt.title('Original image')
plt.subplot(2, 3, 2)
imshow_no_ax(out[0, 0])
plt.title('Grayscale')
plt.subplot(2, 3, 3)
imshow_no_ax(out[0, 1])
plt.title('Edges')
plt.subplot(2, 3, 4)
imshow_no_ax(kitten_cropped, normalize=False)
plt.subplot(2, 3, 5)
imshow_no_ax(out[1, 0])
plt.subplot(2, 3, 6)
imshow_no_ax(out[1, 1])
plt.show()<jupyter_output><empty_output><jupyter_text># Convolution: Naive backward pass
Implement the backward pass for the convolution operation in the function `conv_backward_naive` in the file `cs231n/layers.py`. Again, you don't need to worry too much about computational efficiency.
When you are done, run the following to check your backward pass with a numeric gradient check.<jupyter_code>np.random.seed(231)
x = np.random.randn(4, 3, 5, 5)
w = np.random.randn(2, 3, 3, 3)
b = np.random.randn(2,)
dout = np.random.randn(4, 2, 5, 5)
conv_param = {'stride': 1, 'pad': 1}
dx_num = eval_numerical_gradient_array(lambda x: conv_forward_naive(x, w, b, conv_param)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: conv_forward_naive(x, w, b, conv_param)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: conv_forward_naive(x, w, b, conv_param)[0], b, dout)
out, cache = conv_forward_naive(x, w, b, conv_param)
dx, dw, db = conv_backward_naive(dout, cache)
# Your errors should be around e-8 or less.
print('Testing conv_backward_naive function')
print('dx error: ', rel_error(dx, dx_num))
print('dw error: ', rel_error(dw, dw_num))
print('db error: ', rel_error(db, db_num))<jupyter_output>Testing conv_backward_naive function
dx error: 3.90181171764193e-09
dw error: 3.267434272459827e-10
db error: 1.198721266225107e-10
<jupyter_text># Max-Pooling: Naive forward
Implement the forward pass for the max-pooling operation in the function `max_pool_forward_naive` in the file `cs231n/layers.py`. Again, don't worry too much about computational efficiency.
Check your implementation by running the following:<jupyter_code>x_shape = (2, 3, 4, 4)
x = np.linspace(-0.3, 0.4, num=np.prod(x_shape)).reshape(x_shape)
pool_param = {'pool_width': 2, 'pool_height': 2, 'stride': 2}
out, _ = max_pool_forward_naive(x, pool_param)
correct_out = np.array([[[[-0.26315789, -0.24842105],
[-0.20421053, -0.18947368]],
[[-0.14526316, -0.13052632],
[-0.08631579, -0.07157895]],
[[-0.02736842, -0.01263158],
[ 0.03157895, 0.04631579]]],
[[[ 0.09052632, 0.10526316],
[ 0.14947368, 0.16421053]],
[[ 0.20842105, 0.22315789],
[ 0.26736842, 0.28210526]],
[[ 0.32631579, 0.34105263],
[ 0.38526316, 0.4 ]]]])
# Compare your output with ours. Difference should be on the order of e-8.
print('Testing max_pool_forward_naive function:')
print('difference: ', rel_error(out, correct_out))<jupyter_output>Testing max_pool_forward_naive function:
difference: 4.1666665157267834e-08
<jupyter_text># Max-Pooling: Naive backward
Implement the backward pass for the max-pooling operation in the function `max_pool_backward_naive` in the file `cs231n/layers.py`. You don't need to worry about computational efficiency.
Check your implementation with numeric gradient checking by running the following:<jupyter_code>np.random.seed(231)
x = np.random.randn(3, 2, 8, 8)
dout = np.random.randn(3, 2, 4, 4)
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
dx_num = eval_numerical_gradient_array(lambda x: max_pool_forward_naive(x, pool_param)[0], x, dout)
out, cache = max_pool_forward_naive(x, pool_param)
dx = max_pool_backward_naive(dout, cache)
# Your error should be on the order of e-12
print('Testing max_pool_backward_naive function:')
print('dx error: ', rel_error(dx, dx_num))<jupyter_output>Testing max_pool_backward_naive function:
dx error: 3.27562514223145e-12
<jupyter_text># Fast layers
Making convolution and pooling layers fast can be challenging. To spare you the pain, we've provided fast implementations of the forward and backward passes for convolution and pooling layers in the file `cs231n/fast_layers.py`.
The fast convolution implementation depends on a Cython extension; to compile it you need to run the following from the `cs231n` directory:
```bash
python setup.py build_ext --inplace
```
The API for the fast versions of the convolution and pooling layers is exactly the same as the naive versions that you implemented above: the forward pass receives data, weights, and parameters and produces outputs and a cache object; the backward pass recieves upstream derivatives and the cache object and produces gradients with respect to the data and weights.
**NOTE:** The fast implementation for pooling will only perform optimally if the pooling regions are non-overlapping and tile the input. If these conditions are not met then the fast pooling implementation will not be much faster than the naive implementation.
You can compare the performance of the naive and fast versions of these layers by running the following:<jupyter_code># Rel errors should be around e-9 or less
from cs231n.fast_layers import conv_forward_fast, conv_backward_fast
from time import time
np.random.seed(231)
x = np.random.randn(100, 3, 31, 31)
w = np.random.randn(25, 3, 3, 3)
b = np.random.randn(25,)
dout = np.random.randn(100, 25, 16, 16)
conv_param = {'stride': 2, 'pad': 1}
t0 = time()
out_naive, cache_naive = conv_forward_naive(x, w, b, conv_param)
t1 = time()
out_fast, cache_fast = conv_forward_fast(x, w, b, conv_param)
t2 = time()
print('Testing conv_forward_fast:')
print('Naive: %fs' % (t1 - t0))
print('Fast: %fs' % (t2 - t1))
print('Speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('Difference: ', rel_error(out_naive, out_fast))
t0 = time()
dx_naive, dw_naive, db_naive = conv_backward_naive(dout, cache_naive)
t1 = time()
dx_fast, dw_fast, db_fast = conv_backward_fast(dout, cache_fast)
t2 = time()
print('\nTesting conv_backward_fast:')
print('Naive: %fs' % (t1 - t0))
print('Fast: %fs' % (t2 - t1))
print('Speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('dx difference: ', rel_error(dx_naive, dx_fast))
print('dw difference: ', rel_error(dw_naive, dw_fast))
print('db difference: ', rel_error(db_naive, db_fast))
# Relative errors should be close to 0.0
from cs231n.fast_layers import max_pool_forward_fast, max_pool_backward_fast
np.random.seed(231)
x = np.random.randn(100, 3, 32, 32)
dout = np.random.randn(100, 3, 16, 16)
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
t0 = time()
out_naive, cache_naive = max_pool_forward_naive(x, pool_param)
t1 = time()
out_fast, cache_fast = max_pool_forward_fast(x, pool_param)
t2 = time()
print('Testing pool_forward_fast:')
print('Naive: %fs' % (t1 - t0))
print('fast: %fs' % (t2 - t1))
print('speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('difference: ', rel_error(out_naive, out_fast))
t0 = time()
dx_naive = max_pool_backward_naive(dout, cache_naive)
t1 = time()
dx_fast = max_pool_backward_fast(dout, cache_fast)
t2 = time()
print('\nTesting pool_backward_fast:')
print('Naive: %fs' % (t1 - t0))
print('fast: %fs' % (t2 - t1))
print('speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('dx difference: ', rel_error(dx_naive, dx_fast))<jupyter_output>Testing pool_forward_fast:
Naive: 0.008496s
fast: 0.008562s
speedup: 0.992203x
difference: 0.0
Testing pool_backward_fast:
Naive: 0.966685s
fast: 0.017047s
speedup: 56.708066x
dx difference: 0.0
<jupyter_text># Convolutional "sandwich" layers
Previously we introduced the concept of "sandwich" layers that combine multiple operations into commonly used patterns. In the file `cs231n/layer_utils.py` you will find sandwich layers that implement a few commonly used patterns for convolutional networks. Run the cells below to sanity check they're working.<jupyter_code>from cs231n.layer_utils import conv_relu_pool_forward, conv_relu_pool_backward
np.random.seed(231)
x = np.random.randn(2, 3, 16, 16)
w = np.random.randn(3, 3, 3, 3)
b = np.random.randn(3,)
dout = np.random.randn(2, 3, 8, 8)
conv_param = {'stride': 1, 'pad': 1}
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
out, cache = conv_relu_pool_forward(x, w, b, conv_param, pool_param)
dx, dw, db = conv_relu_pool_backward(dout, cache)
dx_num = eval_numerical_gradient_array(lambda x: conv_relu_pool_forward(x, w, b, conv_param, pool_param)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: conv_relu_pool_forward(x, w, b, conv_param, pool_param)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: conv_relu_pool_forward(x, w, b, conv_param, pool_param)[0], b, dout)
# Relative errors should be around e-8 or less
print('Testing conv_relu_pool')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))
from cs231n.layer_utils import conv_relu_forward, conv_relu_backward
np.random.seed(231)
x = np.random.randn(2, 3, 8, 8)
w = np.random.randn(3, 3, 3, 3)
b = np.random.randn(3,)
dout = np.random.randn(2, 3, 8, 8)
conv_param = {'stride': 1, 'pad': 1}
out, cache = conv_relu_forward(x, w, b, conv_param)
dx, dw, db = conv_relu_backward(dout, cache)
dx_num = eval_numerical_gradient_array(lambda x: conv_relu_forward(x, w, b, conv_param)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: conv_relu_forward(x, w, b, conv_param)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: conv_relu_forward(x, w, b, conv_param)[0], b, dout)
# Relative errors should be around e-8 or less
print('Testing conv_relu:')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))<jupyter_output>Testing conv_relu:
dx error: 3.5600610115232832e-09
dw error: 2.2497700915729298e-10
db error: 1.3087619975802167e-10
<jupyter_text># Three-layer ConvNet
Now that you have implemented all the necessary layers, we can put them together into a simple convolutional network.
Open the file `cs231n/classifiers/cnn.py` and complete the implementation of the `ThreeLayerConvNet` class. Remember you can use the fast/sandwich layers (already imported for you) in your implementation. Run the following cells to help you debug:## Sanity check loss
After you build a new network, one of the first things you should do is sanity check the loss. When we use the softmax loss, we expect the loss for random weights (and no regularization) to be about `log(C)` for `C` classes. When we add regularization the loss should go up slightly.<jupyter_code>model = ThreeLayerConvNet()
N = 50
X = np.random.randn(N, 3, 32, 32)
y = np.random.randint(10, size=N)
loss, grads = model.loss(X, y)
print('Initial loss (no regularization): ', loss)
model.reg = 0.5
loss, grads = model.loss(X, y)
print('Initial loss (with regularization): ', loss)<jupyter_output>Initial loss (no regularization): 2.3025856489084204
Initial loss (with regularization): 2.5086653405569037
<jupyter_text>## Gradient check
After the loss looks reasonable, use numeric gradient checking to make sure that your backward pass is correct. When you use numeric gradient checking you should use a small amount of artifical data and a small number of neurons at each layer. Note: correct implementations may still have relative errors up to the order of e-2.<jupyter_code>num_inputs = 2
input_dim = (3, 16, 16)
reg = 0.0
num_classes = 10
np.random.seed(231)
X = np.random.randn(num_inputs, *input_dim)
y = np.random.randint(num_classes, size=num_inputs)
model = ThreeLayerConvNet(num_filters=3, filter_size=3,
input_dim=input_dim, hidden_dim=7,
dtype=np.float64)
loss, grads = model.loss(X, y)
# Errors should be small, but correct implementations may have
# relative errors up to the order of e-2
for param_name in sorted(grads):
f = lambda _: model.loss(X, y)[0]
param_grad_num = eval_numerical_gradient(f, model.params[param_name], verbose=False, h=1e-6)
e = rel_error(param_grad_num, grads[param_name])
print('%s max relative error: %e' % (param_name, rel_error(param_grad_num, grads[param_name])))<jupyter_output>W1 max relative error: 1.380104e-04
W2 max relative error: 1.822723e-02
W3 max relative error: 3.064049e-04
b1 max relative error: 3.477652e-05
b2 max relative error: 2.516375e-03
b3 max relative error: 7.945660e-10
<jupyter_text>## Overfit small data
A nice trick is to train your model with just a few training samples. You should be able to overfit small datasets, which will result in very high training accuracy and comparatively low validation accuracy.<jupyter_code>np.random.seed(231)
num_train = 100
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
model = ThreeLayerConvNet(weight_scale=1e-2)
solver = Solver(model, small_data,
num_epochs=15, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=True, print_every=1)
solver.train()<jupyter_output>(Iteration 1 / 30) loss: 2.414060
(Epoch 0 / 15) train acc: 0.200000; val_acc: 0.137000
(Iteration 2 / 30) loss: 3.102925
(Epoch 1 / 15) train acc: 0.140000; val_acc: 0.087000
(Iteration 3 / 30) loss: 2.270330
(Iteration 4 / 30) loss: 2.096705
(Epoch 2 / 15) train acc: 0.240000; val_acc: 0.094000
(Iteration 5 / 30) loss: 1.838880
(Iteration 6 / 30) loss: 1.934188
(Epoch 3 / 15) train acc: 0.510000; val_acc: 0.173000
(Iteration 7 / 30) loss: 1.827912
(Iteration 8 / 30) loss: 1.639574
(Epoch 4 / 15) train acc: 0.520000; val_acc: 0.188000
(Iteration 9 / 30) loss: 1.330082
(Iteration 10 / 30) loss: 1.756115
(Epoch 5 / 15) train acc: 0.630000; val_acc: 0.167000
(Iteration 11 / 30) loss: 1.024162
(Iteration 12 / 30) loss: 1.041826
(Epoch 6 / 15) train acc: 0.750000; val_acc: 0.229000
(Iteration 13 / 30) loss: 1.142777
(Iteration 14 / 30) loss: 0.835706
(Epoch 7 / 15) train acc: 0.790000; val_acc: 0.247000
(Iteration 15 / 30) loss: 0.587786
(Iteration 16 / 30) loss: 0.645509
(Epoch 8 / 15) tr[...]<jupyter_text>Plotting the loss, training accuracy, and validation accuracy should show clear overfitting:<jupyter_code>plt.subplot(2, 1, 1)
plt.plot(solver.loss_history, 'o')
plt.xlabel('iteration')
plt.ylabel('loss')
plt.subplot(2, 1, 2)
plt.plot(solver.train_acc_history, '-o')
plt.plot(solver.val_acc_history, '-o')
plt.legend(['train', 'val'], loc='upper left')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()<jupyter_output><empty_output><jupyter_text>## Train the net
By training the three-layer convolutional network for one epoch, you should achieve greater than 40% accuracy on the training set:<jupyter_code>model = ThreeLayerConvNet(weight_scale=0.001, hidden_dim=500, reg=0.001)
solver = Solver(model, data,
num_epochs=1, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=True, print_every=20)
solver.train()<jupyter_output>(Iteration 1 / 980) loss: 2.304740
(Epoch 0 / 1) train acc: 0.103000; val_acc: 0.107000
(Iteration 21 / 980) loss: 2.098229
(Iteration 41 / 980) loss: 1.949788
(Iteration 61 / 980) loss: 1.888398
(Iteration 81 / 980) loss: 1.877093
(Iteration 101 / 980) loss: 1.851877
(Iteration 121 / 980) loss: 1.859353
(Iteration 141 / 980) loss: 1.800181
(Iteration 161 / 980) loss: 2.143292
(Iteration 181 / 980) loss: 1.830573
(Iteration 201 / 980) loss: 2.037280
(Iteration 221 / 980) loss: 2.020304
(Iteration 241 / 980) loss: 1.823728
(Iteration 261 / 980) loss: 1.692679
(Iteration 281 / 980) loss: 1.882594
(Iteration 301 / 980) loss: 1.798261
(Iteration 321 / 980) loss: 1.851960
(Iteration 341 / 980) loss: 1.716323
(Iteration 361 / 980) loss: 1.897655
(Iteration 381 / 980) loss: 1.319744
(Iteration 401 / 980) loss: 1.738790
(Iteration 421 / 980) loss: 1.488866
(Iteration 441 / 980) loss: 1.718409
(Iteration 461 / 980) loss: 1.744440
(Iteration 481 / 980) loss: 1.605460
(Iteration 501 / 980) loss: [...]<jupyter_text>## Visualize Filters
You can visualize the first-layer convolutional filters from the trained network by running the following:<jupyter_code>from cs231n.vis_utils import visualize_grid
grid = visualize_grid(model.params['W1'].transpose(0, 2, 3, 1))
plt.imshow(grid.astype('uint8'))
plt.axis('off')
plt.gcf().set_size_inches(5, 5)
plt.show()<jupyter_output><empty_output><jupyter_text># Spatial Batch Normalization
We already saw that batch normalization is a very useful technique for training deep fully-connected networks. As proposed in the original paper (link in `BatchNormalization.ipynb`), batch normalization can also be used for convolutional networks, but we need to tweak it a bit; the modification will be called "spatial batch normalization."
Normally batch-normalization accepts inputs of shape `(N, D)` and produces outputs of shape `(N, D)`, where we normalize across the minibatch dimension `N`. For data coming from convolutional layers, batch normalization needs to accept inputs of shape `(N, C, H, W)` and produce outputs of shape `(N, C, H, W)` where the `N` dimension gives the minibatch size and the `(H, W)` dimensions give the spatial size of the feature map.
If the feature map was produced using convolutions, then we expect every feature channel's statistics e.g. mean, variance to be relatively consistent both between different images, and different locations within the same image -- after all, every feature channel is produced by the same convolutional filter! Therefore spatial batch normalization computes a mean and variance for each of the `C` feature channels by computing statistics over the minibatch dimension `N` as well the spatial dimensions `H` and `W`.
[1] [Sergey Ioffe and Christian Szegedy, "Batch Normalization: Accelerating Deep Network Training by Reducing
Internal Covariate Shift", ICML 2015.](https://arxiv.org/abs/1502.03167)## Spatial batch normalization: forward
In the file `cs231n/layers.py`, implement the forward pass for spatial batch normalization in the function `spatial_batchnorm_forward`. Check your implementation by running the following:<jupyter_code>np.random.seed(231)
# Check the training-time forward pass by checking means and variances
# of features both before and after spatial batch normalization
N, C, H, W = 2, 3, 4, 5
x = 4 * np.random.randn(N, C, H, W) + 10
print('Before spatial batch normalization:')
print(' Shape: ', x.shape)
print(' Means: ', x.mean(axis=(0, 2, 3)))
print(' Stds: ', x.std(axis=(0, 2, 3)))
# Means should be close to zero and stds close to one
gamma, beta = np.ones(C), np.zeros(C)
bn_param = {'mode': 'train'}
out, _ = spatial_batchnorm_forward(x, gamma, beta, bn_param)
print('After spatial batch normalization:')
print(' Shape: ', out.shape)
print(' Means: ', out.mean(axis=(0, 2, 3)))
print(' Stds: ', out.std(axis=(0, 2, 3)))
# Means should be close to beta and stds close to gamma
gamma, beta = np.asarray([3, 4, 5]), np.asarray([6, 7, 8])
out, _ = spatial_batchnorm_forward(x, gamma, beta, bn_param)
print('After spatial batch normalization (nontrivial gamma, beta):')
print(' Shape: ', out.shape)
print(' Means: ', out.mean(axis=(0, 2, 3)))
print(' Stds: ', out.std(axis=(0, 2, 3)))
np.random.seed(231)
# Check the test-time forward pass by running the training-time
# forward pass many times to warm up the running averages, and then
# checking the means and variances of activations after a test-time
# forward pass.
N, C, H, W = 10, 4, 11, 12
bn_param = {'mode': 'train'}
gamma = np.ones(C)
beta = np.zeros(C)
for t in range(50):
x = 2.3 * np.random.randn(N, C, H, W) + 13
spatial_batchnorm_forward(x, gamma, beta, bn_param)
bn_param['mode'] = 'test'
x = 2.3 * np.random.randn(N, C, H, W) + 13
a_norm, _ = spatial_batchnorm_forward(x, gamma, beta, bn_param)
# Means should be close to zero and stds close to one, but will be
# noisier than training-time forward passes.
print('After spatial batch normalization (test-time):')
print(' means: ', a_norm.mean(axis=(0, 2, 3)))
print(' stds: ', a_norm.std(axis=(0, 2, 3)))<jupyter_output>After spatial batch normalization (test-time):
means: [-0.08034398 0.07562874 0.05716365 0.04378379]
stds: [0.96718652 1.02997042 1.02887526 1.0058548 ]
<jupyter_text>## Spatial batch normalization: backward
In the file `cs231n/layers.py`, implement the backward pass for spatial batch normalization in the function `spatial_batchnorm_backward`. Run the following to check your implementation using a numeric gradient check:<jupyter_code>np.random.seed(231)
N, C, H, W = 2, 3, 4, 5
x = 5 * np.random.randn(N, C, H, W) + 12
gamma = np.random.randn(C)
beta = np.random.randn(C)
dout = np.random.randn(N, C, H, W)
bn_param = {'mode': 'train'}
fx = lambda x: spatial_batchnorm_forward(x, gamma, beta, bn_param)[0]
fg = lambda a: spatial_batchnorm_forward(x, gamma, beta, bn_param)[0]
fb = lambda b: spatial_batchnorm_forward(x, gamma, beta, bn_param)[0]
dx_num = eval_numerical_gradient_array(fx, x, dout)
da_num = eval_numerical_gradient_array(fg, gamma, dout)
db_num = eval_numerical_gradient_array(fb, beta, dout)
#You should expect errors of magnitudes between 1e-12~1e-06
_, cache = spatial_batchnorm_forward(x, gamma, beta, bn_param)
dx, dgamma, dbeta = spatial_batchnorm_backward(dout, cache)
print('dx error: ', rel_error(dx_num, dx))
print('dgamma error: ', rel_error(da_num, dgamma))
print('dbeta error: ', rel_error(db_num, dbeta))<jupyter_output>dx error: 2.78664820066917e-07
dgamma error: 7.0974817113608705e-12
dbeta error: 3.275608725278405e-12
<jupyter_text># Group Normalization
In the previous notebook, we mentioned that Layer Normalization is an alternative normalization technique that mitigates the batch size limitations of Batch Normalization. However, as the authors of [2] observed, Layer Normalization does not perform as well as Batch Normalization when used with Convolutional Layers:
>With fully connected layers, all the hidden units in a layer tend to make similar contributions to the final prediction, and re-centering and rescaling the summed inputs to a layer works well. However, the assumption of similar contributions is no longer true for convolutional neural networks. The large number of the hidden units whose
receptive fields lie near the boundary of the image are rarely turned on and thus have very different
statistics from the rest of the hidden units within the same layer.
The authors of [3] propose an intermediary technique. In contrast to Layer Normalization, where you normalize over the entire feature per-datapoint, they suggest a consistent splitting of each per-datapoint feature into G groups, and a per-group per-datapoint normalization instead.

**Visual comparison of the normalization techniques discussed so far (image edited from [3])**
Even though an assumption of equal contribution is still being made within each group, the authors hypothesize that this is not as problematic, as innate grouping arises within features for visual recognition. One example they use to illustrate this is that many high-performance handcrafted features in traditional Computer Vision have terms that are explicitly grouped together. Take for example Histogram of Oriented Gradients [4]-- after computing histograms per spatially local block, each per-block histogram is normalized before being concatenated together to form the final feature vector.
You will now implement Group Normalization. Note that this normalization technique that you are to implement in the following cells was introduced and published to ECCV just in 2018 -- this truly is still an ongoing and excitingly active field of research!
[2] [Ba, Jimmy Lei, Jamie Ryan Kiros, and Geoffrey E. Hinton. "Layer Normalization." stat 1050 (2016): 21.](https://arxiv.org/pdf/1607.06450.pdf)
[3] [Wu, Yuxin, and Kaiming He. "Group Normalization." arXiv preprint arXiv:1803.08494 (2018).](https://arxiv.org/abs/1803.08494)
[4] [N. Dalal and B. Triggs. Histograms of oriented gradients for
human detection. In Computer Vision and Pattern Recognition
(CVPR), 2005.](https://ieeexplore.ieee.org/abstract/document/1467360/)## Group normalization: forward
In the file `cs231n/layers.py`, implement the forward pass for group normalization in the function `spatial_groupnorm_forward`. Check your implementation by running the following:<jupyter_code>np.random.seed(231)
# Check the training-time forward pass by checking means and variances
# of features both before and after spatial batch normalization
N, C, H, W = 2, 6, 4, 5
G = 2
x = 4 * np.random.randn(N, C, H, W) + 10
x_g = x.reshape((N*G,-1))
print('Before spatial group normalization:')
print(' Shape: ', x.shape)
print(' Means: ', x_g.mean(axis=1))
print(' Stds: ', x_g.std(axis=1))
# Means should be close to zero and stds close to one
gamma, beta = np.ones((1,C,1,1)), np.zeros((1,C,1,1))
bn_param = {'mode': 'train'}
out, _ = spatial_groupnorm_forward(x, gamma, beta, G, bn_param)
out_g = out.reshape((N*G,-1))
print('After spatial group normalization:')
print(' Shape: ', out.shape)
print(' Means: ', out_g.mean(axis=1))
print(' Stds: ', out_g.std(axis=1))<jupyter_output>Before spatial group normalization:
Shape: (2, 6, 4, 5)
Means: [9.72505327 8.51114185 8.9147544 9.43448077]
Stds: [3.67070958 3.09892597 4.27043622 3.97521327]
After spatial group normalization:
Shape: (2, 6, 4, 5)
Means: [-2.14643118e-16 5.25505565e-16 2.65528340e-16 -3.38618023e-16]
Stds: [0.99999963 0.99999948 0.99999973 0.99999968]
<jupyter_text>## Spatial group normalization: backward
In the file `cs231n/layers.py`, implement the backward pass for spatial batch normalization in the function `spatial_groupnorm_backward`. Run the following to check your implementation using a numeric gradient check:<jupyter_code>np.random.seed(231)
N, C, H, W = 2, 6, 4, 5
G = 2
x = 5 * np.random.randn(N, C, H, W) + 12
gamma = np.random.randn(1,C,1,1)
beta = np.random.randn(1,C,1,1)
dout = np.random.randn(N, C, H, W)
gn_param = {}
fx = lambda x: spatial_groupnorm_forward(x, gamma, beta, G, gn_param)[0]
fg = lambda a: spatial_groupnorm_forward(x, gamma, beta, G, gn_param)[0]
fb = lambda b: spatial_groupnorm_forward(x, gamma, beta, G, gn_param)[0]
dx_num = eval_numerical_gradient_array(fx, x, dout)
da_num = eval_numerical_gradient_array(fg, gamma, dout)
db_num = eval_numerical_gradient_array(fb, beta, dout)
_, cache = spatial_groupnorm_forward(x, gamma, beta, G, gn_param)
dx, dgamma, dbeta = spatial_groupnorm_backward(dout, cache)
#You should expect errors of magnitudes between 1e-12~1e-07
print('dx error: ', rel_error(dx_num, dx))
print('dgamma error: ', rel_error(da_num, dgamma))
print('dbeta error: ', rel_error(db_num, dbeta))<jupyter_output>dx error: 7.413109384854475e-08
dgamma error: 9.468195772749234e-12
dbeta error: 3.354494437653335e-12
|
no_license
|
/assignment2/ConvolutionalNetworks.ipynb
|
diler5/cs231n
| 18 |
<jupyter_start><jupyter_text># Detect OutliersIn our EDA in R, we determined that the ids 524 692 1183 1299 (R counts start at 1!) had very large GrLivArea, while 31 496 534 917 969 had very low SalePrice for their size, relative to the rest of the population. We want to determine what sets of points can be dropped in order to increase prediction accuracy on a validation set.<jupyter_code># we decrement by 1 in order to conform with python counting
pot_outliers = [524-1, 692-1, 1183-1, 1299-1, 31-1, 496-1, 534-1, 917-1, 969-1]
import itertools
import numpy as np
import pandas as pd
pd.set_option('display.precision',20)
from sklearn import linear_model
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import cross_val_predict, KFold, cross_val_score, GridSearchCV, \
ShuffleSplit
# def to compare goodness of fit on training set
def rmse(y_true, y_pred):
return np.sqrt(mean_squared_error(y_true, y_pred))<jupyter_output><empty_output><jupyter_text>We import the preprocessed data set that includes all data points.<jupyter_code>df = pd.read_csv("input/train_tidy_000000000.csv")<jupyter_output><empty_output><jupyter_text>The columns GarageAge and GarageAgeLin have NAs. We have to drop them unless we drop the rows with NoGarage == 1 instead. For now, we just drop GarageAge and GarageAgeLin.<jupyter_code>df.drop(['GarageAge', 'GarageAgeLin'], axis=1, inplace=True)<jupyter_output><empty_output><jupyter_text>We want to split this into a training and validation set. We want the potential outliers to be in the training set.<jupyter_code>outlier_df = df.iloc[pot_outliers]
nooutlier_df = df.drop(pot_outliers)
ss = ShuffleSplit(n_splits=1, test_size=0.20, random_state=89)
X = nooutlier_df.values
for train_idx, validation_idx in ss.split(X):
train_df = nooutlier_df.iloc[train_idx]
validation_df = nooutlier_df.iloc[validation_idx]
train_df = train_df.append(outlier_df)<jupyter_output><empty_output><jupyter_text>We'll set up the matrices we use for the validation set, since these won't change as we drop outliers. <jupyter_code>y_validation = validation_df['SalePrice'].values
x_validation = validation_df.drop(['HouseId', 'SalePrice'],axis=1).values<jupyter_output><empty_output><jupyter_text>We will use the LassoLarsCV model and RMS error as our metric. This is because, as we will see, linear models do reasonably well on this problem and the regularization hyperparameter is automatically selected by CV on the training data.<jupyter_code># Cross-validation sets
kfold = KFold(n_splits=10, random_state=7)
lr = linear_model.LassoLarsCV(verbose=False, max_iter=5000,precompute='auto', cv=kfold, max_n_alphas=1000, n_jobs=-1)<jupyter_output><empty_output><jupyter_text>We want to set a baseline value by training on the full dataset and then predicting on the validation set.<jupyter_code>y_train = train_df['SalePrice'].values
x_train = train_df.drop(['HouseId', 'SalePrice'],axis=1).values
lr.fit(x_train, y_train)
y_pred = lr.predict(x_validation)
baseline = rmse(y_validation, y_pred)
baseline<jupyter_output><empty_output><jupyter_text>We'll examine dropping all possible sets of outliers. There are 512 total combinations including the baseline where we don't drop any points. train_df is still indexed by HouseId - 1<jupyter_code>comb_drop_results_df = pd.DataFrame(dtype = 'float64')
count = 0
for L in range(0, len(pot_outliers)+1):
for subset in itertools.combinations(pot_outliers, L):
drop_pts = list(subset)
comb_drop_results_df.loc[count, 'Dropped'] = str([x+1 for x in drop_pts])
y_train = train_df['SalePrice'].drop(drop_pts).values
x_train = train_df.drop(['HouseId', 'SalePrice'],axis=1).drop(drop_pts).values
lr.fit(x_train, y_train)
y_pred = lr.predict(x_validation)
error = rmse(y_validation, y_pred)
comb_drop_results_df.loc[count, 'RMSE'] = error
comb_drop_results_df.loc[count, 'Diff from Base'] = error - baseline
count += 1
comb_drop_results_df.sort_values(['RMSE'])
comb_drop_results_df.sort_values(['RMSE']).to_csv('comb_drop_results.csv', header=True)<jupyter_output><empty_output>
|
no_license
|
/.ipynb_checkpoints/DetectOutliers-checkpoint.ipynb
|
richcorrado/ART
| 8 |
<jupyter_start><jupyter_text># Practical Statistics for Data Scientists (Python)
# Chapter 1. Exploratory Data Analysis
> (c) 2019 Peter C. Bruce, Andrew Bruce, Peter GedeckImport required Python packages.<jupyter_code>%matplotlib inline
from pathlib import Path
import pandas as pd
import numpy as np
from scipy.stats import trim_mean
from statsmodels import robust
import wquantiles
import seaborn as sns
import matplotlib.pylab as plt
try:
import common
DATA = common.dataDirectory()
except ImportError:
DATA = Path().resolve() / 'data'<jupyter_output><empty_output><jupyter_text>Define paths to data sets. If you don't keep your data in the same directory as the code, adapt the path names.<jupyter_code>AIRLINE_STATS_CSV = DATA / 'airline_stats.csv'
KC_TAX_CSV = DATA / 'kc_tax.csv.gz'
LC_LOANS_CSV = DATA / 'lc_loans.csv'
AIRPORT_DELAYS_CSV = DATA / 'dfw_airline.csv'
SP500_DATA_CSV = DATA / 'sp500_data.csv.gz'
SP500_SECTORS_CSV = DATA / 'sp500_sectors.csv'
STATE_CSV = DATA / 'state.csv'<jupyter_output><empty_output><jupyter_text># Estimates of Location
## Example: Location Estimates of Population and Murder Rates<jupyter_code># Table 1-2
state = pd.read_csv(STATE_CSV)
print(state.head(8))<jupyter_output> State Population Murder.Rate Abbreviation
0 Alabama 4779736 5.7 AL
1 Alaska 710231 5.6 AK
2 Arizona 6392017 4.7 AZ
3 Arkansas 2915918 5.6 AR
4 California 37253956 4.4 CA
5 Colorado 5029196 2.8 CO
6 Connecticut 3574097 2.4 CT
7 Delaware 897934 5.8 DE
<jupyter_text>Compute the mean, trimmed mean, and median for Population. For `mean` and `median` we can use the _pandas_ methods of the data frame. The trimmed mean requires the `trim_mean` function in _scipy.stats_.<jupyter_code>state = pd.read_csv(STATE_CSV)
print(state['Population'].mean())
print(trim_mean(state['Population'], 0.1))
print(state['Population'].median())<jupyter_output>4436369.5
<jupyter_text>Weighted mean is available with numpy. For weighted median, we can use the specialised package `wquantiles` (https://pypi.org/project/wquantiles/).<jupyter_code>print(state['Murder.Rate'].mean())
print(np.average(state['Murder.Rate'], weights=state['Population']))
print(wquantiles.median(state['Murder.Rate'], weights=state['Population']))<jupyter_output>4.4
<jupyter_text># Estimates of Variability<jupyter_code># Table 1-2
print(state.head(8))<jupyter_output> State Population Murder.Rate Abbreviation
0 Alabama 4779736 5.7 AL
1 Alaska 710231 5.6 AK
2 Arizona 6392017 4.7 AZ
3 Arkansas 2915918 5.6 AR
4 California 37253956 4.4 CA
5 Colorado 5029196 2.8 CO
6 Connecticut 3574097 2.4 CT
7 Delaware 897934 5.8 DE
<jupyter_text>Standard deviation<jupyter_code>print(state['Population'].std())<jupyter_output>6848235.347401142
<jupyter_text>Interquartile range is calculated as the difference of the 75% and 25% quantile.<jupyter_code>print(state['Population'].quantile(0.75) - state['Population'].quantile(0.25))<jupyter_output>4847308.0
<jupyter_text>Median absolute deviation from the median can be calculated with a method in _statsmodels_<jupyter_code>print(robust.scale.mad(state['Population']))
print(abs(state['Population'] - state['Population'].median()).median() / 0.6744897501960817)<jupyter_output>3849876.1459979336
3849876.1459979336
<jupyter_text>## Percentiles and Boxplots
_Pandas_ has the `quantile` method for data frames.<jupyter_code>print(state['Murder.Rate'].quantile([0.05, 0.25, 0.5, 0.75, 0.95]))
# Table 1.4
percentages = [0.05, 0.25, 0.5, 0.75, 0.95]
df = pd.DataFrame(state['Murder.Rate'].quantile(percentages))
df.index = [f'{p * 100}%' for p in percentages]
print(df.transpose())<jupyter_output> 5.0% 25.0% 50.0% 75.0% 95.0%
Murder.Rate 1.6 2.425 4.0 5.55 6.51
<jupyter_text>_Pandas_ provides a number of basic exploratory plots; one of them are boxplots<jupyter_code>ax = (state['Population']/1_000_000).plot.box(figsize=(3, 4))
ax.set_ylabel('Population (millions)')
plt.tight_layout()
plt.show()<jupyter_output><empty_output><jupyter_text>## Frequency Table and Histograms
The `cut` method for _pandas_ data splits the dataset into bins. There are a number of arguments for the method. The following code creates equal sized bins. The method `value_counts` returns a frequency table.<jupyter_code>binnedPopulation = pd.cut(state['Population'], 10)
print(binnedPopulation.value_counts())
# Table 1.5
binnedPopulation.name = 'binnedPopulation'
df = pd.concat([state, binnedPopulation], axis=1)
df = df.sort_values(by='Population')
groups = []
for group, subset in df.groupby(by='binnedPopulation'):
groups.append({
'BinRange': group,
'Count': len(subset),
'States': ','.join(subset.Abbreviation)
})
print(pd.DataFrame(groups))<jupyter_output> BinRange Count \
0 (526935.67, 4232659.0] 24
1 (4232659.0, 7901692.0] 14
2 (7901692.0, 11570725.0] 6
3 (11570725.0, 15239758.0] 2
4 (15239758.0, 18908791.0] 1
5 (18908791.0, 22577824.0] 1
6 (22577824.0, 26246857.0] 1
7 (26246857.0, 29915890.0] 0
8 (29915890.0, 33584923.0] 0
9 (33584923.0, 37253956.0] 1
States
0 WY,VT,ND,AK,SD,DE,MT,RI,NH,ME,HI,ID,NE,WV,NM,N...
1 KY,LA,SC,AL,CO,MN,WI,MD,MO,TN,AZ,IN,MA,WA
2 VA,NJ,NC,GA,MI,OH
3 PA,IL
4 FL
5 NY
6 TX
7
8
9 [...]<jupyter_text>_Pandas_ also supports histograms for exploratory data analysis.<jupyter_code>ax = (state['Population'] / 1_000_000).plot.hist(figsize=(4, 4))
ax.set_xlabel('Population (millions)')
plt.tight_layout()
plt.show()<jupyter_output><empty_output><jupyter_text>## Density Estimates
Density is an alternative to histograms that can provide more insight into the distribution of the data points. Use the argument `bw_method` to control the smoothness of the density curve.<jupyter_code>ax = state['Murder.Rate'].plot.hist(density=True, xlim=[0, 12],
bins=range(1,12), figsize=(4, 4))
state['Murder.Rate'].plot.density(ax=ax)
ax.set_xlabel('Murder Rate (per 100,000)')
plt.tight_layout()
plt.show()<jupyter_output><empty_output><jupyter_text># Exploring Binary and Categorical Data<jupyter_code># Table 1-6
dfw = pd.read_csv(AIRPORT_DELAYS_CSV)
print(100 * dfw / dfw.values.sum())<jupyter_output> Carrier ATC Weather Security Inbound
0 23.022989 30.400781 4.025214 0.122937 42.428079
<jupyter_text>_Pandas_ also supports bar charts for displaying a single categorical variable.<jupyter_code>ax = dfw.transpose().plot.bar(figsize=(4, 4), legend=False)
ax.set_xlabel('Cause of delay')
ax.set_ylabel('Count')
plt.tight_layout()
plt.show()<jupyter_output><empty_output><jupyter_text># Correlation
First read the required datasets<jupyter_code>sp500_sym = pd.read_csv(SP500_SECTORS_CSV)
sp500_px = pd.read_csv(SP500_DATA_CSV, index_col=0)
# Table 1-7
# Determine telecommunications symbols
telecomSymbols = sp500_sym[sp500_sym['sector'] == 'telecommunications_services']['symbol']
# Filter data for dates July 2012 through June 2015
telecom = sp500_px.loc[sp500_px.index >= '2012-07-01', telecomSymbols]
telecom.corr()
print(telecom)<jupyter_output> T CTL FTR VZ LVLT
2012-07-02 0.422496 0.140847 0.070879 0.554180 -0.519998
2012-07-03 -0.177448 0.066280 0.070879 -0.025976 -0.049999
2012-07-05 -0.160548 -0.132563 0.055128 -0.051956 -0.180000
2012-07-06 0.342205 0.132563 0.007875 0.140106 -0.359999
2012-07-09 0.136883 0.124279 -0.023626 0.253943 0.180000
... ... ... ... ... ...
2015-06-25 0.049342 -1.600000 -0.040000 -0.187790 -0.330002
2015-06-26 -0.256586 0.039999 -0.070000 0.029650 -0.739998
2015-06-29 -0.098685 -0.559999 -0.060000 -0.504063 -1.360000
2015-06-30 -0.503298 -0.420000 -0.070000 -0.523829 0.199997
2015-07-01 -0.019737 0.080000 -0.050000 0.355811 0.139999
[754 rows x 5 columns]
<jupyter_text>Next we focus on funds traded on major exchanges (sector == 'etf'). <jupyter_code>etfs = sp500_px.loc[sp500_px.index > '2012-07-01',
sp500_sym[sp500_sym['sector'] == 'etf']['symbol']]
print(etfs.head())<jupyter_output> XLI QQQ SPY DIA GLD VXX USO \
2012-07-02 -0.376098 0.096313 0.028223 -0.242796 0.419998 -10.40 0.000000
2012-07-03 0.376099 0.481576 0.874936 0.728405 0.490006 -3.52 0.250000
2012-07-05 0.150440 0.096313 -0.103487 0.149420 0.239991 6.56 -0.070000
2012-07-06 -0.141040 -0.491201 0.018819 -0.205449 -0.519989 -8.80 -0.180000
2012-07-09 0.244465 -0.048160 -0.056445 -0.168094 0.429992 -0.48 0.459999
IWM XLE XLY XLU XLB XTL \
2012-07-02 0.534641 0.028186 0.095759 0.098311 -0.093713 0.019076
2012-07-03 0.926067 0.995942 0.000000 -0.044686 0.337373 0.000000
2012-07-05 -0.171848 -0.460387 0.306431 -0.151938 0.103086 0.019072
2012-07-06 -0.229128 0.206706 0.153214 0.080437 0.018744 -0.429213
2012-07-09 -0.190939 -0.234892 -0.201098 -0.035751 -0.168687 0.000000
XLV XLP XLF XLK
2012-07-02 -0.0[...]<jupyter_text>Due to the large number of columns in this table, looking at the correlation matrix is cumbersome and it's more convenient to plot the correlation as a heatmap. The _seaborn_ package provides a convenient implementation for heatmaps.<jupyter_code>fig, ax = plt.subplots(figsize=(5, 4))
ax = sns.heatmap(etfs.corr(), vmin=-1, vmax=1,
cmap=sns.diverging_palette(20, 220, as_cmap=True),
ax=ax)
plt.tight_layout()
plt.show()<jupyter_output><empty_output><jupyter_text>The above heatmap works when you have color. For the greyscale images, as used in the book, we need to visualize the direction as well. The following code shows the strength of the correlation using ellipses.<jupyter_code>from matplotlib.collections import EllipseCollection
from matplotlib.colors import Normalize
def plot_corr_ellipses(data, figsize=None, **kwargs):
''' https://stackoverflow.com/a/34558488 '''
M = np.array(data)
if not M.ndim == 2:
raise ValueError('data must be a 2D array')
fig, ax = plt.subplots(1, 1, figsize=figsize, subplot_kw={'aspect':'equal'})
ax.set_xlim(-0.5, M.shape[1] - 0.5)
ax.set_ylim(-0.5, M.shape[0] - 0.5)
ax.invert_yaxis()
# xy locations of each ellipse center
xy = np.indices(M.shape)[::-1].reshape(2, -1).T
# set the relative sizes of the major/minor axes according to the strength of
# the positive/negative correlation
w = np.ones_like(M).ravel() + 0.01
h = 1 - np.abs(M).ravel() - 0.01
a = 45 * np.sign(M).ravel()
ec = EllipseCollection(widths=w, heights=h, angles=a, units='x', offsets=xy,
norm=Normalize(vmin=-1, vmax=1),
transOffset=ax.transData, array=M.ravel(), **kwargs)
ax.add_collection(ec)
# if data is a DataFrame, use the row/column names as tick labels
if isinstance(data, pd.DataFrame):
ax.set_xticks(np.arange(M.shape[1]))
ax.set_xticklabels(data.columns, rotation=90)
ax.set_yticks(np.arange(M.shape[0]))
ax.set_yticklabels(data.index)
return ec
m = plot_corr_ellipses(etfs.corr(), figsize=(5, 4), cmap='bwr_r')
cb = fig.colorbar(m)
cb.set_label('Correlation coefficient')
plt.tight_layout()
plt.show()<jupyter_output><empty_output><jupyter_text>## Scatterplots
Simple scatterplots are supported by _pandas_. Specifying the marker as `$\u25EF$` uses an open circle for each point.<jupyter_code>ax = telecom.plot.scatter(x='T', y='VZ', figsize=(4, 4), marker='$\u25EF$')
ax.set_xlabel('ATT (T)')
ax.set_ylabel('Verizon (VZ)')
ax.axhline(0, color='grey', lw=1)
ax.axvline(0, color='grey', lw=1)
plt.tight_layout()
plt.show()
ax = telecom.plot.scatter(x='T', y='VZ', figsize=(4, 4), marker='$\u25EF$', alpha=0.5)
ax.set_xlabel('ATT (T)')
ax.set_ylabel('Verizon (VZ)')
ax.axhline(0, color='grey', lw=1)
print(ax.axvline(0, color='grey', lw=1))<jupyter_output>Line2D(_line1)
<jupyter_text># Exploring Two or More Variables
Load the kc_tax dataset and filter based on a variety of criteria<jupyter_code>kc_tax = pd.read_csv(KC_TAX_CSV)
kc_tax0 = kc_tax.loc[(kc_tax.TaxAssessedValue < 750000) &
(kc_tax.SqFtTotLiving > 100) &
(kc_tax.SqFtTotLiving < 3500), :]
print(kc_tax0.shape)<jupyter_output>(432693, 3)
<jupyter_text>## Hexagonal binning and Contours
### Plotting numeric versus numeric dataIf the number of data points gets large, scatter plots will no longer be meaningful. Here methods that visualize densities are more useful. The `hexbin` method for _pandas_ data frames is one powerful approach.<jupyter_code>ax = kc_tax0.plot.hexbin(x='SqFtTotLiving', y='TaxAssessedValue',
gridsize=30, sharex=False, figsize=(5, 4))
ax.set_xlabel('Finished Square Feet')
ax.set_ylabel('Tax Assessed Value')
plt.tight_layout()
plt.show()<jupyter_output><empty_output><jupyter_text>The _seaborn_ kdeplot is a two-dimensional extension of the density plot. <jupyter_code>fig, ax = plt.subplots(figsize=(4, 4))
sns.kdeplot(data=kc_tax0, x='SqFtTotLiving', y='TaxAssessedValue', ax=ax)
ax.set_xlabel('Finished Square Feet')
ax.set_ylabel('Tax Assessed Value')
plt.tight_layout()
plt.show()<jupyter_output><empty_output><jupyter_text>## Two Categorical Variables
Load the `lc_loans` dataset<jupyter_code>lc_loans = pd.read_csv(LC_LOANS_CSV)
# Table 1-8(1)
crosstab = lc_loans.pivot_table(index='grade', columns='status',
aggfunc=lambda x: len(x), margins=True)
print(crosstab)
# Table 1-8(2)
df = crosstab.copy().loc['A':'G',:]
df.loc[:,'Charged Off':'Late'] = df.loc[:,'Charged Off':'Late'].div(df['All'], axis=0)
df['All'] = df['All'] / sum(df['All'])
perc_crosstab = df
print(perc_crosstab)<jupyter_output>status Charged Off Current Fully Paid Late All
grade
A 0.021548 0.690454 0.281528 0.006470 0.160746
B 0.040054 0.709013 0.235401 0.015532 0.293529
C 0.049828 0.735702 0.191495 0.022974 0.268039
D 0.067410 0.717328 0.184189 0.031073 0.164708
E 0.081657 0.707936 0.170929 0.039478 0.077177
F 0.118258 0.654371 0.180409 0.046962 0.028614
G 0.126196 0.614008 0.198396 0.061401 0.007187
<jupyter_text>## Categorical and Numeric Data
_Pandas_ boxplots of a column can be grouped by a different column.<jupyter_code>airline_stats = pd.read_csv(AIRLINE_STATS_CSV)
airline_stats.head()
ax = airline_stats.boxplot(by='airline', column='pct_carrier_delay',
figsize=(5, 5))
ax.set_xlabel('')
ax.set_ylabel('Daily % of Delayed Flights')
plt.suptitle('')
plt.tight_layout()
plt.show()<jupyter_output><empty_output><jupyter_text>_Pandas_ also supports a variation of boxplots called _violinplot_. <jupyter_code>fig, ax = plt.subplots(figsize=(5, 5))
sns.violinplot(data=airline_stats, x='airline', y='pct_carrier_delay',
ax=ax, inner='quartile', color='white')
ax.set_xlabel('')
ax.set_ylabel('Daily % of Delayed Flights')
plt.tight_layout()
plt.show()<jupyter_output><empty_output><jupyter_text>## Visualizing Multiple Variables<jupyter_code>zip_codes = [98188, 98105, 98108, 98126]
kc_tax_zip = kc_tax0.loc[kc_tax0.ZipCode.isin(zip_codes),:]
kc_tax_zip
def hexbin(x, y, color, **kwargs):
cmap = sns.light_palette(color, as_cmap=True)
plt.hexbin(x, y, gridsize=25, cmap=cmap, **kwargs)
g = sns.FacetGrid(kc_tax_zip, col='ZipCode', col_wrap=2)
g.map(hexbin, 'SqFtTotLiving', 'TaxAssessedValue',
extent=[0, 3500, 0, 700000])
g.set_axis_labels('Finished Square Feet', 'Tax Assessed Value')
g.set_titles('Zip code {col_name:.0f}')
plt.tight_layout()
plt.show()<jupyter_output><empty_output>
|
non_permissive
|
/practical-statistics-for-data-scientists/python/notebooks/Chapter 1 - Exploratory Data Analysis.ipynb
|
MargoSolo/Data_science_study
| 28 |
<jupyter_start><jupyter_text># 7. Write a program to scrap all the available details of top 10 gaming laptops from digit.in. <jupyter_code>driver = webdriver.Chrome(r"E:\Aniket\chromedriver_win32\chromedriver.exe")
url="https://www.digit.in/top-products/best-gaming-laptops-40.html"
driver.get(url)
Brands=[]
Products_Description=[]
Specification=[]
Price=[]
br=driver.find_elements_by_xpath("//div[@class='TopNumbeHeading active sticky-footer']")
len(br)
for i in br:
Brands.append(str(i.text).replace("\n",""))
Brands
sp=driver.find_elements_by_xpath("//div[@class='Specs-Wrap']")
len(sp)
for i in sp:
Specification.append(str(i.text).replace("\n",""))
Specification
des=driver.find_elements_by_xpath("//div[@class='Section-center']")
len(des)
for i in des:
Products_Description.append(str(i.text).replace("\n",""))
Products_Description
pri=driver.find_elements_by_xpath("//td[@class='smprice']")
len(pri)
for i in pri:
Price.append(str(i.text).replace("\n",""))
Price
digit_lap=pd.DataFrame([])
digit_lap['Brands']=Brands[0:10]
digit_lap['Price']=Price[0:10]
digit_lap['Specification']=Specification[0:10]
digit_lap['Description']=Products_Description[0:10]
digit_lap<jupyter_output><empty_output><jupyter_text># 6. Write a program to scrap details of all the funding deals for second quarter (i.e. July 20 – September 20) from trak.in.<jupyter_code>driver = webdriver.Chrome(r"E:\Aniket\chromedriver_win32\chromedriver.exe")
url1="https://trak.in/india-startup-funding-investment-2015/"
driver.get(url1)
Dates=[]
Company=[]
Industry=[]
Investor_Name=[]
Investment_Type=[]
Amount=[]
#scraping the company_name
companies=driver.find_elements_by_xpath("//td[@class='column-3']")
for i in companies:
if i.text is None :
Company.append("--")
else:
Company.append(i.text)
print(len(Company),Company)
#scraping the Industry
Ind=driver.find_elements_by_xpath("//td[@class='column-4']")
for i in Ind:
if i.text is None :
Industry.append("--")
else:
Industry.append(i.text)
print(len(Industry),Industry)
#scraping the Dates
dt=driver.find_elements_by_xpath("//td[@class='column-2']")
for i in dt:
if i.text is None :
Dates.append("--")
else:
Dates.append(i.text)
print(len(Dates),Dates)
#scraping the Investor_Name
IN=driver.find_elements_by_xpath("//td[@class='column-7']")
for i in IN:
if i.text is None :
Investor_Name.append("--")
else:
Investor_Name.append(i.text)
print(len(Investor_Name),Investor_Name)
#scraping the Investment_Type
IT=driver.find_elements_by_xpath("//td[@class='column-8']")
for i in IT:
if i.text is None :
Investment_Type.append("--")
else:
Investment_Type.append(i.text)
print(len(Investment_Type),Investment_Type)
#scraping the Amount
Price=driver.find_elements_by_xpath("//td[@class='column-9']")
for i in Price:
if i.text is None :
Amount.append("--")
else:
Amount.append(i.text)
print(len(Amount),Amount)
Funding=pd.DataFrame([])
Funding['Company']=Company
Funding['Industry']=Industry
Funding['Investor_Name']=Investor_Name
Funding['Amount Invested']=Amount
Funding['Specification']=Investment_Type
Funding['Dates']=Dates
Funding<jupyter_output><empty_output><jupyter_text>Slice Data With Condition On Dates Where 01/07/2020 to 30/09/2020 <jupyter_code># 5. Write a program to scrap geospatial coordinates (latitude, longitude) of a city searched on google maps.<jupyter_output><empty_output><jupyter_text>driver = webdriver.Chrome(r"E:\Aniket\chromedriver_win32\chromedriver.exe")# opening google maps
driver.get("https://www.google.co.in/maps")
time.sleep(3)
city = input('Enter City Name : ') # Enter city to be searched
search = driver.find_element_by_id("searchboxinput") # locating search bar
search.clear() # clearing search bar
time.sleep(2)
search.send_keys(city) # entering values in search bar
button = driver.find_element_by_id("searchbox-searchbutton") # locating search button
button.click() # clicking search button
time.sleep(3)
try:
url_string = driver.current_url
print("URL Extracted: ", url_string)
lat_lng = re.findall(r'@(.*)data',url_string)
if len(lat_lng):
lat_lng_list = lat_lng[0].split(",")
if len(lat_lng_list)>=2:
lat = lat_lng_list[0]
lng = lat_lng_list[1]
print("Latitude = {}, Longitude = {}".format(lat, lng))
except Exception as e:
print("Error: ", str(e))<jupyter_code># 4. Write a python program to search for a smartphone(e.g.: Oneplus Nord, pixel 4A, etc.) on www.flipkart.com and scrape following details for all the search results displayed on 1st page.
Details to be scraped: “Brand Name”, “Smartphone name”, “Colour”, “RAM”,
“Storage(ROM)”, “Primary Camera”, “Secondary Camera”, “Display Size”, “Display
Resolution”, “Processor”, “Processor Cores”, “Battery Capacity”, “Price”, “Product URL”.
Incase if any of the details is missing then replace it by “- “. Save your results in a dataframe
and CSV.<jupyter_output><empty_output><jupyter_text>driver = webdriver.Chrome(r"E:\Aniket\chromedriver_win32\chromedriver.exe")
url4="https://www.flipkart.com/search?q=smartphone&otracker=search&otracker1=search&marketplace=FLIPKART&as-show=on&as=off"
driver.get(url4)Brand_Name=[]
Colour=[]
Storage_RAM_ROM=[]
P_F_Camera=[]
Display_size_Resolution=[]
ProcessorAndCores=[]
Battery=[]
Price=[]
Product_URL=[]
#scraping the Brand_Name
BName=driver.find_elements_by_xpath("//div[@class='_4rR01T']")
for i in BName:
if i.text is None :
Brand_Name.append("--")
else:
Brand_Name.append(i.text)
print(len(Brand_Name),Brand_Name)#scraping the Storage_RAM_ROM
ram=driver.find_elements_by_xpath("//ul[@class='_1xgFaf']//li[1]")
for i in ram:
if i.text is None :
Storage_RAM_ROM.append("--")
else:
Storage_RAM_ROM.append(i.text)
print(len(Storage_RAM_ROM),Storage_RAM_ROM)#scraping the P_F_Camera
PC=driver.find_elements_by_xpath("//ul[@class='_1xgFaf']//li[3]")
for i in PC:
if i.text is None :
P_F_Camera.append("--")
else:
P_F_Camera.append(i.text)
print(len(P_F_Camera),P_F_Camera)#scraping the Display_size_Resolution
DS=driver.find_elements_by_xpath("//ul[@class='_1xgFaf']//li[2]")
for i in DS:
if i.text is None :
Display_size_Resolution.append("--")
else:
Display_size_Resolution.append(i.text)
print(len(Display_size_Resolution),Display_size_Resolution)#scraping the ProcessorAndCores
P=driver.find_elements_by_xpath("//ul[@class='_1xgFaf']//li[5]")
for i in P:
if i.text is None :
ProcessorAndCores.append("--")
else:
ProcessorAndCores.append(i.text)
print(len(ProcessorAndCores),ProcessorAndCores)#scraping the Battery
B=driver.find_elements_by_xpath("//ul[@class='_1xgFaf']//li[4]")
for i in B:
if i.text is None :
Battery.append("--")
else:
Battery.append(i.text)
print(len(Battery),Battery)#scraping the Price
price=driver.find_elements_by_xpath("//div[@class='_30jeq3 _1_WHN1']")
for i in price:
if i.text is None :
Price.append("--")
else:
Price.append(i.text)
print(len(Price),Price)FlipKart=pd.DataFrame([])
FlipKart['Brand_Name']=Brand_Name
FlipKart['Storage_RAM_ROM']=Storage_RAM_ROM
FlipKart['Amount P_F_Camera']=P_F_Camera
FlipKart['Display_size_Resolution']=Display_size_Resolution
FlipKart['ProcessorAndCores']=ProcessorAndCores
FlipKart['Battery']=Battery
FlipKart['Price']=Price
FlipKart<jupyter_code># 3. Write a python program to access the search bar and search button on images.google.com and scrape 100 images each for keywords ‘fruits’, ‘cars’ and ‘Machine Learning’.<jupyter_output><empty_output><jupyter_text>driver.get('https://images.google.com/')search_bar = driver.find_element_by_xpath('//*[@id="sbtc"]/div/div[2]/input') # Finding the search bar using it's xpath
search_bar.send_keys("fruits") # Inputing "banana" keyword to search rock images
search_button = driver.find_element_by_xpath('//*[@id="sbtc"]/button') # Finding the xpath of search button
search_button.click() # Clicking the search buttonprint("start scrolling to generate more images on the page...")
# 500 time we scroll down by 10000 in order to generate more images on the website
for _ in range(500):
driver.execute_script("window.scrollBy(0,10000)") images = driver.find_elements_by_xpath('//img[@class="rg_i Q4LuWd"]')img_urls = []
img_data = []
for image in images:
source= image.get_attribute('src')
if source is not None:
if(source[0:4] == 'http'):
img_urls.append(source)
len(img_urls)for i in range(len(img_urls)):
if i >= 100:
break
print("Downloading {0} of {1} images" .format(i, 100))
response= requests.get(img_urls[i])
file = open("H:/Flip ROBO/banana/img"+str(i)+".jpg", "wb")
file.write(response.content)<jupyter_code># Quetions 1 & 2<jupyter_output><empty_output><jupyter_text>1. Write a python program which searches all the product under a particular product vertical from www.amazon.in. The product verticals to be searched will be taken as input from user.
For e.g. If user input is ‘guitar’. Then search for guitars.
2. In the above question, now scrape the following details of each product listed in first 3 pages
of your search results and save it in a dataframe and csv. In case if any product vertical has
less than 3 pages in search results then scrape all the products available under that product
vertical. Details to be scraped are: "Brand Name", "Name of the Product", "Rating", "No. of
Ratings", "Price", "Return/Exchange", "Expected Delivery", "Availability", "Other Details"
and “Product URL”. In case, if any of the details are missing for any of the product then
replace it by “-“.<jupyter_code>driver.get('https://www.amazon.in/')
inputU = input('please enter product here--->')
search_bar = driver.find_element_by_xpath('//*[@id="twotabsearchtextbox"]') # Finding the search bar using it's xpath
search_bar.send_keys(inputU) # Inputing keyword to search
search_button = driver.find_element_by_xpath('//*[@id="nav-search-submit-button"]') # Finding the xpath of search button
search_button.click() # Clicking the search button
productName=[]
#scraping the Product_Name
PName=driver.find_elements_by_xpath("//span[@class='a-size-medium a-color-base a-text-normal']")
for i in PName:
if i.text is None :
productName.append("--")
else:
productName.append(i.text)
print(len(productName),productName)<jupyter_output>23 ['DIGITEK DBH 006 Over-Ear Bluetooth 5.0 Headphone | with Extra Bass | Upto 10 Hrs. Playtime | Dual Pairing | in-Built Mic | and Noise Cancellation (Black) (DBH 006)', 'COUCOU Sports Wireless Headphones | IPX7 Water Proof Earphones with Strong Bass Mic Qualcomm chip | Bluetooth Earbuds are Comfortable Fit Compact Design Easy to Carry and Playtime Up to 10h (Black)', 'boAt Bassheads 900 On Ear Wired Headphones(Carbon Black)', 'boAt Bassheads 100 in Ear Wired Earphones with Mic(Black)', 'boAt Rockerz 450 Bluetooth On-Ear Headphone with Mic(Luscious Black)', 'Fire-Boltt Blast 1400 Over -Ear Bluetooth Wireless Headphones with 25H Playtime, Thumping Bass, Lightweight Foldable Compact Design with Google/Siri Voice Assistance', 'Sony MDR-ZX110A On-Ear Stereo Headphones (White), without mic', 'pTron Tangent Lite Bluetooth 5.0 Wireless Headphones with Hi-Fi Stereo Sound, 6Hrs Playtime, Lightweight Ergonomic Neckband, Sweat-Resistant Magnetic Earbuds, Voice Assistant & Mic - (Black)', 'JBL C1[...]<jupyter_text># Quetion - 2<jupyter_code>start_page = 0
end_page = 3
urls = []
for page in range(start_page,end_page+1):
try:
page_urls = driver.find_elements_by_xpath('//a[@class="a-link-normal s-no-outline"]')
# appending all the urls on current page to urls list
for url in page_urls:
url = url.get_attribute('href') # Scraping the url from webelement
if url[0:4]=='http': # Checking if the scraped data is a valid url or not
urls.append(url) # Appending the url to urls list
print("Product urls of page {} has been scraped.".format(page+1))
# Moving to next page
nxt_button = driver.find_element_by_xpath('//li[@class="a-last"]/a') # Locating the next_button which is active
if nxt_button.text == 'Next→': # Checking if the button located is next button
nxt_button.click() # Clicking the next button
time.sleep(5) # time delay of 5 seconds
# If the current active button is not next button, the we will check if the next button is inactive or not
elif driver.find_element_by_xpath('//li[@class="a-disabled a-last"]/a').text == 'Next→':
print("No new pages exist. Breaking the loop") # Printing message and breakinf loop if we have reached the last page
break
except StaleElementReferenceException as e: # Handling StaleElement Exception
print("Stale Exception")
next_page = nxt_button.get_attribute('href') # Extracting the url of next page
driver.get(next_page) # ReLoading the next page
prod_dict = {}
prod_dict['Brand']=[]
prod_dict['Name']=[]
prod_dict['Rating']=[]
prod_dict['No. of ratings']=[]
prod_dict['Price']=[]
prod_dict['Return/Exchange']=[]
prod_dict['Expected Delivery']=[]
prod_dict['Availability']=[]
prod_dict['Other Details']=[]
prod_dict['URL']=[]
for url in urls[:4]:
driver.get(url) # Loading the webpage by url
print("Scraping URL = ", url)
#time.sleep(2)
try:
brand = driver.find_element_by_xpath('//a[@id="bylineInfo"]') # Extracting Brand from xpath
prod_dict['Brand'].append(brand.text)
except NoSuchElementException:
prod_dict['Brand'].append('-')
try:
name = driver.find_element_by_xpath('//h1[@id="title"]/span') # Extracting Name from xpath
prod_dict['Name'].append(name.text)
except NoSuchElementException:
prod_dict['Name'].append('-')
try:
rating = driver.find_element_by_xpath('//span[@id="acrPopover"]') # Extracting Ratings from xpath
prod_dict['Rating'].append(rating.get_attribute("title"))
except NoSuchElementException:
prod_dict['Rating'].append('-')
try:
n_rating = driver.find_element_by_xpath('//a[@id="acrCustomerReviewLink"]/span') # Extracting no. of Ratings from xpath
prod_dict['No. of ratings'].append(n_rating.text)
except NoSuchElementException:
prod_dict['No. of ratings'].append('-')
try:
price = driver.find_element_by_xpath('//span[@id="priceblock_ourprice"]') # Extracting Price from xpath
prod_dict['Price'].append(price.text)
except NoSuchElementException:
prod_dict['Price'].append('-')
try: # Extracting Return/Exchange policy from xpath
ret = driver.find_element_by_xpath('//div[@data-name="RETURNS_POLICY"]/span/div[2]/a')
prod_dict['Return/Exchange'].append(ret.text)
except NoSuchElementException:
prod_dict['Return/Exchange'].append('-')
try:
delivry = driver.find_element_by_xpath('//div[@id="ddmDeliveryMessage"]/b') # Extracting Expected Delivery from xpath
prod_dict['Expected Delivery'].append(delivry.text)
except NoSuchElementException:
prod_dict['Expected Delivery'].append('-')
try:
avl = driver.find_element_by_xpath('//div[@id="availability"]/span') # Extracting Availability from xpath
prod_dict['Availability'].append(avl.text)
except NoSuchElementException:
prod_dict['Availability'].append('-')
try: # Extracting Other Details from xpath
dtls = driver.find_element_by_xpath('//ul[@class="a-unordered-list a-vertical a-spacing-mini"]')
prod_dict['Other Details'].append(' || '.join(dtls.text.split('\n')))
except NoSuchElementException:
prod_dict['Other Details'].append('-')
prod_dict['URL'].append(url) # Saving url
time.sleep(2)
prod_df = pd.DataFrame.from_dict(prod_dict)
prod_df
#saving data to csv
prod_df.to_csv('Amazon_{}.csv'.format(inputU))<jupyter_output><empty_output>
|
no_license
|
/FlipRobo_Webscrapping_3_All_Updated.ipynb
|
Swarna-ashik/FlipRobo
| 8 |
<jupyter_start><jupyter_text># Two Sample T-Test - Lab
## Introduction
The two-sample t-test is used to determine if two population means are equal. A common application is to test if a new process or treatment is superior to a current process or treatment.
## Objectives
You will be able to:
* Understand the t-statistic, p-value, and t-test for 2 sample t-test
* Calculate the t-statistic and p-value using formulas as well as Scipy functions
* Visually represent the t-test and p-value using the t-distribution
* Understand how the t-test and frequentist hypothesis testing relate to the concepts of signal and noise
## Example:
Consider the following experimental settings for clinical trials of a new blood pressure medicine.
In the context of controlled experiments, you will often see talk about the "control" group and the "experimental" or "treatment" group. In a drug test example, the control group is the group given the placebo and the treatment group is given the actual drug. Researchers are interested in the average difference in blood pressure levels between the treatment and control groups.
>The 50 subjects in the control group have an average systolic blood pressure of 121.38 who have been given a placebo drug.
>The 50 subjects in the experimental / treatment group have an average systolic blood pressure of 111.56 after treatment with the drug being tested.
The apparent difference between experimental and control groups is -9.82 points. But with 50 subjects in each group, how confident can a researcher be that this measured difference is real? You can perform a two sample t-test to evaluate this.
First, you will calculate a t-statistic for 2 sample t-test, followed by calculation of p-value.
You can set up the experimental and control observations below as numpy arrays. First, make sure to import necessary libraries<jupyter_code>import numpy as np
from scipy import stats
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_style('whitegrid')
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
# Use this sample data to conduct experimentation
control = np.array([166, 165, 120, 94, 104, 166, 98, 85, 97, 87, 114, 100, 152,
87, 152, 102, 82, 80, 84, 109, 98, 154, 135, 164, 137, 128,
122, 146, 86, 146, 85, 101, 109, 105, 163, 136, 142, 144, 140,
128, 126, 119, 121, 126, 169, 87, 97, 167, 89, 155])
experimental = np.array([ 83, 100, 123, 75, 130, 77, 78, 87, 116, 116, 141, 93, 107,
101, 142, 152, 130, 123, 122, 154, 119, 149, 106, 107, 108, 151,
97, 95, 104, 141, 80, 110, 136, 134, 142, 135, 111, 83, 86,
116, 86, 117, 87, 143, 104, 107, 86, 88, 124, 76])
<jupyter_output><empty_output><jupyter_text>It is always a good idea to draw the probability distributions for samples to visually inspect the differences present between mean and standard deviation.
Plot both samples' distributions and inspect the overlap using seaborn to get an idea how different the samples might be from one another. <jupyter_code># Draw a plot showing overlapping of distribution means and sds for incpection<jupyter_output><empty_output><jupyter_text>There are some slight differences between the mean and standard deviation of the control and experimental groups. This is a good sign to further our experimentation and to calculate whether the difference is significant, or not. As a reminder the five steps to performing a hypothesis test are:
1) Set up null and alternative hypotheses
2) Choose a significance level
3) Calculate the test statistic
4) Determine the critical or p-value (find the rejection region)
5) Compare t-value with critical t-value to reject or fail to reject the null hypothesis
## The Null Hypothesis
In thus drug efficacy experiment example, you can define the null hypothesis to be that there is no difference between a subject taking a placebo and the treatment drug.
>**$H_{0}$: The mean difference between treatment and control groups is zero. i.e. $H_{0} = H_{1}$**
## The Alternate Hypothesis
In this example the alternative hypothesis is that there is in fact a mean difference in blood pressure between the treatment and control groups.
>**$H_{1}$ (2-tailed): The parameter of interest, our mean difference between treatment and control, is different than zero.**
>**$H_{1}$ (1-tailed, >): The parameter of interest, our mean difference between treatment and control, is greater than zero.**
>**$H_{1}$ (1-tailed, <): The parameter of interest, our mean difference between treatment and control, is less than zero.**
NOTE: The null hypothesis and alternative hypothesis are concerned with the true values, or in other words the parameter of the overall population. Through the process of experimentation/hypothesis testing and statistical analysis of the results, we will make an inference about this population parameter.
Now, calculate the mean difference between both groups.<jupyter_code># -9.819999999999993<jupyter_output><empty_output><jupyter_text>What is the probability that you would observe this data GIVEN a specified mean difference in blood pressure?
You obviously don't know the true mean difference in blood pressure resulting from administration the drug. The whole point of conducting the experiment is to evaluate the drug. Instead you must assume that the true mean difference is zero: the null hypothesis $H_{0}$ is assumed to be true:
## Calculating the t-statistic
When comparing the difference between groups, we can calculate the two-sample t-statistic like so:
$$\large t = \frac{\bar{x}_{1} - \bar{x}_{2}}{\sqrt{s^{2}_{p} (\frac{1}{n_{1}} + \frac{1}{n_{2}}) } } $$
Where $s^{2}_{p}$ is the pooled sample variance, calculated as:
$$\large s^{2}_{p} = \frac{(n_{1} -1)s^{2}_{1} + (n_{2} -1)s^{2}_{2}}{n_{1} + n_{2} - 2} $$
Where $s^{2}_{1}$ and $s^{2}_{2}$ are the variances for each sample given by the formula
$$ \large s^{2} = \frac{\sum_{i=1}^{n}(x_{i} - \bar{x})^{2}}{n-1} $$
## Calculating pooled sample variance
The $s^2_{p}$ denotes the sample variance. In this version of the t-test you are assuming equal variances in our experimental and control groups in the overall population. There is another way to calculate the t-test where equal variance is not assumed, but in this case it is a reasonable assumption.
This approach combines the variance of the two group's variance measurements into a single, pooled metric.
Now, create some functions to calculate the t-statistic. The first function to create is one that calculates the variance for a single sample.<jupyter_code>def sample_variance(sample):
return None<jupyter_output><empty_output><jupyter_text>Using `sample_variance`, you can now write another function `pooled_variance` to calculate $S_{p}^{2}$<jupyter_code>def pooled_variance(sample1, sample2):
return None<jupyter_output><empty_output><jupyter_text>Now that you have $S_{p}^{2}$, create a function `twosample_tstatistic` to calculate the two sample t-statistic using the formula given earlier. <jupyter_code>def twosample_tstatistic(expr, ctrl):
return None
t_stat = None
# -1.8915462966190268<jupyter_output><empty_output><jupyter_text>Using the data from the samples, you can now determine the critical values with the t-statistic and calculate the area under the curve to determine the p-value.
Write a function `visualize_t` that uses matplotlib to display a standard t-distribution with vertical lines identifying each critical value that signifies the rejection region.<jupyter_code># Visualize t and p_value
def visualize_t(t_stat, n_control, n_experimental):
# initialize a matplotlib "figure"
# generate points on the x axis between -4 and 4:
# use stats.t.pdf to get values on the probability density function for the t-distribution
# Draw two sided boundary for critical-t
return None
n_control = None
n_experimental = None
visualize_t(t_stat, n_control, n_experimental)<jupyter_output><empty_output><jupyter_text>Now that you have defined your boundaries for significance, you can simply calculate p_value by calculating the total area under curve using `stats.t.cdf()`.
Given a t-value and a degrees of freedom, you can use the "survival function" sf of scipy.stats.t (aka the complementary CDF) to compute the one-sided p-value. For the two-sided p-value, just double the one-sided p-value.<jupyter_code>## Calculate p_value
# Lower tail comulative density function returns area under the lower tail curve
lower_tail = stats.t.cdf(-1.89, (50+50-2), 0, 1)
# Upper tail comulative density function returns area under upper tail curve
upper_tail = 1. - stats.t.cdf(1.89, (50+50-2), 0, 1)
p_value = lower_tail+upper_tail
print(p_value)<jupyter_output><empty_output><jupyter_text>To verify these results, you can use SciPy's functions to calculate the p_value in a one liner. <jupyter_code>## your code here
'''
Calculates the T-test for the means of *two independent* samples of scores.
This is a two-sided test for the null hypothesis that 2 independent samples
have identical average (expected) values. This test assumes that the
populations have identical variances by default.
'''
stats.ttest_ind(experimental, control)<jupyter_output><empty_output>
|
non_permissive
|
/index.ipynb
|
dmart49/dsc-two-sample-t-tests-lab-houston-ds-060319
| 9 |
<jupyter_start><jupyter_text>### Load Amazon Data into Spark DataFrame<jupyter_code>from pyspark import SparkFiles
url = "https://s3.amazonaws.com/amazon-reviews-pds/tsv/amazon_reviews_us_Video_Games_v1_00.tsv.gz"
spark.sparkContext.addFile(url)
df = spark.read.option("encoding", "UTF-8").csv(SparkFiles.get(""), sep="\t", header=True, inferSchema=True)
df.show(10)<jupyter_output>+-----------+-----------+--------------+----------+--------------+--------------------+----------------+-----------+-------------+-----------+----+-----------------+--------------------+--------------------+-----------+
|marketplace|customer_id| review_id|product_id|product_parent| product_title|product_category|star_rating|helpful_votes|total_votes|vine|verified_purchase| review_headline| review_body|review_date|
+-----------+-----------+--------------+----------+--------------+--------------------+----------------+-----------+-------------+-----------+----+-----------------+--------------------+--------------------+-----------+
| US| 12039526| RTIS3L2M1F5SM|B001CXYMFS| 737716809|Thrustmaster T-Fl...| Video Games| 5| 0| 0| N| Y|an amazing joysti...|Used this for Eli...| 2015-08-31|
| US| 9636577| R1ZV7R40OLHKD|B00M920ND6| 569686175|Tonsee 6 buttons ...| Video Games| 5| [...]<jupyter_text>### Create DataFrames to match tables<jupyter_code>from pyspark.sql.functions import to_date
# Read in the Review dataset as a DataFrame
df.select("review_id", "customer_id", "product_parent", "review_date").show(10)
# Create the customers_table DataFrame
# customers_df = df.groupby("").agg({""}).withColumnRenamed("", "customer_count")
customers_df = df.groupby("customer_id").agg({"customer_id":"count"}).withColumnRenamed("count(customer_id)", "customer_count")
customers_df.show(5)
## Create the products_table DataFrame and drop duplicates.
# products_df = df.select([]).drop_duplicates()
products_df = df.select(["product_id", "product_title"]).drop_duplicates()
products_df.show()
# Create the review_id_table DataFrame.
# Convert the 'review_date' column to a date datatype with to_date("review_date", 'yyyy-MM-dd').alias("review_date")
# review_id_df = df.select([, to_date("review_date", 'yyyy-MM-dd').alias("review_date")])
#review_id_table = df.select("review_id", "customer_id", "product_id","product_parent", "review_date")
review_id_df = df.select(["review_id","customer_id","product_id","product_parent", to_date("review_date", 'yyyy-MM-dd').alias("review_date")])
review_id_df.show()
# Create the vine_table. DataFrame
# vine_df = df.select([])
vine_df = df.select(["review_id","star_rating", "helpful_votes", "total_votes", "vine", "verified_purchase"])
vine_df.show()<jupyter_output>+--------------+-----------+-------------+-----------+----+-----------------+
| review_id|star_rating|helpful_votes|total_votes|vine|verified_purchase|
+--------------+-----------+-------------+-----------+----+-----------------+
| RTIS3L2M1F5SM| 5| 0| 0| N| Y|
| R1ZV7R40OLHKD| 5| 0| 0| N| Y|
|R3BH071QLH8QMC| 1| 0| 1| N| Y|
|R127K9NTSXA2YH| 3| 0| 0| N| Y|
|R32ZWUXDJPW27Q| 4| 0| 0| N| Y|
|R3AQQ4YUKJWBA6| 1| 0| 0| N| Y|
|R2F0POU5K6F73F| 5| 0| 0| N| Y|
|R3VNR804HYSMR6| 5| 0| 0| N| Y|
| R3GZTM72WA2QH| 5| 0| 0| N| Y|
| RNQOY62705W1K| 4| 0| 0| N| [...]<jupyter_text>### Connect to the AWS RDS instance and write each DataFrame to its table. <jupyter_code>#from getpass import getpass
#password = getpass('Enter your database password')
# Configure settings for RDS
mode = "append"
jdbc_url="jdbc:postgresql://<endpoint>:port/database_name"
config = {"user":"postgres",
"password": password,
"driver":"org.postgresql.Driver"}
# Write review_id_df to table in RDS
review_id_df.write.jdbc(url=jdbc_url, table='review_id_table', mode=mode, properties=config)
# Write products_df to table in RDS
# about 3 min
products_df.write.jdbc(url=jdbc_url, table='products_table', mode=mode, properties=config)
# Write customers_df to table in RDS
# 5 min 14 s
customers_df.write.jdbc(url=jdbc_url, table='customers_table', mode=mode, properties=config)
# Write vine_df to table in RDS
# 11 minutes
vine_df.write.jdbc(url=jdbc_url, table='vine_table', mode=mode, properties=config)
<jupyter_output><empty_output>
|
no_license
|
/Amazon_Reviews_ETL_starter_code_RSD.ipynb
|
Rubysd/Amazon-Vine-Analysis
| 3 |
<jupyter_start><jupyter_text>
3 different feature based approaches
1. bag of visual features:
* Create 4000 dim histogram of centroids the features are assigned to. (per descriptor)
2. BoV with spatio-temporal pyramid.
* concatenate the 6 4000 dim histograms together. split video into 2 time blocks, 3 horiziontal strips.
3. Fisher Vectors (using pre-computed IDTFs quantized to 4000 codewords)
* PCA to reduce descriptor dimensions by 2
* create k=256 GMMs randomly sampling subset of 256,000 features from training set
* Create 2DK FV for each descriptor.
* concatenate the FVs together for one video.
4. FVs as in 3, but with spatio-temporal pyramid
5. FVs (recomputing the IDTFs), compare performance to 3.
<jupyter_code>#python $SRC"consolidateFiles.py" $UCF_DIR -l $UCF_FULL | python $SRC"gmm.py" 256 $PROJ_DIR -s 0.005
import pandas as pd
import numpy as np
import matplotlib, os
%pylab inline<jupyter_output>Populating the interactive namespace from numpy and matplotlib
<jupyter_text>#(1) BoVs
## Read in the pre-computed IDTFs into a data frame per video
## Histogram the traj_index, hog_index, hof_index, and mbh_index into 4 video level 4000 dimensional histograms<jupyter_code>train_list = "../../data/ucf_recognition_20/lists_IDTF/train_list.txt"
test_list = "../../data/ucf_recognition_20/lists_IDTF/test_list.txt"
def np_hist(series, normalize=True):
"""
normalize: divides the histogram by the sum of the elements.
"""
hist = np.zeros((4000))
for _,row in series.iteritems():
hist[row] += 1
if normalize:
hist *= (1000/sum(hist))
return hist
def get_vectors(data_list):
list_df = pd.read_csv(data_list, delimiter = ' ', header = None, names = ['filename', 'class_id'])
list_df['video_name'] = list_df.filename.apply(lambda x: os.path.basename(x).split('.')[0])
#vectors = {}
num_videos = list_df.shape[0]
data = np.zeros((num_videos,16000))
true_label = np.zeros((num_videos))
video_names =
for index, row in list_df.iterrows():
if index % 50 == 0:
print "processed %d videos" % index
df = pd.read_csv(row.filename, delimiter = '\t', header = None, index_col=False,\
names = ['Frame_num', 'mean_x', 'mean_y', 'Traj_index', 'HOG_index', 'HOF_index', 'MBH_index'])
hists = []
for column in ['Traj_index', 'HOG_index', 'HOF_index', 'MBH_index']:
hists.append(np_hist(df[column]))
hist_vector = np.hstack(hists)
vectors[row.video_name] = (vid_vector,row.class_id)
return vectors
train_data = get_vectors(train_list)
test_data = get_vectors(test_list)
np.savez('./features_bov', train=train_data, test=test_data)
plt.bar(range(16000), vid_vector)
plt.show()<jupyter_output><empty_output>
|
no_license
|
/examples/ucf_recognition_20/.ipynb_checkpoints/buildFVs-checkpoint.ipynb
|
anenbergb/seniorThesis
| 2 |
<jupyter_start><jupyter_text>## OpenCV Image Processing<jupyter_code>import cv2
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
img1 = cv2.imread('DATA/dog_backpack.png')
img2 = cv2.imread('DATA/watermark_no_copy.png')<jupyter_output><empty_output><jupyter_text>When reading from cv2.imread, The images are imported as BGR so use
**cv2.cvtColor(img, cv2.COLOR_BGR2RGB)** to convert to RBG to use plt.imshow<jupyter_code>img1 = cv2.cvtColor(img1, cv2.COLOR_BGR2RGB)
img2 = cv2.cvtColor(img2, cv2.COLOR_BGR2RGB)<jupyter_output><empty_output><jupyter_text>## Resizing
img1 =cv2.resize(img1,(x,y)) ----------- width, height<jupyter_code>img1 =cv2.resize(img1,(1200,1200))
img2 =cv2.resize(img2,(1200,1200))<jupyter_output><empty_output><jupyter_text>### Blending the Image
Blending images with same shape:
$$ img1 * \alpha + img2 * \beta + \gamma $$
**cv2.addWeighted()**<jupyter_code>blended = cv2.addWeighted(src1=img1,alpha=0.9,src2=img2,beta=0.1,gamma=0)
plt.imshow(blended)<jupyter_output><empty_output><jupyter_text>---
### Overlaying Images of Different Sizes<jupyter_code>img1 = cv2.imread('DATA/dog_backpack.png')
img2 = cv2.imread('DATA/watermark_no_copy.png')
img2 =cv2.resize(img2,(600,600))
img1 = cv2.cvtColor(img1, cv2.COLOR_BGR2RGB)
img2 = cv2.cvtColor(img2, cv2.COLOR_BGR2RGB)
large_img = img1
small_img = img2
x_offset=0
y_offset=0
x_end = x_offset+small_img.shape[1]
y_end = y_offset+small_img.shape[0]
large_img[y_offset:y_end, x_offset:x_end] = small_img
plt.imshow(large_img)<jupyter_output><empty_output><jupyter_text>### Creating a Mask<jupyter_code>img2gray = cv2.cvtColor(img2,cv2.COLOR_BGR2GRAY)
mask_inv = cv2.bitwise_not(img2gray)
plt.imshow(mask_inv,cmap='gray')
#Converting to 3 channel
white_background = np.full(img2.shape, 255, dtype=np.uint8)<jupyter_output><empty_output><jupyter_text>---
## Image Thresholding<jupyter_code>img = cv2.imread('DATA/rainbow.jpg',0) # put 0 to import as grayscale
plt.imshow(img,cmap='gray')<jupyter_output><empty_output><jupyter_text>### Simple Thresholding <jupyter_code>#Binary
ret,thresh1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
#Binary Inverse
ret,thresh2 = cv2.threshold(img,127,255,cv2.THRESH_BINARY_INV)
# Truncation
ret,thresh3 = cv2.threshold(img,127,255,cv2.THRESH_TRUNC)
#Threshold to zero
ret,thresh4 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO)
#Threshold to zero Inverse
ret,thresh5 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO_INV)
fig = plt.figure(figsize=(12,10))
plt.subplot(2,3,1),plt.imshow(thresh1,cmap = 'gray'),plt.title('Binary')
plt.subplot(2,3,2),plt.imshow(thresh2,cmap = 'gray'),plt.title('Binary Inv')
plt.subplot(2,3,3),plt.imshow(thresh3,cmap = 'gray'),plt.title('Truncated')
plt.subplot(2,3,4),plt.imshow(thresh4,cmap = 'gray'),plt.title('To Zero')
plt.subplot(2,3,5),plt.imshow(thresh5,cmap = 'gray'),plt.title('To Zero Inverse')
plt.show()
def show_pic(img):
fig = plt.figure(figsize=(15,15))
ax = fig.add_subplot(111)
ax.imshow(img,cmap='gray')<jupyter_output><empty_output><jupyter_text>### Adaptive Threshold
cv2.adaptiveThreshold(src, maxValue, adaptiveMethod, thresholdType, blockSize, C[, dst]) → dst**src** – Source 8-bit single-channel image.
**dst** – Destination image of the same size and the same type as src.
**maxValue** – Non-zero value assigned to the pixels for which the condition is satisfied. See the details below.
**adaptiveMethod** – Adaptive thresholding algorithm to use, ADAPTIVE_THRESH_MEAN_C or ADAPTIVE_THRESH_GAUSSIAN_C . See the details below.
**thresholdType** – Thresholding type that must be either THRESH_BINARY or THRESH_BINARY_INV .
**blockSize** – Size of a pixel neighborhood that is used to calculate a threshold value for the pixel: 3, 5, 7, and so on.
**C** – Constant subtracted from the mean or weighted mean (see the details below). Normally, it is positive but may be zero or negative as well.<jupyter_code>img = cv2.imread("DATA/crossword.jpg",0)
th2 = cv2.adaptiveThreshold(img,255,cv2.ADAPTIVE_THRESH_MEAN_C,cv2.THRESH_BINARY,11,8)
show_pic(img)
show_pic(th2)<jupyter_output><empty_output><jupyter_text>---
## Blurring and Smooting<jupyter_code>def load_img():
img = cv2.imread('DATA/bricks.jpg').astype(np.float32) / 255
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
font = cv2.FONT_HERSHEY_COMPLEX
cv2.putText(img,text='bricks',org=(10,600), fontFace=font,fontScale= 10,color=(255,0,0),thickness=4)
return img
def display_img(img):
fig = plt.figure(figsize=(12,10))
ax = fig.add_subplot(111)
ax.imshow(img)
img = load_img()
fig = plt.figure(figsize=(12,10))
ax = fig.add_subplot(1,1,1)
ax.imshow(img)<jupyter_output>Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
<jupyter_text>### Gamma Correction : Practical Effect of Increasing Brightness
Low gamma = brighter image
High gamma = darker image
**np.power(image,gamma_value)**<jupyter_code>fig = plt.figure(figsize=(12,10))
gamma_effect1 = np.power(img,1/4)
gamma_effect2 = np.power(img,2)
fig = plt.figure(figsize=(12,10))
plt.subplot(2,2,1),plt.imshow(gamma_effect1,cmap = 'gray'),plt.title('Gamma 1/4')
plt.subplot(2,2,2),plt.imshow(gamma_effect2,cmap = 'gray'),plt.title('Gamma 2')
plt.show()
<jupyter_output>Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
<jupyter_text>## Low Pass filter with convolution
cv2.filter2D(img,-1,kernel)<jupyter_code>img = load_img()
kernel = np.ones(shape=(5,5),dtype=np.float32)/25
dst = cv2.filter2D(img,-1,kernel)
display_img(dst)<jupyter_output>Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
<jupyter_text>---
## Blurring
**Gaussian Blurring** - cv2.GaussianBlur(img,(k,k),SigmaX) # SigmaX is std in X direction. SigmaY is calculated
**Median Blurring** - cv2.medianBlur(img,5)
Median Blur helps in Noise Reduction<jupyter_code>blurred_img = cv2.GaussianBlur(img,(5,5),10)
display_img(blurred_img)
noise_img = cv2.imread('../DATA/sammy_noise.jpg')
display_img(noise_img)
median = cv2.medianBlur(noise_img,5)
display_img(median)<jupyter_output><empty_output><jupyter_text>---
### Bilateral Filtering
Highly effective at noise removal while preserving edges<jupyter_code>blur = cv2.bilateralFilter(noise_img,9,75,75)
display_img(blur)<jupyter_output><empty_output><jupyter_text>---
## Morphological Operation
In image processing the term morphology deals with developing tools for extracting Form and Structure of image regions
The structuring element is sized 3×3 and has its origin at the center pixel<jupyter_code>def load_img():
blank_img =np.zeros((600,600))
font = cv2.FONT_HERSHEY_SIMPLEX
cv2.putText(blank_img,text='ABCDE',org=(50,300), fontFace=font,fontScale= 5,color=(255,255,255),thickness=25,lineType=cv2.LINE_AA)
return blank_img
def display_img(img):
fig = plt.figure(figsize=(12,10))
ax = fig.add_subplot(111)
ax.imshow(img,cmap='gray')
img = load_img()
display_img(img)<jupyter_output><empty_output><jupyter_text>## Erosion
Erodes away boundaries of foreground objects. Works best when foreground is light color (preferrably white) and background is dark.<jupyter_code>fig = plt.figure(figsize=(12,10))
############################################################
kernel = np.ones((5,5),np.uint8)
erosion1 = cv2.erode(img,kernel,iterations = 1)
erosion5 = cv2.erode(img,kernel,iterations = 5)
############################################################
fig = plt.figure(figsize=(12,10))
plt.subplot(2,2,1),plt.imshow(img,cmap = 'gray'),plt.title('Original')
plt.subplot(2,2,2),plt.imshow(erosion1,cmap = 'gray'),plt.title('Erosion1')
plt.subplot(2,2,3),plt.imshow(erosion5,cmap = 'gray'),plt.title('Erosion5')
plt.show()<jupyter_output><empty_output><jupyter_text># Dilation
Increases the white region in the image or size of foreground object increases. <jupyter_code>fig = plt.figure(figsize=(12,10))
############################################################
dilation1 = cv2.dilate(img,kernel,iterations = 1)
dilation5 = cv2.dilate(img,kernel,iterations = 5)
############################################################
fig = plt.figure(figsize=(12,10))
plt.subplot(2,2,1),plt.imshow(img,cmap = 'gray'),plt.title('Original')
plt.subplot(2,2,2),plt.imshow(dilation1,cmap = 'gray'),plt.title('Dilation1')
plt.subplot(2,2,3),plt.imshow(dilation5,cmap = 'gray'),plt.title('Dilation5')
plt.show()<jupyter_output><empty_output><jupyter_text># Opening
Opening is just another name of **Erosion followed by Dilation**. It is useful in removing noise, as we explained above. Here we use the function, cv2.morphologyEx()
Useful in removing background noise!
# Closing
Closing is reverse of Opening, **Dilation followed by Erosion**. It is useful in closing small holes inside the foreground objects, or small black points on the object.
Useful in removing noise from foreground objects, such as black dots on top of the white text.
**cv2.morphologyEx(img, cv2.MORPH_OPEN/cv2.MORPH_CLOSE, kernel)**<jupyter_code>################# Opening ################################
img = load_img()
white_noise = np.random.randint(low=0,high=2,size=(600,600))
white_noise = white_noise*255
noise_img = white_noise+img
fig = plt.figure(figsize=(12,10))
############################################################
opening = cv2.morphologyEx(noise_img, cv2.MORPH_OPEN, kernel)
############################################################
plt.subplot(2,2,1),plt.imshow(noise_img,cmap = 'gray'),plt.title('Noise_Image')
plt.subplot(2,2,2),plt.imshow(opening,cmap = 'gray'),plt.title('Opening')
plt.show()
img = load_img()
black_noise = np.random.randint(low=0,high=2,size=(600,600))
black_noise= black_noise * -255
black_noise_img = img + black_noise
black_noise_img[black_noise_img==-255] = 0
#######################################
closing = cv2.morphologyEx(black_noise_img, cv2.MORPH_CLOSE, kernel)
#######################################
fig = plt.figure(figsize=(12,10))
plt.subplot(2,2,1),plt.imshow(black_noise_img,cmap = 'gray'),plt.title('Noise_Image')
plt.subplot(2,2,2),plt.imshow(closing,cmap = 'gray'),plt.title('Closing')
plt.show()<jupyter_output><empty_output><jupyter_text>---
## Morphological Gradient
It is the difference between dilation and erosion of an image.
cv2.morphologyEx(img, cv2.MORPH_GRADIENT, kernel)<jupyter_code>gradient = cv2.morphologyEx(img,cv2.MORPH_GRADIENT,kernel)
display_img(gradient)<jupyter_output><empty_output>
|
no_license
|
/Image_Proceesing_Part_I.ipynb
|
sagunkayastha/OpenCV_Image_Processing
| 19 |
<jupyter_start><jupyter_text>
# Overview of some tools applied to COVID-19 data
The purpose of this short overview is to give you a sense of the utility of some of the tools you will study later in this course and to check that you already have (or can install) some of modules we shall use later.
In this demo, with a few lines of code, we obtain and visualize data on our most pressing current issue: the progression of COVID-19 disease worldwide. The data on COVID-19 (which is changing in as yet unknown ways) will be used on several occasions as this course progresses. We will proceed to
- download today's data on COVID-19 from a cloud repository,
- make a structured array out of the data,
- use a geospatial module to put the data on a world map,
- download county maps from US Census Bureau, and
- visualize the COVID-19 data restricted to Oregon.
If you are new to the modules used below, don't try to digest every element of the code here yet: again, the material here is intended just to give you an overview of the various tools we will learn in depth later.
## The modules you need
We have already seen how to install python modules. Make sure you have the following modules installed before proceeding. (By now, you should know how to install missing modules.)
- `matplotlib` (all sorts of plotting & visualization in python)
- `descartes` (for visualizing map objects within matplotlib)
- `gitpython` (to work in python with Git repositories)
- `pandas` (to make data frame structures out of raw data)
- `geopandas` (for analysis of geospatial data)
- `urllib` (for fetching resources at an internet url)<jupyter_code>import pandas as pd
import os
from git import Repo
import matplotlib.pyplot as plt
import geopandas as gpd
import urllib
import shutil
%matplotlib inline<jupyter_output><empty_output><jupyter_text>## Get the data
The Johns Hopkins University Center for Systems Science and Engineering
has curated data on COVID-19 from multiple sources and provided it online
at the "GitHub" cloud repository https://github.com/CSSEGISandData/COVID-19. These days, as the disease progresses, new data is being pushed into this repository every day.
GitHub provides code and data in an efficient distributed version control system called `git`. We don't need to get into details here on how git does it magic. It suffices to know that git repositories in the cloud, or a remote server, can be *cloned* to
get an identical local copy on our computers.
Let us begin by cloning a copy of the Johns Hopkins COVID-19 data repository into a location in your computer. You specify this location in your computer in the variable called `covidfolder` below. Once you have cloned the repository, the next time you run the same line of code, it does not clone it again. Instead, it pulls only the updates from the cloud.<jupyter_code># your local folder into which you want to download the covid data
covidfolder = '../../data_external/covid19'
if os.path.isdir(covidfolder): # if repo exists, pull newest data
repo = Repo(covidfolder)
repo.remotes.origin.pull()
else: # otherwise, clone from remote
repo = Repo.clone_from('https://github.com/CSSEGISandData/COVID-19.git',
covidfolder)
datadir = repo.working_dir + '/csse_covid_19_data/csse_covid_19_daily_reports'<jupyter_output><empty_output><jupyter_text>The folder `datadir` contains many files (all of which can be listed here using the command `os.listdir(datadir)` if needed). The filenames begin with a date like `03-27-2020` and ends in `.csv`. The ending suffix `csv` stands for "comma separated values", a common simple format for storing uncompressed data.## Examine the data
The module `pandas` can make a `DataFrame` object out of each such `.csv` files. Let us pick a recent data and examine the data for that date.<jupyter_code>c = pd.read_csv(datadir+'/03-27-2020.csv')<jupyter_output><empty_output><jupyter_text>The `DataFrame` object `c` has over 3000 rows. An examination of the first five rows already tells us a lot about the data layout:<jupyter_code>c.head()<jupyter_output><empty_output><jupyter_text>This object `c` looks like a structured array. Each row corresponds to a location, specified in latitude `Lat` and longitude `Long_`. The columns "Confirmed", "Deaths", and
"Recovered" represents the number of confirmed cases, deaths, and recovered cases due to COVID-19 at that location.## Put the data on a mapData like that in `c` contains geographical information. One way to visualize geospatial data is to somehow indicate the quantity of interest on a map. We shall visualize the data in the "Confirmed" column by positioning a marker at a geographical location and make the marker size correspond to the number of confirmed cases at that position. The module `geopandas` (`gpd`) is well-suited for visualizing geospatial data. It is built on top of the `pandas` library. So it is easy to convert our `pandas` object `c` to a `geopandas` object.
<jupyter_code>geo = gpd.points_from_xy(c['Long_'], c['Lat']) # make a geometry object from Lat, Long
gc = gpd.GeoDataFrame(c, geometry=geo) # give it to geopandas together with c
gc.head()<jupyter_output><empty_output><jupyter_text>The only difference between `gc` and `c` is the last column, which contains the new geometry objects representing points on the globe. Next, we place markers at these points on a map of the world. Here is how we get a simple map: <jupyter_code>world = gpd.read_file(gpd.datasets.get_path('naturalearth_lowres'))
world.plot();<jupyter_output><empty_output><jupyter_text>On top of such a map, we can now put the markers whose size is proportional to the number of confirmed cases. <jupyter_code>base = world.plot(alpha=0.3)
msz = 500 * gc['Confirmed'] / gc['Confirmed'].max()
gc.plot(ax=base, column='Confirmed', markersize=msz, alpha=0.7); <jupyter_output><empty_output><jupyter_text>## Restricting to OregonRestricting the COVID-19 data in `c` to Oregon is very easy:<jupyter_code>co = c[c['Province_State']=='Oregon']<jupyter_output><empty_output><jupyter_text>However, to visualize this, we need a map of Oregon.
Unfortunately, `geopandas` does not appear to carry any
information about Oregon and its counties.
However this information is available from the [United States Census Bureau](https://www.census.gov/). (By the way, the 2020 census is happening now! Do not forget to respond to their survey. They are one of our authoritative sources of quality data.)
To extract the COVID-19 information for Oregon and visualize it on a map of Oregon, we need to get the county boundary information from the census bureau. This situation illustrates a common situation that arises when trying to analyze data: it is often necessary to procure and merge data from multiple sources in order to
understand a data set.
A quick google search reveals the census page with county information. The information is now in an online file `cb_2018_us_county_500k.zip`, not in a git repository as before.
Let us download this file, without leaving this notebook using python's `urllib` module.<jupyter_code># url of the data
census_url = 'https://www2.census.gov/geo/tiger/GENZ2018/shp/cb_2018_us_county_500k.zip'
# location of your download
your_download_folder = '../../data_external'
if not os.path.isdir(your_download_folder):
os.mkdir(your_download_folder)
us_county_file = your_download_folder + '/cb_2018_us_county_500k.zip'
# download if the file doesn't already exist
if not os.path.isfile(us_county_file):
with urllib.request.urlopen(census_url) as response, open(us_county_file, 'wb') as out_file:
shutil.copyfileobj(response, out_file)<jupyter_output><empty_output><jupyter_text>Now, your local computer has a zip file, which has among its contents, files with geometry information on the county boundaries, which can be read by `geopandas`.
We let `geopandas` directly read in the zip file (as suggested in [[DN]](http://blog.danwin.com/census-places-cartodb-geopandas-mapping/)) as it seems to know which information to extract from the zip archive to make a data frame with geometry. <jupyter_code>us_counties = gpd.read_file(f"zip://{us_county_file}")
us_counties.head()<jupyter_output><empty_output><jupyter_text>The object `us_counties` has information about all the counties. Now, we need to restrict this data to just that of Oregon. Looking at the columns, we find something called STATEFP. Searching through the [government pages](https://www.census.gov/programs-surveys/geography/technical-documentation/records-layout/nlt-record-layouts.html), we find that STATEFP refers to a 2-character state FIPS code.
The FIPS code refers to [Federal Information Processing Standard](https://en.wikipedia.org/wiki/FIPS_county_code)
which was a "standard" at one time, then deemed obsolete, but still continues to be used today. Anyway, suffices to say that it is easy to find that Oregon's FIPS code is 41. Once we know this, python makes it is easy to restrict the data to Oregon: <jupyter_code>ore = us_counties[us_counties['STATEFP']=='41']
ore.plot();<jupyter_output><empty_output><jupyter_text>Now we have the Oregon data in two data frames, `ore` and `co`. We must merge them -- a situation so often encountered when dealing with real data that there is a facility for it in `pandas` called `merge`. Both data has FIPS codes: in `ore` you find it under column GEOID, and in `co` you find it called `FIPS`. The merged data frame is `orco` below:<jupyter_code>ore = ore.astype({'GEOID': 'int64'}).rename(columns={'GEOID' : 'FIPS'})
co = co.astype({'FIPS': 'int64'})
orco = pd.merge(ore, co.iloc[:,:-1], on='FIPS')<jupyter_output><empty_output><jupyter_text>The `orco` object now has both the geometry information as well as the COVID-19 information, making it extremely easy to visualize.<jupyter_code># plot coloring counties by number of confirmed cases
fig, ax = plt.subplots(figsize=(15, 12))
orco.plot(ax=ax, column='Confirmed', legend=True,
legend_kwds={'label': '# confimed cases', 'orientation':'horizontal'})
# label the counties
for x, y, county in zip(orco['Long_'], orco['Lat'], orco['NAME']):
ax.text(x, y, county, color='grey')<jupyter_output><empty_output>
|
no_license
|
/jupyter/01_Overview_of_tools_applied_to_COVID-19_example.ipynb
|
gomezlis/mth271content
| 13 |
<jupyter_start><jupyter_text>### Задания модуля 1#### 1) Загрузите файл mate.txt из папки data.1 способ<jupyter_code>path='../data/'
file = open(path+'mate.txt', mode='r')
file.read()<jupyter_output><empty_output><jupyter_text>2 способ<jupyter_code>file = open(path+'mate.txt', mode='r')
for line in file:
print(line)
file.close()<jupyter_output>Well done, mate!
You opened your first file!
<jupyter_text>3 способ<jupyter_code>with open(path+'mate.txt', mode='r') as t_file:
for line in t_file:
print(line)<jupyter_output>Well done, mate!
You opened your first file!
<jupyter_text>#### 2) Сортировка по длине<jupyter_code>names = ['Jack', 'Juliya', 'Vladimir', 'Sanya', 'Оля']
sorted(names, key=len)<jupyter_output><empty_output><jupyter_text>#### 3) Выведите список из 100 чисел через запятую. Циклами пользоваться нельзя.<jupyter_code>counts= list(range(1, 100, 5))
counts<jupyter_output><empty_output><jupyter_text>#### 4) Напишите цикл для того чтобы убрать цифры из строки "Python курс 2020"<jupyter_code>stroke = 'Python курс 2020'
stroke1 =''
for i in stroke:
if i.isalpha() == True:
stroke1 += i
elif i == ' ':
stroke1 += i
else: pass
stroke1.strip()
b = ''
for i in stroke:
if i.isdigit() == False:
b += i
else: pass
b.strip()
print(''.join(c for c in stroke if c.isdigit()==False))
stroke = 'Python курс 2020'
stroke1 = [char for char in stroke if char.isdigit()==False]
print(stroke1)<jupyter_output>['P', 'y', 't', 'h', 'o', 'n', ' ', 'к', 'у', 'р', 'с', ' ']
|
no_license
|
/Task on Python-Module1.ipynb
|
Katty-K/task-python
| 6 |
<jupyter_start><jupyter_text># **Finding Lane Lines on the Road**
***
In this project, you will use the tools you learned about in the lesson to identify lane lines on the road. You can develop your pipeline on a series of individual images, and later apply the result to a video stream (really just a series of images). Check out the video clip "raw-lines-example.mp4" (also contained in this repository) to see what the output should look like after using the helper functions below.
Once you have a result that looks roughly like "raw-lines-example.mp4", you'll need to get creative and try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video "P1_example.mp4". Ultimately, you would like to draw just one line for the left side of the lane, and one for the right.
---
Let's have a look at our first image called 'test_images/solidWhiteRight.jpg'. Run the 2 cells below (hit Shift-Enter or the "play" button above) to display the image.
**Note** If, at any point, you encounter frozen display windows or other confounding issues, you can always start again with a clean slate by going to the "Kernel" menu above and selecting "Restart & Clear Output".
---**The tools you have are color selection, region of interest selection, grayscaling, Gaussian smoothing, Canny Edge Detection and Hough Tranform line detection. You are also free to explore and try other techniques that were not presented in the lesson. Your goal is piece together a pipeline to detect the line segments in the image, then average/extrapolate them and draw them onto the image for display (as below). Once you have a working pipeline, try it out on the video stream below.**
---
Your output should look something like this (above) after detecting line segments using the helper functions below
Your goal is to connect/average/extrapolate line segments to get output like this
<jupyter_code>#importing some useful packages
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np
import cv2
%matplotlib inline
#reading in an image
image = mpimg.imread('test_images/solidWhiteRight.jpg')
#printing out some stats and plotting
print('This image is:', type(image), 'with dimesions:', image.shape)
plt.imshow(image) #call as plt.imshow(gray, cmap='gray') to show a grayscaled image<jupyter_output>This image is: <class 'numpy.ndarray'> with dimesions: (540, 960, 3)
<jupyter_text>**Some OpenCV functions (beyond those introduced in the lesson) that might be useful for this project are:**
`cv2.inRange()` for color selection
`cv2.fillPoly()` for regions selection
`cv2.line()` to draw lines on an image given endpoints
`cv2.addWeighted()` to coadd / overlay two images
`cv2.cvtColor()` to grayscale or change color
`cv2.imwrite()` to output images to file
`cv2.bitwise_and()` to apply a mask to an image
**Check out the OpenCV documentation to learn about these and discover even more awesome functionality!**## The following is the Bresenham line algorithmFind all interior points for given two end points in a grid space.<jupyter_code>def bresenham(x1,y1,x2,y2): #x1,y1,x2,y2 are all integers
dx=x2-x1
dy=y2-y1
if dx >=0 and dy >=0:
if abs(dx)-abs(dy) >=0:
delta_a=abs(dx)
delta_b=abs(dy)
else:
delta_a=abs(dy)
delta_b=abs(dx)
if dx >=0 and dy <0:
if abs(dx)-abs(dy) >=0:
delta_a=abs(dx)
delta_b=abs(dy)
else:
delta_a=abs(dy)
delta_b=abs(dx)
if dx <0 and dy >=0:
if abs(dx)-abs(dy) >=0:
delta_a=abs(dx)
delta_b=abs(dy)
else:
delta_a=abs(dy)
delta_b=abs(dx)
if dx <0 and dy <0:
if abs(dx)-abs(dy) >=0:
delta_a=abs(dx)
delta_b=abs(dy)
else:
delta_a=abs(dy)
delta_b=abs(dx)
S=[]
S.append(2*delta_b-delta_a)
while len(S)<delta_a:
if S[-1]>=0:
S.append(S[-1]+2*delta_b-2*delta_a)
else:
S.append(S[-1]+2*delta_b)
def M1(S):
x=S[-1][0]
y=S[-1][1]
S.append([x+1,y])
return S
def M2(S):
x=S[-1][0]
y=S[-1][1]
S.append([x+1,y+1])
return S
def M3(S):
x=S[-1][0]
y=S[-1][1]
S.append([x,y+1])
return S
def M4(S):
x=S[-1][0]
y=S[-1][1]
S.append([x-1,y+1])
return S
def M5(S):
x=S[-1][0]
y=S[-1][1]
S.append([x-1,y])
return S
def M6(S):
x=S[-1][0]
y=S[-1][1]
S.append([x-1,y-1])
return S
def M7(S):
x=S[-1][0]
y=S[-1][1]
S.append([x,y-1])
return S
def M8(S):
x=S[-1][0]
y=S[-1][1]
S.append([x+1,y-1])
return S
pts_of_line=[]
pts_of_line.append([x1,y1])
for i in range(len(S)):
if dx>=0 and dy>=0:
if abs(dx)-abs(dy)>=0:
if S[i]<0:
pts_of_line=M1(pts_of_line)
else:
pts_of_line=M2(pts_of_line)
else:
if S[i]<0:
pts_of_line=M3(pts_of_line)
else:
pts_of_line=M2(pts_of_line)
if dx>=0 and dy<0:
if abs(dx)-abs(dy)>=0:
if S[i]<0:
pts_of_line=M1(pts_of_line)
else:
pts_of_line=M8(pts_of_line)
else:
if S[i]<0:
pts_of_line=M7(pts_of_line)
else:
pts_of_line=M8(pts_of_line)
if dx<0 and dy>=0:
if abs(dx)-abs(dy)>=0:
if S[i]<0:
pts_of_line=M5(pts_of_line)
else:
pts_of_line=M4(pts_of_line)
else:
if S[i]<0:
pts_of_line=M3(pts_of_line)
else:
pts_of_line=M4(pts_of_line)
if dx<0 and dy<0:
if abs(dx)-abs(dy)>=0:
if S[i]<0:
pts_of_line=M5(pts_of_line)
else:
pts_of_line=M6(pts_of_line)
else:
if S[i]<0:
pts_of_line=M7(pts_of_line)
else:
pts_of_line=M6(pts_of_line)
return pts_of_line<jupyter_output><empty_output><jupyter_text>Below are some helper functions to help get you started. They should look familiar from the lesson!<jupyter_code>import math
from sklearn import linear_model
def grayscale(img):
"""Applies the Grayscale transform
This will return an image with only one color channel
but NOTE: to see the returned image as grayscale
you should call plt.imshow(gray, cmap='gray')"""
return cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
def canny(img, low_threshold, high_threshold):
"""Applies the Canny transform"""
return cv2.Canny(img, low_threshold, high_threshold)
def gaussian_blur(img, kernel_size=3):
"""Applies a Gaussian Noise kernel"""
return cv2.GaussianBlur(img, (kernel_size, kernel_size), 0)
def region_of_interest(img, vertices):
"""
Applies an image mask.
Only keeps the region of the image defined by the polygon
formed from `vertices`. The rest of the image is set to black.
"""
#defining a blank mask to start with
mask = np.zeros_like(img)
#defining a 3 channel or 1 channel color to fill the mask with depending on the input image
if len(img.shape) > 2:
channel_count = img.shape[2] # i.e. 3 or 4 depending on your image
ignore_mask_color = (255,) * channel_count
else:
ignore_mask_color = 255
#filling pixels inside the polygon defined by "vertices" with the fill color
cv2.fillPoly(mask, vertices, ignore_mask_color)
#returning the image only where mask pixels are nonzero
masked_image = cv2.bitwise_and(img, mask)
return masked_image
def draw_lines(img, lines, color=[255, 0, 0], thickness=15):
"""
NOTE: this is the function you might want to use as a starting point once you want to
average/extrapolate the line segments you detect to map out the full
extent of the lane (going from the result shown in raw-lines-example.mp4
to that shown in P1_example.mp4).
Think about things like separating line segments by their
slope ((y2-y1)/(x2-x1)) to decide which segments are part of the left
line vs. the right line. Then, you can average the position of each of
the lines and extrapolate to the top and bottom of the lane.
This function draws `lines` with `color` and `thickness`.
Lines are drawn on the image inplace (mutates the image).
If you want to make the lines semi-transparent, think about combining
this function with the weighted_img() function below
"""
width=img.shape[1]
hight=img.shape[0]
right_line_train=[]
left_line_train=[]
for line in lines:
for x1,y1,x2,y2 in line:
if x1 >= int(np.round(width/2)) and x2 >= int(np.round(width/2)):
# collect pts to right_line
right_line_train=right_line_train+bresenham(x1,y1,x2,y2)
if x1 <=int(np.round(width/2)) and x2 <= int(np.round(width/2)):
# collect pts to left_line
left_line_train=left_line_train+bresenham(x1,y1,x2,y2)
#cv2.line(img, (x1, y1), (x2, y2), color, thickness)
#print(right_line_train)
#print(left_line_train)
left_X=[]
left_y=[]
right_X=[]
right_y=[]
for i in range(len(left_line_train)):
left_X.append([left_line_train[i][0]])
left_y.append([left_line_train[i][1]])
for i in range(len(right_line_train)):
right_X.append([right_line_train[i][0]])
right_y.append([right_line_train[i][1]])
def find_end_point(m,b,y1,y2):
x1=int(np.round((y1-b)/m))
x2=int(np.round((y2-b)/m))
return [x1,y1,x2,y2]
y1=350
y2=540
mylines=[]
if not not left_X and not not left_y:
reg_left = linear_model.LinearRegression()
reg_left.fit(left_X, left_y)
mylines.append(find_end_point(reg_left.coef_,reg_left.intercept_,y1,y2))
if not not right_X and not not right_y:
reg_right = linear_model.LinearRegression()
reg_right.fit(right_X, right_y)
mylines.append(find_end_point(reg_right.coef_,reg_right.intercept_,y1,y2))
#print(mylines)
for line in mylines:
x1=line[0]
y1=line[1]
x2=line[2]
y2=line[3]
#print(x1,y1,x2,y2)
cv2.line(img, (x1, y1), (x2, y2), color, thickness)
def old_draw_lines(img, lines, color=[255, 0, 0], thickness=15):
for line in lines:
#print(line)
for x1,y1,x2,y2 in line:
cv2.line(img, (x1, y1), (x2, y2), color, thickness)
def hough_lines(img, rho=1, theta=np.pi/180, threshold=10, min_line_len=50, max_line_gap=100):
"""
`img` should be the output of a Canny transform.
Returns an image with hough lines drawn.
"""
lines = cv2.HoughLinesP(img, rho, theta, threshold, np.array([]), minLineLength=min_line_len, maxLineGap=max_line_gap)
#line_img = np.zeros((*img.shape, 3), dtype=np.uint8)
line_img = np.zeros((img.shape[0],img.shape[1], 3), dtype=np.uint8)
draw_lines(line_img, lines)
return line_img
# Python 3 has support for cool math symbols.
def weighted_img(img, initial_img, alpha=0.8, beta=1., lamda=0.):
"""
`img` is the output of the hough_lines(), An image with lines drawn on it.
Should be a blank image (all black) with lines drawn on it.
`initial_img` should be the image before any processing.
The result image is computed as follows:
initial_img * α + img * β + λ
NOTE: initial_img and img must be the same shape!
"""
return cv2.addWeighted(initial_img, alpha, img, beta, lamda)
def pipeline(image):
m=image.shape[0] #540
n=image.shape[1] #960
gray_img=grayscale(image)
gaussian_img=gaussian_blur(gray_img)
high_threshold, thresh_im = cv2.threshold(gaussian_img, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
low_threshold = 0.5*high_threshold
#low_threshold=80 # Last submit, I used the following parameters
#high_threshold=255
canny_img=canny(gaussian_img,low_threshold, high_threshold)
vertices = np.array([[(n/10,m),((n/2)-20,int(np.round(m*0.6))), ((n/2)+20,int(np.round(m*0.6))), (n-(n/20),m)]], dtype=np.int32)
masked_img=region_of_interest(canny_img, vertices)
line_img=hough_lines(masked_img)
lines_edges=weighted_img(line_img, image)
return lines_edges
plt.imshow(pipeline(image))<jupyter_output><empty_output><jupyter_text>## Test on Images
Now you should build your pipeline to work on the images in the directory "test_images"
**You should make sure your pipeline works well on these images before you try the videos.**<jupyter_code>import os
filestr="test_images"
#dir=os.listdir("test_images/")
dir=os.listdir(filestr+"/")
<jupyter_output><empty_output><jupyter_text>run your solution on all test_images and make copies into the test_images directory).<jupyter_code>for i in range(len(dir)):
imgstr=filestr+'/'+dir[i]
savestr=filestr+'/result_'+dir[i]
image = mpimg.imread(imgstr)
result=pipeline(image)
plt.imsave(savestr,result)<jupyter_output><empty_output><jupyter_text>## Test on Videos
You know what's cooler than drawing lanes over images? Drawing lanes over video!
We can test our solution on two provided videos:
`solidWhiteRight.mp4`
`solidYellowLeft.mp4`<jupyter_code># Import everything needed to edit/save/watch video clips
from moviepy.editor import VideoFileClip
from IPython.display import HTML
def process_image(image):
# NOTE: The output you return should be a color image (3 channel) for processing video below
# TODO: put your pipeline here,
# you should return the final output (image with lines are drawn on lanes)
result=pipeline(image)
return result<jupyter_output><empty_output><jupyter_text>Let's try the one with the solid white lane on the right first ...<jupyter_code>white_output = 'white.mp4'
clip1 = VideoFileClip("solidWhiteRight.mp4")
white_clip = clip1.fl_image(process_image) #NOTE: this function expects color images!!
%time white_clip.write_videofile(white_output, audio=False)<jupyter_output>[MoviePy] >>>> Building video white.mp4
[MoviePy] Writing video white.mp4
<jupyter_text>Play the video inline, or if you prefer find the video in your filesystem (should be in the same directory) and play it in your video player of choice.<jupyter_code>HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(white_output))<jupyter_output><empty_output><jupyter_text>**At this point, if you were successful you probably have the Hough line segments drawn onto the road, but what about identifying the full extent of the lane and marking it clearly as in the example video (P1_example.mp4)? Think about defining a line to run the full length of the visible lane based on the line segments you identified with the Hough Transform. Modify your draw_lines function accordingly and try re-running your pipeline.**Now for the one with the solid yellow lane on the left. This one's more tricky!<jupyter_code>yellow_output = 'yellow.mp4'
clip2 = VideoFileClip('solidYellowLeft.mp4')
yellow_clip = clip2.fl_image(process_image)
%time yellow_clip.write_videofile(yellow_output, audio=False)
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(yellow_output))<jupyter_output><empty_output><jupyter_text>## Reflections
Congratulations on finding the lane lines! As the final step in this project, we would like you to share your thoughts on your lane finding pipeline... specifically, how could you imagine making your algorithm better / more robust? Where will your current algorithm be likely to fail?
Please add your thoughts below, and if you're up for making your pipeline more robust, be sure to scroll down and check out the optional challenge video below!
Answer:
* 1) This is my second submission, I have totally revised the line average method. This time, I used the linear regression to fit the points generated from the Houge Trans. That is, using the end points of Houge tranform, I can generate the interior points by Bresenham's line algorithm.
* 2) The challenge file is more difficult because there are shadows in the video. Besides, the resolution is also different.## Submission
If you're satisfied with your video outputs it's time to submit! Submit this ipython notebook for review.
## Optional Challenge
Try your lane finding pipeline on the video below. Does it still work? Can you figure out a way to make it more robust? If you're up for the challenge, modify your pipeline so it works with this video and submit it along with the rest of your project!<jupyter_code>challenge_output = 'extra.mp4'
clip2 = VideoFileClip('challenge.mp4')
challenge_clip = clip2.fl_image(process_image)
%time challenge_clip.write_videofile(challenge_output, audio=False)
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(challenge_output))<jupyter_output><empty_output>
|
no_license
|
/P1-e2.ipynb
|
yychiang/CarND-LaneLines-P1
| 10 |
<jupyter_start><jupyter_text># Первая попытка ([2017-06-17, 11:22])
Экспериментируем с Jupyter и pandas.<jupyter_code>import pandas as pd
props = pd.read_csv("http://www.firstpythonnotebook.org/_static/committees.csv")
props.head(3)
props.info()
contribs = pd.read_csv("http://www.firstpythonnotebook.org/_static/contributions.csv")
contribs.head()
contribs.info()
props.prop_name.value_counts().reset_index()
props.prop_name.value_counts()
prop = props[props.prop_name == "PROPOSITION 064- MARIJUANA LEGALIZATION. INITIATIVE STATUTE."]
prop.head()
prop.info()
contribs.info()
merged = pd.merge(prop, contribs, on="calaccess_committee_id")
merged.head()
merged.info()
merged.prop_name.value_counts()
merged.amount.sum()
merged.committee_position.value_counts()
support = merged[merged.committee_position == "SUPPORT"]
support.info()
oppose = merged[merged.committee_position == "OPPOSE"]
oppose.info()
support.amount.sum()
oppose.amount.sum()
support.amount.sum() / merged.amount.sum()
merged.sort_values("amount", ascending=False)
merged.groupby("committee_name_x").amount.sum().reset_index().sort_values("amount", ascending=False)
merged.groupby(["contributor_firstname", "contributor_lastname", "committee_position"]).amount.sum().reset_index().sort_values("amount", ascending=False)<jupyter_output><empty_output>
|
no_license
|
/prop-64-analysis.ipynb
|
olgapavlova/first-python-notebook
| 1 |
<jupyter_start><jupyter_text>
# Sprint Challenge
## *Data Science Unit 4 Sprint 1*
After a week of Natural Language Processing, you've learned some cool new stuff: how to process text, how turn text into vectors, and how to model topics from documents. Apply your newly acquired skills to one of the most famous NLP datasets out there: [Yelp](https://www.yelp.com/dataset/challenge). As part of the job selection process, some of my friends have been asked to create analysis of this dataset, so I want to empower you to have a head start.
The real dataset is massive (almost 8 gigs uncompressed). I've sampled the data for you to something more managable for the Sprint Challenge. You can analyze the full dataset as a stretch goal or after the sprint challenge. As you work on the challenge, I suggest adding notes about your findings and things you want to analyze in the future.
## Challenge Objectives
*Successfully complete these all these objectives to earn a 2. There are more details on each objective further down in the notebook.*
* Part 1: Write a function to tokenize the yelp reviews
* Part 2: Create a vector representation of those tokens
* Part 3: Use your tokens in a classification model on yelp rating
* Part 4: Estimate & Interpret a topic model of the Yelp reviews<jupyter_code>import pandas as pd
yelp = pd.read_json('./data/review_sample.json', lines=True)
yelp.head()
yelp.shape
yelp.dtypes
import re
import string
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import spacy
import spacy
nlp = spacy.load("en_core_web_lg")<jupyter_output><empty_output><jupyter_text>## Part 1: Tokenize Function
Complete the function `tokenize`. Your function should
- accept one document at a time
- return a list of tokens
You are free to use any method you have learned this week.<jupyter_code>STOPWORDS = set(STOPWORDS).union(set(['yelp']))
def tokenize(text):
return [token for token in simple_preprocess(text) if token not in STOPWORDS]
tokenize("Hello World! This a test of the tokenization method")
#this is different tokenizer method then bellow
yelp['tokens'] = yelp['text'].apply(lambda x: tokenize(x))
df = yelp.copy()
from spacy.tokenizer import Tokenizer
tokenizer = Tokenizer(nlp.vocab)
tokens = []
# Make the tokens
for doc in nlp.pipe(df['text']):
doc_tokens = []
for token in doc:
if (token.is_stop==False) & (token.is_punct==False):
doc_tokens.append(token.text)
tokens.append(doc_tokens)
df['tokens'] = tokens
df.head()<jupyter_output><empty_output><jupyter_text>## Part 2: Vector Representation
1. Create a vector representation of the reviews
2. Write a fake review and query for the 10 most similiar reviews, print the text of the reviews. Do you notice any patterns?
- Given the size of the dataset, it will probably be best to use a `NearestNeighbors` model for this. <jupyter_code>from sklearn.feature_extraction.text import TfidfVectorizer
# Instantiate vectorizer object
tf = TfidfVectorizer(stop_words = 'english')
# Create a vocabulary and get word counts per document
sparse = tf.fit_transform(df.text)
# Print word counts
# Get feature names to use as dataframe column headers
dtm = pd.DataFrame(sparse.todense(), columns=tf.get_feature_names())
# View Feature Matrix as DataFrame
dtm.head()
# Instantiate
from sklearn.neighbors import NearestNeighbors
# Fit on TF-IDF Vectors
nn = NearestNeighbors(n_neighbors=10, algorithm='ball_tree')
nn.fit(dtm)
fake_review = [""" Wow this is absolute crap I cannot believe I wasted
my money on this, if I don't get a full refund someone is going to get sued
someone should literally be fired for this. you are shit."""]
# Query for Sim of Random doc to BBC
new = tf.transform(fake_review)
nn.kneighbors(new.todense())
df['text'][6847]
df['text'][3330]
#this one is not relevant
df['text'][5260]
df['text'][5081]
df['text'][1021]<jupyter_output><empty_output><jupyter_text>## Part 3: Classification
Your goal in this section will be to predict `stars` from the review dataset.
1. Create a piepline object with a sklearn `CountVectorizer` or `TfidfVector` and any sklearn classifier. Use that pipeline to estimate a model to predict `stars`. Use the Pipeline to predict a star rating for your fake review from Part 2.
2. Tune the entire pipeline with a GridSearch<jupyter_code># Import Statements
from sklearn.pipeline import Pipeline
from sklearn.ensemble import RandomForestClassifier
# Create Pipeline
vect = TfidfVectorizer(stop_words='english')
sgdc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
pipe = Pipeline([('vect', vect), ('clf', sgdc)])
# Fit Pipeline
pipe.fit(df.text, df.stars)
# 1 star makes absolute sense!
fake_star = pipe.predict(fake_review)
fake_star
# Experiment Management
from sklearn.model_selection import GridSearchCV
parameters = {
}
grid_search = GridSearchCV(pipe, parameters, cv=5, n_jobs=-1, verbose=1)
grid_search.fit(df.text, df.stars)
fake_stars2 = grid_search.predict(fake_review)
fake_stars2<jupyter_output><empty_output><jupyter_text>## Part 4: Topic Modeling
Let's find out what those yelp reviews are saying! :D
1. Estimate a LDA topic model of the review text
2. Create 1-2 visualizations of the results
- You can use the most important 3 words of a topic in relevant visualizations. Refer to yesterday's notebook to extract.
3. In markdown, write 1-2 paragraphs of analysis on the results of your topic model
__*Note*__: You can pass the DataFrame column of text reviews to gensim. You do not have to use a generator.<jupyter_code>import numpy as np
import gensim
import os
import re
from gensim.utils import simple_preprocess
from gensim.parsing.preprocessing import STOPWORDS
from gensim import corpora
from gensim.models.ldamulticore import LdaMulticore
id2word = corpora.Dictionary(yelp['tokens'])
id2word.doc2bow(tokenize("This is a sample message Darcy England England England"))
import sys
sys.getsizeof(id2word)
len(id2word.keys())
# Let's remove extreme values from the dataset
id2word.filter_extremes(no_below=10, no_above=0.75)
len(id2word.keys())
import warnings
warnings.filterwarnings('ignore')
corpus = [id2word.doc2bow(text) for text in yelp['tokens']]
lda = LdaMulticore(corpus=corpus,
id2word=id2word,
random_state=723812,
num_topics = 5,
passes=10,
workers=4
)
lda.print_topics()
words = [re.findall(r'"([^"]*)"',t[1]) for t in lda.print_topics()]
topics = [' '.join(t[0:5]) for t in words]
print(topics[0])
for t in topics:
print(t)
print("\n")
import warnings
warnings.filterwarnings('ignore')
import pyLDAvis.gensim
pyLDAvis.enable_notebook()
pyLDAvis.gensim.prepare(lda, corpus, id2word)
### hmmm i a pretty thrown that all the topics are positive seeming and seem so close related...
# i was almost expecting topics to be broken up by star
# that there would be one super positive, one super negative, and some middle ones... hmmmm
# it is very possible i did not make enough topics and most reviews are more postitive then not...
# i guess i could check that with star distribution
## wow wrote that top piece while visualiztion was loading... now that it is loaded i am pretty impressed by it
# the topics were not associated with the star rating of the review but rather what was being reviewed
# and it seems to have done a pretty awesome job of splitting the topics.
# for the five it seems like there is bar, bar-type food, asian food, coffee shop, and retail store
#with bar and bar food are overlapped
<jupyter_output><empty_output>
|
no_license
|
/sprint-challenge/LS_DS_415_Sprint_Challenge.ipynb
|
jtkernan7/DS-Unit-4-Sprint-1-NLP
| 5 |
<jupyter_start><jupyter_text># Logistic and linear regression with deterministic and stochastic first order methods
Lab 2 : Optimisation - DataScience Master
Authors : Robert Gower, Alexandre Gramfort, Pierre Ablin, Mathurin Massias
The aim of this lab is to implement and compare various batch and stochastic algorithms for linear and logistic regression with ridge penalization.
The following methods are compared in this notebook.
**Batch (deterministic) methods**
- gradient descent (GD)
- accelerated gradient descent (AGD)
- L-BFGS
- conjugate gradient (CG)
**Stochastic algorithms**
- stochastic gradient descent (SGD)
- stochastic averaged gradient (SAG)
- stochastic variance reduced gradient (SVRG)
Note that we consider as use-cases logistic and linear regression with ridge penalization only, although most of the algorithms below can be used with many other models, and other types of penalization, eventually non-smooth ones, such as the $\ell_1$ penalization.
## VERY IMPORTANT
- This work **must be done by pairs of students**.
- **Each** student must send their work **before the 26th of november at 23:55**, using the **moodle platform**.
- This means that **each student in the pair sends the same file**
- The **name of the file must be** constructed as in the next cell
### How to construct the name of your file<jupyter_code># Change here using YOUR first and last names
fn1 = "soufiane"
ln1 = "moutei"
fn2 = "mohammed"
ln2 = "barrahma-tlemcani"
filename = "_".join(map(lambda s: s.strip().lower(),
["lab2", ln1, fn1, "and", ln2, fn2])) + ".ipynb"
print(filename)<jupyter_output>lab2_moutei_soufiane_and_barrahma-tlemcani_mohammed.ipynb
<jupyter_text># Gentle reminder: no evaluation if you don't respect this EXACTLY### Table of content
[1. Loss functions, gradients and step-sizes](#loss)
[2. Generate a dataset](#data)
[3. Deterministic methods](#batch)
[4. Stochastic methods](#stoc)
[5. Numerical comparison](#comp)
[6. Conclusion](#conc)<jupyter_code>%matplotlib inline
from time import time
import numpy as np
from scipy.linalg import norm
import matplotlib.pyplot as plt
from numba import njit
# choose a large font size by default and use tex for math
usetex = True # change this to True if you have a working LaTeX install
fontsize = 16
params = {'axes.labelsize': fontsize + 2,
'font.size': fontsize + 2,
'legend.fontsize': fontsize + 2,
'xtick.labelsize': fontsize,
'ytick.labelsize': fontsize,
'text.usetex': usetex}
plt.rcParams.update(params)<jupyter_output><empty_output><jupyter_text>
## 1. Loss functions, gradients and step-sizes
We want to minimize
$$
\frac 1n \sum_{i=1}^n \ell(a_i^\top x, b_i) + \frac \lambda 2 \|x\|_2^2
$$
where
- $\ell(z, b) = \frac 12 (b - z)^2$ (least-squares regression)
- $\ell(z, b) = \log(1 + \exp(-bz))$ (logistic regression).
We write it as a minimization problem of the form
$$
\frac 1n \sum_{i=1}^n f_i(x)
$$
where
$$
f_i(x) = \ell(a_i^\top x, b_i) + \frac \lambda 2 \|x\|_2^2.
$$
For both cases, the gradients are
$$
\nabla f_i(x) = (a_i^\top x - b_i) a_i + \lambda x
$$
and
$$
\nabla f_i(x) = - \frac{b_i}{1 + \exp(b_i a_i^\top x)} a_i + \lambda x.
$$
Denote by $L$ (resp. $L_i$) the Lipschitz constant of $f$ (resp. $f_i$) and $\mathbf A^\top = [a_1, \ldots, a_n].$
One can easily see (using $\|\cdot\|_{2}$ for the matrix spectrale norm) that for linear regression
$$
L = \frac{ \|\mathbf A^\top \mathbf A \|_{2}}{n} + \lambda \quad \text{ and } L_i = \| a_i \|_2^2 + \lambda
$$
while for logistic regression it is
$$
L = \frac{ \|\mathbf A^\top \mathbf A \|_{2}}{4 n} + \lambda \quad \text{ and } L_i = \frac 14 \| a_i \|_2^2 + \lambda.
$$
For full-gradient methods, the theoretical step-size is $1 / L$, while for SAG and SVRG (see below) it can be taken as
$1 / (\max_{i=1,\ldots,n} L_i)$We now introduce functions that will be used for the solvers.
<jupyter_code>@njit
def grad_i_linreg(i, x, A, b, lbda):
"""Gradient with respect to a sample"""
a_i = A[i]
tmp = a_i.dot(x)
tmp -= b[i]
tmp *= a_i
tmp += lbda * x
return tmp
@njit
def grad_linreg(x, A, b, lbda):
"""Full gradient"""
g = np.zeros_like(x)
for i in range(n):
g += grad_i_linreg(i, x, A, b, lbda)
return g / n
def loss_linreg(x, A, b, lbda):
return norm(A.dot(x) - b) ** 2 / (2. * n) + lbda * norm(x) ** 2 / 2.
def lipschitz_linreg(A, b, lbda):
return norm(A, ord=2) ** 2 / n + lbda
@njit
def grad_i_logreg(i, x, A, b, lbda):
"""Gradient with respect to a sample"""
a_i = A[i]
b_i = b[i]
return - a_i * b_i / (1. + np.exp(b_i * np.dot(a_i, x))) + lbda * x
@njit
def grad_logreg(x, A, b, lbda):
"""Full gradient"""
g = np.zeros_like(x)
for i in range(n):
g += grad_i_logreg(i, x, A, b, lbda)
return g / n
def loss_logreg(x, A, b, lbda):
bAx = b * np.dot(A, x)
return np.mean(np.log(1. + np.exp(- bAx))) + lbda * norm(x) ** 2 / 2.
def lipschitz_logreg(A, b, lbda):
return norm(A, ord=2) ** 2 / (4. * n) + lbda<jupyter_output><empty_output><jupyter_text>
## 2. Generate a dataset
We generate datasets for the least-squares and the logistic cases. First we define a function for the least-squares case.<jupyter_code>from numpy.random import multivariate_normal, randn
from scipy.linalg.special_matrices import toeplitz
def simu_linreg(x, n, std=1., corr=0.5):
"""Simulation for the least-squares problem.
Parameters
----------
x : ndarray, shape (d,)
The coefficients of the model
n : int
Sample size
std : float, default=1.
Standard-deviation of the noise
corr : float, default=0.5
Correlation of the features matrix
Returns
-------
A : ndarray, shape (n, d)
The design matrix.
b : ndarray, shape (n,)
The targets.
"""
d = x.shape[0]
cov = toeplitz(corr ** np.arange(0, d))
A = multivariate_normal(np.zeros(d), cov, size=n)
noise = std * randn(n)
b = A.dot(x) + noise
return A, b
def simu_logreg(x, n, std=1., corr=0.5):
"""Simulation for the logistic regression problem.
Parameters
----------
x : ndarray, shape (d,)
The coefficients of the model
n : int
Sample size
std : float, default=1.
Standard-deviation of the noise
corr : float, default=0.5
Correlation of the features matrix
Returns
-------
A : ndarray, shape (n, d)
The design matrix.
b : ndarray, shape (n,)
The targets.
"""
A, b = simu_linreg(x, n, std=1., corr=corr)
return A, np.sign(b)
d = 50
n = 10000
idx = np.arange(d)
# Ground truth coefficients of the model
x_model_truth = (-1)**idx * np.exp(-idx / 10.)
_A, _b = simu_linreg(x_model_truth, n, std=1., corr=0.1)
#_A, _b = simu_logreg(x_model_truth, n, std=1., corr=0.7)
plt.stem(x_model_truth);<jupyter_output><empty_output><jupyter_text>### Numerically check loss and gradient<jupyter_code>from scipy.optimize import check_grad
lbda = 1. / n ** (0.5)
A, b = simu_linreg(x_model_truth, n, std=1., corr=0.1)
# Check that the gradient and the loss numerically match
check_grad(loss_linreg, grad_linreg, np.random.randn(d), A, b, lbda)
lbda = 1. / n ** (0.5)
A, b = simu_logreg(x_model_truth, n, std=1., corr=0.1)
# Check that the gradient and the loss numerically match
check_grad(loss_logreg, grad_logreg, np.random.randn(d), A, b, lbda)<jupyter_output><empty_output><jupyter_text>### Choice of the model<jupyter_code>A, b = simu_linreg(x_model_truth, n, std=1., corr=0.9)
loss = loss_linreg
grad = grad_linreg
grad_i = grad_i_linreg
lipschitz_constant = lipschitz_linreg
lbda = 1. / n ** (0.5)<jupyter_output><empty_output><jupyter_text>### Compute the theoretical step-size for gradient descent<jupyter_code>step = 1. / lipschitz_constant(A, b, lbda)
print("step = %s" % step)<jupyter_output>step = 0.06319118838478469
<jupyter_text>### Get a very precise minimum to compute distances to minimum<jupyter_code>from scipy.optimize import fmin_l_bfgs_b
x_init = np.zeros(d)
x_min, f_min, _ = fmin_l_bfgs_b(loss, x_init, grad, args=(A, b, lbda), pgtol=1e-30, factr=1e-30)
print(f_min)
print(norm(grad_linreg(x_min, A, b, lbda)))<jupyter_output><empty_output><jupyter_text>
## 3. Deterministic/Batch methods (GD, AGD, BFGS)### Define a class to monitor iterations<jupyter_code>class monitor:
def __init__(self, algo, loss, x_min, args=()):
self.x_min = x_min
self.algo = algo
self.loss = loss
self.args = args
self.f_min = loss(x_min, *args)
def run(self, *algo_args, **algo_kwargs):
t0 = time()
_, x_list = self.algo(*algo_args, **algo_kwargs)
self.total_time = time() - t0
self.x_list = x_list
self.err = [norm(x - self.x_min) for x in x_list]
self.obj = [self.loss(x, *self.args) - self.f_min for x in x_list]
# Number of iterations
n_iter = 50<jupyter_output><empty_output><jupyter_text>### Gradient descent (GD)
We recall that an iteration of batch gradient writes
$$
x_{k+1} \gets x_k - \eta \nabla f(x_k)
$$
where $\eta$ is the step-size (that can be chosen in theory as $\eta = 1 / L$, with $L$ the Lipshitz constant of $\nabla f$, see above)
*QUESTION*:
- Fill in the iteration of the GD solver in the cell below<jupyter_code>@njit
def gd(x_init, grad, n_iter=100, step=1., store_every=1, args=()):
"""Gradient descent algorithm."""
x = x_init.copy()
x_list = []
A, b, lbda = args
for i in range(n_iter):
### TODO
x -= step * grad(x, A, b, lbda)
### END TODO
if i % store_every == 0:
x_list.append(x.copy())
return x, x_list
step = 1. / lipschitz_linreg(A, b, lbda)
x_init = np.zeros(d)
monitor_gd = monitor(gd, loss, x_min, (A, b ,lbda))
monitor_gd.run(x_init, grad, n_iter, step, args=(A, b, lbda))<jupyter_output><empty_output><jupyter_text>### Accelerated Gradient Descent (AGD)
We recall that an iteration of AGD (see FISTA) writes:
$$
\begin{align*}
x_{k+1} &\gets y_k - \eta \nabla f(y_k) \\
t_{k+1} &\gets \frac{1 + \sqrt{1 + 4 t_k^2}}{2} \\
y_{k+1} &\gets x_{k+1} + \frac{t_k-1}{t_{k+1}} (x_{k+1} - x_k)
\end{align*}
$$
where $\eta$ is the step-size (that can be chosen in theory as $\eta = 1 / L$, with $L$ the Lipshitz constant of $\nabla f$, see above)
*QUESTION*:
- Fill in the iteration of the AGD solver in the cell below<jupyter_code>@njit
def agd(x_init, grad, n_iter=100, step=1., args=(), store_every=1):
"""Accelerated Gradient Descent algorithm."""
x = x_init.copy()
y = x_init.copy()
t = 1.
x_list = []
A, b, lbda = args
for i in range(n_iter):
if i % store_every == 0:
x_list.append(x.copy())
### TODO
x_new = y - step * grad(y, A, b, lbda)
t_new = (1 + np.sqrt(1 + 4 * (t ** 2))) / 2.
y = x_new + ((t - 1) / t_new) * (x_new - x)
t = t_new
x = x_new.copy()
### END TODO
return x, x_list
step = 1. / lipschitz_linreg(A, b, lbda)
x_init = np.zeros(d)
monitor_agd = monitor(agd, loss, x_min, (A, b ,lbda))
monitor_agd.run(x_init, grad, n_iter, step, args=(A, b, lbda))<jupyter_output><empty_output><jupyter_text>### scipy.optimize's conjuguate gradient
Let's compare with ``scipy.optimize``'s nonlinear conjuguate gradient solver. First, define a function to run scipy algorithms and return the list of iterates.<jupyter_code>class callback():
def __init__(self):
self.x_list = []
def __call__(self, x):
self.x_list.append(x.copy())
def scipy_runner(scipy_algo):
def run(*args, **kwargs):
cb = callback()
x = scipy_algo(*args, **kwargs, callback=cb)
return x, cb.x_list
return run
# Nonlinear Conjugate gradient algorithm
from scipy.optimize import fmin_cg
x_init = np.zeros(d)
monitor_cg = monitor(scipy_runner(fmin_cg), loss, x_min, (A, b ,lbda))
monitor_cg.run(loss, x_init, grad, maxiter=n_iter, args=(A, b, lbda), gtol=1e-9)<jupyter_output>Warning: Maximum number of iterations has been exceeded.
Current function value: 0.529788
Iterations: 50
Function evaluations: 81
Gradient evaluations: 81
<jupyter_text>### scipy.optimize's L-BFGS
Let's compare with ``scipy.optimize``'s L-BFGS solver<jupyter_code># L-BFGS algorithm
from scipy.optimize import fmin_l_bfgs_b
x_init = np.zeros(d)
monitor_bfgs = monitor(scipy_runner(fmin_l_bfgs_b), loss, x_min, (A, b ,lbda))
monitor_bfgs.run(loss, x_init, grad, maxiter=n_iter, args=(A, b, lbda), pgtol=1e-30)<jupyter_output><empty_output><jupyter_text>### A first numerical comparison of deterministic solversFirst, define some plotting functions.<jupyter_code>def plot_epochs(monitors, solvers):
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
for monit in monitors:
plt.semilogy(monit.obj, lw=2)
plt.title("Loss")
plt.xlabel("Epoch")
plt.ylabel("objective")
plt.legend(solvers)
plt.subplot(1, 2, 2)
for monit in monitors:
plt.semilogy(monit.err, lw=2)
plt.title("Distance to optimum")
plt.xlabel("Epoch")
plt.ylabel("$\|x_k - x^*\|_2$")
plt.legend(solvers)
plt.show()
def plot_time(monitors, solvers):
for monit in monitors:
objs = monit.obj
plt.semilogy(np.linspace(0, monit.total_time, len(objs)), objs, lw=2)
plt.title("Loss")
plt.xlabel("Timing")
plt.ylabel("$f(x_k) - f(x^*)$")
plt.legend(solvers)
plt.show()
monitors = [monitor_gd, monitor_agd, monitor_cg, monitor_bfgs]
solvers = ["GD", "AGD", "CG", "BFGS"]
plot_epochs(monitors, solvers)
plot_time(monitors, solvers)<jupyter_output><empty_output><jupyter_text>### First conclusions
*QUESTIONS*:
- Give some first conclusions about the batch solver studied here
- What do you observe about AGD? is it suprising ?<jupyter_code>print(step)<jupyter_output>0.06319118838478469
<jupyter_text>
COMMENT
We can see that scipy.optimize algorithms have the highest convergence rate and converge to better values comparing to AGD and Gradient Descent. L-BFGS becomes faster (larger convergence rate) than the Conjuguate Gradient after a few iterations. The Gradient Descent is really slow due to its huge computation of the gradient. In terms of timing, scipy.optimize algorithms are the fastest.
We can see that the convergence of AGD (aka. FISTA) is not linear. In addition, as we saw in the previous lab and since we have a high correlation coefficient ($0.9$), the step value is low and thus the step update towards the minimum. The slow convergence speed (low convergence rate) can be explained also using Beck-Teboulle theorem (the convergence of objective function is upper-bounded by $L$).
## 4. Stochastic methods<jupyter_code>n_iter = 50
# generate indices of random samples
iis = np.random.randint(0, n, n * n_iter)<jupyter_output><empty_output><jupyter_text>### SGD
We recall that an iteration of SGD writes
- Pick $i$ uniformly at random in $\{1, \ldots, n\}$
- Apply
$$
x_{t+1} \gets x_t - \frac{\eta_0}{\sqrt{t+1}} \nabla f_i(x_t)
$$
where $\eta_0$ is a step-size to be tuned by hand.
*QUESTION*:
- Fill in the iteration of the SGD solver in the cell below<jupyter_code>@njit
def sgd(x_init, iis, grad_i, n_iter=100, step=1., store_every=n, args=()):
"""Stochastic gradient descent algorithm."""
x = x_init.copy()
x_list = []
A, b, lbda = args
for idx in range(n_iter):
i = iis[idx]
### TODO
tmp = grad_i(i, x, A, b, lbda)
tmp *= step
tmp /= np.sqrt(idx + 1)
x -= tmp
### END TODO
# Update metrics after each iteration.
if idx % store_every == 0:
x_list.append(x.copy())
return x, x_list
step0 = 1e-1
x_init = np.zeros(d)
monitor_sgd = monitor(sgd, loss, x_min, (A, b ,lbda))
monitor_sgd.run(x_init, iis, grad_i, n_iter * n, step0, args=(A, b, lbda))<jupyter_output><empty_output><jupyter_text>### SAG
We recall that an iteration of SAG writes
For $t=1, \ldots, $ until convergence
1. Pick $i_t$ uniformly at random in $\{1, \ldots, n\}$
2. Update the average of gradients
$$
G_t \gets \frac 1n \sum_{i=1}^n g_i^t
$$
where
$$
g_i^t =
\begin{cases}
\nabla f_{i}(x_t) &\text{ if } i = i_t \\
g_i^{t-1} & \text{ otherwise.}
\end{cases}
$$
3. Apply the step
$$x_{t+1} \gets x_t - \eta G_t$$
where $\eta$ is the step-size (see code below).
*QUESTION*:
- Fill in the iteration of the SAG solver in the cell below<jupyter_code>@njit
def sag(x_init, iis, grad_i, n_iter=100, step=1., store_every=n, args=()):
"""Stochastic average gradient algorithm."""
x = x_init.copy()
# Old gradients
gradient_memory = np.zeros((n, d))
averaged_gradient = np.zeros(d)
x_list = []
A, b, lbda = args
for idx in range(n_iter):
i = iis[idx]
### TODO
tmp = grad_i(i, x, A, b, lbda)
# Since we change only the i-th line, we can just replace it by the new one
# instead of summing each time
averaged_gradient += (tmp - gradient_memory[i, :]) / n
gradient_memory[i, :] = tmp
x -= step * averaged_gradient
### END OF TODO
# Update metrics after each iteration.
if idx % store_every == 0:
x_list.append(x.copy())
return x, x_list
max_squared_sum = np.max(np.sum(A ** 2, axis=1))
step = 1.0 / (max_squared_sum + lbda)
x_init = np.zeros(d)
monitor_sag = monitor(sag, loss, x_min, (A, b ,lbda))
monitor_sag.run(x_init, iis, grad_i, n_iter * n, step, args=(A, b, lbda))<jupyter_output><empty_output><jupyter_text>### SVRG
We recall that an iteration of SVRG writes
For $k=1, \ldots, $ until convergence
1. Set $\tilde x \gets \tilde x^{(k)}$ and $x_1^{(k)} \gets \tilde x$
2. Compute $\mu_k \gets \nabla f(\tilde x)$
3. For $t=1, \ldots, n$
4. Pick $i$ uniformly at random in $\{1, \ldots, n\}$
5. Apply the step
$$
x_{t+1}^{(k)} \gets x_t^{(k)} - \eta \big(\nabla f_{i}(x_t^{(k)}) - \nabla f_{i}(\tilde x) + \mu_k \big)
$$
6. Set $\tilde x^{(k+1)} \gets x_{n+1}^{(k)}$
where $\eta$ is the step-size (see code below).
*QUESTION*:
- Fill in the iteration of the SVRG solver in the cell below<jupyter_code>@njit
def svrg(x_init, iis, grad, grad_i, n_iter=100, step=1., store_every=n, args=()):
"""Stochastic variance reduction gradient algorithm."""
x = x_init.copy()
x_old = x.copy()
x_list = []
A, b, lbda = args
for idx in range(n_iter):
### TODO
if idx % n == 0:
x_old = x.copy()
mu = grad(x_old, A, b, lbda)
i = iis[idx]
tmp = grad_i(i, x, A, b, lbda)
tmp -= grad_i(i, x_old, A, b, lbda)
tmp += mu
x -= step * tmp
### END TODO
# Update metrics after each iteration.
if idx % store_every == 0:
x_list.append(x.copy())
return x, x_list
x_init = np.zeros(d)
monitor_svrg = monitor(svrg, loss, x_min, (A, b ,lbda))
monitor_svrg.run(x_init, iis, grad, grad_i, n_iter * n, step, args=(A, b, lbda))
monitors = [monitor_sgd, monitor_sag, monitor_svrg]
solvers = ["SGD", "SAG", "SVRG"]
plot_epochs(monitors, solvers)
plot_time(monitors, solvers)<jupyter_output><empty_output><jupyter_text>
## 5. Numerical comparison<jupyter_code>monitors = [monitor_gd, monitor_agd, monitor_cg, monitor_bfgs,
monitor_sgd, monitor_sag, monitor_svrg]
solvers = ["GD", "AGD", "CG", "BFGS", "SGD", "SAG", "SVRG"]
plot_epochs(monitors, solvers)
plot_time(monitors, solvers)<jupyter_output><empty_output><jupyter_text>
## 6. Conclusion
*QUESTIONS*:
- Compare and comment your results
- Change the value of the ridge regularization (the ``lbda`` parameter) to low ridge $\lambda = 1 / n$ and high ridge regularization $\lambda = 1 / \sqrt n$ and compare your results. Comment.
- Play also with the level of correlation between features (parameter ``corr`` above), and compare results with low and high correlation.
- Conclude
Compare and comment your results
ANSWER
SVRG and SAG are the best algorithms to converge to the optimum, even better than scipy.optimize algorithms that we saw before. In terms of convergence rate, SVRG and SAG become the fastest after few iterations (SGD, is faster than SAG in the beginning but converges fast to a higher error). We can see also that SVRG is a lot better than SAG. We know that these two algorithms have similar convergence rates but SVRG does not store a full table of gradients (Low Storage Cost) and it works out the full gradient occasionally. Besides, SGD suffers from higher variance leading the algorithm to converge to a higher error but it is still better than GD and AGD. Speaking of the timing, all the algorithms converge fast but SAG requires more time in performance.
Change the value of the ridge regularization (the ``lbda`` parameter) to low ridge $\lambda = 1 / n$ and high ridge regularization $\lambda = 1 / \sqrt n$ and compare your results. Comment.
NOTE
We are going to write a function to perform all the algorithms given the parameters.
<jupyter_code>def performs_all(A, b, lbda, use_logreg=False):
if (use_logreg):
step = 1. / lipschitz_logreg(A, b, lbda)
else:
step = 1. / lipschitz_linreg(A, b, lbda)
# Working out the minimum and the minimizer
x_init = np.zeros(d)
x_min, f_min, _ = fmin_l_bfgs_b(loss, x_init, grad, args=(A, b, lbda), pgtol=1e-30, factr=1e-30)
x_init = np.zeros(d)
# Gradient Descent
monitor_gd = monitor(gd, loss, x_min, (A, b ,lbda))
monitor_gd.run(x_init, grad, n_iter, step, args=(A, b, lbda))
# AGD
monitor_agd = monitor(agd, loss, x_min, (A, b ,lbda))
monitor_agd.run(x_init, grad, n_iter, step, args=(A, b, lbda))
# CG
monitor_cg = monitor(scipy_runner(fmin_cg), loss, x_min, (A, b ,lbda))
monitor_cg.run(loss, x_init, grad, maxiter=n_iter, args=(A, b, lbda), gtol=1e-9)
# L-BGFS
monitor_bfgs = monitor(scipy_runner(fmin_l_bfgs_b), loss, x_min, (A, b ,lbda))
monitor_bfgs.run(loss, x_init, grad, maxiter=n_iter, args=(A, b, lbda), pgtol=1e-30)
# SGD
step0 = 1e-1
monitor_sgd = monitor(sgd, loss, x_min, (A, b ,lbda))
monitor_sgd.run(x_init, iis, grad_i, n_iter * n, step0, args=(A, b, lbda))
# SAG
max_squared_sum = np.max(np.sum(A ** 2, axis=1))
step = (1.0 / (max_squared_sum + lbda)) if not(use_logreg) else (4.0 / (max_squared_sum + 4.0 * lbda))
monitor_sag = monitor(sag, loss, x_min, (A, b ,lbda))
monitor_sag.run(x_init, iis, grad_i, n_iter * n, step, args=(A, b, lbda))
# SVRG
monitor_svrg = monitor(svrg, loss, x_min, (A, b ,lbda))
monitor_svrg.run(x_init, iis, grad, grad_i, n_iter * n, step, args=(A, b, lbda))
monitors = [monitor_gd, monitor_agd, monitor_cg, monitor_bfgs,
monitor_sgd, monitor_sag, monitor_svrg]
plot_epochs(monitors, solvers)
plot_time(monitors, solvers)
# We're going to use a correlation of 0.5
A, b = simu_linreg(x_model_truth, n, std=1., corr=0.5)
print("--- lambda = 1/sqrt(n) ---")
lbda = 1. / n ** (0.5)
performs_all(A, b, lbda)
print("--- lambda = 1/n ---")
lbda = 1. / n
performs_all(A, b, lbda)<jupyter_output>--- lambda = 1/sqrt(n) ---
Warning: Desired error not necessarily achieved due to precision loss.
Current function value: 0.534189
Iterations: 35
Function evaluations: 97
Gradient evaluations: 86
<jupyter_text>
COMMENT
The algorithms are not much affected by the choice of $\lambda$. By looking at the loss vs. timing, the CG algorithm becomes faster when decreasing $\lambda$.
Play also with the level of correlation between features (parameter ``corr`` above), and compare results with low and high correlation.
<jupyter_code>loss = loss_linreg
grad = grad_linreg
grad_i = grad_i_linreg
lipschitz_constant = lipschitz_linreg
for corr in [0.1, 0.5, 0.9]:
A, b = simu_linreg(x_model_truth, n, std=1., corr=corr)
lbda = 1. / n ** (0.5)
print("--- Correlation = ", corr, " ---")
performs_all(A, b, lbda)<jupyter_output>--- Correlation = 0.1 ---
Warning: Desired error not necessarily achieved due to precision loss.
Current function value: 0.529308
Iterations: 13
Function evaluations: 16
Gradient evaluations: 15
<jupyter_text>
COMMENT
With low correlations, the deterministic/batch algorithms are better (in terms of convergence error) than the stochastic ones. We can see that AGD become non-monotonic and fluctuates while converging. The GD is better than SGD. In terms of the convergence rate, SAG and SVRG are the slowest one while scipy.optimize algorithms and SGD are the fastest.
Using a medium correlation ($0.5$), SVRG is the best at convergening to the optimum but still has a low convergence rate in the beginning; we can say that it increases with the correlation coefficient. SGD seems not to be affected by the correlation.
With high correlations, SVRG and SAG are the best at converging and their convergence rate is a lot better than with low correlations. scipy.optimize algorithms become slower when increasing the correlation. Speaking of the timing, scipy.optimize algorithms become slower while SVRG gets faster.
SVRG convergence to the optimum is better using a low correlation
In terms of timing, we can see that SAG is better than SVRG when the correlation is not high. scipy.optimize algorithms are the fastest when the correlation is not high but SVRG and SAG are the fastest on high correlations.
BONUS
Let's see the impact of the ridge regularization parameter and the correlation using logistic regression.
<jupyter_code># We're going to use a correlation of 0.5
A, b = simu_logreg(x_model_truth, n, std=1., corr=0.5)
loss = loss_logreg
grad = grad_logreg
grad_i = grad_i_logreg
lipschitz_constant = lipschitz_logreg
print("--- lambda = 1/sqrt(n) ---")
lbda = 1. / n ** (0.5)
performs_all(A, b, lbda)
print("--- lambda = 1/n ---")
lbda = 1. / n
performs_all(A, b, lbda)
print("-" * 100)
for corr in [0.1, 0.5, 0.9]:
A, b = simu_logreg(x_model_truth, n, std=1., corr=corr)
lbda = 1. / n ** (0.5)
print("--- Correlation = ", corr, " ---")
performs_all(A, b, lbda)<jupyter_output>--- lambda = 1/sqrt(n) ---
Optimization terminated successfully.
Current function value: 0.461824
Iterations: 34
Function evaluations: 69
Gradient evaluations: 69
|
no_license
|
/lab2_moutei_soufiane_and_barrahma-tlemcani_mohammed.ipynb
|
soufianemoutei/Optimization-for-Data-Science
| 23 |
<jupyter_start><jupyter_text># PARAMS: Data sources config<jupyter_code>INPUT_DIR = '../input/'
OUTPUT_DIR = './'
!ls -lh {INPUT_DIR}<jupyter_output><empty_output><jupyter_text># Imports<jupyter_code>%load_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np, pandas as pd
import matplotlib.pyplot as plt
from IPython.display import display
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.metrics import accuracy_score
import graphviz<jupyter_output><empty_output><jupyter_text># ETL## Load<jupyter_code>def display_all(df):
with pd.option_context("display.max_rows", 1000, "display.max_columns", 1000):
display(df)
# load
df_raw = pd.read_csv(f'{INPUT_DIR}train.csv', low_memory=False)
# quick sanity check that it loaded the right thing
display_all(df_raw.tail().T)
# types
df_raw.dtypes
# missing values
display_all(df_raw.isnull().sum().sort_index() / len(df_raw))
for n, c in df_raw.items():
if pd.api.types.is_numeric_dtype(c):
if pd.isnull(c).sum():
print("Column %s has %d missing values" % (
n, pd.isnull(c).sum()))<jupyter_output><empty_output><jupyter_text>## Categories<jupyter_code>def convert_cats(df, extra_cats):
"""Convert string values + what we know is category, to categorical vars"""
for n, c in df.items():
if pd.api.types.is_string_dtype(c) or n in extra_cats:
df[n] = c.astype('category').cat.as_ordered()
convert_cats(df_raw, extra_cats={'Pclass'})
df_raw.dtypes<jupyter_output><empty_output><jupyter_text>## uEDA<jupyter_code>display_all(df_raw.describe(include='all').T)<jupyter_output><empty_output><jupyter_text>## Fill missing<jupyter_code>df = df_raw.copy()
def fix_missing(df):
for n, c in df.items():
if pd.api.types.is_numeric_dtype(c):
if pd.isnull(c).sum():
df[n] = c.fillna(c.median())
fix_missing(df)<jupyter_output><empty_output><jupyter_text>## Fully numericalize<jupyter_code>def numericalize(df):
"""Numericalize categories and get rid of -1's for NaNs"""
for n, c in df.items():
if not pd.api.types.is_numeric_dtype(c):
df[n] = df[n].cat.codes + 1 # +1: NaNs -1 -> 0
numericalize(df)
df.dtypes<jupyter_output><empty_output><jupyter_text>## Split X/Y & training/validation<jupyter_code>y = df.Survived.values
df.drop('Survived', axis=1, inplace=True)
VAL_FR = 0.2
trn_sz = int(len(df) * (1 - VAL_FR))
x_trn = df.iloc[:trn_sz]
y_trn = y[:trn_sz]
x_val = df.iloc[trn_sz:]
y_val = y[trn_sz:]<jupyter_output><empty_output><jupyter_text>## Final processing function<jupyter_code>def proc_df(df):
convert_cats(df, extra_cats={'Pclass'})
fix_missing(df)
numericalize(df)<jupyter_output><empty_output><jupyter_text># Model## Create & Train<jupyter_code>m = DecisionTreeClassifier(max_depth=5)
m.fit(x_trn, y_trn)
print("Training score: %.2f%%" % (m.score(x_trn, y_trn) * 100))<jupyter_output><empty_output><jupyter_text>## Explain/Visualize<jupyter_code>dot_data = export_graphviz(
m,
out_file=None,
feature_names=df.columns,
class_names=['died', 'survived'],
filled=True,
rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph<jupyter_output><empty_output><jupyter_text>## Validate<jupyter_code># y_pred = m.predict(x_val)
# accuracy_score(y_val, y_pred)
print("Validation score: %.2f%%" % (m.score(x_val, y_val) * 100))<jupyter_output><empty_output><jupyter_text># Final train & predict## Train on entire data
Nothing left for validation in this case.<jupyter_code>M = DecisionTreeClassifier(max_depth=5)
M.fit(df, y)
print("Final training score: %.2f%%" % (M.score(df, y) * 100))<jupyter_output><empty_output><jupyter_text>## Load final test data<jupyter_code>df_test = pd.read_csv(f'{INPUT_DIR}test.csv')
proc_df(df_test)
print(df_test.dtypes)
df_test.head()<jupyter_output><empty_output><jupyter_text>## Predict<jupyter_code>y_pred_final = M.predict(df_test)
result = pd.DataFrame({'PassengerId': df_test.PassengerId,
'Survived': y_pred_final})
result.head()
result.to_csv(f'{OUTPUT_DIR}results.csv', index=False)<jupyter_output><empty_output>
|
no_license
|
/Notebooks/py/neuronq/simplest-imaginable-decision-tree-model/simplest-imaginable-decision-tree-model.ipynb
|
nischalshrestha/automatic_wat_discovery
| 15 |
<jupyter_start><jupyter_text>## 1. Write a Python Program to Check if a Number is Positive, Negative or Zero?<jupyter_code>def number_check(num):
if num < 0:
return 'Negative'
elif num > 0:
return 'Positive'
else:
return 'Zero'
num = float(input("Enter a Number: "))
print(f'{num} is a {number_check(num)} number')<jupyter_output>Enter a Number: 6
6.0 is a Positive number
<jupyter_text>## 2. Write a Python Program to Check if a Number is Odd or Even?<jupyter_code>def odd_or_even(num):
if num % 2 == 0:
return 'Even'
else:
return 'Odd'
num = float(input("Enter a Number: "))
print(f'{num} is a {odd_or_even(num)} number')<jupyter_output>Enter a Number: 9
9.0 is a Odd number
<jupyter_text>## 3. Write a Python Program to Check Leap Year?<jupyter_code>def leap_check(year):
if year % 4 == 0:
return "Leap Year"
else:
return "Not a Leap Year"
num = int(input("Enter a Year: "))
print(f'{num} is a {leap_check(num)}')<jupyter_output>Enter a Year: 2020
2020 is a Leap Year
<jupyter_text>## 4. Write a Python Program to Check Prime Number?<jupyter_code>def prime_check(num):
flag = False
for i in range(2,num):
if num % i == 0:
flag = True
if flag == True:
return 'Non-Prime'
else:
return 'Prime'
num = int(input("Enter a Number: "))
if num == 1:
print('1 is not a Prime Number')
else:
print(f'{num} is a {prime_check(num)} number')<jupyter_output>Enter a Number: 7
7 is a Prime number
<jupyter_text>## 5. Write a Python Program to Print all Prime Numbers in an Interval of 1-10000?<jupyter_code>min = 1
max = 10000
print('Prime Numbers between 1 and 10000 are: ')
for num in range(min,max+1):
if num > 1:
for i in range(2,num):
if num % i == 0:
break
else:
print(num)<jupyter_output>Prime Numbers between 1 and 10000 are:
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97
101
103
107
109
113
127
131
137
139
149
151
157
163
167
173
179
181
191
193
197
199
211
223
227
229
233
239
241
251
257
263
269
271
277
281
283
293
307
311
313
317
331
337
347
349
353
359
367
373
379
383
389
397
401
409
419
421
431
433
439
443
449
457
461
463
467
479
487
491
499
503
509
521
523
541
547
557
563
569
571
577
587
593
599
601
607
613
617
619
631
641
643
647
653
659
661
673
677
683
691
701
709
719
727
733
739
743
751
757
761
769
773
787
797
809
811
821
823
827
829
839
853
857
859
863
877
881
883
887
907
911
919
929
937
941
947
953
967
971
977
983
991
997
1009
1013
1019
1021
1031
1033
1039
1049
1051
1061
1063
1069
1087
1091
1093
1097
1103
1109
1117
1123
1129
1151
1153
1163
1171
1181
1187
1193
1201
1213
1217
1223
1229
1231
1237
1249
1259
1277
1279
1283
1289
1291
1297
1301
1303
1307
1319
1321
1327
1361
1367
1373
1381
1399
1409
1423
1427
1429
1433
1439
1447
1451
1453
14[...]
|
no_license
|
/Programming_Assingment3.ipynb
|
anuj-mahawar/Ineuron_Full_Stack_Data_Science
| 5 |
<jupyter_start><jupyter_text>## Observations and Insights <jupyter_code># Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import scipy.stats as st
from scipy.stats import linregress
# Study data files
mouse_metadata_path = "data/Mouse_metadata.csv"
study_results_path = "data/Study_results.csv"
# Read the mouse data and the study results
mouse_metadata = pd.read_csv(mouse_metadata_path)
study_results = pd.read_csv(study_results_path)
# Combine the data into a single dataset
df_merged = pd.merge(study_results, mouse_metadata, on='Mouse ID', how='left')
# Display the data table for preview
df_merged.head()
# Checking the number of mice.
len(set(df_merged['Mouse ID']))
# Getting the duplicate mice by ID number that shows up for Mouse ID and Timepoint.
df=df_merged
#gives us a set of duplicates
set_dups = set(df.loc[df.duplicated(subset=['Mouse ID','Timepoint']), "Mouse ID"])
print(set_dups)
# Optional: Get all the data for the duplicate mouse ID.
df=df_merged
#identify duplicate mouse from set variable to id mouse data
dup_mouse_data = df.loc[df['Mouse ID'].isin(set_dups)]
dup_mouse_data
# Create a clean DataFrame by dropping the duplicate mouse by its ID.
df=df_merged
#dropping dups by using set(created to id dup mouse)
df_clean = df_merged[ ~df_merged['Mouse ID'].isin(set_dups) ]
#df_clean
# Checking the number of mice in the clean DataFrame.
len(set(df_clean['Mouse ID']))<jupyter_output><empty_output><jupyter_text>## Summary Statistics<jupyter_code># Generate a summary statistics table of mean, median, variance, standard deviation, and SEM of the tumor volume for each regimen
# Use groupby and summary statistical methods to calculate the following properties of each drug regimen:
# mean, median, variance, standard deviation, and SEM of the tumor volume.
# Assemble the resulting series into a single summary dataframe.
#group, aggrigate, combine
tumor_grp = df_clean['Tumor Volume (mm3)'].groupby(df_clean['Drug Regimen'])
df_sum_stats = pd.DataFrame({
'mean': tumor_grp.mean(),
'median': tumor_grp.median(),
'var': tumor_grp.var(),
'std': tumor_grp.std(),
'sem': tumor_grp.sem(), })
df_sum_stats
# Generate a summary statistics table of mean, median, variance, standard deviation, and SEM of the tumor volume for each regimen
# Using the aggregation method, produce the same summary statistics in a single line
tumor_grp.agg(['mean', 'median','var','std','sem'])<jupyter_output><empty_output><jupyter_text>## Bar and Pie Charts<jupyter_code># Generate a bar plot showing the total number of unique mice tested on each drug regimen using pandas.
#This question is BADLY worded. It is my understanding you are not actually looking for the number of UNIQUE mice tested but the number of times mice were tested on each regimen.
#groupby Drug Regimen, count mice in df_clean
df = df_clean[['Mouse ID']].groupby(df_clean['Drug Regimen'], as_index=True).count()
df
df.sort_values('Mouse ID', ascending=False, inplace=True)
df.plot(kind="bar", figsize=(8,5), legend=False)
#formatting
plt.title('Number of Mice Tested in each Regimen')
plt.ylabel('Number of Mice')
df_regimentests=df
# Generate a bar plot showing the total number of unique mice tested on each drug regimen using pyplot.
df=df_regimentests
plt.figure(figsize=(8,5))
plt.bar(df.index.values, df['Mouse ID'] )
plt.xticks(range(len(df)), df.index.values, rotation="vertical")
plt.title('Total Number of Mice for Each Regimen')
plt.ylabel('Number of Mice')
plt.show()
# Generate a pie plot showing the distribution of female versus male mice using pandas
sex_count_list = list(df_clean[['Mouse ID', 'Sex']].groupby('Sex').count()['Mouse ID'])
sex_labels = list(df_clean[['Mouse ID', 'Sex']].groupby('Sex').count().index)
df_sex = pd.DataFrame(
{
'Gender Count':sex_count_list
}, index=sex_labels
)
df_sex.plot.pie(y='Gender Count', figsize=(4, 4))
# Generate a pie plot showing the distribution of female versus male mice using pyplot
plt.pie( sex_count_list,labels=sex_labels,autopct='%1.1f%%')
plt.title('Gender Distribution')
plt.axis('equal')
plt.show()<jupyter_output><empty_output><jupyter_text>## Quartiles, Outliers and Boxplots<jupyter_code># Calculate the final tumor volume of each mouse across four of the treatment regimens:
# Capomulin, Ramicane, Infubinol, and Ceftamin
# Start by getting the last (greatest) timepoint for each mouse
df = df_clean[['Drug Regimen','Mouse ID','Timepoint']].groupby(['Drug Regimen','Mouse ID'], as_index=False).max()
df = df[
df['Drug Regimen'].isin(['Capomulin','Ramicane','Infubinol','Ceftamin'])
]
# Merge this group df with the original dataframe to get the tumor volume at the last timepoint
df = pd.merge(df_clean, df, on=['Mouse ID','Timepoint'], how="inner",suffixes=('', '_x'))
df = df[['Drug Regimen','Mouse ID','Timepoint', 'Tumor Volume (mm3)']]
df.sort_values('Drug Regimen', inplace=True)
df_greatest_timepoints=df
# Put treatments into a list for for loop (and later for plot labels)
treatment_list = list(df_greatest_timepoints['Drug Regimen'].unique())
print(treatment_list)
# Create empty list to fill with tumor vol data (for plotting)
tumor_list = []
# Calculate the IQR and quantitatively determine if there are any potential outliers.
quartiles = df_greatest_timepoints['Tumor Volume (mm3)'].quantile([.25,.5,.75])
lowerq = quartiles[0.25]
upperq = quartiles[0.75]
iqr = upperq-lowerq
lower_bound = lowerq - (1.5*iqr)
upper_bound = upperq + (1.5*iqr)
# Locate the rows which contain mice on each drug and get the tumor volumes
df_greatest_timepoints['1QT'] = lowerq
df_greatest_timepoints['3QT'] = upperq
df_greatest_timepoints['IQR'] = iqr
# add subset
# Determine outliers using upper and lower bounds
df_greatest_timepoints['LBR'] = lower_bound
df_greatest_timepoints['UBR'] = upper_bound
# Generate a box plot of the final tumor volume of each mouse across four regimens of interest
df=df_greatest_timepoints
d1=df[df['Drug Regimen']=='Capomulin']['Tumor Volume (mm3)']
d2=df[df['Drug Regimen']=='Ceftamin']['Tumor Volume (mm3)']
d3=df[df['Drug Regimen']=='Infubinol']['Tumor Volume (mm3)']
d4=df[df['Drug Regimen']=='Ramicane']['Tumor Volume (mm3)']
tlist=[d1,d2,d3,d4]
fig = plt.figure(figsize =(3, 3))
plt.boxplot(tlist)
plt.show()<jupyter_output><empty_output><jupyter_text>## Line and Scatter Plots<jupyter_code># Generate a line plot of tumor volume vs. time point for a mouse treated with Capomulin
df=df_clean[df_clean['Mouse ID']=='b128']
df.plot.line(x='Timepoint', y='Tumor Volume (mm3)')
# Generate a scatter plot of average tumor volume vs. mouse weight for the Capomulin regimen
df=df_clean[df_clean['Drug Regimen']=='Capomulin']
df=df.groupby('Mouse ID')
plt.scatter( df['Weight (g)'].mean() , df['Tumor Volume (mm3)'].mean() )
plt.show() <jupyter_output><empty_output><jupyter_text>## Correlation and Regression<jupyter_code># Calculate the correlation coefficient and linear regression model
# for mouse weight and average tumor volume for the Capomulin regimen
df=df_clean[df_clean['Drug Regimen']=='Capomulin']
df=df.groupby('Mouse ID').mean()
correlation = st.pearsonr(df['Tumor Volume (mm3)'], df['Weight (g)'])
print(f"The correlation between both factors is {round(correlation[0],2)}")
df_capo_tumor_avg = df
df=df_capo_tumor_avg
#reshape variables
tumor_volume = df['Tumor Volume (mm3)']
mouse_wght = df['Weight (g)']
#Linear regression model
x_values = mouse_wght
y_values = tumor_volume
(slope, intercept, rvalue, pvalue, stderr) = linregress(x_values, y_values)
regress_values = x_values * slope + intercept
line_eq = "y = " + str(round(slope,2)) + "x + " + str(round(intercept,2))
plt.scatter(x_values,y_values)
plt.plot(x_values,regress_values,"r-")
plt.annotate(line_eq,(6,10),fontsize=15,color="red")
plt.xlabel('Weight')
plt.ylabel('Average Tumor Volume (mm3)')
print(f"The r-squared is: {rvalue**2}")
plt.show()<jupyter_output>The r-squared is: 0.7088568047708717
|
no_license
|
/01-Case-Assignment/Pymaceuticals/.ipynb_checkpoints/pymaceuticals_starter-checkpoint.ipynb
|
citizendez/Matplotlib_Challenge
| 6 |
<jupyter_start><jupyter_text>## 1. Model Creation
1.1 Define the three-compartment model above using a system of ODEs<jupyter_code>def equations(y, t, p):
"""
Define system of ODEs describing the three compartment model
:var: y = list of concentrations in all 3 compartents ([C1, C2, C3])
:params: p = list of rate constants between comparments ([k10, k12, k13, k21, k31])
:return: dydt = list of all differentials to be solved ([dc1dt, dc2dt, dc3dt])
"""
# Define variables and parameters
C1, C2, C3 = y
k10, k12, k13, k21, k31 = p
# Define ODEs
dc1dt = -(k10 + k12 + k13)*C1 + k21*C2 + k31*C3
dc2dt = k12*C1 - k21*C2
dc3dt = k13*C1 - k31*C3
dydt = np.asarray([dc1dt, dc2dt, dc3dt])
return dydt<jupyter_output><empty_output><jupyter_text>1.2 Solve the system of ODEs using a Forward Euler solver<jupyter_code>def ForwardEuler(function, t0, tf, y0, n, p):
"""
"""
h = (tf - t0)/n # Time interval
t = t0
y = np.empty((n, 3))
y[0] = y0
for i in range(n-1):
y[i+1] = y[i] + h*function(y[i], t, p)
t += h
return y
t0 = 0 # Starting time
tf = 1 # Final time
y0 = [10, 0, 0] # Initial conditions for [C1, C2, C3]
n = 1000 # Number of data points
p = [1, 6, 9, 6, 9] # Parameter values for [k10, k12, k13, k21, k31]
model = ForwardEuler(equations, t0, tf, y0, n, p)
def calculate_model_data(function, t0, tf, y0, n, p):
model = ForwardEuler(function, t0, tf, y0, n, p)
I = np.asarray(model.i)
I_model = I[:-1]
return I_model
C1 = model[:,0]
C2 = model[:, 1]
C3 = model[:, 2]
times = np.linspace(0, 1, 1000)<jupyter_output><empty_output><jupyter_text>1.3 Plot concentration-time profiles for each compartment<jupyter_code>plt.figure(figsize=(14,6))
plt.xlabel('Time (s)')
plt.ylabel('Concentration')
plt.plot(times, C1, label='C1')
plt.plot(times, C2, label='C2')
plt.plot(times, C3, label='C3')
plt.legend(loc='best')
plt.show()<jupyter_output><empty_output><jupyter_text>## 2. Data Generation
2.1 Add normally-distributed random noise to the model to simulate real-life noisy data<jupyter_code>data = model + np.random.normal(size=model.shape)/3
C1 = data[:,0]
C2 = data[:, 1]
C3 = data[:, 2]<jupyter_output><empty_output><jupyter_text>2.2 Plot concentration-time profile of data<jupyter_code>plt.figure(figsize=(14,6))
plt.xlabel('Time (s)')
plt.ylabel('Concentration')
plt.plot(times, C1, label='C1')
plt.plot(times, C2, label='C2')
plt.plot(times, C3, label='C3')
plt.legend(loc='best')
plt.show()<jupyter_output><empty_output><jupyter_text>## 3. Parameter InferenceProbability of variables<jupyter_code># p += [0.247] # add standard deviation
# print(p)
lower_bounds = [0, 4, 7, 4, 7, 0.1]
upper_bounds = [3, 7, 11, 7, 11, 0.8]
# prob = []
# for i in range(len(upper_bounds)):
# if (p[i] <= upper_bounds[i] and p[i] >= lower_bounds[i]):
# prob.append(1)
# else:
# prob.append(0)
# prob = np.asarray(prob)
# print(prob)
# prob = np.prod(prob)
# print(prob)
def probability_of_variables(p):
prob = []
for i in range(len(upper_bounds)):
if (p[i] <= upper_bounds[i] and p[i] >= lower_bounds[i]):
prob.append(1)
else:
prob.append(0)
prob = np.asarray(prob)
prob = np.prod(prob)
return prob<jupyter_output><empty_output><jupyter_text>Define objective function<jupyter_code># difference = data - model
# sum_of_squares = np.sum(np.square(difference))
# print(sum_of_squares)
def objective_function(function, t0, tf, y0, n, p):
difference = data - model
sum_of_squares = np.sum(np.square(difference))
return sum_of_squares<jupyter_output><empty_output><jupyter_text>Normal Distribution Sampler<jupyter_code>def normal_dist_sampler(mean, standDev):
temp = []
maxIndex = mean.shape
for i in range(maxIndex[0]):
temp.append(np.random.normal(mean[i], standDev[i]))
return temp
def likelihood(function, t0, tf, y0, n, p):
k10, k12, k13, k21, k31, standDev = p
A = 1/(np.sqrt(2*np.pi*(standDev**2)))
power = -objective_function(function, t0, tf, y0, n, p)/(2*(standDev**2))
tmp = tf*np.log(A)
likely = tmp + power
return likely
# def metropolisHastings():
# a = [1]
# print(p)
# p0 = np.array([2, 5, 8, 5, 7]) #initial guess of parameters
# means = np.asarray(p[0])
# print(p)
# print(means)
# covariance = np.array([])
p0 = np.array([[2, 5, 8, 5, 7, 0.247]])
p += [0.247]
def metropolisHastings(p0):
a = [1.0] # initial guess of parameters
means = np.asarray(p0[0])
covariance = np.array([50, 50, 50, 50, 50, 0.02])
t = 1
indices = 100
while t <= indices:
p_temp = np.asarray([normal_dist_sampler(p0[-1], a[-1]*covariance)])
if probability_of_variables(p_temp[0]) != 0:
if np.log(np.random.uniform(0, 1)) < (likelihood(equations, t0, tf, y0, n, p_temp[0]) - likelihood(equations, t0, tf, y0, n, p0[-1])):
p0 = np.append(p0, p_temp, axis=0)
if t % 50 == 0:
print('Iteration: ', t)
print('Burn in k10: ', p0[-1][0])
print('Burn in k12: ', p0[-1][1])
print('Burn in k13: ', p0[-1][2])
print('Burn in k21: ', p0[-1][3])
print('Burn in k31: ', p0[-1][4])
print('Burn in Standard Deviation: ', p0[-1][5])
np.save('samples', p0)
t += 1
while t < indices*4:
s = t - indices
gammaS = (s+1)**(-0.6)
p_temp = np.asarray([normal_dist_sampler(p0[-1], a[-1]*covariance)])
if probability_of_variables(p_temp[0]) != 0:
if np.log(np.random.uniform(0,1)) < likelihood(equations, t0, tf, y0, n, p_temp[0]) - likelihood(equations, t0, tf, y0, n, p0[-1]):
p0 = np.append(p0, p_temp, axis=0)
accepted = 1
else:
p0 = np.append(p0, [p0[-1]], axis=0)
accepted = 0
else:
p0 = np.append(p0, [p0[-1]], axis=0)
accepted = 0
temp = p0[-1] - means
covariance = ((1 - gammaS)*covariance + gammaS*np.square(temp))
means = (1 - gammaS)*means + gammaS*p0[-1]
a.append(np.exp(np.log(a[-1]) + gammaS*(accepted - 0.25)))
if t % 50 == 0:
print('total iteration: ', t)
print('sampling iteration: ', s)
print('fitted k10: ', p0[-1][0])
print('fitted k12: ', p0[-1][1])
print('fitted k13: ', p0[-1][2])
print('fitted k21: ', p0[-1][3])
print('fitted k31: ', p0[-1][4])
print('fitted standard deviation: ', p0[-1][5])
np.save('samples', p0)
t += 1
comparison = objective_function(equations, t0, tf, y0, n, p)
print('Objective Function with original parameters: ', comparison)
print('Initial k10: ', p[0])
print('Initial k12: ', p[1])
print('Initial k13: ', p[2])
print('Initial k21: ', p[3])
print('Initial k31: ', p[4])
print('Initial Standard Deviation: ', p[5])
print('Likelihood with original parameters: ', likelihood(equations, t0, tf, y0, n, p))
print('Data: ', data)
print('Initial k10: ', p0[0][0])
print('Initial k12: ', p0[0][1])
print('Initial k13: ', p0[0][2])
print('Initial k21: ', p0[0][3])
print('Initial k31: ', p0[0][4])
print('Initial Standard Deviation: ', p0[0][5])
comparison = objective_function(equations, t0, tf, y0, n, p0[0])
print('Initial Objective Function: ', comparison)
print('Initial Likelihood: ', likelihood(equations, t0, tf, y0, n, p0[0]))
metropolisHastings(p0)<jupyter_output>Iteration: 50
Burn in k10: 0.49011291758749387
Burn in k12: -83.16844367414484
Burn in k13: -45.75276763288603
Burn in k21: -89.55024587625286
Burn in k31: -27.437199737415902
Burn in Standard Deviation: 0.27327942581335213
Iteration: 100
Burn in k10: 1.3385262776192768
Burn in k12: 0.38669937825999057
Burn in k13: 27.64863201965735
Burn in k21: 27.073569068104426
Burn in k31: 25.789437683734864
Burn in Standard Deviation: 0.31671661981354565
total iteration: 150
sampling iteration: 50
fitted k10: 1.047328838652071
fitted k12: nan
fitted k13: nan
fitted k21: nan
fitted k31: nan
fitted standard deviation: 0.31986987046788123
total iteration: 200
sampling iteration: 100
fitted k10: 0.8506769552388742
fitted k12: nan
fitted k13: nan
fitted k21: nan
fitted k31: nan
fitted standard deviation: 0.3198751294565778
total iteration: 250
sampling iteration: 150
fitted k10: 1.5640862665019912
fitted k12: nan
fitted k13: nan
fitted k21: nan
fitted k31: nan
fitte[...]
|
no_license
|
/Numerical Methods Practice.ipynb
|
annaraegeorge/pkpd-practice
| 8 |
<jupyter_start><jupyter_text>#### Buid the Model<jupyter_code>model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.summary()
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10))
model.summary()
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
history = model.fit(train_images, train_labels, epochs=10,
validation_data=(test_images, test_labels))
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
print(test_acc)
y_pred = model.predict(test_images)
y_pred
y_pred_labels = model.predict_classes(test_images)
y_pred_labels
plt.imshow(test_images[1])
print(y_pred_labels[1])
print(test_labels)
from sklearn.metrics import confusion_matrix,classification_report
print(confusion_matrix(test_labels,y_pred_labels))
print(classification_report(test_labels,y_pred_labels))
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck']
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(test_images[i], cmap=plt.cm.binary)
# The CIFAR labels happen to be arrays,
# which is why you need the extra index
plt.xlabel(class_names[y_pred_labels[i]])
plt.show()
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck']
plt.figure(figsize=(10,10))
for i in range(9):
plt.subplot(3,3,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(test_images[i], cmap=plt.cm.binary)
# The CIFAR labels happen to be arrays,
# which is why you need the extra index
plt.xlabel(f'Actual-{class_names[test_labels[i][0]]}, Predicted-{class_names[y_pred_labels[i]]}')
plt.show()
print(class_names[test_labels[i][0]])<jupyter_output><empty_output>
|
no_license
|
/CIFAR10_CNN_Image_Classification.ipynb
|
blazingphoenix13/CIFAR10_CNN_Image_Classification
| 1 |
<jupyter_start><jupyter_text>## Saving data from torchtext<jupyter_code>NGRAMS = 2
DATADIR = "./data"
BATCH_SIZE = 16
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")
if not os.path.isdir(DATADIR):
os.mkdir(DATADIR)
train_dataset, test_dataset = text_classification.DATASETS['AG_NEWS'](
root=DATADIR, ngrams=NGRAMS, vocab=None)<jupyter_output><empty_output><jupyter_text>## Define the model<jupyter_code>class TextSentiment(nn.Module):
def __init__(self, vocab_size, embed_dim, num_class):
super().__init__()
self.embedding = nn.EmbeddingBag(vocab_size, embed_dim, sparse=True)
self.fc = nn.Linear(embed_dim, num_class)
self.init_weights()
def init_weights(self):
initrange = 0.5
self.embedding.weight.data.uniform_(-initrange, initrange)
self.fc.weight.data.uniform_(-initrange, initrange)
self.fc.bias.data.zero_()
def forward(self, text, offsets):
embedded = self.embedding(text, offsets)
return self.fc(embedded)<jupyter_output><empty_output><jupyter_text>## Create torchdataset from csv<jupyter_code>def _csv_iterator(data_path, ngrams, yield_cls=False):
tokenizer = get_tokenizer("basic_english")
with io.open(data_path, encoding="utf8") as f:
reader = unicode_csv_reader(f)
for row in reader:
tokens = ' '.join(row[1:])
tokens = tokenizer(tokens)
if yield_cls:
yield int(row[0]) - 1, ngrams_iterator(tokens, ngrams)
else:
yield ngrams_iterator(tokens, ngrams)
def _create_data_from_iterator(vocab, iterator, include_unk):
data = []
labels = []
with tqdm(unit_scale=0, unit='lines') as t:
for cls, tokens in iterator:
if include_unk:
tokens = torch.tensor([vocab[token] for token in tokens])
else:
token_ids = list(filter(lambda x: x is not Vocab.UNK, [vocab[token]
for token in tokens]))
tokens = torch.tensor(token_ids)
if len(tokens) == 0:
logging.info('Row contains no tokens.')
data.append((cls, tokens))
labels.append(cls)
t.update(1)
return data, set(labels)
train_csv_path = "../data/ag_news_csv/train.csv"
test_csv_path = "../data/ag_news_csv/test.csv"
ngrams = 2
vocab = build_vocab_from_iterator(_csv_iterator(train_csv_path, ngrams))
train_iterator = _csv_iterator(train_csv_path, ngrams, yield_cls=True)
test_iterator = _csv_iterator(train_csv_path, ngrams, yield_cls=True)
train_data_set, labels = _create_data_from_iterator(vocab, train_iterator, include_unk=False)
test_data_set, test_labels = _create_data_from_iterator(vocab, test_iterator, include_unk=False)<jupyter_output>120000lines [00:14, 8464.71lines/s]
120000lines [00:14, 8526.46lines/s]
<jupyter_text>## Initiate an instance<jupyter_code>VOCAB_SIZE = len(vocab)
EMBED_DIM = 32
NUM_CLASS = len(labels)
model = TextSentiment(VOCAB_SIZE, EMBED_DIM, NUM_CLASS).to(DEVICE)<jupyter_output><empty_output><jupyter_text>## Functions used to generate batch<jupyter_code>def generate_batch(batch):
label = torch.tensor([entry[0] for entry in batch])
text = [entry[1] for entry in batch]
offsets = [0] + [len(entry) for entry in text]
offsets = torch.tensor(offsets[:-1]).cumsum(dim=0)
text = torch.cat(text)
return text, offsets, label<jupyter_output><empty_output><jupyter_text>## Define functions to train the model and evaluate results<jupyter_code>def train_func(sub_train_):
# Train the model
train_loss = 0
train_acc = 0
data = DataLoader(sub_train_, batch_size=BATCH_SIZE, shuffle=True, collate_fn=generate_batch)
for i, (text, offsets, cls) in enumerate(data):
optimizer.zero_grad()
text, offsets, cls = text.to(DEVICE), offsets.to(DEVICE), cls.to(DEVICE)
output = model(text, offsets)
loss = criterion(output, cls)
train_loss += loss.item()
loss.backward()
optimizer.step()
train_acc += (output.argmax(1) == cls).sum().item()
# Adjust the learning rate
scheduler.step()
return train_loss / len(sub_train_), train_acc / len(sub_train_)
def test(data_):
loss = 0
acc = 0
data = DataLoader(data_, batch_size=BATCH_SIZE, collate_fn=generate_batch)
for text, offsets, cls in data:
text, offsets, cls = text.to(DEVICE), offsets.to(DEVICE), cls.to(DEVICE)
with torch.no_grad():
output = model(text, offsets)
loss = criterion(output, cls)
loss += loss.item()
acc += (output.argmax(1) == cls).sum().item()
return loss / len(data_), acc / len(data_)<jupyter_output><empty_output><jupyter_text>## Split the dataset and run the model<jupyter_code>N_EPOCHS = 5
min_valid_loss = float('inf')
criterion = torch.nn.CrossEntropyLoss().to(DEVICE)
optimizer = torch.optim.SGD(model.parameters(), lr=4.0)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 1, gamma=0.9)
train_len = int(len(train_data_set) * 0.95)
sub_train_, sub_valid_ = random_split(train_data_set, [train_len, len(train_data_set) - train_len])
for epoch in range(N_EPOCHS):
start_time = time.time()
train_loss, train_acc = train_func(sub_train_)
valid_loss, valid_acc = test(sub_valid_)
secs = int(time.time() - start_time)
mins = secs / 60
secs = secs % 60
print('Epoch: %d' %(epoch + 1), "time in %d minutes, %d seconds" %(mins, secs))
print(f'\tLoss: {train_loss:.4f}(train)\t|\tAcc: {train_acc * 100:.1f}%(train)')
print(f'\tLoss: {valid_loss:.4f}(valid)\t|\tAcc: {valid_acc * 100:.1f}%(valid)')<jupyter_output>Epoch: 1 time in 0 minutes, 24 seconds
Loss: 0.0123(train) | Acc: 93.4%(train)
Loss: 0.0000(valid) | Acc: 92.1%(valid)
Epoch: 2 time in 0 minutes, 24 seconds
Loss: 0.0070(train) | Acc: 96.3%(train)
Loss: 0.0001(valid) | Acc: 92.7%(valid)
Epoch: 3 time in 0 minutes, 24 seconds
Loss: 0.0038(train) | Acc: 98.1%(train)
Loss: 0.0001(valid) | Acc: 93.3%(valid)
Epoch: 4 time in 0 minutes, 24 seconds
Loss: 0.0022(train) | Acc: 99.0%(train)
Loss: 0.0000(valid) | Acc: 93.8%(valid)
Epoch: 5 time in 0 minutes, 25 seconds
Loss: 0.0015(train) | Acc: 99.4%(train)
Loss: 0.0000(valid) | Acc: 93.7%(valid)
<jupyter_text>## Evaluate the model with test dataset<jupyter_code>test_loss, test_acc = test(test_data_set)
print(f'\tLoss: {test_loss:.4f}(test)\t|\tAcc: {test_acc * 100:.1f}%(test)')<jupyter_output> Loss: 0.0000(test) | Acc: 99.4%(test)
<jupyter_text>## Test on a random news<jupyter_code>ag_news_label = {1 : "World",
2 : "Sports",
3 : "Business",
4 : "Sci/Tec"}
def predict(text, model, vocab, ngrams):
tokenizer = get_tokenizer("basic_english")
with torch.no_grad():
text = torch.tensor([vocab[token] for token in ngrams_iterator(tokenizer(text), ngrams)])
output = model(text, torch.tensor([0]))
return output.argmax(1).item() + 1
ex_text_str = "MEMPHIS, Tenn. – Four days ago, Jon Rahm was \
enduring the season’s worst weather conditions on Sunday at The \
Open on his way to a closing 75 at Royal Portrush, which \
considering the wind and the rain was a respectable showing. \
Thursday’s first round at the WGC-FedEx St. Jude Invitational \
was another story. With temperatures in the mid-80s and hardly any \
wind, the Spaniard was 13 strokes better in a flawless round. \
Thanks to his best putting performance on the PGA Tour, Rahm \
finished with an 8-under 62 for a three-stroke lead, which \
was even more impressive considering he’d never played the \
front nine at TPC Southwind."
print("This is a %s news" %ag_news_label[predict(ex_text_str, model, vocab, 2)])<jupyter_output>This is a Sports news
|
no_license
|
/notebooks/[Step 1] Follow PyTorch Tutorial.ipynb
|
kangeugine/nlp-getting-started
| 9 |
<jupyter_start><jupyter_text># Psedorandom number generators
While psuedorandom numbers are generated by a deterministic algorithm, we can mostly treat them as if they were true random numbers and we will drop the “pseudo” prefix. Fundamentally, the algorithm generates random integers which are then normalized to give a floating point number from the standard uniform distribution. Random numbers from other distributions are in turn generated using these uniform random deviates, see later.
## Linear congruential generators (LCG)
[LCG](https://en.wikipedia.org/wiki/Linear_congruential_generator) is among the simplest and most popular pseudo random number generators. It relies on the recursive and fully deterministic relation:
$$
z_{i+1}=(a z_i+c)\mod{m}
$$
Hull-Dobell Theorem: The LCG will have a period $m$ for all seeds if and only if
* $c$ and $m$ are relatively prime,
* $a−1$ is divisible by all prime factors of $m$
* $a−1$ is a multiple of 4 if $m$ is a multiple of $4$.
The number $z_0$ is called the *seed*, and setting it allows us to have a reproducible sequence of (pseudo) random numbers. The LCG is typically coded to return $z/m$, a floating point number in $(0, 1)$. Obviosuly, this can be easily scaled to any other range $(a,b)$.
Note that $z \le m-1$ always holds, the yielded $z/m$ result is thus on purpose strictly smaller than 1.
<jupyter_code>def lcg(m=2**32, a=1103515245, c=12345):
lcg.current = (a*lcg.current + c) % m
return lcg.current/m
# setting the seed
lcg.current = 12346
[lcg() for i in range(10)]
rn=[lcg() for i in range(1000)]
print (np.mean(rn))
print (np.std(rn),1/np.sqrt(12))
plt.plot(rn,"o")
<jupyter_output>0.491719525189139
0.29179423488886796 0.2886751345948129
<jupyter_text>LCG though is not sufficiently "random" for several complex modern applications. There are nowadays better performing algorithms, like [Mersenne twister](https://en.wikipedia.org/wiki/Mersenne_Twister), a generalized feedback shift-register generator, is used, in particular the numpy random package features it.
Numpy uses as default [PCG-64](https://numpy.org/doc/stable/reference/random/bit_generators/index.html) of the [PCG family](https://www.pcg-random.org/), which are considered the ultimate random number generators.
# Non-uniform random numbers
In several cases the actual random process occur with non-uniform probability, i.e. with a given probability density function (pdf), different from the uniform distribution. Several methods are available, we will see a few of them
### Inverse transform method
Let'start from a uniform distribution $u(z)$:
$$
\left\{
\begin{array}{ll}
1 & 0\leq z\leq 1 \\
0 & {\rm elsewhere}
\end{array}
\right.
$$
and let's look for a function $x(z)$ such that $x$ is distributed accordingly to a given pdf $p(x)$. The probability to find $x$ between $x$ and $x+dx$ is equal to:
$$
p(x)dx = dz
$$
and thus:
$$
\int_{-\infty}^{x(z)} p(x') dx' = \int_0^z dz'= z
$$
If (a) we could solve the integral and (b) solve for $x$, then we are done. For most of the pdf at least one of the two is not possible.. The typical solvable analitical example is:
$$
p(x) = \mu e^{-\mu x}
$$
$$
\int_{0}^{x(z)} p(x') dx' = 1 - e^{-\mu x} = z
$$
and thus:
$$
x(z) = - \frac{1}{\mu}\log{(1-z)}
$$<jupyter_code>def expon_pdf(x, mu=1):
"""PDF of exponential distribution."""
return mu*np.exp(-mu*x)
def expon_cdf(x, mu=1):
"""CDF of exponetial distribution."""
return 1 - np.exp(-mu*x)
def expon_icdf(p, mu=1):
"""Inverse CDF of exponential distribution - i.e. quantile function."""
return -np.log(1-p)/mu
dist = stats.expon()
x = np.linspace(0,4,100)
y = np.linspace(0,1,100)
plt.figure(figsize=(12,4))
plt.subplot(121)
plt.plot(x, expon_cdf(x))
plt.axis([0, 4, 0, 1])
for q in [0.5, 0.8]:
plt.arrow(0, q, expon_icdf(q)-0.1, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(expon_icdf(q), q, 0, -q+0.1, head_width=0.1, head_length=0.05, fc='b', ec='b')
plt.ylabel('1: Generate a (0,1) uniform PRNG')
plt.xlabel('2: Find the inverse CDF')
plt.title('Inverse transform method');
plt.subplot(122)
u = np.random.random(10000)
v = expon_icdf(u)
plt.hist(v, histtype='step', bins=100, density=True, linewidth=2)
plt.plot(x, expon_pdf(x), linewidth=2)
plt.axis([0,4,0,1])
plt.title('Histogram of exponential PRNGs');<jupyter_output><empty_output><jupyter_text>### Box-Muller for generating normally distributed random numbers
The inverse method is not applicable even for the gaussian distribution:
$$
\frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{x} \exp{-\frac{x'^2}{2\sigma^2}} dx' = z
$$
is not solvable. The trick is to consider a two dimensional gaussian function with the same $\sigma$ on both coordinates:
$$
p(x)dx \times p(y)dy = \frac{1}{\sqrt{2\pi\sigma^2}} \exp{-\frac{x^2}{2\sigma^2}} \times \frac{1}{\sqrt{2\pi\sigma^2}} \exp{-\frac{y^2}{2\sigma^2}} = \frac{1}{2\pi\sigma^2} \exp{-\frac{(x^2+y^2)}{2\sigma^2}}dxdy
$$
which written in radial coordinates:
$$
x=r\cos{\theta};\,\,\,
y=r\sin{\theta}
$$
$$
p(r,\theta)dr d\theta = \frac{r}{\sigma^2} \exp{-\frac{r^2}{2\sigma^2}} dr \times \frac{d\theta}{2\pi} = p(r)dr \times p(\theta)d\theta
$$
with both $p(r)$ and $p(\theta)$ normalized to 1. Now, the latter is a simple uniform distribution, whereas the latter is solvable:
$$
\frac{1}{\sigma^2} \int_{0}^{r} \exp{-\frac{r^2}{2\sigma^2}} rdr = z
$$
which gives:
$$
r=\sqrt{-2\sigma^2\log{1-z}}
$$
<jupyter_code>n = 10000
z = np.random.random(n)
theta = 2*np.pi*np.random.random(n)
r_squared = -2*np.log(z)
r = np.sqrt(r_squared)
x = r*np.cos(theta)
y = r*np.sin(theta)
sns.jointplot(x,y, kind='scatter');
<jupyter_output><empty_output><jupyter_text>### Creating a random number generator for arbitrary distributions
Suppose we have some random samples with an unknown distribution. We can still use the inverse transform method to create a random number generator from a random sample, by estimating the inverse CDF function using interpolation.<jupyter_code>from scipy.interpolate import interp1d
def extrap1d(interpolator):
"""From StackOverflow http://bit.ly/1BjyRfk"""
xs = interpolator.x
ys = interpolator.y
def pointwise(x):
if x < xs[0]:
return ys[0]+(x-xs[0])*(ys[1]-ys[0])/(xs[1]-xs[0])
elif x > xs[-1]:
return ys[-1]+(x-xs[-1])*(ys[-1]-ys[-2])/(xs[-1]-xs[-2])
else:
return interpolator(x)
def ufunclike(xs):
return np.array(list(map(pointwise, np.array(xs))))
return ufunclike
from statsmodels.distributions.empirical_distribution import ECDF
# Make up some random data
x = np.concatenate([np.random.normal(0, 1, 10000),
np.random.normal(4, 1, 10000)])
ecdf = ECDF(x)
inv_cdf = extrap1d(interp1d(ecdf.y, ecdf.x,
bounds_error=False, assume_sorted=True))
r = np.random.uniform(0, 1, 1000)
ys = inv_cdf(r)
plt.hist(x, 25, histtype='step', color='red', density=True, linewidth=1)
plt.hist(ys, 25, histtype='step', color='blue', density=True, linewidth=1);<jupyter_output><empty_output><jupyter_text>### Rejection sampling (Accept-reject method)
Suppose we want to sample from the (truncated) T distribution with 10 degrees of freedom.
We use the uniform as a proposal distibution (highly inefficient)
<jupyter_code>x = np.linspace(-4, 4)
dist = stats.cauchy()
upper = dist.pdf(0)
plt.figure(figsize=(12,4))
plt.subplot(121)
plt.plot(x, dist.pdf(x))
plt.axhline(upper, color='grey')
px = 1.0
plt.arrow(px,0,0,dist.pdf(1.0)-0.01, linewidth=1,
head_width=0.2, head_length=0.01, fc='g', ec='g')
plt.arrow(px,upper,0,-(upper-dist.pdf(px)-0.01), linewidth=1,
head_width=0.3, head_length=0.01, fc='r', ec='r')
plt.text(px+.25, 0.2, 'Reject', fontsize=16)
plt.text(px+.25, 0.01, 'Accept', fontsize=16)
plt.axis([-4,4,0,0.4])
plt.title('Rejection sampling concepts', fontsize=20)
plt.subplot(122)
n = 100000
# generate from sampling distribution
u = np.random.uniform(-4, 4, n)
# accept-reject criterion for each point in sampling distribution
r = np.random.uniform(0, upper, n)
# accepted points will come from target (Cauchy) distribution
v = u[r < dist.pdf(u)]
plt.plot(x, dist.pdf(x), linewidth=2)
# Plot scaled histogram
factor = dist.cdf(4) - dist.cdf(-4)
hist, bin_edges = np.histogram(v, bins=100, density=True)
bin_centers = (bin_edges[:-1] + bin_edges[1:]) / 2.
plt.step(bin_centers, factor*hist, linewidth=2)
plt.axis([-4,4,0,0.4])
plt.title('Histogram of accepted samples', fontsize=20);
<jupyter_output><empty_output><jupyter_text>### Mixture representations
Sometimee, the target distribution from which we need to generate random numbers can be expressed as a mixture of “simpler” distributions that we already know how to sample from
$$
f(x)=\int g(x|y)p(y)dy
$$
For example, if $y$ is drawn from the $\chi^2_\nu$ distrbution, then ${\cal N}(0,\nu/y)$ is a sample from the Student’s T distribution with $\nu$ degrees fo freedom.<jupyter_code>n = 10000
df = 5
dist = stats.t(df=df)
y = stats.chi2(df=df).rvs(n)
r = stats.norm(0, df/y).rvs(n)
plt.plot(x, dist.pdf(x), linewidth=2)
# Plot scaled histogram
factor = dist.cdf(4) - dist.cdf(-4)
hist, bin_edges = np.histogram(v, bins=100, density=True)
bin_centers = (bin_edges[:-1] + bin_edges[1:]) / 2.
plt.step(bin_centers, factor*hist, linewidth=2)
plt.axis([-4,4,0,0.4])
plt.title('Histogram of accepted samples', fontsize=20);<jupyter_output><empty_output><jupyter_text>### Draw from an analytic pdf
Obviously scipy stats module features all possible pdf that can come to your mind. You can draw random data from each of them<jupyter_code>from scipy.stats import gamma
a = 1.99
x = np.linspace(gamma.ppf(0.01, a),
gamma.ppf(0.99, a), 100)
rv = gamma(a)
fig, ax = plt.subplots(1, 1)
ax.plot(x, rv.pdf(x), 'k-', lw=2)
r = gamma.rvs(a, size=1000)
_ = ax.hist(r, density=True, histtype='stepfilled', alpha=0.2)<jupyter_output><empty_output><jupyter_text># Monte Carlo integration
Monte Carlo integration is typically less accurate than other integration methods, but very often is the only available tool, e.g. when the integrand has very rapid variations or singular points, or, most importantly, when dealing with high dimensional integrals.
The idea is simple, let's the area under the function be $I$ whereas the all possible outcomes lay in a box of area $A$. The probability for a point to fall under the function is $p=I/A$. If we generate $N$ random points, the fraction $k$ which fall under the curve is $k/N$ and approximate $I/A$, thus:
$$
I\simeq\frac{k A}{N}
$$
Let's try this with the function $f(x) =\sin^2{\frac{1}{x(2-x)}}$<jupyter_code>def f(x):
return (np.sin(1/(x*(2-x))))**2
x=np.linspace(0.001,1.999,1000)
plt.plot(x,f(x),'r-')
# Monte Carlo integration
N=100000
count=0
for i in range(N):
x=2*np.random.random()
y=np.random.random()
if y<f(x): count+=1
I=2*count/N
print(I)<jupyter_output>1.451
<jupyter_text>### The mean value method
Let's take the integral:
$$
I=\int_a^b f(x) dx
$$
defining $\langle f \rangle$ as the mean of $f$:
$$
\langle f \rangle = \frac{1}{b-a}\int_a^b f(x) dx
$$
and estimating $\langle f \rangle$ by uniformely probing at random the function domain, such as
$$
\langle f \rangle = \frac{1}{N} \sum_{i=1}^{N} f(x_i)
$$
we get:
$$
I=\frac{b-a}{N} \sum_{i=1}^{N} f(x_i)
$$
this easily generalize to higher dimensions:
$$
I=\frac{V}{N} \sum_{i=1}^{N} f(\vec{r}_i)
$$
where the sampling points $\vec{r}_i$ are drawn uniformly at random from integration space of volume $V$.
It can be proven that the standard deviation of the method scales $1/\sqrt{N}$:
$$
\sigma = V\frac{\sqrt{{\rm var}\, f}}{\sqrt{N}}
$$### Importance sampling
There are several general techinques for variance reduction, sometimes known as Monte Carlo swindles since these methods improve the accuracy and convergene rate of Monte Carlo integration without increasing the number of Monte Carlo samples. *Importance sampling* is among the most commonly used.
We can define a weighted average of a function $g(x)$:
$$
\langle g_w \rangle = \frac{\int_a^b w(x) g(x)dx}{\int_a^b w(x)dx}
$$
Consider again the integral of $f(x)$:
$$
I=\int_a^b f(x)dx
$$
Setting $g(x)=f(x)/w(x)$ we have:
$$
\left\langle \frac{f(x)}{w(x)}\right\rangle = \frac{\int_a^b w(x)f(x)/w(x) )dx}{\int_a^b w(x)dx} = \frac{I}{\int_a^b w(x)dx}
$$
and thus:
$$
I = \left\langle \frac{f(x)}{w(x)}\right\rangle \int_a^b w(x)dx \simeq \frac{1}{N}\sum_{i=1}^N \frac{f(x_i)}{w(x_i)}\int_a^b w(x)dx
$$
which generalizes the mean value method if $w(x)$ is the uniform distribution between $a$ and $b$
### Example
Suppose we want to estimate the tail probability of ${\cal N}(0,1)$ for $P(x>5)$. Regular MC integration using samples from ${\cal N}(0,1)$ is hopeless since nearly all samples will be rejected. However, we can use the exponential density truncated at 5 as the importance function and use importance sampling.<jupyter_code>x = np.linspace(4, 10, 100)
plt.plot(x, stats.expon(5).pdf(x))
plt.plot(x, stats.norm().pdf(x));
%precision 10
h_true =1 - stats.norm().cdf(5)
h_true
n = 1000000
y = stats.norm().rvs(n)
h_mc = 1.0/n * np.sum(y > 5)
# estimate and relative error
h_mc, np.abs(h_mc - h_true)/h_true
n = 10000
y = stats.expon(loc=5).rvs(n)
print(y)
h_is = 1.0/n * np.sum(stats.norm().pdf(y)/stats.expon(loc=5).pdf(y))
print(h_is)
# estimate and relative error
h_is, np.abs(h_is- h_true)/h_true<jupyter_output>[ 5.1349936033 10.6016142628 5.1042250624 ... 5.4666308803 5.6565102841
5.0898766291]
2.911795800408398e-07
|
no_license
|
/08_MonteCarlo.ipynb
|
chelseaphilippa/LaboratoryOfComputationalPhysics_Y3
| 9 |
<jupyter_start><jupyter_text>1)As per the table, it is observed that the charges for smoker is quite high in comparison with non-smoker.
2)The charges increases as the age of the person increases and it is comparatively higher in case of smokers.
3)The charges increase as the bmi of the person increases. Also,the charges are very high in obese smokers (bmi > 30)
4)Heatmap also suggests positive correlation of charges with age and bmi.<jupyter_code>sns.distplot(data['charges'])
plt.show()
sns.distplot(data['age'])
plt.show()
sns.distplot(data['bmi'])
sns.boxplot(x=data['charges'],data=data)
sns.distplot(np.log(data['charges']))
##encoding of categorical variables
data['sex']=np.where(data['sex']=='female',0,1)
data['smoker']=np.where(data['smoker']=='yes',1,0)
data.corr()
plt.figure(figsize=(8,8))
sns.heatmap(data.corr())
# dropping region column
# As children is also a categorical variable, converting it into dummy variable
# As the saleprice is right skewed and we will use lograthmic tranformation to overcome this
dataset=data.copy()
dataset=dataset.drop(columns=['region'])
dataset['charges']=np.log(data['charges'])
dataset.head()<jupyter_output><empty_output><jupyter_text>#### Feature Scaling<jupyter_code>from sklearn.preprocessing import MinMaxScaler
scaler=MinMaxScaler()
fea_scale=['age','bmi']
scaler.fit(dataset[fea_scale])
data_x=dataset.drop(columns=['age','bmi'])
dataset=pd.concat([data_x,pd.DataFrame(scaler.transform(dataset[fea_scale]),columns=fea_scale)],axis=1)
dataset.head()
dataset.info()
#setting up dependent and independent data
y=dataset['charges']
x=dataset.drop(columns='charges')
<jupyter_output><empty_output><jupyter_text>##### PredictionModel used for the prediction:
1) KNeighbors Regression
2) Linear Regression
3) Random Forest Regression
4) Support Vector Regression<jupyter_code>from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.svm import SVR
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import r2_score
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25)
knn=KNeighborsRegressor(n_neighbors=9)
knn.fit(x_train,y_train)
y_pred=knn.predict(x_test)
r2=r2_score(y_test,y_pred)
print('r2 score for knn Regression is %0.4f'%r2)
print('score for training set %.2f'%(knn.score(x_train,y_train)))
print('score for test set %.2f'%(knn.score(x_test,y_test)))
lr=LinearRegression()
lr.fit(x_train,y_train)
y_pred=lr.predict(x_test)
r2=r2_score(y_test,y_pred)
print('r2 score for Linear Regression is %0.4f'%r2)
print('score for training set %.2f'%(lr.score(x_train,y_train)))
print('score for test set %.2f'%(lr.score(x_test,y_test)))
rbf=RandomForestRegressor(n_estimators=100)
rbf.fit(x_train,y_train)
y_pred=rbf.predict(x_test)
r2=r2_score(y_test,y_pred)
print('r2 score for RandomForestRegression is %0.4f'%r2)
print('score for training set %.2f'%(rbf.score(x_train,y_train)))
print('score for test set %.2f'%(rbf.score(x_test,y_test)))
<jupyter_output>r2 score for RandomForestRegression is 0.8179
score for training set 0.97
score for test set 0.82
<jupyter_text>The accuracy has improved using RandomForestRegression but we are likely to be overfitting. To reduce overfitting, we could apply pre-pruning by changing the max_depth.<jupyter_code>rbf=RandomForestRegressor(n_estimators=100,max_depth=6)
rbf.fit(x_train,y_train)
y_pred=rbf.predict(x_test)
r2=r2_score(y_test,y_pred)
print('r2 score for RandomForestRegression is %0.4f'%r2)
print('score for training set %.2f'%(rbf.score(x_train,y_train)))
print('score for test set %.2f'%(rbf.score(x_test,y_test)))<jupyter_output>r2 score for RandomForestRegression is 0.8431
score for training set 0.88
score for test set 0.84
<jupyter_text>The model accuracy slightly improved using pre-pruning method by setting max_depth=6<jupyter_code>param_grid={'gamma':[0.0001,0.01,0.1,1,10],'C':[0.01,1,10,100,1000]}
grid_search=GridSearchCV(SVR(),param_grid=param_grid,cv=5)
grid_search.fit(x_train,y_train)
score=grid_search.score(x_test,y_test)
print('score: %.3f'%score)
grid_search.best_params_
<jupyter_output>score: 0.833
|
no_license
|
/insurance.ipynb
|
mahewashabdi/Insurance-Forecast
| 5 |
<jupyter_start><jupyter_text># Preliminaries
Write requirements to file, anytime you run it, in case you have to go back and recover dependencies.
Requirements are hosted for each notebook in the companion github repo, and can be pulled down and installed here if needed. Companion github repo is located at https://github.com/azunre/transfer-learning-for-nlp<jupyter_code>!pip freeze > kaggle_image_requirements.txt<jupyter_output><empty_output><jupyter_text># Read and Preprocess Fake News Data
The data preprocessing steps are the same as those in sections 4.2/4.4
Read in the "true" and "fake" data
In quotes, because that has the potential to simply replicate the biases of the labeler, so should be carefully evaluated<jupyter_code>import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Read the data into pandas DataFrames
DataTrue = pd.read_csv("/kaggle/input/fake-and-real-news-dataset/True.csv")
DataFake = pd.read_csv("/kaggle/input/fake-and-real-news-dataset/Fake.csv")
print("Data labeled as True:")
print(DataTrue.head())
print("\n\n\nData labeled as Fake:")
print(DataFake.head())<jupyter_output>Data labeled as True:
title \
0 As U.S. budget fight looms, Republicans flip t...
1 U.S. military to accept transgender recruits o...
2 Senior U.S. Republican senator: 'Let Mr. Muell...
3 FBI Russia probe helped by Australian diplomat...
4 Trump wants Postal Service to charge 'much mor...
text subject \
0 WASHINGTON (Reuters) - The head of a conservat... politicsNews
1 WASHINGTON (Reuters) - Transgender people will... politicsNews
2 WASHINGTON (Reuters) - The special counsel inv... politicsNews
3 WASHINGTON (Reuters) - Trump campaign adviser ... politicsNews
4 SEATTLE/WASHINGTON (Reuters) - President Donal... politicsNews
date
0 December 31, 2017
1 December 29, 2017
2 December 31, 2017
3 December 30, 2017
4 December 29, 2017
Data labeled as Fake:
titl[...]<jupyter_text>Assemble the two different kinds of data (1000 samples from each of the two classes)<jupyter_code>Nsamp =1000 # number of samples to generate in each class - 'true', 'fake'
DataTrue = DataTrue.sample(Nsamp)
DataFake = DataFake.sample(Nsamp)
raw_data = pd.concat([DataTrue,DataFake], axis=0).values
# combine title, body text and topics into one string per document
#raw_data = [sample[0].lower() + sample[1].lower() + sample[3].lower() for sample in raw_data]
print("Length of combined data is:")
print(len(raw_data))
print("Data represented as numpy array (first 5 samples) is:")
print(raw_data[:5])
# corresponding labels
Categories = ['True','False']
header = ([1]*Nsamp)
header.extend(([0]*Nsamp))<jupyter_output>Length of combined data is:
2000
Data represented as numpy array (first 5 samples) is:
[['Long speech, lots of tea: party meeting with Chinese characteristics'
" BEIJING (Reuters) - The speech was long, the refreshments austere, but Zhang Weiguo, a Communist Party official from Hubei province in central China, was thrilled. It was strongly persuasive, infectious, cohesive, and had rally-appeal, Zhang said after Chinese President and party boss Xi Jinping gave a nearly three-and-a-half hour speech in Beijing s cavernous Great Hall of the People to kick off the 19th Communist Party Congress. I came out of the auditorium feeling infected, my motivation infinitely enhanced. The scene is a far cry from a convention of the Democratic or Republican Party in the United States, with their rock concert-like atmosphere, balloons falling from the rafters and raucous cheering crowds. Instead, most delegates wore conservative business suits, turned pages of the speech in unison, and clappe[...]<jupyter_text>Shuffle data, split into train and test sets...<jupyter_code># function for shuffling data
def unison_shuffle(a, b):
p = np.random.permutation(len(b))
data = np.asarray(a)[p]
header = np.asarray(b)[p]
return data, header
raw_data, header = unison_shuffle(raw_data, header)
# split into independent 70% training and 30% testing sets
idx = int(0.7*raw_data.shape[0])
# 70% of data for training
train_x = raw_data[:idx]
train_y = header[:idx]
# remaining 30% for testing
test_x = raw_data[idx:]
test_y = header[idx:]
print("train_x/train_y list details, to make sure it is of the right form:")
print(len(train_x))
#print(train_x)
print(train_y[:5])
print(train_y.shape)<jupyter_output>train_x/train_y list details, to make sure it is of the right form:
1400
[1 1 0 1 1]
(1400,)
<jupyter_text># ULMFiT Experiments
Import the fast.ai library, written by the ULMFiT authors<jupyter_code>from fastai.text import *<jupyter_output><empty_output><jupyter_text>## Data Bunch Class for Language Model/Task Classifier ConsumptionWe prepare train and test/validation dataframes first.<jupyter_code>train_df = pd.DataFrame(data=[train_y,train_x]).T
test_df = pd.DataFrame(data=[test_y,test_x]).T<jupyter_output><empty_output><jupyter_text>Check their shape:<jupyter_code>train_df.shape
test_df.shape<jupyter_output><empty_output><jupyter_text>Data in fast.ai is consumed using the *TextLMDataBunch* class. Construct an instance of this class for language model consumption.<jupyter_code>data_lm = TextLMDataBunch.from_df(train_df = train_df, valid_df = test_df, path = "")<jupyter_output><empty_output><jupyter_text>Construct an instance of this object for task-specific classifier consumption.<jupyter_code>data_clas = TextClasDataBunch.from_df(path = "", train_df = train_df, valid_df = test_df, vocab=data_lm.train_ds.vocab, bs=32)<jupyter_output><empty_output><jupyter_text>## Fine-Tune Language Model
In ULMFiT, language models are trained using the *language_model_learner* class.
We initialize an instance of this class, opting to go with ASGD Weight-Dropped LSTM (AWD_LSTM) model architecture. This is just the usual LSTM with some weights randomly set to 0, analogously to what is done to activations in Dropout layers. More info can be found here - https://docs.fast.ai/text.models.awdlstm<jupyter_code>learn = language_model_learner(data_lm, AWD_LSTM, drop_mult=0.3)<jupyter_output>Downloading https://s3.amazonaws.com/fast-ai-modelzoo/wt103-fwd.tgz
<jupyter_text>Note that the initialization of this model also loads weights pretrained on the Wikitext 103 benchmark dataset (The WikiText Long Term Dependency Language Modeling Dataset - https://www.salesforce.com/products/einstein/ai-research/the-wikitext-dependency-language-modeling-dataset/). You can see the execution log above for confirmation of this.
We can find a suggested maximum learning rate using the following commands. Instead of selecting the lowest point on the curve, note that the chosen point is where the curve is changing the fastest.<jupyter_code>learn.lr_find() # find best rate
learn.recorder.plot(suggestion=True) # plot it<jupyter_output><empty_output><jupyter_text>Fetch the optimal rate as follows.<jupyter_code>rate = learn.recorder.min_grad_lr
print(rate)<jupyter_output>0.03981071705534969
<jupyter_text>We fine-tune using slanted trangular learning rates, which are already built into the *fit_one_cycle()* method in fast.ai<jupyter_code>learn.fit_one_cycle(1, rate)<jupyter_output><empty_output><jupyter_text>### Discriminative Fine-Tuning
The call *learn.unfreeze()* makes all the layers trainable. We can use the *slice()* function to train the last layer at a specified rate, while the layers below will have reducing learning rates. We set the lower bound of the range at two orders of magnitude smaller, i.e., divide the maximum rate by 100.<jupyter_code>learn.unfreeze()
learn.fit_one_cycle(1, slice(rate/100,rate))<jupyter_output><empty_output><jupyter_text>As you can see, the accuracy slightly increased!
We can use the resulting language model to predict some words in a sequence using the following command (predicts next 10 words)<jupyter_code>learn.predict("This is a news article about", n_words=10)<jupyter_output><empty_output><jupyter_text>Plausible!
Save the fine-tuned language model!<jupyter_code>learn.save_encoder('fine-tuned_language_model')<jupyter_output><empty_output><jupyter_text>## Target Task Classifier Fine-tuning
In ULMFiT, target task classifier fine-tuning is carried out using the *text_classifier_learner* class. Recall that the target task here is predicting whether a given article is "fake news" or not.
We instantiate it below, using the same settings as the language model we fine-tuned above, so we can load that fine-tuned model without issues. We also load the fine-tuned language model into the instance below.<jupyter_code>learn = text_classifier_learner(data_clas, AWD_LSTM, drop_mult=0.3) # use the same settings as the language model we fine-tuned, so we can load without problems
learn.load_encoder('fine-tuned_language_model')<jupyter_output><empty_output><jupyter_text>Figure out the learning best rate as before.<jupyter_code>learn.lr_find() # find best rate
learn.recorder.plot(suggestion=True) # plot it
rate = learn.recorder.min_grad_lr
print(rate)<jupyter_output>0.0006918309709189362
<jupyter_text>Train the fake news classifier<jupyter_code>learn.fit_one_cycle(1, rate)<jupyter_output><empty_output><jupyter_text>A nearly perfect score is achieved!### Gradual Unfreezing
The idea is to keep the initial layers of model as untrainable in the beginning, slowly decreasing how many are untrainable as the training process proceeds.
We can use the following command to only unfreeze the last layer:<jupyter_code>learn.freeze_to(-1)<jupyter_output><empty_output><jupyter_text>We can use the following command to only unfreeze the last two layers<jupyter_code>learn.freeze_to(-2)<jupyter_output><empty_output><jupyter_text>Thus, gradual unfreezing to a depth=2 would involve doing something like this:<jupyter_code>depth = 2
for i in range(1,depth+1): # freeze progressively fewer layers, up to a depth of 2, training for one cycle each time
learn.freeze_to(-i)
learn.fit_one_cycle(1, rate)<jupyter_output><empty_output>
|
permissive
|
/Ch6/tl-for-nlp-section6-1.ipynb
|
sahmel/transfer-learning-for-nlp
| 22 |
<jupyter_start><jupyter_text># 1. Define Concrete Dropout and Variational Dropout<jupyter_code>import torch
import torch.nn as nn
import torch.nn.functional as F
class ConcreteDropout(nn.Module):
def __init__(self, p_logit=-2.0, temp=0.01, eps=1e-8):
super(ConcreteDropout, self).__init__()
self.p_logit = nn.Parameter(torch.Tensor([p_logit]))
self.temp = temp
self.eps = eps
@property
def p(self):
return torch.sigmoid(self.p_logit)
def forward(self, x):
if self.train():
unif_noise = torch.rand_like(x)
drop_prob = torch.log(self.p + self.eps) -\
torch.log(1-self.p + self.eps)+\
torch.log(unif_noise + self.eps)-\
torch.log(1-unif_noise + self.eps)
drop_prob = torch.sigmoid(drop_prob/ self.temp)
random_tensor = 1. - drop_prob
retain_prob = 1. - self.p
x *= random_tensor
x /= retain_prob
return x
cdrop = ConcreteDropout()
drop = nn.Dropout(p=0.1)
input = torch.ones([1,10])
output1 = cdrop(input)
input = torch.ones([1,10])
output2 = drop(input)
print(output1)
print(output2)
class VariationalDropout(nn.Module):
def __init__(self, log_alpha=-3.):
super(VariationalDropout, self).__init__()
self.max_log_alpha = 0.0
self.log_alpha = nn.Parameter(torch.Tensor([log_alpha]))
@property
def alpha(self):
return torch.exp(self.log_alpha)
def forward(self, x):
if self.train():
normal_noise = torch.randn_like(x)
self.log_alpha.data = torch.clamp(self.log_alpha.data, max=self.max_log_alpha)
random_tensor = 1. + normal_noise * torch.sqrt(self.alpha)
x *= random_tensor
return x<jupyter_output><empty_output><jupyter_text># 2. Loading and normalizing CIFAR-10<jupyter_code>import torch
import torchvision
import torchvision.transforms as transforms
batch_size = 1000
train_transform = transforms.Compose(
[transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010))])
test_transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=train_transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size,
shuffle=True, num_workers=4)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=test_transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=batch_size,
shuffle=False, num_workers=4)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
print('train set size: {}'.format(len(trainset)))
log_freq = len(trainset)//batch_size
print('log freq: {}'.format(log_freq))
print('test set size: {}'.format(len(testset)))
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
%matplotlib inline
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()
print(images.shape)
# show images
imshow(torchvision.utils.make_grid(images[:4]))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))<jupyter_output>Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
<jupyter_text># 3. Define Lenet with/without dropout<jupyter_code># Lenet with Concrete dropout
class Net_CDO(nn.Module):
def __init__(self, weight_reg_coef=5e-4, dropout_reg_coef=1e-2):
super(Net_CDO, self).__init__()
self.conv1 = nn.Conv2d(3, 192, 5, padding=2)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(192, 192, 5, padding=2)
self.fc1 = nn.Linear(192 * 8 * 8, 1024)
self.fc2 = nn.Linear(1024, 256)
self.fc3 = nn.Linear(256, 10)
self.leaky_relu = nn.LeakyReLU(negative_slope=0.2)
self.cdropout1 = ConcreteDropout()
self.cdropout2 = ConcreteDropout()
self.cdropout3 = ConcreteDropout()
self.cdropout4 = ConcreteDropout()
self.weight_reg_coef = weight_reg_coef
self.dropout_reg_coef = dropout_reg_coef
nn.init.xavier_uniform_(self.conv1.weight)
nn.init.constant_(self.conv1.bias, 0.0)
nn.init.xavier_uniform_(self.conv2.weight)
nn.init.constant_(self.conv2.bias, 0.0)
nn.init.xavier_uniform_(self.fc1.weight)
nn.init.constant_(self.fc1.bias, 0.0)
nn.init.xavier_uniform_(self.fc2.weight)
nn.init.constant_(self.fc2.bias, 0.0)
nn.init.xavier_uniform_(self.fc3.weight)
nn.init.constant_(self.fc3.bias, 0.0)
def forward(self, x):
x = self.pool(self.leaky_relu(self.cdropout1(self.conv1(x))))
x = self.pool(self.leaky_relu(self.cdropout2(self.conv2(x))))
x = x.view(-1, 192 * 8 * 8)
x = self.leaky_relu(self.cdropout3(self.fc1(x)))
x = self.leaky_relu(self.cdropout4(self.fc2(x)))
x = F.softmax(self.fc3(x),dim=1)
return x
def entropy(self,cdropout):
return -cdropout.p * torch.log(cdropout.p+1e-8) \
-(1-cdropout.p) * torch.log(1-cdropout.p+1e-8)
def calc_reg(self):
weight_reg = (self.fc1.weight.norm()**2+self.fc1.bias.norm()**2)/(1-self.cdropout3.p)+\
(self.fc2.weight.norm()**2+self.fc2.bias.norm()**2)/(1-self.cdropout4.p)+\
(self.fc3.weight.norm()**2+self.fc3.bias.norm()**2)+\
(self.conv1.weight.norm()**2+self.conv1.bias.norm()**2)/(1-self.cdropout1.p)+\
(self.conv2.weight.norm()**2+self.conv2.bias.norm()**2)/(1-self.cdropout2.p)
weight_reg *= self.weight_reg_coef
dropout_reg = -self.entropy(self.cdropout1)-self.entropy(self.cdropout2)-\
self.entropy(self.cdropout3)-self.entropy(self.cdropout4)
dropout_reg *= self.dropout_reg_coef
return weight_reg + dropout_reg
# Lenet with Variational dropout
class Net_VDO(nn.Module):
def __init__(self, reg_coef=5e-4):
super(Net_VDO, self).__init__()
self.conv1 = nn.Conv2d(3, 192, 5, padding=2)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(192, 192, 5, padding=2)
self.fc1 = nn.Linear(192 * 8 * 8, 1024)
self.fc2 = nn.Linear(1024, 256)
self.fc3 = nn.Linear(256, 10)
self.leaky_relu = nn.LeakyReLU(negative_slope=0.2)
self.vdropout1 = VariationalDropout()
self.vdropout2 = VariationalDropout()
self.vdropout3 = VariationalDropout()
self.vdropout4 = VariationalDropout()
self.reg_coef = reg_coef
nn.init.xavier_uniform_(self.conv1.weight)
nn.init.constant_(self.conv1.bias, 0.0)
nn.init.xavier_uniform_(self.conv2.weight)
nn.init.constant_(self.conv2.bias, 0.0)
nn.init.xavier_uniform_(self.fc1.weight)
nn.init.constant_(self.fc1.bias, 0.0)
nn.init.xavier_uniform_(self.fc2.weight)
nn.init.constant_(self.fc2.bias, 0.0)
nn.init.xavier_uniform_(self.fc3.weight)
nn.init.constant_(self.fc3.bias, 0.0)
def forward(self, x):
x = self.pool(self.leaky_relu(self.vdropout1(self.conv1(x))))
x = self.pool(self.leaky_relu(self.vdropout2(self.conv2(x))))
x = x.view(-1, 192 * 8 * 8)
x = self.leaky_relu(self.vdropout3(self.fc1(x)))
x = self.leaky_relu(self.vdropout4(self.fc2(x)))
x = F.softmax(self.fc3(x),dim=1)
return x
def kl_prior(self, vdropout):
c1 = 1.16145124
c2 = -1.50204118
c3 = 0.58629921
return -0.5*vdropout.log_alpha - c1*vdropout.alpha \
- c2*vdropout.alpha**2 - c3*vdropout.alpha**3
def calc_reg(self):
return self.reg_coef * (self.kl_prior(self.vdropout1)+self.kl_prior(self.vdropout2)+\
self.kl_prior(self.vdropout3)+self.kl_prior(self.vdropout4))
# Lenet with MCDO
class Net_MCDO(nn.Module):
def __init__(self):
super(Net_MCDO, self).__init__()
self.conv1 = nn.Conv2d(3, 192, 5, padding=2)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(192, 192, 5, padding=2)
self.fc1 = nn.Linear(192 * 8 * 8, 1024)
self.fc2 = nn.Linear(1024, 256)
self.fc3 = nn.Linear(256, 10)
self.leaky_relu = nn.LeakyReLU(negative_slope=0.2)
self.dropout = nn.Dropout(p=0.3)
nn.init.xavier_uniform_(self.conv1.weight)
nn.init.constant_(self.conv1.bias, 0.0)
nn.init.xavier_uniform_(self.conv2.weight)
nn.init.constant_(self.conv2.bias, 0.0)
nn.init.xavier_uniform_(self.fc1.weight)
nn.init.constant_(self.fc1.bias, 0.0)
nn.init.xavier_uniform_(self.fc2.weight)
nn.init.constant_(self.fc2.bias, 0.0)
nn.init.xavier_uniform_(self.fc3.weight)
nn.init.constant_(self.fc3.bias, 0.0)
def forward(self, x):
x = self.pool(self.leaky_relu(self.dropout(self.conv1(x))))
x = self.pool(self.leaky_relu(self.dropout(self.conv2(x))))
x = x.view(-1, 192 * 8 * 8)
x = self.leaky_relu(self.dropout(self.fc1(x)))
x = self.leaky_relu(self.dropout(self.fc2(x)))
x = F.softmax(self.fc3(x),dim=1)
return x<jupyter_output><empty_output><jupyter_text># 4. Define a Loss function and optimizer<jupyter_code>import torch.optim as optim
CE = nn.CrossEntropyLoss()
def train(epoch, net, optimizer, log_freq=log_freq, is_calc_reg=False):
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs
inputs, labels = data
inputs, labels = inputs.to(device), labels.to(device)
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = CE(outputs, labels)
if is_calc_reg:
loss += torch.sum(net.module.calc_reg())
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if (i+1) % log_freq == 0: # print every 2000 mini-batches
print('[Epoch : %d, Iter: %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / log_freq))
return running_loss / log_freq
def test(net):
print('Start test')
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
for data in testloader:
inputs, labels = data
inputs, labels = inputs.to(device), labels.to(device)
output = 0
for i in range(50):
output += net(inputs)/10.
output = torch.log(output)
_, predicted = torch.max(output, 1)
c = (predicted == labels).squeeze()
for i in range(len(labels)):
label = labels[i]
class_correct[label] += c[i].item()
class_total[label] += 1
for i in range(10):
print('Accuracy of %5s : %.2f %%' % (
classes[i], 100 * class_correct[i] / class_total[i]))
test_score = np.mean([100 * class_correct[i] / class_total[i] for i in range(10)])
print(test_score)
return test_score
from tqdm import tqdm_notebook
lenets = [Net_CDO, Net_VDO, Net_MCDO]
epoch_num = 300
test_freq = 10
losses = list()
net_scores = list()
test_scores = list()
cdropout_history = list()
vdropout_history = list()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
is_train = True
# SAVE
def save(name, net):
net_path = './model/'+name+'.pkl'
net = net.cpu()
torch.save(net.state_dict(), net_path)
# Place it to GPU back
net.to(device)
return net
def load(name, net):
net_path = './model/'+name+'.pkl'
# LOAD
net.load_state_dict(torch.load(net_path))
# Place it to GPU
net.to(device)
return net
def main():
for lenet in lenets:
print(lenet.__name__)
net = lenet()
if torch.cuda.device_count() > 1:
print("Let's use",torch.cuda.device_count(),"GPUs!")
net = nn.DataParallel(net)
net.to(device)
if lenet.__name__ == 'Net_CDO':
optimizer = optim.Adam(net.parameters(), lr=5e-4, amsgrad=True)
else:
optimizer = optim.Adam(net.parameters(), lr=5e-4, weight_decay=5e-4, amsgrad=True)
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=2, gamma=0.97)
for i in tqdm_notebook(range(epoch_num)):
scheduler.step()
# net.train()
if lenet.__name__ == 'Net_CDO':
loss_avg = train(epoch=i, net=net, optimizer=optimizer, is_calc_reg=True)
cdropout_history.append((net.module.cdropout1.p.item(),\
net.module.cdropout2.p.item(),
net.module.cdropout3.p.item(),
net.module.cdropout4.p.item()))
elif lenet.__name__ == 'Net_VDO':
loss_avg = train(epoch=i, net=net, optimizer=optimizer, is_calc_reg=True)
vdropout_history.append((net.module.vdropout1.alpha.item(),\
net.module.vdropout2.alpha.item(),
net.module.vdropout3.alpha.item(),
net.module.vdropout4.alpha.item()))
else:
loss_avg = train(epoch=i, net=net, optimizer=optimizer)
losses.append(loss_avg)
if (i+1) % test_freq == 0:
# net.eval()
net_score = test(net)
net_scores.append(net_score)
save(lenet.__name__, net)
if is_train:
main()
sns.set()
epochs = [10*i for i in range((30))]
plt.plot(epochs, net_scores[:30],label='Net_CDO')
plt.plot(epochs, net_scores[30:60],label='Net_VDO')
plt.plot(epochs, net_scores[60:],label='Net_MCDO')
plt.xlabel('epochs')
plt.ylabel('Test accuracy')
plt.legend()
plt.tight_layout()
plt.show()
cdropout1_history = [cdropout_history[i][0] for i in range(30)]
cdropout2_history = [cdropout_history[i][1] for i in range(30)]
cdropout3_history = [cdropout_history[i][2] for i in range(30)]
cdropout4_history = [cdropout_history[i][3] for i in range(30)]
plt.plot(epochs, cdropout1_history,label='cdropout1')
plt.plot(epochs, cdropout2_history,label='cdropout2')
plt.plot(epochs, cdropout3_history,label='cdropout3')
plt.plot(epochs, cdropout4_history,label='cdropout4')
plt.xlabel('epochs')
plt.ylabel('Dropout rate')
plt.legend()
plt.tight_layout()
plt.show()
vdropout1_history = [vdropout_history[i][0] for i in range(30)]
vdropout2_history = [vdropout_history[i][1] for i in range(30)]
vdropout3_history = [vdropout_history[i][2] for i in range(30)]
vdropout4_history = [vdropout_history[i][3] for i in range(30)]
plt.plot(epochs, vdropout1_history,label='vdropout1')
plt.plot(epochs, vdropout2_history,label='vdropout2')
plt.plot(epochs, vdropout3_history,label='vdropout3')
plt.plot(epochs, vdropout4_history,label='vdropout4')
plt.xlabel('epochs')
plt.ylabel('Alpha value')
plt.legend()
plt.tight_layout()
plt.show()<jupyter_output><empty_output>
|
no_license
|
/Concrete_dropout_and_Variational_dropout.ipynb
|
GRE-EXAMINATION/MCDO
| 4 |
<jupyter_start><jupyter_text>
Logistic Regression Table of Contents
In this lab, you will cover logistic regression by using PyTorch.
Logistic Function
Tanh
Relu
Compare Activation Functions
Estimated Time Needed: 15 min
We'll need the following libraries<jupyter_code># Import the libraries we need for this lab
import torch.nn as nn
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
torch.manual_seed(2)<jupyter_output><empty_output><jupyter_text>Logistic FunctionCreate a tensor ranging from -10 to 10: <jupyter_code># Create a tensor
z = torch.arange(-10, 10, 0.1).view(-1, 1)<jupyter_output><empty_output><jupyter_text>When you use sequential, you can create a sigmoid object: <jupyter_code># Create a sigmoid object
sig = nn.Sigmoid()<jupyter_output><empty_output><jupyter_text>Apply the element-wise function Sigmoid with the object:<jupyter_code># Make a prediction of sigmoid function
yhat = sig(z)<jupyter_output><empty_output><jupyter_text>Plot the results: <jupyter_code># Plot the result
plt.plot(z.numpy(),yhat.numpy())
plt.xlabel('z')
plt.ylabel('yhat')<jupyter_output><empty_output><jupyter_text>For custom modules, call the sigmoid from the torch (nn.functional for the old version), which applies the element-wise sigmoid from the function module and plots the results:<jupyter_code># Use the build in function to predict the result
yhat = torch.sigmoid(z)
plt.plot(z.numpy(), yhat.numpy())
plt.show()<jupyter_output><empty_output><jupyter_text>TanhWhen you use sequential, you can create a tanh object:<jupyter_code># Create a tanh object
TANH = nn.Tanh()<jupyter_output><empty_output><jupyter_text>Call the object and plot it:<jupyter_code># Make the prediction using tanh object
yhat = TANH(z)
plt.plot(z.numpy(), yhat.numpy())
plt.show()<jupyter_output><empty_output><jupyter_text>
For custom modules, call the Tanh object from the torch (nn.functional for the old version), which applies the element-wise sigmoid from the function module and plots the results:<jupyter_code># Make the prediction using the build-in tanh object
yhat = torch.tanh(z)
plt.plot(z.numpy(), yhat.numpy())
plt.show()<jupyter_output><empty_output><jupyter_text>ReluWhen you use sequential, you can create a Relu object: <jupyter_code># Create a relu object and make the prediction
RELU = nn.ReLU()
yhat = RELU(z)
plt.plot(z.numpy(), yhat.numpy())<jupyter_output><empty_output><jupyter_text>For custom modules, call the relu object from the nn.functional, which applies the element-wise sigmoid from the function module and plots the results:<jupyter_code># Use the build-in function to make the prediction
yhat = F.relu(z)
plt.plot(z.numpy(), yhat.numpy())
plt.show()<jupyter_output><empty_output><jupyter_text>
Compare Activation Functions <jupyter_code># Plot the results to compare the activation functions
x = torch.arange(-2, 2, 0.1).view(-1, 1)
plt.plot(x.numpy(), F.relu(x).numpy(), label='relu')
plt.plot(x.numpy(), torch.sigmoid(x).numpy(), label='sigmoid')
plt.plot(x.numpy(), torch.tanh(x).numpy(), label='tanh')
plt.legend()<jupyter_output><empty_output><jupyter_text>
Practice Compare the activation functions with a tensor in the range (-1, 1)<jupyter_code># Practice: Compare the activation functions again using a tensor in the range (-1, 1)
x = torch.arange(-1, 1, 0.1).view(-1, 1)
plt.plot(x.numpy(), F.relu(x).numpy(), label = 'relu')
plt.plot(x.numpy(), torch.sigmoid(x).numpy(), label = 'sigmoid')
plt.plot(x.numpy(), torch.tanh(x).numpy(), label = 'tanh')
plt.legend()<jupyter_output><empty_output>
|
no_license
|
/labs/4.3.1lactivationfuction_v2.ipynb
|
Bcopeland64/Data-Science-Notebooks
| 13 |
<jupyter_start><jupyter_text>
Python | Implementation of Movie Recommender System
Recommender System is a system that seeks to predict or filter preferences according to the user’s choices. Recommender systems are utilized in a variety of areas including movies, music, news, books, research articles, search queries, social tags, and products in general.
Recommender systems produce a list of recommendations in any of the two ways –
Collaborative filtering: Collaborative filtering approaches build a model from user’s past behavior (i.e. items purchased or searched by the user) as well as similar decisions made by other users. This model is then used to predict items (or ratings for items) that user may have an interest in.
Content-based filtering: Content-based filtering approaches uses a series of discrete characteristics of an item in order to recommend additional items with similar properties. Content-based filtering methods are totally based on a description of the item and a profile of the user’s preferences. It recommends items based on user’s past preferences.
Let’s develop a basic recommendation system using Python and Pandas.
Let’s focus on providing a basic recommendation system by suggesting items that are most similar to a particular item, in this case, movies. It just tells what movies/items are most similar to user’s movie choice.
<jupyter_code>
# import pandas library
import pandas as pd
# Get the data
column_names = ['user_id', 'item_id', 'rating', 'timestamp']
path = 'https://cdncontribute.geeksforgeeks.org/wp-content/uploads/file.tsv'
df = pd.read_csv(path, sep='\t', names=column_names)
# Check the head of the data
df.head()
# Check out all the movies and their respective IDs
movie_titles = pd.read_csv('https://cdncontribute.geeksforgeeks.org/wp-content/uploads/Movie_Id_Titles.csv')
movie_titles.head()
data = pd.merge(df, movie_titles, on='item_id')
data.head()
# Calculate mean rating of all movies
data.groupby('title')['rating'].mean().sort_values(ascending=False).head()
# Calculate count rating of all movies
data.groupby('title')['rating'].count().sort_values(ascending=False).head()
# creating dataframe with 'rating' count values
ratings = pd.DataFrame(data.groupby('title')['rating'].mean())
ratings['num of ratings'] = pd.DataFrame(data.groupby('title')['rating'].count())
ratings.head()
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('white')
%matplotlib inline
#plot graph of 'num of ratings column'
plt.figure(figsize =(10, 4))
ratings['num of ratings'].hist(bins = 70)
# plot graph of 'ratings' column
plt.figure(figsize =(10, 4))
ratings['rating'].hist(bins = 70)
# Sorting values according to
# the 'num of rating column'
moviemat = data.pivot_table(index ='user_id',
columns ='title', values ='rating')
moviemat.head()
ratings.sort_values('num of ratings', ascending = False).head(10)
# analysing correlation with similar movies
starwars_user_ratings = moviemat['Star Wars (1977)']
liarliar_user_ratings = moviemat['Liar Liar (1997)']
starwars_user_ratings.head()
# analysing correlation with similar movies
similar_to_starwars = moviemat.corrwith(starwars_user_ratings)
similar_to_liarliar = moviemat.corrwith(liarliar_user_ratings)
corr_starwars = pd.DataFrame(similar_to_starwars, columns =['Correlation'])
corr_starwars.dropna(inplace = True)
corr_starwars.head()
# Similar movies like starwars
corr_starwars.sort_values('Correlation', ascending = False).head(10)
corr_starwars = corr_starwars.join(ratings['num of ratings'])
corr_starwars.head()
corr_starwars[corr_starwars['num of ratings']>100].sort_values('Correlation', ascending = False).head()
# Similar movies as of liarliar
corr_liarliar = pd.DataFrame(similar_to_liarliar, columns =['Correlation'])
corr_liarliar.dropna(inplace = True)
corr_liarliar = corr_liarliar.join(ratings['num of ratings'])
corr_liarliar[corr_liarliar['num of ratings']>100].sort_values('Correlation', ascending = False).head()
<jupyter_output><empty_output>
|
no_license
|
/Movie_recommender_system.ipynb
|
AbhishekGladiatorz/Movie_recommender_system
| 1 |
<jupyter_start><jupyter_text># Again for Dec 2006<jupyter_code>#loading files
path = '/ocean/nsoontie/MEOPAR/SalishSea/results/storm-surges/final/dec2006/'
runs = {'all_forcing','tidesonly'}
fUs={}; fVs={}; fTs={};
for key in runs:
fUs[key] = NC.Dataset(path + key +'/SalishSea_4h_20061211_20061217_grid_U.nc','r');
fVs[key] = NC.Dataset(path + key +'/SalishSea_4h_20061211_20061217_grid_V.nc','r');
fTs[key] = NC.Dataset(path + key +'/SalishSea_4h_20061211_20061217_grid_T.nc','r');
#preparing data
run_stations={}
us={}; vs={}; lats={}; lons={}; tmps={}; sals={}; sshs={}; ts={};
for run in runs:
for key in stations:
string = path + run + '/1h_' + key + '.nc'
run_stations[key] = NC.Dataset(string,'r');
tim = run_stations[key].variables['time_counter']
t_count=np.arange(0, tim.shape[0])
t=nc_tools.timestamp(run_stations[key],t_count)
tlist=[]
for a in t:
tlist.append(a.datetime)
ts[run]=tlist
[us[run], vs[run], lats[run], lons[run], tmps[run], sals[run], sshs[run]] = stormtools.combine_data(run_stations)
run_stations={};
#Observations and tidal predictions
start='31-Dec-2005'; end='02-Jan-2007'
wlev_meas={}; ttide={}; msl={}
for key in stations:
location=key
#filename for predictions
filename='/data/nsoontie/MEOPAR/analysis/storm_surges/data/'+location+'_t_tide_compare8_' +start+'_'+end+'.csv'
[ttide[key], msl[key]] = stormtools.load_tidal_predictions(filename)
wlev_meas[key] = stormtools.load_observations(start,end,location)
#ssh forcing
date_ssh = '01-Dec-2006'
time_ssh={}; ssh_forc={}
[ssh_forc['Tofino'], time_ssh['Tofino']] = stormtools.get_SSH_forcing('west',date_ssh)
[ssh_forc['Port Hardy'],time_ssh['Port Hardy']] = stormtools.get_SSH_forcing('north',date_ssh)
#plotting details
x_ax = ['Dec 13, 2006', 'Dec 18, 2006']
start='11-Dec-2006'; end='18-Dec-2006' #for CGRF
start_EC='01-Dec-2006'
end_EC='31-Dec-2006'
unaware=datetime.datetime.strptime(start,"%d-%b-%Y")
sdt = unaware.replace(tzinfo=tz.tzutc())
unaware=datetime.datetime.strptime(end,"%d-%b-%Y")
edt = unaware.replace(tzinfo=tz.tzutc())
(fig,axs)= plt.subplots(3,1,figsize=(6,7))
plot_station('PointAtkinson',axs)
<jupyter_output>PointAtkinson
Maximum wind speed: 24.1666666667
Time of maximum wind: 2006-12-15 12:00:00+00:00
<jupyter_text># Again for Feb 2006<jupyter_code>#loading files
path = '/ocean/nsoontie/MEOPAR/SalishSea/results/storm-surges/final/feb2006/'
runs = {'all_forcing','tidesonly'}
fUs={}; fVs={}; fTs={};
for key in runs:
fUs[key] = NC.Dataset(path + key +'/SalishSea_4h_20060201_20060207_grid_U.nc','r');
fVs[key] = NC.Dataset(path + key +'/SalishSea_4h_20060201_20060207_grid_V.nc','r');
fTs[key] = NC.Dataset(path + key +'/SalishSea_4h_20060201_20060207_grid_T.nc','r');
#preparing data
run_stations={}
us={}; vs={}; lats={}; lons={}; tmps={}; sals={}; sshs={}; ts={};
for run in runs:
for key in stations:
string = path + run + '/1h_' + key + '.nc'
run_stations[key] = NC.Dataset(string,'r');
tim = run_stations[key].variables['time_counter']
t_count=np.arange(0, tim.shape[0])
t=nc_tools.timestamp(run_stations[key],t_count)
tlist=[]
for a in t:
tlist.append(a.datetime)
ts[run]=tlist
[us[run], vs[run], lats[run], lons[run], tmps[run], sals[run], sshs[run]] = stormtools.combine_data(run_stations)
run_stations={};
#Observations and tidal predictions
start='31-Dec-2005'; end='02-Jan-2007'
wlev_meas={}; ttide={}; msl={}
for key in stations:
location=key
#filename for predictions
filename='/data/nsoontie/MEOPAR/analysis/storm_surges/data/'+location+'_t_tide_compare8_' +start+'_'+end+'.csv'
[ttide[key], msl[key]] = stormtools.load_tidal_predictions(filename)
wlev_meas[key] = stormtools.load_observations(start,end,location)
#ssh forcing
date_ssh = '01-Feb-2006'
time_ssh={}; ssh_forc={}
[ssh_forc['Tofino'], time_ssh['Tofino']] = stormtools.get_SSH_forcing('west',date_ssh)
[ssh_forc['Port Hardy'],time_ssh['Port Hardy']] = stormtools.get_SSH_forcing('north',date_ssh)
#plotting details
x_ax = ['Feb 1, 2006', 'Feb 7, 2006']
start='2-Feb-2006'; end='7-Feb-2006' #for CGRF
start_EC='01-Feb-2006'
end_EC='28-Feb-2006'
unaware=datetime.datetime.strptime(start,"%d-%b-%Y")
sdt = unaware.replace(tzinfo=tz.tzutc())
unaware=datetime.datetime.strptime(end,"%d-%b-%Y")
edt = unaware.replace(tzinfo=tz.tzutc())
(fig,axs)= plt.subplots(3,1,figsize=(6,7))
plot_station('PointAtkinson',axs)<jupyter_output>PointAtkinson
Maximum wind speed: 18.0555555556
Time of maximum wind: 2006-02-04 13:00:00+00:00
<jupyter_text># Again for Nov 2006<jupyter_code>#loading files
path = '/ocean/nsoontie/MEOPAR/SalishSea/results/storm-surges/final/nov2006/'
runs = {'all_forcing','tidesonly'}
fUs={}; fVs={}; fTs={};
for key in runs:
fUs[key] = NC.Dataset(path + key +'/SalishSea_4h_20061112_20061118_grid_U.nc','r');
fVs[key] = NC.Dataset(path + key +'/SalishSea_4h_20061112_20061118_grid_V.nc','r');
fTs[key] = NC.Dataset(path + key +'/SalishSea_4h_20061112_20061118_grid_T.nc','r');
#preparing data
run_stations={}
us={}; vs={}; lats={}; lons={}; tmps={}; sals={}; sshs={}; ts={};
for run in runs:
for key in stations:
string = path + run + '/1h_' + key + '.nc'
run_stations[key] = NC.Dataset(string,'r');
tim = run_stations[key].variables['time_counter']
t_count=np.arange(0, tim.shape[0])
t=nc_tools.timestamp(run_stations[key],t_count)
tlist=[]
for a in t:
tlist.append(a.datetime)
ts[run]=tlist
[us[run], vs[run], lats[run], lons[run], tmps[run], sals[run], sshs[run]] = stormtools.combine_data(run_stations)
run_stations={};
#Observations and tidal predictions
start='31-Dec-2005'; end='02-Jan-2007'
wlev_meas={}; ttide={}; msl={}
for key in stations:
location=key
#filename for predictions
filename='/data/nsoontie/MEOPAR/analysis/storm_surges/data/'+location+'_t_tide_compare8_' +start+'_'+end+'.csv'
[ttide[key], msl[key]] = stormtools.load_tidal_predictions(filename)
wlev_meas[key] = stormtools.load_observations(start,end,location)
#ssh forcing
date_ssh = '01-Nov-2006'
time_ssh={}; ssh_forc={}
[ssh_forc['Tofino'], time_ssh['Tofino']] = stormtools.get_SSH_forcing('west',date_ssh)
[ssh_forc['Port Hardy'],time_ssh['Port Hardy']] = stormtools.get_SSH_forcing('north',date_ssh)
#plotting details
x_ax = ['Nov 12, 2006', 'Nov 19, 2006']
start='11-Nov-2006'; end='19-Nov-2006' #for CGRF
start_EC='01-Nov-2006'
end_EC='30-Nov-2006'
unaware=datetime.datetime.strptime(start,"%d-%b-%Y")
sdt = unaware.replace(tzinfo=tz.tzutc())
unaware=datetime.datetime.strptime(end,"%d-%b-%Y")
edt = unaware.replace(tzinfo=tz.tzutc())
(fig,axs)= plt.subplots(3,1,figsize=(6,7))
plot_station('PointAtkinson',axs)<jupyter_output>PointAtkinson
Maximum wind speed: 20.0
Time of maximum wind: 2006-11-15 17:00:00+00:00
<jupyter_text># Dec 2012<jupyter_code>#loading files
path = '/ocean/nsoontie/MEOPAR/SalishSea/results/storm-surges/final/dec2012/'
runs = {'CGRF/all_forcing','tidesonly'}
fUs={}; fVs={}; fTs={};
for key in runs:
fUs[key] = NC.Dataset(path + key +'/SalishSea_4h_20121214_20121218_grid_U.nc','r');
fVs[key] = NC.Dataset(path + key +'/SalishSea_4h_20121214_20121218_grid_V.nc','r');
fTs[key] = NC.Dataset(path + key +'/SalishSea_4h_20121214_20121218_grid_T.nc','r');
#preparing data
run_stations={}
us={}; vs={}; lats={}; lons={}; tmps={}; sals={}; sshs={}; ts={};
#fUs['all_forcing'] = fUs['CGRF/all_forcing']
#fVs['all_forcing'] = fVs['CGRF/all_forcing']
#fTs['all_forcing'] = fTs['CGRF/all_forcing']
#runs = {'all_forcing','tidesonly'}
for run in runs:
for key in stations:
string = path + run + '/1h_' + key + '.nc'
run_stations[key] = NC.Dataset(string,'r');
tim = run_stations[key].variables['time_counter']
t_count=np.arange(0, tim.shape[0])
t=nc_tools.timestamp(run_stations[key],t_count)
tlist=[]
for a in t:
tlist.append(a.datetime)
ts[run]=tlist
[us[run], vs[run], lats[run], lons[run], tmps[run], sals[run], sshs[run]] = stormtools.combine_data(run_stations)
run_stations={};
sshs['all_forcing']=sshs['CGRF/all_forcing']
ts['all_forcing']=ts['CGRF/all_forcing']
#Observations and tidal predictions
start='31-Dec-2011'; end='02-Jan-2013'
wlev_meas={}; ttide={}; msl={}
for key in stations:
location=key
#filename for predictions
filename='/data/nsoontie/MEOPAR/analysis/storm_surges/data/'+location+'_t_tide_compare8_' +start+'_'+end+'.csv'
[ttide[key], msl[key]] = stormtools.load_tidal_predictions(filename)
wlev_meas[key] = stormtools.load_observations(start,end,location)
#ssh forcing
date_ssh = '01-Dec-2012'
time_ssh={}; ssh_forc={}
[ssh_forc['Tofino'], time_ssh['Tofino']] = stormtools.get_SSH_forcing('west',date_ssh)
[ssh_forc['Port Hardy'],time_ssh['Port Hardy']] = stormtools.get_SSH_forcing('north',date_ssh)
#plotting details
x_ax = ['Dec 13, 2012', 'Dec 19, 2012']
start='11-Dec-2012'; end='18-Dec-2012' #for CGRF
start_EC='01-Dec-2012'
end_EC='31-Dec-2012'
unaware=datetime.datetime.strptime(start,"%d-%b-%Y")
sdt = unaware.replace(tzinfo=tz.tzutc())
unaware=datetime.datetime.strptime(end,"%d-%b-%Y")
edt = unaware.replace(tzinfo=tz.tzutc())
(fig,axs)= plt.subplots(3,1,figsize=(6,7))
plot_station('PointAtkinson',axs)<jupyter_output>PointAtkinson
Maximum wind speed: 15.5555555556
Time of maximum wind: 2012-12-15 18:00:00+00:00
|
permissive
|
/FigureScripts/Nov 2009 -weather compare.ipynb
|
ChanJeunlam/storm-surge
| 4 |
<jupyter_start><jupyter_text> Word Analogies Task
- In the word analogy task, we complete the sentence "a is to b as c is to ___". An example is 'man is to woman as king is to queen'.In detail, we are trying to find
a word d,such that the associated word vectors ea,eb,ec,ed are related in the following manner: eb-ea=ed-ec. We will measure
the similarity between eb-ea and ed-ec using cosine similarity.<jupyter_code>import gensim
from gensim.models import word2vec, KeyedVectors
from sklearn.metrics.pairwise import cosine_similarity
word_vectors=KeyedVectors.load_word2vec_format('GoogleNews-vectors-negative300.bin',binary=True)
type(word_vectors.vocab)
def predict_word(a,b,c,word_vectors):
a,b,c=a.lower(),b.lower(),c.lower()
#similarity between |b-a| =|d-c| should be max
max_similarity = -100
d = None
words = word_vectors.vocab.keys()
wa,wb,wc= word_vectors[a],word_vectors[b],word_vectors[c]
#to find d s.t similiarity (|b-a|,|d-c|) should be max
for w in words:
if w in [a,b,c]:
continue
wv=word_vectors[w]
sim= cosine_similarity([wb-wa],[wv-wc])
if sim> max_similarity:
max_similarity= sim
d = w
return d
triad_2=("man","woman","prince")
predict_word(*triad_2,word_vectors)<jupyter_output><empty_output><jupyter_text>Using the most similar method<jupyter_code>word_vectors.most_similar(positive=['woman','king'], negative=['man'],topn=1)<jupyter_output><empty_output>
|
no_license
|
/DS_Practice/Word2Vec/Word Analogies.ipynb
|
The-Nightwing/DataScience
| 2 |
<jupyter_start><jupyter_text># Nike Inc. (NKE) Stock Prices, Dividends and Splits<jupyter_code>## import library
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import quandl
import numpy as np
import matplotlib.pyplot as plt #for plotting
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
from sklearn import preprocessing,cross_validation
from sklearn.svm import SVR
#from mlxtend.regressor import StackingRegressor
from sklearn.model_selection import cross_val_score
from sklearn import metrics
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import RobustScaler
from sklearn.base import BaseEstimator, TransformerMixin, RegressorMixin, clone
from sklearn.model_selection import KFold, cross_val_score, train_test_split
from sklearn.metrics import mean_squared_error
## data source
quandl.ApiConfig.api_key = "zuiQMfguw3rRgLvkCzxk"
df=quandl.get('EOD/NKE')
##data summary
df.head()
## redefining data adding removin feture
### create the specfic ammount of label and feture
df1=df[['Adj_Open','Adj_High','Adj_Low','Adj_Close','Adj_Volume']]
###redefining the data
### adding some feture to the datasets
df1['volatility']=(df1['Adj_High']-df1['Adj_Close'])/df1['Adj_Close']
df1['PCT_Change']=(df1['Adj_Close']-df1['Adj_Open'])/df1['Adj_Open']
## making final dataframe
df1=df1[['Adj_Close','volatility','PCT_Change','Adj_Open','Adj_Volume']]
## setting the target column
forcast_col='Adj_Close'
## deal with the null data
df1.fillna(-999999,inplace=True)
## for predicting one percent of the data
import math
forcast_out = int(math.ceil(.1*(len(df1))))
print forcast_out
## displaying the previous output
Y=df1[forcast_col]
X=range(len(df1[forcast_col]))
fig_size=[30,5]
plt.rcParams["figure.figsize"] = fig_size
plt.plot(X,Y)
##storing the previous data in a dataframe
df1['label'] = df[forcast_col].shift(-forcast_out)
y1 = df1['label']
x1=range(len(df1['label']))
fig_size=[30,5]
plt.rcParams["figure.figsize"] = fig_size
plt.plot(x1,y1)
## dropping the first column which is the output
X=np.array(df1.drop(['label'],1))
##scale the data
X=preprocessing.scale(X)
X=X[:-forcast_out] ##data what is known
X_lately=X[-forcast_out:] ##data we predict
df1.dropna(inplace=True)
Y=np.array(df1['label'])
##split the training and testing data
xtrain,xtest,ytrain,ytest=cross_validation.train_test_split(X,Y,test_size=0.2)
## training separtely the classifier
##first knn
n_neighbors=1
clf1 = KNeighborsRegressor(n_neighbors) # create a classifire object
clf1.fit(xtrain,ytrain) # train data related with fir() method
accuracy1=clf1.score(xtest,ytest) # test data related with score() method
print "the accuracy is "+str(accuracy1)
## second linear regression
from sklearn.linear_model import LinearRegression
clf2 = LinearRegression() # create a classifire object
clf2.fit(xtrain,ytrain) # train data related with fir() method
accuracy2=clf2.score(xtest,ytest) # test data related with score() method
print "the accuracy is "+str(accuracy2)
## third support vector machine
from sklearn import svm
clf3 = svm.SVR() # create a classifire object
clf3.fit(xtrain,ytrain) # train data related with fir() method
accuracy3=clf3.score(xtest,ytest) # test data related with score() method
print "the accuracy is "+str(accuracy3)
clf4 = RandomForestRegressor(max_depth=2, random_state=0,n_estimators=100)
clf4.fit(xtrain,ytrain) # train data related with fir() method
accuracy4=clf4.score(xtest,ytest) # test data related with score() method
print "the accuracy is "+str(accuracy4)<jupyter_output>the accuracy is 0.9297961855367103
<jupyter_text># applying the stacking method we developed<jupyter_code>class AveragingModels(BaseEstimator, RegressorMixin, TransformerMixin):
def __init__(self, models):
self.models = models
# we define clones of the original models to fit the data in
def fit(self, X, y):
self.models_ = [clone(x) for x in self.models]
# Train cloned base models
for model in self.models_:
model.fit(X, y)
return self
#Now we do the predictions for cloned models and average them
def predict(self, X):
predictions = np.column_stack([
model.predict(X) for model in self.models_
])
return np.mean(predictions, axis=1)
averaged_models = AveragingModels(models = (clf1, clf2, clf3, clf4))
averaged_models.fit(xtrain,ytrain)
accuracy=averaged_models.score(xtest,ytest)
accuracy<jupyter_output><empty_output><jupyter_text>## This is better than the individual one<jupyter_code>
df2=pd.DataFrame()
df3=pd.DataFrame()
df4=pd.DataFrame()
df5=pd.DataFrame()
df6=pd.DataFrame()
forcast_set1=clf1.predict(X_lately)
forcast_set2=clf2.predict(X_lately)
forcast_set3=clf3.predict(X_lately)
forcast_set4=clf4.predict(X_lately)
final_forcast_set=averaged_models.predict(X_lately)
df2['forcast']=np.array(forcast_set1)
df3['forcast']=np.array(forcast_set2)
df4['forcast']=np.array(forcast_set3)
df5['forcast']=np.array(forcast_set4)
df6['forcast']=np.array(final_forcast_set)
fig_size=[30,30]
plt.rcParams["figure.figsize"] = fig_size
df2['forcast'].plot()
df3['forcast'].plot()
df4['forcast'].plot()
df5['forcast'].plot()
df6['forcast'].plot()
plt.legend(loc=4)
plt.ylabel('Price')<jupyter_output><empty_output>
|
no_license
|
/stock_market/Nike.ipynb
|
tanviredu/REGRESSION
| 3 |
<jupyter_start><jupyter_text>## Random sampling<jupyter_code>rs = pd.read_pickle('../../Resources/random-sampling.pkl')
rs.groupby(['run', 'set', 'metric']).count()['epoch'].describe()
43617 / np.round(rs.epoch.max())
rs_rolled = rolling(rs, window=700, skip=50)
p_rs = {
'style': 'set',
'dashes': True,
'markers': True,
'hue': 'seed',
'hue_order': list(map(lambda i: str(i), range(5))), # ['2', '3', '4']
'xticks_every': 5,
'xticks_minor': 5,
'ncol': 2,
}
fig, axes = accuracy_plots_per_model(data=rs_rolled,
style_order=['train', 'val', 'test'],
**p_rs,)
add_n_empty_items_to_legend(2, axes[0, 1])
fig.savefig('../../Resources/Thesis/random-sampling-classification-accuracy.pdf', format='pdf');
fig, axes = accuracy_plots_per_model(data=rs_rolled,
style_order=['train', 'val', 'test'],
**p_rs,)
add_n_empty_items_to_legend(2, axes[0, 1])
fig.savefig('../../Resources/Thesis/random-sampling-classification-accuracy.pdf', format='pdf');
fig, axes = cross_loss_plots_per_model(data=rs_rolled,
style_order=['train', 'val', 'test'],
**p_rs)
add_n_empty_items_to_legend(2, axes[0, 1])
fig.savefig('../../Resources/Thesis/random-sampling-classification-loss.pdf', format='pdf');
fig, axes = cross_loss_plots_per_model(data=rs_rolled[~((rs_rolled.model == 'N-BEATS') & (rs_rolled.set == 'test'))],
style_order=['train', 'val', 'test'],
**p_rs)
add_n_empty_items_to_legend(2, axes[0, 1])
fig.savefig('../../Resources/Thesis/random-sampling-classification-loss-no-nbeats-test.pdf', format='pdf');
fig, axes = mse_loss_plots_per_model(data=rs_rolled,
style_order=['train', 'val'],
**p_rs,)
add_n_empty_items_to_legend(2, axes[0, 1])
fig.savefig('../../Resources/Thesis/random-sampling-forecasting-loss-no-test.pdf', format='pdf');
fig, axes = mse_loss_plots_per_model(data=rs_rolled,
style_order=['train', 'val', 'test'],
**p_rs,)
add_n_empty_items_to_legend(2, axes[0, 1])
fig.savefig('../../Resources/Thesis/random-sampling-forecasting-loss.pdf', format='pdf');
fig, axes = triplet_loss_plots_per_model(data=rs_rolled[~((rs_rolled.model == 'N-BEATS') & (rs_rolled.set == 'test'))],
style_order=['train', 'val', 'test'],
**p_rs,)
add_n_empty_items_to_legend(2, axes[0, 1])
fig.savefig('../../Resources/Thesis/random-sampling-featurization-loss-no-nbeats-test.pdf', format='pdf');
fig, axes = triplet_loss_plots_per_model(data=rs_rolled,
style_order=['train', 'val', 'test'],
**p_rs,)
add_n_empty_items_to_legend(2, axes[0, 1])
fig.savefig('../../Resources/Thesis/random-sampling-featurization-loss.pdf', format='pdf');<jupyter_output><empty_output><jupyter_text>## Feature Freeze<jupyter_code>def pre_task_loss_plots_per_model(df: pd.DataFrame, task: str, **kwargs):
plot_f = {
'classification': cross_loss_plots_per_model,
'forecasting': mse_loss_plots_per_model,
'featurization': triplet_loss_plots_per_model,
}
return plot_f[task](
data=df[df.task == task],
hue_order=list(filter(lambda s: s != task, tasks)),
**kwargs
)
ff = pd.read_pickle('../../Resources/feature-freeze.pkl')
ff.groupby(['run', 'set', 'metric']).count()['epoch'].describe()
41250 / np.round(ff.epoch.max())
ff_rolled = rolling(ff, window=500, skip=20)
p_ff = {
'hue': 'pre-training task',
'style': 'set',
'dashes': True,
'markers': True,
'xticks_every': 2,
'xticks_minor': 2,
'ncol': 2,
}
fig, axes = accuracy_plots_per_model(
data=ff_rolled,
style_order=['train', 'val', 'test'],
hue_order=list(filter(lambda s: s != 'classification', tasks)),
**p_ff
)
fig.savefig('../../Resources/Thesis/feature-freeze-classification-accuracy.pdf', format='pdf');
fig, axes = pre_task_loss_plots_per_model(ff_rolled,
task='classification',
style_order=['train', 'val', 'test'],
**p_ff)
fig.savefig('../../Resources/Thesis/feature-freeze-classification-loss.pdf', format='pdf');
fig, axes = pre_task_loss_plots_per_model(ff_rolled[~((ff_rolled.model == 'N-BEATS') & (ff_rolled.set == 'test'))],
task='classification',
style_order=['train', 'val', 'test'],
**p_ff)
fig.savefig('../../Resources/Thesis/feature-freeze-classification-loss-no-nbeats-test.pdf', format='pdf');
fig, axes = pre_task_loss_plots_per_model(ff_rolled,
task='forecasting',
style_order=['train', 'val'],
**p_ff)
fig.savefig('../../Resources/Thesis/feature-freeze-forecasting-loss-no-test.pdf', format='pdf');
fig, axes = pre_task_loss_plots_per_model(ff_rolled,
task='forecasting',
style_order=['train', 'val', 'test'],
**p_ff)
fig.savefig('../../Resources/Thesis/feature-freeze-forecasting-loss.pdf', format='pdf');<jupyter_output><empty_output><jupyter_text>## Prober<jupyter_code>pr = pd.read_pickle('../../Resources/prober.pkl')
pr.groupby(['run', 'set', 'metric']).count()['epoch'].describe()
50625 / np.round(pr.epoch.max())
pr_rolled = rolling(pr, window=500, skip=20)
pr_rolled['task(s)'] = (pr_rolled['pre-training task'] + ' -> ' + pr_rolled['task'])\
.str.replace('none -> ', '')\
.str.replace('classification', 'clas.')\
.str.replace('forecasting', 'fore.')\
.str.replace('featurization', 'feat.')
prober_tasks = sorted(pr_rolled['task(s)'].unique(), key=lambda s: (len(s.split('->')), s))
p_pr = {
'style': 'set',
'style_order': ['train', 'val', 'test'],
'hue': 'task(s)',
'markers': True,
'dashes': True,
'xticks_every': 2,
'ncol': 2,
}
fig, axes = accuracy_plots_per_model(data=pr_rolled, **p_pr)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/prober-classification-accuracy.pdf', format='pdf');
fig, axes = cross_loss_plots_per_model(
data=pr_rolled[~((pr_rolled.model == 'N-BEATS') & (pr_rolled.set == 'test'))],
legend_pos=2, **p_pr
)
add_n_empty_items_to_legend(1, axes[1, 0])
fig.savefig('../../Resources/Thesis/prober-classification-loss-no-nbeats-test.pdf', format='pdf');
fig, axes = cross_loss_plots_per_model(
data=pr_rolled, **p_pr
)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/prober-classification-loss.pdf', format='pdf');
fig, axes = mse_loss_plots_per_model(
data=pr_rolled, **p_pr
)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/prober-forecasting-loss.pdf', format='pdf');
fig, axes = mse_loss_plots_per_model(
data=pr_rolled, **p_pr
)
add_n_empty_items_to_legend(2, axes[0, 1])
fig.savefig('../../Resources/Thesis/prober-forecasting-loss-no-test.pdf', format='pdf');
fig, axes = triplet_loss_plots_per_model(
data=pr_rolled, **p_pr
)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/prober-featurization-loss.pdf', format='pdf');
fig, axes = triplet_loss_plots_per_model(
data=pr_rolled[~((pr_rolled.model == 'N-BEATS') & (pr_rolled.set == 'test'))], legend_pos=2, **p_pr
)
add_n_empty_items_to_legend(1, axes[1, 0])
fig.savefig('../../Resources/Thesis/prober-featurization-loss-no-nbeats-test.pdf', format='pdf');<jupyter_output><empty_output><jupyter_text>## Few Shot (Sprott)<jupyter_code>fs = pd.read_pickle('../../Resources/few-shot.pkl')
fs.groupby(['run', 'set', 'metric']).count()['value'].describe()
2726 / np.round(fs.epoch.max())
fs_rolled = rolling(fs, window=100, skip=5)
p_fs = {
'x': 'epoch',
'hue': 'attractors, pre-training',
'style': 'set',
'xticks_every': 2,
'dashes': True,
'markers': True,
#'ncol': 3,
}
fs_filtered = fs_rolled[fs_rolled['pre-training'] != 'none'].copy()
fs_filtered['attractors, pre-training'] = fs_filtered['attractors'] + ', ' + fs_filtered['pre-training']
fig, axes = accuracy_plots_per_model(data=fs_filtered,
style_order=['train', 'val', 'test'],
**p_fs)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/few-shot-classification-accuracy.pdf', format='pdf');
fig, axes = plots_per_model(
data=fs_filtered[fs_filtered.metric == 'SprottE.sensitivity'],
style_order=['train', 'val', 'test'],
y='value', ylabel='SprottE sensitivity', ylogscale=False,
**p_fs
)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/few-shot-sprott-sensitivity.pdf', format='pdf');
fig, axes = plots_per_model(
data=fs_filtered[fs_filtered.metric == 'SprottE.specificity'],
style_order=['train', 'val', 'test'],
y='value', ylabel='SprottE specificity', ylogscale=False,
**p_fs
)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/few-shot-sprott-specificity.pdf', format='pdf');
fig, axes = cross_loss_plots_per_model(data=fs_filtered,
style_order=['train', 'val', 'test'],legend_pos=2,
**p_fs)
add_n_empty_items_to_legend(1, axes[1, 0])
fig.savefig('../../Resources/Thesis/few-shot-classification-loss.pdf', format='pdf');
fig, axes = mse_loss_plots_per_model(data=fs_filtered,
style_order=['train', 'val', 'test'],
**p_fs)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/few-shot-forecasting-loss.pdf', format='pdf');
fig, axes = plots_per_model(
data=fs_filtered[fs_filtered.metric == 'SprottE.loss.mse'],
style_order=['train', 'val', 'test'],
y='value', ylabel='SprottE MSE', ylogscale=True,
**p_fs
)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/few-shot-sprott-mse.pdf', format='pdf');
fig, axes = plots_per_model(
data=fs_filtered[fs_filtered.metric == 'SprottE.feature.std'],
style_order=['train', 'val', 'test'],
y='value', ylabel='Feature standard deviation', ylogscale=False,
**p_fs
)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/few-shot-sprott-feature-std.pdf', format='pdf');
fig, axes = plots_per_model(
data=fs_filtered[fs_filtered.metric == 'loss.triplet'],
style_order=['train', 'val', 'test'],
y='value', ylabel='Triplet loss', ylogscale=True,
**p_fs
)
add_n_empty_items_to_legend(1, axes[0, 1])
fig.savefig('../../Resources/Thesis/few-shot-featurisation-loss.pdf', format='pdf');<jupyter_output><empty_output>
|
no_license
|
/notebooks/Plot Results.ipynb
|
streitlua/esa_ecodyna
| 4 |
<jupyter_start><jupyter_text>Loss Surfaces, Mode Connectivity, and Fast Ensembling of DNNs
Timur Garipov, Pavel Izmailov, Dmitrii Podoprikhin, Dmitry Vetrov, Andrew Gordon Wilson
Classification with Wide ResNet and CIFAR10<jupyter_code>import os
import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import torch
import torch.nn as nn
import torch.nn.functional as F
m = nn.Softplus()
from google.colab import drive
drive.mount('/content/drive')
import torchvision
import torchvision.transforms as transforms
data_dir = '/content/drive/My Drive/AALTO/cs4875-research/data/'
transform = transforms.Compose([
transforms.ToTensor(), # Transform to tensor
transforms.Normalize((0.5,), (0.5,)) # Min-max scaling to [-1, 1]
])
trainset = torchvision.datasets.CIFAR10(root=data_dir, train=True, download=True, transform=transform)
testset = torchvision.datasets.CIFAR10(root=data_dir, train=False, download=True, transform=transform)
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
trainloader = torch.utils.data.DataLoader(trainset, batch_size=32, shuffle=True)
testloader = torch.utils.data.DataLoader(testset, batch_size=5, shuffle=False)
class Block(nn.Module):
def __init__(self, in_channels, out_channels, dropout_rate, stride=1):
"""
Args:
in_channels: Number of input channels.
out_channels: Number of output channels.
dropout_rate: Dropout Rate
stride: Controls the stride.
"""
super(Block, self).__init__()
self.conv = nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.ReLU(inplace = True),
nn.Conv2d(in_channels, out_channels, kernel_size=3, bias=False, padding = 1),
nn.Dropout(p = dropout_rate),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace = True),
nn.Conv2d(out_channels, out_channels, kernel_size=3, bias=False, stride = stride, padding = 1)
)
self.skip = nn.Sequential()
if stride != 1 or in_channels != out_channels:
self.skip = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride, bias=False),
)
def forward(self, x):
out = self.conv(x)
out += self.skip(x)
return out
class GroupOfBlocks(nn.Module):
def __init__(self, in_channels, out_channels, n_blocks, dropout_rate, stride=1):
super(GroupOfBlocks, self).__init__()
strides = [stride] + [1]*(int(n_blocks) - 1)
self.in_channels = in_channels
group = []
for stride in strides:
group.append(Block(self.in_channels, out_channels, dropout_rate, stride))
self.in_channels = out_channels
self.group = nn.Sequential(*group)
def forward(self, x):
return self.group(x)
class WideResNet(nn.Module):
def __init__(self, depth, widen_factor, dropout_rate, num_classes=10):
super(WideResNet, self).__init__()
assert ((depth-4)%6 == 0), "Depth should be 6n+4."
n = (depth - 4)/6
k = widen_factor
nStages = [16, 16*k, 32*k, 64*k]
self.conv1 = nn.Conv2d(in_channels=3, out_channels=nStages[0], kernel_size=3, stride=1, padding=1, bias=False)
self.group1 = GroupOfBlocks(nStages[0], nStages[1], n, dropout_rate)
self.group2 = GroupOfBlocks(nStages[1], nStages[2], n, dropout_rate, stride=2)
self.group3 = GroupOfBlocks(nStages[2], nStages[3], n, dropout_rate, stride=2)
self.bn1 = nn.BatchNorm2d(nStages[3])
self.relu = nn.ReLU(inplace=True)
self.fc = nn.Linear(nStages[3], num_classes)
self.nStage3 = nStages[3]
# Initialize weights
for m in self.modules():
if isinstance(m, nn.Conv2d):
n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, np.sqrt(2. / n))
elif isinstance(m, nn.BatchNorm2d):
m.weight.data.fill_(1)
m.bias.data.zero_()
def forward(self, x):
x = self.conv1(x)
x = self.group1(x)
x = self.group2(x)
x = self.group3(x)
x = self.relu(self.bn1(x))
x = F.avg_pool2d(x, 8)
x = x.view(-1, self.nStage3)
return self.fc(x)
# code adapted from https://github.com/timgaripov/dnn-mode-connectivity
def learning_rate_schedule(base_lr, epoch, total_epochs):
alpha = epoch / total_epochs
if alpha <= 0.5:
factor = 1.0
elif alpha <= 0.9:
factor = 1.0 - (alpha - 0.5) / 0.4 * 0.99
else:
factor = 0.01
return factor * base_lr
def adjust_learning_rate(optimizer, lr):
for param_group in optimizer.param_groups:
param_group['lr'] = lr
return lr
def cyclic_learning_rate(epoch, cycle, alpha_1, alpha_2):
def schedule(iter):
t = ((epoch % cycle) + iter) / cycle
if t < 0.5:
return alpha_1 * (1.0 - 2.0 * t) + alpha_2 * 2.0 * t
else:
return alpha_1 * (2.0 * t - 1.0) + alpha_2 * (2.0 - 2.0 * t)
return schedule
def save_checkpoint(dir, epoch, name='checkpoint', **kwargs):
state = {
'epoch': epoch,
}
state.update(kwargs)
filepath = os.path.join(dir, '%s-%d.pt' % (name, epoch))
torch.save(state, filepath)
def compute_accuracy(net, testloader):
net.eval()
correct = 0
total = 0
with torch.no_grad():
for images, labels in testloader:
images, labels = images.to(device), labels.to(device)
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
return correct / total
device = torch.device('cuda:0')
loss_func = nn.CrossEntropyLoss()
m = nn.LogSoftmax(dim=1)
def compute_brier_score(p, y):
brier_score = torch.mean((y-torch.argmax(p, 1).float())**2)
return brier_score
def ensembleEndpoint(model, optimizer):
running_loss = 0.0
running_brier = 0.0
startEpoch = 1
for epoch in range(startEpoch, numEpochs+1):
model.train()
learning_rate = learning_rate_schedule(0.01, epoch, numEpochs)
adjust_learning_rate(optimizer, learning_rate)
brier_score = 0.0
total = 0
for iter, (x, y) in enumerate(trainloader):
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
output = model(x)
batch_brier_score = compute_brier_score(output, y)
brier_score += torch.sum(batch_brier_score, 0).cpu().numpy().item()
loss = loss_func(output, y)
loss.backward()
optimizer.step()
total += y.size(0)
if epoch == (numEpochs-1):
running_loss = loss.item()
print('Loss at epoch {} is {}'.format(epoch, loss.item()))
print('Brier score at epoch {} is {}'.format(epoch, brier_score/total))
return running_loss, brier_score/total
numEpochs = 100
lr = 0.1
model = WideResNet(28, 4, 0.5)
model.to(device)
optimizer = torch.optim.SGD(
filter(lambda param: param.requires_grad, model.parameters()),
lr=lr,
momentum=0.9,
weight_decay=5e-4
)
t0 = time.time()
loss, brier = ensembleEndpoint(model, optimizer)
# print('NLL Loss is {}'.format(loss))
# print('Brier score is {}'.format(brier))
# print('Training endpoint time: {} seconds'.format(time.time() - t0))
# accuracy = compute_accuracy(model, testloader)
# print('Accuracy of the network on the test images: %.3f' % accuracy)
torch.save(model.state_dict(), '/content/drive/My Drive/AALTO/cs4875-research/archive/fge_ensemble-wrn28-4-100.pth')
print('Model saved to %s.' % ('fge_ensemble-wrn28-4-100.pth'))
device = torch.device('cuda:0')
loss_func = nn.CrossEntropyLoss()
m = nn.LogSoftmax(dim=1)
def compute_brier_score(p, y):
brier_score = torch.mean((y-torch.argmax(p, 1).float())**2)
return brier_score
def ensembleEndpoint(model, optimizer):
running_loss = 0.0
running_brier = 0.0
startEpoch = 1
for epoch in range(startEpoch, numEpochs+1):
model.train()
# learning_rate = learning_rate_schedule(0.01, epoch, numEpochs)
# adjust_learning_rate(optimizer, learning_rate)
brier_score = 0.0
total = 0
for iter, (x, y) in enumerate(trainloader):
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
output = model(x)
batch_brier_score = compute_brier_score(output, y)
brier_score += torch.sum(batch_brier_score, 0).cpu().numpy().item()
loss = loss_func(output, y)
loss.backward()
optimizer.step()
total += y.size(0)
if epoch == (numEpochs-1):
running_loss = loss.item()
print('Loss at epoch {} is {}'.format(epoch, loss.item()))
print('Brier score at epoch {} is {}'.format(epoch, brier_score/total))
return running_loss, brier_score/total
numEpochs = 40
lr = 0.1
model = WideResNet(28, 4, 0.5)
model.to(device)
# optimizer = torch.optim.SGD(
# filter(lambda param: param.requires_grad, model.parameters()),
# lr=lr,
# momentum=0.9,
# weight_decay=5e-4
# )
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
t0 = time.time()
loss, brier = ensembleEndpoint(model, optimizer)
print('Training time: {} seconds'.format(time.time() - t0))
# print('NLL Loss is {}'.format(loss))
# print('Brier score is {}'.format(brier))
# print('Training endpoint time: {} seconds'.format(time.time() - t0))
# accuracy = compute_accuracy(model, testloader)
# print('Accuracy of the network on the test images: %.3f' % accuracy)
torch.save(model.state_dict(), '/content/drive/My Drive/AALTO/cs4875-research/archive/fge_ensemble-adam-40.pth')
print('Model saved to %s.' % ('fge_ensemble-adam-40.pth'))
def ensembleFGE(model, optimizer):
startEpoch = 1
cycle=4
ensemble_size = 0
t0 = time.time()
for epoch in range(startEpoch, numEpochs+1):
num_iters = len(trainloader)
model.train()
lr_schedule = cyclic_learning_rate(epoch, cycle, lr_1, lr_2)
learning_rate = learning_rate_schedule(0.01, epoch, numEpochs)
adjust_learning_rate(optimizer, learning_rate)
total = 0
for iter, (x, y) in enumerate(trainloader):
lr = lr_schedule(iter / num_iters)
adjust_learning_rate(optimizer, lr)
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
output = model(x)
loss = loss_func(output, y)
loss.backward()
optimizer.step()
total += y.size(0)
if epoch == (numEpochs-1):
running_loss = loss.item()
print('Training loss at epoch {} is {}'.format(epoch, loss.item()))
if (epoch % cycle + 1) == cycle // 2:
ensemble_size += 1
accuracy = compute_accuracy(model, testloader)
print('Testing accuracy at epoch {} is {}'.format(epoch, accuracy))
print('Training FGE time: {} seconds with {} emsemble size'.format((time.time() - t0), ensemble_size))
if (epoch + 1) % (cycle // 2) == 0:
save_checkpoint(
'/content/drive/My Drive/AALTO/cs4875-research/archive/fge2/',
startEpoch + epoch,
name='fge',
model_state=model.state_dict(),
optimizer_state=optimizer.state_dict()
)
print('Number of models in ensemble is {}'.format(ensemble_size))
return running_loss
numEpochs = 40
training_loss = []
training_brier = []
lr_1=0.05
lr_2=0.01
optimizer = torch.optim.SGD(
filter(lambda param: param.requires_grad, model.parameters()),
lr=lr_1,
momentum=0.9,
weight_decay=5e-4
)
loss = ensembleFGE(model, optimizer)
torch.save(model.state_dict(), '/content/drive/My Drive/AALTO/cs4875-research/archive/fge2_ensemble-80-0112.pth')
print('Model saved to %s.' % ('fge2_ensemble-80-0112.pth'))
# train to get data - training time and accuracy
def load_model(model, filename, device):
model.load_state_dict(torch.load(filename, map_location=lambda storage, loc: storage))
print('Model loaded from %s.' % filename)
model.to(device)
model.eval()
device = torch.device('cuda:0')
loss_func = nn.CrossEntropyLoss()
fge2_ensemble = WideResNet(28, 4, 0.5)
load_model(fge2_ensemble, '/content/drive/My Drive/AALTO/cs4875-research/archive/fge2_ensemble-80-0112.pth', device)
def ensembleFGE(model, optimizer):
startEpoch = 1
cycle=4
ensemble_size = 0
t0 = time.time()
for epoch in range(startEpoch, numEpochs+1):
num_iters = len(trainloader)
model.train()
lr_schedule = cyclic_learning_rate(epoch, cycle, lr_1, lr_2)
learning_rate = learning_rate_schedule(0.01, epoch, numEpochs)
adjust_learning_rate(optimizer, learning_rate)
total = 0
for iter, (x, y) in enumerate(trainloader):
lr = lr_schedule(iter / num_iters)
adjust_learning_rate(optimizer, lr)
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
output = model(x)
loss = loss_func(output, y)
loss.backward()
optimizer.step()
total += y.size(0)
if epoch == (numEpochs-1):
running_loss = loss.item()
print('Training loss at epoch {} is {}'.format(epoch, loss.item()))
if (epoch % cycle + 1) == cycle // 2:
ensemble_size += 1
accuracy = compute_accuracy(model, testloader)
print('Testing accuracy at epoch {} is {}'.format(epoch, accuracy))
print('Training FGE time: {} seconds with {} emsemble size'.format((time.time() - t0), ensemble_size))
if (epoch + 1) % (cycle // 2) == 0:
save_checkpoint(
'/content/drive/My Drive/AALTO/cs4875-research/archive/fge3/',
startEpoch + epoch,
name='fge',
model_state=model.state_dict(),
optimizer_state=optimizer.state_dict()
)
print('Number of models in ensemble is {}'.format(ensemble_size))
return running_loss
numEpochs = 30
training_loss = []
training_brier = []
lr_1=0.05
lr_2=0.01
optimizer = torch.optim.SGD(
filter(lambda param: param.requires_grad, fge2_ensemble.parameters()),
lr=lr_1,
momentum=0.9,
weight_decay=5e-4
)
loss = ensembleFGE(fge2_ensemble, optimizer)
torch.save(model.state_dict(), '/content/drive/My Drive/AALTO/cs4875-research/archive/fge2_ensemble-100-0113.pth')
print('Model saved to %s.' % ('fge2_ensemble-100-0113.pth'))
def ensembleFGE(model, optimizer):
startEpoch = 1
cycle=4
ensemble_size = 0
t0 = time.time()
for epoch in range(startEpoch, numEpochs+1):
num_iters = len(trainloader)
model.train()
lr_schedule = cyclic_learning_rate(epoch, cycle, lr_1, lr_2)
learning_rate = learning_rate_schedule(0.01, epoch, numEpochs)
adjust_learning_rate(optimizer, learning_rate)
total = 0
for iter, (x, y) in enumerate(trainloader):
lr = lr_schedule(iter / num_iters)
adjust_learning_rate(optimizer, lr)
x, y = x.to(device), y.to(device)
optimizer.zero_grad()
output = model(x)
loss = loss_func(output, y)
loss.backward()
optimizer.step()
total += y.size(0)
if epoch == (numEpochs-1):
running_loss = loss.item()
print('Training loss at epoch {} is {}'.format(epoch, loss.item()))
if (epoch % cycle + 1) == cycle // 2:
ensemble_size += 1
accuracy = compute_accuracy(model, testloader)
print('Testing accuracy at epoch {} is {}'.format(epoch, accuracy))
print('Training FGE time: {} seconds with {} emsemble size'.format((time.time() - t0), ensemble_size))
if (epoch + 1) % (cycle // 2) == 0:
save_checkpoint(
'/content/drive/My Drive/AALTO/cs4875-research/archive/fge/',
startEpoch + epoch,
name='fge',
model_state=model.state_dict(),
optimizer_state=optimizer.state_dict()
)
print('Number of models in ensemble is {}'.format(ensemble_size))
return running_loss
numEpochs = 40
training_loss = []
training_brier = []
lr_1=0.05
lr_2=0.01
optimizer = torch.optim.SGD(
filter(lambda param: param.requires_grad, model.parameters()),
lr=lr_1,
momentum=0.9,
weight_decay=5e-4
)
loss = ensembleFGE(model, optimizer)
torch.save(model.state_dict(), '/content/drive/My Drive/AALTO/cs4875-research/archive/fge_ensemble-140-0111.pth')
print('Model saved to %s.' % ('fge_ensemble-140-0111.pth'))
<jupyter_output><empty_output>
|
no_license
|
/FastGeometricEnsemble.ipynb
|
zhiheng-qian/cs4875-research-project
| 1 |
<jupyter_start><jupyter_text>## Python statistics essential training - 04_04_testingStandard imports<jupyter_code>import math
import io
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as pp
%matplotlib inline
import scipy.stats
import scipy.optimize
import scipy.spatial
pumps = pd.read_csv('pumps.csv')
pumps
cholera = pd.read_csv('cholera.csv')
cholera.shape
cholera.loc[0::20]
pp.figure(figsize=(6,6))
pp.scatter(pumps.x,pumps.y,color='b')
pp.scatter(cholera.x,cholera.y,color='r',s=3)
img = matplotlib.image.imread('london.png')
pp.figure(figsize=(10,10))
pp.imshow(img,extent=[-0.38,0.38,-0.38,0.38])
pp.scatter(pumps.x,pumps.y,color='b')
pp.scatter(cholera.x,cholera.y,color='r',s=3)
cholera.closest.value_counts()
cholera.groupby('closest').deaths.sum()
def simulate(n):
return pd.DataFrame({'closest': np.random.choice([0,1,4,5],size=n,p=[0.65,0.15,0.10,0.10])})
simulate(489).closest.value_counts()
sampling = pd.DataFrame({'counts': [simulate(489).closest.value_counts()[0] for i in range(10000)]})
sampling.counts.hist(histtype='step')
scipy.stats.percentileofscore(sampling.counts,340)
100 - 98.14<jupyter_output><empty_output>
|
no_license
|
/Unit8/Exercise Files/chapter4/04_04/.ipynb_checkpoints/04_04_testing_end-checkpoint.ipynb
|
varsha2509/Springboard-DS
| 1 |
<jupyter_start><jupyter_text>We now have a representation of a deck of cards, with each card as a string.
This is ... not ideal.Object oriented Cards
WHAT DO WE WANT THE Cards to be able to do??
* card should be able to return its own rank
* card should be able to return its own suit
* card should be able to print its value as a string, e.g. '2 of Hearts'<jupyter_code># DON'T USE THIS CODE
class Card:
SUITS = ['Hearts', 'Clubs', 'Diamonds', 'Spades']
RANKS = ['2', '3', '4', '5', '6', '7', '8', '9', '10', 'J', 'Q', 'K', 'A']
def __init__(self, rank, suit):
self.rank = rank
self.suit = suit
<jupyter_output><empty_output><jupyter_text>Turns out, the cards print themselves in an ugly way if we use the code above.
Let's try it..<jupyter_code>#This does the same thing ==> c1 = Card('2', 'Hearts')
c1 = Card(rank='2', suit='Hearts')
print(c1) #we just get the memory address
print(c1.rank) #but this works nicely
print(c1.suit) #so does this<jupyter_output>Hearts
<jupyter_text>So, let's try again!!<jupyter_code># DON'T USE THIS CODE
class Card:
SUITS = ['Hearts', 'Clubs', 'Diamonds', 'Spades']
RANKS = ['2', '3', '4', '5', '6', '7', '8', '9', '10', 'J', 'Q', 'K', 'A']
def __init__(self, rank, suit):
self.rank = rank
self.suit = suit
def print_yourself(self):
return f'{self.rank} of {self.suit}'
c2.print() # this doesn't work
c2 = Card(rank='2', suit='Hearts')
print(c2)
c2.print_yourself()
That looks better!!
But I hate having to invoke 'print_yourself()' every time!<jupyter_output><empty_output><jupyter_text>### I wonder if the Grand High Exalted Mystic Ruler thought of another way to do this?????<jupyter_code># Let's look at what we get for free when we make our Card class
dir(Card)<jupyter_output><empty_output><jupyter_text>Turns out, there is a MAGIC/DUNDER METHOD that tells an object to print itself: '__str__'By default, this method '__str__' just says 'print the type of object I am and also my memory address'
BUT WE CAN CHANGE IT!!!
In Python, we are allowed to OVERRIDE the default behavior of any MAGIC METHOD to fit our needs, so that the class we create behaves how we want it to.<jupyter_code># DON'T USE THIS CODE
#So, this is the proper pythonic way to write the Card class so it prints itself:
class Card:
SUITS = ['Hearts', 'Clubs', 'Diamonds', 'Spades']
RANKS = ['2', '3', '4', '5', '6', '7', '8', '9', '10', 'J', 'Q', 'K', 'A']
def __init__(self, rank, suit):
self.rank = rank
self.suit = suit
def __str__(self): #this tells the class how we want it to print itself as a string!
return f'{self.rank} of {self.suit}'
c3 = Card(rank='2', suit='Hearts')
print(c3)
c3.rank
c3.suit<jupyter_output><empty_output><jupyter_text>There's one more thing that I left off of the original list for the card class.
It needs to know when two cards are equal!
Right now, it doesn't!
It will just check the id, and if the id's are not the same, it will say the two cards are not equal!<jupyter_code>c3 = Card(rank='2', suit='Hearts')
c4 = Card(rank='2', suit='Hearts')
# We would like Python to know that these two cards are EQUAL.
c3 == c4 # compares ids of c3 and c4. BAD. It gives an answer that doesn't make sense to us, the designers of this class
id(c3) == id(c4)<jupyter_output><empty_output><jupyter_text>### I wonder if the Grand High Exalted Mystic Ruler thought of a way to fix this problem, too?????##### Spoiler: He did. Can you guess what we have to add to our code to do it???<jupyter_code>class Card:
SUITS = ['Hearts', 'Clubs', 'Diamonds', 'Spades']
RANKS = ['2', '3', '4', '5', '6', '7', '8', '9', '10', 'J', 'Q', 'K', 'A']
def __init__(self, rank, suit):
self.rank = rank
self.suit = suit
def __str__(self): #this tells the class how we want it to print itself as a string!
return f'{self.rank} of {self.suit}'
dir(Card)
class Card:
SUITS = ['Hearts', 'Clubs', 'Diamonds', 'Spades']
RANKS = ['2', '3', '4', '5', '6', '7', '8', '9', '10', 'J', 'Q', 'K', 'A']
def __init__(self, rank, suit):
self.rank = rank
self.suit = suit
def __str__(self): #this tells the class how we want it to print itself as a string!
return f'{self.rank} of {self.suit}'
# def __eq__(self, other):
# if self.rank == other.rank and self.suit == other.suit:
# return True
# else:
# return False
def __eq__(self, other):
return self.rank == other.rank and self.suit == other.suit
c5 = Card(rank='2', suit='Hearts')
c6 = Card(rank='2', suit='Hearts')
c5 == c6
id(c5), id(c6)
class Card:
SUITS = ['Hearts', 'Clubs', 'Diamonds', 'Spades']
RANKS = ['2', '3', '4', '5', '6', '7', '8', '9', '10', 'J', 'Q', 'K', 'A']
def __init__(self, rank, suit):
self.rank = rank
self.suit = suit
def __str__(self): #this tells the class how we want it to print itself as a string!
return f'{self.rank} of {self.suit}'
def __eq__(self, other):
return self.rank == other.rank and self.suit == other.suit
### Let's move on to the Deck class
# what do we want the Deck object to be able to do??
class Deck:
pass
* __init__
* shuffle
* deal
#DON'T USE THIS CODE
class Deck:
def __init__(self):
self.deck = []
for suit in Card.SUITS:
for rank in Card.RANKS:
c = Card(rank, suit)
self.deck.append(c)
# deck = []
# for suit in SUITS:
# for rank in RANKS:
# deck.append(f'{rank} of {suit}')
d1 = Deck()
d1
d1.deck
len(d1.deck)
import random
random.shuffle??
#DON'T USE THIS CODE
import random
class Deck:
def __init__(self):
self.deck = []
for suit in Card.SUITS:
for rank in Card.RANKS:
c = Card(rank, suit)
self.deck.append(c)
def shuffle(self):
random.shuffle(self.deck)
d2 = Deck()
d2<jupyter_output><empty_output>
|
no_license
|
/cards.ipynb
|
seanreed1111/oop-2
| 7 |
<jupyter_start><jupyter_text>_Note: heainit must already be running in the terminal you run this from if you want to make and run XSPEC scripts!_<jupyter_code>from astropy.table import Table, Column
import numpy as np
import os
import subprocess
from scipy.fftpack import fftfreq
# from scipy.stats import binned_statistic
import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager
from matplotlib.ticker import MultipleLocator
import matplotlib.patches as patches
from matplotlib.collections import PatchCollection
from matplotlib.ticker import ScalarFormatter, NullFormatter
from matplotlib.colors import cnames as mcolors
import matplotlib.colors as colors
from matplotlib._color_data import XKCD_COLORS as xkcdcolor
from xcor_tools import geom_rb, find_nearest
%matplotlib inline
font_prop = font_manager.FontProperties(size=20)
homedir = os.path.expanduser("~")
maxi_dir = homedir+"/Dropbox/Research/MAXIJ1535_QPO"
os.chdir(maxi_dir)
cs1_file = maxi_dir+"/out/MAXIJ1535_64sec_256dt_ratecut_cs.fits"
assert os.path.isfile(cs1_file), "Fits file with cross spectrum does not exist."
cs1_tab = Table.read(cs1_file, format='fits')
print(cs1_tab.info)
# print(cs1_tab.meta)
cs2_file = maxi_dir+"/out/MAXIJ1535_64sec_256dt_window2_cs.fits"
cs2_tab = Table.read(cs2_file, format='fits')
cs3_file = maxi_dir+"/out/MAXIJ1535_64sec_256dt_window3_cs.fits"
cs3_tab = Table.read(cs3_file, format='fits')
cs4_file = maxi_dir+"/out/MAXIJ1535_64sec_256dt_window4_cs.fits"
cs4_tab = Table.read(cs4_file, format='fits')
rebin_by = 1.06
fileroot = cs1_file.replace('.fits','').replace('_cs', '')
print(fileroot)
fit_with_noise = False
# fit_with_noise = True
if fit_with_noise:
out_file_df = fileroot+"-wnoise.txt"
flx2xsp_cmd_file = fileroot+"-wnoise_flx2xsp.sh"
else:
out_file_df = fileroot+"-nonoise.txt"
flx2xsp_cmd_file = fileroot+"-nonoise_flx2xsp.sh"
if "hard" in cs1_file:
spec_type = "hard"
elif "window4" in cs1_file:
spec_type="win4"
else:
spec_type = "normal"
print(fit_with_noise)
print(spec_type)
n_seg = cs1_tab.meta['N_SEG']
df = cs1_tab.meta['DF']
dt = cs1_tab.meta['DT']
n_bins = cs1_tab.meta['N_BINS']
n_chans = cs1_tab.meta['N_CHANS']
pos_freq = cs1_tab['FREQUENCY'][0:int(n_bins/2)]
# power = cs1_tab['PSD_REF'][0:int(n_bins/2)]
power1 = cs1_tab['PSD_BROAD'][0:int(n_bins/2)]/ cs1_tab.meta['RATE_BROAD'] ** 2
error1 = power1 / np.sqrt(n_seg) ## computing it in linear re-binning
hf = int(find_nearest(pos_freq, 50)[1])
power2 = cs2_tab['PSD_BROAD'][0:int(n_bins/2)]/ cs2_tab.meta['RATE_BROAD'] ** 2
error2 = power2 / np.sqrt(n_seg)
power3 = cs3_tab['PSD_BROAD'][0:int(n_bins/2)]/ cs3_tab.meta['RATE_BROAD'] ** 2
error3 = power3 / np.sqrt(n_seg)
power4 = cs4_tab['PSD_BROAD'][0:int(n_bins/2)]/ cs4_tab.meta['RATE_BROAD'] ** 2
error4 = power4 / np.sqrt(n_seg)
if not fit_with_noise:
noise_level1 = np.mean(power1[hf:int(n_bins/2)])
print(noise_level1)
power1 -= noise_level1
print(noise_level1)
noise_level2 = np.mean(power2[hf:int(n_bins/2)])
power2 -= noise_level2
noise_level3 = np.mean(power3[hf:int(n_bins/2)])
power3 -= noise_level3
noise_level4 = np.mean(power4[hf:int(n_bins/2)])
power4 -= noise_level4
rb_freq, rb_power1, rb_err1, f_min, f_max = geom_rb(pos_freq, \
power1, error1, rebin_const=rebin_by)
f_bin_span = f_max - f_min
fpf_psd1 = rb_power1 * rb_freq
fpf_err1 = rb_freq * rb_err1
rb_freq, rb_power2, rb_err2, t1, t2 = geom_rb(pos_freq, \
power2, error2, rebin_const=rebin_by)
fpf_psd2 = rb_power2 * rb_freq
fpf_err2 = rb_err2 * rb_freq
rb_freq, rb_power3, rb_err3, t1, t2 = geom_rb(pos_freq, \
power3, error3, rebin_const=rebin_by)
fpf_psd3 = rb_power3 * rb_freq
fpf_err3 = rb_err3 * rb_freq
rb_freq, rb_power4, rb_err4, t1, t2 = geom_rb(pos_freq, \
power4, error4, rebin_const=rebin_by)
fpf_psd4 = rb_power4 * rb_freq
fpf_err4 = rb_err4 * rb_freq
fig, ax = plt.subplots(1, 1, figsize=(9, 6.75), dpi=300, tight_layout=True)
# ax.plot(rb_freq, fpf_psd1, color=xkcdcolor['xkcd:fuchsia'], linestyle='dashed', lw=2, zorder=3, label="Days 20-23")
# ax.plot(rb_freq, fpf_psd2, color=xkcdcolor['xkcd:tangerine'], lw=2, zorder=2, label="Days 23-26")
# ax.plot(rb_freq, fpf_psd3, color=xkcdcolor['xkcd:deep green'], lw=2, zorder=1, label="Days 26-30")
# ax.plot(rb_freq, fpf_psd4, color=xkcdcolor['xkcd:electric blue'], linestyle='dotted', lw=2, zorder=4, label="Days 36-39")
# ax.errorbar(rb_freq, fpf_psd3, yerr=fpf_err3, color=xkcdcolor['xkcd:deep green'], lw=2, zorder=3, label="Days 20-23")
# ax.errorbar(rb_freq, fpf_psd2, yerr=fpf_err2, color=xkcdcolor['xkcd:tangerine'], lw=2, zorder=2, label="Days 23-26")
# ax.errorbar(rb_freq, fpf_psd1, yerr=fpf_err1, color=xkcdcolor['xkcd:fuchsia'], linestyle='dashed', lw=2, zorder=1, label="Days 26-30")
# ax.errorbar(rb_freq, fpf_psd4, yerr=fpf_err4, color=xkcdcolor['xkcd:electric blue'], linestyle='dotted', lw=2, zorder=4, label="Days 36-39")
# ax.errorbar(rb_freq, fpf_psd2, yerr=fpf_err2, color='black', lw=2)
ax.errorbar(rb_freq, fpf_psd1, yerr=fpf_err1, color=xkcdcolor['xkcd:violet'], lw=2)
# ax.errorbar(rb_freq, fpf_psd1, yerr=fpf_err1, color=xkcdcolor['xkcd:violet'], lw=2)
# ax.errorbar(rb_freq, fpf_psd2, yerr=fpf_err2, color='green', lw=2)
ax.set_xlim(0.1, 20)
ax.set_ylim(1e-5, 1e-1)
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel("Frequency (Hz)", fontproperties=font_prop)
ax.set_ylabel(r"Power $\times$ freq. (frac. rms$^2$) ", fontproperties=font_prop)
ax.tick_params(axis='both', labelsize=20)
ax.xaxis.set_major_formatter(ScalarFormatter())
ax.tick_params(axis='x', labelsize=20, bottom=True, top=True,
labelbottom=True, labeltop=False, direction="in")
ax.tick_params(axis='y', labelsize=20, left=True, right=True,
labelleft=True, labelright=False, direction="in")
ax.tick_params(which='major', width=1.5, length=9, direction='in')
ax.tick_params(which='minor', width=1.5, top=True, right=True, length=6, direction='in')
for axis in ['top', 'bottom', 'left', 'right']:
ax.spines[axis].set_linewidth(1.5)
# handles, labels = ax.get_legend_handles_labels()
# ax.legend(handles, labels, loc='upper left', fontsize=16,
# borderpad=0.5, labelspacing=0.5, borderaxespad=0.5)
# plt.savefig("./out/count_compare_psds.eps")
# plt.savefig("./out/count_compare_psds.png")
# if not fit_with_noise:
# plt.savefig("./out/hr_psds.eps")
plt.show()<jupyter_output>/anaconda3/envs/maxij1535/lib/python3.6/site-packages/matplotlib/figure.py:2267: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
warnings.warn("This figure includes Axes that are not compatible "
<jupyter_text>## Now putting it into XSPEC format (only the first one from above)<jupyter_code>psd_df = fpf_psd1 * f_bin_span
err_df = fpf_err1 * f_bin_span
out_tab_df = np.vstack((f_min, f_max, psd_df, err_df))
out_tab_df = out_tab_df.T
n_psd = int((np.shape(out_tab_df)[-1]-2)/2.)
print("Number of spectra for fitting: %d" % n_psd)
np.savetxt(out_file_df, out_tab_df)
print("Saved to %s" % out_file_df)<jupyter_output>Saved to /Users/abbie/Dropbox/Research/MAXIJ1535_B-QPO/out/MAXIJ1535_64sec_256dt_ratecut_5-10-nonoise.txt
<jupyter_text>### Converting the power spectrum into a .pha file type for XSPEC
Need to copy-paste the printed stuff into a terminal. For some reason, flx2xsp isn't working in subprocess.Popen.<jupyter_code>basename = os.path.basename(out_file_df)[:-4]
print("heainit")
print("cd %s/out" % maxi_dir)
print("flx2xsp %s.txt %s.pha %s.rsp nspec=%d clobber=yes" % (basename, basename, basename, n_psd))
# os.chdir("%s/out" % maxi_dir)
# p = subprocess.Popen("flx2xsp %s.txt %s.pha %s.rsp nspec=%d clobber=yes" % (basename, basename, basename, n_psd), shell=True)
# p.communicate()<jupyter_output>heainit
cd /Users/abbie/Dropbox/Research/MAXIJ1535_B-QPO/out
flx2xsp MAXIJ1535_64sec_256dt_ratecut_5-10-nonoise.txt MAXIJ1535_64sec_256dt_ratecut_5-10-nonoise.pha MAXIJ1535_64sec_256dt_ratecut_5-10-nonoise.rsp nspec=1 clobber=yes
<jupyter_text>### Making the XSPEC script<jupyter_code>os.chdir(maxi_dir)
# extras = "_newpar"
extras= ""
xspec_fit_script = "./out/"+basename+extras+"_fitcmd.xcm"
## need +1 in these loop limits because starting at 1
with open(xspec_fit_script, mode='w') as out:
out.write("mdefine lorf E*sigma/(2*3.14159265359)/((E-lineE)**2+((sigma/2)**2)) \n")
out.write("data %s.pha \n" % basename)
if fit_with_noise:
out.write("ignore 1:1-2 \n")
else:
out.write("ignore 1:**-0.1 20.0-** \n")
out.write("notice 1:0.1-20.0 \n")
out.write("setplot energy \n")
## For fitting with noise
if fit_with_noise:
out.write("mod pow+lorf+lorf+lorf+lorf & -1 -1 & 3e-4 1e-7 1e-6 1e-6 1e-2 1e-2 " +
"& 0.488466 -1 & 1e-22 -1 & 2e-4 1e-6 1e-6 1e-6 1e-1 1e-1" +
"& 2.86 -1 & 5.72 -1 5.6 5.6 5.9 5.9 & 1e-3 4e-4 1e-6 1e-6 1e-1 1e-1 " +
"& 2.01016 -1 & 11.0637 -1 & 6e-5 1e-6 1e-6 1e-6 1e-2 1e-2" +
"& 2.77615 -1 & 0.569405 -1 & 8e-4 1e-6 1e-6 1e-6 1e-1 1e-1 \n")
## For fitting without noise
else:
out.write("mod pow+lorf+lorf+lorf+lorf & -1 -1 & 0 -1 " +
"& 0.488466 -1 & 1e-22 -1 & 2e-4 1e-6 1e-6 1e-6 1e-1 1e-1" +
"& 2.86 -1 & 5.72 -1 5.6 5.6 5.9 5.9 & 4e-4 1e-6 1e-6 1e-6 1e-1 1e-1 " +
"& 2.01016 -1 & 11.0637 -1 & 6e-5 1e-6 1e-6 1e-6 1e-2 1e-2" +
"& 2.77615 -1 & 0.569405 -1 & 8e-4 1e-6 1e-6 1e-6 1e-1 1e-1 \n")
out.write("chatter 4 \n")
out.write("query no \n")
out.write("log %s%s_fit.log \n" % (basename, extras))
out.write("fit 500 \n")
if not fit_with_noise and spec_type is "normal":
out.write("thaw 3,6,7,9,10,12,13 \n")
elif not fit_with_noise and spec_type in ["hard","win4"]:
out.write("thaw 3,6,9,10,12,13 \n")
elif fit_with_noise and spec_type is "hard":
out.write("newpar 3 1.31002 0.01 1.28443 1.28443 1.33554 1.33554 \n")
out.write("newpar 7 5.72 -1 \n")
out.write("newpar 9 8.02921 0.1 7.91818 7.91818 8.13992 8.13992 \n")
out.write("newpar 10 12.8523 0.01 12.7974 12.7974 12.907 12.907 \n")
out.write("newpar 12 1.23515 0.01 1.22498 1.22498 1.24529 1.24529 \n")
out.write("newpar 13 2.62491E-02 0.0001 0.0260111 0.0260111 0.0264878 0.0264878 \n")
elif fit_with_noise and spec_type is "normal":
out.write("newpar 3 0.49 0.01 0.270007 0.270007 0.842672 0.842672 \n")
out.write("newpar 7 5.72 0.001 5.63638 5.63638 5.77905 5.77905 \n")
out.write("newpar 9 2.0 0.1 1.17258 1.17258 4.41898 4.41898 \n")
out.write("newpar 10 11.06 0.01 10.5608 10.5608 11.454 11.454 \n")
out.write("newpar 12 2.78 0.01 2.58634 2.58634 3.01183 3.01183 \n")
out.write("newpar 13 0.57 0.01 0.368511 0.368511 0.758069 0.758069 \n")
elif fit_with_noise and spec_type is "win4":
out.write("newpar 3 0.502378 0.01 0.23793 0.23793 1.05434 1.05434 \n")
out.write("newpar 7 5.72 -1 \n")
out.write("newpar 9 7.14139 0.1 4.91461 4.91461 12.4191 12.4191 \n")
out.write("newpar 10 13.0496 0.01 11.6948 11.6948 14.1218 14.1218 \n")
out.write("newpar 12 1.22875 0.01 1.00223 1.00223 1.69227 1.69227 \n")
out.write("newpar 13 0.333533 0.01 0.0956063 0.0956063 0.608401 0.608401 \n")
out.write("newpar 6 =7/2. \n")
out.write("fit 500 \n")
out.write("newpar 0 \n")
out.write("chain burn 2000 \n")
out.write("chain walkers 1000 \n")
out.write("chain length 100000 \n")
out.write("chain run %s%s_MCMC.fits \n" % (basename, extras))
out.write("y \n")
# out.write("n \n")
if fit_with_noise and (spec_type is "normal"):
out.write("error maximum 10000. 2.706 2-14 \n")
else:
out.write("error maximum 10000. 3. 2-14 \n")
out.write("save all %s%s_all.xcm \n" % (basename, extras))
out.write("y \n")
out.write("save mod %s%s_mod.xcm \n" % (basename, extras))
out.write("y \n")
out.write("newpar 0 \n")
out.write("cpd /xw \n")
out.write("setplot delete all \n")
out.write("iplo ufspec ratio \n")
out.write("la T \n")
out.write("la x Frequency (Hz) \n")
out.write("la y Power x freq. (frac. rms\\u2\\d)\n")
out.write("time off \n")
if fit_with_noise:
out.write("r x 0.03 128 \n")
out.write("r y 1e-5 0.08 \n")
else:
out.write("r x 0.1 20 \n")
out.write("r y 1e-5 1e-3 \n")
out.write("cs 1.75 \n")
out.write("la pos y 3.0 \n")
out.write("ma size 3 \n")
out.write("lw 6 \n")
out.write("lw 6 on 1,2,3,4,5,6,7,8,9,10,11,12 \n")
out.write("co 11 on 5 \n")
out.write("co 2 on 4 \n")
out.write("co 2 on 7 \n")
out.write("co 12 on 1 \n")
out.write("ls 1 on 5 \n")
out.write("ls 3 on 6 \n")
out.write("win 1 \n")
out.write("view 0.15 0.35 0.9 0.9 \n")
out.write("win 2 \n")
out.write("view 0.15 0.1 0.9 0.35 \n")
out.write("co 12 on 8 \n")
if fit_with_noise:
out.write("r x 0.03 128 \n")
out.write("r y 0.85 1.15 \n")
else:
out.write("r x 0.1 20 \n")
out.write("r y 0.5 1.5 \n")
out.write("lw 6 \n")
out.write("lw 6 on 1,2,3,4 \n")
out.write("la x Frequency (Hz) \n")
out.write("win 1 \n")
out.write("hardcopy %s%s_fit-w-ratio.eps/cps \n" % (basename, extras))
out.write("exit \n")
out.write("exit \n")
print(xspec_fit_script)<jupyter_output>./out/MAXIJ1535_64sec_256dt_ratecut_5-10-nonoise_fitcmd.xcm
<jupyter_text>### Executing the XSPEC script
This only works if heainit is already running in the same terminal window!<jupyter_code>os.chdir("%s/out" % maxi_dir)
p = subprocess.Popen("xspec < %s" % (os.path.basename(xspec_fit_script)), shell=True)
p.communicate()
print("xspec < %s" % (os.path.basename(xspec_fit_script)))
print("Check log file: %s%s_fit.log" % (basename, extras))
print("And saved best-fit model file: %s%s_mod.xcm" % (basename, extras))
print("And plot: %s%s_fit-w-ratio.eps" % (basename, extras))<jupyter_output>xspec < MAXIJ1535_64sec_256dt_ratecut_5-10-nonoise_fitcmd.xcm
Check log file: MAXIJ1535_64sec_256dt_ratecut_5-10-nonoise_fit.log
And saved best-fit model file: MAXIJ1535_64sec_256dt_ratecut_5-10-nonoise_mod.xcm
And plot: MAXIJ1535_64sec_256dt_ratecut_5-10-nonoise_fit-w-ratio.eps
<jupyter_text>### Reading in the parameter data and computing the rms (in the FWHM) of the QPO<jupyter_code>class Weak_B_Pow_Model(object):
def __init__(self, pars, n_bins=8192, dt=0.0001220703125):
"""
Parameters
----------
pars : 1-D np.array of floats
Parameters from fitting cross spectra.
pars[0] = power law index (from XSPEC pow mod)
pars[1] = power law normalization (from XSPEC pow mod)
pars[2] = BBN1 FWHM (from LORF mod )
pars[3] = BBN1 centroid (from LORF mod)
pars[4] = BBN1 normalization (from LORF mod)
pars[5] = QPO FWHM (from LORF mod)
pars[6] = QPO centroid frequency (from LORF mod)
pars[7] = QPO normalization (from LORF mod)
pars[8] = Harmonic FWHM (from LORF mod)
pars[9] = Harmonic centroid frequency (from LORF mod)
pars[10] = Harmonic normalization (from LORF mod)
pars[11] = BBN2 FWHM (from LORF mod)
pars[12] = BBN2 centroid frequency (from LORF mod)
pars[13] = BBN2 normalization (from LORF mod)
n_bins : int
Number of bins in one Fourier transform segment (pos & neg freq).
dt : float
Time steps of the light curve.
Attributes
----------
pos_freq :
qpo :
continuum :
qpo_filt :
"""
self.pos_freq = np.abs(fftfreq(n_bins, d=dt)[0:int(n_bins/2+1)])
self.pos_freq[0] = 1e-14
powerlaw = self.__xspec_powerlaw(pars[0], pars[1])
bbn1 = self.__lorf(pars[2], pars[3], pars[4])
self.qpo = self.__lorf(pars[5], pars[6], pars[7])
self.qpo /= self.pos_freq
harmonic = self.__lorf(pars[8], pars[9], pars[10])
bbn2 = self.__lorf(pars[11], pars[12], pars[13])
self.continuum = powerlaw + bbn1 + bbn2 + self.qpo + harmonic
# nf_continuum = self.continuum[1:-1]
# whole_continuum = np.concatenate((self.continuum,
# nf_continuum[::-1]), axis=0)
# nf_qpo = self.qpo[1:-1]
# whole_qpo = np.concatenate((self.qpo, nf_qpo[::-1]), axis=0)
# ## This filter is multiplied by both the real and imaginary components
# ## of the Fourier transform, in order to preserve the phase.
# ## Avoiding divide-by-zero errors
# whole_qpo[whole_continuum == 0] = 1e-14
# whole_continuum[whole_continuum == 0] = 1e-14
# ## It's an optimal filter!
# ## The ratio here applied to the cross spectrum is the same as
# ## the sqrt of the ratio applied to the FFT. Apply this here to the cs.
# self.qpo_filt = whole_qpo / whole_continuum
def __lorf(self, sigma, lineE, norm):
"""
The lorentz function times frequency, for fitting f*P(f).
Note that sigma here is the full width half max, and lineE is the
centroid frequency.
sigma :
lineE :
norm :
Returns
-------
The Lorentzian function times frequency evaluated at every input
frequency.
"""
temp = norm * self.pos_freq * sigma / (2*3.14159265359) /\
((self.pos_freq - lineE) **2 + ((sigma / 2.) **2))
return temp
def __xspec_powerlaw(self, phoindex, norm):
"""
The powerlaw function as defined by XSPEC.
Note that phoindex is automatically made negative in here, so a negative
phoindex input returns a positive slope!
phoindex :
norm :
Returns
-------
The powerlaw function evaluated at every input frequency.
norm*freq**(-phoindex)
"""
temp = norm * self.pos_freq ** (-phoindex)
return temp
def get_qpo_rms(psd_mod_file, n_bins, dt, df):
"""
Reads in the parameters for the band power spectrum model to compute the
rms of the QPO over the FWHM range.
Designed to read in from the '_mod.xcm' file from the 'save mod xx_mod.xcm'
XSPEC command.
:param psd_mod_file:
:param n_bins:
:param dt:
:return:
"""
f = open(psd_mod_file, 'r')
f.seek(210)
j = int(0) # index in 'pars' array
pars = np.zeros(14)
pow_mod = Weak_B_Pow_Model(pars, n_bins=n_bins, dt=dt)
for line in f:
# print(line)
element0 = line.split()[0]
# print(element0)
if element0 != '=' and element0 != "newpar" and element0 != '/':
pars[j] = element0
j += 1
elif str(element0) == '/':
pars[j] = 2.85532
j += 1
else:
j += 1
if j == 14:
pow_mod = Weak_B_Pow_Model(pars, n_bins=n_bins, dt=dt)
lf = 0
hf = -1
# lf_val = 4.28
# hf_val = 7.13
lf_val = pow_mod.pos_freq[1]
hf_val = pow_mod.pos_freq[-1]
# lf_val = 1.5
# hf_val = 15
# lf_val = pars[6] - (pars[5] / 2.)
# hf_val = pars[6] + (pars[5] / 2.)
print(pars[6] - (pars[5] / 2.))
print(pars[6] + (pars[5] / 2.))
lf = int(find_nearest(pow_mod.pos_freq, lf_val)[1])
hf = int(find_nearest(pow_mod.pos_freq, hf_val)[1])
rms = np.sqrt(np.sum(pow_mod.qpo[lf:hf] * df))
return rms, lf_val, hf_val
# psd_mod_file = maxi_dir+"/out/MAXIJ1535_64sec_256dt_ratecut-wnoise_mod.xcm"
psd_mod_file = maxi_dir+"/out/MAXIJ1535_64sec_256dt_ratecut_5-10-nonoise_mod.xcm"
# psd_mod_file = maxi_dir+"/out/MAXIJ1535_64sec_256dt_hard-wnoise_mod.xcm"
# psd_mod_file = maxi_dir+"/out/MAXIJ1535_64sec_256dt_window4-wnoise_mod.xcm"
assert os.path.isfile(psd_mod_file), "Psd model file does not exist: %s" % psd_mod_file
qpo_rms, lo_fwhm, hi_fwhm = get_qpo_rms(psd_mod_file, n_bins, dt, df)
print("QPO rms: %.6f" % qpo_rms)
print("FWHM: %.5f - %.5f" % (lo_fwhm, hi_fwhm))<jupyter_output>4.472110000000001
7.32743
QPO rms: 0.029212
FWHM: 0.01562 - 128.00000
|
permissive
|
/psd_fitting.ipynb
|
astrojuan/MAXIJ1535_QPO
| 6 |
<jupyter_start><jupyter_text>## Generate 2D synthetic data<jupyter_code># 2D random data
x, y = make_classification(n_samples=1000,
n_features=2,
n_informative=1,
n_redundant=0,
n_clusters_per_class=1,
random_state=2020)
# normalize
x_norm = (x - x.min(axis=0)) / x.ptp(axis=0)<jupyter_output><empty_output><jupyter_text>## Plot data<jupyter_code>plt.figure()
plt.scatter(x_norm[:, 0], x_norm[:, 1], marker='.', c=y, s=25, edgecolor='face')
plt.grid(False)
plt.xlim(0, 1.0)
plt.ylim(0, 1.0)
plt.show()<jupyter_output><empty_output><jupyter_text>## Split train and test data<jupyter_code>train_indices = np.random.choice(len(x_norm), round(len(x_norm)*0.8), replace=False)
test_indices = np.array(list(set(range(len(x))) - set(train_indices)))
# one hot encoding
y_one = np.eye(len(set(y)))[y]
# x_train = tf.Variable(x_norm[train_indices], dtype=tf.float32)
# x_test = tf.Variable(x_norm[test_indices], dtype=tf.float32)
# y_train = tf.Variable(y_one[train_indices], dtype=tf.int32)
# y_test = tf.Variable(y_one[test_indices], dtype=tf.int32)
x_train = x_norm[train_indices]
x_test = x_norm[test_indices]
y_train = y_one[train_indices]
y_test = y_one[test_indices]
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
print(x_train[1])
print(y_train[1])<jupyter_output>(800, 2)
(800, 2)
(200, 2)
(200, 2)
[0.58974866 0.73700764]
[0. 1.]
<jupyter_text>## kNN <jupyter_code>k = 9
# prediction
d0 = tf.expand_dims(x_test, axis=1)
print(d0.shape)
d1 = tf.subtract(x_train, d0)
print(d1.shape)
distance = tf.reduce_sum(tf.abs(d1), axis=2)
_, top_k_indices = tf.nn.top_k(tf.negative(distance), k=k)
top_k_labels = tf.gather(y_train, top_k_indices)
sum_predictions = tf.reduce_sum(top_k_labels, axis=1)
predictions = tf.argmax(sum_predictions, axis=1, output_type=tf.int32)<jupyter_output>(200, 1, 2)
(200, 800, 2)
<jupyter_text>## Computing the accuracy<jupyter_code># get labels from test set
actual = tf.Variable(y[test_indices], dtype=tf.int32)
correct_count = tf.reduce_sum(tf.dtypes.cast(tf.math.equal(predictions, actual), tf.int32))
accuracy = correct_count / y_test.shape[0] * 100
print("Accuracy = ",accuracy.numpy(),"%")<jupyter_output>Accuracy = 89.5 %
<jupyter_text>## Linear model<jupyter_code>model = keras.Sequential([
keras.layers.Dense(2, activation='softmax', input_shape=[2])
])
model.summary()
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=200, verbose=1)
model.evaluate(x_test, y_test, verbose=2)<jupyter_output>200/1 - 0s - loss: 0.3035 - accuracy: 0.8950
<jupyter_text>## Adversarial Examples<jupyter_code>print(x_test[:1])
print(y_test[0])
prediction = model.predict(x_test[:1])
prediction[0]
loss_func = keras.losses.BinaryCrossentropy()
def create_adversarial_perturbation(input_clean, input_label):
input_tensor = tf.constant(input_clean, dtype=tf.float32)
with tf.GradientTape() as tape:
tape.watch(input_tensor)
pred = model(input_tensor)
loss = loss_func(input_label, pred)
gradient = tape.gradient(loss, input_tensor)
return tf.sign(gradient)<jupyter_output><empty_output><jupyter_text>### Creating single adversarial example<jupyter_code>perturbation = create_adversarial_perturbation(x_test[:1], y_test[0])
perturbation
epsilon = 0.15
x_ad = x_test[:1] + epsilon * perturbation
print(x_test[:1])
print(x_ad.numpy())
pred_ad = model.predict(x_ad)
pred_ad<jupyter_output><empty_output><jupyter_text>### Adversarial examples from full test set<jupyter_code>perturbations = create_adversarial_perturbation(x_test, y_test)
print(perturbations[:10])
x_ad = x_test + epsilon * perturbations
print(x_test[:10])
print(x_ad[:10])
model.evaluate(x_ad, y_test, verbose=2)<jupyter_output>200/1 - 0s - loss: 0.7776 - accuracy: 0.4100
<jupyter_text>### Plot graph<jupyter_code>test_positive_indices = [idx for idx, val in enumerate(y_test) if val[0] == 1]
print(len(test_positive_indices))
print(x_test[list(test_positive_indices)][:10])
print(len(x_ad))
ad_pred = model.predict(x_ad)
ad_result = tf.math.argmax(ad_pred, axis=1)
print(ad_result.numpy())
len(ad_result.numpy()[list(test_positive_indices)])
plt.figure()
plt.scatter(x_test[list(test_positive_indices)][:, 0],
x_test[list(test_positive_indices)][:, 1],
marker='.',
c=y[test_indices][list(test_positive_indices)],
s=25,
edgecolor='face')
plt.grid(False)
plt.ylim(0, 1.0)
plt.xlim(0, 1.0)
plt.title('Test data with positive label')
plt.show()
plt.figure()
plt.scatter(x_ad.numpy()[list(test_positive_indices)][:, 0],
x_ad.numpy()[list(test_positive_indices)][:, 1],
marker='.',
c=ad_result.numpy()[list(test_positive_indices)],
s=25,
edgecolor='face')
plt.grid(False)
plt.ylim(0, 1.0)
plt.xlim(0, 1.0)
plt.title('Adversarial exmaples')
plt.show()
<jupyter_output><empty_output><jupyter_text>## Applicability Domain<jupyter_code># implementing 3-step AD
def check_applicability(input_data):
applicability = 1.0
return applicability
def check_reliability(input_data):
reliability = 1.0
return reliability
def check_decidability(input_data):
decidability = 1.0
return decidability
threshold_applicability = 0.6
threshold_reliability = 0.6
threshold_decidability = 0.6
# Applicability Domain pipline
def check_AD(sample):
result = False
applicability = check_applicability(sample)
if applicability >= threshold_applicability:
reliability = check_reliability(sample)
if reliability >= threshold_reliability:
decidability = check_decidability(sample)
if decidability >= threshold_decidability:
print('Passed AD test')
return True
else:
print(f'Failed Decidability Test (Decidability = {decidability:4.3f}, Threshold = {threshold_decidability:4.3f})')
return False
else:
print(f'Failed Reliability Test (Reliability = {reliability:4.3f}, Threshold = {threshold_reliability:4.3f})')
return False
else:
print(f'Failed Applicability Test (Applicability = {applicability:4.3f}, Threshold = {threshold_applicability:4.3f})')
return False
print(x_ad[0])
print(check_AD(x_ad[0]))<jupyter_output>tf.Tensor([0.5888299 0.39302254], shape=(2,), dtype=float32)
Passed AD test
True
|
no_license
|
/toy_dataset.ipynb
|
changx03/jupyter_tensorflow
| 11 |
<jupyter_start><jupyter_text># **Mental Health Prediction**
## **1. Library and data loading** ##<jupyter_code>import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt
import seaborn as sns
from collections import Counter
from scipy import stats
from scipy.stats import randint
# prep
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.datasets import make_classification
from sklearn.preprocessing import binarize, LabelEncoder, MinMaxScaler
# models
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
# Validation libraries
from sklearn import metrics
from sklearn.metrics import accuracy_score, mean_squared_error, precision_recall_curve
from sklearn.model_selection import cross_val_score
#Neural Network
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import RandomizedSearchCV
#Bagging
from sklearn.ensemble import BaggingClassifier, AdaBoostClassifier
from sklearn.neighbors import KNeighborsClassifier
#Naive bayes
from sklearn.naive_bayes import GaussianNB
#Stacking
from mlxtend.classifier import StackingClassifier
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
# from subprocess import check_output
# print(check_output(["ls", "./input"]).decode("utf8"))
# Any results you write to the current directory are saved as output.
#reading in CSV's from a file path
train_df = pd.read_csv('./input/survey.csv')
#Pandas: whats the data row count?
print(train_df.shape)
#Pandas: whats the distribution of the data?
print(train_df.describe())
#Pandas: What types of data do i have?
print(train_df.info())
<jupyter_output>(1259, 27)
Age
count 1.259000e+03
mean 7.942815e+07
std 2.818299e+09
min -1.726000e+03
25% 2.700000e+01
50% 3.100000e+01
75% 3.600000e+01
max 1.000000e+11
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1259 entries, 0 to 1258
Data columns (total 27 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Timestamp 1259 non-null object
1 Age 1259 non-null int64
2 Gender 1259 non-null object
3 Country 1259 non-null object
4 state 744 non-null object
5 self_employed 1241 non-null object
6 family_history 1259 non-null object
7 treatment 1259 non-null object
8 work_interfere 995 non-null object
9 no_employees 1259 non-null object
10 remote_work 1259 non-n[...]<jupyter_text>
## **2. Data cleaning** ##<jupyter_code>#missing data
total = train_df.isnull().sum().sort_values(ascending=False)
percent = (train_df.isnull().sum()/train_df.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)
print(missing_data)
#dealing with missing data
#Let’s get rid of the variables "Timestamp",“comments”, “state” just to make our lives easier.
train_df = train_df.drop(['comments'], axis= 1)
train_df = train_df.drop(['state'], axis= 1)
train_df = train_df.drop(['Timestamp'], axis= 1)
train_df.isnull().sum().max() #just checking that there's no missing data missing...
train_df.head(5)<jupyter_output><empty_output><jupyter_text>**Cleaning NaN**<jupyter_code># Assign default values for each data type
defaultInt = 0
defaultString = 'NaN'
defaultFloat = 0.0
# Create lists by data tpe
intFeatures = ['Age']
stringFeatures = ['Gender', 'Country', 'self_employed', 'family_history', 'treatment', 'work_interfere',
'no_employees', 'remote_work', 'tech_company', 'anonymity', 'leave', 'mental_health_consequence',
'phys_health_consequence', 'coworkers', 'supervisor', 'mental_health_interview', 'phys_health_interview',
'mental_vs_physical', 'obs_consequence', 'benefits', 'care_options', 'wellness_program',
'seek_help']
floatFeatures = []
# Clean the NaN's
for feature in train_df:
if feature in intFeatures:
train_df[feature] = train_df[feature].fillna(defaultInt)
elif feature in stringFeatures:
train_df[feature] = train_df[feature].fillna(defaultString)
elif feature in floatFeatures:
train_df[feature] = train_df[feature].fillna(defaultFloat)
else:
print('Error: Feature %s not recognized.' % feature)
train_df.head(5)
#clean 'Gender'
#Slower case all columm's elements
gender = train_df['Gender'].str.lower()
#print(gender)
#Select unique elements
gender = train_df['Gender'].unique()
#Made gender groups
male_str = ["male", "m", "male-ish", "maile", "mal", "male (cis)", "make", "male ", "man","msle", "mail", "malr","cis man", "Cis Male", "cis male"]
trans_str = ["trans-female", "something kinda male?", "queer/she/they", "non-binary","nah", "all", "enby", "fluid", "genderqueer", "androgyne", "agender", "male leaning androgynous", "guy (-ish) ^_^", "trans woman", "neuter", "female (trans)", "queer", "ostensibly male, unsure what that really means"]
female_str = ["cis female", "f", "female", "woman", "femake", "female ","cis-female/femme", "female (cis)", "femail"]
for (row, col) in train_df.iterrows():
if str.lower(col.Gender) in male_str:
train_df['Gender'].replace(to_replace=col.Gender, value='male', inplace=True)
if str.lower(col.Gender) in female_str:
train_df['Gender'].replace(to_replace=col.Gender, value='female', inplace=True)
if str.lower(col.Gender) in trans_str:
train_df['Gender'].replace(to_replace=col.Gender, value='trans', inplace=True)
#Get rid of bullshit
stk_list = ['A little about you', 'p']
train_df = train_df[~train_df['Gender'].isin(stk_list)]
print(train_df['Gender'].unique())
#complete missing age with mean
train_df['Age'].fillna(train_df['Age'].median(), inplace = True)
# Fill with media() values < 18 and > 120
s = pd.Series(train_df['Age'])
s[s<18] = train_df['Age'].median()
train_df['Age'] = s
s = pd.Series(train_df['Age'])
s[s>120] = train_df['Age'].median()
train_df['Age'] = s
#Ranges of Age
train_df['age_range'] = pd.cut(train_df['Age'], [0,20,30,65,100], labels=["0-20", "21-30", "31-65", "66-100"], include_lowest=True)
#There are only 0.014% of self employed so let's change NaN to NOT self_employed
#Replace "NaN" string from defaultString
train_df['self_employed'] = train_df['self_employed'].replace([defaultString], 'No')
print(train_df['self_employed'].unique())
#There are only 0.20% of self work_interfere so let's change NaN to "Don't know
#Replace "NaN" string from defaultString
train_df['work_interfere'] = train_df['work_interfere'].replace([defaultString], 'Don\'t know' )
print(train_df['work_interfere'].unique())<jupyter_output>['Often' 'Rarely' 'Never' 'Sometimes' "Don't know"]
<jupyter_text>
## **3. Encoding data**<jupyter_code>#Encoding data
labelDict = {}
for feature in train_df:
le = preprocessing.LabelEncoder()
le.fit(train_df[feature])
le_name_mapping = dict(zip(le.classes_, le.transform(le.classes_)))
train_df[feature] = le.transform(train_df[feature])
# Get labels
labelKey = 'label_' + feature
labelValue = [*le_name_mapping]
labelDict[labelKey] =labelValue
for key, value in labelDict.items():
print(key, value)
#Get rid of 'Country'
train_df = train_df.drop(['Country'], axis= 1)
train_df.head()
<jupyter_output>label_Age [18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 53, 54, 55, 56, 57, 58, 60, 61, 62, 65, 72]
label_Gender ['female', 'male', 'trans']
label_Country ['Australia', 'Austria', 'Belgium', 'Bosnia and Herzegovina', 'Brazil', 'Bulgaria', 'Canada', 'China', 'Colombia', 'Costa Rica', 'Croatia', 'Czech Republic', 'Denmark', 'Finland', 'France', 'Georgia', 'Germany', 'Greece', 'Hungary', 'India', 'Ireland', 'Israel', 'Italy', 'Japan', 'Latvia', 'Mexico', 'Moldova', 'Netherlands', 'New Zealand', 'Nigeria', 'Norway', 'Philippines', 'Poland', 'Portugal', 'Romania', 'Russia', 'Singapore', 'Slovenia', 'South Africa', 'Spain', 'Sweden', 'Switzerland', 'Thailand', 'United Kingdom', 'United States', 'Uruguay', 'Zimbabwe']
label_self_employed ['No', 'Yes']
label_family_history ['No', 'Yes']
label_treatment ['No', 'Yes']
label_work_interfere ["Don't know", 'Never', 'Often', 'Rarely', 'Sometimes']
label_no_emp[...]<jupyter_text>### Testing there aren't any missing data<jupyter_code>#missing data
total = train_df.isnull().sum().sort_values(ascending=False)
percent = (train_df.isnull().sum()/train_df.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)
print(missing_data)<jupyter_output> Total Percent
age_range 0 0.0
obs_consequence 0 0.0
Gender 0 0.0
self_employed 0 0.0
family_history 0 0.0
treatment 0 0.0
work_interfere 0 0.0
no_employees 0 0.0
remote_work 0 0.0
tech_company 0 0.0
benefits 0 0.0
care_options 0 0.0
wellness_program 0 0.0
seek_help 0 0.0
anonymity 0 0.0
leave 0 0.0
mental_health_consequence 0 0.0
phys_health_consequence 0 0.0
coworkers 0 0.0
supervisor 0 0.0
mental_health_interview 0 0.0
phys_health_interview 0 0.0
mental_vs_physical 0 [...]<jupyter_text>Features Scaling
We're going to scale age, because is extremely different from the othere ones.
## **4. Correlation Matrix. Variability comparison between categories of variables** <jupyter_code>#correlation matrix
corrmat = train_df.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);
plt.show()
#treatment correlation matrix
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'treatment')['treatment'].index
cm = np.corrcoef(train_df[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
<jupyter_output><empty_output><jupyter_text>
## **5. Some Visualization to see data relationship** Distribiution and density by Age<jupyter_code># Processing age
train_df['Age'] = pd.to_numeric(train_df['Age'], errors='coerce')
def age_process(age):
if age>=0 and age<=100:
return age
else:
return np.nan
train_df['Age'] = train_df['Age'].apply(age_process)
(train_df['Age']<0).sum()
(train_df['Age']>100).sum()
(train_df['Age']<60).sum()
train_df['Age'].isnull().sum()
# Distribiution and density by Age
plt.figure(figsize=(12,8))
sns.distplot(train_df["Age"], bins=24)
plt.title("Distribuition and density by Age")
plt.xlabel("Age")
# Age vs Family-History
train_df['Age_Group'] = pd.cut(train_df['Age'].dropna(),
[0, 18, 25, 35, 45, 99],
labels=['<18','18-24','25-34','35-44','45+'])
fig,ax = plt.subplots(figsize=(8, 6))
sns.countplot(data=train_df, x = 'Age_Group', hue = 'family_history', ax = ax)
plt.plot('Age vs Family History')
#Age group vs Treatment
fig,ax = plt.subplots(figsize=(8, 6))
sns.countplot(data = train_df, x = 'Age_Group', hue='treatment')
plt.title('Age Group vs Treatment')
#Age vs No. of Employees
fig,ax = plt.subplots(figsize=(8, 6))
sns.barplot(data = train_df, x = train_df['no_employees'], y = train_df['Age'], ax = ax)
plt.title('Age Group vs Group size')
plt.xlabel('Group size at Work')
plt.ylabel('Age')
ticks = plt.setp(ax.get_xticklabels(), rotation=90)
total = train_df['no_employees'].dropna().shape[0] * 1.0
employee_count = Counter(train_df['no_employees'].dropna().tolist())
for key,val in employee_count.items():
employee_count[key] = employee_count[key] / total
employee_group = np.asarray(list(employee_count.keys()))
employee_val = np.asarray(list(employee_count.values()))
sns.barplot(x = employee_group , y = employee_val)
plt.title('employee group ratio')
plt.ylabel('ratio')
plt.xlabel('employee group')
fig,ax = plt.subplots(figsize=(8, 6))
sns.countplot(data=train_df, x='no_employees', hue='tech_company', ax=ax)
ticks = plt.setp(ax.get_xticklabels(),rotation=45)
plt.title('no_employee vs tech_company')
# Remote Work vs employee grp
fig,ax = plt.subplots(figsize=(8, 6))
sns.countplot(data = train_df, x = 'no_employees', hue = 'remote_work', ax=ax)
ticks = plt.setp(ax.get_xticklabels(), rotation=45)
plt.title('No. Employees vs Remote Work')<jupyter_output><empty_output><jupyter_text>Separate by treatment<jupyter_code># Separate by treatment or not
g = sns.FacetGrid(train_df, col='treatment', size=5)
g = g.map(sns.distplot, "Age")<jupyter_output>C:\ProgramData\Anaconda3\lib\site-packages\seaborn\axisgrid.py:243: UserWarning: The `size` parameter has been renamed to `height`; please update your code.
warnings.warn(msg, UserWarning)
<jupyter_text>How many people has been treated?<jupyter_code># Let see how many people has been treated
plt.figure(figsize=(12,8))
labels = labelDict['label_Gender']
g = sns.countplot(x="treatment", data=train_df)
g.set_xticklabels(labels)
plt.title('Total Distribuition by treated or not')<jupyter_output><empty_output><jupyter_text>Draw a nested barplot to show probabilities for class and sex<jupyter_code>o = labelDict['label_age_range']
g = sns.factorplot(x="age_range", y="treatment", hue="Gender", data=train_df, kind="bar", ci=None, size=5, aspect=2, legend_out = True)
g.set_xticklabels(o)
plt.title('Probability of mental health condition')
plt.ylabel('Probability x 100')
plt.xlabel('Age')
# replace legend labels
new_labels = labelDict['label_Gender']
for t, l in zip(g._legend.texts, new_labels): t.set_text(l)
# Positioning the legend
g.fig.subplots_adjust(top=0.9,right=0.8)
plt.show()<jupyter_output>C:\ProgramData\Anaconda3\lib\site-packages\seaborn\categorical.py:3669: UserWarning: The `factorplot` function has been renamed to `catplot`. The original name will be removed in a future release. Please update your code. Note that the default `kind` in `factorplot` (`'point'`) has changed `'strip'` in `catplot`.
warnings.warn(msg)
C:\ProgramData\Anaconda3\lib\site-packages\seaborn\categorical.py:3675: UserWarning: The `size` parameter has been renamed to `height`; please update your code.
warnings.warn(msg, UserWarning)
<jupyter_text>Barplot to show probabilities for family history<jupyter_code>o = labelDict['label_family_history']
g = sns.factorplot(x="family_history", y="treatment", hue="Gender", data=train_df, kind="bar", ci=None, size=5, aspect=2, legend_out = True)
g.set_xticklabels(o)
plt.title('Probability of mental health condition')
plt.ylabel('Probability x 100')
plt.xlabel('Family History')
# replace legend labels
new_labels = labelDict['label_Gender']
for t, l in zip(g._legend.texts, new_labels): t.set_text(l)
# Positioning the legend
g.fig.subplots_adjust(top=0.9,right=0.8)
plt.show()<jupyter_output><empty_output><jupyter_text>Barplot to show probabilities for care options<jupyter_code>o = labelDict['label_care_options']
g = sns.factorplot(x="care_options", y="treatment", hue="Gender", data=train_df, kind="bar", ci=None, size=5, aspect=2, legend_out = True)
g.set_xticklabels(o)
plt.title('Probability of mental health condition')
plt.ylabel('Probability x 100')
plt.xlabel('Care options')
# replace legend labels
new_labels = labelDict['label_Gender']
for t, l in zip(g._legend.texts, new_labels): t.set_text(l)
# Positioning the legend
g.fig.subplots_adjust(top=0.9,right=0.8)
plt.show()<jupyter_output><empty_output><jupyter_text>Barplot to show probabilities for benefits<jupyter_code>o = labelDict['label_benefits']
g = sns.factorplot(x="care_options", y="treatment", hue="Gender", data=train_df, kind="bar", ci=None, size=5, aspect=2, legend_out = True)
g.set_xticklabels(o)
plt.title('Probability of mental health condition')
plt.ylabel('Probability x 100')
plt.xlabel('Benefits')
# replace legend labels
new_labels = labelDict['label_Gender']
for t, l in zip(g._legend.texts, new_labels): t.set_text(l)
# Positioning the legend
g.fig.subplots_adjust(top=0.9,right=0.8)
plt.show()<jupyter_output><empty_output><jupyter_text>Barplot to show probabilities for work interfere<jupyter_code>o = labelDict['label_work_interfere']
g = sns.factorplot(x="work_interfere", y="treatment", hue="Gender", data=train_df, kind="bar", ci=None, size=5, aspect=2, legend_out = True)
g.set_xticklabels(o)
plt.title('Probability of mental health condition')
plt.ylabel('Probability x 100')
plt.xlabel('Work interfere')
# replace legend labels
new_labels = labelDict['label_Gender']
for t, l in zip(g._legend.texts, new_labels): t.set_text(l)
# Positioning the legend
g.fig.subplots_adjust(top=0.9,right=0.8)
plt.show()<jupyter_output><empty_output><jupyter_text>
## **6. Scaling and fitting** ##
Features Scaling
We're going to scale age, because is extremely different from the othere ones.<jupyter_code># Scaling Age
scaler = MinMaxScaler()
train_df['Age'] = scaler.fit_transform(train_df[['Age']])
train_df.head()
<jupyter_output><empty_output><jupyter_text>Spliltting the dataset<jupyter_code># define X and y
feature_cols = ['Age', 'Gender', 'family_history', 'benefits', 'care_options', 'anonymity', 'leave', 'work_interfere']
X = train_df[feature_cols]
y = train_df.treatment
# split X and y into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=0)
# Create dictionaries for final graph
# Use: methodDict['Stacking'] = accuracy_score
methodDict = {}
rmseDict = ()
# Build a forest and compute the feature importances
forest = ExtraTreesClassifier(n_estimators=250,
random_state=0)
forest.fit(X, y)
importances = forest.feature_importances_
std = np.std([tree.feature_importances_ for tree in forest.estimators_],
axis=0)
indices = np.argsort(importances)[::-1]
labels = []
for f in range(X.shape[1]):
labels.append(feature_cols[f])
# Plot the feature importances of the forest
plt.figure(figsize=(12,8))
plt.title("Feature importances")
plt.bar(range(X.shape[1]), importances[indices],
color="r", yerr=std[indices], align="center")
plt.xticks(range(X.shape[1]), labels, rotation='vertical')
plt.xlim([-1, X.shape[1]])
plt.show()<jupyter_output><empty_output><jupyter_text>
## **7. Tuning**
### **Evaluating a Classification Model.**
This function will evalue:
* **Classification accuracy: **percentage of correct predictions
* **Null accuracy:** accuracy that could be achieved by always predicting the most frequent class
* **Percentage of ones**
* **Percentage of zero**s
* **Confusion matrix: **Table that describes the performance of a classification model
True Positives (TP): we correctly predicted that they do have diabetes
True Negatives (TN): we correctly predicted that they don't have diabetes
False Positives (FP): we incorrectly predicted that they do have diabetes (a "Type I error")
Falsely predict positive
False Negatives (FN): we incorrectly predicted that they don't have diabetes (a "Type II error")
Falsely predict negative
* **False Positive Rate**
* **Precision of Positive value**
* **AUC:** is the percentage of the ROC plot that is underneath the curve
.90-1 = excellent (A)
.80-.90 = good (B)
.70-.80 = fair (C)
.60-.70 = poor (D)
.50-.60 = fail (F)
And some others values for tuning processes.
More information: [http://www.ritchieng.com/machine-learning-evaluate-classification-model/]:
<jupyter_code>def evalClassModel(model, y_test, y_pred_class, plot=False):
#Classification accuracy: percentage of correct predictions
# calculate accuracy
print('Accuracy:', metrics.accuracy_score(y_test, y_pred_class))
#Null accuracy: accuracy that could be achieved by always predicting the most frequent class
# examine the class distribution of the testing set (using a Pandas Series method)
print('Null accuracy:\n', y_test.value_counts())
# calculate the percentage of ones
print('Percentage of ones:', y_test.mean())
# calculate the percentage of zeros
print('Percentage of zeros:',1 - y_test.mean())
#Comparing the true and predicted response values
print('True:', y_test.values[0:25])
print('Pred:', y_pred_class[0:25])
#Conclusion:
#Classification accuracy is the easiest classification metric to understand
#But, it does not tell you the underlying distribution of response values
#And, it does not tell you what "types" of errors your classifier is making
#Confusion matrix
# save confusion matrix and slice into four pieces
confusion = metrics.confusion_matrix(y_test, y_pred_class)
#[row, column]
TP = confusion[1, 1]
TN = confusion[0, 0]
FP = confusion[0, 1]
FN = confusion[1, 0]
# visualize Confusion Matrix
sns.heatmap(confusion,annot=True,fmt="d")
plt.title('Confusion Matrix')
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()
#Metrics computed from a confusion matrix
#Classification Accuracy: Overall, how often is the classifier correct?
accuracy = metrics.accuracy_score(y_test, y_pred_class)
print('Classification Accuracy:', accuracy)
#Classification Error: Overall, how often is the classifier incorrect?
print('Classification Error:', 1 - metrics.accuracy_score(y_test, y_pred_class))
#False Positive Rate: When the actual value is negative, how often is the prediction incorrect?
false_positive_rate = FP / float(TN + FP)
print('False Positive Rate:', false_positive_rate)
#Precision: When a positive value is predicted, how often is the prediction correct?
print('Precision:', metrics.precision_score(y_test, y_pred_class))
# IMPORTANT: first argument is true values, second argument is predicted probabilities
print('AUC Score:', metrics.roc_auc_score(y_test, y_pred_class))
# calculate cross-validated AUC
print('Cross-validated AUC:', cross_val_score(model, X, y, cv=10, scoring='roc_auc').mean())
##########################################
#Adjusting the classification threshold
##########################################
# print the first 10 predicted responses
# 1D array (vector) of binary values (0, 1)
print('First 10 predicted responses:\n', model.predict(X_test)[0:10])
# print the first 10 predicted probabilities of class membership
print('First 10 predicted probabilities of class members:\n', model.predict_proba(X_test)[0:10])
# print the first 10 predicted probabilities for class 1
model.predict_proba(X_test)[0:10, 1]
# store the predicted probabilities for class 1
y_pred_prob = model.predict_proba(X_test)[:, 1]
if plot == True:
# histogram of predicted probabilities
# adjust the font size
plt.rcParams['font.size'] = 12
# 8 bins
plt.hist(y_pred_prob, bins=8)
# x-axis limit from 0 to 1
plt.xlim(0,1)
plt.title('Histogram of predicted probabilities')
plt.xlabel('Predicted probability of treatment')
plt.ylabel('Frequency')
# predict treatment if the predicted probability is greater than 0.3
# it will return 1 for all values above 0.3 and 0 otherwise
# results are 2D so we slice out the first column
y_pred_prob = y_pred_prob.reshape(-1,1)
y_pred_class = binarize(y_pred_prob, 0.3)[0]
# print the first 10 predicted probabilities
print('First 10 predicted probabilities:\n', y_pred_prob[0:10])
##########################################
#ROC Curves and Area Under the Curve (AUC)
##########################################
#Question: Wouldn't it be nice if we could see how sensitivity and specificity are affected by various thresholds, without actually changing the threshold?
#Answer: Plot the ROC curve!
#AUC is the percentage of the ROC plot that is underneath the curve
#Higher value = better classifier
roc_auc = metrics.roc_auc_score(y_test, y_pred_prob)
# IMPORTANT: first argument is true values, second argument is predicted probabilities
# we pass y_test and y_pred_prob
# we do not use y_pred_class, because it will give incorrect results without generating an error
# roc_curve returns 3 objects fpr, tpr, thresholds
# fpr: false positive rate
# tpr: true positive rate
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pred_prob)
if plot == True:
plt.figure()
plt.plot(fpr, tpr, color='darkorange', label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.rcParams['font.size'] = 12
plt.title('ROC curve for treatment classifier')
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('True Positive Rate (Sensitivity)')
plt.legend(loc="lower right")
plt.show()
# define a function that accepts a threshold and prints sensitivity and specificity
def evaluate_threshold(threshold):
#Sensitivity: When the actual value is positive, how often is the prediction correct?
#Specificity: When the actual value is negative, how often is the prediction correct?print('Sensitivity for ' + str(threshold) + ' :', tpr[thresholds > threshold][-1])
print('Specificity for ' + str(threshold) + ' :', 1 - fpr[thresholds > threshold][-1])
# One way of setting threshold
predict_mine = np.where(y_pred_prob > 0.50, 1, 0)
confusion = metrics.confusion_matrix(y_test, predict_mine)
print(confusion)
return accuracy<jupyter_output><empty_output><jupyter_text>### **Tuning with cross validation score**<jupyter_code>##########################################
# Tuning with cross validation score
##########################################
def tuningCV(knn):
# search for an optimal value of K for KNN
k_range = list(range(1, 31))
k_scores = []
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
k_scores.append(scores.mean())
print(k_scores)
# plot the value of K for KNN (x-axis) versus the cross-validated accuracy (y-axis)
plt.plot(k_range, k_scores)
plt.xlabel('Value of K for KNN')
plt.ylabel('Cross-Validated Accuracy')
plt.show()
<jupyter_output><empty_output><jupyter_text>### **Tuning with GridSearchCV** ###<jupyter_code>def tuningGridSerach(knn):
#More efficient parameter tuning using GridSearchCV
# define the parameter values that should be searched
k_range = list(range(1, 31))
print(k_range)
# create a parameter grid: map the parameter names to the values that should be searched
param_grid = dict(n_neighbors=k_range)
print(param_grid)
# instantiate the grid
grid = GridSearchCV(knn, param_grid, cv=10, scoring='accuracy')
# fit the grid with data
grid.fit(X, y)
# view the complete results (list of named tuples)
grid.cv_results_
# examine the first tuple
print(grid.cv_results_[0].parameters)
print(grid.cv_results_[0].cv_validation_scores)
print(grid.cv_results_[0].mean_validation_score)
# create a list of the mean scores only
grid_mean_scores = [result.mean_validation_score for result in grid.cv_results_]
print(grid_mean_scores)
# plot the results
plt.plot(k_range, grid_mean_scores)
plt.xlabel('Value of K for KNN')
plt.ylabel('Cross-Validated Accuracy')
plt.show()
# examine the best model
print('GridSearch best score', grid.best_score_)
print('GridSearch best params', grid.best_params_)
print('GridSearch best estimator', grid.best_estimator_)
<jupyter_output><empty_output><jupyter_text>### **Tuning with RandomizedSearchCV** ###<jupyter_code>def tuningRandomizedSearchCV(model, param_dist):
#Searching multiple parameters simultaneously
# n_iter controls the number of searches
rand = RandomizedSearchCV(model, param_dist, cv=10, scoring='accuracy', n_iter=10, random_state=5)
rand.fit(X, y)
rand.cv_results_
# examine the best model
print('Rand. Best Score: ', rand.best_score_)
print('Rand. Best Params: ', rand.best_params_)
# run RandomizedSearchCV 20 times (with n_iter=10) and record the best score
best_scores = []
for _ in range(20):
rand = RandomizedSearchCV(model, param_dist, cv=10, scoring='accuracy', n_iter=10)
rand.fit(X, y)
best_scores.append(round(rand.best_score_, 3))
print(best_scores)<jupyter_output><empty_output><jupyter_text>### **Tuning with searching multiple parameters simultaneously** ###<jupyter_code>def tuningMultParam(knn):
#Searching multiple parameters simultaneously
# define the parameter values that should be searched
k_range = list(range(1, 31))
weight_options = ['uniform', 'distance']
# create a parameter grid: map the parameter names to the values that should be searched
param_grid = dict(n_neighbors=k_range, weights=weight_options)
print(param_grid)
# instantiate and fit the grid
grid = GridSearchCV(knn, param_grid, cv=10, scoring='accuracy')
grid.fit(X, y)
# view the complete results
print(grid.cv_results_)
# examine the best model
print('Multiparam. Best Score: ', grid.best_score_)
print('Multiparam. Best Params: ', grid.best_params_)<jupyter_output><empty_output><jupyter_text>
## **8. Evaluating models**
### Logistic Regression<jupyter_code>def logisticRegression():
# train a logistic regression model on the training set
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
# make class predictions for the testing set
y_pred_class = logreg.predict(X_test)
print('########### Logistic Regression ###############')
accuracy_score = evalClassModel(logreg, y_test, y_pred_class, True)
#Data for final graph
methodDict['Log. Regres.'] = accuracy_score * 100<jupyter_output><empty_output><jupyter_text>
<jupyter_code>logisticRegression()<jupyter_output>########### Logistic Regression ###############
Accuracy: 0.7962962962962963
Null accuracy:
0 191
1 187
Name: treatment, dtype: int64
Percentage of ones: 0.4947089947089947
Percentage of zeros: 0.5052910052910053
True: [0 0 0 0 0 0 0 0 1 1 0 1 1 0 1 1 0 1 0 0 0 1 1 0 0]
Pred: [1 0 0 0 1 1 0 1 0 1 0 1 1 0 1 1 1 1 0 0 0 0 1 0 0]
<jupyter_text>
### KNeighbors Classifier<jupyter_code>def Knn():
# Calculating the best parameters
knn = KNeighborsClassifier(n_neighbors=5)
# From https://github.com/justmarkham/scikit-learn-videos/blob/master/08_grid_search.ipynb
#tuningCV(knn)
#tuningGridSerach(knn)
#tuningMultParam(knn)
# define the parameter values that should be searched
k_range = list(range(1, 31))
weight_options = ['uniform', 'distance']
# specify "parameter distributions" rather than a "parameter grid"
param_dist = dict(n_neighbors=k_range, weights=weight_options)
tuningRandomizedSearchCV(knn, param_dist)
# train a KNeighborsClassifier model on the training set
knn = KNeighborsClassifier(n_neighbors=27, weights='uniform')
knn.fit(X_train, y_train)
# make class predictions for the testing set
y_pred_class = knn.predict(X_test)
print('########### KNeighborsClassifier ###############')
accuracy_score = evalClassModel(knn, y_test, y_pred_class, True)
#Data for final graph
methodDict['KNN'] = accuracy_score * 100
<jupyter_output><empty_output><jupyter_text>KNEIGHBORSCLASSIFIER<jupyter_code>Knn()<jupyter_output>Rand. Best Score: 0.8209714285714286
Rand. Best Params: {'weights': 'uniform', 'n_neighbors': 27}
[0.815, 0.821, 0.821, 0.815, 0.82, 0.816, 0.823, 0.821, 0.816, 0.811, 0.821, 0.819, 0.821, 0.823, 0.818, 0.815, 0.816, 0.815, 0.813, 0.823]
########### KNeighborsClassifier ###############
Accuracy: 0.8042328042328042
Null accuracy:
0 191
1 187
Name: treatment, dtype: int64
Percentage of ones: 0.4947089947089947
Percentage of zeros: 0.5052910052910053
True: [0 0 0 0 0 0 0 0 1 1 0 1 1 0 1 1 0 1 0 0 0 1 1 0 0]
Pred: [1 0 0 0 1 1 0 1 1 1 0 1 1 0 1 1 1 1 0 0 0 0 1 0 0]
<jupyter_text>
### Decision Tree classifier<jupyter_code>def treeClassifier():
# Calculating the best parameters
tree = DecisionTreeClassifier()
featuresSize = feature_cols.__len__()
param_dist = {"max_depth": [3, None],
"max_features": randint(1, featuresSize),
"min_samples_split": randint(2, 9),
"min_samples_leaf": randint(1, 9),
"criterion": ["gini", "entropy"]}
tuningRandomizedSearchCV(tree, param_dist)
# train a decision tree model on the training set
tree = DecisionTreeClassifier(max_depth=3, min_samples_split=8, max_features=6, criterion='entropy', min_samples_leaf=7)
tree.fit(X_train, y_train)
# make class predictions for the testing set
y_pred_class = tree.predict(X_test)
print('########### Tree classifier ###############')
accuracy_score = evalClassModel(tree, y_test, y_pred_class, True)
#Data for final graph
methodDict['Tree clas.'] = accuracy_score * 100
treeClassifier()<jupyter_output>Rand. Best Score: 0.8305206349206349
Rand. Best Params: {'criterion': 'entropy', 'max_depth': 3, 'max_features': 6, 'min_samples_leaf': 7, 'min_samples_split': 8}
[0.83, 0.831, 0.829, 0.817, 0.831, 0.831, 0.831, 0.831, 0.827, 0.826, 0.831, 0.831, 0.83, 0.831, 0.831, 0.829, 0.831, 0.831, 0.831, 0.83]
########### Tree classifier ###############
Accuracy: 0.8068783068783069
Null accuracy:
0 191
1 187
Name: treatment, dtype: int64
Percentage of ones: 0.4947089947089947
Percentage of zeros: 0.5052910052910053
True: [0 0 0 0 0 0 0 0 1 1 0 1 1 0 1 1 0 1 0 0 0 1 1 0 0]
Pred: [1 0 0 0 1 1 0 1 1 1 0 1 1 0 1 1 1 1 0 0 0 0 1 0 0]
<jupyter_text>
### Random Forests<jupyter_code>results=[]
def randomForest():
# Calculating the best parameters
forest = RandomForestClassifier(n_estimators = 20)
featuresSize = feature_cols.__len__()
param_dist = {"max_depth": [3, None],
"max_features": randint(1, featuresSize),
"min_samples_split": randint(2, 9),
"min_samples_leaf": randint(1, 9),
"criterion": ["gini", "entropy"]}
tuningRandomizedSearchCV(forest, param_dist)
# Building and fitting my_forest
forest = RandomForestClassifier(max_depth = None, min_samples_leaf=8, min_samples_split=2, n_estimators = 20, random_state = 1)
my_forest = forest.fit(X_train, y_train)
# make class predictions for the testing set
y_pred_class = my_forest.predict(X_test)
results = pd.DataFrame({'Index': X_test.index, 'Treatment': y_pred_class})
print('********************Results********************')
print(results)
results.to_csv('results.csv', index=False)
print('########### Random Forests ###############')
accuracy_score = evalClassModel(my_forest, y_test, y_pred_class, True)
#Data for final graph
methodDict['R. Forest'] = accuracy_score * 100
randomForest()<jupyter_output>Rand. Best Score: 0.8305206349206349
Rand. Best Params: {'criterion': 'entropy', 'max_depth': 3, 'max_features': 6, 'min_samples_leaf': 7, 'min_samples_split': 8}
[0.831, 0.834, 0.831, 0.831, 0.831, 0.834, 0.832, 0.831, 0.831, 0.831, 0.831, 0.834, 0.831, 0.831, 0.831, 0.831, 0.831, 0.832, 0.831, 0.831]
********************Results********************
Index Treatment
0 5 1
1 494 0
2 52 0
3 984 0
4 186 1
.. ... ...
373 1084 1
374 506 0
375 1142 1
376 1124 0
377 689 1
[378 rows x 2 columns]
########### Random Forests ###############
Accuracy: 0.8121693121693122
Null accuracy:
0 191
1 187
Name: treatment, dtype: int64
Percentage of ones: 0.4947089947089947
Percentage of zeros: 0.5052910052910053
True: [0 0 0 0 0 0 0 0 1 1 0 1 1 0 1 1 0 1 0 0 0 1 1 0 0]
Pred: [1 0 0 0 1 1 0 1 1 1 0 1 1 0 1 1 1 1 0 0 0 0 1 0 0]
<jupyter_text>
## **9. Success method plot**<jupyter_code>def plotSuccess():
s = pd.Series(methodDict)
s = s.sort_values(ascending=False)
plt.figure(figsize=(12,8))
#Colors
ax = s.plot(kind='bar')
for p in ax.patches:
ax.annotate(str(round(p.get_height(),2)), (p.get_x() * 1.005, p.get_height() * 1.005))
plt.ylim([70.0, 90.0])
plt.xlabel('Method')
plt.ylabel('Percentage')
plt.title('Success of methods')
plt.show()
plotSuccess()<jupyter_output><empty_output>
|
no_license
|
/mental_health_prediction.ipynb
|
avurity/Mental-Health-Prediction
| 28 |
<jupyter_start><jupyter_text>
*Esta libreta contiene material del Taller de Python que se lleva a cabo como parte del
evento [Data Challenge Industrial 4.0](www.lania.mx/dci). El contenido ha sido adaptado
por HTM y GED a partir del libro [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do)
de Jake VanderPlas y se mantiene la licencia sobre el texto,
[CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode),
y sobre el codigo [MIT license](https://opensource.org/licenses/MIT).*
# Cálculos con Arrays 1. Ufuncs## Los Loops son Lentooosss<jupyter_code>import numpy as np
np.random.seed(0)
def compute_reciprocals(values):
output = np.empty(len(values))
for i in range(len(values)):
output[i] = 1.0 / values[i]
return output
values = np.random.randint(1, 10, size=5)
compute_reciprocals(values)
big_array = np.random.randint(1, 100, size=1000000)
%timeit compute_reciprocals(big_array)<jupyter_output>1 loop, best of 3: 2.91 s per loop
<jupyter_text>## UFuncs
Operaciones *vectorizadas*<jupyter_code>print(compute_reciprocals(values))
print(1.0 / values)
%timeit (1.0 / big_array)
np.arange(5) / np.arange(1, 6)
x = np.arange(9).reshape((3, 3))
2 ** x<jupyter_output><empty_output><jupyter_text>Cálculos usando vectorizacion a través de ufuncs son en general más eficientes que la implementación usando loops## Exploración de UFuncs
Ufuncs:
- *unary ufuncs*, operan sobre una sola entrada
- *binary ufuncs*, operan sobre dos entradas.### Aritmética de Array
Las operaciones aritméticas de adición, substracción, multiplicación y división standard:<jupyter_code>x = np.arange(4)
print("x =", x)
print("x + 5 =", x + 5)
print("x - 5 =", x - 5)
print("x * 2 =", x * 2)
print("x / 2 =", x / 2)
print("x // 2 =", x // 2) # floor division<jupyter_output>x = [0 1 2 3]
x + 5 = [5 6 7 8]
x - 5 = [-5 -4 -3 -2]
x * 2 = [0 2 4 6]
x / 2 = [ 0. 0.5 1. 1.5]
x // 2 = [0 0 1 1]
<jupyter_text>Negation, operador de exponencia ``**`` y operador de módulo ``%``:<jupyter_code>print("-x = ", -x)
print("x ** 2 = ", x ** 2)
print("x % 2 = ", x % 2)<jupyter_output>-x = [ 0 -1 -2 -3]
x ** 2 = [0 1 4 9]
x % 2 = [0 1 0 1]
<jupyter_text>Orden standard de las operaciones:<jupyter_code>-(0.5*x + 1) ** 2<jupyter_output><empty_output><jupyter_text>El operador ``+`` es un wrapper para la función ``add``:<jupyter_code>np.add(x, 2)<jupyter_output><empty_output><jupyter_text>The siguiente tabla enlista los operadores aritméticos implementados en NumPy:
| Operator | Equivalent ufunc | Description |
|---------------|---------------------|---------------------------------------|
|``+`` |``np.add`` |Addition (e.g., ``1 + 1 = 2``) |
|``-`` |``np.subtract`` |Subtraction (e.g., ``3 - 2 = 1``) |
|``-`` |``np.negative`` |Unary negation (e.g., ``-2``) |
|``*`` |``np.multiply`` |Multiplication (e.g., ``2 * 3 = 6``) |
|``/`` |``np.divide`` |Division (e.g., ``3 / 2 = 1.5``) |
|``//`` |``np.floor_divide`` |Floor division (e.g., ``3 // 2 = 1``) |
|``**`` |``np.power`` |Exponentiation (e.g., ``2 ** 3 = 8``) |
|``%`` |``np.mod`` |Modulus/remainder (e.g., ``9 % 4 = 1``)|
Adicionalmente, hay operadores Boolean; exploraremos éstos en [Comparaciones, mascaras y logica booleana](01.06-Boolean-Arrays-and-Masks.ipynb).### Valor Absoluto
<jupyter_code># Python abs
x = np.array([-2, -1, 0, 1, 2])
abs(x)
np.absolute(x)
np.abs(x)<jupyter_output><empty_output><jupyter_text>Esta ufunc puede operar sobre números complejos:<jupyter_code>x = np.array([3 - 4j, 4 - 3j, 2 + 0j, 0 + 1j])
np.abs(x)<jupyter_output><empty_output><jupyter_text>### Funciones Trigonometricas
<jupyter_code>theta = np.linspace(0, np.pi, 3)
print("theta = ", theta)
print("sin(theta) = ", np.sin(theta))
print("cos(theta) = ", np.cos(theta))
print("tan(theta) = ", np.tan(theta))
x = [-1, 0, 1]
print("x = ", x)
print("arcsin(x) = ", np.arcsin(x))
print("arccos(x) = ", np.arccos(x))
print("arctan(x) = ", np.arctan(x))<jupyter_output>x = [-1, 0, 1]
arcsin(x) = [-1.57079633 0. 1.57079633]
arccos(x) = [ 3.14159265 1.57079633 0. ]
arctan(x) = [-0.78539816 0. 0.78539816]
<jupyter_text>### Exponentes y Logaritmos
<jupyter_code>x = [1, 2, 3]
print("x =", x)
print("e^x =", np.exp(x))
print("2^x =", np.exp2(x))
print("3^x =", np.power(3, x))
x = [1, 2, 4, 10]
print("x =", x)
print("ln(x) =", np.log(x))
print("log2(x) =", np.log2(x))
print("log10(x) =", np.log10(x))
# for small input
x = [0, 0.001, 0.01, 0.1]
print("exp(x) - 1 =", np.expm1(x))
print("log(1 + x) =", np.log1p(x))<jupyter_output>exp(x) - 1 = [ 0. 0.0010005 0.01005017 0.10517092]
log(1 + x) = [ 0. 0.0009995 0.00995033 0.09531018]
<jupyter_text>### Ufuncs especializadas
<jupyter_code>from scipy import special
# Gamma functions (generalized factorials) and related functions
x = [1, 5, 10]
print("gamma(x) =", special.gamma(x))
print("ln|gamma(x)| =", special.gammaln(x))
print("beta(x, 2) =", special.beta(x, 2))
# Error function (integral of Gaussian)
# its complement, and its inverse
x = np.array([0, 0.3, 0.7, 1.0])
print("erf(x) =", special.erf(x))
print("erfc(x) =", special.erfc(x))
print("erfinv(x) =", special.erfinv(x))<jupyter_output>erf(x) = [ 0. 0.32862676 0.67780119 0.84270079]
erfc(x) = [ 1. 0.67137324 0.32219881 0.15729921]
erfinv(x) = [ 0. 0.27246271 0.73286908 inf]
<jupyter_text>## Propiedades Avanzadas de Ufunc
### Especificando la salida
Todas las ufuncs pueden usar el argumento ``out`` para indicar donde asignar el resultado<jupyter_code>x = np.arange(5)
y = np.empty(5)
np.multiply(x, 10, out=y)
print(y)
y = np.zeros(10)
np.power(2, x, out=y[::2])
print(y)
# lo mismo pero crea un array temporal para guardar el resultado de 2**x,
# seguido de una segunda operacion que copia esos valores a y
# que puede ser costoso para arrays grandes
y = np.zeros(10)
y[::2] = 2**x<jupyter_output><empty_output><jupyter_text>### Agregaciones
<jupyter_code>x = np.arange(1, 6)
np.add.reduce(x)
np.multiply.reduce(x)
np.add.accumulate(x)
np.multiply.accumulate(x)<jupyter_output><empty_output><jupyter_text>Exploraremos un poco mas en [Agregaciones: Min, Max, etc.](01.04-Computation-on-arrays-aggregates.ipynb).### Productos exteriores
<jupyter_code>x = np.arange(1, 6)
np.multiply.outer(x, x)<jupyter_output><empty_output>
|
no_license
|
/01_03_Computation_on_arrays_ufuncs.ipynb
|
htapiagroup/introduccion-a-numpy-DoddyRafael
| 14 |
<jupyter_start><jupyter_text>### In this notebook, we display wordclouds using a stopwrod list composed of a combination from stopword dictionaries via spaCy, WordCloud, and NLTK packages.
* Three wordclouds are displayed: a full dataset wordcloud, followed by a positive sentiment only wordcloud, and a negative sentiment only wordcloud.
* The only further customization of the stopwords list is the exclusion of the word 'not'.<jupyter_code>import pandas as pd
from wordcloud import WordCloud
import matplotlib.pyplot as plt
import nltk<jupyter_output><empty_output><jupyter_text>## Some EDA<jupyter_code>df = pd.read_csv('IMDB Dataset.csv')
# Extend width of dataframe view
pd.options.display.max_colwidth = 100
df.head()<jupyter_output><empty_output><jupyter_text>### Review examples from each sentiment.<jupyter_code>print(df['review'][3])
print('')
print('Sentiment:',df['sentiment'][3])
print(df['review'][1])
print('')
print('Sentiment:',df['sentiment'][1])
# Check for balanced dataset
df['sentiment'].value_counts()<jupyter_output><empty_output><jupyter_text>## Pre-processing: Tokenize, Stopwords, Lemmatize, etc.#### Remove html coding<jupyter_code>df['review'] = df['review'].str.replace('<.*?>','')<jupyter_output><empty_output><jupyter_text>#### Make everything lower case<jupyter_code>df['review'] = df['review'].str.lower()<jupyter_output><empty_output><jupyter_text>#### Remove stop words<jupyter_code>import spacy
sp = spacy.load('en_core_web_sm')
all_stopwords = sp.Defaults.stop_words
# # After seeing the word counts, update stop words
# sp.Defaults.stop_words |= {'movie', 'film', 'like'}
# Import custom list and merge with spaCy list.
import pickle
with open('wordcloud_sw.data', 'rb') as file:
load_f = pickle.load(file)
a = list(all_stopwords)
b = list(load_f)
c = [i for i in b if i not in a]
d = [j for j in a if j not in b]
master_stop = a+b+c+d
len(master_stop)
# Convert set to list for the purpose of removing duplicates
master_set = set(master_stop)
master_set.remove('not')
len(master_set)
# Apply function to remove stopwords
df['review'] = df['review'].apply(lambda x: ' '.join([word for word in x.split() if word not in (master_set)]))<jupyter_output><empty_output><jupyter_text>#### Remove all puncuation and special characters<jupyter_code>df['review'] = df['review'].str.replace('[^\w\s]','')<jupyter_output><empty_output><jupyter_text>#### Tokenize & lemmatize<jupyter_code>w_tokenizer = nltk.tokenize.WhitespaceTokenizer()
lemmatizer = nltk.stem.WordNetLemmatizer()
def lemmatize_text(text):
return [lemmatizer.lemmatize(w) for w in w_tokenizer.tokenize(text)]
df['lemma_review'] = df.review.apply(lemmatize_text)
df['review'][0]
print(df['lemma_review'][0])
# Get word counts and make sure stopwords didnt re-enter the data after lemmatizing
cloudcount = dict(df.lemma_review.explode().value_counts())
cleancloud = dict((key, value) for key, value in cloudcount.items() if key not in master_set)
{k: cleancloud[k] for k in list(cleancloud)[:15]}
wordcloud = WordCloud(width=1500, height=750, max_words=100, background_color="black", max_font_size=325,
colormap='Accent', font_path='/System/Library/Fonts/Supplemental/DIN Condensed Bold.ttf').generate_from_frequencies(cleancloud)
plt.figure(figsize=(20,10), facecolor='k')
plt.imshow(wordcloud, interpolation="bilinear")
plt.axis("off")
plt.savefig('full_set_cloud.png')
plt.show()
pos_df = df[df['sentiment'] == 'positive']
neg_df = df[df['sentiment'] == 'negative']
pos_cloud = dict(pos_df.lemma_review.explode().value_counts())
pos_clean = dict((key, value) for key, value in pos_cloud.items() if key not in master_set)
{k: pos_clean[k] for k in list(pos_clean)[:10]}
wordcloud = WordCloud(width=1500, height=750, max_words=100, background_color="black", max_font_size=325,
colormap='Accent', font_path='/System/Library/Fonts/Supplemental/DIN Condensed Bold.ttf').generate_from_frequencies(pos_clean)
plt.figure(figsize=(20,10), facecolor='k')
plt.imshow(wordcloud, interpolation="bilinear")
plt.axis("off")
plt.savefig('pos_cloud.png')
plt.show()
neg_cloud = dict(neg_df.lemma_review.explode().value_counts())
neg_clean = dict((key, value) for key, value in neg_cloud.items() if key not in master_set)
{k: neg_clean[k] for k in list(neg_clean)[:10]}
wordcloud = WordCloud(width=1500, height=750, max_words=100, background_color="black", max_font_size=325,
colormap='Accent', font_path='/System/Library/Fonts/Supplemental/DIN Condensed Bold.ttf').generate_from_frequencies(neg_clean)
plt.figure(figsize=(20,10), facecolor='k')
plt.imshow(wordcloud, interpolation="bilinear")
plt.axis("off")
plt.savefig('neg_cloud.png')
plt.show()<jupyter_output><empty_output>
|
no_license
|
/EDA/Full, Pos, Neg Wordclouds.ipynb
|
jasonli19/Capstone-II
| 8 |
<jupyter_start><jupyter_text>
1D Numpy in PythonWelcome! This notebook will teach you about using Numpy in the Python Programming Language. By the end of this lab, you'll know what Numpy is and the Numpy operations.Table of Contents
Preparation
What is Numpy?
Type
Assign Value
Slicing
Assign Value with List
Other Attributes
Numpy Array Operations
Array Addition
Array Multiplication
Product of Two Numpy Arrays
Dot Product
Adding Constant to a Numpy Array
Mathematical Functions
Linspace
Estimated time needed: 30 min
Preparation<jupyter_code># Import the libraries
import time
import sys
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Plotting functions
def Plotvec1(u, z, v):
ax = plt.axes()
ax.arrow(0, 0, *u, head_width=0.05, color='r', head_length=0.1)
plt.text(*(u + 0.1), 'u')
ax.arrow(0, 0, *v, head_width=0.05, color='b', head_length=0.1)
plt.text(*(v + 0.1), 'v')
ax.arrow(0, 0, *z, head_width=0.05, head_length=0.1)
plt.text(*(z + 0.1), 'z')
plt.ylim(-2, 2)
plt.xlim(-2, 2)
def Plotvec2(a,b):
ax = plt.axes()
ax.arrow(0, 0, *a, head_width=0.05, color ='r', head_length=0.1)
plt.text(*(a + 0.1), 'a')
ax.arrow(0, 0, *b, head_width=0.05, color ='b', head_length=0.1)
plt.text(*(b + 0.1), 'b')
plt.ylim(-2, 2)
plt.xlim(-2, 2)<jupyter_output><empty_output><jupyter_text>Create a Python List as follows:<jupyter_code># Create a python list
a = ["0", 1, "two", "3", 4]<jupyter_output><empty_output><jupyter_text>We can access the data via an index:We can access each element using a square bracket as follows: <jupyter_code># Print each element
print("a[0]:", a[0])
print("a[1]:", a[1])
print("a[2]:", a[2])
print("a[3]:", a[3])
print("a[4]:", a[4])<jupyter_output>a[0]: 0
a[1]: 1
a[2]: two
a[3]: 3
a[4]: 4
<jupyter_text>What is Numpy?A numpy array is similar to a list. It's usually fixed in size and each element is of the same type. We can cast a list to a numpy array by first importing numpy: <jupyter_code># import numpy library
import numpy as np <jupyter_output><empty_output><jupyter_text> We then cast the list as follows:<jupyter_code># Create a numpy array
a = np.array([0, 1, 2, 3, 4])
a<jupyter_output><empty_output><jupyter_text>Each element is of the same type, in this case integers: As with lists, we can access each element via a square bracket:<jupyter_code># Print each element
print("a[0]:", a[0])
print("a[1]:", a[1])
print("a[2]:", a[2])
print("a[3]:", a[3])
print("a[4]:", a[4])<jupyter_output>a[0]: 0
a[1]: 1
a[2]: 2
a[3]: 3
a[4]: 4
<jupyter_text>TypeIf we check the type of the array we get numpy.ndarray:<jupyter_code># Check the type of the array
type(a)<jupyter_output><empty_output><jupyter_text>As numpy arrays contain data of the same type, we can use the attribute "dtype" to obtain the Data-type of the array’s elements. In this case a 64-bit integer:
<jupyter_code># Check the type of the values stored in numpy array
a.dtype<jupyter_output><empty_output><jupyter_text>We can create a numpy array with real numbers:<jupyter_code># Create a numpy array
b = np.array([3.1, 11.02, 6.2, 213.2, 5.2])<jupyter_output><empty_output><jupyter_text>When we check the type of the array we get numpy.ndarray:<jupyter_code># Check the type of array
type(b)<jupyter_output><empty_output><jupyter_text>If we examine the attribute dtype we see float 64, as the elements are not integers: <jupyter_code># Check the value type
b.dtype<jupyter_output><empty_output><jupyter_text>Assign valueWe can change the value of the array, consider the array c:<jupyter_code># Create numpy array
c = np.array([20, 1, 2, 3, 4])
c<jupyter_output><empty_output><jupyter_text>We can change the first element of the array to 100 as follows:<jupyter_code># Assign the first element to 100
c[0] = 100
c<jupyter_output><empty_output><jupyter_text>We can change the 5th element of the array to 0 as follows:<jupyter_code># Assign the 5th element to 0
c[4] = 0
c<jupyter_output><empty_output><jupyter_text>SlicingLike lists, we can slice the numpy array, and we can select the elements from 1 to 3 and assign it to a new numpy array d as follows:<jupyter_code># Slicing the numpy array
d = c[1:4]
d<jupyter_output><empty_output><jupyter_text>We can assign the corresponding indexes to new values as follows: <jupyter_code># Set the fourth element and fifth element to 300 and 400
c[3:5] = 300, 400
c<jupyter_output><empty_output><jupyter_text>Assign Value with ListSimilarly, we can use a list to select a specific index.
The list ' select ' contains several values:
<jupyter_code># Create the index list
select = [0, 2, 3]<jupyter_output><empty_output><jupyter_text>We can use the list as an argument in the brackets. The output is the elements corresponding to the particular index:<jupyter_code># Use List to select elements
d = c[select]
d<jupyter_output><empty_output><jupyter_text>We can assign the specified elements to a new value. For example, we can assign the values to 100 000 as follows:<jupyter_code># Assign the specified elements to new value
c[select] = 100000
c<jupyter_output><empty_output><jupyter_text>Other AttributesLet's review some basic array attributes using the array a:<jupyter_code># Create a numpy array
a = np.array([0, 1, 2, 3, 4])
a<jupyter_output><empty_output><jupyter_text>The attribute size is the number of elements in the array:<jupyter_code># Get the size of numpy array
a.size<jupyter_output><empty_output><jupyter_text>The next two attributes will make more sense when we get to higher dimensions but let's review them. The attribute ndim represents the number of array dimensions or the rank of the array, in this case, one:<jupyter_code># Get the number of dimensions of numpy array
a.ndim<jupyter_output><empty_output><jupyter_text>The attribute shape is a tuple of integers indicating the size of the array in each dimension:<jupyter_code># Get the shape/size of numpy array
a.shape
# Create a numpy array
a = np.array([1, -1, 1, -1])
# Get the mean of numpy array
mean = a.mean()
mean
# Get the standard deviation of numpy array
standard_deviation=a.std()
standard_deviation
# Create a numpy array
b = np.array([-1, 2, 3, 4, 5])
b
# Get the biggest value in the numpy array
max_b = b.max()
max_b
# Get the smallest value in the numpy array
min_b = b.min()
min_b<jupyter_output><empty_output><jupyter_text>Numpy Array OperationsArray AdditionConsider the numpy array u:<jupyter_code>u = np.array([1, 0])
u<jupyter_output><empty_output><jupyter_text>Consider the numpy array v:<jupyter_code>v = np.array([0, 1])
v<jupyter_output><empty_output><jupyter_text>We can add the two arrays and assign it to z:<jupyter_code># Numpy Array Addition
z = u + v
z<jupyter_output><empty_output><jupyter_text> The operation is equivalent to vector addition:<jupyter_code># Plot numpy arrays
Plotvec1(u, z, v)<jupyter_output><empty_output><jupyter_text>Array MultiplicationConsider the vector numpy array y:<jupyter_code># Create a numpy array
y = np.array([1, 2])
y<jupyter_output><empty_output><jupyter_text>We can multiply every element in the array by 2:<jupyter_code># Numpy Array Multiplication
z = 2 * y
z<jupyter_output><empty_output><jupyter_text> This is equivalent to multiplying a vector by a scaler: Product of Two Numpy ArraysConsider the following array u:<jupyter_code># Create a numpy array
u = np.array([1, 2])
u<jupyter_output><empty_output><jupyter_text>Consider the following array v:<jupyter_code># Create a numpy array
v = np.array([3, 2])
v<jupyter_output><empty_output><jupyter_text> The product of the two numpy arrays u and v is given by:<jupyter_code># Calculate the production of two numpy arrays
z = u * v
z<jupyter_output><empty_output><jupyter_text>Dot ProductThe dot product of the two numpy arrays u and v is given by:<jupyter_code># Calculate the dot product
np.dot(u, v)<jupyter_output><empty_output><jupyter_text>Adding Constant to a Numpy ArrayConsider the following array: <jupyter_code># Create a constant to numpy array
u = np.array([1, 2, 3, -1])
u<jupyter_output><empty_output><jupyter_text>Adding the constant 1 to each element in the array:<jupyter_code># Add the constant to array
u + 1<jupyter_output><empty_output><jupyter_text> The process is summarised in the following animation:Mathematical Functions We can access the value of pie in numpy as follows :<jupyter_code># The value of pie
np.pi<jupyter_output><empty_output><jupyter_text> We can create the following numpy array in Radians:<jupyter_code># Create the numpy array in radians
x = np.array([0, np.pi/2 , np.pi])<jupyter_output><empty_output><jupyter_text>We can apply the function sin to the array x and assign the values to the array y; this applies the sine function to each element in the array: <jupyter_code># Calculate the sin of each elements
y = np.sin(x)
y<jupyter_output><empty_output><jupyter_text>Linspace A useful function for plotting mathematical functions is "linespace". Linespace returns evenly spaced numbers over a specified interval. We specify the starting point of the sequence and the ending point of the sequence. The parameter "num" indicates the Number of samples to generate, in this case 5:<jupyter_code># Makeup a numpy array within [-2, 2] and 5 elements
np.linspace(-2, 2, num=5)<jupyter_output><empty_output><jupyter_text>If we change the parameter num to 9, we get 9 evenly spaced numbers over the interval from -2 to 2: <jupyter_code># Makeup a numpy array within [-2, 2] and 9 elements
np.linspace(-2, 2, num=9)<jupyter_output><empty_output><jupyter_text>We can use the function line space to generate 100 evenly spaced samples from the interval 0 to 2π: <jupyter_code># Makeup a numpy array within [0, 2π] and 100 elements
x = np.linspace(0, 2*np.pi, num=100)<jupyter_output><empty_output><jupyter_text>We can apply the sine function to each element in the array x and assign it to the array y: <jupyter_code># Calculate the sine of x list
y = np.sin(x)
# Plot the result
plt.plot(x, y)<jupyter_output><empty_output><jupyter_text>Quiz on 1D Numpy ArrayImplement the following vector subtraction in numpy: u-v<jupyter_code># Write your code below and press Shift+Enter to execute
u = np.array([1, 0])
v = np.array([0, 1])
z = u-v
z<jupyter_output><empty_output><jupyter_text>Double-click __here__ for the solution.
<!-- Your answer is below:
u - v
-->Multiply the numpy array z with -2:<jupyter_code># Write your code below and press Shift+Enter to execute
z = np.array([2, 4])
z = z*2
z<jupyter_output><empty_output><jupyter_text>Double-click __here__ for the solution.
<!-- Your answer is below:
-2 * z
-->Consider the list [1, 2, 3, 4, 5] and [1, 0, 1, 0, 1], and cast both lists to a numpy array then multiply them together:<jupyter_code># Write your code below and press Shift+Enter to execute
p = np.array([1, 2, 3, 4, 5])
q = np.array([1, 0, 1, 0, 1])
o = p*q
o<jupyter_output><empty_output><jupyter_text>Double-click __here__ for the solution.
<!-- Your answer is below:
a = np.array([1, 2, 3, 4, 5])
b = np.array([1, 0, 1, 0, 1])
a * b
-->Convert the list [-1, 1] and [1, 1] to numpy arrays a and b. Then, plot the arrays as vectors using the fuction Plotvec2 and find the dot product:<jupyter_code># Write your code below and press Shift+Enter to execute
x = np.array([-1, 1])
y = np.array([1, 1])
Plotvec2(x,y)
print("The dot product is:", np.dot(x,y))<jupyter_output>The dot product is: 0
<jupyter_text>Double-click __here__ for the solution.
<!-- Your answer is below:
a = np.array([-1, 1])
b = np.array([1, 1])
Plotvec2(a, b)
print("The dot product is", np.dot(a,b))
-->Convert the list [1, 0] and [0, 1] to numpy arrays a and b. Then, plot the arrays as vectors using the function Plotvec2 and find the dot product:<jupyter_code># Write your code below and press Shift+Enter to execute
a = np.array([1, 0])
b = np.array([0, 1])
Plotvec2(a,b)
print("The dot product is:", np.dot(a,b))<jupyter_output>The dot product is: 0
<jupyter_text>Double-click __here__ for the solution.
<!--
a = np.array([1, 0])
b = np.array([0, 1])
Plotvec2(a, b)
print("The dot product is", np.dot(a, b))
-->Convert the list [1, 1] and [0, 1] to numpy arrays a and b. Then plot the arrays as vectors using the fuction Plotvec2 and find the dot product:<jupyter_code># Write your code below and press Shift+Enter to execute
a = np.array([1, 1])
b = np.array([0, 1])
Plotvec2(a,b)
print("The dot product is:", np.dot(a,b))<jupyter_output>The dot product is: 1
<jupyter_text>Double-click __here__ for the solution.
<!--
a = np.array([1, 1])
b = np.array([0, 1])
Plotvec2(a, b)
print("The dot product is", np.dot(a, b))
print("The dot product is", np.dot(a, b))
-->Why are the results of the dot product for [-1, 1] and [1, 1] and the dot product for [1, 0] and [0, 1] zero, but not zero for the dot product for [1, 1] and [0, 1]? Hint: Study the corresponding figures, pay attention to the direction the arrows are pointing to.<jupyter_code># Write your code below and press Shift+Enter to execute<jupyter_output><empty_output>
|
no_license
|
/5.1-Numpy1D.ipynb
|
anuraj76/Python-Programming
| 49 |
<jupyter_start><jupyter_text># Logistic Regression with a Neural Network mindset
Welcome to your first (required) programming assignment! You will build a logistic regression classifier to recognize cats. This assignment will step you through how to do this with a Neural Network mindset, and so will also hone your intuitions about deep learning.
**Instructions:**
- Do not use loops (for/while) in your code, unless the instructions explicitly ask you to do so.
**You will learn to:**
- Build the general architecture of a learning algorithm, including:
- Initializing parameters
- Calculating the cost function and its gradient
- Using an optimization algorithm (gradient descent)
- Gather all three functions above into a main model function, in the right order.## 1 - Packages ##
First, let's run the cell below to import all the packages that you will need during this assignment.
- [numpy](www.numpy.org) is the fundamental package for scientific computing with Python.
- [h5py](http://www.h5py.org) is a common package to interact with a dataset that is stored on an H5 file.
- [matplotlib](http://matplotlib.org) is a famous library to plot graphs in Python.
- [PIL](http://www.pythonware.com/products/pil/) and [scipy](https://www.scipy.org/) are used here to test your model with your own picture at the end.<jupyter_code>import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset
%matplotlib inline<jupyter_output>/opt/conda/lib/python3.5/site-packages/matplotlib/font_manager.py:273: UserWarning: Matplotlib is building the font cache using fc-list. This may take a moment.
warnings.warn('Matplotlib is building the font cache using fc-list. This may take a moment.')
/opt/conda/lib/python3.5/site-packages/matplotlib/font_manager.py:273: UserWarning: Matplotlib is building the font cache using fc-list. This may take a moment.
warnings.warn('Matplotlib is building the font cache using fc-list. This may take a moment.')
<jupyter_text>## 2 - Overview of the Problem set ##
**Problem Statement**: You are given a dataset ("data.h5") containing:
- a training set of m_train images labeled as cat (y=1) or non-cat (y=0)
- a test set of m_test images labeled as cat or non-cat
- each image is of shape (num_px, num_px, 3) where 3 is for the 3 channels (RGB). Thus, each image is square (height = num_px) and (width = num_px).
You will build a simple image-recognition algorithm that can correctly classify pictures as cat or non-cat.
Let's get more familiar with the dataset. Load the data by running the following code.<jupyter_code># Loading the data (cat/non-cat)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()<jupyter_output><empty_output><jupyter_text>We added "_orig" at the end of image datasets (train and test) because we are going to preprocess them. After preprocessing, we will end up with train_set_x and test_set_x (the labels train_set_y and test_set_y don't need any preprocessing).
Each line of your train_set_x_orig and test_set_x_orig is an array representing an image. You can visualize an example by running the following code. Feel free also to change the `index` value and re-run to see other images. <jupyter_code># Example of a picture
index = 54
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") + "' picture.")<jupyter_output>y = [1], it's a 'cat' picture.
<jupyter_text>Many software bugs in deep learning come from having matrix/vector dimensions that don't fit. If you can keep your matrix/vector dimensions straight you will go a long way toward eliminating many bugs.
**Exercise:** Find the values for:
- m_train (number of training examples)
- m_test (number of test examples)
- num_px (= height = width of a training image)
Remember that `train_set_x_orig` is a numpy-array of shape (m_train, num_px, num_px, 3). For instance, you can access `m_train` by writing `train_set_x_orig.shape[0]`.<jupyter_code>### START CODE HERE ### (≈ 3 lines of code)
m_train = train_set_x_orig.shape[0]
m_test = test_set_x_orig.shape[0]
num_px = train_set_x_orig.shape[1]
### END CODE HERE ###
print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))<jupyter_output>Number of training examples: m_train = 209
Number of testing examples: m_test = 50
Height/Width of each image: num_px = 64
Each image is of size: (64, 64, 3)
train_set_x shape: (209, 64, 64, 3)
train_set_y shape: (1, 209)
test_set_x shape: (50, 64, 64, 3)
test_set_y shape: (1, 50)
<jupyter_text>**Expected Output for m_train, m_test and num_px**:
**m_train**
209
**m_test**
50
**num_px**
64
For convenience, you should now reshape images of shape (num_px, num_px, 3) in a numpy-array of shape (num_px $*$ num_px $*$ 3, 1). After this, our training (and test) dataset is a numpy-array where each column represents a flattened image. There should be m_train (respectively m_test) columns.
**Exercise:** Reshape the training and test data sets so that images of size (num_px, num_px, 3) are flattened into single vectors of shape (num\_px $*$ num\_px $*$ 3, 1).
A trick when you want to flatten a matrix X of shape (a,b,c,d) to a matrix X_flatten of shape (b$*$c$*$d, a) is to use:
```python
X_flatten = X.reshape(X.shape[0], -1).T # X.T is the transpose of X
```<jupyter_code># Reshape the training and test examples
### START CODE HERE ### (≈ 2 lines of code)
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0] , -1).T
test_set_x_flatten = test_set_x_orig.reshape((num_px*num_px*test_set_x_orig.shape[3]),m_test)
### END CODE HERE ###
print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
print ("sanity check after reshaping: " + str(train_set_x_flatten[0:5,0]))<jupyter_output>train_set_x_flatten shape: (12288, 209)
train_set_y shape: (1, 209)
test_set_x_flatten shape: (12288, 50)
test_set_y shape: (1, 50)
sanity check after reshaping: [17 31 56 22 33]
<jupyter_text>**Expected Output**:
**train_set_x_flatten shape**
(12288, 209)
**train_set_y shape**
(1, 209)
**test_set_x_flatten shape**
(12288, 50)
**test_set_y shape**
(1, 50)
**sanity check after reshaping**
[17 31 56 22 33]
To represent color images, the red, green and blue channels (RGB) must be specified for each pixel, and so the pixel value is actually a vector of three numbers ranging from 0 to 255.
One common preprocessing step in machine learning is to center and standardize your dataset, meaning that you substract the mean of the whole numpy array from each example, and then divide each example by the standard deviation of the whole numpy array. But for picture datasets, it is simpler and more convenient and works almost as well to just divide every row of the dataset by 255 (the maximum value of a pixel channel).
Let's standardize our dataset.<jupyter_code>train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.<jupyter_output><empty_output><jupyter_text>
**What you need to remember:**
Common steps for pre-processing a new dataset are:
- Figure out the dimensions and shapes of the problem (m_train, m_test, num_px, ...)
- Reshape the datasets such that each example is now a vector of size (num_px \* num_px \* 3, 1)
- "Standardize" the data## 3 - General Architecture of the learning algorithm ##
It's time to design a simple algorithm to distinguish cat images from non-cat images.
You will build a Logistic Regression, using a Neural Network mindset. The following Figure explains why **Logistic Regression is actually a very simple Neural Network!**
**Mathematical expression of the algorithm**:
For one example $x^{(i)}$:
$$z^{(i)} = w^T x^{(i)} + b \tag{1}$$
$$\hat{y}^{(i)} = a^{(i)} = sigmoid(z^{(i)})\tag{2}$$
$$ \mathcal{L}(a^{(i)}, y^{(i)}) = - y^{(i)} \log(a^{(i)}) - (1-y^{(i)} ) \log(1-a^{(i)})\tag{3}$$
The cost is then computed by summing over all training examples:
$$ J = \frac{1}{m} \sum_{i=1}^m \mathcal{L}(a^{(i)}, y^{(i)})\tag{6}$$
**Key steps**:
In this exercise, you will carry out the following steps:
- Initialize the parameters of the model
- Learn the parameters for the model by minimizing the cost
- Use the learned parameters to make predictions (on the test set)
- Analyse the results and conclude## 4 - Building the parts of our algorithm ##
The main steps for building a Neural Network are:
1. Define the model structure (such as number of input features)
2. Initialize the model's parameters
3. Loop:
- Calculate current loss (forward propagation)
- Calculate current gradient (backward propagation)
- Update parameters (gradient descent)
You often build 1-3 separately and integrate them into one function we call `model()`.
### 4.1 - Helper functions
**Exercise**: Using your code from "Python Basics", implement `sigmoid()`. As you've seen in the figure above, you need to compute $sigmoid( w^T x + b) = \frac{1}{1 + e^{-(w^T x + b)}}$ to make predictions. Use np.exp().<jupyter_code># GRADED FUNCTION: sigmoid
def sigmoid(z):
"""
Compute the sigmoid of z
Arguments:
z -- A scalar or numpy array of any size.
Return:
s -- sigmoid(z)
"""
### START CODE HERE ### (≈ 1 line of code)
s = None
s = 1/(1+np.exp(-z))
### END CODE HERE ###
return s
print ("sigmoid([0, 2]) = " + str(sigmoid(np.array([0,2]))))<jupyter_output>sigmoid([0, 2]) = [ 0.5 0.88079708]
<jupyter_text>**Expected Output**:
**sigmoid([0, 2])**
[ 0.5 0.88079708]
### 4.2 - Initializing parameters
**Exercise:** Implement parameter initialization in the cell below. You have to initialize w as a vector of zeros. If you don't know what numpy function to use, look up np.zeros() in the Numpy library's documentation.<jupyter_code># GRADED FUNCTION: initialize_with_zeros
def initialize_with_zeros(dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
Argument:
dim -- size of the w vector we want (or number of parameters in this case)
Returns:
w -- initialized vector of shape (dim, 1)
b -- initialized scalar (corresponds to the bias)
"""
### START CODE HERE ### (≈ 1 line of code)
w = np.zeros((dim,1))
b = 0
### END CODE HERE ###
assert(w.shape == (dim, 1))
assert(isinstance(b, float) or isinstance(b, int))
return w, b
dim = 2
w, b = initialize_with_zeros(dim)
print ("w = " + str(w))
print ("b = " + str(b))<jupyter_output>w = [[ 0.]
[ 0.]]
b = 0
<jupyter_text>**Expected Output**:
** w **
[[ 0.]
[ 0.]]
** b **
0
For image inputs, w will be of shape (num_px $\times$ num_px $\times$ 3, 1).### 4.3 - Forward and Backward propagation
Now that your parameters are initialized, you can do the "forward" and "backward" propagation steps for learning the parameters.
**Exercise:** Implement a function `propagate()` that computes the cost function and its gradient.
**Hints**:
Forward Propagation:
- You get X
- You compute $A = \sigma(w^T X + b) = (a^{(1)}, a^{(2)}, ..., a^{(m-1)}, a^{(m)})$
- You calculate the cost function: $J = -\frac{1}{m}\sum_{i=1}^{m}y^{(i)}\log(a^{(i)})+(1-y^{(i)})\log(1-a^{(i)})$
Here are the two formulas you will be using:
$$ \frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T\tag{7}$$
$$ \frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})\tag{8}$$<jupyter_code># GRADED FUNCTION: propagate
def propagate(w, b, X, Y):
"""
Implement the cost function and its gradient for the propagation explained above
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)
Return:
cost -- negative log-likelihood cost for logistic regression
dw -- gradient of the loss with respect to w, thus same shape as w
db -- gradient of the loss with respect to b, thus same shape as b
Tips:
- Write your code step by step for the propagation. np.log(), np.dot()
"""
m = X.shape[1]
# FORWARD PROPAGATION (FROM X TO COST)
### START CODE HERE ### (≈ 2 lines of code)
A = sigmoid(np.dot(w.T,X) + b) # compute activation
cost = -(1/m)*(np.dot(Y,np.log(A).T)+ np.dot((1-Y),np.log(1-A).T)) # compute cost
### END CODE HERE ###
# BACKWARD PROPAGATION (TO FIND GRAD)
### START CODE HERE ### (≈ 2 lines of code)
dw = (1/m)*np.dot(X,(A-Y).T)
db = (1/m)*np.sum(A-Y)
### END CODE HERE ###
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
grads = {"dw": dw,
"db": db}
return grads, cost
w, b, X, Y = np.array([[1.],[2.]]), 2., np.array([[1.,2.,-1.],[3.,4.,-3.2]]), np.array([[1,0,1]])
grads, cost = propagate(w, b, X, Y)
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
print ("cost = " + str(cost))<jupyter_output>dw = [[ 0.99845601]
[ 2.39507239]]
db = 0.00145557813678
cost = 5.801545319394553
<jupyter_text>**Expected Output**:
** dw **
[[ 0.99845601]
[ 2.39507239]]
** db **
0.00145557813678
** cost **
5.801545319394553
### 4.4 - Optimization
- You have initialized your parameters.
- You are also able to compute a cost function and its gradient.
- Now, you want to update the parameters using gradient descent.
**Exercise:** Write down the optimization function. The goal is to learn $w$ and $b$ by minimizing the cost function $J$. For a parameter $\theta$, the update rule is $ \theta = \theta - \alpha \text{ } d\theta$, where $\alpha$ is the learning rate.<jupyter_code># GRADED FUNCTION: optimize
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
This function optimizes w and b by running a gradient descent algorithm
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- True to print the loss every 100 steps
Returns:
params -- dictionary containing the weights w and bias b
grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
Tips:
You basically need to write down two steps and iterate through them:
1) Calculate the cost and the gradient for the current parameters. Use propagate().
2) Update the parameters using gradient descent rule for w and b.
"""
costs = []
for i in range(num_iterations):
# Cost and gradient calculation (≈ 1-4 lines of code)
### START CODE HERE ###
grads, cost = propagate(w, b, X, Y)
### END CODE HERE ###
# Retrieve derivatives from grads
dw = grads["dw"]
db = grads["db"]
# update rule (≈ 2 lines of code)
### START CODE HERE ###
w = w - learning_rate*dw
b = b - learning_rate*db
### END CODE HERE ###
# Record the costs
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training iterations
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
params = {"w": w,
"b": b}
grads = {"dw": dw,
"db": db}
return params, grads, costs
params, grads, costs = optimize(w, b, X, Y, num_iterations= 100, learning_rate = 0.009, print_cost = False)
print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))<jupyter_output>w = [[ 0.19033591]
[ 0.12259159]]
b = 1.92535983008
dw = [[ 0.67752042]
[ 1.41625495]]
db = 0.219194504541
<jupyter_text>**Expected Output**:
**w**
[[ 0.19033591]
[ 0.12259159]]
**b**
1.92535983008
**dw**
[[ 0.67752042]
[ 1.41625495]]
**db**
0.219194504541
**Exercise:** The previous function will output the learned w and b. We are able to use w and b to predict the labels for a dataset X. Implement the `predict()` function. There are two steps to computing predictions:
1. Calculate $\hat{Y} = A = \sigma(w^T X + b)$
2. Convert the entries of a into 0 (if activation 0.5), stores the predictions in a vector `Y_prediction`. If you wish, you can use an `if`/`else` statement in a `for` loop (though there is also a way to vectorize this). <jupyter_code># GRADED FUNCTION: predict
def predict(w, b, X):
'''
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Returns:
Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
'''
m = X.shape[1]
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0], 1)
# Compute vector "A" predicting the probabilities of a cat being present in the picture
### START CODE HERE ### (≈ 1 line of code)
A = sigmoid(np.dot(w.T,X)+b)
### END CODE HERE ###
Y_prediction = A[0]>0.5
assert(Y_prediction.shape == (1, m))
return Y_prediction
w = np.array([[0.1124579],[0.23106775]])
b = -0.3
X = np.array([[1.,-1.1,-3.2],[1.2,2.,0.1]])
print ("predictions = " + str(predict(w, b, X)))<jupyter_output>predictions = [ True True False]
<jupyter_text>**Expected Output**:
**predictions**
[[ 1. 1. 0.]]
**What to remember:**
You've implemented several functions that:
- Initialize (w,b)
- Optimize the loss iteratively to learn parameters (w,b):
- computing the cost and its gradient
- updating the parameters using gradient descent
- Use the learned (w,b) to predict the labels for a given set of examples## 5 - Merge all functions into a model ##
You will now see how the overall model is structured by putting together all the building blocks (functions implemented in the previous parts) together, in the right order.
**Exercise:** Implement the model function. Use the following notation:
- Y_prediction_test for your predictions on the test set
- Y_prediction_train for your predictions on the train set
- w, costs, grads for the outputs of optimize()<jupyter_code># GRADED FUNCTION: model
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
"""
Builds the logistic regression model by calling the function you've implemented previously
Arguments:
X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
print_cost -- Set to true to print the cost every 100 iterations
Returns:
d -- dictionary containing information about the model.
"""
### START CODE HERE ###
# initialize parameters with zeros (≈ 1 line of code)
w, b = initialize_with_zeros(X_train.shape[0])
# Gradient descent (≈ 1 line of code)
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost = False)
# Retrieve parameters w and b from dictionary "parameters"
w = parameters["w"]
b = parameters["b"]
# Predict test/train set examples (≈ 2 lines of code)
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
### END CODE HERE ###
# Print train/test Errors
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d<jupyter_output><empty_output><jupyter_text>Run the following cell to train your model.<jupyter_code>d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)<jupyter_output>train accuracy: 99.04306220095694 %
test accuracy: 66.0 %
<jupyter_text>**Expected Output**:
**Cost after iteration 0 **
0.693147
$\vdots$
$\vdots$
**Train Accuracy**
99.04306220095694 %
**Test Accuracy**
70.0 %
**Comment**: Training accuracy is close to 100%. This is a good sanity check: your model is working and has high enough capacity to fit the training data. Test error is 68%. It is actually not bad for this simple model, given the small dataset we used and that logistic regression is a linear classifier. But no worries, you'll build an even better classifier next week!
Also, you see that the model is clearly overfitting the training data. Later in this specialization you will learn how to reduce overfitting, for example by using regularization. Using the code below (and changing the `index` variable) you can look at predictions on pictures of the test set.<jupyter_code># Example of a picture that was wrongly classified.
index = 10
plt.imshow(test_set_x[:,index].reshape((num_px, num_px, 3)))
print ("y = " + str(test_set_y[0,index]) + ", you predicted that it is a \"" + classes[d["Y_prediction_test"][0,index]].decode("utf-8") + "\" picture.")<jupyter_output><empty_output><jupyter_text>Let's also plot the cost function and the gradients.<jupyter_code># Plot learning curve (with costs)
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()<jupyter_output><empty_output><jupyter_text>**Interpretation**:
You can see the cost decreasing. It shows that the parameters are being learned. However, you see that you could train the model even more on the training set. Try to increase the number of iterations in the cell above and rerun the cells. You might see that the training set accuracy goes up, but the test set accuracy goes down. This is called overfitting. ## 6 - Further analysis (optional/ungraded exercise) ##
Congratulations on building your first image classification model. Let's analyze it further, and examine possible choices for the learning rate $\alpha$. #### Choice of learning rate ####
**Reminder**:
In order for Gradient Descent to work you must choose the learning rate wisely. The learning rate $\alpha$ determines how rapidly we update the parameters. If the learning rate is too large we may "overshoot" the optimal value. Similarly, if it is too small we will need too many iterations to converge to the best values. That's why it is crucial to use a well-tuned learning rate.
Let's compare the learning curve of our model with several choices of learning rates. Run the cell below. This should take about 1 minute. Feel free also to try different values than the three we have initialized the `learning_rates` variable to contain, and see what happens. <jupyter_code>learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
print ("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations (hundreds)')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()<jupyter_output>learning rate is: 0.01
train accuracy: 99.52153110047847 %
test accuracy: 66.0 %
-------------------------------------------------------
learning rate is: 0.001
train accuracy: 88.99521531100478 %
test accuracy: 66.0 %
-------------------------------------------------------
learning rate is: 0.0001
train accuracy: 68.42105263157895 %
test accuracy: 48.0 %
-------------------------------------------------------
<jupyter_text>**Interpretation**:
- Different learning rates give different costs and thus different predictions results.
- If the learning rate is too large (0.01), the cost may oscillate up and down. It may even diverge (though in this example, using 0.01 still eventually ends up at a good value for the cost).
- A lower cost doesn't mean a better model. You have to check if there is possibly overfitting. It happens when the training accuracy is a lot higher than the test accuracy.
- In deep learning, we usually recommend that you:
- Choose the learning rate that better minimizes the cost function.
- If your model overfits, use other techniques to reduce overfitting. (We'll talk about this in later videos.)
## 7 - Test with your own image (optional/ungraded exercise) ##
Congratulations on finishing this assignment. You can use your own image and see the output of your model. To do that:
1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
2. Add your image to this Jupyter Notebook's directory, in the "images" folder
3. Change your image's name in the following code
4. Run the code and check if the algorithm is right (1 = cat, 0 = non-cat)!<jupyter_code>## START CODE HERE ## (PUT YOUR IMAGE NAME)
my_image = "cat_in_iran.jpg" # change this to the name of your image file
## END CODE HERE ##
# We preprocess the image to fit your algorithm.
fname = "images/" + my_image
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(num_px,num_px)).reshape((1, num_px*num_px*3)).T
my_predicted_image = predict(d["w"], d["b"], my_image)
plt.imshow(image)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your algorithm predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") + "\" picture.")<jupyter_output>y = True, your algorithm predicts a "cat" picture.
|
permissive
|
/Neural Networks and Deep Learning/week2/Logistic+Regression+with+a+Neural+Network+mindset+v5.ipynb
|
mukul54/Coursera-Deep-Learning
| 17 |
<jupyter_start><jupyter_text># Basic Text Classification with Naive Bayes
***
In the mini-project, you'll learn the basics of text analysis using a subset of movie reviews from the rotten tomatoes database. You'll also use a fundamental technique in Bayesian inference, called Naive Bayes. This mini-project is based on [Lab 10 of Harvard's CS109](https://github.com/cs109/2015lab10) class. Please free to go to the original lab for additional exercises and solutions.<jupyter_code>%matplotlib inline
import numpy as np
import scipy as sp
import matplotlib as mpl
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from six.moves import range
# Setup Pandas
pd.set_option('display.width', 500)
pd.set_option('display.max_columns', 100)
pd.set_option('display.notebook_repr_html', True)
# Setup Seaborn
sns.set_style("whitegrid")
sns.set_context("poster")<jupyter_output><empty_output><jupyter_text># Table of Contents
* [Rotten Tomatoes Dataset](#Rotten-Tomatoes-Dataset)
* [Explore](#Explore)
* [The Vector Space Model and a Search Engine](#The-Vector-Space-Model-and-a-Search-Engine)
* [In Code](#In-Code)
* [Naive Bayes](#Naive-Bayes)
* [Multinomial Naive Bayes and Other Likelihood Functions](#Multinomial-Naive-Bayes-and-Other-Likelihood-Functions)
* [Picking Hyperparameters for Naive Bayes and Text Maintenance](#Picking-Hyperparameters-for-Naive-Bayes-and-Text-Maintenance)
* [Interpretation](#Interpretation)
## Rotten Tomatoes Dataset<jupyter_code>critics = pd.read_csv('./critics.csv')
#let's drop rows with missing quotes
critics = critics[~critics.quote.isnull()]
critics.head()<jupyter_output><empty_output><jupyter_text>### Explore<jupyter_code>n_reviews = len(critics)
n_movies = critics.rtid.unique().size
n_critics = critics.critic.unique().size
print("Number of reviews: {:d}".format(n_reviews))
print("Number of critics: {:d}".format(n_critics))
print("Number of movies: {:d}".format(n_movies))
df = critics.copy()
df['fresh'] = df.fresh == 'fresh'
grp = df.groupby('critic')
counts = grp.critic.count() # number of reviews by each critic
means = grp.fresh.mean() # average freshness for each critic
means[counts > 100].hist(bins=10, edgecolor='w', lw=1)
plt.xlabel("Average Rating per critic")
plt.ylabel("Number of Critics")
plt.yticks([0, 2, 4, 6, 8, 10]);<jupyter_output><empty_output><jupyter_text>
Exercise Set I
Exercise: Look at the histogram above. Tell a story about the average ratings per critic. What shape does the distribution look like? What is interesting about the distribution? What might explain these interesting things?
There is not a normal distribution of average rating per critic; it appears as though few critics only post poor ratings and most critics post ratings that are both good and poor. In addition, more critics are posting more positive reviews than negative reviews (because the distribution is skewed towards the right. Perhaps most critics post more positive ratings than they truly feel the movie deserves, in part due to their own reputation; if the critic always rates movies poorly, the credibility of that critic may decrease. Alternatively, perhaps critics are more likely to go see movies that they think they will enjoy, so they are more likely to post higher ratings if they only see movies that they think they will enjoy in the first place. Another explanation may be that simply all movies are becoming 'better' or are broadly accepted by most people.## The Vector Space Model and a Search EngineAll the diagrams here are snipped from [*Introduction to Information Retrieval* by Manning et. al.]( http://nlp.stanford.edu/IR-book/) which is a great resource on text processing. For additional information on text mining and natural language processing, see [*Foundations of Statistical Natural Language Processing* by Manning and Schutze](http://nlp.stanford.edu/fsnlp/).
Also check out Python packages [`nltk`](http://www.nltk.org/), [`spaCy`](https://spacy.io/), [`pattern`](http://www.clips.ua.ac.be/pattern), and their associated resources. Also see [`word2vec`](https://en.wikipedia.org/wiki/Word2vec).
Let us define the vector derived from document $d$ by $\bar V(d)$. What does this mean? Each document is treated as a vector containing information about the words contained in it. Each vector has the same length and each entry "slot" in the vector contains some kind of data about the words that appear in the document such as presence/absence (1/0), count (an integer) or some other statistic. Each vector has the same length because each document shared the same vocabulary across the full collection of documents -- this collection is called a *corpus*.
To define the vocabulary, we take a union of all words we have seen in all documents. We then just associate an array index with them. So "hello" may be at index 5 and "world" at index 99.
Suppose we have the following corpus:
`A Fox one day spied a beautiful bunch of ripe grapes hanging from a vine trained along the branches of a tree. The grapes seemed ready to burst with juice, and the Fox's mouth watered as he gazed longingly at them.`
Suppose we treat each sentence as a document $d$. The vocabulary (often called the *lexicon*) is the following:
$V = \left\{\right.$ `a, along, and, as, at, beautiful, branches, bunch, burst, day, fox, fox's, from, gazed, grapes, hanging, he, juice, longingly, mouth, of, one, ready, ripe, seemed, spied, the, them, to, trained, tree, vine, watered, with`$\left.\right\}$
Then the document
`A Fox one day spied a beautiful bunch of ripe grapes hanging from a vine trained along the branches of a tree`
may be represented as the following sparse vector of word counts:
$$\bar V(d) = \left( 4,1,0,0,0,1,1,1,0,1,1,0,1,0,1,1,0,0,0,0,2,1,0,1,0,0,1,0,0,1,1,1,0,0 \right)$$
or more succinctly as
`[(0, 4), (1, 1), (5, 1), (6, 1), (7, 1), (9, 1), (10, 1), (12, 1), (14, 1), (15, 1), (20, 2), (21, 1), (23, 1),`
`(26, 1), (29,1), (30, 1), (31, 1)]`
along with a dictionary
``
{
0: a, 1: along, 5: beautiful, 6: branches, 7: bunch, 9: day, 10: fox, 12: from, 14: grapes, 15: hanging, 19: mouth, 20: of, 21: one, 23: ripe, 24: seemed, 25: spied, 26: the, 29:trained, 30: tree, 31: vine,
}
``
Then, a set of documents becomes, in the usual `sklearn` style, a sparse matrix with rows being sparse arrays representing documents and columns representing the features/words in the vocabulary.
Notice that this representation loses the relative ordering of the terms in the document. That is "cat ate rat" and "rat ate cat" are the same. Thus, this representation is also known as the Bag-Of-Words representation.
Here is another example, from the book quoted above, although the matrix is transposed here so that documents are columns:

Such a matrix is also catted a Term-Document Matrix. Here, the terms being indexed could be stemmed before indexing; for instance, `jealous` and `jealousy` after stemming are the same feature. One could also make use of other "Natural Language Processing" transformations in constructing the vocabulary. We could use Lemmatization, which reduces words to lemmas: work, working, worked would all reduce to work. We could remove "stopwords" from our vocabulary, such as common words like "the". We could look for particular parts of speech, such as adjectives. This is often done in Sentiment Analysis. And so on. It all depends on our application.
From the book:
>The standard way of quantifying the similarity between two documents $d_1$ and $d_2$ is to compute the cosine similarity of their vector representations $\bar V(d_1)$ and $\bar V(d_2)$:
$$S_{12} = \frac{\bar V(d_1) \cdot \bar V(d_2)}{|\bar V(d_1)| \times |\bar V(d_2)|}$$

>There is a far more compelling reason to represent documents as vectors: we can also view a query as a vector. Consider the query q = jealous gossip. This query turns into the unit vector $\bar V(q)$ = (0, 0.707, 0.707) on the three coordinates below.

>The key idea now: to assign to each document d a score equal to the dot product:
$$\bar V(q) \cdot \bar V(d)$$
Then we can use this simple Vector Model as a Search engine.### In Code<jupyter_code>from sklearn.feature_extraction.text import CountVectorizer
text = ['Hop on pop', 'Hop off pop', 'Hop Hop hop']
print("Original text is\n{}".format('\n'.join(text)))
vectorizer = CountVectorizer(min_df=0)
# call `fit` to build the vocabulary
vectorizer.fit(text)
# call `transform` to convert text to a bag of words
x = vectorizer.transform(text)
# CountVectorizer uses a sparse array to save memory, but it's easier in this assignment to
# convert back to a "normal" numpy array
x = x.toarray()
print("")
print("Transformed text vector is \n{}".format(x))
# `get_feature_names` tracks which word is associated with each column of the transformed x
print("")
print("Words for each feature:")
print(vectorizer.get_feature_names())
# Notice that the bag of words treatment doesn't preserve information about the *order* of words,
# just their frequency
def make_xy(critics, vectorizer=None):
#Your code here
if vectorizer is None:
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(critics.quote)
X = X.tocsc() # some versions of sklearn return COO format
y = (critics.fresh == 'fresh').values.astype(np.int)
return X, y
X, y = make_xy(critics)<jupyter_output><empty_output><jupyter_text>## Naive BayesFrom Bayes' Theorem, we have that
$$P(c \vert f) = \frac{P(c \cap f)}{P(f)}$$
where $c$ represents a *class* or category, and $f$ represents a feature vector, such as $\bar V(d)$ as above. **We are computing the probability that a document (or whatever we are classifying) belongs to category *c* given the features in the document.** $P(f)$ is really just a normalization constant, so the literature usually writes Bayes' Theorem in context of Naive Bayes as
$$P(c \vert f) \propto P(f \vert c) P(c) $$
$P(c)$ is called the *prior* and is simply the probability of seeing class $c$. But what is $P(f \vert c)$? This is the probability that we see feature set $f$ given that this document is actually in class $c$. This is called the *likelihood* and comes from the data. One of the major assumptions of the Naive Bayes model is that the features are *conditionally independent* given the class. While the presence of a particular discriminative word may uniquely identify the document as being part of class $c$ and thus violate general feature independence, conditional independence means that the presence of that term is independent of all the other words that appear *within that class*. This is a very important distinction. Recall that if two events are independent, then:
$$P(A \cap B) = P(A) \cdot P(B)$$
Thus, conditional independence implies
$$P(f \vert c) = \prod_i P(f_i | c) $$
where $f_i$ is an individual feature (a word in this example).
To make a classification, we then choose the class $c$ such that $P(c \vert f)$ is maximal.
There is a small caveat when computing these probabilities. For [floating point underflow](http://nlp.stanford.edu/IR-book/html/htmledition/naive-bayes-text-classification-1.html) we change the product into a sum by going into log space. This is called the LogSumExp trick. So:
$$\log P(f \vert c) = \sum_i \log P(f_i \vert c) $$
There is another caveat. What if we see a term that didn't exist in the training data? This means that $P(f_i \vert c) = 0$ for that term, and thus $P(f \vert c) = \prod_i P(f_i | c) = 0$, which doesn't help us at all. Instead of using zeros, we add a small negligible value called $\alpha$ to each count. This is called Laplace Smoothing.
$$P(f_i \vert c) = \frac{N_{ic}+\alpha}{N_c + \alpha N_i}$$
where $N_{ic}$ is the number of times feature $i$ was seen in class $c$, $N_c$ is the number of times class $c$ was seen and $N_i$ is the number of times feature $i$ was seen globally. $\alpha$ is sometimes called a regularization parameter.### Multinomial Naive Bayes and Other Likelihood Functions
Since we are modeling word counts, we are using variation of Naive Bayes called Multinomial Naive Bayes. This is because the likelihood function actually takes the form of the multinomial distribution.
$$P(f \vert c) = \frac{\left( \sum_i f_i \right)!}{\prod_i f_i!} \prod_{f_i} P(f_i \vert c)^{f_i} \propto \prod_{i} P(f_i \vert c)$$
where the nasty term out front is absorbed as a normalization constant such that probabilities sum to 1.
There are many other variations of Naive Bayes, all which depend on what type of value $f_i$ takes. If $f_i$ is continuous, we may be able to use *Gaussian Naive Bayes*. First compute the mean and variance for each class $c$. Then the likelihood, $P(f \vert c)$ is given as follows
$$P(f_i = v \vert c) = \frac{1}{\sqrt{2\pi \sigma^2_c}} e^{- \frac{\left( v - \mu_c \right)^2}{2 \sigma^2_c}}$$
Exercise Set II
Exercise: Implement a simple Naive Bayes classifier:
split the data set into a training and test set
Use `scikit-learn`'s `MultinomialNB()` classifier with default parameters.
train the classifier over the training set and test on the test set
print the accuracy scores for both the training and the test sets
What do you notice? Is this a good classifier? If not, why not?
<jupyter_code>import sklearn.model_selection as modselect # for train test split
import sklearn.naive_bayes as naiveb # for multinomial
X_train, X_test, y_train, y_test = modselect.train_test_split(X, y, random_state=42)
# split the data
classifier = naiveb.MultinomialNB() # set up a classifier
classifier.fit(X_train, y_train) # fit the training data
pred = classifier.predict(X_test) # predict with the test data
print('Training Score: ' + str(round(classifier.score(X_train, y_train), ndigits=2))) # print training score
print('Testing Score: ' + str(round(classifier.score(X_test, y_test), ndigits=2))) # print testing score<jupyter_output>Training Score: 0.92
Testing Score: 0.78
<jupyter_text>This model is much better at predicting the training data compared to the test data. However, there is still a ~78% chance of getting the correct estimates on the test data. Perhaps there are data in the test data that were not also in the training dataset; values that the model had not yet seen. Because there is such a difference in the test and trainign data, it may also be that the model is overfit, and it is simply memorizing the training data.### Picking Hyperparameters for Naive Bayes and Text MaintenanceWe need to know what value to use for $\alpha$, and we also need to know which words to include in the vocabulary. As mentioned earlier, some words are obvious stopwords. Other words appear so infrequently that they serve as noise, and other words in addition to stopwords appear so frequently that they may also serve as noise.First, let's find an appropriate value for `min_df` for the `CountVectorizer`. `min_df` can be either an integer or a float/decimal. If it is an integer, `min_df` represents the minimum number of documents a word must appear in for it to be included in the vocabulary. If it is a float, it represents the minimum *percentage* of documents a word must appear in to be included in the vocabulary. From the documentation:>min_df: When building the vocabulary ignore terms that have a document frequency strictly lower than the given threshold. This value is also called cut-off in the literature. If float, the parameter represents a proportion of documents, integer absolute counts. This parameter is ignored if vocabulary is not None.
Exercise Set III
Exercise: Construct the cumulative distribution of document frequencies (df). The $x$-axis is a document count $x_i$ and the $y$-axis is the percentage of words that appear less than $x_i$ times. For example, at $x=5$, plot a point representing the percentage or number of words that appear in 5 or fewer documents.
Exercise: Look for the point at which the curve begins climbing steeply. This may be a good value for `min_df`. If we were interested in also picking `max_df`, we would likely pick the value where the curve starts to plateau. What value did you choose?
<jupyter_code>new_df = list(sorted((X > 0).sum(axis=0).reshape(-1).tolist()[0]))
# make a list of summed X values (how often a particular word
# appears in documents). Sort those values and only keep those that
# are greater than 0. Reformat into a long, vertical list.
rows, features = X.shape # save the shape of X into rows (quotes)
# and features (unique words)
height, axis = np.histogram(new_df, bins=len(np.unique(new_df)))
# make a histogram of the new list where the bins are the number
# of unique values in the new summed X values
cumhist = np.cumsum(height * 1, axis=0) / features
# use a cumulative sum to get a proportion of words (divide by
# total features for a proportion)
axis = np.insert(axis, 0, 0) # add 0s to the x axis
cumhist = np.insert(cumhist, 0, 0) # add 0s to the y axis
plt.plot(axis[:-1], cumhist) # all y values and the x values
# minus the last value
plt.xlim(-.1, 5) # set xlimits so that we can see the slope better
plt.xlabel("document count") # xlabel
plt.ylabel("percent of words") # ylabel
plt.show() # show plot<jupyter_output><empty_output><jupyter_text>It appears that most words occur in 1 or fewer documents (the CDF slope is steepest around 0.5 documents) and plateaus by the time it hits 1 document. In this case, the min_df might be best around 0.5 documents and the max_df might be best around 1 document. However, we must either use the proportion of total documetns (float) or an interger for absolute counts. Therefore, min_df might be best at either 0 or 1, and the max_df is likely best around 1 or 2. In general, most words appear to be uncommon across different reviews; there are few words that are commonly used more than once.The parameter $\alpha$ is chosen to be a small value that simply avoids having zeros in the probability computations. This value can sometimes be chosen arbitrarily with domain expertise, but we will use K-fold cross validation. In K-fold cross-validation, we divide the data into $K$ non-overlapping parts. We train on $K-1$ of the folds and test on the remaining fold. We then iterate, so that each fold serves as the test fold exactly once. The function `cv_score` performs the K-fold cross-validation algorithm for us, but we need to pass a function that measures the performance of the algorithm on each fold. <jupyter_code>from sklearn.model_selection import KFold
def cv_score(clf, X, y, scorefunc):
result = 0.
nfold = 5
for train, test in KFold(nfold).split(X): # split data into train/test groups, 5 times
clf.fit(X[train], y[train]) # fit the classifier, passed is as clf.
result += scorefunc(clf, X[test], y[test]) # evaluate score function on held-out data
return result / nfold # average<jupyter_output><empty_output><jupyter_text>We use the log-likelihood as the score here in `scorefunc`. The higher the log-likelihood, the better. Indeed, what we do in `cv_score` above is to implement the cross-validation part of `GridSearchCV`.
The custom scoring function `scorefunc` allows us to use different metrics depending on the decision risk we care about (precision, accuracy, profit etc.) directly on the validation set. You will often find people using `roc_auc`, precision, recall, or `F1-score` as the scoring function.<jupyter_code>def log_likelihood(clf, x, y):
prob = clf.predict_log_proba(x)
rotten = y == 0
fresh = ~rotten
return prob[rotten, 0].sum() + prob[fresh, 1].sum()<jupyter_output><empty_output><jupyter_text>We'll cross-validate over the regularization parameter $\alpha$.Let's set up the train and test masks first, and then we can run the cross-validation procedure.<jupyter_code>from sklearn.model_selection import train_test_split
_, itest = train_test_split(range(critics.shape[0]), train_size=0.7)
mask = np.zeros(critics.shape[0], dtype=np.bool)
mask[itest] = True<jupyter_output><empty_output><jupyter_text>
Exercise Set IV
Exercise: What does using the function `log_likelihood` as the score mean? What are we trying to optimize for?
Exercise: Without writing any code, what do you think would happen if you choose a value of $\alpha$ that is too high?
Exercise: Using the skeleton code below, find the best values of the parameter `alpha`, and use the value of `min_df` you chose in the previous exercise set. Use the `cv_score` function above with the `log_likelihood` function for scoring.
<jupyter_code>from sklearn.naive_bayes import MultinomialNB
#the grid of parameters to search over
alphas = [.1, 1, 5, 10, 50]
best_min_df = 0 # YOUR TURN: put your value of min_df here.
#Find the best value for alpha and min_df, and the best classifier
best_alpha = None
maxscore=-np.inf
for alpha in alphas:
vectorizer = CountVectorizer(min_df=best_min_df)
Xthis, ythis = make_xy(critics, vectorizer)
Xtrainthis = Xthis[mask]
ytrainthis = ythis[mask]
classifier = MultinomialNB(alpha=alpha)
score = cv_score(classifier, Xtrainthis, ytrainthis, log_likelihood)
if score > maxscore:
maxscore = score
best_alpha = alpha
print("alpha: {}".format(best_alpha))<jupyter_output>alpha: 1
<jupyter_text>By choosing the score of log-likelihood, we are trying to find the alpha value that gives us the absolute minimum log-likelihood value. This ensures that the model chosen gives us the best idea of parameters that explain the trends in the data that are not due to random chance. Our regularization parameter (alpha) is used to prevent overfitting. If we make alpha too large, the resulting penalties from a large alpha will make the model results less useful (alpha is a way to mitigate overfitting). From these results, it seems that the best alpha for this example is 1.
Exercise Set V: Working with the Best Parameters
Exercise: Using the best value of `alpha` you just found, calculate the accuracy on the training and test sets. Is this classifier better? Why (not)?
<jupyter_code>vectorizer = CountVectorizer(min_df=best_min_df)
X, y = make_xy(critics, vectorizer)
xtrain=X[mask]
ytrain=y[mask]
xtest=X[~mask]
ytest=y[~mask]
clf = MultinomialNB(alpha=best_alpha).fit(xtrain, ytrain)
#Print the accuracy on the test and training dataset
training_accuracy = clf.score(xtrain, ytrain)
test_accuracy = clf.score(xtest, ytest)
print("Accuracy on training data: {:2f}".format(training_accuracy))
print("Accuracy on test data: {:2f}".format(test_accuracy))<jupyter_output>Accuracy on training data: 0.929535
Accuracy on test data: 0.727965
<jupyter_text>This classifier is not better, but actually worse. The previous classifier with no set alpha produced an accuracy on the training data of ~91% and an accuracy on the test data of about 78%. Here, the score is even lower for the test data, meaning the model is overfitted and that the model has just begun to learn and memorize the training dataset.<jupyter_code>from sklearn.metrics import confusion_matrix
print(confusion_matrix(ytest, clf.predict(xtest)))<jupyter_output>[[1859 2412]
[ 551 6070]]
<jupyter_text>So this means that 1830 values were true positives, 508 values were false positives, 2469 values were false negatives and 6085 values were true negatives.## Interpretation### What are the strongly predictive features?
We use a neat trick to identify strongly predictive features (i.e. words).
* first, create a data set such that each row has exactly one feature. This is represented by the identity matrix.
* use the trained classifier to make predictions on this matrix
* sort the rows by predicted probabilities, and pick the top and bottom $K$ rows<jupyter_code>words = np.array(vectorizer.get_feature_names())
x = np.eye(xtest.shape[1])
probs = clf.predict_log_proba(x)[:, 0]
ind = np.argsort(probs)
good_words = words[ind[:10]]
bad_words = words[ind[-10:]]
good_prob = probs[ind[:10]]
bad_prob = probs[ind[-10:]]
print("Good words\t P(fresh | word)")
for w, p in zip(good_words, good_prob):
print("{:>20}".format(w), "{:.2f}".format(1 - np.exp(p)))
print("Bad words\t P(fresh | word)")
for w, p in zip(bad_words, bad_prob):
print("{:>20}".format(w), "{:.2f}".format(1 - np.exp(p)))<jupyter_output>Good words P(fresh | word)
powerful 0.97
mood 0.95
delight 0.95
chan 0.94
kubrick 0.94
brilliantly 0.94
rare 0.94
entertaining 0.94
stunning 0.93
stands 0.93
Bad words P(fresh | word)
sadly 0.13
lame 0.13
bland 0.12
uninspired 0.11
thin 0.11
witless 0.11
intended 0.10
supposed 0.10
pointless 0.10
unfortunately 0.06
<jupyter_text>
Exercise Set VI
Exercise: Why does this method work? What does the probability for each row in the identity matrix represent
This method likely works because most critic ratings are greater than 0.6. Therefore, one would expect that the most commonly used words would be associated with the reviews from higher-rated films (good reviews). Alternatively, there are few critics that consistently give bad ratings, so words associated with bad ratings are less probable (bad words). The above exercise is an example of *feature selection*. There are many other feature selection methods. A list of feature selection methods available in `sklearn` is [here](http://scikit-learn.org/stable/modules/classes.html#module-sklearn.feature_selection). The most common feature selection technique for text mining is the chi-squared $\left( \chi^2 \right)$ [method](http://nlp.stanford.edu/IR-book/html/htmledition/feature-selectionchi2-feature-selection-1.html).### Prediction Errors
We can see mis-predictions as well.<jupyter_code>x, y = make_xy(critics, vectorizer)
prob = clf.predict_proba(x)[:, 0]
predict = clf.predict(x)
bad_rotten = np.argsort(prob[y == 0])[:5]
bad_fresh = np.argsort(prob[y == 1])[-5:]
print("Mis-predicted Rotten quotes")
print('---------------------------')
for row in bad_rotten:
print(critics[y == 0].quote.iloc[row])
print("")
print("Mis-predicted Fresh quotes")
print('--------------------------')
for row in bad_fresh:
print(critics[y == 1].quote.iloc[row])
print("")<jupyter_output>Mis-predicted Rotten quotes
---------------------------
Nava, who started his feature-film career with El Norte, is a good director who invariably finds a strong rapport with his actors. He's not much of a writer, though, and he should think twice about creating dialogue for his future projects.
Apparently left by director Michael Caton-Jones to his own devices, De Niro's familiar, tight-lipped intensity is entertaining and watchable. But in this Boy's Life Magazine context, it hovers close to cartoonlike.
After winning a well-deserved Oscar for his role as a high-strung football player in Jerry Maguire, this talented actor has become an intolerable screen presence.
Malkovich does such wonderfully unexpected things, especially with his line readings, that he leaves us dumbfounded. No other performer is more effortlessly unnerving than this perversely gifted actor.
There is scarcely a moment in the movie when the story works as fiction; I was always aware of the casting, of the mood[...]<jupyter_text>
Exercise Set VII: Predicting the Freshness for a New Review
Exercise:
Using your best trained classifier, predict the freshness of the following sentence: *'This movie is not remarkable, touching, or superb in any way'*
Is the result what you'd expect? Why (not)?
<jupyter_code>text = 'This movie is not remarkable, touching, or superb in any way'
clf = MultinomialNB(alpha=best_alpha).fit(xtrain, ytrain)
clf.predict_proba(vectorizer.transform([text]))<jupyter_output><empty_output><jupyter_text>Because this model does not account for negative connotations of words (like 'not'), one would expect this sentence to get a high probability of freshness, because it contains words like remarkable, touching, and superb. The result above indicates that there's a 0.001 probability that the value is 0 (negative words) and a 0.999 probability that the value is 1 (positive words). So, although this result supports the logic that corresponds to the model, it doesn't really make sense from a human standpoint. The critic meant that the movie was unremarkable, boring, and dull. However, he or she decided to use the antonym of those words with the addition of 'not'. Although we can see that the author did not mean positive things, most of the words within the sentence are positive words.### Aside: TF-IDF Weighting for Term Importance
TF-IDF stands for
`Term-Frequency X Inverse Document Frequency`.
In the standard `CountVectorizer` model above, we used just the term frequency in a document of words in our vocabulary. In TF-IDF, we weight this term frequency by the inverse of its popularity in all documents. For example, if the word "movie" showed up in all the documents, it would not have much predictive value. It could actually be considered a stopword. By weighing its counts by 1 divided by its overall frequency, we downweight it. We can then use this TF-IDF weighted features as inputs to any classifier. **TF-IDF is essentially a measure of term importance, and of how discriminative a word is in a corpus.** There are a variety of nuances involved in computing TF-IDF, mainly involving where to add the smoothing term to avoid division by 0, or log of 0 errors. The formula for TF-IDF in `scikit-learn` differs from that of most textbooks:
$$\mbox{TF-IDF}(t, d) = \mbox{TF}(t, d)\times \mbox{IDF}(t) = n_{td} \log{\left( \frac{\vert D \vert}{\vert d : t \in d \vert} + 1 \right)}$$
where $n_{td}$ is the number of times term $t$ occurs in document $d$, $\vert D \vert$ is the number of documents, and $\vert d : t \in d \vert$ is the number of documents that contain $t$<jupyter_code># http://scikit-learn.org/dev/modules/feature_extraction.html#text-feature-extraction
# http://scikit-learn.org/dev/modules/classes.html#text-feature-extraction-ref
from sklearn.feature_extraction.text import TfidfVectorizer
tfidfvectorizer = TfidfVectorizer(min_df=1, stop_words='english')
Xtfidf=tfidfvectorizer.fit_transform(critics.quote)<jupyter_output><empty_output><jupyter_text>
Exercise Set VIII: Enrichment (Optional)
There are several additional things we could try. Try some of these as exercises:
Build a Naive Bayes model where the features are n-grams instead of words. N-grams are phrases containing n words next to each other: a bigram contains 2 words, a trigram contains 3 words, and 6-gram contains 6 words. This is useful because "not good" and "so good" mean very different things. On the other hand, as n increases, the model does not scale well since the feature set becomes more sparse.
Try a model besides Naive Bayes, one that would allow for interactions between words -- for example, a Random Forest classifier.
Try adding supplemental features -- information about genre, director, cast, etc.
Use word2vec or [Latent Dirichlet Allocation](https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation) to group words into topics and use those topics for prediction.
Use TF-IDF weighting instead of word counts.
Exercise: Try at least one of these ideas to improve the model (or any other ideas of your own). Implement here and report on the result.
<jupyter_code>vectorizer = CountVectorizer(min_df=best_min_df, ngram_range=(2,2))
# ngram_range allows for bigrams instead of one word
X, y = make_xy(critics, vectorizer) # get the vector values
xtrain=X[mask]
ytrain=y[mask]
xtest=X[~mask]
ytest=y[~mask]
clf = MultinomialNB(alpha=best_alpha).fit(xtrain, ytrain) # fit the model
# Print the accuracy on the test and training dataset
training_accuracy = clf.score(xtrain, ytrain)
test_accuracy = clf.score(xtest, ytest)
print ("Accuracy on training data: %0.2f" % (training_accuracy))
print ("Accuracy on test data: %0.2f" % (test_accuracy))
# Re-test the text given in the previous example
text = 'This movie is not remarkable, touching, or superb in any way'
clf = MultinomialNB(alpha=best_alpha).fit(xtrain, ytrain)
clf.predict_proba(vectorizer.transform([text]))<jupyter_output><empty_output>
|
no_license
|
/Naive_Bayes/Mini_Project_Naive_Bayes-EB.ipynb
|
echelleburns/SpringBoard
| 17 |
<jupyter_start><jupyter_text># Regular Expressions
- Definition
- Match Vs Search
- Substitute substrings
- Find all
- Meta Vs Literal characters
- Various identifiers
- Back referencing example
- Exercise<jupyter_code>import re
a = "This is Learnbay class9"
mObj = re.match("Learnbay",a)
print(mObj)
mObj = re.match("This",a)
print(mObj)
mObj = re.match("This",a)
print(mObj)
mObj = re.match("(This) (is)",a)
if mObj:
print(mObj.group())
print(mObj.group(1))
print(mObj.group(2))
print(mObj.groups())<jupyter_output>This is
This
is
('This', 'is')
<jupyter_text># Using Search<jupyter_code>a = "This is Learnbay class9"
sObj = re.search("Learnbay",a)
if sObj:
print(sObj.group())<jupyter_output>Learnbay
<jupyter_text>#### use of flag <jupyter_code>a = "This is LeaRNBay class9"
sObj = re.search("Learnbay",a,re.I)
if sObj:
print(sObj.group())
a = "This is LexyNBay class9"
sObj = re.search("Le..nbay",a,re.I)
if sObj:
print(sObj.group())
a = "This is Lea\nNBay class9"
sObj = re.search("Lea.nbay",a,re.I|re.S)
if sObj:
print(sObj.group())<jupyter_output>Lea
NBay
<jupyter_text># Use of findall<jupyter_code>a = "This is Learnbay LeARNbay LearnBAY LEArnbay class9"
re.findall("learnbay",a,re.I)
len(re.findall("learnbay",a,re.I))<jupyter_output><empty_output><jupyter_text># Use of substitute<jupyter_code>a = "This is Learnbay LeARNbay LearnBAY LEArnbay class9"
re.sub("learnbay","LB",a,flags=re.I)
re.sub("learnbay","LB",a,count=2,flags=re.I)<jupyter_output><empty_output><jupyter_text># Use of all pattern descriptors<jupyter_code>a = "asdfasdfs37456347345#@$%^#&$@%$"
sObj = re.search("\w+",a)
if sObj:
print(sObj.group())
sObj = re.search("\W+",a)
if sObj:
print(sObj.group())
sObj = re.search("([aA-zZ]+)(\d+)(\W+)",a) # [a-z],[A-Z],[aA-zZ],[0-9]
if sObj:
print(sObj.group())
print(sObj.groups())
a = "asdfasdfs37456347345#@$%^#&$@%$sdhfhs23642356"
sObj = re.search("([aA-zZ]+)(\d+)(\W+)(\w+)?",a) # [a-z],[A-Z],[aA-zZ],[0-9]
if sObj:
print(sObj.group())
print(sObj.groups())
bill = """The 1994 State of the Union address was given by President Bill Clinton to a joint session of the 103rd United States Congress on Tuesday, January 25, 1994. The speech was Clinton's first official State of the Union address, although he had similarly addressed a joint session of Congress a year prior shortly after taking office.
The president discussed the federal budget deficit, taxes, defense spending, crime, foreign affairs, education, the economy, free trade, the role of government, campaign finance reform, welfare reform, and promoting the Clinton health care plan. President Clinton threatened to veto any legislation that did not guarantee every American private health insurance. He proposed for policies to fight crime: a three strikes law for repeat violent offenders; 100,000 more police officers on the streets; expand gun control to further prevent criminals from being armed and ban assault weapons; additional support for drug treatment and education.
The president began the speech with an acknowledgment of former Speaker Tip O'Neill, who died on January 5, 1994. While discussing additional community policing, the president honored Kevin Jett, a New York City cop attending the address who had been featured in a New York Times story in December 1993.[1]
The speech lasted 63 minutes[2] and consisted of 7,432 words.[3] It was the longest State of the Union speech since Lyndon B. Johnson's 1967 State of the Union Address. Republican Representative Henry Hyde criticized the speech as "interminable".[4]
The Republican Party response was delivered by Senator Bob Dole of Kansas.[5] Dole argued that health care in the United States was not in crisis, the Republican opposition to Clinton's plans in the previous year had been popular, and the deficit reduction was the temporary result of tax increases.[4]
Mike Espy, the Secretary of Agriculture, served as the designated survivor.
Contrary to common belief,[6] Clinton did not have to recite the speech from memory because the teleprompter was loaded with the wrong speech. This had happened the previous year: in a speech Clinton gave to Congress on 22 September 1993 detailing the Clinton health care plan, the teleprompter was loaded with the wrong speech. Specifically, the one he gave to a joint session of Congress shortly after he was sworn-in in 1993. Teleprompter operators practiced with the old speech and it was accidentally left in, forcing Clinton to ad-lib for almost ten minutes.[7][8][9][10] The two incidents are often conflated. What happened is that President Clinton simply referenced the September 1993 incident. """
print(re.findall("\d+",bill))
print(re.findall("\w+",bill))
print(re.findall(" \w\w\w\w ",bill))
print(re.findall(" \w{3} ",bill))
print(re.findall(" \w{3,6} ",bill))
print(re.findall(" \d{4} ",bill))
print(re.findall(" \w{6,} ",bill))
print(re.findall(" \w{6} ",bill))<jupyter_output>[' United ', ' speech ', ' taking ', ' budget ', ' health ', ' health ', ' repeat ', ' police ', ' expand ', ' speech ', ' former ', ' speech ', ' speech ', ' Lyndon ', ' speech ', ' argued ', ' health ', ' United ', ' result ', ' served ', ' common ', ' recite ', ' speech ', ' memory ', ' loaded ', ' speech ', ' health ', ' loaded ', ' speech ', ' almost ', ' simply ']
<jupyter_text># Multiple pattern searching<jupyter_code>a = "This is class CLASS cLass"
print(re.findall("(class|CLASS)",a))
print(re.findall("(class|CLASS)",a,flags=re.I))<jupyter_output>['class', 'CLASS', 'cLass']
<jupyter_text># Back referencing<jupyter_code>a = "111 222 111 222 222 "
sObj = re.search("111 222 111 ",a)
if sObj:
print(sObj.group())
sObj = re.search("(111 )(222 )\\1(222 )",a)
if sObj:
print(sObj.group())
sObj = re.search("(111 )(222 )\\1\\2",a)
if sObj:
print(sObj.group())<jupyter_output>111 222 111 222
<jupyter_text># Exercise###### Open the test5.txt file and print all the non-empty lines. Then later print only those lines which is ending with even numbers. Do this with or without regex<jupyter_code>fh = open("test5.txt")
for line in fh:
if line != "\n":
print(line)
fh = open("test5.txt")
for line in fh:
if line != "\n" and int(line[-2])%2 == 0:
print(line)<jupyter_output>This is Line2
This is Line4
This is Line6
This is Line8
<jupyter_text># Using regular expression<jupyter_code>fh = open("test5.txt")
for line in fh:
sObj = re.search("[02468]$",line)
if sObj:
print(line)<jupyter_output>This is Line2
This is Line4
This is Line6
This is Line8
|
no_license
|
/PYTHON-PAN-VITTHAL_SEP_2019/09-FILE-IO_REGEX-DONE/14_RegularExpression.ipynb
|
vitthalkcontact/Python
| 10 |
<jupyter_start><jupyter_text># String Formatter<jupyter_code>name = 'KGB Talkie'
print('The Youtube channel is {}'.format(name))
print(f'The Youtube channel is {name}')
# Minimum width and alignment between columns
# lets say we have to colums
# day value
# 1 10
# 10 11
data_science_tuts = [('Python for beginners', 19),
('Feature selection for machine learning',10),
('Machine Learning Tutorials', 11),
('Deep learning Tutorials', 19)]
data_science_tuts
for info in data_science_tuts:
print(info)
# aligning the two collumns
for info in data_science_tuts:
print(f'{info[0]:{50}} {info[1]:{10}}')
for info in data_science_tuts:
print(f'{info[0]:>{50}} {info[1]:{10}}')
for info in data_science_tuts:
print(f'{info[0]:^{50}} {info[1]:.>{10}}')<jupyter_output> Python for beginners ........19
Feature selection for machine learning ........10
Machine Learning Tutorials ........11
Deep learning Tutorials ........19
<jupyter_text>### Working with .CSV or . TSV<jupyter_code>import pandas as pd
data = pd.read_csv('train.tsv', sep ='\t')
data.head()<jupyter_output><empty_output><jupyter_text>0 - negative
1 - somewhat negative
2 - neutral
3 - somewhat positive
4 - positive<jupyter_code>data.shape
data['Sentiment'].value_counts()
pos = data[data['Sentiment']== 4]
pos.drop(['PhraseId', 'SentenceId'],axis = 1, inplace = True)
pos.to_csv('pos.tsv', sep= '\t', index = False)
pd.read_csv('pos.tsv', sep = '\t')
# built in magic command in jupyter %% writefile
# an easy way to write a file. Only possible in jupyter
%%writefile text1.txt
Hello this is an NLP lesson
# appending
%%writefile -a text1.txt
This is the appended tex<jupyter_output>Appending to text1.txt
<jupyter_text>#### Using python's inbuilt command to read and write text files<jupyter_code>file = open('text1.txt', 'r')
file
file.read()
# setting the pointer
file.seek(0)
file.read()
file.readline()
file.seek(0)
file.readlines()
# closing file
file.close()
file.readlines()
# another file which does not need to close file separately
with open('text1.txt') as file:
text_data = file.readlines()
print(text_data)
for temp in text_data:
print(temp)
# to remove new lines and spaces
for temp in text_data:
print(temp.strip())
for i, temp in enumerate(text_data):
print(str(i) + ' ---> ' +temp.strip())<jupyter_output>0 ---> Hello this is an NLP lesson
1 ---> This is the appended tex
<jupyter_text>### file writing<jupyter_code>file = open('text2.txt', 'w')
file
file.write('This is just another lesson of NLP')
# this must be done to complete the write operation
file.close()
# shortcut
with open('text3.txt', 'w') as file:
file.write(' This si the file')
# append mode
with open('text3.txt', 'a') as file:
file.write(' This si the file')<jupyter_output><empty_output>
|
no_license
|
/Working with text files.ipynb
|
daynoh/Natural-language-processing-using-Tensorflow-and-spacy
| 5 |
<jupyter_start><jupyter_text># Dataset<jupyter_code>#To ignore warnings.
import warnings
warnings.filterwarnings("ignore")
#Load the dataset.
import pandas as pd
df=pd.read_csv("Dataset/spam.csv", encoding='latin-1')
#Remove unwanted columns.
df = df.drop(labels = ["Unnamed: 2", "Unnamed: 3", "Unnamed: 4"], axis = 1)
#Name the columns.
df.columns = ["label", "text"]
df.head()<jupyter_output><empty_output><jupyter_text># Data preprocessing<jupyter_code>import nltk,string
#Getting the english stopwords.
stopwords = nltk.corpus.stopwords.words('english')
#Function to clean the text.
def clean_text(text):
#remove punctuation
text = "".join([word.lower() for word in text if word not in string.punctuation])
#separate into tokens
tokens = text.split()
#remove stopwords
text = [word for word in tokens if word not in stopwords]
return text
#Apply the clean_text function
df["cleaned_text"]=df["text"].apply(clean_text)
df.head()<jupyter_output><empty_output><jupyter_text># word2vec<jupyter_code>from sklearn.model_selection import train_test_split
#Split the data (train, test).
X_train, X_test, y_train, y_test = train_test_split(df["cleaned_text"],df['label'],test_size=0.2)
import gensim
print("Gensim version:",gensim.__version__)
import numpy as np
#Train the word2vec model.
w2v_model=gensim.models.Word2Vec(X_train,vector_size=100,window=5,min_count=2)
#Vocab.
words=set(w2v_model.wv.index_to_key)
#Covert text into learned word vector.
train_vec=np.array([np.array([w2v_model.wv[i] for i in row if i in words]) for row in X_train ])
test_vec=np.array([np.array([w2v_model.wv[i] for i in row if i in words]) for row in X_test ])
#Taking average for all the word vectors in a single sentences (Train datapoints).
avg_train_vec=[]
for vec in train_vec:
if vec.size:
avg_train_vec.append(vec.mean(axis=0))
else:
avg_train_vec.append(np.zeros(100,dtype=float))
#Taking average for all the word vectors in a single sentences (Test datapoints).
avg_test_vec=[]
for vec in test_vec:
if vec.size:
avg_test_vec.append(vec.mean(axis=0))
else:
avg_test_vec.append(np.zeros(100,dtype=float)) <jupyter_output><empty_output><jupyter_text># Lets build the model !<jupyter_code>from sklearn.ensemble import RandomForestClassifier
#Build the Random Forest Classifier.
rf=RandomForestClassifier()
#Fit the model with training data.
rf_model=rf.fit(avg_train_vec,y_train)
#Predict the output for testing data.
y_pred=rf_model.predict(avg_test_vec)<jupyter_output><empty_output><jupyter_text># Evaluation<jupyter_code>#Calculate precision score and recall score.
from sklearn.metrics import precision_score, recall_score,accuracy_score
#Precision - ability of the classifier to find all the positive samples.
precision = precision_score(y_test, y_pred, pos_label='spam')
#Recall - ability of the classifier to find true positive samples.
recall = recall_score(y_test, y_pred, pos_label='spam')
print("Precision score: ",precision)
print("Recall score: ",recall)
import numpy as np
y_pred=np.where(y_pred == "spam", 1, 0)
y_test=np.where(np.array(y_test)== "spam", 1, 0)
#Test datapoints accuracy.
accuracy=accuracy_score(y_test, y_pred)
print("Test Accuracy: ",accuracy)
<jupyter_output>Test Accuracy: 0.9327354260089686
|
no_license
|
/word2vec.ipynb
|
Susheel-1999/NLP-spam_ham_classification_using_different_techniques
| 5 |
<jupyter_start><jupyter_text>## problem1<jupyter_code>#aaaaaaaaadaaa
z1<-c(0,1,rep(0,99))
#constant effect for first ten periods
z2<-c(0,rep(1,10),rep(0,90))
#gradual decrease
z3<-c(0,1,0.75,0.5,0.25,rep(0,96))
#white noise
e<-rnorm(101)
#
model1<-function(a0,a1,z,e){
#ar1 with intervention
y<-rep(0,101)
for (i in 1:100){
y[i+1]<-a0+a1*y[i]+z[i]+e[i]
}
return (y)
}
a0<-0
a1<-0.5
ts.plot(model1(a0,a1,z1,e))
ts.plot(model1(a0,a1,z2,e))
ts.plot(model1(a0,a1,z3,e))
a0<-0
a1<--0.5
ts.plot(model1(a0,a1,z1,e))
ts.plot(model1(a0,a1,z2,e))
ts.plot(model1(a0,a1,z3,e))
a0<-0
a1<-1
ts.plot(model1(a0,a1,z1,e))
ts.plot(model1(a0,a1,z2,e))
<jupyter_output><empty_output>
|
no_license
|
/time_series/applied_econometric_time_series/chapter4_original_problem.ipynb
|
owari-taro/statistics
| 1 |
<jupyter_start><jupyter_text># End to end 2D CNN for GTzan music classification EnvCNN
WINDOWED Version
Adapted by AL Koerich
To GTzan 3-fold
11 December 2018<jupyter_code>import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import os, sys
import soundfile as sf
from sklearn.utils import shuffle
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import normalize
from sklearn.preprocessing import scale
from keras import regularizers
import os, sys
from keras.utils import np_utils
from keras.models import Model
from keras.layers import Conv1D, Dense, MaxPool1D, Flatten
from keras.callbacks import TensorBoard
from keras.utils import np_utils, to_categorical
from keras import optimizers
from keras.layers.normalization import BatchNormalization
from keras.layers.core import Dropout
import keras.initializers as init
os.environ["CUDA_VISIBLE_DEVICES"]="0"
import tensorflow as tf
config = tf.ConfigProto( )
config.gpu_options.allow_growth = True
sess = tf.Session(config=config)
import keras.backend.tensorflow_backend as tf_bkend
tf_bkend.set_session(sess)
#controling_Hyper parameters
batch_size = 50 #100
nb_classes = 10
nb_epoch = 150
#frame_size = 110250
#Indicate folds
train_fold = [1, 2]
test_fold = 3
str_train_fold = "fold"+str(train_fold[0])+"-"+str(train_fold[1])
print(str_train_fold)
X_train = np.load( "folds_mf/2_GTzan_Xs_train_"+str_train_fold+"_110250_75_frozen.npy" )
Y_train = np.load( "folds_mf/2_GTzan_Ys_train_"+str_train_fold+"_110250_75_frozen.npy" )
X_train.min(), X_train.max()
X_train.shape
# Adapt 1D data to 2D CNN
X_train = np.squeeze(X_train)
X_train = np.expand_dims(X_train, axis = 3)
X_train.shape
import gc
gc.collect()
f = X_train.shape[1]
g = X_train.shape[2]
def model_generator_GTzannet2D_1a():
from keras.layers import Input, Dense, Conv2D, AveragePooling1D, LeakyReLU, MaxPool2D, Flatten
from keras.layers.core import Dropout
from keras.models import Model
from keras import initializers, optimizers, regularizers
from keras.callbacks import ModelCheckpoint
from keras.utils import multi_gpu_model
from keras.layers.normalization import BatchNormalization
import keras.initializers as init
from kapre.utils import Normalization2D
from kapre.augmentation import AdditiveNoise
sr = 22050
inp = Input(shape = (f, g, 1))
#----------------------
conv1 = Conv2D(filters = 32, kernel_size = (3, 3), activation = 'relu')(inp)
norm1 = BatchNormalization()(conv1)
#----------------------
conv2 = Conv2D(filters = 32, kernel_size = (3, 3) )(norm1)
act2 = LeakyReLU(alpha = 0.2)(conv2)
pool2 = MaxPool2D(pool_size = 2, strides = 2)(act2)
drop2 = Dropout(0.05)(pool2)
#----------------------
conv3 = Conv2D(filters = 64, kernel_size = (3, 3) )(drop2)
act3 = LeakyReLU(alpha = 0.2)(conv3)
#----------------------
conv4 = Conv2D(filters = 64, kernel_size = (3, 3) )(act3)
act4 = LeakyReLU(alpha = 0.2)(conv4)
pool4 = MaxPool2D(pool_size = 4, strides = 2)(act4)
#----------------------
flat = Flatten()(pool4)
#----------------------
#dense1 = Dense(1024, activation='relu', kernel_initializer = initializers.glorot_uniform( seed = 0))(flat)
#drop1 = Dropout(0.80)(dense1)
#----------------------
#dense2 = Dense(128, activation='relu', kernel_initializer = initializers.glorot_uniform( seed = 0))(flat)
#drop2 = Dropout(0.80)(dense2)
#----------------------
dense3 = Dense(1024, activation='relu', kernel_initializer = initializers.glorot_uniform(seed = 0))(flat)
drop3 = Dropout(0.80)(dense3)
#----------------------
dense4 = Dense(nb_classes, activation='softmax')(drop3)
#----------------------
model = Model(inp, dense4)
model.compile(loss = 'categorical_crossentropy',
optimizer = optimizers.Adadelta(lr = 1.0, rho = 0.95, epsilon = 1e-08, decay = 0.0),
metrics = ['accuracy'] )
model.summary()
return model
import time
from keras.callbacks import ModelCheckpoint
from livelossplot import PlotLossesKeras
from keras import optimizers
hist = []
model = model_generator_GTzannet2D_1a()
#checkpoints
str0 = "weights/"
str1 = "weights_3_GTzan_3f_"+str_train_fold+"_20p_110250_75_frozen"
str2 = ".best.hdf5"
filepath = str0+str1+str2
print(filepath)
checkpoint = ModelCheckpoint( filepath, monitor = 'val_acc', verbose = 1, save_best_only = True, mode = 'max' )
callbacks_list = [checkpoint, PlotLossesKeras()]
#fitting the model
batch_size = 100
hist.append(model.fit(X_train, Y_train,
batch_size = batch_size,
epochs = nb_epoch,
verbose = 1,
shuffle = True,
callbacks = callbacks_list,
validation_split = 0.2
))
filepath<jupyter_output><empty_output>
|
no_license
|
/3_GTzan_3f_CNN_2D_75w-Load-110250_frozen.ipynb
|
karlmiko/IJCNN2020
| 1 |
<jupyter_start><jupyter_text># Thinkful Prep Course: Unit 3.1
## Project 5: Describing Data<jupyter_code>import pandas as pd
import numpy as np
import statistics as statistics<jupyter_output><empty_output><jupyter_text>#### 1. Greg was 14, Marcia was 12, Peter was 11, Jan was 10, Bobby was 8, and Cindy was 6 when they started playing the Brady kids on The Brady Bunch. Cousin Oliver was 8 years old when he joined the show. What are the mean, median, and mode of the kids' ages when they first appeared on the show? What are the variance, standard deviation, and standard error?<jupyter_code>df = pd.DataFrame([['Greg',14],
['Marcia',12,],
['Peter',11],
['Jan',10],
['Bobby',8],
['Cindy',6],
['Cousin Oliver',8]])
df.columns = (['Name','Age'])
df
#THE STATISTICS
mean = np.mean(df['Age'])
median = np.median(df['Age'])
mode = statistics.mode(df['Age'])
variance = np.var(df['Age'])
std = np.std(df['Age'])
n = len(df)
se = std/(n**.5)
#Print the results
print('When the kids started the show:\nThe mean age was {}\nThe median was {}\nThe mode was {}'.
format(round(mean, 2), median, mode))
print ('\nThe variance is {}\nThe standard deviation is {}\nThe standard error is {}'.
format(round(variance, 2), round(std, 2), round(se, 2)))<jupyter_output>When the kids started the show:
The mean age was 9.86
The median was 10.0
The mode was 8
The variance is 6.41
The standard deviation is 2.53
The standard error is 0.96
<jupyter_text>#### 2. Using these estimates, if you had to choose only one estimate of central tendency and one estimate of variance to describe the data, which would you pick and why?If I had to pick one estimate of central tendency I would pick the mean because it will be the best representation of data. Both the mean and the median are the close with less than 2 years difference. There are no outliers in the set to skew the data.
For estimate in variance, I would select the standard deviations to describe the data. Apart from Bobby and Cousin Oliver, who are the same age, the difference between the next olderst is 1-2 years; relatively the same as the standard deviation.#### 3. Next, Cindy has a birthday. Update your estimates- what changed, and what didn't?<jupyter_code>df2 = pd.DataFrame([['Greg',14],
['Marcia',12,],
['Peter',11],
['Jan',10],
['Bobby',8],
['Cindy',7],
['Cousin Oliver',8]])
df2.columns = (['Name','Age'])
#THE STATISTICS
mean = np.mean(df2['Age'])
median = np.median(df['Age'])
mode = statistics.mode(df2['Age'])
variance = np.var(df['Age'])
std = np.std(df2['Age'])
n = len(df2)
se = std/(n**.5)
#Print the results
print('When Cindy has a birthday:\nThe mean is {}\nThe median is {}\nThe mode was {}'.
format(round(mean, 2), median, mode))
print ('\nThe variance is {}\nThe standard deviation is {}\nThe standard error is {}'.
format(round(variance, 2), round(std, 2), round(se, 2)))<jupyter_output>When Cindy has a birthday:
The mean is 10.0
The median is 10.0
The mode was 8
The variance is 6.41
The standard deviation is 2.33
The standard error is 0.88
<jupyter_text>The change in data is not that significant. When Cindy turns 7 central tendency statistics did not change significantly with the mean only increasing by .14 and the mode and median remaining the same.
Cindy's birthday causes the minimum age to change as she is the youngest in the data set. As the ages come closer together, the deviatoin and standar error also decrease. #### 4. Nobody likes Cousin Oliver. Maybe the network should have used an even younger actor. Replace Cousin Oliver with 1-year-old Jessica, then recalculate again. Does this change your choice of central tendency or variance estimation methods?<jupyter_code>df2.iloc[6,:] =('Jessica',1)
#THE STATISTICS
mean = np.mean(df['Age'])
median = np.median(df2['Age'])
#mode = statistical error because there is no re-occuring number in the data.
variance = np.var(df2['Age'])
std = np.std(df2['Age'])
n = len(df2)
se = std/(n**.5)
#Print update results
print('When the kids started the show:\nThe mean age was {}\nThe median was {}\nThe mode was {}'.
format(round(mean, 2), median, mode))
print ('\nThe variance is {}\nThe standard deviation is {}\nThe standard error is {}'.
format(round(variance, 2), round(std, 2), round(se, 2)))<jupyter_output>When the kids started the show:
The mean age was 9.86
The median was 10.0
The mode was 8
The variance is 15.43
The standard deviation is 3.93
The standard error is 1.48
|
no_license
|
/Thinkful Prep Course_Unit 3.1_ Project 5 Drill - Describing Data.ipynb
|
jmniet36/Thinkful-Prep-Course-Data-Science
| 4 |
<jupyter_start><jupyter_text># **INFO5731 Assignment Four**
In this assignment, you are required to conduct topic modeling, sentiment analysis based on **the dataset you created from assignment three**.# **Question 1: Topic Modeling**(30 points). This question is designed to help you develop a feel for the way topic modeling works, the connection to the human meanings of documents. Based on the dataset from assignment three, write a python program to **identify the top 10 topics in the dataset**. Before answering this question, please review the materials in lesson 8, especially the code for LDA and LSA. The following information should be reported:
(1) Features (top n-gram phrases) used for topic modeling.
(2) Top 10 clusters for topic modeling.
(3) Summarize and describe the topic for each cluster.
<jupyter_code>import pandas as pd
data = pd.read_csv("/content/CleanData2.csv")
data = data.head(10000)
#Data cleaning
from nltk.corpus import stopwords
import nltk
nltk.download('stopwords')
from nltk.tokenize import RegexpTokenizer
#from stop_words import get_stop_words
from nltk.stem.porter import PorterStemmer
tokenizer = RegexpTokenizer(r'\w+')
en_stop = stopwords.words('english')
p_stemmer = PorterStemmer()
data['Lower Case'] = data['cleaned_text'].apply(lambda x: " ".join(x.lower() for x in str(x).split()))
data['Tokenization'] = data['Lower Case'].apply(lambda x: tokenizer.tokenize(x))
data['Tokens'] = data['Tokenization'].apply(lambda x: [i for i in x if not i in en_stop])
data['Stemming'] = data['Tokens'].apply(lambda x: [p_stemmer.stem(i) for i in x])
texts = []
for line in data['Stemming']:
texts.append(line)
#Bigrams & Trigrams
from gensim import corpora, models
bigram = models.Phrases(texts, min_count=5, threshold=100)
trigram = models.Phrases(bigram[texts], threshold=100)
bigram_mod = models.phrases.Phraser(bigram)
trigram_mod = models.phrases.Phraser(trigram)
print(trigram_mod[bigram_mod[texts[0]]])
def make_bigrams(texts):
return [bigram_mod[doc] for doc in texts]
def make_trigrams(texts):
return [trigram_mod[bigram_mod[doc]] for doc in texts]
def lemmatization(texts, allowed_postags=['NOUN', 'ADJ', 'VERB', 'ADV']):
texts_out = []
for sent in texts:
doc = nlp(" ".join(sent))
texts_out.append([token.lemma_ for token in doc if token.pos_ in allowed_postags])
return texts_out
import spacy
data_words_bigrams = make_bigrams(texts)
nlp = spacy.load('en', disable=['parser', 'ner'])
data_lemmatized = lemmatization(data_words_bigrams, allowed_postags=['NOUN', 'ADJ', 'VERB', 'ADV'])
print(data_lemmatized[:1])
#Preparing corpus & dictionary
id2word = corpora.Dictionary(data_lemmatized)
texts = data_lemmatized
corpus = [id2word.doc2bow(text) for text in texts]
print(corpus[:1])
id2word[0]
[[(id2word[id], freq) for id, freq in cp] for cp in corpus[:1]]
#LDA
lda_model = models.ldamodel.LdaModel(corpus=corpus,
id2word=id2word,
num_topics = 10,
random_state=100,
update_every=1,
chunksize=100,
passes=10,
alpha='auto',
per_word_topics=True)
from pprint import pprint
pprint(lda_model.print_topics())
doc_lda = lda_model[corpus]
from gensim.models import CoherenceModel
print('\nPerplexity: ', lda_model.log_perplexity(corpus))
coherence_model_lda = CoherenceModel(model=lda_model, texts=data_lemmatized, dictionary=id2word, coherence='c_v')
coherence_lda = coherence_model_lda.get_coherence()
print('\nCoherence Score: ', coherence_lda)<jupyter_output>
Perplexity: -5.171446191463546
Coherence Score: 0.4745583360236491
<jupyter_text>
LDA
1. Co in china fails to stop wuhanvirus
2. Asian co right maybe a problem for some says flumanchu
3. Canadian co irresponsible in fight against poiltical shutdown
4. vaccine delay could hold the olympics
5. Heate problems calls fundamentalists to shutdown warefhouse in Canada
6. Promotion message thanks, calls for helps and remembers the wuhanvirus victims
7. Wuhancoronavirus real time confirmed cases
8. Words thanks bedside nurses for help during the spread
9. Message promotes getting vaccine, wearing a mask
10. Today say rest to spreader lockdowns and get vaccines<jupyter_code>#LSA
lsamodel = models.LsiModel(corpus, num_topics = 10, id2word = id2word)
pprint(lsamodel.print_topics(num_topics = 10))
coherence_values = []
model_list = []
for num_topics in range(2, 12, 1):
model = models.LsiModel(corpus, num_topics = 10, id2word = id2word)
model_list.append(model)
coherencemodel = CoherenceModel(model= model, texts = data['Stemming'], dictionary = id2word, coherence='c_v')
coherence_values.append(coherencemodel.get_coherence())<jupyter_output>/usr/local/lib/python3.7/dist-packages/gensim/topic_coherence/direct_confirmation_measure.py:195: RuntimeWarning: divide by zero encountered in double_scalars
m_lr_i = np.log(numerator / denominator)
/usr/local/lib/python3.7/dist-packages/gensim/topic_coherence/indirect_confirmation_measure.py:317: RuntimeWarning: invalid value encountered in double_scalars
return cv1.T.dot(cv2)[0, 0] / (_magnitude(cv1) * _magnitude(cv2))
<jupyter_text>LSA
1. Real time wuhancoronavirus map case
2. World thanks for spread of the call of help against asian hate
3. Co hate problems calls world to help
4. Hate problem calls for allowing mix to get vaccine
5. vaccine amplitude is still not normal, people refuse to get vaccinated and wer a mask against "covidiot"
6. Old people that are sick are prevented bedside meeting in nursing homes
7. With covid cases on rise, get a mask and wear a mask
8. Allows vaccines to enter foreign cases of patients with diabetes
9. Foreign vaccine contract could simplify mainland china hold and supply
10. Political shutdown in Canada to stop the curb of wuhanvirus# **Question 2: Sentiment Analysis**(30 points). Sentiment analysis also known as opinion mining is a sub field within Natural Language Processing (NLP) that builds machine learning algorithms to classify a text according to the sentimental polarities of opinions it contains, e.g., positive, negative, neutral. The purpose of this question is to develop a machine learning classifier for sentiment analysis. Based on the dataset from assignment three, write a python program to implement a sentiment classifier and evaluate its performance. Notice: **80% data for training and 20% data for testing**.
(1) Features used for sentiment classification and explain why you select these features.
(2) Select two of the supervised learning algorithm from scikit-learn library: https://scikit-learn.org/stable/supervised_learning.html#supervised-learning, to build a sentiment classifier respectively.
(3) Compare the performance over accuracy, precision, recall, and F1 score for the two algorithms you selected. Here is the reference of how to calculate these metrics: https://towardsdatascience.com/accuracy-precision-recall-or-f1-331fb37c5cb9. <jupyter_code>import pandas as pd
data = pd.read_csv("/content/CleanData2.csv")
data = data.head(10000)
import nltk
nltk.download('punkt')
nltk.download('stopwords')
data = data.dropna()
def review_classification(rating):
if rating == 3:
return 'Positive'
elif rating == 2:
return 'Neutral'
elif rating == 1:
return 'Negative'
rating_classification = data['Sentiment'].map(review_classification)
data['document'] = rating_classification
import seaborn as sns
print(data['Sentiment'].value_counts())
sns.countplot(data.Sentiment)
#Data cleaning
from nltk.corpus import stopwords
from textblob import TextBlob
data['Cleaned Text'] = data['cleaned_text'].apply(lambda x: " ".join(x.lower() for x in x.split()))
data['Cleaned Text'] = data['Cleaned Text'].str.replace('[^\w\s]','')
stop = stopwords.words('english')
data['Cleaned Text'] = data['Cleaned Text'].apply(lambda x: " ".join(x for x in x.split() if x not in stop))
#Feature selection
from sklearn.preprocessing import LabelEncoder
from sklearn.feature_extraction.text import TfidfVectorizer
Tfidfvector = TfidfVectorizer(ngram_range=(1,2), max_features=1000)
Tfidfvector.fit(data['cleaned_text'])
x_values = Tfidfvector.transform(data['cleaned_text'])
encoder = LabelEncoder()
y_values = encoder.fit_transform(data['Sentiment'])<jupyter_output><empty_output><jupyter_text>I selected TF-IDF for feature selection. TF-IDF feature selection is easy to compute and reduces complexity by making it simple to compute similarities between cleaned_text and Sentiment. <jupyter_code>#Splitting train and test data separately
from sklearn import model_selection
X_train, x_test, y_train, y_test = model_selection.train_test_split(x_values, y_values, test_size=0.2)
from sklearn.metrics import accuracy_score
#SVM
from sklearn.metrics import classification_report
from sklearn import svm
svm_model = svm.SVC(kernel='linear')
svm_model.fit(X_train, y_train)
predicted = svm_model.predict(x_test)
print("Accuracy score is {0}".format(accuracy_score(y_test, predicted)))
report = classification_report(y_test, predicted, output_dict=True)
report
from sklearn import model_selection
X_train, x_test, y_train, y_test = model_selection.train_test_split(x_values, y_values, test_size=0.2)
#Naive Bayes
from sklearn import naive_bayes
nb = naive_bayes.MultinomialNB()
nb.fit(X_train, y_train)
predicted_nb = nb.predict(x_test)
print("Accuracy score is {0}".format(accuracy_score(y_test, predicted_nb)))
report_nb = classification_report(y_test, predicted_nb, output_dict=True)
report_nb<jupyter_output>Accuracy score is 0.6875
<jupyter_text>- I selected Support Vector Machine (SVM) and Naive Bayes as my Superpvised Models
- SVM:
1. Accuracy: 81.2%
2. Precision: 27.0%
3. F1 score: 29.8%
4. Recall: 33.3%
- Naive Bayes
1. Accuracy: 68.75%
2. Precision: 34.3%
3. F1 score: 40.0%
4. Recall: 50.0%# **Question 3: House price prediction**(40 points). You are required to build a **regression** model to predict the house price with 79 explanatory variables describing (almost) every aspect of residential homes. The purpose of this question is to practice regression analysis, an supervised learning model. The training data, testing data, and data description files can be download here: https://github.com/unt-iialab/info5731_spring2021/blob/main/assignment/assignment4-question3-data.zip. Here is an axample for implementation: https://towardsdatascience.com/linear-regression-in-python-predict-the-bay-areas-home-price-5c91c8378878.
<jupyter_code>import pandas as pd
#Reading Data from csv
train_dataset = pd.read_csv("/content/train.csv")
test_dataset = pd.read_csv("/content/test.csv")
train_dataset.head()
test_dataset.head()
#Train_dataset
train_dataset.describe()
#Null values
print(train_dataset.isnull().sum())
#Null values
print(test_dataset.isnull().sum())
#Performing EDA
%matplotlib inline
import matplotlib.pyplot as plt
train_dataset.hist(bins=50, figsize=(20,15))
plt.savefig("attribute_histogram_plots")
plt.show()
#Sorting
corr_matrix = train_dataset.corr()
corr_matrix["SalePrice"].sort_values(ascending=False)
#Scatter plot
train_dataset.plot(kind="scatter", x="OverallQual", y="SalePrice", alpha=0.5)
#Scatter plot
train_dataset.plot(kind="scatter", x="GrLivArea", y="SalePrice", alpha=0.5)
#Scatter plot
train_dataset.plot(kind="scatter", x="GarageCars", y="SalePrice", alpha=0.5)
train_dataset.boxplot(column=['OverallQual', 'GrLivArea', 'GarageCars', 'GarageArea'])
train_dataset.boxplot(column=['TotalBsmtSF', '1stFlrSF', 'FullBath', 'SalePrice'])
train_dataset.fillna(train_dataset.mean(), inplace = True)
test_dataset.fillna(test_dataset.mean(), inplace = True)
print(train_dataset.isnull().sum())
print(test_dataset.isnull().sum())
#Data Encoding
from sklearn.preprocessing import LabelEncoder
columns = ('GarageCond', 'LandContour', 'RoofStyle', 'RoofMatl', 'Heating', 'MiscFeature', 'SaleType', 'GarageType', 'Electrical', 'SaleCondition', 'Foundation', 'Exterior1st', 'Exterior2nd', 'MasVnrType', 'FireplaceQu', 'LotConfig', 'Neighborhood', 'Condition1', 'Condition2', 'Utilities', 'BldgType', 'HouseStyle','PoolQC', 'BsmtQual', 'BsmtCond', 'GarageQual','BsmtExposure', 'ExterQual', 'ExterCond','HeatingQC', 'KitchenQual', 'BsmtFinType1','BsmtFinType2', 'Functional', 'Fence', 'GarageFinish', 'LandSlope','LotShape', 'PavedDrive', 'Street', 'Alley', 'CentralAir', 'MSSubClass', 'OverallCond', 'YrSold', 'MoSold', 'MSZoning')
for column in columns:
encoder = LabelEncoder()
encoder.fit(list(train_dataset[column].values))
train_dataset[column] = encoder.transform(list(train_dataset[column].values))
for column in columns:
encoder_test = LabelEncoder()
encoder_test.fit(list(test_dataset[column].values))
test_dataset[column] = encoder_test.transform(list(test_dataset[column].values))
x_values = train_dataset[train_dataset.columns[:80]]
x_test_values = test_dataset[test_dataset.columns[:80]]
y_values = train_dataset['SalePrice']
#Training Regression model
from sklearn.linear_model import LinearRegression
reg_model = LinearRegression()
reg_model.fit(x_values, y_values)
reg_model.score(x_values, y_values)
#Predicting House sale price
predicted = reg_model.predict(x_test_values)
pd.DataFrame({'Predicted House Price Values': predicted})<jupyter_output><empty_output>
|
no_license
|
/Rubab_INFO5731_Assignment_Four.ipynb
|
rubabshz/Rubab_INFO5731_Spring2020
| 5 |
<jupyter_start><jupyter_text><jupyter_code>kingdoms = ['Bacteria', 'Protozoa', 'Chromista', 'Plantae', 'Fungi', 'Animalia']
kingdoms[0]
kingdoms
<jupyter_output><empty_output>
|
no_license
|
/Lab2/Chuong.ipynb
|
VinhPhucs/Python-
| 1 |
<jupyter_start><jupyter_text>## Task 3.1<jupyter_code>%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def arbitrary_poly(params):
poly_model = lambda x: sum([p*(x**i) for i, p in enumerate(params)])
return poly_model
# params: [theta_0, theta_1, theta_2]
true_params = [3,-7,2, 20, -13]
y_model = arbitrary_poly(true_params)
# Plot true model
x = np.linspace(start=-1, stop=1, num=20)
plt.figure()
plt.plot(x, y_model(x))
plt.xlabel("x")
plt.ylabel("y")
plt.title("Model");
from scipy.stats import norm, laplace
# Hyperparameters for the type of noise-generating distribution.
loc = 0 # location (mean) parameter
scale = 1 # scaling (std dev) parameter
magnitude = 1.2 # noise magnitude
N = 10 # number of samples
# Generate data points
range_low, range_high = -1, 1
u = np.sort(np.random.uniform(range_low,range_high,N))
y_true = y_model(u)
# Generate noise
pdf = laplace.pdf
alpha = 0
laplaceBeta = 1
normVariance = 1
gamma = 0.1
noiseLaplace = magnitude * np.random.laplace(loc, laplaceBeta, int((1-alpha)*N))
noiseGaussian = magnitude * np.random.normal(loc, normVariance, int(alpha*N))
y = y_true + noiseLaplace
# Plot measured data
plt.scatter(u, y, label=r"Measured data")
u0 = np.linspace(-1, max(u), N)
plt.plot(u0, y_model(u0), "k", alpha=0.3, lw=3, label="True model")
plt.legend()
plt.xlabel("x")
plt.ylabel("y");<jupyter_output><empty_output>
|
no_license
|
/Assignment 3/.ipynb_checkpoints/Assignment3 TTK4260 - martkaa-checkpoint.ipynb
|
martkaa/TTK4260-multimod
| 1 |
<jupyter_start><jupyter_text># COGS 108 - Final Project # OverviewThis project investigates whether nearby restaurants in North Carolina share similar sanitary conditions and whether such similarities are caused by the socio-economic conditions of the restaurants' area. The underlying data did not follow any clear distributions, so the methods for analysis were mostly non-parametric (K-Nearest Neighbors and Mann Whitney U). The Results demonstrated that while nearby restaurants did share similar sanitary conditions, the socio-economic conditions of the areas did not significantly impact these similarities. However, the significance of the conclusions was slightly compromised due to the data being very skewed and having very little variance.### Name & PID
- Name: Carlos Eduardo Matos Ribeiro
- PID: A14032489# Research QuestionDo nearby restaurants (same city, ZIP code, or similar coordinates) in North Carolina share similar sanitary conditions (inspection scores and number of critical violations)? Are such trends caused by the socio-economic conditions (i.e income per capita) of said restaurants' area?## Background and Prior WorkIn North Carolina, restaurants and other food establishments are inspected by local county professionals between one and four times annually$^{1}$. In these inspections, violations are counted and tabulated, each with its own point value depending on its severity; the points are then subtracted from 100 to give a restaurant's final score, which is then used to determine its letter grade$^{1}$. This simple system allows for a straightforward way to quantify the sanitary conditions of restaurants, making it possible to carry out data analyses to investigate general trends and determining factors of said conditions.
With that in mind, I have decided to investigate whether the sanitary conditions of restaurants in North Carolina are related to their location, and more specifically if said locations' socio-economic condition have a considerable impact in this relationship. Certain characteristics about neighborhoods, including how busy it is and the average spending potential of its residents and by passers can greatly affect key factors for a restaurant's success, including the amount of customers it can expect to have and the amount of revenue that it can generate. Customer traffic and revenue in turn can affect many factors related to sanitary conditions, including: how much staff a restaurant can hire (and how overworked said staff is), how well trained the staff is, the quality of the equipment, the quality of the produce, how often produce has to be restocked, how much attention managers can devote to health and safety practices, etc. Therefore, it is reasonable to expect that the socio-economic conditions of a restaurant's area will somehow affect its health and safety conditions.
The most relevant research related to my investigation was a study conducted by the Environmental Health Specialists Network, based on several US states, which aimed to identify which factors most impacted safe food preparation practices in a restaurant. The study concluded that some of the main factors were the time pressure the employees felt, the quality of their equipment, the resources they had available and the emphasis managers gave to food safety$^{2}$. As discussed in the previous paragraph, many of these factors can be impacted by a restaurant's location and its socio-economic conditions, so this study helps corroborate that my research question holds promise and is worth investigating.
References:
- 1) https://www.forsyth.cc/PublicHealth/EnvironmentalHealth/aboutInspections.aspx
- 2) https://www.cdc.gov/nceh/ehs/ehsnet/docs/Factors_Impacting_Food_Workers_Food_Prep_FPT_journal.pdf# Hypothesis
I expect that there will be patterns in the sanitary conditions of restaurants in North Carolina that are close to each other. Additionally, I expect that there will be a positive relationship between the socio-economic characteristics of a restaurant's location, and its overall sanitary conditions, with restaurants in wealthier neighborhoods having fewer health/safety violations then restaurants in low-income, emptier neighborhoods. The reason for that premise was hinted at in the previous section: restaurants in wealthier neighborhoods are more likely to have a constant influx of customers with sufficient spending power to drive their business, thus have the ability to have an adequately-sized staff that is properly trained and equipped to maintain appropriate health conditions. Conversely, restaurants in low-income neighborhoods are less likely to have sufficient customers/revenue to adequately train and equip their staff, and it might face financial hardships that would lead it to overlook sanitary issues.# Dataset(s)- Dataset Name: Inspections
- Link to the dataset: data/inspections.csv
- Number of observations: 18466
In this dataset, each row is a restaurant inspection and each column holds information either about the specific inspection, or the restaurant being inspected. For each inspection there is a myriad of information, including the restaurant's name, address, zip code, coordinate location, the inspection date, number of critical/non-critical violation and overall score, to name a few.
- Dataset Name: Zip
- Link to the dataset: data/zip.csv
- Number of observations: 38
This dataset gathers general socio-economic indicators for various zip codes in North Carolina. Each row is a specific zip code and each column is a different indicator, such as per capita income, median family income and the percent of families living below the poverty line.
The datasets can be combined via the zip codes, with the Zip dataset being used to identify the socio-economic indicators of the neighborhood of each particular inspection.# Setup<jupyter_code>import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
import random
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error
from scipy.stats import mannwhitneyu<jupyter_output><empty_output><jupyter_text># Data CleaningFirst I loaded and examined the inspections dataset:<jupyter_code>df_inspections = pd.read_csv('data/inspections.csv')
print(df_inspections.columns)
df_inspections.head()<jupyter_output>Index(['hsisid', 'date', 'name', 'address1', 'address2', 'city', 'state',
'postalcode', 'phonenumber', 'restaurantopendate',
'days_from_open_date', 'facilitytype', 'x', 'y', 'geocodestatus', 'zip',
'type', 'description', 'inspectedby', 'inspection_num', 'inspector_id',
'previous_inspection_date', 'days_since_previous_inspection',
'previous_inspection_by_same_inspector', 'score', 'num_critical',
'num_non_critical', 'num_critical_previous',
'num_non_critical_previous', 'num_critical_mean_previous',
'num_non_critical_mean_previous', 'avg_neighbor_num_critical',
'avg_neighbor_num_non_critical', 'top_match', 'second_match',
'critical'],
dtype='object')
<jupyter_text>Clearly there are several columns that are not needed for my analysis, some of which have some unnecessary personal information (more on this later in the ethics & privacy section), so the first step was to narrow it down to the potentially relevant columns, including city, zip, coordinates, overall sanitary score and number of each type (critical/non-critical) of violation.<jupyter_code>df_inspections = df_inspections[['hsisid','city','zip','score','num_critical','num_non_critical','x','y','geocodestatus',]]<jupyter_output><empty_output><jupyter_text>Next I ensured that, within the relevant columns, there was no null data to worry about:<jupyter_code>pd.isna(df_inspections).any().any()
<jupyter_output><empty_output><jupyter_text>Finally, I decided to add a column with each restaurant's letter grade (A >= 90, B >= 80, C >= 70), since they usually are the main takeaway from each inspection and could later be useful for analysis.<jupyter_code># First define a function for the transformation
def to_letter_grade(score):
if score >= 90:
return 'A'
if score >= 80:
return 'B'
# Min score in dataset was 72
else:
return 'C'
# Then apply function and assign to new column
df_inspections['grade'] = df_inspections['score'].apply(to_letter_grade)
# Reorder columns to keep grade near score so its meaning is more clear
df_inspections = df_inspections[['hsisid','city','zip','score','grade','num_critical','num_non_critical','x','y','geocodestatus',]]<jupyter_output><empty_output><jupyter_text>Then, I loaded and inspected the zip dataset<jupyter_code>df_zipcodes = pd.read_csv('data/zipcodes.csv')
print(df_zipcodes.columns)
df_zipcodes.head()<jupyter_output>Index(['zip', 'median_family_income_dollars',
'median_household_income_dollars', 'per_capita_income_dollars',
'percent_damilies_below_poverty_line', 'percent_snap_benefits',
'percent_supplemental_security_income', 'percent_nonwhite'],
dtype='object')
<jupyter_text>Observing the columns, I noticed that some had information that was either unnecessary, redundant, and/or problematic (more on the ethics and privacy section), so there were all removed. The remaining columns were all somehow related, so for simplicity I decided to keep only income per capita. Finally, I ensured that there was no null data to worry about.<jupyter_code>df_zipcodes = df_zipcodes.rename(columns={"percent_damilies_below_poverty_line": "percent_families_below_poverty_line"})
df_zipcodes = df_zipcodes[['zip','per_capita_income_dollars']]
pd.isna(df_zipcodes).any().any()<jupyter_output><empty_output><jupyter_text>With both datasets in structured, tidy, format, streamlined to keep only potentially relevant information, and free of null values, they were both ready for analysis and no further cleaning was required.# Data Analysis & Results### Analysis preambleBack in the datasets portion, I noticed that the two datasets that I am using are very unbalanced in terms of size, since one has around 18000 observations and the other only 38. Before analyzing the data, I thought it was prudent to better understand that disparity by looking closer to the information that they shared.<jupyter_code>insp_zips = df_inspections['zip'].unique()
zips = df_zipcodes['zip'].unique()
print("Zips in inspections dataset %d" %len(insp_zips))
print("Zips in zipcodes dataset %d" %len(zips))
count = 0
for elem in insp_zips:
if elem in zips:
count += 1
print("Zips shared by both datasets %d" %count)<jupyter_output>Zips in inspections dataset 51
Zips in zipcodes dataset 38
Zips shared by both datasets 37
<jupyter_text>As shown above, the disparity in number of observations between the datasets is not very problematic, since the inspection dataset does not have that many unique zip codes, and many of them are shared between both data sets. However, it is still likely that many observations in the inspection datasets will not have corresponding information in the zip codes dataset.
With that in mind, I decided to break my analysis into different parts. First, I will use only the inspection dataset to examine whether restaurants that are close to each other share similar sanitary conditions. Then, I will combine the datasets, keeping only the data from zip codes shared by both, to analyze to what extent said location trends can be explained by the available socio-economic indicators.### Distribution of grades, scores and violationsFirstly, lets take a look at the general distribution of scores and grades of all the restaurants in the dataset<jupyter_code>plt.figure(figsize=(10, 8))
graph = sns.countplot(x='grade',data=df_inspections)
graph.set_title("Most North Carolina restaurants have an A grade",fontsize=20)
graph.set_xlabel("Inspection grade ",fontsize=14);
graph.set_ylabel("Number of restaurants",fontsize=14)
plt.show()
plt.figure(figsize=(8, 6))
graph = sns.distplot(df_inspections['score'], bins=25, kde=False);
graph.set_title("Distribution of restaurant inspection scores in North Carolina is skewed to the right",fontsize=20)
graph.set_xlabel("Inspection score",fontsize=14);
graph.set_ylabel("Number of restaurants",fontsize=14)
plt.show()<jupyter_output><empty_output><jupyter_text>From the graphs above we can observe that the distribution is very skewed ($\textbf{not normally distributed}$), with the vast majority of restaurants in our dataset in the A range, and the median being around 95. The scores being so high and generally close together is rather discouraging for analysis, since it is harder to investigate factors that impact scores when all of the scores are so similar. For the same reason, the letter grades are even less informative, since virtually every restaurant has an A.
Therefore, let's use more histograms to examine the distribution of other metrics for health/safety conditions: the number of critical/non-critical violations<jupyter_code>plt.figure(figsize=(8, 6))
graph = sns.distplot(df_inspections['num_critical'], bins=25, kde=False);
graph.set_title("Distribution of number of critical violations per restaurant in North Carolina is skewed to the left",fontsize=20)
graph.set_xlabel("Number of critical violations",fontsize=14);
graph.set_ylabel("Number of restaurants",fontsize=14)
plt.show()
plt.figure(figsize=(8, 6))
graph = sns.distplot(df_inspections['num_non_critical'], bins=25, kde=False);
graph.set_title("Distribution of number of non-critical violations per restaurant in North Carolina is skewed to the left",fontsize=20)
graph.set_xlabel("Number of non-critical violations",fontsize=14);
graph.set_ylabel("Number of restaurants",fontsize=14)
plt.show()<jupyter_output><empty_output><jupyter_text>These histograms show that the number of violations follow a similar skewed (though inverted) pattern, with most of the inspections falling within a lower range of violations (they are also not normally distributed). Note that the distribution of number of critical violations matches the distribution of scores more closely, which is expected since the critical violations have a higher impact on the score in the North Carolina system. Since the critical violations are the ones which most significantly affects a restaurant's health and safety conditions, I will focus on them and disregard non critical violations for the rest of the analysis.### Scores and number of violations per cityHaving obtained a general idea of the distribution of scores in the dataset overall, we can start looking at how those numbers change based on the location of the inspected restaurant. We start that analysis by examining patterns when grouping restaurants at the city level.<jupyter_code>by_city = df_inspections.groupby('city').mean()
print("Average score of city with highest score is: %f" %by_city['score'].max())
print("Average score of city with lowest score is: %f" %by_city['score'].min())
print("Average score per city: ")
by_city['score']<jupyter_output>Average score of city with highest score is: 98.250000
Average score of city with lowest score is: 94.750000
Average score per city:
<jupyter_text>The average score per city did not differ much, with the range of averages per city being less than 4 points (out of 100), showing that there is not a significant difference between overall inspection scores between cities.
Repeating the process for number of critical violations:<jupyter_code>print("Max average number of critical violations is: %f" %by_city['num_critical'].max())
print("Min average number of critical violations is: %f" %by_city['num_critical'].min())
print("Average number of critical violations per city: ")
by_city['num_critical']<jupyter_output>Max average number of critical violations is: 6.000000
Min average number of critical violations is: 0.500000
Average number of critical violations per city:
<jupyter_text>The average number of critical violations table showed greater variation, suggesting that there are differences in the overall sanitary conditions of restaurants in each city. For example, restaurants in Angier have on average 12 times more critical violations than restaraunts in Creedmoor, a significant difference.
However, closer examination of the each of these cities, as shown below, reveals that they each have a very small number of observations, so it's mathematically more likely that they would have outlier values and they do not tell us much about the relationship we investigating.<jupyter_code>print("Number of observations in Angier: %d" %df_inspections.loc[df_inspections['city'] == 'angier'].shape[0])
print("Number of observations in Creedmoor: %d" %df_inspections.loc[df_inspections['city'] == 'creedmoor'].shape[0])<jupyter_output>Number of observations in Creedmoor: 2
<jupyter_text>Given the above realization, it is possible that the variability in number of critical violations could have been simply due to outliers whose averages are less reliable due to their much smaller sample size. To verify this possibility, we can remove cities with too few (less than 100) observations from the dataset, then check the result for the remaining ones.<jupyter_code># First get the count for each city and determine cities to drop
by_city_count = df_inspections.groupby('city').count()['score']
drop_city = []
for key in by_city_count.keys():
if by_city_count[key] < 100:
drop_city.append(key)
# Then use list to drop from the dataframe
df_inspections = df_inspections[~df_inspections['city'].isin(drop_city)]
# Repeat previous procedure
by_city = df_inspections.groupby('city').mean()
print("Max average number of critical violations is: %f" %by_city['num_critical'].max())
print("Min average number of critical violations is: %f" %by_city['num_critical'].min())
print("Average number of critical violations per city: ")
by_city['num_critical']<jupyter_output>Max average number of critical violations is: 4.231081
Min average number of critical violations is: 2.124088
Average number of critical violations per city:
<jupyter_text>Removing the outliers really narrowed the range of average number of critical violations (from 5.5 to about 1.9), and even amongst the remaining cities there is still a considerable disparity in number of observations, potentially affecting the numbers. However, given that a single critical violation by itself can pose a health/safety hazard, the variation in the table above is sufficient to determine that on average the city in which a restaurant is located does have some relationship, albeit a small one, to its sanitary conditions.### Predicting score and number of violations based on coordinate locationWhile the above results were a good starting point, to further investigate the relationship between restaurants' locations and their sanitary conditions, we must move closer than the city level. One way to accomplish this is to look at similarity in results among restaurants that are close together based on their actual geographical proximity, using the X and Y coordinates from the dataset. To do so, we can use K-Nearest Neighbors regression models to predict restaurant scores/number of critical violations, splitting the data into train and test, then use Mean Squared Error on the test predictions to assess the efficiency of the models. K-Nearest Neighbors is a good choice for this task since it works on non-parametric data (such as the one in this dataset).<jupyter_code># First shuffle dataframe in case observations are in some location-related order
df_inspections_shuffled = df_inspections.sample(frac=1)
# Extract relevant columns
X_coords = df_inspections_shuffled['x'].tolist()
Y_coords = df_inspections_shuffled['y'].tolist()
zip_codes = df_inspections_shuffled['zip'].tolist()
scores = df_inspections_shuffled['score'].tolist()
num_critical = df_inspections_shuffled['num_critical'].tolist()
# 80/20 split for train and test
train_len = int(0.8 * len(X_coords))
X_train = X_coords[:train_len]
X_test = X_coords[train_len:]
Y_train = Y_coords[:train_len]
Y_test = Y_coords[train_len:]
zip_train = zip_codes[:train_len]
zip_test = zip_codes[train_len:]
train_score = scores[:train_len]
test_score = scores[train_len:]
train_num_critical = num_critical[:train_len]
test_num_critical = num_critical[train_len:]
# Separating into test and train array
train_array = []
for i in range(0,len(X_train)):
train_array.append([X_train[i],Y_train[i]])
test_array = []
for i in range(0,len(X_test)):
test_array.append([X_test[i],Y_test[i]])
# the 'distance' option gives greatest weight to the closer neighbors,
# helping to ensure that the data points that impact the predictions
# are actually nearby
KNN = KNeighborsRegressor(weights='distance')
# Training, and predicting results
KNN.fit(train_array,train_num_critical)
num_critical_prediction = KNN.predict(test_array)
<jupyter_output><empty_output><jupyter_text>To evaluate the accuracy of the predictions, we can examine their Mean Squared Error.<jupyter_code>print("Mean squared error of predictions for number of critical violations: %.3f" %mean_squared_error(test_num_critical,num_critical_prediction))<jupyter_output>Mean squared error of predictions for number of critical values: 7.372
<jupyter_text>Repeating the process for the restaurant scores:<jupyter_code>KNN = KNeighborsRegressor(weights='distance')
# Training, predicting, and evaluating results
KNN.fit(train_array,train_score)
score_prediction = KNN.predict(test_array)
print("Mean squared error of predictions for inspection scores: %.3f" %mean_squared_error(test_score,score_prediction))<jupyter_output>Mean squared error of predictions for inspection scores: 5.305
<jupyter_text>To help quantify the performance of the models, we can compare them to semi-random educated predictions, that guess values within the range in which most of the data lies (94-100 for score and 0-10 for number of critical violations)<jupyter_code>random_scores = []
for i in range(0,len(test_score)):
random_scores.append(random.randint(94,100))
random_num_critical = []
for i in range(0,len(test_num_critical)):
random_num_critical.append(random.randint(0,10))
print("Mean squared error of guesses for number of critical violations: %.3f" %mean_squared_error(test_num_critical,random_num_critical))
print("Mean squared error of guesses for inspection scores: %.3f" %mean_squared_error(test_score,random_scores))
<jupyter_output>Mean squared error of guesses for number of critical violations: 22.349
Mean squared error of guesses for inspection scores: 11.521
<jupyter_text>It can now be observed that the nearest neighbor models considerably outperformed the educated guesses. The difference was more significant for the number of critical violations, as expected given that the range that captures most of its values is larger. This result demonstrates that the sanitary conditions of neighboring restaurants can be reliably used to predict a given restaurant's own sanitary conditions with reasonable accuracy, $\textbf{indicating that nearby restaurants in North Carolina do indeed share similar sanitary conditions}$, as hypothesized.
Having established that, the next step is to explore whether those similarities are caused by the socio-economic conditions of the restaurants' locations.### Distribution of income per capitaTo start this part of the analysis, it is helpful to again observe general patterns related to the new variable. The histogram below shows its distribution <jupyter_code># Joining the datasets
df_joined = df_inspections.set_index('zip').join(other=df_zipcodes.set_index('zip'))
df_joined = df_joined.dropna()
df_joined.head()
plt.figure(figsize=(8, 6))
graph = sns.distplot(df_joined['per_capita_income_dollars'], bins=25, kde=False);
graph.set_title("Income per capita of restaurant ZIP codes in North Carolina is not normally distributed",fontsize=20)
graph.set_xlabel("ZIP code Income per capita (US \$)",fontsize=14);
graph.set_ylabel("Number of restaurants",fontsize=14)
plt.show()<jupyter_output><empty_output><jupyter_text>Based on the histogram above, we can see that income per capita is not as skewed as the inspection-related metrics. However, it appears somewhat bi-modal and does not look normally distributed.
Plotting income per capita of zip codes against the inspection-related metrics of restaurants will help determine any potential relationships between them.<jupyter_code>plt.figure(figsize=(8, 6))
graph = sns.scatterplot(x='per_capita_income_dollars',y='score',data=df_joined, alpha=0.3);
graph.set_title("No clear pattern between restaurant inspection score and corresponding ZIP code income per capita",fontsize=20)
graph.set_xlabel("ZIP code Income per capita (US \$)",fontsize=14);
graph.set_ylabel("Restaurant inspection score",fontsize=14)
plt.show()<jupyter_output><empty_output><jupyter_text>The above plot does not demonstrate any meaningful relationship between the variables, seen as most of the points on the graph are in the above 90 range and the ones that fall below seem randomly spread across different income per capita values.<jupyter_code>plt.figure(figsize=(8, 6))
graph = sns.scatterplot(x='per_capita_income_dollars',y='num_critical',data=df_joined, alpha=0.5);
graph.set_title("No clear pattern between restaurant number of critical violations and corresponding ZIP code income per capita",fontsize=20)
graph.set_xlabel("ZIP code Income per capita (US \$)",fontsize=14);
graph.set_ylabel("Number of critical violations ",fontsize=14)
plt.show()<jupyter_output><empty_output><jupyter_text>While at first glance the above plot might look slightly parabolic, with the higher values towards the middle, referring back to the histogram of per capita income shows that the plot more or less follows its shape. It is natural to expect that there would be more outliers in the range of income per capita that has more observations, so this scatter plot similarly does not show any meaningful relationships.
The scatter plots did not demonstrate any relationships, though they were not very easy to visualize due to the sheer number of points and the overlap between them. To address that problem, we can instead use a scatter plot to observe average values of inspections by income per capita. <jupyter_code>by_income = df_joined.groupby('per_capita_income_dollars').mean()
plt.figure(figsize=(8, 6))
graph = sns.scatterplot(x='per_capita_income_dollars',y='score',data=by_income.reset_index());
graph.set_title("No clear pattern between ZIP code income per capita and inspection score of restaurants in ZIP code",fontsize=20)
graph.set_xlabel("ZIP code Income per capita (US \$)",fontsize=14);
graph.set_ylabel("Average restaurant inspection score ",fontsize=14)
plt.show()
plt.figure(figsize=(10, 8))
graph = sns.scatterplot(x='per_capita_income_dollars',y='num_critical',data=by_income.reset_index());
graph.set_title("No clear pattern between ZIP code income per capita and number of critical violations of restaurants in ZIP code",fontsize=20)
graph.set_xlabel("ZIP code Income per capita (US \$)",fontsize=14);
graph.set_ylabel("Average restaurant number of critical violations ",fontsize=14)
plt.show()<jupyter_output><empty_output><jupyter_text>As shown above, plotting averages seemed to corroborate the initial impression that there is no relationship between the income per capita of a particular zip code and the sanitary conditions of restaurants in said zip code.
However, we can make use of a more involved statistical test to further investigate if there is indeed no relationship between the aforementioned variables.### Mann-Whitney U TestThe Mann-Whitney U test is useful in this situation because it works even if the related variables are not normally distributed, which, as previously discussed, is the case for my data. I will perform the test across several groups of scores/number of critical violations from areas with different income per capita values, then use that information to deduce whether said income per capita values affect the underlying distributions.
For the following tests, the null hypothesis will be that each pair of scores and pair of number of critical violations come from the same underlying distribution, with the alternative being that they come from different distributions (indicating that the income per capita affects the distribution). The alpha value used will be 5%.<jupyter_code># Splitting dataset more or less along the middle based on income per capita
# values were chosen so that each group was about the same size
over_35 = df_joined[df_joined['per_capita_income_dollars'] >= 35000]
over_35_scores = over_35['score']
over_35_num_critical = over_35['num_critical']
under_30 = df_joined[df_joined['per_capita_income_dollars'] <= 30000]
under_30_scores = under_30['score']
under_30_num_critical = under_30['num_critical']
# Carrying out test
_, p_score = mannwhitneyu(list(over_35_scores), list(under_30_scores))
_, p_num_crit = mannwhitneyu(list(over_35_num_critical), list(under_30_num_critical))
print("P value of test for inspection scores: %.3f" %p_score)
print("P value of test for number of critical violations: %.3f" %p_num_crit)<jupyter_output>P value of test for inspection scores: 0.123
P value of test for number of critical violations: 0.033
<jupyter_text>For the above tests, we fail to reject the null hypothesis for the scores test, but we are able to reject the null for the number of critical violations test, suggesting that the number of critical violations per restaurant of each group comes from different underlying distribution. This seems to indicate that the income per capita of a zip code is related to the number of critical violations of restaurants in that zip code.
Let us repeat the test using different values to generate the groups:<jupyter_code># Splitting dataset into groups of extreme values of income per capita
# values were chosen so that each group was more or less the same size
over_50 = df_joined[df_joined['per_capita_income_dollars'] >= 50000]
over_50_scores = over_50['score']
over_50_num_critical = over_50['num_critical']
under_18 = df_joined[df_joined['per_capita_income_dollars'] <= 18000]
under_18_scores = under_18['score']
under_18_num_critical = under_18['num_critical']
# Carrying out test
_, p_score = mannwhitneyu(list(over_50_scores), list(under_18_scores))
_, p_num_crit = mannwhitneyu(list(over_50_num_critical), list(under_18_num_critical))
print("P value of test for inspection scores: %.3f" %p_score)
print("P value of test for number of critical violations: %.3f" %p_num_crit)<jupyter_output>P value of test for inspection scores: 0.020
P value of test for number of critical violations: 0.006
|
no_license
|
/final_project/FinalProject_cribeiro23.ipynb
|
COGS108/individual_sp20
| 24 |
<jupyter_start><jupyter_text># Image features exercise
*Complete and hand in this completed worksheet (including its outputs and any supporting code outside of the worksheet) with your assignment submission. For more details see the [assignments page](http://vision.stanford.edu/teaching/cs231n/assignments.html) on the course website.*
We have seen that we can achieve reasonable performance on an image classification task by training a linear classifier on the pixels of the input image. In this exercise we will show that we can improve our classification performance by training linear classifiers not on raw pixels but on features that are computed from the raw pixels.
All of your work for this exercise will be done in this notebook.<jupyter_code>import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
from __future__ import print_function
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# for auto-reloading extenrnal modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2<jupyter_output><empty_output><jupyter_text>## Load data
Similar to previous exercises, we will load CIFAR-10 data from disk.<jupyter_code>from cs231n.features import color_histogram_hsv, hog_feature
def get_CIFAR10_data(num_training=49000, num_validation=1000, num_test=1000):
# Load the raw CIFAR-10 data
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# Subsample the data
mask = list(range(num_training, num_training + num_validation))
X_val = X_train[mask]
y_val = y_train[mask]
mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]
return X_train, y_train, X_val, y_val, X_test, y_test
# Cleaning up variables to prevent loading data multiple times (which may cause memory issue)
try:
del X_train, y_train
del X_test, y_test
print('Clear previously loaded data.')
except:
pass
X_train, y_train, X_val, y_val, X_test, y_test = get_CIFAR10_data()<jupyter_output><empty_output><jupyter_text>## Extract Features
For each image we will compute a Histogram of Oriented
Gradients (HOG) as well as a color histogram using the hue channel in HSV
color space. We form our final feature vector for each image by concatenating
the HOG and color histogram feature vectors.
Roughly speaking, HOG should capture the texture of the image while ignoring
color information, and the color histogram represents the color of the input
image while ignoring texture. As a result, we expect that using both together
ought to work better than using either alone. Verifying this assumption would
be a good thing to try for your interests.
The `hog_feature` and `color_histogram_hsv` functions both operate on a single
image and return a feature vector for that image. The extract_features
function takes a set of images and a list of feature functions and evaluates
each feature function on each image, storing the results in a matrix where
each column is the concatenation of all feature vectors for a single image.<jupyter_code>from cs231n.features import *
num_color_bins = 10 # Number of bins in the color histogram
feature_fns = [hog_feature, lambda img: color_histogram_hsv(img, nbin=num_color_bins)]
X_train_feats = extract_features(X_train, feature_fns, verbose=True)
X_val_feats = extract_features(X_val, feature_fns)
X_test_feats = extract_features(X_test, feature_fns)
# Preprocessing: Subtract the mean feature
mean_feat = np.mean(X_train_feats, axis=0, keepdims=True)
X_train_feats -= mean_feat
X_val_feats -= mean_feat
X_test_feats -= mean_feat
# Preprocessing: Divide by standard deviation. This ensures that each feature
# has roughly the same scale.
std_feat = np.std(X_train_feats, axis=0, keepdims=True)
X_train_feats /= std_feat
X_val_feats /= std_feat
X_test_feats /= std_feat
# Preprocessing: Add a bias dimension
X_train_feats = np.hstack([X_train_feats, np.ones((X_train_feats.shape[0], 1))])
X_val_feats = np.hstack([X_val_feats, np.ones((X_val_feats.shape[0], 1))])
X_test_feats = np.hstack([X_test_feats, np.ones((X_test_feats.shape[0], 1))])<jupyter_output>Done extracting features for 1000 / 49000 images
Done extracting features for 2000 / 49000 images
Done extracting features for 3000 / 49000 images
Done extracting features for 4000 / 49000 images
Done extracting features for 5000 / 49000 images
Done extracting features for 6000 / 49000 images
Done extracting features for 7000 / 49000 images
Done extracting features for 8000 / 49000 images
Done extracting features for 9000 / 49000 images
Done extracting features for 10000 / 49000 images
Done extracting features for 11000 / 49000 images
Done extracting features for 12000 / 49000 images
Done extracting features for 13000 / 49000 images
Done extracting features for 14000 / 49000 images
Done extracting features for 15000 / 49000 images
Done extracting features for 16000 / 49000 images
Done extracting features for 17000 / 49000 images
Done extracting features for 18000 / 49000 images
Done extracting features for 19000 / 49000 images
Done extracting features for 20000 / 49000 images
Done extr[...]<jupyter_text>## Train SVM on features
Using the multiclass SVM code developed earlier in the assignment, train SVMs on top of the features extracted above; this should achieve better results than training SVMs directly on top of raw pixels.<jupyter_code># Use the validation set to tune the learning rate and regularization strength
from cs231n.classifiers.linear_classifier import LinearSVM
'''
learning_rates = [1e-9, 1e-8, 1e-7]
regularization_strengths = [5e4, 5e5, 5e6]
'''
learning_rates =[5e-9, 7.5e-9, 1e-8]
regularization_strengths = [(5+i)*1e6 for i in range(-3,4)]
results = {}
best_val = -1
best_svm = None
from tqdm import tqdm, trange
################################################################################
# TODO: #
# Use the validation set to set the learning rate and regularization strength. #
# This should be identical to the validation that you did for the SVM; save #
# the best trained classifer in best_svm. You might also want to play #
# with different numbers of bins in the color histogram. If you are careful #
# you should be able to get accuracy of near 0.44 on the validation set. #
################################################################################
for rates in tqdm(learning_rates):
for strengths in tqdm(regularization_strengths):
tmp_svm = LinearSVM()
print(X_train.shape)
tmp_svm.train(X_train_feats,y_train,learning_rate = rates,reg = strengths,num_iters = 1500,batch_size = 200,verbose=False)
train_acc = np.mean(tmp_svm.predict(X_train_feats)==y_train)
val_acc = np.mean(tmp_svm.predict(X_val_feats)==y_val)
if best_val<val_acc:
best_svm = tmp_svm
best_val = val_acc
# Print out results.
for lr, reg in sorted(results):
train_accuracy, val_accuracy = results[(lr, reg)]
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_accuracy, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)
# Evaluate your trained SVM on the test set
y_test_pred = best_svm.predict(X_test_feats)
test_accuracy = np.mean(y_test == y_test_pred)
print(test_accuracy)
# An important way to gain intuition about how an algorithm works is to
# visualize the mistakes that it makes. In this visualization, we show examples
# of images that are misclassified by our current system. The first column
# shows images that our system labeled as "plane" but whose true label is
# something other than "plane".
examples_per_class = 8
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
for cls, cls_name in enumerate(classes):
idxs = np.where((y_test != cls) & (y_test_pred == cls))[0]
idxs = np.random.choice(idxs, examples_per_class, replace=False)
for i, idx in enumerate(idxs):
plt.subplot(examples_per_class, len(classes), i * len(classes) + cls + 1)
plt.imshow(X_test[idx].astype('uint8'))
plt.axis('off')
if i == 0:
plt.title(cls_name)
plt.show()<jupyter_output><empty_output><jupyter_text>### Inline question 1:
Describe the misclassification results that you see. Do they make sense?## Neural Network on image features
Earlier in this assigment we saw that training a two-layer neural network on raw pixels achieved better classification performance than linear classifiers on raw pixels. In this notebook we have seen that linear classifiers on image features outperform linear classifiers on raw pixels.
For completeness, we should also try training a neural network on image features. This approach should outperform all previous approaches: you should easily be able to achieve over 55% classification accuracy on the test set; our best model achieves about 60% classification accuracy.<jupyter_code># Preprocessing: Remove the bias dimension
# Make sure to run this cell only ONCE
print(X_train_feats.shape)
X_train_feats = X_train_feats[:, :-1]
X_val_feats = X_val_feats[:, :-1]
X_test_feats = X_test_feats[:, :-1]
print(X_train_feats.shape)
from cs231n.classifiers.neural_net import TwoLayerNet
input_dim = X_train_feats.shape[1]
hidden_dim = 500
num_classes = 10
net = TwoLayerNet(input_dim, hidden_dim, num_classes)
best_net = None
################################################################################
# TODO: Train a two-layer neural network on image features. You may want to #
# cross-validate various parameters as in previous sections. Store your best #
# model in the best_net variable. #
################################################################################
# Run your best neural net classifier on the test set. You should be able
# to get more than 55% accuracy.
test_acc = (best_net.predict(X_test_feats) == y_test).mean()
print(test_acc)<jupyter_output><empty_output>
|
no_license
|
/CS231N/assignment1/.ipynb_checkpoints/features-checkpoint.ipynb
|
3375786734/ML_exercise
| 5 |
<jupyter_start><jupyter_text># Confidence Intervals<jupyter_code>import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as st<jupyter_output><empty_output><jupyter_text>## Challenge 1
We want to estimate the average size of the men of a country with a confidence level of 80%. Assuming that the standard deviation of the sizes in the population is 4, get the confidence interval with a sample of men selected randomly, whose heights are:
````
heights = [167, 167, 168, 168, 168, 169, 171, 172, 173, 175, 175, 175, 177, 182, 195]
````
**Hint**: function `stats.norm.interval` from `scipy` can help you get through this exercise. <jupyter_code>heights = [167, 167, 168, 168, 168, 169, 171, 172, 173, 175, 175, 175, 177, 182, 195]
st.norm.interval(0.80, loc=np.mean(heights), scale=st.sem(heights))<jupyter_output><empty_output><jupyter_text>## Challenge 2
In a sample of 105 shops selected randomly from an area, we note that 27 of them have had losses in this month. Get an interval for the proportion of businesses in the area with losses to a confidence level of 80% and a confidence level of 90%.
**Hint**: function `stats.norm.interval` from `scipy` can help you get through this exercise. <jupyter_code>shops_ok=np.ones(78)
shops_losses=np.zeros(27)
st.norm.interval<jupyter_output><empty_output><jupyter_text>## Challenge 3 - More practice
For the same example in challenge 1, calculate a confidence interval for the variance at 90% level.
**Hint**: function `stats.chi2.interval` from `scipy` can help you get through this exercise. <jupyter_code>stats.chi2.interval<jupyter_output><empty_output><jupyter_text>## Challenge 4 - More practice
The sulfuric acid content of 7 similar containers is 9.8, 10.2, 10.4, 9.8, 10.0, 10.2 and 9.6 liters. Calculate a 95% confidence interval for the average content of all containers assuming an approximately normal distribution.
```
acid = [9.8, 10.2, 10.4, 9.8, 10.0, 10.2, 9.6]
```
**Hint**: function `stats.t.interval` from `scipy` can help you get through this exercise. <jupyter_code># your code here<jupyter_output><empty_output><jupyter_text>## Bonus Challenge
The error level or sampling error for the first challenge is given by the following expression:
$$Error = z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt n}$$
Where z represents the value for N(0,1)
Suppose that with the previous data of challenge 1, and with a confidence level of
99% (that is, almost certainly) we want to estimate the average population size, so that the error level committed is not greater than half a centimeter.
#### 1.- Determine what size the selected sample of men should be.<jupyter_code># your code here<jupyter_output><empty_output><jupyter_text>#### 2.- For the second challenge, we have the following error:
$$ Error = z_{\frac{\alpha}{2}}\sqrt{\frac{p\times q}{n}} $$
#### Determine the sample size required to not exceed an error of 1% with a confidence of 80%.<jupyter_code># your code here<jupyter_output><empty_output><jupyter_text>## Bonus Challenge
Let's consider the following problem:
Build a confidence interval of 94% for the real difference between the durations of two brands of spotlights, if a sample of 40 spotlights taken randomly from the first mark gave an average duration of 418 hours, and a sample of 50 bulbs of another brand gave a duration average of 402 hours. The standard deviations of the two
populations are 26 hours and 22 hours, respectively.
Sometimes, we will be interested in the difference of two different groups of random variables. We can also build a confidence interval for that! We have some different cases regarding the variance but for this specific case (the variance are different and known), we have that:
$$\overline{X} - \overline{Y} \sim N(\mu_{X} - \mu_{Y} , \sqrt{\frac{\sigma_{X}^2}{n_X}+\frac{\sigma_{Y}^2}{n_Y}})$$
Solve the problem with this information.<jupyter_code># your code here<jupyter_output><empty_output>
|
no_license
|
/Labs/module_2/Confidence-Intervals/your-code/main.ipynb
|
sachadolle/806_Repo
| 8 |
<jupyter_start><jupyter_text># 輸入與輸出(Input and Output)2019.9.19
單元學習目標:
python輸入:input(), raw_input()
python輸出: print()
python格式化輸出技術 老師說很重要 必考題## 基本輸入:讀取使用者的輸入
```
使用input時,會從標準輸入(stdin)中讀取輸入資料
這些資料是string字串型態{重要}
```
stdin==Standard Input<jupyter_code>x = input('你的名字:')
print('哈囉, ' + x)
a = input("請輸入:")
a<jupyter_output>請輸入:100
<jupyter_text>### Python內建的type()函數可以顯示資料型態str==string==字串資料型態<jupyter_code>type(a)<jupyter_output><empty_output><jupyter_text>### 錯誤的做法:請指出底下程式的錯誤TypeError ==資料型態錯誤
Type==資料型態==data type<jupyter_code>#輸入100看看會怎樣
a = input("請輸入:")
a
type(a)
b=a+1
b<jupyter_output>請輸入:100
<jupyter_text>## 基本輸入:讀取使用者輸入的整數
使用eval()函數<jupyter_code>c=int(input("請輸入:"))
type(c)
a = eval(input("請輸入:"))
type(a)
b=a+1
b<jupyter_output><empty_output><jupyter_text>## 超級重要:可以一次輸入多(兩)個資料
<jupyter_code>a,b = eval(input("請輸入兩個數位:"))
a,b<jupyter_output>請輸入兩個數位:11,22
<jupyter_text>### 高階技巧:<jupyter_code>x, y, z = [int(x) for x in input("Enter three value: ").split()]
print("First Number is: ", x)
print("Second Number is: ", y)
print("Third Number is: ", z)
print()
x, y, z = [int(x) for x in input("Enter three value: ").split(",")]
print("First Number is: ", x)
print("Second Number is: ", y)
print("Third Number is: ", z)
print()
a, b = input("Enter a two value: ").split()
print("First number is {} and second number is {}".format(a, b))
print()
<jupyter_output><empty_output>
|
no_license
|
/Python_1_IO.ipynb
|
iE019/CS4high_4080E019
| 6 |
<jupyter_start><jupyter_text>
Area Plots, Histograms, and Bar Plots## Introduction
In this lab, we will continue exploring the Matplotlib library and will learn how to create additional plots, namely area plots, histograms, and bar charts.## Table of Contents
1. [Exploring Datasets with *pandas*](#0)
2. [Downloading and Prepping Data](#2)
3. [Visualizing Data using Matplotlib](#4)
4. [Area Plots](#6)
5. [Histograms](#8)
6. [Bar Charts](#10)
# Exploring Datasets with *pandas* and Matplotlib
Toolkits: The course heavily relies on [*pandas*](http://pandas.pydata.org/) and [**Numpy**](http://www.numpy.org/) for data wrangling, analysis, and visualization. The primary plotting library that we are exploring in the course is [Matplotlib](http://matplotlib.org/).
Dataset: Immigration to Canada from 1980 to 2013 - [International migration flows to and from selected countries - The 2015 revision](http://www.un.org/en/development/desa/population/migration/data/empirical2/migrationflows.shtml) from United Nation's website.
The dataset contains annual data on the flows of international migrants as recorded by the countries of destination. The data presents both inflows and outflows according to the place of birth, citizenship or place of previous / next residence both for foreigners and nationals. For this lesson, we will focus on the Canadian Immigration data.# Downloading and Prepping Data Import Primary Modules. The first thing we'll do is import two key data analysis modules: *pandas* and **Numpy**.<jupyter_code>import numpy as np # useful for many scientific computing in Python
import pandas as pd # primary data structure library<jupyter_output><empty_output><jupyter_text>Let's download and import our primary Canadian Immigration dataset using *pandas* `read_excel()` method. Normally, before we can do that, we would need to download a module which *pandas* requires to read in excel files. This module is **xlrd**. For your convenience, we have pre-installed this module, so you would not have to worry about that. Otherwise, you would need to run the following line of code to install the **xlrd** module:
```
!conda install -c anaconda xlrd --yes
```Download the dataset and read it into a *pandas* dataframe.<jupyter_code>df_can = pd.read_excel('https://ibm.box.com/shared/static/lw190pt9zpy5bd1ptyg2aw15awomz9pu.xlsx',
sheet_name='Canada by Citizenship',
skiprows=range(20),
skip_footer=2
)
print('Data downloaded and read into a dataframe!')<jupyter_output>Data downloaded and read into a dataframe!
<jupyter_text>Let's take a look at the first five items in our dataset.<jupyter_code>df_can.head()<jupyter_output><empty_output><jupyter_text>Let's find out how many entries there are in our dataset.<jupyter_code># print the dimensions of the dataframe
print(df_can.shape)<jupyter_output>(195, 43)
<jupyter_text>Clean up data. We will make some modifications to the original dataset to make it easier to create our visualizations. Refer to `Introduction to Matplotlib and Line Plots` lab for the rational and detailed description of the changes.#### 1. Clean up the dataset to remove columns that are not informative to us for visualization (eg. Type, AREA, REG).<jupyter_code>df_can.drop(['AREA', 'REG', 'DEV', 'Type', 'Coverage'], axis=1, inplace=True)
# let's view the first five elements and see how the dataframe was changed
df_can.head()<jupyter_output><empty_output><jupyter_text>Notice how the columns Type, Coverage, AREA, REG, and DEV got removed from the dataframe.#### 2. Rename some of the columns so that they make sense.<jupyter_code>df_can.rename(columns={'OdName':'Country', 'AreaName':'Continent','RegName':'Region'}, inplace=True)
# let's view the first five elements and see how the dataframe was changed
df_can.head()<jupyter_output><empty_output><jupyter_text>Notice how the column names now make much more sense, even to an outsider.#### 3. For consistency, ensure that all column labels of type string.<jupyter_code># let's examine the types of the column labels
all(isinstance(column, str) for column in df_can.columns)<jupyter_output><empty_output><jupyter_text>Notice how the above line of code returned *False* when we tested if all the column labels are of type **string**. So let's change them all to **string** type.<jupyter_code>df_can.columns = list(map(str, df_can.columns))
# let's check the column labels types now
all(isinstance(column, str) for column in df_can.columns)<jupyter_output><empty_output><jupyter_text>#### 4. Set the country name as index - useful for quickly looking up countries using .loc method.<jupyter_code># Important
df_can.set_index('Country', inplace=True)
# let's view the first five elements and see how the dataframe was changed
df_can.head()<jupyter_output><empty_output><jupyter_text>Notice how the country names now serve as indices.#### 5. Add total column.<jupyter_code>df_can['Total'] = df_can.sum(axis=1)
# let's view the first five elements and see how the dataframe was changed
df_can.head()<jupyter_output><empty_output><jupyter_text>Now the dataframe has an extra column that presents the total number of immigrants from each country in the dataset from 1980 - 2013. So if we print the dimension of the data, we get:<jupyter_code>print ('data dimensions:', df_can.shape)<jupyter_output>data dimensions: (195, 38)
<jupyter_text>So now our dataframe has 38 columns instead of 37 columns that we had before.<jupyter_code># finally, let's create a list of years from 1980 - 2013
# this will come in handy when we start plotting the data
years = list(map(str, range(1980, 2014)))
years<jupyter_output><empty_output><jupyter_text># Visualizing Data using MatplotlibImport `Matplotlib` and **Numpy**.<jupyter_code># use the inline backend to generate the plots within the browser
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.style.use('ggplot') # optional: for ggplot-like style
# check for latest version of Matplotlib
print ('Matplotlib version: ', mpl.__version__) # >= 2.0.0<jupyter_output>Matplotlib version: 2.2.2
<jupyter_text># Area PlotsIn the last module, we created a line plot that visualized the top 5 countries that contribued the most immigrants to Canada from 1980 to 2013. With a little modification to the code, we can visualize this plot as a cumulative plot, also knows as a **Stacked Line Plot** or **Area plot**.<jupyter_code>df_can.sort_values(['Total'], ascending=False, axis=0, inplace=True)
# get the top 5 entries
df_top5 = df_can.head()
# transpose the dataframe
df_top5 = df_top5[years].transpose()
df_top5.head()<jupyter_output><empty_output><jupyter_text>Area plots are stacked by default. And to produce a stacked area plot, each column must be either all positive or all negative values (any NaN values will defaulted to 0). To produce an unstacked plot, pass `stacked=False`. <jupyter_code>df_top5.index = df_top5.index.map(int) # let's change the index values of df_top5 to type integer for plotting
df_top5.plot(kind='area',
stacked=False,
figsize=(20, 10), # pass a tuple (x, y) size
)
plt.title('Immigration Trend of Top 5 Countries')
plt.ylabel('Number of Immigrants')
plt.xlabel('Years')
plt.show()<jupyter_output><empty_output><jupyter_text>The unstacked plot has a default transparency (alpha value) at 0.5. We can modify this value by passing in the `alpha` parameter.<jupyter_code>df_top5.plot(kind='area',
alpha=0.25, # 0-1, default value a= 0.5
stacked=False,
figsize=(20, 10),
)
plt.title('Immigration Trend of Top 5 Countries')
plt.ylabel('Number of Immigrants')
plt.xlabel('Years')
plt.show()<jupyter_output><empty_output><jupyter_text>### Two types of plotting
As we discussed in the video lectures, there are two styles/options of ploting with `matplotlib`. Plotting using the Artist layer and plotting using the scripting layer.
**Option 1: Scripting layer (procedural method) - using matplotlib.pyplot as 'plt' **
You can use `plt` i.e. `matplotlib.pyplot` and add more elements by calling different methods procedurally; for example, `plt.title(...)` to add title or `plt.xlabel(...)` to add label to the x-axis.
```python
# Option 1: This is what we have been using so far
df_top5.plot(kind='area', alpha=0.35, figsize=(20, 10))
plt.title('Immigration trend of top 5 countries')
plt.ylabel('Number of immigrants')
plt.xlabel('Years')
```**Option 2: Artist layer (Object oriented method) - using an `Axes` instance from Matplotlib (preferred) **
You can use an `Axes` instance of your current plot and store it in a variable (eg. `ax`). You can add more elements by calling methods with a little change in syntax (by adding "*set_*" to the previous methods). For example, use `ax.set_title()` instead of `plt.title()` to add title, or `ax.set_xlabel()` instead of `plt.xlabel()` to add label to the x-axis.
This option sometimes is more transparent and flexible to use for advanced plots (in particular when having multiple plots, as you will see later).
In this course, we will stick to the **scripting layer**, except for some advanced visualizations where we will need to use the **artist layer** to manipulate advanced aspects of the plots.<jupyter_code># option 2: preferred option with more flexibility
ax = df_top5.plot(kind='area', alpha=0.35, figsize=(20, 10))
ax.set_title('Immigration Trend of Top 5 Countries')
ax.set_ylabel('Number of Immigrants')
ax.set_xlabel('Years')<jupyter_output><empty_output><jupyter_text>**Question**: Use the scripting layer to create a stacked area plot of the 5 countries that contributed the least to immigration to Canada **from** 1980 to 2013. Use a transparency value of 0.45.<jupyter_code>### type your answer here
#df_can.sort_values(['Total'], ascending=False, axis=0, inplace=True)
#df_bottom5 = df_can.head()
#df_bottom5 = df_bottom5[years].transpose()
#df_bottom5.plot(kind='area',
# alpha=0.35,
# figsize=(20,10))
df_least5 = df_can.tail(5)
df_least5 = df_least5[years].transpose()
df_least5.head()
df_least5.index = df_least5.index.map(int) # let's change the index values of df_least5 to type integer for plotting
df_least5.plot(kind='area', alpha=0.45, figsize=(20, 10))
plt.title('Immigration Trend of 5 Countries that contributed the least to immigrate')
plt.ylabel('Number of Immigrants')
plt.xlabel('Years')
plt.show()<jupyter_output><empty_output><jupyter_text>Double-click __here__ for the solution.
<!-- The correct answer is:
\\ # get the 5 countries with the least contribution
df_least5 = df_can.tail(5)
-->
<!--
\\ # transpose the dataframe
df_least5 = df_least5[years].transpose()
df_least5.head()
-->
<!--
df_least5.index = df_least5.index.map(int) # let's change the index values of df_least5 to type integer for plotting
df_least5.plot(kind='area', alpha=0.45, figsize=(20, 10))
-->
<!--
plt.title('Immigration Trend of 5 Countries with Least Contribution to Immigration')
plt.ylabel('Number of Immigrants')
plt.xlabel('Years')
-->
<!--
plt.show()
-->**Question**: Use the artist layer to create an unstacked area plot of the 5 countries that contributed the least to immigration to Canada **from** 1980 to 2013. Use a transparency value of 0.55.<jupyter_code>### type your answer here
ax = df_least5.plot(kind='area', alpha=0.35, figsize=(20, 10))
ax.set_title('Immigration trends of 5 least contributing countries')
ax.set_ylabel('Number of Immigrants')
ax.set_xlabel('Years')
<jupyter_output><empty_output><jupyter_text>Double-click __here__ for the solution.
<!-- The correct answer is:
\\ # get the 5 countries with the least contribution
df_least5 = df_can.tail(5)
-->
<!--
\\ # transpose the dataframe
df_least5 = df_least5[years].transpose()
df_least5.head()
-->
<!--
df_least5.index = df_least5.index.map(int) # let's change the index values of df_least5 to type integer for plotting
-->
<!--
ax = df_least5.plot(kind='area', alpha=0.55, stacked=False, figsize=(20, 10))
-->
<!--
ax.set_title('Immigration Trend of 5 Countries with Least Contribution to Immigration')
ax.set_ylabel('Number of Immigrants')
ax.set_xlabel('Years')
--># Histograms
A histogram is a way of representing the *frequency* distribution of numeric dataset. The way it works is it partitions the x-axis into *bins*, assigns each data point in our dataset to a bin, and then counts the number of data points that have been assigned to each bin. So the y-axis is the frequency or the number of data points in each bin. Note that we can change the bin size and usually one needs to tweak it so that the distribution is displayed nicely.**Question:** What is the frequency distribution of the number (population) of new immigrants from the various countries to Canada in 2013?Before we proceed with creating the histogram plot, let's first examine the data split into intervals. To do this, we will us **Numpy**'s `histrogram` method to get the bin ranges and frequency counts as follows:<jupyter_code># let's quickly view the 2013 data
df_can['2013'].head()
# np.histogram returns 2 values
count, bin_edges = np.histogram(df_can['2013'])
print(count) # frequency count
print(bin_edges) # bin ranges, default = 10 bins<jupyter_output>[178 11 1 2 0 0 0 0 1 2]
[ 0. 3412.9 6825.8 10238.7 13651.6 17064.5 20477.4 23890.3 27303.2
30716.1 34129. ]
<jupyter_text>By default, the `histrogram` method breaks up the dataset into 10 bins. The figure below summarizes the bin ranges and the frequency distribution of immigration in 2013. We can see that in 2013:
* 178 countries contributed between 0 to 3412.9 immigrants
* 11 countries contributed between 3412.9 to 6825.8 immigrants
* 1 country contributed between 6285.8 to 10238.7 immigrants, and so on..
We can easily graph this distribution by passing `kind=hist` to `plot()`.<jupyter_code>df_can['2013'].plot(kind='hist', figsize=(8, 5))
print(df_can['2013'].sort_values(ascending=False))
plt.title('Histogram of Immigration from 195 Countries in 2013') # add a title to the histogram
plt.ylabel('Number of Countries') # add y-label
plt.xlabel('Number of Immigrants') # add x-label
plt.show()<jupyter_output>Country
China 34129
India 33087
Philippines 29544
Pakistan 12603
Iran (Islamic Republic of) 11291
United States of America 8501
United Kingdom of Great Britain and Northern Ireland 5827
France 5623
Iraq 4918
Republic of Korea 4509
Algeria 4331
Nigeria 4172
Egypt 4165
Haiti 4152
Mexico 3996
Bangladesh 3789
[...]<jupyter_text>In the above plot, the x-axis represents the population range of immigrants in intervals of 3412.9. The y-axis represents the number of countries that contributed to the aforementioned population.
Notice that the x-axis labels do not match with the bin size. This can be fixed by passing in a `xticks` keyword that contains the list of the bin sizes, as follows:<jupyter_code># 'bin_edges' is a list of bin intervals
count, bin_edges = np.histogram(df_can['2013'])
df_can['2013'].plot(kind='hist', figsize=(8, 5), xticks=bin_edges)
plt.title('Histogram of Immigration from 195 countries in 2013') # add a title to the histogram
plt.ylabel('Number of Countries') # add y-label
plt.xlabel('Number of Immigrants') # add x-label
plt.show()<jupyter_output><empty_output><jupyter_text>*Side Note:* We could use `df_can['2013'].plot.hist()`, instead. In fact, throughout this lesson, using `some_data.plot(kind='type_plot', ...)` is equivalent to `some_data.plot.type_plot(...)`. That is, passing the type of the plot as argument or method behaves the same.
See the *pandas* documentation for more info http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.plot.html.We can also plot multiple histograms on the same plot. For example, let's try to answer the following questions using a histogram.
**Question**: What is the immigration distribution for Denmark, Norway, and Sweden for years 1980 - 2013?<jupyter_code># let's quickly view the dataset
df_can.loc[['Denmark', 'Norway', 'Sweden'], years]
# generate histogram
df_can.loc[['Denmark', 'Norway', 'Sweden'], years].plot.hist()<jupyter_output><empty_output><jupyter_text>That does not look right!
Don't worry, you'll often come across situations like this when creating plots. The solution often lies in how the underlying dataset is structured.
Instead of plotting the population frequency distribution of the population for the 3 countries, *pandas* instead plotted the population frequency distribution for the `years`.
This can be easily fixed by first transposing the dataset, and then plotting as shown below.
<jupyter_code># transpose dataframe
df_t = df_can.loc[['Denmark', 'Norway', 'Sweden'], years].transpose()
df_t.head()
# generate histogram
df_t.plot(kind='hist', figsize=(10, 6))
plt.title('Histogram of Immigration from Denmark, Norway, and Sweden from 1980 - 2013')
plt.ylabel('Number of Years')
plt.xlabel('Number of Immigrants')
plt.show()<jupyter_output><empty_output><jupyter_text>Let's make a few modifications to improve the impact and aesthetics of the previous plot:
* increase the bin size to 15 by passing in `bins` parameter
* set transparency to 60% by passing in `alpha` paramemter
* label the x-axis by passing in `x-label` paramater
* change the colors of the plots by passing in `color` parameter<jupyter_code># let's get the x-tick values
count, bin_edges = np.histogram(df_t, 15)
# un-stacked histogram
df_t.plot(kind ='hist',
figsize=(10, 6),
bins=15,
alpha=0.6,
xticks=bin_edges,
color=['coral', 'darkslateblue', 'mediumseagreen']
)
plt.title('Histogram of Immigration from Denmark, Norway, and Sweden from 1980 - 2013')
plt.ylabel('Number of Years')
plt.xlabel('Number of Immigrants')
plt.show()<jupyter_output><empty_output><jupyter_text>Tip:
For a full listing of colors available in Matplotlib, run the following code in your python shell:
```python
import matplotlib
for name, hex in matplotlib.colors.cnames.items():
print(name, hex)
```If we do no want the plots to overlap each other, we can stack them using the `stacked` paramemter. Let's also adjust the min and max x-axis labels to remove the extra gap on the edges of the plot. We can pass a tuple (min,max) using the `xlim` paramater, as show below.<jupyter_code>count, bin_edges = np.histogram(df_t, 15)
xmin = bin_edges[0] - 10 # first bin value is 31.0, adding buffer of 10 for aesthetic purposes
xmax = bin_edges[-1] + 10 # last bin value is 308.0, adding buffer of 10 for aesthetic purposes
# stacked Histogram
df_t.plot(kind='hist',
figsize=(10, 6),
bins=15,
xticks=bin_edges,
color=['coral', 'darkslateblue', 'mediumseagreen'],
stacked=True,
xlim=(xmin, xmax)
)
plt.title('Histogram of Immigration from Denmark, Norway, and Sweden from 1980 - 2013')
plt.ylabel('Number of Years')
plt.xlabel('Number of Immigrants')
plt.show()<jupyter_output><empty_output><jupyter_text>**Question**: Use the scripting layer to display the immigration distribution for Greece, Albania, and Bulgaria for years 1980 - 2013? Use an overlapping plot with 15 bins and a transparency value of 0.35.<jupyter_code>### type your answer here
df_t = df_can.loc[['Greece','Albania','Bulgaria'], years].transpose()
count, bin_edges = np.histogram(df_t, 15)
df_t.plot(kind='hist',
figsize=(10, 6),
bins=15,
alpha=0.35,
stacked=False,
xticks=bin_edges
)
plt.title('Histogram of Immigration from Greece, Albania, and Bulgaria from 1980 - 2013')
plt.ylabel('Number of Years')
plt.xlabel('Number of Immigrants')
plt.show()<jupyter_output><empty_output><jupyter_text>Double-click __here__ for the solution.
<!-- The correct answer is:
\\ # create a dataframe of the countries of interest (cof)
df_cof = df_can.loc[['Greece', 'Albania', 'Bulgaria'], years]
-->
<!--
\\ # transpose the dataframe
df_cof = df_cof.transpose()
-->
<!--
\\ # let's get the x-tick values
count, bin_edges = np.histogram(df_cof, 15)
-->
<!--
\\ # Un-stacked Histogram
df_cof.plot(kind ='hist',
figsize=(10, 6),
bins=15,
alpha=0.35,
xticks=bin_edges,
color=['coral', 'darkslateblue', 'mediumseagreen']
)
-->
<!--
plt.title('Histogram of Immigration from Greece, Albania, and Bulgaria from 1980 - 2013')
plt.ylabel('Number of Years')
plt.xlabel('Number of Immigrants')
-->
<!--
plt.show()
--># Bar Charts (Dataframe)
A bar plot is a way of representing data where the *length* of the bars represents the magnitude/size of the feature/variable. Bar graphs usually represent numerical and categorical variables grouped in intervals.
To create a bar plot, we can pass one of two arguments via `kind` parameter in `plot()`:
* `kind=bar` creates a *vertical* bar plot
* `kind=barh` creates a *horizontal* bar plot**Vertical bar plot**
In vertical bar graphs, the x-axis is used for labelling, and the length of bars on the y-axis corresponds to the magnitude of the variable being measured. Vertical bar graphs are particuarly useful in analyzing time series data. One disadvantage is that they lack space for text labelling at the foot of each bar.
**Let's start off by analyzing the effect of Iceland's Financial Crisis:**
The 2008 - 2011 Icelandic Financial Crisis was a major economic and political event in Iceland. Relative to the size of its economy, Iceland's systemic banking collapse was the largest experienced by any country in economic history. The crisis led to a severe economic depression in 2008 - 2011 and significant political unrest.
**Question:** Let's compare the number of Icelandic immigrants (country = 'Iceland') to Canada from year 1980 to 2013. <jupyter_code># step 1: get the data
df_iceland = df_can.loc['Iceland', years]
df_iceland.head()
# step 2: plot data
df_iceland.plot(kind='bar', figsize=(10, 6))
plt.xlabel('Year') # add to x-label to the plot
plt.ylabel('Number of immigrants') # add y-label to the plot
plt.title('Icelandic immigrants to Canada from 1980 to 2013') # add title to the plot
plt.show()<jupyter_output><empty_output><jupyter_text>The bar plot above shows the total number of immigrants broken down by each year. We can clearly see the impact of the financial crisis; the number of immigrants to Canada started increasing rapidly after 2008.
Let's annotate this on the plot using the `annotate` method of the **scripting layer** or the **pyplot interface**. We will pass in the following parameters:
- `s`: str, the text of annotation.
- `xy`: Tuple specifying the (x,y) point to annotate (in this case, end point of arrow).
- `xytext`: Tuple specifying the (x,y) point to place the text (in this case, start point of arrow).
- `xycoords`: The coordinate system that xy is given in - 'data' uses the coordinate system of the object being annotated (default).
- `arrowprops`: Takes a dictionary of properties to draw the arrow:
- `arrowstyle`: Specifies the arrow style, `'->'` is standard arrow.
- `connectionstyle`: Specifies the connection type. `arc3` is a straight line.
- `color`: Specifes color of arror.
- `lw`: Specifies the line width.
I encourage you to read the Matplotlib documentation for more details on annotations:
http://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.annotate.<jupyter_code>df_iceland.plot(kind='bar', figsize=(10, 6), rot=90) # rotate the bars by 90 degrees
plt.xlabel('Year')
plt.ylabel('Number of Immigrants')
plt.title('Icelandic Immigrants to Canada from 1980 to 2013')
# Annotate arrow
plt.annotate('', # s: str. Will leave it blank for no text
xy=(32, 70), # place head of the arrow at point (year 2012 , pop 70)
xytext=(28, 20), # place base of the arrow at point (year 2008 , pop 20)
xycoords='data', # will use the coordinate system of the object being annotated
arrowprops=dict(arrowstyle='->', connectionstyle='arc3', color='blue', lw=2)
)
plt.show()<jupyter_output><empty_output><jupyter_text>Let's also annotate a text to go over the arrow. We will pass in the following additional parameters:
- `rotation`: rotation angle of text in degrees (counter clockwise)
- `va`: vertical alignment of text [‘center’ | ‘top’ | ‘bottom’ | ‘baseline’]
- `ha`: horizontal alignment of text [‘center’ | ‘right’ | ‘left’]<jupyter_code>df_iceland.plot(kind='bar', figsize=(10, 6), rot=90)
plt.xlabel('Year')
plt.ylabel('Number of Immigrants')
plt.title('Icelandic Immigrants to Canada from 1980 to 2013')
# Annotate arrow
plt.annotate('', # s: str. will leave it blank for no text
xy=(32, 70), # place head of the arrow at point (year 2012 , pop 70)
xytext=(28, 20), # place base of the arrow at point (year 2008 , pop 20)
xycoords='data', # will use the coordinate system of the object being annotated
arrowprops=dict(arrowstyle='->', connectionstyle='arc3', color='blue', lw=2)
)
# Annotate Text
plt.annotate('2008 - 2011 Financial Crisis', # text to display
xy=(28, 30), # start the text at at point (year 2008 , pop 30)
rotation=72.5, # based on trial and error to match the arrow
va='bottom', # want the text to be vertically 'bottom' aligned
ha='left', # want the text to be horizontally 'left' algned.
)
plt.show()<jupyter_output><empty_output><jupyter_text>**Horizontal Bar Plot**
Sometimes it is more practical to represent the data horizontally, especially if you need more room for labelling the bars. In horizontal bar graphs, the y-axis is used for labelling, and the length of bars on the x-axis corresponds to the magnitude of the variable being measured. As you will see, there is more room on the y-axis to label categetorical variables.
**Question:** Using the scripting layter and the `df_can` dataset, create a *horizontal* bar plot showing the *total* number of immigrants to Canada from the top 15 countries, for the period 1980 - 2013. Label each country with the total immigrant count.Step 1: Get the data pertaining to the top 15 countries.<jupyter_code>### type your answer here
df_15 = df_can.head(15)
df_15 = df_15[years].transpose()<jupyter_output><empty_output><jupyter_text>Double-click __here__ for the solution.
<!-- The correct answer is:
\\ # sort dataframe on 'Total' column (descending)
df_can.sort_values(by='Total', ascending=True, inplace=True)
-->
<!--
\\ # get top 15 countries
df_top15 = df_can['Total'].tail(15)
df_top15
-->Step 2: Plot data:
1. Use `kind='barh'` to generate a bar chart with horizontal bars.
2. Make sure to choose a good size for the plot and to label your axes and to give the plot a title.
3. Loop through the countries and annotate the immigrant population using the anotate function of the scripting interface.<jupyter_code>### type your answer here
df_15.plot(kind='barh', figsize=(12, 12))
plt.title('Top 15 countries contributing to immigration')
plt.xlabel('Year')
plt.ylabel('No. of immigrants')
plt.show()<jupyter_output><empty_output>
|
permissive
|
/Jupyter notebook/IBM/Data visualization with python/DV0101EN-Exercise-Area-Plots-Histograms-and-Bar-Charts-py.ipynb
|
p-s-vishnu/Documents
| 32 |
<jupyter_start><jupyter_text>## Transfer Learning (Tensorflow + VGG16 + CIFAR10)
The code below performs a complete task of transfer learning. All of it was made thinking of an easy way to learn this subject and an easy way to modify it in order to resolve other tasks.
---
Forked from https://github.com/clebeson/Deep_Learning/blob/master/Transfer-Learning/Transferlearning.ipynb
---###All the necessary imports
Note that this code was made for running on [Google Colab](https://colab.research.google.com/notebooks/welcome.ipynb). Then, its usage outside this plataform requires adaptations. As taking off all the Google Colab dependencies and download manually the VGG16 model and put it into the folder "./model". The model can be downloaded [here](https://github.com/ry/tensorflow-vgg16/blob/master/vgg16-20160129.tfmodel.torrent):<jupyter_code>%matplotlib inline
import pickle
import numpy as np
import os
from urllib.request import urlretrieve
import tarfile
import zipfile
import sys
import tensorflow as tf
import numpy as np
from time import time
import skimage as sk
from skimage import transform
from skimage import util
import random
import math
import os.path
from random import shuffle
import logging
from matplotlib import pyplot as plt
from sklearn.metrics import confusion_matrix
# from google.colab import files
from itertools import product
# !pip install googledrivedownloader
logging.getLogger("tensorflow").setLevel(logging.ERROR)
<jupyter_output><empty_output><jupyter_text>---
### Class that defines the principals hyperparameters used by the model
<jupyter_code>class Hyperparameters:
def __init__(self):
self.image_size = 32
self.image_channels = 3
self.num_classes = 10
self.initial_learning_rate = 1e-4
self.decay_steps = 1e3
self.decay_rate = 0.98
self.cut_layer = "pool5"
self.hidden_layers = [512]
self.batch_size = 128
self.num_epochs = 200
self.check_points_path= "./tensorboard/cifar10_vgg16"
self.keep = 1.0
self.fine_tunning = False
self.bottleneck = True
<jupyter_output><empty_output><jupyter_text>### Class that provides same utilities for the model, such as downloads files, gets dataset, does data augmentation, generates bottlenecks files and creates a confusion matrix from the model.<jupyter_code>class utils:
def get_or_generate_bottleneck( sess, model, file_name, dataset, labels, batch_size = 128):
path_file = os.path.join("./data_set",file_name+".pkl")
if(os.path.exists(path_file)):
print("Loading bottleneck from \"{}\" ".format(path_file))
with open(path_file, 'rb') as f:
return pickle.load(f)
bottleneck_data = []
original_labels = []
print("Generating Bottleneck \"{}.pkl\" ".format(file_name) )
count = 0
amount = len(labels) // batch_size
indices = list(range(len(labels)))
for i in range(amount+1):
if (i+1)*batch_size < len(indices):
indices_next_batch = indices[i*batch_size: (i+1)*batch_size]
else:
indices_next_batch = indices[i*batch_size:]
batch_size = len(indices_next_batch)
data = dataset[indices_next_batch]
label = labels[indices_next_batch]
input_size = np.prod(model["bottleneck_tensor"].shape.as_list()[1:])
tensor = sess.run(model["bottleneck_tensor"], feed_dict={model["images"]:data, model["bottleneck_input"]:np.zeros((batch_size,input_size)), model["labels"]:label,model["keep"]:1.0})
for t in range(batch_size):
bottleneck_data.append(np.squeeze(tensor[t]))
original_labels.append(np.squeeze(label[t]))
bottleneck = {
"data":np.array(bottleneck_data),
"labels":np.array(original_labels)
}
with open(path_file, 'wb') as f:
pickle.dump(bottleneck, f)
print("Done")
return bottleneck
def get_data_set(name="train"):
x = None
y = None
folder_name = 'cifar_10'
main_directory = "./data_set"
url = "http://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz"
utils.maybe_download_and_extract(url, main_directory,folder_name, "cifar-10-batches-py")
f = open(os.path.join(main_directory,folder_name,"batches.meta"), 'rb')
f.close()
if name is "train":
for i in range(5):
f = open('./data_set/'+folder_name+'/data_batch_' + str(i + 1), 'rb')
datadict = pickle.load(f, encoding='latin1')
f.close()
_X = datadict["data"]
_Y = datadict['labels']
_X = np.array(_X, dtype=float) / 255.0
_X = _X.reshape([-1, 3, 32, 32])
_X = _X.transpose([0, 2, 3, 1])
if x is None:
x = _X
y = _Y
else:
x = np.concatenate((x, _X), axis=0)
y = np.concatenate((y, _Y), axis=0)
elif name is "test":
f = open('./data_set/'+folder_name+'/test_batch', 'rb')
datadict = pickle.load(f, encoding='latin1')
f.close()
x = datadict["data"]
y = np.array(datadict['labels'])
x = np.array(x, dtype=float) / 255.0
x = x.reshape([-1, 3, 32, 32])
x = x.transpose([0, 2, 3, 1])
return x, utils._dense_to_one_hot(y)
def _dense_to_one_hot( labels_dense, num_classes=10):
num_labels = labels_dense.shape[0]
index_offset = np.arange(num_labels) * num_classes
labels_one_hot = np.zeros((num_labels, num_classes))
labels_one_hot.flat[index_offset + labels_dense.ravel()] = 1
return labels_one_hot
def maybe_download_and_extract( url, main_directory,filename, original_name):
def _print_download_progress( count, block_size, total_size):
pct_complete = float(count * block_size) / total_size
msg = "\r --> progress: {0:.1%}".format(pct_complete)
sys.stdout.write(msg)
sys.stdout.flush()
if not os.path.exists(main_directory):
os.makedirs(main_directory)
url_file_name = url.split('/')[-1]
zip_file = os.path.join(main_directory,url_file_name)
print("Downloading ",url_file_name)
try:
file_path, _ = urlretrieve(url=url, filename= zip_file, reporthook=_print_download_progress)
except:
os.system("rm -r "+main_directory)
print("An error occurred while downloading: ",url)
if(original_name == 'vgg16-20160129.tfmodel'):
print("This could be for a problem with github. We will try downloading from the Google Drive")
from google_drive_downloader import GoogleDriveDownloader as gdd
gdd.download_file_from_google_drive(file_id='1xJZDLu_TK_SyQz-SaetAL_VOFY7xdAt5',
dest_path='./models/vgg16-20160129.tfmodel',
unzip=False)
else: print("This could be for a problem with the storage site. Try again later")
return
print("\nDownload finished.")
if file_path.endswith(".zip"):
print( "Extracting files.")
zipfile.ZipFile(file=file_path, mode="r").extractall(main_directory)
elif file_path.endswith((".tar.gz", ".tgz")):
print( "Extracting files.")
tarfile.open(name=file_path, mode="r:gz").extractall(main_directory)
os.remove(file_path)
os.rename(os.path.join(main_directory,original_name), os.path.join(main_directory,filename))
print("Done.")
def data_augmentation(images, labels):
def random_rotation(image_array):
# pick a random degree of rotation between 25% on the left and 25% on the right
random_degree = random.uniform(-15, 15)
return sk.transform.rotate(image_array, random_degree)
def random_noise(image_array):
# add random noise to the image
return sk.util.random_noise(image_array)
def horizontal_flip(image_array):
# horizontal flip doesn't need skimage, it's easy as flipping the image array of pixels !
return image_array[:, ::-1]
print("Augmenting data...")
aug_images = []
aug_labels = []
aug_images.extend( list(map(random_rotation, images)) )
aug_labels.extend(labels)
aug_images.extend( list(map(random_noise, images)) )
aug_labels.extend(labels)
aug_images.extend( list(map(horizontal_flip, images)) )
aug_labels.extend(labels)
return np.array(aug_images), np.array(aug_labels)
def generate_confusion_matrix( predictions, class_names):
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = 100 * cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm.shape)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
symbol = "%" if normalize else ""
for i, j in product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt)+symbol,
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('Real')
plt.xlabel('Predicted')
# Compute confusion matrix
cnf_matrix = confusion_matrix(predictions["labels"],predictions["classes"])
np.set_printoptions(precision=2)
# # Plot normalized confusion matrix
plt.figure(figsize=(10,7))
plot_confusion_matrix(cnf_matrix, classes=class_names, normalize=True,
title='Normalized confusion matrix')
plt.grid('off')
#plt.savefig("./confusion_matrix.png") #Save the confision matrix as a .png figure.
plt.show()
# <jupyter_output><empty_output><jupyter_text>###The function "get_vgg16" returns a pretrained vgg16 model.
All the work of loading and restoring the weights of the model is responsibility of tensorflow. We just need to choose which layer we want to cut and pass it as parameter for the function "get_vgg16". In transfer learning it is common to dispose the fully connected layer and reuse only the convolutional ones. It occurs because the new problem/dataset used to be different from the original (such one that was used for training the model), and the numbers of classes is often different as well.
In a CNN, the first layers are responsible for selecting borders, the middle layers for selecting some kinds of patterns, based on combinations of those edges obtained previously and the last ones for composing patterns with a high level of representation, also known as semantic layers. Thereby, when the new dataset is much different of the original, the last layers are not indicated to be used. Since these ones likely represents particular patterns that will not help the new dataset. So, it is common to use the first layers in the transfer learning or fine tuning and add new fully connected ones in order to be trained from scratch.<jupyter_code>
def get_vgg16(input_images, cut_layer = "pool5", scope_name = "vgg16", fine_tunning = False):
file_name = 'vgg16-20160129.tfmodel'
main_directory = "./models/"
vgg_path = os.path.join(main_directory,file_name)
if not os.path.exists(vgg_path):
vgg16_url = "https://media.githubusercontent.com/media/pavelgonchar/colornet/master/vgg/tensorflow-vgg16/vgg16-20160129.tfmodel"
utils.maybe_download_and_extract(vgg16_url, main_directory, file_name, file_name)
with open(vgg_path, mode='rb') as f:
content = f.read()
graph_def = tf.GraphDef()
graph_def.ParseFromString(content)
graph_def = tf.graph_util.extract_sub_graph(graph_def, ["images", cut_layer])
tf.import_graph_def(graph_def, input_map={"images": input_images})
del content
graph = tf.get_default_graph()
vgg_node = "import/{}:0".format(cut_layer) #It is possible to cut the graph in other node.
#For this, it is necessary to see the name of all layers by using the method
#"get_operations()": "print(graph.get_operations())"
vgg_trained_model = graph.get_tensor_by_name("{}/{}".format(scope_name, vgg_node) )
if not fine_tunning:
print("Stopping gradient")
vgg_trained_model = tf.stop_gradient(vgg_trained_model) #Just use it in case of transfer learning without fine tunning
# print(graph.get_operations())
return vgg_trained_model, graph
<jupyter_output><empty_output><jupyter_text>###Creating the model
The function "transfer_learning_model" is responsible for creating the model that will be used for recognizing the CIFAR10 images.
The first scope ("placeholders_variables") defines:
* ** input images** - the images that will feed the model
* **labels** - each image that feeds the input placeholder, need to have a correspondent label, wich will feed this placeholder when the loss was calculated.
* **dropout_keep** - it defines a percent of neurons that will not be activated in each fully connected layer. The number to be fed is between 0 and 1.
* **global_step** - As the train process is running, this variable stores the value of the current step. This value can be used for saving a checkpoint in an specific step, and, when restored, all the model continues the training process from this point/step.
* **learning rate** - it defines the learning rate to be used by the optimizer. In this case, the global step is used in order to provide a decay point even whether the training is restarted or not. It starts from an initial learning rate and decays according to an specific rate, with each number of steps.
These parameters are able to influence directly the success of the training, so they are defined as hyperparameters of the model (class "Hyperparameters"), and must be treated and chosen carefully.
<jupyter_code>def transfer_learning_model(params = None, fine_tunning = False, bottleneck = False):
if params is None:
params = Hyperparameters()
with tf.name_scope('placeholders_variables'):
input_images = tf.placeholder(tf.float32, shape=[None,params.image_size, params.image_size, params.image_channels], name='input')
labels = tf.placeholder(tf.float32, shape=[None, params.num_classes], name='labels')
dropout_keep = tf.placeholder(tf.float32, name='dropout_keep')
global_step = tf.train.get_or_create_global_step()
learning_rate = tf.train.exponential_decay(params.initial_learning_rate, global_step,
params.decay_steps,params.decay_rate, staircase=True)
with tf.name_scope('vgg16'):
# Create a VGG16 model and reuse its weights.
vgg16_out,_ = get_vgg16(input_images=input_images,cut_layer = params.cut_layer, fine_tunning = fine_tunning)
with tf.name_scope("flatten"):
flatten = tf.layers.flatten(vgg16_out, name="flatten")
if (not fine_tunning) and bottleneck:
out_list = flatten.shape.as_list()
BOTTLENECK_TENSOR_SIZE = np.prod(out_list[1:]) # All input layer size, less the batch size
with tf.name_scope('bottleneck'):
bottleneck_tensor = flatten
bottleneck_input = tf.placeholder(tf.float32,
shape=[None, BOTTLENECK_TENSOR_SIZE],
name='InputPlaceholder')
with tf.name_scope('fully_conn'):
logits = fc_model(bottleneck_input, params.hidden_layers) #Create a fully connected model that will be fed by the bottleneck
else:
with tf.name_scope('fully_conn'):
logits = fc_model(flatten, params.hidden_layers) #Create a fully connected model that will be fed by the vgg16
with tf.name_scope('loss'):
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=logits, labels=labels))
# loss = regularize(loss)
tf.summary.scalar("loss", loss)
with tf.name_scope('sgd'):
update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.control_dependencies(update_ops):
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(loss, global_step=global_step)
with tf.name_scope('train_accuracy'):
acc = tf.equal(tf.argmax(logits, 1), tf.argmax(labels, 1))
acc = tf.reduce_mean(tf.cast(acc, tf.float32))
tf.summary.scalar("accuracy", acc)
predictions = {
"classes": tf.argmax(logits, 1),
"probs" : tf.nn.softmax(logits),
"labels": tf.argmax(labels, 1)
}
model = {
"global_step": global_step,
"images": input_images,
"labels": labels,
"loss" : loss,
"optimizer": optimizer,
"accuracy": acc,
"predictions":predictions,
"keep": dropout_keep
}
if (not fine_tunning) and bottleneck:
model.update({"bottleneck_tensor":bottleneck_tensor})
model.update({"bottleneck_input":bottleneck_input})
return model
def get_fc_weights(w_inputs, w_output, id=0):
weight= tf.Variable(tf.truncated_normal([w_inputs, w_output]), name="{}/weight".format(id))
bias = tf.Variable(tf.truncated_normal([w_output]), name="{}/bias".format(id))
return weight, bias
def logits_layer(fc_layer, n_classes):
out_shape = fc_layer.shape.as_list()
w, b = get_fc_weights(np.prod(out_shape[1:]), n_classes, "logits/weight")
logits = tf.add(tf.matmul(fc_layer, w), b, name="logits")
return logits
def fc_layer(input_layer, number_of_units, keep = None, layer_id = "fc"):
pl_list = input_layer.shape.as_list()
input_size = np.prod(pl_list[1:])
w, b = get_fc_weights(input_size, number_of_units, layer_id)
fc_layer = tf.matmul(input_layer, w, name="{}/matmul".format(layer_id))
fc_layer = tf.nn.bias_add(fc_layer, b, name="{}/bias-add".format(layer_id))
if keep is not None:
fc_layer = tf.nn.dropout(fc_layer, keep, name="{}/dropout".format(layer_id))
else:
print("Dropout was disabled.")
fc_layer = tf.nn.relu(fc_layer, name="{}/relu".format(layer_id))
return fc_layer
def regularize(loss, type = 1, scale = 0.005, scope = None):
if type == 1:
regularizer = tf.contrib.layers.l1_regularizer( scale=scale, scope=scope)
else:
regularizer = tf.contrib.layers.l2_regularizer( scale=scale, scope=scope)
weights = tf.trainable_variables() # all vars of your graph
regularization_penalty = tf.contrib.layers.apply_regularization(regularizer, weights)
regularized_loss = loss + regularization_penalty
return regularized_loss
def fc_model(flatten, hidden_layers = [512], keep = None):
fc = flatten
id = 1
for num_neurons in hidden_layers:
fc = fc_layer(fc, num_neurons, keep, "fc{}".format(id) )
id = id+1
logits = logits_layer(fc, params.num_classes)
return logits
<jupyter_output><empty_output><jupyter_text>### Creating a session
The function "create_monitored_session" creates a tensorflow session able to restore weights and/or save them. The parameter "checkpoint_dir" represents where the weights were saved or where one wants to save them. All the save/restore process is performed automatically by tensorflow.
As default, tensorflow allocates all GPU memory in the first called to the session run, thus the "tf.ConfigProto()", by setting the "True" to the "gpu_options.allow_growth", allows the gradual increasing of memory. In other words, it allows to allocate the GPU memory by demanding. This is important mainly when more than one training or prediction process is running on the same GPU.
<jupyter_code>def create_monitored_session(model,iter_per_epoch, checkpoint_dir):
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
sess = tf.train.MonitoredTrainingSession(checkpoint_dir=checkpoint_dir,
save_checkpoint_secs=120,
log_step_count_steps=iter_per_epoch,
save_summaries_steps=iter_per_epoch,
config=config)
return sess<jupyter_output><empty_output><jupyter_text>### Testing the model
The function "test" is responsible for applying the test dataset through the trained model. Thus, it is possible to monitor the model progress. This function could be change in order to do a validation test, which uses the validation dataset, rather than just a test. It would be helpful for problems that do not release a labeled test dataset.<jupyter_code>def test(sess, model,input_data_placeholder, data, labels, batch_size = 128):
global_accuracy = 0
predictions = {
"classes":[],
"probs":[],
"labels":[]
}
size = len(data)//batch_size
indices = list(range(len(data)))
for i in range(size+1):
begin = i*batch_size
end = (i+1)*batch_size
end = len(data) if end >= len(data) else end
next_bach_indices = indices[begin:end]
batch_xs = data[next_bach_indices]
batch_ys = labels[next_bach_indices]
pred = sess.run(model["predictions"],
feed_dict={input_data_placeholder: batch_xs, model["labels"]: batch_ys, model["keep"]:1.0})
predictions["classes"].extend(pred["classes"])
predictions["probs"].extend(pred["probs"])
predictions["labels"].extend(pred["labels"])
correct = list (map(lambda x,y: 1 if x==y else 0, predictions["labels"] , predictions["classes"]))
acc = np.mean(correct ) *100
mes = "--> Test accuracy: {:.2f}% ({}/{})"
print(mes.format( acc, sum(correct), len(data)))
return predictions
<jupyter_output><empty_output><jupyter_text>###Training the model: the mainly function
The "train" function is responsible for training the model. It starts checking the hyperparameters and resetting the default graph. Then, the dataset is loaded by using the class "util". The next step consists of creating the model, where the tensorflow graph is created. Now, a monitored season is created too. This kind of session will save and restore the model automatically, which will be very important when an unexpected event occurs and the model stop the training (such as a power outage or when the Google Colab finishes the session during the training).
With the model and the session created, you are able, if you want, to generate or load the bottlenecks files. This is what the next lines are doing. One of the most important results of theses lines is obtaining the tensor "input_data_placeholder". It is important because when the bottleneck option is chosen, the "feed_dict" must feed the placeholder of the "bottleneck" rather than the one that feeds the VVG16 inputs. Thus, if the bottleneck is chosen, the input placeholder will be the "model[bottleneack_input]", else, it will be the input tensor of the vgg16, "model[images]".
In the the beginning of each epoch, in order to ensure the randomness of the baths, a list containing the dataset indices is shuffled. So, at every batch, a new range of indices is taken and the batch may feed the placeholder.
Therefore, the session can call the optimizer and train the model. Finally, the last two steps consiste of calling the test funtion for checking the training result every epoch, and generate a confusion matrix with the result of the last one.
<jupyter_code>def train(params = None):
if params is None:
params = Hyperparameters()
tf.reset_default_graph()
train_data, train_labels = utils.get_data_set("train")
train_data, train_labels = utils.data_augmentation(train_data, train_labels)
test_data, test_labels = utils.get_data_set("test")
model = transfer_learning_model(params, params.fine_tunning, params.bottleneck)
steps_per_epoch = int(math.ceil(len(train_data) / params.batch_size))
sess = create_monitored_session(model,steps_per_epoch, params.check_points_path)
if (not params.fine_tunning) and params.bottleneck:
indices = list( range(len(train_data)) )
shuffle(indices)
shuffled_data = train_data[indices]
shuffled_labels = train_labels[indices]
bottleneck_train = utils.get_or_generate_bottleneck(sess, model, "bottleneck_vgg16_{}_train".format(params.cut_layer), shuffled_data, shuffled_labels)
bottleneck_test = utils.get_or_generate_bottleneck(sess, model, "bottleneck_vgg16_{}_test".format(params.cut_layer), test_data, test_labels)
train_data, train_labels = bottleneck_train["data"], bottleneck_train["labels"]
test_data, test_labels = bottleneck_test["data"], bottleneck_test["labels"]
del bottleneck_train, bottleneck_test
input_data_placeholder = model["bottleneck_input"]
else:
input_data_placeholder = model["images"]
indices = list( range(len(train_data)) )
msg = "--> Global step: {:>5} - Last batch acc: {:.2f}% - Batch_loss: {:.4f} - ({:.2f}, {:.2f}) (steps,images)/sec"
for epoch in range(params.num_epochs):
start_time = time()
print("\n*************************************************************")
print("Epoch {}/{}".format(epoch+1,params.num_epochs))
shuffle(indices)
for s in range(steps_per_epoch):
indices_next_batch = indices[s * params.batch_size : (s+1) * params.batch_size]
batch_data = train_data[indices_next_batch]
batch_labels = train_labels[indices_next_batch]
_, batch_loss, batch_acc,step = sess.run(
[model["optimizer"], model["loss"], model["accuracy"], model["global_step"],],
feed_dict={input_data_placeholder: batch_data, model["labels"]: batch_labels, model["keep"]:params.keep})
duration = time() - start_time
print(msg.format(step, batch_acc*100, batch_loss, (steps_per_epoch / duration), (steps_per_epoch*params.batch_size / duration) ))
_ = test(sess, model, input_data_placeholder, test_data, test_labels )
predictions = test(sess, model, input_data_placeholder, test_data, test_labels )
sess.close()
class_names = ["airplane","automobile","bird","cat","deer","dog","frog","horse","ship","truck"]
utils.generate_confusion_matrix(predictions, class_names)<jupyter_output><empty_output><jupyter_text>This part of code instantiates a "Hyperparameters" class, changes it and passes it as parameter to the train function. Thus, the training can be started.<jupyter_code>if __name__ == "__main__":
params = Hyperparameters()
params.num_epochs = 100
params.hidden_layers = [1024]
params.initial_learning_rate = 1e-3
params.cut_layer = "pool4"
train(params)
<jupyter_output>Downloading cifar-10-python.tar.gz
--> progress: 100.0%
Download finished.
Extracting files.
Done.
Augmenting data...
Downloading vgg16-20160129.tfmodel
--> progress: 7.8%
|
no_license
|
/transfer_learning/example.ipynb
|
hsneto/ufes-redes-neurais-profundas
| 9 |
<jupyter_start><jupyter_text># Data Science Academy - Python Fundamentos - Capítulo 8
## Download: http://github.com/dsacademybr## Matplotlib
Para atualizar o Matplotlib abra o prompt de comando ou terminal e digite: pip install matplotlib -U## Construindo Plots<jupyter_code># O matplotlib.pyplot é uma coleção de funções e estilos que fazem com que o Matplotlib funcione como o Matlab.
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
mpl.__version__
# O método plot() define os eixos do gráfico
plt.plot([1, 3, 5], [2, 5, 7])
plt.show()
x = [1, 4, 5]
y = [3, 7, 2]
plt.plot(x, y)
plt.xlabel('Variável 1')
plt.ylabel('Variável 2')
plt.title('Teste Plot')
plt.show()
x2 = [1, 2, 3]
y2 = [11, 12, 15]
plt.plot(x2, y2, label = 'Primeira Linha')
plt.legend()
plt.show()<jupyter_output><empty_output><jupyter_text>## Gráficos de Barras<jupyter_code>x = [2,4,6,8,10]
y = [6,7,8,2,4]
plt.bar(x, y, label = 'Barras', color = 'r')
plt.legend()
plt.show()
x2 = [1,3,5,7,9]
y2 = [7,8,2,4,2]
plt.bar(x, y, label = 'Barras1', color = 'r')
plt.bar(x2, y2, label = 'Barras2', color = 'y')
plt.legend()
plt.show()
idades = [22,65,45,55,21,22,34,42,41,4,99,101,120,122,130,111,115,80,75,54,44,64,13,18,48]
ids = [x for x in range(len(idades))]
plt.bar(ids, idades)
plt.show()
bins = [0,10,20,30,40,50,60,70,80,90,100,110,120,130]
plt.hist(idades, bins, histtype = 'bar', rwidth = 0.8)
plt.show()
plt.hist(idades, bins, histtype = 'stepfilled', rwidth = 0.8)
plt.show()<jupyter_output><empty_output><jupyter_text>## Scatterplot<jupyter_code>x = [1,2,3,4,5,6,7,8]
y = [5,2,4,5,6,8,4,8]
plt.scatter(x, y, label = 'Pontos', color = 'r', marker = 'o', s = 100)
plt.legend()
plt.show()<jupyter_output><empty_output><jupyter_text>## Stack Plots<jupyter_code>dias = [1,2,3,4,5]
dormir = [7,8,6,77,7]
comer = [2,3,4,5,3]
trabalhar = [7,8,7,2,2]
passear = [8,5,7,8,13]
plt.stackplot(dias, dormir, comer, trabalhar, passear, colors = ['m','c','r','k','b'])
plt.show()<jupyter_output><empty_output><jupyter_text>## Pie Chart<jupyter_code>fatias = [7, 2, 2, 13]
atividades = ['dormir','comer','trabalhar','passear']
colunas = ['c','m','r','k']
plt.pie(fatias, labels = atividades, colors = colunas, startangle = 90, shadow = True, explode = (0,0.1,0,0))
plt.show()<jupyter_output><empty_output><jupyter_text>## Pylab<jupyter_code># Visualizando os gráfico dentro do Jupyter Notebook
# O Pylab combina funcionalidades do pyplot com funcionalidades do Numpy
from pylab import *
%matplotlib inline
x = linspace(0, 5, 10)
y = x ** 2
fig = plt.figure()
# Definindo os eixos
axes = fig.add_axes([0.1, 0.1, 0.8, 0.8])
axes.plot(x, y, 'r')
axes.set_xlabel('x')
axes.set_ylabel('y')
axes.set_title('Gráfico de Linha');
# Gráficos com 2 figuras
x = linspace(0, 5, 10)
y = x ** 2
fig = plt.figure()
axes1 = fig.add_axes([0.1, 0.1, 0.8, 0.8]) # eixos da figura principal
axes2 = fig.add_axes([0.2, 0.5, 0.4, 0.3]) # eixos da figura secundária
# Figura principal
axes1.plot(x, y, 'r')
axes1.set_xlabel('x')
axes1.set_ylabel('y')
axes1.set_title('Figura Principal')
# Figura secundária
axes2.plot(y, x, 'g')
axes2.set_xlabel('y')
axes2.set_ylabel('x')
axes2.set_title('Figura Secundária');
# Gráficos em Paralelo
fig, axes = plt.subplots(nrows = 1, ncols = 2)
for ax in axes:
ax.plot(x, y, 'r')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Título')
fig.tight_layout()<jupyter_output><empty_output><jupyter_text>## Gráficos a partir do NumPy<jupyter_code>import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
plt.scatter(np.arange(50), np.random.randn(50))
plt.show()
# Plot e Scatter
fig = plt.figure()
ax1 = fig.add_subplot(1,2,1)
ax1.plot(np.random.randn(50), color='red')
ax2 = fig.add_subplot(1,2,2)
ax2.scatter(np.arange(50), np.random.randn(50))
plt.show()
# Plots diversos
_, ax = plt.subplots(2,3)
ax[0,1].plot(np.random.randn(50), color = 'green', linestyle = '-')
ax[1,0].hist(np.random.randn(50))
ax[1,2].scatter(np.arange(50), np.random.randn(50), color = 'red')
plt.show()
# Controle dos eixos
fig, axes = plt.subplots(1, 3, figsize = (12, 4))
axes[0].plot(x, x**2, x, x**3)
axes[0].set_title("Eixos com range padrão")
axes[1].plot(x, x**2, x, x**3)
axes[1].axis('tight')
axes[1].set_title("Eixos menores")
axes[2].plot(x, x**2, x, x**3)
axes[2].set_ylim([0, 60])
axes[2].set_xlim([2, 5])
axes[2].set_title("Eixos customizados");
# Escala
fig, axes = plt.subplots(1, 2, figsize=(10,4))
axes[0].plot(x, x**2, x, exp(x))
axes[0].set_title("Escala Padrão")
axes[1].plot(x, x**2, x, exp(x))
axes[1].set_yscale("log")
axes[1].set_title("Escala Logaritmica (y)");
# Grid
fig, axes = plt.subplots(1, 2, figsize=(10,3))
# Grid padrão
axes[0].plot(x, x**2, x, x**3, lw = 2)
axes[0].grid(True)
# Grid customizado
axes[1].plot(x, x**2, x, x**3, lw = 2)
axes[1].grid(color = 'b', alpha = 0.5, linestyle = 'dashed', linewidth = 0.5)
# Gráfico de Linhas Gêmeas
fig, ax1 = plt.subplots()
ax1.plot(x, x**2, lw=2, color="blue")
ax1.set_ylabel("Area", fontsize=18, color="blue")
for label in ax1.get_yticklabels():
label.set_color("blue")
ax2 = ax1.twinx()
ax2.plot(x, x**3, lw=2, color="red")
ax2.set_ylabel("Volume", fontsize=18, color="red")
for label in ax2.get_yticklabels():
label.set_color("red")
# Diferentes estilos de Plots
xx = np.linspace(-0.75, 1., 100)
n = np.array([0,1,2,3,4,5])
fig, axes = plt.subplots(1, 4, figsize=(12,3))
axes[0].scatter(xx, xx + 0.25*randn(len(xx)))
axes[0].set_title("scatter")
axes[1].step(n, n**2, lw=2)
axes[1].set_title("step")
axes[2].bar(n, n**2, align="center", width=0.5, alpha=0.5)
axes[2].set_title("bar")
axes[3].fill_between(x, x**2, x**3, color="green", alpha=0.5);
axes[3].set_title("fill_between");
# Histogramas
n = np.random.randn(100000)
fig, axes = plt.subplots(1, 2, figsize=(12,4))
axes[0].hist(n)
axes[0].set_title("Histograma Padrão")
axes[0].set_xlim((min(n), max(n)))
axes[1].hist(n, cumulative=True, bins=50)
axes[1].set_title("Histograma Cumulativo")
axes[1].set_xlim((min(n), max(n)));
# Color Map
alpha = 0.7
phi_ext = 2 * np.pi * 0.5
def ColorMap(phi_m, phi_p):
return ( + alpha - 2 * np.cos(phi_p)*cos(phi_m) - alpha * np.cos(phi_ext - 2*phi_p))
phi_m = np.linspace(0, 2*np.pi, 100)
phi_p = np.linspace(0, 2*np.pi, 100)
X,Y = np.meshgrid(phi_p, phi_m)
Z = ColorMap(X, Y).T
fig, ax = plt.subplots()
p = ax.pcolor(X/(2*np.pi), Y/(2*np.pi), Z, cmap=cm.RdBu, vmin=abs(Z).min(), vmax=abs(Z).max())
cb = fig.colorbar(p, ax=ax)<jupyter_output><empty_output><jupyter_text># Gráficos 3D<jupyter_code>from mpl_toolkits.mplot3d.axes3d import Axes3D
fig = plt.figure(figsize=(14,6))
ax = fig.add_subplot(1, 2, 1, projection='3d')
p = ax.plot_surface(X, Y, Z, rstride=4, cstride=4, linewidth=0)
ax = fig.add_subplot(1, 2, 2, projection='3d')
p = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm, linewidth=0, antialiased=False)
cb = fig.colorbar(p, shrink=0.5)
# Wire frame
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(1, 1, 1, projection = '3d')
p = ax.plot_wireframe(X, Y, Z, rstride=4, cstride=4)
# Countour Plot com projeção
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(1,1,1, projection='3d')
ax.plot_surface(X, Y, Z, rstride=4, cstride=4, alpha=0.25)
cset = ax.contour(X, Y, Z, zdir='z', offset=-pi, cmap=cm.coolwarm)
cset = ax.contour(X, Y, Z, zdir='x', offset=-pi, cmap=cm.coolwarm)
cset = ax.contour(X, Y, Z, zdir='y', offset=3*pi, cmap=cm.coolwarm)
ax.set_xlim3d(-pi, 2*pi);
ax.set_ylim3d(0, 3*pi);
ax.set_zlim3d(-pi, 2*pi);<jupyter_output><empty_output>
|
no_license
|
/Cap08/Notebooks/.ipynb_checkpoints/DSA-Python-Cap08-03-Matplotlib-Plots-e-Graficos-checkpoint.ipynb
|
GuilhermeLis/FAD
| 8 |
<jupyter_start><jupyter_text># SparkSession
https://spark.apache.org/docs/2.4.4/api/python/pyspark.html
https://spark.apache.org/docs/2.4.4/api/python/pyspark.sql.html<jupyter_code>import findspark
findspark.init()
import spark_utils
from pyspark import SparkContext, SparkConf
from pyspark.sql import SparkSession
sc = SparkContext("yarn", "My App", conf=spark_utils.get_spark_conf())
se = SparkSession(sc)
spark_utils.print_ui_links()<jupyter_output>NameNode: http://ec2-52-73-202-8.compute-1.amazonaws.com:50070
YARN: http://ec2-52-73-202-8.compute-1.amazonaws.com:8088
Spark UI: http://ec2-52-73-202-8.compute-1.amazonaws.com:20888/proxy/application_1589891955781_0001
<jupyter_text># Register all tables for sql queries<jupyter_code>from IPython.display import display
tables = ["clicks_test", "clicks_train",
"documents_categories", "documents_entities", "documents_meta", "documents_topics",
"events", "page_views", "page_views_sample", "promoted_content"]
for name in tqdm.tqdm(tables):
df = se.read.parquet("s3://ydatazian/{}.parquet".format(name))
df.registerTempTable(name)
print(name)
display(df.limit(3).toPandas())<jupyter_output><empty_output><jupyter_text># Prepare dataset for VW
We will predict a *click* based on:
- ad_id
- document_id
- campaign_id
- advertiser_id<jupyter_code>%%time
se.sql("""
select
clicks_train.clicked,
clicks_train.display_id,
clicks_train.ad_id,
promoted_content.document_id,
promoted_content.campaign_id,
promoted_content.advertiser_id
from clicks_train join promoted_content on clicks_train.ad_id = promoted_content.ad_id
""").write.parquet("/train_features.parquet", mode='overwrite')
se.read.parquet("/train_features.parquet").show(5)
# Format: [Label] [Importance] [Base] [Tag]|Namespace Features |Namespace Features ... |Namespace Features
# https://github.com/VowpalWabbit/vowpal_wabbit/wiki/Input-format
def vw_row_mapper(row):
clicked = None
features = []
for k, v in row.asDict().items():
if k == 'clicked':
clicked = '1' if v == '1' else '-1'
else:
features.append(k + "_" + v)
tag = row.display_id + "_" + row.ad_id
return "{} {}| {}".format(clicked, tag, " ".join(features))
r = se.read.parquet("/train_features.parquet").take(1)[0]
print(r)
print(vw_row_mapper(r))
%%time
! hdfs dfs -rm -r /train_features.txt
(
se.read.parquet("/train_features.parquet")
.rdd
.map(vw_row_mapper)
.saveAsTextFile("/train_features.txt")
)
# copy file to local master node
! rm /mnt/train.txt
! hdfs dfs -getmerge /train_features.txt /mnt/train.txt
# preview local file
! head -n 5 /mnt/train.txt<jupyter_output>rm: cannot remove ‘/mnt/train.txt’: No such file or directory
-1 | ad_id_42337 document_id_938164 campaign_id_5969 advertiser_id_1499
-1 | ad_id_139684 document_id_1085937 campaign_id_17527 advertiser_id_2563
1 | ad_id_144739 document_id_1337362 campaign_id_18488 advertiser_id_2909
-1 | ad_id_156824 document_id_992370 campaign_id_7283 advertiser_id_1919
-1 | ad_id_279295 document_id_1670176 campaign_id_27524 advertiser_id_1820
<jupyter_text># Train VW
https://vowpalwabbit.org/tutorials/getting_started.html
https://github.com/JohnLangford/vowpal_wabbit/wiki/Command-line-arguments<jupyter_code>! ./vw -d /mnt/train.txt -b 24 -c -k --ftrl --passes 1 -f model --holdout_off --loss_function logistic --random_seed 42 --progress 8000000
# make prediction with VW
! echo "? tag1| ad_id_144739 document_id_1337362 campaign_id_18488 advertiser_id_2909" > /mnt/test.txt
! echo "? tag2| ad_id_156824 document_id_992370 campaign_id_7283 advertiser_id_1919" >> /mnt/test.txt
! ./vw -d /mnt/test.txt -i model -t -k -p /mnt/predictions.txt --progress 1000000 --link=logistic
# predicted probabilities of "1" class
! cat /mnt/predictions.txt<jupyter_output>only testing
predictions = /mnt/predictions.txt
Enabling FTRL based optimization
Algorithm used: Proximal-FTRL
ftrl_alpha = 0.005
ftrl_beta = 0.1
Num weight bits = 24
learning rate = 0.5
initial_t = 0
power_t = 0.5
using no cache
Reading datafile = /mnt/test.txt
num sources = 1
average since example example current current current
loss last counter weight label predict features
warning: ? is not a good float, replacing with 0
warning: ? is not a good float, replacing with 0
finished run
number of examples = 2
weighted example sum = 2.000000
weighted label sum = 0.000000
average loss = 5.685139
total feature number = 10
0.318580 tag1
0.036084 tag2
<jupyter_text># Homework 2: Baseline VW model
Train a baseline model using the following features:
- **clicked**
- geo_location features (country, state, dma)
- day_of_week (from timestamp, use *date.isoweekday()*)
- ad_id
- campaign_id
- advertiser_id
- ad_document_id
- display_document_id
- platform
Make submission to Kaggle to know your leaderboard score
If you want to create a dev set, make a 90%/10% split of training data by display_id<jupyter_code># YOUR CODE HERE<jupyter_output><empty_output><jupyter_text># Submitting to Kaggle
Obtain Kaggle API token: https://github.com/Kaggle/kaggle-api#api-credentials
Making a submission: https://github.com/Kaggle/kaggle-api#submit-to-a-competition<jupyter_code>! mkdir ~/.kaggle
! touch ~/.kaggle/kaggle.json
! echo '{"username":"?","key":"?"}' > ~/.kaggle/kaggle.json
! cat ~/.kaggle/kaggle.json
! chmod 600 /home/hadoop/.kaggle/kaggle.json
! aws s3 cp s3://ydatazian/sample_submission.csv .
# https://www.kaggle.com/c/outbrain-click-prediction/overview/evaluation
# For each display_id in the test set, you must predict a space-delimited list of ad_ids,
# ordered by decreasing likelihood of being clicked.
! head -n 5 ./sample_submission.csv
%%time
se.sql("""
select
"0" as clicked,
clicks_test.display_id,
clicks_test.ad_id,
promoted_content.document_id,
promoted_content.campaign_id,
promoted_content.advertiser_id
from clicks_test join promoted_content on clicks_test.ad_id = promoted_content.ad_id
""").write.parquet("/test_features.parquet", mode='overwrite')
%%time
! hdfs dfs -rm -r /test_features.txt
(
se.read.parquet("/test_features.parquet")
.rdd
.map(vw_row_mapper)
.saveAsTextFile("/test_features.txt")
)
# copy file to local master node
! rm /mnt/test.txt
! hdfs dfs -getmerge /test_features.txt /mnt/test.txt
# preview local file
! head -n 5 /mnt/test.txt
! ./vw -d /mnt/test.txt -i model -t -k -p /mnt/predictions.txt --progress 1000000 --link=logistic
# predicted probabilities of "1" class
! head -n 5 /mnt/predictions.txt
! wc -l /mnt/predictions.txt
from collections import defaultdict
scores_by_display_id = defaultdict(dict)
for line in tqdm.tqdm(open('/mnt/predictions.txt')):
score, tag = line.strip().split(" ")
score = float(score)
display_id, ad_id = tag.split("_")
scores_by_display_id[display_id][ad_id] = score
with open("submission.txt", "w") as f:
f.write("display_id,ad_id\n")
for k, vs in tqdm.tqdm_notebook(scores_by_display_id.items()):
f.write("{},{}\n".format(
k,
" ".join([v[0] for v in sorted(vs.items(), key=lambda x: -x[1])])
))
! kaggle competitions submit -f submission.txt outbrain-click-prediction -m "baseline"<jupyter_output>100%|████████████████████████████████████████| 260M/260M [00:03<00:00, 81.9MB/s]
Successfully submitted to Outbrain Click Prediction
|
no_license
|
/spark-hw2.ipynb
|
erezKeidan/ydata_lsml
| 6 |
<jupyter_start><jupyter_text>Copyright Jana Schaich Borg/Attribution-NonCommercial 4.0 International (CC BY-NC 4.0)# MySQL Exercise 4: Summarizing your Data
Last week you practiced retrieving and formatting selected subsets of raw data from individual tables in a database. In this lesson we are going to learn how to use SQL to run calculations that summarize your data without having to output all the raw rows or entries. These calculations will serve as building blocks for the queries that will address our business questions about how to improve Dognition test completion rates.
These are the five most common aggregate functions used to summarize information stored in tables:
You will use COUNT and SUM very frequently.
COUNT is the only aggregate function that can work on any type of variable. The other four aggregate functions are only appropriate for numerical data.
All aggregate functions require you to enter either a column name or a "\*" in the parentheses after the function word.
Let's begin by exploring the COUNT function.
## 1. The COUNT function
**First, load the sql library and the Dognition database, and set dognition as the default database.**<jupyter_code>%load_ext sql
%sql mysql://studentuser:studentpw@mysqlserver/dognitiondb<jupyter_output><empty_output><jupyter_text>The Jupyter interface conveniently tells us how many rows are in our query output, so we can compare the results of the COUNT function to the results of our SELECT function. If you run:
```mySQL
SELECT breed
FROM dogs
```
Jupyter tells that 35050 rows are "affected", meaning there are 35050 rows in the output of the query (although, of course, we have limited the display to only 1000 rows at a time).
**Now try running:**
```mySQL
SELECT COUNT(breed)
FROM dogs
```<jupyter_code>%%sql SELECT COUNT(DISTINCT breed)
FROM dogs<jupyter_output>1 rows affected.
<jupyter_text>COUNT is reporting how many rows are in the breed column in total. COUNT should give you the same output as Jupyter's output without displaying the actual rows of data that are being aggregated.
You can use DISTINCT (which you learned about in MySQL Exercise 3) with COUNT to count all the unique values in a column, but it must be placed inside the parentheses, immediately before the column that is being counted. For example, to count the number of distinct breed names contained within all the entries in the breed column you could query:
```SQL
SELECT COUNT(DISTINCT breed)
FROM dogs
```
What if you wanted to know how many indivdual dogs successfully completed at least one test?
Since every row in the complete_tests table represents a completed test and we learned earlier that there are no NULL values in the created_at column of the complete_tests table, any non-null Dog_Guid in the complete_tests table will have completed at least one test. When a column is included in the parentheses, null values are automatically ignored. Therefore, you could use:
```SQL
SELECT COUNT(DISTINCT Dog_Guid)
FROM complete_tests
```
**Question 1: Try combining this query with a WHERE clause to find how many individual dogs completed tests after March 1, 2014 (the answer should be 13,289):**<jupyter_code>%%sql SELECT COUNT(DISTINCT dog_guid)
FROM complete_tests
WHERE created_at > '2014-03-01' ;<jupyter_output>1 rows affected.
<jupyter_text>You can use the "\*" in the parentheses of a COUNT function to count how many rows are in the entire table (or subtable). There are two fundamental difference between COUNT(\*) and COUNT(column_name), though.
The first difference is that you cannot use DISTINCT with COUNT(\*).
**Question 2: To observe the second difference yourself first, count the number of rows in the dogs table using COUNT(\*):**
<jupyter_code>%%sql SELECT COUNT(*)
FROM dogs;<jupyter_output>1 rows affected.
<jupyter_text>**Question 3: Now count the number of rows in the exclude column of the dogs table:**<jupyter_code>%%sql SELECT COUNT(exclude)
FROM dogs;<jupyter_output>1 rows affected.
<jupyter_text>The output of the second query should return a much smaller number than the output of the first query. That's because:
> When a column is included in a count function, null values are ignored in the count. When an asterisk is included in a count function, nulls are included in the count.
This will be both useful and important to remember in future queries where you might want to use SELECT(\*) to count items in multiple groups at once.
**Question 4: How many distinct dogs have an exclude flag in the dogs table (value will be "1")? (the answer should be 853)**<jupyter_code>%%sql SELECT COUNT(DISTINCT dog_guid)
FROM dogs
WHERE exclude = 1; <jupyter_output>1 rows affected.
<jupyter_text>## 2. The SUM Function
The fact that the output of:
```mySQL
SELECT COUNT(exclude)
FROM dogs
```
was so much lower than:
```mySQL
SELECT COUNT(*)
FROM dogs
```
suggests that there must be many NULL values in the exclude column. Conveniently, we can combine the SUM function with ISNULL to count exactly how many NULL values there are. Look up "ISNULL" at this link to MySQL functions I included in an earlier lesson:
http://www.w3resource.com/mysql/mysql-functions-and-operators.php
You will see that ISNULL is a logical function that returns a 1 for every row that has a NULL value in the specified column, and a 0 for everything else. If we sum up the number of 1s outputted by ISNULL(exclude), then, we should get the total number of NULL values in the column. Here's what that query would look like:
```mySQL
SELECT SUM(ISNULL(exclude))
FROM dogs
```
It might be tempting to treat SQL like a calculator and leave out the SELECT statement, but you will quickly see that doesn't work.
>*Every SQL query that extracts data from a database MUST contain a SELECT statement.*
**Try counting the number of NULL values in the exclude column:**
<jupyter_code>%%sql SELECT SUM(ISNULL(exclude))
FROM dogs;<jupyter_output>1 rows affected.
<jupyter_text>The output should return a value of 34,025. When you add that number to the 1025 entries that have an exclude flag, you get a total of 35,050, which is the number of rows reported by SELECT COUNT(\*) from dogs.
## 3. The AVG, MIN, and MAX Functions
AVG, MIN, and MAX all work very similarly to SUM.
During the Dognition test, customers were asked the question: "How surprising were [your dog’s name]’s choices?” after completing a test. Users could choose any number between 1 (not surprising) to 9 (very surprising). We could retrieve the average, minimum, and maximum rating customers gave to this question after completing the "Eye Contact Game" with the following query:
```mySQL
SELECT test_name,
AVG(rating) AS AVG_Rating,
MIN(rating) AS MIN_Rating,
MAX(rating) AS MAX_Rating
FROM reviews
WHERE test_name="Eye Contact Game";
```
This would give us an output with 4 columns. The last three columns would have titles reflecting the names inputted after the AS clauses. Recall that if you want to title a column with a string of text that contains a space, that string will need to be enclosed in quotation marks after the AS clause in your query.
**Question 5: What is the average, minimum, and maximum ratings given to "Memory versus Pointing" game? (Your answer should be 3.5584, 0, and 9, respectively)**<jupyter_code>%%sql SELECT test_name, AVG(rating), MIN(rating), MAX(rating)
FROM reviews
WHERE test_name ="Memory versus Pointing";<jupyter_output>1 rows affected.
<jupyter_text>What if you wanted the average rating for each of the 40 tests in the Reviews table? One way to do that with the tools you know already is to write 40 separate queries like the ones you wrote above for each test, and then copy or transcribe the results into a separate table in another program like Excel to assemble all the results in one place. That would be a very tedious and time-consuming exercise. Fortunately, there is a very simple way to produce the results you want within one query. That's what we will learn how to do in MySQL Exercise 5. However, it is important that you feel comfortable with the syntax we have learned thus far before we start taking advantage of that functionality. Practice is the best way to become comfortable!
## Practice incorporating aggregate functions with everything else you've learned so far in your own queries.
**Question 6: How would you query how much time it took to complete each test provided in the exam_answers table, in minutes? Title the column that represents this data "Duration."** Note that the exam_answers table has over 2 million rows, so if you don't limit your output, it will take longer than usual to run this query. (HINT: use the TIMESTAMPDIFF function described at: http://www.w3resource.com/mysql/date-and-time-functions/date-and-time-functions.php. It might seem unkind of me to keep suggesting you look up and use new functions I haven't demonstrated for you, but I really want you to become confident that you know how to look up and use new functions when you need them! It will give you a very competative edge in the business world.)
<jupyter_code>%%sql SELECT TIMESTAMPDIFF(minute, start_time,end_time) AS DURATION
FROM exam_answers
LIMIT 10;<jupyter_output>10 rows affected.
<jupyter_text>**Question 7: Include a column for Dog_Guid, start_time, and end_time in your query, and examine the output. Do you notice anything strange?** <jupyter_code>%%sql SELECT dog_guid, start_time, end_time, TIMESTAMPDIFF(minute,start_time,end_time) AS Duration
FROM exam_answers
LIMIT 2000;<jupyter_output>2000 rows affected.
<jupyter_text>If you explore your output you will find that some of your calculated durations appear to be "0." In some cases, you will see many entries from the same Dog_ID with the same start time and end time. That should be impossible. These types of entries probably represent tests run by the Dognition team rather than real customer data. In other cases, though, a "0" is entered in the Duration column even though the start_time and end_time are different. This is because we instructed the function to output the time difference in minutes; unless you change your settings, it will output "0" for any time differences less than the integer 1. If you change your function to output the time difference in seconds, the duration in most of these columns will have a non-zero number.
**Question 8: What is the average amount of time it took customers to complete all of the tests in the exam_answers table, if you do not exclude any data (the answer will be approximately 587 minutes)?**<jupyter_code>%%sql SELECT AVG(TIMESTAMPDIFF(minute,start_time,end_time)) AS AvgDuration
FROM exam_answers;<jupyter_output>1 rows affected.
<jupyter_text>**Question 9: What is the average amount of time it took customers to complete the "Treat Warm-Up" test, according to the exam_answers table (about 165 minutes, if no data is excluded)?**<jupyter_code>%%sql SELECT AVG(TIMESTAMPDIFF(minute,start_time,end_time)) AS AvgDuration
FROM exam_answers
WHERE test_name = "Treat Warm-Up";<jupyter_output>1 rows affected.
<jupyter_text>**Question 10: How many possible test names are there in the exam_answers table?**<jupyter_code>%%sql SELECT COUNT(DISTINCT test_name)
FROM exam_answers;<jupyter_output>1 rows affected.
<jupyter_text>You should have discovered that the exam_answers table has many more test names than the completed_tests table. It turns out that this table has information about experimental tests that Dognition has not yet made available to its customers.
**Question 11: What is the minimum and maximum value in the Duration column of your query that included the data from the entire table?**<jupyter_code>%%sql SELECT MAX(TIMESTAMPDIFF(minute, start_time, end_time)) AS MaxAvgTime,
MIN(TIMESTAMPDIFF(minute, start_time, end_time)) AS MinAvgTime
FROM exam_answers;<jupyter_output>1 rows affected.
<jupyter_text>The minimum Duration value is *negative*! The end_times entered in rows with negative Duration values are earlier than the start_times. Unless Dognition has created a time machine, that's impossible and these entries must be mistakes.
**Question 12: How many of these negative Duration entries are there? (the answer should be 620)**<jupyter_code>%%sql SELECT COUNT(TIMESTAMPDIFF(minute, start_time, end_time))
FROM exam_answers
WHERE TIMESTAMPDIFF(minute, start_time, end_time)<jupyter_output>1 rows affected.
<jupyter_text>**Question 13: How would you query all the columns of all the rows that have negative durations so that you could examine whether they share any features that might give you clues about what caused the entry mistake?**<jupyter_code>%%sql SELECT *
FROM exam_answers
WHERE TIMESTAMPDIFF(minute, start_time, end_time);<jupyter_output>129165 rows affected.
<jupyter_text>**Question 14: What is the average amount of time it took customers to complete all of the tests in the exam_answers table when 0 and the negative durations are excluded from your calculation (you should get 11233 minutes)?**<jupyter_code>%%sql SELECT AVG(TIMESTAMDIFF(mu))<jupyter_output><empty_output>
|
no_license
|
/MySQL_Exercise_04_Summarizing_Your_Data.ipynb
|
vinisan/MySQLCourse
| 17 |
<jupyter_start><jupyter_text># Earth Engine analysis<jupyter_code>from urllib.request import urlopen
import zipfile
import rasterio
import json
import requests
from pprint import pprint
import matplotlib.pyplot as plt
from IPython import display
import numpy as np
import pandas as pd
import folium
import os
import ee<jupyter_output><empty_output><jupyter_text>Initialize the Earth Engine client.<jupyter_code>ee.Initialize()
image_name = 'users/iker/Resilience/total_carbon_africa'
geometry = {
"type": "FeatureCollection",
"features": [
{
"type": "Feature",
"properties": {},
"geometry": {
"type": "Polygon",
"coordinates": [
[
[
15.1171875,
2.5479878714713835
],
[
13.1396484375,
-1.845383988573187
],
[
15.644531250000002,
-4.696879026871413
],
[
21.708984375,
-3.425691524418062
],
[
20.9619140625,
1.3182430568620136
],
[
15.1171875,
2.5479878714713835
]
]
]
}
}
]
}
r = json.dumps(geometry)
r = json.loads(r)
polygon = ee.Geometry.Polygon(r.get('features')[0].get('geometry').get('coordinates'))
image = ee.Image(image_name).clip(ee.Geometry(polygon))<jupyter_output><empty_output><jupyter_text>**Inspect the data**<jupyter_code>def show_image(image):
display.display(display.Image(ee.data.getThumbnail({
'image': image.serialize(),
'dimensions': '360'
})))
show_image(image.visualize(min=0,max=15000))<jupyter_output><empty_output><jupyter_text>## Download data<jupyter_code>def download_image(image):
download_zip = 'data.zip'
url = image.getDownloadUrl()
print('Downloading image...')
print("url: ", url)
data = urlopen(url)
with open(download_zip, 'wb') as fp:
while True:
chunk = data.read(16 * 1024)
if not chunk: break
fp.write(chunk)
# extract the zip file transformation data
z = zipfile.ZipFile(download_zip, 'r')
target_folder_name = download_zip.split('.zip')[0]
z.extractall(target_folder_name)
# remove directory
os.remove(download_zip)
print('Download complete!')
download_image(image)<jupyter_output>Downloading image...
url: https://earthengine.googleapis.com/api/download?docid=1ba9fe9f153317bfc501b28e620b833d&token=dd983769351ab44c4fb1417b24c77c58
Download complete!
<jupyter_text>**Load data**<jupyter_code># Load tiff file data
with rasterio.open('./data/total_carbon_africa.b1.tif') as src:
data = src.read()
profile = src.profile
transform = src.transform
data[data==data.min()]=np.nan
fig, ax = plt.subplots(figsize=(5,5))
ax.imshow(data[0,:,:], vmax=15000);<jupyter_output><empty_output><jupyter_text>### Google Cloud Function ([getting started](https://medium.com/@timhberry/getting-started-with-python-for-google-cloud-functions-646a8cddbb33))
To create a Google Cloud Function we need a [Google Cloud Project](https://cloud.google.com/resource-manager/docs/creating-managing-projects) and [gcloud SDK](https://cloud.google.com/sdk/docs/).
If we have already some projects we can check them by typing:
`gcloud projects list`
```
PROJECT_ID NAME PROJECT_NUMBER
gef-ld-toolbox gef-ld-toolbox 1080184168142
gfw-apis Global Forest Watch API 872868960419
resource-watch Resource Watch 312603932249
skydipper-196010 skydipper 230510979472
soc-platform SOC Platform 345072612231
```
and select one by:
`gcloud config set project gef-ld-toolbox`
Then create a function by creating a `main.py` file with some python code on it:
```python
import ee
import json
service_account = '[email protected]'
credentials = ee.ServiceAccountCredentials(service_account, 'privatekey.json')
ee.Initialize(credentials)
def serializer(url):
return {
'download_url': url
}
def download_image(request):
request = request.get_json()
polygon = ee.Geometry.Polygon(request['geometry'].get('features')[0].get('geometry').get('coordinates'))
image = ee.Image(request['assetId']).clip(ee.Geometry(polygon))
url = image.getDownloadUrl()
return json.dumps(serialize_response(url))
```
In the same directory include the `privatekey.json` with the [service account keys](https://cloud.google.com/iam/docs/creating-managing-service-account-keys) and the `requirements.txt` file.
Finally cd to that directory and deploy the cloud Function with the following command:
`gcloud beta functions deploy download_image --runtime python37 --trigger-http`
Note that the cloud function name matches the name of the function we defined in code: `download_image`.<jupyter_code>import json
import requests
from pprint import pprint
payload = {
"assetId": "projects/SPARC_team/Birds/total_carbon_africa",
"geometry": {
"type": "FeatureCollection",
"features": [{
"type": "Feature",
"properties": {},
"geometry": {
"type": "Polygon",
"coordinates": [
[
[
15.1171875,
2.5479878714713835
],
[
13.1396484375,
-1.845383988573187
],
[
15.644531250000002,
-4.696879026871413
],
[
21.708984375,
-3.425691524418062
],
[
20.9619140625,
1.3182430568620136
],
[
15.1171875,
2.5479878714713835
]
]
]
}
}
]
}
}
url = f'https://us-central1-gef-ld-toolbox.cloudfunctions.net/download_image'
headers = {'Content-Type': 'application/json'}
r = requests.post(url, data=json.dumps(payload), headers=headers)
pprint(r.json())<jupyter_output><empty_output><jupyter_text>## Histogram<jupyter_code>geometry = {
"type": "FeatureCollection",
"features": [
{
"type": "Feature",
"properties": {},
"geometry": {
"type": "Polygon",
"coordinates": [
[
[
20.126953125,
4.8282597468669755
],
[
16.083984375,
-12.897489183755892
],
[
30.937499999999996,
-17.392579271057766
],
[
38.49609375,
-13.2399454992863
],
[
36.38671875,
1.4939713066293239
],
[
20.126953125,
4.8282597468669755
]
]
]
}
}
]
}
geometry = json.dumps(geometry)
geometry = json.loads(geometry)
image = ee.Image(image_name)
regReducer = {
'collection': ee.FeatureCollection(geometry.get('features')),
'reducer': ee.Reducer.histogram(maxBuckets= 20)
}
hist = image.reduceRegions(**regReducer).toList(10000).getInfo()
count = np.array(hist[0].get('properties').get('histogram').get('histogram'))
bucketWidth = hist[0].get('properties').get('histogram').get('bucketWidth')
x_min = np.arange(len(count))*bucketWidth
x_max = np.arange(len(count))*bucketWidth + bucketWidth
plt.figure(figsize=(10,5))
width = 0.35
plt.bar(x_min.astype(np.str), count)<jupyter_output><empty_output><jupyter_text>### Google Cloud Function ([getting started](https://medium.com/@timhberry/getting-started-with-python-for-google-cloud-functions-646a8cddbb33))
`main.py`
```python
import ee
import json
import numpy as np
import pandas as pd
service_account = '[email protected]'
credentials = ee.ServiceAccountCredentials(service_account, 'privatekey.json')
ee.Initialize(credentials)
def serializer(hist):
bucketWidth = hist[0].get('properties').get('histogram').get('bucketWidth')
count = np.array(hist[0].get('properties').get('histogram').get('histogram'))
x_min = np.arange(len(count))*bucketWidth
x_max = np.arange(len(count))*bucketWidth + bucketWidth
df = pd.DataFrame({'min': x_min, 'max': x_max, 'count': count, 'percent': count/count.sum()})
return {'rows': df.to_dict(orient='record'),
'fields': {
'min': {'type': "number"},
'max': {'type': "number"},
'count': {'type': "number"},
'percent': {'type': "number"}
},
'total_rows': len(count)
}
def image_hist(request):
request = request.get_json()
image = ee.Image(request['assetId']).clip(ee.Geometry(polygon))
regReducer = {
'collection': ee.FeatureCollection(request['geometry'].get('features')),
'reducer': ee.Reducer.histogram(maxBuckets= 20)
}
hist = image.reduceRegions(**regReducer).toList(10000).getInfo()
return json.dumps(serializer(hist))
```<jupyter_code>payload = {
"assetId": "projects/SPARC_team/Birds/total_carbon_africa",
"geometry": {
"type": "FeatureCollection",
"features": [{
"type": "Feature",
"properties": {},
"geometry": {
"type": "Polygon",
"coordinates": [
[
[
30.849609375,
-3.162455530237848
],
[
35.33203125,
-3.162455530237848
],
[
35.33203125,
0.4394488164139768
],
[
30.849609375,
0.4394488164139768
],
[
30.849609375,
-3.162455530237848
]
]
]
}
}
]
}
}
%%time
url = f'https://us-central1-gef-ld-toolbox.cloudfunctions.net/histogram'
headers = {'Content-Type': 'application/json'}
r = requests.post(url, data=json.dumps(payload), headers=headers)
pprint(r.json())
payload = {"assetId":"projects/SPARC_team/Birds/total_carbon_africa","geometry":{"type":"FeatureCollection","features":[{"type":"Feature","properties":{},"geometry":{"type":"Polygon","coordinates":[[[18.500977,10.876465],[17.402344,9.838979],[16.21582,9.709057],[15.908203,9.362353],[16.083984,9.058702],[16.083984,8.798225],[15.380859,8.624472],[14.458008,8.711359],[14.326172,8.276727],[14.282227,7.449624],[13.842773,6.708254],[13.31543,6.926427],[12.963867,6.708254],[12.963867,5.922045],[13.227539,5.703448],[14.414063,5.659719],[14.326172,4.784469],[13.666992,4.740675],[13.359375,3.995781],[13.40332,3.469557],[13.974609,3.162456],[14.853516,3.118576],[14.80957,2.547988],[14.018555,2.24064],[13.447266,1.933227],[13.40332,1.493971],[13.447266,0.615223],[14.194336,0.527336],[14.985352,0.263671],[15.029297,-0.747049],[16.303711,-0.307616],[16.435547,2.108899],[16.831055,1.318243],[16.831055,0.57128],[16.831055,-0.439449],[16.655273,-0.747049],[15.46875,-1.537901],[14.106445,-1.493971],[13.710938,-1.933227],[13.710938,-3.250209],[14.370117,-3.688855],[16.259766,-4.696879],[16.743164,-3.294082],[18.808594,-4.872048],[17.885742,-3.513421],[19.191742,-3.688855],[19.543304,-2.196727],[18.752289,-1.889306],[19.367523,-0.922812],[20.114594,-2.372369],[20.378265,-3.908099],[20.070648,-4.696879],[19.499359,-5.484768],[18.312836,-5.965754],[17.09816,-6.993563],[19.288216,-7.38596],[20.914192,-6.86269],[22.05677,-6.51352],[25.264778,-4.63289],[24.078255,-3.931733],[27.330208,-3.010584],[26.407356,-2.132572],[28.165169,-1.166187],[25.253792,0.035706],[27.451057,0.56304],[29.077034,1.485734],[28.154182,1.705376],[26.879768,1.968912],[27.758675,2.759248],[29.648323,2.847033],[29.648323,3.987561],[32.197151,6.132362],[32.153206,7.267119],[31.933479,8.35554],[33.163948,8.442488],[33.911018,9.180736],[33.42762,10.090558],[32.109261,11.47195],[28.945198,11.945288],[28.022346,11.902291],[28.154182,11.170318],[27.978401,9.917449],[27.495003,8.876931],[27.05555,7.833452],[26.132698,8.485955],[25.078011,10.609319],[24.33094,11.428879],[20.490704,9.50663],[22.204571,11.58027],[21.018047,11.967456],[20.227032,11.408014],[19.523907,10.63159],[18.500977,10.876465]]]}}]}}
%%time
url = f'https://us-central1-gef-ld-toolbox.cloudfunctions.net/get_hist'
headers = {'Content-Type': 'application/json'}
r = requests.post(url, data=json.dumps(payload), headers=headers)
pprint(r.json())
url = f'https://us-central1-gef-ld-toolbox.cloudfunctions.net/download_image'
headers = {'Content-Type': 'application/json'}
r = requests.post(url, data=json.dumps(payload), headers=headers)
pprint(r.json())<jupyter_output>{'download_url': 'https://earthengine.googleapis.com/api/download?docid=ecbf83dbf52ed6decc7a115bbbb1f23b&token=3ca1344193855b47273626a90ab59844'}
|
permissive
|
/resilience/EE_analysis.ipynb
|
Vizzuality/notebooks
| 8 |
<jupyter_start><jupyter_text># DonorsChoose
DonorsChoose.org receives hundreds of thousands of project proposals each year for classroom projects in need of funding. Right now, a large number of volunteers is needed to manually screen each submission before it's approved to be posted on the DonorsChoose.org website.
Next year, DonorsChoose.org expects to receive close to 500,000 project proposals. As a result, there are three main problems they need to solve:
How to scale current manual processes and resources to screen 500,000 projects so that they can be posted as quickly and as efficiently as possible
How to increase the consistency of project vetting across different volunteers to improve the experience for teachers
How to focus volunteer time on the applications that need the most assistance
The goal of the competition is to predict whether or not a DonorsChoose.org project proposal submitted by a teacher will be approved, using the text of project descriptions as well as additional metadata about the project, teacher, and school. DonorsChoose.org can then use this information to identify projects most likely to need further review before approval.
## About the DonorsChoose Data Set
The `train.csv` data set provided by DonorsChoose contains the following features:
Feature | Description
----------|---------------
**`project_id`** | A unique identifier for the proposed project. **Example:** `p036502`
**`project_title`** | Title of the project. **Examples:**Art Will Make You Happy!First Grade Fun
**`project_grade_category`** | Grade level of students for which the project is targeted. One of the following enumerated values: Grades PreK-2Grades 3-5Grades 6-8Grades 9-12
**`project_subject_categories`** | One or more (comma-separated) subject categories for the project from the following enumerated list of values: Applied LearningCare & HungerHealth & SportsHistory & CivicsLiteracy & LanguageMath & ScienceMusic & The ArtsSpecial NeedsWarmth **Examples:** Music & The ArtsLiteracy & Language, Math & Science
**`school_state`** | State where school is located ([Two-letter U.S. postal code](https://en.wikipedia.org/wiki/List_of_U.S._state_abbreviations#Postal_codes)). **Example:** `WY`
**`project_subject_subcategories`** | One or more (comma-separated) subject subcategories for the project. **Examples:** LiteracyLiterature & Writing, Social Sciences
**`project_resource_summary`** | An explanation of the resources needed for the project. **Example:** My students need hands on literacy materials to manage sensory needs!
**`project_essay_1`** | First application essay*
**`project_essay_2`** | Second application essay*
**`project_essay_3`** | Third application essay*
**`project_essay_4`** | Fourth application essay*
**`project_submitted_datetime`** | Datetime when project application was submitted. **Example:** `2016-04-28 12:43:56.245`
**`teacher_id`** | A unique identifier for the teacher of the proposed project. **Example:** `bdf8baa8fedef6bfeec7ae4ff1c15c56`
**`teacher_prefix`** | Teacher's title. One of the following enumerated values: nanDr.Mr.Mrs.Ms.Teacher.
**`teacher_number_of_previously_posted_projects`** | Number of project applications previously submitted by the same teacher. **Example:** `2`
* See the section Notes on the Essay Data for more details about these features.
Additionally, the `resources.csv` data set provides more data about the resources required for each project. Each line in this file represents a resource required by a project:
Feature | Description
----------|---------------
**`id`** | A `project_id` value from the `train.csv` file. **Example:** `p036502`
**`description`** | Desciption of the resource. **Example:** `Tenor Saxophone Reeds, Box of 25`
**`quantity`** | Quantity of the resource required. **Example:** `3`
**`price`** | Price of the resource required. **Example:** `9.95`
**Note:** Many projects require multiple resources. The `id` value corresponds to a `project_id` in train.csv, so you use it as a key to retrieve all resources needed for a project:
The data set contains the following label (the value you will attempt to predict):
Label | Description
----------|---------------
`project_is_approved` | A binary flag indicating whether DonorsChoose approved the project. A value of `0` indicates the project was not approved, and a value of `1` indicates the project was approved.### Notes on the Essay Data
Prior to May 17, 2016, the prompts for the essays were as follows:
__project_essay_1:__ "Introduce us to your classroom"
__project_essay_2:__ "Tell us more about your students"
__project_essay_3:__ "Describe how your students will use the materials you're requesting"
__project_essay_3:__ "Close by sharing why your project will make a difference"
Starting on May 17, 2016, the number of essays was reduced from 4 to 2, and the prompts for the first 2 essays were changed to the following:
__project_essay_1:__ "Describe your students: What makes your students special? Specific details about their background, your neighborhood, and your school are all helpful."
__project_essay_2:__ "About your project: How will these materials make a difference in your students' learning and improve their school lives?"
For all projects with project_submitted_datetime of 2016-05-17 and later, the values of project_essay_3 and project_essay_4 will be NaN.
<jupyter_code>%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
warnings.simplefilter("ignore")
warnings.warn("ignore")
import sqlite3
import pandas as pd
import numpy as np
import nltk
import string
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.metrics import confusion_matrix
from sklearn import metrics
from sklearn import model_selection
from sklearn.metrics import roc_curve, auc
from nltk.stem.porter import PorterStemmer
import re
# Tutorial about Python regular expressions: https://pymotw.com/2/re/
import string
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from nltk.stem.wordnet import WordNetLemmatizer
from gensim.models import Word2Vec
from gensim.models import KeyedVectors
import pickle
from tqdm import tqdm
import os
from sklearn.metrics import accuracy_score
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve, auc
from sklearn import preprocessing
from keras.preprocessing.text import one_hot
from keras.preprocessing.sequence import pad_sequences
from keras.models import Sequential
from keras.layers.core import Activation, Dropout, Dense ,Reshape
from keras.layers import Flatten, LSTM,Lambda
from keras.models import Model
from keras.layers.embeddings import Embedding
from keras.preprocessing.text import Tokenizer
from keras.layers import Input
from keras.layers import Concatenate
from keras.utils import to_categorical
from keras.layers import Conv1D, MaxPooling1D<jupyter_output><empty_output><jupyter_text>## 1.1 Reading Data<jupyter_code>#https://stackabuse.com/python-for-nlp-creating-multi-data-type-classification-models-with-keras/
#https://www.pyimagesearch.com/2019/01/21/regression-with-keras/
#https://github.com/mmortazavi/EntityEmbedding-Working_Example/blob/master/EntityEmbedding.ipynb
#https://www.pyimagesearch.com/2019/02/04/keras-multiple-inputs-and-mixed-data/
#https://machinelearningmastery.com/cnn-models-for-human-activity-recognition-time-series-classification/
preprocessed_data = pd.read_csv('preprocessed_data.csv')
print("Number of data points in preprocessed data", preprocessed_data.shape)
preprocessed_data=preprocessed_data.sample(n=50000)
preprocessed_data.head()
X=preprocessed_data.drop(columns=['project_is_approved'],axis=1)
y=preprocessed_data['project_is_approved']
label_encoder = preprocessing.LabelEncoder()
y = label_encoder.fit_transform(y)
X_1, X_test, y_1, y_test = model_selection.train_test_split(X, y, test_size=0.2, random_state=0,stratify=y)
# split the train data set into cross validation train and cross validation test
X_train, X_cv, y_train, y_cv = model_selection.train_test_split(X_1, y_1, test_size=0.2, random_state=0,stratify=y_1)
y_train = to_categorical(y_train)
y_cv = to_categorical(y_cv)
y_test = to_categorical(y_test)
tokenizer = Tokenizer()
tokenizer.fit_on_texts(X_train['essay'].values)
X1_tr = np.array(tokenizer.texts_to_sequences(X_train['essay'].values))
X1_cv = np.array(tokenizer.texts_to_sequences(X_cv['essay'].values))
X1_test = np.array(tokenizer.texts_to_sequences(X_test['essay'].values))
vocab_size = len(tokenizer.word_index) + 1
maxlen = 200
X1_tr = pad_sequences(X1_tr, padding='post', maxlen=maxlen)
X1_cv = pad_sequences(X1_cv, padding='post', maxlen=maxlen)
X1_test = pad_sequences(X1_test, padding='post', maxlen=maxlen)
print(X1_tr.shape)
print(X1_cv.shape)
print(X1_test.shape)
with open('glove_vectors', 'rb') as f:
model = pickle.load(f)
glove_words = set(model.keys())
embeddings_dictionary = dict()
for word in glove_words:
vector_dimensions = model[word]
embeddings_dictionary [word] = vector_dimensions
embedding_matrix = np.zeros((vocab_size, 300))
for word, index in tokenizer.word_index.items():
embedding_vector = embeddings_dictionary.get(word)
if embedding_vector is not None:
embedding_matrix[index] = embedding_vector
embedding_matrix.shape
input_1 = Input(shape=(maxlen,),name='essay_input')
print(input_1.shape)
input_1_embedding = Embedding(vocab_size, 300, weights=[embedding_matrix], trainable=False )(input_1)
print(input_1_embedding.shape)
input_1_lstm = LSTM(128,return_sequences=True)(input_1_embedding)
print(input_1_lstm.shape)
input_1_flatten=Flatten()(input_1_lstm)
print(input_1_flatten.shape)
categoricals=['school_state','teacher_prefix','project_grade_category','clean_categories','clean_subcategories']
numericals=['teacher_number_of_previously_posted_projects','price']
embed_cols=[i for i in X_train[categoricals]]
for i in embed_cols:
print(i,X_train[i].nunique())
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()
X2_tr = vectorizer.fit_transform(X_train['school_state'].values).toarray()
X2_cv = vectorizer.transform(X_cv['school_state'].values).toarray()
X2_test = vectorizer.transform(X_test['school_state'].values).toarray()
cat_emb_name= 'school_state_Embedding'
no_of_unique_cat = X_train['school_state'].nunique()
embedding_size = int(min(np.ceil((no_of_unique_cat)/2), 50 ))
input_2 = Input(shape=(X2_tr.shape[1],),name='school_state_input')
print(input_2.shape)
input_2_embedding = Embedding(no_of_unique_cat, embedding_size,input_length=X2_tr.shape[1], name=cat_emb_name)(input_2)
print(input_2_embedding.shape)
input_2_flatten=Flatten()(input_2_embedding)
print(input_2_flatten.shape)
print(X2_tr.shape)
print(X2_cv.shape)
print(X2_test.shape)
vectorizer = CountVectorizer()
X3_tr = vectorizer.fit_transform(X_train['teacher_prefix'].values.astype('U')).toarray()
X3_cv = vectorizer.transform(X_cv['teacher_prefix'].values.astype('U')).toarray()
X3_test = vectorizer.transform(X_test['teacher_prefix'].values.astype('U')).toarray()
cat_emb_name= 'teacher_prefix_Embedding'
no_of_unique_cat = X_train['teacher_prefix'].nunique()
embedding_size = int(min(np.ceil((no_of_unique_cat)/2), 50 ))
input_3 = Input(shape=(X3_tr.shape[1],),name='teacher_prefix_input')
print(input_3.shape)
input_3_embedding = Embedding(no_of_unique_cat, embedding_size,input_length=X3_tr.shape[1], name=cat_emb_name)(input_3)
print(input_3_embedding.shape)
input_3_flatten=Flatten()(input_3_embedding)
print(input_3_flatten.shape)
print(X3_tr.shape)
print(X3_cv.shape)
print(X3_test.shape)
vectorizer = CountVectorizer()
X4_tr = vectorizer.fit_transform(X_train['project_grade_category'].values).toarray()
X4_cv = vectorizer.transform(X_cv['project_grade_category'].values).toarray()
X4_test = vectorizer.transform(X_test['project_grade_category'].values).toarray()
cat_emb_name= 'project_grade_category_Embedding'
no_of_unique_cat = X_train['project_grade_category'].nunique()
embedding_size = int(min(np.ceil((no_of_unique_cat)/2), 50 ))
input_4 = Input(shape=(X4_tr.shape[1],),name='project_grade_category_input')
print(input_4.shape)
input_4_embedding = Embedding(no_of_unique_cat, embedding_size,input_length=X4_tr.shape[1],name=cat_emb_name)(input_4)
print(input_4_embedding.shape)
input_4_flatten=Flatten()(input_4_embedding)
print(input_4_flatten.shape)
print(X4_tr.shape)
print(X4_cv.shape)
print(X4_test.shape)
vectorizer = CountVectorizer()
X5_tr = vectorizer.fit_transform(X_train['clean_categories'].values).toarray()
X5_cv = vectorizer.transform(X_cv['clean_categories'].values).toarray()
X5_test = vectorizer.transform(X_test['clean_categories'].values).toarray()
cat_emb_name= 'clean_categories_Embedding'
no_of_unique_cat = X_train['clean_categories'].nunique()
embedding_size = int(min(np.ceil((no_of_unique_cat)/2), 50 ))
input_5 = Input(shape=(X5_tr.shape[1],),name='clean_categories_input')
print(input_5.shape)
input_5_embedding = Embedding(no_of_unique_cat, embedding_size,input_length=X5_tr.shape[1], name=cat_emb_name)(input_5)
print(input_5_embedding.shape)
input_5_flatten=Flatten()(input_5_embedding)
print(input_5_flatten.shape)
print(X5_tr.shape)
print(X5_cv.shape)
print(X5_test.shape)
vectorizer = CountVectorizer()
X6_tr = vectorizer.fit_transform(X_train['clean_subcategories'].values).toarray()
X6_cv = vectorizer.transform(X_cv['clean_subcategories'].values).toarray()
X6_test = vectorizer.transform(X_test['clean_subcategories'].values).toarray()
cat_emb_name= 'clean_subcategories_Embedding'
no_of_unique_cat = X_train['clean_subcategories'].nunique()
embedding_size = int(min(np.ceil((no_of_unique_cat)/2), 50 ))
input_6 = Input(shape=(X6_tr.shape[1],),name='clean_subcategories_input')
print(input_6.shape)
input_6_embedding = Embedding(no_of_unique_cat, embedding_size,input_length=X6_tr.shape[1], name=cat_emb_name)(input_6)
print(input_6_embedding.shape)
input_6_flatten=Flatten()(input_6_embedding)
print(input_6_flatten.shape)
print(X6_tr.shape)
print(X6_cv.shape)
print(X6_test.shape)
X7_tr = preprocessing.normalize(X_train[['teacher_number_of_previously_posted_projects', 'price']])
X7_cv = preprocessing.normalize(X_cv[['teacher_number_of_previously_posted_projects', 'price']])
X7_test = preprocessing.normalize(X_test[['teacher_number_of_previously_posted_projects', 'price']])
input_7 = Input(shape=(len(X_train[numericals].columns),),name='numerical_input')
print(input_7.shape)
input_7_dense = Dense(128)(input_7)
print(input_7_dense.shape)
print(X7_tr.shape)
print(X7_cv.shape)
print(X7_test.shape)
#At the end we concatenate altogther and add other Dense layers
output_1 = Concatenate()([input_1_flatten,input_2_flatten,input_3_flatten,input_4_flatten,input_5_flatten,input_6_flatten,input_7_dense])
output_1 = Dense(256,activation='relu')(output_1)
output_1= Dropout(0.4)(output_1)
output_1 = Dense(128,activation='relu')(output_1)
output_1= Dropout(0.3)(output_1)
output_1 = Dense(64,activation='relu')(output_1)
output_1 = Dense(2, activation='softmax')(output_1)
#https://stackoverflow.com/questions/41032551/how-to-compute-receiving-operating-characteristic-roc-and-auc-in-keras
import tensorflow as tf
def auroc(y_true, y_pred):
return tf.py_func(roc_auc_score, (y_true, y_pred), tf.double)
from keras import optimizers
model = Model(inputs=[input_1,input_2,input_3,input_4,input_5,input_6,input_7], outputs=output_1)
model.compile(loss='binary_crossentropy', optimizer=optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.9) ,metrics=[auroc])
model.summary()
from keras.utils import plot_model
plot_model(model, to_file='model_1.png', show_shapes=True, show_layer_names=True)
history = model.fit(x=[X1_tr,X2_tr,X3_tr,X4_tr, X5_tr, X6_tr,X7_tr], y=y_train, validation_data=([X1_cv,X2_cv,X3_cv,X4_cv, X5_cv, X6_cv,X7_cv],y_cv),epochs=12,batch_size=500,verbose=2)
score = model.evaluate(x=[X1_test,X2_test,X3_test,X4_test, X5_test, X6_test, X7_test], y=y_test, verbose=2)
print("Test Loss:", score[0])
print("Test AUC:", score[1])
plt.plot(history.history['auroc'])
plt.plot(history.history['val_auroc'])
plt.title('model auc')
plt.ylabel('auc')
plt.xlabel('epoch')
plt.legend(['train','test'], loc='upper left')
plt.show()
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train','test'], loc='upper left')
plt.show()
# serialize weights to HDF5
model.save_weights("model_1.h5")
print("Saved model to disk")<jupyter_output>Saved model to disk
<jupyter_text>## Model 2<jupyter_code>from sklearn.feature_extraction.text import TfidfVectorizer
import seaborn as sns
vectorizer = TfidfVectorizer()
vectorizer.fit(X_train['essay'].values)
plt.boxplot(list(vectorizer.idf_))
plt.xlabel('Essay')
plt.ylabel('IDF Value')
plt.show()
tenth_percentile=np.quantile((vectorizer.idf_),0.10)
ninty_percentile=np.quantile((vectorizer.idf_),0.90)
print(tenth_percentile)
print(ninty_percentile)
dictionary = dict(zip(vectorizer.get_feature_names(), list(vectorizer.idf_)))
filterred_words=[]
for k,v in dictionary.items():
if v > tenth_percentile and v < ninty_percentile:
filterred_words.append(k)
len(filterred_words)
tokenizer = Tokenizer()
tokenizer.fit_on_texts(filterred_words)
X8_tr = np.array(tokenizer.texts_to_sequences(X_train['essay'].values))
X8_cv = np.array(tokenizer.texts_to_sequences(X_cv['essay'].values))
X8_test = np.array(tokenizer.texts_to_sequences(X_test['essay'].values))
vocab_size = len(tokenizer.word_index) + 1
maxlen = 200
X8_tr = pad_sequences(X8_tr, padding='post', maxlen=maxlen)
X8_cv = pad_sequences(X8_cv, padding='post', maxlen=maxlen)
X8_test = pad_sequences(X8_test, padding='post', maxlen=maxlen)
print(X8_tr.shape)
print(X8_cv.shape)
print(X8_test.shape)
with open('glove_vectors', 'rb') as f:
model = pickle.load(f)
glove_words = set(model.keys())
embeddings_dictionary = dict()
for word in glove_words:
vector_dimensions = model[word]
embeddings_dictionary [word] = vector_dimensions
embedding_matrix = np.zeros((vocab_size, 300))
for word, index in tokenizer.word_index.items():
embedding_vector = embeddings_dictionary.get(word)
if embedding_vector is not None:
embedding_matrix[index] = embedding_vector
embedding_matrix.shape
input_8 = Input(shape=(maxlen,),name='essay_tfidf_input')
print(input_8.shape)
input_8_embedding = Embedding(vocab_size, 300, weights=[embedding_matrix], trainable=False )(input_8)
print(input_8_embedding.shape)
input_8_lstm = LSTM(128,return_sequences=True)(input_8_embedding)
print(input_8_lstm.shape)
input_8_flatten=Flatten()(input_8_lstm)
print(input_8_flatten.shape)
#At the end we concatenate altogther and add other Dense layers
output_2 = Concatenate()([input_8_flatten,input_2_flatten,input_3_flatten,input_4_flatten,input_5_flatten,input_6_flatten,input_7_dense])
output_2 = Dense(256, kernel_initializer="uniform",activation='relu')(output_2)
output_2= Dropout(0.4)(output_2)
output_2 = Dense(128, kernel_initializer="uniform",activation='relu')(output_2)
output_2= Dropout(0.3)(output_2)
output_2 = Dense(64, kernel_initializer="uniform", activation='relu')(output_2)
output_2 = Dense(2, activation='softmax')(output_2)
model_2 = Model(inputs=[input_8,input_2,input_3,input_4,input_5,input_6,input_7], outputs=output_2)
model_2.compile(loss='binary_crossentropy', optimizer=optimizers.Adam(lr=0.0001) ,metrics=[auroc])
model_2.summary()
plot_model(model_2, to_file='model_2.png', show_shapes=True, show_layer_names=True)
history = model_2.fit(x=[X8_tr,X2_tr,X3_tr,X4_tr, X5_tr, X6_tr,X7_tr], y=y_train, validation_data=([X8_cv,X2_cv,X3_cv,X4_cv, X5_cv, X6_cv,X7_cv],y_cv),epochs=2,batch_size=300,verbose=2)
score = model_2.evaluate(x=[X8_test,X2_test,X3_test,X4_test, X5_test, X6_test, X7_test], y=y_test, verbose=2)
print("Test Loss:", score[0])
print("Test AUC:", score[1])
plt.plot(history.history['auroc'])
plt.plot(history.history['val_auroc'])
plt.title('model auc')
plt.ylabel('auc')
plt.xlabel('epoch')
plt.legend(['train','test'], loc='upper left')
plt.show()
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train','test'], loc='upper left')
plt.show()
# serialize weights to HDF5
model_2.save_weights("model_2.h5")
print("Saved model to disk")<jupyter_output>Saved model to disk
<jupyter_text>## Model 3<jupyter_code>from sklearn.preprocessing import StandardScaler
scalar = StandardScaler()
X9_tr = scalar.fit_transform(X_train['price'].values.reshape(-1,1)) # finding the mean and standard deviation of this data
X9_cv = scalar.transform(X_cv['price'].values.reshape(-1,1))
X9_test = scalar.transform(X_test['price'].values.reshape(-1,1))
print(X9_tr.shape)
print(X9_cv.shape)
print(X9_test.shape)
scalar = StandardScaler()
X10_tr = scalar.fit_transform(X_train['teacher_number_of_previously_posted_projects'].values.reshape(-1, 1))
X10_cv = scalar.transform(X_cv['teacher_number_of_previously_posted_projects'].values.reshape(-1, 1))
X10_test = scalar.transform(X_test['teacher_number_of_previously_posted_projects'].values.reshape(-1, 1))
print(X10_tr.shape)
print(X10_cv.shape)
print(X10_test.shape)
numeric_tr = np.hstack((X2_tr,X3_tr,X4_tr,X5_tr,X6_tr,X9_tr,X10_tr))
numeric_cv = np.hstack((X2_cv,X3_cv,X4_cv,X5_cv,X6_cv,X9_cv,X10_cv))
numeric_test = np.hstack((X2_test,X3_test,X4_test,X5_test,X6_test,X9_test,X10_test))
print(numeric_tr.shape)
print(numeric_cv.shape)
print(numeric_test.shape)
numeric_tr=np.expand_dims(numeric_tr,axis=2)
numeric_cv=np.expand_dims(numeric_cv,axis=2)
numeric_test=np.expand_dims(numeric_test,axis=2)
print(numeric_tr.shape)
print(numeric_cv.shape)
print(numeric_test.shape)
input_9 = Input(shape=(numeric_tr.shape[1],numeric_tr.shape[2],),name='combined_input')
print(input_9.shape)
#At the end we concatenate altogther and add other Dense layers
#output_3=tf.reshape(output_3,[-1,output_3.shape[1],output_3.shape[1]])
#print(output_3.shape)
output_3 = Conv1D(128, 5, strides=1,activation="relu")(input_9)
output_3 = MaxPooling1D(pool_size=5)(output_3)
output_3 = Conv1D(64, 5, activation="relu")(output_3)
output_3 = MaxPooling1D(pool_size=5)(output_3)
output_3 = Flatten()(output_3)
output_4 = Concatenate()([input_1_flatten,output_3])
output_4 = Dense(256, kernel_initializer="uniform",activation='relu')(output_4)
output_4= Dropout(0.4)(output_4)
output_4 = Dense(128, kernel_initializer="uniform",activation='relu')(output_4)
output_4= Dropout(0.3)(output_4)
output_4 = Dense(64, kernel_initializer="uniform", activation='relu')(output_4)
output_4 = Dense(2, activation='softmax')(output_4)
from keras import optimizers
model_3 = Model(inputs=[input_1,input_2,input_3,input_4,input_5,input_6,input_9], outputs=output_4)
model_3.compile(loss='binary_crossentropy', optimizer=optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.9) ,metrics=[auroc])
model_3.summary()
plot_model(model_3, to_file='model_3.png', show_shapes=True, show_layer_names=True)
history = model_3.fit(x=[X8_tr,X2_tr,X3_tr,X4_tr, X5_tr, X6_tr,numeric_tr], y=y_train, validation_data=([X8_cv,X2_cv,X3_cv,X4_cv, X5_cv, X6_cv,numeric_cv],y_cv),epochs=2,batch_size=300,verbose=2)
score = model_3.evaluate(x=[X8_test,X2_test,X3_test,X4_test, X5_test, X6_test, numeric_test], y=y_test, verbose=2)
print("Test Loss:", score[0])
print("Test AUC:", score[1])
plt.plot(history.history['auroc'])
plt.plot(history.history['val_auroc'])
plt.title('model auc')
plt.ylabel('auc')
plt.xlabel('epoch')
plt.legend(['train','test'], loc='upper left')
plt.show()
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train','test'], loc='upper left')
plt.show()
# serialize weights to HDF5
model_3.save_weights("model_3.h5")
print("Saved model to disk")<jupyter_output>Saved model to disk
|
no_license
|
/.ipynb_checkpoints/DonorsChoose_LSTM-checkpoint.ipynb
|
chetanmedipally/Recurring-Neural-Networks_LSTM
| 4 |
<jupyter_start><jupyter_text><jupyter_code>class Array2D:
def __init__(self, renglones, columnas):
self._reng = renglones
self._col = columnas
self._array = [[0 for y in range(self._col)] for x in range(self._reng)]
def clear(self, dato):
for ren in range(self._reng):
for col in range(self._col):
self._array[ren][col] = dato
def get_tam_reng(self):
return self._reng
def get_tam_col(self):
return self._col
def set_item(self, reng, col, dato):
self._array[reng][col] = dato
def get_item(self, reng, col):
return self._array[reng][col]
def to_string(self):
return self._array
class JuegoDeLaVida:
CELULA_VIVA = 1
CELULA_MUERTA = 0
def __init__(self, renglones, columnas, generaciones, poblacion):
self._largo = columnas
self._alto = renglones
self._grid = Array2D(self._alto, self._largo)
self._grid.clear(self.CELULA_MUERTA)
self._gen = generaciones
for cel in poblacion:
self._grid.set_item(cel[0], cel[1], self.CELULA_VIVA)
def imprime_grid(self):
for i in range(self._alto):
for j in range(self._largo):
if self._grid.get_item(i, j) == 0:
print(" ░░", end="")
else:
print(" ▓▓", end="")
print("")
def get_num_reng(self):
return self._alto
def get_num_col(self):
return self._largo
def set_celula_muerta(self, reng, col):
self._grid.set_item(reng, col, self.CELULA_MUERTA)
def set_celula_viva(self, reng, col):
self._grid.set_item(reng, col, self.CELULA_VIVA)
def get_is_viva(self, reng, col):
if self._grid.get_item(reng, col) == self.CELULA_VIVA:
return True
else:
return False
def get_is_muerta(self, reng, col):
if self._grid.get_item(reng, col) == self.CELULA_MUERTA:
return True
else:
return False
def get_numero_vecinos_vivos(self, reng, col):
cont_vecinos = 0
try:
for i in range(reng - 1, reng + 2):
for j in range(col - 1, col + 2):
if self._grid.get_item(i, j) == self.CELULA_VIVA and (i, j) != (reng, col):
cont_vecinos += 1
except Exception as e:
cont_vecinos = 0
return cont_vecinos
def evolucionar(self):
self.imprime_grid()
print("")
sig_gen_viva = []
sig_gen_revive = []
sig_gen_muerta = []
for gen in range(self._gen):
for ren in range(self._alto):
for col in range(self._largo):
if (self.get_numero_vecinos_vivos(ren, col) == 2 or self.get_numero_vecinos_vivos(ren,col) == 3) and self.get_is_viva(ren, col):
sig_gen_viva.append((ren, col))
if self.get_numero_vecinos_vivos(ren, col) == 3 and self.get_is_muerta(ren, col):
sig_gen_revive.append((ren, col))
if self.get_numero_vecinos_vivos(ren, col) < 2 or self.get_numero_vecinos_vivos(ren, col) > 3:
sig_gen_muerta.append((ren, col))
for i in sig_gen_viva:
self.set_celula_viva(i[0],i[1])
for i in sig_gen_revive:
self.set_celula_viva(i[0], i[1])
for i in sig_gen_muerta:
self.set_celula_muerta(i[0],i[1])
sig_gen_viva = []
sig_gen_revive = []
sig_gen_muerta = []
print(f"generacion {gen+1}")
self.imprime_grid()
print("")
a = JuegoDeLaVida(7, 7, 6, [(1, 2), (2, 1), (2, 2), (2, 3)])
a.evolucionar()<jupyter_output> ░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ▓▓ ░░ ░░ ░░ ░░
░░ ▓▓ ▓▓ ▓▓ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
generacion 1
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ▓▓ ▓▓ ▓▓ ░░ ░░ ░░
░░ ▓▓ ▓▓ ▓▓ ░░ ░░ ░░
░░ ░░ ▓▓ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
generacion 2
░░ ░░ ▓▓ ░░ ░░ ░░ ░░
░░ ▓▓ ░░ ▓▓ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ▓▓ ▓▓ ▓▓ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
generacion 3
░░ ░░ ▓▓ ░░ ░░ ░░ ░░
░░ ░░ ▓▓ ░░ ░░ ░░ ░░
░░ ▓▓ ░░ ▓▓ ░░ ░░ ░░
░░ ░░ ▓▓ ░░ ░░ ░░ ░░
░░ ░░ ▓▓ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
generacion 4
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ▓▓ ▓▓ ▓▓ ░░ ░░ ░░
░░ ▓▓ ░░ ▓▓ ░░ ░░ ░░
░░ ▓▓ ▓▓ ▓▓ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
generacion 5
░░ ░░ ▓▓ ░░ ░░ ░░ ░░
░░ ▓▓ ░░ ▓▓ ░░ ░░ ░░
▓▓ ░░ ░░ ░░ ▓▓ ░░ ░░
░░ ▓▓ ░░ ▓▓ ░░ ░░ ░░
░░ ░░ ▓▓ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
░░ ░░ ░░ ░░ ░░ ░░ ░░
gener[...]
|
no_license
|
/JuegoDeLaVida_1358.ipynb
|
CarlosMelendezMejia/edd_1358_2021
| 1 |
<jupyter_start><jupyter_text># 線形回帰|重回帰分析## Wine Quality Data Set の赤ワインのデータセットを読み込み<jupyter_code>!wget https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv<jupyter_output>--2020-07-16 10:22:54-- https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv
Resolving archive.ics.uci.edu (archive.ics.uci.edu)... 128.195.10.252
Connecting to archive.ics.uci.edu (archive.ics.uci.edu)|128.195.10.252|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 84199 (82K) [application/x-httpd-php]
Saving to: ‘winequality-red.csv.2’
winequality-red.csv 0%[ ] 0 --.-KB/s
winequality-red.csv 100%[===================>] 82.23K --.-KB/s in 0.1s
2020-07-16 10:22:54 (571 KB/s) - ‘winequality-red.csv.2’ saved [84199/84199]
<jupyter_text>## データフレームに読み込み<jupyter_code>import pandas as pd
df = pd.read_csv('winequality-red.csv', sep=';')
df.head()
# 説明変数(密度と揮発酸)
X = df[['density', 'volatile acidity']]
x1 = df[['density']]
x2 = df[['volatile acidity']]
# 目的変数(アルコール度数)
y = df[['alcohol']]
print(X.shape)
print(y.shape)
# x1, x2, y を3次元プロット
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig=plt.figure()
ax=Axes3D(fig)
ax.scatter3D(x1, x2, y)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_zlabel("y")
plt.show()<jupyter_output><empty_output><jupyter_text>## 重回帰分析|正規化なし### 学習<jupyter_code># ライブラリの読み込み
from sklearn.linear_model import LinearRegression
import numpy as np
# 学習
model = LinearRegression()
model.fit(X, y)<jupyter_output><empty_output><jupyter_text>### 結果の視覚化<jupyter_code># 平面 を3次元プロット
fig=plt.figure()
ax=Axes3D(fig)
ax.scatter3D(x1, x2, y)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_zlabel("y")
mesh_x1 = np.arange(x1.min()[0], x1.max()[0], (x1.max()[0]-x1.min()[0])/20)
mesh_x2 = np.arange(x2.min()[0], x2.max()[0], (x2.max()[0]-x2.min()[0])/20)
mesh_x1, mesh_x2 = np.meshgrid(mesh_x1, mesh_x2)
mesh_y = model.coef_[0][0] * mesh_x1 + model.coef_[0][1] * mesh_x2 + model.intercept_[0]
ax.plot_wireframe(mesh_x1, mesh_x2, mesh_y)
plt.show()
print('偏回帰係数', model.coef_)
print('切片', model.intercept_)
print('決定係数', model.score(X, y))<jupyter_output><empty_output><jupyter_text>### 予測<jupyter_code># 元データをモデルに当てはめた予測
model.predict(X)<jupyter_output><empty_output><jupyter_text>----## 重回帰分析|正規化あり### 正規化<jupyter_code>from sklearn import preprocessing
# 分散を使った正規化
sscaler = preprocessing.StandardScaler()
sscaler.fit(X)
Xss = sscaler.transform(X)
sscaler.fit(y)
yss = sscaler.transform(y)
print('説明変数の正規化')
print(Xss)
print('目的変数の正規化')
print(yss)
# 説明変数 平均 0 の確認
Xss.mean()
# 説明変数 標準偏差1の確認
Xss.std()
# 目的変数 平均 0 の確認
yss.mean()
# 目的変数 標準偏差1の確認
yss.std()<jupyter_output><empty_output><jupyter_text>### 学習<jupyter_code># 学習
model_std = LinearRegression()
model_std.fit(Xss, yss)<jupyter_output><empty_output><jupyter_text>### 結果<jupyter_code>print('標準化偏回帰係数', model_std.coef_)
print('切片', model_std.intercept_)
print('決定係数',model_std.score(Xss, yss))<jupyter_output>標準化偏回帰係数 [[-0.49196281 -0.19145194]]
切片 [1.1769986e-14]
決定係数 0.28283042699952887
<jupyter_text>### 予測<jupyter_code># モデルに当てはめた予測
model_std.predict(Xss)<jupyter_output><empty_output><jupyter_text>データが正規化されている場合、当然、本来求めたい値と結果が異なります。
この場合、正規化する前のモデルで逆変換して戻す必要があるので、scikit-learn のinverse_transform を用いて逆変換を行って確認します。
<jupyter_code># 予測を正規化前の状態で表示
sscaler.inverse_transform(model_std.predict(Xss))<jupyter_output><empty_output>
|
no_license
|
/MultipleLinearRegression.ipynb
|
koichi-inoue/JupyterNotebook
| 10 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.