id
stringlengths 1
5
| image
stringlengths 2
572
| answer
stringlengths 0
5.86k
| solution
stringclasses 1
value | level
stringclasses 12
values | question
stringlengths 3
2.02k
| options
stringlengths 2
1.99k
| subject
stringclasses 13
values | analysis
stringlengths 0
5.86k
|
|---|---|---|---|---|---|---|---|---|
20416
|
[]
|
D
|
null
|
高二
|
已知中心在原点, 焦点在 $\mathrm{y}$ 轴上的双曲线的离心率为 $\sqrt{3}$, 则它的渐近线方程为 ( )
|
A. $y= \pm 2 x$
B. $y= \pm \frac{\sqrt{5}}{2} x$
$y= \pm \frac{1}{2} x$
D. $y= \pm \sqrt{2} x$
|
解析几何
|
答案:D
【解析】因为双曲线焦点在 $\mathrm{y}$ 轴上, 由双曲线 $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{e}$ 的关系得, $\sqrt{1+\left(\frac{a}{b}\right)^{2}}=\sqrt{3}$, 解得 $\frac{a}{b}=\sqrt{2}$,所以它的渐近线方程为 $y= \pm \sqrt{2} x$, 故选 D。
【点评】基础题, 作为选择题, 可以利用结合选项代人验证。
|
20417
|
[]
|
D
|
null
|
高二
|
已知直线 $y=k(x+a)(a>0)$ 与 $\mathrm{x}$ 轴交于点 $\mathrm{A}$, 与直线 $\mathrm{x}=\mathrm{c}(\mathrm{c}>0, \mathrm{c}<\mathrm{a})$ 交于点 $\mathrm{M}$, 椭圆 $\mathrm{C}$ 以 $\mathrm{A}$ 为左顶点, 以 $\mathrm{F}(\mathrm{c}, 0)$ 为右焦点, 且过点 $\mathrm{M}$, 当 $\frac{1}{\frac{1}{3}}<k<\frac{1}{2}$ 时, 椭圆 $\mathrm{M}$ 的离心率的范围是()
|
A. $\left(0, \frac{2}{3}\right)$
B. $\left(\frac{2}{3}, 1\right)$
C. $\left(\frac{1}{2}, 1\right)$
D.$\left(\frac{1}{2}, \frac{2}{3}\right)$
|
解析几何
|
答案:D
【解析】
解答】因为给定的直线 $y=k(x+a)(a>0)$ 与 $x$ 轴交于点 $A$, 与直线 $x=c(c>0, c<a)$ 交于点 $M$, 粗圆 $C$ 以 $A$ 为左顶点, 以 $F(c, 0)$ 为右焦点, 且过点 $M(\mathrm{c}, \mathrm{k}(\mathrm{c}+\mathrm{a}))$ 设椭圆的方程为 $\frac{x^{2}}{m^{2}}+\frac{y^{2}}{n^{2}}=1(m>n>0)$, 则可知有 $m^{2}-n^{2}=\left(\frac{c+a}{2}\right)^{2}$, 同时由于点 $\mathrm{M}$ 在曲线上可知, $\frac{c^{2}}{m^{2}}+\frac{(a+c)^{2}}{4 n^{2}}=1(m>n>0)$, 同时利用勾股定理得到 $\sqrt{k^{2}+1}(a+c)-k(a+c)=2 m$, 联立方程组得到关系式, 进而利用 $\frac{1}{3}<k<\frac{1}{2}$, 得到离心率的范围 $\left(\frac{1}{2}, \frac{2}{3}\right)$, 故选 D.
【分析】解决该试题的关键是对于直线的斜率与椭圆的参数 a,b,c 的关系式的运用, 结合粗圆的方程来分析得到, 属于基础题。
|
20426
|
[]
|
A
|
null
|
高二
|
过抛物线 $C: y^{2}=4 x$ 的焦点作直线交抛物线于 $A\left(x_{1}, y_{1}\right), B\left(x_{2}, y_{2}\right)$, 如果 $x_{1}+x_{2}=6$, 那么 $|A B|=$
|
A. 8
B. 10
C. 6
D. 4
|
解析几何
|
答案:A
【解析】【解答】根据抛物线的定义可知, 抛物线上的点到焦点的距离等于到抛物线准线的距离,
所以 $|A B|=x_{1}+x_{2}+p=6+2=8$, 故答案为: A.
【分析】灵活运用抛物线的性质:抛物线上的点到焦点的距离等于它到准线的距离, 从而得到答案。
|
20427
|
["9358.jpg"]
|
B
|
null
|
高二
|
已知圆 C: $(x+3)^{2}+y^{2}=100$ 和点 $\mathrm{B}(3,0), \mathrm{P}$ 是圆上一点, 线段 $\mathrm{BP}$ 的垂直平分线交 $\mathrm{CP}$ 于 $\mathrm{M}$ 点,则 $\mathrm{M}$ 点的轨迹方程是 ( )
|
A. $y^{2}=6 x$
B. $\frac{x^{2}}{25}+\frac{y^{2}}{16}=1$
C. $\frac{x^{2}}{25}-\frac{y^{2}}{16}=1$
D. $x^{2}+y^{2}=25$
|
解析几何
|
答案:B
【解析】【解答】如图所示, 因为 $\mathrm{M}$ 是线段 $\mathrm{BP}$ 中垂线上的点, 所以 $\mathrm{MP}=\mathrm{MB}$, 即 $\mathrm{M}$ 满足 $M C+M B=M C+M P=10>B C$, 所以, $M$ 点的轨迹是以 $B, C$ 为焦点的粗圆, 且 $2 a=10,2 c=6$, 所以, $b^{2}=16$,故 M 点的轨迹方程是 $\frac{x^{2}}{25}+\frac{y^{2}}{16}=1$, 选 B。
<ImageHere>
【分析】典型题, 利用平面几何知识, 认识到 M 点满足的几何条件, 明确所求轨迹为粗圆, 进一步求得几何量 a,b,c, 达到解题目的。
4. 答案:C
【解析】【解答】因为抛物线 $\mathrm{y}^{2}=2 \mathrm{Px}$, 过点 A $(2,4), \mathrm{F}$ 为焦点, 那么可知 $16=4 \mathrm{p}, \mathrm{p}=4$, 可知其方程为 $\mathrm{y}^{2}=8 \mathrm{x}$, 焦点 $(2,0)$ 准线 $\mathrm{x}=-2, \mathrm{~A}$ 到准线距离为 4 , 所以 $|A F|=4,|B F|=\sqrt{(8-2)^{2}+(-8-0)^{2}}=10$那么 $|A F|:|B F|=2: 5$ , 故选 C.
【分析】解决抛物线的问题, 一般都要考查其定义的运用, 也就是抛物线上任意一点到其焦点的距离等于其到准线的距离来表示焦半径的长度, 属于基础题。
|
20428
|
["9359.jpg"]
|
C
|
null
|
高二
|
<ImageHere>
|
A. $1: 4$
B. $1: 2$
C. 2: 5
D. 3: 8
|
解析几何
|
【解答】因为抛物线 $\mathrm{y}^{2}=2 \mathrm{Px}$, 过点 A $(2,4), \mathrm{F}$ 为焦点, 那么可知 $16=4 \mathrm{p}, \mathrm{p}=4$, 可知其方程为 $\mathrm{y}^{2}=8 \mathrm{x}$, 焦点 $(2,0)$ 准线 $\mathrm{x}=-2, \mathrm{~A}$ 到准线距离为 4 , 所以 $|A F|=4,|B F|=\sqrt{(8-2)^{2}+(-8-0)^{2}}=10$那么 $|A F|:|B F|=2: 5$ , 故选 C.【分析】解决抛物线的问题, 一般都要考查其定义的运用, 也就是抛物线上任意一点到其焦点的距离等于其到准线的距离来表示焦半径的长度, 属于基础题。
|
20429
|
[]
|
D
|
null
|
高二
|
抛物线 $y^{2}=2 x$ 的准线方程是( )
|
A. $y=\frac{1}{2}$
B. $y=-\frac{1}{2}$
C. $x=\frac{1}{2}$
D. $x=-\frac{1}{2}$
|
解析几何
|
答案:D
【解析】【解答】由抛物线方程 $\mathrm{y}^{2}=2 \mathrm{x}$, 则 $\frac{p}{2}=\frac{1}{2}$, 所以该抛物线的准线方程为 $x=-\frac{1}{2}$, 选 D.
|
20430
|
[]
|
D
|
null
|
高二
|
抛物线 $y^{2}=x$ 的准线方程为 ( )
|
A. $x=\frac{1}{2}$
B. $x=\frac{1}{4}$
C. $x=-\frac{1}{2}$
D. $x=-\frac{1}{4}$
|
解析几何
|
答案:D
【解析】【解答】抛物线 $y^{2}=x$ 的焦点在 $x$ 轴上, 且开口向右, $2 p=1, \therefore \frac{p}{2}=\frac{1}{4}, \therefore$ 抛物线 $y^{2}=x$的准线方程为 $x=-\frac{1}{4}$,故答案为: D.
【分析】由抛物线的方程求出 $\mathrm{p}$, 再得到准线方程.
|
20431
|
[]
|
A
|
null
|
高二
|
设 $\mathrm{F}_{1} 、 \mathrm{~F}_{2}$ 是双曲线 $\frac{x^{2}}{4}-y^{2}=1$ 的两个焦点, $\mathrm{P}$ 在双曲线上, 且满足 $\angle \mathrm{F}_{1} \mathrm{PF}_{2}=90^{\circ}$, 则 $\triangle \mathrm{PF}_{1} \mathrm{~F}_{2}$ 的面积是( )
|
A. 1
B. $\frac{\sqrt{5}}{2}$
C. 2
D. $\sqrt{5}$
|
解析几何
|
答案:A
【解析】【解答】设 $\left|\mathrm{PF}_{1}\right|=\mathrm{x},\left|\mathrm{PF}_{2}\right|=\mathrm{y}$, 根据根据双曲线性质可知 $\mathrm{x}-\mathrm{y}$ 的值, 再根据 $\angle \mathrm{F}_{1} \mathrm{PF}_{2}=90^{\circ}$, 求得 $\mathrm{x}^{2}+\mathrm{y}^{2}$ 的值, 进而根据 $2 \mathrm{xy}=x^{2}+y^{2}-(\mathrm{x}-\mathrm{y})^{2}$ 求得 $\mathrm{xy}$, 进而可求得 $\therefore \triangle \mathrm{F}_{1} \mathrm{PF}_{2}$ 的面积. 【解答】设 $\left|\mathrm{PF}_{1}\right|=\mathrm{x}$, $\left|\mathrm{PF}_{2}\right|=\mathrm{y}, \quad(\mathrm{x}>\mathrm{y})$, 根据双曲线性质可知 $\mathrm{x}-\mathrm{y}=4, \because \angle \mathrm{F}_{1} \mathrm{PF}_{2}=90^{\circ}, \quad \therefore x^{2}+y^{2}=20, \quad \therefore 2 \mathrm{xy}=x^{2}+y^{2}$.
$(\mathrm{x}-\mathrm{y})^{2}=4, \quad \therefore \mathrm{xy}=2, \quad \therefore \triangle \mathrm{F}_{1} \mathrm{PF}_{2}$ 的面积为 ${ }^{\frac{1}{2} x y}=1$, 故选 $\mathrm{A}$
【分析】本题主要考查了双曲线的简单性质.要灵活运用双曲线的定义及焦距、实轴、虚轴等之间的关
|
20432
|
[]
|
A
|
null
|
高二
|
粗圆 ${ }^{\frac{x^{2}}{36}}+\frac{y^{2}}{9}=1$ 上有两个动点 $\mathrm{P} 、 \mathrm{Q}, \mathrm{E}(3,0), E P \perp E Q$, 则 $\overrightarrow{E P} \cdot \overrightarrow{Q P}_{\text {的最小值为 ( ) }}$
|
A. 6
B. $3-\sqrt{3}$
C. 9
D. $12-6 \sqrt{3}$
|
解析几何
|
答案:A
【解析】【解答】根据题意, 由于椭圆 $\frac{x^{2}}{36}+\frac{y^{2}}{9}=1$ 上有两个动点 $P 、 Q, E(3,0), E P \perp E Q$, $\mathrm{a}=6, \mathrm{~b}=3, \mathrm{c}=3 \sqrt{3}$, 那么结合粗圆的定义可知,
则 $\overline{E P} \cdot \overrightarrow{Q P}=\overrightarrow{E P} \cdot(\overline{E P}-\overline{E Q})=\overline{E P}^{2}-\overrightarrow{E P} \cdot \overline{E Q}=\overline{E P}^{2}$ 取得最小值, 即为两点距离的最小为
$\because \frac{x^{2}}{36}+\frac{y^{2}}{9}=1 \therefore \sqrt{(x-3)^{2}+\mathrm{y}^{2}}=\sqrt{(x-3)^{2}+9\left(1-\frac{x^{2}}{36}\right)}$ 故可知 $\overline{E P} \cdot \overline{Q P}$ 的最小值为 6 故答案为 A.
【分析】主要是考查了粗圆的方程与性质的运用, 属于基础题。
|
20451
|
[]
|
A
|
null
|
高二
|
若存在过点 $(1,0)$ 的直线与曲线 $y=x^{3}$ 和 $^{y=a x^{2}+\frac{15}{4} x-9}$ 都相切, 则 $\mathrm{a}=\quad$ ( )
|
A. $-1_{\text {或 }}-\frac{25}{64}$
B. -1 或 $\frac{21}{4}$
C. $-^{\frac{7}{4}}$ 或 $-\frac{25}{64}$
D. ${ }^{-\frac{7}{4}}$ 或 7
|
解析几何
|
答案:A
【解析】【解答】由 ${ }^{y=x^{3}}$ 求导得 $y^{\prime}=3 x^{2}$
设曲线 $y=x^{3}$ 上的任意一点 $\left(x_{0}, x_{0}{ }^{3}\right)$ 处的切线方程为 $y-x_{0}{ }^{3}=3 x_{0}{ }^{2}\left(x-x_{0}\right)$, 将点 $(1,0)$ 代入方程得 $x_{0}=0_{\text {或 }} x_{0}=\frac{3}{2}$.
(1)当 $x_{0}=0$ 时: 切线为 $y=0$, 所以 $a x^{2}+\frac{15}{4} x-9=0$ 仅有一解, 得 $a=-\frac{25}{64}$
(2) 当 $x_{0}=\frac{3}{2}$ 时: 切线为 $y=\frac{27}{4} x-\frac{27}{4}$, 由 $\left\{\begin{array}{l}y=\frac{27}{4} x-\frac{27}{4} \\ y=\alpha x^{2}+\frac{15}{4} x-9\end{array}\right.$ 得 $x^{2}-3 x-\frac{4}{9}=0$ 仅有一解, 得 $a=-1$.
综上知 $a=-1$ 或 $a=-\frac{25}{64}$. 选 A.
|
20461
|
[]
|
A
|
null
|
高二
|
若存在过点 $(1,0)$ 的直线与曲线 $y=x^{3}$ 和 $y=a x^{2}+\frac{15}{4} x-9$ 都相切, 则 $\mathrm{a}=\quad(\quad)$
|
A. -1 或 $-\frac{25}{64}$
B. -1 或 $\frac{21}{4}$
C. $-\frac{7}{4}$ 或 $-\frac{25}{64}$
D. $-\frac{7}{4}$ 或 7
|
解析几何
|
答案:A 解: 由 $y=x^{3}$ 求导得 $y^{\prime}=3 x^{2}$, 设曲线 $y=x^{3}$ 上的任意一点 $\left(x_{0}, x_{0}^{3}\right)$ 处的切线方程为 $y-x_{0}^{3}=3 x_{0}^{2}\left(x-x_{0}\right)$, 将点 $(1,0)$ 代入方程得 $x_{0}=0$ 或 $x_{0}=\frac{3}{2}$.
(1)当 $x_{0}=0$ 时: 切线为 $y=0$, 所以 $a x^{2}+\frac{15}{4} x-9=0$ 仅有一解, 得 $a=-\frac{25}{64}$
(2) 当 $x_{0}=\frac{3}{2}$ 时: 切线为 $y=\frac{27}{4} x-\frac{27}{4}$, 由 $\left\{\begin{array}{l}y=\frac{27}{4} x-\frac{27}{4} \\ y=a x^{2}+\frac{15}{4} x-9\end{array}\right.$ 得 $a x^{2}-3 x-\frac{4}{9}=0$ 仅有一解, 得 $a=-1$. 综上知 $a=-1$ 或 $a=-\frac{25}{64}$. 选 A.
|
19006
|
[]
|
A
|
null
|
高二
|
(2018 四川成都七中 3 月模拟) 在 $\triangle A B C$ 中, 角 $B$ 为 $\frac{3 \pi}{4}, B C$ 边上的高恰为 $B C$ 边长的一半,则 $\cos A=$
|
A. $\frac{2 \sqrt{5}}{5}$
B. $\frac{\sqrt{5}}{5}$
C. $\frac{2}{3}$
D. $\frac{\sqrt{5}}{3}$
|
度量几何学
|
作 $A H \perp B C$, 垂足点 $H$ 在 $C B$ 的延长线上, $\triangle A H B$ 为等腰直角三角形, 设 $B C=2 a$, 则 $A B=\sqrt{2} a, A H=a, C H=3 a$, 由勾股定理得 $A C=\sqrt{10} a$, 由余弦定理得 $\cos A=\frac{2 a^{2}+10 a^{2}-4 a^{2}}{2 \times \sqrt{2} a \times \sqrt{10} a}=\frac{2 \sqrt{5}}{5}$, 故选 A.
|
19015
|
[]
|
B
|
null
|
高二
|
(2018 合肥三模)若 $\triangle A B C$ 的三个内角 $A, B, C$ 所对的边分别是 $a, b, c$, 若 $\sin (C-A)=\frac{1}{2} \sin B$, 且 $b=4$, 则 $c^{2}-a^{2}=$
|
A. 10
B. 8
C. 7
D. 4
|
度量几何学
|
$\sin (C-A)=\frac{1}{2} \sin B=\frac{1}{2} \sin (A+C)$ ,
即 $2 \sin C \cos A-2 \cos C \sin A=\sin A \cos C+\cos A \sin C$, 即 $\sin C \cos A=3 \sin A \cos C$, 由正弦
定理和余弦定理得: $c \cdot \frac{b^{2}+c^{2}-a^{2}}{2 b c}=3 a \cdot \frac{a^{2}+b^{2}-c^{2}}{2 a b}$, 即 $b^{2}+c^{2}-a^{2}=3 a^{2}+3 b^{2}-3 c^{2}$,
即 $4 c^{2}-4 a^{2}=2 b^{2}=2 \times 16=32$, 则 $c^{2}-a^{2}=8$, 故选 B.
|
19022
|
[]
|
C
|
null
|
高二
|
(2018:浙江高考模拟)在 $\triangle A B C$ 中, 内角 $A, B, C$ 所对的边分别是 $a, b, c$, 若 $a \sin A=b \sin B+(c-b) \sin C$, 则角 $A$ 的值为 ( )
|
A. $\frac{\pi}{6}$
B. $\frac{\pi}{4}$
C. $\frac{\pi}{3}$
D. $\frac{2 \pi}{3}$
|
度量几何学
|
在 $\triangle A B C$ ,因为 $a \sin A=b \sin B+(c-b) \sin C$
由正弦定理可化简得 $a^{2}=b^{2}+c^{2}-b c$ ,所以 $b^{2}+c^{2}-a^{2}=b c$,
由余弦定理得 $\cos A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}=\frac{1}{2}$, 从而 $A=\frac{\pi}{3}$, 故选 C.
|
19034
|
[]
|
C
|
null
|
高二
|
(2018 全国卷III) $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 若 $\triangle A B C$ 的面积为
$$
\frac{a^{2}+b^{2}-c^{2}}{4}
$$
则 $C=(\quad)$
|
A. $\frac{\pi}{2}$
B. $\frac{\pi}{3}$
c. $\frac{\pi}{4}$
D. $\frac{\pi}{6}$
|
度量几何学
|
根据题意及三角形的面积公式知 $\frac{1}{2} a b \sin C=\frac{a^{2}+b^{2}-c^{2}}{4}$,
所以 $\sin C=\frac{a^{2}+b^{2}-c^{2}}{2 a b}=\cos C$, 所以在 $\triangle A B C$ 中, $C=\frac{\pi}{4}$. 故选 C.
|
19035
|
[]
|
A
|
null
|
高二
|
(2016 年天津) 在 $\triangle A B C$ 中, 若 $A B=\sqrt{13}, B C=3, \angle C=120^{\circ}$, 则 $A C=$
|
A. 1
B. 2
C. 3
D. 4
|
度量几何学
|
由余弦定理得 $13=9+A C^{2}+3 A C \Rightarrow A C=1$, 选 $\mathrm{A}$.
|
18115
|
[]
|
C
|
null
|
高二
|
已知扇形的周长是 6 , 面积是 2 , 则扇形的圆心角的弧度数 $\alpha$ 是 $($ )
|
A. 1
B. 4
C. 1 或 4
D. 2 或 4
|
度量几何学
|
解析:设此扇形的半径为 $r$ ,弧长为 $l$ ,
则 $\left\{\begin{array}{l}2 r+l=6 , \\ \frac{1}{2} r l=2 ,\end{array}\right.$ 解得 $\left\{\begin{array}{l}r=1 , \\ l=4\end{array}\right.$ 或 $\left\{\begin{array}{l}r=2 , \\ l=2 .\end{array}\right.$
从而 $\alpha=\frac{l}{r}=\frac{4}{1}=4$ 或 $\alpha=\frac{l}{r}=\frac{2}{2}=1$.
答案: C
|
18141
|
[]
|
D
|
null
|
高二
|
若 $\theta \in\left[\frac{\pi}{4}, \frac{\pi}{2}\right], \sin 2 \theta=\frac{3 \sqrt{7}}{8}$, 则 $\sin \theta=$
|
A.$\frac{3}{5} \text { B. } \frac{4}{5} \text { C. } \frac{\sqrt{7}}{4} \text { D. } \frac{3}{4}$
|
度量几何学
|
解析: $\because \theta \in\left[\frac{\pi}{4} , \frac{\pi}{2}\right], \therefore 2 \theta \in\left[\frac{\pi}{2} , \pi\right]$,
$\therefore \cos 2 \theta=-\sqrt{1-\sin ^{2} 2 \theta}=-\sqrt{1-\left(\frac{3 \sqrt{7}}{8}\right)^{2}}=-\frac{1}{8}$.
$\therefore \sin ^{2} \theta=\frac{1-\cos 2 \theta}{2}=\frac{1-\left(-\frac{1}{8}\right)}{2}=\frac{9}{16}, \therefore \sin \theta=\frac{3}{4}$.
答案: D
|
18143
|
[]
|
C
|
null
|
高二
|
已知等腰三角形顶角的余弦值等于 $\frac{4}{5}$, 则这个三角形底角的正弦值为 ( )
|
A. $\frac{\sqrt{10}}{10}$
B. $-\frac{\sqrt{10}}{10}$
C. $\frac{3 \sqrt{10}}{10}$
D. $-\frac{3 \sqrt{10}}{10}$
|
度量几何学
|
解析: 设这个等腰三角形的顶角为 $2 \alpha$ ,底角为 $\beta$ ,
则 $2 \alpha+2 \beta=\pi$ 且 $\cos 2 \alpha=\frac{4}{5} , \therefore \alpha+\beta=\frac{\pi}{2}$.
$\therefore \sin \beta=\sin \left(\frac{\pi}{2}-\alpha\right)=\cos \alpha=\sqrt{\frac{1+\cos 2 \alpha}{2}}=\frac{3 \sqrt{10}}{10}$.
答案: C
|
18158
|
[]
|
C
|
null
|
高二
|
某人在无风条件下骑自行车的速度为 $v_{1}$, 风速为 $v_{2}\left(\left|v_{1}\right|>\left|v_{2}\right|\right)$, 则逆风行驶的速度的大小为
|
A. $v_{1}-v_{2}$
B. $v_{1}+v_{2}$
C. $\left|v_{1}\right|-\left|v_{2}\right|$
D. $\frac{v_{1}}{v_{2}}$
|
度量几何学
|
解析:题目要求的是速度的大小,即向量的大小,而不是求速度,速度是向量,速度的大小是实数.
答案: C
|
18165
|
[]
|
C
|
null
|
高二
|
设 $\boldsymbol{a}, \boldsymbol{b}$ 是两个非零向量, 下列说法正确的是
|
A. 若 $|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}|-|\boldsymbol{b}|$, 则 $\boldsymbol{a} \perp \boldsymbol{b}$
B. 若 $\boldsymbol{a} \perp \boldsymbol{b}$, 则 $|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}|-|\boldsymbol{b}|$
C. 若 $|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}|-|\boldsymbol{b}|$, 则存在实数 $\lambda$, 使得 $\boldsymbol{b}=\lambda \boldsymbol{a}$
D. 若存在实数 $\lambda$, 使得 $\boldsymbol{b}=\lambda \boldsymbol{a}$, 则 $|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}|-|\boldsymbol{b}|$
|
度量几何学
|
解析: 若 $|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}|-|\boldsymbol{b}|$, 则 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 共线,且 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 反向,故选项 A, B 不对,选项 C 正确. 若 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 同向,则 $|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}|+|\boldsymbol{b}|$ ,故选项 D 不对.
答案: C
|
18756
|
[]
|
D
|
null
|
高二
|
在 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别是 $a, b, c$, 若 $A: B: C=1: 2: 3$, 则 $a: b: c$ 等于( )
|
A. $1: 2: 3$
B. $2: 3: 4$
C. $3: 4: 5$
D. $1: \sqrt{3}: 2$
|
度量几何学
| |
19049
|
["9190.jpg"]
|
D
|
null
|
高二
|
如图, 在 $\triangle A B C$ 中, $D$ 是边 $A C$ 上的点, 且 $A B=A D, 2 A B=\sqrt{3} B D, B C=2 B D$, 则 $\sin C$的值为 ( )
<ImageHere>
|
A. $\frac{\sqrt{3}}{3}$
B. $\frac{\sqrt{3}}{6}$
C. $\frac{\sqrt{6}}{3}$
D. $\frac{\sqrt{6}}{6}$
|
度量几何学
|
设 $A B=c$, 则 $A D=c, B D=\frac{2 c}{\sqrt{3}}, B C=\frac{4 c}{\sqrt{3}}$, 在 $\triangle A B D$ 中, 由余弦定理得 $\cos A=\frac{c^{2}+c^{2}-\frac{4}{3} c^{2}}{2 c^{2}}=\frac{1}{3}$, 则 $\sin A=\frac{2 \sqrt{2}}{3}$, 在 $\triangle A B C$ 中,
由正弦定理得 $\frac{C}{\sin C}=\frac{B C}{\sin A}=\frac{\frac{4 C}{\sqrt{3}}}{\frac{2 \sqrt{2}}{3}}$
|
19050
|
[]
|
C
|
null
|
高二
|
在 $\triangle A B C$ 中, $\cos A: 2 \cos B: 3 \cos C=2: 4: 21$, 则 $\cos C=(\quad)$
|
A. $\frac{7}{12}$
B. $\frac{7}{10}$
C. $\frac{7}{8}$
D. $\frac{7}{16}$
|
度量几何学
|
析】由已知得: $\frac{\cos A}{\cos B}=1$, 所以 $A=B$ 是等腰三角形, $\frac{\cos \mathrm{A}}{3 \cos C}=\frac{2}{21} \Rightarrow 7 \cos A=2 \cos C \Rightarrow 7 \cos \left(\frac{\pi-C}{2}\right)=2 \cos C$ 整理得: $4 \sin ^{2} \frac{C}{2}+7 \sin \frac{C}{2}-1=0$ 解之得: $\sin \frac{C}{2}=\frac{1}{4}$ 所以 $\cos C=1-2 \sin ^{2} \frac{C}{2}=\frac{7}{8}$, 解得 $\sin C=\frac{\sqrt{6}}{6}$.
|
19075
|
[]
|
A
|
null
|
高二
|
在 $\triangle A B C$ 中, 角 $B$ 为 $\frac{3 \pi}{4}, B C$ 边上的高恰为 $B C$ 边长的一半, 则 $\cos A=(\quad)$
|
A. $\frac{2 \sqrt{5}}{5}$
B. $\frac{\sqrt{5}}{5}$
C. $\frac{2}{3}$
D. $\frac{\sqrt{5}}{3}$
|
度量几何学
|
作 $A H \perp B C$, 垂足点 $H$ 在 $C B$ 的延长线上, $\triangle A H B$ 为等腰直角三角形, 设 $B C=2 a$, 则 $A B=\sqrt{2} a, A H=a, C H=3 a$, 由勾股定理得 $A C=\sqrt{10} a$, 由余弦定理得 $\cos A=\frac{2 a^{2}+10 a^{2}-4 a^{2}}{2 \times \sqrt{2} a \times \sqrt{10} a}=\frac{2 \sqrt{5}}{5}$, 故选 A.
|
18770
|
[]
|
B
|
null
|
高二
|
在 $\triangle A B C$ 中, $a=2, b=\sqrt{3}, c=1$, 则最小角为 $(\quad)$
|
A. $\frac{\pi}{12}$
B. $\frac{\pi}{6}$
C. $\frac{\pi}{4}$
D. $\frac{\pi}{3}$
|
度量几何学
|
$[\because a>b>c, \therefore C$ 最小.
$\because \cos C=\frac{a^{2}+b^{2}-c^{2}}{2 a b}=\frac{2^{2}+(\sqrt{3})^{2}-1^{2}}{2 \times 2 \times \sqrt{3}}=\frac{\sqrt{3}}{2}$,
又 $\because 0<C<\pi, \quad \therefore C=\frac{\pi}{6}$.
|
18791
|
[]
|
D
|
null
|
高二
|
在 $\triangle A B C$ 中, $B=30^{\circ}, A B=\sqrt{3}, A C=1$, 则 $\triangle A B C$ 的面积是( )
|
A. $\frac{\sqrt{3}}{4}$
B. $\frac{\sqrt{3}}{2}$
C. $\sqrt{3}$ 或 $\frac{\sqrt{3}}{2}$
D. $\frac{\sqrt{3}}{2}$ 或 $\frac{\sqrt{3}}{4}$
|
度量几何学
|
[由余弦定理 $A C^{2}=A B^{2}+B C^{2}-2 A B \cdot B C \cos B$,
$\therefore 1^{2}=(\sqrt{3})^{2}+B C^{2}-2 \times \sqrt{3} \times B C \times \frac{\sqrt{3}}{2}$.
整理得: $B C^{2}-3 B C+2=0$.
$\therefore B C=1$ 或 2 .
当 $B C=1$ 时, $S_{\triangle A B C}=\frac{1}{2} A B \cdot B C \sin B=\frac{1}{2} \times \sqrt{3} \times 1 \times \frac{1}{2}=\frac{\sqrt{3}}{4}$.
当 $B C=2$ 时, $S_{\triangle A B C}=\frac{1}{2} A B \cdot B C \sin B=\frac{1}{2} \times \sqrt{3} \times 2 \times \frac{1}{2}=\frac{\sqrt{3}}{2}$.]
|
19086
|
[]
|
A
|
null
|
高二
|
已知 $\frac{\sin \theta+\cos \theta}{\sin \theta-2 \cos \theta}=\frac{1}{2}$, 则 $\tan \theta$ 的值为 ( )
|
-4
B. $-\frac{1}{4}$
C. $\frac{1}{4}$
D. 4
|
度量几何学
|
由题 $\frac{\sin \theta+\cos \theta}{\sin \theta-2 \cos \theta}=\frac{1}{2}=\frac{\tan \theta+1}{\tan \theta-2}$, 解得 $\tan \theta=-4$. 故选 A.
|
19096
|
[]
|
A
|
null
|
高二
|
函数 $f(x)=\frac{1}{3} \tan \left(\frac{\pi}{2} x+\frac{\pi}{4}\right)$ 单调递增区间
|
A. $\left(2 k-\frac{3}{2}, 2 k+\frac{1}{2}\right) k \in Z$
B. $\left(2 k-\frac{1}{2}, 2 k+\frac{1}{2}\right), k \in Z$
C. $\left(4 k-\frac{1}{2}, 4 k+\frac{1}{2}\right), k \in Z$
D. $\left(4 k-\frac{3}{2}, 4 k+\frac{1}{2}\right), k \in Z$
|
度量几何学
|
$-\frac{\pi}{2}+k \pi<\frac{\pi}{2} x+\frac{\pi}{4}<\frac{\pi}{2}+k \pi$, 所以 $-\frac{3}{2}+2 k<x<\frac{1}{2}+2 k$. 故选 A
|
17493
|
[]
|
A
|
null
|
高二
|
$\cos 285^{\circ}$ 等于 ( A )
|
A. $\frac{\sqrt{6}-\sqrt{2}}{4}$
B. $\frac{\sqrt{6}+\sqrt{2}}{4}$
C. $\frac{\sqrt{2}-\sqrt{6}}{4}$
D. $-\frac{\sqrt{2}+\sqrt{6}}{4}$
|
度量几何学
|
[解析] $\cos 285^{\circ}=\cos 75^{\circ}=\cos \left(45^{\circ}+30^{\circ}\right)=\frac{\sqrt{6}-\sqrt{2}}{4}$.
|
17494
|
[]
|
D
|
null
|
高二
|
在 $\triangle A B C$ 中, 若 $\sin A \sin B<\cos A \cos B$, 则 $\triangle A B C$ 是( D )
|
A. 等边三角形
B. 直角三角形
C. 锐角三角形
D. 钝角三角形
|
度量几何学
|
[解析] 由题意, 得 $\cos A \cos B-\sin A \sin B>0$.
即 $\cos (A+B)>0,-\cos C>0, \cos C<0$.
又 $0<C<\pi$, 故 $\frac{\pi}{2}<C<\pi, \triangle A B C$ 为钝角三角形.
|
17497
|
[]
|
B
|
null
|
高二
|
若 $\sin \alpha \cdot \sin \beta=1$, 则 $\cos (\alpha-\beta)$ 的值为( B )
|
A. 0
B. 1
C. $\pm 1$
D. -1
|
度量几何学
|
析] $\because \sin \alpha \sin \beta=1, \therefore\left\{\begin{array}{l}\sin \alpha=-1 \\ \sin \beta=-1\end{array}\right.$ 或 $\left\{\begin{array}{l}\sin \alpha=1 \\ \sin \beta=1\end{array}\right.$,
由 $\cos ^{2} \alpha+\sin ^{2} \alpha=1$ 得 $\cos \alpha=0$,
$\therefore \cos (\alpha-\beta)=\cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta=0+1=1$.
|
17514
|
[]
|
A
|
null
|
高二
|
已知 $\sin \alpha=\frac{\sqrt{5}}{5}$, 则 $\sin ^{4} \alpha-\cos ^{4} \alpha$ 的值为( )
|
A. $-\frac{3}{5}$
B. $-\frac{1}{5}$
C. $\frac{1}{5}$
D. $\frac{3}{5}$
|
度量几何学
|
[解析] $\sin ^{4} \alpha-\cos ^{4} \alpha=-\left(\sin ^{2} \alpha+\cos ^{2} \alpha\right)\left(\cos ^{2} \alpha-\sin ^{2} \alpha\right)=-\cos 2 \alpha=2 \sin ^{2} \alpha-1=-\frac{3}{5}$.
|
17516
|
[]
|
A
|
null
|
高二
|
已知 $\sin 2 \alpha=\frac{2}{3}$, 则 $\cos ^{2}\left(\alpha+\frac{\pi}{4}\right)=(\quad)$
|
A. $\frac{1}{6}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. $\frac{2}{3}$
|
度量几何学
|
析]本题考查半角公式及诱导公式.
由倍角公式可得, $\cos ^{2}\left(\alpha+\frac{\pi}{4}\right)=\frac{1+\cos \left(2 \alpha+\frac{\pi}{2}\right)}{2}=\frac{1-\sin 2 \alpha}{2}=\frac{1-\frac{2}{3}}{2}=\frac{1}{6}$, 故选 A.
|
17356
|
[]
|
D
|
null
|
高二
|
已知 $\alpha$ 是第二象限角, 且 $\cos \alpha=-\frac{12}{13}$, 则 $\tan \alpha$ 的值是 $(\quad)$
|
A. $\frac{12}{13}$
B. $-\frac{12}{13}$
C. $\frac{5}{12}$
D. $-\frac{5}{12}$
|
度量几何学
|
$\because \alpha$ 为第二象限角, $\therefore \sin \alpha=\sqrt{1-\cos ^{2} \alpha}=\sqrt{1-\left(-\frac{12}{13}\right)^{2}}=\frac{5}{13}, \therefore \tan \alpha=\frac{\sin \alpha}{\cos \alpha}=\frac{\frac{5}{13}}{-\frac{12}{13}}=-\frac{5}{12}$.
答案: D
|
17529
|
[]
|
D
|
null
|
高二
|
最大值为 $\frac{1}{2}$, 最小正周期为 $\frac{2 \pi}{3}$, 初相为 $\frac{\pi}{6}$ 的函数表达式是( )
|
A. $ y=\frac{1}{2} \sin \left(\frac{x}{3}+\frac{\pi}{6}\right)$
B $\cdot y=\frac{1}{2} \sin \left(\frac{x}{3}-\frac{\pi}{6}\right)$
C $\cdot y=\frac{1}{2} \sin \left(3 x-\frac{\pi}{6}\right)$
D $\cdot y=\frac{1}{2} \sin \left(3 x+\frac{\pi}{6}\right)$
|
度量几何学
|
解析: 由最小正周期为 $\frac{2 \pi}{3}$, 排除 A、B; 由初相为 $\frac{\pi}{6}$, 排除 C.
## 答案: D
|
17557
|
[]
|
B
|
null
|
高二
|
设 $\alpha \in\left(0, \frac{\pi}{2}\right)$, 若 $\sin \alpha=\frac{3}{5}$, 则 $\sqrt{2} \cos \left(\alpha+\frac{\pi}{4}\right)$ 等于(B )
|
A. $\frac{7}{5}$
B. $\frac{1}{5}$
C. $-\frac{7}{5}$
D. $-\frac{1}{5}$
|
度量几何学
|
[解析] $\sqrt{2} \cos \left(\alpha+\frac{\pi}{4}\right)=\sqrt{2}\left(\cos \alpha \cdot \frac{\sqrt{2}}{2}-\sin \alpha \cdot \frac{\sqrt{2}}{2}\right)=\frac{4}{5}-\frac{3}{5}=\frac{1}{5}$.
|
17559
|
[]
|
C
|
null
|
高二
|
$\sqrt{3} \cos \frac{\pi}{12}-\sin \frac{\pi}{12}$ 的值是 (C)
|
A. 0
B. $\sqrt{2}$
C. $-\sqrt{2}$
D. 2
|
度量几何学
|
[解析] $\sqrt{3} \cos \frac{\pi}{12}-\sin \frac{\pi}{12}=2\left(\frac{\sqrt{3}}{2} \cos \frac{\pi}{12}-\frac{1}{2} \sin \frac{\pi}{12}\right)=2\left(\sin \frac{\pi}{3} \cos \frac{\pi}{12}-\cos \frac{\pi}{3} \sin \frac{\pi}{12}\right)=2 \sin \left(\frac{\pi}{3}-\frac{\pi}{12}\right)=2 \sin \frac{\pi}{4}=\sqrt{2}$.
|
17579
|
[]
|
C
|
null
|
高二
|
已知 $A_{1}, A_{2}, \cdots A_{n}$ 为凸多边形的内角, 且 $\lg \sin A_{1}+\lg \sin A_{2}+\cdots+\lg \sin A_{n}=0$, 则这个多边形是 $(\quad)$
|
A. 正六边形
B. 梯形
$\mathrm{C} \cdot$ 矩形
D. 含锐角菱形
|
度量几何学
|
解析:由题意,得 $\sin A_{1} \cdot \sin A_{2} \cdot \cdots \cdot \sin A_{n}=1$,
$\therefore \sin A_{1}=\sin A_{2}=\cdots=\sin A_{n}=1$,
$\therefore A_{1}=A_{2}=\cdots=A_{n}=90^{\circ}$.
根据多边形的内角和得 $n \times 90^{\circ}=(n-2) \times 180^{\circ}$,
解得 $n=4$.
答案: C
|
17471
|
[]
|
B
|
null
|
高二
|
$ \tan \frac{7 \pi}{6}=(\quad)$
|
A.$\frac{\sqrt{3}}{3}$B. $\frac{\sqrt{3}}{3} \\$
C. $-\sqrt{3}$ D. $ \sqrt{3}$
|
度量几何学
|
解析: $\tan \frac{7 \pi}{6}=\tan \left(\pi+\frac{\pi}{6}\right)=\tan \frac{\pi}{6}=\frac{\sqrt{3}}{3}$.
答案: B
|
17475
|
[]
|
C
|
null
|
高二
|
给出下列各函数值:
(1) $\sin \left(-1000^{\circ}\right)$; (2) $\cos \left(-2200^{\circ}\right)$; (3) $\tan (-10)$; (4) $\frac{\sin \frac{7 \pi}{10} \cos \pi}{\tan \frac{17 \pi}{9}}$. 其中符号为负的是( )
|
A.(1) B. (2)
C. (3) D. (4)
|
度量几何学
|
解析: $\sin \left(-1000^{\circ}\right)=\sin 80^{\circ}>0$;
$\cos \left(-2200^{\circ}\right)=\cos \left(-40^{\circ}\right)=\cos 40^{\circ}>0 ;$
$\tan (-10)=\tan (3 \pi-10)<0$;
$\frac{\sin \frac{7 \pi}{10} \cos \pi}{\tan \frac{17 \pi}{9}}=\frac{-\sin \frac{7 \pi}{10}}{\tan \frac{17 \pi}{9}}$
$\because \sin \frac{7 \pi}{10}>0, \tan \frac{17 \pi}{9}<0, \therefore$ 原式>
|
17606
|
[]
|
C
|
null
|
高二
|
化简 $\left(\sin \frac{\alpha}{2}+\cos \frac{\alpha}{2}\right)^{2}+2 \sin ^{2}\left(\frac{\pi}{4}-\frac{\alpha}{2}\right)$ 得( )
|
A.$ 2+\sin \alpha$
B. $2+\sqrt{2} \sin \left(\alpha-\frac{\pi}{4}\right)$
$\mathrm{C} \cdot 2$
D. $2+\sqrt{2} \sin \left(\alpha+\frac{\pi}{4}\right)$
|
度量几何学
|
解析: 原式 $=1+2 \sin \frac{\alpha}{2} \cos \frac{\alpha}{2}+1-\cos \left[2\left(\frac{\pi}{4}-\frac{\alpha}{2}\right)\right]=2+\sin \alpha-\cos \left(\frac{\pi}{2}-\alpha\right)=2+\sin \alpha-\sin \alpha=2$.
答案: C
|
19105
|
[]
|
B
|
null
|
高二
|
中国传统折扇文化有着极其深厚的底蕴, 一般情况下, 折扇可看作是由从一个圆面中剪下的扇形制作而
成, 设扇形的面积为 $S_{1}$, 圆面中剩余部分的面积为 $S_{2}$, 当 $S_{1}$ 与 $S_{2}$ 的比值为 $\frac{\sqrt{5}-1}{2} \approx 0,.618$ (黄金分割比)时,
扇面看上去形状较为美观,那么此时扇形的圆心角的度数约为()
|
A. $127,.50^{\circ}$
B. $137,.50^{\circ}$
C. $147,.50^{\circ}$
D. $150,.50^{\circ}$
|
度量几何学
|
$\frac{x}{360-x}=0,.618, x=137,.50$
|
19116
|
["9199.jpg"]
|
D
|
null
|
高二
|
(2011 天津) 如图, 在 $\triangle A B C$ 中, $D$ 是边 $A C$ 上的点, 且 $A B=A D, 2 A B=\sqrt{3} B D, B C=2 B D$,则 $\sin C$ 的值为 ( )
<ImageHere>
|
A. $\frac{\sqrt{3}}{3}$
B. $\frac{\sqrt{3}}{6}$
c. $\frac{\sqrt{6}}{3}$
D. $\frac{\sqrt{6}}{6}$
|
度量几何学
|
设 $A B=c$, 则 $A D=c, B D=\frac{2 c}{\sqrt{3}}, B C=\frac{4 c}{\sqrt{3}}$, 在 $\triangle A B D$ 中, 由余弦定理得 $\cos A=\frac{c^{2}+c^{2}-\frac{4}{3} c^{2}}{2 c^{2}}=\frac{1}{3}$, 则 $\sin A=\frac{2 \sqrt{2}}{3}$, 在 $\triangle A B C$ 中,
由正弦定理得 $\frac{c}{\sin C}=\frac{B C}{\sin A}=\frac{\frac{4 c}{\sqrt{3}}}{\frac{2 \sqrt{2}}{3}}$, 解得 $\sin C=\frac{\sqrt{6}}{6}$.
|
19157
|
["9203.jpg"]
|
C
|
null
|
高二
|
已知函数 $f(x)=2 \sin (\omega x+\varphi)(\omega>0,|\varphi|<\pi)$ 的部分图像如右图所示, 且 $A\left(\frac{\pi}{2}, 1\right), B(\pi,-1)$, 则 $\varphi$ 的值为 ()
|
A. $\frac{5 \pi}{6}$\nB. $\frac{\pi}{6}$\nC. $-\frac{5 \pi}{6}$\nD. $-\frac{\pi}{6}$<ImageHere>
|
度量几何学
|
由已知得: $T=2 \pi, \omega=1$, 图像经过 $A\left(\frac{\pi}{2}, 1\right), B(\pi,-1) \varphi=-\frac{5 \pi}{6}$
|
19152
|
[]
|
C
|
null
|
高二
|
(2018 辽宁朝阳三模) 已知函数 $f(x)=\sin \left(\omega x+\frac{\pi}{3}\right)(\omega>0), f\left(\frac{\pi}{6}\right)=f\left(\frac{\pi}{3}\right)$, 且 $f(x)$ 在区间 $\left(\frac{\pi}{6}, \frac{\pi}{3}\right)$ 上有最小值, 无最大值, 则 $\omega$ 的值为 ( )
|
A. $\frac{2}{3}$
B. $\frac{11}{3}$
C. $\frac{14}{3}$
D. $\frac{7}{3}$
|
度量几何学
|
因为 $f(x)=\sin \left(\omega x+\frac{\pi}{3}\right), f\left(\frac{\pi}{6}\right)=f\left(\frac{\pi}{3}\right)$, 又 $f(x)$ 在区间 $\left(\frac{\pi}{6}, \frac{\pi}{3}\right)$ 上有最小值, 无最大值,所以 $f(x)$ 在 $\frac{1}{2}\left(\frac{\pi}{6}+\frac{\pi}{3}\right)=\frac{\pi}{4}$ 处取得最小值, 所以 $\omega \cdot \frac{\pi}{4}+\frac{\pi}{3}=2 k \pi-\frac{\pi}{2}$, 得 $\omega=8 k-\frac{10}{3}(k \in Z)$,当 $k=2$ 时, $\omega=\frac{28}{3}$, 此时函数 $f(x)$ 在区间 $\left(\frac{\pi}{6}, \frac{\pi}{3}\right)$ 内存在最大值, 当 $k=1$ 时, $\omega=\frac{14}{3}$ 符合题意.故选 C.
|
17733
|
[]
|
D
|
null
|
高二
|
下列说法中, 正确的是
|
A. 第二象限的角都是针角\n\nB. 第二象限角大于第一象限的角\n\nC. 若角 $\alpha$ 与角 $\beta$ 不相等, 则 $\alpha$ 与 $\beta$ 的终边不可能重合\n\nD. 若角 $\alpha$ 与角 $\beta$ 的终边在一条直线上, 则 $\alpha-\beta=k \cdot 180^{\circ}(k \in \mathbf{Z})$\n\n
|
度量几何学
|
D
|
17720
|
[]
|
B
|
null
|
高二
|
若 $\varphi$ 是第二象限角, 则 $\frac{\varphi}{2}$ 和 $90^{\circ}-\varphi$ 都不是
|
A. 第一象限角
B. 第二象限角
C. 第三象限角
D. 第四象限角
|
度量几何学
|
解析: $\because \varphi$ 是第二象限角,
$\therefore k \cdot 360^{\circ}+90^{\circ}<\varphi<k \cdot 360^{\circ}+180^{\circ}, k \in \mathbf{Z}$,
$\therefore k \cdot 180^{\circ}+45^{\circ}<\frac{\varphi}{2}<k \cdot 180^{\circ}+90^{\circ}, \quad k \in \mathbf{Z}$,
即 $\frac{\varphi}{2}$ 是第一或第三象限角.
而一 $\varphi$ 显然是第三象限角,
$\therefore 90^{\circ}-\varphi$ 是第四象限角. 故选 B.
答案: B
|
17725
|
[]
|
C
|
null
|
高二
|
在(1) $160^{\circ}$; (2) $480^{\circ}$; (3) $-960^{\circ}$; (4) $1530^{\circ}$ 这四个角中, 属于第二象限角的是 ( )
|
A. (1)
B. (1)(2)
C. (1)(2)(3)
D. (1)(2)(3)(4)
|
度量几何学
| |
17726
|
[]
|
A
|
null
|
高二
|
下列各角中, 与 $60^{\circ}$ 角终边相同的角是
|
A. $-300^{\circ}$
B. $-60^{\circ}$
C. $600^{\circ}$
D. $1380^{\circ}$
|
度量几何学
| |
17728
|
[]
|
B
|
null
|
高二
|
已知 $A=\{$ 第一象限角 $\}, B=\{$ 锐角 $\}, C=\left\{\right.$ 小于 $90^{\circ}$ 的角 $\}$, 则 $A, B, C$ 关系正确的是
|
A. $B=A \cap C$
B. $B \cup C=C$
C. $A C$
D. $A=B=C$
|
度量几何学
| |
19648
|
[]
|
A
|
null
|
高二
|
设 $\triangle A B C$ 的内角 $A, B, C$ 所对边分别为 $a, b, c$ 若 $a=3, b=\sqrt{3}, A=\frac{\pi}{3}$, 则 $B=(\quad)$
|
A. $\frac{\pi}{6}$
B. | |
| :---: |
| $\frac{5 \pi}{6}$ |
C. $\frac{\pi}{6}$ 或 $\frac{5 \pi}{6}$
D. $\frac{2 \pi}{3}$
|
度量几何学
|
$: \mathrm{a}=3, \quad b=\sqrt{3}, A=\frac{\pi}{3}, \therefore$ 由正弦定理可得 $\sin \mathrm{B}=\frac{b \sin A}{a}=\frac{\sqrt{3} \times \frac{\sqrt{3}}{2}}{3}=\frac{1}{2}$, $\because \mathrm{a}>\mathrm{b}, \therefore \mathrm{B}$ 为锐角, $\mathrm{B}=\frac{\pi}{6}$.
|
19656
|
[]
|
B
|
null
|
高二
|
在 $\triangle A B C$ 中, $a=2 \sqrt{3}, c=2 \sqrt{2}, A=60^{\circ}$, 则 $C=(\quad)$
|
A. $30^{\circ}$
B. $45^{\circ}$
C. $45^{\circ}$ 或 $135^{\circ}$
D. $60^{\circ}$
|
度量几何学
|
$: \because \mathrm{a}=2 \sqrt{3}, \mathrm{c}=2 \sqrt{2}, \mathrm{~A}=60^{\circ}$,
$\therefore$ 由正弦定理可得 $: \sin C=\frac{c \sin A}{a}=\frac{2 \sqrt{2} \times \frac{\sqrt{3}}{2}}{2 \sqrt{3}}=\frac{\sqrt{2}}{2}, \because \mathrm{c}<\mathrm{a}$, 可得 $: 0<\mathrm{C}<60^{\circ}, \therefore \mathrm{C}=45^{\circ}$
|
19667
|
[]
|
B
|
null
|
高二
|
在 $\triangle A B C$ 中, 角 $A 、 B 、 C$ 所对的边分别是 $a 、 b 、 c$, 若 $a=\sqrt{6}, b=2, A=60^{\circ}$,则 $B=(\quad)$
|
A. $30^{\circ}$
B. $45^{\circ}$
C. $135^{\circ}$
D. $45^{\circ}$ 或 $135^{\circ}$
|
度量几何学
|
在 $\triangle \mathrm{ABC}$ 中, 角 $\mathrm{A} 、 \mathrm{~B} 、 \mathrm{C}$ 所对的边分别是 $\mathrm{a} 、 \mathrm{~b} 、 \mathrm{c}$, 若 $a=\sqrt{6}, \mathrm{~b}=2, \mathrm{~A}=60^{\circ}$,可知 $a>b$, 可得 $A>B$,
由正弦定理考试 $\sin \mathrm{B}=\frac{b \sin A}{a}=\frac{2 \times \frac{\sqrt{3}}{2}}{\sqrt{6}}=\frac{\sqrt{2}}{2}$,
所以 $\mathrm{B}=45^{\circ}$.
$8 . A$
解析: 根据题意, $\triangle \mathrm{ABC}$ 中, 有 $\frac{a}{\sin A}=\frac{b}{\sin B}$, 则 $\mathrm{b}=\frac{a \cdot \sin B}{\sin A}$,
又由 $\mathrm{A}=45^{\circ}, \mathrm{B}=30^{\circ}, \mathrm{a}=10$,
则 $\mathrm{b}=\frac{a \cdot \sin B}{\sin A}=\frac{10 \times \frac{1}{2}}{\frac{\sqrt{2}}{2}}=5 \sqrt{2}$;
|
19675
|
["9254.jpg"]
|
D
|
null
|
高二
|
某观察站 $C$ 与两灯塔 $A 、 B$ 的距离分别为 $x$ 米和 3 千米, 测得灯塔 $A$ 在观察站 $C$ 的正西方向, 灯塔 $B$ 在观察站 $C$ 西偏南 $30^{\circ}$, 若两灯塔 $A 、 B$ 之间的距离恰好为 $\sqrt{3}$ 千米,则 $x$ 的值为 ( )
|
A. 3
B. $\sqrt{3}$
C. $2 \sqrt{3}$
D. $\sqrt{3}$ 或 $2 \sqrt{3}$
|
度量几何学
|
如图所示,
在 $\triangle \mathrm{ABC}$ 中, 由余弦定理可得:
$(\sqrt{3})^{2}=3^{2}+\mathrm{x}^{2}-2 \times 3 \times \mathrm{X} \times \cos 30^{\circ}$,
<ImageHere>
化为 $x^{2}-3 \sqrt{3} x+6=0$, 解得 $\mathrm{x}=\sqrt{3}$ 或 $2 \sqrt{3}$. 故选: $\mathrm{D}$.
|
19678
|
[]
|
A
|
null
|
高二
|
已知 $\triangle A B C$ 的面积为 $\frac{1}{4}\left(a^{2}+b^{2}-c^{2}\right)$, 则角 $C$ 的度数是 ( )
|
A. 45
B. 60
C. 120
D. 135
|
度量几何学
|
$\because \triangle \mathrm{ABC}$ 的面积为 $\frac{1}{4}\left(\mathrm{a}^{2}+\mathrm{b}^{2}-\mathrm{c}^{2}\right)=\frac{1}{2} \mathrm{ab} \cdot \sin \mathrm{C}$,
$\therefore \mathrm{c}^{2}=\mathrm{a}^{2}+\mathrm{b}^{2}-2 \mathrm{ab} \cdot \sin \mathrm{C}$. 又根据余弦定理得: $\mathrm{c}^{2}=\mathrm{a}^{2}+\mathrm{b}^{2}-2 \mathrm{ab} \cdot \cos \mathrm{C}$,
$\therefore-2 a b s i n C=-2 a b \cos C$, 即 $\sin C=\cos C, \therefore \tan C=1, \therefore C=45^{\circ}$, 故选: A.
|
19682
|
[]
|
B
|
null
|
高二
|
在 $\triangle A B C$ 中, 若 $\frac{\sin A}{a}=\frac{\cos B}{b}$, 则 $\angle B$ 等于()
|
A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D. $90^{\circ}$
|
度量几何学
|
B
|
19689
|
["9255.jpg"]
|
B
|
null
|
高二
|
在 $\triangle A B C$ 中, 内角 $A, B, C$ 的对边分别为 $a, b, c$, 若 $b^{2}-a^{2}$
<ImageHere>
$=(b-c) c, c=3, \triangle A B C$ 的面积为 $\frac{3 \sqrt{3}}{2}$, 则 $b=(\quad)$
|
A. 1
B. 2
C. $\sqrt{2}$
D. 4
|
度量几何学
|
由 $b^{2}-a^{2}=(b-c) c$, 得 $b^{2}+c^{2}-a^{2}=b c$,
$\therefore \cos A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}=\frac{b c}{2 b c}=\frac{1}{2}, \therefore \sin A=\sqrt{1-\cos ^{2} A}=\frac{\sqrt{3}}{2}$,
$\therefore S_{\triangle A B C}=\frac{1}{2} b c \sin A=\frac{1}{2} \times b \times 3 \times \frac{\sqrt{3}}{2}=\frac{3 \sqrt{3}}{2}$, 得 $\mathrm{b}=2$, 故选 $\mathrm{B}$.
|
18479
|
[]
|
C
|
null
|
高二
|
若点 $P$ 在点 $Q$ 的北偏西 $45^{\circ} 10^{\prime}$ 方向上, 则点 $Q$ 在点 $P$ 的( )
|
A. 南偏西 $45^{\circ} 10^{\prime}$
C. 南偏东 $45^{\circ} 10^{\prime}$
B. 南偏西 $44^{\circ} 50^{\prime}$
D. 南偏东 $44^{\circ} 50^{\prime}$
|
度量几何学
| |
18483
|
[]
|
B
|
null
|
高二
|
台风中心从 $A$ 地以每小时 20 千米的速度向东北方向移动, 离台风中心 30 千米内的地区为危险区,城市 $B$ 在 $A$ 的正东 40 千米处, $B$ 城市处于危险区内的持续时间为( )
|
A. 0.5 小时
B. 1 小时
C. 1.5 小时
D. 2 小时
|
度量几何学
|
解析 设 $t$ 小时时, $B$ 市恰好处于危险区, 则由余弦定理得:
$(20 t)^{2}+40^{2}-2 \times 20 t \times 40 \cdot \cos 45^{\circ}=30^{2}$.
化简得: $4 t^{2}-8 \sqrt{2} t+7=0$,
$\therefore t_{1}+t_{2}=2 \sqrt{2}, t_{1} \cdot t_{2}=\frac{7}{4}$.
从而 $\left|t_{1}-t_{2}\right|=\sqrt{\left(t_{1}+t_{2}\right)^{2}-4 t_{1} t_{2}}=1$.
|
18487
|
["9110.jpg"]
|
A
|
null
|
高二
|
如图所示, 设 $A 、 B$ 两点在河的两岸, 一测量者在 $A$ 的同侧, 在 $A$ 所在的河岸边选定一点 $C$, 测出 $A C$ 的距离为 $50 \mathrm{~m}, \angle A C B=45^{\circ}, \angle C A B=105^{\circ}$ 后, 就可以计算 $A 、 B$ 两点的距离为( )
<ImageHere>
|
A. $50 \sqrt{2} \mathrm{~m}$
B. $50 \sqrt{3} \mathrm{~m}$
C. $25 \sqrt{2} \mathrm{~m}$
D. $\frac{25 \sqrt{2}}{2} \mathrm{~m}$
|
度量几何学
|
解析 由题意知 $\angle A B C=30^{\circ}$, 由正弦定理 $\frac{A C}{\sin \angle A B C}=\frac{A B}{\sin \angle A C B}$,
$\therefore A B=\frac{A C \cdot \sin \angle A C B}{\sin \angle A B C}=\frac{50 \times \frac{\sqrt{2}}{2}}{\frac{1}{2}}=50 \sqrt{2}$ (m).
|
18488
|
["9111.jpg"]
|
B
|
null
|
高二
|
如图, 一货轮航行到 $M$ 处, 测得灯塔 $S$ 在货轮的北偏东 $15^{\circ}$, 与灯塔 $S$ 相距 20 海里,随后货轮按北偏西 $30^{\circ}$ 的方向航行 30 分钟后到达 $N$ 处, 又测得灯塔在货轮的东北方向, 则货轮的速度为(
|
A. $20(\sqrt{6}+\sqrt{2})$ 海里/小时
<ImageHere>
B. $20(\sqrt{6}-\sqrt{2})$ 海里/小时
C. $20(\sqrt{6}+\sqrt{3})$ 海里/小时
D. $20(\sqrt{6}-\sqrt{3})$ 海里/小时
|
度量几何学
|
解析由题意,
$\angle S M N=45^{\circ}, \angle S N M=105^{\circ}, \angle N S M=30^{\circ}$.
由正弦定理得 $\frac{M N}{\sin 30^{\circ}}=\frac{M S}{\sin 105^{\circ}}$.
$\therefore M N=\frac{M S \sin 30^{\circ}}{\sin 105^{\circ}}=\frac{10}{\frac{\sqrt{6}+\sqrt{2}}{4}}=10(\sqrt{6}-\sqrt{2})$.
则 $v_{\text {化 }}=20(\sqrt{6}-\sqrt{2})$ 海里/小时.
|
18493
|
[]
|
B
|
null
|
高二
|
从 $A$ 处望 $B$ 处的仰角为 $\alpha$, 从 $B$ 处望 $A$ 处的俯角为 $\beta$, 则 $\alpha$ 与 $\beta$ 的关系为 (
|
A. $\alpha>\beta$
B. $\alpha=\beta$
C. $\alpha<\beta$
D. $\alpha+\beta=90^{\circ}$
|
度量几何学
| |
18500
|
["9120.jpg"]
|
A
|
null
|
高二
|
如图, 为测一树的高度, 在地面上选取 $A 、 B$ 两点, 从 $A 、 B$ 两点分别测得望树尖的仰角为 $30^{\circ}, 45^{\circ}$, 且 $A 、 B$ 两点之间的距离为 $60 \mathrm{~m}$, 则树的高度为 $(\quad)$
<ImageHere>
|
A. $30+30 \sqrt{3} \mathrm{~m}$
B. $30+15 \sqrt{3} \mathrm{~m}$
C. $15+30 \sqrt{3} \mathrm{~m}$
D. $15+3 \sqrt{3} \mathrm{~m}$
|
度量几何学
|
解析 在 $\triangle P A B$ 中, 由正弦定理可得
$\frac{60}{\sin \left(45^{\circ}-30^{\circ}\right)}=\frac{P B}{\sin 30^{\circ}}$,
$P B=\frac{60 \times \frac{1}{2}}{\sin 15^{\circ}}=\frac{30}{\sin 15^{\circ}}$,
$h=P B \sin 45^{\circ}=(30+30 \sqrt{3}) \mathrm{m}$.
|
18501
|
["9121.jpg"]
|
A
|
null
|
高二
|
从高出海平面 $h$ 米的小岛看正东方向有一只船俯角为 $30^{\circ}$, 看正南方向一只船俯角为 $45^{\circ}$, 则此时两船间的距离为( )
|
A. $2 h$ 米
B. $\sqrt{2} h$ 米
C. $\sqrt{3} h$ 米
D. $2 \sqrt{2} h$ 米
<ImageHere>
|
度量几何学
|
解析 如图所示,
$B C=\sqrt{3} h, A C=h$,
$\therefore A B=\sqrt{3 h^{2}+h^{2}}=2 h$.
|
18502
|
["9122.jpg"]
|
B
|
null
|
高二
|
在某个位置测得某山峰仰角为 $\theta$, 对着山峰在平行地面上前进 $600 \mathrm{~m}$ 后测仰角为原来的 2 倍, 继续在平行地面上前进 $200 \sqrt{3} \mathrm{~m}$ 后, 测得山峰的仰角为原来的 4 倍, 则该山峰的高度是( )
|
A. $200 \mathrm{~m}$
B. $300 \mathrm{~m}$
C. $400 \mathrm{~m}$
D. $100 \sqrt{3} \mathrm{~m}$
|
度量几何学
|
解析 如图所示, $600 \cdot \sin 2 \theta=200 \sqrt{3} \cdot \sin 4 \theta$,
<ImageHere>
$\therefore \cos 2 \theta=\frac{\sqrt{3}}{2}, \therefore \theta=15^{\circ}$,
$\therefore h=200 \sqrt{3} \cdot \sin 4 \theta=300(\mathrm{~m})$.
|
18525
|
[]
|
B
|
null
|
高二
|
$\triangle A B C$ 中, 三内角 $A 、 B 、 C$ 成等差数列, 则角 $B$ 等于 $(\quad)$
|
A. $30^{\circ}$
B. $60^{\circ}$
C. $90^{\circ}$
D. $120^{\circ}$
|
度量几何学
| |
18539
|
[]
|
D
|
null
|
高二
|
已知数列 $\left\{a_{n}\right\}$ 为等差数列且 $a_{1}+a_{7}+a_{13}=4 \pi$, 则 $\tan \left(a_{2}+a_{12}\right)$ 的值为 $(\quad)$
|
A. $\sqrt{3}$
B. $\pm \sqrt{3}$
C. $-\frac{\sqrt{3}}{3}$
D. $-\sqrt{3}$
|
度量几何学
|
解析 由等差数列的性质得 $a_{1}+a_{7}+a_{13}=3 a_{7}=4 \pi$,
$\therefore a_{7}=\frac{4 \pi}{3}$.
$\therefore \tan \left(a_{2}+a_{12}\right)=\tan \left(2 a_{7}\right)=\tan \frac{8 \pi}{3}$
$=\tan \frac{2 \pi}{3}=-\sqrt{3}$.
|
18673
|
["9150.jpg", "9151.jpg"]
|
D
|
null
|
高二
|
<ImageHere>
是 9, 那么实数 $a$ 的值为 $(\quad)$
|
A. $3 \sqrt{2}+2$
B. $-3 \sqrt{2}+2$
C. -5
D. 1
<ImageHere>
|
度量几何学
|
解析 区域如图,
易求得 $A(-2,2), B(a, a+4)$,
$C(a,-a)$.
$S_{\triangle A B C}=\frac{1}{2}|B C| \cdot|a+2|=(a+2)^{2}=9$, 由题意得 $a=1$.
|
18174
|
["9063.jpg"]
|
A
|
null
|
高二
|
已知函数 $f(x)=A \sin \left(\frac{\pi}{3} x+\frac{\pi}{6}\right), x \in R, A>0, y=f(x)$ 的部分图象如图, $P, Q$ 分别为该图象的最高点和最低点,点 $P$ 的横坐标为 1 . 若点 $R$ 的坐标为 $(1,0), \angle P R Q=\frac{2 \pi}{3}$, 则 $A=(\quad)$
<ImageHere>
|
A. $\sqrt{3}$
B. 2
C. 1
D. $2 \sqrt{3}$
|
度量几何学
|
函数 $f(x)$ 的周期为 $T=\frac{2 \pi}{\frac{\pi}{3}}=6, \therefore Q(4,-A)$. 又 $\angle P R Q=\frac{2 \pi}{3}, \therefore$ 直线 $R Q$ 的倾斜角为 $\frac{5 \pi}{6}$, $\therefore \frac{A}{1-4}=-\frac{\sqrt{3}}{3}, A=\sqrt{3}$. 故选 A.
|
18195
|
[]
|
D
|
null
|
高二
|
函数 $y=\sqrt{2 \cos x+1}$ 的定义域是()
|
A. $\left[2 k \pi-\frac{\pi}{3}, 2 k \pi+\frac{\pi}{3}\right](k \in Z)$
B. $\left[2 k \pi+\frac{\pi}{3}, 2 k \pi+\frac{2 \pi}{3}\right](k \in Z)$
C. $\left[2 k \pi-\frac{\pi}{6}, 2 k \pi+\frac{\pi}{6}\right](k \in Z)$
D. $\left[2 k \pi-\frac{2 \pi}{3}, 2 k \pi+\frac{2 \pi}{3}\right](k \in Z)$
|
度量几何学
|
由 $2 \cos x+1 \geqslant 0$ 得 $\cos x \geqslant-\frac{1}{2}, \therefore 2 k \pi-\frac{2 \pi}{3} \leqslant x \leqslant 2 k \pi+\frac{2 \pi}{3}, \mathrm{k} \in \mathrm{Z}$.
故选 $\mathrm{D}$.
|
17611
|
[]
|
A
|
null
|
高二
|
半径为 2 , 弧长为 $\frac{\pi}{5}$ 的扇形的面积为 ( )
$\begin{array}{llll}\text {
|
A. } \frac{\pi}{5} & \text { B. } \frac{2 \pi}{5} & \text { C. } \frac{\pi^{2}}{5} & \text { D. } \frac{2 \pi^{2}}{5}\end{array}$
|
度量几何学
|
扇形的面积为 $\frac{1}{2} \times 2 \times \frac{\pi}{5}=\frac{\pi}{5}$, 故选 A.
|
17614
|
["8929.jpg"]
|
C
|
null
|
高二
|
将函数 $f(x)=2 \sin (\omega x+\varphi)\left(\omega>0,|\varphi|<\frac{\pi}{2}\right)$ 的图象向左平移 $\frac{\pi}{2}$ 个单位长度后得到的部分图象如图所示, 有下列四个结论: (1) $f(0)=1$; (2) $y=f(x)-\sqrt{3}$ 在
$[0, \pi]$ 上有两个零点; (3) $f(x)$ 的图象关于直线 $x=-\frac{\pi}{6}$ 对称; (4) $f(x)$ 在区间 $\left[\frac{2 \pi}{3}, \frac{8 \pi}{3}\right]$ 上单调递减, 其中所有正确结论的个数为 ( )
<ImageHere>
|
A. 1
B. 2
C. 3
D. 4
|
度量几何学
|
$f(x)=2 \sin (\omega x+\varphi)\left(\omega>0,|\varphi|<\frac{\pi}{2}\right)$ 的图象向左平移 $\frac{\pi}{2}$ 个单位长度后得:
$g(x)=2 \sin \left[\omega\left(x+\frac{\pi}{2}\right)+\varphi\right]=2 \sin \left(\omega x+\frac{\omega \pi}{2}+\varphi\right)\left(\omega>0,|\varphi|<\frac{\pi}{2}\right)$,
由图象知 $g(x)$ 的周期 $T$ 满足 $\frac{T}{4}=\frac{7 \pi}{6}-\frac{\pi}{6}$,
$\therefore T=4 \pi, \quad \therefore \omega=\frac{2 \pi}{T}=\frac{1}{2}$,
又 $g\left(\frac{\pi}{6}\right)=2, \therefore \frac{1}{2} \times \frac{\pi}{6}+\frac{1}{2} \times \frac{\pi}{2}+\varphi=2 k \pi+\frac{\pi}{2}(k \in \mathbf{Z})$, 即 $\varphi=2 k \pi+\frac{\pi}{6}(k \in \mathbf{Z})$.
又 $|\varphi|<\frac{\pi}{2}, \therefore \varphi=\frac{\pi}{6}, \therefore f(x)=2 \sin \left(\frac{1}{2} x+\frac{\pi}{6}\right)$,
对于(1), $f(0)=2 \sin \frac{\pi}{6}=1$, 故(1)正确;
对于(2), 令 $f(x)-\sqrt{3}=0$, 则 $\sin \left(\frac{1}{2} x+\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}$,
又 $x \in[0, \pi]$, 所以 $\frac{1}{2} x+\frac{\pi}{6} \in\left[\frac{\pi}{6}, \frac{2 \pi}{3}\right]$, 则 $\frac{1}{2} x+\frac{\pi}{6}=\frac{\pi}{3}$ 或 $\frac{2 \pi}{3}$, 即 $x=\frac{\pi}{3}$ 或 $\pi$,
故 $y=f(x)-\sqrt{3}$ 在 $[0, \pi]$ 上有两个零点, 所以(2)正确;
对于(3), 令 $\frac{x}{2}+\frac{\pi}{6}=k \pi+\frac{\pi}{2}(k \in \mathbf{Z})$, 解得 $x=2 k \pi+\frac{2 \pi}{3}(k \in \mathbf{Z})$,
$\therefore f(x)$ 的图象不关于直线 $x=-\frac{\pi}{6}$ 对称, 故(3)错误;
对于(4), 令 $2 k \pi+\frac{\pi}{2} \leq \frac{1}{2} x+\frac{\pi}{6} \leq 2 k \pi+\frac{3 \pi}{2}(k \in Z)$,
解得 $4 k \pi+\frac{2 \pi}{3} \leq x \leq 4 k \pi+\frac{8 \pi}{3}(k \in Z)$,即 $f(x)$ 的单调递减区间为 $\left[4 k \pi+\frac{2 \pi}{3}, 4 k \pi+\frac{8 \pi}{3}\right]$,
令 $k=0$, 得 $f(x)$ 在区间 $\left[\frac{2 \pi}{3}, \frac{8 \pi}{3}\right]$ 上单调递减,
综上所述, (1)(2)(4)正确, 故选 C.
|
17622
|
[]
|
C
|
null
|
高二
|
$675^{\circ}$ 用弧度制表示为 ( )
|
A. $\frac{11}{4} \pi$ B. $\frac{13}{4} \pi$ C. $\frac{15}{4} \pi$ D. $\frac{17}{4} \pi$
|
度量几何学
|
因为 $180^{\circ}=\pi$ 弧度, 所以 $675^{\circ}=675 \times \frac{\pi}{180}=\frac{15 \pi}{4}$, 故选 C.
|
17626
|
[]
|
C
|
null
|
高二
|
下列各角中, 与 $2021^{\circ}$ 终边相同的角为 ( )
|
A. $41^{\circ}$ B. $139^{\circ}$
C. $221^{\circ}$
D. $-41^{\circ}$
|
度量几何学
|
与 $2021^{\circ}$ 终边相同的角为 $\alpha=k \cdot 360^{\circ}+2021^{\circ}$,
当 $k=-5$ 时, $\alpha=221^{\circ}$, 故选 C.
|
17630
|
[]
|
A
|
null
|
高二
|
函数 $f(x)=\frac{1}{2} \tan \left(\frac{\pi}{2} x+\frac{\pi}{4}\right)+1$ 的单调递增区间为 ( )
|
A. $\left(2 k-\frac{3}{2}, 2 k+\frac{1}{2}\right), k \in \mathrm{Z} \quad$ B. $\left(2 k-\frac{1}{2}, 2 k+\frac{1}{2}\right), k \in \mathrm{Z}$
C. $\left(4 k-\frac{1}{2}, 4 k+\frac{1}{2}\right), k \in \mathrm{Z} \quad$ D. $\left(4 k-\frac{3}{2}, 4 k+\frac{1}{2}\right), k \in \mathrm{Z}$
|
度量几何学
|
由 $k \pi-\frac{\pi}{2}<\frac{\pi}{2} x+\frac{\pi}{4}<k \pi+\frac{\pi}{2}$, 得 $2 k-\frac{3}{2}<x<2 k+\frac{1}{2}, k \in \mathbf{Z}$,
增区间为 $\left(2 k-\frac{3}{2}, 2 k+\frac{1}{2}\right), k \in \mathbf{Z}$
故选 A.
|
17633
|
[]
|
B
|
null
|
高二
|
3 弧度的角终边在 ( )
|
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
|
度量几何学
|
因为 $\frac{\pi}{2}<3<\pi$, 所以 3 弧度的角终边在第二象限, 故选 B.
|
17643
|
[]
|
D
|
null
|
高二
|
若角 $\alpha$ 与角 $\beta$ 的终边关于 $y$ 轴对称, 则必有 ( )
|
A. $\alpha+\beta=90^{\circ}$
B. $\alpha+\beta=k \cdot 360^{\circ}+90^{\circ}(k \in \mathbf{Z})$
C. $\alpha+\beta=k \cdot 360^{\circ}(k \in \mathbf{Z})$
D. $\alpha+\beta=(2 k+1) \cdot 180^{\circ}(k \in \mathrm{Z})$
|
度量几何学
|
角 $\alpha$ 与角 $\beta$ 的终边关于 $y$ 轴对称,
所以 $\alpha-\left(90 ? 360\right.$ 按 $\left.k_{1}\right)=90 ? 360$ 按 $k_{2}-\beta, k_{1}, k_{2} ? \mathrm{Z}$,
$\alpha+\beta=90 ? 360$ 按 $k_{2}+90 ? 360$ 按 $k_{1}=360 ?\left(k_{1} \quad k_{2}\right)+180 ?, k_{1}, k_{2} \in \mathrm{Z}$,
即 $\alpha+\beta=360$ 按 $k+180$ 轱 $(2 k+1) \times 180, k \hat{\mathrm{I}} \mathrm{Z}$,
故选 D.
|
17647
|
[]
|
C
|
null
|
高二
|
$\theta$ 是第二象限角, 则下列选项中一定为负值的是 ( )
|
A. $\sin \frac{\theta}{2}$
B. $\cos \frac{\theta}{2}$
C. $\sin 2 \theta$
D. $\cos 2 \theta$
|
度量几何学
|
因为 $\theta$ 是第二象限角,
所以 $2 k \pi+\frac{\pi}{2}<\theta<2 k \pi+\pi, k \in \mathrm{Z}$, 则 $4 k \pi+\pi<2 \theta<4 k \pi+2 \pi, k \in \mathrm{Z}$,
所以 $2 \theta$ 为第三或第四象限角或终边在 $y$ 轴负半轴上, 所以 $\sin 2 \theta<0$,
而 $k \pi+\frac{\pi}{4}<\frac{\theta}{2}<k \pi+\frac{\pi}{2}, k \in \mathrm{Z}, \frac{\theta}{2}$ 是第一象限或第三象限角, 正弦余弦值不一定是负数,
故选 C.
|
17648
|
[]
|
C
|
null
|
高二
|
如果角 $\alpha$ 的终边过点 $P\left(2 \sin 30^{\circ},-2 \cos 30^{\circ}\right)$, 则 $\sin \alpha$ 的值等于()
|
A. $B. -\frac{1}{2} \text { C. }-\frac{\sqrt{3}}{2} \text { D. }-\frac{\sqrt{3}}{3}$
|
度量几何学
|
由题意得 $P(1,-\sqrt{3})$, 它与原点的距离 $r=\sqrt{1+(\sqrt{3})^{2}}=2$,
所以 $\sin \alpha=\frac{y}{r}=\frac{-\sqrt{3}}{2}=-\frac{\sqrt{3}}{2}$, 故选 C.
|
18199
|
[]
|
A
|
null
|
高二
|
已知 $\alpha \in\left(\frac{\pi}{2}, \pi\right), \tan \left(\alpha+\frac{\pi}{4}\right)=\frac{1}{7}$, 那么 $\sin \alpha+\cos \alpha$ 的值为().
|
A. $-\frac{1}{5}$
B. $\frac{7}{5}$
C. $-\frac{7}{5}$
D. $\frac{3}{4}$
|
度量几何学
|
$\because \tan \left(\alpha+\frac{\pi}{4}\right)=\frac{\tan \alpha+1}{1-\tan \alpha}=\frac{1}{7}$,
$\therefore \tan \alpha=-\frac{3}{4}$,
又 $\because \alpha \in\left(\frac{\pi}{2}, \pi\right)$,
$\therefore \cos \alpha=-\frac{4}{5}, \sin \alpha=\frac{3}{5}$,
$\therefore \sin \alpha+\cos \alpha=-\frac{1}{5}$.
故选 A.
|
18214
|
[]
|
D
|
null
|
高二
|
$\cos 585^{\circ}$ 的值为 $(\quad)$
|
A. $\frac{\sqrt{3}}{2}$
B. $-\frac{\sqrt{3}}{2}$
C. $\frac{\sqrt{2}}{2}$
D. $-\frac{\sqrt{2}}{2}$
|
度量几何学
|
$\cos 585^{\circ}=\cos \left(360^{\circ}+225^{\circ}\right)=\cos 225^{\circ}=\cos \left(180^{\circ}+45^{\circ}\right)=-\cos 45^{\circ}=-\frac{\sqrt{2}}{2}$.
|
18216
|
[]
|
B
|
null
|
高二
|
已知角 $\alpha$ 的顶点在坐标原点, 始边与 $X$ 轴正半轴重合, 终边经过点 $P(-\sqrt{2}, 1)$, 则 $\cos 2 \alpha=(\quad)$
|
A. $\frac{2 \sqrt{2}}{3}$
B. $\frac{1}{3}$
C. $-\frac{1}{3}$
D. $-\frac{2 \sqrt{2}}{3}$
|
度量几何学
|
因为角 $\alpha$ 的顶点在坐标原点, 始边与 $X$ 轴正半轴重合, 终边经过点 $P(-\sqrt{2}, 1)$,
所以 $\cos \alpha=\frac{-\sqrt{2}}{\sqrt{2+1}}=-\frac{\sqrt{6}}{3}$,
因此 $\cos 2 \alpha=2 \cos ^{2} \alpha-1=\frac{1}{3}$.
故选 B
|
17654
|
[]
|
C
|
null
|
高二
|
若锐角 $\alpha, \beta$ 满足 $\cos \alpha=\frac{4}{5}, \cos (\alpha+\beta)=\frac{3}{5}$, 则 $\sin \beta$ 的值是()
|
A. $\frac{17}{25} $ B. $\frac{3}{5}$ C. $\frac{7}{25}$ D. $ \frac{1}{5}$
|
度量几何学
|
$\because \cos \alpha=\frac{4}{5}, \cos (\alpha+\beta)=\frac{3}{5}, \alpha, \beta \in\left(0, \frac{\pi}{2}\right), \therefore 0<\alpha+\beta<\frac{\pi}{2}$,
$\therefore \sin \alpha=\frac{3}{5}, \sin (\alpha+\beta)=\frac{4}{5}$,
$\therefore \sin \beta=\sin [(\alpha+\beta)-\alpha]=\sin (\alpha+\beta) \cos \alpha-\cos (\alpha+\beta) \sin \alpha=\frac{4}{5} \times \frac{4}{5}-\frac{3}{5} \times \frac{3}{5}$
$=\frac{7}{25}$,
故选 C.
|
17665
|
[]
|
B
|
null
|
高二
|
$\sin 245^{\circ} \sin 125^{\circ}+\sin 155^{\circ} \sin 35^{\circ}$ 的值是 ( )
|
A. $-\frac{\sqrt{3}}{2}$
B. $-\frac{1}{2}$ C. $\frac{1}{2}$
D. $\frac{\sqrt{3}}{2}$
|
度量几何学
|
原式 $=-\sin 65^{\circ} \sin 55^{\circ}+\sin 25^{\circ} \sin 35^{\circ}=-\cos 25^{\circ} \cos 35^{\circ}+\sin 25^{\circ} \sin 35^{\circ}$
$=-\cos \left(35^{\circ}+25^{\circ}\right)=-\cos 60^{\circ}=-\frac{1}{2}$,
故选 B.
|
18238
|
[]
|
C
|
null
|
高二
|
若 $f(x)=\cos x-\sin x$ 在 $[0, a]$ 上是减函数, 则 $a$ 的最大值是 $(\quad)$
|
A. $\frac{\pi}{4}$
B. $\frac{\pi}{2}$
C. $\frac{3}{4} \pi$
D. $\pi$
|
度量几何学
|
由题意, $f(x)=\cos x-\sin x=-\sqrt{2} \sin \left(x-\frac{\pi}{4}\right)$,当 $x-\frac{\pi}{4} \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$, 即 $x \in\left[-\frac{\pi}{4}, \frac{3 \pi}{4}\right]$ 时, $y=\sin \left(x-\frac{\pi}{4}\right)$ 单调递增,则 $f(x)=-\sqrt{2} \sin \left(x-\frac{\pi}{4}\right)$ 在 $\left[-\frac{\pi}{4}, \frac{3 \pi}{4}\right]$ 上单调递减,
$\therefore x \in\left[-\frac{\pi}{4}, \frac{3 \pi}{4}\right]$ 是 $f(x)$ 在原点附近的单调递减区间,结合条件得 $[0, a] \subset\left[-\frac{\pi}{4}, \frac{3 \pi}{4}\right], \therefore a \leq \frac{3}{4} \pi$, 即 $a$ 的最大值为 $\frac{3}{4} \pi$.故选 C.
|
18241
|
[]
|
B
|
null
|
高二
|
若 $\frac{\sin \alpha+\cos \alpha}{\sin \alpha-\cos \alpha}=\frac{1}{2}$, 则 $\tan 2 \alpha$ 等于 ( )
|
A. $-\frac{3}{4}$
B. $\frac{3}{4}$
C. $-\frac{4}{3}$
D. $\frac{4}{3}$
|
度量几何学
|
$\frac{\sin \alpha+\cos \alpha}{\sin \alpha-\cos \alpha}=\frac{\tan \alpha+1}{\tan \alpha-1}=\frac{1}{2}, \tan \alpha=-3, \tan 2 \alpha=\frac{2 \tan \alpha}{1-\tan ^{2} \alpha}=\frac{-6}{-8}=\frac{3}{4}$.
|
18254
|
[]
|
A
|
null
|
高二
|
已知 $\sin \alpha=\frac{\sqrt{5}}{5}$, 则 $\sin ^{4} \alpha-\cos ^{4} \alpha$ 的值为
|
A. $-\frac{3}{5}$
B. $-\frac{1}{5}$
C. $\frac{1}{5}$
D. $\frac{3}{5}$
|
度量几何学
|
$\sin ^{4} \alpha-\cos ^{4} \alpha=\left(\sin ^{2} \alpha-\cos ^{2} \alpha\right)\left(\sin ^{2} \alpha+\cos ^{2} \alpha\right)=\sin ^{2} \alpha-\cos ^{2} \alpha=2 \sin ^{2} \alpha-1=-\frac{3}{5}$.
|
18260
|
[]
|
C
|
null
|
高二
|
下列三角函数值的符号判断错误的是( )
|
A. $\sin 165^{\circ}>0$
B. $\cos 280^{\circ}>0$
C. $\tan 170^{\circ}>0$
D. ${ }^{\tan 310^{\circ}<0}$
|
度量几何学
|
$165^{\circ}$ 是第二象限角,因此 $\sin 165^{\circ}>0$ 正确; $280^{\circ}$ 是第四象限角,因此 $\cos 280^{\circ}>0$ 正确; $170^{\circ}$ 是第二象限角,因此 $\tan 170^{\circ}<0$ ,故 C 错误; $310^{\circ}$ 是第四象限角,因此 $\tan 310^{\circ}<0$ 正确.
|
18261
|
[]
|
B
|
null
|
高二
|
角 $A$ 为 $\triangle A B C$ 的一个内角,若 $\sin A+\cos A=\frac{2}{3}$ ,则这个三角形为
|
A.锐角三角形
B.钝角三角形
C.等腰直角三角形
D.等腰三角形
|
度量几何学
|
$\because \sin A+\cos A=\frac{2}{3}$ ,
$\therefore(\sin A+\cos A)^{2}=1+2 \sin A \cos A=\frac{4}{9}$,
$\therefore \sin A \cos A=-\frac{5}{18}<0$ ,
又 $0<A<\pi$ ,
$\therefore \frac{\pi}{2}<A<\pi$ ,即 $A$ 为钝角,
$\therefore \triangle A B C$ 为钝角三角形. 故选 $B$.
|
18262
|
[]
|
D
|
null
|
高二
|
已知 $\sin x+\cos x=\frac{\sqrt{3}-1}{2} , x \in(0, \pi)$ ,则 $\tan x=(\quad)$
|
A. $-\frac{\sqrt{3}}{3}$
B. $\frac{\sqrt{3}}{3}$
c. $\sqrt{3}$
D. $-\sqrt{3}$
|
度量几何学
|
$\sin x+\cos x=\frac{\sqrt{3}-1}{2}$ ,且 $x \in(0 , \pi) , \therefore 1+2 \sin x \cos x=1-\frac{\sqrt{3}}{2} , \therefore 2 \sin x \cos x=-\frac{\sqrt{3}}{2}<0 , \therefore x$ 为钝角, $\therefore \sin x$
$-\cos x=\sqrt{(\sin x-\cos x)^{2}}=\frac{1+\sqrt{3}}{2}, \therefore \sin x=\frac{\sqrt{3}}{2}, \cos x=-\frac{1}{2}, \tan x=\frac{\sin x}{\cos x}=-\sqrt{3}$
故选 D.
|
18263
|
[]
|
B
|
null
|
高二
|
若 $\tan \alpha=\frac{1}{2}$ ,则 $\sin ^{4} \alpha-\cos ^{4} \alpha$ 的值为()
|
A. $-\frac{1}{5}$
B. $\frac{-3}{5}$
c. $\frac{1}{5}$
D. $\frac{3}{5}$
|
度量几何学
|
$\because \tan \alpha=\frac{1}{2}$ ,则 $\sin ^{4} \alpha-\cos ^{4} \alpha=\left(\sin ^{2} \alpha+\cos ^{2} \alpha\right)\left(\sin ^{2} \alpha-\cos ^{2} \alpha\right)=\sin ^{2} \alpha-$ $\cos ^{2} \alpha \frac{\sin ^{2} \alpha-\cos ^{2} \alpha}{\sin ^{2} \alpha+\cos ^{2} \alpha}=\frac{\tan ^{2} \alpha-1}{\tan ^{2} \alpha+1}=-\frac{3}{5}$ 选 B.
|
18264
|
[]
|
C
|
null
|
高二
|
若 $\sin x \cdot \cos x=\frac{1}{8}$ 且 $\frac{\pi}{4}<x<\frac{\pi}{2}$ ,则 $\cos x-\sin x$ 的值是( )
|
A. $\pm \frac{\sqrt{3}}{2}$
B. $\frac{\sqrt{3}}{2}$
C. $-\frac{\sqrt{3}}{2}$
D. $\pm \frac{1}{2}$
|
度量几何学
|
$\because \frac{\pi}{4}<x<\frac{\pi}{2}, \therefore \cos x-\sin x<0 ,$
$\therefore(\cos x-\sin x)^{2}=1-2 \sin x \cos x=1-2 \times \frac{1}{8}=\frac{3}{4}$,
$\therefore \cos x-\sin x=-\frac{\sqrt{3}}{2}$. 故选 C.
|
18283
|
[]
|
A
|
null
|
高二
|
已知 $\alpha \in{ }^{\left(\frac{\pi}{2}, \pi\right)}, \tan \alpha=-\frac{3}{4}$, 则 $\sin \alpha$ 为 $(\square)$
|
A. $\frac{3}{5}$ B. $-\frac{3}{5} \quad$ C. ${\frac{4}{5}}$ D.$-\frac{4}{5}$
|
度量几何学
|
$\because \alpha \in^{\left(\frac{\pi}{2}, \pi\right)}$, $\tan \alpha=-\frac{3}{4}=\frac{\sin \alpha}{\cos \alpha}$, 且 $\sin ^{2} \alpha+\cos ^{2} \alpha=1, \sin \alpha>0, \cos \alpha<0, \therefore \sin \alpha=\frac{3}{5}$.
|
18286
|
[]
|
D
|
null
|
高二
|
下列命题中正确的是 ( )
|
A. 终边在 $\mathrm{x}$ 轴负半轴上的角是零角
B. 第二象限角一定是钝角
C.第四象限角一定是负角
D. 若 $\beta=\alpha+k^{\cdot} 360^{\circ}(k \in Z)$, 则 $\alpha$ 与 $\beta$ 终边相同
|
度量几何学
|
终边在 $\mathrm{x}$ 轴负半轴上的角是 $\alpha=2 k \pi+\pi, k \in z$, 零角是没有旋转的角, 所以 $\mathrm{A}$ 错误; 第二象限角应表示为 $\left(2 k \pi+\frac{\pi}{2}, 2 k \pi+\pi\right), k \in z$, 是由无数多个区间的并集构成, 所以 $\mathrm{B}$ 错误; 第四象限角表示为 $\left(2 k \pi+\frac{3 \pi}{2}, 2 k \pi+2 \pi\right), k \in z$, 当 $k \geq 0$ 时, 就是正角, 所以 C 错误; 故选 D.
|
18287
|
["9072.jpg", "9073.jpg"]
|
A
|
null
|
高二
|
已知圆 $O$ 与直线 $l$ 相切于 $A$, 点 $P, Q$ 同时从点 $A$ 出发, $P$ 沿着直线 $l$ 向右、 $Q$ 沿着圆周按逆时针以相同的速度运动, 当 $Q$ 运动到点 $A$ 时, 点 $P$ 也停止运动, 连接 $O Q, O P$ (如图), 则阴影部分面积 $S_{1}, S_{2}$ 的大小关系是 ( )
<ImageHere>
|
A. $S_{1}=S_{2}$
B. $S_{1} \leq S_{2}$
C. $S_{1} \geq S_{2}$
D. 先 $S_{1}<S_{2}$, 再 $S_{1}=S_{2}$, 最后 $S_{1}>S_{2}$
|
度量几何学
|
如图所示, 因为直线 $l$ 与圆 $O$ 相切, 所以 $O A \perp A P$,
所以扇形的面积为 $S_{\text {扇形 } A O Q}=\frac{1}{2} \cdot A Q \cdot r=\frac{1}{2} \cdot A Q \cdot O A, S_{\triangle A O P}=\frac{1}{2} \cdot O A \cdot A P$,
因为 $A Q=A P$, 所以扇形 $A O Q$ 的面积 $S_{\text {扇形AOQ }}=S_{\triangle A O P}$,
即 $S_{\text {扇形AOQ }}-S_{\text {扇形AOB }}=S_{\triangle A O P}-S_{\text {扇形 } A O B}$,
所以 $S_{1}=S_{2}$,
<ImageHere>
|
18311
|
["9081.jpg"]
|
A
|
null
|
高二
|
如图所示, 用两种方案将一块顶角为 $120^{\circ}$, 腰长为 2 的等腰三角形钢板 $O A B$ 裁剪成扇形, 设方案一、二扇形的面积分别为 $\mathrm{S}_{1}, \mathrm{~S}_{2}$, 周长分别为 $l_{1}, l_{2}$, 则 ( )\n\n<ImageHere>(方案一)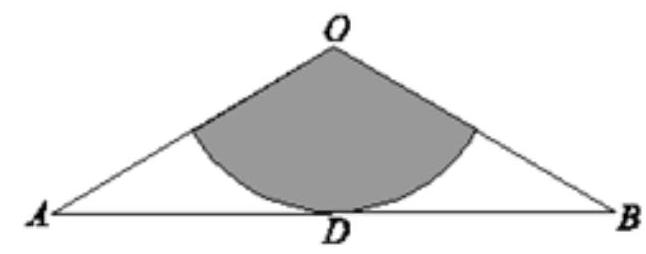\n\n(方案二)
|
A. $S_{1}=S_{2}, l_{1}>l_{2}$\nB. $S_{1}=S_{2}, l_{1}<l_{2}$\nC. $S_{1}>S_{2}, l_{1}=l_{2}$\nD. $S_{1}<S_{2}, l_{1}=l_{2}$\n\n
|
度量几何学
|
$\because \triangle A O B$ 为顶角为 $120^{\circ}$, 腰长为 2 的等腰三角形,\n\n$\therefore A=B=30^{\circ}=\frac{\pi}{6}, O D=1$,\n\n方案一中扇形的周长 $l_{1}=2+2+2 \times \frac{\pi}{6}=4+\frac{\pi}{3}$ ,\n\n方案二中扇形的周长 $l_{2}=1+1+1 \times \frac{2 \pi}{3}=2+\frac{2 \pi}{3}$,\n\n方案一中扇形的面积 $S_{1}=\frac{1}{2} \times 2 \times 2 \times \frac{\pi}{6}=\frac{\pi}{3}$,\n\n方案一中扇形的面积 $S_{2}=\frac{1}{2} \times 1^{2} \times \frac{2 \pi}{3}=\frac{\pi}{3}$,\n\n所以 $S_{1}=S_{2}, l_{1}>l_{2}$.\n\n故选 A.
|
18296
|
[]
|
A
|
null
|
高二
|
若 $\alpha$ 是第二象限的角, 则 $2 \alpha$ 不可能在 ( )
|
A. 第一二象限
B. 第三四象限
C. 第一四象限
D. 第二三象限
|
度量几何学
|
因为 $\alpha$ 是第二象限的角,
所以 $2 k \pi<\alpha<2 k \pi+\frac{\pi}{2}, k \in Z$,
$4 k \pi<2 \alpha<4 k \pi+\pi, k \in Z$
所以 $2 \alpha$ 在三四象限或者在 $y$ 轴的正半轴,
即 $2 \alpha$ 不可能在一二象限, 故选 A.
|
18304
|
[]
|
B
|
null
|
高二
|
若 $\alpha$ 是第三象限的角, 则 $\pi-\frac{\alpha}{2}$ 是( )
|
A. 第一或第二象限的角 B. 第一或第三象限的角 C. 第二或第三象限的角 D. 第二或第四象限的角
|
度量几何学
|
$\because \alpha$ 是第三象限角, $\therefore 2 k \pi+\pi<\alpha<2 k \pi+\frac{3 \pi}{2}, k \in Z, \therefore k \pi+\frac{\pi}{2}<\frac{\alpha}{2}<k \pi+\frac{3 \pi}{4}$, $\therefore-k \pi-\frac{3 \pi}{4}<-\frac{\alpha}{2}<-k \pi-\frac{\pi}{2}, \therefore-k \pi+\frac{\pi}{4}<\pi-\frac{1}{2} \alpha<-k \pi+\frac{\pi}{2}$, 故当 $k$ 为偶数时, $\pi-\frac{1}{2} \alpha$ 是第一象限角; 故当 $k$ 为奇数时, $\pi-\frac{1}{2} \alpha$ 是第三象限角, 故选 B.
|
18305
|
[]
|
B
|
null
|
高二
|
若扇形的面积为 $\frac{3 \pi}{8}$ 、半径为 1 , 则扇形的圆心角为 ( )
|
A. $\frac{3 \pi}{2}$
B. $\frac{3 \pi}{4}$
C. $\frac{3 \pi}{8}$
D. $\frac{3 \pi}{16}$
|
度量几何学
|
设扇形的圆心角为 $\alpha$, 则 $\because$ 扇形的面积为 $\frac{3 \pi}{8}$, 半径为 1 ,
$\therefore \frac{3 \pi}{8}=\frac{1}{2} \alpha l^{2} \therefore \alpha=\frac{3 \pi}{4}$
故选 B
|
Subsets and Splits
Algebra Questions Without Images
Retrieves test entries with no image and focuses on algebra questions across multiple grades, providing limited analytical value through basic filtering.
Algebra Questions Without Images
Finds questions in algebra from specified levels without images, which provides a basic overview of text-based questions.