problem
stringlengths 10
7.44k
| answer
stringlengths 1
270
| difficulty
stringclasses 8
values |
|---|---|---|
$\mathrm{Az}$
$$
a_{n}=\frac{(n+3)^{2}+3}{n(n+1)(n+2)} \cdot \frac{1}{2^{n+1}}
$$
is a sequence defined by its general term. We form the sequence
$$
b_{n}=\sum_{k=1}^{n} a_{k}
$$
Determine the limit of the sequence $b_{n}$ as $n \rightarrow+\infty$.
|
1
|
4/8
|
4. Let $H$ be the orthocenter of $\triangle A B C$ and let $A_{1}, B_{1}, C_{1}$ be the feet of the altitudes dropped from $A, B, C$ respectively. Let $\frac{\overline{A H}}{\overline{H A_{1}}}+\frac{\overline{B H}}{\overline{H B_{1}}}+\frac{\overline{C H}}{\overline{H C_{1}}}=2008$. Calculate the product $\frac{\overline{A H}}{\overline{H A_{1}}} \cdot \frac{\overline{B H}}{\overline{H B_{1}}} \cdot \frac{\overline{C H}}{\overline{H C_{1}}}$.
|
2010
|
2/8
|
The curve \( L \) divides an equilateral triangle \( ABC \) with side length \( a \) into two parts of equal area. Prove that the length \( l \) of the curve \( L \) satisfies the inequality \( l \geqslant \frac{\sqrt{\pi}}{2 \sqrt[4]{3}} a \).
|
l \geqslant \frac{\sqrt{\pi}}{2 \sqrt[4]{3}} a
|
0/8
|
\section*{Task 4 - 121224}
In a city, a network of at least two bus lines is to be established. This network must satisfy the following conditions:
(1) Each line has exactly three stops.
(2) Each line has exactly one stop in common with every other line.
(3) It is possible to reach any stop from any other stop with one line, without having to change lines in between.
Determine all possibilities for the number of bus lines in such a network.
|
7
|
3/8
|
The conductance of a $0.0015 \mathrm{M}$ aqueous solution of a weak monobasic acid was determined by using a conductivity cell consisting of platinized Pt electrodes. The distance between the electrodes is $120 \mathrm{~cm}$ with an area of cross section of $1 \mathrm{~cm}^{2}$. The conductance of this solution was found to be $5 \times 10^{-7} \mathrm{~S}$. The $\mathrm{pH}$ of the solution is 4 . The value of limiting molar conductivity $\left(\Lambda_{m}^{o}\right)$ of this weak monobasic acid in aqueous solution is $Z \times 10^{2} \mathrm{~S} \mathrm{~cm}^{-1} \mathrm{~mol}^{-1}$. What is the value of $Z$?
Please give the answer directly without any intermediate steps.
|
6
|
0/8
|
13. From the consecutive natural numbers $1,2,3, \cdots, 2014$, select $n$ numbers such that these $n$ numbers satisfy: taking any two of them, one will not be 5 times the other. Try to find the maximum value of $n$, and explain the reason.
|
1679
|
4/8
|
Murashkin M.V.
On each cell of a $10 \times 10$ board, there is a chip. It is allowed to choose a diagonal with an even number of chips and remove any chip from it.
What is the maximum number of chips that can be removed from the board using such operations?
|
90
|
0/8
|
B3. We start with a square with side 1. In the first minute, squares with side $\frac{1}{3}$ grow in the middle of the vertical sides. In the next minute, squares with sides of $\frac{1}{3}$ of the length of those line segments grow in the middle of all vertical line segments of the new figure. See below for the situation after 0, 1, and 2 minutes.
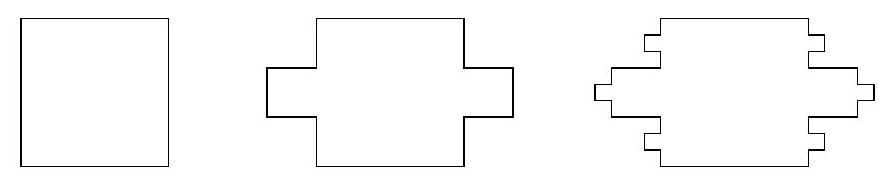
This process continues. Every minute, a square with a side of $\frac{1}{3}$ of the length of each vertical line segment grows in the middle of each vertical line segment. After an hour, squares have grown 60 times.
What is the perimeter of the figure after an hour?
|
84
|
0/8
|
1. Given the function $f(x)=[x[x[x]]]$, where $[x]$ denotes the greatest integer not exceeding $x$. If its domain is $[0,4]$, then its range is $\qquad$ .
|
\{0, 1, 8, 9, 12, 13, 14, 27, 28, 29, 33, 34, 35, 36, 40, 41, 42, 43, 64\}
|
4/8
|
Insert two digits into the number 2019 so that the resulting six-digit number
- starts with 2 and ends with 9,
- is composed of six different digits,
- is divisible by three,
- its first three-digit number is divisible by three,
- its first four-digit number is divisible by four,
- the sum of the inserted digits is odd.
Determine the difference between the largest and smallest six-digit number with the given properties.
(L. Růžičková)
|
69180
|
2/8
|
Example 2. In space, there are 10 points, 4 of which lie on the same plane, and no other set of 4 points are coplanar; find the number of circular cones (not necessarily right circular cones) with one of the points as the vertex and a circle passing through 3 other points as the base.
|
836
|
1/8
|
For any set $A=\left\{a_{1}, a_{2}, a_{3}, a_{4}\right\}$ of four distinct positive integers with sum $s_{A}=a_{1}+a_{2}+a_{3}+a_{4}$, let $p_{A}$ denote the number of pairs $(i, j)$ with $1 \leq i<j \leq 4$ for which $a_{i}+a_{j}$ divides $s_{A}$. Among all sets of four distinct positive integers, determine those sets $A$ for which $p_{A}$ is maximal. Answer. The sets $A$ for which $p_{A}$ is maximal are the sets the form $\{d, 5 d, 7 d, 11 d\}$ and $\{d, 11 d, 19 d, 29 d\}$, where $d$ is any positive integer. For all these sets $p_{A}$ is 4.
|
\{d, 5d, 7d, 11d\}
|
0/8
|
12th Chinese 1997 Problem B2 Let X be the set of residues mod 17. We regard two members of X as adjacent if they differ by 1, so 0 and 16 are adjacent. We say that a permutation of X is dispersive if it never takes two adjacent values to two adjacent values, and connective if it always takes two adjacent values to two adjacent values. What is the largest N for which we can find a permutation p on X such that p, p 2 , ... , p N-1 are all dispersive and p N is connective?
|
8
|
3/8
|
Two cones have a common vertex, and the generatrix of the first cone is the height of the second. The angle at the vertex of the axial section of the first cone is $\arccos \frac{1}{3}$, and that of the second is $-120^{\circ}$. Find the angle between the generatrices at which the lateral surfaces of the cones intersect.
|
60^\circ
|
1/8
|
4. Let the function be
$$
\begin{array}{l}
f(x)=\sqrt{10-6 \cos x}+\sqrt{\frac{17}{8}-\frac{3 \sqrt{2}}{2} \sin x}+ \\
\sqrt{19-2 \sqrt{2} \cos x-8 \sin x} \text {. } \\
\end{array}
$$
For all real numbers $x$, the minimum value of $f(x)$ is
$\qquad$ .
|
\dfrac{21\sqrt{2}}{4} - 1
|
0/8
|
12. (12 points) Person A and Person B start from points A and B respectively at the same time, moving towards each other at a constant speed. When A and B meet at point C, Person C starts from B, moving at a constant speed towards A. When A and C meet at point D, A immediately turns around and reduces their speed to 80% of the original speed. When A and C arrive at A at the same time, B is still 720 meters away from A. If the distance between C and D is 900 meters, then the distance between A and B is $\qquad$ meters.
|
5265
|
1/8
|
133. Digits and Prime Numbers. Using each of the nine digits once and only once, form prime numbers (numbers that do not divide evenly by any integer except 1 and themselves) whose sum is the smallest.
For example, four prime numbers
61
+283
47
59
450
contain all nine digits once and only once, and their sum is 450, but it can be significantly reduced. This is a very simple puzzle.
|
207
|
0/8
|
The non-parallel sides of a trapezoid are extended until they intersect, and a line parallel to the bases of the trapezoid is drawn through this point of intersection. Find the length of the segment of this line that is limited by the extensions of the diagonals if the lengths of the bases of the trapezoid are $a$ and $b$.
|
\dfrac{2ab}{|a - b|}
|
1/8
|
15. Given the function $f(x)=x^{2}+x-2$.
(1) Try to find the analytical expression of the function $g(x)=\frac{|f(x)|-f(x)}{2}$;
(2) If $a>0$, when the line $y=a x+b$ intersects the curve $y=g(x)$ at three different points, try to determine the relationship between $a$ and $b$, and draw a diagram to represent the region where the point $(a, b)$ lies with $a$ and $b$ as coordinates.
|
g(x) = \begin{cases} 0 & \text{if } x \leq -2 \text{ or } x \geq 1, \\ -x^2 - x + 2 & \text{if } -2 < x < 1. \end{cases}
|
2/8
|
5. (10 points) On a horizontal straight line, a square and two isosceles right triangles are placed. If the area of the square placed diagonally is 6 square centimeters, then the total area of the shaded parts is $\qquad$ square centimeters.
|
3
|
0/8
|
There is a $2n\times 2n$ rectangular grid and a chair in each cell of the grid. Now, there are $2n^2$ pairs of couple are going to take seats. Define the distance of a pair of couple to be the sum of column difference and row difference between them. For example, if a pair of couple seating at $(3,3)$ and $(2,5)$ respectively, then the distance between them is $|3-2|+|3-5|=3$. Moreover, define the total distance to be the sum of the distance in each pair. Find the maximal total distance among all possibilities.
|
4n^3
|
5/8
|
A variable tangent $t$ to the circle $C_1$, of radius $r_1$, intersects the circle $C_2$, of radius $r_2$ in $A$ and $B$. The tangents to $C_2$ through $A$ and $B$ intersect in $P$.
Find, as a function of $r_1$ and $r_2$, the distance between the centers of $C_1$ and $C_2$ such that the locus of $P$ when $t$ varies is contained in an equilateral hyperbola.
[b]Note[/b]: A hyperbola is said to be [i]equilateral[/i] if its asymptotes are perpendicular.
|
\sqrt{2} r_1
|
1/8
|
323. Find the area of the triangle formed by the intersection of a sphere of radius $R$ with a trihedral angle, the dihedral angles of which are equal to $\alpha, \beta$ and $\gamma$, and the vertex coincides with the center of the sphere.
|
(\alpha + \beta + \gamma - \pi) R^2
|
2/8
|
6. Five spherical surfaces can divide space into $\qquad$ parts.
|
30
|
2/8
|
19. In base five, there is $(\overline{a b b})_{5} \times(\overline{a c d})_{5}=(\overline{b a e c a})_{5}$, where the same letters represent the same digits, and different letters represent different digits. Then, the product of this equation converted to a decimal number is . $\qquad$
|
2021
|
3/8
|
6. A triangular piece of paper of area 1 is folded along a line parallel to one of the sides and pressed flat. What is the minimum possible area of the resulting figure?
|
\dfrac{2}{3}
|
0/8
|
Let us call a natural number useful if it does not contain any zeros or repeated digits in its decimal notation, and the product of all its digits is a multiple of their sum. Do there exist two consecutive three-digit useful numbers?
|
Yes
|
0/8
|
8. Hexagon $A B C D E F$ has a circumscribed circle and an inscribed circle. If $A B=9, B C=6, C D=2$, and $E F=4$. Find $\{D E, F A\}$.
|
\{1, 8\}
|
0/8
|
## Task A-2.2.
A 2021-digit number is written. Each two-digit number formed by two consecutive digits of this number (without changing the order) is divisible by 17 or 23. The unit digit of this number is 7. What is its first digit?
|
4
|
0/8
|
1. Given circles $\odot O_{1}$ and $\odot O_{2}$ intersect at points $A$ and $B$, with radii $5$ and $7$ respectively, and $O_{1} O_{2}=6$. A line through point $A$ intersects $\odot O_{1}$ and $\odot O_{2}$ at points $C$ and $D$, respectively. Points $P$ and $O$ are the midpoints of segments $CD$ and $O_{1} O_{2}$, respectively. Find the length of $OP$.
|
2\sqrt{7}
|
5/8
|
2.203. $\frac{\sqrt{\sqrt{\frac{x-1}{x+1}}+\sqrt{\frac{x+1}{x-1}}-2} \cdot\left(2 x+\sqrt{x^{2}-1}\right)}{\sqrt{(x+1)^{3}}-\sqrt{(x-1)^{3}}}$.
2.203. $\frac{\sqrt{\sqrt{\frac{x-1}{x+1}}+\sqrt{\frac{x+1}{x-1}}-2} \cdot\left(2 x+\sqrt{x^{2}-1}\right)}{\sqrt{(x+1)^{3}}-\sqrt{(x-1)^{3}}}$.
The expression is already in a mathematical form and does not require translation. However, if you need the problem statement in English, it would be:
2.203. $\frac{\sqrt{\sqrt{\frac{x-1}{x+1}}+\sqrt{\frac{x+1}{x-1}}-2} \cdot\left(2 x+\sqrt{x^{2}-1}\right)}{\sqrt{(x+1)^{3}}-\sqrt{(x-1)^{3}}}$.
Simplify the expression above.
|
(x^2 - 1)^{-1/4}
|
0/8
|
Let \( a_{1}, a_{2}, \ldots, a_{k} \) be fixed numbers and \( u_{n+k} = a_{1} u_{n+k-1} + \ldots + a_{k} u_{n} \). Suppose that \( x_{1}, \ldots, x_{k} \) are pairwise distinct roots of the equation \( x^{k} = a_{1} x^{k-1} + a_{2} x^{k-2} + \ldots + a_{k} \). Prove that \( u_{n} = c_{1} x_{1}^{n-1} + \ldots + c_{k} x_{k}^{n-1} \) for some fixed numbers \( c_{1}, \ldots, c_{k} \).
|
u_n = c_1 x_1^{n-1} + c_2 x_2^{n-1} + \ldots + c_k x_k^{n-1}
|
5/8
|
2. The sum of 16 consecutive natural numbers, including the number $n$, is fifteen times greater than the number $n$. Determine all numbers $n$ for which this is possible.
|
24
|
0/8
|
Consider a sequence where the \( n \)-th term is the first digit of the number \( 2^n \). Prove that the number of different "words" of length 13—sets of 13 consecutive digits—is 57.
|
57
|
3/8
|
A point on the hypotenuse, equidistant from both legs, divides the hypotenuse into segments of lengths 30 cm and 40 cm. Find the legs of the triangle.
|
42\,
|
0/8
|
The highway from Lishan Town to the provincial capital is 189 kilometers long, passing through the county town. It is 54 kilometers from Lishan Town to the county town. At 8:30 AM, a bus left from Lishan Town to the county town and arrived at 9:15 AM. After a 15-minute stop, it continued to the provincial capital and arrived at 11:00 AM. Another bus left from the provincial capital to Lishan Town on the same morning at 8:50 AM, traveling at 60 kilometers per hour. What is the time when the two buses meet?
|
10:08
|
3/8
|
In a scalene triangle, two of the medians are equal to two of the altitudes. Find the ratio of the third median to the third altitude.
|
3.5
|
0/8
|
Inside a grid rectangle with a perimeter of 50 cells, a rectangular hole with a perimeter of 32 cells is cut along the boundaries of the cells (the hole does not contain boundary cells). If you cut this figure along all the horizontal lines of the grid, you get 20 strips, each 1 cell in width. How many strips will you get if, instead, you cut it along all the vertical lines of the grid? (Note: A $1 \times 1$ cell is also considered a strip!)
|
21
|
0/8
|
A set of identical square tiles with side length 1 is placed on a (very large) floor. Every tile after the first shares an entire edge with at least one tile that has already been placed.
- What is the largest possible perimeter for a figure made of 10 tiles?
- What is the smallest possible perimeter for a figure made of 10 tiles?
- What is the largest possible perimeter for a figure made of 2011 tiles?
- What is the smallest possible perimeter for a figure made of 2011 tiles?
|
180
|
1/8
|
Let \( f: \mathbb{N} \rightarrow \mathbb{N} \) be a function satisfying the following conditions:
(a) \( f(1)=1 \).
(b) \( f(a) \leq f(b) \) whenever \( a \) and \( b \) are positive integers with \( a \leq b \).
(c) \( f(2a)=f(a)+1 \) for all positive integers \( a \).
How many possible values can the 2014-tuple \((f(1), f(2), \ldots, f(2014))\) take?
|
1007
|
0/8
|
Let $\omega_1$ and $\omega_2$ be two circles intersecting at points $P$ and $Q$. The tangent line closer to $Q$ touches $\omega_1$ and $\omega_2$ at $M$ and $N$ respectively. If $PQ = 3$, $QN = 2$, and $MN = PN$, what is $QM^2$?
|
5
|
0/8
|
A paper cup has a base that is a circle with radius $r$, a top that is a circle with radius $2r$, and sides that connect the two circles with straight line segments. This cup has height $h$ and volume $V$. A second cup, exactly the same shape as the first, is held upright inside the first cup so that its base is a distance of $\frac{h}{2}$ from the base of the first cup. The volume of liquid that will fit inside the first cup and outside the second cup can be written as $\frac{m}{n} \cdot V$, where $m$ and $n$ are relatively prime positive integers. Find $m + n$.
|
93
|
4/8
|
On $2020 \times 2021$ squares, cover the whole area with several L-Trominos and S-Tetrominos (Z-Tetrominos) along the square so that they do not overlap. The tiles can be rotated or flipped over. Find the minimum possible number of L-Trominos to be used.
|
2020
|
4/8
|
Let $\triangle ABC$ be acute with $\angle BAC = 45^{\circ}$. Let $\overline{AD}$ be an altitude of $\triangle ABC$, let $E$ be the midpoint of $\overline{BC}$, and let $F$ be the midpoint of $\overline{AD}$. Let $O$ be the center of the circumcircle of $\triangle ABC$, let $K$ be the intersection of lines $DO$ and $EF$, and let $L$ be the foot of the perpendicular from $O$ to line $AK$. If $BL = 6$ and $CL = 8$, find $AL^2$.
|
48
|
0/8
|
Evan, Larry, and Alex are drawing whales on the whiteboard. Evan draws 10 whales, Larry draws 15 whales, and Alex draws 20 whales. Michelle then starts randomly erasing whales one by one. The probability that she finishes erasing Larry's whales first can be expressed as $\frac{p}{q}$. Compute $p+q$.
|
137
|
0/8
|
Five identical circles are placed in a line inside a larger circle as shown. If the shown chord has a length of $16$, find the radius of the large circle.
|
10
|
1/8
|
A unit circle is centered at $(0, 0)$ on the $(x, y)$ plane. A regular hexagon passing through $(1, 0)$ is inscribed in the circle. Two points are randomly selected from the interior of the circle, and horizontal lines are drawn through them, dividing the hexagon into at most three pieces. The probability that each piece contains exactly two of the hexagon's original vertices can be written as \[ \frac{2\left(\frac{m\pi}{n}+\frac{\sqrt{p}}{q}\right)^2}{\pi^2} \] for positive integers $m$, $n$, $p$, and $q$ such that $m$ and $n$ are relatively prime and $p$ is squarefree. Find $m+n+p+q$.
|
11
|
1/8
|
For a positive integer $n$, consider all its divisors (including $1$ and itself). Suppose that $p\%$ of these divisors have their unit digit equal to $3$.
For example, if $n = 117$, it has six divisors: $1, 3, 9, 13, 39, 117$. Two of these divisors, namely $3$ and $13$, have unit digits equal to $3$. Hence, for $n = 117$, $p = 33.33\ldots$.
Find the maximum possible value of $p$ for any positive integer $n$.
|
50
|
2/8
|
Let $ABCDEF$ be a regular hexagon with side length 10 inscribed in a circle $\omega$. $X$, $Y$, and $Z$ are points on $\omega$ such that $X$ is on minor arc $AB$, $Y$ is on minor arc $CD$, and $Z$ is on minor arc $EF$, where $X$ may coincide with $A$ or $B$ (and similarly for $Y$ and $Z$). Compute the square of the smallest possible area of $\triangle XYZ$.
|
7500
|
4/8
|
Tim has a working analog 12-hour clock with two hands that run continuously. He also has a clock that runs at half the correct rate. At noon one day, both clocks show the exact time. At any given instant, the hands on each clock form an angle between $0^\circ$ and $180^\circ$ inclusive. At how many times during that day are the angles on the two clocks equal?
|
33
|
1/8
|
We color all the sides and diagonals of a regular polygon $P$ with 43 vertices either red or blue. Each vertex is an endpoint of 20 red segments and 22 blue segments. A triangle formed by vertices of $P$ is called monochromatic if all of its sides have the same color. Suppose there are 2022 blue monochromatic triangles. How many red monochromatic triangles are there?
|
859
|
2/8
|
How many ways are there to express $1,000,000$ as a product of exactly three integers greater than $1$? For the purpose of this problem, $abc$ is not considered different from $bac$, etc.
|
114
|
0/8
|
In how many rearrangements of the numbers $1, 2, 3, 4, 5, 6, 7, 8, 9$ do the numbers form a \textit{hill}? A \textit{hill} is defined as a sequence where the numbers increase to a peak and then decrease, such as in $129876543$ or $258976431$.
|
254
|
4/8
|
In triangle $ABC$, points $D$, $E$, and $F$ are on sides $BC$, $CA$, and $AB$ respectively, such that $BF = BD = CD = CE = 5$ and $AE - AF = 3$. Let $I$ be the incenter of $\triangle ABC$. The circumcircles of $\triangle BFI$ and $\triangle CEI$ intersect at $X \neq I$. Find the length of $DX$.
|
3
|
0/8
|
There were 35 yellow and white dandelions growing on the lawn. After eight white dandelions flew away, and two yellow ones turned white, the number of yellow dandelions became twice the number of white ones. How many white and how many yellow dandelions were there on the lawn at first?
#
|
20
|
2/8
|
## Task 1 - 290721
Susi goes shopping. From the money her mother gave her, she spends $30 \%$ at the butcher's; at the dairy, she pays with a quarter of the amount her mother gave her. At the greengrocer's, she needs exactly four fifths of the amount she paid at the butcher's.
At the bakery, she finally spends twice as much money as the remaining amount she brings back home. Her mother gives her half of this remaining amount, which is exactly $1.05 \mathrm{M}$, so she can buy a soft ice cream.
Determine the amount of money Susi initially received from her mother!
|
30
|
3/8
|
In a country with $n$ cities, all direct airlines are two-way. There are $r>2014$ routes between pairs of different cities that include no more than one intermediate stop (the direction of each route matters). Find the least possible $n$ and the least possible $r$ for that value of $n$.
|
2016
|
1/8
|
2. Ivan Semenovich leaves for work at the same time every day, drives at the same speed, and arrives exactly at 9:00. One day he overslept and left 40 minutes later than usual. To avoid being late, Ivan Semenovich drove at a speed 60% faster than usual and arrived at 8:35. By what percentage should he have increased his usual speed to arrive exactly at 9:00?
|
30
|
3/8
|
6. 15 cards, each card has 3 different Chinese characters, any 2 cards do not have exactly the same characters; among any 6 cards, there must be 2 cards that have a common character. Question: What is the maximum number of different Chinese characters on these 15 cards?
|
35
|
0/8
|
Six. (20 points) As shown in Figure 3, let
$$
P_{1}(1, \sqrt{3}), P_{2}(4,2 \sqrt{3}), \cdots, P_{n}\left(x_{n}, y_{n}\right)
$$
$\left(0<y_{1}<y_{2}<\cdots<y_{n}\right)$ be $n$ points on the curve $C: y^{2}=3 x(y \geqslant 0)$. Points $A_{i}(i=1,2, \cdots, n)$ are on the positive $x$-axis, satisfying that $\triangle A_{i-1} A_{i} P_{i}$ is an equilateral triangle ($A_{0}$ is the origin).
(1) Find the expression for the $x$-coordinate $a_{n}$ of point $A_{n}\left(a_{n}, 0\right)$ in terms of $n$;
(2) Evaluate
$$
\left[\frac{4}{5}+\frac{1}{\sqrt[4]{a_{1}}}+\frac{1}{\sqrt[4]{a_{2}}}+\cdots+\frac{1}{\sqrt[4]{a_{2000}}}\right]
$$
where [a] denotes the integer part of the number. When $2005 < c < 2005.6$, take $\sqrt{c}=44.78$; when $2006 < c < 2006.5$, take $\sqrt{c}=44.785$. $\sqrt{2}=1.4$.
|
88
|
4/8
|
19. Sesame Street has 100 households, and their house numbers are not consecutive, but are arranged according to the following pattern:
$$
1,2,4,5,7,9,10,12,14,16,17,19,21,23,25, \cdots \cdots
$$
Among these 100 house numbers, there are $\qquad$ odd numbers.
|
49
|
4/8
|
2・-110 Let the sequence of positive real numbers $x_{0}, x_{1}, \cdots, x_{1995}$ satisfy the following two conditions:
(1) $x_{0}=x_{1995}$;
(2) $x_{i-1}+\frac{2}{x_{i-1}}=2 x_{i}+\frac{1}{x_{i}}, i=1,2, \cdots, 1995$.
Find the maximum value of $x_{0}$ for all sequences that satisfy the above conditions.
|
2^{997}
|
0/8
|
8.4. The steamship "Raritet" after leaving the city moves at a constant speed for three hours, then drifts for an hour, moving with the current, then moves for three hours at the same speed, and so on. If the steamship starts its journey from city A and heads to city B, it takes 10 hours. If it starts from city B and heads to city A, it takes 15 hours. How long would it take to travel from city A to city B on a raft?
|
60
|
1/8
|
8. A parallel beam of light falls normally on a thin lens with a focal length of $F=150$ cm. Behind the lens, there is a screen on which a circular spot of a certain diameter is visible. If the screen is moved 40 cm, a spot of the same diameter will again be visible on the screen. Determine the initial distance from the lens to the screen. (15 points)
|
170
|
1/8
|
4. (10 points) Person A leaves location $A$ to find person B, and after walking 80 kilometers, arrives at location $B$. At this point, person B had left for location $C$ half an hour earlier. Person A has been away from location $A$ for 2 hours, so A continues to location $C$ at twice the original speed. After another 2 hours, both A and B arrive at location $C$ simultaneously. What is the speed of person B in kilometers per hour?
|
64
|
5/8
|
10.251. Five circles are inscribed in an angle of $60^{\circ}$ such that each subsequent circle (starting from the second) touches the previous one. By what factor is the sum of the areas of all five corresponding circles greater than the area of the smallest circle?
|
7381
|
3/8
|
Let \( f(n) \) satisfy \( f(0) = 0 \) and \( f(n) = n - f(f(n-1)) \) for \( n = 1, 2, 3, \cdots \). Determine all real-coefficient polynomials \( g(x) \) such that
\[ f(n) = \lfloor g(n) \rfloor \text{ for } n = 0, 1, 2, \cdots, \]
where \( \lfloor g(n) \rfloor \) denotes the greatest integer less than or equal to \( g(n) \).
|
\frac{\sqrt{5} - 1}{2} (x + 1)
|
3/8
|
3. In a convex quadrilateral $A B C D$, points $E$ and $F$ are the midpoints of sides $B C$ and $C D$ respectively. Segments $A E, A F$, and $E F$ divide the quadrilateral into 4 triangles, the areas of which are consecutive natural numbers. What is the maximum possible value of the area of triangle $A B D$?
|
6
|
0/8
|
In the right triangle \( \triangle ABC \), with \( \angle ACB = 90^\circ \), \( BC = a \), and \( CA = b \) (where \( a > 0 \) and \( b > 0 \)), point \( P \) lies on side \( AB \). The right triangle \( \triangle ABC \) is folded along line \( PC \) to form the tetrahedron \( PACB \). Find the maximum possible volume of this tetrahedron.
|
\dfrac{a^2 b^2}{6 \left( a^{2/3} + b^{2/3} \right)^{3/2}}
|
0/8
|
Consider 2021 lines in the plane, no two of which are parallel and no three of which are concurrent. Let E be the set of their intersection points. We want to assign a color to each point in E such that any two points on the same line, and whose connecting segment contains no other point of E, are of different colors.
How many colors are needed at a minimum to achieve such a coloring?
|
3
|
5/8
|
Consider two mirrors placed at a right angle to each other and two points A at $ (x,y)$ and B at $ (a,b)$. Suppose a person standing at point A shines a laser pointer so that it hits both mirrors and then hits a person standing at point B (as shown in the picture). What is the total distance that the light ray travels, in terms of $ a$, $ b$, $ x$, and $ y$? Assume that $ x$, $ y$, $ a$, and $ b$ are positive.
[asy]draw((0,4)--(0,0)--(4,0),linewidth(1));
draw((1,3)--(0,2),MidArrow);
draw((0,2)--(2,0),MidArrow);
draw((2,0)--(3,1),MidArrow);
dot((1,3));
dot((3,1));
label("$A (x,y)$", (1,3),NE);
label("$B (a,b)$", (3,1),NE);[/asy]
|
\sqrt{(x + a)^2 + (y + b)^2}
|
3/8
|
5. Let $P$ be the vertex of a cone, and $A, B, C$ be three points on the circumference of its base, satisfying $\angle A B C=90^{\circ}$, $M$ is the midpoint of $A P$. If $A B=1, A C=2, A P=\sqrt{2}$, then the size of the dihedral angle $M-B C-A$ is $\qquad$ .
|
\arctan\left(\dfrac{2}{3}\right)
|
0/8
|
Define the Fibonacci numbers via $F_0=0$, $f_1=1$, and $F_{n-1}+F_{n-2}$.
Olivia flips two fair coins at the same time, repeatedly, until she has flipped a tails on both, not necessarily on the same throw. She records the number of pairs of flips $c$ until this happens (not including the last pair, so if on the last flip both coins turned up tails $c$ would be $0$). What is the expected value $F_c$?
|
\dfrac{19}{11}
|
0/8
|
1. Line segment $A B$ divides a square into two polygons (points $A$ and $B$ are on the sides of the square), each polygon has an inscribed circle, one of which has a radius of 6, while the other has a radius greater than 6. What is the difference between the side length of the square and twice the length of line segment $A B$?
|
12
|
1/8
|
Example 21 Given three lines $l_{1}, l_{2}, l_{3}$ on a plane that do not pass through the origin, their equations are:
$$
\begin{array}{l}
l_{1}: a_{1} x+b_{1} y+c_{1}=0, \\
\iota_{2}: a_{2} x+b_{2} y+c_{2}=0, \\
\iota_{3}: a_{3} x+b_{3} y+c_{3}=0 .
\end{array}
$$
A moving line $l$ passing through the origin intersects the lines $l_{1}, l_{2}, l_{3}$ at points $A\left(x_{1}, y_{1}\right), B\left(x_{2}\right.$, $\left.y_{2}\right), C\left(x_{3}, y_{3}\right)$. Let $\left|\overrightarrow{O A}_{i}\right|=\rho_{i}(i=1,2,3),$ and $P$ be a point on the line $l$, with $|\overrightarrow{O P}|=$ $\rho$, and satisfies: $\frac{1}{\rho_{1}}+\frac{1}{\rho_{2}}+\frac{1}{\rho_{3}}=\frac{1}{\rho}$. Try to find the equation of the trajectory of the moving point $P(x, y)$.
|
\left(\frac{a_{1}}{c_{1}}+\frac{a_{2}}{c_{2}}+\frac{a_{3}}{c_{3}}\right)x + \left(\frac{b_{1}}{c_{1}}+\frac{b_{2}}{c_{2}}+\frac{b_{3}}{c_{3}}\right)y + 1 = 0
|
0/8
|
11. Given a function $f(x)$ defined on $[0,1]$, $f(0)=0, f(1)=1$, and satisfies the following conditions:
(a) For any $x \in[0,1], f(x) \geq 0$;
(b) For any two numbers $x_{1} \geq 0, x_{2} \geq 0, x_{1}+x_{2} \leq 1$, it holds that $f\left(x_{1}+x_{2}\right) \geq f\left(x_{1}\right)+f\left(x_{2}\right)$.
Find the smallest positive number $c$, such that for any function $f(x)$ satisfying the above conditions and for any $x \in[0,1]$, we have $f(x) \leq c x$.
|
2
|
3/8
|
9.6. Waiting for customers, a watermelon seller sequentially weighed 20 watermelons (weighing 1 kg, 2 kg, 3 kg, ..., 20 kg), balancing the watermelon on one scale pan with one or two weights on the other pan (possibly identical). In the process, the seller wrote down on a piece of paper the weights he used. What is the smallest number of different numbers that could have appeared in his notes, if the weight of each weight is an integer number of kilograms?
|
6
|
3/8
|
In an isosceles triangle, the angle at the apex is $36^{\circ}$, and the angle bisector of the base angle is equal to $\sqrt{20}$. Find the lengths of the sides of the triangle.
|
2\sqrt{5}
|
4/8
|
13. (15 points) As shown in the figure, ten points are evenly marked on the circumference of a circle. Place the ten natural numbers $1 \sim 10$ on these ten points. Rotate a line passing through the center of the circle. When the line does not pass through any marked points, it divides the numbers 1 to 10 into two groups. For each arrangement, there are five ways to divide the numbers as the line rotates. For each division, there is a product of the sums of the two groups, and the smallest of these five products is denoted as $K$. What is the maximum value of $K$ among all possible arrangements?
|
756
|
0/8
|
30 Given that the three sides of $\triangle A B C$ are all integers, $\angle A=2 \angle B, \angle C>90^{\circ}$. Find the minimum perimeter of $\triangle A B C$.
|
77
|
4/8
|
13.150. In the manuscript of an arithmetic problem book, an example was written in which a given number had to be multiplied by 3 and 4 subtracted from the result. In the printing house, a misprint was made: instead of the multiplication sign, a division sign was placed, and instead of a minus sign, a plus sign. Nevertheless, the final result did not change. What example was intended to be placed in the problem book?
|
3 \times 3 - 4
|
0/8
|
In the picture, you can see a pool with a long step on one of its walls. We started filling the empty pool with a constant flow and observed the water level. After
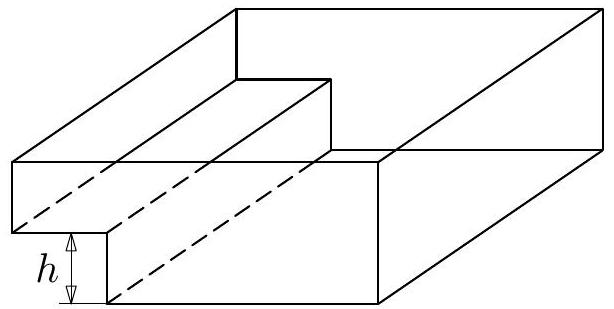
8 min, the water level had risen to a height of $20 \mathrm{~cm}$ and had not yet reached the level of the step. After $23 \mathrm{~min}$ of filling, the water level was at $55 \mathrm{~cm}$ and the step had already been submerged for some time. After 35.5 min of filling, the pool was filled to a height of $80 \mathrm{~cm}$. At what height $h$ from the bottom of the pool is the step located?
(L. Šimünek)
|
45
|
3/8
|
Let $n$ be a positive integer, and denote by $f(n)$ the smallest positive integer $k$ such that $\left[\frac{n^{2}}{k}\right]=\left[\frac{n^{2}}{k+1}\right]$. Determine the value of $\left[\frac{n^{2}}{f(n)}\right]+f(n)$!
|
2n
|
0/8
|
The base of the pyramid is a square $ABCD$ with a side length of 1.5, the lateral edge $SC$ is perpendicular to the base plane and equals 1.75. Points $S, B$, and $D$ lie on the lateral surface of a cone with the vertex at point $A$, and point $C$ lies in the base plane of this cone. Find the lateral surface area of the cone.
|
\dfrac{15\sqrt{22}}{11} \pi
|
1/8
|
8. There are 9 representatives, each from different countries, with 3 people from each country. They randomly sit at a round table with 9 chairs. The probability that each representative is seated next to at least one representative from another country is $\qquad$ .
|
\dfrac{41}{56}
|
5/8
|
Let $n$ and $k$ be two natural numbers that are coprime, with $1 \leq k \leq n-1$, and let $M$ be the set $\{1,2, \ldots, n-1\}$. Each element of $M$ is colored with one of two colors. It is assumed that for every $i$ in $M$, $i$ and $n-i$ have the same color, and if $i \neq k$, $i$ and $|i-k|$ have the same color. Show that all elements of $M$ are of the same color.
|
\text{All elements of } M \text{ are the same color.}
|
0/8
|
As shown in the figure, the side length of the shaded small square is 2, and the side length of the outermost large square is 6. Determine the area of the square \(ABCD\).
|
20
|
0/8
|
Good morning, I.v.
Vasya has 100 bank cards. Vasya knows that one of the cards has 1 ruble, another has 2 rubles, and so on, with the last card having 100 rubles, but he does not know how much money is on which card. Vasya can insert a card into an ATM and request a certain amount. The ATM dispenses the requested amount if it is available on the card, and does nothing if the money is not there, while swallowing the card in either case. The ATM does not show how much money was on the card. What is the largest amount of money Vasya can guarantee to get?
|
2550
|
0/8
|
Let \((1+x+x^2)^n = a_0 + a_1x + a_2x^2 + \ldots + a_{2n}x^{2n}\) be an identity in \(x\). If we let \(s = a_0 + a_2 + a_4 + \ldots + a_{2n}\), the original answer is in the form \(\frac{k \cdot 3^n + m}{n}\), where n cannot be divisible by 2. Please find the value of \(k + m + n\).
|
4
|
0/8
|
Ali and Veli go hunting. The probability that each will successfully hit a duck is \(\frac{1}{2}\) on any given shot. During the hunt, Ali shoots 12 times, and Veli shoots 13 times. What is the probability that Veli hits more ducks than Ali? Express your answer in the form \(\frac{k}{m}\), where \(\frac{k}{m}\) is in simplest form, and find the value of k + m.
|
3
|
4/8
|
A six-digit number (base 10) is considered "squarish" if it satisfies the following conditions:
1. None of its digits are zero.
2. It is a perfect square.
3. The first two digits, the middle two digits, and the last two digits of the number are all perfect squares when considered as two-digit numbers.
How many squarish numbers are there? Provide your answer as an integer.
|
2
|
1/8
|
Squares $ABCD$ and $EFGH$ are congruent, $AB=10$, and $G$ is the center of square $ABCD$. Find the area of the region in the plane covered by these squares.
|
175
|
3/8
|
How many integer pairs $(m,n)$ are there satisfying the equation $4mn(m+n-1)=(m^2+1)(n^2+1)$? Provide your answer as an integer.
|
5
|
2/8
|
Five equilateral triangles, each with side $2\sqrt{3}$, are arranged so they are all on the same side of a line containing one side of each. Along this line, the midpoint of the base of one triangle is a vertex of the next. What is the area of the region of the plane that is covered by the union of the five triangular regions? Express your answer in the form of $a\sqrt{b}$, where $a$ and $b$ are integers. Please provide the value of a + b.
|
15
|
1/8
|
An observer stands on the side of the front of a stationary train. When the train starts moving with constant acceleration, it takes $5$ seconds for the first car to pass the observer. If the time it takes for the $10^{\text{th}}$ car to pass is $x$ seconds, find the value of $100x$.
|
81
|
0/8
|
When simplified, \( (x^{-1} + y^{-1})^{-1} \) is equal to what expression in the form \(\frac{kx}{my}\)? Please find the value of k + m.
|
2
|
3/8
|
What is the probability of having $2$ adjacent white balls or $2$ adjacent blue balls in a random arrangement of $3$ red, $2$ white, and $2$ blue balls? Provide your answer in the form \(\frac{k}{m}\), where the fraction is in simplest form. Calculate the value of \(k + m\).
|
31
|
5/8
|
In $\triangle ABC$, $AB = 10$, $AC = 8$, and $BC = 6$. Circle $P$ is the circle with the smallest radius that passes through $C$ and is tangent to $AB$. Let $Q$ and $R$ be the points of intersection, distinct from $C$, of circle $P$ with sides $AC$ and $BC$, respectively. If the length of segment $QR$ is $x$, what is the value of $10x$?
|
48
|
4/8
|
Pikachu, Charmander, and Vulpix are three of the four equally-skilled players in a Pokemon bracket tournament. Because they are equally skilled, whenever any two of the players battle, they are equally likely to win. In the bracket tournament, the four players are randomly paired into two rounds, each round consisting of two players. The winners of the first two rounds then play each other in the final round. The winner of the final match ranks first; the loser of the final round ranks second; and the two losers of the previous rounds jointly rank third. What is the probability that Charmander plays Vulpix in a round, but ranks lower than Pikachu? Express your answer in the form \(\frac{k}{m}\) where the fraction is in simplest form, and provide the value of \(k + m\).
|
9
|
0/8
|
1. Use the numbers $2,3, \cdots, 2019$ to form 1009 fractions, with each number appearing only once in either the numerator or the denominator. From these 1009 fractions, select the largest one. Find the minimum value of this number.
|
\dfrac{1010}{2019}
|
1/8
|
Subsets and Splits
Filtered Answers A-D
Retrieves 100 rows where the answer is a single letter from A to D, providing basic filtering of the dataset.