problem
stringlengths 10
7.44k
| answer
stringlengths 1
270
| difficulty
stringclasses 8
values |
|---|---|---|
Two isosceles triangles are placed side-by-side with their bases on the same line. If $\triangle ABC$ and $\triangle DEF$ are such triangles with $AB = AC$, $DE = DF$, $\angle BAC = 25^\circ$, and $\angle EDF = 40^\circ$, find the sum $\angle DAC + \angle ADE$.
|
147.5^\circ
|
3/8
|
The planet Zeta follows an elliptical orbit with its sun at one focus. At its closest approach (perigee), it is 3 astronomical units (AU) from the sun, and at its farthest point (apogee), it is 15 AU away. Calculate the distance from the sun to Zeta when Zeta is exactly halfway along its orbit from perigee to apogee.
|
9 \text{ AU}
|
2/8
|
A circular dartboard is divided into sectors. The probability of a dart randomly landing in one of the smaller sectors is $\frac{1}{8}$. There are 3 smaller sectors with equal probabilities and one larger sector. What is the central angle, in degrees, of one of the smaller sectors?
|
45^\circ
|
1/8
|
A unit cube is cut once along a diagonal of one face and then along the diagonal of the opposite parallel face creating four triangular prisms. One of these prisms is cut again along a plane passing through one of its longest edges and the midpoint of its opposite edge. This results in six pieces in total. What is the volume of the triangular prism that includes vertex $W$ on the original cube?
|
\frac{1}{8}
|
2/8
|
8 Arrange fifteen students numbered $1,2,3, \ldots, 15$ in a circle facing inward, in numerical order. The first time, the student numbered 1 turns around. The second time, the students numbered 2 and 3 turn around. The third time, the students numbered $4,5,6$ turn around, .... The 15th time, all students turn around. When the 12th turn is completed, how many students are still facing outward?
|
12
|
0/8
|
1. Given a set of data consisting of seven positive integers, the only mode is 6, and the median is 4. Then the minimum value of the sum of these seven positive integers is $\qquad$ .
|
26
|
3/8
|
2.149. $\frac{6}{\sqrt{2}+\sqrt{3}+\sqrt{5}}$.
Express the above text in English, keeping the original text's line breaks and format, and output the translation result directly.
2.149. $\frac{6}{\sqrt{2}+\sqrt{3}+\sqrt{5}}$.
|
\dfrac{3\sqrt{2} + 2\sqrt{3} - \sqrt{30}}{2}
|
2/8
|
65. Suppose you have forgotten one digit of a phone number you need and dial it at random. What is the probability that you will have to make no more than two calls?
|
\dfrac{1}{5}
|
3/8
|
4. As shown in Figure 4, in $\triangle A B C$, $A B=A C$, $\angle B=40^{\circ}$, $B D$ is the angle bisector of $\angle B$, and $B D$ is extended to $E$ such that $D E=A D$. Then the degree measure of $\angle E C A$ is
|
30
|
0/8
|
9. As shown in Figure 3, the center of the equilateral triangle $\triangle A_{1} B_{1} C_{1}$ with side length 1 is $O$. Rotate $\triangle A_{1} B_{1} C_{1}$ around the center $O$ to $\triangle A_{2} B_{2} C_{2}$ such that $A_{2} B_{2} \perp B_{1} C_{1}$. Then the area of the common part (i.e., the hexagon $A B C D E F$) of the two triangles is
|
\dfrac{3 - \sqrt{3}}{4}
|
0/8
|
Example 5 As shown in Figure 5, in $\triangle A B C$, $A C=7, B C=$ $4, D$ is the midpoint of $A B$, $E$ is a point on side $A C$, and $\angle A E D=$ $90^{\circ}+\frac{1}{2} \angle C$. Find the length of $C E$.
|
\dfrac{11}{2}
|
2/8
|
1.7 density, 400 gr weight liquid is mixed with 1.2 density $600 \mathrm{gr}$ solution. Measuring the density $D$ of the newly formed solution, we find that $D=1.4$. What is the contraction that occurs when mixing the two initial liquids?
|
21
|
5/8
|
Amanda has two identical cubes. Each cube has one integer on each face so that the following statements are all true:
- Three adjacent faces of each cube have the numbers 15,9 and 4 as shown.
- The numbers on all pairs of opposite faces have the same sum $s$.
- When both cubes are rolled and the numbers on the top faces are added, the probability that the sum equals 24 is $\frac{1}{12}$.
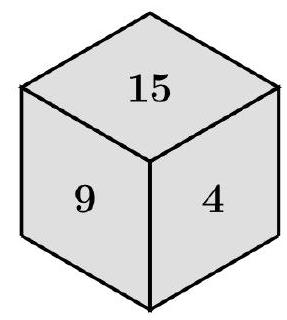
Determine the sum of all possible values of $s$.
|
64
|
1/8
|
3. In the city of hedgehogs, there are 1000 identical buildings, each with 1000 floors, and exactly one hedgehog lives on each floor. Each resident in the city wears a hat colored in one of 1000 possible colors, and any two residents in the same building have hats of different colors. We say that two hedgehogs are $\bar{u} p u j a \bar{u} e l i$ if they wear hats of the same color and live on consecutive floors (in different buildings). Determine the maximum possible number of (unordered) pairs of hedgehogs that are friends.
|
250000000
|
0/8
|
6. (15 points) A capacitor with capacitance $C_{1}=20$ μF is charged to a voltage $U_{1}=20$ V. A second capacitor with capacitance $C_{2}=5$ μF is charged to a voltage $U_{2}=5$ V. The capacitors are connected with their oppositely charged plates. Determine the voltage that will establish across the plates.
|
15
|
3/8
|
13.236. The master is giving a simultaneous chess exhibition on several boards. By the end of the first two hours, he won $10 \%$ of the total number of games played, while 8 opponents drew their games with the master. Over the next two hours, the master won $10 \%$ of the games with the remaining opponents, lost two games, and drew the remaining 7 games. On how many boards was the game being played?
|
20
|
2/8
|
9. The military district canteen needs 1000 pounds of rice and 200 pounds of millet for dinner. The quartermaster goes to the rice store and finds that the store is having a promotion. “Rice is 1 yuan per pound, and for every 10 pounds purchased, 1 pound of millet is given as a gift (no gift for less than 10 pounds); millet is 2 yuan per pound, and for every 5 pounds purchased, 2 pounds of rice are given as a gift (no gift for less than 5 pounds).” What is the minimum amount of money the quartermaster needs to pay to buy enough rice and millet for dinner?
|
1168
|
3/8
|
Example 6 Let $a_{1}, a_{2}, \cdots, a_{n}(n \geqslant 2)$ be $n$ distinct real numbers, $a_{1}^{2}+a_{2}^{2}+\cdots+a_{n}^{2}=S$. Try to find $\max \min _{1 \leqslant i<j \leqslant n}\left(a_{i}-a_{j}\right)^{2}$.
|
\dfrac{12S}{n(n^2 -1)}
|
3/8
|
2. In 8 "Y" grade, there are quite a few underachievers, but Vovochka performs the worst of all. The pedagogical council decided that either Vovochka must correct his failing grades by the end of the quarter, or he will be expelled. If Vovochka corrects his grades, then 24% of the class will be underachievers, but if he is expelled, the percentage of underachievers will be 25%. What is the current percentage of underachievers in 8 "Y"?
#
|
28
|
4/8
|
10. There is a sequence of numbers +1 and -1 of length $n$. It is known that the sum of every 10 neighbouring numbers in the sequence is 0 and that the sum of every 12 neighbouring numbers in the sequence is not zero.
What is the maximal value of $n$ ?
|
15
|
0/8
|
An 8-inch by 8-inch square is folded along a diagonal creating a triangular region. This resulting triangular region is then folded so that the right angle vertex just meets the midpoint of the hypotenuse. What is the area of the resulting trapezoidal figure in square inches?
[asy]
fill((0,0)--(10,0)--(10,10)--(0,10)--cycle,gray(.7));
draw((0,0)--(10,0)--(10,10)--(0,10)--cycle,linewidth(1));
fill((20,0)--(20,10)--(30,10)--cycle,gray(0.7));
draw((20,0)--(20,10)--(30,10)--cycle,linewidth(1));
draw((20,0)--(30,0)--(30,10),dashed);
fill((40,0)--(40,5)--(45,10)--(50,10)--cycle,gray(0.7));
draw((40,0)--(40,5)--(45,10)--(50,10)--cycle,linewidth(1));
draw((40,5)--(45,5)--(45,10));
draw((40,5)--(40,10)--(45,10),dashed);
draw((40,0)--(50,0)--(50,10),dashed);
draw((12,5)--(18,5),Arrow);
draw((32,5)--(38,5),Arrow);
[/asy]
|
24
|
4/8
|
Find all solutions to the equation $\sqrt{3x+6}=x+2$. If there are multiple solutions, order them from least to greatest, separated by comma(s).
|
1
|
0/8
|
$A$, $B$ and $C$ are circular regions as shown. There are 7 items in circle $C$. There are exactly 20 items in $A$ and 10 of those items are not in $B$. How many items are in $B$, but not in $C$?
[asy]
draw(Circle((0,0),50));
label("$A$",(39,39));
draw(Circle((10,-10),32));
label("$B$",(-16,16));
draw(Circle((5,-5),20));
label("$C$",(22,-22));
[/asy]
|
3
|
4/8
|
In the diagram, four circles of radius 1 with centres $P$, $Q$, $R$, and $S$ are tangent to one another and to the sides of $\triangle ABC$, as shown. [asy]
size(250);
pair A, B, C, P, Q, R, S;
R=(0,0);
Q=(-2,0);
S=(2,0);
P=(1,1.732);
B=(-5.73,-1);
C=(3.732,-1);
A=(1.366,3.098);
draw(A--B--C--A);
draw(circle(P, 1));
draw(circle(Q, 1));
draw(circle(R, 1));
draw(circle(S, 1));
label("A", A, N);
label("B", B, SW);
label("C", C, SE);
dot(P);
dot(Q);
dot(R);
dot(S);
label("P", P, N);
label("Q", Q, SW);
label("R", R, SW);
label("S", S, SE);
[/asy]
The radius of the circle with center $R$ is decreased so that
$\bullet$ the circle with center $R$ remains tangent to $BC$,
$\bullet$ the circle with center $R$ remains tangent to the other three circles, and
$\bullet$ the circle with center $P$ becomes tangent to the other three circles.
The radii and tangencies of the other three circles stay the same. This changes the size and shape of $\triangle ABC$. $r$ is the new radius of the circle with center $R$. $r$ is of the form $\frac{a+\sqrt{b}}{c}$. Find $a+b+c$.
|
6
|
0/8
|
Points \( M \) and \( N \) are the midpoints of sides \( BC \) and \( AD \), respectively, of quadrilateral \( ABCD \). The segments \( AM \), \( DM \), \( BN \), and \( CN \) divide quadrilateral \( ABCD \) into seven parts (six of which are triangles, and the seventh is a quadrilateral). Prove that if the areas of these six parts are odd natural numbers, then all six parts are triangles.
|
\text{All six parts are triangles.}
|
4/8
|
The area of the large square $\mathrm{ABCD}$ is 18 square centimeters, and the side $\mathrm{MN}$ of the gray square $\mathrm{MNPQ}$ lies on the diagonal $\mathrm{BD}$, with vertex $\mathrm{P}$ on side $\mathrm{BC}$ and $\mathrm{Q}$ on side $\mathrm{CD}$. What is the area of the gray square $\mathrm{MNPQ}$ in square centimeters?
|
4
|
4/8
|
Let $ABCD$ be a rhombus with angle $\angle A = 60^\circ$. Let $E$ be a point, different from $D$, on the line $AD$. The lines $CE$ and $AB$ intersect at $F$. The lines $DF$ and $BE$ intersect at $M$. Determine the angle $\angle BMD$ as a function of the position of $E$ on $AD.$
|
60^\circ
|
1/8
|
The line \( x + y = 1 \) intersects the ellipse \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \) at points \( A \) and \( B \). \( C \) is the midpoint of the line segment \( AB \). If \( |AB| = 2 \sqrt{2} \) and the slope of the line \( OC \) is \( k_C = \frac{1}{\sqrt{2}} \), find the equation of the ellipse.
|
\dfrac{x^2}{3} + \dfrac{2y^2}{3\sqrt{2}} = 1
|
4/8
|
B5. Simon has 2017 blue blocks numbered from 1 to 2017. He also has 2017 yellow blocks numbered from 1 to 2017. Simon wants to arrange his 4034 blocks in a row. He wants to do so in such a way that for every $k=1,2, \ldots, 2017$ the following conditions are met:
- to the left of the blue block with number $k$ there are $k$ or more yellow blocks;
- to the right of the yellow block with number $k$ there are $k$ or fewer blue blocks.
Determine all possible numbers of the 1000th block from the left in the row.
## C-problems
For the C-problems, not only the answer is important; your reasoning and the way of solving it must also be clearly written down. Solve each C-problem on a separate sheet of paper. Each correctly worked out C-problem is worth 10 points. Partial solutions can also earn points. Therefore, write everything clearly and submit your scratch paper (for each problem!) as well.
|
500
|
1/8
|
$\begin{array}{l}\text { 1. Let } g(x)=\ln \left(2^{x}+1\right) \text {. Then } \\ g(-4)-g(-3)+g(-2)-g(-1)+ \\ g(1)-g(2)+g(3)-g(4) \\ =\end{array}$
|
-2 \ln 2
|
4/8
|
8. A three-digit number has 3 digits, none of which are 0, and its square is a six-digit number that has exactly 3 digits as 0. Write down one such three-digit number: $\qquad$
|
448
|
1/8
|
There is a parabola and two of its tangents. Through the points of tangency, we draw chords parallel to the tangents. In what ratio does the intersection point divide the chords?
|
\dfrac{1}{3}
|
1/8
|
One. (40 points) Let $n(n>1)$ be a given positive integer, and $x_{1}, x_{2}, \cdots, x_{n}$ be any real numbers, satisfying $\sum_{i=1}^{n} x_{i}^{2}=1$. Find the maximum value of $\sum_{k=1}^{n} k x_{k}^{2}+\sum_{1 \leqslant i<j \leqslant n}(i+j) x_{i} x_{j}$.
|
\frac{n(n+1)}{4} + \frac{n}{2} \sqrt{ \frac{(n+1)(2n+1)}{6} }
|
0/8
|
5. A person is walking parallel to a railway track at a constant speed. A train also passes by him at a constant speed. The person noticed that depending on the direction of the train, it passes by him either in $t_{1}=1$ minute or in $t_{2}=2$ minutes. Determine how long it would take the person to walk from one end of the train to the other.
## $(15$ points)
|
4
|
4/8
|
7. Let the set $T=\left\{(a, b, c) \mid a, b, c \in \mathbf{N}^{*}\right.$, and $a, b, c$ can form the side lengths of some triangle $\}$. Then the value of $\sum_{(a, b, c) \in T} \frac{2^{a}}{3^{b} \cdot 5^{c}}$ is $\qquad$.
|
\dfrac{17}{21}
|
3/8
|
## Task B-4.3.
If $26!=403291 x 6112660563558 x y 00000$, determine the digits $x$ and $y$.
|
4
|
0/8
|
4. Let $O$ be the center of the base $\triangle ABC$ of the regular tetrahedron $P-ABC$. The dihedral angles between each pair of lateral edges are $\alpha$, and the angle between $PC$ and the plane $PAB$ is $\beta$. Denote the distance from point $O$ to each face as $d$. A moving plane through point $O$ intersects $PC$ at point $S$, and the extensions of $PA$ and $PB$ at points $Q$ and $R$, respectively. Then $\frac{1}{PQ}+\frac{1}{PR}+\frac{1}{PS}$ $\begin{array}{lllll}= & & & \end{array}$ $\qquad$ (the result should be expressed in terms of $\alpha, \beta, d$).
|
\dfrac{\sin \beta}{d}
|
0/8
|
Evie and Odette are playing a game. Three pebbles are placed on the number line; one at -2020 , one at 2020, and one at $n$, where $n$ is an integer between -2020 and 2020. They take it in turns moving either the leftmost or the rightmost pebble to an integer between the other two pebbles. The game ends when the pebbles occupy three consecutive integers.
Odette wins if their sum is odd; Evie wins if their sum is even. For how many values of $n$ can Evie guarantee victory if:
(a) Odette goes first;
(b) Evie goes first?
|
2021
|
1/8
|
2. Given that $A$ is a two-digit number, the remainder when $A^{2}$ is divided by 15 is 1, then the number of $A$ that satisfies the condition is $($ )
The translation preserves the original text's line breaks and format.
|
24
|
5/8
|
Five. (Total 20 points) Given the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ passes through the fixed point $A(1,0)$, and the foci are on the $x$-axis. The ellipse intersects the curve $|y|=x$ at points $B$ and $C$. There is a parabola with $A$ as the focus, passing through points $B$ and $C$, and opening to the left, with the vertex coordinates $M(m, 0)$. When the eccentricity $e$ of the ellipse satisfies $1>e^{2}>\frac{2}{3}$, find the range of the real number $m$.
---
The given ellipse is $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ and it passes through the point $A(1,0)$. The foci of the ellipse are on the $x$-axis. The ellipse intersects the curve $|y|=x$ at points $B$ and $C$. A parabola with $A$ as the focus, passing through points $B$ and $C$, and opening to the left, has the vertex coordinates $M(m, 0)$. When the eccentricity $e$ of the ellipse satisfies $1>e^{2}>\frac{2}{3}$, find the range of the real number $m$.
|
\left(1, \dfrac{3 + \sqrt{2}}{4}\right)
|
4/8
|
2.3. Determine all functions $f: \mathbb{Z} \longrightarrow \mathbb{Z}$, where $\mathbb{Z}$ is the set of integers, such that
$$
f(m+f(f(n)))=-f(f(m+1))-n
$$
for all integers $m$ and $n$.
|
f(n) = -n - 1
|
0/8
|
Find all integers $n$ such that $20n+2$ divides $2003n+2002$.
The original text has been translated into English while preserving the original line breaks and format.
|
-42
|
1/8
|
1. As shown in Figure 1, it is known that rectangle $A B C D$ can be exactly divided into seven small rectangles of the same shape and size. If the area of the small rectangle is 3, then the perimeter of rectangle $A B C D$ is
|
19
|
1/8
|
(5) A bag contains one black ball and one white ball. Each time a ball is randomly drawn from the bag, the drawn ball is not returned, but another black ball is added instead. The probability of drawing a black ball on the $n$-th draw is $a=$ $\qquad$ .
|
1 - \dfrac{1}{2^n}
|
2/8
|
Let $a$ and $b$ be real numbers. Define $f_{a,b}\colon R^2\to R^2$ by $f_{a,b}(x;y)=(a-by-x^2;x)$. If $P=(x;y)\in R^2$, define $f^0_{a,b}(P) = P$ and $f^{k+1}_{a,b}(P)=f_{a,b}(f_{a,b}^k(P))$ for all nonnegative integers $k$.
The set $per(a;b)$ of the [i]periodic points[/i] of $f_{a,b}$ is the set of points $P\in R^2$ such that $f_{a,b}^n(P) = P$ for some positive integer $n$.
Fix $b$. Prove that the set $A_b=\{a\in R \mid per(a;b)\neq \emptyset\}$ admits a minimum. Find this minimum.
|
-\dfrac{(b + 1)^2}{4}
|
4/8
|
Ana baked 15 pasties. She placed them on a round plate in a circular
way: 7 with cabbage, 7 with meat and 1 with cherries in that exact order
and put the plate into a microwave. She doesn’t know how the plate has been rotated
in the microwave. She wants to eat a pasty with cherries. Is it possible for Ana, by trying no more than three pasties, to find exactly where the pasty with cherries is?
|
Yes
|
5/8
|
Subject 2. The arithmetic mean of the distinct natural numbers $a_{1}, a_{2}, a_{3}, \ldots, a_{2014}$, 2014, and 2016 is 2015.
a. Find the arithmetic mean of the numbers $a_{1}, a_{2}, a_{3}, \ldots, a_{2014}$.
b. If the numbers $a_{1}, a_{2}, a_{3}, \ldots, a_{2014}$ are even, show that $a_{1} \cdot a_{2} \cdot a_{3} \cdot \ldots \cdot a_{2014}=0$
|
2015
|
1/8
|
Rubanov I.S.
Petya came up with 1004 reduced quadratic trinomials $f_{1}, \ldots, f_{1004}$, among the roots of which are all integers from 0 to 2007. Vasya considers all possible equations $f_{i}=f_{j}$ ( $i \neq j$ ), and for each root found, Petya pays Vasya one ruble. What is the smallest possible income for Vasya?
|
0
|
2/8
|
12. (17 points) A rectangular wooden board, if 4 decimeters are cut off from both the longer and shorter sides, the area is reduced by 168 square decimeters. Please ask: What is the original perimeter of the rectangle in decimeters?
|
92
|
5/8
|
## Task 15/66
For the calculation of the square root of a number $z=p^{2}+a$ with $0 \leq a \leq 2 p+1$, the approximation formula is
$$
\sqrt{z}=\sqrt{p^{2}+a} \approx p+\frac{a}{2 p+1}
$$
How large is the maximum error of this approximation in dependence on $a$? How does this change in dependence on $p$?
|
\dfrac{1}{8p + 4}
|
3/8
|
The natural numbers $1,2,3, \ldots, 10$ are written on a board. It is allowed to write the number $a^{2}$ if the number $a$ is already on the board, or write the least common multiple (LCM) of the numbers $a$ and $b$ if the numbers $a$ and $b$ are already on the board. Is it possible to obtain the number 1,000,000 using these operations?
|
\text{No}
|
4/8
|
Viswam walks half a mile to get to school each day. His route consists of $10$ city blocks of equal length and he takes $1$ minute to walk each block. Today, after walking $5$ blocks, Viswam discovers he has to make a detour, walking $3$ blocks of equal length instead of $1$ block to reach the next corner. From the time he starts his detour, at what speed, in mph, must he walk, in order to get to school at his usual time? If the answer is \(x\) mph, what is the value of \(10x\)?
|
42
|
4/8
|
Sonya the frog chooses a point uniformly at random lying within the square \([0, 6] \times [0, 6]\) in the coordinate plane and hops to that point. She then randomly chooses a distance uniformly at random from \([0, 1]\) and a direction uniformly at random from \{north, south, east, west\}. All of her choices are independent. Find the probability that she lands outside the square. The original answer is in \(\frac{k}{m}\) format, please give the value of k + m.
|
13
|
5/8
|
A lampshade is made in the form of the lateral surface of the frustum of a right circular cone. The height of the frustum is \(3\sqrt{3}\) inches, its top diameter is 6 inches, and its bottom diameter is 12 inches. A bug is at the bottom of the lampshade and there is a glob of honey on the top edge of the lampshade at the spot farthest from the bug. The bug wants to crawl to the honey, but it must stay on the surface of the lampshade. The original answer is in the form \(k\sqrt{m} + n\pi\). Please give the value of k + m + n.
|
10
|
1/8
|
Recall that in any row of Pascal's Triangle, the first and last elements of the row are $1$ and each other element in the row is the sum of the two elements above it from the previous row. With this in mind, define the *Pascal Squared Triangle* as follows:
- In the $n^{\text{th}}$ row, where $n \geq 1$, the first and last elements of the row equal $n^2$.
- Each other element is the sum of the two elements directly above it.
The first few rows of the Pascal Squared Triangle are shown below.
\[
\begin{array}{c@{\hspace{7em}} c@{\hspace{2pt}}c@{\hspace{2pt}}c@{\hspace{4pt}}c@{\hspace{2pt}} c@{\hspace{2pt}}c@{\hspace{2pt}}c@{\hspace{2pt}}c@{\hspace{3pt}}c@{\hspace{2pt}} c@{\hspace{2pt}}c}
\vspace{4pt}
\text{Row 1: } & & & & & & 1 & & & & & \\
\vspace{4pt}
\text{Row 2: } & & & & & 4 & & 4 & & & & \\
\vspace{4pt}
\text{Row 3: } & & & & 9 & & 8 & & 9 & & & \\
\vspace{4pt}
\text{Row 4: } & & &16& &17& &17& & 16& & \\
\vspace{4pt}
\text{Row 5: } & &25 & &33& &34 & &33 & &25 &
\end{array}
\]
Let $S_n$ denote the sum of the entries in the $n^{\text{th}}$ row. For how many integers $1 \leq n \leq 10^6$ is $S_n$ divisible by $13$?
|
76926
|
2/8
|
Let $p$ and $q$ be prime numbers such that $(p-1)^{q-1}-1$ is a positive integer that divides $(2q)^{2p}-1$. Compute the sum of all possible values of $pq$.
|
85
|
1/8
|
There are $15$ (not necessarily distinct) integers chosen uniformly at random from the range from $0$ to $999$, inclusive. Yang then computes the sum of their units digits, while Michael computes the last three digits of their sum. The probability of them getting the same result is $\frac{m}{n}$ for relatively prime positive integers $m, n$. Find $100m + n$.
|
200
|
3/8
|
The number $S$ is the result of the following sum: $1 + 10 + 19 + 28 + 37 + \ldots + 10^{2013}$. If one writes down the number $S$, how often does the digit $5$ occur in the result?
|
4022
|
1/8
|
Three friends play a game of marbles, agreeing that the loser of each round will double the number of marbles the other players have, meaning he gives the other two a number of marbles such that they end up with twice what they had at the beginning of the round. The first player lost the first round, the second player the second, the third player the third, and they all ended up with 64 marbles each. How many marbles did each of the three friends start with?
|
104,56,32
|
0/8
|
8.3. In a cinema, five friends took seats numbered 1 to 5 (the leftmost seat is number 1). During the movie, Anya left to get popcorn. When she returned, she found that Varya had moved one seat to the right, Galia had moved three seats to the left, and Diana and Elia had swapped places, leaving the edge seat for Anya. Which seat did Anya occupy before she got up?
|
3
|
2/8
|
17. What odd digit can the sum of two prime numbers end with, if it is not a single-digit number?
|
1,3,5,9
|
3/8
|
## 53. Two Sisters
The age difference between two sisters is 4 years. If the cube of the age of the first one minus the cube of the age of the second one equals 988, how old is each sister?
|
7,\quad11
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Arnold`, `Bob`, `Alice`, `Eric`, `Peter`, `Carol`
- People have unique favorite sports: `volleyball`, `soccer`, `basketball`, `baseball`, `swimming`, `tennis`
- Each person has a unique hobby: `gardening`, `cooking`, `painting`, `woodworking`, `knitting`, `photography`
- Each mother is accompanied by their child: `Bella`, `Meredith`, `Alice`, `Samantha`, `Fred`, `Timothy`
- Each person has a unique birthday month: `feb`, `jan`, `mar`, `may`, `sept`, `april`
- Everyone has something unique for lunch: `stir fry`, `grilled cheese`, `pizza`, `spaghetti`, `stew`, `soup`
## Clues:
1. The person who loves soccer is somewhere to the right of Eric.
2. The person who paints as a hobby is somewhere to the left of the woodworking hobbyist.
3. The person whose birthday is in February is not in the third house.
4. The person who is the mother of Timothy is directly left of Arnold.
5. The person who loves cooking is somewhere to the left of the person's child is named Fred.
6. Alice is the person who paints as a hobby.
7. The person's child is named Alice is the person who loves cooking.
8. The person whose birthday is in March is the person's child is named Samantha.
9. The person who loves the soup is the person whose birthday is in May.
10. Carol is somewhere to the right of the person whose birthday is in May.
11. The person whose birthday is in March and the person who is a pizza lover are next to each other.
12. The person whose birthday is in February is not in the fourth house.
13. There are two houses between the person who loves baseball and the person who loves the stew.
14. The person whose birthday is in May is somewhere to the left of the person who loves volleyball.
15. The person whose birthday is in January is somewhere to the right of Arnold.
16. The person who loves cooking is not in the third house.
17. The person who enjoys knitting is the person whose birthday is in September.
18. The person who enjoys gardening is the person's child is named Meredith.
19. The person who is a pizza lover is the person who loves swimming.
20. There is one house between the person who loves basketball and the person whose birthday is in May.
21. The person who loves the soup is directly left of the person who loves the spaghetti eater.
22. The person who loves the stew is the person's child is named Bella.
23. The person who enjoys knitting is somewhere to the left of the person who loves the soup.
24. Bob is somewhere to the left of the person who loves the stew.
25. Arnold is the person who loves stir fry.
26. The woodworking hobbyist is directly left of the person who loves the soup.
What is the value of attribute Hobby for the person whose attribute Birthday is mar? Please reason step by step, and put your final answer within \boxed{}
|
painting
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Arnold`, `Bob`, `Alice`, `Eric`, `Carol`
- The mothers' names in different houses are unique: `Holly`, `Aniya`, `Kailyn`, `Janelle`, `Penny`, `Sarah`
- Everyone has something unique for lunch: `stir fry`, `stew`, `spaghetti`, `soup`, `pizza`, `grilled cheese`
- The people keep unique animals: `dog`, `horse`, `cat`, `fish`, `rabbit`, `bird`
- Everyone has a favorite smoothie: `watermelon`, `desert`, `lime`, `cherry`, `blueberry`, `dragonfruit`
- Each person lives in a unique style of house: `mediterranean`, `craftsman`, `victorian`, `colonial`, `modern`, `ranch`
## Clues:
1. The person whose mother's name is Penny is the person residing in a Victorian house.
2. The person in a modern-style house is The person whose mother's name is Kailyn.
3. The person in a modern-style house is somewhere to the right of the person residing in a Victorian house.
4. The person who drinks Blueberry smoothies is not in the sixth house.
5. The person whose mother's name is Sarah is the person who drinks Blueberry smoothies.
6. The person who likes Cherry smoothies is not in the third house.
7. The person who likes Cherry smoothies is Eric.
8. The person whose mother's name is Janelle is not in the third house.
9. The person who loves the spaghetti eater is in the third house.
10. The fish enthusiast is The person whose mother's name is Holly.
11. The person who keeps horses is in the first house.
12. The person in a Mediterranean-style villa is the person who loves the stew.
13. The bird keeper is in the third house.
14. The person living in a colonial-style house is the person who drinks Blueberry smoothies.
15. Carol is the person who keeps horses.
16. There are two houses between the Desert smoothie lover and Peter.
17. The person who loves eating grilled cheese is the Dragonfruit smoothie lover.
18. The person who is a pizza lover is somewhere to the right of the Dragonfruit smoothie lover.
19. The person whose mother's name is Janelle is somewhere to the left of Arnold.
20. Carol is directly left of The person whose mother's name is Aniya.
21. The person in a ranch-style home is The person whose mother's name is Aniya.
22. Arnold is somewhere to the right of the person in a Craftsman-style house.
23. The cat lover is Bob.
24. There is one house between the Watermelon smoothie lover and the person who is a pizza lover.
25. There are two houses between the cat lover and the person who loves stir fry.
26. Arnold is the rabbit owner.
27. Peter is The person whose mother's name is Janelle.
What is the value of attribute House for the person whose attribute Mother is Aniya? Please reason step by step, and put your final answer within \boxed{}
|
2
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Alice`, `Arnold`, `Carol`, `Bob`, `Eric`, `Peter`
- People use unique phone models: `iphone 13`, `samsung galaxy s21`, `xiaomi mi 11`, `oneplus 9`, `google pixel 6`, `huawei p50`
- Each person has a unique birthday month: `april`, `mar`, `feb`, `may`, `jan`, `sept`
- Each person has an occupation: `nurse`, `doctor`, `engineer`, `teacher`, `artist`, `lawyer`
## Clues:
1. The person who uses a Google Pixel 6 is directly left of the person whose birthday is in March.
2. The person who is a nurse is Eric.
3. Arnold is directly left of the person whose birthday is in April.
4. Alice and the person whose birthday is in January are next to each other.
5. The person who is an artist is the person whose birthday is in May.
6. The person whose birthday is in September is not in the sixth house.
7. There is one house between the person whose birthday is in March and the person who is a nurse.
8. The person whose birthday is in March is the person who is a lawyer.
9. The person who uses a Xiaomi Mi 11 is directly left of the person who is a nurse.
10. The person who is a teacher is not in the sixth house.
11. Eric is the person who uses an iPhone 13.
12. The person who is an engineer and Peter are next to each other.
13. The person whose birthday is in January is in the third house.
14. The person who uses a Samsung Galaxy S21 is Bob.
15. The person who is a lawyer and the person whose birthday is in April are next to each other.
16. The person who uses a OnePlus 9 is somewhere to the right of the person who is a doctor.
What is the value of attribute PhoneModel for the person whose attribute House is 6? Please reason step by step, and put your final answer within \boxed{}
|
iphone 13
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Arnold`, `Carol`, `Alice`, `Eric`, `Bob`
- People have unique favorite music genres: `pop`, `hip hop`, `rock`, `jazz`, `classical`, `country`
- The people keep unique animals: `fish`, `dog`, `cat`, `rabbit`, `horse`, `bird`
- Each person lives in a unique style of house: `modern`, `colonial`, `mediterranean`, `ranch`, `victorian`, `craftsman`
- Each person has a unique hobby: `gardening`, `woodworking`, `knitting`, `cooking`, `painting`, `photography`
- The people are of nationalities: `brit`, `german`, `norwegian`, `swede`, `dane`, `chinese`
## Clues:
1. The cat lover is the person in a Mediterranean-style villa.
2. The person who loves country music is somewhere to the right of the rabbit owner.
3. The person who loves pop music is not in the second house.
4. Alice is somewhere to the right of Arnold.
5. The person who loves jazz music and the photography enthusiast are next to each other.
6. The person who loves rock music is the German.
7. The woodworking hobbyist is somewhere to the right of the person in a modern-style house.
8. The person who loves hip-hop music is the Norwegian.
9. The cat lover is somewhere to the left of the woodworking hobbyist.
10. Alice is the person who paints as a hobby.
11. The person in a Craftsman-style house is Carol.
12. Peter is the fish enthusiast.
13. The person who loves hip-hop music is not in the fifth house.
14. The person who loves pop music is not in the sixth house.
15. The person who loves cooking is somewhere to the left of the Swedish person.
16. The Dane is directly left of the person who keeps horses.
17. The rabbit owner is somewhere to the left of the British person.
18. There is one house between Alice and the person who loves country music.
19. The person who paints as a hobby is the person living in a colonial-style house.
20. The German is somewhere to the left of the photography enthusiast.
21. Eric is the Norwegian.
22. The person residing in a Victorian house is directly left of the person who enjoys gardening.
23. There are two houses between the person who loves cooking and the person who loves classical music.
24. The bird keeper is the person who loves cooking.
25. The cat lover is directly left of Bob.
26. Eric is not in the first house.
27. Carol is somewhere to the right of the German.
28. The rabbit owner is directly left of the person in a modern-style house.
What is the value of attribute MusicGenre for the person whose attribute Hobby is gardening? Please reason step by step, and put your final answer within \boxed{}
|
hip hop
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Alice`, `Arnold`, `Peter`, `Eric`, `Bob`, `Carol`
- People have unique favorite sports: `baseball`, `tennis`, `swimming`, `basketball`, `soccer`, `volleyball`
## Clues:
1. The person who loves tennis is Eric.
2. The person who loves volleyball is in the fifth house.
3. Arnold is somewhere to the right of Carol.
4. Carol is not in the first house.
5. The person who loves baseball is Bob.
6. There is one house between the person who loves swimming and the person who loves basketball.
7. Alice is in the fourth house.
8. The person who loves swimming is Peter.
9. Alice and Arnold are next to each other.
10. Peter is somewhere to the right of Eric.
11. The person who loves swimming is not in the sixth house.
What is the value of attribute House for the person whose attribute Name is Bob? Please reason step by step, and put your final answer within \boxed{}
|
6
|
2/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Bob`, `Carol`, `Peter`, `Alice`, `Eric`, `Arnold`
- They all have a unique favorite flower: `daffodils`, `iris`, `lilies`, `roses`, `tulips`, `carnations`
- People have unique hair colors: `gray`, `red`, `blonde`, `auburn`, `brown`, `black`
- Each person has a favorite color: `white`, `blue`, `green`, `purple`, `red`, `yellow`
- People own unique car models: `tesla model 3`, `ford f150`, `honda civic`, `toyota camry`, `chevrolet silverado`, `bmw 3 series`
- The mothers' names in different houses are unique: `Janelle`, `Holly`, `Kailyn`, `Sarah`, `Penny`, `Aniya`
## Clues:
1. There is one house between Arnold and the person who loves blue.
2. The person whose mother's name is Janelle is directly left of the person who has auburn hair.
3. The person who owns a Chevrolet Silverado and the person who owns a BMW 3 Series are next to each other.
4. Carol is the person who loves a carnations arrangement.
5. The person who loves the boquet of iris is the person who has gray hair.
6. The person who loves the rose bouquet is The person whose mother's name is Kailyn.
7. Bob is the person who loves the boquet of lilies.
8. The person who loves a bouquet of daffodils is somewhere to the left of the person who owns a Chevrolet Silverado.
9. Bob is in the third house.
10. The person who owns a Honda Civic is in the sixth house.
11. The person who loves the vase of tulips is somewhere to the left of The person whose mother's name is Penny.
12. The person who has brown hair is in the fourth house.
13. The person who has brown hair is somewhere to the left of the person who has blonde hair.
14. The person whose mother's name is Holly is Bob.
15. The person who owns a Ford F-150 is in the third house.
16. Eric is directly left of the person who has auburn hair.
17. The person who owns a Tesla Model 3 is the person who loves yellow.
18. There are two houses between the person who loves purple and The person whose mother's name is Aniya.
19. The person who loves purple is in the first house.
20. The person whose favorite color is green is not in the fourth house.
21. The person who has gray hair is the person who owns a BMW 3 Series.
22. The person who has gray hair is somewhere to the left of Alice.
23. The person whose mother's name is Holly is somewhere to the left of the person who loves the vase of tulips.
24. The person who has red hair is the person who loves white.
What is the value of attribute Name for the person whose attribute House is 5? Please reason step by step, and put your final answer within \boxed{}
|
Peter
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Eric`, `Alice`, `Arnold`, `Carol`, `Peter`, `Bob`
- Each person has a unique level of education: `high school`, `trade school`, `bachelor`, `doctorate`, `master`, `associate`
- Each person has a favorite color: `purple`, `blue`, `white`, `red`, `green`, `yellow`
- Each person prefers a unique type of vacation: `cultural`, `cruise`, `beach`, `mountain`, `camping`, `city`
- People have unique favorite book genres: `science fiction`, `biography`, `historical fiction`, `fantasy`, `romance`, `mystery`
## Clues:
1. Alice is the person with a master's degree.
2. There is one house between the person with an associate's degree and Peter.
3. The person who loves historical fiction books is somewhere to the left of the person who loves biography books.
4. The person who loves historical fiction books is the person with a high school diploma.
5. Bob is the person with a bachelor's degree.
6. Carol is somewhere to the right of Eric.
7. The person with a master's degree is somewhere to the right of the person who enjoys camping trips.
8. The person who loves science fiction books is somewhere to the left of the person who loves yellow.
9. The person who loves historical fiction books is somewhere to the left of the person whose favorite color is green.
10. The person with a high school diploma is not in the second house.
11. The person who loves beach vacations is the person with a doctorate.
12. The person who loves mystery books is somewhere to the left of the person with a bachelor's degree.
13. The person with a doctorate is in the first house.
14. The person with a high school diploma is directly left of the person who enjoys camping trips.
15. The person who loves romance books is not in the third house.
16. There is one house between the person who loves purple and the person with a bachelor's degree.
17. The person who loves biography books is the person whose favorite color is red.
18. There is one house between the person who loves fantasy books and the person who loves blue.
19. The person who goes on cultural tours is the person who loves blue.
20. Carol is not in the fifth house.
21. The person who loves purple is the person with a doctorate.
22. The person who enjoys mountain retreats is somewhere to the right of the person who loves science fiction books.
23. The person who prefers city breaks is the person whose favorite color is green.
What is the value of attribute Color for the person whose attribute House is 4? Please reason step by step, and put your final answer within \boxed{}
|
yellow
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Carol`, `Alice`, `Eric`, `Peter`, `Arnold`, `Bob`
- The mothers' names in different houses are unique: `Penny`, `Janelle`, `Aniya`, `Sarah`, `Holly`, `Kailyn`
- Everyone has a unique favorite cigar: `blends`, `dunhill`, `blue master`, `prince`, `yellow monster`, `pall mall`
- Each person has a unique type of pet: `cat`, `dog`, `rabbit`, `hamster`, `bird`, `fish`
- The people keep unique animals: `bird`, `horse`, `cat`, `rabbit`, `dog`, `fish`
- Everyone has a favorite smoothie: `desert`, `watermelon`, `lime`, `cherry`, `blueberry`, `dragonfruit`
## Clues:
1. The dog owner is not in the third house.
2. The fish enthusiast is not in the fourth house.
3. The person who owns a dog is Eric.
4. The cat lover is not in the second house.
5. The person who smokes Blue Master is somewhere to the right of The person whose mother's name is Sarah.
6. The cat lover is not in the fourth house.
7. There are two houses between Carol and the person who owns a rabbit.
8. The person whose mother's name is Penny is the person with a pet hamster.
9. The person whose mother's name is Kailyn is somewhere to the right of the person with a pet hamster.
10. The dog owner and the person who drinks Lime smoothies are next to each other.
11. The Prince smoker is somewhere to the right of The person whose mother's name is Janelle.
12. There is one house between The person whose mother's name is Penny and Bob.
13. There are two houses between the person partial to Pall Mall and The person whose mother's name is Penny.
14. Peter is somewhere to the left of the person who drinks Lime smoothies.
15. The bird keeper is the Watermelon smoothie lover.
16. The person with a pet hamster is the Prince smoker.
17. The person who smokes Yellow Monster is the person who drinks Lime smoothies.
18. The person whose mother's name is Sarah is the person who smokes Yellow Monster.
19. The Dunhill smoker is somewhere to the left of the Watermelon smoothie lover.
20. The person whose mother's name is Holly is directly left of the person who owns a dog.
21. The bird keeper is The person whose mother's name is Kailyn.
22. The person whose mother's name is Sarah is not in the third house.
23. The person who smokes many unique blends is the rabbit owner.
24. The person who has a cat is somewhere to the right of the person with an aquarium of fish.
25. The person who smokes Yellow Monster is Eric.
26. The person who keeps a pet bird is the Desert smoothie lover.
27. Alice is The person whose mother's name is Kailyn.
28. The Dragonfruit smoothie lover is Carol.
29. The person who keeps horses is the person who likes Cherry smoothies.
What is the value of attribute Mother for the person whose attribute House is 2? Please reason step by step, and put your final answer within \boxed{}
|
Sarah
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Alice`, `Bob`, `Arnold`, `Eric`, `Carol`
- People own unique car models: `tesla model 3`, `honda civic`, `toyota camry`, `chevrolet silverado`, `bmw 3 series`, `ford f150`
## Clues:
1. Alice is not in the fifth house.
2. Carol is somewhere to the left of the person who owns a Chevrolet Silverado.
3. The person who owns a Toyota Camry is Bob.
4. The person who owns a BMW 3 Series is not in the second house.
5. The person who owns a Honda Civic is somewhere to the right of Arnold.
6. There is one house between the person who owns a BMW 3 Series and the person who owns a Chevrolet Silverado.
7. There is one house between Arnold and Bob.
8. The person who owns a Tesla Model 3 is not in the sixth house.
9. The person who owns a Toyota Camry is not in the third house.
10. The person who owns a Tesla Model 3 is Peter.
11. The person who owns a Honda Civic and the person who owns a Toyota Camry are next to each other.
12. The person who owns a Toyota Camry is not in the fifth house.
13. The person who owns a Chevrolet Silverado is not in the second house.
What is the value of attribute House for the person whose attribute Name is Eric? Please reason step by step, and put your final answer within \boxed{}
|
5
|
1/8
|
There are 4 houses, numbered 1 to 4 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Alice`, `Arnold`, `Eric`, `Peter`
- People have unique heights: `short`, `very short`, `average`, `tall`
- Each person has a favorite color: `yellow`, `white`, `red`, `green`
- They all have a unique favorite flower: `lilies`, `roses`, `daffodils`, `carnations`
- The people keep unique animals: `bird`, `fish`, `horse`, `cat`
## Clues:
1. The person who loves a carnations arrangement is somewhere to the left of the bird keeper.
2. Peter is not in the first house.
3. The person who loves the rose bouquet is directly left of Eric.
4. The person who loves a carnations arrangement and the person who loves the rose bouquet are next to each other.
5. Alice is directly left of the bird keeper.
6. The person who keeps horses is Peter.
7. The fish enthusiast is the person who loves a bouquet of daffodils.
8. The person whose favorite color is red is the person who loves a bouquet of daffodils.
9. The person who is tall is in the third house.
10. The person who has an average height is somewhere to the left of the person who loves white.
11. The person whose favorite color is green is not in the second house.
12. The person who is short is somewhere to the left of the person who is tall.
13. The person who is short is the person whose favorite color is green.
What is the value of attribute House for the person whose attribute Animal is bird? Please reason step by step, and put your final answer within \boxed{}
|
2
|
2/8
|
There are 3 houses, numbered 1 to 3 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Arnold`, `Eric`
- People have unique favorite sports: `soccer`, `basketball`, `tennis`
- The people keep unique animals: `cat`, `bird`, `horse`
- Each person has a unique favorite drink: `water`, `tea`, `milk`
- The people are of nationalities: `swede`, `dane`, `brit`
## Clues:
1. The person who likes milk is not in the first house.
2. The person who keeps horses is somewhere to the left of Eric.
3. The person who loves basketball is Peter.
4. The Swedish person is somewhere to the left of the one who only drinks water.
5. The person who loves tennis is the tea drinker.
6. The person who loves soccer is the bird keeper.
7. The cat lover is the British person.
8. Peter is not in the third house.
9. The person who likes milk is the person who loves soccer.
What is the value of attribute House for the person whose attribute Animal is bird? Please reason step by step, and put your final answer within \boxed{}
|
3
|
2/8
|
There are 3 houses, numbered 1 to 3 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Arnold`, `Eric`
- Each mother is accompanied by their child: `Bella`, `Meredith`, `Fred`
- People use unique phone models: `samsung galaxy s21`, `iphone 13`, `google pixel 6`
- People have unique favorite book genres: `romance`, `science fiction`, `mystery`
- Everyone has a unique favorite cigar: `blue master`, `prince`, `pall mall`
- People have unique heights: `short`, `very short`, `average`
## Clues:
1. Eric is directly left of the Prince smoker.
2. The person who has an average height is somewhere to the right of Peter.
3. The person who uses a Samsung Galaxy S21 is in the second house.
4. The person who smokes Blue Master is in the third house.
5. The person who uses a Google Pixel 6 is Eric.
6. Arnold is somewhere to the right of the person who loves science fiction books.
7. The person who uses an iPhone 13 is the person's child is named Bella.
8. The person who is short is the Prince smoker.
9. The person who loves mystery books is the person who uses a Google Pixel 6.
10. The person's child is named Meredith and the person who is short are next to each other.
What is the value of attribute Children for the person whose attribute House is 1? Please reason step by step, and put your final answer within \boxed{}
|
Meredith
|
2/8
|
There are 3 houses, numbered 1 to 3 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Arnold`, `Peter`, `Eric`
- Each person has a unique birthday month: `sept`, `jan`, `april`
- Each person has a unique hobby: `photography`, `cooking`, `gardening`
- Everyone has something unique for lunch: `grilled cheese`, `spaghetti`, `pizza`
- People have unique favorite book genres: `science fiction`, `romance`, `mystery`
- The mothers' names in different houses are unique: `Janelle`, `Holly`, `Aniya`
## Clues:
1. The person whose birthday is in April is the person who enjoys gardening.
2. The person whose mother's name is Janelle is not in the third house.
3. The photography enthusiast is in the first house.
4. The person whose mother's name is Janelle is the person who loves mystery books.
5. The person who loves science fiction books and Eric are next to each other.
6. Arnold is not in the third house.
7. The person whose mother's name is Holly is the person whose birthday is in September.
8. The person whose birthday is in January is The person whose mother's name is Aniya.
9. The person whose mother's name is Holly is the person who loves science fiction books.
10. The person who loves eating grilled cheese is The person whose mother's name is Aniya.
11. The person who loves the spaghetti eater is Arnold.
What is the value of attribute Food for the person whose attribute Mother is Holly? Please reason step by step, and put your final answer within \boxed{}
|
spaghetti
|
0/8
|
There are 3 houses, numbered 1 to 3 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Eric`, `Arnold`
- Everyone has something unique for lunch: `pizza`, `grilled cheese`, `spaghetti`
- Everyone has a favorite smoothie: `desert`, `watermelon`, `cherry`
- Each person has a unique type of pet: `fish`, `dog`, `cat`
## Clues:
1. The person who likes Cherry smoothies is the person with an aquarium of fish.
2. The person who loves the spaghetti eater is directly left of the person who has a cat.
3. The person who has a cat is Eric.
4. The Watermelon smoothie lover is Arnold.
5. The person who owns a dog is directly left of the person who is a pizza lover.
6. The Desert smoothie lover is not in the third house.
What is the value of attribute Food for the person whose attribute House is 2? Please reason step by step, and put your final answer within \boxed{}
|
pizza
|
2/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Alice`, `Arnold`, `Carol`, `Peter`, `Eric`, `Bob`
- Each person has a unique type of pet: `cat`, `bird`, `fish`, `dog`, `hamster`, `rabbit`
- People have unique heights: `super tall`, `average`, `tall`, `very short`, `very tall`, `short`
- People have unique favorite sports: `baseball`, `tennis`, `soccer`, `swimming`, `basketball`, `volleyball`
## Clues:
1. There is one house between the person who has an average height and the person who is short.
2. The person with an aquarium of fish is in the fifth house.
3. The person who has a cat is the person who is tall.
4. The person who is very tall is the person who loves soccer.
5. Peter is in the first house.
6. The person who loves tennis is in the sixth house.
7. Carol is somewhere to the right of the person who is very tall.
8. The person who loves volleyball is directly left of the person who loves soccer.
9. The person who loves baseball is directly left of the person who is super tall.
10. Carol and Bob are next to each other.
11. The person who is super tall is not in the sixth house.
12. The person who is short is not in the fourth house.
13. There is one house between the person who loves swimming and Bob.
14. The person who loves basketball is somewhere to the left of the person who owns a dog.
15. The person who owns a rabbit is somewhere to the left of the person who is short.
16. The person who keeps a pet bird is the person who is short.
17. Arnold is not in the second house.
18. Bob is directly left of Eric.
19. The person who owns a rabbit and the person who is very tall are next to each other.
What is the value of attribute House for the person whose attribute FavoriteSport is swimming? Please reason step by step, and put your final answer within \boxed{}
|
3
|
0/8
|
There are 5 houses, numbered 1 to 5 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Arnold`, `Bob`, `Alice`, `Eric`, `Peter`
- People have unique heights: `very tall`, `average`, `tall`, `very short`, `short`
- Everyone has something unique for lunch: `stew`, `grilled cheese`, `spaghetti`, `pizza`, `stir fry`
## Clues:
1. Alice is the person who is short.
2. The person who is tall is in the third house.
3. The person who has an average height is not in the second house.
4. The person who has an average height is somewhere to the left of the person who loves the stew.
5. The person who loves stir fry is Arnold.
6. The person who is a pizza lover is the person who is tall.
7. Eric is the person who is tall.
8. Bob is somewhere to the right of Arnold.
9. The person who loves eating grilled cheese is somewhere to the right of Eric.
10. The person who is very short is somewhere to the left of Arnold.
What is the value of attribute Food for the person whose attribute Name is Bob? Please reason step by step, and put your final answer within \boxed{}
|
grilled cheese
|
2/8
|
There are 3 houses, numbered 1 to 3 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Eric`, `Arnold`, `Peter`
- People have unique favorite music genres: `pop`, `rock`, `classical`
- People have unique favorite sports: `tennis`, `soccer`, `basketball`
- Everyone has a unique favorite cigar: `blue master`, `pall mall`, `prince`
- The mothers' names in different houses are unique: `Holly`, `Aniya`, `Janelle`
## Clues:
1. The person who loves basketball is somewhere to the right of the person partial to Pall Mall.
2. The Prince smoker is not in the third house.
3. Eric is The person whose mother's name is Holly.
4. The person whose mother's name is Aniya is the person who loves pop music.
5. Arnold is directly left of the Prince smoker.
6. The person who loves tennis is the person who smokes Blue Master.
7. The Prince smoker is somewhere to the right of the person who loves classical music.
8. The person whose mother's name is Aniya is not in the second house.
What is the value of attribute House for the person whose attribute MusicGenre is pop? Please reason step by step, and put your final answer within \boxed{}
|
3
|
1/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Alice`, `Eric`, `Bob`, `Peter`, `Arnold`, `Carol`
- People have unique heights: `very tall`, `tall`, `super tall`, `average`, `very short`, `short`
- People use unique phone models: `oneplus 9`, `google pixel 6`, `samsung galaxy s21`, `iphone 13`, `huawei p50`, `xiaomi mi 11`
## Clues:
1. Bob is directly left of the person who is tall.
2. Peter is somewhere to the left of the person who uses an iPhone 13.
3. The person who is very short is somewhere to the right of the person who uses a Google Pixel 6.
4. Carol is the person who is very tall.
5. There is one house between the person who uses a Google Pixel 6 and the person who is short.
6. The person who uses a Samsung Galaxy S21 is not in the first house.
7. The person who uses a OnePlus 9 is directly left of the person who is short.
8. The person who is tall is Arnold.
9. The person who is super tall is in the first house.
10. The person who uses a Xiaomi Mi 11 is Carol.
11. The person who uses a Google Pixel 6 is somewhere to the right of Eric.
12. The person who is short is in the sixth house.
What is the value of attribute House for the person whose attribute Height is super tall? Please reason step by step, and put your final answer within \boxed{}
|
1
|
0/8
|
There are 5 houses, numbered 1 to 5 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Eric`, `Alice`, `Peter`, `Bob`, `Arnold`
- Each person has a unique type of pet: `hamster`, `fish`, `cat`, `dog`, `bird`
- Each person has an occupation: `doctor`, `engineer`, `artist`, `lawyer`, `teacher`
- Each person has a favorite color: `green`, `blue`, `yellow`, `red`, `white`
- The people keep unique animals: `bird`, `cat`, `horse`, `fish`, `dog`
## Clues:
1. The person who owns a dog is Arnold.
2. The bird keeper is in the fourth house.
3. The person who keeps a pet bird is directly left of the dog owner.
4. The person who loves white is somewhere to the left of the person who is a lawyer.
5. The person who loves yellow is directly left of the person whose favorite color is green.
6. The cat lover is Bob.
7. The cat lover is somewhere to the left of Eric.
8. The person who keeps horses is in the fifth house.
9. The person who is a lawyer is directly left of the person who is a teacher.
10. The person who is a doctor is in the first house.
11. Alice is the person who loves yellow.
12. The person who loves blue is directly left of the person with an aquarium of fish.
13. The person who loves yellow is in the first house.
14. The person with a pet hamster is the person who is an artist.
15. Eric is the dog owner.
What is the value of attribute House for the person whose attribute Name is Bob? Please reason step by step, and put your final answer within \boxed{}
|
2
|
1/8
|
There are 4 houses, numbered 1 to 4 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Alice`, `Arnold`, `Peter`, `Eric`
- Everyone has a unique favorite cigar: `pall mall`, `blue master`, `prince`, `dunhill`
- People have unique favorite sports: `soccer`, `swimming`, `tennis`, `basketball`
- Each person lives in a unique style of house: `ranch`, `colonial`, `craftsman`, `victorian`
- Everyone has a favorite smoothie: `watermelon`, `desert`, `cherry`, `dragonfruit`
## Clues:
1. The Dunhill smoker is in the first house.
2. The person who smokes Blue Master is the Watermelon smoothie lover.
3. The person in a ranch-style home is the person who loves basketball.
4. The person who loves soccer is in the second house.
5. The Dunhill smoker is the person who likes Cherry smoothies.
6. The person who loves swimming is somewhere to the right of the person who smokes Blue Master.
7. The Dragonfruit smoothie lover is Alice.
8. The Prince smoker is the Dragonfruit smoothie lover.
9. The Watermelon smoothie lover is not in the second house.
10. Arnold is the person who smokes Blue Master.
11. The person who loves swimming is the person living in a colonial-style house.
12. The person who loves swimming is Peter.
13. The person in a Craftsman-style house is directly left of the person in a ranch-style home.
What is the value of attribute House for the person whose attribute Cigar is blue master? Please reason step by step, and put your final answer within \boxed{}
|
3
|
1/8
|
On an $8 \times 8$ board, several dominoes (rectangles of $2 \times 1$) can be placed without overlapping. Let $N$ be the number of ways to place 32 dominoes in this manner, and $T$ be the number of ways to place 24 dominoes in this manner. Which is greater: $-N$ or $M$? Configurations that can be derived from one another by rotating or reflecting the board are considered distinct.
|
T
|
2/8
|
In a carriage, any group of $m \ (m \geq 3)$ passengers have only one common friend (where if A is a friend of B, then B is also a friend of A; no one is their own friend). What is the maximum number of friends that the person with the most friends in this carriage can have?
|
m
|
4/8
|
We intersected the unit cube $ABCDEFGH$ with a plane such that it intersects the edges $AB$ and $AD$ at the internal points $P$ and $Q$, respectively, both at a distance $x$ from $A$, and it intersects the edge $BF$ at the point $R$. What is the distance $BR$ if $\angle QPR = 120^\circ$?
|
1-x
|
3/8
|
Given positive integers \( x, y, z \) and real numbers \( a, b, c, d \) such that \( x \leqslant y \leqslant z, x^a = y^b = z^c = 70^d \), and \( \frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{d} \), determine the relationship between \( x + y \) and \( z \). Fill in the blank with “ \( > \)”, “ \( < \)” or “ \( = \)”.
|
=
|
4/8
|
Given natural numbers \( m \) and \( n \). There are two piles on the table: the first pile contains \( n \) stones, and the second pile contains \( m \) stones. Petya and Vasya play the following game. Petya starts. In one move, a player can break one of the available piles on the table into several smaller piles. The player who cannot make a move loses. For which values of \( m \) and \( n \) can Petya ensure victory regardless of Vasya's play?
|
m \neq n
|
4/8
|
There are three piles of stones. Each time A moves one stone from one pile to another, A earns a reward from B. The reward is equal to the difference in the number of stones between the pile to which A moves the stone and the pile from which A takes the stone. If this difference is negative, A must pay B that amount instead (if A doesn’t have enough money, A can owe it temporarily). At a certain moment, all the stones are in the piles where they initially started. Determine the maximum possible amount of money A can have by that moment.
|
0
|
3/8
|
Several non-intersecting line segments are placed on a plane. Is it always possible to connect their endpoints with additional line segments so that a closed, non-self-intersecting polygonal chain is formed?
|
\text{No}
|
3/8
|
A three-digit natural number was written on the board. We wrote down all other three-digit numbers that can be obtained by rearranging its digits. Therefore, there were three new numbers in addition to the original number on the board. The sum of the smallest two of all four numbers is 1088. What digits does the original number contain?
|
0, 5, 8
|
1/8
|
6. A point on the coordinate plane whose both horizontal and vertical coordinates are integers is called an integer point. The number of integer points in the region enclosed by the parabola $y=x^{2}+1$ and the line $2 x-y+81=0$ is $\qquad$ .
|
988
|
4/8
|
Four, (Full marks 20 points) As shown in the figure, the side length of the equilateral $\triangle ABC$ is $1$, and points $R, P, Q$ on $AB, BC, CA$ satisfy $AR + BP + CQ = 1$ while moving. Let $BP = x, CQ = y$, $AR = z$, and the area of $\triangle PQR$ be $S$. Try to express $S$ in terms of $x, y, z$.
---
The translation retains the original text's line breaks and formatting.
|
S = \dfrac{\sqrt{3}}{4}(xy + yz + zx)
|
2/8
|
A person moves in the $x-y$ plane moving along points with integer co-ordinates $x$ and $y$ only. When she is at a point $(x,y)$, she takes a step based on the following rules:
(a) if $x+y$ is even she moves to either $(x+1,y)$ or $(x+1,y+1)$;
(b) if $x+y$ is odd she moves to either $(x,y+1)$ or $(x+1,y+1)$.
How many distinct paths can she take to go from $(0,0)$ to $(8,8)$ given that she took exactly three steps to the right $((x,y)$ to $(x+1,y))$?
|
462
|
1/8
|
Let's determine the largest of the $A$ numbers for which the following statement holds. No matter how we write down the first 100 positive integers, there will always be ten consecutive numbers in the sequence whose sum is at least $A$.
|
505
|
2/8
|
[ The sum of the angles of a triangle. The theorem about the exterior angle.] [ Criteria and properties of an isosceles triangle. ]
On the side $B C$ of the isosceles triangle $A B C(A B=B C)$, points $N$ and $M$ ( $N$ is closer to $B$ than $M$) are taken such that $N M=A M$ and $\angle M A C=\angle B A N$.
Find $\angle C A N$.
|
60^\circ
|
0/8
|
Adrian has $2n$ cards numbered from $ 1$ to $2n$. He gets rid of $n$ cards that are consecutively numbered. The sum of the numbers of the remaining papers is $1615$. Find all the possible values of $n$.
|
34
|
0/8
|
Show that \(X\) is an element of \(\mathcal{F}^{*}\) of order \(r\).
Also, introduce the notion of introspection as described by the authors of the AKS algorithm.
#### Definition 2.4.7.
An integer \(k\) is said to be introspective for a polynomial \(P(X) \in(\mathbb{Z} / p \mathbb{Z})[X]\) if \(P\left(X^{k}\right) \equiv P(X)^{k}\) \((\bmod H(X), p)\).
|
r
|
3/8
|
11.1. Solve the system $\left\{\begin{array}{c}x^{2}+4 \sin ^{2} y-4=0 \\ \cos x-2 \cos ^{2} y-1=0\end{array}\right.$.
|
(0, \frac{\pi}{2} + k\pi)
|
1/8
|
2. Solve the equation $\cos \left(\pi x^{2}\right)-\cos ^{2}\left(\frac{\pi x^{2}}{2}\right)+1+\cos \left(\pi x^{2}-4 \pi x\right)=\sin ^{2}\left(\frac{\pi x^{2}}{2}\right)$. In your answer, specify the third term of the increasing sequence of all positive roots of the equation.
|
\dfrac{3}{4}
|
3/8
|
For a positive integer $n$, there is a school with $2n$ people. For a set $X$ of students in this school, if any two students in $X$ know each other, we call $X$ [i]well-formed[/i]. If the maximum number of students in a well-formed set is no more than $n$, find the maximum number of well-formed set.
Here, an empty set and a set with one student is regarded as well-formed as well.
|
3^n
|
4/8
|
Subsets and Splits
Filtered Answers A-D
Retrieves 100 rows where the answer is a single letter from A to D, providing basic filtering of the dataset.