output_description
stringlengths 15
956
| submission_id
stringlengths 10
10
| status
stringclasses 3
values | problem_id
stringlengths 6
6
| input_description
stringlengths 9
2.55k
| attempt
stringlengths 1
13.7k
| problem_description
stringlengths 7
5.24k
| samples
stringlengths 2
2.72k
|
|---|---|---|---|---|---|---|---|
Print N lines.
The first line should contain K, the number of colors used.
The (i+1)-th line (1 \le i \le N-1) should contain c_i, the integer
representing the color of the i-th edge, where 1 \le c_i \le K must hold.
If there are multiple colorings with the minimum number of colors that satisfy
the condition, printing any of them will be accepted.
* * *
|
s003051255
|
Accepted
|
p02850
|
Input is given from Standard Input in the following format:
N
a_1 b_1
a_2 b_2
\vdots
a_{N-1} b_{N-1}
|
n = int(input())
ikeru = [[] for _ in range(n)]
for i in range(n - 1):
a, b = map(int, input().split())
ikeru[a - 1].append((b - 1, i))
settansaku = set([])
setmada = {0}
listmada = [(0, None)] # left: Vertex, right: Color
kouho = 1
num = [0 for _ in range(n - 1)]
while kouho != 0:
for i, cnt in listmada[:]:
colors = {cnt}
settansaku.add(i)
setmada.remove(i)
listmada.remove((i, cnt))
kouho -= 1
c = 0
for k, j in ikeru[i]:
if not k in setmada:
if not k in settansaku:
setmada.add(k)
while True:
if c not in colors:
listmada.append((k, c))
colors.add(c)
num[j] = c
break
c += 1
kouho += 1
print(max(num) + 1)
print("\n".join([str(i + 1) for i in num]))
|
Statement
Given is a tree G with N vertices. The vertices are numbered 1 through N, and
the i-th edge connects Vertex a_i and Vertex b_i.
Consider painting the edges in G with some number of colors. We want to paint
them so that, for each vertex, the colors of the edges incident to that vertex
are all different.
Among the colorings satisfying the condition above, construct one that uses
the minimum number of colors.
|
[{"input": "3\n 1 2\n 2 3", "output": "2\n 1\n 2\n \n\n* * *"}, {"input": "8\n 1 2\n 2 3\n 2 4\n 2 5\n 4 7\n 5 6\n 6 8", "output": "4\n 1\n 2\n 3\n 4\n 1\n 1\n 2\n \n\n* * *"}, {"input": "6\n 1 2\n 1 3\n 1 4\n 1 5\n 1 6", "output": "5\n 1\n 2\n 3\n 4\n 5"}]
|
Print N lines.
The first line should contain K, the number of colors used.
The (i+1)-th line (1 \le i \le N-1) should contain c_i, the integer
representing the color of the i-th edge, where 1 \le c_i \le K must hold.
If there are multiple colorings with the minimum number of colors that satisfy
the condition, printing any of them will be accepted.
* * *
|
s580000706
|
Accepted
|
p02850
|
Input is given from Standard Input in the following format:
N
a_1 b_1
a_2 b_2
\vdots
a_{N-1} b_{N-1}
|
N = int(input())
edge = []
# bとして振られる番号
d_col = [0] * N
# b先に振り分ける番号
e_col = [1] * N
for i in range(N - 1):
a, b = map(int, input().split())
edge.append([a, b, i, 0])
edge = sorted(edge)
for j, e in enumerate(edge):
a, b, i, ans = e
if d_col[a - 1] == e_col[a - 1]:
edge[j][3] = e_col[a - 1] + 1
e_col[a - 1] += 1
else:
edge[j][3] = e_col[a - 1]
d_col[b - 1] = e_col[a - 1]
e_col[a - 1] += 1
edge = sorted(edge, key=lambda x: x[2])
col = []
for e in edge:
col.append(e[3])
print(max(col))
for i in col:
print(i)
|
Statement
Given is a tree G with N vertices. The vertices are numbered 1 through N, and
the i-th edge connects Vertex a_i and Vertex b_i.
Consider painting the edges in G with some number of colors. We want to paint
them so that, for each vertex, the colors of the edges incident to that vertex
are all different.
Among the colorings satisfying the condition above, construct one that uses
the minimum number of colors.
|
[{"input": "3\n 1 2\n 2 3", "output": "2\n 1\n 2\n \n\n* * *"}, {"input": "8\n 1 2\n 2 3\n 2 4\n 2 5\n 4 7\n 5 6\n 6 8", "output": "4\n 1\n 2\n 3\n 4\n 1\n 1\n 2\n \n\n* * *"}, {"input": "6\n 1 2\n 1 3\n 1 4\n 1 5\n 1 6", "output": "5\n 1\n 2\n 3\n 4\n 5"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s654700431
|
Accepted
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
import math, string, itertools, fractions, heapq, collections, re, array, bisect, sys, random, time, copy, functools
sys.setrecursionlimit(10**7)
inf = 10**20
eps = 1.0 / 10**10
mod = 10**9 + 7
dd = [(0, -1), (1, 0), (0, 1), (-1, 0)]
ddn = [(0, -1), (1, -1), (1, 0), (1, 1), (0, 1), (-1, -1), (-1, 0), (-1, 1)]
def LI():
return [int(x) for x in sys.stdin.readline().split()]
def LI_():
return [int(x) - 1 for x in sys.stdin.readline().split()]
def LF():
return [float(x) for x in sys.stdin.readline().split()]
def LS():
return sys.stdin.readline().split()
def I():
return int(sys.stdin.readline())
def F():
return float(sys.stdin.readline())
def S():
return input()
def pf(s):
return print(s, flush=True)
def main():
n = I()
a = LI()
b = [a[0]]
for c in a[1:]:
b.append(b[-1] + c)
d = [0] * n
d[-1] = a[-1]
for i in range(n - 2, -1, -1):
d[i] = d[i + 1] + a[i]
g = [[] for _ in range(n)]
g[0] = [0, inf]
j = 0
for i in range(1, n):
t = b[i]
k = abs((b[i] - b[j]) - b[j])
while j < i - 1 and k > abs((b[i] - b[j + 1]) - b[j + 1]):
k = abs((b[i] - b[j + 1]) - b[j + 1])
j += 1
g[i].append(b[j])
g[i].append(b[i] - b[j])
g[-1] = [0, inf]
g[-2] = [0, inf]
j = n - 1
for i in range(n - 2, -1, -1):
t = d[i]
k = abs((d[i] - d[j]) - d[j])
while j > i + 1 and k > abs((d[i] - d[j - 1]) - d[j - 1]):
k = abs((d[i] - d[j - 1]) - d[j - 1])
j -= 1
g[i - 1].append(d[i] - d[j])
g[i - 1].append(d[j])
r = inf
for i in range(n):
t = max(g[i]) - min(g[i])
if r > t:
r = t
return r
print(main())
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s393750532
|
Accepted
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n = int(input())
s = list(map(int, input().split()))
a = [0]
c = 0
for si in s:
c += si
a.append(c)
ans = []
f = 1
g = 3
for i in range(2, n - 1):
while abs(a[f] - (a[i] - a[f])) > abs(a[f + 1] - (a[i] - a[f + 1])):
f += 1
while abs(a[g] - a[i] - (a[n] - a[g])) > abs(a[g + 1] - a[i] - (a[n] - a[g + 1])):
g += 1
ls = [a[f], a[i] - a[f], a[g] - a[i], a[n] - a[g]]
ans.append(max(ls) - min(ls))
print(min(ans))
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s599935687
|
Wrong Answer
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n = int(input())
a = list(map(int, input().split()))
b = [0 for _ in range(n + 1)]
for i in range(n):
b[i + 1] = b[i] + a[i]
# b[i] = sum(a[:i])
suma = sum(a)
border = suma / 4
def func1(start_index, bit, seq_num):
# bit: 0 -> border を超えない, 1 -> border を超える
end_index = start_index + 1
if bit == 0:
while b[end_index] - b[start_index] < border and end_index < n - 3 + seq_num:
end_index += 1
if end_index == start_index + 1:
return end_index, b[end_index] - b[start_index]
else:
return end_index - 1, b[end_index - 1] - b[start_index]
elif bit == 1:
while b[end_index] - b[start_index] < border and end_index < n - 3 + seq_num:
end_index += 1
return end_index, b[end_index] - b[start_index]
def func2(bits):
# bits: 0~7
starts = [0]
sums = []
for i in range(3):
f = func1(starts[-1], bits % 2, i)
bits = bits // 2
starts.append(f[0])
sums.append(f[1])
sums.append(b[n] - b[f[0]])
return max(sums) - min(sums)
candidates = []
for i in range(8):
candidates.append(func2(i))
print(min(candidates))
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s166677275
|
Accepted
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from collections import deque
N = int(input())
A = list(map(int, input().split()))
L = [(10**18, 10**18, 10**18)] * (N + 1)
left = 0
right = 0
que = deque([])
for i, a in enumerate(A, start=1):
right += a
que.append(a)
while len(que) > 1 and abs(right - left) > abs((right - que[0]) - (left + que[0])):
q = que.popleft()
left += q
right -= q
L[i] = (abs(left - right), left, right)
R = [(10**18, 10**18, 10**18)] * (N + 1)
left = 0
right = 0
que = deque([])
for i, a in enumerate(A[::-1], start=1):
right += a
que.append(a)
while len(que) > 1 and abs(right - left) > abs((right - que[0]) - (left + que[0])):
q = que.popleft()
left += q
right -= q
R[i] = (abs(left - right), left, right)
# for i in range(1, N + 1):
# L[i] = min(L[i], L[i - 1])
# R[i] = min(R[i], R[i - 1])
R = R[::-1]
ans = 10**18
for mid in range(1, N):
X = [L[mid + 1][1], L[mid + 1][2], R[mid + 1][1], R[mid + 1][2]]
if min(X) == 0:
continue
ans = min(ans, max(X) - min(X))
print(ans)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s375541748
|
Accepted
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from sys import exit, setrecursionlimit, stderr
from functools import reduce
from itertools import *
from collections import defaultdict
from bisect import bisect
def read():
return int(input())
def reads():
return [int(x) for x in input().split()]
N = read()
A = reads()
psum = [0] * (N + 1)
for i in range(N):
psum[i + 1] = psum[i] + A[i]
# print(psum, file=stderr)
ans = 10**20
for i in range(2, N - 1):
lmid = psum[i] / 2
k = bisect(psum, lmid)
if abs(psum[k - 1] - lmid) < abs(psum[k] - lmid):
k = k - 1
rmid = (psum[N] + psum[i]) / 2
l = bisect(psum, rmid)
if abs(psum[l - 1] - rmid) < abs(psum[l] - rmid):
l = l - 1
m = min(psum[k], psum[i] - psum[k], psum[l] - psum[i], psum[N] - psum[l])
M = max(psum[k], psum[i] - psum[k], psum[l] - psum[i], psum[N] - psum[l])
ans = min(ans, M - m)
print(ans)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s350010745
|
Accepted
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from bisect import bisect_right, bisect_left
from itertools import accumulate
N = int(input())
A = list(map(int, input().split()))
A = [0] + A
a = list(accumulate(A))
answer = a[-1]
# 切り口はN-1個, 真ん中の選び方はN-3
for i in range(N - 3):
left = a[i + 2]
right = a[-1] - left
p = bisect_left(a, left // 2)
P1 = a[p]
Q1 = left - P1
P2 = a[p - 1]
Q2 = left - P2
if abs(P1 - Q1) <= abs(P2 - Q2):
P = P1
Q = Q1
else:
P = P2
Q = Q2
s = bisect_right(a, a[-1] - right // 2)
S1 = a[-1] - a[s - 1]
R1 = right - S1
S2 = a[-1] - a[s]
R2 = right - S2
if abs(S1 - R1) <= abs(S2 - R2):
S = S1
R = R1
else:
S = S2
R = R2
answer = min(answer, max(P, Q, R, S) - min(P, Q, R, S))
print(answer)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s927489083
|
Runtime Error
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N, *A = map(int, open(0).read().split())
a = A[0]
b = A[1]
c = A[2]
d = sum(A[3:])
x = 0
m = c
n = d
df2 = max(m, n) - min(m, n)
for i in range(3, N - 1):
m += A[i]
n -= A[i]
if df2 > max(m, n) - min(m, n):
df2 = max(m, n) - min(m, n)
c, d = m, n
y = i
ans = max(a, b, c, d) - min(a, b, c, d)
for i in range(2, N - 2):
b += A[i]
c -= A[i]
df1 = max(a, b) - min(a, b)
df2 = max(c, d) - min(c, d)
while True:
na = a + A[x + 1]
nb = b - A[x + 1]
if df1 < max(na, nb) - min(na, nb):
break
df1 = max(na, nb) - min(na, nb)
a, b = na, nb
x += 1
while True:
nc = c + A[y + 1]
nd = d - A[y + 1]
if df2 < max(nc, nd) - min(nc, nd):
break
df2 = max(nc, nd) - min(nc, nd)
c, d = nc, nd
y += 1
ans = min(ans, max(a, b, c, d) - min(a, b, c, d))
print(ans)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s977794803
|
Wrong Answer
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from numpy import *
from scipy import *
from sys import *
n = int(input())
a = array(list(map(int, input().split())))
border = sum(a) / 4.0
a = cumsum(a)
ans = inf
b = searchsorted(a[0:-4], border, side="left")
c = searchsorted(a[b + 1 : -3] - a[b], border, side="left") + b + 1
d = searchsorted(a[c + 1 : -2] - a[c], border, side="left") + c + 1
ans = min(
ans,
abs(
min(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
- max(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
),
)
d = max(c + 1, d - 1)
ans = min(
ans,
abs(
min(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
- max(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
),
)
c = max(b + 1, c - 1)
d = searchsorted(a[c + 1 : -2] - a[c], border, side="left") + c + 1
ans = min(
ans,
abs(
min(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
- max(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
),
)
d = max(c + 1, d - 1)
ans = min(
ans,
abs(
min(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
- max(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
),
)
b = max(0, b - 1)
c = searchsorted(a[b + 1 : -3] - a[b], border, side="left") + b + 1
d = searchsorted(a[c + 1 : -2] - a[c], border, side="left") + c + 1
ans = min(
ans,
abs(
min(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
- max(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
),
)
d = max(c + 1, d - 1)
ans = min(
ans,
abs(
min(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
- max(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
),
)
c = max(b + 1, c - 1)
d = searchsorted(a[c + 1 : -2] - a[c], border, side="left") + c + 1
ans = min(
ans,
abs(
min(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
- max(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
),
)
d = max(c + 1, d - 1)
ans = min(
ans,
abs(
min(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
- max(a[b], a[c] - a[b], a[d] - a[c], a[-1] - a[d])
),
)
print(ans)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s947428835
|
Wrong Answer
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
# coding: utf-8
# Your code here!
n = int(input())
a = list(map(int, input().split()))
ac = []
s = 0
for i in range(n):
s += a[i]
ac.append(s)
ans = n * 10**9
l = 0
r = 2
last = ac[n - 1]
for i in range(1, n - 2):
mid = ac[i]
while ac[l + 1] <= mid / 2 and l < i - 1:
l += 1
while ac[r + 1] - mid <= (last - mid) / 2 and r < n - 2:
r += 1
ans = min(
ans,
max(ac[l], ac[i] - ac[l], ac[r] - ac[i], ac[n - 1] - ac[r])
- min(ac[l], ac[i] - ac[l], ac[r] - ac[i], ac[n - 1] - ac[r]),
)
# print(l,i,r,ans)
print(ans)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s219619357
|
Accepted
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N = int(input())
A = [int(i) for i in input().split()]
S = [0 for i in range(N + 1)]
for i in range(N):
S[i + 1] = S[i] + A[i]
B = A[::-1]
T = [0 for i in range(N + 1)]
for i in range(N):
T[i + 1] = T[i] + B[i]
F = [0 for i in range(N)]
G = [0 for i in range(N)]
for i in range(N):
LS = S[i + 1]
k = 0
if i != 0:
k = F[i - 1]
if k != 0:
k -= 1
tmp = LS
for j in range(k, i + 1):
L = S[j]
R = LS - S[j]
if abs(R - L) <= tmp:
F[i] = j
else:
break
tmp = abs(R - L)
if F[i] <= 0:
F[i] = 0
for i in range(N):
RS = T[i + 1]
k = 0
if i != 0:
k = G[i - 1]
if k != 0:
k -= 1
tmp = LS
for j in range(k, i + 1):
L = T[j]
R = RS - T[j]
if abs(R - L) <= tmp:
G[i] = j
else:
break
tmp = abs(R - L)
if G[i] <= 0:
G[i] = 0
ans = S[N]
for i in range(N):
A = [0 for i in range(4)]
k = 0
if i != 0:
k = F[i - 1]
A[0] = S[k]
A[1] = S[i] - S[k]
A[2] = T[N - i] - T[G[N - i - 1]]
A[3] = T[G[N - i - 1]]
score = max(A) - min(A)
if ans > score:
ans = score
print(ans)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s445419802
|
Runtime Error
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n=int(input())
l=[0]+list(map(int,input().split()))
from itertools import accumulate
l=list(accumulate(l))
from bisect import bisect, bisect_left, bisect_right
ans=10**15
for i in range(2,n-1):
x=bisect_left(l,l[i]//2)
p1=l[x]
p2=l[x-1]
if abs(l[i]-p1*2)>=abs(l[i]-p2*2):
p=p2
else:
p=p1
q=l[i]-p
x=bisect_left(l,(l[n]-l[i])//2+l[i])
r1=l[x]-l[i]
r2=l[x-1]-l[i]
if abs(l[n]-l[i]-r1*2)>=abs(l[n]-l[i]-r2*2):
r=r2
else:
r=r1
s=l[n]-l[i]-r
ans=min(ans,max(p,q,r,s)-min(p,q,r,s))
print(ans)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s907703811
|
Runtime Error
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
mp.put(ps.RunID, ps)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s276336046
|
Runtime Error
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N=int(input())
L=list(map(int,input().split()))
T=sum(L)//4
i=0
while K<=T:
K=K+L[i]
i=i+1
X=K-L[i-1]
a=min(abs(X-T),abs(T-K))
if a==abs(X-T):
i=i-1
While K<=T:
K=K+L[i]
i=i+1
X=K-L[i-1]
b=min(abs(X-T),abs(T-K))
if b==abs(X-T):
i=i-1
While K<=T:
K=K+L[i]
i=i+1
X=K-L[i-1]
c=min(abs(X-T),abs(T-K))
if c==abs(X-T):
i=i-1
While K<=T:
K=K+L[i]
i=i+1
X=K-L[i-1]
d=min(abs(X-T),abs(T-K))
if d==abs(X-T):
i=i-1
N=[a,b,c,d]
print(max(N)-min(N))
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s427656007
|
Wrong Answer
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n, *a = map(int, open(0).read().split())
m = sum(a) / 4
mx, mn = 0, 1e18
cnt = a[0]
for i in range(1, n):
if abs(cnt - m) < abs(cnt + a[i] - m):
mx = max(mx, cnt)
mn = min(mn, cnt)
cnt = a[i]
else:
cnt += a[i]
print(mx - mn)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Find the minimum possible absolute difference of the maximum and the minimum
among P,Q,R,S.
* * *
|
s613368837
|
Runtime Error
|
p03312
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from libc.stdio cimport scanf
cdef:
long long N, i
long long A[202020], a
scanf("%lld", &N)
A[0] = 0
for i in range(N):
scanf("%lld", & A[i+1])
A[i+1] += A[i]
cdef long long ans = 10 ** 18
cdef long long mid, l = 1, r = 3
cdef long long Ldif, Rdif, mx, mn
for mid in range(2, N - 1):
Ldif = abs(A[mid] + A[0] - 2 * A[l])
while l + 1 < mid and abs(A[mid] + A[0] - 2 * A[l+1]) <= Ldif:
Ldif = abs(A[mid] + A[0] - 2 * A[l+1])
l += 1
r = max(r, mid + 1)
Rdif = abs(A[N] + A[mid] - 2 * A[r])
while r + 1 < N and abs(A[N] + A[mid] - 2 * A[r+1]) <= Rdif:
Rdif = abs(A[N] + A[mid] - 2 * A[r+1])
r += 1
mx = max(A[l] - A[0], A[mid] - A[l], A[r] - A[mid], A[N] - A[r])
mn = min(A[l] - A[0], A[mid] - A[l], A[r] - A[mid], A[N] - A[r])
ans = min(ans, mx - mn)
print(ans)
|
Statement
Snuke has an integer sequence A of length N.
He will make three cuts in A and divide it into four (non-empty) contiguous
subsequences B, C, D and E. The positions of the cuts can be freely chosen.
Let P,Q,R,S be the sums of the elements in B,C,D,E, respectively. Snuke is
happier when the absolute difference of the maximum and the minimum among
P,Q,R,S is smaller. Find the minimum possible absolute difference of the
maximum and the minimum among P,Q,R,S.
|
[{"input": "5\n 3 2 4 1 2", "output": "2\n \n\nIf we divide A as B,C,D,E=(3),(2),(4),(1,2), then P=3,Q=2,R=4,S=1+2=3. Here,\nthe maximum and the minimum among P,Q,R,S are 4 and 2, with the absolute\ndifference of 2. We cannot make the absolute difference of the maximum and the\nminimum less than 2, so the answer is 2.\n\n* * *"}, {"input": "10\n 10 71 84 33 6 47 23 25 52 64", "output": "36\n \n\n* * *"}, {"input": "7\n 1 2 3 1000000000 4 5 6", "output": "999999994"}]
|
Print the sum of the scores over all possible permutations, modulo 10^9+7.
* * *
|
s704564137
|
Accepted
|
p03365
|
Input is given from Standard Input in the following format:
N
|
import sys
input = lambda: sys.stdin.readline().rstrip()
sys.setrecursionlimit(max(1000, 10**9))
write = lambda x: sys.stdout.write(x + "\n")
n = int(input())
M = 10**9 + 7 # 出力の制限
N = n + 3 # 必要なテーブルサイズ
g1 = [None] * (N + 1) # 元テーブル
g2 = [None] * (N + 1) # 逆元テーブル
inverse = [None] * (N + 1) # 逆元テーブル計算用テーブル
g1[0] = g1[1] = g2[0] = g2[1] = 1
inverse[0], inverse[1] = [0, 1]
for i in range(2, N + 1):
g1[i] = (g1[i - 1] * i) % M
inverse[i] = (
-inverse[M % i] * (M // i)
) % M # ai+b==0 mod M <=> i==-b*a^(-1) <=> i^(-1)==-b^(-1)*aより
g2[i] = (g2[i - 1] * inverse[i]) % M
def cmb(n, r, M):
if r < 0 or r > n:
return 0
r = min(r, n - r)
return (g1[n] * g2[r] * g2[n - r]) % M
ans = 0
prev = 0
# s = 0
for i in range((n + 1) // 2, n):
tmp = cmb(i - 1, n - i - 1, M) * g1[i] * g1[n - 1 - i]
ans += i * (tmp - prev)
prev = tmp
# print(i, tmp, g1[i], g1[n-1-i])
ans %= M
print(ans)
|
Statement
There are N squares lining up in a row, numbered 1 through N from left to
right. Initially, all squares are white. We also have N-1 painting machines,
numbered 1 through N-1. When operated, Machine i paints Square i and i+1
black.
Snuke will operate these machines one by one. The order in which he operates
them is represented by a permutation of (1, 2, ..., N-1), P, which means that
the i-th operated machine is Machine P_i.
Here, the _score_ of a permutation P is defined as the number of machines that
are operated before all the squares are painted black for the first time, when
the machines are operated in the order specified by P. Snuke has not decided
what permutation P to use, but he is interested in the scores of possible
permutations. Find the sum of the scores over all possible permutations for
him. Since this can be extremely large, compute the sum modulo 10^9+7.
|
[{"input": "4", "output": "16\n \n\nThere are six possible permutations as P. Among them, P = (1, 3, 2) and P =\n(3, 1, 2) have a score of 2, and the others have a score of 3. Thus, the\nanswer is 2 \\times 2 + 3 \\times 4 = 16.\n\n* * *"}, {"input": "2", "output": "1\n \n\nThere is only one possible permutation: P = (1), which has a score of 1.\n\n* * *"}, {"input": "5", "output": "84\n \n\n* * *"}, {"input": "100000", "output": "341429644"}]
|
Print the sum of the scores over all possible permutations, modulo 10^9+7.
* * *
|
s366617229
|
Runtime Error
|
p03365
|
Input is given from Standard Input in the following format:
N
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef vector<ll> vl;
typedef long double ld;
typedef vector<ld> vd;
typedef bool bl;
typedef vector<bl> vb;
typedef unordered_map<ll,unordered_map<ll,ll>> graph;
const ll e5 = 1 << 20;
const ll mod = 1000000007;
const ll e3 = 1 << 13;
const ll INF = 1ll << 62;
ll factorial(ll n,ll mod = mod){
static ll dp[100000];
if(dp[n]) return dp[n];
if(n == 0) return dp[n] = 1;
return dp[n] = (n*factorial(n-1))%mod;
}
ll powl(ll x,ll r,ll mod = mod){
ll ret = 1;
for(;r != 0;r >>= 1){
if(r&1 != 0) ret *= x,ret %= mod;
x *= x,x %= mod;
}
return ret;
}
ll inverse(ll x,ll mod = mod){
return powl(x,mod-2,mod);
}
ll combination(ll n,ll m,ll mod = mod){
if(n < m) return 0;
return (((factorial(n)*inverse(factorial(m)))%mod)*inverse(factorial(n-m)))%mod;
}
ll n;
ll ans = 0;
ll solve(ll k){
return (((combination(k-1,n-1-k)*factorial(k))%mod)*factorial(n-1-k))%mod;
}
int main(){
cin >> n;
if(n == 2){
cout << 1 << endl;
return 0;
}
for(ll i = 2;i <= n-1;i++){
ans += ((((solve(i)-solve(i-1)+mod)%mod)*i)%mod);
ans %= mod;
}
cout << ans << endl;
}
|
Statement
There are N squares lining up in a row, numbered 1 through N from left to
right. Initially, all squares are white. We also have N-1 painting machines,
numbered 1 through N-1. When operated, Machine i paints Square i and i+1
black.
Snuke will operate these machines one by one. The order in which he operates
them is represented by a permutation of (1, 2, ..., N-1), P, which means that
the i-th operated machine is Machine P_i.
Here, the _score_ of a permutation P is defined as the number of machines that
are operated before all the squares are painted black for the first time, when
the machines are operated in the order specified by P. Snuke has not decided
what permutation P to use, but he is interested in the scores of possible
permutations. Find the sum of the scores over all possible permutations for
him. Since this can be extremely large, compute the sum modulo 10^9+7.
|
[{"input": "4", "output": "16\n \n\nThere are six possible permutations as P. Among them, P = (1, 3, 2) and P =\n(3, 1, 2) have a score of 2, and the others have a score of 3. Thus, the\nanswer is 2 \\times 2 + 3 \\times 4 = 16.\n\n* * *"}, {"input": "2", "output": "1\n \n\nThere is only one possible permutation: P = (1), which has a score of 1.\n\n* * *"}, {"input": "5", "output": "84\n \n\n* * *"}, {"input": "100000", "output": "341429644"}]
|
Print the sum of the scores over all possible permutations, modulo 10^9+7.
* * *
|
s890889759
|
Wrong Answer
|
p03365
|
Input is given from Standard Input in the following format:
N
|
def permutations(L):
if L == []:
return [[]]
else:
return [
[h] + t for i, h in enumerate(L) for t in permutations(L[:i] + L[i + 1 :])
]
n = int(input())
perm_list = []
for i in range(n - 1):
perm_list.append(str(i + 1))
perm_result = permutations(perm_list)
# print(perm_result)
score = 0
for p in perm_result:
m = [0] * n
for j in range(len(p)):
m[int(p[j]) - 1] = 1
m[int(p[j])] = 1
mini_score = 0
for i in range(n - 1):
mini_score += m[i]
if mini_score == n - 1:
score += j + 1
break
print(score)
|
Statement
There are N squares lining up in a row, numbered 1 through N from left to
right. Initially, all squares are white. We also have N-1 painting machines,
numbered 1 through N-1. When operated, Machine i paints Square i and i+1
black.
Snuke will operate these machines one by one. The order in which he operates
them is represented by a permutation of (1, 2, ..., N-1), P, which means that
the i-th operated machine is Machine P_i.
Here, the _score_ of a permutation P is defined as the number of machines that
are operated before all the squares are painted black for the first time, when
the machines are operated in the order specified by P. Snuke has not decided
what permutation P to use, but he is interested in the scores of possible
permutations. Find the sum of the scores over all possible permutations for
him. Since this can be extremely large, compute the sum modulo 10^9+7.
|
[{"input": "4", "output": "16\n \n\nThere are six possible permutations as P. Among them, P = (1, 3, 2) and P =\n(3, 1, 2) have a score of 2, and the others have a score of 3. Thus, the\nanswer is 2 \\times 2 + 3 \\times 4 = 16.\n\n* * *"}, {"input": "2", "output": "1\n \n\nThere is only one possible permutation: P = (1), which has a score of 1.\n\n* * *"}, {"input": "5", "output": "84\n \n\n* * *"}, {"input": "100000", "output": "341429644"}]
|
Print the minimum possible value.
* * *
|
s378627377
|
Accepted
|
p03735
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
n = int(input())
lis = []
a, b = [], []
for i in range(n):
X, Y = map(int, input().split())
lis.append([min(X, Y), max(X, Y)])
a.append(min(X, Y))
b.append(max(X, Y))
lis.sort()
answer = (max(a) - min(a)) * (max(b) - min(b))
a_max, b_min = max(a), min(b)
current = float("inf")
for i in range(n):
if lis[i][0] > b_min:
current = min(current, a_max - b_min)
break
current = min(current, a_max - lis[i][0])
a_max = max(a_max, lis[i][1])
print(min(answer, current * (max(b) - min(a))))
|
Statement
There are N bags, each containing two white balls. The i-th box contains two
balls with integers x_i and y_i written on them, respectively.
For each of these bags, you will paint one of the balls red, and paint the
other blue.
Afterwards, the 2N balls will be classified according to color.
Then, we will define the following:
* R_{max}: the maximum integer written on a ball painted in red
* R_{min}: the minimum integer written on a ball painted in red
* B_{max}: the maximum integer written on a ball painted in blue
* B_{min}: the minimum integer written on a ball painted in blue
Find the minimum possible value of (R_{max} - R_{min}) \times (B_{max} -
B_{min}).
|
[{"input": "3\n 1 2\n 3 4\n 5 6", "output": "15\n \n\nThe optimal solution is to paint the balls with x_1, x_2, y_3 red, and paint\nthe balls with y_1, y_2, x_3 blue.\n\n* * *"}, {"input": "3\n 1010 10\n 1000 1\n 20 1020", "output": "380\n \n\n* * *"}, {"input": "2\n 1 1\n 1000000000 1000000000", "output": "999999998000000001"}]
|
Print the minimum possible value.
* * *
|
s000207197
|
Accepted
|
p03735
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
from collections import deque
N = int(input())
Ball = deque([])
m, M = float("inf"), 0
for i in range(N):
a, b = map(int, input().split())
if a > b:
a, b = b, a
if a < m:
m = a
mp = i
if b > M:
M = b
Mp = i
Ball.append((a, b))
s = max([a[0] for a in Ball])
t = min([a[1] for a in Ball])
ans = (s - m) * (M - t)
if mp == Mp:
print(ans)
exit()
l = min(Ball[mp][1], Ball[Mp][0])
r = max(Ball[mp][1], Ball[Mp][0])
for i in range(2 * N):
if Ball:
a, b = Ball.popleft()
if l <= a <= r or l <= b <= r:
pass
elif a > r:
r = a
elif b < l:
l = b
elif a < l and b > r:
Ball.append((a, b))
else:
break
if Ball:
Ball = sorted(list(Ball), key=lambda x: (x[0], -x[1]))
Max = [r]
for i in range(len(Ball)):
Max.append(max(Max[-1], Ball[i][1]))
for i in range(len(Ball)):
ans = min(ans, (M - m) * (Max[i] - Ball[i][0]))
ans = min(ans, (M - m) * (Max[len(Ball)] - l))
else:
ans = min(ans, (M - m) * (r - l))
print(ans)
|
Statement
There are N bags, each containing two white balls. The i-th box contains two
balls with integers x_i and y_i written on them, respectively.
For each of these bags, you will paint one of the balls red, and paint the
other blue.
Afterwards, the 2N balls will be classified according to color.
Then, we will define the following:
* R_{max}: the maximum integer written on a ball painted in red
* R_{min}: the minimum integer written on a ball painted in red
* B_{max}: the maximum integer written on a ball painted in blue
* B_{min}: the minimum integer written on a ball painted in blue
Find the minimum possible value of (R_{max} - R_{min}) \times (B_{max} -
B_{min}).
|
[{"input": "3\n 1 2\n 3 4\n 5 6", "output": "15\n \n\nThe optimal solution is to paint the balls with x_1, x_2, y_3 red, and paint\nthe balls with y_1, y_2, x_3 blue.\n\n* * *"}, {"input": "3\n 1010 10\n 1000 1\n 20 1020", "output": "380\n \n\n* * *"}, {"input": "2\n 1 1\n 1000000000 1000000000", "output": "999999998000000001"}]
|
Print the minimum possible value.
* * *
|
s864156932
|
Wrong Answer
|
p03735
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
# coding: utf-8
import array, bisect, collections, heapq, itertools, math, random, re, string, sys, time
sys.setrecursionlimit(10**7)
INF = 10**20
MOD = 10**9 + 7
def II():
return int(input())
def ILI():
return list(map(int, input().split()))
def IAI(LINE):
return [ILI() for __ in range(LINE)]
def IDI():
return {key: value for key, value in ILI()}
def solve(N, x, y):
state = [x[0], x[0], y[0], y[0]]
for i in range(1, N):
state_1 = [
max(state[0], x[i]),
min(state[1], x[i]),
max(state[2], y[i]),
min(state[3], y[i]),
]
state_2 = [
max(state[0], y[i]),
min(state[1], y[i]),
max(state[2], x[i]),
min(state[3], x[i]),
]
dif_1 = (state_1[0] - state_1[1]) * (state_1[2] - state_1[3])
dif_2 = (state_2[0] - state_2[1]) * (state_2[2] - state_2[3])
if dif_1 > dif_2:
state = state_2
else:
state = state_1
ans = (state[0] - state[1]) * (state[2] - state[3])
return ans
def main():
N = II()
x, y = [], []
for __ in range(N):
a, b = ILI()
x.append(a)
y.append(b)
print(solve(N, x, y))
if __name__ == "__main__":
main()
|
Statement
There are N bags, each containing two white balls. The i-th box contains two
balls with integers x_i and y_i written on them, respectively.
For each of these bags, you will paint one of the balls red, and paint the
other blue.
Afterwards, the 2N balls will be classified according to color.
Then, we will define the following:
* R_{max}: the maximum integer written on a ball painted in red
* R_{min}: the minimum integer written on a ball painted in red
* B_{max}: the maximum integer written on a ball painted in blue
* B_{min}: the minimum integer written on a ball painted in blue
Find the minimum possible value of (R_{max} - R_{min}) \times (B_{max} -
B_{min}).
|
[{"input": "3\n 1 2\n 3 4\n 5 6", "output": "15\n \n\nThe optimal solution is to paint the balls with x_1, x_2, y_3 red, and paint\nthe balls with y_1, y_2, x_3 blue.\n\n* * *"}, {"input": "3\n 1010 10\n 1000 1\n 20 1020", "output": "380\n \n\n* * *"}, {"input": "2\n 1 1\n 1000000000 1000000000", "output": "999999998000000001"}]
|
Print the minimum possible value.
* * *
|
s478195848
|
Wrong Answer
|
p03735
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
n = int(input())
xy = [list(map(int, input().split())) for i in range(n)]
amin, amax, bmin, bmax = float("inf"), 0, float("inf"), 0
for i, j in xy:
amin = min(amin, min(i, j))
amax = max(amax, min(i, j))
bmin = min(bmin, max(i, j))
bmax = max(bmax, max(i, j))
print((amax - amin) * (bmax - bmin))
|
Statement
There are N bags, each containing two white balls. The i-th box contains two
balls with integers x_i and y_i written on them, respectively.
For each of these bags, you will paint one of the balls red, and paint the
other blue.
Afterwards, the 2N balls will be classified according to color.
Then, we will define the following:
* R_{max}: the maximum integer written on a ball painted in red
* R_{min}: the minimum integer written on a ball painted in red
* B_{max}: the maximum integer written on a ball painted in blue
* B_{min}: the minimum integer written on a ball painted in blue
Find the minimum possible value of (R_{max} - R_{min}) \times (B_{max} -
B_{min}).
|
[{"input": "3\n 1 2\n 3 4\n 5 6", "output": "15\n \n\nThe optimal solution is to paint the balls with x_1, x_2, y_3 red, and paint\nthe balls with y_1, y_2, x_3 blue.\n\n* * *"}, {"input": "3\n 1010 10\n 1000 1\n 20 1020", "output": "380\n \n\n* * *"}, {"input": "2\n 1 1\n 1000000000 1000000000", "output": "999999998000000001"}]
|
Print the minimum possible value.
* * *
|
s945915696
|
Accepted
|
p03735
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
import sys
input = sys.stdin.readline
def solve():
INF = float("inf")
N = int(input())
Ls = []
Rs = []
for _ in range(N):
x, y = map(int, input().split())
if x > y:
x, y = y, x
Ls.append(x)
Rs.append(y)
minAll = min(Ls)
maxAll = max(Rs)
ans1 = (max(Ls) - minAll) * (maxAll - min(Rs))
ans2 = INF
LRs = []
min1, max1 = INF, -INF
for L, R in zip(Ls, Rs):
if L != minAll:
if R != maxAll:
LRs.append((L, R))
else:
min1 = min(min1, L)
max1 = max(max1, L)
else:
if R != maxAll:
min1 = min(min1, R)
max1 = max(max1, R)
else:
print(ans1)
return
if not LRs:
print(ans1)
return
LRs.sort()
d1 = maxAll - minAll
maxL = LRs[-1][0]
minR, maxR = INF, -INF
ans2 = INF
for L, R in LRs:
minL = L
diff = max(maxL, maxR, max1) - min(minL, minR, min1)
ans2 = min(ans2, d1 * diff)
minR = min(minR, R)
maxR = max(maxR, R)
minL, maxL = INF, -INF
diff = max(maxL, maxR, max1) - min(minL, minR, min1)
ans2 = min(ans2, d1 * diff)
print(min(ans1, ans2))
solve()
|
Statement
There are N bags, each containing two white balls. The i-th box contains two
balls with integers x_i and y_i written on them, respectively.
For each of these bags, you will paint one of the balls red, and paint the
other blue.
Afterwards, the 2N balls will be classified according to color.
Then, we will define the following:
* R_{max}: the maximum integer written on a ball painted in red
* R_{min}: the minimum integer written on a ball painted in red
* B_{max}: the maximum integer written on a ball painted in blue
* B_{min}: the minimum integer written on a ball painted in blue
Find the minimum possible value of (R_{max} - R_{min}) \times (B_{max} -
B_{min}).
|
[{"input": "3\n 1 2\n 3 4\n 5 6", "output": "15\n \n\nThe optimal solution is to paint the balls with x_1, x_2, y_3 red, and paint\nthe balls with y_1, y_2, x_3 blue.\n\n* * *"}, {"input": "3\n 1010 10\n 1000 1\n 20 1020", "output": "380\n \n\n* * *"}, {"input": "2\n 1 1\n 1000000000 1000000000", "output": "999999998000000001"}]
|
Print the minimum possible value.
* * *
|
s757052178
|
Wrong Answer
|
p03735
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
import sys
read = sys.stdin.buffer.read
readline = sys.stdin.buffer.readline
readlines = sys.stdin.buffer.readlines
n = int(readline())
xy = list(map(int, read().split()))
if n == 1:
print(0)
exit()
max_num = max(xy)
min_num = min(xy)
max_ind = -1
min_ind = -1
same = False
big = []
small = []
for i in range(n):
x, y = xy[i * 2 : i * 2 + 2]
if x > y:
x, y = y, x
if (x == min_num) & (y == max_num):
same = True
if x == min_num:
min_ind = i
if y == max_num:
max_ind = i
big.append(y)
small.append(x)
# 最大と最小を違う色に塗る
ans = (max(big) - min(big)) * (max(small) - min(small))
if same:
print(ans)
exit()
# 同じ色に塗る
r = max_num - min_num
if xy[min_ind * 2] == min_num:
min_pair = xy[min_ind * 2 + 1]
else:
min_pair = xy[min_ind * 2]
if xy[max_ind * 2] == max_num:
max_pair = xy[max_ind * 2 + 1]
else:
max_pair = xy[max_ind * 2]
nums = []
for i in range(n):
if (i == min_ind) | (i == max_ind):
continue
x, y = xy[i * 2 : i * 2 + 2]
if x > y:
x, y = y, x
nums.append((x, y))
if len(nums) == 0:
b = abs(max_pair - min_pair)
ans = min(ans, r * b)
print(ans)
exit()
nums.sort()
b = max(nums[-1][0], max_pair, min_pair) - min(nums[0][0], max_pair, min_pair)
ans = min(ans, r * b)
min_up = nums[0][1]
max_up = nums[0][1]
for i in range(n - 3):
min_up = min(min_up, nums[i][1])
max_up = min(max_up, nums[i][1])
b = max(nums[-1][0], max_pair, min_pair, max_up) - min(
nums[i + 1][0], max_pair, min_pair, min_up
)
ans = min(ans, r * b)
min_up = min(min_up, nums[-1][1])
max_up = min(max_up, nums[-1][1])
b = max(max_pair, min_pair, max_up) - min(max_pair, min_pair, min_up)
ans = min(ans, r * b)
print(ans)
|
Statement
There are N bags, each containing two white balls. The i-th box contains two
balls with integers x_i and y_i written on them, respectively.
For each of these bags, you will paint one of the balls red, and paint the
other blue.
Afterwards, the 2N balls will be classified according to color.
Then, we will define the following:
* R_{max}: the maximum integer written on a ball painted in red
* R_{min}: the minimum integer written on a ball painted in red
* B_{max}: the maximum integer written on a ball painted in blue
* B_{min}: the minimum integer written on a ball painted in blue
Find the minimum possible value of (R_{max} - R_{min}) \times (B_{max} -
B_{min}).
|
[{"input": "3\n 1 2\n 3 4\n 5 6", "output": "15\n \n\nThe optimal solution is to paint the balls with x_1, x_2, y_3 red, and paint\nthe balls with y_1, y_2, x_3 blue.\n\n* * *"}, {"input": "3\n 1010 10\n 1000 1\n 20 1020", "output": "380\n \n\n* * *"}, {"input": "2\n 1 1\n 1000000000 1000000000", "output": "999999998000000001"}]
|
Print the minimum possible value.
* * *
|
s847338924
|
Runtime Error
|
p03735
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
import math,string,itertools,fractions,heapq,collections,re,array,bisect,sys,random,time,copy,functools
sys.setrecursionlimit(10**7)
inf = 10**20
mod = 10**9 + 7
def LI(): return [int(x) for x in sys.stdin.readline().split()]
def LI_(): return [int(x)-1 for x in sys.stdin.readline().split()]
def LF(): return [float(x) for x in sys.stdin.readline().split()]
def LS(): return sys.stdin.readline().split()
def I(): return int(sys.stdin.readline())
def F(): return float(sys.stdin.readline())
def S(): return input()
def main():
n = I()
if n == 1:
return 0
a = sorted([sorted(LI()) + [_] for _ in range(n)])
b = sorted(a, key=lambda x: x[1])
r = (a[-1][0]-a[0][0]) * (b[-1][1]-b[0][1])
bm = b[-1][1] - a[0][0]
bmi = b[0][2]
am = a[-1][1]
at = 0
k = [[inf,0]]
for i in range(n-1):
kk = []
kk.append(min(k[-1][0], b[i][0], b[i+1][1]))
kk.append(max(k[-1][1], b[i][0]))
if kk[0] == k[-1][0]:
k[-1][1] = kk[1]
else:
k.append(kk)
k = k[1:]
kl = len(k)
am = b[-1][1] - a[0][0]
ami = a[0][2]
bm = 0
mtm = 0
bt = b[0][1]
for i in range(n-1,0,-1):
tm = b[i][0]
if mtm < tm
mtm = tm
if ami == b[i][2]:
break
if tm < bt:
bt = tm
if tm < b[i-1][1]:
tm = b[i-1][1]
bm = mtm
if tm > bm:
bm = tm
tr = am * (bm-bt)
if r > tr:
r = tr
for j in range(kl):
ki,km = k[j]
tr = am * (max(km,bm)-min(ki,bt))
if r > tr:
r = tr
if km >= bm:
break
return r
print(main())
|
Statement
There are N bags, each containing two white balls. The i-th box contains two
balls with integers x_i and y_i written on them, respectively.
For each of these bags, you will paint one of the balls red, and paint the
other blue.
Afterwards, the 2N balls will be classified according to color.
Then, we will define the following:
* R_{max}: the maximum integer written on a ball painted in red
* R_{min}: the minimum integer written on a ball painted in red
* B_{max}: the maximum integer written on a ball painted in blue
* B_{min}: the minimum integer written on a ball painted in blue
Find the minimum possible value of (R_{max} - R_{min}) \times (B_{max} -
B_{min}).
|
[{"input": "3\n 1 2\n 3 4\n 5 6", "output": "15\n \n\nThe optimal solution is to paint the balls with x_1, x_2, y_3 red, and paint\nthe balls with y_1, y_2, x_3 blue.\n\n* * *"}, {"input": "3\n 1010 10\n 1000 1\n 20 1020", "output": "380\n \n\n* * *"}, {"input": "2\n 1 1\n 1000000000 1000000000", "output": "999999998000000001"}]
|
Print the minimum possible value.
* * *
|
s445275110
|
Accepted
|
p03735
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
n = int(input())
x, y = zip(*sorted(sorted(map(int, input().split())) for _ in range(n)))
a = x[-1]
b = d = 2 * 10**9
for i in range(n - 1):
a = max(a, y[i])
b = min(b, y[i])
d = min(d, a - min(b, x[i + 1]))
print(min((x[-1] - x[0]) * (max(y) - min(y)), (max(y) - x[0]) * d))
|
Statement
There are N bags, each containing two white balls. The i-th box contains two
balls with integers x_i and y_i written on them, respectively.
For each of these bags, you will paint one of the balls red, and paint the
other blue.
Afterwards, the 2N balls will be classified according to color.
Then, we will define the following:
* R_{max}: the maximum integer written on a ball painted in red
* R_{min}: the minimum integer written on a ball painted in red
* B_{max}: the maximum integer written on a ball painted in blue
* B_{min}: the minimum integer written on a ball painted in blue
Find the minimum possible value of (R_{max} - R_{min}) \times (B_{max} -
B_{min}).
|
[{"input": "3\n 1 2\n 3 4\n 5 6", "output": "15\n \n\nThe optimal solution is to paint the balls with x_1, x_2, y_3 red, and paint\nthe balls with y_1, y_2, x_3 blue.\n\n* * *"}, {"input": "3\n 1010 10\n 1000 1\n 20 1020", "output": "380\n \n\n* * *"}, {"input": "2\n 1 1\n 1000000000 1000000000", "output": "999999998000000001"}]
|
Print any uniforming state of the given network if T = 1, or any non-
uniforming state if T = 2. If the required state doesn't exist, output `-1`.
* * *
|
s457611377
|
Wrong Answer
|
p02827
|
Input is given from Standard Input in the following format:
N M T
x_1 y_1
x_2 y_2
:
x_M y_M
|
N, M, T = map(int, input().split())
xy = [list(map(int, input().split())) for _ in range(M)]
state_u = list(range(N))
state_d = list(range(N))
for j, (xj, yj) in enumerate(xy):
state_u[xj - 1] = yj - 1
state_d[yj - 1] = xj - 1
ans_u = [None] * N
ans_d = [None] * N
for i in range(N):
idx = i
while state_u[idx] != idx:
idx = state_u[idx]
ans_u[i] = state_u[idx]
#
idx = i
while state_d[idx] != idx:
idx = state_d[idx]
ans_d[i] = state_d[idx]
print("#", state_u, ans_u)
print("#", state_d, ans_d)
if ans_u.count(ans_u[0]) == N:
print("^" * N)
elif ans_d.count(ans_d[0]) == N:
print("v" * N)
else:
print(-1)
|
Statement
A _balancing network_ is an abstract device built up of N wires, thought of as
running from left to right, and M _balancers_ that connect pairs of wires. The
wires are numbered from 1 to N from top to bottom, and the balancers are
numbered from 1 to M from left to right. Balancer i connects wires x_i and y_i
(x_i < y_i).
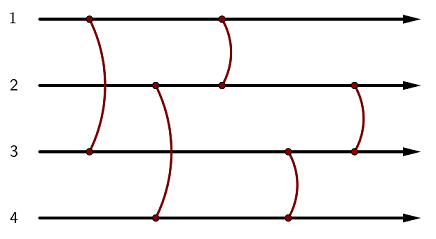
Each balancer must be in one of two states: _up_ or _down_.
Consider a token that starts moving to the right along some wire at a point to
the left of all balancers. During the process, the token passes through each
balancer exactly once. Whenever the token encounters balancer i, the following
happens:
* If the token is moving along wire x_i and balancer i is in the down state, the token moves down to wire y_i and continues moving to the right.
* If the token is moving along wire y_i and balancer i is in the up state, the token moves up to wire x_i and continues moving to the right.
* Otherwise, the token doesn't change the wire it's moving along.
Let a state of the balancing network be a string of length M, describing the
states of all balancers. The i-th character is `^` if balancer i is in the up
state, and `v` if balancer i is in the down state.
A state of the balancing network is called _uniforming_ if a wire w exists
such that, regardless of the starting wire, the token will always end up at
wire w and run to infinity along it. Any other state is called _non-
uniforming_.
You are given an integer T (1 \le T \le 2). Answer the following question:
* If T = 1, find any uniforming state of the network or determine that it doesn't exist.
* If T = 2, find any non-uniforming state of the network or determine that it doesn't exist.
Note that if you answer just one kind of questions correctly, you can get
partial score.
|
[{"input": "4 5 1\n 1 3\n 2 4\n 1 2\n 3 4\n 2 3", "output": "^^^^^\n \n\nThis state is uniforming: regardless of the starting wire, the token ends up\nat wire 1.\n\n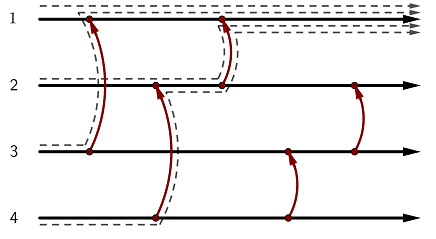\n\n* * *"}, {"input": "4 5 2\n 1 3\n 2 4\n 1 2\n 3 4\n 2 3", "output": "v^^^^\n \n\nThis state is non-uniforming: depending on the starting wire, the token might\nend up at wire 1 or wire 2.\n\n\n\n* * *"}, {"input": "3 1 1\n 1 2", "output": "-1\n \n\nA uniforming state doesn't exist.\n\n* * *"}, {"input": "2 1 2\n 1 2", "output": "-1\n \n\nA non-uniforming state doesn't exist."}]
|
If \\{A_i\\} is pairwise coprime, print `pairwise coprime`; if \\{A_i\\} is
setwise coprime, print `setwise coprime`; if neither, print `not coprime`.
* * *
|
s894658152
|
Accepted
|
p02574
|
Input is given from Standard Input in the following format:
N
A_1 \ldots A_N
|
import sys
sys.setrecursionlimit(10**6)
int1 = lambda x: int(x) - 1
p2D = lambda x: print(*x, sep="\n")
def II():
return int(sys.stdin.readline())
def MI():
return map(int, sys.stdin.readline().split())
def LI():
return list(map(int, sys.stdin.readline().split()))
def LLI(rows_number):
return [LI() for _ in range(rows_number)]
def SI():
return sys.stdin.readline()[:-1]
class Sieve:
def __init__(self, n):
self.plist = [2] # n以下の素数のリスト
min_prime_factor = [2, 0] * (n // 2 + 5)
for x in range(3, n + 1, 2):
if min_prime_factor[x] == 0:
min_prime_factor[x] = x
self.plist.append(x)
if x**2 > n:
continue
for y in range(x**2, n + 5, 2 * x):
if min_prime_factor[y] == 0:
min_prime_factor[y] = x
self.min_prime_factor = min_prime_factor
def isprime(self, x):
return self.min_prime_factor[x] == x
# これが素因数分解(prime factorization)
def pfct(self, x):
pp, ee = [], []
while x > 1:
mpf = self.min_prime_factor[x]
if pp and mpf == pp[-1]:
ee[-1] += 1
else:
pp.append(mpf)
ee.append(1)
x //= mpf
return pp
mx = 10**6 + 5
n = II()
aa = LI()
sv = Sieve(mx)
use = [0] * mx
ispair = True
for a in aa:
pp = sv.pfct(a)
for p in pp:
if use[p]:
ispair = False
use[p] += 1
if ispair:
print("pairwise coprime")
elif max(use) < n:
print("setwise coprime")
else:
print("not coprime")
|
Statement
We have N integers. The i-th number is A_i.
\\{A_i\\} is said to be pairwise coprime when GCD(A_i,A_j)=1 holds for every
pair (i, j) such that 1\leq i < j \leq N.
\\{A_i\\} is said to be setwise coprime when \\{A_i\\} is not pairwise coprime
but GCD(A_1,\ldots,A_N)=1.
Determine if \\{A_i\\} is pairwise coprime, setwise coprime, or neither.
Here, GCD(\ldots) denotes greatest common divisor.
|
[{"input": "3\n 3 4 5", "output": "pairwise coprime\n \n\nGCD(3,4)=GCD(3,5)=GCD(4,5)=1, so they are pairwise coprime.\n\n* * *"}, {"input": "3\n 6 10 15", "output": "setwise coprime\n \n\nSince GCD(6,10)=2, they are not pairwise coprime. However, since\nGCD(6,10,15)=1, they are setwise coprime.\n\n* * *"}, {"input": "3\n 6 10 16", "output": "not coprime\n \n\nGCD(6,10,16)=2, so they are neither pairwise coprime nor setwise coprime."}]
|
If \\{A_i\\} is pairwise coprime, print `pairwise coprime`; if \\{A_i\\} is
setwise coprime, print `setwise coprime`; if neither, print `not coprime`.
* * *
|
s102915935
|
Wrong Answer
|
p02574
|
Input is given from Standard Input in the following format:
N
A_1 \ldots A_N
|
N = int(input())
A = list(map(int, input().split()))
sumA = sum(A) % (1000000007)
square = 0
for i in range(N):
square -= ((A[i] % (1000000007)) ** 2) % (1000000007)
if square < 0:
square = square + 1000000007
res = (((sumA * sumA + square) % (1000000007)) * ((1000000007 + 1) / 2)) % 1000000007
print(round(res))
|
Statement
We have N integers. The i-th number is A_i.
\\{A_i\\} is said to be pairwise coprime when GCD(A_i,A_j)=1 holds for every
pair (i, j) such that 1\leq i < j \leq N.
\\{A_i\\} is said to be setwise coprime when \\{A_i\\} is not pairwise coprime
but GCD(A_1,\ldots,A_N)=1.
Determine if \\{A_i\\} is pairwise coprime, setwise coprime, or neither.
Here, GCD(\ldots) denotes greatest common divisor.
|
[{"input": "3\n 3 4 5", "output": "pairwise coprime\n \n\nGCD(3,4)=GCD(3,5)=GCD(4,5)=1, so they are pairwise coprime.\n\n* * *"}, {"input": "3\n 6 10 15", "output": "setwise coprime\n \n\nSince GCD(6,10)=2, they are not pairwise coprime. However, since\nGCD(6,10,15)=1, they are setwise coprime.\n\n* * *"}, {"input": "3\n 6 10 16", "output": "not coprime\n \n\nGCD(6,10,16)=2, so they are neither pairwise coprime nor setwise coprime."}]
|
If \\{A_i\\} is pairwise coprime, print `pairwise coprime`; if \\{A_i\\} is
setwise coprime, print `setwise coprime`; if neither, print `not coprime`.
* * *
|
s175465840
|
Wrong Answer
|
p02574
|
Input is given from Standard Input in the following format:
N
A_1 \ldots A_N
|
n = int(input())
1 / (n > 2)
|
Statement
We have N integers. The i-th number is A_i.
\\{A_i\\} is said to be pairwise coprime when GCD(A_i,A_j)=1 holds for every
pair (i, j) such that 1\leq i < j \leq N.
\\{A_i\\} is said to be setwise coprime when \\{A_i\\} is not pairwise coprime
but GCD(A_1,\ldots,A_N)=1.
Determine if \\{A_i\\} is pairwise coprime, setwise coprime, or neither.
Here, GCD(\ldots) denotes greatest common divisor.
|
[{"input": "3\n 3 4 5", "output": "pairwise coprime\n \n\nGCD(3,4)=GCD(3,5)=GCD(4,5)=1, so they are pairwise coprime.\n\n* * *"}, {"input": "3\n 6 10 15", "output": "setwise coprime\n \n\nSince GCD(6,10)=2, they are not pairwise coprime. However, since\nGCD(6,10,15)=1, they are setwise coprime.\n\n* * *"}, {"input": "3\n 6 10 16", "output": "not coprime\n \n\nGCD(6,10,16)=2, so they are neither pairwise coprime nor setwise coprime."}]
|
If \\{A_i\\} is pairwise coprime, print `pairwise coprime`; if \\{A_i\\} is
setwise coprime, print `setwise coprime`; if neither, print `not coprime`.
* * *
|
s416968239
|
Wrong Answer
|
p02574
|
Input is given from Standard Input in the following format:
N
A_1 \ldots A_N
|
print("not coprime")
|
Statement
We have N integers. The i-th number is A_i.
\\{A_i\\} is said to be pairwise coprime when GCD(A_i,A_j)=1 holds for every
pair (i, j) such that 1\leq i < j \leq N.
\\{A_i\\} is said to be setwise coprime when \\{A_i\\} is not pairwise coprime
but GCD(A_1,\ldots,A_N)=1.
Determine if \\{A_i\\} is pairwise coprime, setwise coprime, or neither.
Here, GCD(\ldots) denotes greatest common divisor.
|
[{"input": "3\n 3 4 5", "output": "pairwise coprime\n \n\nGCD(3,4)=GCD(3,5)=GCD(4,5)=1, so they are pairwise coprime.\n\n* * *"}, {"input": "3\n 6 10 15", "output": "setwise coprime\n \n\nSince GCD(6,10)=2, they are not pairwise coprime. However, since\nGCD(6,10,15)=1, they are setwise coprime.\n\n* * *"}, {"input": "3\n 6 10 16", "output": "not coprime\n \n\nGCD(6,10,16)=2, so they are neither pairwise coprime nor setwise coprime."}]
|
If \\{A_i\\} is pairwise coprime, print `pairwise coprime`; if \\{A_i\\} is
setwise coprime, print `setwise coprime`; if neither, print `not coprime`.
* * *
|
s507554967
|
Wrong Answer
|
p02574
|
Input is given from Standard Input in the following format:
N
A_1 \ldots A_N
|
print("pairwise coprime")
|
Statement
We have N integers. The i-th number is A_i.
\\{A_i\\} is said to be pairwise coprime when GCD(A_i,A_j)=1 holds for every
pair (i, j) such that 1\leq i < j \leq N.
\\{A_i\\} is said to be setwise coprime when \\{A_i\\} is not pairwise coprime
but GCD(A_1,\ldots,A_N)=1.
Determine if \\{A_i\\} is pairwise coprime, setwise coprime, or neither.
Here, GCD(\ldots) denotes greatest common divisor.
|
[{"input": "3\n 3 4 5", "output": "pairwise coprime\n \n\nGCD(3,4)=GCD(3,5)=GCD(4,5)=1, so they are pairwise coprime.\n\n* * *"}, {"input": "3\n 6 10 15", "output": "setwise coprime\n \n\nSince GCD(6,10)=2, they are not pairwise coprime. However, since\nGCD(6,10,15)=1, they are setwise coprime.\n\n* * *"}, {"input": "3\n 6 10 16", "output": "not coprime\n \n\nGCD(6,10,16)=2, so they are neither pairwise coprime nor setwise coprime."}]
|
If \\{A_i\\} is pairwise coprime, print `pairwise coprime`; if \\{A_i\\} is
setwise coprime, print `setwise coprime`; if neither, print `not coprime`.
* * *
|
s035201145
|
Wrong Answer
|
p02574
|
Input is given from Standard Input in the following format:
N
A_1 \ldots A_N
|
N = int(input())
Alist = list(map(int,input().split()))
# import time
# import random
# Alist = [random.randint(1,1000000) for i in range(1000000)]
# tt = time.time()
def GCD(a,b):
if a>b:
a = a%b
if a == 0:
return(b)
else:
return GCD(a,b)
else:
b = b%a
if b == 0:
return(a)
else:
return GCD(a,b)
isPC = True
isSC = False
kouyaku = 1
skipindex = 0
prod = 1
for i,x in enumerate(Alist[1:]):
prod*=Alist[i-1]
if GCD(x,prod)>1:
isPC = False
kouyaku = GCD(x,prod)
break
if kouyaku > 1:
for x in Alist:
kouyaku = GCD(x,kouyaku)
if kouyaku == 1:
isSC = True
break
if isPC:
print('pairwise coprime')
elif isSC:
print('setwise coprime')
else:
print('not coprime')
# print(time.time() - tt)
|
Statement
We have N integers. The i-th number is A_i.
\\{A_i\\} is said to be pairwise coprime when GCD(A_i,A_j)=1 holds for every
pair (i, j) such that 1\leq i < j \leq N.
\\{A_i\\} is said to be setwise coprime when \\{A_i\\} is not pairwise coprime
but GCD(A_1,\ldots,A_N)=1.
Determine if \\{A_i\\} is pairwise coprime, setwise coprime, or neither.
Here, GCD(\ldots) denotes greatest common divisor.
|
[{"input": "3\n 3 4 5", "output": "pairwise coprime\n \n\nGCD(3,4)=GCD(3,5)=GCD(4,5)=1, so they are pairwise coprime.\n\n* * *"}, {"input": "3\n 6 10 15", "output": "setwise coprime\n \n\nSince GCD(6,10)=2, they are not pairwise coprime. However, since\nGCD(6,10,15)=1, they are setwise coprime.\n\n* * *"}, {"input": "3\n 6 10 16", "output": "not coprime\n \n\nGCD(6,10,16)=2, so they are neither pairwise coprime nor setwise coprime."}]
|
If \\{A_i\\} is pairwise coprime, print `pairwise coprime`; if \\{A_i\\} is
setwise coprime, print `setwise coprime`; if neither, print `not coprime`.
* * *
|
s425207271
|
Wrong Answer
|
p02574
|
Input is given from Standard Input in the following format:
N
A_1 \ldots A_N
|
n=int(input())
aa=list(map(int,input().split()))
a=[x for x in aa if x!=1]
n=len(a)
if n<=1:
print('pairwise coprime')
exit()
# 素因数分解
def factorization(n):
arr = []
temp = n
for i in range(2, int(-(-n**0.5//1))+1):
if temp%i==0:
cnt=0
while temp%i==0:
cnt+=1
temp //= i
arr.append([i, cnt])
if temp!=1:
arr.append([temp, 1])
if arr==[]:
arr.append([n, 1])
return arr
tmp=[i for i,j in factorization(min(a))]
not_flg=False
for t in tmp:
flg=True
for x in a:
if x%t==0:
pass
else:
flg=False
break
if flg:
not_flg=flg
break
if not_flg:
print('not coprime')
exit()
#if n>78499:
if n>99999:
print('setwise coprime')
exit()
ary=set(())
for x in a:
tmp={i for i,j in factorization(x)}
for t in tmp:
if t in ary:
print('setwise coprime')
exit()
else:
ary.add(t)
print('pairwise coprime')
|
Statement
We have N integers. The i-th number is A_i.
\\{A_i\\} is said to be pairwise coprime when GCD(A_i,A_j)=1 holds for every
pair (i, j) such that 1\leq i < j \leq N.
\\{A_i\\} is said to be setwise coprime when \\{A_i\\} is not pairwise coprime
but GCD(A_1,\ldots,A_N)=1.
Determine if \\{A_i\\} is pairwise coprime, setwise coprime, or neither.
Here, GCD(\ldots) denotes greatest common divisor.
|
[{"input": "3\n 3 4 5", "output": "pairwise coprime\n \n\nGCD(3,4)=GCD(3,5)=GCD(4,5)=1, so they are pairwise coprime.\n\n* * *"}, {"input": "3\n 6 10 15", "output": "setwise coprime\n \n\nSince GCD(6,10)=2, they are not pairwise coprime. However, since\nGCD(6,10,15)=1, they are setwise coprime.\n\n* * *"}, {"input": "3\n 6 10 16", "output": "not coprime\n \n\nGCD(6,10,16)=2, so they are neither pairwise coprime nor setwise coprime."}]
|
For each randomAccess, print $a_p$ in a line.
|
s888458126
|
Accepted
|
p02431
|
The input is given in the following format.
$q$
$query_1$
$query_2$
:
$query_q$
Each query $query_i$ is given by
0 $x$
or
1 $p$
or
2
where the first digits 0, 1 and 2 represent pushBack, randomAccess and popBack
operations respectively.
randomAccess and popBack operations will not be given for an empty array.
|
li = []
for i in range(int(input())):
req = list(map(int, input().split()))
if req[0] == 0:
li.append(req[1])
elif req[0] == 1:
print(li[req[1]], end="\n")
else:
del li[len(li) - 1]
|
Vector
For a dynamic array $A = \\{a_0, a_1, ...\\}$ of integers, perform a sequence
of the following operations:
* pushBack($x$): add element $x$ at the end of $A$
* randomAccess($p$):print element $a_p$
* popBack(): delete the last element of $A$
$A$ is a 0-origin array and it is empty in the initial state.
|
[{"input": "8\n 0 1\n 0 2\n 0 3\n 2\n 0 4\n 1 0\n 1 1\n 1 2", "output": "1\n 2\n 4"}]
|
For each randomAccess, print $a_p$ in a line.
|
s959104929
|
Accepted
|
p02431
|
The input is given in the following format.
$q$
$query_1$
$query_2$
:
$query_q$
Each query $query_i$ is given by
0 $x$
or
1 $p$
or
2
where the first digits 0, 1 and 2 represent pushBack, randomAccess and popBack
operations respectively.
randomAccess and popBack operations will not be given for an empty array.
|
class Operation:
def __init__(self, num_list):
self.num_list = num_list
def ope(self, queries):
q = queries[0]
# print(queries, self.num_list)
if q == 0:
self.pushBack(queries[1])
elif q == 1:
self.randomAccess(queries[1])
elif q == 2:
self.popBack()
def pushBack(self, x):
# print("pushBack")
self.num_list.append(x)
def randomAccess(self, p):
# print(len(self.num_list), p + 1)
if len(self.num_list) >= p + 1:
print(self.num_list[p])
def popBack(self):
if len(self.num_list) > 0:
self.num_list.pop(-1)
x = int(input())
op = Operation(list())
for i in range(x):
op.ope(list(map(int, input().split())))
|
Vector
For a dynamic array $A = \\{a_0, a_1, ...\\}$ of integers, perform a sequence
of the following operations:
* pushBack($x$): add element $x$ at the end of $A$
* randomAccess($p$):print element $a_p$
* popBack(): delete the last element of $A$
$A$ is a 0-origin array and it is empty in the initial state.
|
[{"input": "8\n 0 1\n 0 2\n 0 3\n 2\n 0 4\n 1 0\n 1 1\n 1 2", "output": "1\n 2\n 4"}]
|
For each randomAccess, print $a_p$ in a line.
|
s225005306
|
Accepted
|
p02431
|
The input is given in the following format.
$q$
$query_1$
$query_2$
:
$query_q$
Each query $query_i$ is given by
0 $x$
or
1 $p$
or
2
where the first digits 0, 1 and 2 represent pushBack, randomAccess and popBack
operations respectively.
randomAccess and popBack operations will not be given for an empty array.
|
line_num = int(input())
array = []
for i in range(line_num):
line = [int(i) for i in input().split()]
if line[0] == 0:
array.append(line[1])
elif line[0] == 2:
array.pop()
else:
print(array[line[1]])
|
Vector
For a dynamic array $A = \\{a_0, a_1, ...\\}$ of integers, perform a sequence
of the following operations:
* pushBack($x$): add element $x$ at the end of $A$
* randomAccess($p$):print element $a_p$
* popBack(): delete the last element of $A$
$A$ is a 0-origin array and it is empty in the initial state.
|
[{"input": "8\n 0 1\n 0 2\n 0 3\n 2\n 0 4\n 1 0\n 1 1\n 1 2", "output": "1\n 2\n 4"}]
|
For each randomAccess, print $a_p$ in a line.
|
s621457761
|
Accepted
|
p02431
|
The input is given in the following format.
$q$
$query_1$
$query_2$
:
$query_q$
Each query $query_i$ is given by
0 $x$
or
1 $p$
or
2
where the first digits 0, 1 and 2 represent pushBack, randomAccess and popBack
operations respectively.
randomAccess and popBack operations will not be given for an empty array.
|
n = int(input())
a = []
for i in range(n):
x = list(map(int, input().split()))
if x[0] == 0:
a.append(x[1])
if x[0] == 1:
print(a[x[1]])
if x[0] == 2:
a.pop()
|
Vector
For a dynamic array $A = \\{a_0, a_1, ...\\}$ of integers, perform a sequence
of the following operations:
* pushBack($x$): add element $x$ at the end of $A$
* randomAccess($p$):print element $a_p$
* popBack(): delete the last element of $A$
$A$ is a 0-origin array and it is empty in the initial state.
|
[{"input": "8\n 0 1\n 0 2\n 0 3\n 2\n 0 4\n 1 0\n 1 1\n 1 2", "output": "1\n 2\n 4"}]
|
Print the index of the place where the palace should be built.
* * *
|
s090894866
|
Accepted
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
"""
半ば強引に二分探査で書いた。
"""
# 入力
n = int(input())
t, a = map(int, input().split())
h = list(map(int, input().split()))
h_not_sorted = h
h = sorted(h)
x = abs((t - a) / 0.006)
# 二分探査
l = 0
r = n - 1
x_index = 0
while l + 1 != r:
middle = (l + r) // 2
if h[middle] == x:
x_index = middle
break
elif h[middle] < x:
x_index = middle + 1
l = middle
else:
x_index = middle - 1
r = middle
# x_indexが両橋の場合とそれ以外で場合わけ。
res = abs(a - (t - 0.006 * h[x_index]))
ans = x_index
flag_r = True
flag_l = True
if x_index == n - 1:
flag_r = False
elif x_index == 0:
flag_l = False
else:
pass
# x_indexの両橋と比較。x_indexが際数値でない可能性があるため。
if flag_r:
if abs(a - (t - 0.006 * h[x_index + 1])) < res:
res = abs(a - (t - 0.006 * h[x_index + 1]))
ans += 1
if flag_l:
if abs(a - (t - 0.006 * h[x_index - 1])) < res:
res = abs(a - (t - 0.006 * h[x_index - 1]))
ans -= 1
print(h_not_sorted.index(h[ans]) + 1)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s444316710
|
Wrong Answer
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
import numpy as np
def find_nearest(array, value):
min_value = np.abs(max(array))
min_idx = 0
j = 0
for i in array:
j += 1
if min_value > np.abs(value - i):
min_value = np.abs(value - i)
min_idx = j
return min_idx
input_N = input()
input_two = input().split()
input_three = input().split()
N = int(input_N)
T = int(input_two[0])
A = float(input_two[1])
H_f = [float(s) for s in input_three]
j = 0
degree_list = list(range(j))
for i in H_f:
degree_list.append(T - i * 0.006)
print(find_nearest(degree_list, A))
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s385668515
|
Wrong Answer
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
#!usr/bin/env python3
from collections import defaultdict
from collections import deque
from heapq import heappush, heappop
import sys
import math
import bisect
import random
import itertools
sys.setrecursionlimit(10**5)
stdin = sys.stdin
def LI():
return list(map(int, stdin.readline().split()))
def LF():
return list(map(float, stdin.readline().split()))
def LI_():
return list(map(lambda x: int(x) - 1, stdin.readline().split()))
def II():
return int(stdin.readline())
def IF():
return float(stdin.readline())
def LS():
return list(map(list, stdin.readline().split()))
def S():
return list(stdin.readline().rstrip())
def IR(n):
return [II() for _ in range(n)]
def LIR(n):
return [LI() for _ in range(n)]
def FR(n):
return [IF() for _ in range(n)]
def LFR(n):
return [LI() for _ in range(n)]
def LIR_(n):
return [LI_() for _ in range(n)]
def SR(n):
return [S() for _ in range(n)]
def LSR(n):
return [LS() for _ in range(n)]
mod = 1000000007
inf = float("INF")
# A
def A():
x, y = LI()
print(x + y // 2)
return
# B
def B():
II()
a, t = LI()
h = LI()
ans = [0, inf]
for num, i in enumerate(h):
if ans[1] > abs(t - a - i * 0.006):
ans = [num, abs(t - a - i * 0.006)]
print(ans[0] + 1)
return
# C
def C():
n, m = LI()
py = LIR(m)
pya = py[::1]
py.sort(key=lambda x: x[1])
city = [1 for i in range(n)]
dicity = {}
for p, y in py:
dicity[(p, y)] = city[p - 1]
city[p - 1] += 1
for p, y in pya:
a = "00000" + str(p)
a = a[-6:]
b = "00000" + str(dicity[(p, y)])
b = b[-6:]
print(a + b)
return
# D
def D():
return
# Solve
if __name__ == "__main__":
B()
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s157119581
|
Accepted
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
I = lambda: map(int, input().split())
a = lambda l: l.index(min(l))
N = I()
T, A = I()
print(a([abs(T - i * 0.006 - A) for i in I()]) + 1)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s858855865
|
Accepted
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
def htemp(t, x):
return float(t - 0.006 * x)
input()
lt, la = [int(x) for x in input().split()]
h_ary = [int(x) for x in input().split()]
maxdiff = float("inf")
goodpoint = 0
for i, h in enumerate(h_ary):
diff = abs(la - htemp(lt, h))
if diff < maxdiff:
maxdiff = diff
goodpoint = i
print(goodpoint + 1)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s765404254
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
N = int(input())
T,A = [int(i) for i in input().split(' ')]
H = [int(i) for i in input().split(' ')]
minTemp = 600
for i,h in enumerate(H):
temp = T - h * 0.006
if abs(temp-A) < minTemp:
minTemp = abs(temp-A)
place = i+1
print(place)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s810364234
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
n = int(input())
t, a = map(int, input().split())
h = list(map(int, input().split()))
ans_num = 1
ans_para = h[0]
for i, r in enumerate(h):
deg = t - (r * 0.006)
ans_para_deg = t - (ans_para * 0.006)
if abs(a - ans_para_deg) >= abs(a - deg):
ans_para = r
ans_num = i+1
print(ans_num
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s128854943
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
#include "bits/stdc++.h"
using namespace std;
using ll = long long;
using Graph = vector<vector<int>>;
#define int ll
#define double long double
#define YES {cout<<"YES"<<'\n';}
#define NO {cout<<"NO"<<'\n';}
#define Yes {cout<<"Yes"<<'\n';}
#define No {cout<<"No"<<'\n';}
#define yes {cout<<"yes"<<'\n';}
#define no {cout<<"no"<<'\n';}
void YN(bool flg){cout<<(flg?"YES":"NO")<<'\n';}
void Yn(bool flg){cout<<(flg?"Yes":"No")<<'\n';}
void yn(bool flg){cout<<(flg?"yes":"no")<<'\n';}
#define SORT(a) sort(a.begin(),a.end())
#define REVERSE(a) reverse(a.begin(),a.end())
#define REP(i, n) for(int i = 0; i < n; i++)
#define REPR(i, n) for(int i = n; i >= 0; i--)
#define FOR(i, m, n) for(int i = m; i < n; i++)
#define out(n) {cout << n << '\n';}
typedef vector<int> VI;
typedef vector<string> VS;
typedef vector<bool> VB;
typedef vector<VI> VVI;
const int MOD = 1000000007;
const long long INF = 10e10;
const double PI = acos(-1.0);
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }
template<class T>auto MAX(const T& a) { return *max_element(a.begin(),a.end()); }
template<class T>auto MIN(const T& a) { return *min_element(a.begin(),a.end()); }
template<class T, class U>U SUM(const T& a, const U& v) { return accumulate(a.begin(),a.end(), v); }
template<class T, class U>U COUNT(const T& a, const U& v) { return count(a.begin(),a.end(), v); }
template<class T, class U>int LOWER(const T& a, const U& v) { return lower_bound(a.begin(),a.end(), v) - a.begin(); }
template<class T, class U>int UPPER(const T& a, const U& v) { return upper_bound(a.begin(),a.end(), v) - a.begin(); }
int GCD(int a, int b) { return b ? GCD(b, a%b) : a; }
int LCM(int a, int b) { int g = GCD(a, b); return a / g * b; }
int POW(int a, int n) { int r = 1; while (n > 0) { if (n & 1)r *= a; a *= a; n /= 2; }return r; }
int isPrime(int n){if(n<2){return 0;}for(int i=2; i*i<=n; i++){if(n%i==0){return 0;}}return 1;}
/*素因数分解*/map< int, int >prime_factor(int n){map< int, int > ret;for(int i = 2; i * i <= n; i++) {while(n % i == 0) {ret[i]++;n /= i;}}if(n != 1) ret[n] = 1;return ret;}
/*約数列挙*/vector<int> divisor(int n){vector<int> v; for(int i=1; i*i<=n; i++){if(n%i==0){v.push_back(i);if(i!=n/i){v.push_back(n/i);}}}sort(v.begin(),v.end()); return v;}
//----------------ライブラリとか----------------
signed main(){
cin.tie(0);
ios::sync_with_stdio(0);
cout<<fixed<<setprecision(15);
int n,t,a; cin >> n >> t >> a;
VI h(n); REP(i,n) cin >> h[i];
//hをxに近づける
int x = 6*(t-a)/1000;
int ans , tmp = INF;
REP(i,n){if(tmp>abs(h[i]-x)){tmp=abs(h[i]-x); ans=i+1;}}
out(ans);
return 0;
}
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s526214161
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
N = input()
T, A = map(int, input().split())
temperatures = list(map(int, input().split()))
r = 50000000
results = ''
list = [T - t * 0.006 for t in temperatures]
for index, avg_temp in enumerate(list):
if avg_temp < 0:
avg_temp = avg_temp * -1
ondo_sa = A - avg_temp
if r > ondo_sa:
r = ondo_sa
results = index + 1
print(results)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s418759550
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
N = int(input())
T,A = int(i) for i in input().split()
Hi = [int(i) for i in input().split()]
Ave = [T - i*0.006 for i in Hi]
Result = [abs(i) for i in Ave - A]
print(index(min(result)) + 1)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s186148807
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
n input()
t, a = map(int,input().split())
ary=[int(x) for x in input().split()]
x = (t-a)/0.006
def getNearestValue(list, num):
idx = np.abs(np.asarray(list) - num).argmin()
return list[idx]
if __name__ == "__main__":
print(getNearestValue(ary, x))
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s701541537
|
Wrong Answer
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
from sys import stdin
n = int(stdin.readline().rstrip())
t, a = [int(x) for x in stdin.readline().rstrip().split()]
hs = [int(x) for x in stdin.readline().rstrip().split()]
answers = [t - h * 0.006 for h in hs]
answers = [abs(an - a) for an in answers]
print(min(answers))
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s895634273
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
s = int(input())
w = input().split()
hight = input().split()
m = []
for i in hight:
m.append(abs(floot(w[0]) - floot(i) * 0.006 - floot(w[1])))
print(m.min())
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s554394247
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
N = int(input())
T,A = int(i) for i in input().split()
Hi = [int(i) for i in input().split()]
Ave = T - i*0.006 for i in Hi
Result = [abs(i) for i in (Ave - A)]
print(index(min(Result))+1)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s762042141
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
N = int(input())
T, A = (int(i) for i in input().split())
H = [int(input(i)) for i in range(N)]
print(int(H.index(min(abs((T-0.006*H[i]) - A) for i in range[N])))
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s968654902
|
Wrong Answer
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
(
n,
(T, A),
*D,
) = [list(map(int, s.split())) for s in open(0)]
n = n[0]
D = D[0]
di = {}
for i in range(len(D)):
di[i] = abs(A - D[i] * 0.006)
di = sorted(di.items(), key=lambda x: x[1])
print(di[0][0] + 1)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s266642951
|
Accepted
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
# -*- coding:utf-8 -*-
def Palace():
input()
T, A = [int(n) for n in input().split()]
candidate = [int(n) for n in input().split()]
index = 1
_min = float("inf")
for i, elevation in enumerate(candidate, start=1):
temp = T - elevation * 0.006
diff = abs(A - temp)
if diff < _min:
_min = diff
index = i
print(index)
if __name__ == "__main__":
Palace()
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s890908764
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
import sys
def solve(N, T, A, ls_H):
dosi = []
titen = []
titen1 = []
ti = 100000
for x in ls_H :
do = T - x * 0.006
dosi.append(do)
#print(dosi)
for y in dosi :
ti = A - y
titen.append(ti)
#print(titen)
for z in titen :
titen1.append(abs(z))
#print(titen1)
for i in titen1 :
if ti > i :
ti = i
#print(ti)
return titen1.index(ti) + 1
def readQuestion():
ws = sys.stdin.readline().strip().split()
N = int(ws[0])
ws = sys.stdin.readline().strip().split()
T = int(ws[0])
A = int(ws[1])
ws = sys.stdin.readline().strip().split()
ls_H = list(map(int, ws))
return (N, T, A, ls_H)
def main():
print(solve(*readQuestion()))
# Uncomment before submission
main()
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s988868733
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
N = int(input())
T, A = map(int, input().split())
H = list(map(int, input().split()))
min = float('inf')
idx = None
for i in range(len(H)):
if min > abs(A - T + H[i] * 0.006):
idx = i + 1å
print(i)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s387444378
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
n=int(input())
t,a=map(int,input().split())
h=list(map(int,input().split()))
ans=[]
for i in range(n):
ans.append(a-abs(t−h[i]×0.006))
print(min(ans))
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s713295818
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
n = int(input())
t, a = map(int, input().split())
places = map(int, [input() for _ in range(n)]
k = places.map(lambda x: abs(a - t - (H * 0.006)) // が最小となるindex
target = enumerate(k)
ans = (0, 99999)
for i in target:
if i[1] < ans[1]:
ans = i
print(i[0])
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s502541634
|
Runtime Error
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
N¥N = int(input())
T, A = map(int, input().split())
H = list(map(int, input().split()))
a = []
def cal(n):
ans = T - n * 0.006
return ans
for i in H:
a.append(int(abs(A - cal(i))))
print(a.index(min(a)) + 1)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s039850230
|
Accepted
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
N = int(input())
T, A = [int(s) for s in input().split(" ")]
Ht = [T - int(s) * 0.006 - A for s in input().split(" ")]
# for i, ta in zip(range(1, len(Ht)+1), Ht):
ret = min(zip(range(1, len(Ht) + 1), Ht), key=(lambda x: abs(x[1])))
print(ret[0])
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s195588309
|
Accepted
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
i = lambda: map(int, input().split())
i()
t, a = i()
c = [abs(t - 0.006 * b - a) for b in i()]
print(c.index(min(c)) + 1)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s942977504
|
Wrong Answer
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
N = int(input())
list = input().split()
T = list[0]
A = list[1]
print("Tは{}".format(T))
print("Aは{}".format(A))
list2 = input().split()
H = []
T_mean = []
minimum = []
for i in range(N):
H.append(list2[i])
T_mean.append(int(T) - int(H[i]) * 0.006)
minimum.append(abs(T_mean[i] - int(A)))
print(minimum.index(min(minimum)) + 1)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
Print the index of the place where the palace should be built.
* * *
|
s057380204
|
Wrong Answer
|
p03220
|
Input is given from Standard Input in the following format:
N
T A
H_1 H_2 ... H_N
|
# coding:UTF-8
num = int(input())
s = input()
ss = s.split(" ")
t = int(ss[0])
a = int(ss[1])
high = input()
high_list = high.split(" ")
calc_list = list()
for i in range(num):
high_work = int(high_list[i])
work = t - high_work * 0.006
calc_list.append(abs(a - work))
print(calc_list)
print(calc_list.index(min(calc_list)) + 1)
|
Statement
A country decides to build a palace.
In this country, the average temperature of a point at an elevation of x
meters is T-x \times 0.006 degrees Celsius.
There are N places proposed for the place. The elevation of Place i is H_i
meters.
Among them, Princess Joisino orders you to select the place whose average
temperature is the closest to A degrees Celsius, and build the palace there.
Print the index of the place where the palace should be built.
It is guaranteed that the solution is unique.
|
[{"input": "2\n 12 5\n 1000 2000", "output": "1\n \n\n * The average temperature of Place 1 is 12-1000 \\times 0.006=6 degrees Celsius.\n * The average temperature of Place 2 is 12-2000 \\times 0.006=0 degrees Celsius.\n\nThus, the palace should be built at Place 1.\n\n* * *"}, {"input": "3\n 21 -11\n 81234 94124 52141", "output": "3"}]
|
If the number of non-negative integers i satisfying the following condition is
finite, print the maximum value of such i; if the number is infinite, print
`-1`.
* * *
|
s337954150
|
Wrong Answer
|
p02962
|
Input is given from Standard Input in the following format:
s
t
|
print(1)
|
Statement
Given are two strings s and t consisting of lowercase English letters.
Determine if the number of non-negative integers i satisfying the following
condition is finite, and find the maximum value of such i if the number is
finite.
* There exists a non-negative integer j such that the concatenation of i copies of t is a substring of the concatenation of j copies of s.
|
[{"input": "abcabab\n ab", "output": "3\n \n\nThe concatenation of three copies of t, `ababab`, is a substring of the\nconcatenation of two copies of s, `abcabababcabab`, so i = 3 satisfies the\ncondition.\n\nOn the other hand, the concatenation of four copies of t, `abababab`, is not a\nsubstring of the concatenation of any number of copies of s, so i = 4 does not\nsatisfy the condition.\n\nSimilarly, any integer greater than 4 does not satisfy the condition, either.\nThus, the number of non-negative integers i satisfying the condition is\nfinite, and the maximum value of such i is 3.\n\n* * *"}, {"input": "aa\n aaaaaaa", "output": "-1\n \n\nFor any non-negative integer i, the concatenation of i copies of t is a\nsubstring of the concatenation of 4i copies of s. Thus, there are infinitely\nmany non-negative integers i that satisfy the condition.\n\n* * *"}, {"input": "aba\n baaab", "output": "0\n \n\nAs stated in Notes, i = 0 always satisfies the condition."}]
|
If the number of non-negative integers i satisfying the following condition is
finite, print the maximum value of such i; if the number is infinite, print
`-1`.
* * *
|
s100916544
|
Wrong Answer
|
p02962
|
Input is given from Standard Input in the following format:
s
t
|
print(-1)
|
Statement
Given are two strings s and t consisting of lowercase English letters.
Determine if the number of non-negative integers i satisfying the following
condition is finite, and find the maximum value of such i if the number is
finite.
* There exists a non-negative integer j such that the concatenation of i copies of t is a substring of the concatenation of j copies of s.
|
[{"input": "abcabab\n ab", "output": "3\n \n\nThe concatenation of three copies of t, `ababab`, is a substring of the\nconcatenation of two copies of s, `abcabababcabab`, so i = 3 satisfies the\ncondition.\n\nOn the other hand, the concatenation of four copies of t, `abababab`, is not a\nsubstring of the concatenation of any number of copies of s, so i = 4 does not\nsatisfy the condition.\n\nSimilarly, any integer greater than 4 does not satisfy the condition, either.\nThus, the number of non-negative integers i satisfying the condition is\nfinite, and the maximum value of such i is 3.\n\n* * *"}, {"input": "aa\n aaaaaaa", "output": "-1\n \n\nFor any non-negative integer i, the concatenation of i copies of t is a\nsubstring of the concatenation of 4i copies of s. Thus, there are infinitely\nmany non-negative integers i that satisfy the condition.\n\n* * *"}, {"input": "aba\n baaab", "output": "0\n \n\nAs stated in Notes, i = 0 always satisfies the condition."}]
|
If the number of non-negative integers i satisfying the following condition is
finite, print the maximum value of such i; if the number is infinite, print
`-1`.
* * *
|
s323931582
|
Accepted
|
p02962
|
Input is given from Standard Input in the following format:
s
t
|
import sys
sys.setrecursionlimit(2147483647)
INF = float("inf")
MOD = 10**9 + 7
input = lambda: sys.stdin.readline().rstrip()
class UnionFind(object):
def __init__(self, n):
self.__par = list(range(n))
self.__rank = [0] * n
self.__size = [1] * n
def root(self, k):
if self.__par[k] == k:
return k
self.__par[k] = self.root(self.__par[k])
return self.__par[k]
def unite(self, i, j):
i = self.root(i)
j = self.root(j)
par = self.__par
rank = self.__rank
size = self.__size
if i == j:
return False
if rank[i] > rank[j]:
par[j] = i
size[i] += size[j]
else:
par[i] = j
size[j] += size[i]
if rank[i] == rank[j]:
rank[j] += 1
return True
def size(self, k):
return self.__size[self.root(k)]
class RollingHash(object):
__base1 = 1007
__mod1 = 10**9 + 9
__base2 = 1009
__mod2 = 10**9 + 7
def __init__(self, s):
n = len(s)
self.__s = s
self.__n = n
b1 = self.__base1
m1 = self.__mod1
b2 = self.__base2
m2 = self.__mod2
H1, H2 = [0] * (n + 1), [0] * (n + 1)
P1, P2 = [1] * (n + 1), [1] * (n + 1)
for i in range(n):
H1[i + 1] = (H1[i] * b1 + ord(s[i])) % m1
H2[i + 1] = (H2[i] * b2 + ord(s[i])) % m2
P1[i + 1] = P1[i] * b1 % m1
P2[i + 1] = P2[i] * b2 % m2
self.__H1 = H1
self.__H2 = H2
self.__P1 = P1
self.__P2 = P2
def hash(self, l, r):
m1 = self.__mod1
m2 = self.__mod2
assert 0 <= l <= r <= self.__n
return (
(self.__H1[r] - self.__P1[r - l] * self.__H1[l] % m1) % m1,
(self.__H2[r] - self.__P2[r - l] * self.__H2[l] % m2) % m2,
)
def resolve():
from math import ceil
s = input()
t = input()
n = len(s)
m = len(t)
s = s * ceil(m / n)
s = s * 2
ok = [0] * n
uf = UnionFind(n)
rhs = RollingHash(s)
rht = RollingHash(t)
t = rht.hash(0, m)
for i in range(n):
if rhs.hash(i, i + m) == t:
ok[i] = 1
for i in range(n):
if ok[i] and ok[(i + m) % n]:
if not uf.unite(i, (i + m) % n):
print(-1)
return
ans = 0
for i in range(n):
if ok[i]:
ans = max(ans, uf.size(i))
print(ans)
resolve()
|
Statement
Given are two strings s and t consisting of lowercase English letters.
Determine if the number of non-negative integers i satisfying the following
condition is finite, and find the maximum value of such i if the number is
finite.
* There exists a non-negative integer j such that the concatenation of i copies of t is a substring of the concatenation of j copies of s.
|
[{"input": "abcabab\n ab", "output": "3\n \n\nThe concatenation of three copies of t, `ababab`, is a substring of the\nconcatenation of two copies of s, `abcabababcabab`, so i = 3 satisfies the\ncondition.\n\nOn the other hand, the concatenation of four copies of t, `abababab`, is not a\nsubstring of the concatenation of any number of copies of s, so i = 4 does not\nsatisfy the condition.\n\nSimilarly, any integer greater than 4 does not satisfy the condition, either.\nThus, the number of non-negative integers i satisfying the condition is\nfinite, and the maximum value of such i is 3.\n\n* * *"}, {"input": "aa\n aaaaaaa", "output": "-1\n \n\nFor any non-negative integer i, the concatenation of i copies of t is a\nsubstring of the concatenation of 4i copies of s. Thus, there are infinitely\nmany non-negative integers i that satisfy the condition.\n\n* * *"}, {"input": "aba\n baaab", "output": "0\n \n\nAs stated in Notes, i = 0 always satisfies the condition."}]
|
If the number of non-negative integers i satisfying the following condition is
finite, print the maximum value of such i; if the number is infinite, print
`-1`.
* * *
|
s462970998
|
Accepted
|
p02962
|
Input is given from Standard Input in the following format:
s
t
|
def getTableMP(Ss):
lenS = len(Ss)
table = [-1] * (lenS + 1)
j = -1
for i in range(lenS):
while j >= 0 and Ss[i] != Ss[j]:
j = table[j]
j += 1
table[i + 1] = j
return table
Ss = input()
Ts = input()
lenS, lenT = len(Ss), len(Ts)
num = (lenT + lenS - 1 + lenS - 1) // lenS
S2s = Ss * num
tableMP = getTableMP(Ts + "$" + S2s)
isFounds = [False] * lenS
for i in range(2 * lenT + 1, 2 * lenT + lenS + 1):
if tableMP[i] >= lenT:
isFounds[i - 2 * lenT - 1] = True
ans = 0
numDone = 0
for i in range(lenS):
if not isFounds[i]:
i = (i + lenT) % lenS
for num in range(lenS + 1):
if not isFounds[i]:
ans = max(ans, num)
numDone += num + 1
break
i = (i + lenT) % lenS
else:
ans = -1
break
if numDone < lenS:
ans = -1
print(ans)
|
Statement
Given are two strings s and t consisting of lowercase English letters.
Determine if the number of non-negative integers i satisfying the following
condition is finite, and find the maximum value of such i if the number is
finite.
* There exists a non-negative integer j such that the concatenation of i copies of t is a substring of the concatenation of j copies of s.
|
[{"input": "abcabab\n ab", "output": "3\n \n\nThe concatenation of three copies of t, `ababab`, is a substring of the\nconcatenation of two copies of s, `abcabababcabab`, so i = 3 satisfies the\ncondition.\n\nOn the other hand, the concatenation of four copies of t, `abababab`, is not a\nsubstring of the concatenation of any number of copies of s, so i = 4 does not\nsatisfy the condition.\n\nSimilarly, any integer greater than 4 does not satisfy the condition, either.\nThus, the number of non-negative integers i satisfying the condition is\nfinite, and the maximum value of such i is 3.\n\n* * *"}, {"input": "aa\n aaaaaaa", "output": "-1\n \n\nFor any non-negative integer i, the concatenation of i copies of t is a\nsubstring of the concatenation of 4i copies of s. Thus, there are infinitely\nmany non-negative integers i that satisfy the condition.\n\n* * *"}, {"input": "aba\n baaab", "output": "0\n \n\nAs stated in Notes, i = 0 always satisfies the condition."}]
|
If the number of non-negative integers i satisfying the following condition is
finite, print the maximum value of such i; if the number is infinite, print
`-1`.
* * *
|
s698784934
|
Wrong Answer
|
p02962
|
Input is given from Standard Input in the following format:
s
t
|
S = list(input())
T = list(input())
len0 = len(S)
while len(S) < len(T):
S = S + S
S = S + S
p = 26
mod = (1 << 21) + 1 # 互いに素なものを指定
TABLE = [0] # Rolling Hashのテーブル. 最初は0
LEN = len(S)
for i in range(LEN):
TABLE.append((p * TABLE[-1] % mod + ord(S[i]) - 97) % mod) # テーブルを埋める
NOW = 0
LEN2 = len(T)
for i in range(LEN2):
NOW = (p * NOW % mod + ord(T[i]) - 97) % mod
TH = NOW
def hash_ij(i, j): # [i,j)のハッシュ値を求める
return (TABLE[j] - TABLE[i] * pow(p, j - i, mod)) % mod
OK = [0] * LEN
for i in range(LEN2, LEN):
if hash_ij(i - LEN2, i) == TH:
OK[i - LEN2] = 1
OK = OK[:len0]
ANS = 0
ST = [-1] * len0
for i in range(len0):
if OK[i] == 1 and ST[i] == -1:
j = i
count = 0
while OK[j] == 1:
if ST[j] != -1:
count += ST[j]
break
count += 1
ST[j] = 1
j = (j + LEN2) % len0
if j == i:
print(-1)
import sys
sys.exit()
ST[i] = count
ANS = max(ANS, count)
print(ANS)
|
Statement
Given are two strings s and t consisting of lowercase English letters.
Determine if the number of non-negative integers i satisfying the following
condition is finite, and find the maximum value of such i if the number is
finite.
* There exists a non-negative integer j such that the concatenation of i copies of t is a substring of the concatenation of j copies of s.
|
[{"input": "abcabab\n ab", "output": "3\n \n\nThe concatenation of three copies of t, `ababab`, is a substring of the\nconcatenation of two copies of s, `abcabababcabab`, so i = 3 satisfies the\ncondition.\n\nOn the other hand, the concatenation of four copies of t, `abababab`, is not a\nsubstring of the concatenation of any number of copies of s, so i = 4 does not\nsatisfy the condition.\n\nSimilarly, any integer greater than 4 does not satisfy the condition, either.\nThus, the number of non-negative integers i satisfying the condition is\nfinite, and the maximum value of such i is 3.\n\n* * *"}, {"input": "aa\n aaaaaaa", "output": "-1\n \n\nFor any non-negative integer i, the concatenation of i copies of t is a\nsubstring of the concatenation of 4i copies of s. Thus, there are infinitely\nmany non-negative integers i that satisfy the condition.\n\n* * *"}, {"input": "aba\n baaab", "output": "0\n \n\nAs stated in Notes, i = 0 always satisfies the condition."}]
|
If the number of non-negative integers i satisfying the following condition is
finite, print the maximum value of such i; if the number is infinite, print
`-1`.
* * *
|
s322150347
|
Runtime Error
|
p02962
|
Input is given from Standard Input in the following format:
s
t
|
S = input()
T = input()
if T * len(S) == S * len(T):
print(-1)
|
Statement
Given are two strings s and t consisting of lowercase English letters.
Determine if the number of non-negative integers i satisfying the following
condition is finite, and find the maximum value of such i if the number is
finite.
* There exists a non-negative integer j such that the concatenation of i copies of t is a substring of the concatenation of j copies of s.
|
[{"input": "abcabab\n ab", "output": "3\n \n\nThe concatenation of three copies of t, `ababab`, is a substring of the\nconcatenation of two copies of s, `abcabababcabab`, so i = 3 satisfies the\ncondition.\n\nOn the other hand, the concatenation of four copies of t, `abababab`, is not a\nsubstring of the concatenation of any number of copies of s, so i = 4 does not\nsatisfy the condition.\n\nSimilarly, any integer greater than 4 does not satisfy the condition, either.\nThus, the number of non-negative integers i satisfying the condition is\nfinite, and the maximum value of such i is 3.\n\n* * *"}, {"input": "aa\n aaaaaaa", "output": "-1\n \n\nFor any non-negative integer i, the concatenation of i copies of t is a\nsubstring of the concatenation of 4i copies of s. Thus, there are infinitely\nmany non-negative integers i that satisfy the condition.\n\n* * *"}, {"input": "aba\n baaab", "output": "0\n \n\nAs stated in Notes, i = 0 always satisfies the condition."}]
|
For each find operation, print the value.
|
s088268036
|
Wrong Answer
|
p02348
|
n q
query1
query2
:
queryq
In the first line, n (the number of elements in A) and q (the number of
queries) are given. Then, _i_ th query queryi is given in the following
format:
0 s t x
or
1 i
The first digit represents the type of the query. '0' denotes update(s, t, x)
and '1' denotes find(i).
|
#!/usr/bin/env python3
# DSL_2_D: Range Update Query
class SegmentTree:
def __init__(self, n):
size = 1
while size < n:
size *= 2
self.size = 2 * size - 1
self.data = [-1] * self.size
self.data[0] = 2**31 - 1
def set_range(self, lo, hi, v):
def _set_range(r, i, j, vv):
if j < lo or i > hi:
if vv != -1:
self.data[r] = vv
elif lo <= i and j <= hi:
self.data[r] = v
else:
if self.data[r] != -1:
vv = self.data[r]
self.data[r] = -1
mid = i + (j - i) // 2
_set_range(r * 2 + 1, i, mid, vv)
_set_range(r * 2 + 2, mid + 1, j, vv)
_set_range(0, 0, self.size // 2, -1)
def get(self, i):
def _get(r, lo, hi):
if self.data[r] != -1:
return self.data[r]
mid = lo + (hi - lo) // 2
if i <= mid:
return _get(r * 2 + 1, lo, mid)
else:
return _get(r * 2 + 2, mid + 1, hi)
return _get(0, 0, self.size // 2)
def run():
n, q = [int(x) for x in input().split()]
t = SegmentTree(n)
for _ in range(q):
com, *args = [x for x in input().split()]
if com == "0":
i, j, v = [int(x) for x in args]
t.set_range(i, j, v)
elif com == "1":
i = int(args[0])
print(t.get(i))
if __name__ == "__main__":
run()
|
Range Update Query (RUQ)
Write a program which manipulates a sequence A = {a0, a1, . . . , an−1} with
the following operations:
* update(s, t, x): change as, as+1, ..., at to x.
* find(i): output the value of ai.
Note that the initial values of ai (i = 0, 1, . . . , n−1) are 231-1.
|
[{"input": "3 5\n 0 0 1 1\n 0 1 2 3\n 0 2 2 2\n 1 0\n 1 1", "output": "1\n 3"}, {"input": "1 3\n 1 0\n 0 0 0 5\n 1 0", "output": "2147483647\n 5"}]
|
For each find operation, print the value.
|
s798258073
|
Wrong Answer
|
p02348
|
n q
query1
query2
:
queryq
In the first line, n (the number of elements in A) and q (the number of
queries) are given. Then, _i_ th query queryi is given in the following
format:
0 s t x
or
1 i
The first digit represents the type of the query. '0' denotes update(s, t, x)
and '1' denotes find(i).
|
#! -*- coding:utf-8 -*-
n, q = map(int, input().split())
query = [0] * q
for i in range(q):
query[i] = input()
arr = [2**31 - 1] * n
for i in range(q):
if len(query[i]) == 7:
tmp = list(query[i].split())
s = int(tmp[1])
t = int(tmp[2])
for i in range(s, t + 1):
arr[i] = tmp[3]
else:
tmp = list(query[i].split())
print(arr[int(tmp[1])])
|
Range Update Query (RUQ)
Write a program which manipulates a sequence A = {a0, a1, . . . , an−1} with
the following operations:
* update(s, t, x): change as, as+1, ..., at to x.
* find(i): output the value of ai.
Note that the initial values of ai (i = 0, 1, . . . , n−1) are 231-1.
|
[{"input": "3 5\n 0 0 1 1\n 0 1 2 3\n 0 2 2 2\n 1 0\n 1 1", "output": "1\n 3"}, {"input": "1 3\n 1 0\n 0 0 0 5\n 1 0", "output": "2147483647\n 5"}]
|
For each find operation, print the value.
|
s019070923
|
Accepted
|
p02348
|
n q
query1
query2
:
queryq
In the first line, n (the number of elements in A) and q (the number of
queries) are given. Then, _i_ th query queryi is given in the following
format:
0 s t x
or
1 i
The first digit represents the type of the query. '0' denotes update(s, t, x)
and '1' denotes find(i).
|
from math import log2, ceil
class SegmentTree:
def __init__(self, n):
tn = 2 ** ceil(log2(n))
self.a = [2**31 - 1] * (tn * 2)
def find(self, c, l, r, i):
if self.a[c] != -1:
return self.a[c]
mid = (l + r) // 2
if i <= mid:
return self.find(c * 2, l, mid, i)
else:
return self.find(c * 2 + 1, mid + 1, r, i)
def update(self, c, l, r, s, t, x):
if l == s and r == t:
self.a[c] = x
return
cv = self.a[c]
if cv != -1:
self.a[c * 2] = self.a[c * 2 + 1] = cv
self.a[c] = -1
mid = (l + r) // 2
if t <= mid:
self.update(c * 2, l, mid, s, t, x)
elif s > mid:
self.update(c * 2 + 1, mid + 1, r, s, t, x)
else:
self.update(c * 2, l, mid, s, mid, x)
self.update(c * 2 + 1, mid + 1, r, mid + 1, t, x)
n, q = map(int, input().split())
st = SegmentTree(n)
for _ in range(q):
query = input().split()
if query[0] == "0":
s, t, x = map(int, query[1:])
st.update(1, 0, n - 1, s, t, x)
else:
print(st.find(1, 0, n - 1, int(query[1])))
|
Range Update Query (RUQ)
Write a program which manipulates a sequence A = {a0, a1, . . . , an−1} with
the following operations:
* update(s, t, x): change as, as+1, ..., at to x.
* find(i): output the value of ai.
Note that the initial values of ai (i = 0, 1, . . . , n−1) are 231-1.
|
[{"input": "3 5\n 0 0 1 1\n 0 1 2 3\n 0 2 2 2\n 1 0\n 1 1", "output": "1\n 3"}, {"input": "1 3\n 1 0\n 0 0 0 5\n 1 0", "output": "2147483647\n 5"}]
|
For each find operation, print the value.
|
s736422939
|
Accepted
|
p02348
|
n q
query1
query2
:
queryq
In the first line, n (the number of elements in A) and q (the number of
queries) are given. Then, _i_ th query queryi is given in the following
format:
0 s t x
or
1 i
The first digit represents the type of the query. '0' denotes update(s, t, x)
and '1' denotes find(i).
|
class SegmentTreeDual:
def __init__(self, arr, op=lambda x, y: y if y != -1 else x, ie=-1):
self.h = (len(arr) - 1).bit_length()
self.n = 2**self.h
self.ie = ie
self.op = op
self.val = [ie for _ in range(len(arr))]
self.laz = [ie for _ in range(2 * self.n)]
for i in range(len(arr)):
self.val[i] = arr[i]
def propagate(self, k):
if self.laz[k] == self.ie:
return
if self.n <= k:
self.val[k - self.n] = self.op(self.val[k - self.n], self.laz[k])
self.laz[k] = self.ie
else:
self.laz[(k << 1)] = self.op(self.laz[(k << 1)], self.laz[k])
self.laz[(k << 1) + 1] = self.op(self.laz[(k << 1) + 1], self.laz[k])
self.laz[k] = self.ie
def update(self, left, right, f):
left += self.n
right += self.n
for i in reversed(range(self.h + 1)):
self.propagate(left >> i)
for i in reversed(range(self.h + 1)):
self.propagate((right - 1) >> i)
while right - left > 0:
if right & 1:
right -= 1
self.laz[right] = self.op(self.laz[right], f)
if left & 1:
self.laz[left] = self.op(self.laz[left], f)
left += 1
left >>= 1
right >>= 1
def get(self, index):
res = self.val[index]
index += self.n
while index:
res = self.op(res, self.laz[index])
index //= 2
return res
INF = 2**31 - 1
N, Q = map(int, input().split())
A = [INF for _ in range(N)]
sg = SegmentTreeDual(A)
ans = []
for _ in range(Q):
q = list(map(int, input().split()))
if q[0] == 0:
s, t, x = q[1:]
sg.update(s, t + 1, x)
else:
i = q[1]
ans.append(sg.get(i))
print("\n".join(map(str, ans)))
|
Range Update Query (RUQ)
Write a program which manipulates a sequence A = {a0, a1, . . . , an−1} with
the following operations:
* update(s, t, x): change as, as+1, ..., at to x.
* find(i): output the value of ai.
Note that the initial values of ai (i = 0, 1, . . . , n−1) are 231-1.
|
[{"input": "3 5\n 0 0 1 1\n 0 1 2 3\n 0 2 2 2\n 1 0\n 1 1", "output": "1\n 3"}, {"input": "1 3\n 1 0\n 0 0 0 5\n 1 0", "output": "2147483647\n 5"}]
|
For each find operation, print the value.
|
s177702599
|
Accepted
|
p02348
|
n q
query1
query2
:
queryq
In the first line, n (the number of elements in A) and q (the number of
queries) are given. Then, _i_ th query queryi is given in the following
format:
0 s t x
or
1 i
The first digit represents the type of the query. '0' denotes update(s, t, x)
and '1' denotes find(i).
|
import sys
INF = 2**31 - 1
class RUQ:
def __init__(self, n):
tmp = 1
while tmp < n:
tmp *= 2
self.n = tmp * 2
self.A = [INF] * (2 * self.n - 1)
def update(self, a, b, x=-1, k=0, l=0, r=0):
if r <= a or b <= l:
return
if a <= l and r <= b:
if x >= 0:
self.A[k] = x
return
if self.A[k] != INF:
self.A[k * 2 + 1] = self.A[k * 2 + 2] = self.A[k]
self.A[k] = INF
self.update(a, b, x, k * 2 + 1, l, (l + r) / 2)
self.update(a, b, x, k * 2 + 2, (l + r) / 2, r)
line = sys.stdin.readline()
n, q = map(int, line.split())
ruq = RUQ(n)
for i in range(q):
line = sys.stdin.readline()
if line[0] == "0":
com, s, t, x = map(int, line.split())
ruq.update(s, t + 1, x, 0, 0, ruq.n)
else:
com, i = map(int, line.split())
ruq.update(i, i + 1, -1, 0, 0, ruq.n)
print(ruq.A[i + ruq.n - 1])
|
Range Update Query (RUQ)
Write a program which manipulates a sequence A = {a0, a1, . . . , an−1} with
the following operations:
* update(s, t, x): change as, as+1, ..., at to x.
* find(i): output the value of ai.
Note that the initial values of ai (i = 0, 1, . . . , n−1) are 231-1.
|
[{"input": "3 5\n 0 0 1 1\n 0 1 2 3\n 0 2 2 2\n 1 0\n 1 1", "output": "1\n 3"}, {"input": "1 3\n 1 0\n 0 0 0 5\n 1 0", "output": "2147483647\n 5"}]
|
Output the converted Celsius temperature in a line.
|
s175519960
|
Accepted
|
p00375
|
The input is given in the following format.
$F$
The input line provides a temperature in Fahrenheit $F$ ($30 \leq F \leq
100$), which is an integer divisible by $2$.
|
kashi = int(input())
sesshi = int((kashi - 30) / 2)
print(sesshi)
|
Celsius/Fahrenheit
In Japan, temperature is usually expressed using the Celsius (℃) scale. In
America, they used the Fahrenheit (℉) scale instead. $20$ degrees Celsius is
roughly equal to $68$ degrees Fahrenheit. A phrase such as "Today’s
temperature is $68$ degrees" is commonly encountered while you are in America.
A value in Fahrenheit can be converted to Celsius by first subtracting $32$
and then multiplying by $\frac{5}{9}$. A simplified method may be used to
produce a rough estimate: first subtract $30$ and then divide by $2$. Using
the latter method, $68$ Fahrenheit is converted to $19$ Centigrade, i.e.,
$\frac{(68-30)}{2}$.
Make a program to convert Fahrenheit to Celsius using the simplified method:
$C = \frac{F - 30}{2}$.
|
[{"input": "68", "output": "19"}, {"input": "50", "output": "10"}]
|
Output the converted Celsius temperature in a line.
|
s397126311
|
Accepted
|
p00375
|
The input is given in the following format.
$F$
The input line provides a temperature in Fahrenheit $F$ ($30 \leq F \leq
100$), which is an integer divisible by $2$.
|
print(int(input()) // 2 - 15)
|
Celsius/Fahrenheit
In Japan, temperature is usually expressed using the Celsius (℃) scale. In
America, they used the Fahrenheit (℉) scale instead. $20$ degrees Celsius is
roughly equal to $68$ degrees Fahrenheit. A phrase such as "Today’s
temperature is $68$ degrees" is commonly encountered while you are in America.
A value in Fahrenheit can be converted to Celsius by first subtracting $32$
and then multiplying by $\frac{5}{9}$. A simplified method may be used to
produce a rough estimate: first subtract $30$ and then divide by $2$. Using
the latter method, $68$ Fahrenheit is converted to $19$ Centigrade, i.e.,
$\frac{(68-30)}{2}$.
Make a program to convert Fahrenheit to Celsius using the simplified method:
$C = \frac{F - 30}{2}$.
|
[{"input": "68", "output": "19"}, {"input": "50", "output": "10"}]
|
Output the converted Celsius temperature in a line.
|
s570164530
|
Accepted
|
p00375
|
The input is given in the following format.
$F$
The input line provides a temperature in Fahrenheit $F$ ($30 \leq F \leq
100$), which is an integer divisible by $2$.
|
C = int(input())
F = (C - 30) / 2
print(int(F))
|
Celsius/Fahrenheit
In Japan, temperature is usually expressed using the Celsius (℃) scale. In
America, they used the Fahrenheit (℉) scale instead. $20$ degrees Celsius is
roughly equal to $68$ degrees Fahrenheit. A phrase such as "Today’s
temperature is $68$ degrees" is commonly encountered while you are in America.
A value in Fahrenheit can be converted to Celsius by first subtracting $32$
and then multiplying by $\frac{5}{9}$. A simplified method may be used to
produce a rough estimate: first subtract $30$ and then divide by $2$. Using
the latter method, $68$ Fahrenheit is converted to $19$ Centigrade, i.e.,
$\frac{(68-30)}{2}$.
Make a program to convert Fahrenheit to Celsius using the simplified method:
$C = \frac{F - 30}{2}$.
|
[{"input": "68", "output": "19"}, {"input": "50", "output": "10"}]
|
Output the converted Celsius temperature in a line.
|
s374776677
|
Accepted
|
p00375
|
The input is given in the following format.
$F$
The input line provides a temperature in Fahrenheit $F$ ($30 \leq F \leq
100$), which is an integer divisible by $2$.
|
x = input()
x = int(x)
y = (x - 30) / 2
print(int(y))
|
Celsius/Fahrenheit
In Japan, temperature is usually expressed using the Celsius (℃) scale. In
America, they used the Fahrenheit (℉) scale instead. $20$ degrees Celsius is
roughly equal to $68$ degrees Fahrenheit. A phrase such as "Today’s
temperature is $68$ degrees" is commonly encountered while you are in America.
A value in Fahrenheit can be converted to Celsius by first subtracting $32$
and then multiplying by $\frac{5}{9}$. A simplified method may be used to
produce a rough estimate: first subtract $30$ and then divide by $2$. Using
the latter method, $68$ Fahrenheit is converted to $19$ Centigrade, i.e.,
$\frac{(68-30)}{2}$.
Make a program to convert Fahrenheit to Celsius using the simplified method:
$C = \frac{F - 30}{2}$.
|
[{"input": "68", "output": "19"}, {"input": "50", "output": "10"}]
|
Output the converted Celsius temperature in a line.
|
s466298205
|
Wrong Answer
|
p00375
|
The input is given in the following format.
$F$
The input line provides a temperature in Fahrenheit $F$ ($30 \leq F \leq
100$), which is an integer divisible by $2$.
|
print((int(input()) - 30) / 2)
|
Celsius/Fahrenheit
In Japan, temperature is usually expressed using the Celsius (℃) scale. In
America, they used the Fahrenheit (℉) scale instead. $20$ degrees Celsius is
roughly equal to $68$ degrees Fahrenheit. A phrase such as "Today’s
temperature is $68$ degrees" is commonly encountered while you are in America.
A value in Fahrenheit can be converted to Celsius by first subtracting $32$
and then multiplying by $\frac{5}{9}$. A simplified method may be used to
produce a rough estimate: first subtract $30$ and then divide by $2$. Using
the latter method, $68$ Fahrenheit is converted to $19$ Centigrade, i.e.,
$\frac{(68-30)}{2}$.
Make a program to convert Fahrenheit to Celsius using the simplified method:
$C = \frac{F - 30}{2}$.
|
[{"input": "68", "output": "19"}, {"input": "50", "output": "10"}]
|
If M popular items can be selected, print `Yes`; otherwise, print `No`.
* * *
|
s181784604
|
Wrong Answer
|
p02718
|
Input is given from Standard Input in the following format:
N M
A_1 ... A_N
|
# coding: utf-8
# Your code here!
# coding: utf-8
import sys
sys.setrecursionlimit(10000000)
# const
dxdy = ((1, 0), (0, 1))
# my functions here!
def pin(type=int):
return map(type, input().rstrip().split())
def resolve():
N, M = pin()
A = sorted(list(pin()))
A.reverse()
p = (sum(A)) // (4 * M)
# print(sum(A),A)
print(["No", "Yes"][A[M - 1] > p])
"""
#printデバッグ消した?
#前の問題の結果見てないのに次の問題に行くの?
"""
"""
お前カッコ閉じ,るの忘れてるだろ
"""
import sys
from io import StringIO
import unittest
class TestClass(unittest.TestCase):
def assertIO(self, input, output):
stdout, stdin = sys.stdout, sys.stdin
sys.stdout, sys.stdin = StringIO(), StringIO(input)
resolve()
sys.stdout.seek(0)
out = sys.stdout.read()[:-1]
sys.stdout, sys.stdin = stdout, stdin
self.assertEqual(out, output)
def test_入力例_1(self):
input = """4 1
5 4 2 1"""
output = """Yes"""
self.assertIO(input, output)
def test_入力例_2(self):
input = """3 2
380 19 1"""
output = """No"""
self.assertIO(input, output)
def test_入力例_3(self):
input = """12 3
4 56 78 901 2 345 67 890 123 45 6 789"""
output = """Yes"""
self.assertIO(input, output)
if __name__ == "__main__":
resolve()
|
Statement
We have held a popularity poll for N items on sale. Item i received A_i votes.
From these N items, we will select M as popular items. However, we cannot
select an item with less than \dfrac{1}{4M} of the total number of votes.
If M popular items can be selected, print `Yes`; otherwise, print `No`.
|
[{"input": "4 1\n 5 4 2 1", "output": "Yes\n \n\nThere were 12 votes in total. The most popular item received 5 votes, and we\ncan select it.\n\n* * *"}, {"input": "3 2\n 380 19 1", "output": "No\n \n\nThere were 400 votes in total. The second and third most popular items\nreceived less than \\dfrac{1}{4\\times 2} of the total number of votes, so we\ncannot select them. Thus, we cannot select two popular items.\n\n* * *"}, {"input": "12 3\n 4 56 78 901 2 345 67 890 123 45 6 789", "output": "Yes"}]
|
If M popular items can be selected, print `Yes`; otherwise, print `No`.
* * *
|
s570566257
|
Wrong Answer
|
p02718
|
Input is given from Standard Input in the following format:
N M
A_1 ... A_N
|
print("Yes")
|
Statement
We have held a popularity poll for N items on sale. Item i received A_i votes.
From these N items, we will select M as popular items. However, we cannot
select an item with less than \dfrac{1}{4M} of the total number of votes.
If M popular items can be selected, print `Yes`; otherwise, print `No`.
|
[{"input": "4 1\n 5 4 2 1", "output": "Yes\n \n\nThere were 12 votes in total. The most popular item received 5 votes, and we\ncan select it.\n\n* * *"}, {"input": "3 2\n 380 19 1", "output": "No\n \n\nThere were 400 votes in total. The second and third most popular items\nreceived less than \\dfrac{1}{4\\times 2} of the total number of votes, so we\ncannot select them. Thus, we cannot select two popular items.\n\n* * *"}, {"input": "12 3\n 4 56 78 901 2 345 67 890 123 45 6 789", "output": "Yes"}]
|
If M popular items can be selected, print `Yes`; otherwise, print `No`.
* * *
|
s667142880
|
Accepted
|
p02718
|
Input is given from Standard Input in the following format:
N M
A_1 ... A_N
|
size, comp = input().split()
size = int(size)
comp = int(comp)
vote_list = list(map(int, input().split()))
data = len(list(filter(lambda x: x >= (sum(vote_list) / (4 * comp)), vote_list)))
print("Yes" if data >= comp else "No")
|
Statement
We have held a popularity poll for N items on sale. Item i received A_i votes.
From these N items, we will select M as popular items. However, we cannot
select an item with less than \dfrac{1}{4M} of the total number of votes.
If M popular items can be selected, print `Yes`; otherwise, print `No`.
|
[{"input": "4 1\n 5 4 2 1", "output": "Yes\n \n\nThere were 12 votes in total. The most popular item received 5 votes, and we\ncan select it.\n\n* * *"}, {"input": "3 2\n 380 19 1", "output": "No\n \n\nThere were 400 votes in total. The second and third most popular items\nreceived less than \\dfrac{1}{4\\times 2} of the total number of votes, so we\ncannot select them. Thus, we cannot select two popular items.\n\n* * *"}, {"input": "12 3\n 4 56 78 901 2 345 67 890 123 45 6 789", "output": "Yes"}]
|
If M popular items can be selected, print `Yes`; otherwise, print `No`.
* * *
|
s816845479
|
Wrong Answer
|
p02718
|
Input is given from Standard Input in the following format:
N M
A_1 ... A_N
|
n, m = map(int, input().split())
aaa = list(map(int, input().split()))
border = sum(aaa) // (4 * m)
selectable = sum(1 for a in aaa if a >= border)
print("Yes" if selectable >= m else "No")
|
Statement
We have held a popularity poll for N items on sale. Item i received A_i votes.
From these N items, we will select M as popular items. However, we cannot
select an item with less than \dfrac{1}{4M} of the total number of votes.
If M popular items can be selected, print `Yes`; otherwise, print `No`.
|
[{"input": "4 1\n 5 4 2 1", "output": "Yes\n \n\nThere were 12 votes in total. The most popular item received 5 votes, and we\ncan select it.\n\n* * *"}, {"input": "3 2\n 380 19 1", "output": "No\n \n\nThere were 400 votes in total. The second and third most popular items\nreceived less than \\dfrac{1}{4\\times 2} of the total number of votes, so we\ncannot select them. Thus, we cannot select two popular items.\n\n* * *"}, {"input": "12 3\n 4 56 78 901 2 345 67 890 123 45 6 789", "output": "Yes"}]
|
If M popular items can be selected, print `Yes`; otherwise, print `No`.
* * *
|
s407911753
|
Accepted
|
p02718
|
Input is given from Standard Input in the following format:
N M
A_1 ... A_N
|
n, m, *a = map(int, open(0).read().split())
print("YNeos"[len([i for i in a if sum(a) <= 4 * i * m]) < m :: 2])
|
Statement
We have held a popularity poll for N items on sale. Item i received A_i votes.
From these N items, we will select M as popular items. However, we cannot
select an item with less than \dfrac{1}{4M} of the total number of votes.
If M popular items can be selected, print `Yes`; otherwise, print `No`.
|
[{"input": "4 1\n 5 4 2 1", "output": "Yes\n \n\nThere were 12 votes in total. The most popular item received 5 votes, and we\ncan select it.\n\n* * *"}, {"input": "3 2\n 380 19 1", "output": "No\n \n\nThere were 400 votes in total. The second and third most popular items\nreceived less than \\dfrac{1}{4\\times 2} of the total number of votes, so we\ncannot select them. Thus, we cannot select two popular items.\n\n* * *"}, {"input": "12 3\n 4 56 78 901 2 345 67 890 123 45 6 789", "output": "Yes"}]
|
If M popular items can be selected, print `Yes`; otherwise, print `No`.
* * *
|
s239026261
|
Accepted
|
p02718
|
Input is given from Standard Input in the following format:
N M
A_1 ... A_N
|
n, m = list(map(int, input().split()))
arr = list(map(int, input().split()))
arr.sort(reverse=True)
total = sum(arr)
print("Yes" if arr[m - 1] * 4 * m >= total else "No")
|
Statement
We have held a popularity poll for N items on sale. Item i received A_i votes.
From these N items, we will select M as popular items. However, we cannot
select an item with less than \dfrac{1}{4M} of the total number of votes.
If M popular items can be selected, print `Yes`; otherwise, print `No`.
|
[{"input": "4 1\n 5 4 2 1", "output": "Yes\n \n\nThere were 12 votes in total. The most popular item received 5 votes, and we\ncan select it.\n\n* * *"}, {"input": "3 2\n 380 19 1", "output": "No\n \n\nThere were 400 votes in total. The second and third most popular items\nreceived less than \\dfrac{1}{4\\times 2} of the total number of votes, so we\ncannot select them. Thus, we cannot select two popular items.\n\n* * *"}, {"input": "12 3\n 4 56 78 901 2 345 67 890 123 45 6 789", "output": "Yes"}]
|
For each dataset, print a line having a decimal integer indicating the minimum
number of moves along a route from the start to the goal. If there are no such
routes, print -1 instead. Each line should not have any character other than
this number.
|
s507099804
|
Wrong Answer
|
p00725
|
The input is a sequence of datasets. The end of the input is indicated by a
line containing two zeros separated by a space. The number of datasets never
exceeds 100.
Each dataset is formatted as follows.
> _the width(=w) and the height(=h) of the board_
> _First row of the board_
> ...
> _h-th row of the board_
>
The width and the height of the board satisfy: 2 <= _w_ <= 20, 1 <= _h_ <= 20.
Each line consists of _w_ decimal numbers delimited by a space. The number
describes the status of the corresponding square.
> 0 | vacant square
> ---|---
> 1 | block
> 2 | start position
> 3 | goal position
The dataset for Fig. D-1 is as follows:
> 6 6
> 1 0 0 2 1 0
> 1 1 0 0 0 0
> 0 0 0 0 0 3
> 0 0 0 0 0 0
> 1 0 0 0 0 1
> 0 1 1 1 1 1
>
|
while ():
w, h = map(int, input().split())
if w == 0 or h == 0:
break
field = []
for y in range(h):
field.append(map(int, input().split()))
print(-1)
|
D: Curling 2.0
On Planet MM-21, after their Olympic games this year, curling is getting
popular. But the rules are somewhat different from ours. The game is played on
an ice game board on which a square mesh is marked. They use only a single
stone. The purpose of the game is to lead the stone from the start to the goal
with the minimum number of moves.
Fig. D-1 shows an example of a game board. Some squares may be occupied with
blocks. There are two special squares namely the start and the goal, which are
not occupied with blocks. (These two squares are distinct.) Once the stone
begins to move, it will proceed until it hits a block. In order to bring the
stone to the goal, you may have to stop the stone by hitting it against a
block, and throw again.
Fig. D-1: Example of board (S: start, G: goal)
The movement of the stone obeys the following rules:
* At the beginning, the stone stands still at the start square.
* The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
* When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. D-2(a)).
* Once thrown, the stone keeps moving to the same direction until one of the following occurs:
* The stone hits a block (Fig. D-2(b), (c)).
* The stone stops at the square next to the block it hit.
* The block disappears.
* The stone gets out of the board.
* The game ends in failure.
* The stone reaches the goal square.
* The stone stops there and the game ends in success.
* You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.
Fig. D-2: Stone movements
Under the rules, we would like to know whether the stone at the start can
reach the goal and, if yes, the minimum number of moves required.
With the initial configuration shown in Fig. D-1, 4 moves are required to
bring the stone from the start to the goal. The route is shown in Fig. D-3(a).
Notice when the stone reaches the goal, the board configuration has changed as
in Fig. D-3(b).
Fig. D-3: The solution for Fig. D-1 and the final board configuration
|
[{"input": "1\n 3 2\n 6 6\n 1 0 0 2 1 0\n 1 1 0 0 0 0\n 0 0 0 0 0 3\n 0 0 0 0 0 0\n 1 0 0 0 0 1\n 0 1 1 1 1 1\n 6 1\n 1 1 2 1 1 3\n 6 1\n 1 0 2 1 1 3\n 12 1\n 2 0 1 1 1 1 1 1 1 1 1 3\n 13 1\n 2 0 1 1 1 1 1 1 1 1 1 1 3\n 0 0", "output": "4\n -1\n 4\n 10\n -1"}]
|
For each dataset, print a line having a decimal integer indicating the minimum
number of moves along a route from the start to the goal. If there are no such
routes, print -1 instead. Each line should not have any character other than
this number.
|
s508325891
|
Runtime Error
|
p00725
|
The input is a sequence of datasets. The end of the input is indicated by a
line containing two zeros separated by a space. The number of datasets never
exceeds 100.
Each dataset is formatted as follows.
> _the width(=w) and the height(=h) of the board_
> _First row of the board_
> ...
> _h-th row of the board_
>
The width and the height of the board satisfy: 2 <= _w_ <= 20, 1 <= _h_ <= 20.
Each line consists of _w_ decimal numbers delimited by a space. The number
describes the status of the corresponding square.
> 0 | vacant square
> ---|---
> 1 | block
> 2 | start position
> 3 | goal position
The dataset for Fig. D-1 is as follows:
> 6 6
> 1 0 0 2 1 0
> 1 1 0 0 0 0
> 0 0 0 0 0 3
> 0 0 0 0 0 0
> 1 0 0 0 0 1
> 0 1 1 1 1 1
>
|
from queue import Queue as q
from copy import deepcopy as cp
def l_move(data):
global flag
field, n, i, j = data[0], data[1], data[2], data[3]
if j == 0 or field[i][j - 1] == 1 or n == 0:
return None
field[i] = cp(field[i])
while j:
if field[i][j - 1] == 0:
field[i][j] = 0
j -= 1
field[i][j] = 2
elif field[i][j - 1] == 3:
flag = True
print(11 - n)
return None
else:
field[i][j - 1] = 0
n -= 1
return [field, n, i, j]
return None
def u_move(data):
global x
global flag
field, n, i, j = data[0], data[1], data[2], data[3]
if i == 0 or field[i - 1][j] == 1 or n == 0:
return None
for _ in range(x):
field[i][_] = cp(field[i][_])
while i:
if field[i - 1][j] == 0:
field[i][j] = 0
i -= 1
field[i][j] = 2
elif field[i - 1][j] == 3:
flag = True
print(11 - n)
return None
else:
field[i - 1][j] = 0
n -= 1
return [field, n, i, j]
return None
def r_move(data):
global flag
field, n, i, j = data[0], data[1], data[2], data[3]
global y
if j == y - 1 or field[i][j + 1] == 1 or n == 0:
return None
field[i] = cp(field[i])
while j < y - 1:
if field[i][j + 1] == 0:
field[i][j] = 0
j += 1
field[i][j] = 2
elif field[i][j + 1] == 3:
flag = True
print(11 - n)
return None
else:
field[i][j + 1] = 0
n -= 1
return [field, n, i, j]
return None
def d_move(data):
global flag
field, n, i, j = data[0], data[1], data[2], data[3]
global x
if i == x - 1 or field[i + 1][j] == 1 or n == 0:
return None
for _ in range(x):
field[i][_] = cp(field[i][_])
while i < x - 1:
if field[i + 1][j] == 0:
field[i][j] = 0
i += 1
field[i][j] = 2
elif field[i + 1][j] == 3:
flag = True
print(11 - n)
return None
else:
field[i + 1][j] = 0
n -= 1
return [field, n, i, j]
return None
while True:
flag = False
y, x = map(int, input().split())
lis = q()
if x == 0:
break
field = []
for i in range(x):
field.append(list(map(int, input().split())))
for i in range(x):
for j in range(y):
if field[i][j] == 2:
start_x, start_y = i, j
data = [field, 10, start_x, start_y]
lis.put(data)
while lis.qsize():
d = lis.get()
tmp = l_move(d)
if flag:
break
if tmp != None:
lis.put(tmp)
tmp = u_move(d)
if flag:
break
if tmp != None:
lis.put(tmp)
tmp = d_move(d)
if flag:
break
if tmp != None:
lis.put(tmp)
tmp = r_move(d)
if flag:
break
if tmp != None:
lis.put(tmp)
if not flag:
print(-1)
|
D: Curling 2.0
On Planet MM-21, after their Olympic games this year, curling is getting
popular. But the rules are somewhat different from ours. The game is played on
an ice game board on which a square mesh is marked. They use only a single
stone. The purpose of the game is to lead the stone from the start to the goal
with the minimum number of moves.
Fig. D-1 shows an example of a game board. Some squares may be occupied with
blocks. There are two special squares namely the start and the goal, which are
not occupied with blocks. (These two squares are distinct.) Once the stone
begins to move, it will proceed until it hits a block. In order to bring the
stone to the goal, you may have to stop the stone by hitting it against a
block, and throw again.

Fig. D-1: Example of board (S: start, G: goal)
The movement of the stone obeys the following rules:
* At the beginning, the stone stands still at the start square.
* The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
* When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. D-2(a)).
* Once thrown, the stone keeps moving to the same direction until one of the following occurs:
* The stone hits a block (Fig. D-2(b), (c)).
* The stone stops at the square next to the block it hit.
* The block disappears.
* The stone gets out of the board.
* The game ends in failure.
* The stone reaches the goal square.
* The stone stops there and the game ends in success.
* You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.

Fig. D-2: Stone movements
Under the rules, we would like to know whether the stone at the start can
reach the goal and, if yes, the minimum number of moves required.
With the initial configuration shown in Fig. D-1, 4 moves are required to
bring the stone from the start to the goal. The route is shown in Fig. D-3(a).
Notice when the stone reaches the goal, the board configuration has changed as
in Fig. D-3(b).

Fig. D-3: The solution for Fig. D-1 and the final board configuration
|
[{"input": "1\n 3 2\n 6 6\n 1 0 0 2 1 0\n 1 1 0 0 0 0\n 0 0 0 0 0 3\n 0 0 0 0 0 0\n 1 0 0 0 0 1\n 0 1 1 1 1 1\n 6 1\n 1 1 2 1 1 3\n 6 1\n 1 0 2 1 1 3\n 12 1\n 2 0 1 1 1 1 1 1 1 1 1 3\n 13 1\n 2 0 1 1 1 1 1 1 1 1 1 1 3\n 0 0", "output": "4\n -1\n 4\n 10\n -1"}]
|
Print the number of different altars that Ringo can build.
* * *
|
s022683672
|
Accepted
|
p03559
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
B_1 ... B_N
C_1 ... C_N
|
from _collections import deque
from _ast import Num
def parser():
while 1:
data = list(input().split(" "))
for number in data:
if len(number) > 0:
yield (number)
input_parser = parser()
def gw():
global input_parser
return next(input_parser)
def gi():
data = gw()
return int(data)
MOD = int(1e9 + 7)
import numpy
from collections import deque
from math import sqrt
from math import floor
# https://atcoder.jp/contests/arc067/tasks/arc067_a
# C - Factors of Factorial
"""
need to consider the case that ticket is not enough to lower everything
"""
N = gi()
A = [0] * N
B = [0] * N
C = [0] * N
sB = [0] * N
sC = [0] * N
for i in range(N):
A[i] = gi()
A.sort()
for i in range(N):
B[i] = gi()
B.sort()
nai = 0
for i in range(N):
while nai < N and A[nai] < B[i]:
nai += 1
sB[i] = nai
if i > 0:
sB[i] += sB[i - 1]
for i in range(N):
C[i] = gi()
C.sort()
nbi = 0
for i in range(N):
while nbi < N and B[nbi] < C[i]:
nbi += 1
if nbi:
sC[i] = sB[nbi - 1]
if i > 0:
sC[i] += sC[i - 1]
print(sC[-1])
|
Statement
The season for Snuke Festival has come again this year. First of all, Ringo
will perform a ritual to summon Snuke. For the ritual, he needs an altar,
which consists of three parts, one in each of the three categories: upper,
middle and lower.
He has N parts for each of the three categories. The size of the i-th upper
part is A_i, the size of the i-th middle part is B_i, and the size of the i-th
lower part is C_i.
To build an altar, the size of the middle part must be strictly greater than
that of the upper part, and the size of the lower part must be strictly
greater than that of the middle part. On the other hand, any three parts that
satisfy these conditions can be combined to form an altar.
How many different altars can Ringo build? Here, two altars are considered
different when at least one of the three parts used is different.
|
[{"input": "2\n 1 5\n 2 4\n 3 6", "output": "3\n \n\nThe following three altars can be built:\n\n * Upper: 1-st part, Middle: 1-st part, Lower: 1-st part\n * Upper: 1-st part, Middle: 1-st part, Lower: 2-nd part\n * Upper: 1-st part, Middle: 2-nd part, Lower: 2-nd part\n\n* * *"}, {"input": "3\n 1 1 1\n 2 2 2\n 3 3 3", "output": "27\n \n\n* * *"}, {"input": "6\n 3 14 159 2 6 53\n 58 9 79 323 84 6\n 2643 383 2 79 50 288", "output": "87"}]
|
Print the number of different altars that Ringo can build.
* * *
|
s683272075
|
Wrong Answer
|
p03559
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
B_1 ... B_N
C_1 ... C_N
|
N = int(input("How many parts does Ringo have for each category? (under 10 000) "))
Astring = input(
"Set up the sizes of the top parts A, separated by a space, under 10⁹ : "
)
A = Astring.split()
Bstring = input(
"Set up the sizes of the middle parts B, separated by a space, under 10⁹ : "
)
B = Bstring.split()
Cstring = input(
"Set up the sizes of the bottom parts C, separated by a space, under 10⁹ : "
)
C = Cstring.split()
ncomb = 0
for k in range(len(C)):
for j in range(len(B)):
if C[k] > B[j]:
for i in range(len(A)):
if B[j] > A[i]:
ncomb += 1
print("Ringo can build ", end="")
print(ncomb, end="")
print(" different altars.")
|
Statement
The season for Snuke Festival has come again this year. First of all, Ringo
will perform a ritual to summon Snuke. For the ritual, he needs an altar,
which consists of three parts, one in each of the three categories: upper,
middle and lower.
He has N parts for each of the three categories. The size of the i-th upper
part is A_i, the size of the i-th middle part is B_i, and the size of the i-th
lower part is C_i.
To build an altar, the size of the middle part must be strictly greater than
that of the upper part, and the size of the lower part must be strictly
greater than that of the middle part. On the other hand, any three parts that
satisfy these conditions can be combined to form an altar.
How many different altars can Ringo build? Here, two altars are considered
different when at least one of the three parts used is different.
|
[{"input": "2\n 1 5\n 2 4\n 3 6", "output": "3\n \n\nThe following three altars can be built:\n\n * Upper: 1-st part, Middle: 1-st part, Lower: 1-st part\n * Upper: 1-st part, Middle: 1-st part, Lower: 2-nd part\n * Upper: 1-st part, Middle: 2-nd part, Lower: 2-nd part\n\n* * *"}, {"input": "3\n 1 1 1\n 2 2 2\n 3 3 3", "output": "27\n \n\n* * *"}, {"input": "6\n 3 14 159 2 6 53\n 58 9 79 323 84 6\n 2643 383 2 79 50 288", "output": "87"}]
|
Print the number of different altars that Ringo can build.
* * *
|
s136583468
|
Accepted
|
p03559
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
B_1 ... B_N
C_1 ... C_N
|
N = int(input())
A = [[int(a), "A"] for a in input().split()]
B = [[int(b), "B"] for b in input().split()]
C = [[int(c), "C"] for c in input().split()]
parts = A + B + C
parts.sort(key=lambda x: x[1])
parts.sort(reverse=True, key=lambda x: x[0])
A_pat = [0]
B_pat = [0]
C_count = 0
for s, t in parts:
if t == "C":
C_count += 1
elif t == "B":
B_pat.append(C_count + B_pat[-1])
elif t == "A":
A_pat.append(B_pat[-1] + A_pat[-1])
print(A_pat[-1])
|
Statement
The season for Snuke Festival has come again this year. First of all, Ringo
will perform a ritual to summon Snuke. For the ritual, he needs an altar,
which consists of three parts, one in each of the three categories: upper,
middle and lower.
He has N parts for each of the three categories. The size of the i-th upper
part is A_i, the size of the i-th middle part is B_i, and the size of the i-th
lower part is C_i.
To build an altar, the size of the middle part must be strictly greater than
that of the upper part, and the size of the lower part must be strictly
greater than that of the middle part. On the other hand, any three parts that
satisfy these conditions can be combined to form an altar.
How many different altars can Ringo build? Here, two altars are considered
different when at least one of the three parts used is different.
|
[{"input": "2\n 1 5\n 2 4\n 3 6", "output": "3\n \n\nThe following three altars can be built:\n\n * Upper: 1-st part, Middle: 1-st part, Lower: 1-st part\n * Upper: 1-st part, Middle: 1-st part, Lower: 2-nd part\n * Upper: 1-st part, Middle: 2-nd part, Lower: 2-nd part\n\n* * *"}, {"input": "3\n 1 1 1\n 2 2 2\n 3 3 3", "output": "27\n \n\n* * *"}, {"input": "6\n 3 14 159 2 6 53\n 58 9 79 323 84 6\n 2643 383 2 79 50 288", "output": "87"}]
|
Print the number of different altars that Ringo can build.
* * *
|
s277166888
|
Runtime Error
|
p03559
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
B_1 ... B_N
C_1 ... C_N
|
# -*- coding: cp932 -*-
import sys
import os
import re
import datetime
import bisect
def Test(value):
a = [1,3,5]
#x = 4
insert_index = bisect.bisect_left(a, value)
print("insert_index = ", insert_index)
if False:
while(True):
Test(int(input('? ')));
sys.exit()
N = int(input())
partsNumA = sorted(map(int, input().split()))
partsNumB = sorted(map(int, input().split()))
partsNumC = sorted(map(int, input().split()))
# Bに対してAの個数のBによるループ
partsNumSumBa = []
sumA = 0
#for i in range(N):
for curPartsB in partsNumB:
indexA = bisect.bisect_left(partsNumA, curPartsB)
numA = indexA
sumA += numA
partsNumSumBa.append(sumA)
if False:
print("Sorted A" , partsNumA)
print("Sorted B" , partsNumB)
print("Sorted C" , partsNumC)
print("B loop" , partsNumSumBa)
# Cに対してBの個数のCによるループ
sumBAll = 0
for curPartsC in partsNumC:
indexB = bisect.bisect_left(partsNumB, curPartsC)
if indexB == 0:
continue
numB = partsNumSumBa[indexB - 1]
sumBAll += numB
print(sumBAll)
|
Statement
The season for Snuke Festival has come again this year. First of all, Ringo
will perform a ritual to summon Snuke. For the ritual, he needs an altar,
which consists of three parts, one in each of the three categories: upper,
middle and lower.
He has N parts for each of the three categories. The size of the i-th upper
part is A_i, the size of the i-th middle part is B_i, and the size of the i-th
lower part is C_i.
To build an altar, the size of the middle part must be strictly greater than
that of the upper part, and the size of the lower part must be strictly
greater than that of the middle part. On the other hand, any three parts that
satisfy these conditions can be combined to form an altar.
How many different altars can Ringo build? Here, two altars are considered
different when at least one of the three parts used is different.
|
[{"input": "2\n 1 5\n 2 4\n 3 6", "output": "3\n \n\nThe following three altars can be built:\n\n * Upper: 1-st part, Middle: 1-st part, Lower: 1-st part\n * Upper: 1-st part, Middle: 1-st part, Lower: 2-nd part\n * Upper: 1-st part, Middle: 2-nd part, Lower: 2-nd part\n\n* * *"}, {"input": "3\n 1 1 1\n 2 2 2\n 3 3 3", "output": "27\n \n\n* * *"}, {"input": "6\n 3 14 159 2 6 53\n 58 9 79 323 84 6\n 2643 383 2 79 50 288", "output": "87"}]
|
Print the number of different altars that Ringo can build.
* * *
|
s777172084
|
Accepted
|
p03559
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
B_1 ... B_N
C_1 ... C_N
|
# python3
# utf-8
parts_nr = int(input())
a_part_idx___size = sorted([int(x) for x in input().split()], reverse=True)
b_part_idx___size = sorted([int(x) for x in input().split()], reverse=True)
c_part_idx___size = sorted([int(x) for x in input().split()], reverse=True)
b_part_idx___good_c_nr = []
curr_nr = 0
for b_part_idx in range(parts_nr):
while (
curr_nr < parts_nr
and c_part_idx___size[curr_nr] > b_part_idx___size[b_part_idx]
):
curr_nr += 1
b_part_idx___good_c_nr.append(curr_nr)
curr_b_part_idx = 0
curr_ans = 0
a_part_idx___ans = []
for a_part_idx in range(parts_nr):
while (
curr_b_part_idx < parts_nr
and a_part_idx___size[a_part_idx] < b_part_idx___size[curr_b_part_idx]
):
curr_ans += b_part_idx___good_c_nr[curr_b_part_idx]
curr_b_part_idx += 1
a_part_idx___ans.append(curr_ans)
print(sum(a_part_idx___ans))
|
Statement
The season for Snuke Festival has come again this year. First of all, Ringo
will perform a ritual to summon Snuke. For the ritual, he needs an altar,
which consists of three parts, one in each of the three categories: upper,
middle and lower.
He has N parts for each of the three categories. The size of the i-th upper
part is A_i, the size of the i-th middle part is B_i, and the size of the i-th
lower part is C_i.
To build an altar, the size of the middle part must be strictly greater than
that of the upper part, and the size of the lower part must be strictly
greater than that of the middle part. On the other hand, any three parts that
satisfy these conditions can be combined to form an altar.
How many different altars can Ringo build? Here, two altars are considered
different when at least one of the three parts used is different.
|
[{"input": "2\n 1 5\n 2 4\n 3 6", "output": "3\n \n\nThe following three altars can be built:\n\n * Upper: 1-st part, Middle: 1-st part, Lower: 1-st part\n * Upper: 1-st part, Middle: 1-st part, Lower: 2-nd part\n * Upper: 1-st part, Middle: 2-nd part, Lower: 2-nd part\n\n* * *"}, {"input": "3\n 1 1 1\n 2 2 2\n 3 3 3", "output": "27\n \n\n* * *"}, {"input": "6\n 3 14 159 2 6 53\n 58 9 79 323 84 6\n 2643 383 2 79 50 288", "output": "87"}]
|
Print `Heisei` if the date represented by S is not later than April 30, 2019,
and print `TBD` otherwise.
* * *
|
s716553099
|
Accepted
|
p03109
|
Input is given from Standard Input in the following format:
S
|
print("TBD" if input() > "2019/04/30" else "Heisei")
|
Statement
You are given a string S as input. This represents a valid date in the year
2019 in the `yyyy/mm/dd` format. (For example, April 30, 2019 is represented
as `2019/04/30`.)
Write a program that prints `Heisei` if the date represented by S is not later
than April 30, 2019, and prints `TBD` otherwise.
|
[{"input": "2019/04/30", "output": "Heisei\n \n\n* * *"}, {"input": "2019/11/01", "output": "TBD"}]
|
Print `Heisei` if the date represented by S is not later than April 30, 2019,
and print `TBD` otherwise.
* * *
|
s626440168
|
Accepted
|
p03109
|
Input is given from Standard Input in the following format:
S
|
print("TBD") if input() > "2019/04/30" else print("Heisei")
|
Statement
You are given a string S as input. This represents a valid date in the year
2019 in the `yyyy/mm/dd` format. (For example, April 30, 2019 is represented
as `2019/04/30`.)
Write a program that prints `Heisei` if the date represented by S is not later
than April 30, 2019, and prints `TBD` otherwise.
|
[{"input": "2019/04/30", "output": "Heisei\n \n\n* * *"}, {"input": "2019/11/01", "output": "TBD"}]
|
Print `Heisei` if the date represented by S is not later than April 30, 2019,
and print `TBD` otherwise.
* * *
|
s172520556
|
Runtime Error
|
p03109
|
Input is given from Standard Input in the following format:
S
|
s = input()
if s[5] = "1":
print("TBD")
elif int(s[6]) >= 5:
print("TBD")
else:
print("Heisei")
|
Statement
You are given a string S as input. This represents a valid date in the year
2019 in the `yyyy/mm/dd` format. (For example, April 30, 2019 is represented
as `2019/04/30`.)
Write a program that prints `Heisei` if the date represented by S is not later
than April 30, 2019, and prints `TBD` otherwise.
|
[{"input": "2019/04/30", "output": "Heisei\n \n\n* * *"}, {"input": "2019/11/01", "output": "TBD"}]
|
Print `Heisei` if the date represented by S is not later than April 30, 2019,
and print `TBD` otherwise.
* * *
|
s878933356
|
Runtime Error
|
p03109
|
Input is given from Standard Input in the following format:
S
|
y, m, d = int(input().split("/"))
print("Heisei" if y <= 2019 and m <= 4 and d <= 30 else "TBD")
|
Statement
You are given a string S as input. This represents a valid date in the year
2019 in the `yyyy/mm/dd` format. (For example, April 30, 2019 is represented
as `2019/04/30`.)
Write a program that prints `Heisei` if the date represented by S is not later
than April 30, 2019, and prints `TBD` otherwise.
|
[{"input": "2019/04/30", "output": "Heisei\n \n\n* * *"}, {"input": "2019/11/01", "output": "TBD"}]
|
Print `Heisei` if the date represented by S is not later than April 30, 2019,
and print `TBD` otherwise.
* * *
|
s373995110
|
Runtime Error
|
p03109
|
Input is given from Standard Input in the following format:
S
|
lst = list(map(int, input().split('/'))
if lst[1] >= 5:
print('TBD')
else:
print('Heisei')
|
Statement
You are given a string S as input. This represents a valid date in the year
2019 in the `yyyy/mm/dd` format. (For example, April 30, 2019 is represented
as `2019/04/30`.)
Write a program that prints `Heisei` if the date represented by S is not later
than April 30, 2019, and prints `TBD` otherwise.
|
[{"input": "2019/04/30", "output": "Heisei\n \n\n* * *"}, {"input": "2019/11/01", "output": "TBD"}]
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.