output_description
stringlengths 15
956
| submission_id
stringlengths 10
10
| status
stringclasses 3
values | problem_id
stringlengths 6
6
| input_description
stringlengths 9
2.55k
| attempt
stringlengths 1
13.7k
| problem_description
stringlengths 7
5.24k
| samples
stringlengths 2
2.72k
|
|---|---|---|---|---|---|---|---|
Print `YES` if the objective is achievable; print `NO` otherwise.
* * *
|
s757604564
|
Runtime Error
|
p03685
|
Input is given from Standard Input in the following format:
R C N
x_{1,1} y_{1,1} x_{1,2} y_{1,2}
:
x_{N,1} y_{N,1} x_{N,2} y_{N,2}
|
r, c, n = map(int, input().split())
l = []
for i in range(n):
x1, y1, x2, y2 = map(int, input().split())
if (x1 == 0 or x1 == r or y1 == 0 or y1 == c) and (
x2 == 0 or x2 == r or y2 == 0 or y2 == c
):
if x1 == 0:
l.append((y1, i))
elif y1 == c:
l.append((c + x1, i))
elif x1 == r:
l.append((c * 2 + r - y1, i))
else:
l.append((r * 2 + c * 2 - x1, i))
if x2 == 0:
l.append((y2, i))
elif y2 == c:
l.append((c + x2, i))
elif x2 == r:
l.append((c * 2 + r - y2, i))
else:
l.append((r * 2 + c * 2 - x2, i))
l.sort()
s = [l[0][1]]
for x, i in l[1:]:
s.append(0)
s.append(i)
r = [0] * len(s)
i, j = 0, 0
while i < len(s):
while i - j >= 0 and i + j < len(s) and s[i - j] == s[i + j]:
j += 1
r[i] = j
k = 1
while i - k >= 0 and k + r[i - k] < j:
r[i + k] = r[i - k]
k += 1
i += k
j -= k
for i in range(1, len(s), 2):
p = r[i]
if i == p - 1:
m = (len(s) - p * 2) // 2
if m == -1 or (m > 0 and r[-m] == m):
print("YES")
exit(1)
print("NO")
|
Statement
Snuke is playing a puzzle game. In this game, you are given a rectangular
board of dimensions R × C, filled with numbers. Each integer i from 1 through
N is written twice, at the coordinates (x_{i,1},y_{i,1}) and
(x_{i,2},y_{i,2}).
The objective is to draw a curve connecting the pair of points where the same
integer is written, for every integer from 1 through N. Here, the curves may
not go outside the board or cross each other.
Determine whether this is possible.
|
[{"input": "4 2 3\n 0 1 3 1\n 1 1 4 1\n 2 0 2 2", "output": "YES\n \n\n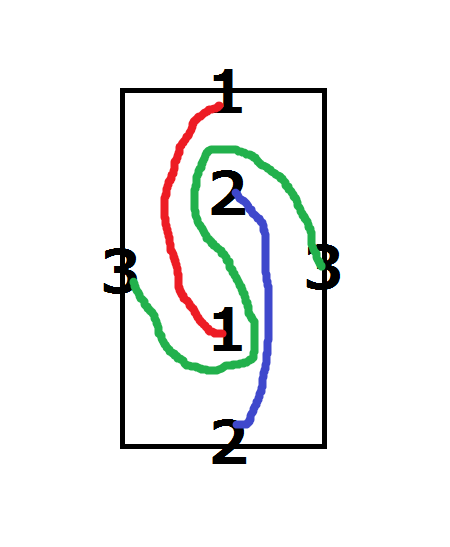\n\nThe above figure shows a possible solution.\n\n* * *"}, {"input": "2 2 4\n 0 0 2 2\n 2 0 0 1\n 0 2 1 2\n 1 1 2 1", "output": "NO\n \n\n* * *"}, {"input": "5 5 7\n 0 0 2 4\n 2 3 4 5\n 3 5 5 2\n 5 5 5 4\n 0 3 5 1\n 2 2 4 4\n 0 5 4 1", "output": "YES\n \n\n* * *"}, {"input": "1 1 2\n 0 0 1 1\n 1 0 0 1", "output": "NO"}]
|
Print `YES` if the objective is achievable; print `NO` otherwise.
* * *
|
s165181035
|
Accepted
|
p03685
|
Input is given from Standard Input in the following format:
R C N
x_{1,1} y_{1,1} x_{1,2} y_{1,2}
:
x_{N,1} y_{N,1} x_{N,2} y_{N,2}
|
import os
import sys
from collections import deque, Counter
if os.getenv("LOCAL"):
sys.stdin = open("_in.txt", "r")
sys.setrecursionlimit(10**9)
INF = float("inf")
IINF = 10**18
MOD = 10**9 + 7
# MOD = 998244353
R, C, N = list(map(int, sys.stdin.buffer.readline().split()))
XY = [list(map(int, sys.stdin.buffer.readline().split())) for _ in range(N)]
# 入力と答えの制約より、もし長方形の制限がなければ任意の点まで行ける
# 長方形の辺上にある点だけ考えればいい
p1 = []
p2 = []
p3 = []
p4 = []
for i, (x1, y1, x2, y2) in enumerate(XY):
for x, y in ((x1, y1), (x2, y2)):
if y == 0:
p1.append((x, i))
elif x == R:
p2.append((y, i))
elif y == C:
p3.append((x, i))
elif x == 0:
p4.append((y, i))
# 順番に並ぶようにする
p1.sort()
p2.sort()
p3.sort(reverse=True)
p4.sort(reverse=True)
points = p1 + p2 + p3 + p4
counts = Counter([i for _, i in points])
que = deque()
for _, i in points:
if counts[i] <= 1:
continue
if que and que[-1] == i:
que.pop()
else:
que.append(i)
while len(que) >= 2 and que[0] == que[-1]:
que.popleft()
que.pop()
ok = len(que) == 0
if ok:
print("YES")
else:
print("NO")
|
Statement
Snuke is playing a puzzle game. In this game, you are given a rectangular
board of dimensions R × C, filled with numbers. Each integer i from 1 through
N is written twice, at the coordinates (x_{i,1},y_{i,1}) and
(x_{i,2},y_{i,2}).
The objective is to draw a curve connecting the pair of points where the same
integer is written, for every integer from 1 through N. Here, the curves may
not go outside the board or cross each other.
Determine whether this is possible.
|
[{"input": "4 2 3\n 0 1 3 1\n 1 1 4 1\n 2 0 2 2", "output": "YES\n \n\n\n\nThe above figure shows a possible solution.\n\n* * *"}, {"input": "2 2 4\n 0 0 2 2\n 2 0 0 1\n 0 2 1 2\n 1 1 2 1", "output": "NO\n \n\n* * *"}, {"input": "5 5 7\n 0 0 2 4\n 2 3 4 5\n 3 5 5 2\n 5 5 5 4\n 0 3 5 1\n 2 2 4 4\n 0 5 4 1", "output": "YES\n \n\n* * *"}, {"input": "1 1 2\n 0 0 1 1\n 1 0 0 1", "output": "NO"}]
|
Print `YES` if the objective is achievable; print `NO` otherwise.
* * *
|
s973309902
|
Wrong Answer
|
p03685
|
Input is given from Standard Input in the following format:
R C N
x_{1,1} y_{1,1} x_{1,2} y_{1,2}
:
x_{N,1} y_{N,1} x_{N,2} y_{N,2}
|
print("YES")
|
Statement
Snuke is playing a puzzle game. In this game, you are given a rectangular
board of dimensions R × C, filled with numbers. Each integer i from 1 through
N is written twice, at the coordinates (x_{i,1},y_{i,1}) and
(x_{i,2},y_{i,2}).
The objective is to draw a curve connecting the pair of points where the same
integer is written, for every integer from 1 through N. Here, the curves may
not go outside the board or cross each other.
Determine whether this is possible.
|
[{"input": "4 2 3\n 0 1 3 1\n 1 1 4 1\n 2 0 2 2", "output": "YES\n \n\n\n\nThe above figure shows a possible solution.\n\n* * *"}, {"input": "2 2 4\n 0 0 2 2\n 2 0 0 1\n 0 2 1 2\n 1 1 2 1", "output": "NO\n \n\n* * *"}, {"input": "5 5 7\n 0 0 2 4\n 2 3 4 5\n 3 5 5 2\n 5 5 5 4\n 0 3 5 1\n 2 2 4 4\n 0 5 4 1", "output": "YES\n \n\n* * *"}, {"input": "1 1 2\n 0 0 1 1\n 1 0 0 1", "output": "NO"}]
|
Print `YES` if the objective is achievable; print `NO` otherwise.
* * *
|
s579477166
|
Runtime Error
|
p03685
|
Input is given from Standard Input in the following format:
R C N
x_{1,1} y_{1,1} x_{1,2} y_{1,2}
:
x_{N,1} y_{N,1} x_{N,2} y_{N,2}
|
#include "bits/stdc++.h"
#define _overload3(_1,_2,_3,name,...) name
#define _rep(i,n) repi(i,0,n)
#define repi(i,a,b) for(int i=int(a),i##_len=(b);i<i##_len;++i)
#define BUGAVOID(x) x
#define rep(...) BUGAVOID(_overload3(__VA_ARGS__,repi,_rep,_rep)(__VA_ARGS__))
#define sz(c) (int)(c.size())
#define all(c) c.begin(),c.end()
#define mp make_pair
#define write(x) cout<<(x)<<"\n"
using namespace std; typedef long long ll;
typedef vector<int> vi; typedef vector<ll> vll; template<class T, class U>using vp = vector<pair<T, U>>;
template<class T>using vv = vector<vector<T>>; template<class T, class U>using vvp = vv<pair<T, U>>;
template<class T>vv<T> vvec(size_t n, size_t m, T v) { return vv<T>(n, vector<T>(m, v)); }
template<class T>bool chmax(T& a, const T& b) { return a < b ? a = b, 1 : 0; }
template<class T>bool chmin(T& a, const T& b) { return b < a ? a = b, 1 : 0; }
constexpr int INF = 1 << 28, MAX = 1e5 + 5, MOD = 1e9 + 7;
constexpr ll LINF = 1ll << 60; constexpr double EPS = 1e-6;
constexpr int dy[4] = { 0,1,0,-1 }, dx[4] = { 1,0,-1,0 };
struct aaa { aaa() { cin.tie(0); ios::sync_with_stdio(0); }; }aaaa;
int R, C, N;
vi X1, X2, Y1, Y2;
int main() {
cin >> R >> C >> N;
X1.resize(N);
X2.resize(N);
Y1.resize(N);
Y2.resize(N);
rep(i, N) {
cin >> X1[i] >> Y1[i] >> X2[i] >> Y2[i];
}
// 両端が辺に乗ってるもののみ
// 左上0反時計回りに座標振る
vp<int, int> sepa;
rep(i, N) {
if ((X1[i] % C && Y1[i] % R) || (X2[i] % C && Y2[i] % R)) continue;
int crd1 = Y1[i] == 0 ? X1[i] :
(X1[i] == C ? C + Y1[i] :
(Y1[i] == R ? R + C + C - X1[i] :
R + 2 * C + R - Y1[i]));
int crd2 = Y2[i] == 0 ? X2[i] :
(X2[i] == C ? C + Y2[i] :
(Y2[i] == R ? R + C + C - X2[i] :
R + 2 * C + R - Y2[i]));
if (crd1 > crd2) swap(crd1, crd2);
sepa.emplace_back(crd1, crd2);
}
sort(all(sepa));
bool ans = true;
if (!sepa.empty()) {
int i = 0;
while (i < sepa.size()) {
int border = sepa[i].second;
int j = i + 1;
for (; j < sepa.size(); ++j) {
if (sepa[j].first > border) break;
else if (sepa[j].second > sepa[j - 1].second) {
ans = false;
}
}
i = j;
}
}
write(ans ? "YES" : "NO");
}
|
Statement
Snuke is playing a puzzle game. In this game, you are given a rectangular
board of dimensions R × C, filled with numbers. Each integer i from 1 through
N is written twice, at the coordinates (x_{i,1},y_{i,1}) and
(x_{i,2},y_{i,2}).
The objective is to draw a curve connecting the pair of points where the same
integer is written, for every integer from 1 through N. Here, the curves may
not go outside the board or cross each other.
Determine whether this is possible.
|
[{"input": "4 2 3\n 0 1 3 1\n 1 1 4 1\n 2 0 2 2", "output": "YES\n \n\n\n\nThe above figure shows a possible solution.\n\n* * *"}, {"input": "2 2 4\n 0 0 2 2\n 2 0 0 1\n 0 2 1 2\n 1 1 2 1", "output": "NO\n \n\n* * *"}, {"input": "5 5 7\n 0 0 2 4\n 2 3 4 5\n 3 5 5 2\n 5 5 5 4\n 0 3 5 1\n 2 2 4 4\n 0 5 4 1", "output": "YES\n \n\n* * *"}, {"input": "1 1 2\n 0 0 1 1\n 1 0 0 1", "output": "NO"}]
|
Print `YES` if the objective is achievable; print `NO` otherwise.
* * *
|
s312002604
|
Runtime Error
|
p03685
|
Input is given from Standard Input in the following format:
R C N
x_{1,1} y_{1,1} x_{1,2} y_{1,2}
:
x_{N,1} y_{N,1} x_{N,2} y_{N,2}
|
# coding: utf-8
import array, bisect, collections, copy, heapq, itertools, math, random, re, string, sys, time
sys.setrecursionlimit(10 ** 7)
INF = 10 ** 20
MOD = 10 ** 9 + 7
def II(): return int(input())
def ILI(): return list(map(int, input().split()))
def IAI(LINE): return [ILI() for __ in range(LINE)]
def IDI(): return {key: value for key, value in ILI()}
def read():
R, C, N = ILI()
num_point = []
for __ in range(N):
x_1, y_1, x_2, y_2 = ILI()
num_point.append([(x_1, y_1), (x_2, y_2)])
return R, C, N, num_point
# 周上を (0, 0) を原点として反時計回りに 1 本の数直線とした時の point の座標を返す.
# 周上にあるかの判定も行う.
def change_edge_point(R, C, point):
x, y = point
if 0 < x < C or 0 < y < R:
return False
if y == 0:
return x
elif y == R:
return C + R + C - x
if x == 0:
return C + y
elif x == R:
return C + R + C + R - y
def solve(R, C, N, num_point):
point_double = []
for point in num_point:
p_1, p_2 = point
ret_1 = change_edge_point(R, C, p_1)
ret_2 = change_edge_point(R, C, p_2)
if ret_1 is False or ret_2 is False:
continue
point_double.append((min(ret_1, ret_2), max(ret_1, ret_2)))åç
for p_1, p_2 in itertools.combinations(point_double, 2):
if p_1[0] == p_2[0] or p_1[1] == p_2[1]:
return "NO"
if p_1[0] < p_2[0]:
if p_1[1] > p_2[1]:
continue
else:
return "NO"
elif p_1[0] > p_2[0]:
if p_1[1] < p_2[1]:
continue
else:
return "NO"
return "YES"
def main():
params = read()
print(solve(*params))
if __name__ == "__main__":
main()
|
Statement
Snuke is playing a puzzle game. In this game, you are given a rectangular
board of dimensions R × C, filled with numbers. Each integer i from 1 through
N is written twice, at the coordinates (x_{i,1},y_{i,1}) and
(x_{i,2},y_{i,2}).
The objective is to draw a curve connecting the pair of points where the same
integer is written, for every integer from 1 through N. Here, the curves may
not go outside the board or cross each other.
Determine whether this is possible.
|
[{"input": "4 2 3\n 0 1 3 1\n 1 1 4 1\n 2 0 2 2", "output": "YES\n \n\n\n\nThe above figure shows a possible solution.\n\n* * *"}, {"input": "2 2 4\n 0 0 2 2\n 2 0 0 1\n 0 2 1 2\n 1 1 2 1", "output": "NO\n \n\n* * *"}, {"input": "5 5 7\n 0 0 2 4\n 2 3 4 5\n 3 5 5 2\n 5 5 5 4\n 0 3 5 1\n 2 2 4 4\n 0 5 4 1", "output": "YES\n \n\n* * *"}, {"input": "1 1 2\n 0 0 1 1\n 1 0 0 1", "output": "NO"}]
|
Print `YES` if the objective is achievable; print `NO` otherwise.
* * *
|
s425603531
|
Accepted
|
p03685
|
Input is given from Standard Input in the following format:
R C N
x_{1,1} y_{1,1} x_{1,2} y_{1,2}
:
x_{N,1} y_{N,1} x_{N,2} y_{N,2}
|
def main():
from bisect import bisect_left as bl
class BIT:
def __init__(self, member):
self.member_list = sorted(member)
self.member_dict = {v: i + 1 for i, v in enumerate(self.member_list)}
self.n = len(member)
self.maxmember = self.member_list[-1]
self.minmember = self.member_list[0]
self.maxbit = 2 ** (len(bin(self.n)) - 3)
self.bit = [0] * (self.n + 1)
self.allsum = 0
# 要素iにvを追加する
def add(self, i, v):
x = self.member_dict[i]
self.allsum += v
while x < self.n + 1:
self.bit[x] += v
x += x & (-x)
# 位置0からiまでの和(sum(bit[:i]))を計算する
def sum(self, i):
ret = 0
x = i
while x > 0:
ret += self.bit[x]
x -= x & (-x)
return ret
# 位置iからjまでの和(sum(bit[i:j]))を計算する
def sum_range(self, i, j):
return self.sum(j) - self.sum(i)
# 和がw以上となる最小のインデックスを求める
def lowerbound(self, w):
if w <= 0:
return 0
x, k = 0, self.maxbit
while k:
if x + k <= self.n and self.bit[x + k] < w:
w -= self.bit[x + k]
x += k
k //= 2
return x
# vに一番近いv以上の値を求める
def greater(self, v):
if v > self.maxmember:
return None
p = self.sum(bl(self.member_list, v))
if p == self.allsum:
return None
return self.member_list[self.lowerbound(p + 1)]
# vに一番近いv以下の値を求める
def smaller(self, v):
if v < self.minmember:
return None
b = bl(self.member_list, v)
if b == self.n:
b -= 1
elif self.member_list[b] != v:
b -= 1
p = self.sum(b + 1)
if p == 0:
return None
return self.member_list[self.lowerbound(p)]
r, c, n = map(int, input().split())
xyzw = [list(map(int, input().split())) for _ in [0] * n]
outer = []
for x, y, z, w in xyzw:
if x in [0, r] or y in [0, c]:
if z in [0, r] or w in [0, c]:
if y == 0:
p = x
elif x == r:
p = r + y
elif y == c:
p = 2 * r + c - x
else:
p = 2 * r + 2 * c - y
if w == 0:
q = z
elif z == r:
q = r + w
elif w == c:
q = 2 * r + c - z
else:
q = 2 * r + 2 * c - w
if p > q:
p, q = q, p
outer.append((p, q))
member = [i for i, j in outer] + [j for i, j in outer] + [-1] + [2 * r + 2 * c + 1]
bit = BIT(member)
bit.add(-1, 1)
bit.add(2 * r + 2 * c + 1, 1)
outer.sort(key=lambda x: x[0] - x[1])
for a, b in outer:
if bit.greater(a) < b:
print("NO")
return
bit.add(a, 1)
bit.add(b, 1)
print("YES")
main()
|
Statement
Snuke is playing a puzzle game. In this game, you are given a rectangular
board of dimensions R × C, filled with numbers. Each integer i from 1 through
N is written twice, at the coordinates (x_{i,1},y_{i,1}) and
(x_{i,2},y_{i,2}).
The objective is to draw a curve connecting the pair of points where the same
integer is written, for every integer from 1 through N. Here, the curves may
not go outside the board or cross each other.
Determine whether this is possible.
|
[{"input": "4 2 3\n 0 1 3 1\n 1 1 4 1\n 2 0 2 2", "output": "YES\n \n\n\n\nThe above figure shows a possible solution.\n\n* * *"}, {"input": "2 2 4\n 0 0 2 2\n 2 0 0 1\n 0 2 1 2\n 1 1 2 1", "output": "NO\n \n\n* * *"}, {"input": "5 5 7\n 0 0 2 4\n 2 3 4 5\n 3 5 5 2\n 5 5 5 4\n 0 3 5 1\n 2 2 4 4\n 0 5 4 1", "output": "YES\n \n\n* * *"}, {"input": "1 1 2\n 0 0 1 1\n 1 0 0 1", "output": "NO"}]
|
Print `YES` if the objective is achievable; print `NO` otherwise.
* * *
|
s317961987
|
Wrong Answer
|
p03685
|
Input is given from Standard Input in the following format:
R C N
x_{1,1} y_{1,1} x_{1,2} y_{1,2}
:
x_{N,1} y_{N,1} x_{N,2} y_{N,2}
|
w, h, n = map(int, input().split())
vec = []
for i in range(n):
x, y, x1, y1 = map(int, input().split())
vec.append([x, y, i])
vec.append([x1, y1, i])
sorted_node = []
vec.sort(key=lambda x: x[1])
for p in vec:
if p[0] == 0:
p[0] = -1
p[1] = -1
sorted_node.append(p)
vec.sort(key=lambda x: x[0])
for p in vec:
if p[1] == h:
p[0] = -1
p[1] = -1
sorted_node.append(p)
vec.sort(key=lambda x: x[1], reverse=True)
for p in vec:
if p[0] == w:
p[0] = -1
p[1] = -1
sorted_node.append(p)
vec.sort(key=lambda x: x[0], reverse=True)
for p in vec:
if p[1] == 0:
p[0] = -1
p[1] = -1
sorted_node.append(p)
print("ok")
|
Statement
Snuke is playing a puzzle game. In this game, you are given a rectangular
board of dimensions R × C, filled with numbers. Each integer i from 1 through
N is written twice, at the coordinates (x_{i,1},y_{i,1}) and
(x_{i,2},y_{i,2}).
The objective is to draw a curve connecting the pair of points where the same
integer is written, for every integer from 1 through N. Here, the curves may
not go outside the board or cross each other.
Determine whether this is possible.
|
[{"input": "4 2 3\n 0 1 3 1\n 1 1 4 1\n 2 0 2 2", "output": "YES\n \n\n\n\nThe above figure shows a possible solution.\n\n* * *"}, {"input": "2 2 4\n 0 0 2 2\n 2 0 0 1\n 0 2 1 2\n 1 1 2 1", "output": "NO\n \n\n* * *"}, {"input": "5 5 7\n 0 0 2 4\n 2 3 4 5\n 3 5 5 2\n 5 5 5 4\n 0 3 5 1\n 2 2 4 4\n 0 5 4 1", "output": "YES\n \n\n* * *"}, {"input": "1 1 2\n 0 0 1 1\n 1 0 0 1", "output": "NO"}]
|
Print `YES` if the objective is achievable; print `NO` otherwise.
* * *
|
s891762984
|
Runtime Error
|
p03685
|
Input is given from Standard Input in the following format:
R C N
x_{1,1} y_{1,1} x_{1,2} y_{1,2}
:
x_{N,1} y_{N,1} x_{N,2} y_{N,2}
|
import sys
R, C, N = [int(i) for i in input().split()]
lec = [[0] * (C + 1) for i in range(R + 1)]
x1 = [0] * N
x2 = [0] * N
y1 = [0] * N
y2 = [0] * N
ngx1 = []
ngx2 = []
ngy1 = []
ngy2 = []
for i in range(0, N):
x1[i], y1[i], x2[i], y2[i] = [int(i) for i in input().split()]
for i in range(0, N):
if (x1[i] in [0, R] or y1[i] in [0, C]) and (x2[i] in [0, R] or y2[i] in [0, C]):
ngx1.append(x1[i])
ngx2.append(x2[i])
ngy1.append(y1[i])
ngy2.append(y2[i])
if len(ngx1) in [0, 1]:
print("YES")
sys.exit()
else:
for j in range(1, len(ngx1)):
for i in range(j, len(ngx1)):
tc = (ngx1[0] - ngx2[0]) * (ngy1[i] - ngy1[0]) + (ngy1[0] - ngy2[0]) * (
ngx1[0] - ngx1[i]
)
td = (ngx1[0] - ngx2[0]) * (ngy2[i] - ngy1[0]) + (ngy1[0] - ngy2[0]) * (
ngx1[0] - ngx2[i]
)
if tc * td < 0:
print("NO")
sys.exit()
print("YES")
|
Statement
Snuke is playing a puzzle game. In this game, you are given a rectangular
board of dimensions R × C, filled with numbers. Each integer i from 1 through
N is written twice, at the coordinates (x_{i,1},y_{i,1}) and
(x_{i,2},y_{i,2}).
The objective is to draw a curve connecting the pair of points where the same
integer is written, for every integer from 1 through N. Here, the curves may
not go outside the board or cross each other.
Determine whether this is possible.
|
[{"input": "4 2 3\n 0 1 3 1\n 1 1 4 1\n 2 0 2 2", "output": "YES\n \n\n\n\nThe above figure shows a possible solution.\n\n* * *"}, {"input": "2 2 4\n 0 0 2 2\n 2 0 0 1\n 0 2 1 2\n 1 1 2 1", "output": "NO\n \n\n* * *"}, {"input": "5 5 7\n 0 0 2 4\n 2 3 4 5\n 3 5 5 2\n 5 5 5 4\n 0 3 5 1\n 2 2 4 4\n 0 5 4 1", "output": "YES\n \n\n* * *"}, {"input": "1 1 2\n 0 0 1 1\n 1 0 0 1", "output": "NO"}]
|
For each dataset, prints the score in the corresponding inning.
|
s812636742
|
Accepted
|
p00103
|
The input consists of several datasets. In the first line, the number of
datasets _n_ is given. Each dataset consists of a list of events (strings) in
an inning.
|
a = 0
while 1:
OUT = 0
R = 0
P = 0
SET = 0
if a == 0:
b = int(input())
a += 1
if b == 0:
break
while OUT <= 2:
n = input()
if n == "HIT":
R += 1
if R > 3:
P += 1
R = 3
if n == "OUT":
OUT += 1
if n == "HOMERUN":
P += R + 1
R = 0
b -= 1
print(P)
P = 0
|
Baseball Simulation
Ichiro likes baseball and has decided to write a program which simulates
baseball.
The program reads events in an inning and prints score in that inning. There
are only three events as follows:
Single hit
* put a runner on the first base.
* the runner in the first base advances to the second base and the runner in the second base advances to the third base.
* the runner in the third base advances to the home base (and go out of base) and a point is added to the score.
Home run
* all the runners on base advance to the home base.
* points are added to the score by an amount equal to the number of the runners plus one.
Out
* The number of outs is increased by 1.
* The runners and the score remain stationary.
* The inning ends with three-out.
Ichiro decided to represent these events using "HIT", "HOMERUN" and "OUT",
respectively.
Write a program which reads events in an inning and prints score in that
inning. You can assume that the number of events is less than or equal to 100.
|
[{"input": "HIT\n OUT\n HOMERUN\n HIT\n HIT\n HOMERUN\n HIT\n OUT\n HIT\n HIT\n HIT\n HIT\n OUT\n HIT\n HIT\n OUT\n HIT\n OUT\n OUT", "output": "0"}]
|
For each dataset, prints the score in the corresponding inning.
|
s087038211
|
Runtime Error
|
p00103
|
The input consists of several datasets. In the first line, the number of
datasets _n_ is given. Each dataset consists of a list of events (strings) in
an inning.
|
a = int(input().rstrip())
b = 0
while a > b:
c = 0
runner = 0
point = 0
while c < 3:
x = input().rstrip()
if x == "HIT":
if runner == 3:
point += 1
else:
runner += 1
elif x == "HOMERUN":
point = point + runner + 1
runner = 0
else:
c += 1
print(point)
|
Baseball Simulation
Ichiro likes baseball and has decided to write a program which simulates
baseball.
The program reads events in an inning and prints score in that inning. There
are only three events as follows:
Single hit
* put a runner on the first base.
* the runner in the first base advances to the second base and the runner in the second base advances to the third base.
* the runner in the third base advances to the home base (and go out of base) and a point is added to the score.
Home run
* all the runners on base advance to the home base.
* points are added to the score by an amount equal to the number of the runners plus one.
Out
* The number of outs is increased by 1.
* The runners and the score remain stationary.
* The inning ends with three-out.
Ichiro decided to represent these events using "HIT", "HOMERUN" and "OUT",
respectively.
Write a program which reads events in an inning and prints score in that
inning. You can assume that the number of events is less than or equal to 100.
|
[{"input": "HIT\n OUT\n HOMERUN\n HIT\n HIT\n HOMERUN\n HIT\n OUT\n HIT\n HIT\n HIT\n HIT\n OUT\n HIT\n HIT\n OUT\n HIT\n OUT\n OUT", "output": "0"}]
|
For each dataset, prints the score in the corresponding inning.
|
s458579989
|
Accepted
|
p00103
|
The input consists of several datasets. In the first line, the number of
datasets _n_ is given. Each dataset consists of a list of events (strings) in
an inning.
|
def hit(point, base, out_count):
new_base = (base << 1) + 1
return point + (new_base > 0b111), new_base & 0b111, out_count
def homerun(point, base, out_count):
return point + (bin(base & 0b111).count("1") + 1), 0, out_count
def out(point, base, out_count):
return point, base, out_count - 1
F = {"HIT": hit, "HOMERUN": homerun, "OUT": out}
i, point, base, out_count = int(input()), 0, 0, 3
while i:
point, base, out_count = F[input().strip()](point, base, out_count)
if not out_count:
i -= 1
print(point)
point, base, out_count = 0, 0, 3
|
Baseball Simulation
Ichiro likes baseball and has decided to write a program which simulates
baseball.
The program reads events in an inning and prints score in that inning. There
are only three events as follows:
Single hit
* put a runner on the first base.
* the runner in the first base advances to the second base and the runner in the second base advances to the third base.
* the runner in the third base advances to the home base (and go out of base) and a point is added to the score.
Home run
* all the runners on base advance to the home base.
* points are added to the score by an amount equal to the number of the runners plus one.
Out
* The number of outs is increased by 1.
* The runners and the score remain stationary.
* The inning ends with three-out.
Ichiro decided to represent these events using "HIT", "HOMERUN" and "OUT",
respectively.
Write a program which reads events in an inning and prints score in that
inning. You can assume that the number of events is less than or equal to 100.
|
[{"input": "HIT\n OUT\n HOMERUN\n HIT\n HIT\n HOMERUN\n HIT\n OUT\n HIT\n HIT\n HIT\n HIT\n OUT\n HIT\n HIT\n OUT\n HIT\n OUT\n OUT", "output": "0"}]
|
For each dataset, prints the score in the corresponding inning.
|
s031985373
|
Wrong Answer
|
p00103
|
The input consists of several datasets. In the first line, the number of
datasets _n_ is given. Each dataset consists of a list of events (strings) in
an inning.
|
num = int(input())
for i in range(num):
outcount = 0
HIT = 0
HOMWRUN = 0
COUNT = 0
while True:
a = input()
if a == "HIT":
HIT += 1
if HIT == 4:
COUNT += 1
HIT = 1
if a == "HOMERUN":
COUNT += HIT + 1
if a == "OUT":
outcount += 1
if outcount == 3:
break
print(COUNT)
|
Baseball Simulation
Ichiro likes baseball and has decided to write a program which simulates
baseball.
The program reads events in an inning and prints score in that inning. There
are only three events as follows:
Single hit
* put a runner on the first base.
* the runner in the first base advances to the second base and the runner in the second base advances to the third base.
* the runner in the third base advances to the home base (and go out of base) and a point is added to the score.
Home run
* all the runners on base advance to the home base.
* points are added to the score by an amount equal to the number of the runners plus one.
Out
* The number of outs is increased by 1.
* The runners and the score remain stationary.
* The inning ends with three-out.
Ichiro decided to represent these events using "HIT", "HOMERUN" and "OUT",
respectively.
Write a program which reads events in an inning and prints score in that
inning. You can assume that the number of events is less than or equal to 100.
|
[{"input": "HIT\n OUT\n HOMERUN\n HIT\n HIT\n HOMERUN\n HIT\n OUT\n HIT\n HIT\n HIT\n HIT\n OUT\n HIT\n HIT\n OUT\n HIT\n OUT\n OUT", "output": "0"}]
|
For each dataset, prints the score in the corresponding inning.
|
s910118990
|
Wrong Answer
|
p00103
|
The input consists of several datasets. In the first line, the number of
datasets _n_ is given. Each dataset consists of a list of events (strings) in
an inning.
|
inn = int(input())
o = 0
i = 0
s = []
sc = 0
ba = []
while i < inn:
b = input()
if b == "OUT":
o += 1
if o % 3 == 0 and o > 0:
s.append(sc)
sc = 0
i += 1
o = 0
ba = []
elif b == "HIT":
ba.append(1)
if len(ba) >= 4:
sc += 1
ba = [1, 1, 1, 1]
elif b == "HOMERUN":
ba.append(1)
sc += len(ba)
ba = []
[print(i) for i in s]
|
Baseball Simulation
Ichiro likes baseball and has decided to write a program which simulates
baseball.
The program reads events in an inning and prints score in that inning. There
are only three events as follows:
Single hit
* put a runner on the first base.
* the runner in the first base advances to the second base and the runner in the second base advances to the third base.
* the runner in the third base advances to the home base (and go out of base) and a point is added to the score.
Home run
* all the runners on base advance to the home base.
* points are added to the score by an amount equal to the number of the runners plus one.
Out
* The number of outs is increased by 1.
* The runners and the score remain stationary.
* The inning ends with three-out.
Ichiro decided to represent these events using "HIT", "HOMERUN" and "OUT",
respectively.
Write a program which reads events in an inning and prints score in that
inning. You can assume that the number of events is less than or equal to 100.
|
[{"input": "HIT\n OUT\n HOMERUN\n HIT\n HIT\n HOMERUN\n HIT\n OUT\n HIT\n HIT\n HIT\n HIT\n OUT\n HIT\n HIT\n OUT\n HIT\n OUT\n OUT", "output": "0"}]
|
For each dataset, prints the score in the corresponding inning.
|
s404712534
|
Accepted
|
p00103
|
The input consists of several datasets. In the first line, the number of
datasets _n_ is given. Each dataset consists of a list of events (strings) in
an inning.
|
SCORE = []
preSCORE = 0
OUTcount = 0
BASE = [False] * 3
n = int(input())
for i in range(n):
while OUTcount < 3:
spam = input()
if "HIT" in spam:
if BASE[2] == True:
preSCORE += 1
BASE[2] = BASE[1]
BASE[1] = BASE[0]
BASE[0] = True
elif "OUT" in spam:
OUTcount += 1
elif "HOMERUN" in spam:
preSCORE += sum(x for x in BASE) + 1
BASE = [False] * 3
SCORE.append(preSCORE)
BASE = [False] * 3
OUTcount = 0
preSCORE = 0
for i in SCORE:
print(i)
|
Baseball Simulation
Ichiro likes baseball and has decided to write a program which simulates
baseball.
The program reads events in an inning and prints score in that inning. There
are only three events as follows:
Single hit
* put a runner on the first base.
* the runner in the first base advances to the second base and the runner in the second base advances to the third base.
* the runner in the third base advances to the home base (and go out of base) and a point is added to the score.
Home run
* all the runners on base advance to the home base.
* points are added to the score by an amount equal to the number of the runners plus one.
Out
* The number of outs is increased by 1.
* The runners and the score remain stationary.
* The inning ends with three-out.
Ichiro decided to represent these events using "HIT", "HOMERUN" and "OUT",
respectively.
Write a program which reads events in an inning and prints score in that
inning. You can assume that the number of events is less than or equal to 100.
|
[{"input": "HIT\n OUT\n HOMERUN\n HIT\n HIT\n HOMERUN\n HIT\n OUT\n HIT\n HIT\n HIT\n HIT\n OUT\n HIT\n HIT\n OUT\n HIT\n OUT\n OUT", "output": "0"}]
|
Print the maximum number of points you can gain.
* * *
|
s103759105
|
Runtime Error
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
n = int(input())
num = list(map(int, input().split()))
ans = 0
frag = 0
A = 0
B = 0
C = 0
for i in range(n - 1):
for a in range(i, i + 5):
for b in range(a, i + 5):
for c in range(b, i + 5):
if num[a] == num[b] == num[c]:
frag = 1
A = a
B = b
C = c
ans += 1
break
if frag == 1:
break
if frag == 1:
break
if frag == 1:
del num[A]
del num[B]
del num[C]
frag = 0
if num[0] == num[1] == num[2]:
ans += 1
print(ans)
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s839770935
|
Runtime Error
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
n = int(input())
l = list(map(int, input().split()))
l.sort()
c = 0
for i in range(n - 2):
if l[i] == i[i + 1] == l[i + 2]:
c += 1
print(c)
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s321840697
|
Wrong Answer
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
##main#######################################
## INPUT ####################################
N = int(input())
# A = list(map(int,list(input().split())))
A = input()
AA = A.replace(" ", "")
## PROCESSING ###############################
ans = 0
# for idx in range(N*3):
# print("first:"+ AA)
while len(AA) > 0:
# print(AA)
AAA = AA[0:5]
AAAA = list(AAA)
AAAA.sort()
c = 0
i = 0
deletieNumFlg = 0
while i < len(AAAA):
CHAR1 = AAAA[i]
c = AAA.count(CHAR1)
# print("dddd1")
# print(CHAR1)
# print("c:" + str( c))
# print("dddd2")
if c >= 3:
AAAA.remove(CHAR1)
AAAA.remove(CHAR1)
AAAA.remove(CHAR1)
ans = ans + 1
deletieNumFlg = 1
i = 99
else:
i = i + c
# print("flg:" + str(deletieNumFlg))
# print("next(bef):" + AA)
if deletieNumFlg == 1:
AA = "".join(AAAA) + AA[5:]
else:
AA = AA[3:]
# print("next(aft):" + AA)
## OUTPUT ###################################
# print("++++OUTPUT++++")
print(ans)
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s321847479
|
Wrong Answer
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
N = int(input())
cards = list(map(int, input().split()))
five_cards = []
start_index = 0
end_index = 5
if N == 1:
five_cards = cards
points = 0
for _ in range(N - 1):
five_cards = cards[start_index:end_index]
five_cards = sorted(five_cards, key=five_cards.count, reverse=True)
if five_cards.pop(0) == five_cards.pop(0) == five_cards.pop(0):
points += 1
start_index += 3
end_index += 3
if len(set(five_cards)) == 1:
points += 1
print(points)
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s916535259
|
Wrong Answer
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
n = int(input())
print(n)
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s927011367
|
Wrong Answer
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
n = int(input())
array = list(map(int, input().strip().split()))
s = list(set(array))
l = len(s)
f = 0
for i in range(l):
f += array.count(s[i]) // 3
print(f)
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s865914095
|
Runtime Error
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
# 途中まで
N = int(input())
A = list(map(int, input().split()))
DP = [[-1] * (N + 1) for _ in range(N + 1)]
R = {}
for i in range(5):
a = A[i]
if a in R:
R[a] += 1
else:
R[a] = 1
Flag = 0
for i in R.keys():
if R[i] >= 3:
Flag = 1
R[i] -= 3
L = []
for i in R.keys():
if R[i] == 2:
DP[i][i] = Flag
elif R[i] == 1:
L.append(R[i])
for i in range(len(L) - 1):
for j in range(i + 1, len(L)):
DP[L[i]][L[j]] = Flag
print(DP)
for i in range(5, N * 3, 3):
R = {}
for j in range(i, i + 3):
pass
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s952536303
|
Wrong Answer
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
a = [input().split() for l in range(2)]
c = a[1]
N = int(a[0][0])
p = 0
for i in range(N):
suff = c[:5]
for j in range(N):
if suff.count(j) == 5:
p = p + 1
suff.remove(j)
suff.append(j)
suff.append(j)
elif suff.count(j) == 4:
p = p + 1
suff.remove(j)
suff.append(j)
elif suff.count(j) == 3:
p = p + 1
suff.remove(j)
s = c[:8]
for k in range(N):
if s.count(k) > 2:
p = p + 1
i = i + 1
del s[:6]
c[:5] = suff
print(p)
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s735106828
|
Accepted
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
n = int(input())
a = [*map(int, input().split())]
for i in range(n * 3):
a[i] -= 1
INF = 1 << 30
dp = [[-INF] * n for i in range(n)]
mx = [-INF] * n
mx_all = -INF
add_all = 0
dp[a[0]][a[1]] = dp[a[1]][a[0]] = 0
mx[a[0]] = mx[a[1]] = 0
mx_all = 0
for i in range(n - 1):
x, y, z = sorted(a[i * 3 + 2 : i * 3 + 5])
update = []
# パターン1
if x == y == z:
add_all += 1
continue
# パターン2
if x == y:
for j in range(n):
update.append((j, z, dp[j][x] + 1))
if y == z:
for j in range(n):
update.append((j, x, dp[j][y] + 1))
# パターン3
update.append((y, z, dp[x][x] + 1))
update.append((x, z, dp[y][y] + 1))
update.append((x, y, dp[z][z] + 1))
# パターン2-2
for j in range(n):
update.append((j, x, mx[j]))
update.append((j, y, mx[j]))
update.append((j, z, mx[j]))
# パターン3-2
update.append((y, z, mx_all))
update.append((x, z, mx_all))
update.append((x, y, mx_all))
# in-place にするために更新を遅延させる
for j, k, val in update:
if dp[j][k] < val:
dp[j][k] = dp[k][j] = val
if mx[j] < val:
mx[j] = val
if mx[k] < val:
mx[k] = val
if mx_all < val:
mx_all = val
# 最後の 1 回
if mx_all < dp[a[-1]][a[-1]] + 1:
mx_all = dp[a[-1]][a[-1]] + 1
print(mx_all + add_all)
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s011760629
|
Runtime Error
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
from functools import lru_cache
(N,) = [int(x) for x in input().split()]
A = [int(x) for x in input().split()]
# O(N^3), should TLE
@lru_cache(maxsize=None)
def dp(a, b, i):
# Best you can do with [a] + [b] + A[i:]
# Where len(A[i:]) is 3 * K - 5
assert (3 * N - i) % 3 == 1
assert a <= b
if i == 3 * N - 1:
return int(a == b == A[-1])
best = 0
temp = [a] + [b] + A[i : i + 3]
assert len(temp) == 5
for x in temp:
if temp.count(x) >= 3:
# If found any triple, alway take the points
for j in range(3):
temp.remove(x)
assert len(temp) == 2
if temp[0] > temp[1]:
temp[1], temp[0] = temp[0], temp[1]
best = 1 + dp(temp[0], temp[1], i + 3)
break
else:
# keep any two
temp.sort()
for j in range(5):
for k in range(j + 1, 5):
best = max(best, dp(temp[j], temp[k], i + 3))
return best
for i in reversed(range(2, 3 * N, 3)):
for a in range(1, N + 1):
for b in range(a, N + 1):
dp(a, b, i)
print(dp(A[0], A[1], 2))
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s927897340
|
Runtime Error
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
import copy
import itertools
n = int(input())
a = list(map(int, input().split()))
dp1 = [[0] * (n + 1) for i in range(n + 1)]
f = copy.deepcopy(dp1)
for k in list(itertools.permutations(a[0:5])):
x = k[2] == k[3] and k[2] == k[4]
dp1[k[0]][k[1]] = int(x)
f[k[0]][k[1]] = 1
dp2 = copy.deepcopy(dp1)
x = 0
for i in range(1, n - 1):
p, q, r = sorted(a[(3 * i + 2) : (3 * i + 5)])
if p == r:
x += 1
elif p == q:
for j in range(n):
if f[j + 1][p] == 1:
dp2[j + 1][r] = dp1[j + 1][p] + 1
dp2[r][j + 1] = dp1[j + 1][p] + 1
f[j + 1][r], dp2[r][j + 1] = 1, 1
if f[r][r] == 1:
dp2[p][p] = dp1[r][r] + 1
f[p][p] = 1
elif q == r:
for j in range(n):
if f[j + 1][q] == 1:
dp2[j + 1][p] = dp1[j + 1][q] + 1
dp2[p][j + 1] = dp1[j + 1][q] + 1
f[j + 1][p], dp2[p][j + 1] = 1, 1
if f[p][p] == 1:
dp2[q][q] = dp1[p][p] + 1
f[q][q] = 1
else:
if f[r][r] == 1:
dp2[p][q] = dp1[r][r] + 1
f[p][q] = 1
if f[p][p] == 1:
dp2[q][r] = dp1[p][p] + 1
f[q][r] = 1
if f[p][p] == 1:
dp2[q][r] = dp1[p][p] + 1
f[q][r] = 1
dp1 = copy.deepcopy(dp2)
if f[a[-1]][a[-1]] == 1:
dp1[a[-1]][a[-1]] += 1
print(x + max(sum(dp1, [])))
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s560048672
|
Wrong Answer
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
import sys
INF = 1 << 60
MOD = 10**9 + 7 # 998244353
sys.setrecursionlimit(2147483647)
input = lambda: sys.stdin.readline().rstrip()
from collections import defaultdict
def resolve():
n = int(input())
A = list(map(int, input().split()))
dp = defaultdict(int)
dp[(A[0], A[1])] = 0
for i in range(n - 1):
ndp = defaultdict(int)
k = max(dp.values())
for key, val in dp.items():
if val != k:
continue
B = list(key)
for j in range(3 * i + 2, 3 * i + 5):
B.append(A[j])
B.sort()
for s in range(5):
for t in range(s + 1, 5):
C = B[:]
C.remove(B[s])
C.remove(B[t])
if len(set(C)) == 1:
ndp[B[s], B[t]] = max(ndp[B[s], B[t]], val + 1)
else:
ndp[B[s], B[t]] = max(ndp[B[s], B[t]], val)
dp = ndp
ans = 0
for key, val in dp.items():
if key[0] == key[-1] == A[-1]:
val += 1
ans = max(ans, val)
print(ans)
resolve()
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the maximum number of points you can gain.
* * *
|
s542071998
|
Accepted
|
p02581
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \cdots A_{3N}
|
import sys
input = sys.stdin.buffer.readline
n = int(input())
a = list(map(int, input().split()))
a.append(n + 1)
a.append(n + 1)
dp = [[-1] * (n + 2) for i in range(n + 2)]
ma = [-1] * (n + 2)
dp[a[0]][a[1]] = 0
ma[a[0]] = 0
ma[a[1]] = 0
after = 0
for i in range(n):
x, y, z = a[3 * i + 2], a[3 * i + 3], a[3 * i + 4]
if x == z:
y, z = z, y
if y == z:
x, z = z, x
if x == z:
after += 1
continue
tank = []
if x != y:
for i in range(n + 1):
tank.append((i, x, ma[i]))
tank.append((i, y, ma[i]))
tank.append((i, z, ma[i]))
tank.append((x, y, max(max(ma), dp[z][z] + 1)))
tank.append((x, z, max(max(ma), dp[y][y] + 1)))
tank.append((y, z, max(max(ma), dp[x][x] + 1)))
else:
for i in range(n + 1):
tank.append((i, x, ma[i]))
tank.append((i, y, ma[i]))
tmp = ma[i]
if dp[i][x] != -1:
tmp = max(tmp, dp[i][x] + 1)
if dp[x][i] != -1:
tmp = max(tmp, dp[x][i] + 1)
tank.append((i, z, tmp))
tank.append((x, y, max(max(ma), dp[z][z] + 1)))
tank.append((x, z, max(max(ma), dp[y][y] + 1)))
tank.append((y, z, max(max(ma), dp[x][x] + 1)))
for p, q, c in tank:
dp[p][q] = max(dp[p][q], c)
ma[p] = max(ma[p], c)
ma[q] = max(ma[q], c)
res = 0
for i in range(n + 2):
for j in range(n + 2):
res = max(res, dp[i][j])
print(res + after)
|
Statement
We have 3N cards arranged in a row from left to right, where each card has an
integer between 1 and N (inclusive) written on it. The integer written on the
i-th card from the left is A_i.
You will do the following operation N-1 times:
* Rearrange the five leftmost cards in any order you like, then remove the three leftmost cards. If the integers written on those three cards are all equal, you gain 1 point.
After these N-1 operations, if the integers written on the remaining three
cards are all equal, you will gain 1 additional point.
Find the maximum number of points you can gain.
|
[{"input": "2\n 1 2 1 2 2 1", "output": "2\n \n\nLet us rearrange the five leftmost cards so that the integers written on the\nsix cards will be 2\\ 2\\ 2\\ 1\\ 1\\ 1 from left to right.\n\nThen, remove the three leftmost cards, all of which have the same integer 2,\ngaining 1 point.\n\nNow, the integers written on the remaining cards are 1\\ 1\\ 1.\n\nSince these three cards have the same integer 1, we gain 1 more point.\n\nIn this way, we can gain 2 points - which is the maximum possible.\n\n* * *"}, {"input": "3\n 1 1 2 2 3 3 3 2 1", "output": "1\n \n\n* * *"}, {"input": "3\n 1 1 2 2 2 3 3 3 1", "output": "3"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s442961607
|
Runtime Error
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
import sys
input = sys.stdin.readline
def linput(ty=int, cvt=list):
return cvt(map(ty,input().split()))
def gcd(a: int, b: int):
while b: a, b = b, a%b
return a
def lcm(a: int, b: int):
return a * b // gcd(a, b)
def main():
#n=int(input())
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s952328387
|
Runtime Error
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
s = sorted(list(map(int, input().split())))
a = s.pop(-1)
b, c = a // 2, a - (a // 2)
d = s[0] * a[1]
print(abs(d * b - d * c))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s630946133
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
V = list(map(int, input().split()))
V.sort()
L = V[2] // 2
print(V[0] * V[1] * (V[2] - L - L))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s049456188
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
A, B, C = [int(x) for x in input().split()]
x = abs((A // 2) * B * C - ((A - (A // 2)) * B * C))
y = abs((B // 2) * A * C - ((B - (B // 2)) * A * C))
z = abs((C // 2) * A * B - ((C - (C // 2)) * A * B))
print(min(x, y, z))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s695305797
|
Wrong Answer
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
L = list(map(int, input().split()))
L = sorted(L)
print(L[0] * L[1] * (L[2] // 2))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s314111636
|
Runtime Error
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
str = input()
num = list(map(int,str.split(' ')))
if !(num[0]%2)*(num[1]%2)*(num[2]):
print(0)
else:
num.sort()
print(num[0]*num[1])
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s389347935
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
abc = [int(i) for i in input().split()]
abc.sort()
red = abc[0] * abc[1] * abc[2]
abc[2] = abc[2] // 2
blue = abc[0] * abc[1] * abc[2] * 2
print(red - blue)
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s942337674
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
a, b, c = (int(s) for s in input().strip().split(" "))
print("0" if a * b * c % 2 == 0 else str(min(a * b, a * c, b * c)))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s649116430
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
x, y, z = map(int, input().split())
s = x * y * (z // 2)
ss = x * y * (z - z // 2)
l = abs(s - ss)
c = y * z * (x // 2)
cc = y * z * (x - x // 2)
r = abs(c - cc)
d = z * x * (y // 2)
dd = z * x * (y - y // 2)
p = abs(d - dd)
print(min(r, l, p))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s537529399
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
A = sorted(list(map(int, input().split())))
print(0 if any([a % 2 == 0 for a in A]) else A[0] * A[1])
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s436471343
|
Runtime Error
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
a, b, c = map(int, input().split())
print(min(B * C,C * A,A * B))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s986759089
|
Wrong Answer
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
A, B, C = map(int, input().split(" "))
# 一番長い辺で切れば断面の数は最小
L = max(A, B, C) // 2
print(abs((A * B * L) - (A * B * (C - L))))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s569173133
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
I = input().split()
a = [int(x) for x in I]
ans = 10**20
for i in range(0, 2):
for j in range(i + 1, 3):
s = a[i] * a[j]
k = 3 - (i + j)
A = s * ((a[k] + 1) // 2)
B = s * ((a[k]) // 2)
ans = min(ans, A - B)
print(ans)
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s993966385
|
Runtime Error
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0; i<(n); i++)
#define rrep(i,n) for(int i=1; i<=(int)(n); i++)
#define pb push_back
#define all(v) v.begin(),v.end()
#define fi first
#define se second
#define bigger (char)toupper
#define smaller (char)tolower
using namespace std;
typedef pair<int,int> pii;
typedef vector<int> vi;
typedef vector<vi> vii;
typedef vector<string> vs;
typedef vector<char> vc;
typedef long long ll;
typedef unsigned long long ull;
int main() {
ll A,B,C;
cin>>A>>B>>C;
if(A%2==0||B%2==0||C%2==0) cout<<0<<endl;
else {
vector<ll> v;
v.pb(A);
v.pb(B);
v.pb(C);
sort(all(v));
cout<<v[0]*v[1]<<endl;
}
}
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s372838131
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
l = sorted(list(map(int, input().split())))
print(((l[2] + 1) // 2 - l[2] // 2) * l[0] * l[1])
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s788152401
|
Wrong Answer
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
n = sorted(map(int, input().split()))
print(n[0] * n[1])
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s964849111
|
Runtime Error
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
a=list(map(int,input().split()))
a.sort()
if a%2!=0 and b%2!=0 and c%2!=0:
print(a[0]*a[1])
elif:
print("0")
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s050203675
|
Wrong Answer
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
A = list(sorted(map(int, input().split())))
tmp = A[-1] // 2
print(A[0] * A[1] * (tmp - (A[-1] - tmp)))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s739324662
|
Wrong Answer
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
a, b = sorted(map(int, input().split()))[:2]
print(a * b if a * b % 2 else 0)
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s933927633
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
import math
A, B, C = map(int, input().split())
# A-B Partern
base1 = A * B
part1_a = math.ceil(C / 2)
part1_b = C - part1_a
ans1 = abs((base1 * part1_a) - (base1 * part1_b))
# A-C Partern
base2 = A * C
part2_a = math.ceil(B / 2)
part2_b = B - part2_a
ans2 = abs((base2 * part2_a) - (base2 * part2_b))
# B-C Partern
base3 = B * C
part3_a = math.ceil(A / 2)
part3_b = A - part3_a
ans3 = abs((base3 * part3_a) - (base3 * part3_b))
print(min(ans1, ans2, ans3))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s447316080
|
Runtime Error
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
a,b,c=map(int,input().split())
m=a*b*c
k=max(a,b,c)
if m%2==0:
print(int(0))
else:
n=k//2
h=m/k
print(int((k-2n)*h))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s128647241
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
i, j, k = sorted(map(int, input().split()))
print(i * j * (k % 2))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s946442505
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
d = list(map(int, input().split()))
d.sort()
s = d[0] * d[1]
print(s * (d[2] % 2))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s732492866
|
Accepted
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
A, B, C = sorted([int(x) for x in input().strip().split()])
print(A * B * (C % 2))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s916052211
|
Runtime Error
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
a,b,c=map(int,input().split())
print(min(a%*b*c,a*b%*c,a*b*c%))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
Print the minimum possible difference between the number of red blocks and the
number of blue blocks.
* * *
|
s309691044
|
Runtime Error
|
p04005
|
The input is given from Standard Input in the following format:
A B C
|
a,b,c=map(int,input().split())
print(min(a%*b*c,b%*a*c,c%*a*b))
|
Statement
We have a rectangular parallelepiped of size A×B×C, built with blocks of size
1×1×1. Snuke will paint each of the A×B×C blocks either red or blue, so that:
* There is at least one red block and at least one blue block.
* The union of all red blocks forms a rectangular parallelepiped.
* The union of all blue blocks forms a rectangular parallelepiped.
Snuke wants to minimize the difference between the number of red blocks and
the number of blue blocks. Find the minimum possible difference.
|
[{"input": "3 3 3", "output": "9\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 9 red blocks and 18 blue blocks, thus the difference is 9.\n\n\n\n* * *"}, {"input": "2 2 4", "output": "0\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 8 red blocks and 8 blue blocks, thus the difference is 0.\n\n\n\n* * *"}, {"input": "5 3 5", "output": "15\n \n\nFor example, Snuke can paint the blocks as shown in the diagram below. There\nare 45 red blocks and 30 blue blocks, thus the difference is 9.\n\n"}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s864109797
|
Wrong Answer
|
p03390
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
def examC():
ABC = LI()
ABC.sort()
judge = ABC[2] * 2 - ABC[1] - ABC[0]
ans = judge // 2 + (judge % 2) * 2
print(ans)
return
def examD():
def judge(A, B):
cur = int((A * B) ** 0.5)
if cur**2 == A * B:
return (cur - 1) * 2 - 1
if cur * (cur + 1) >= A * B:
return cur * 2 - 2
else:
return cur * 2 - 1
Q = I()
ans = []
for _ in range(Q):
a, b = LI()
ans.append(judge(a, b))
for v in ans:
print(v)
return
import sys, copy, bisect, itertools, heapq, math
from heapq import heappop, heappush, heapify
from collections import Counter, defaultdict, deque
def I():
return int(sys.stdin.readline())
def LI():
return list(map(int, sys.stdin.readline().split()))
def LSI():
return list(map(str, sys.stdin.readline().split()))
def LS():
return sys.stdin.readline().split()
def SI():
return sys.stdin.readline().strip()
global mod, inf
mod = 10**9 + 7
inf = 10**18
if __name__ == "__main__":
examD()
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s819070100
|
Wrong Answer
|
p03390
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
N = int(input())
lis = []
for T in range(N):
c = list(map(int, input().split()))
pro = c[0] * c[1]
sq = int(pro**0.5)
if c[0] == c[1]:
n = (sq - 1) * 2
elif (c[0] % 2 != 0 and c[1] % 2 == 0) or (c[1] % 2 != 0 and c[0] % 2 == 0):
n = (sq - 1) * 2
elif c[0] % 2 == 0 and c[1] % 2 == 0:
n = (sq * 2) - 1
else:
n = (sq * 2) - 2
lis.append(n)
for i in lis:
print(i)
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s860563637
|
Runtime Error
|
p03390
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
# t=int(input())
t = 1
for i in range(t):
x, y, z = map(int, input().split())
ma = max(x, y, z)
mi = min(x, y, z)
if x == ma:
if y < z:
m = x - y
n = x - z
else:
m = x - z
n = x - y
elif y == ma:
if x < z:
m = y - x
n = y - z
else:
m = y - z
n = y - x
else:
if x < y:
m = z - x
n = z - y
else:
m = z - y
n = z - x
ans = n + (m - n) // 2
if (m - n) % 2 == 1:
ans += 2
print(ans)
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s487529182
|
Runtime Error
|
p03390
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
from math import sqrt
Q = int(input())
for i in range(Q):
A,B = map(int, input().split())
m=A*B
if A==B or B=A+1:
ans = 2*A-2
elif A=B+1
ans = 2*B-2
C = int(sqrt(m))
if C*C==m:
C=C-1
if C*(C+1)<m:
ans = 2*C-1
else:
ans = 2*C-2
print(ans)
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
Print the minimum possible sum of the integers written on the last two cards
remaining.
* * *
|
s302463083
|
Wrong Answer
|
p02978
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
def prob_a():
n = int(input())
a_list = [int(a) for a in input().split()]
ans = a_list[0] + a_list[-1]
a_list = a_list[1:-1]
if n >= 3:
for i in range(n - 3):
if min(a_list[0] / 2, a_list[-1] / 2) <= min(a_list):
if a_list[0] <= a_list[-1]:
x = a_list[0]
a_list = a_list[1:]
a_list[0] += x
ans += x
else:
x = a_list[-1]
a_list = a_list[:-1]
a_list[-1] += x
ans += x
else:
x = min(a_list)
ind = a_list.index(x)
a_list[ind - 1] += x
a_list[ind + 1] += x
a_list.pop(ind)
# print(a_list)
ans += a_list[0] * 2
else:
pass
print(str(ans))
prob_a()
|
Statement
There is a stack of N cards, each of which has a non-negative integer written
on it. The integer written on the i-th card from the top is A_i.
Snuke will repeat the following operation until two cards remain:
* Choose three consecutive cards from the stack.
* Eat the middle card of the three.
* For each of the other two cards, replace the integer written on it by the sum of that integer and the integer written on the card eaten.
* Return the two cards to the original position in the stack, without swapping them.
Find the minimum possible sum of the integers written on the last two cards
remaining.
|
[{"input": "4\n 3 1 4 2", "output": "16\n \n\nWe can minimize the sum of the integers written on the last two cards\nremaining by doing as follows:\n\n * Initially, the integers written on the cards are 3, 1, 4, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 1 written on it, add 1 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 4, 5, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 5 written on it, add 5 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 9 and 7 from top to bottom.\n * The sum of the integers written on the last two cards remaining is 16.\n\n* * *"}, {"input": "6\n 5 2 4 1 6 9", "output": "51\n \n\n* * *"}, {"input": "10\n 3 1 4 1 5 9 2 6 5 3", "output": "115"}]
|
Print the minimum possible sum of the integers written on the last two cards
remaining.
* * *
|
s671259065
|
Wrong Answer
|
p02978
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n = int(input())
a = sorted(map(int, input().split()))
r = a.pop()
for n, i in zip(a, range(n - 1, 0, -1)):
r += n * i
print(r)
|
Statement
There is a stack of N cards, each of which has a non-negative integer written
on it. The integer written on the i-th card from the top is A_i.
Snuke will repeat the following operation until two cards remain:
* Choose three consecutive cards from the stack.
* Eat the middle card of the three.
* For each of the other two cards, replace the integer written on it by the sum of that integer and the integer written on the card eaten.
* Return the two cards to the original position in the stack, without swapping them.
Find the minimum possible sum of the integers written on the last two cards
remaining.
|
[{"input": "4\n 3 1 4 2", "output": "16\n \n\nWe can minimize the sum of the integers written on the last two cards\nremaining by doing as follows:\n\n * Initially, the integers written on the cards are 3, 1, 4, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 1 written on it, add 1 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 4, 5, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 5 written on it, add 5 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 9 and 7 from top to bottom.\n * The sum of the integers written on the last two cards remaining is 16.\n\n* * *"}, {"input": "6\n 5 2 4 1 6 9", "output": "51\n \n\n* * *"}, {"input": "10\n 3 1 4 1 5 9 2 6 5 3", "output": "115"}]
|
Print the minimum possible sum of the integers written on the last two cards
remaining.
* * *
|
s208270160
|
Wrong Answer
|
p02978
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n = int(input())
p = input().rstrip().split(" ")
S = 0
if len(p) == 2:
print(int(p[0]) + int(p[1]))
elif len(p) == 3:
print((int(p[1]) * 2) + int(p[0]) + int(p[2]))
else:
l = []
for i in range(0, len(p)):
l.append(int(p[i]))
S = list(l)
while len(l) >= 3:
t = min(l)
C = l.index(t)
if C == 0:
l[C] = l[C] + l[C + 1]
l[C + 2] = l[C + 2] + l[C + 1]
del l[C + 1]
elif C == len(l) - 1:
l[C - 2] = l[C - 2] + l[C - 1]
l[C] = l[C] + l[C - 1]
del l[C - 1]
else:
l[C - 1] = l[C - 1] + l[C]
l[C + 1] = l[C + 1] + l[C]
del l[C]
A = l[0] + l[1]
S.reverse()
l = S
while len(l) >= 3:
t = min(l)
C = l.index(t)
if C == 0:
l[C] = l[C] + l[C + 1]
l[C + 2] = l[C + 2] + l[C + 1]
del l[C + 1]
elif C == len(l) - 1:
l[C - 2] = l[C - 2] + l[C - 1]
l[C] = l[C] + l[C - 1]
del l[C - 1]
else:
l[C - 1] = l[C - 1] + l[C]
l[C + 1] = l[C + 1] + l[C]
del l[C]
B = l[0] + l[1]
print(min(A, B))
|
Statement
There is a stack of N cards, each of which has a non-negative integer written
on it. The integer written on the i-th card from the top is A_i.
Snuke will repeat the following operation until two cards remain:
* Choose three consecutive cards from the stack.
* Eat the middle card of the three.
* For each of the other two cards, replace the integer written on it by the sum of that integer and the integer written on the card eaten.
* Return the two cards to the original position in the stack, without swapping them.
Find the minimum possible sum of the integers written on the last two cards
remaining.
|
[{"input": "4\n 3 1 4 2", "output": "16\n \n\nWe can minimize the sum of the integers written on the last two cards\nremaining by doing as follows:\n\n * Initially, the integers written on the cards are 3, 1, 4, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 1 written on it, add 1 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 4, 5, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 5 written on it, add 5 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 9 and 7 from top to bottom.\n * The sum of the integers written on the last two cards remaining is 16.\n\n* * *"}, {"input": "6\n 5 2 4 1 6 9", "output": "51\n \n\n* * *"}, {"input": "10\n 3 1 4 1 5 9 2 6 5 3", "output": "115"}]
|
Print the minimum possible sum of the integers written on the last two cards
remaining.
* * *
|
s800089275
|
Wrong Answer
|
p02978
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
size = int(input())
nums = list(map(int, input().split()))
# size = 10
# nums = list(map(int, "3 1 4 1 5 9 2 6 5 3".split()))
fnums = nums[1 : size - 1]
rnums = list(reversed(fnums))
tmp = nums[1 : size - 1]
tmp.sort()
tmps = len(tmp)
idxs = []
for num in tmp:
fix = fnums.index(num)
lix = rnums.index(num)
if fix <= lix:
# print("fix")
# print("{} {}".format(tmps, fix))
idxs.append(fix)
fnums[fix] = -1
rnums[tmps - fix - 1] = -1
else:
# aaaa
# print("lix")
idxs.append(tmps - lix - 1)
fnums[tmps - lix - 1] = -1
rnums[lix] = -1
# print(fnums)
# print(rnums)
first = 0
# print(idxs)
for i in range(0, len(idxs)):
idx = idxs[i]
# print("{} {}".format(idx, nums))
n = nums.pop(idx + 1)
nums[idx] += n
nums[idx + 1] += n
for j in range(0, len(idxs)):
idxs[j] -= 1 if idxs[j] > idx else 0
print(sum(nums))
# 5 2 4 1 6 9
# 5 2 5 7 9
# 7 7 7 9
# 14 14 9
# 28 23
# 51
|
Statement
There is a stack of N cards, each of which has a non-negative integer written
on it. The integer written on the i-th card from the top is A_i.
Snuke will repeat the following operation until two cards remain:
* Choose three consecutive cards from the stack.
* Eat the middle card of the three.
* For each of the other two cards, replace the integer written on it by the sum of that integer and the integer written on the card eaten.
* Return the two cards to the original position in the stack, without swapping them.
Find the minimum possible sum of the integers written on the last two cards
remaining.
|
[{"input": "4\n 3 1 4 2", "output": "16\n \n\nWe can minimize the sum of the integers written on the last two cards\nremaining by doing as follows:\n\n * Initially, the integers written on the cards are 3, 1, 4, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 1 written on it, add 1 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 4, 5, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 5 written on it, add 5 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 9 and 7 from top to bottom.\n * The sum of the integers written on the last two cards remaining is 16.\n\n* * *"}, {"input": "6\n 5 2 4 1 6 9", "output": "51\n \n\n* * *"}, {"input": "10\n 3 1 4 1 5 9 2 6 5 3", "output": "115"}]
|
Print the minimum possible sum of the integers written on the last two cards
remaining.
* * *
|
s464570617
|
Wrong Answer
|
p02978
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
import sys
MAX_INT = int(10e9)
MIN_INT = -MAX_INT
mod = 1000000007
sys.setrecursionlimit(1000000000)
def IL():
return list(map(int, input().split()))
def SL():
return input().split()
def I():
return int(sys.stdin.readline())
def S():
return input()
def tami(visited, x, cnt, List):
global ans
# print(a)
# print("visited=",visited)
# print("List=",List)
# print("-----------")
if cnt == N - 2:
ans = min(ans, List[0] + List[-1])
return
else:
for j in range(1, N - 1): # 次の探索 j
if j in visited:
continue
else:
if x < j:
for v in range(x + 1, j): # x→j 間に未探索 → ダメ
if v not in visited:
break
else:
for k in range(j - 1, -1, -1): # listの更新
if k not in visited:
left = k
break
for k in range(j + 1, N):
if k not in visited:
right = k
break
l = (
List[:left]
+ [List[left] + List[j]]
+ List[left + 1 : right]
+ [List[right] + List[j]]
+ List[right + 1 :]
)
tami(visited + [j], j, cnt + 1, l)
else:
for k in range(j - 1, -1, -1): # listの更新
if k not in visited:
left = k
break
for k in range(j + 1, N):
if k not in visited:
right = k
break
l = (
List[:left]
+ [List[left] + List[j]]
+ List[left + 1 : right]
+ [List[right] + List[j]]
+ List[right + 1 :]
)
tami(visited + [j], j, cnt + 1, l)
N = I()
a = IL()
ans = MAX_INT
for i in range(1, N - 1):
l = a[: i - 1] + [a[i - 1] + a[i]] + [a[i]] + [a[i + 1] + a[i]] + a[i + 2 :]
# print(l)
tami([i], i, 1, l)
print(ans)
|
Statement
There is a stack of N cards, each of which has a non-negative integer written
on it. The integer written on the i-th card from the top is A_i.
Snuke will repeat the following operation until two cards remain:
* Choose three consecutive cards from the stack.
* Eat the middle card of the three.
* For each of the other two cards, replace the integer written on it by the sum of that integer and the integer written on the card eaten.
* Return the two cards to the original position in the stack, without swapping them.
Find the minimum possible sum of the integers written on the last two cards
remaining.
|
[{"input": "4\n 3 1 4 2", "output": "16\n \n\nWe can minimize the sum of the integers written on the last two cards\nremaining by doing as follows:\n\n * Initially, the integers written on the cards are 3, 1, 4, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 1 written on it, add 1 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 4, 5, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 5 written on it, add 5 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 9 and 7 from top to bottom.\n * The sum of the integers written on the last two cards remaining is 16.\n\n* * *"}, {"input": "6\n 5 2 4 1 6 9", "output": "51\n \n\n* * *"}, {"input": "10\n 3 1 4 1 5 9 2 6 5 3", "output": "115"}]
|
Print the minimum possible sum of the integers written on the last two cards
remaining.
* * *
|
s150257101
|
Accepted
|
p02978
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from functools import lru_cache
def solve(n, aaa):
@lru_cache(maxsize=None)
def search_min(li, ri, lc, rc):
w = ri - li
if w == 1:
return 0
lrc = lc + rc
if w == 2:
return aaa[li + 1] * lrc
if w == 3:
a1, a2 = aaa[li + 1], aaa[li + 2]
return (a1 + a2) * lrc + min(a1 * lc, a2 * rc)
ret = min(
aaa[i] * lrc + search_min(li, i, lc, lrc) + search_min(i, ri, lrc, rc)
for i in range(li + 1, ri)
)
return ret
return search_min(0, n - 1, 1, 1) + aaa[0] + aaa[-1]
n = int(input())
aaa = list(map(int, input().split()))
print(solve(n, aaa))
|
Statement
There is a stack of N cards, each of which has a non-negative integer written
on it. The integer written on the i-th card from the top is A_i.
Snuke will repeat the following operation until two cards remain:
* Choose three consecutive cards from the stack.
* Eat the middle card of the three.
* For each of the other two cards, replace the integer written on it by the sum of that integer and the integer written on the card eaten.
* Return the two cards to the original position in the stack, without swapping them.
Find the minimum possible sum of the integers written on the last two cards
remaining.
|
[{"input": "4\n 3 1 4 2", "output": "16\n \n\nWe can minimize the sum of the integers written on the last two cards\nremaining by doing as follows:\n\n * Initially, the integers written on the cards are 3, 1, 4, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 1 written on it, add 1 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 4, 5, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 5 written on it, add 5 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 9 and 7 from top to bottom.\n * The sum of the integers written on the last two cards remaining is 16.\n\n* * *"}, {"input": "6\n 5 2 4 1 6 9", "output": "51\n \n\n* * *"}, {"input": "10\n 3 1 4 1 5 9 2 6 5 3", "output": "115"}]
|
Print the minimum possible sum of the integers written on the last two cards
remaining.
* * *
|
s917667959
|
Wrong Answer
|
p02978
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
import time
import random
N = int(input())
A = [int(a) for a in input().split()]
sTime = time.time()
def calc(X):
# print("X =", X)
if len(X) == 2:
return sum(X)
mi = min(X[1:-1])
T = [i for i in range(1, len(X) - 1) if X[i] == mi]
# print("len =", len(T))
mii = random.randrange(len(T))
# print("T =", T)
# print("mii =", mii)
k = T[mii]
if random.randrange(10) == 0:
k = random.randrange(len(X) - 2) + 1
Y = [
X[i] + (X[k] if i == k - 1 or i == k + 1 else 0)
for i in range(len(X))
if i != k
]
return calc(Y)
ans = 10**30
while time.time() - sTime < 1.7:
ans = min(ans, calc(A))
print(ans)
|
Statement
There is a stack of N cards, each of which has a non-negative integer written
on it. The integer written on the i-th card from the top is A_i.
Snuke will repeat the following operation until two cards remain:
* Choose three consecutive cards from the stack.
* Eat the middle card of the three.
* For each of the other two cards, replace the integer written on it by the sum of that integer and the integer written on the card eaten.
* Return the two cards to the original position in the stack, without swapping them.
Find the minimum possible sum of the integers written on the last two cards
remaining.
|
[{"input": "4\n 3 1 4 2", "output": "16\n \n\nWe can minimize the sum of the integers written on the last two cards\nremaining by doing as follows:\n\n * Initially, the integers written on the cards are 3, 1, 4, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 1 written on it, add 1 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 4, 5, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 5 written on it, add 5 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 9 and 7 from top to bottom.\n * The sum of the integers written on the last two cards remaining is 16.\n\n* * *"}, {"input": "6\n 5 2 4 1 6 9", "output": "51\n \n\n* * *"}, {"input": "10\n 3 1 4 1 5 9 2 6 5 3", "output": "115"}]
|
Print the minimum possible sum of the integers written on the last two cards
remaining.
* * *
|
s060864967
|
Runtime Error
|
p02978
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from collections import deque
N = int(input())
ai = [int(x) for x in input().split()]
queue = deque([ai])
log = []
while queue:
ai = queue.popleft()
ind = list(range(1, len(ai) - 1))
for index in ind:
pi = ai[:]
pi[index - 1] += pi[index]
pi[index + 1] += pi[index]
si = pi[0:index]
si.extend(pi[index + 1 :])
if len(si) == 2:
log.append(si)
else:
queue.append(si)
print(min([sum(i) for i in log]))
|
Statement
There is a stack of N cards, each of which has a non-negative integer written
on it. The integer written on the i-th card from the top is A_i.
Snuke will repeat the following operation until two cards remain:
* Choose three consecutive cards from the stack.
* Eat the middle card of the three.
* For each of the other two cards, replace the integer written on it by the sum of that integer and the integer written on the card eaten.
* Return the two cards to the original position in the stack, without swapping them.
Find the minimum possible sum of the integers written on the last two cards
remaining.
|
[{"input": "4\n 3 1 4 2", "output": "16\n \n\nWe can minimize the sum of the integers written on the last two cards\nremaining by doing as follows:\n\n * Initially, the integers written on the cards are 3, 1, 4, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 1 written on it, add 1 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 4, 5, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 5 written on it, add 5 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 9 and 7 from top to bottom.\n * The sum of the integers written on the last two cards remaining is 16.\n\n* * *"}, {"input": "6\n 5 2 4 1 6 9", "output": "51\n \n\n* * *"}, {"input": "10\n 3 1 4 1 5 9 2 6 5 3", "output": "115"}]
|
Print the minimum possible sum of the integers written on the last two cards
remaining.
* * *
|
s495625702
|
Runtime Error
|
p02978
|
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from collections import deque
n = int(input())
a = deque([int(i) for i in input().split()])
while len(a) != 2:
a_left = a.popleft()
a_right = a.pop()
m = min(a)
min_index = [i for i, x in enumerate(a) if x == min(a)]
a.append(a_right)
a.appendleft(a_left)
tmp = 0
tmp_index = 0
for i in min_index:
if tmp < a[i] + a[i + 2]:
tmp = a[i] + a[i + 2]
tmp_index = i
b = a.copy()
a = deque([])
for i in range(len(b)):
if i == tmp_index:
a.append(b[i] + m)
elif i == tmp_index + 2:
a.append(b[i] + m)
elif i != tmp_index + 1:
a.append(b[i])
a1 = a.popleft()
a2 = a.popleft()
print(a1 + a2)
|
Statement
There is a stack of N cards, each of which has a non-negative integer written
on it. The integer written on the i-th card from the top is A_i.
Snuke will repeat the following operation until two cards remain:
* Choose three consecutive cards from the stack.
* Eat the middle card of the three.
* For each of the other two cards, replace the integer written on it by the sum of that integer and the integer written on the card eaten.
* Return the two cards to the original position in the stack, without swapping them.
Find the minimum possible sum of the integers written on the last two cards
remaining.
|
[{"input": "4\n 3 1 4 2", "output": "16\n \n\nWe can minimize the sum of the integers written on the last two cards\nremaining by doing as follows:\n\n * Initially, the integers written on the cards are 3, 1, 4, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 1 written on it, add 1 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 4, 5, and 2 from top to bottom.\n * Choose the first, second, and third card from the top. Eat the second card with 5 written on it, add 5 to each of the other two cards, and return them to the original position in the stack. The integers written on the cards are now 9 and 7 from top to bottom.\n * The sum of the integers written on the last two cards remaining is 16.\n\n* * *"}, {"input": "6\n 5 2 4 1 6 9", "output": "51\n \n\n* * *"}, {"input": "10\n 3 1 4 1 5 9 2 6 5 3", "output": "115"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s860517825
|
Runtime Error
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
import sys
stdin = sys.stdin
sys.setrecursionlimit(10**5)
def li(): return map(int, stdin.readline().split())
def li_(): return map(lambda x: int(x)-1, stdin.readline().split())
def lf(): return map(float, stdin.readline().split())
def ls(): return stdin.readline().split()
def ns(): return stdin.readline().rstrip()
def lc(): return list(ns())
def ni(): return int(stdin.readline())
def nf(): return float(stdin.readline())
l,n = li()
x = [ni() for _ in range(n)]
dp = [[0,0] for _ in range(n+1)] for _ in range(n+1)]
left = [0] + x
right = [l] + x[::-1]
for total in range(1,n+1):
for ccw in range(total+1):
cw = total - ccw
if ccw == 0:
dp[ccw][cw][1] = dp[ccw][cw-1][1] + (right[cw-1] + l - right[cw]) % l
elif cw == 0:
dp[ccw][cw][0] = dp[ccw-1][cw][0] + (left[ccw] + l - left[ccw-1]) % l
else:
dp[ccw][cw][0] = max(dp[ccw-1][cw][1] + (left[ccw] + l - right[cw]) % l,
dp[ccw-1][cw][0] + (left[ccw] + l - left[ccw-1]) % l)
dp[ccw][cw][1] = max(dp[ccw][cw-1][1] + (right[cw-1] + l - right[cw]) % l,
dp[ccw][cw-1][0] + (left[ccw] + l - right[cw]) % l)
ans = 0
for ccw in range(n+1):
cw = n - ccw
ans = max(ans, dp[ccw][cw][0], dp[ccw][cw][1])
print(ans)
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s594155318
|
Accepted
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
ln, kn, *ki = map(int, open(0).read().split())
# 順回転
pa = ki[-1]
ky = [pa]
kigu = 1
for ys in range(2, kn + 1):
# 要素数が偶数の場合
if kigu == 1:
pa += ki[kn - ys] * 2 + ln - ki[-(ys // 2)] * 2
# 要素数が奇数の場合
else:
pa += ki[kn - ys] * 2 - ki[-(ys // 2) - 1] + ln - ki[-(ys // 2)]
ky.append(pa)
kigu *= -1
# 逆回転
pa = ln - ki[0]
ky.append(pa)
kigu = 1
for ys in range(2, kn + 1):
# 要素数が偶数の場合
if kigu == 1:
pa += (ln - ki[ys - 1]) * 2 - ln + ki[ys // 2 - 1] * 2
# 要素数が奇数の場合
else:
pa += (ln - ki[ys - 1]) * 2 + ki[ys // 2] - ln + ki[ys // 2 - 1]
ky.append(pa)
kigu *= -1
print(max(ky))
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s091529533
|
Runtime Error
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
l,n=map(int,input().split())
tree=[]
for i in range(n):
k=int(input())
tree.append(k)
reverse_tree=[l-i for i in tree]
position=0
ans=0
while len(tree)>0:
if (tree[0]-position >= reverse_tree[0]+position):
ans+= tree[0]-position
position=tree.pop(tree[0])
reverse_tree.pop(reverse_tree[-1])
else:
ans+= reverse_tree[0]+position
position=l-reverse_tree.pop(reverse_tree[0])
tree.pop(tree[-1])
print(ans)
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s897854395
|
Runtime Error
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
l = int(input())
n = int(input())
x = [int(i) for i in input().split()]
k = 0
sum = 0
while i > 1
if 10 + k - x[n-i] < x[i] - k:
k = x[i]
sum = sum + x[i] - k
del x[i]
n = n - 1
else:
k = x[n-i]
sum = sum + 10 + k - x[n-i]
del x[n-i]
n = n - 1
print(sum)
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s912107968
|
Runtime Error
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
[L, N] = list(map(int, input().split(" ")))
TreeList = []
for i in range(N):
TreeList.append(int(input()))
maxLengthDict = {}
def maxLength(current, left, right):
if (
current in maxLengthDict
and left in maxLengthDict[current]
and right in maxLengthDict[current][left]
):
return maxLengthDict[current][left][right]
if left == right:
if current not in maxLengthDict:
maxLengthDict[current] = {}
if left not in maxLengthDict[current]:
maxLengthDict[current][left] = {}
leftDist = (TreeList[left] - current) % L
rightDist = (current - TreeList[right]) % L
maxLengthDict[current][left][right] = max(leftDist, rightDist)
return maxLengthDict[current][left][right]
leftDist = (TreeList[left] - current) % L
rightDist = (current - TreeList[right]) % L
if current not in maxLengthDict:
maxLengthDict[current] = {}
if left not in maxLengthDict[current]:
maxLengthDict[current][left] = {}
maxLengthDict[current][left][right] = max(
leftDist + maxLength(TreeList[left], left + 1, right),
rightDist + maxLength(TreeList[right], left, right - 1),
)
return maxLengthDict[current][left][right]
left = 0
right = N - 1
current = 0
ret = maxLength(current, left, right)
print(ret)
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s446212232
|
Wrong Answer
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
l, n = map(int, input().split())
k = n - 1
a = []
b = []
c = []
for i in range(n):
t = int(input())
a.append(t)
b.append(l - t)
c.append(1)
p = 0
q = 0
res = 0
f = 0
x = 0
for i in range(n):
if i == n - 1:
res += max(a[p], abs(b[k - q]))
else:
if a[p] >= abs(b[k - q]):
res += a[p]
f += a[p]
if i == 0:
x = 0
else:
x = a[p - 1]
p += 1
if c[p] == 1:
a[p] -= f
c[p] += 1
if c[k - p] == 1:
b[k - q] += f
c[k - p] += 1
# b[k-q] -=x
else:
res += b[k - q]
f -= b[k - q]
if i == 0:
x = 0
else:
x = b[k - q - 1]
q += 1
if c[p] == 1:
a[p] += f
c[p] += 1
if c[k - p] == 1:
b[k - q] -= f
c[k - p] += 1
# a[p] -=x
print(res)
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s467363200
|
Accepted
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
l, n = [int(item) for item in input().split()]
right = []
left = []
for i in range(n):
a = int(input())
right.append(a)
left.append(l - a)
left.reverse()
rsum = [0] * (n + 1)
lsum = [0] * (n + 1)
for i in range(n):
rsum[i + 1] += rsum[i] + right[i]
lsum[i + 1] += lsum[i] + left[i]
# Take all from left or right
ans = max(right[-1], left[-1])
# Take from left first, then ping pong
for i in range(n - 1):
val = left[i] * 2
rest = n - (i + 1)
val += rsum[(rest + 1) // 2] * 2
val += (lsum[rest // 2 + i + 1] - lsum[i + 1]) * 2
if rest % 2 == 0:
val -= left[rest // 2 + i]
else:
val -= right[(rest + 1) // 2 - 1]
ans = max(ans, val)
# Take from right first, then ping pong
for i in range(n - 1):
val = right[i] * 2
rest = n - (i + 1)
val += lsum[(rest + 1) // 2] * 2
val += (rsum[rest // 2 + i + 1] - rsum[i + 1]) * 2
if rest % 2 == 0:
val -= right[rest // 2 + i]
else:
val -= left[(rest + 1) // 2 - 1]
ans = max(ans, val)
print(ans)
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s481986071
|
Wrong Answer
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
import copy
"""
l, n = [10, 6]
x = [1, 2, 3, 6, 7, 9]
"""
l, n = [int(i) for i in input().split()]
x = [0 for _ in range(n)]
for i in range(n):
x[i] = int(input())
x.sort()
"""
x = queue.Queue
for i in range(n):
x.get(_x[i])
"""
"""
count = 0
prev = 0
while len(x) > 0:
if prev <= x[0] <= x[-1]:
if x[0] - prev > prev + l - x[-1]:
count += x[0] - prev
prev = x[0]
x = x[1:]
else:
count += prev + l - x[-1]
prev = x[-1]
x = x[:-1]
elif x[0] <= prev <= x[-1]:
if prev - x[0] >= x[-1] - prev:
count += prev - x[0]
prev = x[0]
x = x[1:]
else:
count += x[-1] - prev
prev = x[-1]
x = x[:-1]
else:
if prev - x[-1] > x[0] + l - prev:
count += prev - x[-1]
prev = x[-1]
x = x[:-1]
else:
count += x[0] + l - prev
prev = x[0]
x = x[1:]
print("x:{} prev:{} count:{}".format(x, prev, count))
"""
def right(i, j):
# iからjまでの時計回りの距離
if i < j:
return i + l - j
else:
return i - j
def left(i, j):
# iからjまでの反時計回りの距離
if i < j:
return j - i
else:
return j + l - i
_max = 0
for i in range(1, n - 1):
# x[i],x[i+1]は通らない
# x[i+1]->x[i-1]->x[i+2]->x[i-2]
_x = copy.deepcopy(x)
_x = _x[i + 2 : n] + _x[0 : i + 1]
# print(_x)
count = 0
prev = x[i + 1]
while len(_x) > 0:
# print("i:{} count:{} prev:{}".format(i, count, prev))
count += left(prev, _x[-1])
prev = _x[-1]
_x = _x[:-1]
if len(_x) > 0:
# print("i:{} count:{} prev:{}".format(i, count, prev))
count += right(prev, _x[0])
prev = _x[0]
_x = _x[1:]
# print("i:{} count:{}".format(i, count + min(abs(l - prev), prev)))
_max = max(_max, count + min(abs(l - prev), prev))
"""
_x = copy.deepcopy(x)
_x = _x[i+3:n]+_x[0:i+2]
count = 0
prev = x[i]
while len(_x) > 0:
# print("i:{} count:{} prev:{}".format(i, count, prev))
count += right(prev, _x[0])
prev = _x[0]
_x = _x[1:]
if len(_x) > 0:
# print("i:{} count:{} prev:{}".format(i, count, prev))
count += left(prev, _x[-1])
prev = _x[-1]
_x = _x[:-1]
print("i:{} count:{}".format(i, count + min(abs(l - prev), prev)))
_max = max(_max, count + min(abs(l - prev), prev))
"""
print(_max)
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s634478491
|
Runtime Error
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
L, N = (int(i) for i in input().split())
X = [int(input()) for _ in range(N)]
X.insert(0, 0)
X_c = [L - i for i in X]
def f(L, N, X, p, l, r, d_r):
w = 0
for _ in range(N - (l + r)):
if d_r: # L
l += 1
w += X[l] - p
p = X[l]
d_r = False
else: # R
r += 1
w += L - X[-r] + p
p = X[-r] - L
d_r = True
return w
len_l = [X[i] + f(L, N, X, X[i], i, 0, True) for i in range(1, N)]
len_r = [X_c[-i] + f(L, N, X, X[-i] - L, 0, i, False) for i in range(1, N)]
max_l = max(len_l)
max_r = max(len_r)
print(max(max_l, max_r))
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s868397834
|
Runtime Error
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
f = input().split()
L = int(f[0])
N = int(f[1])
ls = []
dis = []
for i in range(N):
ls.append(int(input()))
for l in ls:
dis.append(L - l)
for_lst = []
dist_lst = []
for i in range(2**N):
dist_lst.append(0)
for i in range(len(dist_lst)):
for_lst.append(bin(i)[2:].zfill(N))
# ls_lst = [ls for r in range(len(dist_lst))]
# dis_lst = [dis for r in range(len(dist_lst))]
dist_lst[int(len(dist_lst) / 2) :] += ls[0]
dist_lst[: int(len(dist_lst) / 2)] += dis[-1]
# 毎回全体の1/4について各操作を行えばいい
for i in range(len(dist_lst)):
dist = dis
lst = ls
for j in range(1, N):
if for_lst[i][j - 1 : j + 1] == "00":
dist_lst[i] += lst[1] - lst[0]
dist = dist[1:]
lst = lst[1:]
elif for_lst[i][j - 1 : j + 1] == "01":
dist_lst[i] += lst[0] + dist[-1]
dist = dist[1:]
lst = lst[1:]
elif for_lst[i][j - 1 : j + 1] == "10":
dist_lst[i] += lst[0] + dist[-1]
dist = dist[:-1] # len(dist) - 1]
lst = lst[:-1] # len(dist) - 1]
else:
dist_lst[i] += dist[-2] - dist[-1]
dist = dist[: len(dist) - 1]
lst = lst[: len(lst) - 1]
print(max(dist_lst))
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the longest possible total distance Takahashi walks during the process.
* * *
|
s575760910
|
Wrong Answer
|
p03187
|
Input is given from Standard Input in the following format:
L N
X_1
:
X_N
|
l, n = map(int, input().split())
t = []
pt = []
p = 0
for i in range(n):
t.append(int(input()))
pt.append(t)
pt.append(list(map(lambda x: abs(x - l), t)))
y = 0
for i in range(n):
if min(pt[0]) > min(pt[1]):
t = min(pt[0])
y += t
x = pt[0].index(t)
pt[0].pop(x)
pt[1].pop(x)
pt[0] = list(map(lambda x: abs(x - t), pt[0]))
pt[1] = list(map(lambda x: abs(x - l), pt[0]))
else:
t = min(pt[1])
y += t
x = pt[1].index(t)
pt[0].pop(x)
pt[1].pop(x)
pt[0] = list(map(lambda x: abs(x + t), pt[0]))
pt[1] = list(map(lambda x: abs(x - l), pt[0]))
print(y)
|
Statement
Takahashi Lake has a perimeter of L. On the circumference of the lake, there
is a residence of the lake's owner, Takahashi. Each point on the circumference
of the lake has a coordinate between 0 and L (including 0 but not L), which is
the distance from the Takahashi's residence, measured counter-clockwise.
There are N trees around the lake; the coordinate of the i-th tree is X_i.
There is no tree at coordinate 0, the location of Takahashi's residence.
Starting at his residence, Takahashi will repeat the following action:
* If all trees are burnt, terminate the process.
* Specify a direction: clockwise or counter-clockwise.
* Walk around the lake in the specified direction, until the coordinate of a tree that is not yet burnt is reached for the first time.
* When the coordinate with the tree is reached, burn that tree, stay at the position and go back to the first step.
Find the longest possible total distance Takahashi walks during the process.
|
[{"input": "10 3\n 2\n 7\n 9", "output": "15\n \n\nTakahashi walks the distance of 15 if the process goes as follows:\n\n * Walk a distance of 2 counter-clockwise, burn the tree at the coordinate 2 and stay there.\n * Walk a distance of 5 counter-clockwise, burn the tree at the coordinate 7 and stay there.\n * Walk a distance of 8 clockwise, burn the tree at the coordinate 9 and stay there.\n\n* * *"}, {"input": "10 6\n 1\n 2\n 3\n 6\n 7\n 9", "output": "27\n \n\n* * *"}, {"input": "314159265 7\n 21662711\n 77271666\n 89022761\n 156626166\n 160332356\n 166902656\n 298992265", "output": "1204124749"}]
|
Print the maximum number of robots that we can keep.
* * *
|
s350068576
|
Accepted
|
p02796
|
Input is given from Standard Input in the following format:
N
X_1 L_1
X_2 L_2
\vdots
X_N L_N
|
#!/usr/bin/env python3
(n,), *r = [[*map(int, i.split())] for i in open(0)]
s = sorted([[x + l, x - l] for x, l in r])
c = 1
p = s[0][0]
for i in s[1:]:
if i[1] >= p:
c += 1
p = i[0]
print(c)
|
Statement
In a factory, there are N robots placed on a number line. Robot i is placed at
coordinate X_i and can extend its arms of length L_i in both directions,
positive and negative.
We want to remove zero or more robots so that the movable ranges of arms of no
two remaining robots intersect. Here, for each i (1 \leq i \leq N), the
movable range of arms of Robot i is the part of the number line between the
coordinates X_i - L_i and X_i + L_i, excluding the endpoints.
Find the maximum number of robots that we can keep.
|
[{"input": "4\n 2 4\n 4 3\n 9 3\n 100 5", "output": "3\n \n\nBy removing Robot 2, we can keep the other three robots.\n\n* * *"}, {"input": "2\n 8 20\n 1 10", "output": "1\n \n\n* * *"}, {"input": "5\n 10 1\n 2 1\n 4 1\n 6 1\n 8 1", "output": "5"}]
|
Print the maximum number of robots that we can keep.
* * *
|
s402363225
|
Accepted
|
p02796
|
Input is given from Standard Input in the following format:
N
X_1 L_1
X_2 L_2
\vdots
X_N L_N
|
n = int(input())
arms = [input().split(" ") for _ in range(n)]
for a in arms:
for i in range(2):
a[i] = int(a[i])
arms.sort(key=lambda x: x[0])
res = []
for x, l in arms:
left, right = x - l, x + l
if not res or res[-1] <= left:
res.append(right)
elif res[-1] > right:
res[-1] = right
print(len(res))
|
Statement
In a factory, there are N robots placed on a number line. Robot i is placed at
coordinate X_i and can extend its arms of length L_i in both directions,
positive and negative.
We want to remove zero or more robots so that the movable ranges of arms of no
two remaining robots intersect. Here, for each i (1 \leq i \leq N), the
movable range of arms of Robot i is the part of the number line between the
coordinates X_i - L_i and X_i + L_i, excluding the endpoints.
Find the maximum number of robots that we can keep.
|
[{"input": "4\n 2 4\n 4 3\n 9 3\n 100 5", "output": "3\n \n\nBy removing Robot 2, we can keep the other three robots.\n\n* * *"}, {"input": "2\n 8 20\n 1 10", "output": "1\n \n\n* * *"}, {"input": "5\n 10 1\n 2 1\n 4 1\n 6 1\n 8 1", "output": "5"}]
|
Print the maximum number of robots that we can keep.
* * *
|
s887358008
|
Accepted
|
p02796
|
Input is given from Standard Input in the following format:
N
X_1 L_1
X_2 L_2
\vdots
X_N L_N
|
import collections
I = [int(_) for _ in open(0).read().split()]
N = I[0]
X = I[1::2]
L = I[2::2]
coord = [[x - l, x + l] for x, l in zip(X, L)]
x_i = collections.defaultdict(int)
for lr in coord:
x_i[lr[0]] = x_i[lr[1]] = 0
for i, v in enumerate(sorted(x_i.keys())):
x_i[v] = i
for i in range(N):
coord[i][0] = x_i[coord[i][0]]
coord[i][1] = x_i[coord[i][1]]
class SegmentTree:
def __init__(self, array, f, ti):
"""
Parameters
----------
array : list
to construct segment tree from
f : func
binary operation of the monoid
ti :
identity element of the monoid
"""
self.f = f
self.ti = ti
self.n = n = 2 ** (len(array).bit_length())
self.dat = dat = [ti] * n + array + [ti] * (n - len(array))
for i in range(n - 1, 0, -1): # build
dat[i] = f(dat[i << 1], dat[i << 1 | 1])
def update(self, p, v): # set value at position p (0-indexed)
f, n, dat = self.f, self.n, self.dat
p += n
dat[p] = v
while p > 1:
p >>= 1
dat[p] = f(dat[p << 1], dat[p << 1 | 1])
def query(self, l, r): # result on interval [l, r) (0-indexed)
f, ti, n, dat = self.f, self.ti, self.n, self.dat
res = ti
l += n
r += n
while l < r:
if l & 1:
res = f(res, dat[l])
l += 1
if r & 1:
r -= 1
res = f(dat[r], res)
l >>= 1
r >>= 1
return res
array = [-1] * len(x_i)
# array[r]: 腕が動く範囲が[l, r) となるロボットが存在するlの最大値
for l, r in coord:
array[r] = max(array[r], l)
now = 0
ans = 0
for i in range(len(array)):
if array[i] != -1 and array[i] >= now:
now = i
ans += 1
print(ans)
|
Statement
In a factory, there are N robots placed on a number line. Robot i is placed at
coordinate X_i and can extend its arms of length L_i in both directions,
positive and negative.
We want to remove zero or more robots so that the movable ranges of arms of no
two remaining robots intersect. Here, for each i (1 \leq i \leq N), the
movable range of arms of Robot i is the part of the number line between the
coordinates X_i - L_i and X_i + L_i, excluding the endpoints.
Find the maximum number of robots that we can keep.
|
[{"input": "4\n 2 4\n 4 3\n 9 3\n 100 5", "output": "3\n \n\nBy removing Robot 2, we can keep the other three robots.\n\n* * *"}, {"input": "2\n 8 20\n 1 10", "output": "1\n \n\n* * *"}, {"input": "5\n 10 1\n 2 1\n 4 1\n 6 1\n 8 1", "output": "5"}]
|
Print the maximum number of robots that we can keep.
* * *
|
s335326444
|
Wrong Answer
|
p02796
|
Input is given from Standard Input in the following format:
N
X_1 L_1
X_2 L_2
\vdots
X_N L_N
|
N = int(input())
List = [list(map(int, input().split())) for i in range(N)]
List.sort()
cnt = 0
for i in range(len(List) - 2):
migi = int(List[i - cnt][0] + List[i - cnt][1])
hidari = int(List[i + 2 - cnt][0] - List[i + 2 - cnt][1])
if migi > hidari:
List.pop(i - cnt)
cnt = cnt + 1
cnt = 0
for i in range(len(List) - 2):
if i > 1:
migi = int(List[i - 2 - cnt][0] + List[i - 2 - cnt][1])
hidari = int(List[i - cnt][0] - List[i - cnt][1])
if migi > hidari:
List.pop(i - cnt)
cnt = cnt + 1
cnt = 0
for i in range(len(List) - 1):
if i > 0:
hidari_1 = int(List[i - cnt][0] - List[i - cnt][1])
migi_1 = int(List[i - 1 - cnt][0] + List[i - 1 - cnt][1])
migi_2 = int(List[i - cnt][0] + List[i - cnt][1])
hidari_2 = int(List[i + 1 - cnt][0] - List[i + 1 - cnt][1])
if hidari_1 < migi_1 and migi_2 > hidari_2:
List.pop(i - cnt)
cnt = cnt + 1
cnt = 0
for i in range(len(List) - 1):
hidari = int(List[i + 1 - cnt][0] - List[i + 1 - cnt][1])
migi = int(List[i - cnt][0] + List[i - cnt][1])
if hidari < migi:
List.pop(i - cnt)
cnt = cnt + 1
length = len(List)
print(length)
|
Statement
In a factory, there are N robots placed on a number line. Robot i is placed at
coordinate X_i and can extend its arms of length L_i in both directions,
positive and negative.
We want to remove zero or more robots so that the movable ranges of arms of no
two remaining robots intersect. Here, for each i (1 \leq i \leq N), the
movable range of arms of Robot i is the part of the number line between the
coordinates X_i - L_i and X_i + L_i, excluding the endpoints.
Find the maximum number of robots that we can keep.
|
[{"input": "4\n 2 4\n 4 3\n 9 3\n 100 5", "output": "3\n \n\nBy removing Robot 2, we can keep the other three robots.\n\n* * *"}, {"input": "2\n 8 20\n 1 10", "output": "1\n \n\n* * *"}, {"input": "5\n 10 1\n 2 1\n 4 1\n 6 1\n 8 1", "output": "5"}]
|
Print the maximum number of robots that we can keep.
* * *
|
s659997274
|
Wrong Answer
|
p02796
|
Input is given from Standard Input in the following format:
N
X_1 L_1
X_2 L_2
\vdots
X_N L_N
|
N = int(input())
p = []
for _ in range(N):
x, n = [int(i) for i in input().split()]
p.append((x - n, x + n))
p.sort()
cc = [0 for _ in range(N)]
i = 0
j = 1
c = 0
while i < N and j < N:
# print(p[i][0],p [j][0], p[i][1])
if p[i][0] <= p[j][0] < p[i][1]:
# print("!")
j += 1
cc[j - 1] += 1
cc[i] += 1
else:
i += 1
j = i + 1
co = [int(i > 1) for i in cc]
# print(co)
if all([i == 0 for i in co]):
# print("!")
if all([i == 0 for i in cc]):
print(N)
else:
print(1)
quit()
print(N - sum(co))
|
Statement
In a factory, there are N robots placed on a number line. Robot i is placed at
coordinate X_i and can extend its arms of length L_i in both directions,
positive and negative.
We want to remove zero or more robots so that the movable ranges of arms of no
two remaining robots intersect. Here, for each i (1 \leq i \leq N), the
movable range of arms of Robot i is the part of the number line between the
coordinates X_i - L_i and X_i + L_i, excluding the endpoints.
Find the maximum number of robots that we can keep.
|
[{"input": "4\n 2 4\n 4 3\n 9 3\n 100 5", "output": "3\n \n\nBy removing Robot 2, we can keep the other three robots.\n\n* * *"}, {"input": "2\n 8 20\n 1 10", "output": "1\n \n\n* * *"}, {"input": "5\n 10 1\n 2 1\n 4 1\n 6 1\n 8 1", "output": "5"}]
|
Print the number of combinations in a line.
|
s491083170
|
Accepted
|
p02329
|
The input is given in the following format.
N V
a1 a2 ... aN
b1 b2 ... bN
c1 c2 ... cN
d1 d2 ... dN
|
from collections import Counter
n, v = map(int, input().split())
a, b, c, d = (tuple(map(int, input().split())) for _ in range(4))
ab = [ai + bi for ai in a for bi in b]
cd = [ci + di for ci in c for di in d]
abc, cdc = Counter(ab), Counter(cd)
ans = 0
for k, t in abc.items():
if v - k in cdc:
ans += t * cdc[v - k]
print(ans)
|
Coin Combination Problem
You have 4 bags A, B, C and D each of which includes N coins (there are
totally 4N coins). Values of the coins in each bag are ai, bi, ci and di
respectively.
Find the number of combinations that result when you choose one coin from each
bag (totally 4 coins) in such a way that the total value of the coins is V.
You should distinguish the coins in a bag.
|
[{"input": "3 14\n 3 1 2\n 4 8 2\n 1 2 3\n 7 3 2", "output": "9"}, {"input": "5 4\n 1 1 1 1 1\n 1 1 1 1 1\n 1 1 1 1 1\n 1 1 1 1 1", "output": "625"}]
|
For each print operation, print a list of keys obtained by inorder tree walk
and preorder tree walk in a line respectively. Put a space character _before
each key_.
|
s908806240
|
Wrong Answer
|
p02283
|
In the first line, the number of operations $m$ is given. In the following $m$
lines, operations represented by insert $k$ or print are given.
|
Binary Search Tree I
Search trees are data structures that support dynamic set operations including
insert, search, delete and so on. Thus a search tree can be used both as a
dictionary and as a priority queue.
Binary search tree is one of fundamental search trees. The keys in a binary
search tree are always stored in such a way as to satisfy the following binary
search tree property:
* Let $x$ be a node in a binary search tree. If $y$ is a node in the left subtree of $x$, then $y.key \leq x.key$. If $y$ is a node in the right subtree of $x$, then $x.key \leq y.key$.
The following figure shows an example of the binary search tree.
For example, keys of nodes which belong to the left sub-tree of the node
containing 80 are less than or equal to 80, and keys of nodes which belong to
the right sub-tree are more than or equal to 80. The binary search tree
property allows us to print out all the keys in the tree in sorted order by an
inorder tree walk.
A binary search tree should be implemented in such a way that the binary
search tree property continues to hold after modifications by insertions and
deletions. A binary search tree can be represented by a linked data structure
in which each node is an object. In addition to a key field and satellite
data, each node contains fields _left_ , _right_ , and _p_ that point to the
nodes corresponding to its left child, its right child, and its parent,
respectively.
To insert a new value $v$ into a binary search tree $T$, we can use the
procedure insert as shown in the following pseudo code. The insert procedure
is passed a node $z$ for which $z.key = v$, $z.left = NIL$, and $z.right =
NIL$. The procedure modifies $T$ and some of the fields of $z$ in such a way
that $z$ is inserted into an appropriate position in the tree.
1 insert(T, z)
2 y = NIL // parent of x
3 x = 'the root of T'
4 while x ≠ NIL
5 y = x // set the parent
6 if z.key < x.key
7 x = x.left // move to the left child
8 else
9 x = x.right // move to the right child
10 z.p = y
11
12 if y == NIL // T is empty
13 'the root of T' = z
14 else if z.key < y.key
15 y.left = z // z is the left child of y
16 else
17 y.right = z // z is the right child of y
Write a program which performs the following operations to a binary search
tree $T$.
* insert $k$: Insert a node containing $k$ as key into $T$.
* print: Print the keys of the binary search tree by inorder tree walk and preorder tree walk respectively.
You should use the above pseudo code to implement the insert operation. $T$ is
empty at the initial state.
|
[{"input": "8\n insert 30\n insert 88\n insert 12\n insert 1\n insert 20\n insert 17\n insert 25\n print", "output": "1 12 17 20 25 30 88\n 30 12 1 20 17 25 88"}]
|
|
For each print operation, print a list of keys obtained by inorder tree walk
and preorder tree walk in a line respectively. Put a space character _before
each key_.
|
s455878540
|
Accepted
|
p02283
|
In the first line, the number of operations $m$ is given. In the following $m$
lines, operations represented by insert $k$ or print are given.
|
m = int(input())
l, r = {}, {}
def insertnode(num, x):
"""xには毎回rootを設定(rootから順に比較してし、適した場所に追加)"""
if num < x:
if x in l:
if l[x] != 3000000000:
insertnode(num, l[x])
else:
l[x] = num
return
else:
l[x] = num
return
else:
if x in r:
if r[x] != 3000000000:
insertnode(num, r[x])
else:
r[x] = num
return
else:
r[x] = num
return
def inorder(num):
if num == 3000000000:
return
if num in l:
inorder(l[num])
else:
l[num] = 3000000000
inorder(l[num])
print(" " + str(num), end="")
if num in r:
inorder(r[num])
else:
r[num] = 3000000000
inorder(r[num])
def preorder(num):
if num == 3000000000:
return
print(" " + str(num), end="")
if num in l:
preorder(l[num])
else:
l[num] = 3000000000
preorder(l[num])
if num in r:
preorder(r[num])
else:
r[num] = 3000000000
preorder(r[num])
for i in range(m):
order = input()
if i == 0:
global root
root = int(order[7:])
continue
if order[0] == "i":
num = int(order[7:])
insertnode(num, root)
else:
inorder(root)
print()
preorder(root)
print()
|
Binary Search Tree I
Search trees are data structures that support dynamic set operations including
insert, search, delete and so on. Thus a search tree can be used both as a
dictionary and as a priority queue.
Binary search tree is one of fundamental search trees. The keys in a binary
search tree are always stored in such a way as to satisfy the following binary
search tree property:
* Let $x$ be a node in a binary search tree. If $y$ is a node in the left subtree of $x$, then $y.key \leq x.key$. If $y$ is a node in the right subtree of $x$, then $x.key \leq y.key$.
The following figure shows an example of the binary search tree.

For example, keys of nodes which belong to the left sub-tree of the node
containing 80 are less than or equal to 80, and keys of nodes which belong to
the right sub-tree are more than or equal to 80. The binary search tree
property allows us to print out all the keys in the tree in sorted order by an
inorder tree walk.
A binary search tree should be implemented in such a way that the binary
search tree property continues to hold after modifications by insertions and
deletions. A binary search tree can be represented by a linked data structure
in which each node is an object. In addition to a key field and satellite
data, each node contains fields _left_ , _right_ , and _p_ that point to the
nodes corresponding to its left child, its right child, and its parent,
respectively.
To insert a new value $v$ into a binary search tree $T$, we can use the
procedure insert as shown in the following pseudo code. The insert procedure
is passed a node $z$ for which $z.key = v$, $z.left = NIL$, and $z.right =
NIL$. The procedure modifies $T$ and some of the fields of $z$ in such a way
that $z$ is inserted into an appropriate position in the tree.
1 insert(T, z)
2 y = NIL // parent of x
3 x = 'the root of T'
4 while x ≠ NIL
5 y = x // set the parent
6 if z.key < x.key
7 x = x.left // move to the left child
8 else
9 x = x.right // move to the right child
10 z.p = y
11
12 if y == NIL // T is empty
13 'the root of T' = z
14 else if z.key < y.key
15 y.left = z // z is the left child of y
16 else
17 y.right = z // z is the right child of y
Write a program which performs the following operations to a binary search
tree $T$.
* insert $k$: Insert a node containing $k$ as key into $T$.
* print: Print the keys of the binary search tree by inorder tree walk and preorder tree walk respectively.
You should use the above pseudo code to implement the insert operation. $T$ is
empty at the initial state.
|
[{"input": "8\n insert 30\n insert 88\n insert 12\n insert 1\n insert 20\n insert 17\n insert 25\n print", "output": "1 12 17 20 25 30 88\n 30 12 1 20 17 25 88"}]
|
For each print operation, print a list of keys obtained by inorder tree walk
and preorder tree walk in a line respectively. Put a space character _before
each key_.
|
s943401447
|
Accepted
|
p02283
|
In the first line, the number of operations $m$ is given. In the following $m$
lines, operations represented by insert $k$ or print are given.
|
# coding: utf-8
Node = list()
n = int(input())
def insertKey(k):
idx = len(Node)
Node.append([k, -1, -1])
if idx > 0:
pPrv = -1
pTmp = 0
while pTmp != -1:
pPrv = pTmp
if k < Node[pTmp][0]:
pTmp = Node[pTmp][1]
else:
pTmp = Node[pTmp][2]
if Node[-1][0] < Node[pPrv][0]:
Node[pPrv][1] = idx
else:
Node[pPrv][2] = idx
def inOrder(num):
if num == -1:
return
inOrder(Node[num][1])
print(" {}".format(Node[num][0]), end="")
inOrder(Node[num][2])
def preOrder(num):
if num == -1:
return
print(" {}".format(Node[num][0]), end="")
preOrder(Node[num][1])
preOrder(Node[num][2])
for i in range(n):
temp = input().strip()
if temp[:6] == "insert":
insertKey(int(temp[7:]))
else:
inOrder(0)
print("")
preOrder(0)
print("")
|
Binary Search Tree I
Search trees are data structures that support dynamic set operations including
insert, search, delete and so on. Thus a search tree can be used both as a
dictionary and as a priority queue.
Binary search tree is one of fundamental search trees. The keys in a binary
search tree are always stored in such a way as to satisfy the following binary
search tree property:
* Let $x$ be a node in a binary search tree. If $y$ is a node in the left subtree of $x$, then $y.key \leq x.key$. If $y$ is a node in the right subtree of $x$, then $x.key \leq y.key$.
The following figure shows an example of the binary search tree.

For example, keys of nodes which belong to the left sub-tree of the node
containing 80 are less than or equal to 80, and keys of nodes which belong to
the right sub-tree are more than or equal to 80. The binary search tree
property allows us to print out all the keys in the tree in sorted order by an
inorder tree walk.
A binary search tree should be implemented in such a way that the binary
search tree property continues to hold after modifications by insertions and
deletions. A binary search tree can be represented by a linked data structure
in which each node is an object. In addition to a key field and satellite
data, each node contains fields _left_ , _right_ , and _p_ that point to the
nodes corresponding to its left child, its right child, and its parent,
respectively.
To insert a new value $v$ into a binary search tree $T$, we can use the
procedure insert as shown in the following pseudo code. The insert procedure
is passed a node $z$ for which $z.key = v$, $z.left = NIL$, and $z.right =
NIL$. The procedure modifies $T$ and some of the fields of $z$ in such a way
that $z$ is inserted into an appropriate position in the tree.
1 insert(T, z)
2 y = NIL // parent of x
3 x = 'the root of T'
4 while x ≠ NIL
5 y = x // set the parent
6 if z.key < x.key
7 x = x.left // move to the left child
8 else
9 x = x.right // move to the right child
10 z.p = y
11
12 if y == NIL // T is empty
13 'the root of T' = z
14 else if z.key < y.key
15 y.left = z // z is the left child of y
16 else
17 y.right = z // z is the right child of y
Write a program which performs the following operations to a binary search
tree $T$.
* insert $k$: Insert a node containing $k$ as key into $T$.
* print: Print the keys of the binary search tree by inorder tree walk and preorder tree walk respectively.
You should use the above pseudo code to implement the insert operation. $T$ is
empty at the initial state.
|
[{"input": "8\n insert 30\n insert 88\n insert 12\n insert 1\n insert 20\n insert 17\n insert 25\n print", "output": "1 12 17 20 25 30 88\n 30 12 1 20 17 25 88"}]
|
If the elements of the sequence are pairwise distinct, print `YES`; otherwise,
print `NO`.
* * *
|
s686177671
|
Accepted
|
p02779
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
|
# -*- coding: utf-8 -*-
import sys
def input():
return sys.stdin.readline().strip()
def list2d(a, b, c):
return [[c] * b for i in range(a)]
def list3d(a, b, c, d):
return [[[d] * c for j in range(b)] for i in range(a)]
def list4d(a, b, c, d, e):
return [[[[e] * d for j in range(c)] for j in range(b)] for i in range(a)]
def ceil(x, y=1):
return int(-(-x // y))
def INT():
return int(input())
def MAP():
return map(int, input().split())
def LIST(N=None):
return list(MAP()) if N is None else [INT() for i in range(N)]
def Yes():
print("Yes")
def No():
print("No")
def YES():
print("YES")
def NO():
print("NO")
sys.setrecursionlimit(10**9)
INF = 10**18
MOD = 10**9 + 7
N = INT()
A = LIST()
if len(A) == len(set(A)):
YES()
else:
NO()
|
Statement
Given is a sequence of integers A_1, A_2, ..., A_N. If its elements are
pairwise distinct, print `YES`; otherwise, print `NO`.
|
[{"input": "5\n 2 6 1 4 5", "output": "YES\n \n\nThe elements are pairwise distinct.\n\n* * *"}, {"input": "6\n 4 1 3 1 6 2", "output": "NO\n \n\nThe second and fourth elements are identical.\n\n* * *"}, {"input": "2\n 10000000 10000000", "output": "NO"}]
|
If the elements of the sequence are pairwise distinct, print `YES`; otherwise,
print `NO`.
* * *
|
s142859855
|
Wrong Answer
|
p02779
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
|
i = input
print(["YES", "NO"][int(i()) == len(set(i().split()))])
|
Statement
Given is a sequence of integers A_1, A_2, ..., A_N. If its elements are
pairwise distinct, print `YES`; otherwise, print `NO`.
|
[{"input": "5\n 2 6 1 4 5", "output": "YES\n \n\nThe elements are pairwise distinct.\n\n* * *"}, {"input": "6\n 4 1 3 1 6 2", "output": "NO\n \n\nThe second and fourth elements are identical.\n\n* * *"}, {"input": "2\n 10000000 10000000", "output": "NO"}]
|
If the elements of the sequence are pairwise distinct, print `YES`; otherwise,
print `NO`.
* * *
|
s332511996
|
Wrong Answer
|
p02779
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
|
print("YES")
|
Statement
Given is a sequence of integers A_1, A_2, ..., A_N. If its elements are
pairwise distinct, print `YES`; otherwise, print `NO`.
|
[{"input": "5\n 2 6 1 4 5", "output": "YES\n \n\nThe elements are pairwise distinct.\n\n* * *"}, {"input": "6\n 4 1 3 1 6 2", "output": "NO\n \n\nThe second and fourth elements are identical.\n\n* * *"}, {"input": "2\n 10000000 10000000", "output": "NO"}]
|
If the elements of the sequence are pairwise distinct, print `YES`; otherwise,
print `NO`.
* * *
|
s673528472
|
Runtime Error
|
p02779
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
|
N, K = input().split()
P = input().split()
max_sum = 0
for i in range(int(N) - int(K) + 1):
sum = 0
for k in range(i, i + int(K)):
print(k)
p = int(P[k])
sum += (p / 2) + 0.5
if max_sum < sum:
max_sum = sum
print(float(max_sum))
|
Statement
Given is a sequence of integers A_1, A_2, ..., A_N. If its elements are
pairwise distinct, print `YES`; otherwise, print `NO`.
|
[{"input": "5\n 2 6 1 4 5", "output": "YES\n \n\nThe elements are pairwise distinct.\n\n* * *"}, {"input": "6\n 4 1 3 1 6 2", "output": "NO\n \n\nThe second and fourth elements are identical.\n\n* * *"}, {"input": "2\n 10000000 10000000", "output": "NO"}]
|
If the elements of the sequence are pairwise distinct, print `YES`; otherwise,
print `NO`.
* * *
|
s116976974
|
Runtime Error
|
p02779
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
|
N, K = map(int, input().split())
p = list(map(int, input().split()))
max = 0
for i in range(N - K + 1):
s = 0
for j in range(i, i + K):
s += p[j]
if s > max:
max = s
print((max + K) / 2)
|
Statement
Given is a sequence of integers A_1, A_2, ..., A_N. If its elements are
pairwise distinct, print `YES`; otherwise, print `NO`.
|
[{"input": "5\n 2 6 1 4 5", "output": "YES\n \n\nThe elements are pairwise distinct.\n\n* * *"}, {"input": "6\n 4 1 3 1 6 2", "output": "NO\n \n\nThe second and fourth elements are identical.\n\n* * *"}, {"input": "2\n 10000000 10000000", "output": "NO"}]
|
If the elements of the sequence are pairwise distinct, print `YES`; otherwise,
print `NO`.
* * *
|
s099358182
|
Accepted
|
p02779
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
|
print("YNEOS"[int(input()) > len(set(input().split())) :: 2])
|
Statement
Given is a sequence of integers A_1, A_2, ..., A_N. If its elements are
pairwise distinct, print `YES`; otherwise, print `NO`.
|
[{"input": "5\n 2 6 1 4 5", "output": "YES\n \n\nThe elements are pairwise distinct.\n\n* * *"}, {"input": "6\n 4 1 3 1 6 2", "output": "NO\n \n\nThe second and fourth elements are identical.\n\n* * *"}, {"input": "2\n 10000000 10000000", "output": "NO"}]
|
If the elements of the sequence are pairwise distinct, print `YES`; otherwise,
print `NO`.
* * *
|
s699306905
|
Accepted
|
p02779
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
|
n = int(input())
xx = input().split()
x = []
for k in range(len(xx)):
x.append(int(xx[k]))
x = sorted(x)
ok = "YES"
for k in range(len(x) - 1):
if x[k] == x[k + 1]:
ok = "NO"
break
print(ok)
|
Statement
Given is a sequence of integers A_1, A_2, ..., A_N. If its elements are
pairwise distinct, print `YES`; otherwise, print `NO`.
|
[{"input": "5\n 2 6 1 4 5", "output": "YES\n \n\nThe elements are pairwise distinct.\n\n* * *"}, {"input": "6\n 4 1 3 1 6 2", "output": "NO\n \n\nThe second and fourth elements are identical.\n\n* * *"}, {"input": "2\n 10000000 10000000", "output": "NO"}]
|
If the elements of the sequence are pairwise distinct, print `YES`; otherwise,
print `NO`.
* * *
|
s431903924
|
Accepted
|
p02779
|
Input is given from Standard Input in the following format:
N
A_1 ... A_N
|
def merge(l, r, a):
l1 = len(l)
r1 = len(r)
i, j, k = 0, 0, 0
while j < l1 and k < r1:
if l[j] < r[k]:
a[i] = l[j]
j += 1
elif l[j] == r[k]:
a[i] = l[j]
j += 1
global res
print("NO")
quit()
return 0
else:
a[i] = r[k]
k += 1
i += 1
while j < l1:
a[i] = l[j]
j += 1
i += 1
while k < r1:
a[i] = r[k]
k += 1
i += 1
return a
def mergeSort(a):
n = len(a)
if n == 1:
return a
else:
mid = n // 2
left = []
right = []
for i in range(mid):
left.append(a[i])
for i in range(mid, n):
right.append(a[i])
mergeSort(left)
mergeSort(right)
merge(left, right, a)
return a
n = int(input())
a = list(map(int, input().split()))
res = True
s = mergeSort(a)
if res:
print("YES")
else:
print("NO")
|
Statement
Given is a sequence of integers A_1, A_2, ..., A_N. If its elements are
pairwise distinct, print `YES`; otherwise, print `NO`.
|
[{"input": "5\n 2 6 1 4 5", "output": "YES\n \n\nThe elements are pairwise distinct.\n\n* * *"}, {"input": "6\n 4 1 3 1 6 2", "output": "NO\n \n\nThe second and fourth elements are identical.\n\n* * *"}, {"input": "2\n 10000000 10000000", "output": "NO"}]
|
Print the probability of having more heads than tails. The output is
considered correct when the absolute error is not greater than 10^{-9}.
* * *
|
s850665597
|
Accepted
|
p03168
|
Input is given from Standard Input in the following format:
N
p_1 p_2 \ldots p_N
|
def wczytaj_liste():
wczytana_lista = input()
lista_znakow = wczytana_lista.split()
ostateczna_lista = []
for element in lista_znakow:
ostateczna_lista.append(int(element))
return ostateczna_lista
def wczytaj_rzeczywiste():
wczytana_lista = input()
lista_znakow = wczytana_lista.split()
ostateczna_lista = []
for element in lista_znakow:
ostateczna_lista.append(float(element))
return ostateczna_lista
def rzuc_grosza_wiedzminowi_migusiem():
N = wczytaj_liste()[0]
prawdopodopienstwa = wczytaj_rzeczywiste()
przed_rzutem = [1.0]
for moneta in prawdopodopienstwa:
po_rzucie = []
for i in range(len(przed_rzutem)):
if i > 0:
po_rzucie.append(
przed_rzutem[i] * (1 - moneta) + przed_rzutem[i - 1] * (moneta)
)
else:
po_rzucie.append(przed_rzutem[0] * (1 - moneta))
po_rzucie.append(przed_rzutem[-1] * moneta)
przed_rzutem = po_rzucie
odp = sum(przed_rzutem[N // 2 + 1 :])
print(odp)
rzuc_grosza_wiedzminowi_migusiem()
|
Statement
Let N be a positive odd number.
There are N coins, numbered 1, 2, \ldots, N. For each i (1 \leq i \leq N),
when Coin i is tossed, it comes up heads with probability p_i and tails with
probability 1 - p_i.
Taro has tossed all the N coins. Find the probability of having more heads
than tails.
|
[{"input": "3\n 0.30 0.60 0.80", "output": "0.612\n \n\nThe probability of each case where we have more heads than tails is as\nfollows:\n\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Head) is 0.3 \u00d7 0.6 \u00d7 0.8 = 0.144;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Tail, Head, Head) is 0.7 \u00d7 0.6 \u00d7 0.8 = 0.336;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Tail, Head) is 0.3 \u00d7 0.4 \u00d7 0.8 = 0.096;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Tail) is 0.3 \u00d7 0.6 \u00d7 0.2 = 0.036.\n\nThus, the probability of having more heads than tails is 0.144 + 0.336 + 0.096\n+ 0.036 = 0.612.\n\n* * *"}, {"input": "1\n 0.50", "output": "0.5\n \n\nOutputs such as `0.500`, `0.500000001` and `0.499999999` are also considered\ncorrect.\n\n* * *"}, {"input": "5\n 0.42 0.01 0.42 0.99 0.42", "output": "0.3821815872"}]
|
Print the probability of having more heads than tails. The output is
considered correct when the absolute error is not greater than 10^{-9}.
* * *
|
s247144868
|
Runtime Error
|
p03168
|
Input is given from Standard Input in the following format:
N
p_1 p_2 \ldots p_N
|
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ff first
#define ss second
#define pb push_back
#define pf push_front
#define mp make_pair
#define pu push
#define pp pop_back
#define in insert
#define MOD 1000000007
#define endl "\n"
#define sz(a) (int)((a).size())
#define all(x) (x).begin(), (x).end()
#define trace(x) cerr << #x << ": " << x << " " << endl;
#define prv(a) for(auto x : a) cout << x << ' ';cout << '\n';
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define OTP(s) cout<<s<<endl;
#define FOR(i,j,k,l) for(int i=j;i<k;i+=l)
#define REP(i,j) FOR(i,0,j,1)
inline ll add(ll a, ll b){a += b; if(a >= MOD)a -= MOD; return a;}
inline ll sub(ll a, ll b){a -= b; if(a < 0)a += MOD; return a;}
inline ll mul(ll a, ll b){return (ll)((ll) a * b %MOD);}
typedef vector<ll> vl;
typedef vector<vl> vvl;
typedef pair<ll,ll> pll;
typedef vector<pll> vpll;
ll min(ll a,ll b)
{
return a>b?b:a;
}
ll max(ll a,ll b)
{
return a>b?a:b;
}
ll n;
double q[3000][3000];
double p[10000];
int main()
{
IOS
cin>>n;
REP(i,n)
{
cin>>p[i+1];
}
double prod=1;
q[0][0]=1;
FOR(i,1,n+1,1)
{
prod*=0;
q[0][i]=prod;
}
prod=1;
REP(i,n)
{
prod*=p[i+1];
q[i+1][0] = prod;
}
FOR(i,1,n+1,1)
{
FOR(j,1,i+1,1)
{
q[i][j] = p[i]*q[i-1][j] + (1-p[i])*q[i-1][j-1];
}
}
// REP(i,n+1)
// {
// REP(j,n+1)
// {
// cout<<q[i][j]<<" ";
// }
// cout<<endl;
// }
double ans = 0;
REP(i,(n-1)/2+1)
{
ans+=q[n][i];
}
cout<<fixed<<setprecision(12)<<ans<<endl;
}
|
Statement
Let N be a positive odd number.
There are N coins, numbered 1, 2, \ldots, N. For each i (1 \leq i \leq N),
when Coin i is tossed, it comes up heads with probability p_i and tails with
probability 1 - p_i.
Taro has tossed all the N coins. Find the probability of having more heads
than tails.
|
[{"input": "3\n 0.30 0.60 0.80", "output": "0.612\n \n\nThe probability of each case where we have more heads than tails is as\nfollows:\n\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Head) is 0.3 \u00d7 0.6 \u00d7 0.8 = 0.144;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Tail, Head, Head) is 0.7 \u00d7 0.6 \u00d7 0.8 = 0.336;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Tail, Head) is 0.3 \u00d7 0.4 \u00d7 0.8 = 0.096;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Tail) is 0.3 \u00d7 0.6 \u00d7 0.2 = 0.036.\n\nThus, the probability of having more heads than tails is 0.144 + 0.336 + 0.096\n+ 0.036 = 0.612.\n\n* * *"}, {"input": "1\n 0.50", "output": "0.5\n \n\nOutputs such as `0.500`, `0.500000001` and `0.499999999` are also considered\ncorrect.\n\n* * *"}, {"input": "5\n 0.42 0.01 0.42 0.99 0.42", "output": "0.3821815872"}]
|
Print the probability of having more heads than tails. The output is
considered correct when the absolute error is not greater than 10^{-9}.
* * *
|
s938853869
|
Accepted
|
p03168
|
Input is given from Standard Input in the following format:
N
p_1 p_2 \ldots p_N
|
# -*- coding: utf-8 -*-
#############
# Libraries #
#############
import sys
input = sys.stdin.readline
import math
# from math import gcd
import bisect
import heapq
from collections import defaultdict
from collections import deque
from collections import Counter
from functools import lru_cache
#############
# Constants #
#############
MOD = 10**9 + 7
INF = float("inf")
AZ = "abcdefghijklmnopqrstuvwxyz"
#############
# Functions #
#############
######INPUT######
def I():
return int(input().strip())
def S():
return input().strip()
def IL():
return list(map(int, input().split()))
def SL():
return list(map(str, input().split()))
def ILs(n):
return list(int(input()) for _ in range(n))
def SLs(n):
return list(input().strip() for _ in range(n))
def ILL(n):
return [list(map(int, input().split())) for _ in range(n)]
def SLL(n):
return [list(map(str, input().split())) for _ in range(n)]
######OUTPUT######
def P(arg):
print(arg)
return
def Y():
print("Yes")
return
def N():
print("No")
return
def E():
exit()
def PE(arg):
print(arg)
exit()
def YE():
print("Yes")
exit()
def NE():
print("No")
exit()
#####Shorten#####
def DD(arg):
return defaultdict(arg)
#####Inverse#####
def inv(n):
return pow(n, MOD - 2, MOD)
######Combination######
kaijo_memo = []
def kaijo(n):
if len(kaijo_memo) > n:
return kaijo_memo[n]
if len(kaijo_memo) == 0:
kaijo_memo.append(1)
while len(kaijo_memo) <= n:
kaijo_memo.append(kaijo_memo[-1] * len(kaijo_memo) % MOD)
return kaijo_memo[n]
gyaku_kaijo_memo = []
def gyaku_kaijo(n):
if len(gyaku_kaijo_memo) > n:
return gyaku_kaijo_memo[n]
if len(gyaku_kaijo_memo) == 0:
gyaku_kaijo_memo.append(1)
while len(gyaku_kaijo_memo) <= n:
gyaku_kaijo_memo.append(
gyaku_kaijo_memo[-1] * pow(len(gyaku_kaijo_memo), MOD - 2, MOD) % MOD
)
return gyaku_kaijo_memo[n]
def nCr(n, r):
if n == r:
return 1
if n < r or r < 0:
return 0
ret = 1
ret = ret * kaijo(n) % MOD
ret = ret * gyaku_kaijo(r) % MOD
ret = ret * gyaku_kaijo(n - r) % MOD
return ret
######Factorization######
def factorization(n):
arr = []
temp = n
for i in range(2, int(-(-(n**0.5) // 1)) + 1):
if temp % i == 0:
cnt = 0
while temp % i == 0:
cnt += 1
temp //= i
arr.append([i, cnt])
if temp != 1:
arr.append([temp, 1])
if arr == []:
arr.append([n, 1])
return arr
#####MakeDivisors######
def make_divisors(n):
divisors = []
for i in range(1, int(n**0.5) + 1):
if n % i == 0:
divisors.append(i)
if i != n // i:
divisors.append(n // i)
return divisors
#####MakePrimes######
def make_primes(N):
max = int(math.sqrt(N))
seachList = [i for i in range(2, N + 1)]
primeNum = []
while seachList[0] <= max:
primeNum.append(seachList[0])
tmp = seachList[0]
seachList = [i for i in seachList if i % tmp != 0]
primeNum.extend(seachList)
return primeNum
#####GCD#####
def gcd(a, b):
while b:
a, b = b, a % b
return a
#####LCM#####
def lcm(a, b):
return a * b // gcd(a, b)
#####BitCount#####
def count_bit(n):
count = 0
while n:
n &= n - 1
count += 1
return count
#####ChangeBase#####
def base_10_to_n(X, n):
if X // n:
return base_10_to_n(X // n, n) + [X % n]
return [X % n]
def base_n_to_10(X, n):
return sum(int(str(X)[-i - 1]) * n**i for i in range(len(str(X))))
def base_10_to_n_without_0(X, n):
X -= 1
if X // n:
return base_10_to_n_without_0(X // n, n) + [X % n]
return [X % n]
#####IntLog#####
def int_log(n, a):
count = 0
while n >= a:
n //= a
count += 1
return count
#############
# Main Code #
#############
N = I()
P = [0] + list(map(float, input().split()))
dp = [[0 for j in range(N + 1)] for i in range(N + 1)]
dp[0][0] = 1
for i in range(1, N + 1):
for j in range(i + 1):
if j:
dp[i][j] = dp[i - 1][j] * (1 - P[i]) + dp[i - 1][j - 1] * P[i]
else:
dp[i][j] = dp[i - 1][j] * (1 - P[i])
print(sum(dp[-1][-(-N // 2) :]))
|
Statement
Let N be a positive odd number.
There are N coins, numbered 1, 2, \ldots, N. For each i (1 \leq i \leq N),
when Coin i is tossed, it comes up heads with probability p_i and tails with
probability 1 - p_i.
Taro has tossed all the N coins. Find the probability of having more heads
than tails.
|
[{"input": "3\n 0.30 0.60 0.80", "output": "0.612\n \n\nThe probability of each case where we have more heads than tails is as\nfollows:\n\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Head) is 0.3 \u00d7 0.6 \u00d7 0.8 = 0.144;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Tail, Head, Head) is 0.7 \u00d7 0.6 \u00d7 0.8 = 0.336;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Tail, Head) is 0.3 \u00d7 0.4 \u00d7 0.8 = 0.096;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Tail) is 0.3 \u00d7 0.6 \u00d7 0.2 = 0.036.\n\nThus, the probability of having more heads than tails is 0.144 + 0.336 + 0.096\n+ 0.036 = 0.612.\n\n* * *"}, {"input": "1\n 0.50", "output": "0.5\n \n\nOutputs such as `0.500`, `0.500000001` and `0.499999999` are also considered\ncorrect.\n\n* * *"}, {"input": "5\n 0.42 0.01 0.42 0.99 0.42", "output": "0.3821815872"}]
|
Print the probability of having more heads than tails. The output is
considered correct when the absolute error is not greater than 10^{-9}.
* * *
|
s975986929
|
Wrong Answer
|
p03168
|
Input is given from Standard Input in the following format:
N
p_1 p_2 \ldots p_N
|
n = int(input())
v = list(map(float, input().split()))
dp = [[0.0] * (len(v) + 1) for i in range(len(v))]
for x in range(n):
for a in range(x + 2):
if x == 0 and a == 0:
dp[x][a] = v[x]
elif x == 0 and a == 1:
dp[x][a] = 1 - v[x]
elif a > n / 2:
dp[x][a] = dp[x - 1][a] * v[x]
else:
dp[x][a] = dp[x - 1][a] * v[x] + dp[x - 1][a - 1] * (1 - v[x])
# import numpy
# print(numpy.matrix(dp));
print(sum(dp[n - 1]))
|
Statement
Let N be a positive odd number.
There are N coins, numbered 1, 2, \ldots, N. For each i (1 \leq i \leq N),
when Coin i is tossed, it comes up heads with probability p_i and tails with
probability 1 - p_i.
Taro has tossed all the N coins. Find the probability of having more heads
than tails.
|
[{"input": "3\n 0.30 0.60 0.80", "output": "0.612\n \n\nThe probability of each case where we have more heads than tails is as\nfollows:\n\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Head) is 0.3 \u00d7 0.6 \u00d7 0.8 = 0.144;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Tail, Head, Head) is 0.7 \u00d7 0.6 \u00d7 0.8 = 0.336;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Tail, Head) is 0.3 \u00d7 0.4 \u00d7 0.8 = 0.096;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Tail) is 0.3 \u00d7 0.6 \u00d7 0.2 = 0.036.\n\nThus, the probability of having more heads than tails is 0.144 + 0.336 + 0.096\n+ 0.036 = 0.612.\n\n* * *"}, {"input": "1\n 0.50", "output": "0.5\n \n\nOutputs such as `0.500`, `0.500000001` and `0.499999999` are also considered\ncorrect.\n\n* * *"}, {"input": "5\n 0.42 0.01 0.42 0.99 0.42", "output": "0.3821815872"}]
|
Print the probability of having more heads than tails. The output is
considered correct when the absolute error is not greater than 10^{-9}.
* * *
|
s847154120
|
Accepted
|
p03168
|
Input is given from Standard Input in the following format:
N
p_1 p_2 \ldots p_N
|
def wolne_mnozenie_wielomianu(wielomian1, wielomian2):
odp = [0.0] * (len(wielomian1) + len(wielomian2) - 1)
for i in range(len(wielomian1)):
for j in range(len(wielomian2)):
odp[i + j] += wielomian1[i] * wielomian2[j]
while len(odp) > 1 and odp[-1] == 0.0:
odp.pop()
return odp
def wyrownaj(wielomian1, wielomian2):
if len(wielomian1) > len(wielomian2):
wielomian2 = wielomian2 + [0.0] * (len(wielomian1) - len(wielomian2))
if len(wielomian2) > len(wielomian1):
wielomian1 = wielomian1 + [0.0] * (len(wielomian2) - len(wielomian1))
return wielomian1, wielomian2
def dodawanie_wielomianu(wielomian1, wielomian2):
wielomian1, wielomian2 = wyrownaj(wielomian1, wielomian2)
odp = [0.0] * len(wielomian2)
for i in range(len(wielomian1)):
odp[i] = wielomian1[i] + wielomian2[i]
while len(odp) > 1 and odp[-1] == 0.0:
odp.pop()
return odp
def odejmowanie_wielomianu(wielomian1, wielomian2):
wielomian1, wielomian2 = wyrownaj(wielomian1, wielomian2)
odp = [0.0] * len(wielomian2)
for i in range(len(wielomian1)):
odp[i] = wielomian1[i] - wielomian2[i]
while len(odp) > 1 and odp[-1] == 0.0:
odp.pop()
return odp
def szybkie_mnozenie_wielomianu(wielomian1, wielomian2):
wielomian1, wielomian2 = wyrownaj(wielomian1, wielomian2)
if len(wielomian1) < 3:
return wolne_mnozenie_wielomianu(wielomian1, wielomian2)
k = len(wielomian1) // 2
a = wielomian1[k:]
b = wielomian1[:k]
c = wielomian2[k:]
d = wielomian2[:k]
ac = szybkie_mnozenie_wielomianu(a, c)
bd = szybkie_mnozenie_wielomianu(b, d)
w = szybkie_mnozenie_wielomianu(
dodawanie_wielomianu(a, b), dodawanie_wielomianu(c, d)
)
w_ac_bd = odejmowanie_wielomianu(w, dodawanie_wielomianu(ac, bd))
ac = [0.0] * 2 * k + ac
w_ac_bd = [0.0] * k + w_ac_bd
odp = dodawanie_wielomianu(ac, dodawanie_wielomianu(bd, w_ac_bd))
while len(odp) > 1 and odp[-1] == 0.0:
odp.pop()
return odp
def wczytaj_liste():
wczytana_lista = input()
lista_znakow = wczytana_lista.split()
ostateczna_lista = []
for element in lista_znakow:
ostateczna_lista.append(int(element))
return ostateczna_lista
def wczytaj_rzeczywiste():
wczytana_lista = input()
lista_znakow = wczytana_lista.split()
ostateczna_lista = []
for element in lista_znakow:
ostateczna_lista.append(float(element))
return ostateczna_lista
def wymnoz_duzo_wielomianow(wielomiany):
if len(wielomiany) == 1:
return wielomiany[0]
k = (len(wielomiany) + 1) // 2
lewo = wymnoz_duzo_wielomianow(wielomiany[:k])
prawo = wymnoz_duzo_wielomianow(wielomiany[k:])
return szybkie_mnozenie_wielomianu(lewo, prawo)
def rzuc_grosza_wiedzminowi_natychmiast():
N = wczytaj_liste()[0]
prawdopodopienstwa = wczytaj_rzeczywiste()
rzuty = []
for moneta in prawdopodopienstwa:
rzut = [1 - moneta, moneta]
rzuty.append(rzut)
po_rzutach = wymnoz_duzo_wielomianow(rzuty)
odp = sum(po_rzutach[N // 2 + 1 :])
print(odp)
rzuc_grosza_wiedzminowi_natychmiast()
|
Statement
Let N be a positive odd number.
There are N coins, numbered 1, 2, \ldots, N. For each i (1 \leq i \leq N),
when Coin i is tossed, it comes up heads with probability p_i and tails with
probability 1 - p_i.
Taro has tossed all the N coins. Find the probability of having more heads
than tails.
|
[{"input": "3\n 0.30 0.60 0.80", "output": "0.612\n \n\nThe probability of each case where we have more heads than tails is as\nfollows:\n\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Head) is 0.3 \u00d7 0.6 \u00d7 0.8 = 0.144;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Tail, Head, Head) is 0.7 \u00d7 0.6 \u00d7 0.8 = 0.336;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Tail, Head) is 0.3 \u00d7 0.4 \u00d7 0.8 = 0.096;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Tail) is 0.3 \u00d7 0.6 \u00d7 0.2 = 0.036.\n\nThus, the probability of having more heads than tails is 0.144 + 0.336 + 0.096\n+ 0.036 = 0.612.\n\n* * *"}, {"input": "1\n 0.50", "output": "0.5\n \n\nOutputs such as `0.500`, `0.500000001` and `0.499999999` are also considered\ncorrect.\n\n* * *"}, {"input": "5\n 0.42 0.01 0.42 0.99 0.42", "output": "0.3821815872"}]
|
Print the probability of having more heads than tails. The output is
considered correct when the absolute error is not greater than 10^{-9}.
* * *
|
s546088438
|
Accepted
|
p03168
|
Input is given from Standard Input in the following format:
N
p_1 p_2 \ldots p_N
|
#!/usr/bin/env python3
# vim: set fileencoding=utf-8
# pylint: disable=unused-import, invalid-name, missing-docstring, bad-continuation
"""Module docstring
"""
import functools
import heapq
import itertools
import logging
import math
import random
import string
import sys
from argparse import ArgumentParser
from collections import defaultdict, deque
from copy import deepcopy
def prob(i, values):
result = 1
idx = 0
for idx, v in enumerate(values):
i, rest = divmod(i, 2)
if rest == 1:
result *= v
else:
result *= 1 - v
idx += 1
return result
def solve(values, nb):
LOG.debug((values))
dp = [[0] * (nb + 1) for _ in range(nb // 2 + 1)]
dp[0][0] = 1
for j in range(1, nb + 1):
dp[0][j] = dp[0][j - 1] * (1 - values[j - 1])
total = dp[0][-1]
for i in range(1, nb // 2 + 1):
for j in range(i, nb + 1):
dp[i][j] = (
dp[i - 1][j - 1] * values[j - 1] + (1 - values[j - 1]) * dp[i][j - 1]
)
total += dp[i][-1]
# LOG.debug(("\n" + "\n".join(map(str, dp))))
return 1 - total
def do_job():
"Do the work"
LOG.debug("Start working")
# first line is number of test cases
N = int(input())
values = list(map(float, input().split()))
# values = []
# for _ in range(N):
# values.append(input().split())
result = solve(values, N)
# 6 digits float precision {:.6f} (6 is the default value)
print("{:.10g}".format(result))
def configure_log():
"Configure the log output"
log_formatter = logging.Formatter("L%(lineno)d - " "%(message)s")
handler = logging.StreamHandler(sys.stdout)
handler.setFormatter(log_formatter)
LOG.addHandler(handler)
LOG = None
# for interactive call: do not add multiple times the handler
if not LOG:
LOG = logging.getLogger("template")
configure_log()
def main(argv=None):
"Program wrapper."
if argv is None:
argv = sys.argv[1:]
parser = ArgumentParser()
parser.add_argument(
"-v",
"--verbose",
dest="verbose",
action="store_true",
default=False,
help="run as verbose mode",
)
args = parser.parse_args(argv)
if args.verbose:
LOG.setLevel(logging.DEBUG)
do_job()
return 0
if __name__ == "__main__":
import doctest
doctest.testmod()
sys.exit(main())
class memoized:
"""Decorator that caches a function's return value each time it is called.
If called later with the same arguments, the cached value is returned, and
not re-evaluated.
"""
def __init__(self, func):
self.func = func
self.cache = {}
def __call__(self, *args):
try:
return self.cache[args]
except KeyError:
value = self.func(*args)
self.cache[args] = value
return value
except TypeError:
# uncachable -- for instance, passing a list as an argument.
# Better to not cache than to blow up entirely.
return self.func(*args)
def __repr__(self):
"""Return the function's docstring."""
return self.func.__doc__
def __get__(self, obj, objtype):
"""Support instance methods."""
return functools.partial(self.__call__, obj)
|
Statement
Let N be a positive odd number.
There are N coins, numbered 1, 2, \ldots, N. For each i (1 \leq i \leq N),
when Coin i is tossed, it comes up heads with probability p_i and tails with
probability 1 - p_i.
Taro has tossed all the N coins. Find the probability of having more heads
than tails.
|
[{"input": "3\n 0.30 0.60 0.80", "output": "0.612\n \n\nThe probability of each case where we have more heads than tails is as\nfollows:\n\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Head) is 0.3 \u00d7 0.6 \u00d7 0.8 = 0.144;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Tail, Head, Head) is 0.7 \u00d7 0.6 \u00d7 0.8 = 0.336;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Tail, Head) is 0.3 \u00d7 0.4 \u00d7 0.8 = 0.096;\n * The probability of having (Coin 1, Coin 2, Coin 3) = (Head, Head, Tail) is 0.3 \u00d7 0.6 \u00d7 0.2 = 0.036.\n\nThus, the probability of having more heads than tails is 0.144 + 0.336 + 0.096\n+ 0.036 = 0.612.\n\n* * *"}, {"input": "1\n 0.50", "output": "0.5\n \n\nOutputs such as `0.500`, `0.500000001` and `0.499999999` are also considered\ncorrect.\n\n* * *"}, {"input": "5\n 0.42 0.01 0.42 0.99 0.42", "output": "0.3821815872"}]
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.