output_description
stringlengths 15
956
| submission_id
stringlengths 10
10
| status
stringclasses 3
values | problem_id
stringlengths 6
6
| input_description
stringlengths 9
2.55k
| attempt
stringlengths 1
13.7k
| problem_description
stringlengths 7
5.24k
| samples
stringlengths 2
2.72k
|
|---|---|---|---|---|---|---|---|
Print the area of the triangle ABC.
* * *
|
s302098114
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
n = int(input())
arr = list(map(int, input().split()))
print(max(arr) * n - sum(arr) + min(arr))
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s269033218
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
|AB|,|BC|,|CA|=map(int, input().split())
ans=(|AB|*|BC|*|CA|/max(|AB|,|BC|,|CA|))/2
print(ans)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s752776478
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
a, b, c= input().split()
a, b, c = int(a), int(b), int(c)
if a>b and a>c:
print(int((1/2 * b * c)))
if b>a and b>c:
print(int((1/2 * a * c)))
else:
print(int((1/2 * a *b))
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s787964356
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
a = int(input())
b = int(input())
c = int(input())
print(a*c)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s365075272
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
A = int(input())
p = A
C = []
while A not in C:
C.append(A)
if A % 2 == 0:
A = A // 2
else:
A = A * 3 + 1
print(len(C) + 1)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s577814502
|
Wrong Answer
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
triangulo = input()
lados = triangulo.split()
AB = lados[0]
BC = lados[1]
area = (int(AB) * int(BC)) / 2
print(area)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s552351050
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
#! /usr/bin/env python3
# -*- coding: utf-8 -*-
ls = [int(x) for x in input().split()]
ls.sort()
print(int((ls[0]*ls[1])/2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s543550039
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
a = int(input())
b = int(input())
c = int(input())
print(a*c)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s533940477
|
Wrong Answer
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
# -*- coding:utf-8 -*
n_list = list(map(int, input().split()))
print((n_list[0] * n_list[1]) / 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s224316745
|
Wrong Answer
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
p = input().split()
k = []
for i in p:
k.append(int(i))
k.sort()
print(k[0] * k[1] / 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s441059770
|
Wrong Answer
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
in1 = list(map(int, input().split(" ")))
in1.sort()
print(in1)
print((in1[0] * in1[1]) / 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s218081151
|
Accepted
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
N = list(map(int, input().split()))
d = sorted(N)
print(int(N[0] * N[1] / 2))
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s025978751
|
Accepted
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
aD = sorted(int(_) for _ in input().split())
print(aD[0] * aD[1] // 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s956564197
|
Accepted
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
print([int(i[0]) * int(i[1]) // 2 for i in [input().split()]][0])
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s307995190
|
Accepted
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
e = [int(i) for i in input().split()]
e.sort()
print(e[0] * e[1] // 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s268927382
|
Accepted
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
a_b, b_c, c_a = map(int, input().split())
print((a_b * b_c) // 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s226861530
|
Accepted
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
(*abc,) = sorted(map(int, input().split()))
print(abc[0] * abc[1] // 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s894332385
|
Wrong Answer
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
As = list(sorted(map(int, input().split())))
print((As[0] + As[1] // 2))
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s394201155
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
|ab|,|bc|,|ca|=map(int,input().split())
print((|ab|*|bc|)//2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s781666872
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
a,b,c=map(int,input().split())
print(min(a,b)*min(max(a,b),c))//2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s695091725
|
Wrong Answer
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
list = list(map(int, input().split()))
print(list[0] * list[1] / 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s928269050
|
Wrong Answer
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
arr = list(map(int, sorted(input().split())))
print(int(arr[0] * arr[1] / 2))
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s797446530
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
AB BC CD = map(int, input().split())
print(int(AB*BC*0.5))
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s086311256
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
N = list(int, input().split())
N.sort()
print(N[0] * N[1] // 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s905531622
|
Accepted
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
N, M, L = map(int, input().split())
print(int(N * M / 2))
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s855224411
|
Accepted
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
a = input().split()
b = int(a[0])
c = int(a[1])
print(b * c // 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s031463140
|
Wrong Answer
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
a, b, c = list(map(int, (input()).split()))
print((a) * (b) / 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s065480916
|
Wrong Answer
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
N = input().split()
a = int(N[0]) * int(N[1]) / 2
print(str(a))
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s227771779
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
x, y, z = map(int, input()split())
print(x * y / 2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s050267806
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
A = [int(n) for n in input().split())
print(A[0]*A[1]/2)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s821505021
|
Runtime Error
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
# ABC117 A
T, X = map(int, input().split())
print(T / X)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print the area of the triangle ABC.
* * *
|
s615168553
|
Wrong Answer
|
p03145
|
Input is given from Standard Input in the following format:
|AB| |BC| |CA|
|
a, b, c = list(input().split())
A = int(a) * int(b) / 2
print(A)
|
Statement
There is a right triangle ABC with ∠ABC=90°.
Given the lengths of the three sides, |AB|,|BC| and |CA|, find the area of the
right triangle ABC.
It is guaranteed that the area of the triangle ABC is an integer.
|
[{"input": "3 4 5", "output": "6\n \n\n\n\nThis triangle has an area of 6.\n\n* * *"}, {"input": "5 12 13", "output": "30\n \n\nThis triangle has an area of 30.\n\n* * *"}, {"input": "45 28 53", "output": "630\n \n\nThis triangle has an area of 630."}]
|
Print N lines. The i-th line must contain the niceness when the headquarters
are set up in Vertex i.
* * *
|
s288439302
|
Wrong Answer
|
p03515
|
Input is given from Standard Input in the following format:
N
a_1 b_1 c_1
:
a_{N-1} b_{N-1} c_{N-1}
|
import sys
sys.setrecursionlimit(10**7)
def solve():
n = int(sys.stdin.readline())
adj = [[] for i in range(n + 1)]
dp = [dict() for i in range(n + 1)]
cnt = [dict() for i in range(n + 1)]
for i in range(n - 1):
ai, bi, ci = map(int, sys.stdin.readline().split())
if ci > 2:
return
adj[ai].append((bi, ci))
adj[bi].append((ai, ci))
def cnt_node(v, p):
if p in cnt[v]:
return cnt[v][p]
cnt[v][p] = 1
for u, c in adj[v]:
if u == p:
continue
cnt[v][p] += cnt_node(u, v)
return cnt[v][p]
def dfs(v, p):
if p in dp[v]:
return dp[v][p]
dp[v][p] = 0
for u, c in adj[v]:
if u == p:
continue
if c == 1:
dp[v][p] += cnt_node(u, v)
else:
dp[v][p] += dfs(u, v) + 2
return dp[v][p]
for i in range(1, n + 1):
# print(dp)
# print(cnt)
ans = dfs(i, -1)
print(ans)
if __name__ == "__main__":
solve()
|
Statement
Snuke Festival 2017 will be held in a tree with N vertices numbered 1,2,
...,N. The i-th edge connects Vertex a_i and b_i, and has _joyfulness_ c_i.
The staff is Snuke and N-1 black cats. Snuke will set up the headquarters in
some vertex, and from there he will deploy a cat to each of the other N-1
vertices.
For each vertex, calculate the _niceness_ when the headquarters are set up in
that vertex. The niceness when the headquarters are set up in Vertex i is
calculated as follows:
* Let X=0.
* For each integer j between 1 and N (inclusive) except i, do the following:
* Add c to X, where c is the smallest joyfulness of an edge on the path from Vertex i to Vertex j.
* The niceness is the final value of X.
|
[{"input": "3\n 1 2 10\n 2 3 20", "output": "20\n 30\n 30\n \n\n * The figure below shows the case when headquarters are set up in each of the vertices 1, 2 and 3.\n * The number on top of an edge denotes the joyfulness of the edge, and the number below an vertex denotes the smallest joyfulness of an edge on the path from the headquarters to that vertex.\n\n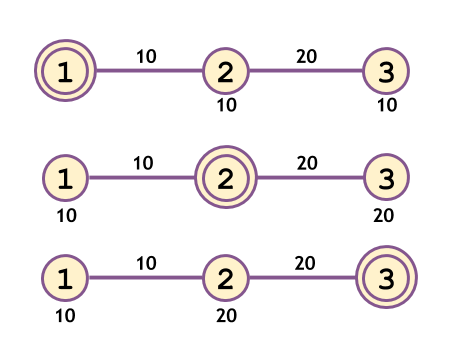\n\n* * *"}, {"input": "15\n 6 3 2\n 13 3 1\n 1 13 2\n 7 1 2\n 8 1 1\n 2 8 2\n 2 12 2\n 5 2 2\n 2 11 2\n 10 2 2\n 10 9 1\n 9 14 2\n 4 14 1\n 11 15 2", "output": "16\n 20\n 15\n 14\n 20\n 15\n 16\n 20\n 15\n 20\n 20\n 20\n 16\n 15\n 20\n \n\n* * *"}, {"input": "19\n 19 14 48\n 11 19 23\n 17 14 30\n 7 11 15\n 2 19 15\n 2 18 21\n 19 10 43\n 12 11 25\n 3 11 4\n 5 19 50\n 4 11 19\n 9 12 29\n 14 13 3\n 14 6 12\n 14 15 14\n 5 1 6\n 8 18 13\n 7 16 14", "output": "103\n 237\n 71\n 263\n 370\n 193\n 231\n 207\n 299\n 358\n 295\n 299\n 54\n 368\n 220\n 220\n 319\n 237\n 370"}]
|
For each dataset, print the minimum number of votes required to be the winner
of the presidential election in a line. No output line may include any
characters except the digits with which the number is written.
|
s320998418
|
Wrong Answer
|
p00769
|
The entire input looks like:
> _the number of datasets (=n)_
> _1st dataset_
> _2nd dataset_
> …
> _n-th dataset_
>
The number of datasets, _n_ , is no more than 100.
The number of the eligible voters of each district and the part-whole
relations among districts are denoted as follows.
* An electoral district of the first stage is denoted as [_c_], where _c_ is the number of the eligible voters of the district.
* A district of the _k_ -th stage (_k_ > 1) is denoted as [_d_ 1 _d_ 2… _d m_], where _d_ 1, _d_ 2, …, _d m_ denote its sub-districts of the (_k_ − 1)-th stage in this notation.
For instance, an electoral district of the first stage that has 123 eligible
voters is denoted as [123]. A district of the second stage consisting of three
sub-districts of the first stage that have 123, 4567, and 89 eligible voters,
respectively, is denoted as [[123][4567][89]].
Each dataset is a line that contains the character string denoting the
district of the final stage in the aforementioned notation. You can assume the
following.
* The character string in each dataset does not include any characters except digits ('0', '1', …, '9') and square brackets ('[', ']'), and its length is between 11 and 10000, inclusive.
* The number of the eligible voters of each electoral district of the first stage is between 3 and 9999, inclusive.
The number of stages is a nation-wide constant. So, for instance,
[[[9][9][9]][9][9]] never appears in the input. [[[[9]]]] may not appear
either since each district of the second or later stage must have multiple
sub-districts of the previous stage.
|
def calc_majority(l):
l.sort()
result = 0
for i in range(len(l) // 2 + 1):
result += l[i]
return result
# 過半数になるような値を求めてそれを返す
def calc_fisrt_majority(l):
people_num = list(map(int, l))
people_num.sort()
n = 0
for i in range(len(people_num) // 2 + 1):
n += int(people_num[i]) // 2 + 1
return n
# 括弧と括弧の間の数値を返す
def get_num(l, lp, rp):
# print(lp, end="")
# print(" ", end="")
# print(rp)
s = ""
for i in range(lp + 1, rp):
s += l[i]
return s
# 左かっこに対応する右かっこのインデックスを返す
def getRp(char_list, n):
count = 1
i = 0
while count:
c = char_list[i]
i += 1
if c == "[":
count += 1
elif c == "]":
count -= 1
else:
continue
return i + n
# かっこの位置全てのリストを返す
def brackets(s):
lp = []
rp = []
n = 0
bucket_nest = 0
l = list(s)
for i in l:
if i == "[":
bucket_nest += 1
if i != "[":
break
for i in l:
n += 1
if i == "[":
lp.append(n - 1)
rp.append(getRp(l[n:], n - 1))
for i in range(1, len(lp)):
return lp, rp, bucket_nest
def main():
N = int(input())
lp = []
rp = []
tmp_result = []
result = 0
people_num = []
nest = 0
n = 0
while N != 0:
s = input()
l = list(s)
N -= 1
lp, rp, nest = brackets(s)
n = 0
for i in lp:
if l[i + 1] != "[": # 次が[でないなら必ず数字が来る
people_num.append(get_num(l, lp[n], rp[n]))
if l[rp[n] + 1] == "]": # ネストの終わり
tmp_result.append(calc_fisrt_majority(people_num))
people_num.clear()
n += 1
print(tmp_result)
if nest == 2:
result = tmp_result[0]
while nest != 2:
result = calc_majority(tmp_result)
nest -= 1
print(result)
if __name__ == "__main__":
main()
# [[[37][95][31][77][15]][[43][5][5][5][85]][[71][3][51][89][29]]
# [[57][95][5][69][31]][[99][59][65][73][31]]]
# [[43][9][43][48][79]]=9+43+43=95
|
Hierarchical Democracy
The presidential election in Republic of Democratia is carried out through
multiple stages as follows.
1. There are exactly two presidential candidates.
2. At the first stage, eligible voters go to the polls of his/her electoral district. The winner of the district is the candidate who takes a majority of the votes. Voters cast their ballots only at this first stage.
3. A district of the _k_ -th stage (_k_ > 1) consists of multiple districts of the (_k_ − 1)-th stage. In contrast, a district of the (_k_ − 1)-th stage is a sub-district of one and only one district of the _k_ -th stage. The winner of a district of the _k_ -th stage is the candidate who wins in a majority of its sub-districts of the (_k_ − 1)-th stage.
4. The final stage has just one nation-wide district. The winner of the final stage is chosen as the president.
You can assume the following about the presidential election of this country.
* Every eligible voter casts a vote.
* The number of the eligible voters of each electoral district of the first stage is odd.
* The number of the sub-districts of the (_k_ − 1)-th stage that constitute a district of the _k_ -th stage (_k_ > 1) is also odd.
This means that each district of every stage has its winner (there is no tie).
Your mission is to write a program that finds a way to win the presidential
election with the minimum number of votes. Suppose, for instance, that the
district of the final stage has three sub-districts of the first stage and
that the numbers of the eligible voters of the sub-districts are 123, 4567,
and 89, respectively. The minimum number of votes required to be the winner is
107, that is, 62 from the first district and 45 from the third. In this case,
even if the other candidate were given all the 4567 votes in the second
district, s/he would inevitably be the loser. Although you might consider this
election system unfair, you should accept it as a reality.
|
[{"input": "[[123][4567][89]]\n [[5][3][7][3][9]]\n [[[99][59][63][85][51]][[1539][7995][467]][[51][57][79][99][3][91][59]]]\n [[[37][95][31][77][15]][[43][5][5][5][85]][[71][3][51][89][29]][[57][95][5][69][31]][[99][59][65][73][31]]]\n [[[[9][7][3]][[3][5][7]][[7][9][5]]][[[9][9][3]][[5][9][9]][[7][7][3]]][[[5][9][7]][[3][9][3]][[9][5][5]]]]\n [[8231][3721][203][3271][8843]]", "output": "7\n 175\n 95\n 21\n 3599"}]
|
For each dataset, print the minimum number of votes required to be the winner
of the presidential election in a line. No output line may include any
characters except the digits with which the number is written.
|
s110238492
|
Accepted
|
p00769
|
The entire input looks like:
> _the number of datasets (=n)_
> _1st dataset_
> _2nd dataset_
> …
> _n-th dataset_
>
The number of datasets, _n_ , is no more than 100.
The number of the eligible voters of each district and the part-whole
relations among districts are denoted as follows.
* An electoral district of the first stage is denoted as [_c_], where _c_ is the number of the eligible voters of the district.
* A district of the _k_ -th stage (_k_ > 1) is denoted as [_d_ 1 _d_ 2… _d m_], where _d_ 1, _d_ 2, …, _d m_ denote its sub-districts of the (_k_ − 1)-th stage in this notation.
For instance, an electoral district of the first stage that has 123 eligible
voters is denoted as [123]. A district of the second stage consisting of three
sub-districts of the first stage that have 123, 4567, and 89 eligible voters,
respectively, is denoted as [[123][4567][89]].
Each dataset is a line that contains the character string denoting the
district of the final stage in the aforementioned notation. You can assume the
following.
* The character string in each dataset does not include any characters except digits ('0', '1', …, '9') and square brackets ('[', ']'), and its length is between 11 and 10000, inclusive.
* The number of the eligible voters of each electoral district of the first stage is between 3 and 9999, inclusive.
The number of stages is a nation-wide constant. So, for instance,
[[[9][9][9]][9][9]] never appears in the input. [[[[9]]]] may not appear
either since each district of the second or later stage must have multiple
sub-districts of the previous stage.
|
def rec(s, l, now=0):
if s[now].isdigit():
res = ""
while now < l and s[now] != "]":
res += s[now]
now += 1
return int(res) // 2 + 1, now + 1
else:
g = []
while now < l and s[now] == "[":
res, now = rec(s, l, now + 1)
g.append(res)
g.sort()
return sum(g[: len(g) // 2 + 1]), now + 1
for _ in range(int(input())):
s = input()
l = len(s)
print(rec(s, l)[0])
|
Hierarchical Democracy
The presidential election in Republic of Democratia is carried out through
multiple stages as follows.
1. There are exactly two presidential candidates.
2. At the first stage, eligible voters go to the polls of his/her electoral district. The winner of the district is the candidate who takes a majority of the votes. Voters cast their ballots only at this first stage.
3. A district of the _k_ -th stage (_k_ > 1) consists of multiple districts of the (_k_ − 1)-th stage. In contrast, a district of the (_k_ − 1)-th stage is a sub-district of one and only one district of the _k_ -th stage. The winner of a district of the _k_ -th stage is the candidate who wins in a majority of its sub-districts of the (_k_ − 1)-th stage.
4. The final stage has just one nation-wide district. The winner of the final stage is chosen as the president.
You can assume the following about the presidential election of this country.
* Every eligible voter casts a vote.
* The number of the eligible voters of each electoral district of the first stage is odd.
* The number of the sub-districts of the (_k_ − 1)-th stage that constitute a district of the _k_ -th stage (_k_ > 1) is also odd.
This means that each district of every stage has its winner (there is no tie).
Your mission is to write a program that finds a way to win the presidential
election with the minimum number of votes. Suppose, for instance, that the
district of the final stage has three sub-districts of the first stage and
that the numbers of the eligible voters of the sub-districts are 123, 4567,
and 89, respectively. The minimum number of votes required to be the winner is
107, that is, 62 from the first district and 45 from the third. In this case,
even if the other candidate were given all the 4567 votes in the second
district, s/he would inevitably be the loser. Although you might consider this
election system unfair, you should accept it as a reality.
|
[{"input": "[[123][4567][89]]\n [[5][3][7][3][9]]\n [[[99][59][63][85][51]][[1539][7995][467]][[51][57][79][99][3][91][59]]]\n [[[37][95][31][77][15]][[43][5][5][5][85]][[71][3][51][89][29]][[57][95][5][69][31]][[99][59][65][73][31]]]\n [[[[9][7][3]][[3][5][7]][[7][9][5]]][[[9][9][3]][[5][9][9]][[7][7][3]]][[[5][9][7]][[3][9][3]][[9][5][5]]]]\n [[8231][3721][203][3271][8843]]", "output": "7\n 175\n 95\n 21\n 3599"}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s472569641
|
Runtime Error
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
N, A, B = map(int, input().split())
blue = [1] * A
red = [-1] * B
ball = (blue + red) * N
X = ball[0:N]
print(X)
print(X.count(1))
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s498074194
|
Runtime Error
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
H, A, B = map(int, input().split())
l = []
s = 0
while True:
for i in range(A):
if s == H:
print(l.count("b"))
exit()
s += 1
list.append("b")
for j in range(B):
if s == H:
print(l.count("b"))
exit()
s += 1
list.append("a")
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s151371510
|
Accepted
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
a, b, c = map(int, (input().split()))
d = (a // (b + c)) * b + min((a % (b + c)), b)
print(d)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s380881571
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
n, m, l = map(int, input().split())
x = n // (m + l)
y = n % (m + l)
if y <= m:
print(x * m + y)
else:
print(x * m + y)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s862119481
|
Accepted
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
import glob
# 問題ごとのディレクトリのトップからの相対パス
REL_PATH = "ABC\\158\\B"
# テスト用ファイル置き場のトップ
TOP_PATH = "C:\\AtCoder"
class Common:
problem = []
index = 0
def __init__(self, rel_path):
self.rel_path = rel_path
def initialize(self, path):
file = open(path)
self.problem = file.readlines()
self.index = 0
return
def input_data(self):
try:
IS_TEST
self.index += 1
return self.problem[self.index - 1]
except NameError:
return input()
def resolve(self):
pass
def exec_resolve(self):
try:
IS_TEST
for path in glob.glob(TOP_PATH + "\\" + self.rel_path + "/*.txt"):
print("Test: " + path)
self.initialize(path)
self.resolve()
print("\n\n")
except NameError:
self.resolve()
class Solver(Common):
def resolve(self):
q = [int(i) for i in self.input_data().split()]
N = q[0]
A = q[1]
B = q[2]
shou = int(N / (A + B))
amari = N % (A + B)
if amari <= A:
result = shou * A + amari
else:
result = (shou + 1) * A
print(str(result))
solver = Solver(REL_PATH)
solver.exec_resolve()
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s103638667
|
Accepted
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
a = list(map(int, input().split()))
N = a[0]
A = a[1]
B = a[2]
count = 0
i = N % (A + B)
j = N // (A + B)
if i >= A:
i = A
count = j * A + i
print(count)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s271648555
|
Accepted
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
N, A, B = [int(x) for x in input().strip().split()]
p = N // (A + B) * A
q = N % (A + B)
if q > A:
q = A
print(p + q)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s179098045
|
Runtime Error
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
number, b, r = map(int, input().split())
ans = ""
for i in range(10):
ans = ans + ("b" * b) + ("r" * r)
answer = ans[:number]
answer = answer.replace("r", "")
print(len(answer))
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s139217757
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
quant, azul, verm = input().split()
quant, azul, verm = int(quant), int(azul), int(verm)
eq = azul + (quant - (azul + verm))
if azul == 0:
eq = 0
print(eq)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s294859084
|
Accepted
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
N, A, B = map(int, input().split(sep=" "))
print((N // (A + B) * A) + min(N % (A + B), A))
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s879634697
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
n, r, b = [int(i) for i in input().split()]
k = n * b // (r + b)
l = min(n % (r + b), b)
print(k + l)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s123155868
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
[N, A, B] = list(map(int, input().split()))
C = A + B
print(A * N // C + min(N % C, A))
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s974496101
|
Runtime Error
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
import numpy as np
def cumsum(x):
return list(np.cumsum(x))
def cumsum_number(N, K, x):
ans = [0] * (N - K + 1)
number_cumsum = cumsum(x)
number_cumsum.insert(0, 0)
for i in range(N - K + 1):
ans[i] = number_cumsum[i + K] - number_cumsum[i]
return ans
"""
int #整数
float #小数
#for
for name in fruits: #fruitの頭から操作
print(name)
#リスト
list0 = [] #リスト生成
list0 = [1,2,3,4] #初期化
list0 = [0]*10 #[0,0,0,0,0,0,0,0,0,0]
list1= [i for i in range(10)] #>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
list1 = list(map(int, input().split())) # 複数の入力をリストに入れる
number=[int(input()) for i in range(int(input()))] #複数行の入力をリストに
list1 = list1 + [6, 7, 8] #リストの追加
list2.append(34) #リストの追加 最後に()内が足される
list.insert(3,10) #リストの追加 任意の位置(追加したい位置,追加したい値)
len(list4) #リストの要素数
max(sa) #list saの最小値
list5.count(2) #リスト(文字列も可)内の2の数
list1.sort() #並び替え小さい順
list1.sort(reverse=True) #並び替え大きい順
set(list1) #list1内の重複している要素を削除し、小さい順に並べる
sum([2,3, ,3]) #リストの合計
abs(a) #aの絶対値
max(a,b) min(a,b) #最大値 最小値
text1 = text1.replace("34","test") #text1内の"34"を"test"に書き換える(文字列内の文字を入れ替える)
exit(0) #強制終了
cumsum(リスト) #累積和をリストで返す
cumsum_number(N,K,x) #N個の数が含まれるリストx内のK個からなる部分和をリストで返す
"""
N, A, B = map(int, input().split())
S = N // (A + B) # SはA+Bのセット数
M = N - S * (A + B) # Mは残り
if A <= M:
print(A + S * A)
else:
print(M + S * A)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s660257974
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
li = list(map(int, input().split()))
a = 0
b = 0
out = 0
isA = True
for i in range(li[0]):
if isA:
a += 1
out += 1
if a >= li[1]:
isA = False
a = 0
else:
b += 1
if b >= li[2]:
isA = True
b = 0
print(out)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s153644749
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
import sys
N, A, B = map(int, input().split(" "))
Result = 0
Count_Blue = 0
if 1 <= N <= 10**18 and A >= 0 and B >= 0 and 0 < A + B <= 10**18:
LoopCount = 10**100
for Count in range(LoopCount):
Result = Result + (1 * A)
Count_Blue += 1 * A
Result = Result + (1 * B)
if Result > N:
Count_Blue = Count_Blue - (Result - (1 * B) - N)
print(Count_Blue)
sys.exit()
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s596893946
|
Runtime Error
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
import unittest
from solution import Solution
class TestSolution(unittest.TestCase):
def test_001(self):
# class under test
solution = Solution()
# actual
N, A, B = 6, 2, 4
actual = solution.solve(N, A, B)
# expect
expect = 2
# assert
self.assertEqual(actual, expect)
def test_002(self):
# class under test
solution = Solution()
# actual
N, A, B = 10**18, 5, 5
actual = solution.solve(N, A, B)
# expect
expect = 5 * 10**17
# assert
self.assertEqual(actual, expect)
if __name__ == "__main__":
unittest.main()
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s736052200
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
N, A, B = map(int, input().split())
co = 0
i = 0
while (A + B) * i < N:
co = co + A
i += 1
print(co)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s896149861
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
n, a, b = map(int, input().split())
abc = 0
list_a = [a, b]
ans = 0
while abc < 1:
for i in range(10000000000000000000000000000):
if i % 2 == 0:
n -= a
ans += a
else:
n -= b
if n <= 0:
ans += n
abc += 1
break
print(ans)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s462298129
|
Runtime Error
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
N, A, B = map(int, input().split())
a = list()
a = ["blue"] * A + ["red"] * B
for i in range(N):
a = a + a
del a[N:]
print(a.count("blue"))
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s780184443
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
i = input()
j = i.split(" ")
print(int(j[0]) - int(j[2]))
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s270597643
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
N, B, A = map(int, input().split())
print(N - A)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s704743782
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
n, A, B = list(map(lambda x: int(x), input().split(" ")))
x = n % (A + B)
r = min(x, A)
ans = (n - x) * A / (A + B) + r
print(int(ans))
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s682729092
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
a_list = input().split()
n = int(a_list[0])
a = int(a_list[1])
b = int(a_list[2])
# print(n)
# print(a)
# print(b)
group = int(a + b)
# print(group)
c = n % group
d = n - c
e = d / group
parta = a * e
if a >= c:
f = c
else:
f = a
print(int(f) + int(parta))
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s455739914
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
i = input()
a = i.split(" ")
n = len(i)
if n == 5:
N = int(a[0])
A = int(a[1])
B = int(a[2])
if A == 0:
print("0")
elif N - (A + B) == 0:
print(A)
elif A + B != N:
x = N - (A + B)
print(A + x)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s953125162
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
p = list(map(int, input().split()))
n = p[0]
a = p[1]
b = p[2]
d = n % (a + b)
s = (n - d) / (a + b)
if d < a:
ans_d = d
else:
ans_d = a
ans = s * a + ans_d
print(int(ans))
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s181769580
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
s = list(map(int, input().split()))
n = s[0]
a = s[1]
b = s[2]
if n % (a + b) < a:
print(int(n / (a + b) * a) + int(n % (a + b)))
else:
print(int(n / (a + b) * a) + a)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s106184415
|
Wrong Answer
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
print(0)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of blue balls that will be there among the first N balls in
the row of balls.
* * *
|
s169723823
|
Accepted
|
p02754
|
Input is given from Standard Input in the following format:
N A B
|
n, b, r = list(map(int, input().split()))
block = n // (b + r)
count_b = block * b
extra_b = n % (b + r)
if extra_b <= b:
count_b += extra_b
else:
count_b += b
print(count_b)
|
Statement
Takahashi has many red balls and blue balls. Now, he will place them in a row.
Initially, there is no ball placed.
Takahashi, who is very patient, will do the following operation 10^{100}
times:
* Place A blue balls at the end of the row of balls already placed. Then, place B red balls at the end of the row.
How many blue balls will be there among the first N balls in the row of balls
made this way?
|
[{"input": "8 3 4", "output": "4\n \n\nLet `b` denote a blue ball, and `r` denote a red ball. The first eight balls\nin the row will be `bbbrrrrb`, among which there are four blue balls.\n\n* * *"}, {"input": "8 0 4", "output": "0\n \n\nHe placed only red balls from the beginning.\n\n* * *"}, {"input": "6 2 4", "output": "2\n \n\nAmong `bbrrrr`, there are two blue balls."}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s084125404
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N=int(input())
s=list(map(int,input().split()))
s=list(sorted(s))
if N%2==1:
s.remove(0)
for i in range(n-1)
a = []
for i in range(n//2):
a.append(2*i+1)
if s[0::2]==s[1::2] and s[0::2] ==a :
print((2**((len(s))//2))%(10**9+7))
else:
print(0)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s843991734
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
import sys
from collections import deque
p=10**9+7
def main(n,a):
h=n//2
g=n%2
a.sort()
c=[2*(x//2)+g+1 for x in range(n-g)]
if g==1:
c.insert(0,0)
if a!=c:
return 0
return 2**(h%(p-1))
if __name__='__main__':
n=int(input())
a=list(map(int,sys.stdin.readline().strip().split()))
print(main(n,a))
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s910577294
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N = int(input())
A = list(map(int, input().split()))
ans = 0
A_test = sorted(list(set(A)))
if N % 2 == 1:
judge = [i for i in range(0,N,2)]
if A_test == judge:
ans = 2**(N//2)
else:
judge = [i for i in range(1,N,2)]
if A_test == judge:
ans = 2**(N//2)]
ans = ans % (10**9 + 7)
print(ans)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s965445196
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from collections import Counter
n = int(input())
lst = [int(i) for i in input().split()]
mod = 10**9 + 7
lst_c = Counter(lst)
lst_c = sorted(lst_c.items(),key = lambda x:x[0])
ideal = []
if n%2!=0:
ideal.append((0,1))
for i in range(1,n//2+1):
ideal.append((2*i,2))
else:
for i in range(n//2):
ideal.append((2*i+1,2))
if lst_c != ideal:
print(0)
else:
l = len(ideal)
if n%2!=0:
l -= 1
print(2**l % mod)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s789752761
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N = int(input())
L = input().split()
if N % 2 == 0:
sc = 0
for i in range(0, N):
n = L.count(str(i))
if n ¥= 2:
sc += 1
break
else:
pass
if sc ==0:
ss = 2 * (N / 2)
print(ss)
else:
n = L.count("0")
if n % 2 ¥= 0:
print(0)
else:
for i in range(0, N):
n = L.count(str(i))
if n ¥= 2:
sc += 1
break
else:
pass
if sc ==0:
ss = 2 * (N / 2)
print(ss)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s353251522
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
import sys
stdin = sys.stdin
ns = lambda : stdin.readline().rstrip()
ni = lambda : int(ns())
na = lambda : list(map(int, stdin.readline().split()))
def main():
n = ni()
a = na()
if n % 2 == 0:
if 0 in a:
print(0)
return
else:
print(2 ** len(list(set(a))))
else:
zero = 0
for aa in a:
if aa == 0:
zero += 1
if zero > 1:
print(0)
return
else:
if zero == 1:
print(2 ** (len(list(set(a)) - 1))
else:
print(2 ** len(list(set(a)))
main()
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s992332830
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n = int(input())
a = list(map(int, input().split()))
import(sys)
cnt = [0] * n
for x in a:
a[x] += 1
ok = True
for i in range(0, n):
if n % 2 == 1 && i % 2 == 0:
if i == 0 && cnt[i] != 1 or cnt[i] != 2:
ok = False
elif n % 2 == 0 && i % 2 == 0:
if cnt[i] != 2:
ok = False
if not ok:
print(0)
else:
res = 1
for i in range(0, n // 2):
res *= 2
res %= 1000000007
print(res)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s920506558
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n = int(input())
*a, = map(int, input().split())
a.sort()
if n % 2:
for k in range(n):
if a[k] != (k+1)//2*2:
print(0)
break
else:
print(2**((n-1)//2) % (10**9+7))
else:
for k in range(n):
if a[k] != k//2*2+1:
print(0)
break
else:
print(2**(n//2) % (10**9+7))
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s240180943
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N = int(input())
nums = list(map(int, input().split()))
n_dict = {}
idx = 0
mod = !(N%2)
while True:
if 2*idx + mod > N:
break
else:
n_dict[2*idx+mod] = 0
for num in nums:
if num in n_dict:
n_dict[num] += 1
else:
print(0)
exit()
for key, value in n_dict.items():
if value != 2:
print(0)
exit()
print((2**(N//2))%(10**9+7))
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s576173078
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
mod = 10**9 + 7
n = int(input())
a = sorted(list(map(int,input().split())))
if n % 2 == 0:
for i in range(n//2):
if not a[2*i] == a[2*i+1] == 2*i+1:
print(0)
exit()
else:
if a[0] != 0:
print(0)
exit()
for i in range(n//2):
if not a[2*i+1] == a[2*i+2] == 2*i+2
print(0)
exit()
print(pow(2, n//2) % mod)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s176078742
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N = int(input())
A = list(map(int,input().split()))
Nc = 1
if A.count(0) >= 2:
Nc *= 0
else:
for i in range(N):
if (N-A[i]) >=1
if A.count(i+1) == 2:
Nc = Nc*2%1000000007
elif A.count(i+1) == 0:
Nc *= 1
else:
Nc *= 0
break
else:
Nc *= 0
break
print(Nc)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s871112406
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
import math
n=int(input())
arr=list(map(int,input().split()))
ans=True
if n%2!=0:
zero=0
[zero+=1 for c in arr if c==0]
if zero[0]!=1:
ans=False
elif len(set(arr))!=int(n/2)+1:
ans=False
else:
if 0 in arr:
ans=False
elif len(set(arr))!=int(n/2):
ans=False
if ans:
print(2**math.floor(n/2)%((10**9)+7))
else:
print(0)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s680852220
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n=int(input())
a=[int(x) for x in input().split()]
a.sort()
even=[]
odd=[]
for i in range(0,n // 2):
even.append(2*i+1)
even=even+even
even.sort()
for j in range(1,(n-1 // 2)+1):
odd.append(2*j)
odd =odd + odd
odd.append(0)
odd.sort()
if n % 2 == 1:
if a == odd:
print(pow(2,n-1 // 2,10**9+7)
else:
print(0)
else:
if a == even:
print(2,n // 2,10**9+7)
else:
print(0)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s606327716
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N = int(input())
A = list(map(int,input().split()))
Nc = 1
if A.count(0) >= 2:
Nc *= 0
else:
for i in range(N):
if (N-A[i]-1) >= 0:
if A.count(i+1) == 2:
Nc = Nc*2
elif A.count(i+1) == 0:
else:
Nc *= 0
break
else:
Nc *= 0
break
print(Nc%1000000007)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s278131304
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from collections import Counter
N= int(input())
Alist = list(map(int, input().split()))
count = Counter(Alist)
res = 1
if N % 2 ==0:
for i in range(1,N,2):
if count[i] != 2:
print(0)
exit()
else:
if count[0] != 1:
print(0)
exit()
else:
for i in range(2,N,2):
if count[i] != 2
print(0)
exit()
print(2**(N//2) % (10**9+7))
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s374939335
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n = int(input())
a = [int(i) for i in input().split()]
# aの各数値の個数をdictで保持(数値:個数)
a_dict = {}
for v in a:
if v in a_dict:
a_dict[v] += 1
else:
a_dict[v] = 1
# a_dictの中になければならない数値のリストを作成
possible_list = {i: True for i in range(1, n, 2)}
can = True
if n % 2 == 0:
for k, v in a_dict.items():
# 数値が2個でない、もしくはkがpossible_list内に存在しないならFalse
if v != 2 or k not in possible_list:
can = False
break
else:
if a_dict[0] != 1:
can = False
else:
for k, v in a_dict.items():
if v != 2 or k not in possible_list:
can = False
break
if can:
print(2 ** (n // 2) % (10 ** 9 + 7))
else:
print(0)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s025359599
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N = int(input())
A = list(map(int,input().split()))
d = {}
for i in set(A):
d[i] = 0
if N % 2 == 1:
for i in A:
d[i] += 1
for k,v in d.items():
if k == 0:
if v != 1:
print(0)
exit()
continue
if v != 2:
print(0)
exit()
else:
for i in A:
d[i] += 1
for k,v in d.items():
if k == 0:
if v != 0:
print(0)
exit()
if v != 2:
print(0)
exit()
ans = 2
M = 10**9 + 7
if N % 2 == 1:
ans = 2**((N-1)/2) % M
else:
ans = 2**(N/2) % M
print(int(ans))
~
~
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s753507282
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N=int(input())
A=[int(i) for i in input().split()]
A.sort()
miss=0
if N%2==0:
for i in range(int(N/2)):
if miss==1:
for j in range(2):
if A[0]==2*i+1:
A.pop(0)
else:
miss=1
if miss==1:
print(0)
else:
print(int((2**int(N/2))%(10e9+7)))
if N%2==1:
if A[0]!=0:
miss=1
A.pop(0)
else:
A.pop(0)
for i in range(int((N-1)/2)):
if miss==1:
for j in range(2):
if A[0]==2*i+2:
A.pop(0)
else:
miss=1
if miss==1:
print(0)
else:
print(int((2**int((N-1)/2))%(10e9+7)))
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s098325448
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N = int(input())
input_list = sorted([int(i) for i in input().split()])
mod = 10 ** 9 + 7
if N = 1 and input_list[0] == 0:
print(1)
else:
if N % 2 == 1:
if input_list[0] != 0:
print(0)
else:
flag = 2
limit = (N - 1) // 2
for i in range(1, limit, 2):
if input_list[i] == flag and input_list[i+1] == flag:
flag += 2
if i == limit-1:
print((2**limit) % mod)
else:
print(0)
break
elif N % 2 == 0:
flag = 1
limit = N // 2
for i in range(0, limit, 2):
if input_list[i] == flag and input_list[i+1] == flag:
flag += 2
if i == limit-2:
print((2**limit) % mod)
else:
print(0)
break
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s738685702
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
import sys
input=sys.stdin.readline
N=int(input())
A=list(map(int,input().split()))
Devide_N=10**9+7
Rem_2_32_DN=(2**32)%Devide_N
if N%2==1:
if A.count(0)!=1:
print(0)
else:
for ch_n in range(1,(N-1)//2+1):
if A.count(ch_n*2)!=2:
break
else:
A.remove(ch_n*2)
A.remove(ch_n*2)
else:
#exp=(N-1)//2
#exp_quotient_32=exp//32
#exp_rem_32=exp%32
#Rem_ans_Devide_N=1
#for _ in range(exp_quotient_32):
# Rem_ans_Devide_N=(Rem_ans_Devide_N*Rem_2_32_DN)%Devide_N
#print((Rem_ans_Devide_N*2**(exp_rem_32))%Devide_N)
sys.exit()
print(0)
else:
for ch_n in range(1,N//2+1):
if A.count(ch_n*2-1)!=2:
break
else:
A.remove(ch_n*2-1)
A.remove(ch_n*2-1)
else:
#exp=N//2
#exp_quotient_32=exp//32
#exp_rem_32=exp%32
#Rem_ans_Devide_N=1
#for _ in range(exp_quotient_32):
# Rem_ans_Devide_N=(Rem_ans_Devide_N*Rem_2_32_DN)%Devide_N
#print((Rem_ans_Devide_N*2**(exp_rem_32))%Devide_N)
#sys.exit()
print(0)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s642048790
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
N = int(input())
input_list = sorted([int(i) for i in input().split()])
mod = 10 ** 9 + 7
if N = 1 and input_list[0] == 0:
print(1)
if N % 2 == 1:
if input_list[0] != 0:
print(0)
else:
flag = 2
limit = (N - 1) // 2
for i in range(1, limit, 2):
if input_list[i] == flag and input_list[i+1] == flag:
flag += 2
if i == limit-1:
print((2**limit) % mod)
else:
print(0)
break
elif N % 2 == 0:
flag = 1
limit = N // 2
for i in range(0, limit, 2):
if input_list[i] == flag and input_list[i+1] == flag:
flag += 2
if i == limit-2:
print((2**limit) % mod)
else:
print(0)
break
# 5
# 4 2 0 2 4
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s056953847
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
import math
n=int(input())
a=list(map(int,input().split()))
flg = True
if n%2==0:
if 0 in a or len(set(a))!=n//2:
flg=False
else:
if len([0 for i in a if a==0])!=1 or len(set(a))!~n//2+1:
flg=False
if flg:
print(2**(n//2)%(10**9+7))
else:
print(0)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s348498680
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
from collections import Counter
import math
N = int(input())
A = list(map(int,input().split()))
A_count = Counter(A)
count_item = list(A_count.items())
count_item.sort()
start = 1 - (N % 2)
for i in range(math.ceil(N / 2)):
if i == 0 and N % 2 == 1:
if count_item[i][0] == 0 and count_item[i][1] != 1:
print("0")
exit()
else:
if count_item[i][0] != i * 2 + (1 - (N % 2)) or count_item[i][1] != 2:
print("0")
exit()
print(2 ** (N // 2) % (10 ** 9 + 7)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s171284947
|
Runtime Error
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
# -*- coding: utf-8 -*-
import sys
import copy
import collections
from bisect import bisect_left
from bisect import bisect_right
from collections import defaultdict
from heapq import heappop, heappush, heapify
import math
import itertools
import random
# NO, PAY-PAY
#import numpy as np
#import statistics
#from statistics import mean, median,variance,stdev
INF = float('inf')
def inputInt(): return int(input())
def inputMap(): return map(int, input().split())
def inputList(): return list(map(int, input().split()))
def main():
N = inputInt()
A = inputList()
base = []
base_flg = []
if N % 2 == 1:
for i in range(0,N,2):
base.append(i)
base_flg.append(False)
else:
for i in range(1,N,2):
base.append(i)
base_flg.append(False)
dic = {}
for i in A:
if i in dic:
dic[i] += 1
else:
dic[i] = 1
for k, v in dic.items():
if k in base:
if v == 2 ans k != 0:
ind = base.index(k)
if base_flg[ind] == False:
base_flg[ind] = True
else:
print(0)
sys.exit()
else:
if k == 0 and v == 1:
ind = base.index(k)
if base_flg[ind] == False:
base_flg[ind] = True
else:
print(0)
sys.exit()
else:
print(0)
sys.exit()
else:
print(0)
sys.exit()
for i in base_flg:
if i == False:
print(0)
sys.exit()
tmp = N // 2
print(2**tmp)
if __name__ == "__main__":
main()
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of the possible orders in which they were standing, modulo
10^9+7.
* * *
|
s023152143
|
Wrong Answer
|
p03846
|
The input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
|
n, l = int(input()), list(input())
f = any(l.count(l[i]) != 2 and l.count(0) == 1 for i in range(n))
print(2 ** (n // 2) % 1000000007 if f is True else 0)
|
Statement
There are N people, conveniently numbered 1 through N. They were standing in a
row yesterday, but now they are unsure of the order in which they were
standing. However, each person remembered the following fact: the absolute
difference of the number of the people who were standing to the left of that
person, and the number of the people who were standing to the right of that
person. According to their reports, the difference above for person i is A_i.
Based on these reports, find the number of the possible orders in which they
were standing. Since it can be extremely large, print the answer modulo
10^9+7. Note that the reports may be incorrect and thus there may be no
consistent order. In such a case, print 0.
|
[{"input": "5\n 2 4 4 0 2", "output": "4\n \n\nThere are four possible orders, as follows:\n\n * 2,1,4,5,3\n * 2,5,4,1,3\n * 3,1,4,5,2\n * 3,5,4,1,2\n\n* * *"}, {"input": "7\n 6 4 0 2 4 0 2", "output": "0\n \n\nAny order would be inconsistent with the reports, thus the answer is 0.\n\n* * *"}, {"input": "8\n 7 5 1 1 7 3 5 3", "output": "16"}]
|
Print the number of intersections in a line.
|
s076136264
|
Accepted
|
p02304
|
In the first line, the number of segments $n$ is given. In the following $n$
lines, the $i$-th segment is given by coordinates of its end points in the
following format:
$x_1 \; y_1 \; x_2 \; y_2$
The coordinates are given in integers.
|
import bisect
import sys
from typing import List, Tuple, Set
class BIT(object):
def __init__(self, n: int) -> None:
self.tree = [0] * (n + 1)
self.n = n
def add(self, i: int, v: int) -> None:
while i <= self.n:
self.tree[i] += v
i += i & -i
def _sum(self, i: int) -> int:
ret = 0
while i:
ret += self.tree[i]
i -= i & -i
return ret
def sum(self, l: int, h: int) -> int:
return self._sum(h) - self._sum(l - 1)
if __name__ == "__main__":
n = int(input())
vx: List[Tuple[int, int, int]] = []
x_init_set: Set[int] = set()
for _ in range(n):
x1, y1, x2, y2 = map(lambda x: int(x), input().split())
if x1 == x2:
if y1 > y2:
y1, y2 = y2, y1
vx.append((y1, -sys.maxsize, x1))
vx.append((y2, sys.maxsize, x1))
x_init_set.add(x1)
else:
if x1 > x2:
x1, x2 = x2, x1
vx.append((y1, x1, x2))
vx.sort()
bit = BIT(len(x_init_set))
xs = [-sys.maxsize] + sorted(x_init_set)
ix = {v: i for i, v in enumerate(xs)}
ans = 0
for y, j, x2 in vx:
if j == -sys.maxsize:
bit.add(ix[x2], 1)
elif j == sys.maxsize:
bit.add(ix[x2], -1)
else:
i1 = bisect.bisect_left(xs, j)
i2 = bisect.bisect(xs, x2) - 1
ans += bit.sum(i1, i2)
print(ans)
|
Segment Intersections: Manhattan Geometry
For given $n$ segments which are parallel to X-axis or Y-axis, find the number
of intersections of them.
|
[{"input": "6\n 2 2 2 5\n 1 3 5 3\n 4 1 4 4\n 5 2 7 2\n 6 1 6 3\n 6 5 6 7", "output": "3"}]
|
Print T lines. The i-th line should contain the answer to the i-th test case.
* * *
|
s040921481
|
Wrong Answer
|
p02611
|
Input is given from Standard Input in the following format:
T
\mathrm{case}_1
\vdots
\mathrm{case}_T
Each case is given in the following format:
N
|
t, *n = map(int, open(0))
for k in n:
print(
sum(
[
k**j
* [
0,
765144583,
346175634,
347662323,
5655049,
184117322,
927321758,
444014759,
542573865,
237315285,
417297686,
471090892,
183023413,
660103155,
727008098,
869418286,
539588932,
729548371,
700407153,
404391958,
962779130,
184117322,
927321758,
444014759,
542573865,
237315285,
417297686,
471090892,
183023413,
660103155,
727008098,
869418286,
][(k & 1 << 4) + j]
for j in range(16)
]
)
% (10**9 + 7)
)
|
Statement
Given is an integer N. Snuke will choose integers s_1, s_2, n_1, n_2, u_1,
u_2, k_1, k_2, e_1, and e_2 so that all of the following six conditions will
be satisfied:
* 0 \leq s_1 < s_2
* 0 \leq n_1 < n_2
* 0 \leq u_1 < u_2
* 0 \leq k_1 < k_2
* 0 \leq e_1 < e_2
* s_1 + s_2 + n_1 + n_2 + u_1 + u_2 + k_1 + k_2 + e_1 + e_2 \leq N
For every possible choice (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2), compute
(s_2 − s_1)(n_2 − n_1)(u_2 − u_1)(k_2 - k_1)(e_2 - e_1), and find the sum of
all computed values, modulo (10^{9} +7).
Solve this problem for each of the T test cases given.
|
[{"input": "4\n 4\n 6\n 10\n 1000000000", "output": "0\n 11\n 4598\n 257255556\n \n\n * When N=4, there is no possible choice (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2). Thus, the answer is 0.\n * When N=6, there are six possible choices (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2) as follows:\n * (0,1,0,1,0,1,0,1,0,1)\n * (0,2,0,1,0,1,0,1,0,1)\n * (0,1,0,2,0,1,0,1,0,1)\n * (0,1,0,1,0,2,0,1,0,1)\n * (0,1,0,1,0,1,0,2,0,1)\n * (0,1,0,1,0,1,0,1,0,2)\n * We have one choice where (s_2 \u2212 s_1)(n_2 \u2212 n_1)(u_2 \u2212 u_1)(k_2 - k_1)(e_2 - e_1) is 1 and five choices where (s_2 \u2212 s_1)(n_2 \u2212 n_1)(u_2 \u2212 u_1)(k_2 - k_1)(e_2 - e_1) is 2, so the answer is 11.\n * Be sure to find the sum modulo (10^{9} +7)."}]
|
Print T lines. The i-th line should contain the answer to the i-th test case.
* * *
|
s026426163
|
Accepted
|
p02611
|
Input is given from Standard Input in the following format:
T
\mathrm{case}_1
\vdots
\mathrm{case}_T
Each case is given in the following format:
N
|
m = 10**9 + 7
x = [
[
0,
765144583,
346175634,
347662323,
5655049,
184117322,
927321758,
444014759,
542573865,
237315285,
417297686,
471090892,
183023413,
660103155,
727008098,
869418286,
],
[
539588932,
729548371,
700407153,
404391958,
962779130,
184117322,
927321758,
444014759,
542573865,
237315285,
417297686,
471090892,
183023413,
660103155,
727008098,
869418286,
],
]
for _ in range(int(input())):
n = int(input())
print(sum([n**j * x[n & 1][j] for j in range(16)]) % m)
|
Statement
Given is an integer N. Snuke will choose integers s_1, s_2, n_1, n_2, u_1,
u_2, k_1, k_2, e_1, and e_2 so that all of the following six conditions will
be satisfied:
* 0 \leq s_1 < s_2
* 0 \leq n_1 < n_2
* 0 \leq u_1 < u_2
* 0 \leq k_1 < k_2
* 0 \leq e_1 < e_2
* s_1 + s_2 + n_1 + n_2 + u_1 + u_2 + k_1 + k_2 + e_1 + e_2 \leq N
For every possible choice (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2), compute
(s_2 − s_1)(n_2 − n_1)(u_2 − u_1)(k_2 - k_1)(e_2 - e_1), and find the sum of
all computed values, modulo (10^{9} +7).
Solve this problem for each of the T test cases given.
|
[{"input": "4\n 4\n 6\n 10\n 1000000000", "output": "0\n 11\n 4598\n 257255556\n \n\n * When N=4, there is no possible choice (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2). Thus, the answer is 0.\n * When N=6, there are six possible choices (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2) as follows:\n * (0,1,0,1,0,1,0,1,0,1)\n * (0,2,0,1,0,1,0,1,0,1)\n * (0,1,0,2,0,1,0,1,0,1)\n * (0,1,0,1,0,2,0,1,0,1)\n * (0,1,0,1,0,1,0,2,0,1)\n * (0,1,0,1,0,1,0,1,0,2)\n * We have one choice where (s_2 \u2212 s_1)(n_2 \u2212 n_1)(u_2 \u2212 u_1)(k_2 - k_1)(e_2 - e_1) is 1 and five choices where (s_2 \u2212 s_1)(n_2 \u2212 n_1)(u_2 \u2212 u_1)(k_2 - k_1)(e_2 - e_1) is 2, so the answer is 11.\n * Be sure to find the sum modulo (10^{9} +7)."}]
|
Print T lines. The i-th line should contain the answer to the i-th test case.
* * *
|
s712270254
|
Accepted
|
p02611
|
Input is given from Standard Input in the following format:
T
\mathrm{case}_1
\vdots
\mathrm{case}_T
Each case is given in the following format:
N
|
import sys
import numpy as np
read = sys.stdin.buffer.read
readline = sys.stdin.buffer.readline
readlines = sys.stdin.buffer.readlines
MOD = 10**9 + 7
def fft_convolve(f, g):
"""
数列 (多項式) f, g の畳み込みの計算.上下 15 bitずつ分けて計算することで,
30 bit以下の整数,長さ 250000 程度の数列での計算が正確に行える.
"""
Lf, Lg = f.shape[-1], g.shape[-1]
Lg = g.shape[-1]
L = Lf + Lg - 1
fft_len = 1 << L.bit_length()
fh, fl = f >> 15, f & (1 << 15) - 1
gh, gl = g >> 15, g & (1 << 15) - 1
def conv(f, g):
Ff = np.fft.rfft(f, fft_len)
Fg = np.fft.rfft(g, fft_len)
h = np.fft.irfft(Ff * Fg)
return np.rint(h)[..., :L].astype(np.int64) % MOD
x = conv(fl, gl)
z = conv(fh, gh)
y = conv(fl + fh, gl + gh) - x - z
return (x + (y << 15) + (z << 30)) % MOD
def coef_of_generating_function(P, Q, N):
"""compute the coefficient [x^N] P/Q of rational power series.
Parameters
----------
P : np.ndarray
numerator.
Q : np.ndarray
denominator
Q[0] == 1 and len(Q) == len(P) + 1 is assumed.
N : int
The coefficient to compute.
"""
assert Q[0] == 1 and len(Q) == len(P) + 1
def convolve(f, g):
return fft_convolve(f, g)
while N:
Q1 = np.empty_like(Q)
Q1[::2] = Q[::2]
Q1[1::2] = MOD - Q[1::2]
P = convolve(P, Q1)[N & 1 :: 2]
Q = convolve(Q, Q1)[::2]
N >>= 1
return P[0]
den = np.array([1, -1], np.int64)
for _ in range(5):
den = np.convolve(den, np.array([1, -2, 0, 2, -1]))
num = np.zeros_like(den)[:-1]
num[5] = 1
def f(N):
return coef_of_generating_function(num, den, N)
T = int(readline())
nums = map(int, read().split())
for n in nums:
print(f(n))
|
Statement
Given is an integer N. Snuke will choose integers s_1, s_2, n_1, n_2, u_1,
u_2, k_1, k_2, e_1, and e_2 so that all of the following six conditions will
be satisfied:
* 0 \leq s_1 < s_2
* 0 \leq n_1 < n_2
* 0 \leq u_1 < u_2
* 0 \leq k_1 < k_2
* 0 \leq e_1 < e_2
* s_1 + s_2 + n_1 + n_2 + u_1 + u_2 + k_1 + k_2 + e_1 + e_2 \leq N
For every possible choice (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2), compute
(s_2 − s_1)(n_2 − n_1)(u_2 − u_1)(k_2 - k_1)(e_2 - e_1), and find the sum of
all computed values, modulo (10^{9} +7).
Solve this problem for each of the T test cases given.
|
[{"input": "4\n 4\n 6\n 10\n 1000000000", "output": "0\n 11\n 4598\n 257255556\n \n\n * When N=4, there is no possible choice (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2). Thus, the answer is 0.\n * When N=6, there are six possible choices (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2) as follows:\n * (0,1,0,1,0,1,0,1,0,1)\n * (0,2,0,1,0,1,0,1,0,1)\n * (0,1,0,2,0,1,0,1,0,1)\n * (0,1,0,1,0,2,0,1,0,1)\n * (0,1,0,1,0,1,0,2,0,1)\n * (0,1,0,1,0,1,0,1,0,2)\n * We have one choice where (s_2 \u2212 s_1)(n_2 \u2212 n_1)(u_2 \u2212 u_1)(k_2 - k_1)(e_2 - e_1) is 1 and five choices where (s_2 \u2212 s_1)(n_2 \u2212 n_1)(u_2 \u2212 u_1)(k_2 - k_1)(e_2 - e_1) is 2, so the answer is 11.\n * Be sure to find the sum modulo (10^{9} +7)."}]
|
Print T lines. The i-th line should contain the answer to the i-th test case.
* * *
|
s201475971
|
Wrong Answer
|
p02611
|
Input is given from Standard Input in the following format:
T
\mathrm{case}_1
\vdots
\mathrm{case}_T
Each case is given in the following format:
N
|
import numpy as np
conv = np.convolve
def beki(P, Q, n):
while n:
Q1 = Q.copy()
Q1[1::2] = -Q[1::2]
P = conv(P, Q1)[n & 1 :: 2]
Q = conv(Q, Q1)[::2]
n >>= 1
return P[0]
mod = 10**9 + 7
t = int(input())
p = [0, 0, 0, 0, 0, 1]
q = [1]
for _ in range(16):
q = conv(q, [-1, 1])
for _ in range(5):
q = conv(q, [1, 1])
for i in range(t):
n = int(input())
print(beki(p, q, n) % mod)
|
Statement
Given is an integer N. Snuke will choose integers s_1, s_2, n_1, n_2, u_1,
u_2, k_1, k_2, e_1, and e_2 so that all of the following six conditions will
be satisfied:
* 0 \leq s_1 < s_2
* 0 \leq n_1 < n_2
* 0 \leq u_1 < u_2
* 0 \leq k_1 < k_2
* 0 \leq e_1 < e_2
* s_1 + s_2 + n_1 + n_2 + u_1 + u_2 + k_1 + k_2 + e_1 + e_2 \leq N
For every possible choice (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2), compute
(s_2 − s_1)(n_2 − n_1)(u_2 − u_1)(k_2 - k_1)(e_2 - e_1), and find the sum of
all computed values, modulo (10^{9} +7).
Solve this problem for each of the T test cases given.
|
[{"input": "4\n 4\n 6\n 10\n 1000000000", "output": "0\n 11\n 4598\n 257255556\n \n\n * When N=4, there is no possible choice (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2). Thus, the answer is 0.\n * When N=6, there are six possible choices (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2) as follows:\n * (0,1,0,1,0,1,0,1,0,1)\n * (0,2,0,1,0,1,0,1,0,1)\n * (0,1,0,2,0,1,0,1,0,1)\n * (0,1,0,1,0,2,0,1,0,1)\n * (0,1,0,1,0,1,0,2,0,1)\n * (0,1,0,1,0,1,0,1,0,2)\n * We have one choice where (s_2 \u2212 s_1)(n_2 \u2212 n_1)(u_2 \u2212 u_1)(k_2 - k_1)(e_2 - e_1) is 1 and five choices where (s_2 \u2212 s_1)(n_2 \u2212 n_1)(u_2 \u2212 u_1)(k_2 - k_1)(e_2 - e_1) is 2, so the answer is 11.\n * Be sure to find the sum modulo (10^{9} +7)."}]
|
Print T lines. The i-th line should contain the answer to the i-th test case.
* * *
|
s896091902
|
Wrong Answer
|
p02611
|
Input is given from Standard Input in the following format:
T
\mathrm{case}_1
\vdots
\mathrm{case}_T
Each case is given in the following format:
N
|
T = int(input())
mod = 10**9 + 7
for case in range(T):
n = int(input())
k = n // 2
ans = (
(
(k + 1)
* (k + 2)
* (k + 3)
* (k + 4)
* (k + 5)
* (
-50050 * n**9 * k
+ 386100 * n**8 * k**2
- 2413125 * n**8 * k
- 1801800 * n**7 * k**3
+ 16216200 * n**7 * k**2
- 49849800 * n**7 * k
+ 5605600 * n**6 * k**4
- 65165100 * n**6 * k**3
+ 285985700 * n**6 * k**2
- 576425850 * n**6 * k
- 12108096 * n**5 * k**5
+ 171531360 * n**5 * k**4
- 966125160 * n**5 * k**3
+ 2749546800 * n**5 * k**2
- 4088037954 * n**5 * k
+ 18345600 * n**4 * k**6
- 305454240 * n**4 * k**5
+ 2086302400 * n**4 * k**4
- 7557336150 * n**4 * k**3
+ 15640447550 * n**4 * k**2
- 18305945385 * n**4 * k
- 19219200 * n**3 * k**7
+ 366912000 * n**3 * k**6
- 2934072960 * n**3 * k**5
+ 12806757600 * n**3 * k**4
- 33368162100 * n**3 * k**3
+ 53348049300 * n**3 * k**2
- 51266409740 * n**3 * k
+ 13305600 * n**2 * k**8
- 286070400 * n**2 * k**7
+ 2614953600 * n**2 * k**6
- 13296679200 * n**2 * k**5
+ 41391926800 * n**2 * k**4
- 82078221750 * n**2 * k**3
+ 105034352450 * n**2 * k**2
- 85482724200 * n**2 * k
- 5491200 * n * k**9
+ 131155200 * n * k**8
- 1346822400 * n * k**7
+ 7797283200 * n * k**6
- 28086983904 * n * k**5
+ 65754247440 * n * k**4
- 102157331940 * n * k**3
+ 106855669500 * n * k**2
- 75640798296 * n * k
+ 1025024 * k**10
- 26906880 * k**9
+ 306324480 * k**8
- 1985860800 * k**7
+ 8100701952 * k**6
- 21735549360 * k**5
+ 39163472320 * k**4
- 48125918400 * k**3
+ 41580305424 * k**2
- 26358665760 * k
+ 3003 * n**10
+ 165165 * n**9
+ 3963960 * n**8
+ 54504450 * n**7
+ 473792319 * n**6
+ 2708871165 * n**5
+ 10261040790 * n**4
+ 25253728500 * n**3
+ 38298988728 * n**2
+ 31917805920 * n
+ 10897286400
)
)
% mod
) * pow(1307674368000, mod - 2, mod)
ans %= mod
print(ans)
|
Statement
Given is an integer N. Snuke will choose integers s_1, s_2, n_1, n_2, u_1,
u_2, k_1, k_2, e_1, and e_2 so that all of the following six conditions will
be satisfied:
* 0 \leq s_1 < s_2
* 0 \leq n_1 < n_2
* 0 \leq u_1 < u_2
* 0 \leq k_1 < k_2
* 0 \leq e_1 < e_2
* s_1 + s_2 + n_1 + n_2 + u_1 + u_2 + k_1 + k_2 + e_1 + e_2 \leq N
For every possible choice (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2), compute
(s_2 − s_1)(n_2 − n_1)(u_2 − u_1)(k_2 - k_1)(e_2 - e_1), and find the sum of
all computed values, modulo (10^{9} +7).
Solve this problem for each of the T test cases given.
|
[{"input": "4\n 4\n 6\n 10\n 1000000000", "output": "0\n 11\n 4598\n 257255556\n \n\n * When N=4, there is no possible choice (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2). Thus, the answer is 0.\n * When N=6, there are six possible choices (s_1,s_2,n_1,n_2,u_1,u_2,k_1,k_2,e_1,e_2) as follows:\n * (0,1,0,1,0,1,0,1,0,1)\n * (0,2,0,1,0,1,0,1,0,1)\n * (0,1,0,2,0,1,0,1,0,1)\n * (0,1,0,1,0,2,0,1,0,1)\n * (0,1,0,1,0,1,0,2,0,1)\n * (0,1,0,1,0,1,0,1,0,2)\n * We have one choice where (s_2 \u2212 s_1)(n_2 \u2212 n_1)(u_2 \u2212 u_1)(k_2 - k_1)(e_2 - e_1) is 1 and five choices where (s_2 \u2212 s_1)(n_2 \u2212 n_1)(u_2 \u2212 u_1)(k_2 - k_1)(e_2 - e_1) is 2, so the answer is 11.\n * Be sure to find the sum modulo (10^{9} +7)."}]
|
Print the total weight of the minimum spanning tree of $G$.
|
s036254469
|
Wrong Answer
|
p02241
|
In the first line, an integer $n$ denoting the number of vertices in $G$ is
given. In the following $n$ lines, a $n \times n$ adjacency matrix $A$ which
represents $G$ is given. $a_{ij}$ denotes the weight of edge connecting vertex
$i$ and vertex $j$. If there is no edge between $i$ and $j$, $a_{ij}$ is given
by -1.
|
Minimum Spanning Tree
For a given weighted graph $G = (V, E)$, find the minimum spanning tree (MST)
of $G$ and print total weight of edges belong to the MST.
|
[{"input": "5\n -1 2 3 1 -1\n 2 -1 -1 4 -1\n 3 -1 -1 1 1\n 1 4 1 -1 3\n -1 -1 1 3 -1", "output": "5"}]
|
|
Print the total weight of the minimum spanning tree of $G$.
|
s177987977
|
Accepted
|
p02241
|
In the first line, an integer $n$ denoting the number of vertices in $G$ is
given. In the following $n$ lines, a $n \times n$ adjacency matrix $A$ which
represents $G$ is given. $a_{ij}$ denotes the weight of edge connecting vertex
$i$ and vertex $j$. If there is no edge between $i$ and $j$, $a_{ij}$ is given
by -1.
|
a = input()
matrix = []
for i in range(int(a)):
matrix.append(list(map(int, input().split())))
# ?????????O(n)????????£?????????
class union_find(object):
"""union-find tree"""
def __init__(self, length):
self.length = length
self.unionnumber = 0
self.unionlist = [[]]
self.num = list(-1 for i in range(length))
def unite(self, i, j):
if self.num[i] == -1:
if self.num[j] == -1:
self.unionlist[self.unionnumber].extend([i, j])
self.num[i] = self.unionnumber
self.num[j] = self.unionnumber
self.unionnumber += 1
self.unionlist.append([])
else:
tmp = i
i = j
j = tmp
if self.num[i] != -1:
if self.num[j] != -1:
if self.num[i] == self.num[j]:
pass
else:
self.unionlist[self.num[i]].extend(self.unionlist[self.num[j]])
tmp = self.num[j]
for k in self.unionlist[self.num[j]]:
self.num[k] = self.num[i]
self.unionlist[tmp] = "del"
else:
self.num[j] = self.num[i]
self.unionlist[self.num[i]].append(j)
def same(self, i, j):
if self.num[i] == -1 or self.num[j] == -1:
return False
else:
return self.num[i] == self.num[j]
# ?????????=-1
def Kruskal(matrix):
length = len(matrix)
edgelist = []
for i in range(length):
for j in range(i + 1):
if matrix[i][j] != -1:
edgelist.append([j, i, matrix[i][j]])
edgelist.sort(key=lambda x: x[2], reverse=True)
result = [[-1 for i in range(length)] for j in range(length)]
union = union_find(length)
while edgelist != []:
edge = edgelist.pop()
i, j, score = edge
if union.same(i, j):
pass
else:
union.unite(i, j)
result[i][j] = score
result[j][i] = score
return result
a = Kruskal(matrix)
count = 0
for i in range(len(a)):
for j in range(i):
if a[i][j] != -1:
count += a[i][j]
print(count)
|
Minimum Spanning Tree
For a given weighted graph $G = (V, E)$, find the minimum spanning tree (MST)
of $G$ and print total weight of edges belong to the MST.
|
[{"input": "5\n -1 2 3 1 -1\n 2 -1 -1 4 -1\n 3 -1 -1 1 1\n 1 4 1 -1 3\n -1 -1 1 3 -1", "output": "5"}]
|
Print the total weight of the minimum spanning tree of $G$.
|
s391388296
|
Wrong Answer
|
p02241
|
In the first line, an integer $n$ denoting the number of vertices in $G$ is
given. In the following $n$ lines, a $n \times n$ adjacency matrix $A$ which
represents $G$ is given. $a_{ij}$ denotes the weight of edge connecting vertex
$i$ and vertex $j$. If there is no edge between $i$ and $j$, $a_{ij}$ is given
by -1.
|
n = int(input())
a = []
for i in range(n):
inp = input()
if "-1" in inp:
inp = inp.replace("-1", "10000")
a.append(list(map(int, inp.split())))
w = 0
v = set()
v.add(0)
while len(v) < n:
print(v)
min_w = 10000
min_idx = 0
i = 0
for node in v:
if min_w > min(a[node]):
min_w = min(a[node])
i = node
min_idx = a[i].index(min_w)
if min_idx in v:
a[i][min_idx] = 10000
continue
else:
w += min_w
v.add(min_idx)
print(w)
|
Minimum Spanning Tree
For a given weighted graph $G = (V, E)$, find the minimum spanning tree (MST)
of $G$ and print total weight of edges belong to the MST.
|
[{"input": "5\n -1 2 3 1 -1\n 2 -1 -1 4 -1\n 3 -1 -1 1 1\n 1 4 1 -1 3\n -1 -1 1 3 -1", "output": "5"}]
|
Print the total weight of the minimum spanning tree of $G$.
|
s836996787
|
Wrong Answer
|
p02241
|
In the first line, an integer $n$ denoting the number of vertices in $G$ is
given. In the following $n$ lines, a $n \times n$ adjacency matrix $A$ which
represents $G$ is given. $a_{ij}$ denotes the weight of edge connecting vertex
$i$ and vertex $j$. If there is no edge between $i$ and $j$, $a_{ij}$ is given
by -1.
|
def memoize(f):
cache = {}
def helper(x):
if x not in cache:
cache[x] = f(x)
return cache[x]
return helper
def split_apex(a):
if len(a) == 2:
yield (a[0],), (a[1],)
else:
for i in range(0, len(a)):
yield (a[i],), a[:i] + a[i + 1 :]
@memoize
def wait(a):
global g
if len(a) == 1:
return 0
return min(calc_wait(apex, apices) for apex, apices in split_apex(a))
def calc_wait(apex, apices):
global g
w = [g[apex[0]][i] for i in apices if g[apex[0]][i] != -1]
return wait(apex) + wait(apices) + (min(w) if len(w) else 200000)
n = int(input())
g = [None] + [[None] + list(map(int, input().split())) for _ in range(n)]
a = tuple(i + 1 for i in range(n))
wait(a)
|
Minimum Spanning Tree
For a given weighted graph $G = (V, E)$, find the minimum spanning tree (MST)
of $G$ and print total weight of edges belong to the MST.
|
[{"input": "5\n -1 2 3 1 -1\n 2 -1 -1 4 -1\n 3 -1 -1 1 1\n 1 4 1 -1 3\n -1 -1 1 3 -1", "output": "5"}]
|
Print the total weight of the minimum spanning tree of $G$.
|
s960137931
|
Accepted
|
p02241
|
In the first line, an integer $n$ denoting the number of vertices in $G$ is
given. In the following $n$ lines, a $n \times n$ adjacency matrix $A$ which
represents $G$ is given. $a_{ij}$ denotes the weight of edge connecting vertex
$i$ and vertex $j$. If there is no edge between $i$ and $j$, $a_{ij}$ is given
by -1.
|
import heapq
class MST:
"""Given weighted graph, find minimum spanning tree.
>>> mst = MST([[-1, 2, 3, 1, -1], \
[2, -1, -1, 4, -1], \
[3, -1, -1, 1, 1], \
[1, 4, 1, -1, 3], \
[-1, -1, 1, 3, -1]]);
>>> mst.weight()
5
"""
MAX_WEIGHT = 2001
def __init__(self, graph):
self.graph = graph
self.size = len(graph)
self.tree = []
self._search()
def weight(self):
return sum([self.graph[i][j] for i, j in self.tree])
def _search(self):
visited = [0]
while len(visited) < self.size:
h = []
for node in visited:
for i, w in enumerate(self.graph[node]):
if w == -1:
continue
if i in visited:
continue
heapq.heappush(h, (w, node, i))
weight, src, dst = heapq.heappop(h)
visited.append(dst)
self.tree.append((src, dst))
def run():
n = int(input())
nodes = []
for _ in range(n):
nodes.append([int(i) for i in input().split()])
mst = MST(nodes)
print(mst.weight())
if __name__ == "__main__":
run()
|
Minimum Spanning Tree
For a given weighted graph $G = (V, E)$, find the minimum spanning tree (MST)
of $G$ and print total weight of edges belong to the MST.
|
[{"input": "5\n -1 2 3 1 -1\n 2 -1 -1 4 -1\n 3 -1 -1 1 1\n 1 4 1 -1 3\n -1 -1 1 3 -1", "output": "5"}]
|
Print the total weight of the minimum spanning tree of $G$.
|
s922503345
|
Accepted
|
p02241
|
In the first line, an integer $n$ denoting the number of vertices in $G$ is
given. In the following $n$ lines, a $n \times n$ adjacency matrix $A$ which
represents $G$ is given. $a_{ij}$ denotes the weight of edge connecting vertex
$i$ and vertex $j$. If there is no edge between $i$ and $j$, $a_{ij}$ is given
by -1.
|
n = int(input())
adj = [list(map(int, input().split())) for i in range(n)]
def mst():
T = [0]
gross_weight = 0
cnt = n - 1
while cnt:
ew = 2001
for i in range(len(T)):
for tv, tew in enumerate(adj[T[i]]):
if (tv not in T) and (tew != -1):
if tew < ew:
v, ew = tv, tew
T.append(v)
gross_weight += ew
cnt -= 1
print(gross_weight)
mst()
|
Minimum Spanning Tree
For a given weighted graph $G = (V, E)$, find the minimum spanning tree (MST)
of $G$ and print total weight of edges belong to the MST.
|
[{"input": "5\n -1 2 3 1 -1\n 2 -1 -1 4 -1\n 3 -1 -1 1 1\n 1 4 1 -1 3\n -1 -1 1 3 -1", "output": "5"}]
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.