output_description
stringlengths 15
956
| submission_id
stringlengths 10
10
| status
stringclasses 3
values | problem_id
stringlengths 6
6
| input_description
stringlengths 9
2.55k
| attempt
stringlengths 1
13.7k
| problem_description
stringlengths 7
5.24k
| samples
stringlengths 2
2.72k
|
|---|---|---|---|---|---|---|---|
Print the original password.
* * *
|
s937938444
|
Accepted
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
print("".join([a + b for a, b in zip(input(), input() + "\n")]).split("\n")[0])
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s145370806
|
Wrong Answer
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
print("".join([a + b for a, b in zip(input(), input())]))
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s386162035
|
Runtime Error
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
a=lst(input())
b=input()
i=0
for j in b:
a[i:i]=j
i+=1
print(*a)
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s701696902
|
Runtime Error
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
odds = input()
evens = input()
password = "".join(a + b for (a, b) in zip(odds, evens)
if len(odds) > len(evens):
password += odds[-1]
print(password)
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s862445113
|
Runtime Error
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
o=list(input())
e=list(input())
p=list(o + e)
for i in range(len(p)):
if i % 2 = 1 :
p[i-1]=o[int((i-1)/2)]
else:
p[i-1]=o[int((i/2)-1)]
print("".join(pass))
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s377566944
|
Runtime Error
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
o=list(input())
e=list(input())
p=list(o + e)
for i in range(len(p)):
if i % 2 == 1 :
p[i-1]=o[int((i-1)/2)]
else:
p[i-1]=o[int((i/2)-1)]
print("".join(pass))
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s723301355
|
Wrong Answer
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
#!/usr/bin/python3
# ABC058_B
"""
∵∴∵
"""
test = True
def restore():
"""
奇数番目の文字の文字列 O
偶数番目の文字の文字列 E
からもとの文字列を復元する関数
"""
O = input() # 奇数番目の文字
E = input() # 偶数番目の文字
password = "" # もとのパスワード
len_O = len(O)
if test:
print(len_O)
for i in range(len_O):
password += O[i]
try:
password += E[i]
except IndexError:
pass
return password
def main():
"""
main関数
"""
print(restore())
if __name__ == "__main__":
main()
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s512494721
|
Wrong Answer
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
print(*[a + b for a, b in zip(input(), input())], sep="")
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s761633187
|
Accepted
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
if __name__ == "__main__":
X = input()
Y = input()
N = len(X) + len(Y)
res = ""
cnt1 = 0
cnt2 = 0
for x in range(N):
if x % 2 == 0:
res += X[cnt1]
cnt1 += 1
else:
res += Y[cnt2]
cnt2 += 1
print(res)
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s583947291
|
Accepted
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
A = list(input())
B = list(input())
C = list()
if len(A) == len(B):
for i in range(len(A)):
C.append(A[i] + B[i])
print("".join(C))
else:
for i in range(len(B)):
C.append(A[i] + B[i])
C.append(A[-1])
print("".join(C))
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s574802298
|
Accepted
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
while True:
try:
o, e = [input() for _ in range(2)]
s = ""
for i in range(len(e)):
s += o[i] + e[i]
if len(o) != len(e):
s += o[len(o) - 1]
print(s)
except EOFError:
exit()
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s627685335
|
Accepted
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
print("".join("".join(x) for x in zip(input(), input() + " ")).strip())
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s906990990
|
Runtime Error
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
o = input().split("")
e = input().split("")
j = 0
k = 0
ans = ""
for i in range(len(o) + len(e)):
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s721582922
|
Accepted
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
s_odd = input()
s_even = input()
o = s_odd.__len__()
e = s_even.__len__()
s = [(s_odd[i] + s_even[i]) for i in range(e)]
if o - e == 1:
s += s_odd[-1]
print("".join(s))
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s579769602
|
Accepted
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
###
### atcorder test program
###
import sys
### math class
class math:
### pi
pi = 3.14159265358979323846264338
### GCD
def gcd(self, a, b):
if b == 0:
return a
return self.gcd(b, a % b)
### LCM
def lcm(self, a, b):
return (a * b) // self.gcd(a, b)
### Prime number search
def Pnum(self, a):
if a == 1:
return False
for i in range(2, int(a**0.5) + 1):
if a % i == 0:
return False
return True
### Circle area
def caria(self, r):
return r * r * self.pi
math = math()
### output class
class output:
### list
def list(self, l):
l = list(l)
print(" ", end="")
for i, num in enumerate(l):
print(num, end="")
if i != len(l) - 1:
print(" ", end="")
print()
output = output()
### input sample
# i = input()
# A, B, C = [x for x in input().split()]
# inlist = [int(w) for w in input().split()]
# R = float(input())
# A = [int(x) for x in input().split()]
# for line in sys.stdin.readlines():
# x, y = [int(temp) for temp in line.split()]
### output sample
# print("{0} {1} {2:.5f}".format(A//B, A%B, A/B))
# print("{0:.6f} {1:.6f}".format(R*R*math.pi,R*2*math.pi))
# print(" {}".format(i), end="")
# A, B, C = [int(x) for x in input().split()]
O = input()
E = input()
for i in range(len(O)):
print(O[i], end="")
if len(E) > i:
print(E[i], end="")
print("")
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
Print the original password.
* * *
|
s761394320
|
Accepted
|
p03760
|
Input is given from Standard Input in the following format:
O
E
|
# Author: cr4zjh0bp
# Created: Sat Mar 28 10:36:41 UTC 2020
import sys
stdin = sys.stdin
inf = 1 << 60
mod = 1000000007
ni = lambda: int(ns())
nin = lambda y: [ni() for _ in range(y)]
na = lambda: list(map(int, stdin.readline().split()))
nan = lambda y: [na() for _ in range(y)]
nf = lambda: float(ns())
nfn = lambda y: [nf() for _ in range(y)]
nfa = lambda: list(map(float, stdin.readline().split()))
nfan = lambda y: [nfa() for _ in range(y)]
ns = lambda: stdin.readline().rstrip()
nsn = lambda y: [ns() for _ in range(y)]
ncl = lambda y: [list(ns()) for _ in range(y)]
nas = lambda: stdin.readline().split()
o = ns()
e = ns()
s = []
i = 0
for i, j in zip(o, e):
s.append(i)
s.append(j)
if len(o) > len(e):
s.append(o[-1])
elif len(e) > len(o):
s.append(e[-1])
print(*s, sep="")
|
Statement
Snuke signed up for a new website which holds programming competitions. He
worried that he might forget his password, and he took notes of it. Since
directly recording his password would cause him trouble if stolen, he took two
notes: one contains the characters at the odd-numbered positions, and the
other contains the characters at the even-numbered positions.
You are given two strings O and E. O contains the characters at the odd-
numbered positions retaining their relative order, and E contains the
characters at the even-numbered positions retaining their relative order.
Restore the original password.
|
[{"input": "xyz\n abc", "output": "xaybzc\n \n\nThe original password is `xaybzc`. Extracting the characters at the odd-\nnumbered positions results in `xyz`, and extracting the characters at the\neven-numbered positions results in `abc`.\n\n* * *"}, {"input": "atcoderbeginnercontest\n atcoderregularcontest", "output": "aattccooddeerrbreeggiunlnaerrccoonntteesstt"}]
|
If the minimum possible sum of the wrongness of all the squares is x, print x.
* * *
|
s809638148
|
Runtime Error
|
p03330
|
Input is given from Standard Input in the following format:
N C
D_{1,1} ... D_{1,C}
:
D_{C,1} ... D_{C,C}
c_{1,1} ... c_{1,N}
:
c_{N,1} ... c_{N,N}
|
4 3
0 12 71
81 0 53
14 92 0
1 1 2 1
2 1 1 2
2 2 1 3
1 1 2 2
428
k-mbp:ABC99 kaibe$ cat D.py
N,C = map(int,input().split())
D = []
c = []
for i in range(C):
D.append(list(map(int,input().split())))
for i in range(N):
c.append(list(map(int,input().split())))
c1 = []
c2 = []
c3 = []
from itertools import product
for i,j in product(range(N),repeat=2):
if (i+j)%3 == 0:
c1.append(c[i][j])
elif (i+j)%3 == 1:
c2.append(c[i][j])
else:
c3.append(c[i][j])
val=[]
cnt=[[],[],[]]
for j in range(C):
cnt[0].append(c1.count(j+1))
cnt[1].append(c2.count(j+1))
cnt[2].append(c3.count(j+1))
for i in product(range(C),repeat=3):
dif = 0
if i[0]!=i[1] and i[1]!=i[2] and i[2]!=i[0]:
for j in range(C):
dif += D[j][i[0]] * cnt[0][j]
dif += D[j][i[1]] * cnt[1][j]
dif += D[j][i[2]] * cnt[2][j]
val.append(dif)
print(min(val))
|
Statement
There is a grid with N rows and N columns of squares. Let (i,j) be the square
at the i-th row from the top and the j-th column from the left.
These squares have to be painted in one of the C colors from Color 1 to Color
C. Initially, (i,j) is painted in Color c_{i,j}.
We say the grid is a _good_ grid when the following condition is met for all
i,j,x,y satisfying 1 \leq i,j,x,y \leq N:
* If (i+j) \% 3=(x+y) \% 3, the color of (i,j) and the color of (x,y) are the same.
* If (i+j) \% 3 \neq (x+y) \% 3, the color of (i,j) and the color of (x,y) are different.
Here, X \% Y represents X modulo Y.
We will repaint zero or more squares so that the grid will be a good grid.
For a square, the _wrongness_ when the color of the square is X before
repainting and Y after repainting, is D_{X,Y}.
Find the minimum possible sum of the wrongness of all the squares.
|
[{"input": "2 3\n 0 1 1\n 1 0 1\n 1 4 0\n 1 2\n 3 3", "output": "3\n \n\n * Repaint (1,1) to Color 2. The wrongness of (1,1) becomes D_{1,2}=1.\n * Repaint (1,2) to Color 3. The wrongness of (1,2) becomes D_{2,3}=1.\n * Repaint (2,2) to Color 1. The wrongness of (2,2) becomes D_{3,1}=1.\n\nIn this case, the sum of the wrongness of all the squares is 3.\n\nNote that D_{i,j} \\neq D_{j,i} is possible.\n\n* * *"}, {"input": "4 3\n 0 12 71\n 81 0 53\n 14 92 0\n 1 1 2 1\n 2 1 1 2\n 2 2 1 3\n 1 1 2 2", "output": "428"}]
|
If the minimum possible sum of the wrongness of all the squares is x, print x.
* * *
|
s038999329
|
Runtime Error
|
p03330
|
Input is given from Standard Input in the following format:
N C
D_{1,1} ... D_{1,C}
:
D_{C,1} ... D_{C,C}
c_{1,1} ... c_{1,N}
:
c_{N,1} ... c_{N,N}
|
def sol():
n,c=map(int,input().split())
d=[[int(i) for i in input().split()] for i in range(c)]
t=[[int(i) for i in input().split()] for i in range(n)]
ans=-1
for i in range(c):
for j in range(c):
for k in range(c):
q=[i,j,k]
if len(set(q))<3: break
chk=0
for p in range(n**2):
h,w=p//n,p%n
x=(h+w+2)%3
chk+=d[t[h][w]-1][q[x]]
if ans==-1: ans=chk
ans=min(ans,chk)
print(ans)
if __name__="__main__":
sol()
|
Statement
There is a grid with N rows and N columns of squares. Let (i,j) be the square
at the i-th row from the top and the j-th column from the left.
These squares have to be painted in one of the C colors from Color 1 to Color
C. Initially, (i,j) is painted in Color c_{i,j}.
We say the grid is a _good_ grid when the following condition is met for all
i,j,x,y satisfying 1 \leq i,j,x,y \leq N:
* If (i+j) \% 3=(x+y) \% 3, the color of (i,j) and the color of (x,y) are the same.
* If (i+j) \% 3 \neq (x+y) \% 3, the color of (i,j) and the color of (x,y) are different.
Here, X \% Y represents X modulo Y.
We will repaint zero or more squares so that the grid will be a good grid.
For a square, the _wrongness_ when the color of the square is X before
repainting and Y after repainting, is D_{X,Y}.
Find the minimum possible sum of the wrongness of all the squares.
|
[{"input": "2 3\n 0 1 1\n 1 0 1\n 1 4 0\n 1 2\n 3 3", "output": "3\n \n\n * Repaint (1,1) to Color 2. The wrongness of (1,1) becomes D_{1,2}=1.\n * Repaint (1,2) to Color 3. The wrongness of (1,2) becomes D_{2,3}=1.\n * Repaint (2,2) to Color 1. The wrongness of (2,2) becomes D_{3,1}=1.\n\nIn this case, the sum of the wrongness of all the squares is 3.\n\nNote that D_{i,j} \\neq D_{j,i} is possible.\n\n* * *"}, {"input": "4 3\n 0 12 71\n 81 0 53\n 14 92 0\n 1 1 2 1\n 2 1 1 2\n 2 2 1 3\n 1 1 2 2", "output": "428"}]
|
If the minimum possible sum of the wrongness of all the squares is x, print x.
* * *
|
s461234218
|
Runtime Error
|
p03330
|
Input is given from Standard Input in the following format:
N C
D_{1,1} ... D_{1,C}
:
D_{C,1} ... D_{C,C}
c_{1,1} ... c_{1,N}
:
c_{N,1} ... c_{N,N}
|
x = input().split()
n = int(x[0])
c = int(x[1])
dlist = [0] * (c * c)
clist = [0] * (n * n)
cost1 = []
cost2 = []
cost3 = []
x = 0
for i in range(c):
a = input().split()
for i in a:
dlist[x] = i
x = x + 1
x = 0
for i in range(n):
a = input().split()
for i in a:
clist[x] = i
x += 1
x = 0
list1 = []
list2 = []
list3 = []
y = 0
yy = 0
while y < n:
while yy < n:
if (y + yy) % 3 == 0:
list1.append(clist[y * n + yy])
elif (y + yy) % 3 == 1:
list2.append(clist[y * n + yy])
elif (y + yy) % 3 == 2:
list3.append(clist[y * n + yy])
yy = yy + 1
y = y + 1
yy = 0
y = 1
y2 = 1
y3 = 1
mini = 99999999999999999999
while y <= c:
cost = 0
for i in list1:
if i != y:
cost = cost + dlist[(i - 1) * c + y - 1]
cost1.append(cost)
y = y + 1
while y2 <= c:
cost = 0
for i in list2:
if i != y2:
cost = cost + dlist[(i - 1) * c + y2 - 1]
cost2.append(cost)
y2 = y2 + 1
while y3 <= c:
cost = 0
for i in list3:
if i != y3:
cost = cost + dlist[(i - 1) * c + y3 - 1]
cost3.append(cost)
y3 = y3 + 1
x = 1
x2 = 2
x3 = 3
while x <= c:
while x2 <= c:
if x2 == x:
x2 += 1
if x2 > c:
break
while x3 <= c:
if x3 == x or x3 == x2:
x3 += 1
if x3 == x or x3 == x2:
x3 += 1
if x3 > c:
break
mini = min(mini, cost1[x - 1] + cost2[x2 - 1] + cost3[x3 - 1])
x3 += 1
x2 += 1
x3 = 1
x += 1
x2 = 1
x3 = 1
print(mini)
|
Statement
There is a grid with N rows and N columns of squares. Let (i,j) be the square
at the i-th row from the top and the j-th column from the left.
These squares have to be painted in one of the C colors from Color 1 to Color
C. Initially, (i,j) is painted in Color c_{i,j}.
We say the grid is a _good_ grid when the following condition is met for all
i,j,x,y satisfying 1 \leq i,j,x,y \leq N:
* If (i+j) \% 3=(x+y) \% 3, the color of (i,j) and the color of (x,y) are the same.
* If (i+j) \% 3 \neq (x+y) \% 3, the color of (i,j) and the color of (x,y) are different.
Here, X \% Y represents X modulo Y.
We will repaint zero or more squares so that the grid will be a good grid.
For a square, the _wrongness_ when the color of the square is X before
repainting and Y after repainting, is D_{X,Y}.
Find the minimum possible sum of the wrongness of all the squares.
|
[{"input": "2 3\n 0 1 1\n 1 0 1\n 1 4 0\n 1 2\n 3 3", "output": "3\n \n\n * Repaint (1,1) to Color 2. The wrongness of (1,1) becomes D_{1,2}=1.\n * Repaint (1,2) to Color 3. The wrongness of (1,2) becomes D_{2,3}=1.\n * Repaint (2,2) to Color 1. The wrongness of (2,2) becomes D_{3,1}=1.\n\nIn this case, the sum of the wrongness of all the squares is 3.\n\nNote that D_{i,j} \\neq D_{j,i} is possible.\n\n* * *"}, {"input": "4 3\n 0 12 71\n 81 0 53\n 14 92 0\n 1 1 2 1\n 2 1 1 2\n 2 2 1 3\n 1 1 2 2", "output": "428"}]
|
If the minimum possible sum of the wrongness of all the squares is x, print x.
* * *
|
s868682060
|
Runtime Error
|
p03330
|
Input is given from Standard Input in the following format:
N C
D_{1,1} ... D_{1,C}
:
D_{C,1} ... D_{C,C}
c_{1,1} ... c_{1,N}
:
c_{N,1} ... c_{N,N}
|
N,C = list(map(int,input().split()))
D = [ list(map(int,input().split())) for i in range(C)]
c = [ list(map(int,input().split())) for i in range(N)]
sep = {0:[0 for i in range(C)],1:[0 for i in range(C)],2:[0 for i in range(C)]}
for i,cx in enumerate(c):
for j,cy in enumerate(cx):
sep[(i + j) % 3][cy] + = 1
minimums = [[],[],[]]
for key,values in sep.tems():
for i in range(C):
m0 = 0
am0 = 0
m1 = 0
am1 = 1
deposit = 0
for j,value in enumerate(values):
deposit += D[j][i] * valuea
sep[key].append(deposit)
min0 = min(sep[0])
min1 = min(sep[1])
min2 = min(sep[2])
min3 = min(sep[2])
print(min1 + min2 + min3)
|
Statement
There is a grid with N rows and N columns of squares. Let (i,j) be the square
at the i-th row from the top and the j-th column from the left.
These squares have to be painted in one of the C colors from Color 1 to Color
C. Initially, (i,j) is painted in Color c_{i,j}.
We say the grid is a _good_ grid when the following condition is met for all
i,j,x,y satisfying 1 \leq i,j,x,y \leq N:
* If (i+j) \% 3=(x+y) \% 3, the color of (i,j) and the color of (x,y) are the same.
* If (i+j) \% 3 \neq (x+y) \% 3, the color of (i,j) and the color of (x,y) are different.
Here, X \% Y represents X modulo Y.
We will repaint zero or more squares so that the grid will be a good grid.
For a square, the _wrongness_ when the color of the square is X before
repainting and Y after repainting, is D_{X,Y}.
Find the minimum possible sum of the wrongness of all the squares.
|
[{"input": "2 3\n 0 1 1\n 1 0 1\n 1 4 0\n 1 2\n 3 3", "output": "3\n \n\n * Repaint (1,1) to Color 2. The wrongness of (1,1) becomes D_{1,2}=1.\n * Repaint (1,2) to Color 3. The wrongness of (1,2) becomes D_{2,3}=1.\n * Repaint (2,2) to Color 1. The wrongness of (2,2) becomes D_{3,1}=1.\n\nIn this case, the sum of the wrongness of all the squares is 3.\n\nNote that D_{i,j} \\neq D_{j,i} is possible.\n\n* * *"}, {"input": "4 3\n 0 12 71\n 81 0 53\n 14 92 0\n 1 1 2 1\n 2 1 1 2\n 2 2 1 3\n 1 1 2 2", "output": "428"}]
|
If the minimum possible sum of the wrongness of all the squares is x, print x.
* * *
|
s943211809
|
Wrong Answer
|
p03330
|
Input is given from Standard Input in the following format:
N C
D_{1,1} ... D_{1,C}
:
D_{C,1} ... D_{C,C}
c_{1,1} ... c_{1,N}
:
c_{N,1} ... c_{N,N}
|
n, b = map(int, input().split())
d = [list(map(int, input().split())) for _ in [0] * b]
c = [list(map(int, input().split())) for _ in [0] * n]
mods = [{}, {}, {}]
for i in range(n):
for j in range(n):
m = (i + j) % 3
cij = c[i][j]
if cij in mods[m].keys():
mods[m][cij] += 1
else:
mods[m][cij] = 1
mins = [[], [], []]
for i in range(b):
for l in [0, 1, 2]:
mins[l] += [sum([d[k - 1][i] * v for (k, v) in mods[l].items()])]
r = 1000000
for i in range(b):
for j in range(b):
for k in range(b):
if i != j and j != k and k != i:
r = min(mins[0][i] + mins[1][j] + mins[2][k], r)
print(r)
|
Statement
There is a grid with N rows and N columns of squares. Let (i,j) be the square
at the i-th row from the top and the j-th column from the left.
These squares have to be painted in one of the C colors from Color 1 to Color
C. Initially, (i,j) is painted in Color c_{i,j}.
We say the grid is a _good_ grid when the following condition is met for all
i,j,x,y satisfying 1 \leq i,j,x,y \leq N:
* If (i+j) \% 3=(x+y) \% 3, the color of (i,j) and the color of (x,y) are the same.
* If (i+j) \% 3 \neq (x+y) \% 3, the color of (i,j) and the color of (x,y) are different.
Here, X \% Y represents X modulo Y.
We will repaint zero or more squares so that the grid will be a good grid.
For a square, the _wrongness_ when the color of the square is X before
repainting and Y after repainting, is D_{X,Y}.
Find the minimum possible sum of the wrongness of all the squares.
|
[{"input": "2 3\n 0 1 1\n 1 0 1\n 1 4 0\n 1 2\n 3 3", "output": "3\n \n\n * Repaint (1,1) to Color 2. The wrongness of (1,1) becomes D_{1,2}=1.\n * Repaint (1,2) to Color 3. The wrongness of (1,2) becomes D_{2,3}=1.\n * Repaint (2,2) to Color 1. The wrongness of (2,2) becomes D_{3,1}=1.\n\nIn this case, the sum of the wrongness of all the squares is 3.\n\nNote that D_{i,j} \\neq D_{j,i} is possible.\n\n* * *"}, {"input": "4 3\n 0 12 71\n 81 0 53\n 14 92 0\n 1 1 2 1\n 2 1 1 2\n 2 2 1 3\n 1 1 2 2", "output": "428"}]
|
If the minimum possible sum of the wrongness of all the squares is x, print x.
* * *
|
s014190892
|
Runtime Error
|
p03330
|
Input is given from Standard Input in the following format:
N C
D_{1,1} ... D_{1,C}
:
D_{C,1} ... D_{C,C}
c_{1,1} ... c_{1,N}
:
c_{N,1} ... c_{N,N}
|
import copy
N , C = map(int, input().split())
ds =[list(map(int, input().split())) for i in range(C)]
cs =[list(map(int, input().split())) for i in range(N)]
c0 = []
c1 = []
c2 = []
for i in range(N):
for j in range(N):
if (i+j) % 3 == 0:
c0.append(cs[i][j])
elif (i+j) % 3 == 1:
c1.append(cs[i][j])
else:
c2.append(cs[i][j])
d = 10**9
l0 = len(c0)
l1 = len(c1)
l2 = len(c2)
for i in range(C):
d0 = 0
for l in range(l0):
if (c0[l]-1) != i:
d0 += ds[c0[l]-1][i]
for j in range(C):
if i == j:
continue
d1 = copy,copy(d0)
for h in range(l1):
if (c1[h]-1) != j:
d1 += ds[c1[h]-1][j]
for k in range(C):
if i == k or j == k:
continue
d2 = copy.copy(d1)
for l in range(l2):
if (c2[l]-1) != k:
d2 += ds[c2[l]-1][k]
if d > d2:
d = d2
print(d)
|
Statement
There is a grid with N rows and N columns of squares. Let (i,j) be the square
at the i-th row from the top and the j-th column from the left.
These squares have to be painted in one of the C colors from Color 1 to Color
C. Initially, (i,j) is painted in Color c_{i,j}.
We say the grid is a _good_ grid when the following condition is met for all
i,j,x,y satisfying 1 \leq i,j,x,y \leq N:
* If (i+j) \% 3=(x+y) \% 3, the color of (i,j) and the color of (x,y) are the same.
* If (i+j) \% 3 \neq (x+y) \% 3, the color of (i,j) and the color of (x,y) are different.
Here, X \% Y represents X modulo Y.
We will repaint zero or more squares so that the grid will be a good grid.
For a square, the _wrongness_ when the color of the square is X before
repainting and Y after repainting, is D_{X,Y}.
Find the minimum possible sum of the wrongness of all the squares.
|
[{"input": "2 3\n 0 1 1\n 1 0 1\n 1 4 0\n 1 2\n 3 3", "output": "3\n \n\n * Repaint (1,1) to Color 2. The wrongness of (1,1) becomes D_{1,2}=1.\n * Repaint (1,2) to Color 3. The wrongness of (1,2) becomes D_{2,3}=1.\n * Repaint (2,2) to Color 1. The wrongness of (2,2) becomes D_{3,1}=1.\n\nIn this case, the sum of the wrongness of all the squares is 3.\n\nNote that D_{i,j} \\neq D_{j,i} is possible.\n\n* * *"}, {"input": "4 3\n 0 12 71\n 81 0 53\n 14 92 0\n 1 1 2 1\n 2 1 1 2\n 2 2 1 3\n 1 1 2 2", "output": "428"}]
|
If the minimum possible sum of the wrongness of all the squares is x, print x.
* * *
|
s492916279
|
Runtime Error
|
p03330
|
Input is given from Standard Input in the following format:
N C
D_{1,1} ... D_{1,C}
:
D_{C,1} ... D_{C,C}
c_{1,1} ... c_{1,N}
:
c_{N,1} ... c_{N,N}
|
#include <iostream>
#include <vector>
#include <algorithm>
#include <utility>
#include <string>
#include <queue>
#include <stack>
using namespace std;
typedef long long int ll;
typedef pair<int, int> Pii;
const ll mod = 1000000007;
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
int n, c;
cin >> n >> c;
vector<vector<int> > d(c, vector<int>(c));
for (auto &x: d) {
for (auto &y: x) cin >> y;
}
vector<vector<int> > a(n, vector<int>(n));
for (auto &x: a) {
for (auto &y: x) {
cin >> y;
y--;
}
}
vector<int> c0Count(c), c1Count(c), c2Count(c);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if ((i + j) % 3 == 0) c0Count[a[i][j]]++;
else if ((i + j) % 3 == 1) c1Count[a[i][j]]++;
else if ((i + j) % 3 == 2) c2Count[a[i][j]]++;
}
}
int ans = 1000000007;
for (int c0 = 0; c0 < c; c0++) {
for (int c1 = 0; c1 < c; c1++) {
if (c0 == c1) continue;
for (int c2 = 0; c2 < c; c2++) {
if (c0 == c2 || c1 == c2) continue;
int cost = 0;
for (int i = 0; i < c; i++) {
cost += d[i][c0] * c0Count[i];
cost += d[i][c1] * c1Count[i];
cost += d[i][c2] * c2Count[i];
}
if (cost < ans) ans = cost;
}
}
}
cout << ans << endl;
return 0;
}
|
Statement
There is a grid with N rows and N columns of squares. Let (i,j) be the square
at the i-th row from the top and the j-th column from the left.
These squares have to be painted in one of the C colors from Color 1 to Color
C. Initially, (i,j) is painted in Color c_{i,j}.
We say the grid is a _good_ grid when the following condition is met for all
i,j,x,y satisfying 1 \leq i,j,x,y \leq N:
* If (i+j) \% 3=(x+y) \% 3, the color of (i,j) and the color of (x,y) are the same.
* If (i+j) \% 3 \neq (x+y) \% 3, the color of (i,j) and the color of (x,y) are different.
Here, X \% Y represents X modulo Y.
We will repaint zero or more squares so that the grid will be a good grid.
For a square, the _wrongness_ when the color of the square is X before
repainting and Y after repainting, is D_{X,Y}.
Find the minimum possible sum of the wrongness of all the squares.
|
[{"input": "2 3\n 0 1 1\n 1 0 1\n 1 4 0\n 1 2\n 3 3", "output": "3\n \n\n * Repaint (1,1) to Color 2. The wrongness of (1,1) becomes D_{1,2}=1.\n * Repaint (1,2) to Color 3. The wrongness of (1,2) becomes D_{2,3}=1.\n * Repaint (2,2) to Color 1. The wrongness of (2,2) becomes D_{3,1}=1.\n\nIn this case, the sum of the wrongness of all the squares is 3.\n\nNote that D_{i,j} \\neq D_{j,i} is possible.\n\n* * *"}, {"input": "4 3\n 0 12 71\n 81 0 53\n 14 92 0\n 1 1 2 1\n 2 1 1 2\n 2 2 1 3\n 1 1 2 2", "output": "428"}]
|
If the minimum possible sum of the wrongness of all the squares is x, print x.
* * *
|
s078063002
|
Accepted
|
p03330
|
Input is given from Standard Input in the following format:
N C
D_{1,1} ... D_{1,C}
:
D_{C,1} ... D_{C,C}
c_{1,1} ... c_{1,N}
:
c_{N,1} ... c_{N,N}
|
# -*- coding: utf-8 -*-
import bisect
import heapq
import math
import random
import sys
from collections import Counter, defaultdict
from decimal import ROUND_CEILING, ROUND_HALF_UP, Decimal
from functools import lru_cache, reduce
from itertools import combinations, combinations_with_replacement, product, permutations
sys.setrecursionlimit(50000)
def read_int():
return int(input())
def read_int_n():
return list(map(int, input().split()))
def read_float():
return float(input())
def read_float_n():
return list(map(float, input().split()))
def read_str():
return input()
def read_str_n():
return list(map(str, input().split()))
def error_print(*args):
print(*args, file=sys.stderr)
def mt(f):
import time
def wrap(*args, **kwargs):
s = time.time()
ret = f(*args, **kwargs)
e = time.time()
error_print(e - s, "sec")
return ret
return wrap
@mt
def slv(N, CN, D, C):
# for d in D:
# error_print(d)
# for c in C:
# error_print(c)
T = [[], [], []]
for i, r in enumerate(C):
for j, c in enumerate(r):
T[(i + j) % 3].append((i, j, c))
TC = [[], [], []]
for j, t in enumerate(T):
for i in range(CN):
s = 0
for c in t:
s += D[c[2] - 1][i - 1]
TC[j].append(s)
ans = sys.maxsize
for i, j, k in permutations(range(CN), 3):
ans = min(ans, sum([TC[0][i], TC[1][j], TC[2][k]]))
return ans
def main():
N, CN = read_int_n()
D = [read_int_n() for _ in range(CN)]
C = [read_int_n() for _ in range(N)]
print(slv(N, CN, D, C))
if __name__ == "__main__":
main()
|
Statement
There is a grid with N rows and N columns of squares. Let (i,j) be the square
at the i-th row from the top and the j-th column from the left.
These squares have to be painted in one of the C colors from Color 1 to Color
C. Initially, (i,j) is painted in Color c_{i,j}.
We say the grid is a _good_ grid when the following condition is met for all
i,j,x,y satisfying 1 \leq i,j,x,y \leq N:
* If (i+j) \% 3=(x+y) \% 3, the color of (i,j) and the color of (x,y) are the same.
* If (i+j) \% 3 \neq (x+y) \% 3, the color of (i,j) and the color of (x,y) are different.
Here, X \% Y represents X modulo Y.
We will repaint zero or more squares so that the grid will be a good grid.
For a square, the _wrongness_ when the color of the square is X before
repainting and Y after repainting, is D_{X,Y}.
Find the minimum possible sum of the wrongness of all the squares.
|
[{"input": "2 3\n 0 1 1\n 1 0 1\n 1 4 0\n 1 2\n 3 3", "output": "3\n \n\n * Repaint (1,1) to Color 2. The wrongness of (1,1) becomes D_{1,2}=1.\n * Repaint (1,2) to Color 3. The wrongness of (1,2) becomes D_{2,3}=1.\n * Repaint (2,2) to Color 1. The wrongness of (2,2) becomes D_{3,1}=1.\n\nIn this case, the sum of the wrongness of all the squares is 3.\n\nNote that D_{i,j} \\neq D_{j,i} is possible.\n\n* * *"}, {"input": "4 3\n 0 12 71\n 81 0 53\n 14 92 0\n 1 1 2 1\n 2 1 1 2\n 2 2 1 3\n 1 1 2 2", "output": "428"}]
|
If the minimum possible sum of the wrongness of all the squares is x, print x.
* * *
|
s647195262
|
Accepted
|
p03330
|
Input is given from Standard Input in the following format:
N C
D_{1,1} ... D_{1,C}
:
D_{C,1} ... D_{C,C}
c_{1,1} ... c_{1,N}
:
c_{N,1} ... c_{N,N}
|
###############################################################################
from sys import stdout
from bisect import bisect_left as binl
from copy import copy, deepcopy
from collections import defaultdict
mod = 1
def intin():
input_tuple = input().split()
if len(input_tuple) <= 1:
return int(input_tuple[0])
return tuple(map(int, input_tuple))
def intina():
return [int(i) for i in input().split()]
def intinl(count):
return [intin() for _ in range(count)]
def modadd(x, y):
global mod
return (x + y) % mod
def modmlt(x, y):
global mod
return (x * y) % mod
def lcm(x, y):
while y != 0:
z = x % y
x = y
y = z
return x
def combination(x, y):
assert x >= y
if y > x // 2:
y = x - y
ret = 1
for i in range(0, y):
j = x - i
i = i + 1
ret = ret * j
ret = ret // i
return ret
def get_divisors(x):
retlist = []
for i in range(1, int(x**0.5) + 3):
if x % i == 0:
retlist.append(i)
retlist.append(x // i)
return retlist
def get_factors(x):
retlist = []
for i in range(2, int(x**0.5) + 3):
while x % i == 0:
retlist.append(i)
x = x // i
retlist.append(x)
return retlist
def make_linklist(xylist):
linklist = {}
for a, b in xylist:
linklist.setdefault(a, [])
linklist.setdefault(b, [])
linklist[a].append(b)
linklist[b].append(a)
return linklist
def calc_longest_distance(linklist, v=1):
distance_list = {}
distance_count = 0
distance = 0
vlist_previous = []
vlist = [v]
nodecount = len(linklist)
while distance_count < nodecount:
vlist_next = []
for v in vlist:
distance_list[v] = distance
distance_count += 1
vlist_next.extend(linklist[v])
distance += 1
vlist_to_del = vlist_previous
vlist_previous = vlist
vlist = list(set(vlist_next) - set(vlist_to_del))
max_distance = -1
max_v = None
for v, distance in distance_list.items():
if distance > max_distance:
max_distance = distance
max_v = v
return (max_distance, max_v)
def calc_tree_diameter(linklist, v=1):
_, u = calc_longest_distance(linklist, v)
distance, _ = calc_longest_distance(linklist, u)
return distance
###############################################################################
def main():
n, c = intin()
dlistlist = [None]
for _ in range(c):
dlist = [None]
dlist.extend(intina())
dlistlist.append(dlist)
clistlist = []
for _ in range(n):
clistlist.append(intina())
costs0 = []
costs1 = []
costs2 = []
for cc in range(1, c + 1):
costs = [0, 0, 0]
for i in range(n):
for j in range(n):
costs[(i + j) % 3] += dlistlist[clistlist[i][j]][cc]
costs0.append((costs[0], cc))
costs1.append((costs[1], cc))
costs2.append((costs[2], cc))
costs0.sort()
costs1.sort()
costs2.sort()
ans = float("inf")
for cost0, c0 in costs0[:3]:
for cost1, c1 in costs1[:3]:
for cost2, c2 in costs2[:3]:
if c0 == c1 or c1 == c2 or c2 == c0:
continue
ans = min(ans, cost0 + cost1 + cost2)
print(ans)
if __name__ == "__main__":
main()
|
Statement
There is a grid with N rows and N columns of squares. Let (i,j) be the square
at the i-th row from the top and the j-th column from the left.
These squares have to be painted in one of the C colors from Color 1 to Color
C. Initially, (i,j) is painted in Color c_{i,j}.
We say the grid is a _good_ grid when the following condition is met for all
i,j,x,y satisfying 1 \leq i,j,x,y \leq N:
* If (i+j) \% 3=(x+y) \% 3, the color of (i,j) and the color of (x,y) are the same.
* If (i+j) \% 3 \neq (x+y) \% 3, the color of (i,j) and the color of (x,y) are different.
Here, X \% Y represents X modulo Y.
We will repaint zero or more squares so that the grid will be a good grid.
For a square, the _wrongness_ when the color of the square is X before
repainting and Y after repainting, is D_{X,Y}.
Find the minimum possible sum of the wrongness of all the squares.
|
[{"input": "2 3\n 0 1 1\n 1 0 1\n 1 4 0\n 1 2\n 3 3", "output": "3\n \n\n * Repaint (1,1) to Color 2. The wrongness of (1,1) becomes D_{1,2}=1.\n * Repaint (1,2) to Color 3. The wrongness of (1,2) becomes D_{2,3}=1.\n * Repaint (2,2) to Color 1. The wrongness of (2,2) becomes D_{3,1}=1.\n\nIn this case, the sum of the wrongness of all the squares is 3.\n\nNote that D_{i,j} \\neq D_{j,i} is possible.\n\n* * *"}, {"input": "4 3\n 0 12 71\n 81 0 53\n 14 92 0\n 1 1 2 1\n 2 1 1 2\n 2 2 1 3\n 1 1 2 2", "output": "428"}]
|
If the minimum possible sum of the wrongness of all the squares is x, print x.
* * *
|
s943915854
|
Wrong Answer
|
p03330
|
Input is given from Standard Input in the following format:
N C
D_{1,1} ... D_{1,C}
:
D_{C,1} ... D_{C,C}
c_{1,1} ... c_{1,N}
:
c_{N,1} ... c_{N,N}
|
from itertools import permutations
def solve(p, query):
# the cost of group's all color change to i
group_a = [0] * (color + 1)
group_b = [0] * (color + 1)
group_c = [0] * (color + 1)
for c_a, c_b, c_c in zip(mod_1, mod_2, mod_0):
for i in range(1, color + 1):
group_a[i] += d[c_a][i]
group_b[i] += d[c_b][i]
group_c[i] += d[c_c][i]
top_3_group_a = sorted(
list(zip(list(range(color + 1)), group_a[1:]))[:3], key=lambda x: x[1]
)
top_3_group_b = sorted(
list(zip(list(range(color + 1)), group_b[1:]))[:3], key=lambda x: x[1]
)
top_3_group_c = sorted(
list(zip(list(range(color + 1)), group_c[1:]))[:3], key=lambda x: x[1]
)
ans = float("inf")
for i in top_3_group_a:
for j in top_3_group_b:
if i[0] != j[0]:
for k in top_3_group_c:
if i[0] != k[0] and j[0] != k[0]:
ans = min(ans, i[1] + j[1] + k[1])
return ans
if __name__ == "__main__":
n, color = map(int, input().split())
c, d = [], []
d.append([0] * (color + 1))
for _ in range(color):
d.append([0] + list(map(int, input().split())))
_c = []
for _ in range(n):
_c.append(list(map(int, input().split())))
mod_1, mod_2, mod_0 = [], [], []
for i in range(n):
for j in range(n):
if (i + j) % 3 == 1:
mod_1.append(_c[i][j])
elif (i + j) % 3 == 2:
mod_2.append(_c[i][j])
else:
mod_0.append(_c[i][j])
if n % 3 == 1:
mod_1.append(0)
mod_2.append(0)
if n % 3 == 2:
mod_0.append(0)
mod_2.append(0)
print(solve(c, d))
|
Statement
There is a grid with N rows and N columns of squares. Let (i,j) be the square
at the i-th row from the top and the j-th column from the left.
These squares have to be painted in one of the C colors from Color 1 to Color
C. Initially, (i,j) is painted in Color c_{i,j}.
We say the grid is a _good_ grid when the following condition is met for all
i,j,x,y satisfying 1 \leq i,j,x,y \leq N:
* If (i+j) \% 3=(x+y) \% 3, the color of (i,j) and the color of (x,y) are the same.
* If (i+j) \% 3 \neq (x+y) \% 3, the color of (i,j) and the color of (x,y) are different.
Here, X \% Y represents X modulo Y.
We will repaint zero or more squares so that the grid will be a good grid.
For a square, the _wrongness_ when the color of the square is X before
repainting and Y after repainting, is D_{X,Y}.
Find the minimum possible sum of the wrongness of all the squares.
|
[{"input": "2 3\n 0 1 1\n 1 0 1\n 1 4 0\n 1 2\n 3 3", "output": "3\n \n\n * Repaint (1,1) to Color 2. The wrongness of (1,1) becomes D_{1,2}=1.\n * Repaint (1,2) to Color 3. The wrongness of (1,2) becomes D_{2,3}=1.\n * Repaint (2,2) to Color 1. The wrongness of (2,2) becomes D_{3,1}=1.\n\nIn this case, the sum of the wrongness of all the squares is 3.\n\nNote that D_{i,j} \\neq D_{j,i} is possible.\n\n* * *"}, {"input": "4 3\n 0 12 71\n 81 0 53\n 14 92 0\n 1 1 2 1\n 2 1 1 2\n 2 2 1 3\n 1 1 2 2", "output": "428"}]
|
Output the number of cakes I can enjoy.
|
s754684193
|
Accepted
|
p00377
|
The input is given in the following format.
$N$ $C$
$p_1$ $p_2$ ... $p_C$
The first line provides the number of my friends $N$ ($1 \leq N \leq 100$) and
the number of those among them who brought one or more pieces of cake with
them $C$ ($1 \leq C \leq N$). The second line provides an array of integers
$p_i$ ($1 \leq p_i \leq100$), each of which shows the number of cakes of the
$i$-th friend of mine who was willing to come up with one or more pieces of
cake.
|
n, c = list(map(int, input().split()))
pli = list(map(int, input().split()))
for i in range(c):
p = sum(pli)
mycake = p // (n + 1)
if p % (n + 1) > 0:
mycake += 1
print(mycake)
|
Cake Party
I’m planning to have a party on my birthday. Many of my friends will come to
the party. Some of them will come with one or more pieces of cakes, but it is
not certain if the number of the cakes is a multiple of the number of people
coming.
I wish to enjoy the cakes equally among the partiers. So, I decided to apply
the following rules. First, all the party attendants are given the same number
of cakes. If some remainder occurs, a piece goes on a priority basis to the
party host (that’s me!). How many pieces of cake can I enjoy?
Given the number of my friends and cake information, make a program to
calculate how many pieces of cake I can enjoy. Note that I am not counted in
the number of my friends.
|
[{"input": "5 4\n 5 5 6 5", "output": "4"}, {"input": "7 5\n 8 8 8 8 8", "output": "5"}, {"input": "100 3\n 3 3 3", "output": "1"}]
|
If it is possible to remove all the stones from the boxes, print `YES`.
Otherwise, print `NO`.
* * *
|
s996337960
|
Runtime Error
|
p03808
|
The input is given from Standard Input in the following format:
N
A_1 A_2 … A_N
|
n = int(input())
a = [int(i) for i in input().split()]
def get_inv_diff(a):
prev_val = a[-1]
idx_lst = []
for idx, cur_val in enumerate(a):
# print("cur,pre",cur_val,prev_val)
if cur_val <= prev_val:
idx_lst.append(idx)
if idx != 0 and prev_val - cur_val > 3:
for prev_val - cur_val / 4:
idx_lst.append(idx)
# print("detect!")
prev_val = cur_val
return idx_lst
def check_sum(a):
sum = 0
for val in a:
sum += val
cmp = [i+1 for i in range(n)]
cmp_sum = 0
for val in cmp:
cmp_sum += val
if sum % cmp_sum != 0:
return -1
else:
result = sum / cmp_sum
return result
result = check_sum(a)
if result == -1:
print("NO")
else:
indices = get_inv_diff(a)
if len(indices) != result:
print("NO")
else:
# print("indices:", indices)
test_lst = [0 for i in range(n)]
for begin_idx in indices:
for count in range(n):
# print("count:",count)
test_lst[(begin_idx + count) % n] += count+1
# print(test_lst)
if test_lst == a:
print("YES")
else:
print("NO")
|
Statement
There are N boxes arranged in a circle. The i-th box contains A_i stones.
Determine whether it is possible to remove all the stones from the boxes by
repeatedly performing the following operation:
* Select one box. Let the box be the i-th box. Then, for each j from 1 through N, remove exactly j stones from the (i+j)-th box. Here, the (N+k)-th box is identified with the k-th box.
Note that the operation cannot be performed if there is a box that does not
contain enough number of stones to be removed.
|
[{"input": "5\n 4 5 1 2 3", "output": "YES\n \n\nAll the stones can be removed in one operation by selecting the second box.\n\n* * *"}, {"input": "5\n 6 9 12 10 8", "output": "YES\n \n\n* * *"}, {"input": "4\n 1 2 3 1", "output": "NO"}]
|
If it is possible to remove all the stones from the boxes, print `YES`.
Otherwise, print `NO`.
* * *
|
s354485281
|
Runtime Error
|
p03808
|
The input is given from Standard Input in the following format:
N
A_1 A_2 … A_N
|
#n,a,b,c,d=map(int,input().split())
n=int(input())
a=[int(i) for i in input().split()]
ans=False
c=[]
t=sum(a)//((n*(n+1))//2)
if sum(a)%((n*(n+1))//2)!=0:
ans=False
else:
for i in range(n):
if i==0:
d=a[0]-a[-1]
else:
d=a[i]-a[i-1]
if (t-d)%n!=0:
ans=False
break
s=(t-d)//n
c.append(s)
if sum(c)==t:
#ans=True
if n==1:
ans=True
print('YES' if ans else 'NO')
|
Statement
There are N boxes arranged in a circle. The i-th box contains A_i stones.
Determine whether it is possible to remove all the stones from the boxes by
repeatedly performing the following operation:
* Select one box. Let the box be the i-th box. Then, for each j from 1 through N, remove exactly j stones from the (i+j)-th box. Here, the (N+k)-th box is identified with the k-th box.
Note that the operation cannot be performed if there is a box that does not
contain enough number of stones to be removed.
|
[{"input": "5\n 4 5 1 2 3", "output": "YES\n \n\nAll the stones can be removed in one operation by selecting the second box.\n\n* * *"}, {"input": "5\n 6 9 12 10 8", "output": "YES\n \n\n* * *"}, {"input": "4\n 1 2 3 1", "output": "NO"}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s326517709
|
Accepted
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
def genP(W):
P = []
D = [0] * (W - 1)
P.append(D[:])
for i in range(2 ** (W - 1) - 1):
d = 0
while D[d] == 1:
D[d] = 0
d += 1
D[d] = 1
if any(D[i] == 1 and D[i + 1] == 1 for i in range(W - 2)):
continue
P.append(D[:])
return P
def make_swap(p, W):
base = [x for x in range(0, W)]
b = base[:]
for w in range(len(p)):
if p[w] == 1:
b[w], b[w + 1] = b[w + 1], b[w]
return b
if 0 == 1:
W = 4
base = [x - 1 for x in range(1, W + 1)]
for p in genP(W):
print(*base)
print("", *p)
print(*make_swap(p, W))
print()
def solve(H, W, K):
swaps = []
for p in genP(W):
s = make_swap(p, W)
swaps.append(s)
count = [[0] * W for i in range(H + 1)]
count[0][0] = 1
for h in range(0, H):
for w in range(0, W):
for swap in swaps:
count[h + 1][w] += count[h][swap[w]]
count[h + 1][w] %= 1000000007
# print(count[H])
print(count[H][K - 1])
def main():
H, W, K = map(int, input().split())
solve(H, W, K)
main()
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.
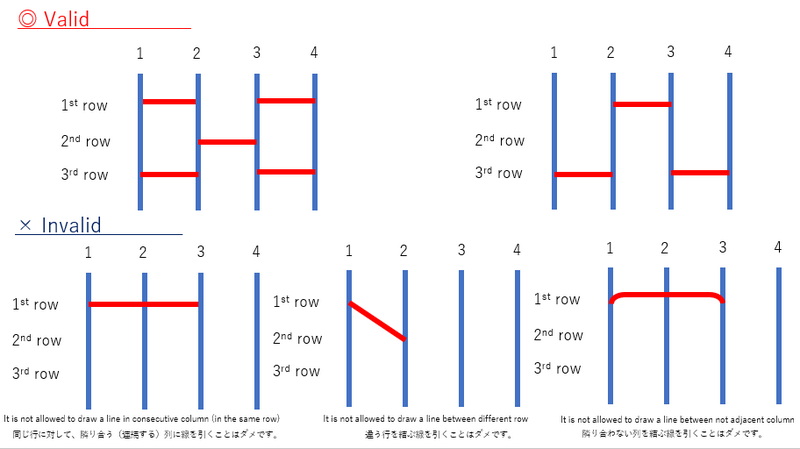
Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s963240742
|
Accepted
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
H, W, K = [int(_) for _ in input().split()]
MOD = 1000000007
P = [""]
for i in range(W - 1):
Q = []
for p in P:
Q.append(p + "0")
if len(p) == 0 or p[-1] == "0":
Q.append(p + "1")
P = Q
rs = [1] + [0] * (W - 1)
for j in range(H):
nrs = [0] * W
for p in P:
drs = rs[:]
for i, c in enumerate(p):
if c == "1":
drs[i], drs[i + 1] = drs[i + 1], drs[i]
for i in range(W):
nrs[i] = (nrs[i] + drs[i]) % MOD
rs = nrs
print(rs[K - 1])
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s755270001
|
Accepted
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
from itertools import product
h, w, k = list(map(int, input().split()))
seqs = [
s for s in product([0, 1], repeat=w - 1) if not any(x & y for x, y in zip(s, s[1:]))
]
cache = {}
def f(x, y):
if y > h:
return int(x == k)
if (x, y) in cache:
return cache[(x, y)]
r = 0
for s in seqs:
nx = x
if x < w and s[x - 1]:
nx += 1
elif x > 1 and s[x - 2]:
nx -= 1
r = (r + f(nx, y + 1)) % (10**9 + 7)
cache[(x, y)] = r
return r
print(f(1, 1))
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s826901298
|
Accepted
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
#!/usr/bin/env python3
from copy import deepcopy
MOD = 10**9 + 7
def main():
h, w, k = map(int, input().split())
ways = []
for way in range(2 ** (w - 1)):
if isvalid(way):
ways.append(way)
dp = [0 for i in range(w)]
dp[0] = 1
for i in range(h):
dppre = deepcopy(dp)
dp = [0 for i in range(w)]
for j in range(w):
for way in ways:
dp[j] += dppre[apply(way, j)]
dp[j] %= MOD
print(dp[k - 1])
def apply(way, fr):
logic = [False]
for d in range(8):
logic.append(bool(way & 1))
way >>= 1
if logic[fr]:
to = fr - 1
elif logic[fr + 1]:
to = fr + 1
else:
to = fr
return to
def isvalid(way):
logic = []
for d in range(7):
logic.append(bool(way & 1))
way >>= 1
for d in range(6):
if logic[d] & logic[d + 1]:
return False
return True
if __name__ == "__main__":
main()
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s768268942
|
Wrong Answer
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
from numpy import matrix
H, W, K = [int(i) for i in input().split()]
p = 10**9 + 7
F = [[0] * W for i in range(W)] # a→bへの写像の個数
def dfs(i, T, flag):
if i >= W - 1:
for j, t in enumerate(T):
F[j][t] += 1
return None
dfs(i + 1, T[:], False)
if not flag:
T[i], T[i + 1] = T[i + 1], T[i]
dfs(i + 1, T[:], True)
dfs(0, [i for i in range(W)], False)
F = matrix(F)
A = matrix([[0] * W for i in range(H + 1)]) # (h, w)の場合の数
A.itemset(0, 1)
print((A * F**H)[:, K - 1].sum() % p)
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s314107985
|
Runtime Error
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
import numpy as np
from numpy.linalg import matrix_power
H, W, K = map(int, input().split())
def c(i, j):
f = [1, 1, 2, 3, 5, 8, 13, 21]
a = 0
if i == j + 1:
a = f[j] * f[W - i - 1]
if j in (i, i + 1):
a = f[i] * f[W - j - 1]
return a
def mp(m, n, p):
a = m % p
if n == 0:
return np.identity(m.diagonal().size, dtype="int32")
if n == 1:
return a
else:
q, r = divmod(n, 2)
x = np.matmul(a, a) % p
if r == 1:
return np.matmul(a, mp(x, q, p)) % p
else:
return mp(x, q, p) % p
m = mp(np.array([[c(i, j) for i in range(W)] for j in range(W)]), H, 1000000007)
x = np.array([[c(i, j) for i in range(W)] for j in range(W)])
print(m[0, K - 1])
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s117088476
|
Accepted
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
def DP(H, W, K):
res = [[0 for i in range(W)] for j in range(H + 1)]
res[0][0] += 1
for step in range(1, H + 1):
for i in range(2 ** (W - 1)):
s = "{:08b}".format(i)[::-1]
# print()
# print(s)
if "11" in s:
continue
for x in range(0, W):
if x == 0:
if s[x] == "0":
res[step][x] += res[step - 1][x]
elif s[x] == "1":
res[step][x + 1] += res[step - 1][x]
elif x == W - 1:
if s[x - 1] == "0":
res[step][x] += res[step - 1][x]
elif s[x - 1] == "1":
res[step][x - 1] += res[step - 1][x]
else:
# right
if s[x] == "0" and s[x - 1] == "0":
res[step][x] += res[step - 1][x]
elif s[x] == "1":
res[step][x + 1] += res[step - 1][x]
elif s[x - 1] == "1":
res[step][x - 1] += res[step - 1][x]
# print(res[step])
for i in range(W):
res[step][i] = res[step][i] % MOD
return res[step][K - 1]
H, W, K = map(int, input().split(" "))
MOD = 1000000007
print(DP(H, W, K))
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s320802632
|
Accepted
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
H, W, K = map(int, input().split())
MOD = 10**9 + 7
L = [0] * (W - 1)
row = 0
for i in range(2 ** (W - 1)):
LL = format(i, "08b")
Lf = 0
for j in range(len(LL) - 1):
if LL[j] == "1" and LL[j + 1] == "1":
Lf = 1
if Lf == 0:
row += 1
LL = LL[8 - (W - 1) :]
for k in range(W - 1):
if LL[k] == "1":
L[k] += 1
# print(LL,Lf)
B = [] # Bridge
for _ in range(W):
B.append([0, 0, 0])
for i in range(W):
if i != 0:
B[i][0] = L[i - 1]
else:
B[i][0] = 0
if i != W - 1:
B[i][2] = L[i]
else:
B[i][2] = 0
B[i][1] = row - B[i][0] - B[i][2]
A = [[0] * (W + 2)]
for _ in range(H):
A.append([0] * (W + 2))
A[0][1] = 1
for i in range(H):
for j in range(1, W + 1):
A[i + 1][j - 1] += A[i][j] * (B[j - 1][0])
A[i + 1][j] += A[i][j] * (B[j - 1][1])
A[i + 1][j + 1] += A[i][j] * (B[j - 1][2])
print(A[H][K] % MOD)
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s018001738
|
Accepted
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
"""3/18 AtCoder(漸化式dp)
一番左の棒からスタートして、K番目の棒に到達するようなあみだくじは
何通り作れますかという趣旨の問題
まず、この問題を解くうえで一番重要なのは、
「ある高さh、棒jに至る経路の総数を求める漸化式が立てられる」ということ
高さh、棒jに至る経路の総数をdp[h][j]とすれば、
高さh-1からこの位置に至ることができるのは、
棒j-1,j,j+1のいずれかしかない
さらに、そこに至る経路数というのは結局
「ほかの棒にどんな風に架け橋(横棒)がかかっているか」の場合の数なので、
それをdp[h-1][j-1],dp[h-1][j],dp[h-1][j+1]にかけていく必要がある
例えば、dp[h-1][j]を見てみる これは、同じ棒から下ってくることを
意味しているが、換言すれば「高さi-1とiには、棒jから伸びる横棒はない」
ということである
つまり、この高さにおける横棒の架かり方というのは
「棒1~j-1までの架かり方」と「棒j+1~棒Wまでの架かり方」の
二パターンしかないということになる
ある高さにおける横棒のかかり方も漸化式で求められる
高さhにおける(横一列にかけ橋が並んでいる状況を考える)、
n本の棒の間にかかる橋の場合の数の総数をf(n)と置くと、
f(n) = f(n-1)+f(n-2)と書くことができる
これは、f(n)が
①n本目とn-1本目の棒の間に橋が架かっていない→場合の数はf(n-2)と同じ
②n本目とn-1本目の棒の間に橋が架かっている→場合の数はf(n-1)と同じ
の二パターンの合計だからである
だから、dp[h-1][j]に掛ける数はいくつかということを考えたら、
j-1本の棒の間にかかる橋の場合の数f(j-1)と、
W-j本の棒の間にかかる橋の場合の数f(W-j)本ということになる
これと同様に、残り二本に対してもいくつかければよいかを考えて、
dp[h][j]]に対する漸化式を立てればよい
"""
H, W, K = map(int, input().split())
dp = []
for i in range(H + 1): # 高さ0の分を余分に持っておく
L = [0] * W
dp.append(L)
fb = [1, 1] # フィボナッチ(f(n)=f(n-1)+f(n-2))
for i in range(W - 2):
fb.append(fb[i] + fb[i + 1])
dp[0][0] = 1 # 左端の棒の高さ0は初期位置なので1に
if W != 1: # 棒が一本以上あるときは
for i in range(1, H + 1):
for j in range(W): # 棒が左端、右端、それ以外で場合分け
if 1 <= j <= W - 2:
dp[i][j] = (
dp[i - 1][j - 1] * fb[j - 1] * fb[W - j - 1]
+ dp[i - 1][j] * fb[j] * fb[W - j - 1]
+ dp[i - 1][j + 1] * fb[j] * fb[W - j - 2]
)
elif j == 0:
dp[i][j] = dp[i - 1][j] * fb[W - 1] + dp[i - 1][j + 1] * fb[W - 2]
else:
dp[i][j] = dp[i - 1][j] * fb[W - 1] + dp[i - 1][j - 1] * fb[W - 2]
else:
dp[H][0] = 1
print(dp[H][K - 1] % (10**9 + 7)) # 高さH(一番下)、K-1番目の棒を調べる
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s779479677
|
Runtime Error
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
#include <iostream>
#include <cmath>
#include <vector>
#include <map>
#include <string>
#include <algorithm>
typedef long long ll;
const ll INF = (ll)1e18 + 1;
const ll MOD = (ll)1e9 + 7;
// print(x, y, z);
void print(){ std::cout << std::endl; }
template <typename Head> void print(Head&& head) { std::cout << head << std::endl; }
template <typename Head, typename... Tail> void print(Head&& head, Tail&&... tail)
{
std::cout << head << " ";
print(std::forward<Tail>(tail)...); // or print(tail...);
}
int main(int argc, char* argv[])
{
ll H, W, K;
std::cin >> H >> W >> K;
K--;
// dp[h][w] = 横線をh段引いたときに0がwに来る場合の数
std::vector< std::vector<ll> > dp(H+1, std::vector<ll>(W, 0LL));
dp[0][0] = 1;
for (ll h = 0; h < H; h++) {
for (ll bit = 0; bit < (1 << (W - 1)); bit++) {
// 2 つの横線がつながっていないか調べる
bool judge = true;
for (ll line = 0; line < W - 2; line++) {
if ((1 << line & bit) && (1 << (line + 1) & bit)) judge = false;
}
if (!judge) continue;
// あみだ処理
std::vector<ll> amida(W, 0LL);
for (ll line = 0; line < W; line++) {
amida[line] = line;
}
for (ll line = 0; line < W-1; line++) {
if ((1 << line) & bit) std::swap(amida[line], amida[line+1]);
}
// 動的計画法の処理
for (ll line = 0; line < W; line++) {
dp[h + 1][amida[line]] += dp[h][line];
dp[h + 1][amida[line]] %= MOD;
}
}
}
print(dp[H][K]);
return 0;
}
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s045680369
|
Accepted
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
H, W, K = [int(x) for x in input().split()]
p = 10**9 + 7
# H = 1, 縦棒W本のあみだくじの数 →フィボナッチ数列
h1amida = [1, 1, 2] + [None] * 6
for i in range(3, 9):
h1amida[i] = h1amida[i - 2] + h1amida[i - 1]
# dp[h][k] = 縦棒の長さh+1、縦棒の本数W、ゴールの棒kとなるあみだの数
# dp[0][*]とdp[*][0]はダミー
dp = [[0 for _ in range(W + 1)] for _ in range(H + 1)]
for k in range(1, W + 1):
if k == 1:
dp[1][k] = h1amida[W - 1]
elif k == 2:
dp[1][k] = h1amida[W - 2]
else:
dp[1][k] = 0
for h in range(2, H + 1):
for k in range(1, W + 1):
if k > 1:
dp[h][k] += (dp[h - 1][k - 1] * h1amida[k - 2] % p) * h1amida[W - k] % p
dp[h][k] += (dp[h - 1][k] * h1amida[k - 1] % p) * h1amida[W - k] % p
if k < W:
dp[h][k] += (dp[h - 1][k + 1] * h1amida[k - 1] % p) * h1amida[W - k - 1] % p
dp[h][k] %= p
print(dp[H][K])
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s338774761
|
Runtime Error
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
from sys import exit
H,W,K = [int(n) for n in input().split()]
memo = [[0 for _ in range(H+1)] for __ in range(W)]
memo[0][0] = 1
for h in range(1,H+1):
for pt in range((1 << W-1)):#1 == 線あり 0 == 線なし とする
pts = bin(pt)[2:]
pts = pts[::-1]#反転
if "11" in pts: continue
# print(pts)
#各パターンの時の各線の計算
for i in range(W):
if i < len(pts) and pts[i] == "1":
# print(i)
memo[i][h] += memo[i+1][h-1]
memo[i+1][h] += memo[i][h-1]
i+=1#よみとばす
else:
memo[i][h] += memo[i][h-1]
for wt in range(0,W):
# print(memo[wt])
print(memo[K-1][H])
# for wt in range(0,W):
# print(memo[wt])
# for i in range(0,N):
# if(bit & (1 << i)):#1が一本たっていて、iだけ横にシフトするものとマスクとの共通部分
# print(i)
# print("BIT:", end="")
# print(bin(1 << i))
exit()
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s305412900
|
Wrong Answer
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
print(1)
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s648117453
|
Wrong Answer
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
print(0)
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
Print the number of the amidakuji that satisfy the condition, modulo 1\ 000\
000\ 007.
* * *
|
s532407828
|
Runtime Error
|
p03222
|
Input is given from Standard Input in the following format:
H W K
|
H,W,K = map(int, input().split())
# HとWは道の数を決定
dp = [[0]*W for _ in range(H+1)]
dp[0][0] = 1
if W==1:
print(1)
else:
for i in range(H):
for j in range(2**(W-1)):
flag = True
for k in range(W-1):
if k != W-2:
# 二桁連続で1の場合は処理を省く
if (((j >> k) & 1)&((j >> k+1) & 1)):
flag = False
break
if flag:
#print(bin(j)[2:].zfill(W-1))
for l in range(W-1):
if ((j >> l) & 1):
dp[i+1][l] += dp[i][l+1]
dp[i+1][l+1] += dp[i][l]
else:
dp[i+1][l] += dp[i][l]
#print(dp[i+1])
print(dp[-1][K-1]%(1000000007)
|
Statement
Amidakuji is a traditional method of lottery in Japan.
To make an amidakuji, we first draw W parallel vertical lines, and then draw
horizontal lines that connect them. The length of each vertical line is H+1
[cm], and the endpoints of the horizontal lines must be at 1, 2, 3, ..., or H
[cm] from the top of a vertical line.
A _valid amidakuji_ is an amidakuji that satisfies the following conditions:
* No two horizontal lines share an endpoint.
* The two endpoints of each horizontal lines must be at the same height.
* A horizontal line must connect adjacent vertical lines.

Find the number of the valid amidakuji that satisfy the following condition,
modulo 1\ 000\ 000\ 007: if we trace the path from the top of the leftmost
vertical line to the bottom, always following horizontal lines when we
encounter them, we reach the bottom of the K-th vertical line from the left.
For example, in the following amidakuji, we will reach the bottom of the
fourth vertical line from the left.

|
[{"input": "1 3 2", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "1 3 1", "output": "2\n \n\nOnly the following two amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "2 3 3", "output": "1\n \n\nOnly the following one amidakuji satisfies the condition:\n\n\n\n* * *"}, {"input": "2 3 1", "output": "5\n \n\nOnly the following five amidakuji satisfy the condition:\n\n\n\n* * *"}, {"input": "7 1 1", "output": "1\n \n\nAs there is only one vertical line, we cannot draw any horizontal lines. Thus,\nthere is only one amidakuji that satisfies the condition: the amidakuji with\nno horizontal lines.\n\n* * *"}, {"input": "15 8 5", "output": "437760187\n \n\nBe sure to print the answer modulo 1\\ 000\\ 000\\ 007."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s650940120
|
Accepted
|
p03388
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
import sys
def input():
return sys.stdin.readline().strip()
def prod_max(a, d, b, e, n):
"""
初項a、公差dの等差数列および初項b、公差eの等差数列を各項ごとに
掛け合わせた時の第0項から第n項までの最大値を返す。
a>0, d>0, b>0, e<0を仮定する。
"""
if n < 0:
return 0
idx = round((-(b / e) - (a / d)) / 2)
if idx < 0:
return a * b
if idx <= n:
return (a + idx * d) * (b + idx * e)
return (a + n * d) * (b + n * e)
def main():
"""
解説放送にしたがって決め打ち二分探索による実装。
まずa<=bを仮定しても良い。a*bよりも小さい積がX個作れるかを考える。
これは1, 2, ..., a-1, a+1, ...からX個、1, 2, ..., b-1, b+1, ...からX個選んで
小さいものと大きいもののペアで積を取ったものが全てa*b未満であることをいえば良い。
積を実際に全て計算していては間に合わないが、実質これは等差数列の積なので
これらの積のうち最大値はO(1)で計算可能。
"""
Q = int(input())
for _ in range(Q):
a, b = map(int, input().split())
if a > b:
a, b = b, a
# 決め打ち二分探索
left = a - 1
right = 10**10
while right - left > 1:
mid = (left + right) // 2
if mid < b:
"""
この時ペアリングは
1*mid, 2*(mid-1), ..., (a-1)*(mid-a+1), (a+1)*(mid-a), ..., (mid+1)*1
前半後半でそれぞれ最大値を取得する。
"""
cand1 = prod_max(1, 1, mid, -1, a - 2)
cand2 = prod_max(a + 1, 1, mid - a + 1, -1, mid - a)
if cand1 < a * b and cand2 < a * b:
left = mid
else:
right = mid
# print("case1 left={}, right={}".format(left, right))
elif mid < a + b - 1:
"""
この時ペアリングは
1*(mid+1), 2*mid, ..., (mid-b+1)*(b+1),
(mid-b+2)*(b-1), ..., (a-1)*(mid-a+2),
(a+1)*(mid-a+1), ..., (mid+1)*1
より3つに分けて最大値を求める。
"""
cand1 = prod_max(1, 1, mid + 1, -1, mid - b)
cand2 = prod_max(mid - b + 2, 1, b - 1, -1, a + b - mid - 3)
cand3 = prod_max(a + 1, 1, mid - a + 1, -1, mid - a)
if cand1 < a * b and cand2 < a * b and cand3 < a * b:
left = mid
else:
right = mid
# print("case2 left={}, right={}".format(left, right))
else:
"""
この時ペアリングは
1*(mid+1), 2*mid, ..., (mid-a+3)*(a-1),
(a+1)*(mid-a+2), ..., (mid-b+2)*(b+1),
(mid-b+3)*(b-1), ..., (mid+1)*1
より3つに分けて最大値を求める。
"""
cand1 = prod_max(1, 1, mid + 1, -1, a - 2)
cand2 = prod_max(a + 1, 1, mid - a + 2, -1, mid - a - b + 1)
cand3 = prod_max(mid - b + 3, 1, b - 1, -1, b - 2)
if cand1 < a * b and cand2 < a * b and cand3 < a * b:
left = mid
else:
right = mid
# print("case3 left={}, right={}".format(left, right))
print(left)
if __name__ == "__main__":
main()
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s155147617
|
Wrong Answer
|
p03388
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
#!/usr/bin/env python3
from collections import defaultdict
from collections import deque
from heapq import heappush, heappop
import sys
import math
import bisect
import random
import itertools
sys.setrecursionlimit(10**5)
stdin = sys.stdin
bisect_left = bisect.bisect_left
bisect_right = bisect.bisect_right
def LI():
return list(map(int, stdin.readline().split()))
def LF():
return list(map(float, stdin.readline().split()))
def LI_():
return list(map(lambda x: int(x) - 1, stdin.readline().split()))
def II():
return int(stdin.readline())
def IF():
return float(stdin.readline())
def LS():
return list(map(list, stdin.readline().split()))
def S():
return list(stdin.readline().rstrip())
def IR(n):
return [II() for _ in range(n)]
def LIR(n):
return [LI() for _ in range(n)]
def FR(n):
return [IF() for _ in range(n)]
def LFR(n):
return [LI() for _ in range(n)]
def LIR_(n):
return [LI_() for _ in range(n)]
def SR(n):
return [S() for _ in range(n)]
def LSR(n):
return [LS() for _ in range(n)]
mod = 1000000007
inf = float("INF")
# A
def A():
s = S()
s.sort()
if s == ["a", "b", "c"]:
print("Yes")
else:
print("No")
return
# B
def B():
a, b, k = LI()
ans = []
for i in range(a, min(a + k, b + 1)):
ans.append(i)
for i in range(max(b - k + 1, a + k), b + 1):
ans.append(i)
for i in ans:
print(i)
return
# C
def C():
abc = LI()
abc.sort()
a, b, c = abc
a1 = (c - a) % 2
b1 = (c - b) % 2
if a1 and b1:
print((c - a) // 2 + (c - b) // 2 + 1)
return
if a1 or b1:
print((c - a) // 2 + (c - b) // 2 + 2)
return
print((c - a) // 2 + (c - b) // 2)
return
# D
# 解説AC
# a <= b として一般性を失わない
# 1: a = b のとき
# (a-k)*(a+k) = a*a - k*k < a*a
# であることを考えると0<k<aのすべてをとれて、
# 1回目にa-k,2回目にa+kもしくは2回目にa-k,1回目にa+kをとっている場合
# 満たすことがわかるこれは2*a-2人である
# ここでa*a > n*k を考えるとn,kどちらかはa-1以下である
# また、a+1以上である場合、もう一方がa-1以下であることが確定するため
# 片方がa+1以上である場合の個数はもう一方がa-1以下である場合に数えている
# よって個数の上限が2*a-2人であるためこれが解であることがわかる
#
# 2: c*c < a*b かつ c*(c+1) >= a*b を満たすcを考えるとき
# 1回目,2回目どちらかはc以下をとる必要があるゆえに上と同様に考えれば
# (c-k)*(c+k)を考えると0<=k<=c-1を考えればよくk=0で同じ組になることから
# 2*c-1人に見えるがc-k = aとなるときは除去しなければならないため
# 2*c-2人が解になる
#
# 3: c*c < a*b かつ c*(c+1) < a*b を満たす最大のcを考えるとき
# 2と同様に(c-k)*(c+k)を考えるのではなく(c-k)*(c+1+k)の組として
# 考えればよく0<=k<c-1を考えてよく2*c人に見えるが、c-k=aのときだけ
# 除外する必要があるので2*c-1人が解になる
def D():
for _ in range(II()):
a, b = LI()
c = int(math.sqrt(a * b - 1))
print(2 * a - 2 if a == b else 2 * c - 1 - (c * (c + 1) >= a * b))
return
# Solve
if __name__ == "__main__":
D()
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s092271978
|
Runtime Error
|
p03388
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
import math
q = int(input())
for i in range(q):
a,b = map(int,input().split())
if a == b:
print(a*2-2)
continue
y = max(a,b)
z = min(a,b)
ind = int(math.sqrt(a*b))
if ind.is_integer():
ind -= 1
cnt = 0
else:
if ind*(ind+1) < a*b:
if ind >= z:
cnt = 1
if ind+1 >= y:
cnt = 2
print(2*ind-cnt)
else:
if ind >= z:
cnt = 1
print(2*ind-1-cnt)
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s704653210
|
Runtime Error
|
p03388
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
#include <iostream>
using namespace std;
typedef unsigned long long ll;
ll get_upper(ll lower, ll a, ll b) {
ll upper = a*b/lower;
if (upper*lower == a*b) --upper;
return upper;
}
// index が条件を満たすかどうか
bool isOK(ll lower, ll a, ll b) {
ll upper = get_upper(lower, a, b);
return lower <= upper;
}
int binary_search(ll a, ll b) {
ll left = a;
ll right = b-1;
/* どんな二分探索でもここの書き方を変えずにできる! */
while (right - left > 1) {
int mid = left + (right - left) / 2;
if (isOK(mid, a, b)) left = mid;
else right = mid;
}
/* left は条件を満たす最大の値、right は条件を満たさない最小の値になっている */
return left;
}
void solve(ll a, ll b) {
if (a > b) swap(a, b);
ll ans = 2*(a-1); // (a未満, bより大)の数
ll lower = binary_search(a, b);
ll upper = get_upper(lower, a, b);
if (lower < a || upper >= b) {}
else if (lower == a) {
if (lower < upper && upper < b) ++ans;
}
else {
++ans; // (a, b-1)
if (lower == upper) ans += (lower-a-1)*2+1;
else ans += (lower-a)*2;
}
// cout << a << " " << b << " " << lower << " " << upper << " " << ans << endl;
cout << ans << endl;
}
int main() {
ll q;
cin >> q;
for (ll i = 0; i < q; ++i) {
ll a, b;
cin >> a >> b;
solve(a, b);
}
}
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s247072245
|
Runtime Error
|
p03388
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <map>
#include <functional>
#include <cmath>
using namespace std;
typedef long long int ll;
#define repi(i,a,b) for(ll i=a;i<b;i++)
#define rep(i,a) repi(i,0,a)
#define rrep(i,a) for(ll i=a-1;i>=0;i--)
ll solve(ll a, ll b){
ll sqrtab = sqrt(a * b - 1);
if(sqrtab * (sqrtab - 1) < a * b)
return sqrtab * 2 - 1;
else
return sqrtab * 2 - 2;
}
int main(){
ll Q;
cin >> Q;
rep(i, Q){
ll a, b;
cin >> a >> b;
cout << solve(a, b) << endl;
}
return 0;
}
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s728343173
|
Runtime Error
|
p03388
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
t= int(input())
for i in range(t):
k=input().split()
a=int(k[0])
b=int(k[1])
c=a*b
d=int(c**.5)
print(2*d-1-((d*d)==c)-(c==d*d and a!=b))
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s891900830
|
Wrong Answer
|
p03388
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
#!/usr/bin/env python3
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s091463502
|
Wrong Answer
|
p03388
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
Q = int(input())
for n in range(Q):
li = list(map(int, input().split()))
x, y = map(int, sorted(li))
z = x + int((x * y) // (x + 1)) - 1
print(z)
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
For each query, print the maximum possible number of participants whose scores
are smaller than Takahashi's.
* * *
|
s536053859
|
Accepted
|
p03388
|
Input is given from Standard Input in the following format:
Q
A_1 B_1
:
A_Q B_Q
|
# PROBLEM D
Q = int(input())
for _ in range(Q):
a, b = sorted([int(s) for s in input().split()])
c_max = int((a * b) ** 0.5)
if c_max * c_max == a * b:
c_max -= 1
sol = 2 * c_max
if a <= c_max:
sol -= 1
if (c_max * c_max < a * b) and (c_max * (c_max + 1) >= a * b):
sol -= 1
print(sol)
|
Statement
10^{10^{10}} participants, including Takahashi, competed in two programming
contests. In each contest, all participants had distinct ranks from first
through 10^{10^{10}}-th.
The _score_ of a participant is the product of his/her ranks in the two
contests.
Process the following Q queries:
* In the i-th query, you are given two positive integers A_i and B_i. Assuming that Takahashi was ranked A_i-th in the first contest and B_i-th in the second contest, find the maximum possible number of participants whose scores are smaller than Takahashi's.
|
[{"input": "8\n 1 4\n 10 5\n 3 3\n 4 11\n 8 9\n 22 40\n 8 36\n 314159265 358979323", "output": "1\n 12\n 4\n 11\n 14\n 57\n 31\n 671644785\n \n\nLet us denote a participant who was ranked x-th in the first contest and y-th\nin the second contest as (x,y).\n\nIn the first query, (2,1) is a possible candidate of a participant whose score\nis smaller than Takahashi's. There are never two or more participants whose\nscores are smaller than Takahashi's, so we should print 1."}]
|
Print the number of integers satisfying the condition, modulo 10^9+7.
* * *
|
s701811999
|
Wrong Answer
|
p02960
|
Input is given from Standard Input in the following format:
S
|
# from collections import *
# from itertools import *
# from bisect import *
# from heapq import *
# import copy
# import math
# N=int(input())
# X,Y=map(int,input().split())
# S=list(map(int,input().split()))
# S=[list(map(int,input().split())) for i in range(N)]
S = input()
mod = 10**9 + 7
Scount = S.count("?")
X = pow(10, Scount)
count = (X - 5) // 13
amari = (X - 5) % 13
print((count - 1) % mod)
|
Statement
Given is a string S. Each character in S is either a digit (`0`, ..., `9`) or
`?`.
Among the integers obtained by replacing each occurrence of `?` with a digit,
how many have a remainder of 5 when divided by 13? An integer may begin with
0.
Since the answer can be enormous, print the count modulo 10^9+7.
|
[{"input": "??2??5", "output": "768\n \n\nFor example, 482305, 002865, and 972665 satisfy the condition.\n\n* * *"}, {"input": "?44", "output": "1\n \n\nOnly 044 satisfies the condition.\n\n* * *"}, {"input": "7?4", "output": "0\n \n\nWe may not be able to produce an integer satisfying the condition.\n\n* * *"}, {"input": "?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???", "output": "153716888"}]
|
Print the number of integers satisfying the condition, modulo 10^9+7.
* * *
|
s739226119
|
Runtime Error
|
p02960
|
Input is given from Standard Input in the following format:
S
|
n = int(input())
l = list(map(int, input().split()))
l.sort()
count = 0
for i in range(n - 2):
for j in range(i + 1, n - 1):
k = j + 1
while k < n and l[k] < l[i] + l[j]: # whileでlist indexはみ出さないように注意
count += 1
k += 1
|
Statement
Given is a string S. Each character in S is either a digit (`0`, ..., `9`) or
`?`.
Among the integers obtained by replacing each occurrence of `?` with a digit,
how many have a remainder of 5 when divided by 13? An integer may begin with
0.
Since the answer can be enormous, print the count modulo 10^9+7.
|
[{"input": "??2??5", "output": "768\n \n\nFor example, 482305, 002865, and 972665 satisfy the condition.\n\n* * *"}, {"input": "?44", "output": "1\n \n\nOnly 044 satisfies the condition.\n\n* * *"}, {"input": "7?4", "output": "0\n \n\nWe may not be able to produce an integer satisfying the condition.\n\n* * *"}, {"input": "?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???", "output": "153716888"}]
|
Print the number of integers satisfying the condition, modulo 10^9+7.
* * *
|
s518101605
|
Runtime Error
|
p02960
|
Input is given from Standard Input in the following format:
S
|
ip = list(str(input()))
a = [0] * len(ip)
for i in range(len(ip)):
if ip[i] == "?":
a[i] += 1
tmp = []
s = ""
def nums0(s):
if len(s) < sum(a):
s += "0"
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
tmp.append(s)
def nums1(s):
if len(s) < sum(a):
s += "1"
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
tmp.append(s)
def nums2(s):
if len(s) < sum(a):
s += "2"
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
tmp.append(s)
def nums3(s):
if len(s) < sum(a):
s += "3"
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
tmp.append(s)
def nums4(s):
if len(s) < sum(a):
s += "4"
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
tmp.append(s)
def nums5(s):
if len(s) < sum(a):
s += "5"
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
tmp.append(s)
def nums6(s):
if len(s) < sum(a):
s += "6"
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
tmp.append(s)
def nums7(s):
if len(s) < sum(a):
s += "7"
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
tmp.append(s)
def nums8(s):
if len(s) < sum(a):
s += "8"
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
tmp.append(s)
def nums9(s):
if len(s) < sum(a):
s += "9"
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
tmp.append(s)
if a[0] == 0:
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
else:
nums0(s)
nums1(s)
nums2(s)
nums3(s)
nums4(s)
nums5(s)
nums6(s)
nums7(s)
nums8(s)
nums9(s)
tmp = set(tmp)
ans = 0
# ip = [?,?,2,?,?,5]
# a = [1,1,0,1,1,0]
for i in tmp:
nums = list(i)
tmpstr = ""
jj = 0
for j in range(len(ip)):
if a[j] == 1:
tmpstr += nums[jj]
jj += 1
else:
tmpstr += ip[j]
if int(tmpstr) % 13 == 5:
ans += 1
ans = ans % (10**9 + 1)
print(ans)
|
Statement
Given is a string S. Each character in S is either a digit (`0`, ..., `9`) or
`?`.
Among the integers obtained by replacing each occurrence of `?` with a digit,
how many have a remainder of 5 when divided by 13? An integer may begin with
0.
Since the answer can be enormous, print the count modulo 10^9+7.
|
[{"input": "??2??5", "output": "768\n \n\nFor example, 482305, 002865, and 972665 satisfy the condition.\n\n* * *"}, {"input": "?44", "output": "1\n \n\nOnly 044 satisfies the condition.\n\n* * *"}, {"input": "7?4", "output": "0\n \n\nWe may not be able to produce an integer satisfying the condition.\n\n* * *"}, {"input": "?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???", "output": "153716888"}]
|
Print the number of integers satisfying the condition, modulo 10^9+7.
* * *
|
s691995178
|
Accepted
|
p02960
|
Input is given from Standard Input in the following format:
S
|
s = input()[::-1]
p = [1] + [0] * 12
q = 1
t = [[(i * k) % 13 for i in range(10)] for k in range(13)]
for i in s:
if i != "?":
i = int(i)
g = t[q][i]
p = p[-g:] + p[:-g]
else:
d = [0] * 13
for j in t[q]:
r = p[-j:] + p[:-j]
d = [(r[i] + d[i]) % (10**9 + 7) for i in range(13)]
p = d
q = (q * 10) % 13
print(p[5] % (10**9 + 7))
|
Statement
Given is a string S. Each character in S is either a digit (`0`, ..., `9`) or
`?`.
Among the integers obtained by replacing each occurrence of `?` with a digit,
how many have a remainder of 5 when divided by 13? An integer may begin with
0.
Since the answer can be enormous, print the count modulo 10^9+7.
|
[{"input": "??2??5", "output": "768\n \n\nFor example, 482305, 002865, and 972665 satisfy the condition.\n\n* * *"}, {"input": "?44", "output": "1\n \n\nOnly 044 satisfies the condition.\n\n* * *"}, {"input": "7?4", "output": "0\n \n\nWe may not be able to produce an integer satisfying the condition.\n\n* * *"}, {"input": "?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???", "output": "153716888"}]
|
Print the number of integers satisfying the condition, modulo 10^9+7.
* * *
|
s892907662
|
Accepted
|
p02960
|
Input is given from Standard Input in the following format:
S
|
s = input()
a = [0] * 13
a[0] = 1
for i in s:
b = [0] * 13
for j, k in enumerate(a):
b[(j * 10) % 13] += k
a = b[:]
b = [0] * 13
if i == "?":
for l in range(10):
for j, k in enumerate(a):
b[(j + l) % 13] += k
else:
for j, k in enumerate(a):
b[(j + int(i)) % 13] += k
a = [j % (10**9 + 7) for j in b]
print(a[5] % (10**9 + 7))
|
Statement
Given is a string S. Each character in S is either a digit (`0`, ..., `9`) or
`?`.
Among the integers obtained by replacing each occurrence of `?` with a digit,
how many have a remainder of 5 when divided by 13? An integer may begin with
0.
Since the answer can be enormous, print the count modulo 10^9+7.
|
[{"input": "??2??5", "output": "768\n \n\nFor example, 482305, 002865, and 972665 satisfy the condition.\n\n* * *"}, {"input": "?44", "output": "1\n \n\nOnly 044 satisfies the condition.\n\n* * *"}, {"input": "7?4", "output": "0\n \n\nWe may not be able to produce an integer satisfying the condition.\n\n* * *"}, {"input": "?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???", "output": "153716888"}]
|
Print the number of integers satisfying the condition, modulo 10^9+7.
* * *
|
s703784861
|
Accepted
|
p02960
|
Input is given from Standard Input in the following format:
S
|
import sys
from io import StringIO
import unittest
import os
# 再帰処理上限(dfs作成時に設定するのが面倒なので限度近い値を組み込む)
sys.setrecursionlimit(999999999)
# 実装を行う関数
def resolve(test_def_name=""):
s = list(input())
s.reverse()
devval = pow(10, 9) + 7
dp = [[0 for i in range(13)] for i in range(100001)]
# 初期値設定
if s[0] == "?":
for j in range(10):
dp[0][j] += 1
else:
dp[0][int(s[0]) % 13] += 1
# DP
for i in range(1, len(s)):
for j in range(10):
if s[i] != "?" and s[i] != str(j):
continue
# ここを改善しないと無理。pow(10,100万)とか不可能・・。TLE・・。
aaa = j * pow(10, i, 13)
# 前DPの値を今DPに加算
for k in range(13):
dp[i][(aaa + k) % 13] = (
dp[i][(aaa + k) % 13] + dp[i - 1][k] % devval
) % devval
# 余り5の要素数が答え
print(dp[len(s) - 1][5])
# テストクラス
class TestClass(unittest.TestCase):
def assertIO(self, assert_input, output):
stdout, sat_in = sys.stdout, sys.stdin
sys.stdout, sys.stdin = StringIO(), StringIO(assert_input)
resolve(sys._getframe().f_back.f_code.co_name)
sys.stdout.seek(0)
out = sys.stdout.read()[:-1]
sys.stdout, sys.stdin = stdout, sat_in
self.assertEqual(out, output)
def test_input_1(self):
test_input = """??2??5"""
output = """768"""
self.assertIO(test_input, output)
def test_input_2(self):
test_input = """?44"""
output = """1"""
self.assertIO(test_input, output)
def test_input_3(self):
test_input = """7?4"""
output = """0"""
self.assertIO(test_input, output)
def test_input_4(self):
test_input = """?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???"""
output = """153716888"""
self.assertIO(test_input, output)
# 自作テストパターンのひな形(利用時は「tes_t」のアンダーバーを削除すること
def test_1original_1(self):
test_input = """?"""
output = """1"""
self.assertIO(test_input, output)
# 実装orテストの呼び出し
if __name__ == "__main__":
if os.environ.get("USERNAME") is None:
# AtCoder提出時の場合
resolve()
else:
# 自PCの場合
unittest.main()
|
Statement
Given is a string S. Each character in S is either a digit (`0`, ..., `9`) or
`?`.
Among the integers obtained by replacing each occurrence of `?` with a digit,
how many have a remainder of 5 when divided by 13? An integer may begin with
0.
Since the answer can be enormous, print the count modulo 10^9+7.
|
[{"input": "??2??5", "output": "768\n \n\nFor example, 482305, 002865, and 972665 satisfy the condition.\n\n* * *"}, {"input": "?44", "output": "1\n \n\nOnly 044 satisfies the condition.\n\n* * *"}, {"input": "7?4", "output": "0\n \n\nWe may not be able to produce an integer satisfying the condition.\n\n* * *"}, {"input": "?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???", "output": "153716888"}]
|
Print the number of integers satisfying the condition, modulo 10^9+7.
* * *
|
s481401506
|
Accepted
|
p02960
|
Input is given from Standard Input in the following format:
S
|
X = [1] + [0] * 12
for s in input():
X = [
sum([X[(i - k) * 9 % 13] for i in (range(10) if s > "9" else [int(s)])])
% (10**9 + 7)
for k in range(13)
]
print(X[5])
|
Statement
Given is a string S. Each character in S is either a digit (`0`, ..., `9`) or
`?`.
Among the integers obtained by replacing each occurrence of `?` with a digit,
how many have a remainder of 5 when divided by 13? An integer may begin with
0.
Since the answer can be enormous, print the count modulo 10^9+7.
|
[{"input": "??2??5", "output": "768\n \n\nFor example, 482305, 002865, and 972665 satisfy the condition.\n\n* * *"}, {"input": "?44", "output": "1\n \n\nOnly 044 satisfies the condition.\n\n* * *"}, {"input": "7?4", "output": "0\n \n\nWe may not be able to produce an integer satisfying the condition.\n\n* * *"}, {"input": "?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???", "output": "153716888"}]
|
Print the number of integers satisfying the condition, modulo 10^9+7.
* * *
|
s389164233
|
Accepted
|
p02960
|
Input is given from Standard Input in the following format:
S
|
S = input()
A = [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
a = 10**9 + 7
for i in range(len(S)):
B = A[:]
if S[i] == "?":
A[0] = (
B[0] + B[9] + B[5] + B[1] + B[10] + B[6] + B[2] + B[11] + B[7] + B[3]
) % a
A[1] = (
B[4] + B[0] + B[9] + B[5] + B[1] + B[10] + B[6] + B[2] + B[11] + B[7]
) % a
A[2] = (
B[8] + B[4] + B[0] + B[9] + B[5] + B[1] + B[10] + B[6] + B[2] + B[11]
) % a
A[3] = (
B[12] + B[8] + B[4] + B[0] + B[9] + B[5] + B[1] + B[10] + B[6] + B[2]
) % a
A[4] = (
B[3] + B[12] + B[8] + B[4] + B[0] + B[9] + B[5] + B[1] + B[10] + B[6]
) % a
A[5] = (
B[7] + B[3] + B[12] + B[8] + B[4] + B[0] + B[9] + B[5] + B[1] + B[10]
) % a
A[6] = (
B[11] + B[7] + B[3] + B[12] + B[8] + B[4] + B[0] + B[9] + B[5] + B[1]
) % a
A[7] = (
B[2] + B[11] + B[7] + B[3] + B[12] + B[8] + B[4] + B[0] + B[9] + B[5]
) % a
A[8] = (
B[6] + B[2] + B[11] + B[7] + B[3] + B[12] + B[8] + B[4] + B[0] + B[9]
) % a
A[9] = (
B[10] + B[6] + B[2] + B[11] + B[7] + B[3] + B[12] + B[8] + B[4] + B[0]
) % a
A[10] = (
B[1] + B[10] + B[6] + B[2] + B[11] + B[7] + B[3] + B[12] + B[8] + B[4]
) % a
A[11] = (
B[5] + B[1] + B[10] + B[6] + B[2] + B[11] + B[7] + B[3] + B[12] + B[8]
) % a
A[12] = (
B[9] + B[5] + B[1] + B[10] + B[6] + B[2] + B[11] + B[7] + B[3] + B[12]
) % a
else:
s = int(S[i])
for i in range(13):
A[i] = B[(i * 4 + 9 * s) % 13]
print(A[5])
|
Statement
Given is a string S. Each character in S is either a digit (`0`, ..., `9`) or
`?`.
Among the integers obtained by replacing each occurrence of `?` with a digit,
how many have a remainder of 5 when divided by 13? An integer may begin with
0.
Since the answer can be enormous, print the count modulo 10^9+7.
|
[{"input": "??2??5", "output": "768\n \n\nFor example, 482305, 002865, and 972665 satisfy the condition.\n\n* * *"}, {"input": "?44", "output": "1\n \n\nOnly 044 satisfies the condition.\n\n* * *"}, {"input": "7?4", "output": "0\n \n\nWe may not be able to produce an integer satisfying the condition.\n\n* * *"}, {"input": "?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???", "output": "153716888"}]
|
Print the number of integers satisfying the condition, modulo 10^9+7.
* * *
|
s513507273
|
Accepted
|
p02960
|
Input is given from Standard Input in the following format:
S
|
M = 10**9 + 7
# リストに入力(文字列)
text = input()
lst = list(text)
lst.reverse()
digit = len(lst)
six = [[0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0]]
for i in range(digit):
if lst[i] == "?":
six[i % 6][1] = six[i % 6][1] + 1
else:
six[i % 6][0] = (six[i % 6][0] + int(lst[i])) % 13
rem = (
-(
six[0][0]
+ 10 * six[1][0]
+ 9 * six[2][0]
+ 12 * six[3][0]
+ 3 * six[4][0]
+ 4 * six[5][0]
- 5
)
% 13
)
######(?のいじったもの)+rem=0(mod13)
######(?*1+?*10+?*9+?*12+?*3+?*4)+rem=0
modulos = [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
def mat1(ls):
val_ls = [0] * 13
for i in range(13):
val_ls[i] = (
ls[i]
+ ls[(i - 1) % 13]
+ ls[(i - 2) % 13]
+ ls[(i - 3) % 13]
+ ls[(i - 4) % 13]
+ ls[(i - 5) % 13]
+ ls[(i - 6) % 13]
+ ls[(i - 7) % 13]
+ ls[(i - 8) % 13]
+ ls[(i - 9) % 13]
) % M
return val_ls
def mat10(ls):
val_ls = [0] * 13
for i in range(13):
val_ls[i] = (
ls[i]
+ ls[(i - 10) % 13]
+ ls[(i - 20) % 13]
+ ls[(i - 30) % 13]
+ ls[(i - 40) % 13]
+ ls[(i - 50) % 13]
+ ls[(i - 60) % 13]
+ ls[(i - 70) % 13]
+ ls[(i - 80) % 13]
+ ls[(i - 90) % 13]
) % M
return val_ls
def mat100(ls):
val_ls = [0] * 13
for i in range(13):
val_ls[i] = (
ls[i]
+ ls[(i - 9) % 13]
+ ls[(i - 18) % 13]
+ ls[(i - 27) % 13]
+ ls[(i - 36) % 13]
+ ls[(i - 45) % 13]
+ ls[(i - 54) % 13]
+ ls[(i - 63) % 13]
+ ls[(i - 72) % 13]
+ ls[(i - 81) % 13]
) % M
return val_ls
def mat1000(ls):
val_ls = [0] * 13
for i in range(13):
val_ls[i] = (
ls[i]
+ ls[(i + 1) % 13]
+ ls[(i + 2) % 13]
+ ls[(i + 3) % 13]
+ ls[(i + 4) % 13]
+ ls[(i + 5) % 13]
+ ls[(i + 6) % 13]
+ ls[(i + 7) % 13]
+ ls[(i + 8) % 13]
+ ls[(i + 9) % 13]
) % M
return val_ls
def mat10000(ls):
val_ls = [0] * 13
for i in range(13):
val_ls[i] = (
ls[i]
+ ls[(i - 3) % 13]
+ ls[(i - 6) % 13]
+ ls[(i - 9) % 13]
+ ls[(i - 12) % 13]
+ ls[(i - 15) % 13]
+ ls[(i - 18) % 13]
+ ls[(i - 21) % 13]
+ ls[(i - 24) % 13]
+ ls[(i - 27) % 13]
) % M
return val_ls
def mat100000(ls):
val_ls = [0] * 13
for i in range(13):
val_ls[i] = (
ls[i]
+ ls[(i - 4) % 13]
+ ls[(i - 8) % 13]
+ ls[(i - 12) % 13]
+ ls[(i - 16) % 13]
+ ls[(i - 20) % 13]
+ ls[(i - 24) % 13]
+ ls[(i - 28) % 13]
+ ls[(i - 32) % 13]
+ ls[(i - 36) % 13]
) % M
return val_ls
for j in range(six[0][1]):
modulos = mat1(modulos)
for j in range(six[1][1]):
modulos = mat10(modulos)
for j in range(six[2][1]):
modulos = mat100(modulos)
for j in range(six[3][1]):
modulos = mat1000(modulos)
for j in range(six[4][1]):
modulos = mat10000(modulos)
for j in range(six[5][1]):
modulos = mat100000(modulos)
print(modulos[rem])
|
Statement
Given is a string S. Each character in S is either a digit (`0`, ..., `9`) or
`?`.
Among the integers obtained by replacing each occurrence of `?` with a digit,
how many have a remainder of 5 when divided by 13? An integer may begin with
0.
Since the answer can be enormous, print the count modulo 10^9+7.
|
[{"input": "??2??5", "output": "768\n \n\nFor example, 482305, 002865, and 972665 satisfy the condition.\n\n* * *"}, {"input": "?44", "output": "1\n \n\nOnly 044 satisfies the condition.\n\n* * *"}, {"input": "7?4", "output": "0\n \n\nWe may not be able to produce an integer satisfying the condition.\n\n* * *"}, {"input": "?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???", "output": "153716888"}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s541498353
|
Wrong Answer
|
p03672
|
Input is given from Standard Input in the following format:
S
|
st = input()
for i in range(2, len(st), 2):
r = st[0:i]
if r[0 : i // 2] == r[i // 2 :]:
print(i)
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s178230516
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
s=list(input())
while len(s) != 0:
s.pop()
if len(s)%2==0 and s[:len(s)//2]==s[len(s)//2:]:
print(len(s)
exit()
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s445442775
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
S = input().strip()
while len(S) > 0:
S = S[:-1]
mid = len(S)//2
if S[:mid] == S[mid:]:
print(len(S))
break
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s810040491
|
Wrong Answer
|
p03672
|
Input is given from Standard Input in the following format:
S
|
S = input()
for i in range(1, len(S)):
S2 = S[0 : len(S) - i]
flag = True
if S2.count("a") % 2 == 1:
flag = False
elif S2.count("b") % 2 == 1:
flag = False
elif S2.count("b") % 2 == 1:
flag = False
elif S2.count("c") % 2 == 1:
flag = False
elif S2.count("d") % 2 == 1:
flag = False
elif S2.count("e") % 2 == 1:
flag = False
elif S2.count("f") % 2 == 1:
flag = False
elif S2.count("g") % 2 == 1:
flag = False
elif S2.count("h") % 2 == 1:
flag = False
elif S2.count("i") % 2 == 1:
flag = False
elif S2.count("j") % 2 == 1:
flag = False
elif S2.count("k") % 2 == 1:
flag = False
elif S2.count("l") % 2 == 1:
flag = False
elif S2.count("m") % 2 == 1:
flag = False
elif S2.count("n") % 2 == 1:
flag = False
elif S2.count("o") % 2 == 1:
flag = False
elif S2.count("p") % 2 == 1:
flag = False
elif S2.count("q") % 2 == 1:
flag = False
elif S2.count("r") % 2 == 1:
flag = False
elif S2.count("s") % 2 == 1:
flag = False
elif S2.count("t") % 2 == 1:
flag = False
elif S2.count("u") % 2 == 1:
flag = False
elif S2.count("v") % 2 == 1:
flag = False
elif S2.count("w") % 2 == 1:
flag = False
elif S2.count("x") % 2 == 1:
flag = False
elif S2.count("y") % 2 == 1:
flag = False
elif S2.count("z") % 2 == 1:
flag = False
if flag:
print(len(S2))
break
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s777012289
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
python-scipy-connected-components/
# from scipy.sparse import csr_matrix
# import string
import sys
sys.setrecursionlimit(10 ** 5 + 10)
def input(): return sys.stdin.readline().strip()
def resolve():
s= str(input())
ls=len(s)
cur=ls//2
i=0
while True:
i+=1
cur-=1
if s[:cur]==s[cur:ls-i*2]:
print(ls-i*2)
break
resolve()
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s185366389
|
Wrong Answer
|
p03672
|
Input is given from Standard Input in the following format:
S
|
#!/usr/bin/env python3
import sys
# import time
# import math
# import numpy as np
# import scipy.sparse.csgraph as cs # csgraph_from_dense(ndarray, null_value=inf), bellman_ford(G, return_predecessors=True), dijkstra, floyd_warshall
# import random # random, uniform, randint, randrange, shuffle, sample
# import string # ascii_lowercase, ascii_uppercase, ascii_letters, digits, hexdigits
# import re # re.compile(pattern) => ptn obj; p.search(s), p.match(s), p.finditer(s) => match obj; p.sub(after, s)
# from bisect import bisect_left, bisect_right # bisect_left(a, x, lo=0, hi=len(a)) returns i such that all(val<x for val in a[lo:i]) and all(val>-=x for val in a[i:hi]).
# from collections import deque # deque class. deque(L): dq.append(x), dq.appendleft(x), dq.pop(), dq.popleft(), dq.rotate()
# from collections import defaultdict # subclass of dict. defaultdict(facroty)
# from collections import Counter # subclass of dict. Counter(iter): c.elements(), c.most_common(n), c.subtract(iter)
# from datetime import date, datetime # date.today(), date(year,month,day) => date obj; datetime.now(), datetime(year,month,day,hour,second,microsecond) => datetime obj; subtraction => timedelta obj
# from datetime.datetime import strptime # strptime('2019/01/01 10:05:20', '%Y/%m/%d/ %H:%M:%S') returns datetime obj
# from datetime import timedelta # td.days, td.seconds, td.microseconds, td.total_seconds(). abs function is also available.
# from copy import copy, deepcopy # use deepcopy to copy multi-dimentional matrix without reference
# from functools import reduce # reduce(f, iter[, init])
# from functools import lru_cache # @lrucache ...arguments of functions should be able to be keys of dict (e.g. list is not allowed)
# from heapq import heapify, heappush, heappop # built-in list. heapify(L) changes list in-place to min-heap in O(n), heappush(heapL, x) and heappop(heapL) in O(lgn).
# from heapq import nlargest, nsmallest # nlargest(n, iter[, key]) returns k-largest-list in O(n+klgn).
# from itertools import count, cycle, repeat # count(start[,step]), cycle(iter), repeat(elm[,n])
# from itertools import groupby # [(k, list(g)) for k, g in groupby('000112')] returns [('0',['0','0','0']), ('1',['1','1']), ('2',['2'])]
# from itertools import starmap # starmap(pow, [[2,5], [3,2]]) returns [32, 9]
# from itertools import product, permutations # product(iter, repeat=n), permutations(iter[,r])
# from itertools import combinations, combinations_with_replacement
# from itertools import accumulate # accumulate(iter[, f])
# from operator import itemgetter # itemgetter(1), itemgetter('key')
# from fractions import gcd # for Python 3.4 (previous contest @AtCoder)
def main():
mod = 1000000007 # 10^9+7
inf = float("inf") # sys.float_info.max = 1.79...e+308
# inf = 2 ** 64 - 1 # (for fast JIT compile in PyPy) 1.84...e+19
sys.setrecursionlimit(10**6) # 1000 -> 1000000
def input():
return sys.stdin.readline().rstrip()
def ii():
return int(input())
def mi():
return map(int, input().split())
def mi_0():
return map(lambda x: int(x) - 1, input().split())
def lmi():
return list(map(int, input().split()))
def lmi_0():
return list(map(lambda x: int(x) - 1, input().split()))
def li():
return list(input())
def check_even_string(s):
n = len(s)
assert n >= 2 and n % 2 == 0
for i in range(n // 2):
if s[i] != s[i + n // 2]:
return False
return True
s = input()
n = len(s)
for i in range(2, n - 1, 2):
if check_even_string(s[:i]):
print(i)
exit()
if __name__ == "__main__":
main()
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s830582102
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
n = input()[:-1]
while n[:len(n)//2] != [len(n)//2:]:
n = n[:-1]
print(len(n))
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s090111769
|
Wrong Answer
|
p03672
|
Input is given from Standard Input in the following format:
S
|
s = input()
print(len(s) / 2)
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s913044042
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
#include <iostream>
#include <vector>
#include <algorithm>
#include <utility>
#include <string>
#include <queue>
#include <stack>
using namespace std;
typedef long long int ll;
typedef pair<int, int> Pii;
const ll mod = 1000000007;
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
string s;
cin >> s;
int n = s.length();
int ans = 0;
for (int i = 1; i * 2 < n; i++) {
bool good = true;
for (int j = 0; j < i; j++) {
if (s[j] != s[j+i]) {
good = false;
break;
}
}
if (good) ans = i * 2;
}
cout << ans << endl;
return 0;
}
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s735112571
|
Wrong Answer
|
p03672
|
Input is given from Standard Input in the following format:
S
|
s = list(input())
c = 0
max_len = 0
s.pop(len(s) - 1)
for i in range((len(s) // 2 + len(s) % 2)):
if len(s) % 2 == 0:
for j in range(len(s) // 2):
if s[j] == s[j + len(s) // 2]:
c += 1
if c == len(s) // 2 and max_len < c:
max_len = c
c = 0
s.pop(len(s) - 1)
print(max_len * 2)
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s987642854
|
Accepted
|
p03672
|
Input is given from Standard Input in the following format:
S
|
import re
print(len(re.match(r"(.+)\1", input()[:-1]).group()))
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s248017569
|
Wrong Answer
|
p03672
|
Input is given from Standard Input in the following format:
S
|
s = input().strip()
for i in range(1000):
r = -2 * i
s2 = s[:r]
half = len(s2) // 2
if s2[half:] == s2[: half * -1]:
print(r)
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s771533113
|
Accepted
|
p03672
|
Input is given from Standard Input in the following format:
S
|
import sys
## io ##
def IS():
return sys.stdin.readline().rstrip()
def II():
return int(IS())
def MII():
return list(map(int, IS().split()))
def MIIZ():
return list(map(lambda x: x - 1, MII()))
## dp ##
def DD2(d1, d2, init=0):
return [[init] * d2 for _ in range(d1)]
def DD3(d1, d2, d3, init=0):
return [DD2(d2, d3, init) for _ in range(d1)]
## math ##
def to_bin(x: int) -> str:
return format(x, "b") # rev => int(res, 2)
def to_oct(x: int) -> str:
return format(x, "o") # rev => int(res, 8)
def to_hex(x: int) -> str:
return format(x, "x") # rev => int(res, 16)
MOD = 10**9 + 7
def divc(x, y) -> int:
return -(-x // y)
def divf(x, y) -> int:
return x // y
def gcd(x, y):
while y:
x, y = y, x % y
return x
def lcm(x, y):
return x * y // gcd(x, y)
def enumerate_divs(n):
"""Return a tuple list of divisor of n"""
return [(i, n // i) for i in range(1, int(n**0.5) + 1) if n % i == 0]
def get_primes(MAX_NUM=10**3):
"""Return a list of prime numbers n or less"""
is_prime = [True] * (MAX_NUM + 1)
is_prime[0] = is_prime[1] = False
for i in range(2, int(MAX_NUM**0.5) + 1):
if not is_prime[i]:
continue
for j in range(i * 2, MAX_NUM + 1, i):
is_prime[j] = False
return [i for i in range(MAX_NUM + 1) if is_prime[i]]
## libs ##
from itertools import (
accumulate as acc,
combinations as combi,
product,
combinations_with_replacement as combi_dup,
)
from collections import deque, Counter
from heapq import heapify, heappop, heappush
from bisect import bisect_left
# ======================================================#
def main():
s = IS()
n = len(s)
for i in range(2, n, 2):
si = s[: n - i]
sl = si[: (n - i) // 2]
sr = si[(n - i) // 2 :]
if sl == sr:
print(n - i)
return None
if __name__ == "__main__":
main()
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s988991759
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
Beta
paiza.IO
新規コード
一覧
ウェブ開発
New!
日本語 サインアップ ログイン
Python3 Split Button!
Enter a title here
Main.py
Success
1
2
3
4
5
6
7
8
9
10
11
12
13
def chunked(iterable, n):
return [iterable[x:x + n] for x in range(0, len(iterable), n)]
s=input()
for i in range(1,len(s)):
a=s[:(-1*i)]
if len(a)>1:
li=chunked(a,(len(a)+1)//2)
if li[0]==li[1]:
print(len(a))
quit()
実行 (Ctrl-Enter) Split Button!
出力
入力
コメント 0
(0.04 sec)
2
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s979878969
|
Wrong Answer
|
p03672
|
Input is given from Standard Input in the following format:
S
|
S = input()
len_s = len(S)
for i in range(2, len_s, 2):
deleted_str = S[:-i]
center = (len_s - i) // 2
mae = deleted_str[:center]
ato = deleted_str[center:]
if mae == ato:
print(len(deleted_str))
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s708429319
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
S = input()
result = ''
for i in range(1, len(S)):
s = S[0:len(S) - i]
if len(s) % 2 == 0 and s[0:len(s)//2] == s[len(s)//2:]:
result = len(s)
break
print(result)
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s020171589
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
s=input()
n=len(s)
for i in range(1,n+1):
if s[0:i]==s[i:i+i]:
print(i)
break:
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s339678620
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
s = input()
for k in range(len(s)//2-1, 0, -1)
if s[:k] == s[k:2*k]: break
print(k)
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s940390708
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
S = input()
for i in range(len(S) - 1, 0, -1):
if(S[0:i//2] == S[i//2:i]):
print(i)
break
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s166052640
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
#!/usr/bin
# -*- coding:"utf-8" -*-
s = input()
sn = len(s)
if sn % 2 == 1:
sn = sn -1
for i in range(sn, 0, -2)
if s[:i/2] == s[i/2:]:
break
print(s[:i])
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s523415196
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
S = gets.chomp.split("")
L = S.length
while L > 0
L -= 1
A = S[0...L/2]
B = S[L/2...L]
if A == B
puts L
break
end
end
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s341089540
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
s = list(str(input()))
s_rev = list(reversed(s))
n = len(s_rev)
for i in range(len(s_rev)):
del s_rev[0]
if len(s_rev) % 2 == 1:
continue
elif s[0:len(s_rev) // 2] != s[len(s_rev) // 2:len(s_rev)]:
continue
elif len(s_rev) != 0:
print(len(s_rev))
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s223782423
|
Wrong Answer
|
p03672
|
Input is given from Standard Input in the following format:
S
|
l = list(input())
for i in range(len(l)):
del l[-1]
if len(l) % 2 != 0:
del l[-1]
# print('1',l)
if len(l) % 2 == 0:
if l[: len(l) // 2] == l[len(l) // 2 :]:
# print('2',l,'len(l)',len(l))
exit()
else:
del l[-1]
# print('3',l)
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print the length of the longest even string that can be obtained.
* * *
|
s993013890
|
Runtime Error
|
p03672
|
Input is given from Standard Input in the following format:
S
|
import sys, re
from collections import deque, defaultdict, Counter
from math import ceil, sqrt, hypot, factorial, pi, sin, cos, radians, log2
from itertools import accumulate, permutations, combinations, product, groupby
from operator import itemgetter, mul
from copy import deepcopy
from string import ascii_lowercase, ascii_uppercase, digits
from bisect import bisect, bisect_left
from fractions import gcd
from heapq import heappush, heappop
from functools import reduce
def input(): return sys.stdin.readline().strip()
def INT(): return int(input())
def MAP(): return map(int, input().split())
def LIST(): return list(map(int, input().split()))
def ZIP(n): return zip(*(MAP() for _ in range(n)))
sys.setrecursionlimit(10 ** 9)
INF = float('inf')
mod = 10 ** 9 + 7
S = input()
for i in range(1, len(S)):
T = S[:-2*i]
if T[:len(T)//2] == T[len(T//2:)]:
print(len(T))
break
|
Statement
We will call a string that can be obtained by concatenating two equal strings
an _even_ string. For example, `xyzxyz` and `aaaaaa` are even, while `ababab`
and `xyzxy` are not.
You are given an even string S consisting of lowercase English letters. Find
the length of the longest even string that can be obtained by deleting one or
more characters from the end of S. It is guaranteed that such a non-empty
string exists for a given input.
|
[{"input": "abaababaab", "output": "6\n \n\n * `abaababaab` itself is even, but we need to delete at least one character.\n * `abaababaa` is not even.\n * `abaababa` is not even.\n * `abaabab` is not even.\n * `abaaba` is even. Thus, we should print its length, 6.\n\n* * *"}, {"input": "xxxx", "output": "2\n \n\n * `xxx` is not even.\n * `xx` is even.\n\n* * *"}, {"input": "abcabcabcabc", "output": "6\n \n\nThe longest even string that can be obtained is `abcabc`, whose length is 6.\n\n* * *"}, {"input": "akasakaakasakasakaakas", "output": "14\n \n\nThe longest even string that can be obtained is `akasakaakasaka`, whose length\nis 14."}]
|
Print all elements of the list in order after performing given operations.
Print an element in a line.
|
s662351968
|
Runtime Error
|
p02433
|
The input is given in the following format.
$q$
$query_1$
$query_2$
:
$query_q$
Each query $query_i$ is given by
0 $x$
or
1 $d$
or
2
where the first digits 0, 1 and 2 represent insert, move and erase operations
respectively.
|
# coding=utf-8
A = []
cursor = 0
N = int(input())
for i in range(N):
query = map(int, input().split())
if query[0] == 0:
A.insert(cursor, query[1])
elif query[0] == 1:
cursor += query[1]
elif query[0] == 2:
A.pop(cursor)
[print(x) for x in A]
|
List
For a dynamic list $L$ of integers, perform a sequence of the following
operations. $L$ has a special element called END at the end of the list and an
element of $L$ is indicated by a cursor.
* insert($x$): Insert $x$ before the element indicated by the cursor. After this operation, the cursor points the inserted element.
* move($d$): Move the cursor to the end by $d$, if $d$ is positive. Move the cursor to the front by $d$, if $d$ is negative.
* erase(): Delete the element indicated by the cursor. After this operation, the cursor points the element next to the deleted element. In case there is no such element, the cursor should point END.
In the initial state, $L$ is empty and the cursor points END.
|
[{"input": "5\n 0 1\n 0 2\n 0 3\n 1 1\n 2", "output": "3\n 1"}]
|
Print Q lines. The i-th line should contain the response to the i-th query.
* * *
|
s071616836
|
Accepted
|
p02599
|
Input is given from Standard Input in the following format:
N Q
c_1 c_2 \cdots c_N
l_1 r_1
l_2 r_2
:
l_Q r_Q
|
import sys
import io, os
input = io.BytesIO(os.read(0, os.fstat(0).st_size)).readline
from operator import itemgetter
N, Q = map(int, input().split())
C = [0] + list(map(int, input().split()))
QU = [list(map(int, input().split())) + [i] for i in range(Q)]
QU.sort(key=itemgetter(0))
# BIT(BIT-indexed tree)
LEN = N + 3
BIT = [0] * (LEN + 1) # 1-indexedなtree
def update(v, w): # index vにwを加える
while v <= LEN:
BIT[v] += w
v += v & (-v) # 自分を含む大きなノードへ. たとえばv=3→v=4
def getvalue(v): # [1,v]の区間の和を求める
ANS = 0
while v != 0:
ANS += BIT[v]
v -= v & (-v) # 自分より小さい2ベキのノードへ. たとえばv=3→v=2へ
return ANS
NUM = [[] for i in range(N + 1)]
for i, c in enumerate(C):
if i == 0:
continue
if NUM[c] == []:
update(i, 1)
NUM[c].append(i)
NUMIND = [0] * (N + 1)
ANS = [-1] * Q
ia = 1
for x, y, ind in QU:
while ia != x:
update(NUM[C[ia]][NUMIND[C[ia]]], -1)
NUMIND[C[ia]] += 1
if NUMIND[C[ia]] < len(NUM[C[ia]]):
update(NUM[C[ia]][NUMIND[C[ia]]], 1)
ia += 1
# print(x,y,ind)
# print([getvalue(i) for i in range(1,N+1)])
ANS[ind] = getvalue(y)
sys.stdout.write(" ".join(map(str, ANS)) + "\n")
|
Statement
We have N colored balls arranged in a row from left to right; the color of the
i-th ball from the left is c_i.
You are given Q queries. The i-th query is as follows: how many different
colors do the l_i-th through r_i-th balls from the left have?
|
[{"input": "4 3\n 1 2 1 3\n 1 3\n 2 4\n 3 3", "output": "2\n 3\n 1\n \n\n * The 1-st, 2-nd, and 3-rd balls from the left have the colors 1, 2, and 1 \\- two different colors.\n * The 2-st, 3-rd, and 4-th balls from the left have the colors 2, 1, and 3 \\- three different colors.\n * The 3-rd ball from the left has the color 1 \\- just one color.\n\n* * *"}, {"input": "10 10\n 2 5 6 5 2 1 7 9 7 2\n 5 5\n 2 4\n 6 7\n 2 2\n 7 8\n 7 9\n 1 8\n 6 9\n 8 10\n 6 8", "output": "1\n 2\n 2\n 1\n 2\n 2\n 6\n 3\n 3\n 3"}]
|
Print Q lines. The i-th line should contain the response to the i-th query.
* * *
|
s151682250
|
Accepted
|
p02599
|
Input is given from Standard Input in the following format:
N Q
c_1 c_2 \cdots c_N
l_1 r_1
l_2 r_2
:
l_Q r_Q
|
from sys import stdin
class BIT:
def __init__(self, n):
self.data = [0] * (n + 10)
def upd(self, pos, val=1):
pos += 1
while pos < len(self.data):
self.data[pos] += val
pos += pos & -pos
def get(self, pos):
ans = 0
pos += 1
while pos > 0:
ans += self.data[pos]
pos -= pos & -pos
return ans
def get_range(self, l, r):
return self.get(r) - self.get(l - 1)
def main():
n, q = map(int, stdin.readline().split())
color = list(map(int, stdin.readline().split()))
queries = []
for i in range(q):
l, r = map(int, stdin.readline().split())
queries.append((l, r, i))
queries.sort(key=lambda val: val[1])
ans = [0] * q
prev_pos = [0] * (n + 1)
bit = BIT(n + 1)
f = 0
for cur_pos, color in enumerate(color, 1):
bit.upd(prev_pos[color], -1)
bit.upd(cur_pos, 1)
prev_pos[color] = cur_pos
while f < q and queries[f][1] == cur_pos:
ans[queries[f][2]] = bit.get_range(queries[f][0], queries[f][1])
f += 1
print("\n".join(map(str, ans)))
main()
|
Statement
We have N colored balls arranged in a row from left to right; the color of the
i-th ball from the left is c_i.
You are given Q queries. The i-th query is as follows: how many different
colors do the l_i-th through r_i-th balls from the left have?
|
[{"input": "4 3\n 1 2 1 3\n 1 3\n 2 4\n 3 3", "output": "2\n 3\n 1\n \n\n * The 1-st, 2-nd, and 3-rd balls from the left have the colors 1, 2, and 1 \\- two different colors.\n * The 2-st, 3-rd, and 4-th balls from the left have the colors 2, 1, and 3 \\- three different colors.\n * The 3-rd ball from the left has the color 1 \\- just one color.\n\n* * *"}, {"input": "10 10\n 2 5 6 5 2 1 7 9 7 2\n 5 5\n 2 4\n 6 7\n 2 2\n 7 8\n 7 9\n 1 8\n 6 9\n 8 10\n 6 8", "output": "1\n 2\n 2\n 1\n 2\n 2\n 6\n 3\n 3\n 3"}]
|
Print Q lines. The i-th line should contain the response to the i-th query.
* * *
|
s662958571
|
Accepted
|
p02599
|
Input is given from Standard Input in the following format:
N Q
c_1 c_2 \cdots c_N
l_1 r_1
l_2 r_2
:
l_Q r_Q
|
# From: https://github.com/cheran-senthil/PyRival/blob/master/pyrival/data_structures/SegmentTree.py
class SegmentTree:
def __init__(self, data, default=0, func=max):
"""initialize the segment tree with data"""
self._default = default
self._func = func
self._len = len(data)
self._size = _size = 1 << (self._len - 1).bit_length()
self.data = [default] * (2 * _size)
self.data[_size : _size + self._len] = data
for i in reversed(range(_size)):
self.data[i] = func(self.data[i + i], self.data[i + i + 1])
def __delitem__(self, idx):
self[idx] = self._default
def __getitem__(self, idx):
return self.data[idx + self._size]
def __setitem__(self, idx, value):
idx += self._size
self.data[idx] = value
idx >>= 1
while idx:
self.data[idx] = self._func(self.data[2 * idx], self.data[2 * idx + 1])
idx >>= 1
def __len__(self):
return self._len
def query(self, start, stop):
"""func of data[start, stop)"""
start += self._size
stop += self._size
res_left = res_right = self._default
while start < stop:
if start & 1:
res_left = self._func(res_left, self.data[start])
start += 1
if stop & 1:
stop -= 1
res_right = self._func(self.data[stop], res_right)
start >>= 1
stop >>= 1
return self._func(res_left, res_right)
def __repr__(self):
return "SegmentTree({0})".format(self.data)
import io
import os
from collections import defaultdict
def solve(N, Q, C, LR):
# Bucket sort queries by right endpoint
LByR = defaultdict(list)
for i, (l, r) in enumerate(LR):
LByR[r].append((i, l))
# Segment tree stores a 1 at position i if the ith element is the rightmost of its dupes
segTree = SegmentTree([0] * (N + 1), 0, lambda x, y: x + y)
lastSeen = {}
ans = [0] * Q
for r, x in enumerate(C):
if x in lastSeen:
# Clear the previous rightmost bit
segTree[lastSeen[x]] -= 1
# Add a new rightmost bit
segTree[r] += 1
lastSeen[x] = r
for queryIndex, l in LByR[r]:
ans[queryIndex] = segTree.query(l, r + 1)
return "\n".join(map(str, ans))
if __name__ == "__main__":
input = io.BytesIO(os.read(0, os.fstat(0).st_size)).readline
N, Q = [int(x) for x in input().split()]
C = [int(x) for x in input().split()]
# 0-indexed, inclusive inclusive
LR = [[int(x) - 1 for x in input().split()] for i in range(Q)]
print(solve(N, Q, C, LR))
|
Statement
We have N colored balls arranged in a row from left to right; the color of the
i-th ball from the left is c_i.
You are given Q queries. The i-th query is as follows: how many different
colors do the l_i-th through r_i-th balls from the left have?
|
[{"input": "4 3\n 1 2 1 3\n 1 3\n 2 4\n 3 3", "output": "2\n 3\n 1\n \n\n * The 1-st, 2-nd, and 3-rd balls from the left have the colors 1, 2, and 1 \\- two different colors.\n * The 2-st, 3-rd, and 4-th balls from the left have the colors 2, 1, and 3 \\- three different colors.\n * The 3-rd ball from the left has the color 1 \\- just one color.\n\n* * *"}, {"input": "10 10\n 2 5 6 5 2 1 7 9 7 2\n 5 5\n 2 4\n 6 7\n 2 2\n 7 8\n 7 9\n 1 8\n 6 9\n 8 10\n 6 8", "output": "1\n 2\n 2\n 1\n 2\n 2\n 6\n 3\n 3\n 3"}]
|
Print Q lines. The i-th line should contain the response to the i-th query.
* * *
|
s511219725
|
Accepted
|
p02599
|
Input is given from Standard Input in the following format:
N Q
c_1 c_2 \cdots c_N
l_1 r_1
l_2 r_2
:
l_Q r_Q
|
import sys
input = sys.stdin.readline
def solve():
def makeBIT(numEle):
numPow2 = 2 ** (numEle - 1).bit_length()
data = [0] * (numPow2 + 1)
return data, numPow2
def addValue(iA, A):
iB = iA + 1
while iB <= numPow2:
data[iB] += A
iB += iB & -iB
def getSum(iA):
iB = iA + 1
ans = 0
while iB > 0:
ans += data[iB]
iB -= iB & -iB
return ans
def getRangeSum(iFr, iTo):
return getSum(iTo) - getSum(iFr - 1)
N, Q = map(int, input().split())
cs = list(map(lambda x: int(x) - 1, input().split()))
LRs = []
Lss = [[] for _ in range(N)]
for i in range(Q):
L, R = map(int, input().split())
L, R = L - 1, R - 1
LRs.append((L, R))
Lss[R].append((L, i))
data, numPow2 = makeBIT(Q)
anss = [0] * Q
posRights = [-1] * N
for R, c in enumerate(cs):
if posRights[c] != -1:
addValue(posRights[c], -1)
addValue(R, 1)
posRights[c] = R
for L, i in Lss[R]:
anss[i] = getRangeSum(L, R)
print("\n".join(map(str, anss)))
solve()
|
Statement
We have N colored balls arranged in a row from left to right; the color of the
i-th ball from the left is c_i.
You are given Q queries. The i-th query is as follows: how many different
colors do the l_i-th through r_i-th balls from the left have?
|
[{"input": "4 3\n 1 2 1 3\n 1 3\n 2 4\n 3 3", "output": "2\n 3\n 1\n \n\n * The 1-st, 2-nd, and 3-rd balls from the left have the colors 1, 2, and 1 \\- two different colors.\n * The 2-st, 3-rd, and 4-th balls from the left have the colors 2, 1, and 3 \\- three different colors.\n * The 3-rd ball from the left has the color 1 \\- just one color.\n\n* * *"}, {"input": "10 10\n 2 5 6 5 2 1 7 9 7 2\n 5 5\n 2 4\n 6 7\n 2 2\n 7 8\n 7 9\n 1 8\n 6 9\n 8 10\n 6 8", "output": "1\n 2\n 2\n 1\n 2\n 2\n 6\n 3\n 3\n 3"}]
|
Print Q lines. The i-th line should contain the response to the i-th query.
* * *
|
s746167382
|
Runtime Error
|
p02599
|
Input is given from Standard Input in the following format:
N Q
c_1 c_2 \cdots c_N
l_1 r_1
l_2 r_2
:
l_Q r_Q
|
class SegmentTree:
def __init__(self, l):
nb = bin(len(l))[2:]
b = sum([int(d) for d in nb])
if b == 1:
self.end_leaves = pow(2, len(nb) - 1)
else:
self.end_leaves = pow(2, len(nb))
self.tree = [set() for _ in range(self.end_leaves * 2)]
for i in range(len(l)):
self.tree[self.end_leaves + i].add(l[i])
def union(self, a):
if a >= self.end_leaves // 2:
self.tree[a] = self.tree[a * 2] | self.tree[a * 2 + 1]
return self.tree[a]
else:
self.tree[a] = self.union(a * 2) | self.union(a * 2 + 1)
return self.tree[a]
def query(self, l, r):
x = l + self.end_leaves
y = r + self.end_leaves
tl = set()
tr = set()
while y - x > 1:
if x % 2 == 1:
tl = tl | self.tree[x]
x += 1
if y % 2 == 0:
tr = self.tree[y] | tr
y -= 1
x >>= 1
y >>= 1
if y - x == 0:
print(len(tl | tr | self.tree[x]))
else:
print(len(tl | tr | self.tree[x] | self.tree[y]))
N, Q, *f = map(int, open(0).read().split())
c = f[:N]
lr = [f[N + i * 2 : N + i * 2 + 2] for i in range(Q)]
st = SegmentTree(c)
st.union(1)
for l, r in lr:
st.query(l - 1, r - 1)
|
Statement
We have N colored balls arranged in a row from left to right; the color of the
i-th ball from the left is c_i.
You are given Q queries. The i-th query is as follows: how many different
colors do the l_i-th through r_i-th balls from the left have?
|
[{"input": "4 3\n 1 2 1 3\n 1 3\n 2 4\n 3 3", "output": "2\n 3\n 1\n \n\n * The 1-st, 2-nd, and 3-rd balls from the left have the colors 1, 2, and 1 \\- two different colors.\n * The 2-st, 3-rd, and 4-th balls from the left have the colors 2, 1, and 3 \\- three different colors.\n * The 3-rd ball from the left has the color 1 \\- just one color.\n\n* * *"}, {"input": "10 10\n 2 5 6 5 2 1 7 9 7 2\n 5 5\n 2 4\n 6 7\n 2 2\n 7 8\n 7 9\n 1 8\n 6 9\n 8 10\n 6 8", "output": "1\n 2\n 2\n 1\n 2\n 2\n 6\n 3\n 3\n 3"}]
|
Print Q lines. The i-th line should contain the response to the i-th query.
* * *
|
s982529284
|
Runtime Error
|
p02599
|
Input is given from Standard Input in the following format:
N Q
c_1 c_2 \cdots c_N
l_1 r_1
l_2 r_2
:
l_Q r_Q
|
N, Q = map(int, input().split())
N = 5 * 10**5
value_to_index = [[] for i in range(N)]
C = list(map(int, input().split()))
for i, v in reversed(list(enumerate(C))):
value_to_index[v - 1].append(i)
LR = [list(map(int, input().split())) + [i] for i in range(Q)]
LR.sort()
# セグ作成
segtree = [[0] * N.bit_length() for i in range(N.bit_length())]
for num, arr in enumerate(value_to_index):
if arr:
v = arr[-1]
for i in range(len(segtree)):
p2 = 2**i
segtree[i][v // p2] += 1
# セグ取得
def seg_range(l, r):
r += 1
ans = []
tmp = 1
# 大きくしていくゾーン
while True:
while l % (tmp * 2) == 0 and tmp <= r:
tmp *= 2
if l + tmp <= r:
ans.append((tmp.bit_length() - 1, l // tmp))
l += tmp
else:
break
# 小さくしていくゾーン
tmp //= 2
while tmp > 0:
if l + tmp <= r:
ans.append((tmp.bit_length() - 1, l // tmp))
l += tmp
tmp //= 2
return ans
tmp = 0
ans = [0] * N
for l, r, idx in LR:
while tmp < l - 1:
v = C[tmp] - 1
tmp += 1
old = value_to_index[v].pop()
if value_to_index[v]:
new = value_to_index[v][-1]
for i in range(len(segtree)):
p2 = 2**i
segtree[i][new // p2] += 1
for i in range(len(segtree)):
p2 = 2**i
segtree[i][old // p2] -= 1
ans[idx] = sum([segtree[i][j] for i, j in seg_range(l - 1, r - 1)])
print(*ans[:Q], sep="\n")
|
Statement
We have N colored balls arranged in a row from left to right; the color of the
i-th ball from the left is c_i.
You are given Q queries. The i-th query is as follows: how many different
colors do the l_i-th through r_i-th balls from the left have?
|
[{"input": "4 3\n 1 2 1 3\n 1 3\n 2 4\n 3 3", "output": "2\n 3\n 1\n \n\n * The 1-st, 2-nd, and 3-rd balls from the left have the colors 1, 2, and 1 \\- two different colors.\n * The 2-st, 3-rd, and 4-th balls from the left have the colors 2, 1, and 3 \\- three different colors.\n * The 3-rd ball from the left has the color 1 \\- just one color.\n\n* * *"}, {"input": "10 10\n 2 5 6 5 2 1 7 9 7 2\n 5 5\n 2 4\n 6 7\n 2 2\n 7 8\n 7 9\n 1 8\n 6 9\n 8 10\n 6 8", "output": "1\n 2\n 2\n 1\n 2\n 2\n 6\n 3\n 3\n 3"}]
|
Print Q lines. The i-th line should contain the response to the i-th query.
* * *
|
s897287688
|
Runtime Error
|
p02599
|
Input is given from Standard Input in the following format:
N Q
c_1 c_2 \cdots c_N
l_1 r_1
l_2 r_2
:
l_Q r_Q
|
def main():
# 一点更新・一点取得の加法BIT
class BIT:
def __init__(self, n):
self.n = n
self.maxbit = 2 ** (len(bin(n)) - 3)
self.bit = [0] * (n + 1)
self.allsum = 0
# 初期化する
def make_bit(self, a):
n, bit = self.n, self.bit
for i, j in enumerate(a):
x = i + 1
self.allsum += j
while x < n + 1:
bit[x] += j
x += x & (-x)
# 位置iに値vを足す
def add(self, i, v):
x, n, bit = i + 1, self.n, self.bit
self.allsum += v
while x < n + 1:
bit[x] += v
x += x & (-x)
# 位置0からiまでの和(sum(bit[:i]))を計算する
def sum(self, i):
ret, x, bit = 0, i, self.bit
while x > 0:
ret += bit[x]
x -= x & (-x)
return ret
# 位置iからjまでの和(sum(bit[i:j]))を計算する
def sum_range(self, i, j):
return self.sum(j) - self.sum(i)
# 和がw以上となる最小のインデックスを求める
def lowerbound(self, w):
if w <= 0:
return 0
x, k, n, bit = 0, self.maxbit, self.n, self.bit
while k:
if x + k <= n and bit[x + k] < w:
w -= bit[x + k]
x += k
k //= 2
return x
n, q = map(int, input().split())
c = list(map(int, input().split()))
lastappend = [-1] * n
lr = [list(map(int, input().split())) for _ in [0] * q]
ilr = [(i, l - 1, r - 1) for i, (l, r) in enumerate(lr)]
ilr.sort(key=lambda x: (x[2], x[1], x[0]))
bit = BIT(n)
ans = [-1] * q
r_now = -1
for i, l, r in ilr:
if r > r_now:
for j in range(r_now + 1, r + 1):
last = lastappend[c[j]]
if last != -1:
bit.add(last, -1)
lastappend[c[j]] = j
bit.add(j, 1)
r_now = r
ans[i] = bit.sum_range(l, r + 1)
for i in ans:
print(i)
main()
|
Statement
We have N colored balls arranged in a row from left to right; the color of the
i-th ball from the left is c_i.
You are given Q queries. The i-th query is as follows: how many different
colors do the l_i-th through r_i-th balls from the left have?
|
[{"input": "4 3\n 1 2 1 3\n 1 3\n 2 4\n 3 3", "output": "2\n 3\n 1\n \n\n * The 1-st, 2-nd, and 3-rd balls from the left have the colors 1, 2, and 1 \\- two different colors.\n * The 2-st, 3-rd, and 4-th balls from the left have the colors 2, 1, and 3 \\- three different colors.\n * The 3-rd ball from the left has the color 1 \\- just one color.\n\n* * *"}, {"input": "10 10\n 2 5 6 5 2 1 7 9 7 2\n 5 5\n 2 4\n 6 7\n 2 2\n 7 8\n 7 9\n 1 8\n 6 9\n 8 10\n 6 8", "output": "1\n 2\n 2\n 1\n 2\n 2\n 6\n 3\n 3\n 3"}]
|
Print Q lines. The i-th line should contain the response to the i-th query.
* * *
|
s604057920
|
Wrong Answer
|
p02599
|
Input is given from Standard Input in the following format:
N Q
c_1 c_2 \cdots c_N
l_1 r_1
l_2 r_2
:
l_Q r_Q
|
def query(ind, start, end, q1, q2, s):
if q1 > end or q2 < start:
return 0
if q1 <= start and q2 >= end:
for i in segment[ind][0]:
s.add(i)
return 0
mid = (start + end) // 2
(
query(2 * ind + 1, start, mid, q1, q2, s)
+ query(2 * ind + 2, mid + 1, end, q1, q2, s)
)
return len(s)
def build(ind, start, end):
if start == end:
segment[ind] = [[l[start]], 1]
return
mid = (start + end) // 2
build(2 * ind + 1, start, mid)
build(2 * ind + 2, mid + 1, end)
a = set()
for i in segment[2 * ind + 1][0]:
a.add(i)
for i in segment[2 * ind + 2][0]:
a.add(i)
segment[ind] = [list(a), len(a)]
n, m = map(int, input().split())
l = list(map(int, input().split()))
segment = [0] * (4 * n)
build(0, 0, n - 1)
for _ in range(m):
a, b = map(int, input().split())
print(query(0, 0, n - 1, a - 1, b - 1, set()))
|
Statement
We have N colored balls arranged in a row from left to right; the color of the
i-th ball from the left is c_i.
You are given Q queries. The i-th query is as follows: how many different
colors do the l_i-th through r_i-th balls from the left have?
|
[{"input": "4 3\n 1 2 1 3\n 1 3\n 2 4\n 3 3", "output": "2\n 3\n 1\n \n\n * The 1-st, 2-nd, and 3-rd balls from the left have the colors 1, 2, and 1 \\- two different colors.\n * The 2-st, 3-rd, and 4-th balls from the left have the colors 2, 1, and 3 \\- three different colors.\n * The 3-rd ball from the left has the color 1 \\- just one color.\n\n* * *"}, {"input": "10 10\n 2 5 6 5 2 1 7 9 7 2\n 5 5\n 2 4\n 6 7\n 2 2\n 7 8\n 7 9\n 1 8\n 6 9\n 8 10\n 6 8", "output": "1\n 2\n 2\n 1\n 2\n 2\n 6\n 3\n 3\n 3"}]
|
Print Q lines. The i-th line should contain the response to the i-th query.
* * *
|
s176179593
|
Runtime Error
|
p02599
|
Input is given from Standard Input in the following format:
N Q
c_1 c_2 \cdots c_N
l_1 r_1
l_2 r_2
:
l_Q r_Q
|
from functools import cmp_to_key
import sys
input = sys.stdin.readline
N, P = map(int, input().split())
(*C,) = map(int, input().split())
Q = [tuple(map(int, input().split())) for _ in range(P)]
Q = [(i, l, r) for i, (l, r) in enumerate(Q)]
block = int(N**0.5)
def compare(a, b):
_, la, ra = a
_, lb, rb = b
if (la - 1) // block != (lb - 1) // block:
return -1 if (la - 1) // block < (lb - 1) // block else 1
return -1 if ra < rb else 1
Q.sort(key=cmp_to_key(compare))
ans = [0] * P
cl = cr = 0
S = dict()
S[C[0]] = set([0])
cnt = 1
for i, l, r in Q:
l -= 1
r -= 1
while cl < l:
x = C[cl]
if x in S:
if len(S[x]) == 1:
del S[x]
cnt -= 1
else:
S[x].remove(cl)
cl += 1
while l < cl:
x = C[cl - 1]
if x in S:
S[x].add(cl - 1)
else:
S[x] = set([cl - 1])
cnt += 1
cl -= 1
while cr < r:
x = C[cr + 1]
if x in S:
S[x].add(cr + 1)
else:
S[x] = set([cr + 1])
cnt += 1
cr += 1
while r < cr:
x = C[cr]
if x in S:
if len(S[x]) == 1:
del S[x]
cnt -= 1
else:
S[x].remove(cr)
cr -= 1
ans[i] = cnt
print("\n".join(map(str, ans)))
|
Statement
We have N colored balls arranged in a row from left to right; the color of the
i-th ball from the left is c_i.
You are given Q queries. The i-th query is as follows: how many different
colors do the l_i-th through r_i-th balls from the left have?
|
[{"input": "4 3\n 1 2 1 3\n 1 3\n 2 4\n 3 3", "output": "2\n 3\n 1\n \n\n * The 1-st, 2-nd, and 3-rd balls from the left have the colors 1, 2, and 1 \\- two different colors.\n * The 2-st, 3-rd, and 4-th balls from the left have the colors 2, 1, and 3 \\- three different colors.\n * The 3-rd ball from the left has the color 1 \\- just one color.\n\n* * *"}, {"input": "10 10\n 2 5 6 5 2 1 7 9 7 2\n 5 5\n 2 4\n 6 7\n 2 2\n 7 8\n 7 9\n 1 8\n 6 9\n 8 10\n 6 8", "output": "1\n 2\n 2\n 1\n 2\n 2\n 6\n 3\n 3\n 3"}]
|
Print Q lines. The i-th line should contain the response to the i-th query.
* * *
|
s280984639
|
Runtime Error
|
p02599
|
Input is given from Standard Input in the following format:
N Q
c_1 c_2 \cdots c_N
l_1 r_1
l_2 r_2
:
l_Q r_Q
|
n, q = list(map(int, input().split()))
cl = list(map(int, input().split()))
for i in range(n):
flg = [1] * n
l, r = list(map(int, input().split()))
pt = 0
for j in range(l - 1, r):
pt += flg[cl[j]]
flg[cl[j]] = 0
print(pt)
|
Statement
We have N colored balls arranged in a row from left to right; the color of the
i-th ball from the left is c_i.
You are given Q queries. The i-th query is as follows: how many different
colors do the l_i-th through r_i-th balls from the left have?
|
[{"input": "4 3\n 1 2 1 3\n 1 3\n 2 4\n 3 3", "output": "2\n 3\n 1\n \n\n * The 1-st, 2-nd, and 3-rd balls from the left have the colors 1, 2, and 1 \\- two different colors.\n * The 2-st, 3-rd, and 4-th balls from the left have the colors 2, 1, and 3 \\- three different colors.\n * The 3-rd ball from the left has the color 1 \\- just one color.\n\n* * *"}, {"input": "10 10\n 2 5 6 5 2 1 7 9 7 2\n 5 5\n 2 4\n 6 7\n 2 2\n 7 8\n 7 9\n 1 8\n 6 9\n 8 10\n 6 8", "output": "1\n 2\n 2\n 1\n 2\n 2\n 6\n 3\n 3\n 3"}]
|
Print an integer representing the minimum number of minutes needed to make N
pieces of takoyaki.
* * *
|
s232092918
|
Runtime Error
|
p02576
|
Input is given from Standard Input in the following format:
N X T
|
from collections import deque
H, W = map(int, input().split())
Ch, Cw = map(int, input().split())
Dh, Dw = map(int, input().split())
Ch -= 1
Cw -= 1
Dh -= 1
Dw -= 1
S = []
for i in range(H):
s = list(input())
S.append([-1 if i == "." else i for i in s])
dq = deque()
dq.append((Ch, Cw))
S[Ch][Cw] = 0
while dq:
a = dq.pop()
if a[0] - 1 >= 0 and (
S[a[0] - 1][a[1]] == -1
or (S[a[0] - 1][a[1]] != "#" and S[a[0] - 1][a[1]] > S[a[0]][a[1]])
):
S[a[0] - 1][a[1]] = S[a[0]][a[1]]
dq.appendleft((a[0] - 1, a[1]))
if a[0] + 1 < H and (
S[a[0] + 1][a[1]] == -1
or (S[a[0] + 1][a[1]] != "#" and S[a[0] + 1][a[1]] > S[a[0]][a[1]])
):
S[a[0] + 1][a[1]] = S[a[0]][a[1]]
dq.appendleft((a[0] + 1, a[1]))
if a[1] - 1 >= 0 and (
S[a[0]][a[1] - 1] == -1
or (S[a[0]][a[1] - 1] != "#" and S[a[0]][a[1] - 1] > S[a[0]][a[1]])
):
S[a[0]][a[1] - 1] = S[a[0]][a[1]]
dq.appendleft((a[0], a[1] - 1))
if a[1] + 1 < W and (
S[a[0]][a[1] + 1] == -1
or (S[a[0]][a[1] + 1] != "#" and S[a[0]][a[1] + 1] > S[a[0]][a[1]])
):
S[a[0]][a[1] + 1] = S[a[0]][a[1]]
dq.appendleft((a[0], a[1] + 1))
for i in range(5):
for j in range(5):
if (
a[0] - 2 + i >= 0
and a[0] - 2 + i < H
and a[1] - 2 + j >= 0
and a[1] - 2 + j < W
and (
S[a[0] - 2 + i][a[1] - 2 + j] == -1
or (
S[a[0] - 2 + i][a[1] - 2 + j] != "#"
and S[a[0] - 2 + i][a[1] - 2 + j] >= S[a[0]][a[1]] + 1
)
)
):
S[a[0] - 2 + i][a[1] - 2 + j] = S[a[0]][a[1]] + 1
dq.append((a[0] - 2 + i, a[1] - 2 + j))
print(S[Dh][Dw])
|
Statement
Takahashi loves takoyaki - a ball-shaped snack.
With a takoyaki machine, he can make at most X pieces of takoyaki at a time,
taking T minutes regardless of the number of pieces to make.
How long does it take to make N takoyaki?
|
[{"input": "20 12 6", "output": "12\n \n\nHe can make 12 pieces of takoyaki in the first 6 minutes and 8 more in the\nnext 6 minutes, so he can make 20 in a total of 12 minutes.\n\nNote that being able to make 12 in 6 minutes does not mean he can make 2 in 1\nminute.\n\n* * *"}, {"input": "1000 1 1000", "output": "1000000\n \n\nIt seems to take a long time to make this kind of takoyaki."}]
|
Print an integer representing the minimum number of minutes needed to make N
pieces of takoyaki.
* * *
|
s244443404
|
Wrong Answer
|
p02576
|
Input is given from Standard Input in the following format:
N X T
|
s = input()
max = 0
count = 0
for i in range(3):
if s[i]=="R":
count+=1
else:
if max < count:
max = count
count = 0
if max < count:
max = count
print(max)
|
Statement
Takahashi loves takoyaki - a ball-shaped snack.
With a takoyaki machine, he can make at most X pieces of takoyaki at a time,
taking T minutes regardless of the number of pieces to make.
How long does it take to make N takoyaki?
|
[{"input": "20 12 6", "output": "12\n \n\nHe can make 12 pieces of takoyaki in the first 6 minutes and 8 more in the\nnext 6 minutes, so he can make 20 in a total of 12 minutes.\n\nNote that being able to make 12 in 6 minutes does not mean he can make 2 in 1\nminute.\n\n* * *"}, {"input": "1000 1 1000", "output": "1000000\n \n\nIt seems to take a long time to make this kind of takoyaki."}]
|
Print an integer representing the minimum number of minutes needed to make N
pieces of takoyaki.
* * *
|
s628928399
|
Runtime Error
|
p02576
|
Input is given from Standard Input in the following format:
N X T
|
H, W, M = map(int, input().split())
row_boms = [0 for i in range(H)]
col_boms = [0 for i in range(W)]
boms = [[0 for j in range(W)] for i in range(H)]
for i in range(M):
h, w = map(int, input().split())
boms[h - 1][w - 1] = 1
row_boms[h - 1] += 1
col_boms[w - 1] += 1
row_max = max(row_boms)
col_max = max(col_boms)
rowmax_h = []
colmax_w = []
for i in range(H):
if row_boms[i] == row_max:
rowmax_h += [i]
for i in range(W):
if col_boms[i] == col_max:
colmax_w += [i]
rows = len(rowmax_h)
cols = len(colmax_w)
tf = 0
for i in rowmax_h:
for j in colmax_w:
if boms[i][j] == 0:
tf = 1
break
if tf == 1:
print(row_max + col_max)
else:
print(row_max + col_max - 1)
|
Statement
Takahashi loves takoyaki - a ball-shaped snack.
With a takoyaki machine, he can make at most X pieces of takoyaki at a time,
taking T minutes regardless of the number of pieces to make.
How long does it take to make N takoyaki?
|
[{"input": "20 12 6", "output": "12\n \n\nHe can make 12 pieces of takoyaki in the first 6 minutes and 8 more in the\nnext 6 minutes, so he can make 20 in a total of 12 minutes.\n\nNote that being able to make 12 in 6 minutes does not mean he can make 2 in 1\nminute.\n\n* * *"}, {"input": "1000 1 1000", "output": "1000000\n \n\nIt seems to take a long time to make this kind of takoyaki."}]
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.