output_description
stringlengths 15
956
| submission_id
stringlengths 10
10
| status
stringclasses 3
values | problem_id
stringlengths 6
6
| input_description
stringlengths 9
2.55k
| attempt
stringlengths 1
13.7k
| problem_description
stringlengths 7
5.24k
| samples
stringlengths 2
2.72k
|
|---|---|---|---|---|---|---|---|
If Kizahashi can complete all the jobs in time, print `Yes`; if he cannot,
print `No`.
* * *
|
s936510044
|
Wrong Answer
|
p02996
|
Input is given from Standard Input in the following format:
N
A_1 B_1
.
.
.
A_N B_N
|
nb = int(input())
somme = 0
mmax = 0
for loop in range(nb):
n, m = map(int, input().split())
somme += n
if m > mmax:
mmax = m
if somme <= mmax:
print("yes")
else:
print("no")
|
Statement
Kizahashi, who was appointed as the administrator of ABC at National Problem
Workshop in the Kingdom of AtCoder, got too excited and took on too many jobs.
Let the current time be time 0. Kizahashi has N jobs numbered 1 to N.
It takes A_i units of time for Kizahashi to complete Job i. The deadline for
Job i is time B_i, and he must complete the job before or at this time.
Kizahashi cannot work on two or more jobs simultaneously, but when he
completes a job, he can start working on another immediately.
Can Kizahashi complete all the jobs in time? If he can, print `Yes`; if he
cannot, print `No`.
|
[{"input": "5\n 2 4\n 1 9\n 1 8\n 4 9\n 3 12", "output": "Yes\n \n\nHe can complete all the jobs in time by, for example, doing them in the\nfollowing order:\n\n * Do Job 2 from time 0 to 1.\n * Do Job 1 from time 1 to 3.\n * Do Job 4 from time 3 to 7.\n * Do Job 3 from time 7 to 8.\n * Do Job 5 from time 8 to 11.\n\nNote that it is fine to complete Job 3 exactly at the deadline, time 8.\n\n* * *"}, {"input": "3\n 334 1000\n 334 1000\n 334 1000", "output": "No\n \n\nHe cannot complete all the jobs in time, no matter what order he does them in.\n\n* * *"}, {"input": "30\n 384 8895\n 1725 9791\n 170 1024\n 4 11105\n 2 6\n 578 1815\n 702 3352\n 143 5141\n 1420 6980\n 24 1602\n 849 999\n 76 7586\n 85 5570\n 444 4991\n 719 11090\n 470 10708\n 1137 4547\n 455 9003\n 110 9901\n 15 8578\n 368 3692\n 104 1286\n 3 4\n 366 12143\n 7 6649\n 610 2374\n 152 7324\n 4 7042\n 292 11386\n 334 5720", "output": "Yes"}]
|
If Kizahashi can complete all the jobs in time, print `Yes`; if he cannot,
print `No`.
* * *
|
s855695971
|
Wrong Answer
|
p02996
|
Input is given from Standard Input in the following format:
N
A_1 B_1
.
.
.
A_N B_N
|
N = input()
for i in range(int(N)):
input()
print("Yes")
|
Statement
Kizahashi, who was appointed as the administrator of ABC at National Problem
Workshop in the Kingdom of AtCoder, got too excited and took on too many jobs.
Let the current time be time 0. Kizahashi has N jobs numbered 1 to N.
It takes A_i units of time for Kizahashi to complete Job i. The deadline for
Job i is time B_i, and he must complete the job before or at this time.
Kizahashi cannot work on two or more jobs simultaneously, but when he
completes a job, he can start working on another immediately.
Can Kizahashi complete all the jobs in time? If he can, print `Yes`; if he
cannot, print `No`.
|
[{"input": "5\n 2 4\n 1 9\n 1 8\n 4 9\n 3 12", "output": "Yes\n \n\nHe can complete all the jobs in time by, for example, doing them in the\nfollowing order:\n\n * Do Job 2 from time 0 to 1.\n * Do Job 1 from time 1 to 3.\n * Do Job 4 from time 3 to 7.\n * Do Job 3 from time 7 to 8.\n * Do Job 5 from time 8 to 11.\n\nNote that it is fine to complete Job 3 exactly at the deadline, time 8.\n\n* * *"}, {"input": "3\n 334 1000\n 334 1000\n 334 1000", "output": "No\n \n\nHe cannot complete all the jobs in time, no matter what order he does them in.\n\n* * *"}, {"input": "30\n 384 8895\n 1725 9791\n 170 1024\n 4 11105\n 2 6\n 578 1815\n 702 3352\n 143 5141\n 1420 6980\n 24 1602\n 849 999\n 76 7586\n 85 5570\n 444 4991\n 719 11090\n 470 10708\n 1137 4547\n 455 9003\n 110 9901\n 15 8578\n 368 3692\n 104 1286\n 3 4\n 366 12143\n 7 6649\n 610 2374\n 152 7324\n 4 7042\n 292 11386\n 334 5720", "output": "Yes"}]
|
If Kizahashi can complete all the jobs in time, print `Yes`; if he cannot,
print `No`.
* * *
|
s561044462
|
Wrong Answer
|
p02996
|
Input is given from Standard Input in the following format:
N
A_1 B_1
.
.
.
A_N B_N
|
print("Yes")
|
Statement
Kizahashi, who was appointed as the administrator of ABC at National Problem
Workshop in the Kingdom of AtCoder, got too excited and took on too many jobs.
Let the current time be time 0. Kizahashi has N jobs numbered 1 to N.
It takes A_i units of time for Kizahashi to complete Job i. The deadline for
Job i is time B_i, and he must complete the job before or at this time.
Kizahashi cannot work on two or more jobs simultaneously, but when he
completes a job, he can start working on another immediately.
Can Kizahashi complete all the jobs in time? If he can, print `Yes`; if he
cannot, print `No`.
|
[{"input": "5\n 2 4\n 1 9\n 1 8\n 4 9\n 3 12", "output": "Yes\n \n\nHe can complete all the jobs in time by, for example, doing them in the\nfollowing order:\n\n * Do Job 2 from time 0 to 1.\n * Do Job 1 from time 1 to 3.\n * Do Job 4 from time 3 to 7.\n * Do Job 3 from time 7 to 8.\n * Do Job 5 from time 8 to 11.\n\nNote that it is fine to complete Job 3 exactly at the deadline, time 8.\n\n* * *"}, {"input": "3\n 334 1000\n 334 1000\n 334 1000", "output": "No\n \n\nHe cannot complete all the jobs in time, no matter what order he does them in.\n\n* * *"}, {"input": "30\n 384 8895\n 1725 9791\n 170 1024\n 4 11105\n 2 6\n 578 1815\n 702 3352\n 143 5141\n 1420 6980\n 24 1602\n 849 999\n 76 7586\n 85 5570\n 444 4991\n 719 11090\n 470 10708\n 1137 4547\n 455 9003\n 110 9901\n 15 8578\n 368 3692\n 104 1286\n 3 4\n 366 12143\n 7 6649\n 610 2374\n 152 7324\n 4 7042\n 292 11386\n 334 5720", "output": "Yes"}]
|
If Kizahashi can complete all the jobs in time, print `Yes`; if he cannot,
print `No`.
* * *
|
s405285857
|
Accepted
|
p02996
|
Input is given from Standard Input in the following format:
N
A_1 B_1
.
.
.
A_N B_N
|
(N,) = list(map(int, input().split()))
d = {}
for i in range(N):
ai, bi = list(map(int, input().split()))
if bi in d:
d[bi].append(ai)
else:
d[bi] = [ai]
B = list(d.keys())
B.sort()
ret = "Yes"
s = 0
for b in B:
s += sum(d[b])
if s > b:
ret = "No"
print(ret)
|
Statement
Kizahashi, who was appointed as the administrator of ABC at National Problem
Workshop in the Kingdom of AtCoder, got too excited and took on too many jobs.
Let the current time be time 0. Kizahashi has N jobs numbered 1 to N.
It takes A_i units of time for Kizahashi to complete Job i. The deadline for
Job i is time B_i, and he must complete the job before or at this time.
Kizahashi cannot work on two or more jobs simultaneously, but when he
completes a job, he can start working on another immediately.
Can Kizahashi complete all the jobs in time? If he can, print `Yes`; if he
cannot, print `No`.
|
[{"input": "5\n 2 4\n 1 9\n 1 8\n 4 9\n 3 12", "output": "Yes\n \n\nHe can complete all the jobs in time by, for example, doing them in the\nfollowing order:\n\n * Do Job 2 from time 0 to 1.\n * Do Job 1 from time 1 to 3.\n * Do Job 4 from time 3 to 7.\n * Do Job 3 from time 7 to 8.\n * Do Job 5 from time 8 to 11.\n\nNote that it is fine to complete Job 3 exactly at the deadline, time 8.\n\n* * *"}, {"input": "3\n 334 1000\n 334 1000\n 334 1000", "output": "No\n \n\nHe cannot complete all the jobs in time, no matter what order he does them in.\n\n* * *"}, {"input": "30\n 384 8895\n 1725 9791\n 170 1024\n 4 11105\n 2 6\n 578 1815\n 702 3352\n 143 5141\n 1420 6980\n 24 1602\n 849 999\n 76 7586\n 85 5570\n 444 4991\n 719 11090\n 470 10708\n 1137 4547\n 455 9003\n 110 9901\n 15 8578\n 368 3692\n 104 1286\n 3 4\n 366 12143\n 7 6649\n 610 2374\n 152 7324\n 4 7042\n 292 11386\n 334 5720", "output": "Yes"}]
|
If Kizahashi can complete all the jobs in time, print `Yes`; if he cannot,
print `No`.
* * *
|
s469798944
|
Accepted
|
p02996
|
Input is given from Standard Input in the following format:
N
A_1 B_1
.
.
.
A_N B_N
|
def s0():
return input()
def s1():
return input().split()
def s2(n):
return [input() for x in range(n)]
def s3(n):
return [input().split() for _ in range(n)]
def s4(n):
return [[x for x in s] for s in s2(n)]
def n0():
return int(input())
def n1():
return [int(x) for x in input().split()]
def n2(n):
return [int(input()) for _ in range(n)]
def n3(n):
return [[int(x) for x in input().split()] for _ in range(n)]
def t3(n):
return [tuple(int(x) for x in input().split()) for _ in range(n)]
def p0(b, yes="Yes", no="No"):
print(yes if b else no)
# from sys import setrecursionlimit
# setrecursionlimit(1000000)
# from collections import Counter,deque,defaultdict
# import itertools
# import math
# import networkx as nx
# from bisect import bisect_left,bisect_right
# from heapq import heapify,heappush,heappop
n = n0()
AB = n3(n)
AB.sort(key=lambda x: x[1])
time = 0
f = True
for a, b in AB:
time += a
if time <= b:
pass
else:
f = False
break
p0(f)
|
Statement
Kizahashi, who was appointed as the administrator of ABC at National Problem
Workshop in the Kingdom of AtCoder, got too excited and took on too many jobs.
Let the current time be time 0. Kizahashi has N jobs numbered 1 to N.
It takes A_i units of time for Kizahashi to complete Job i. The deadline for
Job i is time B_i, and he must complete the job before or at this time.
Kizahashi cannot work on two or more jobs simultaneously, but when he
completes a job, he can start working on another immediately.
Can Kizahashi complete all the jobs in time? If he can, print `Yes`; if he
cannot, print `No`.
|
[{"input": "5\n 2 4\n 1 9\n 1 8\n 4 9\n 3 12", "output": "Yes\n \n\nHe can complete all the jobs in time by, for example, doing them in the\nfollowing order:\n\n * Do Job 2 from time 0 to 1.\n * Do Job 1 from time 1 to 3.\n * Do Job 4 from time 3 to 7.\n * Do Job 3 from time 7 to 8.\n * Do Job 5 from time 8 to 11.\n\nNote that it is fine to complete Job 3 exactly at the deadline, time 8.\n\n* * *"}, {"input": "3\n 334 1000\n 334 1000\n 334 1000", "output": "No\n \n\nHe cannot complete all the jobs in time, no matter what order he does them in.\n\n* * *"}, {"input": "30\n 384 8895\n 1725 9791\n 170 1024\n 4 11105\n 2 6\n 578 1815\n 702 3352\n 143 5141\n 1420 6980\n 24 1602\n 849 999\n 76 7586\n 85 5570\n 444 4991\n 719 11090\n 470 10708\n 1137 4547\n 455 9003\n 110 9901\n 15 8578\n 368 3692\n 104 1286\n 3 4\n 366 12143\n 7 6649\n 610 2374\n 152 7324\n 4 7042\n 292 11386\n 334 5720", "output": "Yes"}]
|
If Kizahashi can complete all the jobs in time, print `Yes`; if he cannot,
print `No`.
* * *
|
s067162054
|
Wrong Answer
|
p02996
|
Input is given from Standard Input in the following format:
N
A_1 B_1
.
.
.
A_N B_N
|
import sys
input = sys.stdin.readline
def my_sort(L, C, p, q):
if p < q:
mid = (p + q) // 2
my_sort(L, C, p, mid)
my_sort(L, C, mid + 1, q)
i = p
j = mid + 1
k = p
tmp = 0
while k <= q:
if i > mid:
tmp = L[j]
j += 1
elif j > q:
tmp = L[i]
i += 1
else:
if L[i][1] <= L[j][1]:
tmp = L[i]
i += 1
else:
tmp = L[j]
j += 1
C[k] = tmp
k += 1
for i in range(p, q + 1):
L[i] = C[i]
n = int(input())
task = []
time_total = [0 for i in range(n)]
for i in range(n):
task.append([int(i) for i in input().split()])
task_sorted = [[0, 0] for i in range(n)]
my_sort(task, task_sorted, 0, n - 1)
time_total[0] = task_sorted[0][0]
for i in range(n - 1):
time_total[i + 1] = time_total[i] + task_sorted[i + 1][0]
while i < n:
if time_total[i] > task_sorted[i][1]:
print("No")
sys.exit()
i += 1
print("Yes")
|
Statement
Kizahashi, who was appointed as the administrator of ABC at National Problem
Workshop in the Kingdom of AtCoder, got too excited and took on too many jobs.
Let the current time be time 0. Kizahashi has N jobs numbered 1 to N.
It takes A_i units of time for Kizahashi to complete Job i. The deadline for
Job i is time B_i, and he must complete the job before or at this time.
Kizahashi cannot work on two or more jobs simultaneously, but when he
completes a job, he can start working on another immediately.
Can Kizahashi complete all the jobs in time? If he can, print `Yes`; if he
cannot, print `No`.
|
[{"input": "5\n 2 4\n 1 9\n 1 8\n 4 9\n 3 12", "output": "Yes\n \n\nHe can complete all the jobs in time by, for example, doing them in the\nfollowing order:\n\n * Do Job 2 from time 0 to 1.\n * Do Job 1 from time 1 to 3.\n * Do Job 4 from time 3 to 7.\n * Do Job 3 from time 7 to 8.\n * Do Job 5 from time 8 to 11.\n\nNote that it is fine to complete Job 3 exactly at the deadline, time 8.\n\n* * *"}, {"input": "3\n 334 1000\n 334 1000\n 334 1000", "output": "No\n \n\nHe cannot complete all the jobs in time, no matter what order he does them in.\n\n* * *"}, {"input": "30\n 384 8895\n 1725 9791\n 170 1024\n 4 11105\n 2 6\n 578 1815\n 702 3352\n 143 5141\n 1420 6980\n 24 1602\n 849 999\n 76 7586\n 85 5570\n 444 4991\n 719 11090\n 470 10708\n 1137 4547\n 455 9003\n 110 9901\n 15 8578\n 368 3692\n 104 1286\n 3 4\n 366 12143\n 7 6649\n 610 2374\n 152 7324\n 4 7042\n 292 11386\n 334 5720", "output": "Yes"}]
|
If Kizahashi can complete all the jobs in time, print `Yes`; if he cannot,
print `No`.
* * *
|
s645729668
|
Accepted
|
p02996
|
Input is given from Standard Input in the following format:
N
A_1 B_1
.
.
.
A_N B_N
|
n, *t = map(int, open(0).read().split())
c = f = 0
for b, a in sorted(zip(t[1::2], t[::2])):
c += a
f |= c > b
print("YNeos"[f::2])
|
Statement
Kizahashi, who was appointed as the administrator of ABC at National Problem
Workshop in the Kingdom of AtCoder, got too excited and took on too many jobs.
Let the current time be time 0. Kizahashi has N jobs numbered 1 to N.
It takes A_i units of time for Kizahashi to complete Job i. The deadline for
Job i is time B_i, and he must complete the job before or at this time.
Kizahashi cannot work on two or more jobs simultaneously, but when he
completes a job, he can start working on another immediately.
Can Kizahashi complete all the jobs in time? If he can, print `Yes`; if he
cannot, print `No`.
|
[{"input": "5\n 2 4\n 1 9\n 1 8\n 4 9\n 3 12", "output": "Yes\n \n\nHe can complete all the jobs in time by, for example, doing them in the\nfollowing order:\n\n * Do Job 2 from time 0 to 1.\n * Do Job 1 from time 1 to 3.\n * Do Job 4 from time 3 to 7.\n * Do Job 3 from time 7 to 8.\n * Do Job 5 from time 8 to 11.\n\nNote that it is fine to complete Job 3 exactly at the deadline, time 8.\n\n* * *"}, {"input": "3\n 334 1000\n 334 1000\n 334 1000", "output": "No\n \n\nHe cannot complete all the jobs in time, no matter what order he does them in.\n\n* * *"}, {"input": "30\n 384 8895\n 1725 9791\n 170 1024\n 4 11105\n 2 6\n 578 1815\n 702 3352\n 143 5141\n 1420 6980\n 24 1602\n 849 999\n 76 7586\n 85 5570\n 444 4991\n 719 11090\n 470 10708\n 1137 4547\n 455 9003\n 110 9901\n 15 8578\n 368 3692\n 104 1286\n 3 4\n 366 12143\n 7 6649\n 610 2374\n 152 7324\n 4 7042\n 292 11386\n 334 5720", "output": "Yes"}]
|
If Kizahashi can complete all the jobs in time, print `Yes`; if he cannot,
print `No`.
* * *
|
s888079394
|
Accepted
|
p02996
|
Input is given from Standard Input in the following format:
N
A_1 B_1
.
.
.
A_N B_N
|
import io
import sys
def IN_S():
return input()
def IN_I():
return int(input())
def IN_L_I():
return list(map(int, input().split()))
def IN_L_S():
return list(map(str, input().split()))
def STR_SPLIT(s, n):
for l in range(0, len(s), n):
yield s[0 + l : n + l]
def T_IN():
global test_str
sys.stdin = io.StringIO(test_str[1:-1])
test_str = """
30
384 8895
1725 9791
170 1024
4 11105
2 6
578 1815
702 3352
143 5141
1420 6980
24 1602
849 999
76 7586
85 5570
444 4991
719 11090
470 10708
1137 4547
455 9003
110 9901
15 8578
368 3692
104 1286
3 4
366 12143
7 6649
610 2374
152 7324
4 7042
292 11386
334 5720
"""
def MAIN():
# T_IN()
if A():
print("Yes")
else:
print("No")
def A():
n = IN_I()
# [[a, b]]
md = list([IN_L_I() for i in range(0, n)])
md.sort(key=lambda x: (x[1]))
total = 0
for item in md:
total += item[0]
if total > item[1]:
return False
return True
def B():
return None
def C():
return None
MAIN()
|
Statement
Kizahashi, who was appointed as the administrator of ABC at National Problem
Workshop in the Kingdom of AtCoder, got too excited and took on too many jobs.
Let the current time be time 0. Kizahashi has N jobs numbered 1 to N.
It takes A_i units of time for Kizahashi to complete Job i. The deadline for
Job i is time B_i, and he must complete the job before or at this time.
Kizahashi cannot work on two or more jobs simultaneously, but when he
completes a job, he can start working on another immediately.
Can Kizahashi complete all the jobs in time? If he can, print `Yes`; if he
cannot, print `No`.
|
[{"input": "5\n 2 4\n 1 9\n 1 8\n 4 9\n 3 12", "output": "Yes\n \n\nHe can complete all the jobs in time by, for example, doing them in the\nfollowing order:\n\n * Do Job 2 from time 0 to 1.\n * Do Job 1 from time 1 to 3.\n * Do Job 4 from time 3 to 7.\n * Do Job 3 from time 7 to 8.\n * Do Job 5 from time 8 to 11.\n\nNote that it is fine to complete Job 3 exactly at the deadline, time 8.\n\n* * *"}, {"input": "3\n 334 1000\n 334 1000\n 334 1000", "output": "No\n \n\nHe cannot complete all the jobs in time, no matter what order he does them in.\n\n* * *"}, {"input": "30\n 384 8895\n 1725 9791\n 170 1024\n 4 11105\n 2 6\n 578 1815\n 702 3352\n 143 5141\n 1420 6980\n 24 1602\n 849 999\n 76 7586\n 85 5570\n 444 4991\n 719 11090\n 470 10708\n 1137 4547\n 455 9003\n 110 9901\n 15 8578\n 368 3692\n 104 1286\n 3 4\n 366 12143\n 7 6649\n 610 2374\n 152 7324\n 4 7042\n 292 11386\n 334 5720", "output": "Yes"}]
|
Print the minimum necessary amount of money in order to build roads so that it
will be possible to travel between every pair of towns by traversing roads.
* * *
|
s119362788
|
Runtime Error
|
p03684
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
s UnionFind(object):
def __init__(self, n):
self.n = n
self.par = list(range(n))
self.rank = [1] * n
def is_same(self, a, b):
return self.root(a) == self.root(b)
def root(self, x):
if self.par[x] == x:
return x
self.par[x] = self.root(self.par[x])
return self.par[x]
def unite(self, x, y):
x = self.root(x)
y = self.root(y)
if x == y:
return
if self.rank[x] > self.rank[y]:
self.par[y] = x
elif self.rank[x] < self.rank[y]:
self.par[x] = y
else:
self.par[y] = x
self.rank[x] += 1
N = int(input())
X = []
Y = []
for i in range(N):
x, y = map(int, input().split())
X.append((x, i))
Y.append((y, i))
X = sorted(X)
Y = sorted(Y)
graph = []
for i in range(N - 1):
graph.append((X[i + 1][0] - X[i][0], X[i][1], X[i + 1][1]))
graph.append((Y[i + 1][0] - Y[i][0], Y[i][1], Y[i + 1][1]))
graph.sort()
uf = UnionFind(N)
total_cost = 0
for cost, a, b in graph:
if not uf.is_same(a, b):
uf.unite(a, b)
total_cost += cost
print(total_cost)
|
Statement
There are N towns on a plane. The i-th town is located at the coordinates
(x_i,y_i). There may be more than one town at the same coordinates.
You can build a road between two towns at coordinates (a,b) and (c,d) for a
cost of min(|a-c|,|b-d|) yen (the currency of Japan). It is not possible to
build other types of roads.
Your objective is to build roads so that it will be possible to travel between
every pair of towns by traversing roads. At least how much money is necessary
to achieve this?
|
[{"input": "3\n 1 5\n 3 9\n 7 8", "output": "3\n \n\nBuild a road between Towns 1 and 2, and another between Towns 2 and 3. The\ntotal cost is 2+1=3 yen.\n\n* * *"}, {"input": "6\n 8 3\n 4 9\n 12 19\n 18 1\n 13 5\n 7 6", "output": "8"}]
|
Print the minimum necessary amount of money in order to build roads so that it
will be possible to travel between every pair of towns by traversing roads.
* * *
|
s309252473
|
Runtime Error
|
p03684
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
vs = $stdin.each_line.drop(1).map { |row| row.split(' ').map { |c| c.to_i } }.map.with_index do |row, i|
[i, row[0], row[1]]
end
v_new = []
v_new.push(vs.pop)
e_cost_sum = 0
while !vs.empty? do
v = vs.pop
edge_min = v_new.map { |u| [(u[1] - v[1]).abs, (u[2] - v[2]).abs].min }.min
v_new.push(v)
e_cost_sum += edge_min
end
puts e_cost_sum
|
Statement
There are N towns on a plane. The i-th town is located at the coordinates
(x_i,y_i). There may be more than one town at the same coordinates.
You can build a road between two towns at coordinates (a,b) and (c,d) for a
cost of min(|a-c|,|b-d|) yen (the currency of Japan). It is not possible to
build other types of roads.
Your objective is to build roads so that it will be possible to travel between
every pair of towns by traversing roads. At least how much money is necessary
to achieve this?
|
[{"input": "3\n 1 5\n 3 9\n 7 8", "output": "3\n \n\nBuild a road between Towns 1 and 2, and another between Towns 2 and 3. The\ntotal cost is 2+1=3 yen.\n\n* * *"}, {"input": "6\n 8 3\n 4 9\n 12 19\n 18 1\n 13 5\n 7 6", "output": "8"}]
|
Print the minimum necessary amount of money in order to build roads so that it
will be possible to travel between every pair of towns by traversing roads.
* * *
|
s524785096
|
Runtime Error
|
p03684
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
import sys
sys.setrecursionlimit(100000)
d = 10**9 + 7
def factorial(n):
if n > 1:
return (n % d) * factorial(n - 1)
return 1
n, m = map(int, input().split())
ans = (factorial(n) % d) * (factorial(m) % d)
ans %= d
if n == m:
ans *= 2
print(ans)
|
Statement
There are N towns on a plane. The i-th town is located at the coordinates
(x_i,y_i). There may be more than one town at the same coordinates.
You can build a road between two towns at coordinates (a,b) and (c,d) for a
cost of min(|a-c|,|b-d|) yen (the currency of Japan). It is not possible to
build other types of roads.
Your objective is to build roads so that it will be possible to travel between
every pair of towns by traversing roads. At least how much money is necessary
to achieve this?
|
[{"input": "3\n 1 5\n 3 9\n 7 8", "output": "3\n \n\nBuild a road between Towns 1 and 2, and another between Towns 2 and 3. The\ntotal cost is 2+1=3 yen.\n\n* * *"}, {"input": "6\n 8 3\n 4 9\n 12 19\n 18 1\n 13 5\n 7 6", "output": "8"}]
|
Print the minimum necessary amount of money in order to build roads so that it
will be possible to travel between every pair of towns by traversing roads.
* * *
|
s157106082
|
Wrong Answer
|
p03684
|
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
|
# 定数
INF = 1000000
# 入力
N = int(input())
xy = [[int(j) for j in input().split()] for i in range(N)]
# x,y座標とその街を、小さい順に並べる
xCity = [[xy[i][0], i] for i in range(N)]
yCity = [[xy[i][1], i] for i in range(N)]
xCity.sort()
yCity.sort()
# 連結済みのx,yの列の最大
xIndex = 0
yIndex = 0
# 連結済みの町
linked = []
if xCity[0][1] == yCity[0][1]:
linked.append(xCity[0][1])
N -= 1
else:
linked.append(xCity[0][1])
linked.append(yCity[0][1])
N -= 2
# 所要金額
ans = 0
for roop in range(N):
# 連結済みじゃ無い街を指すまで続ける
while xCity[xIndex][1] in linked:
xIndex += 1
while yCity[yIndex][1] in linked:
yIndex += 1
# 同じ街を見ている場合
if xCity[xIndex][1] == yCity[yIndex][1]:
linked.append(xCity[xIndex][1])
ans += min(
xCity[xIndex][0] - xCity[xIndex - 1][0],
yCity[yIndex][0] - yCity[yIndex - 1][0],
)
continue
# 違う街を見ている場合
xDist = xCity[xIndex][0] - xCity[xIndex - 1][0]
yDist = yCity[yIndex][0] - yCity[yIndex - 1][0]
if xDist < yDist:
linked.append(xCity[xIndex][1])
ans += xDist
else:
linked.append(yCity[yIndex][1])
ans += yDist
print(ans)
|
Statement
There are N towns on a plane. The i-th town is located at the coordinates
(x_i,y_i). There may be more than one town at the same coordinates.
You can build a road between two towns at coordinates (a,b) and (c,d) for a
cost of min(|a-c|,|b-d|) yen (the currency of Japan). It is not possible to
build other types of roads.
Your objective is to build roads so that it will be possible to travel between
every pair of towns by traversing roads. At least how much money is necessary
to achieve this?
|
[{"input": "3\n 1 5\n 3 9\n 7 8", "output": "3\n \n\nBuild a road between Towns 1 and 2, and another between Towns 2 and 3. The\ntotal cost is 2+1=3 yen.\n\n* * *"}, {"input": "6\n 8 3\n 4 9\n 12 19\n 18 1\n 13 5\n 7 6", "output": "8"}]
|
For each dataset, print the table with sums of rows and columns. Each item of
the table should be aligned to the right with a margin for five digits. Please
see the sample output for details.
|
s598985056
|
Accepted
|
p00102
|
The input consists of several datasets. Each dataset consists of:
_n_ (the size of row and column of the given table)
1st row of the table
2nd row of the table
:
:
_n_ th row of the table
The input ends with a line consisting of a single 0.
|
if __name__ == "__main__":
while True:
n = int(input())
if n == 0:
break
A = [[0 for _ in range(n + 1)] for _ in range(n)]
B = [0 for _ in range(n + 1)]
for i in range(n):
tmp = list(map(int, input().split()))
for j, k in enumerate(tmp):
A[i][j] += k
B[j] += k
A[i][n] = sum(A[i])
B[n] = sum(B[:n])
for m in A:
tmp2 = ""
for g in m:
tmp2 += "{:>5}".format(str(g))
print(tmp2)
tmp3 = ""
for y in B:
tmp3 += "{:>5}".format(str(y))
print(tmp3)
|
Matrix-like Computation
Your task is to develop a tiny little part of spreadsheet software.
Write a program which adds up columns and rows of given table as shown in the
following figure:
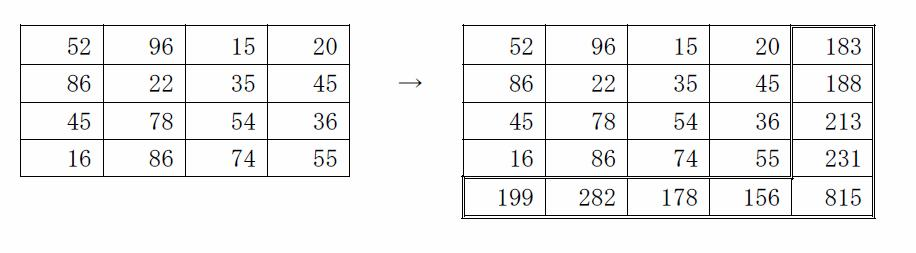
|
[{"input": "52 96 15 20\n 86 22 35 45\n 45 78 54 36\n 16 86 74 55\n 4\n 52 96 15 20\n 86 22 35 45\n 45 78 54 36\n 16 86 74 55\n 0", "output": "96 15 20 183\n 86 22 35 45 188\n 45 78 54 36 213\n 16 86 74 55 231\n 199 282 178 156 815\n 52 96 15 20 183\n 86 22 35 45 188\n 45 78 54 36 213\n 16 86 74 55 231\n 199 282 178 156 815"}]
|
Print the answer.
* * *
|
s242800177
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
def resolve():
H, W, M = list(map(int, input().split()))
HW = [list(map(int, input().split())) for _ in range(M)]
rowsum = [0 for _ in range(H)]
colsum = [0 for _ in range(W)]
for h, w in HW:
rowsum[h - 1] += 1
colsum[w - 1] += 1
rmax = 0
ridx = []
for i, r in enumerate(rowsum):
if rmax < r:
rmax = r
ridx = [i]
elif rmax == r:
ridx.append(i)
maxr = [False for _ in range(H)]
for i in ridx:
maxr[i] = True
cmax = 0
cidx = []
for j, c in enumerate(colsum):
if cmax < c:
cmax = c
cidx = [j]
elif cmax == c:
cidx.append(j)
maxc = [False for _ in range(W)]
for i in cidx:
maxc[i] = True
cnt = 0
for h, w in HW:
if maxr[h - 1] and maxc[w - 1]:
cnt += 1
print(rmax + cmax if cnt < len(cidx) * len(ridx) else rmax + cmax - 1)
if "__main__" == __name__:
resolve()
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s478981767
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
from sys import stdin
def input():
return stdin.readline().strip()
h, w, m = map(int, input().split())
dic_h = {}
dic_w = {}
s = set([])
for _ in range(m):
i, j = map(int, input().split())
s.add((i, j))
try:
dic_h[i] += 1
except:
dic_h[i] = 1
try:
dic_w[j] += 1
except:
dic_w[j] = 1
max_h = 0
lh = []
max_w = 0
lw = []
for i, j in dic_h.items():
if max_h < j:
max_h = j
lh = [i]
elif max_h == j:
lh.append(i)
for i, j in dic_w.items():
if max_w < j:
max_w = j
lw = [i]
elif max_w == j:
lw.append(i)
for i in lh:
for j in lw:
if (i, j) not in s:
print(max_h + max_w)
exit()
print(max_h + max_w - 1)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s851951182
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
import sys
from collections import Counter
INF = 10**18
sys.setrecursionlimit(10**6)
def li():
return [int(x) for x in input().split()]
H, W, M = li()
PH = []
PW = []
for i in range(M):
h, w = li()
PH.append(h)
PW.append(w)
most_common_h = Counter(PH).most_common(1)
most_common_w = Counter(PW).most_common(1)
most_common_h_value = most_common_h[0][0]
most_common_h_cnt = most_common_h[0][1]
most_common_w_value = most_common_w[0][0]
most_common_w_cnt = most_common_w[0][1]
is_same = False
for i in range(M):
if PH[i] == most_common_h_value and PW[i] == most_common_w_value:
is_same = True
cnt = most_common_h_cnt + most_common_w_cnt
if is_same:
cnt -= 1
print(cnt)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s055201324
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
from collections import deque
H, W = map(int, input().split())
CY, CX = map(lambda x: int(x) - 1, input().split())
DY, DX = map(lambda x: int(x) - 1, input().split())
gridgraph = [input() for _ in range(H)]
q = deque()
q.append([CY, CX])
# 更新されるなら追加
adjacent = [[1, 0], [0, 1], [-1, 0], [0, -1]]
INF = float("inf")
distant = [[INF] * W for _ in range(H)]
distant[CY][CX] = 0
visited = set()
while len(q):
cy, cx = q.popleft()
if (cy, cx) in visited:
continue
visited.add((cy, cx))
for dy, dx in adjacent:
ny, nx = cy + dy, cx + dx
if ny < 0 or ny >= H or nx < 0 or nx >= W:
continue
if gridgraph[ny][nx] == "." and distant[ny][nx] > distant[cy][cx]:
distant[ny][nx] = distant[cy][cx]
q.appendleft([ny, nx])
for i in range(-2, 3, 1):
for j in range(-2, 3, 1):
target_y, target_x = cy + i, cx + j
if target_y < 0 or target_y >= H or target_x < 0 or target_x >= W:
continue
if (
gridgraph[target_y][target_x] == "."
and distant[target_y][target_x] > distant[cy][cx] + 1
):
distant[target_y][target_x] = distant[cy][cx] + 1
q.append([target_y, target_x])
if distant[DY][DX] == INF:
print(-1)
else:
print(distant[DY][DX])
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s641211973
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
#!/usr/bin/env python3
from collections import deque
H, W = list(map(int, input().split()))
ch, cw = list(map(int, input().split()))
dh, dw = list(map(int, input().split()))
ch -= 1
cw -= 1
dh -= 1
dw -= 1
S = [list((str(input()))) for i in range(H)]
def check(h, w):
if h < 0 or h >= H:
return False
if w < 0 or w >= W:
return False
if S[h][w] == "#":
return False
return True
def main():
map_ = [[10**10] * W for i in range(H)]
# map_[ch][cw] = 0
dq = deque([[ch, cw, 0]])
while len(dq) > 0:
# print(dq)
h, w, value = dq.popleft()
map_value = map_[h][w]
if map_value <= value:
continue
map_[h][w] = value
for i in [-2, -1, 0, 1, 2]:
for j in [-2, -1, 0, 1, 2]:
if i == 0 and j == 0:
continue
if abs(i) + abs(j) == 1:
if check(h + i, w + j):
# print(h+i, w+)
if map_[h + i][w + j] > value:
dq.appendleft([h + i, w + j, value])
else:
if check(h + i, w + j):
if map_[h + i][w + j] > value + 1:
dq.append([h + i, w + j, value + 1])
# for i in map_:
# print(i)
ans = map_[dh][dw]
if ans == 10**10:
print(-1)
else:
print(ans)
if __name__ == "__main__":
main()
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s530215141
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
h, w = map(int, input().split())
ch, cw = map(int, input().split())
dh, dw = map(int, input().split())
s = [0] * h
for i in range(h):
s[i] = input()
s[i] = list(s[i])
def clear_maze(sx, sy, gx, gy, maze):
INF = 100000000
field_x_length = len(maze)
field_y_length = len(maze[0])
distance = [[INF for i in range(field_y_length)] for j in range(field_x_length)]
# distance = [[INF]*field_y_length]*field_x_length
def bfs():
count = 0
queue = []
queue.insert(0, (sx, sy))
distance[sx][sy] = 0
while len(queue):
x, y = queue.pop()
if x == gx and y == gy:
break
for i in range(0, 24):
if i <= 3:
nx, ny = x + [1, 0, -1, 0][i], y + [0, 1, 0, -1][i]
if i >= 4:
nx, ny = (
x
+ [
-1,
1,
1,
-1,
-2,
-1,
0,
1,
2,
2,
2,
2,
2,
1,
0,
-1,
-2,
-2,
-2,
-2,
][i - 4],
y
+ [
1,
1,
-1,
-1,
2,
2,
2,
2,
2,
1,
0,
-1,
-2,
-2,
-2,
-2,
-2,
-1,
0,
1,
][i - 4],
)
if (
i <= 3
and 0 <= nx
and nx < field_x_length
and 0 <= ny
and ny < field_y_length
and maze[nx][ny] != "#"
and distance[nx][ny] == INF
):
count += 1
queue.insert(0, (nx, ny))
distance[nx][ny] = distance[x][y]
if (
i >= 4
and count == 0
and 0 <= nx
and nx < field_x_length
and 0 <= ny
and ny < field_y_length
and maze[nx][ny] != "#"
and distance[nx][ny] == INF
):
queue.insert(0, (nx, ny))
distance[nx][ny] = distance[x][y] + 1
count = 0
return distance[gx][gy]
return bfs()
if clear_maze(ch - 1, cw - 1, dh - 1, dw - 1, s) == 100000000:
print(-1)
else:
print(clear_maze(ch - 1, cw - 1, dh - 1, dw - 1, s))
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s749271672
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
N = int(input())
if N % 9 == 0:
print("Yes")
else:
print("No")
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s834399755
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
import numpy as np
m = np.zeros((3 * 10**4, 3 * 10**4))
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s555156337
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
from sys import stdin
input = stdin.readline
H, W, M = map(int, input().split())
sum_row = [0] * H
sum_col = [0] * W
bomb_row = [0] * M
bomb_col = [0] * M
for i in range(M):
h, w = map(int, input().split())
sum_row[h - 1] += 1
sum_col[w - 1] += 1
bomb_row[i] = h - 1
bomb_col[i] = w - 1
maxcol = max(sum_col)
maxcollist = [False] * W
for col in range(W):
if sum_col[col] == maxcol:
maxcollist[col] = True
maxrow = max(sum_row)
maxrowlist = [False] * H
for row in range(H):
if sum_row[row] == maxrow:
maxrowlist[row] = True
# 最高行または最高列上にあり、
# かつ最高行と最高列の交点にない爆弾があるかをチェック
cross_cnt = sum(maxrowlist) * sum(maxcollist)
for i in range(M):
h, w = bomb_row[i], bomb_col[i]
if maxrowlist[h] and maxcollist[w]:
cross_cnt -= 1
if cross_cnt > 0:
print(maxcol + maxrow)
else:
print(maxcol + maxrow - 1)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s718772557
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
h, w, m = map(int, input().split())
R = [0] * h
C = [0] * w
XY = [tuple(map(lambda x: int(x) - 1, input().split())) for i in range(m)]
for x, y in XY:
R[x] += 1
C[y] += 1
maxR, maxC = max(R), max(C)
cnt0 = R.count(maxR) * C.count(maxC)
cnt1 = sum(R[x] == maxR and C[y] == maxC for x, y in XY)
print(maxR + maxC - int(cnt0 == cnt1))
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s200952120
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
H, W, M = map(int, input().split())
HW = [tuple(map(int, input().split())) for i in range(M)]
HW = [(h - 1, w - 1) for h, w in HW]
st = set(HW)
countH = [0] * H
countW = [0] * W
for h, w in HW:
countH[h] += 1
countW[w] += 1
maxH = max(countH)
maxW = max(countW)
candiH = []
candiW = []
for i in range(H):
if maxH == countH[i]:
candiH.append(i)
for i in range(W):
if maxW == countW[i]:
candiW.append(i)
count = 0
ans = maxH + maxW - 1
add = 0
for i in candiH:
for j in candiW:
if (i, j) not in st:
add = 1
if count > 300000:
break
count += 1
print(ans + add)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s748099213
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
h, w, m = map(int, input().split())
HW = set()
for _ in range(m):
x, y = map(int, input().split())
HW.add((x - 1, y - 1))
sum_h = [[0, 0] for _ in range(h)] # [sum, index]
sum_w = [[0, 0] for _ in range(w)]
for h, w in HW:
sum_h[h][0] += 1
sum_w[w][0] += 1
sum_h[h][1] = h
sum_w[w][1] = w
h_num_ix = {}
for num, ix in sum_h:
if not num in h_num_ix:
h_num_ix[num] = set()
h_num_ix[num].add(ix)
w_num_ix = {}
for num, ix in sum_w:
if not num in w_num_ix:
w_num_ix[num] = set()
w_num_ix[num].add(ix)
max_h_num = max(h_num_ix)
max_w_num = max(w_num_ix)
max_num = max_h_num + max_w_num - 1
for h_ix in h_num_ix[max_h_num]:
for w_ix in w_num_ix[max_w_num]:
num = max_h_num + max_w_num
if (h_ix, w_ix) in HW:
continue
max_num += 1
print(max_num)
exit()
print(max_num)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s219357362
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
H, W, M = map(int, input().split())
dicti = {}
dictj = {}
bomb = []
for i in range(M):
h, w = map(int, input().split())
bomb.append((h, w))
if h in dicti:
dicti[h] += 1
if h not in dicti:
dicti[h] = 1
if w in dictj:
dictj[w] += 1
if w not in dictj:
dictj[w] = 1
LI = sorted(dicti.items(), key=lambda x: x[1], reverse=True)
LJ = sorted(dictj.items(), key=lambda x: x[1], reverse=True)
answer = 0
for i in range(min(len(LI), 10)):
for j in range(min(len(LJ), 10)):
ans = LI[i][1] + LJ[j][1]
if (LI[i][0], LJ[j][0]) in bomb:
ans -= 1
answer = max(ans, answer)
print(answer)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s796338936
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
import sys
H, W, M = map(int, input().split())
hList = {i + 1: 0 for i in range(H)}
wList = {i + 1: 0 for i in range(W)}
pList = set()
# print(hList, wList, pList)
for _ in range(M):
h, w = list(map(int, input().split()))
# print(h, w)
hList[h] += 1
wList[w] += 1
pList.add((h, w))
# print(hList, wList, pList)
maxHCount = max(hList.values())
maxHList = [h for h, count in hList.items() if count == maxHCount]
maxWCount = max(wList.values())
maxWList = [w for w, count in wList.items() if count == maxWCount]
# counterList = []
# for maxH in maxHList:
# for maxW in maxWList:
# counterList.append(hList[maxH] + wList[maxW] - (1 if ((maxH, maxW) in pList) else 0))
# print(max(counterList))
# print(max(((hList[maxH] + wList[maxW] - (1 if ((maxH, maxW) in pList) else 0)) for maxH in maxHList for maxW in maxWList)))
# print(max(((hList[maxH] + wList[maxW] - (1 if ((maxH, maxW) in pList) else 0)) for maxH in maxHList for maxW in maxWList)))
if M < len(maxHList) * len(maxWList):
print(maxHCount + maxWList)
sys.exit(0)
for maxH in maxHList:
for maxW in maxWList:
if (maxH, maxW) in pList:
print(maxHCount + maxWList - 1)
sys.exit(0)
print(maxHCount + maxWList)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s312884957
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
h,w,m=map(int,input().split())
item=[list(map(int,input().split())) for i in range(m)]
row=[0]*h
col=[0]*w
for i in range(m):
x,y=item[i]
row[x-1]+=1
col[y-1]+=1
mr,mc=max(row),max(col)
xr=set([i for i in range(h) if row[i]==mr])
xc=set([i for i in range(w) if col[i]==mc])
check=len(xr)*len(xc)
for i in range(m):
r,c=item[i]
if r-1 in xr and c-1 in xc:
check-=1
print(mr+mc if check>0 else mr+mc-1)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s405184718
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
h, w, m = map(int, input().split())
a = [0] * m
hc = [0] * w
wc = [0] * h
for i in range(m):
x, y = map(int, input().split())
a[i] = [x - 1, y - 1]
hc[y - 1] += 1
wc[x - 1] += 1
hcm = max(hc)
wcm = max(wc)
hk = []
wk = []
for i in range(len(hc)):
if hc[i] == hcm:
hk.extend([i])
for i in range(len(wc)):
if wc[i] == wcm:
wk.extend([i])
for i in range(len(a)):
if a[i][0] not in wk:
if a[i][1] not in hk:
print(hcm + wcm)
exit()
print(hcm + wcm - 1)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s563296994
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
x, y, m = map(int, input().split())
mat = set()
r = [0] * x
c = [0] * y
smx = 0
smy = 0
for _ in range(m):
p, q = map(int, input().split())
p -= 1
q -= 1
mat.add((p, q))
r[p] += 1
c[q] += 1
smx = max(smx, r[p])
smy = max(smy, c[q])
xs = []
ys = []
for i in range(x):
if smx == r[i]:
xs.append(i)
for i in range(y):
if smy == c[i]:
ys.append(i)
ans = smx + smy - 1
for h in xs:
for w in ys:
if (h, w) in mat:
continue
print(ans + 1)
exit()
print(ans)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s035068237
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
a, b, c = map(int, input().split())
d = [input().split() for l in range(c)]
counter_x = {}
counter_y = {}
for n in range(c):
if d[n][0] in counter_x.keys():
counter_x[d[n][0]] += 1
else:
counter_x[d[n][0]] = 1
if d[n][1] in counter_y.keys():
counter_y[d[n][1]] += 1
else:
counter_y[d[n][1]] = 1
max_x = max(counter_x, key=counter_x.get)
max_y = max(counter_y, key=counter_y.get)
for l in d:
if l == [max_x, max_y]:
u = 1
else:
pass
print(int(max(counter_x.values())) + int(max(counter_y.values())) - u)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s286877492
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
n, m, k = map(int, input().split())
c = {}
e = {}
for i in range(k):
a, b = map(int, input().split())
t = str(a) + "x"
s = str(b) + "y"
e[t + s] = 1
if t in c:
c[t] += 1
else:
c[t] = 1
if s in c:
c[s] += 1
else:
c[s] = 1
d = sorted(c.items(), key=lambda x: x[1], reverse=True)
p, r = d[0]
w = ""
p = list(p)
m = r
if p[1] == "x":
for i in range(len(d)):
u, v = d[i]
u = list(u)
if u[1] == "y":
m += v
w += "".join(p) + "".join(u)
break
else:
for i in range(len(d)):
u, v = d[i]
u = list(u)
if u[1] == "x":
m += v
w += "".join(u) + "".join(p)
break
if w in e:
print(m - 1)
else:
print(m)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s397498763
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
H, W, M = map(int, input().split())
a = [[0] * W for i in range(H)]
hh = [0] * H
ww = [0] * W
for i in range(M):
h, w = map(lambda a: int(a) - 1, input().split())
hh[h] += 1
ww[w] += 1
a[h][w] = 1
Maxh = 0
Maxw = 0
argh = 0
argw = 0
for h in range(H):
if Maxh <= hh[h]:
argh = h
Maxh = hh[h]
for w in range(W):
if Maxw <= ww[w]:
argw = w
Maxw = hh[w]
print(Maxw + Maxh - a[argh][argw])
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s592232443
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
hwm = list(map(int, input().split()))
H, W, M = hwm[0], hwm[1], hwm[2]
ls1 = [[0] * W for _ in range(H)]
ls2 = [[0] * H for _ in range(W)]
hls = []
wls = []
for m in range(M):
ls = list(map(int, input().split()))
ls1[ls[0] - 1][ls[1] - 1] = 1
ls2[ls[1] - 1][ls[0] - 1] = 1
for h in range(H):
hls.append(sum(ls1[h]))
for w in range(W):
wls.append(sum(ls2[w]))
maxbomb = 0
for h in range(H):
for w in range(W):
if ls1[h][w] == 0:
sumbomb = hls[h] + wls[w]
else:
sumbomb = hls[h] + wls[w] - 1
if maxbomb < sumbomb:
maxbomb = sumbomb
print(maxbomb)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s360003614
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
# E - Bomber
target = []
hsetting = []
wsetting = []
hcount = 0
wcount = 0
xcount = 1
append = target.append
happend = hsetting.append
wappend = wsetting.append
# 入力
H, W, M = map(int, input().split())
for hwinput in range(M):
h, w = map(int, input().split())
append([h, w])
happend(h)
wappend(w)
# h_target = sorted(hsetting)
# w_target = sorted(wsetting)
max_bomb_out = 0
w_max_bomb_out = 0
h_max_bomb_out = 0
h_index_count = 0
w_index_count = 0
h_index = [0]
w_index = [0]
targetcount = target.count
hsetcount = hsetting.count
wsetcount = wsetting.count
h_index_ap = h_index.append
h_index_cl = h_index.clear
w_index_ap = w_index.append
w_index_cl = w_index.clear
h_index_index = h_index.index
w_index_index = w_index.index
h_index_p = []
w_index_p = []
h_index_p_ap = h_index_p.append
w_index_p_ap = w_index_p.append
for i in range(1, H + 1):
h_index_ap(hsetcount(i))
h_max_bomb_out = max(h_index)
for j in range(1, W + 1):
w_index_ap(wsetcount(j))
w_max_bomb_out = max(w_index)
max_bomb_out = h_max_bomb_out + w_max_bomb_out - xcount
# 出力
print(max_bomb_out)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s364698558
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
r = input().split()
H = int(r[0])
W = int(r[1])
M = int(r[2])
d = [input().split() for i in range(M)]
D = []
for i in range(M):
D_pre = [int(s) for s in d[i]]
D.append(D_pre)
gyou = [0] * H
retu = [0] * W
for i in range(M):
gyou[D[i][0] - 1] += 1
retu[D[i][1] - 1] += 1
g_Max = max(gyou)
r_Max = max(retu)
g = []
r = []
for i in range(H):
if gyou[i] == g_Max:
g.append(i)
for i in range(W):
if retu[i] == r_Max:
r.append(i)
x = 0
for i in g:
for j in r:
if [i + 1, j + 1] not in D:
x += 1
print(g_Max + r_Max)
break
if x == 0:
print(g_Max + r_Max - 1)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s941432978
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
import collections
h, w, m = (int(each) for each in input().split())
bombs = []
for each in range(m):
bombs.append(tuple(int(each) for each in input().split()))
hbombs = [each[0] for each in bombs]
wbombs = [each[1] for each in bombs]
# h方向で行番号と対象の数のタプル
hbombs_cnt = collections.Counter(hbombs).most_common()
wbombs_cnt = collections.Counter(wbombs).most_common()
hbombs_max = hbombs_cnt[0][1]
wbombs_max = wbombs_cnt[0][1]
# h方向で一番多い行番号と対象の数のタプル
hbombs_most_common = [each for each in hbombs_cnt if each[1] == hbombs_max]
wbombs_most_common = [each for each in wbombs_cnt if each[1] == wbombs_max]
# print(hbombs_most_common)
# print(wbombs_most_common)
result = hbombs_max + wbombs_max
pos = [0]
# 爆破位置に爆弾があるか
for _h in hbombs_most_common:
for _w in wbombs_most_common:
# print(_h[0], _w[0])
if (_h[0], _w[0]) in bombs:
pos.append(1)
# print(pos)
print(result - max(pos))
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s614766246
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
H,W,M=map(int,input().split())
l = [ list(map(int,input().split(" "))) for i in range(M)]
h=[0]*H
w=[0]*W
for i in range(M):
h[l[i][0]-1]=h[l[i][0]-1]+1
w[l[i][1]-1]=w[l[i][1]-1]+1
maxh=max(h)
maxw=max(w)
max_h=[i for i,k in enumerate(h) if k==maxh]
max_w=[i for i,k in enumerate(w) if k==maxw]
flag=0
for i in max_h:
for j in max_w:
c=0
for k in range(M):
if i==l[k][0]-1 or j==l[k][1]-1:
c=1
if c==0:
flag=1
print(maxh+maxw)
if flag==1:
break
if flag==1:
break
if flag==0:
print(maxh+maxw-1)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s089499953
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
H, W, M = map(int, input().split())
HW = [[0] * W for i in range(H)]
H_list = [0] * H
W_list = [0] * W
for i in range(M):
h, w = map(int, input().split())
HW[h - 1][w - 1] = 1
H_list[h - 1] += 1
W_list[w - 1] += 1
# print(HW, H_list, W_list)
H_max = max(H_list)
W_max = max(W_list)
H_index = []
W_index = []
for i in range(H):
if H_list[i] == H_max:
H_index.append(i)
for i in range(W):
if W_list[i] == W_max:
W_index.append(i)
x = 1
for i in H_index:
for j in W_index:
if HW[i][j] == 0:
x = 0
print(H_max + W_max - x)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s709467029
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
# E - Bomber
H, W, M = map(int, input().split())
bomb = set()
height = dict()
width = dict()
for i in range(M):
h, w = map(int, input().split())
bomb.add((h, w))
if h in height:
height[h] += 1
else:
height[h] = 1
if w in width:
width[w] += 1
else:
width[w] = 1
hei = dict()
wi = dict()
for h in height:
if height[h] in hei:
hei[height[h]].append(h)
else:
hei[height[h]] = [h]
for w in width:
if width[w] in wi:
wi[width[w]].append(w)
else:
wi[width[w]] = [w]
max_h = max(hei)
max_w = max(wi)
tmp = 1
for h in hei[max_h]:
for w in wi[max_w]:
if (h, w) not in bomb:
tmp = 0
break
print(max_h + max_w - tmp)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s113802116
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
h, w, m = list(map(int, input().split()))
hl = []
wl = []
hc = [0] * h
wc = [0] * w
mp = [0] * (h * w)
for j in range(m):
h1, w1 = [int(j) for j in input().split()]
hl.append(h1)
wl.append(w1)
for i in range(m):
x = hl[i] - 1
y = wl[i] - 1
z = y * h + x
hc[x] += 1
wc[y] += 1
mp[z] += 1
mx = max(hc)
my = max(wc)
lmx = []
lmy = []
for p in range(h):
if hc[p] == mx:
lmx.append(p)
for q in range(w):
if wc[q] == my:
lmy.append(q)
zzx = len(lmx)
zzy = len(lmy)
zzz = 1
if zzx * zzy <= 300000:
for s in range(zzx):
ss = lmx[s]
for t in range(zzy):
tt = lmy[t]
uu = tt * h + ss
if mp[uu] == 0:
zzz = 0
else:
zzz = 0
print(mx + my - zzz)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s333950959
|
Runtime Error
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
h, w, m = list(map(int, input().split()))
b = []
r = [0] * (10**5 + 1)
c = [0] * (10**5 + 1)
for i in range(m):
h, w = list(map(int, input().split()))
r[h] = r[h] + 1
c[w] = c[w] + 1
b.append([h, w])
if max(r) > max(c):
j = r.index(max(r))
for i in range(len(b)):
if b[i][0] == j:
c[b[i][1]] = c[b[i][1]] - 1
i = c.index(max(c))
else:
i = c.index(max(c))
for j in range(len(b)):
if b[j][1] == i:
r[b[j][0]] = r[b[j][0]] - 1
j = r.index(max(r))
print(r[j] + c[i])
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s240837486
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
h, w, m = (int(i) for i in input().split())
l1 = []
l2 = [0] * h
l3 = [0] * w
for i in range(m):
x, y = (int(i) for i in input().split())
l1.append((x, y))
l2[x - 1] += 1
l3[y - 1] += 1
m1 = max(l2)
m2 = max(l3)
m3 = max(m1, m2)
if m3 == m1:
l4 = [0] * w
k = l2.index(m1)
for i in range(m):
if l1[i][0] != k + 1:
l4[l1[i][1] - 1] += 1
k1 = max(l4)
print(m1 + k1)
else:
l4 = [0] * h
k = l3.index(m2)
for i in range(m):
if l1[i][1] != k + 1:
l4[l1[i][0] - 1] += 1
k1 = max(l4)
print(m2 + k1)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s191809428
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
#!/usr/bin/python3
# -*- coding: utf-8 -*-
h, w, m = map(int, input().split())
bom_set = set()
h_dict = {}
w_dict = {}
for i in range(m):
hh, ww = map(int, input().split())
bom_set.add(tuple([hh, ww]))
if hh in h_dict:
h_dict[hh] += 1
else:
h_dict[hh] = 1
if ww in w_dict:
w_dict[ww] += 1
else:
w_dict[ww] = 1
h_max_count = max(h_dict.values())
w_max_count = max(w_dict.values())
hh_dict = {}
ww_dict = {}
for hh in h_dict:
if h_dict[hh] == h_max_count:
hh_dict[hh] = h_max_count
for ww in w_dict:
if w_dict[ww] == w_max_count:
ww_dict[ww] = w_max_count
flag = 0
for hh in hh_dict:
for ww in ww_dict:
if tuple([hh, ww]) not in bom_set:
flag = 1
break
if flag == 1:
break
if flag == 1:
print(h_max_count + w_max_count)
else:
print(h_max_count + w_max_count - 1)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s610657177
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
H,W,M = list(map(int, input().split()))
s = []
Hlist = [0 for i in range(H)]
Wlist = [0 for i in range(W)]
for i in range(M):
s.append(list(map(int, input().split())))
Hlist[s[i][0]-1] += 1
Wlist[s[i][1]-1] += 1
Hmax = max(Hlist)
Wmax = max(Wlist)
Hmaxindex = [i for i, v in enumerate(Hlist) if v == Hmax]
Wmaxindex = [i for i, v in enumerate(Wlist) if v == Wmax]
print(Hmax + Wmax)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s717526105
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
H,W,M=map(int,input().split())
bomb=[]
h=[0]*H
w=[0]*W
for i in range(M):
hi,wi=map(int,input().split())
h[hi-1] += 1
w[wi-1] += 1
bomb.append([hi,wi])
maxh = max(h)
maxw = max(w)
ans = maxh + maxw
lh=[]
lw=[]
for i in range(len(h)):
if h[i] == maxh:
lh.append(i+1)
for i in range(len(w)):
if w[i] == maxw:
lw.append(i+1)
a = 0
for i in range(M):
if ans == h[bomb[i][0]-1]+w[bomb[i][1]-1]:
a += 1
if a == len(lh)*len(lw):
print(ans-1)
else:
print(ans)
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s225295045
|
Wrong Answer
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
# -*- coding: utf-8 -*-
from collections import Counter, defaultdict
import sys
# sys.setrecursionlimit(10**6)
# buff_readline = sys.stdin.buffer.readline
buff_readline = sys.stdin.readline
readline = sys.stdin.readline
INF = 2**62 - 1
def read_int():
return int(buff_readline())
def read_int_n():
return list(map(int, buff_readline().split()))
def read_float():
return float(buff_readline())
def read_float_n():
return list(map(float, buff_readline().split()))
def read_str():
return readline().strip()
def read_str_n():
return readline().strip().split()
def error_print(*args):
print(*args, file=sys.stderr)
def mt(f):
import time
def wrap(*args, **kwargs):
s = time.time()
ret = f(*args, **kwargs)
e = time.time()
error_print(e - s, "sec")
return ret
return wrap
@mt
def slv(H, W, M, HW):
g = defaultdict(dict)
for h, w in HW:
g[h][w] = 1
h = Counter(h for h, w in HW)
w = Counter(w for h, w in HW)
h = list(h.items())
h.sort(reverse=True, key=lambda x: x[1])
w = list(w.items())
w.sort(reverse=True, key=lambda x: x[1])
ans = 0
for k, v in h:
for kk, vv in w:
if k in g and kk in g[k]:
ans = max(ans, v + vv - 1)
else:
return ans
return ans
def main():
H, W, M = read_int_n()
HW = [read_int_n() for _ in range(M)]
print(slv(H, W, M, HW))
if __name__ == "__main__":
main()
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer.
* * *
|
s304586349
|
Accepted
|
p02580
|
Input is given from Standard Input in the following format:
H W M
h_1 w_1
\vdots
h_M w_M
|
from collections import defaultdict as dd
def solve():
h, w, m = map(int, input().split())
targets = set()
rows = dd(int)
cols = dd(int)
for _ in range(m):
r, c = map(int, input().split())
rows[r] += 1
cols[c] += 1
targets.add((r, c))
best_rows = []
best_cols = []
best_row = max(rows.values())
best_col = max(cols.values())
best = best_row + best_col - 1
for k, v in rows.items():
if v == best_row:
best_rows.append(k)
for k, v in cols.items():
if v == best_col:
best_cols.append(k)
for row in best_rows:
for col in best_cols:
if (row, col) not in targets:
print(best + 1)
return
print(best)
solve()
|
Statement
We have a two-dimensional grid with H \times W squares. There are M targets to
destroy in this grid - the position of the i-th target is \left(h_i, w_i
\right).
Takahashi will choose one square in this grid, place a bomb there, and ignite
it. The bomb will destroy all targets that are in the row or the column where
the bomb is placed. It is possible to place the bomb at a square with a
target.
Takahashi is trying to maximize the number of targets to destroy. Find the
maximum number of targets that can be destroyed.
|
[{"input": "2 3 3\n 2 2\n 1 1\n 1 3", "output": "3\n \n\nWe can destroy all the targets by placing the bomb at \\left(1, 2\\right).\n\n* * *"}, {"input": "3 3 4\n 3 3\n 3 1\n 1 1\n 1 2", "output": "3\n \n\n* * *"}, {"input": "5 5 10\n 2 5\n 4 3\n 2 3\n 5 5\n 2 2\n 5 4\n 5 3\n 5 1\n 3 5\n 1 4", "output": "6"}]
|
Print the answer modulo 1\,000\,000\,007 (=10^9+7).
* * *
|
s774543354
|
Runtime Error
|
p04004
|
The input is given from Standard Input in the following format:
N M K
|
#include<iostream>
#define MOD 1000000007
#define N 1000
using namespace std;
typedef long long LL;
LL mod_pow(LL base, LL exp)
{
if(exp==0) return 1;
if(exp&1) return (mod_pow(base,exp-1)*base)%MOD;
else return mod_pow((base*base)%MOD,exp/2);
}
LL fac[3*N+1];
LL fac_inv[3*N+1];
LL C(LL n, LL k)
{
if(k < 0 || n < k) return 0;
LL num = fac[n];
LL den = (fac_inv[n-k]*fac_inv[k])%MOD;
return (num*den)%MOD;
}
int main()
{
fac[0] = 1;
for(LL n = 1; n <= 3*N; n++)
fac[n] = (fac[n-1]*n)%MOD;
fac_inv[3*N] = mod_pow(fac[3*N],MOD-2);
for(LL n = 3*N-1; n >= 0; n--)
fac_inv[n] = (fac_inv[n+1]*(n+1))%MOD;
LL a, b, c; cin >> a >> b >> c;
a++;
//WLOG, b > c
if(!(b>c))
{
b = b^c;
c = b^c;
b = b^c;
}
LL ans = 0;
LL sum = 1;
LL pull = 0;
for(LL n = a; n <= a+b+c; n++)
{
LL sub = 0;
sub = (sub+sum-pull)%MOD;
sub = (sub*C(n-2,a-2))%MOD;
sub = (sub*mod_pow(3,a+b+c-n))%MOD;
ans = (ans+sub)%MOD;
sum = (2*sum-C(n-a,c))%MOD;
pull = (2*pull+C(n-a,n-a-b))%MOD;
}
cout<<(ans+MOD)%MOD<<endl;
return 0;
}
|
Statement
Alice, Bob and Charlie are playing _Card Game for Three_ , as below:
* At first, each of the three players has a deck consisting of some number of cards. Alice's deck has N cards, Bob's deck has M cards, and Charlie's deck has K cards. Each card has a letter `a`, `b` or `c` written on it. The orders of the cards in the decks cannot be rearranged.
* The players take turns. Alice goes first.
* If the current player's deck contains at least one card, discard the top card in the deck. Then, the player whose name begins with the letter on the discarded card, takes the next turn. (For example, if the card says `a`, Alice takes the next turn.)
* If the current player's deck is empty, the game ends and the current player wins the game.
There are 3^{N+M+K} possible patters of the three player's initial decks.
Among these patterns, how many will lead to Alice's victory?
Since the answer can be large, print the count modulo 1\,000\,000\,007
(=10^9+7).
|
[{"input": "1 1 1", "output": "17\n \n\n * If Alice's card is `a`, then Alice will win regardless of Bob's and Charlie's card. There are 3\u00d73=9 such patterns.\n * If Alice's card is `b`, Alice will only win when Bob's card is `a`, or when Bob's card is `c` and Charlie's card is `a`. There are 3+1=4 such patterns.\n * If Alice's card is `c`, Alice will only win when Charlie's card is `a`, or when Charlie's card is `b` and Bob's card is `a`. There are 3+1=4 such patterns.\n\nThus, there are total of 9+4+4=17 patterns that will lead to Alice's victory.\n\n* * *"}, {"input": "4 2 2", "output": "1227\n \n\n* * *"}, {"input": "1000 1000 1000", "output": "261790852"}]
|
Print the number of candies given to Takahashi when both Tozan and Gezan
perform the operations optimally.
* * *
|
s297559198
|
Accepted
|
p03391
|
Input is given from Standard Input in the following format:
N
A_1 B_1
:
A_N B_N
|
INF = float("inf")
N, *AB = map(int, open(0).read().split())
A, B = AB[::2], AB[1::2]
sum_a = sum(A)
mi = min((b for a, b in zip(A, B) if a > b), default=sum_a)
print(sum_a - mi)
|
Statement
You are given sequences A and B consisting of non-negative integers. The
lengths of both A and B are N, and the sums of the elements in A and B are
equal. The i-th element in A is A_i, and the i-th element in B is B_i.
Tozan and Gezan repeats the following sequence of operations:
* If A and B are equal sequences, terminate the process.
* Otherwise, first Tozan chooses a positive element in A and decrease it by 1.
* Then, Gezan chooses a positive element in B and decrease it by 1.
* Then, give one candy to Takahashi, their pet.
Tozan wants the number of candies given to Takahashi until the process is
terminated to be as large as possible, while Gezan wants it to be as small as
possible. Find the number of candies given to Takahashi when both of them
perform the operations optimally.
|
[{"input": "2\n 1 2\n 3 2", "output": "2\n \n\nWhen both Tozan and Gezan perform the operations optimally, the process will\nproceed as follows:\n\n * Tozan decreases A_1 by 1.\n * Gezan decreases B_1 by 1.\n * One candy is given to Takahashi.\n * Tozan decreases A_2 by 1.\n * Gezan decreases B_1 by 1.\n * One candy is given to Takahashi.\n * As A and B are equal, the process is terminated.\n\n* * *"}, {"input": "3\n 8 3\n 0 1\n 4 8", "output": "9\n \n\n* * *"}, {"input": "1\n 1 1", "output": "0"}]
|
Print the eventual sequence that will be produced, in a line.
* * *
|
s371781206
|
Wrong Answer
|
p03811
|
The input is given from Standard Input in the following format:
N
A_1 A_2 … A_N
|
def gcd(a, b):
return gcd(b, a % b) if b else a
def merge(a, us, vs):
i, j, res = 0, 0, []
while i < len(us) and j < len(vs):
if a[us[i]] >= a[vs[j]]:
res.append(us[i])
i += 1
else:
res.append(vs[j])
j += 1
return res + us[i:] + vs[j:]
def dfs(g, a, u, vis):
vis[u] = True
res = []
for v in g[u]:
if not vis[v]:
res = merge(a, res, dfs(g, a, v, vis))
return [u] + res
while 1:
try:
n = int(input())
a = sorted(map(int, input().split()))
except:
break
g = [[j for j in range(n) if i != j and gcd(a[i], a[j]) != 1] for i in range(n)]
# vis=[False]*n
# res=[]
# for u in range(n):
# if not vis[u]:
# res=merge(a,res,dfs(g,a,u,vis))
# print(' '.join(str(a[u]) for u in res))
|
Statement
There are N integers written on a blackboard. The i-th integer is A_i.
Takahashi and Aoki will arrange these integers in a row, as follows:
* First, Takahashi will arrange the integers as he wishes.
* Then, Aoki will repeatedly swap two adjacent integers that are coprime, as many times as he wishes.
We will assume that Takahashi acts optimally so that the eventual sequence
will be lexicographically as small as possible, and we will also assume that
Aoki acts optimally so that the eventual sequence will be lexicographically as
large as possible. Find the eventual sequence that will be produced.
|
[{"input": "5\n 1 2 3 4 5", "output": "5 3 2 4 1\n \n\nIf Takahashi arranges the given integers in the order (1,2,3,4,5), they will\nbecome (5,3,2,4,1) after Aoki optimally manipulates them.\n\n* * *"}, {"input": "4\n 2 3 4 6", "output": "2 4 6 3"}]
|
Print the eventual sequence that will be produced, in a line.
* * *
|
s278872893
|
Runtime Error
|
p03811
|
The input is given from Standard Input in the following format:
N
A_1 A_2 … A_N
|
import math, string, itertools, fractions, heapq, collections, re, array, bisect, sys, random, time
sys.setrecursionlimit(10**7)
inf = 10**20
mod = 10**9 + 7
def LI():
return list(map(int, input().split()))
def II():
return int(input())
def LS():
return input().split()
def S():
return input()
def main():
n = II()
a = LI()
a.sort()
i = n - 1
m = {}
def g(a, b):
if (a, b) in m:
return m[(a, b)]
c = math.gcd(a, b)
if c == 1:
m[(a, b)] = True
else:
m[(a, b)] = False
return c == 1
def f(i):
ai = a[i]
ii = i
ff = False
while ii > 0:
j = ii - 1
aj = a[j]
mj = ii
while g(ai, a[j]) and j >= 0:
if a[j] < ai:
mj = j
j -= 1
if mj != ii:
a[mj : ii + 1] = [ai] + a[mj:ii]
ff = True
ii = mj
else:
if f(ii - 1):
continue
else:
break
return ff
for i in range(n - 1, -1, -1):
while f(i):
pass
sa = a[:]
for _ in range(100):
random.shuffle(a)
for i in range(n - 1, -1, -1):
while f(i):
pass
if a < sa:
sa = a[:]
return " ".join(map(str, sa))
print(main())
|
Statement
There are N integers written on a blackboard. The i-th integer is A_i.
Takahashi and Aoki will arrange these integers in a row, as follows:
* First, Takahashi will arrange the integers as he wishes.
* Then, Aoki will repeatedly swap two adjacent integers that are coprime, as many times as he wishes.
We will assume that Takahashi acts optimally so that the eventual sequence
will be lexicographically as small as possible, and we will also assume that
Aoki acts optimally so that the eventual sequence will be lexicographically as
large as possible. Find the eventual sequence that will be produced.
|
[{"input": "5\n 1 2 3 4 5", "output": "5 3 2 4 1\n \n\nIf Takahashi arranges the given integers in the order (1,2,3,4,5), they will\nbecome (5,3,2,4,1) after Aoki optimally manipulates them.\n\n* * *"}, {"input": "4\n 2 3 4 6", "output": "2 4 6 3"}]
|
For each dataset, output the number of successful applicants in a line.
|
s520702609
|
Accepted
|
p01085
|
The input consists of multiple datasets. Each dataset is formatted as follows.
> _m_ _n_ min _n_ max
> _P_ 1
> _P_ 2
> ...
> _P m_
>
The first line of a dataset contains three integers separated by single
spaces. _m_ represents the number of applicants, _n_ min represents the
minimum number of successful applicants, and _n_ max represents the maximum
number of successful applicants. Each of the following _m_ lines contains an
integer _P i_, which represents the score of each applicant. The scores are
listed in descending order. These numbers satisfy 0 < _n_ min < _n_ max < _m_
≤ 200, 0 ≤ _P i_ ≤ 10000 (1 ≤ _i_ ≤ _m_) and _P_ _n_ min > _P_ _n_ max+1.
These ensure that there always exists an _n_ satisfying the conditions.
The end of the input is represented by a line containing three zeros separated
by single spaces.
|
while True:
m, nmin, nmax = map(int, input().split())
if m + nmin + nmax == 0:
break
P = [int(input()) for i in range(m)]
gap = 0
for i in range(nmin, nmax + 1):
if gap <= P[i - 1] - P[i]:
gap = P[i - 1] - P[i]
n = i
print(n)
|
Entrance Examination
The International Competitive Programming College (ICPC) is famous for its
research on competitive programming. Applicants to the college are required to
take its entrance examination.
The successful applicants of the examination are chosen as follows.
* The score of any successful applicant is higher than that of any unsuccessful applicant.
* The number of successful applicants _n_ must be between _n_ min and _n_ max, inclusive. We choose _n_ within the specified range that maximizes the _gap._ Here, the _gap_ means the difference between the lowest score of successful applicants and the highest score of unsuccessful applicants.
* When two or more candidates for _n_ make exactly the same _gap,_ use the greatest _n_ among them.
Let's see the first couple of examples given in Sample Input below. In the
first example, _n_ min and _n_ max are two and four, respectively, and there
are five applicants whose scores are 100, 90, 82, 70, and 65. For _n_ of two,
three and four, the gaps will be 8, 12, and 5, respectively. We must choose
three as _n_ , because it maximizes the gap.
In the second example, _n_ min and _n_ max are two and four, respectively, and
there are five applicants whose scores are 100, 90, 80, 75, and 65. For _n_ of
two, three and four, the gap will be 10, 5, and 10, respectively. Both two and
four maximize the gap, and we must choose the greatest number, four.
You are requested to write a program that computes the number of successful
applicants that satisfies the conditions.
|
[{"input": "2 4\n 100\n 90\n 82\n 70\n 65\n 5 2 4\n 100\n 90\n 80\n 75\n 65\n 3 1 2\n 5000\n 4000\n 3000\n 4 2 3\n 10000\n 10000\n 8000\n 8000\n 4 2 3\n 10000\n 10000\n 10000\n 8000\n 5 2 3\n 100\n 80\n 68\n 60\n 45\n 0 0 0", "output": "4\n 2\n 2\n 3\n 2"}]
|
For each dataset, output the number of successful applicants in a line.
|
s141453435
|
Runtime Error
|
p01085
|
The input consists of multiple datasets. Each dataset is formatted as follows.
> _m_ _n_ min _n_ max
> _P_ 1
> _P_ 2
> ...
> _P m_
>
The first line of a dataset contains three integers separated by single
spaces. _m_ represents the number of applicants, _n_ min represents the
minimum number of successful applicants, and _n_ max represents the maximum
number of successful applicants. Each of the following _m_ lines contains an
integer _P i_, which represents the score of each applicant. The scores are
listed in descending order. These numbers satisfy 0 < _n_ min < _n_ max < _m_
≤ 200, 0 ≤ _P i_ ≤ 10000 (1 ≤ _i_ ≤ _m_) and _P_ _n_ min > _P_ _n_ max+1.
These ensure that there always exists an _n_ satisfying the conditions.
The end of the input is represented by a line containing three zeros separated
by single spaces.
|
N = input().split(" ")
a = [input() for i in range(int(N[0]))]
ma = int(N[2])
mi = int(N[1])
gap = []
x = mi
while x != ma + 1:
value = int(a[x - 1]) - int(a[x])
gap.append(value)
x = x + 1
import numpy as np
gapIndex = np.array(gap)
maxIndex = [i for i, x in enumerate(gapIndex) if x == max(gapIndex)]
print(int(maxIndex[0]) + 2)
|
Entrance Examination
The International Competitive Programming College (ICPC) is famous for its
research on competitive programming. Applicants to the college are required to
take its entrance examination.
The successful applicants of the examination are chosen as follows.
* The score of any successful applicant is higher than that of any unsuccessful applicant.
* The number of successful applicants _n_ must be between _n_ min and _n_ max, inclusive. We choose _n_ within the specified range that maximizes the _gap._ Here, the _gap_ means the difference between the lowest score of successful applicants and the highest score of unsuccessful applicants.
* When two or more candidates for _n_ make exactly the same _gap,_ use the greatest _n_ among them.
Let's see the first couple of examples given in Sample Input below. In the
first example, _n_ min and _n_ max are two and four, respectively, and there
are five applicants whose scores are 100, 90, 82, 70, and 65. For _n_ of two,
three and four, the gaps will be 8, 12, and 5, respectively. We must choose
three as _n_ , because it maximizes the gap.
In the second example, _n_ min and _n_ max are two and four, respectively, and
there are five applicants whose scores are 100, 90, 80, 75, and 65. For _n_ of
two, three and four, the gap will be 10, 5, and 10, respectively. Both two and
four maximize the gap, and we must choose the greatest number, four.
You are requested to write a program that computes the number of successful
applicants that satisfies the conditions.
|
[{"input": "2 4\n 100\n 90\n 82\n 70\n 65\n 5 2 4\n 100\n 90\n 80\n 75\n 65\n 3 1 2\n 5000\n 4000\n 3000\n 4 2 3\n 10000\n 10000\n 8000\n 8000\n 4 2 3\n 10000\n 10000\n 10000\n 8000\n 5 2 3\n 100\n 80\n 68\n 60\n 45\n 0 0 0", "output": "4\n 2\n 2\n 3\n 2"}]
|
For each dataset, output the number of successful applicants in a line.
|
s112909257
|
Wrong Answer
|
p01085
|
The input consists of multiple datasets. Each dataset is formatted as follows.
> _m_ _n_ min _n_ max
> _P_ 1
> _P_ 2
> ...
> _P m_
>
The first line of a dataset contains three integers separated by single
spaces. _m_ represents the number of applicants, _n_ min represents the
minimum number of successful applicants, and _n_ max represents the maximum
number of successful applicants. Each of the following _m_ lines contains an
integer _P i_, which represents the score of each applicant. The scores are
listed in descending order. These numbers satisfy 0 < _n_ min < _n_ max < _m_
≤ 200, 0 ≤ _P i_ ≤ 10000 (1 ≤ _i_ ≤ _m_) and _P_ _n_ min > _P_ _n_ max+1.
These ensure that there always exists an _n_ satisfying the conditions.
The end of the input is represented by a line containing three zeros separated
by single spaces.
|
da = list(map(int, input().split()))
k = []
while sum(da) != 0:
for i in range(da[0]):
k.append(int(input()))
for i in range(da[0]):
k[da[0] - 1 - i] = k[da[0] - 1 - i] - k[da[0] - 2 - i]
pp = k[da[1] : da[2] + 1]
print(pp)
qq = min(pp)
for i in range(len(pp)):
if pp[i] == qq:
jj = i
print(da[1] + jj)
da = list(map(int, input().split()))
k = []
|
Entrance Examination
The International Competitive Programming College (ICPC) is famous for its
research on competitive programming. Applicants to the college are required to
take its entrance examination.
The successful applicants of the examination are chosen as follows.
* The score of any successful applicant is higher than that of any unsuccessful applicant.
* The number of successful applicants _n_ must be between _n_ min and _n_ max, inclusive. We choose _n_ within the specified range that maximizes the _gap._ Here, the _gap_ means the difference between the lowest score of successful applicants and the highest score of unsuccessful applicants.
* When two or more candidates for _n_ make exactly the same _gap,_ use the greatest _n_ among them.
Let's see the first couple of examples given in Sample Input below. In the
first example, _n_ min and _n_ max are two and four, respectively, and there
are five applicants whose scores are 100, 90, 82, 70, and 65. For _n_ of two,
three and four, the gaps will be 8, 12, and 5, respectively. We must choose
three as _n_ , because it maximizes the gap.
In the second example, _n_ min and _n_ max are two and four, respectively, and
there are five applicants whose scores are 100, 90, 80, 75, and 65. For _n_ of
two, three and four, the gap will be 10, 5, and 10, respectively. Both two and
four maximize the gap, and we must choose the greatest number, four.
You are requested to write a program that computes the number of successful
applicants that satisfies the conditions.
|
[{"input": "2 4\n 100\n 90\n 82\n 70\n 65\n 5 2 4\n 100\n 90\n 80\n 75\n 65\n 3 1 2\n 5000\n 4000\n 3000\n 4 2 3\n 10000\n 10000\n 8000\n 8000\n 4 2 3\n 10000\n 10000\n 10000\n 8000\n 5 2 3\n 100\n 80\n 68\n 60\n 45\n 0 0 0", "output": "4\n 2\n 2\n 3\n 2"}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s320097841
|
Wrong Answer
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
A, B, Q = (int(i) for i in input().split())
slist = [int(input()) for i in range(A)]
tlist = [int(input()) for i in range(B)]
qlist = [int(input()) for i in range(Q)]
for j in range(Q):
sl = [qlist[j] - slist[i] for i in range(A) if qlist[j] - slist[i] >= 0]
sr = [abs(qlist[j] - slist[i]) for i in range(A) if qlist[j] - slist[i] < 0]
tl = [qlist[j] - tlist[i] for i in range(B) if qlist[j] - tlist[i] >= 0]
tr = [abs(qlist[j] - tlist[i]) for i in range(B) if qlist[j] - tlist[i] < 0]
sl.sort()
sr.sort()
tl.sort()
tr.sort()
if sl == []:
if tl == []:
L = [sr[0] + tr[0]]
elif tr == []:
L = [sr[0] * 2 + tl[0], sr[0] + tl[0] * 2]
else:
L = [sr[0] + tr[0], sr[0] * 2 + tl[0], sr[0] + tl[0] * 2]
elif sr == []:
if tl == []:
L = [sl[0] * 2 + tr[0], sl[0] + tr[0] * 2]
elif tr == []:
L = [sl[0] + tl[0]]
else:
L = [sl[0] + tl[0], sl[0] * 2 + tr[0], sl[0] + tr[0] * 2]
else:
if tl == []:
L = [sl[0] * 2 + tr[0], sl[0] + tr[0] * 2, sr[0] + tr[0]]
elif tr == []:
L = [sr[0] * 2 + tl[0], sr[0] + tl[0] * 2, sl[0] + tl[0]]
else:
L = [
sl[0] * 2 + tr[0],
sl[0] + tr[0] * 2,
sr[0] + tr[0],
sr[0] * 2 + tl[0],
sr[0] + tl[0] * 2,
sl[0] + tl[0],
]
print(min(L))
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s121716651
|
Accepted
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
# お約束
INF = float("inf")
MOD = int(1e9 + 7)
def int1(n):
return int(n) - 1
def parse(args, *params):
return tuple(p(v) for p, v in zip(params, next(args).split()))
# 二分探索
def bsr(a, v, lo=0, hi=None):
if hi == None:
hi = len(a) - 1
if hi < lo:
return lo
mi = (lo + hi) // 2
if v < a[mi]:
return bsr(a, v, lo, mi - 1)
else:
return bsr(a, v, mi + 1, hi)
# エントリーポイント
def main(args):
A, B, Q = parse(args, int, int, int)
S = list(int(next(args)) for _ in range(A))
T = list(int(next(args)) for _ in range(B))
X = tuple(int(next(args)) for _ in range(Q))
s = [-INF] + S + [INF]
t = [-INF] + T + [INF]
for x in X:
sr = bsr(s, x)
sl = sr - 1
tr = bsr(t, x)
tl = tr - 1
min_cost = INF
for st in [s[sl], s[sr]]:
for tt in [t[tl], t[tr]]:
min_cost = min(min_cost, abs(st - x) + abs(tt - st))
min_cost = min(min_cost, abs(tt - x) + abs(tt - st))
print(min_cost)
import sys
if __name__ == "__main__":
main(iter(sys.stdin.read().split("\n")))
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s211601765
|
Wrong Answer
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
import numpy as np
A, B, C = map(int, input().split())
s = np.array([int(input()) for _ in range(A)])
t = np.array([int(input()) for _ in range(B)])
x = np.array([int(input()) for _ in range(C)])
for i in x:
si = i - s
asi = list(abs(si))
min_si = min(asi)
s_idx = asi.index(min_si)
ti = i - t
ati = list(abs(ti))
min_ti = min(ati)
t_idx = ati.index(min_ti)
if si[s_idx] * ti[t_idx] < 0:
if min_si <= min_ti:
print(min_si * 2 + min_ti)
else:
print(min_ti * 2 + min_si)
else:
print(max(min_si, min_ti))
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s337280569
|
Wrong Answer
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
N = list(map(int, input().split()))
# A = [[0] * (N[0]+N[1]+N[2])]*2
A = [[10**11 + 1] * 4 for i in range((N[0] + N[1] + N[2]))]
# print(A)
for i in range(N[0]):
A[i][0] = int(input())
A[i][1] = 0
for i in range(N[0], N[0] + N[1]):
A[i][0] = int(input())
A[i][1] = 1
r = 0
for i in range(N[0] + N[1], N[0] + N[1] + N[2]):
A[i][0] = int(input())
A[i][1] = 2
A[i][2] = r
r += 1
A = sorted(A)
# print(A)
L0 = 10**11 + 1
R0 = 10**11 + 1
L1 = 10**11 + 1
R1 = 10**11 + 1
j = 0
for i in range(N[0] + N[1] + N[2]):
k = i
R0 = 10**11 + 1
R1 = 10**11 + 1
if A[i][1] == 0:
L0 = A[i][0]
if A[i][1] == 1:
L1 = A[i][0]
if A[i][1] == 2:
for j in range(k, N[0] + N[1] + N[2]):
if A[j][1] == 0:
R0 = A[j][0]
if A[j][1] == 1:
R1 = A[j][0]
if (R0 != (10**11 + 1)) & (R1 != (10**11 + 1)):
break
LA01 = abs(L0 - A[i][0])
RA01 = abs(R0 - A[i][0])
LA11 = abs(L1 - A[i][0])
RA11 = abs(R1 - A[i][0])
LA02 = LA01 * 2
RA02 = RA01 * 2
LA12 = LA11 * 2
RA12 = RA11 * 2
# print(min(max(LA01,LA11),LA01+RA12,RA01+LA12,max(RA01,RA11),max(LA01,LA11),LA02+RA11,RA02+LA11,max(RA01,RA11)))
A[i][3] = min(
max(LA01, LA11),
LA01 + RA12,
RA01 + LA12,
max(RA01, RA11),
max(LA01, LA11),
LA02 + RA11,
RA02 + LA11,
max(RA01, RA11),
)
A = sorted(A, key=lambda x: x[2])
for i in range(N[2]):
print(A[i][3])
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s335274871
|
Accepted
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
A, B, Q = map(int, input().split())
S = [-int(1e10)] + [int(input()) for _ in range(A)] + [int(2e10)]
T = [-int(1e10)] + [int(input()) for _ in range(B)] + [int(2e10)]
for _ in range(Q):
x = int(input())
seq = False
teq = False
su = A + 1
sl = 0
while su - sl > 1:
t = (su + sl) // 2
if S[t] == x:
seq = True
break
if S[t] > x:
su = t
else:
sl = t
tu = B + 1
tl = 0
while tu - tl > 1:
t = (tu + tl) // 2
if T[t] == x:
teq = True
break
if T[t] > x:
tu = t
else:
tl = t
if seq and teq:
print(0)
elif seq:
print(min(x - T[tl], T[tu] - x))
elif teq:
print(min(x - S[sl], S[su] - x))
else:
SU = S[su] - x
TU = T[tu] - x
SL = x - S[sl]
TL = x - T[tl]
print(
min(
[
max(SU, TU),
max(SL, TL),
SU * 2 + TL,
TL * 2 + SU,
TU * 2 + SL,
SL * 2 + TU,
]
)
)
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s188046333
|
Accepted
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
a, b, q = list(map(int, input().split()))
s = [int(input()) for _ in range(a)]
t = [int(input()) for _ in range(b)]
x = [int(input()) for _ in range(q)]
def bs(z, st):
l = 0
r = len(st) - 1
while r - l != 1:
m = (l + r) // 2
if st[m] <= z:
l = m
else:
r = m
return l
for xi in x:
tmps = []
tmpt = []
if xi <= s[0]:
tmps.append(s[0] - xi)
elif s[-1] <= xi:
tmps.append(s[-1] - xi)
else:
tmp = bs(xi, s)
tmps.append(s[tmp] - xi)
tmps.append(s[tmp + 1] - xi)
if xi <= t[0]:
tmpt.append(t[0] - xi)
elif t[-1] <= xi:
tmpt.append(t[-1] - xi)
else:
tmp = bs(xi, t)
tmpt.append(t[tmp] - xi)
tmpt.append(t[tmp + 1] - xi)
anss = []
for i in tmps:
for j in tmpt:
if i // abs(i) == j // abs(j):
anss.append(max(abs(i), abs(j)))
else:
maxij = max(abs(i), abs(j))
minij = min(abs(i), abs(j))
anss.append(abs(maxij + minij * 2))
anss.sort()
print(anss[0])
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s455549909
|
Runtime Error
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
a, b, q = map(int, input().split())
shrine = []
temple = []
question = []
for i in range(a):
shrine.append(int(input()))
for i in range(b):
temple.append(int(input()))
for i in range(q):
question.append(int(input()))
shrine.sort()
temple.sort()
def ans(ls, rs, lt, rt, q_i):
ans_list = []
if ls != 0 and lt != 0:
ans_list.append(abs(min(ls, lt) - q_i))
if rs != 0 and ls != 0:
ans_list.append(abs(max(rs, rt) - q_i))
if ls != 0 and rt != 0:
ans_list.append(2 * abs(ls - q_i) + abs(rt - q_i))
ans_list.append(2 * abs(rt - q_i) + abs(ls - q_i))
if lt != 0 and rs != 0:
ans_list.append(2 * abs(rs - q_i) + abs(lt - q_i))
ans_list.append(2 * abs(lt - q_i) + abs(rs - q_i))
return min(ans_list)
for q_i in question:
ls = 0
rs = 0
lt = 0
rt = 0
for n, s_i in enumerate(shrine):
if s_i > q_i:
ls = shrine[n - 1]
ts = s_i
break
for n, t_i in enumerate(temple):
if t_i > q_i:
lt = temple[n - 1]
rt = t_i
break
print(ans(ls, rs, lt, rt, q_i))
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s486913107
|
Runtime Error
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
def search(x, r):
low = 0
high = len(r) - 1
mid = (low + high) // 2
while low <= high:
rr = r[mid] - x
ll = r[mid + 1] - x
if rr * ll <= 0:
return (abs(rr), abs(ll))
elif r[mid] - x > 0:
high = mid
mid = (low + high) // 2
else:
low = mid
mid = (low + high) // 2
a, b, q = [int(i) for i in input().split()]
s = []
for i in range(a):
s.append(int(input()))
t = []
for i in range(b):
t.append(int(input()))
x = []
for i in range(q):
x.append(int(input()))
for xx in x:
s_l = float("inf")
s_r = float("inf")
if s[-1] - xx <= 0:
s_l = abs(s[-1] - xx)
elif s[0] - xx >= 0:
s_r = abs(s[0] - xx)
else:
s_l, s_r = search(xx, s)
t_l = float("inf")
t_r = float("inf")
if t[-1] - xx <= 0:
t_l = abs(t[-1] - xx)
elif t[0] - xx >= 0:
t_r = abs(t[0] - xx)
else:
t_l, t_r = search(xx, t)
# print(s_l,s_r,t_l,t_r)
# l = max(s_l,t_l)
# r = max(s_r,t_r)
if s_l <= t_l:
l = t_l
lr = s_l * 2 + t_r
else:
r = s_l
lr = t_l * 2 + s_r
if s_r <= t_r:
r = t_r
rl = s_r * 2 + t_l
else:
r = s_r
rl = t_r * 2 + s_l
ans = min(l, r, lr, rl)
print(ans)
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s108944417
|
Accepted
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
import bisect
def main():
a, b, q = map(int, input().split())
s = [0 for _ in range(a)]
for i in range(a):
s[i] = int(input())
t = [0 for _ in range(b)]
for i in range(b):
t[i] = int(input())
x = [0 for _ in range(q)]
for i in range(q):
x[i] = int(input())
ans = [10**18 for _ in range(q)]
for i in range(q):
next1 = bisect.bisect(s, x[i])
if next1 > 0:
d1 = x[i] - s[next1 - 1]
next2 = bisect.bisect(t, s[next1 - 1])
if next2 > 0:
d2 = d1 + (s[next1 - 1] - t[next2 - 1])
if d2 < ans[i]:
ans[i] = d2
if next2 < b:
d2 = d1 + (t[next2] - s[next1 - 1])
if d2 < ans[i]:
ans[i] = d2
if next1 < a:
d1 = s[next1] - x[i]
next2 = bisect.bisect(t, s[next1])
if next2 > 0:
d2 = d1 + (s[next1] - t[next2 - 1])
if d2 < ans[i]:
ans[i] = d2
if next2 < b:
d2 = d1 + (t[next2] - s[next1])
if d2 < ans[i]:
ans[i] = d2
next1 = bisect.bisect(t, x[i])
if next1 > 0:
d1 = x[i] - t[next1 - 1]
next2 = bisect.bisect(s, t[next1 - 1])
if next2 > 0:
d2 = d1 + (t[next1 - 1] - s[next2 - 1])
if d2 < ans[i]:
ans[i] = d2
if next2 < a:
d2 = d1 + (s[next2] - t[next1 - 1])
if d2 < ans[i]:
ans[i] = d2
if next1 < b:
d1 = t[next1] - x[i]
next2 = bisect.bisect(s, t[next1])
if next2 > 0:
d2 = d1 + (t[next1] - s[next2 - 1])
if d2 < ans[i]:
ans[i] = d2
if next2 < a:
d2 = d1 + (s[next2] - t[next1])
if d2 < ans[i]:
ans[i] = d2
for i in range(q):
print(ans[i])
if __name__ == "__main__":
main()
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s099820142
|
Accepted
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
import bisect
a, b, q = map(int, input().split())
s = [int(input()) for i in range(a)]
s.sort()
t = [int(input()) for i in range(b)]
t.sort()
"""
sとtのどちらを先にするか
左右どちらに走るか
の都合4パターンの最小値を選べばよい
"""
def minl(x):
# sを選択
idx = bisect.bisect_left(s, x)
ret = 3 * 10**10
if idx == 0:
first = s[0] - x
now = s[0]
idx = bisect.bisect_left(t, now)
if idx == 0:
second = t[0] - now
elif idx == b:
second = now - t[b - 1]
else:
second = min(now - t[idx - 1], t[idx] - now)
ret = min(ret, first + second)
elif idx == a:
first = x - s[a - 1]
now = s[a - 1]
idx = bisect.bisect_left(t, now)
if idx == 0:
second = t[0] - now
elif idx == b:
second = now - t[b - 1]
else:
second = min(now - t[idx - 1], t[idx] - now)
ret = min(ret, first + second)
else:
for first_g in [s[idx - 1], s[idx]]:
first = abs(first_g - x)
now = first_g
idx = bisect.bisect_left(t, now)
if idx == 0:
second = t[0] - now
elif idx == b:
second = now - t[b - 1]
else:
second = min(now - t[idx - 1], t[idx] - now)
ret = min(ret, first + second)
# tを選択
idx = bisect.bisect_left(t, x)
if idx == 0:
first = t[0] - x
now = t[0]
idx = bisect.bisect_left(s, now)
if idx == 0:
second = s[0] - now
elif idx == a:
second = now - s[a - 1]
else:
second = min(now - s[idx - 1], s[idx] - now)
ret = min(ret, first + second)
elif idx == b:
first = x - t[b - 1]
now = t[b - 1]
idx = bisect.bisect_left(s, now)
if idx == 0:
second = s[0] - now
elif idx == a:
second = now - s[a - 1]
else:
second = min(now - s[idx - 1], s[idx] - now)
ret = min(ret, first + second)
else:
for first_g in [t[idx - 1], t[idx]]:
first = abs(first_g - x)
now = first_g
idx = bisect.bisect_left(s, now)
if idx == 0:
second = s[0] - now
elif idx == a:
second = now - s[a - 1]
else:
second = min(now - s[idx - 1], s[idx] - now)
ret = min(ret, first + second)
return ret
for i in range(q):
x = int(input())
print(minl(x))
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s956679551
|
Accepted
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
# coding: utf-8
# https://atcoder.jp/contests/abc119
def leq_search(xs, x, s, t):
# x以下で最大のindex
if t - s <= 3:
res = 0
for i in range(s, t):
if xs[i] <= x:
res = i
return res
i = (s + t) // 2
if xs[i] <= x:
return leq_search(xs, x, i, t)
else:
return leq_search(xs, x, s, i)
def geq_search(xs, x, s, t):
# x以上で最小のindex
if t - s <= 3:
res = 0
for i in range(t - 1, s - 1, -1):
if xs[i] >= x:
res = i
return res
i = (s + t) // 2
if xs[i] >= x:
return geq_search(xs, x, s, i + 1)
else:
return geq_search(xs, x, i + 1, t)
def nearest_search(xs, x, s, t):
# xにもっとも近いindex
if t - s <= 3:
res = s
for i in range(s, t):
if abs(x - xs[i]) < abs(x - xs[res]):
res = i
return res
i = (s + t) // 2
if xs[i] <= x:
return nearest_search(xs, x, i, t)
else:
return nearest_search(xs, x, s, i + 1)
def main():
A, B, Q = map(int, input().split())
s = [None] * A
t = [None] * B
xs = [None] * Q
for i in range(A):
s[i] = int(input())
for i in range(B):
t[i] = int(input())
for i in range(Q):
xs[i] = int(input())
S, T = 0, 1
st = [[s[i], S, i] for i in range(A)]
st.extend([[t[i], T, i] for i in range(B)])
# st = [[s[i], S, i] for i in range(A)].extend([[t[i], T, i] for i in range(B)])
st = sorted(st, key=lambda x: x[0])
st_retrieval = [x[0] for x in st]
# 各神社から最寄りの寺を求める
s_near_t = [None] * A
for i in range(A):
s_near_t[i] = t[nearest_search(t, s[i], 0, B)]
# 各寺から最寄りの神社を求める
t_near_s = [None] * B
for i in range(B):
t_near_s[i] = s[nearest_search(s, t[i], 0, A)]
for x in xs:
# left
near_i = leq_search(st_retrieval, x, 0, A + B)
val, mark, i = st[near_i]
# val: 座標
# mark: S or T
# i: 元の列 s or t の中での index
cand1 = abs(val - x)
if mark == S:
near_t = s_near_t[i]
cand1 += abs(near_t - val)
else:
near_s = t_near_s[i]
cand1 += abs(near_s - val)
# right
near_i = geq_search(st_retrieval, x, 0, A + B)
val, mark, i = st[near_i]
# val: 座標
# mark: S or T
# i: 元の列 s or t の中での index
cand2 = abs(val - x)
if mark == S:
near_t = s_near_t[i]
cand2 += abs(near_t - val)
else:
near_s = t_near_s[i]
cand2 += abs(near_s - val)
print(min(cand1, cand2))
main()
# print(main())
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s835238403
|
Accepted
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
import bisect
SList = []
TList = []
QList = []
minpos = -1 * (10**10)
maxpos = 10 * (10**10)
def ans(x):
index = bisect.bisect_left(SList, x)
s = [SList[index - 1], SList[index]]
index = bisect.bisect_left(TList, x)
t = [TList[index - 1], TList[index]]
min1 = abs(x - s[0]) + abs(t[0] - s[0])
diff = abs(x - s[0]) + abs(t[1] - s[0])
if diff < min1:
min1 = diff
diff = abs(x - s[1]) + abs(t[0] - s[1])
if diff < min1:
min1 = diff
diff = abs(x - s[1]) + abs(t[1] - s[1])
if diff < min1:
min1 = diff
diff = abs(x - t[0]) + abs(s[0] - t[0])
if diff < min1:
min1 = diff
diff = abs(x - t[0]) + abs(s[1] - t[0])
if diff < min1:
min1 = diff
diff = abs(x - t[1]) + abs(s[0] - t[1])
if diff < min1:
min1 = diff
diff = abs(x - t[1]) + abs(s[1] - t[1])
if diff < min1:
min1 = diff
return min1
A, B, Q = map(int, input().split())
for _ in range(A):
SList.append(int(input()))
for _ in range(B):
TList.append(int(input()))
for _ in range(Q):
QList.append(int(input()))
SList.insert(0, minpos)
SList.append(maxpos)
TList.insert(0, minpos * 2)
TList.append(maxpos * 2)
for q in QList:
print(ans(q))
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s485561596
|
Accepted
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
# -*- coding: utf-8 -*-
A, B, Q = list(map(int, input().rstrip().split()))
s_list = [-(10**11)] + [int(input().strip()) for _ in range(A)] + [10**11]
t_list = [-(10**11)] + [int(input().strip()) for _ in range(B)] + [10**11]
x_list = [int(input().strip()) for _ in range(Q)]
# -----
# x_dic={ x : [a1,a2,b1,b2]}
# 距離xに対して、最も近い神社・寺のindexを保存
# a1(xより西の最寄りの神社)、a2(xより東の最寄りの神社)
# b1(xより西の最寄りの寺)、 b2(xより東の最寄りの寺)
x_dic = {}
x_sort = sorted(x_list)
i_x = 0
for i in range(len(s_list) - 1):
while s_list[i] <= x_sort[i_x] <= s_list[i + 1]:
x_dic[x_sort[i_x]] = [i, (i + 1)]
i_x += 1
if i_x > len(x_sort) - 1:
break
if i_x > len(x_sort) - 1:
break
i_x = 0
for i in range(len(t_list) - 1):
while t_list[i] <= x_sort[i_x] <= t_list[i + 1]:
x_dic[x_sort[i_x]].extend([i, (i + 1)])
i_x += 1
if i_x > len(x_sort) - 1:
break
if i_x > len(x_sort) - 1:
break
for x in x_list:
dist_min = 10**11
for s in x_dic[x][0:2]:
for t in x_dic[x][2:4]:
diff1 = abs(s_list[s] - x) + abs(t_list[t] - s_list[s])
diff2 = abs(t_list[t] - x) + abs(s_list[s] - t_list[t])
dist_min = min(dist_min, diff1, diff2)
print(dist_min)
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s099990488
|
Wrong Answer
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
a, b, q = [int(i) for i in input().split(" ")]
s = [0] * a
t = [0] * b
x = [[0, 0]] * q
# a, b, q = [2, 3, 4]
# s = [100, 600]
# t = [400, 900, 1000]
# x = [[0, 150], [1, 2000], [2, 899], [3, 799]]
sd = 0
td = 0
for i in range(0, a):
s[i] = int(input())
for i in range(0, b):
t[i] = int(input())
for i in range(0, q):
x[i] = [i, int(input())]
x = sorted(x, key=lambda k: k[1])
ans = [[0, 0]] * q
def sdd(i, x):
if i < 0 or i >= a:
return 10**10 + 1
else:
return abs(s[i] - x)
def tdd(i, x):
if i < 0 or i >= b:
return 10**10 + 1
else:
return abs(t[i] - x)
for j in range(0, q):
bf = False
for i in range(sd, a):
if s[i] > x[j][1]:
sd = i
bf = True
break
if not bf:
sd = a
bf = False
for i in range(td, b):
if t[i] > x[j][1]:
td = i
bf = True
break
if not bf:
td = b
xj = x[j][1]
a1 = min(max(sdd(sd - 1, xj), tdd(td - 1, xj)), max(sdd(sd, xj), tdd(td, xj)))
a2 = min(
2 * sdd(sd - 1, xj) + tdd(td, xj),
2 * tdd(td - 1, xj) + sdd(sd, xj),
sdd(sd - 1, xj) + 2 * tdd(td, xj),
tdd(td - 1, xj) + 2 * sdd(sd, xj),
)
ans[j] = [x[j][0], min(a1, a2)]
ans = sorted(ans, key=lambda k: k[0])
for i in range(0, q):
print(ans[i][1])
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s035441136
|
Wrong Answer
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
a, b, q = map(int, input().split())
s = [int(input()) for _ in range(a)]
t = [int(input()) for _ in range(b)]
x = [int(input()) for _ in range(q)]
s.sort()
t.sort()
import bisect
# a=[0,2,3,4,67,8]
# a.sort()
for item in x:
ss = bisect.bisect_left(s, item)
tmp = []
if ss > 0:
tmp.append(s[ss - 1])
if ss < len(s):
tmp.append(s[ss])
tmp2 = []
tt = bisect.bisect_left(t, item)
if tt > 0:
tmp2.append(t[tt - 1])
if tt < len(t):
tmp2.append(t[tt])
result = 10**9
for item2 in tmp:
for item3 in tmp2:
# print(item,item2,item3)
result = min(
result,
abs(item - item3) + abs(item3 - item2),
abs(item - item2) + abs(item3 - item2),
)
print(result)
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s058925907
|
Runtime Error
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
import bisect
A, B, Q = [int(e) for e in input().split()]
ss = [int(input()) for _ in range(A)]
tt = [int(input()) for _ in range(B)]
xx = [int(input()) for _ in range(Q)]
for x in xx:
buf = []
# s right, t
idx_s_right = min(bisect.bisect_left(ss, x), A - 1)
s_right = ss[idx_s_right]
idx_st_right = min(bisect.bisect_left(tt, s_right), B - 1)
idx_st_left = max(0, idx_st_right - 1)
t_right = tt[idx_st_right]
t_left = tt[idx_st_left]
buf.append(abs(s_right - x) + abs(t_right - s_right))
buf.append(abs(s_right - x) + abs(t_left - s_right))
s_right = None
t_right = None
s_left = None
t_left = None
# s left, t
idx_s_left = max(0, idx_s_right - 1)
if idx_s_left != idx_s_right:
s_left = ss[idx_s_left]
idx_st_right = min(bisect.bisect_left(tt, s_left), B - 1)
idx_st_left = max(0, idx_st_right - 1)
t_right = tt[idx_st_right]
t_left = tt[idx_st_left]
buf.append(abs(s_left - x) + abs(t_right - s_left))
buf.append(abs(s_left - x) + abs(t_left - s_left))
s_right = None
t_right = None
s_left = None
t_left = None
# t right, r
idx_t_right = min(bisect.bisect_left(tt, x), B - 1)
t_right = tt[idx_t_right]
idx_ts_right = min(bisect.bisect_left(ss, t_right), A - 1)
idx_ts_left = max(0, idx_ts_right - 1)
s_right = ss[idx_ts_right]
s_left = ss[idx_ts_left]
buf.append(abs(t_right - x) + abs(s_right - t_right))
buf.append(abs(t_right - x) + abs(s_left - t_right))
s_right = None
t_right = None
s_left = None
t_left = None
# s left, t
idx_t_left = max(0, idx_t_right - 1)
if idx_t_left != idx_t_right:
t_left = ss[idx_t_left]
idx_ts_right = min(bisect.bisect_left(ss, t_left), A - 1)
idx_ts_left = max(0, idx_ts_right - 1)
s_right = tt[idx_ts_right]
s_left = tt[idx_ts_left]
buf.append(abs(t_left - x) + abs(s_right - t_left))
buf.append(abs(t_left - x) + abs(s_left - t_left))
print(min(buf))
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s093014370
|
Wrong Answer
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
from bisect import bisect_left
abq = list(map(int, input().split()))
s = sorted([int(input()) for i in range(abq[0])])
t = sorted([int(input()) for i in range(abq[1])])
x = [int(input()) for i in range(abq[2])]
for i in range(abq[2]):
s_r_i = bisect_left(s, x[i])
if s_r_i < len(s):
s_r = s[s_r_i]
else:
s_r = None
t_r_i = bisect_left(t, x[i])
if t_r_i < len(t):
t_r = t[t_r_i]
else:
t_r = None
s_l_i = bisect_left(s, x[i]) - 1
if 0 <= s_l_i < len(s):
s_l = s[s_l_i]
else:
s_l = None
t_l_i = bisect_left(t, x[i]) - 1
if 0 <= t_l_i < len(t):
t_l = t[t_l_i]
else:
t_l = None
if s_r != None and t_r != None:
route1 = max(abs(x[i] - s_r), abs(x[i] - t_r))
else:
route1 = 10**10
if s_r != None and t_l != None:
route2 = min(abs(x[i] - s_r), abs(x[i] - t_l)) * 2 + max(
abs(x[i] - s_r), abs(x[i] - t_l)
)
else:
route2 = 10**10
if s_l != None and t_r != None:
route3 = min(abs(x[i] - s_l), abs(x[i] - t_r)) * 2 + max(
abs(x[i] - s_l), abs(x[i] - t_r)
)
else:
route3 = 10**10
if s_l != None and t_l != None:
route4 = max(abs(x[i] - s_l), abs(x[i] - t_l))
else:
route4 = 10**10
print(min(route1, route2, route3, route4))
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s948122806
|
Wrong Answer
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
A, B, Q = map(int, input().split())
s = [0] * A
t = [0] * B
for i in range(A):
s[i] = int(input())
for i in range(B):
t[i] = int(input())
INF = 10**12
for _ in range(Q):
x = int(input())
flg_sh = 0
if x <= s[0]:
dis_sh_r = s[0] - x
dis_sh_l = INF
flg = -1
elif x > s[-1]:
dis_sh_l = x - s[-1]
dis_sh_r = INF
flg = 1
else:
flg_sh = 1
for j in range(A):
if x > s[j]:
dis_sh_l = x - s[j]
dis_sh_r = s[j + 1] - x
break
flg_te = 0
if x <= t[0]:
dis_te_r = t[0] - x
dis_te_l = INF
flg = -1
elif x > t[-1]:
dis_te_l = x - t[-1]
dis_te_r = INF
flg = 1
else:
flg_te = 1
for j in range(A):
if x > t[j]:
dis_te_l = x - t[j]
dis_te_r = t[j + 1] - x
break
path_l = max(dis_sh_l, dis_te_l)
path_r = max(dis_sh_r, dis_te_r)
if flg_sh and flg_te:
if (t[j] - s[j]) * (t[j + 1] - s[j + 1]) > 0:
l_min, r_min = min(dis_sh_l, dis_te_l), min(dis_sh_r, dis_te_r)
path_m = l_min + r_min + min(l_min, r_min)
else:
path_m = dis_sh_l + dis_te_r + min(dis_sh_l, dis_te_r)
path_m = min(path_m, dis_sh_r + dis_te_l + min(dis_sh_r, dis_te_l))
elif flg_sh and not flg_te:
path_m = min(dis_te_l, dis_te_r)
if flg == -1:
path_m += min(dis_sh_l, path_m) + dis_sh_l
else:
path_m += min(dis_sh_r, path_m) + dis_sh_r
elif flg_te and not flg_sh:
path_m = min(dis_sh_l, dis_sh_r)
if flg == -1:
path_m += min(dis_te_l, path_m) + dis_te_l
else:
path_m += min(dis_te_r, path_m) + dis_te_r
else:
a, b = min(dis_sh_l, dis_sh_r), min(dis_te_l, dis_te_r)
path_m = a + b + min(a, b)
ans = min(path_l, path_r)
ans = min(ans, path_m)
print(ans)
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s602660029
|
Runtime Error
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
if __name__ == "__main__":
A, B, Q = map(int, input().split())
s_list = [int(input()) for i in range(A)]
t_list = [int(input()) for i in range(B)]
x_list = [int(input()) for i in range(Q)]
for xi in x_list:
distance_ti_right_xi = [ti - xi for ti in t_list if ti >= xi]
distance_ti_left_xi = [xi - ti for ti in t_list if ti <= xi]
distance_si_right_xi = [si - xi for si in s_list if si >= xi]
distance_si_left_xi = [xi - si for si in s_list if si <= xi]
first_move = min(
distance_si_left_xi,
distance_si_right_xi,
distance_ti_left_xi,
distance_ti_right_xi,
)
if first_move == distance_ti_left_xi or first_move == distance_si_left_xi:
first_move = -1 * first_move
xi += first_move
if (
abs(first_move) == distance_si_left_xi
or abs(first_move) == distance_si_right_xi
):
distance_ti_right_xi = [ti - xi for ti in t_list if ti >= xi]
distance_ti_left_xi = [xi - ti for ti in t_list if ti <= xi]
second_move = min(distance_ti_left_xi, distance_ti_right_xi)
if (
abs(first_move) == distance_ti_left_xi
or abs(first_move) == distance_ti_right_xi
):
distance_si_right_xi = [si - xi for si in s_list if si >= xi]
distance_si_left_xi = [xi - si for si in s_list if si <= xi]
second_move = min(distance_si_left_xi, distance_si_right_xi)
answer = abs(first_move) + abs(second_move)
print(answer)
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s365856431
|
Wrong Answer
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
a, b, q = map(int, input().split())
s = [int(input()) for i in range(a)]
t = [int(input()) for i in range(b)]
x = [int(input()) for i in range(q)]
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
Print Q lines. The i-th line should contain the answer to the i-th query.
* * *
|
s973891518
|
Runtime Error
|
p03112
|
Input is given from Standard Input in the following format:
A B Q
s_1
:
s_A
t_1
:
t_B
x_1
:
x_Q
|
n = int(input())
|
Statement
Along a road running in an east-west direction, there are A shrines and B
temples. The i-th shrine from the west is located at a distance of s_i meters
from the west end of the road, and the i-th temple from the west is located at
a distance of t_i meters from the west end of the road.
Answer the following Q queries:
* Query i (1 \leq i \leq Q): If we start from a point at a distance of x_i meters from the west end of the road and freely travel along the road, what is the minimum distance that needs to be traveled in order to visit one shrine and one temple? (It is allowed to pass by more shrines and temples than required.)
|
[{"input": "2 3 4\n 100\n 600\n 400\n 900\n 1000\n 150\n 2000\n 899\n 799", "output": "350\n 1400\n 301\n 399\n \n\nThere are two shrines and three temples. The shrines are located at distances\nof 100, 600 meters from the west end of the road, and the temples are located\nat distances of 400, 900, 1000 meters from the west end of the road.\n\n * Query 1: If we start from a point at a distance of 150 meters from the west end of the road, the optimal move is first to walk 50 meters west to visit a shrine, then to walk 300 meters east to visit a temple.\n * Query 2: If we start from a point at a distance of 2000 meters from the west end of the road, the optimal move is first to walk 1000 meters west to visit a temple, then to walk 400 meters west to visit a shrine. We will pass by another temple on the way, but it is fine.\n * Query 3: If we start from a point at a distance of 899 meters from the west end of the road, the optimal move is first to walk 1 meter east to visit a temple, then to walk 300 meters west to visit a shrine.\n * Query 4: If we start from a point at a distance of 799 meters from the west end of the road, the optimal move is first to walk 199 meters west to visit a shrine, then to walk 200 meters west to visit a temple.\n\n* * *"}, {"input": "1 1 3\n 1\n 10000000000\n 2\n 9999999999\n 5000000000", "output": "10000000000\n 10000000000\n 14999999998\n \n\nThe road is quite long, and we may need to travel a distance that does not fit\ninto a 32-bit integer."}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s472910503
|
Accepted
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
*a, b = map(int, input().split())
print("NYoe s"[sum(a) >= b :: 2])
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s834371771
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a,b,c = map(int, input().split())
print("Yes") if c =< a+b else print("No")
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s589059546
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a,b,c=map(int,input.split())
if a+b=>c:
print('Yes')
else:
print('No')
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s110108092
|
Accepted
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
# __author__ = "tatuo"
# __date__ = "$Mar 3, 2018 12:34:20 PM$"
import math
import re
import sys
def getinputdata():
# 配列初期化
array_result = []
data = input()
array_result.append(data.split(" "))
flg = 1
try:
while flg:
data = input()
array_temp = []
if data != "":
array_result.append(data.split(" "))
flg = 1
else:
flg = 0
finally:
return array_result
arr_data = getinputdata()
a = int(arr_data[0][0])
b = int(arr_data[0][1])
c = int(arr_data[0][2])
if a + b >= c:
print("Yes")
else:
print("No")
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s617013789
|
Accepted
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
import sys
## io ##
def IS():
return sys.stdin.readline().rstrip()
def II():
return int(IS())
def MII():
return list(map(int, IS().split()))
def MIIZ():
return list(map(lambda x: x - 1, MII()))
## dp ##
def DD2(d1, d2, init=0):
return [[init] * d2 for _ in range(d1)]
def DD3(d1, d2, d3, init=0):
return [DD2(d2, d3, init) for _ in range(d1)]
## math ##
def to_bin(x: int) -> str:
return format(x, "b") # rev => int(res, 2)
def to_oct(x: int) -> str:
return format(x, "o") # rev => int(res, 8)
def to_hex(x: int) -> str:
return format(x, "x") # rev => int(res, 16)
MOD = 10**9 + 7
def divc(x, y) -> int:
return -(-x // y)
def divf(x, y) -> int:
return x // y
def gcd(x, y):
while y:
x, y = y, x % y
return x
def lcm(x, y):
return x * y // gcd(x, y)
def enumerate_divs(n):
"""Return a tuple list of divisor of n"""
return [(i, n // i) for i in range(1, int(n**0.5) + 1) if n % i == 0]
def get_primes(MAX_NUM=10**3):
"""Return a list of prime numbers n or less"""
is_prime = [True] * (MAX_NUM + 1)
is_prime[0] = is_prime[1] = False
for i in range(2, int(MAX_NUM**0.5) + 1):
if not is_prime[i]:
continue
for j in range(i * 2, MAX_NUM + 1, i):
is_prime[j] = False
return [i for i in range(MAX_NUM + 1) if is_prime[i]]
## libs ##
from itertools import accumulate as acc
from collections import deque, Counter
from heapq import heapify, heappop, heappush
from bisect import bisect_left
# ======================================================#
def main():
a, b, c = MII()
if a + b >= c:
print("Yes")
else:
print("No")
if __name__ == "__main__":
main()
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s219914652
|
Accepted
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
import math
import queue
import bisect
import heapq
import time
import itertools
mod = int(1e9 + 7)
def swap(a, b):
return (b, a)
def my_round(a, dig=0):
p = 10**dig
return (a * p * 2 + 1) // 2 / p
def gcd(a, b): # 最大公約数
if a < b:
a, b = swap(a, b)
if b == 0:
return a
else:
return gcd(b, a % b)
def lcm(a, b): # 最小公倍数
return a / gcd(a, b) * b
def divisors(a): # 約数列挙
divisors = []
for i in range(1, int(a**0.5) + 1):
if a % i == 0:
divisors.append(i)
if i != a // i:
divisors.append(a // i)
return divisors
def is_prime(a): # 素数判定
if a < 2:
return False
elif a == 2:
return True
elif a % 2 == 0:
return False
sqrt_num = int(a**0.5)
for i in range(3, sqrt_num + 1, 2):
if a % i == 0:
return False
return True
def prime_num(a): # 素数列挙
pn = [2]
for i in range(3, int(a**0.5), 2):
prime = True
for j in pn:
if i % j == 0:
prime = False
break
if prime:
pn.append(i)
return pn
def prime_fact(a): # 素因数分解
sqrt = math.sqrt(a)
res = []
i = 2
if is_prime(a):
res.append(a)
else:
while a != 1:
while a % i == 0:
res.append(i)
a //= i
i += 1
return res
def main():
a, b, c = map(int, input().split())
if a + b >= c:
print("Yes")
else:
print("No")
return
if __name__ == "__main__":
main()
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s439297065
|
Accepted
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
###############################################################################
from sys import stdout
from bisect import bisect_left as binl
from copy import copy, deepcopy
from collections import defaultdict
mod = 1
def intin():
input_tuple = input().split()
if len(input_tuple) <= 1:
return int(input_tuple[0])
return tuple(map(int, input_tuple))
def intina():
return [int(i) for i in input().split()]
def intinl(count):
return [intin() for _ in range(count)]
def modadd(x, y):
global mod
return (x + y) % mod
def modmlt(x, y):
global mod
return (x * y) % mod
def lcm(x, y):
while y != 0:
z = x % y
x = y
y = z
return x
def combination(x, y):
assert x >= y
if y > x // 2:
y = x - y
ret = 1
for i in range(0, y):
j = x - i
i = i + 1
ret = ret * j
ret = ret // i
return ret
def get_divisors(x):
retlist = []
for i in range(1, int(x**0.5) + 3):
if x % i == 0:
retlist.append(i)
retlist.append(x // i)
return retlist
def get_factors(x):
retlist = []
for i in range(2, int(x**0.5) + 3):
while x % i == 0:
retlist.append(i)
x = x // i
retlist.append(x)
return retlist
def make_linklist(xylist):
linklist = {}
for a, b in xylist:
linklist.setdefault(a, [])
linklist.setdefault(b, [])
linklist[a].append(b)
linklist[b].append(a)
return linklist
def calc_longest_distance(linklist, v=1):
distance_list = {}
distance_count = 0
distance = 0
vlist_previous = []
vlist = [v]
nodecount = len(linklist)
while distance_count < nodecount:
vlist_next = []
for v in vlist:
distance_list[v] = distance
distance_count += 1
vlist_next.extend(linklist[v])
distance += 1
vlist_to_del = vlist_previous
vlist_previous = vlist
vlist = list(set(vlist_next) - set(vlist_to_del))
max_distance = -1
max_v = None
for v, distance in distance_list.items():
if distance > max_distance:
max_distance = distance
max_v = v
return (max_distance, max_v)
def calc_tree_diameter(linklist, v=1):
_, u = calc_longest_distance(linklist, v)
distance, _ = calc_longest_distance(linklist, u)
return distance
class UnionFind:
def __init__(self, n):
self.parent = [i for i in range(n)]
def root(self, i):
if self.parent[i] == i:
return i
self.parent[i] = self.root(self.parent[i])
return self.parent[i]
def unite(self, i, j):
rooti = self.root(i)
rootj = self.root(j)
if rooti == rootj:
return
if rooti < rootj:
self.parent[rootj] = rooti
else:
self.parent[rooti] = rootj
def same(self, i, j):
return self.root(i) == self.root(j)
###############################################################################
def main():
a, b, c = intin()
if a + b >= c:
print("Yes")
else:
print("No")
if __name__ == "__main__":
main()
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s379811484
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
def main():
import sys
input = sys.stdin.readline
import bisect
import numpy as np
n = int(input())
a = list(map(int, input().split()))
b = list(map(int, input().split()))
x = max(max(a), max(b)).bit_length() + 1
b = np.array(b, dtype=np.int32)
ans = 0
for i in range(1, x + 1):
d = sorted(b & (1 << i) - 1)
t = 1 << (i - 1)
anstmp = 0
for j in range(n):
y = a[j] & (1 << i) - 1
t1 = np.searchsorted(d, t - y)
t2 = np.searchsorted(d, 2 * t - y)
t3 = np.searchsorted(d, 3 * t - y)
anstmp += (t2 - t1) + (n - t3)
if anstmp % 2:
ans += t
print(ans)
main()
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s435859235
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
blue = int(input())
b = []
r = []
count = []
for i in range(blue):
b.append(input())
red = int(input())
for i in range(red):
r.append(input())
for i in b:
count.append(b.count(i) - r.count(i))
if max(count) < 0:
print(0)
else:
print(max(count))
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s545381371
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
n = int(input())
reds = sorted([list(map(int,input().split())) for i in range(n)] key = lambda reds: -reds[1])
blues = sorted([list(map(int,input().split())) for i in range(n)])
res = 0
for c,d in blues:
for a,b in reds:
if a<c and b<d:
reds.remove([a,b])
res+=1
break
print(res)
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s124792732
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a=int(input());
b=int(input());
c=int(input());
if(a+b>c) print("Yes");
else print("No");
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s033167554
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
import sys
def spam(ab, cd, count=0):
ab = ab[:]
cd = cd[:]
for x in ab:
for y in cd:
if x[0] < y[0] and x[1] < y[1]:
ab.remove(x)
cd.remove(y)
return spam(ab, cd, count + 1)
return count
def main():
N = int(sys.stdin.readline())
ab = [[int(x) for x in sys.stdin.readline().split()] for _ in range(N)]
cd = [[int(x) for x in sys.stdin.readline().split()] for _ in range(N)]
ab1 = sorted(ab, key=lambda x: (x[0], x[1]))
cd1 = sorted(cd, key=lambda x: (x[0], x[1]))
ab2 = sorted(ab, key=lambda x: (x[1], x[0]))
cd2 = sorted(cd, key=lambda x: (x[1], x[0]))
print(max([spam(ab1, cd1), spam(ab2, cd2)]))
if __name__ == "__main__":
main()
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s005477892
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a,b,c=map(int,input().split())
print('Yes':if a+b>=c,else:'No')
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s934286668
|
Wrong Answer
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a, b, x = map(int, input().split())
print("Yes" if a + b > x else "No")
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s956912987
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a,b,c=map(int,input().split())
print('No'ifa+b<c else'Yes')
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s157368462
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a,b,c=map(int,input().split())
if("Yes" if a+b>=c else "No")
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s490885584
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
50 100 120
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s901811481
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a,b,c=map(int,input().split())
print("Yes"a+b>=c else"No")
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s346321599
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a=map(int,input().split())
print("YES" if a[0)+a[1]>=a[3] else "NO")
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s727544582
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
19 123 143
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s169732693
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
x = [int(input()) for i in range(4)]
print(min(x[0], x[1]) + min(x[2], x[3]))
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s961536991
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a=map(int, input().split)
print("YES" if a[0)+a[1]>=a[3] else "NO")
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s894554952
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
a, b, c = map(int, input().split())
if a+b >= c
print("Yes")
else:
print("No")
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
If Takahashi can buy the toy, print `Yes`; if he cannot, print `No`.
* * *
|
s437388935
|
Runtime Error
|
p03407
|
Input is given from Standard Input in the following format:
A B C
|
A,B,C = map(int,input().split())
if A + 2B <= C:
print("Yes")
else:
print("No")
|
Statement
An elementary school student Takahashi has come to a variety store.
He has two coins, A-yen and B-yen coins (yen is the currency of Japan), and
wants to buy a toy that costs C yen. Can he buy it?
Note that he lives in Takahashi Kingdom, and may have coins that do not exist
in Japan.
|
[{"input": "50 100 120", "output": "Yes\n \n\nHe has 50 + 100 = 150 yen, so he can buy the 120-yen toy.\n\n* * *"}, {"input": "500 100 1000", "output": "No\n \n\nHe has 500 + 100 = 600 yen, but he cannot buy the 1000-yen toy.\n\n* * *"}, {"input": "19 123 143", "output": "No\n \n\nThere are 19-yen and 123-yen coins in Takahashi Kingdom, which are rather hard\nto use.\n\n* * *"}, {"input": "19 123 142", "output": "Yes"}]
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.