output_description
stringlengths 15
956
| submission_id
stringlengths 10
10
| status
stringclasses 3
values | problem_id
stringlengths 6
6
| input_description
stringlengths 9
2.55k
| attempt
stringlengths 1
13.7k
| problem_description
stringlengths 7
5.24k
| samples
stringlengths 2
2.72k
|
|---|---|---|---|---|---|---|---|
Print the total distance traveled by Takahashi throughout the game when
Takahashi and Aoki acts as above. It is guaranteed that K is always an integer
when L_i,R_i are integers.
* * *
|
s111005819
|
Accepted
|
p03333
|
Input is given from Standard Input in the following format:
N
L_1 R_1
:
L_N R_N
|
import sys
sys.setrecursionlimit(10**7) # 再帰関数の上限,10**5以上の場合python
import math
from copy import copy, deepcopy
from copy import deepcopy as dcp
from operator import itemgetter
from bisect import bisect_left, bisect, bisect_right # 2分探索
# bisect_left(l,x), bisect(l,x)#aはソート済みである必要あり。aの中からx未満の要素数を返す。rightだと以下
from collections import deque, defaultdict
# deque(l), pop(), append(x), popleft(), appendleft(x)
# q.rotate(n)で → にn回ローテート
from collections import Counter # 文字列を個数カウント辞書に、
# S=Counter(l),S.most_common(x),S.keys(),S.values(),S.items()
from itertools import accumulate, combinations, permutations, product # 累積和
# list(accumulate(l))
from heapq import heapify, heappop, heappush
# heapify(q),heappush(q,a),heappop(q) #q=heapify(q)としないこと、返り値はNone
from functools import reduce, lru_cache # pypyでもうごく
# @lru_cache(maxsize = None)#maxsizeは保存するデータ数の最大値、2**nが最も高効率
from decimal import Decimal
def input():
x = sys.stdin.readline()
return x[:-1] if x[-1] == "\n" else x
def printe(*x):
print("## ", *x, file=sys.stderr)
def printl(li):
_ = print(*li, sep="\n") if li else None
def argsort(s, return_sorted=False):
inds = sorted(range(len(s)), key=lambda k: s[k])
if return_sorted:
return inds, [s[i] for i in inds]
return inds
def alp2num(c, cap=False):
return ord(c) - 97 if not cap else ord(c) - 65
def num2alp(i, cap=False):
return chr(i + 97) if not cap else chr(i + 65)
def matmat(A, B):
K, N, M = len(B), len(A), len(B[0])
return [
[sum([(A[i][k] * B[k][j]) for k in range(K)]) for j in range(M)]
for i in range(N)
]
def matvec(M, v):
N, size = len(v), len(M)
return [sum([M[i][j] * v[j] for j in range(N)]) for i in range(size)]
def T(M):
n, m = len(M), len(M[0])
return [[M[j][i] for j in range(n)] for i in range(m)]
def binr(x):
return bin(x)[2:]
def bitcount(x): # xは64bit整数
x = x - ((x >> 1) & 0x5555555555555555)
x = (x & 0x3333333333333333) + ((x >> 2) & 0x3333333333333333)
x = (x + (x >> 4)) & 0x0F0F0F0F0F0F0F0F
x += x >> 8
x += x >> 16
x += x >> 32
return x & 0x7F
def main():
# C - Interval Game
mod = 1000000007
# w.sort(key=itemgetter(1),reverse=True) #二個目の要素で降順並び替え
N = int(input())
# N, K = map(int, input().split())
# A = tuple(map(int, input().split())) #1行ベクトル
# L = tuple(int(input()) for i in range(N)) #改行ベクトル
S = tuple(tuple(map(int, input().split())) for i in range(N)) # 改行行列
base = N
ls = []
rs = []
for i, (l, r) in enumerate(S):
heappush(ls, -l * base + i)
heappush(rs, r * base + i)
dset = set()
cur = 0
tot = 0
f = 0
lsc = ls.copy()
rsc = rs.copy()
while ls and rs:
while ls:
l, i = divmod(heappop(ls), base)
l *= -1
if i in dset:
dset.remove(i)
elif cur < l:
tot += l - cur
dset.add(i)
cur = l
break
else:
f = 1
break
if f:
break
while rs:
r, i = divmod(heappop(rs), base)
if i in dset:
dset.remove(i)
elif cur > r:
tot += cur - r
cur = r
dset.add(i)
break
else:
f = 1
break
if f:
break
tot += abs(cur)
ls = lsc
rs = rsc
dset = set()
cur = 0
tot2 = 0
f = 0
while ls and rs:
while rs:
r, i = divmod(heappop(rs), base)
if i in dset:
dset.remove(i)
elif cur > r:
tot2 += cur - r
cur = r
dset.add(i)
break
else:
f = 1
break
if f:
break
while ls:
l, i = divmod(heappop(ls), base)
l *= -1
if i in dset:
dset.remove(i)
elif cur < l:
tot2 += l - cur
dset.add(i)
cur = l
break
else:
f = 1
break
if f:
break
tot2 += abs(cur)
print(max(tot, tot2))
if __name__ == "__main__":
main()
|
Statement
Takahashi and Aoki will play a game with a number line and some segments.
Takahashi is standing on the number line and he is initially at coordinate 0.
Aoki has N segments. The i-th segment is [L_i,R_i], that is, a segment
consisting of points with coordinates between L_i and R_i (inclusive).
The game has N steps. The i-th step proceeds as follows:
* First, Aoki chooses a segment that is still not chosen yet from the N segments and tells it to Takahashi.
* Then, Takahashi walks along the number line to some point within the segment chosen by Aoki this time.
After N steps are performed, Takahashi will return to coordinate 0 and the
game ends.
Let K be the total distance traveled by Takahashi throughout the game. Aoki
will choose segments so that K will be as large as possible, and Takahashi
walks along the line so that K will be as small as possible. What will be the
value of K in the end?
|
[{"input": "3\n -5 1\n 3 7\n -4 -2", "output": "10\n \n\nOne possible sequence of actions of Takahashi and Aoki is as follows:\n\n * Aoki chooses the first segment. Takahashi moves from coordinate 0 to -4, covering a distance of 4.\n * Aoki chooses the third segment. Takahashi stays at coordinate -4.\n * Aoki chooses the second segment. Takahashi moves from coordinate -4 to 3, covering a distance of 7.\n * Takahashi moves from coordinate 3 to 0, covering a distance of 3.\n\nThe distance covered by Takahashi here is 14 (because Takahashi didn't move\noptimally). It turns out that if both players move optimally, the distance\ncovered by Takahashi will be 10.\n\n* * *"}, {"input": "3\n 1 2\n 3 4\n 5 6", "output": "12\n \n\n* * *"}, {"input": "5\n -2 0\n -2 0\n 7 8\n 9 10\n -2 -1", "output": "34"}]
|
Print the total distance traveled by Takahashi throughout the game when
Takahashi and Aoki acts as above. It is guaranteed that K is always an integer
when L_i,R_i are integers.
* * *
|
s376000149
|
Accepted
|
p03333
|
Input is given from Standard Input in the following format:
N
L_1 R_1
:
L_N R_N
|
import math, string, itertools, fractions, heapq, collections, re, array, bisect, sys, random, time, copy, functools
sys.setrecursionlimit(10**7)
inf = 10**20
eps = 1.0 / 10**10
mod = 10**9 + 7
def LI():
return [int(x) for x in sys.stdin.readline().split()]
def LI_():
return [int(x) - 1 for x in sys.stdin.readline().split()]
def LF():
return [float(x) for x in sys.stdin.readline().split()]
def LS():
return sys.stdin.readline().split()
def I():
return int(sys.stdin.readline())
def F():
return float(sys.stdin.readline())
def S():
return input()
def pf(s):
return print(s, flush=True)
def main():
n = I()
a = [LI() + [_] for _ in range(n)]
r = 0
la = sorted(a, key=lambda x: [-x[0], -x[0]])
ra = sorted(a, key=lambda x: [x[1], x[0]])
u = set()
li = 0
ri = 0
tr = 0
c = 0
for i in range(len(a) // 2 + len(a) % 2):
while li < n and la[li][2] in u:
li += 1
if c < la[li][0]:
tr += la[li][0] - c
c = la[li][0]
u.add(la[li][2])
while ri < n and ra[ri][2] in u:
ri += 1
if ri == n:
break
if c > ra[ri][1]:
tr += c - ra[ri][1]
c = ra[ri][1]
u.add(ra[ri][2])
r = tr + abs(c)
u = set()
li = 0
ri = 0
tr = 0
c = 0
for i in range(len(a) // 2 + len(a) % 2):
while ri < n and ra[ri][2] in u:
ri += 1
if c > ra[ri][1]:
tr += c - ra[ri][1]
c = ra[ri][1]
u.add(ra[ri][2])
while li < n and la[li][2] in u:
li += 1
if li == n:
break
if c < la[li][0]:
tr += la[li][0] - c
c = la[li][0]
u.add(la[li][2])
if tr + abs(c) > r:
r = tr + abs(c)
return r
print(main())
|
Statement
Takahashi and Aoki will play a game with a number line and some segments.
Takahashi is standing on the number line and he is initially at coordinate 0.
Aoki has N segments. The i-th segment is [L_i,R_i], that is, a segment
consisting of points with coordinates between L_i and R_i (inclusive).
The game has N steps. The i-th step proceeds as follows:
* First, Aoki chooses a segment that is still not chosen yet from the N segments and tells it to Takahashi.
* Then, Takahashi walks along the number line to some point within the segment chosen by Aoki this time.
After N steps are performed, Takahashi will return to coordinate 0 and the
game ends.
Let K be the total distance traveled by Takahashi throughout the game. Aoki
will choose segments so that K will be as large as possible, and Takahashi
walks along the line so that K will be as small as possible. What will be the
value of K in the end?
|
[{"input": "3\n -5 1\n 3 7\n -4 -2", "output": "10\n \n\nOne possible sequence of actions of Takahashi and Aoki is as follows:\n\n * Aoki chooses the first segment. Takahashi moves from coordinate 0 to -4, covering a distance of 4.\n * Aoki chooses the third segment. Takahashi stays at coordinate -4.\n * Aoki chooses the second segment. Takahashi moves from coordinate -4 to 3, covering a distance of 7.\n * Takahashi moves from coordinate 3 to 0, covering a distance of 3.\n\nThe distance covered by Takahashi here is 14 (because Takahashi didn't move\noptimally). It turns out that if both players move optimally, the distance\ncovered by Takahashi will be 10.\n\n* * *"}, {"input": "3\n 1 2\n 3 4\n 5 6", "output": "12\n \n\n* * *"}, {"input": "5\n -2 0\n -2 0\n 7 8\n 9 10\n -2 -1", "output": "34"}]
|
Print the total distance traveled by Takahashi throughout the game when
Takahashi and Aoki acts as above. It is guaranteed that K is always an integer
when L_i,R_i are integers.
* * *
|
s919029311
|
Wrong Answer
|
p03333
|
Input is given from Standard Input in the following format:
N
L_1 R_1
:
L_N R_N
|
N = int(input())
L = [0 for i in range(N)]
R = [0 for i in range(N)]
P = []
for i in range(N):
L[i], R[i] = map(int, input().split())
if L[i] <= 0 <= R[i]:
P.append(0)
elif 0 < L[i]:
P.append(L[i])
else:
P.append(R[i])
P.sort()
X = []
Y = []
for i in range(N):
# 0<=i<N
if i < N // 2:
X.append(P[i])
else:
Y.append(P[i])
Y.sort(reverse=True)
# len(X)<=len(Y)
if N % 2 == 1:
X.append(Y[len(Y) - 1])
K1 = 0
K2 = 0
D1 = 0
D2 = 0
M = len(X)
for i in range(M):
K1 += abs(X[i] - D1)
K2 += abs(Y[i] - D2)
D1 = X[i]
D2 = Y[i]
K1 += abs(Y[i] - D1)
K2 += abs(X[i] - D2)
D1 = Y[i]
D2 = X[i]
K1 += abs(D1)
K2 += abs(D2)
print(max([K1, K2]))
|
Statement
Takahashi and Aoki will play a game with a number line and some segments.
Takahashi is standing on the number line and he is initially at coordinate 0.
Aoki has N segments. The i-th segment is [L_i,R_i], that is, a segment
consisting of points with coordinates between L_i and R_i (inclusive).
The game has N steps. The i-th step proceeds as follows:
* First, Aoki chooses a segment that is still not chosen yet from the N segments and tells it to Takahashi.
* Then, Takahashi walks along the number line to some point within the segment chosen by Aoki this time.
After N steps are performed, Takahashi will return to coordinate 0 and the
game ends.
Let K be the total distance traveled by Takahashi throughout the game. Aoki
will choose segments so that K will be as large as possible, and Takahashi
walks along the line so that K will be as small as possible. What will be the
value of K in the end?
|
[{"input": "3\n -5 1\n 3 7\n -4 -2", "output": "10\n \n\nOne possible sequence of actions of Takahashi and Aoki is as follows:\n\n * Aoki chooses the first segment. Takahashi moves from coordinate 0 to -4, covering a distance of 4.\n * Aoki chooses the third segment. Takahashi stays at coordinate -4.\n * Aoki chooses the second segment. Takahashi moves from coordinate -4 to 3, covering a distance of 7.\n * Takahashi moves from coordinate 3 to 0, covering a distance of 3.\n\nThe distance covered by Takahashi here is 14 (because Takahashi didn't move\noptimally). It turns out that if both players move optimally, the distance\ncovered by Takahashi will be 10.\n\n* * *"}, {"input": "3\n 1 2\n 3 4\n 5 6", "output": "12\n \n\n* * *"}, {"input": "5\n -2 0\n -2 0\n 7 8\n 9 10\n -2 -1", "output": "34"}]
|
Print the total distance traveled by Takahashi throughout the game when
Takahashi and Aoki acts as above. It is guaranteed that K is always an integer
when L_i,R_i are integers.
* * *
|
s346660597
|
Accepted
|
p03333
|
Input is given from Standard Input in the following format:
N
L_1 R_1
:
L_N R_N
|
N = int(input())
LRs = []
for i in range(N):
L, R = map(int, input().split())
LRs += [(L, R, i)]
Ls = sorted(LRs)
Rs = sorted(LRs, key=lambda x: x[1])
# 1手目がマイナス方向の場合
done = [False] * N
iL = N - 1
iR = 0
ans1 = 0
xNow = 0
while True:
# マイナス方向に移動
while iR < N and done[Rs[iR][2]]:
iR += 1
if iR == N:
break
xNext = Rs[iR][1]
if xNow < xNext:
break
ans1 += xNow - xNext
xNow = xNext
done[Rs[iR][2]] = True
# プラス方向に移動
while iL >= 0 and done[Ls[iL][2]]:
iL -= 1
if iL < 0:
break
xNext = Ls[iL][0]
if xNext < xNow:
break
ans1 += xNext - xNow
xNow = xNext
done[Ls[iL][2]] = True
ans1 += abs(xNow)
# 1手目がプラス方向の場合
done = [False] * N
iL = N - 1
iR = 0
ans2 = 0
xNow = 0
while True:
# プラス方向に移動
while iL >= 0 and done[Ls[iL][2]]:
iL -= 1
if iL < 0:
break
xNext = Ls[iL][0]
if xNext < xNow:
break
ans2 += xNext - xNow
xNow = xNext
done[Ls[iL][2]] = True
# マイナス方向に移動
while iR < N and done[Rs[iR][2]]:
iR += 1
if iR == N:
break
xNext = Rs[iR][1]
if xNow < xNext:
break
ans2 += xNow - xNext
xNow = xNext
done[Rs[iR][2]] = True
ans2 += abs(xNow)
print(max(ans1, ans2))
|
Statement
Takahashi and Aoki will play a game with a number line and some segments.
Takahashi is standing on the number line and he is initially at coordinate 0.
Aoki has N segments. The i-th segment is [L_i,R_i], that is, a segment
consisting of points with coordinates between L_i and R_i (inclusive).
The game has N steps. The i-th step proceeds as follows:
* First, Aoki chooses a segment that is still not chosen yet from the N segments and tells it to Takahashi.
* Then, Takahashi walks along the number line to some point within the segment chosen by Aoki this time.
After N steps are performed, Takahashi will return to coordinate 0 and the
game ends.
Let K be the total distance traveled by Takahashi throughout the game. Aoki
will choose segments so that K will be as large as possible, and Takahashi
walks along the line so that K will be as small as possible. What will be the
value of K in the end?
|
[{"input": "3\n -5 1\n 3 7\n -4 -2", "output": "10\n \n\nOne possible sequence of actions of Takahashi and Aoki is as follows:\n\n * Aoki chooses the first segment. Takahashi moves from coordinate 0 to -4, covering a distance of 4.\n * Aoki chooses the third segment. Takahashi stays at coordinate -4.\n * Aoki chooses the second segment. Takahashi moves from coordinate -4 to 3, covering a distance of 7.\n * Takahashi moves from coordinate 3 to 0, covering a distance of 3.\n\nThe distance covered by Takahashi here is 14 (because Takahashi didn't move\noptimally). It turns out that if both players move optimally, the distance\ncovered by Takahashi will be 10.\n\n* * *"}, {"input": "3\n 1 2\n 3 4\n 5 6", "output": "12\n \n\n* * *"}, {"input": "5\n -2 0\n -2 0\n 7 8\n 9 10\n -2 -1", "output": "34"}]
|
Print the total distance traveled by Takahashi throughout the game when
Takahashi and Aoki acts as above. It is guaranteed that K is always an integer
when L_i,R_i are integers.
* * *
|
s774378211
|
Wrong Answer
|
p03333
|
Input is given from Standard Input in the following format:
N
L_1 R_1
:
L_N R_N
|
N = int(input())
P = []
Q = []
R = []
for i in range(N):
l, r = map(int, input().split())
if r < 0:
P.append((l, r))
elif l > 0:
Q.append((l, r))
else:
R.append((l, r))
P.sort(key=lambda x: (x[1], x[0]), reverse=1)
Q.sort()
ans = 0
M = min(len(P), len(Q))
for i in range(M):
lp, rp = P.pop()
lq, rq = Q.pop()
ans += (-rp + lq) * 2
if P:
rest = N - 2 * M
cnt = min((rest + 1) // 2, len(P))
R.extend(P[:-cnt])
P = P[-cnt:]
R.sort()
if cnt:
lp, rp = P.pop()
ans += (-rp) * 2
for i in range(cnt - 1):
lp, rp = P.pop()
lr, rr = R.pop()
if not rp < lr:
break
ans += (-rp) * 2 - (-lr) * 2
if Q:
rest = N - 2 * M
cnt = min((rest + 1) // 2, len(Q))
R.extend(Q[:-cnt])
Q = Q[-cnt:]
R.sort(key=(lambda x: (x[1], x[0])), reverse=1)
if cnt:
lq, rq = Q.pop()
ans += lq * 2
for i in range(cnt - 1):
lq, rq = Q.pop()
lr, rr = R.pop()
if not rr < lq:
break
ans += lq * 2 - rr * 2
print(ans)
|
Statement
Takahashi and Aoki will play a game with a number line and some segments.
Takahashi is standing on the number line and he is initially at coordinate 0.
Aoki has N segments. The i-th segment is [L_i,R_i], that is, a segment
consisting of points with coordinates between L_i and R_i (inclusive).
The game has N steps. The i-th step proceeds as follows:
* First, Aoki chooses a segment that is still not chosen yet from the N segments and tells it to Takahashi.
* Then, Takahashi walks along the number line to some point within the segment chosen by Aoki this time.
After N steps are performed, Takahashi will return to coordinate 0 and the
game ends.
Let K be the total distance traveled by Takahashi throughout the game. Aoki
will choose segments so that K will be as large as possible, and Takahashi
walks along the line so that K will be as small as possible. What will be the
value of K in the end?
|
[{"input": "3\n -5 1\n 3 7\n -4 -2", "output": "10\n \n\nOne possible sequence of actions of Takahashi and Aoki is as follows:\n\n * Aoki chooses the first segment. Takahashi moves from coordinate 0 to -4, covering a distance of 4.\n * Aoki chooses the third segment. Takahashi stays at coordinate -4.\n * Aoki chooses the second segment. Takahashi moves from coordinate -4 to 3, covering a distance of 7.\n * Takahashi moves from coordinate 3 to 0, covering a distance of 3.\n\nThe distance covered by Takahashi here is 14 (because Takahashi didn't move\noptimally). It turns out that if both players move optimally, the distance\ncovered by Takahashi will be 10.\n\n* * *"}, {"input": "3\n 1 2\n 3 4\n 5 6", "output": "12\n \n\n* * *"}, {"input": "5\n -2 0\n -2 0\n 7 8\n 9 10\n -2 -1", "output": "34"}]
|
Print the total distance traveled by Takahashi throughout the game when
Takahashi and Aoki acts as above. It is guaranteed that K is always an integer
when L_i,R_i are integers.
* * *
|
s227427422
|
Wrong Answer
|
p03333
|
Input is given from Standard Input in the following format:
N
L_1 R_1
:
L_N R_N
|
N = int(input())
LR = []
for i in range(N):
LR.append([int(x) for x in input().split()])
# print(LR)
distance = []
for lr in LR:
if lr[0] > 0:
distance.append([lr[0], lr[0], lr[1]])
elif lr[1] < 0:
distance.append([lr[1], lr[0], lr[1]])
else:
distance.append([0, lr[0], lr[1]])
# print(distance)
distance.sort(key=lambda x: x[0])
count = 0
x = 0
dict = 0 if abs(distance[0][0]) >= abs(distance[-1][0]) else -1
while distance:
if distance[dict][1] > x:
next = distance[dict][1]
elif distance[dict][2] < x:
next = distance[dict][2]
else:
next = x
count += abs(next - x)
x = next
if dict == 0:
distance = distance[1:]
dict = -1
else:
distance = distance[:-1]
dict = 0
count += abs(x)
print(count)
|
Statement
Takahashi and Aoki will play a game with a number line and some segments.
Takahashi is standing on the number line and he is initially at coordinate 0.
Aoki has N segments. The i-th segment is [L_i,R_i], that is, a segment
consisting of points with coordinates between L_i and R_i (inclusive).
The game has N steps. The i-th step proceeds as follows:
* First, Aoki chooses a segment that is still not chosen yet from the N segments and tells it to Takahashi.
* Then, Takahashi walks along the number line to some point within the segment chosen by Aoki this time.
After N steps are performed, Takahashi will return to coordinate 0 and the
game ends.
Let K be the total distance traveled by Takahashi throughout the game. Aoki
will choose segments so that K will be as large as possible, and Takahashi
walks along the line so that K will be as small as possible. What will be the
value of K in the end?
|
[{"input": "3\n -5 1\n 3 7\n -4 -2", "output": "10\n \n\nOne possible sequence of actions of Takahashi and Aoki is as follows:\n\n * Aoki chooses the first segment. Takahashi moves from coordinate 0 to -4, covering a distance of 4.\n * Aoki chooses the third segment. Takahashi stays at coordinate -4.\n * Aoki chooses the second segment. Takahashi moves from coordinate -4 to 3, covering a distance of 7.\n * Takahashi moves from coordinate 3 to 0, covering a distance of 3.\n\nThe distance covered by Takahashi here is 14 (because Takahashi didn't move\noptimally). It turns out that if both players move optimally, the distance\ncovered by Takahashi will be 10.\n\n* * *"}, {"input": "3\n 1 2\n 3 4\n 5 6", "output": "12\n \n\n* * *"}, {"input": "5\n -2 0\n -2 0\n 7 8\n 9 10\n -2 -1", "output": "34"}]
|
Print the total distance traveled by Takahashi throughout the game when
Takahashi and Aoki acts as above. It is guaranteed that K is always an integer
when L_i,R_i are integers.
* * *
|
s745212002
|
Wrong Answer
|
p03333
|
Input is given from Standard Input in the following format:
N
L_1 R_1
:
L_N R_N
|
N = int(input())
arr = [[int(i) for i in input().split()] for i in range(N)]
cor = 0
sum = 0
print(arr)
Larr = sorted(arr, key=lambda x: (x[0]), reverse=True)
Rarr = sorted(arr, key=lambda x: (x[1]))
for i in range(N):
if Larr[0][0] - cor < cor - Rarr[0][1]:
if Rarr[0][0] > cor or cor > Rarr[0][1]:
sum += cor - Rarr[0][1]
cor = Rarr[0][1]
Larr.remove(Rarr[0])
Rarr.pop(0)
else:
if Larr[0][0] > cor or cor > Larr[0][1]:
sum += Larr[0][0] - cor
cor = Larr[0][0]
Rarr.remove(Larr[0])
Larr.pop(0)
sum += abs(cor)
print("{}".format(sum))
|
Statement
Takahashi and Aoki will play a game with a number line and some segments.
Takahashi is standing on the number line and he is initially at coordinate 0.
Aoki has N segments. The i-th segment is [L_i,R_i], that is, a segment
consisting of points with coordinates between L_i and R_i (inclusive).
The game has N steps. The i-th step proceeds as follows:
* First, Aoki chooses a segment that is still not chosen yet from the N segments and tells it to Takahashi.
* Then, Takahashi walks along the number line to some point within the segment chosen by Aoki this time.
After N steps are performed, Takahashi will return to coordinate 0 and the
game ends.
Let K be the total distance traveled by Takahashi throughout the game. Aoki
will choose segments so that K will be as large as possible, and Takahashi
walks along the line so that K will be as small as possible. What will be the
value of K in the end?
|
[{"input": "3\n -5 1\n 3 7\n -4 -2", "output": "10\n \n\nOne possible sequence of actions of Takahashi and Aoki is as follows:\n\n * Aoki chooses the first segment. Takahashi moves from coordinate 0 to -4, covering a distance of 4.\n * Aoki chooses the third segment. Takahashi stays at coordinate -4.\n * Aoki chooses the second segment. Takahashi moves from coordinate -4 to 3, covering a distance of 7.\n * Takahashi moves from coordinate 3 to 0, covering a distance of 3.\n\nThe distance covered by Takahashi here is 14 (because Takahashi didn't move\noptimally). It turns out that if both players move optimally, the distance\ncovered by Takahashi will be 10.\n\n* * *"}, {"input": "3\n 1 2\n 3 4\n 5 6", "output": "12\n \n\n* * *"}, {"input": "5\n -2 0\n -2 0\n 7 8\n 9 10\n -2 -1", "output": "34"}]
|
Print the number of such ways to paint the dominoes, modulo 1000000007.
* * *
|
s821108321
|
Runtime Error
|
p03626
|
Input is given from Standard Input in the following format:
N
S_1
S_2
|
N = int(input())
S1 = input()
S2 = input()
i = 1
if S1[0] == S2[0]:
ans = 3
state = 0
else:
i+= 1
ans = 6
state = 1
mod = 10**9 + 7
while N > i:
if S1[i] != S2[i] and state == 0:
ans *= 2
i+=2
state = 1
elif S1[i] != S2[i] and state == 1:
ans *= 3
i+=2
elif S1[i] == S2[i] and state == 0:
ans *= 2
i+= 1
elif S1[i] == S2[i] and state == 1:
ans *= 1
i+=1
state = 0
ans %= mod
print(ans)
~
|
Statement
We have a board with a 2 \times N grid. Snuke covered the board with N
dominoes without overlaps. Here, a domino can cover a 1 \times 2 or 2 \times 1
square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and
green. Two dominoes that are adjacent by side should be painted by different
colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S_1 and S_2 in
the following manner:
* Each domino is represented by a different English letter (lowercase or uppercase).
* The j-th character in S_i represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
|
[{"input": "3\n aab\n ccb", "output": "6\n \n\nThere are six ways as shown below:\n\n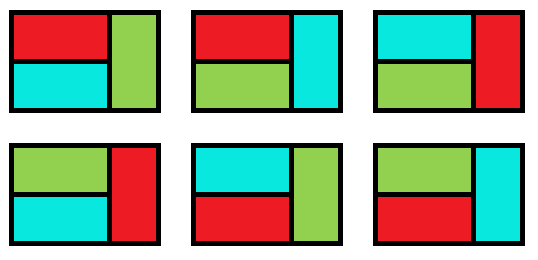\n\n* * *"}, {"input": "1\n Z\n Z", "output": "3\n \n\nNote that it is not always necessary to use all the colors.\n\n* * *"}, {"input": "52\n RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn\n RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn", "output": "958681902"}]
|
Print the number of such ways to paint the dominoes, modulo 1000000007.
* * *
|
s191447650
|
Accepted
|
p03626
|
Input is given from Standard Input in the following format:
N
S_1
S_2
|
n, s, t = open(0)
a = 3
for i in range(1, int(n)):
if i < 2 or s[i - 1] == t[i - 1]:
a *= 2
elif s[i - 1] != s[i] != t[i]:
a *= 3
print(a % (10**9 + 7))
|
Statement
We have a board with a 2 \times N grid. Snuke covered the board with N
dominoes without overlaps. Here, a domino can cover a 1 \times 2 or 2 \times 1
square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and
green. Two dominoes that are adjacent by side should be painted by different
colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S_1 and S_2 in
the following manner:
* Each domino is represented by a different English letter (lowercase or uppercase).
* The j-th character in S_i represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
|
[{"input": "3\n aab\n ccb", "output": "6\n \n\nThere are six ways as shown below:\n\n\n\n* * *"}, {"input": "1\n Z\n Z", "output": "3\n \n\nNote that it is not always necessary to use all the colors.\n\n* * *"}, {"input": "52\n RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn\n RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn", "output": "958681902"}]
|
Print the number of such ways to paint the dominoes, modulo 1000000007.
* * *
|
s919715156
|
Accepted
|
p03626
|
Input is given from Standard Input in the following format:
N
S_1
S_2
|
# -*- coding: utf-8 -*-
#############
# Libraries #
#############
import sys
input = sys.stdin.readline
import math
# from math import gcd
import bisect
from collections import defaultdict
from collections import deque
from functools import lru_cache
#############
# Constants #
#############
MOD = 10**9 + 7
INF = float("inf")
#############
# Functions #
#############
######INPUT######
def I():
return int(input().strip())
def S():
return input().strip()
def IL():
return list(map(int, input().split()))
def SL():
return list(map(str, input().split()))
def ILs(n):
return list(int(input()) for _ in range(n))
def SLs(n):
return list(input().strip() for _ in range(n))
def ILL(n):
return [list(map(int, input().split())) for _ in range(n)]
def SLL(n):
return [list(map(str, input().split())) for _ in range(n)]
######OUTPUT######
def P(arg):
print(arg)
return
def Y():
print("Yes")
return
def N():
print("No")
return
def E():
exit()
def PE(arg):
print(arg)
exit()
def YE():
print("Yes")
exit()
def NE():
print("No")
exit()
#####Shorten#####
def DD(arg):
return defaultdict(arg)
#####Inverse#####
def inv(n):
return pow(n, MOD - 2, MOD)
######Combination######
kaijo_memo = []
def kaijo(n):
if len(kaijo_memo) > n:
return kaijo_memo[n]
if len(kaijo_memo) == 0:
kaijo_memo.append(1)
while len(kaijo_memo) <= n:
kaijo_memo.append(kaijo_memo[-1] * len(kaijo_memo) % MOD)
return kaijo_memo[n]
gyaku_kaijo_memo = []
def gyaku_kaijo(n):
if len(gyaku_kaijo_memo) > n:
return gyaku_kaijo_memo[n]
if len(gyaku_kaijo_memo) == 0:
gyaku_kaijo_memo.append(1)
while len(gyaku_kaijo_memo) <= n:
gyaku_kaijo_memo.append(
gyaku_kaijo_memo[-1] * pow(len(gyaku_kaijo_memo), MOD - 2, MOD) % MOD
)
return gyaku_kaijo_memo[n]
def nCr(n, r):
if n == r:
return 1
if n < r or r < 0:
return 0
ret = 1
ret = ret * kaijo(n) % MOD
ret = ret * gyaku_kaijo(r) % MOD
ret = ret * gyaku_kaijo(n - r) % MOD
return ret
######Factorization######
def factorization(n):
arr = []
temp = n
for i in range(2, int(-(-(n**0.5) // 1)) + 1):
if temp % i == 0:
cnt = 0
while temp % i == 0:
cnt += 1
temp //= i
arr.append([i, cnt])
if temp != 1:
arr.append([temp, 1])
if arr == []:
arr.append([n, 1])
return arr
#####MakeDivisors######
def make_divisors(n):
divisors = []
for i in range(1, int(n**0.5) + 1):
if n % i == 0:
divisors.append(i)
if i != n // i:
divisors.append(n // i)
return divisors
#####MakePrimes######
def make_primes(N):
max = int(math.sqrt(N))
seachList = [i for i in range(2, N + 1)]
primeNum = []
while seachList[0] <= max:
primeNum.append(seachList[0])
tmp = seachList[0]
seachList = [i for i in seachList if i % tmp != 0]
primeNum.extend(seachList)
return primeNum
#####GCD#####
def gcd(a, b):
while b:
a, b = b, a % b
return a
#####LCM#####
def lcm(a, b):
return a * b // gcd(a, b)
#####BitCount#####
def count_bit(n):
count = 0
while n:
n &= n - 1
count += 1
return count
#####ChangeBase#####
def base_10_to_n(X, n):
if X // n:
return base_10_to_n(X // n, n) + [X % n]
return [X % n]
def base_n_to_10(X, n):
return sum(int(str(X)[-i - 1]) * n**i for i in range(len(str(X))))
#####IntLog#####
def int_log(n, a):
count = 0
while n >= a:
n //= a
count += 1
return count
#############
# Main Code #
#############
N = I()
S = S()
B = []
prev = None
Hold = False
for s in S:
if Hold:
if s == prev:
B.append(2)
Hold = False
else:
B.append(1)
else:
Hold = True
prev = s
if Hold:
B.append(1)
ans = 1
prev = None
for b in B:
if b == 1:
if prev == None:
ans = 3
elif prev == 1:
ans *= 2
ans %= MOD
else:
if prev == None:
ans = 6
elif prev == 1:
ans *= 2
ans %= MOD
else:
ans *= 3
ans %= MOD
prev = b
print(ans)
|
Statement
We have a board with a 2 \times N grid. Snuke covered the board with N
dominoes without overlaps. Here, a domino can cover a 1 \times 2 or 2 \times 1
square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and
green. Two dominoes that are adjacent by side should be painted by different
colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S_1 and S_2 in
the following manner:
* Each domino is represented by a different English letter (lowercase or uppercase).
* The j-th character in S_i represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
|
[{"input": "3\n aab\n ccb", "output": "6\n \n\nThere are six ways as shown below:\n\n\n\n* * *"}, {"input": "1\n Z\n Z", "output": "3\n \n\nNote that it is not always necessary to use all the colors.\n\n* * *"}, {"input": "52\n RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn\n RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn", "output": "958681902"}]
|
Print the number of such ways to paint the dominoes, modulo 1000000007.
* * *
|
s053043586
|
Accepted
|
p03626
|
Input is given from Standard Input in the following format:
N
S_1
S_2
|
MOD = 10**9 + 7
N = int(input())
S = iter(input() + " ")
prev = next(S)
count = 0
counts = []
for c in S:
count += 1
if prev != c:
counts.append(count)
count = 0
prev = c
counts = iter(counts)
prev = next(counts)
ans = 3 * prev
for count in counts:
if prev == 1:
ans *= 2
elif count == 2:
ans *= 3
prev = count
print(ans % MOD)
|
Statement
We have a board with a 2 \times N grid. Snuke covered the board with N
dominoes without overlaps. Here, a domino can cover a 1 \times 2 or 2 \times 1
square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and
green. Two dominoes that are adjacent by side should be painted by different
colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S_1 and S_2 in
the following manner:
* Each domino is represented by a different English letter (lowercase or uppercase).
* The j-th character in S_i represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
|
[{"input": "3\n aab\n ccb", "output": "6\n \n\nThere are six ways as shown below:\n\n\n\n* * *"}, {"input": "1\n Z\n Z", "output": "3\n \n\nNote that it is not always necessary to use all the colors.\n\n* * *"}, {"input": "52\n RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn\n RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn", "output": "958681902"}]
|
Print the number of such ways to paint the dominoes, modulo 1000000007.
* * *
|
s911845314
|
Runtime Error
|
p03626
|
Input is given from Standard Input in the following format:
N
S_1
S_2
|
n = int(input())
s = [input() for _ in range(2)]
if n == 1:
print(3)
exit()
law = 10**9 + 7
dp = [[0 for _ in range(2)] for _ in range(n)] # 直前の色と同じかどうか
dp[0][0] = 3
dp[0][1] = 0
dp[1][0] = 0
dp[1][1] = 6
sideway = s[0][1] == s[0][2]
for i in range(2, n):
if sideway:
sideway = False
if s[0][i - 2] == s[1][i - 2]: # |=
dp[i][0] = 0
dp[i][1] = sum(dp[i - 1])
else: # ==
dp[i][0] = 0
dp[i][1] = dp[i - 1][0] * 2 + dp[i - 1][1]
else:
if s[0][i] == s[1][i]:
sideway = False
if s[0][i - 1] == s[1][i - 1]: # ||
dp[i][0] = 0
dp[i][1] = sum(dp[i - 1]) * 2
else: # =|
dp[i][0] = 0
dp[i][1] = sum(dp[i - 1])
else:
sideway = True
if s[0][i - 1] == s[1][i - 1]: # |-
dp[i][0] = 0
dp[i][1] = sum(dp[i - 1]) * 2
else: # =-
dp[i][0] = sum(dp[i - 1])
dp[i][1] = 2 * sum(dp[i - 2]) - dp[i][0]
dp[i][0] %= law
dp[i][1] %= law
print(sum(dp[i - 1]))
|
Statement
We have a board with a 2 \times N grid. Snuke covered the board with N
dominoes without overlaps. Here, a domino can cover a 1 \times 2 or 2 \times 1
square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and
green. Two dominoes that are adjacent by side should be painted by different
colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S_1 and S_2 in
the following manner:
* Each domino is represented by a different English letter (lowercase or uppercase).
* The j-th character in S_i represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
|
[{"input": "3\n aab\n ccb", "output": "6\n \n\nThere are six ways as shown below:\n\n\n\n* * *"}, {"input": "1\n Z\n Z", "output": "3\n \n\nNote that it is not always necessary to use all the colors.\n\n* * *"}, {"input": "52\n RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn\n RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn", "output": "958681902"}]
|
Print the number of such ways to paint the dominoes, modulo 1000000007.
* * *
|
s923846266
|
Runtime Error
|
p03626
|
Input is given from Standard Input in the following format:
N
S_1
S_2
|
N = int(input())
S = [input() for _ in range(2)]
M = 1000000007
if S[0][0] == S[1][0]:
last_kind = 0
ans = 3
i = 1
else:
last_kind = 1
ans = 6
i = 2
while i < N:
if last_kind == 0 and S[0][i] == S[1][i]:
ans *= 2
last_kind = 0
i += 1
elif last_kind == 1 and S[0][i] == S[1][i]:
last_kind = 0
i += 1
elif last_kind == 0 and S[0][i] == S[0][i+1]:
ans *= 2
last_kind = 1
i += 2
elif last_kind == 1 and S[0][i] == S[0][i+1]:
ans *= 3
last_kind = 1
i +=
ans %= M
print(ans)
|
Statement
We have a board with a 2 \times N grid. Snuke covered the board with N
dominoes without overlaps. Here, a domino can cover a 1 \times 2 or 2 \times 1
square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and
green. Two dominoes that are adjacent by side should be painted by different
colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S_1 and S_2 in
the following manner:
* Each domino is represented by a different English letter (lowercase or uppercase).
* The j-th character in S_i represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
|
[{"input": "3\n aab\n ccb", "output": "6\n \n\nThere are six ways as shown below:\n\n\n\n* * *"}, {"input": "1\n Z\n Z", "output": "3\n \n\nNote that it is not always necessary to use all the colors.\n\n* * *"}, {"input": "52\n RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn\n RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn", "output": "958681902"}]
|
Print the number of such ways to paint the dominoes, modulo 1000000007.
* * *
|
s408093361
|
Accepted
|
p03626
|
Input is given from Standard Input in the following format:
N
S_1
S_2
|
def read_line(*types):
return [f(a) for a, f in zip(input().split(), types)]
(n,) = read_line(int)
m = 1000000007
domino = []
domino.append(input())
domino.append(input())
# print(domino[0])
# print(domino[1])
def compress(line):
x = [line[0]]
for c in line[1:]:
if x[-1] != c:
x.append(c)
return x
domino[0] = compress(domino[0])
domino[1] = compress(domino[1])
xs = []
for i in range(len(domino[0])):
xs.append(domino[0][i] != domino[1][i])
# print(xs)
patterns = None
if xs[0]:
patterns = 6
else:
patterns = 3
lastX = xs[0]
for x in xs[1:]:
if x:
# T -> T
if lastX:
patterns *= 3
else:
# F -> T
patterns *= 2
else:
# T -> F
if lastX:
patterns *= 1
else: # F -> F
patterns *= 2
lastX = x
print(patterns % m)
# T -> T
# 6 * 4 = 24
# 0|1120
# 1|2002
# 0
# 2
# 1
# 0
# 1
# 2
# 2
# 0
# 2
# 1
# F -> T
# 3 * 2 = 6
# 0|12
# 0|21
#
# 1|02
# 1|20
#
# 2|10
# 2|01
# T -> F
# 6 * 1 = 6
# 0|2
# 1|2
# 0|1
# 2|1
# 1|2
# 0|2
# 1|0
# 2|0
# 2|1
# 0|1
# 2|0
# 1|0
# F -> F
# 3 * 2 = 6
# 0 | 12
# 1 | 02
# 2 | 01
|
Statement
We have a board with a 2 \times N grid. Snuke covered the board with N
dominoes without overlaps. Here, a domino can cover a 1 \times 2 or 2 \times 1
square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and
green. Two dominoes that are adjacent by side should be painted by different
colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S_1 and S_2 in
the following manner:
* Each domino is represented by a different English letter (lowercase or uppercase).
* The j-th character in S_i represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
|
[{"input": "3\n aab\n ccb", "output": "6\n \n\nThere are six ways as shown below:\n\n\n\n* * *"}, {"input": "1\n Z\n Z", "output": "3\n \n\nNote that it is not always necessary to use all the colors.\n\n* * *"}, {"input": "52\n RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn\n RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn", "output": "958681902"}]
|
Print the number of such ways to paint the dominoes, modulo 1000000007.
* * *
|
s098214297
|
Runtime Error
|
p03626
|
Input is given from Standard Input in the following format:
N
S_1
S_2
|
n = int(input())
s1 = str(input())
s2 = str(input())
def mult(prev,now):
if (prev == 1)&(now==0:
return 1
else:
return 2
if n == 1:
ans = 3
elif n == 2:
ans = 6
else:
i = 0
flag = 0
ans = 6
while (i <= n - 1):
if s1[i] != s2[i]:
pat = 1
i +=2
flag += 1
else:
pat = 0
flag += 1
i += 1
if flag == 1:
prev = pat
continue
elif (flag == 2) & (i == 2):
prev = pat
else:
now = pat
ans *= mult(prev,now)
prev = now
print(int(ans))
|
Statement
We have a board with a 2 \times N grid. Snuke covered the board with N
dominoes without overlaps. Here, a domino can cover a 1 \times 2 or 2 \times 1
square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and
green. Two dominoes that are adjacent by side should be painted by different
colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S_1 and S_2 in
the following manner:
* Each domino is represented by a different English letter (lowercase or uppercase).
* The j-th character in S_i represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
|
[{"input": "3\n aab\n ccb", "output": "6\n \n\nThere are six ways as shown below:\n\n\n\n* * *"}, {"input": "1\n Z\n Z", "output": "3\n \n\nNote that it is not always necessary to use all the colors.\n\n* * *"}, {"input": "52\n RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn\n RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn", "output": "958681902"}]
|
Print the number of such ways to paint the dominoes, modulo 1000000007.
* * *
|
s133989785
|
Runtime Error
|
p03626
|
Input is given from Standard Input in the following format:
N
S_1
S_2
|
#include <bits/stdc++.h>
using namespace std;
#define rep(i,N) for(int i=0,i##_max=(N);i<i##_max;++i)
#define repp(i,l,r) for(int i=(l),i##_max=(r);i<i##_max;++i)
#define per(i,N) for(int i=(N)-1;i>=0;--i)
#define perr(i,l,r) for(int i=r-1,i##_min(l);i>=i##_min;--i)
#define all(arr) (arr).begin(), (arr).end()
#define SP << " " <<
#define SPF << " "
#define SPEEDUP cin.tie(0);ios::sync_with_stdio(false);
#define MAX_I INT_MAX //1e9
#define MIN_I INT_MIN //-1e9
#define MAX_UI UINT_MAX //1e9
#define MAX_LL LLONG_MAX //1e18
#define MIN_LL LLONG_MIN //-1e18
#define MAX_ULL ULLONG_MAX //1e19
typedef long long ll;
typedef pair<int,int> PII;
typedef pair<char,char> PCC;
typedef pair<ll,ll> PLL;
typedef pair<char,int> PCI;
typedef pair<int,char> PIC;
typedef pair<ll,int> PLI;
typedef pair<int,ll> PIL;
typedef pair<ll,char> PLC;
typedef pair<char,ll> PCL;
inline void YesNo(bool b){ cout << (b?"Yes" : "No") << endl;}
inline void YESNO(bool b){ cout << (b?"YES" : "NO") << endl;}
inline void Yay(bool b){ cout << (b?"Yay!" : ":(") << endl;}
template<int MOD> struct Fp {
ll val;
constexpr Fp(ll v = 0) noexcept : val(v % MOD) {
if (val < 0) v += MOD;
}
constexpr int getmod() { return MOD; }
constexpr Fp operator - () const noexcept {
return val ? MOD - val : 0;
}
constexpr Fp operator + (const Fp& r) const noexcept { return Fp(*this) += r; }
constexpr Fp operator - (const Fp& r) const noexcept { return Fp(*this) -= r; }
constexpr Fp operator * (const Fp& r) const noexcept { return Fp(*this) *= r; }
constexpr Fp operator / (const Fp& r) const noexcept { return Fp(*this) /= r; }
constexpr Fp& operator += (const Fp& r) noexcept {
val += r.val;
if (val >= MOD) val -= MOD;
return *this;
}
constexpr Fp& operator -= (const Fp& r) noexcept {
val -= r.val;
if (val < 0) val += MOD;
return *this;
}
constexpr Fp& operator *= (const Fp& r) noexcept {
val = val * r.val % MOD;
return *this;
}
constexpr Fp& operator /= (const Fp& r) noexcept {
long long a = r.val, b = MOD, u = 1, v = 0;
while (b) {
long long t = a / b;
a -= t * b; swap(a, b);
u -= t * v; swap(u, v);
}
val = val * u % MOD;
if (val < 0) val += MOD;
return *this;
}
constexpr bool operator == (const Fp& r) const noexcept {
return this->val == r.val;
}
constexpr bool operator != (const Fp& r) const noexcept {
return this->val != r.val;
}
friend constexpr ostream& operator << (ostream &os, const Fp<MOD>& x) noexcept {
return os << x.val;
}
friend constexpr istream& operator >> (istream &is, Fp<MOD>& x) noexcept {
return is >> x.val;
}
friend constexpr Fp<MOD> modpow(const Fp<MOD> &a, long long n) noexcept {
if (n == 0) return 1;
auto t = modpow(a, n / 2);
t = t * t;
if (n & 1) t = t * a;
return t;
}
};
//const int MOD = 998244353;
//const int MOD = 1e6 + 3;
const int MOD = 1e9 + 7;
const int N_MAX = 1e5+5;
//mint:mod演算のための型
using mint = Fp<MOD>;
//型変換
#define MINT (mint)
//mod MOD上での階乗
mint fact[N_MAX];
void init(){
fact[0] = fact[1] = MINT 1;
for(int i = 2; i < N_MAX; i++){
fact[i] = fact[i-1] * i;
}
}
//mod MOD上での逆元
inline mint inv(mint n){
return modpow(n,MOD-2);
}
//二項係数の計算(mod MOD上)
inline mint COM(int n, int k){
if(n<k) return 0;
return fact[n]/(fact[k]*fact[n-k]);
}
int main(void){
SPEEDUP
cout << setprecision(15);
int N;cin >> N;
string s1,s2;cin >> s1 >> s2;
mint ans = 3;
int pre = (s1[0] == s2[0]) ? 1:2;
ans*=pre;
repp(i,1,N){
if(pre==2)++i;
if(pre == 1) ans*=2;
else if(s1[i] != s2[i]) ans*=3;
pre = (s1[i] == s2[i]) ? 1:2;
}
cout << ans << endl;
return 0;
}
|
Statement
We have a board with a 2 \times N grid. Snuke covered the board with N
dominoes without overlaps. Here, a domino can cover a 1 \times 2 or 2 \times 1
square.
Then, Snuke decided to paint these dominoes using three colors: red, cyan and
green. Two dominoes that are adjacent by side should be painted by different
colors. Here, it is not always necessary to use all three colors.
Find the number of such ways to paint the dominoes, modulo 1000000007.
The arrangement of the dominoes is given to you as two strings S_1 and S_2 in
the following manner:
* Each domino is represented by a different English letter (lowercase or uppercase).
* The j-th character in S_i represents the domino that occupies the square at the i-th row from the top and j-th column from the left.
|
[{"input": "3\n aab\n ccb", "output": "6\n \n\nThere are six ways as shown below:\n\n\n\n* * *"}, {"input": "1\n Z\n Z", "output": "3\n \n\nNote that it is not always necessary to use all the colors.\n\n* * *"}, {"input": "52\n RvvttdWIyyPPQFFZZssffEEkkaSSDKqcibbeYrhAljCCGGJppHHn\n RLLwwdWIxxNNQUUXXVVMMooBBaggDKqcimmeYrhAljOOTTJuuzzn", "output": "958681902"}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s810238408
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
n = int(input())
aaa = list(map(float, input().split()))
mot = 0.0
for i in aaa:
mot += 1 / i
print(1 / mot)
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s202640009
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
def solve():
a = read()
result = think(a)
write(result)
def read():
n = read_int(1)[0]
return read_int(n)
def read_int(n):
return list(map(lambda x: int(x), read_line().split(" ")))[:n]
def read_float(n):
return list(map(lambda x: float(x), read_line().split(" ")))[:n]
def read_line(n=0):
if n == 0:
return input().rstrip()
else:
return input().rstrip()[:n]
def think(a):
buf = 0
for d in a:
buf += 1 / d
return 1 / buf
def write(result):
print(result)
if __name__ == "__main__":
solve()
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s661426911
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
from functools import reduce
def gcd_base(x, y):
while y != 0:
x, y = y, x % y
return x
def gcd(num):
return reduce(gcd_base, num)
def lcm_base(x, y):
return (x * y) // gcd_base(x, y)
def lcm(num):
return reduce(lcm_base, num, 1)
def calc_denom(l, numer):
cnt = 0
for x in l:
cnt += numer // x
return cnt
N = int(input())
l = list(map(int, input().split()))
numer = lcm(l)
denom = calc_denom(l, numer)
print(numer / denom)
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s236123068
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
n, *a = map(int, open(0).read().split())
print(1 / sum([1 / x for x in a]))
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s743861816
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
n = int(input())
sums = 0
for num in input().split():
sums += 1 / int(num)
print(1 / sums)
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s602579359
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
_ = input()
print("{:.16g}".format(1 / sum(1 / x for x in map(int, input().split()))))
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s462068980
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
_, a = int(input()), input()
inv_a = map(lambda x: 1 / int(x), a.split())
print(1 / sum(inv_a))
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s962982286
|
Runtime Error
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
a, b = map(int, input().split())
print((b - 2) // (a - 1) + 1)
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s682727751
|
Runtime Error
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
n = int(input())
a = [int(input()) for i in range(n)]
for result in range(n):
1 // (1 // (a * n))
print(result)
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s137733377
|
Runtime Error
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
n1 = int(input())
n2 = list(map(int, input().split()))
print(1 / ((1 / n2[0] + 1 / n2[1])))
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s022894525
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
input_a = int(input())
input_list = list(map(int, input().split()))
sum_a = 0
for i in range(input_a):
sum_a += 1 / input_list[i]
sum_b = 1 / sum_a
print(sum_b)
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s192173148
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
total_number = int(input())
numbers = list(map(int, input().split()))
reversed = 0
for i in range(total_number):
reversed += 1 / numbers[i]
sol = 1 / reversed
print(sol)
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s451704963
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
n = int(input())
resistors = [int(i) for i in input().split()]
reverse = []
for i in range(len(resistors)):
reverse.append(1 / resistors[i])
print(1 / sum(reverse))
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s762261651
|
Accepted
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
n = int(input())
an = input().split(" ")
an = list(map(int, an))
# print(an[0],an[1])
bn = list(map(lambda x: 1 / x, an))
# print(an, bn)
print(1 / sum(bn))
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s080453770
|
Wrong Answer
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
N = int(input())
A = list(map(int, input().split()))
a_max = max(A)
c = []
for x in range(N):
if A[x] < a_max:
c.append(int(a_max / A[x]))
else:
c.append(1)
print(a_max / int(sum(c)))
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print a decimal number (or an integer) representing the value of
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
Your output will be judged correct when its absolute or relative error from
the judge's output is at most 10^{-5}.
* * *
|
s395370554
|
Wrong Answer
|
p02934
|
Input is given from Standard Input in the following format:
N
A_1 A_2 \ldots A_N
|
n = int(input())
list_a = list(map(float, input().split()))
list_b = [1 / i for i in list_a]
# print(list_b)
print(sum(list_b))
|
Statement
Given is a sequence of N integers A_1, \ldots, A_N.
Find the (multiplicative) inverse of the sum of the inverses of these numbers,
\frac{1}{\frac{1}{A_1} + \ldots + \frac{1}{A_N}}.
|
[{"input": "2\n 10 30", "output": "7.5\n \n\n\\frac{1}{\\frac{1}{10} + \\frac{1}{30}} = \\frac{1}{\\frac{4}{30}} = \\frac{30}{4}\n= 7.5.\n\nPrinting `7.50001`, `7.49999`, and so on will also be accepted.\n\n* * *"}, {"input": "3\n 200 200 200", "output": "66.66666666666667\n \n\n\\frac{1}{\\frac{1}{200} + \\frac{1}{200} + \\frac{1}{200}} =\n\\frac{1}{\\frac{3}{200}} = \\frac{200}{3} = 66.6666....\n\nPrinting `6.66666e+1` and so on will also be accepted.\n\n* * *"}, {"input": "1\n 1000", "output": "1000\n \n\n\\frac{1}{\\frac{1}{1000}} = 1000.\n\nPrinting `+1000.0` and so on will also be accepted."}]
|
Print the minimum time required to light K candles.
* * *
|
s065781680
|
Wrong Answer
|
p03276
|
Input is given from Standard Input in the following format:
N K
x_1 x_2 ... x_N
|
n, k, *a = map(int, open(0).read().split())
print(sum(list(sorted(map(abs, a)))[:k]))
|
Statement
There are N candles placed on a number line. The i-th candle from the left is
placed on coordinate x_i. Here, x_1 < x_2 < ... < x_N holds.
Initially, no candles are burning. Snuke decides to light K of the N candles.
Now, he is at coordinate 0. He can move left and right along the line with
speed 1. He can also light a candle when he is at the same position as the
candle, in negligible time.
Find the minimum time required to light K candles.
|
[{"input": "5 3\n -30 -10 10 20 50", "output": "40\n \n\nHe should move and light candles as follows:\n\n * Move from coordinate 0 to -10.\n * Light the second candle from the left.\n * Move from coordinate -10 to 10.\n * Light the third candle from the left.\n * Move from coordinate 10 to 20.\n * Light the fourth candle from the left.\n\n* * *"}, {"input": "3 2\n 10 20 30", "output": "20\n \n\n* * *"}, {"input": "1 1\n 0", "output": "0\n \n\n * There may be a candle placed at coordinate 0.\n\n* * *"}, {"input": "8 5\n -9 -7 -4 -3 1 2 3 4", "output": "10"}]
|
Print the minimum time required to light K candles.
* * *
|
s632678832
|
Runtime Error
|
p03276
|
Input is given from Standard Input in the following format:
N K
x_1 x_2 ... x_N
|
a = [list(map(int, input().split())) for i in range(2)]
k = a[0][1]
num_list = a[1]
positive_list = []
negative_list = []
ans_positive = []
ans_negative = []
ans_list = []
for _ in num_list:
if _ > 0:
positive_list.append(_)
elif _ < 0:
negative_list.insert(0, _)
else:
if num_list != [0]:
k -= 1
for _ in list(range(len(positive_list))):
if not 0 <= k - _ - 2 < len(negative_list):
continue
ans_positive.append(2 * positive_list[_] - negative_list[k - _ - 2])
for _ in list(range(len(negative_list))):
if not 0 <= k - _ - 2 < len(positive_list):
continue
ans_negative.append(-2 * negative_list[_] + positive_list[k - _ - 2])
if ans_positive:
ans_list.append(min(ans_positive))
if ans_negative:
ans_list.append(min(ans_negative))
if k <= len(positive_list):
ans_list.append(positive_list[k - 1])
if k <= len(negative_list):
ans_list.append(-1 * negative_list[k - 1])
if ans_list == []:
print(0)
else:
print(min(ans_list))
|
Statement
There are N candles placed on a number line. The i-th candle from the left is
placed on coordinate x_i. Here, x_1 < x_2 < ... < x_N holds.
Initially, no candles are burning. Snuke decides to light K of the N candles.
Now, he is at coordinate 0. He can move left and right along the line with
speed 1. He can also light a candle when he is at the same position as the
candle, in negligible time.
Find the minimum time required to light K candles.
|
[{"input": "5 3\n -30 -10 10 20 50", "output": "40\n \n\nHe should move and light candles as follows:\n\n * Move from coordinate 0 to -10.\n * Light the second candle from the left.\n * Move from coordinate -10 to 10.\n * Light the third candle from the left.\n * Move from coordinate 10 to 20.\n * Light the fourth candle from the left.\n\n* * *"}, {"input": "3 2\n 10 20 30", "output": "20\n \n\n* * *"}, {"input": "1 1\n 0", "output": "0\n \n\n * There may be a candle placed at coordinate 0.\n\n* * *"}, {"input": "8 5\n -9 -7 -4 -3 1 2 3 4", "output": "10"}]
|
Print the minimum time required to light K candles.
* * *
|
s029259391
|
Wrong Answer
|
p03276
|
Input is given from Standard Input in the following format:
N K
x_1 x_2 ... x_N
|
def main(N, K, xs):
if xs[0] >= 0:
return xs[K - 1]
if xs[-1] <= 0:
return abs(xs[-1 * K])
for i, x in enumerate(xs):
if x == 0:
xs.pop(i)
if K == 1:
return 0
K = K - 1
N = N - 1
if x > 0:
zi = i
break
result = None
if zi - K >= 0:
result = xs[zi - K]
if zi + K - 1 <= N - 1:
if result == None:
result = xs[zi + K - 1]
result = min(result, xs[zi + K - 1])
for i in range(K - 1):
if zi - K + i + 1 < 0:
continue
if zi - 1 + i + 1 > N - 1:
continue
l = abs(xs[zi - K + i + 1])
r = abs(xs[zi - 1 + i + 1])
if result == None:
result = 2 * min(l, r) + max(l, r)
else:
if result > 2 * min(l, r) + max(l, r):
result = 2 * min(l, r) + max(l, r)
return result
N, K = [int(i) for i in input().split(" ")]
xs = [int(i) for i in input().split(" ")]
print(main(N, K, xs))
|
Statement
There are N candles placed on a number line. The i-th candle from the left is
placed on coordinate x_i. Here, x_1 < x_2 < ... < x_N holds.
Initially, no candles are burning. Snuke decides to light K of the N candles.
Now, he is at coordinate 0. He can move left and right along the line with
speed 1. He can also light a candle when he is at the same position as the
candle, in negligible time.
Find the minimum time required to light K candles.
|
[{"input": "5 3\n -30 -10 10 20 50", "output": "40\n \n\nHe should move and light candles as follows:\n\n * Move from coordinate 0 to -10.\n * Light the second candle from the left.\n * Move from coordinate -10 to 10.\n * Light the third candle from the left.\n * Move from coordinate 10 to 20.\n * Light the fourth candle from the left.\n\n* * *"}, {"input": "3 2\n 10 20 30", "output": "20\n \n\n* * *"}, {"input": "1 1\n 0", "output": "0\n \n\n * There may be a candle placed at coordinate 0.\n\n* * *"}, {"input": "8 5\n -9 -7 -4 -3 1 2 3 4", "output": "10"}]
|
Print the minimum time required to light K candles.
* * *
|
s245600604
|
Runtime Error
|
p03276
|
Input is given from Standard Input in the following format:
N K
x_1 x_2 ... x_N
|
import statistics
def Medi(Arra, Haba):
re = []
for i_M in range(len(Arra) - Haba + 1):
re.append(statistics.median_high(Arra[i_M : i_M + Haba]))
return re
N = int(input())
A = list(map(int, input().split()))
print(A)
ans = []
if N == 1:
ans.append(A[0])
else:
kuri = max(N // 2, 10)
for i in range(1, N + 1):
ans += Medi(A, i)
so = ans
so.sort()
print(so)
print(statistics.median_high(ans))
|
Statement
There are N candles placed on a number line. The i-th candle from the left is
placed on coordinate x_i. Here, x_1 < x_2 < ... < x_N holds.
Initially, no candles are burning. Snuke decides to light K of the N candles.
Now, he is at coordinate 0. He can move left and right along the line with
speed 1. He can also light a candle when he is at the same position as the
candle, in negligible time.
Find the minimum time required to light K candles.
|
[{"input": "5 3\n -30 -10 10 20 50", "output": "40\n \n\nHe should move and light candles as follows:\n\n * Move from coordinate 0 to -10.\n * Light the second candle from the left.\n * Move from coordinate -10 to 10.\n * Light the third candle from the left.\n * Move from coordinate 10 to 20.\n * Light the fourth candle from the left.\n\n* * *"}, {"input": "3 2\n 10 20 30", "output": "20\n \n\n* * *"}, {"input": "1 1\n 0", "output": "0\n \n\n * There may be a candle placed at coordinate 0.\n\n* * *"}, {"input": "8 5\n -9 -7 -4 -3 1 2 3 4", "output": "10"}]
|
Print the minimum time required to light K candles.
* * *
|
s722333169
|
Accepted
|
p03276
|
Input is given from Standard Input in the following format:
N K
x_1 x_2 ... x_N
|
N, K = list(map(int, input().split()))
X = list(map(int, input().split()))
left = []
right = []
for x in X:
if x < 0:
left.append(-x)
if x == 0:
K -= 1
if x > 0:
right.append(x)
left = list(reversed(left))
left.insert(0, 0)
right.insert(0, 0)
def solve(left, right):
result = float("inf")
for i in range(min(len(left), K)):
# print(i,left,right)
tmp_time = 2 * left[i]
tmp_count = i
if i + len(right) - 1 < K:
continue
tmp_result = tmp_time + right[K - i]
result = min(result, tmp_result)
return result
if K == 0:
print(0)
exit()
print(min(solve(left, right), solve(right, left)))
|
Statement
There are N candles placed on a number line. The i-th candle from the left is
placed on coordinate x_i. Here, x_1 < x_2 < ... < x_N holds.
Initially, no candles are burning. Snuke decides to light K of the N candles.
Now, he is at coordinate 0. He can move left and right along the line with
speed 1. He can also light a candle when he is at the same position as the
candle, in negligible time.
Find the minimum time required to light K candles.
|
[{"input": "5 3\n -30 -10 10 20 50", "output": "40\n \n\nHe should move and light candles as follows:\n\n * Move from coordinate 0 to -10.\n * Light the second candle from the left.\n * Move from coordinate -10 to 10.\n * Light the third candle from the left.\n * Move from coordinate 10 to 20.\n * Light the fourth candle from the left.\n\n* * *"}, {"input": "3 2\n 10 20 30", "output": "20\n \n\n* * *"}, {"input": "1 1\n 0", "output": "0\n \n\n * There may be a candle placed at coordinate 0.\n\n* * *"}, {"input": "8 5\n -9 -7 -4 -3 1 2 3 4", "output": "10"}]
|
Print the minimum time required to light K candles.
* * *
|
s525729151
|
Runtime Error
|
p03276
|
Input is given from Standard Input in the following format:
N K
x_1 x_2 ... x_N
|
#!/usr/bin/env python3
import sys
def append_zero(x):
if 0 in x:
return
if x[0] > 0:
x.insert(0, 0)
return
if x[len(x) - 1] < 0:
x.appnd(0)
return
for i in range(1, len(x)):
if x[i - 1] < 0 and x[i] > 0:
x.insert(i, 0)
return
def solve(N, K, x):
y = [0]
append_zero(x)
n = len(x)
z = 0
for i in range(1, n):
y.append(y[i - 1] + x[i] - x[i - 1])
if x[i] == 0:
z = i
# print(x)
# print(y)
if n == K:
if n - 1 == z or z == 0:
return y[n - 1]
else:
l = y[z] + y[n - 1]
r = y[n - 1] - y[z] + y[n - 1]
return min(l, r)
ans = 10e20
for i in range(n - K):
k = i + K
if k <= z:
ans = min(ans, y[z] - y[i])
if z <= i:
ans = min(ans, y[k] - y[z])
if i <= z and z < k:
l = y[z] - y[i] + y[k] - y[i]
r = y[k] - y[z] + y[k] - y[i]
ans = min(ans, l, r)
return ans
def main():
def iterate_tokens():
for line in sys.stdin:
for word in line.split():
yield word
tokens = iterate_tokens()
N = int(next(tokens)) # type: int
K = int(next(tokens)) # type: int
x = [int(next(tokens)) for _ in range(N)] # type: "List[int]"
print(solve(N, K, x))
if __name__ == "__main__":
main()
|
Statement
There are N candles placed on a number line. The i-th candle from the left is
placed on coordinate x_i. Here, x_1 < x_2 < ... < x_N holds.
Initially, no candles are burning. Snuke decides to light K of the N candles.
Now, he is at coordinate 0. He can move left and right along the line with
speed 1. He can also light a candle when he is at the same position as the
candle, in negligible time.
Find the minimum time required to light K candles.
|
[{"input": "5 3\n -30 -10 10 20 50", "output": "40\n \n\nHe should move and light candles as follows:\n\n * Move from coordinate 0 to -10.\n * Light the second candle from the left.\n * Move from coordinate -10 to 10.\n * Light the third candle from the left.\n * Move from coordinate 10 to 20.\n * Light the fourth candle from the left.\n\n* * *"}, {"input": "3 2\n 10 20 30", "output": "20\n \n\n* * *"}, {"input": "1 1\n 0", "output": "0\n \n\n * There may be a candle placed at coordinate 0.\n\n* * *"}, {"input": "8 5\n -9 -7 -4 -3 1 2 3 4", "output": "10"}]
|
Print the minimum time required to light K candles.
* * *
|
s993846838
|
Wrong Answer
|
p03276
|
Input is given from Standard Input in the following format:
N K
x_1 x_2 ... x_N
|
n, k = map(int, input().split())
x = list(map(int, input().split()))
b = None
for i in range(n):
if x[i] == 0:
b = i
start = True
break
elif x[i] > 0:
b = i
start = False
break
if not b:
m = abs(x[-k])
else:
if start:
del x[b]
k -= 1
n -= 1
if k == 0:
m = 0
else:
if b >= k:
m1 = abs(x[b - k])
else:
m1 = None
if n - b >= k:
m2 = abs(x[b + k - 1])
else:
m2 = None
m = max(abs(2 * x[0]), abs(2 * x[-1]))
for i in range(1, k):
if b - i >= 0 and b - i + k - 1 < n:
m = min(
2 * abs(x[b - i]) + abs(x[b - i + k - 1]),
abs(x[b - i]) + 2 * abs(x[b - i + k - 1]),
m,
)
if m1:
m = min(m, m1)
if m2:
m = min(m, m2)
print(m)
|
Statement
There are N candles placed on a number line. The i-th candle from the left is
placed on coordinate x_i. Here, x_1 < x_2 < ... < x_N holds.
Initially, no candles are burning. Snuke decides to light K of the N candles.
Now, he is at coordinate 0. He can move left and right along the line with
speed 1. He can also light a candle when he is at the same position as the
candle, in negligible time.
Find the minimum time required to light K candles.
|
[{"input": "5 3\n -30 -10 10 20 50", "output": "40\n \n\nHe should move and light candles as follows:\n\n * Move from coordinate 0 to -10.\n * Light the second candle from the left.\n * Move from coordinate -10 to 10.\n * Light the third candle from the left.\n * Move from coordinate 10 to 20.\n * Light the fourth candle from the left.\n\n* * *"}, {"input": "3 2\n 10 20 30", "output": "20\n \n\n* * *"}, {"input": "1 1\n 0", "output": "0\n \n\n * There may be a candle placed at coordinate 0.\n\n* * *"}, {"input": "8 5\n -9 -7 -4 -3 1 2 3 4", "output": "10"}]
|
Print the minimum number of vertices that you need to remove in order to
produce a good tree.
* * *
|
s508913083
|
Accepted
|
p04049
|
The input is given from Standard Input in the following format:
N K
A_1 B_1
A_2 B_2
:
A_{N-1} B_{N-1}
|
N, K = map(int, input().split())
G = [[] for i in range(N)]
a = [0 for i in range(N - 1)]
b = [0 for i in range(N - 1)]
for i in range(N - 1):
a[i], b[i] = map(int, input().split())
a[i] -= 1
b[i] -= 1
G[a[i]].append(b[i])
G[b[i]].append(a[i])
d = [[-1 for i in range(N)] for j in range(N)]
for i in range(N):
q = [i]
d[i][i] = 0
while len(q) > 0:
r = q[-1]
q.pop()
for p in G[r]:
if d[i][p] != -1:
continue
d[i][p] = d[i][r] + 1
q.append(p)
# dia=max([max([d[i][j] for i in range(N)]) for j in range(N)])
if K % 2 == 0:
t = [[d[i][j] for i in range(N)] for j in range(N)]
D = K // 2
ans = [0 for i in range(N)]
for i in range(N):
for j in range(N):
if t[i][j] > D:
ans[i] += 1
print(min(ans))
else:
t = [[min([d[a[i]][j], d[b[i]][j]]) for j in range(N)] for i in range(N - 1)]
ans = [0 for i in range(N - 1)]
D = (K - 1) // 2
for i in range(N - 1):
for j in range(N):
if t[i][j] > D:
ans[i] += 1
print(min(ans))
|
Statement
Given an undirected tree, let the distance between vertices u and v be the
number of edges on the simple path from u to v. The diameter of a tree is the
maximum among the distances between any two vertices. We will call a tree
_good_ if and only if its diameter is at most K.
You are given an undirected tree with N vertices numbered 1 through N. For
each i (1≦i≦N-1), there is an edge connecting vertices A_i and B_i.
You want to remove zero or more vertices from the tree, so that the resulting
tree is good. When a vertex is removed, all incident edges will also be
removed. The resulting graph must be connected.
Find the minimum number of vertices that you need to remove in order to
produce a good tree.
|
[{"input": "6 2\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "2\n \n\nThe tree is shown below. Removing vertices 5 and 6 will result in a good tree\nwith the diameter of 2.\n\n\n\n* * *"}, {"input": "6 5\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "0\n \n\nSince the given tree is already good, you do not need to remove any vertex."}]
|
Print the minimum number of vertices that you need to remove in order to
produce a good tree.
* * *
|
s004303402
|
Accepted
|
p04049
|
The input is given from Standard Input in the following format:
N K
A_1 B_1
A_2 B_2
:
A_{N-1} B_{N-1}
|
n, k = map(int, input().split())
g = [[] for _ in range(n)]
for i in range(n - 1):
a, b = map(int, input().split())
g[a - 1].append(b - 1)
g[b - 1].append(a - 1)
if k % 2 == 0:
ans = 100000
for i in range(n):
s = [i]
d = [-1] * n
d[i] = 0
while s:
p = s.pop()
for node in g[p]:
if d[node] == -1:
s.append(node)
d[node] = d[p] + 1
c = 0
for i in range(n):
if d[i] > k // 2:
c += 1
ans = min(ans, c)
else:
ans = 100000
for i in range(n):
for j in g[i]:
s = [i, j]
d = [-1] * n
d[i] = 0
d[j] = 0
while s:
p = s.pop()
for node in g[p]:
if d[node] == -1:
s.append(node)
d[node] = d[p] + 1
c = 0
for p in range(n):
if d[p] > k // 2:
c += 1
ans = min(ans, c)
print(ans)
|
Statement
Given an undirected tree, let the distance between vertices u and v be the
number of edges on the simple path from u to v. The diameter of a tree is the
maximum among the distances between any two vertices. We will call a tree
_good_ if and only if its diameter is at most K.
You are given an undirected tree with N vertices numbered 1 through N. For
each i (1≦i≦N-1), there is an edge connecting vertices A_i and B_i.
You want to remove zero or more vertices from the tree, so that the resulting
tree is good. When a vertex is removed, all incident edges will also be
removed. The resulting graph must be connected.
Find the minimum number of vertices that you need to remove in order to
produce a good tree.
|
[{"input": "6 2\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "2\n \n\nThe tree is shown below. Removing vertices 5 and 6 will result in a good tree\nwith the diameter of 2.\n\n\n\n* * *"}, {"input": "6 5\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "0\n \n\nSince the given tree is already good, you do not need to remove any vertex."}]
|
Print the minimum number of vertices that you need to remove in order to
produce a good tree.
* * *
|
s915240473
|
Wrong Answer
|
p04049
|
The input is given from Standard Input in the following format:
N K
A_1 B_1
A_2 B_2
:
A_{N-1} B_{N-1}
|
n, k = [int(v) for v in input().split()]
node_list = [[int(v) - 1 for v in input().split()] for i in range(n - 1)]
node_type = [0 for i in range(n)]
connect_list = [[] for i in range(n)]
for i in node_list:
a, b = i
connect_list[a].append(b)
connect_list[b].append(a)
node_type[a] += 1
node_type[b] += 1
leaf_set = [i for i in range(n) if node_type[i] == 1]
def bfs(p):
search_list = [p]
color_list = ["W" for i in range(n)]
color_list[p] = "B"
for _ in range(k):
new_search_list = []
for i in search_list:
for j in connect_list[i]:
if color_list[j] == "W":
color_list[j] = "B"
new_search_list.append(j)
search_list = new_search_list
return n - color_list.count("B")
ans_list = [bfs(i) for i in leaf_set]
print(min(ans_list))
|
Statement
Given an undirected tree, let the distance between vertices u and v be the
number of edges on the simple path from u to v. The diameter of a tree is the
maximum among the distances between any two vertices. We will call a tree
_good_ if and only if its diameter is at most K.
You are given an undirected tree with N vertices numbered 1 through N. For
each i (1≦i≦N-1), there is an edge connecting vertices A_i and B_i.
You want to remove zero or more vertices from the tree, so that the resulting
tree is good. When a vertex is removed, all incident edges will also be
removed. The resulting graph must be connected.
Find the minimum number of vertices that you need to remove in order to
produce a good tree.
|
[{"input": "6 2\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "2\n \n\nThe tree is shown below. Removing vertices 5 and 6 will result in a good tree\nwith the diameter of 2.\n\n\n\n* * *"}, {"input": "6 5\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "0\n \n\nSince the given tree is already good, you do not need to remove any vertex."}]
|
Print the minimum number of vertices that you need to remove in order to
produce a good tree.
* * *
|
s989027159
|
Runtime Error
|
p04049
|
The input is given from Standard Input in the following format:
N K
A_1 B_1
A_2 B_2
:
A_{N-1} B_{N-1}
|
n, k = map(int, input().split())
tree = [[] for i in range(n)]
for _ in range(n - 1):
a, b = sorted(map(int, input().split()))
tree[a - 1].append(b - 1)
tree[b - 1].append(a - 1)
def search(tree, pos, past=None, depth=0):
"""
子孫ノードを探索して、最深のノードとその深さを返す
"""
# 子ノードを探索する
ress = [] # 子ノードの探索結果
for next_node in tree[pos]:
# next_nodeが親なら探索しない
if next_node == past:
continue
res = search(tree, next_node, pos, depth + 1)
ress.append(res)
ress.sort(reverse=True)
# 子ノードがいないならばこのノードとその深さを返す
if len(ress) == 0:
ress = [[depth, pos]]
return ress[0]
def countChildren(tree, pos):
"""
ノードposを根ノードとした場合の
深さ毎のノードを数える
"""
def dfs(tree, pos, child_list=[], past=None, depth=0):
child_list += [0] * (depth + 1 - len(child_list))
child_list[depth] += 1
# 子ノードを探索する
for next_node in tree[pos]:
# next_nodeが親なら探索しない
if next_node == past:
continue
dfs(tree, next_node, child_list, pos, depth + 1)
child_list = []
dfs(tree, pos, child_list)
return child_list[:]
# 最遠頂点対 u,vと直径diameterを求める
_, u = search(tree, 0)
diameter, v = search(tree, u)
# u,vを頂点ノードとしたときの深さ毎のノードを数える
u_list = countChildren(tree, u)
v_list = countChildren(tree, v)
removed_nodes = 0
while diameter > k:
if u_list[-1] < v_list[-1]:
removed_nodes += u_list[-1]
u_list.pop()
else:
removed_nodes += v_list[-1]
v_list.pop()
diameter -= 1
print(removed_nodes)
|
Statement
Given an undirected tree, let the distance between vertices u and v be the
number of edges on the simple path from u to v. The diameter of a tree is the
maximum among the distances between any two vertices. We will call a tree
_good_ if and only if its diameter is at most K.
You are given an undirected tree with N vertices numbered 1 through N. For
each i (1≦i≦N-1), there is an edge connecting vertices A_i and B_i.
You want to remove zero or more vertices from the tree, so that the resulting
tree is good. When a vertex is removed, all incident edges will also be
removed. The resulting graph must be connected.
Find the minimum number of vertices that you need to remove in order to
produce a good tree.
|
[{"input": "6 2\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "2\n \n\nThe tree is shown below. Removing vertices 5 and 6 will result in a good tree\nwith the diameter of 2.\n\n\n\n* * *"}, {"input": "6 5\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "0\n \n\nSince the given tree is already good, you do not need to remove any vertex."}]
|
Print the minimum number of vertices that you need to remove in order to
produce a good tree.
* * *
|
s021807684
|
Wrong Answer
|
p04049
|
The input is given from Standard Input in the following format:
N K
A_1 B_1
A_2 B_2
:
A_{N-1} B_{N-1}
|
class tree_unit:
def __init__(self, name):
self.name = name
self.conn = []
def add_conn(self, vectex):
self.conn.append(vectex)
def search(self, vectex):
if vectex in self.conn:
conn = self.conn[:].remove(vectex)
return conn
else:
return []
def __repr__(self):
return str(self.name)
N, K = [int(x) for x in input().split()]
units = [tree_unit(0)]
for vec in range(1, N + 1):
units.append(tree_unit(vec))
for i in range(N - 1):
A, B = [int(x) for x in input().split()]
units[A].add_conn(B)
units[B].add_conn(A)
start = 1
for i in range(1, N + 1):
if len(units[i].conn) == 1:
start = i
cur = units[start].conn[0]
stack = [cur]
visited = [False for i in range(N + 1)]
depth = [0 for i in range(N + 1)]
depth[start] = 1
depth[cur] = 2
depth_var = 3
visited[start] = True
while stack:
cur = stack.pop()
visited[cur] = True
exist = False
for vec in units[cur].conn:
if not visited[vec]:
stack.append(vec)
depth[vec] = depth_var
exist = True
if exist:
depth_var += 1
max_depth = max(depth)
if max_depth <= K:
print(0)
else:
dif = max_depth - K
count_up, count_down = 0, 0
for v in depth[1:]:
if v > max_depth - dif:
count_up += 1
elif v <= dif:
count_down += 1
print(min(count_up, count_down))
|
Statement
Given an undirected tree, let the distance between vertices u and v be the
number of edges on the simple path from u to v. The diameter of a tree is the
maximum among the distances between any two vertices. We will call a tree
_good_ if and only if its diameter is at most K.
You are given an undirected tree with N vertices numbered 1 through N. For
each i (1≦i≦N-1), there is an edge connecting vertices A_i and B_i.
You want to remove zero or more vertices from the tree, so that the resulting
tree is good. When a vertex is removed, all incident edges will also be
removed. The resulting graph must be connected.
Find the minimum number of vertices that you need to remove in order to
produce a good tree.
|
[{"input": "6 2\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "2\n \n\nThe tree is shown below. Removing vertices 5 and 6 will result in a good tree\nwith the diameter of 2.\n\n\n\n* * *"}, {"input": "6 5\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "0\n \n\nSince the given tree is already good, you do not need to remove any vertex."}]
|
Print the minimum number of vertices that you need to remove in order to
produce a good tree.
* * *
|
s532382604
|
Runtime Error
|
p04049
|
The input is given from Standard Input in the following format:
N K
A_1 B_1
A_2 B_2
:
A_{N-1} B_{N-1}
|
import sys
sys.setrecursionlimit(5000000)
input = sys.stdin.readline
n,k = map(int,input().split())
edge = [[] for i in range(n)]
alledge = []
for i in range(n-1):
a,b = map(int,input().split())
edge[a-1].append(b-1)
edge[b-1].append(a-1)
alledge.append((a-1,b-1))
if n==2:
print(0)
exit()
def f(x,y,c):
c += 1
for e in edge[x]:
if e != y:
if c > d:
used[e] = 1
f(e,x,c)
if k % 2 == 0:
d = k//2
res = []
for i in range(n):
used = [0]*n
f(i,-1,0)
res.append(sum(used))
print(min(res))
else:
d = (k-1)//2
res = []
for e1 in alledge:
used = [0]*n
f(e1[0],e1[1],0)
f(e1[1],e1[0],0)
res.append(sum(used))
print(min(res))
|
Statement
Given an undirected tree, let the distance between vertices u and v be the
number of edges on the simple path from u to v. The diameter of a tree is the
maximum among the distances between any two vertices. We will call a tree
_good_ if and only if its diameter is at most K.
You are given an undirected tree with N vertices numbered 1 through N. For
each i (1≦i≦N-1), there is an edge connecting vertices A_i and B_i.
You want to remove zero or more vertices from the tree, so that the resulting
tree is good. When a vertex is removed, all incident edges will also be
removed. The resulting graph must be connected.
Find the minimum number of vertices that you need to remove in order to
produce a good tree.
|
[{"input": "6 2\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "2\n \n\nThe tree is shown below. Removing vertices 5 and 6 will result in a good tree\nwith the diameter of 2.\n\n\n\n* * *"}, {"input": "6 5\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "0\n \n\nSince the given tree is already good, you do not need to remove any vertex."}]
|
Print the minimum number of vertices that you need to remove in order to
produce a good tree.
* * *
|
s549402182
|
Wrong Answer
|
p04049
|
The input is given from Standard Input in the following format:
N K
A_1 B_1
A_2 B_2
:
A_{N-1} B_{N-1}
|
from collections import defaultdict
def computeDist(tree, nk, i):
visited = [0] * (nk[0] + 1)
queue = []
visited[i] = 1
queue.append(i)
dist = [0] * (nk[0] + 1)
dist[i] = 0
while queue:
s = queue.pop(0)
for u in tree[s]:
if not visited[u]:
queue.append(u)
visited[u] = 1
dist[u] = dist[s] + 1
return len([i for i in dist if i > nk[1] // 2])
def minimumNodesToBeRemoved(tree, nk):
noOfNodesAtDistKBy2 = [0] * (nk[0] + 1)
for i in range(1, nk[0] + 1):
noOfNodesAtDistKBy2[i] = computeDist(tree, nk, i)
return min(noOfNodesAtDistKBy2[1:])
def start():
nk = [int(i) for i in input().split()]
tree = defaultdict(list)
for i in range(nk[0] - 1):
uv = [int(i) for i in input().split()]
tree[uv[0]].append(uv[1])
tree[uv[1]].append(uv[0])
return minimumNodesToBeRemoved(tree, nk)
print(start())
|
Statement
Given an undirected tree, let the distance between vertices u and v be the
number of edges on the simple path from u to v. The diameter of a tree is the
maximum among the distances between any two vertices. We will call a tree
_good_ if and only if its diameter is at most K.
You are given an undirected tree with N vertices numbered 1 through N. For
each i (1≦i≦N-1), there is an edge connecting vertices A_i and B_i.
You want to remove zero or more vertices from the tree, so that the resulting
tree is good. When a vertex is removed, all incident edges will also be
removed. The resulting graph must be connected.
Find the minimum number of vertices that you need to remove in order to
produce a good tree.
|
[{"input": "6 2\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "2\n \n\nThe tree is shown below. Removing vertices 5 and 6 will result in a good tree\nwith the diameter of 2.\n\n\n\n* * *"}, {"input": "6 5\n 1 2\n 3 2\n 4 2\n 1 6\n 5 6", "output": "0\n \n\nSince the given tree is already good, you do not need to remove any vertex."}]
|
Print the given integer n and :. Then, print prime factors in ascending order.
If n is divisible by a prime factor several times, the prime factor should be
printed according to the number of times. Print a space before each prime
factor.
|
s019204190
|
Wrong Answer
|
p02467
|
n
An integer n is given in a line.
|
X = int(input())
temp = X
ret = repr(X) + ":"
for cnt in range(2, X):
while temp % cnt == 0:
temp = temp / cnt
ret += " " + repr(cnt)
cnt += 1
print(ret)
|
Prime Factorization
Factorize a given integer n.
|
[{"input": "12", "output": "12: 2 2 3"}, {"input": "126", "output": "126: 2 3 3 7"}]
|
Print the given integer n and :. Then, print prime factors in ascending order.
If n is divisible by a prime factor several times, the prime factor should be
printed according to the number of times. Print a space before each prime
factor.
|
s459321876
|
Accepted
|
p02467
|
n
An integer n is given in a line.
|
arr = []
n = int(input())
temp = n
for i in range(2, int(-(-(n**0.5) // 1)) + 1):
if temp % i == 0:
cnt = 0
while temp % i == 0:
cnt += 1
temp //= i
arr.append([i, cnt])
if temp != 1:
arr.append([temp, 1])
if arr == []:
arr.append([n, 1])
k = []
for a, s in arr:
k += [a] * s
print(str(n) + ":", *k, sep=" ")
|
Prime Factorization
Factorize a given integer n.
|
[{"input": "12", "output": "12: 2 2 3"}, {"input": "126", "output": "126: 2 3 3 7"}]
|
Print the given integer n and :. Then, print prime factors in ascending order.
If n is divisible by a prime factor several times, the prime factor should be
printed according to the number of times. Print a space before each prime
factor.
|
s249603344
|
Accepted
|
p02467
|
n
An integer n is given in a line.
|
n = int(input())
m = str(n) + ":"
a = True
l = n
i = 2
while a:
if l % i == 0:
l /= i
m += " " + str(i)
i -= 1
a = i < l**0.5
i += 1
if l != 1:
m += " " + str(int(l))
print(m)
|
Prime Factorization
Factorize a given integer n.
|
[{"input": "12", "output": "12: 2 2 3"}, {"input": "126", "output": "126: 2 3 3 7"}]
|
Print the minimum possible value taken by N after Aoki does the operation zero
or more times.
* * *
|
s584271689
|
Wrong Answer
|
p02719
|
Input is given from Standard Input in the following format:
N K
|
nums = [int(e) for e in input().split()]
Min = nums[0]
y = nums[1]
t = True
while t:
if abs(Min - y) < Min:
Min = Min - y
elif abs(Min - y) > Min:
break
print(Min)
|
Statement
Given any integer x, Aoki can do the operation below.
Operation: Replace x with the absolute difference of x and K.
You are given the initial value of an integer N. Find the minimum possible
value taken by N after Aoki does the operation zero or more times.
|
[{"input": "7 4", "output": "1\n \n\nInitially, N=7.\n\nAfter one operation, N becomes |7-4| = 3.\n\nAfter two operations, N becomes |3-4| = 1, which is the minimum value taken by\nN.\n\n* * *"}, {"input": "2 6", "output": "2\n \n\nN=2 after zero operations is the minimum.\n\n* * *"}, {"input": "1000000000000000000 1", "output": "0"}]
|
Print the minimum possible value taken by N after Aoki does the operation zero
or more times.
* * *
|
s863216014
|
Runtime Error
|
p02719
|
Input is given from Standard Input in the following format:
N K
|
n, m = map(int, input().split())
# 商品iをそれぞれN個入力
num = [int(i) for i in input().split()]
# 降順で並び替え
num = sorted(num, reverse=True)
# 総得票数
sum_num = sum(num)
# m-1番目つまり人気商品の中の一番人気がない商品が
# 総得票数の1/4Mは未満は人気商品と言えないNo
if num[m - 1] < sum_num / (4 * m):
print("No")
else:
print("Yes")
|
Statement
Given any integer x, Aoki can do the operation below.
Operation: Replace x with the absolute difference of x and K.
You are given the initial value of an integer N. Find the minimum possible
value taken by N after Aoki does the operation zero or more times.
|
[{"input": "7 4", "output": "1\n \n\nInitially, N=7.\n\nAfter one operation, N becomes |7-4| = 3.\n\nAfter two operations, N becomes |3-4| = 1, which is the minimum value taken by\nN.\n\n* * *"}, {"input": "2 6", "output": "2\n \n\nN=2 after zero operations is the minimum.\n\n* * *"}, {"input": "1000000000000000000 1", "output": "0"}]
|
Print the minimum possible value taken by N after Aoki does the operation zero
or more times.
* * *
|
s750262315
|
Wrong Answer
|
p02719
|
Input is given from Standard Input in the following format:
N K
|
# 振動し始めたら終わり
N, K = map(int, input().split())
A = []
i = 0
if N - K >= 0:
A.append(N - K)
N = N - K
else:
A.append(K - N)
N = K - N
if N - K >= 0:
A.append(N - K)
N = N - K
else:
A.append(K - N)
N = K - N
if N - K >= 0:
A.append(N - K)
N = N - K
else:
A.append(K - N)
N = K - N
i = 2
if A[i - 2] == A[i]:
print(min(A))
else:
while A[i - 2] != A[i]:
if K == 1:
print("0")
break
elif N - K >= 0:
A.append(N - K)
N = N - K
i += 1
if A[i - 2] != A[i]:
print(min(A))
break
else:
A.append(K - N)
N = K - N
i += 1
if A[i - 2] != A[i]:
print(min(A))
break
|
Statement
Given any integer x, Aoki can do the operation below.
Operation: Replace x with the absolute difference of x and K.
You are given the initial value of an integer N. Find the minimum possible
value taken by N after Aoki does the operation zero or more times.
|
[{"input": "7 4", "output": "1\n \n\nInitially, N=7.\n\nAfter one operation, N becomes |7-4| = 3.\n\nAfter two operations, N becomes |3-4| = 1, which is the minimum value taken by\nN.\n\n* * *"}, {"input": "2 6", "output": "2\n \n\nN=2 after zero operations is the minimum.\n\n* * *"}, {"input": "1000000000000000000 1", "output": "0"}]
|
Print the minimum possible value taken by N after Aoki does the operation zero
or more times.
* * *
|
s696150343
|
Runtime Error
|
p02719
|
Input is given from Standard Input in the following format:
N K
|
str = input().split()
a1 = int(str[0])
a2 = int(str[1])
diff = abs(a1 - a2)
if diff > a2:
larger = diff
smaller = a2
else:
larger = a2
smaller = diff
print(larger % smaller)
|
Statement
Given any integer x, Aoki can do the operation below.
Operation: Replace x with the absolute difference of x and K.
You are given the initial value of an integer N. Find the minimum possible
value taken by N after Aoki does the operation zero or more times.
|
[{"input": "7 4", "output": "1\n \n\nInitially, N=7.\n\nAfter one operation, N becomes |7-4| = 3.\n\nAfter two operations, N becomes |3-4| = 1, which is the minimum value taken by\nN.\n\n* * *"}, {"input": "2 6", "output": "2\n \n\nN=2 after zero operations is the minimum.\n\n* * *"}, {"input": "1000000000000000000 1", "output": "0"}]
|
Print the minimum possible value taken by N after Aoki does the operation zero
or more times.
* * *
|
s805247778
|
Runtime Error
|
p02719
|
Input is given from Standard Input in the following format:
N K
|
x, y, z = map(int, input().split())
print(z, x, y)
|
Statement
Given any integer x, Aoki can do the operation below.
Operation: Replace x with the absolute difference of x and K.
You are given the initial value of an integer N. Find the minimum possible
value taken by N after Aoki does the operation zero or more times.
|
[{"input": "7 4", "output": "1\n \n\nInitially, N=7.\n\nAfter one operation, N becomes |7-4| = 3.\n\nAfter two operations, N becomes |3-4| = 1, which is the minimum value taken by\nN.\n\n* * *"}, {"input": "2 6", "output": "2\n \n\nN=2 after zero operations is the minimum.\n\n* * *"}, {"input": "1000000000000000000 1", "output": "0"}]
|
Print the minimum possible value taken by N after Aoki does the operation zero
or more times.
* * *
|
s576120458
|
Wrong Answer
|
p02719
|
Input is given from Standard Input in the following format:
N K
|
NK = list(map(int, input().split()))
N = NK[0]
K = NK[1]
old = max(NK)
new = 0
while old > new:
old = new
for i in range(10):
if i == 0:
temp = []
temp.append(abs(N - K))
temp.append(abs(K - N))
else:
temp1 = []
temp1.append(abs(temp - K))
temp1.append(abs(temp - N))
temp = temp1
temp = min(temp)
new = temp
print(temp)
|
Statement
Given any integer x, Aoki can do the operation below.
Operation: Replace x with the absolute difference of x and K.
You are given the initial value of an integer N. Find the minimum possible
value taken by N after Aoki does the operation zero or more times.
|
[{"input": "7 4", "output": "1\n \n\nInitially, N=7.\n\nAfter one operation, N becomes |7-4| = 3.\n\nAfter two operations, N becomes |3-4| = 1, which is the minimum value taken by\nN.\n\n* * *"}, {"input": "2 6", "output": "2\n \n\nN=2 after zero operations is the minimum.\n\n* * *"}, {"input": "1000000000000000000 1", "output": "0"}]
|
Print the minimum possible value taken by N after Aoki does the operation zero
or more times.
* * *
|
s352447917
|
Runtime Error
|
p02719
|
Input is given from Standard Input in the following format:
N K
|
n, k = list(map(int, input().split()))
# print(n, k)
min_result = n
flag = 0
dic = {}
z = n // k
zz = n // z
result = zz
while flag == 0:
result = abs(result - k)
print("result", result)
print("min_result", min_result)
if result <= min_result:
min_result = result
dic[result] = dic.get(result, 0) + 1
if dic[result] > 1:
flag = 1
print(min_result)
|
Statement
Given any integer x, Aoki can do the operation below.
Operation: Replace x with the absolute difference of x and K.
You are given the initial value of an integer N. Find the minimum possible
value taken by N after Aoki does the operation zero or more times.
|
[{"input": "7 4", "output": "1\n \n\nInitially, N=7.\n\nAfter one operation, N becomes |7-4| = 3.\n\nAfter two operations, N becomes |3-4| = 1, which is the minimum value taken by\nN.\n\n* * *"}, {"input": "2 6", "output": "2\n \n\nN=2 after zero operations is the minimum.\n\n* * *"}, {"input": "1000000000000000000 1", "output": "0"}]
|
Print the minimum possible value taken by N after Aoki does the operation zero
or more times.
* * *
|
s786227501
|
Accepted
|
p02719
|
Input is given from Standard Input in the following format:
N K
|
c, d = [int(i) for i in input().split()]
c %= d
print(min(c, abs(c - d)))
|
Statement
Given any integer x, Aoki can do the operation below.
Operation: Replace x with the absolute difference of x and K.
You are given the initial value of an integer N. Find the minimum possible
value taken by N after Aoki does the operation zero or more times.
|
[{"input": "7 4", "output": "1\n \n\nInitially, N=7.\n\nAfter one operation, N becomes |7-4| = 3.\n\nAfter two operations, N becomes |3-4| = 1, which is the minimum value taken by\nN.\n\n* * *"}, {"input": "2 6", "output": "2\n \n\nN=2 after zero operations is the minimum.\n\n* * *"}, {"input": "1000000000000000000 1", "output": "0"}]
|
Print the minimum possible value taken by N after Aoki does the operation zero
or more times.
* * *
|
s495360839
|
Wrong Answer
|
p02719
|
Input is given from Standard Input in the following format:
N K
|
N, K = map(int, input().split()) # 複数の数字
print(N % K)
|
Statement
Given any integer x, Aoki can do the operation below.
Operation: Replace x with the absolute difference of x and K.
You are given the initial value of an integer N. Find the minimum possible
value taken by N after Aoki does the operation zero or more times.
|
[{"input": "7 4", "output": "1\n \n\nInitially, N=7.\n\nAfter one operation, N becomes |7-4| = 3.\n\nAfter two operations, N becomes |3-4| = 1, which is the minimum value taken by\nN.\n\n* * *"}, {"input": "2 6", "output": "2\n \n\nN=2 after zero operations is the minimum.\n\n* * *"}, {"input": "1000000000000000000 1", "output": "0"}]
|
Print the minimum possible value taken by N after Aoki does the operation zero
or more times.
* * *
|
s500417298
|
Wrong Answer
|
p02719
|
Input is given from Standard Input in the following format:
N K
|
def replacing(a, b):
new = a - b
new1 = abs(new) - b
return abs(new1)
|
Statement
Given any integer x, Aoki can do the operation below.
Operation: Replace x with the absolute difference of x and K.
You are given the initial value of an integer N. Find the minimum possible
value taken by N after Aoki does the operation zero or more times.
|
[{"input": "7 4", "output": "1\n \n\nInitially, N=7.\n\nAfter one operation, N becomes |7-4| = 3.\n\nAfter two operations, N becomes |3-4| = 1, which is the minimum value taken by\nN.\n\n* * *"}, {"input": "2 6", "output": "2\n \n\nN=2 after zero operations is the minimum.\n\n* * *"}, {"input": "1000000000000000000 1", "output": "0"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s995840761
|
Accepted
|
p03558
|
Input is given from Standard Input in the following format:
K
|
from collections import deque
def main():
"""K の正の倍数の 10 進法での各桁の和としてありうる最小の値を求めてください。
2 ≤ K ≤ 10^5
min: 1が1つと他が0 -> 10^n, e.g.: 5*2, 25*4
10倍しても元のKと和は変わらない
1-9倍とは限らない?: 入力例 2 11111=41×271, 4+1=5では?
"""
K = int(input())
ans = sum_digits(K)
for i in range(2, 10):
ans = min(ans, sum_digits(K * i))
print(ans)
def sum_digits(n):
return sum(map(int, list(str(n))))
def main2():
import sys
debug = sys.argv[-1] == "debug"
K = int(input())
q = deque([1])
inf = float("inf")
dp = [inf for _ in range(K)]
dp[1] = 0
# 01BFS
# cost 0 の辺の遷移は deque の先頭に要素を追加
# cost 1 の辺の遷移は deque の末尾に要素を追加
while q:
idx = q.popleft()
x = dp[idx]
m1 = (idx * 10) % K
m2 = (idx + 1) % K
if dp[m1] > x:
dp[m1] = x
q.appendleft(m1)
if dp[m2] > x + 1:
dp[m2] = x + 1
q.append(m2)
if debug:
print((m1, m2), dp, q, file=sys.stderr)
print("-" * 10, file=sys.stderr)
print(dp[0] + 1)
if __name__ == "__main__":
main2()
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s335194463
|
Runtime Error
|
p03558
|
Input is given from Standard Input in the following format:
K
|
# coding: utf-8
N = int(input())
array = []
X = int(100000/N)
for i in range(X):
Y = N*(i+1)
STR = str(Y)
a_list = list(map(float,STR))
ddd = sum(a_list)
array.append(sum(ddd)
sum_list = min(array)
print(int(sum_list)
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s201519540
|
Runtime Error
|
p03558
|
Input is given from Standard Input in the following format:
K
|
import heapq
def small_multiple(k):
# kの倍数で各桁の総数が最も小さくなるような、各桁の総数
dist = [float("inf")] * k
q = []
# kで割った余りが1になるような最小の数は1
heapq.heappush(q, (1, 1))
while q:
n, c = heapq.heappop(q)
if dist[n] <= c:
continue
print(n, c)
dist[n] = c
if dist[(n+1) % k] > c + 1:
heapq.heappush(q, ((n + 1) % k, c + 1))
if dist[(n*10) % k] > c:
heapq.heappush(q, ((n * 10) % k, c))
print(dist[0])
def main():
k = int(input())
small_multiple(k)
if __name__ == "__main__":
main()
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s319278503
|
Wrong Answer
|
p03558
|
Input is given from Standard Input in the following format:
K
|
n = int(input())
num = int((n) ** (1 / 2))
print((num) ** 2)
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s767617257
|
Runtime Error
|
p03558
|
Input is given from Standard Input in the following format:
K
|
k = int(input())
ans= 10*10
for i in range(2,10*5):
o = list(str(i*k))
sumorder = sum(o)
if sumorder < ans:
ans = sumorder
print(ans)
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s445270064
|
Wrong Answer
|
p03558
|
Input is given from Standard Input in the following format:
K
|
n = int(input())
ans = 0
temp = n
while n < 10:
n += temp
temp = n % 9
print(temp if temp != 0 else sum([int(x) for x in str(n)]))
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s091218762
|
Runtime Error
|
p03558
|
Input is given from Standard Input in the following format:
K
|
k = int(input())
from collections import deque
d = deque([1])
discovered = {1:1}
while true:
q = d.popleft()
if q == 0:
print(discovered[q])
quit()
if (q*10)%k not in discovered:
if (q*10)%k == 0:
d.appendleft((q*10)%k)
discovered[(q*10)%k] = discovered[q]
if q+1 not in discoverd:
d.append(q+1)
discovered[q+1] = discovered[q]+1
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s619649362
|
Wrong Answer
|
p03558
|
Input is given from Standard Input in the following format:
K
|
n = input()
c = 0
for i in n:
c += int(i)
for i in range(1, 10 ** len(n)):
d = 0
l = str(int(n) * (i + 1))
for j in l:
d += int(j)
c = min(c, d)
print(c)
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s742300454
|
Wrong Answer
|
p03558
|
Input is given from Standard Input in the following format:
K
|
K = int(input())
A = [1]
B = [[x, 0] for x in range(K)]
C = [1]
B[1][1] = 1
while B[0][1] == 0:
for x in C:
b = (10 * x) % K
c = (x + 1) % K
if b == 0:
B[0][1] = B[x][1]
break
elif c == 0:
B[0][1] = B[x][1] + 1
break
else:
if b in C:
pass
else:
C += [b]
B[b][1] = B[x][1]
if c in C:
pass
else:
C += [c]
B[c][1] = B[x][1] + 1
print(B[0][1])
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s631716218
|
Wrong Answer
|
p03558
|
Input is given from Standard Input in the following format:
K
|
# D-small multiple
k = int(input())
maxi = 10**10
for i in range(1, 5 * 10**5 + 1):
a = str(k * i)
sums = 0
for j in range(len(a)):
sums += int(a[j])
maxi = min(maxi, sums)
print(maxi)
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s201126844
|
Accepted
|
p03558
|
Input is given from Standard Input in the following format:
K
|
# -*- coding: utf-8 -*-
#############
# Libraries #
#############
import sys
input = sys.stdin.readline
import math
# from math import gcd
import bisect
import heapq
from collections import defaultdict
from collections import deque
from collections import Counter
from functools import lru_cache
#############
# Constants #
#############
MOD = 10**9 + 7
INF = float("inf")
AZ = "abcdefghijklmnopqrstuvwxyz"
#############
# Functions #
#############
######INPUT######
def I():
return int(input().strip())
def S():
return input().strip()
def IL():
return list(map(int, input().split()))
def SL():
return list(map(str, input().split()))
def ILs(n):
return list(int(input()) for _ in range(n))
def SLs(n):
return list(input().strip() for _ in range(n))
def ILL(n):
return [list(map(int, input().split())) for _ in range(n)]
def SLL(n):
return [list(map(str, input().split())) for _ in range(n)]
######OUTPUT######
def P(arg):
print(arg)
return
def Y():
print("Yes")
return
def N():
print("No")
return
def E():
exit()
def PE(arg):
print(arg)
exit()
def YE():
print("Yes")
exit()
def NE():
print("No")
exit()
#####Shorten#####
def DD(arg):
return defaultdict(arg)
#####Inverse#####
def inv(n):
return pow(n, MOD - 2, MOD)
######Combination######
kaijo_memo = []
def kaijo(n):
if len(kaijo_memo) > n:
return kaijo_memo[n]
if len(kaijo_memo) == 0:
kaijo_memo.append(1)
while len(kaijo_memo) <= n:
kaijo_memo.append(kaijo_memo[-1] * len(kaijo_memo) % MOD)
return kaijo_memo[n]
gyaku_kaijo_memo = []
def gyaku_kaijo(n):
if len(gyaku_kaijo_memo) > n:
return gyaku_kaijo_memo[n]
if len(gyaku_kaijo_memo) == 0:
gyaku_kaijo_memo.append(1)
while len(gyaku_kaijo_memo) <= n:
gyaku_kaijo_memo.append(
gyaku_kaijo_memo[-1] * pow(len(gyaku_kaijo_memo), MOD - 2, MOD) % MOD
)
return gyaku_kaijo_memo[n]
def nCr(n, r):
if n == r:
return 1
if n < r or r < 0:
return 0
ret = 1
ret = ret * kaijo(n) % MOD
ret = ret * gyaku_kaijo(r) % MOD
ret = ret * gyaku_kaijo(n - r) % MOD
return ret
######Factorization######
def factorization(n):
arr = []
temp = n
for i in range(2, int(-(-(n**0.5) // 1)) + 1):
if temp % i == 0:
cnt = 0
while temp % i == 0:
cnt += 1
temp //= i
arr.append([i, cnt])
if temp != 1:
arr.append([temp, 1])
if arr == []:
arr.append([n, 1])
return arr
#####MakeDivisors######
def make_divisors(n):
divisors = []
for i in range(1, int(n**0.5) + 1):
if n % i == 0:
divisors.append(i)
if i != n // i:
divisors.append(n // i)
return divisors
#####MakePrimes######
def make_primes(N):
max = int(math.sqrt(N))
seachList = [i for i in range(2, N + 1)]
primeNum = []
while seachList[0] <= max:
primeNum.append(seachList[0])
tmp = seachList[0]
seachList = [i for i in seachList if i % tmp != 0]
primeNum.extend(seachList)
return primeNum
#####GCD#####
def gcd(a, b):
while b:
a, b = b, a % b
return a
#####LCM#####
def lcm(a, b):
return a * b // gcd(a, b)
#####BitCount#####
def count_bit(n):
count = 0
while n:
n &= n - 1
count += 1
return count
#####ChangeBase#####
def base_10_to_n(X, n):
if X // n:
return base_10_to_n(X // n, n) + [X % n]
return [X % n]
def base_n_to_10(X, n):
return sum(int(str(X)[-i - 1]) * n**i for i in range(len(str(X))))
def base_10_to_n_without_0(X, n):
X -= 1
if X // n:
return base_10_to_n_without_0(X // n, n) + [X % n]
return [X % n]
#####IntLog#####
def int_log(n, a):
count = 0
while n >= a:
n //= a
count += 1
return count
#############
# Main Code #
#############
N = I()
graph = [[] for i in range(N)]
for i in range(N):
graph[i].append((1, (i + 1) % N))
for i in range(N):
graph[i].append((0, (i * 10) % N))
def bfs(graph, start):
N = len(graph)
d = [INF] * N
d[start] = 0
q = deque([start])
while q:
u = q.popleft()
for c, v in graph[u]:
if d[v] <= d[u] + c:
continue
d[v] = d[u] + c
if c:
q.append(v)
else:
q.appendleft(v)
return d
d = bfs(graph, 1)
print(d[0] + 1)
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s912295987
|
Accepted
|
p03558
|
Input is given from Standard Input in the following format:
K
|
import sys
# import math
# import queue
# import copy
# import bisect#2分探索
from collections import deque
def input():
return sys.stdin.readline()[:-1]
def inputi():
return int(input())
K = inputi()
vals = [10**5 + 1] * K
visit = []
vals[1] = 0
q = deque([1])
flag = False
while len(q) > 0:
s = q.popleft()
vs = vals[s]
if s == 0:
print(vs + 1)
flag = True
break
# visit.append(s)
s0 = (10 * s) % K
if vs < vals[s0]:
vals[s0] = vs
q.appendleft(s0)
s1 = (s + 1) % K
if vs + 1 < vals[s1]:
vals[s1] = vs + 1
q.append(s1)
# print(q,s,s0,s1,vals)
# if flag==False:
# print(vals[0]+1)
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s675566555
|
Wrong Answer
|
p03558
|
Input is given from Standard Input in the following format:
K
|
p = int(input())
if p % 5 == 0 and p % 2 == 0:
print(1)
else:
m = 1000000000000000
for i in range(1, 100001):
v = p * i
s = 0
for j in range(10000):
s += v % 10
v //= 10
if v == 0:
break
if v >= 100000:
s += 1
m = min(m, s)
print(m)
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s429305859
|
Runtime Error
|
p03558
|
Input is given from Standard Input in the following format:
K
|
# coding: utf-8
# Your code here!
from datetime import datetime
K = int(input())
start = datetime.now()
def KSum(n):
k = 0
for i in str(n):
k += int(i)
return k
m = KSum(K)
j = 1
while((datetime.now()-start).total_seconds() < 1.8):
for x in range(100):
P = KSum(K*j)
if m > P:
m = P
j += 1
print(m)
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s271307245
|
Wrong Answer
|
p03558
|
Input is given from Standard Input in the following format:
K
|
def digit_sum(n: int) -> int:
ans = 0
while n > 0:
ans += n % 10
n //= 10
return ans
def judge(n: int) -> int:
pow2 = [2**i for i in range(21)]
pow5 = [5**i for i in range(11)]
pow10 = [10**i for i in range(7)]
if n % 99999 == 0:
return 9 * 5
elif n % 9999 == 0:
return 9 * 4
elif n % 999 == 0:
return 9 * 3
elif n % 99 == 0:
return 9 * 2
elif n % 33 == 0:
return 6
elif n in pow2:
return 1
elif n in pow5:
return 1
elif n in pow10:
return 1
else:
ans = 10**10
for i in range(1, 100000):
ans = min(ans, digit_sum(i * n))
return ans
n = int(input())
print(judge(n))
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s258936495
|
Wrong Answer
|
p03558
|
Input is given from Standard Input in the following format:
K
|
import heapq
def main():
k = int(input())
if k == 2:
print(1)
elif k == 3:
print(3)
elif k == 8:
print(1)
elif k == 9:
print(9)
else:
brdict = {}
for i in range(1, k):
if i == k - 1:
brdict[i] = [(0, 1)]
else:
brdict[i] = [((i * 10) % k, 0)]
if (i * 10) % k != i + 1:
brdict[i] += [(i + 1, 1)]
start = 1
cost = [i for i in range(k)]
cost[0] = k
fixed = [False] * k
fixed[start] = True
akouho = [(1, start)]
heapq.heapify(akouho)
while not all(fixed):
(fnode, fcost) = heapq.heappop(akouho)
if fnode == 0:
break
fixed[fnode] = True
for br in brdict[fnode]:
if not fixed[br[0]]:
if cost[br[0]] > fcost + br[1]:
cost[br[0]] = fcost + br[1]
heapq.heappush(akouho, (br[0], cost[br[0]]))
print(cost[0])
if __name__ == "__main__":
main()
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
Print the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
* * *
|
s161680838
|
Wrong Answer
|
p03558
|
Input is given from Standard Input in the following format:
K
|
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**6)
############ ---- Input Functions ---- ############
def in_int():
return int(input())
def in_list():
return list(map(int, input().split()))
def in_str():
s = input()
return list(s[: len(s) - 1])
def in_ints():
return map(int, input().split())
n = in_int()
while n % 2 == 0:
n = n // 2
while n % 5 == 0:
n = n // 5
ans = sum(list(map(int, list(str(n)))))
for i in range(1, n):
x = sum(list(map(int, list(str(n * i)))))
ans = min(x, ans)
print(ans)
|
Statement
Find the smallest possible sum of the digits in the decimal notation of a
positive multiple of K.
|
[{"input": "6", "output": "3\n \n\n12=6\u00d72 yields the smallest sum.\n\n* * *"}, {"input": "41", "output": "5\n \n\n11111=41\u00d7271 yields the smallest sum.\n\n* * *"}, {"input": "79992", "output": "36"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s993687298
|
Wrong Answer
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
A, B = map(int, input().split())
if A != 0:
A = A - 1
def ruiseki_XOR(N):
if (N + 1) % 2 == 0:
if ((N + 1) // 2) % 2 == 0:
return 0
else:
return 1
else:
if ((N + 1) // 2) % 2 == 0:
return N
else:
return 1 ^ N
a = ruiseki_XOR(A)
b = ruiseki_XOR(B)
print(a ^ b)
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s823093402
|
Runtime Error
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
N, M = map(int, input().split())
ils = [map(int, input().split()) for _ in range(M)]
par = [i for i in range(N)]
size = [1] * N
def root(x):
if par[x] == x:
return x
else:
par[x] = root(par[x])
def unit(x, y):
x = root(x)
y = root(y)
if x == y:
return
par[x] = y
size[y] += size[x]
size[x] = size[y]
inconv = N * (N - 1) // 2
inconvs = [inconv]
for A, B in ils[::-1]
inconv -= size(root(A)) * size(root(B))
unite(A, B)
inconvs.insert(0, inconv)
print('\n'.join(inconvs))
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s668736953
|
Accepted
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
n, m = list(map(int, input().split()))
isla = [0 for i in range(n + 1)]
bri = []
crus = [[] for i in range(n)]
num = [0 for i in range(n)]
score = []
crusmax = 0
plusnum = -1
minusnum = -1
newnum = -1
plusval = [0, 0]
minusval = [0, 0]
for i in range(m):
a, b = list(map(int, input().split()))
bri.append([a, b])
bri.reverse()
# print(bri)
for i in range(m):
a = bri[i][0]
b = bri[i][1]
if isla[a] == 0 and isla[b] == 0:
crusmax += 1
crus[crusmax].append(a)
crus[crusmax].append(b)
isla[a] = crusmax
isla[b] = crusmax
num[crusmax] = 2
[plusnum, minusnum, newnum] = [0, 0, crusmax]
elif isla[a] == 0:
isla[a] = isla[b]
crus[isla[b]].append(a)
num[isla[b]] += 1
[plusnum, minusnum, newnum] = [isla[b], 0, 0]
plusval = [num[isla[b]] - 1, num[isla[b]]]
elif isla[b] == 0:
isla[b] = isla[a]
crus[isla[a]].append(b)
num[isla[a]] += 1
[plusnum, minusnum, newnum] = [isla[a], 0, 0]
plusval = [num[isla[a]] - 1, num[isla[a]]]
elif isla[a] < isla[b]:
color = isla[b]
dif = len(crus[isla[b]])
for j in range(len(crus[isla[b]])):
isla[crus[color][j]] = isla[a]
crus[isla[a]].append(crus[color][j])
crus[color] = []
num[isla[a]] += num[color]
num[color] = 0
[plusnum, minusnum, newnum] = [isla[a], color, 0]
plusval = [num[isla[a]] - dif, num[isla[a]]]
minusval = [dif, 0]
elif isla[a] > isla[b]:
color = isla[a]
dif = len(crus[isla[a]])
for j in range(len(crus[isla[a]])):
isla[crus[color][j]] = isla[b]
crus[isla[b]].append(crus[color][j])
crus[color] = []
num[isla[b]] += num[color]
num[color] = 0
[plusnum, minusnum, newnum] = [isla[b], color, 0]
plusval = [num[isla[b]] - dif, num[isla[b]]]
minusval = [dif, 0]
else:
[plusnum, minusnum, newnum] = [0, 0, 0]
# print("bri[i]",bri[i])
# print("isla",isla)
# print("crus",crus)
# print("num",num)
if i == 0:
total = 0
else:
total = score[-1]
if newnum != 0:
total += 1
if plusnum != 0:
total += (plusval[1] * (plusval[1] - 1)) // 2
total -= (plusval[0] * (plusval[0] - 1)) // 2
if minusnum != 0:
total += (minusval[1] * (minusval[1] - 1)) // 2
total -= (minusval[0] * (minusval[0] - 1)) // 2
score.append(total)
# print("total",total)
# print()
score.reverse()
for i in range(len(score)):
score[i] = (n * (n - 1)) // 2 - score[i]
score.append((n * (n - 1)) // 2)
score = score[1:]
for i in range(len(score)):
print(score[i])
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s618152763
|
Accepted
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
n, m = map(int, input().split())
ab = [list(map(int, input().split())) for i in range(m)]
tree = [[] for i in range(n + 1)]
parent = [0] * (n + 1)
count = [0] * m
for i in range(1, m + 1):
a, b = ab[-i]
A = parent[a]
B = parent[b]
if A == 0 and B == 0:
parent[a] = a
parent[b] = a
tree[a].append(b)
count[-i] = 1
elif A == 0:
count[-i] = len(tree[B]) + 1
parent[a] = B
tree[B].append(a)
elif B == 0:
count[-i] = len(tree[A]) + 1
parent[b] = A
tree[A].append(b)
elif parent[a] == parent[b]:
count[-i] = 0
else:
A = parent[a]
B = parent[b]
u = len(tree[A])
v = len(tree[B])
count[-i] = (u + 1) * (v + 1)
if u < v:
A, B = B, A
a, b = b, a
for u in tree[B]:
parent[u] = A
parent[B] = A
tree[A].append(B)
tree[A] += tree[B]
tree[B] = []
sum = 0
for i in range(0, m):
sum += count[i]
print(sum)
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s636171595
|
Accepted
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
n, m = map(int, input().split())
ab = []
for _ in range(m):
ab.append(list(map(lambda x: int(x) - 1, input().split())))
ab.reverse()
pre = [i for i in range(n)]
num = [1 for _ in range(n)]
ans = n * (n - 1) // 2
out = []
for i in range(m):
out.append(ans)
x, y = ab[i]
X = []
while pre[x] != x:
X.append(x)
x = pre[x]
Y = []
while pre[y] != y:
Y.append(y)
y = pre[y]
if x != y:
ans -= num[x] * num[y]
if num[x] >= num[y]:
win = x
pre[y] = x
num[x] += num[y]
else:
win = y
pre[x] = y
num[y] += num[x]
for xx in X:
pre[xx] = win
for yy in Y:
pre[yy] = win
out.reverse()
for o in out:
print(o)
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s593550610
|
Accepted
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
sn, bn = map(int, input().split(" "))
fu = [int(sn * (sn - 1) / 2)]
gr_si = [n for n in range(sn + 1)]
siL_gr = [[n] for n in range(sn + 1)]
siL_br = []
for _ in range(bn):
siL_br.append(list(map(int, input().split(" "))))
siL_br = siL_br[::-1]
for bri in range(bn - 1):
si1, si2 = siL_br[bri]
gr1 = gr_si[si1]
gr2 = gr_si[si2]
if gr1 == gr2:
fu.append(fu[bri])
else:
lengr1 = len(siL_gr[gr1])
lengr2 = len(siL_gr[gr2])
if lengr1 < lengr2:
gr1, gr2 = gr2, gr1
fu.append(fu[bri] - lengr1 * lengr2)
for si in siL_gr[gr2]:
gr_si[si] = gr1
siL_gr[gr1] += siL_gr[gr2]
siL_gr[gr2] = []
print(*fu[::-1], sep="\n")
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s829061270
|
Accepted
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
class Node:
def __init__(self, key):
self.key = key
self.parent = None
self.rank = 0
self.elements_count = 1
class DisjointSet:
def __init__(self, nodes):
self.nodes = nodes
def find_set(self, key):
pivot = self.nodes[key]
while pivot.key != pivot.parent.key:
pivot = pivot.parent
self.nodes[key].parent = pivot
return pivot.key
def elements_count(self, key):
repr_key = self.find_set(key)
return self.nodes[repr_key].elements_count
def same(self, x, y):
return self.find_set(x) == self.find_set(y)
def unite(self, x, y):
y_root = self.find_set(y)
x_root = self.find_set(x)
if self.nodes[x].rank > self.nodes[y].rank:
self.nodes[y_root].parent = self.nodes[x_root]
self.nodes[x_root].elements_count += self.nodes[y_root].elements_count
elif self.nodes[x].rank < self.nodes[y].rank:
self.nodes[x_root].parent = self.nodes[y_root]
self.nodes[y_root].elements_count += self.nodes[x_root].elements_count
else:
self.nodes[x_root].parent = self.nodes[y_root]
self.nodes[y_root].rank = self.nodes[y_root].rank + 1
self.nodes[y_root].elements_count += self.nodes[x_root].elements_count
def comb_pair(n):
return (n * (n - 1)) // 2
def m():
N, M = [int(i) for i in input().split()]
nodes = [Node(i) for i in range(0, N)]
for node in nodes:
node.parent = node
ds = DisjointSet(nodes)
convenience = [0] * (M + 1)
inputs = [input().split() for _ in range(M)]
inputs = [(int(x[0]) - 1, int(x[1]) - 1) for x in inputs]
reversed_inputs = list(reversed(inputs))
for i in range(M):
a, b = reversed_inputs[i]
if ds.same(a, b):
convenience[i + 1] = convenience[i]
next
else:
before = comb_pair(ds.elements_count(a)) + comb_pair(ds.elements_count(b))
ds.unite(a, b)
after = comb_pair(ds.elements_count(a))
diff = after - before
convenience[i + 1] = convenience[i] + diff
maximum = convenience[-1]
for c in convenience[-2::-1]:
print(maximum - c)
if __name__ == "__main__":
m()
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s126532269
|
Wrong Answer
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
sn, bn = map(int, input().split(" "))
fubensa = [int(sn * (sn - 1) / 2)]
if bn > 1:
br = []
for _ in range(bn):
br.append(list(map(int, input().split(" "))))
br = br[::-1]
sg = [0 for n in range(sn + 1)]
sg[br[0][0]] = 1
sg[br[0][1]] = 1
gn = 1
fubensa.append(fubensa[0] - 1)
sgc = [0, 2]
for bri in range(1, bn - 1):
si1 = br[bri][0]
si2 = br[bri][1]
sg1 = sg[si1]
sg2 = sg[si2]
if sg1 + sg2 == 0:
gn += 1
sg[si1], sg[si2] = gn, gn
sgc.append(2)
fubensa.append(fubensa[bri] - 1)
elif sg1 == 0:
fubensa.append(fubensa[bri] - sgc[sg2])
sg[si1] = sg2
sgc[sg2] += 1
elif sg2 == 0:
fubensa.append(fubensa[bri] - sgc[sg1])
sg[si2] = sg1
sgc[sg1] += 1
elif sg1 != sg2:
fubensa.append(fubensa[bri] - sgc[sg1] * sgc[sg2])
sg = [sg1 if x == sg2 else x for x in sg]
else:
fubensa.append(fubensa[bri])
for x in fubensa[::-1]:
print(x)
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s062806819
|
Wrong Answer
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
n, m = map(int, input().split())
lst = [list(map(int, input().split())) for _ in range(m)]
lst = list(reversed(lst))
possible_route = n * (n - 1) / 2
ans = [possible_route]
route_lst = []
for pair in lst:
new_route_lst = []
index0 = -1
index1 = -1
for k, route in enumerate(route_lst):
if pair[0] in route:
index0 = k
if pair[1] in route:
index1 = k
if index0 >= 0 and index1 >= 0 and index1 != index0:
route = set(route_lst[index0]) | set(route_lst[index1])
new_route_lst.append(list(route))
elif index0 >= 0:
route = set(route_lst[index1]) | set(pair)
new_route_lst.append(list(route))
elif index1 >= 0:
route = set(route_lst[index1]) | set(pair)
new_route_lst.append(list(route))
else:
new_route_lst.append(pair)
for k, route in enumerate(route_lst):
if k == index0 or k == index1:
pass
else:
new_route_lst.append(route)
count = 0
for k in new_route_lst:
m = len(k)
count += m * (m - 1) / 2
ans.append(possible_route - count)
route_lst = new_route_lst
for i in reversed(ans):
print(int(i))
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s334225425
|
Wrong Answer
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
n, m = map(int, input().split())
ab = []
for _ in range(m):
a, b = map(int, input().split())
ab.append([a, b])
# %%
# n, m, ab = 4, 5, [[1, 2], [3, 4], [1, 3], [2, 3], [1, 4]]
# %%
import math
# %%
n_comb = math.factorial(n) // (math.factorial(n - 2) * math.factorial(2))
# %%
ans_list = [n_comb]
# %%
group_sets = []
for abi in ab[::-1]:
ai, bi = abi
difficulty = 0
flag_new = True
flag_double = 0
for g in group_sets:
if ai in g or bi in g:
# check double
difficulty2 = 0
for g2 in group_sets:
if ai in g2 or bi in g2:
flag_double += 1
difficulty2 += len(g2)
if flag_double >= 2:
difficulty += difficulty2
continue
elif ai in g:
difficulty += len(g)
g.add(bi)
flag_new = False
elif bi in g:
difficulty += len(g)
g.add(ai)
flag_new = False
if flag_new:
group_sets.append({ai, bi})
difficulty += 1
ans_list.append(max(ans_list[-1] - difficulty, 0))
# %%
ans_list = ans_list[:-1]
for i in ans_list[::-1]:
print(i)
# %%
# %%
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s446299718
|
Wrong Answer
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
N, M = [int(e) for e in input().split(" ")]
ABs = []
for _ in range(M):
ABs.append([int(e) for e in input().split(" ")])
maxValue = N * (N - 1) // 2
ans = [maxValue]
buf_sets = []
flagSkip = False
for i in range(M - 1):
a, b = ABs[M - 1 - i]
# print("a,b", a, b)
if flagSkip is True:
ans.append(0)
continue
idx_a = None
idx_b = None
if len(buf_sets) > 0:
for j, s in enumerate(buf_sets):
if a in s:
idx_a = j
if b in s:
idx_b = j
if idx_a is not None and idx_b is not None:
break
if idx_a is None and idx_b is None:
s_new = set([a, b])
buf_sets.append(s_new)
elif idx_a is not None and idx_b is None:
buf_sets[idx_a].add(a)
buf_sets[idx_a].add(b)
elif idx_a is None and idx_b is not None:
buf_sets[idx_b].add(a)
buf_sets[idx_b].add(b)
else:
s_a = buf_sets[idx_a]
s_b = buf_sets[idx_b]
buf_sets[idx_a] = s_a | s_b
buf_sets.pop(idx_b)
# for s in buf_sets:
# print(s)
# print("---")
count = 0
for s in buf_sets:
n = len(s)
count = count + (n * (n - 1) // 2)
d = maxValue - count
ans.append(d)
if d == 0:
flagSkip = True
for a in reversed(ans):
print(a)
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s618111249
|
Accepted
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
class UnionFindNode(object):
def __init__(self, group_id, parent=None, value=None):
self.group_id = group_id
self.parent_ = parent
self.value = value
self.size_ = 1
def __str__(self):
return (
"UnionFindNode(group_id: {}, \n\tparent: {}, value: {}, size: {})".format(
self.group_id, self.parent_, self.value, self.size_
)
)
def is_root(self):
return not self.parent_
def parent(self):
parent = self
while parent.parent_:
parent = parent.parent_
if not self.is_root():
self.parent_ = parent
return parent
def find(self):
parent = self.parent()
return parent.group_id
def size(self):
parent = self.parent()
return parent.size_
def unite(self, unite_node):
parent = self.parent()
unite_parent = unite_node.parent()
if parent.group_id != unite_parent.group_id:
if parent.size() > unite_parent.size():
unite_parent.parent_ = parent
parent.size_ = parent.size_ + unite_parent.size_
else:
parent.parent_ = unite_parent
unite_parent.size_ = parent.size_ + unite_parent.size_
[N, M] = list(map(int, input().split(" ")))
bridge_list = []
for _ in range(M):
[a, b] = list(map(int, input().split(" ")))
bridge_list.append((a - 1, b - 1))
node_list = [UnionFindNode(i) for i in range(N)]
combination_num = N * (N - 1) // 2
combination_list = [combination_num]
for bridge in bridge_list[:0:-1]:
# print(bridge)
if node_list[bridge[0]].find() != node_list[bridge[1]].find():
combination_num = (
combination_num - node_list[bridge[0]].size() * node_list[bridge[1]].size()
)
node_list[bridge[0]].unite(node_list[bridge[1]])
combination_list.append(combination_num)
# print(combination_num)
for value in combination_list[::-1]:
print(value)
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s960242554
|
Runtime Error
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
import numpy as np
lst = input().split(" ")
N = int(lst[0])
M = int(lst[1])
mat = np.eye(N)
bridges = []
for i in range(M):
pair = input().split(" ")
A = int(pair[0]) - 1
B = int(pair[1]) - 1
mat[A][B] = 1
mat[B][A] = 1
bridges.append([A, B])
# print(mat)
for i in range(M):
a = bridges[i][0]
b = bridges[i][1]
mat[a][b] = 0
mat[b][a] = 0
# print(mat)
connected = np.eye(N)
for j in range(N):
connected = np.dot(connected, mat)
connected = np.where(connected > 0, 1, 0)
# print(connected)
print(int((N**2 - np.sum(connected)) / 2))
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s581666360
|
Wrong Answer
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
# -*- coding: utf-8 -*-
import sys
# ----------------------------------------------------------------
# Use Solve Function
def solve(lines):
N, M = map(int, lines.pop(0).split(" "))
NLIST = []
for i in range(M):
A, B = map(int, lines.pop(0).split(" "))
NLIST.append((A, B))
res = N * (N - 1) // 2
R = [res]
sets = []
for i in range(M - 1, 0, -1):
x = NLIST[i]
print(x)
n1 = {x[0]}
n2 = {x[1]}
delete_idx = []
for j, y in enumerate(sets):
if x[0] in y:
n1 = y
delete_idx.append(j)
if x[1] in y:
n2 = y
if not j in delete_idx:
delete_idx.append(j)
delete_idx.sort(reverse=True)
for k in delete_idx:
sets.pop(k)
if n1 != n2:
res -= len(n1) * len(n2)
n1 = n1.union(n2)
sets.append(n1)
R.append(res)
print(R)
lines = [x.strip() for x in sys.stdin.readlines()]
#
# solve !!
#
solve(lines)
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s927360655
|
Runtime Error
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
from math import factorial
N, M = map(int, input().split())
AB_list = [[]]
for i in range(M):
A, B = map(int, input().split())
AB_list.append([A, B])
del AB_list[0]
AB_list.reverse()
S_list = []
result = []
mixed = []
i = 0
while i < M:
S_list.append(AB_list[i])
if len(S_list) == 1:
val_c = int(
factorial(len(S_list[0])) / factorial(2) / factorial(len(S_list[0]) - 2)
)
result.append(val_c)
else:
count = 0
change = 1
switch = 0
while change != 0 and switch == 0:
change = 0
for k in range(len(S_list) - 1):
list_and = list(set(S_list[k]) & set(S_list[len(S_list) - 1]))
if not len(list_and) == 0:
val = list(set(S_list[k]) | set(S_list[len(S_list) - 1]))
S_list.insert(k, val)
del S_list[k + 1 : k + 2]
del S_list[len(S_list) - 1]
change += 1
switch += 1
break
else:
pass
while change != 0 and switch != 0:
change = 0
for k in range(len(S_list) - 1):
list_and = list(set(S_list[k + 1]) & set(S_list[0]))
if not len(list_and) == 0:
val = list(set(S_list[k + 1]) | set(S_list[0]))
del S_list[k + 1 : k + 2]
S_list.insert(0, val)
del S_list[1]
change += 1
break
else:
pass
# print(S_list)
val_total = 0
for j in range(len(S_list)):
val_c = int(
factorial(len(S_list[j])) / factorial(2) / factorial(len(S_list[j]) - 2)
)
val_total += val_c
result.append(val_total)
i += 1
result.reverse()
base_result = int(factorial(N) / factorial(2) / factorial(N - 2))
for i in range(1, M):
print(base_result - result[i])
print(base_result)
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
In the order i = 1, 2, ..., M, print the inconvenience just after the i-th
bridge collapses. Note that the answer may not fit into a 32-bit integer type.
* * *
|
s330577245
|
Wrong Answer
|
p03108
|
Input is given from Standard Input in the following format:
N M
A_1 B_1
A_2 B_2
\vdots
A_M B_M
|
class UnionFind:
def __init__(self, size: int):
self.__root = [-1 for _ in range(size)]
self.__size = [1 for _ in range(size)]
def find(self, v: int) -> int:
if self.__root[v] == -1:
return v
return self.find(self.__root[v])
def size(self, v: int) -> int:
root = self.find(v)
return self.__size[root]
def unite(self, u: int, v: int):
ur, vr = self.find(u), self.find(v)
if ur > vr:
ur, vr = vr, ur
self.__size[ur] += self.__size[vr]
self.__root[vr] = ur
def connected(self, u: int, v: int):
return self.find(u) == self.find(v)
def print(self):
print("-" * 5 + " root " + "-" * 5)
print(self.__root)
print("-" * 5 + " size " + "-" * 5)
print(self.__size)
def decayed_bridges(N: int, M: int, edges: list) -> list:
ret = [0 for _ in range(M + 1)]
uf = UnionFind(N + 1)
m = M
ret[m] = N * (N - 1) // 2
m -= 1
for u, v in reversed(edges):
if uf.connected(u, v):
ret[m] = ret[m + 1]
else:
n1, n2 = uf.size(u), uf.size(v)
ret[m] = ret[m + 1] - n1 * n2
uf.unite(u, v)
m -= 1
return ret
if __name__ == "__main__":
N, M = [int(s) for s in input().split()]
edges = []
for _ in range(M):
a, b = [int(s) for s in input().split()]
edges.append((a, b))
answers = decayed_bridges(N, M, edges)
for a in answers:
print(a)
|
Statement
There are N islands and M bridges.
The i-th bridge connects the A_i-th and B_i-th islands bidirectionally.
Initially, we can travel between any two islands using some of these bridges.
However, the results of a survey show that these bridges will all collapse
because of aging, in the order from the first bridge to the M-th bridge.
Let the **inconvenience** be the number of pairs of islands (a, b) (a < b)
such that we are no longer able to travel between the a-th and b-th islands
using some of the bridges remaining.
For each i (1 \leq i \leq M), find the inconvenience just after the i-th
bridge collapses.
|
[{"input": "4 5\n 1 2\n 3 4\n 1 3\n 2 3\n 1 4", "output": "0\n 0\n 4\n 5\n 6\n \n\nFor example, when the first to third bridges have collapsed, the inconvenience\nis 4 since we can no longer travel between the pairs (1, 2), (1, 3), (2, 4)\nand (3, 4).\n\n* * *"}, {"input": "6 5\n 2 3\n 1 2\n 5 6\n 3 4\n 4 5", "output": "8\n 9\n 12\n 14\n 15\n \n\n* * *"}, {"input": "2 1\n 1 2", "output": "1"}]
|
For each query, output in a line the era name and the era-based year number
corresponding to the western year given, separated with a single whitespace.
In case you cannot determine the era, output “Unknown” without quotes.
|
s879596365
|
Wrong Answer
|
p01359
|
The input contains multiple test cases. Each test case has the following
format:
_N Q_
_EraName_ 1 _EraBasedYear_ 1 _WesternYear_ 1
.
.
.
_EraName_ _N_ _EraBasedYear_ _N_ _WesternYear_ _N_
_Query_ 1 .
.
.
_Query_ _Q_
The first line of the input contains two positive integers _N_ and _Q_ (1 ≤
_N_ ≤ 1000, 1 ≤ _Q_ ≤ 1000). _N_ is the number of database entries, and Q is
the number of queries.
Each of the following N lines has three components: era name, era-based year
number and the corresponding western year (1 ≤ _EraBasedYear_ _i_ ≤
_WesternYear_ _i_ ≤ 109 ). Each of era names consist of at most 16 Roman
alphabet characters. Then the last _Q_ lines of the input specifies queries (1
≤ _Query_ _i_ ≤ 109 ), each of which is a western year to compute era-based
representation.
The end of input is indicated by a line containing two zeros. This line is not
part of any dataset and hence should not be processed.
You can assume that all the western year in the input is positive integers,
and that there is no two entries that share the same era name.
|
inputnum, outputnum = (int(n) for n in input().split(" "))
data = {}
while True:
for i in range(inputnum):
temp = input().split(" ")
data[temp[0]] = [int(temp[2]) - int(temp[1]) + 1, int(temp[2])]
for o in range(outputnum):
targ = int(input())
for k, v in data.items():
if v[0] <= targ <= v[1]:
print(k + " " + str(targ - v[0] + 1))
break
else:
print("Unknown")
inputnum, outputnum = (int(n) for n in input().split(" "))
if inputnum == outputnum == 0:
break
|
A: Era Name
As many of you know, we have two major calendar systems used in Japan today.
One of them is Gregorian calendar which is widely used across the world. It is
also known as “Western calendar” in Japan.
The other calendar system is era-based calendar, or so-called “Japanese
calendar.” This system comes from ancient Chinese systems. Recently in Japan
it has been a common way to associate dates with the Emperors. In the era-
based system, we represent a year with an era name given at the time a new
Emperor assumes the throne. If the era name is “A”, the first regnal year will
be “A 1”, the second year will be “A 2”, and so forth.
Since we have two different calendar systems, it is often needed to convert
the date in one calendar system to the other. In this problem, you are asked
to write a program that converts western year to era-based year, given a
database that contains association between several western years and era-based
years.
For the simplicity, you can assume the following:
1. A new era always begins on January 1st of the corresponding Gregorian year.
2. The first year of an era is described as 1.
3. There is no year in which more than one era switch takes place.
Please note that, however, the database you will see may be incomplete. In
other words, some era that existed in the history may be missing from your
data. So you will also have to detect the cases where you cannot determine
exactly which era the given year belongs to.
|
[{"input": "3\n meiji 10 1877\n taisho 6 1917\n showa 62 1987\n heisei 22 2010\n 1868\n 1917\n 1988\n 1 1\n universalcentury 123 2168\n 2010\n 0 0", "output": "meiji 1\n taisho 6\n Unknown\n Unknown"}]
|
Print the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
* * *
|
s654564302
|
Accepted
|
p03364
|
Input is given from Standard Input in the following format:
N
S_{1,1}S_{1,2}..S_{1,N}
S_{2,1}S_{2,2}..S_{2,N}
:
S_{N,1}S_{N,2}..S_{N,N}
|
# -*- coding: utf-8 -*-
#############
# Libraries #
#############
import sys
input = sys.stdin.readline
import math
# from math import gcd
import bisect
import heapq
from collections import defaultdict
from collections import deque
from collections import Counter
from functools import lru_cache
#############
# Constants #
#############
MOD = 10**9 + 7
INF = float("inf")
AZ = "abcdefghijklmnopqrstuvwxyz"
#############
# Functions #
#############
######INPUT######
def I():
return int(input().strip())
def S():
return input().strip()
def IL():
return list(map(int, input().split()))
def SL():
return list(map(str, input().split()))
def ILs(n):
return list(int(input()) for _ in range(n))
def SLs(n):
return list(input().strip() for _ in range(n))
def ILL(n):
return [list(map(int, input().split())) for _ in range(n)]
def SLL(n):
return [list(map(str, input().split())) for _ in range(n)]
######OUTPUT######
def P(arg):
print(arg)
return
def Y():
print("Yes")
return
def N():
print("No")
return
def E():
exit()
def PE(arg):
print(arg)
exit()
def YE():
print("Yes")
exit()
def NE():
print("No")
exit()
#####Shorten#####
def DD(arg):
return defaultdict(arg)
#####Inverse#####
def inv(n):
return pow(n, MOD - 2, MOD)
######Combination######
kaijo_memo = []
def kaijo(n):
if len(kaijo_memo) > n:
return kaijo_memo[n]
if len(kaijo_memo) == 0:
kaijo_memo.append(1)
while len(kaijo_memo) <= n:
kaijo_memo.append(kaijo_memo[-1] * len(kaijo_memo) % MOD)
return kaijo_memo[n]
gyaku_kaijo_memo = []
def gyaku_kaijo(n):
if len(gyaku_kaijo_memo) > n:
return gyaku_kaijo_memo[n]
if len(gyaku_kaijo_memo) == 0:
gyaku_kaijo_memo.append(1)
while len(gyaku_kaijo_memo) <= n:
gyaku_kaijo_memo.append(
gyaku_kaijo_memo[-1] * pow(len(gyaku_kaijo_memo), MOD - 2, MOD) % MOD
)
return gyaku_kaijo_memo[n]
def nCr(n, r):
if n == r:
return 1
if n < r or r < 0:
return 0
ret = 1
ret = ret * kaijo(n) % MOD
ret = ret * gyaku_kaijo(r) % MOD
ret = ret * gyaku_kaijo(n - r) % MOD
return ret
######Factorization######
def factorization(n):
arr = []
temp = n
for i in range(2, int(-(-(n**0.5) // 1)) + 1):
if temp % i == 0:
cnt = 0
while temp % i == 0:
cnt += 1
temp //= i
arr.append([i, cnt])
if temp != 1:
arr.append([temp, 1])
if arr == []:
arr.append([n, 1])
return arr
#####MakeDivisors######
def make_divisors(n):
divisors = []
for i in range(1, int(n**0.5) + 1):
if n % i == 0:
divisors.append(i)
if i != n // i:
divisors.append(n // i)
return divisors
#####MakePrimes######
def make_primes(N):
max = int(math.sqrt(N))
seachList = [i for i in range(2, N + 1)]
primeNum = []
while seachList[0] <= max:
primeNum.append(seachList[0])
tmp = seachList[0]
seachList = [i for i in seachList if i % tmp != 0]
primeNum.extend(seachList)
return primeNum
#####GCD#####
def gcd(a, b):
while b:
a, b = b, a % b
return a
#####LCM#####
def lcm(a, b):
return a * b // gcd(a, b)
#####BitCount#####
def count_bit(n):
count = 0
while n:
n &= n - 1
count += 1
return count
#####ChangeBase#####
def base_10_to_n(X, n):
if X // n:
return base_10_to_n(X // n, n) + [X % n]
return [X % n]
def base_n_to_10(X, n):
return sum(int(str(X)[-i - 1]) * n**i for i in range(len(str(X))))
def base_10_to_n_without_0(X, n):
X -= 1
if X // n:
return base_10_to_n_without_0(X // n, n) + [X % n]
return [X % n]
#####IntLog#####
def int_log(n, a):
count = 0
while n >= a:
n //= a
count += 1
return count
#############
# Main Code #
#############
N = I()
data = SLs(N)
data = [i * 2 for i in data] * 2
ans = 0
for i in range(N):
oy, ox = 0, i
flag = 1
for j in range(N):
for k in range(N):
if data[oy + j][ox + k] != data[oy + k][ox + j]:
flag = 0
break
if not flag:
break
if flag:
ans += 1
print(ans * N)
|
Statement
Snuke has two boards, each divided into a grid with N rows and N columns. For
both of these boards, the square at the i-th row from the top and the j-th
column from the left is called Square (i,j).
There is a lowercase English letter written in each square on the first board.
The letter written in Square (i,j) is S_{i,j}. On the second board, nothing is
written yet.
Snuke will write letters on the second board, as follows:
* First, choose two integers A and B ( 0 \leq A, B < N ).
* Write one letter in each square on the second board. Specifically, write the letter written in Square ( i+A, j+B ) on the first board into Square (i,j) on the second board. Here, the k-th row is also represented as the (N+k)-th row, and the k-th column is also represented as the (N+k)-th column.
After this operation, the second board is called a _good_ board when, for
every i and j ( 1 \leq i, j \leq N ), the letter in Square (i,j) and the
letter in Square (j,i) are equal.
Find the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
|
[{"input": "2\n ab\n ca", "output": "2\n \n\nFor each pair of A and B, the second board will look as shown below:\n\n\n\nThe second board is a good board when (A,B) = (0,1) or (A,B) = (1,0), thus the\nanswer is 2.\n\n* * *"}, {"input": "4\n aaaa\n aaaa\n aaaa\n aaaa", "output": "16\n \n\nEvery possible choice of A and B makes the second board good.\n\n* * *"}, {"input": "5\n abcde\n fghij\n klmno\n pqrst\n uvwxy", "output": "0\n \n\nNo possible choice of A and B makes the second board good."}]
|
Print the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
* * *
|
s549508350
|
Runtime Error
|
p03364
|
Input is given from Standard Input in the following format:
N
S_{1,1}S_{1,2}..S_{1,N}
S_{2,1}S_{2,2}..S_{2,N}
:
S_{N,1}S_{N,2}..S_{N,N}
|
n = int(input())
s = [input() for i in range(n)]
def check
def yoi(s, b):
for i in range(n):
for j in range(i+1, n):
if s[i % n][(j + b) % n] != s[j % n][(i + b) % n]:
return 0
return 1
sol = sum(yoi(s, b) for b in range(n))
print(sol * n)
|
Statement
Snuke has two boards, each divided into a grid with N rows and N columns. For
both of these boards, the square at the i-th row from the top and the j-th
column from the left is called Square (i,j).
There is a lowercase English letter written in each square on the first board.
The letter written in Square (i,j) is S_{i,j}. On the second board, nothing is
written yet.
Snuke will write letters on the second board, as follows:
* First, choose two integers A and B ( 0 \leq A, B < N ).
* Write one letter in each square on the second board. Specifically, write the letter written in Square ( i+A, j+B ) on the first board into Square (i,j) on the second board. Here, the k-th row is also represented as the (N+k)-th row, and the k-th column is also represented as the (N+k)-th column.
After this operation, the second board is called a _good_ board when, for
every i and j ( 1 \leq i, j \leq N ), the letter in Square (i,j) and the
letter in Square (j,i) are equal.
Find the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
|
[{"input": "2\n ab\n ca", "output": "2\n \n\nFor each pair of A and B, the second board will look as shown below:\n\n\n\nThe second board is a good board when (A,B) = (0,1) or (A,B) = (1,0), thus the\nanswer is 2.\n\n* * *"}, {"input": "4\n aaaa\n aaaa\n aaaa\n aaaa", "output": "16\n \n\nEvery possible choice of A and B makes the second board good.\n\n* * *"}, {"input": "5\n abcde\n fghij\n klmno\n pqrst\n uvwxy", "output": "0\n \n\nNo possible choice of A and B makes the second board good."}]
|
Print the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
* * *
|
s505267547
|
Runtime Error
|
p03364
|
Input is given from Standard Input in the following format:
N
S_{1,1}S_{1,2}..S_{1,N}
S_{2,1}S_{2,2}..S_{2,N}
:
S_{N,1}S_{N,2}..S_{N,N}
|
N = int(input())
S = []
for i in range(N):
S.append(input())
def check(S, A, B):
for i in range(N):
for j in range(i+1, N):
if j + B < N:
b = j + B
else:
b = j + B - N
if i + B < N:
d = i + B
else:
d = i + B - N
if S[a][b] != S[c][d]:
return 0
return 1
cnt = 0
for i in range(N):
cnt += check(S, 0, i):
print(cnt * N)
|
Statement
Snuke has two boards, each divided into a grid with N rows and N columns. For
both of these boards, the square at the i-th row from the top and the j-th
column from the left is called Square (i,j).
There is a lowercase English letter written in each square on the first board.
The letter written in Square (i,j) is S_{i,j}. On the second board, nothing is
written yet.
Snuke will write letters on the second board, as follows:
* First, choose two integers A and B ( 0 \leq A, B < N ).
* Write one letter in each square on the second board. Specifically, write the letter written in Square ( i+A, j+B ) on the first board into Square (i,j) on the second board. Here, the k-th row is also represented as the (N+k)-th row, and the k-th column is also represented as the (N+k)-th column.
After this operation, the second board is called a _good_ board when, for
every i and j ( 1 \leq i, j \leq N ), the letter in Square (i,j) and the
letter in Square (j,i) are equal.
Find the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
|
[{"input": "2\n ab\n ca", "output": "2\n \n\nFor each pair of A and B, the second board will look as shown below:\n\n\n\nThe second board is a good board when (A,B) = (0,1) or (A,B) = (1,0), thus the\nanswer is 2.\n\n* * *"}, {"input": "4\n aaaa\n aaaa\n aaaa\n aaaa", "output": "16\n \n\nEvery possible choice of A and B makes the second board good.\n\n* * *"}, {"input": "5\n abcde\n fghij\n klmno\n pqrst\n uvwxy", "output": "0\n \n\nNo possible choice of A and B makes the second board good."}]
|
Print the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
* * *
|
s798919390
|
Runtime Error
|
p03364
|
Input is given from Standard Input in the following format:
N
S_{1,1}S_{1,2}..S_{1,N}
S_{2,1}S_{2,2}..S_{2,N}
:
S_{N,1}S_{N,2}..S_{N,N}
|
N = int(input())
S = []
for i in range(N):
S.append(input())
def check(S, A, B):
for i in range(N):
for j in range(i+1, N):
if S[i][j] != S[j][i]:
return 0
else return 1
cnt = 0
for i in range(N):
cnt += check(S[i:] + S[:i], 0, i)
print(cnt * N)
|
Statement
Snuke has two boards, each divided into a grid with N rows and N columns. For
both of these boards, the square at the i-th row from the top and the j-th
column from the left is called Square (i,j).
There is a lowercase English letter written in each square on the first board.
The letter written in Square (i,j) is S_{i,j}. On the second board, nothing is
written yet.
Snuke will write letters on the second board, as follows:
* First, choose two integers A and B ( 0 \leq A, B < N ).
* Write one letter in each square on the second board. Specifically, write the letter written in Square ( i+A, j+B ) on the first board into Square (i,j) on the second board. Here, the k-th row is also represented as the (N+k)-th row, and the k-th column is also represented as the (N+k)-th column.
After this operation, the second board is called a _good_ board when, for
every i and j ( 1 \leq i, j \leq N ), the letter in Square (i,j) and the
letter in Square (j,i) are equal.
Find the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
|
[{"input": "2\n ab\n ca", "output": "2\n \n\nFor each pair of A and B, the second board will look as shown below:\n\n\n\nThe second board is a good board when (A,B) = (0,1) or (A,B) = (1,0), thus the\nanswer is 2.\n\n* * *"}, {"input": "4\n aaaa\n aaaa\n aaaa\n aaaa", "output": "16\n \n\nEvery possible choice of A and B makes the second board good.\n\n* * *"}, {"input": "5\n abcde\n fghij\n klmno\n pqrst\n uvwxy", "output": "0\n \n\nNo possible choice of A and B makes the second board good."}]
|
Print the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
* * *
|
s791251604
|
Runtime Error
|
p03364
|
Input is given from Standard Input in the following format:
N
S_{1,1}S_{1,2}..S_{1,N}
S_{2,1}S_{2,2}..S_{2,N}
:
S_{N,1}S_{N,2}..S_{N,N}
|
import numpy as np
n=int(input())
s=[chr(i) for i in range(97, 97+26)]
aa_cij=np.array([[s.index(i)+1 for i in list(input())] for _ in range(n)],dtype='int8')
ans=0
for i in range(n):
aa_cij=np.concatenate( [ aa_cij[1:,:], aa_cij[[0],:] ], axis=0)
if np.allclose(aa_cij 、aa_cij.T):
ans+=1
print(ans*n)
|
Statement
Snuke has two boards, each divided into a grid with N rows and N columns. For
both of these boards, the square at the i-th row from the top and the j-th
column from the left is called Square (i,j).
There is a lowercase English letter written in each square on the first board.
The letter written in Square (i,j) is S_{i,j}. On the second board, nothing is
written yet.
Snuke will write letters on the second board, as follows:
* First, choose two integers A and B ( 0 \leq A, B < N ).
* Write one letter in each square on the second board. Specifically, write the letter written in Square ( i+A, j+B ) on the first board into Square (i,j) on the second board. Here, the k-th row is also represented as the (N+k)-th row, and the k-th column is also represented as the (N+k)-th column.
After this operation, the second board is called a _good_ board when, for
every i and j ( 1 \leq i, j \leq N ), the letter in Square (i,j) and the
letter in Square (j,i) are equal.
Find the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
|
[{"input": "2\n ab\n ca", "output": "2\n \n\nFor each pair of A and B, the second board will look as shown below:\n\n\n\nThe second board is a good board when (A,B) = (0,1) or (A,B) = (1,0), thus the\nanswer is 2.\n\n* * *"}, {"input": "4\n aaaa\n aaaa\n aaaa\n aaaa", "output": "16\n \n\nEvery possible choice of A and B makes the second board good.\n\n* * *"}, {"input": "5\n abcde\n fghij\n klmno\n pqrst\n uvwxy", "output": "0\n \n\nNo possible choice of A and B makes the second board good."}]
|
Print the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
* * *
|
s567461211
|
Accepted
|
p03364
|
Input is given from Standard Input in the following format:
N
S_{1,1}S_{1,2}..S_{1,N}
S_{2,1}S_{2,2}..S_{2,N}
:
S_{N,1}S_{N,2}..S_{N,N}
|
def getN():
return int(input())
def getNM():
return map(int, input().split())
def getList():
return list(map(int, input().split()))
def getArray(intn):
return [int(input()) for i in range(intn)]
def input():
return sys.stdin.readline().rstrip()
def rand_N(ran1, ran2):
return random.randint(ran1, ran2)
def rand_List(ran1, ran2, rantime):
return [random.randint(ran1, ran2) for i in range(rantime)]
def rand_ints_nodup(ran1, ran2, rantime):
ns = []
while len(ns) < rantime:
n = random.randint(ran1, ran2)
if not n in ns:
ns.append(n)
return sorted(ns)
def rand_query(ran1, ran2, rantime):
r_query = []
while len(r_query) < rantime:
n_q = rand_ints_nodup(ran1, ran2, 2)
if not n_q in r_query:
r_query.append(n_q)
return sorted(r_query)
from collections import defaultdict, deque, Counter
from sys import exit
from decimal import *
from heapq import heapify, heappop, heappush
import math
import random
import string
from copy import deepcopy
from itertools import combinations, permutations, product
from operator import mul, itemgetter
from functools import reduce
from bisect import bisect_left, bisect_right
import sys
sys.setrecursionlimit(1000000000)
mod = 10**9 + 7
#############
# Main Code #
#############
# N <= 300 O(n ** 3)まで
# 何通り dp or combo
N = getN()
# 1つ目の譜面
B = [list(input()) for i in range(N)]
# 2つ目にはなにも書かれてない
# 2つ目の盤面に縦にi、横にjずらして数字を記入する
# 対角線に対して線対称なものの数を求める
# 整数a, bの選び方が何通りあるか
def judge(a, b):
res = [[""] * N for i in range(N)]
# 盤面1のB[i][j]を盤面2に書き込む
for i in range(N):
for j in range(N):
res[(i + a) % N][(j + b) % N] = B[i][j]
for i in range(N):
for j in range(N):
if res[i][j] != res[j][i]:
return 0
else:
continue
break
else:
return 1
# 全てのa, bについて調べるなら1つの(a, b)についてO(N)で求める必要がある
# 判定する際、節約出来ないか?
# N * N のゾーンをずらしていく
# a [b a] b
# c [a c] a
# a b a b
# c a c a 対称軸がずれる 軸は2N - 1本ある
# 良い盤面になる条件
# 斜めにずらしていくことで前の結果を利用できる
# 1本の軸について判定した時、1つの盤面が良い盤面なら他全ても良い盤面
# 軸に刺さっている盤面の数を求めればいい
# 軸は2N - 1本ある
# 縦に対角線をずらす
ans = 0
for i in range(N):
# 軸(0, i)にはN - i本の盤面が連なっている
# 連なっている全ての盤面は全てTrueか全てFalse
ans += (N - i) * judge(i, 0)
# 横に対角線をずらす
for i in range(1, N):
ans += (N - i) * judge(0, i)
print(ans)
|
Statement
Snuke has two boards, each divided into a grid with N rows and N columns. For
both of these boards, the square at the i-th row from the top and the j-th
column from the left is called Square (i,j).
There is a lowercase English letter written in each square on the first board.
The letter written in Square (i,j) is S_{i,j}. On the second board, nothing is
written yet.
Snuke will write letters on the second board, as follows:
* First, choose two integers A and B ( 0 \leq A, B < N ).
* Write one letter in each square on the second board. Specifically, write the letter written in Square ( i+A, j+B ) on the first board into Square (i,j) on the second board. Here, the k-th row is also represented as the (N+k)-th row, and the k-th column is also represented as the (N+k)-th column.
After this operation, the second board is called a _good_ board when, for
every i and j ( 1 \leq i, j \leq N ), the letter in Square (i,j) and the
letter in Square (j,i) are equal.
Find the number of the ways to choose integers A and B ( 0 \leq A, B < N )
such that the second board is a good board.
|
[{"input": "2\n ab\n ca", "output": "2\n \n\nFor each pair of A and B, the second board will look as shown below:\n\n\n\nThe second board is a good board when (A,B) = (0,1) or (A,B) = (1,0), thus the\nanswer is 2.\n\n* * *"}, {"input": "4\n aaaa\n aaaa\n aaaa\n aaaa", "output": "16\n \n\nEvery possible choice of A and B makes the second board good.\n\n* * *"}, {"input": "5\n abcde\n fghij\n klmno\n pqrst\n uvwxy", "output": "0\n \n\nNo possible choice of A and B makes the second board good."}]
|
Print the maximum possible total value of the selected items.
* * *
|
s722011557
|
Runtime Error
|
p03734
|
Input is given from Standard Input in the following format:
N W
w_1 v_1
w_2 v_2
:
w_N v_N
|
n, w = [int(v) for v in input().split()]
knapsack = [[int(v) for v in input().split()] for i in range(n)]
dp_list = [[None for i in range(4 * n + 1)] for i in range(n + 1)]
dp_list[0][0] = 0
base = knapsack[0][0]
for wi, vi in knapsack:
wi -= base
for i in range(n - 1, -1, -1):
for j in range(4 * n, -1, -1):
if 0 <= j - wi < 4 * n + 1 and 0 <= j < 4 * n + 1:
if dp_list[i][j - wi] is not None:
if dp_list[i + 1][j] is None:
dp_list[i + 1][j] = dp_list[i][j - wi] + vi
else:
dp_list[i + 1][j] = max(
dp_list[i][j - wi] + vi, dp_list[i + 1][j]
)
ans_list = [0]
for i in range(1, n + 1):
l = w - i * base
for j in range(l + 1):
if dp_list[i][j] is not None:
ans_list.append(dp_list[i][j])
print(max(ans_list))
|
Statement
You have N items and a bag of strength W. The i-th item has a weight of w_i
and a value of v_i.
You will select some of the items and put them in the bag. Here, the total
weight of the selected items needs to be at most W.
Your objective is to maximize the total value of the selected items.
|
[{"input": "4 6\n 2 1\n 3 4\n 4 10\n 3 4", "output": "11\n \n\nThe first and third items should be selected.\n\n* * *"}, {"input": "4 6\n 2 1\n 3 7\n 4 10\n 3 6", "output": "13\n \n\nThe second and fourth items should be selected.\n\n* * *"}, {"input": "4 10\n 1 100\n 1 100\n 1 100\n 1 100", "output": "400\n \n\nYou can take everything.\n\n* * *"}, {"input": "4 1\n 10 100\n 10 100\n 10 100\n 10 100", "output": "0\n \n\nYou can take nothing."}]
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.