path
stringlengths 8
204
| content_id
stringlengths 40
40
| detected_licenses
list | license_type
stringclasses 2
values | repo_name
stringlengths 8
100
| repo_url
stringlengths 27
119
| star_events_count
int64 0
6.26k
| fork_events_count
int64 0
3.52k
| gha_license_id
stringclasses 10
values | gha_event_created_at
timestamp[ns] | gha_updated_at
timestamp[ns] | gha_language
stringclasses 12
values | language
stringclasses 1
value | is_generated
bool 1
class | is_vendor
bool 1
class | conversion_extension
stringclasses 6
values | size
int64 172
10.2M
| script
stringlengths 367
7.46M
| script_size
int64 367
7.46M
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
/Day23/.ipynb_checkpoints/作業解答23-checkpoint.ipynb
|
05e29e3e269fed80b24a9bfcff55db41dd4d80b4
|
[] |
no_license
|
hochinchang/python60days
|
https://github.com/hochinchang/python60days
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 3,640,417 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="xp4Wh9IFK_Ps"
# 目標: 學習並了解Bokeh 如何應用
#
# 重點:
#
# 初步了解 BOKEH 互動式GUIDE LINE
#
# 自定義和組織資料數據可視化
#
# 為可視化添加交互姓 --- CustomJS/Render
#
# 作業:
#
# 1.建立簡單的水果資料集
# fruits = ['Apples', 'Pears', 'Nectarines', 'Plums', 'Grapes', 'Strawberries']
#
# counts = [5, 3, 4, 2, 4, 6]
#
# 2. 利用 Source 建立字典, 再用figure 輸出 BAR 圖
# source = ColumnDataSource(data=dict(fruits=fruits, counts=counts, color=Spectral6))
#
# 3. Bokeh官方有提供sample_data給大家練習,gallery豐富的範例都取自sample_data,對比官方的資料格式就能輕鬆模仿應用, 下載 股市資料
#
# 4. 使用HoverTool(游標滑過時顯示資料); Click_policy (藉由標籤控制數值顯示)
#
# + [markdown] colab_type="text" id="A7MvttnXP40Z"
# # 利用 Bokeh 與 Python 製作網頁互動視覺化
#
# 設定資料與輸出檔案
# output_file(“out.html”)
# 利用 Bokeh 繪製圖表
# p = figure()
# p.line([1,2,3,4,5], [5,4,3,2,1])
# 開啟產生的 HTML 檔 ( HTML + JavaScript ,自動生成 )
# show(p)
# + colab={} colab_type="code" id="fE_sd_KzP40Z"
from bokeh.plotting import figure, output_file, show
from bokeh.models import widgets
from bokeh.io import output_notebook
import numpy as np
# 讓網頁直接輸出在NOTEBOOK
output_notebook()
# + colab={"base_uri": "https://localhost:8080/", "height": 852} colab_type="code" id="yiUh9I2kP40f" outputId="a96b2eaf-b1f4-4ef4-d0e9-2339ba2b75d5"
#Bokeh官方有提供sample_data給大家練習,gallery豐富的範例都取自sample_data。
#下載sample_data指令為bokeh.sampledata.download(),直接貼在jupyter執行。檔案會下載到bokeh module裡。
import bokeh.sampledata
bokeh.sampledata.download()
# + colab={"base_uri": "https://localhost:8080/", "height": 267} colab_type="code" id="eUGPEX5pV1jA" outputId="0d31a441-a236-4528-9d1e-d14d6dce4b19"
from bokeh.models import ColumnDataSource
from bokeh.palettes import Spectral6
from bokeh.models import ColumnDataSource, HoverTool
from bokeh.plotting import figure
fruits = ['Apples', 'Pears', 'Nectarines', 'Plums', 'Grapes', 'Strawberries']
counts = [5, 3, 4, 2, 4, 6]
source = ColumnDataSource(data=dict(fruits=fruits, counts=counts, color=Spectral6))
p = figure(x_range=fruits, plot_height=250, y_range=(0, 9), title="Fruit Counts")
p.vbar(x='fruits', top='counts', width=0.9, color='color', legend_field="fruits", source=source)
p.xgrid.grid_line_color = None
p.legend.orientation = "horizontal"
p.legend.location = "top_center"
show(p)
# + colab={"base_uri": "https://localhost:8080/", "height": 267} colab_type="code" id="ejwc4XFJt4V4" outputId="0a00d34c-98e7-4bd7-8b12-8074995866e2"
from bokeh.models import FactorRange
from bokeh.transform import factor_cmap
fruits = ['Apples', 'Pears', 'Nectarines', 'Plums', 'Grapes', 'Strawberries']
years = ['2015', '2016', '2017']
data = {'fruits' : fruits,
'2015' : [2, 1, 4, 3, 2, 4],
'2016' : [5, 3, 3, 2, 4, 6],
'2017' : [3, 2, 4, 4, 5, 3]}
# this creates [ ("Apples", "2015"), ("Apples", "2016"), ("Apples", "2017"), ("Pears", "2015), ... ]
x = [ (fruit, year) for fruit in fruits for year in years ]
counts = sum(zip(data['2015'], data['2016'], data['2017']), ()) # like an hstack
source = ColumnDataSource(data=dict(x=x, counts=counts))
p = figure(x_range=FactorRange(*x), plot_height=250, title="Fruit Counts by Year")
#p.vbar(x='x', top='counts', width=0.9, source=source)
p.vbar(x='x', top='counts', width=0.9, source=source, line_color="white",
# use the palette to colormap based on the the x[1:2] values
fill_color=factor_cmap('x', palette=['firebrick', 'olive', 'navy'], factors=years, start=1, end=2))
p.y_range.start = 0
p.x_range.range_padding = 0.1
p.xaxis.major_label_orientation = 1
p.xgrid.grid_line_color = None
show(p)
# + colab={"base_uri": "https://localhost:8080/", "height": 417} colab_type="code" id="FIsyxA8hvYOd" outputId="01790929-23d8-48eb-90b4-70454b7211d9"
import bokeh.io
from bokeh.resources import INLINE
from bokeh.models import HoverTool
from bokeh.palettes import Spectral4
from bokeh.plotting import figure, output_file, show, output_notebook, ColumnDataSource
from bokeh.sampledata.stocks import AAPL, GOOG, IBM, MSFT
import pandas as pd
# 環境 settings
bokeh.io.reset_output()
bokeh.io.output_notebook(INLINE)
# set hover
## HoverTool
# 游標滑過時顯示資料,date格式需要轉換,不然會是timestamp
hover = HoverTool(
tooltips = [
("date", "@date"),
("close", "@open"),
("close", "@close"),
("high", "@high"),
("low", "@low"),
("volume","@volume")
],
formatters={"@date":"datetime"}
)
# set figure
p = figure(
plot_width=1000,
plot_height=400,
x_axis_type="datetime",
tools=[hover,"pan,box_zoom,reset,save"],
)
p.title.text = 'Stock_Price--Click on legend entries to mute the corresponding lines and show daily details in hover'
# use ColumnDataSource to control
# click_policy
# 藉由標籤控制數值顯示
# hide為隱藏,mute為切換自訂顯示模式
# 可在muted_color控制顏色, muted_alpha控制顏色濃淡
for data, name, color in zip([AAPL, IBM, MSFT, GOOG], ["AAPL", "IBM", "MSFT", "GOOG"], Spectral4):
df = pd.DataFrame(data)
df['date'] = pd.to_datetime(df['date'])
source = ColumnDataSource(df)
p.line(x="date",y="close", line_width=2, color=color, alpha=0.8,
muted_color=color, muted_alpha=0.2, legend_label=name,source=source)
p.legend.location = "top_left"
# use hide or mute
p.legend.click_policy="mute"
# output_file("interactive_legend.html", title="interactive_legend.py example")
show(p)
output_notebook()
n=lon, lat=lat, name=name, units=units)
# append to list
gmobj_m_mon_nlt.append(gmobj_tmp_nlt)
gmobj_m_mon_lt.append(gmobj_tmp_lt)
gmobj_m_mon_kpp.append(gmobj_tmp_kpp)
gmobj_m_mon_epbl.append(gmobj_tmp_epbl)
gmobj_m_mon_smc.append(gmobj_tmp_smc)
# tmp list
gmobj_stat_tmp = []
# loop over turbulent methods
for i in np.arange(nm):
if diag_type == 'D':
# difference
diag1 = tmp[i,:] - diag0_nlt
elif diag_type == 'R':
# ratio
diag1 = tmp[i,:] / diag0_nlt
# create GOTMMap object
gmobj_tmp = GOTMMap(data=diag1, lon=lon, lat=lat, name=name, units=units)
# append to list
gmobj_stat_tmp.append(gmobj_tmp)
# append to list
gmobj_stat_arr.append(gmobj_stat_tmp)
# +
# figure 1: Statistics of the ratio to the median or mean
f = plt.figure()
f.set_size_inches(6, 4)
pbdata0 = []
xshift = list((np.arange(nm)-nm/2)*1)
for k in np.arange(nm):
pdata = np.concatenate([gmobj_stat_arr[i][k].data for i in np.arange(12)])
tmp = pdata
pdata0 = pdata[~np.isnan(tmp)]
pbdata0.append(pdata0)
# all the non-Langmuir cases
pdata1 = np.concatenate(pbdata0[0:5])
# all the Langmuir cases
pdata2 = np.concatenate(pbdata0[5:])
pbdata0.append(pdata1)
pbdata0.append(pdata2)
# add color for non-Lanmguir and Langmuir cases
pbcolor = bcolor
pbcolor.append('lightgray')
pbcolor.append('darkgray')
# add label for non-Lanmguir and Langmuir cases
label_list = legend_list
label_list.append('Non-Langmuir')
label_list.append('Langmuir')
# reference line
plt.axhline(y=y_ref, linewidth=1, color='gray')
# plot
xx = np.arange(nm+2)+1
position_arr = xx
pbox0 = plt.boxplot(pbdata0, whis=[5, 95], showfliers=False, positions=position_arr,
widths=0.3, patch_artist=True)
tmp_arr = [item.get_ydata() for item in pbox0['whiskers']]
label_b = tmp_arr[20][1]
label_a = tmp_arr[15][1]
plt.xlim([0,nm+3])
ax = plt.gca()
if diag_type == 'D':
ylims = [-13,32]
panel = '(a)'
label_a_str = r'$\uparrow${:4.1f}'.format(label_a)
label_b_str = r'$\downarrow${:4.1f}'.format(label_b)
elif diag_type == 'R':
ylims = [0.75,1.4]
panel = '(c)'
label_a_str = r'$\uparrow${:4.2f}'.format(label_a)
label_b_str = r'$\downarrow${:4.2f}'.format(label_b)
plt.ylim(ylims)
if label_a > ylims[1]:
plt.text(0.58, 0.96, label_a_str, transform=ax.transAxes,
fontsize=10, color='k', va='top')
if label_b < ylims[0]:
plt.text(0.79, 0.07, label_b_str, transform=ax.transAxes,
fontsize=10, color='k', va='top')
plt.text(0.06, 0.91, panel, transform=ax.transAxes, fontsize=14, color='k', va='top')
# color for the boxes
for patch, color in zip(pbox0['boxes'], pbcolor):
patch.set_facecolor(color)
# x- and y-labels
plt.setp(ax, xticks=xx, xticklabels=label_list)
plt.ylabel(y_label)
# reduce margin
plt.tight_layout()
# auto adjust the x-axis label
plt.gcf().autofmt_xdate()
# save figure
figname = fig_root+'/'+fig_prefix+'_'+diagname+'_all.png'
plt.savefig(figname, dpi = 300)
# print info
print('Max for KPPLT-R16: {:4.2f}'.format(label_a))
print('Min for OSMOSIS: {:4.2f}'.format(label_b))
print('Standard deviation of non-Langmuir: {:6.4f}'.format(np.std(pdata1)))
print('Standard deviation of Langmuir: {:6.4f}'.format(np.std(pdata2)))
# +
# figure 1b: Statistics of the ratio to the median or mean
# mean of all non-Langmuir and Langmuir cases, respectivly
f = plt.figure()
f.set_size_inches(6, 4)
pbdata0 = []
xshift = list((np.arange(nm)-nm/2)*1)
for k in np.arange(nm):
pdata = np.concatenate([gmobj_stat_arr[i][k].data for i in np.arange(12)])
tmp = pdata
pdata0 = pdata[~np.isnan(tmp)]
pbdata0.append(pdata0)
# mean of the non-Langmuir cases
pdata = np.concatenate([gmobj_m_mon_nlt[i].data for i in np.arange(12)])
tmp = pdata
pdata1 = pdata[~np.isnan(tmp)]
# mean of the Langmuir cases
pdata = np.concatenate([gmobj_m_mon_lt[i].data for i in np.arange(12)])
tmp = pdata
pdata2 = pdata[~np.isnan(tmp)]
pbdata0.append(pdata1)
pbdata0.append(pdata2)
# add color for non-Lanmguir and Langmuir cases
pbcolor = bcolor
pbcolor.append('lightgray')
pbcolor.append('darkgray')
# add label for non-Lanmguir and Langmuir cases
label_list = legend_list
label_list.append('Non-Langmuir')
label_list.append('Langmuir')
# reference line
plt.axhline(y=y_ref, linewidth=1, color='gray')
# plot
xx = np.arange(nm+2)+1
position_arr = xx
pbox0 = plt.boxplot(pbdata0, whis=[5, 95], showfliers=False, positions=position_arr,
widths=0.3, patch_artist=True)
plt.ylim([ymin,ymax])
plt.xlim([0,nm+3])
# color for the boxes
for patch, color in zip(pbox0['boxes'], pbcolor):
patch.set_facecolor(color)
# x- and y-labels
ax = plt.gca()
plt.setp(ax, xticks=xx, xticklabels=label_list)
plt.ylabel(y_label)
# reduce margin
plt.tight_layout()
# auto adjust the x-axis label
plt.gcf().autofmt_xdate()
# save figure
figname = fig_root+'/'+fig_prefix+'_'+diagname+'_all_b.png'
plt.savefig(figname, dpi = 300)
# +
# figure 1c: Statistics of the ratio to the median or mean
# Ratio of Langmuir over non-Langmuir for KPP, ePBL and SMC, and mean of all
f = plt.figure()
f.set_size_inches(2.5, 4)
pbdata0 = []
xshift = list((np.arange(4)*1))
# Langmuir effects in KPP
pdata = np.concatenate([gmobj_m_mon_kpp[i].data for i in np.arange(12)])
tmp = pdata
pdata1 = pdata[~np.isnan(tmp)]
# Langmuir effects in ePBL
pdata = np.concatenate([gmobj_m_mon_epbl[i].data for i in np.arange(12)])
tmp = pdata
pdata2 = pdata[~np.isnan(tmp)]
# Langmuir effects in SMC
pdata = np.concatenate([gmobj_m_mon_smc[i].data for i in np.arange(12)])
tmp = pdata
pdata3 = pdata[~np.isnan(tmp)]
# mean of the Langmuir cases
pdata = np.concatenate([gmobj_m_mon_lt[i].data for i in np.arange(12)])
tmp = pdata
pdata4 = pdata[~np.isnan(tmp)]
pbdata0.append(pdata1)
pbdata0.append(pdata2)
pbdata0.append(pdata3)
pbdata0.append(pdata4)
# add color for non-Lanmguir and Langmuir cases
pbcolor = ['deepskyblue','forestgreen','firebrick','darkgray']
# add label for non-Lanmguir and Langmuir cases
label_list = ['KPPLT-LF17', 'ePBL-LT', 'SMCLT-H15', 'Langmuir']
# reference line
plt.axhline(y=y_ref, linewidth=1, color='gray')
# plot
xx = np.arange(4)+1
position_arr = xx
pbox0 = plt.boxplot(pbdata0, whis=[5, 95], showfliers=False, positions=position_arr,
widths=0.3, patch_artist=True)
plt.xlim([0,5])
ax = plt.gca()
if diag_type == 'D':
plt.ylim([-12,32])
plt.text(0.14, 0.91, '(b)', transform=ax.transAxes, fontsize=14, color='k', va='top')
# label
elif diag_type == 'R':
plt.ylim([0.75,1.4])
plt.text(0.14, 0.91, '(d)', transform=ax.transAxes, fontsize=14, color='k', va='top')
# color for the boxes
for patch, color in zip(pbox0['boxes'], pbcolor):
patch.set_facecolor(color)
# x- and y-labels
plt.setp(ax, xticks=xx, xticklabels=label_list)
# plt.ylabel(y_label+'$^\prime$')
# reduce margin
plt.tight_layout()
# auto adjust the x-axis label
plt.gcf().autofmt_xdate()
# save figure
figname = fig_root+'/'+fig_prefix+'_'+diagname+'_all_c.png'
plt.savefig(figname, dpi = 300)
# print info
medians_arr = [item.get_ydata() for item in pbox0['medians']]
whiskers_arr = [item.get_ydata() for item in pbox0['whiskers']]
for i, var in enumerate(label_list):
print('{}:'.format(var))
print(' Mean: {:4.2f}'.format(pbdata0[i].mean()))
print(' Median: {:4.2f}'.format(medians_arr[i][0]))
ii = i*2
print(' 50% range: {:4.2f} - {:4.2f}'.format(whiskers_arr[ii][0], whiskers_arr[ii+1][0]))
print(' 90% range: {:4.2f} - {:4.2f}'.format(whiskers_arr[ii][1], whiskers_arr[ii+1][1]))
# +
# figure 1d: Legend
f = plt.figure()
f.set_size_inches(6, 1.2)
# add color for non-Lanmguir and Langmuir cases
pbcolor = bcolor
pbcolor.append('lightgray')
pbcolor.append('darkgray')
# add label for non-Lanmguir and Langmuir cases
label_list = legend_list
label_list.append('Non-Langmuir')
label_list.append('Langmuir')
# plot
xx = np.arange(nm+2)+1
yy = np.ones(xx.size)
sct = plt.scatter(xx, yy, s=60, c=pbcolor, edgecolors='k')
plt.xlim([0,nm+3])
for i in np.arange(nm+2):
plt.text(xx[i], yy[i]-0.05, label_list[i], color='black',
fontsize=11, rotation=30, va='top', ha='right')
# x- and y-labels
ax = plt.gca()
ax.spines['bottom'].set_color('white')
ax.spines['top'].set_color('white')
ax.spines['right'].set_color('white')
ax.spines['left'].set_color('white')
ax.axes.get_yaxis().set_visible(False)
ax.axes.get_xaxis().set_visible(False)
# plt.setp(ax, xticks=xx, xticklabels=label_list)
# reduce margin
plt.tight_layout()
# auto adjust the x-axis label
plt.gcf().autofmt_xdate()
plt.gcf().subplots_adjust(bottom=0.65)
plt.gcf().subplots_adjust(left=0.1)
# save figure
figname = fig_root+'/legend.png'
plt.savefig(figname, dpi = 300)
# +
# figure 1e: Legend2
f = plt.figure()
f.set_size_inches(6, 1.2)
# plot
xx = np.arange(nm)+1
yy = np.ones(xx.size)
sct = plt.scatter(xx, yy, s=80, c=bcolor, edgecolors='k', linewidth=1)
plt.xlim([0,nm+1])
for i in np.arange(nm):
plt.text(xx[i], yy[i]-0.05, legend_list[i], color='black',
fontsize=11, rotation=30, va='top', ha='right')
# x- and y-labels
ax = plt.gca()
ax.spines['bottom'].set_color('white')
ax.spines['top'].set_color('white')
ax.spines['right'].set_color('white')
ax.spines['left'].set_color('white')
ax.axes.get_yaxis().set_visible(False)
ax.axes.get_xaxis().set_visible(False)
# reduce margin
plt.tight_layout()
# auto adjust the x-axis label
plt.gcf().autofmt_xdate()
plt.gcf().subplots_adjust(bottom=0.65)
plt.gcf().subplots_adjust(left=0.1)
# save figure
figname = fig_root+'/legend_2.png'
plt.savefig(figname, dpi = 300)
# -
def mask_forcing_regime(pdata, pfreg):
hist = np.zeros(14)
pdata_S0= pdata[pfreg==1]
pdata_S1 = pdata[pfreg==-1]
hist[0] = pdata_S0.size
hist[1] = pdata_S1.size
pdata_L0= pdata[pfreg==2]
pdata_L1 = pdata[pfreg==-2]
hist[2] = pdata_L0.size
hist[3] = pdata_L1.size
pdata_C0= pdata[pfreg==3]
pdata_C1 = pdata[pfreg==-3]
hist[4] = pdata_C0.size
hist[5] = pdata_C1.size
pdata_SL0= pdata[pfreg==4]
pdata_SL1 = pdata[pfreg==-4]
hist[6] = pdata_SL0.size
hist[7] = pdata_SL1.size
pdata_SC0 = pdata[pfreg==5]
pdata_SC1 = pdata[pfreg==-5]
hist[8] = pdata_SC0.size
hist[9] = pdata_SC1.size
pdata_LC0 = pdata[pfreg==6]
pdata_LC1 = pdata[pfreg==-6]
hist[10] = pdata_LC0.size
hist[11] = pdata_LC1.size
pdata_SLC0 = pdata[pfreg==7]
pdata_SLC1 = pdata[pfreg==-7]
hist[12] = pdata_SLC0.size
hist[13] = pdata_SLC1.size
masked_data = [pdata_S0, pdata_S1, pdata_L0, pdata_L1, pdata_C0, pdata_C1, \
pdata_SL0, pdata_SL1, pdata_SC0, pdata_SC1, pdata_LC0, pdata_LC1, \
pdata_SLC0, pdata_SLC1]
hist_pct = hist/np.sum(hist)*100
return masked_data, hist_pct
# +
# figure 2: sort the differences by forcing regime
# forcing regimes
pfreg = np.concatenate([gmobj_freg_mon[i].data for i in np.arange(12)])
f, axarr = plt.subplots(2)
f.set_size_inches(8, 6)
# reference line
axarr[0].axhline(y=y_ref, linewidth=1, color='gray')
axarr[1].axhline(y=y_ref, linewidth=1, color='gray')
xshift = list((np.arange(nm)-nm/2)*0.07+0.035)
for k in np.arange(nm):
pdata = np.concatenate([gmobj_stat_arr[i][k].data for i in np.arange(12)])
tmp = pdata
pfreg0 = pfreg[~np.isnan(tmp)]
pdata0 = pdata[~np.isnan(tmp)]
if k == 0:
pbdata0, hist_pct = mask_forcing_regime(pdata0, pfreg0)
else:
pbdata0, tmp = mask_forcing_regime(pdata0, pfreg0)
xx = np.arange(hist_pct.size/2)+1
position_arr = xx+xshift[k]
pbox0 = axarr[0].boxplot(pbdata0[0::2], whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.05, patch_artist=True)
pbox1 = axarr[1].boxplot(pbdata0[1::2], whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.05, patch_artist=True)
for patch in pbox0['boxes']:
patch.set_facecolor(bcolor[k])
for patch in pbox1['boxes']:
patch.set_facecolor(bcolor[k])
# x- and y-labels
plt.setp(axarr[0], xticks=xx,
xticklabels=['S', 'L', 'C', 'SL', 'SC', 'LC', 'SLC'])
plt.setp(axarr[1], xticks=xx,
xticklabels=['S*','L*','C*','SL*','SC*','LC*', 'SLC*'])
axarr[0].set_ylabel(y_label)
axarr[1].set_ylabel(y_label)
axarr[0].set_xlim([0.5,np.max(xx)+0.5])
axarr[1].set_xlim([0.5,np.max(xx)+0.5])
axarr[0].set_ylim([ymin,ymax])
axarr[1].set_ylim([ymin,ymax])
# frequency of occurrence
par1 = axarr[0].twinx()
par1.bar(xx, hist_pct[0::2], width=0.4, color='lightgray')
par1.set_ylabel('$\%$')
par1.set_ylim([0, 25])
axarr[0].set_zorder(par1.get_zorder()+1)
axarr[0].patch.set_visible(False)
par2 = axarr[1].twinx()
par2.bar(xx, hist_pct[1::2], width=0.4, color='lightgray')
par2.set_ylabel('$\%$')
par2.set_ylim([0, 25])
axarr[1].set_zorder(par2.get_zorder()+1)
axarr[1].patch.set_visible(False)
# reduce margin
plt.tight_layout()
# save figure
figname = fig_root+'/'+fig_prefix+'_'+diagname+'_forc_reg.png'
plt.savefig(figname, dpi = 300)
print(hist_pct)
# +
# figure 2b: sort the differences by forcing regime, only including L LC and C
# forcing regimes
pfreg = np.concatenate([gmobj_freg_mon[i].data for i in np.arange(12)])
f, axarr = plt.subplots(2)
f.set_size_inches(8, 8)
# reference line
axarr[0].axhline(y=y_ref, linewidth=1, color='gray')
axarr[1].axhline(y=y_ref, linewidth=1, color='gray')
xshift = list((np.arange(nm+2)-nm/2-1)*0.06+0.03)
pbdata0s0_nlt = []
pbdata0s1_nlt = []
pbdata0s0_lt = []
pbdata0s1_lt = []
for k in np.arange(nm):
pdata = np.concatenate([gmobj_stat_arr[i][k].data for i in np.arange(12)])
tmp = pdata
pfreg0 = pfreg[~np.isnan(tmp)]
pdata0 = pdata[~np.isnan(tmp)]
if k == 0:
pbdata0, hist_pct = mask_forcing_regime(pdata0, pfreg0)
else:
pbdata0, tmp = mask_forcing_regime(pdata0, pfreg0)
xx = np.arange(3)+1
position_arr = xx+xshift[k]
pbdata0s0 = [pbdata0[i] for i in [2,10,4]]
pbox0 = axarr[0].boxplot(pbdata0s0, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.04, patch_artist=True)
pbdata0s1 = [pbdata0[i] for i in [3,11,5]]
pbox1 = axarr[1].boxplot(pbdata0s1, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.04, patch_artist=True)
for patch in pbox0['boxes']:
patch.set_facecolor(bcolor[k])
for patch in pbox1['boxes']:
patch.set_facecolor(bcolor[k])
# save the data for non-Langmuir and Langmuir groups
if k < 5:
pbdata0s0_nlt.append(pbdata0s0)
pbdata0s1_nlt.append(pbdata0s1)
else:
pbdata0s0_lt.append(pbdata0s0)
pbdata0s1_lt.append(pbdata0s1)
# process data for non-Langmuir and Langmuir cases
pbdata1s0_nlt = []
pbdata1s1_nlt = []
pbdata1s0_lt = []
pbdata1s1_lt = []
for k in np.arange(3):
pbdata0s0 = np.concatenate([pbdata0s0_nlt[i][k] \
for i in np.arange(len(pbdata0s0_nlt))])
pbdata1s0_nlt.append(pbdata0s0)
pbdata0s1 = np.concatenate([pbdata0s1_nlt[i][k] \
for i in np.arange(len(pbdata0s1_nlt))])
pbdata1s1_nlt.append(pbdata0s1)
pbdata0s0 = np.concatenate([pbdata0s0_lt[i][k] \
for i in np.arange(len(pbdata0s0_lt))])
pbdata1s0_lt.append(pbdata0s0)
pbdata0s1 = np.concatenate([pbdata0s1_lt[i][k] \
for i in np.arange(len(pbdata0s1_lt))])
pbdata1s1_lt.append(pbdata0s1)
pbcolor = ['lightgray', 'darkgray']
# plot non-Langmuir cases
position_arr = xx+xshift[nm]
pbox0 = axarr[0].boxplot(pbdata1s0_nlt, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.04, patch_artist=True)
pbox1 = axarr[1].boxplot(pbdata1s1_nlt, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.04, patch_artist=True)
for patch in pbox0['boxes']:
patch.set_facecolor(pbcolor[0])
for patch in pbox1['boxes']:
patch.set_facecolor(pbcolor[0])
# plot Langmuir cases
position_arr = xx+xshift[nm+1]
pbox0 = axarr[0].boxplot(pbdata1s0_lt, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.04, patch_artist=True)
pbox1 = axarr[1].boxplot(pbdata1s1_lt, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.04, patch_artist=True)
for patch in pbox0['boxes']:
patch.set_facecolor(pbcolor[1])
for patch in pbox1['boxes']:
patch.set_facecolor(pbcolor[1])
# x- and y-labels
plt.setp(axarr[0], xticks=xx, xticklabels=['L', 'LC', 'C'])
plt.setp(axarr[1], xticks=xx, xticklabels=['L*','LC*','C*'])
axarr[0].set_ylabel(y_label)
axarr[1].set_ylabel(y_label)
axarr[0].set_xlim([0.5,np.max(xx)+0.5])
axarr[1].set_xlim([0.5,np.max(xx)+0.5])
axarr[0].set_ylim([ymin,ymax])
axarr[1].set_ylim([ymin,ymax])
# frequency of occurrence
par1 = axarr[0].twinx()
hist_pcts1 = [hist_pct[i] for i in [2,10,4]]
par1.bar(xx, hist_pcts1, width=0.4, color='lightgray')
par1.set_ylabel('$\%$')
par1.set_ylim([0, 45])
axarr[0].set_zorder(par1.get_zorder()+1)
axarr[0].patch.set_visible(False)
# label
axarr[0].text(0.02, 0.12, '(a) Destablizing', fontsize=13, color='k', va='top',
transform=axarr[0].transAxes)
par2 = axarr[1].twinx()
hist_pcts2 = [hist_pct[i] for i in [3,11,5]]
par2.bar(xx, hist_pcts2, width=0.4, color='lightgray')
par2.set_ylabel('$\%$')
par2.set_ylim([0, 45])
axarr[1].set_zorder(par2.get_zorder()+1)
axarr[1].patch.set_visible(False)
# label
axarr[1].text(0.02, 0.12, '(b) Stabilizing', fontsize=13, color='k', va='top',
transform=axarr[1].transAxes)
# reduce margin
plt.tight_layout()
# add legend
plt.subplots_adjust(bottom=0.2)
# add color for non-Lanmguir and Langmuir cases
pbcolor = bcolor
pbcolor.append('lightgray')
pbcolor.append('darkgray')
# add label for non-Lanmguir and Langmuir cases
label_list = legend_list
label_list.append('Non-Langmuir')
label_list.append('Langmuir')
# plot
xshift = 0.15
xx = np.arange(nm+2)*0.06+xshift
yy = -np.ones(xx.size)*0.3
for i in np.arange(nm+2):
axarr[1].text(xx[i], yy[i], legend_list[i], color='black',
transform=axarr[1].transAxes, fontsize=11, rotation=30,
va='top', ha='right')
axarr[1].scatter(xx[i], yy[i]+0.07, s=60, c=bcolor[i], edgecolors='k', linewidth=1,
transform=axarr[1].transAxes, clip_on=False)
# save figure
figname = fig_root+'/'+fig_prefix+'_'+diagname+'_forc_reg_s.pdf'
plt.savefig(figname, dpi = 300)
# print info
print('Percentage of each regime:')
print(' L: {:6.2f}%, LC: {:6.2f}%, C: {:6.2f}%'.format(hist_pcts1[0], hist_pcts1[1], hist_pcts1[2]))
print(' L*: {:6.2f}%, LC*: {:6.2f}%, C*: {:6.2f}%'.format(hist_pcts2[0], hist_pcts2[1], hist_pcts2[2]))
print('Total: {:6.2f}%'.format(sum(hist_pcts1)+sum(hist_pcts2)))
# +
# figure 2c: sort the effects of LT by forcing regime, only including L LC and C
f, axarr = plt.subplots(2)
f.set_size_inches(5, 6)
# add color for non-Lanmguir and Langmuir cases
pbcolor = ['deepskyblue','forestgreen','firebrick','darkgray']
# add label for non-Lanmguir and Langmuir cases
label_list = ['KPPLT-LF17', 'ePBL-LT', 'SMCLT-H15', 'Langmuir']
# reference line
axarr[0].axhline(y=y_ref, linewidth=1, color='gray')
axarr[1].axhline(y=y_ref, linewidth=1, color='gray')
xshift = list((np.arange(4)-2)*0.10+0.05)
# forcing regimes
pfreg = np.concatenate([gmobj_freg_mon[i].data for i in np.arange(12)])
gmobj_list = []
# Langmuir effects in KPP
gmobj_list.append(gmobj_m_mon_kpp)
# Langmuir effects in ePBL
gmobj_list.append(gmobj_m_mon_epbl)
# Langmuir effects in SMC
gmobj_list.append(gmobj_m_mon_smc)
# mean of the Langmuir cases
gmobj_list.append(gmobj_m_mon_lt)
for k in np.arange(4):
pdata = np.concatenate([gmobj_list[k][i].data for i in np.arange(12)])
tmp = pdata
pfreg0 = pfreg[~np.isnan(tmp)]
pdata0 = pdata[~np.isnan(tmp)]
pbdata0, tmp = mask_forcing_regime(pdata0, pfreg0)
xx = (np.arange(3)+1)*0.7
position_arr = xx+xshift[k]
pbdata0s0 = [pbdata0[i] for i in [2,10,4]]
pbox0 = axarr[0].boxplot(pbdata0s0, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.06, patch_artist=True)
pbdata0s1 = [pbdata0[i] for i in [3,11,5]]
pbox1 = axarr[1].boxplot(pbdata0s1, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.06, patch_artist=True)
for patch in pbox0['boxes']:
patch.set_facecolor(pbcolor[k])
for patch in pbox1['boxes']:
patch.set_facecolor(pbcolor[k])
# x- and y-labels
plt.setp(axarr[0], xticks=xx, xticklabels=['L', 'LC', 'C'])
plt.setp(axarr[1], xticks=xx, xticklabels=['L*','LC*','C*'])
axarr[0].set_ylabel(y_label)
axarr[1].set_ylabel(y_label)
axarr[0].set_xlim([0.3,np.max(xx)+0.4])
axarr[1].set_xlim([0.3,np.max(xx)+0.4])
if diag_type == 'R':
ymin1 = 0.9
ymax1 = 1.4
elif diag_type == 'D':
ymin1 = -5
ymax1 = 35
axarr[0].set_ylim([ymin1,ymax1])
axarr[1].set_ylim([ymin1,ymax1])
# frequency of occurrence
par1 = axarr[0].twinx()
hist_pcts1 = [hist_pct[i] for i in [2,10,4]]
par1.bar(xx, hist_pcts1, width=0.4, color='lightgray')
par1.set_ylabel('$\%$')
par1.set_ylim([0, 45])
axarr[0].set_zorder(par1.get_zorder()+1)
axarr[0].patch.set_visible(False)
# label
axarr[0].text(0.05, 0.92, '(a) Destablizing', transform=axarr[0].transAxes,
fontsize=13, color='k', va='top')
par2 = axarr[1].twinx()
hist_pcts2 = [hist_pct[i] for i in [3,11,5]]
par2.bar(xx, hist_pcts2, width=0.4, color='lightgray')
par2.set_ylabel('$\%$')
par2.set_ylim([0, 45])
axarr[1].set_zorder(par2.get_zorder()+1)
axarr[1].patch.set_visible(False)
# label
axarr[1].text(0.05, 0.92, '(b) Stablizing', transform=axarr[1].transAxes,
fontsize=13, color='k', va='top')
# legend
xshift = 0.63
xx = np.arange(4)
xx = xx*0.1+xshift
yy = np.ones(xx.size)*0.90
for i in np.arange(4):
axarr[1].text(xx[i], yy[i], label_list[i], color='black',
transform=axarr[1].transAxes, fontsize=10, rotation=30,
va='top', ha='right')
axarr[1].scatter(xx[i], 0.92, s=60, c=pbcolor[i], edgecolors='k',
linewidth=1, transform=axarr[1].transAxes)
# reduce margin
plt.tight_layout()
# save figure
figname = fig_root+'/'+fig_prefix+'_'+diagname+'_forc_reg_s_c.pdf'
plt.savefig(figname, dpi = 300)
# print info
print('Destablizing:')
medians_arr = [item.get_ydata() for item in pbox0['medians']]
whiskers_arr = [item.get_ydata() for item in pbox0['whiskers']]
for i, var in enumerate(['L', 'LC', 'C']):
print('{}:'.format(var))
print(' Mean: {:4.2f}'.format(pbdata0s0[i].mean()))
print(' Median: {:4.2f}'.format(medians_arr[i][0]))
ii = i*2
print(' 50% range: {:4.2f} - {:4.2f}'.format(whiskers_arr[ii][0], whiskers_arr[ii+1][0]))
print(' 90% range: {:4.2f} - {:4.2f}'.format(whiskers_arr[ii][1], whiskers_arr[ii+1][1]))
print('Stablizing:')
medians_arr = [item.get_ydata() for item in pbox1['medians']]
whiskers_arr = [item.get_ydata() for item in pbox1['whiskers']]
for i, var in enumerate(['L', 'LC', 'C']):
print('{}:'.format(var))
print(' Mean: {:4.2f}'.format(pbdata0s1[i].mean()))
print(' Median: {:4.2f}'.format(medians_arr[i][0]))
ii = i*2
print(' 50% range: {:4.2f} - {:4.2f}'.format(whiskers_arr[ii][0], whiskers_arr[ii+1][0]))
print(' 90% range: {:4.2f} - {:4.2f}'.format(whiskers_arr[ii][1], whiskers_arr[ii+1][1]))
# -
def mask_latitude(pdata, lat):
hist = np.zeros(7)
pdata_S3 = pdata[lat<=-50]
hist[0] = pdata_S3.size
pdata_S2 = pdata[(lat>-50) & (lat<=-30)]
hist[1] = pdata_S2.size
pdata_S1 = pdata[(lat>-30) & (lat<=-10)]
hist[2] = pdata_S1.size
pdata_EQ = pdata[(lat>-10) & (lat<10)]
hist[3] = pdata_EQ.size
pdata_N1 = pdata[(lat>=10) & (lat<30)]
hist[4] = pdata_N1.size
pdata_N2 = pdata[(lat>=30) & (lat<50)]
hist[5] = pdata_N2.size
pdata_N3 = pdata[lat>=50]
hist[6] = pdata_N3.size
masked_data = [pdata_S3, pdata_S2, pdata_S1, pdata_EQ, pdata_N1, pdata_N2, pdata_N3]
hist_pct = hist/np.sum(hist)*100
return masked_data, hist_pct
# +
# figure 3: sort the differences by latitude
plat = np.concatenate([gmobj_m_mon_nlt[i].lat for i in np.arange(12)])
f = plt.figure()
f.set_size_inches(8, 3.5)
# reference line
plt.axhline(y=y_ref, linewidth=1, color='gray')
xshift = list((np.arange(nm)-nm/2)*0.07+0.035)
for k in np.arange(nm):
pdata = np.concatenate([gmobj_stat_arr[i][k].data for i in np.arange(12)])
tmp = pdata
plat0 = plat[~np.isnan(tmp)]
pdata0 = pdata[~np.isnan(tmp)]
pbdata0, hist_pct = mask_latitude(pdata0, plat0)
xx = np.arange(hist_pct.size)+1
position_arr = xx+xshift[k]
pbox0 = plt.boxplot(pbdata0, whis=[5, 95], showfliers=False, positions=position_arr,
widths=0.05, patch_artist=True)
for patch in pbox0['boxes']:
patch.set_facecolor(bcolor[k])
# x- and y-labels
ax = plt.gca()
plt.setp(ax, xticks=xx, xticklabels=['70$^\circ$S-50$^\circ$S',
'50$^\circ$S-30$^\circ$S',
'30$^\circ$S-10$^\circ$S',
'10$^\circ$S-10$^\circ$N',
'10$^\circ$N-30$^\circ$N',
'30$^\circ$N-50$^\circ$N',
'50$^\circ$N-70$^\circ$N'])
plt.ylabel(y_label)
plt.xlim([0.5,np.max(xx)+0.5])
plt.ylim([ymin,ymax])
# frequency of occurrence
par1 = ax.twinx()
par1.bar(xx, hist_pct, width=0.4, color='lightgray')
par1.set_ylabel('$\%$')
par1.set_ylim([0, 25])
ax.set_zorder(par1.get_zorder()+1)
ax.patch.set_visible(False)
# reduce margin
plt.tight_layout()
# auto adjust the x-axis label
plt.gcf().autofmt_xdate()
# save figure
figname = fig_root+'/'+fig_prefix+'_'+diagname+'_lat.png'
plt.savefig(figname, dpi = 300)
# +
# figure 4: sort the differences by month
f, axarr = plt.subplots(3)
f.set_size_inches(12, 9)
# reference line
axarr[0].axhline(y=y_ref, linewidth=1, color='gray')
axarr[1].axhline(y=y_ref, linewidth=1, color='gray')
axarr[2].axhline(y=y_ref, linewidth=1, color='gray')
xx = np.arange(12)+1
xshift = list((np.arange(nm)-nm/2)*0.07+0.035)
for k in np.arange(nm):
pbdata0 = []
pbdata1 = []
pbdata2 = []
for i in np.arange(12):
plat = gmobj_stat_arr[i][k].lat
# south of 30S
pdata = gmobj_stat_arr[i][k].data[plat<=-30]
pdata = pdata[~np.isnan(pdata)]
pbdata0.append(pdata)
# 30S-30N
pdata = gmobj_stat_arr[i][k].data[(plat>-30) & (plat<30)]
pdata = pdata[~np.isnan(pdata)]
pbdata1.append(pdata)
# north of 30N
pdata = gmobj_stat_arr[i][k].data[plat>=30]
pdata = pdata[~np.isnan(pdata)]
pbdata2.append(pdata)
position_arr = xx+xshift[k]
pbox0 = axarr[0].boxplot(pbdata0, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.05, patch_artist=True)
pbox1 = axarr[1].boxplot(pbdata1, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.05, patch_artist=True)
pbox2 = axarr[2].boxplot(pbdata2, whis=[5, 95], showfliers=False,
positions=position_arr, widths=0.05, patch_artist=True)
for patch in pbox0['boxes']:
patch.set_facecolor(bcolor[k])
for patch in pbox1['boxes']:
patch.set_facecolor(bcolor[k])
for patch in pbox2['boxes']:
patch.set_facecolor(bcolor[k])
# x- and y-labels
month_labels = ['JAN', 'FEB', 'MAR', 'APR', 'MAY', 'JUN', \
'JUL', 'AUG', 'SEP', 'OCT', 'NOV', 'DEC']
plt.setp(axarr[0], xticks=xx, xticklabels=month_labels)
plt.setp(axarr[1], xticks=xx, xticklabels=month_labels)
plt.setp(axarr[2], xticks=xx, xticklabels=month_labels)
axarr[0].set_ylabel(y_label)
axarr[1].set_ylabel(y_label)
axarr[2].set_ylabel(y_label)
axarr[0].set_xlim([0.5,np.max(xx)+0.5])
axarr[1].set_xlim([0.5,np.max(xx)+0.5])
axarr[2].set_xlim([0.5,np.max(xx)+0.5])
axarr[0].set_ylim([ymin,ymax])
axarr[1].set_ylim([ymin,ymax])
axarr[2].set_ylim([ymin,ymax])
# reduce margin
plt.tight_layout()
# save figure
figname = fig_root+'/'+fig_prefix+'_'+diagname+'_mon.png'
plt.savefig(figname, dpi = 300)
# -
| 34,059 |
/analysis/average_project_length/brian/Census_Exploration-All-Data.ipynb
|
54f18993ada0513a63b8de5f5bf0de53e81ecc33
|
[] |
no_license
|
brgoggin/datasci-housing-pipeline
|
https://github.com/brgoggin/datasci-housing-pipeline
| 2 | 0 | null | 2017-08-28T18:15:41 | 2017-05-18T03:14:47 | null |
Jupyter Notebook
| false | false |
.py
| 2,263,596 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
pd.set_option('display.max_columns', 100)
pd.set_option('display.max_rows', 100)
# +
#Loading and compiling dataset
df_schools = pd.read_csv("Masterlist of Schools.csv", index_col="school.id")
df_location = pd.read_csv("Schools Location Data.csv",
encoding = "latin-1",
index_col="School ID",
usecols=["School ID", "Enrolment", "Latitude", "Longitude"])
df_rooms = pd.read_csv('Rooms data.csv', index_col="School ID")
df_teachers = pd.read_csv("Teachers data.csv", index_col="school.id")
df_elementary = pd.read_csv("Enrollment Master Data_2015_E.csv")[:-1].astype(int).set_index("School ID")
df_secondary = (pd.read_csv('Enrollment Master Data_2015_S.csv')[:-1]
.replace(",", "", regex=True)
.astype(int)
.replace("SPED NG Male", "SPED NG Male SS")
.replace("SPED NG Female", "SPED NG Female SS")
.set_index("School ID"))
df_mooe = (pd.read_csv('MOOE data.csv', index_col="school.id", usecols=["school.id", " school.mooe "])
.replace(",", "", regex=True).astype(float))
# -
#Saving all datasets into one data frame
df_all = pd.concat([df_schools, df_location, df_rooms, df_teachers, df_elementary, df_secondary, df_mooe], axis=1)
df_all
#Checking the shape
df_all.shape
#Checking for missing values
df_all.isna().sum()
#Checking for duplicates
df_all[df_all.index.duplicated(keep=False)]
#Checking the columns
df_all.columns
# Let's try to explore the data for both elementary and secondary school
# Obtain all numeric features and school.classification
df_numeric = df_all[['school.region', 'school.cityincome','rooms.standard.academic', 'rooms.standard.unused',
'rooms.nonstandard.academic', 'rooms.nonstandard.unused',
'teachers.instructor', 'teachers.mobile', 'teachers.regular',
'teachers.sped','Enrolment', ' school.mooe ', 'school.classification']]
# +
# Combine all rooms and all teachers
df_numeric["rooms_total"] = (df_numeric['rooms.standard.academic'] +
df_numeric['rooms.standard.unused'] +
df_numeric['rooms.nonstandard.academic'] +
df_numeric['rooms.nonstandard.unused'])
df_numeric["teachers_total"] = (df_numeric['teachers.instructor'] +
df_numeric['teachers.mobile'] +
df_numeric['teachers.regular'] +
df_numeric['teachers.sped'])
df_numeric['student_teacher_ratio'] = df_numeric['Enrolment']/df_numeric["teachers_total"]
df_numeric['student_room_ratio'] = df_numeric['Enrolment']/df_numeric["rooms_total"]
df_numeric['student_mooe_ratio'] = df_numeric['Enrolment']/df_numeric[' school.mooe ']
df_numeric = df_numeric.dropna()
# Removing (statistical) outliers for MOOE
Q1 = df_numeric[' school.mooe '].quantile(0.25)
Q3 = df_numeric[' school.mooe '].quantile(0.75)
IQR = Q3 - Q1
df_outlier_removed = (df_numeric[(df_numeric[' school.mooe '] >= Q1 - 1.5*IQR) &
(df_numeric[' school.mooe '] <= Q3 + 1.5*IQR)])
df_outlier_removed.columns
# -
#Checking the dataset
df_numeric ["school.cityincome"] = df_numeric["school.cityincome"].replace(['P 55 M or more'],'P 55 M or more but less than P 80 M')
df_numeric
#reordering categories
df_numeric["school.cityincome"] = df_numeric["school.cityincome"].astype('category')
df_numeric["school.cityincome"].cat.reorder_categories(['Below P 15 M', 'P 15 M or more but less than P 25 M',
'P 25 M or more but less than P 35 M',
'P 35 M or more but less than P 45 M',
'P 45 M or more but less than P 55 M',
'P 55 M or more but less than P 80 M',
'P 80 M or more but less than P 160 M',
'P 160 M or more but less than P 240 M',
'P 240 M or more but less than P 320 M',
'P 320 M or more but less than P 400 M',
'P 400 M or more',
'Special Class'])
#Getting the no. of students per city classified by income
students_per_city_income = df_numeric.groupby("school.cityincome").agg(Enrolment=("Enrolment", sum))
students_per_city_income
#Plotting the bar graph for students per city classified by income
plt.figure(figsize=(12,6), dpi = 80)
plt.barh(students_per_city_income.index, students_per_city_income["Enrolment"].values)
plt.title("Students")
plt.ticklabel_format(axis="x", style="plain")
plt.show
#Getting the no. of teachers per city classified by income
teachers_per_city_income = df_numeric.groupby("school.cityincome").agg(Teachers=("teachers_total", sum))
teachers_per_city_income
#Plotting the bar graph for teachers per city classified by income
plt.figure(figsize=(12,6), dpi = 80)
plt.barh(teachers_per_city_income.index, teachers_per_city_income["Teachers"].values)
plt.title("Teachers")
plt.ticklabel_format(axis="x", style="plain")
plt.show
#Getting the no. of rooms per city classified by income
rooms_per_city_income = df_numeric.groupby("school.cityincome").agg(Rooms=("rooms_total", sum))
rooms_per_city_income
#Plotting the bar graph for rooms per city classified by income
plt.figure(figsize=(12,6), dpi=80)
plt.barh(rooms_per_city_income.index, rooms_per_city_income["Rooms"].values)
plt.title("Rooms")
plt.ticklabel_format(axis="x", style="plain")
plt.show
#Getting the total MOOE per city classified by income
mooe_per_city_income = df_numeric.groupby("school.cityincome").agg(MOOE_per_city_income=(" school.mooe ",sum))
mooe_per_city_income
#Plotting the bar graph for total MOOE per city classified by income
plt.figure(figsize=(12,6), dpi = 80)
plt.barh(mooe_per_city_income.index, mooe_per_city_income ["MOOE_per_city_income"].values)
plt.title("Total MOOE")
plt.ticklabel_format(axis="x", style="plain")
plt.show
rs','21 years', '22 to 24 years',
'25 to 29 years','30 to 34 years','35 to 39 years']
middle=['40 to 44 years','45 to 49 years','50 to 54 years','55 to 59 years']
old=['60 and 61 years','62 to 64 years','65 and 66 years','67 to 69 years',
'70 to 74 years','75 to 79 years','80 to 84 years','85 years and over']
teen_cats=[]
adult_cats=[]
middle_cats=[]
old_cats=[]
for cat in teen:
teen_cats.append(male+cat)
teen_cats.append(female+cat)
for cat in adult:
adult_cats.append(male+cat)
adult_cats.append(female+cat)
for cat in middle:
middle_cats.append(male+cat)
middle_cats.append(female+cat)
for cat in old:
old_cats.append(male+cat)
old_cats.append(female+cat)
tracts['teen']=tracts[teen_cats].sum(axis=1)
tracts['adult']=tracts[adult_cats].sum(axis=1)
tracts['middle']=tracts[middle_cats].sum(axis=1)
tracts['old']=tracts[old_cats].sum(axis=1)
# +
#Consolidate "moved-in" categories
times=['Moved in 2015 or later', 'Moved in 2010 to 2014', 'Moved in 2000 to 2009','Moved in 1990 to 1999', 'Moved in 1980 to 1989', 'Moved in 1979 or earlier']
for period in times:
tracts['total: '+period]=tracts['Estimate; Owner occupied: - '+ period]+tracts['Estimate; Renter occupied: - '+ period]
# -
#Create variables to explore
tracts['perc_old']=(tracts['old']/tracts['Estimate; Total:_B01001'])*100
tracts['perc_white']=(tracts['Estimate; Total: - White alone']/tracts['Estimate; Total:_B02001'])*100
tracts['perc_rich']=(tracts['>100']/tracts['Estimate; Total:_B01001'])*100
tracts['pop_density']=tracts['Estimate; Total:_B01001']/(tracts['ALAND']*(0.000000386102)) #convert to pop per square miles (from square meters)
tracts['perc_owner']=(tracts['Estimate; Total: - Owner occupied']/tracts['Estimate; Total:_B25003'])*100
tracts['median_age']=tracts['Total; Estimate; SUMMARY INDICATORS - Median age (years)']
tracts['median_income']=tracts['Households; Estimate; Median income (dollars)']
tracts.loc[(tracts['median_age']=='-'), 'median_age'] = 'nan'
tracts.loc[(tracts['median_income']=='-'), 'median_income'] = 'nan'
tracts.loc[(tracts['median_income']=='(X)'), 'median_income'] = 'nan'
tracts['median_age']=tracts['median_age'].astype(float)
tracts['median_income']=tracts['median_income'].astype(float)
tracts['median_homevalue']=tracts['Estimate; Median value (dollars)']
tracts.loc[(tracts['median_homevalue']=='-'), 'median_homevalue'] = 'nan'
tracts.loc[(tracts['median_homevalue']=='2,000,000+'), 'median_homevalue'] = '2000000' #round down to 2 million for these
tracts['median_homevalue']=tracts['median_homevalue'].astype(float)
#percentage pre-2000 and pre-1990 move-in
tracts['perc_pre_2000']=((tracts['total: Moved in 1980 to 1989']+tracts['total: Moved in 1990 to 1999']+tracts['total: Moved in 1979 or earlier'])/tracts['Estimate; Total:_B25038'])*100
tracts['perc_pre_1990']=((tracts['total: Moved in 1980 to 1989']+tracts['total: Moved in 1979 or earlier'])/tracts['Estimate; Total:_B25038'])*100
#tracts['perc_pre_2000'].describe(percentiles=[.1, .2, .3, .4, .5, .6, .7, .8,.9])
#tracts['perc_pre_1990'].describe(percentiles=[.1, .2, .3, .4, .5, .6, .7, .8,.9])
#make series of scatter plots, correlation graphs. Population density, age, income, tenure, race, home age.
varlist=['GEOID', 'geometry', 'perc_owner', 'pop_density', 'perc_old', 'perc_rich', 'perc_white',
'median_age', 'median_income', 'median_homevalue', 'perc_pre_2000', 'perc_pre_1990'] #keep only certain variables
tracts=tracts[varlist]
# +
#Check plots
#tracts.plot(column='perc_rich', cmap='OrRd')
#plt.xlim([-122.58, -122.18])
#plt.ylim([37.7, 37.82])
# -
#First, spatial join between points and neighborhood boundaries. Set 'how' to 'left' to preserve all developments
df = gpd.sjoin(devs, tracts, how = 'inner', op='within')
# +
# a few projects appear to be outside tract boundaries so they are dropped here. not too many so I'm not worried about them too much.
#base=tracts.plot(color='white', linewidth=.1)
#devs.plot(ax=base)
#plt.xlim([-122.58, -122.18])
#plt.ylim([37.7, 37.82])
# -
df.head()
# # Joint Scatter Plot Graphs
df['years_per_unit']=df['project_time_years']/df['units']
df[pd.notnull(df['project_time_years'])].shape
df_export.head()
# # Interuption: Export Shapefile
# +
def permit_time(value):
returnval=np.nan
if pd.notnull(value['BP_date']) & pd.notnull(value['first_date']):
returnval=((dateutil.parser.parse(value['BP_date']) - dateutil.parser.parse(value['first_date'])).days)/365
return returnval
def bp_time(value):
returnval=np.nan
if pd.notnull(value['con_date']) & pd.notnull(value['BP_date']):
returnval=((dateutil.parser.parse(value['con_date']) - dateutil.parser.parse(value['BP_date'])).days)/365
return returnval
def con_time(value):
returnval=np.nan
if pd.notnull(value['comp_date']) & pd.notnull(value['con_date']):
returnval=((dateutil.parser.parse(value['comp_date']) - dateutil.parser.parse(value['con_date'])).days)/365
return returnval
df_export['permit_time']=df_export.apply(permit_time, axis=1)
df_export['bp_time']=df_export.apply(bp_time, axis=1)
df_export['con_time']=df_export.apply(con_time, axis=1)
# -
df_export['years_per_unit']=df_export['project_time_years']/df_export['units']
df_export['ptime_per_unit']=df_export['permit_time']/df_export['units']
#df_export=df[pd.notnull(df['project_time_years'])]
df_export=df_export[['address', 'apn', 'x', 'y', 'geometry', 'years_per_unit', 'ptime_per_unit']]
df_export.to_file(driver='ESRI Shapefile',filename=output+"dots.shp")
df_export.to_csv(output+"dots.csv")
# # End Interuption
# +
def joint_scatter(variable, title, yaxis,file, df=df, color='blue'):
fig, ax = plt.subplots(4, 2, figsize=(14,20), sharey=True)
sample_size=df[pd.notnull(df[variable])][variable].count()
plt.suptitle(title+ " n="+str(sample_size), fontsize=20)
#plt.ylim([0,25])
for m in range(4):
for n in range(2):
ax[m, n].tick_params(axis='both', which='major', labelsize=13)
ax[m, n].get_xaxis().set_major_formatter(mpl.ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
dotsize=50
ax[0, 0].scatter(df['pop_density'], df[variable], s=dotsize, color=color, edgecolors='black')
ax[0, 0].set_xlabel('Population Density', fontsize=18)
ax[0, 0].set_ylabel(yaxis, fontsize=14)
ax[1, 0].scatter(df['perc_owner'], df[variable], s=dotsize, color=color, edgecolors='black')
ax[1, 0].set_xlabel('Percentage Owner', fontsize=18)
ax[1, 0].set_ylabel(yaxis, fontsize=14)
ax[2, 0].scatter(df['perc_white'], df[variable], s=dotsize, color=color, edgecolors='black')
ax[2, 0].set_xlabel('Percentage White', fontsize=18)
ax[2, 0].set_ylabel(yaxis, fontsize=14)
ax[0, 1].scatter(df['median_age'], df[variable], s=dotsize, color=color, edgecolors='black')
ax[0, 1].set_xlabel('Median Age', fontsize=18)
ax[1, 1].scatter(df['median_income'], df[variable], s=dotsize, color=color, edgecolors='black')
ax[1, 1].set_xlabel('Median Income', fontsize=18)
ax[2, 1].scatter(df['median_homevalue'], df[variable], s=dotsize, color=color, edgecolors='black')
ax[2, 1].set_xlabel('Median Home Value', fontsize=18)
ax[3, 0].scatter(df['perc_pre_2000'], df[variable], s=dotsize, color=color, edgecolors='black')
ax[3, 0].set_xlabel('Percentage Pre 2000', fontsize=18)
ax[3, 0].set_ylabel(yaxis, fontsize=14)
ax[3, 1].scatter(df['perc_pre_1990'], df[variable], s=dotsize, color=color, edgecolors='black')
ax[3, 1].set_xlabel('Percentage Pre 1990', fontsize=18)
export_folder = output+"/census_scatterplots"
plt.savefig(export_folder+'/'+file+'.png')
#ax[0, 1].scatter(df['perc_old'], df[variable], s=60)
#ax[0, 1].set_xlabel('Percentage Old', fontsize=18)
#ax[1, 1].scatter(df['perc_rich'], df[variable], s=60)
#ax[1, 1].set_xlabel('Percentage Rich', fontsize=18)
joint_scatter('project_time_years','Scatter Plots: Time to Completion (Years)', 'Time (Years)', 'all_years')
# -
joint_scatter('years_per_unit', 'Scatter Plots: Time to Completion (Years per Unit)', 'Time (Years per Unit)', 'all_years_per_unit')
# ## Scatter Entitlement Times
df2 = df[pd.notnull(df['BP_date'])]
#scatter plots by entitlement times
df2['permit_time']=df2.apply(lambda x: ((dateutil.parser.parse(x['BP_date']) - dateutil.parser.parse(x['first_date'])).days)/365, axis=1)
df2['permit_time_per_unit']=df2['permit_time']/df2['units']
joint_scatter('permit_time', 'Scatter Plots: Permit Time (Years)', 'Time (Years)','all_ent_years', df=df2, color='red')
joint_scatter('permit_time_per_unit', 'Scatter Plots: Permit Time (Years per Unit)', 'Time (Years per Unit)','all_ent_years_per_unit', df=df2, color='red')
# ## Big Project Scatter Plots
df_big=df[df['units']>=10]
joint_scatter('project_time_years', 'Big Projects: Time to Completion (Years)', 'Time (Years)', 'big', df=df_big, color='green')
df_big=df_big[pd.notnull(df_big['BP_date'])] #drop all without BP date for permitting time graphs
df_big['permit_time']=df_big.apply(lambda x: ((dateutil.parser.parse(x['BP_date']) - dateutil.parser.parse(x['first_date'])).days)/365, axis=1)
joint_scatter('permit_time', 'Big Projects: Permit Time (Years)', 'Time (Years)', 'big_ent', df=df_big, color='green')
# # Regressions
import statsmodels.formula.api as smf
import numpy as np
from sklearn import linear_model
df.head()
mod = smf.ols(formula='project_time_years ~ units + pop_density + median_age + median_income + median_homevalue + perc_pre_1990', data=df)
res = mod.fit()
print(res.summary())
mod = smf.ols(formula='permit_time ~ units + pop_density + median_age + median_income + median_homevalue + perc_pre_1990', data=df2)
res = mod.fit()
print(res.summary())
mod = smf.ols(formula='permit_time ~ units + median_age', data=df2)
res = mod.fit()
print(res.summary())
mod = smf.ols(formula='years_per_unit ~ pop_density + median_age + median_income + median_homevalue + perc_pre_1990', data=df)
res = mod.fit()
print(res.summary())
| 16,247 |
/hw5/hw5.ipynb
|
cedd282325bfb5fb80d6932aa79f4add61acff11
|
[] |
no_license
|
JialiangZJU/csmath
|
https://github.com/JialiangZJU/csmath
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 6,966 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Collect 10 sentences as a corpus
# Make a word vectors of this corpus
corpus = ['king is a strong man',
'queen is a wise woman',
'boy is a young man',
'girl is a young woman',
'prince is a young king',
'princess is a young queen',
'man is strong',
'woman is pretty',
'prince is a boy will be king',
'princess is a girl will be queen']
# +
# Remove Stop word. The words which are more frequent in sentence are called stop word, i.e. is,a,the,will
def remove_stop_words(corpus):
stop_words = ['is','a','will','be']
results = []
#print(corpus)
for sentence in corpus:
words_in_sentence = sentence.split(' ')
for stp_w in stop_words:
if stp_w in words_in_sentence:
words_in_sentence.remove(stp_w)
results.append(" ".join(words_in_sentence))
return results
# +
corpus = remove_stop_words(corpus)
corpus
# make a word list with unique value
word_list = []
for sentence in corpus:
for word in sentence.split(' '):
word_list.append(word)
word_list = set(word_list)
#word_list
# +
# Generation of data.
word2int = {}
for i,word in enumerate(word_list):
word2int[word] = i
#word2int
# generate multidimentional array. it contains word of each sentence in a array.
sentences = []
for sentence in corpus:
sentences.append(sentence.split())
# Findout neighbors of window size 2.
WINDOW_SIZE = 2
data = []
for sentence in sentences:
for idx, word in enumerate(sentence):
# print(idx,word)
# print(sentence[max(idx - WINDOW_SIZE, 0) : min(idx + WINDOW_SIZE, len(sentence)) + 1])
for neighbor in sentence[max(idx - WINDOW_SIZE, 0) : min(idx + WINDOW_SIZE, len(sentence)) + 1] :
if neighbor != word:
data.append([word, neighbor])
#data
# +
#preparing Dataframe using panda
import pandas as pd
# for text in corpus:
# print(text)
df = pd.DataFrame(data, columns = ['input', 'label'])
df
# +
# Gererate one hot encoding for every piece of data (input, label)
import tensorflow as tf
import numpy as np
ONE_HOT_ENCODE = len(word_list)
# function for generating one hot encoding
def one_hot_encoding(word_index):
one_hot_encoding = np.zeros(ONE_HOT_ENCODE)
one_hot_encoding[word_index] = 1 #place 1 for the specified word
return one_hot_encoding
X = [] # input array
Y = [] # target array
for x,y in zip(df['input'],df['label']):
X.append(one_hot_encoding(word2int[x]))
Y.append(one_hot_encoding(word2int[y]))
# convert them to numpy arrays
X_train = np.asarray(X)
Y_train = np.asarray(Y)
# making placeholders for X_train and Y_train
x = tf.placeholder(tf.float32, shape=(None, ONE_HOT_ENCODE))
y_label = tf.placeholder(tf.float32, shape=(None, ONE_HOT_ENCODE))
# word embedding will be 2 dimension for 2d visualization
EMBEDDING_DIM = 2
# hidden layer: which represents word vector eventually
W1 = tf.Variable(tf.random_normal([ONE_HOT_ENCODE, EMBEDDING_DIM]))
b1 = tf.Variable(tf.random_normal([1])) #bias
hidden_layer = tf.add(tf.matmul(x,W1), b1)
# output layer
W2 = tf.Variable(tf.random_normal([EMBEDDING_DIM, ONE_HOT_ENCODE]))
b2 = tf.Variable(tf.random_normal([1]))
prediction = tf.nn.softmax(tf.add( tf.matmul(hidden_layer, W2), b2))
# loss function: cross entropy
loss = tf.reduce_mean(-tf.reduce_sum(y_label * tf.log(prediction), axis=[1]))
# training operation
train_op = tf.train.GradientDescentOptimizer(0.05).minimize(loss)
# +
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
iteration = 20000
for i in range(iteration):
# input is X_train which is one hot encoded word
# label is Y_train which is one hot encoded neighbor word
sess.run(train_op, feed_dict={x: X_train, y_label: Y_train})
if i % 3000 == 0:
print('iteration '+str(i)+' loss is : ', sess.run(loss, feed_dict={x: X_train, y_label: Y_train}))
# -
# Now the hidden layer (W1 + b1) is actually the word look up table
vectors = sess.run(W1 + b1)
print(vectors)
w2v_df = pd.DataFrame(vectors, columns = ['x1', 'x2'])
w2v_df['word'] = word_list
w2v_df = w2v_df[['word', 'x1', 'x2']]
w2v_df
#word vector in 2d chart. Graphically showing how words are similar to each other
| 4,576 |
/Visualization Data.ipynb
|
9e558c386b53e7754e2420b96b81d2223aaf183b
|
[] |
no_license
|
mominur0rabbi/MyProject
|
https://github.com/mominur0rabbi/MyProject
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 282,391 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# showign graph in notebook
housing = pd.read_csv('house_prices.csv')
housing.shape
housing.head()
housing.columns
# Analyze the spread of the 'lotArea' column
sns.distplot(housing['LotArea'], kde=False)
sns.distplot(housing['LotArea'], kde=True)
plot = sns.countplot(x='Exterior1st', data=housing)
plot = sns.countplot(x='Exterior1st', data=housing)
plot.set_xticklabels(plot.get_xticklabels(), rotation=40);
sns.regplot(x="LotArea", y = "SalePrice", data= housing)
# +
# Are outliers hewing the relationship. Redraw the relationship after removing very large value
housing['LotArea'].quantile([0.5, 0.95, 0.99])
# -
# Plot after Removeing highest and lowest values
housing_sub = housing.loc[housing['LotArea']< housing['LotArea'].quantile(0.95)]
sns.regplot(x="LotArea", y = "SalePrice", data= housing_sub)
# # Plotting multiple graphs
# # Q: Analyze the relationship between SalesPrice and all "Square Feet(SF)" related Columns
#
#
sf_cols =[col_name for col_name in housing.columns if "SF" in col_name]
len(sf_cols)
sf_cols
fig, axs = plt.subplots(nrows = 3, ncols = 3, figsize=(10,10))
for i in range(0, len(sf_cols)):
rows = i//3
cols = i%3
print(rows, cols)
fig, axs = plt.subplots(nrows = 3, ncols = 3, figsize=(10,10))
for i in range(0, len(sf_cols)):
rows = i//3
cols = i%3
ax = axs[rows, cols]
plot = sns.regplot(x=sf_cols[i], y ='SalePrice', data = housing, ax=ax)
### Is the price of the house impacted by the Exterior covering on house
housing['Exterior1st'].value_counts()
fig, axs = plt.subplots(figsize = (10,10))
sns.boxplot(Data = housing, x ="Exterior1st", y = "SalePrice", ax=axs);
plot.set_xticklabels(plot.get_xticklabels(), rotation=40);
| 2,099 |
/testing/main.ipynb
|
3c2856e97371a930fefdaca26c185c96c0a70f07
|
[] |
no_license
|
Dark417/Kaggle_titanic
|
https://github.com/Dark417/Kaggle_titanic
| 2 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 21,128 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from matplotlib.colors import ListedColormap
from sklearn import model_selection, datasets, linear_model, metrics
import numpy as np
# -
# %pylab
def plot_2d_dataset(data, colors):
pyplot.figure(figsize(8, 8))
pyplot.scatter(list(map(lambda x: x[0], data[0])), list(map(lambda x: x[1], data[0])), c = data[1], cmap = colors)
# +
#генерация датаседа для регрессии
reg_data, reg_target = datasets.make_regression(n_features = 2, n_informative = 1, n_targets = 1,
noise = 5., random_state = 7)
plot_2d_dataset([reg_data, reg_target], ListedColormap(['red', 'blue']))
# -
train_data, test_data, train_labels, test_labels = model_selection.train_test_split(reg_data, reg_target,
test_size = 0.3,
random_state = 1)
#Линейная регрессия (минимум среднеквадратичной ошибки)
linear_regressor = linear_model.LinearRegression()
linear_regressor.fit(train_data, train_labels)
predictions = linear_regressor.predict(test_data)
#Линейная регрессия (минимум асолютной ошибки) -- отсеивает признаки, некритично реагирует на выбросы
lasso_regressor = linear_model.Lasso(random_state = 3)
lasso_regressor.fit(train_data, train_labels)
lasso_predictions = lasso_regressor.predict(test_data)
# +
#Линейная регрессия (минимум асолютной ошибки) со встроенной кросс-валидацией
alphas = np.arange(1, 100, 5)# вектор коэффициентов регуляризации
lasso_cv_regressor = linear_model.LassoCV(alphas=alphas, cv=3)# кросс-валидация с 3 фолдами
lasso_cv_regressor.fit(train_data, train_labels)
alphas_p = lasso_cv_regressor.alphas_ #лучше брать вектор коэффициентов из модели, он может измениться
mse_p = lasso_cv_regressor.mse_path_.mean(axis=1) #среднеквадратичная ошибка
# -
#Регрессия стохастический градиентный спуск
sgd_regressor = linear_model.SGDRegressor(random_state = 0)
sgd_regressor.fit(train_data, train_labels)
predictions = sgd_regressor.predict(test_data)
009E": "Population 25 and Over w/ 5th Grade",
"B15003_010E": "Population 25 and Over w/ 6th Grade",
"B15003_011E": "Population 25 and Over w/ 7th Grade",
"B15003_012E": "Population 25 and Over w/ 8th Grade",
"B15003_013E": "Population 25 and Over w/ 9th Grade",
"B15003_014E": "Population 25 and Over w/ 10th Grade",
"B15003_015E": "Population 25 and Over w/ 11th Grade",
"B15003_016E": "Population 25 and Over w/ 12th Grade, no diploma",
"B15003_017E": "Population 25 and Over w/ Regular High School diploma",
"B15003_018E": "Population 25 and Over w/ GED or alternative credential",
"B15003_019E": "Population 25 and Over w/ Some college, less than 1 year",
"B15003_020E": "Population 25 and Over w/ Some college, 1 or more years",
"B15003_021E": "Population 25 and Over w/ Associate's degree",
"B15003_022E": "Population 25 and Over w/ Bachelor's degree",
"B15003_023E": "Population 25 and Over w/ Master's degree",
"B15003_024E": "Population 25 and Over w/ Professional school degree",
"B15003_025E": "Population 25 and Over w/ Doctorate degree",
})
# Dataframe to be cleaned is put to screen
census_raw.head()
# -
# Check for duplicate zip codes
len(census_raw[census_raw.duplicated(["Zip Code Tabulation Area"])])
# Rows with empty values are dropped
census_no_na = census_raw.dropna()
census_no_na.head()
# Force all dtypes to float
census_no_na = census_no_na.astype(float)
census_no_na.dtypes
# +
# All rows containing a negative value are dropped
# Empty array for indeces to drop is initialized
indeces_to_drop = []
# Every row is checked for a negative value
# Iterate through the rows
for index, row in census_no_na.iterrows():
# Ensure that only 1 index is given per row
unique = True
# Loop through columns
for col in row:
# If a value is negative, add its index to the array be dropped and flip boolean to ensure only 1 entry
if ((col < 0) & unique):
indeces_to_drop.append(index)
unique = False
# Delete each row whose
for index in indeces_to_drop:
census_no_na.drop(index, inplace=True)
census_no_na.head()
# +
# All rates are calculated
# Rate Poverty
census_no_na["Poverty Rate"] = census_no_na["Poverty Count"] / census_no_na["Population"]
# Rate over 25 less than 1st grade
census_no_na["Rate 25 and Over w/ less than 1st grade"] =\
(census_no_na["Population 25 and Over w/ No Schooling"] +\
census_no_na["Population 25 and Over w/ Nursery School"] +\
census_no_na["Population 25 and Over w/ Kindergarten"]) / census_no_na["Population 25 and Over"]
# Rate over 25 with some or completed elementary school (1st through 6th grade)
census_no_na["Rate 25 and Over w/ Some or Completed Elementary School"] =\
(census_no_na["Population 25 and Over w/ 1st Grade"] +\
census_no_na["Population 25 and Over w/ 2nd Grade"] +\
census_no_na["Population 25 and Over w/ 3rd Grade"] +\
census_no_na["Population 25 and Over w/ 4th Grade"] +\
census_no_na["Population 25 and Over w/ 5th Grade"] +\
census_no_na["Population 25 and Over w/ 6th Grade"]) / census_no_na["Population 25 and Over"]
# Rate over 25 with some or completed middle school (7th and 8th grade)
census_no_na["Rate 25 and Over w/ Some or Completed Middle School"] =\
(census_no_na["Population 25 and Over w/ 7th Grade"] +\
census_no_na["Population 25 and Over w/ 8th Grade"]) / census_no_na["Population 25 and Over"]
# Rate over 25 with some high school (9th through 12th grade)
census_no_na["Rate 25 and Over w/ Some High School"] =\
(census_no_na["Population 25 and Over w/ 9th Grade"] +\
census_no_na["Population 25 and Over w/ 10th Grade"] +\
census_no_na["Population 25 and Over w/ 11th Grade"] +\
census_no_na["Population 25 and Over w/ 12th Grade, no diploma"]) / census_no_na["Population 25 and Over"]
# Rate over 25 with completed high school or equivalent
census_no_na["Rate 25 and Over w/ Completed High School or Equivalent"] =\
(census_no_na["Population 25 and Over w/ Regular High School diploma"] +\
census_no_na["Population 25 and Over w/ GED or alternative credential"]) / census_no_na["Population 25 and Over"]
# Rate 25 and Over w/ Some college, less than 1 year
census_no_na["Rate 25 and Over w/ Some college, less than 1 year"] =\
census_no_na["Population 25 and Over w/ Some college, less than 1 year"] / census_no_na["Population 25 and Over"]
# Rate 25 and Over w/ Some college, 1 or more years
census_no_na["Rate 25 and Over w/ Some college, 1 or more years"] =\
census_no_na["Population 25 and Over w/ Some college, 1 or more years"] / census_no_na["Population 25 and Over"]
# Rate 25 and Over w/ Associate's degree
census_no_na["Rate 25 and Over w/ Associate's degree"] =\
census_no_na["Population 25 and Over w/ Associate's degree"] / census_no_na["Population 25 and Over"]
# Rate 25 and Over w/ Bachelor's degree
census_no_na["Rate 25 and Over w/ Bachelor's degree"] =\
census_no_na["Population 25 and Over w/ Bachelor's degree"] / census_no_na["Population 25 and Over"]
# Rate 25 and Over w/ Master's degree
census_no_na["Rate 25 and Over w/ Master's degree"] =\
census_no_na["Population 25 and Over w/ Master's degree"] / census_no_na["Population 25 and Over"]
# Rate 25 and Over w/ Professional school degree
census_no_na["Rate 25 and Over w/ Professional school degree"] =\
census_no_na["Population 25 and Over w/ Professional school degree"] / census_no_na["Population 25 and Over"]
# Rate 25 and Over w/ Doctorate degree
census_no_na["Rate 25 and Over w/ Doctorate degree"] =\
census_no_na["Population 25 and Over w/ Doctorate degree"] / census_no_na["Population 25 and Over"]
# +
# Final DataFrame is made
census_df = census_no_na[["Zip Code Tabulation Area", "Population", "Median Age", "Household Income",
"Per Capita Income", "Poverty Rate", "Population 25 and Over",
"Rate 25 and Over w/ less than 1st grade",
"Rate 25 and Over w/ Some or Completed Elementary School",
"Rate 25 and Over w/ Some or Completed Middle School",
"Rate 25 and Over w/ Some High School",
"Rate 25 and Over w/ Completed High School or Equivalent",
"Rate 25 and Over w/ Some college, less than 1 year",
"Rate 25 and Over w/ Some college, 1 or more years",
"Rate 25 and Over w/ Associate's degree",
"Rate 25 and Over w/ Bachelor's degree",
"Rate 25 and Over w/ Master's degree",
"Rate 25 and Over w/ Professional school degree",
"Rate 25 and Over w/ Doctorate degree"]]
# Output Dataframe to csv and screen
census_df.to_csv("acs5_2018.csv", index=False)
census_df.head()
# -
beta_1, beta_2))
criterion = nn.BCEWithLogitsLoss()
cur_step = 0
classifier_losses = []
# classifier_val_losses = []
for epoch in range(n_epochs):
# Dataloader returns the batches
for real, labels in tqdm(dataloader):
real = real.to(device)
labels = labels[:, label_indices].to(device).float()
class_opt.zero_grad()
class_pred = classifier(real)
class_loss = criterion(class_pred, labels)
class_loss.backward() # Calculate the gradients
class_opt.step() # Update the weights
classifier_losses += [class_loss.item()] # Keep track of the average classifier loss
## Visualization code ##
if cur_step % display_step == 0 and cur_step > 0:
class_mean = sum(classifier_losses[-display_step:]) / display_step
print(f"Step {cur_step}: Classifier loss: {class_mean}")
step_bins = 20
x_axis = sorted([i * step_bins for i in range(len(classifier_losses) // step_bins)] * step_bins)
sns.lineplot(x_axis, classifier_losses[:len(x_axis)], label="Classifier Loss")
plt.legend()
plt.show()
torch.save({"classifier": classifier.state_dict()}, filename)
cur_step += 1
# Uncomment the last line to train your own classfier - this line will not work in Coursera.
# If you'd like to do this, you'll have to download it and run it, ideally using a GPU
# train_classifier("filename")
# + [markdown] colab_type="text" id="Iu1TcEA3aSSI"
# ## Loading the Pretrained Models
# You will then load the pretrained generator and classifier using the following code. (If you trained your own classifier, you can load that one here instead.)
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="OgrLujk_tYDu" outputId="57924502-e734-46fc-da2e-df18dd807fb3"
import torch
gen = Generator(z_dim).to(device)
gen_dict = torch.load("pretrained_celeba.pth", map_location=torch.device(device))["gen"]
gen.load_state_dict(gen_dict)
gen.eval()
n_classes = 40
classifier = Classifier(n_classes=n_classes).to(device)
class_dict = torch.load("pretrained_classifier.pth", map_location=torch.device(device))["classifier"]
classifier.load_state_dict(class_dict)
classifier.eval()
print("Loaded the models!")
opt = torch.optim.Adam(classifier.parameters(), lr=0.01)
# + [markdown] colab_type="text" id="_aq53cc1nZgq"
# ## Training
# Now you can start implementing a method for controlling your GAN!
# + [markdown] colab_type="text" id="ZJuga5nC-b3a"
# #### Update Noise
# For training, you need to write the code to update the noise to produce more of your desired feature. You do this by performing stochastic gradient ascent. You use stochastic gradient ascent to find the local maxima, as opposed to stochastic gradient descent which finds the local minima. Gradient ascent is gradient descent over the negative of the value being optimized. Their formulas are essentially the same, however, instead of subtracting the weighted value, stochastic gradient ascent adds it; it can be calculated by `new = old + (∇ old * weight)`, where ∇ is the gradient of `old`. You perform stochastic gradient ascent to try and maximize the amount of the feature you want. If you wanted to reduce the amount of the feature, you would perform gradient descent. However, in this assignment you are interested in maximize your feature using gradient ascent, since many features in the dataset are not present much more often than they're present and you are trying to add a feature to the images, not remove.
#
# Given the noise with its gradient already calculated through the classifier, you want to return the new noise vector.
#
# <details>
#
# <summary>
# <font size="3" color="green">
# <b>Optional hint for <code><font size="4">calculate_updated_noise</font></code></b>
# </font>
# </summary>
#
# 1. Remember the equation for gradient ascent: `new = old + (∇ old * weight)`.
#
# </details>
# + colab={} colab_type="code" id="U9WLR8Oy1rxU"
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: calculate_updated_noise
def calculate_updated_noise(noise, weight):
'''
Function to return noise vectors updated with stochastic gradient ascent.
Parameters:
noise: the current noise vectors. You have already called the backwards function on the target class
so you can access the gradient of the output class with respect to the noise by using noise.grad
weight: the scalar amount by which you should weight the noise gradient
'''
#### START CODE HERE ####
new_noise = noise + ( noise.grad * weight)
#### END CODE HERE ####
return new_noise
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="8s2RbF5F3_lL" outputId="e165d0bb-a937-4ce0-9f78-3a094513487c"
# UNIT TEST
# Check that the basic function works
opt.zero_grad()
noise = torch.ones(20, 20) * 2
noise.requires_grad_()
fake_classes = (noise ** 2).mean()
fake_classes.backward()
new_noise = calculate_updated_noise(noise, 0.1)
assert type(new_noise) == torch.Tensor
assert tuple(new_noise.shape) == (20, 20)
assert new_noise.max() == 2.0010
assert new_noise.min() == 2.0010
assert torch.isclose(new_noise.sum(), torch.tensor(0.4) + 20 * 20 * 2)
print("Success!")
# -
# Check that it works for generated images
opt.zero_grad()
noise = get_noise(32, z_dim).to(device).requires_grad_()
fake = gen(noise)
fake_classes = classifier(fake)[:, 0]
fake_classes.mean().backward()
noise.data = calculate_updated_noise(noise, 0.01)
fake = gen(noise)
fake_classes_new = classifier(fake)[:, 0]
assert torch.all(fake_classes_new > fake_classes)
print("Success!")
# + [markdown] colab_type="text" id="tj-c9LT5lIRC"
# #### Generation
# Now, you can use the classifier along with stochastic gradient ascent to make noise that generates more of a certain feature. In the code given to you here, you can generate smiling faces. Feel free to change the target index and control some of the other features in the list! You will notice that some features are easier to detect and control than others.
#
# The list you have here are the features labeled in CelebA, which you used to train your classifier. If you wanted to control another feature, you would need to get data that is labeled with that feature and train a classifier on that feature.
# + colab={"base_uri": "https://localhost:8080/", "height": 597} colab_type="code" id="kASNj6nLz7kh" outputId="50c4dfce-5925-4c85-e601-fb92c4ed5299"
# First generate a bunch of images with the generator
n_images = 8
fake_image_history = []
grad_steps = 10 # Number of gradient steps to take
skip = 2 # Number of gradient steps to skip in the visualization
feature_names = ["5oClockShadow", "ArchedEyebrows", "Attractive", "BagsUnderEyes", "Bald", "Bangs",
"BigLips", "BigNose", "BlackHair", "BlondHair", "Blurry", "BrownHair", "BushyEyebrows", "Chubby",
"DoubleChin", "Eyeglasses", "Goatee", "GrayHair", "HeavyMakeup", "HighCheekbones", "Male",
"MouthSlightlyOpen", "Mustache", "NarrowEyes", "NoBeard", "OvalFace", "PaleSkin", "PointyNose",
"RecedingHairline", "RosyCheeks", "Sideburn", "Smiling", "StraightHair", "WavyHair", "WearingEarrings",
"WearingHat", "WearingLipstick", "WearingNecklace", "WearingNecktie", "Young"]
### Change me! ###
target_indices = feature_names.index("Smiling") # Feel free to change this value to any string from feature_names!
noise = get_noise(n_images, z_dim).to(device).requires_grad_()
for i in range(grad_steps):
opt.zero_grad()
fake = gen(noise)
fake_image_history += [fake]
fake_classes_score = classifier(fake)[:, target_indices].mean()
fake_classes_score.backward()
noise.data = calculate_updated_noise(noise, 1 / grad_steps)
plt.rcParams['figure.figsize'] = [n_images * 2, grad_steps * 2]
show_tensor_images(torch.cat(fake_image_history[::skip], dim=2), num_images=n_images, nrow=n_images)
# + [markdown] colab_type="text" id="PmETsfun7bLc"
# ## Entanglement and Regularization
# You may also notice that sometimes more features than just the target feature change. This is because some features are entangled. To fix this, you can try to isolate the target feature more by holding the classes outside of the target class constant. One way you can implement this is by penalizing the differences from the original class with L2 regularization. This L2 regularization would apply a penalty for this difference using the L2 norm and this would just be an additional term on the loss function.
#
# Here, you'll have to implement the score function: the higher, the better. The score is calculated by adding the target score and a penalty -- note that the penalty is meant to lower the score, so it should have a negative value.
#
# For every non-target class, take the difference between the current noise and the old noise. The greater this value is, the more features outside the target have changed. You will calculate the magnitude of the change, take the mean, and negate it. Finally, add this penalty to the target score. The target score is the mean of the target class in the current noise.
#
# <details>
#
# <summary>
# <font size="3" color="green">
# <b>Optional hints for <code><font size="4">get_score</font></code></b>
# </font>
# </summary>
#
# 1. The higher the score, the better!
# 2. You want to calculate the loss per image, so you'll need to pass a dim argument to [`torch.norm`](https://pytorch.org/docs/stable/generated/torch.norm.html).
# 3. Calculating the magnitude of the change requires you to take the norm of the difference between the classifications, not the difference of the norms.
#
# </details>
# + colab={} colab_type="code" id="qabLcvEL7X-J"
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: get_score
def get_score(current_classifications, original_classifications, target_indices, other_indices, penalty_weight):
'''
Function to return the score of the current classifications, penalizing changes
to other classes with an L2 norm.
Parameters:
current_classifications: the classifications associated with the current noise
original_classifications: the classifications associated with the original noise
target_indices: the index of the target class
other_indices: the indices of the other classes
penalty_weight: the amount that the penalty should be weighted in the overall score
'''
# Steps: 1) Calculate the change between the original and current classifications (as a tensor)
# by indexing into the other_indices you're trying to preserve, like in x[:, features].
# 2) Calculate the norm (magnitude) of changes per example.
# 3) Multiply the mean of the example norms by the penalty weight.
# This will be your other_class_penalty.
# Make sure to negate the value since it's a penalty!
# 4) Take the mean of the current classifications for the target feature over all the examples.
# This mean will be your target_score.
#### START CODE HERE ####
other_distances = current_classifications[:,other_indices] - original_classifications[:,other_indices]
# Calculate the norm (magnitude) of changes per example and multiply by penalty weight
other_class_penalty = -torch.norm(other_distances, dim=1).mean() * penalty_weight
# Take the mean of the current classifications for the target feature
target_score = current_classifications[:, target_indices].mean()
#### END CODE HERE ####
return target_score + other_class_penalty
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="5-vTjn__EKQT" outputId="f48d4b7e-f9bc-403f-822d-a222f868ebd4"
# UNIT TEST
assert torch.isclose(
get_score(torch.ones(4, 3), torch.zeros(4, 3), [0], [1, 2], 0.2),
1 - torch.sqrt(torch.tensor(2.)) * 0.2
)
rows = 10
current_class = torch.tensor([[1] * rows, [2] * rows, [3] * rows, [4] * rows]).T.float()
original_class = torch.tensor([[1] * rows, [2] * rows, [3] * rows, [4] * rows]).T.float()
# Must be 3
assert get_score(current_class, original_class, [1, 3] , [0, 2], 0.2).item() == 3
current_class = torch.tensor([[1] * rows, [2] * rows, [3] * rows, [4] * rows]).T.float()
original_class = torch.tensor([[4] * rows, [4] * rows, [2] * rows, [1] * rows]).T.float()
# Must be 3 - 0.2 * sqrt(10)
assert torch.isclose(get_score(current_class, original_class, [1, 3] , [0, 2], 0.2),
-torch.sqrt(torch.tensor(10.0)) * 0.2 + 3)
print("Success!")
# + [markdown] colab_type="text" id="CkrGr-NUGwC8"
# In the following block of code, you will run the gradient ascent with this new score function. You might notice a few things after running it:
#
# 1. It may fail more often at producing the target feature when compared to the original approach. This suggests that the model may not be able to generate an image that has the target feature without changing the other features. This makes sense! For example, it may not be able to generate a face that's smiling but whose mouth is NOT slightly open. This may also expose a limitation of the generator.
# Alternatively, even if the generator can produce an image with the intended features, it might require many intermediate changes to get there and may get stuck in a local minimum.
#
# 2. This process may change features which the classifier was not trained to recognize since there is no way to penalize them with this method. Whether it's possible to train models to avoid changing unsupervised features is an open question.
# + colab={"base_uri": "https://localhost:8080/", "height": 597} colab_type="code" id="l3SshFjn-soX" outputId="4d97c409-589c-46b7-97b3-8d0483e968d5"
fake_image_history = []
### Change me! ###
target_indices = feature_names.index("Smiling") # Feel free to change this value to any string from feature_names from earlier!
other_indices = [cur_idx != target_indices for cur_idx, _ in enumerate(feature_names)]
noise = get_noise(n_images, z_dim).to(device).requires_grad_()
original_classifications = classifier(gen(noise)).detach()
for i in range(grad_steps):
opt.zero_grad()
fake = gen(noise)
fake_image_history += [fake]
fake_score = get_score(
classifier(fake),
original_classifications,
target_indices,
other_indices,
penalty_weight=0.1
)
fake_score.backward()
noise.data = calculate_updated_noise(noise, 1 / grad_steps)
plt.rcParams['figure.figsize'] = [n_images * 2, grad_steps * 2]
show_tensor_images(torch.cat(fake_image_history[::skip], dim=2), num_images=n_images, nrow=n_images)
# -
| 24,806 |
/Python/Numpy_basics.ipynb
|
84367c1cb97a0a4276d9f094fdb7aedc96d0d066
|
[] |
no_license
|
rachelrliu/Machine_Learning_Notes
|
https://github.com/rachelrliu/Machine_Learning_Notes
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 16,120 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# #Python NumPy: Arrays and Vectorized Computation
#
# This is a personal study note for Data Wrangling. It is meant to be a both a quick guide and reference for further research into these topics.
#
# *Reference: Python for Data Analysis by Wes McKinny*
#
# ##Array
#
# A numpy array is a grid of values, all of the **same type**, and is indexed by a tuple of nonnegative integers. The number of dimensions is the rank of the array; the **shape** of an array is a tuple of integers indicating the size of each dimension. Arrays also have a "size" attribute. For a 1-dimensional array this is equivalent to its length. It is essentially a product of the dimensions.
#
# The easiest way to create an array is to use the *array* function. This accepts any se- quence-like object (including other arrays) and produces a new NumPy array containing the passed data.
#
import numpy as np
a = np.array([1, 2, 3]) # Create a rank 1 array
print type(a), a.ndim, a.shape, a.size
a[0] = 5 # Change an element of the array
print a
b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print b
print b.ndim, b.shape, b.size
# More on array creation: [Array creation routine](http://docs.scipy.org/doc/numpy/reference/routines.array-creation.html)
# ##Datatypes
#
# Numpy tries to guess a datatype when you create an array, but functions that construct arrays usually also include an optional argument to explicitly specify the datatype.
# +
x = np.array([1, 2]) # Let numpy choose the datatype
y = np.array([1, 2], dtype=np.int64) # Force a particular datatype
z = x.astype(np.float64) #Cast an array from one dtype to another
print x.dtype, y.dtype, z.dtype
# -
# More on dtype: [documentation](http://docs.scipy.org/doc/numpy/reference/arrays.dtypes.html)
# ##Array Indexing
#
# ###Slicing
# Similar to Python lists, numpy arrays can be sliced. A slice of an array is a view into the *same data*. Since arrays may be multidimensional, you must specify a slice for each dimension of the array.
# +
# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
print b
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print a[0, 1]
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print a[0, 1]
# +
c = np.array([[[1],[2],[3]], [[4],[5],[6]]])
print c.shape
#If the number of objects in the selection tuple is less than ndim ,
#then : is assumed for any subsequent dimensions.
d = c[1:2,0:2]
print d,d.shape
# -
# ###Integer array indexing
# When you index into numpy arrays using slicing, the resulting array view will always be a subarray of the original array. In contrast, integer array indexing allows you to construct arbitrary arrays using the data from another array. Here is an example:
# +
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print a[[0, 1, 2], [0, 1, 0]]
# The above example of integer array indexing is equivalent to this:
print np.array([a[0, 0], a[1, 1], a[2, 0]])
# When using integer array indexing, you can reuse the same
# element from the source array:
print a[[0, 0], [1, 1]]
# Equivalent to the previous integer array indexing example
print np.array([a[0, 1], a[0, 1]])
# -
# We can also mix integer indexing with slice indexing. However, doing so will yield an array of lower rank than the original array.
# +
# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1,:] # Rank 1 view of the second row of a
row_r2 = a[1:2,:] # Rank 2 view of the second row of a
print row_r1, row_r1.shape, row_r1.ndim
print row_r2, row_r2.shape, row_r2.ndim
# -
# ###Boolean array indexing
#
# Boolean array indexing lets you pick out arbitrary elements of an array. Frequently this type of indexing is used to select the elements of an array that satisfy some condition. Here is an example:
#
#
a = np.array([[1,2], [3, 4], [5, 6]])
bool_idx = (a > 2) # Find the elements of a that are bigger than 2;
# this returns a numpy array of Booleans of the same
# shape as a, where each slot of bool_idx tells
# whether that element of a is > 2.
bool_idx
# We can use boolean array indexing to construct a *rank 1* array consisting of the elements of a corresponding to the True values of bool_idx:
# +
print a[bool_idx]
# We can do all of the above in a single concise statement:
print a[a > 2]
# -
# We can use what NumPy calls "Boolean indexing", combined with the sum function, to count the number of True values in the array:
#number of elements in array that are greater than 2
print ((a > 2) == True).sum()
# ##Array Math
#
# Basic mathematical functions (universal functions) operate **elementwise** on arrays, and are available both as operator overloads and as functions in the numpy module.
#
# [Universal functions documentation](http://docs.scipy.org/doc/numpy/reference/ufuncs.html)
# ##Sorting
#
# Sorting works much like it does with built-in lists. The np.sort() function is a pure function that returns a sorted copy of the array while leaving the original array untouched, whereas the .sort() method is a modifier that sorts the array in place.
#
#
# +
int_arr = np.random.randint(0,10,8) #generate 8 interger from range(10)
print int_arr
np.sort(int_arr)
print np.sort(int_arr)
print int_arr
# -
int_arr.sort()
print int_arr
# We can sort multidimensional arrays by passing in the axis along which you want to sort. For a 2D array, this means passing in axis 0 if you want to sort by columns and axis 1 if you want to sort by rows:
# +
twod_int_arr = np.random.randint(0,10,(4,4))
print twod_int_arr
print np.sort(twod_int_arr,0) #sort by column
print np.sort(twod_int_arr,1) #sort by row
# -
# np.argsort returns the indices that would sort an array.
# +
arr = np.random.randint(0,10,10)
print arr
print arr.argsort()
print arr.argsort()[::-1] #reverse
# -
# ##Some Useful NumPy Functions
#
# numpy.where(condition[, x, y]) return elements, either from x or y, depending on condition. When True, yield x, otherwise yield y.
# +
a = np.array([[1,2],[3,4]])
b = np.array([[9,8],[7,6]])
c = np.array([[True,False],[True,False]])
print np.where(c,a,b)
# -
# in1d() function tests a set of input values for membership in a given array or set it returns an array of Booleans indicating which of the input set can be found in the target:
# +
arr = np.random.randint(0,10,10)
print arr
print np.in1d([3,9,6],arr)
# -
# unique() function returns a sorted list of unique values found in the input array:
# +
arr = np.random.randint(0,10,10)
print arr
print np.unique(arr)
# -
# More:
# [NumPy Reference](http://docs.scipy.org/doc/numpy/reference/routines.html)
| 7,682 |
/Functions_2.ipynb
|
b2b6e8e5ce5b07a5502cf3f6254102647c933386
|
[] |
no_license
|
vincedlbr/ort-ms2i-vdelabre
|
https://github.com/vincedlbr/ort-ms2i-vdelabre
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 1,839 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
mylistVeloEuro=[
500, 650, 800, 950, 1100, 1250, 1400, 1550, 1700, 1850,
2000, 2150, 2300, 2450, 2600, 2750, 2900, 3050, 3200, 3350,
3500, 3650, 3800, 3950, 4100, 4250, 4400, 4550, 4700, 4850,
5000, 5150, 5300, 5450, 5600, 5750, 5900, 6050, 6200, 6350,
6500, 6650, 6800, 6950, 7100, 7250, 7400, 7550, 7700, 7850,
8000, 8150, 8300, 8450, 8600, 8750, 8900, 9050, 9200, 9350
]
def countVelo(tab, sup, c=None) :
nb_velo=0
for euro in tab :
if (euro > sup) :
nb_velo=nb_velo+1
return len(tab), nb_velo, c
print(countVelo)
NbTotalVelo, NbVeloSup, test = countVelo(mylistVeloEuro, 4000)
print(NbTotalVelo)
print(NbVeloSup)
print(test)
NbTotalVelo, NbVeloSup, test = countVelo(mylistVeloEuro, 4000, "blop")
print(NbTotalVelo)
print(NbVeloSup)
print(test)
| 1,082 |
/analysis/EWAS/blood/modeling_linear_XGboost/blood_testing_models_by_sex.ipynb
|
bb293656718dab11a5aed001a93fd0a828713e12
|
[] |
no_license
|
AC297rDNAMethylation2021/Healthy-Aging
|
https://github.com/AC297rDNAMethylation2021/Healthy-Aging
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 1,459,229 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import requests
from bs4 import BeautifulSoup
resp = requests.get("http://blog.castman.net/py-scraping-analysis-book/ch1/connect.html")
soup = BeautifulSoup(resp.text, "html.parser")
print(soup.find("h1").text)
# +
import requests
from bs4 import BeautifulSoup
def main():
url01 = 'http://blog.castman.net/py-scraping-analysis-book/ch1/connect.html'
bad_url = 'http://non-existed.domin/connect.html'
text01 = get_tag_text(url01,'h1')
print(text01)
text02 = get_tag_text(url01,'h2')
print(text02)
text03 = get_tag_text(bad_url,'h1')
print(text03)
def get_tag_text(url,tag):
try:
resp = requests.get(url)
if resp.status_code == 200:
soup = BeautifulSoup(resp.text, 'html.parser')
return soup.find(tag).text
except Exception as e:
print('Exception: %s' %(e))
return None
if __name__ =='__main__':
main()
# -
the we created installed.
import age_predict.Loading_EWAS_Aging_Data as le
import age_predict.Regression as rg
import age_predict.Pickle_unpickle as pu
# View working directory
os.getcwd()
# #### Set paths
data_path = '../../data/'
cpg_path = '../saved_features/'
save_models_path = '../saved_models/'
# #### Get Saved imputed whole blood data 2263 cpgs
# * The dataframes imported here were created with the "blood_feature_selection_by_XGBoost_importance_scores_gender" notebook
df_train = pd.read_csv(data_path + 'df_train_ranked_gen.csv', index_col=0)
df_test = pd.read_csv(data_path + 'df_test_ranked_gen.csv', index_col=0)
# #### Get Saved blood cpg rankings
# * The list of top ranked cpgs imported here was created with the "blood_feature_selection_by_XGBoost_importance_scores_gender" notebook and pickled
cpgs_XGboost_blood_ranked_gender = pu.get_pickled_object(cpg_path + 'cpgs_XGboost_blood_ranked_gender')
top_100 = cpgs_XGboost_blood_ranked_gender[:100]
top_1000 = cpgs_XGboost_blood_ranked_gender[:1000]
s = pd.Series(list(df_train.age) + list(df_test.age))
# #### Looking at the age distributions in the data
# Histogram of ages in train + test data
plt.figure(figsize=(6,4))
s.hist(bins=20,histtype='bar', ec='black' )
plt.xlabel('Age', fontsize=14)
plt.xlim(0,120)
plt.ylabel('Count', fontsize=14)
plt.grid(True, lw=1, ls = '--', alpha=0.2)
plt.title('Blood DNA meythylation dataset', fontsize=16)
plt.show()
# Histogram of ages in train data
plt.figure(figsize=(6,4))
df_train.age.hist(bins=20,histtype='bar', ec='black' )
plt.xlabel('Age', fontsize=14)
plt.xlim(0,120)
plt.ylabel('Count', fontsize=14)
plt.grid(True, lw=1, ls = '--', alpha=0.2)
plt.title('Histogram of Ages Train data', fontsize=16)
plt.show()
# Histogram of ages in test data
plt.figure(figsize=(6,4))
df_test.age.hist(bins=20, histtype='bar', ec='black')
plt.xlabel('Age')
plt.ylabel('Count')
plt.title('Histogram of Ages Test data')
plt.show()
# ## 1 = Male, 0 = Female
df_train
df_test
# #### Training Linear, XGboost, Ridge, Lasso models using the top 100 ranked cpgs
from sklearn.model_selection import train_test_split
X = df_train[top_100]
y = df_train.age
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state = 2021)
wb_mod_100, rms_train, rms_test, r2_train, r2_test = rg.linear_regress(X_train, y_train, X_test, y_test, plot=True)
wb_mod_XG_100, rms_train, rms_test, r2_train, r2_test, feature_importances_ = rg.xgboost_regress(X_train, y_train, X_test, y_test, early_stopping_rounds=10)
wb_mod_lasso_100, rms_train, rms_test, r2_train, r2_test = rg.lassoCV_regress(X_train, y_train, X_test, y_test, plot=True, alphas=[1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 1, 1e1, 1e2, 1e3, 1e4, 1e5],cv=5)
wb_mod_ridge_100, rms_train, rms_test, r2_train, r2_test = rg.ridgeCV_regress(X_train, y_train, X_test, y_test, plot=True, alphas=[1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 1, 1e1, 1e2, 1e3, 1e4, 1e5],cv=5)
wb_mod_kNN_100, rms_train, rms_test, r2_train, r2_test = rg.kNN_regress(X_train, y_train, X_test, y_test, plot=True, ks=[1, 2, 3, 5, 10, 15, 20, 30, 50],cv=5)
# #### Testing Linear, XGboost, Ridge, Lasso models using the top 100 ranked cpgs on both sexes separately.
df_male = df_test[df_test.sex == 1]
df_female = df_test[df_test.sex == 0
# +
X_test_male = df_male[top_100]
y_test_male = df_male.age
X_test_female = df_female[top_100]
y_test_female = df_female.age
# -
preds, MSE, rms, r2, MAE, r_corr = rg.test_model_on_heldout_data(X_test_male, y_test_male, wb_mod_100, mtype='Linear Regression', figsize=(8,4))
preds, MSE, rms, r2, MAE, r_corr = rg.test_model_on_heldout_data(X_test_female, y_test_female, wb_mod_100, mtype='Linear Regression', figsize=(8,4))
preds, MSE, rms, r2, MAE, r_corr = rg.test_model_on_heldout_data(X_test_male, y_test_male, wb_mod_XG_100, mtype='XGboost Regression', figsize=(8,4))
preds, MSE, rms, r2, MAE, r_corr = rg.test_model_on_heldout_data(X_test_female, y_test_female, wb_mod_XG_100, mtype='XGboost Regression', figsize=(8,4))
preds, MSE, rms, r2, MAE, r_corr = rg.test_model_on_heldout_data(X_test_male, y_test_male, wb_mod_lasso_100, mtype='Lasso Regression', figsize=(8,4))
preds, MSE, rms, r2, MAE, r_corr = rg.test_model_on_heldout_data(X_test_female, y_test_female, wb_mod_lasso_100, mtype='Lasso Regression', figsize=(8,4))
preds, MSE, rms, r2, MAE, r_corr = rg.test_model_on_heldout_data(X_test_male, y_test_male, wb_mod_ridge_100, mtype='Ridge Regression', figsize=(8,4))
preds, MSE, rms, r2, MAE, r_corr = rg.test_model_on_heldout_data(X_test_female, y_test_female, wb_mod_ridge_100, mtype='Ridge Regression', figsize=(8,4))
| 5,802 |
/.ipynb_checkpoints/day_3-checkpoint.ipynb
|
fa0f16afd158e7995ca92cccaa00b9a0934e7bd8
|
[] |
no_license
|
appdulrahman/60DaysofUdacity
|
https://github.com/appdulrahman/60DaysofUdacity
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 6,991 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# import the necessary libraries
import pickle
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.sparse as sparse
import skimage.io as skio
import copy as cp
# ### Creating Training Data
# open the training data array
tempfile = open('Variables/trainImagePatchArray.pckl', 'rb')
# load through the pickle library
trainImagePatchArray = pickle.load(tempfile)
tempfile.close()
# convert all values to integer
trainingDataIn= trainImagePatchArray.astype(int)
# open the output image obtained from the k-means++ clustering
tempfile = open('Variables/trainingOutputImage.pckl', 'rb')
# load the output image through the pickle library
trainingOutputImage = pickle.load(tempfile)
tempfile.close()
# taking the entire left half of the input image except the first pixel
trainingOutputImage = trainingOutputImage[1:300,1:224]
# reshaping the image
trainout = trainingOutputImage.reshape(((trainingOutputImage.shape[0]*trainingOutputImage.shape[1]),3))
trainout
# open the file containing the centers of the clusters
tempfile = open('Variables/clusters.pckl', 'rb')
# load the clusters using pickle
clusters = pickle.load(tempfile)
tempfile.close()
# from the clusters dictionary, get the list of centers of the colors
colorlist = list(clusters.keys())
# and convert to a numpy array
colors = np.asarray(colorlist,dtype=int)
colors
trainingDataIn
# initialize an array of zeros with the length of trainout
trainingDataOut = np.zeros((len(trainout),5),dtype=int)
# for all pixels in the training image
for index,pixel in enumerate(trainout):
# reassign the values to the array to 1 if the colors array is equal to the pixel's column
trainingDataOut[index,np.where((colors == pixel).all(axis=1))] = 1
trainingDataOut
# convert the training input data into a dataframe
Trainingdataframe = pd.DataFrame(data=trainingDataIn,index=range(1,len(trainingDataIn)+1), columns= ["px"+str(i) for i in range(1,10)] )
# converting the training output data to a coordinate matrix, detailing the colors from the clusters
arr = sparse.coo_matrix(trainingDataOut)
# and adding that to the dataframe
Trainingdataframe['Color'] = arr.toarray().tolist()
Trainingdataframe
# ### Creating Testing Data.
# open the test data from the pickle file
tempfile = open('Variables/testImagePatchArray.pckl', 'rb')
# loading it
testImagePatchArray = pickle.load(tempfile)
tempfile.close()
# converting it into integer data type
testDataX = testImagePatchArray.astype(int)
# load the expected test output image
tempfile = open('Variables/expectedtestingOutputImage.pckl', 'rb')
testOutputImage = pickle.load(tempfile)
tempfile.close()
# taking the entire test image except the first pixel
testOutputImage = testOutputImage[1:300,1:224]
# and reshaping it to incorporate the R, G, B channels
testout = testOutputImage.reshape(((testOutputImage.shape[0]*testOutputImage.shape[1]),3))
testDataX
testout
# initialize an array of zeros with the length of the test output data
testDataY = np.zeros((len(testout),5),dtype=int)
# for all pixels in the test output image
for index,pixel in enumerate(testout):
# assign a value of 1 for all the indices where the column of the pixel represents the color from the clusters
testDataY[index,np.where((colors == pixel).all(axis=1))] = 1
testDataY
# create a dataframe for the test data with each pixel from the above
Testingdataframe = pd.DataFrame(data=testDataX,index=range(1,len(testDataX)+1), columns= ["px"+str(i) for i in range(1,10)] )
# convert the array into a sparse coordinate matrix
arr = sparse.coo_matrix(testDataY)
# and add that to the dataframe
Testingdataframe['Color'] = arr.toarray().tolist()
Testingdataframe
# ### Defining Functions for Multiclass Logistic Regression
# +
def softmax(XW):
"""
implementing the softmax function for logistic regression
"""
XW -= np.max(XW)
# returns the softmax value based on teh formula for the softmax function
prob = (np.exp(XW).T/ np.sum(np.exp(XW),axis=1)).T
return prob
def loss(W,X,Y,lambd):
"""
implements the loss function
"""
# compute the softmax function by taking the dot product of input data and the weights
prob = softmax(np.dot(X,W))
N = len(Y)
# compute the loss based on the formula for loss of logistic regression
lvalue = ((-1 / N) * np.sum(Y * np.log(prob))) + lambd*(0.5)*np.sum(np.dot(W,W.T))
# return the loss value
return lvalue
def gradient(W,X,Y,lambd):
"""
implements gradient descent
"""
# get the probability from the softmax function
prob = softmax(np.dot(X,W))
N = len(Y)
# compute gradient of the loss function
galue = ((-1 / N) * np.dot(X.T,(Y - prob))) + lambd*W
return galue
def predict(prob):
"""
predict the colors
"""
# get indices of max probabilities in the columns
preds = np.argmax(prob,axis=1)
# get the color predictions based on the indices obtained above
predcolors = [colors[index] for index in preds]
# and return the predictions as an array
return np.asarray(predcolors)
def accuracy(predicted,actual):
"""
computes the accuracy of the prediction
"""
# get the average of all values that are same as the actual value
accuracy = (np.sum(np.equal(predicted,actual).all(axis=1))/len(actual))*100
# and return
return accuracy
def minibatch(X,Y,batchSize):
"""
returns mini batches
"""
# choose a random data point for Y
initialpoint = np.random.randint(0, Y.shape[0] - batchSize - 1)
# get all X points from the initial point until the length of the batch size
Xbatch = X[initialpoint:(initialpoint + batchSize)]
# get all Y points from the initial point until the length of the batch size
Ybatch = Y[initialpoint:(initialpoint + batchSize)]
return Xbatch,Ybatch
def getbestparameters(dataDictionary):
"""
gets the best parameters (weights, test accuracy and hyperparameters) for the model
"""
# set test accuracy to 0 initially
test_accuracy = 0
# initialize an array of zeros for the weights initially
W = np.zeros((9,5))
# set hyperparameters to 0 initially
hyperparameters = (0,0,0)
for key in dataDictionary.keys():
# if the updated test accuracy is more than the previous test accuracy obtained
if dataDictionary.get(key).get("test_accuracy") > test_accuracy:
# update weights
W = dataDictionary.get(key).get("W")
# update hyperparameters
hyperparameters = dataDictionary.get(key).get("hyper_parameters")
# update test accuracy
test_accuracy = dataDictionary.get(key).get("test_accuracy")
return(W,test_accuracy,hyperparameters)
# +
# dictionary for the data
data = {}
# list of batch sizes for the data
batchsizes = [1, 10 , 100, 1000]
# list of values for alpha (learning rate)
alphas = [10, 1, 0.1]
# values for lambda (regularization constant)
lambds = [0, 5, 10]
times = 0
# run for 10 iterations
for iteration in range(0,10):
# for all lambda values
for lambd in lambds:
# for all batch sizes
for batchSize in batchsizes:
# for all alpha values
for ogalpha in alphas:
# randomly choose an index from the training input data
shuffledindex = np.random.choice(range(0,len(trainingDataIn)),len(trainingDataIn),replace=False)
# take 80% of these samples as the training data
trainingindices = shuffledindex[:int(.80*len(trainingDataIn))]
# take remaining samples as the validation data
validationindices = shuffledindex[int(.80*len(trainingDataIn)):]
# normalize the training data
trainingDataInNorm = (trainingDataIn - np.mean(trainingDataIn,axis=0))/np.std(trainingDataIn,axis=0)
# add a column of ones to the normalized training data
trainingDataInNorm = np.column_stack((np.ones((len(trainingDataInNorm),1),dtype=int),trainingDataInNorm))
# get the normalized validation data using the indices defined above
validationDataXnorm = trainingDataInNorm[validationindices]
# get the output validation data from the expected training data output
validationDataY = trainingDataOut[validationindices]
# get the normalized training input data from the above
trainingDataXnorm = trainingDataInNorm[trainingindices]
# get the output training data
trainingDataY = trainingDataOut[trainingindices]
# reshape the data using a normal Gaussian distribution
W = np.reshape(np.random.normal(0, 1/50, 50),(10,5))
# initiaize previous validation loss to 0
previousValLoss = 0
# maximum number of iterations is 100
maxiter = 100
i = 1
# keep a copy of the current value of alpha
alpha = cp.copy(ogalpha)
# run for 100 iterations
while (i < maxiter):
# get the mini batch from the normalized data
minibatchX,minibatchY = minibatch(trainingDataXnorm,trainingDataY,batchSize)
# run gradient descent on this mini batch
gred = gradient(W,minibatchX,minibatchY,lambd)
alpha = alpha/np.sqrt(i+1)
# update the weights
W = W - (alpha*gred)
# get the validation loss
valLoss = loss(W,validationDataXnorm,validationDataY,lambd)
# get the accuracy of the prediction
valaccuracy = accuracy(predict(softmax(np.dot(validationDataXnorm,W))),trainout[validationindices])
# checks if difference between the previous validation loss and current validation loss is not significant
# or if the validation loss is NaN
if (np.abs(previousValLoss - valLoss) < 0.00001*previousValLoss) or (np.isnan(valLoss)):
# if so, break out of the loop
break
# otherwise, update the validation loss
previousValLoss = valLoss
# inrease i for the next iteration
i = i+1
# print both validation loss and validation accuracy
print("validation loss :: " + str(valLoss) + " ; Validation accuracy :: " + str(valaccuracy))
# normalize the test data
testDataX1 = (testDataX - np.mean(testDataX,axis=0))/np.std(testDataX,axis=0)
# append a column of 1s to the test data
testDataX1 = np.column_stack((np.ones((len(testDataX1),1),dtype=int),testDataX1))
# get the test accuracy
testaccuracy = accuracy(predict(softmax(np.dot(testDataX1,W))),testout)
# and print it
print("Test accuracy :: " + str(testaccuracy))
times = times + 1
print((ogalpha,batchSize,lambd))
# update the data dictionary for the next batch size
data.update({times:{"W" : W, "test_accuracy" : testaccuracy, "hyper_parameters" : (ogalpha,batchSize,lambd)}})
# -
# getting the test accuracy from the model
W,test_accuracy,parameters = getbestparameters(data)
test_accuracy
# get the prediction
prediction = predict(softmax(np.dot(testDataX1,W)))
prediction.shape
# get the predicted image
predictionImage = prediction.reshape((299,223,3))
# display the predicted image
plt.imshow(predictionImage)
# get expected output test image
expectedtestingOutputImage = skio.imread(fname="expectedtestingOutputImage.jpg")
# display it
plt.imshow(expectedtestingOutputImage)
| 12,275 |
/.ipynb_checkpoints/Data by Asset Class-checkpoint.ipynb
|
1db7246577f2fe497b60469987cd40f6339c3cfc
|
[] |
no_license
|
snhuber/iblocal
|
https://github.com/snhuber/iblocal
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 158,021 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/resh1604/SIT742/blob/master/Part2half.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="Vn6NE6IBT02O" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 33} outputId="039fc790-ee7b-408b-e6c2-3a0a47076ad0"
# !pip install wget
# + id="urEVJeYIT3w6" colab_type="code" colab={}
import wget
link_to_data = 'https://github.com/tulip-lab/sit742/raw/master/Assessment/2019/data/wine.json'
DataSet = wget.download(link_to_data)
link_to_data = 'https://github.com/tulip-lab/sit742/raw/master/Assessment/2019/data/stopwords.txt'
DataSet = wget.download(link_to_data)
# + id="KVj3VLr5T9vn" colab_type="code" colab={}
import json
import pandas as pd
import matplotlib.pyplot as plt
# + id="0UsZmmxzT_x6" colab_type="code" colab={}
import re
import nltk
from nltk.tokenize import RegexpTokenizer
from nltk.probability import *
from itertools import chain
#from tqdm import tqdm
import codecs
# + id="14tTLtKCT5vC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 100} outputId="0a72aab4-ee54-4322-d90f-b445582e5ef7"
nltk.download('punkt')
nltk.download('reuters')
# + id="7XuGu7UHUH-Q" colab_type="code" colab={}
file = 'wine.json'
# + id="xM9Q2ZmkUKnz" colab_type="code" colab={}
df = pd.read_json(file, orient='columns')
#df.head(10)
#print(df)
#print(df.to_json(orient='index', lines='True'))
df
# + id="9o6IBIsIUpj8" colab_type="code" colab={}
data1 = df[['description']]
data1
# + id="cW3X3Z6-Usgf" colab_type="code" colab={}
data2 =data1.loc[:,].tail(100)
data2
# + id="Ucc2d4MeUuxX" colab_type="code" colab={}
data2.iloc[0,0]
# + id="xQaRkH0eU6Ws" colab_type="code" colab={}
data3 = []
for index, row in data2.iterrows():
data3.append(row['description'].lower())
#print(ans)
with open('your_file1.txt', 'w') as f:
for item in data3:
f.write("%s\n" % item)
#print(row['description'])
# + id="P6SIpq5EXkbY" colab_type="code" colab={}
data4 = ''.join(map(str, data3))
data4
# + id="bYuX5Px0afBZ" colab_type="code" colab={}
data5 = re.sub(r'[^\w]', ' ', data4)
data5
# + id="Ozb5iFiYX2aF" colab_type="code" colab={}
with open('stopwords.txt') as f:
stop_words = f.read().splitlines()
stop_words = set(stop_words)
stop_words
# + id="9zmTc3orX5gN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 70} outputId="fcc5bd8e-9a1c-4772-8641-e4eea5be67e9"
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize
word_tokens = word_tokenize(data5)
data6 = [w for w in word_tokens if not w in stop_words]
data6 = []
for w in word_tokens:
if w not in stop_words:
data6.append(w)
print(word_tokens)
print(data6)
# + id="eEU_7i_zfZya" colab_type="code" colab={}
data6.sort()
# + id="aAJt3ZRsevk-" colab_type="code" colab={}
fd_1 = FreqDist(data6)
fd_2 = fd_1.most_common(50)
# + id="rH-rfQBelLP1" colab_type="code" colab={}
with open("top.txt", "w") as output:
output.write(str(fd_2))
# + id="UMsR2_7RFlAP" colab_type="code" colab={}
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(min_df=1)
X = vectorizer.fit_transform(data6)
idf = vectorizer._tfidf.idf_
data7 = dict(zip(vectorizer.get_feature_names(), idf))
data7
grid(True)
plt.title('GAMMA = 10')
fig.colorbar(cax, ticks=[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, .75,.8,.85,.90,.95,1])
plt.show()
| 3,780 |
/atv03/3.1 entrega/03_entrega.ipynb
|
26e8b7d23a9919d3340345a289048fd32baebe73
|
[] |
no_license
|
adrielnardi/mestrado-renear
|
https://github.com/adrielnardi/mestrado-renear
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 42,477 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="1-aLH0rksl7A"
# ### Mestrado Profissional em Computação Aplicada
#
# #### **Disciplina**: Redes Neurais Artificiais
# #### **Professor**: Dr. Francisco de Assis Boldt
# #### **Aluno**: Adriel Monti De Nardi
#
# ------
#
#
# + [markdown] id="OZOvm7fzhOH_"
# ### Trabalho 03: Plotar a região de decisão de uma ELM
#
# Para concluir a atividade proposta devemos plotar a região de decisão da ELM mostrada no vídeo.
#
#
# + [markdown] id="TFBi7oQRiagi"
# #Função gera dataset, plota dataset e hiperplano
# + colab={"base_uri": "https://localhost:8080/", "height": 298} id="-z7A1LpojWfm" outputId="ef926e73-2c11-44a4-ca49-e45d9b4d7334"
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.preprocessing import label_binarize
def geradataset(tamanho=20, centros=[[0,0],[1,0],[1,1],[0,1]]):
X, y = make_blobs(n_samples=tamanho, centers=centros, cluster_std=0.2)
y = np.array(y%2, dtype=int)
return X, y
def plotadataset(X, y):
plt.xlabel('X1')
plt.ylabel('X2')
for k in set(y):
plt.plot(X[:,0][y==k],X[:,1][y==k], "o", alpha=0.3)
def plotahiperplano(vetor, bias=0, xmin=0, xmax=1):
xs = np.linspace(xmin, xmax, num=2)
ys = (-vetor[0] / vetor[1]) * xs - bias / vetor[1]
plt.plot(xs,ys)
X, y = geradataset()
plotadataset(X, y)
plt.show()
y
# + [markdown] id="jgaFAqyAjg76"
# #Funções de Custo
#
# + id="6qhwsxToji-P"
class CustoPerceptron():
@staticmethod
def erro(y, ypred):
return y - ypred
@staticmethod
def custo(y, ypred):
return np.sum(CustoPerceptron.erro(y, ypred)**2)
@staticmethod
def gradiente(y, ypred, X):
return np.matmul(X.T, CustoPerceptron.erro(y, ypred))
class Adaline():
def __init__(self):
self.preactivated = True
@staticmethod
def erro(y, ypred):
return y - ypred
@staticmethod
def custo(y, ypred):
return np.sum((1 - Adaline.erro(y, ypred))**2)
@staticmethod
def gradiente(y, ypred, X):
return np.matmul(X.T, Adaline.erro(y, ypred))
# + [markdown] id="R0Ht-X56jn8Y"
# #Algoritmos
# + id="FpihARbxjpd1"
class DescidaGradiente():
def __init__(self, custo=Adaline(), maxiter=1000, alpha=0.005):
self.custo = custo
self.maxiter = maxiter
self.alpha = alpha
def getW(self, X, y, activation=lambda a: a):
w = np.random.uniform(-1, -1, size=(X.shape[1], y.shape[1]))
for _ in range(self.maxiter):
ypred = activation(np.matmul(X, w))
custo = self.custo.custo(y, ypred)
if custo == 0:
break
w = w + self.alpha * self.custo.gradiente(y, ypred, X)
return w
class PseudoInversa():
def __init__(self):
pass
def getW(self, X, y):
pinv = np.linalg.pinv(X)
w = np.matmul(pinv, y)
return w
# + [markdown] id="bnI4_plKjvNi"
# #Extreme Learning Machine
# + id="82VNzSFQjzJ8"
from sklearn.base import BaseEstimator, ClassifierMixin
from scipy.special import expit
def tanh(a):
return expit(a) * 2 - 1
class ExtremeLearningMachine(BaseEstimator, ClassifierMixin):
def __init__(self, algoritmo=PseudoInversa()):
self.wih = None
self.w = None
self.threshold = 0
self.activation = tanh
self.algoritmo = algoritmo
@staticmethod
def includebias(X):
bias = np.ones((X.shape[0],1))
Xb = np.concatenate((bias,X), axis=1)
return Xb
def fit(self, X, y):
self.wih = np.random.uniform(-1, 1, size=(X.shape[1],X.shape[0]//3))
Xh = np.matmul(X, self.wih)
Xho = self.activation(Xh)
X = ExtremeLearningMachine.includebias(Xho)
self.labels = list(set(y))
y = label_binarize(y, classes=self.labels)*2-1
if len(self.labels) == 2 :
y = y[:,0:1]
# treinamento
if hasattr(self.algoritmo, 'custo') and not (hasattr(self.algoritmo.custo, 'preactivated') and self.algoritmo.custo.preactivated):
self.w = self.algoritmo.getW(X, y, self.activation)
else:
self.w = self.algoritmo.getW(X, y)
def predict(self, X):
Xh = np.matmul(X, self.wih)
Xho = self.activation(Xh)
Xb = ExtremeLearningMachine.includebias(Xho)
a = np.matmul(Xb, self.w)
if self.w.shape[1] > 1:
idx = np.argmax(a, axis=1)
else:
idx = np.array(self.activation(a) > self.threshold, dtype=int)[:,0]
ypred = np.array([self.labels[i] for i in idx])
return ypred
# + colab={"base_uri": "https://localhost:8080/"} id="wy9i2-e5kXWy" outputId="fceeec36-ca83-4dc2-b0d2-bbc0dfcb79a2"
elm = ExtremeLearningMachine()
elm.fit(X, y)
ypred = elm.predict(X)
print(sum(y == ypred)/len(y))
# + [markdown] id="qQ9Tv9M9kjT6"
# #Plotting Decision Regions
#
# Aqui será plotado a região de decisão da ELM
# + colab={"base_uri": "https://localhost:8080/", "height": 587} id="amx1C7cknsey" outputId="19f73d83-d9c8-4611-81ec-94cafa2e6c1f"
from mlxtend.plotting import plot_decision_regions
# !pip install mlxtend
plot_decision_regions(X, ypred, clf=elm, legend=len(set(y)))
plt.xlabel('X1')
plt.ylabel('X2')
plt.title("Plotando Decisão de Região")
plt.show()
# + [markdown] id="ngeLd99OicIQ"
# #Referência:
#
# - [Como faço para instalar pacotes Python no Colab do Google?](https://qastack.com.br/programming/51342408/how-do-i-install-python-packages-in-googles-colab) (data de acesso: 01.09.2021)
# - [Installing mlxtend](http://rasbt.github.io/mlxtend/installation/) (data de acesso: 01.09.2021)
# - [Plotting Decision Regions](http://rasbt.github.io/mlxtend/user_guide/plotting/plot_decision_regions/)
# (data de acesso: 01.09.2021)
#
#
| 6,011 |
/Mini 3/.ipynb_checkpoints/Untitled-checkpoint.ipynb
|
6a40ad54e409bb716365cdccc7f8ea0e1fdb68e9
|
[] |
no_license
|
jannesgg/statistical-learning-big-data
|
https://github.com/jannesgg/statistical-learning-big-data
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 492,933 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Viewing Example Augmentations
# %reload_ext autoreload
# %autoreload 2
# +
import sys
sys.path.append("..")
import numpy as np
from src.data.prepare_data import *
from src.models.model import *
from src.visualization.exploration import grid_augmentations_show
from PIL import Image
from torchvision.transforms import ToPILImage
# -
SEED = 1
np.random.seed(SEED)
train = pd.read_csv("../data/internal/train.csv")
test = pd.read_csv("../data/internal/test.csv")
sub = pd.read_csv("../data/internal/sample_submission.csv")
transform = ImageTransform(128, True)
dataset_train = MelanomaDataset("../data/internal/train", train, transform=transform, phase='visualize_augmentations')
sample_images = []
for i, idx in enumerate(np.random.randint(0, len(train), size=20)):
print(i + 1)
sample_images.append(dataset_train[idx]['inputs'])
fig = grid_augmentations_show(sample_images, 16, 16, 4, 5)
fig.savefig('../images/augmentation_example.png')
random((5, 3))
random_array_2
random_array_2.shape
random_array_3 = np.random.rand(5, 3)
random_array_3
# Pseudo-random numbers
np.random.seed(seed = 99999)
random_array_4 = np.random.randint(10, size = (5, 3))
random_array_4
np.random.seed(7)
random_array_5 = np.random.random((5, 3))
random_array_5
random_array_5 = np.random.random((5, 3))
random_array_5
random_array_4.shape
# ## 3. Viewing arrays and matrices
np.unique(random_array_4)
a1
a2
a3
a1[0]
a2[0]
a3[0]
a2
a2[1]
a3[:2, :2, :2]
a4 = np.random.randint(10, size = (2, 3, 4, 5))
a4
a4.shape, a4.ndim
# Get the first 4 numbers of the inner most arrays
a4[:, :, :, :1]
# ## 4. Manipulating & comparing arrays
# ### Arithmetic
a1
ones = np.ones(3)
ones
a1 + ones
a1 - ones
a1 * ones
a2
a1 * a2
a3
# How can you reshape a2 to be compatible with a3?
# Search: "How to reshape numpy array"
a1 / ones
a2 / a1
# Floor division removes the decimales (rounds down)
a2 // a1
a2 ** 2
np.square(a2)
np.add(a1, ones)
a1 % 2
a1 / 2
a2 % 2
np.exp(a1)
np.log(a1)
# ## Aggregation
#
# Aggregation = performing the same operation on a number of things
listy_list = [1, 2, 3]
type(listy_list)
sum(listy_list)
sum(a1)
np.sum(a1)
# Use Python's methods (`sum()`) on Python datatypes and use Numpy's methods on Numpy arrays (`np.sum()`).
#Creative a massive Numpy array
massive_array = np.random.random(100000)
massive_array.size
massive_array[:10]
# %timeit sum(massive_array) # Python's sum()
# %timeit np.sum(massive_array) # Numpy's np.sum()
a2
np.mean(a2)
np.max(a2)
np.min(a2)
# Standart deviation = a measure o how spread out a group of numbers is from the mean
np.std(a2)
# Variance = measure of the average degree to which each number is different to the mean
# Higher variance = wider range of numbers
# Lower variance = lower range of numbers
np.var(a2)
# Standard deviation = squareroot of variance
np.sqrt(np.var(a2))
# Demo of std and var
high_var_array = np.array([1, 100, 200, 300, 4000, 5000])
low_var_array = np.array([2, 4, 6, 8, 10])
np.var(high_var_array), np.var(low_var_array)
np.std(high_var_array), np.std(low_var_array)
np.mean(high_var_array), np.mean(low_var_array)
# %matplotlib inline
import matplotlib.pyplot as plt
plt.hist(high_var_array)
plt.show()
plt.hist(low_var_array)
plt.show()
# ### Reshaping & transposing
a2
a2.shape
a3
a3.shape
a2 * a3
a2.reshape(2, 3, 1)
a2_reshape = a2.reshape(2, 3, 1)
a2_reshape
a2_reshape * a3
a2
# Transpose
a2.shape
# Transpose = switches the axis'
a2.T
a2.T.shape
a3
a3.shape
a3.T
a3.T.shape
# ## Dot product
# +
np.random.seed(0)
mat1 = np.random.randint(10, size = (5, 3))
mat2 = np.random.randint(10, size = (5, 3))
mat1
# -
mat2
mat1.shape, mat2.shape
# Element-wise multiplication (Hadamard product)
mat1 * mat2
# Dot product
np.dot(mat1, mat2)
# Transpose mat1
mat1.T
mat1.shape, mat2.T.shape
mat3 = np.dot(mat1, mat2.T)
mat3
mat3.shape
| 4,169 |
/notebooks/utkrisht44sharma/a-study-of-personality-using-nlp-techniques.ipynb
|
dbf9677a0f13ae9344becfe424e3bdc083694a29
|
[] |
no_license
|
Sayem-Mohammad-Imtiaz/kaggle-notebooks
|
https://github.com/Sayem-Mohammad-Imtiaz/kaggle-notebooks
| 5 | 6 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 6,976 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] _uuid="b6ae14c08e1660d5be189ead001c6b2c7d7162e4"
# **A study of personality using NLP techniques**
#
# I am trying to find out whether personality is a factor determining how a person writes. I am using the Word2Vec model by [Mikolov et. al. ](https://github.com/svn2github/word2vec) to calculate word similarites by getting the cosine similarites ( dot product ) of the word vectors trained by the Word2Vec model. The [four temperament model by David Kiersey](https://keirsey.com/temperament-overview/) takes temperamance as a factor and divides people into 4 groups (Artisan , Guardian , Idealist, Rational) . In the given article he draws parallel between Jungian types and his temperaments as follows (Artisan -SP , Guardian - SJ , Idealist - NF , Rational -NT). I have performed an one way anova with four groups with the following results.
# + _uuid="6fa1b3f88439be97d977946cd2f7fb6c5936965a"
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# + _uuid="6d5eb033a91ba5a3b8f974e74cfd02bffc59717a"
import pandas as pd
text=pd.read_csv("../input/mbti_1.csv")
# + _uuid="ee0d26642c00dfa6546bddf4eabdb8e9a190b2b3"
posts=text.values.tolist()
# + _uuid="c0b8ab63ff7222eee3d31d177410a92005a83db6"
mbti_list=['ENFJ','ENFP','ENTJ','ENTP','ESFJ','ESFP','ESTJ','ESTP','INFJ','INFP','INTJ','INTP','ISFJ','ISFP','ISFP','ISTP']
values = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
index = np.arange(len(mbti_list))
# + _uuid="01c94fead6ea9b6ac446ea987bcaf61b2dacb6a4"
for post in posts:
for i in range(0,len(mbti_list)):
if post[0] == mbti_list[i]:
values[i]=values[i]+1
# + _uuid="a1d4eb272fafeeeda181bc8cb012ed656cb65fda"
plt.bar(index,values)
plt.xlabel('Personality Type',fontsize=3)
plt.ylabel('No of persons',fontsize=5)
plt.xticks(index,mbti_list,fontsize=8,rotation=35)
plt.title('Distribution of types among Dataset(1 person=50 tweets)')
plt.show()
# + [markdown] _uuid="5f29b1169a17366574fc19675078e4506128855d"
# This plot shows the number of people present for each type present in the dataset.
# + [markdown] _uuid="db0e4ea16e37a7532f3805ebf26179b6f037b6a7"
# This function performs the various pre-processing tasks and trains the Word2Vec model and then saves it in a binary file.
# + _uuid="20b49a3ccacaa71945b329da86aedb22d1160fbf"
from nltk.tokenize import word_tokenize
from gensim.models import Word2Vec
import re
def train_w2v_using_key(temp):# I'm too lazy to learn regex in python
perlist=list()
if temp=="SJ":
for i in posts:
if i[0]=='ISFJ' or i[0]=='ISTJ' or i[0]=='ESFJ' or i[0]=='ESTJ':
perlist.append(i[1])
if temp == 'SP':
for i in posts:
if i[0]=='ISFP' or i[0]=='ISTP' or i[0]=='ESFP' or i[0]=='ESTP':
perlist.append(i[1])
else:
for i in posts:
if temp in i[0]:
perlist.append(i[1])
for i in range(0,len(perlist)): # using some code https://www.kaggle.com/prnvk05/rnn-mbti-predictor for filtering out links and numbers from the text
tempstr = ''.join(str(e) for e in perlist[i])
post=tempstr.lower()
post=post.replace('|||',"")
post = re.sub(r'''(?i)\b((?:https?://|www\d{0,3}[.]|[a-z0-9.\-]+[.][a-z]{2,4}/)(?:[^\s()<>]+|\(([^\s()<>]+|(\([^\s()<>]+\)))*\))+(?:\(([^\s()<>]+|(\([^\s()<>]+\)))*\)|[^\s`!()\[\]{};:'".,<>?«»“”‘’]))''', '', post, flags=re.MULTILINE)
puncs1=['@','#','$','%','^','&','*','(',')','-','_','+','=','{','}','[',']','|','\\','"',"'",';',':','<','>','/']
for punc in puncs1:
post=post.replace(punc,'')
puncs2=[',','.','?','!','\n']
for punc in puncs2:
post=post.replace(punc,' ')
post=re.sub( '\s+', ' ', post ).strip()
perlist[i]=post
word_tokens=[]
for i in range(0,len(perlist)):
word_tokens.append(word_tokenize(perlist[i]))
model = Word2Vec(word_tokens, min_count=1)
model.save(temp+".bin")
# + _uuid="f3c621cad5ff87da5496d9a64fa5f65365896516"
train_w2v_using_key("NT")
# + _uuid="aae641fa80754da63c473b847e2c6db9b7597f96"
train_w2v_using_key("NF")
# + _uuid="fcccd8e77a36791f8d6306b9ed89e528d588580e"
train_w2v_using_key("SP")
# + _uuid="fcef7b7a052d69aa1063d5824f37b732bbe2f9e5"
train_w2v_using_key("SJ")
# + [markdown] _uuid="ca162b05e3a4ce2e5afd0882f1cadedd742a7def"
# **Similarities**
#
# model.wv.similarity('word1','word2') returns the cosine similarity of the vectors of the words word1 and word2.
# The higher the cosine similarity between the more similar the words.
# + _uuid="a49c01a9abfe8b6a55eb5f33147f7f26bf713508"
model=Word2Vec.load("NT.bin")
model.wv.similarity("defend","justify")
# + [markdown] _uuid="2b64516eda5f5e7c98122b686dc8ea403bb5f863"
# The following shows that **temperamannce is a factor** that determines writing as the F-value obtained is larger than the critical value with the p-value being much smaller than the significance level for the hypothesis test.
# 
#
| 5,294 |
/tutorials/3_03_Example_qixiang_topop_output.ipynb
|
041948f2a6dd784f03bb8323bca991c2795e44eb
|
[
"MIT"
] |
permissive
|
NengLu/UWG_QiXiang
|
https://github.com/NengLu/UWG_QiXiang
| 3 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 678,807 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: "py37\u3000"
# language: python
# name: py37
# ---
# # A work example for qixiang.TopoGrid, qixiang.Flow, qixiang.Stream
#
# These codes (*topogrid.py, flow.py, stream.py*) are written by reorganizing the codes (*grid.py, flow.py, network.py*) from repo [geolovic/topopy](https://github.com/geolovic/topopy) by [José Vicente Pérez Peña](https://scholar.google.es/citations?user=by5rTEUAAAAJ&hl=es) from Universidad de Granada, Granada, Spain, and adding some functions which function like *klargestconncomps.m* and *trunk.m* from TopoToolbox matlab codes by Wolfgang Schwanghart.
#
# Cite:
#
# Schwanghart, W., Scherler, D., 2014. Short Communication: TopoToolbox 2 - MATLAB-based software for topographic analysis and modeling in Earth surface sciences. Earth Surf. Dyn. 2, 1–7. https://doi.org/10.5194/esurf-2-1-2014
#
# +
import sys
sys.path.append("..")
from qixiang import TopoGrid
from qixiang import Flow
from qixiang import Stream
# +
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
# %matplotlib inline
# -
# # 1. TopoGrid
#
# Class for holding and manipulating gridded data.
#
# This class is reorganized the Class PRaster(), Grid(), DEM() in grid.py from repo [geolovic/topopy](https://github.com/geolovic/topopy)
input_file = "../data/dem/TRR_Earth2014.TBI2014.1min.order10800.tif"
topo = TopoGrid(input_file)
topo.plot()
# # 2. Flow
#
# Class that define a network object (topologically sorted giver-receiver cells).
#
# This class is reorganized the Class Flow() in flow.py from repo [geolovic/topopy](https://github.com/geolovic/topopy)
#
# The algoritm to created the topologically sorted network has been adapted to Python from FLOWobj.m by Wolfgang Schwanghart (version of 17. August, 2017) included in TopoToolbox matlab codes.
# ### How the pixels are sorted in flow.py from repo [geolovic/topopy](https://github.com/geolovic/topopy)
#
# Sort the pixels and get _ix (giver) and _ixc (receiver)
#
# ```python
# class Flow(PRaster):
#
# def __init__(self, dem="", auxtopo=False, filled=False, verbose=False, verb_func=print):
#
# self._ix, self._ixc = sort_pixels(dem, auxtopo=auxtopo, filled=filled, verbose=verbose, verb_func=verb_func)
# ```
#
# 1. Fill the sinks
#
# Algoritm: skimage.morphology.reconstruction
#
#
# 2. Get the flats and sills
#
# Flats are defined as cells without downward neighboring cells. Sills are cells where flat regions spill over into lower terrain.
#
# Algoritm: identifyflats.m in TopoToolbox (ndimage.morphology.grey_erosion, ndimage.morphology.grey_dilation)
#
#
# 3. Get presills
#
# presills are pixels immediately upstream to sill pixels.
#
# ```python
# presills_pos = get_presills(dem_arr, flats, sills)
# ```
#
# Algoritm: from TopoToolbox
#
#
# 4. Get the auxiliar topography for the flats areas
#
# ```python
# topodiff = get_aux_topography(topodiff.astype(np.float32), flats.astype(np.int8))
# ```
#
# 5. Get the weights inside the flat areas
#
# Calculate weights in the flats areas by doing a cost-distance analysis.It uses presill positions as seed locations, and an auxiliar topography as friction surface.
#
# ```python
# weights = get_weights(flats, topodiff, presills_pos)
# ```
#
# Algoritm: from TopoToolbox (skimage.graph.MCP_Geometric)
#
#
# 6. Sort pixels (givers)
#
# ```python
# ix = sort_dem(dem_arr, weights)
# ```
#
# Algoritm: from TopoToolbox
#
#
# 7. Get receivers
#
# ```python
# ixc = get_receivers(ix, dem_arr, cellsize)
# ```
# Algoritm: from TopoToolbox
flow = Flow(topo, auxtopo=False, filled=False, verbose=True, verb_func=print)
#flow = Flow(topo, auxtopo=False, filled=True, verbose=True, verb_func=print)
# +
flowcc = flow.get_flow_accumulation()
extent = flowcc.get_extent()
res_area = 2
xticks_area = np.arange(extent[0],extent[1]+res_area/2,res_area)
yticks_area = np.arange(extent[2],extent[3]+res_area,res_area)
# +
#flow_arr = flowcc.read_array()
if flowcc._nodata:
mask = flowcc._array == flowcc._nodata
flow_arr = flowcc._array.copy()
flow_arr[mask] = flow_arr.min()
#flow_arr = np.ma.array(flowcc._array, mask = mask)
fig = plt.figure(figsize=(8, 6))
ax = plt.subplot(111)
ax.set(xlabel='Longitude', ylabel='Latitude', yticks=yticks_area, xticks=xticks_area)
ax.set_title('The flow path of the rivers in the TRR-topopy')
#im = ax.imshow(flow_arr,extent=extent,cmap=cm.Blues,vmin=0, vmax=2000)
im = ax.imshow(np.log10(flow_arr),extent=extent,cmap=cm.Blues,vmin=0, vmax=5)
cbar= plt.colorbar(im,fraction=0.046, pad=0.04)
cbar.set_label('Discharge (log10)')
plt.savefig(('TRR_Flowpath_nofill.png'),dpi=300)
plt.show()
# -
# # 3. Stream
#
# Class that define a stream network object, defined by applying a threshold to a flow accumulation raster derived from the *Flow* (Flow.get_flow_accumulation()).
#
# This class is based on the Class Network() in network.py from repo [geolovic/topopy](https://github.com/geolovic/topopy), and added some new funtions which can function as *klargestconncomps.m* and *trunk.m* from TopoToolbox matlab codes by Wolfgang Schwanghart.
#
# +
# min_area = 0.0005
# threshold = int(flow._ncells * min_area)
threshold = 500
stream = Stream(dem=topo, flow=flow, threshold=threshold, verbose=False, thetaref=0.45, npoints=5)
#streams = stream.get_streams(asgrid=False)
#streams_seg = stream.get_stream_segments(asgrid=False)
#streams_or = stream.get_stream_order(kind="shreeve", asgrid=False)
str_or0 = stream.get_stream_order(kind="strahler", asgrid=False)
# -
print(threshold)
print(flow._ix.shape)
print(stream._ix.shape)
# ## Test get_klargestconncomps
ccs_arr,ccs_id = stream.get_klargestconncomps(k=5,asgrid=False)
#ccs_arr = ccs._array.copy()
#extent = stream.get_extent()
ccs_id
# +
data_img = ccs_arr
fig = plt.figure(figsize=(8, 6))
ax = plt.subplot(111)
ax.set(xlabel='Longitude', ylabel='Latitude', yticks=yticks_area, xticks=xticks_area)
ax.set_title('The biggest basin of the TRR')
ax.imshow(data_img,extent=extent,cmap=cm.tab20b)
# -
# ## Test get_trunk
ccs_arr,ccs_id = stream.get_klargestconncomps(k=5,asgrid=False)
ccs_id
trunk_arr2 = stream.get_trunk(ccs_arr,ccs_id)
stream.get_trunk_output(trunk_arr2,path='../data/data_rivers/qixiang/')
# +
data_img = trunk_arr2
fig = plt.figure(figsize=(8, 6))
ax = plt.subplot(111)
ax.set(xlabel='Longitude', ylabel='Latitude', yticks=yticks_area, xticks=xticks_area)
ax.set_title('The Basins of the TRR')
ax.imshow(data_img,extent=extent,cmap=cm.tab20b)
# +
import cartopy
import cartopy.crs as ccrs
import cartopy.feature as cfeature
# cartopy parameters
rivers = cfeature.NaturalEarthFeature('physical', 'rivers_lake_centerlines', '50m',
edgecolor='Blue', facecolor="none")
coastline = cfeature.NaturalEarthFeature('physical', 'coastline', '50m',
edgecolor=(0.0,0.0,0.0),facecolor="none")
lakes = cfeature.NaturalEarthFeature('physical', 'lakes', '50m',
edgecolor="blue", facecolor="blue")
prj_base = ccrs.PlateCarree()
# w = ccs_arr
# flow_arr2 = flow_arr.copy()
# flow_arr2[np.where(w==0)]=0
# data_img = np.flipud(flow_arr2)
w = trunk_arr2
flow_arr2 = flow_arr.copy()
flow_arr2[np.where(w==0)]=0
data_img2 = np.flipud(flow_arr2)
fig = plt.figure(figsize=(8, 6))
ax = plt.subplot(111, projection=prj_base)
ax.set_extent(extent)
ax.set(xlabel='Longitude', ylabel='Latitude', yticks=yticks_area, xticks=xticks_area)
ax.set_title('The flow path of the rivers in the TRR')
#ax.imshow(data_img,extent=extent,cmap=cm.Blues,vmin=0, vmax=2000,transform=prj_base)
ax.imshow(data_img2,extent=extent,cmap=cm.Blues,vmin=0, vmax=2000,transform=prj_base,alpha=0.5)
ax.add_feature(coastline, linewidth=1.5, edgecolor="Black", zorder=5)
ax.add_feature(rivers, linewidth=0.5, edgecolor="r", zorder=6)
ax.add_feature(lakes, linewidth=0, edgecolor="Blue", facecolor="#4477FF", zorder=7, alpha=0.5)
plt.show()
#plt.savefig(('TRR_Flowpath.png'),dpi=300)
# -
fig = plt.figure(figsize=(8, 6))
ax = plt.subplot(111)
ax = plt.axes(projection=prj_base)
ax.set(xlabel='Longitude', ylabel='Latitude', yticks=yticks_area, xticks=xticks_area)
ax.set_title('The flow path of the rivers in the TRR')
labels = np.arange(1,len(ccs_id)+1)
colors =['b','y','c','r','g']
for i in range(0,len(labels)):
fname_load = '../data/data_rivers/qixiang/river'+str(labels[i])+'.txt'
river = np.loadtxt(fname_load)
ax.scatter(river[:,0],river[:,1],label=labels[i],color=colors[i],s =5)
plt.legend(loc = 'lower right',prop = {'size':8})
ax.add_feature(coastline, linewidth=1.5, edgecolor="Black", zorder=5)
ax.add_feature(rivers, linewidth=1.0, edgecolor="r", zorder=6)
ax.add_feature(lakes, linewidth=0, edgecolor="Blue", facecolor="#4477FF", zorder=7, alpha=0.5)
| 9,111 |
/DSE210x/HW_9_Weather Data.ipynb
|
0d1fa3ca10663314d8f4d5f9f5d6ea5049f03d60
|
[] |
no_license
|
FayeAlangi/UCSanDiegoX
|
https://github.com/FayeAlangi/UCSanDiegoX
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 106,458 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import scipy.stats
import matplotlib.pyplot as plt
# +
# # This sets the size and properties of the plots when using matplotlib.pyplot
# plt.style.use([{"figure.figsize":(30,5),
# # "xtick.labelsize": "medium",
# # "ytick.labelsize": "medium",
# # "legend.fontsize": "large",
# # "axes.labelsize": "large",
# # "axes.titlesize": "large",
# # "axes.spines.top": False,
# # "axes.spines.right": False,
# # "ytick.major.right":False,
# # "xtick.major.top":False
# },'seaborn-poster'])
# -
#Loading data
data=pd.read_csv("temperature.csv")
data.head()
Detroit_data=data[['datetime','Detroit']].copy()
Detroit_data.head()
rows_before=Detroit_data.shape[0]
rows_before
Detroit_data=Detroit_data.dropna()
rows_after=Detroit_data.shape[0]
rows_after
plt.hist(Detroit_data['Detroit'],bins=100,density=True)
plt.show()
scipy.stats.norm.cdf(Detroit_data['Detroit'])
Detroit_data['Detroit'].describe()
hist = np.histogram(Detroit_data['Detroit'], bins=100)
#hist_dist = scipy.stats.rv_histogram.mean(hist)
hist_dist=scipy.stats.rv_histogram(hist)
hist_dist
Detroit_data['Detroit'].plot.density(bw_method=0.1)
Detroit_data['Detroit'].plot.kde()
0.5*0.7794+0.5*0.0228
(291-276)/6.5
(291-293)/6
0.5*0.9893+0.5*0.3707
0.68-0.4011
| 1,574 |
/python/modis_et/et_extract.ipynb
|
c1eb22defad5774f0640ec0bff7f35830c4c7a2a
|
[] |
no_license
|
hydrosense-uva/codes
|
https://github.com/hydrosense-uva/codes
| 0 | 2 | null | 2023-04-17T14:20:15 | 2022-09-24T00:50:04 |
Python
|
Jupyter Notebook
| false | false |
.py
| 17,868 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/neerajthandayan/Tensorflow-2.0/blob/main/CNN_CIFAR.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="-RBrKGon-DXX"
# importing Libraries
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Dense, Flatten, Dropout, Input
# + id="zeTEhrxl_Ki3"
# Fetching Dataset
data = tf.keras.datasets.cifar10
(J_train,k_train), (J_test,k_test) = data.load_data()
J_train, J_test = J_train/255, J_test/255
k_train, k_test = k_train.flatten(), k_test.flatten()
# + colab={"base_uri": "https://localhost:8080/"} id="6N8NYHPt_0hq" outputId="419cfc89-3246-491a-a38c-eed81fd76616"
# Checking Shape of Data
J_train.shape
# + colab={"base_uri": "https://localhost:8080/"} id="oWZw2AfBALmd" outputId="0d8843bd-8256-4083-88f1-b7881eeba69b"
# Finding number of classes
print(f'Number of classes: {len(set(k_train))}')
# + id="_BTnymS9AghG"
# Constructing Model
i = Input(shape=J_train[0].shape)
x = Conv2D(32, (3,3), strides=2, activation='relu')(i)
x = Conv2D(64, (3,3), strides=2, activation='relu')(x)
x = Conv2D(128, (3,3), strides=2, activation='relu')(x)
x = Flatten()(x)
x = Dropout(0.5)(x)
x = Dense(512, activation='relu')(x)
x = Dropout(0.2)(x)
x = Dense(1024, activation='relu')(x)
x = Dropout(0.2)(x)
x = Dense(10, activation='softmax')(x)
clf = Model(i,x)
# + colab={"base_uri": "https://localhost:8080/"} id="FnmgXW1gCZIL" outputId="0f736ec2-0819-4cc2-95eb-9926406ec973"
# Compiling Data
clf.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
result = clf.fit(J_train,k_train, validation_data=(J_test,k_test), epochs=15)
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="wzj9yOvqD1I4" outputId="f0f1fa65-f375-405d-ee50-39d62267e473"
# Checking Loss
import matplotlib.pyplot as plt
plt.plot(result.history['loss'], label='loss')
plt.plot(result.history['val_loss'], label='val_loss')
plt.legend()
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="Z48xh5hAFz9-" outputId="60ebde19-311f-4b20-a225-782292f47adc"
# Checking Accuracy
plt.plot(result.history['accuracy'], label='Accuracy')
plt.plot(result.history['val_accuracy'], label='val_accuracy')
plt.legend()
# + colab={"base_uri": "https://localhost:8080/", "height": 496} id="TjZsvpJuGZmO" outputId="7bae94cb-d7f0-4a48-ad88-fedc38df8762"
# Plot confusion matrix
from sklearn.metrics import confusion_matrix
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
p_test = clf.predict(J_test).argmax(axis=1)
cm = confusion_matrix(k_test, p_test)
plot_confusion_matrix(cm, list(range(10)))
# + id="PvBgBfsiGeRE"
# label mapping
labels = '''airplane
automobile
bird
cat
deer
dog
frog
horse
ship
truck'''.split()
# + colab={"base_uri": "https://localhost:8080/", "height": 281} id="QK7bs4LSGg8g" outputId="5d4587a6-b09e-4bdb-c207-b870bb14af71"
# Show some misclassified examples
# TODO: add label names
misclassified_idx = np.where(p_test != k_test)[0]
i = np.random.choice(misclassified_idx)
plt.imshow(J_test[i], cmap='gray')
plt.title("True label: %s Predicted: %s" % (labels[k_test[i]], labels[p_test[i]]));
random variables with mean of 0, stddev of 0.01
# b is initialized to 0
# shape of w depends on the dimension of X and Y so that Y = tf.matmul(X, w)
# shape of b depends on Y
w = tf.Variable(tf.random_normal(shape=[784, 10], stddev=0.01), name='weights')
b = tf.Variable(tf.zeros([1, 10]), name="bias")
# Step 4: build model
# the model that returns the logits.
# this logits will be later passed through softmax layer
logits = tf.matmul(X, w) + b
# Step 5: define loss function
# use cross entropy of softmax of logits as the loss function
entropy = tf.nn.softmax_cross_entropy_with_logits(logits=logits,labels=Y, name='loss')
loss = tf.reduce_mean(entropy) # computes the mean over all the examples in the batch
# Step 6: define training op
# using gradient descent with learning rate of 0.01 to minimize loss
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
with tf.Session() as sess:
# to visualize using TensorBoard
writer = tf.summary.FileWriter('./logistic_reg', sess.graph)
start_time = time.time()
sess.run(tf.global_variables_initializer())
n_batches = int(mnist.train.num_examples/batch_size)
for i in range(n_epochs): # train the model n_epochs times
total_loss = 0
for _ in range(n_batches):
X_batch, Y_batch = mnist.train.next_batch(batch_size)
_, loss_batch = sess.run([optimizer, loss], feed_dict={X: X_batch, Y:Y_batch})
total_loss += loss_batch
print ('Average loss epoch {0}: {1}'.format(i, total_loss/n_batches))
print ('Total time: {0} seconds'.format(time.time() - start_time))
print('Optimization Finished!') # should be around 0.35 after 25 epochs
# test the model
n_batches = int(mnist.test.num_examples/batch_size)
total_correct_preds = 0
for i in range(n_batches):
X_batch, Y_batch = mnist.test.next_batch(batch_size)
_, loss_batch, logits_batch = sess.run([optimizer, loss, logits], feed_dict={X: X_batch, Y:Y_batch})
preds = tf.nn.softmax(logits_batch)
correct_preds = tf.equal(tf.argmax(preds, 1), tf.argmax(Y_batch, 1))
accuracy = tf.reduce_sum(tf.cast(correct_preds, tf.float32))
total_correct_preds += sess.run(accuracy)
print ('Accuracy {0}'.format(total_correct_preds/mnist.test.num_examples))
writer.close()
# -
# Answer:
# ---
# Learning Rate: 0.1
#
# Batch Size : 150
#
# Total Time: 12.00
#
# Accuracy : 0.915
ax, lat_roi_min])
dst_ds = None
print(mos_file_name)
# -
# _______________________________________________________________________________________________________________________________________________________________________
# Step 5: Seperate the individual files corresponding to each month
jan_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 1]
feb_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 2]
mar_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 3]
apr_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 4]
may_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 5]
jun_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 6]
jul_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 7]
aug_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 8]
sep_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 9]
oct_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 10]
nov_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 11]
dec_files = [name for name in os.listdir('.') if name.endswith('.tif') and 'ctd' not in name and pd.to_datetime(name[date_start:date_end],format='%Y%j').month == 12]
# _______________________________________________________________________________________________________________________________________________________________________
# Step 6: Create function to convert 8-day to monthly value
def non_empty_month():
if len(jan_files) != 0:
return jan_files
if len(feb_files) != 0:
return feb_files
if len(mar_files) != 0:
return mar_files
if len(apr_files) != 0:
return apr_files
if len(may_files) != 0:
return may_files
if len(jun_files) != 0:
return jun_files
if len(jul_files) != 0:
return jul_files
if len(aug_files) != 0:
return aug_files
if len(sep_files) != 0:
return sep_files
if len(oct_files) != 0:
return oct_files
if len(nov_files) != 0:
return nov_files
if len(dec_files) != 0:
return dec_files
# +
profile = rasterio.open(non_empty_month()[0]).profile
raster_shape = rasterio.open(non_empty_month()[0]).shape
def monthly(file_list):
data = np.empty((raster_shape[0],raster_shape[1],1))
if len(file_list) > 0:
for i in range(len(file_list)):
file_open = rasterio.open(file_list[i])
file = file_open.read(1)
file = np.reshape(file,(file.shape[0], file.shape[1], 1))
data = np.append(data,file, axis=2)
data_new = np.delete(data, 0, axis=2)
data_new[data_new > nodata] = np.nan
data_mean = np.nanmean(data_new, axis=2)
data_final = (data_mean/8)*scale_factor*pd.to_datetime(file_list[0][date_start:date_end],format='%Y%j').days_in_month
with rasterio.open('MODIS_ET_'+ str(pd.to_datetime(file_list[0][date_start:date_end],format='%Y%j').year) + str(pd.to_datetime(file_list[0][date_start:date_end],format='%Y%j').month).zfill(2) + '.tif', 'w', **profile) as dst:
dst.write(data_final.astype(rasterio.int16), 1)
# -
# _______________________________________________________________________________________________________________________________________________________________________
# Step 7: Use the function to create monthly files for the whole time series
monthly(jan_files)
monthly(feb_files)
monthly(mar_files)
monthly(apr_files)
monthly(may_files)
monthly(jun_files)
monthly(jul_files)
monthly(aug_files)
monthly(sep_files)
monthly(oct_files)
monthly(nov_files)
monthly(dec_files)
| 11,693 |
/NLP_Job_Descriptions.ipynb
|
473720e8c41b8e96b41a763401f95122180a9c7f
|
[] |
no_license
|
larzeitlin/JupyterNotebooks
|
https://github.com/larzeitlin/JupyterNotebooks
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 595,997 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Applying various NLP processes to Reed.com job description dataset
# ...to identify categorized key terms
#
# Note: various cells have been commented out because they are time consuming. To rerun these processes simply uncomment them. Their work should be saved to disk, so they can be safely recommented to avoid repeating work
import pandas as pd
import spacy
from spacy.matcher import Matcher
from pprint import pprint
import math
import string
import warnings
from sklearn.feature_extraction.stop_words import ENGLISH_STOP_WORDS
import re
import gensim
from gensim.corpora import Dictionary
from gensim.corpora import MmCorpus
from gensim.utils import simple_preprocess
import pyLDAvis
import pyLDAvis.gensim
import pickle
warnings.filterwarnings('ignore')
# ## First some preprocessing
#
# We want to have all the job descriptions lemmatized, with common n-gram terms identified.
#
# Load up the file containing job posting and create a list of all the job description contents...
df = pd.read_csv("reed_uk.csv")
raw_jds = df['job_description'].tolist()
# %%capture
# Lemmatization, bigram, trigram, stopword removal, etc. Uncomment to rerun
'''
def jd_to_words(jds):
for jd in jds:
yield(gensim.utils.simple_preprocess(str(jd), deacc=True))
data_words = list(jd_to_words(raw_jds))
bigram = gensim.models.Phrases(data_words, min_count=5, threshold=100)
bigram.save("bg_model")
trigram = gensim.models.Phrases(bigram[data_words], threshold=100)
trigram.save("tg_model")
'''
bigram = gensim.models.phrases.Phrases.load("bg_model")
trigram = gensim.models.phrases.Phrases.load("tg_model")
bigram_mod = gensim.models.phrases.Phraser(bigram)
trigram_mod = gensim.models.phrases.Phraser(trigram)
# +
def remove_stopwords(text):
return([word for word in simple_preprocess(str(text)) if word not in ENGLISH_STOP_WORDS])
def lemmatization(text, allowed_postags):
doc = nlp_1(" ".join(text))
text_out = [token.lemma_ for token in doc if token.pos_ in allowed_postags]
text_out = " ".join(text_out)
return(text_out)
# -
# %%capture
'''
nlp_1 = spacy.load('en', disable=['parser', 'ner'])
df['lemmatized'] = ''
total_rows = df.shape[0]
for index, row in df.iterrows():
jd = row['job_description'].encode('ascii', errors='ignore').decode()
jd_no_stops = remove_stopwords(jd)
jd_tg = trigram_mod[bigram_mod[jd_no_stops]]
lemmatized = lemmatization(jd_tg, allowed_postags=['NOUN', 'ADJ', 'VERB', 'ADV'])
df.at[index, "lemmatized"] = lemmatized
df.to_csv("reed_jobs_jd_lemmatized.csv")
'''
df = pd.read_csv("reed_jobs_jd_lemmatized.csv")
# ## LDA Modeling
#
# Now let's build a LDA model to identify parts of job descriptions that do not pertain to relevent skills information. Then we can then safely ignore these sentences.
# +
# %%capture
# uncomment this to rerun
'''
jds_list_lemmatized = df['lemmatized'].tolist()
split_jds = [jd.split() for jd in jds_list_lemmatized]
gensim_dict = Dictionary(split_jds)
gensim_dict.save("jd_gensim.dict")
corpus = [gensim_dict.doc2bow(text) for text in split_jds]
MmCorpus.serialize("mmcorpus.mm", corpus)
'''
# +
# load up the "here's some I made earlier" components
gensim_dict = Dictionary.load("jd_gensim.dict")
corpus = MmCorpus("mmcorpus.mm")
# +
# %%capture
# uncomment this to rerun
'''
lda_model = gensim.models.ldamodel.LdaModel(corpus=corpus,
id2word=gensim_dict,
num_topics=25,
random_state=100,
update_every=1,
chunksize=100,
passes=10,
alpha='auto',
per_word_topics=True)
lda_model.save("reed_jd_lda_1")
'''
# -
lda_model = gensim.models.ldamodel.LdaModel.load("reed_jd_lda_1")
# We can load this up into LDAvis to have a look at the topics that have been identified.
# We are mainly interested in the general job description ones here (so that we can exclude them) but we'll name as many as possible anyway
# +
# %%capture
# uncomment this to rerun
'''
LDAvis_prepared = pyLDAvis.gensim.prepare(lda_model,
corpus,
gensim_dict)
with open("lda_vis_prep", 'wb') as f:
pickle.dump(LDAvis_prepared, f)
'''
# +
with open("lda_vis_prep", 'rb') as f:
LDAvis_prepared = pickle.load(f)
pyLDAvis.display(LDAvis_prepared)
pyLDAvis.display(LDAvis_prepared)
# -
topic_tags = {
1 : "exclude",
2 : "Customer Service",
3 : "exclude",
4 : "Project Managment",
5 : "managment",
6 : "exclude",
7 : "exclude",
8 : "sales",
9 : "Finance Administration",
10 : "exclude",
11 : "Health and Safety",
12 : "Manufacturing",
13 : "Recruitment",
14 : "Finance Regulatory",
15 : "Digital Marketing",
16 : "Technician",
17 : "Charity / Fundraising",
18 : "Graduate",
19 : "Hospitality",
20 : "Care",
21 : "Catering",
22 : "Transport",
23 : "Education",
24 : "Unknown Topic 1",
25 : "exclude"}
bigram = gensim.models.phrases.Phrases.load("bg_model")
trigram = gensim.models.phrases.Phrases.load("tg_model")
bigram_mod = gensim.models.phrases.Phraser(bigram)
trigram_mod = gensim.models.phrases.Phraser(trigram)
nlp_1 = spacy.load('en', disable=['parser', 'ner'])
def is_exclude_sent(sent):
sent = sent.encode('ascii', errors='ignore').decode()
sent_no_stops = remove_stopwords(sent)
sent_tg = trigram_mod[bigram_mod[sent_no_stops]]
lemmatized = lemmatization(sent_tg, allowed_postags=['NOUN', 'ADJ', 'VERB', 'ADV'])
bow = gensim_dict.doc2bow(lemmatized.split())
vector = lda_model[bow][0]
topics_df = pd.DataFrame(vector, columns=['topic', 'freq'])
topics_df = topics_df.sort_values('freq', ascending=False)
# topics_df = topics_df[topics_df["freq"] > min_topic_freq]
topics_df['topic'] = topics_df['topic'].apply(lambda x : topic_tags[x])
topics_df = topics_df.set_index('topic')
return(topics_df)
is_exclude_sent("Key Accountabilities & Responsibilities In association with content editors, support the online delivery of marketing campaigns to drive interest and salesTake ownership of on-site journey, identifying design problems and devise elegant solutions, driving the implementation of these initiatives to continually increase conversion and overall revenue")
# Now we'll make some helper functions to identify term frequency in a job description, inverse document frequency accross the corpus, and industry key terms (per industry)
# ## Term Frequency
# Calculates the ratio of the number of times a word appears to the total length of the job description:
#
# $f_{t, d}$
def TF(description):
description = description.split() # splits on whitespace
desc_length = len(description)
lemmas_dict = {}
for token in description:
if token not in lemmas_dict:
lemmas_dict[token] = 1
else:
lemmas_dict[token] += 1
TF_dict = {k:v/desc_length for k, v in lemmas_dict.items()}
return(TF_dict)
# ## Inverse Document Frequency
# Calculates the natural log of the ratio of the number of descriptions a word appears in to the total number of descriptions.
#
#
# $\log \frac{N} {n_{t}}$
#
# Uncomment the below 3 cells to re-process (lengthy)
# %%capture
'''
def IDF(desc_list):
idf_dict = {}
for ind, desc in enumerate(desc_list):
desc = desc.split()
lemmas = []
for token in desc:
lemmas.append(token)
lemmas = list(set(lemmas))
for l in lemmas:
if l not in idf_dict:
idf_dict[l] = 1
else:
idf_dict[l] += 1
idf_dict = {k:math.log(len(desc_list) / v) for k, v in idf_dict.items()}
return(idf_dict)
idf_dict = IDF(df['lemmatized'].tolist())
print(len(idf_dict.keys()))
IDF_df = pd.DataFrame.from_dict(idf_dict, orient="index", columns=['IDF'])
IDF_df = IDF_df.sort_values(by=['IDF'], ascending=False)
IDF_df.to_csv("IDF.csv")
'''
IDF_df = pd.read_csv("IDF.csv", index_col=0)
# ## TF-IDF
# The product of the two functions above, roughly represents the importance of the word in that JD
#
# $f_{t, d} \times \log \frac{N} {n_{t}}$
def TFIDF(JD):
JD_TF = TF(JD) # note this assumed a preprocessed job description
TF_df = pd.DataFrame.from_dict(JD_TF, orient="index", columns=["TF"])
for index, row in TF_df.iterrows():
try:
TF_df.at[index, 'TFIDF'] = row['TF'] * IDF_df.at[row.name, "IDF"]
except KeyError as e:
# print("KeyError, ", e)
TF_df.at[index, 'IFIDF'] = 0.0
TF_df = TF_df.sort_values(by=['TFIDF'], ascending=False)
return(TF_df)
# ## Identify Key Terms by Industry
#
# We want to have a list of key terms that are especially relevent to each industry.
# We can use the same principles as TF-IDF, but simply treat all the job descriptions from a specific industry as a single "document" for the TF component.
# eg: Term Frequency accross industry * Inverse Document Frequency
#
# $f_{t, i} \times \log \frac{N} {n_{t}}$
# +
def TFI(list_jds):
lemmas_dict = {}
total_words = 0
total_jds = len(list_jds)
for ind, jd in enumerate(list_jds):
desc = jd.split() # splits on whitespace
desc_length = len(desc)
total_words += desc_length
for token in desc:
if token not in lemmas_dict:
lemmas_dict[token] = 1
else:
lemmas_dict[token] += 1
TF_dict = {k:v/total_words for k, v in lemmas_dict.items()}
return(TF_dict)
def TFI_IDF(JDs_list):
TFI_dict = TFI(JDs_list)
TFI_df = pd.DataFrame.from_dict(TFI_dict, orient="index", columns=["TF"])
total_rows = TFI_df.shape[0]
for index, row in TFI_df.iterrows():
try:
TFI_df.at[index, 'TFI_IDF'] = row['TF'] * IDF_df.at[row.name, "IDF"]
except KeyError as e:
# print("KeyError, ", e)
TFI_df.at[index, 'IFI_IDF'] = 0.0 # If something goes wrong here, we just give it a value of zero
output_df = TFI_df.sort_values(by=['TFI_IDF'], ascending=False)
return(output_df)
# -
# ## Make the industry word lists
#
# We'll run this process on each industry and save it to disk as a csv
# +
industries_list = list(set(df['category'].tolist()))
for ind in industries_list:
ind_df = df[df['category'] == ind]
ind_JDs = ind_df['lemmatized'].tolist()
tfi_idf_df = TFI_IDF(ind_JDs)
tfi_idf_df.to_csv("key_terms_for_{}.csv".format(ind.replace(' ', '_')))
# -
# ## Compound Terms
#
# We've found some n-gram terms with the preprocessing above. We can also consider noun chunks and pattern matching to itentify key terms indise the job descriptions
# +
nlp = spacy.load("en")
def noun_chunks(JD, threshold):
desc = nlp(JD)
exclude_list = []
for ent in desc.ents:
if ent.label_ in ['PERSON', 'GPE', 'DATE', 'TIME', 'MONEY', 'LOC']:
exclude_list.append(ent.text)
tfidf = TFIDF(JD)
noun_chunks = [chunk for chunk in desc.noun_chunks if len(chunk) > 1]
nc_df = pd.DataFrame()
nc_df['chunks'] = pd.Series(noun_chunks)
for index, row in nc_df.iterrows():
tfidf_score = 0
for i in row['chunks']:
try:
tfidf_score += tfidf.at[i.lemma_, 'TFIDF']
except KeyError:
pass
nc_df.at[index, 'tfidf_score'] = tfidf_score / len(row['chunks'])
nc_df = nc_df.sort_values(by=['tfidf_score'], ascending=False)
exc_tags = ['DT', 'PP', 'SYM', 'ADP', 'PRP', 'PRP$', 'POS' ]
nc_df['chunks'] = nc_df['chunks'].apply(lambda x : '_'.join([w.text for w in x if (not w.is_punct and w.tag_ not in exc_tags)]))
nc_df = nc_df[(nc_df['tfidf_score'] > threshold)]
noun_chunks = set(list(nc_df['chunks'].tolist()))
chunks = ' '.join(noun_chunks)
return(chunks)
# -
threshold = 0.01
df['noun_chunks'] = ''
num_rows = df.shape[0]
for index, row in df.iterrows():
# print("working on row {} of {}".format(index, num_rows))
jd = row['job_description'].encode('ascii', errors='ignore').decode()
df.at[index, 'noun_chunks'] = noun_chunks(jd, threshold)
df.to_csv("job_lem_noun_chunks.csv")
def pattern_match(JD, threshold):
tfidf = TFIDF(JD)
matcher = Matcher(nlp.vocab)
pattern = [{'TAG' : 'NN'},
{'TAG' : 'VBG'}]
matcher.add("noun_verb_pair", None, pattern)
desc = nlp(JD)
matches = matcher(desc)
score_dict = {}
for match_id, start, end in matches:
string_id = nlp.vocab.strings[match_id]
span = desc[start:end]
word_list = nlp(span.text)
score = 0
for token in word_list:
try:
score = tfidf.at[token.lemma_, 'TFIDF']
except KeyError:
pass
score = score / len(word_list)
score_dict[span.text] = score
return_list = [k for k, v in score_dict.items() if v > threshold]
return(return_list)
threshold = 0.01
df['pattern_matches'] = ''
num_rows = df.shape[0]
for index, row in df.iterrows():
# print("working on row {} of {}".format(index, num_rows))
jd = row['job_description'].encode('ascii', errors='ignore').decode()
df.at[index, 'noun_chunks'] = pattern_match(jd, threshold)
df.to_csv("job_lem_chunks_patterns.csv")
# ## Filter out unwanted tags
# such as peoples names, dates, times, etc
def single_word_filter(JD, threshold):
desc = nlp(JD)
single_word_tfidf = TFIDF(JD)
exclude_list = []
for ent in desc.ents:
if ent.label_ in ['PERSON', 'GPE', 'DATE', 'TIME', 'MONEY', 'LOC']:
exclude_list.append(ent.text)
exclude_list = [x.split() for x in exclude_list]
exclude_list = [item for sublist in exclude_list for item in sublist]
tag_include = ['NN', 'NNS', 'VB', 'VBS', 'VBP', 'VBN', 'VBG']
token_list = [t for t in desc if t.text not in exclude_list]
token_list = [t for t in desc if t.tag_ in tag_include]
return_list = []
for t in token_list:
try:
tfidf = single_word_tfidf.at[t.lemma_, 'TFIDF']
except KeyError:
continue
if tfidf > threshold:
return_list.append(t.lemma_)
return(list(set(return_list)))
def key_tags(JD):
threshold = 0.01
JD = JD.encode('ascii', errors='ignore').decode()
chunks = noun_chunks(JD, threshold)
pattern_matches = pattern_match(JD, threshold)
single_word_tags = single_word_filter(JD, threshold)
tags = chunks + pattern_matches + single_word_tags
tags = [t for t in tags if t.lower() not in global_exclude]
tags = [t for t in tags if len(t) > 1]
tags = [t for t in tags if len(t.split()) < 5]
return(tags)
# ## Let's test it out on some JDs...
#
# uncomment to run.
# %%capture
'''
for index, row in df.iterrows():
if row['category'] == 'hr jobs':
print(row['job_title'])
print(key_tags(row['job_description']))
'''
# Run cell below to add TFIDF tags to all the job postings
# %%capture
'''
for index, row in df.iterrows():
print(index)
if index % 50 == 0:
df.to_csv("jobs_jd_tags_temp.csv")
tags = key_tags(row['job_description'])
tags = [x.lower().replace(' ', '_') for x in tags]
tags_str = ' '.join(tags)
df.at[index, 'tags'] = tags_str
df.to_csv("jobs_jd_tags.csv")
'''
# ## Outcome
#
# This method has produced some interesting tags, with a lot that are clearly skills. However, there is also a lot of noise, and no clear way to filter it out. This might be improved by training a new Spacy classifier on a labeled dataset. [DataTurks](https://dataturks.com/) is a potential tool for this
# ## Second Pass: Latent Dirichlet Allocation / Topic Modeling
#
# Using topic modeling to identify key areas of the corpus and the accociated topics might yield valuble results / help with the process of categorizing job descriptions.
raw_jds = df['job_description'].tolist()
def sent_to_words(sentences):
for sentence in sentences:
yield(gensim.utils.simple_preprocess(str(sentence), deacc=True))
data_words = list(sent_to_words(raw_jds))
# Rather than using the more complicated noun clustering approach to compound tags, we'll simply use statistical bigram and trigram identification. Any tags longer than three words will not be caught in this process
bigram = gensim.models.Phrases(data_words, min_count=5, threshold=100)
trigram = gensim.models.Phrases(bigram[data_words], threshold=100)
bigram_mod = gensim.models.phrases.Phraser(bigram)
trigram_mod = gensim.models.phrases.Phraser(trigram)
# Some utility functions for processing the text
# +
def remove_stopwords(texts):
return([[word for word in simple_preprocess(str(doc)) if word not in ENGLISH_STOP_WORDS] for doc in texts])
def make_bigrams(texts):
return([bigram_mod[doc] for doc in texts])
def make_trigrams(texts):
return([trigram_mod[bigram_mod[doc]] for doc in texts])
def lemmatization(texts, allowed_postags):
texts_out = []
n_texts = len(texts)
for en, sent in enumerate(texts):
print("{} out of {} lemmatized".format(en, n_texts), end='\r')
doc = nlp_1(" ".join(sent))
texts_out.append([token.lemma_ for token in doc if token.pos_ in allowed_postags])
return(texts_out)
# -
# NB: The below is a somewhat lengthy process, once run, comment it out and rely on the saved data that id loaded up two cells below
data_words_nostops = remove_stopwords(data_words)
# data_words_bigrams = make_bigrams(data_words_nostops)
data_words_trigrams = make_trigrams(data_words_nostops)
nlp_1 = spacy.load('en', disable=['parser', 'ner'])
data_lemmatized = lemmatization(data_words_bigrams, allowed_postags=['NOUN', 'ADJ', 'VERB', 'ADV'])
# Create a dictionary of terms from th job descriptions. Corpus is a matrix of the descriptions in which they appear
gensim_dict = Dictionary(data_lemmatized)
gensim_dict.save("jd_gensim.dict")
corpus = [gensim_dict.doc2bow(text) for text in data_lemmatized]
MmCorpus.serialize("mmcorpus.mm", corpus)
gensim_dict = Dictionary.load("jd_gensim.dict")
corpus = MmCorpus("mmcorpus.mm")
mallet_path = "mallet-2.0.8"
lda_model = gensim.models.ldamodel.LdaModel(corpus=corpus,
id2word=gensim_dict,
num_topics=25,
random_state=100,
update_every=1,
chunksize=100,
passes=10,
alpha='auto',
per_word_topics=True)
lda_model.save("reed_jd_lda")
# Using LDAVis we can have a look at the clusters which represent topics
# +
LDAvis_prepared = pyLDAvis.gensim.prepare(lda_model,
corpus,
gensim_dict)
with open("lda_vis_prep", 'wb') as f:
pickle.dump(LDAvis_prepared, f)
# -
with open("lda_vis_prep", 'rb') as f:
LDAvis_prepared = pickle.load(f)
pyLDAvis.display(LDAvis_prepared)
pyLDAvis.display(LDAvis_prepared)
def lda_desc(text, min_topic_freq=0.05):
parsed_text = nlp(text)
ug_parsed_text = [t.lemma_ for t in parsed_text if not t.is_punct]
tg_parsed_text = trigram_mod[ug_parsed_text]
tg_parsed_text = [t for t in tg_parsed_text if t not in ENGLISH_STOP_WORDS]
text_bow = gensim_dict.doc2bow(tg_parsed_text)
text_lda = lda_model[text_bow][0]
topics_df = pd.DataFrame(text_lda, columns=['topic', 'freq'])
topics_df = topics_df.sort_values('freq', ascending=False)
topics_df = topics_df[topics_df["freq"] > min_topic_freq]
topics_df['topic'] = topics_df['topic'].apply(lambda x : topic_names[x])
topics_df = topics_df.set_index('topic')
return(topics_df)
import textract
text = textract.process("test.docx").decode()
lda_desc(text)
| 20,503 |
/second_dataset_python_code/.ipynb_checkpoints/Prediction - EU Sales-checkpoint.ipynb
|
d353a4f615ce26b4c0d840152e22da6ff671342f
|
[] |
no_license
|
akulisek/game_sales_information_retrieval
|
https://github.com/akulisek/game_sales_information_retrieval
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 105,870 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import pandas as pd
from sklearn import linear_model
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
import operator
ITERATION_FAKTOR = 20
GROUP_OF_PREDICTION = 'EU_Sales'
def get_whole_dataset():
column_names = ['Name', 'Series', 'Platform', 'Year_of_Release', 'Genre', 'Publisher', 'NA_Sales', 'EU_Sales', 'JP_Sales', 'Other_Sales', 'Global_Sales', 'Critic_Score', 'Critic_Count', 'User_Score', 'User_Count', 'Rating', 'Predecessors_Count', 'Predecessors_Global_Sales_Mean', 'Predecessors_JP_Sales_Mean', 'Predecessors_EU_Sales_Mean', 'Predecessors_NA_Sales_Mean', 'Predecessors_Other_Sales_Mean']
raw_data = pd.read_csv('../dataset/video_games_sales_with_predecessors2.csv', usecols = column_names, sep = ';')
return raw_data
show_data = get_whole_dataset()
#show_data.head()
show_data
# -
# ## Prepare data
# Niektoré časti pre spracovanie ako spracovanie predchodcov boli vyhodnotené za pomoci ElasticSearch.
#remove not used columns
def remove_unused_columns(dataset):
dataset = dataset.drop('Series', axis = 1)
dataset = dataset.drop('Rating', axis = 1)
dataset = dataset.drop('Publisher', axis = 1)
return dataset
# +
# Years in dataset
# min(prepared_data.Year_of_Release) # 1985
# max(prepared_data.Year_of_Release) # 2016
genres = ['Sports', 'Platform', 'Racing', 'Role-Playing',
'Puzzle', 'Misc','Shooter', 'Simulation', 'Action',
'Fighting', 'Adventure','Strategy']
platforms = ['Wii', 'DS', 'X360', 'PS3', 'PS2', 'PS4',
'3DS','PS', 'X', 'PC', 'PSP', 'WiiU', 'GC',
'GBA', 'XOne', 'PSV', 'DC']
def get_decade(row):
if row['Year_of_Release'] <= 1990:
return 1980
elif row['Year_of_Release'] <= 2000:
return 1990
elif row['Year_of_Release'] <= 2010:
return 2000
else:
return 2010
def label_genres(row, genre):
if(row['Genre'] == genre):
return 1
else:
return 0
def label_platforms(row, platform):
if(row['Platform'] == platform):
return 1
else:
return 0
def set_means(row, means):
return means[row['Genre']]
def calculate_means(data, group):
# get mean of sales for each genre in group(NA,EU,...)
means = {}
for genre in genres:
genre_only = data[data['Genre'] == genre]
means[genre] = genre_only[group].mean()
return means
def mean_sales_of_genre_for_group(data):
means = calculate_means(data,'Global_Sales')
data['Global_Mean_Sale_For_Genre'] = data.apply(lambda row: set_means(row,means), axis=1)
means = calculate_means(data,'NA_Sales')
data['NA_Mean_Sale_For_Genre'] = data.apply(lambda row: set_means(row,means), axis=1)
means = calculate_means(data,'EU_Sales')
data['EU_Mean_Sale_For_Genre'] = data.apply(lambda row: set_means(row,means), axis=1)
means = calculate_means(data,'JP_Sales')
data['JP_Mean_Sale_For_Genre'] = data.apply(lambda row: set_means(row,means), axis=1)
means = calculate_means(data,'Other_Sales')
data['Other_Mean_Sale_For_Genre'] = data.apply(lambda row: set_means(row,means), axis=1)
def get_filtered_data():
data = get_whole_dataset()
data = remove_unused_columns(data)
# remove data with no user count with score
data = data[data.User_Count != 0]
# remove data with no critic count with score
data = data[data.Critic_Count != 0]
# remove all null columns
data = data.dropna()
# add Decade column
data = data.copy()
data['Decade'] = data.apply(get_decade,axis=1)
# add count of genre for each part
#add 0/1 to
for genre in genres:
data[genre] = data.apply(lambda row: label_genres(row,genre), axis=1)
# remove genre column
mean_sales_of_genre_for_group(data)
data = data.drop('Genre', axis = 1)
#add 0/1 to
for platform in platforms:
data[platform] = data.apply(lambda row: label_platforms(row,platform), axis=1)
# remove platform column
data = data.drop('Platform', axis = 1)
# remove name column
data = data.drop('Name', axis = 1)
return data
# -
# ## Linear Regression - Global Sales
# +
def data_for_global():
data = get_filtered_data()
data = data.drop('NA_Sales', axis = 1)
# data = data.drop('EU_Sales', axis = 1)
data = data.drop('JP_Sales', axis = 1)
data = data.drop('Other_Sales', axis = 1)
data = data.drop('Global_Sales', axis = 1)
data = data.drop('NA_Mean_Sale_For_Genre', axis = 1)
# data = data.drop('EU_Mean_Sale_For_Genre', axis = 1)
data = data.drop('JP_Mean_Sale_For_Genre', axis = 1)
data = data.drop('Other_Mean_Sale_For_Genre', axis = 1)
data = data.drop('Global_Mean_Sale_For_Genre', axis = 1)
data = data.drop('Predecessors_JP_Sales_Mean', axis = 1)
# data = data.drop('Predecessors_EU_Sales_Mean', axis = 1)
data = data.drop('Predecessors_NA_Sales_Mean', axis = 1)
data = data.drop('Predecessors_Other_Sales_Mean', axis = 1)
data = data.drop('Predecessors_Global_Sales_Mean', axis = 1)
return data
def print_model(coef, labels, rsq_error, mean_error, alpha = None):
# View the R-Squared score
alpha_str = '' if alpha is None else 'Alpha = ' + str(alpha) + ' '
print alpha_str + 'R-Squared score: ' + str(rsq_error) + '\n'
df = pd.DataFrame(coef, index = labels, columns = ['Coefficient'])
df = df[df.Coefficient != 0]
df = df.sort_values(by = 'Coefficient', ascending = False)
print df
alpha_str = '\n' if alpha is None else '\nAlpha = ' + str(alpha) + ' '
print alpha_str + 'Mean squared error: ' + str(mean_error),
print '\n__________________________________________________\n'
# View the R-Squared score
def get_rsq_error(model,X_test,Y_test):
return model.score(X_test, Y_test)
# View the mean square error score
def get_mean_sq_error(model,X_test,Y_test):
Y_pred = model.predict(X_test)
return mean_squared_error(y_true = Y_test, y_pred = Y_pred)
# +
data = data_for_global()
count_of_coef = (len(data.columns)-1) # -1, one column(y) will be deleted
coef_array = [0] * count_of_coef
rsq_error = 0
mean_error = 0
for _ in range(ITERATION_FAKTOR):
# create train set 80% and train set 20%
train_set, test_set = train_test_split(data, test_size = 0.2)
# training set
Y_train = train_set[GROUP_OF_PREDICTION]
X_train = train_set.drop(GROUP_OF_PREDICTION, axis = 1)
# test set
Y_test = test_set[GROUP_OF_PREDICTION]
X_test = test_set.drop(GROUP_OF_PREDICTION, axis = 1)
lin_regresion = linear_model.LinearRegression()
model = lin_regresion.fit(X_train, Y_train)
coef_array = map(operator.add,coef_array,model.coef_)
rsq_error += get_rsq_error(model,X_test,Y_test)
mean_error += get_mean_sq_error(model,X_test,Y_test)
coef_array = map(operator.truediv,coef_array,[ITERATION_FAKTOR]*count_of_coef)
rsq_error = rsq_error / ITERATION_FAKTOR
mean_error = mean_error / ITERATION_FAKTOR
print_model(coef_array, list(X_train), rsq_error, mean_error)
# # Run the model on X_test and show the first five results
# print list(model.predict(X_test)[0:5])
# # View the first five test Y values
# print list(Y_test)[0:5]
# -
# ## Lasso - Global Sales
# +
data = data_for_global()
for alpha in [.0001, .1, 10]:
count_of_coef = (len(data.columns)-1) # -1, one column(y) will be deleted
coef_array = [0] * count_of_coef
rsq_error = 0
mean_error = 0
for _ in range(ITERATION_FAKTOR):
# create train set 80% and train set 20%
train_set, test_set = train_test_split(data, test_size = 0.2)
# training set
Y_train = train_set[GROUP_OF_PREDICTION]
X_train = train_set.drop(GROUP_OF_PREDICTION, axis = 1)
# test set
Y_test = test_set[GROUP_OF_PREDICTION]
X_test = test_set.drop(GROUP_OF_PREDICTION, axis = 1)
lasso = linear_model.Lasso(alpha = alpha)
model = lasso.fit(X_train, Y_train)
coef_array = map(operator.add,coef_array,model.coef_)
rsq_error += get_rsq_error(model,X_test,Y_test)
mean_error += get_mean_sq_error(model,X_test,Y_test)
coef_array = map(operator.truediv,coef_array,[ITERATION_FAKTOR]*count_of_coef)
rsq_error = rsq_error / ITERATION_FAKTOR
mean_error = mean_error / ITERATION_FAKTOR
print_model(coef_array, list(X_train), rsq_error, mean_error, alpha)
# -
# ## Ridge - Global Sales
# +
data = data_for_global()
count_of_coef = (len(data.columns)-1) # -1, one column(y) will be deleted
coef_array = [0] * count_of_coef
rsq_error = 0
mean_error = 0
for _ in range(ITERATION_FAKTOR):
# create train set 80% and train set 20%
train_set, test_set = train_test_split(data, test_size = 0.2)
# training set
Y_train = train_set[GROUP_OF_PREDICTION]
X_train = train_set.drop(GROUP_OF_PREDICTION, axis = 1)
# test set
Y_test = test_set[GROUP_OF_PREDICTION]
X_test = test_set.drop(GROUP_OF_PREDICTION, axis = 1)
ridge = linear_model.Ridge()
model = ridge.fit(X_train, Y_train)
coef_array = map(operator.add,coef_array,model.coef_)
rsq_error += get_rsq_error(model,X_test,Y_test)
mean_error += get_mean_sq_error(model,X_test,Y_test)
coef_array = map(operator.truediv,coef_array,[ITERATION_FAKTOR]*count_of_coef)
rsq_error = rsq_error / ITERATION_FAKTOR
mean_error = mean_error / ITERATION_FAKTOR
print_model(coef_array, list(X_train), rsq_error, mean_error)
# -
# ## Elastic Net - Global Sales
# +
data = data_for_global()
count_of_coef = (len(data.columns)-1) # -1, one column(y) will be deleted
coef_array = [0] * count_of_coef
rsq_error = 0
mean_error = 0
for _ in range(ITERATION_FAKTOR):
# create train set 80% and train set 20%
train_set, test_set = train_test_split(data, test_size = 0.2)
# training set
Y_train = train_set[GROUP_OF_PREDICTION]
X_train = train_set.drop(GROUP_OF_PREDICTION, axis = 1)
# test set
Y_test = test_set[GROUP_OF_PREDICTION]
X_test = test_set.drop(GROUP_OF_PREDICTION, axis = 1)
elasticNet = linear_model.ElasticNet()
model = elasticNet.fit(X_train, Y_train)
coef_array = map(operator.add,coef_array,model.coef_)
rsq_error += get_rsq_error(model,X_test,Y_test)
mean_error += get_mean_sq_error(model,X_test,Y_test)
coef_array = map(operator.truediv,coef_array,[ITERATION_FAKTOR]*count_of_coef)
rsq_error = rsq_error / ITERATION_FAKTOR
mean_error = mean_error / ITERATION_FAKTOR
print_model(coef_array, list(X_train), rsq_error, mean_error)
| 10,866 |
/machine-learning/sdca/SDCA.ipynb
|
9f1a0b125fa65be457d2468e6bfcfbeaaf6fde8f
|
[] |
no_license
|
MichaelKarpe/ponts-paristech-projects
|
https://github.com/MichaelKarpe/ponts-paristech-projects
| 0 | 0 | null | 2022-12-08T06:19:06 | 2020-03-02T06:36:20 |
Jupyter Notebook
|
Jupyter Notebook
| false | false |
.py
| 133,415 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Stochastic Dual Coordinate Ascent
#
# #### Guillaume DESFORGES, Michaël KARPE, Matthieu ROUX
# ###### Libraries importation
# +
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize_scalar, minimize
# import bigfloat
# from lightning.classification import SDCAClassifier
# from lightning.regression import SDCARegressor
from copy import deepcopy
from malaptools import *
import warnings
warnings.filterwarnings('ignore')
# -
# ###### Global variables
# +
n = 500
d = 1
T = 500 # 500
lamb = 1
# X = np.random.rand(n,d)
# Y = np.random.rand(n)
# X = np.random.normal(0, 1, (n,d))
# Y = np.random.normal(0, 1, n)
def gen_linear(a, b, eps, nbex):
X = np.array([np.random.uniform(-5, 5) for i in range(nbex)])
Y = np.array([a * x + b + np.random.normal(0, np.sqrt(eps)) for x in X])
return X.reshape(-1, 1), Y.reshape(-1, 1)
# X,Y = gen_linear(1,0,1,1000)
# plt.scatter(X,Y)
ratio = 0.8
n_train = n
n_test = n // 10 * 2 # car gen_arti doit avoir un nb d'échantillons pair...
X_train, y_train = gen_arti(data_type=0, sigma=0.5, nbex=n_train, epsilon=0.1)
X_test, y_test = gen_arti(data_type=0, sigma=0.5, nbex=n_test, epsilon=0.1)
plot_data(X_train, y_train)
plt.show()
# print(X_train)
# -
# ###### Loss function
def phi(y, a, loss):
if loss == "square_loss":
return np.array([(a - y[i]) ** 2 for i in range(len(y))]).reshape(-1, 1)
elif loss == "hinge_loss":
return np.array([max(0, 1 - y[i] * a) for i in range(len(y))]).reshape(-1, 1)
elif loss == "logistic_loss":
return np.array([np.log(1 + np.exp(-y[i] * a)) for i in range(len(y))]).reshape(
-1, 1
)
elif loss == "absolute_loss":
return np.array([np.abs(a - y[i]) for i in range(len(y))]).reshape(-1, 1)
elif loss == "smoothed_hinge_loss":
return np.array([max(0, 1 - a) for i in range(len(y))]).reshape(-1, 1)
# ###### Convex conjugate in theory
def phi_star_theoric(y, u, loss):
phi_0 = []
for i in range(len(y)):
def phi_i(z):
return phi(y, z, loss)[i]
def f(z):
return -(z * u - phi_i(z))
phi_0.append(-minimize_scalar(f).fun)
return np.array(phi_0).reshape(-1, 1)
# ###### Convex conjugate for classic losses with closed forms
def phi_star(y, a, loss):
if loss == "square_loss":
return np.array([a * y[i] + a ** 2 / 4 for i in range(len(y))]).reshape(-1, 1)
elif loss == "hinge_loss":
return np.array([a * y[i] for i in range(len(y))]).reshape(-1, 1)
elif loss == "logistic_loss":
return np.array(
[
a * y[i] * np.log(-a * y[i]) + (1 + a * y[i]) * np.log(1 + a * y[i])
for i in range(len(y))
]
).reshape(-1, 1)
elif loss == "absolute_loss":
return np.array([a * y[i] for i in range(len(y))]).reshape(-1, 1)
elif loss == "smoothed_hinge_loss":
return np.array([a * y[i] + gamma * a ** 2 / 2 for i in range(len(y))]).reshape(
-1, 1
)
# ###### Illustration of 'minimize_scalar' function: How does it work?
# def f(x):
# return (x - 2) * x * (x + 2)**2
#
# X = np.linspace(-2,2,100)
# plt.plot(X,[f(x) for x in X])
# plt.show()
#
# res = minimize_scalar(f)
#
# print(res)
# print(res.x)
# print(res.fun)
# ###### Computation of objective functions
def primal(y, x, w, loss):
n = len(y)
return (
sum([phi(y, np.dot(x[i].T, w), loss)[i] for i in range(n)]) / n
+ lamb * np.linalg.norm(w) ** 2 / 2
)
def w(alpha, x):
n = len(alpha)
d = len(x[0])
# return np.vdot(alpha,x)/(lamb*n)
# print("alpha x", [alpha[i]*x[i] for i in range(n)])
return np.array(sum([[alpha[i] * x[i] for i in range(n)][j] for j in range(d)])) / (
lamb * n
)
def dual(y, x, alpha, loss):
n = len(y)
return (
-sum([phi_star(y, -alpha[i], loss)[i] for i in range(n)]) / n
- lamb * np.linalg.norm(w(alpha, x)) ** 2 / 2
)
def nb_iter(L_lipschitz, eps_p):
return (
max(0, np.ceil(n * np.log(lamb * n / (2 * L_lipschitz ** 2))))
+ n
+ 20 * L_lipschitz ** 2 / (lamb * eps_p)
)
def duality_gap(y, x, w_hat, alpha_hat, loss):
return primal(y, x, w_hat, loss) - dual(y, x, alpha_hat, loss)
# ###### Closed forms for $\Delta \alpha_i$
# +
gamma = 1
def incr_solution(y, a, loss, x, w):
if loss == "square_loss":
# print("x", x)
# print("w", w)
# print(np.dot(x.T,w))
return (y - np.dot(x.T, w) - a / 2) / (0.5 + np.linalg.norm(x) ** 2 / (lamb * n))
elif loss == "hinge_loss":
return y * max(0, min(1, (1 - np.dot(x.T, w) * y) / (np.linalg.norm(x) ** 2 / (lamb * n)) + a * y)) - a
elif loss == "absolute_loss":
return max(-1, min(1, (y - np.dot(x.T, w) * y) / (np.linalg.norm(x) ** 2 / (lamb * n)) + a)) - a
elif loss == "logistic_loss":
return (y / (1 + np.exp(np.dot(x.T, w) * y)) - a) / max(1, 0.25 + np.linalg.norm(x) ** 2 / (lamb * n))
elif loss == "smoothed_hinge_loss":
return y * max(
0,
min(1, (1 - np.dot(x.T, w) * y - gamma * a * y) / (np.linalg.norm(x) ** 2 / (lamb * n) + gamma)+ a * y)
) - a
# -
# ###### Computation of SDCA
def SDCA(y, loss, x, T_0, output_type, verbose=False):
n = len(x)
alpha = np.zeros(n)
# alpha = np.random.rand(n)
alpha_t = [0] * (T + 1)
alpha_t[0] = alpha
alpha_coefs = [[alpha[i]] for i in range(len(alpha))]
w_t = [0] * (T + 1)
w_t[0] = w(alpha, x)
for t in range(1, T + 1):
i = np.random.randint(n)
def f(z):
return (
phi_star(y, -(alpha_t[t - 1][i] + z), loss)[i]
+ lamb * n / 2 * np.linalg.norm(w_t[t - 1] + z * x[i] / (lamb * n)) ** 2
)
delta_i = incr_solution(
y[i], alpha_t[t - 1][i], loss, x[i], w_t[t - 1]
) # minimize(f, 0, method='nelder-mead').x #minimize_scalar(f).x
w_t[t] = w_t[t - 1] + delta_i * x[i] / (lamb * n)
alpha_t[t] = deepcopy(alpha_t[t - 1])
alpha_t[t][i] += delta_i
if verbose:
for i in range(len(alpha)):
alpha_coefs[i].append(alpha_t[t][i])
sum_alpha_coefs = [
sum([alpha_coefs[i][j] for i in range(len(alpha_coefs))])
for j in range(len(alpha_coefs[0]))
]
if verbose:
for i in range(len(alpha[:20])):
plt.subplot(1, 2, 1)
plt.plot(range(1, len(alpha_coefs[i]) + 1), alpha_coefs[i])
plt.title("Evolution of alpha coefs at each iteration")
plt.xlabel("t")
plt.ylabel("alpha")
plt.subplot(1, 2, 2)
plt.plot(
range(1, len(sum_alpha_coefs)),
[
abs(sum_alpha_coefs[i + 1] - sum_alpha_coefs[i])
for i in range(len(sum_alpha_coefs) - 1)
],
label="Evolution of alpha",
)
plt.title("Evolution of alpha coefs variation at each iteration")
plt.xlabel("t")
plt.ylabel("Variation")
plt.legend()
plt.subplots_adjust(bottom=0.2, right=2, top=1, wspace=0.3, hspace=0.3)
plt.show()
if output_type == "averaging":
# return sum([alpha_t[i] for i in range(T_0,T)])/(T-T_0), sum([w_t[i] for i in range(T_0,T)])/(T-T_0)
# return alpha_t[-1], w_t[-1]
return alpha_t, w_t
elif output_type == "random":
# return alpha_t[np.random.randint(T-T_0)+T_0+1], w_t[np.random.randint(T-T_0)+T_0+1]
# return alpha_t[-1], w_t[-1]
return alpha_t, w_t
# ###### List of losses and outputs
# +
losses = [
"square_loss",
"hinge_loss",
"absolute_loss",
"logistic_loss",
"smoothed_hinge_loss",
]
outputs = ["averaging", "random"]
chosen_loss = losses[2]
chosen_output = outputs[0]
# -
# ###### Prediction and error
# +
def predict_y(w, X):
# ones=np.array([1 for i in range(len(X))]).reshape(-1,1)
# return np.dot(np.concatenate((ones,X), axis=1),w)
return np.dot(X, w)
def mse(yhat, y):
n = len(y)
return sum([(yhat[i] - y[i]) ** 2 for i in range(n)]) / n
# -
# ###### Execution of SDCA on data
# +
alpha_hat, w_hat = SDCA(y_train, chosen_loss, X_train, T // 2, chosen_output, True)
alpha_hat, w_hat = alpha_hat[-1], w_hat[-1]
y_hat = predict_y(w_hat, X_train)
print(mse(y_hat, y_train))
y_train_predict = predict_y(w_hat, X_train)
y_test_predict = predict_y(w_hat, X_test)
# -
# ###### Display results for gen_arti
# +
def predict(X):
Y_pred = np.dot(X, w_hat)
Y_pred[Y_pred > 0] = 1
Y_pred[Y_pred <= 0] = -1
return Y_pred
plot_frontiere(X_train, predict, step=200)
plot_data(X_train, y_train)
plt.show()
# -
# ###### Plot train and test error
def plot_mse_data(y, loss, x, output_type, label, verbose=False):
MSE = []
for i in range(1, T // 5):
MSEbis = []
# Boucle permettant "d'annuler" l'effet de l'aléatoire
for j in range(5):
alpha_hat, w_hat = SDCA(y, loss, x, T // 2, output_type, verbose)
w_hat = w_hat[5 * i]
y_hat = predict_y(w_hat, x)
MSEbis.append(mse(y_hat, y))
MSE.append(np.mean(MSEbis))
plt.plot([5 * i for i in range(1, T // 5)], MSE, label=label)
# print(MSE)
plt.xlabel("Nombre d'itérations")
plt.ylabel("Erreur moyenne des moindres carrés")
plt.legend()
plot_mse_data(
y_train, chosen_loss, X_train, chosen_output, label="Train error", verbose=False
)
plot_mse_data(
y_test, chosen_loss, X_test, chosen_output, label="Test error", verbose=False
)
plt.show()
# ###### Display optimal primal and dual value and duality gap
print("Optimal primal value :", primal(y_train, X_train, w_hat, chosen_loss))
print("Optimal dual value :", dual(y_train, X_train, alpha_hat, chosen_loss))
print(
"Duality gap for optimal values :",
duality_gap(y_train, X_train, w_hat, alpha_hat, chosen_loss),
)
print("Minimum number of iterations :", nb_iter(1, 0.1))
CCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIuAABK2QEBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAgYYKELDSUG4WhgACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIEDACnkAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAoKECBKw0lJuFIYAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCBCwQh5AAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQaKgAASsN5WZhCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgSskAcQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEGipAwEpDuVkYAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAEr5AEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQACBhgoQsNJQbhaGAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgggQMAKeQABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEECgoQIErDSUm4UhgAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIELBCHkAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBoqAABKw3lZmEIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACBKyQBxBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQaKkDASkO5WRgCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAASvkAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIGGChCw0lBuFoYAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCBAwAp5AAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQKChAgSsNJSbhSGAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggQsEIeQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEGioAAErDeVmYQgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIErJAHEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBoqQMBKQ7lZGAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggEAaAgQQQAABBBBAAAEEEEBgJQLlGiMlagxjEAIIIIAAAggggAACCCCAAAIIIIAAAggggAACywkQsLKcEL8jgAACCCCAAAIIIICAC8SDU6Lgleg9/ls9rmjcer8zHIHtKLCSfWc7uqzXOlPurJck80Hg1QlQTr46e5aMAAIIbJQA52gbJct8GyHAuUkjlFkGAghsJwECVrbT1mZdEUAAAQQQQAABBBBYRwGvZIxqGldYYxONvo7JYFYIIIDAkgKUO0vy8CMCCCCAQFxguYPGCs9547PkMwINEVgu70aJaJI8vNLkRsnmHYFmEdAuRP7d+K2B8cYYN8khYGNWronmulny72ryw2rGXcumIGBlLWpMgwACCCCAAAIIIIDANhQo6YorvEKpXKiEH1Z6MbbS8bYhL6uMAAIbJEC5s0GwzBYBBBDYigKVk9ytuHKs05YW2GR5l/OzLZ0bWTkEXlqAMuKlCZnBKxTYLPlX6VzN6cNqxl0tPwErqxVjfAQQQAABBBBAAAEEtqGAX2wlzEpmViqZefBK6JDcyCuWbWjNKiOAAAIIIIAAAggggAACCCCAAAIIIIAAAg0RWKZuN1E2SyXMNqoOmICVhmxlFoIAAggggAACCCCAwOYXKJTMRsam7fmzISsUy2aJhCUSyRXH4y9z7bP5gVgDBBBA4KUEovuwovelZhaVqNH7UuPyGwIIIIDA8gJR2Ru915siKnej93rjMRyBRgpE+TZ6r7fsKN9G7/XGYzgCjRZQ3l0u/ypNyrvk30ZvHZa3lECUb6P3pcaN8m70vtS4/IZAIwTKQcmraJRlXsly0bo7W23vrn7r7GxbZuzV/0zAyurNmAIBBBBAAAEEEEAAgW0loMsW/WXnSnb11xv2l798ZcWi6omSPrzoX5YhCa99uCxfxomfX0pgqUvshXlvqTFrJWHh1LXGYBgC6yMQz5vR54SVPQvqn2hYuLSqr+uThtU0A7BvrJf5Zp/PclkxUZ1312mFl1vu0osh/y7ts31+nc8J8RwVfC4notw7/5vGTwQF8ytEmk/1K0wEi24aAeXP+TwaJCvhB/QwJ8dSmrDwxCI2bKmP1fNdatzlfwtybpC2BIEHy4NtizHUYFo2K+ummPkVDnKeBizMg5S/80Zb+9PC7d4c6xrLoJUERenU+/zvPjSefeOfK+OVK58qs9vwD/Np3PBFbesFRPmiuRGCfLp0WqO8nCoX7MSRg/a7zz+1UydPWjq9vnmJgJXmziukDgEEEEAAAQQQQACBphDwC5SkKuyTpp5WypayhAUBKyuqrw+vY5a+DGqKVSURm1ogyGjV1T7e1JRIVLouLRWLVtazrcwsmVQvQWE1aNBxkH+P/1M9v/hvL/VZ7QUvNQMmXk7Ac8SmQY5X+CjRQc4rqbE0DBD0fOvd8AZNPOWy8vE6r+CKZxelN3pfvDXq/7J4XIZsXoGls0zZEt4jW8JKpaKV1RgVVueHH61mg+UKy8ell70SU3LpSpS2+jhBLkjY/M2lJUWkeCms8jeRSlqxVLRSqeANqqlEylLJ5CtoZIpviRXuJPFJ+LylBRaEViWCXB2VkR4M4DEi4XCPDdA/y5FohPUtJytzW9FF5HLp4/fNLOB5Icyrnhk1oJJBojVLWKkcnD9EoyaSOnNYPHJwXrFspo5m/BLvUSKj95eYFZPWEIi2YfReY5RXMmh+ey88d12YzvlvwfglK/n5bzqV9nNhJV11afMF8PwUjVmtaD2i98YsdfssJdqe0Xvzr3l0/lCd0ugw7Wuic4iyymOzUrFkJa9PS1VPEnzXBGvIXgSs1OZkKAIIIIAAAggggAACCIQCutaI/vQkIAWsWCJluuDOtLRYS0vLslZ+gbPsWIyAwMsJeD7zO6HjV8dBo7+GlIoFy83NWamUM90xrWCVjs7OWNCKxtWjruLTB2nyudQY/jIpZr94Gb2VT7t4a6582oaOGWTgcJH6olxXtlIiacVE0vLFomVnZkxBKqqoT7ekrTXToqezretrvsF2udlGC16+0TYac7k58vvmE4jKsSDHRt+C9dA35WHPo+Wy599iseABg2pU6ujosFQ6HQS0hLWawR3WQSXnwrlV2YQZf8lxqiZZ/DXKmdH74jEYsj0EPAeUFbASNCAlEjrZLZkCBgsJs0K5bMXZGSsXdZZQtnQ6Y+2ZNksn61TUN4QtyrfRe0MWykKaVaAcnDMoedE5q8rH4K9ss7NZKxTyViyXveG0vaMjuIZb2KFFVQtTVMJG7+uz8kGODfNt1Bq2PrNmLptMQIdyXXdVcph/10oEQ9Qwms8XLDubtWIhZ8lkwusfVAeRTqtpU/moVhmo67kNxKjk241cyAamv+lnrYKpkiuaK7W+7ee3+/ynIJlRqoP3hEJVbDY7a7ncnJ9TqKPiTGurdbS3R6V1Jb97EEz1DDdi7cm/G6Eam6e2/qKDa+z3JvtYuZkgyrVB+sK1sEKpaLl83ubyOUsoeFBnyKXy0gEra1xFAlbWCMdkCCCAAAIIIIAAAghsRwHdGa1I+mSqbJmWlPX3ddu+vbtiFMEV9oZWEMWWxkcE6gnEL7e94t7MJqembXDwmU0V82blknW0Z+z40X2Wacl4AEAwr6CCszpoxedRqdypt9RVDvfdJUjpKqdk9FUJbJ670MMSNKy4DPKGAlZyxbKNT07awMCkqYeg1nTGdvR02IH9e8MK+1WBLD3yauvX1HvG0nPk120g4LlVFZ7+IWh8ipduquh89PixTU1PWz6Xs2SibEcP77XOzi5vgKqUud6YWqf9aYGjdxWwYMjqv0Q5N3pf/RyYYusIqG3MSzPl47ChTOXvbKFo41MzNjj4xGaLBWtJt1h/T7ft3b3LOtraXjEAefcVb4CmWXysyT8IWAnCBb1I1g0Hjx49trGxccvlcmZWtAO7+23Xzn5P/4J2Yb+Ii5fe8c/x1a03PD5O7c/BIqK8G73XHpehW1zAD+VhHoiyQiUPJq1QLNn4+JQNDg7a5GTO+3jt6+6y/v4d1tXV4TgJ9YIVMVXOSTc4YKWyxMqSoxTwvi4CUfkSva/LTNdhJrHtveh6aT6tlaDBctJ7o3j6dNCeP39hhWLRUlay3Tu67PDhg7GAlSBpDQtY8cXF1mUdZJhFtcB8fqj+pdm+R1dtniM82UHeUA+DChqcmpmx4dFRez405Nd50eWeglbW+0XAynqLMj8EEEAAAQQQQAABBLawgFcI6cKlVLbOjjZ7/dQR++I3HwVrHG878rujggsdLoW3cIZoslWL8preo8tnvSvOpFAq28NHI/btufM2l5u1YnHO+vu67A9/97l1dnZaKq0qojDPRjOKrV+NQbFfX+5jlNaXmwtTVwts5DarXta6fQ8zQzztxYTZxHTJbt25Y48f3LZysWDdHZ322vFD9sVvP7OO9uV7uVq39NWZUTy9dUZh8DYQ8EZPBZxUlcGlhNnYeM7++Oe/2IOHD21ubsbaMmn74rcf2cED+zxgUHlIf74LqBFgiUwV/bRuZee6zWgbbOQtvIpRHoyvou6Enpgp24NHg/bnP41YfnrGOjsydvzwAfv0w/dtz+4d8dH5jMArE4jKRSUgKtL0rh5V8gWzf/nnr+3mdNZKc3kvXz94+7S9++7rPrKmDW+w9vTHPy+5QvGFLjniwh+XKt8rY8YDGSoD+bClBaL8FL4rH87Nle3Bg2f23XfnLTs5aWlL2pED++yds6ft8OEDft5Qq5HfZxHNb53RotkG79G3dV4Is/OSbMVl0Svwqmz5BeeswaMElRyVv/pTm/635y7a1NioTU3nLZ0ye/3EYfu7v/3cU52szGh+JXzQigrK+Wn4hMBaBaIsGLwHNx94/k3oHMLs8dNxu3ztmo2OjlluLhs+3jUeJrvWJS+ejoCVxSYMQQABBBBAAAEEEEAAgToCum5WV7wldZueKFs6WbaO1ugSp/ZE8V/jn2uPzVAE1i5QK395RZEq7FMJy6Q1hroxDYYmrGgt6ZK1ZRLWkgrCVfRLvVet+dcbl+EIrEWgVh7TgylyLQnLpMzS3rF00dKJkmWSZWtLm/+tZVlMg8B6Cijvev5VdEr4UrCg8q/eZzNpS4XnEDqPSCSK1pIqW2tL2KtVOE00dfQezSt6rzc8+p13BNZTQOcEuRaVsylLJxOWLJctWSpbJpmg/F1PaOb18gI1CkflX93pX2oxyygPJxLmD7EqFcNziDBUu8bJb41BC9JYY3ELfl/yy0o6vnupBSy5dH5sIoH4Zo4+x/Oens7WGpa/yrt6aFvSytaaTlhn63zPKpo2Pt1Gr6KWF/1t9LK26/yjHlKbff09WNszb5ADo3TrW5QnM8q4paIl1FNxMriG6wzr0HzSGitZb3iNURmEwLoIBHku+Fd5N3g4pllbpsVa9Ri2ZNIKCWVmBavo/GH9cykBK+uyKZkJAggggAACCCCAAALbS0CXJkl1uVvpdnf59V//y5nll8kYCCjfeX6NGlN1q1a8Bqlc9uCr6kvuqIIpEiT/RhK8b5TAknnMM2RQTR9U10djV+fUjUod80VghQJR1owac2Lf9VjBsgJaKo9XU3msMnjlVZ7K8bFZrjBRjIbA2gS8hFWGC+rnrZwo+58yYRD8WmO+ZNAaKAx6VQJeZnoeLlkpUTL9Z4miWaI035NVjTxbY9C6rsJGz39dE8vMNlxA+aE6Tywsf8NHtQVduXneVbEcvaqnjYZv1Hujl7dR69HM85Wx54EmTqTngzAzBGeyC3OG0q+/qOwNSuCSnz/Ex4x/buLVJWnbSEB5Un9e+5Aom3oC8us17/knzLHL9QKkzL/KzE3AyjbKZKwqAggggAACCCCAAALrJaBrj2QyaanU/J1N6zVv5oPAegvMX3CXgzYnNZD6fSG6hg4DWMKFatx619arvN5e0WpoWbw2TmAjttnGpXaZOZcTVvaG/mSlwV89XW2pdVyGgJ83gUBVhoy+qqxVvKAeKVhSe6nanvRfOEI03krKxJWMswmkSOImEFBeC/4UnhKEqETDPPlRxt0E60ISt5dAlE+j96Lpv4IVEwVLlYNCmOy7vfJEM69tPC/qs/Ktv/xxK0GwSjlRsnIiaQn1ihmbIPoYvUeTbvR7o5e30evTjPPfLMbxdOpzJf9WziGUd8tWUtBrpd+KefFo/Ph85n/lEwKNEVA+jOfB6LPXl8VydTA8+nV90xYPRFzfOTM3BBBAAAEEEEAAAQQQ2JIC/ixh76Wi7A1OW3IlWaktJaDL6eCSOqgOCpr4w4tsbzSNfg9Wu/rye3769WepXtb6L2H7znGr2Ebr4WFWHrTi9zpFrajbdwOz5k0lEOXT6kQtGK4iWEFXHngVPQoo4YGE0XQaf8E00Q+8I/AKBaJwlShkRb0FkVFf4QZh0csKLCpHw8fw+HWc95IZNZEuOytGQKDhAovyrzf8JyodtEXnCrXGa0RiX9VyG7FuLOPlBarzh5/+VoJXNH/K35dXZg4bLTBfzpa8R0w/99VC4xGDtRLxEtmbHlZqgTIMAQQQQAABBBBAAAEEFgnUuy6pviBfNCEDEGgCgei6uZxQZed8/yp+h3/0YyydjczXjVxWbBX52MwCUZ6MZY6gWV8Dkt7TinpbCf5r5hUhbdtOIMq70YqrC2nVbVba94NMrbyb9P8Wt/trFrGsH82JdwRejYDf3J+whMrcKNhKPbVV5/VXkzqWikAgEM+PYQHqZW/UNBoGC1aCtv0cAjwEmlcgyr9e7paTYRkcvS8Mdm3etSBl20ogdgIb5V+t//zn6MpN77Vf9YbXHpuhCGysQJB3lbGDkO2NXZoZASsbLcz8EUAAAQQQQAABBBDYQgJ6bun8K6q4nx/CJwSaWcB7qAgfBhRV2HsDVN0qo2ZeG9K2ZQXijU5hxWdQ8ipQJRlWF6mXlfB26S0LwYptOoGgPnNRsnXqEOTh6Bwi6GXFq+2jQbGpagyK/cpHBBonoLzof97YHyw3ClQhnzZuO7CkFQrEzx8q5W68/A17aAsekLnCmTIaAg0UCM97tcSg7FU7aRCkovfoc1QONzBlLAqBpQXi5e+iMaOzCeVh9VaxaAQfwHlFbReGvlqBhPJsmGnrZN11SyABK+tGyYwQQAABBBBAAAEEENj6AgsvUPRt4ZCtL8Aabm6BqBooqDSKvm3udSL120EgKm2Dx1JojYMh5OHtsPW3xjoGQYIL16X+/aULx+MbAq9awM92PWhbPbRFr/lP0RDeEWhugeD8V6EAlL/NvaW2beqqTmyDs109STB4HFDYydW25WHFN6+AnwdHvbRRAm/eDbkNU67yV6/gXHhjAQhY2Vhf5o4AAggggAACCCCAwKYXiOqN/Ppaa6Mbo6mj3/TbdbutQFBFH/wbZuPtRsD6bhYBZdOojA07UfGb+xNlK/tzVcL3MGhls6wW6dwGAtEJQ3xV43lYw+eLYc4l4k58bnqBcjkMGQw6CKoU002fcBK4fQRqlcGVU4oo2CoaKXrfPjys6eYS8GCVhFkpUfa/4FxYwSvhucTmWh1Su80EPP+G6xz17FpOqKfMMANH13qRC0VyJMF7kwkozwb5eT7T6px4I06ECVhpso1PchBAAAEEEEAAAQQQ2EwCXFdvpq21TdOq6+ooo5b1GKv5rxtxkb1NlVnt9RaI8myloUkLCKqKzKJueecrjdZ78cwPgTULxPJuNI8gx8bujtYP0XjxMjqagHcEmkjAS9oo8CpeJkd5uInSSlK2sYDyY3RaEObN6KtUgs9qdCLiahvnkk216sqz+tM5hJ9HeNaNX8htqtUhsdtaIHocW8ISiWTQvwrnENs6R2yulQ/PHTzRG5txtafwQgABBBBAAAEEEEAAAQQQQAABBBDYFAJRRVH0vikSTSIRQACBLSMQDwTYMivFimx+AU4LNv82ZA0WC1TyNSXvYhyGbAYBPVElkVCwSpiZo/fNkHjSiEADBQhYaSA2i0IAAQQQQAABBBBAAAEEEEAAAQTWJFCp7IwqPdc0FyZCAAEEEFiFgJqXvJGp0miq2/7LPNJqFYaMigACCLycgB7JFpbFLzcjpkYAAQQQaFIBAlaadMOQLAQQQAABBBBAAAEEEEAAAQQQQMAFvKE0ai2N3rFBAAEEEGiYQDl8FAV3RjeMnAUhgMD2FlCQSrkqQDChx1pRDm/vjMHaI4DAlhQgYGVLblZWCgEEEEAAAQQQQAABBBBAAAEEtpIAdfNbaWtuv3WJd+RfTpjfKb39FFjjzSwQz8ObeT1IOwIIILCpBKoLX+K2N9XmI7EIIIDASgUIWFmpFOMhgAACCCCAAAIIIIAAAggggAACCCCAwJoE/E7pNU3JRAgggAACCCCAAAIIIIAAAltVgICVrbplWS8EEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQKBJBQhYadINQ7IQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIGtKkDAylbdsqwXAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCDQpAIErDTphiFZCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIDAVhUgYGWrblnWCwEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQaFIBAlaadMOQLAQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAYKsKELCyVbcs64UAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCDSpAAErTbphSBYCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIILBVBQhY2apblvVCAAEEEEAAAQQQQAABBBBAAIEtLJDYwuvGqiGAAAIIIIAAAggggAACCCCAwHYQIGBlO2xl1hEBBBBAAAEEEEAAAQQQQAABBLaQAMEqW2hjsioIIIAAAggggAACCCCAAAIIbFsBAla27aZnxRFAAAEEEEAAAQQQQAABBBBAYHMJKFCFYJXNtc1ILQIIIIAAAggggAACCCCAAAII1BMgYKWeDMMRQAABBBBAAAEEEEAAAQQQQACBphQgaKUpNwuJQgABBBBAAAEEEEAAAQQQQACBVQkQsLIqLkZGAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQeFkBAlZeVpDpEUAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBFYlQMDKqrgYGQEEEEAAAQQQQAABBBBAYFMJVD05pWxm+lvwWjRgwa98QQABBBBAAAEEEECg+QVi572xj0G6owHRe/OvDSlEAAEEtoTAfHUDBfCW2KCsxIYIpDdkrswUAQQQQAABBBBAAAEEEEAAgSYS8EAV1Q+FdUReaZSIDWiitJIUBBBAAAEEEEAAAQTWTyCxOGB7/WbOnBDYEAG/UkskzC/Zymbl8nyz/4YskJkisFaBsI4hmjyqZYgPns+98aHRFLwjgAA9rJAHEEAAAQQQQAABBBBAAAEEtrTAfOVQsJrlsI4oGB5VJ21pAlYOAQQQQAABBBBAYJsJVJ/l6ty3+rx4m5GwuptMIOHRKpss0SQXgZgA4SkxDD4isIQAAStL4PATAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgg0UKAScRVr8ifiqoEbgEUhgAACjRMgYKVx1iwJAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQSWEVAPK0EnK2UeCbSMFT8jgAACm1mAgJXNvPVIOwIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAJbUKBcVrDKFlwxVgkBBBBAoCJAwEqFgg8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACjRAgYKURyiwDAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAoCJAwEqFgg8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACjRAgYKURyiwDAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAoCJAwEqFgg8IIIAAAggggAACCCCAAAIIIIAAAidzceAAACAASURBVAgggAACCCCAAAIIIIAAAggggAACjRAgYKURyiwDAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAoCJAwEqFgg8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACjRAgYKURyiwDAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAoCJAwEqFgg8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACjRAgYKURyiwDAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAoCJAwEqFgg8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACjRAgYKURyiwDAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAoCJAwEqFgg8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACjRAgYKURyiwDAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAoCJAwEqFgg8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACjRAgYKURyiwDAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAoCJAwEqFgg8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACjRAgYKURyiwDAQQQQAABBBBAAAEEEGg6gXLTpYgEIYCAmbFrkg0QQAABBBBAAAEEEEAAAQQQQGCbCKS3yXqymggggAACCCCAAAIIIIAAAhWBUtgqnjCzevcxRK3mGocXAgg0VEC7H7teQ8lZGAIIIIAAAghsJYHoWiZaJ06sIgneEUAAAQQQaDYBAlaabYuQHgQQQAABBBBAAAEEEEBgwwUUpKKglXrBKkoAlbobvhlYAAIIIIAAAggggAACCGyAANcyG4DKLBFAAAEEENgQgaVqJzdkgcwUAQQQQAABBBBAAAEEEECgGQS4HGyGrUAaEEAAAQQQQAABBBBAAAEEEEAAAQQQ2K4C9LCyXbc8640AAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIbCWB+NOA6GhlK21Z1gUBBBBAYIsKcEvdFt2wrBYCCCCAAAIIIIAAAgisg0C8snMdZscsEEAAAQQQaHoBjn1Nv4lI4DYRYF9svg3NNmm+bVIrRQpSif5q/c4wBBBAYKUC8XI//nml0zMeAgisSICAlRUxMRICCCCAAAIIIIAAAghsR4FSsWqtl6qgWOq3qtlsiq9an+ivZFYuBn8+bFOsQJMlsip/lEtNlj6SgwAC20ugqkzaXivP2jaNQDwfxj9HCaw1LPpti7/rPKFYLBrnCw3e0MpzUb7Tu87XonO2slk5+q3ByWJxoUB8+6wRJdqEZTbmGgWZbEsKrMO+1RAXlceVndiCY2T0vQEJ8GNyA5fXgFViEQg0jQCPBGqaTUFCEEAAAQQQQAABBBBA4FULKCgjm81ZoViwcqlklihbe3u7tbSkLaG79FQ5sU26lc7nyjaXy1uxULBkKmHJZMJaWlKWybS86s20aZdfKpYsny9YLpfzdUin09bS0mKpVNISyW2SsTbt1iPhCLykQL3jR73hL7m45SYvlcpertc8plEcLcfH7+slEM9r8c/RfhEftl7L3AzzKZvNzc1ZLjfnARKJRMJSqZR1dnSYcfvpxm7BhJkC1mdnc5bP561cKvt5WkdHu6VaEsH1wMamgLkvJbDGMkHXddls1goKAiuXLan9qbOz5iFwqcXzGwJbVmCN+1ajPXR6MJfV8TFnpVLJEkmz1tY2a2tr3Zh6Gi2wbDYznbdcLu/1Qzoet7VmrKU1dkCOzlsaDcLyENhCAgSsbKGNyaoggAACCCCAAAIIIIDA2gV0t8zU9Kz98svPNjEx4Xe1ppIJO3nyhO0/sN96e3uWbiRQBXdJt15aJfjAg1zWnqRXN2XJ7OnTIXv0+KGNjgxbyYrW09Nthw8dtCNHDlu6JfXq0raJlzw+PmFPHj+2e/fveWV5V1e37d27144fP27t7W0bU8m2ib1IOgJbSkANAaXwOKHYx2TQ8KkbvF/NsSJhxVI5aKxT2spWP4BlS20IVqapBMrz+4QCY6PWYzUoK0hju77Gxsbt0aNH9uzZoAeuKLh1x44d9sYbb1hPT0/Fabv6bOR6FwtlGx8bt7t379nwyIj7ZzIZO3r0iB06dNC6ezo3cvHMeyUC3tNN0DqsxuqVvMbHJ+278+e9kVvH3/a2Njtx4oTt27vPOjrbVzILxkFg8wtUBVUUC+pONrgxpXLMbeJDr24uGhkZs4GBARv04+OspZJJO3nqpL355pt+k826b6Sy2exc3q7+es2ePh300xQFMB44sM8O7N9nvX09wSKb2G3dTZghAhskQMDKBsEyWwQQQAABBBBAAAEEENhcAqqvmZicsG/PnbMnTx5boVCwTDpt+cLfmColPGClziopUGV2dtbGJyY8aKU102pdXZ3Wmsn4XT91JnvFg1Vjpdfi2pVcrmwPBx7bhR9+tLv3blmxlLODBw/YZ599YgcP7idgJZRbzZsa30ZGRuzK1av21Vd/NfW2smv3bjtz5ozt2rXLWtJpS2e4RF+NKeMisJkECvmSTU9N2+TUpCdbd3brTz14vYqXyqSZ7IxlZ2ZsLj9nrZk26+ro9OMdPTi8ii2yPZc5MzNj09PTNjs753dHa59ob+8IerTbniS+7qOjI3bt2lW7cuWKTU5OWltbmx0+fMT27NljHR0dln5F5cZ22CT5XN6Ghobsp59/snt379nk5JQHNHzyycceXNzd3Vnr1Hk70LzadawEt5VtamrKZmayfnOBAr47O7tMQUU1g1fCBvqx0Qn7l3/5V8vOZr2Bu3dHr+VyBWtv6yRg5dVuWZb+CgRyc3k/9k5PT1kqlfZ6Cx171XNIM8eKFotmL14M26VLV/wYqbobBbv+ofh7e/31173npPXm1Pmyejy7ePGi/XLxoj8Xrm/HDnvvvbPW2pqx3h0Eka63OfPbvgKv5qp4+3qz5ggggAACCCCAAAIIINCkAqVy2Stufvnlot28ecMKhbx3vX702FE7deqk94iRUHDH4vgOy2bn7MHAI7tz5453H76zv99ef+2U7dzZb5nWZn6ETo2VMbNCoWSPHj/yyvqLl34ys6Kvz9Ejh9xBvdHUrBRu0m3bDMmS2ejoqN28ecu+/vpb0x1tBw4e8Ox09uw73nDtASv144iaYTVIAwIIrFFgdGTUHgw8tAcDD7wL8yNHjtjxY8ds9+6da5zjy02mR108G3xuDwYG7NnzZ7Z75y47cviIHT1yxNo6My83c6ZGYAUCc7N5e/LkmT148MAGnz61ffv2eQ8WOjZ2dnaYlcLHr9Q+VVnBEjbpKAkFUE/Zrdt37Ntz503BK2pIfO21F/bZb35je/fuMz1S0F/bzaYBm1SPmVDPKpcvX7HLV67Y6Nio9fb0WF9fn506dcpKpSOWpKPBBmyJxYvQ4z8UcHL/wYA9evzYZmambc+evXbs6FHbvXuX95rivZbFe10J95GJqSk7f/6CTamBPpm0Xbt22v59B+y1114zsz2LF8YQBLaiQMKskC94710DDx/a4OCgP/742LFjdvjQIevu6W7qtVYZMDI6Zrdu3bEffvzZhoeGrGxFO3HiuJX0LDeLFc5Vvcm8zIrpRqbrN27YV19/bWXddLJzp5+nnDxxYmGALcfkl2FmWgSMgBUyAQIIIIAAAggggAACCCDgAmUrJ8I6h0TC9KAEPeFnuVd2Jmd37z6wf/5ff7RLly9ZNjvtvZH84z/+vZ19523bs2d35RFBy82rYb8v8wyKcqJk+jP9WVlPighe+vDKHl8RJWJzvovcykn/K+s96IA57OFGjz6oKG/OFSTVCCBQV0CPmLj263X79ttz3gA6l8/ZW2fO2Bef/9b+5ne/s9a2xlbPFYtlG3j4yL766mv7/vsLNvjsuR3Yt88++fhjy6Qzduz4EUs0Nkl17TbFD/Him8aKFW2yUsFsfGzSvj//o+dDPfpmz97d9sEH79kXX3xub7yhO6VXNKstN5KfLiSSVrKklW3+XZ/1bMrwQV5bbr2ba4USfk1Q0mmbrgnU5UBCAVTJpu59oLkM1zk1CbNcPm9Png7a//cv/2LXrl2zmWzWDuw/YL/78gv78IP37eiRw0tun7Ki7XWx5+HiFNbrvIU25+yi43d1dqg3fHOuZSXVpULRRkZG7ceffrLvL1ywmzdveg9en336qX3+28/t7DvvWKqJH/0bHP+CeppyWe86UVBdhT5Xvaq3adXPK/+q+Ze9XkjX876csBuaSi2JBq7b8laesi03phwjSzy33OZdyQpx+bkSJcZBAAEEEEAAAQQQQACBLS3g18Z+URxUSEeNAeoCNvpcD0BdUg8+fWE3btyxe3cHbGp6wqanZ+zMmQd+x596WUknl7/0KpeK/jghPT86mVKjxNqv0tWbh3rwSKXCinXNKt6/b/xzjRUrlxWwUvQ7lspW8q5vo9HWnqpoDtvwPazcCirWgqCVoLee1MLtsg1pmnuVFbDlO09zJ5PUNbdA2SyXy/tz73VH6I1btyxXKHi35YcOHbQvCgWzUlrt0A17+R2qI6N2794Du379lo2Ojtvk+JTt27PPxsaDR9ulXuIY1LAVacYF6YRCr21zsFQ5Weu1RNnpj/Ywm56etYEHj+3atZs2MTFmY2Pjpm721a3/qZMnLJXevj39BI1vCSt5AHUQuKKu7YJz0q2SuZpzZ/FrAjOd/XqgSikZNoR60EpyG+3btfbrVztMPYONjo3Z9Zu37Nebtyyfy9no+IQdPXrUTp08uWTiPHDcG7XD/cmSpnPxGs3cS86HH7emgK6dS8Wi32SSTDbwhKzBnKof0CO1Bh49tNt37tide3dN66vH0548cdLeeO0160h1NvScdBGBCuElDnNRGa0gTg/kVOCKrrWDnXzR7F56gOqDwvl70jxwMSw5NECvJdIbjrGF3qKVfrkV11yKxaKVtPOVE15fltxWjlsoS6zjqixfa7qOC2NWCCCAAAIIIIAAAggggECzCcxfcgd3z0Tf9R599rsq69RE5PM5m8lO23R2xkplBZ0UbXZ21iYmJmwuNxerPNHcYlfhsa+z2VkbHR2zQrFgHe0d1tvbE3T3Ho4epSM2dV1GPdt5fHzcJicmra0tY91dnabnuydSS9yqrAWoJkYNI2pIUsBKuP5e+eM9z0SpqLtofogLiCu2weQoVf3nuh6TpBH0IWkKZuHVbAJbt8K62aS3enpUIatyPpvNevBKoVS0mekZbzRQ8IgXv41E8CCanM3OZm0uN+ulUi43Z3Nzs/44vKDSnzJpzZtkW9GtoZwMffToRT3eYzabtWKxYDqfyob7SbFULxBmzVtlc03ojWNK8nxzugKao//8/GLTn5Y14Y4SuXsDpc7YwlelB8aF53bRz7w3QEDXJ8Wi5XN5m5mattzsnD9eT5+zMzNWyOXrJ6KyIatG8QD+JsyHVcnk6wYKqOeeubyfj01PT1tba5t1dXd5ryPL3N+xgYnauFnrEcj5Qt7rKlRPoXNQnaPq/FR/Cgorl0qWaOKgneBqOghQ0fmzXj4sDCxZ7+0WzVt2QXWJettSuRGWHVEREr1v3OZrkjmvz4pqvxubmPB9T/tdb3ePdXS0WxNnvSbx39rJIGBla29f1g4BBBBAAAEEEEAAAQRWIFCpxwyvvyvfNa03ENS4o1IjJczaO9qtd0ev9fZ2Wyqd8gqe1rZW27lzp7W36aI7aswJJ6hKz9xc0R4/GbQff/zRg0wOHT5k7737nk+fbgkStJJqAc1dfyOjo3bl8hW7fv269fZ02bvvnrXjx45aR2dn/d48tICodkcz8fgVdX0bVAnp5+iupaCCpmol+LqkgG8bNXYkgjt2S3r8T/B/2BgSBK0sORN+RACBzSmQMGtpabGenh7/a2tttXypaH39fbazf6dXeuspBY186bEW3d3dnp7Ozg6bnZu1ru5OP5Z1dXWGFfGNTNEmX9ZKDtKbfBXXO/k65WhtzVh3d6d1dnVYdnbKGwh7erqtt6fHWlriVdY6im4z5PCcTG8L1lxfFgxY7y3D/OICzh0Fq+gHvyaIjxGce7NJFpps1Ld0MmUdbe3Wv2OHdXV02NzcnO3o6bH+HX3W2dGx/GK9x6IgRp8daXmu7TBGqVC24eERu3b1qt2+fdv27d9vZ86csSNHjlhLOm3JVHUhvLlV0um0dXR0WG9Pr+8zqqfQMD/29vZYe3v7fJ1AU6zqwuP/gvs7woLXqy7C6+qNSnJQI6J/Q574sYADwOrZS2Yvhkbs8pWr9uv163bowAF7792z3jtxJqMeaFc/S6bYGgLxs/+tsUasBQIIIIAAAggggAACCCCwBoGyggjCoI/oPaiWqDOz8EK6ra3NDh7Yb59+9ont6OuxmZlp27t3j739zjveva6CWGq+FLxQMpuanrH7Dx7a9xd+sNGRUXt74m07euSY9fbusPSCBpuac6kMVOrzhZI/duLS5ct24fsLtm/fHtu9e5ft27fXOrq6KuPW/BCsvlfEhB+9ssA/R7cvRRNSiRBJrOpdlqpoc9MwgMUDhbz2DdRVYTIyAptIoDWTtpMnT9qnn45bZ0+XFYpFO/3mG3bmrTOmAMdGV8yqAWbPnj327nvv+rKfvXhuh/YfsHfeecsfyeINNJGvCiyKp0iD93USSKXNent77e233/K7up89e+bnKm+/fcYOHTpkKY3Aq2rn047IztiIbBF/9FJwChw8MrR62X4+F147sGWqddb5e9msNZOxvXt222effGr9ff1eduzfv99Ov/mmH7v8OU61dpPonHtRkthqi0i204BycB3+8OEj++mnn+3S5Uv+SLr+/p12+PCRIDJhi2WRVCrlwSqnT5+2XD5ve/bstdbWVnvv3Xft8KHD1pLJ+GORmj0bVMpebZ/oy0Ym2nvfCsJW1DNqdANPdEPPRi56y827ZDaXK9mjR0/sl18u24UffrA3XjtpB/bvs8OHDpol6tSdbTkIVqiWAGf/tVQYhgACCCCAAAIIIIAAAttQIHpG/XxQgSqs45XWtVB0F/DefXvs008/tkOHDvjz1NXbyonjx627Ox4ksvgW+lyhaKNjI3b7zi27c++OTU8FwS56TIMeLWS29CWb6mf0p7oaBb/MzeXt8eMndufufbt3/4GVyyWbmJyyfEHzMtMjgv2m3XjlWzQTjRAN94offYn+fECt1WfYigUiy+g9NmEiyGk+RD/zWl4gyvjLj7nyMTZinitf+tYe81XYRsVWfJ+K0hG9N0o9aXbkyCFLppK2/8B+L7cPHNhvhw8etHR68bGhbrJWk+5a6x/OWM+I7+vr82CB/p39NjY+Znt27rJ9e/b4I+nCzh2CA8xqllk34Q3+YYl1b3BKmm9xr3J7xpedMFPvPqdPv+m9/YyOjlpf3w7bv3+f7d692xb2OhTfiZuPdKNTVMnO1Tf6bzWWeP5YL9TVzrPaVE/L1J//l/R/a82yerL1Sj7ziQmot7JMxnsm++STj+zo0cM2Oztn/f39fne+eowIGq6DR5zGpqz5sToWv+ZIm3VgpdDYrCvQoHQnzCanpuzxkyd249ZNu3f/vvX09tjU1KTv+JVzoQYlZ9FiahU28ZHWsp2TZh0dnXbq1OvW2dltr5183TKZjN98s2/fPkuoR5nlXtFyNd4KRl9ydtG8VjWfYORo0iXnX+/HaOKVLHdB7y0rmaDeQhkugWLJ/PGPDx48tFu3b9uDgQHr7e6y6emslUvRhlmBlUat3hy1hq1gVozSPAJL1342TzpJCQIIIIAAAggggAACCCDQYIEwgMWXWn01HCRFASB64k9Pd7v1dB+z48eP+LOgU8mktaR1983SSZ6dy9rQyAu7efuGjU+MWTKRtLKVfLpE2ONLdN2uBsbql67JS6WyJZMJD1iZzc7aw0eP7dmz55bLFaxY0p1AqmYPGkRrzMIrd4PnMYfRL+GFvu4civ68W5DqhfP9pQTEHLzK5ts63N7R0Pn3OjUvdQbPT7eaT1Fq4jmkagFes1/dWraaZYTj1lqUfqo3vM4idEdbdHdbnVFWPXgj5rnqRGzGCaJtF6U9no00LLwrUSXRoorFaJr1fg+X6c2MNdKz7OKiddK08c/LTlh/hL6dPdbd02PHjx+zVLrF0umUpZLBowmWPFbElu9ldbSI+HrFxvGfy0EQo+Zbc956nF17ix09csT0GDrl/Uw6ZTrO6Ljm20nzjOar9/jyojQ06XvUEOlJjqd7NesRHzf+eU3rHJtB7GPFN57G1c5f89Orah4eoFodC+X7RThq1fjhXFb+Vme5S84gvu4ls3RagVwHTMFbuVzeH53V0pLg5lohhtsq6pYt4l7Sd6kfq2cQ3/7Rb/FhS82r1m8rmYfGqbcMPYIyDAypO06t5UbDouXre2wZvh+s8mbtsh4b4wVn2CVeOQhX0TlHtJilViVKUvx9vU6h4vNs2s8RUmw7rEtadTxLJ6y9q83ePP26nTp50gqFvD/ORI808UsdX3aNBWt4lK5KYhYNqPyy9IdwOs+wWlat5a0saGbp5YRprjH7ynRKSq3fo7I+nvdrrW6taSszf4kP8WVt1DJeInnxSScnp0w9fA0ODvrjEUulkl+Ly3Vh4GR8qnX8HNuGC47b2oa60SS+DVez2Ggb1PBPK3h67x7bs2uPFQpFU71FOr2KY6/OMcP5J6P0ReeO0fKi9VoiHfPHudWtZ+W8Npq37ypasOouVoCk6eSrKarHj+a5aLgmCI8JK1jEdhxlpdfRhWLZpqazdv/BgPcMrPoqbYikNob+fBuEG2LRBqqS9Y04Pyw4j6gqF6vGmR97gz6FSfe567POxaNh1flKIy312wYlsZlnS8BKM28d0oYAAggggAACCCCAAAINFNAV5HxldLDgWsPmkxSvyNK1ZqZFd19WtxDNjx99KhZKppbKXD5nE5OTNvDwoU3PzFh3V7dXPOoxQpqf/vzaPZqw6l2pU7CK3kvlsmWzczYw8MifxZ1IpiyZSnsDgOqQ9PLr4aiXlXBYpULOFxbcSarAGQ9W8WCXyERLqfMKp63zK4MrAkF+qq5dVgWP/mpXWIQVN9X81d8ry1jLh1oziw2LMmKtWa9228dmG2TwcKbx4bWWUzUsUSuCq2qc1X5dNE+tW63XKtNaaxZNM0zZLgr+WW69Io9a49UaFq2k1z8uNUI0Yuy93rLqDY8m1e9aVL1lVicjGj+aPnqPj6ddUOVmrd+iYSt8T7eYdabaFleQr3B6HXOUFvWopZcCJhfU5UbrkzDzRgRt3xplfrQ4tfGlLBk0PGha1RlHFauhYzTuZnqPH5sXpFvrFBkt+CH8Uus3DdOr1m/hT9Vv8VG9oTo8lvt4lYwU5tXqiVf7PVqn+ELjy4vPLxy30s4a/221n+PrscS0dZel6bWfmllLMmEtLZngywrnu8Qit+BPC1GCs77VraaX89FxM8rTmkX0eeEiVjdzjV1v+vDUxn+uN45Pv8KGxlopC8tDrUqU36IyYEFjb9U+UmtWQVLmA7aDUJXAacF5WjjxUqtUPf8obdXDt+T31cCsFKAqr6YzKQ/8rDQGrnD7zi8u2pNWm9hw/PjBd9HGXe0851O14NNKZlNrvXVuoBlVmVXmvZL5VkZew4do/tHy1zCLjZ5ESdP50cTEpL0YGrbhkVEPnPQkJ5JWLJb83MgDeWvEH0WrFq3qmtIbzSScOJ6l/PgYBYPUm/lyC6/3exgXoA7+UmHEyYKyst7yNFxpToZt8Cp7o3XQsuLL02f9Fh9WPd/wHGAFVSeVKX12uqmmMiQo9/V14dDYCLU+RsuO/abObXVevWDmlfkGaJWbJcL1rv5ePW1s9lv7Y3QtucRaRtcuxaJZdnbOA8VGRkc9ozinb9ew8FJwUHwj15pv9PsK8lll8nC71Z23XxevMlitevlKV7ScaMHxtGpY9L36czT+Nn4nYGUbb3xWHQEEEEAAAQQQQAABBOoLRDfR+PVm/KKy/iQLrj0ro1VfxOoaNZm0QrFk4xOT9uTpoA0Nj9rsXN66ulRLkvLGSL+oDyvIomve6mTou/5UX6RglcFnz+358xc2OTXjlfZeneS19sGUlYZIJU6DqtMWXqSrUr7yt+iKu7JmfFiFQCUfRTcOOX+0BdUKHfwQbRK9q+JMPeXkczkPTMq0tlimNT1fCRJs1lWkYnWjqiI3ly/YbDbrjzJpaWnxbqO9Mi+a1UukQXm8VsVgNOu1vC9qM1jFTOLTat0L+YI/371QKFR6Mmpra7WWdIsl411mv4TBKpK3MaN6/WtiYVBDlAnjS/QMHA6I/17Wo8jmLJ/PW7FY9EC39vYO06PSaheI8Zku8Vmm1cvU6HWstb30SLS5uVnfX9S9eaY1Y5lMaxC4UW9RNeaneeXzJcvlcpZIJE0BhOmUAgCDmXhIYo3p6i2ierjKYeU1vXw2+hw3rZ531XdNr+znk8R+0/6k+aqnipxvk4Lfed6SabHWTKultEli40efPSnRcH3RAUXr6j+EqY9+D79u6rc661IsmD9eQtu9XCpZKpWy1rY2y2TSlW1fb71FpT/NWnzFQtlyuWC/0LxaPT+q7PDcU282axse305ls0JB+Tdnc3M5a21rtUymxVJVjV5e1q1tactPpTIhV/RyYXZuLnDMZKy1NWPpZNIfr+JQworSrs91tsvyC9ziY0Q7qq/m2pHiAZna/sVCwbeRGmVVXre2ti08rq0Ta7SJq2en3gH1OBftb+rRQPtbW1ub97Kz1mjNxQAAIABJREFU4ByjesLoezjj4DwlyG9aFzUetra2+rlSdb5feR6bfxholDWD9zCQJUpD+K6kqPzQPqfHeablmWkJzm9i40bxQrFBW/NjVTZVfivkS36ekC/k/XGlXr62ti04ti6LUTVfHz8aFr0vOZMg06jvyeA/lTsrmnDJuerYq/XT+YfOFzXL9vZ2PwdZh9kvLCfjKdHq6FwgDExVeZqTcy7v6dANDcExIBUUuS+/qvGl1/xcKMhhzssXjeDnYi0ZS6bDhYdprjlxgwdqn52cmrUnT5/59fNMds4fVVI23TSiv6SfG5frHLarOde0atUzqf7+MiZLzSv2m/Ko8lDltcyKLIgj0Hxi84rPw/f7QnBOqv2+VCx5fmhty1hLSzCmL3YFcQmV+YYfosAU7cexOdVOS/XE+q40V03qg2utSzR+bFU16fyyw3lpYL3pa6WhmYeFgaYy8jIsYVYsln3f1v6ttU+ldN7Q6sc6rbd6JVtq9Z0nGQTcz2Sz9uDBgD0fGrLs7IxfZ6m8EqBvltVaxhYcpbeaV3UqKqdn52Y9SEvXiC2Z+QmVX31fiG3v6nnU+x5Nu+D3+VlXBhfzurksa3O5Ob++1Pl5RnUrrS1bJ+9U1nbtHwhYWbsdUyKAAAIIIIAAAggggMA2EdB1c71rZ1XATGezNjo6ajMzM1YqFi3T2mo7+/utq7PTK98rlSIJNSaVTN0PPx8etms3rtu1X2/YxNSU5Qsly+WLNjY+aXfv3vdABTX86uK5WCp5JUAymfQKAj1juqe3zYdNzeRtdHTcHwV08dJlG3z2whsBVBmcnZ31rlZv3rpt42MTQU2Kavf1oCCvIEpY344+27WrP7hQjio+4wErumNmm2znxqxmqBm+uW5ZFTRJy+fLNjMz689Tn5qasqnpGZuZnrbZ7Jyl1A16R8Y6OlXBn7b2tlbr7u62vr7+lw8OCFc8m80Hy56c9IYXNb6oYkXPclfea29vs66uTm9U6ujosM6uTuvq7LJUKrmoYWYpSzWoTk/P2PDwkDdWlcsly7RkbNeuXdbV2WGpljq1w0vMVPPTXVqTeu58uWytLYFPb2+vqXJ0uZfSlJ3N2sT4uM3MTFt2JuvrrgY1r3wvqkEtaZ2dWv9Wr6RTg0RXV5cbtHe0r3vwzXJpXs/fPZhNje2FkjuMjclhxssKPeu+t7fHG2BUrqhBZmJiwv8mJydtcmLSVPmo4conMpdTR0e7KZ90d2taNYaufLuqmJqZnvU7Xqdnpivz7e3dYe3tQeu7epDOzsza+Pi4b3ttu+kp7S9Zb6TRttm9e7edPHWykj9VqRhVLKoM1DxmprOebzStB3vklO9nbWYm6wW/KjXVkKoG95ZM2i36+nqtva1tVZtA5fTY2IRbqUeszvYO6+3psR29vZ4+LxJiha3SqbsQp6amfR21L8q/r6/P9/3W1sBT4+i57yMjI6btMT4xYVOTkzY7O+vbTOXEzl077cTxE5VGAiU8my3ZyOiwjU+OW7GUt0w6bT2d3dbfu8NaO9uCY4LXHK9qNZtnZM8fc/b8xXM/JqohW3lyz+49HoSiVcvni0FeHp9wY9kp35dLZT92d3R2eM9nXd1d1tnV5faRe7SiykMFbYOZGZuYnPBtMD09Zfqbm53z/NbR3mGdKjM72n3f6O/vt472dkulEkF+XPmu4Yv1vKEya2bGzyeUXz3vKlBldtb3Yd/+He2eB4LAm4xpPXq6uq2zsz1KfvBe7wRHv5bNJiaD8lU2alTY0dNrPT3d1t4R9Bak9VeZqXObsbExGx+Xw5SnoyWTse6uTtu9a5edOHHMMlHklweGlW1oeMTGJ8atVC5ZOp10p96eLk/rwkRuz29RuaB3lVmrfakxXcfy6akpm5wc97JNAYZqXNdxs1gseECb8ro3PrW2Wnt7p+3o7/M8uqLgkTDAVseBFy+Cc1AdCzo7u2zX7p3W2hr09pfPFW18bCzY5yYn/V3lmgJN1PjV2dXhx9Pu7i4/N+3q6rbW1tSihhzl//HxaZvwfDbhPRWq/FajaDKZ9uOOjs8dHW2+v+3Y0ev7fsuqzi3KlgjPf73vxPBxBWqS0/J1zqDyVr0zKK/rvEF/CtxUAJD2Ne3jfuxoa7Oenh7r0HFwlfv6ard3M4yvY5LOZVUWTE9PB+VRNiiXFEypQkUB0B2dnR4oJSOVkdru2m461i4KNopWTAFxs1l78fy5H6N1/qh57ejr9+NiS+vy53uaVXRoC97XsGOZ2djYlB83JiZU3k/7PqbzRe2nvTt6/XxZ66MyUMf6zs4OP/ZEq7Lce3D817nyiJ+HqhcqnV+p7G1tDRp2Z7O6ppz0fUHnClPTyoszfm4d5MNOL1PTLSnr6e62HTt2WHd355rKkur06sYL5X9dr+Tmcr7MKTnoGkIBv5bw6+C29jbfDxS8onNDnZvJIrURAZzViazxXWXizEzOzy/v3x+wa7/+6kErekxJOZGyyemsPXz0xK5fv22tLQo8006rnBLklnS6xcsTnV+qHB0b07XHlC9JeVnbun9nnz/yscbiaw4aHZs2nXfrPEKPRdEje3xevT2ej+ruD1VzU4P46NiYDQ0N+Y0num5pb2u3Xm33rs7K44VKebPR0Qk/f1cDvm5S2dHbYzt29Fh7dP5XNW99VbmnIAOVeQp6VN7WsV3bU3Hqsp2amvM8qXzpeXJq2rJZ5UndmKPt3+n7eUtLyrp7uv2curur6pykxrLjgyrHwmhHjv+4gs/at2azORsbH/PrBj1aLHgsUnCO3dPb49tgUc8v0YJ1EKj10uC1FSe15vZqhunaoxRcp+vcbHJiwgrFgp9Hq04iuDY0L3fb/by20+u9dP6g8+Surg6vo1Ae1iuSEtnUVM5GRsdM+90PP/7k5wuatwLadK336NEju379hrW16mYDVUqVrFwu+nEznc5YT0+v9fXvtHRLfWTlwVyuZDPTOj9Wfcas5fLBtbzqU/xaKp3yPKiySeWkyqUdfdpHuoLrsfqzX7BNpqdUb6BzENWxWVgv0+fp9x6LPDg46MVJ9YSjY6NhPUPWe7PUOUJff58dOnTIduzo8xsLFixgm34hYGWbbnhWGwEEEEAAAQQQQAABBKoEoitqv7heeKWqbwuHzE+roIJbt2/b119/bffu3fdKy107d9rvf/97O3v2bW8wVWV3NANV7l28dMm+u/C9Xbpy1e4+uO+9o6jRSxfWulCfGBv3C2k1sKkiXw0KqjBTZV9bW7v9p//jP9lHH31krW1Ju3P3vv3ww4/208+/2LVr172COF8omp4H/OzZC/uXP/7Rvv/+vE8X3PsS3IpXKuatq7Pbfvub39of/vAH29HXu+Du2hjHfDVdPYh6OPNMfIoLVLyCDx5C5I2C03b37l27dPmyXbt6zR8VpWAAf754KuF3DLe3BxXWx44etbPvnrVPP/nE+r3yZpWtIPENrIbbgtmDgUd27do1u3r1qj179jxobJiaDu8ESvhdQGpQ2Ldvjx05etTOnDljZ8+e9UpwNQRF9XjxVa31eXR0zG7evGnnz5+3hw8HvJFn185d9h/+wz/a6dOnra+/t9ZkC4cp/aGjHrF15849O3f+vKdfjfUH9u+zD95/3z755BM7sH+/JeI9oiyckwctZGdz9uTJoP31r3+169ev2+DTp74va/+Leg/RZKrYUqCCGg2OHT1ib54+7Wl+7dQp78nAK9gq27dqQS/7Vbc1+it6f9kZLp5ePSI8fvzE/vSnP9n9+/e9hfTkyZNeTmibq/yZnJy2787/YD/99KPduHHDg/UUrKK7DVXG6I5eBR8dPHjQjh87Zm+/846dPHHC+vt3LF5gnSHq2efW3bv2l7/8xZehoJHffPYb++jDj+zEySOmG/Gmp3Ne6fnzTz/b+fPf2eCzZ56XFDSowA5tI+0j//c//ZN1dQfBf8ozqjTV9EHAy5yX25cvX7ar1656D1VqfFGwioKVSkXdRZj0dVLe37N7l338ycf2+ee/8XyVTld1XVFnfTRY+/V3352327fvuJRMPvzgA/vit59bW1um0pAQzUIVxmr003Tnvztv9+7f84bY337+ub3//vt2/OgBL5v1HPhbt27ZuXPnTOuhBuOowUoVyP19fXbmrbfsn/7pn0yBANpPte4PBgbsu+/O2aUrF21iasJ2dPfYh++9b3/z5Zd2oO1A0MuKslpVWRGlr9nfFYyidfx//tt/s8HBp/7IGeXlf/iHv7f9+/Z7TwzDw8N24cIFu3jxkt2+fduGhoa9twcVLjr+BgFYO+zwkcP21ltv2d/8ze9s3/79lgmfXqOyOx8GFalM+/nnn+3ar9fs0aPHYaBbwf08yLC9zXb299mxY8fs7//9v7dTJ09aT0+n996UWmXXC8rD0zNZT/PFXy7Znbt37cXzFx6spECVoMwqeE8PasxVcOHefXvtnbfftvffe9/efvvMyjZf2Wx2rmA3bty0v371ld28fdsb3X/72WeeBxWAovykwIdbN2/bhQs/2JUrV3xfVAOuetFQD0V9fTvs7Dtv23/9r/+XZTJdvmw1GKlh7c9/+Yt9d/68ZbPT1tvbbadPv2mffPyRvf76a37Oo+3Aa/UC2seVrVQ+6DirsuHG9Rv25MljDyhSo03Uu4mMVVZEQX7Hjx+3v/v939nJU6esvS3j81kuBWpovXPnjv2P//k/Pf9rfqffPGP/4T/+ox08sMeDutQg+9VXX9tPP/5kd+7e8YZuHWMVwKcgMfVMomAuLf/DDz60t996y48j7R0Lmy+Ud5Qnf/ghyG9Pnjzx/U09tShDqmFfdy7rOKTzFJXXp06dsv6+bi/OVpSjvNzz28Z9nknvZSvl5UIuX/bGZZn+8stFP+8YHR3xYDE1vumlAJWd/TvtwMEDdurUa/b+++/ZkSNHrKuzTkBF7JxmOetm/316etbLpm+//dauXbtqL14M2Ux2xnut8/OERMIbh2WqgI7+nTvt6JEjdvads77fHzx4wDo7W2uupgJCHj8ZtP/+3/+73bt3z8+PlWc++eRje+edd9zYL7lWtJG1iBWPuCA92dmyXbp8zX766Sf79ZoCHp56A74CaFToq9xVYMnu3bu8MfKDDz+0N9543c+fV1rca5+6fOWK/fWvX/l5mfLUxx9/bB988IEdPbLPy96ng4N25fIVu3jxol8/KmBFQUE6J1PvagoCVOCDgrbefPMN+/TTT73s1rXE2tZ8nmFycsauXv3Vy5ZHDx/a0PCQDb0Y8mBZXbdqZ9M5s65d1dB84MABO3MmOGc+ceKEX3c2unjXbqbz/bv37tmFH360c+d0HfLQg571KF2Z3Lv3wCYnpuz78xd8ZaMH46p88cCOHTvs9ddft3/3b/9gAw8H7Ny5bz0v6nxBN5S8887b9g//8A/WVScPzwsGn1SeXbp02b759pzduHnLWtIpbzg/cviQ/eY3n9lbb52x7u4lAjrC3jBkOTwyYt9884398z//s5fvKodl/bd/+zd2+s3T1tndbgpqGRx8bue/v+DH68ePHpv2xfffO2uffPKRvfP2W5bK1Di31XnH9Iz965/+ZFeuXPVABgVD/9s//Ds7c/qM7ezvskKhHFzHXrpkV65etYcDD4OAppx6YdQ5iXr8y1hbR7sHqnz22We+7545/dqKjjMVO63sgswT5ebovTJmzQ86tx4YGPDrUF3zjY+OeY9ICtr54ssv7ZOPP65/LZpQjpg/MZ7/tObipGYaX9nAhOoEynbv/gP74Yfv/RxZQcgedDSX9+AVpU35XYGmba1ttqOvzw4eOuRl3JnTb9rRo4etv2/htbzqGW7cvOH73A8//mz3Hzy0iUkFKyc8mEmPtP5//8f/sG++/sbnrc2rPFMuFfx4rvJPZd+/+Tf/xoPwoxst4k7aFrO5kj9qSOc7Fy/+4vu3bmzwm1Gysx5Uqryj6zfdgKIgPu1jX375hZ8vdHQExx7Na7ncpF5idA3x008/e8+GZ8++69cJJ06ctNZE0GOyelNWHeH333/v12qq69O5sQpI3cxx4sRx+/t/+Hsvl3ft6ouvzrb9vPCMb9sysOIIIIAAAggggAACCCCwXQUWX4xqSFBJrcbXxb8vlAru0J6y+/cf2a2bd/0uq4l9U/b++2N+V6sqt6JamCuXr9m35875n+5QGp2c9LtdfXnqfaVY9OnVUJzUXcgapt5VvJvVhDf86C5t3QX+8PFj+/X6r/bHf/1XezjwyMbGJ2xqasZ7Y9GFuBoBdFFcLMzZ2OhoMD+/M7QYPGvGStbZ0WXHjh/3nlh6St2W0C1cWuFk0FgXVAbpc0gS9k6wUIBvaxFQtkil05ZuafXH7uhOIzV4Xrp0yRv7tM3U4JfPF7yCVNtADedq/Hv+fCjsOeeW/fLzRa/AUUPk4SOHKttqyTRFtWuloAeHF8Oj9tU333rFu/Ke7opVo4D+1PAZtPAE+aDlxZBXBF2/cdMban786Wf74vPPvfF1584dK7p7WAE4qvxSgNfdu3dscnLCK3lV0apuclfUohTbMRWcpfw/MPDEbty4Y1OTEzYzNWMH9h+w2Wxw52C9PTmXN7t8+Yr9+NNP9ssvv3hDm+4c1B2HWndVUEfTqkFNvQvorjE1bA8ODtrVq9f8rqxDhw7af/kv/8WOHTvqvXAs6b/cj7F1WzhquCNWgOqOuHCyVXxTfhsdG/fgJVWcq3cn3UX75um3LdM6ZC+Ghuyrr77ySreng0/9bnndvabxtOFU3ilfK0/dH3hkF69ctUvXrnlgxm8+/cyOHjnsDSiVVaiTNpV7I+Pjdm9gwK7fvOl3s+7dt89ee+1173XkybNhO3fue/vl51/s5q2b9sJ70Zj1itSS342XND3HRY8JyhfVyBAUw16ZOTtrd+/es19/vW6//vqrb8fhoSEvV9UTga9PUb1Qqdcjde+f8H1v8FnCKz4HHj70htK3zpyx3/3uS29cVU8Zy70UHKFGkus3rlcqK48ePjI/WVXtqNKsRiftK1qmtod6QTh+4qS9/kbW5gpmDx8+svPffWcK2lHg5Kj2IXXHXyyG22LGG6JVrqsMCQ8rfpesypfHT57Y9Ru3/C7TXX19tmfXXt+XFJThgZZK3fKrNr8OTfRJx9OpmWm7/+CBN0yoAVGP43v2/LkpMOvJk6f23bnvvNxVsIfukFavZEFFsryCyvjxyRkbGhm3e/cH7NbtW/bl7760Tz751Hp72mx6puANswrUUPnx+PFjLz8VNKJgJz0exPeJZNLvpnz+7Lk3PA48GPBgv48++tA+/PCDZdWUF/SnLtmvXfvVrl675oFcAw8fec8601PBHfVRcJ033PtOVvaGKAUC6Jzhwf0HPv3Zs+/YRx9+YIcPHfS7YX3UOtta5bXKZjUuKEhAjZ/79x+w4ydPeaPG8xcv3FGBszdu3rTxsHcm5V15a/3T6bQHJagxX4FYfuNt0ixXKNrTwec+36npSdu1s98DzSYmp+Ybo6r2i2WxtswIa9/x1HuAGtAVTKFgNt21rGOWzgkVOKByTmVbkE9UNiaDfDI0bk8Gh7zsVtmrhtePvKH9TWvNVEqEmsLKJ9qH7t9/4H/afxQs88WXX/j8r1//1f7yl//t+4seXanGIz/GRucjSkMiaePjU/bs2ZDdvXPfbt++60GnCj7t6Gjxu6YVnPXHP/7Ry1EFqoyNj3tPQ4oTiBoRle/Uo9fw6KifTymQRgEjH3/8kZ06eSLswWOFvl52BmWBGuieD72woZFhbxS+d/euDT5/7ndMz85mreDnDMGxY2Ji2l68GLWBh0/s8uVf7dKlK/bhRx94MNbhwwcW976wwuTUxG+SgSoPv//+QtAwd/Om9/Kg3idU3qo3Sm0fvyYK06syTecLz54P+bmXzsV27txpb791xv7zf/4/rae7a2EvHP7Im4I/9vTO/Yf26/XbfozUNIeOHLNTp2a9nF0thx5lUfcVK3/0cXhkxtRrpQJEFbA7+OSpl/kKdFUDqnrH0OO39K5zaR1v7t2/b3fv3w8CBt9/3wNH1NuWgkmWennZOzrq09+5e8/v3lfD8OHDR/ya7sqVy95YqmDLZ8+eeW+Ivl970IwO3UEkgxpmh4Y6fXvcuXPXb3L47W9+4+ft6lEjusZbKi3x37JzJbt86bKdP/+9/fzLzzYyMuy9QercSYFwegxesJ21LwSBnzpOPHz00APVhoaHra293XvXWM4gvtyX/azLGfXioIALHbNv3rxtL4aGPUBZQdI6Zuul46kctf20HfVSIJLWRWWmerbs7Or2G0NUzql3MZ1TamqVR+pl9YMPP7LWQ4eCXu2K4WMWfU6L/9Eibt0KAj6fvxj2XiXUkK3lq9eHg4cOLh2wojKqHPRuonPF6zdu2O07d3yfUwC5ArrUm6qOw8G6lC1fLNizoRd25/49DzDR8P5dffbmmTc9oHpRKrVyfk5a9MBuXb8NjwzbzuERO3Xydevp7rXhoTb78ccfPHjq/oN7fj6qHneC81GtVvDMFZXPCnRQel4Mjdily1ftrTNv2pdffOHnJJ0dmfAxpRp/6XPQShy/RgvrSippV5o1fZh2/5owm8nm/cYEBfYoiGB4aNjTqMDaM6dP+/Woeg6pPvcNZ+Ozi36LL7+y3E38YWIya3fv3bc//enPduPGdRscfOI9COlaSuWRnx+Hj85R3g/275Q9fzHkPf3q/PTPf/6TffDBe/b73/+dHT16zNpaW+zxkxd+/Je3elcZHhnz84O8bnYoJ6xYSpoeyfX4yVPPXzo2aN5lPcfHSv7ouJ07++3osWO+XVTHlVaBGxbdOq98Ojjs55IK3lNZ8/z5M7+hQkFWlXNjvzYK8oX2Oz+mv3hhz54/8+vB19943a/r3n77betsrx00Gd+86llFAeo699VjhHt7+2xoaMSOHT9pk9NzHsyn4LE7t+/Y8+fP/RxJ+4OOh8qY6m1I1x0KslXgD69AgIAVcgICCCCAAAIIIIAAAgggUKkPUfVeePVbedf1sKopar/UUDs3F1Sgjk9M+V1ZnR3d3lDqF/a6Ilb8iwV3E+turAf379tsoWA53VZlieDu0kqDVNHyZTWMF62cSFpRlWRhH+IpPeqkXDZd5uoxRI+ePLX7Dwb87kU1ZOml9OtCX3esqm5Iva3olUxpKv1W9MqwhOkRRLngThOfLqrq19jzafZnVUcVdr4e9S18QfwTCsgpyksLUXwbhdtKXeirIfrWzVtegaaAETV8qMJXDS66Q1IV+qok1XPpczNzNjebs8mp6SBo4ulz75Jb3XGrK17doa6uv5d7qT57djpnt+/ctQs//WzffPed96gxNjpmqkBSJY5Sr54qWlvbPACqUFBj/ow3NCm3vHgx7JVUqlTV3Wjvnj1rx44dXG7RXuGlrqFVwR88OmLce45QI68qxFb7Ul6fyxVsaipro2NT3h15T9ekP+qlqPlph6jxmpkpeiDAX/73//ZGFt1VOTuX84ZSrbfuBOzsaHMDbQ8Zq0J+di7vn5V+Ba2oK2wNV4VYVLldY3HrNEhbpXa+Wo8FqBJQ20aPGFGjsd47Op/ag4GH9ujxM+8d5LwqeIeHvZt/VSaqW/eWsKJNwRLT2Vn/G5+atuTwsI1MjNv4pB5HMWVf/va3dvjQIb/zOCxWFiVbW6tYLls2N2fjk5M2MjZqc7lZUyPHi+Fhe/ho0C58/5P99a/feoORHoWj7ry9xl7tP+pBRC0TybS1d3YFjeZhGawiV9tJDfcXvv/efrl4yRsbNUwNLCrvFCyou1L1WAyV4fmctvucP2pIj9XQ45DU4Pps8Jk/0iCTabMjhw8su1nUaKcGY93pFwUUKjBqwauq2FDezs7O+bbQI680j9HxcXdItbTYt9984wErKj+0H7qDCNT4m0xaMZf39Vd31ypPlHO0CF+vQt576Rgfn7TRsUlrSbX4dzXc1NllFiS12b/ITsc/lZUK8pSHeuG5ceuWNz7dVdn3/Q82Mjwa7LuplLVkWr2SXNtH5a3KFd2tOemPpxq20bERP7Yq8ke946i3HO0P574950Ex6tlGtulUS9CrmT8GMO+PsCiWiv54NzXqK3hAPU0pQE934B84uN9aMy1LkgbbreQNUVqm7nBWnlBgjlfuWzK4m7211dpaWjzISo8H8rw7p95OSt79v4JPVJGvXUU9u6i3rkxr/WVrv5hTeT2tRxZMWGur9sURb+i7P/DQfrhwwb7++hu/u1/HD09nGDClu7a1XNmrJwXtJAowVIOuEqDfVMboUYhTUxN+F616jlFjYbBDBWdfG1fiLUneBD+ubc1VTjx98tSPa3rchR4PoXLdb+qVbDJlmZZWa29ttYQl/U58lYF6jIfyuvaXkdERb+xRT1Nd3T12cP9+a9Pjeeq8dE6g7ab9bWJSPcOp162E99am85o///nP9vPPv3iDrn5Tr0N6tEaL8ogCEXR8LeZtZmbOg1ZGRvQ4mazlcwUvi/VIMzWgffPN1/btuW88EGBG50oKkkymrK1Vj+VL+PlLrpCzYj7nj19TA7KOEXq0YT6fs96ebtu7Z7elwsYopTsKSq21av6rAmCSSe/OXz0IqacYBSyoe38PTvM0BD1xBZ5Fm50tWDY7ZWPj05ZIDJnWR67qNe+TTz8y9Z7Q09NZOZpXFf21ktK8w8q6vpm2G7du2//6X//swQxqnNPd8drHg142Wn3/lqca7HScyeVylp/L2azy3dSUB2Lv3TNmu3fv9HJNZXh1jtP8coWSjU9lbWRi2hsJky1tNjM758Gp644U7oI6Zx4em7Hvf/zZvjn3nf144YKN6lE9s8Ed+zoX0qMhFSCg4HINn8nOhuXmmOd7PRJCZb96cHvj9VO2d/dOS+k5KtUvZQY/TusRjXM2NjHhjwXSvvjo8RO7dfuON5L+6c//6gFpQ0Mv/Fii8lznrepdKJ1SwO6cFXJ5m53NWy6f9/3y2fORmqk5AAAgAElEQVQXHqiqR2jpwPHWmdPWscLHsczly56OixcVrBL0TKbem3RtoOBMzU+BHQrq1v6ifUtBXHppP1H+VyO0zp09iMF/adw/yk8qGxVY+uDBAy9DlA91Ha9jqPJm8FJDuR6lpkeMhYcivXkDetlvJFGZlUyl/ZGXenSZzm9zhbwp+Gnw2XMv93b29duOHYsDH+JrrHPS4eFRe/jokffyOJPNWbGQ80fp6DpEgTA6ZzxwYN/iILf4jJT0snkgrgJZFXgeXY9oPn39/ZWAFdUGqG5hZm7Wxqem/BxdAJN6lJS2V8QQn79m70ExwTFbZfzoyKgPGxh4aOlk2vfnr7/+q92/rzSPmc55dATXNaSCeDTj7NycL6M4m/Np9bjBFy9G/Hxax4W//d3v7M03TgaBZ5UDVp0EhenT7hIEjujGijAILNyH/IRE44U+s3NlD4RUwJJ6+dSxSXlRj3dST1jqjVABua1V50Q+u6pkVC+iimtzfI1Wwntjy/n58R//+K927tx33jPh3FzWA9pSSfXWpKAKPa5Nx+ySX6/rmKp9Sudx6klEvbPqkWN79u4OrhHDi4mZqWn7/9l77+e2kizP94AEARCg90YS5b0plfdVPT1vunvmjYl4sW/3l4335+2LeDszu9O7M1PdPd1V1eW6vJFKKnlHb0RvAJJ48fnmTeACBEhQpeoqSfcqKFybN/PkSXPP+eb33L59S99ehDijDydhXr+Zr1MF8rlOaGzm0JynLvn2RlHWAThn1/XtpG9H6iJUH4RUHhsfE4Px2+++a/SJhPkVQwtttY75fcIam5o03q8TPpOFOfTTy5vqGxmzhkeG3Zy1vt6effqpQh2GXlU4xw55WlxeNr6jGM8Id8Qfc+WLFy9ogcd777+vsEHIirLRN5J55i7YW5iPEbazQW2kJPkn9qDCqPjEyiIqeCSBSAKRBCIJRBKIJBBJIJJAJIFIApEEKkvAf9BXuCoDjmLsOmMOn9nO8OUcg+FHABRgCIFKeG1jw+aXlrUClA98Noz3LU1N1tfTo3i6AioEq7pIlA9u4j2zEj6TSlpvV6cdP3zIeru65ESfx+A7Mma57JoMVU2ZtHV3YTBrsVSKkBiY5WUeEHAFAz9hO4jhS9oYAVxRgwLHnPmO57RtIwd3Q/T/ThLwIkSiGDeo+w8/+tiuXb1q09NTepwVdcSaJ5Yyq29wnuNMwsCMs+P+HCuTlmxZhpZxy21syCnNKrwTx49ac2vzTtkwcEvQ/f7uP35vv/ndf9jo+IRz/NTXGSs/ocjNNKWlh81NLcorzlicigsLc6KFxkiFoXJ0dDRwiOF87bRMY0rOyGqZkAy8rvlfGUO54iVU7elq551mYwDCKM2v/1fpCWxgACDe/+ADhQFCFmyEvKHs/LW2tVprS6sM/xhSV5dXZDheWV4SQGVpccGWlhYFtiH+NHVWXwNYqFJ+fjLnUExWxIptKSYHJnLCOY5BjpXqOF3QScLjNGWIR+/0hH6CkGc48aCyZ6Xt0vKi3Z++b98sfW3T4xMW29i0V155WeEZGqFdprrLLYGBGrACDeeUnFs4zBcWbWR42NZW1+x3v/utXb58Vefov6CebszgLEoIQLO6sqwQA0N791hDPC7nvDO2O5AgLAPOITsjAyKOJsJhwB6RaW4SfX1zc4v6Rdod4R5w+uL4hG6fcsJM0tX9sbW1dahfl9+pvCxbKhY9lZCDK9V1nrvQYRmGA6abtVzOFpaWtHrw3vCwmAbu3L4tJiEAAalUuyimif+O4woD6b59e40QC6xm9W9DroUtyHPRWfPgrbCQ5k9sh7LhmJqeuS+n+cLcnBgoMFA3ZZqsq7tLITza24khHxdYBQcUQArnOF+2NVYkT0wqjMBabt2SiaQcHjg+AL/glCX8UnNTs9IkHj0r2wGl0CZwOuHEIV0M3DgdY/V11t/fb3/xF29aT3fntlKT1sRiRt5npqZsfm5W4NPmTMbS6Yz6anSYPgsmHvIDuAqACgAznIU4DQkZBXCKEBGEAuxob1P5q78cJ5DTWbQG9iN0EP3DafXvb70lwCXjA/lg3KIdwWiDYwPwD8xTzDU4x4b6+flGeIUy+hltFSTgiBIqXKh8ij4TMKzqfXZWoDvCcmQybk6Bg5X+DV2lIqSTC4taMU8ftyygRVasTThUCGUDu19fT0flF/qzwVyReoR9ELAIgJl7d+7Ye398TyAW3sm7CZfC+IETCRYvwKvo6uz9Oc1vcNTDGsXGanccYv/xH7+zd975g8Zd2OY629utpbVVut/S1Cx9WwXoOD+ncFOkCZMUx7AOMC84dvSopRsbNYaFFmj7EhR/mZsEfSP6j/MV9pibN24q7fHxMek7jk7SY67W3tYq5oClxRUTgF1AzQWNF4RLWf5y0SanJmx5ZcnefON1O3LksKWSzjUTvKr4/kdhD73czAuEduv2LTFXwFqwAEAwRiiapNGntne0izkpnXagNXSK+kRHYbygjvjLrq3KsT4wOKgQlKSxdaskKTf/23pvrWcqpVn67NJyTuEsYA8gdAt9cH1dneq+s6PNWlqbxWSBTgMOXZifE4iUfn9hcUFALhiqALvC/AfLVCPy2SZUIv56dJb2ASMGc25A0l9++YXaNKECmSPQ3xKKtqm5yQhdmG5Ma+yhT15eWpb+TU5PaU7GGAC70fLSksCSPHegaajyXKxUBAKrfPrZZ/Y//se/2JUrV8WmBVAFgIzGvaa0QmYyJyOsDXmHPYA5E85h8tM/MCAGi+bm5gKgouw1P9ihY0isF4sPofnS6SYBgnCgAyCFpZRvbR/+kTqNxRyzor6Rgy+UttZ2O3hgyDKZRtVjX3+f1cXrbQNgcwDMAbSyd3CPtRKOshx1FSohIffo56hX2gSAN/pPMcQtLmqchcGGa5lMast0OZSU5tKAcpnXCBQYj1u6qUltqrW1RQBV3R+ACLQfqH6tYy/3aV7KIor1dYGvbt+5LZaSudlZu3TpW9kXCEPINxFza81J0hnNIwDC0zfCigngFkAi8yNCAmaza9bV1WmDA33W0poBZcBsoaSIOx8EJaFcvlDB/tpaXnO4jz/5REBjWGg21tclH8LR/uVf/lyhH2nPFbue8pfv3G2UP/GTPgY0RdhSQIfMFzc31sX6AbMJrELMGxob05ZoYMxel67Tb/Ntxi/tm1/CKjEXpi8EmIqYmH/09vQaYTk7u3tsdTVrUzP3tehlY9mBYtKppA329QTjaL3qX6w8eQd6bmttVt+BrcyBPoriBHS2urJic7P3bXRkxHLrWY0hsHQxx2cOQZ9DvhjP+T5lXgCbLd+09IeMR4T4ee/992QXI4RWqjFpEGiiSjtVN99VtH+Yh65cuWz//u//JiYnFhMwFhKmlu+0dJr+uUEgP87vGRzU90fDDoxbxdI+/nsRYOXxr+OohJEEIglEEogkEEkgkkAkgUgCkQQiCTxMCZR9tWKfFwzEO8m9o1yO802t3MLQxXbi5EnFkv4v/+U/29Lqml2AOvWdd+23v/2tsXKurbXVnj53zv7ub/7GDh06KMcPRvKC0VZhYVzMd1ZO7Rvot7988w1b38zb+NS0/emTT+2f/vGf7ObSoiUbGmzP4ID97f/5K8U87+nukROaFXgwEWxursswBmilsbGh8CXu7TtFSw/+DJ5xFp+wnethivXxTgupOvYGb/GANQdnHzTfGGQwIDc3ZeTAeOP110SJPtDvVt17Uzw0/jjN/+XX/9s++OhPYtfJxzblVL1y9bqxioeQChiJYtUMH3IwEOM5Z7/+3//L3nn3jzY8PGp5q5PRua+/106fPmU/+4s3bWhon3QSY7iMQasrMoRiLH///Q/ELoDxEecY4TAwSmP8fvqpp6y1vXlbC4/XM//rQRIyQu1kFaqiLE7K7qJ3NHGk5LgYSpcF/MSt/2//73+TsQr1xtl75MgRxXonBMHAwIBWd6H/tEGM3YAlMHDx7Oeff24Xv71o0Ej/7Gc/s6bm7ctcJds/qdNOhqwg3ZATCoAEgJUPPvzAYKthBX26MWWvvfaavfTSi3b61Gk5bARwYTXt+roc4l98+aXAQJ99/pkc9rm1nHT3w48+tOaWJgHv9g/tK6kTLwjpBHq6QTgmbnErsjEqQrvcEL+plfYY8Ht6uwxDM2wXR1mx3N9rjY1JOcxYmZfONFpjKuGTlhOH9nHgwAHV9ZWrV+W8OHXqlD3zzDMCE2JUxKDIilAM8rD+EDIGHceQe+3KVbXdjY2cffXVRevp6bfz585bV2e71VcnqggpYBloJRYyyId01K8YrQNwU18nIBaMIRj3CWc0Ozdr12/esI3cuvX29YrK/KlzT4nmn2OcgwATcChBL+8ZPJxMJeWCXPwOwI5SQI2/8uj+unAPMYHuAGvgQFzPZgVEo42/+sqrGiNp+9Q7fRGrIFkFf+nyd/Zv//qWffrZpwb1N6xkUJ+jCzj2Ce1Df5BMJNR3v/Lyy/bUuXM2ODAowzT9PGM4oBX6zLfffUchHEh7Nbtud+4M229+81s7ffqE+m76mEqbhmAxXtUJ/LF37x6FwQI4durUaXv66WfsqaeekkMBxwD6QgcMY8bY2Lh9c/GCvfWb34j6n/ziRIS6nZBA/AHYqbQJ5KXwEn7lMoxwmzY7P2fXrl9TH0/IGZiC+nrRwZN27qlzdvToEYG4cG5QVhgHmprTLvyQI3ATsNf3ydLGcNHD+5Uy9gSdw+nrt/C+P1fpF8Bab0+PQrABqsSJAugEJjT6S8BD6A69q1Yz5/Ny1n700Uf229/9zj7/4jOtwMexDhvBO+++qxXo3T0dAv9Vrh43U/HtTSv4l1fs//vv/902YMAys/6+PvvLv/w/7PnnnrcDB/bL0U578wAGwLt/fO99x8Qyy+r9TRseHbW3fvsb+/yLL7TiG0caDA7Hjx2z119/3V5++WUBBdAxAUvyeYWu++STT+yDDz40xiIcWTijAdh+9Kc/aV6DUxpnVMVBKOTrJN+Ma4C/AC5SHQCxAP+88vJL6juQKcAvQGKEusC7RaiRy5e/s4/+9LHaOH0HQE7CuL33/gfKM2PNvr39larw0ThHW66P2dLCon399TcaHxUaJxazjo52jUl/9Ytf2LFjR3XsgPFOTwAW0zcSmo1wmIRxoC85efKknTt7TrpRrT/clXBoPpUVtuZk1tY2tXr/3XfetUvfXrT52fsCMjDXOHnyuL366iv25htvCOggoAZA041NMcZQrt/87nd289ZNsWbAzoMOMtfu7uraFrBCBmEZ8H+A/27evGljo6MaqQGkHti/X2FBn3v+WQGB0WuFYCMc3Sbtekkh5P7pn/9ZbI6E4ESHyQfgExi+ABRu56BHhMurGwKf/eM//pPqiTAbPINDmv7k6afP24svvGCHDh4QGA1wIu0XBzZ9CGBnQjDuG9qnPqijs0Nz6por4SHcCKi4q7PV/v7v/t5++Ytf2sqqGx/feeddgZAuX7osRoZDhw7YL3/5V/bqKy8bTmT6Fua4Yr6sqxezCixqhCmbnY2rbwSUkYU5VaGE5sTmBjB6i/oFJ9Stx0xj9BdffqV24EAmLjQIzBCA9ph70m8NARrM7NlWCrncphZBwOIjtspYnfHtv3fPXquPh1YHbJvK9hfJvv+j3waMBRCLkERaLFMXs0OHjir8GfoAmAcnvYALsXp9V9wbGTHCyf7P//lrsdzQZ7AIgzB2sHCxaOe1V14MFj64ucz2uQquxoLv7Ao3Z9fydvfusH300cf29tvv2s2b19T/AJg8f/68/cXPfqZ2BJByO4BRhaQf7VNB30iEGsb/3//hbQEyQWsyxh09csj+4e//Tv0yIGy+0QFbMNYyH6EPmpmeUbhMFjZ8++23dvDgfjtx/LjCUHmWH1go/8v//Z/FQrSykrW7wyP2+7fftXfeeUff04ydhw4M2f/1D39nL77wvEJuoWdsZJG/uvqYJVOwFxa/6YJbLN1YH/Qtx2ULwdaFDePcuXOqX4Dh1C39EsAS/uibrt+4bv/+72/pex6gC/aMe3fvaTyi7yY0UEtzWq8Jmq5/ZcVfgHl37tyxzz/7zK5evWKEuuT7i+8L8nLmzBk7eOiQAMC0d9hDyRO2E5nZKqb65J2MACtPXp1HJY4kEEkgkkAkgUgCkQQiCUQSiCQQSeD7SKDM8OnAHFhwAlaHYEWcN+iEv0CTybglE02GTyq1um6tLS1ajeasP44mNJFMGEYBYk43NSWKliHyHF5siNG8LmFpYj1Dp76ek7HUGXjdijAMADgtWZXS2dHqPvqDlV7VPrxJi9VTbDISeAeagDicddd0Q/Tf7iQQiA5nhww92ZwtQX27mZfR+fz5c/bC88/b4UMHrKe725oypd5vWFFYLfSrX/3SWto67D/efsdu3bwhg+fM7KwAJNAbQ3nfiQOyTFeV2bzZ9MycnAuXvvtOjAPocEM8aSdOHDOM3i+99IIN7d9nLS1NlkjUSV9JatMy1s6K/M526+nttY8//lSrh6anJw3D7PUbN+x//+u/ynEJm1B9PU7O6iIqgkpwYACiCjnuqz+27RXKQrgJ/WLorygEc87mu3dEz47BjdWAGO3/4e//Voa5/r5ea8o0qm35JsCL880Ztafurk7Dafzqa6/I8cdqTbdafdvsPRIXUVNRpAe5xUmCsw5nPobIN15/Q055QB9y0sWReXBzHh1ttkaYalpbtf/NhW8EYsGQBysDqxoxviNjDHXVQEqqQ2SucFgbMmyvLK+I9QQQxunTJ2WIfOaZp7VCjdXt6UzK4nGztuYm9VUwXEAWw+Z7Loye1B3Ozt6+Pusf6Lf+vn7r6ekR64TCcAVO9U1L6jlWz6MjNCpijX/6yWcC7wDYun37rl248K298MKz1tSwU8zzoEEU2gW58n+Fk4Ew3RUcykB3uAu6dsJ4IUf0Ftr/s2fO2DPnn1ad7BlwK/VwpDU0xKy9rc02BE7EyVpsDfRBftPbS15dcuBve+R+y8E3hKLZXMsq9AgrQI8cPmyvvPqq5LZ33z7VfbwoFttoaxaDAkwqrW0t9i//69e2ka+Xcx0QF47AjVzOOjs67eTxE/azn71hx44dk17Td9AmfLvY2GySY50wToC+CEWFLoul6u5dAZA6O2Dq6asuZwCrdSYw6y9jfyVgYEtLi3V391hvb691dXULqMI9eq/8U2npbSrdqHXK77z9toAqrEJlFejIyIgLi7DGatRE6RyDnBC5h36U8A6E2mKCsJGXA5LV1FyDkQYjPEDF5559Tmw+zF9Yfc4C6Y2NNpUJ3C4rVf1WHvwNPeR9vEf7/sbot4IEtpcQINO9e/faz3/+cznhmBcyp+jr6xNwANCh5pOObV/pM294+aUXBPjb2MzZlWvX1O+zavrevXuq88OHD1lne4vqJ1SVW/KntheEj5ibnRMYF9DCX//yr+3smbPqrzPNqRLH4MZGs7388ksKyxWnj/30UzESAa4an5gQ0AwGDlZ7M08CHHbixHEb6O+zZGPRvYFkCNOH0x7GNPrM7y5fFiU/4Yq++vIrO3v6tMZ7B1jRpDcAZW8pSsExByMeDibGgqGhIXv++eft2WeesYMHD1hXR4dCSAhYhmAAwGbSmovBLkJIto8/+Vj9NsDj0dExgTRgv2L8od/ZTp5bc/XTOoOjmTHJASQ3rSmdlsPyP/2n/yRHHSwriWQw/gTyoZ7oTmAD6erqEqgFMCEr4AcH+y2RdCvzH0pJt28uodlB5bdNTE7a5198aZcuXxITIqMxc/E333zDXnrhRTtz5rQNDvRbIlHvSCFIJm9a0Q/rCSwXf3zvPYX9BDQJ0xfgDeZAXV0d6rv9WFGSAymUC68DaIUxLJ/NiqKqvbXVjpw/r3kMTlXmNLBmMe7zGLLll+/JFKv6M032L7/+tX399dcKlwETEf3/9es3jBAygwMDFk/4iVwxF150N27csAsXLwpUQJtkDgbgijEPZ/+pkycNkH1La4sl4uTZpdHe1i6WnT1799rZs2cF7AbkTZsgf3+uTd+2Cg1ilkkn9JfNEapoTeAo2HLIDmA4mG+o33bYSRsTOsc1hbMTgL2Y6waYUVtaxJRGSB3mBTDwTU5OiVVnfT1vifBHRFBm1ZEBWFmzazduCARNnwX4FZAHgOTZ2ftifQDwMzk1Zfv27anaUWSzmwoT5UJHZtVHM7fu6e2xvv4AFOcrs5j9B9jjW61oJYD9h8UXqYaE2u6ZM6fshReet5MnAUYOyAbBnLtQ1TGzxswRsRiSr3/6p38WAHh5aV1l5TsSABtjkRbY7CKHrngub3of/20yBzG7dfuewli99dZv7d7IsIBFMH2xQINx59Spk2JJCk2N1Yb5Vv9z6ukuivvQbgWscn92XuwzLAwA7ER/Q3v95S/+yp579mkB+z0bWPjFeUtrfIfJF6DXG2+8qsVWftyLB5M+5n9NzQBNEpZrziiEG6xtAppa3upjeYvXxay5KW2dHe2Wbk6FX1PYpx0rHFdBodwl6p5vzrNnz9j/81//q/rCnp5uzXsAZGMLC8/veaqtrVnjOe2EdvfWW28JxAJoBaAYcxDGeg9Y4RneU/bqQt7YmZicEPsMc2zmTvSryPHVV19VWox19JvxuPum21gHPONYqh53PSsR1A4HxRndDjdGlyMJRBKIJBBJIJJAJIFIApEEIglEEogk8HhLYLtP0O1KjiGm+rPhK9oPTvDjV8251INUAoNa4bmQ4bEkF570JHDw4NzFuMMncAwDC7/BPXpXycNFY6ZOh77AZfAJWGKclaaQk8iLVCbDWg9DEgxMHW5lEo7keL5Oq85xvrNaF+d7RgbSstQxPteZpdIAS07YRj5mM3NzWmWfnZmx1ZU1GUhZTX9w/34Zl0q8g0Fy2dymVvK98+47NoLRLrtmgKS6OrvsxRdfsNffeNWOHz9sRG7w+ZZOBHipTGODZfb2O4pdnEHZnH366Sei+4Z+//PPv7CXX3pZFMu9vZVX7aNIGJ2w/MiIrB32/ZvKyl7joYw9AFb0h7Xca74vSTEhWAbGRsdsnZjzUKonU9bb2yPnHr8Y3NlkZ/aPBw4AVnglG9uso7vNbPNw8TXF5B/pPXqPTWjJiR9OTyJe+k2tBj7/1FP287/4mRwTmXSytIsIxN3YWG979xJqLCljJMCKXDZrhES4PztnN2/etmv7bjhq6M4O6V9YYBK3HOUuQRkoN/O2MDdvxEEHDIMz9pVXXrIXnn9BzBbJJCw4RUtiMrnVA6h01e+adXR0WqoxbQcOHpAzJZHY6hzz8Ck0oTFRb3v39NmLL74oZyPsFPNzC7ae2xBDD+EQAJyZVQasOHVXrxwuag379BXOg09+MGxOTk4ozBFOWVbtvfbKq2JOOHhgvyUTrpTIjPaQ0HEp8I2X0kaKLdxLpobsPEK3uJHZyQ4UBHpMPeCQwnF/7vxT9sYbr2sfp1TYp0QxAT51d2Xs/NNP2eLykv3pk4/FMAXwKruWtbWVVetoaxfYkL4TJ01ne5vFGwK0k5eVmNHMBgc77emN83JmEYKMNDCMs8oTxibCEmwLWCG9mIlWvbWlTc/i9AOUJecgRfUoEAoaZIM+e8+eQRn5J8bHBdKbn5szHOcz92f13pWVNa2AFnjM5zvQEM0jOBeAcTc28gqfQHg62Ir2Dw3Zq6+8Yi8895zCrTQCHvAqxXxmq/qF3lC6qyHge44DpSk+nkc7jZQNccBqLXb2zGkBQQEGpmETCZzIkkqQiLoCMwOvtGdPn9XVPW2ED5m+P6OQJmvZnML1ANJijAewUmmj2op/AQgEtcnnxawCuwvtjZXElZiocBTuGeyw3Po5hb+4c/e2ra7BjLJgq6vrlsutic0LoOQvf/kLORjbCdkRLlOgs+lU3Ib27rX1bE6rpSfHJ2x5eVXglTt376rPZlxik0OyoLBbS4Yqcw+MGfSb3V3dWnX9szffVNtvackISKbORQm6TMQTMevpbbdk6qRAraurywIX43xeXFiwm7duiXXi6JEjAuGUO9O25uSne4bwSFOTkwL08P2RzmQ0Rj/99NNioRBjQVhpGZ8Qk4A9cWvKdNqege1Dou1ceqVY/bZAP7fe4L6Xtp53Z1ZWcwLjfP3NNwJuATQEtHT40EF7/bXXDDa+3p4OlcW3JT2JY74xbvv27hHDBKBu+nrCQwDsgV2RVf8HDxyw5uZWASO25KEgM/fNAGMJHTEhePoH+gTaArhF/86cJ9wWfF6Yy/f3dVp7+0su5NbsrI2Pj0uXAdwSlnR4ZEQsIfHE1vkLOPLllazBPgLIRgxl6zkBTgCw/c1f/0rzot6eTtcOygrBeNja2qS/fXsH3Zyx7J4/96GGJ80xmeMzcKIcxKlDJx2bIsB3Msux33TOYSDUlVI9ADYBPuzbN2R3h0c1LwTQAyAUWcE+lkg0avws6X/NbHVtU99tw/eG5dwGLA0DIeA+5pQzM1M6T33B6EZdlAAqfMZgwFleths3boo5B8ABbEaAq/v7B8WAE7rVj+zuVzomiQS3hPdLn9IRcyk/Rkt2JvbFdEuj+sPXX3/Nzj91zvr6eg2yqUpbprHOhob6xAwIYIpvsRs3r6v/YB4EoA/gD+CFumpsoaGEybGKESwc4hLHVGkul7ex0Ql9m37w0Yd2+btLYuog7CsA/Ndfe10gSuaElWVLSjvIJJSXR3EXffFhI2ERZa5cFzc7cOCgPf/8c9bX01UAoJWXD8mkxHrSZeXf/NKTCqKjaQkgRhOTLtEHs7nf8rl44Z2FPjz4wAkuuLp3IdYY99tbCenbYmnYg7fZwNK0tzUL9C8Wza++VB+PXQDWnxvXr9va6kqh9itqgu8+YmC58/rGpZ9fz+UEIoS582c/e9POAdZrSpf00WStHpBgHpT5Nhl9Ai8Ve90nsPBRkSMJRBKIJBBJIJJAJIFIApEEIglEEogk8P0lgBPMfTzLCTur0akAACAASURBVMhHJ0ac4OPTucjcoS4FL/TONP/rP8605sJ/ffvMhR/05/j1DwWOdd1WeNYZ4DDGaQUL38NBnsJJVN2XYcBbB6ploOrT0QXVQyAG7RdliNNZhpx8Xqtyh/YN2tkzp+zIkUPW3MRqvpD4eDacFk7oZEwGasKgsFIHCnqo1Qm9gCEcR2S1yl7ACHPzpqjyWYnHc8SbP378qL3++qt29sxhS4TAKuSkXG3ITldHs+htMcRg6EunM8rm1PSMER+cVXJbHgyJQw6gzU3JAaNiwQAaKvpud70NVc7pwkHlVDAoYUwm0zLsJqAZTglkkWiAgj0QIYUP10G5MGiD5ecqv/IROgtjSr1Mh2BVYFVg5SeOwueee1a6h/NT/Qll93++hAFQQuGhzp+3p546J4M56ayuZRUS4bsr39nw8D2xTfjHwr9KUgA8l3jM6rTqD0MqOv/C88/Z66+9YqdOHbHGxljBYV9Ig8e22ajjtpaM9fd2WzLhrOq+mn1zCxeLcxwf2D8gObBiHOc+52lvs3NzakvbvNJdEn5ih8yFE1EmAuCQMhELqN4JudBpb7zxhr380ot25PCBAliFx3fs630hHz/lLUhPwDXKVxjLHFsIfdWBgweNMFAwSQFWQV4FkQQpONegWxXK6vVTJ0/I8chlmEVgt+ns7FT4Gxw0rAqNJ4Ox3ydWVtX9/b324ksvaiUy+uNZpeiL6JNqIZmCeaClNWPtHS2WSBKeIJgL8GqwImV9EllIJesVIvDQoUMCxRAyCNaU5ZVVm5tjzFgr5KUgwGCHorh5jJsP0FevE1MtD8tAi0KivPbaqwIQlIBVeL6s/OVpbz12ggs/Ft7fev/je8bPHR+ohDhj682aW9LW2tZk6UwFsErgKFL6wVwS4BOsTK+9+qr19PSqIyEUHCwEiwuLCl1YLT9adR8wxqEj1CTzT8AyR48etVdeeVXtpcSJ6ZSrJMn+vi6tziekUTqdEmMa4YXYunu67dTpk2KBgzmwMAaVpOAOEgLttIlJCRYiWCZYSb64tCwnMmwp2shDhQ4zrHearwTj4N59e+3M6dNiOmppzlR2cvpy5WFaabQTJ44KjHxgaEiOulwuZyPDw3b1ylU5pjku5MXtPVL/A2QiZBoyRVaEpIKRDWd+IbwGAvV/lC4s4GqlRY5btnAioYsV7y1ed5er3VT5/PoG4aWmDYDh1evXBQbIb24o3BYgPcaE7i5C21RUIQ0qrKTv6+uy48eOa4U9oScZmwAhADC4e29Y4VA2NyrnQQxrAKY2NwVSRL6trS0K/QdQEhaLVCr80VAsc3gvlYwJ2Hr48GExZNTx3bCxqXcDhoCJaMsgKFa3TRseHlE4oOvXrsuRizNWY9mLL9jf//3f2EBfZbBK+P3sV2hm5bf8YMe827O+FHSP+b/0kP4K+QOm39Scl6O6gPqI3sdjQX0GXY8EsLXeWppb5dwHQIpiA24j5NLMDExsC07XQ9/rdL2kzzfYtWvXFHaT8H3JZMK6e7rs1OlTBZDJwsKiQKaz9+e0QKDSpw3nlpZXFPIPRit0hbAthOQjXNPAwKB7YWFuEG5Dft//+hJu9+vu9fYL5kJdXZ12/NhRAbhgtijp5yskRX2gk7ADHT5yRDJDt9Et5kJTk1PqTyo8WnKKUERs5Ej9NEx6EMFtwkiYV8jcjz/9zP7wzjticiGMUTKVtMOHDtvrr79hL7/ysu3Zu0eAr5KEg0SZJ/2oirslUw//BH0M+groaX1jQ22hvo6wdxmBsRAuc9NKurddbmQTq3CD0tGYHrS7YHxnvsDfln7CNU2lpOoIIVp0adOZwxrqHXtSf39ndbBKkBZ50FoMsYI26bv24MGDlkolpUvZbFbgQuY/220O7ujaA3KENRFbDIUg1NQvfvFX9srLL1pz81awSiFdHo+2EgmEusuS89FBJIFIApEEIglEEogkEEkgkkAkgUgCkQSeMAk82Bej+/DeXlQlKYc+vPUUx4FPvGgNcOGF3JWtthLeGTwmmv9wkvr8x1mA40BUto5xQmmVZCRkfCg779/LS1S+wolopyYJ+MqpcLOMJFhJWFlTXy8qXVZqQoFO7Hl33StEhQQCKykGN2i1CSOBgQUDqZxKi6ziDZwfFR6/deu2aL1n5+e02hfLDKFUXn/jNTGMVHhkyymvLuSXlYA4QVtb2xwbh5mxEvXq1Wu2thY4hMpTkFI5lhV0lD82jFvbiK48lQrH6H0AgpHuVk8tk84oJJfei1E+m9UKRuQzO7tQ6jj2BfY3h48r5OLRP+VXlbqVlNRLR0e74oETyodVa6y+CwPmtpRZoJU6a2tvU/gfjOawMQCumluYt/Exx/SAo7zqFlSfjOJBeCfo5VmR/vTT562nt9s5C6tXc9WkucBj4UeDZqliUcX+j3v9Pr/Nzc3W1U34FRfaa3V11Rk24R3fduNpv4X3/bkKv4qb5d/u2gjhPbq7uuz0qVP6I9SHQG7hwlRIauupGvOw9cFH4oyM5fQp6mPIsnOe4wgfGtqv1e1hX0QlaXCOVZhNzY4xACYmpzgOxIXsaRMAWrQ613uxilVWIquGuGl1Pg5HVsnDsALgiZBb6JHs8F4xd1Of4XvL3s0lTkHnDsAEwA7GdMIb8G5Wg+Os9P1wSYaDA7roQl+9CX17nbW1ttnhgwcN4GR/b59YufSiSgnsdI4MVtjkuKhyrcLt0amaJRAoWTAWFx6LmZymhLjAWZVMJgVsQk9XVlbEfFK4d8uOH9PdvNHrCyvZATvCxqA2Ul6f/jjQYUKawB4Fi4ULGefYszbzm0oDev2CXvhnt+TFAbfSjY0KUchcCWcwYOH1jXU5kZeXl5TRSk61cLIKgwUDTUODWCj27d2rkEYAUUqdsn7CHMg2GF0Ih5FKNtiBA0O2Z8+ANTamjD6cNj88Mmy3b91WeDAVIfziCmX6SZ4ScI3QCs2a05LHufl5GxsfFygju4pcygbbWstZ6b5ATx6eLMozV0yZehoZGRUbysTEpHSnMZ12gPFnnlHoVpi4CptPyv8GwGf6dcYddAdWlUTShRqERWJsfEJsEgUAlU9M5UQADhaA0qOrhHrtDsYdwOKEmt2232VMCsYlAJaEPmxtaVW6uZwDowFcVFdQQd4wyly4cEEsYAAJcCgnEgkBcGDcC/mOfc4fuV8n5UrZriCQstvor1rb2mz/0H7JFXA3/eXM/RmFBxEwnmdUn+5hwBRssFp8e+mSxn7e1NLSLMZAQoUROkRjtZnABKOjozY6NmaAqMo36o7++c6duw5QBBgvb1pM4MKPBJOA8gcLM9stF2o84b4VkqmU3oXDH8AjLHbh8lZKTDKPwTw3oD/6V/QbEBXAdtoG4YZq3rRuyAFxGR8QwejYuH3w4Uf21m9+o3BesN3AcnHs6FF74cUX7MUXXrCe7p7KYJWaX/zo3wjgiHA6zZkmIwQmYBWAPbCwXr9+3bLZdY25W4AkWzr2GmURqLBrd+6AfQekZq+0vWybasDWte094YvupSoPfRd/qCtzHsL30LfBqkQbBqSb28aeEk6WUvBNSGccb2iwoX1DYlU5cGC/m6+Eb472d5RABFjZUUTRDZEEIglEEogkEEkgkkAkgUgCkQQiCUQSeMgSKLE3lRzIyFNwHJVdCueisKqIe3Rf8BUeGKDycv67cyJZLUtrq+EhnLrfL3vIn45+H4oEMGxi5B8c2GNdHV2WaWyUc1SrAAObTcGeGK5eH2e9MSnK5ERD3Fj1ifN/ZXnVsVb458tyOjE1acOjI24VFQwvqaQc/4QkgrZbW43VDhMLxskjRw6L0h6zOiuMoHSemJy0+bn5yoCngvI5B1eJsb3Gd5cVy2U7DFKR9T1kpC2TR3tHmw0MDsgxBnAIZ/HI6JiYZy5+e8kmJqaNmPCbYBB2YTOtlK9H7Ryi0io36kIMNDE5SHDOY1Avqa8yuZaUNUaYiXrr6e21wT2D1kEoiPo6W1uF1WFe9PQY2SuuLKb++PPAO4VoiQsowgphnJ9NmbR73XZ5KMlQ8aBczVyZXdHC1wIRFMyyHEPbDvgGZ5bF8pbNYVxfrI1hxTfowktqyLzuDZxWebNEQ0JOWFaz7hkYsEy68YHlUJTI47tH83X1mJdBua29XQ7H3p5egZMwjPqFx9SGrxH/i2TSyZTCYBHnHr2kNqiHzq5O/aXScZdIkJDvfsqlSteXTDRYa0uzpVIYxukDN21paVmrpwvqUdCP8hSCDPqMhn8r3BpeFcu4glOIMAHxekJgxeSAxYmzHcOKki2Afih+3pBDX0+vHD8HhvYLXFDh9TWd8ivbqaWC3ApjRE1JRDftSgIoV0A3EEZsBWls4sBpiFsymZLzBup+dBQGAICd1bZC3XFDcMDqdJzqOMnTPoScT8Drrj8OfnEewdABEwUgE/Wz+bwcSwP9/QKIoR61qEiioUGOOAAw8QZYw9yAjuN9aXFJTAqVEnL9RZChoCNg7Ors7FB5Ors6KjCr+EwFD9DrxAjNCbitztrbW62vr8d6urvcOLjGODin0CFr2TUvsjJpPAKH+bz19vYK8Mx8EtmxwhxWknfe/aNduXbdpmeWbC0b6tRKBPxjljGUpwrZoP8kFNb4xITNLy4I5Nfc0mK9vX3W0wtYJFX6lNdp/xtKnudgRSN8DH0ojvml5WWbmpqy5ZUVzclLE3NHXs/pr2ED5J2wWRASqK292TFs0aK92pUn4vNCwMJk3Jqbmq2puVl3Ad4CsAiLh2f7Kn8cMOO9e/cE6GaezObCqRwwnLEl7b784Z/8sVdEB6ryonK/MZqv/vwcofyX+5gGMh52dLarfwBoR3/J98/01IxYLyUG/ypAsHVmkJQRjunKlauFxQOAoQFkAxCnr+nscGGyCL8HWIV6gIGkfMvlNm1hft4AtcCSoTE6ldC3GWmRz4e5ASzhHxv7HhhI+CvmN9pCuu9OlP0fAA0ASvCncIR5UztYWVlVuEIxuZU9ttMh+gh2HCDYF19+ZX94+w92/cZ1W1lZtpbmZjFjvfzyi/bMM+c1DySM5sOWz055/Kldb6iPCbgDc2Qq5b4n6A++u3LF3nn3Xbty7apNzcwI4FzaTzzAIpNALwoyD0D5eRg1oQdUR1a46kTFYdkpL8Mqp/3lmn8BETa1tKiPZYZP/7yyuuJYfsrzHEpVl5S/GOSuYoSjHbOogpCzzPWV94eV0dC7H+fdMA70cS5nVLZIApEEIglEEogkEEkgkkAkgUgCkQQiCfxgEnAOl9qTx6BSzZZTS1rh7159Jwevdt/9YaO533fvK3+umgGgaPnk+drLFd1ZuwS0UhLASjpjXRixM03G6vsdN18fgAHi9Vqtyy/MIqwEYmXa+rqLxV4pLUIG3Z+ddQ7cmAmw0dPbY/0DvZZK4ZhyDkkACztt3MFqT1ZPd3Z2yRlM7Gecn3OzszJwd3a2yTmzNS2exkDFFbdydOs9uz1TbFWFvYC1pbw0rDpkZd/AwICNjo/b6uqKTUxM2PsffKTVZEtLK3boAMamVks3phW6icVThXD2vADr9WO6yVAfGOPRBcKdtLW1ihUCHSmoB3IoF64HCATdDywrOCxJY2x01LJrq3LQiIIaR836uiXqt8YadyxRAQ91XZ2cp6wQhs0Ch028wYXkKX99oe7L6sbfV36d8/4cLCs0HxiLWI3PKjvlQz5YRzW+trZqrJqXJ8Ogj9+w3HpWToKyV25zyFt9jra5LbgUyzsHAbJPJZLW3dll+/bskaG/ZIX3zkk9OXcEIhbrGDUsH32dZZoycgQRUqR8c+OvqxdfO7SFJOwKnZ0KjcUzOFdwqsNO1dycKbaHIEGNxeWJBzWO45tVvoSiEubJTOxYOTxYfvMv98c7/Qb05jhqNjc2BJ7a2Fy3jQ3SJMRX3DbzMa3CRq8JBwGYYINxI5cTEAGwYbWtcCVw4KGDANj2Dw1ZR3ubfS8dVDgm/wb/Wy0n0fnvJQFCixDyQmETHBMfTDv0c25VcV7O0/nFJYUFIKxErM6BKeint7BAhDJTGBM4F7BBsHKbvr+ltVV9bMk9oWfZpea92tfH6y2dbhTAqr4uZusxF3oD5yt9v0C9/qHwg2VpAkYFrJJKAtIidcpJe1uRM4q+vTCOV0jHaaMbyAALtLS0ypmM47Ow6abwoMgVPz64FDiTSQM06LC+3m4bGR22bHZNQFnmZAA3mbc1NDyCk4q6OoFV9uxx4/L42IRl19cV6ub3f3hbgAiY+PYMDkp2rGBPJOJGqBz6v6pbhfqoeu/3vlCsJ58UqrGWyxpshPwxt+auTKZJgA/aDICTXA5mCDdvDibQAmzlmRtsrqsdxeoa1M8y76f/x+nLH2CRmZn7YtghveqbG78AjwHiYk7V0elCERWeqSbL0HnyCWsS4ZrIK++EZYtyeCahQnrBDm0eEDoAL8aoGAxv3d3WP9Cv+uQ2zQnZCb2rPJ2f5LFWfvi6Dz7MfRmcyAugFeXfXysrDIA0GKm6u7sUrokwQEtLiwr5Mzc7b/mgagv9X8xsYXFZLESwLCFjdANAOGBsABxdnV3W19drI8N3xWw1NTltY6NjLiRk2fsBiE1NTdv0zJQxP+U99J+EYuvo6Ci7+3seBn27r2ve1djYqPwSRq6AOdjmNYjRSx2wC3klzOJGfkNzb4CR9IuEp6l9I9U6AeBnl5fs4sWL9tFHH9kXX3yh7w1A5vv37bPnnn3Wnn/+OTt0sDSMZu3veczupCJgWm3NWH9fv+Z10zPTtplds9t37th777+nby0B5AcHrKOt3WCZApzI+O7g27uQCe8LKp/mp12UqKA4gGA43kWa4VsrPEf/5MDbxdBqzIN0nl9AlisrwbHrz5gXwSxDH8mzCr0Zfk9ov1AGNLC+Tn0ATHDMfWBS3LrxRIWMbr3xiT1TiznsiRVOVPBIApEEIglEEogkEEkgkkAkgUgCkQQiCdQkAX2thu/MO1+mnDulH6Xcqtv5Ug5vZYf6ci4/F75/y777yOdD333sOyM7liudK7enb3nenZDdIAAQYECL1h5VEdRDOI0zKJVKWaYxbawELmxQAqA2papTuOzVgvrheZhatGJzE8f5um0E8aALD4R2XHxlF6ca3YDhBQeQf79eixJU23g5+at3BiCcn329vTJcs7Iuu7oqxwsMGpOTk3b44H63nDCUnrSqYPSsk6FWFlbu2ebVoSS+9y4OE4zuT58/b3/6+GMbGR0RS8bly5dsfm7O7ty+bWdOn7ajR44qBnxXZ6dlMNIlWQEWMtB/75z8RBNQf+GAROgZq93TmbThSKTrcjpIz+JWoaoUQd1xTXoU9HWNjWnRLbOqV6soA2YHwgawktI5akL6T2K8A3YV/gScceFcCEMFdbNACFX6tJ1UqNJ13gGF+FpuXSsx11bXjFXvyzhpaFMCrzgn0/DwiBxNOH1V1lhMbRA57Wbj2do3f3dMDieM74DdAD08/M2/6+Gn/OdM0Y9dbkxEKV09wYwC0E7s3X48DjTarx5VVQZhqFDmhkTcUo2NhfEQR7j67iBsSnm5vCO2kiS5htNQbSl4fzabK3FE7VKVBLIiBBsr4FeWl/W7ll2xXC6rlaJEEcDofm942ObnF9SB4fykMdP+GD98qy4vS/GYBucaN05nwHwd7e0GoEBjAr723TWB4J1bpbTrZIqZfOz3nLQeTEJywuQ2BEpZXVkNftdscWlJlScHdjanY1h/2NTfK8zkpoCxnKv09pi5sVzzxhhgBNfecK6nGlNa9V5X1s2HK4tyka7TxE05enDuM2bADCTWlUxGAJTwc9r3D5ddgJ0FBz9tDYAWfQBtfH3dgRF31vngDspTX1do84RhZJrF7LqiMMrywSH9BW2GVewwMgBWwFG9vLSs8EAAWBoaArasCs//lE+1d3TYgf1DduzoEYVRWFxYVhgTwkMCBD52/KidOnnSjhw+bL19vXLst7W6EJi77esethwq6TLvQE9WV1ZsaXFR/SmADvrMhkRCwI1bt28LpED4E/WfPrxl8JsHpYCS1AFSabDs+oaNT4yr3hk/aGs45ucXFhzDynqpcx7QI2pNPgAW8kt7iDfEBTgBJLDbDcZA2hP9twAqm6a00UM3BgQphtoT4F1kQF7ZYOiCNQldhilEbRZcsXddVxPobjP7Y9wfyrt2qyFPy/IG+KqxMWk9Pd0GGP7O3Tu2md20ublZm5qeMhhS0pkmi9cRotCzq7iQWbR/5rkwQAFYOXhwv6WSjdbb020DA/128UJS/cTCwrwWATAXLd9YhDA8PCxQEXpFv4d+HDp4UGw4hTYWqtfyNB7oWGaGmMALzS3Nyr/eVQPuzs+RUsl6haERCJxIRoAqA52XsGrMGEUDVEjffu3adfvD22/bx3/62O7fvy9ZEO7l2WeftV/96pe2Z3DAkn6BRjDuFGRU4/seu9tiJhDPqVMnbGxiTAyYMJHBADQxOWFnT5+xkydPGAyX/X191tffJ12P11DX5bKijvWnC26fHkTfUFREqB2WPFvtfPimsI7DtrNJyN91g0mQsMn0Y7AQAdTWd13Qt8LIMzMzo3tlQ4MxNk/fy/wYo0f1gvJKbcx56uKWaWoywnrBtlS5LLUUxCf6ZP7+EF+2T6Yko1JHEogkEEkgkkAkgUgCkQQiCUQSiCTwhEtg6wfo1jPBtysX/EU+zotfu4EMi44hZw0MiZbnwh/kwbGMjTh5MQR4o79P2tMl+HeGktt2l/t3+8y2CUYXkadz6LBiOC6GlEZWl2H5rXFzVeIqp1DfHCpsOKuFMK6UbhhJ17IbiguuePWBjhB7HPpaZ5CBQqT0uS1HwXs4j8ER5y/04I2NKWds0vk6hSa6Pz2jldxb0tAJl//Sa15zS8/ufOQMXKwQxxjvgAOuHVR7Fmf1QP+A/fVf/0pAjM8//9yu37hhyytQtE9qBfa94Xv25Zdf2r59QwpDABtLf3+fAD4YlqFRZvMOPYUuqPbCR+S8rxW6JRyOyJQ/Vo9iAGdFnQy7KrqHBJQWzkmleA4dyzQ1a2Wyi/FtYgMiHAKrQTGwl28e1MSqO/aRMQAvdBWHHw4fb/Auf7bSMS2CNHx3y35ufVOhC6Ymp7TKeXZ21ubm5+Q8xKCJ859QPxg2cdpguFTIq5kZGxkZlcOH0Gsb+bwDG5DoA2/hTj2ciDOdckZ3xMxamlsEFGCVf7msw08+2L4vQ7X8PFiqP85Tviyu3uVsbIgbzmb63vDm5Biz+mAZJb0H/7yG+2PvQPeGdVaq44guGZNDCYfrp0SiuuCverBp6EG/qzG9yOzkS7SWNa1AxhmDQ3h2bk6O78WFRVtcWhToKru2ovYF4Ar2htwGDrQ5m5iYdEAw9LWav31rZoMccSEvAAHG+NbWFhdeyBfF5/v7/vqCft90nrDn1QUF/Rydw3p2Qw5xHDFjExO2sLSsPm1+YVHOTRw4gAZZXUw/DA0+v4QKuX79hgsvsYkjifmJ64erVbWrMq66iSd5wdHe3NSkEGplTW5rzZToHJdhg8F56RxayYRrtyJF8E9Xy4y/HvT7bmLDPIFyuDQpK2mzRrx84hOUQqn4to/vmlXljGfxBseqoUdD7yrtkEvndLFYvTU0JC2ZbHQseHkXQhHZO4aVEMNSOM1HYB8s0NGjR+zv/vZvLdOYsW+//c5GR8fEYkPIm5UvVuz27dtiWRkaGrK9+/bansE91t/fa+3tbQIDi2Gwhvr8IcRR6bWM+R78p9Ak6KKZ+tvPPv/c7t67q/mvn2+WONeDhojjXXOp+rjYIphjjI6Na75AKESAikvLsOvgFK1SsgDcrXmXEV4qbpl0RjKr8kT104WCBi5Zf8y7K2SAME4wXcDCQnsBWFFndQKraNwL3uTy5hOr/vqf2hUVm+6KrFfKfqVzFQpRHzeBNQgzCgsU/QLfZsgOwMrU/RkbCPoNHqcbunv3ro0Mj9gGYKHNTevq7BCQoq2tRR9znZ3t+t6Ix+tteWnV0B3A0sP3hi2ROGTpxnih5+La3Xv3VE/0V2I86erSt4pCRtZYjgpF23rK98lQEBEeke/ARINAiYQ53MavvzWtQOwC/insW8C6iS4KJFCtUXh99bYSQGH1Cq343XdX7de//l924ZsLkhlJIY8D+/fbqZMnrL+315IJ1zer2reRDW/f5nLF8jyqJ5ET4X1htQHc+cmnnwjgTB84OztvX31z0e4Oj9oXX14Qy+XQvn36HRzst+6uToVohe2VTfYoD0CpIEG1O24sCNd/5/grVeodtQjwLLrDVz+2D4HmHDB7dTWnUG4wQ83cv2+AvfiWA4TLNz4AMhYk0D+TV+Y8XAeYw5wIWQg0Rb8c3FOtXoOeVJf5XmCOwJwHUKD/nqj2bHS+ugRKv9Cq3xddiSQQSSCSQCSBSAKRBCIJRBKIJBBJIJJAJIGqEpDZI7jK56v/2A6fLz6MgafwnS7zOdfcGT3B9fCj4ZuLtxYTDPb4yC48GCQAfEG5KU9jy9M+kWoXovMPRQKBalBXOD9ZaQtdfSEEj1edHV5WdKSGjK0yvDr3SvnjGJqh/eZvLQu1udNSnC9aBSTlKX+qwrF0rHge+xSU+42plDXUE+ICy1FMFOeEfHFAmOL94T2S4rXuV/+HL+9i3yUilfdPkdwOW1NT0o4dParVi9BSwyIyPDoiIydOX8ALE5OTdnd42K5eu6ZVZThavKGut6fLmpqbHDtNre1rhzz9JC4jzgD4Rr/EP+KaO1YIACwul65n2b7gXCXMAc6NZKpRKyBJAKOoVu2uZRXCJFxunyLvRZ+8s1SOmkzaYFnZDViFtL16oxZr2U2bmZm28fEJGx0dtXv3hm1sbMzR3i8tyUlLWCtWHWfX1txKZC+PWEyrq8UMEygvaTqnlc95uDQPYV/+X+e05T0YQhtTjWIceKhvJDElWA3F8BDK8udMQn2ALxRhcWJiWsC5Uh9aFupk6P732Qv3xNtu3QAAIABJREFUr1zZNLfKEp3XnYETEeYH/koGdJ9I2a9/g+ua/CyhONi786GHghOF9qYQFXmbvj9r4+PjWlF97949429mesYAIq4T3mcta7nsmm1sEB4uK6e8fEuxOjm0uC6HgvQ3yI3mJFty4NoNp9WA/EpYs/qGuAG0BMgmjI8vXCj7O+1WekTntmZjp6SeuOuBFm4pN7pCVa2u5WxxYUHAOoCXODNv3x22OYAqSwAkVuUsB4xHmA8cNoA33GhMf4azdV7nXXVQM24s2PLS0AmvUjzjwCabYibCieP1OHT7NrtudNE4JN0DHNtQuwOIDKjfpO26tFwjdeUgb4W0VcDggSBHwnj7blDzKpzMjl0Dhg2Am9pUqOBGpbNNkWL1lkgkNZbCdEMe1gFFwHTDeOOBm+F0KjWSbV7xY14i5N+Z06cE7mxpbbfvLl+xkZEROe0B1DGfwoHIeNt9tUfsEbCywHYAELi3G3aKFquPl30g/TkKFZZ58D7YA2G/AEzEqnwcmMzT5+fnbW11VWUTS1UVxVa4CzndXZgIVuszp1hbdeAP0gOospbNWXad1f6lQHOfJf06tVXOADAw32Y+VkAs7FJGalJl+fbvCycF0xwgR8IhbcAAQwStujpryjSJFcN9XIaeeIT0NZRr7VL+SjLAQe7roFrxOJ/OOIYVGCsBxeL4BkA6NT0jlo/e3l6zWIP6Z/paQgGNjY0aYCieJ2QW7SGZcH1LW3ur9fX2CNAFUxphf5iv3r07bN09vZZubDN12WZyygOEgkGTfg0Wwn1796o9hck7a5mnlMul8rGTFCrEvIq5eUOiwbZj0Kqcju+Vgy/SgoCLc41qz4XHGu6J1dVrvPvTRx9roQEMn7Q39BWhC3iwsakvX57Vqwrv2/qWSrqw9a7H4AwyQB51Zm1tTUb4trp4nSVTCbt8+TuBVmbuzyqE1fziqo2OT9u94VG7du2GDfT32dDQXtu/f6/2e7q7rKOt1erj8WARThUBl5wOZjPBOE9m/Ii9nXSDbBcALLSFubklm5icFijQz40J+bu8tKS2wfccfXlhvBXgymWG8JksoKA9itmzFG+6XVaCfsONWyziIWSSQK3oXrQ9kAQiwMoDiS16KJJAJIFIApEEIglEEogkEEkgkkAkgUgCD1kChRApboWRc4DW/o4S44q+v51DzBvlvV19J4OVSydITUZ978SsPS/RnTtLACAHdYxRA4cnRj9t3gqzcxKqGOrXPYfeuDQqGXtwjsAagaFGKyWD53C+AEYos11v/3avbNhnWHWccE50jJbkgbLBTgGdcCXACq92fy6nhTJs/9aqV6XjwarpimkFoi1PgLwDWiH0T0tzk3V1d9l3V67YrVu3ZBiGvQBK+DsLd7Sq8WpTkyi/MQQfOnxQK4pZtdfb2yPHbXn6j+oxtaKVZ/Jy54sG6Xi8zGEYrLivIl9ffsiDinruGHBIH4rm9fVc4Cj1d4d+fZ8Y8FygX6lkSg7QnfqxUCra9fqNzwVD9sWL39qlS9/ajRs3bGxs3Gamp6Wv6C9tESM3q+MIJcFvXX1cTkoYYgDQ5LQimtV5zkgJQ9IOYnBZ8m2nPIM7HftGQ2gKhRioC+LHB4b3nZ6v4Tr590CNGm5/5G6hbDgYCakgYN2OJXDSoMroV9BZVt2zjz45Xakrgg13TK/oECv00VLMQHO0zDuUSJlCrazmbXJq0i5cvGDfffed3bx5U6u0p6bQ3WUlDuOL2IfqcCxSXkeTL2BNIqm+n9Xy9Muu33TvC2cjlAPtetXjV86EfF66h8MUx6lIK8ofqvlY0n14Slzzex/tGz3cqVIpcut5AQOg8v/666/s+vXrBmhlYnLKVgGrwlZV74FWgALrFeaEtkFIBc8Uhh5pTuEqPujfypTSZyAY0+UY5JxrNNIxAHb03Q+6+bYiJ9gDOICk5x5w6DPh86tjMuv6cX/Z/0rl6RWDsYhyABgQSCt4zCmv94D6J0t/wSKQhsbBRML1JwKsuLAwnsWLp8gvm5O9y1ppaj/No3i8TiwRL7zwvLW1dVh/f79dvXLFbt68JdY6VrADopqdvW+379wRI8WV/j6t0id0yfFjR+3ggQNiD8PhX+hXqqjcDy0FzVFWCSOx6ljWYBeR75txYMOywRze60al/IgNiPxDniMwmQv9AuiW9GF+CLMTVkqj5FwMoHu9JZKu/UpVvNO1Rjk57XL/+7RLj4o6B7h9cXFJTl6FxoD7o65O+W6IV4jvRUI15sO/+3H5BWfV3tZmnZ2dCpWSXZtUaDXYrQjZkwsAaUyrF5eW9Y0xOTUlNivqlG8J2oEXHywN3T3dNjg4IIc7IcS4n7B+h48esa7uNolueSWnUCbTU1MKAYheEaoPtgyA+FW3LZVe9c4tF7zO8wuIi8UXD8om4bPhf93LfAddejacET8u+HPMYfh2o3+ZGB/Xab4X+MZwALNhu37jusLeEJasMV0b0Nin/1j/BkpH/9bR0WxPt5wXi9PePXvt8ndX7OrVqzY5NR2wT67Y3YV5G7l3165dTVt3d6fC3xw+fNCOHTliR48eFrNPOp3R/LO63Hip//N3Va9vf0ehT+WEbyxGm1q1azdu2Ndff2NXr1yzkdFRAcKmpqfd2Buv1zyE/otx3M2T3XyHuUU8X2/5WN7y8w5sS9/qwgg6O4feT/ZC7/R54tfnXP0zoHi+CavcG34u2q8sgQefMVZOLzobSSCSQCSBSAKRBCIJRBKIJBBJIJJAJIHHVwIVPj516qF+lbrP3t0kqScKK0YDMABrVArnXJr6AKd2ghVjJcXBPiRjuTOYu2eDE9W+0B/fmv7hShYInRV2GPsUYgLHUFjG3FNSOVuz4wyG3FZ6o5wdrrpLHuIuDJm6FHqEXW98LHmgxgOflP/1j8mQWVeeO3/1B/j1DuWyVarko4I4lAHOk+90usEOHTpkPb29durUKbt+7boMmzdv3bLbt26LiQPwzeLigladEyv+ypXv7OLFi3bu3Fl75pln7NzZszLkl8vhByjpnyVJ+gpWBGMUphZZbYxuFZiAvIr+gAUO150AJPUASBxwZLevZZ1bbtNsZmbW3n//A8W2v3L1igz9OAtx1uLsZ3UsDoe2tlYx7sAg0dCQsPp6DJxxi9XH7fad2/b1NxdsbmFewBVWRjtnTjVN81VGrv2fP1fbr2tPdQUwTUODW9Fa29Pb36UcMeDsZtDZPsmfxFV0F51FdoWNUFc1Or1DT2lwJC2xRhSAnPJAFhzMhXdU2fHaQTq0L479uZ06/GzWbHRszD799BP743t/tGvXrglkRUgJjOrNTc3W09NrrOLGGYouZzKNouoHrBJvSOjvzp079u23l+zSt98G8wN41Iu5qJL1Lad5pwBdnmliyx27PYF3YPf52O1bHsf7/ZCHgz+3bgr9883X39jvf/97u3r1O5sUzf2qHDRt7e3W0dlpXZ1d1tbWLrAqTnM5l2BIq6+XXrAK+Y/vvWc3blyXs7qos7uvI/rWkja4i0qg6TLm5NE3AWh2r647q/cOfV8wX3bt3wG9dlEE3RrOgyQoYK+bazvZ0Nt42dJn1e3UJew2Cz/s/WRdYAqz1pZGO3f2tBgezp45ZTdu3JQj+dbNW3bj5k2NubCWTE5OOfDK7duaTwHCe+b8U3b27Fk7eGC/NaZTP2yed0pdPnOYGRw7g+snY9bX22t79gxaW2ub+l4AXtvqt/p6V7f+Ps3F84RSSWjO0dPdbYlkomqO1P4QMd8MMP3AaNEQD0A9JSNV1TS44O8kPbcFc3Qd+3PFJFy7D3S+cDkob3hcLT7y5O0hl0CwMAkSsrKrq8uxni0vS98BlcKk1NySEfvVrdu3bWx8XGFIeBaWyv37h2xo717XDSjMTkLsKvuGhgSYX1hctIWFRc0DYK/M5fYa7Cmz9+8bYbfm5h0jFgl0dHbYiRPHLZmoACrSZ71mR7vvTKndALwnXQ50gP7qx1AH6bFvn7E6A7Rz//60vnXFaGN5AdTX1lbVD8Foytj34osvWDLZbXWRV3xLe3Whfs1OHD8qsNTJEyfsuytXjbnjrVu3Dd0dHxuzleUlm5ubtcXFeRsbH7Obt24I2HLy1gl74fnnBT6EMcv3OSUvKvQlxVGv5Pp2B6EE2SWp3IbZhW8v2Ttvv2Mff/xJoc7RDxhsO/Vd12Htbe2aH2eamsT66cG0hJudvn/frly5YnNz7ruOjHsQVqG7rJCvAs48ACRqDYPyWPbtUeHZ6FR1CURNs7psoiuRBCIJRBKIJBBJIJJAJIFIApEEIglEEthRAiFb1Y736oayj+2KD4XuqXi9/GTw8e+NoVwmiYIBCQMTJ0PspFteEZzQDw96G/6WG8tfHh0/iAScwdppT9jwt9u0tMpsO2tKkCBOWlbEs7KI9/GHMSfH6jPRSNf45gr6QCkIKQD9MsZ9HPs4wQixE9bJ6m+okGj1mytekSN5cyMIYYDzcwcnQtHGrPQSDXXW2tJi6ca0HBH7hvbZibExu337jijsFTt+eFhOYlbcjk+41ZPz8ws2Ozdv2bWcnTlzylqa0xXz9yidpDZ8vVGf6Co6kvO0+NA21LIFnSMLS13oCReKBL1DHwlrw4pzv6K/JEnf/wRuffLDfQLMPIC6bGyaTYxP2TcXLthHH34khgpWvZLmQH+/VgiKLaev1zo7O6y5uVn5w5FQz0piDPJ0oHV19tnnX9jI6JhWiedIOHAA7Nb0WnsxHPCCeoAZxAMuPIio4C0pEeD3O5AjwI0a3y+hH/Vpx3qg4VFjmjS7oNsPkjUP2CowRxXSrS018uL/anvC3TUyOi6a+z/+8T0Z1e/fn5FTe++ePYZDa9/efdY/MChHGSuz0+lGSzWmrL6eMEhxF4rL6uzLr76yqckp+1bJSjJBjnaTGz+/CDTYJ0MStSt14YUPIo/Cw0/gjhNxWOhurkc/Oz09qxXGH374oX1z4aLNzd1XleC8I9zE/gP7bXBgwLq6uq25uUXU9axCB5Qnp2NdvYCKhA26fPmy3bxxQ356zRcCANhuRK5xJJhrME0pzEl3l4gDgxYepuw1KpqUi3sr3+/zt1126AsBb9L/Ei6Aec7mBkwXxad2yhH3ZtfdOLiWXRPQgRAWOMqYlxGmzPfrLtWdUiy++0ffq5DVZDJmXV1tAs11d3XJeTl6fNTu3LmrEGa3795RSLP5+TmxUGTvZW1+bsHmZmfllGc+SXghsayEqy68/wMX3IeAwqkJ6E/zlHxeTHwAlY8dOx6c33k+JD1TfkNjOQxu9fUK7dc/0C/2uEpFCqs96YiNUXIIUI87yYT6YSu7j0Oftm7x9wW384ODn3m8K78rJ6FVmAMTfu6J2iroucofkmsmnbHurm7r6+2z69dvWHZtVQw1MKPMLyxYa3u7LS2v2JWrV216ZkbfX4QX6+ntsa7OTsuk026CEDNriNcrpA/99oVvLtjExITkDtBrenpa7aa1JSOwCiwugDJ4GNBMV2eH5rXoV9WtAJqtUPFVH9Jk14Fdg/CI6KT6Lq9M2z1b5VrB6b/leki4W665E4LewH4n9qOYpdPNYr88dvSYwnl98cXndvfObYUgpf/5+OOPra29TSGMunscS02VpGs+raLvnNWa0/uxb6QoDXHAh4S83ScQFgxYhKRy38R3tZiDELqEVwWAODo6LqY/9Jpj/p46d07fUQWMeImq8Rb/t4sSh9ohuwtLWY0rb7/zrn322WcK1Ubf1NLaYnv3DNrhI4cVfq6bkHNtrWIdAtDtwSrobz5WZ7fv3FUYLwDdhNeUwazGOvX6S37oH2XfYYFQDbaZXZT8ibo1Aqw8UdUdFTaSQCSBSAKRBCIJRBKIJBBJIJJAJIGdJFDj9+lOydR4HRcojtBgCacMiM4p+yC2HxkzvaNXIBXntOd8LZu/i/woT4XfWp6O7qlJAiGDjTdmIHcv+5rSCN8USi98urAfXEcFZKRJJp3zMlg9Sox64jv7vJQ8V0OmSH51dcOgDl/fWBfTBKAY3tXW5lagFtIM7fA+2XLK8/8ABp78plkum7Ncbl2GosJC5dD7atmN15sAPanGLutob7OBgQHbv3+/GFbu3RtWaAVCyIyMjNj9mfs2e3/OVlfWZOTKb2wa8btTyb2WSDwmppbAoI2zjnBSGCBz6+uWrK++Ergg56Beqc5szjk4VlfXVD/0RzhAcITgrKtsVPetIqyEDkj3IPWLM3dkZNTef/9D+/bSZZuenrJ4fdy6urvt/FPn5Rw7dOigdXS0W1NTpmDMbEwl1TgVHYnCxczu3L2r/OPgBcDg+t1wPgtSKN3xbbFc50vvKhx5biBSdu3FObt8fw5L0/fbKsn4+6X4KDztR7fd5dXJSnVdNl67sXL3qZU/UdL1UbWqeLOVlQ0xFHz99df27bcXjVBlhCXp6+uz55591s6cOWP79g1Ze3uHQpMRToM+KB5HN91bMKiT/t179+TQKn93zccOA1RyO+nqPcG7Si7WcOAkW8ONT9gttRLOeLETCgin5oULF+2rr7+x8fFxOT0HB/q02v7ZZ5+xffv2GI6blpYWSyZTlkjQ/8bd/COoCMKmzc0vqm+W48UrJjrp93dRF67N7OKBsltd+wr6umBMKrul8mG4ewz01suq+MDWM8VrxT36X0AU2VzOYDVa39goGbdq6QMIJwZzDXMuNuQCYAV2G+ZLzJsY25Qjn/faslfM6I+9F8o3xWluTlpTpkcg0D2DA3b40CExRMC0QpiJu3fvKmwDfdr4xLitra5orINtZO/evQobVO/DZf6ZywaTCQAC79wELJrf3BDApKe7x06dPKlwPn7+oqJXbB+hflgOTTeOu5ARroJhAWD+uWXT5bASFPcrvmpLAtVOFD4UCzcI/F44cjuJZFLgXcYUhUOEqTGfV/hEdPnx2IJ5pR9w/XyrDKBH/RalX7nkAPUBnvT39Qnsgz4zbwZkMj83b2sra7a0uGQ3rt+w2dlZgd9SiYTC1MDuR7hCv6EPgE8JrQXjH+Fb6XsmJib1tzC/YC3NGfX5AFgAlbMBvIdFpLW1VSGsfHoVfymU/6t4w/YnpfNAuWVv2P7e3V1F0jtJu5giOlmXz1t7R7vGupdfetkOHz4kmdNmF+bnBfKZmblvFy9dsu7eHktnMpbOnLZMpjILzda3bz2zmzwWc/vo7DkdTFhzU6f1dnfaQF+vWIBg9Ll+44a+iWEiJeTg7NycQhEuLCzZxvqGJRsSBnPU3j37LJUKZByI0H/DlNgduMZEsjBp3VkF+ASanp4Rq8oXX3xhd+7es/Vs1poyGTt54ridf/opO3vmtBiHWgDoNqY0zgJWAcvla5RlB7QtGDU1HwryoPz5MbmGatN3mvqNGm6ObtlWAsWecNvboouRBCIJRBKIJBBJIJJAJIFIApEEIglEEngCJOCsL/qI9R+yP1SpMXC71fL1hRXfvJ4PebfSchc50De+W3kn50DgRCXv/ri8HHqX/iu/4o5lO6h8KTr7MCQQVG+JweZhpFueRkiNoFiHQQSwAAY+nE+rKyuikvaGGT3OM0FbKFh0ytMNjgGL4GxYWV4WuwpOGZLGCYMDFR0v32TUKYSrcj4w/37/u9N7labC1jh2FwAVGND1fPkLazkOyYndVCpuqVSrdXe2ynFy9OhRGb9Y6fjFF1/aN19fsLHRcVtZWbPbN2/b2sqqPX3+vHV2EHLh4azaqyXbP8Q9VL3qKLBkw7KyuLgoJ0Uum7XkNtT15flBF7JrawXACw5Q+iTSwKDemIIFopKnxqXkqsWxAemMHJZeOcvfVv0YcMfw8Kh98MEHMvZzJ/TQBw8csNdee1XGTcAqCVZS+xAQCtvl0kTPUWW0mVX2y0vLBssG+UPHoY6mXDtt/g791lAMgVa2MZjW4ijdKU/R9R9PAl4fCjlAJ8pO4ti6efOGXb92VU4X2Io6OvrtxPHj9pc//7kdPXrM2tszBTs/z5OEd2hi1CdsDOoppqP19VAHX+zqC3moslOWrSp3fY/TNbSH75H6o/VoIItaZU794rAkzMT1Gzft7t17ls2ta4X+kSNH7bVXX7WXX37R0hnYVGCLoM8NUndTAfVv6MzmRt6ya1nL5QChulBwEl6tmQlLOggjJ2f3gzyP0vLcbsB52+lR4VphJ5zb6vtqQ45pbG11Ve0omag+bpUklDcDBAQzyypj4cqyMR6JjS5eL+BmU1OzQJKF5x5EVoWHf8SdCvlm3EynATG3WU9Pmw0N7RMDwulTp+za9Wv2ycef2MWLF2xsbExsFJe/+046+vQzz9ih5AHLNIRCA+2y2r6PJGCmYo4iYG0iqfEdUIfqP7sm52dTJi0mAl9ssuezGD5XSz78/bXc6/r2bSYGtSRS6R4yH8oIzIOUn+8GQJIaRPJ5g1kQXS5sPOMLXpZG4Z6f4k7gH3ffyX7MdICi8m+JkFiqliSZiFlHe7vCRiGzpcUFfWNNTUwq1MjS0rJkB1Brfn5efUJja4udPnNKQMLCFDKQYboxJfB8Z4cDo+KcB5QIGJHnBwb7FI4FAHYW5iYzsax1dXcJcFhIr2qOuSCOkm3vqHgRJfR1rn66FglVTKn6SZ9+9TtcFoJXHzx40H7xi7+y5555Vm0XUA/AMMZDQjLBckNoxU8++0zsYq3tbXb40AG14W1eEVziJeEyutl3NRvLzuk9WncAQGxvbbKWpibbt3ePHTiw306cOGHXrl+3Tz75xC5dvqxFAcvLK3b16jVraW4Sc2VXZ7dCUxVMAQrL6boSScBPVAPpeglzuqL+er2rc5B+2Ivefe89u3tvWHOgpnRaYO5XX33FXnn5Rds3NLhF0P4d/gLfdYR1xY7AAg2nVG6MLqn18gd9Aq4gQSfoAVzR11mJeHZ5EAFWdimw6PZIApEEIglEEogkEEkgkkAkgUgCkQQeVwnUYBl5GEX3r/Ffwfl8wGbiTCHFFfu1v6zwDa0Pf3/kX1RqYtGHuL/F/1Z6VfFxXS07rPREdM5LALluIzAMXDi5Cw5uKGnDD2xXL/4dD/ALLS8riAh3wvt55+LikuJ+yzjr30vet+JMKr4R3+fY2LhAL4AR6uP1cjY0NzdVZVjBgMhq4gaFqnCxz1FdqPJFt0/ok1rCzgAs2ITBI2cYyXDYkQdtMmptUwkVS1P5ZCoZt3hHu1b7suKxr6/f+nr77a1/+61NTIxbNremOPWXLl2yoX17HnnACmqA/H34E2y0a2tZAYI2ghA4lSUVOhvoEuAP6gbjOsZA7wSA3YRV/qlUo1a0hZ78QXZn5xYU15z45IC10o2NRqiCY8eO2dDQkHV0dFiiIV4I86Dsh1Z246vZCPxDAnnNztrm+kaBg0p6p/63cvZJLxBJ5Rsqnq2uvwUj+e4TrfimwsmHnV4h4Ud952ELhnF/+3GCISGXy9vs/JwRAmh+YV4sVvSdewYHjbAUOGiamzOFldRSwXI/Eq8B0JDNixafFd/qHlUlRedcdW0r6i555j7asW/LSoYLD1tEj7rKfI/870aUOII2cw5UCBOYQk3k1sXe0dnZZQcOHLBDhw5ZBuYoVvDLC+TeoDqkXwv1dfRlKysAQHPF8VTVC1NELRODUk0itEphLHkAmZTo2QM8X3gklC3XTgKkjjS6usS9rvMLMHdpaUmhOZoyISBF4SUVdmIufBBgMcbB+/dnbRPKL4X9aNBKf5gZABK5NkReAqBOheR+cqeqi25rVmNmyWSddXV1iD1iYKDfhWJMN9p7771vi0uLcixPsIL/+g058TPIebt3bHdtaw5qPgOzCywMsKxQN4R6gHVlYQG2hinLZdcsnymGgFS/qL7RZRdWq6AmS94ZUsPC+Ur3FS5W3KmUSsUbd3ESYHAg6oCRi+auuXqiQf0J5cehS/kBMTPd1lQ9aEo8LyzcLt76o96ad2UGPEb7pmtUGeocCBkwNd9NtaoY3SiMPMwnAZnMz81Kn8fGRhVOdHxsXOFEYWgEFEj6zIOPHDksdj99d+EvB2Bab9ZQXycAzODgoHXduKXvjIUFN5eF5WJpcY9ArJobrOf0TcfcgDCXhAOsLeO1lq56TQmvUv3yrq947fahVsoT0HV14gxnjEvuG7q/v8/OnT0jRppEQ8zqWprtyOHD9uabb9rG5qZ98803tryyorA2XzR/ZS2trfpOhVEzkXgAgEEgOp/f8nw+dsd1rr2jt+h3YzqtPpowWCxQ+dOfPlaoVBhWpqemxSR0+tQZSzdmLJkqAjzBnyIz6o1NY3zAuuptIcGlKiLU07oGCOzmjZv6vmR+go2Db7pDBw9ad093ledLT5Ma8+LZOcd65PLg8ubzWPpE9SOe2u0z1VN7cq/UMtN8cqUTlTySQCSBSAKRBCIJRBKIJBBJIJJAJIEnVAKBFaLG0stYwcd2cD92FL9fkkRw0hvGBE6RowBDGc/ntaLVO+1Lnt3pABCEjGvOeMPtMADgfNCKEZ1wdnB2q5VQH9tc9daCgG1Ary/jqK9YRt0Y/Vci4IJRpigXb9CQLvjTP7BAqVvCAQwODAoswmsxOrPiDErftdUgJj35qCUvebOV1RW7fPmyYlvn1nNSG5xfTc1Nxio/xxbkC+h+4w0NWp2aTKUCYErMNqFtXliQI4hV3Xp/DXnAqUb89smpyQAQsal2VGsRSnNW+YgmSpSfdCpufT09duLYMXv6/NPW3z8g4zTtHaaVe3fv2ezsXOVEHpGzRbk54WPCRUehHIdOe2V1tcDcsGORgn4QBp7RkVGtCsVph+5DNd/a1mZQ/9eFnKWkubXaXd9Y6cqOeQjSm5qatImpSYGaSA3qdYzVe/fuE9MKoKSybFRMem3d5HScm501wkBhVJNhLdT/V3ywcLIo4cKpbXfwIPlnyiTjOuttn67tokufbqrauFBbOj/1u36CpdNQW6zIgoMmOAW4am5u1u7Pztri0pLaDg5EHGJ7BveIQQM/93ZgfbcxAAAgAElEQVQb9UofhTN4LgCOuftx8rgXOc0K6VdNotrt/dvlMrr2fSSAg4hQE4BHceBQ34y9hOUjdFRPT48lGhKOJirUyrnPt3rtxxwAdHhk1JZCAEP6bMb1MLBla369tzt0xbP9+flk6FLJboVHue60M1Dg4MSOqlnTDU73VfyQGpfkqeyAuTRsR1PTUzY3N1cYjnh8pyTU/haXBJqcGB/XnLwh7uZBhC8AEOHnhG4SVfbyx+gQEATO4eaWpPX2dotd4uy5s9bX32cNiaStb24KSH37zh3p4Jai71i/W554sBMxs3h9ndgCcYISPos2BXhwZGTYZu7P2HouW2hNTldhXHOfT8wL/LlwlsPn/P5uM6i2upPS+UTDL/fnqvxKlwPwCbfQbNFNz4bHNybfpzB8OJaPxWJKoeeKJ3/6ewDq1L8FfRX7zHlhXCj5PquxKLAHdnZ2Sp/Rm42NdY27fBuMjo6J7QOmj/VcTqFLAKP09fYJRK1X+M/vPEC3Oo3xe/YMWmdXh77nAeYzH4el5datWwo3BOMf/RNMf4QxHRzcs8N8tqg8bs9r4vbKonuDW6Qrvuf7PpPHwitdir43dfmqLvRK1x1YqF39C8Ap+hnGwLNnz9j580/Z/gMHVNfMpW7evGmfff65Xbp02YEIg7UO1d9YdkVjmp9DlV173A/r6Bdi1pxptN5ewqOdslMnT9vQvv2WSjSa5WNiFBoeGRb4le97bUEVM6+lbcH0Rp+qsU/9BzYrrhWmJZUlGcwnlhZZLHJf72IxBWkB/qS9dHR2Wiq1NXxtQd3KUnahuyZDTK0B27HAUGU3Vzn0+VZz0IsqaWmVh6PTJRKIACsl4ogOIglEEogkEEkgkkAkgUgCkQQiCUQSeHIlUGoxLxiPEUi1L1wvLDkrix+mOET1xS32lOJ53Y4xihVbsZiMUY5m2SXER302u2Zr2aytwyG+iw3wSzIwqGLwAayCwQ3jIs4MbTuVw79vy32c8OXwv/7m6HcnCTiJORlipPmxNnLQ39dv+4eGLJFwXk6MNBiev/76azlFS/K2Q1azubzCAV2+fElpoGtYuFtam62zq1OGwkpMLTjOGhvTLp50vWNY2djYkBOI1cuEXNmxzQUZZbUcgBsMYwuL8zKCOWvXDpkvKWjtB9Aid3W22L69+6y3p0flgK0GY/HCwqKtroZo0mtP9qd1p1Q16A/xFW7mDdplwk1gdAdQpBVyiLiamIMuMLuWt7HxCdE1T05Oqj8ifjirSrs6Oy2ZTBkOg503rMk7vLBCZniCvC4sLtji4oJt5F1fiOMllUrJsZAiD5R5m82Xd2J8yiZwCi8sKs4KWBL+kNHOWy33lKeiEpQKOgwiLL99V8ek7f+KD5aMfcXTj/ieq2AP0PhpFSZQvgo6yDhOCJGl5SUZ0sm3jPLpRmtpbbF43LUdhpVqQws1vL6RF7CPcAKwPIQ3rrNp3hLsb/8T6Iz0kBdvf3d09YeXAKvHCdExOzcnPVEbjsXkvIFRDcdp+ZiqapNnJchfzIWOgnUNECp6wj2kVfirVpQKusv7HqQvKU2KRMIqxtXSO6pl6WGfZz49c/++QEGE5qDLh2GiWrvz7+c6GNyZmWkbHxuz6ZlpI3RiYyopdhEcqji5vw8LjX/XT/63rK8AbAdQZWj/kHV2dwnAymCcXV+XEzlXZS4IsK8sqR+s6NRPV1eXwRoIuJZ2ce/ePbt27aoA3+F8eO3crYaWrQWooSy199ZKzGfI/+70hqBQ3M58DVAFAGPAkszzAYnfvn1bcvDp05XUAvrd6dV/zuv0T7D9xeMNAdOf6+v4Hsllc7a+nttVNDLynkwmrbOzQ0BBwikhSr5TAJ0Oj4zY8L17trK8ojlje3u7mCBaW4pjubq3oJ7IX3MmY729vZqriuknv6nvLuQP2GJqckpAbJz/ADYGYGPp6tqhm/Ray4toTMGfr8xqlRBudyShZAK2uFp1q2LaPj/BhJqEd90o8gYrUjxgxeE1sNQkknGFpjl79qydOXPa2jvaNYeamplWGJtPP/vM7ty9Z8vL2a0589kqvxKUNSh5+dXH7LhQ0aXlor3XmxEGq7u7VQBqmEcbU2kxuAKsWpifd8ycAWDFp8RCCOax2CEEWAnGdMZF2l4B4FL6RncUqCwHLJhh0Q0LVxhn1Z4bGqytvc2SKcK4VUpg67mllaxNTU/rO9eFFnaha8X0Gnrf1ieLZ7yq6HbNq3xpi/dEe7VLoBarQO2pRXdGEogkEEkgkkAkgUgCkQQiCUQSiCQQSeCxkYD//KRAzmhevWhVvmjDxp0gGZeGW6kab6gPDNWczQtYsrqaNf7Waw29EaQL8CWdbnRG7/ym6KtZwbW2uqaPeffe4v8qXbiI5MA7vQDgbG7K+V90xAZf/sFP8Npigo/QnreD+d8/V9Yl7pD8trx3u2tbbkZjWN3FFjxYVp8VHhFVNLGnMaqK3jtwwkDHDnBFG5YCktwhPxiKWOV3+/YdGaZ4FoP+iePHFYYgkaxscoDdArAAQAFRbsdiMlIBhiB8jBhWSGyH9+MsgpUFdhiMt/NzcwG7Sg2CcCV94P8xtDU3t7hV6wZNcp0MZBj0f9jthy9bef5xzM3NztnI6Kj+1ta8cXCbOoqZgV+6f3/O7t29a2Ojo8YqUKqU1br9/f02MDAoA3s5w4p7P+XEAikMVCFLBQaKwpnwTmWFgRkdVh/qBoOmmAIUR73OGgBuhR+rJt6YczoC7Lp69apjagk6zN2B0HyrDZu6yUA4E75M/pwz3scM0E5xGWi1rPqnt/t1zwYy1tuL+98n3e3e+We/FhTJS7H0/eWDc+nVSkfFdFzCrvctyq3SM+FzPF9Mwzt7wneU7svRzSpvnlMIN9rUuoz5gOQY8wurUUsf1ZF36pLOysqq3RsesRs3b9nExGRwt8+RH0c4zdvKN19G/+uvB/eWFMpfq/1Xa5QF7i00+eDh75lw7Vn4id7py+9/XTYruap1RzBvK1ZhTE5RehrpT1nV8oxngyBljgFWEGriw48+ErBC52v1+ujF/iX8hkIs+NM1Spq8qEzcz7Ph53c5cSukoxTL233Jmwq5K38l799c37T7MzM2Njpmk1PTBbBKcd5ceHzLDmPEyMiI5ljMyTfWc9bUlLGe7m77/9l7r++4suzMc9/wBh4gQAAE6D3TMysrS6XKqpLU0yqNul9arYeep1Gv+adG89hrHtosjaq6pV6qrOpK74pJJpnJpGfSggbeBsLcWd8+90TcCNxwQACIAL7gAq879nf2PfeYffY5ODKsCkUN7ba0IeTOv4GtO+LxpCTiSVUcQN0G5Z2obtEXKpX/hkLxi4VpKzRGIyCgkpBsCALtFFitGBockpATllw2r0pLH/zhI61LoVPTyE+jsFHbI+Qc59V+mq2SUqB5o4JltloQZfdNU8K8CcV4S++pvz6w/tBWv3DhvIyOjmh/FX1DTOrevHlTrl69Zl5UhIWFGKVdP6z3tj6iaoMSCLamhGIOOsFoI0JpHsr8mHTPZUttrpqZ8XgmE2GBIgqsrGDLFADClppQ2IaiExTssR0QJsOh9H761GlVLCxVeF4sqFiwsCWGbYO6ZXCwX7cNwrarpu/1WL797rpamIDCIvr/sKbV092t7w62FdrcrygYDXiHNRp/+6EBL9voBAsHoFjo/0GJBduKHTt2VF5/43U5d+6sKl/BIsezZy/k008/k2+uXlWFfL+/mueKyFYaW3gfa0bSLg9tPqunB2sO8P4kkwkzthAOSyQclUg0XrQaDGSqx2EVXeIx/Qbqoi1vkVU2l1NFsWw2r9tibYixyN2kCcpmsCoExW6bSpWBfN5TfNkQQtkNvGL43b17T27dvKUW1GAFFN97k9b6gyGO64j9M6HZlJgr/r85AsGjR5sLi75IgARIgARIgARIgARIgARIoGMJ2ElHDN1hwMr8dLTQN3Jeyh76uV5f13MKP5WD4abTW/JVOouEHcHqq/7+Xh1cgm8Mas3Mzsnjp89lYXG5PPyS1w1n8BuNRKSvp1u60ik9z2ezsrCwqFu1YAKi0gCA5lD/8wXnXaMTj9VajoSMUoQ3XmrzXJZvn/eOPa3ksA0Z0UkmjcfSw4UdKLZkG4+4NN1tE2/CM8Jq75WHh7u9vWk5dvSovH3xovT19ulKKKz2u/799/LZ51/IzVv3yj1VuVpZycrNW7fk/ffflydPn+jqbgw8YTX3ez9/Ty68cqGKT6xAjOhq1e4eDKwaU/irK2ty9ZtrcufOXZmentWJM/8LoANLFp0X8uzcoty6c0e++uorNZG9nsUKOVctGJnRK1CHp408suuurK3m6q6O3pCJgkgu6+r2Q7DqMr+4oAOkyPv42Jjunb7BT8tuWDmxx5YF7AvIsLJ1ILhjSzEoEd26dVs+/vgTefT4qSwtZyRfUR6+QARjxljtf+WbK3L58mVVWsFzTEbBOs358xfk0MRE8EC9lqKdWXHF1e3SKupbf2R6vrGMcRt3kcz+/j4dpEa+UNdjIgIm/e/euyeLy8smL3Zs0gvbn73FpXW5dfuOfPzxx3Lnzh2dUDOMjHIfBkn97jckTxNjXOhAqLrGNVJYEXHRs1cW6hazD3jrC+LYUdYAuS56beIEseikmS8DpfqliYDazqnht9VkmVAAB1TM0YYJbs3G0qh7KJzA+lB3V7cqx8EqFWKDBTZMfj148EiWsVK7OLhuB9mNWOE+/hYWM3L37l354A8fyr27982WMUXLEL72TlDC9J4VDHNUBRNw0Ev7zBJp7mibWqae3htS1xyBWq7RnvQVShnqsgvBJCa2loECBFbZaz1XcGV2bl6ePXsu09NzdVcbI8Tr12/Kv/zL+3Lnzj1ZWFhSy2FIIRSXUW+Wx1ot7daVPXqiUs15wH07MW9bSJoG/Od9CwK81LwFiubPyru9U8Wb7zHecShQYCV4LlcQbFVz+fIV+f77m7K0tKKZUzmGn4oflGqXllbl9p078tmnn+kkf3Z9Xdv842OjcubsaTl9+pTE43X29aoIt90u19cKklktSAHKG6Vi35hMywhuPHfLizmZeTkrM9OzankCq+sx+X78+DFJJpKqGOQVnrf/HoK1smgDsseNUZbfMXW41tv6HbU1uk1YuWtMxEK59uyZs3L+/HkZ6B+QaDQuC/NLcuXKVXn//d/L9e++F7u+AEGi7YNyD/rpt99TwoVCgSoV+GTN78fett8Y+06gTtBnwUn2B7HxXJnDvxd6EZu9Z14U00Yx3hOJsJbF2bNn5ciRw5JMJdXR/bv35eOPPpEPP/hc5udWy+NCuDZ/5U9Mm1vTUfFgFy6RT2whAoUQWKHC9xYWSdFnfvDDA1UGKW6pWy99XnkgzEQirnVxX1+vWj6FIuDzF9Py4MFDtbICZRjUqbAyePLkSYlV7utXUcBIH6ysjBwcUSX/RWzl+uyZ3H/wSGbm5vS9gdL85OSE9KJfpcrZ9RJc/hzfjJJIBRSQ9zCk0oP/bbsVSmVoV5eHt/krzbxXYzcZCl6Wih8UAcNhkaGhQTl79rT87L0/FSza6OrqVku22P7uy6/+KH/84yV58RIWQTy9cARl/xBmwLolM27ki9MmvSINbX/pmn5tNottqTem1o6P2SeVlsWwOGFhYV774bAIiPGmnt4+mZg4LD092KIpbr3qEeWRSiVkbAwWWeLatoB1FVivevjosUxNPTf9eBSBvx6xWgwe8u6utAz090kSC3DCjhTcvKysrcjDx49leWXN1nJlR39CkO6Z6SX59JPP5auvLqmVVDzHOwyBxrdI8+4rYvvd8odj6mhHQlo3mzaG97r4nfG8CQLbvfSniaTQKQmQAAmQAAmQAAmQAAmQAAnsDgHTF7U9Ul83U0dg7P3gtJkpFuOn5BN+yidfcKf03Jxjf12YmU6nUrpnOyZRX7ycke9v3JbR0THp7euV3m5MUnk/OzmGgPyBwcJDOCzpZEJ6u7skmUjI0uKiLC8uyg/37svtW3dk8tCkDo5FMC7uTXAVB5i8gZhisBqPHdg3YzY2CZ14NKVRYoizCnzbny2N0E7Lmeh0gNA/MtxkKkoSZnNjVvrUCiYWETk0Pip//stfytTUU1lbXZH1zJq8eG5WmmFv6ZXVn8jx48clmYSZ+hIsDBxlswW1ZPLtd9/JZ599JjCnPDc3p6uZ+vsHBGaXz507JweGeqsmIxIW6e5Oy6HxcRno75e52VlNB7aOufT1Fenu7lXz3INDQxJXk8EmKAyCQWZhLh4m+aEM8fnnn8u1b7/VLTPAE3u+u7rCDqy9vbADUoIBsXv378vL6ZdycGRERkcPyoEDQ5JKJ8zglhUai9YLAwPFjx49kUuXrupe9CsrKzq4BfPDh48c0QmNgOhac6uYFiQOP3v0Llt1UM52H3EzkQHukJGvv74sXd198qMfvSvHTxyTwYFuiXqrapEaoMf2I3D73Xffy+9+93vdXgIyAlPdsK5y9MhRVZrq7urSgeQNybYyp4PPJo/6v5f/zeQa5uxhCjwWj6nVqcx6RrA9CiymHDp0SKKxmCpzeTusqJzZSagnT6fkxo2bmnesxJyfn1f37npGZQVyBoWVasWB9Jqkm8ky4xB3vUl//6R0IAzjzyirwEFpNeEG503dKKXBIlfvHuemgmo3x9630mbFHjebTDtpCP+Glb8sfa9inYjs44B5lbKkWRnH1lU9vb26vZpOqEHhquDqSu1Ll/6oFrOw+r+7G5OIZrtBvKuoK3M5VxVbvr9xU7786mu5dOlreTk9oyuiI5GYuFkjmTau0vekLCme8Lqq1ITpXTtJU1RcUcG3OavwW+fS+ELYNhXWA55sLkwbQscfXTMhaFfvFmkEoLHbRI2MDIupV0O66hgTrzdv3lZz/emuNyWVNBM7/rAwabO4tKL19ceffKqKqwvzi6q0HI06OmmDSdvKSavafD1p0pkfFKVRDCjGC8+2yMtulkItVf/Gb8mLkduSy4ozG6532+Ay3zEzJeufmK3w610iCBsMZNMpGMsLWMkNC0WXv74i0XBE3n33x3LixAkZGByQSAjtD09sXRFY3phfWJC7d+7IBx98IFevXtWJcCi/YAsQTJoeP3ZUrSZ02lYqldRu376r7aLsek5GDg7J+KERVRKFlRT/lg/WH76XUILNZApy/bubcuXrq/Js6plk1tbUGhBk+OgRTCqnpXLHQCtSgTPkVWTJxqt1ltY1tnTxxNRk1o3/CKfJZEQOTx6Wt958Ux7+8INk1tbVouCL5y/lk48/0+vp6Wm5cP6cLkKIRb2ptoLpWGkT3xHJrOVV0Rnth6mpKZ3gxbZuaGvDIkckUjEjXkyid6Ims6zs1smoPxMV58X3wevnQdDN960ifs9fOIT2elzOnz8rT58+kcePH8vczKwuiLjx/U359T/+d5mbXVArLOPjozpxrNveoqWCpEPJO1fQNjq2xYElxHQ6pdZFenu6fEpIFQndgUu8d+hjQNEef7ASkSnAktKsKs/f+P57rTNHDg4LFpngZz9VRTkMSCcU8QeHBmRgYFBS6S5ZXsmoVR7IPaxC5vI5OdA/KCMjB3X7HvRbNvx8RYwtNGE9Bdtn3bx9W1bXMvJyZlaWVtd17ABbZyX6e+XUiZOqNA/lFf2Bvy+cDXHYG2Vu4MmTOfvcOxpnpi7VgPGNcvGtwZOyQCp8NnFZjLr5ME3KiwFopBoKFJMSITl4cETefPMNeTr1TJaWVwX1Fqx6on0PyzToB16ABRZst2jrci9bGqotdL0w8Zj/W5T3JjC10mk+J/L06TO5d/+eWu+BotWhQ+P6XYPVFHz7IVLIJc4xTgAlpUIeyv9ZtbL6zdVv5Pad27K8vKTPoagyPj6pikGwcAm/qA/UihO2zopFVdkEi6xisUjRyuqt23dlfHxCRsfG1WILFFHgF6+fKvgZ4OJERGCdq6e7S/vu2LYWFlpgfej23btapn3dvTI2Mqh9dL8FMyiQzc4aC7HY/vDzz76UJ4+fqLUWjKVZjUNV1PWUdavxNm+DXazmvRveWEU1P7xfnwAVVuozogsSIAESIAESIAESIAESIIE9TsAONZhh8dK0jaoX6KpSr4fsccAV/qy/Eh7cMSZy9anPge+06DwajUlPT68cHB2VhcUlXd2BgbKr165Kb1+PhCMhmTg0pqb/4R+rPbDNDyb5013YT90EhWfRcEhSyYRgwmKgr1eVVbCK6969+xpHb0+fnDxxQtJdKTOA7IhuFYTVZX29vRKLeSnEQU/NxJR/oq6Y8L1yghVldgBqh/JkhsZVshQztifZ7M/v05STkUyd6KkSKPwMDfTIz372p3Lt2jVVbHr86KGsra2pWWQMKD97/kL+7Jd/JgcOHJBYPK5bqWCgFSsPMRgFJaj3f/e+YIDq5csXaiYdKwqPHJ6UX/3lv5bRgyNG0aVaGhyRrnSXnDl9Sr6/fl1mZ6blqSrOZFUpIJfLS77gyokTJ3XgEMoEGETCnvJQNMBKLli5+MMHfxAozszNz0k61aWDzdjLOrNqVnva97T0RpcS9OjJY/nd738vH330oZqIfvW11+Tc2bMmz5hkcbCCUHTlOoagkP9Mdl1N+mMl3kcffipTU48ll83o4DtWS2PyqX+grxRJy8+Qo535Ib8YmETedQuneEzcfFYePHgg//W//TeZX1ySuYW35djRw5JMmPJBxYEtSxYXl+TG9zfkiy++kA8/+kgHhJFqTFJgEurkyRMyNjqmg4gY9/S/grbMTC4xgWIHAj3lDk2RX/Jr87DEsBIPK1RHD47qCtd1VQ6clq8vX5GhoQOCibaJyQld6Yo6IZ/Pqdn7tcyqXLnyjXz22edy6dIlfQe6e3pUKfDRo8clCwSNWh8oVqheyvRltaksz4veLb7MuDKSbHIf7Kc8hPpXCEu/e2XBmbi8D0H9QNrVhZcnowzhZ7eVBFs25lhWFg2KZcmZDQNpM0ob9pk9RiMh6e/r1e86VmPfj8ZU5p48eSqffvqFDA4ekJXVNZVtTJJhchgm8bFlA+r0b7+9pgoIly9/o20MWCxIJxKSza7LUn7dixevGWK0f5V8vDxbWfUdW0UVMZo8Iy787NG73JcHKKZ57Is8jOJQ8dJDBSUItOWgBHpgaEhSyZQsLS+rYicUOjERi20Ascpct44Mw4y+K1jVDCVMTEL/+te/kW+/xfd0Xnp7uyWeSOi2GPNzc6okpTO1drY2sDxMWjXNngAX6/ag4vTcBAVlZQFHiBu+Q+and4K81LhnIkda4DsoKdU8a6xqcdDR7f/wLcR2Iffu3ZVnU09leXlZZmfn5JhaA0loe8lYYsmpcgK2APnjpT/Kb379a3UL3lA8w2Qg2j+TE4fMxGi1BHTCfVfk2+++lT/84SN5/PiJnDlzSt548zXdggMT7dg+0Wz9GDKWf1ys4s9pvfXyxYy2pb786it59vyZZHNZVXQZGxtTRVIorBSLHgWnBQLFbHOqykSe5auN37FgeFrXQgqcgveHgIOlAnqokJuhoX55/bVXBQoMSwsL2saERb/vv7+hyifYJvBXv/pLOTw5IcgzLO6hTtV5XW+rroXFRXn54qX88OAHVZRF2/nUyZPy13/9v0s6lZZIpNwKAVJvpN1+G1AflEy3BKc4OM9ldz3FlxJYE4teFxlb1sYnXKDdBste3333nWRW17Rdh0ni3/72t3of5Xfx4ltqXQTbCEEJI5/P6yTy8sqK9hXu37+vvCYnJuSdd36kCknYsmW3fihbKAqhD4zvKxTJ5t2Cvqt4xz/55FPNx/GVY6rQAMHDO4ztZCAyUCCJRjcqm0A5G1sCweIVwnz+7IW8eP5ct/BDPx6/Q+OHZHxsXLdGLdaTVUBAwX94ZFitOGKBy+rKrPbdVpZXtV0OhD3dPXLq1CnpheVMDA74y7JKuLit71KZ2zrl4X3/i++R9/5Ve4dqRF18ZGO0R/MAicJf8E/dOqbtZNyZ1kixvrDefIGmU7GihdG52Xl9H2dmpuX582dy7dpVGRrsl8F+WASJSnc6GahMVapzfAFXT6ZNRVsfs7m8PHz0UP7pn/5Z7t27p+3Jt3/0tpw4eULbE6jLsKUqtrHStqIqRGPbrDXBmMEXn38hn3/+pdy+fVMtBRuLQMMyOTmpFt+sspdfJo1F1i45MDysCxmgXAsFT2zNA1nGAhhYt0K7BvIM5ZFCPqf1C96peBhWgEV6e3rl/LnzunhmehbvxbLcu3tP311oyLz6yqva/lFFFIElmaxahIXVwa+//loXvbycmZFYIiGHh4fl0cMHnuKkGR/SLa/8iwp8xY5C1XcX3dRi28jIrS6YqSG/bS0QbZA4Kqy0QSEwCSRAAiRAAiRAAiRAAiRAArtPQAc7kQyvM6qDMcUOaCl9zY1LWLO5Jf8402AdmETt0g79O++8I4uLy7K6elcn5G/fuauTBpe+/lomJsbVAgvSs4pBvxfP5W///d/Ij370tnbc7UBXIhaWwf4+efP112TqyVPdCgiDhVgNij2a7965J4cPH5aBQQzGxNSqBlaiwBrGz997TyYmxsoUYMyENba5wCAp/jWX8/Ic88oMchnxMooAZqCjYuyjaVCV/s117bLCYr6udET+zb/5a1WK+ud/+meVKyiKPHj4UPfy/uTTT9VaSF9/vw7UQhEBkzNzs3O6ShirJNezGZ2IgLnfE8dPyE/efVd+8u6PJY2Bvho/jHf2dCXllQsX1Oz27OyszM3N6wTr3NyCfPHlV3Lj1m0ZHh6WwYFBXfmIlboY8Mfk2dzcjCwsLmh6MHgGJQTItt0Ca33NKKwYua0kZBKGdxB7Vc/MzspnX3wpl698oxNJGCRLJZM6kI4tkzBYhvcI7woG1GCVA36WlpZ1AA1KZSeOH1WWR6G8kdw46VADRds9su95wVtVhgHKVCotJ08ck8zasjybmpLZ+QX5zf/47/LBhx/q6lOKvcIAACAASURBVHAo0GFFYjgcUU5wMz39UleSQskIExfgOHrwoKCuu3D+gg6+2zF1VC22HrNAdFAUlXGZKFdeW9fBR3i13rHoGatP/+qv/kr+y3/5r/Ls+XNZW8vIk8dP5R9//Rv54osv5eDIQV1RiMlfmLXGQDYsw+AIU9VQhpo4NCFvX3xbDhwYlv/n7/9eViFrAd+J4BTZuzZlNnX2ftARcPzu7TncNuI/KEz7nbNheQoTduLBmwys4rOjbhfrXS+rinLTOSjx0iAUv/5XbDc0FLTKi+evGJD/2oSCmgurSjGJcvb0aZl6MiUP7j/QCYL1zLpODv+n//T/ygcffCgHD47qKn28a0vLSyq3s7MzOpGIetsJhVWhEPV0PpeTmzduytrqUnHi1yjoBdeVdjJIl8qrzG1Ma0P5rnBkXhuEZWS8VAe0JvyK6Dru0sGEur6TVrw8ZZWAMkBd2pVKyckTJ7VNN/Xsma4wxrcLk8T4bl379pp+U/v6+gQTylBawrcX1iFmZmb0+4aJWHx33333XVnLrOtWUovz87q02X4TqoJU8fHK0yvTUh1Vp0wrjDvoZE9Fvarfc8/kftU0BD7wpSmAXaAXr4rUdzDkSDe2Wxoe1vdsfn5Onj97ppa2sCUitlIEU0woQ1kB3y5YUYBS2ezcjCwtLsjK8rJGA2WVsfExtdYBixxQ7u34H8ouFBIod2LS89nzKfn088+0PdXX36dMYFkNW3DEYeEsA6XjRZU79E9mYCliaVly2XXdGum1116Vv/jzPxdY2MPq+sqfaRvgnfDU5VS0jEKrbb9U+sE16hcTGjzg3cIVjtBKCfJh7uHdSiYcGR0dlj/75S8kv74u2cy6PJ2akvVsVjDxfenSZX3fsB0X2kLYghBbvkJpcHlpSVZWV7VttLa2qhO6OGqbaGxMMFm8oQFUll6bV58Cm1aWGxUlqufCe6KskFnvr+za57uCBy77+7rkzJnT8otf/FyVth788FBWllck7xbk6rVrcvfeXfmHf/gHzdfAQL9EY1Eta7SlYInQ/mFhxU9+8hN55cJ5owhXC74vSdt1iv4Q2n5Y0HHr+C25fv26LC8ZRbT33/+d3LlzWw5NHFIrDvi+rq2uablGIlH5u7/7P2VycmxD0mCkAcoqsNiB9jEUSrKZjFqYAEu0q2G1B0ordiJ9QyC+GyhubPUDBRdsS4XxguXlVbVcAyWmZCqh339M8GNruJC1DqLl6wuoeIoHnoKHd89IBGpZ/+R70YM5wcOS9JhxARcKOKYNaZ5u7v/Su2vShjCrJt+rx01ySu1XJN7kwJcGL8023egLnDt3VutvfPtgpbNQyKrSykcffSSHxsfU4kdsckLiCd9Wbfge+dpuqIc0aE1k9ZT6UtK2p3ndw8zRugnfrbt378mlry+rdT/U3ZCvgYEB3ZoSdTgs+uC7BmVNWCl9+Rz9vSXtU0ejYTl75rRcfOtNrS9g/Q91KH62zwdukQjqlF559ZULMvX0qX4HMM7w+MkTWVpZkVu3b8v4+LgqpEBZBlvpLS4uyIXz5+VXv/qVDER7JRwRmZw4LH/zN3+jY11Y+IU6d35uXrevheWc0ZGDcmD4gOnL5/IyvzCvbZ2ZafTv5rVe6u2H1dAfydtvvy1///f/tzx7+tRsA6gLV5BanxDZovZuFRVT0LnQP+vcOmzbYm/rhFFhpa2Lh4kjARIgARIgARIgARIgARLYCQKm34nOpR10MefFQfOKgfONafJ3TG3n1tfBhQc48W7ZiZl4PKSr+1+58Io8evhYO86wboGJhBcvXurK14ePn0g8GhHHcXVAd21lWX75y1/oQCmsWujPG0dJxKJq5eGV8+d0YhkWAFYzGR0MXlszE13wEwo5ks1mdKUYzCBn1teNqVYMKGDAxxuIsQPCZpmgL9fgYTPhu81TH4GK4scTMyBnZMyIlF9ufH4bOFUp87zbMRIzuofwG/i5IhOHxuXPfvlL6U53qbURrJDEZGcms66DP1BOgXUTDBZByQYWVqCAgAEh5AUrsIeGBuS1116TN15/QweeuruSxb2na6UCg8TJRFQHDjGxCmtA93/4QVeFZ9az8lzlf1kePX6i+7FD3jCYhUmNXG5dt/1JpdMyMTkpr7zyiq7GxcrP+blZmVE43vtWRU6htJVMJXVFNEzTLy2v6ADw7OyCwJw2TBjjXYmEI2rRABYLMPCO/GOFJJQaEumEnDh+TH7yk3flnXfeFqwqawx+LTLt8cyB/WTdlx6moENy9uwZteCE1WeXrlxRCyvTszOqWIctkrB6H4PwsEyysrykq9hQb2BFOlavwuz9W2++Je/++McyMTEhibgZjqq+uLZciq2M6xCxf7VbA7jsWwaLQRiQhNWpa9e+1UlcyDomnLBS9cmTqaISYC6X1VV2WPFdyOdV1sfGxuVf/cW/UlnPrGV05SDqTtSXmHSwE2nVk4SU2D/ryhvktJeBR5MDI9bWv7ln3vlAT3Vuev6LAZTCtfVUnQA65nFpRaypG40s2fxvLhvm22jCMLwaD6fk3rY3jF9844N+qCsnJg7Jm2+8odsKXL9+Q2UXdSaU+O7d/0GeP38p2JYMW5agroIFIcgu3kdMkk9MTKqy2JHDh3XrjWdPn8jUFBTAsFIc8dpKMygFeAw35s+8mV5a63irEprvtgmtNBHkhetzsS9PFUuJeXnbtOIzo202bAspOqmECX8oTCzBCtb8rMC6wfzigqzfz8nUsxe6LRpWN+Obji0BM5k1reMwGXvs2FF5662LamHt9p07srgwLzdQ/I6j37xadVxJrlFiNu0+ycItr7jrl6knB17buyh+Nuj6AXguTDiaNj1trH1Uwu8KLEBAiXVsdFR++tOfalvl5s2bcvnyZWULZR8osT6ZmtLvIKKBUgbeT7RXoBCByXusGj996pRg5fqPLl6Uw5OTOjHacFba2CG22kukkhKNx7Rvgi1L5heW5eXMnMDyE/7QpoLlCSjDQ9ED7UhsAQQ5jMWj0tffI+fOnlHG586fl1g0XNaWtNtJKAbIhf1Dvw2f0eK3rBFQtu41FktQZvirFE/d4skLLh535NTJExJxHLV08elnn2lbAhaJYG1lfn5R5hcW5eX0tCqEwUqDtdQG5Wi0X5FX9L/AI5lKqTIwFL43xlzKg8mXSa9uC9hUPkvhbPUMbKB0/N577wksdn7+2efajsKkP/IG6wj4HqG9+OTpU1VURlsZZY0yx7Zi2paKRU0fE7PXlcC3mshN+oeC0fHjx+TVV1+Rhfk53d4Kip5QLPrhhwc6wY02LroTUALEVn2wZAWl5zK59OJH1tIpWC/t0e1PUbei7KF/FQqF1ZIflJ+xJRCeVemmlOUGSoawkAVLgdiOanlpRd8BKHVBSQpbBul2cKqtUua1xoWpD1EM+ucvj6AXwlP6Mu7NW4P2VakdUSOqBh7ZdJScIo6NP/tOlL4z5j021xvd2zsIHyH2dHXJ8WPH5OJbb8jM9AtdqAHFsmfPngmUVlB2UBAaGTlQJqOlcjJ5Nyo1wWm0cXbCEZZeUSehrQhFuuWVVVlcWpallVW1uBqORPQbCIureL9Rr8FSCSyerq2uilsoqFWp/v4hVcL62c9+qu8SGKL9ip8S8w0doe+HLQrPnsFWY1OCrVdfvnih305sm4Y6E+NgatnF2woT31Jsn7aWwXfDbDtsrOYcUyVbWGbFtkT49kJBDluvIay79+9pHw3vIMJdXVtTxW3ka/jgiPz4xz9WJTooyIyOjMjczLSmo/iJqSxE/3tSfIZtA0tDY012U4uh8MQQoMIKJYEESIAESIAESIAESIAESIAEMFgDk6fhkGDriL6+Hslm4hKNhLWTjo68/dkBD9tfxeQ2Vpz09KSlr7dbV5Cgk56Ix+uunMIiqG5Mep84rhPe4UhYrl//Xl5Oz2iHHJOmGDzD4AwmyDEwhTRiMtlM3JbGOTU9YZGxg6Py+uuv6yDhN99c04FDdNgxsYoBuJWVZQ2v4ObVFDEGfSsnjTGgin2L1Sxrb5/2wLFyFNsJ6ES2zbyFwmNNAsClg9SRiFrLgSUcrFbu7e5W8/wx3cqhOagoM1gdwWo6KEpg4gl7QuM6iqVLGB0KCtKOrbkYUI2qWXoMciIsrGjCCtnnL17oqlAMQmMya3WloINUmGzAXtPpVL9aIBkePqCyCyWEU6dOyvCB4bIJhqpp8NKFQV1MxF68eFEVY765ek0ePnqkFi0w4IT0Y8B4xdueBvFjoi2d7pL+/l5VfDh//ry88cYbkkgm1QLR40ePVM5hMhiTTPq+BJTO4NCgnDlzRq3JwMw5LGmsLK3owLoOxuWysrayoj7tJB0Gu/BegDFWmx06NKZWYl5//VXNR2kwMyDCDrllxAOmkENitquCWXtXLYrAygombLp6elS5aOrZc5mfW9DVdhgERP4x+A4lH6yiTSYSah3n2JEjqtT01ltvyeHJI5JImu2WMBgY9IN4ICwMVII1FF7ww/YAiXhMJxB1AjNIvgMCtM660nE5fvSo/OLn70l/X5/cuHFDoNSHiTNs87C6siSry4sqd4gfA7PIA9xihS3MTr/3p3+qk/9PnjzRbR0gjxjg7e7uUkWngOj1FrKKCQ+8a309vSpneG9NneqbBfAFoDzxfYnF1cpRf1+/cunu6lbFGmNKHyHbHPo81zmFD3zfsE0T9qtHhYF3BubmUX80N/lXJ7LdeOwNHCOPvb1d0t/bo4Pr2O8eFqAgW838IAuYgOzt6dJVofjmgxsmkTB51cwPYZkJkR5dyY36H/IDJbpqv/7ebq2rIat4H27cvCmQQQzKYwJteXlRlpYW9F1FWUKBKpmIy+AArE9Nytmz51RZC5Yg8G7eGB+Vl9PPi2Uetm2KigRATtDGScQT0tPVre8C6gOkQfNuVxlX+Gv0EmGjnsYqXnDAEZMmYI24Nyfdjcbexu5c0cn9dCqhE2dQ0sRWPnhHzfu58Z03E0BhVaJE2xHfb0zePJ16oiuJs7mcrK6t6B/IqhJKyNG2Ktp3hw4dktdfe02/x1iBjjbLvbt39FsLyxF4b1BG1X6o+/UdgYUJWHGJx1UhFO8KwsKvZnn6sgS5QHyoI/HuYuIbk7Jo45SFggDtz/rHsSwiV5VTsc0RVnRjcg31nra7oJhp/dlwVHEbWwBFtD8A5ng3sX3Pq69eEFhWGB8f0+8RLNLB0gZWmqMNppN3Go5rvoOJbn3fUFdgewQonb399kUNK+Ypbfqi7chTfMexxREs5mG7FEz6YuU62nCqnJJZUzaoN4zMhfTbaupBYxkC1mugQP36G68LLM9ga1O/PkOxraCKKegHhb36qFcnHvt6wDkpUSy5r/HD9xpKBGjbwCoM5B5yGgmZ7SVqeBXMu/b1JeSVV87J4OCA9PX3ypXLV1RhEFYGsD0GFFdgwQqKStn1jCeIpl0Uj6fMpHAqpVtPQgHq/LmzcmBoUNu1QXGDQRz1It6Dvl71j3ZQPIZ3qvFtX+z7AC/IL94r1OHoVyJstGv1HQ14F/zpwuTw8WOT2h7p6e5WC3vffXddJ4WXl6H8ltHJbCy6yGY9nw4UkmL6DqH9Njk5ofKCfNi2tT+O3ThPpcKaposX39Ty+/bbb+XBg4e6/SjkFhYWoQSIigXfe7TjUCcoM+hreE04m3a03aKxsFragSwfODCoCwEQFrYCRp0yNg6raL1qacL6CzpCKQL9fdT/Bw+O6LZT6LOgn4J+JOrd8bExVYBDOeLdqPcDd23/JZOCNlF/X49ug4r2tn57kYEAWcAtxJdKJUzdvNyj+UFZ+sdJ6sXvf44wESfkEZY78B5jHEZlHOkI+OE2/HSloRTUrWUG2U4lkirTfi+VIeAan7Gx0YMC5c4XL54rs6dPn6gVDxzv37+nFumgHIG+serv63chJN3plOEVCkkfxkWSybpjPf70tOM5ZKZ/oF9Onz6lyhw/PHig1lSh2IHt26AIjfEjbB+I7yf4o/6B/OObDGukGA/Au33u7DnlOnHokJQ1abXuLhcrWLuZnDyk1ljQ14d1o6dPn+rCFfRB0K7FNwTjVOFQWL+5aErgmX760U+MGutPsO6Kd3JgoE+tyiGt6JeiLlpdXdG2MeQebWPIKsZhoOR16vRpeffdH8vp06dV5I8eOSyzs9OyMDcnPT1dqkxZbetmpAH1s44b9vRKMh7X/h3eI/2mVJHfdpSBdktT7S95u6WW6SEBEiABEiABEiABEiABEiCBbSKAzjcmYI4dPSKwVIKOLia7MaiBCRT/zw6AoLOKji8G548fO6IDrDD9PTA4oCuhMDCo/dWywXN/SCJRVTIZkJ+/9zPBvu2jY6Ny4+YteflyWgd8MUCGgakoJqCSCent7lLT4+iYF4NFgvDninT3pnSvdd0mZfKwfH35sq4Qg+UMTFhoxx+TypjI00mKcUkkEyadXtLQocfqsePHjmrcCByDCkNDByQcxkSSJeB5KCakPG+dcLV9A6Y+RpjIDzk62DI+NqqWSAq5vAwODOiq3a7uLp3caIYXlJcw6YK94BcXFlQGY5GwblkCU+Sw0uxU6/F7k7mIL5kIy7GjEzI29rdy+/ZtuXrtqlz55qpa6MFkKGQGA0aQcwwgppJmgntkeEROnzopr73+qu4zHYsFDJL6EGzIm5eGvr6UvPb6K3Lk6BE5cfKkrlq+c/euTM+YVZt4DzHxhqAwcY/JL0xcYXDpwoXzcurUaRkdHZKZmUU5cuSIKp5gwHMAg1EjI6okEDRmNDkxKj09v1DlgytXrsitW7fUzD+syCA+nXTI5XWQC3nHJBXCAXOY+cbAHkwIj46OSFdXsnwUbkNmO+eGXRWG9wIrQVEvYrIQPygXYZLl9NkzWq98++13cu/uD7KysqaDghiMx2A2JiXACWUwNjYqb7z+upw8eVKGhwc3KMdVkkE5ozrBREp3d1omD0+o0hIG5rG6FytMa02a+sOrFL9ISKSvNym//MXPtW67evWafPnlV/Li+QsdjMUkb96zngPlQcg7FJNOHD8ur776qly8+LYkk1FdMYi6860335QHDx7ooC2sxmAiotYP7/vRI0c9M/gix44e00Fe1LfefG6Zd9zTAdj+fjl+9JgUIJf5ghw9ekSGBg2HINkuC6TKBcoXZXRofFxXtUOpEZOqmIjFfa0X7SzhZiOpEvdO3bbv66kTxwUT/9hGp7evV02+YwK+mR+UBFDmUC7FdzgWjWnZHTgw5Cl+eqFVCl1AJAhrbHRMt6jCQD+UZ7A1ANoR1X5YND1ysF/+t+H3ZHJiUr7++mu5evWqTD1/pop6a5mMrnjVwfhYtKgsdu7sWZ1kR305ODiodfna2rK8cuGc4COByRbEjVX+2BZoww8Tb5GIDPb3y9GjR9VyC95zTL5jywMop9m2h/ptIP82DpQPJp3wXp89fUbbO1CogeIElGW379tsU9DeRyg1aX17+qTMzg6p3GFLJ8hukQ0qS/vDJJIjcmCoR9LpN1Wh86uvvpTvrl/Xempufk6wAhkTTihDTMIgrMGBfq0HsA0QlPKGBrvVagDqbmwBAqtasLSGSVFM1Fb7ob6EMgC21sDkKrbOgGUR1CuqIKYTTdV8l9+HXCDvJ04cM1sMFgo6yY9JTRUxf77LvZorTw5htQj5xNY7J08cV8UwtIGhYNGj29gFyLxuVxBRt0eOHNbJOvQNTp06IWi/DQz2Crb/O3X6pL6H3353XSfIsM0NtlXEDyu3wQMTufhmwbIRtj7Alk1DB/rUIEGpAR+Ugc66B2UVKJ1AoRXtx3v37sn09IxOAGO7CbQh8A3HD/UJvmtYrY9yPnbsmLbl8I0dGR4WfEbx6fF/dnBur9Eugdyif4J2NVb6o02IegQKl8oVEdm6CEdPXpLJlJw+c9pMiDqO9PT2yYGhA6rE0SjxaNyRw0dH5fCRUVUixHY4N2/e0i2OVlZWjVLY6pq2IxEx2lCQ/1QaSl8pGRoc0jScOnlS69EDQ1gUUBG7l2adSO7rk5PHj2u/FOHBwga2mQHHSk4VoZRfuuiHwApTv37H0J7GhDPCw1+j7SrUMSPD/fKLX7yniuqfffa5yv+zZ89160QoreAP7WikF3UA3h/0c/AuwIrO2TNnvC12KjNenuSdvBoY6NKJc7SBDh+ekD9e+lpUAX5lWS0r2vatmRQfkGPHj0sylVZlhqBcQIECW5GcPnPK28Z0Sa1UQgbR14fCCrZasXJdLa+2vw0FVNRbZ8+eVr74JqN/hvKALKFPAgXrEBq6nvxUCxMyiTra1osIG213KOWhnYPn1X6QO+PvmCoHgMeRw5Oq/FXNT/B9vJRQjofCQZ9acYTCCsZNoPgAqzclxeJywkbRqksmDx3SbWKhMAhZhnWMego7CAl//b0pOXPqlCwvLkoqkTBKDosL+h5AfmGdA98ypMFa+MK4CdJ24dw5bUsNDQ3J2MERZRmcx864G406ogom7/1M2w1oM2BramyfA6uiUIpGGxMLn9BHVgW0aETrICisQCkabU30yU+ePKFKzpVyXXmtZBwoAabkrYtvqmxje6Zvrn7jLSSAhTIz/oC2qSqZoK1yaEzbQsXwtB3pyGuvntF2zPlzZ+TjTz6Re/fvqSIplAgRDn6wAhqNmDYJrA6eO39OrX6irxqLObK8tC4Xzp8V180LtgxCfd3b16NKMcWSLBdFfV+OTE7K9OnT2g9GGwjWk7AYAd8q/jZHwHFR4/JHAiRAAiRAAiRAAiRAAiRAAlUIoMOAIdilrCtffHlV/uW3/0sKhbAcOjggb104JT/76VtVfHbWbeQzmyvIixfTOsiKFSX4YYWNrpaImF6qjrl6g6noMGNMbmUV+5Qvyzo69oW8DphgNWcqnZQoBo/8P9sDq+j0ZvMiMKONfYBhVhomxmdnZ2VxYVEH3NPJpA78Dw0O6GARVrcVF1J5Vv21A+9Z+c9mC8Zc+eysTuLDXDP+sOoPk1rwr+aFD47owGFlOpeWM7Iwv6iTSOh0Y5URVpv09NiJPl9GfKf+rLbLOUoSf/cfzsnvPvhY7j16KtnVJTk6Piz/4d/9W2OyuZpyRwszsZLJCVYhwvQwJo2wGlQHcrvMqjYdI6yQi2rRoycP2VtYWNJV9hgchqRhpQ8mSWIJbyKxMgCUVZU4llewRzTMmi/oysKFhQWVa5j9TaWMpQtMKMLCAyYaMLCoFhniWxuUQZLykP/VdZ1IgHIV0jE3O6tpgdl4TND19vTqJBMmJzDAme6C+eKUxCIiuYLoti5YBQarMBi0RNqgvIM9tYPyjHd5ZSWrqycRJ95hlA0GKzHZtroCiyuuKr0g/7CCgEku8EXYGPCNxiKqqBYUfiX6zV6j/p1fdeXG7Yfyj//fb1Rp4cBgn5w/dVh+8dMfSTLlbQ222Qh8/l7OLsi1b2/If/7P/yDXvr1mTKEnYvJ//ce/kz/75Xuq3ISyAi/IHlZSv3g+reUFhQ8dzB/s19XAWLkJOUEZYGI8UiEmtSZb8ijP1TVZXFgSbL+DAUsokUC+8afjgFXk2Jedqqdr6wUtb9S1sK4zPzeneYCpabUoocqBPTrJj4Hznp5eSaVK1gXw7j1/bsxGo+yxfZRZKV0epVaN3vdicWlVlctgJQMTaLC4Alnq7es2ngLeTcgo6oylJZinhz9X4+rC5FcqbSYn4Fsjqv5ul6fKOF/z3jfIOQakMRgPuYacY5KplT/I8PRCQX7zz/8i9x4+keWlRemOOfIf/4+/lYlDw4Hv55bjd0XWMzn9lqIOwfAn8oVt8KB4F4kGW1cIihcKgDD/j+8yJkgxCQ5lDUygY2uxoq5HAzKJpsXc3ILKN1avYkIK6cI3OZ2u/y5nM662E6CAgAkFTNagroaCoVrd6upWSyVIG+pKKBkgjdGYWZG/traudR7kCqtWsTWFWTEeFv2IBABYWVrTuDAhqzKYNNaT8G7ru9ik/NkosjnXvHv4JmILMSjmar2dlkQitp3Vqk1C3SPaDgsrrvzw+KX80//8n7rlB+q2C6eOyJ/86A0ZGR6oG0bTDiC7a1ld0QzLDboNRSisysWYEMHq/Q1wvDJAvYo/1KEw66/f0vl5mZ4220xiyyg4RZ2M7yjqN0xS4s+s0DepxcLmhYVlmZub1e8vLJuhLZxIBjeW8rmCrGbWdVsQbQvnYZnN0cl1TPxU1v+1mCDt8/MLsrqyWlRYhWzr+5ZOlOo7fyBB7x445F19P5ZXV3S7LLfgSle6S+s5WArYwBFhuiLZbF7bIMgL2h/YcgsKZuEorI6h/VXQ9gnSiW1hoPiI98PUpRFVsAFfvCOJZFwtB6DNFG2i3vFnbyvntg38D//jY7l2/ZaWa8xZl3//b/9S3nzjzFaCVr/gkc26+o2CvELm8M1CnbS8jDbqqqyvZ5Qb5A71TTcseqXRRkvrogAooWCbVPwQXnFCsjJ1BZG1TF5mZma1POEO1iIgm6ae8xoalfLgog7HdpfPpKDWXszWj1Bwhl99pyrjCrq2dZ3g+wLrViuaT0y2wxIHZGF2blZZhLWNH9d2PqyaQBbQbsX3B8oFUMBWozAoIKTXn2ZXBLrCy8ursrS0aPhhK85Y3HzD0ilT9yowMDPKWUFJ1nteHCvLBbWIgu0QMfGPbw8UJ3p7kuJUtNGqhoU+VQFbX6H9vKL9RLSbUfbot0IBFu0VbbfjG6TfobQq7eh3LpU0FjSwR06dH5K9mnXl/qNZ+eDDj+TO3Xu61eRbr5yRi6+fk6OTo3VCaPwxihZtBpQpvqn4tmLLI5yjHsCkOayAad95ZESGh4dK/fCAaDLrOW1n4n2A4j++9aEwFLaixrpPAlZaAjxWuaX1ome9CPKmFlZ0sY3pi+F90rZIPayov9COX8Q7infTfBO6u0z7L47+Y5Ufyh1bp+LdRr8TTPD+4Z1OdSWq+Kq8bV8ik9DFxVXta2B7VlimwHcI31j0sQLbvO/s5QAAIABJREFUJK6VvWUd54AsQ+Gmv7dX+gd6y9+jyqh918jL0tKqyi/qJ+QHbbt4NKZxQ1Zt2w5u8XvxcloV3FFBoQ2I+gv1hy7aCOCOnMIr/v7XR5flw0++ksXldUmEcvLeT96Sf/0Xf+JL0e6emjo8o1ZWYKEE/Wn9W1qSlVUo44FRXi0Eal2WThkLYni/UV7JpPZPyuqxRrKE7wfagviWzpmxL7x7+HaojEVgZapH37vhkWGBopBamLS8cdRvvanjdbxrft4by1iQxaVFXSiA/ikWoGF7WLzH6Aug/NA2wXcEZYw0WNnGlrZQzA5ckOPlK5MpaB2Id1zHdaIRtUCEMcBw5fhfIyza2M3DqXm5dO26fH7pimRXV+To+EH5k3cuysnjRyWVCqgz7GuOPNmyajB/AaE16JPOSIAESIAESIAESIAESIAESGCPEYDSxvjoAc2V7Wf5+1gYRMUPHVs7mIqdBbrSCV3BbRVIdGDDW+1qfHj/20DLbpoLzKmH03FJpeIyNDQgY6sjxUFADPph9RtM+WNAAAMzNn71bVeueonFoGMM5tkTUDBJy/roiK6OwQCiKjaoGf6UUajBhLs/k17aMHGGLTTsb+MAMjzVyJD1yGORQDIekUS8R4YGekp9d29yqVieQBpQHsVAcILBfM+s8eBgl+BPf40UR42wU8mYJOIDMjTYrwOYWFGlg3jZnK6wxoohTDYUlZtqhFWW3joXCAYDRt1dMf0rFLByMF9UHoESGAZ6McGPVctmdVe0OJCI4DEu1NMN89ZJI5YNpA1y35WOSle6Xwpuv+SyBbMyNGv254Z1F8g9JvJhgQCTC1BMCNmRFD/vRsqtDod2euyGHHEdRwdZsSofg+2Y6MP8AiZYBrDNSk+XjB88KEvjK2oFBYPNUIbDVg5QxMIEudaVVTJWlPmA5xjET6ex/VKi9DpYxTzr3l8h23sNHhOxkCQGsN1Et2SGh1QZAYpZULrBVgGob5EHTCwF7TKAev/gwUGNTfNh6+CK+FUMPVns7sJEXdK4gLzgzz9ZESCzkFGdROiyioIVEdjLAL/2UdARzuMJyHNMnKH+ICedfw8rLxMROeh907eSIXxTk+m4jKcPBgfTxPuPCZD+gR7pl57gsOrcxQr/gVi39PZ1yXp2WNsJ9tsOBZR4IqGyCyswUNaz8qnBQrkK9XxyQIYODJR/wmvIECY0y1aDV7qtvK6TB/s4GnFkaKhf/5pAaL3v3SNkNxmVwaT3bjYCB2VglalDWE0sMtCf1r+x3IgsLo7pdx0KFTCor1YfkilVgkE5VBYh6uC+PmyRWW5hsBp0TM50RUydDTdIsv1Vhm3vVzuqJYj+HnH7vLZSZQD22h9JUGD6vXJ0ErNfzNZyaJ/rd8mGUcUfFBgOjAyZp4jHFxf8Q/FkcMAo+8Dq2sT4uFpmg+IALBRAoRDWC3dDQSUoS9t5DzywQj0WwzZOSX2fs+t53SIHk+FmlX5OwWOFO5Qk0J5L2gl7lIWfb63EYlubZFjGRr2y8X9D4c+Gg6O/jFWx1GxJU3a/VlzVniHsEL4vYYkluqW/v1vjzWTzRmlHtxnM6op+vGf4s21XbT/701WZTl+ceIe7u5PS3eu1G3zPivnEPW1/+AP1O/TO8dgRSXWFJJXuL3Gq4y0gJL2F+iGZiEoy2SviYptDs+gDk734HsESA140tJlR1tF4VBUS0U/eZJTVktKy+0hXPB6ReLxH+vt71Erj8sqq5gdWGlCOaBdCMQrW9vTbWiP2eCwi8YFeGYASRY1yrhFE2SNjIcfw3gAxKPygewhRt9wU6etP619ZJHUuUO6Dg1Dm3lz7xQRfLgEq490T5Ypq1dLupT+eiEo80SeDYixWFcvCHzTC8Nx7Z2UH5AX1Ff7q/VQxV0RGRtDuN23/snERG1e9gNr4OSytRKNQRk4ILD+tZ3PaZoAymrF2aq2OxnTLPNTj6Cuhb1zkv5n86fcUbcFefe9guRRbyiFeKIFA8Q8W57D1L7bqKw5aVTBH3ZJOQyllSLfhWsfik7U17d9pm0e3NY6roiTCUQU9aBJ5MgP/AwM9+tdoNqBkGY93yeBAVzGcRv3SXXUCdpilugs+IQESIAESIAESIAESIAESIIF9QsAOPqAPbM/Lsg4llLIb5gITUG4evrxeLw5BAej9gAC8W3iMCcpwxJGoN/mOe/ir+avhCGElIzFJprBdhbeSv2Zg5iEGHzE4Zn+aBl8W7X0eGydQLEc/R5/ykw5o4hl+RcfedSMH+IF/f/iN+LNu3IK3agkmzBO6Ssg+KjvaNJbdbN0FBhHjsbDE+3pKA1M2eM2fp7Gz2XzasHxHvHexWEgnXPR2C8P2RdP2pzB97UL4QiFVWIHSiiLH/zAN4eOCAUrsBd8/ADP8nil+yKCVXbjd5M8GYY8avRcWBh7NfTvSWHTVeGxe2nTSJRmTZNKrH+sE5ct+/UnPitTAWgqC14FdPalwsJlLf4Ka9B/0iWoyiPZ2buWvTpmWZSLITz3G9Z6XRVB+odF5SgblT+pfhcOu+bYnoiIOJo98H+z63o0LsGkw/UW59YetGfC98/5nPG8dgUZluIo7KKQMYFLd92vq/d9EOVdJii8F9U9V5pBQ+7PnVhg3FQm+H0149EWv74pNiyf2UEDAdnCp+ED5K7iFz5Mvio48xcRfOBGWeDwpjuNNBvuRgyn+/FWW/3kjuYZ7f9lYP/77eO4P1//Mum/6CI0nePIlHtcOlB2gMJiWXglQ8rJp9afHxm3vWTf2fjNHG0Y1P/7n9hzxaZvPh8k+qxaO/751iyZjWCSOhRLRLnH6PCV6+9zvp0POUcUkklH9k0KPdumLsgRLphWitaPZquTqlWMxfUjMVmRpBzPj56jVuo3b1vXIVGV+rRvvaK2gVM1zJYs64VUEX/XSfJ9sIqo664wH/oKAbKM+g8JVLFJStPcXhC62cUv9mRbl0mx3nNSFD2o1KrD8vQK1AmPL1x5D6Jsa5RtsB7rhZ8u/mAd7Y4PL+jcQJ/62EET9SPafCyqs7L8yZ45JgARIgARIgARIgARIgAQCCKCvib4vFDXsQL7tC1vn1fqjuB8KO6ITklYBQT0H9GKrBeL1d+1je7Rx1zwGRBPo3ufOzj3DnSa1YkwI8YMFJvK1Ix6YoMCbgVHzpiGgxIKwoWzw5xsDr8osyL91XOuZdRNwLHhWTIwweA7sgGExTO+keB0QUCtvqfBVBIi4IbA+Wa5wsfWBI9XN8Myr+/KKd6ayTtgQ9164ofoq2C7F7C+Pfb9h5QnMlYE1G2/rSntdmXcfu8pHjVyXebf1qpY70uIW6+lGwipz45Uv7jl+k/R2gtFzjLyqG987iTShXsQPyi72Z78Z9rryaP3oa25X+Pv8V7qveq0BVKmTa70TQQFWusc1fmXgvXudeKjMR2V+g/JU6aeSh5UR684yCwqrgXsIBrqufjEs81YWvpcBeNL4bSJKPlzU45i9aXFFtWFCCFFX1gelZDR1plncpNJOUxF1kmOvjqne9mouM1pvV9Q3G6Wnepi6nYV+D5rxVT28xp5Yebdx4tq711gAga7wLcOWMGiw44Bti7ANhP6Cgscjex8McY4f7tuk4drytc+Nq/L/CxptaSuX8qd768r2KfyMbA4r2dn7tn6110FH8EXd4ymAqhm4yvCC4vSHZcuonju/H3terAztjQo5sLcRhz98/3kzbuDPXx9Yv0Hh2WeNHOHfCwOKylv5FdtKpmlmPj9bTd9WEtQSv664BdMGBidkB318/BSdfd8bjcvPo16DsdEw4Q5p8suaLUt/fM2Eh+DQRm0mf1uI0ybTsi1Gax/YYyN5gFubFrhvxm9A+MoBYfjDseHbe/Zo77cg3oCkbO8tb+s8LHCq/qt4pn2yinvVPdd/suGd8BYm2CjA157riR+496ziVtVIbTj4huDbb6+reqj+AMm23yIrL029O9WD3tdPqLCyr4ufmScBEiABEiABEiABEiABEqgk4J+ErHxW6xr93Y1zRFvoBdeKrPKZjcZ21u11NXdIK+a0Kp/7rpviUCsgX5g8rUEADFvFcRPhhKy9Y38SNwq0/+nunm8ijw0nGONXATPI+2cQyhVsw+S6BW8roIKYbQ4cY0LZgvTXIa2UXxt+0NGWu06eYmjb3ghyXOUeytdOUPqdFEfKzc1q5a1eK6Kt96qU1adlA6/+BDRwXsm5Ih0NhFB0glXwZb8thFUWTrtetCJ/reBfUf5+S2Zl6Oz3vHizcmDdy5BP+Jygerzov8pJM1z8brWerBJmE7c1SH+4Tfjds04tD3vcYkYD67ImwsYWN5upareW7MoEtkbg8LoYBUwvfH80/nN/4v33/ed+N/bcPrdHex9HbNW04b32O9hj50EMamWx4hsc6BRhogwtx2bjaNZ9YCIauNlIPI24QVSNcGkgSVWdNJqOKgH46xdt62wxvCrR7PBtKLL5ooQi92ZlzheMnvq+2ZWPmr4G6xbzLst3IwlqQfwbm+SbDHST3oKyqRxsmVsH1cLH/Uq31k+7H2HZN6DPW0p2tUyXXGz5bMM7gUreF6r/XG/7bthT//tqvdpn9tp/rPXM767GOWREv0X2m9SCMGtEt28eUWFl3xQ1M0oCJEACJEACJEACJEACJLDnCbCjvOeLmBkkge0lgOViWDEGZRVPacWFwopd4ru9sTcX+hYqvC14LRtEbS7BxvVW4q4V33aFWyvO/fasFYwbDaNRd/utDPZDftut7NstPa2Qgd3K027F2wpm7RQGObZTaZTSspfLpRPy1glpLElL+581w7MZt+2W805Oey2WO5EvG4c91koPnzVEIEj3qCGPdEQCJEACJEACJEACJEACJEACJEACJEACJLDXCMAUutnvB4oq9lztHnfqCsK9VkTMDwmQAAmQAAmQAAmQAAmQAAmQAAnsEQJUWNkjBclskAAJkAAJkAAJkAAJkAAJkAAJkAAJkMBWCWCRmCNm/3CzvbdrtlCwAVNpxZLgkQRIgARIgARIgARIgARIgARIgARIYIsEqLCyRYD0TgIkQAIkQAIkQAIkQAIkQAIkQAIkQALbT2Cn7A27gsEio6wigq3FizFTWWX7i5kxkAAJkAAJkAAJkAAJkAAJkAAJkMA+IkCFlX1U2MwqCZAACZAACZAACZAACZAACZAACZBAhxLYTmWRYtiu6NY/Yo5QVAk5oXILKx2Kj8kmARIgARIgARIgARIgARIgARIgARJoPwJUWGm/MmGKSIAESIAESIAESIAESIAESIAESIAESKCCQNHOScX9Fl66rriFgoiLv7w4rithKKz4oyi78D/gOQmQAAmQAAmQAAmQAAmQAAmQAAmQAAk0R4AKK83xomsSIAESIAESIAESIAESIAESIIE9RoDz73usQPd0drZfWh2BkorotkCILYS9gVSBpWiGZU8TZuZIgARIgARIgARIgARIgARIgARIgAR2jkBk56JiTCRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAu1GwHVFHEckHo/L8PABeeON12RgoE8WFhYlGo3K8ePHpLunS8pNrbRbLpgeEiABEiABEiABEiABEiABEiABEiCBTiNAhZVOKzGmlwRIgARIgARIgARIgARIgARIgARIgARaSgDWUxxJxOMyOjoiP3n3HXnlwjnJZDKCJ8eOHJG+3p6WxsjASIAESIAESIAESIAESIAESIAESIAESIAKK5QBEiABEiABEiABEiABEiABEiCB/UPAt6OK73T/5J853QMEWiy5al3FhBmJhKW3u0f6enul4BakUMBDkWg4bLhxV6A9ID/MAgmQAAmQAAmQAAmQAAmQAAmQAAm0DwEqrLRPWTAlJEACJEACJEACJEACJEACJEACLSbgn1/3n9tonKCb9iGPJNC2BKBg0iLFFX8wjkgobG6EnZCEQxUA/G4rHvGSBEiABEiABEiABEiABEiABEiABEiABJolUDn00Kx/uicBEiABEiABEiABEiABEiABEiCBtiYAnZRAvZTAm22dFSZu3xOAxgi1Rva9GBAACZAACZAACZAACZAACZAACZAACewRAlRY2SMFyWyQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQQKcQoMJKp5QU00kCJEACJEACJEACJEACJEACJLAtBLgt0LZgZaAkQAIkQAIkQAIkQAIkQAIkQAIkQAIkQAIkUJMAFVZq4uFDEiABEiABEiABEiABEiABEiCBfUGA2wPti2JmJkmABEiABEiABEiABEiABEiABEiABEiABNqHABVW2qcsmBISIAESIAESIAESIAESIAESIAESIAESqELAqXKft0mABEiABEiABEiABEiABEiABEiABEigMwlQYaUzy42pJgESIAESIAESIAESIAESIAESIAES2FcEHKEhoH1V4MwsCZAACZAACZAACZAACZAACZAACex5AlRY2fNFzAySAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQQHsRoMJKe5UHU0MCJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACe54AFVb2fBEzgyRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiTQXgSosNJe5cHUkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkMCeJ0CFlT1fxMwgCZAACZAACZAACZAACZAACZAACZAACZAACZAACZAACZAACZAACZAACZAACZAACbQXASqstFd5MDUkQAIkQAIkQAIkQAIkQAIkQAIkQAIkQAIkQAIkQAIkQAIkQAIkQAIkQAIkQAIksOcJUGFlzxcxM0gCJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACJEACJEAC7UWACivtVR5MDQmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAnseQJUWNnzRcwMkgAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkEB7EaDCSnuVB1NDAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAnueABVW9nwRM4MkQAIkQAIkQAIkQAIkQAIkQAIkQAIkQAIksMME3OrxOY4jIvjjjwRIgARIgARIgARIgARIgARIYD8ToMLKfi595p0ESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAEdoEAFVZ2ATqjJAESIAESIAESIAESIAESIAESIAESIIHmCLi0R9EcMLomARIgARIgARIgARIgARIgARIgARJocwJUWGnzAmLySIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESIAESGCvEaDCyl4rUeaHBEiABEiABEiABEiABEiABEigeQJO817ogwR2loArIvjjjwQ6jwCqWFaznVduTDEJkAAJkAAJkAAJkMBWCLAFvBV69NseBIqjEFac7bEyedXuV7oLuKbCSgAU3iIBEiABEiABEiABEiABEiABEtg/BNwtdKr3DyXmdFcJuH5VFTNc5DgQXArvrpYLI2+IgF9K/VLrQgGrOPrZUFB0RAIkQAIkQAIkQAIkQAIkQAIksCMETO/NkZB221z03XQcohQ5brWiS0eFlRJTnpEACZAACZAACZAACZAACZAACZAACZBA2xHQASAX0/vmX0kBoHTWdolmgkjAR8CvqILbKrkq0z5HPCUBEiABEiABEiABEiCBPUTA5eqYPVSa+zUrTklJBcoqTgMKKpsYpqDCyn6VL+abBEiABEiABEiABEiABEiABEiABEigowi4uqSpo5LMxJJAiYDjlGwCWeMqrViOV4qBZyRAAiRAAiRAAiRAAiRAAiRAAi0nsAktlCbSQIWVJmDRKQmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQAAmQwNYJUGFl6wwZAgmQAAmQAAmQAAmQAAmQAAmQQMcQ2N5VIR2DgQklARIgge0kUNNyijElLdwSaDtLgGGTAAmQAAmQAAmQAAmQAAmQQEcQoMJKRxQTE0kCJEACJEACJEACJEACu0+A0/y7XwZMQasIQJop0a2iyXB2ikBNDYCdSgTjIYEtEzA1MOvgLYNkACRAAiRAAiRAAiRAAiRAAiSwBwhQYWUPFCKzQAIkQAIkQAIkQAIkQAI7QsDOlbqc6t8R3oxkewlYed7eWBg6CZAACZAACZAACZAACZAACZAACZAACZAACZBAFQJUWKkChrdJgARIgARIgARIgARIgAQ2EuB66I1MeKfTCJi1/SbVlOhOK739mF7VrXJEXKGW1X4sf+aZBEiABEiABEiABEiABEiABEiABPYyASqs7OXSZd5IgARIgARIgARIgARIgARIgAR8BKig4oPB004j4BNf13feadlgekmgjAD0sKiLVYaEFyRAAiRAAiRAAiRAAiRAAiSwnwhQYWU/lTbzSgIkQAIkQAIkQAIkQAIkQAIkQAIk0LEEoKhi5/btsWMzw4STAHVVKAMkQAIkQAIkQAIkQAIkQAIksO8JUGFl34sAAZAACZAACZAACZAACZBA8wQ4Udo8M/rYfQKuOMXJfqGFit0vEKagKQLFeldl117ZY1NB0TEJ7AIBK6umHvYrX+1CYhglCTROoKzObdwbXZLAbhNArWv/xNfwZRN4t0uG8ZMACew/Ao5Ww7SSuf9KvtNzbHtwxXZE6UbLs0aFlZYjZYAkQAIkQAIkQAIkQAIksHcJaN8Eo5zeSOc29lX2LkTmbEcJ2EH5oux6seNaB4ysgx1NFSMjgcYI2DrWHq2vymt7n0cS2HUCWrluTIXrmza1jQhVWvFZDdroi3dIoJ0IsOZtp9JgWuoTsNWxOfo6cNYrRdqS4LHtCdgOmz1SeNu+yJjADQRKUls6K3eE+9WelbvkFQnsBIGSNKLDFtCOaHEiIi0Oj8GRAAmQAAmQAAmQAAmQAAmQAAmQwO4SKPWs7byopkeHgComR/Xe7qaWsZNATQJ+cYZDew07FT6bQTXD4EMS2BECtkK180neUWXWsZJrUgLpLf58p8V7e+mkPOubz9le57R5Mjvgs1WFuANJ3Y4otpJ9ym39EtkKXxt6BWcE6f/zV7nwUnQOR8ULGxiPJLDTBPwvQTWBtBOmO502xkcCWyXgl2mjwr0xRP87wIp5Ix/e2U4CVvr8kroxPjy1fxuftuIOFVZaQZFhkAAJkAAJkAAJkAAJkMA+I4AOje3U7LOsM7udQCCgp11NXre3y90JsJjGdidgZdSINZVU2r289nX6/HWvd27rXiO5Rs1q382O+rnsawHpvMxb+e28lLc4xZThFgOtCG6b+WrwFcJcvNzmuCtyyksSqEKgGUFsxm2V6HibBHaQgOu4Yv5qjaFBrm3NTBnfweJhVHX1ViGP9q8kpdsBjlsCbQdVhkkCJEACJEACJEACJEACJEACJNAZBOy4UGeklqncZwTKhytLyiq0rLLPBKGTslsazyym2lSz9gGGIu150QlPSKDtCJQ3DyizbVdATFBDBCC5VX81H1b1xQck0AYEKLxtUAhMQg0CaEPYPzR7dRtM3KkpunhY00GNGPmIBLZKoLzli9CMNBq5NNYxt1c+qbCy1TKkfxIgARIgARIgARIgARLYtwQccZ3t7bDsW7TM+BYJbOxsFwMsPnKkYoeKohOekEA7EijVtlaI7bEdU8s0kYAhUJLS0mCnGfDESL4n1SVHxEYCbUHAL5I4L8psW6SOiSCB2gT88guXtva1vszzUqvC3ueRBNqeAMW27YuICSwRMO0HtCHMv9LgAwW5RIln7U7AEaiRhMTRsV/HO25Pqrkl0PZwZagkQAIkQAIkQAIkQAIksKcImIFOs0zEdV0JOY7Rtndds3SEfe49Vd6dn5mNAql3IK4F0bEiSDAmoAqeCHd+npmDvUjATjppVVtxYQZBN8r6XuTAPHU+ASOpqHVdHfaEwiDaEtbeSufnkDnoZAK2ekUeKs9R/9opf7s42jR/Wf92cpnv1bT75bc8jz55tW1fOPbdLnfPKxLYHQJWhnHEX8F1pYAJf2yrIt757iSNsZJAbQIVdaqtXjHu4P+nFW+F29oB8ykJ7B4BrXndghQKOaPCbQV7G5JEhZVtgMogSYAESIAESIAESIAESGAvEtB+iU74uxKOhUw/u9ps/zZ2YvYiW+ZpZwi4BVfcfEEHjELeetNcHkOg5lc5bmTvB6au5sNAHxtuFl+T4skGJ7zRCgItKKtWJKORMDSpnjzYZONoJkdds6IJA/c6aIRjxexqtUgoY9XI8H6rCVjBhWjCBLoXvq7KKyq84oErYSckISvveRFv4V6rU1Q9vCbeC5uP6oGVP2ki6HKPta6aSYSPfa0g7bNG09tkEmzwrTk2ELlRLimPzhryKb+78coGb49wUfCqWLOqFHcMWG3+ok3sd7wxyO3XBWi04ALSxluNEahXxo2FUnK1XUWmoljlvUecmCzFDwsPtG72K62Ukhd4RoOagVh4s8UEIMO2SsUR9S/q2ryr6ir6DEoruIISi3Xb4mQ0HNx2vcuagO3I3HYmuNPS23ApN+EQDDwOevDqY1v/hmChQtDutf25BsPeznJrMAl0tl8IQHLLBQ53CoWC5PNZyWXXdfVXqU3cei5UWGk9U4ZIAiRAAiRAAiRAAiRAAnuSQMEbtUcHBRP/OvQZCsM6ZMM/7bw37Lq+w/LuVH33zbpgepsl1pz7VvNHFHq+AAAgAElEQVStFTtkJRyJSDgclpADk6YhcUIhkVC4OKlq0wO39hxHe47wizJXPKkVa+1nCHcr2xJpEvyJqx3dvn3aSYjsxKo/zTjXqjYckULBFSfkSAiy64TE9eR33xYuM942BGyVWJRdb6Ae1/ZeKBxWpSu0I+C+UHB0wh/nOiHaRHtipzNu89fqeC2bRsJtdtJ4O9K8HWE2knd100DkQYwa8KbBW1mtdB9GUwGVsNcGQPshjGuntsA2U7YaeBv8V5n37UiSn8tOxLeVPKhMtDCRaPP587+VtFX6teHaI55r+j2HaD+o8g36cZqOUHlaWpjPyrTxmgQaIeCXV3uOdrETioiLNi/aDqGwXqNhjKGJej8r1vZYzb3/vanmZifu23S2PD024BZnwgbbKeltcfaLwSkHn8KglV/rwHVNvQuhdVVT2yz+Kg0sWJfBx5bzDY6Gd/cxASNjdkmXAWHlGGNmdhwtl3NVgWW7UFFhZbvIMlwSIAESIAESIAESIAES2IsEMGikA51mZVO+III//dkRC9/kFO7jtnaAfJ14z8eWDzbKrUz6ByWC6TVUOo2vvyw17abnLXlHJC8i2ULeDBKFHSngnitScEJ6tHJq82wG830TC15YNg7rzl5v6VgRdrNhtTQtzUbeAe63iHdnc1iRWFxCVnOoa3GhE6SOuA4UrSC7jsA4L38ksNsEtB7yT8Z6sgz5RTMhky9IruBqXawyLSFZL4is56EMYOpaqASU6QB4Yehhmyq6VltPaKQcoFShefLzquPR8tVjgyw8fHVCNo+tslwtxzYNtdxUPmswqZXeal7bfNljTcfNPvTKxrYrIbu5PP7yajJIN7XyJvsLbkjludkoWuoeEFoN2S0FqYw3E74vDJvfqmEFuLV+qh3LwtqE/2rh+u9rHLYP43+whfNqKG1cWwhavdr6zMaDcCHDxkoFnEDhNSzihqXgOF67wou1VYnYaibof98TUFH02g7aVxMoV0FJMGL+oKziho381qFl34Vy7awAT57DZl6DYtgBwW35VjMJ2XJkLQig09LbgiwHBWHrYDwDEv3TdgWkxW6CCWUrr/1Qyc0KlXffPrbHoDh5jwS2SkCtrnnyChHUP18fJVfANtqO6bCVddS2GvNG/1RY2ciEd0iABEiABEiABEiABEiABKoQ0FXRDjosrmQyWZmem5e7PzwvjWwHLG2FH/y2q6Nt+/VVkrzp20yvQddpfEvCWCp6KKVkCyJTz1/ISmZNTUvDnPRKJiOPnkzJ7EJSwhGs/EfP3PzBZLrVxdIwsTLK233ahLx1CUF4CNu+I6UUt+Zsu8quNanbmVDMwOHWy2qHUqs1JSTN1pg4KzgRWc7k5OXLGZVJyEs2l5e5xWV58PipJOLxBpJnQm3AIZ2QwCYJmPpMTVZBhnXGH1tPGKXA+aVlWVhekWw+L3lxJFtw5cmzl6rEYhQ4ChIKoT70R2+1B/z3WnVutUZ29t3Q7OE/HQhurm4yShR2Y4/qHDRUj2PDMVgc1YM1ehENBmipbtemDc2EqyjqpVvhFkQcLH8GBPgyk6Qrazl59mJWcjmjHpjL5WVxaVmePH0ma2uZQGLF6LxyMGEGOt38zYYytvng4bOYj00EY+TV82g5VIbjRVDtcaVze11Ml99j8aZ1tYWjhusPfAthBXlFWht454K8Vr9n3zqvjkAd44REFasKIgtLy5J3YaUNGoIheTkzJ/cfTpu2r6/FWxm+UdLaRhaVEfJ63xIoft2wOEYcndRfy7ky9XxGVjM5VdZG+2FxaU2mnr2svyebV5M3CrT5KmS73ovmU9JYHpnexjg178qUmOWLK/x5CwwkIrNzC2ol07QrROYXl+Xeg1njDu2O4tfWlj3CMuFpaPZ280mjDxKoS6DgeFsFYrsqNySO6+ifUbIKyfOX0zI3v6hjwDpuVd5Zqxt+Mw4cF6Nw/JEACZAACZAACZAACZAACZBAFQLoMKAbvbjmypd/vCbv//4DyeQKEgk5EguLRNDBgV/bR68RTpVHW7pdJ9pNhm0HfTfpvYa37UlvaZijRtSbetRp6S0JolEHARkorGDrlLyEJJtzJZsrSNhxJSquhPLrEolhqyBsEYTxIphMt0orhqvKty4/bz0Nm8pNFU4dT61PbZ0I2/Xxdox6bBdcTCahRrWT/Z7CioSiak1ldXVVIuGI7n+OtXmxSHF4v0jfnzSTdXOHoz9FRDzZFgKQM8zAwhQbJM/8YRW/E8b2gWHBxH9Bwvo4XMhJPCwSVsttSJD1g2B0ptVLpV+iW5/w3XovNjscize+ESL6yWoQl6knGnPcSNylkLzvaelGS86QXh0rb2DAvExpombsqHfVFoXnygzWu05ElQaxmj+Xy6oZdNTRkRD+ROvioGCVaXOwgoJp4N72RtKMbPgT23CqvAgadu9FUkxXsx79iax7XoylrsvNOmhtDIBhgFi5d1XpCluphGU9l0er16yQzq1JLOxKRHe6QipKKtomL36wRnnAhr3ZvNIfCTREAOLo1e2Q17xEJIdjoSAF18hp1MlL1CnoGET9MBt/yxp3iVjtO2KP9VPSmAubCntszFd9Vzad9ljfR2MubDrtsTFf9V3ZdNpjfR+76aIy96g1TR/fKL7CwiCstcGySlhyEg25EtMGMHzaP+TAhmTybccJdqutuptMGffOEUCfQaUQYqdW66zCCvocISmIIzlXZC2Xk4jk5fjEQfnpO2/IiWNHJJ00NlHKJdcT5U28vrSwsnPlzphIgARIgARIgARIgARIoGMJaAfE68hgsCgUwuAnTPnnJZMvbUhR7Kg0MInQ3jA20btq7wztk9TpVL/m1ZyZYR5MmBacfHGlKQaL0P3Ou3lj6j9bECeHgSWjqFJW+laWK0aKytxskq55X8yQ1iaDqO3NvpC1Xe3pp1pOmDBvYS4t1s1OONdKiqbUyhwcOth+rSAFJyeuC40qmEE3uYF0r8F0kCebNo92ogreS5PW3t7pLSVRKyd8tj8JoD6DFOMtMYpX+r6ECuI6eV3pb57AlasTqCEorMA15NgKcbG+tbLumxtqJVgvmZ7abStDDgzLvN/eIwUT6KzOzeY8Nue6TtSberxdKbDC0lii6rlWGdAVpia9uroUk/0O7LFBflGHhnQiFbKbcwuSV4sr25W/xvJVemkadd+cu2Lu6gH0B+t5asaL33v7nBdzv21JKn2jWxAFVkT7gjF6f5DfsLfVGuQ5JJjzxxZBbi4vWd3XFfm0eTUh+NsipiXtC5inJNByAj7J1ZfCSB0UVrCFoISjKqIhtOfRp8vnZd019XD9pFjZbsClLxn1XdMFCfgJmJYvvskqRp7YoQ2hMottiOE8hH4dtinGNplWUdAvozinIPrJ8nwnCEB+IXdW9iCbZvAX9a4qDzohcZywqsGqlZVtShYVVrYJLIMlARIgARIgARIgARIggb1AAF1mfxfa67eIE8Ie6CEJh6ISiWzsVtiuTucyMDnYjkHa7WRTVlYtgt9p6UW2MdbpWEsVUENRhZWQ5PIFWVvP6Ui9sgrHJJVMSTgcVmWVQsHrqvsUHIodcqsF4JtTbQViT02m4kVrRcgMAwQgv8UybCESyI9d6dmKYM17hv+9/c014YgFEhKSQsGRbDYvK6sr6gZ1cDgclXgsYheiqlEKDceTUZVxvVEaRG1FWhkGCQQRsN9Lc8T/GOyE/Dq6BQXq4ZXVjGTzrrgFs+VaOpWSqC7xd9RUeuldVen1orHya2NV1QJ7saWjfV+2FEiTnkt5bNKj53w7FOU2l5LGfHlVUGOOd9GV1rZ2hSm+Gy7WlJotKbClClZHr2cyqlgFncJQRCQeTek2VruXbKXrfel2LxV7N2bzDe6U/Ok0qVd1GsnABerPsIgTlrX1dVUS1LaLE5JYPCnRKEys2HyW5MnUU7i29zqFAtPZuQTstx6SjG0pTPvXbCsYkvX1dSkUctrmjcTiEgljHAJt5no/K9/13PE5CWyFgF9+vXoT2wnrmIIjmey6ZHIZKcDeqyMSjsQlHovWjdAOP9R1SAcksCUC2AbIjEGg5nVV8EyPDu0B6LZiO+L1HDRe83atzJZirOZ548hyNZe8TwIkQAIkQAIkQAIkQAIkQAIYuvQG9DHJ1NeTluGhwY1csHKvXNVlo5u2v8OB2rYvoioJtEP0dugIFlXcUEiWVsye55g0RWcbJkwPHzookWhEO96FQl6VGzBUao1clE8uImSzW0WVqJu+zWHUppE15cG8xa2fcEH91lqFFbsvilfvaJKN5gkmm7I5kYWFZXn4cElVWmKRqHR3JWT4wKBEwuHilJLPm3IyEmvmnMywU1P46JgEmiQAKxRW6kztBrkLhSOSL7jy4PFTWVxalZybU3P+4wcHBUorqHNVYdBWvBtiNXur29ulOOydzR3Vioa+NPrf5gKhr5oETJF2Bl8ou8IeBX6QDUzWQ1kFA/RLKxl5/vyZZLM5iUXC0p1OyIHBPkkkYjXzv70PLVd73N7Y9lfo/nqsU3IOE/6ltEIqoPCqSq8SksdPpmR+cUkKLiZMCzI8OCj9fd0NKqz4Ai5FwTMSaCEBW48ZhRVUxZDdXMGRpdWMzMzMyPJKRkIF0fGH3p4uSSUSDcQP2W2B/NrkNRAjnexHAp6AqKhZYbFKr468nJmW6dmstifCIVcGetMyciBgDK0Cnb9Or3jESxJoIQGjsGLGCqzCCoI3Vq1WM+syv7As07Pz4kJ7xduerYUJKAZFhZUiCp6QAAmQAAmQAAmQAAmQAAnUIqCTDq4rBZgvDYeluyspp48flZ/++GKwN9tXL3vaggGjsvC268Im3h63Kx6G23oCRk1FS04nTrG6CXugizx8PCUff/K5PJl6Ibn1jAz29sufv/euJFNJtRpUgFUW6AgEWVjxJbS1UmFC65Q3w4eh7U+NDGxDMr2ATZm1quT8UuWpWnmjlAWJyNLSuty990CeP30k+XxeupNdcvLIhLz7zluSTCaLCivIbeDgZuDNbWDDIPctAasQpdWu77VQC1euI3MLS/LBR5/Ig+wTWc6tSVciKu+9+7aMjh7UAVFYXfErCJYppVTIb2sUYu3krv/d27fFx4yrMrZfBnHDbH+5sJxVZauPPp6TudkVScWjcuzwmLz52nk5MDiwu+x87ZXdTcjejL2sHuqALJqqFxP+Zo7eKKtgdbQrv/3dh3Lj9l1Zz2Ql7OTkjVfOyisXzqhDq+Bt6nEzQWVCQUi2QrfHDgDBJHYYAfs99icbUhmS1fWCPHz8TL746ktZXZqXWCwqk+Mjcv7MKRkfHfF7qH6ubYjNy6++C1WaCpt9VpbYFi30qZUWja9OPHX9lyXad7Fd4fqiaNtTL+9GyVUvTI2pWwBBYSUsMErx2Zd/lKXLCzrPH4sU5PSxw/KnP/1xMVtF8QoUU9vCLjrnCQm0loBnXUWtsnnCaEURQ78YO/vuxi2Zn5+TvGCbq9ZG7w+NCit+GjwnARIgARIgARIgARIgARKoSgCdlXyhYBRWpCCRkCNdyYgMdNc3Z1o1UD4ggRYTsJ1rBGv70tiYAgor88mEJKJhiTqu5PM5Cbs56U6FpasrJuGwN1yvCislv/5w/Em1Yfvv8Xx/EfDLWqtzbsPGEX/RUEx60gmJhlxUxHpMxsLSl05IKgWT/uZn5dIe7X0eSWCnCBQNrHgRQn51J/RCSuJhR8JuQcKFvEQkJN2pqPSlzbZWaGPYAVB79KfZvhP+ey0537aAq6cuKH/VXZc/qeRb/rT9rraS13bIDdoOoVBU5ruSahVI3Kw4kpNExJXedIxt4HYoJKZBCVRWZWgH2Po37zqSjEUkFnK0DRxxCtKdjMlgd30LQWxPUMB2k8DKekhmk1Ft9zpuTq1fxSOO9KRiMtRbX35bkvYaL0GNRy2JmoF0EAFUuPjzhAKnaEPgL52ISggNuDwUY3OSiDoykN44NV9Lnmo96yBKTGqbEoC84hd0XFlOSVcyLpEQ5JkWVjxUPJAACZAACZAACZAACZAACew+AdNVtlthdPpExO7zZApaTQAS6hsrKg/e8VZPqxgXxHUL4mKWFHul29El7MxSGmsq91/j/gaHvLHnCZjasLXZtINEVo5t6E5IxAnZvaWhXGUl1vqwLovjpKUbPCOBHSRQ1i7AYlNbp4aMUiBkV6XWdU39axakasWtdXeVF6vK7a3nbNsC3nrSgkIo4xvkgPdaTgDMw2FsrSK65RWsbmDeyayobnl0DJAENkWgVlUGGVYLVrDIEwppC6KRuqRWmJtKJD2RQLMEYOzK244YdXABbQZTAReVXJsNku5JYFsI2ArTO+KAP+29qRwXpIDpfjcPIbYjD/8/e+/BHjmOpel+NOGNvJS2qrp6uqd35+597v7/n7E7M23KZKWRD+/JIHmfDyRCVGQopcxUyH7MDIEGBA5eHIIgcAB8URQb5Bc96aII3CIB6pz5Hstc6i8Hdrle+kHHWS7XOfvc52Zct5g4BSUCIiACIiACIiACIiACIvB0CHgeP1Y8OI6bTdu/3o+Vp0NOKblrAlc27vCCXVrCdqLmTvGD3H6gXxnGXSdG8T0rAlbvqIf5jW3zNBSMaGSVXUgbi27W4JkPS/sicGcEsnKWOmt+VnkXPaXpCXNoOlRlFXhneaOIbkTAVBuMT2OhkmqyLahvFII8icD9EbCqypI2Nc9OwOUvEzNCWvWH+8sZxXwTAqbeQI9ZQWwMVxwus7K4cpNg5EcE7oZAWqVdxJU/TJwE6Y/am+qvLZ8XN2hHBO6RAPXR6qzdX+ioMdSmwVWqu+sUUwYr66SrsEVABERABERABERABETgKRGwXzC5NGXjpHNntCsCD5eAbSBig5ExXFmsaX7RaM8P88XH+cNNiiR74gTyOmibhuKYswKlhoJ2ZJP09YkrwlNL3rLCsijO0riwYXlqaVZ6ng4BUw/Ohvo/nVQpJc+OwIoPumfHQAl+DAQuNPXLe48hLZLxGRBghfZCVS8l2Bpmc7oV7qsN7RIeHTxAAvb7jCptZiU2M6vEmdHrFYp+C+mQwcotQFQQIiACIiACIiACIiACIvBsCXCokzYReCQEHDO6iWNMs2WAuEQQ4uznPZJUSMxnS4DFrfmlBldpg6fK4GerD48t4UZVzUTSpkXfGhAuksHrplVUVoMLJtq5BwJUwtXlqj2bLshmlfUeRFSUIvAVBLKiF+AMbYmdZ2V9nU1fIZq8isC1BBaaulDkVIevvVEeROA+CNiKQi5unkp/tt2B7kKzcz61KwL3S2CF+i4E4mAZlr7r3mSwsm7CCl8EREAEREAEREAEREAEnioBfWc/1Zx93Ola1stsSQqTKDujihMD/GWGK5d7SZcDsDi+9Alv/cgVgdsjQI2z2pg2dHJUXjolhTFWyev27UWrkERgLQSMwSA1moaDdNlxyrWutInAgyFwtT6a6gMcOGZNCtv5dBdN9w8GjgR5DASWVfhS1TWt99rlgB5DciTj8yWwSpWNOmdGV47qD89XOR5pymmk4iQxHNMGsazhjzRREvvpEqCK2jpE4qSfbGZJwfUmmUt0axMBERABERABERABERABERABERCBZ0DAfnUzqZzWP/v4vpTyvB97YdU5e02uCKyPwGXNSxs3U2MVXrl8dX1SKGQRuAUCpqP/Qodtl/8thKwgROCWCNy0TL2pv1sSS8GIwK0QWOogXTq8lSgUiAjcIgGrok46peDFNGx30Gl6i8lQUCKwIHBRe7jYW1zUjgg8FAK28M3kWTpcq5SaYWWteBW4CIiACIiACIiACIiACIiACIjAnRJg+89VX9VmCSsXSeIB/MGDg9S93PmvRqQ7zTNFJgIi8AwImLGllyZGT+BeXV4/AyJK4kMksPr9n7DDNJvUn1JfVc14iCmSTM+QQE6Nja7SRlt6+wwVQUkWARF4GATydQjOIaF5JB5GvkiKlQRydYj0uq312gvWXXn3d52Uwcp34dPNIiACIiACIiACIiACIiACIiACD47Ald/Q7BxlAxGNVKxL4xU1Gj24PJRAnxEwnU1mCvRsSRV1mX7GSCceOgEWzvaXlsfU60tF9qWDh54eyfd8CNDgKjNUyYxXksua+3xQKKWPjoDpasqKXuqtdPfRZaEEFgEReOwEsoEzTIYx2H7s6ZH8T57ARb2XSU0rEWZpzDWmXK1ya4SroEVABERABERABERABERABERABB4aAdsbuuw+NDkljwhcEEjtVEyX08Ua0uYwPXfhU3siIAIiIALrIZD1+K8ncIUqAt9PwFZtvz8khSACIiACInDLBPTVdstAFdyTIyCDlSeXpUqQCIiACIiACIiACIiACIiACIjA1xAwa6N/zQ3yKwIiIAIiIAIiIAIiIAIiIAIiIAIiIAI3IiDD1xthkqdnS0AGK88265VwERABERABERABERABERABERABDUaVDoiACIiACIiACIiACIiACIiACIiACKyHgANwWSBNs7IevAp1rQQWplZmWcz1RSWDlfWxVcgiIAIiIAIiIAIiIAIiIAIiIAIPncCaP7ofevIlnwiIgAiIgAiIgAiIwHMgsOhyeg6JVRpFQARE4N4IqLS9N/SKeF0EHAdsOlvn7MQyWFlX5ilcERABERABERABERABERABERABERABERABERABERABERABEbhvAouR/Zpf8L6zQvGLgAiIgAiIwEMnYAyvjKHK3dQbZLDy0DVC8omACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIjANxPIj/m/m86nbxZVN4qACIiACIiACDwrAjJYeVbZrcSKgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAisl4AMBNfLV6E/FQIyWHkqOal0iIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAI3BsBrsK2WInt3qRQxCLwbQTuw8xKBivflle6SwREQAREQAREQAREQASeHYFk+Ytl+fjZEVGCRUAEROAuCTiXWz1VBt8lfMW1DgLLOrx8vI44FaYIiIAIPEsCKmCfZbYr0SIgAg+DAIvgRTG82HkYskkKEXggBGSw8kAyQmKIgAiIgAiIgAiIgAiIwEMmkB8Z8pnhykMWXLKJgEY2SQeeLAGN23uyWfssEpbVLNRm/yxyW4kUARG4ZwL5j7l7FkXRi4AIiMBzIpB+saUWKwkcOCqPn1P2K61fQUAGK18BS15FQAREQAREQAREQARE4LkRWO5H4gc2NxmtPDdNeNrpvaTnakB62pn9qFOXNnReSsIl5b10RQci8AgIqMB9BJkkEUVABJ4EAVUYnkQ2KhEiIAKPloBtS3u0CZDgIrBmAjJYWTNgBS8CIiACIiACIiACIiACT4qA2jqfVHYqMSIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiJwXwRksHJf5BWvCIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACDxTAjJYeaYZr2SLgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIwH0RkMHKfZFXvCIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiKwdgIOkGh917VjVgQiIAIicCUBlcFXotGFZ09ABivPXgUEQAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQARE4OkTUIfp089jpVAEROBeCCQA+Ms2s2uKXP5R2Wu5yBWBVQRksLKKis6JgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIwJMhoA7TJ5OVSogIiMCjIJDASW1YcoYsj0JwCSkCd0xABit3DFzRiYAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiMBDIrCYLChJwH+ga5z1WV7JYOUhaYBkEQEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREIF7ImAMV2iowvhpsbLGTQYra4SroEVABERABERABERABERABERABERABERABERABERABERABERABERABERABERABERABD4nIIOVz5nojAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIwBoJyGBljXAVtAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIwOcEZLDyOROdEQEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAERWCMBGaysEa6CFgEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAER+JyADFY+Z6IzIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACayQgg5U1wlXQIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACnxOQwcrnTHRGBERABERABERABERABERABERABERABERABERABERABERABERABERABERABERABERgjQT8NYatoEVABERABERABERABERABERABERABERABERABERABERABERABERABERABERABERABB44ASeTz3EcOA7g8B931rhphpU1wlXQIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIvCYCNBYhf+Ns0ajFRmsPCatkKwiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIi8AQIyGDlCWSikiACIiACIiACItxtoMoAACAASURBVCACIiACd0YgSWNyMvfO4lVEIiACIiACIiACIiACIiACIiACIiACIiACIvBICLDtbL0LqTwSEBJTBK4hIIOVawDpsgiIgAiIgAiIgAiIgAg8dwL6uH7uGqD0i4AI3CcBlcH3SV9xi4AIiIAIiIAIiIAI3BeBhANlcoNluDSF6sb3lRuK91oCOeXk7uIwM1pZHF8bkDyIwPMjIIOV55fnSrEIiIAIiIAIiIAIiIAIfDWB/If1pdlV8he+OlTdIAIiIAIi8CUCKmK/REfXREAEREAEREAEREAEnjaBnLUKE6rK8dPO7ieaOqntE81YJetWCchg5VZxKjAREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREAEREIHbI6Bu/9tjqZDuioC09q5IK57HTkAGK489ByW/CIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACDwxAgn4D3DU8//EclbJEQEREIELAjJYuWChPREQAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQgXsmkNBSZbEqkAOHViuyXLnnXFH0IiACInD7BGSwcvtMFaIIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiMA3E7hksfLNoehGERABERCBh01ABisPO38knQiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAiIgAg8OQIyWHlyWaoEiYAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiMDDJiCDlYedP5JOBERABERABERABERABERABERABERABERABERABERABERABERABERABERABERABNZKYLEYW5KA/0DXOLyynk0GK+vhqlBFQAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQAREQARE4FERMIYrNFSh1LRYWeMmg5U1wlXQIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACIiACnxPwPz/1AM5YIx3nlmRheLcV1i2J9OCCscwp2HNiJd14cKoogUTg0RGw5edy2XnV+UeXwLsW2IKzBfQy2GvksbfT21feek3IunzbBGxeKZ9um6zCEwEREAEREAEREAEREAEREAEREAEREAEREAEREAEREIFHQeDeDVZsd5ShZTsueJDf/56ODBvOpYi+Nm+uuvmq818b/j37vxVG95yGa6JfmVPfmG572/VqaX1SuOt9X5MEXRYBEXiIBOxjbl096t+RSxYiXf5iAJwIzgUS52bFqA3CSsHjJ5onK5OWO5nbTXEuc6CH/LZ8PX/t1vZzkTJP7XZJWHvynt1rZMqlxAiaS809C67oRUAEROBuCKwsJm3hqELxbjJBsdw+AavDNmTpsiUh91EQ4PeT3azyWjev3Pac9StXBO6LAPXS6ib1Urp5XzmheL+eQF5zv/5u3SEC900gX/5SFpXB950jiv/mBFT+3pzVY/N57wYrV1ZF7QXrfi/Z2wrnkhxP5NGwbKx7KY06WCbwdZioI193x3J8OhYBEXjABOzjnbm2uq/19r4lzyxM3mvfrxlRJ3/tW8J+evdcR+TS9UsHGYtV59aOiZFm70W7u/Y4vzGCa/jkL1tt/caYdJsIiIAIPEoC+XJw8dp+lCmR0CKQI3BJsXPntSsCj4JAXoHz+xSex6q1PopsfHZCLuvqswOgBD9SAtLcR5pxEjsjsKzBy8cCJQIPl4C09eHmzfdKdu8GK5cSYDUt68u4dO1rD/LfYTbcrw1j4f+7A1iE9FB3OA6DP6Y0/3uo8n63XLeqH0vS2LAXanMbCr0Uhw5FQAQeFAGWn3zS7eNP4dxFGfCgRH0EwqwClye76voVyfoKr1eE8PhOW1QPNu0PVrBvzuunl6JvRqEbb5sAn2cp2G1TVXgiIAIiIAIi8HQIXKr7X1dpuO7608GilDwWAtfopNVvJucar48lxZLziRLQd9sTzdinnqxrClaVwU9dAZ5G+lT+Po18zFLxsAxWLNprykrr7UqXSnqbiroyrMsnLx9dKdmDvBAB4G+e1f89APwxG+zvQQr+rUIxs25p+yzfeWIRPpewWBzcUowKRgRE4KERsGWoffzpPvly9LYzgdAuvfvzb5+rytFLN+TK3ky4pcu3LfKDD89iuwGHr/B6u8mmbDZyujeQ9XYFWF9oTyw56wOlkK8mkH826OsJPR9XJ1pXHh0Bq6ePTnAJLAIiIAJPjIAtj1VfeGIZ+/SS89XfSfYGq+NEIj1/eorx2FKU10cru9VVeyxXBB4ggWXVXVmcLntiOqTfDzA3n6lI0s8nnfH3YrBiV1W9bskE6p4tC1cVnva6zSH6Mf6sZ+taD9/q5sKxsidwFrLZdFhZvzWau76PBioBgEkCDJFgksRwoxhlADXPQ9V1Ucw6Xu9attuOL5eFKz9svirvvuSZEeUiS5BqR+7UbSdN4YmACNwjAb4TaLASAhgkwBgJggTw50ApjlHzXTR8B3zZqhz4QkY56fvezlTjwIWTEeP7dnnLn7Hv4BXelm97+sc5MLaORKb80YiKrHJeFjxWnVtcvKUdymOfFwb5JXluKcpvDsayIxfuc7OMrMtz1p91ec1et256t/6KwDcQkBJ9AzTdcucEqKe2oLSRS3ctCbkiIAIisH4CV5S5tmimSy9XeFu/fIpBBJYIXKeLVmfNbcvKaxV7KUwdisCdE/iCIi+r6Re83rnYilAEqI/UUaun1r1U3K5SWnvTqmvCKgJ3SeALOmj12YrzBa/Wi9wHRuDODVZsZwWVhT8qkd0nG6tUtgykf15nxwYvOjzI/MUJEGfHmWM6Y0znlT2Rer+Vv5TF/kwHZQIUHaCQyWdlv5XI1hwIZWUH6ygBToMEf7ROcTruww0DbPkF/LC1hdfbu/BcJ2W/ZnnuKnimm3nHzeYXVcV2eN5YbXgzJ1DJwso71BFetq4N/6qOwiyofBDaFwEReCQE+Jwb478EOJyM8WEwQHc8QWE2Qz0BftzZwV/3d43ByiNJ0p2Lactiy9KW0V6uhF0uJ/NlNq/ZMCg8J7ZiXcH6ySdoOZz8taeyzzRaltwnz3kClFhfiQGPL6VVL681ArDvQz4rrHskNOrK6k/m3Zir361RjBsHbRlSNvKj/KyHOhHguql+2TRZl/7o36TH1ltvHKM8isAFAeqf3e74UbXRyhWBryNARaXiLiksy0eeWjptwuZ7wH7Xf11k8i0C6yOQL38ZyyrdXV/sClkEvo2A1Vvr2lCWj3l+pU7T48oLNiS5IrAeAnkdze/b2FappfGnOoRFJPeBEKBe2p8VaVl/l4+tP7kicF8ErM5alzpq27R4jkqdX+o+jhNEcYRC4c67k+8LkeJ9BASs/mYqu5DYlrm8Tr3W9ngI3HkJw46KKQ1NkMBDYmb0KLge/JxhBBWJDf+c/WOWaR1n+iiyg8O76AygsQr9sCPGdii4NCJJElQ9js++nY0isMGNsrOzhUYevfEU4+kUm+UStspFMyOJLdjtA3E7sa8vFJMWJDgbT/B7u4V3rWPEoxEOKhVUCj62Gk3USqX1CXDHITMfbR6GSao3FIEGRyU3da1IV+YhA/nCRj2xHXKcZYF6ybC8GKh4FyPKb0s3vyCKLomACNwBAfPMszwBcDYZ458nh/h4egZ/MsVuoWg65f+0t2uMG43h5R3I9JiiID9bbrJuYN7pWbm5XA7z2P6YRu6zLCVXGmFw31x30nMsrp9yWcv0Mb35jefsO4j1p1GYYDidIQjn2CmXsVXyUb3jmp/NX75/hwnQDyIEYYDiPMF2uYKK76DopgYs+bTc1z7lpR7adzh5knMpM1KmoQ0364/1CfrnRn0j3nKmg9lpOSJwIwJ8fvM/e5Mp12z5Zk/KFYGHRiD3QqIes4zkj5t9V3Of17jJWCUDIefBEKC+LpfB1F3+cur9YOSVIM+cQAIkzkVZm9dfkqEu5+sPVpd5bfFNagvk/A3PHKuSfzcErL7Stfs2ZquW1F9b/ub1l4qtOoSlJfc+COR11PZFWT3mNXvd6m1ej1WfuI8cU5x5AlZHqbv82eNlveU9NFbheVtvcD0HjnfHDYp54bUvArk6LstdWwbn9djqbL7spV8ea/t6Ava95TiOqX+Z2fDXXBG701KGSsQOlBOE6PUHiEdjVB0fu81NbNXKpgBkxwAb/rlMTSeKcNLvIwkCbLkeXjebqLlpByBhGT9I0J7N0et3kCA2I4g33AJeNzZQK/rGGOHrs+LyHVR0ysX4+kjw23kH74+P0J+MsFcq4d9fHODf9g9Qdm7PSOayBLd/xDRxhhp2IE2SEP1ggu5khHg8RIXLAwUB5kmyqGjdvgR3HyL1isZGXRrp9PoYzabmQaNuvazVsVkuo3DFrCkLaal4hLdi4+mUJzBAhLPBEMN5hGgeoTSf483mFjYrZVSWRv7bB39FkDolAiLwgAmYcjSrIPHZH4UhepMpuqMxvPEYXqGIYTAz7w/65U/P++UMte/8MesGswDtYIpJFCJOYiROks6WwtZYLhBEgOajyYHruij4Hoq+j7L5Fcz73hi3wkGVRq5OajxgK6m89ynxX5UWVsKtYQhrRb+dHuK43cE0CPCyVMH/8+o1ftpp3umMP7b+NADwe6eP9+0zDIYD1OYJ/v3lK7zZ3sF2xb+Q6Z4fFNYVWpwxaTTCaDJBGMdwkwS1KMZP29toVkpGj1in7SbA2WyG0+EQXjSHjwR1z8dBtY69chnlxRfRPScqfXT09wET4LNrP7ipWzTG57PDHz/WWJ7RhJyNRQu1esDpkWjPjwBLOdtgZHXYGvMZHU6AgpvqL2dXMbN9PT9MSvEDJMCy1+qv0V3qclYGs7zlDHWVpRGmDzAZEukZETBlrZMZqWeG06z/h0jMdwD1mT/qL7+NCnCMa7+NeM00BK/6mHhGHJXU+yHAui31lXVdujNT301MHYK6Tf3kRv01gwvhmDow22qptzzPX9pCkHmWIwJ3RCD/vcZ9DnKhDge40GGe55Yvf/kdx4Ev/Jazepx5kyMCd0bA1nNZ9lrdnSMxbQ68xo1la1p/SOsO1F3Wham3ttxlOa0qRAZMzp0RYNmaL4Pt4MF8PYLXqZ/58tfsZzrMMtgaYN2Z4E8ootRYJTUcpgHLujbznbKuwPPhUllMpwWA94M+PhweYtbqYrdSB7wiapW0YZ+FpjVE+bXTwi/Hh4jGE7wpVbBR+hmlUnFROZ1wRHsc49fuOT58fGcMVhqej1flGmqFIgp+3czccoHPVn0vzuRlXLXPO6zsYwCnCfBfpyf4+7vfMJhNsG2MVGLsb26iUEqNbm4e+qoY7+Yc02Qf8rkPhG6CuQckvovIdTBP4sdvtp7Lbu5StwZIcDif4b+O3qM96MHzPLzyy3APXqLi7aJQ9G/+0mWgWWZzlz/q+Ih6Mh3in+fHOBlNMJvMUJ9HSH4EfH8PpeKdPXZ3o0yKRQSeKQFbWaKbNhA6mDseYs+H4/uYex4ix11YrT9TTF9MNstMGrIaY9B+D+97bXSnY8yjOWKXBisOHL6OaLRipv6lRS+NVVwUCz5KBc4YUkCtWETF81HzCtgsV7FbKaMJBxVE8B3PVEgfw7v5i7Cuupi9i+x7iJX2IRJ8mg7xf44+4P3xMWbhHHvw0CyWsL/RQN3PDGyze68K+jbOM49ZfzpPEvz9/AT/+PQenU4H9TAyhkfVSgWNStN8UJg8vni13kb0Xx0GP9zP4jn+z9kxWp02ZmEIL0nQDCNUS/+BYrlk9InpOgvn+Pv5Gf51fIRCHKGIBLulCqL9F2j4+yhz6hhtIvAlAtkzyPcIdYp1Vc42NUaMUTjFdB6iEAF1t4DdSnUxI+CTLc++xErXHh6B3Psnr8N8r/M9NJzNkIQhSlGMquNiq95AOWshuoPXz8PjJYkeHAHqIXXXNuBTd9nGNI7mmIQBnPncGNi+qNbMDLSOXusPLg+fm0DUWerrRX0hQZ+zKsZzjGj4HwYIwznYnOc7Diquh5pfQKNQRKNYQN3zzEyArEeowf65ac/9p5f6y/ou67osa0dIMIhjDIMA0/kcszhCPJ+b9WPZasrBfhvFIpqlIpqFIqrwzCBD6i6LY/5UJ77/fH1OEtjyl20G1GHWdwdRgMFshkkUIZzPMY9jM9iq4jiouS4ahQI2KlXTVsWZWLmxA1WbCNw1Aeov67psnzO6myQYhgGmYWjK4DiK4CQJfMdF1XHQLPjYLJXQLJRMeUwjQpa7qj/cdc4pPhJI+14Atnkv6hDJHP0pB75GCFj+RpFZgp6TStT4831ssvylDmezYavu8PD16U56zm0DFkdQs8Pi17NzvDs8RNTpI9rcwavdA8yiBKHrmIKTldZWkuAfR4d4d3yEeDIBqnX8f29/MLOCcCkgVnSNAUIc4XQ8xO8nJwjnARq+j6i5jZ+29oxCJq733RVYWwGm1WF3FqI/GWMaR0h8H5PpFN1+H51eD5v75ZU5zvRz44uBPx6zcM9XsjMvN3ZsWHRtRd26Vt7rAjP5Qqv2JMac04k6TtpgkySI+ctkpcuwH+WWwbBpZYHWmk3x++kxTjstFAoFjL0SDkplHNQbqBb9i7RSyW4K0xqsJMAUCTqzAB/aHXzs9jAZjlALQrzc2MR+s4lNGaw8SlWS0E+TgC1L+bhz4yNvy9Lryj1bSWf5YoqLQsGsW8eylDOAuAUfLs9l17+ySDH3PfU/ZGIbrY56Xfx+eoLOaIAomiNhS2uczbISk7ED13HhuF66jmoSIYkjOFxDlY2vXgHNSh0vd/bw4/Y23mw0cFCrou4AfDvb/LqS6WPNoOw9RfG50eWo9vNBH/3pBJM4MgZV3dEInWEfw/EUlWYFXELxLjY+HzMk6E1Zf5qY+tPcBWZxjO6gj96wj9lmA1WX+ftVr91bFZ84+KN1fjsM8fv5OU5OjhHOQ7Mk5cY8xv96+xP2dnbMaD/6Ox+P8L7dwh9nx/CCOUpxjGmtgZfVBuYbMcxaR7cqpQJ7cgSc9HvGjMzLRujxG+hk0MVpu4X+eIRCMMdBuYb/ePUWO406PPcG5dmTA6UEPUgC2XIU/Cbnjw2g/I7vxMCns1OcdjuIxmNU4xgHlSr+9tOfUKxVNLvKg8zM5yWUrQJZ3WXDJ8thzk533O/htN3GYDwBZjNsc3aVN29xsLWFir7jn5eiPKDU2noqdZYD/DhIqsfZpoMYnzpnOGu30Rn0MJyMzICpJEngOS7KnodmpYrdRgMvt7bwdncPu5UKmm46IyU/I76iyesBEZEoj4kAvwf5o/6yX4BlbYeDBAZ9HLVaaPW66A9HGM9mmIczo5MFz0XV97HXbOLF1hZebW3j5eYWmvBMx6nt8L/2G/8xgbpNWfVg3xpNW/6y7dCWvxxw1Q5CnPQ6OOm0cd7pYMC+otkMEWdopcEgO0rLZew2m3i9s4+X2zvYqZSxYdq10u85ZdOtZZMCuoIA9ZflL/WX5S9XHWiz/B0OcNRto9XtojcYmP7NMAyNsVXB91Er+Nip1XGwuYlXW5vYazSwUSwbIwDN/HoFbJ1eCwFbh5hmK2fQ2KodJTjtd3DSbeO01TLfbZPZxBgNshLBAa3NYhnb9Tpe7+7hxfYO9hsNbHIwrJPO4HZdn89aEqNAb0TgTgxWbGcUC8WPkxEO+0N0JjOUObVfpYpiuQzXT40l2MnSS4Dj6RTvz86MpXXF9VEoVVAuV00jrU0ZF6yJXddMYzWNOYWVg0LiImAfFxzTuWUbI9J7vq0qYB8M3l3yPBTYEcmAI04Tz/6IAsp+cWGAYuWja++lSytyUzEfBwj7PWxVytiuVtEsZlPhM8xrRLQvGnLiSIpzWqH3+2aKxM1yBVvVihkxcd1Dx3AufimrdCHQbH9JkBuIlk/26n0GYrdr0mm9fZebxcFoyZ8vZzZGha4LfgIFcBGD++n0fTRIor9L25cSviINvN802Lo+JnBMPIzLT9KphRlcHsOluG5ysHzzChluEsyT8JNncRMO9H8TfwbO1wb+CIiuSr9N5he4rLrt+tSuvuvS2UsHF8/FQpSl69fH+fU+TLlMy3JW2oMAnVYLpUIBLzY3sVXwzaiHz8rSK+TiaTMJCBPAmzLDSr6neM1uV9xuL1/t5gNZQLra+82u5APlvj3OEnCzQG7FV1p2OpgmjnmHJ1E6q4rvuvBczqpCH655r1NMNgKwIdZsZhabBEE8x3gyRuf4BJ9aLbxsNvDz7i7+8uIl9ooF1LIpABfJXMXRImDAq65/R2pt0NcGaz1+gwz2VjbcVUpl+F4BiF0k8wSe58P3PHhcd9aGbW/4jnR96VYbPDWKyzfx+TIz3iSuqUvViiWUCwXTeckcplzX8vlShN94jXGbOgKX+aHR9HRmlvQLEgfzCCjwY2ejhlqtZup6fM+nxqkzdMdjTMM5/PkcRcdFqVjC5sYmfN8zqpam5z5S9Y0wvnDb00jFFxJ4h5f4bFi9yzd8nsUwhnufzk7Q6nYQRnMUZwEmtQZ+2N1HM6ml5eAdyvqUoqIOL+uxLaeeUjrvKi1kx29SO1KP37nvRzO8Oz7G+8OPGAczuMEMzSTBqFbDy9evsYXK9Qakd5UAxfMsCbDs5Y9tVHZGFRpancYRfj87xR8np+h0e5jNI/izAPuI8dP+Hja5/PRjHsjzLHP78Sc6X1+w7ao0VPkYAx/O28Y48Kzfw2QyxiyYgp1NccTWUE6YnBqDnwczHI6GeN/t4WNvaL6Pftho4mWlYpavZKPwZ9+8jx+dUvCACPDbiTNS0NDKDGIdDfD+7AQnZ+cYjMcIgjnm8xhRnJgBKfwyc5wEXcdFKwjwvtfH5vEZ/vTyJX7e3cfbRh27S0utP6DkPlhR0jpwWhs2M/mrEnxtXtnvNZa/1GGWv4cJzKCV90fHaA36ZhnhIAjMIOo4js1AawY8CAJ0gymOJ2O87w6w3+rgx60d/InGg7UKKm62PBDzYfkD5VrJ5EEELhO46nHmtxp1l+4ZErwbzfDb2QmOzk4wnLHuMMM8CBHN56b+YNQxcNF2gNPJBH/0e6gffsSfXr7Az/sH+HFj26w2YY0GVX+4nA86+jYCK4vBhJMrpP2sth/8JEnwrj/EH0efcN6nofYYwWyW1n85SxstApwE43CO3izE6XiKT4MRdjtdvNnexs9bO3hbq6HppUteSX+/Lb/WfddaDVaobPzxxc6KKS34PvT6aE9nGMfsACigUqsbgxUmlJ0FXPevDeDToI/2eGLWD66Xy8YfOwGsItmwzXILrofI9c3SC3PPN0sywPWQODS++L4trcqldQfO1VLzXexsbqE9GGAwm2I7TrC9uYV6Je3ESGNjrGltg3tMF39DpitM8NvZKQaHn/Dn3V1g/wCVYsMYNKyW9HJYPGKFicYvLST4704HvcNPaLoeftzdQ7lcQdHLPjjpeXlbVQliTdWwujDy4Uh23m5/q25bDjp/bKNe3GdPWE88Xly0J3P9pTyVu36V99ydV+6SF+9nHlAX59QVzzfLdsRctsP1MHfTpZDo77O4lk/k5FqOlHHRKCbwCgjdNOzI84xhFWddoE5+82aFWw7gO4JcDurK42UGV3q87gIDstvVgud90fdnPlexWHiyd1uXlgPZRZ76fNcKlLk28Myz6RRPn5Elj4vDXLCLc/eyQ0HstuCRe5B5zZ7P+7X3LLn0Yn/2Nutl+diev7iDd9oS++KsuW9F3DYe3nHJz9URXUT5jXu2LGWjyW/tFt79+iuqpTL+91/+DfXNTXCdb8p18SbJhElPmmuM2ibHpsGUp6ZMvTCCs9e+OTk2kusCsP4o2Gd+rRR5YPacde1NubFKvGRP52+9hX0GzY1uxHLYlJe+UZ0ijQTqVdSrZbicbYUGK4lrGgBosBLFEVgdjZwYQTRDGESYBglG87kxIuhOJhgEIeD6cHZ2UaimSwpeaKWNOctoe2gk+oY0f4ETL9nfQsdtPOZKBpieuLHccewBT3wuNUPMTE/MLTaL6DL3Nhqb2N7awXAWYxpE2HcTbG42USoXL2eniYZ/vjS9iZXFxmKivPIPfds76In1p6oPbDU3sDWZwIWDZjDH7uYmmlV2XvIpizND43yqLqKw4a2WwF617sV96d5lfuYcvWaBmXd31nFFY+AuDQT4ceT5gJeYJR/3Dl6iVqubW7gEGOth/SAwhtU0nub7vVgso1lvYHtzGwUutK7tWRLIqdZF+s0zzcNUL+gn/e5Jvw84q8rhPMEv7OhvnaHd62IymSBxEhSDAI0Cp5kOEdniamUkF9Fp78sE7NNJjNq+ngC5WR1mhz9HmbYS4N1wgn8en+LD2Qna/QHf0PDCEJMkRtn3ME54RpsI3AEB+3Dbhz2LMq+7bLznlOg0tDqNQ/zz6Bi/n53htNvFdMK54Vz4ZqRphFEyR+Ck+nupRsEAl+K4g9QpimdEgCrGeirbsWx5e5QA/906M8aBZ602xlMOwUrgchnUcgG+55vR/THL3JjLrIQYhQF6/Tl6YYLhZIbZeAxvbw/7zbqZrcKqsXWfEWIldR0ElspGGqywPZztLr+MRvjP40Mcnp2g3+2b2b1d+PC8AvxiCb6fIHEixPEcYRSZTqfOaIzz8Qy9KMFoNkey9wKNnaYZc5lrtVhHSp5emHzIzYO++pv76SX421O0XP5Sh1n+/v381HyznZyeYzILzUAqDrLyimV4fgEcdMVZ66MowDgOzTKDnFn2fBqiN5oimMxQOjjAXoPLBKXZobL32/NJd6bfZdTX/GaPWX9gfZffa79PAvzn6Ql+Pz5Gv99GjLmpL3i+B5+DyzyWqI4ZIBhwmSDOijwZw5uH4JfdcD5HNI9R3No1Hf6X6sT5yLUvAl9BLOwqbQAAIABJREFUgLpq9XW5LGQdmMYqnB2Ixir/7A3xX58+4vjsFOPZxPQLePxmK5Th+27aDuvGmJv+AS6zHaE7GKAVBuhMJ5hOpvD3D+A1N+D5zlJL+1cILa9rJbBWgxVKToWbZ+tYt8LQNABMZjPT4eRxPVUaWBRTuzz6oxK254GpvM451T9nMOGaq9U6/MyC2iqxVWhjBGAMAdJuRVYMOJqAv9vYWABzUQcuKbDtAH85eIGy46I96GO/UMRPe3toVtKOsDS+i3jtxyWNGAZIcDQY4NfjY7Tf/Y6yk5ipvXebDbMm/eqC/iIswzL7WOXSNp04xu9nxzh7/wd2SyXUigW83T+gLTpMxl7c+hmGBbtcofCZp1zryxeC+vy2pTDNvTYAm3kr78oqzvRj/Wf+lg6vuvvK8zZak25jv5Aaj1gDEnM+k3tF9FeGu3xhEQ6XV2Jnl/FAvfxSR+ByKJkgy4lePuZtq86tCO7hnLqZwNf6WvZw6dge0GWOrNYr6+sym0UOXpxe7XFxPYthcXyvO1fJas9bl0Jy/xrhrXfr2rRdus0eLDzZgBcn7G1fdOnb/ozHr7v9i2Gvushn04z0oZX5PDQjKv/x/h0qfgFvDvbx0ybHUaYbO9cX5XNOLibd+uF++rt41s1zvzi/SorVWZCLIr2JAfMk3es26++zQHgjT6bvyTTIi4BT7zaCRWrT2FaGdZ0gN7/OWG3MZi9J4MYxGpUiftw/wOu9XRSND8pFoxWWr+n6wEEUmk7czrCH7mCEfjLDNIkwd0KzjuW7s1P4cYyy56JSPMC275hZyHIRXqTR4ri56Jd9foGTvUTX7tubL0W7uLjKp73DhrHwvLjAz0uPSyAlDg4c19RX6n4J02COV6UC3uzuoea5V49uvyTMItgVUuevrd630lEmrhW65QA/bm7D5Tq51RrqYYi3u7vYqtVQcmjUwiftQhOWQ7XhLZ9PRbZXrbvsa8VxzivD4LPMj/lpDIzNCCkepcY/1WIRr/b2UCmlxj7W0GA0C8yIFIczAcFBvVQyU65vFhxj8JaLYoUAOvVUCazMdy5rxvqnm5Z37Fqi0RNH9Z/ToH8yxa/HJ/jl4wcMplOEXHrUGOrxvtRolrOtXP2EPFWaStdDI2AHANjR0mz8PE2A31tt/OvTIT6et8yU6I7vImbB6mRLzS4GRzy0FEmeJ0lgRUFM3aVKUnfZ8Z8OqEpwFE7xy8kxfvnwAe3hAEHEWfwcOGb9NRcOO52SxNgSP0lWStSDJsD3PnWX7YmcAp11hnfdNn758AfOztuYTaemclEuFsCBfo1qFZVyxXxvsN4wDqYYziaYYor5LERn3Mds2EM47sN3gUK1Cr9AcwFtInBLBHKVVZa5/LHOy1ksP4Vz/Oe73/C+dYLhaAjMY5S8IkoFH5VixbT7FysFIBuQMpoG6A2GmMUB5nGMw/NThKMR3OkMO7X/ib1yulSw9PeW8k7BXCJg9Zd1BhqrcIDBb+en+Of7P3B4doZgGhpDQc4iWy0U0aiWUWGZ6hdMh/9oNjZlMJcJCqYB+qMR5pMJ4skIZR9ICi/xslo2S1hfilgHIvANBFj1tdVf275FHaaBNvsjjxPgn58+4t3hITq9HpBEKPhsJy2gViqjUS6jWCqD63RPwxCDyQSj6dS0d3HmoON2G9PRBPPhFI1/r8Bp1rFh2vG+QVjdIgJLBPL6y0vUYbafWWMVDjD4oz/APz78gXcfP2Ae8osuQcH1jA5vVDkjdgXFkm/qEONpgOF4iiGNBIOJmYklnE0xHw7NcvR+wYdfr6OZPTT22VkSS4f3RGCt9TpbQLJRlsv8nAx6Zm3VIAjhui7KhRIalQqKvmcqsVTCEf21z3F6fmI6pLzYMS/+bU6vTiOUDJRR3JwCmws8uYaNcbLDhR0qzcRBoVrG3g9vMZqG2C4WsOk7xqDFymRlpCh8OfDjkgYmHLXbmU7NiFxOJT9DjJAjdZz0I5T35e814WXGNzYsfqzakRWtyQjd2RgTRAjsFElmxLlv4rVhWdeisXLa45Rq6uvy4hXWR+bm+S4HuuSVhyu93+C+SxBWhPsoTiVM/wWB7zGgYigLbIudzynY2L7g5fOb7uHMjeS8lOgrhFxKKJ81nrp8OneU210dIiNNpbs8b8Fl31b+y2cf5pGV1ST9S+mnxyuurzq9OMf7bCREsLiQM3jIrl9nP7i4NY9y5cm8h2/bp66YDhezXn2Ck+EArckYcbGIMEkQOo7puKa/1L7883h4jb88Ag6gT5NLwfO/C3+8bpN16d4sCnvNup/xXVz4XKbFmSv82PisS0nolX+tXFfcugj6tnesLHRJ1EliOPEcXhSh7nl409zAX5tbqOam/E1lTpkyH9kA1otDHPX6+NTu41Org24SYzaLMYwj/NE6Q7NCo84iqjvb4MQXNOpIt8XORcbYS9e4VnZ6szJ96ZZcTKnw2QmWN5/xv+Q5CzWFdKWc9hZW7GhgS4//vrWJH7c2EYQJtj0HW15m0MrLNrzMr3HseRvY4uT1OzYN9Jm/nfJUuBxT4sCrlbFbfYUwjFEMA+xXK6hmU+HyWbt85xVxWrlzkeTjvuKuL57m/VGSjV6NQkwDTikZIIkiU7+rF3xsN+soc3mqrPxgR9dwMsFsOoPjJmYk1Valgr1aXUsGfJH2M72YLcVFMygzyilruD9LgF/OT/Hb8QkOz1tmlHTie/AK/sI4j435HCVttM/q/zPFqGTfLYHlspXvXNZ92PDJhnsaq3yczfDryakZqdfu9TCZBXA5xW61jCSYpPP42pkO71Z8xSYClwhQd9m0aWZIQwKWv3/022YwEZexmsymZtrpQrlojFO4PEWczM0o6aVK06VwdSACayGQFcB0qLtT01kKvOv18E8aV/V7CIIpvCRBs1LG24MDvNrexk6thmolnb0wjGMM5gHOR0MctVs4brfQGw3NjABH4wFKJ0eo1xqo7uygytGB2kTgewnYemqmv6bOALaHJzhhZ+nxIT6eHZtR0TQGrHg+XjQ38Gr3APub29io1lGqFAE3xnQeoheGxhD28PQUp2dn4NxXreEAv5weY7NRx//+008o5b9vv1d+3S8COQJUY/5Yd2Cd93A6wW/HR+gMBphHkSl/G8UCXu/v4+3+HpqlIjbqDZSKRVN3aE85M9AIZ70ejs/baPf6pq5xPOzi/x65KJRo6PIKjWKu/TQXv3ZF4KYELr3BOVlzdoLfbpxdhXXe/z49wu9HHzEYDuA6CQpwsF/fxMutLbzY3MRWuYJSuWQMtln+tmcBTgYDU384PTtG6ACDkIM9z7BdP0Sx8BMq1aJp+8qK/JuKK38icIkA1ZU6ZDfus/5g2/vNssNhhH8df8JJ5xzzJEQSBWiUKnixtY0fXrzCdqWKZq2GCr/j4gi92Qyt8QSn/T4+nR6jM+yDxoNnwz7+fnqEYrmIWqWMiu8bo+1Lz5AVRO69Ebh9gxWrYVlOU8FYOe0lEVrjkRlxRcs8WqDWKhXUSiX4XqqYbMBtJzHOe21MpuPF9H7VYglbjabpYFqlxJaeidrGf6m7xPr4dtd2APE7jh1BTddBwMpFZqzC6oVVbisCXT5cTBcr1p15jPZkjGEYYO65mLtcAsExfuiP96fjx3NymtFo6TFZ0viFBkBDGr/MxhhFIQInwdxzMHcd8wLhTDVc44sbnfyPMuV/lzx9duEiDLPH69yysLOjz5x8MPlb8nJ8dtN9naCA9k2eT5oV/DvkSkzvtaWRBXQNO+NrRdzMe7vlg7BerUs/vH6pumsv5m+0gdG11+3N+Wu3sG+Dz7tWFOsuosl74r71kLk8ZVlYr/Ze690+i/ZWe/06NzUwsmZGDrvOF9FfCHIZF8NkPIu4rBAZ1sX56yK/5esUw/7yQVtZF3LZnVWebeLyAazaz6XZRGrDpF8bbnaOh9xyj1x2JnOsB+Pp8qXbPDJlqSmXU2PCs/EI7ckEoevAZac1l6bJym6Knk8S922yjJuT2WoPZb04fTGjyaX7lsPJ6ZLV4c/SnBfks4tXnGCk2X1MNw+ty9PLQdp30PL5K0K/ldOWC6VLDVZiY7BSmkdoJjDrUzez59FdMlxhWoyxq1fE5tYONmubqNaa+NV1TF1iFkwwmAX40G5hp9HAm51t8w6/kvENU2Q5Mn5u5GXDNOxy3DMvFw6vZRvvt+9/3sefvWzDXJywN1kP9thEmB5w1xqIcGa4WpLWMWilQ6MRzme3WGnIhsObcmHYYL/GXdapfHCUh2xYf+I+F9WJix58P1232RiqRGm6HQvxqsitzHSzpVEYdz6+/D69ZV4v+VkOnn4YDuev4Mf5NAgQzSO4cYRaqWhmw9vkaKksPNbraLAym8/NFMCMs+x5ZraYnVrVpDU1wMliskIsR6zjp0eAeW23vDJm5/i80/C8jQTvgxC/tE/xx/Exzrs9M7OPVyqi1tyA63sIgwnGwx5irsUbR8bYf6HIK8K20coVgdsgQFVeLrpYTrLRnuUfp/V/Nxrit9NTfGy10Br0MZ8HqNSrqDbrKNSqOD09xnw2vbredxuCKgwRWEFguSjmsdFfGjlzlP98jl9ap/jj/Awn3a5pnzHlb7WCQrmM2WyGyXCMJJiaqaaNEqvcXUFap9ZNwNRPzQC4BCfzGH+02zhqnWMa0mDaQbNcxp9fvMDfXr/Bq2YTTdc1s/xx3sIICYYo40WjiY16DYVaBfOTQ0y6XWPI8mnYw975GXb8MhqbdRS8dLDGutOk8J8oAVvwWtd+X5nR/cD7bhe/nR5hxBnXkaBSKuGg2sT/fPEaP+zsYadWR92sDMz2Ew+B76Nfqhgjlmq5Ai6xzsGt0XSGzmyC//z0AXtbm2hsb11a1uqJ0lWy1k7AKm76sucRf/x244Bjzq7yrnVu6gzjYGa+yyolHz8fHOCvr6nDO6i7aZsA22F4b6/YxH6jiaPmJgrlKub+MQbdNjjzyodBGzvdDexVqtjZTgdVsa1Bmwh8FwGruCx/nbQ/krOrHI6H+OfRJ3QnQ0RJhGKhiN1yDf/+4hX+tLuPl/U6GhxI5rMvJG0X6ybA/vYOmhsbgOvitNdGOJlgGMX49ewMO80mtksHqGcDc75Lbt387AnkP7Ns2ct2V7PCSAL81jrDca+LYTBG4iZmZrY329v491dv8OcXL9F0fVR8rpDCvrwCBqUSuo0m9ja3jHGKc36KbreNcDzG4bCHRusM29Uqtnb2zSzsLLfZHK3tYRBY2/uQykXFMlP3AOhOJugMRwiCwEzpUyyWUK+UUC0VzHppZrQLl8zptNDtD82aaByN68Mxo6KbtSJnpVpsF7tONj3rxRkaClzZIboI4et2mJ600E5H4bLSknhpQc7zjN0qdv7B4gieMRIzuwpH8PfGYzO1FlwPgedj6heMQU+a1rQj13Zy2H4bhscfjVVoGcmpQDvJHO3xBOMgxNzxEPpFBIUipp5n/NBWgjKRA8NhmDa8C1KZn0Xrd8qEcZkIM0TmmPv5G7NrdJh+bvTHfbJhfnK0sj3mNd5OhTOj2zN5KJP9XRF8FvptOozp4kfZTBrNn1uKJ0uMCfs7wuWtfI7I0bLkUkM8z2Pr5vPWdgqSNfP92meBsjKgXOcf4+SPlxgGZyPIx3FTSlZ+6gR/dmNYRhfsCevmZLHy2Huta5daskzocuOtNs1WXnvMa/aXef/M4aIvNDjgbAf5sLlPXWb8TA9/djMvtGwKPBPXUme69bdulzJZme0+5SUr42b8bTlg3Ezu/P4lOW1iCc5sPJEe2EscMBtnBofWl9UTHhvDuWwGKeqT5ZjPM6tf5EfdtffTve3NMmKFh2Uzy1JWwjvjMYazGSLHhcvpDz3fLNNgy2XLiKnnfl6X+HzRAMDIbeBfPKDpjCupPjHtZjmILFG2fLQyMUyGwfDJgS7162ImkK+jQVHMxjzKnmebB/aYLjebrnz8jNum07qZ97U4jCMlYEimcXBpoITPtWM4mHzIGNn00WXdwEvIyoFf8lB4sYPRdIDJfAouGTTHDJ3h0IxsmSaJaezifWmcF+WofVbIhddMXmSp5TneQz+Wo3Gz8/RLYxC+38iOeWg33md/JpzsmWBYVg/sdbq81eaFnQ3Gpj0XrA0+DXzpAsPh808ZbXpMfAzbjriw91g3Sx/92x8j4bNJeezGsG1Y9pnmMc/T34JBdu8l/9m9PMelUXgfN9dN5VpkSnb+M8e+p7KPb5sXVl4TbpZ3ZGbfBZaf1S6bZOufctj66nA2NdOrx/M5/CjGZqmCl80NM1Uvw2H9hobBvdkcsyAEK6E+XDQqZezWG9iq1ozuXJLdRnjppA6eJIEv5DV1h2vvniMxI6TZWfrryTH6vQHCcI5KoYzNjU1s7O6acqrdbWE6HIIrA5nVgb4Q9pNkqUQ9CAIsJ6l6tpwcJMBpNMPvvT7+fnSC0/MW+qOhmZGqWangxe4uNra3MfNddFotzM3sKpnyZo4N80EkUEI8SQK2uMy/51n3Z/n7cTTCL6cn+PXkCJwViO/ycqmEZq2B5vYOCuUSzlotBJOZqUexPp8+BTbUJ4lMiXpoBHLfC6w/cLbmk0EXp90WRoM+YidBo1TG681N/M9Xr/CnrU1sw0lnWcy+qeMkPa5xJsDGBpxiAeMwxMlkhkkwQG86w4fWGV5W6+AsgZtVLtCZavtDwyF5HgEBFpH2BZ+1Q3GwJduw2wmMoVW71UYchih6HnYrNfz1xUv87eVL7FXKqJoupot0cqn7sgNUPBeFgxcIo8gYd4/jPiZBgE/tNt6fneGgXMVWrWS+WS/u1p4IfB8BqjLbGtLl2IDT4RCf2i0MRwOjw5ViCa+aG/jb65f4eX8PO65jlkG2fTCMvZBw0FCCEme9evka0zBCEgQYBDP0JgGOOl0cVRt4yfpHuWDK33y7y/elQHc/WwJsA86WUmHdl23ex50Ozs/PMZ8FKLgutkol/JnGVi9e4k2zgg04ZlUJMkvrzo6ZOaXiAeXtbXDigSCO0QljzKMQJ4M+/mi1cFCrY3erbtq/2FamTQRuiwDbeNnuyj71TjDFx/MzDAcDxNPAtDkf1Dfwl4MX+NuLF9gvFkz9l+3wrIrwl5a/QLVchPPqDSLXRRLF6ExmGM5CHHd7+Fhp4YfGJtxicdF2fFvyK5zvI8B+iNvdskoqCzg2bBkjiwRoDUfo8MMqa3UtemU0ub5fwTcFW4DELAd03GljNJ7AcX04SYiS66FeLKDK5YAY9qrN9AJedXHVDV9/zlZW+LDwg5EPDjemjx0i7KDiZtPNtNMvp+5kw16bI9FGIwymE3BqTm5Tx8XUTQ1M2FXOTjl2fDIl/DFMdvyYl0U2swrXuufySueTGVqDEUbjKZzEQegVEfgl8zFAP3ZJE4ZnOtKzjhvb8UT5TLhGEh7YWBmh3bcXM5enlzamxIZl99mBxXRzVhmympBZPDdpq/k+qoljOvYoCwsTk857/TD+QpqX0nvTQ9rzpf9uekfmL58pWUez1TfqEzvUTKUZiXHJnj+yJEdWbktZw4R5LLJrK7LusmCZnjEsxsfRv8xD3sdwiw5MZYXxUMRrw8v8UScoL8NjuHZjmHye6X62ZYHbe+1HAu/njyPgKSdZ8PnjPmWiLnH2ozIc+Hwuc7JbNsvSf56Oi9kwTByZ3IyL+kxZKBc3hm8+qpNMh7PZC3j+Lht6KA9/lJc/wy1XTrFspfz8WT0pZozIxT6HpSxddCg/O7vNx9ICEimTYMqI8TA/OC28VVt6pa6Qgbme3pLmVZZ3HJVr72HcnPWhnJUJlIdlHs8zDP6+fcsiz7SVbJh/dFkmsdLDsvSUFXgu6xFFZurDeVYms1HQc1guU4505hXyWJaRaeZ5/pw4NV5JIq5zn5gORs7UQ0kYN3esHGGmTzzPH9PKsEtsqMl0ih8Z6dIuF++Fm/Age8ZJlxvj5DNo42K+UZ/ZgMTymu8wxsP4qRulzLiGMjFdSQQzExr317olfBOSaFYmZ+9DK4fVi8zHQhSmj2lghwIbtvgGfLWzjfZkhD6XenI9TMIQfa7BGoSISsWF8RDDsrrM8oRseMzzjI+NZNxnHMZf9i4mP1MuZHnqRhE2fM/MaMKy18pIlxvzg/6ZB5ST7LnPkY8XOpHGwXhtXpSzd7g1AuH5lRsjyCKjw0OGy/TQ5cb6ADmRJ39mswIaOZysjE31gvJxIwMbLxnwx2fYpD97z3OfusSyt+YCFaQzujAeysKf5UuZeMzNPjvGIHkhS3ZxhcO4U24XMvCYo57oMux5FKDiFY1O831oDYnIlRujMc9rJgfDTOstqXFxbzzCZDxGEkZwoxg71SpebWyYNJEf08H0nrTaGI9HQBSjWPCxt7GJ/c1NNEtpvTaLzjhM7w2Sl79F+0+BgFX0rD5nZkhEgn+cHeO/PrzHh/Mzs0wolz+tFcrY3dzCzz//G2obTXRGIwy7Xb59zNronrtkHSqlegoa8qDTwDKLasafLXtZlzibD/H3o2P896djfGj3MecoUySoc5T/69f4+e2PKNeq+KPfp/ZmA0vSpJpHQrr7oPP9sQu3Sr2s/vLb9t2gg//7/g/8fniEzniC2BgLFrFfqeGHVz8Yg8FpnGDQG5h6E+tsruOmhoOmjeSxE5L8D5uAKSUXNeUY7qL87SQxjnttdEccK53ORrlXr+Nvr1/hL9vb2IRjllDNf9Nz6XHWedloTwOXsFTF6NUbTPsDY5w9nc9x1O3gqLmN11vbaFZrpsxXnfVha8mDli6nPPw2Y72B7dMf2Vna7RoDbS9KwHbhHza28f/+8CNe+4V0+dj8N2pW9+CgFLZPcMRF8Po1TvoDHE5nZvlBtpW8OznFj40N/Fg7MFjs996DZiThHgUB00aQtaX0kgTH/S5awz7m0RyIQjRLNfzHTz/gry/2sZN19rP85SNg69DGeCVhX1YCt+Bh+OKVaWdgpysNsE56fRzXuhgeHKC+aHF5FHgk5EMlkJXBbANkmx1XvDjnsijdLmbh3LRx1vyCmZHtf/34I95WSuBs1uxPYflp9de4puhN9TfZ3UVrNMVkHGA062KUxPjU7eJjrY6/bNXTmZyzdraHikZyPS4C1GH+Ruy36ffRMoMMAjhhjGqxiP/x5gf8x6s3eFMsmn4otlnbPgvqr5md3fRrOUg4ucP+SwxHU7RPThG5HrqTKY46HfRfByY82/fyuCg9XWnXU5+zI7qzTplBHKM7onHFxEypys+uouuiXi6hUuRkPWnneAcwawHOgsAYTbDzr1Ero1Eur3x18750Szuo1vV1xc9GPiTspOC6hbTkbtGqy3VRCUO8bTTxdmcHZY8Tb6YNe3wx9NmhkST4OJngQ6+L3z8doj8cIHEdOIUCzgZD/Nf79zhvDlCOOYKcJg4xkjhEIQaaxRJ2mpvY26ybD1VOX3s0i8CpO9+dn+G810PieEhcH73JFL8dHyOYh6iZj1KOTI/BdUH9ODYdN41CEX9+8wbNArtfLzpsLMXLrjXiSM9e1fhjCxDTUZQZORg5uwOc93vojQdmev15GIJ0yoUiGsUKGn4ZzWIZO40qDjaqZuQyCxZ2LK1zS3WGf/O/dcb4lWFbsTKdY8MadYmd/D3OqjMaojtKO10nQYhZMEMURSh4vlknk0tt1b0Ctgpl7FRr2K8XzccfC+5FB2UmUsriQj5WyNnZRwOr4/EIh4M+gukU/jxC1XHx17dvsVssrHwWL0K5vEe94XPzaTrDcaeLyYRzWzhoFny8rNbw886m6UC9fFfWMZx94KajMhJ04znOen10hyMM+ZEaBJgnXFs8AW3AfNdD0fdR8TzzstmuVAyDnVrFLOHFTtdU89Pct3GSA+Vk+u2PVshk3o0SnA8naPV76A4HmEVzRFHa3ep5QL1QQqNYwiancazV8aJRRy2r6LlxOmuADZ/xLTO3MnyPa8omdtJmHecso9rjEOeDgRlBNQkDTOYBZlEAJ47hew7Kvo+aX8JGpYadagO71RI2PU6alpYLDJMzHlxsJHR5Y750kgSfOgP0uh2zhiuXeXv74gU2PHaxpVO3deME5/0+2sM++tMxRpy9gMsbmIleXVT8Iqp+ERuFEl5sbGG/WTf305CF+UG9vSTKZTFudMRwLCcaq7Q4JWJWLr/rdNAdDEwFhoowh4Pfj48RhjFqcOEjMcuC0CChlESoeR62qxUcbGxgq5yWWMxX+zPKRJ2i0QcteH0fNE6ZwkmNZMIA58MeujQ4nM4wC6N0/VvPR9EvoOr5qHF6xlod+/UG9squ+XhgTPaF/SU9yueUTXOqzwlajLs3MHH3R1PMwpB97XA9DxUucVcqGAPRjWIBrzY3sVlMG4+KXpoXizTeiPrNPV2kJ41hkQbOlsZZVjI9uEoX7Pk5DetoMOEAG+UyKuUyXM81eRtHc2OUNByPERUvG6wYgwcaLkURPp6eYhiE8F0Xu5UyXm9toOgVjP7QH9fOPOY68J0ORpNJtnTMHMV5jKrr46e9ffx5/wX2S+kzwLQwH4xxR/bBOOQa9MMJOqM+hlMaS4WYzUKEYYQ4SsCypVjwjEFv3fWx12iaZ2Mnyw/ysD9D+QKgOaS+21HEJ+0OeqMp5pQvmOFv+wd4u11fkTmOMfjgx0BrOsZZp2vKWXKgHr7Y2ETJT5fK4nupaxptRjju9DGajjALZ+CMJMUoNmuHvt7cwluuhVsrmkeCjZUDNrR3ezgfjMzaoVUAr7a2sL/RxGbRT98tBLaUHgq7zJHlD+sardEI5wOWzxxpN0MYzRHTgIQNn34R9UIZzVLVzHyyV69hs5AasNgoGK4NmyX7CBHG0wnmQWB0YLtO9hvYrdWM0Sbvs/nZ7nXNrIF8r3A5oNe7e9iupU1N+fetjYPpsPGuyACdegYEqAumnhVM0B8NMB6PwQd+u7GBH3YP8KeXb7C12TQGbcM4QhJybV5Or8J3Cu/WJgJ3S4BlltXtU3bsAAAgAElEQVQ8uiz/pnGMURBgNJkZ42aWt7vNOv706iV+fvMjdkul1Og9DI3xvin5bCA58XlKZWIOiHbXSoB1I9bjhsEUvdEAo9HIGANuNDfwZnsXf33zFtsH+8bP2TQ0BqtUfoe9TWZgB2f1pUm0NhG4OwLUW9vh1JkM0Z9NMJsHZgnVRqVivtfebm5hK2esQgN1u7GxnuUsXQ4a23ASM5L/dHvbLNXeG7D+HKEzm5rfflLLlhOyIcgVgW8kkM2Gadry2L7Y7WAwHsNxPXjJHLvVGt40N7DvF0xbMNs67PeTrRtQlTlYgG0gQeJgCwnevGSH0zCdDdNxTJsXO7JGLw/MchaqW3xjfum2z2qlpg0xG6jCGZnbwyEms5mpC7CzlG0LL5sNbMA1xoJsS7XtdRanLX+TxEHgJDiolXC+tYNOv4dZPzGDqs6HI5z0euAshewnW3efiJVN7tMmwDov2yDZr3E26KPT76ejhuMYzWIRr5sbeJEZq7CvxLa5UmdtGWwMsMzAwLQt+9XuPrqDIUbDAcIkQmcyMoYEgzAx7Wx8BrSJwG0QsOWvafcNp6Z/mX1bbOutFIp4ubGJn3b3TB+l7YNL6xAXtQBb/nKG8ZkDbBd87G5s4aixgcFkhNEsMBNBcIKNjUoFNd/7qv7O20inwriawPL79GqfX3nFdpRxFPKAo5rHYwSzWdphytHcnodaqWI6FaiI7MxoTfoYj0aIghBOxE7CBM1K1Ux1ScWzhaZ1F99idmiuvfCVsn7JO+OgfGxg5lSGXK/7X5x68PgIQZKgGc6RvH6NnY0N+F7RVLL5UmCn1vvJBL+1zvGx28XZeGQK9oANzyzwCz567FxptXDaG4BW5mbqIidGHIUoRcB2uYa3+3MUNmsYxsDHdhe/t05xMh6iOx6b5YASx0fixRhHc2PxO5xN4HOd+yiGG8fGaMWfx6i5LvZqdewd7KNWqCw+Br6U9i9dIxebxzRIGJhpHtmRNzCGCcftjplRhx0/7JiOowhJnMBzXHDqPE57Xi+VsVst49/mL/BmewtbWYMQlZJZeZvZeZthfYkLr5m4viMB5EqdY8c6ubJj8HA0wFGnjdNeF4PxFLNgjmAegYZA5Oq47PNw4RdosOFjs1zBfnMDP27v4M1GE1uea6Z3I1tWRCwP6zI/WaFhXo5ohEBjquMjjAZDFIIQlRjY2t7BRnFjYXV7HQf77LBz83Aywn+fHqHX6ZrbXlRrcPb28OPO5iV5mG7eZ563bI3xdhzjeDAwhmLtXgeD4ch0TEYRjVVgjFVotOI4LjzXRcFzUS54psOaRivsbH270cAPzSa2Cmn1n3Hks8g+4yb94KwbCT6NZjhuneO83zWGZuPJBOGclHg3fzAfFHxZspw6aDTw0/4LMy3kdsE165fSz6LsspGaO2/nD+XmC5ydzBxrxVlBPnQ6ODxvodXtYRbFCMIA4ZyGCRGSJDLW/QWfhiIl1Es06qnjVXMLf9o7wG45/diinvB38cK38qazhfCIBjK9CHjX6+Dj4SdMZ4FZ2zLZ2jRTulK283CO9ydHOGu30RsOzAdeGEcI48QYGrHo9jwPJdc3xj/7/SFebW7gNX/NOtitTsMV6uzXb6l229wynYScSjmY4NdOG3+Q06BvrGrJicu0cZm3eZyka9lPJmY5EJN/LE+jCOU4NkYcXJ+2RGOlpZk6UhnttCAunFIBYdEzU+ByBojTXgsnrXO0+h1j2TudhZhHCSLqLxtvXA8l8vAL2KJObTTxZnsHL2sV7JeKaGaNjl9SJXLnj5rKMqRr1tuFWevxQ+sc7W7PPEPMrzjmTDCU2oHvuShyGj3fQ6NQwJudHbOW9OuNBnY9Ls+XPjOpTnx9blx1hy2DUjeVniNQ7HRj9jnNl1urwrJMKCdnqakXiiiXimYmJ5aPiZNgHkeYBmkHG8OwukFW5v0+m+Ffp2c4G47g0wBhq4lio2qMiFiOdWh81z43Ri1cO948W5yZZx6jMI9RpqGE6+PV1g5i6kb2nmT9hnWCs2mE8/EY58O+MVriEgo04pvHMeYhjeHYMU0T8ASe76RlGTzs1tmZMsSPWzt43WiiUUinm11+LkxWZh+mLA+Oghn+cXaG0zZHs0VojMfYKZfxerv+2TPFe8nB3DeZ4F8nx2YZpaJfxE97EYq1Bqo+P1SB43CCT2dtHJ53cNbpIwhnZlYTRBGK8whbpTIQR9iu1xChaPSR/Hpxgt+7Pbw7OzM62IgT3mLqBM0icy73ckqPFn+twY8xJESCk9kMh61znHY6aA8GGE1GxmCXU5XyXUC9KfB5KpRQpXFstQYa0fxp/wUOKj4a2YxYlhn9c59GXNPxFBGnSoVrZkzZb26hWSqbxn76Mx221IdeB+F0iqLjYLtYMfnerJQ+q1/ZsBeJ0c7zIcDMz20sP1k+7dcaOCoUMXY8FCt1/NsBp5J+hZe7nIw3nTY9LWtjU3bZOoeMVnIwtXsnBKwK06VOsiGy4Vew5VexXSiZafV26jX8sL+Ln1+9wEa5ZPywPp3ELC3TuoN0906yS5GsqEZYHWadiV+BOyXWqasYsE2i3sCrvX38sP8SP+7vmTojv6U4uMroL29m+wTn7jOW6EuIbSVi6bQOReDbCViNvZihk9+wHPLTH40xHo3NdP5OtmQlO/03S2UzG+LiG80GkQnBQ16j/tNYfAvAdqOO42o1HZDDKf6nE7Q44+iilePbU6A7RYAEzLelGcCamDZNdtBPpxMzF6qfJNir1bBfq6WDLfNtZjl8Vnd5iiOf2RbyZnMDh9Uqzjm4yYUZANQaDtEazVBppMsCLT0CuRC1KwI3I0D9tW1qaZ/WGKPxCGEQwJ1HaFB/q03sVutGN21b2XLoVoc5CzVnld5Ggt16DYfVGjrDAYJoZmZ7Pu4P8HJ7F41sQNxyODoWga8lQP3lwEkOSOby6EMOnueAdsfFBtuamw004CxmSGc9ebl9kfrLc/z+Y7v8Qa2I42YDHzkFtwsziLgzGqI1nKK6WZHB69dmkvyvJMDyl60Ipk+D/VyTKfqclSqYwYlC1Co1vNzcNIMSK45j6riLOvCitzOt+zIs9rUXabRtyt86GrW6GcDAdvjhbIaTbg97jQY26lVTnq8U6pmfJEf+2F9hhm/QXfOguqyH4PbJW+XiR89wMsVkMkUUztkPA991UPULqJXKpkCjH3ZmnHVaZtRtPI9M7cCjwUq5YqYYZiGZr3jafQPMzLPGRV7t2dtND+Ngwxun0mKnEzvf33U7CKLIGKzwQeFoM34AcuPI5tY8xL9OPuFfx0c45ZSbcEynJEfc07rAKXiYxDFm0wl6yQSYx/B4idPKxHMUQhb+cxRqTbxIgMPhCP84PsTvJ4cYJ5FZD5yzq8AtAK6PeRJhGAYYB1MzPb0TR+CHrBMn8Odz1F3PdMSO43ixBMRC4TK5b+rY+5jH6YiPtIP/l+4Z/nX0CSctWs9PEdCYJ2HHW6pmtIRL4jlc6oE7MaOX622gF44xDF/hL/sH2HO9xXSQt52bNjyOlLL7N03zTf3ZcE0cpoHLnrlJCHzs0yUZ7Aw9Z0mC3wc9/Hr4yXTOcaai+TxdamSx7JPRrQhxPDedvByFQCOKj8MuTgdd/P/svQeX47iSLvjRyUsppc/Kct11/btz35s5u2/O7v//AXvezJ1r21VlpTfyhnbPF0BIlFLpynT3dJF5lCRBIBAIBIIgIhAxeXaIN9s7aNNIzCq8iQ0x4ySGh07G2acTB7gIZ3g36GNw04M3DVGJUvwblevsfNlltjweLZj5idl48MwJ/kUS4d1ogKvulXhMoBtFWqOzPhVCig/TZDc+Fa4p8M35Jb49PcHx9RVms6l4OBE3uF4JDkOIZA6SNEVKaHS1SCpO6TI3RdV1sVmpYrzLHRc+Op2Fvfq8Z2j0wjAPVml9mmX462CEf5yc4PT8BOPpGHEcI6MbF4bU8H3ZbSdGWFQwjycIBgOcdLu4Gk/R29nFr7Z3UKqVZPHIkuKznEhf8so15VIa4YfLS3x3fIqLmxuMJ1ORDQnlKceh6yBzUmRZjGyWwncmcLMuam6A97Ur2S379d4eDhoVbOhuLOlu7c05xaQtouR3gfNwKrxCOb9Bxe0sxKxaEUPF747f493pMYbDIaKIFHbg+AEyxxFjI3JeFnMHLuCPxzgZjvD+5goXm5sID5/hdactyuCPsdQm9jJZF69XCX64ucJfjt7haNDHMI6QzuWoJ7zEsHXDMMQkoixlKDNX5DPiBOU4xoiewSpVPI8TkaWLSb2hj4TiIv0o0MsBZp6DUwDvLt/j6PgIV9fXGNGQj0hllOG+uLNJY/ZNBNd6FXnfu8bbmzKO+jf4w84O/O0tNGv0n/Xw2NMxRA8U7zPgm8tzfHt8jLObG0ymEyTkZ9LcYyA6464/mcZwZrSVyBCI94w+uJNkFh3A294SL0UaTuazMLM0zBqqCHbE0PxIWc4dRKTeU7l8TMkOALOoReMf18mQSqwm8gHjrZr3klKRNVCuSVzMOMbxaIwTuoF3HcQecJDEqFrDn3+enuH4jOPrCoPhQEBQDtO41g9jlKIEQ3ph8jzhOcLm3IFGHiejEH87P8cPVxfiEWQcz2RMLAwsbBg5jo2Ehog0MEvhxsDZcCy7bq5ubhAdHuLV9i6CgN5/7KTRnoWlrPykEdtlmuLdcCiyKY4SNIaMVT8WviUtdVKvlFZcr9MER8M+rvp9lIIySrUm9hJjAHWFFP958g5HJxe47g4xnUZiBEeZ7CScu8TyIXEQbiH1POlB0pfvgZHj4HQ6xdvREP1+H/VZjP3ODp6HibwLzEhdjCjtahm/Vj5fZRnezUb4y/Ex3p+dodsfYhbHSFUx6rlivEkeRxbBmc7geiO8u7nGcbeL3izEHw5f4HktQIuGnrkPc9KBRmQzeg0IY1Q8H3vtTfFwwzBHenD0jGcz+einJxZ689lvtLDTbMjuKmYlrLzE5HX+XmEV5y+LAuSNKoBX7W2MdvdRS100N9r4zeELHLQaEmaQsohemOhxkZwkck+M7njHr8Ivi2ZFa396CqjsIv8yPF3bDfC8vY14kojRL41VXu1syg4nzvQYipKHzJt5LQAKxv3pe/LLxYAsSP7lV+Bho41o7wD+cCKbMZ7vHWCv00bDcWSth2tSTsaNNpxNK/8a+Ssy+MslY9HyH5EClJicBTBkJWXqmN+x44mslXKOGyQZ2uUqOqUKao7ZEco5LcupzCa6KnlVfletl5V2rYpqrQLH85A4DvrcZToeg+GwEut19UdsblHVL4wCyr9cL5JNC9wUMR6b9SDxmJJhu1bDNj1K5ELPzsmgjEvZbdelyuIlCNim4Wy1Kh5i+U0W0pv7eCKeVnYb5UJhOidicfFkCqwI0PwaxHA6xYRr0dRnMBR0qYy9ehMbji8bQyl/87JX62Ya12wIi94qaHTVrlRAz9SO5yN1XAyjGOf0WhFFiEul21YDCqw4FxS4jwIqN62+hjzHTV+M/NAfjzCbzcRlVcnz0KlWsVNrzHVv9/Evn3EdmJ6sN2n02qjJ+h/nD3EcoT+d4bzXx3arghozFkdBgQ+kAFlYf/wKE50T+Xc6w2gyRppG8Oj1vuRjf6OFBjd5rm5wVgDEwa73UgbzG7DhAJ1aRQwOzwc9xK6LaZzi9KaHl1vbiGq1Qv4+0HdCXl2SNLufHyjx4Y9VV/zhENaUZAP4UcQfxVXU6wGDIbzJFF4SoVYK0HQcNHxfmIsfYohnmFxew6PydzITrxHcqdv2fTQ9XwQk4eUPwpafncSuisbV+3zZx14TNXoIoVJK0IQrk+5ZliJyHNmFQKvFRCLJGqhSbxwjmU6RzULxdkIvAo7ryoATwwJu6KcyChxgrnjIoKKdYYG8oAQ/S0VZUvIY/RsCK51OAbrcL/kSR5meAIwSneF/aDXGHdk+HJfGKtSBukaR5jioOi5KrrE84+I322KXYeYfspaad0y1TNsMPUx5Kre4qH6dZfjbxSn+dnKE46sLTCczJNaygWFaygzVUipJ+8NZKLug6VEgSmP04hh/PXqP65suri6u8O+/+S32K8ZTzWP76OPzUZHPH3vAtI0GDMJbjwTOcjy0vL1dAHkUMxr1BIUyPavQcOIfF+f4P999IyFLplEoRk9cuXAkhBTpGiDwA4QM+UKlX2Y8+EzjGWa9KYZUUI9G6I9GoqTbK5fmIWvmONoL4i4vBSoXswzTLBMlI0OiUO2YMLzJaqF77pUWbE/oOuKCKyRdM8jYEXg54xfmz38UXGfA38/O8Y+jdzg5PwPbT+Wz77soBSWUgwp8lx4UXIn/yXiMUUyvEVwu5wZ/3meYCu2p9Fl0Aq/mbbHuSjVUzH9dnOM/j45xen2FmGEu0hgZvShkmShvJcyI68kH93Q6FQX4LI5wSQXmeIwbxsDr9VD+ze+wXbYeS1jZovp7qLbyaI7kojyT2E/8saWMCfz9dIj/79tv8fb4BAwVFdM4TGKuZ/KBRB4h3jTqCeOZeIagZx4O0yHvpzPQJfBVv4s/vniJ32x3hE8oe8xLgsibBrB+9pPwCvvW983P8zBygMvZFNcnI1xdnuP9+/cIRfluZBRlEr2HeAGNViDeLthHDGsVpglm4RizyVgM+Tj5rRDvVkM+Aj+EfEpNlpX3EelCN55RKKF+GEJqlmSCizEPTUVJKLLUdUSuiq8GxwSTovcqhn4rUyluZYTWQY6S0PY0iJNQQB4Sz0c/nOF43MV//NefMez3RbFO2ruuj1K5jHK5CvgBZmGEkCF6EoZLckQJfxWPMJxNMeleo5b9Gvuv6qJgZ59IexaVz2UPeYIGX5TNpxnw53dv8e3JCa5urjEVoyETYocWM2WOI/Ec4ZodIzGNJDLxHnYxGIhXtEGvi153D79//hzPajXjCSxXr1T8MZ1jOYsgOMaMG+s84+cru/9a0WBp+dG1CuW6vG8hHpjoOSUvC5SfKaciz0PouZiJ9Sgwch10HYbIGeLt+SX+/t0PhjeTUOhAbEgvJ0ng8d2cATWG2yobYxL2hcKny8HTizOcnp9JiK6YRjQSLMGEAyyX2Rdl+H6AcTjCNJpIGB+OM/Ggxnid47GE3amUq2h0NmRc5CnCunRcsj0x2+PQ/SyQ0O7KceQ58/HgmTTjWcvyvR5xTLOs7yEhDbJYjHXD4RjfnR3hn0ffYjig1zzKGVfCjDmcz6QxPHpZsWHZapWyyAqhLenLORONAz3X0NqJRYZFaYowyVBFIoZCaplECvEgHWkITAOso+kA//nDD/jH+yPM6CWIQkzsnDKUyiWZa7jEO6Y8Cc3CqOtiEic4pivq0RiT8QTRi5d4s9Wcvw9V1mXDMTAYoRyGaG5UcdBsoF0uywcOactfRNjXnK+OUY5CbDUaeN3pzEMbEm/Cyx/Km/m04vrLogB5gHzBhfnNzMH/fP0Gv9k/REnCZJq5AvNMMxPmNGN8dGFuGusxdnTBRV8Wx/z8Wkv+pQExF3tebjTQqdVlDtUqO6LsJ2/zHc45DHlX5jM0EhXPVwv+1XfQz6+FBUa/VAroO5482s4c/GbvAIeNloTTrZXKJuQfvwczMeM23u7IxWbrmJknrYYDKhj5l8ouP6t2cU5J7yq9OJGdzPQuy7UPbjDYKFewUamCu0vJ4ypl86zJa6bzJ3MQynCGZ65UUCtXZCNO5nmYJjH604koBXaqZWMl8LOiRIHMfycKkO/4E/7NgAt6kuCGGYas51zCddGp19CuVuxa0z2tE543/MutNg1kaNcbqNfrCCdjCcE8ikLQy0qIbanzHmjFo4ICj6IAeZff/TQY7NELOcPRcx0elL/ARrkqYa24EUHX5tYBVrlMpb94qRBPwAHqlSr8IEDCdRcaXTEqAT1jZ4RIaV0cBQWeSAFlNpW/NpwVN9WOw1B2/6n8bZbLaFerwrt3Gato7SxDHg/goO5kaFbKqFWr6IWMpgDZyH/e7eKrg10kBFYcBQU+kgI6h+BqmEQTmM4wDSMxVKXOvF4q2ZDtxhP8XGKyYP7IzR/ImvTUxk387WYD/lUg695JkuF6NMJgNhNepuf94vh5UMDoIj8xLirQ6DJKFmUPDnCw0RIGkLAKnovNWh37TTqgMi/u/aCM//fNb/DH/eeYcad5kspu9pebm9htGjdrnBiwAIUiy/EnH2f8chPLHsOdTJcZ8idql/rjmPO+GDdwVY5eAhjawtSn+DD+236lin97/gqv9p7hJknRTVN8e3KMix49H4zhRhEY/+359jZ2NzZQ4g5tZGJBzgHoRvQO4aNZrWOTHjM2N7FdKePX4Sv0XeDd1TWOr67Q6w/hRBFa9Rqeb23ixe4Oaq4DBiPgrm9+zPpJJtaQdcYYr9VE4altEVrNqZknGJ+Yp3lyspxO3mgtT2OVv/b7+PvxMU6vrjGdzuBECXbqTex2trC/tSUfxIFYCrvidWWYJjjr3uD4/AyDXl8W58/GM6THZ9hotuE8e4aDsjf3WLPAIo/fh1+b/qSlhP25nnhZiOHKpFQHRZ5GSg3b1VK54sU0TmZJF/6ERpYlFUYe27vSWFY8EjHGa5bhL2fn+MsP30kYoHg2BT/QuLiwu7uNrUYLG7U6KnS97RsPO5yEULl9enOFs5sr3PS7mMLF0bCH8MTBdBbj3158hYNGSXaB5ycm2hbiKfgLaYyRFu8ZToM/fZ7Pn2+bXksZhSV0ccV6XFTlAssYCSm9mJ8wRRlow9u86w/wDT0U3VwhDqeouA72tjZxuLWFvXYblaCMwPGlH6mzpNIzylJM4hmu+zcYXF0inowlvMnh5pbsxMjjzTpZP+scWpr/YzTEX969wyU9GUwnAHfPVyvY29nFwc4uWtW6GAgx/BLL96OZGLacXFzg6vISEyQ4HQ/hXpxhY2MDv9nbx7OKJ4v7SptHn1nBysEk4suxRwUud2L/ZTzEf7x9i7dnFxiNJmLsV/V9dJoNHBLnWg2NShX1SgXchTJLIgzDGW7GUxydXYingyieoZvN8Pfz92KA4zi/wputDTHK8MSsboGI0k1plziuWKYmgY9pGuP747fIwhlmgwHS6QSbdDfI2IKdDlr1OnzfE2M6GoVNkkTcu132BxLa46bXRxiG4pIYl5fYY7/5Piq1ynznwgKTx12xz2WBzgG2vQD/Y+8Zmo0mbpBKuJyjbg9HF5cYD4biXo7vqN++/hXeHOyjKh5WqO1P5efHCRq+h06lhp1GA4Fr+oPMoLxMozF6/HFdD+MoxvHZBa6vrhAOJ6g7PjobbRzu7qLVaKFWroqBAo3lYjiyq4LxE48uznHT7WLGsHGuJzsu/nF+hp12Cy9bm3MvDnkKsH7+jHemDGcZ8JejY/xweoZur4s0DGWCtt1u42BzEzsbG2KwEgSB9Mc4Zl9McNHt4fTyEr3RCMM4xvvhELHno9JoigFRpRwsPsrX8Ggep4eubxe3I1Rk80OlF8/Zbh4cG2w/dxLQq8k0ZJgdB0mUwY0SBJmLjVoDPu1YbBmetO8Q+Iitszby5yBN8F33Wgy6Ls6vMBkMxMiWBgq7nY5YZldo9EODUC5gTKYSFqxl3RISH/Ie3ykMH0XeoSc23rfam9jqbGKzuYFGqYJSEEh4LHp2mTkpBuFUZP+7k1P0BiPEaYR+nOKbqxtsnZ+jGfhoNuvztzfbo2Nz0baFVZV5Rm8zlL2Lxuf7gHQgztxpGYnXqRQxEvSzCN90LzAZDXFycoTRTQ9lh95H2tjb2sEG3TnTqINGXjQGS1Mcbm6i6bsy39DqBAfWT6ytsSJ9q6R8t9ADFBbGRMwruFhZx1BFb2ngenyK74+PMZlO4cYZWn4ZO6029na30eJckWGgPF+MNydRLB8f705O0GWItFmIXhKKca3n0vjxFX690RQ5RzeRrczB77Z3sPUvHqZhKAYwz1tttEqmHTLfBMRb2W83N1H+3/83nDBCp2RiqLLfuRCl+RZULq4KChiZo/NLcUvqekhqdSMjrMcjjkHyD3887LRrPs5tcnEqKPCTUICyXHmYO54rgYM0cMSAk+l8rvJP5H5OwW/kvr4NfhL0i0q/cAqQN/mOpu1fyXHRajRl3UV5VudD5mwmKSKDudiZo53myyUVlwUFPjkFVJ6S32SDCr18zkyYXxoBkm8b5TIaJa6HLGSvIrLKp7xXmJTXZZchlM3Gp9idiTEB3aJznSCScJ7GCEbhFeeCAh9CAeXf3niCmDtIuEZN/gs8+XYsO1xpWjlWmTcngLl+ScNDboDlpptsPJaNh/zmo8EVvx1Xi69AL24LCtxNActr5CH+uLFa1ufpVDtKZNNKlpiNePUSw6uX12xiuxu8hEPPgLIH1KoVcB2Om4PoiXowm4Kbohk0QL8H74ZUPCkocDcFyLvkIf6oJ6FsNAaDnCs4soGUa3c1buR7QGbyuf44d5DQgnQq0Khj2A+phJGNp4PpFJF899lBdDd6xZOCAg9SQLmI+iuGhB/FkWxSFy/1SYaK46JTqQg/al4ByhsOAE20Z57IvzS6qiAT3Rg3jE5dV7yDD2YTzDKuSz+IWpHhR6QA++yzHAQsFkwOUG/U8KpeE+8irIyTUj7jDnVe8yNrCw46jRayRmuOj8eXuWsXx3TWYBcamIm8xPLclW12xy8Y81PymcIiCnJwpUN2blvPHDZZcLFWWzQ6aTZbYg3WRYZzvij6ffSHNNBI4UUR9itl/GF7G687m6DaiTQjDP5Yl16TVtu+IzHmemjgigsnKTAYDNHLenDjGE3HxYt6E3/a3UWHMZnF9ncBQ723sA62h5Zq2i5zZZVIxkWAbdHtE/Hii48fAwyRdAngv05OcHLTxWg2g+f6EhP3d3sH+NXuviitWlZpxTL0RkML5fedNurVCr55d4zueIrRNEQ6muDvJ2ei1N7Y2Zx7VVA8SY9PcrD77E5VwzqOGFPQHR9f6ORH1qksx3p5zx/brnzAeyzdIgcAACAASURBVD5TeqhyTfPQy0J+Q6zCW9cGhUHPCOSX76cx/nl5iffX1whhQhNs1qp41dnEr/cP8azZRqfKBQrjNUd2oNONfJbi+3YLf2/U8N15IDwy4O71QR/JlIZEHdRKOyiVjWJN22V6n3e23dZghQ2YG6swnMw65O9J0zaLkpShRzhuaORFPxaEzaFrqhXYpKG4DSWPdLs4H/YlzFXZd8Xo7ffPDiR01GFjAyVYj0G5PiB/8YV2Md5Ab6OFcDySBRkaczWoyMzhSppzHPBHZegxefnsFCfda0xnDFnloN2oCR//6uAZnu/sokGFrPQ7IWXoZsBRu4VavYrEycQd6XgW4nQywp9Pj9Go19EutcWKM88LOTQed0lC2o8X0oh80kcmsuDP79/ju/ML9CYzOJmDZrmCw3Ybv9rblR/DVdBYjS4o2VbuEqD3jbMoQ63SwtvLU1x2LzAOh7iYjpBenCLwArRbv0ctCGRRgEgq7eZ9auHRU05CjxRU9rvAVfcaWTQVr077W5t4s7mLl3t72KfBCo1VxKsEx01m4nEz5Nl4jH82moi99+jfdDGlW+JZiO+vrrBdqWKzUobnmf5+HMEWuYg3f2w/x3azUkWrXJU+v6QsdT1cdm8wyejeM0QQx3jVquNfN7bQsbgaH1tmcZDTenrF0necjnehi303iIcVeklJUsSDIYI4Qqtcw7ONDXy1tY1f7VDJ30DFNYpwhTFEhtPtbbTqTfzz/ZEYQ4UM95ZM8MP1FdrHNWy3Nm/FVVT5wf7lLjx6J3o3ivHt6TkuxAgoQtXzJM7jm719vNndxYtWa94XxJ0hWyibjze3UGs08M+TEwz6fdnRFw6H2Op2sVWtYau8IWNAeELot6D1U65YZ/6QfjJEXAhZyWBzKgPmC+Wumcu8Y0xb+rMpGKZKQ6j58FHzS2K8RWWxHlKlXZCgoQYNVlLXkfHMkFHfX14iGk8wG4zEQPCg1cLrrU283t5Cu1qXMUKDFSpB0mmIelASAzV6OfM8M88JMmCrUcfrvV1UAl9CTe1s0vCug516Ay3PyBXiwr6UOMkZcLa1h0athT9//x36vT5mUYLLKMbbmxs8b9bxulmfKw/ZHiObcmNV5DcnWtZAROS6lfFKAHtWOggvsf00xpIwJCn69Nh1dYpwMMR0OEA1KOPF1i6+3tnDKxqsVKtocuHQZTijVLxSlX1fXIwSJx7aNvFWZ/FitC2Gacpc42RfvZwJL2h/2pBK5Ol/Xl3j+8srdOkFxYOEjHy9sYk/7B/icG8HrWpJ3guExnbwXcD5UqfWwN+PjnB6c41JOMPlbITvrs/RalSxv9GQMvz4bsoCqIfD3R0pTzwoM9i3nIfxYHtaroNqtYJnlWeSzuf8qctqm7U4FRS4RQHyD3lNjjVyiHM55uEj8e7Fax2cT56BaUXFuaDAp6OA8rDw8QoPU+4q/7JG8QxkLqyfUrn5dMgUkAoKPJECnLvzJ0eOf/UbXpOMStVa1lIGrzuY+a5n6/IXaQUFnkgBshjlKo3xZbNKbDxxMp3fovUgQNXjF85i7q9VaFm955lplNGc05bgGm/Ovg/ZfJIk4gFymiaIxSermYWwTHEUFHgqBcg3/FFESkiKyUQ8ADPFdRxww0eVBlN23XUt/BzzEQ5vDe8CVT+QTQosxzXFaRzL5lgqt+Rbc82YWFtHkVhQYA0FyG+UvbJ2Ss/FaYZJnImHFXKi73gie2uMBPBIXiP/qvzlukGlVIIf0Ds+dRDcdBliliaIZHWEOU3+NegVSQUF7qUA+Vd5mGsLwymNUjnTJfdS/vp2DdPIVaarjF0FnOdbzjX4/Vf1XNHleSNXDKyiJMGQHohEz3M3rFXYxX1BgVUK5F77wpOUwaMkw5R6FQpl7nMkD7se6p63PgRgHoitQGQvNyzQxoBrvuWSGAw6niPyd0T5S4PBe8bCKq7F/eenwPyb/XNURT7hC5xudzgZJX/pwWd5PhKBaies+oyL/+ZVbUvpAwXyU53ziK+gpijqxIUvCAp1o/Dg68ERpTIXoMW6ix+bcNDkAoptP8uSHjxWqwozB1VkohiSXeJ0w58lYKiKEsMIiZtEhgAytCP9DIy5XxGBvUi3FelpqcKlG8lBvCg0RGFOhVp/iHfv3yEcj+FlmXhz+N3hC/zrq9d4Xq2ADu0oEAiJ/Z9kjgiVSrmM1svXsqP6L++O0OOODifDD9eX2O9u4vlWG20qwe2xuNKUDztri9gOGkpwZ/fUyTDwXFx5NNvIUBEhaPqAAotl8vWv6xsrO62BEhVlKRLpoFxJrXwFdaUpP+YY3oWKue/PTnBxZXb2u76DzWYLv9rbwx8Pn4uiuUXL2NwHHvukktFFm4dyewvNjU00Wi38x9/+hh7jEUchziYhvr08RbtZw0apAXoCIkqmPQY5oYvgt7g36GqrF3d3NGfeugUsLZPNXSszRdwsz3ObC3ormiITK+DrQQ9hNJN81XIZXz9/gd+8fIlDvwKatVE+6AIN62If0EtFlS4aa02gZjw4sQc4HmiwsGiv5je8PCAvd7t4f3IiYTecOBbDqd+9eIH/682vsV8qoWyNynRs0+iG9gl+qYrK86+Et//67h2GcU8+mr8/P8WLrW0c1ptolzwEnql/pcl33yqB2Th7rb3A/havMGmIo9NT8VRE459yCrxqb+FPX73G7w92xOCCcoU04I/lEzioMW8A1J7vodWs4c/fJ3h3Ppax3R2P8Zejd/jq+QE6O9ti/KZtziNLWPJTB1dc12Wor+kUQZpge6uDP716gz89ewbyq7wHbL8RTiqyzLhkKzPUzMuXGDCM03SKIeO3OhlOry5x1Wgg7LSRefRBNSdFHpVHXZOEbAfpUBNcTax67rKk9y5HPFIBPmmTw43ljOQ2Fui8z9PTPF+g4HqehDxKoghpEkq4GD/NxGjnT69e46vNjtCDvMv3ovYL+TfIHPhehureJjLXkQ/Xs961MPtFr4dv33v499/90brbX9RJupAnuKBJGXIF4OjmChfXl5jNJlIPvcL8r6/eiLHKDq3i7To8oZB3Qo4d7phu1FCtvwZDZNGjBcNbccfH8fU1Dmt1PG81JSyXvNPY+I88iDsPPZs7Q1Wz4OSad4d5IPSyl4b/bNspq9XrEA1vLgcDDGmoF87gpYxzWRLDCoZ0Is1ZQ56feJ2kiXhNo3BhKIPxcITJsAfMQtSdAK/3n+OPr1/hq62OGNmyD8lTNL7l2a+V5zxGHCWNcwBrlPvHw2f47eEzmQ/wXc25AX+U5TyIA/mA73nK54oHVJ49w82E4XdmGMUjxvrD9bCPm+FAFpTZGtbDw1Atd86HWLJ12Kx3npjNLFHTwNBDkqQYj8YYXHfhzEI0XBdf7+7iX3/9OwmDw7FNOlDOEA/HZ2ljHEhYy/3Ke74HTPXGcJSDz+C8ihT7lLuaaFB4maU4OjtBr3sDJIl4eHm+tYV/ef4a/7K/awzSbF8QGquoZ5QvGbb3dlCpVJF89y1+OH6PzPWEpm+vLvDV3h6adRN2jPgLLXO00rGuuPGefcY26ztY+UnzFOeCAk+lQI7lpOjyveFnHTdPhV3kLyjwWSlAYZuT4cq7PMuXJ8PeSgaT8llxKYAXFHgqBVb496nFi/wFBT43Bcii/DagF9mYIVVShjl2ZaGdIX/p9VXl7n24qASWvRUMJQ5PYDAkBQHEVJTGsQlPyy2snNwWR0GBD6QA+VZ/XKMYjYZIJNQlQ/R6qHFntL9G2c9CdxzkYbIlV2QYNroclGU8sCaGmh9HM/FGxPFSHAUFPpYCKle5HhEmKSIJcUn5a2QnveNKqGm7BvNQfSqDDQ9zr58nntLpXZcBwcMkRkijxJSbeXJrKDomFKGHKiqeFxSwFCDrUB5OQm7ii4WpZKXOC1DKGVs9hrUW/Gs2b1KfJ2t5XP/PEozCKWZpjDR7qtKj6K6CAndTQNbG01i8q1DXxPmvT0Nt6lwYMvsD5C/Xcaul8tzzPzescg5BGUx9gF0Rvhup4smPRgH21Wc/yERUAqwu6qtg1MmsMlv+PEdOM88TzIW8v/M+s1eef8pbxXMO0yasVs8PSSq8tB3ML+hz8pFkkG/AJJOwR1SSkjZzZc+a4cFByvKiFLJKzsB6enAYB5RGK0glpFDJuqSX3b62nOLBs07gFaY+m7dJlPBUxPPJ7YPlIloZI8NZnOHd+QnGk5EYzLRKFbxqU0n9Gs+qFTRsu6jcYd+zLF3ccdGdL0rXyfCHly9w0uuj1+uJh4YRPYRcnGG3HOD5qxdGAab0u43Oh6WkojKTzygarUyyBN9eX2IQx6BrP4be8VxX+lA/rLSPTYXCdbZuXht6uY6HsOxjkEa4HA5w3esiimiGcv9BCPyQo7KVitaz8QQnV5cYjoZw0xSVzMer7V38/tkLvGm1JKQEFWU6eNlTykOkdZaZkA/u7nNZdPjL27cSkoQ7Zt71rrB908RWo4J6iS21vHk/ik96aofFk8poZuEvTqriCNNoKt5duBDDj9JOtY6GZ+KMU0FM3MlX/LFOveYzNU6Z0yY3rpjG/KyLCn4qRC/iWIwjJpMpsjhGNU3xrF7Hv//u99h3TBgPga9KWVueClF+NCfI8PXBIS5HRrE87ffFeOPd5QUOKzU8P9yT/mLdTz4UYYs3X6H0JHOJDP/nm28wmJgwQGXXw3a1gn99+Rq/29vBhjVqUtnLM9vMtlPe0GDEdzL4G00Ef/gDbsZ9DKIeojRBL03EI8F24KHT2RTaEm+W1YNoLdqTIuUiBP1mRjE2qjW83trD7w+eidGMGi2SP4m/HLZdpGuLCv0M2N/cwvXlJcajkSjjh5MxxtMp4oQUVo5XAMRmgYGmPubMOkkP8orPePWpgyxOkYYxXJeeXKiEX3h00bZqbZQgRswv5Lw+S9NUFmTECVeawMsSCUv1b1+/wcuNFmhGpQaF2jfsFzm4YJg52HIyPO90cDHcxtW4h8xzEUfAKIpFTm1yV5E1OGFbeJAac0OmwRDH1xcSUghxjI1mE795/hxf06uH74vHH74j5ocdT/RqRkMsevj4av8Ag0FfFpgI97x7g6NKWdpQ67SNkYY2eg7I4LEmOZfj9iVxF95iQblgHt4wlJgnPKN8o7TSMrznO4nPGSJLDP6mU7w9OUavew0kM7hpjE69BYbyIReRZoqjVsd7j24xKft5SAUpkmiGpl/GV1u7+N9vfoVnGw20afRlZYH2IYvM4bIsXyH2vc1nHHM0hCK+rCv/zudzwmG6tI8XHEo2TvfLg310+10MBj15Pk0jjONQDOM8n3skF+1hUf54mDORyafaptk8POVpQFic/HMxMUtpuJMhjhIZHxuVKr7e3MT/8+tfQ0Ll0DRlDR0UtJBQbx445zHkHIHvZno8Y5/Sk9W781P0hj1x2UjPRAcbHfzh8AV+tb+DjZxRHuGQhqYdgJsZb2JftRq42n8Ghgei0Q/DkZ0PB/jm6D32v3qDWtk3ZeZ0W9BFCGSIOW/FKs3nD4qLggKfiAJmHk7hzPfMCgN+ojoKMAUFfgwK6Dvmx6irqKOgwOeigMjkO9ZHPledBdwvmwI6j+Y3TpyqwQrDztJgxZVwoly4f2iGwOf8ce6qP353MByF5/vykIoAGq2EUQh+yxZy+8vmvU/R+gX/ZpjOpsJXZDaus1LZKeutj6xIYZF/+S1fosLVN6sZfMaVInql5cqrrhk8EnSRraDALQqozOSZ/EVjFSr8KRvpIagUlFAqlWTtSHmTeR86VP4KD9PgxfdlAyRhyEbaKJR1z1vLng8BLp4XFFhDASMbgVlEQygjGbmmEHgefG7atHMD5nsM/7IK5uOso0z5yxBAWSrr4owKwJCCMcrrls7WYFckFRRYTwGVuypbOf8l/5LXhH/9QOa/rkutzeOPJflbsgaHqvdNMwmbRW9BTxkPj6+9yPkhFFjVAH4IjEeVISPdxUz5Z/nruwCTgfRQJhaf2fkHmuFHOiveIvTtYoYqpvRFQGsw/bmyq9+Rnf38YNQf4fA6fzBND60HaQKHLx0xWEngMswQMtm5TUWYKuW0nJ6JCw/FSW7yFZjHa3uL5OVrji5J6ZHiffcKJ5fnYgHsxUC7XMar1gb2q2XxgEGFqmkXS5qQB1TtV2mVzHZmDraRYXdnG1f9HgbdGzFouRyPcNGnYu6F4DlH6RNd8INcWMV1BHfGKjsZ9HA9GcNjH2UOPN8oLsUSValh+UuNVzSUDdFiGievaeAiclJ5WU+mE6TcBXMP3gRJPqHClYq5qyQR7yqD8VgmxPwQ2643cNhs46DSQMf27SqPsD+ZJvCs9wiG8nm5uy+hdXr9nngMuJ4OcNy/xvN+C8+3tz5IGLMOtknP9zTvyY+EFlyUYfghYXbjviOLE6TTCE6cwKXrRPuxSj7P05c48cdDitvrdSfWxY9ahmA6urzA+fWVvAjdNMPBRhu/3T8QYxV6olCjK9PPi/arlxe+Ovf9AHtb2+gPB5iORwjTVPj4vNfDbH8Xnr8Iw7QOn8ekEWf+JKTPoI/3lxeY0Vo6TVH2Arzc3MLLegO7nqmLPJGng45/MWijBwcS2ckwDCrY391DHKUYDcaIXR/vLi9x3GrgZauFwHo3URyXaZ73nJPBjVPsNTbwotXBpuNIeBTSz8gCI5u0n2gwwvbQyKqBTAwKWo0G+oMeJrOZfBzyAzHNzMLZbZ67naI43nUm7jpeRE6mxrsKZ9rSvyllk8Ezz195OoryMOehZPHMKBdJ9SyJ4GSxuFwkPx3WG9i0Cn4aVPHQcrpznq8Odgk9rWz6GdrNBrzARew5SF1PvKD0aBS1sTFXyhMOaUjlPg1Legwr1LvGZe8acZagWi5hd2MDr7d3sVsqiWcVkb8Ghfl/0kQNChsOsFMrY7vTwfWgj954hPF0gqvhABeDPvY77VthiQhIx94c6GMuOMRtPj0L/ShPnWWDFX3Os+Eb807iOKZnJoZ4ejsZ469Hx7jodhGGE3hOikaljBe7u3i5u4u6GCQZ2q+il+m7m+4s+X5N+W4FNhtNfLW9izetBuqOMTgiTxNx8vD8UATnCYbvddxpTEwW0TRmZVv0nmc+l7HB94IDbNYaqFer4A6czHfEVew0jjCJQlT8krzv82gQprlXhIwXE71bzcv8S89SSjQXrhsIgdM4lTGx1drArw+e4XVrA026cxavQPPKFq0mMFsJL7VNiwyrFVoPEotiYtjK+YaEeAtHeHt2jNFkyGByYlj6urOFZ42mGA/Rkxur05+OJ44lzoeI5xjA7kYH27v76F6eIYomGIQhTm9uMDgIsVX2Rc7PaUMLfiGMNmb+xDYj/263z1azLDW4uCko8KEUIGPp70NhFOUKCvxEFDCT+Zx0/4nwKKotKPCRFBBW/kgYRfGCAk+lAGeh8p3HUD12hz83fomynyE25zN4C1mnrbmKdHrK+bj+5Lvc8+Faj8bkb35tc4c/v7vvPNbAvzNv8eDLo0COP3jJH/mKyiYa/XG9lAZX3BjBdTTlTSEUM99z6EyYvMvNm8ZYy0Dguie98864buQFsp6yBPseuMWjggLrKKD8Q7YUgxXyllX6U1FKXl5m4HVQFmmEp/KXvC/X9JBl4XCdKKRhQVKYXC2oVlx9LAX4No/SxXud692e48kGTeXxh+pgPuFf2ewJlFwH5SCwKthMNhkzlCC9VCj3ctw8Fv5D9RfPv1wKkI8ShuqhJ3QaU5N/53MIs6XrsXymPMz1fdmcLJtVzTp0Sk9BaSJ1kdoF//48eI76uJ/NQQZ6DLORefS3QP4xJRe5H3ulUBU3uWflxEASKaCpXDefi/LcTkCYS+5tZVQ28SeTc85v5FoNOUwmgs4rr2zReXv5jD/ZgWyc60stnOjIZMfWma9XYehZ0Lc0NGmam2f9ae7FmfVSIRoyZAu9UnS76Ha74ITN8yBu9bc3NyXUEUsJnnI2bWS9ETxJp3cC3kuohM4WWq0r9K6ukHmOKKoH44l4v+D8jZO5T3WwThqsSOW2d+IoRjINMaHims+osKbw8ty560pjPWHK8SXPI79wJWksGjjI+KOCOaFC63FuWkkrGgJ1J1OcnhvPCBSdtSAQ44ndZhPNsgn9cIseFh+dM/MjjsrUGoDNoIrNZhuX1RtMZjEmYYSbwRDd/gDp5tbc3aDQ5VMReS0cq4knzZXd1uQj7lTm06ipSs8BmYcwBcZJgvfDATanYwRBE20bMoN4s4zSxJLiHi42XS+8nAETGgnRq83NDfr9Ae2/xGBpd2sXLw+eC2zy6lzRbI0UtAmEQ6ciPEjzVqeD6tUVHPJyFGE4nqA/HCNMgMrHSFvHKOY5/tQTz2W/h/5gCBrz0GCtXgrw+tkBWvXq3GDt7tFs8CWhaLTSQobXB4fodweYjCbCF73hAJf0fjSaoNlqCo3XwpPxZDiIzwPHwUG7g/3WhoQEU+MI7SOFwRK8ZjpJw/A4jENYr1QQBCVMwpksmImLYk5Q1vDLvcy0Nv8ikXXrYbqQvLlQnPMZcVN8NW/+nIfBdNMeTpwcUMlPQ6JmrYYXeweo+7RkvwOmDItMpAVpwbZy/DZqNZGvcDxknofIcdAbDRHW6+KRSnHhhwHDz9FoozcdodvvYTzqw00TNBoNbLXb2Oy04bvGwwf5aJWevDe9aNpBI4B2q4lGo47eeCCTt3EYojseiXeKhs+Rt3yw/YaWy+kP3S3RkWOMeHoupr6DnpPiMstEPip8tpdtoJEOvQ1RdvbCCc56A7y/usG70zNMRwO4SYya7+Nlp403O7s4bLfFu00ec8VXzsrLnAzHiYRzapTKIoOfb22i4dIFpulD8gazy7HUAMsI+mzlVpPz9GZa/uOOz3ivaZSJ5UoVDDeV0JAnyxAmCaZc1KiaviQKt9EgZK1REV7Ntegd5mTd9NlGaOadksEJIzRLZRxutMXbVwOuGJ1ysn+r0gW4taRZebzec4SVs5StDE11Mxzi4vIS4SwS47lGrYHdrW3Uq3VpHQ2WdKxqpYu2LOjTqHhiIDvsXiKKuKiZoDeeYDQNETZrYBS/pUM7eB1xc2TVOpfKFjcFBQoKFBQoKFBQoKDAL4QC+h270hzOD1bnAytZituCAh9KAbKWzmdjKoK485Ob1egJkYtvsrs5Z7LyAC/mvwA45eWiPzfRSTGZe2fWi4DWnC/xoa0oyn3JFFBO4rcrvxllzVo8bZv1EtJmzrb3yFM+0h/LiMLfekVlecKnMku8YHhcfSqOggIfToG85OPaCNcjRVlqlRhirEKOnDPvA3Uxn10Gl/UVDgdrvLVYxHDEKJH1rD0sjLXPisSCAjkK5GUlkzl3EL6ya1t899Or9FNYijA5b9CfRw8rUpGZg/C/hLPK4VFcFhT4KApYtS2NqMm/RjY6siZOw1eVqU+tY87LajBoHRoQPnm4OH4+FPgYFeonbwUZ56GDQjX/M/kfU/IhyHc/V+g8m58aq9BowVgUitHKGhDE1SiAWJizFIry1HhGwWKHrtah+QlKdSd8pjCk7WpvoSBpCCPxJ7TEGkRsUp52Wqd5ZFq2fL3IwXI8OEdjCJXrJEN3NMIsjJCVAlEwt5pNbLU7onxmXq2LuC9dG5uQ+QuyUfJRr9VNKAbPQZICkyhCbzhBh8p32yz5zlmgZBD6kP/z3X5G4UjB5HE3NS31qBiOzUKAUISecPRjSCaoC+KzO+cHWYKPZN5qjIeWns8z3r4gbaiYpJeVaZqKkYPsQqDhhu+LknWnXpcwHlS0zqtlQUHSwNR0DmoaAjH8BL1W7G5u47I7wPtuX+JjUuksBkFRBr9srBIJys6/byP4KVJYgT0Uz4W2V58YrwK1zEG7UkO70YJ/eSMhtIbTEP88O0WlWobvufBrdRP6yLaVbSabKGw9LyAvrsiPpDcV3hMaXk1H6E+nCGm4FKfwU0jdW7WK8KiOPYWQhy1Kc4GVCTzXC+CXynD9kvDDbByKkVB+DOTLK8z1ZyWaKTHnESrnZxP0xmMk5Nsshe842KxX8ebFARoSzmYhP5ZgEyR/smBgDEWoDKcXmTe1Fo5aLZxfXIhnjijLMJxM0R2Nsd9qioJaYRGjfDvIRVliXGTWSxXst9rYrpUkbA37Jm8gsAqD6JjQPLAeooxRH/NRWnKnlzFeaSxXuoSBQn3cWXHXsyGILbtIlISV2/srkFeDBDyTMENuAnRqTXx9+EIMsVRCkx9u86sx7COtaBRBgxEa74jRm0tPIy6iNENvOEKybd4dpJ3yJ3mRXiQolyczmmKZJwxz1qrWULGuQGgEQDnF+pUdtFF6z2fEo+R7KAU+MnrccF0wvuM4jjEKQ3S8qhhy5dtBOE+ilxZgxXIwnBmRc5B4LsZIcDYdoZF20LRymOGhZmGISTTDeDbBKJxhGIU4OT9Htz/EdBIiSR34cYS652KvUsP/ev01Xm9uo+mu58V59YoG381ZBj+DeAt62dnCHseA9RqmbeZrd+lYajyhLhJ4lR8HKhO0/whH6U9DHKZzzDONy26lcgWu54sM5zO6RpzGsRjMqfGklp/jpJaUangxf/DAhcvYs8SYsZYSeEmCw3YHr9pb2CqZcc220BORIMisi6beAn7Po1t5CVIPtp8yuj+bYTgcI2Os51IZjVpdZHTJN9UztJvWwfJ6TTh5+pKOxgiMHzj0WuQgylKMowizOEOVL0492P77XuL3PVMYxbmgQEGBggIFBZZkckGOggL/fSnAOUJunpBvyOrkI/+suC4o8AEU0Ck2z/JNIMYqhtG46U02V33AXFS4mP84d6bClJu0uH6VGWVTZMNesKbiKCjwKShADyviLdcaWJH36NU6fxjOzqcsX5Nl5ftbeNWIYvKvEcnWWCWJTdiA+cfpMozirqDAgxS4ixFljZ+LaEYXsOC9ByHOM+jsQXmZYcj5M7C4qSyTtV0aXy3JXyuv54CKi4ICT6AAeUm8U1iPJRDzAAAAIABJREFU5WQnj97VHLMyeRfLr6tiiYdzLrIIg1xr/taVLNIKCjydAioHxSBVZK9MXEUvoTrap0Al/+qP5Wh4qPKXD9Tw9Slj4in1F3mfToGflcHKU9BX5s2XWZeWf/4x18rYKqQFFpVBnLzIBGY99Hw58bBiPyxlGqKTdluUk/C72qD18rn5KWRTWNIE3t1rKasY3qpLErSm1dymXn4wcyd/fzoRZVlG60y+8Bh/0Q/k2QCZGLUwtIqhDVtLzwXWe4GtOHKAPndQhxnSJBGXpHT3FKWphDmhN5BmjWpbc3zAN7kWNd8yKqDUAEXknYtyqYRWrYFWrY5KqQJHwiEYpalgTkFGurM9dpIqgEUZaHHLqGR3EQcupk6CcThDv9tDOAuRRVS73X+QrtwlPkkSTGZTicNaYugJ30fL91Gl28vHdK0NUcG89PhRdoCaX0I5KNOljyx4hGmGaRiJgUalFMgOhVu8cD+6H/A0x6/Skbf5jCmcNjF8w4bn4aCzhaObPiLiOhmhN53gr2/fYtjv42pnG4edbXTKFTQD33jyyCmTH6IV28teoaJzEMeY8gOXfeu68EsVMQwYxEDoZAjE7RgfkX/tRwoBMNaz4xglvg3TQwVyTMsfsVo23oToCWESpmiU8+rqp5NQFqsE70wMmwhXxp4bo+I6aJRKaNg+X14CWFMX8bf0MsZNxkCi4vtioJWKO+AM4ygGjYVY90M8YnrYeKAoZ0ApBeiE46FWa78zH3mWZ+UOThq4o4FGCsSBvwfbtqa59yVJV0oGU6vt2vuK3P9MP2TTDG6UIkgd1DzrkSKHv7ZxAcyEYVF68WwmUWyxi4zj13VFNlBOan8QDnlZPI3Q6C1JxB1jliVG4U7jD2QYpRno9Zljg54xWM603UAyUs7I95GEKANm0Ux4nvHNHS8S44gZdy9xF5NFnKVvt2XRqqdczQ0v6OnGBQbTMf76/Td4e/QOPscVsWHdXFRFhpjuAbNUjMWmcWi82rgeAsfFRqWCFxst/HZ3D6+3trFVLolsmYtti7RpvcFS5HvubcU6m16ADRpJMJyT7T/tIymlAFaJsPLCYjb2E+mmZxqm6DXP/MXSLnNN41CG/6JHs/GEsb/NO5WW3xz/fFcSnqHMmn5QA9k5t9zfGwpH39XMTYM4GqxslivYKldQtwY0agtzZ+cT2CpN1ifdQopFaYBFb240vaJc5VyD7zDQmMb1hQeHEZD4RkZLXayPhS1zsgtkDmLnGuKJhbxF5CnPHUfoSCNOesEqjoICPyUFyLrFUVDgl0QB882k304yg37kW+CXRIWiLQUFCgoUFPgwCui8gGfKU7mXufVikZ2L7fPpts6DV6pjuXWPmCY/CVvOK9ZDl+ta8wqg4ragwEMUMGwkuXKXZg1Ny3LDVZ5v7eeb5Oe/O9iPj/Iw9YabarguJ+tGNOwSAEs5tebiXFDgYQqowLSsyFtZTzDLwEbBadfSHgZmc9iyutbFVLNUZMYC7w3bG32JPLdFl0453JbSi5uCAndQwPAVZaedK4gOzGzM4jOuND8oLaXMSgVznY4pzWkDZbDh5AchrgArbgsKLFNA+VbOS3w152S1H1wueM+dcqfC1rmGuXcMPJ1r3wPnS32ko1rmb2Iv/MAGz09AKOqu/lseSqw88uvS8s8/5ppMTB2IKIdUEZU5Ej7Eyc08mI948Kw/1iu4McFeU1+iC3kmdfFM82h6Ho6mGUswk1Oe20k6XxJLyiYtsOZ8P72Wa9U7nqk3HIdTifFFxTyVPrMsw+lkhP+6PEXJ9SSUgrjGkHrNGy7LTDgKUb7CeAyYlkq4mk4xnI7N21LiktFoJcEoikT5z/A6H3OsltYPJCcF3BSoegFetjfxcmcX7VoDnoTyoULLdJYE9RFjILvoqm3iY1EIsgb+XMzKAbpphLNBDz+EMbpxIoq3h/AnX9EQaBbFiKIImWc8u5QDH7VygIDuqh4Cws7JKVSpVOWO8kq5jHK5JJaIrCdMuaM8xCSOUc2MwYq24ME6HsLhEc91WUV5Kl+EOFccSMifl60mrnd3gTjEeRJhlsxwMxogiiMMZjMcdfvYbjTlt9NqoVUOUIMjSmka6lC4idI/X4GOP5tGHSWVlaL4pZUwHCSuh6NxH97Je6Efw+3QGIkhoji2wBi8dMdLK3jHlV/k+ZiUyjgbjTEcjYxiWezkycszjGYjbDZa8rGzgs49t8u9IWPPyqBpGGI2ozobYmBV8n00SgHK4o/jAZDLYIWvPDgoI0Ml8MSrxiQMRT7Rg9J4FsqYZ1ikJUW9VqMLDnYiWwoC8YLjabrme+DM4Wb6y/QDs1NGinEC3cBZmfoAmA97bKvMiXKdvzwK3oKXeZUAWWS8aGWZyEPyI8UY20fZL3Rc6Qf7lpiPczFTEVeh6u1CKCK8JbuULC8zlTJZ5AfDAoV0GU3h5iL1MvTiCG/7PYS+a8LhSCN1oid7ngxSxIoy2nURug5GSYiL/gCD8Vj6gfJbDCXoiSgxBjNsLZuhZyHW0s0jyMf8+YPvV9sfEUO2DAYYUCbzJ+POyF35yrd5uVDluy4CN0C9WsZGpYGDVhOvNjt4vbmJ7WpJvE4JyXN0v1W14MG4YPSylcB1UpG/9VJpbqzyqI862x7C1x+NJWggx1HL0E0MYzRlqKM4wSxOwbbSm9BM3ns0fIslBNTMD9BPElz3u2Kkw34w7/jFgkaefLzWOrV9el7Nt+7e5OVoW4w4vn1alSrq5bJ4mZE8+uFq++oWrByd78pyq8wK7pTP0zgSA0sarGSuJ57IrsIJ/nZ9jtqwJCHIXH7EqEtzmZcZliZ7ZBK3KMMsCNDPMlyORtZdqSOeg6IsxjSaIkxpKlS4kF7XJ0Xa56dAfozqtZ4/f+1FDQUFPj0FlH/VTEXvP31NBcSCAgUFCgr88iiQl5kyj+Z3dS50bf75Uutz8++ldHuj5ebZNMF+0+k6zcrX3TpQRVpBgadTQBX3UnLOhbfhrHmUY1VdKhBDFbO2awqIXus2tCKloMCTKZDnN7O4YlJk+WkNf95bgW6i4VqHHQOrKzbUKRHsU0HfW2/x8IungOGphZGrfJdZRlNes7d308pu0M+PCdGPcDCQY/mAPwaSuBtK8aSgwKMokOch4VGJKqDcmhOS9oU/z8+LXLbVyvhY85prc2ckr2j6xKyrMHpdpdzte6GZtVcR24TbWT5Jys/WYIWscxevMX1ZaaRs90locicQw9T62M46rK1i3mhFc9zCigNKdolT4WaHxR2z6nnbqTPizTzBQteZkk1X4xfFkefVIiy5Lk3xNWeFsEjVdvBMdKhEokKbRiWiRKJSKYnxvnuFwXRkJmFs57xtBoIo2eTSKtzoMcDz5DcLzU5+GoBQo8sd/Aw9QRWSER0LfD70at52ob19saYZqp6LF/UW/mV7G9uu2UWveYluntd4b1qz6BbeK12GyHCeBaABwfXFlRgvcKf4QwdhUKE5jaK5ZapHXAIP1XIAn+4Cbd2K21qYVolInH0H4h2EynIarIgrFbhCW/HkksSi5KbXAMKU+YY2bi3wj0nMAdYG5JIImclqZNJygH04+N3ePkBFYhrhajJANIvEI8rw5gbvrq6xUatjZ2MDh50OduoNMHTSZqWKpueKdxm2Xdun2LMe0oeHGqyQz4Q+9JiSAe+617ga9UGji4yeTPjneSZcCZXmEtsuFa8X9HyROB5iN0CYOQjDmbjdQ2YU33EWYRwOkaA15x1b/aNPSirls+ksxGw6A43CsjhGuRSg5vvGIOLRUE1GpQf5RQxWAvNaYJ1hnEh4LtKJ9/rLV2E40wx3XhOXwGdM7MfImwUklvWQCc2VRfj0J1F25BFYoHjvlfSRQ0MOw69OmsAnPVx/bkhEvhPeY+bVOiQtA40D+Ig/5iVVzJ0xUJCdb+x3iw3P5Iu5wQoNStIMju8L7XqzKcLLC5wN+qDPH4FujVYMj7J3SWjXhNmyr7YECaYRlfmxGMmw9jhJxTOTeLyxbbAni409rU1czrJ6xyJzohAHukmlARaN9wIXXsY7YyhGPqEbQMZf5c93XJSDAK1SBTvVJl60t7C/0cJuo4y2DQNEKubRMvUZLBZdYUxBaLBCqroOw8T4qAS+8UyzwHCB/qLwPI2w+SMUnuWdmdFTSoZ+kqKfhLiajNCfTDGaxpjMYvGKE8aheLWROPVpJO+/1PURpsbDioRLspwhc4g17pQVCVO/jh5NfdyZ/nPIZ+QP9jv5uO6XUKU3NQuC8HnIe8Nez0+rNOG9FphneviC9KMBD0MEUs7Ss0qYpbgcDTA7jsRISaoSg1IzWmjQI1ecfzjctWTONESMafCSZmIcxNoZ6ipOGQ6I85kIaWGw8nCnFDk+KwV0mMhZxxHPev1Zay+AFxT4tBRY4udPC7qAVlCgoEBBgV88BVSGcgqQVw5xds+Q1o89CIcwFJ6W4/oh58KyjihzeteGCComHUqj4vxxFCAnce3BrG6QB80GQOG9VYbUqu5gP2a/XYTfeqYOMjk9mhdHQYEPokCOuZTXNGnOVUxQPcwHfJzl4ZqxYDX8XJvjksXSSsu81g9qTlHoy6ZAnnd1/kDW5WZQ8YRidXWP5TKFJ0PAzhfMai0hmJ/m+bIpX7T+U1BAeYmcpd7hxTBCDLeNXuQp9Sg8ltFrMw4o0umIIjPe7TXDYwfGU5Ao8j6ZAj9LgxVloLtao7yjZ8NyC8UMy8s739ok3AXnQ9IFNgvyYkkha5WJVlyvwmZ2flhq/E4pLFa0Zvq+aMtKSdaRe8hLudV/orCymezOixUIt27nMG49YYIAlieLq+WM/DymhwfGuOXHBgc42zYejjDrM3iBURyxFJVehjJWqMwtio07fjaOiij2npPRc0UMN07h0HAjiUULfhcey1jdf7cKQ4QdiyRUfKYIogiVMEGjSuXyggrsN20NYcz73+bRNBqlUGGcZMZThYSvoEtKa6DEqkRvtgZNhcny3GHP/lZlLL0GlDxvPnVdasfSzRrAFkfuGQ+CQHBxfE88rbDOME1EEU3LAm3jKpR1VWianteVyT/T9i1G6OLp4spAIR48iHMNwDMfcJ4doloJ8N3VOa6urzEcjhGGkXhFuRr00BsO8P7kGO1qDQedDp5v72B/o41OpYZOyUPLvW20YqsRhTIVolTwSxgfGlFRQToZIxynojBPY6vQF17leCUTk6/p9YOuwywPuwHgBYbnU/ZmDC+J4MQh4pgeSxiiRXxraPWPPiudSEtR4rL9Ieswoag8xwO9pJAP1bhEyrCAFr6jNj7WX+D6CPzA7uByEMWJeDdgnQTFg3nz9ybNyDGGsKGxFg0KSCddnDAl7/6vsE0OawGudc4/Chc43A3paU+kXitgDQ5snbnif/0x9bGHWYAx/OF7xmMNX7RK4zlQAlfApspcAmtb4GLqNsLTwDejSXOwOPtE5JAarDge3MBBEtJb1QizyUSMm4xMYs+wNEvxx0OsREzrKawola18Zpxpn7Iyi5HRs09Co61MFoW0CRbIo0+KOwto883ZtJPwfd9Ds9ZEs1pDkLn0y2UM8TwX9ORTCRjuLABDWTUrNWxWatiqVNDxjOFhlcZ6FiPWtw5XTdNzvgHkYcrf/Ki9nY9YL1J5p1TlCJ0x7B2A6zTDab+Hs14Xl4Meji/PMRxNEMcZHMoNie8dIyWN7cuCnrbgl5E6PuKEkF2R3xCZxHFCIx5zLGOhrTCuDfVukXM5JX9HOOQxGpwqTK79+dbwh/WJnFZhnS/8gdfahnxx5WeGr5vNGPDK5OLCepTE6NErm0HWnO1cSHAWGxV5aOZPNCTjPMMRUyeRxeI5i3I8yZBGMzPfyCNQXBcU+JEpQI69dawMjpXbW9mLhIICPyUFhD/5b4mZl7k2/2j5yU+JeVF3QQEzk1vLk7d4eg211hZck69IKijwBAqQrfjjlJurQfpdzWn6fKF9/iVgAVPIWn5kubzM1arn7DqHYwpRqeV7vqwDaN7iXFDgYylgVh2UmwmNRiuGN8l5/H3IZ6UsEfEjNTGGV9wYGrj5kfKxmP+Cy+cEQ+7yF9zgRzSNLLqGGMK5ki4WJXP5yiTZA7a+2HKFc6Fr1omkrJRbhM3kBmgJB34fvByc5QqKu4ICCwrk2ZgswyVFikqu7smfhJfP51qUvetqwbOLYWKWDM0qHTf6mXgKzFkw6l10LNIfpoBypp7zcwiVuYbHDJ/Jf838EHibjyfqRcy6t9nIqFy7WAV/CFjx/HNT4GdpsKKM8qTG01iDUpiFXSMqqfAQRlwB9EHwrdhlWWPZZYAa8UzpvwxV0MiJasHDGtAoThx4VMEtl7wt3qXOFVhsmH01zFXDWnI1/0rzl26X616+EwsLWy9xVri8pocHCTtBhWaaiFv+ZrWKps+PXFeiAfEFximZ1QcbcJJGchkjG1GI2smaCbWSoJ45OKwzxAvDD1ic2JmKwFILPvRG20pDGSpiU/OzH0yLp+YDSu/1vFqrWUhY5CVM8aZjiLCUXWFYUsgzXtPQIEkYToSdS4U3w4i4cDLGZc0xwBK03I0CziXxkriJVaJ4vTHa1DhOrMGReU6FrH4oKl6is1ZYVoE9v9WLR5yJ1hwm+3N+Y9rE51q3gmMavaNscOLuAfXtPey1Gjhrd3DZ7eK638dgMsFwMsVsFmJAI5MsRi+e4f1ggE69iRedTXy1tY3X7QbosYWKa9aj1bMuXidxiowfuiQ9PXxkQL1URl0ML1zpRyGtHeayY9+OOo5BwqBfjJRmGkSWz7JYfvVqFQfNDTCkCA1KBI428gPOSituqoqjBEmSmQUs14fjB3PFOocL2yEHz3dVbJ/xMV8GrhfAISyPhk0JGAZI2UbBESbzL0CaPuU96UuvNBTFvF7tV4vR0om4mp+ZGhDwXK7Oa1rUtlT4A2/YlsXPGs/NW2SNkCxey229u0LFUIwIGBaNhle+i8Bf9LuQWwFqgSWQpIE+MPQQQ6clrmUBk0f7RNtCm4Y4jpHyIjXGVzTmqJUqqJUrYozFDpXSUth6oBAcmKp188riYmV1UAmx4fvYa7VQgQNfQxvl8VeE8mn3XEttfBXYcmY08T6Fm6Ro1+r47eFzvNk/QDXlKOPPGk9wUdV6V/FpKOW64smmYsOKcSTypy3S8z3oSG5Tg+FelpEJMtcn7PRiubxSnqlWtnHMWOOhUQbcIMNZlOL7s1McXZ7jut+TcF7j0VDaXfFLqJdLKAU+PM98TIrxnBirBEhKVcReCRfXXXS713BLntBnbpW7jND6O+2XxxHhNgwxoCEQkSy3nz+QIq+0B/LkHyu6TOM8gzwtgog84DioeIHwxhwtO55F8LAnaEhrxwybbEaSCekmNqR8v5JnkGEjy7DTaKBeMvKTLTT9nseouC4o8DOhgF0rvRMbDp4PHed3Ai0eFBT4CArk+FEWhW7NZz4CdlG0oMCPSgEK2PwM5UetvKjsC6OAzkV55vcMfT16jjEmofF2mqSybiRrR7Qqv+PIieCl6QE52Xzjc8Ge63lcgnIQeIFZf1rKnQOeB5hLLi4LCtxFAX5Le1xfsiKU34Xk26dKVB0T8p2dJogTbg0xxipumqHkeKjIethi7eUunL7UdKWhtL94na1ng5yMU3rJmhM9zUqIeCDmxk/hYF1xMLODXNFbsJXf9ZymGZI4kc2OZkNaioDrz3Yd8T5Yt4AXCQUF7qAA+YhrjI71IM0w2gkjJdCb9CPXvVRU6JoeN0lOplOzUZeGKrL2FqPkc6Pf3fORO1AskgsK3EkBw7+ebOjntFQ8ZCdm473x8GOXvsik9wjNOQ9bvWvEKA7Ctyxk9CMeN6pSD3YfoDsxLR58Dgr8LA1WntpQYT5r2GB2hAOpQxG8vKyQZ1Ky5RI/60NWvvTAYKP59ZzPZMIBLRfinb4A5u2xhaUq6wJGYxXO86xWb8EuQ9d2GYB8cehhq1jXBM0iZ80nN1I+n8Lr5YMp+uphdu5U5svOkD1D2Q+w12nj1eYWXO5ilkzE0xiscCrHdyQNJ7Q6MVrRPtLwA2mKGhzslKro1GqoMOTDMiqf/I64GUUoTQ6W+4243qbGMgpKm3xZM3WVlprMuct8aSabn1VOi2rNGqyQiFw8oPJZCPoQJnnIK9e0cGBFXJlgJ9hLxZ3366ErhsxgyjHf+ryLOvPPBYKEbOCVTupFDSxw5nnNYwFCXqOBiYSpgYMmgO1yAwd7FVw1G7gYDnA2GuNsMMLNaITJdIJpOMU0mqEbxTgdT3A9HmM44c75A7zsNLHpOaAyW/BZoAqHRiZiGGRaVvYCHGxu4lm7LRMul4KEh9WOmhATTCAkHsLdwjl81ckdrV/SGLU0wW65io16Yx7WyRb64JPBn7XQkMmc08wBfzy0feYFTO2WjtyVKi36ptW2TzNXWMTAoYae5tgLo7pFi1dgSQHDp2KwYg0L5n27JrupwxqrGFY3uKssX+aOOyB8eDLbIu8Iqc8Y0C04m3Q1z9mGOyg4r3xOQ/GaRbloStDmgD89CJPddDddTL2Sb96XsoKoIG6NPs0rGQQwLSYYygriPWKj1cD+1ja2NzpwIvIluTSVDwuWEdwtzbUSO9QtSCO0gzRC3XOxVa2iXamhtFJGy87PROzuhs6zLV/Y1mQpvIRBtFy8rtfxh3IZLTt1JDlZteCdk9eSnqtSnz+Ewu3nnAlTmnti1CDvaJnM3tUc4qyHgUbjw9CGADpOgX9c3+Cbs1Nc9W7EWIUTr2qDRpkVbNZq2KrVUCvRY4yHMr8oxXLFQ+KXEJZqGMJHEn+L3nVXGMh4CDMGGFrz6lnab724CbHmaM4vVovk7smHljJzfjUhznKZHry0vSnj7KHMgm9OqjK/YMCxJAvp5mO45AfCg7/a3UPJNSGKyK+c82VimWk/mpeaaYyJ2JdqSS8GKw7QyBI867TRKJWWyGRb/xDaxfOCAj8qBZQv9by2cvL+vRnWlioSCwp8PgpYe05+6SyJ5s9XYwG5oMDjKGBlJU+rPwEwl6VqLVhw8OMIW+T6YArYd7jyI79v+N1AL6ji/YSrVmmMhG79ZYPCGp7MJ8152GCkt8xCo3ANLURjFX7x0tOqb71UfHAbioJfNAXIW8qChquAUqk8Xx8hceipW9fqmVf58k7C2UwKm2F0w2hmasq4gctB2WMY30DWD++E86U+WCHyg/T+UulkCUNy6cFVocDzxGM5lZn09BpxQw0NBx9aD7NAlG/1zCV5yt8kYSjxRW0+DVbWKUyLDtPuKM5PpABZh5soXVmT5noew7xHSFPrRf6R8MillNn8xRkwm84s73JDWQbfSVHyP7/u7pHoFtn+G1NA5aQ2gXNSykaXa+QJN22bH9eIRTTm1KUsyzQjMvUun2bmJ4xWQMNv2Uwj6o4MHjfDUv4+Uq4rfsX581HgF2CwotxJIilrcmWMnikWKaskNAxsU8nHH3UshoOCWR1kghm9kVCdLfXJlUyyc1hr8VvnVRQNfJMqta9muAVhkWDKLhTbiyd6pTn0fnFmXZy0VStl+B5pzLAQrnwcHG7v4E/PX0k4F896WFBILKcKRU3jOX/o8xLhZ/zxw8Mqi+UFm8/96a4pkFQBSqhCzyeCZxktJ+e8kFtt6BrYFLVUP1LZz/IpvdTIZCDFjALZ6Izl40/rWQNmnqQ0FhhckGACh4XsLPdl0k1LcXVKRMDW3kHqWEJZK7QvBL2dV3bPhdYvVug0SmLhufGKKTiHZ3FkKtPY5coTJKfwBXy06x0c1Nu4yiKcDoY46/Vx0evi7PISo8lEPiBG0zHeDgYY9/qYTsaIXh7C294Uq/U8uqynxJ315GXXhNioBD6+OniG/7G/JwtEIiQFb6MoN+N3+UNccLYL8oo7l+WDJBZepuchqkP57GMP0pReBvzAgxu7yMIMYRpjGkcSEmbed+L3TxdY19RqkSE8TldpKR0m3K0SG7MpGg0wJBUnByvFWXTelnmFJs08mz9dKbl8myu6/GBl/JDmS3Uu537yHeud1y2MfxtfrW/edhZYyaYwFJ7eM+Mi61z1fzeezLwonMtn3dTderiAzszEkXKZY4ShcoyXqwxl18PmxgbePDvEy1Zj7mWIpRVCXvYR1jw9hwUvOQ4In95V6g7PFmfirURiYW2HAlqBs+5WixijOPNOd9IUXprAS1IEcFDKee0haP0Rnl7zrLB4fd+hz5lfr/P5zXthYay1Ls+iZpY0lh0cTzRWYRigbgYc3XTxz/fvcH5+JmOr5PnYqNTwencf+xsb2GnUsV2roxy4qIicW3iIC5FhkAEXAI5bTbgu5xCpxLGnDJAJdh7pW9fEWn+WMusbcqvkUsJKmbtotlRm5Ub7ZSX51q1iS5biNcNC+YEvXsfYu1yI3G138MevvkbTcxBYgxrCJ+0VN2VJrUCbwLPm4ZgpJxkanoMyPUPlWFnLFeeCAj8GBXR88KzXD9arjPxgxiJDQYEfhwIqv+e1qeCVBDOfefi9NS9dXBQU+JlR4NHS+WeGd4HOf2cKUIzKNx4VpuLJ2EGSpgiTzBityPpiroVLcjeXbucX8t2fmVDWYRKDXnd5uFlmvvV8GsYYT6H3gFoGXNwVFMhRgHyjvMOzhPouV+wOaa5xOhJymiG583lzINZeknepKOVKFdeswoghYw0MKrQqHtfbFssSa4EUiWspoOvAax9+wYnkT64P0BiKm2Y8zxeDFXp/pdGKhGbLrS3cRyrOIMjDwsey7hqLLDefcw7om4IhrWSN/j5AxbOCAg9QQOUqeVd0d+Wy6Dt0EYwGgxG9VDwkL3NrDUv8S4OVODIbXW0oKxkjK6HUH0CzeFxQYC0FlH9V/pY8GlP7YrTC9fEkihHFxmjQmKsaMMzPQ8+LVV+TRh5WvVeUJoiiWLxcUT/ppil8xzV6QQunOP30FPgFGKwoS+bYWoxVHPnwWqib8oybIzy59iMOUUsuRoRDENjfAAAgAElEQVS8Awgy/1uAX67MmK/wNbGMG3PlQC7BUrjLMI3xi4ShWa5ikc1eaXnWen9WzWkKEh+m8MwXX1VCGPBjNpVZlxNHKCUpmtyxDEc+TJhPobCctknTFDmFy3uWIVMGrlGO8v5TH2Z/H2tdHFSIy2+R9AB9chnvuFRrvTseLyWTNvzAKpcCCcdCE9goTTGOQoyjGWLuHp97J1nQcgkIb6zhCVvHPqZA5t6Dqe5i4A4Ehs4olVAplcVARmDMdz9aiLyXn+05Gqs81mDF4sD6aTAeZcuGEIoz6aM8oWnKZLZWSSY/8J68QBuMIDNK85pTwlarg5fNDq53dnG6s4v319c4vrrGRZeBOIB+EuKby3OUvAwbJQ+tzS3hL62XMCulkhhfkWLcZTQbTlGKU2yxrjwvq6eBVVpZ/BTnxdmB75ekPraBdWm98/bed5EbGPnxSjilgEpcD5jSbRHAF+4sDuUDnlRVHIwLJAMoB25eK9PII/zRqepMJq+xWJWSTyqlALWK8TyguOtZgZh+tDWSRtYCYjWf5v/5nQXpXC8aviSdOcFfascaIjKJh5yXMtsHuZOlUi7l4y61Op7JY/RKVAlKsgOE3ZBFCbJZCC8M0WCILYbyybWUta/ypcLkM22b5iM9aIxIWaX5xJgoTxd98MSmmbr430g6eT/acG1Sr8qAFfxXq1u9fxoa7tJ7QOym7gI4bzMpuDh0LI2R4WIywdHVOU4vz5FEofFEttHGbw+e49c7e9iplVB3HdRscVZFGScbJqWdDiZ2IU7etY5xPpvSCe2K/LwLzQVmT7iShlOQP6HMJ8wqdLD9Xa2WUatVhS8yfljHMdyY3quADR+oWp42nGOQYI8s98oCuXyTWI/nO/JOURm9yFlcFRT4cSigPKln1qr8rGl6/nEwKmopKPCZKKCM/ZnAF2ALChQUKCjwS6IA56kyV+U3Hje/BIEJSZFlstAuG024y/+RjaYIZl5uUpnRuH42w3Q2FRfr9Aha9rhRxZONMay3OAoKfCgFlHd5psHKRrOBU88X7738ziXvhSENTnLfbLy5g/G4Lkneza9bUeFq1lu5vumgTC9EsgnwQ7EuyhUUWKYA2ZEev8UTrmxyNJ7kozgR/g2jGBk31txzkK314No470UGR6F4GiIPezacVYkh2WxIIC1TnAsKPJUCKn+5HsZ11EatjlJQEvlKOTqLIszCSOQpn689cozLS/6MDM4wSxOMGRJIBLbxqlLzS8b78R0yfG0dRWJBgXsowCVpLzPz33JA71MusigVuTklD4uO0xhY69xhwX7KtaYC3nH+IJu0qZ+k3iuKkMaJrBvLHJsbJQv5e0+P/PiP7n+7/vj4fFSNKjApiY0bfzvnpWRVqZ2vgVz7scdiRAgkHRZ6VvBL2TjycuFF8s9Yjvd6Znle3z7YRqYuP83DWi3DnPnf6vOH7gmbP774mrUKyr4H7oIXwwZ+cEymshu+7nmoUrjk6lPY2jbFY35vm6GeWe5SNimcjzrbulj3/8/eezbJkSPbgiciUuusLMmqItns7tFXvGdrz963/fe7+2Ftbe3tvTNzZ1qwKUuL1Jmh1o4DnhmZlaVYxSbZRJRlIQLC4ThwIBCAwyElyqxXGz9DXXl7UF53SMx8+OPHnExE+D4iz0OUpKJoMgznljMUt+zAgn5ZvjWOmBrkgCTmoCQyx7t4CXzuSs/RZGZOFkevZTFLVCJlrUao5LHVLUXMKM3o4i1NJ8pZiRmFhmvzXQqgLPDHzopNWeSNAy954XBBF2iVylgrltGqN1FttoCDd+ienSMcTXCZRDjo93DU62K7UUMzVxR65Jo4looFo3HMPRppgjQMEUwjWQilFYmilWU2Hi4m8yIfy90Kg5Z/S0W5/6OtXDq8FIdiPo9CMQ/0uYAdYxoDI370kK8M/pZdYzHF1tPczw46dadKSsWm0Ly4aQ0HKQr5HMoFSqYpG/NXXsTzyj/TmIwin+Z0JdJn4THnjnf6U9aybxP1u+oqFupKjDnhqwkezWfe6pjdTC5EYSVvd8ZxZidBQnONo7FYRGmKEta8tFpqdbPsaZnUZZgWjfnpJboN+vBgl3uueASSOQaJSpjc8cf8+GN7zeb94OxuJaAlviYiwVmKogNhKgqejwY4G/Yxiafw0wTVYhHbjSa+7azjWamAJi172L5fT20jvZg/trUUYkGEbTqKJoILJzX4E6UVy9YSC+JL1pj+g69MWrE288GEriac8buCwVmY9s+5gvTRKmcpP0xGE/jjMcqFiihiUYEqe1FGsnQ0zPRq8zDGkXjZyMqTZqiJnesQ+IgIZJrbR8zFkXYIfAIEMv2r2TDwCXhwWToEHAIOgS8UAY5puWBKS4y0Ckuz6BPfR4wUOmEfy9fE7QXkWEO+KbhRJU1l0Ypm0dMkNnkEHgpigXf+nXk7VRfDIZBBgN9R1mI0fTkE4ExSvVSSo044w0KFFc5NctGU37tyUTgz4wX1VldkN7PJajCZYjgayd4sfhfzmNgKN+PdTEbJOdchcCcEKJKUKc4H54OcWAmiiPNICva/Yy76l0szS+W3EVU5NgorEabhFElC+Q1QyhVkc1PAo+qdHN8GpQu/BQGVIa6h1MrlmaV5yiAX66dRLIv3ZqZ/iRgj8aJr+2Xe8kfZHYdTsWzPuTUKP08JKAcF5D3/V56rNWy6/78tBFR2Of7lr+R54PoXFVYohSKH6fwkCpFReq68GOAZZRVZ91IZDuVYNo4feJ5AOZ9DSY7EZB7u+lwQ+G3Vhiw0cBicIqVFCmsJQaTcdrQLwGtLWHYXIt394bo2QpD546efWB+Qft2TRalIF6bsC4A0lumQPaVh6JijScSTsS3/Ul7e33Bli3pDtJVBpqmbBbRWqYZyrgQkvhy/RJNMvckU56OxWPSQxTaWmYv82d9SWVgeXYRkvf3al+gOWQBXfZrfAueD2dX64ECCe8hr+QIqpbIc+UBrH+MwwsVkgmGSiKUSGRQsycgCj77VGuRAhIOJFOiNxhgMB/B4xEuSiHWEcuDLTh0qCOnFW9YFeckHtC1ipC31PCSBj0kaC81FGc0QUEK+WWzVYzH6dlCTyJFAVGigYKxIp+lXuCoZktTKEPnkj8do0HLElufhWbmC73Z28Xx/D9VqRYSPn8KDyQiX/T76Q2oCGxZYVi50NvJ5FDk5w4XghMcvpehOxjiPUlEAmcmy1fBUmdX8SWcuw4Y2i6A8ryjO3by0sLa8zIMDSh7JQgWdWpHtz1hamKYxulGIyzTF2A4kjawYItL32HJr5gxn2eSDiYvrAPqTMaIoFLqUl1IuQLVQsJKgKeduhkWpVobcs2rnxH7FO+V71p8K4xxve/ZnjuQiRrN61ES38TlLcFvEu4QzU1NxxiJXOjs1x3oL7lSkYout2B0gPKeUtcv34CCcojsdYxgba0daJi0O3SwO6k8//S37Gabsfw1c8Lz/A8lkr+XnbNhnca/1rG5GkY0Y02Rxd9jHaDQUIfJTD9VCEeu1OjYaZVRyxtoNMeYl7yIW2tLT8rN99rkTbTo24xo7SJdEqlxhSFz5n2HtStiyh+an7jzc+NyH1jytuSOFGd1M+fiBsHzRR3+Uab4Xq3IeuRk/UfFxMB3jbDTAWBR3ZpCZtkCCSsC6+ih5zYdMc56yTMwqIuvp7h0CDgGHgENgJQKzzn1lqPN0CDgEHAIOgQcgwC6W3//VAKgVi8hzw5i1NtGdTtHloqmdhOf3x00Xx8Oy2IQUo9goDFBhhRoEpSCPWqFoFFZuIuLCHAJ3RICyy/krfst1alWRLfpxewqPPKf89uNUZHL1R5n5pKNc88d5K27OGvEbezTCYDCQxVJucOFGvEalNLMke0cWXTSHwCIC7CQzc2A6/1qlHOd5XJovxzNTFnthiPPpVDZPUi7pd9NF0kaG05mFq2gSgptxOOdRLxRQCXLIfQmTqTcV1IV9Fgho/8tj1dvFiihEcUaOy/3sf3ucIw7N+s4V2WViXtal7Mr8Jtd1ODfJUwCGQ6Qxe3OjcNUsV1DIKKwoCUvJOQ6BeyFA+eE8Oa2msf+tFfIoBIHsyKQ8jpIY59OJyCP739mCxkIupCLbYWdjCB4pyI2lw/EEURwJPR4x3yqXUKGFFSv0Tn4XgPxkD7pW8skYeLSMaVWAix+yKM7BrdHu/hD6SmbFWsqt5OwYZxZPGxo/NHnEhkeNWd8XZRoqq7DB8AXBdKt+JGSa2bwN8pnaZT4HTLa88FiVRhlgmQdlRhud0tNnDb/JVZrMhTvC2z4Xkcrw0wBp4mMaxrgYDHHc70t59IOZ4y2mMUorZrGVzxz8ZX/sJHRwpnndxM9Dwygrv0Y+N/Gp+NOVjzkPWKtUsbWxKSbbqG09nIY46HZxPhhJZ0xcbU1nSJuS8D9/MhCmmSt25ABOLs9xcX6GNIkQpDHKPIKCR70UAjneI8sHaXNQU6/W4Xvkisz5SAMPg8lYjqcgD/xdhx/9+dLgi4DHWRwNh+hzQEMJ5cq6LAjyQXPOFCXjxfjLeTE4W37es21xoZ4vMlqQ2ADwTWcH9RoVVqhTRbN1kTnuJuJ+JHMxLbXl28WyKArlfE8UVqIkxsHpKV4fn83iMl9lTZSwbJ2RxowfJWzjMr70JRn/TEnvdUtarA22E7a/zWoZ662WWIPxAlrkAS4mQ/xy8B4Dnqe6gvqyQpjiy4krfvi/m05EqYeKUtSSZnukRYh6mQpUhiDTXClOxkMV8iT2h3SgK/j+GF4sjtad6ZdtLlRy9H0kVNKyZc0U706sSPxHLLuxbmEVvSwz5D/7o2xQ+UraQKUskzZIjcJKbzzEab8rSljsE/R9o4WRqiVd/pYbXCYfE98ysJBYHx7uitWwTBZ8zipbCa8Pz+bhFDI8ZokpfOxl2P/1BwOMxxN55/M8+Gq+gGaxhDqPGrOWmyiHvLRbtI9Sv8yGin9HF2foj/qisGLizpVfNf5DXMVV3dW0TKFvjrOYknHvGj8Lqd5TrnlcUr1YFPOMPq2PcYJz2Mf781P0uatJxn5GfjnOEBnSxkt2VEfStnkqaV7hixlqpotFcE8OAYeAQ8Ah4BBwCDgEHAIOgU+CAL/Bi1zM5PxbvSq7TDnBwG+Ns+EA5yPOEZlF/+zwdxWzDOe34FA2qUwwGk8Qh7F8/9VprbZaQ8kPQAPrdx2/r8rH+TkEiABliN9yVQ/YyRfM/IQ94pwWfkR+uWhk4aJ8xjQBZC+90880BvEQoQGAy+EIw8EQSRzLPDPnqzqNhuSn6Z3rELgXAlmBy8wb8HB0Wvaul0soFLhlMQFyPi7HY1n74Hz3lQV/m7GS1P7UKAxyk+AE/f4AYuEqjGXz5Fqlgmohj3zGQtG9+HeRHQIZBChzZvwAdLyCbHblHD+nqXmUyml/IOtMPB6Q8sv+d2EMYYV21v+KwmuKYWrklwor3DxLi0DVUgnbax2xUMFkKu8ZdtytQ+DOCIjs2j6Ya30NKpRUKiiXivB9rtMk6I6HeHdxjkFqlV6vUDeSqPKrwVyn5Ji5Oxia/jeJRRFmo1Y3a4Ku/1WoPgtX10o+C2YezASPP0iMIoJYG+Fi9dI6XLYjpvDqs8ajnywcWWRkMeSejJEGr+WOmudhyeKozXcchxjSHNfSWsnK9NaTNLnQVcjlxCRokMsZLckoxDCcYhLRQsS83JaVR3Gk47A7+RsA1usNNBtNeF6A1A9k0Pb69BQnUSw7PRRTk3lmW3OGGy0r3cX4S6Bk0ny8W+VmnsNVn3nYY95x6MuFuVaxgE6jiXyOXbOPaZLgZDDEYbeLyzASjHRAQd6UP7rEj2Ehj3ah1jeVRcIQZ5fnmIyHCJCiks9jo9HA9lobhcBYKFE5pUs+ZOG7VDbHinBQI5MbCS7HQ/Sm5tiZbN5ZHMgDB+LkYYJULAMcnp+JhZcFCysZa0Oz9JYRKYOlQ3r6y+apPLOZ8kOYfFP5hBM6VOig0k2xUEAub9oHG7Uoi4lil8mRAzge+bMOYKPRRK1SETOPXi7A+/Mz/P31K5zCDMr4YmP+qy4O+nichzZ4xmMZpJ6oAKGWnlYlvoeflpPtv+5xp0oDjXpD+oHE99CfTvHD2zcyccWBJ3lmXZA1cylqpixST/aFfQng5ds36A9oD4eLvilqpTLWG02sNWqz3SqkQMyzWBhFwayPze4zdlgO/ohpqZCXgQ9XumlhJUoSOV6JAxnWIUu2qnSr/D5qkSXDxVy1PmayQes7lQrWmg3UajV5mfGYp9N+H29PT3ARJ7O+WV/+QpGEeCkw9plhlBO+o4wcaUQbX9NkHj/kdk7VMsBG84VdxIo/TqZJ2yf/vidKeoJxwuONeA5nKnJH/LOllDhWn49YU1GF/Tgnlal0OKDSH/sxKrwyr0dUiroNaqOINudWeL0t0QPC+dbhjxhxV16rXMbm+rr0dXGcYDCd4vXZCQ4uL9BLUrFWl5Vd0bXMACx4Zd4lytrHLofm41yHwG0IzFvXbTFduEPg80VA+9qbOXQ97834uFCHgEPAITBHgMNZzs3wuG0qlZQ5v5HLwQtyOB+OcMqNQWE8swo7/+6f02CvS3+zocjMz5wP+nKkim93RNOiaqdWQ6taATfxuMsh8FAEKEWco1CFq/VmC+VKRb7yaIn0sHuJ435Pvnk530A5lc1tmYxVdnXeipvxDsWC9EiOO6f8cpNVo8x5q/p8I1mGhrt1CNwZAQqc/an8sv/l5shWrYp6tYp8IS+b285HQxz2+7JBlPJMGeUc0PLFvpf++uumwGmvi16vZyxUJKlYk92s12VzE4+Ac5dD4DEQMOMHD1y7W6s1UK3W4QWBHAl4MR7hZDCYzfNmRF+agORvrblJ/2vXF05lbvJyFifn+aIMs91eQ9EzNvofg3dH42tHwMwFc52Pa3a1YgGNShX5fF7W1y6HQ7w6PcFlGIsSFce3V8e/i9ZVuKbRS4GTXh/nlxcIwynSOJYN8J1aRay4MD93fT4IsA/7wi/7RqfDxWjujvc9RL4nnS93OfNH4cz+sv7ZcAr6bKFXaN4fHk1Gl9973KVAwc/5OTnqhS8D8tmfhOhOJ5jCHD3CBiZh2SytB5VoWFlm0A8U/QB5nyZBjULBiMeBTEYYJkYBhi8VHTTp4EjpZ19G2axuutcyyQKv1XLbbTews9EBl89olaA7DfHy/AL/dXiMg0kMDsa44Bby2CNqwlmLGuRD+WOdMA4/PrROFP+b+HncMEXkcanelRqx5cC0DA9NADvttVlnPE1TnI5HeH1xhve9rmBKnLRuiWWsZ7JZDIlnFykOUuCnt69xcXmGJJ5KHp1yBU9aLWw2GtIxZzsAkS8qQ3EnRM4XpSg/CJAGPpJcgMOLSxx2e2LCkHWkckVX6zRbnxcp8D4FDs7PMBqNjLkRKwNcXFRFDpVL+pEWabCMNG+rbVNlYjlPfZbwzJl0whOV1+IUXkIrLAGKQU5+WmbKMjFf84DdtTVsdtZRKBSBfA69eIpXvXP85/sjHCVmYkdw56Ato4Ai+NNSkm/6DZVlyjMXmlkW8vIYF+WEPItFGXjYrDewt7WDQo415ouy2rvzc/x8forD2Ly4mb/KCnnI1hO1o+WDifU0HOLw+Bij4RBelKAQA/ubW9hZ74hFHubNa7ml2O5pafGcsak4qKE28WfkkEP2zeyXyyVzHqKIJo+z8j30xmN0J+HC5J+WXd1scUhPMPqViqz5SZ5S+0Y2KB9Nz8NWs421RtMs8HueKDH9cHCAl+fnOEtTsahDuZi1PRbGEmW7pMyyTak8U1Z4T3maFXEVEFlQ7nivZTCuZULeazyeidbIzDuOvC7we0f6HyWaZVNoawHmEAqUrAtRLA04AiCmCcZJiEESilY3lfq0bWq7JObsZwYpwM/AozTFL6MRji/OMZ5OZdxABVHZ90jLIo9QuAz7V6lZBZpswGPkmaW3fK/80GVfR+W8zXINz5/so1yqAn4gRwG9G/Tx49kZXncH0o/pGIIYSv9v5YX3Ks/Elv0yd+bxp2nYp5sGvMyNe3YIfEEIfOzG+QVB4Vh1CDgEHAIOAYfAF4mADoTt0JTzFjph36xU0aAVlFIZCHLoTSeyw58bE/RYoFVDAf3OoDI8t6YcJxG4oajf78LzEuT8FPVSAe1qWRTF+Q3jLofAByGgc31WfmnZUhf8tzsdNOu0M8rNbTFO+n0zv2ktk2a/81WO6fI7zhw1bubkXh8do9sfiKUAPwGqxRI69SrWqhXZ2JlpQh9UBJfoK0ZA5wSsEM37Xw/tcgXteg2lYhG0cM0NNMeDPo77Q5lTkPnoJehm8mstWg+Q4jCe4rB7jt6gDy/1kPd9NIpFbDbqqBV4JIW7HAKPgwDlV9YOZLNrE+3mGnw/QJSkuBiNcdDr4SI1Gxp1/owyyx/7Yx07ULY5D8w5yjenZzg5v5ANu36copLLY61Sw3q9JhuIda3lcUrgqHzNCGj/SytX9XwJ7UYDpWIJXKMcRlMcdC9wSOW/1Fg3z65vqPxSrunPMQT73xOuk3YvcNnrIo5COXGCp09wfZSK2xyzuGs1Ato3cPAla3109aSb1Uke7PsFvA8JCy8jOfyvPjbAOtx5HMiCTux5mKQpeAiJz0HALMY8xTIN0s3++KFGJYL7frApDebEPPgsDY2D9SAnJrM4MPGDPHqjMc76AwxiYELWrVIK0zKdXMqo5YX88IzDgh8IPS5cUVmEu+jPBn2xgrHJ8w9FjcS8ZJSnGU2lfQ9X0zJ/WrKopR52KiXs72zhp8MDRDzHLopx0Ovjb2/eIZ94SDfWsVEKxAwk0xEH/lgkdiDsPPjjwp0O8KJ4imLqoerlUP81ewsFKYOJQp/xuvb2PnGXiTBrmYjwgCY87NSr2FrryLmsl5OJnE38+uwMzUIerWIeW9U6amLpZi6zxFMGEjIRkeI4BX48PsDP716jP+zLZEQp8LHTbGK31UKrWBTZ1nolT1o/lC/ufaDJLVrwiWMKZg4H5+d4XT3Bt2sd1HwPJbvgz7Skoy8CDmZEYQbAP96/x8nFJSbTqSg1ZPNjOungMgogWgYuJI7CKYIgJ+fd8kOXVlMoR6ShdIi7vISsVQOaCWXaXjIV5Yt4GkmbK/o5lPNFlPLzcrO8tMbCNrRbqeB4cxvvLi4xSC4QIcZZNML/evkj8pTD9Q1jLcGWmWnJg74I1eVkkVESSREmqSh7VHnu3gf0JQtywoJmyk8tUyrafL/7DKcnpxiHEcIkwcVoiH8cvEMxn0N+ewdr1D7IHIFBfMmrvrDPUuD1eICf3r7BZbeLcDxFPklRL5bw3e4+ttZa8uEvdWUZsqwssJd9MPMUjMXf53mx7rQvLSNFLufLWSKiHOEB5/0eji4usL+1uXBylcpdtlT0409lYlWcbPz73F+lZU00p8bVcOZNMc2lxmQe2/lJex2XZxcYTCdiGemXoyNUSiVRmgxYr3yPWNmgTPDSWmNb1vbMRX5amwmmMUqJh2rgo5RXPkzZM3NTs/eeJXlPhyXSH1UhjZ0NbV8sp/KoZVf3nhk9TnTJXOV8zgn5lD69WEA+z7sUCU0YT8c4H/ZxGacoB0aRlYxQFok3y8n3Ia1jsW3+Ek3w119+xHn3EjyqzPNJy1iLEsFMiZC56ConC4UT61KrQzXtQvzMgwm/LVYmwQNvNSe6xJDWpDjW2PBSfLO7i1fnPYzGY4TjPs7CMX46PUHRL6Lkl7DZyImVMqbR9HT5Iy5ZeeZ7gh/qtHjDvrkW+DKZyjwfKMAPRMAl/xoRUBm9d9k1IV13OQQ+AwRWvoM+A74cCw6BaxGg0Lo+9Fp4XMCnR4DfCJyT5PxYMxeg3Wzi+PIS08EIoyjGUbeLN6en2OFifaEw+27Pci7zbVZR+zIFXp2c4Egs4PbFGme5EKBdKaFdLrkF/yxw7v7BCJj5FmNl5cn6On656OHo9AxRmuKcJv0vL/DucoByrQo/Z+btdSxBlz/5huMxVtzZHwNvj47kuHF+OPN4gPVWUyxIc5OD+VJ+MNuOwNeIgH5XzcqeIAAt+AB5zrEBYgm9Vq1h2h9iMo1wOhji58NDdAr7KNJqc2Y8oXLM/ndh7vX8BEeX5xhPxrJWVSmUsFatYqNWFUsCMh8x48HdOAQ+HAGZTxMrbR7W6y2sr63jzdkpEni4HE/w9uICb06OUVlvI+8VZv2nyi5zZv9LC0I8+uoEwJujY5xddmVtx08SUULcbDZlkxn7+0wT+HDGXcqvHAEjgZRfrnGw/+WxbJ1mC9VKFSEtA4UhzscjvDw6xFqhhFq9Iv0v5S8rg7rezM233FD/rneJ9xenGIxHcjoLT6BYq1ex2ayjWsjJvPxXDv6txWftyDouY35kq+8c031xl3agApQMY40Pl25i+BjSKkUSIxfF6AY+EIU87cGemMmBL3dus9hzUeYRGBInSZGLE5R9X0yyVQv+gsKLNAB7uo0Ax3v9ZZCUeHYhigozXBgvi4WHADw7jhZWuuMxXp9d4KfTU1Q2O4hSTxqIvFisQoKso2Y41UXJcuDLGYdCKwgwjSIxqfiPgwO0ajUEfmGmgEB6rGim5T1/XBhTHAUFfVDXQqPlsI/CH19ELE/bA/bbbXyz+wSv37yRI0nGSYJXx4eIxmNcDAf43dM9bJbzKFkrM8ybWegCZIQUPQBnvQGO379D9+IM7WIJL9a38Oe9nUwNZcB94C2XQE19m8JKdViMtZzMInu/kOUSRhqW9Z7TN0uuJk8jKxo/mwcx5VVlR+wBL7a20O91Mez1ME1iHF+e46/TESbjAf7l+99ju1IFFSHIIzEVpQ1RWknxJknw//3yEn/9+SeMwzHSKJSzMFulEl7QakarLWZll8tHOvpRyWMY2qUKTnJ5TIa0oOOhOxqBVhoq+RJ+/80ztANz/I5lXQYzXAjkAvdPwxH+89Vr/PD2rWg/JjxpmfJHkGSRNV1QBBBvWw7KAyPW4NIAACAASURBVM+j++Hnl2Itqd1qYXtjAzzXk3JEHlWOmI6yxIEU8+ZL6DiN8de//x3nJ2fANJTjlaq5HGqFIkq5nEmbGgUxLm6SVhvAXrOJ950OXtJEbhTK2Y5vT48xGQ5xvLuHPz//Bnul4mxhk/gxb2JPl9cFeegPcHp6gsPDA2xVa3ixuYFvN7ckXOvZxL7nf/YzVmmFfUrLA57XqnjTWceIik39LiZxjJ8P3iGcTsTvX589Rz31ZjyTV/6ogMAJq7+fHePvr17h9cEhwiiGHyeo5wt41l7DbrMF7oEhz4o5OVY5V1d6VHaCVr1gFoMal3bx+C4lVXnUtiOu0LyhLd6F8Io4Kuuy44f9I89Ri2KRzShNcHB2jp9KVexvbKDum0kW9qFMZ6xmGUyIiyk5M/HkXWDe3sb8hYVlBQcrvLJaH4aavLOIw6zNzEYG83yJG3/khfJcTT1sIsWz9XUcHx1iehFhRKWVMMJff/4Z3W4PF7v7+Pfneyinpg2zbFoObU+0/EULPCfdCxyfnSI672KnUsd320+w0ayiSB0fKps9gqUPrfsVwrUCqI/jJThaRSCV4Vm/vSpLYXreCrQMZlDtoezRvGtBrDqlcSKV1B0NZVK5XT9EYWcbsX3ns+7kY9C2zRO2zaP3+Mfb13h3ciLKb1TIJd48Eoc9P00ga8vQvNUlu7zXtiTykyamsmxZluNqETWdYCADUKMUQyz0UlnJ0tCwm1wT37wTSV/wXUpg4rCEqVH6oQl0q7TybHMTo0EPR8MeIi/FwdkZwv4UlxcD/P7FU+yv19EwgztTfkubNIkvlZjP4ymODg5xfnoOP4rxtN3CH3f30C6yN3CXQ+DzRGBlW1vp+Xny77j6ihCYvypMoWfPFFj9Ze++ImxcUT8/BGw/quMaFVe1EqnPNzLu+uIb4XGBD0OAo31+p3GUym//zVoDh+UKzlMP0zTG0fk5/hbHaJfLSHd20PE9OSpTe1t+9/OoYDliNE3xlhYK37xGr9dFGkXIBT4222vYajZllz/zciL9sDpzqecI8BvXKFwBGzyGu17DL/kcxvkcRnGEt+dn+OubV6h+8x22goLMUWbnVzhFw4WmPlK8D1P8588/4uT0GOF4hCCJkU+A/fV12R3NdPw5+Z3j7+7uicCS8PCRfSJ/YvW1VhVZG5ydYxSnuBwN8P/+13+hxg1Ku3vYDGgdeJ4n59XY/3Kx/zQF3o77ePnuLS4uL+UcaS+Ksd5ew3a7hUbR7O7PJJ8TcncOgQ9AQMYPovAKdAKInBVzAaZBIBveuebyH7/8gnLeh9/akLUozmXy0jleY6HYWO//v//2N7w/OsKUylZxhFwMbNfreNJuyzw458md/H5ARbkkKxGgLPGdzk22VBjcKFOxpIlpr4c4DDFNUvzHjz+Aa32VynfYCObrXkqQm8k5huCG0LfhBL8cHuD49FTSc61mrV6XNR+OoUt+IPlpWud+egT47v2iLp04UJeLGjSsYiYWAoRxipPBCP/nP/+Jcj4vShqeLNTYxUR2vj4XUkmBP2PeQRZOEh4fkqAcRditN/Dt5ja+2dmeacqyw+dCsW/T0EniGGliFoLmPFlIU7OASIskldTDbruNg0EPF/0+eheXiL0cDgdD/F8//Ih355dYbzRRLRZll3w66iMIx2JV4/vdPTk3kVTZYFlpTc+XF856u4XT4xNMqZwThvjPN28xCCNs8ozQYkmssPhhBH8yRTAN8f3+PtaKtPQyX2QnFDM4pBBUJvBMuewirQoJOw3mz4UzLoxueSn+bW8P3miE10mE3nCIURLh1eUZzqdj/HR5ilqpiGqpiHKxKJYfElpUiWNMwhDjaYjRdIrxcIgpzTKNhnjR2cB2a2O2PPYYL71s3XhJbLXvUlYg0ti3dWjUDqxUaJHv5SqvaRILbebFc9HSKJajoQTnFRR16ZGy0kw9PC8XMdzclI+x1ydHiKMUp5MRJseHOJxM0arWUS9XUCqVkAsCUZiQY6H6ffA8zdPuJXqjIXyeyZYmWK9U8cfdfTxb30AzyEkdrmBDBhiUcVpw+Ze9Z4imU/xzPJY6DZMY74cDjF+9xMtBF2v1Gqrlspzjyd3/k4h1ORFtxbPLHs66PYxHE1TbDXj5PEKGd7uCC3FnW5MMM4yo9u4F85pMxFQoTs9Qff8ejVoVlVIZlWIJ1EQvlArS7qlgMEmNdZGL4RBnvT6Oz84RTaYoBwE65TK+f7KLnXYb5ZxR8lFFCv2orcHDXgBEe7uI+z28PTvDYDzGJI1xMOxj+PY13vS6qBVKwkO5UEQhn0eCBFEaY0oFl+kUw/EEk9FItD4n/R68nR1sR23ESSKWYjJFvf+tFS7KJxUTuIjLfuxfnz+V40Z+fBNh2OtinMR4y/p/+RN+PjtHo1pFjWdec0E28KW99cYjUZg7ubxEt99HFIYI4hS1IIfnax38j+++w1YpL/0O5WEm15l7lVmPtlhTKnvwcCruQzAX+dR2d1thlT5d9tfSZ1M+uNCfmGeNI7SU8ILnbbnMw5lM+/OGKIjtiEWjw8NDJH4OvTDEfx0eoh+G2N5YR71SQtH34IWh/Br5AnYaTayXSlJGshNTGtNElLJo2Utw4EifHZ7FbcYuvWYPc754x15Ii+fzSXCIgSgSK2Kky3DTW80nZtgvaxgnNJ9Wyujv7yHxUhwmsQzouGBPOe6/+hkvL85QygegCbxSsSBWv2h1gn0z2zq1jkfjESaTMSaTCWrTGLl1D3txJFr2VFqUy1pI0uKoq8F3dZkupQxRoU3OP2VbNRoxLBfbKl3+Hvti3nynsX8OeJY7339UDvPNveVknu3K+qPFjhQ8x5UKf1Qr2Vtbx+FgjJNuH5N+H5MkwUHvEuMf/on3F5dYazTkvRh4KaZxjNE0tJbXujjtXaI/HElF7z3Zk51oPOt4wGO7KFNxgtTKFhljGVQmpDz0i2MgjoCE6hpWakQJZV6U7B3TySXvL7bredub0dQ4d3Q1HaMb2MilHmRHuzOG61netizEXMYacnSbUZD9vrOGcNBFMh7gctRHGCbyXhydHeHdtId6tYR6pYxyuYhCIS8ZRlGMMIwwCaditWs8GWHc7SPhe7RYEgVftTxFHrI7o+5YRBfNIfBgBLLthMTYVlKZKeLRhuxNKJue7AQxRjizLWYp+xuClmK6R4fAoyFAmdVrJs98R+mMpyiEBmL+nO/bj/Eu1/yd6xC4DwJ2dCSjEel7beJENlhwcMgFKB1h3Yeyi+sQeDgC/P6hXPLbn1YHd8tl9NY3cHl2jpNeD5NpiINBH//HTz+j5/n4bmcL63bDCftibg4zyiqQY4P/+e4tzroXiLihKU1R83zsNVvYbjTA71v93no4546CQ8C86zmXxB6UVi33Ww2c7mzhH/+8ROR5uJhO8I+jAyRBgO/3nmK7VpJNecSO411+wXKT1eswxD/fvMYvB28wnQ4QJKFYK90oVfDt+jo2qjUnu07gHhkBWfURuaJlcWP1NYdv1jo4PzpGFMeYhhEuwgn+n1e/YOh5+MPeHtbtvBWZodzT+jct51JZ8B+vfwHnyafjCbw4QS2Xw3azge1WE41Swa41PXIxHLmvEwGZ1zTrlzz+ug5gp1HHd3u7+PnnlxgMxujHMV6enSP3poQBAuy12qgwnWwdS2Wjay8F3scx/vn2DX45PsRoMgLSEAXE2KnX8bzTwlajLoqJ/LabfQN+nai7Uj8KApQiM7PAMSnHAUV4WEeK321tY3TZlfUJriN3J1P8x5vXcsrBn7/9Dmuy2djIISmoZZXDKMRfX73CAU8nGE0Q0GpLroDdRhNPO+toFsti4Yr5MXd3fR4IcD3gi7t0MsGIMLUtEjMflnpIPB+DKMbg4sJMkqnAcfWJP15+bH5cnRJ/mRmWhTIuDhYnE4zDCVqNOvZmTcUIrggwJ+D44wIm6VmFD+2gJQ+SToAgMDsimM1GDtjrrOO038NoOMYUHnpJiuHZOU5HYzSqF6gWSgiSFMnwAsVojCfNOrZ3d+X4Bg72mT81zGgSiQPz3c0NOfokTM0RJCejEYbvD/HLRVfO98rzGKJJiGA0RnEaor2+gVqxhiKLMMPGTCjKTn7x4+SMUY9cbqx8ptCQjwrPwuPCbLWCeH8PuUKA16cnuOz2MIy54NnHcTiE7/soFAoo5s3xCJy7jOIIIbXiplMksigdI4hC5KIIG2mKqR9IF7Wcv2B7j38qK0xCWlJHs0W4dL4AmnLxj4tn9lpOeAMjmoZRZj/JgyCr4goX/syC6DIpTcOcedQLT+DZhodwfV0UESZegsvuBSYh5XKK05ND5M8vpH6LGYUVKk1wQTNOYiS2LLUgj51qFd9ubOIvu0+xSYWPzNEyWly65IP4qJWG5wUfg61ddPtDvDk/RZhO0U8SDEd9HB2MUbkooVQqIlfMS55USJlOxxiNhkhDKugEqNaq2NvfR+L7uLw4x/TiAgkXpe2CaBYL4siXEU0mDoNArCMdcxGXC7SDHvKXeRQLJZTyZZQLZRRKeWn7ojCSUlmqj/FojHASIeGRG36A9VoV33Y6+HZ7S+7ZdrSs6rLMxGST1ibKZUyePkO+UpcdHxfnpxgnU0wmQ5ydTqXRiCxbhRX5kE4oy1OR5ZgLxFQQC0Pk41isPfFjXLsZk/sH/M8ARZzYF/Cjv5B6iMpVTJ7uI/WBX96+wWA6Qi+O0O/3cTAcyzmrPN6pWCiIpRwq1ozHY0zDKaIwAuIUPDKpXa3gaaOJP29t4Q8bHaFPeaQ+CgVD5Zyu/qQkXgzPs9YSRDnQLK5lWL69wFZZgGnY8rWfpQKAKDbJpLGRUSFGBhhZ3dtzWIjBOuelsv79xoaYlqX1EfZdVCw4Hg9xfjDB28lQjsfi7iB/MkEuCvGk3hQFj2aRNn+M1RqyQrpiRUiUH81XKsM1P5utcVbwTqjpzYvpsoqUVOLxLb5cyGRcjUf6xCygjgEf2C/TGsfWtvQnNBHNHXiDaSgfJoNBD+/6XeSohZzPSf/s59iOU0RxgiiJMBmPkVCxzNZBx8+JhYqYsrBUIOV5ydtyeDfH0FCrGxkrHHzV8r3D/pOgPOKl5LSOWHdz5RRa4qJmJ3mZX7KILHWT9TXh9BEFLyvPGxwEr2/hqD/EQRQhjKaiDNWbnON0MkX1vIJyiadyGkUhHu01Hk9ABU6+j3hG59ZGB7979g36oxFesk8Z9JByu5kocjGlkZU5h+aZmEn7EZmx9ch7K2FXuZ+XgXXOA5lkYMXyM51VzGUspr0ufZYPvZ/HtwOjNEaaRlYhZo5vtizkn+noshqoyPk0nyLd3hGF259PjmTCZzydYpRMcHoxhN8F8oUcymIWPS8L/tE0lP45nIZg/8x3I5V4ibpfKGDs+eDbinkbGVSunesQ+MQIWKEUxTQrnAnHqlZW6S60w4WHT8y7y/7rQSAjiFZMZ323gCDfPubNamz2OUH9eoTj8y8pZVZHRrzXn9nJw07WymtG2df4MKaT5c+/hr9wDu23D+feKHFUiN/0gPFaB6fbOxh5nsz90IrmiJvh3r7F+XSCLVGIL8smu2mS4DKe4HjUw/uTYxydnmA0HSNIEjQKRTxttvBNZwOb1frMusUXjppj/3NBwFo0lgUHu9nxSbGIwc4mTk+PcDoaYRRGsjlscvgWl2mCnbZZOMoVc6IoOE4inIVTOcbq+OQYvWFX5idKXiq7rf9tdxfPWi1wAxIXoLTL/lwgcHx82QjwLU/55fxOxFPiadW71cLJ5iYmPEac1tCnCd50LxHSWnyaihUszr3mctxUmuByGuGkP5S5uMPDE4wmU5l/rfgB9tY6eLbRwVajJv27zn982ag57j85ArPBrLFwxccKPHQA/H7vCQb9Pt755xhNQpxOQ6THp+gnHg7HU3B+u1gsyvEMPMWB/S838747PkZ3MkKUhOBmu2Ypjz8+2cLzdgutnH/thuhPjoVj4MtEgBPAdt2S6xxcl+Km3G/KVZxx7SYMMbo4RxhFeN+/xOQdMPQ9bFQbqJbKyNPqFU/zSBOcjkc4vLwU60D94dCsFQY57LdaeNFZxxMajnBfdZ+lnMj48bPk7A5M5cHjDBLkJhFyYYRYJnL5mqflBrucZ3coygobhZ4XFVYk3E420LFHTzC1H0UI4mSmmEE/WiTJpTxXM0UupGJFKMeVUPGjIFqIZiDDuHrpgJkNjIOcJjzs1yrob2xieNHF2ZC71ydIohCDaIJR7xJ+kspif246RN1PUUtjxNwhncvPFj1ZCvPCCfD9+jaGZ11gGqM/pv5YivGQu7l7ZuGNvE0jFMMYDc8XqxNMT964AMgF23wYIT8NpVxBHKPIXeJJjIJndjhredS1KBqlFVko9fCXTgctaga/eY2///ATeuMJQipNRDwKJhbrE2MufOqEjxDRCUwzECx5AUp5H7V8AaXAaDRrnuYzXXOe+97njnXD8hbjGDkpbyyLW1xy5rloXNxjnFkuVjyu5DGLsBhCb6lr5pGkKCYJ8mGMOIxRSFIEtLKSmDwWU86fmD9NvlIDdi8XIL+1jXw+j//6+UccU3lClAwShOEY0WiCPi7mH2bClyfloLwWghx2ajX8t2+/w59297DueaB2OHnMyuk8d7swbF8IrJ0XrRrGe/sYDftiwYeTHonnIRwNcTkcoss85WeO+PFFCSxF0aMCRBW720/w+6ffoB9FeDme4iJKEEcxCmxfGSUEYd1+ENDKTDVNUfU8OZqLCjy04BKOQ0TjCUYsdcrlVDPFKNaSfCoNJDIxw8Ow/MTDZrWC7zY28K/PnuJJoyFKKZqPsi1N3+ZbliOLPPxbZw3ttTX8/d0R/levixF5ttY+KL7haITpcGSK7XMdNwYXkWiNgVYPPJrXjWLUggBV3xcrL7S68FgXeSc1dt5USmilHv5QbaDxuz/Kh86Pb1+jR8sMxC0KxdzfZMBTf1NZsOWCO8/7zecKolSTS4BWsSjHYvzl6VM8q5TEwo7QV4AyEwDMn97kgf1aMUqkPrnLIB/6UvYclU48szRxU7m1HkwfafrzUpKixLYTRZa/VCYgmB/jL1xXPBZCb3xgUpaRg589DxhubePs+FiU7iZUoqOEJQnOjo6Qsg+OQwRhiKofoLIZYdLqwGuvSR0YLDwU0lT4DqZTwSHv+9LPsnwrWV3qYxiHP4MHBNdibNoMd9kX00SU+jjJSOUK1v8CLvbsZrYhNkXuyC9tbqNTa+JvL3/B6+MjDKMRYpHpGOE0QTgaY8D43EEqqhPm/UBrMTny7xnrZDU/QDUXoBQEokGv5VGe9flG0FcEkn/+WBfFKDb1bt9HhTgWTBmm79MVJB7sRbzZ7zL/AvOehnKcWJB4tt9m36IXS6oNY7HUtAxDH/LL4QaPp3lWq2K6v4e035UdjWO+8+MUI1pD6nWNXNhFaOZAGgV5Fxaw2VzDH7/9XnajnZTL6J8e42QyMeOTJELeNwpSy9iQV77rSinbUooCrYywfSbsd42MLXJuyqY4lDgOiNkGY8QcD0Xs12ithZZRTH0pGndxdbxRkHbN9+/UWH0LI+T4brTvReoxsqvU8iiP0k49YI3Hm1WLaH/zHK1aHX/7+Wcc8r0Yc/9oIpYoonGEQTi1SszWCo1UF8cfpm0VUw/VIIeGn0PZ86W9MS/N7y5lcnEcAo+JQFb2eM+2KH2vKIzRohIt9UUzBU6K9Ope6DG5crQcAndAICO8cqvjD5HjRNQBObrgbj26+i7lKyVHQXeXQ+ATIkCZXf5RLAN+K/E7ld8D9icK3LOe9xMy7bL+ehCw/SsdGaPbb4udfIA/7e9hMBnh7WSCQRjK5qGXr1/hzeuXoMn/RqOFQq4gVmDP+peIOFMi3xvcDJKC6iy7rQZ4fPC329to0qqkGwt/PbL1a5TUyi9ll7cVQOYjo2YHvW9e4D9evcLJ+ZlY+j29uMDF+SX+7udQyhVQrpYRpzGGkxEGkzFibhQVpZQEhSRGM1cwVoH/8Ee0PLNYarP7NUrm8viKEFC54rwnj0tP/QB/frqPMa0SjyfoT6ayGffdwXscvn8nfXW93kCpzFlGD2cXl+DcIq22cU7RQyLH3G/UqvjXp0/x/dYW1uyx9ZrXVwSvK+rHQICCZCcKeMufHiv4rFjHcP8p4sTD24NDWWs8617KMVX/+PEHsf5crpTh0TL7eIThdApZA0r53eYhF0eo5wLst9v492+/xU6pIWsCH6MYjuZXjIDtDOlwLphz2zy1ZMMDfr/9BMMwRI8nOniezFefnJ7Kke95zqOXubG+BC7PXQ4GEpfHY3Kene2i6PlYL5bxhyd7+HZjC+08NQvc9TkiwLr/oi4KEj+mZEGGC0zTGLUYaAQBhlGCCBwE2F28LJkorKjL1GbHtNk5Y3txWcAxO5Z5fAsX5hq5/Gwhg2SYkoMUDpDrvodmLsAoTlDhLmikErYg5DYrpiWvBJq7Ira5oLi5gVapjL+/eo13R0foD7rGSgwnpLmL3k9RzPlyjmGrXAONc+pAXyZRrEWIDSrsFMuo//EvoHnPn968wenZiZj+lEV82YHNxp2iVsxhg7S4wKUfvXaxtpomopVeI2xyHAwXcwLZgcz8eMnGbCa0F+MxjB0Hi8pF8yDIof70G+xUGnh1eISji3P0x0MMp2NZ8GdV0JqKWdSjBQBPLAIUgzya5Qq2Wg3sdtbwvLOO/TqHg4a2yZI5LiCsrNzZJb98UXMxrpKkqMQpclGCWtFHJQiQz54FwKxYXisit2WivIqiSGoUiuqeLyYtqe1P02pFKjtZpZib6FHOuNjJ+iBW5U4HO5Uq3p2d4t3ZCY6OTzEcTTANQzmSivIuC9dcvPY8OSqIR01sd9bx3c4Odut1tMBFUFN+4nATkoKTnXDe5OLp9jq2Wv8TP71/i9eHBzg6PwMt+sQ8kkKUTqyySkpFlQCteg2765vY39jCk86G7Na5yOUwzBVx6AUIEaPq+ShRsWRJEYLyRFl63moi/7vfYf34GAdnpzjj8RijIcKQR3DZBU1pysYyDhVU2GbKuTxapQr2Oxt4sbOFvXYLnVxerIUQV72Wq5bPbKN8h3GR+bmXov1kE9+s/e/4+88/SpkHoxEGo6FYoTDCSVMT1ipPahSSSrm8HMGzVavjxeYmnq9vYKdWN7Q180dwVTxJSrRNqXTl+Wj+7s94vrmNV4eHeH98jIt+T47eSqxFKE6+0lJCPqVimI92qynHh+2vdfBiewcdHhFj23SmuV/hWNt/OU3RQA61xEMaJSh7ifSfeZp+p/JdQFm7ue0yH+lLWJY0QSVNUGX7TBJUPB+1XB5FWoqyfAkzNzF3hdvVHsSQMkHlDh6v9KJcROnf/x3/+ctLvHr3HuddTu6xiinntJRE3FLU8nnU83kUPSowGqURMXjBPl5MK3uo+b4oMJH3kr+kfEc4tF8hExl4+KhelMdK4qEZ8Gg7T44c4kRPNfBlkKXWghZKZzFSWWZYDh6q1TK2fv8H/NBs4+DkBGeX58YiURgiohIa5YMZy2WsaQS+h1ohj7VaHVuttuxeet5oYq1WlfpStiVptm6UzB1d1j35lXqAhzqtvFBhMknAPpT9ph1bzlm8I+27RGOxaT2nRCUG7jbkGZe0AgYPDb7TaB3Mnx91RV4yYK3MQvsTWkLbIe1mC5v/7b/hp7dv8Pr9exydnIjin7GcQDUhThJTyQso5nLoVBv4w/Pv8M3uHupFg0/qedgulfA+8NEKcmgWC3KkU7Yp6D3fB1TCLEaRWGOjuW+ec1+FD7ZNxptVd6YErAcqNVZTiILrIKXc+WiXiqjRqpQ3xyGT7NZb5keLJlTg41itjkCsmlS8VKy98b3IstMi3TJffJZ3km1rARWHPaC82UGnUMSr00O8Oz9Fb9AXK0k0zcvyG2sqVknWKqRyAr9eKmOz0ZTjmp52OqJZ3+C5vfaVv9A2by2Zi+AQeAQEbGdKWeePskiZ9xOz2G/efcbyGJVfGc5L+2D76ByHwGeBgMqxyDKVa0WZnEq2fLGGxrIWOeUQOvMN8Fkw75j4+hCwyt/an+pYgAorVL6XfpjK6LJQmtl48/Uh5Ur8iRFgn6rj9Hbq4ZtSEeHzZ/Kd+fLte9lIhJwvVgAiJBgNqBRPC4Lmj4ulVL7it2y1UMCzdgd/3NnF77e25ahx+ab9xGV02f92EWDfauZcOM/p4c9P9sX9IQhwwM1BfiAbhcZJikkSojeQw5ZlDpm2e8X6J4/YThJs1Gr48/4z/GV3X2SXcyIyNmYjcZdD4CMhoP1vSquvhRKip89kjujvP/8km2W4eTr2PDnGOZ6OxOI2Z3m48ZEWxtn/BkmEaj6P/fYa/vBkF3/c3BRlFdls9pH4dmS/UgTsB5l8j9l1u2pKy+8pfr+2AcoxLZm/P3iPSRSJ7Ca5HOI0lTk1HgjEjbkcOnDOknP7fhijU63i+yc7+O8vXmC71JC1Hp2b+EqRdsX+yAjoXDDn4bm2uhv4iPafgjPTP7z8GZe9LmgNKPYDmcMfTydAOBE7+MY6utlU6ocJKrmCWCH84/Yuvt/YwgaVW5R/WqvnuoYbSygin9zle/eLuyg/KrQbxRL+tPsM6402RlxE5xZa8PgVuuYSeWOHPDvHgEMHa4FFllMpwOyJzQ7iegpsl8rYoWas3bFOjSx+yDWDAH/55hm21tcQwkNtEuFFvYU6tRAXJpANHxw+kzqB5kCEZu1lcaxZQ/2773Cys4XuiFpfI0ymtLYSI/B8tLwAW8US9utNVAK744Ek+eNijSgnmEW2Qi5AZXcfm/U6TnuXGMahKDNEITn0wBfTWr6IJ9UGNlpNUVwgPxzcc6F2v92C573A3s62DKxauQC7jTqqBatpxoYre+9Ny1Vk+WKSXen2BcjjSbjY3VingkUdF+MRutEEfVqP4ZEpYSi7vKmkEPiBLEJX/BzqQRHNYhGtShmtchHNfCAKReuGoAAAIABJREFUBiY31qGxdjArvFbsLa7CpdG4iFXm2b+NFv7nX/4F/dEUvh9gLfCwVy+jWizNF2JVPDTxNa5iobwS1yo8bNcb+Pdvv8fz3X2xalOLYvxucxstu9i7mhwz5WIiLU2YRVS6PC+zUS5h48ku9todnG0P0R1PMByPMZmMZDI4H/go53MoF/JoFkpoFohpCevVqljLYD3xYrtRXq3X3LGAsV5LvpEPyjwXcmulPFp7+9jrrOFkOATPi6MJOR5DlNDyRM4Xqzj1II9OpYKNah2dchWNnDlqgQuTpe1drOfyssOnkc9jt1KdWWogT8yefJoXUYASz1Iul3C20UF3MkaPRyJNI0zCBGGcWkUCY8mjlM+jXKAs5bGWy2OrXEGnVkE15wtNocuSMhMLgHQV9l47QgZzcYitmQvXrXIezRff4YLKKtEU/amRZQ7qQrHCkYgyAZWdWFc8+7lVKGCtWMRWtYpGoYSKv9pS0Rz4+91l6491xb6AL1nKHXmutTvYqtRwvLmJy8kY/Ql5DsXikR/HKMsifBGtYgmtQhFrxRLWSmW0C4H0U6TJPOguXHZhQfNn/9HxPfxp9ymeVOsYT0co+B6eUFabTdC6iGm7SkVTmudMVYhcEr+mn8P3Ozto1Gq4HE9QiWLsVGto17jEPas6JfgoLmWDdU4LWiJHz55jf20Np8OhHN8yHQ2AJJKJa1qr6JQq8m7YabZlAptMEAu+cnbba2IN69nOrlG+gYcnrdZMse8KwwqCuPzHMpq3E8vbKeTwP/7wJ0TjPtJojLLv4Vmjg1ZlNqxakGmT3i52UguemshyhJyHRg6ob27hvNFCbzrGMI7Qm0zQn05Fcz5JIlGyyVFe2QbyVIoooU05KRbRoYzkc9I3q4xofos1K8W48z/S0nfj73d3sbbWEstjpTjFWqGMJ2ttefcqVHcmfI+Ipt8GntRK+N++/x2+C8eg8irHAk/rTdSpoX0PeozK+mPb5LFCHEdQUaL5/Dl2KVty9FQk5x7T4pTvBWK9rZoPBPO1QgV7jQ7Wika5hG8GmkbOPdlBu1ISC1Q83q1ZK4uVlWX8JW/wXdeG//3v8O3unijalUcT7G9ur2xLpMF2wDHBs7UO8r//Ay4mE7Hs0IKPvfYaKsX746BYsJ01PQ9/3H+Kzc6GHH1UmoaiMLLebErfs1wOhZz+fBfxx7bGvoLjmkqrhk6lgGdbHXPc1WSC4WSKSRhhQis5bAM+lVEDFKmAlTOKPu1iGWulCtrlIuo5q3immX1MQdM8nOsQUARMt69Ps3cv2zBH4KVcTpTYcoUCyoUC8kEgClma4Lo2o+HOdQj8WghQFrM/vk+4SYJ9b+RT+RSoFAuzzQFuMujXqhmXz7UIsP+173yVXY71OAbmWKMkcxUBglxOxtLslzlf5PrdaxF1AR8RAcomx8H8ZuGcFmfVX1TryD/dR7VaxavTc3RHPYxohTeJkCSenOZJGee8G9OWA1+UvZ+22vh2fR3Pmm1sFvIzuh+RfUf6a0bAjnXZr3JsQFnmt22ys4dqpYpms42jbhe94RCTcCoLpgynTTbZmBf5Ms/XKhawVSnj2846vl3fxG61IfOc2n9rf/41Q+3K/pEQYD9qN3/K+JUbHMtl5Pf25ejw1xfnOBv0xCLQNA4Rp778aOXfL3DjaAEl2fScx9M2+98NvFhbw5NiXuaq2T87+f1Idfe1ks0MVjl+1XUWznnTKn7UWUc+F6DZbODg8kL63+mU6q4eEh7dzVlpL5AN5ty0RkWr9WJJLNjTiv3TWgt19un2++9rhdmV++MjQFFmH0lZ4zdawk2VtPr+9BlqxZJYyD++vJQTR6b29AOev0ClLK49c2M3jSS08gU8abTwzdo6XnQ2sF0qouEb2tL/Oln++JV5zxx0nfaeyX7N6Jme1mZLH/losybiq5WyHGMR2sGvpsi6vNfn67jXcC78cqFJF7mZFy8uqtEkfa2xhheNNRqgl0Ximl1A4cCal5n70ByVquFZFgLFLL2HWjmPp+U1TLCGYQpMoqkorHCBpZnPo+X78hLgJB95UB0cpSyVZy1CFAIPG+02xvyRVhIhFIUV7sjPoZXLo02LALZcbOy8OPDKBx7qnRYm4KKRWXhnh8Dyar48QoQXy6Z4iIf9R15EG006BA+tahHTahETpKBu20R4MkeSMEkQmAUkLqYSby6/Sidk81wUTMVQ3WzO198rTvYbST7weTZZ3vOwvrUJKiHxYt4sK+tby0uwOSV124TqMkfEVZSJUmLaEWs3/NSidR05W9XmudoxJqoYJkobKkuZRc+1ShlhpQQe/sR6phIQlbPy+UAm1piPHHGUaSPEdVWdrebB+LJcLAvTCi+pJwvYW/kmRo0Gppp/FMmxM1RYoXUTWsRgfRJLpqW80/oE5apWzmFv/4l8oDKMOLGemZdpM+ae+bI+OJgq54vYzhcxtXIUsswApjzSJDY1yAWcMhVmrKIJrVAwPemQ9kLZtcKsUGTzFtztRBD9tdzVUh4hf5aHUQrBfxLT9kCCnFgjotULY+qUyi4qUywf+XjsS4shfFr8WCRisEEFp2IJu0W2P4D8SjuMIjlyrFIoiNIB64l9CycPpK4sk6RJzDSP2Y31YFiQmIUIsdxTKQCVrVnfQBmsWvyl07qtEdm82DdRQaBQqYnCDQ/5IJYqS1qfj4aldgzWOghxYP48gmtrbQ3jtTX0iZ0sfMeyyMK2Vc8XUPc8KSOPVyEZ+XnAdrGAVnFN+hbyTp7Jv/YtAuEM2AzgcmsC+J8/4sH3zb9tUF2gLX6kx/cN+7HZtUyPAbRCRNeGMR372u2Ch3XuCAF/KUZWPoZhijgKkcv5oPIblY0oz9qfMD1li+XgffZalX02/LZ7ypPg4wEv6k3s1Xl4numXiQHbEH8L7fg2ovcMFx48oO17YrmDYwnywPJr+/iQ/JmGZeC7m31gJShgu93BpN2RdskBdcR26fkSr5LPo2bfFzKplykHLYtUqjXsVWl1zWDGOpI+mvEohLYymC95p4WsdmcDcccssBTZD2vbzNBmMv6IM9tukRLX2QBxUFqsf+a1XP8ZMtfeMg159VMP39YbeFZvSH76HrgPXfJJesSH1rgqhSK2C0WRZ/LLsYb0edOpySPIoTB7P5j3I/Fbli0L3QzDawvjAhwCj4kABc++i3jL9sa2QuXTnXwR4+YaWvkiCmGIXSoPlitiYYttgHHd5RD4nBCgDPM9IjKcetgr1zBc28CoWBElw+1qTTYo3KfP/5zK53j5jSEwe/GbV7+OVWhpczOXx3fNFhpBHml9gnUq6Veq4PHFjOcGC78xWfhCiqMiy36W8yibnHOo1dGp1rFVa+D44gwXQ7NoGsnxrzKbhYLvo1SgFdoSaAX22fo6tis1NPUbzI0pvhAJ+ELZpODasS7HrvwO49c+v8VarbZsTvrl8Ainl5fojUZmtz83htEatxxRn6JZqWCTVpxbTTxbW0MDvsxtkJ62C35v32Ha6QsF0bH9SRGwQkZHx7lyVHG5hLW9p9ipt3BwcSZWwbvjAdj/ilVw+GKhtszNpKUSOtUKnm9tYLtSlrUZXeeRsqkgf9KCusx/iwhQtNhX8vuLy3pcyN/1UtSbbTyp1/H6+BjH5+foDgam/03MMeC5HJVdfVQLJbSrVew06vhmYx0dOVbbzMll++DfInauTJ8PApQ17X9pabDkp2hvb8mJBu9PT3F8eS4bzKM4EqtWtCxoNoAV0KCV7Vod+zy9olGX/lfXI2clZENx/fAMjs/hhvX9RV6UI3a4FCguGoomYKYky3KmskfXjpczsee3DOdCiCygzb2lYfCRCh5cjBat8NQcs6IgsgEpbbpmb/SciJngMC8JpqFFElWaoLIH8kV4UihTNi72M95sYpoZ2IvRlR4bGpPxTC/mK7Q4wcKfbdT8IJAXlH1ZaXq6fGmRFhdYmQXv9cdw8ZSbFe3XFpi48BIFGDG+BDH1z0Vx0ZDnojADAx58ML9YPpaT+TFv/VlyNuLi0zz13e6YmnSl/BYH8kRFCvKi2JAHXvKhE9Aij/W4h6P5kEaBllfFXoKRKS2FulfJ2pVzBtgPLvIs2Fi+RfbSOaYo8KCF+cV7gTmDJXmiP90brywhG1Hlj5PPXAzkjzvb5eJgJ5/nCr/gSPrMm2kYQ38JtSBtmyGksnhr25hmSZdhdFUWmI7lZxuJta3YBGk+gMefls0qOmlauhqmZVb6yrv6W5L6OMufNCgbzJ/8R5aHWXkyZ43O8rWyLHJteRDCKkvLmc1yvf+NkqJL/rSuyDPlhEeaRJRxieghzbNXMxe9lvsXxUzjiMuIC8CZ0MA3+BJklSuNttB33nHWQGSHWVl6bDvs07Vtqkwt8PbQB8FlLid8ZH7khZaYiCknqFE0uPFW6jWjREE/9Sc7VAagUgtlXNuhygbjza6Fh5mv3GTpET4e4aIX+2q2CblukimbRFNq3YoCmciy6Zt4ZI0UQF56VGew9Wqz0HcDMVH5skGLjlb+anFZjLv0pLwxb6MsYSII1rY/0HIsJX20R5U/AkCFNz3miFiTD4Z/CA8sGy/KAvsRSpK+p9mPIMiZXyYPxVzlRquZNJiecskw/ZE3uSyDQtbKMtsuJ0LIPf1ZzSyTjWrS2f/0Y1klvY3HvPicxWEh0R0fyCt51zIQC81P82SboRIwj7VbeVkgtA2w3LwnXdLjhzf5ZXORJlPSktsy2fwVV0m/Cotrsl/Jk/N0CDwiAhQ9yicld8Pz0GzU8V2jLkq6bIN8r3O8f63sPiIvjpRD4EMQ0H6dctzxgH9f38Af1nmArXm/UI75PcF+310Ogc8CAfvOp8Mf+98WFcNp5fbFiwXFXSp+65jws+DdMfGbR0C/AbSgKqfq8ruOlnAps7SCG3XaGAK4mI4wnkzN/EBgLLVV80UZQ3C+j0rt/OZVeZ59S2hGznUIfCQEKLscC7DDpcvv4vV8Ad/t7WG4t4tBCgwmEULZeJAin8uhWiiikjNz1eyjuYmCssuxhrYRaRNOkD9SrTmyigBFjLLG+QczD+GhDmC71cS01cQYKS7jEMPRCFEYw/N8lPwCmqUyagWOMexmPCv/lGHSc5dD4NEQYKe4QqhUdqWblD7Uk6PDN4I8vtnewWR7RzZ9XU4GmE5DObC8QAuv+SIqgRk3cJ6bfTDHD5RdJ7+PVmuO0B0RoPxyTkzmhGkkwAO26lX8qV7FEPsYxDFGk7EcEcSGQMsqtMJSy1GGzcZyzonrGGJFU7kjJy7ar4EA6+mLuLKDUWVYO0h+rOmVuV3op+mfDVN6mi7rkq6MfjWSTUyw+KO3/OzEcZYu7zUZ3WxY9iXBPNjRaxybxYwNPmv8LI1ZBBvOOEKL+Vp9B8YX/qzLOEprnt4YWaQ/Ly1Xlo/r8rVJFgtKPjIvLuYvC3KWB6WrvHFhiZfyf2teC0jaxPdwSJ84MT9+HDF/8kc+6ae/BZLK7ILnzQ+kQyzpysKZja55317OTOUxrS7gZ7yzdG2UlfVNHj74UsGk4gzv7WInO/fYFkLLYoOlhujHn/rR1R9piL8tEzERDyVk0+ojcdRLlUT4rOF09afxbnKVD0nPByWUTSQMmiDyx59+VCsPsihqZUjlhqR4v8jPTFvkSjmzWT7o3pZjVV0zSNugFlXk3maovK9Ku8CTJs562jPf+bGmfYcGE7NVSTR8lcv4Ig9WJLRv1Dq4L71VeVznp+VnHsSM9a1r5upnxWLWTwg/9LQBHDARh6y8KL7X5Xubv/Yj+n5THrLt4i5Ak9csL5QB4kuX/gzP/shXpmhXwmZ8K0MzD3Oj3oLRUth1j8of8aNM8aLfr3UxL8Vb8rTvUsXnQ/kgBqRLTNS9qc6ymF13fxsvTKdtie9kXnQU4+tw1XSKhdYj0z8WDooBaTM/Yc9mRIUVUTQxLF//3ypzat8w49O+z5lw5mepaPln+cnN9Vm4EIfAp0KAbU37QC7s0yAvf9ouKfdOfD9V7bh8VyKgHboNnL1/+C6yCtQaJSvHCx21E+qV0DrPXx8BfgNIP2xlVxVs6c8xzExUVagzLK7wyoS6W4fA4yFAOaQ88se5GbNRhd92HhopwKNF40J5dqC3xuU3pY6fKef6m3HmhHgGhbt5ZARmnafpRznW5Y9zVRzncl6Cx9KGfC7lkZZkBk76XOl/M3MtOhYmyQzZR2bYkXMIGATYLfJSWaPLPpVySBnm/AXll+OFMPXQDgqIaznZAMVU3KSsSlYkwvTa9ypNm4VzHAIPQ0CFdQUVyprKm8ou+18m4diB/TAt2a+XqkhKtM7mz8YLIu+Z8QPTU4aV3orsnJdD4OMgYDcGU/Gac2VGfs04ghYyp0EOcaUqfTKlmLLLMYQqWfFZZdfJ7/2qSPHiVliul8mWWF04ux+pO8dmfX32V7bf1XuCpT92mKsuBZRhGndVvEU/XcZb9JWWYAku012KKY/ZOMvhDNNGomH00zTZew1fcAmCjUxueUt62UtxUj+lrc8zAtYjm+eVuFc8MomUYCYOeVEW6eq95qHPTLqMg5L7GC7z1Yu8KJ90+XusS8tJV8t6b/pMvHSpl9LVYPVnXh+c3zIxfaarGdqMNL9l97okGm8Z/2x8zWbZTwuk+JGW0rsSN+uhQGT8FtItPKyIlGXWBmd5oJdmoTxdIZldfb0SmMnzIbc30GWQ8qxZ8Jn+5F3vNexers2Xjv7ulf6aelym9SAeb2XIVDJftMxH+1Ims8WbYbWSVDZSBoesXAjQWYIrCV3vySzIG68FutbvWkd5sxGyj4qpuhqmruZFl376u5JXNkEm8Nr4mTg33V5D9qYkjxKmeBipMCQXeNGABc+7ZZ3FRMksptTaXfTl05Xsro86S8w0Wh5Nn+VhFvGGG023kocb0l0bZAtuBreZWMzIlsnYgcmEZW+zDM2TzNoHo9osZq4mXyj7Eh2N41yHwCdDYJVMWqVQfqRpsLbpT8any9ghsAoBFdClMHrz+5z9su3iV48nrkm/RM49OgR+NQTY1/JSGaZ7pf9dIbcrvCwl5zgEHobATbKl8snxAvtaKqVwBzQXoLTvpfyyP2Zc/amczyKRxZsyelgRXGqHwFUE7FhX5/LVEqiOG+jyUvnVflhdG+ycD0BAsf2ApF9lEsVLu0h1CQbvKZMil1axSmYXrXIK5VtllnQYX38LYGrggqd7cAjcAwEKlgrrqmQatmLjPccQXNRXm9skxUtlVV2VZRs8d5z8zrFwdx+GQEY+ryWggmn7VRU7enOjDJVTdPzLMMprtg9WOVZ3IZ8M7QV/97CIwExZxWz09j6i0spnr7CiMptFiH4qmBTA6677y5ulrBkoYc2MLi87+Fikr4EMXgyxqTSphM5jm5dANo7c3xaB4VajbJabprH8XaF5g8eMxg1xrg1akZhe6q0Lwfqs7rX0PkKAQqOks/zdyA8DmXiZgBKiu4LAavqpJWMSrEiWpbryXtOom41EP7I5C1t4yMa8x/0Vouz0byasoTM+mB13xdNd8LyOD1Lgz7Zu3vJJ09rnW2kxXjZNNp36X8fCsr+ldVN/I0k0j+X0fL5vnqto3OpHMwUKtmbJjOeZz++yvrcSvjYCMbmp2NcmvCZAuVX3mmiP4D3nWpVWlOhNGM1TEVY+mdiaRl0BJRvZBqjXLJ5muuCaXpN8aTyVPX2eBUhGM98FKqseGNMeHjdvYwsRqYus1zx/9bnNnae9LeY8nJgoktem1wjzZI9+x+pcOd7SSmOOD+TDlI9ElKi6rOF56WfZaLC6ygPdefSFe3oHjK9p6JGNewNy2WhMnn02yZTwPYhmeV7m2z4Te2XX5LP6fzbOjDfLqD6ru5qCyUfpaLu6Lq7zdwj86ghQOO3P1+P3fnUmXIYOgQcgYDtYjts5ScRH7ZfVnXk8IBuX1CHwYASsrM7oZBaYxC8rvLNI7sYh8OshMOszZ1mq0JoQ/udYlj8VV7r6YzL2wzM6mpwB2ftZhFlG7sYh8OgIcIaDV/b7KztOEDG0VjdVhlXG6S6IaTbCQoDNxDkrEZg1e4fZSnyynipidFfBRT/1136Yllb0XsNIkzSycp/NZ9YXX5fRQmT34BC4AYGs0GWjqTDTz8rZLKoeZ28X/JeT8XkWd+le4pIeLye/FgjnfDACKktZgZsRuxrIaPyxb2WoGU+YdVcjjmZz8jK55ecFAZ/l524+NQKfvcIKBUnFUsHK+l0RNI10nbtM7Eo8S1EzWZWBkfwrKe/jsYrsLP2tPC6+JYQW0yzzlaVzY4aznG+/Wc7j9hTXD8zukPaxorD4HwzHcuIbmFKYl11NkuVB/R7T1Xwfk+aDO+9sofVeGVX3LgxrWsbV+4X09FzwuAvV1XFIRvNYHePuvh/KkuZ/3/RX4s8JXQm6eylujPkYdElDP+J4/xg0b2RacpjLzF3zu2u86/Jmeq2R6+Jk/Rn/+jyV0rwc2bQfen99fh9K8fZ0N5fzRhBuJ36XGDdBSeY0/C607hVnNdqrfa8hvCqy6q6tCruGzLI3kz4g+SI5EvpoGFraj8bsIuvuySHwyRC4TonukzHkMnYI3B0Bdsk6rtNUrptWJJz72SGwLJwcs+i4ZTnss2PeMfQ1I6DiuewuYKKyrJ7ZZ00oAj970JjOdQh8HAS0j/UzSlX0SxIgWB49fBwWvhqqy816+fmrAeJ+BVWYst2lUtAwfaarUsswCc8kXLkpKpuY96uILsdxzw6BD0WA8qUyqa7Sss8ighk5zNxqTOc6BD4RAlkBXmJB5r4TeD433863/aa0o5/aZyvMTqaXsPuMHz97hRVit0qgVvndCecbEzLQRmCHrXHVvTGDO0W6kcIsUEktv0Q0goZnBkUrec3E06QPdj8GzQczdTcCD2L9Homvj3pHawXXE7hbQTXWY9FRejP3ZsJXQq94zAhdc8MENhGdbFtkCn2+QjfjkbmVTLLP2ftrOLiS5qZ42bC70s6mue7+g2gx0QclvI6LX81fuVb342f8GFjdwG02KHt/pxrSz93banOJ8J1BY7rr0hr/60LvnMU9Iv6aeV3L1m1MMFz7nmuJ3DWAxG7L0NK6Ld/ryNAyg44hrotzDbs3R2fozTGuIXtzsjuS1GjqzvK64jELuXLDqPeIfiW983AIfFQEssKZvf+omTriDoFHRCAjtxzNPNqr8xFZdKQcAoJARlavIHJT2JXIzsMh8PgIrBbB1b635s5k+l3AyCvJrPS8lbSL4BC4KwLzGY5FGZxJHm9oXvAulyZS9y5pvvI42S6AUMgJ5sueXzlGy8UXkVwU1+UoC88L0ntX2bxrvIWc3IND4B4IUMbu8kH2IbJ4V9r3YNdF/QoRUNlTdyUE1wTKMVcLva+klhXYa5KsJO88PysEvgiFlU+C2Ocg1HfgYSHKwsMnQc1l6hB4fASW5Xr5+a45fmi6u9J38R6MwG+uin5zBXpwFX/ZBD5VfX5ovh+a7mPU0h14uUOU1Zx9cMLV5JyvQ+CTI+Bk+pNXgWPg8RBw4vx4WDpKvzICTnh/ZcBddh8VASfPHxVeR/yeCFwnj9f5ryJ/n7ir0n/FfqqnIkorXzEOdym6E7O7oOTifPYIfExB/pi0P3tgHYOPhsBD5OghaR+tAI7QYyJwVQXpMak7Wg4Bh4BDwCHgEHAIOAQcAg4Bh4BDwCHgEHAIOAQcAg4Bh4BDwCHgEHAIOAQcAp8EAVVW+SSZu0wdAg4Bh4BDwCHgEHAI3IKAU1i5BSAX7BBwCDgEHAIOAYeAQ8Ah4BBwCDgEHAIOAYeAQ8Ah4BBwCDwyAp4Hz+2OfGRQHTmHgEPAIbCIgFNWWcTDPTkEHAIOAYeAQ8Ah8Pkh4BRWPr86cRw5BBwCDgGHgEPAIeAQcAg4BBwCDgGHgEPAIeAQcAg4BH7TCDhdld909brCOQQcAp8YASqqOGWVT1wJLnuHgEPAIeAQcAg4BO6EgFNYuRNMLpJDwCHgEHAIOAQcAg4Bh4BDwCHgEHAIOAQcAg4Bh4BDwCHgEHAIOAQcAg4Bh4BDwCHgEHAIOAQcAg4Bh8BjIeAUVh4LSUfHIeAQcAg4BBwCDgGHgEPAIeAQcAg4BBwCDgGHgEPAIeAQcAg4BBwCDgGHgEPAIeAQcAg4BBwCDgGHgEPgTgg4hZU7wfT/s3en340jZ57vfyApapdSyr0ya3XZ5a09vYz79tyZ+2Lm3Df3b759Tt/pbne33bbL5XLtVbnvmUqtFFcA9zwBBAlSkEhKpERSX1UpAQKBQOCDhyEsgQCJEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBEYlQIOVUUmSDwIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgggMIUCsST7VRzL/nNDN3BTx7JFNFgZCyuZIoAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAAC0yXgGq5YQxUrdjy+xiqWPQ1Wpis2KC0CCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDD1AjRYmfpdyAYggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAALTJUCDlenaX5QWAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBCYegEarEz9LmQDEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQACB6RKgwcp07S9KiwACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIITL0ADVamfheyAQgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwHQJ0GBluvYXpUUAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBKZegAYrU78L2QDQvrV1AAAgAElEQVQEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQGC6BErTVVxKiwACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDBKgSDNLFCgIJD9KzcyypX05EUPKz0gfEQAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBC6lQLuxStJeJbDWK2P6ocHKmGDJFgEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQCBfgAYr+S5MRQABBBBAAAEEEEAAgYxApw197KZ2PmcSMYoAAggggAACCCCAAAIIIIAAAggggAACCCCAwIACNFgZEIpkCCCAAAIIIIAAAghcdoEgtveWpj82bm1XkvYrfipDBBBAAAEEEEAAAQQQQACBCxaw87b2uVtm3J3DXXDZWD0CCCCAAAIIIJAVoMFKVoNxBBBAAAEEEEAAAQQQ6CuQvfDZNzEJEEAAAQQQQAABBBBAAAEELkQg23CFxioXsgtYKQIIIIAAAgj0EaDBSh8gZiOAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgiMVoAGK6P1JDcEEEAAAQQQQAABBBBAAAEEEEAAAQQQ6CMQxzGvFuxjxGwEEEAAAQQQQAABBBBAYNYFaLAy63uY7UMAAQQQQAABBBBAAAEEEEAAAQQQQGACBeIJLBNFQgABBBBAAAEEEEAAAQQQOD8BGqycnzVrQgABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEJBEgxXCAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQOBcBWiwcq7crAwBBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEECABivEAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgggcIkFYkn2a//E7p9YsY3bP2P6ocHKmGDJFgEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQmCYBa6ziGqpYocfYWMWyp8HKNEUGZUUAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBGZAgAYrM7AT2QQEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQGCaBGiwMk17i7IigAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIzIECDlRnYiWwCAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCAwTQI0WJmmvUVZEUAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQACBGRCgwcoM7EQ2AQEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQmCYBGqxM096irAgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwAwI0GBlBnYim4AAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCEyTQGmaCktZEUAAAQQQQAABBBBAAAEEEEAAAQQQQGBKBeIpLTfFRgABBBBAAAEEEEAAAQQugUCQbmOgQEEg+1duZIzbTg8rY8QlawQQQAABBBBAAAEEEEAAAQQQQAABBBAwAbv06X8RQQABBBBAAAEE+glw3NBPiPkIIIDA2ATajVWS9iqBtV4Z0w8NVsYES7YIIIAAAggggAACCCCAAAIIIIAAAgggkCcwvoudeWtjGgIIIIAAAghMn8AY741OHwYlRgABBGZYgAYrM7xz2TQEEEAAAQQQQAABBMYrwNNO4/Ul99EL2Lso/Pso4vZY13q4h9rFwYcJF/DhPOHFpHgIZAVi18tKpzbOzmMcgYkXoN6d+F1EAXME2ofASQBzuJtjxKSJEuiN0d7PE1VYCoPAMQJJ3CYVcOCuPnAQcQwVkydcIIgDyf2Or6A0WBmfLTkjgAACCCCAAAIIIDDzAna+wg8CkyeQfyHIXSqymA2OaawyeRtCiRDICPi4dkGcXDBKb/xnEjGKwAQLpLHbvmDvYzpbZFdTZycwjsD5C6Rh2D7Mjd2hQ3eNG+TF7/kXlTUicJyAj1A/TJoJpsGd32z7uKyYjsC5Cvi61x01WP2brt19dp/8lHMtFitDYDCBNDxtYDfgC3GkQPYbpsNosHxIhcAFC7g61x0DB0r+G2+BaLAyXl9yRwABBBBAAAEEEEBgZgWSy53JcyIzu5Fs2OQJ+OvsJ5asO1H7k7u5ZI1V0jtPuXlYaruIZEN+EJhUAS7UT+qeufTlOqbqjNsVcSrkroCm7a7aaNlEx2TUTssIAmMQyIagtW9N2rimN0uzMZkdH0M5yBKBEQm4SHX/pMcNsfVxZROI4RERk82YBFzEWpgGgQL79c1W7B1BvCdoTOpkO0oBi2G7AR/EUabRil1noMHKKJ3Ja0QC/tDAD9vZpscLvocVXxe3549upDS6rMgJAQQQQAABBBBAAAEELpuAu5B/2Taa7Z06gXacpufa7c/Hboml4AeByRJIbjHZbaaCbDy5cE+sTtZeojTHXsPsrXjdxdDYOrzqPDrd5sud2J7LCALnJZAeNiS39oNsI+3egD6vErEeBIYT6BwluEq301DFB/dJ2VEVn6TDvHMQSGpaX9+mwziQezXFOayfVSBwFoF2NeuOH+wYInscMUTO7YyGWIakCIxAIAm95NqDxW/OSdsI1tLJggYrHQvGEEAAAQQQQAABBBBAYAgBO10Z6uE8TrSH0J3xpC54TrmNp1zWn17bzdGkoxX/nF5vhvbZgrV3+inLy2IIjEzAYrIgua4q3PN6aSyPbAVkhMDwAgNWlUkyq1uTy522Ips24OLDl4slEBiRQPJAaXqjyW46uSf7CwriC+64nOPqEe3hE7KZoQrK9S8YpL1auV5WBjyPI85OCBBmjU2g67tndW3ya422hzp6IH7HtovIOCPQFa+d6T78InvYILCb/p1YHuo6WidLxhA4VwGL4chit/1rwX5MwI+gZDRYGQEiWSCAAAIIIIAAAgggcDkF/BP+A17wvJxIbHWegL96M75z3a61+tNq11il6zJnMscXp7PQORWss0LGEOgIWEDmhqCPZKtzk7tOuck6OQ02dvQLkCw3kswHKwKpZlcgN7xsot0wdcPMtttn4i4Dwui5CmSDNY1DH6LuqWirdl1H/oFi3y16dplzLWy6sote/0Vs82nXeZq6Jc/3NPn0ljkv3940Z/mclrFdVBtJK1z3Wkz/8SzrYFkERimQ/U5YvNoDBtkAjq3RYOdmv+thJbvMSWUZNN1JeTAPgX4C7XhNElrYdX4LskYr7sa/xbEdQwzyQ+wOokSaswr4cLRhJuay8et7eD11L0EDlpEGKwNCkQwBBBBAAAEEEEAAAQSOCrTPZ3pObo6mZAoCPQL+xLhn8mg+5mfu+lRxZ97+EVO76TSaNZILAiMTyIRvd3hmZqQr6/RVcYa1W7bdK6LRwBk4J2rRoyFzfPF6Y+D4lJ05A+TfDq+0d6vOItZTRaE71tzdqU6KzooYQ+CcBez7kAnFpH+VdJI/cLB4zaQ55xKyumEFJmlfjassPXHriWx17jGDIFDB4tZulnZaA/hkJw9HWebT/L05uXTMnXaBbHxlx227oijpXdD3DCRrdhUNvsW9+Q2+JCkRGImAVbdJ/yrJ7f6Bq19ro0V9OZJ9QCYnCGTrSBs/EnNWB4fJ7+lfbHVCATqzaLDSsWAMAQQQQAABBBBAAAEEThBw1+fd00723uj0Qn4ghTbNljtyYtOT2Riu62fPrXrWxsdJF8iLl5N2aG/6Y9NmEqajNnAXhmIpjpKn+pMXAgXuGuiJN5x8dseub9KhKd+0C7gQTO8tBUGgoP2UtFW7fQIzb7aP6SxMXrrs/Lxxn89pls3L7zynTUuZvbEfDmJk29Zv+4bJ76R1HpdPz/rbH12jFd87m8VyyR06tOdn15WXd27C7EKnGM9bzymyYZEZErA4s7hwx7zpdtmNUqt/3X/ptHHE47CMk1CGYctM+vEJ5MSDv99ZLBZUKhRUtIaC7o9ET4PB8ZXqaM455TyaiCkIyDWwCsNQURS6StkaXMVxpMg3HAQJgUkRSI8n3SDtkc3Grbqz6xD2W7SGK+5cbogLY9SXk7KHL0850pjzoRdHoaKwpbDVTBqt+BljEKHByhhQyRIBBBBAAAEEEEAAgVkUcDf87eQ7tqeakrMUN0xPyPveIBugTcuwbv5cyd2/HXbhi0zvC36RZZi2dQ9sliTMTW7v3o3sglFBQVBUoKIUFLt6WYnSi01HeI6bfiQhExA4m4DVtT7cbOieIbWADgqKLIAlFQpFFYrFoz1UDLDqQXuh7peV+5vQLxHzzyTg9pU1tMut0I5m7fdJ3+Q5CXzMHc31dFP8Kixfn3ehYHWvzUn6q0i6l+5uX+PTDnJMcbqS9SzlC9ozuV3o3unDfD4u72Hy8GnbMH7CGIanLe95lC1vc0dc3nZ2me2xGtfui9oka/BqP4Wg4OpfNy+vXExD4AIE2vGbWbdFrI/TKIwVtiKFob2YIj22yMR6e7GcjPKStdOfcsStZhwZn7I8LDYBAnmxF8eam5tzda7NdsfBdhxRsF7aJqDMFAEBE8jWZZnGKm0cO46IY0VhqDAI1Tr2gkN7ia6RbPZdM/iAwIgEuqrTNOB8HesabBcCFextVhbsY2wwSIOVEe1QskEAAQQQQAABBBBAYNYF3HlLevJiT4ZEClzvKtbDykX+dJ1cXWRBhln3BZsNU9SJS+vtTtrx9tCSe5I/Kb0tYr+tyC5uzkn2W2gqCopqqaBGGCsuJE86jfH8e+IoKdAECmTi2oe63WxqRUlvVtZoJQ5ixa4OLsieNz2pDvYXmsa1pdPWWNCZZozH5TLKfH0cDJLnpG2alcfitx3DChTZ09HpMUQrlpqxVEh7suja1q4Pg2z9BKaZtm2gvF3tpIzD7ilZHRtab+g2190otZ4pAoUK1JrAsKNIIxCYtu/CMZtsxwAujt2xQkHWVCVWUZEiteKCq3+7FrVKO2fbcyZ1LXaaD+7v1TgyPk1hZnCZSTseGIbYh4XFb8Nit1BUZI22rf51x8F2/FuQHUPwg8DECaSNXK1c/jwsjK2hdkE2DIOiwrjgzu0GKbsL82n+Qg+ykaSZHIHsNTQ7hijYcbAFYKBisajIWq24hw/GU2QarIzHlVwRQAABBBBAAAEEEJg9gfTJENuwoFBQqxVqv1LVy63DgbZ1PDc2/dm7Hw5UlAtM5K+s+eEFFmVCVj3cnktTG58b7XW07lOS95oX4uSlP3alKFLJXdh8u73vLg5F7mJ9SfVWrNdvd3VYW1Bprpg8NeJarPTm60vphxOCRzFmQMDHml0d8jdE7UJQMt3+jVVS5bCpvf1K0iOQQjVaLR1Uq3r9dkeLC/NHHHyuSZ5HZo9kQrZOn4ZvRmIyDU/kJnvd7yR7InPQn6T3kkFTjy+dXZZPfqw+LimKi9rZq6haryuM7FZp4G40vdnZ09zCvAqF5FVXybYm3wX7QiS1eCa6MqPHlz69Q5v8kTg+WaaExz8paCscaKU96+lsf8+MM3z05fDDM2R1ZNGzlteXyQ+PrGDEE8ZYXtcmxWIo7QUoKOjgsK7tXTt+sNi0G06RDut1vd3Zc8fDg23caG0SAZ+nHw5WElINKuCfIvbxNuhylu7kfeJ7qhwmx35prba1Bq3ttbubpkkDFWukUq03FdmdJ7v5H0farRzq1dtqu7bul//o549DYfSlnNoc07A9ORInZ+tcY9a097WkVLYBBdWakd7u7qvaaLpjB3vAoFpvuDp5cWmp/wY4h2lR6L85pJgeAavh4qDo4vjgsOYaqVgdbI22K7WmXr6p9d8Yd13DkqVf6P5LkAKB4QX8qZMdvdg1tLjgzsFcD22FQG+3d1Wp1lxDlaSn4vHVqUE8zJnv8JvKEggggAACCCCAAAIIIDADAvYU/0E91m//8IX+33/8J/e0ablU1Hy5qPKcnYj3//G3nnov4p799NtOmEZ90pRXqmHXkZeHOR03vb/hLKYYStU/puQhsnfM3bSkwYo9z2+z7ITbYsMu1BdKZTVCab9Sdw1VgjjSfCnQymJZxVJBResf3Z7ii1quy95kP2VLlx1P0vIvAqMRyNQJLmSTWPM3nuyGv4Kymq1Yu7u77pUqc8VAC3PSYrlovaLn/rRzPWZ+7kLDTPTtCoZZZgLStl0moCy5RXD7q1PK01y2u/CGKy42bBuSBitBsezq4d2DipqtSFEUqRC3tLq04I4h/MN6saJ2/WvtdLrb6lijFvvNVctM9Fdd+yZMy5d0057JIDNqeQyST2YRN+r3nx/2zj/NZ18OPzxNHsct48vph8elO266L5MfHpduVNN9Of1w2Hx9Of2ws3zy3fHTk+MHe7K0GUY6PKwoiloqFgLNlwtanC+q5A8eOlkcM+bzTGaftuRHM+/O9+j8yzml43s6n2yju9EL+jpqhDmnWUb+HCNKGoPEdhwclNwxcOWwplq95V4JZP0Lri6XNV+244vBzkyOk+xYD7c94zUeriyzmPrIKdKEb6Td2LfGrJF74MCiyn6tgWBRzTBWrV5Tq9VUIYjd+dv8XEHlUnrydsy2udh0/xwXvccsyGQEhhbIiTHrUdAq2KCoWr2Z1L8W31HTnb8tL5T7r8Vl65oj9k9LCgROK5A5DnAPfVnjVjsPCwIVSkU1wlCHtboq1brmglAfvXtb/+Mf/k4ff/SBlheTPlFcVZs9a7IJOV+LfkWkh5V+QsxHAAEEEEAAAQQQQAABJ+B64bWb/+4OUqBmq6Ww1dSheylFFik94zlygpL2eJHk5v71JzbZpYcftxV1VjaaPPNy6axjsDLm5XHCHd7exhiDrWQqU+VJ5k3L27hE1WLJxrqN7XKOmxZYgxV7OsQiw3pYSZ8oVVGh/bqLoXIn33YD1d3wd1d2Y8WxXe7vvlOa3DQdtIR5pWYaAicIpLFnKZIoS+LaVwm+wYo1vHJP6ym5eRqFLdUOWwpOuCvhchpX6J5QnZ2wtRMxy7kkzBNRnnYhcvZVd6ONdspjR1yDjn6tOsYUGL74Po5taN3428X6OLCeVpLXWyVVd+B6abP7/e74IojdU/9WB1tLlWQf+ZySL4dr+Npv2zIyg+zndq8umeWSUb816V+ageNl4IRH1jj4hE7ZBl/muJSjLO8oy3WO5bX7SenqXIy5TzbReqew16hYjxT++LeQHCfUmmrUa+mxSH5ZfR3u5vqYzk96yqnT0GPUKTftrIu5sPZ79fSZdRpV5OWVCZzTr2JkS9rfiqSZijXYTo5jkwYrBRWKpeR1QHYTyl7JFsU6qFRVOUy+/12xekyJjjvUGGTZ/CxHWffkr+EyT23vr2EPIi4Ezeoyq2vtGoJ919IGV2n9m/RSYQVLeriq1luq11ruDM+mJudtxxTcfXU73+RjUjEZgTMK+Dv+9nchrVctx8Dq36K9TMUdT1ij2DCKdVirqV7v38OKi20Xw9SXZ9xBLN5XIKl3k2toFnTJa1ytC2J3/hbbeZo9FmbXy8YXjzRY6bujSIAAAggggAACCCCAAAK9Au4pZ7tsVChoobyQme3OqN0JTvs0xk9qp0pO6N0p0ZF57URDjKRPr6RLtNc7RA5Hk8bpU9yWm92ksBTDFTa5iTxoaU63jqPlno4pWcns+HClN9teX/85vWSf3lC3G042pRVJUZikcSfaxYIW5svJDf/AUiR5Zi98utQ+2+EKSGoEBhNwX4Ik9uwmkzWxsp/kJlDySqsoLqkVBgobjSTqC9YrUFHzxfn0Zn/3NykbstnxwQo0WCq/Rj8cbKnJSDXOC21n3cK09hr6b057vX13iE/gh+0lBx45aUmb537tn/TpPGs0aFVvvdF0jVHsdRTW7mR+flGlUsE9MW31rmswaA1W3O2n7MX/pLZ363X/nFTUbALL86S0tipX4/dJlKTrn4gUUylgPfekBbdO0F0EW8NW12AlaeRqT/i3mg3Fkd1StRtQUnnOhn7J/C3vRFdSx/cLx/xcTpp68vpPWnL2543SJo2LXrQhGtAli/oI8MPeDE//2TVOsQYpFsF2/OsqP4tAu4EaqNEMXT3sXncVFFQqlzVXssaE6dH0MVzthg99inb6hit9Mmb28ALtBsWuFdPwy1/AEnauZg1SLF598xJ3RBwX1YoC17uK9XBlaYrFguZKZZXSTl6Tv/PHfad8bhewUazyEgn4vxEWb/4LaMPANVhpNSO1mmFyTFoIVCotJD1c9RNy9bPF9nHx3S8D5iPQX8BFr12DSMPMGq1Y/Ws9rNjr2lpRpLgVKmq15J4r6J/lqVPQYOXUdCyIAAIIIIAAAggggMDlErAW9XaTzxqrWEMV65ViZWle1zY3ciDSq57+ImhXCn9F1A+7Zp7ywzguRmUvDJy2rD0XGPKycauxGXkzT8kxJYudfYuz+8g2utvb5e+SFBQUizqsNfTq7Y7stROKIi2W53T7+qZ7JVCngVFvnmcv5ZTsDop5IQI+3txlIVeC9FKnG09uJM2pGRZUOazr5avXrheKuWJJa0sLurq+4i7c5xXd5Xwe4es3Ia8QR6YNlfjI0iOZ0GsyAUXq3i5fQD/snjsJn7pfm3K0RK7HlHSyazAYFNRohXr24rWiqOkaCVpP/jeurmtxcd4dTySvA0oaq9iinYYm4/j7frTMTEHAfeNcD2zJhXo7LrPeVayxSrXe1M72tprNhqtzlxfL2lhf0fz8XC5cV7Xi7gAkU9y/k/vVzt2WqZzYbj1xWuyuPTiGY/Te/EehbL3/WOXpexi0D0kT2DCOtbW9q8NqXWEYu4ZWVzdWtbaynBw592HyN7HySum2pM/yecsxbcwCyb1y1/xjzGsaSfZ2Y9QaXdnRsAWyhZQdP7SigirVhnZ2dlSv+/p3Qeuri1penB9o3e3qYKDUJELgNAIWt2lF2G5kkvaCFhS0vb2rnZ19RXEse622HT9c3VjvvyL3dUh7f+2fmhQInErARW5a7ybj9q81VikoVKBqvaG9g4r29g+si5XsSdqp1nfSQjRYOUmHeQgggAACCCCAAAIIINAlYA1WXHf9KmptdUU/+dF7+odf/21XmuRGlk1KTtrzLsm6Z1mT2V3LnupD+nqXvPWcKr920dMc3cWH0xTWrhRmS5Ud7y1ZclI4mQ/PnGbbe7cv73NyMTJvztFpeWXwnn6YhFzyNHOat5uVXvwMinry/IX+/Xd/0PNXb9xNp6ura/pf/9d/09LSgopFS+fjO31FhYvh7Loz6zpaSKYgcEqBzJN46ahFmlU9Fsn2SqCDalMPHj7V1usXasWh1pYW9aP37+jv//ZXWlzI9nLVKUI7Wq31QPtDZ/5AYy788xa23gdOk21eXgOVZPhE7sHi3vX1frZsL/IJZNu/nZ9ObdMZ68wd9Vh2zSfn3fm7fnI6V/Omb8nwfVZYV/5hXNDO3oH+97/8xjVaqVcbWpwr6v/8+7/RrZvXrbdptx+66m9f/w7dg8HxZRxkO5LVnYf/8eVkzgUIuEbZduSaHjPYhfo4uVhvN0ufvXytf/u332hnt6KFhSV98N47+uu/+rmubV7JLaz7drVjN6nYXVSdqt7MXQUTTxTwNdCJifrMtGPC3nryrHVDb359ijDU7CS43Ja7kLPGKnazSWqGkf75X/5N9x8+VqVZk+KG/voXn+jnP/ukaw1J3HZNGvwP/bA0/tCnZ3V8HLHAsPtlxKsfNDs7fnD9C6YHl1ZsexVmrRHpybNX+vTTT/X06b6KKur9O3f1i08+1t07twbKPjeuB1qSRAgMJmA9UiQ/SeRazLlGWO61VoF+9/s/6rPPPlc9DF2t/NF7d/Tf/9uvT8g8/RvmqnWXm3to7IQFmIXAGQRcLelq3eQYwuLYjoGLasWBXrx6rW++v6cvv/5GYWS9Cya9uZ1hhccuSoOVY2mYgQACCCCAAAIIIIAAAl0C/jzGTmXs6ZC5otZXl3X7+lo7WfvafHtK/og/pc+fO9zUUeY13JpJPYkCmTBNm0x1rrU3aqtani+qFIQKo7rKhVDXryxrbW1Bc/aQdCy1wrSxStKD+iRuImWaNYHeSsxunKY3NZNLlNLuwYK2txZUVEtR3NJcMdbK4pxubq5reSn/0o7/LvjhKNl8Xe/y7i3/KFd0xryy9xp9mfOyHIdR3npyp/Ws3HP6Ye4y5z1xwMLYptivJfeL2Ge7YVoqrWlxvqS5otQKIpUC6dqVZd2+tuper2K9tnVRdH1IMvR5nvfms77LJ2DhZzdP7Xf/sKRafUXlOYvAlgqFUMuLc7p+ZVU3ry7n42S/BJnvQ35ipo5L4Kx1Rm81NK5yjiLfvG21+LX6txVLS643q1hxZK9ma+jKyoLeubbUterz3t68MncViA9nEjjv/XmWwlqsWnl9mS02bLzajFWrrWixXFBBTRXiWMvzJV27sqo714+pfzMF8fn5YWYWowiMTMDiNfuckp3H+WMIq4PXlxbdcW89aqlQjLS2VNbtayfHb/a8hbpyZLuKjHIErH70vy6W0zQWw/YitmbTrjckPWJGYw7G/KsaOYVmEgIIIIAAAggggAACCCBgAvaEchRF7mZUMZDryj8rM+ZzmOyqGEfgiMBJ8RcEBfc6K/+UfRxFUmxPOqU/aTzbBaL2RaKTMvTLMURglAJpDxX+wpFdLLIK170yJYjSK6L+Mqibm7t2C13LYywhbBm7vweZuwu5pbjYib3b3vv5YkuXrn0iC3U6GduUNDRcBt2fLXYjBS6Gre6Vq3utoYr92k8XRffCYwzmZN38i0BWwJr7q3gAACAASURBVMLPjg1cPLtjAutVKonQOEr6vgqUOX7ILmzj/ovQFdS9ifg86QLTvvus/PZrday9+tJ6yXQ9ZcZ2Hnf0+GHat3fS4+m8yzdN+9PqWx+R2XLb9KL1N2jHDy5uQxUCe1mQT32yqs/LD09OzVwEziCQCTIb9dcX7HDAxa+rg+0FK0l/QsV+q3IL9kvEfATOLmDx6mtUH7s+/Oyz73vQ1uR6nss+EXL21XflQIOVLg4+IIAAAggggAACCCCAwOAC6QV7f1HeFrQzmln7yW7fsNs2ix7DGkxAetsNbje6/dE55bZ7T+5Gqc20X/tsV5fYbxOw1yhCr0DsHt3zwZpcvD82XtMY7hvK7ovRu6acz30zylmGSZdSwELFh1UnWm1a6BoIuqEbT6paF1qWMC/GstN8ZqNSzeY9qjzJZ/oFfPCmDQctTJLfQO76fDrfjiSKViefFEcnzZt+KbZgCgR8/Lqi2s1S+3U19Kgr1CnAoIgTLWCxag1Tkio2qTxt3I1FYdJYxTV6LcjeRlGwxq9pfXzihiVZnZiEmQiMQ8BCzzXEskOF2OLVGm7b/30aXBGz49gd5NlHwMVqpqGVhaGP4YJrZJVkYMfCg1S9fVZ37GwarBxLwwwEEEAAAQQQQAABBBDoL5A5Xel7cp1J2z/jIVL0vkdgiEXHnXRcmzzucvv83T4d10b0DRhfipEOk1dMJ09KFwr2lt6k4VV6SbQ9GOlKyQyBvgL+e9b5XnTGbGGb7654uhtOSb/TyRN6J94w7bdeW8lAT0l1l6ZftuO9lNV/7aS4KIEkTny0+KhOSpPcLLXY6Lph2p0ov+CDpMlf8viplqcv6PGpTjlnHAW2ooytwJlmRqfc5NzFpr+8tgWdrUj2a/LZHzvkbngy0YdB9j0BJyRn1iQK+J04iWXrLZOP1Mx5kZ/kkma2JTgpfn26roV7Vza6z351o8uRnLzAVNU9FggWl/Zj/ya/yedkXjLfxq2HoAEDZ8BknowhAqcScIHqgy2JWssniWIbS87h3NDFr+/PImdtPhs/a6q+x77QDKdRoBO5Vvqg3dOg9dDW7n3YYnmgawenE6DByuncWAoBBBBAAAEEEEAAAQQyp+ButK9I9ylQ3+QkuHgBu2DSOTu9+PIMXAJX8HZqf93HX553n2273LZ1LiW1F2AEgXMX6Fc/JnHqL+VbDPt4PnNRu1bd9eEMWY8qnzMUgUUvXKA7CuzZPesA3X4zz+p1J8ovs6XxFXl+igmbOshGTViRBzuQm6BCj8n4mGxd41Z3vymphX1z174gLr9jMu27MAkQGEYgjbOeujI5XrB80vk2iJPm2vm5n3O8nvPq8rd5VqdOE+7xZfW1rjt2SM/dYnceN6v7je2aToGjMeyapdjkIGliZQ/OJOdvaTduA23o0XwHWoxECAwp0Im0zoFEEr521JseRXRmDZn7YMlpsDKYE6kQQAABBBBAAAEEEEAgV8BuQA3xM+oTHH9W5YdDFGXgpGcp8zjLNcgGnKXsPv9R5GF5nZvF0QL7KXZx03VjakN3wTOJXz/fb3LX8MSZXSn5gMDpBLLfDR9v6bTsrCRzf5PJz/HD063a53mWpVkWgZMEOhFaVOA6/C8pjq3Rim80eNLSmXmdjDITGUVg1AJWCXeCzcbs144Wgjju/Po0naSjLgj5TYTAlO1gfwyR2mU/JuN20ymJ6uQ4eCKQKQQCxwr4uG3f5G83eJ2y7+axW8iMWRGwWLXfbGT6aa6hijVWCax/oKSPoFnZbrZjBgWSLonbwezaB2YDe4ybTIOVMeKSNQIIIIAAAggggAACsySQXDBKtsiP++HA23lOJzoDl2eQhNNYZr9d01x2vw1DD22jj4/MzgVPj+OHA6xoiKQD5EYSBIYU8AHohydF+pBZkxyBcQu4i58Wu/brG7sO84TpuAtI/giYQKd+9R5+inuZlTu88FP80KdkiMAkCyRNVdolPP5QuZ2EEQQuUsCHqHvgwDe0cmd5SW8VF1k21o1Ar4DFq4/Z3qOD2PVqZYcY/ri3N0VvbnxGYDIELFLtrVRu6IoUKx7klUCnDHEarEzGfqcUCCCAAAIIIIAAAghMhUAcuMv17ozFxjqn5VNRfAp5aQROOkP2p9t+2AflpKz6LMpsBIYW6Ik3f+HT5ZM+npe8yjxJ2JN86NWxAALjFrAYteYpxYKNub7Q02MHonfc9uQ/GoHO0W7SK5B7PUX7ptNo1kEuCIxEwKrVrgOHTq6BazRYUCD/Sx3c0WFsUgWy4Zwdn9TyUq7LK5Ae5TqAo1Vx2r1K5rb/5ZViyydeoPfwILZGKp3Di57mr+2YH8V20WBlFIrkgQACCCCAAAIIIIDAjAu4C0TuxMWa19vZil20t6lcOprxXT9jm5eefbef9E8iOPNxxraXzZkVgU5NazGcveg5K1vIdsyygEVtIWi/iIJDh1ne2TO6bf6IN7bmV/ZaQY6AZ3RPz8BmpYe62S1JJmWPHXISZRdgHIEJEnD1rYWsb/NK+E7Q3qEoXqA3LNOQTWf7T72p/NIMEZg8gfb1B9daxX/yvQSNp7y+D87x5E6uCCCAAAIIIIAAAgggMOMC/sRlxjeTzZshgeRCUTtyuW40Q/t29jeFcJ39fTyrW5i8/9wimCie1X0829tlDbYDBRbICgbrDn22Qdi6KRRIOgbKezZ6CjeGIiOAAAIIIIDATAnQYGWmdicbgwACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggMAMCLhXUqSvpbCn/flBAAEEEJg5ARqszNwuZYMQQAABBBBAAAEEEEAAAQQQQAABBBCYbAHXWcVkF5HSIYAAAggggMAECMSuoUrSWCXmtcQTsEcoAgIIIDBaARqsjNaT3BBAAAEEEEAAAQQQQAABBBBAAAEEEECgrwCvpuhLRAIEEEAAAQQQQAABBBBAYMYFaLAy4zuYzUMAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEBgmgSsZxVeAjRNe4yyIoAAAqcToMHK6dxYCgEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQOCUAjRYOSUciyGAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgicToAGK6dzYykEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQACBUwrQYOWUcCyGAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIBAvkCQTvbD/FRMReAyC9Bg5TLvfbYdAQQQQAABBBBAAIFTCQQS59mnkmMhBBBAAAEEEEAAAQQQQAABBBBAAIHLIOAvnvnhZdhmthGB4QVKwy/CEggggAACCCCAAAIIIHBZBYIgkPtVMlTASfdljQW2GwEEEEAAAQQQQAABBBBAAAEEEECgn0Agxf3SMB+ByytADyuXd9+z5QgggAACCCCAAAIIDCeQ0zYlZ9JweZIaAQQQQAABBBBAAAEEEEAAAQQQQACBmRTwV878cCY3ko1C4EwCNFg5Ex8LI4AAAggggAACCCBw2QV4PdBljwC2HwEEEEAAAQQQQAABBBBAAAEEEEAAAQQQOI0ADVZOo8YyCCCAAAIIIIAAAghcMgF7DoRnQS7ZTmdzEUAAAQQQQAABBBBAAAEEEEAAAQQQQACBMQrQYGWMuGSNAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgggcFSABitHTZiCAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgggMEYBGqyMEZesEUAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBI4K0GDlqAlTEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBMYoQIOVMeKSNQIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggMBRARqsHDVhCgIIIIAAAggggAACCCCAwKURiC/NlrKh0y4QKInWYNo3hPIjgAACCCCAwAUJcCxxQfCsFgEELrFA9poD53KXOBDY9BMEaLByAg6zEEAAAQQQQAABBBBAAAEEZkPALhHF2etEsRSnt/9nYwvZisshwAXOy7Gf2UoEEEAAAQRGJxDHyVFvHNhxBMcSo5MlJwQQQKCfQNpMMHstot8izEfgggWOHClkLqZlRkdaShqsjJSTzBBAAAEEEEAAAQQQQAABBCZfwE6/XROWzHDyS00JL7uAv2xkQz9+2U3YfgQQQAABBBAYRMDfK40DKWm4MshSpEEAAQQQGFbAX2nIX47zuHwXpk6yQHIMEcsawHY/CTa6UtNgZXSW5IQAAggggAACCCCAAAIIIDDRAlwcmujdQ+EGECCGB0AiCQIIIIAAAggggAACCCAwAQK+uSCPHEzAzqAIEyxAg5UJ3jkUDQEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQmEUBGqzM4l5lmxBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAgQkWoMHKBO8cioYAAggggAACCCCAAAIIIDAGAfdWFV6tMgZZskQAAQQQQAABBBBAAAEEEEAAAQQQQGBgARqsDExFQgQQQAABBBBAAAEEEEAAgekXCER7lenfi2wBAggggAACCCCAAAIIIIAAAggggMD0C9BgZfr3IVuAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAghMlQANVqZqd1FYBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIHJFvCvIg4UJ329TnZxKR0CFyRAg5ULgme1CCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIzKhD7Riszun1sFgIjEKDByggQyQIBBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIFuARqtdHvwCYFuARqsdHvwCQEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQGDMAjRYGTMw2SOAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgh0C9BgpduDTwgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAJjFqDBypiByR4BBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEECgW4AGK90efEIAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBAYswANVsYMTPYIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAAC3QI0WOn24BMCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIDAmAVosDJmYLJHAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQ6BagwUq3B58QQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEExixAg5UxA5M9AggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAQLcADVa6PfiEAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCMyMQBDPzKawIQgggAACCCAwYwI0WDlph9pB3HEHcifNOylP5iGAAALTKECdN417jTIjgAACCCCAAAKTJZB3fs1x5mTtI0qDAAIIIIAAAjMhEEiy394fGq70ivAZAQSOF8g7gTs+NXMQmA4B4noS9xMNVtxeyVwh86PZeO2d5uf56e08kl3sZw+3w0+3VP468vPKn5qfA1MnR6B7v0WTU7BJK4lBZX/b5esWtMmRYvdfOwkjJ7TO65nljTEbQMC+r5fgO0tMDBALk5fkaM14EWUcJniGSXsR28I6EUAAAQSyArl/Z3xVnp2ZnZadns2McQQuQmCo2CR4L2IXsc4TBAjJE3CYhcDlE8g2XKGxyij2f/YgYRT5kQcCkyzg432Sy0jZLpeAj8meA96ej5fLZDa2tjQbmzGKrchrb5yT7wBBP2BOOZmPalJ+CfKnjmqd5DMuge791v1pXOuc9XwLuc8XzPpWs33nJtD+O1HIf5Tl3AoyhhXZtlENjQH2/LNs78Z2vF7Evm2XYgCATFricAAvkiCAAAITKmDVeaZKb5cyb1p7JiMITLoAATzpe+jSlY+QvHS7nA1GAIHzFKCSPU9t1nXRAsT7Re8B1t8rYDGZc3GYUO2FmrrPNFjJ7jKLcX/jJi+4/Ty/TFearg8+xRDDsy4/xKpIOh0CPt5s2A6PdKT9eTo25VxKeaxJ0Plee1MrUDZ9dvxcCjuJK+kgdIWct8raTWLxJ6VM3imW4nQ8MNpZ6M/Mb1uvdSd0eufweVIFbF9mYtSK6eLUjYy30D6Mzhw2ltGZMxnvtpI7AmcXINDPbkgOFyGQ1PUD1vjZujw7fhEFZ52XUOCEOCUeL2E8sMkIIHCxAr5OzpaCyjirwfjkC2SjmOid/P1FCXsFLIJ7I7f3c+8yfEbgIgTOGpdnXf4itnn210mDlew+Tm/etG/a9Myzj3YD8sj8vHo8u+yw46POr71+ezXFLNw1bW/QbI6kR7axf5tIlAad1aHWYYOvS/1wNhVGv1X+5qz5pt+xwL4OOHZZex6b2EVjH9LY7FqADx0B72Ox5r+/xlaUXJerDtQLz2ZdbFvXFTcdHcYuUKBrv/TEpyuWTbO/L+OsEzOFyIyeqGLp7KcrpvzEdB4DBGZLwAe4Df24fQP872xtLVszewI+apP4tU8Wu/ZHJq3J04Hfcp+iu6L3cxkicF4CPnJ7AvS8Vs96EEAAgUsvYPWwr4v90FB8veyHlx4KgEkRyAvTnLJZMqI3B4ZJFyTQL3DtYralGefFwQvadFY78wL9ort9mEGlPNGxQIMVt3syUdp7JOFn2dDaDWR3p/8WdE1ME/h5Pr3V99l0Np797L4x6YSu6T6DIYbZdftxl2d6gzQ77azrGqJYJB1AIOrc6I5qsaJKrOZBrMhuJJYDzS0FKi1JhfmgJ34GyPsyJfExnm5z3JJi86zGatQS46AolRYDlZalYC5IbtTOZhuCofa8VQmuWugxdBNHXV/YOuweRjq0groGWVN6XByHUtyKFdek+k4s2WfblrI0vx6oWA4UlAKpMGrIoXbx6RMfV2z7+5b+0KDOS0zo0L5vFpf1WNFerLAhhZFk9WHR/31ZOm5Hn3GbMtm6qjbzve86HvJ1T/bPnJ+WV4RMvnmzmYbA1Ai4OE8Dul2ZTk3pKSgCTqBTJdtY51PXTIt1H+rezdfzPYv42QwRGJ+A9caZCTw/2huTvZ/HVyByRuD0Apn69dhMiOVjaZhxkQJW+foK+CLLwboRGFLA6tSeepVTuSENSX6OApl61setrd3G3awZfLX9OeqyqnMUyMZvutrcuten4zDjHHfO2VZFg5Vev3YFLYVx576iq7OzgW3psgHfm4//bMukN4janZvYzT3fU0b7xuwgmflMTx66J/sz23FsOdObVJwTnOx5LnPT3e9u3Iex4qa0/zLS0+8jPfymqai4q5XNSDffW9Z7P17T0magoHwuJZu+lfivki+5ff9aseqvYz29H+qH73fVakjzy6Gu3inqw59vaG2jIC0ESWMJ92X3C1/CofmZmW+EYB5WV8yN3sJunCf1Y9K4w63BGnSUkhvoo1/jmHO0hgBVqfY80m/+eUthrSSVmiquVfTTv72lG3cWNb86G3HW/hNjsWIffLwY8bh76hjzbpzF7F3vcOm+ipuxwr1Y3/4h1ItnNVXrFc0vlXXzgwXd/nhB19/LthQZnYYLE6tL/Hmwff1tov9s94vSOGqfZOTFVyYDV127f0ZXTnJC4HwF0to0/S64v4m+N8dMrJ9vmVgbAgMIuJhN49cnt4b3Ppatbvfnudl6OpaaYai5UtEvxRCBixPw5zxpKLvjj2y8+pKl6dzxlD/O9fMYIjApAhbHvlr2dXE2nv28SSkv5UDgOIFsLGdj+Lj0TEfgogT89Yq0zm0f+2avj1kM2y918EXtJdabJ5A9Bs7Ot8uBdm0ue00ije+ui3nZZRhH4IIE/DVkv/r2tWRf56bXnbum+8QMJ1bg8jZY8QcPmQMH1wtDI1azJjWtMi5K5YVAhWKmIyyr0O2mZCNWVJfCglRckErW44X/8b1kWDp72r4lyX59Eqv8S1Lsnrb3N2Z9QXwmNsz+RchOP2HcL2LDULJeOvxNYffl9PNtmxbtSf9MuU7IllnjF3CVrMWMxU9D2nsd64e/tPTbf/pOjeC1rt8t6ud/d1ubN1Y1vxqrVPYBNf6yTc0afHz7AvuTh1A6eBPp/heR/u2fv1LtMNTqZqCPfrWq6+8sa2VlQcV5v9AlG2bNzKuZ1htpnWU9L0RFac4akuSFnC2fN/04Rkvv90uUrCvcj7W7G6vZlJbWAy1vBJpbmbL6yf1tSHpF2noU6T//v+9V3bPXAdW1ePNQa1fntXZlQfO2XVP848PFb4X7e1hN/875G1Vzct+ngJ6gJmZP+/3lDiusx6mq9M2ndX31xQ/aq2xraaWsn/76usqrt3X9vdWxXUyxV2PZr/s7V08aZ9qJcGRfd4sbaxiX1jXu2KUVK2pKzUZy0mydE9kxmTXYDIqBO06bGGQKgsBZBfzfxvQ70v7bml40yn4+66pYHoEzC7g/LHY1M21saAcIdn6dOVBwjVcsXTaGXT3e01jFL3PmQpEBAgMKpDHnzr99/Nl5uMWrv07ks2ofREkFrp14FYaTLmBxa7Ht4zutiye92JTvsghkAzPdZj/JD22yjWc/+/rYDy8LF9s5OQI+HrPHv5lYdccVvrR2zODT27EwxxBehuFFCvh7lv68zR8f+Fi1sE3rWBsStxe5s1h3roDFqq+DLY4tXtP4dbHrjxEsfm22+2fIe1e5K2bieQlc3gYrPnhTabtJa08c776M9Gq7pZaaWlwt68Y7JS2vF1zvAu7mSZimexXp5ZNIYflAm+/M6cbdZZUW0kztYkc9VrgT682LSPs7sQK7+Ws/6U2ZYE3avFvUymagkt2BaTf1StP5xNmPA4y7gyO//r1YT36IVKvE7uaQHRvZq2UKcy0trQW6+UFZ5SsFeuoYwHXsSdLK1lWwaaXbqsTaf93Qi8f7qkZvFcVF3flgVU17tU3vhbSxF3CKV5B6NirSzqu6nj58q1o11Hol0PqtWLV6Q2G8ILv36f6STfGmnqrott2+oUFLCrcjvXwQae8gViuKXMODpSstvfPhksprPRXnqVaYPn1r9VQzVuNFpPvfR/r+u6eqVBq6+f6K3v/pht798YLmFu0VOhe9XzJH7f0CxGKtKR3uxXrxeE+V3VhxoarVZlWVvZq78d4ms2xHw9nO8jxG2kW2bbV9WI21bfGyHatRTXrKKV1pavPdOW3cHUO3POexkTO4DtdIJP074xqLNGPtvDzUi0fb2jl4o+WVed14b17VytXkQL+9o0eH4bK0xjKtWM3dWC+eRKrtxWq2IkXFquYWW3r3w00tXbUGw4FrGNzairX1KtLWVuwOk4pzsRZWGrp+e0GLG0UF1vCWHwSmWiC54d/+O2zHd1HS2Lzd4N0aac1J1gjQGpHyg8BECKSHR+5YoBkrricPdNhxULvhilXRdprrGhomvUNaLBfmMg0Os4dZE7FhFGLmBdJzQ1fvtmL3YJF/cMnVu+l5kbvgab2pWMyWAxWsd1N7jayvhzkEmflQmfgN9PWnxXR6nO/qXzuOaKaNCe0ioD2sZrHrT82I3YnftbNfwPT4N43bdvxab9N2vmg98drDTRa75TR+idvZD4tp2EJf39qxgh1DWF1rMWvHwo3OtVV3i8euZVrv0aWk/i3YA132mYYr07CnZ7OMFrd2HdcerrdzNotfe72Em5Y2AvCNVEpp3WsPi9kD03Y+Z/Ww1ds2pE6ezRiZ5K3KHjOkda473k3fVNF1DcLq2fS6g3vg0Y6DrU626fxMvAANVvxNt3qsw9eRvvss1FfffaMwqOv23U0tFD/Q0nysOAiSg5FQqryI9N2fQv3pt98pWnyjn/36hlZWfqy1a3Y0HbjK3no22XsS6evfN/Tohy3FjUVFrpuVSMF8U/O3Kvrr//mu3l9eUclOHEdR0dsX1/3xiWU9Fmzdi/T7f9zX9puKIjuQsgP+0p7mV5u6+d6i/m7xY11djFWmp44J+qIm+8luVhRCqdia11y8oWa0p6J9juZUiAP3hPoEFXoyi2LfB/9jr6EIreFYWYVwSaVYKrrH+ucU2oGZfQVH8R3065uaodvydmntoPXgRazP/72mx8+eqlo/VHkl0DsflbSy/omuLs8lTmf5A+/3i11Ia0ivHkT69F9e6l9/80ft79f10c839XeH72n16se6eqOkovW2cJ4/vnxutfYhO8HGTyiPzY7se2q/q24YByUXbyWVu4+LTsjmPDf3VOuyvzP224wVHca6/3moB9+90d7WvuJmoLX3G/r5/7iujbs3Oyczp1oRC41EwIewDf1vKJVai+63GC6qFC0oCMvJVcGRrDQ/EzsZjiqxtp9E+uxf3+jN04oOa3uKy3taWm/p//5//ruW1qy7q1hRVXr7INLXn4X65pt7ihWovFzX1TuR/urXt/Xuwk2VF/PXw1QEpkoge+HT/jbajf/DWIf7sepVKSxKpdVAS5vS0nL6mMhUbSCFnTkBi1nXuCp5SMPq9XA31sFOrOqBVK/GatjDGna8aPFblpYshq8EWlwPVF5LbvzbfHf87Y+J/HDmwNigiROw41i7WH8ohQexa0Bb2Yvdgz6Nf1dJnAAAIABJREFUutSym6VFqViW5pYD1wPkqsXvWtJL7cU3qJ84UQp0UQL+GMKuaaQX7Fv7sSye63bz1GJ4KdDKupJX01o5faOriyoz60UgFXANVfzxhF1bqEn1/VjVw6T3XTs9Xb0eaHnNjiU4BiZwLl7AN65y9W1N7vi3ZjGb1rt2DGEPmLoe2cpyPSzbA8Pu94oULGQav3Lce/E79JKVIHnIPbkWb+dvjZ3YPXBZrSTXHez4Ny7I3acsLQZaWJWL3ZUrBRWW0vM336ClHb92kbH94ZKJsrnnKpC5BmHXiyM71t1L6t/aQaxGQ+4en4VjPCeVlgMtrEmrVwpaWpOKS2njKwtXQvZcd92wK7u8DVYyUvZ6H+td5dXDSF/+55Y+/+aBykuhiiqo9Vdpq8Ny+vRNU3ryXahP//W+/vyHB4qXn2vjVkmBdV1iP1ZP2wWQulR5E+vJd/v66k8vVTsoKbRmt0GkYK6u+Morrd2a1+b1JS0tFJOnHc76ZbF120lqQ6q+iPXVH0J9/ttn2t6yBiuR4ihWq/BWi1ea+uDgin78q3e1/s6incPyMwkC/kailcXGrZV2QyrECwoiu5EYKbBHDNwR8iQUeALL0PsdMsf0pxjLNRwoxPMqKFAQ2Tuzigrcp8v1x8pYEqp0zAZ2YNqUKm9j3f9yV9/de679w30trgU6rM/rl3/3nq7ennMtVL3paYd2c8JWGVVj7W3F2nnd0MFOqDAsa3+noa1Xu9rd2dfG1Y2Tr6elDSesznU//p3ytnG9sdCvsNm80uUDK6j7tfxsJTajo3ckS5vlV22Ny1RQbM3Xw2onztI0R5adlgn+oqjbgVJck57da+rrT1/q9YstqRXo2k5T1z+el+Kbw++HaXGYpnJm95kvt72aJyzJ1YdxWUFUUlH2O4Yr2NmYtzaZe0lDta8/faGn93d1cPhGWnyrjdux/uv/8Te6G867m5xxJdbL+5G+/uMbff7FQ8WKtbje0LuVkt77yapuNa9rLrY6nB8EplQg/W64p0jt+N3dbJIOn0V68jDSkwcH2t0+VFja1do70id/d1t37l7RPI1WpnSHz0CxLWbTC0V2/myvl6u+jvT6caSn9yK9eLqj1y92tLN9oEqtqqBQUHEu0uJyrM3rC3rn/Wu6+6MbuvPhgtavBiraaxLTG1DuadMZILqYTeAv4UDuPn6trrXecPdi7TyN9PxhpKcPWnrx7I22t/ZUOaiq3qiqOBeovFjU0npJN+5s6s77m3r3wzXd/bCguU3rcSVz85RdMNAuINEZBbLH1JaV1cdpTxTWACs6lGr2GuTvIz1+sKft3W1pfk/X7pb1yV+9p/d/suZuRNl5P0/4n3FfsPjpBfzxr11ecb2pJNfareHrs/uRHt6ru+tB1XpFWtnVz379jj785KauXLXH+0+/WpZE4EwCFrcWs9awyh4o2I218yLSo3uRnj060Kvn29p+c6BqtaqoFapQLKgwH+rK9WXdvLuhdz+8rnc/mNfmrYLKV6TCUtCph4nrM+0aFu4j4I9/7ZjB4ncv1uGrWK+eRnr8Q6Tnj3f0+tWW9nYPVLcWV4o1v1B2jbSv3lrW7fc29N5H13Xng5JWrhVUWA7cK4OsF2fq5D72zB6NgI/hlmQdRET7sfaeRXr2INLThwd69viN9nfqqh7W1Wg2VbD3yJdbWlqf09Xba7r7wabe/3hDt+4WtLiZPnxgl76t7qX+Hc0+GnEul7fBSnqxzU7W7CC5+ibWi/uRHn93oN3XTV19p6T5+bLm0+63rY2ANR4I30Z6fs8OpLfdk4/luaIWygtatgtu2craetRqSfXDgqqVQLVqyTrNUKzQvZanWW/p5Q8VbX0Y6tpGQcXl4159kc305L3vymjdeR3Gevs00jefvdXO66ZqVStb0TVYadqN+lKg+mGgqFVy3Y6P/ds5+CZ0EZ68tSOaO0TZjqzRlvU/PbvfTx546CtJd3M8m7HlkMy0p8tju7JgNxotyZGy+4ln6f5i4BJPRkJPlfcHxptm07h0BQWxNVkxx0yDlUnYomxZjymPJcnb3GOSDzY5a9WI1Tooqb4XqF4tqBgU1LCnD8MRrdW+K9Y4xOI4qZoUF5qKgrrrySooBO7mxly5kJzA5W2BLe8a2MRqbNvrdyI1VdfyRklXrtuBdVqf2tfEetfx25eXl02z/JpyPT/sPIl0UI1dT1gbN+e1smFd2FsG1hrG9HN2UnZyZv/Yd9b2lt1o7yyXFsImDUvqV+23Y9jl/XJnGaZteNrvNA2l5mHRNcq0p6rtSZPqQaRWcp4z/DaepWy5y54GOjejo1WuS+Z3SnZn2DS/3uz0/HzHPtX2mTv+SNfki+eKntSFFqNWUhet9t30hWqP+AlnGNoFnjh5am73daz9N/ZEc1HVujRXCrR586oWV1aSJ/KtvE1p902sN89rOrRXG6ql8oo0t7Cg1Y11zc0Xku/2GYrEogicu4CvGtLvYdJIJelVxS4e7T+L9PWfI3375Z4e33+q+mFDYXlLNz8p6va7V3Tz6rrKC+krKUb5/Tx3CFY4VQI+Xq0et/be9VjRbux6wfr+y1D3v6no2cMt7e7uqVo5VK1WU73ZcA1WgmKsUinSy8WKnnxb0b2/7OjdD2/q47+6rnc+Lmj9VkGFRfvrww3U4WMi+cs9/HKXYQmLKPtJK0o7rnDXfaynN6n5OnI9BH77RVMP773U1suKKpWK6vW6mq2mmlFL7pykVNBcuahn37X04Nqu7ry/rp/88q5+9Ms5XX23oOKVJP/2a4LStTJAYOQCvh7259D22dXJsSJ3nTLW24eRfvgi1Gd/fKI3Lys6bBwonH+ld3+6pOvXruv9j1fdazdpIDjyvUOGgwikMWxJ3TN4duPJjifsqeiXsR5+F+rzTxt6/OCx9rb31IoOFV95rRt3VvXeBzeT60d+PZYXx8Feg+G4BdJjCHezfz/W4aNIj76N9PVfqnrycEtvt3Z1UDlUo95Qs9lUFNnrjO26ZqCXTxp68l1F9z7f0oc/uqkPf3Zd7/20pGsfJMe/7lVtxPK49+DlzT8Tu+6e5ptYz74Lde+LSPe+e6tXz3e0u3Ogw6o11q4rtAelVVCpFKo0F+nFD1U9/GJP399+rZ/88o4+/uWm7v6koJId/9orVuz2UyG9IWbKxPLljbVxbbnFsPXcam8NOYhVfxrpiat/D/XkwWu9frmj3d0DtZqxWmHUjmHr8r5YDvTk+wM9/PKtHv/opn70s5v66BfzuvFeUaXVTG9X4yo7+Z5a4HI2WPEHynbDs2GtY2Ptvoj08kGs7ZdSWJvX4tyirqyta3lZsoZZdhXNWnHtP4j04kFVu1stFbWiKyvSlfUNFaxb+t6K2Z1ELkrhsorBkuZcW4NIzXhejfquXt2r6tWDA3340RUtLCTvNezek8ndndie0k8zt1Ukl/QsZbpCW4/9pH+Iwp1Ybx5FenJvV2F9XguFVfekfzNuKI4bKsY1FeIlBVH6R2XAg32/mrzN7J2WlqgzyF1HMtHnm26CW8bll7tMJ8v8MZ9bb4n8dL9U5g/q0OsxaMsnzSNdlV9D75r9GvsNXVsU2+U9P538AsXpXeKj981t7bawzyBp2OJDpCfL9ONZS5zJ1WeVmXTsun3azoa5pWxyz6RsbgOMJxm7hj1pXpZftrGCuSU9qhTdDVw3bqa2S7M3aQdYW26SQTbCb7/PwG+0n+6Hfnry1Xap/Sz7kMy2KZmEPs+Bhz3LWteVLXsV1aoKrRWVokBzUaCiGVnf1z3JB15NT8L2PikFWl0PdP3mFd26vekOMG69s6TrNze0urakYl5nD7avLMzt1SKH0ttHkf7wTy9UC7Z09+N1/eRXd7W4ZH14p0LZ/ZpX/jQ/O/m0uvPb/2jp+ZunKm809MnfvKOPFlZVmEvjqL0dJ7vb3GRf2Qr9SpMp7Y/tvAYcSRd3qW3csvXDk7LILufT+SL5z2cZ+pgJ11SID+1FLkmPY/FcUrxByniW9R+7rK3Y/3b+hvrkHYK0gDawn86MdEIyw9cr3Ul8/mnS9k7xdbFvsu3nDzJMy9OVNK9wfpolPFLorqXdbDuRzBTXXSR0qWyGLZ9soUklO647i76fssXxibPFSrO17651mXuwFatVKasYFTUXHGppMdKPPvlY6xvF5KTX0rdiVbaTV0wUokUFpZaWFkvavLapqzeuqpR33OXXzRCBiRDwX4zsl6HzXXSNN61nFetOeivW9oNIX/0p1Bef2Q3UPW2/bagQSWGppdJCy3V3ahea3KFeem7S7+s/EQwUYroF0jB2fzdcA99Y0U6st/ciffkfob7486EePXyj3d2qO5ieKy5qvriiRWtUWAgURaGajaaq1ab2t2p683hbr35oavdtXZXaLX2ksq6+U1Awn/ZW0fN1mW68cZU+RfJVzLhWM7X5Goz/TY9z7KNd6KxZT7SRHv051Kf/HOn7r5/r1ZsdNZpSqVjWXGlBSyXr/dZ6x5W76BlWIm3vNLTzoq6tx6/19mlLB/s39NNwTXc/KSYN2/POWabWj4JPpEB6zuoO1X09aefD9qT/Vqxn34b64bNIX/5hV999v6N6PVCoghqlppZWGqrtJufQ7jUVfvmJ3FAKNRsCVun2BJrFsE22HzuesGvxO7EOHkXu5uk3f4701V+2tb1dVathTx1Fam0fqr4bKbCHp+wU2x//ptkwQGA8At3x687Z0tcIVp/G+uEPkb74Q6ivvnyund2amqH1qFLWfHlJZTuGSO/hhHGs+n5Dr7Zrev14W3tPQu29quqwclWfFNfd8W/JHrazQxV+EBiXgN37tOsN27Gefhnqy9+G+vJPe3ry9IXq9aarq0ulVS0Ur2iuXFYhKLm6ulmv6+DgUDsvq3rx8I12XrS0t91QM7ypu78ouh5YrKdMV9P7r4wfjmtbyPcSCPQEkXtgOZaaUv15pPufhfr8PyJ9/dULbW3tqd5oKgjmVS7Pa6FUVqFk8RsojFpqHNbdNYrtF4faffFKOy+bOjzY1M+1oZvvFjS3HvCazAmNqMvZYMXvDDtgbsrdpHzzNNbrZy1VDxvuuHp+YU4rawvJu+LtoNieJqvE+ubzSE8evdZhre4eA7t+65rWN+1lxpmLbP643Bq52IWOOFIrCrWysOzeY1gIW6rW5/X80Z6e3dtV7e/XNb/pF/KFs2EyLTvn6JT0eowlt+90JFVexHr2JNbO3oFaUVlrC6sqBwvaae0qUHLw5Prv8mvoqQuyJRjvePfWWDGO/JxUNr9AFqj3pKidYVei9lQ3csKs7oT+U88CaRltas8cv8DgQ8vA8kt/k4+x4jjzaydqftvbOVtKC1R/83GYwmQzO8UWZBdvlyct40nZ2XKZ+ZnRbC79x/36XSuI/smTldraMo2W/GI9ZfKThxoOm4dPb0Xy4z0rzM6yJGP9sRW4xmzWE4017LHGT8kTAtn9deoypPTWGruwHOvm+wX97HBTWvxEzXqoWx8s6YOfXdGVDXvhoCXO+UkvdsTVWM/vR/rXf/xC9eJL/Zfqu7p+Z10371xRYO86K6TvjvVZ9PpaPva0pR3A2xM+e7F+/6+Pdf/pF1p/J9LCaqA7765ocdXHitXzx5Qpuw5Xvj57qk82Pruu73o2y5xtccv4fH1aP/QZ+vn+82mHmXxcAzqV3N8X+15lG4KNJGaGLaOzsQJ2CunHejnaXzpLcHRmbh4nF8cysno4c4PEL+AL4T+fNPRlccvkLWjT3IaelEtnXjYLW6z9d8Rm+N9OcteAL7tMZ1b+mE/ry22p/Hh2GEn1SqyDXaleb7kT4UIh0NLyvD76+K5W1pKMbP12Y97S7R9YQyhpbk5auTKvqzfWtXY17fnIrze/VExF4GIELGBdbOYHqH9CxL373J6Ktiedvgr159+H+vQ/H+rVy7pq1ViFaF4l99jdngq2UJheELqYrWKtl1nAt8OMYnfDf/tppC//GOo3//uNnr14qcPqoXuSdHE+0JWNJW1urmptbU3W60St2tD+XkU7O/va3w9VqzX19Om+tqtbqjT3FQcfaWV5SfNX7VQmcD2fWhtpfvoJWP3if/ulvWzzzcUffCQ3OX0DQesZ6Mk3kX7zT9v68o/PVDmsucbWRWtEv7ao9SuLWl1f0sLispqtUNXDlg726tp+e6Bqvantt4d6+3ZHe9WXioofaX3jHa3eKrgebN2h32WjZnvHKJAeTGRC2a3MHcPbtSG517K1Xkf64S+RPv9dQ9989lhPH79VFJYVaMHVEMV4XkE053pcdl+L9jHKGItO1gj0CLhjX4s9i1u7SJ5eh99/FOmzfw/1xadv9ej+tnZ27B1BBZUCu3ZeVCh7zXAxOXe1PP33oSd/PiIwWoHOOVzSO1tyw7/51urbUP/5m4q+/uKhdg92XUjOz5e0ujav9c2y1teuaL68oDCMtbdX1d7eofb2Yh0cVPXq5b4Oa/vaqbxWXPiRfvFfr2lzrqCi3U/KXMof7baQ26UR6P37bjf605v9dj9z/2mkv/w+1J9+91QPH71SGNU1Xy5oaWlBq+tzWruyoqWlFRWDshr1lvZ2K9rZlvb27cGDmr7+6rm2dre1X9/R/1z7qd790Bp49+h2vjo9M/iIwJAC7WOG5M0o4X6sB1+H+v2/1/XZb+/poLqnVljT3FxR6+urWt9Y0uramhYXlhTFsSr7Nfeaq53dWHuVhra2KqpUD/Rm55FU+pmC4JZulwPXC0ty7W7I8pF8rAKX83JQO+hj16q7+SZ27y5++ey1orCl+cWillfntLxWUjCXXOSwXlhab2Pd/y7W27fWEMS6IYh17dZtrV5ZTnaSPYZjF9rSa0d2XzOOQ9nLKuzu6drqkkqlgiq1pvYaZe3v1fTiyb6ePY60eKOghbLchb3OF8XX9H0uUNt60j9CNrT8nj6pqdGqK1JLN69/rJW5QNs/7CXlTO+5+jY2bmLvH7Yhws6Xsr2I5ZX9OZIgO7MznrJ1Jgw6lu7PtptfX285fH5+vh/66WcZ+l4czpCne9rAb4vPzw2tsUB678PfA3E3xHPuh/j3dAxUDp/Ir/Q4AJ/uuPlnmG6rPin73n2Ypm0vlnWwYvQ65RTNeijq/OYkOO0kz3jS9mTz9tuWTZ8dz6ZNmfx2d5J1xnqSn/jxyFJp2V0MHrNkkDb7tzRHlj9mmZMmu66zS4Hmbxb04/lA199/312AsEYiSxuBCunr2I6szMrqWgJKtbextp7HOtguaO7KYnIxzhqgZJ9ytMJ6ayuQH/cbYTFkT6ftW6PFSG9etHS4X9Rqo+Tya2eVSd9Vpqydz/ukDe+d55fx+Wfnp3lnJx0Z98vbjOz4kYSZCZYub32ZJEOPWqM6+2/QMgy9gnSBbP6922Dz/K/N87+ZdfUukpl1okn+cvlTfYPQrv1hSa1sxyzSKUcmgd+WzsxkzJK4ZJm0vWlO+txe3hL5D3Yg0dMTja2/309vEbKfM8u7uEhveNYqUmU/VqPZUCNqqbwoXb+9rjvvrmthOcnAGqtU3tqFndh1zd+Ka1pakJJ36F5TcT49XupXPuYjMEkC7u9N0mDMdyldfRbrmz+H+vLTir778qnevNlXoCUtlxdUVEmhvWe6UHI9jhVLJdc+vn89MkkbTVmmWiD9O+TqcDtWqkuNZ5HufxHpiz8d6NWrA9UaNZXnQ129tqif/Oyu7rx3RddvlXT1evLEktX326+uaetVU49+eKvH93f18s2e9nZruvfVGy0slbVx/WN9uFJUecH/fZtqNQo/EQJ258cq3aRxutW5dmzx8utQn/8u1NdfPNFBNZQKoVZWC7p1d10f/vimbt5d1ca1QCvLgZpNuVdA772J9eR+rHvfP9OzZ69UqRb07MG+vvzdY62tLujv/9dVBcVAwfxEbDiFmBkBq4DTixs2mjY2t5v97lW2e7G2H0b6/i+h/vTbXT158FI72wfuobqNlU01GoGqTeuWLecnzTpnDpMQGJFA9qQw/dtu16ytl4qa1Hwa6eE3ob7+U6SvPnuu16/2Va/FWl5YVhRGiqJIoQW6u7DTk9eISkg2CPQV8PVuK3Y9WT38MtKffnuoJw/fqFaz+y2H2thc0Acfb+qjT27r6u0lbWwErgf9sCVtv1nT1stYTx9VdO+bZ3r7+kAH+wd6+sOeFheean1tRUtri1pOr4H0LQ8JEBhUwI5/ffxWpYo1VvldqM//+EQvX2zJ+mBbWo516+6S3v3Rdfe61vVrBa2sBO62ZrVqr/Be1vNH1/Xohzf64f5jVaoL2n59qD//7r6uXJvXfOkj3VxKG20PWi7SIZAjYIel9pP8tU//5vuJYaxwL9bzr0N99vuWfvj2hSq1luwa8cpapHfeW9fPfvUjbd5c1sZm4OpTu2VU2VnW1stNPX1Y0/ffPtWrV/s6PDzQi8cH+svvn2rRNdTa0NpqsfNmBg430j1x8YPL2WDFu1uvKYfS7stYr5+G2t3eczeyFxfKWl0vu0YrrpWr9ZSyL718HOvVs30dVppqKVRQbOjaOxta2ywnrWGtsYBdG0l/XJwHkWuw0lJdSytFLdpNltKS5g4W1WjE2npZ14Pvt/TOJze0sCTFQdodXPtL0h5JcvVfWL8SG6Y3gaxdjPUQ8PRRrJcvtl33RwqaunEj0OZSoM9+SO6X2b9B8ki8ey2KuwHds5ps9rnjeeXwCe0PYzr/xK7tsnkMuH5bpJ3UL59ci3Lb4mb66ZbQj/uy+WntTPyMUw59ftn1nCZvv3w6dH5pw4DkNTa23ZmXUlg6+/XrSj937ct0XpplO2l7S9sz0oXbM7IjfgP9irLzTjnus/SL2+qHyN6X1i2SfujNot0Jho9FS9D105nQXnWa1zBlaWfZya4Tc+2Mu3eVWyab3ibY57QTDxvNVCPtVdhIJsuu6Wf94IrTU6bcdeVOPP3a7Qnawmqg+UXp5rVisoGF5PVox9UdFuP2lINdv9iyV7k9bqhVX9Jcsy61ylKUvA7LfRdS1xNLaPVnKNXsicsHkSp7cwobS26aPY1mbRNdHdtuuZJTr6Qr6CFsrzZhO25uO1n3iCX3v8e552Vp07Lp0+v13Zl3Yu7I9DNMcPXWeTVayW6jlTm1cmVIXVySrEfPMmmyri3uSdI1L/9D/hLu5DCzgEvVldQCz35yvu292+ILmi7v6jdbrCu/NLvjBj4PPz+9/p00h7WMfGOVnkx7l/PL27AnaXZWezxbB9sF9kas6kGsykFL9WZdYdzS5pVFvfvBVa1tWK8pyb60dG9eRTqsWAs0u/be0sqVBV2/s6obdxYU242h9koYQWCCBPx3xg/TQLWP7tDbvhN20dMaXN6P9O2fQn352aGe3H+j3e1Qc8Gqrm1c10J5WfVqqLfbO2rE9krICdpGinJJBHzQJUFsx172dN6rB5Eefh3pyYMdVWuBSsU5Xb81r09+dV1//etruvleQatXA5Wtd7qC3OsqqjuxDneKunb9ppbmryv6y5Ze78XafV3X4+92de/D11q7fUM3Fgs85XRJomtcm+nq2nbmQedivfWkuBvr3ueRfvhiR/u7keK4rJWVou58tKj/8g939eEni9q8XdDiWqCSHY+0pFY1Vn0n1p13Yy0vv6NCvKBHj96qcdjU4293tbr6WD/56aY25mNit+3OyNkFLJL9b3LQ7mpkO4awntm2Yj3/JnQ9q3z7+aEefLur/cOm5surunHjhjaWVvX8+aGqOzvt42WOm8++V8ihn4CL0iMniX6qNbaKKlLtcaTvPw319Wf2WrYXevOm4Rprb6ys6PrGunb2atrdP1ClYT1gHXPSa5kS1P12CPOHEfCB6uPKX8ewhlY1acdeRfGXSI++29LeTt31LryyXNJPfnlNv/z1Hf3oF0tavhpocTGQ7E5bJN3ai3W4HevOgxWtLX6srz/b0cs3z3S4+1ZPvjnQo/ffauP2TS1em3OvxnQP9fn1D1N20iLgBdI4dtcj0wfb7Wb/yweR/vKHUC+fHajZjLU8P6/N2wv6+a9v6ce/uqnbHxRUXtX/z957P8lxJOmCX6QoLbq6q1prKAoA5FDsyHtv5/b2ntmZ3d3v948+s7Oz92bFzO5ockgOSKgGWovq6tIiVZx9npmF7IYkCJIAWdVWnaIyQ3h4eES4f+GOVFrJBhnPBdymxuJqgJmZGnxtY/tBG63+CZpHJ7j15x0sLVZRnSvLZlPRv7MME/6NW2Jy/JoUeEwE8wbt8SNgVNe4/WmAB3eaaJw6CAIb2ayNjWsFXP94Ge9+WEJ2SiGbV7K5kVlTb9E71VhaJShwE19+1sLO/iE6PeofOpip1lFbKKFQNWBkVOgtaMK/X7PVvr3Hf5SAldigJSEguhr1/QCnJ210B106nUc2b6E4lUW+mJHOQQWdc6bxcIvxiwcYeS40HJjWAHOLDF0RgkwuKpPJ50pGCbo1dJDNAuUyYKTTyDVSCAYeuo0RHtzex81f1lCcUrCe1SJx703yAydR0SBELzB08XW4G6DZbCOQPA3UFhRmsoQ7+OLyNtwHn0wkWg+f65jMLHEjAk9IXhFKU9bQ4b8wrEZ8Xyoe2eHocYZ26Dip+JjMPr4X1y8xMRw/xnU6DdnRs/Hgy0kgw+XIkeeRDVCM3cxXbIF8KaoPT/mN03qCrXCc55NOkmVkXqEtLXwyTpdpft10480zTCPxiS95VFpJeBYjanMG1taM5crakQYsC2Nzs614Wwz/PEZKDh6SCY7zYWFZsbhy/OEJD0aPCJ/HbS2hiqJX43t8PaKBYoZxWWKaxEmP809knfwtWZyYJ6J3aPQR0AK9GsXtznozD7Z7HEqG6TGdZNlgSNASJhVVKVmSlztPlpspXLgeG6lYDimLHvPquUJEfKkT7o/Gi5YoTZb5QvIvV+aLb0UC7FHaNAgnryKCPbp1MYWvfS1ZRvxKT6+P9RvSivnxG/G97MoZAUFX44QvVeUpAAAgAElEQVTgvB2GSsjA8HIwvCJMJycLSlr3GM1IeD7Bh5JWnC55h7GTR0D3WOPhHQ1nFEAFKZi+BcPNAyPuAgrba1x1phfxeLLSkhdvJHmX1/zh4r3ki8nz+LmY59mv5Tzk9TEvx4xgPV5HKUfc3yT/ZAZR+eL3L/z0Ki7HdHoViT0tDZY/plGyX/F5XvPn6Bi3lcijqN1II6FTOEiELzztf5wX0+N5/GEaCTqPZaPIJC2GjnEZ+CxlE/mc46JhRPnHiUXHiM/HciKS65JOlHeYBtOK5GvUR6QsX4P4QgMSJ3rRgAmDLsOjcY1zhcdoHBdX6hL1gzj/6CiPJM55StqwDgQJdzoa3V4fI78PZXqYnp/D2uUF2FTusKtwyjQCDg81OnSzqxwYtoupuTJml0uo1IyxE5u4OJPjhAKvDQWE4R8fqBXlAsGWjpYQQLu3fXz51wB/+/0edvd2MRqOkMvksTC7hI3VMp04Yn/XRKOl4BPgogNxoR4N1a9Ndd/8grDB+ImP0eXkMKaJjD8yXwKCpsbe/QB7D5toNI/gBgrVqoGNt6bx/s/nce2GCatqQEWeUjjuGkWN4rRCwQXyecAyAceZwfDWIXoDF2cHQ2x9cYCFjSwKxRIKDPn2rPXwpG0mFHgGBc71ZM6bRPZq6JGWuOd3b3vY2z+AjwEseyihRK+9P48PfplHeUnBKJD/OBkJvQaavkKqCuRqGoYF+N60GKoa3TTOTge4+0Udd/8+xI3pLHLFaOWUBLk/o6yTnyYUeDoFyMlcZCTWkJxHDzT6xwEObgf44vce7vx9F7t7h+h0h8jnslhencE710owXc63M9hv0ttzcvHy9Bwnv0wo8M0pQL4lv8U8F0pkuUvQa0ujuU2wdoDP/niC+7f3UW+cIW1nMV9bwgo9bs4p3L2bwcAZoOOQe5+gvY6T/+YFnqQwocAjCoTs+uiafBbNIRiKor4b4MHtEU5O6xi6I2SzJhY3y7jx83W8+2EOxZVo/ht3AQ0JMZ6eg4QzzqUV3OEUHL+Dw5MWGnUHW7frmF6zMbM2i/w01TKRfudRKSZnEwq8OAViEcw3qH+jzcgB+vUAO1sad+48lDAqthWgWM1h8/osbvzDHDbeNWFWEro9AClOP+itYlqhWFbw/CmM+gqjvRZGro29u13xlLmwVsTytDFxhvXirTR58hkUGIvhSP7S7ine8PcC3P27i5PjE/ScFkxTYW4li+s/XcOHv6ygfCkKTxUnQFN0WaE8DRRqBmzLR+CW4Yy6GBxYaNVd7NxpYG4lh8XNZRSrAKykBewZhZz89J1Q4MenDoonD1QajzRceiR5qNFu9uEHPkylkc2ZKJYzyBcjS5QPdBsB7t/tietYL6DCIkCuoFGbM2GXwkkFbT5MXj40wvIrmHAfpuHBsoHKjEJpWuHwqIDANTDqNrG7dYzmyQgzsxlYmQiNG6fD4zjR5M3onEWkcYm7hjrAvVsBGkcDuCMfSvlYWK5gblkhTQNQBFgZb/GMk2P6caeO78noxryjCVPCiEaDcWhMGz+MoB+6dqQynjukVYxOM7Wg1Og5RvJIGPfEWBhfx+3CLGkUZPsQeREbHFk+Cg8qgHjOiaObACvQu8xAwx9oOB5gZxTsXFQOK0onbBBZ+3MiSAO5VJv/5ORRfV7oLDI80Hgg9j6mF+2CleTiur1QYtFDibJIGsJDYbpi8QsUJEQglWgen4hoIJioqA0cvqREWSxKt5QO6UZu5CsspySeKJhW4nZTDKpPIUassBbWIA9IG0XGYfKHE06G+DtdIquUgraicEYpljRSuDyyjz7O20lej/kyqqbwOc9jxSM93PKcgIMu4Hoahh21ez4yDMf1ZJlYRqFn3DDxjwnaJ0jyUqfJJOO6xH2H1ywv+dqN+FzqEsoi/iZtQ0RzWo8BEWKU5rtMR2RMSJhkVi9V1osvMcH4K7+FmZ6HrVx4iY+87Ifvss6kAfmXHl/5YfPYWpTFYpgLqxvyCp8n7UZaFB4nOwFOD3uwVR62DmC6RRhOyBMC1Bo3dUhPMYDQyM+Je5w3n+/rcMfE7QY8R8MyM7B0Coabg0HZ4gBibIyIrogaYz9iyLiIZuw7AroJddyRhT6q09c8sGxxH43lrRg6Wfehhj8CfI5DpoJdDPuaonUzlkFxvdmkLF/i+msW5fV6POY31inuO/E4wfaM+viYp0YhaAQck2wipkNZKLIpbrcnzoKSGUXpkkeTY19MVxo1eM5P3L8pGyOlnMf24rWChLsxcpTNUf+OAJ3ybpwlL2L+5Htsc7qxHxBZLhASmHkFg+AOOyEn4jGNbR2XJz4yzeQ584q+DPVlyMDKow0Tpixs5XepT1QvgrZYFo7xlOGsRzy2EDTFJKlgScr3i/n6QL+pcXam0Rv04WOEbA6YXSli9VIBVuxKn/UeaOzt9nHWbkCrEVK5ALMreVQXc0gVwr7GKiSrJXSc/JtQ4HWgwEXGjGRTHH7usz96+OvvdnH7b4c42usjUD2UptJY3ijiZx/Oi7Ke7qMPj8OZ+9jcRHFzMe3Xob5vdBlI0AlRn9mEMo/VstZrHmjsb2mcnjThuB0JPbtyaQPX/2EZV963YM0oGASrJBTuonzn+s3WyC0buELvACPgtDGNvZ0Ag9YAD748wvrbU5hfKKIw/czSTH6cUOD5FIjnVDxycwPnZG3gb3/xsffwBP1+H7CGSBcUrt68jA9+UcLUphHqMDivk3kzN4pEc2hDwzQUlt81ZC62t1XD6GET7Z6PTkPjt7/5BLWNj7A5n4aO5kTPL+TkiQkFnkMBUdxEz5AXNdA5CvDlX3188m/b2P2yh/rpGfpuC1ZG49qNDXz80TyuXTZx/3MfZopgV19CmWsuUiafCQW+bQqQT2WiyhPyHBUk0VrS0di/HeAP/3KKz//8EMf7ffQHQ1i2h7mVEt67uYgr6wZyKeCo7kPt+wi0P94cEq6CowpMpm3fdktO0qfIjXiXLD2sBzjeZjjyLgaDAVzdx9xsBT/7p+t4++M0ioshWEX0g9Sh8GXqnqmfo75pRmHxmoHr1IP0FtBut9DtOQIAr961sHFjBvmpyQRiwniviAKxCKZezQEOtgPcv9NDu9MDDA+5soHFKwX89NeLWH3HhCmbBR7ptsel0BrGlEL5koFfpYHmYQntZgmHjTO4vRQefnWGhY0Clm7Oh5tdJ7J5TLrJydenwDn2iecOGuifcnNxgMPtJjqdLtygg9yUjQ9+9TZu/HQK5Q0ztEHGGzqZNd/nvyxkDbd41UDvTKPbmsVZ8wS9vovT/SEefHWI936xhMJUtO77+sWevPEtUeCJpppvKa/XJ9lI8Ua3bu2Gxu62Rrc7FHCJVi6y+RwKpQyyudDA7hMJfqzRqHcxcDx4gQ87A8zM5ZDNh/Nw6QzsXewU0jHi6tLdrA8dOPD8LnLFIvIFhZl7JQzaGqNhG+3TIba+OsD03DqyZS2gh/jtZx7j3szdFkOgdxpg646HZqMLz/eQSht4970NVOcVznY4xQ8ttEmM+rmiXswsdkHO1zjQeXThqNGrMzRSgNaZRr/rwhlpDHo9eCMHOghgpiykcmlkijYK0xZqS2nMzBrIlxnb+dEgyLxFERTlOzZOU6nU12gcBrh3r45Bb4RcPoeF1TJmlyyki2pclsGRxtFugMOdEdqdIfoDD57vw0gPkC36WFqZx9VLBdy+7aHbb8OwPKQyCovrFVQXbKQr0S73pJHvIh2S17HRYajhnWnc/cJHs9WHF/ShLA8ziznMrZYxs/Q1u1bclsm8IhW6qUwxKNIviKEt0FYuireuxqCucbgX4PRYo9UYYNQP4LlDKBVI+9sFhUzZRnEmg+pcGosrJpTwbOTuimlFTKAMapOji6TyPn5GjKdaeK1zGKB+EKBVZ9u7YDSW0ciF6zrwPB+pjIF01kQ6awhPL29OYXbZgMG8yVes20UjutyMi8CdxPRcFLlyFtbVoVvxk0DavMPJftNBrzNCrz+CT28zpgc7G6A8ncbMfBlziylMzykxsgrgRegb5h+tIaQsca2T1b7QFC91SeNu2O1CgATd954cBjg51Oi2STsHo6EDZ+QiiAAIqZQFO+OhUDYwPZvH/FoaxRkDYuimSPrWrFWEpkSUED4fU0XYQlg0NpbFbfVSVIleiuRl5yDA7kMXe7uHIByLE4XaUgarl6YEwCdAEOZHfXMrQHdH4+Cuj4M7Gl9+2ka/G8BEGt5oiIOHbfzptzZODiqAFSBQDgLlw9MeVMpBuZrC2uUZlOmmnlivZoD9ewGOtgKJn3x60oNomoMUumcevvpsF46ziGzZQGCMQl5RCoExgJXtYfVSGbWFCrJlKrcJhAnL+ZTu/HxqydgUKXW40I1iPJ/uBKjvEIw4QrvdRX/oCMDSsBQy2TQyeUPC2M3U8piZN1GqGjBZx1gMvYr2en7pzz1xjgavOn+hzSP6eG0t8ujsVKPV9tDrjeAMPQFu+l4A04bIJDujkc77mF0oYnmtgPycdCixVYo8GsukxwscDDUGRwH2todoNnrQ2sDsUgHzaylkuBuBzdbRaBxwPNI42e+j3ephNHTh+xqmpZDOpZAvpYQP51eyqM4byEoYnJAf4928XFSOjgMc72sc7jpoN1z0ewM47kgm2wRkpnMW8sUUpmazmFtKozLLNif7hmOsiIlzjXCuecainuAoyh7KQ0ulie0RABk9GPVPInl1RFDvUDxABL4Py7SQygPpIt3mmyhULMwvZzA1S0VNKLMla6EnZZ8aA4yaZwFaLWAwHCBQI9QWp7GwPiVeUwg4FHAOy+MBpycN9IZtGVvzZQurl6uYWUgJeJUtxM+zqhg9MjlMKPA9UiCSJTxEX+HtIx8HO2donLZhqjSqtQquXJ/DzQ83cP2KIcDMVssH1yQydycIecLs3147xgLl28vhzU6Z9OEaYBiGYqwfuuh3hzDNAKWyicX1PObWTKQIVslG3lEu8ivT4Lw+B2SrCvNrBpaWZ9Gp+zhtBmjXW6jv9mQDR205K2PmRMC/2WzzvZU+7s/RnJrzHAJu6db8qy/aaLeGUjSGdq4tF7FytYTZ9XCd9Rjolk8yPYNrUg1dVphbNnDjuoV6oxzqHUY+du4f4/igjbVuFSY3Mr2oXuF7I9Ik4zeGAhE/i97C1xj1NJonAxzunqF55oHA88XlGVy5uYCf/GQFlzcN0XVpmyKXu3vCzUNvTH0nBX3zKUCeFSVvLIzDBRvnv9TfHe50sLd/CmdkoVjKY3WzhA9+dglvXTZRzio0jjR8hhPUjujRx/qpN58ykxq8aRTgPIIbiTzg7Iie+TV6LRdaByiULMytFbB81UZhLvTOJpvHLO4ktmTOK3pg1pl7jGg0rQBzawoLDy3sbs+g3++g2xqgftCXTXgMTZFKRXr6N41Wk/K+fhQQ/g03cx7tahzsNmCotACoyrM2lq4WsXTFgE19JO10FNU8nFvDhdEk+Js5a+DKVYXDvUWcNk8Az0bz2MXhThN+e050keLReuJl8PXjhTegRCHbyQRCSivrN25O9YDuGfX9BJu48FwXmZzGwloO62+XMb1oiHdM8u3YQ2s8d+b6jbZEpWFUFBbWDKwfpLC3XcXBcIBBp47jvTaOdpsoz1SQK5xj/jeAaj/sIsbmrB92LS/WjswbhDGJT0+5g7GO/qgHrTxxT58rTaFQyouXDr4anGmcHGu0W114rgcdDJFKA9X5sjwjQjnKgwJeNkPQPhN9tQrBIq4ewM6VxIA+O19C88RBZ2hh1A1w/9YRNq8uYWE1DXCX8ZP6SfIe6xB3wshF0il3ve0eCzBDKQelso0r7xRRnDZw9ICaRvZUfphQZLSPDdDJtOWZyHJHJc9QY1jXaB0GOKUxbk9j/+Epzs46AvQZDhx4zgiB50FxNW2asFNpZAopFGdSWNqoYWWzjMUNEwurpigrBXnMfFiHZN7RpNBjqKadAJ/8+0Oc1puYrlRw/cNLKGXLsA0DBBEd36dLPh8P7hxj7+GplMXxAsiffYbCjI/RTYXVSh63fn+C/cM9BNzRnTdx/R9WYJiLWCgbYdgQqfPz/wkJCdzpajR2Avz1306wf7AHDy2k8j7e+WgFhUoaM6rw/MSST0RtOb6VpIlgVW2JkWnokuy0Z9zX04bGg7s0oLZwdHCKZqMNxwnb2YBmM8hOsWwpjalaHnMrRVx5dwHzq4YYFunybQwaCW2cFxoj7CecoNNw3j/QODsMcHYU4HjPl1AsjZNOaEgdjuC6LjzPE08thmUilbKRztnITwFrV/rYeGsOi5smKguhUlB2oI0NxImsWXe6EuGB1eEigSFgOhonD9jmBGY10Gp00T7roNcdwHWJFGCtfRh2gGIpjbnFaaxszGFzM4+lWQWnH7KaaZCWfD5iPfUtKHKi/ineX9oavRONDsFFOwH2twc4ODhFtzNErzfEcDiE77OjUR+qYJqmAKuK5TRqNKxfnsHqtYoo9wuz3Lk6biypw6v4JySPeY59MOqa53ayxBnxufjZ+N7LHJmPq9HaC3Dnzw18+skdAazMrqZx5f0qZuZKKFmhxlfAcl2Nh5/6uPeZh+1bLRw9GKFRZ9srmMqG71k42R9hODjE3r0mtBoiAAErHnw4QLqPhY0i0qkbyCwU0GP/+SrA/S8GONwa4mR/gEGfNbehgzQ6bR/3v2yjfjiClfbFuC673JWGb3aRLnXguptIZ7LIFLKhBxYhHP+9xIf0oIgWbzOhjCGS+Iho+FsB9rZOcHrYRLfXg+O6AlhhO1i2hWzWEq9g1dmS1HHlahlLl0xkZ+jWI/JMJRO1C+ViUV9FW15I9lu7jGhEvgnaGu1DjcY+wXMEdgxQP2nirNlBl+AOgktdyiN6zFGwLQN2CkjnNOaXKji+NouNtyoyaaWrQKHTmLeTgikEcNALT+tA4/Zf6ti+fwjX0bh8fRFZaxE2DDAu7P2vAmzd9bCzdYDD3RMMBo7IJrarYRogGC2bt1GaSWF1s4aNq1WsUjnHHTlWBBShu9mdQBDk2/cb2N+po31GOTGCH7gwTUN26lgpE9lCGtWFHNauzGLtShlLmyay01SIJMBKz2gMVjdmWXpZMXQBfg/wdgPsbwXYuhdg90EDx4eUVwOMBJSqYRimAIAYPjFXslGctrF+bR6bbxWxuElgohIfosJaBHIxkwiEQqBrp93FyOnCsBwsb1awtFZBlgArkp1tPAKctsZZs4mB20Yqa6K2WMTi6gzKlbBtxk31jPpNfppQ4PungPSCUM5G8216IazMmchUBrBLTZTzs7h2Yx7vvL+Ka2+bSE8p+MeBeCwKxK2RB4Ug2rD6kuPL90+I17gEkQs+EVSvcTG/z6KJV0fA6WnUTzQanHuP+jAsHzNzBVlfVDg/5diTHD4T7MrlIT8EIRNQO7OgsLBsY+duFkeNAF7fQeOgh+bxEE4vgywVRlH3+T6rPsn7DaQA+SbmPZ7Lxh6NTiPA9oNDAZkQCGimfcxtFFFdTcPkrrpnacWYDoGDKQgw68p1E3/6NIuTugnX89E+G+Bk9wzt+jQqxYmm/g3kmtezyAkZKGzN6XVWITflwy51kJn2UK7ksfnuPG7+dBWXNwxY3NjV06E+UnuiHUk4vHo96zkp1Q+QAonJgMjPcPzPlBRKs4DKn6E8U8L6ehU3f7KO9z/KolRR0F0NdUwBTsUF/TNzIwQXh7FQ/wGSalKl15MCZDl+qY/uh/Pfet1Dj7pb7aBUSWNhpYjaggGLG53Hc4jISwr5PtJtyHzWguhISgsGaksBpqYLODrqYzjycFbv43i3i7XLRdhFeqhPCP/XkzqTUr0JFKDcJH6qFW5Cqzea4gqf3tem5jJY2JxCejr0LkhePwdWiVkw4mPOkbn5ePWKgYW7Fj65pUETRqc9wulRByf7WsBYmp6t3wTaTMr4mlIg4p5Y/kbOGVoNencdgLbnIHAxVbSwtF7G7IKCSZ1BPOVIThXi80gHxw3ghXmF+VWFynQJp8cu+gMfrdM+9h80sLQ+hezMRP6+TowxHlZfp0J962WJJh6DnsYxPVN0OnB8BzCpvAiQL6WRL2ZhpMJQEGf1QAArdFlIDyJQLtJZhdpCeezCnmPBePcj+1gEXCFYhecGUeIYwUhD4nivriqc7JRx1j1F27Gw/dUJTvf60MMUdD4RNytK64k04dydEygXGDY0DrcDNOoELfSRTSvMMQbougFGHyCOIZxxPeq1BNbI1cURhTfjdUEA+D2Nrb/7uPWHAR5+1UD9uI1uJzTEeUEA1/Ng0dCuLIHBMGQSlA9lDmDYbeze6ePBWgpXbk7hZ//rMmYWQuOcgCWYVzJ/XrNOg9DIv/1VV5CgtaqJuRkPziYR9xon9338/jcu7t3aw9F+UwZK1/clABMMH67Rx7Sn4PRSEg6pe5jB3lcOOoMzpMX7RwYzCyXMb5YhgKOL5XgSwflMtEvLa2rxynD7L2fYOTgG7I6AQC69tQoV2CFhk/V6UnoX7zH9ix96gdAEVNAkmgH8AvoNjfuHAb68FeDuV1vot4fo9QcYOtxFo2Cbpmxq0NqDp32Ytgc708ed4j6279Zx/aMlvPtRFbNZ45ExO5lvohw0tIqXhwFw51MPn//xCLt3u+J9YtAN4I4C+L4jXx2Q/hqGMsT1LNvVZDgmq4cHX53hzt8Pcf2nS/joH+cwvWQ8is+ZpFN8HumpxVYzBPxG2OZ/+p2PW5/RGHwGx6F3H3pW8SVP0zCgtYKvA9TNIQ7vH2Hnyx521xbw0U9mxhs9bCuDkRokPBklKpykwzc5j5Jk+Vu7AT77Twd3Pz/E8e4ArTMHvcEInh+INyBxdaqU1EE6pPZAI5VpuiD/f/n5Aa69v4ibP1vDOx+lkKk+ZffqNykv6R7TPk6HQu0iaZ70XPz81zyK7BrSvaZGfUtj6/M2tLYwHGRRmc1j0A9QKhgQwF8f6Oxp/OFfGvjij/toHXvwhxnowIZSKRiGBS9Ii7eVAV27HTItB1pFXzjwrSY8Z4i33+6ja+dx+zMf//GbLZzsDOB00/DcFIIgJaCZACkMhy6Gx0OcnXahZJe7A59/yodvnCFdbmJtcxqbV4gw+YZ6FNKZX5HnoSer7l6Ae58F+PN/DLG7dYB2oy8eQ1yfhktTPHz4QRCBnDxYVg8P7T6mFo5wea+KwWAVl96xkKuF4VukeZgH2/Biu37NtvteHyeNhkD/WOPz33n48pO6eCoYdHwBiAxdF6QRKxkDruh0BIEg7wSUun9nhPt/Z/iBMn7+v13DpXdysKuh96LxQk3eCdtVAFNDYNTQON5y8eCLDgY9D8rLY3N1HjkA9/4e4He/aWHn4aEAMoZDxppiImwrJTtxDBXANIYwU13s3+niaKuL3ukqPvi5PVYwH90P8B//NsD9L/dlrCU/+17UZlwpEjClA/hcfRouHtxp4uHdFi4/rOH9Xyzj0vUU8lQESqWf31LcmUl+Mk0byrPRPtK43/Pxh9+PsHVnD/WTloDqZOwTkUDFoS8xQy1zBMvUMLIutm+3cLS9hF/80wJmNwzY5TDwbQyKFD2jS08tQLfTguf3JRzQ+pUZzK8YMjdiaUXsDDTq9OrS6cDFAFPlEtYuz6M2n0GKxI7GB1J38plQ4I2iQBSu8cYHFg7r81CZLpYX5/HhzzaxvG7ApqGJC3ObEBXA80fQAWNxRTJNOtIbVePXuLDxwBs88i73Gpf2uyxaPFWQPCn3uRYYafTbGo1TjW5viJE7QipNz5JZzCzkkI8M/vJsuPQNX78w35BhLKeQrhqYXQxkvU30vOso8a7SPB5g0C0jw3Hsu6z0JK8fLgXIwz2gdaJxWidg1oRWAWzuzrtcRmmWQJRHoNmnEoJzDxMwigrVSwaKlYx4nCNAmmL6eKeB+sE8KhulpyYx+WFCgRenQDRGcSIdyVF6ni3WDGxcLeHwcAadZReLK7N46yeLWLpswsqE8lpCx8rrBKwEAlp58XwnT04o8JIUuDDeP7IgRetYC1hcN/D+z9dw0LmD6doMrr29ihs3CijPGzLXYGhmWecJ2IopGHDFE+hjib9kISevTSjwAhQQ+Rnp/mnw7wLiybfZx8ilR/chSpU8Zpej+a99wdhPdUVsa4mykzDvKQ2zpjA9b2BqpoCU1cTAMdA9c2QzaK81j3wt9MbyAqWcPDKhwNMpEOmnuYGWXpMbJ310+4wqYctcgYCV2kpWwqiI0CXP0+h/YfE15mPOgS2F/JqB2ZVANke7tLcNAzTrA+xu1TEzW0OKm9AmnwkFXpYC8VAfy2BG3+hqNE/57Uk0B24+L5ZtLK6VwygeEaoh1jtL1lE6wr/C22E4e4a+qswrlCsFpK02DJgY9QLsPzhD5yzAjGtICKGXLf7kvVdLgR8nYIWTBxdodoHj1imGOIFjNGGmXKTLFrIVIBWhZJUPnPaAeu8IA30i3t00zmAXbMws5mFxNxk9WTxBLod9JPyB58oMZGdOpqywccXA1i0Le0cpwLHRPCGqq4X6QRlz0+G69ElpJptf9NZM2AeaxwEe3tUSLmLo9TFfLeHqO2vIlZTsRPdChxLRCMQyRQWOT6PLcfpRuvRu4QyBh/c6uPP3A+w9bIshVwcGAmolFZBO2yjl8sik6LlCYTD00Os7GNELAN36H3potegZoIHiVArv/GQW1dUoZEUCCSfChG3DZD1AjQAMC9CjPoJeAV4rj/YBd7n7YsT94q9bYkxjyAUERujmifUwCJzwkC8UUSqXBFS0tlDA0e4iOq0Rhg7jTw5kUnipUUJ+hjbFiwQYU+LRCQd9erMZAp0Tja1bAboNBX+UQdr2US7mMFubQ6loP3rnlZyxbCkoncOoZ+CTP/nY2u5hZ3sX3XYbvktrJpDN2MjnC7AMU+5xRz4R4J5jwHUD9AYuBv1DDPo9jJw2fpnfRHHOgCKvx5vB2O788sNseR6BVra36jbB7xYAACAASURBVPjy84eo73vwXQOB+OqkVxAfhWwKuWwRqVRadkEQqTgYBRi5PtyBgzPHRb/fQL1xgmLlF7iZLqGweIHmFy5F6e1qeCcBHnwR4D//p4u7X+1Gbc54zGQQDynbQqU0hWwqJR5euv0+2r0Ogh7DI3XQa/noN7OYrWbgjjTSdg4DgwxGg3JU11d8kL7JPsdY002Nzz65g4d36ug2Ad+1xAsQgRi2baGQySGXzYrR2HMCDAZDDIYKvqvQa/vo9Bj2Zktcn2UL13DtQxWGB2KbXaDZ16/GN07g62cZ0zziK8NlP88jGGbFuwlGGWgvJSGeRBZEk+1eX6Pd7cJxHaRSWdhmGYOhD3pVcqiZU/QqZIjHEZuKZ6rnOGtR9Lyj4Jo20hkbdsoGcYd9hlEb9OS5XDoHFxZ6I0+8RzDcC7XSdjoNy2Ts5DCNwKCnFQ+emUY6n4FpW/K8ECFq76cRhNWOq/7YM6wj6RHJl952gL/+zscnvz/Gg7tnGHEnh+cLyMq2LORzOWTSaQYJw2BIfhnCcRxZMPSdLnqDvnga6XU2cO2DIioEiKUjj0pPLcRjpXrxG1GasgsqYkrS/FV/YlstwU7tM417t49w64sH6Lbp4cukEw9pK8qhdCb8pixLPPn0uwzPQy8lNLr5GA576PZ2cdY6xf9p/SMu5WwYtDHExR7XKQIjUcw6GnqYB4YlBEMXzQNg97bGya6Pf/3NPezvtqT/sjGZbz5LRURaQBj9viMgO4as8wcKZ6MATv8Yo66HUuYy1pcNHOwH+Pd/a+LunYdotwYYDT3xvpRL5VDI5qVOBLi1uwP0GfLIDTAKFI53RnBHBxg6baQy17CZyiJthzuBz7VBXDfejOrHSbpJ0FeQwqCjcf92gNPmAHfvPkC73ZMyB4GHQjaLTDorwNTBcISRM4LnBfA9hvFR2Bv10O3cx0n9ED/7p0u4fGMKpcUIOMO+QaCRD7T6x2gOd+GZp5hZsjG9aCM3pejYSBbJNAaNBsCDgwB9/wRGdojKYgVvvbeC0jSfSwB6Y15O1utchScXEwq8PhQQmxN3J2nArir87B838Nb7SyjkU5iZVTDpmYhzYmKPuTobry3I6BwkEnWZ8HyCGN/wdELL5xOQ4HkCh88YftSD4wayBjRsjeoCPXlaofe/56UktKbXNwIdIbupS1M55DMFOIM0em1PlJ6dlsYU14Lx2uR56f4of4/kgtQ9KRx+lMR4ZqU5v6ZXvrNjuvUP5/MM70NPFfOrUyhMv4h3lXCOQrksni6ngcp0FvlsDqOhD88zcXrYQuOoA+0XQ9DwRLY8s10mP74IBaK+HfMS+S8H8Q75v/zv1+E7GrmiQrEaelaRhZAbhl32iNMPfFnWcPNT+IkTepG8J89MKPA1KUD2ilnt4qs0dtoK6Rng6g0Tmeqvkc7bKJYUijRwcrznuB+xKPXMQRBIcvHKb8zGF9OeXE8o8G1RgB4GndBDG+em3JDkyyZNF+UZhqDPh4DXp+Qf87Os74g95H6jjEKhojA9rZDNZDAIMnCGPdQP2ui2NKYdDVpVJp8JBb4JBUQUU33gACe7Afodzge4US2AlVEoVcNw3iJ7yW7xN5Ep0xAeFtW4gra0gLbLNPpXptA8CaADE/22g92tI1y9XkWKe2wmn6dSYDxETrr44zSKiRPZf0T95QO90wDthsaw74r3dG7uzhYzWFgtI03vKtSb8R2a+GIbWUxfYeKIv3luKaQKCtNVA4V8AZ1RDjroo37QRasxhDPII8vQrpPPa0GBHx9ghbxHgZsGKksKN/9rDdWVHEajoYQSyRUtLG6UMLNkIkbB1i4b+MBcxMq7WXgjwDO6KNUULr87D7o1HAv3RAdjh6FSWtHwKburFTztwjdc2HkL0xsKs0sK+Z0s6v00vAGwe7eJrTvTmHurnHApF038k32GnZEDAY1AgRbvE0fbGgc7PbR7XQToozxXw9XrJXGP5LU1fD90qfiosBf4L+7I0W2pCqtmAIYF5MsmfLMFV50gUzaxsDiPufkqKtUycoU0clkTKZteIsJQSwwbtPOgge2HdbTbLvodYP9BF3/61/uoTE+hOJ1Glp5kWK9k3eJzhlDwCVxJAW4W/iCL/qmBnVsB2j2Nzz69haP6MTJZG6urU5hbmMHUVBG5fBqWDQxxhmLVwvpqEUZJYeMtA/cflrG9b0B7Njp1Fye7PZzsB8gWGYIlGozj/JPkITFIc9KbG137Gp1DjftfHmE0CGDCQjaXwtxyGdW5EvKvKu4Z85Qm5jItjUFXYeduCw+MIU6aexi6LZRn01hfn0dtbgalShHprCnzYQprAo06DY2t28fY3jlEoz1At6Wwe7+LdPYIC0szuJaeQjYOGZKsc0wHHtlfbIVc2YCdG2GkTzFVLaNWq2F2bga12RKKpZSEJTFNBd/T8Bjn/kjjwb0WHtzfCUNHdQIcPWzjL/9+D8XiTbw7rcQt4mM8ENGaiwN6Vtn5MsAn/+ngq7/t46RRx9DpShuvrFewtD6N+aUpTBMhmVYIGLqIu+iaA5zst3C4y3AWLWzd38HZyQJMZDDoM6wX2Y6WIRPQ1iv0MsqOyYlg6FyBO0ntvEK+mkLvzgmCrIXqQhXzSzXU5isoVyKeTSmZK3JXSa8NnO572Ll7iv39E3SHIwzOgO1bTZSm72F25Qqm6aWIQKNX9ZEOfzGxV5j+xaRDxhYGV0QZEHCmDShtQsk58w7dGRuGgpHWoPvMn/7zKt6+vgLV0TC6wO9+O8TtrYcwVQ5WaoCF1Tw2rlWxsJINZSjjzRMRoxz4Rh+FGQtLlysoZIDL75vIlK5Dt4GMA9z5PMDv/rgFP1DQRh+lSoCNd2rY2GS4kijEm+EJYCUw+zAzPaxcKmOqlg2NjE8g17lb5y4SBIl2X4RhjwDvMMCnv/Xxtz8eY+veLjrdIZQxwux8EeubC1hZW0SxrJCiu0UNjPpAs66xv9PGvds7aPXpUt+F9jpQ+j5S2ctIZwrIz18AprEITytToniPnV7klbH2KJlY8vyxFF76BlOl0xLpVzn2LQdGroPAaWG+No/Z+VnU5qqYmimLJ61UhqGAAH+gMWgBx/sO7t0+xO5uA4PREN4pPZ+4+Psne8jNrGL5JuXB+eIlL8XHQcCQUVkEvo3OGfDZH4/hGQM82LkLldJYW5/DxsYSZmfLyGUJeAICHxh2gf1dLuZOsL9bhzsy0O942Ls/xJ//pYftWhb1Mwe3vryLRvsI5ek8NpfnsLq2iEIhg1w2BdsGfE7am8DB9gD37xziqF6Hx50Nxz62jDpWN2ZFgbJQjnYMJ6uTrEx0n5LHCGz4QwsH22c42B/htLuPodvBzFIe84vzWFisIl9MIZPhbuJwbBm0fTSO+9jfruP+wz0Mh4B37KE/OoKVMmCYV3GjWBBPdRRu5FWjoHDtoyoK0yn0e0PkZzQ236kix7Ka0XzAVuJFav09E/93/qegF6GZWhHrb+dkcXFuvPh22CxJscn5UyhAVpIvFXlPeWZyO0GBiFdlbmCF4EHG2y3XMjDYP9JcYIeDgXhmJH1lDsh+Ea4jxsJpwvcJwr6CU+HhCRc/kZLkQZIm8rAy7DB29EDm2vSmaKdNFCpZCd+jYqw+x+iYR5PnzCDalCDTbwtIZ4BCXiGXyeJsYKLfD9DtehgOQgAvlUovNU95YmV+ODdj8oaNk+BdDrSTz3kKkCQa4h3o7ESH+hNNb6AaqbSBmZkiMtx89JyPyG4+Ey0dGRqoPKVQyObQPCPDWmi3HHRaTgjQTXgZek7Sk58nFHgKBciX8c6u8BGRrdS3lYBZhgimPoM6LG7UiAz+Mnfg0ppyWzZgMA2m9Xw+f0pBJrcnFHhxCjyDzTidZQje1AywVkiL/tUc62CVeHWOMwrnwPHVU47PyOspb0xuR+s3EoLkm6zins0SwoceMGxrcJ8bvXtTdwTTR7ZkozCdlg3JsvmVBI15Mj7GhI7WdZKbEc1/iwq5dAbtoSlelOk9YDTQCc+6zy7b5NcJBZ5LAa7jHI2zQy2b5Dgf1nCRThvIF9Nit5JoA7T3nJ9uSNIxG8scmEsyPpdSKJQVatVp9BodDANDgARn9S58bkSdfJ5Lgclq7SkkIsMliUMdjc9Q8aEMdkaMRMCJL224NipzeSjaMuO4l3w/ZlpmEZ2PkyUPmwBtBLSnZDJpGMpC39Fo1PsY9ALR24/LkEzrKUWe3P52KfDjA6yQb7mgyyhMLRvifvDax2UEQVkY2uKkWb7hwo8KZLp9rawaCIJaqBtSNZlgk9HFEBOvA891rhiwQi6PQ5W48NQAyGTFM8vsskKlWsJ+PY/Az+LgYRtbX+3jp/+tFIapeVLrxHlwEUpDrwd0DukxJEDjZAjH85ArA9PLeQkHpOgaVIdGLhlhJEQByxT2vsf6YJw++Y71ChTsNLCynsfmW7MolE2UZjLYuLKI1Y2KxAzLFGhsip6nMnIEMJzFnb9VkfvPEu7eaqLe8tFrurj7eQPvvNfG/HoVWYZg4KDHdy98KIcIWDGDDEydQ+BmcXYQwOsBzd4pTo4byBVtbFybx7UbS1i/Wka1plAsKFgpBVeXBM+TpiEAwNKmgfnFAopfFtHvKgxabdR3+zje7mJlrST8IAt91v8xoiQUti7gtzTO9gMx7vmuLTvoS2UDi2vTqFQVjEwkaJ+QzoVqnr9MPh8puuSWIgglLQrcw/0ORvoEVp7G+SKuXJ/DjQ/XsLhqolhRMKgwFt4I0bTuqcZnv59D9g853LploNP10D1rC2jlzhcnEhZpmW68k3Eyk+WIJibc/b68MYO331tBNpfG4loVyxuzWF4vYXFZIS0eiaIXPS0ejLr7AW5/OgXTUNi+20Sz3cKwP8LtTw+xtrGAa9fnZXdbrIs5R3pRjgO9vQBbXzCdAzROHIw8D5msibnlAj741Tqu/WQKSxsG8gQ/sQ6Rh4pRz8Lu7Ty++mQOX/x5DycHA5yctKH0ECPPlT7BMBj8hhqe803x8lc0aZNo/IZJF6sKV9/bRKN3LLyyurKEtcuzWFyzMDWtYKYfDcwEGrk9jdZDA3/77SysP2axvWsICKix38ZXn+7i+s9WkC9nkaWCNdlWL1/ocExO9v1vkNYLvSqT5bDerAKBKoa2YMAKQSsip8YRVWQiUpgHblYtBAONoBOGibq7ncKtrb5MNIx0H7MbBdz8L3lce8+MFo9Mg5ZAyqfp0IhCmQNgfRpYu2rIrmG6ujdMD7/9cx+BZ8BQPeSnLWy+l8M//NJCke7CiWVQNrShoFVJErEIGqGMoaExHgciAnytpiHt6SjqLMDR3QC3/uRi5+4Zet0hTCPA4moJb3+wgPc+XsbmVSOM00jW5e45FxgdB9j+cgq5bAZ3b++gcdZH98TDnb8do7pQwPTsJtYr3EEalZNlfIXtHdaV/+PvC3HB13+IybP9bKBYMbD+Vg1O0Ee7k8fGpRWsbS5hYdlCpRqFneMYyvYahmGWTh8aqMysYPA/bByeAN7IRq+hcOfzE8xfKWD5Zu3pZYqARfR2ZSAHBuwYDXw8uHcK3+yIa83N92p4/+NNvHt9GnNR6DuShBNtPQD27xu49dclWL/N4njHQX84RL8d4O5nHTzItNFzm2gNuqjMFvD2B4u4/uEG3n43jUw+ku0sHd0itjT2b+dRmVrHJ382UWcIhUEfjcMeHtw+w9xKBdXFbIg4f1KNEm0vfQ9paDeF0+OW1MW3+lhYK0oosmvvLWP9MsGKSgAzsmClnGpbqO/auPt5EerfU9jf6aPT66NVH+LO3xqYrp5gfjWHhTLBv4Cmgt0CNt9LY/XtmhiNOF7Z8TwqYh22rVU1sF5SWLm5IizFkIp8l95Vvm0WexK5JveeQAHyECeXFCSRvH7CU5NbFylA+UVe57hB4EpEQvK19C0CoyNZIwA5GVgM8V54ManJ9augQKSqT8jEV5HqDyoNdvFoTu72gUHXkXWGZZritS5TtESOy/wiOS0dTwdIXF6EH5l2c0OCwfWlQjZLT52cCJsYDgMJ7TgacqMFYJ5/NU5iciRFx3OSmByxMImvf8THiBQyRJEMAUHD9A5EXiYv0iMjec9GoWiG68eY18KfHydeJKNlTskdSQZQKkHAVvRUp7SNQddFv+vJnC8p2x9PbHJnQoEXpcAj2RnPf9n3Zd0Z6Q+EdaPHeC6fuA9IMKAw9GdSDsePTY4TCnynFIjmwJwvpOlYlx/OMSJ+FYOpUpGK4oJiJXp8cng1FIip/Cr1Qa+mZK9PKjFfykbQHjDqOfA8B0r5snkyXTCQEh10ZOxPiGupRfI64vFYjtNekcvRQ3oKZsfCyAnQa4/gcv4r3rGebCN5fagzKclrTYF4MkD56gKdUw2nH4jeQRkB0hkT2ZwFk3Yr6iRicZvk2biCvMcv05T5B5DKAuVyAaYaQvthWKBeaxgCVuK84/cnxydSIBYJT/xxclMoIDLY13C7Gm4P8B0qygDTNpAuWMhy0yN1xDEP88eLPJzkXe4BMyH2t3yRegjGcjPhOBqtpjsGDAomJk4nPkrOk3/fNQWeBIn4rsvw3edHQcuaR8piFWqFH5UjVkrwDjEpWQUznlSTYZ/EtEnBHJ8L6CB2Ysj3AmjlC0iDbotqywRR5HBvy4bnaZycnGD7vobTvoaUhD+OOuDF/GLpxniKA+4aD3B0pNHr92BZGnOLZcwvl5HKsfOOp6Oi8GZp4uTi46OKPzrjoCUeRWjvywKr1wxMlTegsIHCLEEZoeslMdYmd8DJoKhRypm4Sc8Sdgpebwajex3UO0102y72H55i7TCH2mpBQps8yjU6Y3sQOOdrmLBhqrRM3B7u7gDmEJ5qwco4+ODnb+OjX67j8rsmbBpj4919bFqWKULkEUBD9+vzKwrz8zVs32+j33dRP+jgcLsFt1eCUdTn3ffGbUgiRfxBgJCESDrRONzVaHbaQJBHNqMxVc1gaWNa3LKKEuGxSj3nBvOJ8+SjLH7EhxLixwdc38EoGMA327h0ZQ4//ccr+OiXGaRmGO4jmtTSoCf0C0Ej3NH+fspCuVCC66zj9lfHaPZ7aDUG2PrqGMuXayjMTWE6jjWYLEeUPw30dBd05bqJpaVLGHU2MbVowMhGNCfAiwb7mKHoocLTKOVNvD+l4A/LCPp5DAYeHCeNZr2Fg+0G6sezWJzl7CjxiRXjnhZgwsH9AA/udHB4eArXt2GaHhZWS/j5P72Ff/gvOZSXDRiFKH++SzeLecCaUbgyo7C6pLCysIz/8d/PsL/dR384AkNqKGoSVbRzeVzwRDle+jQmQpgAFfL5WQMf/8rGxlu/RLmokGV7pSLDe4wGlT6tZcFuTimkSgofsR3dIs6aedm11+26ONwj7U6xuLaM7PRLF/JrvBjKC6lVkj+T518jtfhReZ3/In4L5VKkfY/lprRPYgJNWtkAjdfSt0eAYRM24MLXHrRyYKRHSBUBM5YHMX2TbMZ8o6/OAioLBL0wDJwyXDAmIni0fajMEGY2L54hKF8Evcu0ovSi4ofVkkrFNbzQnxO3L56KnCUIwQF6Jxq3vwhwsNdAfzCAYbrIl4Bf/x8f4INf2CisRX2dsi7id6ZnlAxcLivMzWbxr//fJXz2lwPsHh2hc9wVT1CzyyUsLM8iw7BAsZyMCy+Ne7FUL3Ed7VLXYwvBS6TxAq/IgioduhT+6FdF3PjwXfFQQNd9grBm/ThpFY1umKDOAWZZYXZK4dezBg525tAf9NFsuXBGAfa26zg6mIJ2quG8IEmTRLuKgUhQlpbIkJHXl7Bj+SkfV66v4v/6f64LCMqIlBdjoUjaeMBy2UKl7COjp/G7/3cE9/gUjueg2R1h2K7DRQOFSoBf/7df4uNfl1DdDMEesnNS+D6sT1DUWMopVMoK2l/BX/9wjN2jvgBotu8dYnEjj+Ura5ibfcSrY9Im6hM3Vdz/Bm4XqfQQixtl/Oqfb+Ddj1OYinmOYyrZzue2TcpZhcWKwtyagbnqMv7nf3fw+Rd34Lsp8ez18PYp5tbymF2blTlUaKCHGIm4OJZisK+zXkl6cyhhXyPAJVHW8TPJZ8eVmpxMKPAGUSDmYfI6efwCn4dyhvfDHyjL5LHkc29QdV/vosaN8XqX8nsvHXmP65ChxnAwBMd5hifMZNNIpS1wh7TIaJKT38d4lTciWsszIfPTUxyxKgztSa+Hw9EI/d4IwwHD4YXeD6WPRK9+73R47QrwGKFfuxK+LgWi19FeV0tYSDKobZsoFPNI0TNFNKeXsj6NpAkeFBmtIGEsspk0GG5Fa4Xh0Mew74cecJ+WzutCkEk53lwKxLzIo6yZnyRzw+qF04hwlj+WwXHN43Ti68lxQoHvggJP4Dth5YnM/C6ofyGPCdEvEESmrzGLCl/yAXrK7WuMRi5835fNmNksQ0/b0fw31IOTmpS5VD8+9olIzfkDp8OmDWRyCpl0Cqbi5sQgzIPhoD37CfPox1Kc3JhQ4PkUoL7YB/pdCP9y/ZaxLeSyBlJp+5ENJ+LLZyUoc18+EOnv0mkbBnUU3EPvBhj0XbgMnx7EkR2eldqP97dzUvdJsuLHS5on1zwAnIHGiN68fV/kq50J5a/okeO3SMtzxI1/iI78jaI62vyaKwB2yhT7ThBQv+GIpyDy8LmB4EIyk8vvlgLJJfp3m/PrklvMtDRwRcissQElFtzx8aJh5Wl1eKLgiXtPuLJkHtVVA0vrStCNKdOGAVt2J//lPxsYNcOOIrvaCCSLX4/zJHgiCk9zuK9xfNxEb9iCF/SxtFrB2uYUFI1mcQvL+/EFE4k6YnQaJyvHqL7yLl8hXbIKpWUDpVUDNKgzfi5BK2MXpLGjCj5LAEOGu6QVNq4ZWF5RKBTSIWAmSKPd6KNz1oM3oOuXqG4sTgQMkbpqYm0ULIMRHA3xHNMenKE9PEV+2sAvfv0OfvXP67h03YTN2NMEbESeccZeBBhigOWhkbuoJN7vyvo86G6dO6wIniFgZX8nEMTemAZJWrNcvI5BKy6w8yDAw4cOvMBHoIbIFjRmF/PYvFJCphx63QmtEOMUX/wk4p2YhSRrTY8gDgLN0CAOFldKePsn87h8M41UlYAN1p/5hiEVZPciwVip0NuLWVNYvmzgxs0iysUiLCOFwLPQbXnot114o6jCPPAbtX/MC0LXNN3PKuTnDVQ2TAEEiFE25oG4b/BdDgLMPxMCB25+ZGJl1UQ2nQHDT2jPQq/l4KzOmIeP+JCvCg/QG8EQ8E809h9o1I8GGDoj+OhjdqmAtz9cwo2fZ1GaD+s3dgHGtk6FtCA9GDIntWDg6nsm3v+4grm5CgxD0Dxhe4iCMWa6F2+iZz/JjhC1HmnJWNNZBXtGYX7DRG7ekL4jxliWkR46+OUuKTsMiyEDqa1QWDZw6W0DtbkKLLryIMotsNA5G6HX0Qjidnt2gb7Rr1FNHqUR88ijO+EZ73+DT5hsIhGtH+tC47LwhPwmcEuNIPCgORNXBJowZA8ZKBKZlO+UCzzGsp7XNIjzyBUl+TWKuEAXieK2RHlQpgfTCmCSp+T5BEiP77Cpo3dl8cn6R1UYl/UFaUJXjUFT42QnwNbdDlrtLoZeD4UphQ9/tYErNy3kl1TY18Xtc9jfSYO4fxKkU7xi4PK7BhaWqkjbaZhIY/9hE3f/foijvQD+MAQbSLEe2537goX9Ph+L2p51ptxLVRUKiwbyBNCVI3nAfkRwBfkjbiMC+UirtBLZ9eFHJlZX5gT8pJCCO2IoriE6HHfjMSmuZ6IxH53Syw7D/A0RGD3UlnL4r//8DuZXDQFySL7SkSNejfiM4M9szRCPJYuLtnjECeDDF3Sih8qMhbfeq+HGxyXMLBoiQwnCCXk9wV8c00oK2SWFzWsG5uamkU2nEfgB+u2RxJF1Ob6+wIf+BQj48hjg1hyhWDOwcWMab39go7xkiMcwoScrzz4k42oku3IhPS+9b+L9922sLc2LVzZnYOBot4f7tw/RYGxbVz+ai8RtGPWdWFxKUflbsthRnueeeYE6TR6ZUOCHQAHOPWX++UOozOtcB/EQRGEz+cQUGFMjIY+pwBkMgaEAvz3QwwqN9Tbj7o1fiFNIHmNBHt2L0zQgoQ1zWSrs0wIyNZQp6zPX9SScxbnxIJnk5HxCgWdRIMly5DcNuK7GcBRI7HPOe6ikLBRyMDlP/DqfRNrcHc1wQpZBz4wWPBcSdtbvJ+baXyftybMTCrxCCkzmD6+QmJOkJhSYUODHR4F4bhtAjKWu48EPuPERyGYz8hXQa/ScyNxYB3mRWvHcIdYJ2UAqDfHUYjA2LEwEnsKgN5L5ysXXJ9cTCnxtCsTrrQDo97UY+wlf1QgkFEoqRQX3C6Ya6yQi2yA9vZeKSgArTCQIFByHa8TQo8sLpjp5bEKBxynwBJ4kbzmOL4BBKuszaVvkrzgpeMLzjycam+iozA4dV3D9xo0z1GdIv/AJWhnBGT3x7cnN74kCFDmTD5k2/iYN7/G9+PgsSr3IM9SY8Dl+6IpoRqG2pMSQnkmlYak0uk0Xf/vTPdmhTC8V40+kcImVd5wQBUONPsMBHWq0Ox1oeMjnbSwuVzC3GHlBifOTKj6hkIkszuXFCz4uhlklRnezFIIWBKgiQIWE4ZdggdiIS7ACd0fnlIBWZmYJWEnBNm0onRFjWr89hO8QCBJ6lYgneFK/qK502oGADUJXpgZo2MsUTCysl/HOR8tYumIiXQvLJkAFGiplZ3YEPpK5X2iQZlmm55WErynmCjAMG8NegMZhH4e7LQx6ESGS9IjPo/IQtEKQEAEue/unYrC0Uj7K1ZQAKUo1Gvei8EgJuo/p+ryT+J34GNnuNL1HELQCB6l0gJVLFaxcK2J6JTSOCuAhYZxlu4kBnfWnYZfAjRmFhRWFmUoFuVQBCGwMO3Tt7YO7zoTuzDeRtxSX12xXppNRAvwRwBK9VCzV8QAAIABJREFUqxBoQT11DFKKzsVYK/dCHkgtGpiuKeSyOZjKFiP6sOuj2eiGQKAkXYTGGn5b4/hhgN37Ac4aI9kRp0xHwiCtvz2F2roBsxiBUyRfGkT9cVmkzKnQqJtZMrB+VaE2l0FGJmbkuUB2iIb1jRs6WZBveM42sEIjrQCm6KWJBvVc2DdIO5YxpjdLIAAI0o0G4RRgTisxWleqBaRTVOan4Hsm2o2RuLYO6GHpWyj6xZqLM5pHRb348yu7pgyQ6kR1EoBJgh/PVTX2viLusSIQEr1XKReBGgldhY7xrt9QjIzpLYXmvYSiOrRZ0VOLByge3dDTStwmsYE90W5x+10kwpO60sVnxtfkeXpX2Q2wfUdjb6eBwciFnVKYWyng/V+uorpmCEBB+lwMtiHfE5hBfuE5wQPTBubXKOdsTJUqMI0Mek2N+t5AwmIxLq6AwqTLR56GxgV5A04S/CAyKReCeNivDAGARbRgm0VyUORT3IakUwrYuGKgWsuLHFDaQuCZGPV99NqhF60xJRL5yb2ICclxvvbhY4RcSWFxo4Sr101k6NlHvNhEwEXJN5KTHJ8IIiwq1BYVZuboCpZClJlYwm+VORvvfDSHGoEvlG/xmMZ0yMsRH7PdGXqOoJWZeYXqrIVynm45TbgDX2LUelwwepFsH1fo8ZNQFgbiecpKB6gs2lh5p4SppVDG0hOdyNOoDCyHOJnhGJ8N62PNKlx5y8CVSxUBmcLPotvUApa6f6eOfifu3FH+cQeJ+1J8nezk8b2Lx8erMLkzocAPjgLj8TCe9P/gavg6VIjChZ/4GF1ODucpEI97AcTbpedTYc/BJYBhKFgWPY7FC5ZwJ+qz2FbWe3xeQr0pUdZblglDMfSVCZ+uf50QsJIcEs4XanI1ocCLU4A8RzDJiIAVYaoAlmUgneHa6sXTOfekUhID3aZXP5lwMnS0IYYmhxsKhNHPvTG5mFDg+6PAy/L591fiSc4TCkwoMKHA90eBWGZyzhBouC7gesHYYGpbJkzLCj0/R/oMmU/wvadMXuX3WJdDWxA3IFE3ZdBgakL7JkZDV+YrkynE99f0b3bOT2A+DYwcwPfDjbq0LdHLINdeL/yJ+wNfoNNzG8hl6fmcP3AXpAnfM8D5L0NaTT4TCrwqCsRrOEYkIWAw0NxUbAj/ioOFWOaSvZN8erEAcdegjcCkdxWAe8INIwq9HSh4jivrOD46kcEXCfj9XHPInHxIAeHKZ5Dieb8/49VHP4WJyGZqGhkFRGFgfbOGXMaGpSwM2gHuf3aMs8MAQT8qVzQOxOnEXiiCjsb+VoDjg1P0Bk1YtovZhRJml8soTRsSPuNip5U+nMDNxGk+dkx2eL4UG5ZoXA3Hukc04z06NYi+AuzwI8OooVAqKBSyeaSsLBTSEhqGBllGFqCSR/Q8F4VLlCeNgjSocSxMpQLMLuSwcbWK9Us2UjToRePseIIYTQKl3kwj+tJImZ1WmFtWqM6VYNu27Kpv110c7bTQO/NALwfnBFNcJqmfFqNycKZBjzanZ6dQykUq52FmIYu5lYrshhc6CTHjlx+j7NNvkB7xJwoJxEuiYAM4MEwPuaKJlc1Z1BYysPMJN8ZCy/Bltk9cD6EtDe1phWJJYapsSrxtRRTsgHHaRqIYjo3YcfbPPUZ8wDYX7zN8IeIDufYYAiPkAQI2Cjkgn83DNCwYKiWT8Xa7My7neGJPHR+9Kfc0DvYC7O910Om2YRgeMlmGAypjYSUFm15lCIwatzfp/Uicsf7S9JEhvzpPTyUKxUJOQr5ocaMQXOwez632Mx8Iu/ejR4Qpo/7CdozoIzSL25pH9ifGKqVzD/HuEP1oKWQYH7KkkE6nYRoGAs9Hp9mFM/SFTmO6Pcr1DT9LEpFY18Qn+dP4diChWTjN4Ie7JoV6MTucS2D80vmTSK/M9wiMC9OJxFuM1uHNF0nrfMovdkW+8DQO9wJsP3BQP22CBqFSsYSVlRVcuWLBYl9nOelVK5a15Bt+KUil0iFokLJ/fl6hNl2FqVLwHAO9louzehfOIHpeSsa6fluVerGqv9RTrGtUd+lTcb/iMWpL/j6mE+nF/sUxiecBkCKIskj9g4+APBNojAYuep2B9MFYfj61fDIuOYAaoTaXxepmBdlZA0Yc6ovgjkfiaDwOMT0CPuwpymKFLF3JKg1Fjz6Gh0qtgEvvrCBF+cY0ks3D87jJeB5NtjN5hXIJKBTKMI00XEdhNAgkFmcsg8f1iN6Lr4Ve0mfoochDNm+jtlDGyua0gFESIvURq8SeeeIycHC2FMor9BxDYCLrZMId+jg77mDrqz0Br4zHmIhX4zJMjhMKTCgwocCEAq85BaKxlcb+IKB3RIK+GbsVojSSsYqync9FY3E8LzlXs4T8l3fohZBfg7v0TImF6ns0DBCw8mhucy6NycWEAi9BgYAhrVxuAOEEUouRybIjJUKCL184aU59bPJ/+Aa9wRLNS0W96zxah79wepMHJxT4FikgK2rO2yefCQUmFJhQYEKBp1JgLCYT8wKeBr4Wgz91R2KbMLmhNkwm1vlEqpHwZuJ9uRH/GB3p5Zke3kyCt2V/fziHcBwPNMxefP2pBZ78MKHA8yggXgYhG4BDztIwTEMM9c97Nfm7sDsZk2GvxEsm7Xjhl0GAAoZucQjqmnBvkm6T829OAZ/2QZ9eMql/8EO9AWVwnHRsA4ivn3SMH+bRACyL3lUog0MFO/XinuuHgKsJCz+Jgt/LvaRJ5XspwGuTKRk3ZuKLhUoybPKcz/E6/sbvXbxm0uO0I0s6jVFpoDiv8NY7BvK5tBh5vKGJxr6H3Xt9dOvczkZjVpQH04/Oabhk2KCHdwIcHdbR6TXw/7P33k92HEma4JfiaVFaowAQJECy2XJ7tm9u53b27Mzu7z27X9Zuz85sbuZmeoZsRbJBEiB0aV1Pi1Rx9nlEvMr3UIUqKDZAZpa9ShXh4eHhEeEZ7uHu54b48M4K5pcrOuyIUW6JgQyVWwY/e7boPndmAua1oRF4z/Udnrm2Q4UVFyRTSkGj/9fp2NuNQpEWyXkfEg6m4JfgOgXEsQMaeHKX9thB+Kmf1sMmspM9QQgvF2FprYzrH86gztAqRe3OSXAydZ1sCwqQ4oWAwmDNweI1Fx/crokb4Ch00TqJsLvRwNFuByF3gduDePCQxVcdJiLpK2zei3F80EMYhoiTPvziAIvXqrh2s6w9Y0zWyYB55RNtUkRBGCFfUJhdLGFhpYpqXe/WtwY7pJvlMVF0st6sAzObnfE5iRMP+K4n3kWCQYRwEELFVPqneOwiZNN8betJ+lAZHAAJDX6GDFWlFcMjHgBQYpx6MgKRUR7CIMGgP5DmGhWXgs/Nm90W440PEARD5PwYi8tFLK1VMDVnvClwV5vFg0BYCcs/5FMJXaE9KpRnHSyvOliYr4lVJp3hsXEllMw4FiN0XuoixTppcKL4Fh4yfYhADa9qJbruR+w/WqGe9jhEaRAoFYGc78Pjqj5jpPeGiENtxCXz60sh+h4mNm0qH4OGdmc0toQ37Wk7AvNcdtisqb4jxguaM+Q/WUqSXQXeueWdYwSXhkXeoCFFCAlH0zwZoj8IkCQxpupTWFhYEGWObAk1PAJ63pIfecr0NdaB/UEMtCAuGqslDx5y4k0p6DnonA4QDkx6GWrTiJyL/Lv5UOYe3TfEy4qZkwTZVJvKWMB7mUjMC544ppYdlEqAx1UCKIRRhF53gE6rfyVDMNdR8Bz2wYGMSWs36+K5heOtjKVEJsVXI37lM2NER2O0HD2oGGu1csnH1FwJtVmOb2ZuS49vBGkNYdh0fOc5sjOHQwN35kDRJb0jxph0f3+1gyaRMamAar2AxbVprFzzNA4yfxrvT1IJDZM7gmTuIf+acD8MybSw6mJtbRH0GJdESjy99E5DhHSPT569DCXWy/6uhnyWKqNARoGMAhkFfgAKyKddog1WOE57nifhgGRnkh23zdzEkxznjfl8Zp9zPhaDFdcYsDMkED25cFEqU/pbMmbn16CA4TcarAhfMRwsP1AdJZ/IrwSZslzK2ErzO+U5V5Raw2HGu69E1yxTRoGMAhkFMgpkFHjXKEBVQEyjFW2s7ToO6GGF8u+Fx0gQnkhhNw6bNX4uRekNc9pgJZKwFxSAJ/JltxkFXoUCRgYm//Igz/qeK2ugNDa56mF1fzY9wWrViwOltLFKFCViGJ55WLFUys5vhAIy/tJgkMaC+ttNePhF4+9FBVuWN2eqSsXoSvqJgyiKQT4WHd5FMLLnPygFzL6QH7TM968wMnRaaEhfp2tz7nNmTnsKoJRiPIP4kDAhqzdcLC5M46RRwbDTB4Z5PL2/j7XbZdTXXW1wQKUc9T0sI1ZIOgon+wp7mwrddg9wQtSm87h5exnT86541BDFTxo/owuSR+fiahLzHRW1k2nMREdENB56Fzu4659pE6UXGOkGjGkHCsmJQr9NbxvchF0Ql89J3EMiVjQphDSZNAJmABGbF0cvLHFxiXEea7Ou/NySVuiJEtukFwLRI4LgbQRIvqMyjzQvApU5BzdvO7j/oI5Ws4ckcHG43cH+Vgurt6YwP2VwIpiR0Y02ykgaCt/9NUHjpKXjVeddzC3Tu0oN0wuUOlPENjRMPXnpS6mG1I00COH4MfLlBDm6X2MkCZY3qjvBM4cp2AogfM904naQrrtNrMGEFoQJKBRT+B6HM4GqASv0sNdMQlmaFuDGM4gYqpAXSDemIw+QV7tAr0shn/YzHHJ8qMTV6dJFCX/TBBhg6JJBj8p1VoBWwDGm5nxMz+VRorcJHjyZyzEwY88ZVkPBqTgoVem+mSnJoDTaicUwQCOrIVi2TMN7nWs2g/QN0sMepBuND2jgY/oKlbtiwELa0dlBqJAMgNaxkjh6hCGjiHIMfa0lhQX6YzsbxX+6fXlt6Wif0zuFeWhfXZkShk+kjcy1tJUBYC3QRzxm0lwZ/lUTku8HwLDHXZlU2tA4yUepUEHBB/otwI+U8LFinDSLt613oru4DD9UJrUYf1GPxb5XgB9HSEIP7eZA+hWNwdJD1VXRfCfSsZFZf/7jdWqcppcUMZKTccQY0bEfcRxin+MwxzB0nJcGwKBPKC48xxdjUYd9i2knGInFpR9p8pPvYsRJT7xsFWuJjLFCWNM+Y5kMyvKMTcjFCRm/WWAowjd36ubLDnJlbtvV7zkcSHXB8gwQXpj8hKFdyTKhy5Fy5JKTBisc2i8T8sjn9DhFYy0v76PAUH4VbQwjRilSLv9ZKpizFG5CFXF8KgLFOjA/P4WD7SG6QwfREAg49pt5QddhBPAMpKla6k12mVHgJ00BvQik5Qd+nD/Xd37S1Mkq/zejAKdZIyhxwZ6eUawMZnGynx/2fuw8yciyUMT5y5qRU8blwqf5zmT6yTxjAH/qNySOnZt/6rSYqP8E31AG1F579EYg8erDuOUT6SagnN2SzDYtz0aW41leMaQVhSYu3NMQPWuWM9plVxkFMgpkFMgokFHgfaWAyL7Gw6BelL3QQ8WlMoWVI7ToK4azWqTQ/zPZ4X1lkncb74gGV9wJYPmOYVAuZdazOjEp9SQiB4s6U3sIGsnFXG41cnYm/p7RLbt6MxTguKjHRs1dwrtWHWb4kie71v5cqZZ3+UIS6hSiI5YHOgHX3OwYLN0jlfY5mNmDH4QCl+kyfhAk3otCLmNWOzLbs6mUvjVGKjSmsAtLVmlVdFCYc3DtAw87B2Wc9jwkiY/NZ4fY357BR7057W7WKirpzSICBqcK+9sJ9nf76A+GKBQczC1XsLpeRXWK4VLOEBh1OlO27o5jffX5JtDzmUZXlIL0ngHtQYPeNAaQGHU0LOh36f5LIQh0jOgoUIhpxDAA0FLY+l6hdRIiiV2IUpCw0/BZeoo0Fhk9h2p1muMoFEs+6lMlVGuert9YmxjC020LL1Pv7ARLDwT0srJ808XC8hRODrvodoc4OWzhYLuL08MQc2uu9shi8xMWJ9++wvBI4dHDHTTabcBNRLHHEDULK3W4VTaoxfzNnS1ZSAXXV8iVXOSKjva6YOk2Ktde2PM4HWiEKIaIjiMOGyhV0GWbKHotzXjmYUFYhfDIu4NRBFPpS9sq0qWvRDFJJfmQivdAiYJSG14Abl/h2SOFbpdM4UGJYjW1xG3LZLlULJOXesCgp90vctZg3WvTRZSrPvy8nZ1SeGqsx/6P2p22RFSmlhlWiuwRi6KaVdSCmliDSJXTqIwBu+zG0ovpCMT8RAEuNDaeaEwfivoKvQ6V5grBQCEcAOEQsH2HinV6q2keAXtbCoMB4/WRZvzpvxHC6bIvw/MdfK/7uSWcQfC8Op3TOJJMAGijwFE2e2Hz2Pt0/W078dlY99WJR1ksjHTe9DUTMg3PNpM9p9Odc80FdI7nUYfjqBI34g5ycFFA1MvhdFPhwR/E2o+OieRHMGnwMr5rFtYodBR2Hym0W+y0dJXnIooidDsdBMMhVFw+w/ccnN75R6bdJDwSvTmZvhL2oPvSkH2J/cqOT5yXTDzVAHCHgBso7G8oeAktH3PwaCSkXLjptjbXo0ek8eiGbUCmUciXcsiX6d5m4rCNxDbmq1ReSSkGKzQT4S+Gn3eRL3J8E92dJCEIDcYCS5ehyxfvKuJlRiERa0G9AyihdTjtYSYPi4c9swzZaawEh1xez4FiUDOW15o5nWVkGjGioic4D8gXHczM1JD3m8KsSeSIV5+IhkKc85mVVbHnMfjZTUaBjALPU4DzvT5eZmHpeTjZk4spYCl8cYrsjZ2LzpnL0sSxU9WlJNUJ7HRgv1P1KpF+N3qWhp9dn0MBUtH+znn9U310Lg/SoyhlJ02v1x1TyaPyk1GaBRre/anSPKt3RoGMAhkFMgpkFPixUYAigxx6jtcqndFDkQPO7mzac85MlJJN9GZEm04vNHFt5UqwbLbsnFFgjAIp7uGluZU1Z6aj3Gq/GlJJx0Ccd0PRmeuN1EUyP/Urwqt8oTNo8VqvyZ8HInuWUeDKFCBP2bGS1/YnAOjVx7y3afjc8OFFZZA/xeiKCazuRM5p4OPe0i+ClT3/4ShgzRp+uBJ/rCWRz9Md5rnbVK+yfUI8rSgxdvjwExePn8xg++AQQeji6KCBg51TdE9nUas4ejc2YVL5HQDNwwS7mwpHh20EQYDZxTxW16cwt2R2aFO3ZI1CSHODm+7HFoHJzm8axxopMJkoVLX3B+7c7x0rNI8TNI8VOk2GbVFoNxW6nT76/R6Gg0AMV4IhN44X4Adl9Bsx2v0egjDRYw1x4W53UWDRii01MFj+MOtJek1JSf2L5Tzq0yWUaRxC/02jwwCUkAhndZXd7rbe2suehEqaXnGxul7DwcYsuu0jdFoRDne6ON7r49agAKd0tgNeFqJosNJWONxJsLt7gu4wguslKFZcrN+ax9wiDYTOqcMIvytcGDxtOzGHfSS5GX4iBxQqnigFqaSUwyYakWN08fygzVep17ZuIsBwsE69GxVO+MZYRfWBpKsQNRQOdxM0j5SEMel2IMr2Xi9ArzdAt8fQI7HeVR95cMI6Ok2FZqePOHGR0GWyeM7RyPM/i7YTDxXRAQ2hevQQoNO4nkK5npO6i5KUldevDCHGqnZGGqmzI+G3imV6WOEDanG1G0eGBBnVO13/EdRXuCAcY4hgw70oGvh0gO5JgsahwsmRQvNUodNS6Hf6GHTp/SLCcBAjHCZQUQ4qzCEYOGi2AnT7CaJE77JW9CpidcdvCudXqOYbyWLxFxfdzzWpLmKinUflynMKxRYIz9qkZyyNfT16+IILI7RomBOwXpBNM7BJwHH9RWntO+JPPgkhfEAvRCFtukCrqhxOjwa491WCpw8SJAiQOCGUQ5c85hCJS8f7kniONGpjPNyInrpctFv9UQzcKI7Q7/UQDhluqGwhvH9noxyg5yYaUHI8ClsKrVOOSQrNEyVz0rBHQ7oQvVYfnXYfwTDRRiuhBzUswFdVHB83gKSgjXoSR4wpZVphu9hyLO/ZM8cqzldG2nU8V4xVcmWJyTNBT51Jeq2BORqzyCAcwz0zEToc13MoFH1tjGgGpRfyEV9yHBA4Djgu8E9M2hQ97NAYcQKliVuCYFHcKe/5QL7AEA9mpeTCwide2FuGiMgxHBWQ8wpwxZOWJ4Z4NMoTT1zp8lM0TT/OrjMKZBTIKJBR4N2kgExN+p94BlOyW+9sN9JojrsUfU4cehIgiHhisuKcJK+zeeJSSmYkupREkkAi5LquxCqnlyDuotOx0K+Wf5TKyjzccS28q2FZT1gsR28OGeXILjIKZBTIKJBRIKNARoH3kQJ2zre6CbPaqD0BXl0CY0oLSta8U/cUeO32BIbbdESIeB+JleH8rlKAn1U00uaPm5WtHHwuvmlmTSewDHxmo2K4WMNluCHRrVg9RTpvdp1R4CUpYJcCmE10HPTqyo3vEiVBr3VfGaTl3XQG6n1EIapfsk+41A269FqeHe8KBTKDlTfSEmZUJ69b7j6vU6TLsu/p9aIErN12MfvnGvx7HoLAE48Le5uneHK/jV8sTemd0lRu0rtJW+F0X+FgL0S720GiIkzP1bB6cxa1GRdOPiUBcc3PWFJa5GzRaXTk2uJuX9CCcqgQdxSau4nsSN96mmDjyT52to7QPG1j0GciD0kcyeChrQ5yIBI5p4Ii6nDCAgK+F4W7NlqhyCbCmlXu2rInz0JQ7ohSWplWNB5QdGaLaarC5pGtpD1zQOIgVwDys8DKuovN+Wns7jahEh/H+wPsPGvi5KCO2ZILj4YNKVx6+wr37ibo9+npIhaPNrNLNazfWkR9jqtTE+WmMHvlyzEUOIAq+AUHubwetEkCs278CkVQqU6kddxBKs5HdTD1FhKb0DVJT+H4CXkgwcGWwtOHu9gjDzS6ohSnpxYal8RcAJTB34UHHz7yyLtDqKiEMGIIjUQEJO0yLoU2y7TlMiTQEBgMqFzXXgMkJFTR096GTJtK3c+ypYDpDwJLG2tJyZAbpJ3iwrj0i0RCAnGR8bWOdHbiljL4Yn8NjxT2n8U42FHYfNzDxpM97O4cYDiIRiGZtJcbeiDy4SIPzynCQxEOCohjHxH7vgkLkCQ6ft+ovV4L+cszk37pKl6e45IUE8BIfj4i6Wx3HV1PpD0fskltAIm5iAV0foazp+fAl/wCS0wNztK+6StbNqNg0SPIEIgjjo+uKG8avTa6wxBwBjpkixOJN45R1cTjDvswf8ZYwVVwkpz82MdC1UWEHoJkgF7gIUoC8edxZqX1pit1Bk/wNIYftq+evX2FK8LieESvKn0gOEpwsKkNN7c323jyZB9H+ycSIk9CbEl4H1LTh+P6cBgcJ8mLV5W8M8RgEMKBB8/NyY/tHtNfJtsl/TsPVdMInAtyBQ+FojZyHE/KQVW7m5chZtRwmtFJE45rnL9ptJnPe/ByLojChUeKZ2wavVuYMPlSrEClH4lyJl2mzZAeMwUHjrGxfMDmcjRYMS7yJ/IS+sQjeaDrYerkwYSd8wy9XRnjBv0YUeCRGiksssuMAhkFMgpkFHhfKMCxnj/6beMcyYWd0YK9nTOvXBkzmTkSTVaHJmVelcClUfabljuvjNf7mJDzaja3XtZyHr3A5Xz4ro+Q36Ixve+ljcAvgzDx3nzr8ZNSS17y8StrDZ4nXxITGbLbjAIZBTIKZBTIKJBR4H2kANdVRA4GlZlW/n0DNTHisEByFHyfmyr1um8m270B+v4UQaR5ytTf5xqd68N1XFl7jONYhwia/HyweXk+5528FoNt7b1a6yf0dxvlbM/w70+R7Fmd3xIFuCmSe0MlDLGOOMDQq1yDSB9cbxeWneRbm4jPJ95p9ZF9qOC5ni7L5snOf3MKZAYrb6QJDJOP95nnIMtruwhnOww3Mxcc+CsuVm46WPpuDlsbbajAwclOF9sPT/DZb+twqBCjRWQIREcKR9sKx+KNpY1i1cHCSgUrN6bg1XQ4IIK3ivqzjqnxPBdN+9Aoj4k8Q7NE+wl2Hyb49qsYW4+Psbd7jMPTQ/QYr8VVyOd9lCsl5HI+cj5/LrxcAa7rI+fUUIwX0D3xcHraQtTrw4modI21FbEh2wg/rvhIwUajZnHiUpATwfEUFH9iHJLyaMKKUoLkwZOFa2HpN6LXlbBAVQfzaw7mV3IoPcqj03HRPA5wsNnD8V6C6oKDUs4YoZAegcLRXoJHD0IMhiFiBChWili5Po+ZpRzckilQ8LKFveSZIFjfc3BnKBi+ZBV9z4Hvn1X30lJSFrAWPJfR5E/ibVuFtymfJyYUZa9CQiX6scLW3Rh3vxpi4/E+Tg7baDZPMRj0xU1OsVRAsZaDn/fhUdnpc4d9DjmXvxKKySIae8DRcQcDiZ/oGlMZxjgxNZiodxgrhHFIda6mCfsJFwDpTSBNZ2u0kyJEGtTosUnn0UCMlpPGAEQbq1gkRqlf7cKAkY2inEQHQPtRgod/jXH/qy529w5wfHSKVqeFQdBFvuCCXoOKxTz8nAPfy8H38sh5ReRQQcGtIQkKODkKcHwyQGDa5CyA5KuhefVcFAh0E8mZCnES91wCXx3qlVJepUkED4uQPqe9X4z6E2FdGeezgrU4ZIxWzh5fCf0rJyJeSgv89K4SxQEUfS1CoVj0Ua3n4RVjOC5DaflIxN0RoZuBmt4+rMGKaR9HeXAZP4hOrpw8IidBYcrF7DUPfsUFGF7OtCvhEMLrHmIrYYCQVEK10QT0AujntY2ldRotVpe2JDSgbCoMdhN892WCJ/ca2N46xMHJMU7bTURJKAYTlWoR+UIOuXwOuVwOvk+jFB++KiEXT6GEaWxvnmLvqAfXKQirUOZVk/PIefhJamkBMX7zfFf6r1nFSPGa8VRixh6pVhqeqZ/eUcM2Ni1xXv1JQvvcktPcE4wGxQf6N8a7Nv0557O8us1cCukSY8gfCkw8AAAgAElEQVTYvqQS6DJeAMTVoer0/ETTFAo7ClEYSCiqMMyjcE720SNbvwsLGqXMLt4ZCqQY5J3BKUMko0BGgTdCATsmG2BcrOeCJ5X+Q3Z9KuojKv7Nx5sdDuy3nL0/Fxl+nGgvYDTSpDG7A/5CuE6CXM5Bjt86aXn/XDjZw4wC51GAzEsGPDvEYMXXZrOOcsVjbRRyA4BOM8oxnu1M9rLPeaa8mABBCNDmRYy3+JjhFX29scSKk2cYZFcZBTIKZBTIKJBRIKPAe0MBCgZGOKBMmvN8cK2Esi/lhzCMYEXgdJ2MWDEhhaRTMCS4QhBQ6QrEsd5EyRQ0WPF8rqlYoWM8X3aXUeDKFKCsavi3kKPBiuYprh1HcYyYi6v8HOOyMdPZ7zcWMMl+Ru61acj3lIEVrb+18kP0e77vgEbb2ZFR4JUpQF60P8OK5FF68OF6Ozecyqb2ONGsZ9OS7S5gPSYRmEzCNArgvuBhxDUIvnXFmItrHDkbOeMCWK9cryzjK1EgM1h5JbK9ZibbmWSCcICcgjftYOUDF+vXV7C/0UMQuWgfDbH/rI3+oUKl7AB5hkFQaO8kONoO0Dw5BRBgZraIpWt1zK/4EvKG4Wl0h5SuOervVCLq39gYMOq8rJVMaqbTx6cK+98n+O7zGF/9aRuHe010hz0o38HU9CxmFiuYXahgeqGMctlHseiiUHCRL9IFCOCrAryewrNvFR48qKAbnCKMOLOZLeQpOtgBZIQskZFJk8gwfQTl0lglQWJtLOwgoqupG8U+k8roR6P/ZkKmR5uZJReL1xLMzNdx3PPRbcc42R3gaLuPpZsVFMsKTl5v/UvawP62wtZWAzSkcP0E9dk8bt5eQXXG0enS5Y4KfAMXFA6kXbSxAHWJZqx+eeCGTlotyv/cJynmiuOwRCBRQvbkVOHofoy//FOMb77dwf7+EYIgQrHkYWZmHrMLZcwsVFGbKaJUyyFX8uAVIEpiCvX0a1DsA/e+SCTcTSfwkDAcj9BrfCWakwd13DRI4jkxXiNEoetol+G2qSWtUQSPI5+6GyXWz4SOtNCk8j9JNVjqMpX7lS6NvIakD4S7Ce7/OcbX/97Dg7v7OOkcSAiQcqWM1eUpzCwUMLNQwdRMBYWyh3w+L3TL5/LIJ9Ld0T1W+ObLgg65FBr3ZFKRs0n3lRC9QiZdjBkzJNzIRYZShtDWQOGq9EynM3XiI/u7AoraMGKUR/O0ZqIr5DZoS8o0LmYQ0jVPtOOKK4B7qSQsz9SZ+c4WtvVYx0Jn56dx404d9WV6V6IcJfs59CAteZXgJrudZchXUnXdr4m9QugMEHsB/HKA+hJQn69I/9TCHAfYsYpfrQpp3NN1MLktGwhs+55nHuni7DOe089NUqGPKUv6VaQkBNBgK8HjrxJ8+a9H2Hh0iNNWC0N0UagXMb8wg7nFKuaX6ijXiyhUcsgVfVGw0UVlLskhPwRKEfD7f57BztGuNp7kTgHOj9SOpXHhEGXxtHgxh3UnT+WE58A1ktRZO6YqS3haNyftkwJjKs6WYrunCkvjMMoweaEnBwNe0LYzvCj+hGjn4Z+CI5l1YTLOCkbm3rCHKAz1o1TG5y9lTOa0zXwyXRlOFEug54g4TmeCOyfJ86VkTzIKZBTIKJBR4G9BAX57cMG+kM+j60SyM48eKuKQXsLO5vHUpUHTyhpmIuHJXMaxDoXIhVM9C8fwfYVCwRejFZaZHRkFXpkCKbmCxrRciBTbbuUgDhMM+8HIYOXCMsirKThyzXsudg6ULNiTw+XgN6bPtRCGcjZMbt9l54wCGQUyCmQUyCiQUeC9owDXOAo5B3k/r720qQBBEGqDldgs1ptaGfHAirlGgHheHqCenx7FqfSn0bZ4qnAc+PR26+v1/veOUBnC7wwFrDG2RahcoMEKw6lQw8JvrxAMGT++dslvMU/kYuFYy7aWqc0aH2HGkZaBz5SH3HwH0KM9DcSzI6PA61KAbGcWuCXsPL+vqMejRoxe6bkGoaMUGN23ZHhBqeRny9iJwiDQRitisOI48BxX6zCzDTMvIOIP/yozWHnbNOcsIDPBeA+S/kLFPMs3HjNWrjlYv57D52AoFAf9noPj3QCbjxPcmXHg1hwkTYX9LYWD3QZa3SY8X2FpdRZL16a08QQnCAInYBb9gvoJDhYtK2vR80SkJPTQ4eMEX38R48t/38X2/i7CMEC5ksPS9Xl89NkKrt2awuKag+lFF+USkCvqkDv0GMOC6ZkkPlLIhREOD/LY3ydeukCqloUsFyFIfAxOVKQxdIJksOQU5FOVM/VNPRm/tOm5gKQUirMOltYdrFybwtOdHPqDBKeHAfY2G7h+Uka9TvWhEtua1l6C3W2Fk2YTcGIUygkW1sq481lFvNtYm4/LUBhH6Gp3hKm9gJCk2svKaAHX0Ee8G1xER1vM2Hvxf2AYRFpinFFMWtoVnTxL8Id/i/GHz5+i0TpGmPRRKLpY/3ARd362hhsfVbCw7GBqzkWh6sApMcSVYTziFyokHSA+DbG1UcJRy0VErxCOqIctdmdnOrbxaPDiiNceviAN2B9C8pP13kwchTh24jkDkb4SdmM6JidviyGxqz0pSBxHTdd0npe+TuNi6hw3FL7/Msaf//0E97/eRqsZIkQfSws1fPjJMj78dAVL1zzMLbmYnnU07QqAGJvR8QztuvoK4eNEwn/tbZVw2nMR08uSVN1U6qWRfdkMlsj2PJnfPj9r88kUz91bej33YvyBYcPxh5feWXxSfPEiQGyvVBbdEZhBq/6f4w6mnYQ3lv9SBJ9P4DooFB0U8nr3suPEUvryyjR+87s8bv7cg8soa2K0orNrDMWG5QyefWieEK3Em0LMIY87NQpAhQZ29B4l1XjzmiCW+dLHJD0nAfDjiMb7tIBuKDy9l+CLf23hm7uP0O8F8HIO5haquPPrdax/uIDltTwWlx1Upx0UKg4czkuUdEiHEGB4M9VWePYgwX/8eQjP4Y5udbaT2+Bjp20xwEnjaDzZCJoM00XPIiSlWGenE05WxPCOSWKmQsNPhomey87nzz0cA8y3ImaMnupW0COFGSdH7865kOQ6NBwXTyi0j/oEgZ+HAp/pYkYAKTcMB0Cno0A3o0SbtPELHkqVoihwRomzix8JBV7Mmz+SSmbVyCiQUYCyOT1HFIBCgcJqgiimIXqIaEjXiWdTlcydpNhoeJBZakRDvpcphGELGQ5xoBAGdE3N0HQxcnkXxWJOFj3PYIyyZxcZBa5OAct69A5UcFAoaS8o/MKPogjdTk/zLiFauWbEt6li0s9SC/Z0NBpwex6FJsruHsNEAvnyhDfQFKjsMqNARoGMAhkFMgpkFHgPKGBlCM9BsQTx3ksv8gznTPmXhq/02p2WH5hlfIlECxDyny+YnmvS9KwSAUHA9Hpzmusr+HlXPKyMeRR/D0iVofhuUkD4zgcqdUf4Kk5iuImHfn+IcBhq8ZU8ybVM8wEnPK3ZdlSpsbVBbiQOgU6XWeiZguvU5F32EbPuOsqZXWQUeE0K0L+D8BaN+fJw3RhhEAn/ykZJGVPNTnaOsRO8y9LtI/Ixdatc8xbdIpcwZJNnDOWE2jCGehdmuADWa9Ymy/6SFMgMVl6SYC+T/Gyn+ZnRwVh+9itODr4jrmkLsy7WbyZYWVrG9tEAg+EAx4cxvv+2gaUbM5hyXITHCnvbCY5POhiGfQkpsnZzDkvXZpCrckXGdEfbK40e+axc9jzrZ0V3XpmAbAIqqwIg6Sg8+S7Gk+/bOD7uYxgOUKm7uPXJLH73j7fx0S9cVGcd+CUHLr2/cGO6THR2wmMxfK69ANBQgEos7rm2Qp0YWmh0bOljZ7uLXc4yh7JStmJjSa90I4ukBoRbcTC75GLlhsLco1kcH/Qw7ChsPT3Gx0ezWFkswxUPK8DG4wTbW33EcYQIPVSnc1i+WcHSDRduUQ9mHOdEoXwlTK6eSNA1wgNHTnt5dQhCOFGA2zzaAIiE19SkoMFD1ttYIAd98sCpwsNvY/zlD09w2ggQOzGmZn1c/2gK/9M/3sEHn7iYXdY0oJGSKIXpsIUGFwRPI13inFeg8XkQhgjjIeIkMLpdJjATQrpZfYgBVKVcgieaYAdJ7GDQjWU3G5XO5CGhRTqfQEv9s7zFiSlSiALGK2fYFXrNePOmv1JnukjvA93dBHf/kGD7aQP9QSghQ+YWavjNP6zjN/9lGdduuijWqUzXRioMVSWszfrYfkTjHBcYEOcogKL1vTGksCZHqdq+hct0aSQmGeOS40XtcUnWV3otg8hZTvK23j5pnp2DD2sy9tjwibZDIPH1T8zkaCCUTpy+PitWX434jRfPH9bwbPSGsETABypVB9UqUMwznI9u+DihN6s8SvM0BKOhSQpx5rXF2HMat/QzMRzQhpGj+YHv0+lHSL25C0HB1HHE22nw6TpMPk/ds1+JEWUEnOwoPPouwcP7++gPQ+RLDhZWa7jz62X8+h+WsbTu6g8y9qucoZmxkhZZlNV2IUKqjHcMssS4Zwk/2KiESxHF0miClinUxmmYzjuW6Oo3Qq4UCi/MSbwsbhMJ9dh4NUB6/KfXKa00pOJQj90XjLGpMu2YZxdekgDoU/8TR7KYkzgRPHpeK3tiMDWBZnabUSCjQEaBjALvAwX4OVcAShUHxXIRjhMgFCPFCINeiCgQN2XcmDc+L0rdxucizsWyI4qLRAypMgCigF5aFPJi4JhDoZTXO/TGs74PlMpwfBcoQMHdyipGBi5UgTqNtmVdxEUSKfS6ffmurMZKws7Kt7z9Bpush4U3Oiu0WwqD/sB8tsUolByUar4YSo++5SbhZPcZBTIKZBTIKJBRIKPAe0MBrnGXag5KlQJyuTwUAgyHIYa9EOFQr1MxdL1dW7tQdKX8YH5U+NNL2zCIxdMF3AT5ko9yNS/K2feGOBmi7xYFjIxKHpRL6uhywNS8g3zRFeV8HHvodwbiZRChguKaqWVMWgAY3ZCuGKEYjualdogpyv5WK0CYRLJ0nst7KNcLKHKzoNVHvluUybB5Hyhg+HcMVQcoVR2Uq/TymkOXqsogFKMr6vbk8Jyxzb1j+dM3hE99XahkzXrANYg4AFw6JXBFt+Bzcy+/BbPjnaBAZrDylpvhvD4nzzjuW2nGXDNUzdyygw8/msdp7xSNjotOJ4eNx6c4OZhG2VM43NHePjpdKsE9zMwXRWFXn9XeTcaqk4Y/9kLfiIKWyKSQlIXEoUJ8onCwqXCyF4AdmXGZZ5YK+OAX0/j0dx5q12moYAxVrIGChWP02srjApCO70yXTYm4fNYePSxq56A1emTBjR68zoUtkLKkMaKgwc3SNQdLi4voNxsYDFo42GrhZL+H/rUSKkV6iQG2niU4PmjAlVWuEHMrVSzdqMClRxFO8OcNaETelvk6eAsYAuLv9YBK7pEsbak7jqS0P0NvDIEhPcs8VdjbbSOMq3BzCtMLOdz5T3O481sP09dc0PBHULORhSya9IhABjO8QHeHw6CPJAmRqFBC8tA6fUQjiwbB+UCx4KBYMLHq6Osm8TDoxRgOlYRlYqghOWy+NI1ZNSq5WbZcK/HOEIUK/NGDAOUocqIGY2mRBvIK18Y7UdJWON1V2H8aod1MZFE/lwNu3pnHx7+dwwe/8pBnf7WToTFcE3xZLOtEL0cOECYQd2VRRLppYo4ZULwCmlfNMhJcpREv8IhzVWAT6VjFN0T1EWQxVhGoFLTHbQ9solGZYl2bQoJtIIn0SrWY6jj0sWTCMJ3HZxboOedRORPvRMGffka4HuAXgWLRQc5ngB/tYWUwaKAzrEIVfHgVQIzCJhfSWZAtzOI4WTdLC763aYmDvbb50ni9iesJY6JzQV6lbOIpfQs42kmwtxmi2UrYRVCreFj5oIbPfreM6z/zUJozRipcNGA+wjfjs6BDLygewD7aH/B1DM9VcGlYaYcDg6hkn6RZqhIyjxiukXZl2qvWh20ksPR/udRWJqkSXu/yKqhYHqAhKQ3iwpC/WJSJsvBCFC4DZKuQUOmo0OvQQ1wsuy24I98rubKzWQwaX69KWe6MAhkFMgpkFPihKWBkCKcAFCtAsVSE6/WRBI7MF4NecLZgbzy4XYoi5w3uLg2AkCE06aUCCoWij0I5h1zBzUKqXErELMG5FLAyCcUXa7fiQjyi1mb1pgonosxDY6kI/S63OOeBkoHGTy0rz50n/xCm4d9uGxj2h/KlQHmyVHJRqnjyHSsi3bkIZg8zCmQUyCiQUSCjQEaB94IClAM8rTAtll34dKOGASIabfcCDHsxELkAH6eOMfHByCWUO2QjLrMMrcI0EIMVehgvVnMiA3uZhi5FyezylShgGZDfcL4Dyr+5kqfjFiQOgmGIQXeAaAAwZOboYD6bVx6SecceyPfboAucnjYR0k2Qo+AXuGmwIF4GZfPCCGB2kVHgFSlgv+dcGgs6KJXJqz4UIgRhhH5vgF53ABWXNYeSTc9hVymdz+1Pxl+g3aR38CHiOIDjJijVcjIG01NQdrw7FDhP1f7uYPdTwoTWj3kH1TkXH//CRX2qJDES48DD8e4QR88SHDxLsLelsLvXQ3/YQ6nqYvlGBbPLRbH6FQWT7dgTtLvSwomZi+jBon2i0DiN0O0NENFNsxtjca2Gm7cXUVtzddgX7lw3u+nGdG300kJtIo0WYoAT2nBAd8/c2UTrFj2aTEx9ExjbQeWCCj2f+uInqYLEuIS0ZtiZOnfnO1heq6FSLiCKYpwed3G03UfnSCE+VQh2SfMeGq22uPv18gmW1mewtD4tc7eFZ5WiFyPxGm9S+BPKc0rvq4K+CimZhot1kcLRvsLJYYBBEEn1qNSdma/gzmcrmFp14dDlsT2Yz8K3MGiBG9HjCAVyxvnmrnuaiWimEfsLm8fAIR9RqPK5MF5meCAFl0ROfPSawLANxDSgIm+ly7R4mPMItjFcUX1g2AWCPvGklx8xVxGjlTQKE6SegHrBrSlD3MbQvVhH4eQgQbfVRRgMkCRDuG6A259cx80PC9pYhRYz6dHXFkxkTL9RNBrqKQz7DLHB2KYvrvMF2L32Y00pDWbEeyOiEfFJK4pUkaN0qWdv6lIGHTIrCyGWxIPjC3+mEKJnaTt+qZ1p2HdcgJZrbfYi+WUXsFnttvDs+bI6vChd6p3wO429Sg4KZbq705ohBz7azT6OD5oIerofSb9M5RUUbP1sPSxeTGd/fGbT2fc/4HkStZcq2jYvMyUKR4cKJydNRElC3ygo1jwsrk/hw09cCfMm4eh8Y2FtC7Z0ICz+GDP4SEnoGmoVfC8P1/NeSTlGo5VLB2SLx2TFjdGKfm0SPZf2uQeTUM7uL0o6yTMT/UCPhRwTPUR9hWEnljBu4tXG0syWkoI1Gn+V0uHWGAe0w4/XDqIkFMGf4zjDMnl0XpMe7yy87JxRIKNARoGMAu8+BSiaFOk9wpEFST/nivF/HLroNRIMOgqUWUey14tqxLmK8lWgMOgqdDtKPIpS4U+5n9+24lL6ojntRbCzdxkFLN/YMylCXVLNwfQ8XaJrC/VEueKKv3E8RNgzAtllLCzfe0p/2w6AdoPGz0NRANCVdKnuozzlj3/fZS2SUSCjQEaBjAIZBTIKvF8UoAyhl+XEQ0Wp7qBcBwpFLtzRm6yDXitG9zSWDa6jNVJTy9SSiTyRtWmzrkJdC9f3Oi2Fbr+HMBnCzyeozvhiGO5lHireL155l7BNyb5ySR7OA1OLLooVfrtRkHURDRz0Wwq9htHbyUK43YGcrlBqAY8AuR95qNBtKhwfN8R7PhdXC0UX07PlceOXNJjsOqPAVSiQ4l8ZfzkMe0CZ42+NoYm5pTpBEiv02xGahwMkA7NJnqxN/eNzg69+pvWDChx/+d3HbzhtsBLJt+HUbAGVWubh6irN9EOmSY1AP2SxWVmTFKCxCd11uXMOPvqFh6mZIgp+AZ4qYdD0sPVA4cm3CXY3FI5PWhgEPRSrwPU7U1hYy0l4kTEF+GQBF9yP+nNqcKBXkdMTusodSPgUWgIHURfzS2UsrhlPLja9VfQaIxBtwKKV8XSgkbShXeYOIsQU0kDfGPQiMCr5AszewGPiaPFkebw2btFoFEEPKTPLLq7dcDAzXYXv+bLTan+jjdOdBNGBwsZ3CY73uugN+ohVgFwRWL05h9UbrhgYncGfwHdU7sTzN3lrhOgLcXiVsog37Uk84ORQoduO4CGnTQHcBLWZAtZu6PAOYiBFi9y0bCNtfDZRcGJIGkpiHNISncYqnsvYczkRlkZkGrGDI/ByJQdTM47EsfdcD2EA7G+1cbrfl9BNwj6mLGYdZTd1FlsGM7qRn+OmNsBpNBQ8J6e9q6TpM0Ik/fCK1yzc4qKAXkcr1qNhhDhmqJEB/HyIWx95qC9Sma7rSAWu/bENpe8QZ3qB4LzbU2idsh/SIw1Zl/3GHFJBe/P2zuJFQspytF6eSgbjCnBkQGEbgDSwP2N0k26nEZasxKgio6cvdTFqX3rGMDldeHCUK4Zxtj3OAyrpbSaeUz8K8Rzv4iRBFCWIAjKwgTLJZOcBf9lnbHcZi4DaLBVBDIPlI0ocHB01sL2xLx8EFKxIS/LBc4KYrYstexJPk09e27ratJN57fM3cBZDJ1veq5Rj8RZLLY3QyXGEdrsnNKLCrFhzUZvLobjg6pAzZiySRYN0/2J2GlKSLwPgcJ/9KoHHGAf0pMOyJun2BmgwAmHpMHqgL6zZ3MTjl77V4F9AZFs3ezYlsM46rwtH+ei0BjjcbuBgK9HKR2sYOImRhWP4UQ0VkpbC6VGCre099IOeGKxwJ1J9poACwwZy3MuOjAIZBTIKZBR49ylgx3hiyqHbhYR/pUvpxRUXhWJONiBEgYPD3S4aRzHCrjFepLMUKzedV1POK/w+7EEbxh9H6A26sjGiNpXD9DwXjCgcnZc5e5ZR4OUpwG8Gd9rB0pqLYtkXA2Xuqxn0E+xsnMguO8rYYyxnbkZdgXIieTuELI4mTW7q6KPT7UNRuHRjzC1VMbNQ0Qa6Y8BeHucsR0aBjAIZBTIKZBR4GxSQ6ekHWkt8G/j/oDBdhrd3kJ9zMDPnoFwpiB4jSVycHvVwsNuSDT/cpDl5jOQHvpB1LW3wSoNtKvyPjhJ0Bl3EKkSp6mN+paJDWzMMeHZkFHhVCrCDm5/oGorA0i0X0/MleB7X9B0EA6B5FOB0ny6SjWf6i8qzjEweZjjXjkLzWKHRbIr863kK5UoOK6tz8Ln50qa/CF72PKPAVSnAeYre6GcdzCw6qE9VQN2gUi46jSF2n52Kp9bRRsv0txf5MM2LZE3RBSgEHRqsAL1eX0ICFQoultdmUJ0qQEICXRW/LN1bp0BmsPKWSXyhLJjuQOxYbAmPC4JAedXBtRsLmJmagaNyGPR8PL3fx/2vE2w8U+j0+/ByDqbmi1i+XkF1xgVdNY8U3qxTurNeUMd0/x3LQucoDElCjyhwZVCgdw0vH8PjJERcrbHExDhgJ0cuVnIxZ+dJjJ0dhW5vCHoN0F4QWNqZovkC9N7g48mait2M0KwwxcVXBwuLJdQrVSD2cbTdw8mOQmNX4em9BK3GAHESi4uz67dWsLg+A+aTHeNXoPMbrMj5oM6p3vkJJ55yZ3xaS0s4rA/PMRCHCgldHNK8Q9pbyQDul3QsRPKBfq7hitLXKjB5w+u+wsN7CXb3FIZhaFqd8Fy49H04qSg2BkW5ioO5RQeLSzOolitQsYduI8buRgOHu4l4bZEF8VTdR5dGmJKYjIzLGCg0jhMc7CmcnrZMZ6OCmt40dOidCcpc/dbSLM0HXKgX607L7QxRE8LLk27GWMXSmSWRxIRjflKPGOgfKmw9Uzg9aSOIInmt20K3x6iPS4aro3z1lERS/1yHhka0qNO5pUiDr8XbwhU+MO9G16TJm8STaLlAPu9LLFnCZqgnenIa9vUXI8uexM3iKGfCYA1NNf2cdnXvuS5YXxW7GtaLFC8axKv9Z7mCI8PUOJhb4mJ6HlP1KeT9EobDBPtbJ/jmLzvoHSfCx0z/3JwiH8BGAKNRhlRq1HRnuKXrYep89vItXNFS3/bvi9retpHtM5ZP7HNbNz5n+AC68Itj8frFkGLKjQA/FmNP0jA9JkvzEgXCMoYXHAvikwT37yXYP2wgTlzjreUN1f+ier4h8OeBeY4fyFZXxcPQmYaEnJ/7nRCHuy3sPD0RgzlF4zkeJt3omhfptoqBxnaCpw8VeoMhIhUgX3Qwu1jF+q0lVOvjbSNwsn8ZBTIKZBTIKPB+UICynw/kyg7mlxxMTVVQyOclhvn+VgvNwyGCPifsVHXS13zMezNv0MiRcs3edoJOh64PKdtEqM3kMLtQRn3ayLkpcNllRoErU0AEQJ1aZCQaXBWB+pyD5dU5FAtFJAnQ7ybYeHwkC+8q5jfxxSXIOyO3c7F+716MdmOIJGFISQXHjbB0bRaLq/TAmkLgYpDZm4wCGQUyCmQUyCiQUeBdpQCnctlcBjgVB1NzDqZnKigVish5BZweDbC32cKQBtuh2eUvdZkQJqz8awy24xOF4/0EzdOODvnuxCjXc1i9PiteBLKQQO8qQ7xHeBneZYxuGlx5s1yXK2K6Xofv5BENHZzs9bC/2ZbNfFp3cU79LCvLmiy9sQCtjQQ720pCiTM8C9fQp2bKuP7BCoqlbMPBOVTMHr0MBcwnlJzITtQPlh3UZhyJ9lApllDwS+i1Imw+OpLN7DRESa8znLsewTUI6jhPFQ53FI4P2ggjvcuGnrPWbsyjPu1qvcLL4JulfasUMOrHt1pGBlwoQAMNPXOYPjjWjyQJO2PBkV1ANz9yMD8/i1gBYajEenfz2Sn29g8xiLooVXwsrkxjcW0GpZpRhLNDc4e5LeASymtsTKL0OiNd5xYd+Nz5T5zEzKSAYcdDv0kDAKMApNDFTUU0TKBlJk22TbsAACAASURBVH8hILutmwqNrQQP6BVmL0BvwEyEZUcTG4LDKFYvwfX1Xo/VdATKYUijsoPFVRdLq7TYK4uiunHYxzEHse0Em48V+t0uEtWFX+zj45+vY3El/2LvKqMS3uLF68oCqfYWoxUrjBBlwz+FkgPGcBPFsBi3uAiHLoYt7UpLlMDWQIXNKkK4FtjpGjxuKHSfJbj/1wQHBzrGIYvRRTlwz2NUw8NuBVhYc7G27mJmukKzKQQDDztPm9h82EbnIJEdbuQ5h/Yg/BGwxYfGNgGQdBXiYxpOKeztKrS73RTjaaMVi9Ert1aKdiSdl4O4K6NBhZIOmYdKSmieKsTG7bR4yhDBzxgamA8YfuyoARAdJdh5nGDjYYJWc4jQhASyjWOa6LVRH6vzCKh+Kkps5cOJc/CSAtyEoZnOlNfW28fobOogXZz8wLRWOWHzETTrfcYIYyhc6YZ4kk8coFj0USqUoOAijlx0OzFajUiPUTS6I04pPEaDri3fwKIw7xeBWq0C16XluYtw4KB9nMiuCWu1+xwsA+eiRW7NGun/Z/1rVFd+SOSAmWsurn/kYmV1GuV8ASr2cbIX4+7vj7B1PxE+Fv7gOJui7wgnqaejjaWkP3IXh/0Z7yzpdhgh8OYv6K3DSQo6NBzbwc4PF53ZTpM/4moPTUIU8h7yPo0rEvEIEg9yiLo5MWCzbSRtnOpbMi6ZfhUfKmx+m+DxoxjNVh/KySFS9LBCt1LniEOmXIvGpeeJPvSi9C8L+kWw7JjNNM/xIgu6qDCZR/QMz/7OkGknO0Ns3muhta+gGI7K9iEDh/CF56jcYdvSg9WpwrPvEzx+2MIwHCJx+qhMuVi6Po31W4soVn4Qn2ovJFH2MqPA+0wB24116Lr3uSYZ7u88BSbmCxGTHB1qj99MNFiZm8+jXCwiCl0c74XYZ+jUQ8qvJhyslTVELjGyOeVz/iift4CTbRplD9DqtAAngkcZbKGI2kIZuerrfuS881TOEHybFLA8bGUys75SnHZw6/YyqpWSdok+9LH7uIvDrVA22Yy+WZjf8LCASPNxyG80hXt/5fdZD1EyhOMOUKy6WFqbxuxCxrtvs2kz2BdQwPL6Ba/tY9s17H12ziiQUSCjQEaBF1CAYyv1K3mIh5X5BQe1Sgm+W0TnNMb+Rg+HOwkCMVrR61lcWWE2GZbtuomRK6gn4SYf8Zp/TA8VEfJ5GsKUsLg6g3LVEe/LL8Aoe5VR4GoUIANS/jWb4qnzWl5ahOtQp+PgZJ8eKroIThnWVXvJHK0ZWn5N6Vao31E9haffJ9h+1pM1R4UQ9Kg8s1jB0npONt/LBsKrYZilyihwPgXsAMrleTP+0hv94hJQrZSR98vod1z5hjvYTMTrj9Y9mc0H5F/zk7VroxtJ6FloT+nx94ghrQbwcgkq0zks0WBwys3G3/Nb5G/29BwNzd8Mlx9dwaI4YkcxSiSz9/3Ceor1GCeUgoObH3lYWtYul5PEQ6+foNHso9luIVEBpmbLWL42h4WlHFxaMqZbMn19YWn6hSj5Ux2aHZuGHPUpB8VSTowKaNBATy+HO10JFcBQJWJFTGsaswBJxahWtivEbYX+VoJn92Lc/2aIg2MqsSIR3RyViBs9mu8IaUSSuwTJV31taP9cdvvccWTHVWXFxeKai5nZqlhLd9sxjnYU9p4p7G91EAyHgDtAoRbg018tYmbhst3iLMCu1j5X+g/7wNb1iqXSCECaxAGm6fawmoNyEiRQiGIHjZM+nj1OpI2prNQTA4VzE/+QBks0FCEPPEtw708xHn57iEajLRbkMmHIP0rxuvHTLCACDhX4tKJcc7F+i4ZbdeT9ApykKFbsD+/u49n9BEMrXBmFqiyE89rgRcGLxip7DxN8/22Cvd1T9INA3JhTUJMj3UmvSKPJZBaEnB2gUGBoF8DNe2KwolBAFOXx+NEAhweJxs+2C8807LT9pw/Q6v7g+wQP7ibYeNJDbxAjppbKYdxJ/QkkNGNeC2cSqZe8T7eBzWoNVpDkgSiHhEIqhVkq/+0vMAIunw9S17znj++N0YQYWRD4a+KdxrVccVCt1KRNw9BBqxHgcK+DoKkEXzGe4Rhly7RnW0meKcjTWwvDUE3T+g9g+Kp+J8HRbl/CMiluADZ5BZbt3mnjG76fPCSxeTjp0YiPWTYN5/KAv+rixscuPrw9g6lqFTm3jF7Tx4O/tPDNF21sPohlQT3hLmbyS9qQwJZLfNgXGaKlp0NhsZ9Ebd0W0l+Z9jxcLYw3cKbBCqK8GF9RMBTemOSPyXvyiuUncz05jNbrDurVMvIuwz/5GLSBxmGAwZE29BKXlhRIebCNrFEFDejYrx4k+Pz3MXb3ThFEgOvQ2CkHRUlYj3wm8w9wYlud0xBvuWnGKuZyWJFxhUZAHqLQw+lBiKffNfD0+xhtYxhIWsr4Spqan/Af6UqXtg8S3PsmwcbGLqI4hJsLMbNUwo2PlrB0LSeKSMk3Vnp2k1Ego0BGgYwC7ywF7GREoYs/X3sBXVh2sLzioF6rAEkOnSaw8fAEG48G6FMuD8y3oZGPKAaJ/GfmZsoEg4MEWw8TbDw9QKvbhuMlqEzlMbtaRW2uCDf/w0/J72w7ZIi9HgXk80kbXLl1Bz/7zMX0VA0uhe+ogMOtITa+P8Hepvk+o4xjeFdENCv/GHmSMs8uv2/vRmg1u4hiGqwEWFqZxsLqNArTdOfyeihnuTMKXJkC6Y9iO1Zflvmq6S6Dk73PKPBOUYBCixVc3inEMmTeZwpYGcIHZhdckX9nZurIeUUMeh72Nwd48E0XreMz+deuldj1E2FLrgMyHGZHYftJgs2nPRydNJAgRK1WwtxiHbPzVeQljPL7TLAM93eJAqJuocLfd7B6zcH19TnZih5FLhrHEbYft7H9LEbUMeGq+K1mhtLR+jk9LnPTYV8hOqT3fIXt7WP9oeZEqM+WsHhtGqV56tYm9JLvEjEyXN4fClg5NTX+1mcdrFxzMTVdRs4vIewzMkaIe1/v43g30frpFO+e8a9ev5bxt6Ww/yzB1pMEp402omSAYtnD7HIN82t1FKvaQOb9IdSPH1P/x1/Fv20NlXH7oCix8Frux3Fif5Rdk5xRPIaHAKYkPIQjiyqHx8eIuFCCELHTh1+IMDVXxOxSFUWGprGtyA5KYDzYuVNiu+67NDtIaZxS78fycZfbooPKlA8vT2MFatTzeHx/H1MzVdy8fgPTt1w4NJRhkBd6kmCZNqbdswRf/H8x7v5pC1tP2xiGBUHJdWKxItY4SI4XfldIRAmH9TZ/xpXG2A5TA0YKmPxnaTH5XLaHm9Ukzqk1B3PLDhZWiph+NoVuO8Du1gm6p7PodAcIowEK5QTzawWs3nBR/KFiqxN/IbFxISL1SFX4ovpN1tfca3qS1xgGh3DMqtxkeobWyAPT8+QBF47LgN1KlPhbT47xxT8/wtzMR5inorNimMiAoyFD0gV27rL9Y9z98zZ2dk+RRAUxKqDbOO0OxdEuECfLZp2MFaVbA5ZvuFi5XsbWdgWHh320mgN899Umuv02gv6v8emvPJRWqPU3tOLCIhX5IRBuKdz/Osaf/r2Nh9/uoXEaS0gi8Rokljm0wKSnBt0tOakJWV6SrmL7wjws2wUYzmhm3kGupOCyP8NFGLj48g/fY2btUwk/lZvVFRdWtIujQ4VgT+H+3Rjf/KGHp/caOGoMkCglC6uOk+g46ZMf4yziJXGeJPuIfgyhoiO5CFDHoaeMHKKei9ZugnZNG2vFDPnFBV3WmSkN7XjmvRyEw27mAYkP5KsO6vMTuwaYT0piLt3PNYQRFAtNEjKtMuMkw6BVp4BqvYSDgxaGQYyTgxBbD1t4eDfG7c885Oe1UYgUQlyooefZjI8WT+KYKxFeAY7bFiU+Y3vuPGnhmz+2US7VMHeH1oQ6L+tF46GLFqVJw0QMvfR4yzGPtRM8JqsmRivscwqVJQef/MrF9uMqmoMCht0ceh0Hn//LfezsV/Hpb1fxX/5xGoU5R0KaST00AaUqwvuBwpDhpLYSPN7YQbNzjLnlGn7121uYX6X7rMsM7s5IfqWrFO9pcyofblJA/ySH5sNYeEDRaw2BGd4SlCfpYHnPnMXrzJwLl9MHaZR3MMsxqZaXHa2hitFuRth80MBf/n0Wv/2vQGHBuPGj/Qk/rMifQ4VwV+HuH2N89XkL3369gWGfwYHz8D0fEUPfpepg63zeM77TXKrnUmlXm9eeLYDJ80R99TxmBx2+dEc0msx67r0QUdOU7+28qsd33YvOzWcfjvJzXAmRgIZxCp12hGcPTvBP//1LnDQ+xC/+bgoLtzztHpF57HjFXcaHCba+SfB//Z97eHL/BN1BB4kzQLGex+qtKdz6ZA7Fiv5IFt5Pl22v7ZmwJ2hkX2XnjAI/agqQ99PHWD/gjX3A0SfzVpQmVXb9Filg+ZLsZ2QmegH1F12s3nKxsFnH3lEZ/X6Cxw8OUJhOUJ//GJ/83IM/BYDTrJmiRNalbM6wfrvaIPuL35/i5LSBKAlRqXrijWv9w0XU5/gRoPNm/y+hgAgSdnyw1L4kz0/xtfkWcasO1j/zcONWBbsHZRy1Wug1Xdz946Z8s/1vMyuozrtwinpPhVCWMqn5ruRi/bOvYnz+bwm2tw/RD3qI0UOt7uF3//WXWFwt6u+CdJP8FOmd1fmdoIBmQ/6XL1CNk/244eNsnH0n2ilD4jIK6G/lFw+rL357WQk/zfepceGnSYAr1ZpDpqxnJoA378ja9OJqHttHRUSdBCcHA/zz//1nVOd+h0KuhNoyF4Ot8Gu+4IwMIZun7ie4+5cEmxv7GIZ9WdudX5nC+q0FzCwYg9eMna/UNlmiyyigZO3b8bijVmHxuotbtxN8+UUVqtdGr9PD0/vH+I9/KsD1ruP6p4A35cr6qSw9yGZLAFQFBcBgT+Gf/nuI7787RrvTFt2kX0hw884aPvp0VYxiKC8zL726ZEdGgdeiANcezPhLvYs/42BFdIMJDptlDIIKgl6Iz//5W1RmPPx9bRHlNSqmGapVj8GybiYbDoyx4Lcx7n6Z4NHDLXT6HSRJiPn5Cm7eWcH0ggevkAnGr9VmbyGzNXV4C6B/oiBN5+BHoKgqVSSKICqb+YQKcrH2sh+MJJM1LqFSjotPvoI35WDxuoOV9RIOGxRmckgQQLld1KYdLF6rYGGlAqdEhfA5HYuPZPu06bBcrCFGYvRBxX0s5cpal8FZoNBYoQB4M8D6Rx52N6bQbA8QDbmLLsG9Px8DQRk3b8+K8lBc/TvAoKfQayu0GsDezikeP9pA87SPUnkK19cWMewFaJ420Gx1oRzOZMnZZDjJKgYf4k/vHmB6J4ZDSwNX4y0f2VaY41mQnwR0wX2a3vRukAPmVh2sXHdQ/66KYbePRruHbi9BLxgiQoD5hSJu/3wJtOyj4lSOC8u0Fbig/PMe27rYd/ZeFORsr0i7XUuikerixTikdBwmB0FqLiRP0uNNZOhrV6INHcmHOaC46OL6bRc37y9h60kfKvbQPorw4I8NeIMjXPtgRlwfl4qOeHUIhxAeODlW2Hx6iK3NfZyetDE7u4Kp6gKGwxiPN5sIowCxSP6xNtSydU6dHXpZKQBzN13c+pnC0dECer1tdPou2icRntxtwRk8xOOv5rGwPIVazUGxCCQxeREYdBQOdwfY3jjG9uYx4tDD/Mw0fLeA/qCHTr8tsazoacWDJ91CiPOyTZfmATGGUHDrwNK6iw/uTKPdOUEQBlCJh6OtIf7wP57idHMF19arosjN+QzhotDrQDx5HO71sbVxhL2dAzjwMb80g+nKMg732zhshehjAKCov36MwYiMHy/TByxvpXEn7U3drZEJxwZO8gFDkm0E+H//jx1UZ7jt1Rq+ncV7d5lZOTJ+MQ+BUYGeuAHghkgKDSx9WMDv/tePsbRalNBnlpEZGsp1aJSTSBx4Wr+MPqENTgLS4ihW4lSGOFi75eLWnQU8e9oAQh+9ZoyN7/r4l2gL29+vYHnVFdeaHHF60RBOqYvZlQJW1qeQr2iDEzE48iHGHL/6uxk8/b6N4YmHaOijdQB8+S9b6B0t4ebtaVSnHPkIHSYJhskJphbyWF6bQY0GJLQoFxw5btF+LwR7GhDINWPcS51J/3R7mWsaHjK+6LVPPHzyuwK6qor+ozbavRjHx0MMv47R3E+wdz9GdTqPSq2AStlFseAgjoDhUGE4AHr9CM1GF0enxzhqbsAp9HHn56v45GPtlUWMsjSmr/7fVHUEQO7pPcsDlI/WMfD1v+5j70lNx4yTuccY7NhMcquJwRA/HOs5NyT8eR141Rb+l//9Z/jgw1n4NBL0gfUPGTapjsePigg6PQz7Lnae9PD7//EEh1srWFguSBtxXgr7CsMe0KUl9c4Azx7vYXfnCN1+Dz//5JdQUR5Hh13sHzfFLZSLPEcCi92ZVx77RIyQgMRNEDtsXbYvx2POURNzEKtljzOQ+gnvJVwYexLzx2L8xHOK823us3MajpTHcVtmcj2OOhYXTWcx7LJ8ls57BhGJ1GkAeAOJxzw9tYwYAzQ6h9j4voVB5ym27i9iZW0RtbqDUgnIeUAYAN2mwvGewvbTU3z/YBPdboDYCZAr9nHjk3nc/tUi1m66Ml+mxZ0UiVOYmMsL8Hw+YfYko8CPhAKW59NjBocTdm96VOM0xWuRL7RR21hSm39sUvmR0Carxt+GAuSpNJPxnt8ilPHy+vt09Y6L9b0ydvensLPVQbc1xMO7DQDPgN513LrjoUgD5byWh0Th31OI9hW+/VOEP38+wMbGHvrDNnwvQX22glsfL+HajWnUpy3T/22q//6UOur8BuXJ+/enJm8NU0sSftd6DtyCgjfn4PZvXOwczeLwLztQUUm8rHzz+T7K+Tp+/dsyZtdc0LjFyis0fGaY253vEvzl9zG+/24HzW4XgeqgUBli6dYMfvm7OUzPsSA9ftu8b61uGeCMApYC5PPRmH12I7K39AG9QYcbYOT72vYL5rHXFlZ2vjoFZEE3o+HVCXb1lFw94VqKloVduC430GW0vjoFX5xShgtNXL2GMBo/XpzvJ/mWY6T5DuNmyvmbLj76tYvtozrCZwqdfg/7G118/v88RdK7g1/9J6CyYvQFzMtNfoFCvK+wfT/Gl18kePL9HhqtBmKni0IlweqHa1i/PYepBVc8DAqv/ySJnVX6zVLATPAcO+klc9bB2m0XP//1Ev745SEaLaB9GOP+Hyn/VpH0ZnD9Y4DeCGVDPJeu6RWIOr4nNLSK8fUXezg8aiGIu3DzPcysFnDjkxlcu6HlX+IvssebrUgG7adKATP+Cl+VHNRWHXzyn13snlbQ7ubR6zk42h3iT/+8AxVU8ff/UEZxyXj6kbw6CgCjLhw+TvDnf4vx4N4BjhoNDJMOqtwgf2sBNz9ekG+4zMPru8domcHKm2wT6mwpYZtDGweEYmwgSlh6GBEFplYomSlk9LFI4US8PPgMiQIsrFM5l+Cb+0OE3CmuAjj+ALPLdazcqGOewlDOKF1tZzYCJycKMUYhLnzncsc/PaVQdSsxSOTbVtKkF1eoDM4BTsXBh5+5ONmr4/hogHB3iCgs4mgvwX8cPcHjb08xPz+DSpXbpxXarT46rT5anQ4anQMoZ4i5uRl8fPs6bnMn05bCvW+7OG6FopQUOqSF4xExDPFkcYl1iJGI0Q8XPRlihUYW2uOLpfPFH9usKw9DALk+U5rS8pPKdcdTYpyxvK4wNz+F5oGLXj/GIBzIjvPECTG/Usenv1qDx7iSbyt6BOlhfuQDXpKHYhXIDnixEFT0UpNal9AVvOQ/G5heVYDYKNK5m54eb+gFYrR4YdpDhOQc4E07+PBnHk72bqJx8BidToSEXix2XPzxaBOPv25gZraOSrmGJFEYDEJ0Oj00Gk10Bg0kaoh6vYxf/vIm5uYc7B8pbBxECOKhhODQhkumeWwNDA7yYeAD/pKLWz9XGPanEfRcbG7k0Gh20G/EuPfnE2x810WtVsH01DRK5RKSKEav10On00aXi4lhAN/1sX5tDaurs3A94AnX03eb0i/pQcSlhwWGt6L1Ow1liMMkP1r8XnS2C6IloLzi4pd/56Jxuoh+N0anDYQ94NFfW9h7NMDS0iIqtRLy+RwQJ2i3WmicttHu9DAIQnj5oYTTuH3nGlamXfzpizIaw0iMLsS6Js0ExPeqONu0rIfUcSIjxyCOFa7mF74NYkhsy5M/nMj4Jfu7JTQRYZzFaD0D50HRW4T0W7b1AKG/i49+XcZHt9ewMFOAy50HBG70IDRW0dyuDRdYR4YiExzFcOasSaT/0dAnr7B4w8WdzxS+/XoOu/sRhkGIxp6Lb05PsP84xOxcDbWpAqKkh1a0heJ8H5/+52XU63XkuIOSxn6sg6+QX3Lxi994+PrzFQyHAVqtDsKeh83ve2jv7eDpVy3U56pAPkYvPsbA2cXtX8zDcwqo1iqyI9Pim7gcZflHY4YQsXgWYn0MY6XJbuhAV41uFfDXgE//3kPgrgC5PJ48OMVgMES3CfSbCTYfPEMh76JcLqJWqaBYLCIMIkkzHIboDfvoh0MESR+h08bMAhBcd4mGJjFJL6RNI6Hb4vL/bCfWwdRjLAMnKQ+OU0Cvm+DJgx6ePKC3GqbVldTXY5ngqBg0WGEHpBlI7EQInWP49X3curOE1dUZ+DQUAlBbd3H7Mxcbj69jeC9CECi0Th20m23sb0SYmipKe5erLoK+wqCboNcZ4qh5hH7QR77g4tr6Iv7n/zaNXhO4+xeF/aN9HcdMRdrHiWkPQTl9TfLJGMrWDBEpGmhwPtJexkYkSec5j0ysiJmfZT6T+dg1koExMLUwxkk1uhOKyuKJnudJPTFqFONOpfswjVG4sWKUy1wws/lJfdAH/AHqcxX8/GerMv49eDSNrd0dbNwfYufhDqrlU0zVq6hUqsjlCiCfyXjV6qA76MsOeddXqE/lsPjBEn71D9fx0c8ryM25er609bmIHpM4ZvcZBX6KFGA/sX2F9Zd+qh/KJcfSc1cxbcasg/0U2eat1HmCleT7lCxJHnQVpj9wcePQxcHOGton+2j1geO9AXrtQ3jBDI63qlhbp9teB9xrEPcVeid0w6vw5ZdDPHqyjU53CDj/P3tv+uTIkd5p/iICR95nVWVW1n2wWCySTTbZ6qZao2NsNNJo1mzNZsx2bXe/7Nf9+/bTmu2aRrYaaVajow+xu6Um2d28ySpWZeWdSAARa69HOBBAApnISiATx5MkKiL8fP3xFw4P99fda1pcinTz/qwevbmhqzbINJPtAjeQgo1PovmmolGqxot/w4Ubp7fOltodTRzOSHffjvTtsxV9/vlV7b4o6GhvT199XNHfVT5T9eVD3bkfumNxS6XA7XB7uCttfR3rlz+N9fFHL/T02a6q9bqCYlXX7szoyY82tP4wVDSXdfOPdbyoBghcAgH3ipv2D2JbMJeO+KSCtLXxlyDd2GSZjoSMTXGGoiDpe23aD3bDCNamuo8p9VCIOHpCWFPQwq7Zi2jejV6xBitxOnbn+8C262/peqAH70T66ssbquyUdPT1C3d8+7/+ZFM6+FKVzQ3duhdqYUEqFQO3mNKOKv/2d7E++ZdEH/7yS71wxwlWNTWXaOPhrO69uarrd6PUUMDqqKWeBltCUh9zAo2hA3u/klbuhHr3x4m+framWiXU4WFNzz4/1If/7VtVXha09fWcVtYCzdi7mKTKQaLdZ4l+88tYv/qwoq+/2Nbh0ZGisKbZZenx+1d17415la7QNo+5Jl1a8Vz7a1MqJdvlKtT996RPP1/VzouKvvpsR4eH0m9/caDq7pfS/j3duBu4DR6KpcDNfFdfJnrxRazPfp3ow198q2+f2wkgNYWluq7bjuBvrurWg3K6QNbm82h/L62uO2WMwUonKudxS98LXae6Fkm1cEvVYFNHcV31cEmKqumxP74z4r8QdrW42SCHdYiWNgLdfj1U4a92tV/ZUi05VHlqT6s3r+j6vXnNr+WszX16WY/TJiRdejbBZiuiC4EO46eKw5cqRFXVw4KS0F4H2vbrst+ayIxDEq28EenJTqJvn8/p5d7n2tuqqV5LVKnX9PnXu/rs688aBjjp8SBmhlJTHOxpbWNBj965pj/6w3nduBnoJ/+9ro8/33MTkbXQJiXtqJO2DpmV3dxMK4tSXJaq4UsdJs+luKSjxCaeD1SPcwYrnl9W7s5V5wOZb3ZvF5+/bdwyH7iB0o0bC/rmk7oODu1Ms6O0fFFVVzfm9eitufRcvnxynTM8u6s3djKZrKG0Ce9AquiF9uvfqJK8UByVpeKRmzRtKe5J8pifcXUT/NJRuK9q8EL18KXb+cAsu+uqSEmxycOkdzvtJLr6ONSPg4I++vW0Pv1kU7vbhzqqB7LdVHa/eqnffWlGWNkgdjYUEprRR1TR1bV5vf3OLf3JXxRUKks//Xld9b/dVFyoKC6UVA8Wm0ZVnljW1/Fjrma4NftapO8vBlpYWNR//atY//KLXT1/fqA4DrRzUNXe4Z6+efZU9dh2KjCznlixnQkU1DUzXdLq+hW986NV3bsfaHdf+mJzX9Wnm05Pa+GC+17VkmmHyaH0euFl6uVqclsdOtapsc9r/6ag7zbntbn1XDu/fqaaQavVdbQtbe68UM0ZH9lkvTPvcEZFxq5cLurmgyv6wR/e11tvF20/FX38WaLg213V97cVh3NuFwQlZnGR6XEvMraHSSuu6WrvZNYcFO17t6lasKlqUlVgumF/bmVW9g3Kfskt+7Q76/dVcQ2IK5FZR7hdocwIIa66Se1aPd0pyCmNpWntU1GqFbacrgcqqxbOqh7MOUMtybaQyvJ0d9k/9h2ZDhSthrr1KNEP/mBFf/1XX+vbp7uq10NVqqF+98WmPvn8UElScQZ0p4w4WQAAIABJREFUcXFT1x+WtfFoxhm2KCmlHRIzXEusE5+ovBHqh39U0vb+tLZ+8Y1q1UhxLdbTF1t6+uIr1T8+Ui2wz7aKC7tauPZY+/u3VKvPqGSrjzODv1rB2t1t1Uwfg4ozCAiiujOYaiparkDZ99QZrcxKq29F+uProe7eu6r/6/8M9fG/fqbtlweq1UOn49XDxB2/8uzFd+m3zjX4tlNNpFqSGn3EQUVxuKekYOcdVRRHsZwAma7mcu/5tlHLacWnbUsUqBrV3e9cTdvydeasYizlXGPVeVDPdmax3yIzo7OjaaqqhRVXb1aW2NqTQrolu7XT974X6Q8qU3q2U9DTr7d1eBgrjmN993JPzzYrzlAuCMzIL1SoosLQLN+qsi0rbz64qT/9szf09g8jPbPzg7+R6r94rjgwfY/cDiEOhsls32Urp4mW1U8tCnQUbuoo+E5H2nU7wSiqpNtt+vBtZW7AtTSydE1P4pJUi7Z1pE2HqhpMux2JzKjO5d2I2OEmk8f9fJfS75B9Z6vBSwVhXbXI2vVD1TXrmn6XQq4cFs8MU6vRSx0G36pW2NHctXm9/UGo5cVAKx+u6uj/3dSXX+657RL3Ki/17IW1caZ/kWNqzK081ubG0Y6m50Pde/O6/vw/fU8P34lUsBdXY2Jlto/JzB8EIHA6gcygzb6yZrBc15FqqigOAkW2w599r+yv8Z3yjUvmzgUC/SZg/Qavd7aX2rJ053Gkg60pPf2yrMqXsQ53j7T58kD/5S//Vv/1r2MtLczo5s3rznh5e3Nfm98duJ3ranHd7dNn6ZWmD3Xj4bre/uEtPfp+0e0u2jjmtt9lGLf07HeVv84EGm1j5m36a10R6/uUpNk7oesHbm8+1t/8P/+qw52K9var+uSjXX36u89Unko0M1vS0tKyW4yxs13Rzsua243FJv7dLqVhornlqt7+0UP9yX+8ne7I4ozgO4uEKwQulEA2JhGHtnTCFk7Y+NFUtrNu833kQmUiMwicRsAaar+jaZD1f5OK6nFq4GoGs42/9na+4cHNMQI5bC1+nqG/tnjy0CCQ9YET26ltXs5o+/1/E2lve1Uvdza1u1nT/r70k5/8q37285+rVKpr4/p1zc/Nqlat69nXO6rsJqrVJOsDm44Xpiu6slHSB3/yut54d0kL69m8jmVKfTTQc9MHAqZPpsO2IPlqoAc/iPSD59dUr9X08UdfqFKt6De/+Uq/+/Rz/dVfJppfLGl+ftGN9+1s72v7ZU31SlFJUlAtOVASHGlmrqaN+7P69//jW7r2wI4OT3eFdYv30d8+VBpJOAJel0x/3eLeRNM3Qn3vR5EOtq/r+XcvdbBb1WFF+vjjL/TRxx+pPBVrZXVJi8tLbjbq6ZdbOtiuK6kVVYltM4lAUbmm+SuJvvfBHT35wZqW7SihbA6W9ne4dA+DlT7XhxvQs8n+YuKO6yktHmhmuarCdF0zy7FKM7ECN3HY1hnJOpKNSW8bk54OtLge6OHbS/rdR091UKloYa2g9Qcz7oxlM2pptzfxXzCTwyVZt8msQMnsjgrzOwqKh5pekqaXEoWlmgK371ETgs/fTSwWE914EunP5uZ159H7+sU/fK7Pf/etdrYPVa8nbpKwsWNMWFehKM3Ol3T9zhW99d5dPX5z3a2ws6NdZtZjzW8cafbpgaZXpfJcku6ykP2AmgRuDtw1RlIyFSielqZWDjW7VVN5KtDUQknlmUhFO5PARUgvx+4bzn501bd0DY/WG/MOpemFQPfuhfril0vaOzhU5WDHveTfunVFN+5eVdGOEBngn68zdwqSnRM/G6i8dKi51YpKQayZ1USludhZA/qJ557E8Z3sklRe3NfM6pFm45rCsK7yfFXFqVpqqJBPzBrsYqBwVlp8EOp/+z9u6cN/2tCvfvpb/ebXX+qoUnXWGTYpXKsdOWML0+vClDS3OKW7D+7ojbfv6s135tKzPBNp6UWiuWs1aftIU8uRynbMh68in3emD+57lBlFmCZHK6EefBCotLSijQdz+td//lTPnm25YyiqtgVIEiuq1xQEVpa6okKstevLuvfaDb3x9h09ehQqKgb67LNYM9cONb1ZUTRVU2m+rqBUV1hKdytyBhtelrNejZnJb9Y2ZTviJtB7f1zQ6vp9/eqnG/rwZ7/U82ebOqqYnJGCqu0AlCiKYnccztRsqNW1eSfzW9+/q3uPIs0uB4oPEs2tH2n2y6rbMaK8UFdUNsO33ARCr6rZKZx/ic3YJ6VAxYU9Fed30wl0FdNmxe+qcioXO7bAKtZ2S0l3cypPJ+5swWgqdkY9jXamGKhmFjnzO5paOXLGO+XlkoqzdVdfDRXI55nJaYYE1gYu3A71B39e0NyVt/ThP36m337ylfYPDmRvhaF7KYzdREsyFWpmoejaKNMFbxTlOic2M2j9lNlATz6IVJi9qRv3FvThT37jdr+pH9WVxLGOEmszra0LNbM0pbmlKRWnI9eBMt1xBktFuYHrmeWjtI4KNU0vxAqLNfc9cTCtDJ57ru0zJ3cMRDFd0XHn3Uj/8+oV/fQfl/Xxr77QN19san//0OmQvQDbzkbOWNAlZrwTZ5A4P1fQ8rVF3bx/U/dfX9W9x1e0drugsJytXO6kB3nGXe+bEV3dmM6btfPCoaaWDzVd2VdSs61c0r9GEZ1BjXdtv2ahglhRYAaPVYXRoQqLsYKpmupRXfZjkX43ExXWAj36INL/tPRIH/7Tnj761ef6+qunqh3FqtetLbB3ssjVZ1SMNTWTaHV9Xm+8c1dvvH1DD14L3Y4ts5VA1x4UNfWPewrnjlRerCks24rZ9HfVl8+J7tpDuZUJ1oZOL+/rKNhXaTpWcda4Z/XZxJMONuSfG/WcHm9kBlfFxX1NLR8pSEJNLccqzwZO7/3veDup/LP/Dpk9WTR3pNKyyWXHBtZVmK84dpHtlpb9XDZ2fzM+Vh77jVna0fTqnoo61PLtI83dDLV4I9T766GWbr2mf/nFmn770Rf65qtvdXRYU1y3Lr6tmDdlT78H07NlLa+v6PG7t/Xkveu69zhyk47uHBMT2ADacSb8QQACvRHwBiu2M0VYUVWHqgWHqgehM8hzLaZvcyxF9/Vq70z1lhWhINAzAdMzUzP7DSkHmlkP9fg9O2l2XX///wX66KOvtPniQHE9VBQnOtop6IuPt2XHUNTq9dQAOI5VTyoqlGItrkzp7usbeu8P7urR+4tu4YDb9c4bV/Kz0XPVEPAkAml/2kK4d0t7t51K3Lb+v//vItWq9/Srf/6tvvl2U5VKqLgWqbKXqHoQau+lLZIx/ZXq9UiBLfQJKipPVbV4tawf/7t39e4fXNeM7SZn75F+VM115k+SCT8IDICA6V2SLi2w1G23Tzuatx5WlRTqCovpGKRrWmlfz1kBTYAZ9nRn2HOmOvHRDavpbWT9X+v7Hqgu+xwqDtPFaI0X24mHBYDBE8i+53axj3UBCoGiBen6G5F+aJvUTj/Q3//dvnZ36qoeFRTHZcWVQE+/rOt5uOPGS2zMzhb92u7TSXiohaWybj5c1uP3r+utH1zV0jUbh85Kk2U5+LKRw8QQyOaCZP1fWwt6VXr7921H9A0VpxJ98skXOqokbjeguFLX3neBDjfNSPDI7SZow6t24oE9h6U9LV4t6cn3b+vHf/q6rtrOQHaEpo03+nzQ4YlRrYsqaGOe1BYGTCXaeD3S7x3ZWtzH+uk//kovXxyochioXp9W7UB68U2sredbzkjb5grtPS5JqqoFu5qdi3Tj3pLe/OFDPfm9G1q1Y2BtjiQbM7+oMpFPbwT8q3VvoQl1OgFroG0iuRxo7Xao3/vDR7p1f0W2KcjVWyXdeG1OM/PF3Eq1XJIWNxtXSeycublAa3dD/dFfPNHjd26qUjt0Ri+3H61qaT2dYG+Oidid/7Nfi2zyvBhodiXQg+8t6n/4X35fQXSQTuCtTevaxpQ7FsPHcnOe2YCOTcDZxGnhWqD1hUDTy4GuXL+jbz+/qa3nB9rfqenw4Ej1uhk+BCrO1DW7GGnxSknXbk3pxv15ra6FCm0yOpBuvBHpg+iR7r6+rJmVRFaGaTMAcT9oJrtNSqbqaIYSxQXpxmuR/vgv3tHL5w9VLBW0fF26dW9JU9PZzgjNwjeK0HrT7dfSZgOaIf3EpBnW2PZ9U1NSFFmAisLgSLfu3dDG7VXXkLnB2mbU/t5ldWbW23ZO/JWNQG//6JYWl+dUi3Y0txro+p1FLV0pqmDGSvbXrYje24pqOlWSFq6EevtHa1q7PaXdvQcKw1h33ljV1fWFY+mkBiP20hgoWpHWvh9pajnQ+p0Hev03N7X9oqLaoe20Euuwsic7DqI0k2h6OXSdmOt3lrRxu6Sl62FjdwQ78/7P//MPdbhnW8hF2ng4p8h2fmkrQ6NqCun8vgUIbJvlGen2dKT5a2XdevBQm88Tbb+U9nZq2t/dUf2ooqhQV3lWml0o6OrNOa3fWdD126HKS4HNr2p9Svq95IEevLUuFSpa2Qi0srbgDG1cmd12Cmef+GmoohXH1NjtMpNoxo6sWTTDs2mt339XL77d0/7WkQ4P6zo8MIOVuoqlROXpUPOrkVZvTGntzoJu3Co4mS2t8DDQWz9a0cLG+9qr3tXK+qzWby3L9LWdXVbtJ188bxPaf3yMUFpeD/TBv72r155cVb0SKzQrDG+s4r4sPrC/2guYl8UST/eMscTdzhl2vE95S8s3Q12/dU2FKTNUsqOXErfaceVmqHf/8L6Wb5fcnt2L1wq6fm9WC4tT6UR3h8kLN1lvrG2yfiXQwmyk92YCXbt+V199ekObm3YslFnb2rFehyqXzfjrSFfvlPTw8brmF4oKrcPj/6zK3VFsiYo3Q71WCjS3uqj1O+9o+/mhDrYOdbhf0WF1z32XSvOxFq4levj2NV1dX0q/j4bJVl7MSuv3Qv2H//T7qh3YAHdNpYV93bm/rqkZb0noM/bc0mfXUXId/iC1SStJV5Yj/WAh0K3Xbmvz2S03kL63nWjPVoTuHeroyAYhAxVKgTMCLEzXNLdS0HLWxl/dKLgzGc0ALijYm7avrFz5c+KcdutjO92z8k5LT36woJW172tv60BBzSx/Uj04LS3zt/RMv9xW1XbETmhGKrvS7JZuv7au0lxqfOK+n6XAGUNMzyR6fSnQ/NV53XrtsZ59fVu7L6s62q/KjIvM6C+aTlReiDS3WtTyWqQ7jxa1fjNUwV6qQmkuDvX6703rP+oDaXpbV++UtXZzOZ10yInv8g3TbTTX7oRu56N7r11zBhzV0lM9enJL5Zl0gK1R3k5ozc0Ka3iK0r3H1jl+W6+/YyvQpYU12y1o0Rl+pm1RI7XjN1n6pm/TS4Huvzmt0sybev0HV93K3/U7i9q4cyXdjcHL4vO3qxlVzUvv/Pi21u6XlEQHWr+1ouW7oQqrgdsd5fFyoOWbS7r3xoKefXVHuy8PdLBrRwPWVCoUNTVb0OxCWXPLJc1ciXX9wbzWbkUqLGSGiO73zKzKMmuwgf54HkeECwRGmYC1EWYAXJoNnaG2HWo+Zf0ga8PP3kUZZRTIPkwErF3PBiVtx7OZW6HetH7Y9JqWV1f06a83tflsW7UDG5wPVK+GzoC0oLoKbpFEVVOzM1pZL+nOa0t6/P6a7jwpa+lmmB4F5EclXMdgmAqOLKNLIOu1Wt/H9NcKYn3JFenao0gfHE1r+cpjffKrLX352Z4O9ivOANo2kTMjXVvQXwpjhdP2vhZqbiXW1dtF3XtrSe/8aE3X70XO2D0/0JnlOLrIkHz0CNhx0dbdtr/MyN6OvrV3qKm5oorlskrTUTrUZi/R7ouQhedyZgJuHCKLlaLkR+vMEH0EA+gbTVNN2xjV9X8DTc1GmjqKFM8X3fux7Z7ccSjKp8X1DARoBM4AywW18Rk3RxLZWIl093s2llPS1Oy7+uyjXT39ale720dSvaxavaKkXlUQxCrbLsvFukrlmmaWZ3Xn9SU9/N6aHnxvSdfuRm6Rs9sSlyo5a5UQvlcCplvZgrWoIC3cD/VWIk3P3tDK6qq++fRAW27Sv+LOQE9snD5JVAhtJ+WKCsXELe5euL6o+++s6vH31/XaW5GipaaxlWvG0eFea4RwvRLIdMr1u1z/NlB0RbrxZiRbnDm/9JY+/ZdtffPFtrZeHqpuO+Tbot5a3RmshIVY5bItHo41uzStm/dm9fCtK24M4tq9UNOLtuigV2EId9EE/NDQRec7nvn5L5PNr00FWrgX6r1bs0rqs64jbl8Et11WnrrFyb/jZM82EWUT9FNTod5ZLympXWm8gLoVaDZg2DJonWXuyWZpWqd/+kqgR3MFPXp3LX1BtS+6GQMUU2tI1/Fvi+7EsPRtcfR0oKU7oRY3Qj05iBTvlrT1ItbebqKqbfRQkGbmAy0s2Q4YNoGZrSD3aYaBrjyMtHp3QUllwU20t3Bo/3ULpciO6Hk91J/cvyolV1vL7stt8Vzc1klfj+DEa8bHwtgLvnvJr0mVinRk2/Ulh0rCfRWnjnTzwbLWbtjb04kpnt/Ty5Q1xHM3Qj25FurJB1dt/zY3Od+oM2Pg+XbLOedvK7/Ka9IbSwW9kaxK4ap74TN3Vy7PMZ+WxbcXR5t8npIWH4ZauBPqjR9Hqm9Oa38n0eGedHC4qFJRmp4P3I4gheW00feD2m7ytSAt3wn17+/ckDPQddsy51aj5fK1bFvEMQdjYsPeK9KVxUirjyLZqT/JQaLqVkEvnpedZbCdVTe3kBppmcGXTaabrvtF/gtzod67Oa0kmU6NxkwOM5rxOnUq1JygudscaufqflDNyMOdtSdtLEa6/nqkeK+o6naira1EBwepoYedkT43H2juim0zGSiwk35MHuNu/0fS/R8VdO+HGwrCjdQgxtqHfluBmmGTTYDbDgtX7Y1sKa0Ir5e58na8zfSlo1+45FhY22CGQ66CYytDosW7od69W9Y7yYNs5UKznXSGMJ0S9HkZB7svJJq7H+r1W6FeO4wUb5W1vZVo11ZJ1qSZ2UDzq4FmbDJ+0RqYlLHTs6x8qZ5aYolK1wLdXiro1luJ4t2iDjZntbOd6OBIzjhlxoyQroQqLWeddNMh+7O2fybQ4t1I/+F/vdUYPLS6Mj1sGWVJs2pV9iwZl5ar+3S3nuWHoZbu25KjdHVHfSdRZauora1Zp0em91MzUnk6UMmupvtmEJjpd5q3pXqywYzL94R/8uI1ZJyRHvx+QQ9+aItISmaCnxokWeBjEU5JPIsTRKvpShOrGzNusmiuLcpwmTHlinTLLKQfR0oOFrT3ItH+bqKjw8TZP5Zm0/ZoZiX9TXK/v76erNmz+PORbr65rqBgHzPkyPSpXW5fr3dCvXd9TornMh26qWCqczvWsaT2vbbvWVlafzvS+pNpJfGtVO9tNxSTIfve98LOwheWQt15J9DtN+cVRPMp8+z33bfBDl+Wt5PLbakovfXHZb2V3EnbEsvf512USmvSrSuRbj6JFB8s6vDFgna2Eh0eJiqXAi2vBCra7322qsJkabSlVleuLl1DlqJwX7aOVHCEAASMgH1nsv65GdYtbgS6aTsWzZRUjxa0di/S/KIN2mftlI8DPQhcJIHs99HafGv/y3dDvTUX6MqNUGt3rurzTwJtfbej/Z0jHVXtGEiz0kwUlerOOPvKxrJuP7iih08WtGH6PZ8ZDOf7tO2/wRdZPvIaMwIdlMm9Z6fHt958P9KV66E27i/pV/88pefPXmp321bqVVWrVVMT/EKg0lSouYUpXb+7qPtPVvT6O5HK9g5gfUDfv/LfjQ5ZjhlUijNsBPw7UvZebIsnzBDw5pNQoS0AmVrWlZtlzS+n78DDJv5IyuMHKfi+n7/6TH8tFdPfaWnmSqDrD0PVVNTq9rSCxStavjbtFud0zsxiZwM6nQPgmiPgWKO3OSKvcFuQimuh7s0GWrsZ6l9+vqDffhS53ZArezUdHlbcwt7ITuYu2jhdWQvLC7p6c1qP31nT7YeRStkCZPfuR328QiUQpScC+ebR7m2nlQVp+fVI379qC6Jn9Ot/ntIXvwv08nnV7eRdt13KbWjCxk4juV3Fr24s6NajZT15f0oL1+1c13Tcwk/coMI91QaB+kDA9LJwVdqYibS2EerXdxf1m38p6usvXrjF7EdHVdVt5UFop3oEKk4VNbNQ0sbtOT18ck23H4aa3wgVzAxgTq0P5SOJJoFBT8E3c5qwu3SiKJswjNOJaWdoYoMa/s+36v5HxD1bZ7uuICykbb/N+rgB7GzrlWz+J50M8gl1uPq0LZrtHDBtRhn2YBNJ2QS9pWvh8jLlknJ+jb5/+mVOSunK7NVrkVbML/N35bV03ERwc4V1Izknvk3sZZOZ2Qo9598mhA38uHOmbcLfdjqxPJycGQu7t09DtkYur3ZjWZixystEv/ttrOcvt3RQ3VFYPtLSug1iLWrZturLD6a+Wk4nx7Iy+aIZRyt/IXET/G4wzHaE8HV2ckotvo5nVu9mDJFuh+GZ+onFlijZW2NmOOFZmx5Z3djq/NlAC7Hcx02iW3ST2U2QH590dUXL9MXVqU2Mmr5kZW7LvemcDcCYg9vow8zajUGUyHRR04Gz7L1+K53It3Cunpwepi++zi3LoLG5RJykum8vxtl3Ks20i0DtAp72bHIUU0Mo932zZAuJonKgcCnQNTM88Pprfu47fnzC142FmJ9tNW15ZsyczP0Q1ctgVZHZMrh2qpzzOK2s3t/K7IvVFt1NhGe/Nk5287fAtttKtiLM1Y2lZe6+nCeU0Tcbeb1wjG2nkblAK9eVtlEZNzehbhN9JkendL1MmZ7bsW5Jku6YMncl0pz12y2e17HcBL2TxbyyHY1cGNtazlVgpuv+u+vzbmOUYmw6GjPbacuxs7YnPfvHBSvYcS4rgWYsuJfb5LK0jZ3T/+y7krF0EX3eaWav9G8+CVeXxtR0x7ahdnqdhcgHPEtOVg5rH/x3OJ+OZ2/5mcGTFdGOT5oJtLAcaN5/r4yJxc8+zggkr1OWps8jM7Bx30Fzz+eXsW18N9zOSbk21J4t3TP8ubS8oVWYpBveWHzfvufrq1u6eRlNr0zXjIOVyf7MrT0dH8fribUpbiexNv20+BbW4NqGPO54w0Czi4FmPF/ztvRNL11ebfXl80qlSf/t5Jb35x4Ck0wg+3649sFewlekhz8o6MFb95QcZf2fcqBoJjM25/s0ydoyHGU3HbTf2CBd6bQxb4bZoZKj69r9bk0vvku0s5O+w9kxjLb7of1Ozy0HmprPDEkZKBqOuhxrKdoaS9fHtA0dsz5kIE3fDfTGRqDXfzing51ZvXyRaOtlki6EMN2dkmbMGH0lcCtMbVGNMwr3/Sx/HWuOFG6oCfg+hJ3Yad36mUBP/qCgN967raR2242r2aC9W8hj+sofBIaJgOmvtc0FO2Y40NqjSH92+7qSyrp7F7Uxv8gW45QtUDfBu3p0i4A7BM5GwMY8LIaND7m7ROFCoLm5QO/fDPV9W+CzvaBn38Ta2ZFqVTuqO9D0rNziRBtLmV4InC67BYpmDJD1Sc4mCKEhcEYC7XpmfeC5RMF0qBtXQl1/kqi6c0V726t68TzRwWF67HypHLgdXhdtF/3VwC0qt/6FGwPMpie7t8lnlJHgEDiJgLW/1gBnOwraHLcZZwc3A71xJdDjDxaUHM3r6VeJXm4lqhwlMoPB0lSg2WxzBVtgX7QF4tl4mhvPdu151qSflD9+l0IAg5W+Y89abj9RZl8Ae3P0DbrlZ1+09j514zk7ssENAmbHuTi/LIAP568nye+jZJNKTg7L2tx9fH/N+l6NR3+TXd2X2aJZWdr//Jfcu7cHsWcL4ww+ur1o5CJZEC9zQ9As8Vywhlfezctw2tXLlE3AxduJnn2T6MsvD7S1u62j+r6mFuq683jVnSsZ2cT6Rf1Z+S07G1Aw3jZpbc/+cxY5sjjOGMClZ5HNMffX9pjzacnT1Um7DtgPhtWtcfR5Zddj6ZiD7WaTNHdMaITpQYZGEKdvWRrtutdIsClP3snpoZM31cNX5ppP1Mtg17ayN/TY/Hw74OM2CpQ6NGXxCWU11ai34+n7pF7pavl72bME3GSZoTFZvR62ydk1ryycu/h0/dUc02awqcvmZP6uXeiaamcPL5OX0UJZG1sI3K4mDRnaw2VyZMFddTV0wuTxg3hZW+XTcTruy2KRfb659Hwj30jDhfMCmHBZRLv4v3yaeUFcYew4oTQv1xakCbiYTld8GpZuSzreI4vrRfDOPmy7u/c/6erjWhiLbxxMRvu9sgffHpyUxil+Tqws7VyR01heZs/fOq6Zrh5LNgvrvNvkdo+N32hLrC22D59z9+2fC2mJ2p9dcmFSx1P+tew6/b69SlqWvU/LczhJHu/XkCFzyOVtRbePM/Cyolh7nTnmsfh7h8Hr6SlFxxsCEOhEwH3jUg//3YwCRXZKnu2U1a1/5b/PnZLEDQKDJmC66g2Rre9lx1TGqdXuwlKkuZvpLpy2g6X9Tpk+F203CjOWLGbvOIOWkfQh0E4g6+803rnMgNiFCRTVEmcMPr0mrVYS1etSIZQKNolqxvDldDGCO0LU+l75jlB7PjxD4KIJeN22PnliOyAHaR8iJ0dD73Nu3ELg8gj4RjTr0Np7vdtxNF1s6foUJpyfqMqCnfnd+/IKSM7jSMD3f63/4CdPp+WMV2ZXbafmUNVKItukwtYSFc3gKju62/WBre9s7bT95V4BMxcuEDgXga4q5dvPbJzPjfHZTvRlM3KVopVA5SNp7jBRrZaKEObe3+wEica4o3l3zehc4hMZAt0JZDrc0ENrg21MwW3OkI5DrC8mWqnKvcNZn9d02Ha58u9w7qQPe4fLfR9chm3dke5C4HORBDBY6TvtnOZ7pbfvQ8755CxbZ34a8XqO3yV161gcqusWAAAgAElEQVSZl0/HX3PBOzjlfLPb9kAn/VDlw9p9jsfxhLu45NNoD3KSX3vY/LOXw67WyaxLle9iffV5rK+/fa6dw23Vw4oWVop6/Xs3tHQlOzYnn8ag7vNlytg6J/sn73fW/E+Ke5Jfp3wsvGeY6ZXb5cLCmp9Pz199Gvny+LDe7yzX9nQ7xe0WJnNvMSroFP8sbpZmjsexqOZvnCyM/3SSLwvXAOjTtAR9eH89lskrOnRIzzl5d7v6+7Nk4ePY1cqRPXvnRlLev+GQ3fiAeQa5dFwoH8bHzZ5dByYfL++fi9O49Tc+jn+2eFmezinvbn72nHfzRgz5/Fy4dsGzAPm4Llx7gq3ptwTPP+TvO5XBy+Ov+fDerddrt7g598ZvlqXp5Tlv+p3i+zzbrz7PzN1d7B/v3oo1Tdn7tafl822L31rvnRL0Ebtc8+l1y7NL1K7OPp2uAbp4tMWzxzanNGJbH6IlTMtDl3xwhgAEuhBo+wLZo7VJ/jtnL9X21xYsc+UCgeEgYPrpBuDTFU+2A4Vtqul1uaG/Fg5dHo46m3QpnNFzE0KS7cJYnJKK+T6919dMd10/1xsSNqNzB4HhImB9CLcDZk4s2t8cDG4vn4BvXNskyfq/Nr5of67N9UH9tS0KjxC4cAJZe+pV0ha42WRoaVEq+T6E9YNz0zuNxWheWB/ZP3OFwDkJ9KRSFsjmwXxeNvFvi/nK0pQd993wyN7ZrL+c02MXraeMfAZcIdAnApnuunGyMFFiHQRbYGn6acbaS4HZrzT/vC5bvE563AzJ3RASwGBlEJXivxQ+7Xxjbn72ybv5cO5qHpmnXfJh/bOFy9yzkC0pHHvwgfz1WICzOOQFaorqUjAv++uWj7n7MFnQrhefhr/6gD5+u7v3P+3q4/sfaLtWEj37KtEXnyZ6+t2m9o4O3NZnV28u6NH31jW/Gsodk2KDU9mL02nZ9MXf87Lrq5a3XZBj6XggFjDzzDt1i9+WTsskdS6p9ujuuS1uxzAtinJChBO8fLpWnJZg9mCfk8rpI5/l2pJJh4je3+efD9Iui3/2wvu4+Th27/3b3Xt97pauj3+avw930vW0NE7yNz/P4qQ8vJ9Py1+9ey9Xi9Mezz/btSPrzLGbjM5K6YTMffonBOkqUz5OL+nkw7vC+AbtzJFbUmp5aE+q/bklcA8P7Vwb6WUe7jl19EGPtUU9ZNMI0kik4dK8sWy8f9M1vfPuDfna9cUCBJ1VyFLIx2tP+yzPvaZzqrxZpp3C9ZrHWeQmLAQg0ErAf8/8tdU3fUqblU4+uEHgYgl44yrTV//pIIEdv+p+CL3u2lGL7QOgHeLhBIG+E/Btq12tO2yq640DO2Xm+0PmZ2MHXTZO7BQVNwhcOAHT66yd7fxe5BXafxEuXEIyhEDzvTqvhifpbj4c/CAwLASy+QE7Gtv1DezZ922tqfUGrl5//XVY5EeOCSCQdQiaXYNmma0/6/XVt79ZP9cHcv0I8ztBd5s5+FhcITAgAl4P/fiDKZ997C/n555Nl/17nvll7XUauO1fH7fNmcfLI4DBykWzP+uXwIfPX/vya9ApkfZveTsc8z8hTGNy1gvbHj/XgHTwOubUKZlObscitjnkxHaNVdZgKU4UH0rVbxJ9/kmsLz59ru3dLSmMtbYxr3uP1jW3ErrtoxqdzrakB/5o5fXI+55Zh4Q7OJ2abXudnDWN9vinZnhagLwAJyTuvfLBT0u6m7+l1ZZO22P62+nzbE+nk7tPoJNfe/x+Pr9yfpclcC+FN9lOKdgp3idGt7i++L2Ic9Ywx2TzmbV5tD12zsbiWiNoV/v0FKlzUjlXL5E5nS/FXmXyOdr1pJ5nTsheBDspTLufFyGXxUm3LdH9g7+eFHFY/DJZmzWUBzBKBRkWoMgBgV4I5L9nFj77rvGV6wUeYS6KgNdHf83ybf5eZEcIZQP6MuMVG2jKB7goWckHAp6A6d+pXUhvnWKR0tHRxpCHT4crBIaNQFtbPGziIQ8EuhJo6K4ftDWHhmPXaHhA4OIJmI5mnQh/dJUJ4dXVrubtn9tf6RoDiD7AxZeAHCeUgOmrFd0m9O2aTf67zYHMw450NY+TjLknFB3FHjICpq/dmlDT6zC/0qDLS1+3+ENW1EkTB4OVQdS4V3Zr4P29z+dYJ8V7dLha3E5ptKfZIerpTp0S6eSWT8n8Twpzkl8+nQu8t4FR60faKj77SxLZCr+kKsV7ifafJvrNz+r6zS+r+u6bZ6rVdjQ9F2rj7jXdfXhVUzPpj3TD6jRL5kIvA8PaIeEOTmcua7c0url3zOBMgdtSaI3b+tQW1B5PDdAhTg9O50q218i9hutB3vMHGZAwfUn2lERO8e7OJhfRbvPttfPK+XdP5BV8zpOuxbWOmgnbpcN2wRK1ZpcrW+72eBjzbALvGtRH7Bagm7uPd9L1pLgtfi0PzRS7ODcD9Hh31nR6Dd8lXNO5edejpASDAATOTIDv2ZmREeFiCZygose8sgHRRt/7WICLFZ3cIHA6gQ5K2sHp9HQIAYFhIYACD0tNTLQcp6ph/8YpJpozhR8ggTYd7aTTndwaEp3o2QjFDQTOR6CpZ827LEX/XtZ8TO8s4LHA3aU4Q9DuieADgTMR6FHrGlsEnSlxAg8BAQxWBlkJnb4/ndxOkuGs4U9Ka5L8bB7TpjPrUnKYaOd5oqCeKAoCJbVEtT1p52msr38b61c/ifXZx0+1u72rUqGutRtl3X1tURt3ZlSYsvP82n7FJ4kjZe2dQL+/q/1Or/eSEPJVCYxMnZmgIyPsCbUxwmUYYdFPqBC8IAABCEAAAt0JjEv3o3sJ8RklAvTFRqm2kBUCEIAABCAwugToc4xu3U2a5OjqpNX4eJcXfR7J+sVgZSSrDaFPJZDt+pRUEu1/l+if/npLh7uxpgozKgShdjel776q6qvPNvXtV99od3tbsfY1fzXQG+/e0MM317WyFigo9nUTglPFJgAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEBgEghgsDIJtTyBZUxsh5W6FB9K+89iffi33+r513sqRdMqBWXt79e0v1fV3t6B9isvFBQPtXK1qNfeva13f/xQt14rK1wIFBQCXepxQBNYdxQZAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAATGnwAGK+Nfx5NZQjNYSRIlR4nqW4lefl7Ssy8PVFCsYpCoUquqFtcURKEWFma0sjGnO48X9Mb7G7r9+rTKq4HCYiDZsZRsHzWZOkSpIQABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEBgYAQwWBkYWhK+VAJmZBJmR/rMBJpb29PMwZbiqqQ4UlF1TRVDzcyXde3Wgu6/cUX33riqWw8Lmr4aKChjpXKp9UfmEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAw1gQwWBnr6p3cwgVmbxJJ4Zx05V6o//y/v6Gt57H2tu1zoEI51MzclOYWQ00tBFpYDTS7HKg0FygoZccAGT7sViZXiSg5BCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQgMjAAGKwNDS8KXSiAzNDHjk8KKdONJpGsHoaqHiaqHRQVFqVAOVJqWO/qnUJYzVFFBCqIuktsxQxiwdIGDMwQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCAw1ARvj5g8CEIAABCAAAQgMEQEMVoaoMhCljwTMsCSRglBSKVC0mO62Uo4DKbbjgtJPEAXu3oWzON0MUujI97FySAoCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAT6TqDL+HaQjW+7IXDGuvuOnQQhAAEIQAACEHh1AhisvDo7Yg47Ad85tw54ZDunBM6IxYkdZLYprod+hoJYWj7dM0QjKAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEDgwgl4YxUMVS4cPRlCAAIQgAAEIHA6AQxWTmdEiDEg0DjmJ5YS23nFjE5slxX+IAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAJjRADblDGqTIoCAQhAAAIQGHMCTNmPeQVTvLYdUWxnlbPuqmIQ/a4q/gpYCEAAAhCAAAQgMIkE/Khn42o3/mESgVDm0SQQKHill4LRLC1SQwACEIAABCAAAQhAAAIQgAAEIAABCEDgTASCQPaf+xvw8C87rJypZgg8kgTyRiZ2n38+S4FeNd5Z8iAsBCAAAQhAAAIQGHICdvZ5o0uFvcqQ1xbinUiA/v2JePCEAAQgAAEIQAACEIAABCAAAQhAAAIQmGACthHEBSxXZIeVCdYxig4BCEAAAhCAAAQgAIGzEGB+/yy0CAsBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAInEcBg5SQ6+EEAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEI9J0ABit9R0qCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAInEcBg5SQ6+EEAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEI9J0ABit9R0qCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAInEcBg5SQ6+EEAAhCAAAQgAAEIQAACEIAABCAAgWEgEAyDEMgAAQhAAAIQgAAEIAABCEAAAhCAAAT6RwCDlf6xJCUIQAACEIAABCAAAQhAAAIQgAAEIDA4AhitDI4tKUMAAhCAAAQgAAEIQAACEIAABCBw4QQwWLlw5GQIAQhAAAIQgAAEIAABCEAAAhCAAAROJpBk3nZNMFQ5GRa+EIAABCAAAQhAAAIQgAAEIAABCIwkAQxWRrLaEBoCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQiMLgEMVka37pAcAhCAAAQgAAEIQAACEIAABCAAgTEl4DdVcVe/3cqYlpViQQACEIAABCAAAQhAAAIQgAAEIDCZBDBYmcx6p9QQgAAEIAABCEAAAhCAAAQgAAEIjAgBb7wiDFdGpMYQEwIQgAAEIAABCEAAAhCAAAQgAIFeCGCw0gslwkAAAhCAAAQgAAEIQAACEIAABCAAgUskEGTGKo0dVzBeucTaIGsIQAACEIAABCAAAQhAAAIQgAAE+kEAg5V+UCQNCEAAAhCAAAQgAAEIQAACEIAABCAwYALeWKWx48qA8yN5CEAAAhCAAAQgAAEIQAACEIAABCAwSAIYrAySLmlDAAIQgAAEIAABCEAAAhCAAAQgAIFXJGCGKRinvCI8okEAAhCAAAQgAAEIQAACEIAABCAw9AQwWBn6KkJACEAAAhCAAAQgAAEIDCEBdxQF06hDWDOIBAEIjBEBa2o5+WeMKpSiQAACEIAABC6FgO9R0Ku4FPxkCgEIQAACEIDAiQQwWDkRD54QgAAEIAABCEAAAhCAwHEC+TX/GK0c54MLBCAAgcEQcNNMAUYsg6FLqhCAAAQgAIFxJ+ANV8a9nJQPAhCAAAQgAIFRIoDByijVFrJCAAIQgAAEIAABCEBgqAjkDVeGSjCEgQAEIDB2BJLMPtAbrdhZQayTHrtqpkAQgAAEIACB/hNwfYiEcwb7T5YUIQABCEAAAhDoAwEMVvoAkSQgAAEIQAACEIAABCAAAQhAAAIQgMDACbRvatX+PHAByAACEIAABCAAAQhAAAIQgAAEIAABCPSPAAYr/WNJShCAAAQgAAEIQAACEIAABCAAAQhAoC8E/O4pbvP+DoYp3r8vmZEIBCAAAQhAAAIQgAAEIAABCEAAAhC4BAIYrFwCdLKEAAQgAAEIQAACEIDA+BBgynR86pKSQAACEIAABCAAAQhAAALjTsAfMzju5aR8Y0Igf5oVww9jUqkUAwIQGCUCF9H0YrAyShqBrBCAAAQgAAEIQAACEIAABCAAAQhMBAG/qYpd03sbJmp+vP9EwKCQEIAABCAAAQhAAAITQ8D1fzNDFd/nbb9ODAwKCgEIQGACCGCwMgGVTBEhAAEIQAACEIAABCAwGAIXYWM/GMlJFQIQgMCoEgic0YpJn6T2K6NaEOSGAAQgAAEIQAACEICAJ3Da8MJp/j4drhCAAAQgcC4CjWUygZTflW2QzTAGK+eqMiJDAAIQgAAEIAABCEBg0gkM8nVl0tlSfghAAAIZgcZW6K1trl9pCicIQAACEIAABCAAAQiMPIHWrm7DOJs+78jXLAWAAARGmIBrmgfcEGOwMsIKgugQgAAEIAABCEAAAhCAAAQgAAEITA6BIBvE99fJKTklhQAEIAABCEAAAhCAAAQgAAEIQGAcCWCwMo61SpkgAAEIQAACEIAABCAAAQhAAAIQGHkCtojp2EImZ7TCcUAjX7kUAAIQgAAEIAABCEAAAhCAAAQgAAFhsIISQAACEIAABCAAAQhAAAIQgAAEIACBISRgtinZpipN6ZwFyzEzlqY/dxCAAAQgAAEIQAACEIAABCAAAQhAYEQIYLAyIhWFmBCAAAQgAAEIQAACEIAABCAAAQhMNoEks1NxV2xWJlsZKD0EIAABCEAAAhCAAAQgAAEIQGAMCGCwMgaVSBEgAAEIQAACEIAABCAAAQhAAAIQGGMCXYxTju2+MsYIKBoEIACB4SDQpUEeDuGQAgIQgMBoE2hvYrNn+ryjXa1IDwEIQOA0AhisnEYIfwhAAAIQgAAEIAABCECghYA7oqJ9IKklBA8QgAAEINBvAn6g3l9d+rTF/cZMehCAAAS6EMg3uHaff+4SBWcIQAACEOidQK5Z9WMO7pql4HcYbOkL9546ISEAAQhAYIgJYLAyxJWDaBCAAAQgAAEIQAACEBhmAn7AaJhlRDYIQAACo0rAD8bnB+rzZfH+eTfuIQABCEBgkAQCyZ/NNshsSBsCEIDAhBPw/V8/5mBX95lwLhQfAhCAwLgSwGBlXGuWckEAAhCAAAQgAAEIQKDPBDpOjnZ07HPGJAeBvhPILd/za6TR5b5TJsHzEWjVUksLJT0fUWJDAAIQ6BMBmuM+gSSZCyOAzl4YajI6P4GGumadYXtO3K5WqUN6f/58SAECgybQ8j7nFLvFZdDZkz4Ezk3Aa6y7NhrncyfbMQEMVjpiwRECEIAABCAAAQhAAAIQ6ETALyod8HtKp6xxg0D/CSRSkCTu0//ESRECr0qgtYW1wSE/UJRP0bm3Bs17cw+BISRgCovSDmHFIFIXAg1tzZb4B9ZvyML6a5eoOEPgEgic1Ma6XsMlyESWEDgPgXxL63U4aLTD50mZuBC4SAKmtQ3NZaugi0RPXucg4FpgN17WTCTfKjdd+3NX6E8ypAIBCEAAAhCAAAQgAAEITByBxij+GUpucQb5hnMGUQg6iQTSgc4kSK/ZU2eVfBX97oQUfe9EBbeuBEzx4qyhzA1suvCZUqJTXenhMcwETH/71bAOczmRbVwJmLGK/eWNVsa1rJRrVAn4NpaOwqjW4OTKne8jdFpjn761pUeyod+TqyejWXKnsfQhRrPykDoj4PsXgwXSqfUfbI6kDgEIQAACEIAABCAAAQiMHAH3epKNDfldVpRN+o9cYRAYAm7SNP/Snb8HDwQum4AfiE+vrU+5Of9GY3zZ8pI/BHohkG9n8/e9xCUMBIaDgG+Ph0MapIDA6QSstXUtLsp7OixCDA2BhromaX/BnlOjwQCFHppaQpDeCTgNdgsSOM6qd2qEvGACba9nvh1Or9b2ej0enFzssDI4tqQMAQhAAAIQgAAEIAABCLQT8G897e48Q2BABBoD9S799Clwp6A3fezumGp6B/N81T+fxqvGJ94EEvBK468ZAqeH5pZtJt0wVsmF66jIE4iQIg8xAVNS36j66xCLi2gQaCHg9TfVXTS4BQ4PQ0Mg1y9okykJktRkOwuCDrcBGqPH7lowrIU8LrG5uI/1eZO0/+t3uhrWUiAXBDoRMCMVp8am0UE6EtEpHG4QuDQCXToErmVOQsk+CrORiOPtdb/kxmClXyRJBwIQgAAEIAABCEAAAhNEIH3htrGjwb2sTBBOijogAsffu82l+fF6fNxaJScQKp6Dwe3FEDiudKlLkK4uTbyBlbkeD3sxMpILBF6VgG+Dz6m7xxv4VxWof/HOWaT+CdKHlODbCtHNknooNulvDbF/bg3KEwQuh4DpY2sjZC7NT6u+tj5djsTkOjgCVr+t2jC4vPqXcqvE9mTNbGDGKv7qyuV8+pctKUFggAR8W9s0WmEMbYC4Sfo8BLyytjbF2a9JarBiRiuD/HXBYOU8FUhcCEAAAhCAAAQgAAEITCiBbI3/hJaeYo8KAXvX9gO27v3bWaiECuIoXSViz0H28n3sxXxUSomcpxHwYy+nheu3v1epfP7ezfLy7g23Yw6pRObf/vFTUOla6X5LTnoQ6B8BU+v0kw5wpvc285StMk0v/cuQlCDQJwIN3c1OoDAjbdeN8Edi2gN/EBgaAsf1saXvkCl06mZvcrzNDU3VIcjJBJy1inWGEwWu/U2aneiTY+ILgUsj4FtkP73vrr77mx11dWnCkTEETiJg/YX8nzMaTBTE1vYO9lArDFby4LmHAAQgAAEIQAACEIAABE4lkNgLtk0wnRqSABC4fAKmp/bObe/X9WqiJLaZp1BJbJ9AYRgpLIyONrePH1w+YSTolUC7lnndbMRvD9DwkMJQKkShwjBQEMdSEiuJY7n2OK8U/r5DWt4rl+y5bjtkca70iDyeBEzv7BPb1R9/HgYKoyg1GOxFkTopr3fz17Pg6yXPXsLk82wPn8nlbRr6PTdxlg3u2kXLi924b+fon/21EbCHm14y7CVMPqsu4V9FvHyy7fc+G5+uXU1360kshU3rKtf20hNux8fzsBDIFNjZBWZGr4l1hON0oskZq/jGaVhkRg4IdCJgza71fd1svz0kin3/t1N43CBwmQR858FkCNK9KOw2DEK3L0WUHariRPRhfcfDHM0te27c+nAuEv9AYEAEvJ75ay4bG3OIa3XVq1UMVnJcuIUABCAAAQhAAAIQgAAELpFAuqA0W2ZqL9JnmS25RLnJGgJGwNQ1DAsKFSkMigoUKU4CJW4GtTk41BOtDi/yXeNlX5mu/mfwOEu2Z0h2IoLmxwIvqsC+vvzV52uy5N3svkW+vKfXH3OzRU1x3Q0UmULbKtPARvBbIvtcjl97DHY8Ii4QeAUCXo0z1U3H4KOCm/Q3t3qSKFbgjAl9d8Lmozr+dVLeTm4dI1+SYyafXay8voyXIY2vixORtXs2BO+TxO3p9ynZfibTLqLXXWtmo0LB1WOcHgYkhem005ny9xVxpkgEhsArEsj0zfV/3YRpwfUZmsZzvoPR3gl5xfyIBoE+E0jbYDNWsb5utlqm0fdtb7H7nDnJQeC8BEyBvdq6I62yI67MraHPbZl0UutObm3ReITAQAhkOhzZAq8wTMfT3DvN4JSSHVYGUpMkCgEIQAACEIAABCAAgfEmYC/ZbseKJHArT3subTZ46sIP7j2nZ3EIOF4EvHr5qy+dPTt9VWybqyiIErfkyWxVjuJE1ViKwtQOwA3kZ4NLPr67tifa4tn5wS1e7fOu1SyI7cz6JNfLbmq86ng57Ord7Jp3t13PG57Zra3ur9kOQQoVBwXFQV2JGVwFRdWTgtPtjuVvm4vyeXYMew5HL/85kiDqmBFwupa1fbapVd0ZqFg7bEeqhM5QpRYnqtXlPm5A3w3gZ4YdmbJ2M/IYlM6dJ91u369u7hdZ5XkZei5jPlI/hE0353vllDr99vVcljPmakW3j7W96e4qdk11N7F22AytTKeza8/JD0rgngUg4FgTyH/Hsu9vqqeZLoe59tf6FGd9hxtreBTu0gnk9de3wYH1GxLFSeT6vdb3tTZYYVGJTuj/XlRhaNMvivTw59Olz2TjD9Z/yTa4crsDxTaO5voSLa98roymUj4pu3oV89fhB4GEo0jA6VymZF7XbEzCdNee0/5CoMAGzMyAcIB/GKwMEC5JQwACEIAABCAAAQhAYJwIuIl8O7M02xK9Hsc6qFS1s+9fq31p/bO/mru96rTNnvrgXCHQJwKmcf7jX7YtaXvZrtaknf091ZKam/BXlE42be8dKiwWVShG7oiVet2mVtOVT273ivSpeWa6e+7tH/8N8NfeYp0QKvcVOiEUXkNIwHQgr5MmotcL7+5ayU4D9gq0cxBrv1JTEBWlOFA9CXVUl3YPqopVdCX26eTTznu4/HymzqOHf/KJdgh+ineHGDiNLYE23fKPZrBSk7SzV9HhUVV1O9EqCJyhyu7+obb36unC6SDp0M42NcyOsEj/b1oUNn3PTzXddcBLnabnnlqdOmd0oiC2E1LnaK/s6oyBehEsNcRstja95NiUt59ie77ptRc5OoTJCWTb6zuueUOnDlF6dfJJ28k/boKpYegq7RzUtbN7kBoHhpEzwLL+7+7BoXb2Z0/NIj2E5dRgBIDAuQiYDjujV5+KnQBk7a99EungqOra4jgMXfu7f3SUvsM55fftiV39vU/IpewfuI4MAd+qjYbAprt5/TUtNP09qCY6ODhyOuuMtZPQLTTYP6p1GIO4wLKOFt4LBDOZWblWM9d0mnrYo/skUuWoJuv/1OqxokA6PKpr28bQWvQo7S2kyWR93SzNlmCTiZhSD5CA09NsnMl0zbfFdrV+8c7+gSp2HJBtOZg7HnMQIgVJeujmINImTQhAAAIQgAAEIAABCEBgTAjYZNPuUaL//o+/1P/9l/9F1XqiqWJB89NlLcxOt5XSvfK0ublXn9RyoM2HRwicm0A2imPDPLbyzq5u/XNga0uTdDVeELrBogSysHYAACAASURBVJc7e6q47SqqKkeBVhfnVCzYNqdeCtNfPyzUerWU3F+PM25ZaJ/wua4uLS/OuVKarMiOW4/1NQgyDR2wussecreNLH3VugH7bHbbtNl0OVZB9aCog0pNL168UKBQpUKo6XKkxdlpRTZw1NBan2MaN5vhd9+IVxv+aZtBaEic3fjs2t3bn52IvQZuj9zn505bNfQ5i4lKzitvQ7+97llbHDrjFFtNWo0TbW5v67BaU1yvqRDXtba8qKlSwRnCBpnBisW2s9JNX+2rm359TQ+tXffGFDnjlVeA3ct3wRXnnG2H2/Ldy+fk9w+vfk25NL9LvZTl9Nw81zRkQ+5XtbTpwq2TrJ3cTpc3206/oQ/WADqTpl6idg+TVrrTOes92F89MAMVmyANtLm5qXqtrkIUaroUanG2rFLBjgY6+S+tLf9FOTksvhA4D4H0pzZtK+333/TYDFSSKNTT715o/7DqegthXNXVpXnNz0z5KdVmJ8V3VhqCeN3114YHN0NPYHTqLEiCbJLUZE5bzTiIVFNBlbr0cmtbh5VD1/7OThU1N110YxGXVgVuRrf5W3xpcpDxUBBwO//4MQjXBzLdMF22XYkT7ewdaHe/4owHw6SmhdkpLc7PZpYBFjb9NLW/9bvb+tSPImcp8k7UD5ijm4ZTA3vzsmHaxH1SY5W0PQ5sa+IkUKVa185hRZs7uyoGdT24dV0//uH39drDe5qd7u+eKP1NbXSrBskhAAEIQAACEIAABCAAgVMI2Lt3fqKkVq9re3dP2y+3usS0V5/839letdtj51PiHgItBPyYi20TnRmtuA3QGwYrNrkZKklCt6WpgoKb+Dw8qunrp8/SM3kbCXrNa9NXt6K9EcjPouYcjt8OYgzIS3c8N1yGmYCvt7xWdXKzAct8GCuTGawoLCkJCm53CrNPOarVVa8daW9n2w1ytsZJU07/zbYfcHDalfgUYo1EvaQdwjuvE/xbovQariXSAB4aBRtA2pOXZHut2lRpqsXGOb03gxXbVcWOA7KPnc0WJzU9ff5dOrwfBgoz44i0n2EGKylL9+xuvZGKZzz4evQy+BzPem219+iXvKkhT1OWdKC5+dx6l+baW979lbddM1rlsqfz8rU0WmU+nkevLqm0KSd37/XPdDa0Nrjg+sCWnvV/d/cqOtjbU9BLIdgdrddqIFxfCGQTTW6HiqztdbuqxEoCM9C2vnKoF5s7ermZ9iHcZGk6S9VBgt7ajw4RcbpEAn0w4bsE6b2uWQNsv212/GVBSVSS2wHT2tJA2t3f157tzmZL/9v+fAptzv1/bGSU/Vj0PwdSHCECqcFK2ue1f1MDFLtkT0Hk2l9rg62PvLW7r52dHWcgkBYz1SOvVnmt8m79xZGlms+ovxmQ2rATaChWqgSZ2UpqZ2Wyu4Es60+kiw/MeNt7WoyGcXufy4nBSp+BkhwEIAABCEAAAhCAAATGmUDTYMVW40aKwlBRVO5c5MbAp38TbrwVdQ6fufrQJwbCEwI5At4wJJ0kTVf1txqspC/d9ThRXLXX8XQXljCSClFBUZQasJh+2wxaqw62622rb04MbiFwfgK2uimb5k8Ts+eiM1qJ7SigeuKOpbDjMMIoUMF2p2jk6nUzvbrvg/NshmgE7fnGp9klgpusPaMhTJekcB5NAr79TaU3XTODFF8Wmyy1MU9bYRqoWveGKHa8YKhiVFQYWn/CjndJ9dS3wz49S6qRnE+2L1f/vfDXviRKIiNKINWzVF+tCNaFtWkm6y/E7mPtr23pn2pjGBVVCEOnv70UeTA63EvOhJkUAvm2uKm/qU7Hps1BLT3WygxZEqlYLKsQRk7PfSubT8O4udaxX1Zhk1IRQ1LOxi/biDQ+vq9guuim+O19LLD2N3LHYMZKFMf1tFWOIkVBwZ1M0Yrb+hONkrd6DeRpROAOpOwk2krAtDbVvcxEJfV2BquBarXY7VBcT0yjA0WFogpuDA0dauXI08USSPUv1VnXU0hbYFtk4PoAqZWg9RniOFYQ2y6Y5td+nFX/pMZgpX8sSQkCEIAABCAAAQhAAAJjTcCN/9jLSzahbwv0ZmamtDw/36Xc/gXcX3sfQGofMO2SAc4QaBDwr9s2WZpO1JuLrSa1q71YBzo8rOrly11VjtIX8ulyUStL8yoWi27HlV4WSqeTVV6nG9mf76bPyZ1PGGJfGgHXRNoQUKoQfqjIdlipxaEODqva3DxybXAUBZqeKml5cc4ZDjZkdvruFSpNIZ1y8m6NkH258Tn0JTESGVkCTe0yJfYfK06qITbpVKvHev7ipQ6Pqk7H7SiV1aU5lUs2NNk4k60Dg7Tv4CcCOgQ4h1Oa9jkSIOoYEXC7AGXlSSf8beo0VC1OZDuybW1vO6OVQhRpulRyR2IWCz0MrbsJqzECRVGGkoBrh7MmzXb+sVv71/agqCfSi82XOqwcqR7HUlzXwtyi5mdnXFn8b7l//7rYSf+hxDnyQjlVyCvFkJcoPY7CC5m43atc3yEOtV+put0oKpUjU13NzkxrbmZaU6Wij5Be7Wg4V/Dsi9DqyxMEBk7AvnK+PbXMrA22vsXW9q5e7uwqrtZUKISam5nR0sLcwOUhAwicTsBpadZbsFGIVGft6ndZqRxVtbt3oJ39A9d/6MsWiV0E66FX3SUmzhCAAAQgAAEIQAACEIDARBGw8U2brLdBzKSeaKpc0v27N/Sj977fhYO3vLdBJwtig0e9DSA1gndJGWcItBNwOuP1y0bcs3N4bajIVkfbYP3X3zzTT376ob59uql69UhL88v60z/+fU1NTSm07VbSRNLVee70iaa++sF7b7DVnv+rPLvUszxfJT5xxo2AtZmmEE2lsLtYRe3uV/Xp51/qb/7mb1WL65qbnteDOzf13jtvOv1tksjHzw+Z9tz8NpM69S7dWaX5LTk1AgHGkICf4HRFS/whBKYVqWb49tcG6v/u7/9BX3/7nSoHhyoWQ/34h+/p2tUrqcGgC9/U/RRVPj1zGYS2tec5hpVEkU4lkGpBuhtF2mdNtc3WQu8dVvXN0+f6+3/4e23vVDRdKuvOjTW9+fg1rSwvnpq2BWj5nvQUo7dA/hvSW2hCnZWANyA9a7zLC59pctaspTtUpMdh/s1/+zt9+vkXOjioSEFd7771SI8fPfRTqk7kRmtoE/8DaW8vj8xk5jyI38xBkWxoX5ZBojiIdFhN9NU33+lnP/+Zvv56T4VCpFsb1/T44X1dX792TJhRKvEx4XEYaQItGpwpovWB7Vjif/rZz/XzD3+lxO2wUtODuzf0we+9f2nldeK1CHxpopDxpRFoKkDgjtE281bbyyo9vtWu1nm1k9eePd/UJ7/7VL/41a/d8cSD3MgKg5VLUwgyhgAEIAABCEAAAhCAwGgR8C8m3mjFVkWvLM7p3q3VngpylgGk5utTT0kTCAINAl7PTIf8x16/axYijvXrmbLCIFY9rmqmFOj2xhXNzswoah7L69Ly6fiE/XO/ddOn6/PhCoE8AdM309+Xu4n293ZUCOqKVZNtSrE0P627N9Y0M32yFvVbZ/PycQ+BPIFOmujb3+82p/XLmbK+CxNV4qrCJNLGtRXdunmtMS16bJcrZzg4GDOVvNzcQ6AbAdPfnf1EURDonwuhdup1FRRrYbas29dXtX5tqVtU5+7bX389MTCeEDgHgfb2155Nf+vZ58MPZ1SMQlWca03XVuZ1/9aKy9HHzeupdzuHSKdGvYg8ThViTAPk63KUimg64WU3/d2vpse1fjJdUhTEKgShFmendGNtRQ9udx6D8PFHqdzIOj4EvP7Z1XTYrr/93awKYazIPnFNy/NTenBz+dILTRt86VUwZAJkO6zk2mHT33Ih0ovvvlMxU5iT9sU8b4EwWDkvQeJDAAIQgAAEIAABCEBgQgjYEUC2y4Q7vzQsuBVOxSg6cSP/V0WTH6x61TSIN3kE8oMuXof8oJG9WEdh6D7NY31sELQut3QkCN2kqY/XTs+n0+7OMwT6RSCvv+1pml8YBArD0LXDaVjb8ao95PHnHoIcj4QLBPpEwOlu1v6GoW3Xb4OhdgZ63W2b7nazyJS0kz6bFzrcp8ogmTMTcPobSlGUtr22OtqOVLH9q0yfT/vzIfz1tPD4Q6CfBKzva/1X+6Tta9r+BrZkWqbH6Z9dXZh+Zn5KWj7vU4Lh/YoEPN9ReX/x8lpx/b1dbezB+r/2DmdX9xdINi7R7c/H7+aPOwQGSaBd/1ra1uwLaX0IC3eZ3892OQfJhLRHh4DXC381ye3exoCtIxHYmFlwQgN8zqJisHJOgESHAAQgAAEIQAACEIDAJBGwlxUbOEpfvP050YMhkH9JGkwOpDruBEyH/ECQf62O40She9EO3BFXNvmUDtqnBivG5CJ17yLzGvf6HsfymX6Y7toYvdug3w0Upe2w02+nv1HXonv97xrgnB7o7zkBjmP0vNLlFMQMVfyZ506f7Wj0xCZPMx0fRxaUaeQJpO2sDdTXnaGVdRDcBKrNlh7bEmjki0sBxoyAta++SbYDMu2jIM76FK2FzTXXrR48jTSBUa5Xkz3tOiSuuU2bXNcqu6NVRrpiEH4iCKTamhU16wY7u6tR/mJORM1NaiGtx3D8QEDXFmeKm/YrfM+i/5z8mF3/UyZFCEAAAhCAAAQgAAEIQGAsCbhXGDd5mrhBpLEsJIUaKwJ+TMgNGsWJArcszz3lNusdqyJTmFEmkI4EtZQgr8OpR5KO4jemolqC8wCB4SCQH890A/U2YZruDGST/m53qyRdZTocAiMFBDoTiG2yPzH9TQ0IO4fCFQLDSaDRFLstrTIjWI5cG87KQqo2AmmnODVvTb3SPnFDq9vC8wiB4SMQJOmCr+ZrW16jh09eJJpUAn7EoVP5032BzHBwkPba7LDSiT1uEIAABCAAAQhAAAIQgEBnAvYO03iPCZQ4S/vOQXGFwDARcGrrDa3chKlNkqZv3F6tG6o9TIIjy2QSaFNGNyzvJpoyvc10tznw2RlTWzKdA+EKgUERyCtgYBP+2TFArith7W9mdzWo/EkXAuckkE6VpttUpDuy+UnShs85cyA6BAZPwDXFSSCbNLV7MxjMN8+Dl4AcIHAOAmbY6oxb03Y3nTY9R3pEhcAFEnBtrY1BuFn+TJcx1r7AGiCr3gl06RnYGoPcp/f0zh4Sg5WzMyMGBCAAAQhAAAIQgAAEIGAEzFgFgxV0YYQIuAHOIJ3wd4NG2WSpG7wfoXIg6pgTyI0VtU6J+tn9TIf9pP+Y46B4I0ogp8eujbV/kliBYoWuHc4mTpk2HdEKHl+xvUmKldDd57q7jUlT02V3JNv4cqBk40Gg0RRnHYrUaMW1yuNRQEoxIQRSBbY+RKq9+ZZ6QhBQzJEi0FlDbZdB6/82WuaRKhPCTigBWzRjKuvOKba+cWft7gcdjgTqB0XSgAAEIAABCEAAAhCAwAQQyBaFuJfsZnF52W6y4G4YCbRoqL1rOyOr9CXb/LxeD6PsyAQBI+C0taHI9pR+so15/WMWEGYQuGQCpqsNfW2qpx/b9AP1fri+EdSrtld6p/iXXBayh0Cmzs5G29FIlCTpBzgQGHYCvn1Nm2W/PNqkZrp02OsO+ZrdWnccm72wNV7a6CCgH6NFwLfFirPdBUdLfKSdUAK+pXXX7EhBM1bx7oPAwg4rg6BKmhCAAAQgAAEIQAACEJgYAoN8XZkYiBR0gATSQfrWDGx/isYyEdvf1C0XaQ3DEwSGhYAb5PRNbbbAybllhivDIidyQOBkArZmLpSS7OoOZXPntB2Plir4cXdcIHABBPLqZ/duYWnW9lqzm+6y0pxMvQCRyAICZydg/Ya8Mrv9/FOb12ze6expEgMCl04gt+XVpcuCABDoTsCaX//61jhPxY05tDfO3dPABwKXRcDrbnrNDF5NGO8xIMHYYWVAYEkWAhCAAAQgAAEIQAACEIAABIaDgJtw8pNONnrvXrQbrm0j+sMhM1JAwAj4uSZ3dYtLzdzK702RMcqrMtggMKQEkhZjFRuO9IqbE9grfM6JWwhcJoGGSrrV/V5rve42fC9TRPKGwIkEvLZaoHRflVRvMVo5ERueQ0zAXuPSxQdDLCSiQSD3HmcGK4HC7JNvlcEEgeEl0M02ZZC9XwxWhlcfkAwCEIAABCAAAQhAAAIjQKDba8wIiI6IE0Wg8WLtV0k3St/wabhwA4FhIuA11K7+fpjkQxYI9E4gr8WpNtOL6J0eIS+HgG93nfZmCuvdLkcicoXA2Qmkxipnj0cMCEAAAhA4HwF3mpVPwvoRdH49Da5DSCCvnvn7ixAVg5WLoEweEIAABCAAAQhAAAIQgAAEIAABCEDgVQm4mdJ85ERJy+hn3o97CEAAAhDoNwHf5mKs0m+ypHc5BC56GupySkmuEIAABC6bQBAE8h8F9CIuuz7If3gJYLAyvHWDZBCAAAQgAAEIQAACEIAABCAAAQhAoEEAG5UGCm4gAAEIXAgB1+66uf1sgt8mm9znQrInEwgMhEDCnOlAuJIoBCAAgTyBpmngsdUH+WDcQwACkh0gyx8EIAABCEAAAhCAAAQgAIGzEeDc87PxIjQEIACB/hDww57MNPWHJ6lAAAIQOJ1A0rZ/vx2vwhErp3MjBAQgAAEIQAAC/v0NEhCAwEkEMFg5iQ5+EIAABCAAAQhAAAIQgAAEIDBGBPwkv7+OUdEoymQRyFSY4c/JqnZKCwEIQAACEOgPAfrC/eFIKhCAAAS6E0hbWjsSqHsYfCAAgZQABitoAgQgAAEIQAACEIAABCBwJgKN3VUSiffuM6Ej8FAQQGuHohoQAgIQmEwCdr4KllaTWfeUGgIQuEQCbQ1v2+MlCkbWEIAABMaaQIC1yljXL4XrHwEMVvrHkpQgAAEIQAACEIAABCAwWQQaliuTVWxKCwEIQAACEIDAqxGwOVLmSV+NHbEgAAEIQAACEIAABEaHQHOpTPNudKRHUghcLAEMVi6WN7lBAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMAYE7AdVthkZYwrmKL1jQAGK31DSUIQgAAEIAABCEAAAhCYRAKsk57EWh/1MqO1o16Dkys/uju5dU/JIQCByyXQ3v62P1+udOQOgdMIoLGnEcIfAhCAwKAJJEnCToODhkz6I0sAg5WRrToEhwAEIAABCEAAAhCAAAQgAIFeCfhh+sR2423syBsoUfrpNR3CQeDyCHjlDaTE9JY/CIwOAdfsNpaX+sH6IN8cj05hkHSyCFiTm5XY9SHsWKtGP2KyUFDaESHgFTYnrjk1nX1/IheAWwgMIYGmzg6hcIgEgVMINNtdu/MdB9rfU7DhPcEEMFiZ4Mqn6BCAAAQgAAEIQAACEOiFAANFvVAizDAT8Dqcn2BKgoAJp2GuNGRrJeBGPFNDldYBz9ZgPEFgmAm4IXpvtOIaZj94P8xSI9skE3BNbxuAfF+izYtHCAwXgaTZYxguwZAGAicTyLe9+XuLxXT/yezwHS4CXn/tatrrjgdqGK8Ml6xIA4HLJoDBymXXAPlDAAIQgAAEIAABCEAAAhCAwMAJ+EEiyyi991kyYepJcIUABCBwsQRofy+WN7m9MoHcLis+DQxXPAmuQ0WgtZN7TDTzzveJjwXAAQJDRSBoWF3R5g5VxSDMqxJAkV+VHPEmgAAGKxNQyRQRAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBMSaQtwPM37sin2LNMsZYKBoEIACByyOQmgra7ipsrnJ5tUDOw08Ag5XhryMkhAAEIAABCEAAAhCAAAQgAIF+EGBFUz8okgYEIAABCEAAAhCAwEgRwFhlpKoLYSEAgbEh4Fpfd0RbgL3K2NQqBRkEAQxWBkGVNCEAAQhAAAIQgAAEIDDmBGzBXsC455jXMsWDAAQgAAEI9JsAnYd+EyU9CEAAAhCAAAQgAIEhJZDv+rLLypBWEmINAwEMVoahFpABAhCAAAQgAAEIQAACEIAABCAAAQhAAAJjTiBJJPvwBwEIQAACEIAABCAAAQhAAAIQMAIYrKAHEIAABCAAAQhAAAIQgMDZCTDZdHZmxIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAIEGAQxWGii4gQAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAKjT8DWGLh1BnaeK38QgAAEIAABCEBgSAkUhlQuxIIABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEOiVQDfjlG7uvaZLOAhAAAIQgAAEIDAgAuywMiCwJAsBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAELoOAP8XVXy9DBvKEAAQgAAEIQGAcCDT2bRtIYTBYGQhWEoUABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAALjQGAwZrAYrIyDblAGCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgMDAC/TdawWBlYJVFwhCAAAQgAAEIQAACEBhfAhyBPr51S8kgAAEIQAACEIAABCAAgfEg0P8ppfHgQikgAAEIXBiBQKItvjDaZDRQAoPT5MJA5SZxCEAAAhCAAAQgAAEIQGDMCNjLSSI5i5XBvaiMGTSKAwEIQAACEIAABCAAAQhA4EIJ5N/W8vcXKgSZQQACEJhwAq79ZdXXhGvBOBV/MD0KdlgZJx2hLBCAAAQgAAEIQAACEBgkgcYL9mBeTgYpOmlDAAIQgAAEIAABCEAAAhCYFAL+jc1fJ6XclBMCEIDAMBHwbbBd/f0wyYcsEBgWAhisDEtNIAcEIAABCEAAAhCAAARGggCv2CNRTQgJAQhAAAIQgAAEIAABCEw8gcaag4knAQAIQAACEIAABIaVAAYrw1ozyAUBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEXoFA3lglf/8KSREFAhCAAAQgAAEIDIwABisDQ0vCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQOByCGCocjncyRUCEICAEQhohFEECPREAIOVnjARCAIQgAAEIAABCEAAAhCAAAQgAAEIXDKBbMAzYeDzkiuC7CEAAQhAAAIQgAAEIAABCEAAAhDoBwEMVvpBkTT+f/beszuOJMkWvCFSSyQ0QIKyqrqquqe6p3tmzpt9+7f3y357b3bfzM68qi5JsiihRSK1zlB7rkd4IpBIkAAJkgBpyQNGhIcL8+vmFu5u5uaCgCAgCAgCgoAgIAgIAoKAICAICAKCgCAgCHwABIIPUIYUIQgIAoKAICAICAKCgCAgCAgCgoAg8G4IBEEA/slPEBAEXo+AGKy8Hh95KwgIAoKAICAICAKCgCAgCAgCMxCQ6fYMUCTohiIg3HxDG+7zI1u8qnx+bS41FgQEgeuLgAwfrm/bCGWCgCDwiSAggvYTaUiphiAgCAgCb0RADFbeCJFEEAQEAUFAEBAEBAFBQBAQBASByVIRFaZaaaqvAo8gcIMQ4OamkHUDYPIw4fAbVBMh9bNCwACESz+rFpfKCgKCwDVA4HVD3de9uwakCwmCwBkE1DhCGPcMLhJw/RAgm55i1diDjIevX3sJRRdEQLysXBAoiXadEKDM1XI3FMV6YUKHXh21YrBydVhKToKAICAICAKCgCAgCAgCgsAnjYCeqFz9tOSThk0qd60QiLg4WvQM1NR7YsFyrSgVYgSBWQiI/J2FioQJAoKAICAICAKCwEUQkHHERVCSONcVAc2/+npd6RS6BIFZCEzWHma9lDBB4DojoI2tjHAhLeTlqydYDFauHlPJURAQBAQBQUAQEAQEAUFAEPjkEZBFok++iaWCgoAgIAgIAoKAICAICAIaAb2hVD/LVRC4yQjEPFbc5GoI7YKAICAI3AgElHPXAEHAvxtBsRApCHxwBMRg5YNDLgUKAoKAICAICAKCgCAgCAgCgoAgIAgIAoKAICAICAKCgCAgCNw0BETPdNNaTOgVBAQBQUAQEAQ+LgIcO9BYZXK2ysclR0oXBK4lAmKwci2bRYgSBAQBQUAQEAQEAUFAEBAEBAFBQBAQBAQBQUAQEAQEAUFAELg2CIhXimvTFEKIICAICAKCgCBwoxAQe5Ub1VxC7IdHQAxWPjzmUqIgIAgIAoKAICAICAKCgCAgCAgCgoAgIAgIAm+HgChM3w43SSUICAKCwBUhIF5WrghIyea9IiDDhfcKr2QuCAgCgsAFERBpfEGgJNpnjoAYrHzmDCDVFwQEAUFAEBAEBAFBQBAQBAQBQUAQEAQEgZuDgHIpTXJl7fPmNJpQKggIAoKAICAIfCQEOFyQIcNHAl+KFQQEgc8aASV/RQB/1jwglb84AmKwcnGsJKYgIAgIAoKAICAICAKCgCAgCAgCgoAgIAgIAtcCAdnhfy2aQYgQBAQBQUAQEASuLQKiJ722TSOECQKCwGeFgMzcPqvmlsq+FQJisPJWsEkiQUAQEAQEAUFAEBAEBAFBQBAQBAQBQUAQEAQEAUFAEBAEBAFBQBAQBAQBQUAQEAQEAUHgLAJBEABir3IWGAm5IQh8OOYVg5UbwhJCpiAgCAgCgoAgIAgIAoKAICAICAKCgCAgCAgCgoAgIAgIAoKAICAICAKCgCAgCAgCgoAgIAgIAu8dAePDGK2Iwcp7b0kpQBAQBAQBQUAQEAQEAUFAEBAEBAFBQBAQBAQBQUAQEAQEAUFAEBAEBAFBQBAQBAQBQeBzQkCp++WMts+pyaWub4GA/RZpPmwSbbgjnfnD4i6lXQwB4c+L4SSxPlEEpAN8og375mqd1/QMl+/1m/G7RjHOa8prROKHJ0WDEi9Z+DqOhtwLAoKAIHA1CGh5KzL2avCUXAQBQUAQiBDQ4pWPImKFLQQBQUAQpLcJdgAAIABJREFUEAQEAUFAEPjICBjRqUAyMPvIDSHFX2cErrfBCmdY/FOdWE+3oh499RiCrAP1lXGvlwQgZfw7Q1mc5OvMMR+dNj+i4O2dA2n8VUbnP8yoqW6k6FWgvzLR80xW86P2fnt6ZxAiQYLAR0UgUFyt+0MAYyJnz0g26B6ru4e+zqzAqf44M8aVBuoa6ExfS5uO9Llfp0GLtxnv9XsB89pzim4q3Wz8Sn2azcYaRjXTlWbrnFdZDUgsmYobf46N5a59QwuBNxuBOM/Oqsl5fDwrroQJAtcNgTfx93WjV+j5zBDgLIZCdkrQTo0HPjNQpLo3BAGyqRaxmmXPXZHSEadY/YZUVcj8RBHQfPuJVk+qJQgIAoLA9UVAjwvOo1DGC+chI+HXDQEZTFy3FrkQPdfbYOWUAOTDlMQ89f5C9f3okUjyKbKnqvTRCfwcCbiQ8GIkHfFUC74BsRNV/hsiymtB4EYicNIbYtJNyzUDOHdh7BrU9oT2GDG6m8eC5HYGAufhNBPUGekl6KMjoJtKXycEnde2kwg37eZMDS9WgTcke8Pri5UhsQSBUwjM6Hya0fhKfoLAtUZgBv9ea3qFOEHgdQhooTuDr7Vcfl1yeScIfFAEZvBpVL7m5NeSQ56+UMTX5iIvBYErRUBE7ZXCKZkJAoKAIHBxBN40Ljh/2HHxMiTmlIJYAHkvCMhg4gph1ZMFXvX9FWYfy+p6G6yQ0FOMFXuI3cbqM3sXzOkIV/t0XvvMom+qPYMAMHQ8fWUcfX+1lH4iuV1E/f16ECfwnmm7yZsJVmdziuLotGeTTNKqvhsYYDvrn2pvpnldOh1ZroLAdUDgbCeI2Fcz8RRDB0Cg3aqQ1XW0eF10mL7G332se9ZT025EdE9V7WORdi3L1W2nryQyfn8tiRaiJghofuc45Ly2O689Z8iESb7X6IZk8qfJPbeeOkIUXwHCyDqDeLi+l6sgcFUITPiPN/pPdz59jcnXab68KjokH0HgnRDQvMur5lt9nZHxNB+/JuqM1BIkCAgCgoAgMEEgLn8ZSIF6IlT100nIJOHpmzdGOB1dngQBQUAQEAQEAUHgE0YgPi6Ynrux2vFp3ycMg1TtOiOgx8CkUTOsvl5nuj8V2mYJhqup2/U3WHljPePgzGDK+GudVzzarPc63mWus/KJl8O8tDI0FpenyhjTNhj6/XT6y9Dz2cYleBpADcIFgGSSqWjxnIyJEiGW/VT86Y+1UtpTca/J4QlCbG9L0yVXQeCaI6B5NyLzpJtMM/9JhGm+J89PfrxnH2BAPHwS4SPc6Dr6kaFN5P07MGOy+brQ+hHgOVMksdCYnXkpATcGAc3vHJdootm20d9MQzPGY2Sd4Br3C/3p1eRymDXz06sj8Do9FtP10/XVOMlVELgqBE7xlmZGdjEetccfmVIzYlTo1ONVkSL5CALvhsAJ/558JE7zL2Mo9tVRNS/r67sRIKkFgStHgKwa/qLJQewQVP1GroLAR0dAMWrErRMhy5vwT99N06n5WyWZfinPgoAgIAgIAhdCQGTphWCSSDcdAQ4WNLPH68IwGUjEEZH7D4oAGVAzZpwZhSnfXzNozDXu76ekm2GwojHQV/LdhPd4wxe0BohA0lc+xpUxjMVoXHOI/+LxGT7JO4o0/T6edvqecSP6lCFKlFZ52XAC+EMgGAYIvJA2IwEYaQNm1ggNGaK009nK8zkI6LbhVbX1aQBVU6r/ovTx+3iWM8IZNAn2zdOeUpj29DpsmJtWAvqAz3YeBAjc8BUNVVRbZwwYyXjmcULkXhC4RghMOsA5NOl+5wGBFwAuEDhAMArCqx8ADFeGeQZgGzBSBswUYCT5HPNkMlUEs35T8VNJLvc4RXswBPx+WAdFV9KAmQnpNPilfK/EXI70jxqbuMV/0898J1jFEbp292r8wfHIKOqrY3482TdPvlGTNpxuy+nna1e7E4JIqrZBMXR/157tZtUjzsvx+5MshbfjWMj91SAw4TV+KEPGPGHP2NxmVmknEWe9lTBB4AMiQGkbMbOa9JI5YwyqjZXjFDF6LEr8ldwLAh8cAS2LJzzJY30nDx+cHClQEHgjAppnFZ9GI14dZoTcO+HgSfhJrpN3J0FyJwh8MARmsORJ2frlSYiMF+JYyP21QmCmLJ3Fw6R6ZuRrVR0h5nNCIM6nb+LNeFyN0ZvS6HhyFQTeGwKxNQhVRsSU5Ffhz/eG+ofI+PobrMSMS5SShago5WfEfGRAbuH3AwRcIFPb4qN3WqDqPCIPF2o9je/Ue6Y7gfoi/ByLfpJQ32lliBn65NBrd6Ahgwu4O304v2+hcVxF4PuwShmk7yyg/PVtmPnkidGKzk+usxHQjcAm5z3bmIpx/swTAaVC+Bj7U0ZLUVSlGziv0RknikfeC9wABvMmH9H4JJ6O8XwfgW8qOqgIdHdbcF8eYXjcRGs8wMgClr+8hdIfNmBVaKk0u2oSKghcRwTI4qdYln1P9TsgGAcIRqHBh9dw4e0ewjuqYdRoottqwzeAVDaLwvwczOUcEusl2CslJf+CRGw5OFbAmfKuEhRmHtGvaB8DzosG9n/4FYlhgHHagLGYReHeEuburMIq0LLmKgn4RPIijvpHfCJMlRepWXjp+LPe6Xzk+n4RYJ91oYxVvKMxnGebONrcRTKw4C+kkbk7j/LDFVj5HJSh1ixqbkr7kd+i8d9knEA2Jf30oBSrR/y9/u6rqjPOiR3BLDQkTBB4ZwTC+U04vtTG7npu8tpx6juXLBkIAu+IgP6uq2xCA6uAgz6Ga/mpLQd1XF7V/O1kXvWOVEhyQeDtEIh4USXWPKuvOsfYWEEHyVUQuFYIkGenJ6oqLKKS8ja6VexMER0FnBpjCK9fq2b91Inxo0maGW0vOMV+5M8438Zfxu8/dZCkfjcTgYh/42Ph11bklIB+bUx5KQhcHQLR2i0zjK+LnSpAy1vyqL4/FUEeBIGPg8BployYU8teTdJ5slV4WSN0ra/X22AlYq5QKRrA74dC0rB8IBEACXsiWNXimDIq8JRhgdKQ2qZSuBiWAX8UhIoLzdVUYuj81YxtimPDdePJZO7CrRilgxmEyh7aJdB4xQ+9q7g7LTR/eIaXz5/Bcx0kl8uYGz1E/vYiktmE8kBw4bI+84hqgd8NPZgEYxqUKDcP4QycxiN0qc4vL/9MC4ZlAhZ5woCRCL07nPvRJW9o/nAArxPAb3TQH3SRKmaRLBdgFa2T7duMzHJomEQyBgG8gzY6P77A9rNX2O824KRtpeHP31qCWU6EvBtb0/3Mm1Oqfy0RYC/SQjMmI3X/4CDXC+D3Arh7QzjP99F79BSdnUP0Gy2MBkO4ozE87lFMJGBnM+jOmUg8rGD1zw/x8L/9LZSTOuvoGnW9ScnvAxol9tlX6RFmGMDdruHlv/0Aq+1gkDVg3a3glvk1ykvzCPL2uaLifdB2k/JU32fygUNZ7AOeDyNhhd50LGNm+96k+n0qtOpeTL7neIRekNzDNmo/PcPv//tnpH0b3q08FsYPkFkrIZvNxPyThJ9D3U1vAiZKP6oX5PldJn+OPQSep8YCHAcEtqU8PU0m6LF4NEANxw4BjKQNJM3QoFgDGQ0RbhImN6HdPisa9SJR7HvK+quxrf4IkofJZNGf4jfNdLzG+PGzwk4qez0QiHhXjac0z0ZhE94kD3POHefXCQ/rSfP1qI5Q8ZkiQFms+ZYQaF4mn0Z/imX5nza++kyhkmpfIwQinlW8GydrFi/zvTbU1mPjiM95mfD35CGeodwLAu8HAWOWoQqL4nwszsfx4S6ZVfj0/TSI5PruCJA3+YuPK6gm4NhBCdrYGCOKKhdB4IMjoOWr5leyJe9jOtIJTeTbSKWmZK+MgyfQyM01QECPF0iK5us4WVruah7mOz2O0Pfx+HJ/rRC4vgYr/Mjz2BwvPFrFb7lwd2pwjbFSHqYXcrDLxdDAg3Hp3r4XwG/24TXaGA1dpEsFWJUSzLwJZ7sJv9VHMPZhmFa4eKYZOj7T0wx9qWaKJWJHsAKMk4BRziC3VIZZiDoPaWwN0d09xvGrXYydMdKDAcxb8/BGnqIpltOlKPgsIlMY8SOqlMw0YArgd3347QH8VhdBf4BgNEIwdgCXZ5NQGBmARaVUIjRwSidhFrIw53LKo42Z5rvwGIRTu8kn/BfAawQYPztE/ddnOOjWkV2ew8oXGyh9c+fkKCdqFHTjMS2PBOoM0Tmoo/ZqF4ftYzgZG7e/eQCMWYHPosWkkp8AApqtJ1WJ5CZ5nN5JaEjobPfh/PQS1b8/xrPHv2HYbsNjHzQMmJYFL/DhIlB/9aqHLFZhrpbwgBO4ScaRnIx1pVPv4vGu4J6iQSkCWSz7a7uP4809mO0heikDKXOE8hdrSskt/TUGOBslknFKFtNocAC41Tb8WlPh5aWhZGx6sQSzmD5ttBLLSm4/HAKqL+nvDq/sv90x2ns1HL7YQiaw4TtlJDbm4Q05HjGgjtGJOuH77IvvDQU9XnADuPtdeMct+N0RkDTgpSwkSlkkl+fVUX2kIegD7tEQfqOOYDBQi/tOCsiszMFemgPS5qkFpxuJyXsDWzK+NALshxwOqqPzQi+Myvja4VF60feQmZLR6NWPjr7okYyG8AmGGSE/6jiXJkASCALvgICeJ6lrAND4Vx0LGR2FSvnLP/74MbG4kYNHopohD9ucn0Xv5SIIfGgE4uNYLzrGdEwPdDH+5WCXC/NU9FP+JsMNL2rTS6R8OqWE+tB1kPI+XwQ0/6pxbnjUeCh/YzwczdeV/OVGulS05hVtppvwNscY+u/zRVRq/hEQOKX31DzNcbE+ZprHqpOPuUcwBQQcQ0Syd7I2I5Oxj9ByUuQZBCJ5q3QVXGPRYwnyMMcQau4WbeSKJ9b8yyvzkJ8g8AEQUHyqZS2vev7GcfD0GkQ0/qUMVusRHAtr4a2vH4BmKUIQmCCgxwvU4VDWOgjXIdQG2ilZqtfQyLe0fiA/W6HCacLHOmMtj/WzXD86AtfaYEUt5FIh2hjBeXGE7f/n72gGAyTXy1j77gEW0nkYGTP0aDECvKMRnGe7ePX7C3RaPdy+t4HKVw9gr1XQ/v+eoP5iD0FnhKSZgBlEyhg1uAh9CHCUMFFgRk3zZp6l1jOc6PlGAC/w0Ld9dAsW8l+s4eu//gOSmaIaqCjPG46J9NhCyjUBx4A1NmA6pEVW7V7bGyiU+DGlENJHjxyO4B3U4e0cofdyB61aTR0/Muz14IwcdUwUjZNM20Yyk4GdTSFVymNudQnFjSVYK2VYC3lYC1lYlQyMbKQpj3YDqoHmGHD3B2j8z5/xH//X/42aP0BisYQv//Uv+OeVFRiJVHhMEIlXx1LFauEayHg28kgihwSGnomkbyI4s0IbMVAsqdwKAtcDASUgI1JOpCFt/FT/GABe3Yfz4+/Y+h9/x96T5+gPu7AsG5lUDolsGlYqCTdw4XgOxr6LcSZAubKAytxC6GWIeemj1FgcfzGjlSjkai8nVQkVKhyYO0CSf74F3wtgOYDFARAXTbTS5WqpuLm5RWxBbIIhecBFn96kfv0dZneERtrD3Dd3cO9f/ohMJqWOaZssMN3cWn8alOu2U8pEG2mPfybSgQHftZDwODa5+TyvDZ6VnHIA5/E2dn56hlG1jX7Ch19MYe7OCu7/059hLxWVzHFrPsY/baP69Cla9arStnaKFtb++jU2kn9AYjEcy+kx36fBEFKLj4WAspXnf8own0bOAfz2GH6nj2DIM0RVJw2/hzRUyVrKANAsZWHmLJjp0Ohy4iHoY1VEyv08EdDDQ44D6OWSmwjanjLW9wcOgpELOLRiobEKYKQMGLkErGIm5GN6riPzTi92xsdnnyeyUusPgQD5Vy3Sh0bXatMT5W9viGAwRjDm6r0fKZoMGGkz5Nsi5W8SRipc8AzUwueHIFjKEASmEFBDhHCh3h8E8DscRwyUYXYw4DpYpO2nsjRpwCyko78UzGxovKIm4iJzp4CVxw+KQLTGq8rUm6GGQNBz4A94xroHIx0AlVD2BvTay2VzynD+hH8jIOTysRFQRgBq7RDwu9xYO1LjCSQAM2PBzKdhlk5OCJjQKzw8gUJuPhAClLVarzbk+GGMoDsMeXZMj9mRgDVNJX/NvA2zlIFZysHkvI6nFcS8tn0gqqUYQSBEgOypDQOpG1ZraI4aAwcDnrjiAr6nNswoY8GsHc7hChmYuQSQDNQ4IuD6GnMUGXxtOevaGqxQDqqjJgY8aqKF1k/PsP2fv6FlO8iP1jF/b00t6AaJpGJWfxgoo5bq98/w8tff0OsNUEnkMHf7nhLGzZf7OPjlmdpFbwfWxGCFvMmyTka9ahis1s/U7mLVdKEhC+eFjBqJ71ONqvqMwZM4fXQsD82ChUowwp37d5G4XQwVs2piaSGLBLJGEqbhww5s2H5Iz6kM9QMz/tw7EHlBT2C6AbyqC3frCMPfXuDo+RZae4dwmh3l6t93XXWl8QjFD11N+qaJgdGFbwG+ZeLw8QsEpTRSSyUU7q5g+S8PMP/NBpKpYjgBIvbEPbI2dbePMNitITcMMAyAcWuI3mEDo4MqMnPrCLSVqWnAUI5dSDBpNmC7QIJ/vgHPN2DxXHfygS7jc2/bCAq5XHcEYoyq5Bh3cIVHZfEonfqjTfT3a0g4PhKGjWJlEUsb61i+exvmQlmZbXuDHpqdFo6MAfIPVrF2+3aoqKBxis5eC1f9/DpYGJf9LLoyqspHp51WgszKi3G46KHS2MiYSaQMdn3KDxuJ8EswK6WEEfdosuP3gP6rKg6+/x1Wd4DjbICRFaByZwXppXnQk5XCmGl0+wiCHw8B3XYu1Dcq6RtIwoDvm7A9Ewa/U4xzY35TjKVP6KMRKRWpwwDHj7fw6t9/RtDso5P04c9l4Lge7n37bWh85wFedQj38R6Ofn6K4+MDwPDQKCeQXK5g+av7sNXA1DiRVzcGn/dLqHTpS+BLVo2+W2qhqA94bRfefgPudhXtrUM0D2sYtXpwhkN4ngvLMuGlLVilLAprC1i4s4rC7RXYqxVY5QT40VI7RqQhLtEQEvWtEYi+DWoTwSj0dunVh/D2mxhuH6GxV0XvuIlhqwtn0FdDLO6K9rM20pUiCusLKG+soHR3FRa9sBWoOJ2Sq8LLb908kvANCESLOdxNyrUjv8njEVvwdqvobO6heXgc8e4QjuuoXaRewoSfS6B8e0XJ38rtVdi3lmEWbZiceJBf9d8bipfXgsA7IaDHELH5l98Yhjy8Gcrf9lEd/WYX49EgHHCQf1Mm0nMFFNfmUdlYRfHeGqz5AqxCEsjEvFa8E3GSWBB4CwTI0zR85RrqGPCaHtztQ3R39tCuNTEcDTEomrj7z9+gcm8NZpbb/GU94S2QliTvCwHqDCKZrDZyNX24L7fQ2NxFq1pDP20gsz6P5S82MJ+/De5TPrVmGY2r3xd5kq8goBDQ4weuQ4wDeG3q1Ybw9o4w2NpFc+8IneMWvP4InsPVcMCybYwzBtLLJcxtLGN+YwWZ2yuw5oswcpTDMn4Q7vpACGg5Sf6lTbYy1HbhVXtwt6robh+isXek1tDGgyFcz4Fh8OQTQ62h5VfnsXB7FfO3l2Etcw2NRrBB6LmNVeA8jmXIGsQHatCLFXM9DVa4mMBBK62lWgHcnRb2Hm2he9zCOE+rAwOJTCY8DFAzLAXuq2M0X+yjc1jF2Ahg2SaMLI8jMDCAi65H4TuAScMBeljR3BgdS2HChGWaSHiA5XswfR9BEBqheAbgmgZcy0Rg8C9u6EIPLaGXFsbuej6GjgXHG8JT/omiM48j5me5llKHUiVKnS2Vo9ziP/WLdUpN6lSMT/+Rg7/IswotlZ1XQziPt9D85Qmqz7fQPD5Gr9+F53lIJpOwbAtGIgHLtGEEhlJmsw1dz1VxPMeF23fQbwNGu4GiO0JytYzS/VUa2qn4qpki7NVg0qahiwE6xWEruYav/gJalUZ/k/Zh4omQi5R+5K+AbRyc2UjIBpxE1+0db9XJy3ig3F8OgZv65dEMEfHR++YFXRzBnZTFG/13omhTCwtjwG+4cJ/uob69j163A49WfsUc5r97iLV/+Ar2nXVwNzi//oEzQno4wIIxglXJIrVUDo83oNGILk9f39TA7KuUDfTARSO2egfuoAM/ZSNdzsOez4cKvPOMVljXM38mbH4DwC+BNng7T3E/E6w3Uf1x3mtSL4rtZahk3lE7BO0RnAaPZhtiNPQwbNPTFZlEE3CZjK8ori76fdT9ykgMRw80rnzvZBIPjQmv3DysNhAbyoiXAxv1L3I1xz52akHliup85dlo13jMOPqOqzI4duCEvBlguNdE77AGe+RikAjUIn0ilYKRp9cUAwGPlGx0MaKxQK2FIY1gLSO0xrcTMBKW8qZ2I/C4coDPZkhe1X+apc7GkpAJAgSJnxPOb7ijiV5V2jyqagzn9x30n75AdWtPLWwOun1lrOK6Dnzfh2mZytia3sp6Lw7QerKD+TurWPnqDlJf3Ya9WlRHnyovFuKscQK53LwDArpT649SxL/qe8+JkBfAp4c9LsrvNOA+3Ubj+S5q24fotFoY0NMlDa6o8Of8h8dXJWwkMmm0nu2hubKLhbvrWPrmDpL3l2EtFWCmo13Tusx3IF+SCgJnECAPR2tG+hhp79iD82Qbw2ebOHq1i9ZBVc1lRhHv+kpgA4FpALaF0atjdB/von17Bbe+foDEF+uwb5VhzVnhWCk+nzlDgAQIAu+AgOZfLX85veoGcDdbcJ7toPNsG/XNA7TqDfQ5hhiNlWdTlsj1Ko4PEpkkWsUcGktbWLp7Cwt/uIP0AxpflcMjrvWg7h3IlKSCwGkEpgcT0TxUB/NRKZ5CfvYO6VV9H91fn2J/exs9jicCB82ygeLqPMor8ycGK6cLkidB4MMgEMliXZhej6SxldJb7XfhPNnE4aPfUd3ZQ6/dRiPto/DlGpKpJCpf3Aq9C+r5mox5NZRyfV8IxMYParMMDQOrPpwXVTV/qz5/iebhEbrNFgb9AVzHge9xwQKwTAsuxw8vM2g93UN1paLGv3NfbSBxdxnWfEJ5W1GetM9bd39f9foU8lULi59CRd5DHWLjBOaupmRc2+UaRIdraEO4Lw7QffISja0DtI9qaLdaGI9GcN0xfM9VczPfNGCmk+gW8ugs7qCzsY7FB7eQ+/IWErfn1OYDegxSntuEh99DQ75bltfSYEVtYlU7Y6mIDOBtN1F/eQBrDGSsDPK5IkqVCmDbinH9UQDvaAhv6xjjoyassYtcKYtSqQCzmFNnBuYrZcytLMJL55SChp4uQn4MZ2c8IsgyLCSNBFIjD0avD3fYw0gZnQTwLQs+jWSKOVUuuT8U4z4CdRdu6fX8ABk7QGHORnmxgnSavmKjlX3dASIDBo5TLB6PrHoftX7RID4+cGEYn/X13dr7dOopIaDKOR3jgz2dVz01CKRrPR47UQvgPNrH4D+fYPuXX+B02vADDyk7AbNQQLZUQDKfgZ1JIplMK+B814c7HsMZjuCpvwHGvR4ClzunAAw9mNxlzsoTZzaDxpu15xHr5RLmludRqMxh6PaQKqVQmp9DqlxQCveZuDEPgwpIKr9D0yg2Pxduw8aMQ8vIYTBfT75bUXA85nvhg/MpmhR9XvtMIsRvNF/F6ddhjBcPj6d7L/csmD1Vof++4HsPlGu6uboauQBhUBy7OKbTFMTjRe+mk59Kwpc6P6adRJ7KiOHsI5GRglcfwHu+j/5xE854CDORRHZ9AYt/+wKpv3wJezF5YjhipAGjFJ4ZyJ0FWh7q6ymCph9CgiZksUlJA4+CO+xh/PNzvKzuAuUslr64g6XiA4AKkuls9LNWaut8VJ1MpbRXvTYIECirROYwnQsTkRL9C3lLPcWDo2QzgnTCU9fz4jF8moJTCS/6cF4BF00/Kx5xVAaFBpKOqY5ASwYJpNwAthf2Ogo0Jddmpb9MWJz+89LFgdLx9TX+7rz0Fw4PDVTDLGdlrAtlhqff840OCU1VaOZKAymGh0Yr4ft4HmfzOUWqjqozPvVyxgPjR3/hVyo0olUUqPFJJDZ1vIvke1kaZpA1CdJ5MWBW2fH30b36tDK+fscreZNjh2oANEZIjDykYWJgGsgVy1hcXoZF17xm6IUlaPWAVhf2yENKbX9KYm5hBXOVeSSzmYihJ1R+tjeTJiHGcbw/W0RmVJy4TIA66W/kSX/Eb1cAZy+A89MeBv/rZ2y/fI52swbPGcG2bNimCdMgb1pKfnpjF95gCL85wPHWAfqbBxjs17E6GKBkPIB9aw5m2uSEIjaInEGXBAkCb0Ig3q/jcaNxkz4uVe2CftnE+O8vcPzjI1Q3dzHodOAFPizDQMIyYZupcE7FhU/O5fp9DI/bGG5V0Xt+gH6thdXRVyiYd2As58PjA+Nlyr0g8BYITItflYUer9LQvR/APXDgPN7F6N9/xs7T52hUq/DGQwSGgRSPE7YsmGZC7WTxHR/ByAM6NbR2j9F7sY/xTgOLrQ4qeAgztxQu2FPmx+X+W9AuSQSBMwhEMnmyJkbFqFqsdzD+fgudHx9h99kLjFpNOJ6n1jNTNo+sTitjq8D34Tlj+P0+xtU2jjcPMXi2j161iaXBEJXEQxirhdDTyrVcGT6DiATcCATIuPqn78ONQGrpm0F+uEvaawXwdodwftvE8OfnqP72O7qtGhx3CNf00an7GHDn/9BRmz11riJvJ0jIzXtAgCx65pOu1xD5kvdOAHoaprGKs9mE+8tLVP/zZxxsbaLfbcPzXfRtR40RBvdvKwMt5RWT9J7J/D1UQrL8vBHQfEpe5TyMmw1aAcaPD+B8/xTHP/+O3Z1NeA7PYQNSlo2kXoMgcp4PZ+zB6bXQPWyi8XwHo4MmVuttrDsujORGuGlGnzjweaN9odpHTaLiigg4BzKCxJ/tS6cAAAAgAElEQVS+8j7aiEjjQHffgfPzHob/9Ribv/2GQbMJ1xkpFxJcf0hpHqZNAQ1caMTSHKC5W8N4s4bBTh0L3T4WzYdImAuwipbSHanypFFC7K/J/x9/WkImjDOF7sHR1TvqYbhzjH6zBdPzkbBsZLJZJEulUOFJl65qh8Ee+vtVOL0+bNNCdq6IRDENpSPNAMtf30GhXIQ54DkWvjJaYbFKpakUkybgh38Bz+B+tYfh7hbG3bFaLLZTGeTX11DibsZcBrAstQgX7ralApOZmSqumzLgFC3YK3mkFstKYTvZlavqSmVo2PvUbmZtoRANgKIoJx00jHqaZeKYnX7zdk/T+U2XOf3+7Uo5N9W52StlaNTGOxwEPsP+7y8w6nbVIpKdziC1MIf5e7cxv76M5GIJRjELI0XluKnOPQ0GIwS9vvobNtpoHhzCaNcxtA3kby1h4dYKTCqj+CMh/KMOmnYCPmCtlpH540PcH4+R6hwjsVDE2p8ewloqKTfWpyqlK6Lw0w8Ri080aqdSvP6B+ehsdJvMCtO0vz63c9/qIs6L8Kb3k3SkTdMXv04ivIcbljPrp4jWL0NiLlwPnZ9Orp/j10tnFk/8pntmHhXAy+vomJVVWN1Tb15L7vTL6WedE/PlH5VuHNe2+hhWm3CGA4w9B6lcBov31pFfn4c1lwjlrxVzlx0/6/JS9QoJUv9TTtLAhBNELjrv1vHq337Az/svkVxfAJJJLH7zACdHumnip65K3gahtW6Er5LHoY+JsJ66vtH7kxwigFR4dK9fMmwqiK9mBOkUp64XjTdJdE55k/fv+4blK69kBhKBoY5RoiEmj5WhlytVc4XTJUCYRfMsYHS+s+IzjO/jcWblcV7a14a/xhhKpWNBLPhsgadD+MSPDccQp9+Ez3HiI4JmZ/taame+ZD5sJ5rJGKGpTDiSIR30BxZRoOLMzOH9BZIEXXV9fU1pZz6tTEMZoeRUAO+whaA/VsceJU0bqaSFQqWM0kJlMjmhMsrvDOD1aOHiwTB4TEUK8yvLmFuch00X1Beg5TVkfrKvpjn3k63oO1RM8ajyHEkD7EAtFjk/v0L1f/wndn7+FY43VsbvNPpMZLLIFvLI5vNIpdMYuy5G3R6GnS6G3S5cd4hhtY7dfg9HnTr+YAPLqT+ECicaasZsKN+BZEkqCJwgEM1PlfdTBwjUcb0dOD89x96/fY/a0SFG/YGSkXY6hUQ2g3Qhi3yuANO21KaBUacLhzv3ui0VtzscodFvo+cO8MA0UM5+TWdXMNLRmPGkdLkTBC6FwJlvUmzeoHdBO8/20fif/4WdHx+h3+vADTzlRS2ZySFTLCgZnEqm1E5TdzCC2482vIz64FrCzk+PcDRo4a7t4c5cHvZCNlT4X4pSiSwIXAwBNYbgIJ3jiAHHtSM4Pz5H9f/9Hkebm+j12spe1UqmkczkkSkUkcnnYCdT6mjBQbuFfrMOc9hTR12NqnVsfv8bmuMh7loGVqyvYC9nYGRjc/aLkSaxBIGLIxDNzZSnXnpWGQI+PbXtduD8/SkOfniMxsttBN0uLN+BbdAruoWEF0Rr92ek+8XLlpiCwCUROMNtXAfgH/UTPMaKxw5THre5qXYPve8fYevvv6G9u4/AGYOHVxmGjZwRIBFYsCjD1RpFuDHuTP6XpE+iCwJvRCAa/zIevVl5NHbd7WHwX79h//vHaO7vYzDuw7BMJDMZZAoFpItFZNLc4mWAHgcH7Q6GXIcYDeCPxjh49AyNeh31TgvfFXOwb8/DLJjqVIs30iMRQgTOLF4KMOchoKAiH7uhd1cabDuPttD495+w+cMvGA778H0XJk9KyaSRzGeRy+eQTqVAg23O4ci/g24P/fEQTqONqvMSx4MWnESAdZ7KkloE9yhQPivVPNfS5HctEPj4BivTMKiPeOQesA+4TzdxvLmjPvqmaSOTS6NQyMHgTkK1UzGAz13+L3fQqdcxoiBNAvnlCuxKDmbegJkzkPrTHSTurSgl50mR+rgHA/BMBL7Fc3/gHQ7gGAGM5iF6HQcufOSyKWTvLiPzT3+AVSkCydA9vNIxac1otEps2AGMpA8zZ8EsZEPhzXqFIxS1KM0d1V4QHhGj91YruqL663uVbIYqS71/11HOeelZqC5Yk824+k8Vfs5/THdevuckmRkcla8GgxwI1kdwn/EsyB10Ww2MAgeJfBaVu7ew8seHKP3DlzDncjBzNFKyAdMMFVHMnO7XXQ/ByEGiN0Cu3kSp1UDPd5AoZlG8swgzz50osTqqOvC/AFbZQPLbdSwsFlDhgkAxD2uJu1kjXaOuwDRul4XidWu08fZgefpZX+NhGn991fRd9qrzVvnwIcqQt/qdDtZlxcNnlafjzXp3kTCdv46rF9H1M6lkGWfKmQqYzif+mu9m5BsrQt1OyomnnY70Ts9kSBLzOsaYUYCum74yyjSN08+z4sSzjvJSl2iAxQmaTwUEd31zMAAfyZSFueWF0LNVMiqEF/5NG6vE87/EvTJW4SSRShMe41HtorN9BK/bByoujLGvvg3KBoAE67rG8YjKU6RF9PGMQ/VPeVcJI2vRriwRlfEFE8ZGMDPyVFnHy42R8LpqajKn45wKf115OuGpBLHCz0ur0135darAKUyupLjpuk5nyn7MMG10oWl4U7rpfPSzTq+fZ10ncfT4YkakqPzwQu8m2i/sCbuGqWJ5qIqciIQJXzPiResT5XH+HElnNGWQo+ukaZhVpk46o7pvFaTzi5epM4q/mxaPhCxm/6OUU/uHStlED2c8ItBOZ1FZW0Lx9opy/6jOTR86CLp9pUh1fQ+ebcLKpzF3axkFntPLSYz8BIGLIKB5Nt5vlBcvjkVpgA2Mf6mi+/3P2H/+DK4zhGMZsAp55FcWsfbwDnKLZdilAgwaU9M1b6sP76CJxtY+jnZ30G83MO4O0Xy5i90ffkeumEep/DUMM0BAt6Z6PHsReiWOIDALAcrZuKxlHMrQaGeT+2gb1Z9+R+vgCP1RH65lIFnIY+HBBorrCygsVZCYK8NIJeH3hvCrTQyPGjh+tYvG/iG6rSZGnQHqj3eQTmeQLRaQ/HIFRiIZ8u8smiRMELg0AloQhwlp7O48P4b79yfYevwUo34PNBcEFziXK1i7fwfltUWkKiUYmRwwduB3+giqHbS39nG4vYOgVoM3ctDZOsLeD0+Rmyth6V//BCtFt6yxcdqlaZUEgsA0Anr1POQrzn3dI1ct1h//509o7OxhMOhhbBpI5nOYv7OB+Y11FFYWYHJzXzoNuhT2q3WMDo5V/MbuPrr1GobNHhpPd2FnMiiUCshn1mFkMieefqdJkWdB4FIIcAARk796bc0P4FPRrzxduXCe7WH463McPn6Jzv4R/OEAuQQNrUx4gQeuxPNYCkMNbC9FgEQWBK4UAbW+oDbTBsrLc+jpqgPn8RbaP/6O/Wev0Kweq4WIfDoP2/MxdIbhceNq4XiKnFj3mHojj4LA1SFAPqP8VZ7Jh8qzyt5vz9E6rsL1XfjpFLLL85jfWMPixhpyCxz/ZpVSJeA6f41r7Yc43tpF9XAP1qAHp9rA/o+/o7KyhNv2d0jmKif77/Tc8epq8OnlZBjqaDBjllz49Gp7uRqRX+O/yNBPHR9I48DnNQx+eYbqqy2MhwOM4MHMZ5BfXsTal/eQXSwiUyYPZwDfg98O1yBau0c43NxBr9FUxiuDrSH2fsgglUlgKZeCmYscYgj/xtH/6PfXzmBFKSPVcUDh+e7+5i661SqsIIBtm8jls8gX8spric+F304A76CF1u6h8rrheY46Zzi7WIJZTsPMGGq3lr2aQuAlQ0FKxWk0hFbjaHYKLiZz14LL3V0W3FdZuGkTfcODS/fGKQvufAaJO2VYywWV52TcHGfqaJFYCR+tg4o+EqE88pXChIpRHkOr1jXUC/qkj+iI5xexiLYs0xzzPhajWbwuero8lqvfndxoat7DVU9qaJTUB7zjDrzNfQzrTfjOCK4ZILdURuXbuyj/7Qskvl4L25pKpQh3w440WQQaFgIvgWCcRTAoI9lfRInnmiUs2HMFmFkauMTqwaTkE8tQJ7IY6QSsxXkEw4o6Bkh57tEKeZ2MAL7rbwJyLKN4vvF7RtEK2Vh0pWSP5xO/j8V77S3LiZelM43CFX/w48Ef84+gPpWE4QzQ5etrlOxil1iO6vZEgTvh0VgU5smzmidFxW/i8eL3jMNnHZeYagv41xCpkrC/x/lGERDLK0ofz/41WZ5+pWgMgeWtzkOTqehVcWLJomeFDYP1+yjRqTHRJKN4RN6feFdQ6XXBUTTmreT0cIygN4A3GoPnvLs0+EhayFWKMLPRUUAsI/rTYo7ZXOqn66ATsW0oq3n+ZnMI76iJ8XELCSNA0jVheUZIn8fz1iLFnU4bXRU+mjaSGN2HRYX/k+WV2j6SRRPjlVl5TYWp/CLcmPWlf1HaU+lCslSb6vY91Z5sbtJ8nqKShMTyUHm/FXGnqAofov5PIFWWk0H42b4wI/X7CdKyMaqzbvNTVT718AYymI/G703p4nE1HbHs433htVlF+SjaddnMh/fEnInPzSBWcMQoKot4PjGa9C0NaFWUKN9J9lre64jx6yRSPPDy91G1Lp6Q5cYTxZ8ZznHdCPAPqvCGQ3VMhWGaSOezKC1XYC2UwvQ0gIsMVjjxcX0fRiaFzPIcSqvzMIvZ0N0/Kbuiul68khLzRiNAPox4kfyojjA99uF+/wj1py8x7jTVDtIgk0Xx7i2s/flLzH37AGYlGxpSpxKA58Jvu/AOelhYWUH6pxRqz1+i3aii3x6g/ugVDucryN29DXs9D5NjEvKp8OqNZp2PSvwp3omOSKQ8paEwlUybNbi/76K5uQ8uZlo8/meuhLkvbuH2375BkhsBFvIw8zkYSRvBwAWPkLSPOkgvzKP4ywscPn0BjDrwj9poPtnBwXIF65U0zNxieHQkxzLyEwTeBoHYuIDrLcrbH8O4pqB25r1C9bfnGDSasAPuyMsheWsBK//4Jda+eQBrpQKzkAZ4vLDrwe868GoDlFeXkM7lkH7yEp2jIwxpNPh0FzulAir378LM0Lg1mqee6kNvUwlJIwhw+MBRechM9M7s00PbTg3uky3UX2zB73WVZ5VkMY/KV3dx6y/fIPPgVugFmMYn5Ec3gNdYgX3cRerpEkrpAg5HT+AP2+jVumg82sHRrSXYCxnkSiswMnohTVpAEHhXBCJBqMfBcc/Ze2M4v25j9Mtz7D5+ikGtDsv3UUrlUcmX0et30B120Hddtb5xanL6rmRJekHgbRBQ+qLQcNtrBHBe1eA+eoXmj6FnoGG7BdsPUC4vYi6dh9Pt4ai5rzxVxIcEsSHK21AhaQSB1yBA7uIvxnFcEuSxKPSusnWM1g+P0T2oKm8pCTulxgsL332BlT/eQ/buGsxSBkaSSjUDAY2262NYW6vIz80h+SPQ3ttHe9RF96iJve+fYH5lCdbinDp5QK1Dn7cWHVH2uV90C53gEGurk8DP824KHL0GrpwYjAJ4NR4F9BK1p1vo1erKIMXIJFHYWMXqd19i6S9fw6pkYOTIw0mltPK7HrzjPipbVaQzWRw/foHj4wOMun20n27jeK6IwsocrKUczIytNjPGu8/n2RDXp9Yf32Blun9SKRItiHlHA7QODpWbSzJNkLKRLufVTkLFRJy4NVx4O8foVhsYj0bwydW2jcz8HMx8GjzokoIzHBgYJ5vjtYIt6hTsBBNSrDCNaVJxwz8TvmEoIwlYQWiwkGScaFFC9aSoURkWCWnqiOiS/pRCJXoZ5muos5KNgN5dTGUso2adOg1p48CI17ACoYKK9YmMKeJlKQpYiUlFLsBoOm9G5ceM5VHR60Zla8U9yyO38KrqF9Zz8lFiPlf103mpjysQDH34jS6aR1U4o4Ey9fEtA0Ue5/PlBuy7q6EnHe5sii1wGtF8W2XH9lbK6wBByoJZKkLZs/C4El2nWfQzvwgj1pWuUnV78DqBWuMUxVVpZuX3ujBqxDWxjMdHnZ/KPzq+JCorblQxaQcSRJojPlThzGtCaEQA89VhqszISCNeD52O9Y6Ou1L0aR5hXM2fUdyJApXYx/uCbhddZkTGmy9RApYTlQcatGk64+HMjLRaCI2MWL5lnih142XH75ku4v1T9Yv64aSsCKcJv7BOrGcQM4qYzvfNFbxQDF20ihx/iPMIwzU2cXyiEpQ8imTbmbZRDaczjmShOiotxoMsi2dfUj7zb+Aj6DvA2FUuLhMwkDZt2MkcAj+pDErUQcOUJ8SJfY3lEyP9d6Hax9qH7c2jgOhCtkeXyG34ezW4/T5SKRs5z0LOsRCMgvDcbicI5Zbq/xFPniqbD7re+o5h/EVH2vCouGiBJfAJQsj3E56JGw6ovsekUV35rLOLco2yjj/Nvmc5un0V7/MMxihMfyOY/aTMkP9V2+p2ni57+nl2yW8RGoKgstdGK6z4pLEjmK+y/Gl8Js+xNtLyie8icgJiE8l9FUb8+CNt59HHLHWfisqZpFHyMeonDJxqKyUjGRb92F6naGB60sB8o5+S+yoflhuE/Bcvn3WZ5HMiaydwhw1xfn10QVNVZjKT3ZW4cQzA/q7jxspX3z72aZWAzRwb91wET50nr3E8YzirekcYTPoBi2SZ6vsS3atGDHlff/NVfBqhqLN6HfjHNYycMRzLhJ+0kF2aQ36xDDPHcVck0wZjBHQVORpgFHgwC0UU760ivVSCmU2Fk5c43XIvCLwJgajzsL+oiTbdn3OxaKeK+qMnqNerGMGHYdsorC9g/R+/QuVf/4zE7WxoFK/7mGEhqKRgzWdhLi8gz2N2XU8dxZfqu+jtHePw15dY/eoe8pUvgBS9DL6JOHkvCJyDgPp+xN6Rj/XYix4vWwHcVwc43tpDs91QHwujUMDcw3Xc+9d/QObPX8FaToVeKKNsgkIS5lwS9loRZmkORSsNdzBEd3dTeWcZHNaw+/glCg9XMVcpwkimYSRjNMitIPCWCFDZz7Gzmjv0ArgHfQyevMDh3q46BihIJJBermDp2wfY+O//CPv2AsxCOK8L5+CmOuLUWszAX56Dkc1iPbCx2RkgOXDRqTZx8PML3PnjK1TmvlResaa70FuSLskEgXBawrGwOlIw3MznblXRfLWLVqsJw/cQZNPIbazg7r9+h9x3f4C9Rm/D0RolMQwMmOUMgltpmJWSMsRa6PTR2dvCoNfG8LCGg8evkLldVmNeIxFuDDx3TiTtIghcBoFonqfGwuNoDMEjgH59hcP/eoS9Z6/UeDhhWFgqL6A8v4rk3BKM/R0Mq0MEY18da0WDLZGtlwFe4l4ZAno+pza4AF7Lg/OyivH/foKtn55gf/MVfG6MMW0UKxXc/vIrmEEC4+0dHDR2Qc/65smKypWRJRkJAq9FQK0/hONf5V2l2of3Yhfbvz9Db9xHYAPpchbzf9jAnX/5Bsmv78FasMK1c52xb8NfyMBcLMCcK2PN8xD0RxjWHCTdAI0XOzh8/ArZjSXY80uKyyfrkToPuZ5FQE0wzgZ/9iHxj3xc7nINrQd4h010f/0dxwf76Iy64C6txEJRbfha+W/fIfmHRbV+QB4MIbZgVRKwllLwlspAIoklJ8DQGaPTGGFca6P+fBfZ2wvI3luCMV8AaLQi62jXhhU/vsGKhkIPZpWSAfDaPpxffkOrVoPrjuFagdrhSoMVu5gPlSncKdMawN+vo99owXUdpa22s1kUlngsRT50464VVVNKIVU0OwXfK8OUIFQ2MYyD4phBgjIwUUoZQyku6L1DKUeUQiw2KdT56SuVSqwbJ5uTAuM9IFKKejyWKFQEq2icmEZYBH0PgevDsCwYGTPshPTuQUxYjjIkiRleMOwiv5hySC1GUrGsFbNj7jgG/IGnLCuNhAmzlISZNkJjGWq1WK7GIV6li5R9kTgRbsHIQ9AZoN/uwHOHIZhJWymdzKUSrLIFU7vhjdpaZR/hoBR7zIvPFvGO7iOl3ySuDg8/teECLduX7UDXlVR+U9EZNbdBrKbroWZjUXvH+Gc62uxnJog1HjMnH1BhqeiIjLm0go00jegSyICZIW/QqChqHx5LZSN0Dc/CYtlOytbEkw90WZoHNO1sV21soI0hWG+WrXEZuIpGxZ/JiD+5UJIM+xAV6MxeCf5ZdEwIOueGdY8Ul8oQQRtTsXwaToxo1MS+b8BI2QoHxQ/JCDc2GfmUdZnm0wgDVX8aAUR1ZL4Ke2LNfjAkD7APmjAyxJuemIyoX1PDG1ZMyYQZdZwRdE5lp4JjCXkbewyNGeIKXfKJ4peIdnUUVogPG4CL/zS44tEWBmWHMmqIPAgpxRhzJyD6z0RAoxWWwSDmT7zH0TFbjgU4JhKBiSQMpGAhq5iOxiomgnG4q1FBTNztmMyY1RZTVVePKnFYPvMjHWwPHgXEP4+LdtsHSMMGu0JmbKLgcDcv4JsBDOJBQzUaidN4UdU77MNni4vqrbyD8C07Og3U7JD/IjxVXxyHRjM8bkz1WeoHU4Ch5RDLTtAwISxLdes47+l6nWrQiCL9TvdL9jfN68SeFvJ94kAXY56ygDeyJky2LQ2J1bcr1q5kbsU8swo7i8KVhihI+d95mL9lacRG8z6xoUyIh1FmaP6PDC+U7GcfSJEfQvmojNvYOOcZ+OgmYVnaWMiN5ErU9JN2ZlzSEBl8KgXJMDxrMxhEie3wW6VkdVoNV8JxRCr0CqT6mc4jqp/Kh99jyjn+jUPPYKoeGahvcmhlEn6PScZMOaT5SteJ5ajvVbgASKMTcohJ/vF8hZ8yfmI8JXNj8nbsK69k2tNYQH4nf1OO0BL0PBqisicXxR/ELMItwlm1rfrORN9e9a1z1FF/Bo9jTIf1puGPHqhxbKLK12zOK/lg4KBJw+dhH0PDh5Ey8eCre8iuLoR9lN2IR4vVW+g2mhi5Y4o1pObymHuwDpPHAfEISvkJAm+DAHlc8zV57XgA78kzdI5rGNNboG0ChTTu/cufMPdP3yBxJxvKcu6KjrOdEcA0DNrjA999gaA7wnyjjdbOCIY7xmDnGI//4+/4x283YJZotav3ZL8N0ZJGEIgQUPxLhX84P1QeL/da8DcP0Ks3MPLG8AwfKxsruPXXr5D96xewFlPhGDn6Fqic/PAbwfGYvZZF0N9ApddDrdeAXx1h3BuivrmH2qtDFFcXYc6lJl4FpC0EgUsjoMcBKmHIv8orY8OF8/ff0Ng9gMtNTpYJL2vj3p8eYv2//wWJBwuhsaCaJ0XrBTwGKwGYnEcmgcTXG/B7Hkqv9tE6GsEZdpWXoEf/63v85d48iku3lBLgFAmXroAkEAROENBjZMXDR134O1W0j2roO0O1uDK/toQ7//wn5P7yBeyl9MkYIspCzQs5J/UM2KsJBMM7yDW6KI166NGroOOhvXWI9nYVyw9uIajkwvWuExLkThB4ewQ4j9Tj4BHgPNtH/T9+xvbPT9HbPUav18XYBjLL87j11TfIrd0FrBSCQROoc+NZoJZa3p4ASSkIvCMCeg3FBdxqF86vL7H7X0/QfLyLzlENg9EIZiqB5Y07ePDtn2B980d4z7Zg16rgBuhowfgdiZDkgsAlEVBzOL1+R+8qVbRebCuvw67pw8inkb63gLv/JxX966GxCtezybOxQaxJvR8D7paB4G9YqbbQG/TR7zWB7ghHv28hc3cZG98uhmkvSaZEFwRmIkAeVDwcrsPTS4r3Ygud/UOMB3048JEo5PDwn7/Dyj99i+SDhZP1B7Iw03IO53EfvQFjAcA3dxC0h1jq9dHsteCOBhge1HH4dAu3/vYVTB7HHeP9mXRJ4AdF4HoYrJCZ+CNzUEnhBvDbAxw++R3jfleZkngcrCZNZHh8S7GgonPhzK93EdRacPp9BL4P006oM1ytAncoJk4mXNzFrJg2LEoxf4wZlccSvo8tEKtbpdQJFe4BGV15bQiV7z7Xk6noYjoOxPWP+eo/ZhJ/F0n/SEWkFuRMKkXpYYWKN54tVxvCo5uuehOjdhe9Hl3U01jCQiKdhJ1OwswlkSrnkKHb2koBVjGhFlk4IVCdLFY3TdaZq8YjUgz5/QAeLS8P6+qYjWGni3F3AIeuwBIG7FwGiXwaVi6FVCGL9Oo8rKUyrKIRGq6wriyX9dX1P1PoJQKYh1KWGcowAW6ooA3gwzMBP2vDzLHekTJal8nr1E8FTSztIoxiba344VSayAW2cqM6gLtdQ2+vhpFhwE8mkF+eQ/HhiloUUEoyYhnKxND4Q2N7Ks/XPTDBacLZlspYhRaF3NXY8OAd1uAdNeB1+hjTunU4VLvb6b7KzKVg51MwiinkVspIri3AyFrhUQYaG02CLiqiW+HscedvG6P9Y9Tbbdo+YGl9FZmNZZjZUClMV+Beowd39xDDGvmzh3FvDIN8Z1qwkrbiT6OQQnIhj8xyGdZiUbUTUmbYV3TZmhZ9PQuB4iW1UEPDER4Bc9SFV23Dq/fgdwdweyM4gxAH0zSBhAWkLZg8wmkuiyTPsFsqITnPXfLmWWtJ0kJ+JdbaKIB98KgHd78Gv9bBsDnAqD+C4zjhWYNpE3YhiVQpA7OURW5lXrnBM/NswsiQTdfpXa7n4RTlqYxs2D+oSFBWpwHc/Qa8egdBuw+3P4TbH2M4GtPGAXYqBTOfgFVIIlnOIFPJw5ovhm6vqcTn10CVqYReaKASeVlR/MEyugG8OvmwBefxAfzNHYx7fZheoOxRxp0exj8/gt84hFNMK0OewAgwTPhwsibsShYLD+/ALNDE5YI/ksM2op3AgG3jqF0N3lYNgx8foXdUQ9qwMPA9eI0ujp5swk6klXGfnwjgmT58K8AwGcAvJNXusbnlBdg5WgycpiLU37PvB6ENADX/voVgEMAnX1S7oXystTDo9NUZ9oq0hAUzmYCR55+N1FwOhUW9x9YAACAASURBVI01mGXuMo6MyFjU6eLCQdh0GKsa8SQbjsYCdDvqHrbh7dfhNVrquzAejjD2PVUu68IBW6qUR6KSQWK5CHshByivUzwjU3f0C2J+mWixeqlSFGOyTGYSK3dGPS9TzCQus+Sf7rf8LJAvajxjtaXwCbp9eMRnNIYzduH7gdr1wsWEIJeAVUojv1JBgu7/5nle+5RyeFJYeMPXijcoI3c7GOxXMai3MbQ8LN1bR3J1CWZk1OA1eXRHA+5+HaN6B8POEN7Ig+d7sG0bVsYGcglkl8tIr8zBXirCmuNW8tjkkEeH8LjD2gDuXg1+tYlht4/xYITxeKw8MtiZNJKFDEBZO59HlsabSwW1q12NVaizjupxLvQqAhXbYQzOR+kpiZYfHIsoQ45mV31zfNa308doOILn+jA5FsmmkMhnkCxlkSjnYC0UYS/zOLDQE9mZcllePFDJ3XDMpz03ecc+vMMGxoc1jDo95a7UHztK/ioZb1swUgmw/lbORrKUQXo+D3ulBKuSCo3GtLxgHVodDLpdjFwHXiqBzEoZSw9vK9mnx3tUPvnNDjqdjmKrRDaHzHIF2VsLsIrp0KX6FE/IoyBwEQRUF9N8zp2l9S6aL7YQjMbqO+OnEkivV1D8cg327Wg8nZgeR4TG0twJpYwSxwlY99ZR3DlGsVZDottBrz1E9fkOnMMGrHIWBscj12OGdxGYJM41Q2AiqqPh4GQzAw2FD+oYH9TCY3jpISifQeHOIvL3l2CvZNQ3yOCmCj3HYmZqwgwgEcD0DFirJfj3V7HwalnJ6FavjXG9i85+Df1aB8X1CpCa+l5cM4yEnBuAAHmPfzRep6F5a4TGkxcYtbowggCeZao5QenhKhL3lmGVzJBvtec7VjGaB0X2+LAWAfv2CsoPvkCz21ZjTWfo4/j5Dlr7x8g/XINZiPKJj3duAFxC4vVAYCJ/FTncOBKugSjPont1OJTB3Z5ajDTyWWQ3FlH+ch32ag5mjoZV0ZyeGVGMqnXGaL3SA6ylNKyH66js7KBXb6HXaqBZa6O7W0f/qIXirUVlpCXsG+In/18RAlQc0UvucQedl7uob23DHHlIZ9IorMzj9l//iOIDeqkqwztuw00EcOGpY6c5CVf8GPH0FVEk2QgCb0Yg4jm1DsT5XH8Mt9pAa2sfvWoN/shBJl/Aypf3cO/br2F/8QWs5RL8/QTGhgefR6aTebnME607TmTr5ObNZEgMQeBSCETzN6VH4Ro+9aZ7NbT2qkiQIU0T5lwO6fsLSNxfgrXAI1nDuVvEpuGaHXnUNKLjhrnBvgj7wX0sHtXVGNh0AgwOGqhtHeBWO4BZ4sY5YexLtZVEniBA3978Z6ovfuQlgLrqEccO9Kx/BK/bg++56sjh1FIZS9/chb0xD7PMsW9Mp0XZTV6nnpIb+emheAGw7qyicFjD3N4e+sdVtDtD9PbraB/UML9QhpkthJsgJ1TJzcdE4HosZ1Km6QEohSs9GjTa2NvagjkeqGNzeCqDmUkhW6KCNafiU3nq15roNbkrlluPPSCZQbqQQSKTgMGdi1pe6vw12jqcz/F7PvLZMNSG6lDvQUdu0WBDWcmGmei1OPWk85guJ8peD1SosacC10IAbqDM+gaK9EZAN+EeDUZacJ+/wMHmFlpHVQxabaVwpqcDw7Bg2hYSiaRyUZ9fLGH5/i2U763AvsOFwkLoZWPKKlJX+dSVOKujPbhbn0YIAdztKryX2ziim9G9I/RpsDIcwPM8+KYJI0ElUQqpYg7ZUh7zD25h8csNJO6vwZyzYWbCRXY2w8wd3qcIeM0DsSSOqh2Yl6kUdLATCKKMKcQMJ9wFrsrjAJLNrdshnn0sbHI7uYki8nnSdpFXCS5wOVSQ91H/6RVefv8bunAR5NNY//YBvl6dh5lJRvwSKjQn5TO/6TLiNJ25j0VmXdg+XFwjj9P99l4H7uY+2i+2cbx3gBHbZjCcGFEoTw7pBJLFDFKVPOY3VrH81V0k7nAAkgsNa4gPd6RrxmV9o8GMuo4B52UNuz88wvbuLhzfh/3nf8CyXYE1b8Oru/B2DzHa2sXh5jYa+0fotzrwHFcthhj8tPAc+0RCGVQVlipYvLeOuYcrSNxdgLVUhMl+GR6JeBoBjX3sqgZYVNj3Aa/pwd1rwCNvbh+gc1jHoNPDqDtQSmnPdRXcXBP3KNVoOLNYQG4jPDZq7Zv7SK2WYeRjOLPuxJoeEyKDD/YDGmy5T7dw/GILjcMaeq0unNEYvu8ro7ggYSCRTSFdysGu5LFw/zaWv9hA4t6achutdvpHR5FdjgdOQzLhx0iPPaGcdEeGfVyEJY+4R2O4m4foPX2BzmEN3VYbg14/VNg74dm/lm3DSNtIFrPIzhdRWK1g5eFtJDaWYS+XYGQjTzQWGcWfeFdRhjxDwD0cw92pwduuYrx9hP7WMUY7NYyGPeXsKcWjzToDbP/9EfznSXhJEzQ09C2gl/ThVdIo3FtBZXkZZv7ivt6V/QPbyQGcV204j7bQerSJ/qtD9Per8Lod2IaBlEcXnR3UnrxA/6gGJ0FeMBDYAZzAVTSYy0UsfXsXKTuJPPk0yQ4R9jfirTGmI5akZyDvWfCbDvxmAG//AOPtfRxu7qJ1XMeARhFjh0spoecm24KVocFkBoWlOax93UTh3jrstQqsiq2MRyZyURc01eSqH1LuRAZaymihOob7ah/jF7uobe6iVq1i1O/DdV14BMc0YKWSSGYzyBSLyKyWMP/FOso8Lm2tAjNvApHySHnBiJd5Hh3xOJe552IU40f5Kg8el0n/prhaZtG7Go2I2lQAD9Xil/tyH829A7SPjzFodTAaDuGMRwonwzdgqu9nAsgmkSjlULmzgsUvbiP/8Jbif7NohJ66SPsULtp4kDw4eHmE7e8f4fjFNnoJH/g//ooV5GAV8/BqXbhbe+g830H15S6atRbG/XFoVEZ5atADlYUgY6O0uoD5B+tY+PI2EvfXQ+NLtpMPeHUfzqtjuC+2cfBiG+39Ywy7PYydsaoP29xOJpHMZJTxV2F1HvP31lD56jbs2/OwysmQ3/QIT8vVN+Cb9E0Uxjb8Do20hvCqxxjv7OF4ew/Ng2o4Jhg76qhEHreWSKWQzmWRruRRWJ7D/N1V5L65B2s5DzMXeltR8p7lkoY4rkr2Aj4nIPzO1emqvw1vaw/Hmzuobu2gzwkJ5ZfvKfnLhR6OyVT9UzSWSSlZVlqbR/beIopfrCBLQ82krWSk3wmPAxpMjvnJY+7+OuxbSwo3TQ9dm3rtLuq9Doa0e5wroLS2gNJyBUbWlknLG/hGXp+DQCSv1ICO32x6/qq1cbx/CLiemmNQHpXvr8BenQNlkPJaqMdok2yjjsNPs23AzAVKtvv31pD4/TcMe3244wHaxw3Udg+wwrFOLjcxRJtkIzeCwAURUBwXmx9Q8HJc4vdG8KvHaDfr6I968CwDuYUyiuuLsBZK4fg+Nk9WxalFej1HoydELmiasNYWUF5bQWdrD612A/5gqBY9B9Um8v01WEW6RLsgwRJNEJiFQMTDagzHtaVmHwc7e3CHA0774CZN5Dfmkb81B7NsTry0TebyzJP8y3wiPqbRoLmYgfX1faRfPoHVqsFzHfTqTbT2jrFS78DMFife5maRJWGCwOsQOCX2aGyiN9TQG2C1hnazicF4iLERIFfJI78+D4sb2LgOpz3KThfATDkmsaCUUvbtJeTWl5Cj0rVZx3gwUGsr7f068n0P3AglRq/TIMrzWyNA/os83hp5C+NiEvWEh3w+h4W1Nax+8xBrf/0jrPlFtQnFb3TUGofHscdkEf2tS5eEgsDbIxAJZF64jmdkLHilFDpZoJM3kSwVMH9/HXf/5Tsk79+HWcmHugEzgENjQ66P6kUQlQkz0hu73p4sSSkIzEKApn0Ry4bffLWGHq6Z8vi/eqOm9JBewkJ2oYTS7ZXQmzA3OUbjXJWv5tWQXdVat5kKEJQM2A83UN7agf/qsdqwOuj2lP5hvF9HKjUvBq+zGkbCLoRAyHYR80XraNR7+co+oIdutYHxKNy0G+TzyG4swLq1CKuUnJyEcdIBwjmcemaWlN8pwFopwr+1ivxcBaN6E954BKfRRXOrirlbqwjm8uEGyAtRLJHeNwJanfG+y7lw/lxUoJLOP6qj1agj51AdyG2/Nux8BuliuIOYi2d+qw//uIZWo6Gsr33l7t1GppRDgt5VtMEKmV3/yKzTzwyL/6I+opz408Ak+qdGH9T4RbutT21an85X5xflpTuKQUUwfHWOIX0MZGEi75jwGg78x7to/fIIW0+eoddqKhdFgced2SSYrmmVmQYcw4JvGWinbBz//AL/P3vvwR1HkqQJfqEyUmcioQVBUBerWNUluqa7RnTfzN28t79139sfsDfv9m5vdnpmWpVmFVmUIEFoZCJ16HufhXsiAAIkKLqr+jqCTIRyaW5u4e72uVnrnVVc+PkNNGkKdKWRmqJ9bsFbF0idufhClDuV3dsJgh+eovMfn2Pz/iN09/YRj6noo5JeuTIgLM20EZgmhpaBjmOJv7rW/Yu49b9/Buf6CoxZOsJTu+pO0vRE9tlbUUApecLnEjX9ZqY3nHyXCEIqw7cdgK5IYgPj7hBJfyQ7wSc78VJSZZNPr7PlyYTJXKqM0+CyuMUFAgrIjo/h/V3sfvEDOvCQ1EuolIupSw7aCVYrW8yCO9tlZUvlx/Rf6WC7kCAcXIxpNSBBcK+N8e+/wsZ399HZ2kHojxHT/ZW0TTooCZNYzGINaGHEdXBw+zH2vn2Eq//bJ6h8sCZ+41OgSGYQw4LpAjI/7v7d7GHw/TMcPnqEse9jaLcQzl1DEkwj+OIH7H7xFZ7eu49w7MEbDBDS6ohgII/S9diClolxaQv9757iydoUVv/hFmY/ugZjYTqdsKY4gZTmugyqPBOAAukvNIjh392B95vPsflgXfgzGPKrBVHexlEkPEMLS1ESITBixIaB0bqN5PEmdjf3UHCLWKiWYNKqhjqkjRUwgBY0wp0EwZ0NHPznH7Hzw0P09w4QUkHsexKDNQzj1AVTaNnwHBsjG9i/s47Ow2e49ncfwb25CkwX5WMo7mEYM8t7OvNXPE+SYDvxp10V0fLOTgLvP+5g+z+/wObjx0g8T9rFj8IU7BexD3OcSQAJL0wcuI64IWi/cwlrn7yL+sc3YM9VgIo2A8iAaa5i2WY/Qu93t/H4D7ex/8M6iqMQ1iiAHcQoJoZYZbAMCwQO9Qns2E7gI4KfEOwGHNoRwpkyWnGIeEj/Hq9AAOkT6a6c/X/7HA//7Usx3eaOQthhiAIIBDBE9IzHI4x3PAz39+EjRkxEuG2K2fqOE8JcaopVimjtEjAdI3Es0SWyNOQ7ynSajKOViWJsoOzRokYb0dNN7Hz5FbYJFhvQ6pQP8h3lY8wGIcvbJkJaPLEs9Eoutr69j4X3roKuHiqfXoNFZC8XayaNmdKApNCPJm3rp9/BcN2D/9tvsfHlt+g/3ULQ62HgDREl8lWUBGLuOjJMBJaFse1gu2Jj995jLG3s4MLffwznwowsxIvVC+Z11LRpO+jMX6FJXimodOhXinF2YPKCtgjWY3/dQvfbh9i6/QCDp7sC5AuUfEySSABm7DAmZVRsIDFMxBa/nyb2v1vHky/vYenWVVz5p5+jcE3tKCQ9+P3kmY3DH/MU92MJvKcH6H77BJ0fHqBjhujNLGG2tYqkVYL3b1/g8Ve3sbu+iXCYWnhhm1qGLZNDVozjCS4yjx5tYf/eBvYebePGr03YFy7ArKcIcv+rTez95g/Y+P4ext2eWGMgkjxmnVQatJrksz4FA4MfSujceYSth8u4+o+foHL9AqwWtSoZ5jqbqpM3hcREaWQg2hkj3n6Czp272Hj4CMPOYWo+NAzBbw2ZiM3qmyY828GelQhIsb4yh+XtHSz/6hM4y02glAKqBCh1gs8YX+QYLRdtefC/WcfOv32J9tY2+u02RoO+WKUxTUt2JLGvEQBFfmfmtLaS2Cb2HROPihbChTIu/P37uPnZh2isrUq70bpKuL0FysLATFCarmPh3ctiGc7UnwK6rBsF6PX6aA97gr6fmm2iuTIPd35KLCSlQC9+mF82sJqQMr/IKZB+5lJ2FYUTAXa0AjU8PITLsX2SwKoWMXtjBdZsJeU1cXOVEi/7bRB5xD7EyXbBELO91uocjGIhlQkc/3g+dh5vYObqMpxFIsbyI6fAa1JAf/t41uNOjkto2XB3H8N+F37oIam4qC5Ni8Uys0ardWfkl06d03EWp5MVA9ZcFeb8DEqlCmwYsIII4902RjsdJIMRkuQVLPGdkW3++K+YAuRdHjxzLk+rddttHB50YAaeuP5DpYCpK/PCiwSikH+fA3YzDfK1/NKNOVY9gXNjEaXfVGE/s2VObnghus92Mdg+QGO5fmZXSAuV/80p8CIKcLzJxUa1u1St0cT9ABEtfBLAHvoYmwEas1WUF5uwpiqpq+KsDOa17gcqO1G4lg1YCxbMxRlUm3W0N0wYYYTh3iE6G3tY6I2QNAl6zce8L2ql/N05KZDhQyqL7LUlXPr0Pdw/3EFreg5rN29g9mfvwZ4rCb8mu1yQiWXjHOe6KZKQ5yxznzPvPFhOgbdFAY4PuIdluo7KO5cwtbkFmxtcGlO49ukHcK6mm49oGZkbFOiXPKQA5lpNzM2DJ4Tx2ypXnk5OgdMoQHbjGgTHD9yAfeCht3uAbv8QFbq7d4sozU+hcWFONjcK2FWLWJ71NdPmUEANSzhWttemEC7Pybq2w02BnL8ddLHz4CmW56ZgVrWi57SC5c9yCpyDAop/xcIg1+GHCeLOCINOTzakUsdkN8qoX1mE1SqJ7k3WyLLDVsXD1H3QsAH52HAMWC0gWphGudHEoVWA6QF+b4yDh5u4cPMK7BUye87D52ilP0uQHxWwoj/bWXlI4Rj3Ohjsb2EIX5BSkWkiKFlwZmowuDOffrEpgMd9dIcd7Pld9IwAoRHCLSaoNVzYZYZTHMuMspnwWmd+JplTN0BUjvAf458J8M6mrdM77Zl6x5RNKhmTCC77wzhG8NsvsLu+js3HTzDu9xBFdMiSwLEc1Mtl2JYjH5zYp3+IBGESIhxHiP0udr99AM8fY8kbYfkfPoSxXE3BOros2bPq/KnSDwieBAi+uIet33+J/fuPMR70gSCEGScomA4Kbhmu68K2ixiNPYy8MQLPk4VFL2hj2w8wHoxw8RfvYvGT6yhcIyAhm+GLr1VxjgUS0qlFftKdQAujlLoAIBAhpOLOizGiNZrdHuxeApPWIYRizyuEj7U9c8q0zUnWmBSEL9g2skhgoeJZqIcW/CgR9zDGiFq2FNDCMBMlMNPOpD9JTy7OfJEGY51FMZpa/Aj3YgTfPUPnf/weWw/XZfdW5FPZT4BGjIJdQKVYhW1a8AJPFNnjwEcceoi8EJ2+hy9GQ8ztbePCpzdRe3dFFISwjszNs5rSl8jnHGB7FqojA5VhjFJkwN0bIfx+A+EPT7H77dd49viRLFTz48FmLjlFuIUiLIs72mOEVOSHIeIwgjXwkHht7PYOME58+FGAlV99CouaQloS4P/st0ANqoTmQQpWCR714X95D/t/+F4UskP6ufU92W1vmkQAJALEKDqumAYLogBmwp3LMcZ+iMQL4cQmWrUpGAVXFsul77MpiOOQLXZA+NSH/8cfsPXvX2D3yQb8bhexorVjmlLHkluCSWBAGMAL+PPh0FXF5j62Rr4A5y63P8T8+1fgrCrlt+4LL2n643xyxl2GPiw3rcEEP2yi/b++wP7thxhs7yEaDeTzaiKGxaUmuwC3VIANU3YA0kIDXRuFfohg7GEneIDewSGmnjzB9V99BHdtHoYAbjKykwu9wxF6Bx0MD7uIPA9GbAotxOKfMtNKUICs9NIaExUSZgJbgUY8O4DvuMInp68Gn1FndicWhTt240SsTATjMRzDQpGuQWLAjIkkoNgxYFumAEYISrBMQ8AyLBbBJIFNC1xFsa7iED0inVblKx0h7bqkW9G0UEosJO0hwq0vsbf+FJtPHsOjdYkkBf8UCi5si2qWBFEcCsCPqkOLFnv6HvqjXTwbBWLl5hIitH55UwAJIh8UP6hs00LwRgMjRgn87/cx/u13WP/dbYwO9hEP+0hCX5DsBaeEguui4BQEOMPdnQKuIlgpCtB/8AwPugN0212s/fIW6u9eElP9HKQxmwk7Ti7Opv9P7g0rIHKZ1q/a2Lm3jmd3H8Aa+Ejo9oUgIpGPNkp07eKWYCUmYi8UdzpjKtliIOh58IM9POl78s1aS26h8vGF46AiTSw2OtsmBNzARjN0EMUukiCCsTVA8O1jwLuPB5//Efvb2/BGHkyCP5wiCo4LxyzAoEu7MBA55SYRwhFlRxu7XoRgEODdz/4WZmtadk9u/vtvsfNgHaPDQ/kW01UP5axDq0CWKZZ94oBpRSJrjd4YfrCLw1FfFOCXTAOVmxdhNa1UxrKdWZdTDr6SX5KgEBsI9nowv7iD7Qf3sbezjUG/iyQMRZ6U3RJsmy5/LHijUaqkoXsgKUeAvr+BO8M+BsMBLv78XVRursGa4QdcZSwoX7UAT3rSzdteBP+rH7Dx/34ufOt7NOfkg4a4XMcVsGHa1xyxMOP7qeUcgjaDKE4XgULA79Lqjg+Dq5u6rt4Y270D9IwQY9dEa6mFpZ/dEPdwEoTfAAEtDtH2+zhIRnArDpZWWqjROlFJdxadIM+6MqcQM3+UU0BTQLMM73ktlpN6SA4OAfYZLmAaJqyqi9mryzAqypLPC9hLJtyKBY2iAbNRQqlZg7fdRiH0YIYR9p9sYXhwiGK0kHOqbov8/GoUULwra+tyncpUWuNMOn2xbkiAuIyhChZKc004rRqMSuo+Tcb1euyr2F/Ymn+YniwYcV5nwGzWUWs0UXEr6IdDhN0hhnsdhJ0enKguO/perfB56JwCRxTQPCybT7q0DnQoLkypiKeZ/ti1UL8wC7NZSi1TnJiTSkpaJvPMH0GDlL/E5DarKBWLSPwx7BhiTrq7dYBGuJauIWTTOypWfpVT4AUU0AI4lZfCw5zz0MVldwSPLn85/ufc0zJQnmuiNEu3x8oPqObTEznI+IGyl9NfFzAjwGxWUWs2UC6UUQpCYBTAa/cRHw6QLBSVWawTCeW3OQVegwLpWk46j7ZaZbjvX8U/TJVQKtfgTDVgTZXEGjTnheLGmG6eOc7gWhatkx7bJfoaBcij5BR4EwrocYBliM7BXprGu//4N7KWRIu39tIMTO7w5xIHwd0B5XgiLtllY6d0AJ3ImxQkj5tT4BUpQFb0EkTP9uH3huIOk+NfFCwUWzVU5qdSy0HUCnPupoYgz+XCdxzTcjNoHTBaNVSrNdi9ISxumhmM0X62g6UBdxuXcyuDzxEwf3AuCojCPV134PhXxsARPU5ESA4HCEayNV7AgG69jMZFWu6noQql2jlNzFLnKPxriGtiGQNXC6i2mqiUaigFI4Rhgv7mPgb7XRRGHqyp8rmKmwf601PgRwOsPCcLFXMRtWfNFlG9tYKbwa/gBgYSy0RQc1C/OC8WREz6tTYBe6mMqV9cQjxbwOxoJAsJznQN1SsLKE5Xxdf7meODLDM/VxgKa1o0OQokoBWR4KcFPqWhGIzRec782OmofKKak0cwGqG/8QztDQ+bnV0cjgdwGkUsrKyhMdNCuVYR354W3eKECaK+j9F+D51n2+ju7MEfdBG0A3TuJbBtB3NrKzBrDgy3pBS9mfx5ybG/mFVKIICIbx5h/4+38eTuPXj9HkL2Y7pLWFpAc7aFarOGYrUE2yjAG44xPOihv7WHncePMR4NEOwfouOF0h40H7rYLMNqFWGcxy2RIpEm0zEqqodc+OROPHOmhPpiC/1HLqw+4EYJxo93cPDNI8w26jDcZZhVA2aRLpeUtQ+mkZL5KOkTmWXWVI/C6PbiE17HkIUo+vujqxCD9ikjukzJ0Fbno59NUtOF0AH0/STA0QUXJKg8GykwwvcbGPzxNja+v4N2r4sxwRhFFzNLy6jPtVBrNVCv1WHQ6owXYNzt43B3H5uPHouFnqDbR/eeJ1Y1ClYBpeY0rNmSuH5h2UVfr8ur6onIhBOZKESJKP5G2/sYffs92l4fT/eeoRcO4EyXsbS6imqjAbdSglukEtMW/gx7Y3R3D7D/+Cn8gw5EqdoN0Lu7iZ1yDQurl2DcWITl8KuSaR9dDlEKK8s/WxG83/2A7c9vY+uH+/APDzFmY7gFFJtN1ObmRFlTqlRQLpaAmICZAOPREN1uB/HwEH7VQelCCzbdIpWOuiTblSZ2Y1kASuB/+xA7f/gGm7SaMDwUQFihUsbs8iqmluZQm2qgWGKfMgUEMz4coL2zh50nGxj1ugj2uxiMx7BMG7ZhYbbKnU5lAeaIDGIraxY4avHzXZE2nAAp/qAboKiTwP9uCwf/13/i0Z27GBy0U7SpEWNqfh5T83OozbTgVMui5LZo0ymIEPZHYqVnf2sL7fY+wsMeet4Yw34PCCLc+MdP4RZXUz+V6TqByFG6GGm8uwSjYiHaX0MttGHujsQlUO/ZJjrjHnyEcMs1LL93A+ZMBXHZRmimLoGGToygWoC70ITswj1fzY9ophaIWx9dglMro9xLYA8MdL6/h/bGEwT+CEMuxNUrqK0sYPnaJfgO0vzN1A3bqJAAU2XUV+dRnK7DoDUi0paHtE0qN4wkhiXuhfrY++ExOoMuDnptDA1P3Ci1luZRm2rCLZVgFxwIbcMQwWiMwcYuehs76B3sw/R9RLtdHHz7GEnRRn1tHrbdkgUZgY3Q2orKnovpAsIgUGuQwL/fQ/D5d3j8xTc4ePYUQ4IsLKDUqmH5yiVU51oosm0tW0AL9Kc7OujiYGMLu3s7CIcj+Bv72ApCAbYUXfolvQSrcgTXAAAAIABJREFUQZcTKlNmfqz+6vlP/cRys625G7ZsYejG2Iy6qBYLqNen0JhOf6VKCfwVi0VYoYF4HMLrDNDf2hcAUm/YA0Yeou0Im1//AGeujMsX6L6pklqBYp/TcpI00TIqNkRGuomBWmwheLqHnUGAnjfA051NJI6J2uISZleWUanVRG6wnexxjPBwhOFuGwfPNjHstBFzl+9eB71xBN+dhlUpo72ziXv3v0dv1Be3YysXV1HngnK1gkKpAMu2gGEIb3+A7tYe9p5twB/0EQzGGPpj7Hz5EI1mE8W5FqxqI/0ekmaa2U60Lx9z/kmASDQe4eDZM6CzhyftLYyNCO5CHXPzC6g26qCsLRRd0L0YLch4vQEG7UPsPHqMUaeDsDdAEPjYiu/ADIFV00K1dkncE0mbcVxA2UtZRgtvwwT+1+s4+PwOnj14gIjxLQPuTAOt1SVMzU6jVK3CdgsCRAvoBssLENHCV2+ATreD/fYehv1DFBYaojgt1CsyaWF+1kINs59eR2G6hqVCjKnry7Dmm+nYkFZirEQUT/ZqFXOfXcN7ywS0OZi7cRG1i9OpOUgOEoR2LyDiCZrmtzkFJhRQ/U54/nCEpMvFolSXSQtghYqL4sIMzKIaE00intllZWwvQO6qi0qzgVHBhTM0xeIY5RvljHxT/hLle6b++eVPgAJa9hHUPubYfIxxf8ThtiDOTddFaaom4zpaFZTx7omJleoCk8pMFKfEMlZL4s6QQEgEw9QyWW+EcJS60pN5+MkEJinlFzkFzkEBysE4QdzzkBz0YJF3yb50p1l0UJul68zS8Q0UOlnNe1zs5PBFbbSg/DXLBtxmFW7RxaibyPrAuN0Hf7L5hONH5q3T0Gnm55wCL6SAZhh9TucitIJLt7seXQAGfrpb37ZQbFRRqJXTOdFRlKMcMs94KZY+rQQJrReXXZjlMlxuwAhNBOMAweEQCa3YhlyQ4cwg5+EjYuZXb0QByk/l1tIo1DDVuAK6exdFE9cm+OPmOWai1uC5XiLrlZMFizcqQR45p8AbUUDGuAUDtP7qXFwUS9MwTXAvJvlY5l7MQeRuuubBG97KT8/L3qgUeeScAmdTQFiPrzO8xg138e4BwtEIpkGZmsAiYKVegdmsiVw+NladJHJKPpTjBL0SLNCckjkhogjB0EOPFjI9WhPKx7+nUC5/dG4KKNlJHhadHQHbQyS9gWxcp71xWvC3qy5qs00YLjd9KS8fZ+Wh5m8Jl9sKHP9aMOplmcPZAwtJSAv9XUT0BMDNx7r/vKgvnJVX/vytUkCrrt5qoi9LTLf/aeG4A9xZIujhBm59sCquX8TnJSdWRQuGY6dC1QScS3XYi7dQ/tt3kIQRDMsCHEuY0KQfNlpikdHBaTmpZ9nC6Gt15vCC//TjF6Ry9OoUppb4/KN+3MFPBZFlGAi8ATY3nqAd+xgXTVQWZzB1Yxk3Pv4AlcsrsKYbKcKFSAn6D+8GqG0cYOqLe9j5/C7a97mr3ENw0Mfg/jYO7m5gbqEGs1EUJZEslrDP6UoQEEFvMr0E4ZM+vK/uYef7B2Lyn4qw4lQdzWsXcPmzD1C5tJL6JC/bsrpe8hLU9sZo3X2Gyv/8rbgKIDDA6IzQvrOOQrOMynwTzfLV1HfdiUXLIyKd44pNR1nFRaGqIebS3YsLqN9tYnTYRkJXLTsH2Pnqnnxwp4sW7JUWMO3CrBxZwzkVsHRKG51aIkU3+k61qaQEfyYImpYFL7pq0nTlOZuuaut0iMrUX8KIuo3YNkO6Iekh/OYBNr68Da99gNhMYDXKqK7M4+IvPsDUO2uwFqdhlFxZZGObFjsRqus7qP6v3+PZ13fQ291F0Pcwur+NPbeMucV5VMqXYRbpKiLD16qsVJgjslCILJRiE1YSwescYGM4xJ4/RFCxUVmaw8yNFdz8m49hLc7ClEUSRzSeMhjqxqg92Ub9N19i/6t7GG3vgIYFxgcj9O9uYePrB1ilr+X688oZKQat1nDXfYfWQ7bR/f1dHPzwEKNuR9xoEaxQujCPmXcvYfH6Goor8zBbDRgFaq+Jao8Qd/tY2NxCdX8LAyNCdXFWlNCULdIMarFSgFt0ifVohAH7wZ2HiHp9hEkAq1VD69oqrn72ESo3L8OabopskUz8BKX2GLVHm6j9x1fY/+4RDvf3cHA4RPv2Y2zXamguz8JqLsOwCumcmwO3195pp5gjMsUiDEE24dMRws/v4fG/f44h2wYREtcRxezcpzex9v47cC5dkPaRAlDZQDdq3QDNe4/R+uoO1r/6HsF+B6OBh+HTPTw87GN6ZgYLcy2YlZpUVZTMLvtfAY3aVdTeXRNAVRLZCO7uw/rtXQG97Po99KMIzlQFjV9/Avv6guyWoaCTPugYYoJNlGz86mT7SprT2X/p6s0EzJKJxmc3UfvgndRt3GECupzvtPfge0OMbAOluTpan1xB/b/8EwxOHk3uAqYZFtLfhOGYMApWqqFne2heUOWhvKT1Irpi83uH2BsNcJCMEddcNC4v4cKta1i6dQ3W0pws8vF7I5XhRGAYovnNOvzf38bG13dgHOyCwmK0c4itb+7j4OPrmKkWYbplJOYxD6MpWIWymYabDhMEX97Hzpd30HmyDnhjxAULhcVpzNy6irVf/RL2yiyMipuWn1YmhiHK24dofPcQzm+/xuHjTXjDAbrbhwKYqTXqWJIy0/qW6gdnU/yn/YZtJfxgwF5ooXV5EfX9RbSqTcxfWMLC5VVUL6/ArJbVAFa582G/3fdQ+WEblX/9HZ7+8ACHh204fozDjT3s/rCOmRtLaFavyhhiQgQt5imgyC8h4ERAkS76DAfJXhsHB23hE6PmYubqBax8eANzH78Ds14Tlx0EusWjBHHbR+n+Juq//w67X99Bp7OPUeDD6PTQ/vYeYivB9uEO+mEP9nwTc+9dxY3PPoazuigTQ45/RHYPEpS2Bqje2YD173/Ewf11xN027LGH4aNtHC5vYv7aMuJFWoVyxHVOuuD3fN/jZ5pjEX7fQm+I8d4IYzNGUDJRuTgrLnQu/ewWrIVZmJUywD5ErBd3EHXHCJ9uo/avNex+fQ/d3R2MxgHC9V3s0JVPtYjr11ZgNZ2Upvymy3dGx08Qfv0Q+3ceY3x4CCOOUJidwexHV3DlVx/BWV6CQfCfsqrHNhFFkBeKnF/c3MKz9XUUN5+hfHEOi9fWUOSYqZCKGOdCHVOzP0Pz7z5IF0RdM5UL7LaUCQS3loDClQbmL/4M88F76STbNWG6HG9qLngVgaXj5OecAhkKEKTSGwmwjONGTrbp0soqu7DoK5eTZ81mlDU89L26nTwj7/KbWrRRatZR4O4+9uEY8A/6SPocRKV9TdI8LZ1smvl1ToFTKCBzMPIi+YcgQz9GMvDFqmYcJzBMC5ZbgF0rwRA3vKlcPSWp448odzkG4jSA85GiC5PAe/YRPxBLWcmYZgRjJLGZjiFP4+EX9ZPjOeZ3f40UIH/oH+Vh30fSHoiFFW5CosLJLrmi8OeGG44JXniQB/nT8tdNZFxGa4cc2HCYEg7GCHscyKvxok7zNP59YWb5y79uCmQYRvGwjLn7Y/jDUQpYIQ8rd+l2mX5WUv6cjCOyBNTJ8cz0ZE5M+evIOhItQXJt0vd8RHS1PQqQBJS/b7J2kS1Afv1XTQHNd1xjIZ/S0jOX7SqFo3VURaCEylSyKefYeuOoIL7JuPmRU+BHpoCsHVAuGkjIw9xNpg+yKHUDPETmcgAgF5mzDpyfcwr8iSigWFBOiv3Erfl+BzEtRzBbI4ZFvQHXpbWFVz5nJM2ypxSP4wtZ1+f8reKIhbZgY0s2c8fjAKNOX8YOks4p8fNHOQXOSwHFxilP0tgCXRIPR+IxgBYG6UnFrrgoNMrpmlhGFB/jP/Jzhqcpu41CIlZejXop3RTJTYzcfEwLRF4kY18Z/56Ie96y5+HeLgV+FMAK237ChNn6cCArIAUDpphcUz7YGYEDBD3x15G5m4tKaA549ZEN+yZMJopLnWh61tkef5q5O61ijKR+k/gqbXEvksTo+gN0EWHx4nVc//XHaP7qQ1HoG7QsImN5Lu6xIyUwqzbMKVo6aGDOacDtBfB2niKmq49OD/e+ug3n+gxml7mLOF0AZCeVoomFhhQQEe2FCO+tY+/RExx29uAnoVgNWPvkFpY+ex/uh5fSjkzFj1YwhzQBVoLZuIy5xQto/Pf/G1//x2+RDIYYHQ6xe3cd7kwV9bVVGKWCDOayAiJDqWOXLFv2IJ30M7HUUuCikAXr4hyal5bE9Up3ewt2HOHg6RPs9/fRePoYN//+E5RuXYG93BAFF9Gf/CoLypOAJ6WkmjCfzuRk5tl7uWbA1JMvJ/RnRRNw0HNx+eBkjJP3ase5uCZQ7fPkAN1Hz7C3swMjDmHWaph/7xqu/eoTuOJmwU3bRyVFsAjNwZrNRUy1/gvK1Wnc/u//goI3QDT0MFjfwcMvvsO7l+eQ1FtpXzop2IVPaUUmBVS5dMUVheh7A4yMCIuXL+Pqr36G2me3ZDelWWL/S2lMmkoZKias1iLMch3F4hT2/vU/0d9/BjsMMN7t4PbvvsT0L26gMV8SZeFkgZB5K2UwFbvR3hjR9w/QXt/AoNuBH4ewy0UsvnMFFz/7AOVPb4o5fLNipj7rSAeWIbKB2SaSiw1cjq/THI64xzIrCqTA5pCyJojHQNxO4P/xW2w/WE9dXxCsUCzg+i8/xto/fwbnyiLMWmqVQkhNfgpSU/xW6xJapQaqTgNbX3yN3s5jsRBw8OApHn/bwpULDTguzeypXaen8sY5HiaG8DAtwsiAc5Qg+OY+tr66A4w9hHQvUqRZ63l88H/8Heof34C91BTLAbIgoNpV5vuNAqypa5haWkRlZh7b//p7bG0+he8PMdo7xOPPv4O72MTs6s+OrCRRfrD/VC0YRVMU1QIqqhdlsQt0UWKmYNSAO2YrtlhZsmYIEEllOpXsx2T4813gxYRQyg2C19LFjrQd6SosMg0xCxdwt6RrIqCMbJhimUlAjMxLvh8KeavzpjzUE0vSSB1U3odJjCCK4EUeOJhZvnUd1/7hY7gfXIdZtyfKdy0bqUQ3RzaMTy7BqLRwwW2g9//8DyRjD34Yo9/p4c4fv0F5voHa3Jq4dZHspG3UN0JZvhLev/MQ7c0tjLzUclhjZQHX/+kXmPnHvxHwEHd2yoxDlP8WksCC1ZqFNdvCSrGGmd98jfXvv8cw6KH3dBs739cxe/0CrNlLsLiTnwfpoGmRPvnp/yUvsszUDLgJ7AszuFj9BBd+dh1mk0CrogAQZKc3q6nXCrhjKzSQ1IowG6sw3DKWoxidP+7Bkp3jEbo7+9he30DjxpUjOrB9NI30Wdz5cZycOt4KwwCjJMDIjnHjo0+w9qtPULhFazZE1ajFXl56hgCfjMpFGOUmZgYhojshgsO0DAf7m/AQoh97KLQq+Piff435X/8c9nxFQJvS3iwP+Zayt1KFOXUd87aLelzA47vfwxuG8Adj9DZ2sbu+iaUrLRitOswJ8OKoavpK74IwCaBNYoyTCGPDwPTqCi7/+mM0PrkJe7GRfm/4zdBlIM/Xi7BmL2JmaRW1qd9h6ze/xZNnj2GEMcK9Hg4ebaL/aAu1qwStGKn/UFGkE5hIX6QRwt0Ogv5APtSJZeO9Tz9B858/gXtrIf2+6DZkgdkGjB86SGam4Kw2cemj61iLIpglS9DyqQW+tLEIWuMYiqA9GT9qy2+6LZkmQXV68VTszJyQVZpQ+TmnwKtQgLJKg90Yj9f9dHd0ktBpGWA5jliXoLwSWaXCTbI5Rf5o+SfWgbhgVKukrsKYX5wgGvmpdQoxR60YPZvOJPH8IqfAOSiQYSHQzebIw5g7/KOQ+57FPZxRsAUQPPneqmRPYzuZ4/M906XcLRZglEqg2zc+SoIQ4cgTl5V0M3r2vOocZc+D5BQQCiQyh4qHHsaHPQGkUyDTUpxdLsMouum84iS1FO9nH3McQb6WTUC8KLliaZFhaD2XloHC4VjGNxJwMoDMppJf5xQ4JwXIYzx4JoBkSNk4FtentCYsY4hSUdb7yJunsKxK4JQTw7sOjCLdjRYEsEK3qpS/4dhDISLqKjMHOiWJ/FFOgXNTQDMnx6qMlOVtPVbmMx1OXR5tr+NLHencueYBcwq8fQqQR7N8rNhSxgXqXcrHGWY+ztrH+PztFzBP8a+eAllRKXoPIGl3EHgj2YpP/RotJhe48bmgmJlxjrPsMTLK/I3raNxEz/GDbcItFWHRZRsjRrGMHxKfpuCPRc1vcgqcnwLkwRP8K4tmYx+h58n4l8oAq1CAww0v3DycXSs+R04yXubGxEoJTsGBQTfdtBI0GiP0aGGFi+0v7g/nyCYP8pYo8KMAVlj2U+UhH+oBABmPjKKZhfc89L1KI+Fz/U4FkQXdUzNQAX4CJy5WEx3mI8GIyqzpKax8chONT2/Bnk/NI4qCim4j+FEQ2hDNk4CKJXuhgvjyKmr3nqE67CHqthEEIQ62dlL/4tmOxg8VM1QfrLhLCx776H1/D71OW3Z6GtUy6jdWMffhFRRurMCspwAPUcjq3c1KHqiVdkTv38DaXgfrX30J0w8R7ByifXcD/TsPUXMvwpwtpZR+k7aQD2LqFsi+MIv4/auYHo5xOB4j7tNnXojocIDhd4/xzV4X9T98h+nLK5i6dgH22lLqnoigJlf8MKULpCf45XRmzDIJmU4dwp/8LL9JpXRimTM/7LTSMCZYw0f43UPsbWxjFPqyIDx7aRlLH92A+8EVWFOOWJERsBaTYPFk8MDFC6ZjI3r3Cq5v7eKLL36PZDwSf/C7D55g5+5DzJcd2Iu1FFCUKUJ6SV+x3OmbgiS8JMTAMOHXXVz8xS1Uf/4ubLYrFSUEI5CWwpwKhcW4NLiyXIZ9ZQWtx0+xN+wgGnThj8do7+zKYEZ4iCRUpJVBPi2AcGPwDsFUT7B37wFGPYJVAiRlFzPvXcXqL2+h9MFl2IuVFKjCcmglZKYoBM+kUoZWECgj0vaaLDKyLxAYs72P/t0HODzYxyjyZbfoyvtXsPjhddiX5mE20l0gUk9NK+FJLtQbcK62EO9ewuz+Pp4dbolbnsH2Pta/u4eZDy+jVS3DKhRTcEFGdumkXnqe9F1u3UsQDxIED0fo3XmM/a1tAfJ7hoHqhUWsfvYB6r98H/Z8WYE1lGKf+fIXpYhA4RG7CtgfYo7mqwMPg60nKEbA3oMnKH4zg9bHN2BNUfmf7voWOUuKSnsrmctrM8UZCW4iiQU8w1Vbg6422DaUHfxP8uufavOX1v1kAKbDxWJttUX6cSLyK04SxIZBA0EIqQTR/EnzcNL+af5SDpKDBT55KBamEoavA5LccYS2Cx/egPvRDVjT9kSJPkmL8cgTisdwpYFkdAP1299gsLkjZu4jP0R3t41g4E94Psv7dI9CMFK04yO4fR/tjW0Mh0N4TLdcwq1ffojWxzdhzbup2VH2c50f25Wymfc0UXpjDfF2D82dPbR3hvBHAfobu3j09R1cWqqi6NBSBi2VqTY5SYef+n3alQWsatEAWbmOZL6aWs9RoEThU/IeD/Ib6Uj8JgFnEeBcm0Hl3goajx7C399HFIbw+gMM23SNFdOXFGhZi/EmMoNpSZKJfLtjgjtiHz753rVRXZrC2t9/nIJVWrTko3hC9xkjESCulGe1gXBtBZW9PRwOejDDQNw+DWgrqVzAtU8/xOytqylYpWyIaxrhfdaFzMm02N78rF1ZRuHRDlp7e9gfduAkCUJaTeoMhadoM5F10PyaEiX9S0CXaZlihIl9iC7X/IINZ7aOxQ+uof7OGuylBibgRCZCgA/Tkz5miBU0m7L7k/cw7/nYPNiGMR5jOBii+2QHG9/cw7VmA6a4rzNSkBjlGmX9/gHGgwGCMBDLZdxlX1laEGsusluUtJP+rhtd3bMtWQi2UWzJj+2rzUHquko5FZ1EDk3aQvEFkyA5mTyBgYo4wj8qyyy98uucAueigOYd4SsVg7w2PlI2kd/sgiuLPedKUyejv13kZRoFqNVgOwUZkwoH0zWi5yPxGJCB8iOnwCtSIMu3Oir5l2MNupYMA3E1Z1l0P+vCFstfitdEoOpIz58pk+XgN5my3XEA1xXAChc9Q4Ku/AABF4yoMNXhn08qf5JT4JwUUAzt+/DHIyTKZr9p23BKnJ+dISdP42UmJeN9QMxKl0twXTedNxMAH0aIx77M5c34ra8UnLO+ebD/X1GAfCjylybUfIRBgDiOZJ3GdhwBrAoPZ8ezJMBp/JslDHnZtgFaaHMcsThkhLTaHMIfeyjT71suf7MUy6//3BQgj8qRM6KmRH7+C6OAkt+nytIJf/+F1Skv7k+bAoqvjm2aiRMEQ7oTDNLFTMOEUyzA4vztnHwo8ze1nijGrwqOuAo3LTu1wBmGMIJI1jq4pp0fOQXehAJqyTkd/3J8SwuAtMIaR6J4cQp26qae6wgvO/QQQp+pHrJpddsV4LdpEnTFNfYYwdhH4mf0NS9LO3//J6fAjwZYeWnNyDUvEqDq/bEgmglfmviPH4BFpYKIyq5xwcLUjQuYfvcinAslUTaLUoprKFwYYXHVeopYCaFHlypgzjRg0M3Lk0cYD/uIIx+jbg/BiOZo1ao2OzgzUz/uao4OfESPd7Bz/xHGgz4sfnDmp9B6/xKKN5ZgzRdgFpWiVyuHJ7RNLY1whzsVZfX1K6h8dxfDIMR4GCDaOsTugw2U1mZgzdCKxvlozWCTLHQUPuSP1na4m37GQnLzIhoRcCkC2nceYdztIAo8mL0xhr1n2H/WFtdIvQdbaF1dRGV1HtbClLiOMGtcXE1SV0k6Q33Web7szC+0VCpVFk6Cs/BM61UPVWltPYNgoujJPvr3n6DXbiM2LRSmGpi6dhHNGxfgLClfrwThaAspTEOATYmYJzQDA/bqLAq33kH1/h2MgwCRF6C3tY+9R88wvboAe0G5fHmuvGmBCFhhg3APZVh2MHVzFY2bF+CsVGCWWdfMjmBJQwGr6Bc5Aqy6AWuhCfPCAtz1hwjHQ7FWMe724A9GYo1FLOBo+stiDF2iEETSQfRwA7vrTxB5QwHW2K0qpj64hNK7F2BfmBJAFek9USyeoL0AJXTdpA+oBtLXMd0ODRA+eoruxpb0n5BuxpoVXPzkPZRurgq/iRKU1kWYfqqrTXd8kvZWAmvagLU6C/vpEqbWH2DYbmO/P0Ln6Q72n+6gTvc6NTe1BHWijLp4p55ZXJaV3ZjXcSI0oyuv4JuHaNPly2AICyZC20T96jKW/+ZdFNYqoJEAsYjCMmboKzzCZzSDRvcDtoPovWtYODhA+2AXcRhhv93F9r11bH9zFwsfvSv+3UUG6fKQEBwBM13KJAKqkSBSYBVaJhEZJaCRjFWjbCVVWpLGOWjC4DykDZRMFLAGtzNmADMhwXxIEIgihHmnlnEkriqrzpq3E8WJfphmI4o/4p1CKrorRUxfX0XznVU4K/RPltZ5wneMqxWIfEXvQ1OAtdLC9IVF+AKAGApYaNwdIhrR59fxOLxnn6ErMMrP8Z2H6O+14XGwVC6icmUJM7QcdXEaVjXt69Imuk7s+5TTBAk5BpKVEsKLS2g9nBfwgBV4iA762Lq3jtmfX4U72wBo/pxlPwf9FVl+GidVXuExsqJ286WFYbYtpZFV/2E8+RkwiaOcAczlaTRmW9g72APiSHZ0j7sDJJxsxdwxfqLKOg268qDvTPJaHMGjWc1qHXPvXYFzYxn2gpkCtZRS44jGlJH0eWAgaQLm0gxK003YWwXEoS/WTULHRKFVx8UPb8JenRfLKtm+LNVnvZgoQSu0hjVrw5yfRqPZQGHTAoE08EL4vTFiL5Ub5Evh3RNVYqfSKhXWyUtiRGUH1dVZzNxcEzd7tDAlfU+Bz6hol3JoWpPvQn5zyoj3LmL6q0UMN57BC8YYHfSwe2cdq1fWYM3VYdHqmeozojMKE7EKwWJFhgGPXUNcgNENGFFYdDvBsvNMAUz75Ky7kcph7hNR6WmeOKK3Ym9dzkn7KSJIJVQY9W6ym1+9O0mu/D6nwGtRQPNgGCIOQyRxjAgmRGGqJ9oyNlHfuRdkQtbUw1D5xnGybafCiubTxcoKLWEE/Ir9dKd4L6hi/uqnQAFhNFUQzb+cV4aRADxFVlqWLHZS2UmFqYhNhn2Z/OR7/aObX8eBbdnyiGM4umSMggC0sJIfOQVemwJZPqR8DWPE5CuCbpmoaR5frH8Z76r0OBYRC1ccdxOwVSjI7jwCBo04FtmbeB5N4b120fOIOQUoEIVPSQpekLfCUOQv1w85DqaVIJPu0LnJKCt6yat8cOzh8WccWxt26mrdsh1YpinAK8pdn/yby9+cCX8sCqTTvMz89McqSJ5vToHXpIAaL1AEZyT5ayaWR8sp8BoU0OMARqXeg5tZCESVtTZucubmRcWo50iey28CVGFYrj3TMkW5dLRwwbSDCLHnIQm5EztfgzgHWfMgp1Egy7t8T12JHwpgJYpSwDYtDL7KhhmOh1OdeEaPRbA2x9ECWOHacozQ95EIsOu0guXPfgwKiOrjx8j4lfPkF/9la1dk7pO/V87ozxBBTUJjGAh57dq4+P41uMszR+5NREmT7kCTpRX2MJl4ptYDCBgxigbM6QbcagU2zSZwZ+XYE3ACfc9K5ybN+GNcJsFNa3tdxOub2NvewjgYo1AqY3ZpEStXL8NqTaVWDKggl91CqasXKpfECkB41Mmtlg1raRHVcg2u7cBhnKGHw+09Mamk83wZRXWTscr6WuKoCYs8FNPRgHOxBPfT62j989+i9cE12YkdlEsYc5e4aYmp1P0nT3H7X/8T//7f/k/8/r/+Czb+5XN4nz+Bf7+HcDtGfJiIcpjgHalXhj6nlZVlOvN44cszY8kLEZq8UrxNsEbcHiARXZOnAAAgAElEQVRaf4p9ts1oCKdQQGthDstrKzCnWxOlI/V2ovDTZ3GzoNKixR4CRi4so9WaQdWtwE4M+P0BDnf24fVHaZ66eJroPFNhmVAVSysTBg0NCIjjnc9+BmuhkVqXYFso6ypacS8LH9SZECTAg21Hv4jzMyiUinAsBzZMxF4ArzdAMvSP9+cJDYB4v4/R5h7223sYR6GYqy3PzWD6ygqsuSbEHYqWXLrsui48My0e+p0ojpXSle/EpQStWXTQv/8Yww5BT4GYFqvPzaBx4xrs2boAggQwomgr15P4guaROpiNEsyFBcxMz6HiFGHFCcL+CO2NHYwO+0h8KsBV/1VFe+lJkfFYOHbpfozR7Tvo7e8hikMa5YFZKWH20grca8spEEW0y6r+TEBbRFAyRdypsP1cQxTs7pU1VGp1uJYDK45xuLmDb37ze0T0Q8kdtayzpqUukJQvLSQXf6kkTxeBtXwgA+jAJ84n0zrx+vTbk4kpBbZpTQYZMRfzZEdYagFikg7Lz1+2GqeWIRU4BGsRhBPYJsxmBUvX12AvzKTj7iwtmIYs+KmdwgSp855rhyUT5ZUllNyimAm3iVMYeIiGHASlAyYR6apclNECVts8wPb6Mwz6PXBAVqrVcfX9W7DmZ6W9pN9TBtN9GNMhgp3yi+6imBbzrwDm7AyMuQWUi2W4piM7Ptn3/d5QFu2P0WZy8zYuUjDDydZ6GylP0lB0f44nGUC1q9CWboB031V9XoCBmk61GppTLVE00KoU+6lP3+2BsmNJWuqK6LMUgvIxVXjQCo9nAIXpBi5/+B6sZjEFizEuwSkEtiQEdClwHUEX7IfEYrSqsBtVkTtMLTYS2OUS6stzsC8uwaw7KWiGVl70d5xnHmRVThaJoaIFljqtKlVg2w5sw0x3SI5GCIkSD0kIFe/kSRQ3aV2YdEgQTKWIxso87NUFmHVXgQJT+Sn0UDSWekg9lUWjkgFzroELN66hVCwL38eej87GNvafbSPuDoSeMjlm+UmDZg12yYVlWeKMx/YDHD7ZQvhkR6xJJb4hLtg4UEoI9JFf2p/pVkV4PiVzWrNj7ZSprC5z5tGxS/1en4+9zG9yCrwmBbL8SD5V4+r0klaSTFE4ndk/T2bL9DjO0v2Z/c+yUmWpsozHPAg+Bft9fuQUeFsU4LdCgNORuANK5wnkR0s2PVDxKUBi5qf582Temf4gl/zDbyLBLmp3kxiW1jwsA56zEjuZeH6fU+AlFOAcQSnhOV/hOEqU/WRZstnLWC37nrzLcYzjiAyXsREx9JwyhREEsKJdjr6kWPnrnAKnUiDDb8KenN/Sgg/5WPiX7tO54JMRrEzoxK3wtSSQyYX3DCcbO2wBvdJNucAOoxiB76e7WF/aKTJp5pc5Bd4qBY4zsvB8pk+81azyxHIKvAkFjrPqiZRypj1BkPz2z0GBLE/q779aI2f2dCnI8S9doZz7YJqZ4DLvc4symNCvBFTr02S4WkvN2f/c5M0DnkKBLP8owHYUR7K2bpqWrB2kE7hT4p72iHM0LnirdXnysMmfXoOgioX8K5u+Tksgf/ZjUOAvB/pGSZgVvj8Gtd5Snvq7QaVoYppwamXMX70Ac7qcfghEGXX0UZBdlKr60m+5i9JKxDWEOVUVhQ+VV3EUIg5CUbrFgzGSqfKRuxTpoAmSMRDvHWK8uSeLKlSmmQUHjVYL5nQKmKGSTyumRJWVpTsBEmJ+IHVDgVIRlWoV1nBfmcL1BJBAix6iSM3GZeGz96fQ87nXpAUf8ie76RPYsyYMZxHTzV+jce8yDr6/j43v7sLojWCOPNhBiAIXPA9DjIZbuP+0g6e/+w7N1QXM3byI5vtXYC+2xLWOUaL7Eu6WUvlky6jzPaWc532kk9BtLu2XjawFJxXWYyBq9zB+toXI9wQywsWIIpWRraa48RCwBePL6lpmfY0JKwEsyVN5Xiqg2ZzC+NkOBnEMMzIQ9sdHLnkYkAXUZ1VYqmOFN2XHfQSUbcx9cBX2TFVZ5lB5qXiTsY6qnNwT1OKaMCoubPpIlh3xCai4H3a6iAcjWC1XKqA/HPx4EEQUH47h9zxZHA9goFivY3ptGaXlOZj1UloGKm208jatwdFfXSf9RBFfSMY4VF7T8sDhEP3dNiLPk0WacqWK6eVFGFVq/NNwPE/AJvy4EWCWTY8kpLWSSlmUtI7pwIEJKwT8zgCxsqghFmsygzxdtBeeNfNIPVNXGsnIh7fbThdDad3EMrH6zjWxmmNyzMiDvJxuuE7vlTUCoXP6RP6KwnjKgLU0jemFeXQOe3ADH6ORh/7mLpJx6oOS8Sbp6TJJCmywlIWE5LqvZt5JXN5n4/Fa8YoEfckfbQFCJytxM/H5XifPXb+CE9CBJ1BwlSfLyHeMryPp/FkdARckYu0hcR1YrRrclQVYDTvltyyIQcfTZ7YTaV+gFQ8DRqMqppoNMowfAeNAXLXQkopZVQVhGZRMjds+4v0ugv5ILOcYsFAsVzB3+RLosk3kIMf/mgc1ETUt9Jnym6j5ckV4MhwSpJKCZTCOQDAjeVroIInqCrzmWeebppgmMnn2mmm+LNrJ9NW97psTHuFzBdiSJLUOl+3ollAoVWGZNgwiOcMYiRelgB6dPomUvRaiJbKQG8QB/CTCmBa1Z+oo3LqeWkRhP5dwaVROCuVgk4sbHbYPXT3ZMErc3cAJo4GI3+JKEfWlGRhl5RaQC9H8zyRUMkyLMlaKxT9Ms2DBKNiCEk93YAYIx2OYymx4doI5qY/id/J8CqoxAMdGoVlFld/HRhkGZYrefaHkl5RF0UROpCVdk5QBa74G653rKH5+G+gdiGlQYxzCo+Wa0QgATQQpYFXZgDVfQoGglYIDu5+IO6P1L28jrphYLDuw5qdg1RygyOozN+WmSYiRIYiWrSpImokqpKZ/+vDor3qdpeux66OQ+VVOgTejQPqpTMfcUSqEyH5cLNLWUc6VgeZZLdPYBaiwUgJC3DnSJVhACyu5Pd5z0TQP9GIKkOf4YeVZLKyE4udZvqvkO1qbyCpMM98qLaEZVV+fmplpCWiR7zheIuAq4ILRyxT+L0z01Jzyh39tFMjwIxfQ6c6KcpJDaS5QFgqFlDtPMinvs4e+l7O6YdpqjMYuIuxI2cx+ohfrs2nk1zkFXocCZDf+ZBMZN8BwUk7WMyfWVTgGmIhDhp3cnJGhfs8z45qmzAO4ks/0KX9j8rFMqnTgM9LKH+cUyCmQUyCnQE6BnAI/XQqoDQcyd5MVNSO1LME1hPOOGXS4zLqkTANpnY0bSLker/LRllx+ugTJS/aXQoHJ2n7E8WmEiDzGOZeV8t0b1YNAFVr0Fl2SLIzLJvYwDOHm4983Iu3bjPyXA1h5m7X+CaRFUACPhJ2t4sKoFWC6qRsLWXtW3w+G0roYTkBFUcWH7FtiJcFEbKcL1qInI1DDC2W3+OQDxPDKwoNYSel5CLoDmFxY4UeGCjPTFJ9zcZdbtkMYljK9P5n1cnmHk1cDSWgjCSyxVAJvnPq+ZdmoHAtC2c1PSy+JHwNFZSaalT1rzpuSIm2VTBh5zHRVXHHPQiAE6y6AjAbMqRJml2cxdXUN0YNt9B9tYbC9D9/3EBC8EwTw/RHQ89BuD9Df2kPt0VMsfnAV9XdWYF+Yhlm2xHqB0DQtRZppJm/9+JXP2bqdElkLYbGWEiRIBmMMDjowwggWBxSWKYCPJAwQ92geJ0MgsclNiU0By+dkGhPx2BRrDclwAMe2UTAdSctie3sRwlEglnaMclpNbV4+JTR3+qe6eRadblHMkgVrpgIJryWGZsps/VgE+aWAKqNA0IwN0FIFqH434BgsH33DhekOIWbONPjxIXuNgaSvlOuJKRZerGoZlflpWNP11J2HBmPo/E6h6+RRtnx8KIuJdL8CoWfYp9nbSEhI6wSFchHJcIiobUoYAd/ouupEmSb7QWwiGZliCYC7mblcZCWGAFbsKEHQHYIAEwG8sKyvdbB9Uxqx78b9sYCyjChElEQILRu1uSm4zdQVEFmA/YNtyEM1R3qRyV/cazhUkAPmdAX1mRYG9xw4gQHLCxAc9MQKDsFpms0y0Y9d8v2kenJxkujHgr/+jdBdLdwxFek8afkEtKK6wqQIOnw2x5NFEwIdBUijELACRK4FNIowqwWQl1lJkc0n4hzFVvJZAAQEJKSWI8iutLoDAkXGlM1kdMVUMjZKxEJKTJDW4QiJFwpgpWAXUCi44mM8obu1ToEJpQSQemQrI7WWQsY9A8lgIOZFCMZgvzOiGNHYh0cLK2Mi3zN0zFbgTa5VcXRJ1CfuTVI8Oy4zSRtLs0F6TzAarc1QJ6ysqog1Gvn+UYlgIPYMJWeGArKUQW9iwOQnj6ZQtFWhs3I3CONMQR4BLfE4FpJKAeI6J+uqLRN/0lKqfwpwhd9G10otslDWIoFdtOFMVVKwH2WtfNRVR9bpKQJPgIE2XUHRFJZCmrNsYSgmDY0oSuWsjqvPukCUh/yRnFy0dmxY1aJY1RLAIb+3Wv7phmVgXQaeKZ7I866h5EkTBbcI27BgxglML0IwGMEfjUGPQLofUU6JlbjFOUzPzMAb9GH4PkZ7bTz6w210vSGWbl5G7eIirLlGOk4qpd9q6Yci7I7S01V7/pwpMF/quuuAul76Pj/nFHgLFJhwneY3nvXOaMWG3NlEpekrHel8WqKk3yM9UGXXSv9RYZqa432llPPAOQVOpYCwsPAvTcWl3wwKUnlOwIr6Dpwa+UUPteyltTBaOVNjOi50xlT4T3YD6oAvSix/l1PgJRQgX4kM5lg+XaScyF8lV2W+k01GmDzzgPfZZwJYIZw2BYFzXUXkvIwjswEzaeSXOQXOS4EsC3EeMxlDcGxupOMHLX/TgXGacjbeWXlpsSpLDJS/ynKLkr/sK0cTrLMSyZ/nFPjzUECz+Z8ntzyXnALnpAAZ8zzy9pzJ5cFyCrx1CnB8y0TVN12zq2wm1gt6fKjHBNnrbGHUOvhkzscxh/pxJYNgcLEyKGMVlalOM5tOfp1T4FUpIHM0ZemVG1tE7GrFzCsmpgcTZFrlUlPYVPRZiYC1c8DVK9L0Txxcq5//xNn8FSb/AgHN7wB/7Gz0m1Uql2CpXTrysVBxdX86jXoShH+40MdJq+yuUFYYOKHlx4LfHmIYOOfkDc9U4o0D+EMPTmLCNUyUvAT2dh/+549h1ooQzR21d1qzNCktzYAQzWAhiUwkQwPxkzbghzCp8IOFOAKCcYBg5MkOT6MoKqrTqnD0TNX36EF69dxjyiXWR6wYcGOpAdN1Yc3Mw7kyh+DSHqz7z1B4vIX+7gF6+20kh13Ew4Eo8LxuB8Ggg/2tbYw6PSz1+pj1rsC+OAtrqnBkjeZkQf5U92wUVpJnCmJ6bhiFGPcGMOMYZcNCHBpwD0YIv3+GuD0U6w0y4GA8/ZME1A3bN7CR0OvPwQhBZyhoRGZAJQZd8oTDsVj+MBsFiSl5qzKwqunSW7oYzR3AhaKbWmzI7qLUNGG2Jw/9jMpZ207NzbHthF1N8U8vi9EK6MD1PVmnJn/Sv+JgiGA8JAJK+NspOSjTygytDmiwis5T01DfZ898x0Odmb9UM6R7FoKDCNwJZUenkyQoehGcvQGCbx4jXHfFasCRwlhXSifCs4HEs5CMDMRbbfjdgbhxkXrGCYL+UPxFvr4faFVw0odKAgHzDBBw92kcw+cH2wTKzTrMclEW/IXIijVY9Ump9TddJykoCraPAaNcgNVspKYBidoiuGEQQKw0+QDKKRknf5noJGEF4jj+KCWSymsSj/eZeJPn573Q+U7OKrFMmnKZzTfz7rRsjr0WoFY6CKJ7lsQ2YVUIVqHJZRX7WISTKWaQO6Q3fSJyUVwHo/UWKmH4I2JBHxS15P3RGMlwBILT+LZi2CgNI4R3NxFvd2EUaXJfV45MoRNQPKlySsY24t0hkp0DJL4/sX1HEMOIgBXKZsoJNod8hDLp/CVcsuDSJ4jySMEp4h5pnCAeJyJDE4LyPP48AWKKtQFaUGF4+vAZG4ie7MLbORSSEmgm3zAB0CkQHWmRpXGWNmxU8gt3ORYKMItE56kIGi1G5TFlYJbttawjqxDRbSkzhEwriWG6DopNWrJSERlXMxDPqu7PlSudKU5KGNE9IHcTJ4m42pm8OOWCSdLCCqvO8YhTLMKplFJT4brwWTrocjAtVTYBtbDIBNGWXPlm2JYNK/FhBOk3J/QoTFQccSuXCADRuXkBU702Dr0RRtu7iEIf/ac7OKS1sY0u5tZ20bowD4fWVuaboFU5s2ILiEyAPxbHBOkHRsqh85hkJhfpn2w9Mo+zlwyiqpV9nF/nFHh9Cmi+U98Yrdw0ntOOvloWMm6aDKC0eKA7x/zIKfAWKaD5l0mqsbxAo0RQErDymhJTp6vO7BfyT32C+V2ydJi3WJ08qb8iCmT5Z8KnicyXUotULxjnnSRTNi2+E0Gb4X2CribJnQx8MrH8PqfAOShA9sqwGD/3tELFIT9lsBbIOoiwOFlPPzgjC74+xqEyjsg8lLmKXjw8I5H8cU6BnAI5BXIKvDoFXiKfXz3BPEZOgTMokPnQ85JzLB6T8UM2mg57Gn/yXfY5r9WYWg8fjpLSCR09ya9yCrwRBdTag+Y5Kg6FBV8lUaYhg2euW6Q6G9nArdJIx8/k3aONOceZ/lUyy8O+TQpktGZvM9kXp6XFWFbuvTjG+d6emS5fvO3MzlekY6F0EVgcwX0Q2OU4KNWqqTnkdAZ6LM6xGyagdKJULknHkh3QZmoalIslcQxCRya7hlh11TljglgCKkYD+GMPBYGYGDD6QxzeXUdvcx+xTVO5tDCQLuikZWaJUw0h72n0i8o9NzRgjyJE/aHsSrdgI05MjEcexsMxEpp0TvdUH6vGG92w3lS2CwFSt0RW0QAaBqzWHOJ3Z1E8/ADVBxuYuvMAew+eorexC+/gEOZoBCsMkHSG2PriDnqdDoa9HtbcT2GWppEUCK44UbqT9ydev/GtZloFJoIXwae7HBqngYlw7KN7fx3jvQ7iogvqWrnrRYrFP2q3f7rwRrMQMYpJAW5iw/QTDLv7CEZ90N88XUZFdCnTGyFmm8VKyaqaNx3DpDdpsQzYTgHFUlHcJk2U9rrMp9CGj/RrKaRlpoMjxbf8wMiOfqJ8udgndVBU1ICV4RCBN4LEpIWZog2bllocMp/KVGtkTimDpKYLoc6yyKPDUmndC5D0fRhhDMe04NISQa8n7qX6TzbF1U6oLSnoeJnGlu9cAhRiU37wQgwPO4hCunKi8jsBXbGINRnudtb1z6Tx0kvVxxlXrEUMQ8SdHnwFWAlIQNNAdSoFrEzANUyY+WXLra/VWfRkdvrBNlwbRq0K00wBFlZsIg4MATsVRj7QTF03TdJnGjo9aW1RXUh15DH/SKHPqKFumzNen+8xiZMS9WRyadE4JE+H40cFOyVlJjORu+kwnn+DJEZoxuKaRdAjkzDZumfT0w3MncLqOtMAQiFZzGZpU3POEpu3CsRAIEkggJVQSF0gwGWvjWf/87cIDchPDCyxgmklNQnSbiSgQaAQmShEBFMFGPY7SJIoBfcBGPeHKVgxJGLFkr5piCzN1uUnfE0Zwb7P4lOWEI8zTBB1Y8R7XUT7fcTtHpLOANFwBK/fx5i/oYeAYDgvghUANr0NDD2EA1oaY381YcbpzoAJcU+SQbUVH5NkVNLFhgHLLcBRwExh+wxDkhWI85s8yqQhHZRAU8UntLpmlwqoTjfFvc9E3jJD1d66SM91L+nQ5Nx0h6S4+CFoLo5R0pHOODNW+o/fVhtWsQCHADiC2TRA8ET+J8uTmsVnZWk1xUGBoBfbhhXQ0lqAaDQWiy9SFYJO2UWYfhEofDQH2B9iNYrx5HchgsMu4PuI2h52/ngHB98+RGV6CtOXlrF4cw3uxUXYCy1YswSuGDLEEDURXfvpbvicAEz7mZCAbaDro8+KNsea5wx65Y9zCpybApOOr2Kwr/M7IAonQxRPr76Lg2PzDA9zXK8ED08CHqDVlsz359zlzQPmFDhJgSwP82NG9z00/WxwHqIE6GvwWjZZgvDjOLUGJnhP8a2uPhQny5Pf5xR4VQpoZlOuTzgAkCE9Qf8EkIvgfIVEuVGIoyamq7oAZboe58uY7jX6xCuUIA/610gB4V/hssnEMbWKovgwOy4gfTTfa1opXtW3k7NalyHLioin/FUblDg3OCvaJH5+kVMgp0BOgZwCr0aBk/L61WLnoXMKvDoF5LueztxkiKrHvmosmxnSvlLa2jqbxJd1zXwN4pUImAc+HwXovketm1N8kt849zr3oWUuJ4DUJaQJKMUCp3PpaFfcbbKvvELS5y5DHvC1KPCjAFbOU1LySMo25wmteO4V45wv5ZOh3g73MhUqqLjL2nELMGx2wsyk82S2vD+ZtZpdirJJzKgwvXQxXJR6Kg255mIK+x7N1Ho+At9XbmKAOPDgdwKEvUPxFCGAFRZl0gBHC+J8JCa/eE4M2DHEDco4jhAYhvzYcARIiCWQbD1etVGzcdW1YBy45s9d1RRa6jnLGlsJLLolKFMRtgB7uYnirWsIH+3C/+YB9h8/Q2//AOFohEM/QLDZwc43j1CabWKhYqJQnkHiHKV5PHuNtjv+9JXudGFPRtLkpYUVz4c3GqEs7RkjDgLESQjf9+EbJrwkToU1rXvIP3KRRhmmvgMHBne2W6LMTuIASezBQ4TITBAiQhjTxIg2saAKk+EtXuofAVVUPqYrcyfCnlWfE/WbmJVVi4OksGVZR8pQhicNqIwOItDNVBiM5aFJl1lO+hPl6Wl5nsVXmTrpIsnYjKw5DJAMfER+IB8ouioKQh+H+zuwDguiiI64iKOpqzpDmlWasOASiJmi6wuCCwJfrDWMEcGLYlHWRhFprdA1Z5VTF+65Mxk9/RhLd6LFiMFQLCeQ90VhbiZwSi6MgtYsp4kImV6Sn8gCURxbMIpFWLZDKJoA0ujuaNjtozz2gCRjJYkJT9pA0YFZih6OLate6jBpkKOanbw/evN6Vwphq4qgcz9XWiIPpV1VobK7301TgAjFWlnJZgILsnU/kQXf6brxWi/2yUIgQQSpcoeyUxLS9NEFJ/9TJo3pyswHLf6wz4XjEbrbvshluowRK+NqDMUgukgcexHgRQMsAlgkCidOMPL7AqAZGxEC04YfBvIrC0/aGbDOifq8tdtsRd8wUSUjBKwSJmIlKdoeIXy2h+DpDvYfPkN7aw+Dgy6CoQe6zaKco1sctg2BOVZiopBYsGNDQIFmFIvrGgFhkppsQ2noE2XVbcvHk2v2QVpYccQyyoSV9HtWXV3rdzKu1u8liyP68HFkAhEtiGW781GQtFDH4mfLqcCAmUzPDDqJlipdGE7CUhFjWzAdW4wACY/xxcky6PhsE7qX4pEyoYxs6GZQQLPkszAUS1NRQD9NWlZoN0LpeMK5MgPg51hzimjff4rDrX2xNDb0BojGIbzNPTw77GH38VNUF2fRvLiIqbUllFemYS00YE+XYZQSAcGIBTYWOFtmTQh9TkuS/31LFMjJ+gJCZohD15tavsgIbuJeRfULJsPw7EuZeMdTJ2Oz46kw4tM37fsyGuS42DLldzxefpdT4A0pwA+Z+CrnJgk92jvBqLzNyt4Tt4p7jwrC8HGMSAG7BT/LPJSZ3qOA+VVOgVekwAnWFN5VVu0IkCJYJdGAldOSfo5ZM4E0jzMPJY6F7zn2F5/oaqyfiZJf5hR4Iwoo+SsL9oKaT02XH1ufYQYn+T6bqeZbHU7494SrIcOEZXEDVzZwNpH8+jQK5NQ6jSoveEaCvYhXVdRzBHlBJvmrnAJ/Bgqck5f/DCXJs8gpcCoFZNwgY1O1DsH1aVmDODX46Q851tUCWY8dxFNsnFpq5nROxsD5+Pd0AuZP34gCXKNWc7iEygCuMQsfqnmY0otIHlom64GZPvOl3vhKvWvAeSBXz7hYwZW5dA0tVZC8UWnzyG+RAj8KYCXLM2fV5TxhsnEZ/lXjSHxG0sI3m4gwLUNkesIkYDbnE9fZ9E68yt7qVKnY/P/Ye9MnOY5kT+yXZ93VV/UFNC7i4M05+Gbe26eVtNo1fZE+6A+VzPRRJpNkuybt7JudeTMckgMQBAE00A30fdRdlbfs5xFRnV3oBhoYECSH2bBCXpEeHh4eEZ7uHu50VmEmDrXlJ1/q7HODrjydKA15xSccbPrPLCz6qIxlKZBEiGK6MNAcT8W2i6zkIys5yCQihnIGUeGSlMmeQA15CF9SIdDwT6cVMZUmcLhjuu4jW2nAblYARm54qeLdIHrGcdKI3DPqgcwl18LJhep87tiWAm4Gx/HgzHlwWnU4iwuwW7NY+XYR1ftPcfDoKdygh/EwxGDrCNvfPkHp6hwWW3XYs5VXM5LgpqlxFp4GR/aItoHmbp1/ylRONChHAUo0VsNCxL6hQ0KlJNFvUqSyuzGjwwqFBO0iKIZFQhbFmY0ks8VhxbFKsFGF66SolFOULs3AnmWKnymDnulcGu3pcKSxlIXB80QBNxlgLPu6fwY+lwJDP3HGyA0x7hSOY2Xg1IsHd3LSkYLKk0n9rDvf9+f1AevUz07pXXg/joA4FOcPudS0tmplGQtMtcPlSzJrSR8qBxG1i06NMjoI8Ey5ItBZqKIcPpwYpQrgrs7CbpZheXlkX5NwrII/Lq5hAoxDOWdIYHr4sHbHdwGXVm4NW6F1cm2qNPd5beDyaHuwvLI4qhCEzCBZgmA8UillzPv5I9/Tf+odVbm4TgmxNX+ph6qkKqLOc+8bOK885uYzxfzC7OKkQflYmU/ylUxBNI9YN8/PwUEeM3KG48DzmeNkCs6Zl2cD1LOnvMESeVCGTBnZgw+YiimmQxlTuTCiioWYKbUaNWR0RLQVNNXrCn0lWmmnJs7n4mRF50fNc4kvDiMuFAkAACAASURBVCuOl6E848BdqAFMrcW5Mo/MmW16Wzf/horYGebH00hFVUl7GaInXUR3H2L/8QaOdvfR3j9An9GZ6Czm+XA9F27Zg+uW4bqO9KdtOfBSD5XMhcOIRd0Bxr1AKpFq8hO2Yq/TRGAhEk7LB7zkTkTLpKRhU/mTcvrVc5tvOl4VMG6HyqB9Tv9oWDKHTq8tmqGU25h6KNFzXtbRxJMw2R5ZRLizkhHa1PrCeiZry3nt4H3tkzchFj8oLFvmzzRhKiz1YSzPdZ2CLunmZ3DmLcCZh1X6BK0by6g93cXhxi6s/X0M2x0EwwHCYR/j8QBBp4fRzhG6j7bRWGth9sYy6jdX4V5pwZkvicPquetDvg3581xXnXF70qziRFFgwt4kFn+GjwoCTSgw4SN9IvxOWcb11BCXFHGxzPlKA6TH/OTFCaiTE01rkpvjkuMui2KJuqf6RKX2cugA7+U+714G8wR6cVZQ4EUKkHf0j98DYOQsyuNZIOkN05iG/5zSiBDOmw/y93kuP73Q8py3GICOBlOmVHTdifOvelr8X1DgNSkgMozmMTqiC++SX6nsjBHHTFXINJ0arjmaasx1nnf1/Gs2WUiUFt6zLCSUpagL4fxr3jWwimNBgdehwGSOVHMwHVFBZ3KRr7k1IYOVKp2KyAMG9qv4znw7EL44lXMs6AhX/I60bbi+0rtMviUN7OI4+bxTSxaJrQiu9EPqbkGm16QASThNOvJpjpenH79mDUXxggI/AAUKrv0BiF5UeRYFqGbjxlTbEX05dYX8dqPTivwZtePJkqbu51mY5+bHU74fhrIhkOsgN1ZajL7JjAW0bebm77NQ+rnfm0QLoS23oNW57CC0ocqcNhHqBmwHKSLhP7WTlxFZz5YhXgBqvgmN0woDA+iNC7SvcGtlRhmbdjW9+fgFGMUNTYHpyeL7I0xOo/n9VfKDQ37VJDB5zpO8e9ZpzJUrSH7mnnynnC54wSuOFRkLHIRM1P0mc7tGxzRBjtqZQdAwhiSWm5zTEzKWKCh0VilVG6iutuAtN4Gyj9S2RelCS3BmyZ7NSeQE5WzANUhVrIzbkAgeGQ3zNQ9Rq4T68hzssk45Y+hhkDTXZx2nyKurOV2ScMwv98TS3GylVBip9jLlgF0vwVm8imhhAc1SHUl3hNFejGQ8RNod4+jpDma29jBzYwllOtpoW6+APhNnXfk0rjlcTk4vVEiKM3UHlQZplorDSGq7sKol1C4vor4yB6vuIWQUGZvKYht0WmFZ/tGUbWhFI6UhD/vHtjIkboZRKYW7WENzbQFWTRvip9tHZZukuhAbpiguuON+koqHlU2/Ixic/58xoJqjWFok8kQOFMnEJlDxTY9fAccFXBnfX8gxl69uGp88yc0zWaDUS7LwSf0qugDxiZiOo17H3M2rqM41kJVsiUjDr2UqgmhMVmm8qCRKVTQLScBx8kHNqhjhInBSBBUbzkIN9eUFWCXmMlLtk6PBSd09/3/Wy+7V7RHlaJxKZCOCoLMK3ZqUB1Cu0ReFT9B8TTwmKMDqYUVHmIxCbK7yPJamKnk314ecFaTunOBlgObf5/lr4HjqVdZJtKhv1uhxuMov77xncDQv5+vj+fRzUy53pNFepVYzDc0DyRU0py+RNimUSpUalFwQHD8Q6PCgPRC0ClLm5sRx4c3OYuGDG3DKnijBmapNmm8ZdylhTsWTmeJLcWjR45g8QmIFToJh3cb8e6soz9UkIs8pZ8JXNM008fWOuoEX7WzSJo+HEOzEMCudzKAp3Qzx8xTRn9ex9ce/YvfpU/THAyRI4VeraMwvoLbUQrlZhV8vw6uV4JVc0IjrWw4qKaNP+UifHWP47SZGvSOZR8VhY7qBeZw0PlJEIlypEcjxJ86diglPPjpM8/MwCWMCRxeQ65OGm0thp7NgEN5JcQVdF5b5kqu1RJThHG4003kkps71u+QU+eMrHFx6fJl7+ukLB/KRRFmZtIuVkxjGqZLI2hL5h/ONVEcovE0/O45bRkfxLThzC/BuzMPbXkN1fRv9jR30NnfR397H+OgY2WiMZBghHuzh+PkhOk+e4/hpC4u7V7H8+fuwbq3A8irKgSiPKXEzNDPH/PPi/LUpQJKa32u//HN9wSvB90pKrskSxHRQZuS0HHteiDSG8JSVmD6LEfMIhbxtZXB8B5avHWMKfr8QSYtCZ1BA+EnP2TznrnuPTleucuhmmlGmfGOKwZzSUyAZpuYx93fqkheiMFUOL5R/uPBYdCz1fOFh+UgueDhHweL0tShAHtNMZ7meOKFTihbpLY10NE8l/Uxkk5NXJmKDnOSZ18ANCIPbS1Q13OwAz4FV8pWCR4+h18K5KFxQYIoCMgVydzQdSeg0KJFdY5k/OYfK/Gt4Ms9zeZ4VIBqwLkuH1ywKJWU05X6ODDg2vFIJDp2uGBWu+HuBAhOy5mnKiWby4IVXihvnUYA0NHQ7RU91W7PqeW8X9wsK/DgpYHj6x4ldgdXPjQIW4JUrKnqaqAoykV2TeKL90zqEHGHyPGzOeTT6wShCNhopG6G2HUW085e4MdIY5XLwitMJBWSpMx8d4rCibHeTAsXJaX6kvYTyr+fJhkiSRzbMRNQf2GqzyymaUS9GKmsZNs+/WlQTZ60wQhbHYvMiW0d8y3cleroorKdkklNVFBfvjAI/D4eVv4Gcir/5v+b0t8C4BprZEaEMlnpcXRS+Rud0005efmHa4yP5ZYCrdq9xZxEjWFRmZ7H04S14n9+B3ayJkkUcBCS/hFaCn6rPXBgFORWahGvB8m3Z4WzPcLHK5TU4Qe00ymddEbwpz6OpzpTNP9f3Tt0yUddZPReDNIPdsOCuVZH2b2Bmu42jbhvD0RBWnKFz1MHgqIOwP0J5ui6hmal4+miQnL5vrqeBmftnH8XYyEgArie7ZhPqDaplLN++juYvP4CzOgN4nIB1OB6z9WAajVPV0hHKhmWngBvBrruw62XYtZKaw/NldVt5y7iMKJ6ZruBs/Cf9pIvLOqwXYXaoqUqiQIj3RQ6OeYfKEY9REXxxzElTClQJEqYK4p/GMffm6VNTyem76ko1TLVbDDrcwemIcxA9KmuzTaz94kM4N6/AnimrKBSskO+xMUawoKQm+GuAXAsnz5jOIwPoD0QD7EIDdlWNg1PG2rPwO+ueoQsNu9xZ5Xni4MDoBUxjwrQ+8XCEUsgl1lPDRvA9C5geS4TJMvovi1Jkw5F4BujqpI5avQarlEsHZF546XEC4WQMv7T8GzzMVXHytr5p+iHvvGLKnxR+5ZkY+rUPutDK0OuisHR5McZPxsAZ1bKcMfR4DlzfhUujUBpJWpbmSgsr//Y3cOabsCr8CtAWf9NOAUkg2ruJfMlndBgQXMXVCszdZvmcBz2JfmWV1HMKa1LsFLwz8LzQrRdWHf0W8XsF4TS9XqhGN83czxgYaTdD+NU6nv/hKxw+2cBw0EVgpZhZWcTSe9ew+N411NeWYc/PwJ6pyXxnlRkFRZEpDTIgBIIvtlE+6ANP6YJmZjzi+QpcZS5jeY00i5s5wLxuQJijaUD+KG1TUDg36MtT9Z/ZLYSpq54cifPkg+ekUrqJvKo9LCHpHQw+cYIkpGeQQvYEWh75HA68nceH7zENEHdsErbtwvMZ8UY77hkwmk1JO0YQYv/Q6ZRHu1aHe+kWvA9voPHsAMnmLuJNOq/soL17gG67jXAcYHg4Qn/YRefoEINojDU7QaN8HZZD+SPXdNMIczQ4FMe3QgHT/W8F2N8jEPId+b3swyuX4FAmo8MKUz0G49Oh91/GozJGT5RF4ig2Gqu0FqzAtpAyCAbTjNJhvPgrKPA2KMCFiCKDZ4shvuSXEPJeGiOlw9Q40DyYm3NNveTn/ARheNiILFxrwlhFaSFMGmJ9T/EwU1u9bDyYOopjQYHzKGD4h8eSB79SFYdBsiF31YVBOOFP+UbTcKbZ9hR4yuyaj7NRgDiKRP6isT+RqHHcbFKW76hT7xUXBQVehwKGd/kOp0buWC55Ev2EGyrSKEEUjJGEoUS7kh0oMofmKjmPkfX8C/JuECIOmX6azvcqOpBfLsluVqPrz0H8+Z1yrOf74udHge+vxTn+zJ0W9P7+KF5AfqcU4ORR/BUU+IEpwMnVsWDVqrBdT9Z6pksPx2NZ+0UPLal8cniexbqEI5vauFEtQxbECAcj2eQmIrFjw2Zk67KvIvnnwBWnBQXemAJaX8wN4JKynrZCbu6n/oEOJ4m2ZbxQwRlMLIyqC9KcF0RIdaRiyazgOHDLZVi+fzqTxwuwixvvUlArHFZ+BPwmxtG3oJXT6whUupATZxI2URxQnEw+eJleplSuIh0PJbJEyEgqNQfu5Vk489wVpAxwepP0+RRihfzjUaIEqPfoT2HTQKi5i34Vpqh+4+UHU3j6yLfOmHsMCqeA8l2W5VFnS7GqFuyFOuy1S6g8qMPpHCPmDsFxKgtuzHQrYjk0FecganLm7ry9U9KHVXJXVqWKSr0OjDuIaJ1FjIiG5sU63LVZWLRBnIHeK5Ghspl95NOZgn1jqYmYk/U5NFUpIjRu+Qn+lZXlccwjaxp60o9st/jdsBiFKSpJymW4HqPzWJLXPg5jRGGMjMFE2H7izCq00+QL6OSr5EPNB1JeQjUDdqMMpv/hwse9cTFShHYM+CmcxRqcpRps7ashSkzCNL88Lcy9fJ1yjwbYDFaJXke5iCMvIPuKG6xL/9EZTFIW6bps2HAzG8N2H5VRJO186VjL4ShgxUM6QzYOkXa7SOJYRfdhFA/XQm22AatSfpHfcnDeiBdNgy58zFXIU/7Iz/qcSmLTJRRZqHBTfaWOUu7CdemCZlDkqn5dECflNRCD18kDdcb75JWyB6/iw3EdZGGAIA4Q2DGcVgXOKh0vtNOFwYnHHH8IMHOdL0My8EOEdTiJiq7C59oh4cUOnkbwjGtTzxmPCFpVb3rljELn3eIrBndTxlwzBdo4Q7J5iODL77C/8QxhMBLBsrHYwLV/+hSrH96Es7Yijpd2mbtcaWRj2zVcRn73CUffF2TVgqeaRC3uVOOmLg1aPJ4ZlSVf4JXngsArS51VYBpNw16G3+X55OIsCOqeisaSweEEmSRIqLymAdLwh6G/ATFND16zMh5F+I8RMxJKHKtIEp4Lv1IWpxUDYnLUsFm1AStyA7MklixYJQf2zDLStTm4N1fgbR9gdnMP7fUdHD7ZQrt3jHE4RrR7jOdfP4Q1U8X1ZhWV6iXYlRMZROqbbscEieKkoMD3TAE9zK16GeVqRdYuh7uRohDRkKn3Mlj05/KnmHQyKPRcb6YnHhOVlSXtdBFHTGuhUlJQUeTSWEpYut7vuXUF+L9DCpD1ZE3J+2yXHKDqo1QpI6HCiOmAwgBpMD4xmJLp5OUcUQxbc02Rn+QzBUP5ZkGIbBggCkO1u5/RAyoluBUaTPkxmYNTnBYUeF0KcBoUGRiwq2X4MzPi0Ap++0eJUrYHkYpUIfKSYdZzKjJzMPmYc3C/j2BEhX2GhN8l5RLcehV0ki549xwaFrcvTgGzhvMoOoCSyNOS2ipMxeE1JP+FSmZ/Bfeerlcr66kDCKj4p8OKGJx8eJQhuEnmtQCeBl9cFRQoKFBQoKBAQYGCAj8wBSgDcyPt/Iw4kzA6v51aCEdjpHRa5Z/RNxhUz1r7Wcb8tPww6g9UhDZG9PcclBuUf32ldzWwimNBgTelAPmQegDacmuUTUvwdPSeJIoQUf4d8xusMmU+OIOBtapaUCH/hgmywVA2jyWpJLSCVymjVKuoKJkEcQaYN21K8d6bU6BwWHlz2r2dN0WZ8nZHhGSXMNhpZY0Yr6hMYdqeCj94K0i7FsZJhF4yRscKUW9YsOeUkcfiLqFptM4btPn7esGT3exab0lUptfBHHrm9PQxDzP/hPfNYpm/z/Ppd9gEmeR4kokTDY2+9sIsyvUafNcHwlR2g6cBw6LGJ7ZKg7CpL98C8wU/Xd80PkQp7+hiYJ5RjriLwaJSQaVWx/ioiyiOEaUBuskQS0xt1LQkes2pdk7wOwvo1D0x8k/1K99/oR0GUc7m5nwK1jmXUjr/isBnnaYi41ygC/G2OSV+3BlcqcD1S+LwmyYZoiBCOAqBmEpuS2WwkUgSfOEcRPK3TR3KLi2Lnl33QOMRd3LSwSHOUgziMQ7HbVyqpHCE1qSNroAH/giD+OaNueZZvt1yrmgtPKjBXAjfKdzFmMvAGSUXVqMqAiGj8Uj0hNjCoD3APOnDOvkzdeXhnHWuy9NDGiJwqhzWkiGIzlMNRljRURHOgqn7VJpq4E/xy1mvmaKvfdRspByctDKYRj9ptqK1pLNiZBRWnC+vK5vgw5NTiJ/GRkhjjPAa1ukSL7nKwWXMEVOnOUrFnBtNOZ4Q17IHp+rDdV3hyTAJMUiGsLxQnFWcGe58U+2cAD0PDcI2eGs6CFGEeHympDZxZDlB7DxoL9w3qE8eyA1T4eSuJvILpfMFLn5O48AISJ4f4+jhBoJeTyLO+I0GarcuY+k3t+HfXIMzVwFTwQlNpW0nDcw4hzBlmswlEQbhWKW/JMOYtE3Eml1iaPgqDC/UvFcBI0Oc4PmqKifPp+s285Xcp/sWYU4Xmrw9OWEpSQqWpMphhfOJRP7R/GZKElQenEZZbnG5iJW3ejQOkCSJOErRKZBRJVz/JREfWI1xWqFjJbuP90oWnBkga5WQLi0huTKDZK2F+aUlNBuz2Hv8BMd7uxiO+2g/28fBw000Lrdw+fKKKPcZ9U3+9ME0ozgWFHhnFBBm1k6WtbJEzSODM1hWxpRAoxHSIed43ywNaoyZcZY7ihMZ50EuejGN/QmiThf8aOcf1z+vVtXGfr0GvLOGFhX9vVCALMefTJuGf3mkH3nFR6nsI3AcWHEq6SSS4RBZwCgrDbVu6vcNDIFjiEO+51pBHuZxHAEjOqwwNZaFzPdg03GX3wLOBWV8A7s4FhTIU8DwruwczSTFrtVswLIp7TBCZYrxYIxgMILLtD6ul2N8zf95eDzXzCw8zLm4N0AwHqsErVkmzlZevaI2V/B78RTzTwMrrgsKvIQCWvwWEYDnnnK6osMgvxPJrIzuwygrcRjAMxPuS0DKI5bjj/MvFfbjUM+/ECdB7pB2uEO6mH9fRcnieUGBggIFBQoKFBT48VJAy8HisDLXlOiVjO3Mze1REIjBn5GnuclL/b1EkNByA8uJvm8YYtDtIM0SiRTLNIK+yL+usr8ZkD9e6hSY/cgpQF2wbMamOqBWgl8tScTulA+SCDF1aIMBEM8AqZv7hssxn5F5hXGV/Kv01bFyWAmUzpoZKbwqdWjKYbv4fvvxMEfhsPJ99EVujLwKvJhmjJHpVYVf+ZwjUo1V8/8ENHHijx6WtbIotS3bFs/KaDhE0OsjHY7hJMwbrj3ZzDvmeF79ZiLgMa+g4TXffd2/i7yTL6OanZukchXqcsY4LGkHSiWUSyX4noc4CfV3eyYh0nJvGhJOKGqeEaRJGWLunXk0lb6MDAJMGzMY+YS7F5t1jB1Xdt2mjC7SHiPrBcgiWlG1BoOHqbadiUPupimfu/XiqaYlQRuyvljo9e4oNE8QlmQaBJ7/ESQXI9+DVa3AYzguZpmiUnsYImwPkA4i5dDyqp3DhKtpc6oRukE0jEq0imZVlIuy6MFCNBqju3uI1WEou5ellZqfJ04nhjA6vYiUeUldusoTfF6HdCQZjbiM0ELP5aoNe7amlK5tGzY3VccpBodtxL0RfAmJxggjJ7xxZnVEiooqKlvp5zIIkPb64rRD/9LYdUQosCl0MsoMaXDen3ZKI0iy+6S9pryhjbnm0RQ661m+3HnnfM+8m/MII5VoBBRDoKmDRXluyhuYuefm1ukjC2S5CBrTAE6XfuEqD1/SE+mUWPn7fIn9IPfU2LfqFTilEpLBEGkaIRyOkRz34KzMAw1ai3RbOFbM+XTlCnUh86SMQZ83pD4SytycBvCK6+k2vLT4GUjy/depmuWFXzNkowzp0TGOD3eQMKVdyUe5UcPStcsoX12FM68MBbav6U3c+L6GwSPTIImgOhhj2O0jTZMJWVXEFBbWfzx9HVzNez+hI8cHh7iwQ5IiHcZI+iEkwJeEvueEkmsQzw2JzJFzCYM8DTNk3SFC2a2ZInUcgAbIsq/COBow5r08XJLaXPOo5zEahmRsNyFh9u1GCfbcIqy5RSwTNo2mOyEORwO0t/ZxtLmL1U+GsBt1JcsYmKbu4lhQ4F1TgLzMYBFMNdgog+ke5eOLESYGIZL9Lix3HpanIkoIz5/Ht1wwOB/SOWwUYdjtidGKoUwT20J5pi6Oj5Ox9K7bWtT390cB8iJZk5lEaz7cWhkW53b+hQmS9hBpb4xsDGSMaqajWvLxKTbmBX+c/438OY6QjccYRwFiK0VWovzpwy4zP9ypt1V9xf8FBV6DAsJu/I/fUY0SrPkGYpsZjG3mBEI6jBAc9FFZjeHQqZbCEPmT7xj2M/KKuc+jOAxmiHsDiXLBHavk30q9Ap87TDkGzPuvgW9RtKDAKQoYPuQ3H6MONsqgQxQdwflnJSmyfgAMItEZgUan877ZDR9TryIyOyOsxsA4AFOEU4YA0yVXPVicf83GtVMIFRcFBQoKFBQoKPACBThXmzn2hYfFjYICPwAFtPwg8qhvwW7VYVeVLpkSBKPXB50BkuM+LK8h0fdfJrgKe2tlfxZA9H3dTgd2miK1bdglH6VGDWD6wkIA/gE6/O+zSmEll9kRSrLZ3Cl5KoJ3CiTDEOPDHtzVBFbF0TzMuTj3AabnZrG30A6QkPlpUwhl00EUBoizBKlrw5upwqYMTB4u/n40FCh644foitwYetPqXyoTWcxDm1O26HMOeO7Qt2fqaLTmYds2fN4cB+hs7yHc3EHaixVKxq75KgSJiEGG3MSfqVvbuczlq0DJcxZ+1V++jKn7vHdM5WwPjQM00Eex7EgJo7F4hZaYIqlShuPpaBLnwXqd+zm88uieAmEekE5c27l7pl7G7OIiHK8Ey3JkB21/6wjjZ/tIjsZiqDgFg+Tm+wYGlWSENSUr8Ln0i+mfXLdN4GmcBa3cef56Uva1T7hCTBHFtN/wDXGuUiFTQ6lShQMbfmYh6gzECDl+vod0SE0LFeJ8Sf8RrPmZe9PHXNViDKLivVGF36ghtRw4loN4EOBwfQvpUU/oLujm6DVRXuZpmXs+2XHHunhf98XkvWmcLnLNfqVdgMpWSWnVRK01Kw49ru3AyyzsPN5Ad+cAIjwmU14j03QRgz2VVZkorNJ+hnTvCHtb2wijELFlwa5UUF1ugc4T4pFt2vsSfOmEdDIRvKTg3/Io14fCz6SxpCLTjJRlsFL+NCoGb/14gqJ5/rfg8rbe1WOX/GLP1GDPNeBUysjY6ZmFoDvE1t3vkHYGgr6kSzlprtqlnG+neUb8zJAj3dhm024pny/4thozxQN0duDPOMawfgqJ03/mNdO/09faWYX4p90hsm4XaTwGpwDP91Fp1jGzOC+GtHwKoMkcyKbqcSpjlGtAmCFtD9BvHwuhsjQVR5Zp1N7etab32wP4diAxUhN5UJMoDSOM2310d46R9pjqQQv2prYzmiHfrjSehxmSToj48VOMhiMkmaUcVipl+E1+JJfUEGR/Gl5kX5MneG2QkDoMM6jb7D/yPvuXzobOkgX/gxbsm1cxv7iEilOS9GhJf4zxcQ8pP0KokDe8ZPAvjgUF3jUFtGzGaD/OYh328hycUhk25Q44iHsB9u8/RdINwAhQ8iGdx/GMMSfGpgBI+wF6xx2MgxGiJEJiZ1hYW0Z9fkZ7xOQBFecFBS5GAbLchO30haynlEHnamgstQCPedCBNIjQ3z5ActRHOopPZI08jHy1Zi1m0UGG9LiPQaeLYaBS1Jbmaqi2mmL0l3U7/25xXlDgdShgGJnygwM4Cy6cy4vIPFdkEUaptMMM7Y19JNwYkv9GNfUYUUTL0yJXkHf5Od7O0D9qYzwaqtKOjUZrDrWF5vlOAwZucSwocBEKmPmXDoMV8nADlYUZMQzRwYRRrjrP9tHbOhSZnY6swtyEbeTfqaM47Ueah497CNsdhNEIKVKUGlXUFmchG1aMU+JF8CzKFBQoKFBQoKBAQYGCAj8eChj9A2XgMuBeXUJltgbbtuAwBeAoxGi/jXD3WDmxGnn3rBZoOUL0qFGGtMfvtx76vQ6CNJYNM26tgoVLKyqdylkwinsFBd6EAtz461iw58uwWzPwa1XZZM0oQePjPg7Wt5ENKdSeofedKDNyMnGi5d/uEOPDI9Ghxdy8WnIxs7YEt1EWG96boFq88/1QgKqj4u9dUuCijiAvw+mcBUWtJRK/Qo1KM0iNUZRGbzpFzDXhLC+hXKnCZx7ycIzezj52Hz5FvHcoRqrJB6/+WD4XHfNcKyGlnF7Uzn3ndR/k4U233dRvYE4/N++aHanjDFm7IwomptyIkcAr+yjXq/CZM/0t/5kuOA/sxJGEzg00xs014F25jHKtAcf2JGXReL+LvcfPEW/tIx2p3bWn4E7T4NRDXfM0Xc5DSN+fBjkp/ppwJu/ldCi8N0FRV8TUJOIBXKJCvIna/DwqpSrKdCTpD9He3MXR0x2k7b6KNHMKiFqgxHBqjKE0gGqjqAhXObxF8e5asGfrmF9dQaXWgOt4YGqc0V4b+/cfI9k9BBhlX/tvnSCcb1HunPAN0Xhu6jvrXu61C51qgZORj+zZCuo31lBtNkCHlRJsDI/a2F9/jvjZ0aTNUr8xCrMSwSmbGIqFJnGG+PkAyeYW+u22irBiWSjPzeDaJ+9PvLBf1XZp6pSfzIXa9YaFhHf4nxixHTgMTU/yExE64sT0bNAITdNfCzPCK6aP3hCPt/KaxoHzgN10YbfmUF+Yh+uVxYkq6I/w5K/fIXi2i7SXSP8J/7Lt+vcCHma+54NcG834F9r28AAAIABJREFUyN97Vd++APtlN0ShryuUyli/dcKT7Au9KXvCn3keNfgShDEOGPwN2DiRFG6OJA8AMjtD5tqyG9DizkBGqVIbDxWm5mNNYOrIBMwuthEg3d5HNBpKKhzbsnXUrJc18Kf4zBDwHNwn/ZSJbdBOM0T9MbrbR0i2D5ANKNVrp5UpUBN+YuQvFhsC6V4Hh989wmhM5TcjZpVQa81jZqkFu147zY96rhY4hG14wYxZAuU5ZQv+KL8YGYaG01l+vNRg16rwHRcly4GXWnBFYT8laE3hfg41itsFBd4uBcxczI9t7g5hqsFWE/W5OTiOB4cOud0Rtr5ZR9pjGi5V/UQuJP/n/8jHZG3uKjlOkDzbwajXRxRHSDgnei4uvXcVbmtWxkr+1eK8oMCbUkD4kd8oZW54qMBeWkC5VofLSJBBhN7zfZGd075KJcc53fDydJ0Ci+t7QKfRBOnuAQb9PmJReGYozzdQW5qB3aiIjDP9fnFdUOC1KGDmYBr8a5x/G2i2FuD7FdkUYQUJDtd3kBwM1IYWOt8aWYR8rH8TnmY6SZYZZIif7GHU7iFJGJuS8igwu7KAmaV5heL0/P1aiBeFf84UID+ZP5kz+b3HHdINB9bCLCqNOjzXh5tZGO4cYbjTBudfcXolf9IR3PAvT/U3lcCk7E2n/aNENqz0OyqkP73Xy7N1NJbnZGOb7JI2SBTHggIFBQoKFBR4KQWKJf+l5CkevkMKTGQIrQelDcFZqKDWmkG9WodPvWcYY7DfRuf5vsi/ItuaTWRn4cqNYJQvYiB+foR0Zx9pHKvPPddFZaaJletrskFN9HZnwSjuFRS4CAUMAxs9MHVo3NROGXVuFr5Xhms5CDt9HD3ZRtody8Zt2dBl5N/peigHM3gBHa46IdL9Y/SO24hFh5aKLWF2bRGVuQas0lsMYjCNR3H92hQoHFZem2Q//hcyibBiRrrGlx+7WuHotJpwrq1iZmUFfqkii01w2MbxvaeIHmwh3hlK6gV+0JqPXjlSiZP7yaLF3eoBB79OCSC713MKnxy5OOdM/3KPT59q9BkRJR1mSLoZUv6GGVI6nbA+LpzTP21ck/tcVFmOitGB2g0Vb3eRPNrEsNdDkEYIbMBp1lCio0i9CjpOyB/rN8jyhuDDDOu5v/zz3O1Tp8zic+rGORfsn7IFZ96Dc30Z9cst+LWKSAVJt4v2o0207z9DvNlXXq26b8TxwNBguu3SfkaVyZCyPPuGxjw9kU/wmmKVczB849sEb6pQkThOg5oYZ8wOopU67CvzqM3T6OIgCQKMdo/QubeJaOMIyVEsjjumPRPeZLv0zwhU0l622Sgg2WiuQR7gtOpwb15GfWkeXsmHk6awemM8++JbdO9tIN4ZCb/JOND8PYGjGyV8piM2SHgxoXMG5oOUuk29eSKcbv6Frvg6x69dt+G+fwP1lRa8Ep0aLKSDMQ6/28ThV4+RHGdCG+lv4mx4gsfUUmGsxxwPmZSNv32K7pNNDEZ9DNIYadlDc62F9355B3aNIdcmXHIhPL/3QkSHOBkldKkk0WaojLOzDPY4BLrsN6WQEz7g+GD7Kaich+A7a6bCwDRjYognPzYsOKszmL9xWdKCeZ4Haxxh8HgH+1+uI/puF8lRquY/rZB8Yf4zcx75kOHuOPY5/5EfQ+VYMBkv59HiDe/nd6famQU/tVFObKlXcNHjUPqEY4b46XH1wjE/ZomPdoiUlBlMm2H4UqJmcT6IBNZEUDV8b+ZG0oA7Yrl+dDJEXz9Ed+M542FK1GtGazFT/xs2/8XX3hlPvVj1yZ1zJp48boxMpEnsZYAzCBA8O0D38Rbi/Z5eb5UskB9P8mEraws91TPEOxHix9vY2djEIBgitqlcL6N5fRnV1TnYNfdkHmb/SDhGhiTP1BotPKsV7ZyrMudE3mAzpE91OifNO5JbhWydJWKwZzhzu6JDOebbeEKQ4qygwLujAHlQDy5Zv2uQ3SGttUtwXLqb2pIS6OjBcyR7PZmfZA6blhu4donsrfk/yJDsHCOhk/loJM6miWPDbVSweH0VzlztgoLnuyNFUdNPiwKnpk+j8GRK2boHe3kBNSqM/AoQJxjvddDbOkbKKCuSqvLEOXoidOXXZH7XdTPE2x0Mn+9gOOwhZWg8z5LoKvXWjOzwv9jH00+LrgW2PwwFjP6DO/RWblxBpVoDI6zQYaX7dA8h+ber5OZTc7A29su3H+VNyticfw8DxPcfYdTtgjvzIm66qPiYW1lAqTUzEVF/mNYWtf7UKTCZf7UMIbopiTLISG3zaMzPoVyuSpTV6LCH4dYxkoO+irRKJ3LyqXZS4VHmYTMHM0LQkAanNoLtffR6HdDklHg2SvMNNFbmRHa33AkWP3VyFvgXFCgoUFCgoEBBgZ8NBU6t3pRPuaGvYcFfbUkkf9kREKnvt+4TRvEP1aZoE+l1Sg8hsi91b4y8TBvCo+doP98W0SLiN2LVR3WpgfrVRXEsKBxWfjas9k4aKpt0ZVN7XaK8lit1eLanIg0/2UNMGbjHdPZ6c6rhX31UOjS1EZ3pi5PdLtLne+KwEiSMEGTDqVcwt7aI0lwdtv9OmlVUckEKFA4rFyTUT6WYiq/ClEDKMDqt8GMOcmfRhnvrKi598hGas/Oy6T1jFIsHG9j+4gGi+xtIuqlOn6MMnROjPT+CzY8GJhoCtVMJo38o5xVlGJVVzHwov5SA2hplyphLGhvpBdfPkByMEO8OkbQzZHQ+GZ4oluTDnLuedJoTcVrQjhnyPkOn9xhNYoz43mPsf/EndNrHiLIUSdlFdXEWtcU5eMy7xwgAmnQGHUXD6ZuTpxc6OSU46DfMPbG/m53jTcC9soD6xzcxt7wI17LgRGN0njzDzpcPMP7qMeKdsTjgyKRMBw0xZJw4a4jjBAUO/mgYpnAx0jRjn7H/tNOKKDIu1IK/vZDwphhH2XLT+pMd9LJ7vmLBuVSDe3sVy+9dgc/Q+Qxb1x1g94sH6N7bRLzVUaHEDQ9I+7lA0aia+1GwYnvJF1TU0HmIjkEU2uggsOTAe/86WnRaadRRsV2UwhS79x/i6R/vIvzmqdTDhU3gaCFOnAT0GJjQ2oTXpaPESNOc9Zv+Mc19XTZiefMOjeo1wPtwBQvXr6DenJHoEG6U4Oi7Taz//i7ip4dIzdg14yHHH3QMSEdAcpQhenSM4OtvsLuxgXE4Rj8JUVqYwcr7V1H58CrsJmNon+4q4QKDz9/OEq8HwbCNObIv61XU6g0hEcMbJoMhhnuHSPbbJ3OEjgAh4yRPz1ztpntyt77H0xMvNuFH+l8wpWjNgrs2D+8XH2BudQnVShWVzEZpEOPpf/0r9v94H/HmQOZDM8/KHMC5Tn5UUmpHFeMIwvFPfuSPfCwx/LXx8633YzYJqc6YNyVxWHHVHKSdusRxRjvPyNwkTgoGZ300c5fhX/FRUj3E/raqFYCRwTjlxTGC3hA99jd3F+q+5hwnTME1hHWwfjpqcS3ZiTH809c42NyElURgtBbtD/M99vlbBv0qhpX1n3xmfmocy2tT71o02sjjDCVYcMcRwu0jHHy7gYRhxvt6PZc19mSd4fqi+E7xV/zgGXpf3kevfYxxHCLzXZSXZrH04VU4izPC4/k5mu9KSgimJRvoOVPWLPKBljPYf2bMmsWKczn7k/N/d4C438MoGiPMIrjVEiozdUi0nUK6fctMV4B7YwpwgHGeL1lwlucw+8H78Cs1+dh2wwzj58foP95Gsj8Suc0YTMny5icyDMeDHjfJs3301zeQRRHo32WXS6gvzcFbZXq0qQhDb4x48WJBAS0D6iiINmX0pXlUl5dE9nJSC2lvjKOnuxhs7mmjv3Yw1IoirsUyffM6UU7VyUGE5MkuDp5tYTTuw2bu6FpZHFaq8w1JgZn/TCj6oaDA30QBfi9wh+msh5mP7sj3k8g+YYLR9hGO1rcRb7fV97GO0DiZeymDUO7Q/Ex5Jdk6QPfuNxj1uojSBInrorE4h7lLC3DmSuJ8VfDv39RjxcuGApQfyL+ah+3lFrylRdTrTUmFmQ3G6G8eYPBkR30fymYVpfeQ7yAjQ4vDipKvqRNLNg7Q2drHgA6DNpD5DsotRriaBXWFhcHJdEBxLChQUKCgQEGBggI/UQpoHQSN8M6VVaxeuyob/7I4xvigh876LqKne0j7icjA/E6TjZ5a7pXzvMP2cSYbZg62d0TM5QY1f7aGxuo8nKWS6DrMvsKfKMUKtH9oCpBnzZ+Rgcm/803Yq8uoNmdQckvAKMLw+SEOv32K5KCr+Fc+3tQ3m+geJt9wmq/Hmei3R0+ei86aDivUoTGd69xaC3azAqbxLv5+PBTIB8//8WD1Y8BERykx33nMbMCf/Jnd/eb6NfGdwIRyLzmxSL8EEF/inznqS3PjFExjrDLlDZ404HCHRpUKRwfuB+9hfmMLg34HwaAtxp/nX32H3niE5cMDtD7+AO7lBQljLgpH4wRDuFzE6EzS5S6NHexvPcPxoA+74uPKJ++hebUFp+kb9BS2Bo8J7uZkqlE55SaN69HGHrbvPsD6w8eYqTfRWlrG3NoyypdXYM9WYZeprdf9Y3DUBKFBLN4aI/zLd+j/9TE6j55h1O8gTCNYlTLql5Yk/cnC5RVYtZIoBEQpZVCTo+rwExqfbtapotMX5CPTz5Z1wkMsl6cHFRGeJTmK7VnAvXUZC9tbaB/sITo+xmg0wv63TzAajXFpdw8rv7gF971LcGY5e59USpAyOUuKBrb9AL3NLRweH2Pgxrj22W3Mra3AmS0rZcQU6Q0kidIjeJs7Fzia9kyOPLHETyDNMjkKDdXtU+2nYMPxxbD5zpyF9Oo8GrevovdsF4NohCgaI9nv4Lv//AUWez1c/e3H8G5egdO0kblkGI0fj+TNkDv+t3F0dIgwibH43iVUlpqw6hUVNYROK0yxM+/A+8dfYOn4GEFvgGjQRylOsHv3MUbDIS6vP8Ol33wK98qSGgc00hoa84QGJC58nRTJzg76W8+x2znEuGLj/X/6BWorLR2pRPe3oY1G96UHIVauhCirLNh0avrsA1w76OOb/QN4mSsRJo4ebOCr/+3/wI1/+hjNj27Du9RQtCFd9dRB56X4WYDo7mMc/P5rHD9cx2DQR5ClCH0bH3x8C1c/uyO5Lrm7igqyU3+GzmyObouZG0+jmyt4CsBbuGB7SAtGnGnWxUAtAQnFYWWM3uYeOn+6i9nSL+C5DRVRRwz3Rumn5otT40+jJWNVs9Pf1AKhjXIcFJgyD5ywqVTHMuYn3u+Z6tsrLVRvXUGj28ZoNIQXRAj223jw//0J+zu7uPmPv0D1k5vqo8DjeNeYmgN5kt7vRwGSnS1sP3+GYRqitDqHK5+9j3KrLh8TdKYiDc+iw5v0EvHgP/55mQV7EIERrey5YxVdwzYTe77O3NiVN7WDhZ2p1D4VF06jDruiRBXOD1ajgnK9jn43lDB+/aM2tr59gpn3VmHZN+C0fPUuaUvwNPCOMkTrI0RfP8bhv97F/tN1pHEI33aQMjqH/NLT8zPxkX4UxHL/qVaypXJm1pxciZeeTmBOIKgVQmQOzoPaockMsJcC0w81TNUD6n+VI0vVMQExqVvdsWwb/HEMx3QmtCzYaYqwP8DG199ikI1xvdPG3K8/hT3rw/JV/8rbdNqLMnEiHf+nL3H0+3vYW98QGIz2YDeraF5ZxOIH107WKTpm8qOX0/QoQ7y5jyd/uYcoijCzvIDlO+/B4e7kqsaP+Jq26ehZfC85zBDd20D3q6+x/fwJhmmAyM7gNiti8LRqKv/oVHMnZChOCgp83xQgjwv/KfFRUlpROHPmXbi3rqGx2MLxqAsrGMDqjvDN7/6EmyULy9VfwZlzlBNjbv0VR2M6Xw8zhH9+hPGXf8Xx7g7CKMAoS1FdaOHqrz6WlC2SFq1g/u+7i39e8Clz6ZC8zlIV9uVFNJ7Po9I+QBIGKqXsTBm3Z6tofngD/I6hclS+m/ntQwdU7Syf7CWIvnmM43/9M44P9xFFI1iVEuYvLWHx2iW4882TaJc/LyoXrX2bFMiJKypCRQa7YcH76Bbm/ngfe3vbcII+sn6AjS+/RVbxsDbzz3DmS7ArmcjHAoL/Ua7Wm3PCuxsY//ErtHd3RXaJrAx2vYyP/vHXqK+2lPyZq/ttNqmA9TOlAGUB2dxgwWmV4VxewszyIqpHu5ImtfN8F/f/5Qt8zJSD71+H03KVMohyAH90thKZHUi2Q0T3nuP4v/4Z+9tbGIQj2I4tuqGF65dQWqQS6uQb/2dK8aLZPyQFzpw/C6H2h+ySou4LUGCaRTNLqWLM9+CZfD0Fl2Wm4UwVKS4LCrwWBbR9Bdw0s7oA98ollGoNeKMUwSBAe30bj/7zn3DL/w2s26tiJ7SoWyYfap6l/YD6h/jZEOP/8/fYfbiOgBFeLQtJycHiNW40vgyJzFbw72t1T1H4FRTQdh/Kpfw+Y5aQ5uoSKsMOgihAMgxx/1/+DMyWsVKrwL1Ug0XbIOVm8iJ1ELKJXQUwiB4eIL73EHsbzxCEAZIUqMzNo3XrmjitWD4VHq/AqXj8TilQOKycIrc2nglzZ2BW4tTKkMgPsotRGaheQ5gQWHqngiiuCTdBnCXIGAJZD4g0pZX9FDIvXuRse5NxZKWIrRQRUokYktrGKUIBM+uNAcYoFnY5A2YteLeWUN66gdqoi6PHARIuPEc9hPc2ERyNMH5wjObSPMrNGizfg+WpkZ/FCTCOkIwDjHsDtA8O8fRoFz0rRu1yC61LSxJS1NQ5OZ4rhOW08ixsGsfykmdsiOHTPex98R368DFobOJ4YQ6NhXlU6lWUyiV4JeLnAS6/6PlegiwMkfbHiI4G2F9/hs7uPka9HiyGsC7ZKF9ewPIvb2Hlk5vwFufEYWSCq1g6deQCWEgsi6jIwpxy4jsjf4SxGwsM4jDhnVTxEGgQ1QZZFjL0kLK6ZiqE6xbc6wuoHFxH67iDnb+GSIMR4m4fnYfPkPZGGG7sY251EY1ZGvcqgMehbDHkALIwQhaECAcjHB4c4uDgAO1oiHC+hJmVBTQX5+FkZVUh61asoulOxxL1SzJ1lhAuy/HPHPXlqYORbUx7ZIEh7dRG/IRwxbEoFwHI0MDAZvsrFtylGtIPr2JuaxfdaIjB3i4QROhtbCMZBYh3u1i49AiVuTrcahnwSkCUym7jLBxjPOjj+fEeOvEQzmwFtVoFpWZFaCVOGMSNC1/TAm4vofn8Fmb7I+w/ego7GiHuDNG7/xxP9/qINtpC68oMd30yRJEjiqAsSoAwQTYMMez2cHS8j+OjfRwmA2SXZnDt4w9Qa+UodIrOufvnneZoLafkOT+DbVnwbs4jPbqN+Z1tdJ88hh2MkB31cfDlQ7i9AIsP9jC7sgyrzpAsVFylkv4k7QUId45wsPEc2+tPEfX7GCYhxlUPrdvXsPKrW/CuLcNyqKzVjh15/AxO0sfqucyTtoXU4Y9znXR8/q3T5wbG6bsXv+J0QWWa7FafQXltCV6tjtF4AAQpop0+nv3LfSTdCM2rq7BnZ7RTV4DQjZDVHDQuL0vahEnIY42yZE1iaGQ9KBgyXE5lcF8QcaENlYt01krFGYJHQuX/SnM4NZbEAUc5rDktG+6vbmJu2EV7NMBgdx9xGCLY2kfUHQCHI8zf3cDM4jy8mpqbRRjjGiJjP0LaH6HX6WCvvY/doz2kDR9Ln93CyntXUZqlw8pU/Ren/jklOfhTcZ6h8weTXSS7Pez8l3tofLeD2LNlDqTjGv0wVEwPBUq5LygyMy0Af6GTYlQC3IU6bv3yY9TfvyI4W9zdfbmFxVs3cPDXHhAESPpD9B9tY+P//hJLjw5QXZmHVadDnqvWgWGArB+it7kjPL+9sQErTXDrylUslup4/OBrhEgRWhloeJCdjPmuNuemXzmH2aoXySdWloLtutBfHhYdeGzOtcphRmZbW8kbImQbQftlgFmvqVqcTlKRLVRgJz0hTwpMARJcUoR2htCyMWYap3IN1XIZjpPhsNPGwdePgaMh0vU2qnNN2PUqUKJjpy3zHnfWZ0ddbH59X0KD9gc9DJHCbdbRunkJqx/TsaouDijmI1ZIReNPAAlh3r73FO3dQxxWKhj+ZRPzi4soN7TMUfYB31X10dFlNEbWHSPd7+L44Qa2NjfQ6R8hdlKUVxawcHsNc9dXYDdctZ5PiRZTFCguCwp8bxQwQ10q4AV5kU6WNQvOlTpmf3kL+6NjdJ714McZButb2P79PdQyD9VPP1COdxXO01yDyPscLymi9S10//BX7D1+gu6wi24aIa6V0bqxhNVffwi7ThnFUs6I31vrCsA/OwoID1uwShnsWQvu7WXMHlxC8/gQg909DDo9tO+u45nj4uYY8G6twVnwVKQJTvoxI6sAyX6C6MsH6P/lLnaerWMUDpC4VBbVsPz+dcxLSqu6Gi8/OyIXDX6rFCDPmm9Mzr+Us5l6d9mB+/F1zBzt4fDht2CUyuHmLnZcF7OlKqqfvC/pORnRUr55KWZRXmlniB/tYPSHb/Dsm4fi7N9HiLDiYvbKAi59/jGcxTnZmfeCs/9bbVgB7OdGAfFf5ze5n8GZteDcXER9/zKqu88RHnUR9kfoPHiGjf/nT7g5zOC9fwNuiwKH5mFuYmIY9P0Y0f2nGP/5G+xtPBUZYmyn8JtVLN9ew/w1fjM3CofBnxuD/ZDt1cKyfBvmvmepQ1VTuIWMhv+JPmZab/lDIl/UXVDgVRRQfKzZ/ERnw9eoEuQD89Dwv5FbXgW6eF5Q4CIU0DruTAz+Vbg3VrD4wQ0cf/stwsFAIlPsfPEtmpUqFkcp3OuXlH3EWIlTIOlkiJ90EH31AOt/vovR0SGGSYSRRyfaBubuXEHzxtqJ7sHw9EXwK8oUFHgVBbixlxHRGxbcyzMo/+IGqv1DDEcDxOMRhs/2sP27r1GLbdT+4Zdw5suwufmRcjPtmfyGO8oQPz1A9K9/xe53T9HudGXDdlrysbC2iEt3rsmGGbtki+rtVSgVz98dBcxU9O5q/DHXRAHBCAtWJo4gNEjJxl5LGdtpVJI5WBvh1begvjeROM5o5EQgyVS+eTqsUFKhkY8yy0UcVs4Eq0yhNBrzJ9EOeDTtEOD6ReKgd2jYDRXtKP3lTazGIUZhhNH2AYLRGPHxGP3j5xg+2ILjOvB9D9VqFW7JE0AJd/yPxxiORgjjQOo6yEKkszVUqw24TGaX8QPjjB0axOeiixjBiGErQ2WYonIcwBkNEaCLfWsTe3Qc4eRl2yiVyqiUK4Ir+ySOIolKEocBMrrOpUJt0KHHKrmors5h8Re3cO3ffALv1iqcRi6ahOlgGgnY+cyIYAER/WBIZ4uG6EmHvtgrfKSVY6lNZxVjruZ7ymDLl/Kk0DYJURJwZ5e77CL78DqWxwnSQQhnaxfjfh/ZIML48Ra2nm5j13XglcqoNxrSfhI2CMfi8RqOA8RRiHEaI8xSxDVudZxHNo5U6qRTteeaYFF+1g4rckYD6pRAnRsmLG1JY3M38+XpeSs/DZfw2a+GAIYIxseBIbi4W22GDlXLqB3fwWoSIk1SpMc9jMcBwo1dbD8/wLZjoVStoFavo1FpIAljBAH5so/+qIt2FiCeKWPu9hrST8cSdUVVrPmSEUQqTJEFeJ/dwqUIsBIbR1vbSIYDpIMIQW8Xjzf24HgeSpUKao0mSnSMSlPEQYAwiBDSOSgKEGQhYivGqOahVKvAzhxkEsIiR9/XPSUtzZ/4YlniNcq0Xv7HV3E5+C1G/zFGd2ML6WiEpD1A+y8P0L27Dq9cQX2Wea7L4uE/Ho4w6HYRjkaI4hBBGgMSCaGOmWuLuPUffoPmpzfgLFRIiEnaFVP95Gj6ShxaLMQyN1pIM+W0ohRkCnGZAyYvvvmJ8It+XRTB5JNyBmepAufGJSxdv4Jw/SnCUQCrF6F9fwP9jT00W/OYW1pC6jo4SnsYlgL4q3V88t/+FpXyVTh1Oh8ZwNpBkfxPXxxGm2BlskX49XAX5SKdGqyE7gjiqkJHDjonnFR4AnOi3PYgwljp02UgeB9rYYTd1Ea/fYw4GMM6HuCo/Q0OvroPzy+jXm+gVqvJHJjEEYajIaIgEAeXkNdWjCEilC8vwr2dwuVgZns5NxtF5gkab3YmXa1jpXN8ZxnKlovkuIvd4w6Y4XTSavKOXgDMNKHRkdkmsRSNhnaCng+4q3OYr8+h9t4V2PRBYZS+6yuo/+pDNLafYbh/iDSKJQXUbucuOnefojbbQH1uBo7lIBpHGPQGGA66GA37GEZjBHYq/LLy689JbFjr95HEKkKHOKzkxxynPrWcCW2EZnTOom8g+V7PleKIyBKGl15GSdNwOqwIDDo1peLMl9hAbKewJlFWCPOshVTVNVnnhdcyRFmsosWIUyVXR0Ndg5xqnKAg/Z8isDKEDOdpuZhfaGFmeQlW2Yf17TcYHnXQPniI3r2nKJWraDQaqNdqcF0b494Qg84Ag35P5IA0i9XcXvXQuHkJlz5/X5ykaPSRNGwcStpfS9b1MEU2SFA+DoCNA7QHIwy+eITnlSp8/qoVNOp1mb9c14GdZhjRwa7TxaDbw2jQwwgJIkbLmq1g9dObuPzZLdTosFKbMtgbMkz17cu6qXhWUOCtUYB8R2MpJ45SBnfBgv+PH2LpcA/940M4vQHG/TE6f32Mx+0xbncz2UFCw5E4Ycch0s4YycYewq+/xe7jh+i3DxFQWeSmaFxpofXZDXh3VmSefJuRs94aDQpAP10K6CWIjpomyop3s4VK+xpWDzrY64yQBX2EO4fYG47RCC20Dgdw6DBc4wKQIRunSI7GSB5vocfIWE8fYzxoI5XIWA00rq1g7bPbcC8xKuHU/P3TpVyB+Q9NAc69XP8pe/KbxctEiel99h4ud46xt7sNqzdCNBhj+PC2V4G8AAAgAElEQVQZHvUD3OnEcBjBc74JeL7SH/QCpNttxH+5h92Hj9A92EeSxAjoLLs8i5VfvgfvfUY91boEylfFX0GBt0UBI0NQ3q0C3tU5ZN2rWHq+i/boKdJeG+PjPnZ+/xUakYPFdoDk2qqS5fmZG6ZIOzGSJ3uI7z3AxoP7CHpdxFmMrFFC6eoilj66gcraEpw68w+/LcQLOAUFXoMC5luNr5Dn+ZPJ25LonXKpU7a9BtSiaEGBd08B4WVuatJsTIXN5KfQER0On+cipRt55d0jXNT490oB0WPS/uUyGiDgXmth9rcfY659BGszkU3OYxr8/+Vr+J0AjcMR7OU5WKWSUoKGCZK9PuKvvsP2V/fQ3dlFFkdgKqC0UcbcR9fQ+ug63EvFZoO/Vx76Idul+JeigNo0wywh/uc3sbi3i6TTx3A3kg2snbsPsdELcHPswL6yDHtuRvFwmiDrJ0ieHSD+5hGe3buH3tExoihG6rqorCygdWcN9ffWYDcZTfyMDds/JAGKurlPvfgTCohgrIzl8qHmxBg4MfpWgsiK4TqpGJIkMgp3iSspWhNPROjzCUmhhRY7FvMyjH1g5GSIuTPSilB1UliMDJIXWM6Hpp7wY5K951sICM/LMLSBkZ0gFCMpLUPaqKVPaWwTQ6qkgVDGev/ODOzGb3F7dRXt//IXbDx4hOHhIawkBaMpIY4wDkYI+l3lviCJ7Cw4li15m+kkA5cumzYs7oQue3Do2MJUA4Ys5qgwOm3Um3rGKuU93mcbiTMjFbgOLM+FFVD3yRB7zEOWIOWPjiRxIk4GrIKvEg4FQxoUGYmaZZimwKlV0Fhp4cZ/80vM//YD+B8sKQ+83EiQiZFAjGHeTia8wN3jY0QYM7aqGBxNZUrgpEJX4UzFboahl6Bvk48iBLYjfaOw0QKsoYmuS7XfUgq169yZ/hnWli9h4Q9/wdO793G4tYUojuGSn9JYjNjMoS00YztJFzpDCQGA0AYCcRLx4HkObN+FzUg5EgVD9MjKHi90Jn+mGLkJ+laMyEpg0xjiaiebqb463ZG6IWwHSSeRNkiLBIEHDN0MfSvF2EpkHDFykdBZ99eEDDRqsn+5i2jeQukf72BhbhbNhRYe/+4LBIeHyIKxOIzQiWUQBhh2OmjbHhgNI80YaShGlESInUToQRuRGgJETiPICukAIj5YjFgyA7v5a1y5/h7K/9d/ws63jzA4PobFQUMeY4QLRuYZDIQt6SrFjxC2NqHzSpYgonOSmyFxVaQRUe6bL5UJU5qWvuZRoy78lVqwafS67MKqfYjbMw0c/Mff4/FXXyMaBnCTVBSp4/EQvU5bnBnELzXLECfRhCahY0nUhJu//hg3/v1v4X9yRSlbPY0smUgY6wRXYQH2EWnHKCd+ir7MkzEGdgLf1i5+dIZJ/SkmP4HzpmdSP18Ww4kFu57BfW8FS//un3BAh4Tne0jjFGBfMUpOr43nm5sIAXTtEbJ5F0vOFdB5p5LEOsxOpuZezs1uhtRJEbgWPJ/zDttoKw/diyA9QZAOIQl6ToIuOP7pkBAjdHRduXICltcyp+sdzLaF0m9vYHHlMmauf4f1//d32N/YRDwawSanpymiUR9Hox7ah44419A5gfyv+ppLTobMs8RJL+WRSwznaJn/pwbeRdp2Vhk9b1hlIChlGDsZMkbfoBJUz0E8iEsn26gDgpjmm3VUDSUVrURGK72hk0zCrbNNQhui7DOcZQneZzdxfW8HT/58F8c7u4ijBG4Uod9uo9s5RrbJedBSDhKcKiXaVQqUXNRXWvj8f/kf4V6/jXjzGNZsU5wvRk6KukQW0n1BJHW/MFWOOH9wbHNedxL0ECNgRKiyA/jOhRyAZDhxLIuzV4LQppyRYmRboJOOZycqCpV4dEi+J+lTcZwSZE46QZxn6HTnKYeQkcyxCTI7Q+SqZTnIYtTNHHTyqqInx3DJxsjP0HdTuL4Hf62Fxifvw15ZxntlGxv3vpW0dHTOC4IA/c6xOKtz+bDhIEstxEkqa0XMYdKsonVrDb/+n/8HlD+9CXfFhV0yva2dpMh/nJC5fvqu4k9ZrtnnQDAciNMljoFjm4NCTyMyfzGmueJx0mTE1FGzVbQ+uIY7//ZXaHx4A85c+bTyx7T7BA1zpzgWFHhnFBB5x8iHFQvenRnMH36KbDDG+h/+LPJs3O9j57uH2Fxfh1OrodpsoFGvIQzGCDs9pP0hvDCeOKaFnoO0WcLtf/srXP6nz2BXaZAtGP2dderPoSK9jsvyw3MqPX061XvIPryG2W6E0W4Xo73niMY9hJ0O7v7u9wj/+K/w61UsLi7B930E7QGG+0fAkA7olEMjJFmMsedi+foqrv7DR6h+9j6cGR0V4OdA26KN74YCnBLNtEiZlfPv9Qay/gd4v93Fw9/9SdKqpqMhdh+vY39nB3atCr9Rx2xzBlEUIuwNER/3YDO6bMI5mDohALM1XP38Q7z3H/5ZoqNOvpk4Vkyd76aVRS1/5xSgzC+f5Zwi52y4ty5hefA5Ms7BT0IEww6y4Qj3fv9HxF98gbTiY3l5CeWyj2QcYrhzDGcYIwlDRHEgOsig7Ehk5Cu/+Qhzn9yWiIgTGaLg379zjvoRNe8sXuOGDtFfcpOIjYz6hbwO70eEfoFKQYEJBTQvy4ZXxJPNzxES2HTepgJF/4lOSKk5zK3iWFDg7VOALCf6WgvU1zpLZXi/uIWbR22sRxn2nz6VdOBHm89wtLsL6/d/gNuooVavwYGNfq+HtDuCNQxhRQnIy9QxR5US6teW8Zv/6b9H7f01ZeinPo8p53Wdb78xBcSfDQXIQ1oHIfzEa9cCN0J615to/MNHQD/EeqcLaxTBjlMcbjzD7v/6vyOtlFBrNmVTO+k1Puwg7g6QjgKxg9F2Fzk2spkKrv32E6x+/hHcy3NnZxf42RD8x9vQnJn+x4vkO8OMk7nPydyC3XQRzpYQNDwkGZXCPtKyA9ulIwZHjLJxqrNXYMhChM2dETUb4xkP4UwJcWjB5rHqIJHoCa9QcGhbu4zdicE4wajmYNTwMY5KyMqsoySGOROC/wWlicHH50RgwVmxYZWuYH62hPKNFp49WEd7ew/xaIwkCJFGkTiGZDpKCQ13tsOd4C4y34XfrOPS2iLmb1/B8kc30LzBXXUqGssrKHPuYzHGMWNCjelxVnAp+SXsSgXt9R30d48w7HUFL4meQsWRpJpgRARl2eeOdYlhQ8cZ30Op2cDi5RWs3LqChTs34F5ZgLvSkB374rwxjYmmEWlnVS3EMx6iZgmW4wl/oOarFEksZ36EwfIUPtk/VQuDuo1R00XqVJG6FpIqnXum3jF163dFz+WpCdldokG0Bav5OW5fa6Hx7SPsbj7DuNdDPA4kugCjfcifOKwwpYarnFCYuqZeweKlZSzcWkPr02tYeP8qnJnaiUGPuBMd0o1+RjVgPOMimCkhShx4c2VkdU+1J9dO9Zp+mQD0giLARCgCbDrm1hwkcyUETR9jy0dStWQc0ZAuYevlBf2fAUcjpI60QqcV3FmCVfVxa2kOBw/Wsbe5jd5BG+FogIxOB3RSSTNxWElsG5HtIbIdePM1NG8sY/WT9zC7xl331VN9ZQy+9DxhGibZOVqfw1L1v8PcvTXsfLuO/e1tDNodRIzUI45quqniBEWHKNKb80YJ/mwNrcuLaNxYQfODNcxeWoBdswVuvplvfG54i/yV6bg2jgX/0zUs1v4Z83cuYeu7Jzh8toVeuyN5+ZSDACM2cHeKjcQpwSlzPNSxsLyA65/cwfyHN+ByzDLKkHY0Ip8rjwOTtkx3vhyISAZ4CYIq+cVDEHviNBbXPMQ0ULP/OAamPsSEt9+AAIY1zKtkVwY+YVogd8WH9Zs7+MhNsPWXb7H98Al63bY4riQ0clsxhC9cC07FgyPzo6P6hbwqTikWUAWCpocojRFUbFh1B6FPBxOzPcLU/pIjEZXxn4lSfDTjI5ypIillyGbKMv5ZnxjsSev8n+lf0o5zLFODXfVhVT/EzcUKFr5+gOffPcao1xfHKUZSSekYJIPPKHIcxY+OA6dSRnWxiZW1RbTuXMXqp7fgzlPK0/0yTdQ8Lued63EuGJq2cl0rJxg1LAybrkTs4KMT8CpNnZkihBf5XJNVRQVTJMksWxRToe0gLmVwZnzEFTU2yVMWd8dyTbhcQ+Pf/wYfLC9g694jbDxalx2yKVOicfcVHVQyOo/Ri8KBVfUwu7yA5ZtXcPWT2/A/vgmrbCMdenCuLSHbGQClFHbdB2zF87LMG/6V9VuROqg5CGZ9hM2SOAFxd2JGp5Xp/jyPhlRW0DHGzzCmPND0MWxUkNIZZ6Yq41McWFm3OIacpuYErLlN3OgsVHNkjUrsBEnTQ8q2VJgax9HzPRlMd4xuDyNMBeyz2RJG1RKs67Nwby3AXWthdubfoH5jCc/uP8LzJ0+F79IwEmcpQU28VlxkFAZqHporC1i5cw3X/uEjeDcvwVlwT7zUuUSZuskvyOA0XXi3LuPWv/sNGiuL2N/YRntnDzHTWiUx2JcqxJqaiuh0lLkWMseDW/IlHd616ytYuHMZi+9fRYUpKOYZgmdCoZMT1l38FRT4ISnAQcOpyczvNQv+h1exECaI4wSbjx5j0O0gi2M4jAoYdhF0h0hdDxnl2ThCRidlCxIlClUPtZUF3P7Nx7jy+YdwV2bU94ueN37IphZ1/51QwCzaujkid4nMpNYwZ7UizqMrowTxlz6SzacI/3/23vy7lRzL87sRJLVLT09v35fMrMqqzKyu7uptxmOfOf7J/p/nHP889rinp92bu1xdXV1bbi/fKj0tJMPni8ANgiGSoiSSIsUPM/UQgeUC+OAGAgHcQOy/C0aMjf2P1jk4sjdvjyzPGuVOaMdH1tCYTJ/Ca+aWb27brRcP7Olffxk+kdXY0YsJcYcK+uxrokTzUQ09i4Tnj6DEcVvpl/ds5+jP7MVh2377L78Mn3S147Z1Dg6te9QOE/Tff/O6fDGm3bGi0wnDwxO9x7DestbNbfv8P35lL/7jl9Z8qM8Kl88T4RnAxzzzUX1KsegEYn9YPj/q87GFNe+smv30ud19d2jFestOfvlLO37/Vm9wmZ2cWHZwaB8OTmxfut/RZ7I7eoco7PJ8omeQrXW7+eKBPfzzz+3ZX39ljXvblmteUMN1H68vOjfKvzAEpHJhyOG6l5djBe18emz6dG1h7fBSTHyeXJiaUdBlIRAMCqXHGifrnb0VsxO9DJd1wnNbnukFnziv6nqewhnkl4ZzDIELEgjz8ZoG1DuAmke9t2HdP/vcnp/IuqSwb7/52k4OD604PDY76YZd5jvZu9Ard7oaOHQs10vRmdlhw8L49/5PXtrL/+VPbePTx2ENIYx91T1rHoIfBCZFQP2ifnK1tqS+taEXvx7Z1mHbnprZr//hH+3o7XsrTk7Crundjye2/+6jHTW+D0m77bYVeo6LhirZxrptPLhtd798aY/+/MfWfKrdXeMzXJkb/84RgUFT+3NUvBkVRZPIWgCNE8qlkcQ9e3b4pa08vRUG0Ot3b9jNl49sdVOmieVnFcID3RhF1PUVFlf11vODXXv8Z59b88EN65y0rXlzw7Y+vW+r2xuV3HBBDpMb15zCW276nMntbXv4s89sc2/XDj8c2Lv1tj35/BPbuBG35VJ8v9AlMx4HPy0AaqcLGUdsNaxx+77ld1fts+d7dvDHV9Z+f2Tt94d29P6jHX08sI4WkiSv1bTG2kqYsMm0lejejm0+vm07T+/a+qPb1riRl295pvkOq88A/3JSqQzI1zNrPli3fP2FPdzdsbuffm8HX/9gB6/fWmf/yLpHJ6ZFNJWto0l+LfA1cuu2cstXm5ZpEW57zVZu7tgNGRM8vWfNJ7ulMYW2fNJidVpOP9ZgU/ogW43bW/bwq09C53i8ktlh02xPC/wbsvAomboMubKeVmfauHfD7v/sE2ve3rb7J4d20jB79PlLy7fWqnbw9khdFSFw1idJ9CbNlgyb9qx5f8MeP9+zW797Yoc/vLeT9wdhkbb94dA66oiL8vNIems9X2tZvrlq+c1N23p81248u28rz+5YYze+8Z4MJkJ+cQGz8ey2PfurL2z15V1rW9fyvQ3b+ex+NCDp6U+v2RxY9PHTRrTivb1tT/70c9u7f8c+Hn60t2sn9vDTZ7a2rbtCnEB0YTFt4C6jlVZmRZwAzDd3rXFn2+49vW17v//e9r95a4fv3ltn/9Dah4d2eHhojUbDuisN66w1rLupLb5u2M6T23bz+T1rPbhtuRZvvXzKM0y8F5bpAVgL2+syVNPniG5Z486mPX5xL2y3K6vM4w8Hps8snRweWzvu6pM1GlasZIF1c2fVVm9t2w3tUKBr4MFNa97aCHrg1avauPIY4yBcDDGeyu6MZA+WZ5a3irBLQuPmI+s83bMnL+7a3X/7o73/9rUdvNuP10Un7IDUWluxfGfdGttr1pJe3N+znU+fWOP2jfBmtni7Ppf5KLO4hWXIN3Y+csJuCqu29fKevTj6ym7sP7eDbts27+7axt2blq81y+snllc1UFXS6oxR++FR1HYqri4lcdjU7k5f2ONb27b75I69+/Z7O9n/GD7XdCSDrlbL2lu5te5v2K3P7tuNO9rqML7JGwc/rSe37Kf/+S8tf3dsJ/r8zP2tMJmXy8gsqcfwQsW+QGLX86ADT//6Z7b58oGdrFrQyXufPrF8Q5ZcPSl9TOJ1GIy5giGNhTeOG3sv7da9bdt+ec8O37wPb3sef9i3o4OPQS+1k5QMMxorK1as5JavrdjKjQ3buH/Tdh7ftg19Euj+rmXKOhiD9fK/0FEsvwaMYTekGy278+Vz+7xh1tzXTilFtQGVGkr9WfWT8VQ0VpGrsKAbcvWJPD3YN7q2v1pYd3fNbj67Vy4EhP5YRol+z7pp+e6X9uThLdt+ft8OX723thbJjo7DzmAneWadVtNsfcVW72wHDrdfPLTWy/ITcIXsIe5v2LP/+U8tf/3ADlsd29HnCLbiDh2xb3elDRPFZnbj+X17cfyV3X322N43jq1xe8PuvXxSGkCl9awqHA88LPQ7atc12/v0iX2iXUpefbRHq0e28fKW3bxzq9ytLMSP19wgWVFxVC6NA+799KV90exa9+DQTjZyW3m+axu31OaJ8ahkxus33Pdvb9qDP/nEjndb4ZN6tz9/aa3nN61xK7fG7T1r3F6zZ4/3bOfXD+zguzd2+O7AOodH4cG1sbpqzc11a21vWLG7ZpuPboX74uqncdcyjZNincv7WVkJ9R0yPMk2Cms+WDH785/Yo4d37e4fvrPXv//Wjt/vh52EuvqsnRaN2jKRzaxoNsK4I1tfsebOmm3cvmF7Lx/Y+rM7YTylsUIwavJ7m/jo59zjKQ4EZk3A+/je7la6eRXWfNi0wl7aPctsZXfLfvjVb+3w1WvrHret0KJTp7Cs27FG1rSTLLN2S0biua3srtvGk9t296fP7eFffGmtF3d7Bqfo+6yb93rm5/1nWrt47yj7VBlYmtnzDcvyL+3JZtO2/3HL3v7bb23/7dvyPtzRd6O74dkkiGmUY5/Oxoo1b++EN/Pu/uyl3fqTl9Z6dju8+RcMDr0PT/PmGALnIeCdrqep6a6e+5r3tNvoI9s9+YWt7WzYN//ya9vXs4PGkJrD72TBmFAj1G7WsKLZMmvK4H/dVh7dtL2fPLUXf/WFtT65Z43t8pmsGm/QDzt53EkRiDoVdoZt6FlIU1gNK37xY7u/2rL1jTV786uy/z3RTrTajfCoa93wCXI9dMkgsGEdPRNo7vHpHbv3s0/tjvrfl3etHEPHOTH0d1KthpwzCFRddapzek5uZOGlSFtdsexk1fK1tpl2FfRnc8lNxylp+jPyJBgCEyUgPUx10efyVjMr1htWrLbCztj5hj43EXfkVQEG6Gx1PUy0gAhbKgKui65fiRvmgNf04nlmrU/vmnW69mJ1xbb+6V/t7e+/taP3++GFT41/9bKMXs3VPG5XL//pawfrK7Zxeyt8BujRn/7Ydn/+Y2ve1guFcQ1hiF4vFX8qe2kCVT8o3fUTPceFl/7LhQPt4m3dp7a70rLPttbs7S9/b/vfvrKDDx/ClxhkqN1td8JLklojsZWVoMft7TXbeHrPbv/kuT3+sx+F8W9jb8VyrQv7tXLpGiBgkgQwWBlAs7Fjln1xz+58etfuxPByYc7C7hrhYhmQbqiXX2yySHy+azcf/cJu+jqwtjbasHIrb7/BDBLkMhSmY82zKN3TLbt99+d2+yR8sCBsv6/tvsINKRrihPhKEzfi8IsxLBzpAxJxYFU0zVY+2bPiyU1b65ppQa/7obDu60PrvnljxceP5XbQG2uWb2+GtzPy7VY5UR5lhO9+1Y1ABtVniJ+K6T+tM4u1HqK1KJfv3LbWZ7ds7djs5rFZd7+wYv/ICr0N9fHIisOPoYPKmvpUyrrlu9thB5uwe8ZqsnuEyifNV5k9s9RVf6W+UItquVnz0YY1bn1uL/7D52VHGeqqT3eUD1TBCEKCkj+FaQH85v09uynuesAKi7tx5xGPm+brxwqLnbPaUTsGaPcL7TDTfPjcVn/xzAp9FeegsO77Q+u+eh22gQ07YqytWa722dmyfFfHskSMu6fozRktVg+aDFadm2arP71nKz+6a7dUFi0sa8MB1VNrnirXqF8aLnlrZs37Lbv/v/4i1EcslX++Xu42pDr2GZC47NQzlktGZPrkVPPOQ1v9kwe2eRTr/7Zj3bdvrfjwPnwDQwOpfKs01GncaJY7p/gNKO4e4tkEV3mpngoLzGWAYtZ6uW6tZ89srf3UtivWx9b94bUVx8flJ6/W18u8djYs38qj0Udp5KR2C8wks1t+EUyTS2nV+sox7CRl6nFi36H2CPlIV9VOmxvWuPuZrfz8M9v60LXuuw/hEwL6rJc1G5ZvbVp+eydYVmtnktJCNVqrhm9bxk1VlE9goX/icdr4akftzHRr1bLN5/bgx8/soQyLtEAdPpFS6nqZeEr/iov+xFlZaPL5YW6NW89s5U+e2e77rnVf/WBdDVra7fANw3xv0xq39bdW1l1v8ipxmPUrwufBvnj5v1txJIOIcvcWN/AYt928T9U3Qlsvd+3Bg/9g97VTVLwGg9x0UD/oslK7hgFZeQ1qYbNxM7P8Z3dt5Sd3bFObqqhv3i+s88NbK96+C2/PhU+mbW5avrkWDPVkhBh2zVFfJ6MctY9cZ3fJppGcYIggo75bTdv6T1/aj/7yiyA1bIWa3m9CI9UyjOoVfD08uqq/P/w4s/CJoXBvEaDSaKX1bM2aD57bvT9/bp03RXgjtviwb8XBQZjYkrFGvrVhjYfb5fUZDHbi/VELxg9atv2/fWVfNH9WXq9qd+mD849FDu0a7wcrXz6y+z96WO2S49d62J1tUN9aq3a4biOz9V88t2dfPQufLlJ9vb8N/bQzSa+9mqwQRWsoj1etee+l/fivX1hxXOqPtr0P9z7VJfmFdouGRq2Hm3br/p/YLft5qXPiq/iqhx5mn21a8+Endv8Xn1jnTde6r99a99378AaGxgD5noxb1sI3cXt9SuxPq/L3+j1/+ygwCEaNhbWerFrz/kNb+fKBbahff19YV2348bDsv45Pyj56TcanW5bvbFq+1TTtDhPGBhrv6JpK9Sk9TurOIQSunICui9DHZ2ZrhbUeNqyx/YndfnTLbvzTr+ybf/6Vvfn2e2vvH1rnWJ93lDHiihX6NONqbq2ddbv18qE9/upTW/npS2vc1H24vGar6+vKK0kBrh2BpD8PddP4XcaSuzIYbll++wu7/XTP1v9ux/7wr78JhrUdfT6lXVhX32XVbpfa7avVsK17N+3OZ0/szlef2cpnjy3X+EY78+nZapx76LWDS4VmQsB1WDqmF0K0S8W93PL/8Kw0MH9x3775h3+xN9/9YMf7h+WuQO2T8BKMXlDQGHt1e8tuPLtn9794YVu/+KnlNxrlTq1xnBa2Qq+NH2dSNzJZHgIaP0iH9UyybtZ60bR89zPbe3rXtv/2H+wPv/6Nvfv+lbU/Hllbu07GyRZ9rrW1tm7bd27Y7vP7YdfN1o+fWfNO3A1xgs+Hy9MY1PSyBLxbDnLiXLI+b5nvNa37aNvseM8a++u2eaNjrd0NM33WvC/RZUtAeghMhoDUMry02izfxursrVnxZNcah/dsc70bXjRY29sp1yCG6PAQ78kUECnLRaA+FxbPfZ5Pc8vZV/etcf+O3X/+wDb+/l/sm3//g+2/eW/dsK6oz6vrc/Od0O+uba7b9r2btvfjZ3brL7+w5tPdcvyr+WWe3ZZLt6Zc26ofrOuwj381B7GqjSC0Dv3EGo/u2sbf/Yu9+qf/z05+98fwcmVbXwnptC3Pc8tXVqyxtmqtrY2wucKjrz6z9Z+8sNaT9XI9V/PIVaZTrhziz00AgxVHJj2VoobFYC0cFeXClYdrfBwXrM6l0FH5/eFSE9RhcSWV6xfJoAtFF6r7x/KFpCqPrM/1OZN1M5MVb5xArBb6PJ0S1C94+cWLXunC86xuOF4+GazET/IUe+tWdNYrg5dwowsLW3GHEmlRkHWBG1ZaP2cSXe0uorecwtv5epAOhhOZFWulEUDjRmZFZ82ssxYW/PoMchRffzLQSBbhQjuoocUvTFrVMnVmzkbrACvlADQswrqeRNmVjFq6sOC4UVim/du9joqjOomzjj1NrQiBZVw0LIJha+SaF2VdupkVq+XOK8WtDSser5cWEZLj9ZKuer0Di7hYXR9QxDJU+ql32X0HBoWpbf28Xs5h51HXwsJvq7DGVqmbXi/Xzz4GQ1gEXfP20k4oHelENLbYyMJCftG5Zda9Vepg5FsucseFTNVfb/XrW7hxLTYU3dslqUfITxPnmmBXXr6IrDrcWjV7cr+8zv/X6rsAACAASURBVFResdSia+Bbsgocg2VKcs1pN5Ikj0sfRt30azpUQzoRP5ei66TQjkl3dsy6O73yqpyqjxswqPwqq9xUD0JnIFLumTRO1P8iygrfY5XMICsyUXslSdL6DvFOo5x9nAgJ7So9D/XQbjmlbjS2G1bcuW2F9EI1kUFObEsZBajeocySpboEHVN6Gf/EBXf5DzPwGlbK2DahTdRfqVw6kSzXTbFKfwP0MASrbKFtomFN+IxMqcShb97OrHF714r2biUt1Mmv/XDtet1KWSG8in2BA5UpLW+8D4UtU7x/Lje6KuMpC28vd+UnGe6m/tFbzRH6bdU/XmOBhdJFP13MYXekFd0Hyk+w2d0NKzob5YXu14n0QwZa3h96fxIMh4rwFm1oH78WvA+NZekrv8JWS/0p84/ljMZAIe6A+rgohSv7QnVSvNCnZ5ap/LG9wiR0aPcq1ekD5ycZktXSora2+izvDWpn9YEDy6MwSQzjDu2GEwvsvCIHyQiL5OKrHYc2GlbcvWlF52Zov6DPqa4pf6X1W57ERtFegVBneStO1G0J07mutZCP+trOtll3q+zvY13L66cc90gHyvzLdOHYmXhmOq/l70G4EJglgT41lK7rXiD91LW3VlhD19HqrjWf/Jk9/evP7fHr99bV1qb7H+3kuG3NViu81ZRvr1t+Q0Zbq5bfWLd8W4uo8ZqQ3L6MZllD8rp2BAbpkvexUdfCfUzdbLOw5v3cGjsPrfXpnu18+HPrSofffLCTDwfWbncta7VsdWvD8hs71tjTywTrlm/os0Aas8XnNOU5KN9rB5cKXRkB6a7GHprrCc8LheU7ma18tmPNRz+zJ3/5uT3+cBCMcztv34WdQVvNprXWVy3f2LRsdyd8ulGfc27satATx27+kCf9ZexxZc27VBlrHKyt0TV+CJ8U3bXWs7+2l/t/Yt0376zz6rUd7x+YvpLaaDatubZmjc0ty2/qb9Pybb3gE/tf6a/rriDSDy+VKs1FZX0M29Lcnl4cfWSfPL1rLw+6Vmi3wbW2NfZWTS9Kop9z0WIUQgR8XKxj9ZsaFoQXIQvb/vPP7aeffWLdg7ZlrY5lGvPqc80ae2gcwg8CsyLgehrn3rTDtenT69qtba1pjVsvbeWLJ7b35kMYPxQfj+348NDa+hRmntuaXoa+sW35zZ3wQrR27C/nQ5OxA+OGWbXmcuQjHXW9Tcen0S+s0azq6xKZtdbXrHHnK3vwF5/YvbcfrKsXet9/CDvtN3Lt0L1m2c6WNW7esHx30/IbK3H+oTeHthxQF7OWWiLhJwLeyfqAWQsvWvDxC0VR1MmHjj76K8zTjaKoOD6pIblpOvkPG7QkeVfi4wUbJqbjAmgwKvCijJJXL6uXS8Kr9elepHAzCxnHMnshYjqdhnLoPJY1GM0k4Z5kpOv17GXdix7ZhAVlbxtl52k04a9jP++l7LVNLE8Qn5ZtUH6e3tOEb01qm5XwUn8ZqrwUnupDmi4s3JUdoD5p01c2b59ReSeywsKG8gn1K3eTCIz76jtCmDPzKO56HnLdzxf+PczLOkw/PV7qRlnS6YBJCiK5HkcTLJJXeXjACNfTyHhAi9TS1QH6WsmUbK+3FoTD+0V5sD9RLqE6pXd/OTydnoXDzjYx2FmrLiPKHa4FZZDGSY9HVPHcQbGsIbugH1p47lrRyssF6FDmAZl7m3o5B0QpW84BK0KtwdQenj4slid1VoCzj8deN506Sve7tKu8Qj8Y20xtV2USSlm1x8D20WK5W4bLldGf0qf18LqOU9gknfos7VoVfkOYBCBVeROOSuR1U7j6FDcsEEdP4/2f4rufXy9BL8rsvQzJ2cUPI9bAKqpGUURDKBXby+HxouunyjhE8Xj1kri/6u+q54mD2w2GKnrgDwZlYhANLEvrxpiBp5F8MdF53U99iv/q4e4v18sSjkuDJu18FQw0Yn8foifi0uR9x16WeP+WoUqYjNPYwGWNkuN8Qlmi/vu4ItVfz0fxE3nhVGG6N0WdD/XzOHL1F3Wuut+EfAUiqU16HL2r6yyJduow0W0x9Ptkv7j+s758VRbVVQzz0rZQVQm/GHYqTzwgMC8EpKu6BnysoQWl9cwau4UV97ase7hpxeGeFccnttqRNVtu2UorfN4rW9O2vOX9Ttdo+ElWlDkvVaQc15yAdE7jG+lglpm+9lNsZtbY27DiZN26H7es+HhiK8f69p766UbQ37Aluu8CKkR+n0J/r7nCzFH1vP8N45DMTLobXoDIreg2rDhet+JwO+zytnZyUhq4a+fWlRXLNOkpI4Fo/O9j8dD/hjFSrKeOlQ8/CEyDgHRXz0cyPJeqyZB+S/1vbkW7acXhhnX3b9iq+l91sup/m3EMIQN+f6FC43zve1P9nUaZkQmBUQRif+njYu0QXdxcKR/w1NHqOTfOCYz1nDkqL8IgMGkCrr9ypaemnaj1XLdqRUfbYKuvjS/MhnHzpAuAPAgMIZDc26v7vaKqT9V4VjsWb2dW3F6x4njPisMdK046ttpuh13+NUjQSwfZ6krYhT68+Kn5f1/SjLo/JHe8IXB+AonOhsTpM5X3tRq/avMGjX81HaGNDO5tWnG0bt39bSuO2rbajpPFrYblayuWrWsuIs6hSU6UW40p0nxKsfw7BwR8OW0OijIfRQh66g+CWgRLlDlMPnin7P7nKXaU2zfBITlx54d4eFrioIsnRq4WVxVHP1/gi6eV4+GVR+0gledB8tOv3NkunsSHW52lBdax+gRP4+Fn5etS03TuF92+G2LMM9Tbuah8tTTpaV+Z0oBxjjUjIKZav09/assRZfaJqhAljRfLn4oa6ziR0SdzUMWTuF6O4Cqux0/jqACu8/L3ONH/vOWr0ktWGLRHmTqv5zuW8BgpKWOydt8ns69NqrxKQx9f26myrMIrn74DNX24VmO8PtlJTMWpRFUHSYRZHFZlTC+GAYVxL3eHlk0R/G9IJA9OXaWqnaepFTTNn/I+pb6ead2tFcSDQ/r0+vaAWvyRp0qjh1MvjM5HyVE8hafx6xl4+lo/23ctpPyVPpXpst2/Lv+i52IV04Ys/CT6VddN4u9c0iJV2bs8xU/SVOGVZxLB47nbixyORulkLergUxU0yg465hMPridD8h0sLJEV+5jQQ0nGuHJq8cKpdD8BWnGvFaKWNORZxVWgR4hucNyvJmvo6Vnx03AxTPj2yUy7MxVN6Xw8ksg4b9/elwcnELhiAkGt9U/YCUxvQ2vxX6uo+ouFU5+j8ZQmmNJfvQ8adi2laTiGwKQIBOUt++VwKD3VG9KNlhWbsoosf6Hv1j9Bh5PnJyWqqbSnwYXApQiM0xe6/sZn1fBmtHZxXV0xu7FSjqm8D1Zf632wx49uKKfLQqcv1WwkPoOA65m6Tp+n8CSx/80aTcs2tvq7VvW/rpvRLfvlmFh+/CAwTwSkk+EBLypnfbwrb++f56nclGW5Cbi6DprjiWHLDYjaT5VAvV90nav1lX3R1LfKCEXj3zVNQmiJOFoCqLBhsBCf13w+QmlcptyQT3Uw1SoifIkIuP66q6onahZUU3PD0kvtONiQccpGb2jg6yY+Bk70N5XTP2BeIr4LUFUMVmqNVOm/LgopdFww6Xuoq6UZ+zReaN7nh3TRT/n6L70e3a/PTSP4sQvw874EtZOqkom/p3PX5SlKekOK5/0XdRToaROxIV4qKw3z40HpPCy6FX+PK9ePdTgoD4UP8nfZsdh+OtSND0h9ojxvdwclVtio8EFp6n59mQ6QN0p+PUznvnFGPR+dK9zT1PLtQ9V3MkhQKadPVDyp2nFIsjO9Yxn7riEv+9DGLjP38oQ8dKJ61OpZ5R8j9+XTJ6CXtvLWQXVSSbrwgRftlMhh/ENhdVf2lJ61F+yUJI9QYShjpPH9uIrad6AswwBBvmnUUlBf3CoT9x0Ux8Mu4VZtVpdfPw95RE85+kvx1ePXz88qo8us4nm7DBE0LHhIdC9+X3DfSczY/SRff35eleuCB5KTlrl+n3Cxnp+7if9AVU3C/bDfdUHulnUKZ+7lblq+fiHjc3AZnl719EkI5ZMsWHj36tl7kqGuZOkzVPEeMzTeqABlpj8fkHvcerndP3Gra0V+LicJH+iXho/KYxwIHsfdVLaO0+vRw8RKx4PS1MszKI7LwYXArAnU9VP5S0el026IFeLET4YpPKYpF0qTAsddpcI1XNdzpan7JUk5hMBZBFxVx1Ijj+R9c7g/ZuVQ1HWxfo9TmpjuXHmdVXDCIZASGEe5ot5Wxt8a08XBUVDRqMN94yXlEQawUYnlJLqeFoFjCEyFgKtedEMeUd/L5/JkHOFx/HpQZPdLjz08DZtK4REKgREEov6d6nPTJOhoSoPjqyIgPfR+U2VI9VLrSApO/XScnl9Vucn3ehNwHUt1s17jdO5B8au45aC4ml9IZXkc93OZ9XP3x4XAeQm4jimd65W7LmvAefDyOXnt/O5xE7d6sVOB/peEn3seP0nL4fQIYLAygK2uk6DkUdOr43h+OolfWf0RKjlpgv4oIcRTp9HCseIODazFrsk9lXdd1qkIo+UFIEma5LCW8JyntXKfSp2Gx90TPO9ekFa16imjh/sr0QV+npfkp6Kqm/g5ZFayzpGm4q40XgB3zyMnjTtOQS6bh5fXuY2TZ1rGs46r8kmw/vRzV4Eewd0YJXU8yJMNCkv9+o6jzp1K60L7IpdFGxJUi9l3KvHnT6ZUacEkIQ8+pazBEvvz8jv+4LihkDEoOB7N3b5aJMXpz6Qe6/Lnnr+7AySOLEI9Xf18gLzxvDQE8pwvKXREcs9hvDJNIFa9LDpXIdJfPY7CPF49rH6eyuk7jhHTvORVT187vzCfVE7MJ12rUNEk24uTRu8r9qAT9ZF6g8wTK86YAvrqMyhNIrMvrpdjUJoQ1h9bZ6lPlaw6cIGXc9M8gqRR8tMwJUx/aVjqz/FUCIB7DKx1HU2TRIDV5HwK1D935rdkT6eJ0PqT9ag8PB0uBM4gIDXSX6qGZyTpj5yO+11QqptRlz0fj1Ll5x5nZkoECAwhIGVKdS49dkVzVyKks5pj0BfY6jNjmuEMOhknIYZkeb4LZpgQ/CEwBgHX71SHlSyeB6evH40XQAhIEvXF6aUfowREgcD0CSRdbqK1/fkqIKp3fwBnEJgRgQHKWXWtGlvUn99mVCyygUAYE3j/WNfTqKSVtw6qk3RtLXpWYXCFwIwInFfnFF96PajPlUoP8o9VUbJhl8qMaks2QwjUH8uHRLvm3snFcEqPk7BTFKqw6qAvymDfvijhRPE831NpTnmcTj/IZ2CygZ6DUg/xS9Inh+ndbXDC/siD44zyTdLrMDmNqU77nBI3RpRTadK8kvTVosKgBCP8EhEjYg0JulTiROYF5fQl6ztJZPthGl7v+dMwxVd43c/ljOUqsQuoZzaWgF7yMaOX0WKenrU80+O6rFFh9bjxXEkGJhvqqQAxcA4uuEww2Na0jKMYPbG9I5cw1E2jpsf1BApL23pU3Hracc/HlHlmtDMjjFugNJ56+BRADBuU1yC/VNSI45FJPdDdEXIuFTSufMVLVXXcdGnhzpnmnNHLnIYlqvnrVK1c805LO/p43IRJvOTwtGwPjK6fVhHl4fwHBlYxQ51ORekFT+xoYB5pOZXToEiD/CZWKgQNIiDk/udqNCgefpGA62gdlvvLrYd5Uo9Th1n3dxl1/3o6ziEwgoDUZ6AKnVe/UiHpccxbXi6yrzgD4vaFcwKBcQicV4+GLiy5BVbtwggWLjW/ccpFHAhMgsBZ+t0X3ndS5q7xxgDvSRQNGRC4NIGom2Op6FiRLl0iBEBgbAKVSlYHSdJBfkkwhxCYKAHXt/ocg/sPymzUYpenS8cQ7jdIFn4QOA+BaenSGXIVfKl5/PPUkbjnIoDByji4zlDwcUScFWcGWZxVBMLPInBVjTTJfCcp6yxeCj8rv7PCx8mjijNRYZXUMw+uKNvB5VJhZlygcbMbN97gil0D3yEAhnhPpcKzzGucCsxbecYp84g4c1edswp0VviIus40aFHKOVMoV5dZ1RyarPAJEHevrliLkXMFb0BxB4W5NfuA6ANv9YNkDEqLHwQuQuC8+jVG/DGiXKSkpIHA+QkM6m9HKeiosPPnTgoIzI4Aujs71uQEAQgsLwH62uVt+3mq+ST0MJWRHlf1HOhZhXIAgakTuIQKXiLp1Ku1zBkMejRfZh7UHQIQgAAEIAABCEAAAhAYgwAPeGNAIgoEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQgMJYDBylA0BEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEITIMABivToIpMCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAIGhBDBYGYqGAAhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBaRDAYGUaVJEJAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIDCUAAYrQ9EQAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAwDQIYrEyDKjIhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABIYSwGBlKBoCIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAASmQQCDlWlQRSYEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAwFACGKwMRUMABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMA0CGCwMg2qyIQABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQGEoAg5WhaAiAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEJgGAQxWpkEVmRCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACQwlgsDIUDQEQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAtMggMHKNKgiEwIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEBgKAEMVoaiIQACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYBoEMFiZBlVkQgACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQgMJYDBylA0BEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAATORyA7X3RiQ2BpCWCwsrRNT8UhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQGDSBAorzMLfpCUjDwLXiwAGK9erPakNBCAAAQhAAAIQgAAEZkJAj9z8ILBIBHizaZFai7JCAAIQgAAEIAABCEAAAhCAAAQgAAEILAMBDFaWoZWpIwQgAAEIQAACEIAABC5JoDJQ0aq/r/y7e0nZJIfAtAmkqhqOC7NMf5UyT7sEyIcABCAAAQhAAAIQgAAEIAABCEBg2QgUYZOVwoK7bJWnvteOwLTm0TBYuXaqQoUgAAEIQAACEIAABCAwHQK+kWllvDKdbJAKgakRkLFKeLh2JU4tWaaWK4IhAAEIQAACEIAABCAAAQhAAAIQWFYCRWm1sqzVp94LSiDMoWWliUplcBXm0SY/mYbByoIqCcWGAAQgAAEIQAACEIDAVRLw9f6rLAN5Q+A8BMrH6VJz/dHa3fPIIS4EIAABCEAAAhCAAAQgAAEIQAACEBiXgAxWwt+4CYgHgSUjgMHKkjU41YUABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgekT4KWv6TMmh8UmgMHKYrcfpYcABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgXkkUH1PZR4LR5kgcPUEMFi5+jagBBCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgcG0I8CHia9OUVGSqBDBYmSpehEMAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAwLIQkKkK5irL0trU87IEMFi5LEHSQwACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCKBwswKPgeEPkDgTAIYrJyJiAgQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBMQlgrDImKKItOwEMVpZdA6g/BCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQmDEBDFZmDJzsIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAwLITwGBl2TWA+kMAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAIEZE8BgZcbAyQ4CEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQgsOwEMVpZdA6g/BCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQGEogGxpymQAMVi5Dj7QQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCwZASKJasv1YUABCAAAQhAAAIQgMB0CGCwMh2uSIUABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAIFrRQBDlWvVnFQGAhCAAAQgAAEIQGBMAtpdxf/GTDJmNAxWxgRFNAhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIHDtCRRmxZSMVFJ2GKykNDiGAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCAwkoLdK9XM3nuJAAAIQgAAEIAABCEDg2hGYzZgXg5VrpzhUCAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCFyGgH8GaHrGKxisXKZ9SAsBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAASuCYEiy6wINiqloUoxxXphsDJFuIiGAAQgAAEIQAACEIAABCAAAQhAAAIQgAAERCB9M296b+fBGgIQgAAEIAABCEAAAhCAAAQmQWA2z20YrEyirZABAQhAAAIQgAAEIACBpSHgi01LU2Eqeu0I6J2Q+F6Ivx7i7rWrKxW6vgTKSSNU9/q28HWrmXTV/1S3oLuzmfu8biipz7QJDO1YU4VNj6ddIORDYJIEou4O1fNJ5oUsCEyAALo6AYiIuFICodtFka+0Dch8bALpCFda65pbWGb6m+YPg5Vp0kU2BCAAAQhAAAIQgAAErjWB6T6sXGt0VG66BNIn6/hOf5mhB3Qts254/M6K8p3/6RYI6RC4OAHX2jBJpC15LTdtzRs0N7gXl01KCMyKQNDjzILudoNbana5xXRaCtf41I9jCFw1AR/zxr73qotD/hAYg4B6U/2C9haZZfrr+fRWocpo/AuBuSQQet2ozKX+Sqddu+eyyBQKAn0ECiusyPTXLV30t48PJ/NHwPvaXslCT5zsltkLmeRRc5LCkAUBCEAAAhCAAAQgAAEIXHcCyYNKWFM6/SgzksBVzi2ds6gj60Hg/BIIehmfpXXc1+6FZVlirBLfEZHRSpg36os7v1WkZEtKwI1UglJP/w2nJaVMtadAIHSx0VhFBirhL3S7Ckl/aWesYzrllA7HMyQQ1U8aWGphZkXRW9/Pqv54hmUiKwiMScB7Vu9Rlaw0VSk74J5eJ69O092OSZdosySQqmV4XgvPbq7hsywJeUHgDAJ1tYzKG7xlrOJGK8HtjSckNdXzM3IhGAL9BKRgU1Kgnlgd6U/7n2gc0V+ESZ5hsDJJmsiCAAQgAAEIQAACEIDAUhHwB5cBlZ7iQ8yA3MbzmuLD3HgFINbUCYyrd1myoWk9Tf3cC917YncfXAjMlkCqm74z0OntKWZbJnKDQJ2A9HREf6ngoMoj4pQxRkao58o5BC5PIO1jozTX1zJIOpn+XT5LJEBgGgSkpQPUeRpZIRMCUyPQGwX4kdy8tHqdWq4IhsA0CdAzT5Pu0siuq1H93LvM8wKRnAFpg5fCfP7hvHLPER+DlXPAIioEIAABCEAAAhCAAAQgMAaB+gPTGEmIAoGJEvAHbXcnKhxhELgqAv56f+xk65NGQyaZrqq05LukBIb0u6m3jv1zbKn/khKj2nNOIMzR63NsmT4mmFk3y31/tp5VwFmKzNh4zlt5wYs3QP9Sr/IjmEGTy85X2wXVTVrklSZKkUxLf4fll+bN8XITCKoqRfF+V66MVvSmPz8IzBGBkf1Z+bKMl9bHwH6OC4GxCIx7L/Z4I3WylqOnSbyVPHjHOYfwKbb6/EMSfxKHGKxMgiIyIAABCEAAAhCAAAQgsLQEzvMUVIM04KGoFmO80/MUYVJ5jlcyYl0lgUQvBjW7/MJ8/bhlHCRk3LTEg8A4BBKdHRS9/AiQJjz9Hf/k2yqeYJieniHbk+NCYGoEQqcb10Ojnp76HJv80dWpNQGCz08gqGrY/Tz2wDJcib1w+YmVKDPq9PlzIAUEJkDA9a/Wf+rUg2QlWFSdbv/iaVWCKnLlM92DWec33dog/TIEarrbL0qdsAxUorHKeT5LMVJufy5zcTbNa2IaLChvT20GFb63hAAAIABJREFU8K3jURT/6yW8Rkf1Cs9z1Qa01zwX90JlU3sMqqe3k4f5uTKppSn1VZ5FfNkgjXyhUo1MhMHKSDwEQgACEIAABCAAAQhAAALnJjDowcf9XJg/CE3qeacu3/NJ3YvkNY7cNA+Or57AWe2scH1GJW5WEQ6zrPcwT5tffRtSglMEemopxS3flQ5KrIBe4Kl0eEBgHgi4mgZVrd7S01ntDWn1xSj0PDQZZagRCGYqYajQM1PpG24E5a4lSk/7IqcBHENgQgQG6GAY8qZGK+G4COtRpeFVkveA9CF0mro7LM+kWBwuL4F+9SgVMaveNkie3a4TIlV6GtdcP8zJEaO8JcshfN07KzLr/SmJh0yuKeZCkldrGjo8yQp6OScpcxayVO5x2Y6qYz3MzyXbj/vqU86daSw87R8GK9MmjHwIQAACEIAABCAAAQhcUwJ6XNGUZ3eM55bwQl98+Ol7Buo7OT+oMbLuCVVe50rQS8rRYhAIeuZF9bYun69j02dhV5Ww3BS29zfrxm3+Ff2S6ug540Jg4gTK3ftlrFIarBTdTtn/TjwnBELgkgS879UtN/a/lUTpb7drRbewQoHh0yoj+t4oq+qfz+qkPe+z4lUFYlyQopjocdIG3iwTlT9hYUlxS8mnPGKGRdeK8CfLq3MsmA6TN+F6IA4CKQFXO12Dscu1LI9G2+PqrwtJBXMMgRkRkPoFFSz0dn95N8niM9wi3FvOi6nvWfa8iUfFF6z6mGxU/DHDptY9LGJ5BzGLw4TM8miwkltY9M9qBtuD0i6y39QUY5GhTKjs02Q7VHYZoPFvnmWWaxwxpR8GK1MCi1gIQAACEIAABCAAAQhcSwKaPAhz9JmVk0VZmAA9T13D5NL0nnFGF+Wq8h1dKkInRUCTQkHBegKjyobJThmqdLvanUJHeblYqknPOGfkcXupe0eoTo8FR9MjMEzPNC+UZ5rk1AYrnXKXFZ1MccJoerVE8nkI1Lq08ySdadxKd6uDcpEp6GwsSTAWjBXKNFmfNeJK1Omi1uvt54n4kCj4x8A0Tj3e6RxKH08zLBz/ixNYJLYqa9/ykRc+KpK62t7HgGSrUhrAXpwOKSEwXQJSYf+TGutPLxoU1g3+vlfbuH3ldEuLdAgMJ6DF0aC/3W7VDw/5qNVwIQsSEgzLVFa/B02q3FMwVvFihs3xlr28bljlUNJ2C/MTmeVZw/KwS2Y5F5FG4RgC0yIwzqU5bBzgY4iwI1s4KUcRE++fkspjsJLA4BACEIAABCAAAQhAAAIQOJuAHlPCRL2mjIrxJuzHeVA6O2diQOBsAnrgDpOaPtenF/rjU3jbGtYpmlZkLSuypnUt/ilOTOcT+INyGvYwPygufhC4LAHXY+lkx6THTetmDetaIxxLj7uWB929bF6kn08Ci3bvrPeRPtEp/W2rn81lIChD1zz8dSwL/oPsrkLdU4EubEBTxZeuq5A0WeXJwWwJROXV4ttC/HwcoHLHhT0dhv63MOsUuRXR0FU7A3Wz3NqWW0ebXi1KHReiISjkpAh4lxkvRSuyRtDhbpGFsUTH8tD/XrX6evkmVe+Jy3FAc1/Qidd85gIdtWes/ret57m8aZ3Q75Zmg+p/Nf7V2OI6/uovX0yijmGcVAc8CcG6ZU7h2li08gql43VXWHxeQfqqPribdUx7ZLaLLOh2mm5Uc9THuaPizkWYQ5iLwpSTQvNWpDqaiV5GsbLjylR0/3NjFKXV+FZup6txsM7zsNlrd4oKicFKXTM4hwAEIAABCEAAAhCAAASGEpCxiv7Pc03cm7U7hbX1JD7ub9ynpnHlzfuT57j1IN5ECUgtwkN2lCqDFX266qSTWdZcNWusWDc7tk43t+OTwo5OCiuyzBp5TCc1j39VweLu/9U5BxCYAoF04TN0b9Hg6rhjdhT629wsXzHLW2EB9aRjdlzvg+kXp9AyiBybQDlMqKJLPTXJeXjSsbY+BaTxQ57bSVHYUbtrR+0ibC2tDVd8/jO8reuT/1GfPawSPOqgPtaon49KS9jkCcyiTxrWxuPm7ekVPx6HifowdjA7Om5beLc/y8IClHRZRlgnolXT+TrAqgieRz0C5xC4LIFKyaL6ug77glNYdGpYljUtk9F2ISPCzE40th1DL71Pvmwx+9KrTGdcO33xr+okljFBfFUludb5uhqq33WdlJ/GuMdhLKzxrxb8szCmUP87zhyEy10keF7/iZY5Xm8TlRmFUd4ShPcRwY39hvRZ8xDqb0tDK+lvZiedrh2eaN+KmMoTD2igRdPhqejDAC4X8zpNcwT6kVmclpRGP4fUGHW0vJ7sku+w2FFYNDTppRp9pFT65Jpkp5LDcWZ20u4Go5Usl+Gr7t1prNGyzxuaFdOUft7SEB8CEIAABCAAAQhAAAIQmDsCehzR200fTgr7r//tH+y//Jf/I1jXr6+s2M7mut3c2TqzzOHBKqseyc+Mf54I/iB1njRnx/WnvHM8bJ4tlBhTJ+Az7+VDdNi+VJ8B0qdU8pYdHB7bd9+/sY9Hbeu2j21jNbdH925Zq9W0RkMT+eWOQaVhVhEexsvJdD29lzsLTb0KZLDcBLKgfeX3zUUiTNK3rMhX7ODwxH7729+aFo5WV5q2vb5qt/duWFOWVn2/UZNIfo30JeBkXgmkFkyTLuNUZpTVV3ZLw5Nw+5Q+N8Pb0TKu+uM339nB0bF12m3T/kBPHty1jbVVy6XCil8ofvk+qnZwS2dNpdVB5IVuy5J1oYQDqLscdwdEKadzBwVc0k95jsr3ouJFd1S/cVG5c5LuLF0PuqE393MLn6pSDxwwSx/zYGh1eHRi3373nR0fH1ur2bCdzVXbu7Flq6utschlE9O/OWFKMeaPQBg/lGNXV0r1oxoDW9a0777/wd7vH9hJu2N50bYHd2/ZjZ3NcOmf2atM4RnOr7F57nv8OaJs7LKPVE/Bb7IExFl9rd7eD/c4PXOFz1dpF6s8PLe9+v57Ozj4YM1GZje2NuzG9oatr7XOKEip2WU7nhF1joLPumVdqKj9Q6oLiRiWaOHKq4pM+DIu+4VSbwOnOK7Q7piN1op998Nb+/71Ozvp5tawY7u1s2F3bu3Egqgw6Z/3yHK9x3G/Ya0wP/6LU9KS2UX1d/SwzhXM3TPaZ8zrszeWHEbZ84tuJTfGTwtdVVyGKlkwVinlK67+9IJiZjJS0bPb63cf7M27D5YXR/byyX37n/7qT+3Tl89tc32ye6JMVtoZ3AmGAAQgAAEIQAACEIAABBaXQHh00UqpHny6hR0dHdmrw4/2/bffDqlUfDCKoeGs98+QNIO9/dFrcOiYvrE448nysrs7Zh5Eu1ICejNET9tqtdDOWjsND+qNait0TXx2izy80fTx6Nj+7Xe/D4YpSiODFf3Kl0bipH8494d+9OFKG/jaZ+5T6tK3UuekcR1rWt5aN2voE1bS09yOTtp2cnxsb96+qVGJutrn25PlcvuCw8mgdKdj4XMVBBan3wl9cOhApU/qj7Udut6KblW7AoVza1m7e2z//rs/Wq4+W+upWpySsUtwXR+rmdYAPpC40Kv+E2ToRQt3mmH6UNZ9WOiF/GO+VfYXEjIq0fkkj9sWpdQx+Zc331GFvGDYWXXz8pUGK+VnL5VVabCiz7CZtvLvqgfOrX1S2Ju3H+zd27dmmfzG+J1VhDFEEAUCowhIxbz/DBodDAD13NawLG+aPgUUjAL0mYoiCwaEX3/z7YCebICyTsNgJY5zBhRgVDVnHFb2DWHRLpR3AJsZl+i6ZifdtMKtV+OYIH5GJewq2OlYUTTCW/6v336wt2/fWDZW/+sL/otBrlpDnkJx07XqSYmfZnnVN0z6ipt8ecs+QloWxsCxxMpH/YYMBvPWSjC80mfYtKOrhhKv3ry1169/iGOIsvfur62PS+Qujg57qSelX1OXExXsvOWu9HJkQm/X8WpRyRwRvXz9b2SmMXVPWu9oWLpy/kE6W14fyqXsi0NInln4hGu3fIlxpRxpjCjl5YIwWLkcP1JDAAIQgAAEIAABCEBgeQgEW5XyQUcTovrEij4N1NInVvp+gx+GyoclD3O3L+HAk95D1sDgsCA2JOSU95myqhRePnerAA7mmkD5wK1HbN9MVG2uBVJNzmsL3qKr6SDF0LpTy5qt3Dqddphe0iJVuVAVZpnmuqYU7roSkA5La92VgUrTulkjbIGurdDDf9rWv6E4zQFrPYN6ukF+zjCGTX4W1zPAnScCfSsWk7vHlZP15WRnqcPdcCIjwSIrd1lpWMOKrnay0i4sHctbjfAptnKGVP1up9zNquyRwyR9OTlbAvTSunHh5LC65NMS/V5yOuRqfKZXnlF9xKC66n5Z9+/3KCX2+4UUA7zkH+p23mLUi3Cpc30aUNZTvQJq7JB1c+sEvVUhs7CmmuW55XnXsrgr1oCOuFcSN+KaQt36LudejhxNgEDQgim02QSKNlBEMNCOw9eyP9bTmq7ThuWNlh2ftMNCqXS4W3St0VyxRl7qevmvV9bdXjbBp3dZ9AIucTRhcZcoyaikXkq5onCazajUhJ2DQDBWkdFK+XJMyTq30mCwZZ3uSbnYX6jfbVijkYfdVs7KYdFazDXurHpdNHzSPJa6vNUNWCPV+Nym+321Q1DvM0Aybe10tYegDK9kqN0M/bJmKXp9S9o6TlauH1+01Uk3aQLjtYjaM23TSZTiPPrgecsdnc6f4UrdlT6XY+GyBnqhwCzLCys6XesU3WjAPYn6nJaBwcppJvhAAAIQgAAEIAABCEAAAgMIhIX++FkUzeU3sszWV1dst/ZJoHIhqXyM88ckF1ee+yOeux462K3mAgYHl4/wyeLCkGhhcqBenmFxS//xyjdaBqGzJKAWC9/fjZl6ewcDlUbTDo/b9vrN+/DN86LbtdVWw27d9O14M8vjxL0e6usq5bJmWR/yWi4CZY8jTXNjlfK4k2k3itwOjk7shx9ehx0pms2Gbay2wmfZZDg4+ufa6+6g2B7m7qA4+F0PAn5vc3cytQpv5skOMKiQ/tEkvKbmG9XuKup/uyfdsFiaWddu3bwZPqkSDFyywrrdciJfy6zlHG8sY9x5ozzz/nky5S/7+lGy5uuaCGshE58AP78OnCbm7VLKUi9W/kLrVhmMNDYKO0JUUWd+4CVOF4cKa1i7Y3Z41Lb9/QPrtDthoXR9rWlbGyvB6HW8gkqP5kuXxis3sRaDQKm95X4/Zf9Z+uj602cxG/b23Qf7+PHYTjrqlXPb3dm2zY21snpBNaN+DjFeXU7t9V5BrhNwdzE0YzFKGUyxkx1WSsbSXRm9Hh537MOHD3Z83LE8b4Rxw/bmmq2vn/VJoMWovZcyaFtUL9c8D7usG8ROeMcSyisCsaWCkYpayQ1XZHulka52pzB7827f3n44CPNRmm/Y3lyPc2hqGd/aIh67TLnVRNikNeKyGkX60QT8Qo7u6MjnCw06MY4+JGU4Q4/KkbrGDnqzq+yPgzbqnzyzk27X9g+P7d3+vtlJu1L78xV8vNgYrIzHiVgQgAAEIAABCEAAAhCAQHic1oKSnlwy29rcsJdPHtrPv/wisDm96ONvSJVTfOGxqvfPWDzjY9bouGFXjNFRFOqLPGPJDOLGeRA8O19izI6AjFXCBqZxcVMTRdJV7bCi76J//e339nf/zz/at69eW7tzZHs3d+0//eWf2sqK3jLVhL7e7NOkkR7UlTROoEZVmN6b7bNjRE7zTkA9VGqwYtbJmvbhqG2//cPX9n/+1+/DzhRba6v25MEd++qnn9vaan2Xq14dS9X1Xs/dXnj/kXS/34ezeSAQ+6MJFqU0JphsYwdpYc691OEiLHrqbVItODXs/cGh/d9/8z/su1dvrGif2Gors7/4+Zd259bN8Ekg6b12XilHDF7ZsowpAfmMNHrwpGO6k5Q1ZpaXihau4rMu5UvlcLHEdSNPSSmLWdOz2ump3EbWbVDikQlOiT/bo8wjSA2LTQ07ODyxb7/7wf72b/+HvX330VZba/b4wS37yWcvbXdXRq9n/crPXp0Vi/D5JDBI6+atpH4VBDeMgcuVaY19ww6DXbP/62/+u/3293+0zseOZd1j+/LHP7NPP3kRqjJWHceKdD4yZXnPl4bY15WAK1jpSjdkMHh8UtjX37yyf/rnf7Zvvt0PL8w8uX/fPv3kqd2/d3ssGC55rMhXGSleyNMobxQ92XE+5Q3zDOWuQKXGSmt7Nn+ZdbRDpmX2d3//T/YP//xLOzzRh14Le/H4of3Zz7+Mu2qWOxKWquctJS2IFkZxPuMqVZO8p0nA23zcPKbTQ8hoRU9t4ZkrfEJQc7mZZY1GmDv71a9/Y7/813/THkFTnS7AYGVcPSAeBCAAAQhAAAIQgAAElp2Ano3Cs7j+yWxttWX3bt+yL370uCJTX7CoHr+S56rksEo37MDTuzso3rjyXIa7g2Tht9gEpAv1vSbU3vrTMqh2pPjNv/7KXr/qWNE9ts1WZp89fWhbm+vWaMa3wxXZba0S1+UsNiFKvygEvF+T3nUys7f72oa3bf8961i707HVRmG3dzft80+e2OZGXevLWroMd4fVXXnwm18CZ7Xf3JU82RxFuqW+t901e/Wmbf/y//6zvX7dtbxo22ojtxeP7tnjR3es9hWWsMNVtDusJkWdQ3D9ZO4qT4GuA4H0fi/9fXdYhDHvP/2jdnE7tmajZXs76/bJ0wd2/+6NaJgzvOZ6sVUqOw21nYbM4TUhZN4J1O/nOtfb/Scds1/+csP+GLbAOrGsOLFH9/bsi08fjFWlaehZep2NVQgiLQ0B12O5H48LW2017Xe/+ZV91z22Rt60vRub9uLxfXv+9M6ZTKahu2dmeokIXl53LyGqL2nKtC/gkideTncvKa5KvjDljQWtNrCINRAPBan/1d/Xf/zGftlo2MlJNxis3Nndtp9+er+q79ABQvkeTS8eRxCYIgG/7jwLjYGlyxsba/bDD6/CZ1y7GKw4HlwIQAACEIAABCAAAQhA4MoJ6Ikls/DdUh029HnTEYUaFTYiWRXk6d2tAi5wMAkZF8iWJFdMwNtdS/paFA1/Db07UljR7Zh129rp1Jrpmr8nSso+wCsJ5RACUyAQX6zT5JH0s9loWLOR20m7HXQ3K7rBv3HJrNHtSwIkeT8BN/RLfDVWaKjflbIFhSu3nc6KTngTNfTPdUWU/kv54+xpn0FsfUY1yevch/V8zy2ABNeNgKuEq5nOs6wIf3r7VGZYGkOoD+69ST2aQvXFwdHRCIXApQi47qZC5Cf9K8O0k5V2Iywsrz5hkcae3XG4rnpd/OwyJqeFIJD2v41gaNUxK7T0n2nfNsutqw8OjvUbdF2MlfAaRVo0BgtTXhV0xAaVGt+WuqxxQzd8fjjX2CHV31GVrfrua6SMVGUuCUhPvd9VAXXcU82i1F3tuBIipTEnWx12WJksT6RBAAIQgAAEIAABCEBgaQjoAUafYKmebOID+0AA/U886dPPwOh4QuBSBGr6ptPysdqPSjfLupZnRfgrV1Jjrr2n8/5iDPPvj8UZBCZGIPSzLq0oP8kmcyt9xkQLqOXkfWpt5ZFxITBnBKIBVihV7EtlhNJbSD1d3p6By+mw4FN27EMCa9703zUgnF6UgI8nghHKWYtJZ4VftBCkg8BFCBTlYpOGDzK6qp7hXNaofvI8/a3LG+X6fWBUHMKWloDUI7zdH/SkNBQsfcrFfi34j1LXpQVHxWdH4Iw+MdVP6avrr1wZXVXhknPK+rUKnV19yGmpCUjjXOtctd3gSm543WvAsGHS0DBYmTRR5EEAAhCAAAQgAAEIQGBpCOj7pfrm7pgVDg/jMa4/BY2Z9Mxo45bhTEFEWHgCo3QrLJjq+7yFFWG2XjP2PoFU2y4InVp4VbguFahUsSjfjHaDlbDSVEh/+UFgvglIh2VkpfFCkYW9KcJx6R8+kT7dClQX0XSzQfq8EPCBgLv1cgXNq3ueed4vTWPgxOdMHVPcJP6ZuREBAuclcFqvK5+gn66kYRRhYdOKehazVNHz5OVFr5d34LkLdndgpAt4VjRPp71MVqPqdhm5p0s5po9vF3EVmZd5Col6WO2lEl4oyLqmlwx6z2wyVtFuK9f0Nw30o/Tsshgpb3l7r4xOerB1VJ4JUjluKEfByfNbmIuoQ+zJuGzzkH5eCHibujsv5TpdDpVQfz0tLXvkchjroafTTcIHg5VJUEQGBCAAAQhAAAIQgAAElpBAeOTOaov8s+Yw/897syZCftKJ8B2J08ohndUUp08XWZaXi6dxITXAO50MphC4UgLlFKcmjTLrFpkVod/Vu07T6H/rE6ZXWvUlzPz6dUCqkf5y7QoULFaSZg1+yfl5D68frvMSIP5AAq4Y7irSmH2boiW7okiC27fmYXeKLCz0l+tSY8qsypiWp/LkAAITInBav1xDgx7HXMJxNB6cUMYXE3O6uBeTcyqVC3b3VITJe0wrq2nJHUnAM3V3ZOQJB6YaG0XLq9BHrOLzW7X12lWUb8LVHSZOVXMUw+LMkz/lja0xGETZlOXLMnphJqh03xya75SZNvo11u950l3KMpJAqtHqevVJQflNUzsxWBnZJARCAAIQgAAEIAABCEAAAqMIhMfqaT6xjMqcMAgMI1DTyTAxFOKWj9jVpGdYldI3KXyiaJhA/CEwQwJS2AE6HIxVNGEfDKwa4a3TdGrzciWcnKTLlWPZUw9o/EVD4qoUdbjsdeMuKuHF7dJwJfinxoKLVk/Ku2AEap3qqNJHHXb1dIMVudqVIpPhStpNjyV6rEijSkUYBCZEoFwwHSgMNR2IBc9ZERikgD4uKj9KoQHy9JdMZ1XfEfkMQjEi+pUHLWN5fbwr+FX9q4PQJB4l7Owa7ZDkV+pwvdX609ZDOYfAVAm4siqTmipWp0F504iTLxGzcpNnikQIQAACEIAABCAAAQgsDYGwcLo0taWii07AJ4jCJJE+SxE/TZFOGpVxyhfb0uNFrzvlvwYE/FMq2lklGq4U4TNX16BuVCEhMN2JwCSj6R7GavRNcvoyf1jw7xmu1CdGp1swpENgTALxyxjS4fCXGFwt1NvvY1aXaNeDQP0O4uc+1vXz4StS14MDtVhsAtXYIVQjbAlkhZU7rYQx8GJXj9JfBwI+OBizLv454rIv7tfwMUUQDQLTJeADhOimWpoeT7MQ7LAyTbrIhgAEIAABCEAAAhCAwHUioAcXbQMZt4LU7L3eceIHgfkjMOSRWq9LxwXTMFlULZr2ajAkZS8CRxCYNoFBShgWSqW1vSWn0BfHBdXLF2lQppeXioQlJpColA6rv1Rn3XOJMVH1BSLg+hpcGb1GxV6gKlDU609Aaln/9XTVlbb2BDcoUV0I5xC4MgKpvpbKWu5zdWUFImMI9AiM1X9mYXc2DRzGit6TzhEEZkfAldPdKmff4arymNoBO6xMDS2CIQABCEAAAhCAAAQgcH0I+DNLOV1UGqmUC6cYrFyfVr7eNQn2VnG5X2/o6Xvo4f1+TRyhxte78a9B7ao+OBx0F+zj9tegAajC+ASko66waaqyE042REeNUzwczyGBRI9dfYMbdHyYos9hPSgSBAKB+BRXlE9wVUed6DmgIDCPBHo7UsRF/4GDjHksOWWCQCRQWQ2WHW7ZG0MHAgtCoNLf6ZcXg5XpMyYHCEAAAhCAAAQgAAEIXDsCPtV57SpGhSAAAQjMLYGeZVVcdprbklIwCNQJFIU2aYs6HI91Hrx6ql1PxjkEroZAsoh/Wj0zy6od266meOQKgfMQ6KmzL5PKp+d7HlnEhcCVETjdGV9ZUcgYAucjQJ97Pl7Eni8CsxsvYLAyXy1PaSAAAQhAAAIQgAAEIDDXBKrFJiY557qdKBwEIHC9CIQ5+r6J+nLBdHbTR9eLJ7WBAAQgcCECmfperfXT+16IH4kgAAEIQAACy0YgDBmCtXacRWMMsWwqQH3HI4DByniciAUBCEAAAhCAAAQgAAEIxMXSYLQSJut5OQ+lgAAEIDBLAr3pzT7rlVkWgbwgcCkCYaeVS0kgMQSumkCvJ77qkpA/BEYR8Me1epzCyv/q/pxDAAIQgMCUCMheJYhmDDElwoi9BgQwWLkGjUgVIAABCEAAAhCAAAQgMAsC9eXRzMr/ZpE3eUAAAhCAQHyr3z+jAhAILCQBjSbqI4qFrAiFXiIC4fNVSX31SSA2WUmAcLhYBOiCF6u9KC0EIAABCEBgCQhgsLIEjUwVIQABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAwDwRwGBlnlqDskAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBCRAIH6BgS6AJkEQEBCAAAQhAAALTIoDByrTIIhcCEIAABCAAAQhAAAIQgAAE5pQA346e04ahWBCAAAQgAAEIQAACEyZQGq1MWCjiIAABCEBgLALhS2y9f8ZKQyQILBsBDFaWrcWpLwQgAAEIQAACEIAABCAAgSUnoJdMs+RN06IIs0dLToXqQwACEIAABCAAAQhAAAIQgAAEIDBpAoUx5zBppsi7XgQwWLle7UltIAABCEAAAhCAAAQgAAEIQGAogazPUGVoNAIgAAEIQGBiBJienxhKBEEAAhCAAASWkwAbZC5nu1NrCEBgaQhgsLI0TU1FIQABCEAAAhCAAAQgAAEIQMDCzirMeKIJEIAABGZBoDJWUbebGe+WzgI6eUAAAhCAAASuAYEwhojjh2tQHaoAAQhAAAIjCGCwMgIOQRCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMDFCWjByf8kpTJiubhIUkIAAhCAAAQgcE0J1McMPm4o4jsHfn5Nq0+1IAABCCwlAQxWlrLZqTQEIAABCEAAAhCAAAQgAAEIQAACEIAABGZMgMWmGQMnOwhAAAIQgMDiE8BIZfF+qSwQAAAgAElEQVTbkBpAAAIQGEUAg5VRdAiDAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEJg4AQxWJo4UgRCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACowhgsDKKDmEQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhMngMHKxJEiEAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEBgFAEMVkbRIQwCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYOIEMFiZOFIEQgACEIAABCAAAQhAAAIQgAAEIAABCEAAAv0Eiv5TziAAAQhAAAIQgAAEIAABCEBg6QlgsLL0KgAACEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgMFsCGKzMlje5QQACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgaUngMHK0qsAACAAAQhAAAIQgAAEIAABCEAAAhBYJAKZmemPHwQWi4A+CeSfBXJ3sWpAaSEAAQgsPoHYFzOQWPympAYQgAAEIACBSRGojQv8tHpqc49J5VeTg8FKDQinEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAwLQIVNOe08oAuRCAAAQgAAEIQAACEIAABCAwCQJZ+drBNJ/iMFiZREMhAwIQgAAEIAABCEAAAhCAAAQgAAEIzJjAlF9ymnFtyO5aE8h8erNge6Br3dBUDgIQgAAEIAABCEAAAhC4TgT8SW6adcJgZZp0kQ0BCEAAAhCAAAQgAAEIQAACEIAABCAAAQgknwMCBgQgAAEIQAACEIAABCAAAQhAoCSAwQqaAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEyRADurTBEuoiEAAQhAAAIQgAAEIAABCCwsAQxWFrbpKDgEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhBYTAIYrCxmu1FqCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgsLAEMFhZ2Kaj4BCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQGAxCWCwspjtRqkhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIDAwhLAYGVhm46CQwACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgcUkgMHKYrYbpYYABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAILSwCDlYVtOgoOAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEFpMABiuL2W6UGgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCCwsAQxWFrbpKDgEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhBYTAIYrCxmu1FqCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgsLAEMFhZ2Kaj4BCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQGAxCWCwspjtRqkhAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIDAwhLAYGVhm46CQwACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgcUkgMHKYrYbpYYABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAILSwCDlYVtOgoOAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEFpMABiuL2W6UGgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCCwsAQxWFrbpKDgEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhMhEA2vpRi/KjEhAAEIAABCEAAAhCAAARGEMBgZQQcgiAAgckT4IF+8kzHkijw/jdWAiJBAAJTI0BHODW0sxGsBuzGTnU2OZILBCAAgfkmcMkbG2PU+W5eSgeBSREozM5hCzCpXJdbziW756WFlyiq36KKxA9FXlrNuAYVz+iIJ9WK3jlMSh5yIHBlBBgsXBl6MoYABPoINPvO5vJEHWb6VHC1hfTue35KdLU8ppa7g1YGY8CeipZ4GWL+U8ljagDnU7AY+t/CWMu5HjjSMfTRo16t66QFPSv/0gJNoR6OqrCuZfG/NMvlOHYKUwA8CKCym1FWg7LH75wEXD2UrGq76qAmLI1ca+QRQTUhnJ5FwFnWEHuyvuBwopUWGavoT3eyhkcNTaqTUpTC9VuYu10sL87CEpB+DtHjha0TBV8AAlI8/5MC+l8seug34zH6uQDtuexFdIVFWaelCUU1AB6HsdpjnHjTKu2Cy3V1VjVAefnGjKo4aGrl8sKRUCqpc8jOVtlUv+kmHNxAN0WlCMKl+Tq614G4xvcU2BQuejg+O2LOmEA5+kov+lJdXYHdVbH6FVkh/T4zLjrZQQACS0dgQWbR047zattofkpytRyWIvcBd2Ta//It7wzdvbzEGUrIFrHUUuT4MBoPzyR2wWr2LhlNMJSTDGfmtXARBOcsQOPEWbiKU+CZEqjrWP08KcyIoCQWh6MI9DqvU7FOd5spcB2n52ny0ynTUI4hAAEIXA8C3oG6m9Sq3j16l1n3T5JwCIGrI4BiXh17cp44gSHqPMR74tkvg0BYTrKVnaa7k5SNLAhMmoD0NOpqqrLp8aSzRB4ELkUgmKgNkDDg+a0W6+wYtQScQmBeCNAnz0tLnLscc7DDirTndPd3yneQkp1Odi4AFxGpLC+Z7bnKuLSRBTkqgZy0rWbVBiHf2Ni0+SU1MbZl2nYLwbRP8YJGLFAPkNCOsPuqM6pJL9E4ZdLyX+WnPQZ0tiDWkaOoxDCnmEDq89JJn8cYMi8RJSnGJaRcaVIn5tRUGOnLNajaaK4jK6jAlEgtcnrqANPc0vDUf8mPheoUmj6PgTF61ILRoifo7aziAxYPKRP0n/WEcASBKRFA5aYEFrFnE9Bd+4z+82whxIDAFRKQ/vqPztRJ4C4ogVSdvQpRrdFuB4I7PwQGKeyAZ7Z6gVHmOhHOZ0YgUb7kcGbZkxEELkRglNEKinwhpCSaTwI+LYFaz2f7jFGqOTBYUSldk8qj/rMYLM9eQK9qF1Q+iRr0c/9hYof5D5KF33gE6k1bZ6wF704UpTD9aVp06AL4ID0ZryhVLIlQnuli+9D8qlSLf+D67zWpt4X7n8v1BlaiRdh1sg4hlNsr4a4+sTNo5fNcZKYfOZbRryGd+k9Lrelya6iPAi/a6C48trFO9efXkF+7nv/CuaF+XqtEkaNXoa+EqJMIqqFPIulEgRcFOoqQqOq38FRDLURJNXK68tSx9HMa9EKmV/1PUjHtRpScVkxU+7r/VRd7kfN3HYuX6YiqjHPdpiOCrlnoALy15PrxiGwIggAEIHCtCMR+T13ooJ93i2eFD0qLHwSmQKB3t9eRn7mijpehpxovNrEgMCUCUkT/1ZXyfCrtUnAhMCMCrrzuKluUdkbwyWaSBLzvdXeSspEFgfMQSLtTpRvVpXpcd0fFHyXnPOUjLgSmQSDV4WnIR+ZMCVyJwYrrUNnX9fd4OtNfGSeGeRR3HVFcM3Z57n2WO278NDsdp+dn5TFv4b5Qk5br7EWbNPZ0j52tuyG3zKxtZsdmdlKUBiQyIlG5VzOz1WELmn1Czl9u6ceJmR0WZocxD+XZzMxWzKw1yljm/NldWYr0OtCx/9ULNC5Oj+euy8lqHrVTjzY/7sACZiYTBF1HCg7XzsB481ONUJKsvH6OzOxIBhWx/DIE0DXkdZlIqSMPXbP+p+tWx7rRKD9dPwtrhODtrY9W139uvxLuSXn4HFLd1EDX14CUdUljnRfRXC+9ZiVberloP/Xp0hH1udIXuaqLdEU6I91RvRaxbgPboqYE3oZy/ed+fu6uJ5XrfyHMAzwi7kAC42HqxVI79M5cZM+nF54PiugJcCEAAQgsF4FeNzm43meFD06FLwSmQqC8l0spUcypAEbobAhIfaXM+qHOEQTOYhDwvtfdxSg1pYRAIJCqbXoMHghcJQHpoo8JVI70uK6nHneQ/1XWgbwhcF4CdR0+b3rizxWBKzNYUX/pfeagxSjXs2BokSy06gFML7L6wrHL8fjj0PV807iD/DxcYSqjFlrzesTzZOwCZ+yKlRYEtTCo4utPxVZ95sH4YhBCx6zFyw+F2Q/HhX39w0d7f9y1rNO1G1nHXtzatpsbTVtrlnWZBNagbzHPrw8L+/UPx9Y5+miN7rFtNnN7fnvX7q43bUPwFunnQNX+WXn9qK6+CKxgr3sSNdRwUPsMqrrHc9fjKI9gtJJexx44565YqD6+qK7rSE2vjtNVoF7feamS2lPlftc1++ZjYX94e2Anhx/NOie2tdq0l3f27M5aIxgFVJ3xJSojVspPRl4Hhdm3B4X97rv3dmSZrXSO7dZqZk/3tm13oxWMzS6R1RUidsuUWISidz8q8vJ6Kq+f/trJT+0hX7/mLloJyXLW4u3XsRt2XFTuVaVTHT4WZm+6hf321bG9OTqxbvvYtu3Enu5u2p2dTdtslPvVXFUZp5lvqS+98ZC3rffHdX1RuPzU/8jtFmZ5dnm9mmYd50W2rr/+KzOWTFBjgA71J/5+zYZ0MY63h4d7UvkrnofPS50px2ITkH75b6DueiAuBK6KgHeC6ju75U5z8lIfWf/RR9aJcH7VBLyPTdS4KpL70fdWSDiYdwJRWet6jQ7Pe8Mtcfm8o43PX05C3h4k/UWHnQzuXBKo9b0qIzo7ly21XIWqK6EPDgZQ0BpRumFwPWmVxDvmyoMDCMwngXQutyqhXwNDFbyKycEcEJi5wYr0Q4qjRarwV5Q7V7TkCoh3gFGBtEDc1m7rXbOGFgS1SpOZdWS0Endh13n4FMM5gLqejkqiOOq05WpBqNUxW/NVCS/rKAFzEibO2qVEi4KHJ11rtztht5Cd1VbgJqOVebtexVx60i7M9q2wrw9O7B9+/4198+7Iuscndq9Z2Hr+1NZaN2ylmVXGA96uF62P6+ZHM/vjQWH/7de/t/bH95a1D+3GatPW11ZsZ2XbNhoXzeEKlCKF0i0XOMN1pXZXNeLgRHqiqB7dSzpuTQfFy9xIRdevDKTy8jp22cprUDoPv0pXZRMT/WQ4pevnXbuwvN2xtSy37ZU81GfmnWgs0ykngellV7nfdQr73ftD+/vf/9E+vH5lefvY7t3Yshvrq3ajtWOrqoAaQYku+NN1oz/1M9rJ5YMV9pv3Hfubf/2N7XfN1juH9mxnzTZaT2xtdddajZ7BzwWzvMJk/RorQxVdT2Idbg/Sed2filLfw/VVx5u01XkrEvrFyHn/uLCPJxaM9rZbmW1FK6r+Ep43h9nG1zV2YKWB0z/+4Tv7/bt3dnJ4YHt2bCs/emFbG2u23pibq2yicPy6kVC/ZsVD9z39dYoijEGkQ3kePzJVlNeOiDR0nFhIqN0Xqe0nCvMywrzvCzsk9Xb7URvoVp93y2tb/ZZ+3la65jtxfKoxonZh03hKaeo7i12meKS97gTUE5y+eqVniWoGCDrnGr/u+rAg9YsKGiY3/T4U+1BpdKq/qpHO/RG60mF56ld5xHMcCMyIgFTPdVV66z/5exjq6VRwF4GAP1u4Xkt/1ffGIWx/FRQpUfDaaX9cziAwaQKx0w0LpVG2661c/Vx/EzWNITgQmA8C0lUf96pE6m/r+iv/1G8+Sk4pIFASqMYNsaP157WUj4KqfljK7CfpcZqAYwhMlUBh+q/c1d6VsZeh1FJ6rZBKn+PLxszT9jjN+9HMV4E0wa9FTb2B//6osIN2YWtW2G4jt73VLEzyS4GkYHpT/32Md3TYtpVmbhubuTXzLCwOvjss7LBdhEXlfMwd2SU3/E7r9KkVhhBFCYrCmp2ubXbb9nBnzdYasX8eJMPlX7Hr9ZQr3m8Lsz98LOy7797Y4eGRrTabYYeSx1ur1tIqy6CfC1HYkCiDkk3CL2CPBgMq/7ujtv3hhzf2u+/fWfvwyA5XCvv84Z496NyoBn+XLaby9Jv1sRX29qhj//b193ay/96yk4+2t96yDy+fW0cr0bMGchmoSdudZKXhxYduYW+OzY67RVhY72rXlVgtOelPi+/n+SXZhWQy9Gp1O2GXhL2tpm3ERcDzyLyKuKp2WJCMu5R8/aFrv3n12uzwo+2tNO3x3g27e2PdNmSEcxUFrOdZA6/y6++oa/bDwUm4dl5/820wWGkfn9j7Z2070YJ4vM1fVqVdTZzbDx8O7de//8Y+dApbbx9a8/aOfX7vrrVvFlYsksFXnXN6Hj9btl+YvWoXdnIs48oiGBKsFx27s9my9eQuWzVRdZAKO/tY/ZM+76T74rf7XfvtNz/Yh+O27a617PHOpj2/tRYMP5WlBmZn/tRYFyzLmbLHjKA6qb99d2T2h+9/sH///gc72n9v77Jj+/LRfTtpF1bo+29Rn6+4uGPWqj9aHbPfZ4KhU/xslsY7+93C3h+aHbULO+6YHUun2idhV6xGnlujkZs+ONXSJ/HyzNabuW2vZbbRzMKuRfJf6M9u9WOb6ZnugWqPMF5ql/q4327bquXWKjLbbGZ2cysLfGVUpGv+bbewg0OztnZ+M7ONvLCdVsO2V9Q2Y16DM60lmc0ngV5vrb5B+pX2ERqbuTGU305O9YN+Az4VMJ81plTXgICeG+KOjdJZN7bUCyXqS6XDUkv9ScP1J/3VfUqGffrTIpX8UdtroA8LWIVKb91QOOl/VR3ppf/pOc91V8eus3J7PfgCQqDIC01A/Wvoe6XDOo6fVvU+2PVYOqtHKemw+mHXYRlbp7/aaRrEMQQmSkC62817+pt+/t3HD8pQ/avGCytZqbc+ZpDrxxMtGMIgMAaBoL+x3w3zB3rRKI55ldyf49Snqu9Vn+s74qZzNZJDvzsGcKJMhEDYaT9+rcLHwD5u0Ln3vWn/qmONGzQXIdf1WP7hhwI7CdyZEnDFc7fX7/q4WOMKLTuFca+Oo/7OtJhkdikCaruZ/XRD1g1dOxV8fVDYr//wnX379p3truT2fHfTVu7dso3wun+5aKBPwfzuoGu/+/qjff/N721jrWmPnzyxnZtNOzgu7Fe/fWWvPhwEo5Us0zKOlLWnsCMrFt6AlYGMxy+NZfrSFIXlhT5B07bVzpH9/+y9Z5ccN9Im+qTP8qZ904oyo5l93e695/7/D/fTnru7r5mRNBIl0bQtb7PS454nMtFdXeymKJEckWLlOVXpgEAgEIgEEIGIXSuH86fPsNf04ZXhH26k/8Bu9AeHHXWQKvx/P17g6Y8/YT4PUK94+L8f7aP25X002vVXMWdjrR//sNFUDiUquULgiIETFz8tF5njIXc95FmO1MqQmgaycrH0bdFjfk0vnsmnEUwkpofEiGAYGTLLA/i74pl1An341xTcNFihscrLhcJfX77EIkoR5wZy0yl28t/Vfzb5QbrN5sOCBusGLgZyuGmIah7jqFnDvzx5DKdmXhl46N5X5HzbVnx3baD5gbxAjyFn8xz/+6dT/M9vv4cVBbjfquLfntxH5euv4PvXHn7eHQZvB4n46zqkBpBYLmKLvOwCKkOYm8gMW5QN74rqbEv+hM8U6WZilZuIYcJUScFnH+2yLqmkj5tcSwX3SCn8vb/EYDAQg0AuCO45Fv7Hk8c4ahaf2Zu5NKw3PxMD0jakcYxS+M+TIf7f//m/EBsWdqsu/ul4B61/+Rqtqi0DszeC/LZIvVEhr09EZSzrlVn87ltITQeZ6SBVOVJlIlOG8PLroXy4b9c5R2PJZ/KNUQC9edGLWJ9huyYKZ6M5ZoslFqsQqyhCGIZQHItYBmzLlJ9vG2hWfew2GzjqNLHf8NH2DNRNoOkUxit6MVqXuT2/hgJmadxXhgN8NlZ4PuijP5/BjCLUTRv3uh3885f7qFuGtN0UCj9MUpxf9LGYLcVQbcctwp492u3gqOX9mhHpa5DbvvrDU4ACYU3xT9lA7z40TgxBw/zCEK1mGmiW3sluiO51IaOvbyT4w1NwW8HfgQJkNfl209Cv5NcVlHjVCzMgyYEso1F0sVDkWQaqLlCDgSrxLZVPvwPq2yK3FBC+JP9yDE/+FaNhKAQxEGXFZg7tJZSjeCqYxEDYMuCXC/ccZ/G3PbYU+D0oIGOFNf6l/OWaxSqlR2UlHqqJFxfryb++aaDmAHXbQLVcwOdQYTtc+D1ab1umHj9wrZe6AXrnXabctAFw7YpCmjKYSlFXATULqNpAxTLEeEUrMbYyeMtLvwcFtL5A8y/Xcjhvi/OSh7nhqgzb7BsGKiZ5lzxchBenERZ5W8tfff496rIt849NAc7D9PKAXFM3UOo49FrDinzLuVtW6MTIj5StZFdPcVNWIX99yxADwlv5lcBvffHHpu+2dr8nBQo9AVmPMpnjCo6NqS/hGnuoFJwUMm/j3M01DXE+IRhv+fX3bLg3LluP9d44w9skJBPReGIChRejEN+eXOJyMsFR3UPDBrKD7lVYBS7WcuL1916G738+xWxwjnbNg793CBM2hiHwY3+I89EMqzSHYVgAYzNsSslSaF4Zs4ixQTGAuFaDkVv1cX1tUEmU5zDyFJUswrGr8OcHR2hWPThu4Z6fuXSOD0k+Eyf+9GBqnlIBM8MgyBBlFrLExPl4jiBOJN2HgbvGWrfFmuAxDPEUwUEgBRE/svQOkRmFh4jrHL/tKkeODDSvKLhCJlFkKbeC3I5g5Dly00WqjMITyW8r5nfLRcrqieEyAy7mS/xw0cckCBFlJpTlSNgt6T80vdWHeDvi/dozecceRe4i5LsP9iE3WaKaRYj22njy4B46uQfPKgbp1znX236zrOtU/6grjQFryIHcOFI4n62wyF2YeYhxlKA/WyBIEqS+KwO3fxRub1qOUJQW1Ny9QiMAy0NmuYCVIacBmGEXodXK1tV1flP4m+l0fs1nmeUANocGJpTKxCgqV6b0n9dzzSbkD+Fe8+eVLblwPp9yoXuSAM8nM7w4u8RisYRjGLjvO/ji6BAHzXo5IS2+Qq/2pTerH8sibcVAJlToBQkmqYHEMGCGKQaLAMPpDFW3gwotZl5zkK/5Y6r132uy3PlKU4YJNKw7E9/ygniwXilDK5lmwSfk1yyBMi0owxRcb8n60TwijXiQPrzmQFr4RlGucDwU48VwgovpEuMgQpyk4slL2ukq9GEO0yhazjYU3GmA570xGg6wW3Fx3Krhs702vjraheMU45PrMQ5Lvj50m/HMN9dcfZ3mU7siD3JyM0oVfh5O8XcxqJ7CjlboOI7Q6Umyj6pV8CsNqn8czvDivI/ZZAE2TddK4eAAe6066JuFE/2blP/UqLqt7xtRoDRWoVzg2FbLhv4sRX88xSxYwc1iHFQsfHW0g2a1Bs80r3lLCxYWpjv1GxW8TbSlwG+nAPmV42MqmuZQGAYKvdkKF8MJZqsIQZggDGNwQ4lLYxXHRNO3sd+q46DVwH6jirZvoFJ6XNl+i357W2xz/joK6HFYEcIUGMUKvXmOi+kM00WAeUCD4VQ2yFiGDbdcqCfv7rfr2GtWsVMz0bAL45VfV/o29ZYCb08BPR/kuFXk7wq4GMcYzpeYLFaYrULEcSybrBiO2TNytKsOdupV7DcbOGw30KkUhu6lE8u3R2oLYUuBN6SA5l/OpSapwmCpcDFZYDRbYEr5G6fIuL4PA7ZhwDdSHLSqMnbYbdWx03BlgwbHD7es/r8hFttkWwr8NgpwNYbrcZS/NLQaJsD5NMJwtsR0vsJsESGKE+QZQzqbqJoZWp6JnUYFh9029lsNtCo0wtpuMvptLbDN9aYUWF/zI9/KWgP5VimMQsjcbbRYYbTkZrmVbJZL0kyMBW3Tgue4siGuW/Ww16hip1lBt+6gzg1ypTHsm+KyTbelwLukgObtYnW81JOUY+LeLEdvOsE4COClCboe18qbONppil5BDF23i7TvsjneG6z3a7BScpHEpSwt+WjpdLlSeDme43QwxmQ2R8fpAoYD07QLYwQFBAAmCng2HOFFfwC1WKBiKtgwZOFAxTHiYIloMUfEbVw0WDH0kFWzL9duqbKhBwkbOWzk3K3N0YP48cjFlwfVYQZNuGkGy59EwyrORp7BYtiMPMYqs5BnmSwIX3mRKIxkf0Ft/wbtx+J4vKOOQzB68Y9UMeULFcPI+Eth5AZUZkOVu9dZ/I2i129eeVni+s5PGuMCsEahaAkUCjwq77QCr3yh0709OteQCJoEEb4olYRU8RZ7Bd++pN8LAmtI9k/jCPEqQLhYiTUt+0fpYqVEjZYqBpRBhbGF3DCF/tI9DAOWwYFMWpr4kFTsZWVn0JWTnREKWRJAZSGCmiP9hyFT7nYBcd0GAkYaYoM59TMm2Eiui34XZ4LWilyVp1DsN/S4RCM28XmeQGV5Qbb3gYeu5+tgM80t7/n4Kjvfy4/taYryQBmlKpsi7x3ouAhel0fayzWNA00DBj8AUr6CMtiHPsZDc8JN3FkXfk2otJmEGYbLBPN5LAYrtSxDnHJaUFb/9qa6CfAN7gSTDGJIaUEh4TcpM2DwnCYwy91It4Eivpxgc4FoQC1TFKJqGWhVXFEm/RoFOz8puhUbyPsAACAASURBVO7jRCGJGDovQd2zUfMscTt9O9VuYkac5CfGcYztZ5ZGKppxr3mLTz7Wg/TiQYU06T+GAj15/HA+wc8XA4ynUyxXIZKUhikGbMeBY9uwbBp5cQySIS9/WZ4jyHMwZM00jzB1TISLhnj/+GynAzh22c9uUozcyDbjAsssoueGHI6Ro2kb6Jbe7Uo0f/2JjcjjZpHlww/7RNS18nUcK/SDCP15gOF8BS8KUKv74m2P/MzqMT37/OU0QH8aYDlfinGzRwdsKodvvQnnf9g02WL3/ikgcq8shrv79cKnzH0GGV5eDtDrDxGsYvjZCo+bLnbrdXheHVRAyWR7E82PsP9tVmF7/+FSQMtK/R2hp6nLBDgbFWFbL8dTjCcTrFYR4jhBElOy0jOYAcc24dkm2vUq9loNHO908Hi3g+OGhY5bhFuj5NS/D5cKW8w+dAqQT28ThbIUUo7DOATmBqqXU4UX/QBnwyGG8zlWqxBRSMPhBHm5IYre7TzHxIvJDN1RBQftJu7vdfB4p4o910B9zVvFh06bLX4fGwVucrMex2tjq36ucDpWOO1PcT6cYDpfiIfGMIqQlXNQuu+3aXTlOeKdsVtf4mgnwePdJu63bOx6xlWYoK38/dj44+PCl/zLH8e7soF1qfByGOO8P8BoNsNiuSrGD1FShmA3YZo0WklxMq2g05hhr1HHo4M9POzWcFAz0VoLFfRxUWOL7cdGAT0G1mtpPaVwNlN42Z/hYjTGZDrHchmIsXaSZKKzoNE2+df3TJG/e+MFjna6Elr+XtvHnk+DrCLslXVT3H9s5Nni+wFSQPMs520B1/9oYLVCYaQ9DtCbzDBbLrCkXigKEScxspSpuYxvwrEc2XRQ8z2Zvx20a7i308JRu45Dyl96vNI6k9sG3h8gTbYoffwUIF+TS/njmIJOMWg/wHWJ5yOFFxcDXAwGmK9C+MkKx3UPyHPs7DRQuXWG+PHT5I9ag/dnsEIuojKUxgXc4W8UuwbpLu1soXDKncSLSNxOeZUG6vW2LGhRD0xFAHcLnIcKZ9MFpmGEmmmhVqmiUfHElbBvWWhWKljWU7g0WCl3YhcNxcJpxFJ4zKCRCkO7hKmJNM6QJzFMo3Cx77vc+QVQv8DwP1QK0ShBDBOIfJ6JK6xK5qLBtI4r97JQzGJ43CWcf+m9qD1ES1doQO6CUxbzyknDvwUHguKkk4szPHu2gZ12E/PJWIwLOGltN5twnTfYV3EbXiy7fM4yeHlbsk2c17KVap/NXGL28AqswulHoWxnjbSBRJH6Dcq+WfAmWuB+dF2HdbKKeakwcWElI9huovwKtNc8WAf+hnB+DX1fU7LwAYuka1hay7bqdeSGDbruzsRghbzP3QxsmmLJIjeK8ByJMhEEIbIsF0txw0jhmBzEKDgWxUihZDVooMDsYvxFYwV6WLHkV/F9WJuKvBvtskGQdVrddi0F/QLjrefbAH9NqxtIFI9pbKPtLNh/XBvNehUVjx5WHNR8C41qBY5lSTpdzJ1FXBf2665eB5jvXve+LEkn08ZGNFaRVi5DWxHnN8ObkH455VV5JWBBUeyfSrmq7ZpugJNUpRwsyriV72/kWSNlmf0u9G5k+4W0a1Bfe0kwxJE/CWdDD0yWj9Qu+hC9P+UljQlonXI38HltKdcvmV8vJFZchoSpoFmrwogyNCoWWrWahHrjTmYpS9ezLFzjy0WiXqbwH2djpJMBDmouPj/cw1GHjvpZBo0juCNkDeMNhDUsbXzx/SjFZNCHl4Z4vNvCvf2uWN4TQgFFI7MG87pqwsZMQYOqIiQca1rk1jnXkr/TS8K/wurGzTst5opXSH8Opn+eK/zX6Rx/f3GG3ngK5KksKLueiarno+r78D0PrkensUqUJ9wtSWOVOMkQxSniOIWKgDBPsUwyxHRjrw06y6HFVd3KAT29N4xzhR8upxgsFqjbwGetCtqHO8Jfv7rW6w20fr0JaB2RzXfv6n6z/Ksy2UvJU+tHkVgMmtmHZeypME2BeQqscgupwUm6jXq9LuMn3xMbvDItMF4m4nqd30eOCSu1CtqtJlr1yiulrZe8vf60KUDO409/P3itF+/7Cvipn+PbF5c4vehjNp2LkXE1W8FJU8xWGXbZxzdJqHn9lRebCbf3Wwr8dgqQZ7UXIC56Xirgvy5z/HRyifPBCPPlElmayBzNNCwYrivG7KlSCNIMWZjiYj7C8+EcO8M5uKsvPt6FsVNB2zXglPyrx9+/HdNtzk+VAmQhLQa1WCQtyLtc1OQaE+XtiN5+5wr//myJH09OMZyMkChuZCrmsxbnxaW3QuZZpgr98Rwvx1M0+2Pcn8yxio6g9lpw68W4+/0tqn2qrfmp15uczOV4Pfsr7rSxykApfNPP8cPLHl6e9TBdrJBycw33i9gmTJtrfPQqXfymS8rfOdzBCu3hCsNFF9G9Duz9Gmp2sVuaMngrfz91vnu7+t8mfzVEjh/0PPjZimsRMZ6enKJ3eYFUNoUaMBXXD20Y5dq+rB4pA9PpCi+nc9SsAS4XEZbRIbDfgt8w4XMdXxeyPW8p8J4oQN4mD1PxT/n7w1Thu5M5fn7+UsI5J/RqpXIJ32zYHP8WnqXDHJiHMfqrKV6MOP5d4slhgNXxDqy9Jjq+UcjdQqX1nrDfgv0UKUCe1UaCg3Lc+1M/xMvLES76E0xmS+R5ApN7Bg0lG1sN8eJqyKbcIM2RxTlUEMOaLNAeOTiezPHFQRfpwS6clg3Tfk2YoE+R6Ns6vx8K0LagnNhxTsfRMQ1VaEBIG4MhnV1MFP7rOcfElxhPJ+LZ34sXSEIXO42qeDHWYxSZLK5PFN8P1luob0mB9zu3pmLSLEJSiKAEMFPA2SSWRaqUu64cF9VaDZVKVdJSacCBANN992yO2SpALpbVlijnOCCl+7+Dho0/P3qIo/0IUc6ZGT2slF4DxP0Jd/MbyA0LLGeSmHh2MUbvYgDLpp+WFK1WHQ+P9tCtexLPigYrhsqKjiDKniIkEFVoXhqjiwztZh02g7m9xcFOUmJaLqv8RnjMVgC7FRu+5uCdBgpNF/jTw3tw8xSrMESzWsUXh100qgzZ8SuPq15+M99rULlaPLqZ4/X11m8JtyiSTzigo+EKxZROcRPqrXdvkHQziZRJIyYp/RoLwufdZvpby918+JsybQL59fcsljhTqVZ3DRx36gg/ewwOQlJ6UKF3o4w9j3Rl5YoQW6nlIoSDeZLjp5+fYzaZF146VIJuu4HDnZYYPtETEXmt0M8X3lZYJruim0bizn6/6qNV8+BohfqNamgMbzzUDX87sXUj8Mxjnbb6Wfnq9af1jGVKhtIhDBOy62inbuLz4wOEKeDGDRzVHDw56qJZdW7f5fz6Al/7VlfrtYn0y1tQ16/Wz2I/xAeyCkVPKyVpuTC1nvAtrzXZ5bxWhl4sI0MUPPIWBd1FoF9TkV+T9jWoEhX2GAm7xNA1hg1luOKLKTc4jCroWxTHf02h1wC94xVzizwH0HWBzw53EAaPMFyE2K86eLLXQKfZFKOH20BoC+QlgNOZwv/64TmS4Tm+Ouhip9nAbrsma/NcdhdnZbcBKWsgdS5DV1Bp9c1pHxcvnqGhYnjWI3S6XVSdora/RGpSZPPHoq+8AJU0ZJpfgnUHyr/7Y+JOmrENaP19vlL49mSFn857GM8WUKYJ17bRqbk47DZx0GXYjyq4m8H3i9FCkirxJpckKVZJhvkywmS2wGo2Es9pB40q9rs7qJbebUgrTS9NX47D6OWuHyr87cUZXvYH2K97qD46xFcHOxIT/C5i3Up/PtTH+rV+ps8akfJeJ914rFP/g84svfi6s21IG9kxlSgs4wRxrmBYNqy8MO7d3+nC5ZhSxqgKQQIJHRDGKTix92wb7XYL7UZDQnLxW/v71u8fRMZtMb+KAuQ1zf/kOU60qQylx6WXgcL35wG+PzlHb7pEEMbIDBeGYyFBhsSwZU7D/BrGrYVvGe9Wsmwfvh0FyHP8htHocUEPUxnwfS/H356doT8cI1itxGDStmxUfRfVig/P9WWHXprn4h6dO/iiVYgwz9GbR8ifnQAJw64e4ovDOprlTr0tC79dW21zr1GAjFvORzT/ctxKY5X//XSE7573sAgCcBZLj3Y0+q64BQ97fkV2+YdxLB7wViE3WqWYrGIsX14gj0JYyT3UHu2h7RmolPPstdK3l1sKvBMK6HmXKEsBDJXC94Mc//70FOe9EYKAxio5LNOA5zmo1SrgRiF6bMwpf5MUQRghWkUIkwy9+QrJTy+RBDM4eIDH+w3YjvHaecA7qcgWyB+eAnp8uv4d5zP+0tJd/2mg8B/P5vjbywsMJ1MxzLZMSzYJVKgb8DxYjicbrOhJNkpjBNESaRRikSb4/uUFIhrIBodo/emeKPy5RsLf9thS4H1RgPKX3tk4Z/thlOO/Xozx81kf0/FcPJWThz3HQa3iiW7Lth3kucIqjrAMFwglVFuK/mKF5OU5osUMTv4QXxx04FcNUWe9L9y3cD9NClDucq1hqhSengX462kfTy/GWK5icRzAhXluUqxWXPieC9dx4DoWTLuIxBAliaxHBFGMJE0wizMsT3sYjydYTedo/NOXsOrFOJtb7Nbl/qdJ8W2t3w8FCmtq8pfM5crxBNduOac7C4Efeyt88+IMZ6M5lqsIDNRu2BaSNERiWshEV7OG3ZZZ14jx4V6+P4OVNQYQRYC46VEShmAwnWMerJCrHBXXQrXiwa/QLKRgQFpIMVzB89NzhEEgu13oCWW/XUPTAeow4LsKtf0aIlUTRcMVictFCcISJaIJpAbwcqkwnnnoMSQOUthGhpZv4vO9Jp7sWPAkdEWxe1ZglfhrBaGdA36Wo1ktLAivyisv1qq7+eqV+0L9tJFj4/aVTHzASm2m27zfyMjX/Hi0YOCrPQv7zmPZqU23zPeaDhpOsSvoF8DchMrExKXEZz0vH20e+hnTrafdTPcm96JMfUuNNyf9m7jchZfgLtr+oha66LvSv0kdfm2adzX5Is5isGICx3UTVbsjfYfOVGjzlaVFkxI/PmONYwtYmIzvbaJ/bmOWx2IcxuBd+7UKvj7cw4ODCiyGKGGG0gBC7CLKa/YdW+WoWqbwW7lh7fVkKMh9O8PcRXydZx2yfnZXnrW0N5KW7vbZd+imcYf9ZM9Hw30AJ4vQcVAoeumd6R3w9Roa15fE+XV4v+7dNZSyqxa7q9YeF231hjBu5Lvu+lePN8Fc3YtbF03Zq+S3XJQ5rjK+2aLDFWTtteUWyHy0Bnbj5o4Mv+LxNezrq7uzv0mau3OT11waICoDj9tA/fP7WEQZmvw+VizQ88q6YxSBZBTGEpxkc1ceB3WDZYL+bAkEMYI4R5JzT2nR50nT12HJdBwo8kfjh0EMXMxW6M1DZHaGVaZErtyE9ypElrP+e6XW5Y7AV56/yYMrxigTbxS/Xscbr27cvElBb55GK0rmucL5OMfLXl9CJ2RxCM+xcdyu4/ODNj4/7KLTqKPGhWO7sMVlu9MMkAqVVNlglIVVVMUiaCNYNCXEW8OxcNSqo2pzP8/Ng9ViexTuEhVGMfCCuyqCBBXXRcBoUmsulTfJsElOga4famKuZ1q/LlFhMp3lltc3Ed640/n4+LV5+VInvpHwmiJ8rV9p7yqap0mfRQxZWEoTjhUVqr6HTr2OVs0XWc/xLI2+JoECY/wqlYOhuejF7mCni0ajfkV/XY5UZ73gjfptb//IFGDD81fwIHmC/EY+ojymN0nZETLK8fR8hGcXQ4zmCzGY4nYnk4Z/WblD+oq5/8j02tbtg6NAKbv4DeM4guGrRkrh+TDF05MeeoMxwmAJW2Wy4Hm008Zuq4pOvYpatQbLMBGlOWZRjMkyQG88w3CywGKxwngZ4efeWL6BtaoPt+VI2N/3tzjxwVF3i9A7poD+7spZi99yHExl6QoKJxHw3ekMT1+8wHwZQ2WJhMXsNGo46DTRrVXQqHqo1GpIc4VFnGIchOhNFxiNxljM54jSFKeDCZqug0algj/fb4jRN8dr22NLgXdDAXJxscpAVtbjBipLn08U/v6ij/5oJsYqSGM0XAcHOx3stRsif5uNuniCTbIc8yjBaEH5O8VgPMViFWMeRngxmKDmueL23+v6Mo/Ufejd1GEL5VOjwG38o+dZsmkjBb69TPDDyxNM50uoNIZn5Nip13DYaWO3UUeTilO/ity0JHztLIlxOZ2iNxhg1B8gSBmGcArfMmTO/Od7Lex7Bt7Ab/in1hzb+r4jClAG0zsQ5e+LBeUvPWFOJCywkcYScm2v08DRTgudqodGvQHH9sRgZRZFGC2X6E+n6A8nWAQRZqsIJ3mGuteHZ3uo2lWRv+8I3S2YLQWEAuRbzt+iBOj1xzg7vcB8HkJlGRriGbiBVrWDdq2CesVHxfNkbdBybBlzBGGCUUj5u0B/PMVkNEaYmRgsYnx/3sfhTgfmg10cVowrncj1qtu2EbYUeFcUKDToeiyh19AYRvtkpvDj+QTPLnq4HE4kegQ3E9qWJZ7JiQH7wfb4OCnwntaEyBIlUxnlBAvAQgGXU4XxfIkwpuspE77noOK7cNyCkTgZEy8sU4XheIIkTmAbChXHxH6rjpZjoCaKFQMdv1j41aTXA2QyMvWkhMXFNVpepXWg5pgwVApDRbCMFHUzwZFv4HPfBP2MML/+aY0GBS6f8Uyn78W5LFEXqBHYPK+/L0iymaK4Z7pb3t94xBse+lzCZl3XDz5eL5bvqHRnfGU6ptvvULViyQelWsZcftuPikZfo6bPm3it3/Oa6TZx3Uzzyv1VhkJDLYYRryS6+4HwxtrrK3Drba/f31YRcW6tE9xx1vnWgZdJ9Std91uS3AH07R/rRTS2tyi9K4WxEiETn7zsg7zhwIa/AAr8ELjcOUZpkbNHKThGio5j4EHVw+eMTW8VfYT1kV9Zsav7su8QB81vQoMy3Y3aaSLdeLh2o/Mw3Xpa/VxXaC3L5uV6Nv1u/ZnGm/hy8ksvRTQG2NuzYKMqz7xSwbterIb1W88aB33+JTi/VLbAuQJ2dSF0K3wLvFqCTnUN++YT3rEfsR0lDR+UiXVKgUq3bWUT3Xi+3mxreV/F5PVP1mHzmvho3np9znf3ltXWddPGbNdP3l05GhLLY5xQOvmqGAzzxp33lsh49ml2Ud3PCwuyomFE0VTu5J/EwGC5wjLlt8GWsCeZsqRNN78nulx91jTX8CgfevMc4yjHMjdQg4XUtMVYVMta5inZQ4O54gud5upFeaFpKqHFNp4VIws+3IS6CaVsnLVkGn+dcu2VfvTOz7oM1pVjkXkM9GcBhvOFxIol5ZuuhS/22/iXe7v4YrcG3ywMY2l8RJzZpoTDazEudIDMMZDUgajdBj3Q8svOHb6US5uHrjel91wB/RWNlkKkykRiOkgMR3a9Uc5pGX0LmGuwBMhj/cwMG5l0ufrMLDqJPheA1oHdfLNehE7FFDdTXUO57cVdMDRebBtRBNAYJWb4pRh5nopngFa9hk6tLp7JWArTLblgNc+QqcJjFL2G1X0Hezsd1CqFFLqB3zoCN16s4b29/INSgF9amkaRCYrG5xVl6BzAWQo8HeZ4enKJl70RxvNAYpR69TpMy0ISxQiXKyjjri/2H5Rs22p9GBQoZRdP/FHhH0LhgptKhlOcDkZYhhGsPEej6uLhXgdfPzzEUauCDo1oGUatXOSfpS4mUQ3PBy38eD7Ci6yPJMjQW4Tw+hPsNuvoeDvwq0WI1quxzIdBiS0WHxEFruQt5yElD1Pm0psVvQP9NMzx48UAw9kMyrDFK9p+o4Kvj/fxcL+Lvbor33zHL7/5mYdRUsXJtIOfPA8nhonpYol5FOBZbyxhHA9366hWDBmjbz/zHxGzfMioCu8W6128JA9zo0AvAp4NV3hxOcQ8TMTzX8118HCvjT89OMbDnQZ2fKBWNcTrJsNWTlMb/cDHi1YDP1creNEbIp6lGAUpnl5M0KnV0HX30Oo4svFhy8MfMmN8+Lhd8Q8nWNwYV67JL6jsnyn8/eISvfFExhSuY6LrOvjz4S6eHO7hsOmjYRlgRCtuPg2VhUnu4HRWwVPfQ5pkIn8XSYTT8Rz/+fxUPMw23dvnwB8+tbYYflAUKMcMxZSNN8WIgvKXBtuDFPh5FOBFb4DJPEKWZfBdG/e6TXx1/wCfH+2i4wI134BjFiGHZ5mNYVjF6bSLp/6lyN9gNsc0pPydoltvYLfiYXfX/oevZX5QtN8i884pQNkrXEzn+YYtu5Jty0Gz5uN4t4UH+10ctpto+y5qriHjYc9mlAwDCRSCzMMw9XAyr+GnXk3Ckc+DCKs4lPnbt6cXaDVraPpVWYPknK/oNe+8KluAnzAFyFN6vZaymHO585QhgHL8dD7C84s+RtM56Im82mjC9jxZp+UGAx1G6BMm30dd9fdksHKTJnqBa5YCF8MZFvSukiv43JXie6i6jii8uahAwTiMFM76C6wiTsIULIMeVWx0mlVUGeOaCru1GFZ6UKzPIpiNwljFZGiP0mjDNrn7nK4kcsDIwTAmdp7Bhy1hhihgNQx2Cn2sX1PhQ4UF0zE9f7+4qLYGgJeZNuYpCxA4pYcAwtU46LPG4+q85tqWHZaHLoK4aIVT+erGie+kjHK30Y2XazeER7oJLcvnGjeNb1GX63Q6PV3ma3yYh0o3TSeeNRyeeehzefvK6eZ7hgQq4zz+Ys4C1BVea3WSOqy13c0yCvx1HQiFvLmuPH0Fydc80OWzrfQ1YfOny9X4rNNHP3sN6F/1ar0sZtS8wGuNj0aKuAq+ipM/BU+VfF56PTCQw85zuHkGD5YYwBAeD11OeSsgWW+WQZjsPzyYTvMq63qVUwNghs2D3beEI8ZKZb/RdJPkt+Vbg6PryrNuD77mvcZJ12UdV4kERjqUSt31PGvg5fK2MnR7sgy+56HTafqs48P3TKvrtnnWcHj+5YOpipTCy1cY/HJO5tN46TPxJo34AdFK9TshyWqxrvEVGhqdO7PxxSv0KWXfOh4agDbWIF66tle0IaCrG53jHZ7L6knoo3cI9gYoLVfLevBEniR5yZOaP67zXE+waSjBSTYNTAaBEoMJhsozLRex6SIyPXmvv6ukIaukeZZtrPsd+wR3mEgYixy4nCkEcSaGM5ltIrZsxHaRhu3EvMRVw9J9S+MpbVzSr3gmwla/vuotTFJUvSTAWopXLsvvG407iIPIshKSzk18iIvGi8/1u1fgveUDwmU7RVBYJEpCHdLFpniZs03sNqp4crSPR/sVdIxihwLx0visk0foVfYDufYM5KIULHaWSbQ8vii9ZLH+bDNaorP8ERe75xFWqYIybaSmh8ytSHuy0fX3WpdPHPS1Pr9CDr4o6atlPMsV/Mq662vyKmGS9vrH+2vzyZvQ+Y55eWgY+sx3PIr8BZ6853uWv/7Tefh+vVzNG0Ij9pEoQpomMLIMjg3stZvoNOtwHfrmK42OVgrjyRQqz4U2VdvCfq2Kg2YFVVawLEMu+LdeiauH24tPgwLiF/CqN1/xGQ34I4W/n6/wnz+/xGWvL+76wXAqzQb293ZgOi5GowmSkDMPze2fBtW2tfx9KUB5KRxXsp2WpeRfGuydjTNcDKZYzBZixVKxDRy3G/jXx/fx5T0fO6YhG0F0LejBq03PhPSSWvNg2AcIohTjLEIYrXA5W+Lnix6Omj5qTh2mU3wHdf7teUuB30SBcrxBCcoxEMfANNp9cTkSz0AG15gQo1ur48vjPfw/fzrEXtUEvZtzfM0w1RwjtGygYwNdn5s39iW8avDsJVTmoD8P8N3LM3z18AE6B654udtK69/UWttMd1BAj2nJj/QQdDnPcTaYYDKdIUkUfNvAYbuBf/v8Ib66V8Oha8hGNQ2OPEwP1e0W0G66qDYY4jjFIA4RLQP0FyFe9Ec4rnvoVrpoloZXOv/2vKXAr6HADflXrh9wHYKhVLgp9WQY4OXZBdIkkTlnw/fxeK+Lf/v8AR50DTRRGJ7IuKOUwR0A7R0TNb8rqHz77CXiBTBPYnzz4hSf37uHw3oLDf9VL6O/Bvdt2i0FblLgei2NcpQG28NA4WVvjOl8gSzK4Fomdmoe/tvjY/zToy6OOU7QaydlZ2hawI4L7DRs+NUjpIaJc4YKmszQmwV4MRjjqOHioL6Dpm/I+upNPLZ3Wwr8NgpwzYubHRly9bP9LlarAC8HYzy5t4fHR3u4v+ujYxdriNSx6nU6yt9MGWhZQMNSaLkm6vUGlotdPLsYYZWmiLMEP1/0cW+3jXvtCtplGPPfhuk215YCJQWuFiFuUkTW0EodRC9VeHoZ4psXFzg5O0cQUjobqHgV3NvfhVOtixfBVRDCMNgLtsfHSoH3ZLBSfNxF0JXKElpB9RdK3FBGYYQsSQAzRcv3wV0Bogwura/7U4Xz3gAZRwaGCdf10KR71rovroLJclSq8CA/81gfHFN3ovmcz9d/ckczK8ZrK32mMD1h6nQlyCsYvCcqHGxzwYPpSv2MWBKu3+u8ctbI8YY6uHLQzoUTup4nzHU8uUNeds/fAHL7DWnLTks4MqAvkzHcihj06IFSmY5GQ8SfB/G16DWjXMgpH1+diBN/xE8MdMo6MwHpLh+zUhmkceBZrmX3h5K8pBHTuqrYccRr4iftV+LHNMTnrkO/k3AzZdp1st6VTz9nWo2X0EmMogpFO3mOHYBlvL4jaCwKqL9YfpmchjsErnmHbcBr4kPFIduDaWh4UeHkrMRD8zdxIs1Y92vvDcShBKwr+SvPRI9lrEO5ui5x54k/4sCftBMTCS9QC6xg5DT6yoUndJrbUCHdmZ9nXWem04pR8rwu70b+EhdBlC/oNckoYGi+ZxLWRbel5q0bldNArypZPNDtQli6KL7R/ZCweOg2Y/uxP1Cpz/ZgnUqSFPQpHl37PgAAIABJREFU0/MZ66rzcYGJ9xpHlqVpwjS6LoRN+sSyH7uA76A00Ct5QYdTIm7rOJdFv3K6SqMRLXPxOdVoYkvySq7iAXHUddFygPjyGfPTk0MBp6gPn7/RUSrb3yQty9N0JJ2urqGkLVgm24Heo9h/tPcRPtO8QKPFNyLWmyD0e6YpG5PVEZlW0kNQKg0NWOf16rIN2XZ6oZ7eki7mCv3pUqzs6Q0ltlyEti2TcAuG8CPpx+IIjxMXyiFdLmFxhx93SQ1ihZPhWOKh021vattYGRYCg2FT2EaGyC/dHvI9uNW4piAsjRHXG6swEiwrfhvt1yqreVPjybrrPst+RWNYpiEudskvInM3vkksjWl4KMo54vQaFMqkv3hi2TQaWibAIlwhh2LED3j0HteuocXYsbg2VtFtoAGvVVXaYv0563qFt0Z+TQ6RB4o2A86mCmfjGZRbEW9rqelgpSxpTxrTsr8UNCrObH96oGP5lBdXTVQixLJ5sH78iRwrZR6TFM+UyDym81SxmEjeIv3XxwSsgya1PjMPrwmLB8/k/7h8wO8IYTENz8SdZTINZS/x4T2/uUle5K+axWISZT0PphNjolBhuQplfGqpVOq926ihVXNllxSNtDIaHUWQ2L0qTWHlDMnl4dFOGx3PkBByxOOVY71Cr7zcPvjjUuC64bU85oL998Mc355cgrv8z8dc9AxF0dnpVPHw8yfo7jcwWwGL8ayYPJDfteH0Ncg/Ltm2NfvdKFCympSvWU2+p+U3bJwAF6MFJrMAaRSLcd/x3j7+fP8IX+756DAWejmW1rBkLqE4ljCwayg82jWwCI/w3WKKSZpIyJWX/SHOdhvo1jzU6XZ1e2wp8LYUKBlYxsxitA08vcwxGC8QxxlMlYsnlS+OdvFPj+7huGqKooljA37Hs9LomfM+jhs5XlE7JmK1J2E1p4MUSZZimub4z6dPcVj9Gp1OMQJYG4q9bS22+T9FCpRjXFZdj2klHFsGnE9CDGcLZGkGI8ux12nj6weH+Oqghj3XAD0oc76lD62AsmT9UyHumhjfO0C8XKAXRggyhiqdobfTxINuC42KLWNtLf81nO15S4FfTYHS0zrnbFQnvRgpXAwmiJMcNBisuxY+2+vif3z1BA/bBhowZB2OYwY5ynVUzk05H89rQPy4K55ie2mKaJlyNo0fzs5xWHWwd792w1hWg9metxR4YwpsCD49/uU4YpwC5+MYA45/E8rfCM1qDX95dIQ/HXWwXxqrMJw8wfBHUc61CruUv591TUyW+4hXEc6DEBEynE+meDFw8Hi3Cc93ZS1jO4Z44xbbJnwNBShLtfflz3cdNLwH+PK4i+OdJtpVjhcKmcuRK3+a72T+ptfsS97NPAP/8tUBhosIwXyOFAaWSYrhPMB0EcLwK1drcq9BaftqS4HXU2BDBjMx+ZFjYXonPgkS/PWkj+/PRjjpz5DFKwlL3G418ejxEzy4v4tFrPDTuUKeAhaFOHl4e3yUFLgaD7419npitcYLmrGoMGA4oMFCYTiZIUlT0XzQhTDjBNddF1SUkZdofT2aJ5jMl4BhiUcU17ZQq/jwHfNKeS5cy4HAWnm6DnzEHwWu6Jo0btS2lAxrKLocpsmKKcYbWnmuYWye2UE42D6dZ+L5JUtyqJw7xgwcNjx0q1q8lz1qHUC5YVzTg7vTL5cJJlGEKImBNJN6HTSbOKh7aKyB0vW8Ald+OEQBo4B5pjBdKCyjTCzVnWSFQ7pirvvwXdauqDKVVRfLHMtFiDxN4JoG9ioODuo+qloLXqJOPPlju40zheFCIQoiqDRBs1rBUdeRyQRxYHsRh9FSiVu7RRRjEUZIlJK280wLNcdF1QKaHneSe2gyvExpnMN6saxbmvGqym97ofGcpQrTZYZpsIKjFHyYqDkWOlUXrYolXn7uKmuTz94EZ+7u13QUvo5JI4VZmEks91UUSVw1hsaq2TYajoO6Y0kc7VbNAl1bki/XmucW5roL47XnRILHBpHXb4trJqRGzxSvRnxGAaEHMEZe7BSm9SLfGSqHqbKr9+Q1XVRZ4lXbSt/Oi0H+PMmgshSOyuGZwPFuU+rKsphfw7jqBhrRctIqsmSlMF8kxWRB0UtSioN2A+2qhRoz6jwakbX6ExceVGJPI+5U0iEgGCosw2G9ht2KK/2CYMg/i1RhFChMghxmGqFq5uhUHXSbvtRBF8cz8Wce9p9RqDAOFJZxBidbYbfmodPwYNEtX2lIMEsUxssc01WEeRRhGSfyUbUsG65lwbeUKLJano1u1cdOxZT+xzpc0aio0q3/QlOxTCkYsuDlwlPRrXQqoTAfacUJGmUWPV9Ngwyr1YJ2hKiZBlqOhZ2KD8+3hVc1AlIma6jL5QsSZ60jMc3moeknzymuS09ZAcuPFcarRGK+LsMEcaqQ0wuCYaLqeajZ7DM2mp4tuxMa2jWsbpzNwj7Se/IW6UGZOxjNAdNGxWQ4GBP7DR+ebcAqGYPtp+PtngaFG96fz4eYLiMoy0FuupiEKX6+nCJFSxZ5bMpu+gHLU9h5IiH4ulUP9U5F+IGGKn325UDh6UWCi9EUEfs0TKzSDGeTKSqndbSqvngwo5woPDJl8PMMXd/DTt0XJYHuqmtscaNVCo81t3CKfqTPpazV/EqjmrlSGK0gfWsZRQiTFGmSinLNp6x1bdQdW0IFNn0HzQpQs2/uzKI7zCuBdAOzX3fDehI3yoRQKcRZBlV6CmPIw7pjoGIVC8x6srjJtuv369fEhHk2D5JGt/9UQjgAL1YK353M0BvPkJkulDIkrv3JYIK/+Q4824LFMDcql++OmWeomIbsHOr4lsihdZkh4YnW5AS/c5NEYRRlCJIMUZojzoAkScRlLnHybUeUlr5hoGlbOGi4spuT34K76q7rxvyUR+T/wUphuQhEBniuK0pOji34vdRppqnCeJFjskqx4KIQkYGJhplhx7ex16pLWC3C5fdgGQLL1QpZmsK3Lew1qpKmXu7Y0+kWK4XZdCYeVlhet+Ljs92ujN2oJLitPXQdtudPjAJkGh5lpxX5DYWX8yWeDca4GM0RZSYafgX3d2p48uAQxw+bMF0DJ3EOymORQTLRppGpBljC3Z62FHjHFCCH8duxPr4k39KwT3aXLuilbYXlKhGFU8O1cL/TxKN2Awd0J22UoTTXxvQCs/yccsde4AH3dy1cdttirBIGC4yWAXqzBSarCHs1V+C846ptwX2CFKDopME7DU7pXeX5xQizIBZnuz4U9uo+HnUbeNgy0N4Ilcx5KfsCv/M0sKUhFu+POyaOj48QLOcS4nqZKzy/7GEwPcSD9s6V195PkNzbKr8LCmx85slzNMCnYTXX5BhWlC75GYqiYls4bNXxZK+Do2oRNl2M8Us8CIo/8rIoUZWByFR4uOugP2hjGkSYLVYYryIxwpoEIXba9WLD1LuoyxbGJ0sBzXuc+3KOxbXok8ECw9kSeRnOeKfq41GnASrxO1axwZFzKP7W57qUwdw8waeLBnB8dIj5MkCworofOBtNcDltIzyuSRgs8vv22FLgXVBA5G+pB+JaMMe/U65Bpxl8C9hvePjyaAfH9WIMIZtxROpeczDXBiSUvDKQGAr3OiZGkzZG0wWWWYBJFKK/CDAKQrQaDtyN9ah3UY8tjE+QAlwzoEFKKVNt10Cz7SCsNdHwzRsb5a+59VU6icFVqf8JWkCjXkPfdpBlMSJlYRYmWKxi+re4IbdfhbR9sqXAb6cA1yHoKfM8WOH5cCSG1kGSivOL424Hj48P8dnDXbSqBk4mgJXRYMWAJXr/13H4b8dpm/P9U+DdjedewwMcSC4jhfFsgdl8hkzRPEXJjtV2tYKqV8Sr5mB2kQOzxRxhGMAwqBrP4Vs26r4LR7yilERhea8pk6luJBHdKfc0c9jBXxFTnmW8zuBqfbBNRd1PgwnOekPMGVNeGTisWPjvj4/RrHauB9ebeHGRrvRwIspDpfDtxQQvhhMZbKs0hmeZ+Mv9Y1j3DlGtF0ozAaNhEZHympcc/M+gcLJS+Pmsj+F4jngVohLN8X99+RAV9wC2awpONLQZpQp/O5+hd3mBOFyh6lj4rF2H/+g+qu2bO9kInxSi0u9iofDdyz5Gg77sOr53sA+rc4waDHFLOgw5Schx1u9jMJ5gFiwRUzEo7kUA2zRRcT1UHFOMaO4f7OB+u4WjhomuU3iPYOm6mprlN+/18zc9sw7kOy5Q0X31pVJ43l/h5dk5BqMJ6irHjmvjuFGH++AAdbcGh1YEv3gU3oPuSqZpR/pReReIJSAVpwoveitcjsYYzueYByvEcSzKB9M04Jq2KN3pFrNTc3F/r4t73ToOqgaaax4ASJfCXOQuDG55/sbEJKNqFXKxwKF7i/QYk6G0lBgryMq1KFLYj67bj9ekAQ9dLPNSgTiJFH647OPFcIYwCsGFwiatyP0v4XU9WRzXsHTeElShrylpehErfENe7g3Ehb6RJqiqBP/y+QN8frQPt1ooLSWvRqYERFzIF8RnniucLBX++vICi+kYWRSgYgP//YvHqDld+I4ladl/+kGG788G+OlyAiMKsONxR0gHfuUBXK804Fkrg/2T/ed0FuPp+QBnoxmcdIWvHhziC/8ItG/jxJ1GB5ejECe9fiEfgyWWYQjTtGEYJizTEg8MVc/GTr2C404Lnx/uoVs1JL4vd1FRiG/SS9PtBg00cclBtBAoM22Q6CqLLDCUPDxRCj8MYpyen2E27oOU2au4eNxtoXp0AMdp0G7i5rEBuDB3upnkNrzZRiyb3nSomJ5AoRconPRmOB+OMJrMsVgyrJyBPM9hGSY8j6HlLLSqFey26rjXaeN+18OOX7hFvinhbuLwMd2JTKM8zxSeDmb49oefkMJCx7XwuFNF5eEhjHpFPJGRjpR9F5nCs1GOp70Jng/m6E+5wB7DMC0oy8Z4FeK7k3OcjsbiLYIeI0yGzFMpvDxBx7Pw5GAXx9X7UF7hKe3HQYLnw6nw9WS2QMowe2Jln+NFfyaGTfxuc/eqqWh/z/B7CWp5isc7Xfzp0X14uxWZKJH+wprCkrdwRMlHSjwPldJPJysVYBw7sL9R3nMgO86As2GM0/4EF8MpgtUKSZqIIUKeZvBcB1XXRc330KgylIuPB4zjuuPLzkQuil31K13WWzKK1FHqSlrxxxrxil5tDGTKLJ8WMvRtiiV09iH+6DLx2TjHj4Mpfh7OcDrhQjf9OFny/VkECZ5djrGaL0s3oDRYUbC5nJinaHH3225bdh+7detKTtNYRdN9phQY8pELOfQW0ZtOJb54QOPVNEOaZRIGksp226RxqI2K7Ui83CfHh6Ko368baNnFpPqK9rfQnIqnSa7w43CGs9NzhKsV6rUavn7yCEdu4aWGPHAZAqf9BU56Q/THM1nU5OISOaiRx3jYquJPD47RaB9JndIcCIIMwWIJlcRi/PZwt429Zg2+e/09JJ8xrCVjTxu5iaplSUin425DDIHXlby3oL999KlRYK0j85K8TU9K1TSFu1rAi2aoVWq4v9vC14+O8eWjHbgOQG9Y4l2P+5cY58so5i9isLLxbf3USLqt7/ulwPUsoPg2F9+p4nsSZNxUkmK+WCKJQ3imEkPsw1YVuzVTDC853tJyUH/3+E3Sz/i+YQCHdQP7nQ760wDL5RJBkmOwDDEKIoR5Xca4a93n/VZ6C/0PRoGCczTvFusBxaaRi14f4SoSw1yXmyZaDRy2amjQ2PuO+ZTmY/IwPTq2LIUnxz7OXriYGyayPJONVhxfT1ZdmYduTon+YATeVud9U6AUfuRh8i/H8/SwMlnkWMwXiFYBjCxGu1YHN6odtCzZYEDF6Lrc1Nf6TG+vdQUc1AwcdFvojeeYzpZYpTGGDA+0DHCc1iTMkJbZ77uqW/h/TAqQ50QGl94uuQbeG02wXCwLPQBy7DcqOGrXJVyFnvsxn+ZXTRneF/IXErLt4YGFy/MqRobBfZ+YLFYYzpeYrBTcWrGOvuVfTb3t+W0oQB6mwSDXbbkJkfosjiGQpmhUbRy36ri/46NuFqF8Cr4v16vKgjX/Uv76ysB+HdhrNXFWrWI0CxCnGaarGJfzFfa7DdS5iWmzE7xNJbZ5P00KrO0I1PLTtoCKVegI+ewVNiPD66N8yRPHxzJ/A1CrVmDbFqKVQm6aiJIUYUS/2m+/hqmL3p63FFingPAgNw8owEtTOMESfrSEbTo4bjfxl0f38eTBHlpeIa8pa1WeQKlMmFw2oa4D3F5/NBR47/Npyjy64p8HEAVGEidQpgJ3FfsOd8K7qLjFR52Tsf44x2yxQJ6nssPbBGOz+mhUfJjc+XuLup5llPL0hpTUz/RZlO1iBMMceWEQU6wI39pgRapCtUQlCQcqg4SKkil6/ZHEdeu5CnutGj6/15GFaE4UNwfIop7Su36pQIqA7y+n+Kk3xWwRQKWRDEoUXLT8Ku7XW4LPjY9IWQmNE5XoUwU8W6b469klej0q3GO00gBfPTgGXTgwC8umEm+cKvw0XOD0YoRwFaDhObLo8qfjwoRnHWeWwR/bg67vno1mOD29RBSGmCoL3c+OcFADzpYK3/w8wY8n51gslojiWBRTsgHUKAw7FHfXmytpb1oLf3vew+d7O/in+/fwl+M6uq4hoVLWy9eNodtNn/XzNznTIEEMoLgTWyl8N8rxzbMzPH/+QhZG910bZruJ+80matUabOcOYxWpDKlRHkSmVJLehhdTcmGBZZNfzpXCj/0cPzw/w9lgILu8Y8b84+xKPA+UISdoNWUsYRsGajbwrD/AV/cO8Zd7h3jctmRXDAcJdKf9To61Kl2B5DPBoyhBbktekOQGBT61KDTAKrxn6O5zE6uinxIKnzOvhFwwgUkG/MC4y5MpnCxBu+Lh/sP7OOh4UscbfCCFFkBIU7bpEgA9RfznyQV6/SHCMOb2fVSyFWzXRrVSRbvaKAb5zH8TsQKX0kqevP18usQ35z1MhwMgDNCpuPj6yRNkJn1MFGWy/wzDVIzV/npyDjMMcFjz4NkOviqLWC+GxXJiQx7ohzGe9sf46bwPOw1h1mqoHR6i5Rp4Pszx08s+Xp5fYrJYIowjpGmKnHLOtCRcFK2iHdsSWeUZY7T9Hl4OJ6I8/mKvBtcpZOedi6xErORXIUfZL694SNP46sH1Bfs/6c3+82Mvx//56QQX52dIllNULAXnaBeG7aBarcCxXyH1NSBBYZ1CN14VN2t4yG7I0jippxS+ucjx7YtT9Ic0FAwQRjGylB6cWGgB11gk4lXEsWeo9oY4rPfx5wfH+Oq4gwcNU3Y7atl8Q67egsqH+oiynH2A/MhdoqeLEN+c9ZHAxq5vwVYtfHm4iypobGCIR7CLSOH/vBjhm5NzvOxPsYKDFPyqGlA01jQtBKlCMl3icroAQ5wgKwxMLFPBUzH2qg5s34VFDzszhW9/PscPZz3ME4VYGciVAYPfG8NFohIMFwlGs4mICpMhdSQwUAo7i1DPY3HLd7S/h0xVhGlucAbFoHgeufH0qknIJsLH5ZkvhCaq4NUxFE7nCt+fDfH8rCdu34MV+YXcTFlb8uliJcZgtm3Dth007QyfH7ax+OwePj9soc09AqUx2FXhb3lBvmM/pWEkJ3m6XyZZjulihWWUIIUn9dssStf5+rnuMDwXUnM9DXmFNebi4N+eT/Dvz8/xkoYqiUIEm+ZDQgvyQJzTw1OK6Xhe0If0p5cdlcDMYnQrjhiefnZ8jPaa1y1Nd4Z7/OY8xQ+XI5yOp5gsFljF9IDE3UecKOSFLGOFxWueKd8ZjudcZHg+nuHxXgdfH+3gvx03RTbe8TWW6rNeswR4MV3ih/MelvMF2q022kcPZPczjVX4jfiPH3p4fn6B4XgqBlo0MDZp9GwYmCUBqpbCA/J7yUtxChnHLKdz5FGEVr0usX67NRNeKWf4TaArSlHWrkJYlotus47DdgudahFzXUKQEegNFmbr6Ba68ULK3/59GhRgy5O3Gdv8L/fbWI524CYrNLst/OufvsDDvQrqliG7qGnsTEktI0oZe7FXl95WPg1ybWv5O1JgU0qR+zimXcbAeDYHPUTmeQbPUtivu9itOmi6xQ7oG+P4sg58VnKw9IEqDHQthZ1GBZ7rIVcmEpgYrRKMVjECOho0r4Z4vyMltkV/zBTQX15+u8UD3AoYTSYII8DMU1QcA/c7LexW/RthTnWdmV8f7BN6HFc3gAd1A1XPBb2k5oaJ1DDFIJyhWnarjasvvs6/PW8p8FsoQLnJkSrlLzdxTBcBVqvCW7KjUuxS/tZc1J3CCxB5dFN+a95lP+B7Gl21DSXeLqsVXzbVcd1isgrRny8QJHtobhWmv6W5tnlIAS04y/WnYvygMKNn4/lS1pMZE9dBLh6u9qqeeLCibTb5k+FyNw/yMH8yhjaAY98Qr9+yCmZaiOIVBrMFLidL7Nbqm9m391sK/GYKkJ0pf+dQGC0CzJch0jSHm+doV1wcNiro2EUoNirW9LiDBa7LYs2/XM+nN7fdhoFmvQbTHiONgUkY44RrItyY6BriveU3I73NuKXABgU0/1GGUia/ImZvY1w+K0O5Mz3z0hCA0S8syyp4nSHhufEu4xa869WujeK3t1sKvBUFyFuUr3Sa8KjbwWR3B1VYMG0f//zlZ7i/WwW963M76II8K/xMTqfOv9AvvBUC28y/GwXem8EKmUofnCCFQYY4oEKeCqwUvqnQ9Aq3/HQFTyFIw5bpeIZoOYNJxRbVKlmGqllDq/SwcgW3vNCy9eq5LrQ88/n6OypoCsOVIgE9rNw8Ssm8NuDgk4LdgUq3A6M+QjQJkDBMSLREf7ES7xEd7+buHHYZim7Wn5NNLpaMlcL5PEcvzDHLHKyMKmA5SA2Fi0WC8+lSQjPwg7CJO/EkHsRHK5N7YSLu9xe5Acv24VRdWF6FeqGrARPLDk0DCzhYwkEEB5wmBHmxQEh417UurlmOKLwMYGnYmCsLMVyMMxMv5woXS4XnpyM8P7vANAiRcXsyAzvZNhzHgcmPmFIS25m7q2PkSPIcy1WG/GKELM6RR4f418864qHiLkZcbzvWf9MbzuZ7SVPiTnqPoPDjTOHffzrF+WCCgMpVv4Zmp4l7R/t4dP8QtaolO8tv8sHaXamsEiONskDSa/Pg/leqerWi8EIp/Odpgr+f9HDZHyCIaJBA5Z0hin56heAHn4YrQZjIDoFE5WK0EI8XCOMT2UUTPriHx/s1GbySL14ZYGwi8qb3utH1eSMfH9/8lVt+r9JRecJ2/+WDqQwuZnd3kfojhFaIKAfyhCF5VhhHLTDsAg/WUQouwTKvLNZwoYbeNlY5+mGKWUZaO7KinaoEL0dzPFqE+FI1JJQM3dddwVlrN73wM8+A/irGMMoQ5QY824dVqcGtNcQdP/stDdUYHTcyHCxgIbRdGGaC0LARGbbgRRqtdyDiy7z0YbAyLCxNG4HpggYAvUjhx3EEP3Hx96fnuOjRiClALCFVLJiuI94faLDCfkPvBDRO45c2URniVYbwdFAYPKXHaD5oXwm4W/uQIFcS8upUEmNNMupkPPPHOohnmVzhu4sc//79zzgbjSWkhu/4aHebYmh0eLQH36N5xKsH+4v0Gb69SnB1cf1IF16CYPvQM8h5pPBfpyG+Ox/gZDDFinImYyg2C6ZpwXI92K4rxhf0nhEmEcJMIWR7JnOEyQtM5wvMj/fx5V4RgoZuOoW/XkX3PT25ru/bFKDbhO1C+RKZQGA4WCoLiWHDyw0saXiSK+E93WdojDKPUyzTXBbTYdkiRFWeCy2ljxgmlEkvZwYMkyZxuXhYoZcVpBYy20Rq2oW3qhQSQoYeQXKL7W6KcQNXOwvbvmLh3nZsMOweLRUKg5UEtGw2MoEui/ukDH/EdYMFXiFV8V7/FzTV+UTe0lsRvQD1E/z9fIBn/REWixCrKEeSAZZpw3VtOC4NVGxEIWVx0e/zOMcqipGeD7CKQ8wXh/j6aA9HdVcUyzf4hYVqxF/B8vUPmI1GU9zR69qknRIPQVGeY7RYYREliJSLjAYjJSieWWt9f7MEvtG/IsV6Wjo5I224Y4e/iK3lVWDmJnK6SCy94ojnGtOG6dfKEF6F5xfQE15mwvBckYvkEVafP9KEZ8q5FRR+7g/x9GKE/jyUb34mBo0mDMuFbZtwRW7SwMxEkjB8YeF1JclTxPMIQXyJeLVAp/IF7B0awBVjqfX66pqyTPL/0nAQGC4WyoFKDIwyA/6C/V/hb88u8LI/wnTO74yBzHQkZJlMpWlAYxowHQe2y+XSgr5JpBAv51DRCjXLwG7FAxdRa1YxOWeVGPhqPlMIlwuJlUrveEfi0akF32R86tu+zxpznnnc3prly+3pD04B9h0aw+35Bv7ts4f4bK8Bv+rhsFuRHaaWQbFJyUpPR/QIVHpXKecqmpvuJNOWve4kzfbFb6MAeY7fE4ajYEzoRRhKOFOVZ7AYXq3mou1bIgNpWyWTlFv4kI8Iq9hhClDp36oYqFarsGm0kgWYhSkmQYRFlCH37Hc33/ltVd/m+ogpoL+4rAK/8zQCnARp8c3nYqahZHPDbrUi3lWKORS/8gXzFiMxfV0QgndMRy98DQCdRh0X/hzLIERuWKLwZ3jXDFuDlY+YdT4Y1EX26k0/HH9GqghLTsUQPRaqDJ2KDYbsZPhOrg8VHPtqFfic4w/+qDCl4WzDN9CoVeFVKjBpKJhmEhpoHqXYpas3Jt4eWwr8GgqsC94yH+UvvQP1GWKe612ynEj5q7BT8dDxi1DzlqJn7tsL03zN13qXf7Piw/d9JCHXPkzMwhi96RyfH9fFAPEOULcXsH26pcAdFCD/isEKPaxG3JBDHubmnlw8xe7VfDG4orgkzzE9u4Hm2fUbvucYQuSvA9TFU4WNzLKxSnMM5hwHx0iqHl6vnLgD2e0mUIZnAAAgAElEQVTjLQXWKPAKH5bMKOu/a+muLsm0zKTl+BUTF7xN/uVPZcWGNOr7DK4hm9y4yDdrfH8FdHuxpcC7oQBlLNWFe66Bf6Z+dHdXohIctKtou4aIzFAZEr642FRfRIeQtW5RVLwbPLZQ/rEUuFXH+a5Q0B/lujLw0AfS/TqO3SNRonBidVhxcNSqom4XoWGoMrtXMREdNHG/7sDmYpjKcY/GBe063GJT8ivorcnSO6WkyF4xPCBWVBWJqdVr1f+Eq3/MxQHyQdtE3fdhGpYoxcMMGC5D9GYrNHarcG8gcy3zWT6VRwxVcDpLMAlicGd1TuWUWCYqjBcBLsczLNSxhCXQZa+D5CCICl1ZOEy5020lk9c0S+E6DrqdJioV54Z1uv7uMG44F8J55poil2UK9SbVaK8e8tYEUuJnOEgtGzMq3E9HSMMFxoM+Vos5mp6Lzk4TdU4cHAeu48KyLTHWWWUZZqsQ4/lSdpEHYYzpIsKzZAROTA66TdTbFrzSy47GQtdd3/Ms304J4VR4+VinC9+TNvyRzvRAQM8QP80V/uP7U5yenIuSiUql3WYNX1OJfbyPg64Lzyo/vuuFrV2vl0O+ETxKfPQ7lkvVAne00ysFd/o/7WX44cU5Ts57iJYLydmq+mg1amjWKxKKwnepIDYwjzPMuVA7X2I8GmJJbzXxAklEjxs0BLoPe8fDriPqi7dfxNWIs553XPOx/hXk4F3Rf+RerIeu6bFGsutLKvCMwq1hVQF7XQeu50NZFrLUFEOq/mIhrjwf+PQNURKWFyVe5FUaT3CyO4yAwSzAMmTYKROKgyPTQGo66C0j9JYhuOOfccbJ1aWt0RU+BMtdRCGN42Jayq8QxhlUpuDZJnZrPhqeLXmZie3KPGJ4pmhJTAOZwkMF3/AdfxpXXZB+zhi99GaQGw71v+ivMmTnA1hKoXd2iiRcoek6/z9779kkOZJkCT5Qh3MSPCJJsS7SbGb3Vm5P7j7cb7/7cjJLZGele5vUTFXyjIgM5tzB7eSpwTzgHh4kSXVXdwOZCMANZmpqampU1VTR322Dp5yCmo+ax00iR/qHeZyKX0iai5zO5oiiBJdpgh+PL9FyfRz2O9hr2TfWNIJTiZS6Iot+T+qQ9agvgyuf7FtEAYDtBwrfn+X4/fM3ePXmjbhUqbsWDtoN/PrxPn6xv4u9tltYh9K0WocphJFKWOUkxmN+RRXLC+uZ+bPtHqcKvz/N8KeXb3F8cYX5fAHEC2y1m2LRoNtqo1EorPBkY5gkslF8NZmKha7ZbIE3YYqYQg/xbfgUj/qOCMINjp/+acq4LNWtWdwf42bSchrSTniSbpFoDShXSBV7c37RdOVY1HMsfNFrwrf3cL6TY2J5ODkf4vJqLL7PaU662wxw0O+g29LjF7mcHE6FFTeL0fYsGYP7noV6AGS7HQw6DUwtX8Y+Kl1FiZLFS83Osd9rY7vXQ9P1xMUQFVTpFogugep5gv12A1uNmvCN4cK75pC6la3SQ5dfK0ywz6V7vGdDhT+/ucSzN6cYzhbgcZWmY6PTDTDoddBu1BDUPDiOizCMMIszXM0icRmUhBkuJgniTCFJ6K6Q/oN3sBtYIphY0t68rDDvKm63/aIgmmZgO54CXSHWPAeRbUs754nyZ+dDdGm5qe9J/0Vfx2aCZrIV2OyU2KbWOrdyHNJV/H0r4HGnjvRwINbRwqCLF+dTnF0MESdUYQGavovddoCnW21Yubb8xfrnCE6XQG3fxZN+Gx1Pm7o1+9fMgzdx9NIImI9gz+cSv9lqot2oo9UIUPd9OJ4Hy6ZlFwuLVGE4m+NyPMVoNEKSpriaJniexdh+dYogeIp6R7t1M/xhaGrqne6I2K9mto/Y8mApB6PURjJUGF1c4sXzF1jQ7ZxtY9CsyYZQgwqiNIGqMtTTCI97bex1mrLJRPj0nf5Vrw77s11RUnky6GC/00LD0eXmcNdQFrZthW+2G+h+fSQWY759tIPDfuN6vLnBG6Qy7xsfTLGq5z8QBaRtst3xhP62h/3+DmxXW+fhnIXNe3lxfiMbQJqHyIPL4XQZqXqpKPDTUoA9F+dmtBpJK13TMEKWpdyxFOWTjrj29fX8SsanzfiQi8n/HEM4blBts1VXaNQ9USaN5hZCKtiGiVjpSuFKXKarrooCH0MBsiXdWY3mieyBcEh2bEss/faaDXF/YvhMj9S6z9V/r0dvfuNczlO0wqfkhH9Qq2E6j5BZNsZUEA5j7TXXAPwYxKu0FQWK2SMFptOYAtMIScYVM3kY4gqXgnuz/yjKAPy4gf8YZISq7H/rPvvfGmoU+kczLBKF8SJFmEDceN7YXKhqo6LAfRQgkxXLHT54s//lWv18rGSdzUDOBWquKxbUm8WBT/LzbRfBCv/ydH/R/7brvuydTaIFlGVhHsVisZjzFeZbXRUFPpYC5CP2tjxUTYVtWpClzIVuWrlXQg8A3WZjpas0vMqnXMsXzcNkc/a/gafQDAJ4fg0q5L5vjPFigUWSIFHa4m4pqYFWPSsKPJgCN/lnLaTcUZY/lcN5Pln23a5lBItYW6/mUTY7z0HjA5Sj8CqDeTCiVcSKAg+gADmM8njKFt1BHWkWCMPVbEvmwCt7aDIPMJ4sKE0gU2vuNOx9HfKAzKsofzUKGHnIT4IAmYobsAMbaO94+Gb7ALE6QFaYlvIVULevFfiJzD8/6uK7R10RvnGGS6UG37aWfrHXO8H13+WCGGY0YRTDaUEPpxj8RwyvTzPreJsh6gZiYctRaDcC2I4LlfHkrovhIsLJcIyn2xST66bAvM3NMKbnZOcypoWVEJMwkQmQ7fLEO4X3VOyY4nQ0xvlMiW9Z8b1F3YwSSoRpNg6HM/pRXGjrDCqnjBtbWz00aWXFWVMkELOMIoaUST2FnVrfQDdfwmU25kmc+Z7bkDLmLidO1F7PEb18gyyeiIuHQd3F53s9fPPZUxwO2ugEejOHGzrEk5YS3i0oSJzg+9dneH02RraYi8ln+2yIL95dYK+2hS5P5JfKWXoVmsofBvKmR4EiVGvP6YPh5CvmyUURLXE8ixX+58sx/tf3z2RxX0OOQSPAb4728E+fHeFJzxHFIAPrOqO73jRm62mEVoUGNvN+vVD4w8t3eHV6iclkAV8pdAMPX+xt4+sn+3i800KjZi2VZUQZIwb+/TjFv34PnA4nWCwWeDeLkbw5R7MeoOPvoj/wC67VpLgL03u/rRN57Td/rgTRYoIwDSGv8ddKZiupBF/2AzQB3q8BtUZDLMzkaYLMc3AxnWE4ncPaZozlIX+ddzFB4kYNT/KfTXKcDaeI4hzK9mG7NqycVmtSTBKtsHI+ydGjEkdhuamMDeuJChk8aXe1ULiaLJDklpgNa/gu9rpNtAo3VSySqVcKSHPLhbJYEor0BdOVUpv4TGPuXJRVXCjbk9N3l/ME48U58vkYAVJRkHm6t4Vff/EUu/0ATSrUF4t7aT858Has8PtnV/jxzQnOkhyJ4+J8tsCzk0scdHvofLuFxrqrnxIOgqQRdClLTgUo1mWpds0AT9qwzZKHfxgq/O7lO3z/6q0o1jRqDva6LXx7uIP/+NkjHLRtEbrJwe8ykZdUKQLJM7qzWcmzHM3UCxWTqOz1fKzdPp2eX4npYyr4dOs1/PrRHr59+giP92poFKMX6UT+oKu1P72O8McfX+E0PhdXN6fjCE52ju12C61gFy0eifzJLpbXEEIrB5mTmp82S23NhCoFVNhSFp+59OumebJ2SZ6DuoX+UQvfHjUxVMAZgH/5c4DZeCpWr2xaiGh28X98+QhfPaqhSSsRRRkIg7xIjudGKN16JXULn/e3REFkrCCu1v7f4ZVYAkKeoFNz8JtH2/j1l7vYqVsyqSR/EBZN87nFmB64135+N9GG/LB+caQuj9bkWdY9hWgXCvjzaYgfj69wcTUTha+m4+DJoIXvHh/gq6e76DY0PqZtjugS7CrHf//zS7w+tkQIdxlZSE5GaAeX6NRb6B40RPFjOVFi9W5Cbh3Z8u8iPsdEnqjpBxb2+j10CqtB8SLHOE7x59dv4aoEvv0Yh10HHdmQ03VguIob0eKKsyzHLufF92LOwAk9x9TfPOngqydtUfi7VMD/8yIQ5bdsMZV6GTQD/ObJNv7vbwda6UKGWG3hhHXGtsd6C+ierJjLMBvhj2Lj8Giri4vhCDVk6HdaeHq0j6OdHexSwZeJlhs+un95PR3g+zdT/OEHrZCXLua4WsT41x9eg+6i9qgoopNJPnw19SZPGu+xPVFUpLIilIuLRYrT4RTDd2cYTyboBC4Otlp4ureLJztb2OnWIZuiVLZPNE/XafWrIO5h08LOF9v4T19sayUcbqay3yxaNfOlRYAv2zaefHOA/OsD+ciT1oTBtiKXqSzze/m89cMyRvXy908BcgH7E/ILrS0p+3ouxW/s0/jU/C49p/aNYjixPFH++ydXVcK/IgXIg7w41nLDnlYrpwn0CX+67aX7QcdCM/AR0HoZeZcse8dF3ibvc7OJ6/vAt1CvaQtodHeYpMAiyRGmmSiXU/Fy2bfeAbf6VFHgNgqQ58jDVJblwRAe2qGrQse20ay56NTry7V42UYF+Z9peZkn38mPnNbQYmOLirC+bJ/qE/5RjDEFWjpZ9beiwCehAPmX6+N5CszCSK+5uGFv2+jWA7R9X9YqkpnpuMtMW8LCzN1pEdB3LDkk4/lU/rZFGDuNcsS0TJjr/ZhqylEiXvX6MAoUvKfnsYXCCi2hzhRSmmuz9Enohu+hVfNlj7+Y7W6GX3TGwrvFHFr3vw4ajQDqai57IGHCw3+06V1dFQU+ngJkO5n/FhZrZwlAHsvyTFy1U9bC+W8rqMm8wHS5fJr3dSwYzv0g6X+pNOu7CII6spmLNA6xSGLEtLZezLs537gN1jrs6ndFgTspsM5IZq5gnkzMOLyLPpdBNKbPQ7dcB/LAPF1jzxcLpEkEW2UiFeHht2a9VvHqnRVQffxYCpA1l3tolM1RWF5iW8qxdEixjyaW3osQrv02yMvKOJXYvhxcvf+VKbCUw/wkeGhDGLKw56YTzWDrk7E6N25YcfJpGIvIMF6TnSNXSPygeNK72OD6aCQJ0GwO61xFoLimFGKy0bE1GqLJpSAKDr1WC81WG+OLGdhN09z+u9FUBOHltGR63uzgeVNIPgq5YRKLOWX6PfZqdGsRYDaZAYmPWZLhxekV2k/7oDWDJXEKwJw40U0JNw5nC4VFmMopCFqnCTwHg24b9XptqelryiBw2EiloZon8SOGmy/Bn7Jm2xJhO83d5rmCCkPxO3q4uy2WFv7D53sY1LRPMXPCg/XKMtOLaLMB1L/qwGu2MIqeYUzrIVmOaarwby9f4xe9Gg7bPannMia6hnTIJiwpCGW4TCYtDqJaWYWn7V/FwH/5/Rl+fPlGdlAdlWLQrOMXB7v437/5DLtNno7S5DX5bMqjjI/BxAiFGZ9plzgUgnMKhl9cKLx5d4FwEcFzbfS8AP/pu6/wzdE2jvoWuoXpVtKJFxVW5KTLExet3jf4lz+/w9vXb7EYj3AZJnh7NcZpt47D9kD4gvxo8C5AfNKHKRvzuM7H/DIh5nl31oxlFpkUAPa7XZy2WhglEXLbwWQRYUJ3L0U82fAuKoO0Zv1y4k4ajRYK08J3KE3PNZst4fXRYorU8cSU+MnlFF+0O5LO0JcYEqRpi7TiMZqnmEc0aafF4M2ah8OtHuqu7m9M6ZhO61sUFl1Ep16rvJWIc4MIq+loHspCknGxnsDLMxztDfCbzx/hV0+3sVvTlhzY/zFfWoFhuTs20OwBjV8O4AdNhNkPGIYpkjjG2XiBPz1/jW8/30KfkvDSVZBPyqzfdWlW27tWWiNNpA0VVmyorPJqrvAvv3uGZ6cXiONIXLntdpr47ukR/rcvH2nLEwWuMpEloQ3BSnjcEigxytFZv9yMo3Wik4XCi/MQJ5djhFEMZAm2Ok38X7/9Ft/utrDfttC0tCYty0ZaMb1fU3Ce1BAEX+B3XoA374ZYzCc4n0d4fn6FQbeBdq0lAhLmXc5/BeWP/nET8s2Q98vE4FuGo5VhCs0FiaDrk6+sDhEe8cl6Upa4naMykkc3EzlVFhknRx0pOkjQtwPprw0PEkPC4c0FMxUCyScU0Nuc9EGhYVtwLe0bklr23LZvWplYdhlAWw0wfZWgyGZAH9VEu+A7Cec4w/7cuJEqnuJSqphHbFJWMdZV3lwpvDkbil9hMj3HoW8/e4zfPtnFN3va1Ya4g2IZisbRdIFgx0av+xn+v//Vwp9fneBqNMU8S/DmaoKd8yscbddRpwKbqS7TsMzvhz6p+FFYmmrDwuf7Hl4PB1hMZzijS7BMW476ffwaw+EQv/nyM3y538O2b4lQhHXCOiAt7QIZ9kmknVwGLyGmDme9UahCSw41Zcn4SDdlPAXh0DWjogFlzQ8NlaBX1BfzkbzYRmSOZomLwWVeRZYGPhVLvnncxaD3aynHoGWh5XOupHEv1hK6/6XAk0oubcD/rAXL+xq/+/EVRkmMKIlxOYtwTP/NW030muUavy4meZA3lbU4J+EcjC4Jf/jhGawshZUs0Kz5+KevP8M3j/bxeBCA1oFY/6QjyZf7egHO8pl2QlpxTkBSFmQsSnr9IF0Ig3E4l+WT6YsquY5YvVUUuIMC6/xFPuLNq9zO2CfKnHstvIhaPSoK/GQUMPxonuxzZZ6WAXGaynhtOzZ8jy7fHLFWUebduxAz/M8nFct9j9bveGjBlrVhnKSI0lTm6yb/u+BV3yoKbKIA+Yv8w5v8G1EZKkr0HJCKuI6NurG8thz3NRffxXeMwTGf9lHrvgfPo2tSPbdcxCnmhcLKXTA24VuFVRS4jQLkJa7VY3G1TQfUXEc5orBCy4FuyR3QfQom5F+zrqPlalpnpqtUbe05EWVBWrpKM7r21uuA2/CqwisK3EcB6RvJuzkwms1ljGcaKgzWgxpqnrakRp7ceK11pORfvU61EDgU+PvFos1CkmeYc4+ZLndXZtMbIVeBFQXupABZz/Av57+LhPOIRMtwuKfjODL/dQtXzuRN3ndd5f7Xc4CaD/h+DXNaHldK5r5xRivimofZLu6DeVd+1beKArdSwDAWn7KxVmI2Mn7xnXMKs09PWea7sUIU86iogq2495uj3wzQbxcHj6+T3pp19aGiwIdSgGxpWJdzgfIUwYQTtvTfSsHi5vkyhc61nMbgsSnMfKuef10K/LT77GWuKVilPPCus4/5vWQYCdBCizVQfzGqMV89MdbCHzkh3a6h2+ng+HIuLnYocD8fTUXrkCbvDVGZlmXhIjNS2tXFaKown8+g0gj1RgOdTgO1Vg/RPJLBYLqI8OztKb446mPL1YtKU1iOJUbgzknTdJ4iXMTI0xycLFG7kWbpqLhSprNJL0+uPnnJc0lpHbb2t0xzDlZKZVBpClfF4vf2F/t7+O0XezhcE6oxHW/iKkI1ZSGxFB7t2DjY20GymGOa5wjzHCcXV5hSgaegcznPMjrLcKJcCDAJmzcHUQZTeEnrDK8jhf/6h2O8fnOCcDoBLatsN2v41dND/McvjsCT1BQ63bo4Kmd8411nzvwEp+JFNnMpjIPCyUiJZZXZbAqVhmIZ4qvDbXz3aBuP+hba1k1lGZ5k92k/wFJIOxbOj3YQTad4O50gzHIcXw7xoungsFvH4y1z9vwGcj/LAFN3fLJt7PTqeNNsYnx1KdYhpotQXCFNE4UuK4ZXIQwkeWWjkS58WL+TCRbzmfgN9T0X2/2ubDqOTt+IMtZwNsPx2RnSJ52lJSe2X3MROnltHCuMZiEWYSxCcm72tOo17PTaYhqavMG8N18U1ZtSbY5xM5TS+BzIYth5Im5WfvnkEL98tIX9miWKcKQNcRU6FcoBPIHKvA5rCuN9H+fTA8xenyKNHNHCP70aiQnfrK4V8daxMmXgU27FJXwmWgOiPGhpizNU+uDUk+3nh5HCf/3TG7x5d6YtqzgWdtpd/PMXT/HLxwfYa2h8TfuxygQuCk48boqbi49F+zU0Il6sEyokMf/jocLphbasQlptt2v45nCArw9a2G/aolRBIbjpZ6kIQBTaVKLwFLBrY7rYx2ge4WIxxTRJRWFlZ9AGfRxu+c6yTzc4/M0/peJJcc0Bhg90PWie4rvwl7BiBkXNjZxOq3Jw0UyBPWnJeuW9ntb8Nt9NXDKWons7HscTV5G0/WI29FfhkM7lE9ise8J9yMV4ho/JL1RwYn97Fiq8PltgOB7L6RRa3nm83cF3hzv4cqeObZ4gLHhE8ioUPYgjFW88X+G7p1uYxDlGkzloaftiNseri0u8PGuhu9+96Y7woUiXCmZowt572wK+O+wjns+RhDQBmyHOElzMM4TpFMP4Ob4/7uBw0MXRVh8HPRsdnsQprHkwe96mLtaJSDrxYhy2E47frG6tAyuDuZ4DCC1YX3reIjxg+OSeumHehE3rIgOeMuppd3VGMUToW+BYoCP5sxLJp4puIp/U8OqsifloiMSyEWUpRtMZpvMQaK5p4Rkg5acwEAthI55Pxe3UoOnj10+/wm+fHIgbMNKtUdS/wYmE4WkR2YwvlfO2ajX0NFnzN8vP67Y0xefqUVHgoyggSnuEQKZbZ8SPglwlrihwOwXYr62zG3/LMJ/xdCkNmTlwXQeu464eODAJb+kc+Zmf2Idyyu/RfaBLP+ja8kWSpUgSKpObmAUyt8C7vRTVl4oCputUSDLoTfZiDuLYDmq12lKB+iHsZTiScTmfqHnkXypb6TVYkuda4CQq3Q+BWNVQRYH7KUC+414Xla7iJJY1FwX+5F8qTNHCMi/huAewHaPIHF76X6tQWOGhHFrTzBEmdGulXVLcj10Vo6LA3RQQ/s2pMBiKdQouvnjQkspSnEc8gGVXMjD867vsg2X3VPbKROCfUeEVyLmgra6KAp+AAuRf7qFEdBudpshTSns0/8r8tfBl9RA+Nrwr/a8NiBd4zn85h1CcYytQaTvjZHu50/AJClGBqChwGwXKE1sThwxaMDTlBZRjzqDEWve/v7rEbD4Xk89yILwRiAvtPjfbeBEer4c0iCJq9ago8FNQQFjR8ONPkUEF8y9CASPz+4tkxkzYd93Vf933/S+GaJGRwZVrQRKLxq76TUsUViz7TATuYZJiOA8xngODhjYjb/p+PulKgcLg4VyJUG0xmyFPY7RqbexSQN5r4PTYRWppIfTLswtMQoW0sFVvYHHqwgkTzR0tYlqaiBAtUqhUIai5oB9m+lL0XW3UlkVYttGSAoDMiJYfHkBRgwAF7nkKT6ViEeXL7S088i0xk0/68Ob4Zi7zTsW2prLQcxUO91q4uGiBp5DSOMJosZDTHOa0sqG3gVF+iusRbjRxRlfgL0L3whqFWFYJFX73aow/PXuB6SKW03ttz8V3j/bx26dH+HLLR6dQBiBsrXpwV65lDBSUxXuZvXwkKlI3tACSAG8vY1HEoWUK386w3fbxi6NtPO5Z6BWWIWosRylbCn8phCXwyFJ4smXhfKuLy6tLTOY8eT7H20sXJ6MedgcNERIa+pYx/Lm+G3Yjj+z2LXSaTbyh0FLRZ30ipy6GkxjNQU2sNJhyMB2VKajMcB7Thc8EYRiKjZNWPcDedg90mfjMoX0Hhel8gbOroShx+MYnbgGM5Ca8DPTRDIznIeKIjpqVnNBg++k16rKBbuIyKdMIy5lCGOTe80mLBmw/gQsc9bv4em8Ljxu2nOrnutrMDQ1byFKlQIQLo702sL/TwY9nQ+QLD1kSYhonmMXa6hI7VqJo0ht0Zc9/iSuppBVWZGOKCl9chAGYGFc8zy/wh+dvgDQCfQJutev49eMDEQA/7mg3QOv7AMzT5LvMqvSiaahd2ZSCBV+WkxtxIZUPIoU3F0OcXw2RJhmatsJRv4nvDgfYb1qgRx9az9CuSrTyA2GTr3TZtdLK030Hz8+6GM+miKcx3s1CHE9muGSdd5ra/+E9OJfx/Hm9U0BvareEWVEJ5Xow9WKemsc0o0gYra2oDC54X/fhpKe5TD/DJ+tK07k0lvMUSJZD5bwt6Z+lfkpKIib/DVibbO59EobJn0+Og3RLdDKlguA7MU9pqRz9hoevd7v4YlDHrkdrPIXSxloOMl4RR2XhaR94tbOFFydniEahKDmdTiZ4fX6GLwcNNOueKPTcyeRr8Nd/kn4yh7CArrLwVRdIHu8jVQ5+OJ1gPpvKyZ04zXF1OsarqxkGZ2M83p7g6c4AB+0GdpsudulqydGwzATO1BHzJI3LdWS+iYJRMX6a+mB8vtu5VjIiTYQu68iXf5tKLNGVijBGjZKfCYNwecnTpCkCiJP0/a5Ct1XHue8hsW1kuSOumeYLsTmmAZT+lsEwWP/WGkhUpqWLn8N+G//0xRE+72hLZuyrDG+XQGm8DJLlDxve16Ot/96QpAqqKPDRFNDzjuv57qqFtI8GXwGoKPBeFNA6rjkyanXKGsYChf4UnK70ieyYVwI2Z8MoMubYdOFJhRUbKs8EfkqhADPkwFVdFQU+kAJkRTNvpPwnTemcmccALFG0osC0vBZ/aDacw/DmfgsVtgiE/TVXWHFGBWSaqn4otCpeRYG7KUA+5h5RIjycynqLPOw5HlzHWVUYvBuUfGWvSv5l/+s6gEP35BJIi8p0zZbKfuND+vEHZFdF+QenAPk3pfWIJNHjOk89S//pwSmfYnkgnQzv1sRCEE1m6jmH8C5opaJSWHkgKatod1CgPPvkPCJl/5vxwFcO26J1QV8r+xURy/HvAKu7Wva/ovhtaQsA3Jor3G/TiiHdDundixKkgs9LIdVrRYGPogBZircYoShDKpiZXMibcgJ6EHgzUXjx9hTzBRVWcrHa/Hiri/1uS9zKE8SHzKnLWVfvFQU+HQUoeyKHV9ffMgX+csvpTbzy0JH9Z6AvC7YAACAASURBVEBhTo55EozKJ52ahX6nqTfpHBdZnmKW5Hg3nGPXa4gLAV00feKYgjUKY6+mGYbjCSJ28kmMbs3FQb+NYGDj33wfqeciiSDuhS6mc8y7LRFmM29enCzpQUOJH3FapojjGE6eohME2O820fa1qwyThoLg2y7i+LAqoPsAbVKJAxrPXHx9tI+Djidm9g2cdVj8TTzMTXcROwMLrVZDTlHnWYI0z2URw3KxfAYWcd7EMjpcuzTKLAexo92IUAnhOAF+/+wK//rHP2M6GsG2LHSbdXy+3cf/+evPcdTSygEGL24sGQEAF/73XxTGalkxYxM/DsoyiS2E7vTPenp5heFojDzL0GvVsTvoY3+rh8DWll24QcBJKS8Dx5SVtGKjbNcsbA0G6A7GmMbniBYzjOYLnI+nmIa7aNavLfncj/dfPwbLSd6hAYwd3xLlKoZl9JOsLEyjFGfjGbZ6NQS25hnSxNCW1nNOhwqjyVSsfji2h367jsOBJiStrSySVHyLUnnsaq4QeBa8oiEsYRUKX+OFwoxWjRKtsNJt1zFot9BgI5eKXaOZDHbXgqNbmXMt2cpP+kxHhm4jwHefP8FO01kqq7DOdUmus1+2m0KppO4AnaYFn8JdHqdyHCjbxmS2QNRt6A6qyJCweBu+0sF6Q1U7c7HA9pPYwALaUsVpCvyP74/xxx9fIg4TBHTt0qzhq90t/OdfPhZLSq2SEoK014JWfJi8TDlWyr78oWOV4zCE/SonwzQzeHx+geHVUFpC3a9hdzDA0W4fdVjXE+qS0pkBTTikGfuZraaFnd0+riZTXIZzcTcymkUYThcIkwZcb7NFGgPr5/y8pt31WxlfUw/lMMbkTfrQ5y5N+dt0oMtAcb9zbTzXxGP9livVwCD8ZR4CghtPum3waeKtPw0+y7QbedTEuvtJ2MRvlAJvz6Y4Pnkn5qubtRoGnSaOdrbRa+n+lvlxHGTZmY4X5WCmD2Z/TKsgg56FrZ0dHM+GSNIEkyjG+Wgi5oUzo7BSpH/vh8m42CCmpZQtWPjlrotGax+OU8OrtwnG00TchuWWhUWU4s3iEqcnp/iD64i7si+P9vDdZ48waFoyD6GSCBW4qJTBcpjL0F7XlOb15bfiI0+zL+ur0IHieGYUQ5fEMgk3PQtm4OEi4ZciDnVbSXDSnK8yTtLAFG9Hu9PhN/Z7jUYTfhBgZk1ko5wm+0MxNbopwxLvyWeFnJs6dHWVJ9jpdPHl/hYOuhZomNQoq9jsv99nBW2YtFRvN7B5SJwbiaqAigLvQ4Fqof0+1KrifnoKmC6Q3R3HTW6iU2ElF1+QekzlyVAZO4rsuTnEsE2XGSeKYUiicG1AZRWxsMIxQuWyNryeaGyCVIVVFLiDAmTYggX5Kvybq0IIpCcldMtMVyg3NurvAFvmW75T2E84xRS4aCM8hV1Mygoc7gBZfaoocC8FhH9lrax3rnKl4BSb8NLXvgefGR42T87faeWC4Lgu4s29Ofldakf3IllFqCiwgQKGNclPnD9w7iBzBCix0KbN9es+2sTdAEaC+J1rXfbZPBjjuZA+3OzlGrf3Scq14Qeb0r4t+yr8H5QCZg4hsoo810pXPLQjllE0Ubin8dBL+LzYb5H5bzFHkT6Xe1ZpJm6HmG91VRT4KSlAXlwu19bGe05jKcPkwdY5PQjECv/2eoaL80skWSIH2Ds1B988PsBup6YP9v2UyFawKwq8LwVEPFHIO+6bYLwv7Cr+X4wCfzmFlb9xJiH6nCRTnt2lSf+ejZrvIkks5MpGmEMUFb7sBsh5/LkQkLGzpyB2poDhLMR8FiJLUrhQ2Kr7OOjYcGk5oBlgMaTCio3IcnByNcZndF/R0ifXmD/HEbGEQFhzhWm4EGGNZ+Vo+Ta2GzW0fI0jJ07lceeTkJ8axcjRqrn4fG8L9ExjXHMwP8mjPLsq1gqkBhmNwiMqEThWDiie3kjlNNJ4PsNkniNo6ukeNzQJpgxK/yhOMCkOnhZy10PsAqPCRNl/+/4c//byLRZhAifPMGgE+OZgG//5u2/FOgMtlREHXro++XdVmFd8vuNRKK2UYogSEeuESkmLVE6IJzSZrRQaQYBuq4V6oPOhG4vM0kJ1nbsuJ2GYm+EUoDbqQC2oA/S5YrtIlIVZnIhiRkY7xO8zOy7h+1O/Ev/yxd9ElTxAC0VdS6HfCNCoNzCOc+SWi1mS4XQ8xWd5H1nhi5l8wJttSCysjOYI6cInS+HbNvb6bey0LNF4H/S7ouiVk/5Rih+OT1H39hFQaF3wEulLS0dzBVBhJZIdRQUrT9Gud8S6Cl2HiAWPIu9yOcy7XlBoQdJykmc+3vG08kzcATW9Or44GqBbs0S5gu2jTDPzzie/kQbSdmipqKaFzNTuz2l6GjlGsxnCqC4N36S9HQ3GsMU0Cc8ZhrDEldnrUOG//PECz9+8QxiSvi76gYdfPt7Hf/jisSgZ0eCTgU+cBFIRYMJX8l0GcrZw3ZoZbD6Zdm7a0MU0wiyif1haMsrRbrfRbbUReDoN4zNvPg3tDWTzNLxWr1nwPEdUKJTtIUwU5osE1FFSpiNYQfjn/8PQjZgKHVf85hZfLa0oSToYWpVLJnQSzTsNxChurMcRaOUMiwiEK3nzWdSrCKyKU9I8bc0NUBOvDLf8TjwMfiX2KEfR72s4MI3wCy0qRQqzKEWcZOKv2q810O100Wv7cIklT7wW6ZlmeRlFw8I6FzcMmg0LnXYLJzbVymwkctOaWSK+t/2iTEsYD31Zw58/lxZJlAW7AXR/O8DzvS6enbzDq9MzjMZThDHpoxXL5paDV+MYF+Ex/nh8iaOtLh5vD/Bku42DjqXdBRXjLenOW1/a2hppZtDQ7YT9F/03kUTXfRnjmHZlICwTLgNKL1RgKwAzT8Lmz1zLb2Shy9iSJ8MKxRY5qV+A8WoOLCr+MpJta3P60jeX8rnttVCYYg5138VBr40nWz10YIkVMo45MhvjnEO/3QZpNdwQazV09ddD4qymqH5VFKgoUFHgb4YC7OL0eKFRlrFX6bknP1BQL3cxDzEFu01Zhd/L3Sbf5S4EpkxHgROFsVSKoVCrnL+BXz0rCnwIBWTeIYJ4bWFF5q0rHPkwqIZvyZs0DsDVPedTbAsMy/JclHMr3n0YPatY91OAvMT+l4okum/MRSmQrtTkek9mMzzM5/VFIT+VBamUyD06Al2NcR23eqso8H4UYP9LQbw57cz+l9aByGEPYt+CHc3egvAwD14Ui1DdvxcHI7iH9H7oVbErCmykgPBZwaPsEsXyn7hXp3xG/zMJ36fHNHC55yIHiGQyoecQzOPOfTGTYfWsKPApKUCmLC7ONygzoSsgyh6vFPDijNZVzsRdlSsWrWv4aq+PXxzuoh9ce3cwMKpnRYGKAhUFPgUF/nIKK58C278iDPbhnCRTzsmT/t26QqfTxiieI0OGMFM4vRpidrSFDPWlwIgTaFpXob2Ay8kcizCSmXndc0TBZLtuifBt0GlhdF5DNLcRwsHJcIyraQdZq3UNSwYPJW4QaEViHkVyEoIuUdo1F9tNHy1HC+jNmGMmRIZ0Ev4hs/jCfKNrWajbFvo1B01bW/kolss3VxzFoWbSjTfXFDUK/eQINxctqbjYWcQxFvSXi0DiEUeiaG6DO596A5NSMhep7WKSAaED/OHlAv9+cobL6QI5XHTrDXx3tIN/fnqEX2w54raIzE481i+T33r4pt+WWlVYIY5UqOCgTqWkaZIiktOHFI9Z8F0XvuPSEwxCuhMiDsXgL5NUZkLhKa33WBZii0oEGiYnq7btQFn0K2wjoYZrmiESzeufr8LKRrqV2g+tAvTqNnrdLiYXE2QpFXEynE/nCDMg44mJQihtrBNNUq3wRb+enM7Trc5et4meZ4kweW93G1dhijAKschyvHx3ice729hperLJQ/oa5bFJDoxmIRZRLIoUDnJ0G3X0Gg1xgcO8WU93XvdGWEvN9kPXKypBw1ZiAYQKINcdsAEoLXSZWNpNIeCmGykqbsjyvtjYJ8/QGgEVpAx3lyHwXfhMXrizStOTVIBykFoWpjnEGs3vXrP9XGE6T2HbHrpNtp8t/ObxDr7oOWgXyl4GNrE17wbZ9d8m3JTM/F5/8juxJ99PYvoe5gkcJSdo6JvYtRx6J8LcV0gKobwUR/qDAho3QhyIshMn1qxrVqIlbY6JfMQp/SenSBIKXEiDdUz+hn+XtAxIT95cbJj31ZLpE3r8qnskxtpce+uh/E2y8TbfrpVWSG8uWLiAv/u6G79S2lK5GMp05sm+ge6w5lRWoQ4kN79sB77riWpCnCnMOUZlaqm0IvQgcoVSD2lEanBBxiYk2fGbZSOFJRabqLCSZDlyCueK/D/kYXA39OOTY6KvLPRpPenAwVZ7H4d723h9PsLJ1QTDyRxRSAUuC7MsxzTOcJGmuIxGOB1FOL6YyGLx8606dmlBjP6QCzqZOpDilhDmuELhCm/hETkpX2yOMLJBtJTmIa8mP6Fx0abZDqmIQssqMnbz3QZSC5jz5umNjFxoi7UolSnQB7neKH9IrloZju286XvYaQbYrXtiuYqWlvTcRNey5tiPqcGH4FPFqSjwCSkglisKTVF5mFb2CfOoQFUUuIcChuvYt7NvplCTF0d6Cuk57q9c/FkK2jSklKPICVPOaTXQIg9Fa9N6PCrBWsmn+lFRYBMFSgxnXvmUWyZAOtGHsNUyDV+KQ3sycZRTfFrJWASnJuNN+FVhFQU+gAJkqdzS82MR+nO9xf2h95y2b+Rh0z6g+3cqXRnFgg9AtUpSUeAGBdj1kq94ccogtx78b8S9K8Cs4qSLJTMXDE34pu+VPYGqD76LjNW3D6CAZqnikM+y571mNL4t+9cHwic/Xyu+6Hmw2C0Wc1cbAH5IJg/EpYr2D0gBw74lxmUvzf07WlahFXYeyP7xMsePx1c4H05FmarpuXi83cevP3+KvaaF+lIK8Q9Iw6rIFQUqCvykFLiWl/6k2fz8gd83/ps5sQiZADR9C7uDHsLxJeZpjCjLcT4caesaqIvlBJaagtiFAs5mdGcyQRwt4Fo5Oo0aBs06ur4eDPZ6Pt7Va5hcUcBj4+xqhItxH+FeS2Y/FLxQYYHC2HGkMJnPxLWQjQw110GnHqDbaIIWIhiX+JoxiE95L7ydvPdsigURDWAqm9hitcCzLcnHLBw21nCRn8GDODG+TYshyoLKtcWUNFdaIFgCUho3l6ECh4sb10Ee1DC2PNhzhfO5wu+/f47JaIIkTkVJ5HB7F7/88jP84qiFpWUVY+hhA9Kb8iPRlrQrvZvylJ90SUQBapyyLEznQDk1LOwaLjIbP05yNGxa79B0g/imZK56mipWDmyF1AZCG6JIcDHNtRUQChfFLUyuT5//LZ58KZSX2OF4sNCrW9gZDPD6YiYCzTmFsIsQk0Qh8mmFR5uho0UaCjUvJwrjWYgkSeBZCl2fClouWtT+tYGjvQF+PLlECFsUht4OxxiGESJ4ctLemLSLoDCaKUxmM8RRKEoktPpD11HtRh1U/vrQq8wPm2BwGUJfvTUqMd1Yg2zkwCUYfiVqnkd3Lgo2tZ5EgFWcRC02AZYJNrxIDlSAcjykboC5DbyZK7w6TvGnH19hNA3pnBWtwMOTnR5++9UBPu9baBdtnSA1x2rgd2O8AYEiaNmmCqUK9pHSdqi0kqS6L2A7cT2EtofjWMEd56CFC0elosjiWLScwstgQUsUtOCgENvAxKYVqgj0A8vWSNqnaSz9b5rRtsxSze52RP9WvoiwyHDfdR0ZypBv+G6ehZaCPr2htRdEcctQ06S7q/iMU45n3vXz7pMhq3FX4WzK08Q331hSbkqRZxaJEp6hMgndY8W2jasMeDFVOItoyUSJgiDjE2GtokP3dvx9vdE7dYCTqcI8jMViGkdRKhlGUYowJk+qj7bKw3Iw2/JFLqTVNj53YKHVBp60PZzubuPFcRNv3l3ifDTFdJFgHnE84OlHhfF0gflkiLMLB8PxEPPwEMlBDwddW5Qz1/Mp5ynjWrne5RS7HuAYvHKtE7/0ke2Wi1pzc2HLOrm+tR/xOAPiRLFrEcUVtkj26xznJi5wOY0RU6OFinRZej3mlvK67VVcFVK5DQqtoCauERueVgS8pgHfCga4DVAVXlHgZ0YBNj3T/JabmSbgZ4Zrhc7fNwXYe5qhQSseioaoCJxunjEtMe4aWQz7mufKZ47PpQFIv5tcV2JWPyoK3E0BMljBOobXzFMSFt8/hLtMGplCkdULwavML2Wiyby5v8F5sCzS7sa1+lpRYBMFCoY1/MYoDCrzMb/J3lHB7OVvm0CaMEnHtAZ4KaHu37VA1rQhk656VhT4aArIXmDBcMJ/Jea7DTijGF5dfdXhZg3LSPxf7NfeBq4KryjwoRTQ3Kr/yn6SuNQu2PA9gBp2FkgyTdAwpUMv2kUR8h5Qq6gVBT6AAmuMxr097tPJHmuhrPJiovDHZ6d4+/YM8XyCukpw0G7h6/0dfPOoI7JH7rStgfoAZKokFQUqClQUuEmBSmHlJk1uDSmLPQIAj/dbOH7tisZ4pBSupguMQ1p4ULCda1P84s5kojCdL5AmMXzXwk6vg36jJsoUNDjyaMvCy2Ydp7YjwriL4RRnwwkm8S5caqEUgiEOIuMQGE0nWCxmIgFqd+qirNJw6QahJJgsJvac+ywXpreW7v4Pcg7asVCv1+CWrauYmZd5ro1Ykn8Bnp/0GXzaidA+AsTnqEgQdSTu+ehF+CpOjGc5NmzHR+YHuEhzvDsJcXpxhYvhHFmcgZb/676PX33zNZ7se6LQYJhcDLusgDSYXQsuJaS84JGVTxFv+b4CRNZRHOBpZWVB4WbCM/s2MsvF+TRE8vodXl2MYWW0DqLdKtHahpwepD0COUVLn+88PWMhoUUJy8E8TjGdh5CIlj55HmYJ4iwVlyl/M1MDko/eJyiYpdKOAvoNKqx0YVlvkCsLYZZjGMWgS5gdP4DvW/pkPq1uJMDZVYjxeIYkitF2HOx2mugHWCojPd63Uf9TgDFs0LLCxSwUiy3TpImOr12ksO2IS61QIYwiZFkCx1KiPNZr1tEIKBZaWRevVvQDfrGot14KoqzSrAXwNfcL76w1l1uTs8V4DoXt5JXiLiyRPAwGza1T68NDYnsYZgov3uV48/YdriYLpLklClVb3RZ++9URHg8sdCzttojl0m3347hOWhKtCRX9FIXdfBf3RBRs0xSx1IGu/4vZAvHrU/x4YsGhCU66VaLBFFFY0dRWtJHBtkkGE8UFR6xUTeMEsyl1w4mzQp4mSGJd71Dswf++LzNesZRCM1qHEuWdEpMXDGvCTR0zzW08JXVYkO7GyWrhaP2xAF3E1I8yTOLH+pc8yx9WUvDHdbs0eTOdaP4nQJRkSytUkzDG83fnGE8muqzLI9qEUyh5iTskQrBFOYW6g1TgiiwX8yjVfq+VA5XliGi1Kc5EYYUpPvZaLyb1ztzCbVGduphKn1LoeMDjJ3WMHx3hZKTw6nyC48sxTkcTXIyn4q6IyitUqFm8OsF0FmI234f9i0N4bVtcDjEv0piXyZdPfVvaGo60Jc0fxQeZK0h8k6iAYR6mXtlOzU0FlCldNOWcnyiMQmAW5WL9KYwT8KalGlq1olIaFVQSuiOzPYzmERazucx7LJt1QpO7D6e2lediVrpVq6HhOWJhhuVeGe+pJFtdFQUqClQUqCjwYAqYvn6ZQAYPHjQolFKLCLcMFctkXDvqOOW/+jNB6D6fMOnmwrgaug/qEnz1UlHgQRQgRxnlP9ljEGtuXK8//CKMlfjCr9rSkNZXoebVTT5/eA5VzIoCmylAruKhMbqPYEdJPqR74A/Z35O0BS8LPxdWlNk+qIRosyNe5fTNSFWhFQUeSIEl/8p6jK7/tHtBrZz6QCBr+8N6W1bPG2Q/gvupyxXvA2FW0SoK3EEBM96Tf/Wt90/4g3NbuVYfd0BbiS4/pKdd6ccLHpY++F5QVYSKAp+MAtx54015CfdYua/3ZqrwP3+8wo8v32AynctBwLZr4VeP9vHrR3vo0rp10TY+GSIVoIoCFQUqCpQoYGT5paDq9T4KUBhC01cHWxaCmgfL4Wl/nibOcTWdYxLmqDfpaEQrMUxT4Hy8wHwRQqUJavUadnsddANf3AtRsrJbt9Bt1OB5rgiOoyQUCwEXkwQN35dZErUdQ0WBUIZ5GCKNI7i2i16rgV6ziYbHZaaeUJky8Ldc5sU8i0mWmYiZaLc/uUrQiwKXSiMUmK/ltZK2yIfwb+QhgYwgYiVx51B2AcAvN9IUmTFc6KqAt5cjRFGM0XiGVNHdCUX6ClmaYjwcIu5vA029qJecCpyWeIqQW5DZXJIbSFzjxU8GT4IhTknOk+T0XU1fPnJ2XrsgSacYzmjNo6AhMogKBTe1lpo5pK2e+hoFHsJJ6U8hz2AVbhtyuhsSYd4G5JYF+/m9UE+ClgRIJ1oXaTvAVtcWQWNC9zQqwzhOcTmbY9EN0CkmTLSIMo0URtMFwihBnmZotjwc9DvghCkAJ0oKXcJsNHHheUjSEIvcwtlkJm619gaBnOinssoiB4aTCPNwgSSJULdz7HRb6NRrYsFDGI9IkmE2XnfwSyn+eu0I+ypaWLHgWdeuRdZZkiAMbxlwJo7JWSmKibVLD9ngZ8SHLGwECVuUohZJhpenCYYXQ4wnc2TcQLAt5GmOaD7F5OIS+dY2PemI9QdTHoOLwe1DnoRFEutSaGGFKBOlClGSiNKJ4/tQliNC7iiKxBIOhfvit0Xare472GaopWZRU40beewBLK3skiqFLEmRZyk8lo9tJ4uhxLrRaj/5IeW4K82yWd8V6af6JhuPuqakyku9m4QuGalAQBT0dA3fWr/8XDosuh6PG066fyuAl+JuKqZJr2txUwwdJvFM5KJtGN4RnklysaJDRT9qw9E11nAaYzGfLUtNdpFWJXCYWt/cllXKFmNXludD2a70tyrLYFMRjP0s/9O6CpP8BBctSXGk4JDB/pFuwowSSIsWV+jurw/stjt4t9/G23GG52eXOL0YYjRZIAxjROECJ9MF/JNzdOseOk93UWuKOqhgXNTIEnuSQUjBei/+XY9st3clBo55mvnIHAqXKXA6zHA6nOB8NMPFeIZZFIm/8jTPRflQ6o0moU09WjYy2wUtsLD8nEdxMiDC0CW2d7+Q56huyolszbHl9uh2kMmk3k1h74Zjom6KVWK/TZ+rsIoCFQUqCvzdUsD096aA7A9lTJXxo+hn7+pAN3TB69FlaVQowVBQqpX4tQVOk2/1rCjwXhTYMHAzSJZKwsR6inCXsHQJggy7/KGxWPKwACVcrbTCyQ7nJVzrVVdFgU9FgYLNhK9EaYUBRuFKL3IenJXhXfNkQvOuRaVaYeXmgYQHZ1FFrCiwpMA1b7Gf1PvU5Dj2vVRauea+ZZLbXzjvKHWthM11rO7Xr1VVSlFuh1V9qSjwHhQgT8meVTGJYLdL2YXeuX8PQAXHm3bBlAJDJsLkYR5k1fuZ7we1il1R4MMpIHt0hWUVyhqprPJ8qPCHNxP8+PYMszCWQ8e9Vh2/OdzCt4c72Ktb14fEPjzrKmVFgYoCFQXupEClsHInea4/6kmx/s0JC09D7/gWOnUf556LJE0RK4XL+VwsRfQbVGmhOxOF4VzhcjRDFCYiBGu6Dna7HREu8Zx/DloyUBi0AjSbAebTUIQ6PHn8bjTH3pYPx7hAoMWJRYqQJ8EpiHUU2nVflF3qnt5TIa6ylr1Gv3gzpShPk25E2hDA+MQyk8UyFVbkhMd6TGa6YZVggs0nUdaQH4VUs1DUIDgGm8WIib+SjZy+VojDCBfn50jiGGlCN0AeUlqpzm2xcPPs5B32OwGaQRtbtHbD0+vMzpCAwMWqCwM25rSSrfmh1V/Mr+snoaR0e5CkUGkqCiZUWfKQiTUNGsmhUJ0WIqh8Igookq+BeL1oE1UgZWurAZ4N5Xnwsxp6NYW+Txc3dCvEHP/a1wNxKMhrKE0hbV0BvaaFdrOGSWwjTy2ECXAxnmO+00caWGKxZkpzdAsqrMzEOpFt5WjVPez3Wmi6QA0U+FpoQmG728JZPcBoNkGsbIF1OVkg6QeiLRxCYRJr10JRlICC6ZoD7LUb6AWuvHMdYvhvnbrEn+uJTdzyIEoojSs3MoX91jMofpfhb4KrHdxoxQx+p7BecCtxsoFhngQtcag0lCuE4QLv3r5GOJ3L75rvIibvWgrjMMG/nV7iYHuAxrYtFqHY563YKDCIlTIwQbcUayWYyco3P6YxkNFaRq7bh8oTuK4D387gqlTqWcTdNLVdnJOUBm0UVgoFOFYge6uc5nzY7lxtcWLbs6WefccWl1MrCH2qH1IozSSk5XttxJRxMMQs6Gt+lqPceJfuVCcokq1EIQzpZQRHE4M1e6N2JR3jm1i649R8ZsIEzApi/MGaYUess16BsYLNA36wMcrGwBLcSiLCTtNMbtF6pAUrS8GzctSpwKTR0TgJ0mZjwfS1UoKivTPMQU4mD3LpX5u2hX5giSKoR6tGK7m/54+7CMETuiVw5RphX+kpCy0X6LeBvZaL3eYOnjWbeHE2xPH5EPMkwixNcDKZ4IcTC08GDbRqLbiudj/HrFcuUVCimocuEb/nRb+3jLt8uWYCBhklMz5nCjiHwtuZwsvjEU7Oh7gajTGj0uF8IYphrmOBt+e4sG0XNpVS2C4dB7nrIHEDTGJasqFyC086Z6CVlaLaV9C+6wfj2zYFRkuW0UQl0g+ouAdEuSv76ltFgYoCFQX+7ikgY5Nlw3HcQliaios66tXfJTNd71/ZLZshRt6ZnkOw9jQEqnS7HDM4AK4n/runclXAT0kBM9uTqQCVWWWyRcVYWw5/ZIUC+3qed7EdYRXsunR1KBZgbQtWTpetdN9amousUqAqbAAAIABJREFUA69+VxR4AAVMH0leJNtyeWIrvZ/FHjRXGdIs10LTW/YmNmVjeNs82ffmdMvJzQ/CEeUrp7DksglCFVZR4OEUIJ8ZHnaXizvuYfEcER2qm9XoLTBNQyh9NkHcz+KtDywRjjhkFyvg3PetrooCH0MB8pm5CYc85TiOWHvnYSbyHvtPw+MPZTkTj7DZ9S6tyhZTXipua+Xtagr8MfVXpX04BXgILVKUWwIjKLyaUVnlCj+8OsF4OIWTxui3fHyx28VvnhziqF9H09WH4ww/Pzy3KmZFgYoCFQUeToFKYeWBtDKTY0YXmRYsdC2FfqeBYFhDPE3FfNbVLMTVIsZhvy4bGlMFXE0VhqMZsiSHbzno+TXstFto+RC/b9zs42nx7W4dg0EXp+MZcsvGKIxxMpzia3RF6YFuM2YicE/EkoecLs5jtAIXrcBDzdMCKuJo8DVPXUz+KkIKe/lGXeI+MjAvWQjYFjzXFuHQSpo7Rit+Kt/XOBCiFkpSd8SAMHGJqQmTvAR1SxQNoixFsqClEoWa76Pba2E0miFUiVi6ef72Hfp10uUpmrv1pbky1t0KzLVfK2W68aOg3Y1wHZBlFLhTkSgDFE/pZ+g2a9jqNNFtN+CoDFZGt0WZPr1P7K1CcGjloixA2liyaUAsC6UV2KipGB1XYbddQ7fmw9W7brdg8pcJ1nS8myYGE8bizTSsA7rEabE8Wx3EsxHCJEGSO7gczzGJMiRtG7SuMlbA5STBZDoTFz6Ba4ty1nY7QMPW7mq4kUOFoMOBh+N2C6Pzc6TKweVkLvBi9EXQStdcdKc1mUeyyUNcCG+vFaBXo8KKXilwPf2wUunSmbi3PQ0N+Cx054UOmn7lr5vfCbd861bOUhv+ucaX8Qxc81yBatEMa4YoWiAJQ7iWjUazjaDVxnA4RJI5mCUJfnx3ie32MTr2ATo7jijoLeHI5oAW8C8JtTGzZYo7X4TebDsphRY0wZCL+x72DZ1GHbudGjq+ozfr+J0nGpi92FYo7FGIggKR4M3OpLjFAkMK5CkGnoVH3TaaQU0UVj4C5VvLY5ouDT5pZRrDFdddL1Es19MqMJbPNJb3x5C03HQqToOk8yTuSRo6aVppGxVEWF8MLWG95Cfznc9rzNhf8bcO0T26Tl2GUU5bfjdw+BS0Sh8ljL9LgJZhRXAmp7K50ap5ptbwsdtu4qATiOBAxi1K0kx9LIFpOmshm94403Th7kFC1RU0LIUt18JWq47AdVaUSkpo3v9awn8lsgmXQvGHZgyiyk0RhrC+aHmFinlNWOgB2OtZ2Ok0ETTqCFOIRaQEOSZpitcXF3g33JH5BRX6zGWyMr+hGVTzAvOyCt4o6EqUlleBGn8THy5qaSqUC9rnNBX6/AIvXrzGcDhBkiRi5YT06rYaMv61Aw+BX4PvumJRy3JdWJ6DzAuwqLXww8kQZ+/OMV3MQOtRtu3DoVLLhutGOUr1KW7SOH6WFfhWCrIBYBVUUaCiQEWBigJ3UsCMu+yVHduBV6sBeSwWyZIslyenZpuvmx8YUr7llKqe2smpa27UexwvyuNu1ZdvJm8VeisFDI/JvJe8S+VZsUSrv3CtzjkLf/Ey8flebJHoD6W/Wu1ZMyPhRgmQpJkobFFh2raV5FGjYdyKZ0uUq14/lAKm/+XeiUOFFa4VeNBLZUjSRNyS36UweF++3LKSw1bSELias0QoSyXwiofvo171/SEUIA/LAQyu/5hAmNpCnCbiCtAE3QurWBubeLLvmvKIkiV9thxasYHAt+RshIlXPSsKfCwFhId55sbVh2/SPEUqVs/1DEJYupQJ5wfrYTLJYGDxjfPmJFHI8lT6dFGyUkr2Smz72hr3EmyRdvm7eqko8D4UMJPdNT5icEwr9ACu6AYoAf71zQT//vINLi6GsCwP3ZqLr3Z6+OfHe/hquy576tyb5LUGrgitHhUFKgpUFPg0FCiJND4NwL9nKNyoYLfMSbevtFug3UEPLy4nGM/mSJWF4SIShRVaVqnBwiwBRvMEk8lUFBlagVZW6dQ8+IXfN7pIoXB2r2tjd7uPP788Rp5bGFNhZTTBMNGndejSZDQHhqMp4iiG59jo1n30m3U0ap6WyRUVYDZo+JNYC+ay+LS0LJerUI4wD16NaoUVTqa4iL3tYj68GMO8F0HL8OsvBRwRsl7H2gTdwLLF1U4mVkxcB+h1W9jd2cbh/i6evT7FybsrTMYzJLDx48kZaqLg8BWetLRVBdZdGTED1zyvsbjtTVRsloMzwZnb5cFxng5nUs5C8wTb3S18+9kjPN6vwaWFjRywi9uQnnkbQTeTcqOM7k8EJxEmAl4O0BpPwwH6gY2AOxd/9evhVCOqjE3ayKY3lUwA7G/3cXZygtkkR5TS/U+CSZRgBhfk9/OpwvlwgtlsJu2u12lip9dGr+4LPXy9byNuhg77Nl50O3hlO8hgYxYmuJwucBUqOAFA5TFaaxnPZkhTcohC3XUEFt1psf54mfrUvz7FX12ZUq/Sf2xYhDwwG6GhKCtp1QDty7pA+hYYwo+lb1IHliUukLZ7bewfHKLdb+HFSwunb2MskhiLFPj+1Vt0bKDpHeJpX/M12U7cv8hurqnREvD3fDX8QOtHpL/v+dpHN9uK42Cn18G3j3fwZBCAJ3PYhq4VVnS5TTuSrPmdwaVCE1WVp6hTgcyxwT5Y+gEd9Sf7q1EpEFrLpYRe6YsU7u7KNLGFpUqwuVvJn/dY77lOTgyKWzofzfxlvErQJWb59/W7VvZY6VRNJg94XsPRdWYUX6Qc5UoswSKOxJZP9reyqcpTVZaFTrOBz4528U9Pe8Lf5FdxJUVY5cIRnmSu6UYSSARGy3hCi0pwFppWjrZtIfA+vM2WUC9emXEJGdadMOnqThxRJh686faMW3JUXvEA7NrA010bF4t9jEaXyOYKaRphNJvjajbDLE6QNTmzuL6Yq7nLDUSX/f4aZFrOK6iswr759ULh98/P8YcfXmMxnUFlOer1BvYHHRz0OtjttbDTaWDQ8lBzaWUFoLseVp4IeqjMyzlN3MXoaijKp0IVUUJibqvXzRDzXZuW5i/DMoTPm7SrrooCFQUqClQU+HAKsO9l38x5Ws114LkebCeHSmPEtHJGJWN2uPdeBpIeb5iEljHTVFtL4wAl+dgOfM9bzsnvBVtFqChwDwXIV74HBIG/nCfQukoUR+KykMkZh7eeGxY/ViYetAFHiwCuzC/4toiUWKeU7Ona0XEQeC68pRr3PYhVnysKbKBAme3Ik5w6cz7r24BLgam4Uk5EWYrbTZuWOEs+JnxhbJ0R+10Dn/P5JAUyfQpEonEtVfM9GkKsrooCH00B0696toVWo44LWqiwHTmwFydUuGJPurZmY0CJZwWJ0m/yPI8rRTy0EfMYhVaucm1L9n0DT7eZj0a+AvAPTQGyoWFF9sFUhPKoSF3swyaJVlp5H4VB0/+KskoOxCn74FRbWeEhOyps0xL0z+Bg6j905f/dFN5w8M0C8Qv5kT0o3QDxINob7u29GuPPz19hMpnIfnnDt/H1owP89tE2frHbRd8rDgwTAK9S33zdYopv1aOiQEWBigIfSYFKYeWBBORERasq6H6Zv6mQstv30Wk38fbknZhGniwSXM4jsQzBE9rjUGEymyKJQ7h5ik7QxH6vg3agBTiEQyEUJzu9GrDVbctGncpihGmGizDE8Uihvg0sFDCeKcxmU2RJjLprY7fbwqDVRMPXJ8DN2MFi8V3/LoeWCmykO6Wgu181HHOC38BfGafuBrDxqxZSrkLhr5tYWxDrvZmCp3Lsd5v4/GgXT452sTew0XQP5PTJs0WELASuFgmenQ3RffYWtc8P4bRsOblOepur9GqC7nlqLf5yOhEsKiDgAM5FvkuRYgRFl00UePo2dn0LDQrlZeNB28ggDAPH0JKZmzC+GxpooSVABQ1CJ9/8LV3lsvKd+FMB53Dg4McgwKVlIclzTKMYo3mISVYXIwB0p0UhbLRYiECz1+xjm1Yyaq60G9KFAle6zei7Cv1mA/V6gEmSY5FEuJwt8G6SoF/zMKN7oSjHZD6BymM0AlcsJPVbTdT9T0NTU1/meaOOZFepXMM3YtwIuIZVvBU7U7r5WtJ36D83kt4IoLlq7s76ro2DQQdfH+3h6IAWViy07X3Y0QKv4xhRDAznCX44u0KzXkejNcCWZ4GOzlasH1wjt8K3NzJeC2Ayk1R426JSgELNC2BbjvgosR0bNbFI5YF+MqngxLM5hUrYCkTCMjy2Tl0d7ku7qSla9/npBNmix0NcCqsjZsy4gSwD1hGVSIViha7clWTlH0K7QkelHC5986reg4FajnadtQAiIhsxXdYRvzLqjVuIW0iZRLmOFnw2Fmwl/3U4Kx/v+EHI7Dt4sy8NaBnJp3sCbl1R0SRHw7Gw09D9ra5rjY8UdQ22nMpaC2PFXPe3jihJUVD3wX1uiRwah0Ith+ESIITTWJi45imhum4YxJu4ce7RdhV2unoDMIpTcOMkEaU/KpwlSJWvXf2Yeiv4hdUjVVTkIbwqpzY1CkRJ2I8vGmHJmNFJZZ7A4KL22ekUr07OMZtHUHEEWlJ5vNXCrz5/hCPOS5o22nUq9mqToYROGATJBXJoKSRKK6pJaKF0RYU43u97FcV532RV/IoCFQUqClQU2EAB01/zE9+59qAgSNY5cQ4VWcjoDjeOwZPOcpW7bumUyz0zP2oHABwDmCTJgJDjV5yIiJ9zvBrnfjyJvUHPtMilelQUuJcC5DzeZs4YuECjHuj5jW0hzXPMwxAxhUXwZE4pQMssW35fm8PIPCZRMvdSMrGiQpeLuutJW1lLei++VYSKAoYC5B32luUn1zz1GpVJarAdOjnWVq7Iv0nhBdWkv/E0wEpzcPa/EfvfJJN+nDNzUVZxXTSCGngo7IPXPTcQqAL+oShQ4jeWm3zMQwvtZkME8VzjZbnCPNRKr+xLV3it3HmW34v1o8wdoDBPFBZhLC7eqHNFC+AN34Vf8e4/FLv9JQrLfaCGp8d47oNym4KKJmEaI6KlFTlapHmd+Kzws0GQbtmLuS8t64sbFlq4yhSywremx/1Q3we3tjbCWGtbBnT1rCjwIAoU/SnZiDzIm/LFIff15grfv53i2eu3mE0msLIY3cDDZ7td/OrxLj7bbourdO6tyn53xYsPInkVqaJARYGPo0ClsPIQ+hUdMicOnGiwr6fQiJt3Awp6mw1QuEo3PvNUYUjLDgmQeRT6KkxnU6g8gWspsYhClwXtmlFe0E8CbakCXqeNaRqJqcRJkuLtcIztQRdxDkwWczkRpLIMQc0R0//del02Edfm9MuSEf3ltUGYufx2z4uBw01EESoJJe5JVPpM/DSOa5JWbkoWAtrbyqDBXAvn6zbweb+D7/YHeDyw0aIyyJ6NON7HZBbi3UmISGU4m8X406tj7DQbCOw+/KYl9VZC68ar4LkRkUJZpfAwsaRHMTHlAinwPbiisOLAynOoJISTLNCwfHRhicIJ+Wj9JhIGXvlp3okO05DvOEm+w8jNjfL8XAIo8jZicZaFbnx22haa9QC24yJRCrMwBt1qsd14LVosUpgtIqRJIuace81AK2i5lmwuCj3ExRCEB/oND51OC9PhDHGiMAojnIyn8Lb7mFDhKwoxX8zFhUij7mPQaaEd1MQCAHHiRZobuhdB7/W4K+3tvPXwLJZWKNiehE+17acHQaBrr1whcF18truF7/a72GXjAdDes7GY7GEeZjg+nyLMFd6OFvCOzzHoteFseXADnftSPc5oaLxnX1DGlbmL8oGnN+IcUVhhZ2sBcQw/TtCGJ8oyVDZjPWmMNRRDb4aZex0+w8kr0m7YiTNRGUg5wUe+i0svwhDEtKKHgGR+Blnz5IclDQ1SD0CMXagI+MuAWKSbaRmib3418a9DBQVB0MTbjCZTlm8hoyg/UGFFH/HTii1FP30LicswimyXWJnfm55MV8aamwf1GoVnVFjRToR54tuOQgQp0PYsBIWS4CZ4DDO8RLjli+GmPyiGpvLnD343ZTf5LgGVC7cMNC/8SHw0lvwrG9cAug0L7XqA0SRCokKxwrLgBkqWyiKUdcTL5GvqzPCcVNu1vtEG7ikAFA/up9B63JkCXl0McTGaIVfaXdd2q4Zf7PXw20cd7FBB075WrmT+ptnxKfsyYB+ukKUZ8izRAxs5uBD8rOZc/aooUFGgokBFgb8WBTjucM1b44Y9BaY2xxgLWZYjCiMt8FSMUZrnGGSXA6weCWihgtMXCp3iXCGKY3HNImMbT/c7DnyncB1gYFTPigLvQwGymtH/LuZP5F26BNWK3ZZYlaCyVEiFq5WdgSLxhvyMrT3OY2SjPyLvsiVYoGfSmu2h7mjllyXbb4BTBVUUuI8C5B/DibpvhByuqdUC2C5n4rYclFvEdBNO6z8P2+Azc3D2v2GqhP/jJAbNZHm2jbrnos69rL/Fjab7iFp9/6tQgPxLC5vthiP75dwrSJXCIo6xiGKx3Mk1/UMutgn2vXRhMU8h6bXCoILv2GiSdzfuhjwEehWnooCmAPnMXGRN7iHWXQs1zxXXmNyDS7MUIa1SJ5xD3C9SI0ze3AMhD/PQTpzRQq5CnuWSR81ztCzBud7zMnhUz4oCD6eA4WDzvD4BYPiQPEjLKmNaVgkV/nQc4oc373B+OQRdrncbAZ4OWvinJ9v4aqeN3Zo+uMr2sNy6voHQAzvyG+mqgIoCFQUqCmymwP2j6+Z0/3ihWh4nAh1OWjixprGCFoBOs46g5iOKPaRwMIkyvJvkyDo2LqczsYhiqQyBa6MT+Og1fDRsfYrbEJIweWq61wD2d7bxcjJGlOUIcxunoykuo44IfKYhT7JxWZojcFxsNeto+g5oapFDBHEqu7sww5TJ577nw4cZDZl/19OY3+Z5f54P9ZOrYFlK/JLSuszRoIejro8+NzgB7PHE9qGNJD7E5PIdZjGwSHIcX03w+1fHCGo1NBvNpWUOI5C8gR8Rv41wIqDVKUz5CIeLI59uoBxbFkyyzrdsREkmShg8/UIJKNNwkGcdMR3r3cBZx4Mo8GZSxmFcXp9SgFqA/OkepcJJ2YuysOyssy4VJeoB/JqHOExB/r6cRbiYKzSpsDJLsAgj2HmGwHPQb9TRazZE2YXwDP/JyU8A/YaFnUEfp5MFVGphGmc4Gc/RRh+jUAn8KIrEpGPD99BtNKTO7qqHT0occdlSIspHAteKXpvUFG4BTHOTdC3le3i01cd+20LXYm8CNKEQPmliEe/javQDskhhvIjw8mKIzvNXaHqP5WQtXaSw7pwl597WWG7BoQg2VGBq4iQKX44lZuAtm3WrMJsvpP6ztA7L1ZYaOGiZ+mJacxv+InjDG+adkZZ7bybju9H78K+UxBQ4iELAJkhlZJd0/HDENA2KfG8Bw2DS2SwySE1DO2Vdq7IY3A3aZXCMX/6t43ARJJCXpjsKEsjn9fjl3xrjTTBN7puf7AM9uuWjkpNrg+MrLFeUH+ZhJGbaO961pRTmafI1eRIyw4i5eS9ef5KHofUKcCJgEDIIrkRY/WHwZRK+B1w8NupwnGmhwARxPZgXx90NeD7NrSGWM2VjM1Qo5ccEpYt9hAhoFHA2U7gazxBFMSybJ4Essdj0xf62LGibdJu4gbaEwRNF3Cg3dyzWYTIRYFo0gcs+8iMHudWylgpRvVYUqChQUaCiwHtTgHMuKgzXHQt134cNKn5z493CNKGSpJLxoWzB8mYm7Jn1vEM262kjQCysJEiSWNa1vsN1FC2Q6nnt2jB0E2QVUlHgDgpwZsOb/EurnhRmkgM5xeAJ/0WSYppmWOSFW9IlLDPLWgbILIpcyS/kXxGYisKKVri1uE51aGHFXq7Xy6mr94oC70sB9n/kN/Iw59RNKuJ7Llxxj23r/jdOwcNtkfJlbb5c65ppfilTBpm5PPmXLlWoMMC5PBVWuA5vuLYcrmIbqfrfEvGq1/emgOEfw7+9piV7pFzjUWmFrsBHixiTWMGrFfviZFLD9Gs5MphrR64jyb9UuIqSRB+HU7kou9LCCveJTN5rIKqfFQUeRAHyD28zfyBPBTyYyvHd5sEsJYon8zSTOUREC84PsMZr+mDDw3GqkMQxVJ7BdyyxVlv3nBVZzgrCFWOvkKP6cRsFDKOYp47H8d/sv9GyCi0mH0fAn15N/n/23rNJciTJEnwgDgecs+CRkayyaHfPzM5en8jJ3Ynsl/t4/3tlb3Znpru6uotX8shgzgnoyVPA3OEeHiRJZGZFGkI8ABjM1NQe1BRG1NTw0+PnOD45RTgbo1x0cH9jC/98dxd/2K2ixrm2nBG4VrAX4a7Df68IsKZQP+vj40OA3+FP/LimaGb6Pt9wkcaLATRKNmrVikza0QtKfxbiaBDiZJqgO55gPB4DYYB62UO7WkK1aM8NFkiWNNW5bAJ3tpooOg5imJiEwPFgiqNxguNxgu5whNAPZMClJBP4DsoFUwYSSYeGNKSVsfvB3+274iMtUywDmiYiWEks2wI5cToIxY9oBQZ2bOCr7SK+fHAXtRqNfCyMI+CHVyf49vkhfj2JMKYbv6zT/roAKWlRZ6Yn7hxIoKMKWqNyZQoHxNgZ6419vOqPcTZKB3NZDg4myES2eEm4nAPmwx/z+P0fiwFoGuyI628D6DSqqDcaMGwbkWFjECRisHJKeR+Nxd04V/10Sh7anotKYeFdhYOQaiCdBl80WNlsN8B5T1qwj4IYr4a+0DvuJ+gNxjKpbUQxKk4RrVoNnp16LHhXsvoh39PlZUhg0GAl4ZZaqYcbLwFKYqyS1p+9ooGv9qv44v4+3GIBsWliGCb4/tlLfPf8EM/7Mdgp42AtG71yZJUhXyfUo3VnqQOZjuI1fzQ4otekctFE0THBsbgwCXHS6+Ko18dgmswNt1QZWSf47pUBC+8VPZ55nw+TiqQqlCKyjsG3CmO9p2/mWNzeLmUjAClvJBegdUHwRSwp3zppuZdymydRJPlU1Rd666B+ImLUqqkJ5HJDjU8VfvmzIiyp2TmnRxxSTkxxdBIGsZxVvHXnNOcF/XVxLgtjeuZaKdLgrYhCgdsHGOBKw7PBEK/6U0zihcyQFsugyq/KpsrF55Rn+SnALmPgDZ4xTx4kz3zmRj3isSzfSmaMPBMplyqUHU0epMGVOb4fyN7H/K5wEKXieagUXWkT5MuZ6twUAyPhOyLFFBWasc35yejLiQQyF7bCc9bR5daEARWs8B4iCWdoeA626q5MCvF7qOqllXkkU1iTf+oPOjTvAakHrTD9Xqo886XPs6OvNQIaAY2ARuD9IZB9AuRLwS0h6y7QqlVREE+ShiysOB6N0fN9jKNEFk3MG2JkU334hGW2NdLB0vQbANk2dzyZyIC9iRj1iodmtYRS0VlO+v6KrHO6ZQiw7cH2SBXARo0GtgxJW89+YuBld4C+Tw8V6bFofyyu+IR3/LHpM0MiWz93ByOMRyPEoQ/LiNGpV9CulWWMZ0n0bxmmujjvDwHKEdv31Ig1J9W/HCNkmz0CF8ZNcTaeYcoJ1Ky9Ltwp5c2bTBiVDLM9Txke+QkmswBhEIGem0sFG81SEdw+i/0lfWgE3gUC1LjcFn2/Y8IrZrIbJbKV1el4irPJTAxQqIOVjObzZRhlVvqPMoabYJQAJ70h+r2+bMFuGglqJRcb9Ai8EPk8GX2tEbgeAhS4bISEsqv0L9sQjWoZpZIH0zQQGQbOJlMcDceyXfJVcwtKtnnmGEh/kqA/GCCYzbjaCKWiLe0Hr2DClgWO12NXx9IIXBcB6lExuE6AARL8Ok3wP3/r4q8//ozj4xMkgY+2V8TXuxv4p/1tPOI2QFyouurhXDVw1fm6DOh4GgGNgEbgNRHgd1gf11G2WeOFYKlJLxqHcGKm7hlo1WswDFM8rIzCBKfjGU7ZEGEj3J/BQoxGxUOr6qHqpFbkzDb/I1026A82uE2KJyvG/dhAbxricBDjsB+iNxwjikI4toWq56DhOjLhrhrnip56qdcpGuNeN56i+zrnd0dbTa1GMJMIBVojR+nEu6ycMoAWDBxUDHx9bwubm1twShX4sHAWxPj5pIe/Pz/Ey2Ha0Tk/OLVSqjnj8wuZFF3dsYDYc8K9JB5yDNQrJbiuC8MqYDgN8fJsiOfHQxkYyOb45hPB6ULynHCtYYG5zzm4OOpKyo/3lmWh4hEjBQDtmiPGRYZp0RQJwwA4nYRi5DMYT8RdOFdtbtcq6NCjUCFNTxoKG74D8djiAa16Aa7riAEMByO7swiHvQQnPe5XzlWc9IJjoVosou7Rw8qiPrKrrGh+rAjKMGsmBzLJzH/Zth6X8ZzKEI1WYthJhCJXo8SAx31ZDYBeERowsF8z8NXdNrY2OyiUK5gmJo5HU/z48gg/Hh7hyE/gZ+7cL8tv3bOUh8V7U1jzXbIx3KpaqFU9uCVHFO3En+G428fh6UAMZdjQZhq+73RUg0Bwuj2GyYnxbHJc0Z2f5xeZ8K1j7h2FSVb8R75WO5xZeJwNls+rc1qMlIN54IKhfFD+WjBQ0YS2ulmQUqSJMb9ZtmnCpEUXD36z4hjTIJCBIEVbypCrX4yq6hux57XQswDbdsSzCl3yxhEwGc/EvamilWZ0/n8+j/NP14eoNJI3DVYcA42yh2qlCuqPWWaw8uz4BN1RKqdCKVc/SEOVReWi6K7nWSG4/qmicd3zUl5rSZ/Ph3U+H5X1gAMjowkwGo8QhlxrxndroVIsygp46lfWB5WfKjdXrtuWlcqmYXFRJaJwvecu5qkGCXlW11wVT4NaIc6NIZIAJRuoOWmnlpNDzG+J6Qwg2skI7wlw2KUXJV/2bxbN+5aeVbIs5CT55wP0tUZAI6AR0Ai8NgLUpTR4pFF4tWhIP9bltkCGDT+McTwY4Ww8xThIB0LnX7B1SjhslJpLAAAgAElEQVRhay1dHS0TTv0AkxmnTmnoG6FWLqJZLaPipR71XptZnUAjkEOAIsgf2yTs57RKBurVKmzbFmNttkVedIeylTPd81M22RaZy3BGK98W4tgBV6YeThOwj0qvt5ws5ThPq1YSg6t1op9jS19qBF4LAfZZON7I/nqzWkTJ82AXCtIOPx6McTwcY5TpXzXpP89gRRgpy6oN3h34GIoMcyFVIqv7W2UXJY5TMlN9aATeEgGKH0WJY3Q1jplXynBdjnFbCBIDx8OJjJlT/1J2uRt02oFcZLyqfym/J1wgOpogpNdxiws2MoOVemW+YGNBQV9pBK6JgPr4Z2fKrhrn5zhprVSA5xZhWhQ6C2fjCQ57A1kkFc7bEOfzIrm8HHPxbHeYoNcfyLwOPQV7jolOvYRy0RJv0+ep6BCNwDUQUMKWyTBTKNlTxiojAE9mwN+eD/D35y9x3B8iirlooIxHu1v4Lwc7+KJTx1bRkN0kUs/qK3mvtC1WnupbjYBGQCPwThBgH14f10FgrpSp8lNPEWkjxkDdAzaaDfzECffExCyI0RtNYbseRuMpwiAUN29cNdaoevDcNL36jqgzG0T0drBZMFArl3FYGGEWGxj7EV71hmJBPhqNkMQhXLcgWxFVSy4K2T6His6c1euU6yOLk6J7EVOqF5Pix1jKZSmfED+646slBh62TZyMO5iOhng6PJP3ctQd4AckaJU8GFYDtmfIIKzKcxU3oS3bE6QZyTYFGQsKa7YAaHnNiWA3AdplA5uNKg7PBjieDTAJprKl048vj2XlldUC6okBN2epytJQllT+0mHLNS6YFxsYrKzM5zYcLIa8Lxr5VE1UqyV5l+yojsNQBr+DoQ2uvIzCQLb92G7W0Sx7KBLw7BCDjcyrELGhx5BGxUC9VoE/nSAMYwz9AK9OpxiMxxJmGQnKRRu1UhFlz4Sd1Z+U5IK2yuOjO4t9SpJuAZJNZF+Xx3SLmnQ41jIMkV3KHg+eafjVMoDPN0z0D7YxDUM8n44RxAmenQ3huSeouC5K+3UYnMEQmTw/uCsPLvintslhfhwc5kFSrD/bNRPbrSrOhiOMgwGCyMCL/gTfH/VQb1eBsolqZijI953TBDLIwbqS/5E2uVT1izJ3sweZsmBw5QViRBa3iUvLSbFNkV/Gi/wpPaZ4YxkkPAvgff5Yvc8/43X6ZtJQFZdhNGJwLBu2RW0SSWebrvzPJj5mmZ5RWOXzV/QZxufEMaUFcL9d8h8bhqzwO576GMUQoybqY0WHZx7qnN1e66TKwMjMn3m7MFC3EmxWXWx2Ghg9P4bvRzibRPjh6ASNVgueV4Jlp3peef0gDSV3KnPSZxh1L8vCPBa/hZSp+K97Jn3SplkJz6Sdz4c7KrEOpNjw6eIgXzQOUfxxQGRE7yQxcHgWYjAcI5xNQXM/DnJUvAK4Oicv68xf/RwbKBaLYqzEraBmcYxRGMr7z6chB0zDg3yRKz6Xd89xGgYKwwYS04Jv2LJiM8i+Z3xH85dtpAPklLEJUhekL6cJfnkxwngyRSzeXrKtgAiMPjQCGgGNgEbgwyFA5Z99k5Tu5zeUA/bNioFqqYShU4DvA0ccsB+OsDero+EV5LtB/Z//kpEcv330AECDZ37DTvwEr057mE6n4pWS37CGV0STE6b22393Pxx4OucPjkDWjFDNFLZb2Gas2Ql2Njs4819Ju8lPTLzoDXE0mmGn7kgfiHJLL4Tq4BXbX2zL85e2YYBfX8ay5S9dCtpGAs+iB5cSmmV6WV00fxQdfdYIvCkClF/22thH57YqnFQ6dl1MxxbORtPUk+8kQdtJt9imzOYHeJX+5ZleUodIcDhLZGxxOBwBcQCbE/6eg2bFQ6moDQbf9F3pdAvlp/Qvxz8KiYGSkWCz1cTL/gSzsy6C0MDRkO2HKe6iLkZZkmbeH170XVUfmv1IGrs+Po7RH4+lL20jgWdbMkbYrpZF9klHHxqB10aAgkNFmTuof8VgkONOroGaV0LBLiK2HPTHgbQhujPqT2Muw0yjDqV/RYYTtiESnCX0oD9Gf9AH4hC2EaFStLFZL4n34Nsy3q8w0OcPgECmBCl/NPJj+3WaAH0keBUA3z3u4ocnz3H06gRG4KNZLuHBRhPf3NvDo20PNdOQeSfKrejlrGpo3foB3qXOUiPwCSOQ78/cOhjemULNEUqSCAknJLPBDDZIqiYNVhwUHAczPxaDlf5wCphDjMYz8f1fdh0xVqmVHbjmYiAvnYxKPwScAComBspGgk6zgWe9CSZs1AcRTrpDxOEM4/EEhpGg5DkyKd+olVEwFwYP2bzP+32XOXyul/HlCVbaiQuSdG1icBiJP/6nB4MUS1KkMPNMTJuGgT/d4RYVB+ieHqPvhxhOpngWdfFX5ykqZRfloiveNdRg7CKji6/Im/qpWEwvFYnb2xSBgy0LR6MW+v0T+HGA/tTHD89eol6twLI7MGtc+Z5OoqYDY9lEaUZQTUzSGwsbCcyP5eLkLw+VJov+uzyxKCwHB7WrDlCtlGAVbFkpQYOV09EQEwPiXcWyTFRLDrYbddRcI91bOVdqGq1wjpN1sQBDGvqb7Tb6vQEG/hCjWYDj0zMZFJ9NJ7KKU7wTVVxU3LQxlkE7p8p79ZsHvuaFpF8l/Jo0rh/9uhkttgXiikBVRnWml5NqwgGvBH+676I33UC338c0CTGKDDw+HcI1n6NTdmE2i6hbqSa8sM5eUADFrTpTFjiYvFVIsL/RwKvhRAbSuPrmZX8M49kxao06Cgc1WAUDysuRSs8z6w35UDqVulDxxefs/FHeZCL9Ar5eJ1jRXk5D7CxwT6oIIQJYYqTA/FlGplmXjs8Yhz91MEyFqzB1VnP63EN3/V4uaUyVH8+CAXF2CnAcB5hMwL2XhrNAsA6xKaudlE5Vne08T+o65c0Ap6aK3C+6YCK2TEzjAC/7I4yzjlG+k8O0+Z8qy3XPLEMeD1r707jqTtvE2WQHL7tD+LMJhsEMP708Qr1eR8k9QLFjZjK9HnvSJZ+r+pbywjxUmdX5uvyqeKRPmVQrGmkgxNfGCTlizJ9jprwpfJiW6dSZ1+xocqKPg3VdDtYdxfj5t+cYDEaIQl9W5rQbVTTKruxDr9JnZOb1wy0acN2ibCNE7zqjaYKz8Rhn0wQGjWlXBgqZnnwpeaS3qzr3IZdtmFJG6fusO6Zb3ATVSvptYxqWjfSE96yjPEaCoxj45SjBL09fYMImEnOg1Y6ALP8U2/qsEfhkEGCdXa23n0zhdUE/WgSULqfu9xIDtB1u1+vonp2iNzpD3/fx7KyH3WYV2/WW9MtE92clYvp5v0a2ogAG9FDRT/Di1THGw5Gk8RxbJpxqrrM02frRAqMZ+90gwPEVboXKrXsf3dvCk+4Iw34fsyjB89Mhnp70sdeqiMdcpYPZ5lEHw1QbjMZWR6MEPz87FK+d3ErFNmK062UxuG8W07adSqvPGoG3RYCyKH2SxECrArQaFRyeVDDrdaUPd9gd4gVluFqHbaVjgkqOmTev2c+RCSsAwwR4Pkjw8qyH0XAA04jhOZYs5KHXSm7/lpf/t+Vfp/+0EaAsceyFfeqDHQdPe00cn3YR0cPKYIwnJ13c2dqAWzNlMQTbD/lDya8ydu0C+OXFKbr9AZI4ku1wm5USNmo11DP9q3uSeQT19dsgoPSvky1M5bZTlUoVg+kAY9/H0WCCp8ddbOw3UTLS739efyr5Ve1gjpG97CV4eXKGQb8PIzFF/7arHnaaNZQyz99vw7NO+wkjsKL8KHf89tOLFY1VX0bAfz6Z4D++/xVH3b6MB1YtEw+3Wvjj3V18vuuJx3X2+fJyrBDNty1U2EqWKlifNQIaAY3AWyNwqw1WzqNDFZtO0qbdN3V9PuZFIen0bKqW2aDmjy46G56BcqmEcZy6tx+NuJVJgGA8ke1HWtWybF3Alc9KqafcLCbxpEGUraDo1D1pDJ0OfXD7iF5/hCTkSmSu5AnBgT3u1ekVVibcSTTLQOWjzlLm3NYI1xkZl7TixkJ9ntQ5RWhB+yLEluOl8VXJl2kxJkMupcmZahVDIvId8i9NSQxp2EFPGxsG8Nm2heMvHuE/fnqCSRxhHIf49fgUzafPUTJ3UN4syVYkS3meZytXuGQ+WZ7nVXWuuC1Qpwzsb5RwfNKQScrZdIr+LMS3vz3DZDJCd7uNz7eqsn0CLbZVY0DxwIbFFMA4TsRd4NFpH/F4gLbr4E6nhWa1gKKa28txdpOXijdVb9Lzm+dIemoAkRhUPKBWr6Ebnkq96Q6GGM+4tUiAklNAvezJyksaVMx54QvIjFWIIW+p0Oi9ZrNdwtNnRfQHI4QxMOQ59BFHEQomVyi5MjBeKqQ1+qKSMC+VHz2DXFRueZQRUfHX08yYzh7y7vL4acQ0Dv8vp1+fx0WhmXFDQtfrMdLy5OgnmacgYsxJCSPBo/0ahrMD/P37nxBwe7JZjCfcWuvJS9jmHorNwtwzRL4cvJ7/Mv0hdZTvS+mg7N2RA9YfWb0LAzsN4M5WR7bS6oURAj/Eq+EM//aPX9DrNfD53hYebLmowJD3reoPkVGdQRoHDMIE3V6EQe8Ms/EIW/Uq9lt1bFbSz16e34sQu074nE5mIEOvFfSIMY24tVWAQ98m3HO8yaeAIxdpDoJJhouiRz3Ges5VmwU79YazzA91X7pVjML6IvlkOuJkwwD3JqfRimlMkBgmBrMAT0+7+P5lhEcbFpqWIe50ObipvnEKY+JLtnnPwSfXNlApFVPX0SZktdTJxMf3z05QdTq4V0oHTmkEQx6ZTv0UzzkYFvItMrNc2vyd5M+trBIDDTPBbtvBztaG6IvRIMTMBH58cYhw5qN31sHD3SY6JRqDpgMJKk91ZkeOkxDcRujspI/peAjXMrHXqmOvWYabKXj1bvK8XHXNPGSgOAGORjEev3yFl68O4Xol1MtltGs1bDfLKDs0AEo9dpEm0ykY1DehmyR4epLgh6M+fnzVw8lpXyIWbROtiof7exvoNKooOebciFLxTMwo+RWX+tZNDVMME9MgxGG3j789OcGXB21sFFODMFUu9d4IgeCerfBknnQhzr/YtPHk1Qm+LT9F4w93ZIso5UWMaehZhu5vuarjyTDB31/O8OPzV+hzi0PTyXhJv+SpRlZcKy6Wz0tP5SWqN7kcT99pBG4bApR0ZbB428r2vssjekSrjothF2FLv93U/7wVL3wWsNkwcFhy0TVN2Xb1yfEpao4pHlbudKpzT3hKV/MbqAwuz5IEvx7H+PbHw7SNHvhwCxY2Gw1sNaqoubZMzqq0FzOon2gErkaAckT5ZfuqDGCnbqDdqOHs9AzhOMIwTPDTiyPU2Nf8bANVK10YwbYL0/LHPgU9U9C7ypNRgn/8NsDRaQ/BzAf3wiy7Fj6/t4dWxZW8tOxe/V5WY2jMVhHJ7pUn36yfXAXQqabbT3dtWyaiXp718e3Pj9HxHmB/o4wGZ5qyg1fsQ1D/cmzpDAmeDhP88PQM3cEIcRyBW4W261XstBriYUX12RQNfdYIvCkClD+lf7kwabsKbLSqePK8CD+0MAoCMVj59pcnKD28A6OSDnCyv8o2B39sP1D/Un4PfU62DsXYld7ZDI6LJwEONvexxYVNmc5+U351Oo2AfPQJA4WP8ktP6rylF3cT2Kyb2Gg0Me2fwkeE3iTA//zue9TtR7C2W2iYalZiIcMcB6EO7nIcZJrgh8cnOKLRFrcUlO0EK9hu1qQNTfW90OApD/q/RuBNEaD+pLEK26/PQ+A/Ho/xnz89x+nIR2wWUK54+Hy3g6/3N3C3U0Q5kz6mU+PqlEe2iXmsyqa6z7eZVViWRJ80Ah8WAdHlhsxv6TG0D/sq3iT3dObuTVL+ztJQcXIaUX4J9xuOYcqkLSdv0y0NrlUk8fCRxqRiZsOYKxHqBQMbjRr6s554dPAnE/iTGOZsCtcxsFktoV0uicvCvBLPK3e+DE7a0uhhp2GA1uLPcIw4jOCHARD7MJIY3LW24hTEJR0nhZhO0cyvjmYY6YtPkjiBGYcwkwhGnMBQE6gJY6QNKkVjCQeZRI3muKXeTRKY5vqJ/rU0MoLMibyacQxkP054MXeesnbhUvaqDOSX+0PTb0GMdL9olYJxFDfMgx0jTvZWEgM7LvDNvQaO+328jKaYjUOcTQKZLKvYFmrePnar6eAo06bcpCxwEpmW+ylz2WR/jjvGVUpP8cnB3I4BPKgb6G82EPo+jn0f4SzCq7M+fD/A2XCKF90WatUKSq4Dx7bAHTqIQRRDtl8ZTafiTWfQH+L05BReOMP9dg01z0OtkrrcvgzrHJtvdMmyqclpEhCMRW747iKYSebdJmtUM24qSZdnl76r9B1RFpgPjVBqjoFWtYThSWqwEocxwskESeCj5NloVypoeA6Kue2vVPkVTSVfrI/bdbosd3FiWbIt0IzbTrBTECYomjaaroemW5TB9yWO5aUqycrKreoRPZKw/vAHa63M5nkSuiLYMeiZiS4fjZgfSzYBU3wVbirdKi8M58AR41GuLdbHOMh4oMykpV81vWMx1I806Y3I4HtDyj+EhzTVat6q/tDTykEVGO+20D0+xmFvjGA6xskoxHcvjuCVSig5G3ArmVFCxrzwTJmhfmV+tNAWvUO5Cee6Sl2o+OygcVugDRN40Cygu1HFz5MBunGEWRTi6UlXVjIcj0M87m+gWiyk3kIKlnQmpUEeJZiFwCwI0B8OMex1MeuewgxmCA92ZCAuEbONJaTf+kb0aaZT2U2NkwSD2MC/Pz/B02FZvPqIwGRaTsxMDHkrqfYSPUv5yjDjtm9xiA3PwWdbm2jXHTFcUVhRJtIBRX7HwvT9IkrlLHv3LJSKr74tDNusGNhp1/Ds5AyRkYhhzYuhj//+4xMcjzaw3eD+uZmsBQkKkY+yxfpZBA28mK8yNqsVgP1OC78edhGMRbowCBJ8+/SVdI6OdtrwChADGDMGzDAUD2ONUkG8JXG1FWVbDhHY1ANQ2tVPLXhoAKSOxVX6LRHdkRjYKwGPtlsIxwM8m44w8QOcdkcIJiHOhj6eDXy0axXUSh5c16QDHNADTxQBYZiIzh1Op+j1exicHCGajtEpe3AKjuwnXMxWLMrryzOhGLvgzCKxfPxxsKIfJnjSG+FvT14hsYsolytoVMdo1Rsou658CwqWCdu2YIr3IgNREiMIA4wDDor4ODzr4fB0gLPBFL4foogAnaqLh50GvtjbRrtclFVseX2s5MDjYKEL7FU9/Fq0MQxjBFGCV2Mf/+PxMU4TG7utGmpuqm9oaGUnEcpI0CkXYNiG0N4AsFWv4PDUw+lwgth0cDgM8Jenp4idGna5+ojeq8hEDExpNOgnOB1FsqLo+fEJeqMxigUHlaqH6XiK0Wwihl2ZaspqynlgWRb5zdtvbNNYmUHYYpSH2L/GqzqfkQ7RCLwnBPJymr/mN0NM3HPNT/EuthTpPTH5e87mEmXAb036vfk9F/DmeacqZ9uQ3+yaARzUDJw0PPROPfRGNPYMxYjScA4xLpSxxza4tJRTPcwJf7pB7yfATycxvntygqcvXoB9ZSuJUfVsHHRa2GnUUNMeKm7+hX5COVBdqn4NjZw7RoL7nSoGpyU8Hw/gJxaed0coWMcoelXc23VR59aJ85GFtP02oGeVEPju2Qi/PX+J6XgEw5/AM0JslWr4Yn8HzVJB8mJ90Wr6KiFTCEnj/4rIKu4V0W7bY0KTjUEoGa6BbXgDp00XZ2UHvTHb11P8fNyF+8sLDK27ONgooMZtfzM5ZB+E+pfeGX/rJfj+2QDPDw8xGQ1hhQHKxQL2mxXsNitolrSHoNsmRh+yPEr/coyHiwnpGfWgaeBlu4wnw2PMIuDVYIrvnh+jWK5gvNfEpmfIWDj5ZhXgohLZxioCvns+xT9+fophd4DE9+EZMZpOAQ+32thsFOcy/yHL/DHnfaEmzXTNx8z7e+UthwcxU21gLpbbrQAPOmUMThycJhyfmeHXwx7+v+ohpqaH+1sealn7lzxT/86y9u/zYYJ/PB3g6ctXGA2GsOIYBdOUtu9eq4Fa0UoXL73XwurMbisCSn8OADxLEvzn0zG+e/wCh2d9JLEJt1RCs93C5v42ik0DExs4ShIZ5zVzdYDyzyOvP/LXVpx6MaSep9F33kN1llSfNAI3goCSw5y4zvMxjHQxJBsSRsQ5tMUCYkZSaVWC1XsVrs8fFgHOY93qg4InPwqqeBbghG2cGj9k90gKc8ODq8FIRZn/qbzpotNNDNSsBLudNp51JxhNZojiGEkcwolDlOwCtioeWiUXLmf6skP4ylUWvgzxIJEAW56BdqUk2/1M/VCsemncYSeJTNrXi0XUXU8aNezEzj8kC/JpuVUji+XnRHfM8iuDlZSD1QrO+3mY4BYCCX+ZwY+RZJNpqiRXn5kT+WQZaQ1Po4eUXjYST7xyuCiK8+JwsjMzWKGtPbczWTrIZzZXxTTiuYSebxIDd6vAV3f3EAU+nvs+ZiFdAPdQsoBGyUG9sgM369gvlZ0ZyAQ7m5qZHC1lurhR5eP7Y55mCQh2G/D9GGEQ4TQMZcLyaOjjZHCMv/32SrZUcL2iWLaywRAEIabTGWazKaazGaIgoMsCJFGIbddGq1yGT+jmoCzyf9dXxIGlVihTvqT+UH5iU4y9LGLGbRwYjxGvy1eSTniTPvezLyZA3QHa1RKeywR6jIgP4hBWHKBS87BZr6JRMlDM9rVn2lxVEvknC5SxkgFsuAaa1QpeFLvwJ6GsIOLsNA0+PLsgxio1x17eXkgVVgqUlodFYgk5aWRxYiOrB0liIo7XG1qdg4F6Jg5FH7DAqcFLim0qWSnfS+9QjKXSEEIsBgpZ+YyIBiusi2n+8hFeSnz+hnnSaIR1iPVHpc/zKoYlOTmn4Y8YX7VN9B4cYPrzU5yEPiYzH7+d9FB2D1EvFLDpNuBwcj0jxhN/YqRCXWvSEwMNdnKGNissKt1AAzyps1wGud8GZlP8bPXFCpzGXofDEIf9l/j3n56j6BRQoZcpz4FTsBBEBiazEBOpQxNEUQAz9OHGATqug4MwQWrakeG6wsP1b1NhZxmV2LNRT0PA1IopQWzEGIUJ/u2nJ2m9mdekXC5GOlW2qDiZwUqSGic6swnuNyrw/qsLr9xe2r6Msm/J1nKpMVRqfEmdGklOeVGm/MqHPtOPezUDD/fr+PuTAgbhDEFioRcC/+unZ/j1VRfteg1N7gHNVt1kADecYqfq4U+f3cduvSB6U72vOr1Y7Tn4/lkdk/EUg4DmhAZ+OeziqD/G358do1mriqEm34UxHaLp2vjiYBcP96pSh8mr4jdFJP3OiPVCDq7VS5aJ6SrUVQbw9U4B4XQT/myGZ8dnCPwIp5MIZ5Mufnh+CrfooFTy5FfMtsTxZz6m1LfTKYIgQBwHMIMpyvywWzYmsGSgTPQNGVgwusrO2ntVNjGm4oCFbWBoOjgJLYxnCZLRCMarMZL4pciObXKrnQK8kosCt9wxaVATYjIey/ZoAY0GLRsx9y9K6F3NQLVg4kGngT/e2caDVlFc3vP9MO+sSgpvvOZ3ccsAHrZN/Nyq47fTHqaxgX4A/O3FGZ70xmjVSuLa3uEKoWAGJwmw6Zj4p7u7aLfL8q1kh/Sz3Q7oTWfw2wuEsSHy/uvREM+O/4rtThP1ag3FoidGQfSW1R9xr+Yh/OlI9GGpWsLuziZq7Zbsn/uk1xfjmYRbJmWKUcGdB1d0C8tGHSjfI54pMyxvvsT5VPpaI/BxI0DJVfKupFja6pRp1gf1eUkFfV4YNqfnu2nNQ/XFVQgojFfjic6+6OFq5Nt8TwwEjPRDkrb008UAnPSnMfNgq4HecBPDZ0cIgileDHz0fnkBv1jFIKbxa2rgwrQ02OSA6fNugm9/PsLjZy8wGI5lIUWZ3lUqLh5sb2CrVkDZTNvEK6J+m9HWZbthBGTsgXlk255+teVi1G/j5PgEo8hGbxbh56M+ZvET9PEA+5smasW07Uz1y5Wpx7MEf/9tJFsZHnd74Jac7KO2yjYedmq433HEs5C0t2+4PLeKvNK36nyrCveGhVGNgSw5oVF9Hq5+3i0Co40Kjo7rmB4NMB7FOJ3O8D9+fArfKWFkbmOnacp2o+wPcMKf+vdJN8aPj/v47ckTDMYTwPdRMhNseAXc6zSwXS+BDi7ScY835F0n0wisIEAZZP+T40Rlth8aJnr7Gzg+fI7BzJSxg/BsiOiXZxgZBTzYqaDlpXLIqqC2wv3rb1P89OtTHB6dIUzSSdFmsYAvNpt4sFmF2o5tpfqscKNv8wiIn1QZxM2HfuLXawSIOpFyzLHRzQLw+ZaJV8d1jMMYvWGMQRTi3385xDApYmTew27TFO+8TMcxIPFu0Uvwy7MRfvzlN/SHI8RBAM800C55uNtuYrdRkzaE1r+fuPy9w+JTlOldpZck+F9PZ/jLz0/x8riHICmgUCigWK6iXK0jsoBXwwRnIy6U4bxDbkSNY9wMXGmjyVQcxybCBHaUwEOAqg082PBkflS3hd/hi9Sk1iOgdPViveI8HsWVBityMB7naVYMVuaR9cVHjcCt1iUiqNmEMwtqhlMk0yGMyBcrKyv0YXKJdSq/oodXdPGlL4+NPAuGNMLLBlccF+GaMYxgAoPeGGjMYsSoOxY2yh6qjiEGKWzw8GDdmeeXc/nJFZRsELXEaMXF4bgnjR16WLGiKZrlkqz+rtNtcp5GRledSJvfF8axY66Un4mnAcOfyX6fsv3AFVM8RpDACqYwZlMYYQQjTD210BgnEXMZldvlZ/LBcpOXQhKK+0Yr8mHROwCNV/jL+CUuvFP4cO6wkEQocDIxnAIh+eeEVWZ8o7JmAlFOaT4sPz2ecDXg1/s2An9X3Pe+PO0hniY4Oevih18StD0bzmYTdbcwlwHhlV5dwnO/D30AACAASURBVAAxvdtw8jsyZSWgTE6rPHNnZi+NWfEoYeBhEyhX29jebOLbHx/j2fExJmLMxGnZghTZn/gY+iGMHjekMGTLp4j58YhoWEQZSxWuZZkoWJasWp/LTS7/m7hkPsxffuFMZJvGF3QCTsMJFoJx+A1IPT5cwQVByt4T41MG6VGoWQS2yi5+NBLM6EWHE5DBFEUzQbNoo1MpiXcHJe9L5Se97EOl9niuIMFG2UW9VMRoNEYSpvWcBi8Nt4i6Uzi/FVSOddZdkVnOW9MAKYrF+IEym1Buo0QaY4yjDsUTz3N5p9wmIayE8uPDiq1UhrJEjEts50eGjcKIz/ljMGkaAWBJPZ4i9mcwLdKjocOcglyodEKfW/1EAexoBuo8RD7sOIAtRi/r0zEveimil5UtO8HXd0sY+NtIQh+nh0P4QYTDV8d4bAF33AJ2Niso0EtQxicntAs0OApniOMZEEyl7Hx/6+oP85NnZMcA2omBUttBuXof9Wdj/O23F3j54hWCIBHnTJysj8MEs+EE5nCcrpA2C7IfchTGYqDEWmZnk3zyPsTAioi8u4PURKfxPYYBLBoTRTPEEb2nqIO5rzu49Yp6U2RUGd1ZMEwbScFBYhfgR/QqtTgUVpRF1hHWQXrjsGJXDPkURaZIS5t+pxQFDnbu1U386dEBvv3HTzgdjOibBWGS4GwwxmA0wVMzEYMj2x+jVQCcnQ581iGDNTaVWb5jTly1jARf3dnCbEIPPFP4lFQaMMwCTF6d4vD4LDWsjHw40RT7rSq22w0EUQUJK2xGz44AM/Clnolxi2AZZsZV5zFkCLnh95IDYPsm4DyoodX8Gn/55SUeP32B/oCGS4xjYhLGmA2n6E1msGy+tUS8LsVRiCjicG4sHTTTpMcrE9S3nJB4F4finoZGpmlmbeZ06yjDtFI5oMcXTuyFwHg4Tb2YGTRKo/ErZSAbReZ7jSN4BRsbtSq+2u3gm/0N3O/YYqySftfVu0+5VzJDuPnOdsrAv3x+H73/+BZH0wkimuNZBQymPsbTCV4eHaUD3TQYtIGo5uGzrTbacRkFK5X5B00D/YMdnPaGePXqBH6cGoSRzRcnXRye9mEYtvRykzhBFEeIQurCEK1aGQcHu/jym02YBcCeejimCx4a+cIU3bqKu5JrOUfUaTPRY4UkQCFhO4zehtJ6xPKmkrVKRd9rBD5eBPIyznaB6A1RYJlRVqYL5FuRFYPeovRxCQKXqPCldlOqOi4h9Ak+okASP/6yNjbFjYb5zcTAvQ0Lw3AXp6MZTs9CBGGIoR/h3779Ht99/zOqbhGNelW+GaOpD25xOwogxpe+PxMj7qIRYb/VwB/u7uDz3QpqhbRPrfX3JyhvN1HkrP7P+3TS5wR2C8DXdzYxmAT4668vpX049kP8eniKk8EA5aKFUtFGqewhiAKM/QCDWYThNBRPqWFAj5kRag7w5Z1t/Pmrz8R4eqk/dxPluVU087U8UzIXle+Kxxclu03h1L1s31P/tqh/m8Dw4QFG0RMchgGmUYhpkuAvP/yKnx8/Rdl1ZKtlGr+z/3YymKA/DcQDqYwzJbFMqO7UKvjT3V18sbch446UYdUWuU346bJ8OAQouyJTCcf8gA2LW7Z76H3+EH97/BLd7kDk98nRGU77Y/zluyLKHKfzHPbUMQl8dCchBrMYvh8hkW2AEpSMGAetJv7bv3yJrXK6rS5L+VqL6D4cLDrn3xECqqvFsdFaYuBOBfjm/i5GETDl4qfAxyTkVj8v8OzwGJ5lol6vwi0WZEz7uDfGOACmfoTJeIgkoYfcRLzp//PDA3y23UY7826V/zL+jiDSrH6ECLDpxDFkbqf2/a9PcdIdyCIzjj9HUYzeWRfjbhdPf7Zg0BO8WpzOwXqOS6sy0T2FjBaTGse4LRmAVR4rrGCCqhljt1FC4b/+CcV2GRXdIFbo6fNNIpDrH6i2q8itGKhwrpgLttP5VNmpIOMll2zB3drAxWN99WEQ4KzNrT7YwKC+pBeHKnxUjBDc8bViWrKKgI0FUbbZViOvA0bqdSH1suJxW4K6iU3PxNAKZGKG1omNArBZKmKrWoaXrRrLD/7N88u+CDyRZ07ib5cN7DdcTE58zPgRgQ/PDLDp1bBZdmSgRDWg5nSyi4yclJ0dXDfmpJ6PMncbN0JUzUga+rZsk5T7IGWdCtKlO9xKEqLKQRkjwYRbA8QxSgYnR1MLTJXPav7qns/540SdnRgo0AIzDlBOAiRGAC+JUKQXBq5UyvHO/PlJZJgjHZwIFTNCBSFivj/Llq0lCuYi3eKrmg305ybdE3ru2CghHHYw6/dkK4xk5qN72sWzZ8/RKRooFTfm2104EVCKQ1QQwRevGiFKsOHEkUyCk791ZWcYn6kGrW0nKO+YaDoH+Om5ixdHJzjrjTDzI4SciE4SsUwVVyOgMVAsBjxieGGbqJRddGoV3GvV8PlGU7anUDgpjG/izDJQZ/O9OYkB10gy+Qno1wM1m8ZYND5IV7Zfy1iFjCrQcoPfXHVRpcGXZ2KjZCKe+fDjELYRoOW52KoU0PQKMompyq7IzMueGcyIrGdGSrsVB4clC91kIh0D1te67WC76skeoZ69kBOhQ6IsdO4gDszTTRJUjAget+VCiLJpwTXOywJJMD75cGCglMl6KZ7BMSNUCxZK9mILHdK/6BBrZj5Uxji07I8TVJMQ0zhAmKR8lA2aPy1v70M+SJtGBZRlL/KlLoeyzop1P4Jj8AO+fORxZRmYdz0xsGsn+GKzirhfBs4MTKchopGPs6MYT0sOyu4BCnUPlpWWnYZirDv0PMVpeddMUDLpESLlK5+P4oC8MJz5cnCZk9D7ToLCfgkd7z5+8go4OhtgMBqLF5Uw8hEHsrmOJGA+NFChFyoTIUpeAQ3XxVapiPutOh7tbqJdduT9rLxmxcI1zyn3/M8f3ze/L/y2lBEiTALkNj66kOZ8QIWFJUPSMYizhlUEN4nE4NG10wl8hQ8/2ql+8kUnJqaJqm2jRCOL7L2nHKqsF/wyLd/NVgH43x9UUTXv46fnL/Hi+AwT7mVKPuhMi0NENBqLAxQKlrw/i+YUGZ+s76SlPEr9YduEZ9xDp1LEz88PMR5NEAQ0PEuAMJZtbcRQNAngWjXxNMb05Izvm64jSxH3Bo7QNyIUjFj2Cea3waZOzOKqEgkf+Xoh35d0RUCxRY9N2/ip5ODZ4QlOegPxCkQjqzCix6oEdGLDwojXLskjQrFgyzZinXIVe60aDtoN3GlX4Wb1VfImw8vgzllad8Go5F1khLiXDHy9swEjCPCyN0Z3NMF4OsPUJ0M0scoG2vjx4420T0LQmxU9PNEDS8ktot1pYKfZwJ2NNg5aZWxXDNTsdLCOea2yyHuGU9fyYds28PWejTB8iJ+eHeL5cU+2G0piGiHSGDVCRGPSJIJl2PCsMhzDQCFJv21kjQPmX2+YKPzxEX58XMGzw1N0+0PEoY8kTAugtBIndvi9KBUd7LRbuLe7jTt7HbS9tMwj18BTkwasU5SQwMlq0Go5yD7Lwa3DakaAquEjSKYoxiGKyQwF0CBm3ZvQYRqBjxgBymymz/I6g1ulyJZvUg+VZ0h2vs/X8Y+4dJq13zMCFMhMp6rvCL/Z9GTIVaaPtgsYz3bx/W8Bjk4DTINA+jczP0R/EuB4PJU2IPs7vs/t7dhni2GbCSqOiTvNOv5wsIGvdppo2Ya0T/jN1IdG4F0jQLmS9nM24UQvQf7DPfhBgicvjjAYjGUyPxz46I8T2DTO7XKyKUIYRgiiGHFiyqA++zS1koNv9vdlsn+3bkm/X8vuu35rnyi9dY1f1a/P9G8HBr7csuEHe/iHkeDps5cYT33pH3MCldtPOzR+t2gkH4M6OeS+03Hax/IcC/utCr7Y7uDr3TY6bublOcvnE0VeF/uGEJC2LcekOEbHMXMPCO5viEflXwwTZ92uyGd/PMNoEsA2TVgcNDIotyFmM+pfW/rUNHSlh+xH21v408Eeduscg0j722yucIxCHxqBN0aA8pP1yxQNBnH8gW0IypqRGPh8w8Q02JKxh9+ezjDxQ8z8AL7vo2+aOJv6sLgoKU4knEMjSRTJwmkaxW7XK3i0vSH6d6diSLtatyEU4vr8LhCg3Cp16I/HstuAkZgwDUtWG0dJOt47m+98oAYgKaysB/QMzxMXLfKnKgbHrvks/XFxe2hGKBdM+Fw4+i6Y1zQ0Am+AwEJXc76aC4l9mLGfLZhOZ2hUnVgiL/KehayNsBRb37xHBPjdvbUHZU2Elp4CbOB+u4bgwT6sMETJsnC300LD82RS/k3lUg2AcBJwowh8vddGzU4Q+IH4Lmk6Fu61qtis0GDFSCdTlK4/3x5K+c1czu1WDXyz34aXDDDlRHkUiMHI3VYDe/UyKmzI52itvkhVJk5a1wsGHmw2xfCE1unloou7rRrKRU6rLz5m6ppnlmnTLeDRRhtNy5KGWK1o406HE47Wucnu1fzVPWkRJ3ZSuFr77kZD9mvkJF1xVsduqymW9GwIqoPxOdfJInow0Ck7sj9po+TJFjkdx8RGvQqvkPHBTHIHb0mPE6HsuNBLhlEDrDubSGZTBOO64EnjAc/zYJimWOyzY8+09HBDF6nf7O8imHCfah+1YgHtUgnFxUL3XI7pJflW5eU8NHmvmkBrw0TH28LzRhlHvZGs0uKKrVkQwpdBMFquptu8cD2Ba1uoOjbaFQ87zTr2GlVslk2ZlBQPFSvlPcfImwZk8qTKQAVBDLntxsOtFgpmjMSy0TKB/U4LVdeVd/tancOMd574o3xK57UC/OHONrYaZRk0LMYRWiUP9zottMsF6SQQ3/lBXvOHkhcSpcvRuoXpbgt24qdeKGCg5jq416xis16GV1js75wnk79mfhycb3kmHmy0hA69htArz16nIdtzKZ6yYgkelFsaMWyWXTzabqPkWHD8MTa9AnY7LdE5Kl0+v3PXGVHhI6vHX+5sYMt1ELMeOw72WX+K5HJxMBnlnxDRvfp22cPn222MKbyBj41aGc1SEQVu5ZOr/3MKGZbMl+82SQw8agL2/gaqsS+rDQv+DC3blK1LZDkLvQFZhrxP8eJQ9fDN3X1MEqAQTLBXKaJRqcg2Z/Oyq3eYm6xjSVR5WRsrBWBr28SOcwcvzgY4HY4xmMww5ER/ECOggybQWCMRGSkYrD8JGpUiOhUPuxUPd+pVtCs2ShlM6l3Ny/sWF8RZ9Fq7BifZxtC/psEKvWdkjEj7nzqKBgqcpDRiOMEMO+Ui2vXqfCssRmedrFqQ/cb/+OCOeMZoFC0ctEpizEDZm+ObK5cKo+EAjQ2qDlB5UEerUsQvNQ+9wRjTMBKL+9Szk4mqEWLLs0TnV11H5JYkSUthSPkomgaqOxbapT3UXRMnvRFGMw7w0wAmkAmqImh0mODBZhvtWnW+xRH5pbx0ipCB00apBH86QS0JsFWryreaGKv8ckWSMOLB5zQS5Oul8WizYqB1r429WgmvegNwAGzI7aJkICFASK80NHKhwaOZSNqK46BVKWO3WcVuo4qNSkG+scRrnvf8Is/FxdeMzh/xonHPBo3/NmiAd4Dn3QmOBkMxWulNJuA4MjuOPIdqizwaX3EVpG3Dsw2UbQt118FOvYa9Zg07DVv2iuW3Veo7XR0qHtWZ7GX1jBgJT8TKMuDdr8h2hT/WT/Gix8kabmcYyNZS9MLkmQnapSLuNRuol8vynpkXja0qBnCH3rE2TWx5u/i5XsOL0y7GkwkCGmPGkXiHoTvGYhKhYptolV0cbG7iYKuBFmc8M9amdQ/T/U30xjNsVRx0avQDlMM9g5hhfMf1AnCvWYG510G/6sjA5sFGAw1upUTva1l8fdIIfPQIqG8gz5ngUl+IsTB1q2XKlnu2bYLGi/y+caugeeSPvoCawduEAGVTtdFq9NbGFQV3K3DMPfzsFXDYG2LiR/BDA2GUwA9D8VTGwVGzYMM2IvGWWHctbNY8fLW3iS+3W9ivOTJYT6NjObQSv01i8+HKsiJHbCeJ/BpAh23uBuA/2EOpUMTjo1OcjWYIQx9REiGkRyvuw8sjpuRD+jtly8ZG2cb9Th3//PAO7jZLsuhCtVO1dhao9L8bQoDyS1ljH4Z9ZGPfQRF70vd+ftLHeBZiRo+S1L/SnKcn3ES2cLYLNKyyxJPVVq2EL3c6+HKrhftNT7wqKt1+Q6xrsp8aAivfc9V+YPfPpPfiKhDc7chWuL+5Ls7G3BKdiz5jhEzL/qg0jC0Ytg3XcGTRV9s1cH+jij/eu4NHW+X5NipK3fOsrj81yHV53xECFwgQx5woxxy72oKBb7YLcMxd6ae96I7QH08wDULEhomxLJCS2X5YZhEGFwvaJtiG2GmU8Girgy93NnG/aaGaeReUmf60ufGOCqLJfOoIUJRF91oWCrKfPFfQc94rlU3iQ4/S3B1CBgy5mFrGo3mrDFY4wBjD4CSUGlTkIDZ/sQHTtmDRoMV2AcvRCvhTF7r3XX6KZTbGTVmXvh49r3OM34xQtGI4VoKCLKROmcuSvG9OdX5vgAC/u7f2UAqaQluHgT/f6+Bf7rXBjV/YKeNEFI0y+PxND1Up1Erz//NhG/HDltSaGNzPjd4pUi8hBFvaP7lGUO5SWCA9hnFiacc20Npz8V/2vhC/CHzmkl42+cWJo+sczHejYOD//nwX+HxXPjMsMyecaIywygNpcjVG0TBxt2Ji65s9xNgTR2A2vUZkadelW+VHxSEP7KDQW8f/9eU2AmwLHywL8SEfq8KYcIsIOzWWuFu1sP3HeyCm3IaJ6bgN01UYEDO+a35POUlbaRl4+Od7kjefMU/SotEErxW/FcvAZy0D+3++C5aZePE5MSO91UOlI00qQM7TysSeGlTghH/FwP1KDSFqmIIea4BRCAwnCaazdLKfdgelAg0rUreZfN/ERk3Gko/5hOQqE+/iXhUkw4L5UbbZsfxvf7wHH+k7oFzTwpxlZJlzya7NBdPwRzy5bVOxaGDzm12RMxIh7nzGPMgDeVl7qMyzDxXjUab2PQOdBy3864Om5EM+xetJ9lywXCWoaGW88ZblPKib2Kpv4l+/2hDPQ3wnlBnyt1p+pqGsxAbwqG3jbntH5J0DSzSEUmVhOh6coGb7cenI8aHCicOmbeD/+dM+EuynHSZVr1beAZPzR7KNgoEvtjzc3boDBwfpRzxLdxWmTM845HnLpD6q4p/2vhTaDCdPxIfl5T1ln9esm19tFXF/6xt5n6yzLDs96SzlSSaZKHcwSPBL0nzZKaTOlrrbqiNADT73g02A/gwYjRNMg0Q6ix7rT9FApZjyRU9V1Dt8T6Qp2bHNvYp3Lv9LLxWvJJSxzonFjmngzw+qSB5Upa+pol1GS9mwMy7ZIUn1YzqWWek5PldxiEebxld36vjjnX+V/PgelC5dwjdjIGNX7ogFM2I8fmMauy6+2T3AlHiGwGiUIPQTMehqFIFW0UCTxg0rOpI01TunTuIWAaW6gfv1XQy5X3oIDMYJgmkiRkoVB2i4BurOoh4IL5le9Sqs/3vitpK0WR7mqepYVpS1J8UL6yUHcellg/V/e6+EaM8TeWH5RjHQHySYBam3kqIDuI6BkpN+nygvZZYrKytlRmG/NuPXCBRaQtdAqWJgt1JGgBI4HDdKUnedMx8IogQT7nwXcYAZcAsG6mV6h4LwptovrJN874pH1qMLvw3sk1Lu7fSdMQ3Tb1CONm083NxALwEGM5U3n8eolyw03bT9pOoRsaZXuqKlsDbwVdXA3WoVY1QxToDxlN80lgGyVVjdNUBZqmQ6ne+JGHNAkjx/2Xbw4P/4av7dpP5W8q4gZr4ME5kwDFR2a/jj7jeiPhhOnUO6LBvj6kMj8HtEgLLMtkUpBupmhE0HmBZi+R40i/R2lXpb+j2WTfN8OxCgjLL9QjnltpF3HaD+sIH9zTp+fHYk3ra4vSBX+4fisYtbaBqyUMFxbGw1Kriz2cLDnQ08bBfRzPri6VjpZR+y24GfLsWHRYDyyzYC2xkcF/inTRM7rU388qqNv//2FKdnZxhN6JGP24umXkQ5kM/2br3i4k6njs92O/h6v4GGlfYx2O5Y1/b+sCXVud9GBFRbmDLH9vAO+7l3ithp3cfffz3Dk8MjHHcHsi0rvQsnbLDLgg726yx0qiXcaTfx2e4m7nVK2Cqk/R7GYt3Qh0bgnSCQHwjhddYx44myS/3LcYOvW8BmvYGDrRr+8fgVjk7OMByOZRsr6t104jRG0S6g7rrYaTXwcLuFr+5U0absZuMEuSxWh5XeSXE0EY0AEcjrSOrfbctAecfBna27+O7xGL88e4lXp6eYRtwmmZ4m6DmZBi4JXMdCvVSSRVFf7O/g3kYZWxyzzI955DPQkGsE3hIB0bfcOl3mAk3EBcDnojhL3GmnE2SGAcM0Uq//siBm7h8ZJs1iZXAx28Y+M2qRLdPZXYsNxFGCIhdaWyZargXPSuYLHN+SfZ1cI/BaCFB9cmzC5cJcI0THjrHhcHzYQsstoMKFM5kez5okr0VfR/4wCPCd3dqDgkjBVQ1jTmJx6IGDCmpCis/fRmAVfZ45ucTJtVgtm0e6BYZMKnEyPd94vwR18jOfVOREkzhUzsqSm0i7hMTSI5aXk1NiFJk94beHuDCv1fKzLAWDG2ykHQrGoxEmseMzobWUQ76bsPRAbkhf5cXJVl7ToIPfxLwhxmpKuuPlQV55yYV8xELwyfG/mm71fp5/RofbGiiO87RYNt7zx4kv5ksDG/VueSYfPK87mI4Hzxnrko+UPeOXmEZJanhEI42owB+xTktG2ozP908alFOVJ58p/rKsbvykyqHqC72GUA6UsQafq3K/CTOqvIIb609Gn/eq7MyDmMixrg7lGFDvlWkop1ytSaMfhRvDKXOkt/49StdYsuJzxuePdZtpiokx1x0Svqb8zEvyUem4Kwp1AcuRy1vlv2Q8wcTrypjxS96VHqF8KvwUrQylOf+8UGk40U0e8rgyncImnzZ/nS8L6wV1AQ+FicJS0cnLLussy04alBmeGW/pOBeQYkDe8r/UcIX1xxD9wQ5eywVi/lhPBY+0vpIH8qXklNfzbNaBtcTQNW6yORWSIm0Sp1FXOix44StcIkwYGZ+Hwk7xyHOef94rtvk9Udin9TF9p6rMikZG+tyJ74C05D1JHUmN4iIOHhUSxA3WF76zhcEYcVx3zOlkPJFmmKQGKQ0bCGuAUTMEm/m7yL6TLF8+PbFguagDeKhvgyr3EgtLNwvOGFfoZvWM3xklLyxfaAFRQ+lb5p/KC9MQF4U5rxVOF2S1yPSKK6bnj7zxJ/eCO7+DqcxQluWbWORu3QaSUvqtI+mUr/RdKMyUHiHe1+KPeoOEcpiTF6ULuP0WDVI2XAOxSx3IfG2REcobdanIi+KfnkRTcuk7ozwl6aB3yLJ4BmIvpcNo3F6QdPhOFbbkm+VgXmwy8TlppuVdYJVlI9jxWvDLZIXxM3ER/hS+Ko0+awR+bwhQhlkXWoaBb7Y87DW+wihKYEex7A/ddm2UHGoufWgE3hMCa4Qt+5yIQmbfUoyKq8D+o02M7m6gO4pkpelkNpU4BcuCZxdQdoqoewXUPUNWlKqFB3N6lGwq9TV5vqfS6mxuOQLUsepg24MuzR0bqO9YuN88wDQ4wGDkYzieIgh8WJYJyi893dXKZTQ8A80iULfSMR7VLlM09VkjcNMIUD1S7thWoK6kF+FS2cD25y2M7rfQmyQ4G44x9ektKIZpGvAsA1XPQa3ooO5y8p+G3mnbnGTy9eKm+df0PyEEVr7nSl/ymy/jNokhCyCaGyYe1Lcxmm3JQr7+aCLergx6nLUtlKwCqm4J9SJQ8wzxHC7jfBmU+SZD/voTQloX9T0hoMYalP6VMRQTaN4t4U87DzCY3cfpIN2eLRKPviaKVoJK0Ua1SB1cQMszULbSRc2kp/Xve3p5n1g21IUcv+MWgv/v//YlJhE3/QYSJXAcz87G4QiNGlNTMCldqs4SnnXTGFnmFuN0voX1gdtlblQsGTdUNPRZI/BeEEjScW2llz9rFtD5p0f485efoRBFKHMrV8dG2U7H/pdkmgyqAHV+L0zrTK6DANuNt/pQjQqeOVlCRcxrpaffReEVPQXm3F5Fyf6q9memKw34JT44+JdN7Mhkc0ZH1R91JglFWoUt0clu2CnganXSyh/keyVIHjOM22uoCUvJR32cMuyW011WmDRHxlf4iCJhMAPzhVDMMZyDSNmkI/nnx5ZhKqeLeFck8meVN/Nn3vR8kc+Wz9U7VOmYH+MzLp/zyNhKbxQj6d25//k0pK3KLvnmsFzES6/U/byg5yjfbAD540E+1I/888hjp/Cf85vFufiUp7wcSzqtGX1mmod2ib4ioZIvPUwnOxlF8Ua6lKH8wVtVnnw40+XJMx5/fG88Ux7kOW+ysHz6/DWjMG8lt0reFF8ZiXyS5es1EZj3HKcVmWTiNUkkTDBgOTLvA+RBhS1nevEdafPdSx3MMluXn6JA+vwJZtlEPOOr8qt4F57zLyNrfHBinYc8ovfB7JrBYl6Ryc18En01Pya8jOkLmbn8gSoT5YQDJzyY1XUOVUzFWlqWRUrS5m9+ZISVkQHfCb81Kn0aVyGgUq1QzWjQ6InvyDPTb410XiRJatyl8mZ09VviRZHPYKUxKPmiQRNxVu9HGRhyUIpHlr28ijSImznxLz0oM6wvPBiWXaYB8/95Kovyq8d5+ZOwDCNVjjR1SnmVPu/V7xzl5WxVdleeSU+Vj9eqbii9QAIkzWf8n57V/TJ5xQLpCU0VsBztfGJFNIun0lNuSULJUfp4EZlX+V8+G0UjrxsVO0JTnJCn9Flmxl9QzlO63jXTqjzzdJSsvS3963GhY2kEbhYByjZ1O9vrHMzslFLDNnav8/KfrwM3fLMf6QAAIABJREFUy5Gm/ikiQB1+mYzxGb8f1O2qbymLK2wgsA1MXBOTmo0gKgGmCds0pI3E7QMdK20f5uV53tBQYF/FgIqnzxqB10RAyTXllz+u9Oe2t03DQOAZiDxgVi1iOiuKlzgz9Z4uW6ZwK1nKO9s987bPFXXlNdnT0TUCVyOQTTKpCXuu9K9TDh0DIb2ylQwMa2X4QVkWmbAPxglTym+RW/fm+/RX56ZjaATeKQLq26/0b5WLXbiAowgEjoFZBZjUy4jisrR7uYCRepdGV9z2leMNiobS5++UQU1MI3AFAhxH41wNZZj6lzLcMQxELjArGhh6RcyioixS5cJEh173bQOemcow+3ladq8AWT9+MwTUYFwmYJS1OmW0zEVy3CAwP+6YyqFKctGZpKhz1aHiqXAly+o+H1el0WeNwI0hQIGk8OX0snjRlIWYHFtPF3pRLhlNyes5fi58cC6mDniPCPA7+0kcSv54vmklqvKaA8sApdnngZdcZAR44mDgOXpZ0ovC11Fm3NVyX55+8ZRX/K1Oha7L543CSFwpmhUCKu9V+Bj+NoeiSxr56zxNhivFlg+X6zdkQOV1QXEX2bwh/QWBN7u6LFs+UzJ0Wbz1OV+egk8VJhfGzD9YFYiVepKPetF1nk/G4Y8D7jzyaVS8dWHq2UVnpiFmV5btIgJZOOkoGgzi/XX5UXHJx4XyfEX+Ks9rRDsXReV/XX6vKhjprMM0n8+18zrH7RUBJJyTPZVnPlXucT743DXj5eOu8rx6v4rLurzTTFRKdc5lzSBmqs7ZNyYXQx7xscKY0an7L5WdlaxUWtLNP8pfp3ky5uLgc37zFIuLJ/mrZSrLd/l4i2sVh+c85oyhnqnYi/vFlTxbl1gluuKcp8Rr/hRGyuCCJNQzRS6fToWpeHKfj3A5aPnk8+vV/OYP1uCUf7Z6rdhQZ4WxOl+WzxItlUAFKoLZ/cqthCoc1z1TZPRZI/DRInCJ4Oa1I6PxnudLkny0xdSM3U4ElFyq0qk+Kyf5vSIHiewluVXxlRyLLCu9LzcZpfy1Iq7PGoEbQGBJz2YGzq5hoMZ9THNtIcajfPOs0mgxvYEXokm+FgKUQfVjQjWBWnQMJM5i7I7bLFNuGVfJ72tlpCNrBN4EgSuUJB+rfr/IJ40AaLDtLi/g4DP1IxtLZNmGyALWNSfehG2dRiNwKQKZvCk5zOtUMSSk/s21H7gImHKu2hAq3aV56IcagbdBIKcXRbfmvv1KT66SVzKbf05ZVfKqzipd/lk+TF3rs0bgRhFQApgX2JV2bl43q+g3ypMm/s4R+CQMVpRyVed3juJ1CDJzVZl4vpSZNMJSFJV2KXA1YxUpH75IsLjKP7/gOu8mhlEya3aVQ8rhBWnXBV+UgEytPlvD6JqgdblcGab4Jz31yyfKP2d42tx8V7kvcrqQ4ioWkmSVqwWdm706z8yFfL8DRs7RVsUm7XMPz2d4UZSLwucUcsW8Mu480fUvSPMquvmikvL5+KmvCsXq+ecX88O4/Fgzbf6jfXGK81XysrhXPWP+1+eX0/eZe6VLCKsyrUY5l88qsKsJ3uT+XCY53U7u1z1fk881o61JeVFQvrDXoJ5F4Ykd6HUpGKbC89cXcZAPV+nyYde9fpu0F+WhaPKskFJhF6VJwxk7i3m9BJeTU09z20plUi9P8lnkr1Wyc99L9WBtZPXwmmcFzGvI8TrKihV1XhfnXFgu7/mzHPTzsDUXr5XPmvQ6SCPwsSJA2V4daPpYedV8fQIIrNHJq/qXq/fZplDfNT7nT6n4efxVWvMHnwCOuogfHgElf7m2mApSMksm83JL9+fXbeN/+AJqDj4FBFb79WpSVMku5Tcv158CJrqMHwEC+Y/+FewwKuWWhxqvym7lRPll+Kqs5+PwOi/rq8/0vUbgphDItxeYB+V0dYItH4fX+tAI3BgCFDAqQx7Zme3Wi+SOUdQzXtPrtuq/UZbVM5JT1+qcZrL4n6e1CNVXGoEbRoACmcm6yknJqDqrcH3+/SGw+j39/ZXgjTn+WFUq+eJnIvtErFQ+qYz5mrdUDBVZna9q2ivwloicq/AqFs9KH6gc8qzk473WtSKiiM4Tr/DF8DVB8+irF4qeor/y/ILgub5Ln+fexTz9FYTn8V7zQpG9MJmKcBHnFyZ8jQcqj+UkDJVc1z9OI98EW/OMr/fq35iFXD7LJb/u3esQUCCe5/b8ExWygHg55Hr8Mafzua1PS/r8XTf+eioLfnl1PVoq54tTXJvOGoO7y/i8+plCfYUDFazOfMzrlWjXp39x2S+moTJXaa/IXPGYI3guxQrJ635JciTXX+bpKnZXY67gt3K7GvuN7tPykrL6rXTJGMzjHDBZ+OucFK3VNFm46kQyqyuzU+xmvPH2yjSr+a67Vzyqs4pzHeJzJlTiXCIVpOjxnHs8D16Np+7XxZ0n0hcagduBAMX9nKhndYD6YUU73Y5C61LcPgQSIIkBw0pldrXdcE7G36yxdPtw0yV6/wioNobSs4tRF9HF52X1/bOoc9QIXIgABVTJcF6PqrBMgHnSsnwhivrBTSPwGsKXxDEMk14ozidaDaGY87cazuKsVIGbLqGmrxFYQkC1ey+Sz6XI+kYjcFMIUDkqZcg88gKpwjMFOtejmUG2Mh5k+NrxB5Ve8c79sTJtPKelnumzRuAGEaDk8Sd6l8K3Kpv5ey2cN/gmbpb0J2yw8gGkVlUkni/Mng9ynwcVjxVOXedlYimM6fIRlx7mU61cr8TjrargK4+YUAWp8yJkhWz+dhE5H7p8fS7OuYBrZTUnuib5KkLzuNmFSqLOS+9iHnnxdB70Li4uJHvhg3eR6wqN9XnNQ+cXK8lu4nYlr6XbpZt3kPlb03sdAufjMiRfcxclWh938fzdX53P8e3yuD49xszpvjfO9hIz8rehuS4tWV59cdcvcI7iGyXK0r9B2quS8PlquXLcvvHlVfmS8Eqclds3zvp8QlLmb01BlzJdujlP5qqQdclVltkzntZFO0daRcqlOxfnTQJIT/Gk0qu81P1F53m8+cUi5jq6i6eLK5WUPPBQ9+qcBeuTRuA2IrBWzHOBucvbWHxdpo8QgQtl7sIHaSFez/tERownpfs/Qiw0S7cQgTVyrILUeW2pL324NoUO1AjcDAJzWZxfLNrON5OjpqoRuDEEuAEQJTknzRfmdVEchr+LUaQLM9YPNALXROAiGb1mch1NI/D2CFAIV8f2SPUi4czCeVJ6dG1UBqo+m0RYG+vt+dcUNAJXIEDJW5K+pZvs4bo6cAVd/fjjQuATNlj5QC9itSKtZWNNpDVBa5MuV9v1Ua4TekV+y4+X765D/kPGuYrb5efLdx+S708y7/cB//vI4xov7yNhQzj9cLx8uJyv8YrWR/kdsry+ICuht7VcK8Vcaeqee3ojASvYrtxenuVrRb6c1NLTj4HuTfGwVFB9oxHQCGgENALvHAHq79fR4fm4+et3zpgmqBG4HgJaDK+Hk46lEdAIaATeJQKm+Xradyl27iZ3+S7Z07Q0AhoBjcDvD4E3VIg0WLn0eEO6l9LUDzUCN4GAltWbQPW90rxSH71XbnRmGgGNgEZAI6AR0AhoBDQCGgGNgEZAI6AR0AhoBDQCGgGNgEZAI6AR0AhoBDQCGgGNgEZAI6AR0AhoBDQCtx4BbbBy61+xLqBGQCOgEdAIaAQ0AhoBjYBGQCOgEdAIaAQ0AhoBjYBGQCOgEdAIaAQ0AhoBjYBGQCOgEdAIaAQ0AhqBjwsBbbDycb0PzY1GQCOgEdAIaAQ0AhoBjYBGQCOgEdAIaAQ0AhoBjYBGQCOgEdAIaAQ0AhoBjYBGQCOgEdAIaAQ0AhqBW4+ANli59a9YF1AjoBHQCGgENAIaAY2ARkAjoBHQCGgENAIaAY2ARkAjoBHQCGgENAIaAY2ARkAjoBHQCGgENAIaAY3Ax4WANlj5/9m7z+dIkjTP70+kglYFlOrqqhbbszO7c3ckX5BGu/+cRjsj+YJ8c8Lm5nZ3RMvSBS1Sy6D9Hg/PDGQlUEAhUUgAX1Rnp4rwcP+Eh8jwJ9xna32QGwQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBA4M4LELBy51cxBUQAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBGZLgICV2Vof5AYBBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEELjzAgSs3PlVTAERQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIHZEiBgZbbWB7lBAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQmEGBZAbzRJYQQAABBBBAAAEEELjNAgSs3Oa1R94RQAABBBBAAAEEEEAAAQQQQAABBBBAAAEErkcgDckmqZke/CGAAAIIIIAAAggggMB0BQhYma4nqSGAAAIIIIAAAggggAACCCCAAAIIIIAAAgjccgH1phIfw6IQtDKk4AUCCCCAAAIIIIAAAtMQIGBlGoqkgQACCCCAAAIIIIAAAggggAACCCCAAAIIIHB7BRSMMikgZcJnDA10e1czOUcAAQQQQAABBBCYLQECVmZrfZAbBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEDgzgsQsHLnVzEFRAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEZkuAgJXZWh/kBgEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQuPMCBKzc+VVMARFAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAgdkSIGBlttYHuUEAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBO68AAErd34VU0AEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQGC2BAhYma31QW4QQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIE7L0DAyp1fxRQQAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBCYLQECVmZrfZAbBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEDgzgsQsHLnVzEFRAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEZkuAgJXZWh/kBgEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQuPMCBKzc+VVMARFAAAEEEEAAAQQQmJ5AqqSSkJ6/nl7SpIQAAggggAACCCCAAAIIIIAAAggggAACCCBwjwQIWLlHK5uiIoAAAggggAACCCAwVYHEjKCVqYqSGAIIIIAAAggggAACCCCAAAIIIIAAAgggcG8ECFi5N6uagiKAAAIIIIAAAgggMD0BAlWmZ0lKCCCAAAIIIIAAAggggAACCCCAAAIIIIDAfRQgYOU+rnXKjAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAII3KAAASs3iM+iEUAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQACB+yhAwMp9XOuUGQEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQuEEBAlZuEJ9FI4AAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAAC91GAgJX7uNYpMwIIIIAAAggggAACVxZIrpwCCSCAAAIIIIAAAh8JcIrxEQkffCEB6t4XgmYxCCCAAAIIIIAAArMqkN5AxghYuQF0FokAAggggAACCCCAwO0WyK7mp1zVv93rkdwjgMDtEkgtsdOXjk6/u12lIbf3S2B4xuCVdvjufiFQ2tshMFY9VWUnnfKy/70dq5NcIoDA3RJg33u31ud9Kw2nwfdtjd+S8o6d+95UrglYuSl5losAAggggAACCCCAwG0U8Cv2+jUTf9HE59tYGPKMAAII3CaB05foT7+7TeUgr/dTILE0X2knRQDcTxhKPcMCpxqWkixwhVPfGV5jZA0BBO68APvgO7+KKSACCNyAwNi+VefA8Tw4/xPuOnNGwMp16pI2AggggAACCCCAAAJ3UWD4a2XsF81dLCtlQgABBGZQYLgbnsG8kSUEzhfQucN4X0Hnz8G3CMyCQNzvxudZyBN5QAABBBBAAAEEEEDgugTiea+e/fU1XgYmYOW61iLpIoAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCEwUIGBlIgsfIoAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCFyXAAEr1yVLuggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAITBQhYmcjChwgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAALXJUDAynXJki4CCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIDARAECViay8CECCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCNy8QHrzWSAHCCCAAALXIkDAyrWwkigCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCFxNIAarxOerpcbcCCCAAAKzJUDAymytD3KDAAIIIIAAAggggAACCCDwJQQSs+RLLIdlIDBFAb9Er4pL5Z2iKkl9WYHQ0EQV/rLqLG26AjSXTteT1BBAAIGLCcS9b3y+2FxMhQACCCAwJYFr3P0SsDKldUQyCCCAAAIIIIAAAgjcP4GUNtP7t9JvT4lzP6RH7fujDxPT6/AIr29P0cjp/RIYNeyPXgUB1dzxz+6XDaWdQYHRrtUzF/e/obaGfXCShucZzD1ZQuACAux3L4DEJDMoEPbH2X5Y+WNXPINriSx9LKCKOqqsib9kP/yxE5/MmsDoHDjca6DzX6+5o+o8a1kmPwgMBeJeNrGBxasO8bPhRFN+QcDKlEFJDgEEEEAAAQQQQACB+yXAr+37tb5nvLSxOsbnj7Kri0T6Mj508SjNXwP9aA4+QGDWBM6s3rOWUfKDQFZZw8XNsN8N++BIk5ze/1K5IwzPNyXwiToYzyKUvU9MelMlYLkIDAVO11Gd74ZPTjWY6qPTEw7n5wUCNy8wuXk0BK3cfO7IAQIXEvB9bLazTXX9ITv/Zd97IT4mujkB7YFDwIqZ9rvh/fXlp3R9SZMyAggggAACCCCAAAIIIIAAAjcvoB/Wuh4ULnlOam7iatHNryVyMBSI1TFU2OHH13+JKLcoXiIwZYHhBU6v37GSjy3kozqf+/6MWXJTjF6el85oqtv56jIOFynhXba6SPk/Mc1pHr0Lj3CP9OlvP5HU9Xw97fqgXM5Asa4H6zNSvQO+KoIXw6tufJe1OkUS1nmU4HkmBcKGGKqpV+SZzCWZQuBCAh5tFer0haZnIgRmRkCBVte7DyZgZWZWNhlBAAEEEEAAAQQQQGD2BZIkMdNj+Jd/PfyQFwjcjICq46eu/+gavT9yE1KNb2Z9sdRLCsSKGp8vOTuTI3DTArk784a9XV20Ol90upsu43UvH4frFR7z9TMF/5++GH2pu6NH7643S2emnjuNOXOaz/lC6d544T4n41Oe5w76qkhqa/Jn/Z/1POVKQ3LTElDVjNVz/LXX4PjltBZIOghcg0DY12q/m4b9blZv9X5Ywa9huSSJwFUFhnVX5w1pwVKLj9N9ZV51OePzE7AyLsJ7BBBAAAEEEEAAAQQQOFdgdH3oen+snJsJvkTgMwVC/dVP8PAXL9zH9zwjMBMCox1tiMEaVtncF1mT00zkl0wgcI6A19oYrJKmHjSoBid1Me1/w2o9rOhZasMvzkmdrxD4EgJJNppKPlSF+vkl5FnG1QWGDU9JDBVMvQH145Tz+2Dq98c+fHL9AqqDo7r30dUGv7tfZxD5unr9uWIJCHyugNdUVeksSCVU4bPqb/x8tA187nKZD4HPFYi1MM4/ClYpWJoUTu2j4zTTelbq/CGAAAIIIIAAAggggAACCCBwdwT8otCoOKMf3fGL+EM7XgyKz6N5eIXArAicrp1hIIqQtxm4w39WkMjH7AjE3WwuR2EfHL5I01HDf75RKkyer+3517nEeInAFxRQ3R0FtmZnE7NSNa8rH9eV7hdcb1NZ1HU5XFe65xQ6LjK0l+pdfIzPNJxy/AveI/CFBGIdzC8u1tfx32/5aXiNwGwKeI32KBX9brtIHZ60Dcxm2cjV3RQYr4ExVFsBhDqP8D+/ESE3Zfz8iiT0sHJFQGZHAAEEEEAAAQQQQOC+CMSfI/5bJFXXkFP6VXJfACnnlxGIFTVbmmpprKl+P/8gdGtq2QUjXTgqFriX48usHJZyIQHV4VhpNUP2Ph0MzAbhQlHREismiSXZnaYXSpeJEPiSArl98XA/rLvykoIlSdGKxaIlheLpUQY9f7kZz8tvfhsZn+6CSYzPxnsEokCsXvFZn4fzXvUKlNogHczGeTB1Pa6y63m+5b7KfixCMtA5Q8HPGwoWniejxTkmf8unCHxJAT9/SM10CuyXHvzufv1u47fbl1wPLOuCAvmTBo2kndXUoq43WNGSdBAGFBxFwo520r4I9r8XlGay6xCI9TdXDX1Pm6Y26Pct9fobbp7JTTLVnBCwMlVOEkMAAQQQQAABBBBA4O4KJPrRrf/5pfrwa4aYlbu7vm97yfwCZ9buH397687+gTfw66e3mvw1Fi9/CMygQO4qkF76/lfZTNUpry7Th3/ex8rnVOJc+jNYerJ0iwVidYxVLBv0x5tNCx6goqAVfRtq8nAnHGeYRtljJi6S1jSXe5Hl3cJpLsOZL57fhXnLfGNZ47OXJzErFFVvwzAUumDvj1tWtvy64fUdF4gVONdgqnNeBbl60Ipeax+s6S5Sj2N602S7yHKnuTzSulUCqnKx2vmZby5QxZtLCdi+VevzXmQ2VthYWPVAofOHcAac2//qZCK3A9R8ubdxdp4R+KIC+fqbDePqy8/OI3SjTDHRvTOKHsx+3eXnmVJmCViZEiTJIIAAAggggAACCCBw1wW8fcn/FwJX9PtEF4yu4XfKpShvevmXyiwTfzGBUD/DxU691s/q3qBvfTU0qRWtkNggKVh3ULBualbOLozG60X5ehU/i8/TLER+OdNMl7Rur0CsZ/G5r7qpa5uFMG70QHf3J4n1reCPcy9yTqhg/tGEzy8t5o23l56LGS4pEOvBJWf74pPHKhWfY75DfxRZw1NSMkuKpsan/iCxfqpHyOrUghvigr+4wPUv8DqKFtdXfJ5qKbKL3FNN85oTyzvotV+SVzkKJa+3PqSVFWyQ6qG6HP7i8zVn71Ty11Ef4gJuojxx2bPyfJt9s59rXj+zZiXv3SqGvA5Uhy8RtB3Tm+a6oY5NU/NupBW3OdWN+BioV1c1+StgRefB2i+n5ue/N1mHbnLZd2Nt38FS5M95VEHUuJ/VZd0wE26aCc+n9r+x4udIqF85DF5eu4CqYL4axvrn1x/8OkTBTD1jFnUtIvY4ODbTlHJJwMqUIEkGAQQQQAABBBBAAIG7LuAXjNQfr+6L9obTxHppYt3hldCbEYg/qG5m6Sx1lgXizUuqor2BWbvbNTX2p8nABklqfUus00/9keqWEV0EVXSA/sZ+tfsP+fxn2WRXfaL+XlXwbs0fq5g/Z5Wjn5h1+qEOW7FkvW7XOv2BP7qDxDpn7INjWsMW1SlTxe1rysmS3C0WyNeJOMa5qrF2q+1eap1e39QZui7Ua5/c6abW7qahwxVd6NcwV1nFjc9xHxnfiyf/epwrDBkw/uktf+/DMJ4+LE0q0ef2epdfb0r3PN9Jyz3vM1+dw53ReVPe8Hexoo1lY5CY9fqqq31vJNW90mo81We9fuLPmmXccCyZa3sbt7NpLuCmyjLNMkwrrdvi69U3bmd61t3R3tBvpjqs71VnQ8N/0fr9bqi/8fwhznsG3BmbxxlT8zEClxdQFYzbm+qb9kPx91u3N/BzBwWtpArYThM/h7jpaxCXLyVz3FWBU/vg2DuFhrLSOXA62v8qaEXnv34Occ7+l33uXa0ps1ku7XvjPjjuf+OzLv92egPrakigJLFCsRh6HfQzi+nXVAJWZrOOkCsEEEAAAQQQQAABBGZOwH/IeIOSWb/ft2q1bn/92492uL9/o3nVD6dPN+PcaBZZ+JcS8N/Moctz70XFg1PS0BNQkli13rS9/V3r9buWFBI7OD6x/+M//d82VylbwQNWUksntvj5wCthzOmxskycfGya894Of+Z/orHgvDT47o4IZJUp9lsVq0TfStZLC3Zca2QXiwpWbTTt77/8arXqsZWKxTMBYhq+jxxWtjMnv/QXYf976dmY4UICcYXF5wvNdKMTxYZur8N+8TO1gRX90er07f2HHWu1O36ntIJX/p//9/+zpcV5S5IQtBICJcJ+WJuD9sf+rL14dqwP04TbWMOe+XSRXWtU8U9/Of4ua9Cd+XOI4YEmjBsfihHqxfArb6O+XF1xv8zqozmzz8PTRUHHgeN88Xn8+xl7n+Z9Q94GSdG6/cQa7Y7Vag0/n2g22/bbyzfWqtdtcb7yiZjAJAtmuQaD2Cg2ZcZLbUNTXvZMJXfLfNNEjUlqAU294V/bd2rqBUg9W5VDnW21LUmK3mPQf/3Tn+3lq5ehHyGPFIh7AT3H+hqe4zfTXT+nlzHdtO97anGNxefZ91BtLWQHNAVWaW/s+99BwWqNju3s7Fl/MLC0Z/by1Wur147tT39auOGCqQ4kk3lfAAAgAElEQVTHenzDWblTi4/1Nj5Pu3DTX2+67qB/qg6x8V89sllSsqRQsbfvt63V6vhwmKrff//pV2vUa1mUlsoZH6Oyjq5xaW8+7Xr28fJGS77qq+n7XjVHzH++gNdZDRkYa2JW3VQHddNirdmyg5MT6/S65iNkFqZdH0f5S9LJV+NGU/AKAQQQQAABBBBAAAEE7rWAfs7q8metndp//q9/tv/zP/1f1u2nViwUNKqKWT+7PeT6frec4x+bds+ZhK/ukYAq4ejHtl/8ye4sTQq6aB9+dGtICq856k5l0AsXlz7R5BQQJ1TyfGvhJaW1bfGHwGmBjxtMdWEzKZYtLeiu6L53f+D3+KcDK6Q+YNDpJD56N6q3/mpSxQtRAB/NeZEPJiV3kfmY5lMCsS7cEuGxIaJ8H6uAEN0RnfVKYd54WvCCq+4WrBf2xR4Mq3KqhsaAldTSgV/+D4GEWR0dXrT3mJVR3VaiQ6nTH58NPQxYOXuS2fpGdSIYxcIGoc/NZZbaJ7z868/ZR9w23wkBCqq/fs5QLPn+N9ZSH9jqEvvfGMz1uWtq0nweYzDpiyl85tvSJ+rFFBYz00ncPt/Qg6D2hL5l+0pUjxRFD1Lp+fhrRe8lM0l7lqTqZzAEuPiKGBY41vLR6vGkRm+n9OqeV7ApKX46metZe59e7uWmUG0YVkE/nivYT+cPRUsL2f5XQYUaGcj7aQv9tV1kKddT07gGcRH7q08z7fp7PbXBc+lJh/yGuqw6XLRisWza/+qRFEv+283Pf9O4/9U8p8uZpRL41Pvg1SHPSOH0cs+Y6BIfX19OL5EJJr2kQJKdpHq9Hf6ey/Zx3tuVAggTH5atZD377tlj+4//6/9iP/zD97a4kPWJoqo0hdVPDyuXXHlMjgACCCCAAAIIIIDAfRPQ7w49iqlZMRlYpeStRNmdz7pqVAoXRi/yA+VzGjw+AR4We5GFfyIhvr5TAqdqRPZGl3vUkcrw97R6pigWst/WF7hgcy0tTneKncJcSSBXB/Mvfb8ZKvGoN5XYIBUa/y+62GHdz6Wv8T889VMbzUVSDBeyLj3bRZJmmqy5RhD5lTXbMKfrQsi3alcMvQmlie/0jS5LhulGpYzz6dxjlOJFYgNHU1/W6fPnvOySPn/6kdDnp3FTc94G38k2o9qYem9Weh9Ko1eF3AnF5Pnjp9cqMM2qkWX0WvMbUW7L863xjfvWUS0NxFqbiZVK8Xwh1N2wjtVD26cLeF31Ieb4tlSF25XP26sbamQ8AwhnEYVh/dVa0G83TfXpuqupr+HyQ6gK1/G78HZVsmvN7dUCcs/L2vT3aKGOjdXHrMeKgQKtiomVs95c/ew2HZ3/TqrHp3N4+t15Jbvcd2P5vdzM50x9Xfk9Z5F8NR2BGGiercK4JrXH1RmEelwpeL3Wfjl+Gxat32n+yemPL50vAlYuTcYMCCCAAAIIIIAAAgjcPwH97igkqS3Pz9mjrQd+p7/GMx0MdLkoXgCNF/E/9hn+HL62K0YfL5NPEEAAAQQyAQ2topfZzviK15KGrFyrH1Jcy4vQIHMtSd+uRHURlPOH27XOyC0CCCBwjsAwnGJaJyTnLOtefhUbD+OJ371ECIW+lsAHnU/HgO97bHtdRff9A/uG6+IlXQROC1zi+kAh7dnmg3VbXFq0Ym5YYvV+NY0/AlamoUgaCCCAAAIIIIAAAgjccQFdL5grF+zF82dWrpS9i95+P3Tbr7551ZDk//zCwqSrC2OXivItp3fcjuIhgAACMykQ76K6YmNGdo1rJotIpu6GgM4qCFi5G+uSUiCAAAIIIPAlBXTn/9iViCsvPlztSK6v95Yr5/D2J8Dvi9u/DinBrAlMuk47nsfRNP5qbEPUUILLS/O2ufnASt5r0Pj8V3ufpOlFOtW82kKYGwEEEEAAAQQQQAABBO6WgEbc1UPtnLrpWT9m4uMiJR373XORWZgGAQQQQOAKAqPLTyGRq+6Hrzr/FYpyr2a9786x3sbne7XyKSwCCCCAAAIIXElA51HTPpe6zHWPK2X+Hs887XV2jykpOgKfJXCR314+TdxYLzLDJ3JCwMongPgaAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAYLoCUxpZaLqZIjUEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQACBuytQurtFo2QIIIAAAggggAACCCBwrQKx68dJC5lCd5CTkuUzBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAgbshQA8rd2M9UgoEEEAAAQQQQAABBL68gIJSJgWmTPrsy+eOJSKAAAIIIIAAAggggAACCCCAAAIIIIAAAgjMsAA9rMzwyiFrCCCAAAIIIIAAAgjcCgECVG7FaiKTCCCAAAIIIIAAAggggAACCCCAAAIIIIDALAnQw8osrQ3yggACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAII3AMBAlbuwUqmiAgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwCwJELAyS2uDvCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAvdAgICVe7CSKSICCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDBLAgSszNLaIC8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggMA9ECBg5R6sZIqIAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgjMkgABK7O0NsgLAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCBwDwQIWLkHK5kiIoAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACsyRAwMosrQ3yggACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAII3AMBAlbuwUqmiAgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwCwJELAyS2uDvCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAvdAgICVe7CSKSICCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDBLAgSszNLaIC8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggMA9ECBg5R6sZIqIAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgjMkgABK7O0NsgLAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCBwDwQIWLkHK5kiIoAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACsyRAwMosrQ3yggACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAII3AMBAlbuwUqmiAgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwCwJELAyS2uDvCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAvdAgICVe7CSKSICCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDBLAgSszNLaIC8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggMA9ECBg5R6sZIqIAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgjMkgABK7O0NsgLAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCBwDwQIWLkHK5kiIoAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACsyRAwMosrQ3yggACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAII3AMBAlbuwUqmiAgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwCwJELAyS2uDvCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAvdAgICVe7CSKSICCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDBLAgSszNLaIC8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggMA9ECBg5R6sZIqIAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgjMkgABK7O0NsgLAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCBwDwQIWLkHK5kiIoAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACsyRAwMosrQ3yggACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAII3AMBAlbuwUqmiAgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwCwJELAyS2uDvCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAvdAgICVe7CSKSICCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDBLAgSszNLaIC8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggMA9ECBg5R6sZIqIAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgjMkgABK7O0NsgLAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCBwDwQIWLkHK5kiIoAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACsyRAwMosrQ3yggACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAII3AMBAlbuwUqmiAgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwCwJELAyS2uDvCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAvdAgICVe7CSKSICCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDBLAgSszNLaIC8IIIAAAggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAggggMA9ECjdgzJSRAQQQAABBBBAAAEEEEAAAQQQuCGB1Mz00F8y9py9HX4f31/mOaY5nEcL++jD4be8QAABBBBA4EIC8diVn3jSZ+d9f9HDUZwuPufT5DUCd1FA29JZp2wztx2kZmmWqUn7gJjf+HwX1xdlmiyg+tBqp1avN/wxGAysUi7bwsK8LS0tWKWcWELFmIzHpwgggEBOgICVHAYvEUAAAQQQQAABBBBAAAEEEEBgugLdgVl/EC70FxKzJB2LJ0lGAS3jS05zrQLxta75Kh291wXgYiG8j9eC4+eeVpw/fjm+AN4jgAACCFxSIO5Y42yzv4MdmNkgDY/YcOjHFH2hhuh8kXLFyX/sr3PfqfSf+v6UUH7i+EV81rFRxzbFW6bhuajP9GF8xGl5RmCWBWI9H9tWlGVtg+nAbJCdEw5y5386rxv+JWaVbJvwz5Rm/vvhhF/gRbbsfhrOZX0/om3fyxm+jOeinsU0Oy/NzlFvLN9fgIZFmOkQ0uuZ7ewd26+/vbKXL19ap92x9fU1e/bVU/v+uxf2YGPFKmW0EEAAAQQ+JUDAyqeE+B4BBBBAAAEEEEAAAQQQQAABBC4toIv77W5qL9+8s529fWs0W35lN7HwTy1xia7yZ40SqVrpvOEwNf0btgT6dGq4K1ghSaxYKNnc3JyVy2Wbr1T8DsbFhXlbW1m0xYUktPTF3Kr1wBsV4gc8I4AAAghMVyBr0Z1uolNLTQ2Kh8cN+7C9Yzu7e9bt9S311uYQ+ahDz+m/JDtshIPT6Ovc57kZ/PusMd2PXcMEc3PGrhly851+qeNiakmaWjFJbH15yR4/3LQnDzetMl/+uLFeSd9UA/7pjPMOgU8KxEb97e19293ds6OjE+sniTf2D/ycMJ6rpZYkqZXKRft3//QHe7SxGKr5TdR1bWNxE9auoGD25vW+vX3/zqq1hn8QzmET35+EALOBFSy1hbmyff/ihT19vMV2+snacbsn6PfNDk869i9/+dF++fWlHR0eWb8/sP3DE6tW69bt9eyPf/idbawvWrF4u8tK7hFAAIHrFiBg5bqFSR8BBBBAAAEEEEAAAQQQQACBeyig6/yd3sA+bO/az7qIW615NyuJN9yNAlWG/WRnvaaohcDbElNv+nM5NQokBQWsFKxQKFi5VLZioWClUtHmKmWrlEu2urLsj8WFBVtbW7XV5SVbXiyFrrhp3LuHNZAiI4DA9QjcROvx55VEu371iFCrd+zNu1376ZdfrdPpeju0jjOhJFmwpPf2kC/bpNf6bDjXqUyFmBQtUQnnjl/66FR0ST7dURIKWCmkAyukqT1++MCSYsHWN9asZGXveWU05Vhyp77gDQI3LDChemtb6w1S2z86sZ9fvbG37z6EHo8UBaJtI80CmRW0VUitWExsdXXN5ua+sbXF0Hw1IdnrLWhugeoR5qSe2qs37+3Hn3+1k2rN0qQQQ21soO1W8dKJWalgtrY0b5vr6/bk8dapLf96M0zqX1pAgVgKzN8/PLJ3H/ZsZ//I2q2OaUigdqfrVbsyV/Z6sLhQssXFypfOIstDAAEEbpUAASu3anWRWQQQQAABBBBAAAEEEEAAAQRuh4A326VmJ7WG7ewf+N2GhULJLM0aKLwfFW/Jm9j6pgaO2NOKplLAinpZ8eAVtW/4OEO6Nzc0EsxXyra0tGirKyv26OGWPdratEebG7a1sWaLC2UrVxIrFLIhFm4HIblEAAEEELiigI4falQ88l5WDq3TVcBK7C3Fj1QhgEWfDRupsxce1BJf6zlOMHqORzEfy8cG5r2FTcizmuT9b7SQsalSK9jAkkHPkmLRnjaa1h0MrD9hqWMz8haB2RTwk7cQw6Wgj1qzY3tHVXu7s++9q4Qu8QqW6LxQQSs+HlZqhcLAXr5+bxvra7a8GII+bqRzimyT7fbMtnfVu8quByY0W+0w1GWmrh6b1LOKAlbKpYL1O4vWanXC0JWaJu4k4m5jNtcWubqkgIIhW52BHR3X7bjWtGa7b4O04MFY+l+j1bGDwyM7Pj6xR5trBKxc0pfJEUDg/gkQsHL/1jklRgABBBBAAAEEEEAAAQQQQODaBXRdXr2hJFaw/iCx3iCxcqEY+lX3i/cKR9H9ifFa/tiV/GGPK2rH0Hd++3s2fWhsVAOIpQMrFhKrtzrWaLX9TseXr9/aXLloG6sr9off/WC/++F7e/hww8eQL5dC4Mq1A7AABBBAAIEbFfD2cvV8oGDJpGiDNLFeP/R+orgRH9Ijy6Hea3qfR59lwSrhcBWOQX6UShXYEo9X8TlMr2breESLfazEKRQkc96feh/TIa2gNBIfIMjzMvDexobhLuclwXcIzI6AbzghO3qpGGM18A+saGmxbKne+Dah7aJgqQetaKK+aUjJdx+27aunD+3F11t2kw1YymW3l9r77W0PPmh1epYmReun4fw19BKYWt8GNhiklvR1ZhsD4mZndZCT6QvoN0iv1/UgyH6/7+tfdToERKZex3vdrnV7Xev7D5bp54EUEUAAgbskcJPH+7vkSFkQQAABBBBAAAEEEEAAAQQQQCAvoKv8HlCioJWiP1I19OnzNLu/XXfTZk0Wgyx4JSQRGva8ic5fqruVrJFRnbD7nbjm3canA2+NtHQwCI0h3oYwsF5/YN3esbX/7W/26u07e/xoy148f2bfPP/KlpfKVtLtumqQVPsifwgggAACFxdI1YiroXZa1mq1bNDv+xBty0uLtjBfMcWHzMJfDBHxxvHs2KOh5TwgREEn2bhAfnTRxEkWVqJpNRSdCuGv1Y7e9wOGZhuo9b2gHiFCr1/ZgS0LSYlLzY51MZ1PgSQaEsgXmx0VtbjECsPgmE8lwPcIzLZAOPNTg776I8kqu58Xqp7rM0WR6ZvUdvf2bXt3z5qdf7SFcmLlMJLkFy+g9nPVWsv29g+sVq9bt9vzgBTF23iPf9kuwoNvPOgtv/1/8eze+AK1u+x2zZrNttXqNUv7fSuXS94D4uLCvCluPe5TbzyzV8yAds0anrRSKXngvPcQlPX6qFqgoa3mF+atUtYwprl6ccXlMjsCCCBwVwVm5OfDXeWlXAgggAACCCCAAAIIIIAAAgjcUwFvHNSFaXX1rivURb+D1gNWsgu5fhG3qMbDENuSlwrBKrrAq0fqdy6q2/XQwBgu/Oq97mpUY6THxgy8CcST0eKb3YG1D07s8LjqPa8cHh5btVqzb158ZQ831029rZQIWMmz8xoBBBD4pECvZz7EzqvXb21vf8867bapMfL7b7/x4MDF5fIn0/hSE+hoUSwWrVIp2+LCghVL+SGBlAu1PKc+lI+G8wnxKWp5DscfBUj6XfN+/En8TvlB2vHpQstrSEON11pOsVTyoUHi0UgNmmHicFD049jEwqeWaGiRJLX5+Xkrl4Oh5uIPgVstMKzEPnCO9b17o3Dy5b0ceY9Cej/wYBZtj41my/YPDmxnd9eePX7o52tf2kDnlc1WavuHh3Z0cmKtTjecaypSIXuErdp3IWGgy6ynpi+d11lYnix6fbPjat3evXtv7969tW6nYyvLS/bNi+f21dMnNr9QDqf1s5DhK+ZBu3YFq6ytLNvqyrIdn1St0+laPxlYqVCwhYV523qwYSsrS8P9+RUXyewIIIDAnRYgYOVOr14KhwACCCCAAAIIIIAAAggggMANCWRBKD7MQtb252ElatQrJDY/V7IHG6u2tDhvpbIuTwxbNEKG/a700K26Gvh0R/tgMPDgFAWoqHvtbq9n7XbbWu2Odbt971Wlp5bUbEgFJaQu2ruDge0dndjB0ZHt7O9avdmwf/r972xzY80WvJHxhoxYLAIIIHALBVrd1PYOjuyvP/5sr1+9tGazYaurq7awsGBrqyu2uKQhP7IerEJ84Y2U0oNVzGxxvmRbG6v2/Nlja3c6IQAy6/kkdGCigJWBB614RrMgFbWs+j/1pGIFP+aoIf3g6Nha6mlhoME/9Jd6A+XSwpxtrK95jwJ+Q312B37sgSUGXfrRLkZvjskUCkV7uLlh6yvLVtLSNcyIenMZm463CNwagWHlHfgwjjYYmOq5bwI6BysVLe0POzzyHYd6zzs+qtqrl2/t8YNNC93ifbkSaxtVLyr1RsN2dnY92FkB0hrqUj3BJMq/hn9R739pfxTo5lkcFvjLZXgGlqRSd7qp7e8f2t/+/pP99NOP1mo17eHWps0vLNjmpp4nBDMK+xaSKRR/Ya5gDzfX7NnTTeu0GnZ0fOzHiblywR4+WLWvnz2xBxvrNjc3NwNriCwggAACsy1AwMpsrx9yhwACCCCAAAIIIIAAAggggMCtFPCL/dn9sn7XehJ6QUlsYKVyxdbXV+yPf/xH+/bF197Apwa/U9ers8ZEpRMaBMJ48Glv4HcwNhpNO6nW7PD42PYPju24WrNarWG1esPa3Z71FeCSmmnEIA1FpKEblM7e4Yn9+V/+aicnVfv3//wH++rJI1teLJnulGR4oFtZ1cg0Agh8QQHtk9vdgdWaLTup1a3V61svNeuph6tEe3j1hHXzwSp5ks31OVv6D3+wf/rDDzYIreT+dRjSw48yfrSKw5GE1lMdkdTrQ3jomFKt1ezd+w/253/7m73f3bdms+m9omgoiErR7Ounm/Yf//f/zdbXVq2k3sPSfghq0ch1OqZ5TxJntc2Olqd558qJzZUSS9Qqyh8Ct0lAm5T+cid13qlKCPGwgoaFVCByalYuFm1pack6LQUed6yvD33YyMSqJw17/eq9/fH3v7eluUXTJvWl/pR1FeOkVrO3795ZrVYzBUTrPFL7kIWFRd+eNURQp+N9/H2prM3scvzY0O5ZtVq3o6MT6/b64TxcFUEn2D4eUC77sZ7kPrptL8tFs/XVOfvnf/zOlhfm7N3799ZqtW11ZdF/X3z37XNbW122ssa04g8BBBBA4FwBAlbO5eFLBBBAAAEEEEAAAQQQQAABBBD4HAFdh/YRFPQcR1fQLffeBDCwJBnYwnzZVpbmbW1Jd6+fatv4aJFKzy/36gbd/px11pasvblhrc5ja7a7Vq037ei4ZnsHh7azd2BHx1WrN5vehXs66Mcb3K2bDuywWrP01VvrKbCl+we/A3J1pZJvW/lo+XyAAAII3HcB7YfVNltvtXzYh8OTmnU0BkRStIEVvHHS99RfsGH5k+tEjeIlPRJbnA/DUcSmQ39WcI0SiR9mCQ7bUrPP+2nBismCHR2UTI2U6kFFgSrqSqZgAysXC7ZQSWx1oWQPVuZCA6UfBP1omPXUks/t2ALVW0N2hPTeWfKT5l9rovFZ89/zGoFZEMjVUe+wKDv30/aiYBV9rYeG6tpYW7NGuWH1WmrNVteDvApWsE6nb4eHJ95jx8pC2ZYWJ/TOcQ1ljdthvZH6UEAKWul0uzbwc9jQq8rW1qYHRh8eHlqnwyap1aDdXSc7Hz8+qfnQT0mh5IEqHkDuwYLXsMJuLMlQj8uFxB5trdviQsWeP3tkvV7fhwpaWpi35eVFq5Rn6YB4Y1gsGAEEEPikAAErnyRiAgQQQAABBBBAAAEEEEAAAQQQ+BwBXfT3nlPS1NSJur9WI4UuWg/6fpetPg/3r19sCWpm0XAAACAASURBVLpJUw/drbi4UNJADD5ju7tmtXrPjk4e2IftFdve3bft/UPbOzy2eqNpvW64+1/DOqiB9fD4xDrtli0uLlqxXLRS5YktLxS/bKtDADp/mbIKY1ZcDGhWp4oNFXehLNM2Vj3INe5NO/lrS++25vvaQHIJ520usp3nZh2+zKcx/PCCL64y7zmLULLdfmq1Rt0OT46t3mz5ew3zpt5VUu3nC7HA5yT0Jb/KbVsTe2jIfZ/P1vjHIUBFPcgkITDH92U6IGn7DUOEqBcVDQ+illsPw9Q0F9nnZWSeVD4Tk16PZ2zSNPosrgZNH1/r8zj/pM/OSuu6Pv+cPGieWIYr5WtqCV0pF3dy5gnrR70LaVtQE79Cl9VxkM79KsWirSwv2nylZJb2rNNt6vTQV3Kv37davWnv3m/b5vqyLS2ufREu1Qxl4fCkavuHx1ZtNK3TV29JIV/lUtG+evzIqrW6HR7sD0PNQsjZhMJ/kVzf7EJkpqCUWrNtJ+rtsNWx3kDruGiWKpgxDUOx5TffK1Fpifq7UiJZGp94OnNXEZatqr20ULLFhVWzrVXf3eobPe7KKfwnhPgaAQQQmIoAAStTYSQRBBBAAAEEEEAAAQQQQAABBBCYLJDdSRvvYh92CW9WGKT+UMPF51xyjheEtdy5kllltWQP1h7Y061V2znYslfvtu1vv7y0dx+6Vu11h0tRU2J3oCEt2vbjry+toDvjF+Zs/umWlbIrJQPl7dzb3CeXdvKnE6526yN/DELhJwGkqXc/n6gb9Ys0ek5e+Jf9dEJR1cozGKhXHXXE8Llr+xPF0HL15y0EudfZy6k+TSrj5y7A60BWF/IV+jLpxbJPmmdSvfpougsWKL8cxZxlsVQMpfUR6ChAIF8fNVlufVxQfULin/5IHQH4eskt79NzjU0R13cuDbXXdnpmJ/Wa7R8d+X60r2X5/ikLzki8VTcMseMFziUwtojb9jbV0HJZo7uvzGyouRCSqSGAtC0PTL16qZF2uD+6LEEk1HznzTthHQ2DU+J3Qo6vlVb22juLUPL59POvP3flKP3LpJPP26eWqWnVAqwuO87qtOBC6WXHJI0FmEvo/GwrHCsmrozGqdWF3Jjjp8pxqe/jMsNyhovVxzELnq/hm0ul/iUn1tngsMe9bBjIYmJWKRVsfXXDBmnH6o2qperGSec/g9RanY69fP3Gvv7qoT18uGaafvh3ymD46ZVfKNlez2z/4Mh29w/spN7w4W00vGSpVDT1nKHhJN9/+GC9bme0UV15ybclgVydzLKsT7p98+E51fNWu5dav2++vnSMULCPD++ZTZ9fjR+VOiYfv/hoYk0Qd5Lahj+aIMzp0SITEonp52fTZ+PvNeukaWOSY89x9visr33/Op722HyXWMTYnNf4NmbKC3GNyyFpBBBAICdAwEoOg5cIIIAAAggggAACCCCAAAIIIDA9Ab/e6Y1L3kwxbNQJF3PV6JQOu4a/6lI9tkQJp2aLcwV7+nDDFpcWbWFpyZaWlu312w92cHRi/V4vtHdZYt1BaofHVXv55u1weKLVFY01b1MOVhkrXbwQrPwOW/vjh9m0Ht2Ru36ur/XweXLpjc2W+ya8DNgffXzlD/LLzS8j/zoupFCwgjcMxg+u4Tm/3PzraS0q+iu9aaavtK6SXszXZ6cTV6SeP5GR/NeT2ovVfnRWI/K01sNtSSc6hN3cKCggciu241NlOWuCmGZcRkwntwqHu5X43Wc+jwe+aBW3Om1vlIxDPhSKJQ/6077MgzliGX2Z8U1WmPhW3/lH+iALQDgVOfGZGb7u2Xy/HBrd40oNwSoqTCjj+Gr5ZJbyJpo4vo9D6Q1TnpBSxnrqm/hZfNaX8XXGfWp6vdHnmiY+fzTBJz6IeY6TXTad8fljOnqO3yl/Xo5YmPxEuenGPv74bbYBefiJhnMKa0yLOS/b2VnMcEHJEPU6g1WU+1x5cy/zH39cxln+JPSyouAF74wpC/Da2ly3dqdhOzs71mz1raCdWFKwvs7Tjo59CLJme2BL82EISS+hPGL9iEXOG8XPLvmsAItqbeBDS2q4yd5AoUoh4bly2TQc0Nrqih0c7HuA2iWTn/7k12Bw2UzKrNHSOfWJ6digngyTNPGh01SHk6QQd5kued62drG6HQt9Rkr+9YTKEGdTAfOvJ0waDU7FvcQPz3n+KEfnpa1sZPm4sUNgdMjnM//6nLLyFQIIIDBNAQJWpqlJWggggAACCCCAAAIIIIAAAgggMBKIV2FHn+iy9eidf597P/rm81+pIb1YsPmiWaG8aMXSCysVK1YuVazf/81OqjXrdhW0ohbj1Frdru0dHNrL10V7vLVuxRdf23p54fOX/9GcKl+8Gpx9ObHIEz8cpRa/js/xm/H3Y4uKk039WcvVssaXf4EFxdni8+RZYkEmL0C9e2jZ8dv4PEzr/MSHk93mFy6kgmeF/8jgQoXTXJOxPP1cGuPpfzTXpVvqc4lf48vxcmhRsSwflWGa+cgWfCp4RG3lWn7MwCWX50lmHZmMz/pRWbLlD6e77DK1nLF1ql12o9Gxk5OG1WoN0+g3hULRkqRoqRUt9aEfin7vu157fEfOewh/KlO5DXn4+ey+8GOYxzzE/jaylerrNaLlsHMvzy3VGdOd8fG5SZ35ZS4xr4OxjuQ+P3Pe87644PzxlGBY/+N88XnCMpRFPYZV8ZxpT82umXLTjt6GDcgDIjzl8I0m1Ss99DeaPvvAk9NUo4FffPpswtyiRjMMUwzz5b448+X48ienO56/s6Y6czFf/otTWQxoqg/qfa3f79nK8pI9WF83BQ3X6nXvjUMt+X0NM1Nv2O7egR0cHtvi0438ah2t4wh3xZIpmV4v9aALLU/7uX4/9QAarfnFxXn7+tlXtry05Ps+Bd7M3F/gHdZl5e8U/5UzfDo1N9N6arTs4OjQqrUTS1MNnqZ9o4ZJC+tZPRfGc7eYhdMpjdfrONX4s+YKA41qmM/4l18T4+mewogz6HlsQqWhx+d2sBjnn5B0fqnD17743CHw3DIM55ryC2Uiv+ApJ09yCCCAwEUFCFi5qBTTIYAAAggggAACCCCAAAIIIIDA1AWGDVdTTlnXXysFs82VghWfP/WL241G23rdN1btN6yXXZxN077Vm03b3tn1bufX1tdseXnBSqNr4BNzFq/tjl3rnjjtR1fEzUx3o6q7dDWE9LOu70O7R2gM09XjkHZqxULBisUke4y6GL8uuzMK8dHHivlRN+/dXurd56ss+vP/x+GMksQbvZPCwEplNfXqTtuilTQyUBoaBS7TMKC01e18tihvVND8Wl16HppcbMV8VKazPvAGl2wYHOVby9FjuMzLLi9LK3aVr+WqE5piIWsoOSc9lV3DFXT7ofEn5C3NBQeEuqMkyqWClUuJp31W2SbVzzitvGNdVcNiaHAa2KA/8AZFDZtVKhQ9SMw91JuObGI5Pm4PiklP5zlUuZBWzizmu6e6ogbRbFiq2LgY6mGoj8Vi0Y3K2VXSXDKfn8fxfGl717AIHuigoLpRMIi8xv/i7HrWNqYGVD080C4z1Z7Cy+P1MLFCMdzNXkgS84G3shFpxtMeb6D76Pv8B7m8aZ/Z1B30RzU7Pq5Zq9m1dOARgr5/Vd56/cS6evRCA2WSqKE33F2vZJXcKMnQZ4WGE/IhhUZf5HMwE6/j+vD9i4/Mkq3I7Iv4vUqnf5f6G598/P1ZicWF5qbXMaXXT63bHfh+ODQUq55kQ7LpWJIUrFhIfF9TUp1RZcn/Kd1cmvmvLvpaSSgv3jitmbRPyPKr+q793HAZZyxL86sc3X7Pt99o6/VbCWT73/mKNqYzcpZtc9pnyqJQUH0c+PNoplGBlYzeZVm1Tlfl6HtQxSA7pmmYGnmWsvEDtQ1qmJi5SimUy7OSTyWmlkHksjo+VdhuwlAq/f7Aer2eFQtF0z5Ki9O+QNtUWH9h3eX3H2cx5BZ5Yy/zZc1nwo8rvZ7NVcq2sb5uWw8e2O7unnW6PZO5ytTudG13b992dg/s6eONycezuPLyiV/ydcyjhj07PDy2o8Njq9dbvp/TUETaXlaXFz1gpVIphSFuVLeyrT6GsF1ysZebPMuk6nN86Ljs29sgHJeVDx96qViwpBCOC6oz2nZUXz51fnuZDCk7GnBTvavsHx7Z4eGRNZqNcB7gCek8RUFJfa/PvW7qedKK1T5Bqy2uujTuJPyzsI/K1+98vkLPVmFgoLjePB2lqW09OyccbsyaSBPk/vzcRsdXnYdn5woDRWG6UejJx/dXxcTm5orjsw9T8uVn53Ta54V6G7bT0lkFyOaO2dKzRi5VL2aphtVzH4XjxON6dn6blSHON8zE575Iw77a61IuDS3Gz+lu0YikuezzEgEEbqkAASu3dMWRbQQQQAABBBBAAAEEEEAAAQRuu0C4yKv/X8+fX7w2s+XFxF48e+wX9+v1mvX6PWu2OqYGIV2RVWNWo9WxN+8+2JMnT2xtddVWV+b94rQ3UE7I3th17wlTjD4aL6HeN9upnVRbVqvXrNlsWLvTsV637wEsagBTo5QacXWte2lpyVZXV215eclWVtRbTHbh+uPr76Mr/6PFT/2Vrzc1pKdmra7uRFaPC7oTuW6DgcrQ94AGLTjx4YDMSuWCLSzO2fz8vC3OL9ri4pKpnbGiYIrxBtNhjkfKWqYCVTqdvnV6asAME2moIW/QS1KreKPCJyKNhmlf/IWW2+2m3qjR6yloQwsfWKkYAonUiLUwp5VywTQVcKKy9FJrq0G2q+YeNYYpkKdg85UQZJLv3SLWIT232qkdV9tWrdWt0WxZs9W0drsVGhc86KVg5WLJ1FCysbFhjx9u2vy8ggIulsW4fvWsklYbPV+39Xrdms2m57fb7XhPReVSyebnF2x+fs4bHFdXV/y1GvMqHqAUTC5Kc0HB0WQTElae253UGs2unVSrVm80rNlqWafT9gYzzazhCVR3FhcW/U553dX/4MGSladZfXJ5a3VSa3d61uv3vf1M23axlHgj91xlNMTFuL22MQ2PUas1rVqtW6fdtXar7WVRPSwWCzY3V7HFxQVbXFiwylzFNGSFHsvzuYiVmJf4PBKc+CqfD5FoH1mtp/Zu58DevP1gh0cn5ttCqm8VOpP4NtntDazZ6lm13jPVkSRRoESoe3HnpKm9DU8N/cWCN/ZXymUrK4rtgvmbmOkb/1CZjwWIz1fLVAhfPCMtBQzmGnx7GpJD+4bjE9vb2/cgj16v73VO+2XfV3pwVtnrverL6vKybWyUhrm+Wm5Hc2v/3Gz3PehAQ7p4k36a2lxZgR1lK5RHw4OM5jodLHJU63hZdIzUfq7dbtugH4aKmV+Ys3nV+4V5e7CxbqtLS1auZClpcSLTfnagfYGOGX33UH1U0EqlXLSFSiUbqm7kq1m1/9Cz/g5PGp4HLVv7Pj331EObpbawsGDlctlUd5WPJ48f2vJSaGoJQUtZJjwzo2VkSfsygkz4pN0zOzg4sWarba1W289Rmo2GH0u1n9XyFCC4sDBvS0uLtrqyZPPzIfgzph6f4zJm4dnLGDMWnzNjf5sqoKFv6aBva6vL9vjRQ/v5l1/8PEIrI+4/Do+qtrt7YO3O91aYC+dGQjzrHO1zyh7XvwKV9vbVU0jDj3NhfaY2X6nY+uqKbW0+8PNJ9QzjGcgqzKh42Qefk4kJ8+RT02sPWu3qmNK3bqfr54/1Wt2Pczqf0DmkYglLc2WrzM3ZXLlkC9kxeq5SsZXligd0jPI7YaEX+ChuK/Vmah92Du23V299mE0FV2qoOAWOKFjFt8Nu6vuESkvbTzYMjsac80iJLNDGA1ZCIGalVLa5uTk/H/IAtwn50b6l2e76uZmOQTqS6rio8mpf4+eWES9XWAXzKE/1Rmq1ettqtZr36tNqNaw/0DrVuWk8H6vYysqSff3VYw8ay2dDSStYSMHDCq7rdLW/DeVTgFC5qIcCYnVOVwyBOvkEMgetz25nYM1mxzqa3yNuCj5kVrmgY2PJg2rnKxc8iRtbxqm3yrQHXYb9nB/bG13ft4bpJBmO0To+VyoVK5V0np07vJ1KkDcIIIDA9AQIWJmeJSkhgAACCCCAAAIIIIAAAggggMCMCegata6zLs0n9vXTR/bPv//BL2i/evPOm5GsoIvqClpJ7aTWsA/bu94Atr6qXlk+708X8bVM/enacF93TvbNmk01Jlbt4ODIjk+qfpFcjem6G1XDFOnCd6ej4YpSb5jSXdveIF2p2PzCvC0uqpFqxdbXVu3Bxqptrq/YXDn56CJ6KFiWgc99mnCRXxe29Xd4NLCDoyO/m/bo5MQDAhrNpnnj2mAQGkh1u6qZ3xmuMhRLRSuXFcRQ9gvgC3PzVikV7MHqqm1trtvG2qqtLM5bITY6jhVCbRonJ01792HbXr1+a90s2KiooB5LPSjj2VeP/Ll4ZgCMZ+lS/1OR1fD69t221416ven1R40RSSG1tZUl++rJQ2/MKJcvuOBEjf8de7+zZ6/evvMGJ61z3UW/vDBn//jD9/Zwa9UbK9QYp4YVBalo2Tu7++5+clKzWqNp9UZoyO33QyOVpi8VQuOIGkhWltQgve6BK5sPHnjdWV4uDO+wlut4g5/q70kttaPjqu0dHNj+wYEHrCgwptVsWbfXtX6v7w1RChZSg4Yawebmyv68tDhna2vL9ujRlm1ubNjSYsV7/LgU/PjEWhG5BqdJX7fVWF9r2/bOvh0cHtrxyYkPJdHuKMCj4/nWNqY/NfyqAd8bxOYqtrS44DZan5sb4S7/hYViCKwYX9hF3ufyqiX+/Otre/v+g7XaHd8rKJBrbW3Fvv/2a3v8cMMbtjSdHu2+WbXWtv3DYw8M0b5CwSr1WsOD2tQgqZ4XLB14zzZqzFLQytx8xSqV0IC+UK7Y1199ZQ83H9jaasXK5YtkejSN8uH7rHZqB4dV29s/8AbcvaMT29k78B5W1M2B9p3e01IaekH4+deXdnCwb4sLCgYIrXGh1wG/5z+U3RvDNICQ2frqqj19+ti+/+bZaOG3+JW2JW9gn1oZchVpLE1tp92BttWe7e8f2OFROK6cqL548GDoocPrS7/vgUHqFUTD483PzXtg2fLiku97t7Ye2Nbmhq0shwE2xvcJY4s+/VaVRX+5rKru1Jsd+7e//M1OqnX/rpD2bG1l0Z49eWIvXnztDbD5oDwFBlYbXTs8PrH9/SMfAkZ1X4EirVbL67z2kyqDAk4UsKJglT/+4R9tYX7ByvGom+VDx6t2L7Xf3ryz7d193xeocTy1gT18sG4/fPfCj6EKHIvbXlM9axy3bH//0I6OTuzg4NAUCKD9h+9Dul0PylTAW6lc8n22tj8PnFl/aw/WV21jY9UeP1aQYNl0fMqxZFAh4EBBdc1W16q1qpdZQWDheNr0HkV0TtDT+YAC0woK9JmzpBCOo/PzFVtaWrCNjTV79OiBPdzasGWNg5j783273k/KQG66m3zpayMdWNrvW5IObHlxwbYebPiz6q2CB7TL7qWp1ZttOzg6se2dQ+9lZT4GreQLcIWyxmrcaKa+/tVbSKvV8eWrCV/d22ysr9mTx49scaFsna53reK9loxCnMTtU+dz9enXceET8q+vdDal3ndqtbYdHte8blarVdN5lwJWdDzQQ4HP7qbzL50blRUsoW1ex2kFMpZsaWHBNh9smLb59bU1W1osXvr4rJhd9ahycFy1HW2r+4e2u3do27sHfuxKrez7QfXzpICVWqtvL99tW7XR8IA11U3lzwMj9NIp9WEWrG2pLS8t2jcvntt3Lx6d6aeg1B9//tWPldo+49b27Mkje/b0sT18sOrxMHF/pnMpBZccV/t+TNve2TPtL2vVup+/dvuqc30/JyormLJgtrayYl8/e2oPNx/68VbBlp79bNPS2tZ52E+/vrKDg2NTkGD4fmCLcxXberBuXz97Yquri1aeEJ3t6Q3M1+lf/vaj1Vtt66u+adr+wCqFog+TpcDjr756bHNz6m3xCpt1ro7VGgo02vNzagX1KthHvUdpUL+KAp7XVuz3v/9HD5Dz3Wss+JlrhC8QQACBqwkQsHI1P+ZGAAEEEEAAAQQQQAABBBBAAIEZFtC1WbWbqgOMjZWCfffia+9ufmdn1xrtgaWJwh3UgNSzeqvjF973D47s66dPbO4z72bUMpWmHhpG46TWt5OTugeq6AK5GhfVoKi7qNWY3tKd496QXggXu72HFQV7qAcPBa2ocT00OChoZX1txR5tbtizxw9t88Gara8u2cJCDJGZ4srIXdjWHcfVeteOTxr2/sOube/u2d7hoR3VatbpdoYNJh7IMFAwQ2i0Uf4LKkOhmPVqoSFkCt6biIZserC6Yl89eWTfv3hulaePbUEtBBOKogaOZrNr2zsH9veffvM75lVSddNfMA1R07P1tWXrb2q4gMl373+OjNZhq9vz4JJffntlR0dV75lHd5vqTv1HWxseqPH00ZZdNGBFaTbaHfuwu29//elX63kjaOixZXVpwe8w39xc9ewqLuH4pO11Rubv3ofeLRpN1R3dWa27i/veyOCBThpuQ713qLeWQsEq5UNb+LDrDVMPHz70xranTzbtwcbSMNBJjUVq0FG+tJ73D5u+jt/v7PowDGpEVR1VA2pfDWNanho2PPCg4OtXd+KqUUxbkxpq11aXbG9/34dOePJwy4NBKupV4XNWguY5Y0bFLakR6vi46QEVH3b27f32vgdUqUcYBYioAUoNMWo484ay0FbmQSty0t3P3uPC/JwP9/Boa9O3f/WYoJ5X5ucmVMhLlEOBBTt7h/bzr6/spFYP9bOQeCOzhpfYWl/zu7BVjna3Z9v7x363+vvtA9/GtK9oNlvWafe8twUNx6QeM2JwhIYCUu88CgrTPsPXe6loByc1++rxI3vyeNMebq7b0lLZG+DOoPQSqQ7oT0NiHBw2vNcpBUkpSEUN6rVm2+9o7yoiQdEGXm8S3967/b43WCpYKAw1U/BKpQCB+AiNuQPfbrXtPnn00ObmF25vwEo2bEPGdr1PHoEQ1p7qSr2V2vae6sqefdje9uAK9XLl26oCyjQUlobT0fBd3hAcgrQKiYIeQmCTeoxYWly0x4+27OmTR/bk0aZtri/b4vynhhGbUFRVnmw/oiE2avWO/fbqve3uH/jERevag7VFr5/qyaxcDFFUKpYa/3cPavZhd8eDEj/sHNhRtWGtZugVSb2aqM4r/ThE3sJcxfppYh0NPeRN36M8KSv9xEwxBdva9n57443aHrCSph5guLamAJ0VPzfQcVq907z7cGjv3u/ah+09DwCq1xvWaYfjm/YjYTig0PuZhlpRcJKGWVEgwIf5fQ/IefBg1aq1mve4ouBS7xUhy5rvf5LR0Fq7e3umx44Cjo5PrK6eZDpd0/al3iMSzTBQbwfatsveh4Rv4+r9oVy09fUle3y4Zc/rT+zZoy1bXZy3+bJ6cshOQM7b2EdcN/ZK60nHLdVVBeAtzJXtwfqaPXq4Zc12x9rdmu9btOLVm4iCNd5+2PZyK9gw/GUVbwql0L663uja3sGRHRwe+/FD61yBEDqv2FhftYebGzZfCcdKNe6rTnmghHrFy3o8UlY+iz5XFK/D3rNVx+vTcbVmB4c1291XIKOC0qrWbne8Zwxt3/pPdVTHZw2B5/nyHuhC7xjabrRf9l5i1lbssR8bHtrDrU1bV289lWyoxk846lT1w27V3r7ftd2DI9MxV3W3VmtZy3sRE0JJZwe+5+8nA2t2U3u/qyDn4ywIVDq5gBXPv9cGdysWUg/8Us+C3754dKZlu9239+937eWbd9ZoNPyY7qkOBrayvGRbCljJ9kk6V/B95u6Bvfuwa++3d/2coVlvWbvVsW67qzNJ/yfMsoJaLbXO1sA2H2xaXzuU3PqJTLE3qddvtu3t+23fdsVfSPu2trzgPTI92NywpWUF1WV/Sif+ZZ2maHtXEPKrt9tW97wULBkMrJwktr667EHDqvNbD9ds4awuZ2KaZz6PCtDqmu3sH9qPv7y0n1++Dj1YZUMnltO+ba4u23y57MMQDuvy8MWZC+ALBBBA4EoCBKxciY+ZEUAAAQQQQAABBBBAAAEEEEBg1gW8YdfM1AHG460le/Jw096sLlt7t+09q6jxXT2saMiOo5Oq7R+od4aabT5Y8TsZL1s+XdONd7/XGgN7/W7b3r3btu3tHe/SXnfF+vA/Wq43puv+WTV+qQE48QYcNeKotc0bxbztSd2km5XLuvv8wHa2t213Z8e+ef7M7958vPXA5uc1zMllczth+tE1bf/SG6+PW/bu/Y798vK1N+b5ne/tlrWyYIvQeF7wBlI18IQWhsQKffUWo2FBdNepGlXCQw1xhXRgJ8fH1m42/S5WdbO/sBQboU7nS54aCkh3sqpxpK3b8RWwYrobNLVGo+nBPgqUmfafhjlR7zu6u/vwUEOhaNl9DyRSLzhatje4XWLBCv5Q44TuTB71VpJYq9mwWqPhdwGr4eXopG1v3ryzl69e29u377zXkxCEEeqDxzlly9U60DAAuju30BtYJwl3/qpxS71k7OwfewNNrf6V/e5339qa7vgthxYIsakXl4PDuv3082/226s3trO3773ndLyxWGtAQTqFYaNtaATXLcs9r6Fap2pUVvDK4dGxB7scHJ5Y9cVz+/bb597bhw9nFfObPV/2KVZPNTJrqJ3jast+/e2l/fbytb3b3nVXGemOczUoavpCUvBtyberXPNXUuj58FtqWtOms1sq2O7uvj/+4ftv7Zvnz+3h1vqpRufL5FdqWr4aX49Oau5SLIchWLRt7x4c23fd1IqVEBC2f3jod2q/ebttewfHVlWDeTcEgIXhDrTew/AJMWAl6Zq1s4akUL7QcFqtNmxnd8+e7m7ZP3z3wp4+eWzrawveQH9We/NIJAAAIABJREFUu5PqgdJttfv25u07+8//7U+eh1ojBEh51U90e7d3JeKSCgTytz60WtMs7Xvjs5c8u3Pet3215so5ST2oqmQDm6/MeUOjnKax67rMuvnsaVUMPeKfMPPv4+fTfhZy1vNNtdbx4Zn+8uMv3kiq3oQa9bo3liorChBUo7Xqg2ZTwKPWkwL7vDE1aYcgJwU4FY/8mPdhe8fUS9UffveNPd1as+Wl+cu1usc6qL2jGoebTTuuqveQY89HMe1Z2u/4sVX778Wl0HyrbVi9mvz060v77dUre7e9YyfVhvUGCoQKWfDADT+CpNY11R99nvq+WD135Y97cfXE53qj6cFWe3uHvu3IQ8OjaN/0/KunVvCeXVJ7837bfvzpV3v7LgQFKhhAhgomHTmGWqr9vYJV/HCTDqxhqdVqBTs4KtiH3ZIdHO7b73743r7/9ht7uKWAtFAZdORQT2u7B1V7++69/fbyle3t7dlxrepDAfV8nYWhnpS29lshzE8BCBpqJAYdheCEo5NjOzw5tqOjI6s/f2bPH295jw5LS/O+3nO7uqw2xop61h4gm+zan+Lyw7POwbSOKyXz49K3L154wIj2f368TRKv2woEev/+gwe4rSzP+Xr3YJGr5FckWXa0f9My1bPOkc4zOuphJfRkpQAp9QilISN13EwU2pAFQlpS9GAVT8eHQMuiEC6ar8iRTa8s6RTnqNryeqKe5RQ4eHisQBUNA6gA0tirms77lEAYes3rfZr68JLKT/AJxzftqLTdqPcYDzbZ3bdnT5/Yt8+f2pPNNVtdXhhaxKx7wI7v4MMnOh9U8O6f//WvVq03veciBaoMBhresZItQaEeEvKzBA+i0fB8Ol8LSWnbUQBIyE+2IYXt0zRUnDb8gfcgo2PD6b6DYs7My1irN72uKFgvBis/PDqxRqPlu2UtZhissndo//rXv5t6WNS5nILDBuqKSTsa39n4WvXtfaDTcR/ismfFUinkO1tPcXXJWuecChJSQNHe/lEINutrHzWwQa/rPbZ5D4q+s8jyrgQ0s/6yY66G/FJQ8a+v3/v+SsNF6txWexzV+3anZSuryza3oN7Uls40yVI94ynkXPuhgxMFx7y3n379zYMeFdiob3UOt1A0e/JgzR482LBK3L/GQp+RMh8jgAAC0xAgYGUaiqSBAAIIIIAAAggggAACCCCAAAIzKRAbYGPm5spm6g3jxVdPbHdn1xujdMFZ/3TXuoIIdGetGtw3NlYudVHYGwqytg9dID86btrLNx/sv//r372Led2t3dadk/oyNi7oYrX3PhIagD3wQS+9n3A12KmhSpNrCJqC9QapNVod75lFXcJruBbdof37331vL54/s+VF9WQSS/uZz7n5FYuwvVuzn3556Q8NraDGd/Wm4I01aszTNXe/6K5hbcreuhAazsPysyYJb8CI7R7BSndN96zV6dri0rI3CkzKsabVn3rDGSQavklBGQW/U1ffdXuh2351oa6G2mn9KW2tKb9dvaDmdS2/YGkhNFR6gIbaOTKDiyw3lFtl0VAqSq9ofW/WUbNk4j1saJgoNdgOCiX724+/eDDGhw/bfoet7sLV8kbLDI1UsdEutokomEN3rIfmqoI1O31rH554Q1etUbVuv20//PAP9vjRmjf6HVdTe/v2vf3y20t7+fqdB+c0W2H4mr42DK+CWQOtGlG93VbvQ6O4lpPqs6RgCk1qdgbW7Wloi3emwImTas3+3R//yXsE0p3cqmKfU0+jn3LU7KS2s1/zYUcUYLN7cGDNdisEoSnDxcQb0dSw7CVQXnW3vAevZA3PyofWoSUeRJH21Hhes1q9ZcfVuq8Hb3j+5pE3kl9kHcdplFf9qaxK35sMC+HOc201CkQ5qTat2uxZZ1Dwnh3+/C//4kFF6olF/gqW8qAkBbN5hyaxt4wwbJjS17bmqzoszrdF1Y+jWtN7B6rW63ZweGT/8P039v23L+zrrzYsi1MKcyij2TYft081EqtnHQ1jpNWvXZbqqxruvFkrC0Tx5btu2D+p8c/3YQpI037M0w49Uajh0OuJDxOhPleyO9azJtUs+zP5FNelNy6OuD7Kq7Y/Xx+hqB99P40PDo8a9vNvr+2//8tfbO9Iw4JouBz1rKC64S3UWa8U2sZ8S8v2F3odjw9qUC7YINU+Z2C9at0aLdX5Yzs52rP/+Y8/2DfPv7LlleWLZTmrP3FibW86dingw/OVDcWjuqz6pHqt/Xi3k9r2btV+/Oln+/GXX703Fh1ftJ9V8F2o2wpmCLthlceLlPVqoeFOlpfUW1TIwHA9xYx4FQtlVXn1vXqgUgOyestSzy6NVtd+efXa/suf/mzVas1qtYb3fqZjsO83fOgSJRiOx8pDoSi7EFBaUG8S6cCHrRnouNjqe/CLekU6Pq7Z//Qf/r1tbi57HjXczPudA/vrTz/7MBwHBwceFOipa7/qx7ew7WgDUh8PWp62bwXV6hM1jms1q8cMDW9ydKwemNp2vHdg9W+/th+++8aeP//a5k71uqaSx4eW5jvrqHRDz6GuemFUNq3j1GxhLrHvv/3Wh3pJdI6m77Qe+31T8JGC+hQItb6+bOUr9n41LLiOAVnPNxoKau/g0IMlvDcxBdgVE2+8f7ChQK4FUwcXXjf9+HfODmG4gIu/iGup2ujZf/vT/7DXb9/bwdGxqVc1D1YNsbq+QSj4JGwQYR/r57I6P1Ai3s1Odsz2489wUmv3zPaPalZrduxAvbWcHNngd99a5flXNr9wOmjY9yFx+9a5Vz+1w5OqfdjdMwWzhsC4EGztAdg+TJzylQU2etF1LFamFLAY8qr17q/9XFjTh2CJNO15Xfd0J9F62TLPQsmKpYoVS3OWFLtex3X80dCaypufPhfNqs3UXr/btf/xr/9mr9+996C5rg+r5zsZD+JR0I+TDaQagtiTtO/b+vx8DI4arcdQmhCw4ue4aQiw0+apAe+0LlRkTaftLQy2NprfX2Wuqt/Ly/P2/Xff2e5h1Zq9xHsr0zFTdVA98qnXH52fKRhtfu5rW1sZjp85luj5bxVeXGum9ubdtvdMo97TOhrGaBCCmjTcpYaL+vr5M3v69IktLpZvUTTp+WXnWwQQmH0BAlZmfx2RQwQQQAABBBBAAAEEEEAAAQQQ+EwBb9yK8/ody2ZbG2v27Okj+8tf56zR7ntDiBru1A6gO791Z7h6WlEX9Brm5DJ/ujithjh12/7Lb2/sbz+/srcf9qzV6pga/nUXarz6qwYPNQaUKyVTV9+VSsWHatDyeoO+dTQ0QLfr3b5rSAQ1TOiuVG+vGCRWb2k4mGO/oN3tda3f79vzr5/axtr8ZbL88bThCrs1WgoIOPEheH59+caHsGm02h40o7zrT/mPwRJ6XyqWTL2O6I5+TaPGAzU89NV4mQU3eLnVgJmalSplW1xesdX1dSuVQxDBxxlSY7ku/KshITSy6r0aE71BPN7JK88ptcOpdErfS6kgGB86Ssv2AYiy3nBCo5CCTy77p+CjpFDyxyALWdHC1IvM4cmJvd/ZsVY3tb///ItpGCl1d69gFU0jBzWYFouqNxWbq1SsVCpbt9OxTkdBDn3vtUXuglP+NHSG2mf6DfUq1LPyXNHmFhatPLdoqytl7x7/599e2S+/vva63+qGISlCi08YnqpUGtVTDaWj9ajltdttr3uyUuOKN9R4UI1Z2uzZ7v6R14G5+XkrFL63xw83fGiay5rF6bVe1CvDuw9H9te//+y9/qj3m2ZbDV2hroRVooaxbPipSsXm5+atUq54vtVg3Ww1ra3tRrfVK+hIjcBZw16v07Pt3UNf32pcV68gXz/ZtDmNLXaJP5loe1W+lG8Fafimk2pfM7DDk7odayiF3UP7299/spcvP1ir0zZtz96g5g3L6mVBjdiJlXV3dW4/oTvEO+3Q+4nqhsqrZXoIXlK0Tj+1ar1t7fau7z80dJCGgNlanwtDM4SJQ4myauz59G2pYFpnlUT3xRc8YEVDk6ghUL3XaLgZ3Y0dk1CDl+pjIamo7THLue8kQpu07ys0ddabQiG1xcUlm/N14tm7hOzNTHrelq7vPmNXMLkgYtKfEtXrbMHvdxTc8Zs35msooOb/z957MDeuZFmDByRAgt7Ju/LPdc98MRvx7W5sxP7/iN2I2flmprufq1dGJe8oetAAG+dmJglSlESpJFXV60QFBZe4efOkQ+GevJchOMQQTAM681fGYHoaGPfXdBqem5L5hF5Dgp4KOcP+SyISdR7ymMbnRgthv410coRw2MeLFy+Qz+fG+WutpncyCCsFTVtgAhkXKVwIfryflHGI/akTDJDpRTg5beDtH++k7dMIzj5MQouEkCIrjpwGhjiTEGyKATUcDaWfMjROiqGNUt6UhxWjnLQ0NmYhqKmx1uEc5IRCHK1fNtFqBzg8PsE/fvkdxyfnKuTZYCBel5g55zIvxTzU3ExcOadxXub8rPqAIu3JfCdG6hBDmY+ZVxK+n8WPP/2ETNYTr0n//fMv4tmA4VGCXiBGbfZbEmn4z/ddeK4n7wJeypeQTsyL3j7omU1IFMyHGHOcHZBEMEDUD/DBAVzHgZ/JSEgid2zTNjVj9qwP3agMYF9wT+w415BgQO855VJKCCL54xP0LxvSBqivhE1pd2VOZGjEzHLxTqTia4uoeAvo9IbixYTeVZiXpuOCRvxatYJyuYSMz9BMZlMeb1QXnFw1d++zl3Yr3Z7kJIaU5Puo8rom5FEZm9knFCGExCq+d9HTkOepdwG+fxGvXjCQEGEMO8j5hDhTS5JHSKEIA7anFjAKkE4yDE6EnZ1nKryhKY7Z66GI7S7BdwHODWlFTOOrBkPmkIAsBEeSN6iBemWREIUMFegmIiFasb1TPxk6WGDZ+D7ME4Y4JIk5C9cjwXP+JjhpMiXHMVMHfEemxxfOjUzD99g/Puzj77/8Lv2u0WrJOxLnMg2GjIESSpGeVPi+OpQ3TcGIc1oulyEfWqWnOhSs+VYcn0QX4invhzxLyLu6emdVY9jkYV2eGK68Qu9zhUIar16+RLM3RKvXR7vVkvGLsyzfyY5Oz1A9OEIhl0UuvYZJ/56PUfyq0hHyXsn3+o97hyABnWEI1YuzIsHmshm8eP4cW5ubKBRy5r8rcVH22CJgEbAIPBoCd/tf1qOpYQVbBCwCFgGLgEXAImARsAhYBCwCFgGLgEXAImAReBoEGIqgUikjl8siGHXgiNWOH5hViAGuZG0227IKO4rMivTbdeMHYbpxb3dGePt+H7/89l48rNC7hXh2iLjukt+GI/gkamR9FPI55AtZZLMZpGlQTykLE41SJANwpSjdgTcaLVkBTy8t4rqbK9CjBHrBEGcXDTEi01NLIukildpCNhOnkdyu+1QKhvbgyvezS/z69j1+++M9jk8v0O4FkkwM7hKKZ4S0l0A2mwXdmZMQwD0NfFz9TSsAV5wzzAGNJTTEB90eeiQKdHsY9AMU8nkJmZAvZJBwx3aAWXXUuRgzmIZIq41GChryaaRQBtsrZgGT9E572hImP7XCW2lHa6o6py1WfneSrBLLc4RI3FBowyMJHxEEd7YjkpyODo6ErELzju+5gnWWWPv8+eBx2qdB2kXAEE1BX7yoMGQAQ1u1210hwYgBRRv82r0h9o/PkMkfIullxDD47sMudj/ti8ce1hVXA2c8F7lMVkKDZHV+zIvkKhrIWA9so+12W7wEtLo9nDOMQjCQqDBioA5DdDr0KlTH27fvwRXqNDS6/v0+SQqpjF5/TlsgwebXt+/AcCgBwyOM6HdnJMZrGrLZFouFAjLEKZsVogbbKIkVNP4ylFO31xv3r2arrQzAYjZOCJnt6KSuQ6hEyPppLNfKcO+oOltrJGFyFElLW9bEoHZ2fomPnw5xeVnHuw8f0Wg2hNDBFf05n94j8shksvCJOYltfkrqnqQVjld9GiR7AejNgd4H6CGi3e2J8ZfeiNgnSBDgOHJ0ci7jjIx92U3kUhOL2aRHqfaZ9pJYW67grz+8kpXy4iGGpKeQYYzquLi4RKvVHBtAabLzki42VqooFfLwUyrsUYKCdSchIUjlSGOgMkxXSwXUquX5Hf8e/eqLPjKB8/PVoCxTKY6aV1rtEX57+xG/MGzNwZHytqDHPyZ3Ew5obGSbL7AO/DT8rC/jBA3ZHE+krfQCGRcUYaMt/ZUKs63Q6099MMC73UM4CQ+eX8DzHY41rLE7bDI2qjmAtc4moAgrCQSjCK3uALgM8P7TvvRjkm+MN7FUwhESSi6fRdb3FUErmQQJKhxzgn4gfZ332EZTSWVTZRZTsBE/EnLkuiKv8YTG9U4wxMlFA3/s7mN/fx97+/vo97vSLv10Ahk/I95lsux72YyMIal0WogTJGv1ej0ZQ9gHLi+bEjJuOFQeFTgn0Vg/CgbA+SWS73eRLVVlDDo+PcG79x/FexHHThrHMykP+SzH2SyyGXpPyCCVTsm7APMkeU2IRsEAbXp+umyIx6puEEhZxFsXjfSjIY7O60ICLZRLQjQqJbPi6ELVnEGIZ3eszztU/V2TsppYr+YfG4ufdrC6UsP+UUlCAIp3ChLnQke8yZyenGFjZQnL1eLVsI0y5txBCyHDKlIhvVExzBLfuagVEUs6SeTSGSzVatKvXO2eisRMJiBhQdiOws7gE2aLH5trt+9NLXluQkgyKTeBaNgXRgbpsq6XhJ/2xLMQyYckVPC9kXOCeYeU+ZnvcZ2eeGAi4ensvI7LZkPO2UaV1x5FKD4970o7ZHsvVVdQLtIj0FVdqRt5xZsrVQy+fyEJCAOJNb3+SMJsMZQdPbeomzJzwPdS2FitolbKwU+lFLFSKl7XPoWQlEkvJ06EcDRAoZDFUqWoxsE5UKonSIQe6Z8K00U/U/Ta1xsMGVUT+0fn+P2Pd+KpjiRVEvM4Vso7eMZHNp0Cwz1l0p4QZOgRioSziITM4QBbG0uolPNwyaQymz7kTggrmpijSyNMHc7P/Mf7ego0T8/d81XQ9xxsrtdw2dyQcJnvu20MWFEctyKg3mhjb18RVirlIti/k3fg1EuYqcYAHz7uifc0hvaU/5sIFTxCzk9ja20Zz3c2sbxcQ+qOBN25BbMXLQIWAYvAHRCYM/Xc4Wmb1CJgEbAIWAQsAhYBi4BFwCJgEbAIWAQsAhYBi8A3goDYFWiASADptCfGh3qzJx4h+EGYH5vpnYJGPXpZEY8WC5aNz5L30qar7cMz/NfPb7H76UBWnIIhA2hMj0IhKKSSDtaWynj5YgcvXzxDbakiBgjKkE0fmPN6o4uDwyO8/7iLdx8+SJgBtTKeK9aVp4ZRs4vf3+0ilUqLgXtnqwZGSZCFrEbu7N5kEPsOTxBoWL5sBni/u4///McvEiKpO+CqV4hBgaYumg65GrecS2FnZx3b29tYXV1FqVSSVen8WM/V6NyYjYQYubzE6ekpjo6OcHR4CIZDWK4VsbGxgrSfFAs2CQk0cvPjfXyjTpRjVBY9aSyQi2I2EJqBnM88G5dzn2MlTq2VNccxTe4s0qhHjMRIqyUI+SbpYv/oFEfHZxhyRX1/ICQnklVooGCohO2tTaysrAjhifwmGnlYN5THdtENQtQvW/j3//hf4kKe4QRoNqLRj6VgaIl6q4eP+/TmMUAuk8He3r6EwSJRisLoWGipXMBrhpF5to1arQIasxJJuvHXHAQ6T0g4aLX6OD47x8eDQ/ztl99wdlZHEIzonwDhiA7oQ/SDELu7+xK2an11BX6qeGcvK6xqtne6sydRheGSTs7OpU9F4UiMXE40RCrtoZbPYmtrC3/5y48ol0pC+KBXGOpu9Cfe1HNv/1CIWT//+jua7a4Y3+gZgZ2nNwSOzy7RD7pYW1kSw3XZeDAyjdFU6ExL4OXJb5JY6oqG92AoRLD/7z//jsEgQLvZlAdoF8tl01hZquLZzg62NzdRq9WQ8lNSVmP8kt7FfhGS3AR83P2Ev//8s4wTo7AvxDaSVpS1zEWrG+Do9Bwf9/axslRDqpiBl7zakqlzIefihzeq7iU0CokvowjtIMR///wW//jlNzSbDSkfFXCTCRRzPv7y/Su8frGDWrmo+jAt92K2U+2TZySYsd2wnUl90NvQDHb2dIIAWw5Dybz/eIC//eM3kNxBDwIk6QmWDEDhANl0Gs+2NvH69UuZV9gPXEZzkNBYamxg26MHhIt6G7/++lY8tewdHivPXdJEEwgTHi6aPbz/dISk66NaWUbSzYoHgIlW8aPrak+NNyql8rgwhOpTjU4gIavefdjD/tGJeHhhiDU3kUAu62N9dQk7WxvY2FjDcq0mpBtOJ9Sf3k1azZZ49xFvQxyTYuoYbTgXyHU9NtJ4zA7GsZD4HZ1d4P/59/+FXq+Dbqcj/rtSqQSqlQK2Ntbx3evXqFVrQnTzPAdJl2FNaJyP5Ec9Dg8P8fsffwiR6LLZFcIPQ2eRPEoPV63eQMiBib//KkROEsrOL+i9YyCjMY3g1UIOz5/t4MXzHWxvbIhnFZJzZPpM8L3ChIFzcHHRxG9v/8Bvv/+B/cMjDEKGMlR1yz7VDgY4uSAJbh8ry0vIZNJIjy3aRMagEwPsix+S+BEhdEg1IOlAhfvbWF/Bp4NDvH33UZECSEccReh1B6hfNIR0xRBks7HaVC0vXiimFyIkQ91cNuTX6XaV5xuGKEqlUStXsFytCemInjb4jMzfEn6HLYstTeHLe5+7UVI65eDFsx28ffsWJ8fHbPjihU6IHLUqNtbWpN1Uy2VFSnMZPkoRKPi8vA8M+e6l+vwvv73F33/5Fe8+fhJPguKpR8L7JdGPIpw32tg/ucD6WV3IU64b71W6RCRVpBz85YeX+P71M8GB3gn5a3YG+P3dRzCMUbd3Im8cYTSUCSqfyeG7F9v4lx9fo1LKiTCl42T+4bnalMcitn96BLuihU4odaDfCem4kD+Wn1NObzhAp89fhL/98is+fNxFt9uVeYdjTNpzdb/bwub6KlaXq6hyzqIHJYb3Gg7FY12n3RbiH4m2HEvnbaq+SdlUnlbUOT22KWIzvfMIaWXew7zGB3SZOB8Wsw6eb62h22nj9OQIly22RaG+oBeMsH94gnTKxdJSBZ63hkKWL4HTcuZlxWz47rR/dIyff/0NJyfnQmLk/E3PU76bwHKliL989wobqyvI59I3//9hXib2mkXAImAR+EwELGHlMwG0j1sELAIWAYuARcAiYBGwCFgELAIWAYuARcAi8G0hwI/aXJFarVZxdNaAI275GU6GYU7oDWQkHgtarRYKWXqUmHxKv66k/BjcH0Y4u2jiP//7Hzg9b4i3lUTSUwwQfiRPuqiU8njz6pmsYFxboTGMK+AZRueqZEVCALxKFvnsM6yuLEnIHxpw/ni3h0azJ8YdflWm0arZ6oqbb1kdnsuhUmSYoRt0n3OLH/v7A4ZbOcG73T2c1VkOGpJoCIiQEJfyEarlAl7urOEv379EtVIWQ45a5cvQC8qwKOKVXRph5CKbrgoJ4sX2uni3YCgZPlMoFGRFNfPgd/dZAwWvz93GhsiZgvCBmUtzn7/lIkUoMZEixkj6iTbmvqywvmN+NCaNf9rWQMsFjaHtbqBwiEIkowjFXBYbayv48fs3WF9bRalYQDpFgyYN/8pII6ppjxo08qS8Iv73//lvqFTL+Ns/fsb+4Rm4clgRVmhASUo4GnoZ8RIOet2e3KfBJuW5eP3iGV6/eo7nWxsoFejhw5W8aLA1HAiTt1vgyu4VFMtFpDMZCSH1afcQne5A9yl65hgJmCen5zg6PpEyJD218viWahjfplGx0QrFOLy7dwiGEGFfpTcSYkcimuck8ObFDn747js8e7aDYkGtjDYkFWnIlKir0c+4SG1volgoolqtSWiQg6NTtHt9IawIqWUQSt/6r7/9jLTnIZ9/KYQeaRyT5jDWc7EDZV1jfVw2m7Kam+2BK+eXqyU8297Em1fPsVStiNeMVNyNhDGN6rw5TpA8xlXRhRxDgawIYe744lIM6Aw/xXBhNFDSC8vJ6RmOTk6QSa2hVEgJFqxTbqY4PCWsKZehJ9TNQVIZ5RgeSVgy0pqUMY5pSVohGc93HWRSysMTk8qRls885HDyR2Ucu68ufF1/qZ7BZmHN+MDnlEs/y1XxDN2g5pVLCQ1BA7EYGhGKN5JauYQfXr/Ci+dqnshnE2LAZf4cjxMkW7AMkSJ9+akcspkfUa1VhARDgkOr08OIIS2YxqEBuo/dvSP8+tsf+P67l1heyi5UdIOTCvuhHlHXHPQZBuuyJYQKzq9sh/QewjGU3qK2N9bw6gWJG6sy7mT9FFyPIX9Ue6L+qaQH3y0KDYrjFfv97EboJtCrI5lPmVCHzaLnIYZfG/Z7INEt63vSh757/Rwvn++gmC8g5SaFWKcjmNBJDEKP4dVouU/DT22gXMpjfW0T//6//oFPB0cS+m7AUFkSFiWSseTj3oGUUUKzDIZIOCHy+Qw2Vpbxw3evsbG2imqphFzWGxPqqKrwvXTnZL1kvCJymZ+wVKvi7z//gncf98SgLZWcZFiWUBHTTs5AomK1UkTaJ0FgGpFZvL7YuZ5MlEGegwUJK0rbWqUg5aTXmX5fefEgBnwHabW6uKDHkHoT/kpxSn0zlk1dvOVkEALN1gBHJ6eg1wmShBgyhnNczvexVKmgXCzKPEgkpS/FRgSO3WqE4Lw+IZDeku3c26bdki+Sz3rYWF1G0KNnvRE2N9exvr4qnldy9A6S8aWNmrmYKpnneRSxb9BpXwL44fULVColrG9s4P/99/9Au9sfh6oj4UaFQ2rh5OwCy7UKOEbEhE101fMNPc1w/mIi4jEcudKu1ZnE9RIiBOcLemUhOTLtOuJFRD016aRj71vyTqfCDQrJY07fnijCIxXKj2qIDIYA9Fx5ZyU5879//hXvP3zE5eWlePui5jCgAAAgAElEQVRLOi6WqmU8397Cdy+fice0XIb9mGG4FJFS/T/ARRimUC3SQxHDq111Y8IySDuQ0FF6Puc7mJBiqZAiDSmqyaSs0/pfvc4iF/NpbG+s4M3rF/jl7QdcNlpCgGMr6wZ9mQ9IQBIPVB49oejwRleETy4I+fb0HO/e7+Lg8Fi9G6jZWeZuklhf7Gzj2dYG8ll/7rg6kWaPLAIWAYvA4yAw53PI42RkpVoELAIWAYuARcAiYBGwCFgELAIWAYuARcAiYBH4KhDQhJVarYr0BxqSmvJxWYgHNDIxZEgQSLgQugany/WbNn5EpiHlvN7Dhw+74umArtgZesR8mOeKyOVKWQxhP37/CqtLNEQrwsF1srUtB2l+7HcT8NMF+D7dv6fhuin89nYXrXZHwu3Q4EMPCOcXF/j4ycPqShWeu4ay66uV2tdlMnM9GAIHx2182DvA0fGpCotEswTDGdGTghNhdamG1y+28SNXYq5x9XtaSAOmrCKSJ2ZzlPHbS9ENewphNoVKqSjGUxp66MHhqjnAPDzZi3yRyz/GQDS5/9hHimCirb7x8l21OSykihi5WAzZFIGF5RoxLpATiuGyXCni5c42Xr14JoaEXC4tJIIpVo+RoWwmIEeJBt61lQIiPJeQEs1mB81WIG2EedD8OxyMEDLslLjgJ/EjISGqXjzbwnevX2J7cx2Voi+GJs1ZEE1NuzSGQZKtcm4CbiqL8NkOBv0hep0AH/eOxKgstjw+GQKnZ3WcnF7gzStV6rv87fUinJ6diweR07MzCcshhmy9QriQz2Jncx3/+tMP2N7eRLmUFaPLVFWJEUnnSpjZtzwHXqqAtP8aJHckXQ/vd/ck5Ad1Dx32rVD6A0OxkBCyspxXTfAuBbiSVhE/Bv2eGPRINtlYXRLPS8+217G6XEM6lRyTY0jYMRuNWgZ/XuPYVaQx0K8hlUlDPFn8989itB6F9MahvBf0gh7OLs5Rr18gWKmINXNKjslAhGqPStpoyJ0yjGpETbuTZzRBhd5TkopEMIV7XK49XhgBQnxy3sSHT3viUaPT64q3KhpBk4kInpfA2toSfvzuDV4+20GtUkIuoyz+rK+xIVgC8qiBin2ZJDW3moLrbomBl54tPnw6BMcJ9oEQoXhfIunh46c9Wc1fLGWRvsbLwNwC6YZlmgn3JM0xhBfD3NDjQdDtiKE4n83IePP65XO82NlCqZjRZCmls0TFYIPiXBI5cF0VckomWGZ+TWPTjyjDNjuzScf+QHJq0EcSIUqFnBBlvn/DcW8NlXJOjR1U2hRAF5JzVVJbVLysh7RXQyZbwsn5JZqdtvQ5eZdwOKar8CIME6imrBBJJ0SlXMDO9ga+l3F2A8VcBil6cdF9zeAZnxdJCvPSDtxkGonEJsJRiHYnQDA8RqfXl9AezIPYMvRLo9GU8DnFQk7mWJFpym8y+ML7KXU0zmw2vM6wQLVKGetrK/i0dyLkRBmPEaFF4t3ZBY5Pz7G8RM8Y9ysIsyTpoN+PcFFvCJmPYRdVU2EfSwixiO9TxWJO6ujGnKQM7J2ft7H8rO9M2sHrV8+k/1Eiw7kVi3khV5HQMoUfE8xccGKWv1IpCTe9hCjhCmHs8PhEyE1UluQyehVptdo4P79At9PFsJibS6RWeVz1GiJzsZlMNCFXVJKQODq9CY8zq6eBS7/DOPGBy9yb2VOE/Ai2AK6vOEnxbHh0dIKg20X9oo7RoC9E3HIxh7/88Ebep+gxLZtWfY5Yy2ZE0B+deCaK98AZBeac6sev1MOcpDdeonedWrWENy9foNUJEA73pG44rvD/J41WG+/e74kHqEzGx8pycbbqx/KFTBQBF40edvcOsPuJ7zaBEKtIOeKYw/Fna2MNz3e2ZA7hu/q1AseS7YFFwCJgEXh4BGLT1sMLtxItAhYBi4BFwCJgEbAIWAQsAhYBi4BFwCJgEbAIfG0I8Ju653kolyvipp8fgdVPGYH5Qbg/6KPfD2RV623681s5PwofH5/ij3fvUa83ENLhPw0B9JKRcFDKZ8U7yk8/fIet9eK01xYjgBmNv3hP5ypGxiTEa4rnbsJL+eh0+/i0f4DLRlu8dfDZTreHk7NTfPy0i3IxK6FF+PF7kU2Fk4nwcf8IDBNRb7bB8AYMt8JyyIrfTApvnm/iLz+8xvNnG6KuGLEXyUAXjx/Ix4Y5vRp5oceNMSSWWOwUsfNHP2SlcvvMjEWMIU9Qlv4pY51at0yS0+bGKr7//hVePNtGzr+mHnlZlvoqgCmD4aBYX6tLRQwGz/Fp9wCDwQmG7Z5aUxsxfABd1jMvRazK+GnQ68+//PVHbG2sophT7vgp3hSbBA+jhbRvfUJ7YcoFlioZbK2vo15v4fDkHP1+Xwgf8pQYTVo4rzfFkwxXos+p0mursNnu4eDoRMJjNZotDEdDceFPLx5eMilhbv7tf/yrkKmyPt38zBE1a4fR+tMjSGrJQ+S8Qn8wFFLHoN4Xwz0LHDkO2t2ehGPZOzhErfp60obnZLPwJXoUQIR0Ki2rvX/6/o2EYapVMsoIyzKMAdf1O0c4xwf2Q4YYWV7OY+S8wqfDI7TbbbQ6HQVFIpJwKs1mE41WE72gixCFKe5TXDSznSIq6XZAaooY5GOJaaJVXgZiF/9pD02FfR4A7NLBCNg/PBbSSKPdwjAklUQNFolEhFIph+fPN/HXv/6ASjGloqOYdj/b1rU6xrZP7km5mICfXRfPO/S40G53ZRKkxwV65OmOAjHi0yvP0lIZ6aoK5zGvZEorfUcbns24ptqwCkfG9thq65A+JMkVstheX8WP378Wz0LVSlqSs1+bti+IGliN7HlKzF5Tjg70+KUEsr/J4KCJbhnfw/rKEv63f/2rkFWyJPxMkqhjk6cBT+djxr1qycWznU2c1+s4r1/IuDRinxhJz9Ch6+joIhLy6epKTTwoff/dKyEl0CxuijdbhKlz8W5BA3MSz3e2cXB8istWB93eufQ/jqdhGElYw2arLe8Dw2EIL6UVj2E6JfcLn7Ds8otxijj2kNjKch4dnUk4FKrJInSDAGcXlzg9u0Cv/0zep5h+IQxnysp+1ukFODu/wMXFJbr0rqXHunTKEw86y0sVZDIJkMOgm8aMlIc/ZVlIpNjeqMmPOSxcPio58wDfubJZR3kYebYtbaMTqNBxigjBMHV9NC4vwZBIDOM4z7OIlnxlJ01LT+hmLpi8V1+dMwTIeQUSQVq8KcdMWcyp8uClz/gu6SQkbFe/P8J5v4F6vU63QzIvlvI5CVf3Lz99h/VVFZJQsjd58ITH8fy1GjftzOM3pbnrPXnXzqWwtbUunvBI7ut02lo5CCHn5OwS7z58QrFYQL5YQG6OJ0jqRv5zJ1BeE0lYYRhFtiSOgxyPfC+JleWaCsG2tiKkuMUb2l1LZtNbBCwCFoGbEZh5zbo5sb1rEbAIWAQsAhYBi4BFwCJgEbAIWAQsAhYBi4BF4FtHgN+lXddBLpdDMpmU1aUMLcCNRngSVoaDoRh3Q4YyuWWTb9wRZMXvp/1D+d5NoxE/CLtuQrwkrK8ti3eVrc2SrCgXggEtJcyT3tPNR/J5H/B1/jTI0LV6IZfExtoy3rx5jmqlhKRLQ4qrQjlEkRhf6Oml3migPxyIPlrEtTvqMBwCvWCI47NzWcHJFbfqgz69fUTIZtLyUfuH719ja3NdCBE0gsRVNsSGazOac0NsHPGv/vHjOenlklnBe58Mr5P5RNdV8VTYAMMEoWGHK5QZzod4em4SpWIeL1+oEB8kHTEcz6IbMVVygEq5iDevX0p4HFpj2NbFHwYV0TLZVsvFPOhdZWWpgnwuCbPKjRAbmMUoaIy3ur8YnWh09V2gWi5hbW0V9GCUonci7SafpI+gPwC9D/UYhmvB8lDNYQjUL5s4PDoWgzBXCI9GQ4yGAzHqUfftjXW8ebUDIasYpfiwAlxdiR/zCnXgL5JoH6hVXKytLqNWLYs3IxrsZGxwHAxHwPHpGT58/CRhswTgeOM3eS661+G1PBrtcxmsry7jX/7yPa6QVTRONF5ylGKWs9lqO6HkzNAG5WIG21ubqFbLinQiCVSbIxGB4VhIZun3BzdqG5drEooRUmugvA4pskoYhTJ2cvyUNmMemN0rxzLT9TKb5ls9Nx4ErtTQ3QvEmafdHUr4h+PTU/SHQyGrcLz3vKSMETtbm7IqvlzSZBVmw8Yx285nKkQ3eWlPDOH0w3cvhXCRydCbmPIQIcZfOOLN4vD4GCcnp3cqBNvJPBjYZjivMoSU73tYWarirz/9gJfPt1Epp8dtnJlxXpKyzLNgzPbt67Qzg5fcVx69xAuQS08tjnis2FxfxYvn6+A4GxF4yqb6nN9i490srjJ3M0wagGc763j2fEfmY6MaMaCXDvk5DtwE+3oWa8tLWKlVxcOD6dNj9fkwy23KPr4xeVdgHy8WSGhcl7A5fI+RcZ1jLR8NI7RbHQm9NxgMJxJmB47JnSc/Mhgx43gVmWOqWi7n8Gx7C346pbw7sT4Y4iwkOTdAo0myzlDO71MA6sAhsNFsy9xCwhbDKiVkPgaKhZzMn/lcRpHBdCZGx/vkeddniIP5TT1r2snURX1iHuC75RAIhwpjztGFgoPv3rzG0lJVvI7wCfHAxVBg4rWnC3qZ4Rx9l02y1GEJqRo3mSs0IVxhSqKsuan3sztzXwTcknbqNolmkRBtWA72AbUfIZNOYWdzDf/3//V/CFmF79HxbKZUMDdMIWba51RansTSXbl3zwtUgSGUinkPO1vr2FxfA9sglZa2R2IOEviwuyekFXquCwYA/7siY2YsX3b/eqOH335/h8PDY5DARu+PfAFzE468e7x6vi0erkoFX5XnEcoUU8keWgQsAhaBaxGY97p3bWJ7wyJgEbAIWAQsAhYBi4BFwCJgEbAIWAQsAhYBi8CfAQESLdLptHxQN6tBTbl4PgpHGNFAONeqzq+5EyILDdkfd+s4OTmTEDrigUC+uNC7SohapYDtzVXxXpF2gUR8ObW4Y1dGMZP/dXvzoV+5igeWq2UxrOdzWTExMiwRf1xdenZRlxAml/XmQsQAGuZ6vZF80D49PZWQSIbUwKKkPA/VShk//fgDarWaIt3MUdToOOfW/EvGOBC/O+9a/D6PtRFkYv2YTfAw50oVGgEnX/B5ND5fRNd5quiV5JMVwsoqxfZGQ24+mxWPIXRbTzID2yvJItduvDfnPttK1nextbmBQiEvYX+U8VSRVmjUITkrm/GxVK2I8Tjre2I0ZjlFrPbeMVu3PJ+9loiAnJ+QtlIqleC6nghhyIFEIintsxcEEhaEHlIW2ajHZWuEk9NznJ3XxQMKjTY0hhETkqmebW/g1ctnSHtzQIhfkgKZgl3FjIasJQnd9UyMXIagQ/rZKHLQ6w/RaLUkNFGgFuIvUgTxfjA7zogq4rkowlK1JCFCMj5DEWiRRu8Fv96a5DI+ZBxsrq2hVqkImY3Y06MNQ4fRqNUlaagbiHFvoQLEE5mM4td091B1ojznzEsmj5h2c22CuOCv45iqPqW65Cr0ggif9o9wyhAdAT0VEQsVZiaZdMSQ/vL5DjZWV8bksjFas21GOuv4rvRvJjHlKuYdbK4vY3N9RcKRSTvhLBdRjz4u6pcSbo5zy6Ib+yjbvPzTBEMaSmkc54jKkEYk09GLFAkj+Zw3RQqgcpyXrgXeKL+oQjpdxFA9jtKDrJCNjVW8ePlMvGdIXszT4Mc82B/NNamDSYaE1ZA22XcZwmZ1ZRWeR+KPUp4EC1Nmn/NoqYTV5SUh9hnRE4mxSuHFOfmZPD1XkRHpYSHluZosxvYBjEhY6XbFWwgN1F/9Ni6nvHWIukSPYYFI3Fxl+JYMjemqfGHkSNnoZeXg6Bid7uLtMo4Fh63+MEKj1cHhEcMOKZKuVHsCKJUKqFUrQlxJcGDV2+y8Z64/6Z7qmHZ6Xca6D4kXPK0+H8mkPWSzvoS7ZNvkewDbDV93hazdJxl0pMgR18mOXSeOHDNir0mxu/rwvqBNYL8qc94VIc2QFKfaPQmh2xtr+OHNC+RzKSF9Tz0Wl3/N8U2qz94jFuO5XuQpEtnN4ExpJCd8lKSV5VoJL19sC8kok8nCSbriSWYofbyP3b1D/PrbezQaPQyH9Jo3kdUfMgxjB3//+Xfs7R+h2eooXMQrXQK1clGI9DtbGygWslfGm4kke2QRsAhYBJ4GgdumtafRwuZiEbAIWAQsAhYBi4BFwCJgEbAIWAQsAhYBi4BF4AkRcBIOUilPeU+I5Wu+9YajEPQwYj56T5LI5+jxskqeDUcRdvf2hSTClb/0JMGNu5SXxPJSSYgApaKvPgjzIbPxmMnNz1y/Yc+kXtIRV/VLtYq4BJfMJF+uPo7EmHNweCzuvweDWwwJzCsEut0+zs8vcHl5iT6t8criKPusn5aV3Ovra2LoEEPiDTre6dYdyj4td46b+ekED3JG9RQUmqYSM8wIOYkJ7rOZ8Afa04axGCWdBPKZDJZrNZSLBVn1f2sW8QSx9sXL9CKQL+SQyaSFvDBOynTa20Uhn5eQNCRXpb2k2GiZzvzuUjySRrK+D9/3J/2LbZPhpSJgMBih2+2BfWyRjWpeNts4rzeELML2zY0eaWiopUFzY21VjMBC6tHlulX2GAidMlL2v2LBw+bGmhhImYeqbgcjOOgPR2i1uzg5OwOJN4tss9nEn6FL/rTnCmGFYUlo/J7eTGFUmafvzT9jfuKJKZ9FNpuF67oKe9IEQnrqicSzyqA/EKPkfCl3u6qHPPUQyWTxx+epPpUgnvgrOp6n9xOpxyZOb1cHhye4uGwi4DJ5rq5n+3AA30+L5wmSVYo5kiMW2UxbUmlZBRRHkhl5XiRNbawvSZgwRepQhtbBaCQhg+iVh6Ep5nI452av5x12IBlqItALD10AMLRKLpsWb05rK8viEYjG2cfeIon2E6mwSk6EVNrF8nINq6vLkyn0Lm2TaXV6qs+waqVSUbyASLFNXwgj8a6Sy2ZknFquVpDPMijTDds8PUx+QtQDGLKG3kckdIuQgzikc8xyJLwLPSiZ8fKGnL6CW2xrVwtMjkgu62NjfQ2FfHZsjGfaYDASzyjsI91ucCNX4roCcgZqdQOZW0jK4tzEjeO+76dQLhfkl/ETU2Sqq5pel8OC103XjO8XfPTGZLH2wnRyqt9L2Vb5DswWo0hl6j1nyHff0UjmiYVBZVfX/fxGfR79ZuydUL9fFYt57GytCanVn0doNcDcQzdpBzc0hsn74QLv4DP5k8zM8TmXcYTs/vz5MywtLSOV9kHCFlsqSSvnFw183N2XuaLTGU48rERAszXC/sExfv/9PeqXLfT76j693eRlLKrhxc4WVmplITGpBjKjiD21CFgELAJPiMCV/wY9Yd42K4uARcAiYBGwCFgELAIWAYuARcAiYBGwCFgELAJfBAEaWGnIVyGBaOChMU3cNsg3+tGIHlZGiLRxfKKksQAo6xpt7rQlHh2foNFoKRmSOBKjHI0edL1eLudltbC+pRZbGlET4Qsf0bBdzCkSSaXMMEMmdElCr750cHh0juMTeqRQq2evFS5eWSIxSjZbbdn3B4PJitkoQj6Xw+rSEgo0gCdmDNLXCn7cG8KBYBY3GAw+R4N5YpXHgFmp81LOppmcK/OtfkYbVYwXAjYM1m02mxGCUDqdWrx4FBn/6SzlEtu758H1XGWcCrl6OhTjNMNjlEtF8YpSzOeRcj+jfrU3FoY2kjbJzNmvtFcFqkSj9ZChqhY0cNGo2Gi1UW/SYN4b90l+1CRhZW1lRVbBM2TVlY3537bF0vAwk6anBBqUs/ASrrgtkiIIOS1Eu9fD6dmFeJ5QdXlbBtfdV6uhaZCtVMooVwqTtmx0mmKCTKr3Oonx60kSetwkUq4rpAQjkmPacDjCYBhKyIT7l0G3ZBFspMc1sMf3RYCkkCDo4/ysjlarI+GvzHhHYzrH49evX6FULIyN+LfnxTqarie5Qi4ZgFIhh5VlkqZ4xrqlJxIH9IfCcESdXiBzw2hRxspUw1LyyIykRHo9qJSKIFlleakC7xbuxu1lWzyFDDsRx1mG58mjXC4jn9MB0ITQokq/uMQJqslEEhk/Ow7nIyOpxsFzXRRyOaytroi3K4H5LpkwrVSYekjEJiJw/FakNHWfZFz+BsORIh6YcZbPfnWbaRcxuorGy6hNLytbm2soleghjMQW9Y9e8OhF5vjkTLXLezhZoXe8i4sGTk7O0Wp3MJB5KVShogpZ8QBUyOdAbzY6auTjIGjqNb5/yJxidc95kxxGEp0UYUVnJOFmlGcSkknlfXhBHaTKNGFqwUc+O5m0nHF/1e3IicTjGr2uOU4EN+lIqD0SUKuV/GSs1G3ss5V4ZAGsNtdR7/oMK7qzvYFiMQuHLENxz+eg0+vh6OQUv797j7PLBnpDEvIA8tRPzi/w4dMe9g4PEfQVCd2JIqSSCdQqJfFspcINZcFXnfH4Emsvj1xEK94iYBGwCEwhYAkrU3DYE4uARcAiYBGwCFgELAIWAYuARcAiYBGwCFgE/uwIyKdt/hGnD/yjVpJLGISIoQLUSnBFTpj3ZdtYFZQMfge+vGyi2+tpJxm0nITwvATyeR9LXL2YSU0+lsceH2N9xw/E/KDjewwLVMXqyjJyuayI4ofqyGHolQTa3QE63QFGjOswbxMgJmVotdpoNFuyalNWaWtyAVdjlopFMWZmfFfclN9R3Xm5f9a1GTv+Z8n6Ug9PNQNZoay9DyQSsqq8Vq0KOeiz9ZMmnoCXSsNLpcTcNwrpPWioSSMRMr4PhpZiOKDPrVsa9hjWiJ5DSG5iW6WRhGZg1huJMv1+X/a3reDmUyRc1RstXDaaYjSnKIYWkZBdwyFI2CLp46p3kvshJyF1Ug6K+QL8lI+EQ3KaGidGUYSgP8DFZUP2xqi6SE7zCDrEulIqCWEonZpBfnzKg/HJIllJahKGaJT0GfqM2I/JUZAxYTQiYWUhcSqRgkBrolaMMwTQPN2uGXHukNm3kNQMoA+va78fot3uiacs1hPENQjDOZFEORIyGD0w+SlNtKAKHPzN7w4VYIwDvu+Ity4SVtSMSCN9QigmbPM06JPQSA8Mt27SPEiUnPw4OZKkQSOyeBWqlMGQZ5VK6bZh4NbsFk0gfYCeC6IEvKSHpdoS8tncld61UM2aRLpfUXYqmUYhV4CbZFg14pgAw6GxnyQ5JqY9GWdJXjFbTIy5NKdLTVcoa4BdN+EmkMn4Mv+zrpiP+iXEQ4YJ9TIR/BUdmQGJKmkQ4pd4jecki6yvrWB5qSpeeRCx5AzbGAppkOEPGY6x0VjM45VBgGN30AtxcnqG45NTDAYkUaoO5LoJyY9h8khc5BYf6dRofLcx2eT75PsZNTlkc472OD+7JLCq8HrSTscexVSJF33Pkjl5uok+ajFNVmavKodnqmdI+Vx6yfHww/evsbq6NNFH3rWEQzu59lBHeo58EHGUpb1gpT2gWs7i9asdbG+RvJWT0G2jaIRhOEKj3cLPv/2O95/2cN4IEIyA88uhkFjeffggfYVjMccgP+WhkMtia4NeZzbFs9Y4DOGDKG6FWAQsAhaB+yMweTu6vwz7pEXAImARsAhYBCwCFgGLgEXAImARsAhYBCwCFoFvBgF+BDYf4vmJmwYeMcyJFwgafIAEjUw0AF0xZU0XsxdEuKg3xSW9uN7nw8bLBA3Gfgp0SU7X/Ve2GUPClfv6gvkoP5Wcxhy6y8+kZZV9oZBHu9PBKOiDTmGSCU88v3Q6fYlbX8wVrhr0KZDCx2FaArTbXWWQJCYsPb19pFIoF4vyo33UYCfqGeWuU95cn1LeXLzbftrgr7/mU5lFdbhbdo+W+jooxNBIY6oDpD0PXNl9ZVW3Ket1Qq7RmivuPfGw4glhhaDRUwPJGaxpeioRTxzGen2NnEUuU0XKpkwvmUTScTCkVwZtxKaHlQHDbS3A9qBtvNdn2IaehEXhI8Qp6TBskYM022apJOGHptolFZ2DkYFvfJtp4hf1Y6wDGrJTHj3cJMRyKsZ342Wl0xMPBlKEOfkYnCaiJ0fmnujgAIVCTkglTHGDqPhj1x7Hi0MPEiQG8EfDr9qUQZt66yq5c558luKMSNH5cxU36n0ze8VSeKxiB8EAl/UGer0AIQmHMicJ7QgkO5BgRpIiQ+vIputE+kC8ESyApzgRczhnkBzgylwV0PuO8FKU97HBKESvPxDC2LUEyNm8TAPhdR6L1wN6d0iC3pCqpYIYTlOzRK1ZOQ987kTsAyTPOKiWy4IlITOwxdVm1nPreDYRqygiGceFn86AYd2EZKQKLjJI4qNHCz+TRoID75xNYJpzXV1Sd/nX/GiAptcskg9kKtQDEsd7jlccY6fnzWuFf8EbMe8qMS0IoamTjA9UKyXxeNLudoSQSxQ4rzRbLZxdXKDRrKFaTk+/n8TkzR4Sqm4vQP2igUajDYdWe/aDpIOMn0KlVEBRxubpuiL2ZjP1YM6v3U+LuDbZU91gW0nSKx87vehm3nQVVU2aEZX5yvSO42PqQcKXjXuEHggxAklHxXwWy8tV5HMZ9ajpHw9crmlx02eSsVE2XoCbjlkMeddRiSiR4YzWV2u4bGyAfaAT9DAIGOInxDAEmt0u/vjwEX42hyj5DG//+AO7ewfinY5DOevcdRQZenN9GTtbG1iuVZC01uGbasLeswhYBJ4YATskPTHgNjuLgEXAImARsAhYBCwCFgGLgEXAImARsAj80yPAVcBf8Eu4MTLQYBt3fS7GPq5kp370DKFXLGub05Vqo5xeb4Sz8zMEA3qM0B4kpGyOrLLOZrISvmG8otpkPueb9pUM9IW5SfXFVArIZbPIZTNgGBbiSof5NOqTGNDpddBoXGJtOS8G/it5kO/B8BPDIdq9AK1uF/QiId/XiYEDZLIZ5PMZZEV0EaUAACAASURBVLNzjEFzlbuSy2ddMFmospkziowff1YWcx8WDMQ4qPJRZjUeqzvKC81D6KBIBJDV+KGsgk2lPWSyKSEMjZWbZD2+dJcDhr9im5ZNVuIrYgk9KtDzioSVuIvAOWlpZJEuRDJMMiEGMbZF1pW0S6JHQ2pIT0ZzBMQvRcBoyFXwA/S6PQwHI0wAiYRQ5no+vHQGwyiBTj9S3ly0jCnx42pimBNlXBatdCJjMg0dtUa73QcSKU88GCi2h0movFz0gx5CxpOYyiSu/PSxyB/joJou2zPrI5v1kUq5Co+xntPP3+VMoa1W0SdIGHKVIVaNY4qQNzZ5L6i/5K94E6r9xytPxvMbNLxPmajXfZ67QY1v6RY9EDVaLfT6fTHKm7GGTSiVTiPt+2KkbPeU1xKWjeQEkjCYZl61jiEd16NKJ8SlBEBezHAQIuPn0A7ofUd7YBJykwoj1e8PxvPDbPXwfDpfc8Y7VEoNDipsThrFQl4Indp/0aR64o9Nrj7ckbC3FG75fBbp9MQ8wtHRZM8MZ8t4rRI6ofLskJT5l5JY5JBh3jSJz/NIYqU3KMM0UnnE87yah7k70YZH1JWkNBlnmTEvMin3Mo5pT3FTJboq/UmumCJw8DXb+NhR3B7Wi7ltyqHLSa88tWoZy0s1HB2foj9U7ygkCbe7PVzUL9FoNTEY1jCPG2yyNHuK70fAWb2JC3rH6wby7sRZimHUCrkMapUi8jkfHmOyGL2MANlTimYWTGFsEpv91EOLnxjMFhAjSdnWtDqyF8KZFsLrMkYAQxJ1+hEGgiHf8UhN1s1mPHgwtX52cY2fPuUYG1UCNiHROoqEfFcqFJDL5iQEmVJOPzB+7vNVluEkNlZQ9Bg5PRZ/FpqauEKOWzGTwObaKlrNDur1hvx6AcN3AoMQ2Ds6RSqziwES+OXXtzg6PRNPcHxvSiBCJu1iuVLEi+dbEiopl/Ovadufj4uVYBGwCFgE7oPA5I3sPk/bZywCFgGLgEXAImARsAhYBCwCFgGLgEXAImARsAjcEQH5tCy8EGOov6OAz0zOj8c00jG0Ad3ADwdDRLIgWn1WFk8XiYQYk2kAvGkLBgNZ3dsfDMQwJYZFGg5Goay25sfyTCYztRJ+bB24SfCC97gamKu2UymGHKIJXNAFo9iTGNDrdVG/rGM0WgcibbiekU27kSKs9NDudpVdkR/daW1zAD/tiWHRcx/A/cZM3gufigUgXj79ZMzGtbCsOySUbImFaQdigDAGNmOlUJjfQew4qZFPoIku65CeUNI0SqfUtXFiHtzcHKeSjk90XxMi1lQ5VH6m/ZDQMra03CefKf1UyfjX/Ki8Ol5cOENaBL1AEVaGQ62fg1EUgj5WokQC3f4QF5ct8UYhTVZlrYpvrEkELpbtRBOV2BACQgmn5aATDBCMhggd9qQQkbihINElQjQaYTQYqvAs8bzGgKsDVVYDKTOnDsokznv04MSwYQzbk/KSQg6bEfEAp8qwyz7O3xgOSibBblzht2c1gW9ydPtT90whS8Inz/L0CtTTVargnTwyPqJHEHr8Ifnum9hIHBmN0At66A8HGEahkEk4HtPo6HkpJF0Xx6dn8CR8j+rHqmurdqZIYhPMZCzXhZcUBkx5KCFkF+bDkHDZbB5eq4dAwoZF4iGJ/YqhifqDkaQ11TM7I6jcVUbqWIWiUn1PkVY4p9L7EkmW9DzGdE+9sVezM2TSHjivzep9qz5GaenIKjWhnPx06QmcTsM6oXeZjJ9GLCKQPMzUpkpuy9tkLTlw/pM50FjqKUcRZRjeRo5vE/ik9xUuajA2JZlRYOYyT/nqsbJUw+rqMv7xy++IOP6GLF2IIUJcNptCzO12u0h52pvGjFhzSpyHADqDCLsHhzi/aKLfp7yRhKvKpJV3lZWligqRN9vItSB66ZFa4571LNsC5dMp5+6MGO5ncDB9jg3FNCvK4DHfZ0k0JsGT3sv4Gw1H8g7Hvs/pi3iRlDYYRej1h2g02xgORzKWKHdKKlPVZowic7X8ii7O6mnegB34nqe8AiZj3g1nMH3Qgui+GO/vk0qc1fOWnPVYIqn0PMdmyN9SpYDe9hbq9Sb6wRDBoInhMJQ6brR7+OPjHk7rDRwfHSFgvFJ67UvSK12EcjGHZ9vrePPqBcrlnPWucks12NsWAYvA0yNgCStPj7nN0SJgEbAIWAQsAhYBi4BFwCJgEbAIWAQsAv+0CPDjuTGePea345sAZr78KD+ghwQSBZJJ0K04DdP83E2vByQN8Df2SHGNQHqK6It3FfUsTcDcEokkXM+TkCJcBS2bsgeo4wf6y4XaDAfA37SuzIyr4gcIer0x5vOypcGjPxohGA5UqBYmEvsXw7jQ+wax4KrxSLyxiM1dp5k1qsyTf69rMayIaLyt3PHT/72zNw+qOlVamPpV92Y1M0/cvFdlYQucFCxePgnVk1RG1JslLXZXtBQDiLZ8MFtaVlnxmiAjbd3EF4krs1gW41Sq1elysdnrzB2HpvZQDLqqMuXG+Lm5B/QSEEbKcN/vYzQaKcwkMUkrQKfbx29v3+FgPy2GZ96iZBbNbGa8Medqb8gaNFyzuVM/EpESMgowBEr9solWpyNjBZ8RWLR1kKQVGjg1j2Va9JwzpY5ImLrLaqB3FelfqtupfKZS3e9EcuMfKZ+WcVWF+wl/hKeIEdUbjYBWc4ROp43+INAWeVJrWEdMw3ZL82180wUdX2JKVcfEl+QIeqJiBIxxI3pELKTNmQKNdVr8YDQM0Qv6GGjD/JgJEUGMkMfHJ/iP//qbeO4YF0MOVGUza7PFj3lNERzUXVLiJHyM9tBCwuL5RR30pCLpSILUTB/2RRq4dU8QGK8rotIplvOYLaU8Oniuh2yG3ismnkaMvg/bAcZS9YEyx6sBIhLCDEP13Hsbg28ksMz6x+FWyAXCKFEh2CQsUOpqeD7z+B32JmtDvuOjUjqdpzrW7IY7yH2QpNc1DN0rTR4GLTmXOUo3L3NDF5K7jJ9EuVhArVrB4IRttA/OK2yPzVYbJ2fnQh6mRziGLrxu48gRjICLRguf9g6FpMVhnZ5GEk4oYRar5aKEk7mNpMvxWzbuqfNDbEaO2evx2xBWGIay0+6i1e4ISZPkFPZLkqbZbwfmPS4MhbTCeZN9V0grcISbEvSHuGy1cNloCrla9QBVGDVf6veThyjPk8ig7upn/nKMoYcVksQea5vkejUHU33cy3H8peRq8luvMC9uGc/BSq2C79+8kpBWDAfEtkxCIdtIs91FN+hjOKIXOnpdZKi3BPJ+Glsba3j14hkq5Rw8z0jUgu3OImARsAh8BQjcMH1/BdpZFSwCFgGLgEXAImARsAhYBCwCFgGLgEXAImAR+PMiMP7a//RF5Ldjem5gGAWGzpEQJQ5XMKpwOm7SlRAp0ySQq3oKYSUI9GpffpZWH4H5HGWQCEBygFzlH/MV+6qoe12hSBJu+HGexBjmZQz03NOI0el2xh4irmQixBQSAxgCYoQRl+rKpldp82O3Ju+IBw5VvCtinvKCkC0I5ANj+ZRlUHmxAOoXLwrr8bZ2dx9dWXW6JY4fJ5YMBcSfEKs+s35VHmPxOszC7NXJ/duOpH/1+2KEG4U0ljOkj9DKZE8PR3sHh/CSNDgaj02xQoybSRxhlWvcu4ghIpF2xpSyEn0wBA17HCvkKm9o4yE9vNBDEw2Bps/fVpbr7kvfNWSh6xLd57rwkxQW1J/+FmLI3Efi4z5DLwAM1TGMcHJxiYODAwnzofxEqHqRWmQMMzIB9GZKqE55Zu6FIP2oXMpjbWUZ6ytJMUZ/wWnHqHzrXryZ0PhMLz8Soo0h3lh/Dnr9Ac7ql+hIGJOYKDGIKpwEAl3Z5IqoTdW/EFEEIkVgE6M/yWFRJJ5dur2+zAcGJ+Gr0ODN9k7CSqhW+otMA/U4D5OX2RsWAs9VuCKObSRYpv00ZE4xSZ9qT5wEK0gotIfUQTDjHym28sTFeZjjLMudTLqgV7R52/yr81Jec00LYJXIb1xORZi55qmv67JpdDNasWgpz0GpmMfa6jIu6F2ir8jPxLbT7Up4lIt6A8vLyxKO8TqPSsSm2x3g7Owcl5d1DAcDIROxX9DbValYQLVSRj6XhbuAVzl5HzH9YEbve53GG4JDb0tAOxii2W6j2+2jcckwj00JGUaPMoEmtpHcNhwNwXmS77RsBEKqlPB7xusOxxEIaWUYhgjoXZD3ZU5VfdW0n2uq4l5FerSH5uFO/CL13lrIF6bCbz2aHrfNrOP3kM/XgPSbPEMDra8IqZbe4DoMm9gLpN/zHT4cqAxJRJKQj25C+s3W5gaWl5eQSs2+CX6+XlaCRcAiYBF4CAQsYeUhULQyLAIWAYuARcAiYBGwCFgELAIWAYuARcAiYBG4HwJf6Ks4V/G32x0x0NHoLMbwBA1MyijoJpOyMpNhO677Fs3v4jSo0+029zRMmXWpNGLQEEYiwLUC7ofY1FPUgSuDmRd/sho+ZkSnhxX5kE0Dxg0bdWcZaJTkp2wJgSMGL4wJDTS4xW0pN4h7vFvGsKLWkit95hktHk+DB5I8Qx7QZWD9JZIkrGjD8wPldp0Y1mcyodrOQ5Jk2P6VSYQ5mFYTP75Oo+nrNLwNGd5gROKI6V3S6EUuPaEEjRbXjSPBviueXGL5EVfRZVru9NkEa9XkDVlLEWCkHNrALSUgacX0l5u71XQ215wxvAuxf5RmHOcLKLqP9jvyubkZjFko1otm8ugyxu9eU+wrl/Vwg/4QOL1o4O3uPk7OzsbhcDisqRZA3SfAi8FY1DC5KgO9E5GwMsT6SlXIWJVSWQgr4+Z4RYObLxjp8VTSvKRtzLsbT3m3Y85JNEDLqnkpN+XT2ByKZzCGsWt3enCEjcL2O8ciqokTKudJfQthJaaO4KcJK0xF72BRpMglqlTsDwyLFSLiqv04/0EAiAmbORyroOd57hRxIynexzjOfYnNoMH5+aHGPVUSPeopzooMfaaEzIfeHjQUj1psGStNIR81p4cVbrCaJ5WOMgr5LNZXV/D+4x7anY7yGhJFCIIhGq0OzutN8TrhpzwkrrF6EZZ2u4ujw2PxVMK2LWTNUYRcxke1XBIvLr7v3neomKf+na9xWAkGES6bfZycn+Po5BTnFw1cNtqiP0k6QRAIKZnjwUiHSBK2hh73ZWaTdsA/HCN4hSjzvVZ5FVOXxcWM1vHuDWdSb3rsVbnducx3eYB5mt+859i3s7ns2EPUvDQPdc306cn8NEHkofKIy/ESQLmQxM72BuoNtvuW8sYliTgGURP1HkOCXC6Txs7OFjY2VpHPf9l2HS+HPbYIWAQsArMIXDN1zyaz5xYBi4BFwCJgEbAIWAQsAhYBi4BFwCJgEbAIWAQeFoGbPjY/bE7T0mj4DIIRGk26Qx8JOSCM6J1Ekz/EsKS8o5A8cNNGkgdX6NKQqAzq2jAghj8VbmhsUL1J0D3uGTsp5dMYJj8ngZEOvWKMVmYvFvHZ7+jasMY0QlgJR4ic2Ocih4QGusqfg8OsrHuU4S6PsJyzWVLvb3ebtBUak9j+iLV4O7ml3T1MmRV2qt0Y7yQPI5lSjCGc5ZpXd4vkxOrliuExUkrY2JMQjejETpVBTHK6jUxGF6PHdH6GYKFa1Lhd6cvjPiMPMRiN0AXEEKRaoTbim044LfxOZ0I00/1rrMedJCySWLMMaLOUsGyLPDM/Dasg3hEFghhZb/5Tt1+lHPIvuO/2AglNc3RyJmGa+LQYWrUhNk5YEcljvgaVU63FQYhkNEDW99Dt9oSUOG8Yu12zm1IoE6UYhm9Kdod71F55QdCev+ihQ7xzJBEOBwIS60Bwl9JKpaocxkSxWF+QCuNtZao2bYzEE7Vpgha9bNHb2IgGfBIrGL6Hz/AXApwb2N8mGRsBc/fS7+bcEbkx8gbVMDrNSf5ol5gn+x7HjsfcWF7mZepwXB0PmqlCcD6W44p+0ByfUpjgB0gIp6VaBeVSAe0OQ5/Qux09YoVo9wKc1RtoNDsSAmxeuCnOFqMQEgpn99O+Ji1rIm7EcEA+atWyEFYUotOlfHQkdabMpxNE+LB7jN29AxwcHeP07ELCAA2GyrMXvaew3DLcjWc95dVHLsqAqvqv9H0NImWTpKM8NyniCt/9yB2TsGv3KaSRHSezTUP3eGfX6Mu+nU6nJV8mmVefD6HU1DhnhuKHyOwGpSmeo9byUh4bmxs4OruU0FZDesLiOB5qX3FRJB4Sl5ZreP5sB7UaPc48RKmtDIuARcAi8DgIxL5APE4GVqpFwCJgEbAIWAQsAhYBi4BFwCJgEbAIWAQsAhaBuQg8juVmblazF4NggP39A3R7PfEEQY8qXDrOEBKu5yKXyyGbZZx3b/bR8Tm/J5vf5Ps0r9BAr8LzjI1746ce/oBeOZTRexIOSHSQEAyGiDDR8IoG/MguH7oZHkkRJ+TzvpBZ1PNqtSatETfIuSL4kS8oqB8lE5bS1K0Y+GX18sNkpdRWWE4ZO8SQZPK4Ss4xdx5nzxI/Ud0KYUJZdmhTk1yvzVoxSOhpwpCTVL1E4upewmExfFcCkEgb4/apBCr5mpUVB04qwWRq9iaBIiEoQ6C6JkZ7CckyQtp1kEmnlYFPPBd9IxYgg/sYI1Per2NP3oCiH9GorMKTiVcPgVfXIRktE6aF9FLDn5CWJBWueli8/qSEEiKDHj4esbxC3KF8rcM9slJPqr8yCvDQ9BMaIF0XvscQXgwOQbKJ+t2clSKrMD1b+xSElKIJMCpsFA34isBJogrbfiIaIZvxkctl4BqvKLPd5mYFJndZhSRxcI6cXP0iRw/dFeLyxnPmk5aMiLLBfGlkH77QbLOpJISssra6gstmC51uDxHoWS6JbjDE0ek5Ts4vUCxkkUnnZYyOa0JUut0IFxcNnJ9fyusZ+w/bI8MBMRRQuViU4/hz5pjPG4RVDzV3Hm4/jICTsx7effyEX39/J8S9VquDXtAXcjRzUu8NEZxQ6U7PPelUWt5dPS8p+1QygZTL0JSKzCyhqDhmOPwlhNxzcdlAs90VgpyURw+mmmK1eKHM+LT4E4+ekvVEMhr7JI//bJuUKYow6PfR63UlpKd4IWMdcq6L1P9nGOqT4U97vR6GQ8b4jCFhGvGfEaBYMe2hRcAi8O0gYAkr305dWU0tAhYBi4BFwCJgEbAIWAQsAhYBi4BFwCJgEXgABPg9Nwj6ODk+QT/oK+OZlssP3CkvJYSVTMaXj/03ZcnvvGI4HFuqaIhTvA4VasiYYG+S8nn3qEOc+CAGTLmmPMYwxAM3MWPJn+n81PdtvTTUGCzkI7/60i8rcUnYEIP99LN/5jPzDV/qkcuy5eM+rxojsUbVJLwXGJOHKV5TJZ6UFzRrvL5XMa55aFK6WAKHJnD1byHbqqQnNrpj6YdopCvkslhZqiLnp+C5miQmOCqii8p1rhba9MgU0/ev4qGN/Mw3GsFLRMhn0yiXShLiI1Yye/gZCEwZFrUBlOOaoVoY0WqIks6oL+lBzVzSp7w5PjTCTRoj7DH2Y9LK5wlnq2T5uefYy3GIbTOfzWJ1qYZyuSRkEjUeXZOXGsLHXlEU8Wq2xSucJLqQ5CY5y0VFWAmRiEIU81ks16rwvPubE1R5FAlSpszprndNIR7v8phY+nhZPLFkA+hTNPSnLRp5Zikd3mR5qaq8jpzX6fgHYeSgNxjhstXF6fkFVpcrqBTzV8ICEZWLi0ucnl5IWB0JoxMBSTeJfM7HUrWCYiEPV9iP15dP0NXvStenuvudEYCjsx7evvuIX9++w+7eoYR0HA0ZkosDQQgST1JuEn7GF1J1JpNBxveRzWSQSqXgpVykPBdpNyl4KcKKCjVItl7kJDEII/zxYRfBoI9mpyNhc2SckRFT6S39c4EiEIuvq7XpPiAeohRhZYFifBtJCLR+tRlFwNl5B6enp2g2W8pDouKqaJKOSsiwoM1WE0dHh6gUssilS8rLiqk4M2R8GwhYLS0CFoE/OQL3f8P8kwNji2cRsAhYBCwCFgGLgEXAImARsAhYBCwCFgGLwJ8TgeEgQqfdQf2ygeGIJgK10SjoJpLy8T+fz8vH/5tW4/N7rxBcUh4S+us+dzymLK5sHA6Hj/YxX4gmZmW8CUmkjSj0TKA8rzDEjCKsTKy3psS63OaUH67H5aChVAlnGYajoRhMTdIvt5/3df1xzSUM98R2It5nxhDpPMWwPk+nxRFiW6E0IUqMjWCfJ3Px3E3Gd3piocQTEpU0LHnmrqWSNqi9MZi2SUE0pKe8JGqVEv760/dYrpbhpz0xzNMoPzHJK+P4fIXnaaMIAuP0Us06HY3/UShemFKug1zWRyo1T8b46S96QM0eSzsjW/eCBysn5dJWnEm5KGTS6OTSUpvMZ0JcUWfSYaYUiGvF1Fxh7iDjp5D2XIgXrQfT9BEF6WJwKB6XiGGxuGI+ilDK5fFyZwdv3rwSDxLS3iWtYaco3VT/MwAZ9BTphXLjmyCqDaESbCJSbmhUX1Jt3qUXipQLLxVzUcN4LDdNkvFM9PEUaeUR2+icrMeXpPwyrswiMU5y/4O5Ig3+9xf7T/8kQ+YlGRbIQaVSRqlETyhpNDuBhHZk/wj6A5ydX6DVbKNfG8BzJ+4kTDigw+NjHJ+coj8w7zSOzCUMM7RUqyKXy8anmieBnf2PBITuIMJvf7zHL7+9xaeDI3S6ffF+R6IKxwOGc8n6LkqlApaXl7G5sYFKpYJ8Lgs/7cu7noRwTDrwEvSTxDFQdzK2S8cBPbh0giHO6w14hyeIIoaU1J3fDBdz2/A9oTAyzf6eYhZ9TL/CquRmXFz04a8p3bw6cFS4uEEIdIMI7z58xO7eHpqthswP7APcOMby/yZRmMBwGKLZ7ODd+48o5bMoF3LShtguBKt5+XxNOFhdLAIWgX8qBCxh5Z+qum1hLQIWAYuARcAiYBGwCFgELAIWAYuARcAiYBGoX/ZwdHQiXlbCkOQSWcIu1kGuUGU4oGKhIGF2brL48juv67rIZGjg0N4dHH4GDoWsMhj00Q+C8er2x0CeqgsxZjAQUoX5YG3ykpApN4Q1Yjoageglhj9+5J5QeCCrNoMgwGAwkA/iRu6X2RPx2Nd1OTS+6KUSb1CL92PP3pAyfks1jQgjGmbFdB6/S5HMn6nuus0QI/Tjhq8yU9K7Cr9DeqO72d/h0TskFcPIfbIQI2USCdeFI4ZxJYSG9Gg0QDjqy0r65VoRmZQjq+0NdsZwxb05psrxYylCTK/Y4VTpeJ3cNqog4YfYGkJd9XdvVlOyv70ToqF+bMUPVXy2fdZNznfwYmcTfiohK8NVBg4iqThWps6fex6yLSj3ILqPy0UhNZHYlM9nsbq8hEI+e1duxRerGk4jNCLLTwMs5JFwBCekl58ElstpaYsEzdTBVNseX5wUQy6ZIXNyWYUEio9wCkKVQkPOZwm5dtilUpvwQDFZtx6KoJlOeetDD5xAYzYh1T2QfJGrQ/OZwZyiDfDz5pAHyvqfQQzbt+tCvKBUSiUhajCkjRoDIISVo+MTnJ0vY22limyGXojUxnApwxHk3e/09Eze+wzRmN65Cvkcaks1GS/kNe4zAZVeaTK/QRa7Gt8uWr0Ie4enQljZOzxBtzeQgFy86ziheH0pFXJ49XwbL57vYG1tFflcDp6bFOKa62rvfjovISREk7GBQyTzSXDYdFwh8yQYHigynsnUwGAIZYu+Ly1QRKkDprvXq9IN2N10i23F/G5K963dYz22uyN8/LSPP959wOnZOQZDEqpDJPT/QxRpfnI+DIGT03N8+LCLYjaDVy935L1/3Dm+NRCsvhYBi8CfFgFLWPnTVq0tmEXAImARsAhYBCwCFgGLgEXAImARsAhYBCwCswjQOHB2doH9/QOM5CNvQnvOiMQzSpqElWxWDAHGMcmsjPh5MpmE7/sqJA+FG48nYSgkj/48osciX/jjmdxwTJvYKBxJXiSuTBNWVJlIqpkyZM7IozqJZEJ+XJ1Ld/FcZU9TB+WTrDIcjiSIy8yjT3s6ZZTWWQuW1Pem7bb785+NPxWGLL8xPJr08RTm2u378VNzK2V893ZBD5biS+S5mPJicEo4SLquWgWuq4DG++Gwj6DbhoMRXAfwEtpAZapp0X62QDoixNXt0le06mOjJm8uIGOxEn+DqVj+B2xCJNDVyllkUpsYDAPxlEKyivYVMCGsTGVq3IPECC2Eku3Cc5FJp8Ww+y2gy6ZkDK3kg4iHBCHlsOghBr0e+p2OhPswbX5u+7tjm7yuGk3znhanU88dw25HWcp4e7JHSBHL+Z6636RUHKP5XWL+1Ztk2nvTCBDjrO+hWimjWq3g+PRcEdYckgojNBpN8Z7XarclbBsjWPGZwRA4PmlISKBury/POE4k4XNIVllariGbzQghZjrHu58tSlYxkkkkaTRb+Ns/fsHx6QW6gSarCCFsJGNXuZDFm5fP8PrFM2yuryKfJ1llMvWocUJJjLdDM0yyuTMN3+nUT5groB8WpuG7I6/LNiVAX7vPjvJixML7iLjfM8xYF+ahynI/RR70KZao149wcnaB3999lH0vCBBFIfiOyneUXC6PQiGPs9NT+T8OWwiJ+e12FweHRyjocIb0TuelHlQ9K8wiYBGwCHw2Apaw8tkQWgEWAYuARcAiYBGwCFgELAIWAYuARcAiYBGwCHztCPBDLz2HdHoRDk/OsX98JsQMRUMgsSMSF+q5bBqlovrgm2Rsils2kkGy2ay4YqdBQH3054d/FUYm6PcRDIfw4UEH5rlF4uK3pUwjRShhPqEmrFBrWTnOEEf0AOP7yth/Q3FY1pTHVbcu+gGRonT16wd99PsDMQYtrt1nppzVlaoo+7PopTRTF8X3CY0ijg67MPvsPVWhGDECRRH6xJdeVkia4Y83lRJju8jdstEFuttDD5DaSp2i5gAAIABJREFU5GuUfwCR9xahcbzheQm55XlIe56E66JFTbVtiDGm1wsQBD2MRkMAntTLA1X/lFaUKf3XwMcLj5HRVK5f34kqtgq3w2Nj+KSHE7OW/96wxB5M+w7S6QyiKCM4G9inEImlN7bJ2ftM8gi8hKlsHuMkmUzAY6g5hnVI0HOQ6iv0MtTtB2h2WqrIxkodx+I6heaCqBPrrmjEzCYVHKfkXr0ydftrOBkXIkZmmttQHkZZg91EmiIAqOtUZqzQJMlCR1clL/TYN5HI4DKDzQ1FZpP3U0ClVMRStQKSjNHvixc0vn8FwQAXl01c1JtYXgkVGdcBgkGE958+4bLZwnAU6hBjEdJeEiSDrK8uI5NO6TBbnwneDfrPk9zvR7i4aOHjhz0hFoSMD8S5jp6WHKCUz+H59ga+f/MKm2srKOb9K3remOXMzVFIbzNDITuzXc4PWDVTJ/MUv/WaKgffhxUb5iFkzmaqC0fRM+WcTfktn/M9l83irN7B7v4R3u8eoNFsYzQYISmwhsikPWyuVrG1uYnfEyHOzy/Q7fYRRg76UYizehPvPx2hXNmH63lCDB0Tb79lcKzuFgGLwJ8GAfNa+6cpkC2IRcAiYBGwCFgELAIWAYuARcAiYBGwCFgELAIWgTgC/JbLj72M+75/dIlPRyc4bzRV6BsJOZKA5yWRTiVRLhWwVKugUvawiIcV10uiUCiAoYQYvkE+zIsLdx1Op98HV/oOaCGQzezjGt7lOPbB3wEGowhcYcmwPQxbw+/1NOiLa/AIYswpFotIJJLXfsunRDfJ8qfgp9NI0pvBKERI//kR0O320On20B/EgwXdRefPS2tsEKZsSpoiqEROhJA/TWMxaT8vx8nTlEeiSqfTwXAwRBQq085TurafaPPnOlL1eY2RiY0yYrt0xNtRzvfhJZNqsbZeBs7dYDBEq9kCw29J3ce6x4OgpfUQW/Otsk3iB8n56xVCQ6quNpo62T9oKOZKffndkyEi9WdKzRN6tElCGW0lRI4KycSwTPKjxwDzM9fie5IwpoQa4V/3niqnPE9C0yU9AkCOnExUEr+tR8JKuyVj3rgiFikSBV/3m3k+nozGA55/25shrTx1KW4dNJ5aoa8oPzNeqr2EvLpuYmUSTvKh6vNp10GRIXwqZQnlQ6It33tInONb0Nn5JY5OzhD0h2A4FD7a7Q/w9t0HNNod8HUs5FweRUi5CZSKOWysrSDrJxRJ9YlRajYHOD2to9XqYjSM5D2DHvP4DsbwX6tLNfzLTz/gxc42SnlfyJOmX5q+eq3Ksc5rYCTxoRf0EfQDxb8dpzEHpm6ulbrQDSVNk1bESxSJK5/B3bouV/G+Z3SPJZpzKXb3qz8kVGbjcTeI8Gn/SLyrHJycq7BRo0jaQzblYn25jJ++e47/83/+K/7tX37AcrUsHsqUN0kHne4Qh8cX+Mevb3F4fIpOb+b/I6Zu4hkbBezeImARsAg8AQKWsPIEINssLAIWAYuARcAiYBGwCFgELAIWAYuARcAiYBH4MgiIQRUA/S+0uhH+6++/4ODoFJGTGK+wjaIReEajxdrKEmrVsii7yLfudAool0viYYUPmWdovh2NQgT9Abq9AMMhNWCCh/sUQxsmOSUBPaAw9JCE8jFmY4YwcZD1M+IWX7zFUDmjoNJG/vIxz00im/WRz2VlVb8yHqn0w9EIw2GIkcjXD5oP2zE5j3koqjuO8q4xowI/uXO18HBALzCKZDPR5fO+vLPI9OLR7dGLhwm5pIA0cM6BdJL913gkRkFTgQqfL1qGeVWkr5EElvYUkYptVPSMhy4A0G4rMhHvSQSFx8J8np4PkZcm4HzROrhDOaKQ4QfooYDDCfukCh9GEaoM30pJ7lDoJ05KAmSxUBDvWAw7x41zCse6wWiIbtBDpzcSw/udVGOl3fa7k8BvIbFpj2b/1Do/1sDx1OX4evLjW5RPgnGxiOVaTbzDqfcfElGARquD0/NL1Bst9AcROv0Ip+d1HByfoN3tSRhIstlIfKNHvaVqGflsSkKqsJRP3VJIVLm8bGEoZBWOqgkhHbOc9C5WzGfFo0yCnkrC++tnuj4xEqJzvy+kvnDeHPSQIIgHp+n3t4dsTSQr8UdkWBRz/pBFeEh97yqL9UYPQR8/neL9xz0JGyUceJY1jJCMImTTKfz45iVeP99CMevgp+/f4PnOlvQRziFOIgn+T6fTH+Lw6BR/vP+Ig6MT+T/EXfWx6S0CFgGLwGMh8HBfSR5LQyvXImARsAhYBCwCFgGLgEXAImARsAhYBCwCFgGLwD0R4GrbYQSc10P88usuPu4eoNlqy4dtfhShqdV1aBRPolLMYWWpIsSV6xb6zqqR8hyUixmUikXlml6+mSfEiMsPyiQ6nF/UhbQys5ZxVtSC5+oTvDE8tDs91OsNNJsdDMUjirkTIp32kM9nkM+ThHL9p3ve8v008vmc/Ay5RX30TwhRg15iLuuXoJMVsW0wm6fctLcEZZMwZdSGiSghhJpgMBBjLr09TDapkHuboBhCqtmiB48BSNyhmT4ufZLPt3w0wfNJSsH6MSCa/TUZ01afybrI5Xyk0ykwVIqY6zRphW2+fsGV6Z3HN7yYLmT2V3Q2be3KjRsv3ALBjc9+iZsSFUt4D2IZVAQ3Wn4jZSyc6n5fQsGvIE8Jj3RtO7ldQXq74pySy2bhJV3lWYjsuQhCHKTHq/39A3S6d/R6ZZrovL1R61trkEbvr3pPUC2w966ieHvVMPppB6VSActLFWT8NPje4jB8Fj1R9Po4rzdxfHqObn+Ei8seDg5P0OQ8wfckOixKqDCIJKusLFeRSn1Gh713wVSrIKm5Rc8vIxKD6bGKKtIrUAjPc2UcKBbycJN8t7zf64xpgSSrBIMROt1ASCujkIExTdvUGMgcba7dv3BKwj0Vvle2ppQ65y9TpffS/LqHWJKeEK56+OP9BxwcHqPVagtpVJB1ImQyKbx4voOdrS1UywW4DkNmeXj5/Llc93317sR3enoWarY7+LR3iA+7ezg95/ttbHhS0F2njr1uEbAIWAQeFQFLWHlUeK1wi4BFwCJgEbAIWAQsAhYBi4BFwCJgEbAIWASeDIGZD600XNCc1+pE2N07xn/+7RecXzQkjAi/z9MgwPA3KTeJfNbHcq2CWqWIXIbu5W/RWufFte+57P/f3pl2N44ja/olJZHaF+9L2rlUVXffnjsf5sz//w1z5s7te7u7liyn90W2dmql5rwBQqJl2ZZsOSurK5hHKYoEgcADEKQRgQgHW5sbYuzBXBl+B1zNGI4RdHq4urxGs9nGkH7YH9ueOHXvkigdvxjiqFZv4ub2Ds1GC8PBSCajZaXxOEQu46OQzyKTZriix5UcPJXJuGLYQuOWBD1ZuFyxakJq0FDj7q6Gi4tLtNoDWGcx9+R64x9mYl70TFKSYBA38FTgOKKE6vX76A+HGHEV8mMbL4wYPpbEHmeyRitAjYY6wyHCWL4LZmGz+oa/40DetlZSUmSrMlWQPYImuv9on0LFJI2p6AEomUqa0Fu8bAxp96vrKm6rNbTbvUWb9pFCnzgsHZD30NsyekKCb+IUa+9E8XgkMBC9q4iHFVfCAomxyhO33zdRia8hxHPPj2dk8FOueFjJZzLwGO6EngPk+UHfVw7aQYCffvkZ9UZteS8rz5Qtp+VmjcZKu7/IdZrmGQJ/7PHjGTiLnY4QplJAIedLCMdCIWfCMoqnDRfDcIxGO8Dp+RWa7S6uq3c4Pb+QdzAaMXPM4ntOJuNjc2NN3v34HrRUV1/0JXGBWtFDHkP00CbNGKyMJ97k/FQS2bSPbDqBZNJ4hVkgy7lJWD++l7bagYR5pJHvaMy35Pv9UjjcPzQ3v8UOmocnvbjQWEa2V46Pi5XLVCurxOJFrjjlYAjUG32cnl3g6MuJGMD3+wOpGh02ptMpuQf+8ucfsLmxDj9F/zxAEsC7vS18/91HOe/x3UkMnlwMhiNc39zi+OQMJyfn6HTpnTDCZd91VlwPzU4JKAElsAgBjl+6KQEloASUgBJQAkpACSgBJaAElIASUAJK4PdPYGYSnHPjXJn465cr/OOfP8uELxUDDGcRjoZwxiESGCPjpbBeLon77GIhJ27hn3BIYjiJi3Ozy7R7u7uyIl7meqk0iRQDXDlL99u3t3V0gv786fMXzKnTe0uzNcTdXR31elNCD4lnEXqeCOkGJUQ+l5GPeEx5pnVTSYhSJJfLwvOS4smChiAUjat+7+7ucHJ6hnqjif6AK3J/i42lRiWLwZGxH3DGDkaDETiJL15QrFLkFSIyC87fs7431Sr6vb5x0U9lPY0WuPiZSuSpRK8o7Vu5dOYGWrVYYs2wRM+JxCHyAj0F5TLwvRRcKgrZz8HwD2Ocn1/g+PQM1apR3i9RwvM1lBs6nuyNGcWL+hb3HdriuWKUZ0Y5OlaJ7oOYMdJK2+Bb5LCITK+AkEo6yGUyyGTSEu7E9nnXScBxEuId4e//+AlXN1V0+xypoo1lxsud/c1k8fP2On7/Qbv2H7Ta8Zb/fezbhrLe1gB4KWB9rYK1tQpy2bT04WQqhWTKl/eU49NzCQ3EMJAXVzcSkpH3Eh8hqYSDbCaNSqUEei+xt4Ut5jkoJt2iqZ/Oje9u/NBQ2HVdMQrkOJtMJpHJZOD7vsj87HvpE8XwnYZ1pJe8avUWnW4X43EohjF8mtr6P5HF0qeYJ3OmsQoNcfgRo5UVF8Z31fvjl2ljCiyvHUtLvvgF9z36LX7dIinZu9rBWPrur0dfcHV9gyAIhGoyASScMTbXy/jh+4/48P4AxVwKNKLndVT60ph+d2cbf/23P4FGXQmXzw8X4dhB0BuIB6LPR1/E8J0hh1bcLItUUdMoASWgBO4RUIOVezj0hxJQAkpACSgBJaAElIASUAJKQAkoASXwtQjYSfpVT5Iyv6A/xuV1F//n//6M//jP/8LR8Qm6vS7CcCRmBq4zRtIFMn4S25tr+O7Te2xvrotr+WVUEEybcIDdnS2zitFLYjQaiiKdyvR+f4RGo4PLq1vx7sJF8lxF+6It0jhwJWSPLsKrdYlBX729E68ijiiSzQrcVNLFu/1d7GxvIpkUPc2TRXKSO5v2UCkVUcwX4HH5crTRYwwNb6gcPT45FWWp2ITMgpKD9qrY90vrG8uC+gi6w2dYmLTvGy8bVPDQow1cdNodCY3U69G3OcOT0JohlgF3eYwyz8o9k4yXMYxUszOWCf2b6t3Ue01kKDG95JnMpgl/H3sraKt5FV1aaRTDysnLtXIR25sbWK+UxFsQlXrU4NFwi3f06fklPn85BkM48f5geUuXGSm3osgr86rxRscI/Y3Ar1BiruamIUUmk0UqlRIlpDCWMW0s3o06QYBufyDt8u3XaIVw7mX1+vZk985mEjjY3xOFPEO2JRgfS7xDJBCOXQnr8PnoWLxITJx3PTa+zYj06L1hr4/df5Mx84/boPdaV38sQCDefxZIvnAS2z+jxzjHo7VKCeuVsoTNoQEG37vGYwe9/hDV2zp++fwFZ+eXaLUCjEZGKZ9McBzzcHCwh3K5YMIJPf9qsLCYyyb0fE+8vYjdRWR8IZ7yAPR6/cggecFc+ewLgbjjFHv7d/o0fqjhHz/+E/VGXYxvOa6b7eU3OMerlJdAsVgwnm5cdzJe8Xk6GI3kHZJe8OT99036RyxTu0uWv+MtGELeu49OTuRvGL6H8+8m/s3Bv19KhSze7W3jw+EeCtmEGNuzurbWTFcupvDdR4YL2kcxn5f7gyn47kQPggwN9NPPn8H33P4g6gMv7wq/Y9oquhJQAt8Cgckj6VsQRmVQAkpACSgBJaAElIASUAJKQAkoASWgBP71CYihSlTNVc2LchK8PwTa3TGqdwGOz67xz58+429//1HitNfqdfGsQi22g1BivHtJR0IAfTjYx3cfDlHmZDuDvy+58YpyMYHN9XVUSiXjAYKrSsMxBsMQrXYPV9d3uLy+ldWSMmE/W8akWBJ5hIp49YC4tWdonsurKq6vb9FstWUSm9dxfj6VSqBSLmF7exOVcnEyiT1bZPw3i2fooLVKGWuVCjLpjFnpK6uRHQxHIRrNFn79coyb21sEvYdeVh6Rejp7Hi9wyX3Kx3pxRTTDFqUkTIb1sAJ0gx7qtQbu7hro9waisHlQBDN5VEiTmqfpr4Ceec4vq7i8uhEPNvQyI5u0k1F60bNE7GC0/+19PaqcnhVVQiw9z2j2sud/k+oz4J/IhJQL2ZSsJN5YryDje8YDkNzJzNnFba0Brqan23zeG2yuSfM8kffsKUEQNauV+oHk9oBNMJvJnN+TFeAiFAswhfCn/cy57Js6RIlpM5H200ilPFmpzb7F8Ywr6DlGcCxqdzpTxdc3VYOvIEzkfUla1zTxiwrlpb5nVscz3Fwhz9XxjhhhcXU8PwwVcXx6IYrM27vuk6HaZAyw8vDb7i8qne3zi6bXdErgKxBg9MVsBiiXi+JBQsJniQcJGkmMxYvEl5NzefeiAYuYuDpmHMukk9jf20ahkH/Rs2KV1UuLwUo6koMGN6G809EbCQ1WukEXgz49lSxRauwe52X9EOJt5vOvv+L49BSdTkcyM7afy2T8UAYWZYyAMmKwQuM6+8xjzvR812y3JQxRn7Es32CbVJcFRtXhscnxNyjzrbKk+L0RcFfv4PjsHCdn57it1cTwh2+fbLO0l8TO1oYYrGxtVJCiPePMJobovoPtjTw+HB5gc2MDnucDDn1LJsSoi+9Ov9Lw8ewC9Xobo+GU30x2+lMJKAEl8OYE1GDlzRFrAUpACSgBJaAElIASUAJKQAkoASWgBJTAAwIyqRzNKj84aeabHz9rznNV+TA0E/Ht3hh3zS7Or6r48fMX/Mff/oH/+Nt/4eTsDI1WU7yeOI4xVqEbbRqm5DI+Dt/t4tPHQ+ztVuD59NowR5gnDlFGXuIlga3NdfFqQk8ldN1OpcMoHKMTDHBdreHs/Fo8djxwvX2vTP64d+Be6VQ8Bt2xhBhifnf1BvqDvswwj8cjOE4oK3X393fF+CST9u9d/9SPtO9irVLE9tYaigUahbjijUbawXHRH4b4cnyGo5ML3Nw2xEAont90pW786OP7VL6IhwyuBqZDlCikyGNXpFJJMGRRqViER4V5JN1oHKLb7+Ou0cTx+SVqzTYGdJEyb5OCHk7I8zANVThXT2OVWiPAz78e4fzyCkHQBVc705U6P7p9XQIknk45qBSL2N7YQKlQFA8f1O6ZO9pBp9vH+dUN/uvv/5TvdhCKg51HesGDCvC+Ytr43cffMr4Mge4AoPOe/sD02QcZzDlg72KbJ/ur7E+MVGwKXryopHMK+kqHKC3bwk/58kkmklIyDfP44X1Ybzbk0+kGv4MarR6cad/Z8BQvK4cr6DfW09je2hQPQ1QIOxhhHA7l2UKl43W1js9H5/jl6BS39Z543prbk+Jd7cknjJGVYzH7PsOH9Pvmeyll+cuqvNqrZuq82swf5jbh/jXLtUaGD8X5QxzheEQvK6VCXrzD8f2AIRBDGnxEnlZubqqoRwbLNKKg1wmGA8plPHlny9Hi5Wu22ZyWSac9ZLPpyXujkd2ECer1B2i1A9T5XjNYwHMYhx++yhKOYxzN0XFGoznE8YnxptFsNDEc8n3RheskgXGUOC7bEkyYlIaXDGHk+T4YlomhN7nxvhgMh6DReKPZRJehiOLlrGBfjGOifEyInlWXsIyQryubVzPKW73Vw+nFNX79corL6yoGtFCkwf2Yf7+4KBdz+HC4j72dTeQzqfse5WIe5viUzvkODt/tyd8nNGJnOzmu8dTF0EAs58vxKS4urxF0B/fzWqbqmlYJKAEl8EoC5i+LV2ailysBJaAElIASUAJKQAkoASWgBJSAElACSmARAqIwSCTgJqj854pxKjsjLwPMIJokj8+Vx6d/uc8P524ZFqcbuUuv1Ru4qd7i8uoaF5dX4g0k6A8xEM8YY3HFQUWfTKonEigVcnh/sId/+/P3skoxXt4i9ZiXZnengm7ve1xdX2NwXcWIsUngIoRjXG+fX8lkPifyt9ZLyGc9MA49F+Xbes/LV45Fbt6bzZGEgPjx8zHOzi4RBH3RTNA4hkYyvp9CpVLChw+HWCuX4U0j+zyatT2Roovxooe9nQ3c3FyhXqui15saa4Rw0Qr6+PHnL6LoSLjA5loeXiopbUm2j222DZmE+1R+cgKeygtyyuVyMonOOjDBbF48TMUUPayUiiX413dooY2RKEWonApx12zix8+/olAoIeGmsF7JwfNo1GA2EY96mZnNykMDqEZ7hOvqrXjr+PzrEW7vaiKny74ahpO8ZrLQn29IgO1Gx0eVYhZ7O9s4v75Ft0flPLV3IUZ0ke+6aLQ7+Nvf/4Fhf4B2qy3KmXIxCy9lwmSxnaUPzJHV9jeq2MR4JbI5GI5oINZHpxOg0+mKiVQ+m8b2Zln66GP5zSniX+KQURCnxANT2s9gMKRhClf+05sUDfOquLwuYW2tiHwuC5/j2xOQnmqT3zMwY5r0uhqQDZ8P21vrqN5t4+r6Bq12iMHAKLI5hvaHDs4uqhgO/h8a9aYoJTc3KsjlUuJZy3hPMHLIUOlAnhOPScYy+cjs9MbS5wN6y+l3JZQEw30wTNETzflYtl/9OOsx3e7/mh5/g73IC9ob5DzJ8mFtfg8tMhF/ZTusNT80QKFHuY2NdZTOL9BsNiOPc8ZomJ4kzP1oPNDxjSCX9bGztY5SMS+e235rgjSaodENjW34DmTeNBw4rovBcASGffz8+Qv+9MNHuLm0GNyI9eAzNGmo0g7odbCJi6sbfP58Il75Em4yuo8TcMYJiLEz84qBeNjPni5M2iKRkJCNvueh2zMebZhpbzDA9c01Lq8usb5WQqmUfeD5j+MTx6vf80Zm/MQwLl0dvoN0eiGuqjX89z9+krCfnaAnD1KGxaSxSqVUwMeDfdA75EbZhElkGChYLyszAvDnWimJj4f78h5Djz2NdiCeulwnIQa/7B/05LVWLiCZrCCd5sN7afH1AiWgBJTAqwiowcqr8OnFSkAJKAEloASUgBJQAkpACSgBJaAElMAyBDiZy/Aq/X4frXYbtVpdDAHErCCm2eQ8qRizRF5KbBghGhVwtWYn4PVB5Ga8h0ajiXqjiVa7g1YnQH8wFCWqmXSnooJKbQdZ38NGpYyDvR386buP2NlcR4aeVV44y0xjEy5yprwZ38Hm+ho+fXwvyvTqbQ0jCgxXQmTc1Zr4fHSMcDxCq7UFuvGmksL3kuJOXZSLc2D2RHkYot0OcHFxiS8nFzg6u8BdrYWB+O82SkhOZq+tlXF4uIed7U3QzfyyG5U/m+sl7O9uot1qot8fiBt3GgVQkU+lwvVtA+4vXzDod/DhnQk7RIOTdDqNZDIlShc7z805dPG+MKJCe4jhcChtH3QDdNodWfnMtv3uu08olWhoQkOm+VLTYIXlUDlFw5V6MoHBmEZBZklxbzDCVfUOP30+Qjgco9fbxdp6EX46IaFMqAux+hAxSojCmfQHDB0AtAJ66LkUrzynZ+dg+/UHA9C9vesmMaTBCj+8+M1MVx6p/HwkLzsqff0rlPMy6R5eRXlDwEs4WCuX8PH9e7TbDDszQisIMB6NMKKKb0RvRn38enwihlC12h32d7dhFO0MY5OUUEIMLUVDANmiPk3DFBpODcc0CBih1+/Lh2NUs9lGvd5Co9lGNu1LGImNjTJo4PVNb082MaG+bEslksj4aWQzGbQ7PZjQWMarQbvTxsX1FQr5NNKpFLbW1pCm1cqcjQYXvJdouCiGanPS/JEP2eajcvfd3g6qNKQ7PkGr1ZZwJzQsGY9dtLsjXN7UMRp+lpBM+7tb2N5eB71rpdMpUchzXOXzj5xl9Ir6PZ/FHJOHoyEG/YEolrv9Eaq1hjyb+QwYhyMc7O/hMPEO2Uxx4Ucl21X+2QE9ek7+K7fpy++qxag8zN/2El5v9h+mWSzvr5VqakJ6v8SXyM0a85NNuxL+cK1SAj2qDEc9hKFjPKKNWaIJ40fvFHBCFPMZHOxvSxhEvvO8bIsupOAvET4qlLnQEV4hn0U+mxEPFzwmBt1gOMaRhLz7+fMRPC+J3e11lIt5pDP+3HclvqPxWdYPHdw12ri4usPJ6SUuLqvCptejpw4gk8lKOD0afcv7UCSPVCdWtWj3SURGXhrYJZHNZuGnfYT1lmkch8+GEbrdAS6urlDIZZFMJMBQZwx7xm0WH40v7LPhd+fULt4fFoE3Q5bPxdtaE78en+H04grtbk8MS4w3HEf6CEMBffpwgI1KCb5nnq9xTnzvthv/RnHHgC8hUEs4eLeL6l0Nw/Nr+RsMoSPe0e7qLZycnqFIgyiP70pFpLxv/SXH1lK/lYAS+FchoAYr/yotqfVQAkpACSgBJaAElIASUAJKQAkoASXwjRGQSezIhbV4EaF/AhqcjMZodRjC4w6j0EU2W384ZS3GBKEYt4zCkXjS4Cp+etSgd4Wg20O7E8in2zW/aaTC/DnhyylwKieoquB3KpkAV7Fu0qBjf0/iuR8e7CLtGe8LL0VndXG8niEcivkUvv9wiHazIYr0eoPhaWi0EaLT7WJw0xdPBM1WG7f1phi4cFVjxvdFoW5CzhhOJtQGRAl5d1cXbx8XFxcSVqjWaEmInjFCuO4YiaSDYi6Dd9ub+PhuH2ulongkWVi7GAHg9HQp72N/ZxtBO0DQoQeUqsS6Fzf1cMSAheFXgqCJRrOOzY11lMtlFItFMVpJpVJwo6WydDtPhQu/TTt1QaU2XcN32i20mg1wNe7mzi7yhQKciUnJwxZJJoF8NiXeaTYqRWFcbw4Qjjlhb8KSdDpDfDm5xKA3RrPdx057E4VCFr5Pbzb0OsCpsDFCKmop1yiUviTtUavh/PJSvPTc3d1Km3kpXxSL4RxcAAAgAElEQVQwmUwOd/W6pGX3sn3bONyPqwceyj33CF3wSzgH5sR9uhkyt4G5V+Ze9fTBuNaHec1ukrFJ5Iwd2A+VGfe2edfeS7DAD8ljNmN6E3JEebJUHSMlOz365LMJvN/fRqtRw2g4kNXH9NJDgxPe+7QPo7KHXlF4j1TvGtjYYIirgij4PM+T/pbyUuDKYjFSGQ4nxlR2fKHhG1fqN5sttNsttFsddIMAVIgW8pkHCrbHiERNGp0mD66dt1yoPOUp+/uxXJY7bpuPuY4FNPun/Jopa/lymXfGT6BSzGO9XBJDwf4gFIUaY1DQiOj6poFk4oKB0tDtjcU7RzKZAL0Usb7ikSUMMRwMZGymYV25lFmukr9R6ilbjtH8xREzzjHyrWITvkJO5sx7M592sLu1juDTBwx6XZyHIzRbHQl5xZalIV2n18Pp1TU6/QC1dgu3zaZ4uMnlMmK4QmMtP+XBTdix0hiq0CCRXrRomNft8nnK8bkLGley//e7baS9JPLZHHa2tqQ2T1XNEhHZRekeDZZypfF0JmPmUgPAyyBKq4iwtly+D5iNxcvH/n5ZEfeuMr3AvHPIiakAcQj3rnnyhxV2TiJmbcrjDm8qPkOmfZHvBbzZTLonMpqT91seEomEvfF2wkHbtANldCXE2zLl8yp+6EWrlMuIt4nTTBo0yujRcoPGElGGjjxjQ3ipBMqlEnZ3tuEll/cYZMuMzLGMUZYMbJMWibfOQtVJpRwUS3ns7++g3e2KMTYvZI7DcIxGu4svZ1dwEkkxrN3aWEehWJDQeAnXeMLgOw3flem5jgbh3cEIF1dV8cR3fkGPeS0MBgMkky5yhTxKlYq81zHsISnRQMaUSEvCh2LbQ0w1b2Pvy3gu1stFrJUKuLm5kZCYvG4MF4MwFMM6xz1Fj57L+iEKhYJ46GN+9BIo779jGhsH8k6Uyfgo5nNicDyvTNP67P+2VSQnSSpy8qXga2xyD/KdyhZmKMlPK94j77YU0f4dwfeXZjvE2cU1jr6col5nONOxGBoyx3TKlb9haHD/bncb+ZzPyHAPN3b9aDigDMyfxoqFHJ8lFdy92zHeDYc9dLv0hOOi0+vjslqD/+UU+WIJnuejnMyYfB6WoEeUgBJQAm9CQA1W3gSrZqoElIASUAJKQAkoASWgBJSAElACSuCPTYATt+5EGcFpZaM84d5wZCbgf/lyhvOrW6SSychrxZQZV1fSQIKGHsNwJB9RLsuE/EAMV4xxiglHISU4rjGU4MpuTgJzEj4cibEKjTnodeT7Tx/w/uAdtja4MtFMKk9Lfdkec5GPA+TSDg7319ENPooMn4/OUGt2RalI44jhyMSLr9bqOD6/FI8RlVIJefFQ4oNeUgyjEfr9IXqDoSiFb+8aqDcaaLZaGA1HonikniIcjWQaPJPysb+9gY+MU7+9iazvigHNREO3YNXoNYKGN9vr6xhKyJ6eGJtwxX23N5Bc6G2l0+1LqAgaceROLsVYhUqgTCaDlOeJpxROlFNBQgUKvVbQoCjodtFsNVFv1o3CGiG2N9YR9IaimBHlEvvOTNPwJ+fls2kH9CBQr9URtNtot9voj+j9hSF7zKrc27s2Wq0TnF/VsHl2hVw+i2yWits0kqmUIBkNTTgietIIel3x2FGt1cSLDUObUFHMMmlMtL25g82NLfztv/+OXq8Pl73ZGkNRHSZKkYmm4nnSkpTtPGO0IloiU3HTf5/ParkUpMsAVdwigxXuiQLR1He5/J5KzUraj9kVAxkpL1Lq87wR5qmM5ByVMmz/tOtgq+Jh9P1HGVF63S5uhgMZJ2jQxrGF7dNs99DqXOH8uoq1SgX5fBZirOL78Dx6nUghkUxGBivWqGo48f7EflWv10Xxx3HHGY+QSriSD5WClJu1e0p8aeZ7acRUw/QXXkjwT+bwLJYnExhjFdMGYrgXtYcU/eSVj5/ktcW8I6v8a7VtCcPWaLXF+IvxHMLxALV6B93eBZqtPs4ub1EuFpHPZuElEnBcR8bywaCPfreLpONikwZF//7pwT3/uBRf8YxtRHZhVp6GXlHjy5hDAyw5HktotY8rEJOhsJhzpZDEv/3pA4bDvoz5vd6ZrIpnmDaaSNAzUH80RP+2hrtWG6eXV2KowjGP3qhk7EsmZVymWMaIMPJ2FQTyPO31aATaQYvGMGMXVPAnnRCVYk76qesuptyX/iVjijEWlRrwIGtix035vdreH2sBYWbv0bHDcY9njSJ+Il8kkkn8usaalG2fBfJt6yclRvd6VPHXFRe7mvmxrczzxMjBcYb/bLmx5N/ALsciPl/FUNI+AkRwdnbWI2quBVHxCt4nubSPjXIRxVwWrRaNsOhlhXFm2G9N+/OdsJAvyJhDb3iz7xnP4bkn0sRIIW6oQO7Lb/TyslbO43/++7+h1mhgMLgEPR2NHYbrccT4pF9vI+h/kVAxaxJWpyzGtHyu0diE9y+fVfwOgkDe0arVO9T47hb04MKV98tCLocfvv+EyvoGrm/vcFO9wYDPNPaYyYvH/L7Dut1jEKsq3xvzGQd7O1uo1es4v7wQo1Ex7HNcDMcuqvU2Or0h7hodXFbrkbe8jLyj01hlODTeF2kox2Ca+3s7+O7TB2QyiYm5h2lJc0eb4s37BOWy7EVG3oP2fnxU6lgFXrhrkNl3muj5IHkZUkZe7pvfs8WwjzL0E7tTfwjxqvL56ERCf/Kd2XXodXAsfZyhTA/f7eLD4T4qpez9EEqxxpmEVpop0ksyNFAa333YF+8qQZfP6q68FYahi1a3jy/n18gXTuRdPpelZzp6KnpU/Nnq6G8loASUwKsIqMHKq/DpxUpACSgBJaAElIASUAJKQAkoASWgBJTAQgRkMtXMepoJXFdiqLeDPmSFqM3ELu6kwQr/jY1BirmGk6acVE+IJwUqqLk5opCYxhtgKQx/kE76WCvmxSsC3Y/v7m5hd2sTxUJWVuTaIlf1zXI5aU/X24d7O0g4CaS8DH765Rj1ZgPd/lD8K3CVe384Rq3RQbvdw2VktJNImLANnNemdxUauHB1ZX9ojD0YUkfCQDg0zhiBSg7PS4h7+IP9Xfz5u094t7uFQtZDitp9CvSCjZdlfQfbmxuyTJOK/dSXM1xdVxH0+pOMh3Q9Pxhj0AjQ6gxwc9sUgyEqpe30PdtI2lDc1HPd9xij8UjqzxAuVLdyBTGVa5y4l27yiMyUiwY1xVwS+zubaDVbEh6jWm/JSmHqpmRzEhiMHOlfveG1KMnpgp5eBuhZgxu9c1CxE0bGUPQAY/iyA9JrDWQV9qcPH3Dw7hC5TA6fP3/GnXRB0xutCZYpdNn/beMYUvKLyjt7eNnszK0w96pplmb1P+Vmm/C4UbaYfVH3TBPPzWuRgyYLw4h52n+ywp0tbGLBxNRLi+Rq0rDP87NRzmH4/lCUcD/+8hkX1zeyKn0sWlCqME2pgxFQrTdRa7WN4odhUVxj2CZKokn/NAZylJr9kIZgVP4ZMjSBMZ5RqDhiG0VDz8KCT5jQqmqyMfcVAJ/kN2dHjGKitrBtTvWt1HtO+mcOUVqGUyoVsqKYvLy8FsOzRrsjXouEi+Mi6I1wcXOHWrODdMqDzzGEN5XL5g/Fy9SoP0Ahk0E4GuOvf/kEcX70xjieqd6Tp20bynf8fhOlO9vSHOR5adcV1YXZ0I6RIed++PQRqZSHdDaLf/50hN7QjJ8y9rmuGLHwOTMYddBsBxJ6g2Mfn7EmRE90Z4gulx4ZQqPU55hI49DhCOGI0huDNmukY41HnwTEk0QQPYqn1bdcjOGIGJI+m9EqE7B88zEymbYyRoerK8eUQANGFmdGDoPEKs5XV1Y8JxnDpUwOTIQflT1tgHjyr75PMawovEemH4pijZriqZYXkYYn2XQKm2sVVErFiZetkO9KUfkcfvhaRI9wG+trJgzjkkVRSpuftHFkcCPDrGOeOdMHK1MutjHfdNrB3u4W/vT9JwnTdXx6MXk3ojEHQ68F/SGubuuoNdvwvBsxDqbBtzH2GIinJBo0c4yVcF8DvtcY92OsPz2EffhwgP/x1z8jkfJB42MaEzaG9WgcsMa4lNu2mr17TF0m9bdVi6rJ5yLfz0r5LBiy5nB/F73ekRioSF5uUsI0ccxiqKJWcAw/dSFhjlgHuvKg3QxDlA16HWS8hISYPDg4QDqdMAaDtszJd2TRR1nZFvbvh0h66VWLN8Mk1+V3okLkuRrCpWGjdArD7qn8+N7PkZHeyG5rLfzjnz/h7PxSDL1NZxsj6TryrPxwsIfDd3vYWCvfN1ZhAdPmerQ43if0Krm9WcL7d7vodDrodAI0Oz3DH5D2Yt8r5nLiHW17qyj5SfYLlPFo4XpCCSgBJbAAATVYWQCSJlECSkAJKAEloASUgBJQAkpACSgBJaAElicgqgmrgY9NdNpdMVCgkgzDR2dbOQ0sytVotlSUbmIQ4cJ1QlEc0+iBE7EMO5FKJWTVaT6bQTmfw+7mOtaoxKiUUC4Vkc+kkHrj2RAqdMslH667g2TKE7nOzi9wc3uLZrslMo+pEA9DUGnbDagEN4r0OGVREhrdl7mGSjCmY11dB9mMLzHs6XHk4+EB3u3toMT487TJIK+XTtSHEIOXUi4J11kXbyJeKoW0l8LldRXtgF5X6EY8CvE0NJ5jGA5k/mZa3K4klS4xHsLlCv7Io4vr0HhF9NlPGm0wJxrjrFeKeH+4Jy7nj8+uUL2tg2FcBsNQ+LDPUPk6CgPpP5TLdR0k6OVBDIKM0pxg+Y+wmDfDlmQzHtbKRTBk1KcPh9ja3BaFbybjIZFwJKQVAZv6m7rNr/dTR22ZZGYVueaYXLVstkxv23vOtSIt+498WB4TjSIlO38bGZ6SeJlzRoRpHY3BhynDEl8mv9m0VN5vrZeQdF34DFmSy4KhDer1hqzSpgKfpXHrD/oAnQNJx6MiyUhHpbwgi7gZIxQjs/QHemoS5Tv71FhCCWXTaaR9X/rqHMxRieYryjY6FuUr9zAPWQ83Ytowbbt7Obz2B5V4k7sqanNT9qT/LqLlmhGDOWYyDjY3Svjwfl/4hldjCSVDEx+a9hhvUiMxJGs7AZKOIyvEWRxDP4TjEcbDIa0kxGvRfVYzBX4LP6PGNvcR/ZpQKRl9m/XpcMbWk8PqBWbxfK5Uyh7G2JdxjOHNrqs11JstUTzS4E5M/hg6bzDCyHEwcIamv4tnGMplRrtJ3xUFL+lbIyY+S9lI9Nw1FiM/emhJp/lcMcZ+T9ZukrFJxazYXyhXNGKa75l0T+a50EkzfptxbXo7GeMY1o/hRuhdKtpHfNxdqICFEonxiATY4PNMWkOEMf0mku4VnT2OLWo140mO/RFsM3qD4ntCKF6hpvVfSPw3TST6e8omIzNHZ/YMu/E345hEcOIVtUme+GZyn2GBCjlsra/h+vpOwrgNRhxr2KdDJJwQqYSDve1NScPSlyxGJDD9maKaujjC3Yx7pn8xxeKNTBmYmoaYDNny6f2BePbi+9J19U4803E8pREz7R3DET3W9SU048T40nHEwFKMLKW+5n7m/ZdwHHjpBBhG6PDwHT59/IC9nTV0Bwyxl0Ehl0en1cRwxHcyMkkKF9OXn4AePxUDmUk7Eury4/tDCV3GMarT7YlBI/nw3ZfhmsSjk4SqoaE2vYgYb1E0xg6HfQwzPnp9hnyMFzSzH3m8ssZnHN0oiulGHMfk18xFK/4pdefYMoLD8ZZjS3RMxp1o7JP+LSZT98tn9Wj8XW928NMvRzg+OUOj3pjw4lMl63tYX6vg4N2+eAfKZBYYi+8XM/kloRUz9JK2Ie/MDC83OL8Cw8PxfXg0hLxPfzk5RSGfRaHwF6R9tpG5YSTU0CQ33VECSkAJrJbAG0/RrFZYzU0JKAEloASUgBJQAkpACSgBJaAElIAS+H0Q4DwxV4RyMpZTyGbOOT7zPDbhe+ziY5nglf9ksjdS44ryzCq4OaFNJYc1OnBdY6jClaO+l0I27SOXy4hxynqlhI1yGVsba8hlM/D9hCj8mMObbVH1qCQQ5WIpCd/fRCbtoZjP4OQsjcurG7SDrkzEcwUsOTE8A+tIZYFVJ04m3CkslebycSR8kidGOR4210s43N/D4f6OeI7JZ5P3V11GOJeqb9Qetg7FbALe3pYo6XMZhtXxcXl9K94suHK3P6BCwbaubbX5JYqxDatD4xTHhZdMyKrotVIRGS8lXnEWEZlp8jlPvMn46Sxy+SK4IpQeYBrNloQfIluRS0QTNYlZcTyi4lKsEBCKMsModBiKyUslkfZT2Fgvi7HKhw9UDmwil03Kyl8arCRpYUMnM1GfNn17EaljTKR4q+yiYtEoUk0uprfH75TYlU/vzhGDh+RjV4JP7kYaq5jwQEaBGC1PfrqEJc5aMpEiUoxjIhMSkTNWwzlyPyiIyWPpeB/n0w78raLc3wypxfBNJ6dnaLY7CIKeWW1OD00MGSX9zpUbyZTMAUr0M6aoiI85ZwzDaADHj5dykU4lsFbMYXtrU8IY8P5+ajP5TFOYLkcmpkx+826JVWmaeEV7MoZIaBdTjpQn9Ywr8l4mAR0VlYo+Pr7fF0Upx+QLMWbroDfoSQg0rpgXj1A0YuGKf9ZLhGI/GMMZGc52PF9RtVefTQwRw9yJWlWMVUZwx1RS0hDM3k8yiK9cBtNfjAcvGq2kUgfIZbM4Pj7HxRUN9u4kZBxDSAwiY0hjAkjFtVFes7M5NBKQm8H0v8lNQOMsPoNcR8ZlL+HKWFjMpbGzvY5KpYJMOrNQvWzf5zhr5KYkJn8z5ljDkYWyWzDRpFRJb3mZyrI88zG/p21l30wWLOTRZJPy5P5if7DjeoR7cvzeMPZofouckDIjowkxVqGRUdQfrTGVKd2yWSTXt0lj+dhnjfnm0WjjuCChmzg2PDO42mvsNy+h95QExNh0e3Mdp2eXuL2tIRx2IwOesRirFDMZeVdaq5RfNfYaww4zFtAwyfQvvvNGN5eVbcFv20JU1O1ulRCGH8WIw//1CLf1uhh+BL2eGHXwZVCeJBICbwSM6EGFz5XIcxrPy/si5J0ml/HFI9YP333A+/cH2N7eQi7jAMEYWd8XLxrVK5pZsM9GhjjLuhCL1ZMG4eViRjyBdIIuUqkzXN3cot1uicdAMVQXoyp61RtjOKbBOh/NNFoxY4aMs24CJgzZ9K3d9pgpZXvEyB1ZdpubjInkHW+aOibmynal7aTv8gnHD41WKII1CGYKGmM97Ns8MxoD7WCEi8sb/OPHn1G9rUk4UKnE2PTbUjGPd3vbEiKpWMgtHcpqtrKUb62cljzb7UD6V73elHdn9q1O0MH5xRUyfgqbGxvgPZXNRCHhpMIzOU6bYeaE/lQCSkAJLEdADVaW46WplYASUAJKQAkoASWgBJSAElACSkAJKIGFCXDqk5P5VKQYLyqRjcBkYpyTsmauczopzcl3mbgWDweOhHShUtNNJJFM0AgkI4YDnpcUYxB6V1ivlMXdOQ1WMhlfjFeyaQ8ZbzqTOt1buALLJZwpgD/TvoO9nZIY0mxvbeD65hbnF5e4uLzEba0uHkFCZyyeQkJqd2XCPp6RWfHOEEc08iiVcrJSdndnAzs7G7JSuJzPShgiel559WYno6NvKoGo3Hi3W0apWMDuzjZOzi5xfnmN65sbqc9gMJgoS1i+UZzQ+41RSPMYV+1bpX3STYgBzPpaCbvbm3j/bg/rlQrSnve0+Fa2yNtAsZBCOlNBqVjG7vaWKKl+PTrG5dW1rBylhxXpX64xWKHS3MgXGQ2IhxdXvPLkMmlsrFewv7ONvb1t7OysC2svZfon+20uQy8zLoJghLEoB+klgyEgTL5PC2/OsonY042CkSuah0jQwxDzkLbn/cKKxiq7SMZPpYmUpaLEjJSavDMpu1nTHCncXqGkssWzfvKRvIdwYerI+rJO5rzZt9cs9U3FnEEl/clLApVSCn76HTY31/Hh8B1Ozy9xcXGJ6yoNmJoY03hJFGIsicr7KV667hfSovjlWRo00eAsgXwujTIN39Yq2N5Yw3q5iAo/pWI0Zj0vOevLjYpkUSaHAxnxGI5IwgZQObvCpo6Ki9qA/WzqDYReM6QNIiW39N0XFM46UaXMsGF723n4/g+olMs4Oj7Fr8dfUK3dSUggw5ptbj9yxMBn/2BIs2QCfiop3gUWhmor+Zt8G2ME42HFPNdM/SIDhUk/ivqY7QArkpVdhSvdi3kHGX8da6USDu52cHl9jZOTU1xVq+JxhcrtUchxatq/+fyQ0YxaabmPzLglHlVA71MufN9DpVgAn1X0VMExulDIyLM1m11sVb+5x6lANh4/eO/znqPXD+mDEwM9a565IjhzsmHtJwYFlEfqTi8kxmjF3HykupqGkr4gxipDONE7D1lzzDfvQqu52a20Uj8pj6yN1zKRQbzJmHF9DpavfsgaQvB5MxkLIxSi2Od989zzx6Kzlbe1iL06JhOOjNeVUgFZP4l+dyThE8nez2RAb3Tr5RLSqdlMbGaLffNq8zylpyWOA2Rt3it4f4rB0uSZ83yecWn8FLC3XRaDtL3dbfxy9AVHx8e4uLwSr3HmAcaxPBpKI268u003JkuGfklic6OMd/s78lzc29sSo85UypHxmx5pchkPhayPpBtiQK938o/v6vf7jpXPNsG9GtmT0UH+9D0Hm2t5pP76F6xVKjg6PsHR0RFqtboYa1NkMVwRgTkqOQhZvkPPiSYsEZ8LNESnMTHznBTD+4le8iLjmsl7jXhq5JgSwg1HcPiRe+OetCv/IbLZ9x1hyHsxevbyePyZMKd0Xn91eYGff/4JpyfHEsJJDAvZvOEAGT+Nnc11fP/pIzY3KmD/WMXG0EAbayV0D3ZRvb3FaNBDo9HCkIakCNHptHFydoLsf/pI/+//hXxuzQxkLNx2BH5PGmYVUmkeSkAJ/NEJOGPOHuimBJSAElACSkAJKAEloASUgBJQAkpACSiBFRLgqkHGZD8+vcTN7Z3xKBKaED4s5v4cp5mwnle8GK5QAUAFr3wS4mGFk9hUKqfEA0JSvCwwdIFMcHNCnituXTOxPS/fr3mME+uMltPvj9HpdiVsyV2tLpPD9LbS6fYlLEZvMECv38c4NF5ApH6phHg14Wp6+eSyKBby4CrLQi4rHkqoeKCXmZVsnCWyM0W2kaJv2n/0+mM02j3UG02wDlxB2253JCRFEASiUKEBi4QMGo+RTCYlrIQJ15SC56eQyaSRz+dQzOfAlaPlYkFWANP4YNmNs1qUK+iO0WwGqNUpVwPtToBur4de33764maf3mxokJBIJOH5HjK+L0qccjGPUiEPKrry+SzSGQ+eL+rdSV/98ZdzWSkcBH0JDUTlKw1dtjcrslKV4agW3RrNvoRXOru4Mm7v6ftAjHrGIsP25oa47Wcffu1GRv0RcHZxi6sr44WGxxIYw0u6orCisUelUkY2583enC8qPhiGuLq+xcXlNVqdrjHIGpK9i0Iug53NCva2N5BOL6h9sX2S0nDf9s1IOo43g+EYXfbPRhONVhvNZhP1ZhOdToBWJ0AnCERJJt53QnpeMfcZlWTmXkuKRxV6ESrw/irmUSjkJdwQQydwtTHHF3pcWaZdKO6PP5/h6uoGDJtlfOiwvcfiielP338QgwB6TlrlFvTGuK42cHF1g1qjKXWnoi9FY5ysL96nNtcryOYWbINZ4Vgx9q3hGK0OcFdvStgz8QjQbsmY1u32MOCYNqQy0hiuefSGlUnL+LVeLotxxMHhlnhImG3X2SK/6m/b52xfC4FuN5Qx5vTyCs1OF4MhY00ZZbWfdCVE24eDfQmh47A57bUrEtyKZL8HAz5nRzLe1RsN3NUb0vf5XOH41+315ZkyHAyl/a0HAj5L+WxNJVPIpPnc9JDNZUFPRfRIxrGQ3wyP5ku/5z2yQHUoGL2G9RniIsDnL1/QbLUxoqcjGuclGHItDbb7+8MDCeOyGjTWaHA6YHJM6PdDeQe5rtYlZJX14pFw6F3Cw1///IOEvXBXcOux6p3uGNVaA19OzhAEXfEgQc4M91LMZcH7bX9vy4QlXEHf6PXGuL1rybOEBrCGAg0WRsimk+BzZGtzA/m8vxrML8yFz5vBELi6vhMPbXxGi0qK4WpSSRTyafHIwZA+k5CNs3xsp6cMs+ciuVgO31FOzm7kWcd3EqblWOt5CXm2vj98hxyfc6/ZxkCzNRYj2fPLSwnvKOKxrISDnJ/Cx8M9eTcQ64VnyopXjUnlnXFo3qE5nlbv7nBbq4H16Ub3dr/XA+9rhgFiJX3fl7BdDFmXzWYlZGSlXDDhMIsFZLO+PLt4h7A82ke32iGur6s4vzjDYNiV+zPjedjb3sL6+hpyufREcl7Dz/QOm5x6sCP5R23e6gxRqzdwe3uHWq2GVruNoNeV+6PX68u7Ad8L+Az2Uh7SvodCLo3NtQr2d7exu70OL2Z4Hi+s2R7j6OQcd42mjHcMJ8T3qCTGWC8X8OnwHbL5NJwXvFvGy3lqnyF0Gp0evpycSxuxTvQuxnueYTtpIMX3q2I+CxoLzW5kdX3bknclhtwcO654/6OHQBrd8D2fLHa2NlDMe8x6ZRv/LmH70AidHlaCbl88E47DoYz3Gd8D340P9nZRLKan9x2Fjm8PqxU/q/tKQAkogYUJqMHKwqg0oRJQAkpACSgBJaAElIASUAJKQAkoASWwDIEwpAJnJCsGuWaPK75lxns2E4lDbw/OzHzyZ+Te3HigYDpjoJFwjJKf87dcWZtM0hvL48oMW8Jv+U2FUn8wBhW53W4fQW+ATpeGKgOIwUqvh5ArQyMvD1TmUIFOw4hcLishgVIpKs0TYHQaKs6ZdqWbnYy231Eb2DKoTKFhQLc7kNWYVKLQKGCewUoqmUQyZT4it58SZS6NVvyoHl6Sq/unc+G2nGW+6TyCehuuDqW+gDyprP78WIQAAA8ySURBVO32AnS7DMHEEDF9DIZ0186+khQ50mkPNEbgJ+3Rg0oSVnkpCueYEEF3hG5/iOEoRNJ1ZeU2w1JJG2X8pdphLMYVA3T7hiHvD9N5Q8PFS4kyd2WGSDCKvG4vxGAwFC8lNCBIUv4Ew2zR00wSzqztwlJ9ix2GPZzr6IHeYIRuj/VjeCZHQjKJkjyRgO8lkPVTLze0sn3Ttk9MzuHQGFH0+0O5zzrdQIyq2kEgisVRZKwiHo3oWcKNlGVeSrzt8H6j1yb2URpY0RCJ9xrvM/nYMpf47rSH6PcHwoWii/hcBo+xeF+iEcwK9VAiWRhx6A1C9If0NGC8x9BbUypBRXFCPJwsrcyz7O03a0HDseEYnT7EMMAYTFApGYjBSnjPYMUTYwgarHFcS6d9eL6LtzDwWKKJHiZl/WL9il2bjzDWMxgMMJB+bTwssV+z19MrAOsURa97mOcbHCF7Kp8HwxBBj8+UnjxXjMGKMVoZMnQbPa6EHGn4/OSz04WXovFQFmJERKOsdHoSdo7PU44/8ox5Su5YP5gkY3/gc67XE05yz9HzQYJjvfGqw/BrHINWs1khphnyCJ8JvV4I3gMch8b09OSMQYMVMdzKpFdqKDUMo+e7PCfIm2OG6Rs0rmX/oNcuGdenor4YAfPn+wQNc+Qed9gLqeg2CmdjYJdE4g0V9gsLHxmT9HqjKPSIuP6ahKFK+/SgF+Vm2dhvHrZNPK/AeLrIcKjXNcYcHLPFWM4dI5V0xQPfq5X+9BASGZT0ekNjB0YBo8c4+1cmk4Ln8cExT+DFjlnDlWAQgs+xHo3Qgi6CbgBrsGI983meLwZoHE9p3Mz7i2EMaXAmoQzpnYnyRQYx/Ob9wb4T9DoY0TuIy3cCV7zdcWxw+WIW29gEy1SH6W0d+C7Q6VB2Y0xnjYp5XzoOjc+T8GhARyPiXFoMvBjOiAwfvNdHgvC9r90do88waAytSY8mroPEOEQ6mZBnizzfVv1wjTHhc4GGH70Bn/FDecfkKGues3zGJqXfyd8n93FOcunxmSLGhQN5D+RbFMMl0TsL35PT/Hg02p9cMt1ZpkGmV032aNjXCQZgODmO0xLoSjjyvchFkt4F097DMSR+P75ShokwuqMElMAfnoAarPzhu4ACUAJKQAkoASWgBJSAElACSkAJKAEl8LYE7CR3fH4zXuKyc502n3vXzT0YL+Xb26fInCymhxCzAp2T1FG4GioGIkULV6Vb4xTWgvW+V/dVV82yjOc7p0Am44cyU5E7GnEVvZlop2KUm6zkFw85ZuUxJ9ypPLKK/5XVxSwtv7f81yjRqcxlyCUqTvhtwlPIKtwklSRm9bvIFKuvhK6K6jyn6rGUq9m1LJnbypgsIpppJlOo3Y9ft3Tl2RCmBrZO8W9mTZ3LI3qbeMmL7TPzR2RkF2S7cmX/kEYqDIMS1ZHf8rH9lF4QEsbwjd/sp49ku5hcs6micuXwSjOeLej5308ge/5ipojXxWYWqxORUnHPcYHGHRwbCJtJ2B5UKMp9x44QjQVyMpbHYoK8cSpbt9liovpz7LYoWBXWTerx2HWz+bzBbxYtys5IGc2xTwzGpBEoXuQ1igOwhBdyRZltx+W4PvTVzWHh2Ho6U16vztvmucA3xYh/eIm01wLXviQJ+cerbrvFm9Q51gfZpPYxaOv4Evnf/Jpo7KURguX0gM28E/bYPAFnMrBJZw7Pu3K5Y8yYH2a88szniBKVZfsUf9LIJOS7lrwr8gg3G3LRjEPW2EzGpCgFx2URm//Zy5gfjaqisZhJ42NAdOlKvjheSh/lOyK9Hw3G0TsjhTFeyygvjWpoUCnGNZax/aYkVv7omDzHo/1JsgjYxDBpcmIlVXk0E9ZE3jH4nHs01eMnbDvb+9iOUxPxY+02yWVycnLkRTvzsrYZPVoEL3r0pL1av5WAElACixNQg5XFWWlKJaAElIASUAJKQAkoASWgBJSAElACSmBZArMTmk/Nis7LOz4ZGuU1m6VcZvNl+rkJ5mX+2xyTCe1IXmsYYcW331YyOmHgJP9LJr9tHi/+jgsTbwdmaM/NHJe6zRYYSxPbNakeyWc2i2d/Mx9+WMCDQqbiSrKozHtco2NSTnS9URpQ0W6U7XNbwV43p8xnZZ5JwKxWkM1MruanVaLMzd9qR2ZPzv6em/PswWktLJr4N7O0n9krV/p7KoZkK3Yp9li0ypwnyMX2WSrL2CfeZLMQbOZvVY7Nf+bbVn3m8Mt+ztZlNpd43WzaGGc5HU/D6/l79thsvl/790uhvfS6Jer3WBG2L8/rx7yGH26m30ceIRiKLIZ/Zc3wmJCRDF/jy9bXlhUf6ibPVHtwcsCmft23LXtlPJ8R52uX94w4j59+TlB7njnE4cWPz+YeTzd7jtc9dX42/VO/Z2VYVb6Tl5dY4basOWXY51b8lNzz9oC91mZnj/O37e88Fj9u077RN2W24xLFs59JcZHMFCluaDM5P7tj6xgZat2rDs+xnvbgV6rnpF1m3iXoCUbqPm+MsfVg/SI5bRM9SB5PG0s/i2aVv+nFidu9/rXKAjQvJaAElECMwLfgEC4mju4qASWgBJSAElACSkAJKAEloASUgBJQAv8yBDi5+tqJ4tkJ2nlZzknzJMN4+tfK92RBc05y0t6WPzOpPSf16/nNzXTBg/fY2Cl0HmQF+H0vgWRqFRILljAvi4eXWl72zMNiHxPHXjGRVC6V/5hpLGMKTuuhKG9zlv+z3qE9fH/9sc1injyTkufs8LroGq6Stm7eH2QTSzcnl6UOPdkuswXP/l6upElqkmNW9sMTrNKbb7Zd+B1pfCYKsJm6/WZKmBW27aM8Yw0wU+3YJa8QZDZTautsx46VILt2rGMSu8Wvj+/b87/H73j9fgP5n8JoDO8iAZlwkphhIGiUZw9OTpga2DrNHH6uenEF9WzaF2Y5m81Svyk+PTvR4c9ks4JMDrx2Z5rhfVz3f722lMlAGsv2Kd6vLu/FGVgeMUFjuxyimGKux61YulcVzwJWldeLBXnuQgrJzwMThbkXsjqTZ7qtmx3v7RXMzm48x6xpOBilM9czkT1pM7IXRd9M8sipmZRP/oxnwf34b144KWb2xEyuk3Sx41HVpkeYx4OD09NvtUemk3aJFTLx9BI7JrusjN2k3qZ2c0WPp7XXvMX3DGDxhBRFc51Xt7cQQfNUAkrgj0tADVb+uG2vNVcCSkAJKAEloASUgBJQAkpACSgBJfD1CTwzGX1PoPgE7SLX2TT2+15msR/PnY8lXfkuy35p+TMTySuX7ckM7RR6VIFl6hC1o4i/zHVWnpdcY6999Duqh6hJmGhqrBL9gisNxXpbAex3LNM5h2Jn5+++5Jr5OX3TR613oHh14/tvLbz0N6uLY2Ffs/DZytmyo3th9vRv8ntWFivjc8I8mu7+PTS5teL5xa+N78fT/J73v1KdHi3m0RMWqk1gv81xGrPYPZvy3vf95PdOfcs/5oltn2QTueclmpx86Y7NlKZAbzD02Oxj4tnxNnboG9idI2hcqse63bzL5h2L5/XY/kuvm81vNh8rO9PZ/dk0s3k8+nvOhXMOTS5/6pxNFEsjxkwxGaeGB0wUS2ivjX8/czqe9Mn9RfJZIM0kyWTHlDrzc1qtByeelPJtTj4mA4+zXSbnJzvTQ3GJpqfjR1e3b/vITI7T/jJzQn8qASWgBFZMQEMCrRioZqcElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACcwncE9POz+JHlUCSkAJKAEloASUgBL4gxCgUbFuSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBJSAEnhzAm/tLODNK6AFKAEloASUgBJQAkpACayMgBqsrAylZqQElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWwCAE1WFmEkqZRAkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASWBkBNVhZGUrNSAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSmARAmqwsgglTaMElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWwMgJqsLIylJqRElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUwCIE1GBlEUqaRgkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSmBlBNRgZWUoNSMloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSiBRQiowcoilDSNElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUwMoIqMHKylBqRkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAKLEFCDlUUoaRoloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSiBlRFQg5WVodSMlIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBBYhoAYri1DSNEpACSgBJaAElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAIrI6AGKytDqRkpASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSkAJLEJADVYWoaRplIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBFZGQA1WVoZSM1ICSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSkAJKAEloASUgBJYhIAarCxCSdMoASWgBJSAElACSkAJKAEloASUgBJQAkpACSgBJaAElIASUAJKQAkoASWgBJSAElACSkAJrIzA/wdKnGEJBfSDDwAAAABJRU5ErkJggg==)
# + id="0VfgNhh2spS5" colab_type="code" outputId="5571f1c6-9bbe-4c42-d611-e7d9f8562b58" colab={"base_uri": "https://localhost:8080/", "height": 275}
import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.externals import joblib
def extract_BoW_features(words_train, words_test, vocabulary_size=5000, cache_dir=cache_dir, cache_file="bow_features.pkl"):
"""Extract Bag-of-Words for a given set of documents, already preprocessed into words."""
# If cache_file is not None, try to read from it first
cache_data = None
if cache_file is not None:
try:
with open(os.path.join(cache_dir, cache_file), "rb") as f:
cache_data = joblib.load(f)
print("Read features from cache file:", cache_file)
except:
pass # unable to read from cache, but that's okay
# If cache is missing, then do the heavy lifting
if cache_data is None:
# Fit a vectorizer to training documents and use it to transform them
# NOTE: Training documents have already been preprocessed and tokenized into words;
# pass in dummy functions to skip those steps, e.g. preprocessor=lambda x: x
vectorizer = CountVectorizer(max_features=vocabulary_size, preprocessor=lambda x: x, tokenizer=lambda x: x) # already preprocessed
features_train = vectorizer.fit_transform(words_train).toarray()
# Apply the same vectorizer to transform the test documents (ignore unknown words)
features_test = vectorizer.transform(words_test).toarray()
# NOTE: Remember to convert the features using .toarray() for a compact representation
# Write to cache file for future runs (store vocabulary as well)
if cache_file is not None:
vocabulary = vectorizer.vocabulary_
cache_data = dict(features_train=features_train, features_test=features_test,
vocabulary=vocabulary)
with open(os.path.join(cache_dir, cache_file), "wb") as f:
joblib.dump(cache_data, f)
print("Wrote features to cache file:", cache_file)
else:
# Unpack data loaded from cache file
features_train, features_test, vocabulary = (cache_data['features_train'],
cache_data['features_test'], cache_data['vocabulary'])
# Return both the extracted features as well as the vocabulary
return features_train, features_test, vocabulary
# Extract Bag of Words features for both training and test datasets
features_train, features_test, vocabulary = extract_BoW_features(words_train, words_test)
# Inspect the vocabulary that was computed
print("Vocabulary: {} words".format(len(vocabulary)))
import random
print("Sample words: {}".format(random.sample(list(vocabulary.keys()), 8)))
# Sample
print("\n--- Preprocessed words ---")
print(words_train[5])
print("\n--- Bag-of-Words features ---")
print(features_train[5])
print("\n--- Label ---")
print(labels_train[5])
# + id="K2l8qoYG1WKp" colab_type="code" outputId="51bbccb4-eb47-459f-9b88-45bc080a55d5" colab={"base_uri": "https://localhost:8080/", "height": 279}
# Plot the BoW feature vector for a training document
plt.plot(features_train[5,:])
plt.xlabel('Word')
plt.ylabel('Count')
plt.show()
# + [markdown] id="20mIiXNO1x6j" colab_type="text"
# ### Zipf yasası
#
# [Zipf yasası](https://en.wikipedia.org/wiki/Zipf%27s_law), çok sayıda yazı içeren bir veri setinde, herhangi bir kelimenin sıklığının frekans tablosundaki sıralamasıyla ters orantılı olduğunu belirten bir yasadır. Bu yüzden, en sık kullanılan kelime, ikinci en sık kullanılan kelimeden yaklaşık iki kat, en sık kullanılan üçüncü kelimeden üç kat sayıda yer alacaktır.
# + id="EbRkuLA515Op" colab_type="code" outputId="c6c92c8f-38ec-42a7-f029-17a02b77a59a" colab={"base_uri": "https://localhost:8080/", "height": 283}
# Find number of occurrences for each word in the training set
word_freq = features_train.sum(axis=0)
# Sort it in descending order
sorted_word_freq = np.sort(word_freq)[::-1]
# Plot
plt.plot(sorted_word_freq)
plt.gca().set_xscale('log')
plt.gca().set_yscale('log')
plt.xlabel('Rank')
plt.ylabel('Number of occurrences')
plt.show()
# + [markdown] id="gQk2qP352Mzp" colab_type="text"
# ### Özellik(Feature) vektörlerini normalize etmek
#
# Bag-of-Words özellikleri, sadece kelime sayıları olduğu için anlaşılması kolaydır. Ancak, sayımlar çok değişkenlik gösterebilir ve öğrenme algoritmaları için iyi bir girdi olmayabilir. Bu yüzden, çok da ilerlemeden, BoW özellik vektörlerini normalize edelim.
#
# Bu şekilde her yazı içinde oranlanmış olacak ve uzun yazıların dominasyon etkisi olmayacaktır.
# + id="mLgM2E2i2Vh8" colab_type="code" colab={}
import sklearn.preprocessing as pr
# Normalize BoW features in training and test set
features_train = pr.normalize(features_train, axis=1)
features_test = pr.normalize(features_test, axis=1)
# + [markdown] id="RgnLnxDV2i26" colab_type="text"
# ## Adım 4: Bag of Words kullanarak Sınıflandırma
#
# Verilerin hepsi doğru bir şekilde dönüştürüldü şimdi bir sınıflandırıcıya aktarabiliriz. Temel bir model elde etmek için, scikit-learn'den (özellikle, [`GaussianNB`]) bir Naive Bayes sınıflandırıcı eğitiyoruz. (http://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.GaussianNB.html) ve test setindeki doğruluğunu değerlendiriyoruz.
#
#
# 
#
#
# 
#
#
#
# 
# + id="d4wHXRU_2qmJ" colab_type="code" outputId="02426e01-e5b6-414b-dd6a-7e4658d282f4" colab={"base_uri": "https://localhost:8080/", "height": 34}
from sklearn.naive_bayes import GaussianNB
# Gaussian Naive Bayes algoritmasını train ediyoruz
clf1 = GaussianNB()
clf1.fit(features_train, labels_train)
# Ortalama accuracy score'u hem train hem test verisi için hesaplıyoruz.
print("[{}] Accuracy: train = {}, test = {}".format(
clf1.__class__.__name__,
clf1.score(features_train, labels_train),
clf1.score(features_test, labels_test)))
# + [markdown] id="litxxnD63JNP" colab_type="text"
# ### Gradient-Boosted Decision Tree classifier - Karar Ağaçları
#
# Ağaç tabanlı algoritmalar, Bag of Words üzerinde oldukça iyi çalışır, kelimelerin süreksiz ve seyrek olmasından dolayı ağaç tabanlı algoritma yapısı ile güzel bir şekilde eşleşir. Şimdiki görevimiz, scikit-learn'ın Gradient-Boostted Decision Tree sınıflandırma algoritmasını kullanarak Naive Bayes sınıflandırıcısının performansını geliştirmeye çalışmak.
# BoW (Bag of Words) verilerini sınıflandırmak için, scikit-learn kütüphanesinden [`GradientBoostingClassifier`] (http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html) kullanıyoruz.
#
# 
# + id="46_RQIAT3fgU" colab_type="code" outputId="148ecd43-2dac-48ac-ce08-7c69661f3a10" colab={"base_uri": "https://localhost:8080/", "height": 34}
from sklearn.ensemble import GradientBoostingClassifier
n_estimators = 32
def classify_gboost(X_train, X_test, y_train, y_test):
# Classifier'ı initialize ediyoruz
clf = GradientBoostingClassifier(n_estimators=n_estimators, learning_rate=1.0, max_depth=1, random_state=0)
# GradientBoostingClassifier kullanarak train ediyoruz.
clf.fit(X_train, y_train)
# Train ve Test veri seti için başarı oranlarını print ediyoruz.
print("[{}] Accuracy: train = {}, test = {}".format(
clf.__class__.__name__,
clf.score(X_train, y_train),
clf.score(X_test, y_test)))
# Model'i return ediyoruz
return clf
clf2 = classify_gboost(features_train, features_test, labels_train, labels_test)
# + [markdown] id="uVQiZtIv4iZb" colab_type="text"
# ## Adım 5: RNN kullanarak Sınıflandırma
#
# Duygu analizi görevinin geleneksel bir makine öğrenme yaklaşımıyla nasıl çözülebileceğini gördük: BoW + doğrusal olmayan bir sınıflandırıcı. Şimdi Keras'ta duyarlılık analizi yapmak için Tekrarlayan Sinir Ağlarını(RNN) ve özellikle LSTM kullanacağız. [IMDB](https://keras.io/datasets/#imdb-movie-reviews-sentiment-classification) verisini ve aynı büyüklükteki sözlüğü kullanarak geliştireceğiz.
# + id="GpqZoSlj42ob" colab_type="code" outputId="d190b0ac-e9bd-4498-a9d6-baf75723d2b7" colab={"base_uri": "https://localhost:8080/", "height": 85}
from keras.datasets import imdb # import the built-in imdb dataset in Keras
# Set the vocabulary size
vocabulary_size = 5000
# Load in training and test data (note the difference in convention compared to scikit-learn)
(X_train, y_train), (X_test, y_test) = imdb.load_data(num_words=vocabulary_size)
print("Loaded dataset with {} training samples, {} test samples".format(len(X_train), len(X_test)))
# + id="bR-6Wntu5qj8" colab_type="code" outputId="1cd23861-a333-4eca-a65e-e81755042d4b" colab={"base_uri": "https://localhost:8080/", "height": 105}
# Inspect a sample review and its label
print("--- Review ---")
print(X_train[7])
print("--- Label ---")
print(y_train[7])
# + [markdown] id="TSpQWvL456Q6" colab_type="text"
# Kullanacağımız etiketler 0 için negatif, 1 için pozitif değeri içermektedir. İncelemenin(review) kendisi bir sayı dizisi olarak saklanır. Bunlar, bireysel kelimelere önceden atanmış kelime id'leridir. Onları tekrar orijinal kelimelerle eşlemek için `imdb.get_word_index ()` tarafından döndürülen sözlüğü kullanabilirsiniz.
# + id="DPXA7VJu5-_a" colab_type="code" outputId="99d37fef-2b95-4148-f09a-6a0a2060fbe0" colab={"base_uri": "https://localhost:8080/", "height": 139}
# Map word IDs back to words
word2id = imdb.get_word_index()
id2word = {i: word for word, i in word2id.items()}
print("--- Review (with words) ---")
print([id2word.get(i, " ") for i in X_train[7]])
print("--- Label ---")
print(y_train[7])
# + [markdown] id="wO55nJHN6fxk" colab_type="text"
# Bir belgedeki her bir kelimenin sayımını basitçe özetlediğimiz Bag of Words yaklaşımından farklı olarak, bu ifade temel olarak sözcük dizisinin tamamını (eksi noktalama, stopwords vb.) korur. Bu, RNN'lerin çalışması için kritiktir. Ama aynı zamanda şimdi özelliklerin(feature) farklı uzunluklarda olabileceği anlamına da geliyor!
#
# ### Pad sequences
#
# Bu verileri RNN'inize beslemek için tüm giriş belgelerinin aynı uzunlukta olması gerekir. Daha uzun incelemeleri keserek ve daha kısa incelemeleri boş bir değerle doldurarak (0) maksimum review uzunluğunu `max_words`'ile sınırlayalım. Bunu Keras'ta [`pad_sequences()`](https://keras.io/preprocessing/sequence/#pad_sequences) fonksiyonunu kullanarak kolayca yapabilirsiniz. Şimdilik, `max_words` ayarını 500’e ayarlayın.
# + id="fdDXYA5A6pQK" colab_type="code" colab={}
from keras.preprocessing import sequence
# Set the maximum number of words per document (for both training and testing)
max_words = 500
# Pad sequences in X_train and X_test
X_train = sequence.pad_sequences(X_train, maxlen=max_words)
X_test = sequence.pad_sequences(X_test, maxlen=max_words)
# + [markdown] id="Q6f_Lbbw7C5z" colab_type="text"
# ### Duygu Analizi için RNN Modeli Dizayn Etme
#
# Input değerimiz, maksimum uzunluk = `max_words` kelimelerinin bir dizisidir (teknik olarak, tamsayı kelime id'leri) ve output'umuz bir ikili duygu etiketidir (0 veya 1).
#
# Simple RNN: Gate yok
#
# Gated Recurrent Unit (GRU): Update gate bulunuyor. Memory bulunmuyor.
#
# Long Short Term Memory Unit (LSTM): Update, Forget ve Output gate bulunuyor.
#
# Daha fazla bilgi için:
# http://colah.github.io/posts/2015-08-Understanding-LSTMs/
#
# http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/
# + id="6AgaQPlY7Qrv" colab_type="code" outputId="5bed47e9-d99c-4e83-bcad-e26f03f4dfa4" colab={"base_uri": "https://localhost:8080/", "height": 394}
from keras.models import Sequential
from keras.layers import Embedding, LSTM, Dense, Dropout
# RNN model
embedding_size = 32
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_size, input_length=max_words))
model.add(LSTM(100))
model.add(Dense(1, activation='sigmoid'))
print(model.summary())
# + [markdown] id="cs0iYl3h8_kf" colab_type="text"
# ### Modelimizi Eğitelim ve Değerlendirelim
#
# Şimdi modelimizi eğitmeye hazırız. Keras dünyasında, öncelikle eğitim sırasında kullanmak istediğimiz loss fonksiyonunu ve optimizasyon fonksiyonunu ve ölçmek istediğimiz değerlendirme metriklerini belirterek modelinizi derlememiz gerekiyor.
# + id="4iLU7GtM9SVO" colab_type="code" outputId="f5285022-8259-4bd6-b5a2-e962b4234591" colab={"base_uri": "https://localhost:8080/", "height": 156}
# Compile our model, specifying a loss function, optimizer, and metrics
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# + [markdown] id="_XTTg7Xd9485" colab_type="text"
# Derlendikten sonra eğitim sürecini başlatabiliriz. Belirlememiz gereken iki önemli eğitim parametresi vardır - ** batch size ** ve ** toplam training adım sayısı(number of training epochs) **, model mimarimizle birlikte toplam eğitim süresini belirler.
#
# Eğitim biraz zaman alabilir! Mümkünse, bir GPU kullanmayı düşünün, çünkü tek bir antrenman CPU üzerinde birkaç saat sürebilir.
#
# > **İpucu**: Eğitim sırasında doğrulama(validation) için kullanılacak eğitim setinin küçük bir kısmını bölebiliriz. Bu, eğitim sürecini izlemeye ve potansiyel overfit tespit etmeye yardımcı olacaktır. `validation_data` parametresini kullanarak `model.fit()` olarak ayarlanmış bir doğrulama sağlayabilir veya Keras'ın bu amaçla bir kenara bırakması için eğitim verilerinin bir kısmını (genellikle% 5-10) yalnızca `validation_split` olarak belirtebiliriz. Doğrulama metrikleri, her dönemin sonunda bir kez değerlendirilir.
# + id="z8XlJwbU-PA0" colab_type="code" outputId="552fa56b-c899-4700-e6b7-dd3706e27cd1" colab={"base_uri": "https://localhost:8080/", "height": 445}
# Specify training parameters: batch size and number of epochs
batch_size = 64
num_epochs = 3
# Reserve/specify some training data for validation (not to be used for training)
X_valid, y_valid = X_train[:batch_size], y_train[:batch_size] # first batch_size samples
X_train2, y_train2 = X_train[batch_size:], y_train[batch_size:] # rest for training
# Train our model
model.fit(X_train2, y_train2, validation_data=(X_valid, y_valid), batch_size=batch_size, epochs=num_epochs)
# + id="ZSfNtCL1OyqI" colab_type="code" colab={}
import os
cache_dir = os.path.join("cache", "sentiment_analysis") # where to store cache files
os.makedirs(cache_dir, exist_ok=True) # ensure cache directory exists
# Save our model, so that we can quickly load it in future (and perhaps resume training)
model_file = "rnn_model.h5" # HDF5 file
model.save(os.path.join(cache_dir, model_file))
# Later we can load it using keras.models.load_model()
#from keras.models import load_model
#model = load_model(os.path.join(cache_dir, model_file))
# + [markdown] id="_8lDfyO8O86s" colab_type="text"
# Modelinizi geliştirdikten sonra, daha önce karşılaşılmayan test verilerinde ne kadar iyi performans gösterdiğini görme zamanı geldi.
#
#
# + id="igfDR9bCPFgu" colab_type="code" outputId="81db2108-cf30-4ab5-a138-48a5a4e36c51" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Evaluate our model on the test set
scores = model.evaluate(X_test, y_test, verbose=0) # returns loss and other metrics specified in model.compile()
print("Test accuracy:", scores[1]) # scores[1] should correspond to accuracy if you passed in metrics=['accuracy']
| 4,725,117 |
/Dataframes.ipynb
|
e934b85b5c1de8137f9d59640d06999ad99e4798
|
[] |
no_license
|
e10lee/Dataframes
|
https://github.com/e10lee/Dataframes
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 16,655 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="U3Yz3s2uio1F"
#
#
# **Q1-1**: Write a program that create a dataframe from the data.
#
# **Q1-2:** Select people that are psychologist or teacher and their number of cars is greater than their family size.
#
# **Q1-3:** Select people who have at most 2 family members and at least 1 car.
#
# **Q1-4:** Write a code that get number of unique jobs in this dataset.
#
#
#
#
# + id="yR8lcOtcjxXD"
import pandas as pd
data = {"name": ["Joseph", "Jacob", "Sam", "Jesee", "Ryan", "Lisa", "Lee"],
"job": ["teacher", "psychologist", "data scientist", "software developer", "psychologist", "psychologist", "teacher"],
"family_size": [3, 2, 1, 4, 2, 3, 2],
"num_cars": [3, 1, 1, 2, 2, 4, 1]}
# + id="Youi5qMaP34p" colab={"base_uri": "https://localhost:8080/"} outputId="67e3292d-3940-492e-afb0-98d66dc18336"
# Type your solution here
#Q1-1
frame = pd.DataFrame(data, columns = ["name", "job", "family_size", "num_cars"], index=["one", "two", "three", "four", "five", "six", "seven"])
print(frame)
# + id="mbzOjeYhx2nn" colab={"base_uri": "https://localhost:8080/", "height": 80} outputId="453502ac-9cd1-41f6-c0a8-d25eaf2e8486"
#Q1-2
frame[((frame["job"] == "teacher") | (frame["job"] == "psychologist")) & (frame["num_cars"] > frame["family_size"])]
# + id="wli5wqK1x9x2" colab={"base_uri": "https://localhost:8080/", "height": 173} outputId="fac483ef-c36c-4fd6-b78e-c3f2ef315083"
#Q1-3
frame[(frame["family_size"] <= 2) & (frame["num_cars"] >= 1)]
# + id="pRJMXnoTyA15" colab={"base_uri": "https://localhost:8080/"} outputId="4f1a5e60-15cc-484c-b6e9-370d21d8ad3e"
#Q1-4
result = pd.value_counts(data["job"])
print(result)
# + [markdown] id="Ow6nG8k4l91X"
# **Q2. Lets consider you have two series like the below cell. Compute the mean of weights of each fruit.**
# + id="u-X_DoOzVLLB"
import numpy as np
fruit = pd.Series(np.random.choice(['apple', 'banana', 'carrot'], 10))
weights = pd.Series(np.linspace(1, 10, 10))
# + id="S419nzYnpU__" colab={"base_uri": "https://localhost:8080/"} outputId="3a6817ec-3c1c-40ea-936a-f8b78fb19c17"
# Type your solution here
results = weights.groupby(fruit).mean()
print(results)
# + [markdown] id="g4lKaPIhtVrt"
# **Q3. Consider the below course_name array:**
#
# **Q3-1**: Write a NumPy program to get the indices of the sorted elements of **course_name** array.
#
# **Q3-2:** Write numpy code to check whether each element of **course_name** array starts with "P".
#
# + id="RUP_jp2KtVrx"
import numpy as np
course_name = np.array(['Python', 'JS', 'examples', 'PHP', 'html'])
# + id="U1i27POxv-o_" colab={"base_uri": "https://localhost:8080/"} outputId="105d99a2-0928-4b1e-97d4-4879d8bd47f5"
# Type your solution here
#Q3-1
indice = np.argsort(course_name)
print(indice)
# + id="TDEJJQtQMH7V" colab={"base_uri": "https://localhost:8080/"} outputId="0a780954-da26-42cc-fd4c-588263225337"
Pstart = np.char.startswith(course_name, "P")
print(Pstart)
# + [markdown] id="sUFItNFOxwkz"
# **Q4. Consider the below student_id array:**
#
# **Q4-1:** Reverse the **student_id** array. Print both original and reversed array.
#
# **Q4-2:** Get the 3-largest values of **student_id** array.
# + id="Rl5qzEjFv0nw" colab={"base_uri": "https://localhost:8080/"} outputId="3465fdf2-bb48-4144-a659-4812de23c8c0"
import numpy as np
#Q4-1
student_id = np.array([1023, 5202, 6230, 1671, 1682, 5241, 4532])
student_id2 = student_id[::-1]
print(student_id)
print(student_id2)
# + id="EetvHGrUxMCC" colab={"base_uri": "https://localhost:8080/"} outputId="65c557bd-f05f-41b5-8e71-0bba6e2bddfe"
# Type your solution here
#Q4-2
sort = np.argsort(student_id)
result = [student_id[sort][-3:]]
print(result)
# + [markdown] id="uKRyDVuW6B19"
# # **Q5: Write a numpy program to print sum of all the multiples of 3 or 5 below 100**
# + id="ZIixq1gz6OK3" colab={"base_uri": "https://localhost:8080/"} outputId="92e49bc9-9a85-46da-935d-84621cd8e34e"
# Type your solution here
# Hint: you can use arange to start off
range = np.arange(1, 100)
multiple = range[(range % 3 == 0) | (range % 5 == 0)]
print(multiple[:1000])
print(multiple.sum())
# + [markdown] id="2CWJOsP24c34"
# **Q6. Consider the below array.**
#
# Q6.1. Write a code to swap column 1 with column 2.
#
# Q6.2. Write a code to swap row 0 with row 1.
# + id="3OG6X5Eg5KSM" colab={"base_uri": "https://localhost:8080/"} outputId="8a66c6e2-f5f2-46e7-dc52-115509391296"
import numpy as np
arr = np.arange(12).reshape(3,4)
arr[:, [1, 0]] = arr[:, [0, 1]]
print(arr)
# + id="Q-Q91DpO5YYW" colab={"base_uri": "https://localhost:8080/"} outputId="a17e754e-4f58-4fc5-cbbf-c05621901e1b"
# Type your solution here
arr = np.arange(12).reshape(3,4)
arr[[1,0],:] = arr[[0,1],: ]
print(arr)
| 4,952 |
/Untitled.ipynb
|
dec5b4926ca931754e771bbc82a18ab34fcde452
|
[] |
no_license
|
piggy2303/chatbot_spech_to_text
|
https://github.com/piggy2303/chatbot_spech_to_text
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 1,028 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
print("hello")
mport fileinput
# +
### data from both ksin and ppin
inp = fileinput.FileInput('input/kinases_human.txt')
pkin = []
for line in inp:
pkin.append(line.split('\n')[0])
d = {}
df = pd.read_csv('input/ksin.csv')
for k, s in zip(df.iloc[:, 0], df.iloc[:, 5]):
if k not in d:
d[k] = {s}
else:
d[k].add(s)
df1 = pd.read_csv('input/ppin.csv')
for p1, p2 in zip(df1.iloc[:, 0], df1.iloc[:, 5]):
if p1 in pkin:
if p1 not in d:
d[p1] = {p2}
else:
d[p1].add(p2)
if p2 in pkin:
if p2 not in d:
d[p2] = {p1}
else:
d[p2].add(p1)
allnp = open('output_cheng_all_human.gmt', 'w+')
fnp = open('output_cheng_fourplusinteractions_human.gmt', 'w+')
uSubs = set()
numKSI = 0
numKins = 0
for k in d:
temp = set()
for x in d[k]:
if x != x:
temp.add(k)
else:
temp.add(x)
allnp.write('{0}_cheng_human\t'.format(k) + '\t'.join(temp) + '\n')
if len(temp) >= 4:
numKSI += len(temp)
numKins += 1
{uSubs.add(x) for x in temp}
fnp.write('{0}_cheng_human\t'.format(k) + '\t'.join(temp) + '\n')
print('{0}\t#kins: {1}\t#ksi: {2}\t#usubs: {3}'.format('human', numKins, numKSI, len(uSubs)))
allnp.close()
fnp.close()
# -
x = [k for k in d if k not in pkin] ## 138 kinases in ksin that aren't defined in pkin
#print(x)
| 1,742 |
/chapter_13/01_fid_numpy.ipynb
|
a14e552dd995e108c48915fe2eff55790dddd373
|
[] |
no_license
|
fenago/generative-adversarial-networks
|
https://github.com/fenago/generative-adversarial-networks
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 2,482 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# example of calculating the frechet inception distance
import numpy
from numpy import cov
from numpy import trace
from numpy import iscomplexobj
from numpy.random import random
from scipy.linalg import sqrtm
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
import warnings
warnings.simplefilter("ignore")
# calculate frechet inception distance
def calculate_fid(act1, act2):
# calculate mean and covariance statistics
mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False)
mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False)
# calculate sum squared difference between means
ssdiff = numpy.sum((mu1 - mu2)**2.0)
# calculate sqrt of product between cov
covmean = sqrtm(sigma1.dot(sigma2))
# check and correct imaginary numbers from sqrt
if iscomplexobj(covmean):
covmean = covmean.real
# calculate score
fid = ssdiff + trace(sigma1 + sigma2 - 2.0 * covmean)
return fid
# define two collections of activations
act1 = random(10*2048)
act1 = act1.reshape((10,2048))
act2 = random(10*2048)
act2 = act2.reshape((10,2048))
# fid between act1 and act1
fid = calculate_fid(act1, act1)
print('FID (same): %.3f' % fid)
# fid between act1 and act2
fid = calculate_fid(act1, act2)
print('FID (different): %.3f' % fid)
| 1,501 |
/.ipynb_checkpoints/Covid_county_analysis_BARCHART-checkpoint.ipynb
|
289cd3abb71ac87fb2544f4b42f23525780c0b3f
|
[] |
no_license
|
alexF3/covidDeathRateBarChart_nov
|
https://github.com/alexF3/covidDeathRateBarChart_nov
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 186,188 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ###### Analysis of Covid-19 death rates at the county level
#
#
# # BLUF (bottom line up front):
# # In November, Covid has made it more deadly to live in more than 600 counties in the US than it was to deploy to Iraq and Afghanistan during the deadliest year of those wars.
#
# ### Let's compare the rate of Covid-19 deaths in various geography to historical death rates by other causes. This will help establish a more intuitive sense of "risk" that is easier to communicate to a general audience.
#
# ### Let's establish the mortality rate for troops deployed to Iraq and Afghanistan during the deadliest years of those wars
#
# ### The commonly used metric for mortality statistics is "deaths per hundred thousand population per year." We'll use data from Statista and a 2018 RAND report to establish a measurement of "deaths per hundred-thousand-deployed-troop-years" for each year.
#
# ### That's a bit of a mouthful...we're summing all of the time spent deployed to the wars by all troops in a year ('hundred thousand troop-years') for each of the years 2001 through 2015.
#
# ### https://www.statista.com/statistics/263798/american-soldiers-killed-in-iraq/
# ### https://www.statista.com/statistics/262894/western-coalition-soldiers-killed-in-afghanistan/
# ### https://www.rand.org/pubs/research_reports/RR1928.html?adbsc=social_20180320_2212921&adbid=975928167633334272&adbpl=tw&adbpr=22545453
# # First, let's walk through the methodology and check it against the Johns Hopkins Covid-19 tracker page
from IPython.core.display import Image, display
import os
display(Image(os.getcwd()+'/math explainer/math explainer.002.jpeg'))
display(Image(os.getcwd()+'/math explainer/math explainer.003.jpeg'))
display(Image(os.getcwd()+'/math explainer/math explainer.004.jpeg'))
# # Change to monthly data
361.4*(30/365)
# # Load libraries and prep for analysis
# +
import os
import wget
import pandas as pd
import geopandas as gpd
import shapely
from shapely.geometry import shape
from shapely.ops import cascaded_union
import numpy as np
import geopy.distance
import shapely
import matplotlib.pyplot as plt
import matplotlib.ticker as mtick
from shapely.geometry import Point
import json
import datetime as dt
# -
# # Load summary of deployment and mortality data from Rand and Statista
warDeaths = pd.read_csv(os.getcwd()+'/data/iraqAfghanWarDeathRates.csv')
warDeaths
# convert deployed years colum from string to float
warDeaths.troop_years_deployed = warDeaths.troop_years_deployed.str.replace(',','').astype(float)
# Check the math for 2007:
100000*((904+117)/282546)
# # Make 2018 MONTHLY rate of death by cause
# ### US 2018 population: http://www2.census.gov/programs-surveys/popest/tables/2010-2018/national/totals/na-est2018-01.xlsx
# ### US 2018 deaths: https://www.cdc.gov/nchs/fastats/deaths.htm
# ### US 2018 traffic deaths: https://crashstats.nhtsa.dot.gov/Api/Public/ViewPublication/812826
usPop2018 = 328082386
usDeathTypes = pd.read_csv(os.getcwd()+'/data/cdc_us2018_deathCounts.csv')
trafficDeaths = pd.DataFrame({'cause':['traffic death'],'deaths':[36560]})
usDeathTypes = pd.concat([usDeathTypes,trafficDeaths])
usDeathTypes['deathRate'] = round((30/365)*100000* usDeathTypes.deaths/usPop2018,1)
usDeathTypes
# ### The deadliest year in the combined war data was 2007 at __361 fatalities per 100,000 troop-years__
# # Load the latest Covid data from JHU Github
# +
fpData = os.getcwd()+'/data/'
## Get daily update of hopkins time series file for confirmed US cases
wget.download('https://github.com/CSSEGISandData/COVID-19/raw/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_US.csv',\
out = fpData +'covid_hopkins_overTime_CONFIRMED.csv')
## if file saves as a ____(01).csv, delete the old file and rename new to "covid_hopkins_overTime_CONFIRMED.csv"
if os.path.exists(fpData + "covid_hopkins_overTime_CONFIRMED (1).csv"):
os.remove(fpData + "covid_hopkins_overTime_CONFIRMED.csv")
os.rename(fpData + "covid_hopkins_overTime_CONFIRMED (1).csv",fpData + "covid_hopkins_overTime_CONFIRMED.csv")
# -
fpData = os.getcwd()+'/data/'
## Get daily update of hopkins time series file for confirmed US cases
wget.download('https://github.com/CSSEGISandData/COVID-19/raw/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_US.csv',\
out = fpData +'covid_hopkins_overTime_DEATHS.csv')
## if file saves as a ____(01).csv, delete the old file and rename new to "covid_hopkins_overTime_CONFIRMED.csv"
if os.path.exists(fpData + "covid_hopkins_overTime_DEATHS (1).csv"):
os.remove(fpData + "covid_hopkins_overTime_DEATHS.csv")
os.rename(fpData + "covid_hopkins_overTime_DEATHS (1).csv",fpData + "covid_hopkins_overTime_DEATHS.csv")
# +
# Read in new US Confirmed Timeseries data
fpData = os.getcwd()+'/data/'
covidData = pd.read_csv(fpData +'covid_hopkins_overTime_CONFIRMED.csv',dtype={'FIPS':str})
covidData.FIPS = covidData.FIPS.str.split('.').str[0].str.zfill(5)
covidDeaths = pd.read_csv(fpData +'covid_hopkins_overTime_DEATHS.csv',dtype={'FIPS':str})
covidDeaths.FIPS = covidDeaths.FIPS.str.split('.').str[0].str.zfill(5)
# collect dates from timeseries file
dates = []
for i in covidData.columns:
if '/' in i:
dates.append(i)
fipsList = covidData[~covidData.FIPS.isnull()].FIPS.unique().tolist()
# -
countyPops = pd.read_csv('/Users/alex/Documents/Compare Hopkins and NYT/co-est2019-alldata.csv',encoding='Latin1',\
dtype={'STATE':str,'COUNTY':str})
countyPops['fips'] = countyPops.STATE + countyPops.COUNTY
countyPops = countyPops[countyPops.COUNTY!='000']
covidData = pd.merge(covidData,countyPops[['fips','POPESTIMATE2019']],left_on='FIPS',right_on='fips',how='left')
covidDeaths = pd.merge(covidDeaths,countyPops[['fips','POPESTIMATE2019']],left_on='FIPS',right_on='fips',how='left')
dates = []
for i in covidDeaths.columns:
if '/' in i:
dates.append(i)
covidDeaths.head()
# # Make comparative rate bar charts
# ### dataframe of annual rates of death in the US from most recent year available
warDeaths
warDeaths.deathsPerHunKyr.max()*(30/365)
# Data: https://www.statista.com/statistics/248622/rates-of-leading-causes-of-death-in-the-us/
# https://crashstats.nhtsa.dot.gov/Api/Public/ViewPublication/812826
{'traffic accident':11.2,'suicide':14.2,'influenza/pneumonia':14.9,\
'cancer':141.9,'heart disease':163.6,'Worst annual Iraq/Afghanistan losses':361.4}
# formatting names for vis later (endlines give spacing off x axis)
df = pd.DataFrame({'cause':['\nUS\ntraffic accident\n(2018)','\nUS\nsuicide\n(2018)','\nUS\ninfluenza/\npneumonia\n(2018)','\nUS\ncancer\n(2018)','\nUS\nheart\ndisease\n(2018)','\ndeployed troops\nworst year of \nIraq/Afghanistan\n(2007)'],\
'monthlyDeathRate':[usDeathTypes[usDeathTypes.cause=='traffic death'].deathRate.item(),\
usDeathTypes[usDeathTypes.cause=='suicide'].deathRate.item(),\
usDeathTypes[usDeathTypes.cause=='flu_pneumonia'].deathRate.item(),\
usDeathTypes[usDeathTypes.cause=='cancer'].deathRate.item(),\
usDeathTypes[usDeathTypes.cause=='heart disease'].deathRate.item(),\
round(warDeaths.deathsPerHunKyr.max()*(30/365),1)]})
df
# ## So: an average month in the deadliest year of the wars in Iraq and Afghanistan had a mortality rate of 29.7 deaths per 100,000 troops
# endDate = dates[-1]
endDate = '11/30/20'
dateTimeEndDay = dt.datetime.strptime(endDate,'%m/%d/%y')
dateTimeBeginDay = dateTimeEndDay - dt.timedelta(days=30)
beginDate = dt.datetime.strftime(dateTimeBeginDay,'%-m/%-d/%y')
print('endDate:{}'.format(endDate))
print('beginDate:{}'.format(beginDate))
# +
# Calculate death rate in the last 30 days in the
# states of ND, SD, MT combined
stateDeathRate = covidDeaths[['Admin2','Province_State',beginDate,endDate,'POPESTIMATE2019']]
stateDeathRate.head()
# -
# Check population sums
stateDeathRate[stateDeathRate.Province_State=='Montana'].POPESTIMATE2019.sum()
# +
# This checks withe the US Census 2019 population of Montana
# https://www.census.gov/quickfacts/MT
# 1,068,778
# +
stateDeathRate['30dayDeaths'] = stateDeathRate[endDate] - stateDeathRate[beginDate]
# -
mtDeaths = stateDeathRate[stateDeathRate.Province_State=='Montana']['30dayDeaths'].sum()
mtPop = stateDeathRate[stateDeathRate.Province_State=='Montana'].POPESTIMATE2019.sum()
mt30dayDeathRate = 100000*(mtDeaths/mtPop)
mt30dayDeathRate
stateDeathRate = pd.DataFrame(stateDeathRate.groupby('Province_State')[['30dayDeaths','POPESTIMATE2019']].sum()).reset_index()
stateDeathRate['30dayDeathRate'] = round(100000*(stateDeathRate['30dayDeaths']/stateDeathRate['POPESTIMATE2019']),1)
stateDeathRate = stateDeathRate[(~stateDeathRate['30dayDeathRate'].isnull())&(stateDeathRate.POPESTIMATE2019>0)]
stateDeathRate.sort_values('30dayDeathRate',ascending=False)
# ### Look at national covid death rate over the 30 day window
stateDeathRate.POPESTIMATE2019.sum()
national30dayDeathRate = 100000*stateDeathRate['30dayDeaths'].sum()/stateDeathRate.POPESTIMATE2019.sum()
national30dayDeathRate
usDeathRate = round(100000*(covidDeaths[endDate].sum() - covidDeaths[beginDate].sum())/covidDeaths.POPESTIMATE2019.sum(),1)
usDeathRate
# +
df = pd.concat([df[:3],pd.DataFrame({'cause':['\nUS\nCovid'],\
'monthlyDeathRate':[usDeathRate]}),
df[3:]])
# -
df
# ## North Dakota and South Dakota had higher Covid-19 death rates in November than an average month in the dealiest year of Iraq and Afghanistan (which was 29.7 fatalities per 100,000 deployed troops per month)
# +
df = df[df.cause!=''] # remove placehoders
dg = pd.DataFrame({'cause':['\nND\nCovid','\nSD\nCovid'],\
'monthlyDeathRate':\
[stateDeathRate[stateDeathRate.Province_State=='North Dakota']['30dayDeathRate'].item(),\
stateDeathRate[stateDeathRate.Province_State=='South Dakota']['30dayDeathRate'].item(),\
]})
df = pd.concat([df,dg])
df
# -
my_colors = ['#968c81','#968c81','#968c81','#cc1212','#968c81','#968c81','#968c81','#cc1212','#cc1212','#cc1212']
# +
fig, ax = plt.subplots(1, figsize=(30, 10))# remove the axis
ax = df.plot.bar(ax=ax,x='cause',y='monthlyDeathRate',rot=0,ylim=((0,100)),fontsize=20,legend=False,color=my_colors)
plt.title('\nDeath Rates (per hundred thousand people per month)\n', fontsize=40)
ax.tick_params(axis='x', which='both', labelsize=25)
ax.get_yaxis().set_major_formatter(
mtick.FuncFormatter(lambda x, p: format(int(x), ',')))
for p in ax.patches:
ax.annotate(str(p.get_height()), (p.get_x() + .07, p.get_height() +3),fontsize=30)
# plt.axis('off')
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.set(yticklabels=[])
ax.set(ylabel=None) # remove the y-axis label
ax.tick_params(left=False) # remove the ticks
ax.set(xlabel=None) # remove the x-axis label
ax.annotate('Data: Johns Hopkins CSSE, NHTSA, CDC', xy=(0.76, .01), xycoords='figure fraction', fontsize=17, color='#555555')
filename = os.getcwd()+ '/deathRateBarChart_NationalWithStates.png'
plt.savefig(filename,dpi=300,bbox_inches="tight",facecolor='white')
barsList = [filename]
# -
| 11,631 |
/SVM, DT and RF.ipynb
|
0dd6575ca6fb03af2b21c5b53804cbd25c7e0fe8
|
[] |
no_license
|
nishchalgpt/powergrid-stock-research
|
https://github.com/nishchalgpt/powergrid-stock-research
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 301,687 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# ## Coursera Assignment: Linear Regression
# +
from __future__ import division, print_function
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Creates a table data structure which is easy to manipulate
df = pd.read_csv("machine_learning_andrewng/ex1data1.csv", header=None)
df.rename(columns={0: 'population', 1: 'profit'}, inplace=True)
df.head()
# -
# visualising the data
fig = plt.figure(num=None, figsize=(12, 8), dpi=80, facecolor='w')
plt.scatter(df['population'], df['profit'], marker='x', color='red', s=20)
plt.xlim([4, 24])
plt.xticks(range(4, 26, 2))
plt.yticks(range(-5, 30, 5))
plt.xlabel("Population in 10,000")
plt.ylabel("Profit in $10,000")
plt.title("Scatter plot of training data\n")
plt.show()
class LinearRegression(object):
"""Performs Linear Regression using Batch Gradient
Descent."""
def __init__(self, X, y, alpha=0.01, n_iterations=5000):
"""Initialise variables.
Parameters
----------
y : numpy array like, output / dependent variable
X : numpy array like, input / independent variables
alpha : float, int. Learning Rate
n_iterations : Number of maximum iterations to perform
gradient descent
"""
self.y = y
self.X = self._hstack_one(X)
self.thetas = np.zeros((self.X.shape[1], 1))
self.n_rows = self.X.shape[0]
self.alpha = alpha
self.n_iterations = n_iterations
print("Cost before fitting: {0:.2f}".format(self.cost()))
@staticmethod
def _hstack_one(input_matrix):
"""Horizontally stack a column of ones for the coefficients
of the bias terms
Parameters
----------
input_matrix: numpy array like (N x M). Where N = number of
examples. M = Number of features.
Returns
-------
numpy array with stacked column of ones (N x M + 1)
"""
return np.hstack((np.ones((input_matrix.shape[0], 1)),
input_matrix))
def cost(self, ):
"""Calculates the cost of current configuration"""
return (1 / (2 * self.n_rows)) * np.sum(
(self.X.dot(self.thetas) - self.y) ** 2)
def predict(self, new_X):
"""Predict values using current configuration
Parameters
----------
new_X : numpy array like
"""
new_X = self._hstack_one(new_X)
return new_X.dot(self.thetas)
def batch_gradient(self, ):
h = self.X.dot(self.thetas) - self.y
h = np.multiply(self.X, h)
h = np.sum(h, axis=0)
return h.reshape(-1, 1)
def batch_gradient_descent(self, ):
alpha_by_m = self.alpha / self.n_rows
for i in range(self.n_iterations):
self.thetas = self.thetas - (alpha_by_m * self.batch_gradient())
cost = self.cost()
print("Iteration: {0} Loss: {1:.5f}\r".format(i + 1, cost), end="")
X = df['population'].values.reshape(-1, 1)
y = df['profit'].values.reshape(-1, 1)
lr = LinearRegression(X, y)
lr.batch_gradient_descent()
# plot regression line
X = np.arange(4, 24, 0.1).reshape(-1, 1)
fig = plt.figure(num=None, figsize=(12, 8), dpi=80, facecolor='w')
plt.scatter(df['population'], df['profit'], marker='x', color='red', s=20, label='Training data')
plt.plot(X, lr.predict(X), color='blue', label='Linear Regression')
plt.xlim([4, 24])
plt.xticks(range(4, 26, 2))
plt.yticks(range(-5, 30, 5))
plt.xlabel("Population in 10,000")
plt.ylabel("Profit in $10,000")
plt.title("Scatter plot of training data\n")
plt.legend()
plt.show()
# +
def cost(theta_0, theta_1):
"""Calculate the cost with given weights
Parameters
----------
theta_0 : numpy array like, weights dim 0
theta_1 : numpy array like, weights dim 1
Returns
-------
float, cost
"""
X = df['population'].values
y = df['profit'].values
X = X.reshape(-1, 1)
y = y.reshape(-1, 1)
X = np.hstack((np.ones((X.shape[0], 1)), X))
n_rows = X.shape[0]
thetas = np.array([theta_0, theta_1]).reshape(-1, 1)
return (1/(2*n_rows)) * sum((X.dot(thetas) - y)**2)[0]
def prepare_cost_matrix(theta0_matrix, theta1_matrix):
"""Prepares cost matrix for various weights to
create a 3D representation of cost. Every value
in the cost matrix represents the cost for theta
values in the theta matrices.
Parameters
----------
theta0_matrix : numpy array like, weights dim 0
theta1_matrix : numpy array like, weights dim 1
"""
J_matrix = np.zeros(theta0_matrix.shape)
row, col = theta0_matrix.shape
for x in range(row):
for y in range(col):
J_matrix[x][y] = cost(theta0_matrix[x][y], theta1_matrix[x][y])
return J_matrix
theta_0 = np.arange(-5, 1, 0.01)
theta_1 = np.arange(0.6, 1.2, 0.001)
theta_0, theta_1 = np.meshgrid(theta_0, theta_1)
J_matrix = prepare_cost_matrix(theta_1, theta_0)
# +
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
fig = plt.figure(num=None, figsize=(12, 8), dpi=80, facecolor='w')
ax = fig.gca(projection='3d')
surf = ax.plot_surface(theta_0, theta_1, J_matrix, cmap=cm.coolwarm,)
ax.zaxis.set_major_locator(LinearLocator(10))
ax.set_xlabel("theta0")
ax.set_ylabel("theta1")
ax.set_zlabel("J(theta)")
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.title("3D plot for theta0, theta1, and the cost function\n")
plt.show()
# -
# ## Linear Regression with multiple variables
#
df = pd.read_csv("machine_learning_andrewng/ex1data2.csv", header=None)
df.head()
X = df.iloc[:, [0, 1]].values
y = df.iloc[:, [2]].values
# +
from sklearn.preprocessing import StandardScaler
scaler_X = StandardScaler()
scaler_Y = StandardScaler()
X = scaler_X.fit_transform(X)
y = scaler_Y.fit_transform(y)
# -
lr = LinearRegression(X, y, alpha=0.1, n_iterations=1000)
lr.batch_gradient_descent()
X_test = np.array([2104, 3]).reshape(1, 2)
print("Testing on : {0}".format(X_test[0]))
X_test = scaler_X.transform(X_test)
prediction = lr.predict(X_test)
print("Prediction(Scaled): {0:.2f}".format(prediction[0][0]))
print("Prediction(Unscaled): {0:.2f}".format(scaler_Y.inverse_transform(prediction)[0][0]))
197536]['X'], cities.iloc[197536]['Y']))
ax.scatter(cities.loc[(cities.clusters == 141)]['X'], cities.loc[(cities.clusters == 141)]['Y'])
# +
from sklearn.neighbors import NearestNeighbors
startlist=[0]
neigh = NearestNeighbors(n_neighbors=1, n_jobs=-1)
# -
neigh
submission_df.head()
cities.iloc[47239]
import hvplot.pandas
import colorcet as cc
allpoints = cities.hvplot.scatter('X', 'Y', width=380, height=350, #datashade=True,
title='All Cities')
colors = list(reversed(cc.kbc))
primedensity = cities[cities.is_prime].hvplot.hexbin(x='X', y='Y', width=420, height=350,
cmap=colors, title='Density of Prime Cities').options(size_index='Count',
min_scale=0.8, max_scale=0.95)
allpoints + primedensity
# +
from sklearn.mixture import GaussianMixture
mclusterer = GaussianMixture(n_components=250, tol=0.01, random_state=66, verbose=1)
cities['mclust'] = mclusterer.fit_predict(cities[['X', 'Y']].values)
nmax = cities.mclust.max()
print("{} clusters".format(nmax+1))
# +
#histo = cities.hvplot.hist('mclust', ylim=(0,14000), color='tan')
# custcolor = cc.rainbow + cc.rainbow
# gausses = cities.hvplot.scatter('X', 'Y', by='mclust', size=5, width=500, height=450,
# # datashade=True,
# dynspread=True, cmap=custcolor)
# display(histo, gausses)
# -
centers = cities.groupby('mclust')['X', 'Y'].agg('mean').reset_index()
# +
from scipy.spatial.distance import pdist, squareform
from ortools.constraint_solver import pywrapcp
from ortools.constraint_solver import routing_enums_pb2
#%% functions
def create_mat(df):
print("building matrix")
mat = pdist(locations)
return squareform(mat)
def create_distance_callback(dist_matrix):
def distance_callback(from_node, to_node):
return int(dist_matrix[from_node][to_node])
return distance_callback
status_dict = {0: 'ROUTING_NOT_SOLVED',
1: 'ROUTING_SUCCESS',
2: 'ROUTING_FAIL',
3: 'ROUTING_FAIL_TIMEOUT',
4: 'ROUTING_INVALID'}
def optimize(df, startnode=None, stopnode=None, fixed=False):
num_nodes = df.shape[0]
mat = create_mat(df)
dist_callback = create_distance_callback(mat)
search_parameters = pywrapcp.RoutingModel.DefaultSearchParameters()
# search_parameters.time_limit_ms = int(1000*60*numminutes)
search_parameters.solution_limit = num_iters
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.LOCAL_CHEAPEST_INSERTION)
search_parameters.local_search_metaheuristic = (
routing_enums_pb2.LocalSearchMetaheuristic.GUIDED_LOCAL_SEARCH)
if fixed:
routemodel = pywrapcp.RoutingModel(num_nodes, 1, [startnode], [stopnode])
else:
routemodel = pywrapcp.RoutingModel(num_nodes, 1, startnode)
routemodel.SetArcCostEvaluatorOfAllVehicles(dist_callback)
print("optimizing {} cities".format(num_nodes))
assignment = routemodel.SolveWithParameters(search_parameters)
print("status: ", status_dict.get(routemodel.status()))
print("travel distance: ", str(assignment.ObjectiveValue()), "\n")
return routemodel, assignment
def get_route(df, startnode, stopnode, fixed):
routemodel, assignment = optimize(df, int(startnode), int(stopnode), fixed)
route_number = 0
node = routemodel.Start(route_number)
route = []
while not routemodel.IsEnd(node):
route.append(node)
node = assignment.Value(routemodel.NextVar(node))
return route
# +
# %%time
#%% parameters
num_iters=100
# main
nnode = int(cities.loc[0, 'mclust'])
locations = centers[['X', 'Y']].values
segment = get_route(locations, nnode, 0, fixed=False)
# -
opoints = centers.loc[segment]
opoints.reset_index(drop=True, inplace=True) #recall ordered points
cities['clustorder'] = cities.groupby('mclust').cumcount()
# +
from sklearn.neighbors import NearestNeighbors
startlist=[0]
neigh = NearestNeighbors(n_neighbors=1, n_jobs=-1)
for i,m in enumerate(opoints.mclust[1:], 0):
neigh.fit(cities.loc[cities.mclust == m, ['X', 'Y']].values)
lastcenter = opoints.loc[i, ['X', 'Y']].values.reshape(1, -1)
closestart = neigh.kneighbors(lastcenter, return_distance=False)
start = cities.index[(cities.mclust == m) & (cities.clustorder == closestart.item())].values[0]
startlist.append(start)
opoints['startpt'] = startlist
# +
stoplist = []
for i,m in enumerate(opoints.mclust, 1):
neigh.fit(cities.loc[cities.mclust == m, ['X', 'Y']].values)
if m != opoints.mclust.values[-1]:
nextstartnode = opoints.loc[i, 'startpt']
else:
nextstartnode = 0
nextstart = cities.loc[nextstartnode, ['X', 'Y']].values.reshape(1, -1)
closestop = neigh.kneighbors(nextstart, return_distance=False)
stop = cities.index[(cities.mclust == m) & (cities.clustorder == closestop.item())].values[0]
stoplist.append(stop)
opoints['stoppt'] = stoplist
display(cities.head(), opoints.head())
# -
coords = cities.loc[opoints.stoppt, ['X', 'Y', 'mclust']]
# +
# %%time
num_iters = 100
seglist = []
total_clusts = cities.shape[0]
for i,m in enumerate(opoints.mclust):
district = cities[cities.mclust == m]
print("begin cluster {}, {} of {}".format(m, i, opoints.shape[0]-1))
clstart = opoints.loc[i, 'startpt']
nnode = district.loc[clstart, 'clustorder']
clstop = opoints.loc[i, 'stoppt']
pnode = district.loc[clstop, 'clustorder']
locations = district[['X', 'Y']].values
segnodes = get_route(locations, nnode, pnode, fixed=False) #output is type list
ord_district = district.iloc[segnodes]
segment = ord_district.index.tolist()
seglist.append(segment)
seglist.append([0])
path = np.concatenate(seglist)
# -
path = pd.DataFrame({'Path': path})
path.to_csv('submission_JM.csv', index=False)
path['is_prime'] = submission_df.Path.apply(is_prime)
primes = submission_df.loc[submission_df.is_prime == True]
non_primes = submission_df.loc[submission_df.is_prime == False]
non_prime_lst = list(non_primes.sort_index(ascending = False)['Path'])
prime_lst = list(primes.sort_index(ascending = False)['Path'])
prime_path = []
for i in log_progress(range(0, len(path))):
if i % 10 == 0 and len(prime_lst) > 0 and i != 0:
prime_path.append(prime_lst.pop())
else:
prime_path.append(non_prime_lst.pop())
prime_path_df = pd.DataFrame({'Path': prime_path})
prime_path_df.to_csv('submission_JM_prime.csv', index=False)
e
from Utilities.utils import gridsearch
model = DecisionTreeClassifier() # Our model
param_grid = {"max_depth": np.arange(2,8,1), # Maximum depth of tree
"max_features": np.arange(3,8,1), # Number of features to consider when looking for the best split
"max_leaf_nodes": np.arange(4,27,1), # Maximum number of leaves in our tree.
"criterion": ["gini", "entropy"], # Splitting criteria
"class_weight": [None, 'balanced',{0: 1.105, 1: 1.15}] # Weights associated with classes.
}
metric = roc_auc_score # Metric to use
tiebreaker = zero_one_loss # Tie breaker metric.
n_best_grids = 10 # 5 best grids
best_score, best_grid, tiebreaker = gridsearch(model, x_train, y_train, x_val, y_val, param_grid, metric,
n_best_grids, loss=False, tiebreaker=tiebreaker)
for a,t,g in zip(best_score, tiebreaker, best_grid):
print("AUC:",a)
print("Tie",t)
print("Grid:",g)
# -
model.set_params(**best_grid[0])
model.fit(x_train,y_train)
c = confusion_matrix(y_val,model.predict(x_val))
sns.heatmap(c, annot=True, xticklabels=xlabel, yticklabels=ylabel)
print(c)
# This seems like a good result and we could naively choose this single tree, or any of the top 10 combinations as they have the same error, as our model. The problem is that every time we run the parameter search another combination of parameters will be the best tree because of the intrinsic variance of decision trees, additionally these trees will have a really good error as well because of the natural low bias of decision trees. Remember that the trees are tuned to the validation set and might, probably wont, generalize good to new data.
# But there is some pattern to what sort of combinations work for the problem. For the entropy criterion trees the best performing ones the maximum depth is between 5 and 7, the maximum number of leaves between 22 and 26, the maximum number of features to consider on each split around 7 and using balanced weighting for the classes. The balanced weighting adjust the weights for the classes inversely proportional to class frequencies, basically counteracting the false positive hypothesis mentioned earlier.
# For the gini criterion trees the best performing ones the maximum depth is around 7, the maximum number of leaves varies a lot but tend to approach higher values (≈25), the maximum number of features to consider on each split around 7 and using the proposed weighting for the classes.
# To decrease variance and try to make our model to generalize we use need to use an ensemble. The first that comes to mind is trying Bootstrap aggregating or a random forest. It should theoretically provide the stability we need and reduces variance.
# # Ensembles
# +
from sklearn.ensemble import BaggingClassifier, RandomForestClassifier
base = DecisionTreeClassifier(criterion='entropy', splitter='best',
max_depth=5, min_samples_split=2, min_samples_leaf=1,
min_weight_fraction_leaf=0.0, max_features=7, random_state=None,
max_leaf_nodes=22, min_impurity_split=1e-07,
class_weight='balanced', presort=False)
model = BaggingClassifier(base_estimator=base, n_estimators=100, max_samples=1.0, max_features=1.0,
bootstrap=True, bootstrap_features=False, oob_score=False, warm_start=False,
n_jobs=1, random_state=None, verbose=0)
model.fit(x_train, y_train)
predictions = model.predict(x_val)
conf = (confusion_matrix(y_val,predictions))
auc = (roc_auc_score(y_val,predictions))
sns.heatmap(conf, annot=True, xticklabels=xlabel, yticklabels=ylabel)
plt.title("AUC " + str(auc))
print(auc)
#plt.savefig('Bagging.eps', format='eps', dpi=1000)
# -
model = RandomForestClassifier(n_estimators=100, criterion='entropy', max_depth=5,
min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0,
max_features='auto', max_leaf_nodes=22, min_impurity_split=1e-07,
bootstrap=True, oob_score=False, n_jobs=1, random_state=None, verbose=0,
warm_start=False, class_weight='balanced')
model.fit(x_train, y_train)
predictions = model.predict(x_val)
conf = (confusion_matrix(y_val,predictions))
auc = (roc_auc_score(y_val,predictions))
sns.heatmap(conf, annot=True, xticklabels=xlabel, yticklabels=ylabel)
plt.title("AUC " + str(auc))
print(auc)
#plt.savefig('randfor.eps', format='eps', dpi=1000)
# The ensembles seems to provide stability and decrease the variance run to run. However they seem to introduce some bias. Looking back at when we compared entropy and gini criterion and looked at the effect of the depth and variance. Remember that the gini trees generally had few false positives while entropy trees had few false negatives. An viable hypothesis might be that the two complement each other, and because we in the ensembles above only use the one or the other. To test the hypothesis we're gonna try an VotingClassifier using the parameters search result we acquired above.
# The voting classifier consists of a 5:4 ratio of entropy and gini trees since the gini trees showed less potential in the grid search. The classification is done using a majority vote rule.
from sklearn.ensemble import VotingClassifier
mods = []
for i in range(1,100): # 100 Trees provides low variance.
# A parameter combination that were sucessfull for entropy trees.
mods.append((str(i),DecisionTreeClassifier(criterion='entropy', splitter='best',
max_depth=5, min_samples_split=2, min_samples_leaf=1,
min_weight_fraction_leaf=0.0, max_features=None, random_state=None,
max_leaf_nodes=22, min_impurity_split=1e-07, class_weight='balanced', presort=False)))
if(i < 80):
# A parameter combination that were sucessfull for gini trees.
mods.append((str(i)+"gi",DecisionTreeClassifier(criterion='gini', splitter='best',
max_depth=7, min_samples_split=2, min_samples_leaf=1,
min_weight_fraction_leaf=0.0, max_features=None, random_state=None,
max_leaf_nodes=25, min_impurity_split=1e-07,
class_weight={0: 1.105, 1: 1.15}, presort=False)))
model = VotingClassifier(estimators=mods, voting='hard', n_jobs=1)
model.fit(x_train, y_train)
predictions = model.predict(x_val)
conf = (confusion_matrix(y_val,predictions))
auc = (roc_auc_score(y_val,predictions))
sns.heatmap(conf, annot=True, xticklabels=xlabel, yticklabels=ylabel)
print(auc)
print((roc_auc_score(y_train,model.predict(x_train))))
# The hypothesis might be true, this is a really good separation and a AUC of nearly 89 for the validation set and 93 for the training set. Thats not a gigantic difference and hopefully the constraints on the trees have prevented the model from overfitting on the training data.
# # Pipeline
# Before giving the test set a go we train our model on the entire training dataset with some imputing. We also put it into a pipeline to automate the work-flow.
# +
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import Imputer,StandardScaler
X = pd.read_csv('input/Train.csv')
Y = X['Outcome']
X = X.drop(["Outcome"], axis=1)
model = VotingClassifier(estimators=mods, voting='hard', n_jobs=1)
pipeline = Pipeline([("imputer", Imputer(missing_values='NaN',
strategy="mean",
axis=0)),
("standardizer", StandardScaler()),
("VotingClassifier", model)])
pipeline.fit(X,Y)
# -
# # Test
# ## No missing values
test = pd.read_csv('input/Test.csv')
test.dropna(inplace = True)
truth = test['Outcome']
test.drop('Outcome', axis = 1, inplace = True)
predictions = pipeline.predict(test)
conf = (confusion_matrix(truth,predictions))
acc = (accuracy_score(truth,predictions))
auc = (roc_auc_score(truth,predictions))
sns.heatmap(conf, annot=True, xticklabels=xlabel, yticklabels=ylabel)
print("accuracy", acc)
print("AUC", auc)
#plt.savefig('test_conf.eps', format='eps', dpi=1000)
# Eureka, this is really good.
# ## Missing values
test = pd.read_csv('input/Test.csv')
truth = test['Outcome']
test.drop('Outcome', axis = 1, inplace = True)
predictions = pipeline.predict(test)
conf = (confusion_matrix(truth,predictions))
acc = (accuracy_score(truth,predictions))
auc = (roc_auc_score(truth,predictions))
sns.heatmap(conf, annot=True, xticklabels=xlabel, yticklabels=ylabel)
print("accuracy", acc)
print("AUC", auc)
# Not as good, but still good.
| 22,125 |
/Deep_Learning_with_TensorFlow/1.4.0/Chapter11/4.1. projector_data_prepare.ipynb
|
5cec94aec4d3715eb284ff97d3ea39fec9b50e2c
|
[
"MIT"
] |
permissive
|
hyphenliu/TensorFlow_Google_Practice
|
https://github.com/hyphenliu/TensorFlow_Google_Practice
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 46,049 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="X1xALvaQWBX_"
# # Práctica G: repositorios locales y remotos
# + [markdown] colab_type="text" id="ciqUoT0yixVA"
# ##### Cookbook [@data_mining_2020_1](https://nbviewer.jupyter.org/github/JacoboGGLeon/data_mining_2020_1/blob/master/README.ipynb)
# + [markdown] colab_type="text" id="EUyHB8zC5ubh"
# ## Resources
# + [markdown] colab_type="text" id="ciPg12iW5wYw"
# * [Git cheatsheet](https://ndpsoftware.com/git-cheatsheet.h)
# * [Installing and using Git and GitHub on Ubuntu Linux: A beginner's guide](https://www.howtoforge.com/tutorial/install-git-and-github-on-ubuntu/)
# * [How to remove origin from git repository](https://stackoverflow.com/questions/9224754/how-to-remove-origin-from-git-repository)
#
#
# + [markdown] colab_type="text" id="703KlDUZIzsb"
# ### Highlights
#
# ```
# vagrant@vagrant:~/test$ git add README
# vagrant@vagrant:~/test$ git commit -m "primer commit"
# [master cc2296c] primer commit
# 1 file changed, 1 insertion(+), 1 deletion(-)
# vagrant@vagrant:~/test$ git push origin master
# Username for 'https://github.com': JacoboGGLeon
# Password for 'https://[email protected]':
# Counting objects: 3, done.
# Writing objects: 100% (3/3), 257 bytes | 85.00 KiB/s, done.
# Total 3 (delta 0), reused 0 (delta 0)
# To https://github.com/JacoboGGLeon/test.git
# c1c7113..cc2296c master -> master
# ```
#
#
# + [markdown] colab_type="text" id="GOljQUJIirjB"
# ## Recipe
# + [markdown] colab_type="text" id="UfPNo8E8WNHm"
# ### Instalación
#
#
# -
# #### En terminal:
# + [markdown] colab_type="text" id="jQXuWaLx4gdB"
# Actualizar el sistema operativo
#
# > ```sudo apt-get update -y && sudo apt-get upgrade -y```
# + [markdown] colab_type="text" id="xQXis9JM4lqf"
# Instalar git
#
# > ```sudo apt-get install git```
# + [markdown] colab_type="text" id="5kXkCzU_4pwM"
# Checar la versión instalada
#
# > ```git --version```
# + [markdown] colab_type="text" id="L0PQqWAV9ufp"
# Actualizar las credenciales de Github
#
# > ```git config --global user.name "user_name"```
#
# > ```git config --global user.email "user_email"```
#
# > ```git config --global user.password "user_password"```
#
# + [markdown] colab_type="text" id="UfPNo8E8WNHm"
# ### Del repositorio local al repositorio remoto
# + [markdown] colab_type="text" id="oXw88Tp0A9Oa"
# Crear un repositorio en la máquina local
#
# > ```git init test```
#
# Respuesta esperada (similar)
#
# > ```Initialized empty Git repository in /home/vagrant/test/.git/```
#
# + [markdown] colab_type="text" id="0SIlYoJsBgKN"
# Crear un archivo
#
# > ```nano README```
#
# Escribir dentro de él: ¡Hola mundo!
#
# + [markdown] colab_type="text" id="WVuSUCDDBqT1"
# Indexar el archivo, o sea, agregarlo
# en una lista para subirlo al repositorio remoto que se encuentra en Github
#
# > ```git add README```
#
# + [markdown] colab_type="text" id="p8WcfehECDdB"
# Avisar que nuestro archivo(s) está listo para subirlo al repositorio remoto
#
# > ```git commit -m "some_message"```
#
# + [markdown] colab_type="text" id="JwXxpHeICeev"
# ### En Github
# + [markdown] colab_type="text" id="KNdbzZ3BCneb"
# Crar un repositorio remoto
#
# > 
# + [markdown] colab_type="text" id="nHv42YcyETH6"
# Sólo llenar el nombre del repositorio: ```test```
#
# > 
# + [markdown] colab_type="text" id="xKyrbbLWE7sj"
# ### En terminal (de nuevo)
# + [markdown] colab_type="text" id="SwQy2fcVEo2-"
# Agregar el origen remoto, o sea, la conexión del repositorio local con el repositorio remoto a.k.a. Github
#
# * Copiar la ruta de el repositorio remoto ```.git```
# > 
#
# Y ese será el "origen"
#
# > ```git remote add origin https://github.com/user_name/test.git```
#
# + [markdown] colab_type="text" id="7EdqvO5DFqbw"
# Subir el archivo que enlistamos para subirse al repositorio remoto
#
# > ```git push origin master```
#
# Nos pedirá dos datos: ```username``` y ```password```
#
# Así sería la respuesta (similar)
#
#
# > ```
# > Username for 'https://github.com':
# > Password for 'https://[email protected]':
# > Counting objects: 3, done.
# > Writing objects: 100% (3/3), 228 bytes | 76.00 KiB/s, done.
# > Total 3 (delta 0), reused 0 (delta 0)
# > To https://github.com/.../test.git
# > * [new branch] master -> master
# > ```
#
# + [markdown] colab_type="text" id="cj2F2aQvGk--"
# ### En Github (de nuevo, ya para acabar)
# + [markdown] colab_type="text" id="UW0okY48GwdV"
# Seleccionar el repositorio ```test``` y ahí debería estar nuestro repositorio
#
# > 
# + [markdown] colab_type="text" id="UfPNo8E8WNHm"
# ### Del repositorio remoto al repositorio local
#
#
# + [markdown] colab_type="text" id="oXw88Tp0A9Oa"
# En Github crear un repositorio remoto
#
# > 
# + [markdown] colab_type="text" id="oXw88Tp0A9Oa"
# En una carpeta raíz
#
# > ```git clone https://github.com/.../test.git```
#
# Respuesta esperada (similar)
#
# > ```Cloning into 'test'...
# warning: You appear to have cloned an empty repository.```
# + [markdown] colab_type="text" id="oXw88Tp0A9Oa"
# Listar los archivos
#
# > ```ls```
#
# Debemos encontrar una carpeta ```test```
#
# Entrar a la carpeta
#
# > ```cd test```
# + [markdown] colab_type="text" id="oXw88Tp0A9Oa"
# Crear archivo y editarlo al mismo tiempo
#
# > ```nano readme.md```
#
# Dentro escribimos un mensaje, el que sea
#
# > *Para salir, escribir* ```ctrl``` + ```x``` *y aceptar los cambios*
# + [markdown] colab_type="text" id="oXw88Tp0A9Oa"
# Agregamos todos los archivos
#
# > ```git add .```
# + [markdown] colab_type="text" id="oXw88Tp0A9Oa"
# Hacemos el *commit*
#
# > ```git commit -m "primer commit"```
#
# Respuesta esperada (similar)
#
# > ```1 file changed, 1 insertion(+)
# create mode 100644 readme.md```
# + [markdown] colab_type="text" id="oXw88Tp0A9Oa"
# Actualizamos el repositorio remoto
#
# > ```git push origin master```
#
# Respuesta esperada (similar)
#
# > ```
# > Username for 'https://github.com':
# > Password for 'https://[email protected]':
# > Counting objects: 3, done.
# > Writing objects: 100% (3/3), 228 bytes | 76.00 KiB/s, done.
# > Total 3 (delta 0), reused 0 (delta 0)
# > To https://github.com/.../test.git
# > * [new branch] master -> master
# > ```
| 6,869 |
/Image classifcation/Intel_Image_classification (1).ipynb
|
f47d2859fe7fe6ac49f619c26491bcf6a4387541
|
[] |
no_license
|
Srinivas1258/ML-DL
|
https://github.com/Srinivas1258/ML-DL
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 100,187 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5" _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19"
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
''''import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
#print(os.path.join(dirname, filename))'''
# You can write up to 5GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All"
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session
# + _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a" _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0"
# !ls /kaggle/input/intel-image-classification/seg_train/seg_train/
# +
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.layers import Conv2D,MaxPool2D,Flatten,BatchNormalization,Dropout,Activation
import pandas as pd
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import matplotlib.pyplot as plt
import numpy as np
from tensorflow.keras.models import load_model
from keras.utils import np_utils
from tensorflow.keras import applications
from keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras import optimizers
# +
train_datagen = ImageDataGenerator(
rescale=1./255, # normalizing the image b/w 0 to 1
shear_range=0.2, # shear transformation
zoom_range=0.2, # zooming the image by 20%
horizontal_flip=True) # rotating
val_datagen = ImageDataGenerator(
rescale=1. / 255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True)
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
'/kaggle/input/intel-image-classification/seg_train/seg_train/',
target_size=(224, 224),
batch_size=32,
class_mode='categorical')
validation_generator = val_datagen.flow_from_directory(
'/kaggle/input/intel-image-classification/seg_test/seg_test/',
target_size=(224, 224),
batch_size=32,
class_mode='categorical')
test_generator=test_datagen.flow_from_directory(
'/kaggle/input/intel-image-classification/seg_pred/',
target_size=(224, 224),
batch_size=32,
class_mode=None)
# +
from tensorflow.keras.applications.inception_v3 import InceptionV3
from tensorflow.keras.models import Model
import tensorflow.keras
inception=InceptionV3(include_top=False,weights='imagenet',input_shape=(224,224,3))
output1=inception.layers[-1].output
output1=tensorflow.keras.layers.Flatten()(output1)
inception=Model(inception.input,output1)
for layers in inception.layers:
layers.trainable=False
inception.summary()
# +
from tensorflow.keras.layers import Conv2D, MaxPool2D, Flatten, Dense, Dropout, InputLayer,BatchNormalization
from tensorflow.keras.models import Sequential
from tensorflow.keras import optimizers
model2 = Sequential()
model2.add(inception)
# model2.add(Conv2D(256,kernel_size=3,padding='same',activation='relu',input_shape=(224,224,3)))
# model2.add(MaxPool2D(pool_size=(2,2)))
# model2.add(Dropout(0.25))
# model2.add(Flatten())
model2.add(Dense(1024, activation='relu', input_dim=(224,224,3)))
# model2.add(Dense(1024,activation='relu'))
# model2.add(BatchNormalization())
model2.add(Dropout(0.25))
''''model2.add(Dense(256, activation='relu'))
# model2.add(BatchNormalization())
model2.add(Dense(64, activation='relu'))
# model2.add(Dropout(0.3))'''
model2.add(Dense(6, activation='softmax'))
model2.compile(loss='categorical_crossentropy',
optimizer=optimizers.Adam(),
metrics=['accuracy'])
model2.summary()
# -
STEP_SIZE_TRAIN=train_generator.n//train_generator.batch_size
STEP_SIZE_VALID=validation_generator.n//validation_generator.batch_size
history=model2.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=validation_generator,
validation_steps=STEP_SIZE_VALID,
epochs=5
)
# +
acc=history.history['accuracy']
val_acc=history.history['val_accuracy']
loss=history.history['loss']
val_loss=history.history['val_loss']
epochs=range(len(acc))
fig = plt.figure(figsize=(20,10))
plt.plot(epochs, acc, 'r', label="Training Accuracy")
plt.plot(epochs, val_acc, 'b', label="Validation Accuracy")
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title('Training and validation accuracy')
plt.legend(loc='lower right')
plt.show()
fig.savefig('../Accuracy_curve_CNN_256.jpg')
fig = plt.figure(figsize=(20,10))
plt.plot(loss)
plt.plot(val_loss)
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
fig.savefig('../loss_curve_CNN_256.jpg')
# -
test_generator.reset()
pred=model2.predict_generator(test_generator,
verbose=1)
print(pred)
# +
import matplotlib.pyplot as plt
predicted_class_indices=np.argmax(pred,axis=1)
labels = (train_generator.class_indices)
labels = dict((v,k) for k,v in labels.items())
predictions = [ print(k) for k in predicted_class_indices]
''''filenames=test_generator.filenames
results=pd.DataFrame({"Image":filenames,
"target":predictions})
results.to_csv("results.csv",index=False)
0.2..
106 '''
# -
for filenames in os.walk('/kaggle/input/intel-image-classification/seg_pred/seg_pred/'):
print(filename)
| 6,249 |
/notebooks/Translate PWN 3.1.ipynb
|
54e1e32024a258c49911065278b68733187aea30
|
[] |
no_license
|
khrystyna-skopyk/wordnet
|
https://github.com/khrystyna-skopyk/wordnet
| 0 | 0 | null | 2021-09-14T14:56:49 | 2021-09-01T21:45:40 | null |
Jupyter Notebook
| false | false |
.py
| 30,568 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
import wn
from google.cloud import translate_v2 as translate
import logging
logger = logging.getLogger("wordnet_translator")
logger.setLevel(logging.INFO)
consoleHandler = logging.StreamHandler()
consoleHandler.setLevel(logging.INFO)
# create formatter
formatter = logging.Formatter('%(asctime)s - %(name)s - %(levelname)s - %(message)s')
# add formatter to ch
consoleHandler.setFormatter(formatter)
# add ch to logger
logger.addHandler(consoleHandler)
# -
wn.download("pwn:3.1")
# +
import pymongo
client = pymongo.MongoClient('mongodb://localhost:27017/')
db = client.wordnet
collection = db["tasks"]
# +
from tqdm.notebook import tqdm
from collections import defaultdict
def populate_tasks_in_mongo(lexicon="pwn:3.1", filter_func=None):
if filter_func is None:
filter_func = lambda synset: True
tasks_created = 0
tasks_updated = 0
for synset in tqdm(wn.synsets(lexicon=lexicon)):
if filter_func(synset):
words = {w.id: w.lemma() for w in synset.words()}
res = (
collection.update_one(
{"_id": synset.id},
{
"$set": {
"ili": synset.ili.id,
"pos": synset.pos,
"words": words,
"definition": list(
map(str.strip, synset.definition().split(";"))
),
}
},
upsert=True,
)
)
if res.upserted_id:
tasks_created += 1
else:
tasks_updated += 1
logger.info(
f"{tasks_created} was created and {tasks_updated} was updated from '{lexicon}'"
)
def filter_only_big_synsets_with_description(synset):
return len(synset.lemmas()) == 5 and synset.definition()
export_samples = defaultdict(lambda: defaultdict(int))
for pos in ["a", "v", "n"]:
for lemmas_count in range(1, 5):
export_samples[pos][lemmas_count] = 2
def filter_to_have_a_nice_sample(synset):
global export_samples
if not synset.definition():
return False
if export_samples[synset.pos][len(synset.lemmas())] > 0:
export_samples[synset.pos][len(synset.lemmas())] -= 1
return True
return False
# populate_tasks_in_mongo(filter_func=filter_only_big_synsets_with_description)
populate_tasks_in_mongo(filter_func=filter_to_have_a_nice_sample)
# +
import requests, uuid, json
from urllib.parse import urljoin
class BingTranslationException(Exception):
pass
class BingTranslator:
translate_path = '/translate'
dictionary_lookup_path = '/dictionary/lookup'
def __init__(self, key_file, endpoint="https://api.cognitive.microsofttranslator.com"):
self.endpoint = endpoint
with open(key_file) as fp:
self.headers = json.load(fp)
def _get_headers(self):
headers = self.headers.copy()
headers['X-ClientTraceId'] = str(uuid.uuid4())
return headers
def _request(self, path, phrase, source_language="en", target_language="uk"):
constructed_url = urljoin(self.endpoint, path)
headers = self._get_headers()
params = {
'api-version': '3.0',
"from": source_language,
'to': target_language
}
body = [{
'text': phrase
}]
request = requests.post(constructed_url, params=params, headers=headers, json=body)
try:
response = request.json()
except json.JSONDecodeError:
raise BingTranslationException(f"Cannot translate phrase '{phrase}' cannot parse the response as json")
if "error" in response:
raise BingTranslationException(f"Cannot translate phrase '{phrase}' because of an error: {response['error']}")
if request.status_code != 200:
raise BingTranslationException(f"Cannot translate phrase '{phrase}', status code was {request.status_code}")
return response
def translate(self, phrase, source_language="en", target_language="uk"):
response = self._request(self.translate_path, phrase, source_language, target_language)
for l in response:
for translation in l.get("translations", []):
return translation["text"]
raise BingTranslationException(f"Cannot find a translation for a phrase '{phrase}'")
def dictionary_lookup(self, word, source_language="en", target_language="uk"):
response = self._request(self.dictionary_lookup_path, word, source_language, target_language)
for l in response:
return l.get("translations", [])
raise BingTranslationException(f"Cannot find a translation for a phrase '{phrase}'")
# +
from time import sleep
import itertools
import re
import html
from collections import Counter
def sliding_window(iterable, n=2):
iterables = itertools.tee(iterable, n)
for iterable, num_skipped in zip(iterables, itertools.count()):
for _ in range(num_skipped):
next(iterable, None)
return zip(*iterables)
class AbstractTranslator:
def __init__(self, source_language="en", target_language="uk"):
self.source_language = source_language
self.target_language = target_language
def generate_samples(self, task):
raise NotImplementedError()
def translate(self, task, sleep_between_samples=1):
raise NotImplementedError()
def parse_results(self, results):
raise NotImplementedError()
def method_id(self):
raise NotImplementedError()
class AbstractSlidingWindowTranslator(AbstractTranslator):
def __init__(
self,
group_by=3,
add_or=True,
add_quotes=True,
combine_in_one=True,
add_aux_words=True,
source_language="en",
target_language="uk",
):
super().__init__(source_language=source_language, target_language=target_language)
self.group_by = group_by
self.add_or = add_or
self.add_quotes = add_quotes
self.combine_in_one = combine_in_one
self.add_aux_words = add_aux_words
def method_id(self):
return f"{type(self).__name__}(group_by={self.group_by},add_or={self.add_or},add_quotes={self.add_quotes},combine_in_one={self.combine_in_one},add_aux_words={self.add_aux_words})"
def generate_samples(self, task):
samples = []
total_samples = 0
words = list(task["words"].values())
if self.add_aux_words:
if task["pos"] == "v":
words = [f"to {w}" for w in words]
elif task["pos"] == "n":
words = [f"the {w}" for w in words]
if self.add_quotes:
words = [f'"{w}"' for w in words]
if len(words) < self.group_by:
chunks = [words]
else:
chunks = sliding_window(words, self.group_by)
for chunk in chunks:
total_samples += len(chunk)
if self.add_or and len(chunk) > 1:
lemmas = ", ".join(chunk[:-1]) + f" or {chunk[-1]}"
else:
lemmas = ", ".join(chunk)
if task["definition"]:
samples.append(f"{lemmas}: {task['definition'][0]}")
else:
samples.append(lemmas)
if self.combine_in_one:
return {"samples": ["<br/>\n\n".join(samples)], "total_lemmas": total_samples}
else:
return {"samples": samples, "total_lemmas": total_samples}
def estimate_tasks(self, tasks, price_per_mb=1.0 / 1024 / 1024):
total_len = 0
for task in tasks:
samples = self.generate_samples(task)["samples"]
for sample in samples:
total_len += len(sample)
return (float(total_len) / 1024 / 1024) * price_per_mb
def _parse_result(self, result):
all_terms = []
all_definitions = []
for l in filter(None, result.replace("<br/>", "\n").split("\n")):
if ":" not in l:
logger.warning("Cannot find a semicolon in the translated text")
continue
terms, definition = l.split(":", 1)
terms = list(map(str.strip, terms.split(",")))
if self.add_or:
for or_word in ["чи то", "чи", "або", "альбо", "or"]:
splits = re.split(f"[,\s]+{or_word}[,\s]+", terms[-1], flags=re.I)
if len(splits) > 1:
terms = terms[:-1] + list(map(lambda x: x.strip(", "), splits))
break
else:
if self.group_by > 1:
logger.warning("Cannot find 'or' in the last chunk")
if self.add_quotes:
terms = [term.strip('"\'"«»') for term in terms]
all_terms += terms
all_definitions.append(definition.strip())
return {"all_terms": all_terms, "all_definitions": all_definitions}
class SlidingWindowGoogleTranslator(AbstractSlidingWindowTranslator):
def __init__(
self,
gcloud_credentials,
group_by=3,
add_or=True,
add_quotes=True,
combine_in_one=True,
add_aux_words=True,
source_language="en",
target_language="uk",
):
self.gtrans_client = translate.Client.from_service_account_json(gcloud_credentials)
super().__init__(
group_by=group_by,
add_or=add_or,
add_quotes=add_quotes,
combine_in_one=combine_in_one,
add_aux_words=add_aux_words,
source_language=source_language,
target_language=target_language,
)
def translate(self, task, sleep_between_samples=1):
results = []
sampled = self.generate_samples(task)
for sample in sampled["samples"]:
results.append(
self.gtrans_client.translate(
sample,
source_language=self.source_language,
target_language=self.target_language,
)
)
sleep(sleep_between_samples)
return self.parse_results(results)
def parse_results(self, results):
terms = Counter()
definitions = Counter()
parsed_results = []
for r in results:
parsed = self._parse_result(html.unescape(r.get("translatedText", "")))
terms.update(parsed["all_terms"])
definitions.update(parsed["all_definitions"])
parsed_results.append(parsed)
return {
"raw": parsed_results,
"terms": terms.most_common(),
"definitions": definitions.most_common(),
"type": "translator",
}
def estimate_tasks(self, tasks, price_per_mb=20):
return super().estimate_tasks(tasks, price_per_mb)
class SlidingWindowBingTranslator(AbstractSlidingWindowTranslator):
def __init__(
self,
bing_apikey,
group_by=3,
add_or=True,
add_quotes=True,
combine_in_one=True,
add_aux_words=True,
source_language="en",
target_language="uk",
):
self.bing_apikey = bing_apikey
self.bing_translator = BingTranslator(self.bing_apikey)
super().__init__(
group_by=group_by,
add_or=add_or,
add_quotes=add_quotes,
combine_in_one=combine_in_one,
add_aux_words=add_aux_words,
source_language=source_language,
target_language=target_language,
)
def estimate_tasks(self, tasks, price_per_mb=10):
return super().estimate_tasks(tasks, price_per_mb)
def translate(self, task, sleep_between_samples=1):
results = []
sampled = self.generate_samples(task)
for sample in sampled["samples"]:
results.append(
self.bing_translator.translate(
sample,
source_language=self.source_language,
target_language=self.target_language,
)
)
sleep(sleep_between_samples)
return self.parse_results(results)
def parse_results(self, results):
terms = Counter()
definitions = Counter()
parsed_results = []
for r in results:
parsed = self._parse_result(html.unescape(r))
terms.update(parsed["all_terms"])
definitions.update(parsed["all_definitions"])
parsed_results.append(parsed)
return {
"raw": parsed_results,
"terms": terms.most_common(),
"definitions": definitions.most_common(),
"type": "translator",
}
class AbstractDictionaryTranslator(AbstractTranslator):
def generate_samples(self, task):
return {"samples": list(task["words"].values()), "total_lemmas": len(task["words"]), "pos": task["pos"]}
class DictionaryBingTranslator(AbstractDictionaryTranslator):
def __init__(
self,
bing_apikey,
source_language="en",
target_language="uk",
):
self.bing_apikey = bing_apikey
self.bing_translator = BingTranslator(self.bing_apikey)
super().__init__(
source_language=source_language,
target_language=target_language,
)
# [ "a", "n", "r", "s", "v" ]
# a ADJ
# r ADV
# c CONJ
# n NOUN
# v VERB
# x OTHER
# DET
# MODAL
# PREP
# PRON
# Марьяна Романишин, [12 жовт. 2021 р., 09:18:00]:
# Так, у цьому випадку adposition - це preposition. У різних мовах прийменники можуть стояти перед іменником (preposition) або після іменника (postposition). Термін adposition об'єднує одне і друге.
# s також можна змапити на ADJ.
def translate(self, task, sleep_between_samples=1):
results = []
sampled = self.generate_samples(task)
for sample in sampled["samples"]:
results.append(
self.bing_translator.dictionary_lookup(
sample,
source_language=self.source_language,
target_language=self.target_language,
)
)
sleep(sleep_between_samples)
return self.parse_results(results)
def parse_results(self, results):
terms = Counter()
parsed_results = []
for r in results:
if "normalizedTarget" in r:
terms.update(r["normalizedTarget"])
parsed_results.append(r)
return {
"raw": parsed_results,
"terms": terms.most_common(),
"definitions": [],
"type": "dictionary",
}
def method_id(self):
return f"{type(self).__name__}()"
translators = [
SlidingWindowGoogleTranslator("../api_keys/dchaplynskyi_gmail_com.json", group_by=1),
SlidingWindowGoogleTranslator("../api_keys/dchaplynskyi_gmail_com.json", group_by=3),
SlidingWindowBingTranslator("../api_keys/khrystyna_skopyk_gmail_com.json", group_by=1),
SlidingWindowBingTranslator("../api_keys/khrystyna_skopyk_gmail_com.json", group_by=3),
DictionaryBingTranslator("../api_keys/khrystyna_skopyk_gmail_com.json"),
]
# tasks = list(collection.find(
# {
# "_id": {
# "$in": [
# # VERBS
# "pwn-00006238-v",
# "pwn-00009140-v",
# "pwn-00014735-v",
# # "pwn-00018151-v",
# # "pwn-00022309-v",
# # "pwn-00023466-v",
# # "pwn-00050369-v",
# # "pwn-00056644-v",
# # "pwn-00058790-v",
# # "pwn-00067045-v",
# # NOUNS:
# "pwn-00109001-n",
# "pwn-00284945-n",
# "pwn-00224850-n",
# # ADJS:
# "pwn-00102561-a",
# ]
# }
# }
# ))
tasks = list(collection.find())
for translator in tqdm(translators):
for t in tqdm(tasks):
if translator.method_id() not in t.get("results", {}):
res = translator.translate(t)
collection.update_one(
{"_id": t["_id"]}, {"$set": {f"results.{translator.method_id()}": res}}, upsert=True
)
# +
from csv import DictWriter
def render_counter(cnt):
return "\n".join(f"{k}: {v}" for k, v in cnt.most_common())
answered = list(collection.find({"results": {"$exists": 1}}))
methods = set()
for l in answered:
methods |= set(l["results"].keys())
columns = ["pwn", "lemmas", "pos", "definition"]
for method in sorted(methods):
columns.append(f"Terms, {method}")
columns.append(f"Definitions, {method}")
columns.append("Terms combined")
columns.append("Definitions combined")
with open("/tmp/translations.csv", "w") as fp:
w = DictWriter(fp, fieldnames=columns)
w.writeheader()
for t in answered:
to_export = {
"pwn": t["_id"],
"definition": "\n".join(t["definition"]),
"pos": t["pos"],
"lemmas": "\n".join(t["words"].values()),
}
combined_terms = Counter()
combined_definitions = Counter()
for method, r in t.get("results", {}).items():
terms = Counter(dict(r.get("terms", [])))
definitions = Counter(dict(r.get("definitions", [])))
combined_terms.update({k.lower(): v for k, v in terms.items()})
combined_definitions.update({k.lower(): v for k, v in definitions.items()})
to_export[f"Terms, {method}"] = render_counter(terms)
to_export[f"Definitions, {method}"] = render_counter(definitions)
to_export["Terms combined"] = render_counter(combined_terms)
to_export["Definitions combined"] = render_counter(combined_definitions)
w.writerow(to_export)
| 18,437 |
/Books/Patterns/Builder.ipynb
|
be948f1b116e145f2b9b9827567c1df127ca36f6
|
[] |
no_license
|
Provinm/baseCs
|
https://github.com/Provinm/baseCs
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 4,888 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
class Account(object):
def __init__(self,account_number,firstname,lastname,account_balance):
self.firstname = firstname
self.lastname = lastname
self.account_balance = account_balance if account_balance > 0 else 0
self.account_number = account_number if account_number > 100001 else 0
def display(self):
print (self.firstname)
print (self.lastname)
print (self.account_balance)
print (self.account_number)
ob = Account(100,"kartik","kumar",32132)
ob.display()
| 812 |
/Abhishek_MT19086/Code/Abhishek19086_code_colab.ipynb
|
464271a9a7d3962e77fcbf73ca025a20461a831d
|
[] |
no_license
|
abhishekvickyvyas/IMDB_score_prediction
|
https://github.com/abhishekvickyvyas/IMDB_score_prediction
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 571,205 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # SDA - lecture 14 - The frequency domain
# +
import logging
logging.basicConfig(level=logging.INFO, format='%(levelname)s: %(asctime)s: %(message)s')
import math
import numpy as np
import matplotlib.pyplot as plt
# Use scipy.fft and not numpy.fft which is slower on real numbers
import scipy.fft as sfft
# %matplotlib inline
# -
# ### Sum of two sine waves (different frequencies)
# * Note the result when one of the frequemcies is an harmonic of the other
x = np.arange(0,4,0.001)
y = np.zeros((x.shape[0],3))
f1, f2 = 4, 2
y[:,0] = np.sin(x*math.pi*2*f1)
y[:,1] = np.sin(x*math.pi*2*f2)
y[:,2] = y[:,0] + y[:,1]
fig, ax = plt.subplots(figsize=(20,5), nrows=1, ncols=3)
titles = [f'Pure {f1} Hz sine wave', f'Pure {f2} Hz sine wave', 'Sum of the two sine waves']
for i in [0,1,2]:
ax[i].plot(x,y[:,i])
ax[i].set_title(titles[i])
ax[i].set_xlabel('Time (s)')
# ### Sum of two sine waves (different phases)
# * Note that decreased sum amplitude as the phase difference increases
# +
x = np.arange(0,4,0.001)
f = 2
phis = [0.1, 0.3, 0.5]
fig, ax = plt.subplots(figsize=(12,4*len(phis)), nrows=len(phis), ncols=2)
for j, phi in enumerate(phis):
y = np.zeros((x.shape[0],3))
y[:,0] = np.sin(x*f*math.pi*2)
y[:,1] = np.sin((x*f+phi)*math.pi*2)
y[:,2] = y[:,0] + y[:,1]
ax[j,0].plot(x,y[:,0],'b')
ax[j,0].plot(x,y[:,1],'r')
ax[j,0].set_title(f'Phase diff {phi} cycle')
ax[j,0].set_ylim(-2,2)
ax[j,1].plot(x,y[:,2])
ax[j,1].set_title(f'Sum')
ax[j,1].set_ylim(-2,2)
# -
# ### Sampling theory
# Plot a sine wave sampled at different rates with their corresponding DFT
# * Note the change when fs < 2*f
# +
f = 4 # Frequency of the sine wave [Hz]
T = 2 # Duration of the sine wave [s]
fss = [100, 20, 10, 6] # Sampling frequencies [samples/s]
fig, ax = plt.subplots(figsize=(16,12), nrows=4, ncols=2)
for i, fs in enumerate(fss):
x = np.arange(0,T,1/fs)
midp = int(x.shape[0] * .5)
y = np.sin(x*f*math.pi*2)
ax[i,0].plot(x,y,'.:')
ax[i,0].set_title(f'fs={fs}Hz f={f}Hz T={T}s')
p = sfft.fft(y)
ax[i,1].step(x[:midp]*fs/T,abs(p[:midp]),where='mid')
# -
# ### DFT - intermediate frequencies
#
# Author: Ori Carmi
N = 64 # number of samples
t = np.arange(N) # time vector
fc = [15,15.5,16]
fig, ax = plt.subplots(figsize=(12,9), nrows=3, ncols=1)
for k,i in enumerate(fc):
x1 = np.cos(2*np.pi*i/N*t)
X1 = sfft.fft(x1)
X1 = abs(X1)
ax[k].plot(np.arange(N), X1, '.')
ax[k].set_title(f'f = {i} [Hz]')
# # Maintaining the magnitude of the fft
# +
x = np.arange(0,4,0.001)
y = np.zeros((x.shape[0],3))
f1, f2 = 4, 2
A1, A2 = 2, 3
y = np.sin(x*math.pi*2*f1)*A1 + np.sin(x*math.pi*2*f2)*A2
Py = np.sum(y**2)
logging.info(f'Total power original signal {Py:.2f}')
Y = sfft.fft(origy)
PY = np.sum(np.abs(Y**2))/len(Y)
logging.info(f'Total power fft {PY:.2f}')
# -
= False)
tf1=tf1.drop(tf1[tf1['content_rating'].isna()].index, inplace = False)
tis=((df.shape[0]-tf1.shape[0])/df.shape[0])*100
print("% of data rows removed on deleting rows null values in `goss`,`budget`,`aspect_ratio`,`content_rating` is "+str(tis))
#only around 24% so now we have deleted all rows
# + [markdown] id="ZxMj3KAMIog8" colab_type="text"
# ['color',
# 'director_name',
# '**num_critic_for_reviews**',
# '**duration**',
# '**director_facebook_likes**',
# '**actor_3_facebook_likes**',
# 'actor_2_name',
# '**actor_1_facebook_likes**',
# 'gross',
# 'genres',
# 'actor_1_name',
# 'movie_title',
# '**num_voted_users**',
# '**cast_total_facebook_likes**',
# 'actor_3_name',
# '**facenumber_in_poster**',
# 'plot_keywords',
# 'movie_imdb_link',
# '**num_user_for_reviews**',
# 'language',
# 'country',
# 'content_rating',
# 'budget',
# 'title_year',
# '**actor_2_facebook_likes**',
# 'imdb_score',
# 'aspect_ratio',
# '**movie_facebook_likes**']
#
# ` Here we can see in table data that bold attributes may take value zero so we convert them into NA and than replace NA value of these columns with mean value of that attribute`
# + [markdown] id="a6Jwgm75OZ3K" colab_type="text"
# **Replace zero with NA**
# + id="BfjrALzFN_0e" colab_type="code" colab={}
#Replace zero with NA
tf2=tf1
ls_zero_to_NA='movie_facebook_likes','actor_2_facebook_likes','num_user_for_reviews','facenumber_in_poster','cast_total_facebook_likes','num_voted_users','actor_1_facebook_likes','actor_3_facebook_likes','director_facebook_likes','duration','num_critic_for_reviews'
for k in ls_zero_to_NA:
tf2[k].replace(0, np.nan, inplace=True)
# + [markdown] id="G0HeukQy9bL5" colab_type="text"
# **Here we are filling NA of columns with mean value**
# + id="Q1Sm-zdd8ww7" colab_type="code" colab={}
for colmn in ls_zero_to_NA:
tf2[colmn]=tf2[colmn].fillna(tf2[colmn].mean())
# tf2
# + id="iYYj8iqs9-lq" colab_type="code" colab={}
tf2_missing=tf2.isna()
tf2_count_missing=tf2_missing.sum()
tf2_per_none_value=tf2_count_missing/len(tf2_count_missing)
tf2_per_none_value.sort_values(ascending=False,inplace=True)
# tf2_per_none_value
#Now we have NA values in only these columns
# + [markdown] id="rjm_9zF9Dp77" colab_type="text"
# **Here only four column are remainng which have NA values we replce them with most frequent values in their column**
# + id="tpvyNoR5D_x1" colab_type="code" colab={}
tf2 = tf2.fillna(tf2.mode().iloc[0])
# + [markdown] id="gjhaELt1T1tE" colab_type="text"
# # **Make Graphs to Visualise the trends in data**
# + id="iSFUJHdSUMgX" colab_type="code" outputId="5eef632a-a2ab-4914-8e1a-47dccf01b451" colab={"base_uri": "https://localhost:8080/", "height": 281}
import matplotlib.pyplot as plt
x = tf2['title_year']
plt.hist(x, bins=20)
plt.ylabel('No of Movies released')
plt.title('No of Movies released per year')
plt.show()
# + id="Pm0drwH8V0Lr" colab_type="code" outputId="e149bc54-87dc-42c0-e9d4-6b858532c803" colab={"base_uri": "https://localhost:8080/", "height": 281}
x = tf2['color']
plt.hist(x, bins=10)
plt.ylabel('No of Movies released')
plt.title('No of Movies released per color where total rows are '+str(len(tf2)))
plt.show()
# + id="M9An3nXCaI-h" colab_type="code" outputId="4307ca07-2c64-4eec-b99e-960efea58c2e" colab={"base_uri": "https://localhost:8080/", "height": 348}
x = tf2['country']
plt.hist(x, bins=20,rwidth=.9)
plt.ylabel('No of Movies released')
plt.title('No of Movies released per country where total rows are '+str(len(tf2)))
plt.xticks(rotation='vertical')
plt.show()
# + id="6zxwqY04cpAE" colab_type="code" outputId="f66c6bb7-d45d-4ff4-ba05-5f28e1b5fb4e" colab={"base_uri": "https://localhost:8080/", "height": 331}
x = tf2['language']
plt.hist(x, bins=20,rwidth=.9)
plt.ylabel('No of Movies released in language')
plt.title('No of Movies released in language where total rows are '+str(len(tf2)))
plt.xticks(rotation='vertical')
plt.show()
# + [markdown] id="A-lB7Sond2RX" colab_type="text"
# **Add profit and profit percentage column for graphs and will drop these columns too before applying algorithems**
# + id="6GVoWcr0d0jd" colab_type="code" colab={}
tf2['profit'] = tf2.apply(lambda row: row.gross - row.budget, axis = 1)
tf2['profit_percentage'] = tf2.apply(lambda row: (row.profit/row.budget)*100, axis = 1)
# tf2
# + id="2NM51VAxihne" colab_type="code" colab={}
group_by_imdb_score = tf2.groupby(by=['imdb_score'])
tf2_avg = group_by_imdb_score.mean()
tf2_count = group_by_imdb_score.count()
# + id="OjgYXx0zlZaJ" colab_type="code" outputId="e17c932f-ac4e-45f2-e263-26f939a6b7a0" colab={"base_uri": "https://localhost:8080/", "height": 296}
tf2_avg['num_critic_for_reviews'].plot(kind='line')
# df.groupby('state')['name'].nunique().plot(kind='bar')
# plt.hist(x, bins=20,rwidth=.9)
plt.ylabel('Average number of critic_for_reviews')
plt.title('Average number of critic_for_reviews per IMDB score')
# plt.xticks(rotation='vertical')
plt.show()
# + id="wB33cFZNrEW6" colab_type="code" outputId="1ba0f03b-7ffd-474f-d417-fa86066625d6" colab={"base_uri": "https://localhost:8080/", "height": 296}
tf2_avg['budget'].plot(kind='line')
# df.groupby('state')['name'].nunique().plot(kind='bar')
# plt.hist(x, bins=20,rwidth=.9)
plt.ylabel('Average budget')
plt.title('Average budget per IMDB score')
# plt.xticks(rotation='vertical')
plt.show()
# + id="QN6-5QPjrlIw" colab_type="code" outputId="fac03c40-2412-4ad8-be76-3a349b617b9a" colab={"base_uri": "https://localhost:8080/", "height": 296}
tf2_avg['gross'].plot(kind='line')
# df.groupby('state')['name'].nunique().plot(kind='bar')
# plt.hist(x, bins=20,rwidth=.9)
plt.ylabel('Average gross')
plt.title('Average gross per IMDB score')
# plt.xticks(rotation='vertical')
plt.show()
# + id="kGWMRT1br_CQ" colab_type="code" outputId="8ae50196-d354-4f83-d8e9-e93d6dd4a87e" colab={"base_uri": "https://localhost:8080/", "height": 296}
tf2_avg['facenumber_in_poster'].plot(kind='line')
# df.groupby('state')['name'].nunique().plot(kind='bar')
# plt.hist(x, bins=20,rwidth=.9)
plt.ylabel('Average facenumber_in_poster')
plt.title('Average facenumber_in_poster per IMDB score')
# plt.xticks(rotation='vertical')
plt.show()
# + id="104W5-WJLsRj" colab_type="code" outputId="fe7bb395-2001-418f-925d-2fbda995c022" colab={"base_uri": "https://localhost:8080/", "height": 296}
tf2_avg['profit'].plot(kind='line')
# df.groupby('state')['name'].nunique().plot(kind='bar')
# plt.hist(x, bins=20,rwidth=.9)
plt.ylabel('Average profit')
plt.title('Average profit per IMDB Score')
# plt.xticks(rotation='vertical')
plt.show()
# + [markdown] id="oE2-RxhkLv9o" colab_type="text"
# From above images we can see that most of the movies are **color** attribute as "color" ,and **country** attribute is "USA",most of the movies in data have **langauge** atribute as "english" so they are not much useful for classification.
#
# Other Attributes as **movie_title** ,**aspect_ratio**,**number of faces**, **movie_imdb_link** (as we have seen in *tableau*) are not affecting IMDB score. we will also remove these attributes.**title_year** is also not afffecting the IMDB score but budget is increasing according to its values so we are not removing it.
#
# + id="5Tl5juLpEao3" colab_type="code" outputId="9491b13b-0a25-4321-d09c-aed6459322a8" colab={"base_uri": "https://localhost:8080/", "height": 34}
unique_count_of_director_name=tf2['director_name'].nunique()
unique_count_of_actor_1_name=tf2['actor_1_name'].nunique()
unique_count_of_actor_2_name=tf2['actor_2_name'].nunique()
unique_count_of_actor_3_name=tf2['actor_3_name'].nunique()
unique_count_of_plot_keywords=tf2['plot_keywords'].nunique()
print(unique_count_of_director_name,unique_count_of_actor_1_name,unique_count_of_actor_2_name,unique_count_of_actor_3_name,unique_count_of_plot_keywords)
# + [markdown] id="3pjhitmtFUgc" colab_type="text"
# **As we can see unique count of above four variable is high so we will also remove these variable too**
# + id="2MKk6_nKZsPR" colab_type="code" colab={}
# # df['movie_title'][6].replace("\xa0", "", regex=True)
# s = pd.Series(df['movie_title'])
# s = pd.Series(df['movie_title'])
# k=s.replace("\xa0", "", regex=True)
# df['movie_title']=k
# #we can see some character at last of it
# + [markdown] id="UaGFpwYg7OIf" colab_type="text"
# **checking affect of Splited genres on IMDB score**
# + id="sO157tjjZsRI" colab_type="code" colab={}
# # Split Genres
genres_tf2 = tf2[["genres", "imdb_score"]].copy()
kp=genres_tf2['genres'].str.split("|", n=-1, expand=False)
kp1=list(map(set,kp))
new_colm=list(set.union(*kp1))
# + [markdown] id="oSDPiUb0hH7V" colab_type="text"
# Add genre colums having value 1 if it is else 0
# + id="pvV7hX7EZsSd" colab_type="code" colab={}
for add_col in new_colm:
if add_col not in genres_tf2.columns:
genres_tf2[add_col]=genres_tf2.apply(lambda row: 1 if (add_col in row.genres) else 0 , axis = 1)
# + id="X669zTUQwI4n" colab_type="code" outputId="203c097e-aa25-4a5f-d59b-f3559c36f987" colab={"base_uri": "https://localhost:8080/", "height": 500}
dict_imdb_genres={}
for k in genres_tf2:
if(k!='imdb_score'):
dict_imdb_genres[k]=genres_tf2.loc[genres_tf2[k] == 1, 'imdb_score'].mean()
x_plot=list(dict_imdb_genres.keys())
y_plot=list(dict_imdb_genres.values())
fig, ax = plt.subplots(figsize=(15, 8))
ax.barh(x_plot, y_plot)
# + [markdown] id="IapmIFoN7rC5" colab_type="text"
# **Here We can see that imdb_score is almost same for all genres so we will drop this column too during applying algorithems and do not and splited genres in main data**
# + id="XPHK3XZxUOeg" colab_type="code" colab={}
to_remove_column=['country','profit','profit_percentage','movie_imdb_link','facenumber_in_poster','aspect_ratio','movie_title','language','color','director_name','actor_1_name','actor_2_name','actor_2_name','actor_3_name','plot_keywords']
for i in to_remove_column:
if i in tf2.columns:
tf2=tf2.drop(columns=[i])
# tf2=tf2.drop(columns=[i])
classification_data=tf2
# classification_data=encode_the_data(kf_test)
# classification_data
# + id="2DE6eW_8Va9D" colab_type="code" colab={}
# classification_data['imdb_score']=classification_data.apply(lambda row:'D' if ( float(row.imdb_score)>=0 and float(row.imdb_score)<5) else ('C' if (float(row.imdb_score)>=5 and float(row.imdb_score)<6) else ('B' if (float(row.imdb_score)>=6 and float(row.imdb_score)<6.5) else ('B+' if (row.imdb_score>=6.5 and float(row.imdb_score)<7) else ('A' if (float(row.imdb_score)>=7 and float(row.imdb_score)<7.5) else ('A+' if (float(row.imdb_score)>=7.5 and float(row.imdb_score)<8) else ('A++' if (float(row.imdb_score)>=8 and float(row.imdb_score)<=10) else 0))) ))) , axis = 1)
# + id="3lUObk3mve7e" colab_type="code" colab={}
classification_data['imdb_score']=classification_data.apply(lambda row:'E' if ( float(row.imdb_score)>=0 and float(row.imdb_score)<5) else ('D' if (float(row.imdb_score)>=5 and float(row.imdb_score)<6) else ('C' if (float(row.imdb_score)>=6 and float(row.imdb_score)<7) else ('B' if (row.imdb_score>=7 and float(row.imdb_score)<8) else ('A' if (float(row.imdb_score)>=8 and float(row.imdb_score)<10) else 0) ))) , axis = 1)
# + id="LJ0aprPqVeLv" colab_type="code" colab={}
# classification_data['imdb_score']=classification_data.apply(lambda row:'E' if ( float(row.imdb_score)>=0 and float(row.imdb_score)<2) else ('D' if (float(row.imdb_score)>=2 and float(row.imdb_score)<4) else ('C' if (float(row.imdb_score)>=4 and float(row.imdb_score)<6) else ('B' if (row.imdb_score>=6 and float(row.imdb_score)<8) else ('A' if (float(row.imdb_score)>=8 and float(row.imdb_score)<10) else 0) ))) , axis = 1)
# + id="-olUYv8pLyRW" colab_type="code" colab={}
# classification_data.groupby('imdb_score').count()
# + id="kBrU_ArQ_n3I" colab_type="code" outputId="0c4b7aea-6483-460d-fdb3-603f174ecfc7" colab={"base_uri": "https://localhost:8080/", "height": 684}
# classification_data
import seaborn as sns
corr = classification_data.corr()
plt.figure(figsize = (16,10))
ax = sns.heatmap(
corr,
vmin=-1, vmax=1, center=0,
cmap=sns.diverging_palette(0, 300,s=90, n=20),
square=True,linewidths=.5,annot=True
)
ax.set_xticklabels(
ax.get_xticklabels(),
rotation=45,
horizontalalignment='right'
);
# plt.figure(figsize = (16,5))
# Var_Corr = classification_data.corr()
# # plot the heatmap and annotation on it
# sns.heatmap(Var_Corr, xticklabels=Var_Corr.columns, yticklabels=Var_Corr.columns)
# + [markdown] id="werMRCf_JEKq" colab_type="text"
# From Attributes Correlation Heatmap we can see that few atributes are highly corelated to each othes as:
#
# 1.cast_total_facebook_likes and actor_1_facebook_likes(.95)
#
# 2.num_voted_users and num_users_for_reviews (.75)
#
# 3.num_voted_users and num_critic_for_reviews (.59)
#
# 4.num_users_for_reviews and num_critic_for_reviews(.56)
# operation =>
#
# A.remove cast_total_facebook_likes
# B.add coulumn others_facebook_likes=sum(actor_2_facebook_likes+actor_3_facebook_likes)
# C. add column num_user_per_critic=num_user_for_reviews/num_critic_for_reviews
# D. remove columns num_user_for_reviews and num_critic_for_reviews
# + id="f6X68OGyW8Yk" colab_type="code" colab={}
backup_classification_data=classification_data
# + id="gyh-JbzJXE6Q" colab_type="code" colab={}
# classification_data=backup_classification_data
# + id="-5pDDWLDD2KU" colab_type="code" colab={}
classification_data['others_facebook_likes'] = classification_data.apply(lambda row: row.actor_2_facebook_likes + row.actor_3_facebook_likes, axis = 1)
classification_data['num_user_per_critic'] = classification_data.apply(lambda row: (row.num_user_for_reviews/row.num_critic_for_reviews), axis = 1)
for col in ["cast_total_facebook_likes","num_user_for_reviews","num_critic_for_reviews","actor_2_facebook_likes","actor_3_facebook_likes","genres"]:
if (col in classification_data.columns):
classification_data=classification_data.drop(columns=[col])
cols = classification_data.columns.tolist()
cols.remove('imdb_score')
cols.append('imdb_score')
classification_data=classification_data[cols]
# tf2
# classification_data
# + id="GdPWIiqfFw3o" colab_type="code" outputId="edbe2b65-e95a-40f2-93a2-85b64dc8d169" colab={"base_uri": "https://localhost:8080/", "height": 677}
import seaborn as sns
corr = classification_data.corr()
plt.figure(figsize = (16,10))
ax = sns.heatmap(
corr,
vmin=-1, vmax=1, center=0,
cmap=sns.diverging_palette(0, 300,s=90, n=20),
square=True,linewidths=.5,annot=True
)
ax.set_xticklabels(
ax.get_xticklabels(),
rotation=45,
horizontalalignment='right'
);
# + [markdown] id="_A05VAlgHDb8" colab_type="text"
# # Algorithem Implementation
# + id="LFEwg8wS0Dkv" colab_type="code" colab={}
# from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
from sklearn import tree
from sklearn.model_selection import cross_val_score,train_test_split
from sklearn import preprocessing
from sklearn import metrics
def encode_the_data(data):
for col in data.columns:
if data.dtypes[col] == "object":
le = preprocessing.LabelEncoder()
# le.fit(data[col])
# data[col] = le.transform(data[col].astype(str))
data[col] = le.fit_transform(data[col].astype(str))
return data
# # classification_data_en
classification_data_en=encode_the_data(classification_data)
# classification_data_en=classification_data
X=classification_data_en.loc[:, classification_data_en.columns != 'imdb_score']
y=classification_data_en['imdb_score']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)
# + id="YV8S2vv5WPGp" colab_type="code" colab={}
# # **GaussianNB Naive_bayes Classifier**
# from sklearn.naive_bayes import GaussianNB
# model=GaussianNB()
# # X_train, X_test, y_train, y_test
# model.fit(X_train,y_train)
# # multinom_naive_bayes,X_train,Y_train
# naive_Y_predict=model.predict(X_test)
# naive_bayes_accuracy=metrics.accuracy_score(y_test,naive_Y_predict)
# naive_bayes_accuracy
# + [markdown] id="95ralG7SWEdx" colab_type="text"
# # **Decision Tree Classifier**
#
# + [markdown] id="PWhITcx08tG2" colab_type="text"
# **Accuracy with Decision Tree Classifier**
# + id="jJnLNsCm-J-W" colab_type="code" colab={}
depth_of_tree_x=[]
accuracy_of_tree_y=[]
depth_of_tree=[]
test_accuracy_of_tree_y=[]
# 5,100,10
for depthis in range(3,10):
decision_tree = tree.DecisionTreeClassifier(criterion = "gini",max_depth=depthis)
decision_tree.fit(X_train,y_train)
decision_tree_score_is = cross_val_score(estimator=decision_tree, X=X_train, y=y_train, cv=5)
depth_of_tree_x.append(depthis)
accuracy_of_tree_y.append(decision_tree_score_is.mean())
# print(decision_tree_score_is)
# print(decision_tree_score_is.mean())
depth_of_tree.append((depthis,decision_tree_score_is.mean()))
# decision_tree_score_is = cross_val_score(estimator=decision_tree, X=X_train, y=Y_train, cv=10, n_jobs=4)
Y_test_pred = decision_tree.predict(X_test)
test_decision_accuracy_is=metrics.accuracy_score(y_test,Y_test_pred)
test_accuracy_of_tree_y.append(test_decision_accuracy_is)
# + id="5IIGoEUs-V7B" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 573} outputId="1cb1316a-5dc8-4700-a7ef-dda36b187dd0"
import matplotlib.pyplot as plt
plt.plot(depth_of_tree_x, accuracy_of_tree_y)
plt.xlabel("Depth")
plt.ylabel("Accuracy")
plt.title('Accuracy of training data with cross validation')
plt.show()
plt.plot(depth_of_tree_x, test_accuracy_of_tree_y)
plt.xlabel("Depth")
plt.ylabel("Accuracy")
plt.title('Accuracy of test data')
plt.show()
# + id="edvzYF91KHad" colab_type="code" outputId="b296eb7c-a1ce-4b73-e297-cb286ac1ff28" colab={"base_uri": "https://localhost:8080/", "height": 34}
decision_tree = tree.DecisionTreeClassifier(criterion = "gini",max_depth=6)
decision_tree.fit(X_train,y_train)
y_test_pred = decision_tree.predict(X_test)
test_decision_accuracy_is=metrics.accuracy_score(y_test,y_test_pred)
# decision_tree_score_is = cross_val_score(estimator=decision_tree, X=X_train, y=Y_train, cv=5)
# depth_of_tree_x.append(depthis)
# accuracy_of_tree_y.append(decision_tree_score_is.mean())
# classification_data_en.columns
test_decision_accuracy_is
# + [markdown] id="AQpgGIP7C6J6" colab_type="text"
# **Cross Validation k-fold**
# + id="F-bFpiTlsXUq" colab_type="code" outputId="daf410f0-bc6c-4862-9567-95527761b9bd" colab={"base_uri": "https://localhost:8080/", "height": 34}
# by using cross validation
decision_tree = tree.DecisionTreeClassifier(criterion = "gini",max_depth=7)
a=X
b=y
decision_tree_score_is = cross_val_score(estimator=decision_tree, X=a, y=b, cv=5)
decision_tree_score_is
# + [markdown] id="d-u9tmrJDFYj" colab_type="text"
# **Decision Tree Creation**
# + id="qJRjODkJh7OE" colab_type="code" colab={}
# from sklearn.tree import export_graphviz
# from sklearn.externals.six import StringIO
# from IPython.display import Image
# import pydotplus
# feature_cols=list(X.columns)
# dot_data = StringIO()
# export_graphviz(decision_tree, out_file=dot_data,
# filled=True, rounded=True,
# special_characters=True,feature_names = feature_cols,class_names=['A++','A+','A','B++','B','C','D'])
# graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
# graph.write_png('IMDB.png')
# Image(graph.create_png())
# + [markdown] id="CMpqEAiK9PNC" colab_type="text"
# # **K-NN Classifier**
# + id="KUOlpPXTt_yD" colab_type="code" colab={}
from sklearn.neighbors import KNeighborsClassifier
range_k=range(1,100)
score_list=[]
for i in range_k:
knn=KNeighborsClassifier(n_neighbors=i)
knn.fit(X_train,y_train)
ypred=knn.predict(X_test)
score_list.append(metrics.accuracy_score(y_test,ypred))
# + id="oLDB9Fhh0zTn" colab_type="code" outputId="ff6e21da-83a4-4358-b169-8ea19f9d9866" colab={"base_uri": "https://localhost:8080/", "height": 296}
plt.plot(range_k,score_list)
plt.xlabel('K in Knn')
plt.ylabel("Testing Accuracy")
# + id="SfBtBmKH6c6Z" colab_type="code" outputId="99d43735-251d-4c83-c8e8-6e013fb2c474" colab={"base_uri": "https://localhost:8080/", "height": 34}
knn=KNeighborsClassifier(n_neighbors=82)
knn.fit(X_train,y_train)
ypred=knn.predict(X_test)
metrics.accuracy_score(y_test,ypred)
# + [markdown] id="PNfns9t-2xwA" colab_type="text"
# Here we can see we are getting best accuracy when k=82
# + [markdown] id="Efw93gcz9o7k" colab_type="text"
# # **Classification using Support Vector Machines**
# + id="Ie42bpTQ3JZI" colab_type="code" outputId="eba53c1d-1ddb-4d8f-be28-43bb51f988b8" colab={"base_uri": "https://localhost:8080/", "height": 34}
from sklearn import svm
#Create a svm Classifier
clf = svm.SVC(gamma='scale')
#Train the model using the training sets
clf.fit(X_train, y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
# + [markdown] id="iqobl_AreboY" colab_type="text"
# # **Random Forest with and without LDA(linear discriminant analysis )**
# + [markdown] id="oET1Qc_ses5V" colab_type="text"
# **Without LDA**
# + id="hyRy0qz5bxug" colab_type="code" outputId="7506a4a4-a1e6-461f-bfa4-bab1895e9e26" colab={"base_uri": "https://localhost:8080/", "height": 88}
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(max_depth=2, random_state=0)
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
# + [markdown] id="wt-S7fZAe0xW" colab_type="text"
# **With LDA**
# + id="QGlHLaaca2xH" colab_type="code" colab={}
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=1)
X_trainlda = lda.fit_transform(X_train, y_train)
X_testlda = lda.transform(X_test)
#LDA tries to reduce dimensions of the feature set while retaining the information that discriminates output classes. LDA tries to find a decision boundary around each cluster of a class.
# + id="XFUa4T3tbqAH" colab_type="code" outputId="5c6327fb-a80e-4921-f52e-62971ad2f6d8" colab={"base_uri": "https://localhost:8080/", "height": 88}
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(max_depth=2, random_state=0)
classifier.fit(X_trainlda, y_train)
y_pred = classifier.predict(X_testlda)
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
# + id="y9W1McdrKM7o" colab_type="code" colab={}
# classification_data['imdb_score'].uniquecount()
# classification_data.groupby('imdb_score').count()
# + id="LSE3CwEcl_DY" colab_type="code" outputId="ebac800b-764c-46f9-896b-6ea6656fd494" colab={"base_uri": "https://localhost:8080/"}
float("7.8")
| 25,920 |
/CNN 2D - FD.ipynb
|
7b2c37f092a059f6b0253c0fb85cc553cd1bcdc4
|
[
"Unlicense"
] |
permissive
|
dmitryanton68/Tracker-fault-diagnosis
|
https://github.com/dmitryanton68/Tracker-fault-diagnosis
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 116,735 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [conda env:dl]
# language: python
# name: conda-env-dl-py
# ---
# +
import warnings
warnings.filterwarnings('ignore')
from model import cnn_model
import numpy as np
import pandas as pd
import keras
import matplotlib.pyplot as plt
import seaborn as sns
import collections as cll
import itertools
import glob
import os
from sklearn.model_selection import train_test_split
from keras.utils import np_utils
from keras.models import Sequential
from keras import regularizers
from keras.layers import Dense, Dropout, Activation, Conv2D, Flatten, BatchNormalization, AveragePooling2D, LSTM
from keras.optimizers import SGD
from keras.optimizers import Adam, Nadam, Adadelta
from keras.models import load_model
from sklearn.metrics import classification_report,confusion_matrix
from keras.datasets import mnist
from keras.utils import Sequence
from keras.preprocessing.sequence import pad_sequences
from keras_lr_finder import LRFinder
class My_generator(Sequence):
def __init__(self, x_set_dir, y_set, batch_size):
self.x, self.y = x_set_dir, y_set
self.batch_size = batch_size
def __len__(self):
return int(np.ceil(len(self.x) / float(self.batch_size)))
def __getitem__(self, idx):
batch_x = self.x[idx * self.batch_size:(idx + 1) * self.batch_size]
batch_y = self.y[idx * self.batch_size:(idx + 1) * self.batch_size]
# read your data here using the batch lists, batch_x and batch_y
x = [np.load(filename) for filename in batch_x]
y = [np.load(filename) for filename in batch_y]
return np.array(x).reshape(self.batch_size,img_rows,img_cols,1), np.array(y)
# -
def cnn_model_big(input_dim, n_classes, init,drop):
model = Sequential()
model.add(Conv2D(128, (4, 4), strides=(1, 1), kernel_initializer=init , padding='same', activation='relu', input_shape=input_dim))
model.add(Conv2D(128, (4, 4), strides=(1, 1), kernel_initializer=init , padding='same', activation='relu'))
model.add(AveragePooling2D(pool_size=(9,1)))
model.add(Dropout(drop))
model.add(Conv2D(256, (3,3), strides=(1, 1), kernel_initializer=init , activation='relu'))
model.add(Conv2D(256, (3,3), strides=(1, 1), kernel_initializer=init , padding='same', activation='relu'))
model.add(AveragePooling2D(pool_size=(7,1)))
model.add(Dropout(drop))
model.add(Conv2D(512, (3,3), strides=(1, 1), kernel_initializer=init , padding='same', activation='relu'))
model.add(Conv2D(512, (3,3), strides=(1, 1), kernel_initializer=init , padding='same', activation='relu'))
model.add(AveragePooling2D(pool_size=(5,1)))
model.add(Dropout(drop))
model.add(Conv2D(768, (3,3), strides=(1, 1), kernel_initializer=init,activation='relu'))
model.add(Conv2D(768, (3,3), strides=(1, 1), kernel_initializer=init, padding='same', activation='relu'))
model.add(AveragePooling2D(pool_size=(3,1)))
model.add(Dropout(drop))
model.add(Flatten())
model.add(Dense(4096, kernel_initializer=init , activation='relu'))
model.add(Dropout(drop*6))
model.add(Dense(768, kernel_initializer=init , activation='relu'))
model.add(Dropout(drop*2))
return model
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
fig = plt.figure()
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes)
plt.yticks(tick_marks, classes)
fmt = '.4f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('Classe correta')
plt.xlabel('Classe prevista')
return fig
img_rows, img_cols = 6410, 8
n_classes = 2
input_shape = (img_rows,img_cols,1)
# # B1
train_path = glob.glob(os.path.join('dados/train/', '*.npy'))
test_path = glob.glob(os.path.join('dados/test', '*.npy'))
y_train_dir = glob.glob(os.path.join('dados/B1_y_train/', '*.npy'))
y_test_dir = glob.glob(os.path.join('dados/B1_y_test/', '*.npy'))
batch_size_train = 1
batch_size_test = 1
my_training_batch_generator = My_generator(train_path, y_train_dir, batch_size_train)
my_validation_batch_generator = My_generator(test_path, y_test_dir, batch_size_test)
init = keras.initializers.he_uniform(42)
init2 = keras.initializers.constant(0.001)
model = cnn_model_big(input_shape,n_classes,init,drop=0.1)
model.add(Dense(n_classes,activation='softmax'))
model.load_weights('PesosB1/cruzinho-CNN.ESSE.hdf5')
model.summary()
# +
sgd = SGD(lr=0.1, decay=0, momentum=0.9, nesterov=True)
adam = Adam(lr=0.0001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0, amsgrad=False)
nadam = Nadam(lr=0.0001, beta_1=0.9, beta_2=0.999, epsilon=None, schedule_decay=0.000001)
adadelta = Adadelta(lr = 1)
filepath = 'PesosB1/cruzinho-CNN-vgg.{epoch:02d}-{loss:.2f}-{acc:.2f}-{val_loss:.2f}-{val_acc:.2f}.hdf5'
cb = keras.callbacks.ModelCheckpoint(filepath, monitor='acc', verbose=0, save_best_only=True, save_weights_only=False, mode='auto', period=1)
model.compile(optimizer = nadam, loss = 'binary_crossentropy', metrics = ['accuracy'])
# -
history = model.fit_generator(generator=my_training_batch_generator,
epochs=50,
verbose=1,
use_multiprocessing=True,
workers = 8,
max_queue_size=84,
validation_data=my_validation_batch_generator,
validation_steps=(len(test_path) // batch_size_test),
steps_per_epoch=(len(train_path) // batch_size_train),
callbacks = [cb],
initial_epoch=0)
# + active=""
# history = model.fit(X_train, y_train, validation_data=(X_test,y_test), batch_size=10, epochs=10, initial_epoch=0,shuffle=True)
# +
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
# Plot training & validation loss values
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Test'], loc='upper left')
plt.show()
# +
y_test = []
y_train = []
for i in y_test_dir:
tmp = np.load(i)
y_test.append(tmp)
for i in y_train_dir:
tmp = np.load(i)
y_train.append(tmp)
# -
#Predict Test
classes = ['sem falha', 'com falha']
y_testing = np.argmax(y_test, axis =1)
pred = model.predict_generator(my_validation_batch_generator, workers=8, use_multiprocessing=True, verbose=1,max_queue_size=64, steps=(len(test_path) // batch_size_test))
pred = np.argmax(pred, axis = 1)
print(classification_report(y_testing,pred,digits=4))
cm = confusion_matrix(y_testing,pred)
cm_plot = plot_confusion_matrix(cm, classes, normalize=True, title='')
cm_plot.savefig('cruzin_b1_test.png',dpi = 'figure', bbox_inches='tight')
#Predict Train
y_training = np.argmax(y_train, axis = 1)
pred = model.predict_generator(my_training_batch_generator, workers=8, use_multiprocessing=True, verbose=1,max_queue_size=64, steps=(len(train_path) // batch_size_train))
pred = np.argmax(pred, axis = 1)
print(classification_report(y_training,pred,digits=4))
cm = confusion_matrix(y_training,pred)
cm_plot = plot_confusion_matrix(cm, classes, normalize=True, title='')
cm_plot.savefig('cruzin_b1_train.png',dpi = 'figure', bbox_inches='tight')
| 8,303 |
/Neural Network.ipynb
|
0d5ecf7871699df6a4388194aa163336767b6716
|
[] |
no_license
|
WHaMoCaTY/Diabetes-130-UShospitals
|
https://github.com/WHaMoCaTY/Diabetes-130-UShospitals
| 2 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 57,826 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import torch
import torch.utils.data
import torch.nn as nn
from torch.autograd import Variable
import torch.optim as optim
import numpy as np
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
# -
# Prepare data
my_data = np.genfromtxt('hospital_ready_shuffle.csv', delimiter=',')[1:]
X = my_data[:,:-1]
Y = my_data[:, -1]
Y = Y-1
scaler = MinMaxScaler()
scaler.fit(X)
X = scaler.transform(X)
X_train = X[:60000,:]
X_test = X[60000:,:]
Y_train = Y[:60000]
Y_test = Y[60000:]
# +
# data loader
tensor_Xtr = torch.from_numpy(X_train).float()
tensor_Ytr = torch.from_numpy(Y_train).long()
tensor_Xva = torch.from_numpy(X_test).float()
tensor_Yva = torch.from_numpy(Y_test).long()
train = torch.utils.data.TensorDataset(tensor_Xtr, tensor_Ytr)
train_loader = torch.utils.data.DataLoader(train, batch_size=256, shuffle=True)
test = torch.utils.data.TensorDataset(tensor_Xva, tensor_Yva)
test_loader = torch.utils.data.DataLoader(test, batch_size=256, shuffle=True)
# +
# define network
# define nnet
class Net(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(73, 200)
self.relu1 = nn.ReLU()
# self.fc2 = nn.Linear(200, 200)
# self.relu2 = nn.ReLU()
self.out = nn.Linear(200, 3)
def forward(self, input_):
a1 = self.fc1(input_)
h1 = self.relu1(a1)
# a2 = self.fc2(h1)
# h2 = self.relu2(a2)
a3 = self.out(h1)
return a3
class Net2(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(73, 200)
self.relu1 = nn.ReLU()
self.fc2 = nn.Linear(200, 200)
self.relu2 = nn.ReLU()
self.out = nn.Linear(200, 3)
def forward(self, input_):
a1 = self.fc1(input_)
h1 = self.relu1(a1)
a2 = self.fc2(h1)
h2 = self.relu2(a2)
a3 = self.out(h2)
return a3
# -
# Create model
net = Net()
net.cuda()
opt = optim.SGD(net.parameters(), lr=0.0001)
criterion = nn.CrossEntropyLoss()
# Test the Model
def test(net, loader):
correct = 0
total = 0
for x, y in loader:
x = Variable(x).cuda()
outputs = net(x)
_, predicted = torch.max(outputs.data, 1)
total += y.size(0)
correct += (predicted.cpu() == y).sum()
return correct.item()/total
# run
best_ac = 0
train_ac = []
test_ac = []
train_loss = []
for epoch in range(20):
for i, (x, y) in enumerate(train_loader):
# Convert torch tensor to Variable
x = Variable(x).cuda()
y = Variable(y).cuda()
# Forward + Backward + Optimize
opt.zero_grad() # zero the gradient buffer
outputs = net(x)
loss = criterion(outputs, y)
loss.backward()
opt.step()
train_loss.append(loss.item())
tr_ac = test(net, train_loader)
te_ac = test(net, test_loader)
train_ac.append(tr_ac)
test_ac.append(te_ac)
if te_ac > best_ac:
torch.save(net.state_dict(), 'model.pb')
best_ac = te_ac
print("Epoch: %d, Loss: %4f, Train AC: %4f, Test AC: %.4f, Best AC: %.4f" % (epoch, loss.item(), tr_ac, te_ac, best_ac))
best_ac
net = Net2()
net.cuda()
opt = optim.SGD(net.parameters(), lr=0.0001)
criterion = nn.CrossEntropyLoss()
# run 2
best_ac2 = 0
train_ac2 = []
test_ac2 = []
train_loss2 = []
for epoch in range(20):
for i, (x, y) in enumerate(train_loader):
# Convert torch tensor to Variable
x = Variable(x).cuda()
y = Variable(y).cuda()
# Forward + Backward + Optimize
opt.zero_grad() # zero the gradient buffer
outputs = net(x)
loss = criterion(outputs, y)
loss.backward()
opt.step()
train_loss2.append(loss.item())
tr_ac = test(net, train_loader)
te_ac = test(net, test_loader)
train_ac2.append(tr_ac)
test_ac2.append(te_ac)
if te_ac > best_ac2:
torch.save(net.state_dict(), 'model.pb')
best_ac2 = te_ac
print("Epoch: %d, Loss: %4f, Train AC: %4f, Test AC: %.4f, Best AC: %.4f" % (epoch, loss.item(), tr_ac, te_ac, best_ac2))
# plot accuracy
plt.plot(np.arange(20)+1, test_ac2, 'r')
plt.plot(np.arange(20)+1, test_ac, 'b')
plt.legend(['1 hidden layer of 200','2 hidden layers of 200'])
plt.title('Accuracy On Test Data')
plt.xlabel('Training Epochs')
plt.ylabel('Accuracy')
plt.savefig('acc.jpg')
# plot loss
plt.plot(np.arange(20)+1, train_loss2, 'r')
plt.plot(np.arange(20)+1, train_loss, 'b')
plt.legend(['1 hidden layer of 200','2 hidden layers of 200'])
plt.title('Accuracy On Test Data')
plt.xlabel('Training Epochs')
plt.ylabel('Accuracy')
plt.savefig('loss.jpg')
best_ac
best_ac2
| 5,016 |
/Module_08_電腦視覺服務應用3/Demo_8-3.ipynb
|
47dddef76a87fc73bb0441568218cc27f53bc3e5
|
[] |
no_license
|
shangxiwu/Azure
|
https://github.com/shangxiwu/Azure
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 134,198 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 特定領域偵測服務操作
# ## domain: celebrities
# +
from azure.cognitiveservices.vision.computervision import ComputerVisionClient
from msrest.authentication import CognitiveServicesCredentials
from IPython.display import Image
from IPython.core.display import HTML
# Set API key.
subscription_key = '390b0e8c9f8b43d9a21e896e74ae1c7b'
# Set endpoint.
endpoint = 'https://aien08cv01.cognitiveservices.azure.com/'
# Call API
computervision_client = ComputerVisionClient(endpoint, CognitiveServicesCredentials(subscription_key))
'''
Detect Domain-specific Content - remote
This example detects celebrites and landmarks in remote images.
'''
print("===== Detect Domain-specific Content - remote =====")
# URL of one or more celebrities
remote_image_url_celebs = "https://upload.wikimedia.org/wikipedia/zh/4/49/Nobi_Nobita.png"
# Call API with content type (celebrities) and URL
detect_domain_results_celebs_remote = computervision_client.analyze_image_by_domain("celebrities", remote_image_url_celebs)
# Print detection results with name
print("Celebrities in the remote image:")
if len(detect_domain_results_celebs_remote.result["celebrities"]) == 0:
print("No celebrities detected.")
else:
for celeb in detect_domain_results_celebs_remote.result["celebrities"]:
print(celeb["name"])
PATH = remote_image_url_celebs #圖片路徑
Image(url=PATH , width=480, height=240)
# -
# ## domain: landmarks
# +
from azure.cognitiveservices.vision.computervision import ComputerVisionClient
from msrest.authentication import CognitiveServicesCredentials
from IPython.display import Image
from IPython.core.display import HTML
# Set API key.
subscription_key = '390b0e8c9f8b43d9a21e896e74ae1c7b'
# Set endpoint.
endpoint = 'https://aien08cv01.cognitiveservices.azure.com/'
# Call API
computervision_client = ComputerVisionClient(endpoint, CognitiveServicesCredentials(subscription_key))
remote_image_url = "https://pic.pimg.tw/anrine910070/1552868712-427881496.jpg"
# Call API with content type (landmarks) and URL
detect_domain_results_landmarks = computervision_client.analyze_image_by_domain("landmarks", remote_image_url)
print()
print("Landmarks in the remote image:")
if len(detect_domain_results_landmarks.result["landmarks"]) == 0:
print("No landmarks detected.")
else:
for landmark in detect_domain_results_landmarks.result["landmarks"]:
print(landmark["name"])
PATH = remote_image_url #圖片路徑
Image(url=PATH , width=850, height=600)
# -
# # 色彩配置偵測服務操作
# +
from azure.cognitiveservices.vision.computervision import ComputerVisionClient
from msrest.authentication import CognitiveServicesCredentials
# Set API key.
subscription_key = '390b0e8c9f8b43d9a21e896e74ae1c7b'
# Set endpoint.
endpoint = 'https://aien08cv01.cognitiveservices.azure.com/'
# Call API
computervision_client = ComputerVisionClient(endpoint, CognitiveServicesCredentials(subscription_key))
'''
Detect Color - remote
This example detects the different aspects of its color scheme in a remote image.
'''
print("===== Detect Color - remote =====")
# Select the feature(s) you want
remote_image_features = ["color"]
# Call API with URL and features
detect_color_results_remote = computervision_client.analyze_image(remote_image_url, remote_image_features)
# Print results of color scheme
print("Getting color scheme of the remote image: ")
print("Is black and white: {}".format(detect_color_results_remote.color.is_bw_img))
print("Accent color: {}".format(detect_color_results_remote.color.accent_color))
print("Dominant background color: {}".format(detect_color_results_remote.color.dominant_color_background))
print("Dominant foreground color: {}".format(detect_color_results_remote.color.dominant_color_foreground))
print("Dominant colors: {}".format(detect_color_results_remote.color.dominant_colors))
# -
# # 智慧裁切縮圖服務操作
# +
import os
import sys
import requests
# If you are using a Jupyter notebook, uncomment the following line.
# %matplotlib inline
import matplotlib.pyplot as plt
from PIL import Image
from io import BytesIO
# Set API key.
subscription_key = '390b0e8c9f8b43d9a21e896e74ae1c7b'
# Set endpoint.
endpoint = 'https://aien08cv01.cognitiveservices.azure.com/'
thumbnail_url = endpoint + "vision/v2.1/generateThumbnail"
# Set image_url to the URL of an image that you want to analyze.
image_url = "https://s2.itislooker.com/imgs/201811/06/12/15414798522851.jpg"
headers = {'Ocp-Apim-Subscription-Key': subscription_key}
params = {'width': '600', 'height': '600', 'smartCropping': 'true'}
data = {'url': image_url}
response = requests.post(thumbnail_url, headers=headers,
params=params, json=data)
response.raise_for_status()
thumbnail = Image.open(BytesIO(response.content))
# Display the thumbnail.
plt.imshow(thumbnail)
plt.axis("off")
# Verify the thumbnail size.
print("Thumbnail is {0}-by-{1}".format(*thumbnail.size))
| 5,205 |
/final_project-master2/Data Cleaning.ipynb
|
4f9e46d01c601d7b0a85079b8f05412f19aa494b
|
[] |
no_license
|
JChicatelli/Primary_Numbers
|
https://github.com/JChicatelli/Primary_Numbers
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 105,601 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
county_facts = "county_facts.csv"
primary_results = "primary_results.csv"
county_facts_df = pd.read_csv(county_facts, encoding="ISO-8859-1")
primary_results_df = pd.read_csv(primary_results, encoding="ISO-8859-1")
# County facts dataframe
county_facts_df.head()
# +
#county_facts_df.count()
# +
# Remove all NaN
county_facts_df = county_facts_df.dropna(how='any')
# Set dataframe to show specific columns
county_facts_cleaned_df = county_facts_df[["fips", "area_name", "PST120214", "POP010210", "POP645213", "VET605213",
"LFE305213", "INC110213", "PVY020213", "SBO001207", "SBO315207", "SBO215207",
"SBO415207", "SBO015207", "MAN450207", "RTN130207", "RTN131207", "BPS030214",
"LND110210", "POP060210"]]
#county_facts_cleaned_df.count()
# -
# Rename columns
county_facts_cleaned_df = county_facts_cleaned_df.rename(columns={"area_name":"County",
"PST120214":"Population % Change",
"POP010210":"2010 Population",
"POP645213":"% Foreign Born",
"VET605213":"Veterans",
"LFE305213":"Mean Travel Time",
"INC110213":"Median Household Income",
"PVY020213":"Below Poverty Level",
"SBO001207":"Total Number of Firms",
"SBO315207":"% Black-owned Firms",
"SBO215207":"% Asian-owned Firms",
"SBO415207":"% Hispanic-owned Firms",
"SBO015207":"% Women-owned Firms",
"MAN450207":"Manufacturers Shipments ($1000)",
"RTN130207":"Retail Sales ($1000)",
"RTN131207":"Retail Sales per Capita",
"BPS030214":"Building permits",
"LND110210":"Land Area (Square Miles)",
"POP060210":"Population per Square Mile"})
county_facts_cleaned_df.head()
# Drop all NaN from primary results dataframe
primary_results_df = primary_results_df.dropna(how='any')
#primary_results_df.count()
# Set dataframe to show specific columns
primary_results_cleaned_df = primary_results_df[["fips", "party", "candidate", "votes", "fraction_votes"]]
#primary_results_cleaned_df
# Rename columns
primary_results_cleaned_df = primary_results_cleaned_df.rename(columns={"party":"Party",
"candidate":"Candidate",
"votes":"Votes",})
fips_merge_df = pd.merge(county_facts_cleaned_df, primary_results_cleaned_df, on="fips")
fips_merge_df
fips_merge_df.to_csv("training_data.csv", index=False, header=True)
# +
# primary_results_alabama_df = primary_results_df.loc[primary_results_df["state"] == "Alabama", :]
# primary_results_republican_df = primary_results_df.loc[primary_results_df["party"] == "Republican", :]
# primary_results_democrat_df = primary_results_df.loc[primary_results_df["party"] == "Democrat", :]
# primary_results_democrat_df.head()
# primary_results_democrat_sorted = primary_results_democrat_df.sort_values(["fips", "votes"], ascending=True)
# primary_results_democrat_sorted = primary_results_democrat_sorted.sort_values(["fips"], ascending=True)
# 8959 rows
# primary_results_democrat_sorted.nlargest(keep="last")
# primary_results_democrat_df.nlargest(100, ["fips", "votes"], keep="first")
| 4,320 |
/EDA/project.ipynb
|
ba5f957ba7e6df1d92efd801785d01a5d7a3d12b
|
[] |
no_license
|
Karsenh/CPSC322FinalProject
|
https://github.com/Karsenh/CPSC322FinalProject
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 923,489 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Importing the Libraries
import pandas as pd
from mysklearn.mypytable import MyPyTable
from mysklearn import myutils
from mysklearn import plot_utils
from mysklearn.myclassifiers import MySimpleLinearRegressor
import matplotlib.pyplot as plt
# # Loading the Dataset
mytable = MyPyTable()
dataset = mytable.load_from_json_file('yelp_academic_dataset_business.json', 30000)
dataset.head()
dataset.get_shape()
dataset.remove_rows_with_missing_values()
dataset.get_shape()
# # Selecting Business Attributes
id_ = dataset.get_column('business_id')
review_count = dataset.get_column('review_count')
attributes = dataset.get_column('attributes')
mytable2 = MyPyTable()
dataset2 = mytable2.load_from_json_file('yelp_academic_dataset_tip.json', 30000)
dataset2.head()
id_2 = dataset2.get_column('business_id')
user_id = dataset2.get_column('user_id')
text = dataset2.get_column('text')
new_id = []
new_user_id = []
new_text = []
for id in id_:
if id in id_2:
new_id.append(id)
index = id_2.index(id)
new_user_id.append(user_id[index])
new_text.append(text[index])
new_id = new_id[:1500]
new_user_id = new_user_id[:1500]
new_text = new_text[:1500]
new_rev_count = []
new_attributes = []
for id in new_id:
index = id_.index(id)
new_rev_count.append(review_count[index])
new_attributes.append(attributes[index])
mytable3 = MyPyTable()
dataset3 = mytable3.load_from_json_file('yelp_academic_dataset_user.json', 250000)
user_id = dataset3.get_column('user_id')
fans = dataset3.get_column('fans')
compliment_plain = dataset3.get_column('compliment_plain')
friends = dataset3.get_column('friends')
useful = dataset3.get_column('useful')
new_fans = []
new_comp_plain = []
new_friends = []
new_useful = []
for id in new_user_id:
if id in user_id:
index = user_id.index(id)
new_fans.append(fans[index])
new_comp_plain.append(compliment_plain[index])
new_friends.append(friends[index])
new_useful.append(useful[index])
new_dataset = [[a, b, c, d, e, f, g] for a, b, c, d, e, f, g in zip(new_rev_count, new_attributes, new_text, new_fans, new_comp_plain, new_friends, new_useful)]
# # Exploratory Data Analysis
# ## Data Preprocessing
columns = ['Review Count', 'Attributes', 'Review Length', 'Fans', 'Compliment Plain', 'Friends', 'Useful']
final_dataset = MyPyTable(columns, new_dataset)
final_dataset.replace_missing_values_with_column_average('Review Count')
final_dataset.replace_missing_values_with_column_average('Attributes')
final_dataset.replace_missing_values_with_column_average('Review Length')
final_dataset.replace_missing_values_with_column_average('Fans')
final_dataset.replace_missing_values_with_column_average('Compliment Plain')
final_dataset.replace_missing_values_with_column_average('Friends')
final_dataset.replace_missing_values_with_column_average('Useful')
final_dataset.get_shape()
final_dataset.remove_rows_with_missing_values()
final_dataset.get_shape()
# ### Saving Trimmed Data To New File
import os
if not os.path.exists('output'):
os.mkdir('output')
final_dataset.save_to_file(filename='output/trimmed_data.csv')
# ### Summarization: Column Names, Minimum, Maximum, Middle, Average, Medium Values
stats = final_dataset.compute_summary_statistics(col_names=['Review Count', 'Fans', 'Compliment Plain', 'Useful'])
stats.pretty_print()
# ## Visualization
# ### Frequency Diagrams
# #### Applying Discretization To Review Count To Generate Frequency Diagram
review_values = final_dataset.get_column('Review Count')
new_review_values = []
review_counts = [0] * 10
ranges = ['≤ 13', '14-50', '51-100', '101-200', '201-400', '401-600', '601-800', '801-1000', '1001-1200', '≥ 1200']
for val in review_values:
if val <= 13:
new_review_values.append('≤ 13')
review_counts[0] += 1
elif 14 <= val <= 50:
new_review_values.append('14-50')
review_counts[1] += 1
elif 51 <= val <= 100:
new_review_values.append('51-100')
review_counts[2] += 1
elif 101 <= val <= 200:
new_review_values.append('101-200')
review_counts[3] += 1
elif 201 <= val <= 400:
new_review_values.append('201-400')
review_counts[4] += 1
elif 401 <= val <= 600:
new_review_values.append('401-600')
review_counts[5] += 1
elif 601 <= val <= 800:
new_review_values.append('601-800')
review_counts[6] += 1
elif 801 <= val <= 1000:
new_review_values.append('801-1000')
review_counts[7] += 1
elif 1001 <= val <= 1200:
new_review_values.append('1001-1200')
review_counts[8] += 1
elif val >= 1200:
new_review_values.append('≥ 1200')
review_counts[9] += 1
x_range = range(len(ranges))
y_range = range(0, max(review_counts)+50, 30)
plot_utils.frequency_diagram(ranges, review_counts, ranges, y_range, 'Total number of counts by categories (1 to 10) of Review Counts', 'Review Count', 'Count')
# #### Applying Discretization To Review Length To Generate Frequency Diagram
review_length = final_dataset.get_column('Review Length')
review_length = [len(str(t)) for t in review_length]
new_review_length = []
review_length_counts = [0] * 5
ranges = ['≤ 20', '21-50', '51-100', '101-200', '≥ 200']
for val in review_length:
if val <= 20:
new_review_values.append('≤ 20')
review_length_counts[0] += 1
elif 14 <= val <= 50:
new_review_values.append('21-50')
review_length_counts[1] += 1
elif 51 <= val <= 100:
new_review_values.append('51-100')
review_length_counts[2] += 1
elif 101 <= val <= 200:
new_review_values.append('101-200')
review_length_counts[3] += 1
elif val > 200:
new_review_values.append('≥ 200')
review_length_counts[4] += 1
x_range = range(len(ranges))
y_range = range(0, max(review_length_counts)+60, 30)
plot_utils.frequency_diagram(ranges, review_length_counts, ranges, y_range, 'Total number of counts by categories (1 to 5) of Review Length', 'Review Length', 'Count')
# #### Applying Discretization To Attributes To Generate Frequency Diagram
attributes = final_dataset.get_column('Attributes')
attributes = [len(k.keys()) if k else 0 for k in attributes]
new_attributes = []
attributes_counts = [0] * 5
ranges = ['≤ 5', '6-10', '11-15', '16-20', '≥ 20']
for val in attributes:
if val <= 5:
new_attributes.append('≤ 5')
attributes_counts[0] += 1
elif 6 <= val <= 10:
new_attributes.append('6-10')
attributes_counts[1] += 1
elif 11 <= val <= 15:
new_attributes.append('11-15')
attributes_counts[2] += 1
elif 16 <= val <= 20:
new_attributes.append('16-20')
attributes_counts[3] += 1
elif val > 20:
new_attributes.append('≥ 20')
attributes_counts[4] += 1
x_range = range(len(ranges))
y_range = range(0, max(attributes_counts)+60, 30)
plot_utils.frequency_diagram(ranges, attributes_counts, ranges, y_range, 'Total number of counts by categories (1 to 5) of Attribute Counts', 'Attribute Counts', 'Count')
# #### Applying Discretization To Fans To Generate Frequency Diagram
fans_values = final_dataset.get_column('Fans')
new_fans_values = []
fans_counts = [0] * 10
ranges = ['0', '1-5', '6-10', '11-20', '21-50', '51-100', '101-200', '201-300', '301-400', '≥ 400']
for val in fans_values:
if val == 0:
new_fans_values.append('0')
fans_counts[0] += 1
elif val <= 13:
new_fans_values.append('1-5')
fans_counts[1] += 1
elif 14 <= val <= 50:
new_fans_values.append('6-10')
fans_counts[2] += 1
elif 51 <= val <= 100:
new_fans_values.append('11-20')
fans_counts[3] += 1
elif 201 <= val <= 400:
new_fans_values.append('21-50')
fans_counts[4] += 1
elif 401 <= val <= 600:
new_fans_values.append('51-100')
fans_counts[5] += 1
elif 601 <= val <= 800:
new_fans_values.append('101-200')
fans_counts[6] += 1
elif 801 <= val <= 1000:
new_fans_values.append('201-300')
fans_counts[7] += 1
elif 1001 <= val <= 1200:
new_fans_values.append('301-400')
fans_counts[8] += 1
elif val >= 1200:
new_fans_values.append('≥ 400')
fans_counts[9] += 1
x_range = range(len(ranges))
y_range = range(0, max(fans_counts)+50, 100)
plot_utils.frequency_diagram(ranges, fans_counts, ranges, y_range, 'Total number of counts by categories (1 to 10) of Fans', 'Fans', 'Count')
# #### Applying Discretization To Compliment Plain To Generate Frequency Diagram
comp_plain_values = final_dataset.get_column('Compliment Plain')
new_comp_plain_values = []
comp_plain_counts = [0] * 10
ranges = ['≤ 13', '14-50', '51-100', '101-200', '201-400', '401-600', '601-800', '801-1000', '1001-1200', '≥ 1200']
for val in comp_plain_values:
if val <= 13:
new_comp_plain_values.append('≤ 13')
comp_plain_counts[0] += 1
elif 14 <= val <= 50:
new_comp_plain_values.append('14-50')
comp_plain_counts[1] += 1
elif 51 <= val <= 100:
new_comp_plain_values.append('51-100')
comp_plain_counts[2] += 1
elif 101 <= val <= 200:
new_comp_plain_values.append('101-200')
comp_plain_counts[3] += 1
elif 201 <= val <= 400:
new_comp_plain_values.append('201-400')
comp_plain_counts[4] += 1
elif 401 <= val <= 600:
new_comp_plain_values.append('401-600')
comp_plain_counts[5] += 1
elif 601 <= val <= 800:
new_comp_plain_values.append('601-800')
comp_plain_counts[6] += 1
elif 801 <= val <= 1000:
new_comp_plain_values.append('801-1000')
comp_plain_counts[7] += 1
elif 1001 <= val <= 1200:
new_comp_plain_values.append('1001-1200')
comp_plain_counts[8] += 1
elif val >= 1200:
new_comp_plain_values.append('≥ 1200')
comp_plain_counts[9] += 1
x_range = range(len(ranges))
y_range = range(0, max(comp_plain_counts)+50, 100)
plot_utils.frequency_diagram(ranges, comp_plain_counts, ranges, y_range, 'Total number of counts by categories (1 to 10) of Compliment Plain', 'Compliment Plain', 'Count')
# #### Applying Discretization To Friends To Generate Frequency Diagram
friends = final_dataset.get_column('Friends')
friends_values = [len(str(f)) for f in friends]
new_friends_values = []
friends_counts = [0] * 10
ranges = ['≤ 100', '101-1000', '1001-10000', '10001-20000', '20001-30000', '30001-40000', '40001-50000', '50001-60000', '60001-70000', '≥ 70000']
for val in friends_values:
if val <= 100:
new_friends_values.append('≤ 100')
friends_counts[0] += 1
elif 101 <= val <= 1000:
new_friends_values.append('101-1000')
friends_counts[1] += 1
elif 1001 <= val <= 10000:
new_friends_values.append('1001-10000')
friends_counts[2] += 1
elif 10001 <= val <= 20000:
new_friends_values.append('10001-20000')
friends_counts[3] += 1
elif 20001 <= val <= 30000:
new_friends_values.append('20001-30000')
friends_counts[4] += 1
elif 30001 <= val <= 40000:
new_friends_values.append('30001-40000')
friends_counts[5] += 1
elif 40001 <= val <= 50000:
new_friends_values.append('40001-50000')
friends_counts[6] += 1
elif 50001 <= val <= 60000:
new_friends_values.append('50001-60000')
friends_counts[7] += 1
elif 60001 <= val <= 70000:
new_friends_values.append('60001-70000')
friends_counts[8] += 1
elif val >= 70000:
new_friends_values.append('≥ 70000')
friends_counts[9] += 1
x_range = range(len(ranges))
y_range = range(0, max(friends_counts)+50, 100)
plot_utils.frequency_diagram(ranges, friends_counts, ranges, y_range, 'Total number of counts by categories (1 to 10) of Friends', 'Friends', 'Count')
# #### Applying Discretization To Useful To Generate Frequency Diagram
useful_values = final_dataset.get_column('Useful')
new_useful_values = []
useful_counts = [0] * 10
ranges = ['≤ 13', '14-50', '51-100', '101-200', '201-400', '401-600', '601-800', '801-1000', '1001-1200', '≥ 1200']
for val in useful_values:
if val <= 13:
new_useful_values.append('≤ 13')
useful_counts[0] += 1
elif 14 <= val <= 50:
new_useful_values.append('14-50')
useful_counts[1] += 1
elif 51 <= val <= 100:
new_useful_values.append('51-100')
useful_counts[2] += 1
elif 101 <= val <= 200:
new_useful_values.append('101-200')
useful_counts[3] += 1
elif 201 <= val <= 400:
new_useful_values.append('201-400')
useful_counts[4] += 1
elif 401 <= val <= 600:
new_useful_values.append('401-600')
useful_counts[5] += 1
elif 601 <= val <= 800:
new_useful_values.append('601-800')
useful_counts[6] += 1
elif 801 <= val <= 1000:
new_useful_values.append('801-1000')
useful_counts[7] += 1
elif 1001 <= val <= 1200:
new_useful_values.append('1001-1200')
useful_counts[8] += 1
elif val >= 1200:
new_useful_values.append('≥ 1200')
useful_counts[9] += 1
x_range = range(len(ranges))
y_range = range(0, max(useful_counts)+50, 30)
plot_utils.frequency_diagram(ranges, useful_counts, ranges, y_range, 'Total number of counts by categories (1 to 10) of Useful', 'Useful', 'Count')
# ### Box and Whisker Plot
plt.figure(figsize=(14, 6))
plt.boxplot([review_counts, attributes_counts])
plt.title('Ditribution Comparison Between Review Count and Attributes Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Review Count', 'Attributes'])
plt.show()
# Review Count is positively skewed in terms of data distribution because its top tail is longer compared to Attributes box plot which has normal or symmetric distribution because of equal top and bottom tails and median being in middle of box. Although, Attributes has median value higher than Review Count which suggests clear disagreement between both features count. Finally, no outliers found in both features which is good for data mining and machine learning algorithms.
plt.figure(figsize=(14, 6))
plt.boxplot([review_counts, useful_counts])
plt.title('Ditribution Comparison Between Review Count and Useful Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Review Count', 'Useful'])
plt.show()
# Similar to Review Count, Useful also has positively skewed data distribution between its top tail is longer but its short in terms of box shape which suggests less dispersed data or less variability in Useful compared to Review Count. And, Useful has median value slightly above than Review Count which suggests disagreement between both features count. Finally, no outliers found in both features.
plt.figure(figsize=(14, 6))
plt.boxplot([review_counts, fans_counts])
plt.title('Ditribution Comparison Between Review Count and Fans Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Review Count', 'Fans'])
plt.show()
# Similar to Review Count, Fans also has positively skewed data distribution because of its longer top tail and median value close to bottom. Both features are in disagreement because Review Count has median value higher than Fans.
plt.figure(figsize=(14, 6))
plt.boxplot([review_counts, review_length_counts])
plt.title('Ditribution Comparison Between Review Count and Review Length Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Review Count', 'Review Length'])
plt.show()
# Compared to Review Count, Review Length has negatively skewed data distribution because of its bottom tail being longer but data is much dispersed and widely spread in Review Length compared to Review Count. And, both features are in disagreement because Review Length has median value higher than Review Count. Finally, no outliers found in both features count.
plt.figure(figsize=(14, 6))
plt.boxplot([review_counts, friends_counts])
plt.title('Ditribution Comparison Between Review Count and Friends Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Review Count', 'Friends'])
plt.show()
# Similar to Review Count, Friends also has positively skewed data distribution because of its longer top tail and median value being at bottom and both have almost same data dispersion. But, both features are in disagreement because Review Count has median value higher than Friends. Finally, one outlier found in Friends which is not good for data mining algorithms and it should be handled by outliers handling methods as outliers show errors in dataset.
plt.figure(figsize=(14, 6))
plt.boxplot([review_counts, comp_plain_counts])
plt.title('Ditribution Comparison Between Review Count and Compliment Plain Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Review Count', 'Compliment Plain'])
plt.show()
# Similar to Review Count, Compliment Plain has positively skewed data distribution because of its median value being at bottom side of box which makes upper part of box bigger. But, data is very less dispersed in compared to Review Count. And, both features are in disagreement because Review Count has median value higher than Compliment Plain. Finally, two outliers found in Compliment Plain which should be handled with methods like outliers deletion or replacement etc.
plt.figure(figsize=(14, 6))
plt.boxplot([attributes_counts, review_length_counts])
plt.title('Ditribution Comparison Between Attributes Count and Review Length Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Attributes', 'Review Length'])
plt.show()
# Attributes is showing normal distribution of dataset compared to Review Length which has negatively skewed distribution because of its bottom tail being longer. Though, first quartile, second quartile, and third quartie of Review Length, all are different and higher than Attributes which suggests complete disgreement between both features, surely because of data being highly dispersed in Review Length compared to Attributes. Finally, no outliers found in both features count.
plt.figure(figsize=(14, 6))
plt.boxplot([attributes_counts, fans_counts])
plt.title('Ditribution Comparison Between Attributes Count and Fans Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Attributes', 'Fans'])
plt.show()
# Compared to Attributes which has normal distribution, Fans has positively skewed (a.k.a skew-right) data distribution but has lower median value than Attributes which suggests disagreement between both features. Finally, one outlier found in Fans which should be handled properly in order to get reliable and accurate results from data mining algorithms.
plt.figure(figsize=(14, 6))
plt.boxplot([attributes_counts, comp_plain_counts])
plt.title('Ditribution Comparison Between Attributes Count and Compliment Plain Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Attributes', 'Compliment Plain'])
plt.show()
# Compared to Attributes which has normal distribution, Compliment Plain has positively skewed (a.k.a skew-right) data distribution but has lower median value than Attributes which suggests disagreement between both features. Finally, two outliers found in Fans which should be handled properly because of reasons mentioned above.
plt.figure(figsize=(14, 6))
plt.boxplot([attributes_counts, friends_counts])
plt.title('Ditribution Comparison Between Attributes Count and Friends Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Attributes', 'Friends'])
plt.show()
# Compared to Attributes which has normal distribution, Friends has positively skewed (a.k.a skew-right) data distribution but has lower median value than Attributes which suggests disagreement between both features. Finally, one outlier found in Fans.
plt.figure(figsize=(14, 6))
plt.boxplot([attributes_counts, useful_counts])
plt.title('Ditribution Comparison Between Attributes Count and Useful Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Attributes', 'Useful'])
plt.show()
# Compared to Attributes which has normal distribution, Useful has positively skewed (a.k.a skewed-right) data distribution and also has lower median value than Attributes which suggests disagreement between both features. Finally, no outliers found in both features.
plt.figure(figsize=(14, 6))
plt.boxplot([review_length_counts, fans_counts])
plt.title('Ditribution Comparison Between Review Length Count and Fans Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Review Length', 'Fans'])
plt.show()
# Review Length is showing negatively skewed (a.k.a skew-left) data distribution because of its bottom tail being longer compared to Fans which has positively skewed (a.k.a skewed-right) data distribution as it has longer top tail and also lower median value compared to Review Length which suggests disagreement between both features. Finally, single outlier found in Fans.
plt.figure(figsize=(14, 6))
plt.boxplot([review_length_counts, comp_plain_counts])
plt.title('Ditribution Comparison Between Review Length Count and Compliment Plain Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Review Length', 'Compliment Plain'])
plt.show()
# Compared to Review Length which has negatively skewed data distribution, Compliment Plain has positively skewed data distribution because of its median value being closer to bottom of box and data is also less dispersed in Compliment Plain with median value being lower compared to Review Length, which ultimately suggests disagreement between both features. Finally, two outliers found in Compliment Plain count.
plt.figure(figsize=(14, 6))
plt.boxplot([review_length_counts, friends_counts])
plt.title('Ditribution Comparison Between Review Length Count and Friends Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Review Length', 'Friends'])
plt.show()
# Compared to Review Length which has negatively skewed data distribution, Friends has positively skewed data distribution because of its median value being closer to bottom of box and top longer tail and data is also less dispersed in Friends with median value being lower compared to Review Length, which shows disagreement between both features. Finally, one outlier found in Friends count.
plt.figure(figsize=(14, 6))
plt.boxplot([review_length_counts, useful_counts])
plt.title('Ditribution Comparison Between Review Length Count and Useful Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Review Length', 'Useful'])
plt.show()
# Compared to Review Length which has negatively skewed data distribution, Useful has positively skewed data distribution because of its top longer tail but data is less dispersed compared to Review Length, also median value of Useful is lower which shows disagreement between both features. Finally, no outliers found in both features count.
plt.figure(figsize=(14, 6))
plt.boxplot([fans_counts, comp_plain_counts])
plt.title('Ditribution Comparison Between Fans Count and Compliment Plain Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Fans', 'Compliment Plain'])
plt.show()
# Fans and Compliment Plain both have postively skewed data distribution because of longer top tail in Fans and median value at bottom of box in Compliment Plain (two reasons which make data positively skewed but Fans has more dispersed distribution compared to Compliment Plain though median values of both are almost similar. We can deduce that both features have some similarities at initial part (e.g. First Quartile and Median) but disagreement in rest. Finally, outliers were found in both features.
plt.figure(figsize=(14, 6))
plt.boxplot([fans_counts, friends_counts])
plt.title('Ditribution Comparison Between Fans Count and Friends Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Fans', 'Friends'])
plt.show()
# Both Fans and Friends have positively skewed data distribution but Fans has slightly more dispersed data. Both features seems to have similar views in first quartile and median but disagree in top part of box because of different third and fourth quartiles including whiskers. Again, outliers found in both features.
plt.figure(figsize=(14, 6))
plt.boxplot([fans_counts, useful_counts])
plt.title('Ditribution Comparison Between Fans Count and Useful Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Fans', 'Useful'])
plt.show()
# Again, both features have positively skewed data distribution but differ in all quartiles including median value and whiskers so they're in disagreement. Although, Fans is slightly more dispersed than Useful. Finally, one outlier was found in Fans count.
plt.figure(figsize=(14, 6))
plt.boxplot([comp_plain_counts, friends_counts])
plt.title('Ditribution Comparison Between Compliment Plain Count and Friends Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Compliment Plain', 'Friends'])
plt.show()
# Both features have data distribution of skew-right but differ in all quartiles and whiskers. Also, Compliment Plain is way less dispersed in terms of distribution than Friends. Finally, outliers were found in both features counts.
plt.figure(figsize=(14, 6))
plt.boxplot([comp_plain_counts, useful_counts])
plt.title('Ditribution Comparison Between Compliment Plain Count and Useful Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Compliment Plain', 'Useful'])
plt.show()
# Again, both features are showing data distribution of skew-right because of median value being closest to bottom part of box in Compliment Plain (which makes upper part bigger) and longer top tail in Useful. And, they differ in all quartiles so they're in complete disagreement. Finally, outliers were found in Compliment Plain.
plt.figure(figsize=(14, 6))
plt.boxplot([friends_counts, useful_counts])
plt.title('Ditribution Comparison Between Friends Count and Useful Count')
plt.xlabel('Feature')
plt.ylabel('Count')
plt.xticks([1, 2], ['Friends', 'Useful'])
plt.show()
# Friends and Useful both have skew-right data distribution, whereas Friends is slightly more dispersed than Useful and have different quartile ranges than Useful which suggest disagreement with Useful. Finally, one outlier was found in Friends.
# ### Histograms
review_count = final_dataset.get_column('Review Count')
plot_utils.histogram(review_count, 10, 'Distribution of Review Count', 'Review Count', 'Count')
# Skew-Right
attributes = final_dataset.get_column('Attributes')
attributes = [len(k.keys()) for k in attributes if k]
plot_utils.histogram(attributes, 10, 'Distribution of Attributes', 'Attributes', 'Count')
# Bidomal
text = final_dataset.get_column('Review Length')
text_length = [len(str(t)) for t in text]
plot_utils.histogram(text_length, 10, 'Distribution of Review Length', 'Review Length', 'Count')
# Skew-Right
compliment_count = final_dataset.get_column('Fans')
plot_utils.histogram(compliment_count, 10, 'Distribution of Fans', 'Fans', 'Count')
# Skew-Right
compliment_count = final_dataset.get_column('Compliment Plain')
plot_utils.histogram(compliment_count, 10, 'Distribution of Compliment Plain', 'Compliment Plain', 'Count')
# Skew-Right
friends = final_dataset.get_column('Friends')
friends = [len(f) for f in friends]
plot_utils.histogram(friends, 10, 'Distribution of Friends', 'Friends', 'Count')
# Skew-Right
useful = final_dataset.get_column('Useful')
plot_utils.histogram(useful, 10, 'Distribution of Useful', 'Useful', 'Count')
# Skew-Right
# ## Simple Linear Regression
# Formula for regression line that best fits dataset:
# $$y = mx + b$$
#
# Slope $m$:
# $$m = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})^2}$$
#
# Intercept $b$:
# $$b = $\bar{y} - m\bar{x}$$
#
# Correlation Coefficient $r$:
# $$r = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2 \sum_{i=1}^{n}(y_i - \bar{y})^2}}$$
#
# Covariance $cov$:
# $$cov = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{n}$$
#
# Standard Error Formula:
# $$stderr = \sqrt{\frac{\sum_{i=1}^{n}(y_i - y^\prime)^2}{n}}$$
# ### Finding Correlation Between Useful and Fans
X = final_dataset.get_column('Useful')
X = [[x] for x in X]
y = final_dataset.get_column('Fans')
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Useful vs Fans Comparison', 'Useful', 'Fans', regression_line, corr, cov, 45500, max(y) - 200)
# Moderate Relationship
# ### Finding Correlation Between Useful and Friends
X = final_dataset.get_column('Useful')
X = [[x] for x in X]
y = final_dataset.get_column('Friends')
y = [len(f) for f in y]
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Useful vs Friends Comparison', 'Useful', 'Friends', regression_line, corr, cov, 0, max(y) + 20000)
# Moderate Relationship
# ### Finding Correlation Between Useful and Review Length
X = final_dataset.get_column('Useful')
X = [[x] for x in X]
y = final_dataset.get_column('Review Length')
y = [len(str(x)) for x in X]
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Useful vs Review Length Comparison', 'Useful', 'Review Length', regression_line, corr, cov, 0, max(y) + 5.5)
# Weak Relationship
# ### Finding Correlatin Between Useful and Compliment Plain
X = final_dataset.get_column('Useful')
X = [[x] for x in X]
y = final_dataset.get_column('Compliment Plain')
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Useful vs Compliment Plain Comparison', 'Useful', 'Compliment Plain', regression_line, corr, cov, 0, max(y) + 1000)
# Strong Relationship
# ### Finding Correlation Between Attributes Count and Review Length
X = final_dataset.get_column('Attributes')
X = [[len(x.keys()) if x else 0] for x in X]
y = final_dataset.get_column('Review Length')
y = [len(str(x)) for x in X]
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Attributes Count vs Review Length Comparison', 'Attributes Count', 'Review Length', regression_line, corr, cov, 0, max(y) + 0.)
# Strong Relationship
# ### Finding Correlation Between Review Count and Review Length
X = final_dataset.get_column('Review Count')
X = [[x] for x in X]
y = final_dataset.get_column('Review Length')
y = [len(str(x)) for x in X]
len(X), len(y)
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Review Count vs Review Length Comparison', 'Review Count', 'Review Length', regression_line, corr, cov, 0, max(y))
# Weak Relationship
# ### Finding Correlation Between Compliment Plain and Review Length
X = final_dataset.get_column('Compliment Plain')
X = [[x] for x in X]
y = final_dataset.get_column('Review Length')
y = [len(str(x)) for x in X]
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Compliment Plain vs Review Length Comparison', 'Compliment Plain', 'Review Length', regression_line, corr, cov, 0, max(y) + 1.5)
# Weak Relationship
# ### Finding Correlation Between Fans and Review Length
X = final_dataset.get_column('Fans')
X = [[x] for x in X]
y = final_dataset.get_column('Review Length')
y = [len(str(x)) for x in X]
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Fans vs Review Length Comparison', 'Fans', 'Review Length', regression_line, corr, cov, 0, max(y) + 4)
# Weak Relationship
# ### Finding Correlation Between Friends and Review Length
X = final_dataset.get_column('Friends')
X = [[len(str(x))] for x in X]
y = final_dataset.get_column('Review Length')
y = [len(str(x)) for x in X]
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Fans vs Review Length Comparison', 'Fans', 'Review Length', regression_line, corr, cov, 0, max(y) + 2)
# Weak Relationship
# ### Finding Correlation Between Fans and Compliment Plain
X = final_dataset.get_column('Fans')
X = [[x] for x in X]
y = final_dataset.get_column('Compliment Plain')
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Fans vs Compliment Plain Comparison', 'Fans', 'Compliment Plain', regression_line, corr, cov, 2350, max(y) + 2000)
# Moderate Relationship
# ### Finding Correlation Between Fans and Friends
X = final_dataset.get_column('Fans')
X = [[x] for x in X]
y = final_dataset.get_column('Friends')
y = [len(f) for f in y]
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Fans vs Friends Comparison', 'Fans', 'Friends', regression_line, corr, cov, 0, max(y) + 40000)
# Weak Relationship
# ### Finding Correlation Between Friends and Compliment Plain
X = final_dataset.get_column('Friends')
X = [[len(x)] for x in X]
y = final_dataset.get_column('Compliment Plain')
regressor = MySimpleLinearRegressor()
regressor.fit(X, y)
m, b = regressor.slope, regressor.intercept
x = [x[0] for x in X]
regression_line = [(m*i)+b for i in x]
corr = myutils.coefficient_correlation(y, regression_line)
cov = myutils.squared_error(y, regression_line)
plot_utils.scatter_plot(x, y, 'Friends vs Compliment Plain Comparison', 'Friends', 'Compliment Plain', regression_line, corr, cov, 120000, max(y) - 500)
# Weak Relationship
| 36,125 |
/Research/cifar10.ipynb
|
b8fd8ecd75c24d77244b03814149dc61064e113c
|
[] |
no_license
|
marksein07/Machine-Learning
|
https://github.com/marksein07/Machine-Learning
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 228,800 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from datetime import datetime
import pandas as pd
df = pd.read_csv("signals_experiment_time/signals_8.csv")
#header=None, names=["TIME", "HR", "RESP", "ABPMean", "ABPSys", "ABPDias", "SpO2", "SOFA"]
# +
df["TIME_"] = df["TIME"].apply(lambda x: datetime.strptime(x, '%H:%M:%S %d/%m/%Y'))
# -
df = df.sort_values(by="TIME_")
df[["TIME", "HR", "RESP", "ABPMEAN", "ABPSYS", "ABPDIAS", "SPO2", "SOFA_SCORE"]].to_csv("signals_experiment_time/signals_8.csv", index=False)
df
atement will fetch `GTC_Loader` module and name it `gtc`.
import FPSDP.Plasma.GTC_Profile.GTC_Loader as gtc
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
pylab.rcParams['figure.figsize'] = (10.0, 8.0)
pylab.rcParams['font.size'] = 20
# ## 2. Define relevant quantities
# Before loading GTC output files, it is convenient to define some quantities for initialization. They are:
# 1.The directory that contains all GTC output files
gtc_path = 'Data/GTC_Outputs/nov6-3/'
# 2.The grid on which all data will be interpolated or extrapolated.
#
# For now, only `Cartesian2D` grids are accepted. `Cartesian2D` grids can be generated by giving __*DownLeft*__ and __*UpRight*__ coordinates (Z,R) of the box (in meter), and __*NR*__ and __*NZ*__ of grid points, or __*ResR*__ and __*ResZ*__ as the resolution on each direction (in meter). For our GTC run, let's make a box that's larger than the simulation domain:
grid2d = gtc.Cartesian2D(DownLeft = (-1,1), UpRight = (1,2.2), ResR = 0.01, ResZ = 0.01)
# 3.The time steps we are interested in
# Valid time steps are the integer number in "*snapXXXXXXX_fpsdp.json*" file names. We should provide a list of integer to `GTC_Loader`, if any of the time steps are not available, an exception will be raised along with the valid time steps information. We'll see the example later.
timesteps = [1,2,3]
# ## 3. Load data files
# Now, we are ready to load the output files:
gtcdata = gtc.GTC_Loader(gtc_path,grid2d,timesteps)
# As we can see, first, our 2D grid are detected and accepted. Then, an error occurs. Since our output files only contain time steps 1 and 2, when we try to aquire time 3, our Loader will complain and tell us only `[1,2]` are available. Let's try again:
timesteps = [1,2]
gtcdata = gtc.GTC_Loader(gtc_path,grid2d,timesteps,Mode = 'full')
# This time, all went well. Now, gtcdata is ready, we can then take a look at it's content.
# ## 4. Exam data
# Python objects use `__dict__` to store all attributes, we can use it's `keys()` method to list all the attribute names.
gtcdata.__dict__.keys()
# That's a LOT of stuff... Fortunately, only some of them are supposed to be used directly. Let me introduce them one by one.
# #### 1.GTC run parameters
# Some relevant GTC run parameters are determined by data in gtc.in.out and gtc.out files. They are: isEM, HaveElectron **(MORE IS TO BE ADDED)**
# `isEM` is a boolean flag showing if the GTC run has **electromagnetic perturbations**.
gtcdata.isEM
# It's shown that our GTC run here has electromagnetic perturbations.
# `HaveElectron` is a boolean flag showing if the GTC run has **non-adiabatic electrons**.
gtcdata.HaveElectron
# Our GTC run apparently includes non-adiabatic electrons as well.
# #### 2.Raw data got from GTC output files
# Second kind of attributes store the raw data read from GTC output files. They are normally named after their data entry names in the output files. They are: **`R_gtc`, `Z_gtc`, `a_gtc`, `R_eq`, `Z_eq`, `a_eq`, `B_phi`, `B_R`, `B_Z`**, and perturbations **`phi`**, **`dne_ad`**,**`nane`**, **`dni`**, **`Te_perp`**, **`Te_para`**, and **`A_para`**.
# `R_gtc`, `Z_gtc` are R,Z coordinates for each mesh grid point in GTC simulation. `a_gtc` is the radial flux coordinate on this mesh. In our case, it's the poloidal magnetic flux $\psi_p$. `theta_gtc` is the poloidal flux coordinate $\theta$ on the same mesh. Let's take a look at them:
fig=plt.figure()
plt.scatter(gtcdata.R_gtc, gtcdata.Z_gtc, s=2, c=gtcdata.a_gtc, linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
fig = plt.figure()
plt.scatter(gtcdata.R_gtc, gtcdata.Z_gtc, s=2, c=gtcdata.theta_gtc, linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
# It is clear that $\psi_p$ is not normalized, and $\theta$ is defined between $[0,2\pi)$
# `R_eq`, `Z_eq` and `a_eq` have similar physical meaning as their `_gtc` counter parts. The difference is that, by definition, they should cover the whole poloidal cross-section, from magnetic axis to the outmost closed flux surface, while `_gtc` quantities only cover GTC simulation region which usually excludes the magnetic axis and edge region. These `_eq` quantities are used to interpolate all equilibrium profiles and magnetic field. While equilibrium electron density and temperature are functions of $\psi_p$ only, i.e. $n_e(\psi_p)$ and $T_e(\psi_p)$, equilibrium magnetic field is a vector field on the whole poloidal cross-section. We use `B_phi`, `B_R` and `B_Z` to store the 3 components of the equilibrium magnetic field. Let's take a look at them: **ISSUE #1 NEEDS TO BE RESOLVED**
fig = plt.figure()
plt.scatter(gtcdata.R_eq,gtcdata.Z_eq, s=2, c= gtcdata.B_phi, linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
fig = plt.figure()
plt.scatter(gtcdata.R_eq,gtcdata.Z_eq, s=2, c= gtcdata.B_R, linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
fig = plt.figure()
plt.scatter(gtcdata.R_eq,gtcdata.Z_eq, s=2, c= gtcdata.B_Z, linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
# `phi` stores the perturbed potential at each requested time step. Let's see snapshot 1:
fig = plt.figure()
plt.scatter(gtcdata.R_gtc,gtcdata.Z_gtc, s=2, c= gtcdata.phi[0], linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
# `dne_ad` is the adiabatic response of the electron density to perturbed potential. `nane` is the non-adiabatic response, it only exist if the run has non-adiabatic electrons. `dni` is the ion density perturbation.
fig = plt.figure()
plt.scatter(gtcdata.R_gtc,gtcdata.Z_gtc, s=2, c= gtcdata.dne_ad[0], linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('dne_ad')
if gtcdata.HaveElectron:
fig = plt.figure()
plt.scatter(gtcdata.R_gtc,gtcdata.Z_gtc, s=2, c= gtcdata.nane[0], linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('nane')
fig = plt.figure()
plt.scatter(gtcdata.R_gtc,gtcdata.Z_gtc, s=2, c= gtcdata.dni[0], linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('dni')
# `Te_perp` and `Te_para` stores perturbed perpendicular and parallel electron temperature respectively. They are both small in our example because we are at the very beginning of the simulation.
fig = plt.figure()
plt.scatter(gtcdata.R_gtc,gtcdata.Z_gtc, s=2, c= gtcdata.Te_perp[0], linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('Te_perp')
fig = plt.figure()
plt.scatter(gtcdata.R_gtc,gtcdata.Z_gtc, s=2, c= gtcdata.Te_para[0], linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('Te_para')
# `A_para` stores perturbed parallel vector potential for electromagnetic runs.
if gtcdata.isEM:
fig = plt.figure()
plt.scatter(gtcdata.R_gtc,gtcdata.Z_gtc, s=2, c= gtcdata.A_para[0], linewidth = 0.1)
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('A_para')
# #### 3. 1D equilibrium profiles
# As mentioned before, equilibrium density and temperature profiles are given as functions of $\psi_p$ only. These functions are specified by a $\psi_p$ array (`a_1D`) and corresponding $n_e$ (`ne0_1D`) and $T_e$ (`Te0_1D`) values.
plt.plot(gtcdata.a_1D,gtcdata.ne0_1D)
plt.xlabel('$\psi$')
plt.ylabel('$n_{e0}$')
plt.plot(gtcdata.a_1D,gtcdata.Te0_1D)
plt.xlabel('$\psi$')
plt.ylabel('$T_{e0}$')
# #### 4. Interpolated and/or extrapolated data
# All interpolated data are stored in `_on_grid` quantities. Let's look at them one by one:
# $\psi_p$ (`a_on_grid`) is interpolated inside the convex hull of points given by `R_eq` and `Z_eq`, and linearly extrapolated outside based on the two partial derivatives on the boundary.
fig = plt.figure()
plt.imshow(gtcdata.a_on_grid, extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
# $n_{e0}$ and $T_{e0}$ are interpolated on $\psi_p$, and then applied to `a_on_grid` to obtain values on grid.
fig = plt.figure()
plt.imshow(gtcdata.ne0_on_grid, extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
fig = plt.figure()
plt.imshow(gtcdata.Te0_on_grid, extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
# `Bphi_on_grid`, `BR_on_grid`, and `BZ_on_grid` are similarly interpolated. The extrapolation is done using $B_{\phi} = R_0B_{\phi 0}/R$, and contravariant expression for $B_R$ and $B_Z$ based on the extrapolated value for $\psi_p$. **(ISSUE #1 NEEDS TO BE RESOLVED)**
fig = plt.figure()
plt.imshow(gtcdata.Bphi_on_grid, extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
fig = plt.figure()
plt.imshow(gtcdata.BR_on_grid, extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
fig = plt.figure()
plt.imshow(gtcdata.BZ_on_grid, extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
# The perturbed quantities, `phi`, `dne_ad`, etc. , are interpolated on `R_gtc` and `Z_gtc`, but not extrapolated. All points outside the simulation grid are assigned 0 values.
fig = plt.figure()
plt.imshow(gtcdata.phi_on_grid[0], extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('phi')
fig = plt.figure()
plt.imshow(gtcdata.dne_ad_on_grid[0], extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('dne_ad')
if gtcdata.HaveElectron:
fig = plt.figure()
plt.imshow(gtcdata.nane_on_grid[0], extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('nane')
fig = plt.figure()
plt.imshow(gtcdata.dni_on_grid[0], extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('dni')
fig = plt.figure()
plt.imshow(gtcdata.Te_perp_on_grid[0], extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('Te_perp')
fig = plt.figure()
plt.imshow(gtcdata.Te_para_on_grid[0], extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('Te_para')
if gtcdata.isEM:
fig = plt.figure()
plt.imshow(gtcdata.A_para_on_grid[0], extent = [1,2.2,-1,1])
plt.colorbar()
fig.axes[0].set_aspect(1)
plt.title('A_para')
| 10,679 |
/.ipynb_checkpoints/Keras_step_1-both-checkpoint.ipynb
|
0043382f91b22bfceda45a669cb0a0e5107e2a27
|
[] |
no_license
|
TejaSreenivas/fashion_mnist_proj
|
https://github.com/TejaSreenivas/fashion_mnist_proj
| 0 | 0 | null | 2018-09-17T12:48:27 | 2018-09-17T12:42:24 |
Jupyter Notebook
|
Jupyter Notebook
| false | false |
.py
| 12,134 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import cv2
#image = cv2.imread('input.jpg', cv2.IMREAD_UNCHANGED)
image = cv2.imread('input.jpg')
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGBA)
image[np.all(image == [0, 0, 0, 255], axis=2)] = [0, 0, 0, 0]
= merger()
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.optimizers import SGD
from keras.utils import print_summary, to_categorical
import sys
import os
batch_size = 64
num_classes = 10
epochs = 10
# +
n_classes = 10
id_mtx = np.identity(n_classes,dtype=np.float32)
mnist['train_y'] = id_mtx[mnist['train_y']]
mnist['test_y'] = id_mtx[mnist['test_y']]
mnist['train_y'].shape, mnist['test_y'].shape
n_classes = 10
id_mtx = np.identity(n_classes,dtype=np.float32)
mnist['train_y'] = id_mtx[merged['train_y']]
mnist['test_y'] = id_mtx[merged['test_y']]
n_classes = 10
id_mtx = np.identity(n_classes,dtype=np.float32)
fashion['train_y'] = id_mtx[fashion['train_y']]
fashion['test_y'] = id_mtx[fashion['test_y']]
mnist['train_y'].shape, mnist['test_y'].shape,fashion['train_y'].shape, fashion['test_y'].shape,merged['train_y'].shape, merged['test_y'].shape
# -
(x_train, y_train), (x_m_test, y_m_test), (x_f_test,y_f_test) = (merged['train_x'],merged['train_y']),(mnist['test_x'],mnist['test_y']),(fashion['test_x'],fashion['test_y'])
# +
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same', input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.3))
model.add(Conv2D(64, (3, 3), padding='same', input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.3))
model.add(Conv2D(128, (3, 3), padding='same', input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.4))
model.add(Flatten())
model.add(Dense(80))
model.add(Activation('relu'))
model.add(Dropout(0.3))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# -
opt = SGD(lr=0.01, momentum=0.9, decay=0, nesterov=False)
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_split=0.2,
shuffle=True)
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
and λSB on the wavelength axis.**
# <img src="https://miro.medium.com/max/1030/1*oUtYY0-j6iEc78Dew3d0uA.png"
# alt="https://miro.medium.com/max/1030/1*oUtYY0-j6iEc78Dew3d0uA.png"
# style="float: left; margin-right: 10px;" />
spectral_bandwidth_2 = librosa.feature.spectral_bandwidth(sample+0.01, sr=sample_rate)[0]
spectral_bandwidth_3 = librosa.feature.spectral_bandwidth(sample+0.01, sr=sample_rate, p=3)[0]
spectral_bandwidth_4 = librosa.feature.spectral_bandwidth(sample+0.01, sr=sample_rate, p=4)[0]
plt.figure(figsize=(15, 9))
librosa.display.waveplot(sample, sr=sample_rate, alpha=0.4)
plt.plot(t, normalize(spectral_bandwidth_2), color='r')
plt.plot(t, normalize(spectral_bandwidth_3), color='g')
plt.plot(t, normalize(spectral_bandwidth_4), color='y')
plt.legend(('p = 2', 'p = 3', 'p = 4'))
# # zero crossinng
#
# **A very simple way for measuring the smoothness of a signal is to calculate the number of zero-crossing within a segment of that signal. **
zero_crossings = librosa.zero_crossings(sample, pad=False)
print(sum(zero_crossings))
# # chromagram
#
# **A chroma feature or vector is typically a 12-element feature vector indicating how much energy of each pitch class, {C, C#, D, D#, E, …, B}, is present in the signal. In short, It provides a robust way to describe a similarity measure between music pieces.**
chromagram = librosa.feature.chroma_stft(sample, sr=sample_rate)
plt.figure(figsize=(15, 5))
librosa.display.specshow(chromagram, x_axis='time', y_axis='chroma', cmap='coolwarm')
| 4,397 |
/lectures/L11/Exercise_1.ipynb
|
486eb51e9253c9e0c944ef4055d863a2b293f229
|
[
"MIT"
] |
permissive
|
crystalzhaizhai/cs207_yi_zhai
|
https://github.com/crystalzhaizhai/cs207_yi_zhai
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 3,038 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Exercise 1
# Read and parse the chemical reactions `.xml` input file `rxns.xml`.
#
#
# 1. Collect the species into a species list. My output is `['H', 'O', 'OH', 'H2', 'O2']`.
#
# Some notes and hints:
# * **Hint:** For this `.xml` format you should have a loop over the `phase` element.
# * **Hint:** You can use the `find()` method to get the species array.
#
# 2. Calculate and print out the Arrhenius reaction rate coefficients using $R = 8.314$ and $T = 1500$.
#
# Some notes and hints:
# * **Hint:** For this `.xml` format you should have loops over the `reactionData` element, the `reaction` element, the `rateCoeff` element, and the `Arrhenius` element using the `findall()` method discussed in lecture.
# * **Hint:** You can use the `find()` method to get the reaction rate coefficients.
# * My solution is:
#
# `k for reaction01 = 6.8678391864294477e+05
# k for reaction02 = 2.3105559199959813e+06`
import xml.etree.ElementTree as ET
tree=ET.parse("rxns.xml")
elementroot=tree.getroot()
elements=elementroot.find('phase').find("speciesArray").text.strip(" ").split(" ")
print(elements)
reactionroot=elementroot.find("reactionData")
for reaction in reactionroot:
coefficients=reaction.find("rateCoeff").find("Arrhenius")
a=float(coefficients.find("A").text)
b=float(coefficients.find("b").text)
e=float(coefficients.find("E").text)
print("k=",a*T**b*math.exp(-e/(R*T)))
| 1,736 |
/HM6(2).ipynb
|
7a43482e0c44ab71ec117187ef1cc82ba059e6cf
|
[] |
no_license
|
mmyd/Machine-Learning-
|
https://github.com/mmyd/Machine-Learning-
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 37,554 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import seaborn as sns
import numpy as np
import sklearn
import matplotlib.pyplot as plt
from pandas import *
from numpy import *
from sklearn import *
import warnings
from sklearn.preprocessing import Imputer
warnings.filterwarnings('ignore')
inf552= pd.read_csv("C:\\Users\\DELL\\Desktop\\INF552\\HM6\\data_banknote_authentication.csv",header=None,names=list(range(0,4))+['class'])
# Choose 472 data points randomly as the test set, and the remaining 900 points as the training set
from sklearn.svm import LinearSVC
test=inf552.sample(n=472,random_state=123 ,axis=0)
train=inf552.drop(index=test.index)
#determine the ranges for λ that keep the accuracy above a threshold (e.g.60%)
cls1 = LinearSVC(penalty='l1',random_state=123,dual=False,C=10**(-3)).fit(train[list(range(0,4))], train['class'])
print('the accuracy for λ = 10−3 is: ',cls1.score(train[list(range(0,4))], train['class']))
cls2 = LinearSVC(penalty='l1',random_state=123,dual=False,C=10**(2)).fit(train[list(range(0,4))], train['class'])
print('the accuracy for λ = 10+2 is: ',cls2.score(train[list(range(0,4))], train['class']))
print('the accuracy will not below 60% for λ = 10−3 and λ = 10+2')
# passive learning
# Train a SVM with a pool of 10 selected data points from the trainset(90 times)
from sklearn.model_selection import GridSearchCV
import sklearn.metrics
errors=[]
for i in range(50):
error=[]
testset=test
trainset=train
train_pool=trainset.sample(n=10,axis=0)
# If all selected data points are from one class, select another set of 10 data points randomly.
while len(train_pool['class'].value_counts())==1:
train_pool=trainset.sample(n=10,axis=0)
trainset=trainset.drop(index=train_pool.index)
# Determine the weight of the SVM penalty
C_range1 = np.logspace(-3, 2, 5)
param_grid1 = dict(C=C_range1)
passive_cls = LinearSVC(penalty='l1',dual=False)
passive_model = GridSearchCV(passive_cls, param_grid=param_grid1, cv=KFold(n_splits=10)).fit(train_pool[list(range(0,4))], train_pool['class'])
test_pred=passive_model.predict(testset[list(range(0,4))]);
error.append(1-metrics.accuracy_score(testset['class'], test_pred))
for i in range(89):
new_pool=trainset.sample(n=10,axis=0)
train_pool=train_pool.append(new_pool)
trainset=trainset.drop(index=new_pool.index)
C_range1 = np.logspace(-3, 2, 5)
param_grid1 = dict(C=C_range1)
passive_cls = LinearSVC(penalty='l1',dual=False)
passive_model = GridSearchCV(passive_cls, param_grid=param_grid1, cv=10).fit(train_pool[list(range(0,4))], train_pool['class'])
test_pred=passive_model.predict(testset[list(range(0,4))]);
error.append(1-metrics.accuracy_score(testset['class'], test_pred))
errors.append(error)
# active learning
# Train a SVM with a pool of 10 selected data points from the trainset(90 times)
errors2=[]
for i in range(50):
error2=[]
testset2=test
trainset2=train
train_pool2=trainset2.sample(n=10,axis=0)
# If all selected data points are from one class, select another set of 10 data points randomly.
while len(train_pool2['class'].value_counts())==1:
train_pool2=trainset2.sample(n=10,axis=0)
trainset2=trainset2.drop(index=train_pool2.index)
# Determine the weight of the SVM penalty
C_range2 = np.logspace(-3, 2, 5)
param_grid2 = dict(C=C_range2)
active_cls = LinearSVC(penalty='l1',dual=False)
active_model = GridSearchCV(active_cls, param_grid=param_grid2, cv=KFold(n_splits=10)).fit(train_pool2[list(range(0,4))], train_pool2['class'])
test_pred2=active_model.predict(testset2[list(range(0,4))]);
error2.append(1-metrics.accuracy_score(testset2['class'], test_pred2))
for j in range(89):
# Choose the 10 closest data points in the training set to the hyperplane of the SVM
aa=(active_model.decision_function(trainset2[list(range(0,4))])).tolist();
w_norm = np.linalg.norm(active_model.best_estimator_.coef_);dist=aa/ w_norm;
ind = np.argsort(dist)[:10];
new_pool2=trainset2.iloc[ind,:]
train_pool2=train_pool2.append(new_pool2)
trainset2=trainset2.drop(index=new_pool2.index)
C_range2 = np.logspace(-3, 2, 5)
param_grid2 = dict(C=C_range2)
active_cls = LinearSVC(penalty='l1',dual=False)
active_model = GridSearchCV(active_cls, param_grid=param_grid2, cv=10).fit(train_pool2[list(range(0,4))], train_pool2['class'])
test_pred2=active_model.predict(testset2[list(range(0,4))]);
error2.append(1-metrics.accuracy_score(testset2['class'], test_pred2))
errors2.append(error2)
# Plot the average test error versus number of training instances
trans_errors=np.transpose(errors);trans_errors2=np.transpose(errors2);
passive_errors=[];active_errors=[];
for i in range(90):
passive_errors.append(trans_errors[i].mean());
active_errors.append(trans_errors2[i].mean());
means={"passive_errors":passive_errors,"active_errors":active_errors}
means=DataFrame(means)
#errors.index = range(10,901,10)
plt.figure(figsize=(10,5))
xlist1 = means.iloc[:,0]
xlist2 = means.iloc[:,1]
ylist = list(range(10,901,10))
plt.title("Plot of passive and active test errors")
plt.xlabel(" number of training instances")
plt.ylabel("test error rate")
plt.plot(ylist,xlist1,"b-o")
plt.plot(ylist,xlist2,"r-o")
plt.legend(loc='best')
plt.show()
print('the conclusion: when the number of trainning instances is small, the passive learning is better than active one.')
print('when the number of instances is large enough, there is a slightly difference between passive and active learning.')
| 5,935 |
/tutorials/map_expansion_tutorial.ipynb
|
2ac44370ee4295ffcaa42afaa5255885704b6202
|
[] |
no_license
|
parkinkon1/nuscenes_test
|
https://github.com/parkinkon1/nuscenes_test
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 4,144,577 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [Root]
# language: python
# name: Python [Root]
# ---
# # MongoDB Tutorial - Monday 6 March 2017
# ## Introduction
# In what follows, we assume that you have installed MongoDB according to the [instructions online](https://docs.mongodb.org/manual/installation/) and started the mongo daemon with the following command.
#
# > mongod
#
# Note that you might have to create a folder `/data/db` with appropriate access rights before the daemon starts successfully.
#
# We also assume that you use Python 3 and have the [pymongo driver](http://api.mongodb.org/python/current/installation.html) installed.
#
# ** Note ** To run the notebook yourself, [install Jupyter](http://jupyter.readthedocs.org/en/latest/install.html), [download](https://raw.githubusercontent.com/mmathioudakis/moderndb/master/2017/mongodb.tutorial.ipynb) the notebook, and [open it](http://jupyter.readthedocs.org/en/latest/running.html) with Jupyter.
#
# ** Note ** This notebook might be updated later. Major updates will be listed at its bottom.
# +
import pymongo as pm
client = pm.MongoClient()
client.drop_database("tutorial")
import bson.son as son
# -
# ## "Hello World!" : Databases, Collections, Documents
#
# *Relational databases* contain *tables* that contain *records*.
#
# A **MongoDB database** contains **collections** that contain **documents**.
# +
# start a client
client = pm.MongoClient()
# connect to a database
db = client.tutorial
# get a collection
coll = db.test_collection
# -
# Documents follow the [JSON](http://json.org/) format and MongoDB stores them in a binary version of it ([BSON](http://bsonspec.org/)).
# <img src = "http://json.org/object.gif">
# <img src = "http://json.org/array.gif">
# <img src = "http://json.org/value.gif">
#
# Below you see examples of JSON documents.
#
# ** JSON example 0 **
# ```
# {}
# ```
#
# ** JSON example 1 **
# ```
# {
# "name" : "Michael",
# "age": 32,
# "grades": [71, 85, 90, 34]
# }
# ```
#
# ** JSON example 2 **
#
# ```
# {
# "first name": "Michael",
# "last name": "Mathioudakis",
# "age": 32,
# "grades": {
# "ModernDB": 69,
# "Data Mining": 71,
# "Machine Learning": 95
# },
# "graduated": true,
# "previous schools": ["NTUA", "UofT"]
# }
# ```
# In Python, JSON documents are represented as dictionaries.
# The examples from above are therefore represented as follows.
example_0 = {}
example_1 = {"name": "Michael", "age": 32, "grades": [71, 85, 90, 34]}
example_2 = \
{"first name": "Michael",
"last name": "Mathioudakis",
"age": 32,
"grades": {
"ModernDB": 69,
"Data Mining": 71,
"Machine Learning": 95
},
"graduated": True,
"previous schools": ["NTUA", "UofT"]
}
# Note that we can also use native Python objects, like the `datetime` object below, to specify values.
import datetime
example_3 = {"name": "Modern Database Systems",
"start": datetime.datetime(2016, 1, 12),
"end": datetime.datetime(2016, 3, 26),
"tags": ["rdbms", "mongodb", "spark"]}
# ### Inserting and finding documents
#
# Our collection `coll` is currently empty. Let's add one document to it.
coll.insert_one(example_0)
# If we call the collection's function `find()`, we get back a cursor.
coll.find()
# We can use the cursor to iterate over all documents in the collection.
for doc in coll.find():
print(doc)
# Notice that the empty document we inserted is not *really* empty, but associated with an "\_id" key, added by MongoDB.
#
# Let's try another one.
coll.insert_one(example_1)
for doc in coll.find():
print(doc)
print()
# Notice how MongoDB added an "\_id" for the new document, as well.
# Let's insert more documents.
coll.insert_many([example_2, example_3])
for doc in coll.find():
print(doc)
print()
# Notice how the document we insert do not follow a schema?
#
# Let us now find documents that match a condition -- let's say we want to find documents that have a field "name" with value "Michael".
query_result = coll.find({"name": "Michael"})
for doc in query_result:
print(doc)
# #### Projecting fields
#
# We can use **find()** not only to retrieve documents that match a condition, but also to project only those fields that we are interested in.
#
# For example, to suppress the "\_id" field from appearing in the results, we can provide a second argument to __find()__, as follows.
query_result = coll.find({"name": "Michael"}, {"_id": 0})
for doc in query_result:
print(doc)
# What if we're interested in keeping only some of the rest of the fields -- let's say, only "grades"?
query_result = coll.find({"name": "Michael"}, {"_id": 0, "grades": 1})
for doc in query_result:
print(doc)
# ## Loading a larger dataset
#
# Download file [primer-dataset.json](https://raw.githubusercontent.com/mongodb/docs-assets/primer-dataset/primer-dataset.json), store it in the same folder as this notebook, and load it into mongodb by running the command below.
# + language="bash"
# mongoimport --db tutorial --collection restaurants --drop --file primer-dataset.json
# -
# Alternatively, you can import the dataset by running the same command on a terminal.
# > mongoimport --db moderndb --collection restaurants --drop --file dataset.json
# The dataset contains documents that look like the one below.
#
# ** Restaurant Example **
#
# ```
# {
# "address": {
# "building": "1007",
# "coord": [ -73.856077, 40.848447 ],
# "street": "Morris Park Ave",
# "zipcode": "10462"
# },
# "borough": "Bronx",
# "cuisine": "Bakery",
# "grades": [
# { "date": { "$date": 1393804800000 }, "grade": "A", "score": 2 },
# { "date": { "$date": 1378857600000 }, "grade": "A", "score": 6 },
# { "date": { "$date": 1358985600000 }, "grade": "A", "score": 10 },
# { "date": { "$date": 1322006400000 }, "grade": "A", "score": 9 },
# { "date": { "$date": 1299715200000 }, "grade": "B", "score": 14 }
# ],
# "name": "Morris Park Bake Shop",
# "restaurant_id": "30075445"
# }
# ```
restaurants = db.restaurants # our new collection
# how many restaurants?
restaurants.count()
# ## Querying the Dataset
# retrieve a cursor over all documents in the collection
cursor = restaurants.find()
# define printing function
def print_my_docs(cursor, num):
for i in range(num): # print only up to num next documents from cursor
try:
print(next(cursor))
print()
except:
break
# let's print a few documents
print_my_docs(cursor, 3)
next(cursor) # get one more document
# ### Specify equality conditions
# +
# top-level field
cursor = restaurants.find({"borough": "Manhattan"})
print_my_docs(cursor, 2)
# +
# nested field (in embedded document)
cursor = restaurants.find({"address.zipcode": "10075"})
print_my_docs(cursor, 2)
# -
# query by field in array
cursor = restaurants.find({"grades.grade": "B"})
# print one document from the query result
next(cursor)['grades']
# exact array match
cursor = restaurants.find({"address.coord": [-73.98513559999999, 40.7676919]})
print_my_docs(cursor, 10)
# ### Specify Range Conditions
cursor = restaurants.find({"grades.score": {"$gt": 30}})
cursor = restaurants.find({"grades.score": {"$lt": 10}})
next(cursor)["grades"]
# ### Multiple Conditions
# logical AND
cursor = restaurants.find({"cuisine": "Italian", "address.zipcode": "10075"})
next(cursor)
# logical OR
cursor = restaurants.find({"$or": [{"cuisine": "Italian"},
{"address.zipcode": "10075"}]})
print_my_docs(cursor, 3)
# logical AND, differently
cursor = restaurants.find({"$and": [{"cuisine": "Italian"},
{"address.zipcode": "10075"}]})
next(cursor)
# ## Sorting
# +
cursor = restaurants.find()
# to sort, specify list of sorting criteria,
# each criterion given as a tuple
# (field_name, sort_order)
# here we have only one
sorted_cursor = cursor.sort([("borough", pm.ASCENDING)])
# -
print_my_docs(cursor, 2)
another_sorted_cursor = restaurants.find().sort([("borough", pm.ASCENDING),
("address.zipcode", pm.DESCENDING)])
print_my_docs(another_sorted_cursor, 3)
# ## Aggregation
#
# Aggregation happens in stages.
# Group Documents by a Field and Calculate Count
cursor = restaurants.aggregate(
[
{"$group": {"_id": "$borough", "count": {"$sum": 1}}}
]
)
print_my_docs(cursor, 10)
# Filter and Group Documents
cursor = restaurants.aggregate(
[
{"$match": {"borough": "Queens", "cuisine": "Brazilian"}},
{"$group": {"_id": "$address.zipcode", "count": {"$sum": 1}}}
]
)
print_my_docs(cursor, 10)
# Filter and Group and then Filter Again documents
cursor = restaurants.aggregate(
[
{"$match": {"borough": "Manhattan", "cuisine": "American"}},
{"$group": {"_id": "$address.zipcode", "count": {"$sum": 1}}},
{"$match": {"count": {"$gt": 1}}}
]
)
print_my_docs(cursor, 10)
# Filter and Group and then Filter Again and then Sort Documents
cursor = restaurants.aggregate(
[
{"$match": {"borough": "Manhattan", "cuisine": "American"}},
{"$group": {"_id": "$address.zipcode", "count": {"$sum": 1}}},
{"$match": {"count": {"$gt": 1}}},
{"$sort": {"count": -1, "_id": -1}}
]
)
print_my_docs(cursor, 10)
# Same but sort by multiple fields
# Filter and Group and then Filter Again and then Sort Documents
cursor = restaurants.aggregate(
[
{"$match": {"borough": "Manhattan", "cuisine": "American"}},
{"$group": {"_id": "$address.zipcode", "count": {"$sum": 1}}},
{"$match": {"count": {"$gt": 1}}},
{"$sort": son.SON([("count", -1), ("_id", 1)])} # order matters!!
]
)
print_my_docs(cursor, 10)
# what will this do?
cursor = restaurants.aggregate(
[
{"$group": {"_id": None, "count": {"$sum": 1}} }
]
)
print_my_docs(cursor, 10)
# projection
# what will this do?
cursor = restaurants.aggregate(
[
{"$group": {"_id": "$address.zipcode", "count": {"$sum": 1}}},
{"$project": {"_id": 0, "count": 1}}
]
)
print_my_docs(cursor, 10)
# what will this do?
cursor = restaurants.aggregate(
[
{"$group": {"_id": {"cuisine": "$cuisine"}, "count": {"$sum": 1}}},
{"$sort": {"count": -1}}
]
)
print_my_docs(cursor, 5)
# what will this do?
cursor = restaurants.aggregate(
[
{"$group": {"_id": {"zip": "$address.zipcode"}, "count": {"$sum": 1}}},
{"$sort": {"count": -1}}
]
)
print_my_docs(cursor, 5)
# what will this do?
cursor = restaurants.aggregate(
[
{"$group": {"_id": {"cuisine": "$cuisine", "zip": "$address.zipcode"}, "count": {"$sum": 1}}},
{"$sort": {"count": -1}}
]
)
print_my_docs(cursor, 5)
# ### Limiting the number of results
# +
# what will this do?
cursor = restaurants.aggregate(
[
{"$group": {"_id": {"cuisine": "$cuisine", "zip": "$address.zipcode"}, "count": {"$sum": 1}}},
{"$sort": {"count": -1}},
{"$limit": 10} # See comment under "In-class questions"
]
)
for doc in cursor:
print(doc["_id"]["cuisine"], doc["_id"]["zip"], doc["count"])
# -
# ### Storing the result as a collection
# We can use operator [\$out](https://docs.mongodb.org/manual/reference/operator/aggregation/out/) in a final stage to store the result of a query into a new collection. The following example selects restaurants from Manhattan and stores them in their own collection in the same database.
restaurants.aggregate(
[
{"$match": {"borough": "Manhattan"}},
{"$out": "manhattan"}
]
)
# ## SQL to Aggregation
#
# Here we explore the correspondence between SQL queries and the aggregation framework.
# ** SQL query **
# ```
# SELECT COUNT(*) AS count
# FROM restaurants
# ```
cursor = restaurants.aggregate(
[
{"$group": {"_id": None, "count": {"$sum": 1}} }
]
)
# ** SQL query **
# ```
# SELECT borough, cuisine, COUNT(*) as count
# FROM restaurants
# GROUP BY borough, cuisine
# ```
cursor = restaurants.aggregate(
[
{"$group": {"_id": {"borough": "$borough", "cuisine": "$cuisine"}, "count": {"$sum": 1}}}
]
)
# ** SQL query **
# ```
# SELECT borough, cuisine, COUNT(*) as count
# FROM restaurants
# GROUP BY borough, cuisine
# HAVING COUNT(*) > 3
# ```
cursor = restaurants.aggregate(
[
{"$group": {"_id": {"borough": "$borough", "cuisine": "$cuisine"}, "count": {"$sum": 1}}},
{"$match": {"count": {"$gt": 3}}}
]
)
# ** SQL Query **
# ```
# SELECT zipcode, cuisine, COUNT(*) as count
# FROM restaurants
# WHERE borough = "Manhattan"
# GROUP BY zipcode, cuisine
# HAVING COUNT(*) > 3
# ```
cursor = restaurants.aggregate(
[
{"$match": {"borough": "Manhattan"}},
{"$group": {"_id": {"zipcode": "$address.zipcode", "cuisine": "$cuisine"}, "count": {"$sum": 1}}},
{"$match": {"count": {"$gt": 3}}}
]
)
print_my_docs(cursor, 5)
# ** SQL Query **
# ```
# SELECT zipcode, cuisine, COUNT(*) as count
# FROM restaurants
# WHERE borough = "Manhattan"
# GROUP BY zipcode, cuisine
# HAVING COUNT(*) > 3
# ORDER BY count
# ```
cursor = restaurants.aggregate(
[
{"$match": {"borough": "Manhattan"}},
{"$group": {"_id": {"zipcode": "$address.zipcode", "cuisine": "$cuisine"}, "count": {"$sum": 1}}},
{"$match": {"count": {"$gt": 3}}},
{"$sort": {"count": 1}}
]
)
# ## Using secondary memory (disk)
cursor = restaurants.aggregate(
[
{"$match": {"borough": "Manhattan"}},
{"$group": {"_id": {"zipcode": "$address.zipcode", "cuisine": "$cuisine"}, "count": {"$sum": 1}}},
{"$match": {"count": {"$gt": 3}}},
{"$sort": {"count": 1}}
],
allowDiskUse = True # this can be useful when data does not fit in memory, e.g., to perform external sorting
)
# ## Indexing
#
# MongoDb automatically creates an index on the `_id` field upon creating a collection.
# We can use `create_index()` to create index on one or more fields of a collection.
# ### Single-field index
# note that the argument is a list of tuples
# [(<field>: <type>), ...]
# here, we specify only one such tuple for one field
restaurants.create_index([("borough", pm.ASCENDING)])
# The index is created only if it does not already exist.
# ### Compound index
# compound index (more than one indexed fields)
restaurants.create_index([
("cuisine", pm.ASCENDING),
("address.zipcode", pm.DESCENDING)
])
# ### Deleting indexes
restaurants.drop_index('borough_1') # drop this index
restaurants.drop_index('cuisine_1_address.zipcode_-1') # drop that index
restaurants.drop_indexes() # drop all indexes!!1
# ### Multi-key index
#
# An index for a fields with array value.
restaurants.find_one()
restaurants.create_index([("address.coord", 1)])
restaurants.create_index([("grades.score", 1)])
restaurants.create_index([("grades.grade", 1), ("grades.score", 1)])
# The following will not work!
# We cannot _currently_ have compound multi-key indexes.
restaurants.create_index([("address.coord", 1), ("grades.score", 1)]) # NOPE!
# ## Retrieving the execution plan
#
# We can retrieve the execution plan for a **find()** query by calling the [explain()](https://docs.mongodb.org/manual/reference/method/cursor.explain/) function on the result cursor. We demonstrate this in the following example.
restaurants.drop_indexes() # we drop all indexes first -- use this with care!
restaurants.create_index([("borough", pm.ASCENDING)]) # build an index on field "borough", in ascending order
my_cursor = restaurants.find({"borough": "brooklyn"}) # submit query to find restaurants from specific borough
my_cursor.explain()["queryPlanner"]["winningPlan"] # ask mongodb to explain execution plan
# As we see in this example, MongoDB makes use of an index (as indicated by keyword "IXSCAN") -- and particularly the index ('borough_1') we constructed to execute the query.
# What if we had not built this index?
restaurants.drop_indexes() # we drop all indexes first -- use this with care!
my_cursor = restaurants.find({"borough": "brooklyn"}) # submit query to find restaurants from specific borough
my_cursor.explain()["queryPlanner"]["winningPlan"] # ask mongodb to explain execution plan
# In that case, MongoDB simply performs a scan over the collection (as indicated by keyword "COLLSCAN").
# ## Joins
#
# Until very recently, MongoDB did not support joins.
# It was up to the user to implement a join if needed -- as in the cell below.
for a in restaurants.find({"borough": "Manhattan"}).limit(7):
for b in restaurants.find({"borough": "Bronx"}).limit(5):
if a["cuisine"] == b["cuisine"]:
print(a["cuisine"], a["address"]["zipcode"], b["address"]["zipcode"])
# ### Joins with \$lookup
#
# This is a new aggregation stage that implements *left outer equi-joins*.
#
# "A [left outer equi-join](https://www.mongodb.com/blog/post/joins-and-other-aggregation-enhancements-coming-in-mongodb-3-2-part-1-of-3-introduction) produces a result set that contains data for all documents from the left table (collection) together with data from the right table (collection) for documents where there is a match with documents from the left table (collection)."
# create first collection
orders_docs = [{ "_id" : 1, "item" : "abc", "price" : 12, "quantity" : 2 },
{ "_id" : 2, "item" : "jkl", "price" : 20, "quantity" : 1 },
{ "_id" : 3 }]
orders = db.orders
orders.drop()
orders.insert_many(orders_docs)
# create second collection
inventory_docs = [
{ "_id" : 1, "item" : "abc", "description": "product 1", "instock" : 120 },
{ "_id" : 2, "item" : "def", "description": "product 2", "instock" : 80 },
{ "_id" : 3, "item" : "ijk", "description": "product 3", "instock" : 60 },
{ "_id" : 4, "item" : "jkl", "description": "product 4", "instock" : 70 },
{ "_id" : 5, "item": None, "description": "Incomplete" },
{ "_id" : 6 }
]
inventory = db.inventory
inventory.drop()
inventory.insert_many(inventory_docs)
result = orders.aggregate([ # "orders" is the outer collection
{
"$lookup":
{
"from": "inventory", # the inner collection
"localField": "item", # the join field of the outer collection
"foreignField": "item", # the join field of the outer collection
"as": "inventory_docs" # name of field with array of joined inner docs
}
}
])
print_my_docs(result, 10)
# ## Questions from tutorial sessions
# ### Question: How do we query for documents with an array field, all the elements of which satisfy a condition?
#
# Two approaches (if you can think of a different approach, please let me know):
# * Use the [**\$not**](https://docs.mongodb.org/manual/reference/operator/query/not/#op._S_not) operators: form a query to express that "there is no element in the array that does not satisfy the condition".
# * In aggregation, combine an [**\$unwind**](https://docs.mongodb.org/manual/reference/operator/aggregation/unwind/) stage with a [**$group**](https://docs.mongodb.org/manual/reference/operator/aggregation/group/) stage.
#
# To provide an example, let's say we want to __find restaurants with 'A' grades only__.
# Below we show how we can use each of the aforementioned approaches.
# #### First approach: using $not
# using the $not operator
# "find restaurants that contain no grades that are not equal to A"
cursor = restaurants.find({"grades.grade": {"$exists": True}, "grades": {"$not": {"$elemMatch": {"grade": {"$ne": "A"}}}}})
print_my_docs(cursor, 3)
# ##### Note on the semantics of the \$not operator
#
# The operator selects documents that _do not match_ the specified condition on the specified field. These documents include ones that _do not contain_ the field.
#
# To demonstrate this, consider the following simple example of a collection.
# +
# simple example of a collection
mycoll = db.mycoll
mycoll.drop()
# insert three documents
mycoll.insert_one({"grades": [7, 7]})
mycoll.insert_one({"grades": [7, 3]})
mycoll.insert_one({"grades": [3, 3]})
mycoll.insert_one({"grades": []})
mycoll.insert_one({})
# -
# The result of the following query contains documents that do not contain the "grades" field.
# find documents that have no "grades" elements that are not equal to "A"
mycursor = mycoll.find({"grades": {"$not": {"$elemMatch": {"$ne": 7}}}})
print_my_docs(mycursor, 10)
# We can remove such documents from the result as a post-processing step. (**Exercise**: how?)
# #### Second approach: aggregation pipeline
# +
# using aggregation
mycursor = restaurants.aggregate(
[
# unwind the grades array
{"$unwind": "$grades"}, #now each document contains one "grades" value
# group by document "_id" and count:
# (i) the total number of documents in each group as `count`
# -- this is the same as the number of elements in the original array
# (ii) the number of documents that satisfy the condition (grade = "A") as `num_satisfied`
{"$group": {"_id": "$_id", "count": {"$sum": 1}, "num_satisfied": {"$sum": {"$cond": [{"$eq": ["$grades.grade", "A"]}, 1, 0]}}}},
# create a field (named `same`) that is 1 if (count = num_satisfied) and 0 otherwise
{"$project": {"_id": 1, "same_count": {"$cond": [{"$eq": ["$count", "$num_satisfied"]} , 1, 0]}}},
# keep only the document ids for which (same = 1)
{"$match": {"same_count": 1}}
]
)
print_my_docs(mycursor, 5)
# -
# ## Question: Does MongoDB optimize the stages of an aggregation pipeline?
#
# The question was asked in relation to the "limit" query we saw above ("Limiting the number of results").
#
# Indeed, MongoDB does optimize the execution of the aggregation pipeline, as explained [here](https://docs.mongodb.org/manual/core/aggregation-pipeline-optimization/). In relation to the aforementioned query, see, in particular, the part on [sort+limit coalescence](https://docs.mongodb.org/manual/core/aggregation-pipeline-optimization/#sort-limit-coalescence).
# ***
# # Credits and references
#
# We used and consulted material from:
# * the offficial [PyMongo tutorial](https://docs.mongodb.org/getting-started/python/) as well as this shorter [one](http://api.mongodb.org/python/current/tutorial.html),
# * the [JSON](http://json.org/) and [BSON](http://bsonspec.org) documentation, as well as [SON](http://api.mongodb.org/python/current/api/bson/son.html#bson.son.SON),
# * these [posts](https://www.mongodb.com/blog/post/joins-and-other-aggregation-enhancements-coming-in-mongodb-3-2-part-1-of-3-introduction) on the MongoDB blog about the new (v.3.2) left outer equi-join functionality,
# * this [StackOverflow thread](http://stackoverflow.com/questions/18123300/mongo-array-query-only-find-where-all-elements-match).
| 23,059 |
/feature_selection.ipynb
|
e40f7a4e358bca79a2645e78a4575db1d84007b8
|
[] |
no_license
|
fetihkaya/data_science
|
https://github.com/fetihkaya/data_science
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 305,289 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas
import matplotlib.pyplot as plt
import numpy as np
# Load INS data
ins_data = pandas.read_csv('csv/1-vectornav-ins.csv')
ins_data = ins_data.drop(columns=['.header.stamp.secs','.header.stamp.nsecs'])
ins_data['time'] = pandas.to_datetime(ins_data['time'])
ins_data['time'] = (ins_data['time'] - ins_data['time'][0]).astype('timedelta64[ns]').astype('int64')*1e-9
ins_data = ins_data.set_index('time')
# Load GPS Fix (raw) data
fix_data = pandas.read_csv('csv/1-vectornav-fix.csv')
fix_data = fix_data.drop(columns=['.header.stamp.secs','.header.stamp.nsecs'])
fix_data['time'] = pandas.to_datetime(fix_data['time'])
fix_data['time'] = (fix_data['time'] - fix_data['time'][0]).astype('timedelta64[ns]').astype('int64')*1e-9
fix_data = fix_data.set_index('time')
# Load IMU Data
imu_data = pandas.read_csv('csv/1-vectornav-imu.csv')
imu_data = imu_data.drop(columns=['.header.stamp.secs','.header.stamp.nsecs'])
imu_data['time'] = pandas.to_datetime(imu_data['time'])
imu_data['time'] = (imu_data['time'] - imu_data['time'][0]).astype('timedelta64[ns]').astype('int64')*1e-9
imu_data = imu_data.set_index('time')
# Load Pacmod Speed Data
# pacmod parsed_txt/vehicle_speed is gets corrupt rows, so we will use as_tx/vehicle_speed
pacmod_speed = pandas.read_csv('csv/1-pacmod-as_tx-vehicle_speed.csv')
pacmod_speed['time'] = pandas.to_datetime(pacmod_speed['time'])
pacmod_speed['time'] = (pacmod_speed['time'] - pacmod_speed['time'][0]).astype('timedelta64[ns]').astype('int64')*1e-9
# Additionally, there is an factor offset between parsed_txt/vehicle_speed and as_tx/vehicle_speed for whatever reason
# Use 2.237
pacmod_speed['.data'] = pacmod_speed['.data']*2.237
pacmod_speed = pacmod_speed.set_index('time')
# Load Pacmod Steer Data
pacmod_steer = pandas.read_csv('csv/1-pacmod-parsed_tx-steer_rpt.csv')
pacmod_steer = pacmod_steer.drop(columns=['.header.stamp.secs','.header.stamp.nsecs'])
pacmod_steer['time'] = pandas.to_datetime(pacmod_steer['time'])
pacmod_steer['time'] = (pacmod_steer['time'] - pacmod_steer['time'][0]).astype('timedelta64[ns]').astype('int64')*1e-9
pacmod_steer = pacmod_steer.set_index('time')
# Add some basic calculations to dataframes ...
# Mangitude of speed
ins_data['.mag_speed'] = (ins_data['.NedVel.y']**2 + ins_data['.NedVel.x']**2)**(1/2)
# Add ins speed to IMU dataframe
imu_data['ins_vel'] = 0.0
for t in imu_data.index:
imu_data.at[t,'ins_vel'] = ins_data.iloc[ins_data.index.get_loc(t,method='nearest')]['.mag_speed']
# ENU Frame - subtract 90 from yaw
yaw = (90 - ins_data['.RPY.z']) * np.pi/180
ins_x_vel = ins_data['.NedVel.y']
ins_y_vel = ins_data['.NedVel.x']
# Local velocity at IMU location
ins_data['.LocalVel.x'] = np.multiply(ins_x_vel,np.cos(yaw)) + np.multiply(ins_y_vel,np.sin(yaw))
ins_data['.LocalVel.y'] = -np.multiply(ins_x_vel,np.sin(yaw)) + np.multiply(ins_y_vel,np.cos(yaw))
del yaw, ins_x_vel, ins_y_vel # clear unused variables
imu_data
# +
plt.style.use('ggplot')
predicted_yaw = [ins_data['.RPY.z'][0]* np.pi/180] # Initialize first heading value to INS heading
for steering,time in zip(pacmod_steer['.manual_input'],pacmod_steer.index):
V = pacmod_speed.iloc[pacmod_speed.index.get_loc(time,method='nearest')]['.data']
prediction = predicted_yaw[-1] - (V/3.4)*np.tan(steering/20.0)*0.033 # updated equation.
prediction = (prediction + np.pi) % (2* np.pi) - np.pi # Wrap to pi
predicted_yaw.append(prediction)
# -
imu_yaw = [ins_data['.RPY.z'][0]* np.pi/180] # Initialize first heading value to INS heading
for i in range(imu_data.index.size - 1):
t0 = imu_data.index[i]
t1 = imu_data.index[i+1]
y0 = imu_data['.Gyro.z'].iloc[i]
integration = imu_yaw[-1] + (y0)*(t1-t0)
integration = (integration + np.pi) % (2* np.pi) - np.pi # Wrap to pi
imu_yaw.append(integration)
# ## Integrating Yaw
plt.figure()
plt.plot(ins_data.index.values,ins_data['.RPY.z'] * np.pi/180,label='INS') # plot yaw
plt.plot(imu_data.index,imu_yaw,label='Imu Integrated',alpha=0.75)
plt.plot(pacmod_steer.index,predicted_yaw[0:-1],label="model predicted")
plt.xlabel('Time [s]')
plt.ylabel('heading [rad]')
plt.title('INS vs. IMU Integrated Heading');
plt.legend()
plt.show();
# Integrated yaw looks pretty good actually. Gyro data is probably less noisy than acceleration data.
# ## Integrating Acceleration for Velocity
# +
# Perform integration, Initialize to ins_data[0]
imu_vel_x = np.asarray([ins_data['.NedVel.x'].iloc[0]])
imu_vel_y = np.asarray([ins_data['.NedVel.y'].iloc[0]])
for i in range(imu_data.index.size - 1):
t0 = imu_data.index[i]
t1 = imu_data.index[i+1]
v_x0 = imu_data['.Accel.x'].iloc[i]
v_y0 = imu_data['.Accel.y'].iloc[i]
vel_x = imu_vel_x[-1] + ( ((v_x0)*(t1-t0)))
vel_y = imu_vel_y[-1] + ( ((v_y0)*(t1-t0)))
imu_vel_x = np.append(imu_vel_x,vel_x)
imu_vel_y = np.append(imu_vel_y,vel_y)
imu_vel = (imu_vel_x**2 + imu_vel_y**2)**(1/2)
# -
# Plot INS vs Imu Integrated velocity
plt.plot(ins_data.index,ins_data['.mag_speed'],label='INS')
plt.plot(imu_data.index,imu_vel,label="IMU Integrated")
plt.xlabel('Time [s]')
plt.ylabel('Velocity [m/s]')
plt.legend()
plt.title('Comparison of IMU integrated vs. INS velocity')
# ### Where does this drift come from?
#
# Let's observe some acceleration data when the velocity of the golfcart is zero (observed when the magnitude of the GPS speed is < 0.01 m/s)
# +
v_is_zero = ins_data['.mag_speed'] < 1e-2
v_is_zero = ins_data[v_is_zero]['.mag_speed'] >= 0.0
v_is_zero = v_is_zero.index[v_is_zero]
imu_when_zeroV = pandas.DataFrame(columns=imu_data.columns)
for t in v_is_zero:
imu = imu_data.iloc[imu_data.index.get_loc(t,method='nearest')]
imu_when_zeroV = imu_when_zeroV.append(imu)
imu_when_zeroV.describe()
# +
plt.figure()
plt.hist(imu_when_zeroV['.Accel.x'],bins=32,alpha=0.5,label="X Acceleration",density=True)
plt.hist(imu_when_zeroV['.Accel.y'],bins=32,alpha=0.5,label="Y Acceleration",density=True)
plt.xlim([-0.75,0.3])
plt.xlabel('Acceleration [m/s^2]')
plt.ylabel('Density')
plt.title('XY Acceleration Distribution with vehicle stopped')
plt.legend()
plt.figure()
plt.hist(imu_when_zeroV['.Accel.z'],bins=50,alpha=0.5,density=True,label="Z Acceleration")
plt.xlim([-9.85,-9.65])
plt.xlabel('Acceleration [m/s^2]')
plt.ylabel('Density')
plt.title('Z Acceleration Distribution with vehicle stopped')
plt.legend();
# +
# Code accelerations by stop
imu_when_zeroV['group'] = None
c_time = imu_when_zeroV.index[0]
group = 0
for t in imu_when_zeroV.index:
if np.abs(c_time - t) > 10: # Seperation time in seconds. Tune according to dataset
group += 1
c_time = t
imu_when_zeroV.at[t,'group'] = group
#print(t,group)
#print(imu_when_zeroV)
for i in range(imu_when_zeroV['group'].max()):
i +=1 # range gives 0 to n, need 1 to n
seq = imu_when_zeroV[imu_when_zeroV['group']==i]['.header.seq']
print("Stop Group # ",i," Start Seq: ",seq.min(), " End Seq: ",seq.max())
# -
plt.title('XY Acceleration Scatter during stops')
plt.scatter(imu_when_zeroV['.Accel.y'],imu_when_zeroV['.Accel.x'],s=1,c=imu_when_zeroV['group'],label='data')
plt.scatter(0.0,0.0,s=45,color='red',label='zero',marker='x')
plt.scatter(imu_when_zeroV['.Accel.y'].mean(),imu_when_zeroV['.Accel.x'].mean(),s=45,marker='^',color='k',label='mean')
plt.xlabel('Y Acceleration [$m/s^2$]')
plt.ylabel('X Acceleration [$m/s^2$]');
plt.legend()
# ## Subtracting out the bias, and re-integrating
# +
bx = imu_when_zeroV['.Accel.x'].mean()
by = imu_when_zeroV['.Accel.y'].mean()
# Perform integration, Initialize to ins_data[0]
imu_vel_x = np.asarray([ins_data['.NedVel.x'].iloc[0]])
imu_vel_y = np.asarray([ins_data['.NedVel.y'].iloc[0]])
for i in range(imu_data.index.size - 1):
t0 = imu_data.index[i]
t1 = imu_data.index[i+1]
v_x0 = imu_data['.Accel.x'].iloc[i] - bx
v_y0 = imu_data['.Accel.y'].iloc[i] - by
vel_x = imu_vel_x[-1] + ( ((v_x0)*(t1-t0)))
vel_y = imu_vel_y[-1] + ( ((v_y0)*(t1-t0)))
imu_vel_x = np.append(imu_vel_x,vel_x)
imu_vel_y = np.append(imu_vel_y,vel_y)
imu_vel = (imu_vel_x**2 + imu_vel_y**2)**(1/2)
# -
# Plot INS vs Imu Integrated velocity
plt.plot(ins_data.index,ins_data['.mag_speed'],label='INS')
plt.plot(imu_data.index,imu_vel,label="IMU Integrated, no bias")
plt.xlabel('Time [s]')
plt.ylabel('Velocity [m/s]')
plt.legend()
plt.title('Comparison of IMU integrated vs. INS velocity');
# +
# Differentiate the INS velX and velY
imu_data['ins_velX'] = 0.0
imu_data['ins_velY'] = 0.0
for t in imu_data.index:
ct = ins_data.index.get_loc(t,method='nearest')
imu_data.at[t,'ins_velX'] = ins_data.iloc[ct]['.LocalVel.x']
imu_data.at[t,'ins_velY'] = ins_data.iloc[ct]['.LocalVel.y']
imu_data['ins_accel_x'] = np.diff(imu_data['ins_velX'],prepend=1e-6)/np.diff(imu_data.index,prepend=1-7)
imu_data['ins_accel_y'] = np.diff(imu_data['ins_velY'],prepend=1e-6)/np.diff(imu_data.index,prepend=1-7)
imu_data.plot(y=['ins_accel_x','.Accel.x'],alpha=0.5)
plt.title('X measurements')
plt.figure()
imu_data.plot(y=['ins_accel_y','.Accel.y'],alpha=0.5)
plt.legend()
plt.title('Y measurements')
plt.figure()
imu_data.plot(y='.Accel.z',alpha=0.5)
plt.plot([0,700],[-9.801,-9.801],label='True Gravity')
plt.legend()
plt.title('Z Measurements')
plt.figure()
plt.scatter(x=imu_when_zeroV.index,y=imu_when_zeroV['.Accel.z'],label='.Accel.z')
plt.plot([0,100],[-9.801,-9.801],label='True Gravity')
plt.legend()
plt.title('Z Measurements (while stopped)')
# +
import numpy.matlib
from scipy import integrate
def xyz_accel_scale_bias(C,B,imu_data_):
""" Returns acceleration with scalefactor C and Bias B """
imu_data_ = imu_data_.copy() # copy to avoid rewriting
c_ = np.zeros((3,3))
c_[0,0] = C[0]
c_[1,1] = C[1]
c_[2,2] = C[2]
c_[0,1] = C[3]
c_[0,2] = C[4]
c_[1,2] = C[5]
c_[1,0] = C[6]
c_[2,0] = C[7]
c_[2,1] = C[8]
#print(c_)
b_ = np.zeros((3,1))
#print(b_)
b_[0] = B[0]
b_[1] = B[1]
b_[2] = B[2]
#print(b_)
xyz_ = np.matmul(c_ ,( np.array([imu_data_['.Accel.x'],imu_data_['.Accel.y'],imu_data_['.Accel.z']]) + b_))
#imu_data_[['.Accel.x','.Accel.y','.Accel.z']] = 0.0
imu_data_[['.Accel.x','.Accel.y','.Accel.z']] = xyz_.T
return imu_data_
def least_square_cost(imu_data_):
diffx = (imu_data_['.Accel.x'] - imu_data_['ins_accel_x'] )**2
diffy = (imu_data_['.Accel.y'] - imu_data_['ins_accel_y'] )**2
diffz = (imu_data_['.Accel.z'] - -9.801)**2 # 9.801 local gravity @ college station
return np.sum( (diffx + diffy + diffz)**(1/2) )
def minimize_fun(theta):
C = theta[0:9]
B = theta[9:12]
# print(C,B)
new_imu_data = xyz_accel_scale_bias(C,B,imu_data)
return least_square_cost(new_imu_data)
def integrate_imu_vel(imu_data_):
imu_data_ = imu_data_.copy() # copy to avoid rewriting
imu_data_['x_vel'] = integrate.cumtrapz(imu_data_['.Accel.x'],x=imu_data_.index,initial=ins_data['.LocalVel.x'][0])
imu_data_['y_vel'] = integrate.cumtrapz(imu_data_['.Accel.y'],x=imu_data_.index,initial=ins_data['.LocalVel.y'][0])
imu_data_['mag_vel'] = (imu_data_['x_vel']**2 + imu_data_['y_vel']**2)**(1/2)
return imu_data_
print(minimize_fun([1,1,1,1,1,1,1,1,1,0,0,0]))
print(minimize_fun([1,1,1,1,1,1,1,1,1,0,0,0]))
# +
import scipy.optimize
from scipy.optimize import Bounds
Bound = Bounds(lb=[0.9,0.9,0.9,-1.0,-1.0,-1.0,-1.0,-1.0,-1.0,-0.2,-0.2,-0.2],ub=[1.1,1.1,1.1,1.1,1.1,1.1,1.1,1.1,1.1,0.2,0.2,0.2])
sol = scipy.optimize.minimize(minimize_fun,[1,1,1,1,1,1,1,1,1,-0.1,0.0,0.1],bounds=Bound)
print(sol)
# +
C = sol.x[0:9]
B = sol.x[9:12]
c_ = np.zeros((3,3))
c_[0,0] = C[0]
c_[1,1] = C[1]
c_[2,2] = C[2]
c_[0,1] = C[3]
c_[0,2] = C[4]
c_[1,2] = C[5]
c_[1,0] = C[6]
c_[2,0] = C[7]
c_[2,1] = C[8]
b_ = np.zeros((3,1))
b_[0] = B[0]
b_[1] = B[1]
b_[2] = B[2]
print("C = \n", np.array_str(c_, precision=2))
print("B = \n", np.array_str(b_, precision=2))
new_imu_data = xyz_accel_scale_bias(C,B,imu_data)
new_imu_data = integrate_imu_vel(new_imu_data)
new_imu_data.plot(y=['mag_vel','ins_vel'])
plt.legend(['IMU integrated','INS'])
plt.ylabel('m/$s^2$')
plt.title('IMU Velocity integrated with bias and scale factor removal')
plt.figure()
plt.plot(imu_data.index,imu_data['.Accel.x'],label='Old',alpha=0.5)
plt.plot(new_imu_data.index,new_imu_data['.Accel.x'],label='New',alpha=0.5)
plt.title('New X measurements')
plt.legend()
plt.figure()
plt.plot(imu_data.index,imu_data['.Accel.y'],label='Old',alpha=0.5)
plt.plot(new_imu_data.index,new_imu_data['.Accel.y'],label='New',alpha=0.5)
plt.title('New Y measurements')
plt.legend()
plt.figure()
plt.plot(imu_data.index,imu_data['.Accel.z'],label='Old',alpha=0.5)
plt.plot(new_imu_data.index,new_imu_data['.Accel.z'],label='New',alpha=0.5)
plt.title('New Z measurements')
plt.legend()
# -
np.mean(new_imu_data['.Accel.z'])
en(group2)))
for i in range(len(group1)):
for j in range(len(group2)):
con_table[i][j] = sum((df[a1] == group1[i]) & (df[a2] == group2[j]))
return con_table, group1, group2
con_table,g1,g2 = calc_contingency_table_T(bank,"y","marital")
print(g1)
print(g2)
con_table
stats.chi2_contingency(con_table)
def calc_chi2_contingency_T(con_table):
con_table = con_table.astype(float)
marginals_col = con_table.sum(axis=0)
marginals_row = con_table.sum(axis=1)
total = con_table.sum()
for i in range(con_table.shape[0]):
for j in range(con_table.shape[1]):
expected = (marginals_row[i]) * (marginals_col[j]) / total
con_table[i][j] = ((con_table[i][j] - expected)**2) / expected
return con_table.sum()
chi2_stat = calc_chi2_contingency_T(con_table)
chi2_stat
bank
le = LabelEncoder()
X = bank.loc[:,'age':'poutcome']
X = X.select_dtypes(include=np.object) # select string columns
X = X.apply(LabelEncoder().fit_transform)
y = le.fit_transform(bank.loc[:,'y'])
chi2, pval=feature_selection.chi2(X, y)
# +
sorted_idx = np.argsort(chi2)[::-1]
sorted_vals = np.sort(chi2)[::-1]
d = {"features":X.columns[sorted_idx], "values":sorted_vals, "p-values":pval[sorted_idx]}
df = pd.DataFrame(d)
df
# -
# ### Mutual Information
# #### Entropy
#
# Given a discrete random variable $X$ with outcomes $\mathcal{X}=\{x_{1},...,x_{n}\}$ which occur with probability ${\displaystyle \mathrm {P} (x_{1}),...,\mathrm {P} (x_{n})}$, the entropy of X is defined as:
# $$
# H(X) = -\sum_{x \in \mathcal{X}}P(x)logP(x)
# $$
# pk[i] is the probability of outcome i
def entropy_T(pk):
S = 0
for i in range(len(pk)):
if pk[i] > 0:
S = S - pk[i]*np.log2(pk[i])
return S
pk = [0.5, 0.5]
print("Entropy of a fair coin:", entropy_T(pk))
pk = [0.1, 0.9]
print("Entropy of a biased fair coin:", entropy_T(pk))
pk = [0, 1]
print("Entropy of a perfect biased fair coin:", entropy_T(pk))
# Entropy of a fair dice
pk = [1/6,1/6,1/6,1/6,1/6,1/6]
print("Entropy of a fair dice:", entropy_T(pk))
pk = [2/6,2/6,0/6,0/6,2/6,0]
print("Entropy of a fair dice:", entropy_T(pk))
pk = [0,0,0,0,0,1]
print("Entropy of a perfect unfair dice:", entropy_T(pk))
# Shape of the entropy function for a variable with two outcomes
x = np.arange(0.01,1,0.01)
s = []
for i in x:
s.append(entropy_T([i,1-i]))
plt.plot(x,s)
# #### Some facts about entropy
#
# - The range of Entropy:
# $0 ≤ Entropy ≤ log(n)$, where n is number of outcomes
# - Minimum entropy ($0$) occurs when one of the probabilities is 1 and rest are 0’s.
# - Maximum entropy ($log(n)$) occurs when all the probabilities are the same, namely, 1/n.
# #### Mutual Information
#
# $$
# I(X;Y) = \sum_{x \in \mathcal{X}}\sum_{y \in \mathcal{Y}}P(x,y)log\frac{P(x,y)}{P(x)P(y)}
# $$
#
# where $P(X,Y)$ is the joint and $P(X)$ and $P(Y)$ are the marginal probability distributions of the random variables $X$ and $Y$.
#
#
def mutual_info_T(df, a1, a2):
con_table, g1, g2 = calc_contingency_table_T(df, a1, a2)
print(con_table)
marginals_col = con_table.sum(axis=0)
marginals_row = con_table.sum(axis=1)
total = con_table.sum()
mi = 0
for i in range(con_table.shape[0]):
for j in range(con_table.shape[1]):
# Calculate joint probability.
p = con_table[i][j] / total
m = (marginals_row[i] / total)*(marginals_col[j] / total)
if (p > 0):
mi += p*np.log(p / m)
return mi
mutual_info_T(bank,"y","marital")
X = bank.loc[:,['marital', 'education', 'y']]
X
X = X.apply(LabelEncoder().fit_transform)
X
importances_mi = mutual_info_classif(X.loc[:,['marital','education']], X.y,discrete_features=True)
importances_mi
le = LabelEncoder()
X = bank.loc[:,'age':'poutcome']
X = X.select_dtypes(include=np.object) # select string columns
X = X.apply(LabelEncoder().fit_transform)
y = le.fit_transform(bank.loc[:,'y'])
importances_mi=mutual_info_classif(X, y,discrete_features=True)
# +
sorted_idx = np.argsort(importances_mi)[::-1]
sorted_vals = np.sort(importances_mi)[::-1]
d = {"features":X.columns[sorted_idx], "values":sorted_vals}
df = pd.DataFrame(d)
df
# -
# # Categorical (nominal), Ordinal, and Numerical Variables
#
# You can read this link for the differences with these types of variables.
#
# https://stats.idre.ucla.edu/other/mult-pkg/whatstat/what-is-the-difference-between-categorical-ordinal-and-numerical-variables/
# ### Be careful in using OrdinalEncoder
# There is some confusion on the use of LabelEncoder and OrdinalEncoder in Pytgon. LabelEncoder is generally used to encode class variable, and OrdinalEncoder is generally used to encode feature en X. However, note that OrdinalEncoder cannot not assign integer based on the inherent order of the values, you have to give these mapping.
oe = OrdinalEncoder()
X = bank.loc[:,'age':'poutcome']
X = X.select_dtypes(include=np.object) # select string columns
oe.fit_transform(X)
X.columns
X.education.unique()
ordinal_map = {'tertiary':3, 'secondary':2, 'primary':1, 'unknown':0}
X
# If you want to give integer labels in the correct order for the feature education, you should do it manually.
X = bank.loc[:,'age':'poutcome']
X['education'] = X.education.map(ordinal_map)
X
| 18,473 |
/2. Algorithms/NeuralNetwork/Neural Network - Convolutional Neural Network with MNIST.ipynb
|
0f92405373aee43a02a8ffea038213290583ebc5
|
[] |
no_license
|
patrick-ytchou/Machine-Learning
|
https://github.com/patrick-ytchou/Machine-Learning
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 28,381 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Neural Network: Convolutional Neural Network (CNN) with MNIST
# ## Introduction to Convolutional Neural Network
#
# <img src="pic/cnnall.jpeg" width=800>
#
# **Convolutional Neural Network (CovNet/CNN)** is now the go-to model on every image related problem. In terms of accuracy they blow competition out of the water. It is also successfully applied to recommender systems, natural language processing, audio recognition, and much much more. CNN is also computationally efficient. The key advantage of CNN lies in its **feature learning** ability. THat is, CNN can capture relevant features from an image /video and detect patterns in part of the image rather than the image as a whole. For normal neural network, it can only see the whole image as a whole.
#
#
# Convolutional neural network is very powerful in image analysis/recognition. You can, in fact, use simple Artificial Neural Network (ANN) to analyze images, for example image recognition. Then why nowadays people often switch to CNN for images?
#
# Say that you have a picture with 100 x 100 pixels. Since each pixel consists of 3 values(R,G,B), this picture will, in turn, have $100 \times 100 \times 3 = 30,000$ dimensions. If the first hidden layer consists of 1,000 nodes, you will have 30 million weights if you use the fully-connected ANN, for only the first layer! Therefore, CNN is a great technique for images since it reduces the parameters needed for neural network. It basically is a technique that utilize prior knowledge to remove some of the weights in the fully-connected neural network.
#
#
#
#
#
#
#
# ---
# ## Why CNN is useful for image analysis?
#
# CNN is extremely useful not only because of its efficency but also because of unique operations that help detect certain patterns . It uses special convolution and pooling operations and performs parameter sharing. This enables CNN models to run on any device, making them universally attractive.
#
#
# Say the neuron below detects whether or not there is a beak.
#
# <img src="pic/bird1.png" width=100>
#
# The advantage of using CNN instead of ANN is as the following:
#
#
# 1. **Pattern learning**. There's no need to see the whole image for image recognition.
#
# In order to know whether this image contains a wheel, you don't see to see the whole image, since from prior knowledge we know that wheels cannot be in the sky. In CNN, each neuron only performs certain work, say detecting whether there is a beak. Therefore, some of the weights in the fully-connected network structure is useless. That is, **a neuron does not have to see the whole image to discover the pattern**. This property can be implemented via **Convolution Layer**.
#
#
# 2. **Weight sharing**. Detecting same items of different positions requires only one neuron.
#
# Another reason why we can remove some of the weights is that **even if the patterns appear in different regions, since they do almost the same thing (say detecting whether there is a beak), they can use the same sets of parameters**, therefore reducing the number of weights required. For example, two images below shows two birds with beaks in different positions. We don't have to train two neurons to detect this two beaks. Instead, we only need one. This property can be implemented via **Convolution Layer**.
#
# <table><tr><td><img src="pic/bird1.png" width=100></td><td><img src="pic/bird2.png" width=100></td></tr></table>
#
#
# 3. **Subsampling**. Enlarging or reducing the size of the image doesn't matter.
#
# One other reason is that **subsampling the pixels will not change the target**. Subsampling means to shrink the size of image to make it smaller. Since the number of pixels decreases, you need fewer weights. This property can be implemented via **Max Pooling Layer**.
#
# ## The process of Convolution Neural Network
#
# <img src="pic/cnnseq.jpeg" width=600>
#
# There is an input image that we’re working with. We perform **a series convolution + pooling operations**, followed by a number of fully connected layers. Note taht the number of iterations (convolution + pooling) is not a fixed number. The ultimate goal of the iteration is the limit the number of digits. For example, the original hand-written number is 28 x 28 digits. After performing two sets of convolution + pooling as stated above, we shrink it to 4 x 4 digits. We can then limit the size of the input neurons.
#
# In this example, since we are dealing with a classification problem, the output layer contains the exact number of nodes as the total number of classes we are going to predict. Since we are performing multiclass classification, the activation function for the output layer should be the softmax function. If we are doing a regression problem, we can simply give the final layer one node representing the value.
#
# Knowing the entire process of CNN, let's now dive into each component.
#
# ### Convolution (沒寫完)
#
# The main building block of Convolutional Neural Network is the convolutional layer. Convolution is a mathematical operation to merge two sets of information. In our case the convolution is applied on the input data using a convolution filter to produce a feature map. There are a lot of terms being used so let’s define and visualize them.
#
# ### Important Elements within Convolutional Neural Network
#
# **The input Image**
#
# Images are made up of pixels. Each pixel is represented by a number between 0 and 255. As stated in the beginning, since each pixel consists of 3 values(R,G,B), this picture will, in turn, have 100×100×3=30,000 dimensions. If the first hidden layer consists of 1,000 nodes, you will have 30 million weights! It's almost impossible to train these gigantic amount of weights in a fully-connected neural network, let alone the fact that most of the weights are useless. This is why CNN is widely used for images in the field of neural network.
#
# **Feature Detector**
#
# The feature detector is a matrix, usually 3x3 (it could also be 7x7). The feature dectector is also widely known as a **filter** or a **kernel**.
#
# **Feature Map**
#
# Say that you have a decent amount of filters. Feature map is the output of matrix representation of the input image that is multiplied element-wise with the feature detector (filter) and the input image. The feature map is also known as a **convolved feature** or an **activation map**. The aim of this step is to reduce the size of the image and make processing faster and easier. Indeed, some of the features of the image are lost in this step, but most of the representations can be captured by the feature detector.
#
#
# Let’s say we have a 32x32x3 image and we use a filter of size 5x5x3 (note that the depth of the convolution filter matches the depth of the image, both being 3). Here we perform the convolution operation described above. The only difference is that this time we do the sum of matrix multiply in 3D instead of 2D, but the result is still a scalar. We slide the filter over the input like above and perform the convolution at every location aggregating the result in a feature map. This feature map is of size 32x32x1, shown as the red slice on the right. If we take another filter, denoted in green, and follow the same process stated above, we can produce another feature map of size 32x32x1. Therefore, the number of filters determines the thickness of the feature map, which is how many individual feature map that we will stack together to form a 3D one.
#
# <img src="pic/conv.png" width=450>
#
#
# **Stride**
#
# **Stride** is the magnitude of slide that filter moves along the input image matrix. The default value for stride is 1. If we want to have less overlap when conducting the element-wise inner product, or want a smaller feature map, we can have bigger strides. This is the parameter that should be set before the model compile. It requires some domain knowledge as well as trial and error.
#
# **Padding**
#
# Another technique used in CNN is called **padding**. Padding is commonly used in CNN to preserve the size of the feature maps, otherwise they would shrink at each layer, which may not be desirable in some cases. Without padding, the size of the feature map is smaller than the input. The picture below demonstrates that fact. If we want to maintain the same dimensionality, we can use padding to surround the input with zeros. We can either pad with **zeros or the values on the edge**.
#
# With proper padding, the height and width of the feature map was the same as the input (both 32x32), and only the depth changed.
#
# ### Process of Convolution
#
# <img src="pic/convo.png" width=600>
#
# On the left side is the input image to the convolution layer. At the middle is the convolution filter. This is called a 3x3 convolution; the size of the filter can be determined by setting parameters. On the right side is the feature map produced by mering the input image and the convolution filter. We perform the convolution operation by sliding this filter over the input. The magnitude of this slide is controlled by the parameter **stride**. At every location, we do element-wise inner product and sum the result. This sum goes into the feature map. This is the result of this Convolution Layer. Below is a wonderful gif from [A Comprehensive Guide to Convolutional Neural Networks — the ELI5 way](https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53) that show the process of convolution.
#
# <img src="pic/conv.gif">
#
# Note that since we have done padding around the original picture, the dimensionaility of the feature map remains the same.
#
# ---
#
#
# The image below clearly demonstrates why the process of convolution is actually a neural network with less weights connected.
#
# <img src="pic/convo2.png" width=600>
#
# When we move the filter frame to the right, since they are using the same filter, what this actually means is that the two neurons share the same weights, making the total weights even less.
#
#
# ### Max Pooling
#
# What Max Pooling really does is **subsampling**. It is done by applying a max filter to subregions of the initial representation. See the picture below.
#
# <img src="pic/maxpool.png" width=400>
#
#
# What Max Pooling does is to take out the maximum value within a subset of the values. The objective is to down-sample an input representation (image, hidden-layer output matrix, etc.) and reduce its dimensionality. This decreases the computational power required to process the data through dimensionality reduction. It also helps overfitting by providing an abstracted form of the representation. As well, it reduces the computational cost by reducing the number of parameters to learn.
#
# Note that in fact there are two types of pooling: **Max Pooling** and **Average Pooling**. In CNN, Max Pooling dominates and is our go-to method for subsampling.
#
#
# Whenever you finish one loop of **Convolution** and **Max Pooling**, what you really get is a new image representing the original input. **The Convolutional Layer and the Max Pooling Layer together form the i-th layer of a Convolutional Neural Network**. Depending on the complexities of the images, the number of such layers may be increased for capturing low-levels details even further, but at the cost of more computational power.
#
# Note that **Max Pooling is not a must-do step in Convolutional Neural Network**. For example, in Alphago's paper, the author states that he uses the strucure of convolutional neural network to detect patterns on the go board. However, in this go example, the author doesn't use this Max Pooling technique to subsample the image.
#
# ### Flatten
#
# Flatten is the process that connects the result from Max Pooling and the fully-connected neural network. Once the pooled featured map is obtained through iterations of convolution and max pooling, the next step is to transform the entire pooled feature map matrix into a single column so that it can be fed to the neural network for processing. The flattening process is shown as the image below.
#
# <img src="pic/flatten.png" width=300>
#
#
# ### Fully-Connected Neural Network
#
# After doing all the work, now we can simply feed the flattened data into the fully-connected neural network (DNN).
#
# <img src="pic/fc.jpeg" width=700>
#
# Remember that a fully-connected neural network can represent any kind of non-linear relationship between input and output. Thus, adding a fully-connected layer is a good way to learn all the non-linear combinations of the high-level features represented by the output of the flatten layer.
# ## Quick Practice in Keras
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers.core import Dense, Dropout
from keras.layers import Flatten, Conv2D, MaxPooling2D
from keras.optimizers import Adam
from keras.utils import np_utils
from keras.datasets import fashion_mnist
from keras import backend
# +
def load_data():
# # X_train = X_train.reshape(-1, 28*28)
# X_train = X_train.astype('float')
# # X_test = X_test.reshape(-1, 28*28)
# X_test = X_test.astype('float')
# input image dimensions
img_rows, img_cols = 28, 28
# the data, split between train and test sets
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()
if backend.image_data_format() == 'channels_first':
X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
# Convert class vectors to binary class matrices
y_train = np_utils.to_categorical(y_train, 10)
y_test = np_utils.to_categorical(y_test, 10)
X_train = X_train
X_test = X_test
# X_test = np.random.normal(X_test)
X_train = X_train / 255 # normalize the pixel
X_test = X_test / 255 # normalize the pixel
return((X_train, y_train),(X_test, y_test), input_shape)
# -
if __name__ == '__main__':
# load training data and testing data
(X_train, y_train), (X_test, y_test), input_shape = load_data()
# define network structure
model = Sequential()
# CNN
model.add(Conv2D(input_shape = input_shape, filters=25, kernel_size=(3,3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(filters=50, kernel_size=(3,3)))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
# ANN
model.add(Dense(units=300, activation='relu'))
model.add(Dense(units=10, activation='softmax'))
# set configurations
model.compile(loss='categorical_crossentropy',
optimizer=Adam(), metrics=['accuracy'])
# train model
history = model.fit(X_train, y_train, batch_size=256, epochs=20, validation_split=0.3)
# evaluate the model and output the accuracy
result_train = model.evaluate(X_train, y_train)
result_test = model.evaluate(X_test, y_test)
print('\n')
print('----------Model Result----------')
print('Train Acc:', result_train[1])
print('Test Acc:', result_test[1])
# ---
# ## What does Convolution Neural Network Learn?
#
# **Before Flatten -- Convolution + Max Pooling**
#
# So after training the model, we get a great result...then what? How can be interpret this neural network?
#
# We all know that when we are training the neural network, we pass an input into the model. Via gradient descent, we find the set of weights and biases that minimize total loss. Now, how can we know what the filters are doing?
#
# Say that the output of the k-th filter is a M x M matrix. Here we can define a matrix called **Degree of Activation**. Here we define the degree of the activation of the k-th filter to be
# $$a^k = \sum \limits_{i=1}^M \sum \limits_{j=1}^M a_{ij}^k$$
# , where $a_{ij}^k$ is the inner-product retrieved after the convolution layer.
#
# The trick we are going to use is to implement **Gradient Ascent** to get find the image that miximize the degree of the activation. That is, we want to find the image that gives the highest total sum after the inner-product is calculated.
# $$x^* = argmax {a^k}$$
#
# We want to find the input $x^*$ that maximize $a^k$, the degree of activation. This way we can find the image that best reflect what the filter is looking for, which is also equivalent to **what the filter is detecting**. If we do this process of several times, say for 12 filters, we can get something like the following.
#
# <img src="pic/cnnlearn.png" width=300>
#
# What does these images mean? For example, the image on the bottom right corner represents the fact that **that particular filter is responsible for detecting that pattern, in this example diagonal stripes.** Therefore, if we input a image containing diagonal stripes, the output of this filter will be larger compared to other filter that is not detecting diagonal stripes.
#
# From the discussion we can know that **the job for each filter is to detect a certain pattern in the image**.
#
# So the aforementioned discuss can tell us what the filters in the convolution & Max Pooling layer is doing. What about the fully-connected part after flattening?
#
# **After Flatten -- Fully-Connected Neural Network**
#
# By repeating the same process, finding the $x^*$ that maximize the degree of activation, we can find out that each neuron in the fully-connected neural network actually performs the following task.
#
# <img src="pic/cnnlearn2.png" width=250>
#
# It's very different from what we have seen before. In the first image that demonstrates what filters in Convolution + Max Pooling learn, it shows some kind of **patterns**. However, in the second image tha shows what neurons in the fully-connected neural network learn is a **full image**, even if you cannot recognize anything from it. This is because what you feed into the fully-connected neural network is not part of the image, but the entire image as a whole. Therefore, it doesn't only detect and learn some kind of patterns. Instead, it learns the whole picture, or you can say is a larger pattern.
#
#
# Now say you want to see what is the does the entire CNN learn. Let's denote the output of the layer to be $y_i$.
# Say that you want to find an input that maximize the degree of activation of $y^i$, denoting as $x^* = argmax {y^i}$. Below is the shocking result.
#
# <img src="pic/cnnlearn3.png" width=250>
#
# Each image is accompanied by what the result is for each image. The top left image is recognized by the CNN as number $0$, while it is arguably irrecognizable by human beings. Therefore, we can say that neural network learns extremely differently from human beings. For more information about this phenomenon, check out this great video on YouTube: [Deep Neural Networks are Easily Fooled](https://www.youtube.com/watch?v=M2IebCN9Ht4).
#
# So how can we overcome this issue? We all know that digits can only fill a portion of the image. A number $2$ can never cover the entire image. There must be pixels that is not white. We can see that in the previous picture, most of the pixels are white. What if we limit the number of white? We can use regularization!
#
# $$ x^* = argmax_x (y^i - \sum \limits_{i,j}|x_{i,j}|) $$
#
# The term $\sum \limits_{i,j}|x_{i,j}|$ in fact represents the overall number of pixels. Thus, in the equation above we want to find an input $x$ that maximize the output $y^i$ but minimize the number of total $x_{i,j}$, which means limiting the total number of $x$. In this case, most of the images should be left black. The result will be something on the right hand side:
#
# <table><tr><td><img src="pic/cnnlearn3.png" width=300></td><td><img src="pic/cnnlearn4.png" width=300></td></tr></table>
#
# The left hand side represents the orginal result. We can clearly see that using regularization, $x^*$ is much more closer to the real number that we human beings can recognize.
# ---
# ## Reference:
#
# [cs231n](http://cs231n.github.io/)
#
# [What is max pooling in convolutional neural networks?](https://www.quora.com/What-is-max-pooling-in-convolutional-neural-networks)
#
# [Applied Deep Learning - Part 4: Convolutional Neural Networks](https://towardsdatascience.com/applied-deep-learning-part-4-convolutional-neural-networks-584bc134c1e2#a86a)
#
# [What are the advantages of a convolutional neural network (CNN) compared to a simple neural network from the theoretical and practical perspective?](https://www.quora.com/What-are-the-advantages-of-a-convolutional-neural-network-CNN-compared-to-a-simple-neural-network-from-the-theoretical-and-practical-perspective)
#
# [A Comprehensive Guide to Convolutional Neural Networks — the ELI5 way](https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53)
| 21,355 |
/python/crawler/page82.ipynb
|
2c3c2392372c593eee24572a418f6a63de14426e
|
[
"MIT"
] |
permissive
|
groovallstar/test2
|
https://github.com/groovallstar/test2
| 0 | 0 |
MIT
| 2020-01-14T08:48:41 | 2020-01-13T01:53:31 |
Jupyter Notebook
|
Jupyter Notebook
| false | false |
.py
| 26,982 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/groovallstar/test2/blob/feature%2Ffrom_colab/page82.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="7dYuYlxLl_2b" colab_type="code" outputId="baac047f-c563-482f-b705-263a81c2a9fc" colab={"base_uri": "https://localhost:8080/", "height": 1000}
import requests
from bs4 import BeautifulSoup
class Content:
def __init__(self, url, title, body):
self.url = url
self.title = title
self.body = body
def print(self):
print('URL: {}'.format(self.url))
print('TITLE: {}'.format(self.title))
print('BODY:\n{}'.format(self.body))
class Website:
def __init__(self, name, url, titleTag, bodyTag):
self.name = name
self.url = url
self.titleTag = titleTag
self.bodyTag = bodyTag
class Crawler:
def getPage(self, url):
try:
req = requests.get(url)
except requests.exceptions.RequestException:
return None
return BeautifulSoup(req.text, 'html.parser')
def safeGet(self, pageObj, selector):
selectedElems = pageObj.select(selector)
if selectedElems is not None and len(selectedElems) > 0:
return '\n'.join([elem.get_text() for elem in selectedElems])
return ''
def parse(self, site, url):
bs = self.getPage(url)
if bs is not None:
title = self.safeGet(bs, site.titleTag)
body = self.safeGet(bs, site.bodyTag)
if title != '' and body != '':
content = Content(url, title, body)
content.print()
crawler = Crawler()
siteData = [
['O\'Reilly Media', 'http://oreilly.com', 'h1', 'section#product-description'],
['Reuters', 'http://reuters.com', 'h1', 'div.StandardArticleBody_body_1gnLA'],
['Brookings', 'http://www.brookings.edu', 'h1', 'div.post-body'],
['New York Times', 'http://nytimes.com', 'h1', 'div.StoryBodyCompanionColumn div p']
]
websites = []
for row in siteData:
websites.append(Website(row[0], row[1], row[2], row[3]))
crawler.parse(websites[0], 'http://shop.oreilly.com/product/0636920028154.do')
crawler.parse(
websites[1], 'http://www.reuters.com/article/us-usa-epa-pruitt-idUSKBN19W2D0')
crawler.parse(
websites[2],
'https://www.brookings.edu/blog/techtank/2016/03/01/idea-to-retire-old-methods-of-policy-education/')
crawler.parse(
websites[3],
'https://www.nytimes.com/2018/01/28/business/energy-environment/oil-boom.html')
.com/science/1999/aug/11/eclipse.uknews4",
"https://www.theguardian.com/science/1999/aug/05/technology1",
"https://www.theguardian.com/science/1999/jul/23/eclipse",
"https://www.theguardian.com/science/1986/jan/30/spaceexploration.columbia",
"https://www.theguardian.com/science/1986/jan/30/spaceexploration.columbia1",
"https://www.theguardian.com/science/2014/nov/10/breakthrough-prize-scientists-23m-science-awards-2015",
"https://www.theguardian.com/technology/2015/jan/16/elon-musk-falcon-9-rapid-unscheduled-disassembly",
"https://www.theguardian.com/science/2014/oct/31/-sp-rosetta-selfie-mars-saturn-a-month-in-space-september-2014",
"https://www.theguardian.com/science/blog/2014/oct/31/pumpkins-halloween-yeti-mental-health-polio-blogs-roundup",
"https://www.theguardian.com/science/2014/nov/09/steven-pinker-twitter-can-hone-writing-skills",
"https://www.theguardian.com/science/2014/nov/12/rosetta-mission-philae-historic-landing-comet",
]
hubble_urls = [
"https://webbtelescope.org/contents/news-releases/2019/news-2019-41",
"https://hubblesite.org/contents/news-releases/2018/news-2018-21.html",
"https://hubblesite.org/contents/news-releases/2018/news-2018-03.html",
"https://hubblesite.org/contents/news-releases/1990/news-1990-23.html",
"https://hubblesite.org/contents/news-releases/1990/news-1990-17.html",
]
space_urls = [
"https://www.space.com/7078-shuttle-astronauts-deploy-satellites-landing.html",
"https://www.space.com/201-explore-colors-stars.html",
"https://www.space.com/9429-cargo-ship-delivers-healthy-halloween-treats-space-station.html",
"https://www.space.com/37172-trappist-1-planet-visualizations-explained.html",
"https://www.space.com/15107-venus-pleiades-april-skywatching-tips.html",
"https://www.space.com/11521-royal-wedding-space-station-astronauts-message.html",
]
nytimes_urls = [
"https://www.nytimes.com/2019/11/09/us/politics/impeachment-state-department.html?action=click&module=Top%20Stories&pgtype=Homepage",
"http://www.nytimes.com/2015/01/02/world/europe/turkey-police-thwart-attack-on-prime-ministers-office.html",
"https://www.nytimes.com/2019/11/09/us/politics/michael-bloomberg-democrats.html?action=click&module=Top%20Stories&pgtype=Homepage",
"https://www.nytimes.com/2019/11/04/science/space/nasa-boeing-starliner-tes.html",
]
# <a id="scrape-articles"></a>
#
# ## 2. [Scrape articles](#scrape-articles)
# +
# # ========= GET SOUP FOR A SINGLE URL (DO NOT DELETE) =========
# link =
# page_response = requests.get(link, timeout=5)
# soup = BeautifulSoup(page_response.content, "lxml")
# print(soup.prettify())
# text, date = get_space_text_from_soup(soup, page_response)
# text
# +
# # ========= DATES FROM SPACE.com (DO NOT DELETE) =========
# dates = []
# for url in space_urls:
# r = requests.get(url)
# soup = BeautifulSoup(r.content, "lxml")
# # print(soup.prettify())
# published_datetime = soup.find("meta", {"name": "pub_date"}).get("content")
# dates.append(published_datetime)
# # print(dates)
# df = pd.DataFrame(pd.Series(dates), columns=["publication_date"])
# df = append_datetime_attrs(df, date_col="publication_date")
# df
# +
# # ========= APPEND SINGLE ARTICLE SCRAPE TO HDF5 FILE (DO NOT DELETE) =========
# l = []
# for site, links in urls.items():
# # print(site)
# for k, link in enumerate(links[:2]):
# # print(f"{site}_{k+1}")
# df_row = pd.DataFrame(np.random.rand(1, 9), columns=list("ABCDEFGHI"))
# df_row["publication"] = site
# df_row.to_hdf(h5_path, key=f"{site}_{k+1}", format="t", mode="a")
# l.append(df_row)
# print(f"Scraped {len(l)} articles")
# pd.concat(
# [
# pd.read_hdf(h5_path, key=f"{site}_{k+1}")
# for site in urls.keys()
# for k, link in enumerate(links[:2])
# ],
# axis=0,
# ignore_index=True,
# )
# -
from requests.adapters import HTTPAdapter
from urllib3.util.retry import Retry
# +
# # ========= TEST SET DATA FROM GUARDIAN (DO NOT DELETE) =========
# guardian_urls = [
# "https://www.theguardian.com/science/2019/dec/09/european-space-agency-to-launch-clearspace-1-space-debris-collector-in-2025",
# "https://www.theguardian.com/science/2019/nov/04/nasa-voyager-2-sends-back-first-signal-from-interstellar-space",
# "https://www.theguardian.com/science/2019/dec/12/spacewatch-esa-awards-first-junk-clean-up-contract-clearspace",
# "https://www.theguardian.com/science/2019/nov/28/spacewatch-you-wait-ages-for-a-rocket-launch-then-",
# "https://www.theguardian.com/science/2019/dec/26/scientists-attempt-to-recreate-overview-effect-from-earth",
# "https://www.theguardian.com/science/2019/dec/15/exomars-race-against-time-to-launch-troubled-europe-mission-to-mars",
# "https://www.theguardian.com/science/2019/nov/06/cosmic-cats-nuclear-interstellar-messages-extraterrestrial-intelligence",
# "https://www.theguardian.com/science/2019/nov/14/spacewatch-boeing-proposes-direct-flights-moon-2024-nasa",
# "https://www.theguardian.com/science/2019/nov/24/mars-robot-will-send-samples-to-earth",
# "https://www.theguardian.com/science/2019/nov/06/daniel-lobb-obituary",
# "https://www.theguardian.com/science/2019/dec/09/european-space-agency-to-launch-clearspace-1-space-debris-collector-in-2025",
# "https://www.theguardian.com/science/2020/feb/27/biggest-cosmic-explosion-ever-detected-makes-huge-dent-in-space",
# "https://www.theguardian.com/science/2020/feb/06/christina-koch-returns-to-earth-after-record-breaking-space-mission",
# "https://www.theguardian.com/science/2020/jan/01/international-space-station-astronauts-play-with-fire-for-research",
# "https://www.theguardian.com/science/2020/jan/05/space-race-moon-mars-asteroids-commercial-launches",
# "https://www.theguardian.com/science/2019/oct/08/nobel-prizes-have-a-point-parking-space",
# "https://www.theguardian.com/science/2019/oct/31/spacewatch-nasa-tests-new-imaging-technology-in-space",
# "https://www.theguardian.com/science/blog/2020/feb/06/can-we-predict-the-weather-in-space",
# "https://www.theguardian.com/science/2019/sep/08/salyut-1-beat-skylab-in-space-station-race",
# "https://www.theguardian.com/science/2020/feb/13/not-just-a-space-potato-nasa-unveils-astonishing-details-of-most-distant-object-ever-visited-arrokoth",
# ]
# l_texts = {}
# for k, link in enumerate([guardian_urls[0]]):
# print(f"Scraping article number {k+1}, Link: {link}")
# # print(site, link)
# start_time = time()
# r_session = requests.Session()
# retries = Retry(
# total=2,
# backoff_factor=0.1,
# status_forcelist=[500, 502, 503, 504],
# )
# r_session.mount("http://", HTTPAdapter(max_retries=retries))
# try:
# page_response = r_session.get(link, timeout=5)
# except Exception as ex:
# print(f"{ex} Error connecting to {link}")
# else:
# try:
# soup = BeautifulSoup(page_response.content, "lxml")
# # print(soup.prettify())
# except Exception as e:
# print(f"Experienced error {str(e)} when scraping {link}")
# text = np.nan
# else:
# text = get_guardian_text_from_soup(soup)
# scrape_minutes, scrape_seconds = divmod(time() - start_time, 60)
# print(
# f"Scraping time: {int(scrape_minutes):d} minutes, {scrape_seconds:.2f} seconds"
# )
# l_texts[link] = [text]
# df = pd.DataFrame.from_dict(l_texts, orient="index").reset_index()
# df.rename(columns={"index": "url", 0: "text"}, inplace=True)
# display(df)
# # df.to_csv("data/guardian_3.csv", index=False)
# -
# First, we will iterate over a Python dictionary of all the news publications and perform the following actions within each iteration
# 1. Scrape page with `BeautifulSoup` and get soup
# 2. Get text and (optionally) date from soup
# 3. Store extracted contents from soup in a dictionary
# 4. Convert dictionary into single row `DataFrame`
# 5. Rename date column
# 6. Apend publication name as column to `DataFrame`
# 7. Export single-row `DataFrame` to HDF file
# - this would be a single listing's details
# 8. Convert dictionary with all rows into `DataFrame`
# - this would be all listings' details
# 9. Append datetime attributes to full `DataFrame`
# 10. Append full `DataFrame` for publication to a list
# +
cell_st = time()
# Main controller loop for scraping article text from url
l = []
for site, links in urls.items():
(Path(data_dir) / site).mkdir(parents=True, exist_ok=True)
# print(site, links)
l_texts = {}
date_published = np.nan
for k, link in enumerate(links[30000:]):
l_texts_single_listing = {}
print(f"Scraping article number {k+1} from {site}, Link: {link}")
# print(site, link)
start_time = time()
try:
# 1. Get soup
page_response = requests.get(link, timeout=5)
soup = BeautifulSoup(page_response.content, "lxml")
# print(soup.prettify())
# 2. Get text (and optionally date)
if site == "guardian":
text = get_guardian_text_from_soup(soup)
elif site == "hubble":
text = get_hubble_text_from_soup(soup)
elif site == "space":
text, date_published = get_space_text_from_soup(soup, page_response)
elif site == "nytimes":
text, date_published = get_nytimes_text_from_soup(soup)
except Exception as e:
print(f"Experienced error {str(e)} when scraping {link} from {site}")
text = np.nan
scrape_minutes, scrape_seconds = divmod(time() - start_time, 60)
print(
f"Scraping time: {int(scrape_minutes):d} minutes, {scrape_seconds:.2f} seconds"
)
# 3. Store text and date in dictionary
l_texts[link] = [text, date_published]
l_texts_single_listing[link] = [text, date_published]
# 4. Convert dictionary of text and date, for single listing, to DataFrame
df_row = pd.DataFrame.from_dict(
l_texts_single_listing, orient="index"
).reset_index()
# 5. Rename publication date column of DataFrame
df_row.rename(
columns={"index": "url", 0: "text", 1: "publication_date"}, inplace=True
)
# 6. Append publication name as column to DataFrame
df_row["publication"] = site
# print(Path(data_dir) / site / f"scrapes_{site}_{k+1}.h5")
# 7. Store DataFrame in HDF file
df_row.to_hdf(
Path(data_dir) / site / f"scrapes_{site}_{k+1}.h5",
key=f"{site}_{k+1}",
format="t",
mode="w",
)
# print(text)
# Delay between scraping urls
delay_between_scrapes = randint(
min_delay_between_scraped, max_delay_between_scraped
)
if (k + 1) < len(links[30000:]):
print(f"Pausing for {delay_between_scrapes} seconds\n")
sleep(delay_between_scrapes)
# 8. Convert dictionary of text and date, for all listings, to DataFrame
df = pd.DataFrame.from_dict(l_texts, orient="index").reset_index()
df.rename(columns={"index": "url", 0: "text", 1: "publication_date"}, inplace=True)
df["publication"] = site
# display(df)
# 9. (Optional) Append datetime attributes for space.com and nytimes publications
if site in ["space", "nytimes"]:
df = append_datetime_attrs(df, date_col="publication_date", publication=site)
else:
for L in [
"year",
"month",
"day",
"dayofweek",
"dayofyear",
"weekofyear",
"quarter",
]:
df[L] = np.nan
# 10. Append DataFrame to list
l.append(df)
total_minutes, total_seconds = divmod(time() - cell_st, 60)
print(
f"Cell exection time: {int(total_minutes):d} minutes, {total_seconds:.2f} seconds"
)
# +
# # ========= LOAD SUBSET (NOT ALL) OF HDF5 FILES (DO NOT DELETE) =========
# pd.concat(
# [
# pd.read_hdf(Path(data_dir) / site / f"scrapes_{site}_{k+1}.h5", key=f"{site}_{k+1}")
# for site, links in urls.items()
# for k, link in enumerate(links[0:10])
# ],
# axis=0,
# ignore_index=True,
# )
# -
# Finally, we'll concatenate the list of `DataFrame`s of scraped text data into a single `DataFrame` and export it to a separate `*.csv` file per publication
dfs = pd.concat(l, axis=0, ignore_index=True).drop_duplicates()
if site == "space":
dfs = dfs[~pd.isnull(dfs["text"])]
display(dfs)
print(dfs.shape)
dfs.to_csv(Path(data_dir) / f"{site}.csv", index=False)
| 15,649 |
/Source Code and Outputs/deprecated_old/mixup/mixup MNIST NN augmentation 0.75_weighted_perturb_loss.ipynb
|
e0dec2dbd6751effe91f9385f8e749813af739b6
|
[] |
no_license
|
DHKLeung/UCL_MSc_CSML_Dissertation
|
https://github.com/DHKLeung/UCL_MSc_CSML_Dissertation
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 14,567 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import torch
from torchvision import transforms, datasets, models
# +
"""
Configuration and Hyperparameters
"""
torch.set_default_tensor_type(torch.cuda.FloatTensor) # default all in GPU
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
batch_size = 128
step_size = 0.01
random_seed = 0
epochs = 100
L2_decay = 1e-4
alpha = 1.
perturb_loss_weight = 0.75
torch.manual_seed(random_seed)
# -
"""
Data
"""
train_set = datasets.MNIST('./data', train=True, download=True, transform=transform)
train_loader = torch.utils.data.DataLoader(train_set, batch_size=batch_size, shuffle=True, num_workers=8)
test_set = datasets.MNIST('./data', train=False, download=True, transform=transform)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size, shuffle=False, num_workers=8)
model = models.resnet18(pretrained=True)
for param in model.parameters():
param.requires_grad = True
model.conv1 = torch.nn.Conv2d(1, 64, 7, stride=2, padding=3, bias=False)
model.fc = torch.nn.Linear(512, 10)
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=step_size, momentum=0.9, weight_decay=L2_decay)
def mixup_MNIST(inputs, labels, alpha):
lmbda = torch.distributions.beta.Beta(alpha, alpha).sample()
batch_size = labels.size(0)
idx = torch.randperm(batch_size)
mixup_inputs = lmbda * inputs + (1 - lmbda) * inputs[idx]
labels_b = labels[idx]
return mixup_inputs, labels, labels_b, lmbda
def mixup_criterion(criterion, predicts, labels, labels_b, lmbda):
mixup_loss = lmbda * criterion(predicts, labels) + (1 - lmbda) * criterion(predicts, labels_b)
return mixup_loss
"""
Training
"""
model.train()
for epoch in range(epochs):
epoch_loss = 0.
epoch_mixup_loss = 0.
epoch_org_loss = 0.
for i, data in enumerate(train_loader, 0):
inputs, labels = data
inputs = inputs.to('cuda')
labels = labels.to('cuda')
mixup_inputs, labels, labels_b, lmbda = mixup_MNIST(inputs, labels, alpha)
optimizer.zero_grad()
outputs = model(mixup_inputs)
mixup_loss = mixup_criterion(criterion, outputs, labels, labels_b, lmbda)
##
outputs_org = model(inputs)
loss_org = criterion(outputs_org, labels)
weighted_total_loss = mixup_loss * perturb_loss_weight + loss_org * (1 - perturb_loss_weight)
epoch_mixup_loss += mixup_loss.item()
epoch_org_loss += loss_org.item()
epoch_loss += (mixup_loss.item() + loss_org.item())
weighted_total_loss.backward()
##
optimizer.step()
print('{}: {} {} {}'.format(epoch, epoch_mixup_loss, epoch_org_loss, epoch_loss))
torch.save(model.state_dict(), './mixup_model_pytorch_mnist_augment')
model = models.resnet18(pretrained=False)
model.conv1 = torch.nn.Conv2d(1, 64, 7, stride=2, padding=3, bias=False)
model.fc = torch.nn.Linear(512, 10)
model.load_state_dict(torch.load('./mixup_model_pytorch_mnist_augment'))
model.eval()
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
inputs, labels = data
inputs = inputs.to('cuda')
labels = labels.to('cuda')
outputs = model(inputs)
_, predicts = torch.max(outputs, 1)
total += labels.size(0)
correct += (predicts == labels).sum().item()
print(correct / total)
model.eval()
correct = 0
total = 0
with torch.no_grad():
for data in train_loader:
inputs, labels = data
inputs = inputs.to('cuda')
labels = labels.to('cuda')
outputs = model(inputs)
_, predicts = torch.max(outputs, 1)
total += labels.size(0)
correct += (predicts == labels).sum().item()
print(correct / total)
| 4,077 |
/2.Math/4. EDA/raw_LiveCoding.ipynb
|
33ec8885feb2f34ffda08c662196fda229436b1d
|
[] |
no_license
|
samil-web/AI
|
https://github.com/samil-web/AI
| 3 | 0 | null | 2021-09-10T07:58:35 | 2021-09-10T07:22:39 |
Jupyter Notebook
|
Jupyter Notebook
| false | false |
.py
| 182,805 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# https://github.com/Swetha14/LTFS---Loan-Default-Challenge/blob/master/train_sample.zip
df = pd.read_csv("data/train_sample.csv")
df.head(10)
df.tail(10)
df1 = pd.read_csv("data/train_sample.csv", index_col=0)
df1
df.dtypes
type(df["Date.of.Birth"][0])
df["Employment.Type"][0]
df["Employment.Type"].unique()
df["loan_default"].unique()
# 1 is bad
#
# 0 is good
df["loan_default"].value_counts()
df["ltv"].hist(bins=25)
df["ltv"].head(10)
df["ltv"].head(100000).hist(bins=10)
df.asset_cost[df["asset_cost"]<0.9*100000].hist(bins=200)
df["asset_cost"].hist(bins=200)
df.asset_cost[df.asset_cost > 0.20*1000000]
df.boxplot(column="asset_cost")
df.boxplot(column="ltv")
df.boxplot(column="asset_cost", by="Employment.Type")
df["Date.of.Birth"]
# +
from datetime import datetime
dateparse = lambda x: datetime.strptime(x, '%Y(-|/)%m(-|/)%d %H:%M:%S')
df2 = pd.read_csv("data/train_sample.csv", parse_dates=['Date.of.Birth'], date_parser=try_parsing_date)
# -
def try_parsing_date(text):
for fmt in ('%d-%m-%y', '%d.%m.%Y', '%d/%m/%Y'):
try:
return datetime.strptime(text, fmt)
except ValueError:
pass
print(text)
raise ValueError('no valid date format found')
str(datetime.strptime("12-12-12", '%d-%m-%y')).split("-")[0]
df2["Date.of.Birth"]
df2["year_of_birth"] = df2["Date.of.Birth"].apply(lambda x: int(str(x).split("-")[0]))
df2["year_of_birth"]
df2[df2.year_of_birth < 1960].boxplot(column="asset_cost", by="year_of_birth")
import seaborn as sns
sns.boxplot(x=df2[df2.year_of_birth == 1960]["asset_cost"])
plt.scatter(df2.year_of_birth, df2.loan_default)
a = df2[df2.year_of_birth<1960].groupby("year_of_birth")["loan_default"].value_counts()
a.plot.bar(stacked=True)
data = pd.DataFrame(a)
data
data.unstack().plot(kind='bar', stacked=True)
| 2,178 |
/Baby_Names_Births_exercise/.ipynb_checkpoints/Birth_example_1_TEST-checkpoint.ipynb
|
8c5f9158d4d83da90af91730403b7404efd2abca
|
[
"MIT"
] |
permissive
|
FelipeChiriboga/Data_Science_Portfolio
|
https://github.com/FelipeChiriboga/Data_Science_Portfolio
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 32,605 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
# %matplotlib inline
# +
#df = names_2000
names_2000 = pd.read_csv('names/yob2000.txt', names=['name','gender', 'count'])
#names_2000.set_index('name', inplace=True)
# -
df.head()
names_2000.head(10)
# +
names_2000[names_2000['count'] > 1000].head()
# -
one_two = names_2000[names_2000['count'].between(1000, 2000)]
one_two.shape
freq_boys = names_2000[(names_2000['count'] > 1000) & (names_2000['gender'] == 1000)]
freq_boys.shape
b = names_2000['gender'] != 'F'
b.head()
def initial(s):
returns[0]
print(initial)
my_functions = [initial, pd.DataFrame, print, zip]
# +
def get_initial(s):
return s[0]
names_2000['initial'] = names_2000['name'].apply(get_initial)
names_2000.head()
# -
# %matplotlib inline
names_2000.groupby('initial') ['count'].sum().plot.bar()
ini = names_2000.groupby(['gender', 'initial'])['count'].sum()
topchars = ini.sort_values(ascending=False).head(10)
topchars.plot.bar()
# +
import pandas as pd
birthnames = []
a = 1880
while a <= 2017:
fl = str("names/yob" + str(a) + ".txt")
bth = pd.read_csv(fl, names=['names', 'sex','birthcnt']) #probably need to add the name column
bth['year'] = a
birthnames.append(bth)
a = a + 1
birthnames = pd.concat(birthnames)
birthnames
# +
#Goal 3
# easy: create a bar plot with 5 names in one year.
# Medium: plot a time series with one name over all years
# hard: plot the number of distinct boy/girl names over time
| 1,729 |
/notebooks/Tutorial: YOLO/Convolutional Neural Networks.ipynb
|
4ddb6b3a31181fc847e6ba27c925020e2f988575
|
[
"Apache-2.0"
] |
permissive
|
gabrielnieves18/tensorflow-tutorials
|
https://github.com/gabrielnieves18/tensorflow-tutorials
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 15,799 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5" _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19"
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
meta_data = pd.read_csv('../input/training_set_metadata.csv')
test_meta_data = pd.read_csv('../input/test_set_metadata.csv')
# + _uuid="2eec377e2ae127bb44b7d0f98bf169f372b897fb"
classes = np.unique(meta_data['target'])
classes_all = np.hstack([classes, [99]])
# create a dictionary {class : index} to map class number with the index
# (index will be used for submission columns like 0, 1, 2 ... 14)
target_map = {j:i for i, j in enumerate(classes_all)}
# create 'target_id' column to map with 'target' classes
target_ids = [target_map[i] for i in meta_data['target']]
meta_data['target_id'] = target_ids
meta_data.head()
#meta_data['hostgal_specz']
# + _uuid="eeb61301f53a373a6114389d785f00027ae5f523"
# Build probability arrays for both the galactic and extragalactic groups
galactic_cut = meta_data['hostgal_specz'] == 0
galactic_data = meta_data[galactic_cut]
extragalactic_data = meta_data[~galactic_cut]
galactic_classes = np.unique(galactic_data['target_id'])
extragalactic_classes = np.unique(extragalactic_data['target_id'])
# add class_99 (index = 14)
galactic_classes = np.append(galactic_classes, 14)
extragalactic_classes = np.append(extragalactic_classes, 14)
# + [markdown] _uuid="49507175719b5752150907f36e4da3165ed90efe"
# ***
# # EDA
# + _uuid="8684abbef947f6f5b080152464ef3a6811ea9275"
plt.figure(figsize=(20,20))
plt.subplot(221)
plt.scatter(meta_data[~galactic_cut]['hostgal_specz'], meta_data[~galactic_cut]['target'])
plt.xlabel('hostgal_specz')
plt.ylabel('classes')
plt.yticks(classes_all)
plt.subplot(222)
plt.scatter(meta_data['hostgal_specz'], meta_data['target'])
plt.xlabel('hostgal_specz')
plt.ylabel('classes')
plt.yticks(classes_all)
plt.show()
# + _uuid="8684abbef947f6f5b080152464ef3a6811ea9275"
plt.figure(figsize=(20,20))
plt.subplot(221)
plt.scatter(meta_data[~galactic_cut]['hostgal_photoz'], meta_data[~galactic_cut]['target'])
plt.xlabel('hostgal_photoz')
plt.ylabel('classes')
plt.yticks(classes_all)
plt.subplot(222)
plt.scatter(meta_data['hostgal_photoz'], meta_data['target'])
plt.xlabel('hostgal_photoz')
plt.ylabel('classes')
plt.yticks(classes_all)
plt.show()
# + _uuid="8684abbef947f6f5b080152464ef3a6811ea9275"
plt.figure(figsize=(20,20))
plt.subplot(221)
plt.scatter(meta_data[~galactic_cut]['distmod'], meta_data[~galactic_cut]['target'])
plt.xlabel('distmod')
plt.ylabel('classes')
plt.yticks(classes_all)
plt.subplot(222)
plt.scatter(meta_data['distmod'], meta_data['target'])
plt.xlabel('distmod')
plt.ylabel('classes')
plt.yticks(classes_all)
plt.show()
# + _uuid="8684abbef947f6f5b080152464ef3a6811ea9275"
plt.figure(figsize=(20,20))
plt.subplot(221)
plt.scatter(meta_data[~galactic_cut]['mwebv'], meta_data[~galactic_cut]['target'])
plt.xlabel('mwebv')
plt.ylabel('classes')
plt.yticks(classes_all)
plt.subplot(222)
plt.scatter(meta_data['mwebv'], meta_data['target'])
plt.xlabel('mwebv')
plt.ylabel('classes')
plt.yticks(classes_all)
plt.show()
# + _uuid="0b4060b5605213dd9c156fa01f656fad77ba9505"
#color = meta_data[meta_data['hostgal_photoz_err'] > 0.35]
meta_data['photoz_big_err'] = 0
meta_data.loc[meta_data['hostgal_photoz_err'] > 0.35, 'photoz_big_err'] = 1
# + _uuid="60075eba967d045bec9450da52cc0ef2ffdfc3a2"
meta_data.describe()
# + _uuid="f7f16964eecb85fb1d3c7122a0213fcc1fb27987"
plt.figure(figsize=(20,20))
color = meta_data['photoz_big_err']
color = meta_data['photoz_big_err']
plt.subplot(221)
plt.scatter(meta_data['hostgal_specz'], meta_data['hostgal_photoz'], c = color)
plt.xlabel('hostgal_specz')
plt.ylabel('hostgal_photoz')
plt.subplot(222)
plt.scatter(meta_data['hostgal_specz'], meta_data['hostgal_photoz_err'], c = color)
plt.xlabel('hostgal_specz')
plt.ylabel('hostgal_photoz_err')
plt.yticks(np.arange(0,2,0.1))
plt.subplot(223)
plt.scatter(meta_data['hostgal_photoz'], meta_data['hostgal_photoz_err'], c = color)
plt.xlabel('hostgal_photoz')
plt.ylabel('hostgal_photoz_err')
# + _uuid="5f66457490e2893dd58d0288f2646d1c1ad7a06c"
#test_meta_data[test_meta_data['hostgal_specz'].isnull()]
# + _uuid="919c17b35dd11b0970a4c4cb78ce4ee429b64e6f"
plt.figure(figsize=(15,15))
plt.subplot(221)
plt.scatter(meta_data['hostgal_photoz'], meta_data['target'])
plt.xlabel('hostgal_photoz')
plt.ylabel('classes')
plt.yticks(classes_all)
plt.subplot(222)
plt.scatter(meta_data[meta_data['photoz_big_err'] == 0]['hostgal_photoz'], meta_data[meta_data['photoz_big_err'] == 0]['target'])
plt.xlabel('hostgal_photoz')
plt.ylabel('classes')
plt.yticks(classes_all)
plt.xticks(np.arange(0,3,0.1))
plt.show()
# + [markdown] _uuid="95cb963b4de429b9e00cd760834b5bd14cac0d80"
# first: (hostgal_specz >= 1.1) => class 88, 95, 99 (10, 13, 14)
#
# second: (hostgal_photoz >= 1.1 & photoz_big_err = 0) => class 88, 95, 99 (10, 13, 14)
#
# third: other even probabilities counted on the previous rounds
#
#
# + [markdown] _uuid="8c0fd28998e6129404bdc622a1535755d7da5ab2"
# ***
# + [markdown] _uuid="9230565e6601845f490801f3a96d1705186bf891"
# # Weights
#
# Weights are based on this discussion: https://www.kaggle.com/c/PLAsTiCC-2018/discussion/67194 , but, apparently, we have different weights for Galactic and Extragalactic groups for the class_99!
#
# It is also good to check this kernel for more precise calculation of weights: https://www.kaggle.com/ganfear/calculate-exact-class-weights
# + _uuid="c464a70b9c725867d0dbc70b8fb2b3d2ac96f85d"
# Weighted probabilities for Milky Way galaxy
galactic_probabilities = np.zeros(15)
for x in galactic_classes:
if(x == 14):
galactic_probabilities[x] = 0.014845745
continue
if(x == 5):
galactic_probabilities[x] = 0.196867058
continue
galactic_probabilities[x] = 0.197071799
# + _uuid="371292863929044eff3ae3602b710b9341a0312b"
# Weighted probabilities for Extra Galaxies
extragalactic_probabilities = np.zeros(15)
for x in extragalactic_classes:
if(x == 14):
extragalactic_probabilities[x] = 0.147286644
continue
if(x == 7):
extragalactic_probabilities[x] = 0.15579259
continue
if(x == 1):
extragalactic_probabilities[x] = 0.155388186
continue
if(x == 10 or x == 13):
extragalactic_probabilities[x] = 0.076512622
continue
extragalactic_probabilities[x] = 0.077701467
# + _uuid="7bf98a4fbd2fc24bcd92ff952bf48ab9ba8d06ed"
# Weighted probabilities for Remote Classes
bigz_probabilities = np.zeros(15)
for x in extragalactic_classes:
if(x == 14):
bigz_probabilities[x] = 0.398923589
continue
if(x == 10 or x == 13):
bigz_probabilities[x] = 0.207233249
continue
if(x == 7):
extragalactic_probabilities[x] = 0.041550573
continue
if(x == 1):
extragalactic_probabilities[x] = 0.041442716
continue
bigz_probabilities[x] = 0.020723325
#p = (1 - (5*0.077340579/2 + 0.154666479/2 + 0.155069005/2 + 0.148880461/2))/2
#p = 0.28867029
# + [markdown] _uuid="80a693faa4fa1bba7b05fb774dac4252b38ae4d1"
# ***
# + _uuid="aa9b04c735c6a13bcb48511747b66780a78abe68"
#test_meta_data['object_id'].count()
#test_meta_data[test_meta_data['hostgal_specz'] >= 1.1]['object_id'].count()
#( np.isnan(row['hostgal_specz']) ) and (row['hostgal_photoz'] >= 1.2 and row['hostgal_photoz_err'] <= 0.3
#test_meta_data[(test_meta_data['hostgal_photoz'] >= 1.1) & (test_meta_data['hostgal_photoz_err'] <= 0.35)]['object_id'].count()
#x = 84239 / 3492890 * 0.7037
#x = int(x)
#y = 1 - x
#print(x, y)
#type(x)
# + _uuid="04fa08c03cf8bb61d4811c316200b95c1d90df18"
# Apply this prediction to test_meta_data table
import tqdm
def do_prediction(table):
probs = []
for index, row in tqdm.tqdm(table.iterrows(), total=len(table)):
if ( row['hostgal_specz'] >= 1.2 ):
prob = bigz_probabilities
elif ( ( np.isnan(row['hostgal_specz']) ) and (row['hostgal_photoz'] >= 1.2 and row['hostgal_photoz_err'] <= 0.3) ):
prob = bigz_probabilities
elif ( row['hostgal_photoz'] == 0 ):
prob = galactic_probabilities
else:
prob = extragalactic_probabilities
probs.append(prob)
return np.array(probs)
test_pred = do_prediction(test_meta_data)
# + _uuid="554ef771214b68cd54053d3d7c5a1557f8e45d54"
test_df = pd.DataFrame(index=test_meta_data['object_id'], data=test_pred, columns=['class_%d' % i for i in classes_all])
test_df.to_csv('./submission_eda.csv')
x_batch, y_true_batch, _, cls_batch = data.train.next_batch(batch_size)
x_valid_batch, y_valid_batch, _, valid_cls_batch = data.valid.next_batch(batch_size)
feed_dict_tr = {
x: x_batch,
y_true: y_true_batch
}
feed_dict_val = {
x: x_valid_batch,
y_true: y_valid_batch
}
session.run(optimizer, feed_dict=feed_dict_tr)
if i % int(data.train.num_examples/batch_size) == 0:
val_loss = session.run(cost, feed_dict=feed_dict_val)
epoch = int(i / int(data.train.num_examples/batch_size))
loss.append(val_loss)
epochs.append(epoch)
accuracy_array.append(session.run(accuracy, feed_dict=feed_dict_tr))
loss_map = {
'loss': loss,
'epochs': epochs,
'accu': accuracy_array
}
# if (epoch > 0) and (epoch % 5) == 0:
# pd_loss = pd.DataFrame(loss_map)
# pd_loss.plot(x="accu", y="loss", kind='line')
# plt.show()
show_progress(epoch,
feed_dict_tr,
feed_dict_val,
val_loss,
session)
saver.save(session, './dogs-cats-model')
total_iterations += num_iteration
# -
| 10,536 |
/preprocessing/.ipynb_checkpoints/prepro_1117-checkpoint.ipynb
|
13967b5842a5e8c00bbe57aab006ffe93c32f903
|
[] |
no_license
|
wttttt-wang/kaggle_housePrices
|
https://github.com/wttttt-wang/kaggle_housePrices
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 60,924 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# PART ONE: Data Reading
import pandas as pd
import numpy as np
from scipy.stats import skew
import matplotlib.pyplot as plt
# %matplotlib inline
def read_data():
#step1:reading csv data
train = pd.read_csv('../input/train.csv')
test = pd.read_csv('../input/test.csv')
#train.head() # take a brief look at training data
all_data = pd.concat((train.loc[:,'MSSubClass':'SaleCondition'],
test.loc[:,'MSSubClass':'SaleCondition'])) # concat training&test data
return train,test,all_data
# +
# PART TWO: Filling missing value
from scipy.stats import mode
# for numeric features, filling with mean(), for categorial features, filling with mode()[most common]
def mean_fill(df,attr):
if df[attr].dtype == 'object':
df[attr].fillna(mode(df[attr]).mode[0],inplace=True)
else:
df[attr].fillna(df[attr].mean(),inplace=True)
# #test for categorial feature
# mean_fill(all_data,'GarageCond')
from sklearn.ensemble import RandomForestRegressor
def randomforest_fill(df,attr):
# get all the numeric features to predict the missing value, because
# that sklearn's random forest algo can only handle numeric features.
# It could be better to transform the categorial features before calling this method
numeric_df = all_data.loc[:,all_data.isnull().any().values==False].select_dtypes(include = ['float64','int64'])
numeric_df[attr]=df[attr]
numeric_df_notnull = numeric_df.loc[(df[attr].notnull())]
numeric_df_isnull = numeric_df.loc[(df[attr].isnull())]
X = numeric_df_notnull.drop(attr,axis=1)
Y = numeric_df_notnull[attr]
# use RandomForest to train data
clf = RandomForestRegressor(n_estimators = 1000, n_jobs = -1) # n_jobs:The number of jobs to run in parallel for both fit and predict. If -1, then the number of jobs is set to the number of cores
clf.fit(X,Y)
predicted_attr = clf.predict(numeric_df_isnull.drop(attr,axis=1))
df.loc[(df[attr].isnull()),attr] = predicted_attr
#randomforest_fill(all_data,'MasVnrArea')
## before filling the missing value
#all_data.loc[234]['MasVnrArea']
''' # output
234 NaN
234 0.0
Name: MasVnrArea, dtype: float64
'''
## after filling the missing value
#all_data.loc[234]['MasVnrArea']
''' # output
234 82.882
234 0.000
Name: MasVnrArea, dtype: float64
'''
# treat the missing value as a different value
def ano_value_for_miss(df,attr):
df[attr].fillna('No_value',inplace=True)
## test
# ano_value_for_miss(all_data, 'Alley')
# +
# PART THREE: Data Tranformation
# data normalization for numeric feature
# whether to use this method depends on the model used
# if distance based model is used, then u need to call this
# It seems that the popular model Xgbost doesnt need normalization
def normalization(df,attr):
# filled when used
pass
# get dummies for one categorial feature
def dummy_one(df,attr):
h_dummies = pd.get_dummies(df[attr],prefix=attr)
df.drop([attr],axis=1,inplace=True)
df = df.join(h_dummies)
return df
# all_data = dummy_one(all_data, 'Alley')
# get dummies for all categorial features in df
def dummy_all(df):
df = pd.get_dummies(df)
return df
#all_data = dummy_all(all_data)
#all_data.info(verbose=True,max_cols=1000)
from scipy.stats import skew
# Attetion here: for log transform to make features more normally distributed and
# this makes linear regression preform better, since linear regression is sensitive to outliers.
# But!! ! note that if a tree-based model is used, then this log transform is not necessary.
# In a word, many preprecessing steps must be contacted to ur model used.
# the predict object or features could be skewed, we can do log tansform for those variables
# do log transform for one feature/target
# threshold: determine whether to do log transform on this feature/target
def log_skewed_one(df, attr, threshold):
# calculate the skewness
skewness = skew(df[attr].dropna())
if skewness > threshold:
df[attr] = np.log1p(df[attr])
#log_skewed_one(train, 'SalePrice', 0.75)
#train['SalePrice'].hist()
def log_skewed_all(df,threshold):
# get index of all numeric features
numeric_feats = df.dtypes[df.dtypes != 'object'].index
# then compute the skewness for each features
skewed_feats = df[numeric_feats].apply(lambda x: skew(x.dropna()))
# get the features whose skeness>0.75
skewed_feats = skewed_feats[skewed_feats>threshold]
skewed_feats = skewed_feats.index
df[skewed_feats] = np.log1p(df[skewed_feats])
#log_skewed_all(train,0.75)
#train['SalePrice'].hist()
# +
# PART FOUR: Feature Decomposition
from sklearn.decomposition import PCA
# Note that the input df must not have categorial features or missing value,
# do this after preprocessing fo filling missing value and feature transformation
def pca_reduc(df, num_fea_toleave='mle'):
# @return type: pd.DataFrame
pca = PCA(n_components=num_fea_toleave)
after_pca = pca.fit_transform(df)
print 'Percentage of variance explained by each of the selected components:'
print(pca.explained_variance_ratio_)
#print pd.DataFrame(new).info()
return pd.DataFrame(after_pca)
#all_data = dummy_all(all_data)
#all_data.fillna(all_data.mean(),inplace=True)
#all_data = pca_reduc(all_data,30)
#all_data.info(verbose=True, max_cols=1000)
from sklearn.decomposition import KernelPCA
# Kernel PCA ==> non-linear dimensionality reduction through the use of kernels
# Somewhat like kernel in SVM
# kernel = “linear” | “poly” | “rbf” | “sigmoid” | “cosine” | “precomputed”
def kernelpca_reduc(df, kernel='linear',num_fea_toleave=50):
kpca = KernelPCA(n_components=num_fea_toleave,kernel = kernel,n_jobs=-1)
after_kpca = kpca.fit_transform(df)
print 'the selected features Eigenvalues in decreasing order:'
print (kpca.lambdas_)
return pd.DataFrame(after_kpca)
#all_data = dummy_all(all_data)
#all_data.fillna(all_data.mean(),inplace=True)
#all_data = kernelpca_reduc(all_data,kernel='rbf',num_fea_toleave=50)
#print all_data.shape
from sklearn.decomposition import TruncatedSVD
# Dimensionality reduction using truncated SVD
def truncatedSVD_reduc(df,num_fea_toleave=50):
# provide a random_state to get stable output
svd = TruncatedSVD(n_components=num_fea_toleave, n_iter=7, random_state=42)
after_trans = svd.fit_transform(df)
print 'Percentage of variance explained by each of the selected components:'
print(svd.explained_variance_ratio_)
return pd.DataFrame(after_trans)
#all_data = dummy_all(all_data)
#all_data.fillna(all_data.mean(),inplace=True)
#all_data = truncatedSVD_reduc(all_data,num_fea_toleave=50)
#print all_data.shape
# +
# PART FIVE: Feature Selection
from sklearn.feature_selection import RFECV
# RFECV: Feature ranking with recursive feature elimination and cross-validated selection of the best number of features.
def fea_sel_rfecv(train_x,train_y,test_x,estimator):
rfecv = RFECV(estimator=estimator,scoring='neg_mean_squared_error',n_jobs=-1)
after_d = rfecv.fit_transform(train_x,train_y)
print("Optimal number of features : %d" % rfecv.n_features_)
# Plot number of features VS. cross-validation scores
plt.figure()
plt.xlabel("Number of features selected")
plt.ylabel("Cross validation score(neg_mean_squared_error)")
plt.plot(range(1, len(rfecv.grid_scores_) + 1), rfecv.grid_scores_)
return pd.DataFrame(after_d),pd.DataFrame(rfecv.transform(test_x))
#alldata_nomissing = pd.read_csv('../input/alldata_after_filling_missing.csv')
#from sklearn import svm
#clf = svm.LinearSVR()
#after_d,after_d_test = (fea_sel_rfecv(alldata_nomissing.iloc[:1460],train['SalePrice'],alldata_nomissing.iloc[1460:],clf))
#print after_d.shape
#print after_d_test.shape
from sklearn.feature_selection import SelectFromModel
# u can see from 'SelectFromModel' that this method use model result to select features, 'Wrapper'
# estimator: a supervised model with fit() method
def fea_sel_tree(train_x,train_y,estimator):
estimator = estimator.fit(train_x,train_x)
print 'feature importances in this model',
print sorted(estimator.feature_importances_,reverse=True)
model = SelectFromModel(estimator,prefit = True)
after_sel = model.transform(train_x)
return pd.DataFrame(after_sel)
#train = dummy_all(train)
#train.fillna(train.mean(),inplace=True)
#from sklearn.ensemble import RandomForestRegressor
#clf = RandomForestRegressor(random_state=0,n_estimators=50)
#print fea_sel_tree(train.iloc[:,1:-1],train['SalePrice'],clf).shape
# -
train,test,all_data = read_data()
print all_data.info()
def missing_data_fill():
train,test,all_data = read_data()
# step1:
# for features that having many missing values(more than half): ano_value_for_missing value
# ir for the features whose NA has special meaning, like BsmtQual
# dummy_na = True means 'Add a column to indicate NaNs'
all_data = pd.get_dummies(all_data,dummy_na=True,columns=['Alley','FireplaceQu','PoolQC','Fence',
'MiscFeature','BsmtQual','GarageFinish'])
# filling missing value with mean()/ mode
for attr in ['MSZoning','LotFrontage','Utilities','BsmtFinSF2','BsmtHalfBath',
'BsmtUnfSF','TotalBsmtSF','Electrical','BsmtFullBath','Functional','GarageType',
'GarageQual','GarageCond','SaleType','Exterior1st','Exterior2nd','MasVnrType','KitchenQual']:
mean_fill(all_data,attr)
# step2:
# along with filling missing values, we do data transformation
all_data = pd.get_dummies(all_data)
# for important feature: randomforest_fill
# could be better to do this after dummies all the object features
for attr in ['MasVnrArea','BsmtFinSF1','GarageYrBlt','GarageCars','GarageArea']:
randomforest_fill(all_data,attr)
all_data.to_csv('../input/alldata_after_filling_missing.csv',index=False)
#all_data.info(verbose=True,max_cols=1000)
## show the columns that containing null value
#all_data.loc[:,all_data.isnull().any().values==True]
## show the columns whose type is 'object'
#all_data.loc[:,all_data.dtypes=='object']
# +
# step3:
# we use feature selection to exclude some very unimportant features firstly.
alldata_nomissing = pd.read_csv('../input/alldata_after_filling_missing.csv')
#print alldata_nomissing.info(verbose=True,max_cols=1000)
from sklearn import svm
clf = svm.LinearSVR()
after_d,after_d_test = (fea_sel_rfecv(alldata_nomissing.iloc[:1460],train['SalePrice'],alldata_nomissing.iloc[1460:],clf))
print after_d.shape
print after_d_test.shape
# -
# lets skip feature transformation first, just fit the model directly.
# xgboost
import xgboost as xgb
#dtrain = xgb.DMatrix(after_d,label=train['SalePrice'])
model_xgb = xgb.XGBRegressor(n_estimators=360, max_depth=2, learning_rate=0.1)
model_xgb.fit(alldata_nomissing.iloc[:1460],train['SalePrice'])
pre_val = pd.DataFrame(model_xgb.predict(alldata_nomissing.iloc[1460:]))
test_label = pd.read_csv('../input/test_id',header=None)
result = pd.DataFrame()
result['Id'] = test_label[0]
result['SalePrice'] = pre_val[0]
result.to_csv('../input/result_xgb_1119_nofeaselec.csv',index=False)
# + active=""
#
# -
from sklearn.pipeline import Pipeline
import xgboost as xgb
from sklearn.decomposition import PCA
from sklearn.decomposition import PCA, NMF
from sklearn.feature_selection import SelectKBest, chi2
from sklearn.model_selection import GridSearchCV
# the key in the dict of Pipeline is the name u want give to the step
pipe = Pipeline([
('reduce_dim',PCA()),
('regression',xgb.XGBRegressor())
])
# optional for feature nums
N_FEATURES_OPTIONS = [i for i in range(30,250,10)]
N_ESTIMATOR_OPTIONS = [i for i in range(300,500,20)]
param_grid=[
{
'reduce_dim': [PCA(iterated_power=7), NMF()],
'reduce_dim__n_components': N_FEATURES_OPTIONS,
'regression__n_estimators': N_ESTIMATOR_OPTIONS
},
{
'reduce_dim': [SelectKBest(chi2)],
'reduce_dim__k': N_FEATURES_OPTIONS,
'regression_n_estimators': N_ESTIMATOR_OPTIONS
}
]
grid = GridSearchCV(pipe, cv=3, n_jobs=-1, param_grid=param_grid)
grid.fit(alldata_nomissing.iloc[:1460],train['SalePrice'])
mean_scores = np.array(grid.cv_results_['mean_test_score'])
# +
# actually, we can do some operations on features, and get more features to select.
# Its shown that results from features may also work.
# for example, alpha = num_buy/num_click do means something in shopping website's analysis.
# +
# dummies之后删除所有值都相同的列 #实际上所有dummies的feature中全为0的column都不存在
| 12,877 |
/train_v1.ipynb
|
bc094210527a7be3397934e635255cbce04b0b09
|
[
"MIT"
] |
permissive
|
abekoh/splatoon_game_winner
|
https://github.com/abekoh/splatoon_game_winner
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 29,075 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] _cell_guid="56fbfcbd-7cee-4054-9142-48ecc8f689c3" _uuid="78d4e02d62194c4b78f419ac6b332e02fd1bf6a7"
# # Predicting sales with a nested KerasRegressor
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
import os
print(os.listdir("../input"))
# Any results you write to the current directory are saved as output.
# + [markdown] _cell_guid="97ff7f5e-de74-4a7c-b034-bcf1432480f2" _uuid="2dd003abe546efb14933e446b6854697ac10dfca"
# ## Create training and test sets
# + _cell_guid="deb3ac11-c600-48dc-b9d7-2b31d802caab" _uuid="6ed50a5c0665dc88ac7a6d0c8f4f9c57187fd2e6"
# First we create a dataframe with the raw sales data, which we'll reformat later
DATA = '../input/'
sales = pd.read_csv(DATA+'sales_train.csv', parse_dates=['date'], infer_datetime_format=True, dayfirst=True)
sales.head()
# + _cell_guid="e64d8618-78fd-41cf-8361-c12f35ee75db" _uuid="9069d629e7479bdae511d9f7303762b8fa85a2c1"
# Let's also get the test data
test = pd.read_csv(DATA+'test.csv')
test.head()
# + _cell_guid="d55fc349-4a95-4d4a-8aaf-827d57bce777" _uuid="6b3e74f88c77bf2e0eb76f00482fce1cf70b3b64"
# Now we convert the raw sales data to monthly sales, broken out by item & shop
# This placeholder dataframe will be used later to create the actual training set
df = sales.groupby([sales.date.apply(lambda x: x.strftime('%Y-%m')),'item_id','shop_id']).sum().reset_index()
df = df[['date','item_id','shop_id','item_cnt_day']]
df = df.pivot_table(index=['item_id','shop_id'], columns='date',values='item_cnt_day',fill_value=0).reset_index()
df.head()
# + _cell_guid="910d25e3-8401-4815-8248-043d44139e13" _uuid="8983b18b147317811bd7d1ceeec0b1502caab8ce"
# Merge the monthly sales data to the test data
# This placeholder dataframe now looks similar in format to our training data
df_test = pd.merge(test, df, on=['item_id','shop_id'], how='left')
df_test = df_test.fillna(0)
df_test.head()
# + _cell_guid="2565c11e-6b3a-4268-becd-5cab11fee861" _uuid="303707b5b9d2c54fc771ecaae2117ce1b33d067c"
# Remove the categorical data from our test data, we're not using it
df_test = df_test.drop(labels=['ID', 'shop_id', 'item_id'], axis=1)
df_test.head()
# + _cell_guid="fde5595e-0cf6-4620-87e2-6031ba8ea68d" _uuid="005d1e880ce7bea66471a7fb0e67d051cc133550"
# Now we finally create the actual training set
# Let's use the '2015-10' sales column as the target to predict
TARGET = '2015-10'
y_train = df_test[TARGET]
X_train = df_test.drop(labels=[TARGET], axis=1)
print(y_train.shape)
print(X_train.shape)
X_train.head()
# + _cell_guid="fe54e321-f3d2-4217-a396-4416285ff1ff" _uuid="846ff06038a2cf228b383d3c3c75989ae3a726be"
# To make the training set friendly for keras, we convert it to a numpy matrix
# X_train = X_train.as_matrix()
# X_train = X_train.reshape((214200, 33, 1))
# y_train = y_train.as_matrix()
# y_train = y_train.reshape(214200, 1)
print(y_train.shape)
print(X_train.shape)
# X_train[:1]
# + _cell_guid="d7e744b1-4707-4df7-b8b4-4c2b92b0856b" _uuid="2214c539e1f1348b9fb5e903df514434c0e4191e"
# Lastly we create the test set by converting the test data to a numpy matrix
# We drop the first month so that our trained LSTM can output predictions beyond the known time range
X_test = df_test.drop(labels=['2013-01'],axis=1)
# X_test = X_test.as_matrix()
# X_test = X_test.reshape((214200, 33, 1))
print(X_test.shape)
# + [markdown] _cell_guid="e8ac0b5c-09f3-4bf1-8ceb-8f54fb81f9a3" _uuid="2c9ac0c8f0f2ba3bf312c5fc6224facce415402e"
# ## Build and Train the model
# + _cell_guid="d59a768d-c77d-44b4-9d48-14a752962b91" _uuid="512b649b54d56cad4651e57083735121808bc459"
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasRegressor
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
# + _cell_guid="6c3898a6-e583-4426-a2bd-27b40e33f0c5" _uuid="37595bce4deffcd88c38c5eef6e0678a5eadbef8"
# Create the model using the NestedLSTM class - two layers are a good starting point
# Feel free to play around with the number of nodes & other model parameters
model = Sequential()
model.add(Dense(64, input_dim=33, init='normal', activation='relu'))
model.add(Dense(32, init='normal', activation='relu'))
model.add(Dense(16, init='normal', activation='relu'))
model.add(Dense(8, init='normal', activation='relu'))
model.add(Dense(4, init='normal', activation='relu'))
model.add(Dense(1, init='normal'))
model.compile(loss='mean_squared_error', optimizer = 'adam')
# model = Sequential()
# model.add(NestedLSTM(64, input_shape=(33, 1), depth=3, dropout=0.2, recurrent_dropout=0.2))
# model.add(Dense(1))
# # The adam optimizer works pretty well, although you might try RMSProp as well
# model.compile(loss='mse',
# optimizer='adam',
# metrics=['mean_squared_error'])
model.summary()
# + _cell_guid="08d56185-5f4e-44d0-8802-8eddac643569" _uuid="51b1a7acdbd3ceb2fef16d24385778ed1d68e4ed"
# It's training time!
BATCH = 2000
print('Training time, it is...')
model.fit(X_train, y_train,
batch_size=BATCH,
epochs=10
)
# + [markdown] _cell_guid="4e4c11ad-2a76-4ced-bfff-a24e8ba5ab5c" _uuid="272b8e352e7c606b1cc3da4f1b12dd2b1c0e4f62"
# ## Get test set predictions and Create submission
# + _cell_guid="71f93b2d-f548-4362-a04d-0f5923eabd06" _uuid="b801abe918b33a85f55f040235c94dbbadb8d045"
# Get the test set predictions and clip values to the specified range
y_pred = model.predict(X_test).clip(0., 20.)
# Create the submission file and submit!
preds = pd.DataFrame(y_pred, columns=['item_cnt_month'])
preds.to_csv('submission.csv',index_label='ID')
# + _uuid="6eeed9ca595753c75fee93a07e5fcd9ae000450a"
3)} => 6/36
#
# 8 {(2,6),(6,2),(3,5),(5,3),(4,4)} => 5/36
#
# 9 {(3,6),(6,3),(5,4),(4,5)} => 4/36
#
# 10 {(4,6),(6,4),(5,5)} => 3/36
#
# 11 {(5,6),(6,5)} => 2/36
#
# 12 {(6,6)} = > 1/36
# + [markdown] id="QTPVMzwCZdb7"
# ## Inference
# + [markdown] id="aLnt8I-_Zmb-"
# ### Sample Mean and population Mean
#
#
# * Let's consider a sample of 500 houses at random from 1460 houses and plot it's mean
# * But the mean of these 500 houses can be near or pretty far away from the mean of the 1460 houses calculated earlier.
# + [markdown] id="SNfsZPebnjrI"
# ## Central Limit Theorem
#
# The central limit theorem states that if you have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population then the distribution of the sample means will be approximately normally distributed.
#
# ## Explanation
#
# Suppose we are interested in estimating average height of a population. We can not measure every person height in the given population. We take a sample from the given population. But when we take the sample 2 important things should be noted, 1. Sample size and 2. Distribution of sample.
#
# The central limit theorem says, if we take the sample in significantly large size, the mean of the sample will be normally distributed. For instance, let us assume the sample size as N to be 3, which means we take 3 data points randomly as groups from the given population data such as [155, 160, 171], [152, 168, 164], [172, 151, 154], and so on. Suppose we collect 1000 such groups from the population and calculate average of every group, we will have 1000 averages. When we plot this 1000 average data we will have a distribution as a normal distribution.
#
# ## Importance of Central Limit Theorem
#
# * Signifies the importance of Sample size
#
# * No matter what the distribution of population, the shape of sample distribution becomes normal when the sample size (N) increases.
#
# * Important for Inferential Statistical Analysis
#
# + [markdown] id="f_ODZu7rp3Cd"
# Creating a varaible and storing sales price data.
# + id="gU0W21uipDqg"
df_SalePrice=df['SalePrice']
df_SalePrice.describe()
# + id="c3kpxBl6eW97"
df_SalePrice.mean()
# + id="9J0ZaRDEgWyx"
# plot all the observation in SalesPrice data
plt.hist(df_SalePrice, bins=100)
plt.xlabel('SalePrice')
plt.ylabel('count')
plt.title('Histogram of Sales frequency')
plt.axvline(x=df_SalePrice.mean(),color='r')
# + [markdown] id="VQNqJ-pB02tS"
# Observation:
#
# * We can see the vertical red line, mean of data, almost at the centre of main distribution.
#
# * Most of the distribution is in normal but not 100%.
#
# * Here, the data point after the 500000 on x-axis is an outlier, and the points around 400000 maybe or maynot be an outlier since they are very close to out main distribution graph.
# + [markdown] id="-BeAbD6v31ZB"
# **Note:-** We can also see from the above plot that the population is not normal, Therefore, we need to draw sufficient samples of different sizes and compute their means (known as sample means). We will then plot those sample means to get a normal distribution.
# + id="PxMhFgU8n6H0"
#We will take sample size=20, 60 & 500
#Calculate the arithmetice mean and plot the mean of sample 500 times
array1 = []
array2 = []
array3 = []
n = 500
for i in range(1,n):
array1.append(df_SalePrice.sample(n=20,replace= True).mean())
array2.append(df_SalePrice.sample(n=60,replace= True).mean())
array3.append(df_SalePrice.sample(n=500,replace= True).mean())
#print(array)
fig , (ax1,ax2,ax3) = plt.subplots(nrows=1, ncols=3,figsize=(25,8))
#plt.figure()
#plt.subplot(311)
ax1.hist(array1, bins=100,color='r')
ax1.set_xlabel('SalePrice')
ax1.set_ylabel('count')
ax1.set_title('Sample size = 20')
ax1.axvline(x=np.mean(array1),color='b') # for giving mean line
#ax2.subplot(312)
ax2.hist(array2, bins=100, color='g')
ax2.set_xlabel('SalePrice')
ax2.set_ylabel('count')
ax2.set_title('Sample size = 60')
ax2.axvline(x=np.mean(array2),color='r') # for giving mean line
#ax3.subplot(313)
ax3.hist(array3,bins=100)
ax3.set_xlabel('SalePrice')
ax3.set_ylabel('count')
ax3.set_title('Sample size = 500')
ax3.axvline(x=np.mean(array3),color='r') # for giving mean line
# + [markdown] id="VTPvcy9kv8W7"
# ## Confidence Interval
#
# **Confidence Interval (CI)** is a type of estimate computed from the statistics of the observed data. This proposes a range of plausible values for an unknown parameter (for example, the mean). The interval has an associated confidence level that the true parameter is in the proposed range.
# + [markdown] id="elLp-G6pxTON"
# The 95% confidence interval defines a range of values that you can be 95% certain contains the population mean. With large samples, you know that mean with much more precision than you do with a small sample, so the confidence interval is quite narrow when computed from a large sample.
# + [markdown] id="bpJz5fxNxb7R"
# ##**Calculating the Confidence Interval**
#
# Step 1: start with
#
# The number of observations n
# Thhe mean X
# The standard deviation s
#
# **Note:** we should use the standard deviation of the entire population, but in many cases we won't know it.
#
# We can use the standard deviation for the sample if we have enough observations (at least n=30, hopefully more)
#
# Step 2:
#
# Decide what Confidence Interval we want: 95% or 99% are common choices. Then find the "Z" value for that Confidence Interval here:
#
# 
#
#
#
# **Step 3:** Use that Z value in this formula for the Confidence Interval
#
# 
#
# **Note:-**The value after the ± is called the margin of error
#
#
# + id="UmGo758awQJ1"
# importing math library
import math
# lets seed the random values
np.random.seed(10)
# lets take a sample size
sample_size = 1000
sample = np.random.choice(a= df['SalePrice'],
size = sample_size)
sample_mean = sample.mean()
print("Sample Mean:",sample_mean)
# Get the z-critical value*
z_critical = stats.norm.ppf(q = 0.95)
# Check the z-critical value
print("z-critical value: ",z_critical)
# Get the population standard deviation
pop_stdev = df['SalePrice'].std()
# checking the margin of error
margin_of_error = z_critical * (pop_stdev/math.sqrt(sample_size))
# defining our confidence interval
confidence_interval = (sample_mean - margin_of_error,
sample_mean + margin_of_error)
# lets print the results
print("Confidence interval:",end=" ")
print(confidence_interval)
print("True mean: {}".format(df['SalePrice'].mean()))
# + [markdown] id="TZilBKNeJ5HS"
# ## Hypothesis Testing
#
# * $Statistical Hypothesis$, sometimes called confirmatory data analysis, is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables. A statistical hypothesis test is a method of statistical inference.
#
# ### Null Hypothesis
#
# * In Inferential Statistics, **The Null Hypothesis is a general statement or default position that there is no relationship between two measured phenomena or no association among groups.**
#
# * Statistical hypothesis tests are based on a statement called the null hypothesis that assumes nothing interesting is going on between whatever variables you are testing.
#
# * Therefore, in our case the Null Hypothesis would be:
# **The Mean of House Prices in OldTown is not different from the houses of other neighborhoods**
#
# ### Alternate Hypothesis
#
# * The alternate hypothesis is just an alternative to the null. For example, if your null is **I'm going to win up to 1000** then your alternate is **I'm going to win more than 1000.** Basically, you're looking at whether there's enough change (with the alternate hypothesis) to be able to reject the null hypothesis
#
# ### The Null Hypothesis is assumed to be true and Statistical evidence is required to reject it in favor of an Alternative Hypothesis.
#
#
# 1. Once you have the null and alternative hypothesis in hand, you choose a significance level (often denoted by the Greek letter α). The significance level is a probability threshold that determines when you reject the null hypothesis.
#
# 2. After carrying out a test, if the probability of getting a result as extreme as the one you observe due to chance is lower than the significance level, you reject the null hypothesis in favor of the alternative.
#
# 3. This probability of seeing a result as extreme or more extreme than the one observed is known as the p-value.
# + [markdown] id="wnQ0lIjWJ9UE"
# ### P Value
#
# * In statistical hypothesis testing, **the p-value or probability value** is the probability of obtaining test results at least as extreme as the results actually observed during the test, assuming that the null hypothesis is correct.
#
# * So now say that we have put a significance (α) = 0.05
# * This means that if we see a p-value of lesser than 0.05, we reject our Null and accept the Alternative to be true
#
# + [markdown] id="q9wfeeEtMG4L"
#
#
# * The pvalue is the Probability that tells that result from sample data occured by chance.
# * The pvalue tells the number of times null hypothesis is true
#
# * Low p-value is good; It indicates data did not occur by chance.
# * For example, a p-value of .01 means there is only a 1% probability that the results from an experiment happened by chance.
# * Usually it is accepted that if the p-value is lower than significance level α (equal to 0.05) , then we should reject the null hypothesis.
#
# + [markdown] id="3HdcFQalPyRe"
# ###**T-Test**
#
# The T-test is a statistical test used to determine whether a numeric data sample differs significantly from the population or whether two samples differ from one another.
#
# **Purpose:**
#
# * It tells us - Is there a significant difference between two sets of data.
#
# * It lets us know if those differences could have happened by chance.
#
# * It doesn't look at only mean but spread of standard deviation to derive conclusion how significant two data sets are
#
# + [markdown] id="G_MEoYqw_974"
# ## Type 1 and Type 2 Error
#
# * In statistical hypothesis testing, a type I error is the rejection of a true null hypothesis.
#
# * Type II error is the rejection of a false null hypothesis.
#
# ### Type 1 and Type 2 Error Example
#
# For example, let's look at the trail of an accused criminal. The null hypothesis is that the person is innocent, while the alternative is guilty.
# * A Type 1 error in this case would mean that the person is not found innocent and is sent to jail, despite actually being innocent.
# * A Type 2 Erroe Example In this case would be, the person is found innocent and not sent to jail despite of him being guilty in real.
| 17,401 |
/Tuesday_Lesson.ipynb
|
5240dff8415e40c195bc9ffcd29031882058ecb6
|
[] |
no_license
|
laurariv01/Hangman-Program
|
https://github.com/laurariv01/Hangman-Program
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 25,233 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import sys
import random
import math
import numpy as np
import skimage.io
import matplotlib
import matplotlib.pyplot as plt
import cv2
# %matplotlib inline
# Root directory of the project
ROOT_DIR = os.getcwd()
# +
# Import Mask RCNN
sys.path.append(ROOT_DIR) # To find local version of the library
from mrcnn import utils
import mrcnn.model as modellib
from mrcnn import visualize
# Import SUN config
sys.path.append(os.path.join(ROOT_DIR, "samples/sun/")) # To find local version
import sun
# Directory to save logs and trained model
MODEL_DIR = os.path.join(ROOT_DIR, "logs")
# Local path to trained weights file
SUN_MODEL_PATH = os.path.join(ROOT_DIR, "mask_rcnn_sun.h5")
# Directory of images to run detection on
IMAGE_DIR = os.path.join(ROOT_DIR, "images")
# -
SUN_MODEL_PATH
# +
# #!wget https://github.com/hateful-kate/Mask_RCNN/releases/download/v3.0/mask_rcnn_sun.h5
# +
class InferenceConfig(sun.SunConfig):
# Set batch size to 1 since we'll be running inference on
# one image at a time. Batch size = GPU_COUNT * IMAGES_PER_GPU
GPU_COUNT = 1
IMAGES_PER_GPU = 1
config = InferenceConfig()
config.display()
# +
# Create model object in inference mode.
model = modellib.MaskRCNN(mode="inference", model_dir=MODEL_DIR, config=config)
# Load weights trained on SUN RGB-D
model.load_weights(SUN_MODEL_PATH, by_name=True)
# -
class_names = ['BG', 'bed', 'books', 'ceiling', 'chair', 'floor',
'furniture', 'objects', 'picture', 'sofa', 'table',
'tv', 'wall', 'window']
# !wget https://preview.ibb.co/cubifS/sh_expo.jpg -P ./images
# +
# Load a random image from the images folder
file_names = next(os.walk(IMAGE_DIR))[2]
image = skimage.io.imread(os.path.join(IMAGE_DIR, 'sh_expo.jpg'))
# Run detection
results = model.detect([image], verbose=1)
# Visualize results
r = results[0]
visualize.display_instances(image, r['rois'], r['masks'], r['class_ids'],
class_names, r['scores'])
# +
# #!mkdir videos
# #!wget https://github.com/hateful-kate/Mask_RCNN/releases/download/v3.0/Achievement.mp4 -P ./videos
# -
# !ls ./videos
# +
def random_colors(N):
np.random.seed(1)
colors = [tuple(255 * np.random.rand(3)) for _ in range(N)]
return colors
def apply_mask(image, mask, color, alpha=0.5):
"""apply mask to image"""
for n, c in enumerate(color):
image[:, :, n] = np.where(
mask == 1,
image[:, :, n] * (1 - alpha) + alpha * c,
image[:, :, n]
)
return image
def display_instances(image, boxes, masks, ids, names, scores):
"""
take the image and results and apply the mask, box, and Label
"""
n_instances = boxes.shape[0]
colors = random_colors(n_instances)
if not n_instances:
print('NO INSTANCES TO DISPLAY')
else:
assert boxes.shape[0] == masks.shape[-1] == ids.shape[0]
for i, color in enumerate(colors):
if not np.any(boxes[i]):
continue
y1, x1, y2, x2 = boxes[i]
label = names[ids[i]]
score = scores[i] if scores is not None else None
caption = '{} {:.2f}'.format(label, score) if score else label
mask = masks[:, :, i]
image = apply_mask(image, mask, color)
image = cv2.rectangle(image, (x1, y1), (x2, y2), color, 2)
image = cv2.putText(image, caption, (x1, y1), cv2.FONT_HERSHEY_COMPLEX, 0.7, color, 2)
return image
# +
batch_size = 1
VIDEO_DIR = os.path.join(ROOT_DIR, "videos")
VIDEO_SAVE_DIR = os.path.join(VIDEO_DIR, "save")
try:
if not os.path.exists(VIDEO_SAVE_DIR):
os.makedirs(VIDEO_SAVE_DIR)
except OSError:
print ('Error: Creating directory of data')
frames = []
frame_count = 0
# -
# !ls ./videos/save
# +
video = cv2.VideoCapture(os.path.join(VIDEO_DIR, 'Achievement.mp4'));
# Find OpenCV version
(major_ver, minor_ver, subminor_ver) = (cv2.__version__).split('.')
if int(major_ver) < 3 :
fps = video.get(cv2.cv.CV_CAP_PROP_FPS)
print("Frames per second using video.get(cv2.cv.CV_CAP_PROP_FPS): {0}".format(fps))
else :
fps = video.get(cv2.CAP_PROP_FPS)
print("Frames per second using video.get(cv2.CAP_PROP_FPS) : {0}".format(fps))
video.release();
# -
frames = []
sec = 226
vidcap = cv2.VideoCapture(os.path.join(VIDEO_DIR, 'Achievement.mp4'))
success,frame = vidcap.read()
count = 226
while success:
# Save each frame of the video to a list
sec += 1
frames.append(frame)
print('frame_count :{0}'.format(sec))
batch_size = 1
VIDEO_DIR = os.path.join(ROOT_DIR, "videos")
VIDEO_SAVE_DIR = os.path.join(VIDEO_DIR, "save")
if len(frames) == batch_size:
results = model.detect(frames, verbose=1)
print('Predicted')
for i, item in enumerate(zip(frames, results)):
frame = item[0]
r = item[1]
frame = display_instances(frame, r['rois'], r['masks'], r['class_ids'], class_names, r['scores'])
name = '{0}.jpg'.format(sec + i - batch_size)
name = os.path.join(VIDEO_SAVE_DIR, name)
cv2.imwrite(name, frame)
print('writing to file:{0}'.format(name))
frames = []
# Clear the frames array to start the next batch
#cv2.imwrite("frame%d.jpg" % count, frame) # save frame as JPEG file
success,frame = vidcap.read()
print('Read a new frame: ', success)
count += 1
# +
def make_video(outvid, images=None, fps=30, size=None,
is_color=True, format="FMP4"):
"""
Create a video from a list of images.
"""
from cv2 import VideoWriter, VideoWriter_fourcc, imread, resize
fourcc = VideoWriter_fourcc(*format)
vid = None
for image in images:
if not os.path.exists(image):
raise FileNotFoundError(image)
img = imread(image)
if vid is None:
if size is None:
size = img.shape[1], img.shape[0]
vid = VideoWriter(outvid, fourcc, float(fps), size, is_color)
if size[0] != img.shape[1] and size[1] != img.shape[0]:
img = resize(img, size)
vid.write(img)
vid.release()
return vid
import glob
import os
# Directory of images to run detection on
ROOT_DIR = os.getcwd()
VIDEO_DIR = os.path.join(ROOT_DIR, "videos")
VIDEO_SAVE_DIR = os.path.join(VIDEO_DIR, "save")
images = list(glob.iglob(os.path.join(VIDEO_SAVE_DIR, '*.*')))
# Sort the images by integer index
images = sorted(images, key=lambda x: float(os.path.split(x)[1][:-3]))
outvid = os.path.join(VIDEO_DIR, "out.mp4")
make_video(outvid, images, fps=30)
# -
# !ls -lah ./videos/
hould be [7, 9, 4.9]
import statistics
nums= [2,7,4.2,1.6,9,4.4,4.9]
x=statistics.mean(nums)
print("mean is:", x)
new_nums= list(filter(lambda nums: True if nums <=4.5875 else False, nums))
print(new_nums)
#Presentation Code
# -
# ## Reduce() <br>
# <p>Be very careful when using this function, as of Python 3 it's been moved to the 'functools' library and no longer is a built-in function.<br>The creator of Python himself, says to just use a for loop instead.</p>
# #### Syntax
# +
from functools import reduce
# reduce(func, list)
#Presentation Code
# use for loop below instead to calculate sum of list, rather than reduce which may cause errors
# reduce functions passed in must accept two parameters
l_1= [1,2,3,4,5]
def subtractNums (num1,num2):
return num1 - num2
result = reduce(subtractNums, l_1)
print(result)
def addNums (num1,num2):
return num1 + num2
result2=reduce(addNums, l_1)
print(result2)
#Presentation Code
# -
# #### Using Lambda's with Reduce()
#Presentation Code
result=reduce(lambda x,y: x+y, l_1)
print(result)
# #### In-Class Exercise #4 <br>
# <p>Use the reduce function to multiply the numbers in the list below together with a lambda function.</p>
# +
#Presentation Code
# output should be 24
mylist=[1,2,3,4]
result=reduce(lambda x,y: x*y, mylist)
print(result)
#Presentation Code
# -
# ## Recursion <br>
# <p>Recursion means that a function is calling itself, so it contanstly executes until a base case is reached. It will then push the returning values back up the chain until the function is complete. A prime example of recursion is computing factorials... such that 5! (factorial) is 5*4*3*2*1 which equals 120.</p>
# #### Implementing a Base Case
# +
# must always have a base case, otherwise it will infinitely loop
#Presentation Code
def addNums(num):
#set base case here
if num <=1:
print("addNums(1)=1")
return num
else:
print("addNums({}) = {} + addNums({})".format(num,num,num-1))
return num + addNums(num-1)
addNums(7)
# addNums(3) = 3 + addNums(2) = 3 + 2 + addNums(1) = 3 + 2 + 1 = 6
# addNums(2) = 2 + addNums(1) = 2 + 1 = 3
# addNums(1) = 1
#Presentation Code
# -
# #### Writing a Factorial Function
# +
# 5! = 5 * 4 * 3 * 2 * 1 = 120
#Presentation Code
def factorial(num):
if num <= 1:
return 1
else: return num * factorial (num-1)
factorial(5)
# -
# #### In-Class Exercise #5 <br>
# <p>Write a recursive function that subtracts all numbers to the argument given.</p>
# +
# result of passing in 3 should equal 2... we're not subtracting 3 - 2 - 1, we're getting the result of 3 - subNums(2)
# subNums(2) = 2 - subNums(1) and subNums(1) = 1, so the result is subNums(3) = 3 - 1 which is 2
#result should be 3-2-1
def subtractNums(num):
#set base case here
if num <=1:
print("subtractNums(1)=1")
return num
else:
print("subtractNums({}) = {} - subtractsNums({})".format(num,num,num-1))
return num - subtractNums(num-1)
print(subtractNums(5))
# -
# ## Generators <br>
# <p>Generators are a type of iterable, like lists or tuples. They do not allow indexing, but they can still be iterated through with for loops. They are created using functions and the yield statement.</p>
# #### Yield Keyword <br>
# <p>The yield keyword denotes a generator, it doesn't return so it won't leave the function and reset all variables in the function scope, instead it yields the number back to the caller.</p>
# +
# using a for loop
#Presentation Code
def my_range(stop,start = 0, step = 1):
while start < stop:
yield start
start += step
for i in my_range(13, start=1):
print(i)
# for i in my_range(10, start=2):
# print(i)
# -
# #### Infinite Generator
# +
# bad, never create infinite loops
# -
# #### In-Class Exercise #6 <br>
# <p>Create a generator that takes a number argument and yields that number squared, then prints each number squared until zero is reached.</p>
# +
# always create a base case
def squared(num):
while num > 0:
yield num **2
num -= 1
for i in squared(10):
print (i)
# -
# # Exercises
# ### Exercise #1 <br>
# <p>Filter out all of the empty strings from the list below</p>
# +
places = ["","Argentina", "", "San Diego","","","","Boston","New York"]
list(filter(None, places))
# -
# ### Exercise #2 <br>
# <p>Write an anonymous function that sorts this list by the last name...<br><b>Hint: Use the ".sort()" method and access the key"</b></p>
author = ["Joel Carter", "Victor aNisimov", "Andrew P. Garfield","David hassELHOFF","Gary A.J. Bernstein"]
author.sort(key=lambda name: name.split(" ")[-1].lower())
print (author)
# ### Exercise #3 <br>
# <p>Convert the list below from Celsius to Farhenheit, using the map function with a lambda...</p>
# +
# F = (9/5)*C + 32
places = [('Nashua',32),("Boston",12),("Los Angelos",44),("Miami",29)]
celsius_to_farhenheit= lambda data: (data[0], (9/5)*data[1] + 32)
list(map(celsius_to_farhenheit, places))
# -
# ### Exercise #4 <br>
# <p>Write a recursion function to perform the fibonacci sequence up to the number passed in.</p>
# +
#example: 0,1,1,2,3,5,8,13
def fibonacci(n):
#this is my base case
if n <= 1:
return n
else:
return(fibonacci(n-1) + fibonacci(n-2))
nterms = 8
for i in range(nterms):
print(fibonacci(i))
| 12,357 |
/tempConverter.ipynb
|
28eff434e9145ac7cad95c6727aa96d060eb29a5
|
[] |
no_license
|
sealdakota/Python-Examples
|
https://github.com/sealdakota/Python-Examples
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 1,731 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#Dakota Seal
#takes input farenheit temperature and converts it to celsius.
fahrenheit = input("input a temperature in farenheit that you would like converted to celsius: ")
#While loop that checks if temperature is less than or equal to 0 kelvin.
belowZero = True
while belowZero == True:
if float(fahrenheit) <= float(-459.67):
fahrenheit = input("Sorry, but temperatures don't go that low, please enter something more reasonable: ")
belowZero = True
else:
belowZero = False
#converts fahrenheit to celsius
celsius = (float(fahrenheit)-32) * 5/9
print(str("%.2f" % celsius))
# -
| 889 |
/Getting and Knowning your data/Chipotle/Excercise with solutions .ipynb
|
57add271fc88943784a453027c93f30a8c60b1dc
|
[] |
no_license
|
Siddhesh-Nawale/Pandas-Excercise
|
https://github.com/Siddhesh-Nawale/Pandas-Excercise
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 27,683 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Algoritmos de Machine Learning
# En este Notebook, usaremos los Dataframes creados en el Notebook de Features para entrenar distintos modelos de Machine Learning y predecir si los tweets son reales o no.
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
import warnings
warnings.filterwarnings('ignore')
# -
# ## Carga de dataframes
train_df = pd.read_csv('../Data/train_features.csv', encoding='latin-1',dtype={'id': np.uint16,'target': np.bool})
test_df = pd.read_csv('../Data/test_features.csv', encoding='latin-1',dtype={'id': np.uint16})
sample_submission = pd.read_csv('../Data/sample_submission.csv')
train_df.head(2)
test_df.head(2)
# ## Algoritmos
# ### Random Forest
# ###### Entrenamiento
X = train_df.sort_values(by='id',ascending=True).iloc[:,2:]
Y = train_df.sort_values(by='id',ascending=True).iloc[:,1]
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.2)
# +
from sklearn.ensemble import RandomForestClassifier
rf_classifier = RandomForestClassifier(n_estimators=10000,max_depth=15,min_samples_split=20)
rf_classifier.fit(X_train, Y_train)
Y_pred = rf_classifier.predict(X_test)
# -
print(classification_report(Y_test,Y_pred))
print(accuracy_score(Y_test,Y_pred))
# Analizamos la importancia de los features.
# +
plt.figure(figsize=(20,8))
plt.bar(X.columns, rf_classifier.feature_importances_)
plt.xlabel('Features', fontsize=16, fontweight='bold')
plt.ylabel('Importancia', fontsize=16, fontweight='bold')
plt.title('Importancia de Features con RF', fontsize=20, fontweight='bold')
plt.xticks(rotation=45,weight='bold')
plt.show()
# -
# ###### Predicción
registros_a_predecir = test_df.sort_values(by='id',ascending=True).iloc[:,1:]
prediccion_RF = rf_classifier.predict(registros_a_predecir)
prediccion_RF = prediccion_RF.astype(int)
# Damos el formato para realizar el submit.
resultado_RF = pd.DataFrame({'id':sample_submission['id'].values.tolist(),'target':prediccion_RF})
resultado_RF.head()
resultado_RF.to_csv('..\Predicciones\prediccion_RF.csv',index=False)
# ### XGBoost
# ###### Entrenamiento
from xgboost import XGBClassifier
import xgboost as xgb
xgboost = XGBClassifier(max_depth=1,
objective= 'binary:logistic',
nthread=4,n_estimators=2000,
learning_rate=0.02,
colsample_bytree=0.75)
xgboost.fit(X_train,Y_train)
Y_pred = xgboost.predict(X_test)
print(classification_report(Y_test,Y_pred))
print(accuracy_score(Y_test,Y_pred))
# Analizamos la importancia de los features con XGBOOST.
# +
plt.rcParams['figure.figsize'] = [20, 8]
xgb.plot_importance(xgboost)
plt.xlabel('F Score', fontsize=16, fontweight='bold')
plt.ylabel('Features', fontsize=16, fontweight='bold')
plt.title('Importancia de Features con XGB', fontsize=20, fontweight='bold')
plt.yticks(weight='bold')
plt.show()
# -
# ###### Predicción
registros_a_predecir = test_df.sort_values(by='id',ascending=True).iloc[:,1:]
prediccion_XGB = xgboost.predict(registros_a_predecir)
prediccion_XGB = prediccion_XGB.astype(int)
# Damos el formato para realizar el submit.
resultado_XGB = pd.DataFrame({'id':sample_submission['id'].values.tolist(),'target':prediccion_XGB})
resultado_XGB.head()
resultado_XGB.to_csv('..\Predicciones\prediccion_XGB.csv',index=False)
# ### Perceptrón Multicapa
# ###### Entrenamiento
X = train_df.iloc[:,2:]
Y = train_df.iloc[:,1]
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.2)
# Normalizamos los campos.
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
# +
from sklearn.neural_network import MLPClassifier
mlp = MLPClassifier(hidden_layer_sizes=(10,10,10), max_iter=500,
solver='adam',learning_rate_init=3e-4)
mlp.fit(X_train, Y_train)
Y_pred = mlp.predict(X_test)
# -
print(classification_report(Y_test,Y_pred))
print(accuracy_score(Y_test,Y_pred))
# ###### Predicción
registros_a_predecir = test_df.iloc[:,1:]
registros_a_predecir = scaler.transform(registros_a_predecir)
prediccion_MLP = mlp.predict(registros_a_predecir)
prediccion_MLP = prediccion_MLP.astype(int)
# Damos el formato para realizar el submit.
resultado_MLP = pd.DataFrame({'id':sample_submission['id'].values.tolist(),'target':prediccion_MLP})
resultado_MLP.head()
resultado_MLP.to_csv('..\Predicciones\prediccion_MLP.csv',index=False)
#
# ### Redes Neuronales usando Keras
from keras.models import Sequential, Model
from keras import layers
from keras.callbacks import ModelCheckpoint
from keras.initializers import Constant
from keras.optimizers import Adam
from keras.utils.vis_utils import plot_model
# Importamos los archivos creados en el Notebook de Features para predecir usando Embeddings.
tweets_padded = pd.read_csv('../Data/tweets_padded.csv', encoding='latin-1')
matriz_de_embeddings = pd.read_csv('../Data/matriz_de_embeddings.csv', encoding='latin-1')
tweets_padded = tweets_padded.to_numpy()
matriz_de_embeddings = matriz_de_embeddings.to_numpy()
train_embeddings = tweets_padded[:train_df.shape[0]]
test_embeddings = tweets_padded[train_df.shape[0]:]
# #### Primer modelo (Solo Embeddings)
# ###### Entrenamiento
# +
model = Sequential()
model.add(layers.Embedding(matriz_de_embeddings.shape[0],matriz_de_embeddings.shape[1],\
embeddings_initializer=Constant(matriz_de_embeddings),\
input_length = train_embeddings.shape[1],trainable = False))
model.add(layers.SpatialDropout1D(0.2))
model.add(layers.LSTM(100,dropout=0.2,recurrent_dropout=0.2))
model.add(layers.Dense(1,activation='sigmoid'))
model.compile(loss='binary_crossentropy',optimizer=Adam(learning_rate=3e-4),metrics=['accuracy'])
# -
# Veamos el detalle del modelo que vamos a utilizar.
model.summary()
plot_model(model, to_file='modelo1_plot.png', show_shapes=True, show_layer_names=True)
# Realizamos el split en train y tesr de los dataframes y entrenamos el modelo.
X_train,X_test,Y_train,Y_test = train_test_split(train_embeddings,train_df['target'].values,test_size=0.2)
model.fit(X_train,Y_train,batch_size=32,epochs=20,validation_data=(X_test,Y_test),verbose=2)
score = model.evaluate(X_test,Y_test,verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# ###### Predicción
registros_a_predecir = test_embeddings
prediccion = model.predict(registros_a_predecir)
prediccion = np.round(prediccion).astype(int).reshape(3263)
resultado_EM = pd.DataFrame({'id':sample_submission['id'].values.tolist(),'target':prediccion})
resultado_EM.head()
resultado_EM.to_csv('..\Predicciones\prediccion_EM.csv',index=False)
# #### Segundo modelo (Embeddings + features)
# ###### Entrenamiento
train_features = train_df.iloc[:,2:]
test_features = test_df.iloc[:,1:]
def crear_modelo():
nlp_input = layers.Input(shape=(train_embeddings.shape[1],), name='nlp_input')
x = layers.Embedding(matriz_de_embeddings.shape[0],matriz_de_embeddings.shape[1],\
embeddings_initializer=Constant(matriz_de_embeddings),trainable = False)(nlp_input)
x = layers.SpatialDropout1D(0.2)(x)
nlp_out = layers.LSTM(100,dropout=0.2,recurrent_dropout=0.2)(x)
features_input = layers.Input(shape=(train_features.shape[1],), name='features_input')
features_out = layers.Dense(4, activation="relu")(features_input)
concat = layers.Concatenate(axis=1)
x = concat([nlp_out,features_out])
x = layers.Dense(1, activation='sigmoid')(x)
model = Model(inputs=[nlp_input,features_input], outputs=[x])
model.compile(loss='binary_crossentropy',optimizer=Adam(learning_rate=3e-4),metrics=['accuracy'])
return model
# Veamos el detalle del modelo que vamos a utilizar.
modelo = crear_modelo()
modelo.summary()
plot_model(modelo, to_file='modelo2_plot.png', show_shapes=True, show_layer_names=True)
# Realizamos el split en train y tesr de los dataframes y entrenamos el modelo.
e_train,e_test,f_train,f_test,Y_train,Y_test = train_test_split(train_embeddings,train_features,train_df['target'].values,\
test_size=0.2)
# Normalizamos los features.
scaler = StandardScaler()
scaler.fit(f_train)
f_train = scaler.transform(f_train)
f_test = scaler.transform(f_test)
test_norm = scaler.transform(test_features)
# Usamos un CheckPoint para guardar los pesos óptimos del entrenamiento.
cp = ModelCheckpoint('pesos.h5', monitor='val_loss', save_best_only=True)
modelo.fit([e_train,f_train],Y_train,\
batch_size=32,\
epochs=30,\
validation_data=([e_test,f_test],Y_test),\
callbacks=[cp],\
verbose=2)
modelo.load_weights('pesos.h5')
score = modelo.evaluate([e_test,f_test],Y_test,verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# ###### Predicción
registros_a_predecir = [test_embeddings,test_norm]
prediccion = modelo.predict(registros_a_predecir)
prediccion = np.round(prediccion).astype(int).reshape(3263)
resultado_RN = pd.DataFrame({'id':sample_submission['id'].values.tolist(),'target':prediccion})
resultado_RN.head()
resultado_RN.to_csv('..\Predicciones\prediccion_RN.csv',index=False)
# ###### Majority Voting
# Viendo que los resultados de las predicciones con el modelo suelen ser variadas (no predicen siempre las mismas clases para los mismos ids), vamos a probar hacer un Majority Voting entre las predicciones.
# +
n_iteraciones = 11
prediccion_parcial = np.zeros(3263).astype(int)
for i in range(1,n_iteraciones+1):
modelo = crear_modelo()
e_train,e_test,f_train,f_test,Y_train,Y_test = train_test_split(train_embeddings,train_features,train_df['target'].values,\
test_size=0.2)
scaler = StandardScaler()
scaler.fit(f_train)
f_train = scaler.transform(f_train)
f_test = scaler.transform(f_test)
test_norm = scaler.transform(test_features)
cp = ModelCheckpoint('pesos.h5', monitor='val_loss', save_best_only=True)
history = modelo.fit([e_train,f_train],Y_train,\
batch_size=32,\
epochs=30,\
validation_data=([e_test,f_test],Y_test),\
callbacks=[cp],\
verbose=2)
modelo.load_weights('pesos.h5')
registros_a_predecir = [test_embeddings,test_norm]
prediccion = modelo.predict(registros_a_predecir)
prediccion_parcial = prediccion_parcial + np.round(prediccion).astype(int).reshape(3263)
prediccion_individual = np.round(prediccion).astype(int).reshape(3263)
prediccion_acumulativa = np.round(prediccion_parcial / i).astype(int).reshape(3263)
resultado_individual = pd.DataFrame({'id':sample_submission['id'].values.tolist(),'target':prediccion_individual})
resultado_individual.to_csv('..\Predicciones\prediccionRN'+str(i)+'.csv',index=False)
if ((i % 2 == 1) & (i>= 3)):
resultado_acumulativa = pd.DataFrame({'id':sample_submission['id'].values.tolist(),'target':prediccion_acumulativa})
resultado_acumulativa.to_csv('..\Predicciones\prediccion_MV'+str(i)+'.csv',index=False)
# -
# ### GridSearch Embeddings
# La idea es para nuestro mejor modelo buscar optimizar los hiper-parámetros buscando lograr un mejor score.
# Primero vamos a crear un modelo "sencillo" para realizar una busqueda con GridSearch
def create_model(lstm_p1,dropout_rate=0.2,activation='sigmoid'):
model = Sequential()
model.add(layers.Embedding(matriz_de_embeddings.shape[0],matriz_de_embeddings.shape[1],\
embeddings_initializer=Constant(matriz_de_embeddings),\
input_length = train_embeddings.shape[1],trainable = False))
model.add(layers.SpatialDropout1D(dropout_rate))
model.add(layers.LSTM(lstm_p1,dropout=dropout_rate,recurrent_dropout=dropout_rate))
model.add(layers.Dense(1,activation=activation))
model.compile(loss='binary_crossentropy',optimizer=Adam(learning_rate=3e-4),metrics=['accuracy'])
return model
batch_size = [32,64]
epochs = [32,64]
lstm_p1 = [64,100,128]
param_grid = dict(lstm_p1=lstm_p1,\
batch_size=batch_size, epochs=epochs)
# +
from sklearn.model_selection import GridSearchCV
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasClassifier
from keras.constraints import maxnorm
model = KerasClassifier(build_fn=create_model,verbose=0)
grid = GridSearchCV(estimator=model,param_grid=param_grid,n_jobs=1,cv=3)
# -
X_train,X_test,Y_train,Y_test = train_test_split(train_embeddings,train_df['target'].values,test_size=0.2)
grid_result = grid.fit(X_train,Y_train,validation_data=(X_test,Y_test),verbose=2)
best_model = grid.best_estimator_
grid.best_params_
grid.best_score_
# ## RandomizedSearchCV
# Ahora veamos si podemos agregar algunos hiper-parámetros más y buscar la optimizaciónd e estos con RandomSearch (más eficiente que GridSearch porque no testea TODAS las combinaciones)
def create_model(lstm_p1,dropout_rate=0.2,activation='sigmoid',learn_rate):
model = Sequential()
model.add(layers.Embedding(matriz_de_embeddings.shape[0],matriz_de_embeddings.shape[1],\
embeddings_initializer=Constant(matriz_de_embeddings),\
input_length = train_embeddings.shape[1],trainable = False))
model.add(layers.SpatialDropout1D(dropout_rate))
model.add(layers.LSTM(lstm_p1,dropout=dropout_rate,recurrent_dropout=dropout_rate))
model.add(layers.Dense(1,activation=activation))
model.compile(loss='binary_crossentropy',optimizer=Adam(learning_rate=learn_rate),metrics=['accuracy'])
return model
batch_size = [32,64]
epochs = [32,64]
lstm_p1 = [64,100]
dropout_rate = [0.0, 0.1, 0.2, 0.3]
activation = ['softmax', 'softplus', 'softsign', 'relu', 'tanh', 'sigmoid', 'hard_sigmoid']
learn_rate = [3e-4,0.001, 0.01, 0.1, 0.2, 0.3]
param_rndm = dict(lstm_p1=lstm_p1,dropout_rate=dropout_rate,\
batch_size=batch_size, epochs=epochs,\
activation=activation,learn_rate=learn_rate)
# +
from sklearn.model_selection import RandomizedSearchCV
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasClassifier
from keras.constraints import maxnorm
model = KerasClassifier(build_fn=create_model,verbose=0)
rndm = RandomizedSearchCV(estimator=model,param_distributions=param_rndm,n_jobs=1,cv=3)
# -
X_train,X_test,Y_train,Y_test = train_test_split(train_embeddings,train_df['target'].values,test_size=0.2)
rndm_result = rndm.fit(X_train,Y_train,validation_data=(X_test,Y_test),verbose=2)
best_model = rndm.best_estimator_
rndm.best_params_
rndm.best_score_
# Probemos ahora con estos hiper-parámetros que optuvimos realizar predicciones.
# +
model = Sequential()
model.add(layers.Embedding(matriz_de_embeddings.shape[0],matriz_de_embeddings.shape[1],\
embeddings_initializer=Constant(matriz_de_embeddings),\
input_length = train_embeddings.shape[1],trainable = False))
model.add(layers.SpatialDropout1D(0.2))
model.add(layers.LSTM(64,dropout=0.2,recurrent_dropout=0.2))
model.add(layers.Dense(1,activation='tanh'))
model.compile(loss='binary_crossentropy',optimizer=Adam(learning_rate=3e-4),metrics=['accuracy'])
# -
X_train,X_test,Y_train,Y_test = train_test_split(train_embeddings,train_df['target'].values,test_size=0.2)
model.fit(X_train,Y_train,batch_size=64,epochs=64,validation_data=(X_test,Y_test),verbose=2)
# El score previo para este mismo modelo obtenido fue
# <br>
# Test loss: 0.4567945599555969
# Test accuracy: 0.810899555683136
score = model.evaluate(X_test,Y_test,verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# Podemos observar que mejora el score obtenido para Embeddings con la optimizacion de hiper-parámetros.
registros_a_predecir = test_embeddings
prediccion = model.predict(registros_a_predecir)
prediccion = np.round(prediccion).astype(int).reshape(3263)
resultado_EM = pd.DataFrame({'id':sample_submission['id'].values.tolist(),'target':prediccion})
resultado_EM.head()
resultado_EM.to_csv('..\Predicciones\prediccion_EM_op.csv',index=False)
| 16,777 |
/ANN.ipynb
|
9241ead09a530df632f30e1ca49af20fe70d0ba8
|
[] |
no_license
|
Ak-code15/Deep-learning-project
|
https://github.com/Ak-code15/Deep-learning-project
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 304,914 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import tensorflow as tf
import keras
import matplotlib.pyplot as plt
import seaborn as sn
from keras.models import Sequential
dataset=pd.read_excel('Features_2500RPM_60dB.xlsx')
dataset.shape
x = dataset.iloc[:,:-14].values
y14 = dataset.iloc[:,-1].values
y4 = dataset.iloc[:,-2].values
x.shape
labels=np.unique(y4)
labels
from sklearn.preprocessing import LabelEncoder
lb=LabelEncoder()
y4=lb.fit_transform(y4)
y4
y4.shape
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y4,test_size=0.2,random_state=0)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
x_train = sc.fit_transform(x_train)
x_test = sc.transform(x_test)
model=tf.keras.models.Sequential()
model.add(tf.keras.layers.Dense(units = 84, activation = 'relu'))
model.add(tf.keras.layers.Dense(units = 4, activation = 'softmax'))
model.compile(optimizer='adam', loss="SparseCategoricalCrossentropy", metrics=['accuracy'])
y_test.shape
x_train.shape
y_train
x_test.shape
ann2=model.fit(x_train,y_train,validation_data=(x_test,y_test), batch_size = 32, epochs = 20)
plt.plot(ann2.history['accuracy'])
plt.plot(ann2.history['val_accuracy'])
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.title('Model Accuracy')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
# +
plt.plot(ann2.history['loss'])
plt.plot(ann2.history['val_loss'])
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.title('Model Loss')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
# -
y_pred = model.predict(x_test)
y_pred = (y_pred>0.5)
y_pred = 1*y_pred
y_pred
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred.argmax(axis=1))
cm
df_cm = pd.DataFrame(cm, columns=labels, index = labels)
df_cm.index.name = 'Actual'
df_cm.columns.name = 'Predicted'
plt.figure(figsize = (10,7))
sn.set(font_scale=1.4)
sn.heatmap(df_cm, cmap="Blues", annot=True,annot_kws={"size": 16})
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred.argmax(axis=1)))
# ### 14-CLASS
labels2=np.unique(y14)
labels2
y14=lb.fit_transform(y14)
y14.shape
from sklearn.model_selection import train_test_split
x_train2,x_test2,y_train2,y_test2=train_test_split(x,y14,test_size=0.2,random_state=0)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
x_train2 = sc.fit_transform(x_train2)
x_test2 = sc.transform(x_test2)
model2=tf.keras.models.Sequential()
model2.add(tf.keras.layers.Dense(units = 84, activation = 'relu'))
model2.add(tf.keras.layers.Dense(units = 14, activation = 'softmax'))
model2.compile(optimizer='adam', loss="SparseCategoricalCrossentropy", metrics=['accuracy'])
ann3=model2.fit(x_train2,y_train2,validation_data=(x_test2,y_test2), batch_size = 32, epochs = 20)
plt.plot(ann3.history['accuracy'])
plt.plot(ann3.history['val_accuracy'])
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.title('Model Accuracy')
plt.legend(['train', 'val'], loc='lower right')
plt.show()
# +
plt.plot(ann3.history['loss'])
plt.plot(ann3.history['val_loss'])
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.title('Model Loss')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
# -
y_pred2 = model2.predict(x_test2)
y_pred2=(y_pred2>0.5)
y_pred2 = 1*y_pred2
y_pred2
from sklearn.metrics import confusion_matrix
cm2 = confusion_matrix(y_test2, y_pred2.argmax(axis=1))
cm2
df_cm = pd.DataFrame(cm2, columns=labels2, index =labels2)
df_cm.index.name = 'Actual'
df_cm.columns.name = 'Predicted'
plt.figure(figsize = (10,7))
sn.set(font_scale=1.4)#for label size
sn.heatmap(df_cm, cmap="Blues", annot=True,annot_kws={"size": 16})# font size
# +
from keras.wrappers.scikit_learn import KerasClassifier
from sklearn.model_selection import cross_val_score
from keras.models import Sequential
from keras.layers import Dense
def my_classifier():
classifier = Sequential()
classifier.add(Dense(
units = 84,
activation="relu"
))
classifier.add(Dense(
units = 4,
activation="softmax"
))
classifier.compile(
optimizer = "adam",
loss="SparseCategoricalCrossentropy",
metrics=['accuracy']
)
return classifier
#this classifier will be use to the 10 different training fold
#for k-cross validation on 1 test fold
classifier = KerasClassifier(build_fn = my_classifier,
batch_size = 32,
nb_epoch = 20)
accuracies = cross_val_score(
estimator=classifier,
X = x_train,
y = y_train,
cv=5
)
#the important variable is cv which mean the number of
#fold in cross validation that we will use
#after we got the accuracies, find the mean
mean = accuracies.mean()
variance = accuracies.std()
# -
std = np.sqrt(variance)
std
mean
variance
| 5,136 |
/notebooks/my_rebel.ipynb
|
a7536a2da04c26384f4e5c20bc30403d495cf6f9
|
[
"MIT"
] |
permissive
|
chapmanbe/isys90069_w2020_explore
|
https://github.com/chapmanbe/isys90069_w2020_explore
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 14,332 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Who Are Our Rebels
#
# In this notebook I'm going to use some simple NLP to try to explore who were our favorite rebels. In the process I hope to demonstrate some of the data-wrangling challenges that go along with NLP.
# ### Get Data from Canvas
#
# Canvas has a RESTful API. I'm going to use it to pull down the responses to the homework assignments.
#
# By the way, you can also use the Canvas API to access your data.
#
# The cell below contains the code I used to get the data from Canvas.
# ```Python
# with open(os.path.join(os.path.expanduser("~"), ".canvaslms", "quiz_token")) as f:
# token = f.read()
#
# from canvasapi import Canvas
# from bs4 import BeautifulSoup
# import unicodedata
#
# API_URL = "https://canvas.lms.unimelb.edu.au/"
# canvas = Canvas(API_URL, token)
# bec = canvas.get_user(canvas.get_current_user().id)
# ehealth = canvas.get_course(110024)
#
# # This is the id number for the assignment
# rebel_id = 139157
#
# rebels = ehealth.get_assignment(rebel_id)
#
# rebel_submissions = rebels.get_submissions()
#
# responses = [(b.user_id, b.body) for b in rebel_submissions]
#
#
# len(responses)
#
# len(set([r[0] for r in responses]))
#
# rebel_text = [unicodedata.normalize("NFKC", BeautifulSoup(r[1]).getText()) for r in responses if r[1]]
#
# with open("rebel_text.json", "w") as f:
# json.dump(rebel_text, f)
# ```
# +
import os
from collections import Counter
import json
# get token
import random
import matplotlib.pyplot as plt
# -
# ###
with open("rebel_text.json", "r") as f:
rebel_text = json.load(f)
rebel_text
# ### We are going to use the very popular [Spacy](https://spacy.io/) NLP package.
#
# If you are interested in learning more about Spacy, we have some notebooks [here](https://github.com/Melbourne-BMDS/md3nlp_20020) that you can run online with binder to learn more.
import spacy
from IPython.display import SVG, YouTubeVideo
from spacy import displacy
nlp = spacy.load("en_core_web_sm")
# #### Entity Recognition
#
# Spacy will parse the sentences and then try to recognize different entitites that are named in the text, such as people or organizations or diseases. Let's see how it works.
for txt in rebel_text:
doc = nlp(txt)
displacy.render(doc, style="ent")
print('-'*72)
# ### Spacy seems to do OK
# #### But there are some consistent failures
#
# Sometimes the solitary surnames are recognized as `ORG`s (organizations). This is not surprising because
#
# - Dyson is a vaccum cleaner
# - Tesla is a car company
#
# The answer about Nikola Tesla is particularly problematic where we see Tesla as an organization, a piece of art, and a product---everything except a person.
#
# 
# ### Filtering Entities
#
# Let's reduce the number of the recognized entities by only keeping entities that might conceivably be one of our rebels, which in the Tesla case is a problem. Eventually my algorithm is going to count the number of times a name is mentioned to guess that the most frequently named person is the identified hero.
rebels = []
labels = ['ORG', 'PERSON', 'WORK_OF_ART', 'PRODUCT']
for txt in rebel_text:
doc = nlp(txt)
rebels.append([ent for ent in doc.ents if ent.label_ in labels and ent.string != 'Freeman' and ent.string != 'Dyson'])
rebels
# ### Sort identified entities
#
# I want to sort the identified entities for each document from longest to shortest. This is so that I can combine entities such as "Albert Einstein" and "Einstein".
for r in rebels:
r.sort(key=lambda x:len(x.string), reverse=True)
# ### With our sorted lists, we can try to replace partial names with full names
def get_full_names(r):
n = len(r)
for i in range(n-1):
for j in range(i,n):
if r[j].string in r[i].string:
r[j] = r[i]
return None
# Let's use `get_full_names` to replace all partial names (e.g. 'Albert' or 'Einstein' with the full name e.g. 'Albert Einstein').
for i in range(len(rebels)):
r = rebels[i]
print(i)
print("Before")
print(r)
get_full_names(r)
print("After")
print(r)
print('-'*20)
# ### How well did it work?
#
# Most of the substitutions worked reasonably well, but cases 5 (Venter) and 6 (Tesla) clearly failed. Let's examine those to see what is happening.
#
# We are comparing the `string` attributes (`r[j].string in r[i].string`), so let's look at the strings
for ent in rebels[5]:
print("'%s'"%ent.string)
for ent in rebels[6]:
print("'%s'"%ent.string)
# ### Extra Spaces!
#
# We can see that the `Venter` and `Tesla` strings have an extra space after them so our comparison 'Venter ' in 'John Craig Venter' fails. Similarly with 'Tesla '. If we use the Python `strip` method, we can delete leading and trailing white spaces.
def get_full_names2(r):
n = len(r)
for i in range(n-1):
for j in range(i,n):
if r[j].string.strip() in r[i].string.strip():
r[j] = r[i]
return None
# +
with open("rebel_text.json", "r") as f:
rebel_text = json.load(f)
rebels = []
labels = ['ORG', 'PERSON', 'WORK_OF_ART', 'PRODUCT']
for txt in rebel_text:
doc = nlp(txt)
rebels.append([ent for ent in doc.ents if ent.label_ in labels and ent.string.strip() != 'Freeman' and ent.string.strip() != 'Dyson' and ent.string.strip() != 'Freeman Dyson'])
for r in rebels:
r.sort(key=lambda x:len(x.string), reverse=True)
for i in range(len(rebels)):
r = rebels[i]
print(i)
print("Before")
print(r)
get_full_names2(r)
print("After")
print(r)
print('-'*20)
# -
# ### Count the identified Entities
counted=[Counter(r) for r in rebels]
for c in counted:
print(c.most_common(5))
# ### How did our counting work?
#
# Again, pretty well, but sometimes we have a name that is counted with the same frequency as a non-name entity (e.g. `(Madame Curie, 2), (a Nobel Prize, 2)`. So let's start by selecting the entities that are counted at the top-frequency and then see if we can select entities that are a `PERSON'.
# +
def most_frequent(counted):
count = counted[0][1]
return [c for c in counted if c[1] == count]
top_counted = [most_frequent(c.most_common(5)) for c in counted if c]
top_counted
# -
# ### Return the top `PERSON`
#
# If there is more than one `PERSON`, we'll just return the first one.
def get_top_person(counted):
try:
return [ent for ent in counted if ent[0].label_ == 'PERSON'][0]
except:
return None
top_counted_persons = [c[0] if len(c) == 1 else get_top_person(c) for c in top_counted]
top_counted_persons
identified_rebels = [e[0] for e in top_counted_persons if e]
identified_rebels
identified_rebels.sort(key=lambda x:len(x.string), reverse=True)
identified_rebels
get_full_names2(identified_rebels)
identified_rebels
counted_identified_rebels = Counter(identified_rebels)
counted_identified_rebels.most_common(60)
f, axs = plt.subplots(1,figsize=(15,15))
pd.DataFrame([x.string.strip() for x in identified_rebels])[0].value_counts().head(60).plot.barh(axes=axs)
axs.set_xlabel("Counts")
f.savefig("identified_rebels.png")
# ## Discussion
#
# I took a fairly simplistic approach to identifying the named rebels. The technique was not robust to several textual features, such as typos and misspellings possessive form. Because I was counting mentions of names, if someone used a lot of pronouns to refer to the rebel I might not have identified them properly. Identify the answer you submitted. Did I correctly find your rebel? If not, can you think of things in your writing that could be edited to make the identification task easier?
| 7,940 |
/3.K-Nearest Neighbors/2.Code - Using an API/KNN.ipynb
|
608eb89b191bcf5021578e086c4024963fbf93c6
|
[
"MIT"
] |
permissive
|
ananth-repos/machine-learning
|
https://github.com/ananth-repos/machine-learning
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 50,760 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] hide_input=false id="bb021ec4"
# # IMT 2021
#
# # Ecrêtage de puissance sur une ligne de distribution triphasée BT* par batterie alimentée par une centrale photovoltaïque (élément de correction )
#
#
#
# (*BT Basse Tension <1000V)
# + [markdown] hide_input=false id="227e4f19"
# ### Problématique:
#
# Une ligne de distribution d'énergie électrique voit sa puissance à distribuer augmentée pendant les saisons d'affluence touristique (période mai-aout). Le choix économique permettant d'écrêter cette puissance porte sur un système de batterie électrochimique rechargé par une microcentrale photovoltaïque placé sur site.
# + [markdown] id="7bf92883"
# ### Sprint 1- Evaluation de la consommation du village pendant la période estivale
# + id="eabbb239"
# + [markdown] id="0f573274"
# #### Données:
#
# P10_Olinda.csv: Courbe de charge triphasée (puissance absorbée par le village) toutes les 10 min sur la période mai-aout (les données temps sont en heure locale)
# Puissance limite de la ligne 11kW/par phase.
#
# + [markdown] hide_input=true id="53c3a266"
# #### Resultats attendues:
#
# a- Mise en forme de la puissance en fonction du temps (graphique).
#
# b- Tracer de la monotone de puissance (distribution de la puissance par ordre décroissant).
# En déduire la puissance max absorbée par le village ainsi que les deux contraintes (puissance et énergie) que doit fournir le système de substitution au réseau (batterie).
#
# c- La consommation hebdomadaire (kWh) entre mai et aout en fonction des heures creuses (22 h à 6 H) et pleines(6h-22h)
#
# + [markdown] hide_input=false id="f27cb5b1"
# ##### Résultats
# + [markdown] id="be5865f5"
# Mise en forme de la puissance en foncton du temps
# + hide_input=false cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 460} id="1f137698" executionInfo={"status": "error", "timestamp": 1631960959155, "user_tz": -120, "elapsed": 8, "user": {"displayName": "Stephane Reyes", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "14852497390560645681"}} outputId="e8c51479-80af-4c36-b7ab-4abbb28a6473"
#@title Mise en forme de la puissance en foncton du temps
import pandas as pd
source=pd.read_csv('/Users/srmac/Dropbox/Ecole des Mines Ales/Projet UE energie/Maui_olindaCourbe_charge_maijuinjuilletaoutV1.csv', sep=',' )
source.drop(['date', 'h'], axis = 1, inplace = True)
serie=pd.Series(source.values.ravel('F'))
per1 = pd.date_range(start ='2015-05-01', end ='2015-09-01', freq ='10min')
Conso=pd.DataFrame(serie.values,index=per1[:-1], columns=["Puissance"])
#### graphique production consommation
a=list(Conso['Puissance'])
conso=a
b=list(Conso.index)
time_unix_conso=[(b[i].value)/1E6 for i in range(len(b))]
array_conso=a
dsp_conso=list(map(list, zip(time_unix_conso, array_conso)))
from highcharts import Highstock, Highchart
H = Highstock()
H.add_data_set(dsp_conso,'line','Consommation',tooltip = {
'valueDecimals': 0})
options = {
'rangeSelector' : {
'selected' : 2
},
'title' : {
'text' : 'Consommation(kW)'
},
'lang': {
'shortMonths': [
'Janv', 'Fév', 'Mars', 'Avril',
'Mai', 'Juin', 'Juil', 'Août',
'Sept', 'Oct', 'Nov', 'Déc'
],
'weekdays': [
'Dimanche', 'Lundi', 'Mardi', 'Mercredi',
'Jeudi', 'Vendredi', 'Samedi'
],
},
}
H.set_dict_options(options)
H
# + hide_input=true id="da0ff732" outputId="e8273855-8efb-4554-8add-4929bd357998"
import numpy as np
import matplotlib.pyplot as plt
Plimit=11*3
Monotone_Conso=[x for x in sorted(Conso["Puissance"],reverse=True)]
P_stock=Plimit-Conso[Conso['Puissance']>=Plimit]
NRJ_stock=sum(P_stock['Puissance'])/6
plt.figure(figsize=(15,12))
plt.plot(np.arange(0,len(Monotone_Conso)),Monotone_Conso)
plt.title("Monotone de Puissance absorbée ")
plt.xlabel('Pas de temps 10 minutes')
plt.ylabel('Puissance W')
plt.plot(10, Monotone_Conso[0], 'ro')
plt.vlines(x=10, ymin=0, ymax= Monotone_Conso[0], colors='gray', ls=':', lw=2, label='Puissance max abosrbée')
plt.hlines(y=Plimit, xmin=10, xmax=len(conso), colors='red', ls=':', lw=2, label='Puissance max absorbée')
plt.text(0,Monotone_Conso[0],'Puissance max '+str(round(Monotone_Conso[0],0))+" kW", fontsize=14, c='red')
plt.text(len(Monotone_Conso)/2,Plimit+0.5,'Puissance limite max de la ligne '+str(Plimit)+' kW', fontsize=14, color='red')
plt.plot
#plt.fill_between(Monotone_Conso, 6, where=Monotone_Conso>6, color='#539ecd')
# + hide_input=true id="746107cb" outputId="b7e25d1c-7a1e-4358-8bef-89d98d2cd89b"
print("La puissance maximale absorbée :"+str(round(max(conso),0))+" kW")
print('Puissance max system stockage= ' + str(round(min(P_stock['Puissance']),0))+" kW")
print("Energie stockée à restituer= "+str(round(NRJ_stock,0))+ " kWh")
# + hide_input=true id="88b27b59" outputId="a10a869a-61e4-4db5-85d2-289b957da420"
H = Highchart(width=850, height=500)
Conso_HP=Conso[(Conso.index.hour>=6)&(Conso.index.hour<22)]
Conso_HC=Conso[(Conso.index.hour<6)|(Conso.index.hour>21)]
P_stock_average_weekly=P_stock.groupby(pd.Grouper(freq='W')).sum()/6
Conso_average_weekly_HP=Conso_HP.groupby(pd.Grouper(freq='W')).sum()/6
Conso_average_weekly_HC=Conso_HC.groupby(pd.Grouper(freq='W')).sum()/6
time=list(Conso.index.strftime("%d/%m/%Y"))
data0=list(P_stock_average_weekly['Puissance'])
data1=list(Conso_average_weekly_HP['Puissance'])
data2=list(Conso_average_weekly_HC['Puissance'])
options = {
'chart': {'type': 'column'},
'title': {'text': 'Energie moyenne hebdomadaire'},
'xAxis': {'categories':time},
'yAxis': [{'min': -100,'tickInterval':50,'title': {'text': 'Energie'},'labels': {'format': '{value} kWh'}}],
#{'title': {'text': 'Puissance en HP estimée', 'style': {'color':'#F62114' }},'labels': {'format': '{value} kW'},'opposite': True}],
'legend': {'shadow': False},
'tooltip': {'shared': True},
'plotOptions': {'column': {'stacking':'normal','grouping': False,'shadow': False,'borderWidth': 0,'pointWidth': 25}},
}
H.set_dict_options(options)
#H.add_data_set(data0, 'column', 'Energie stockage ', color='#ff7f00',pointPadding=0.2, pointPlacement=-0.2)
H.add_data_set(data1, 'column', 'Consommation HP ', color='#F5130F',stack='conso',pointPadding=0.2, pointPlacement=-0.2)
H.add_data_set(data2, 'column', 'Consommation HC', color='#4444C8',stack='conso',pointPadding=0.2, pointPlacement=-0.2)
H
# + [markdown] hide_input=true id="0d9c69ba"
# ### Sprint 2- Evaluation de la ressource solaire pendant la période estivale
# + [markdown] id="2bff4dcb"
# #### Données:
#
# point GPS Olinda: 20.80892 (North);-156.28288 (West)
#
# Site pvgis:https://re.jrc.ec.europa.eu/pvg_tools/;
#
# données météo:TMY; Typical Meteorological Year(fichier .csv); Année de réference: 2006-2015
# données sortie de générateur photovoltaique:DONNÉES DU RAYONNEMENT HORAIRES; année ref 2015 lmontage fixe, inclinaison 0°, orientation 0°, 1 kWp,pertes 14%.
#
# Caractéristique module photovoltaïque Q.PEAK DUO-G9 350 W (orie
#
#
#
# + [markdown] hide_input=true id="1715af6a"
# #### Resultats attendues:
#
#
# a- Mise en forme et comparaison de l'énergie (par unité de surface) hebdomadaire solaire (Irradiation) et sortie de générateur photovoltaïque (électrique).
#
# b- Déduire en première approximation la surface au sol de module PV puis la puissance crête du generateur photovoltaïque.
#
# + hide_input=true id="0d230311" outputId="39a5dc4d-872a-4c2d-a267-d414ef6815ea"
import pandas as pd
from datetime import timedelta
source=pd.read_csv('/Users/srmac/Dropbox/Ecole des Mines Ales/Projet UE energie/tmy_20.809_-156.283_2006_2015.csv', sep=',',skip_blank_lines=True,header=16, skipfooter=13)
index=pd.to_datetime(source["time(UTC)"], format='%Y%m%d:%H%M')
prod=pd.DataFrame(source["G(h)"].values, index=index,columns=["Irradiance_Globale"])
prod['Date']=prod.index
prod['Date'] = prod['Date'].apply(lambda x: x.strftime('2015-%m-%d %H:%M'))
prod.reset_index()
prod.set_index(pd.to_datetime(prod['Date']), inplace=True)
prod.index=prod.index-timedelta(hours=10)
prod=prod.loc['2015-05-01':'2015-08-31']
source_elec=pd.read_csv('/Users/srmac/Dropbox/Ecole des Mines Ales/Projet UE energie/Timeseries_20.809_-156.283_NS_1kWp_crystSi_14_0deg_0deg_2015_2015.csv', sep=',',skip_blank_lines=True,header=10, skipfooter=13)
index=pd.to_datetime(source_elec["time"], format='%Y%m%d:%H%M')
prod_elec=pd.DataFrame(source_elec["P"].values, index=index,columns=["Puissance"])
prod_elec.index=prod_elec.index-timedelta(hours=10)
prod_elec=prod_elec.loc['2015-05-01':'2015-08-31']
#### graphique production consommation
a=list(prod['Irradiance_Globale'])
b=list(prod.index)
time_unix_prod=[b[i].value//1E6 for i in range(len(b))]
array_prod=a
dsp_prod=list(map(list, zip(time_unix_prod, array_prod)))
a_elec=list(prod_elec['Puissance'])
b_elec=list(prod.index)
time_unix_prod_elec=[b_elec[i].value//1E6 for i in range(len(b_elec))]
array_prod_elec=[x/((1.637*1.031)/0.35) for x in a_elec]
# + hide_input=true id="3b58d26e" outputId="3b97a61d-9934-4380-cf52-afdd10cd7f02"
dsp_prod_elec=list(map(list, zip(time_unix_prod_elec, array_prod_elec)))
from highcharts import Highstock
H = Highstock()
H.add_data_set(dsp_prod,'line','Irradiance',tooltip = {
'valueDecimals': 0})
H.add_data_set(dsp_prod_elec,'line','Production electrique',tooltip = {
'valueDecimals': 0})
options = {
'rangeSelector' : {
'selected' : 2
},
'title' : {
'text' : 'Irradiance au sol vs Production électrique (W/m2)'
},
'lang': {
'shortMonths': [
'Janv', 'Fév', 'Mars', 'Avril',
'Mai', 'Juin', 'Juil', 'Août',
'Sept', 'Oct', 'Nov', 'Déc'
],
'weekdays': [
'Dimanche', 'Lundi', 'Mardi', 'Mercredi',
'Jeudi', 'Vendredi', 'Samedi'
],
},
}
H.set_dict_options(options)
H
# + hide_input=true id="47b37f04" outputId="829b9829-531b-4a5f-b226-0d530530426c"
H = Highchart(width=850, height=500)
prod_average_weekly=prod.groupby(pd.Grouper(freq='W')).sum()/6
prod_elec_average_weekly=prod_elec.groupby(pd.Grouper(freq='W')).sum()/6
P_stock_average_weekly=P_stock.groupby(pd.Grouper(freq='W')).sum()/6
time=list(prod_average_weekly.index.strftime("%d/%m/%Y"))
data0=[x/1000 for x in list(prod_average_weekly['Irradiance_Globale'])]
data1=[x*(-1) for x in list(round(P_stock_average_weekly.Puissance,0))]
data3=[x/1000 for x in list(prod_elec_average_weekly['Puissance'])]
data2=[data1[i]/data3[i] for i in np.arange(len(data1))]
options = {
'chart': {'type': 'column'},
'title': {'text': 'Irradiation hebdomadaire'},
'xAxis': {'categories':time},
'yAxis': [{'min': 0,'tickInterval':1,'title': {'text': 'Irradiation'},'labels': {'format': '{value} kWh/m2'}},
{'min': 0,'tickInterval':10,'title': {'text': 'Energie à stocker', 'style': {'color':'#FFFFF' }},'labels': {'format': '{value} kWh'},'opposite': True}],
'legend': {'shadow': False},
'tooltip': {'shared': True},
'plotOptions': {'column': {'stacking':'normal','grouping': False,'shadow': False,'borderWidth': 0,'pointWidth': 25}},
}
H.set_dict_options(options)
H.add_data_set(data0,'column', 'Irradiation hebdomadaire ', color='#ff7f00',pointPadding=0.2, pointPlacement=0.2)
H.add_data_set(data1,'column', 'Energie à stocker ', color='#8282DA',yAxis=1,pointPadding=0.2, pointPlacement=-0.2)
H.add_data_set(data2,'scatter', 'Surface ', color='#E82F1C',yAxis=1,pointPadding=0.2, pointPlacement=-0.2)
H.add_data_set(data3,'column', 'Energie surfacique PV hebdomadaire ', color='#f3d440 ',pointPadding=0.2, pointPlacement=0.2)
H
# + [markdown] id="cfa4bda9"
# En première approximation et pour un module de type Q.PEAK DUO-G9 350W
# + [markdown] hide_input=false id="82a77e4c"
# ### Sprint 4- Problématique de transfert de puissance sur ligne électrique de distribution, application
#
#
# + [markdown] id="173ff252"
# #### Données:
#
# longueur de la ligne: 2km
#
# résistivité=3,32 10 -8 Ωm
#
# section: 180 mm2
#
# réactance linéique = 3,0 10-4 Ω/m
#
#
# courbe de charge du village: fichier csv
#
# Phi=0.52 rad
#
# tension du poste de distribution: 250V
#
# charge linéaire (Facteur de puissance = cos phi)
#
# chute de tension < 10% de la tension normalise 230 V
# + [markdown] id="e1d40f1b"
# #### Méthode:
#
# a-Modélisation monophasée de la ligne de distribution triphasée
#
# b-Bilan de puissance
#
# c-Tracer l'équation dans le plan V=f(P), agir sur le paramètre Phi et conclure.
#
# d- Mettre en évidence la problématique de puissance transmissible par cette ligne
# + [markdown] id="55a16bb5"
# a-Modélisation monophasé de la ligne de distribution triphasé
#
# On modélise la ligne sur une phase en tenant compte de ses caractéristiques.
# + hide_input=true id="5cc3ce42" outputId="4b3b3457-a810-482a-a607-a4b8a5b6c70e"
# commentaire ligne avec R+X
# resolution equation seconde degre stav
# version 3
import numpy as np
R=float(input("Saisir la valeur de Rligne="))
X=float(input("Saisir la valeur de Xligne="))
E=float(input("Saisir la valeur de E="))
Phi=float(input("Saisir la valeur de Phi="))
dU=0.1
X1=[]
X2=[]
PB=[]
for Pb in range(0,int(E**2/(X**2+R**2)**0.5),1):
a=1
b=2*X*np.tan(Phi)*Pb+2*Pb*R-E**2
c=((R**2+X**2)/np.cos(Phi)**2)*Pb**2
#calcul de delta
delta=b**2-4*a*c
#affichage
#print("résolution de l'équation ",a," vb² + ",b," vb + ",c)
# condition sur delta dans cet ordre >0 puis ==0 puis <0
if delta>0:
x1=((-b-delta**0.5)/(2*a))**0.5
x2=((-b+delta**0.5)/(2*a))**0.5
#print("Delta est positif donc il y a 2 solutions")
#print("VB1 =",x1)
#print("VB2 =",x2)
#print("Pb =",Pb)
X1.append(x1)
X2.append(x2)
PB.append(Pb)
else:
if delta==0:
x0=(-b/(2*a))**0.5
#print("Delta est nul donc il y a 1 solution unique")
#print("x0 =",x0)
else:
#print("Pas de solution dans l'espace de réel")
break
#représentation graphique
import numpy as np
import matplotlib.pyplot as plt
#encadrement pour le graphique
dU=0.1
Rc=3*230**2/(max(Conso['Puissance'])*1000)
V=list((Rc*PB[i])**0.5 for i in range (len(PB)))
plt.figure(figsize=(15,12))
plt.plot(PB,X1)
plt.plot(PB,X2)
plt.plot(PB,V)
idx1 = np.argwhere(np.isclose(X2, V, atol=0.1)).reshape(-1)
plt.plot(idx1[0], V[idx1[0]], 'ro')
idx2 = np.argwhere(np.isclose(230*(1-dU), X2, atol=0.1)).reshape(-1)
plt.plot(idx2[0], X2[idx2[0]], 'ro')
# single vline with specific ymin and ymax
plt.vlines(x=idx1[0], ymin=0, ymax= V[idx1[0]], colors='gray', ls=':', lw=2, label='P')
plt.text(idx1[0],V[idx1[0]]/2,str(idx1[0])+"W", rotation=90,fontsize=14)
plt.vlines(x=idx2[0], ymin=0, ymax= X2[idx2[0]], colors='black', ls=':', lw=2, label='P maxi-chute de tension')
plt.text(idx2[0],X2[idx2[0]]/2,str(idx2[0])+"W", rotation=90,fontsize=14)
plt.vlines(x=max(PB), ymin=0, ymax= X2[max(PB)], colors='red', ls=':', lw=2, label='P maxi-hors chute de tension')
plt.text(max(PB),X2[max(PB)]/2,str(max(PB))+"W", rotation=90,fontsize=14)
# place legend outside
plt.legend(bbox_to_anchor=(1.0, 1), loc='upper left')
plt.axhline(y=230*(1-dU), color="red")
plt.text(100, 230*(1-dU)+2, 'tension mini='+ str(230*(1-dU))+" V", fontsize=10, color='red')
plt.plot
plt.ylim(ymax = 280, ymin = 0)
plt.title("V=f(P) par phase")
plt.axhline(y=0,color='black')
plt.axvline(x=0,color='black')
plt.xlabel('Puissance active transmise en W') # Légende abscisse
plt.ylabel('Tension en bout de ligne en V')
plt.show() # affiche la figure a l'ecranplt.legend(bbox_to_anchor=(1.0, 1), loc='upper left')
# + hide_input=true colab={"base_uri": "https://localhost:8080/", "height": 17} id="d6bc1eec" executionInfo={"status": "ok", "timestamp": 1631961085188, "user_tz": -120, "elapsed": 265, "user": {"displayName": "Stephane Reyes", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "14852497390560645681"}} outputId="b51717ba-4027-4525-872f-822d15418c01" language="html"
# <script src="https://cdn.rawgit.com/parente/4c3e6936d0d7a46fd071/raw/65b816fb9bdd3c28b4ddf3af602bfd6015486383/code_toggle.js"></script>
#
# + id="5f80ce7d"
# + id="b0d4621d"
annels=128, out_channels=64, kernel_size=3, stride=1, padding=1, bias=True)
self.unpool1 = nn.ConvTranspose2d(in_channels=64, out_channels=64, kernel_size=2, stride=2, padding=0, bias=True)
self.dec1_2 = CBR2d(in_channels=128, out_channels=64, kernel_size=3, stride=1, padding=1, bias=True)
self.dec1_1 = CBR2d(in_channels=64, out_channels=64, kernel_size=3, stride=1, padding=1, bias=True)
self.score_fr = nn.Conv2d(in_channels=64, out_channels=num_classes, kernel_size=1, stride=1, padding=0, bias=True) # Output Segmentation map
def forward(self, x):
enc1_1 = self.enc1_1(x)
enc1_2 = self.enc1_2(enc1_1)
pool1 = self.pool1(enc1_2)
enc2_1 = self.enc2_1(pool1)
enc2_2 = self.enc2_2(enc2_1)
pool2 = self.pool2(enc2_2)
enc3_1 = self.enc3_1(pool2)
enc3_2 = self.enc3_2(enc3_1)
pool3 = self.pool3(enc3_2)
enc4_1 = self.enc4_1(pool3)
enc4_2 = self.enc4_2(enc4_1)
pool4 = self.pool4(enc4_2)
enc5_1 = self.enc5_1(pool4)
enc5_2 = self.enc5_2(enc5_1)
unpool4 = self.unpool4(enc5_2)
cat4 = torch.cat((unpool4, enc4_2), dim=1)
dec4_2 = self.dec4_2(cat4)
dec4_1 = self.dec4_1(dec4_2)
unpool3 = self.unpool3(dec4_1)
cat3 = torch.cat((unpool3, enc3_2), dim=1)
dec3_2 = self.dec3_2(cat3)
dec3_1 = self.dec3_1(dec3_2)
unpool2 = self.unpool2(dec3_1)
cat2 = torch.cat((unpool2, enc2_2), dim=1)
dec2_2 = self.dec2_2(cat2)
dec2_1 = self.dec2_1(dec2_2)
unpool1 = self.unpool1(dec2_1)
cat1 = torch.cat((unpool1, enc1_2), dim=1)
dec1_2 = self.dec1_2(cat1)
dec1_1 = self.dec1_1(dec1_2)
output = self.score_fr(dec1_1)
return output
# +
# 구현된 model에 임의의 input을 넣어 output이 잘 나오는지 test
model = UNet(num_classes=12)
x = torch.randn([1, 3, 512, 512])
print("input shape : ", x.shape)
out = model(x).to(device)
print("output shape : ", out.size())
model = model.to(device)
# -
# ## train, validation, test 함수 정의
def train(num_epochs, model, data_loader, val_loader, criterion, optimizer, saved_dir, val_every, device):
print('Start training..')
best_loss = 9999999
for epoch in range(num_epochs):
model.train()
for step, (images, masks, _) in enumerate(data_loader):
images = torch.stack(images) # (batch, channel, height, width)
masks = torch.stack(masks).long() # (batch, channel, height, width)
# gpu 연산을 위해 device 할당
images, masks = images.to(device), masks.to(device)
# inference
outputs = model(images)
# loss 계산 (cross entropy loss)
loss = criterion(outputs, masks)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# step 주기에 따른 loss 출력
if (step + 1) % 25 == 0:
print('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'.format(
epoch+1, num_epochs, step+1, len(train_loader), loss.item()))
# validation 주기에 따른 loss 출력 및 best model 저장
if (epoch + 1) % val_every == 0:
avrg_loss = validation(epoch + 1, model, val_loader, criterion, device)
if avrg_loss < best_loss:
print('Best performance at epoch: {}'.format(epoch + 1))
print('Save model in', saved_dir)
best_loss = avrg_loss
save_model(model, saved_dir)
def validation(epoch, model, data_loader, criterion, device):
print('Start validation #{}'.format(epoch))
model.eval()
with torch.no_grad():
total_loss = 0
cnt = 0
mIoU_list = []
for step, (images, masks, _) in enumerate(data_loader):
images = torch.stack(images) # (batch, channel, height, width)
masks = torch.stack(masks).long() # (batch, channel, height, width)
images, masks = images.to(device), masks.to(device)
outputs = model(images)
loss = criterion(outputs, masks)
total_loss += loss
cnt += 1
outputs = torch.argmax(outputs.squeeze(), dim=1).detach().cpu().numpy()
mIoU = label_accuracy_score(masks.detach().cpu().numpy(), outputs, n_class=12)[2]
mIoU_list.append(mIoU)
avrg_loss = total_loss / cnt
print('Validation #{} Average Loss: {:.4f}, mIoU: {:.4f}'.format(epoch, avrg_loss, np.mean(mIoU_list)))
return avrg_loss
# ## 모델 저장 함수 정의
# +
# 모델 저장 함수 정의
val_every = 1
saved_dir = './saved'
if not os.path.isdir(saved_dir):
os.mkdir(saved_dir)
def save_model(model, saved_dir, file_name='Unet_best_model.pt'):
check_point = {'net': model.state_dict()}
output_path = os.path.join(saved_dir, file_name)
torch.save(model.state_dict(), output_path)
# -
# ## 모델 생성 및 Loss function, Optimizer 정의
# +
# Loss function 정의
criterion = nn.CrossEntropyLoss()
# Optimizer 정의
optimizer = torch.optim.Adam(params = model.parameters(), lr = learning_rate, weight_decay=1e-6)
# -
train(num_epochs, model, train_loader, val_loader, criterion, optimizer, saved_dir, val_every, device)
# ## 저장된 model 불러오기 (학습된 이후)
# +
# best model 저장된 경로
model_path = './saved/Unet_best_model.pt'
# best model 불러오기
checkpoint = torch.load(model_path, map_location=device)
model.load_state_dict(checkpoint)
# 추론을 실행하기 전에는 반드시 설정 (batch normalization, dropout 를 평가 모드로 설정)
# model.eval()
# +
# 첫번째 batch의 추론 결과 확인
for imgs, image_infos in test_loader:
image_infos = image_infos
temp_images = imgs
model.eval()
# inference
outs = model(torch.stack(temp_images).to(device))
oms = torch.argmax(outs.squeeze(), dim=1).detach().cpu().numpy()
break
i = 3
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(16, 16))
print('Shape of Original Image :', list(temp_images[i].shape))
print('Shape of Predicted : ', list(oms[i].shape))
print('Unique values, category of transformed mask : \n', [{int(i),category_names[int(i)]} for i in list(np.unique(oms[i]))])
# Original image
ax1.imshow(temp_images[i].permute([1,2,0]))
ax1.grid(False)
ax1.set_title("Original image : {}".format(image_infos[i]['file_name']), fontsize = 15)
# Predicted
ax2.imshow(oms[i])
ax2.grid(False)
ax2.set_title("Predicted : {}".format(image_infos[i]['file_name']), fontsize = 15)
plt.show()
# -
# ## submission을 위한 test 함수 정의
def test(model, data_loader, device):
size = 256
transform = A.Compose([A.Resize(256, 256)])
print('Start prediction.')
model.eval()
file_name_list = []
preds_array = np.empty((0, size*size), dtype=np.long)
with torch.no_grad():
for step, (imgs, image_infos) in enumerate(data_loader):
# inference (512 x 512)
outs = model(torch.stack(imgs).to(device))
oms = torch.argmax(outs, dim=1).detach().cpu().numpy()
# resize (256 x 256)
temp_mask = []
for img, mask in zip(np.stack(imgs), oms):
transformed = transform(image=img, mask=mask)
mask = transformed['mask']
temp_mask.append(mask)
oms = np.array(temp_mask)
oms = oms.reshape([oms.shape[0], size*size]).astype(int)
preds_array = np.vstack((preds_array, oms))
file_name_list.append([i['file_name'] for i in image_infos])
print("End prediction.")
file_names = [y for x in file_name_list for y in x]
return file_names, preds_array
# ## submission.csv 생성
# +
# sample_submisson.csv 열기
submission = pd.read_csv('./submission/sample_submission.csv', index_col=None)
# test set에 대한 prediction
file_names, preds = test(model, test_loader, device)
# PredictionString 대입
for file_name, string in zip(file_names, preds):
submission = submission.append({"image_id" : file_name, "PredictionString" : ' '.join(str(e) for e in string.tolist())},
ignore_index=True)
# submission.csv로 저장
submission.to_csv("./submission/Baseline_UNet.csv", index=False)
# -
# ## Reference
#
#
en(index_full[168+window-1:-24], OHC_GLORYS2V3_series_running_mean_sum + OHC_GLORYS2V3_white_running_mean_std,
OHC_GLORYS2V3_series_running_mean_sum - OHC_GLORYS2V3_white_running_mean_std,
alpha=0.3,edgecolor='tomato', facecolor='tomato')
plt.plot(index_full[12+window-1:-12],OHC_SODA3_series_running_mean_sum,'g-',linewidth=2.0,label='SODA3')
plt.fill_between(index_full[12+window-1:-12], OHC_SODA3_series_running_mean_sum + OHC_SODA3_white_running_mean_std,
OHC_SODA3_series_running_mean_sum - OHC_SODA3_white_running_mean_std,
alpha=0.3,edgecolor='lightgreen', facecolor='lightgreen')
#plt.plot(index_full[window-1:-48],OHC_NEMO_series_running_mean_sum,color='darkorange',linestyle='-',linewidth=2.0,label='OGCM Hindcast')
#plt.fill_between(index_full[window-1:-48], OHC_NEMO_series_running_mean_sum + OHC_NEMO_white_running_mean_std,
# OHC_NEMO_series_running_mean_sum - OHC_NEMO_white_running_mean_std,
# alpha=0.3,edgecolor='yellow', facecolor='yellow')
#plt.title('{} ({}) from {}N to {}N with a running mean of {} months'.format(part_title,title_depth,lat_interest_list[i],lat_interest_list[i+1],window))
fig7.set_size_inches(12.5, 6)
plt.xlabel("Time",fontsize=16)
#plt.xticks(np.linspace(0, 444, 38), index_year_full)
plt.xticks(np.arange(13,len(year_ORAS4)*12+12+1,60),index_year,fontsize=16)
#plt.xticks(rotation=60)
plt.ylabel("Ocean Heat Content (1E+22 Joule)",fontsize=16)
plt.yticks(np.arange(-2.0,2.0,0.5),fontsize=16)
plt.legend(frameon=True, loc=2, prop={'size': 14})
props = dict(boxstyle='round', facecolor='white', alpha=0.8)
ax = plt.gca()
ax.text(0.52,0.08,text_content,transform=ax.transAxes,fontsize=14,verticalalignment='top',bbox=props)
plt.show()
fig7.savefig(os.path.join(output_path,'Comp_OHC_lowpss_window_60m_60N_90N.png'), dpi = 200)
| 26,945 |
/ML-model_FastAI.ipynb
|
e386e20b73207847815bfc2ec5cc8d93ca159fc5
|
[] |
no_license
|
Jacobjeevan/NLP-Malayalam
|
https://github.com/Jacobjeevan/NLP-Malayalam
| 0 | 1 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 33,063 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Week 12 Homework
#
# Due Wednesday December 8th.
#
# Try to take this as a practice test with a 3 hour limit.
# ### Exercise 1
#
# Create a function that takes a list of strings and outputs a dictionary where the key is the string and the value is the length of the corresponding string.
# +
def ex1(lst):
return {item: len(item) for item in lst}
try:
assert(ex1(['']) == {'': 0})
assert(ex1(['a']) == {'a': 1})
assert(ex1(['hello', 'world']) == {'hello': 5, 'world': 5})
assert(ex1(['python', 'data', 'science']) == {'python': 6, 'data': 4, 'science': 7})
assert(ex1(['a']) == {'a': 1})
print("solution is correct")
except:
print("solution is incorrect")
# -
# ### Exercise 2
#
# Create a function that outputs all the even numbers under 500 that are also divisible by 9.
# +
def ex2():
# lst2 = []
# for x in range(500):
# if x % 2 == 0 and x % 9 == 0:
# lst2.append(x)
# return lst2
return [x for x in range(500) if x % 18 == 0]
try:
assert(ex2() == [0,18,36,54,72,90,108,126,144,162,180,198,216,234,252,270,288,306,324,342,360,378,396,414,432,450,468,486])
print("solution is correct")
except:
print("solution is incorrect")
# -
# ### Exercise 3
#
# Create a class that implements a linked list.
# +
class Node:
def __init__(self, data):
self.data = data
self.next = None
def __repr__(self):
return f"<Node data: {self.data}>"
class LinkedList:
def __init__(self, node=None):
self.head = node
self.tail = node
def append(self, data):
new_node = Node(data)
if self.tail:
self.tail.next = new_node
self.tail = new_node
else:
self.head = new_node
self.tail = new_node
def output_list(self):
current_node = self.head
while current_node:
print(current_node)
current_node = current_node.next
def __repr__(self):
return f"<Linked List {self.head} {self.tail}>"
node = Node(5)
linked_list = LinkedList(node)
linked_list.append(10)
linked_list.append(15)
linked_list.append(20)
linked_list.append(25)
linked_list.append(30)
linked_list.append(35)
linked_list.append(40)
linked_list.output_list()
# +
# s = [0]
# print(s[-1])
# print(s[0])
# +
# if None:
# print("Hello")
# else:
# print('none is falsy')
# -
# ### Exercise 4
#
# Given the following two sets, assign to variable `m` the numbers that are contained by both sets (the numbers that are in both s and t).
# +
s = {0,2,4,6,8,10}
t = {0,1,3,5,7,9}
m = s.intersection(t)
try:
assert(m == {0})
print("solution is correct")
except:
print("solution is incorrect")
# -
# ### Exercise 5
#
# Fix the following class definition so that the code runs without error. (Only change the class definition).
# +
class Exercise5:
def __init__(self, num, lname, fname):
self.num = num
self.last_name = lname
self.first_name = fname
@property
def get_attrs(self):
return [self.num, self.last_name, self.first_name]
instance = Exercise5('46', 'Biden', 'Joe')
try:
assert(instance.get_attrs == ['46', 'Biden', 'Joe'])
print("solution is correct")
except:
print("solution is incorrect")
# -
# ### Exercise 6
#
# Create a class called `Time` that takes two arguments (`hours` and `minutes`) and sets them as instance attributes. Then create a function that overloads the addition and equality operators so you can add the times together and then check if two instances are equal in time.
# +
class Time:
def __init__(self, hrs, mins):
# instance attributes
self.hrs = hrs
self.mins = mins
# overload the methods, dunder add
#def __add__()
time1 = Time(0, 30)
time2 = Time(1, 30)
time3 = Time(2, 0)
time1 + time2
try:
assert(time1 + time2 == time3)
print("solution is correct")
except:
print("solution is incorrect")
# +
class Time:
def __init__(self, hrs, mins):
# instance attributes
self.hrs = hrs
self.mins = mins
# overload the methods, dunder add
# will take self & other
# what does other refer to ? -> refers to the other instance
def __add__(self, other):
f =self.hrs + other.hrs
g =self.mins + other.mins
if g >= 60:
f += g // 60
#f = f + g // 60
g %= 60 #
#g = g % 60
return f,g
# we want the minutes, handle the overlap with the minutes, should not be getting (1,60) but (2,0)
time1 = Time(0, 30)
time2 = Time(1, 30)
time1 + time2
# time3 = Time(2, 0)
# time1 + time2
# try:
# assert(time1 + time2 == time3)
# print("solution is correct")
# except:
# print("solution is incorrect")
# +
# what can we do with hours and minutes, self.total in the __init__
# normalize two differnet numbers to make comparable, in this call normalized time in minutes to compare and add easily
class Time:
def __init__(self, hrs, mins):
# instance attributes
self.hrs = hrs
self.mins = mins
self.total_time = self.hrs * 60 + self.mins
#print(self.total_time)
#def __repr__(self):
#return f"<Time h:{self.hrs} m:{self.mins}>"
# overload the methods, dunder add
# will take self & other
# what does other refer to ? -> refers to the other instance
def __add__(self, other):
# if other is not instance of Time returns None. function that does not return anything returns NONE
# difference with the addition dunder,
if isinstance(other, Time):
added_time = self.total_time + other.total_time
return Time(added_time // 60, added_time % 60)
# equality for the assert now easily, have to define whats eqaul to us, we could look at the total_time
def __eq__(self, other):
# when checking equality, return a Bool
if isinstance(other, Time):
return self.total_time == other.total_time #will give us True or False
time1 = Time(0, 30)
time2 = Time(1, 30)
time1 + time2
# for the equality to override it
time3 = Time(2, 0)
# time1 + time2, time1 is self.total_time and time2 is other.total_time
try:
assert(time1 + time2 == time3)
print("solution is correct")
except:
print("solution is incorrect")
# +
class Time:
def __init__(self, hrs, mins):
self.hrs = hrs
self.mins = mins
self.total_time = self.hrs * 60 + self.mins
def __add__(self, other):
if isinstance(other, Time):
added_time = self.total_time + other.total_time
return Time(added_time // 60, added_time % 60)
def __eq__(self, other):
# when checking equality, return a Bool
if isinstance(other, Time):
return self.total_time == other.total_time #will give us True or False
elif isinstance(other, tuple):
return other == ()
time1 = Time(0, 30)
time2 = Time(1, 30)
time1 + time2
# for the equality to override it
time3 = Time(2, 0)
# time1 + time2, time1 is self.total_time and time2 is other.total_time
try:
assert(time1 + time2 == time3)
print("solution is correct")
except:
print("solution is incorrect")
# -
5 // 2, 5 % 2
# +
def func():
pass
s=func()
s == None
# +
def func():
pass
s=func("hello")
s == None
# +
class Num:
def __init__(self, n):
self.num = n
def __add__(self, other):
# when we add, want to return a val
#pass
if isinstance(other, Num):
return self.num + other.num
# can also do it like this
#new_num = Num(self.num + other.num)
#return new_num
def __repr__(self):
return f"<Num {self.num}>"
n = Num(5)
e = Num(3)
n + e
# +
class Num:
def __init__(self, n):
self.num = n
def __add__(self, other):
# when we add, want to return a val
#pass
if isinstance(other, Num):
#return self.num + other.num
# can also do it like this
new_num = Num(self.num + other.num)
return new_num
def __repr__(self):
return f"<Num {self.num}>"
n = Num(5)
e = Num(3)
n + e
# +
the __init__ making instance of the class
# -
# # student class, and instance of the student class, that will be object, when we want to use instances, will need a way to refer to instance of
# class, may not know what we want to do, set functions, refer to self doesnt exist yet but will want to use later, __init__ constructor sets up the
# instance, define hours, be able to creat instance of time and have attrs that exist in single instance later
#
# time1 creates instance of the class, create like a function and have
#
# class Space:
# moon = "grey"
# s = Space
# f = Space
#
# s.moon == f.moon
#
#
# ### Exercise 7
#
# Create a function that creates an `m` by `n` matrix (`m` rows and `n` columns) filled with zeros.
def ex7(m,n):
#return [[0 for x in range(m)] for y in range(n)]
return [ [0] * n for x in range(m) ]
try:
assert(ex7(0,0) == [])
assert(ex7(1,1) == [[0]])
assert(ex7(2,2) == [[0,0],[0,0]])
assert(ex7(3,5) == [[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]])
print("solution is correct")
except:
print("solution is incorrect")
# ### Exercise 8
#
# Create a function that takes an arbitrary number of integer arguments and sums them.
# +
def ex8(*args):
#return sum(*args)
return sum(args)
try:
assert(ex8(3,5,7) == 15)
assert(ex8(2,4) == 6)
assert(ex8(*range(10)) == 45)
print("solution is correct")
except:
print("solution is incorrect")
# -
# ### Exercise 9
#
# Create a decorator function that wraps the following function so that the string returned has anchor tags (e.g `<a>hello world</a>`)
# +
def decorator_func(func):
def wrapper():
return f"<a>{func()}</a>"
return wrapper
@decorator_func
def func():
return "hello world"
try:
assert(func() == '<a>hello world</a>')
print("solution is correct")
except:
print("solution is incorrect")
# -
# ### Exercise 10
#
# Using list comprehension, create a list with two for loops that generate the following output:
#
# [('0', '0'), ('0', '1'), ('1', '0'), ('1', '1')]
# +
l = [ (str(x), str(y)) for x in range(2) for y in range(2) ]
try:
assert(l == [('0', '0'), ('0', '1'), ('1', '0'), ('1', '1')])
print("solution is correct")
except:
print("solution is incorrect")
# -
# %load_ext tutormagic
# +
# %%tutor --lang python3
l = [ (str(x), str(y)) for x in range(2) for y in range(2) ]
try:
assert(l == [('0', '0'), ('0', '1'), ('1', '0'), ('1', '1')])
print("solution is correct")
except:
print("solution is incorrect")
# -
# ### Exercise 11
#
# Create a dictionary comprehension that generates the following dictionary:
# ```
# {'a': ['*'], 'b': ['*'], 'c': ['*']}
# ```
# +
#d = { key: ['*'] for key in ['a', 'b', 'c'] }
# too verbose
#d = { key:[val] for key in ['a', 'b', 'c'] for val in ['*'] }
d = { key: ['*'] for key in ('a','b','c') }
try:
assert(d == {'a': ['*'], 'b': ['*'], 'c': ['*']})
print("solution is correct")
except:
print("solution is incorrect")
# -
# ### Exercise 12
#
# Create a lambda expression that takes `a` and `b` and computes `c`:
#
# $$ a^2 + b^2 = c^2 $$
#
# To find c by itself
#
# $$ √ a^2 + b^2 = c^2 $$
# +
#from math import sqrt
#f = lambda a,b: (a ** 2 + b ** 2)
f = lambda a,b: (a ** 2 + b ** 2)**0.5
try:
assert(f(3,4) == 5.0)
assert(f(5,12) == 13.0)
print("solution is correct")
except:
print("solution is incorrect")
# -
# ### Exercise 13
#
# Create a generator function that yields one even number at a time.
# +
# def generator(num):
# return [num*2 for num in range(num)]
# generator(4)
def generator(num):
for x in range(num):
if x % 2 == 0:
yield x
start = generator(2)
# -
next(start)
next(start)
# ### Exercise 14
#
# Write a function that recursively calculates the following if `n` is greater than 0. If `n` is less than 0, return 0.5.
#
# $$ n = (n-1) + (n-1)$$
# $$ n -1 = (n - 1 -1) + (n-2)$$
# $$ n-2 = (n-2-1) + (n-1-1) =(n-3) + (n-3) $$
# We need a base case from recursion, to have terminating point
# if we keep looping thru things, like while, if we don't put in comdition, same goes for the recursion
# calls itself and will continue until reaching condition, condition no longer calling te func, will take
# that result and return, cascade again, keep calling itslef until hit return statement and bubble back up
# to the top.
#
# What would be the exit conditon:
# if less than 0 - exit condition, if less than zero return 0.5
# $$ n! = n * (n-1)! $$
# $$ (n-1)! = (n-1) * (n-2)!$$
#
# Will continue going until we reach 0
# +
# %%timeit
def ex14(n):
if n < 0:
return 0.5
else:
#calculate, start the recursion
return ex14(n-1) + ex14(n-1)
#return 2 * ex14(n-1) # number of less recursion calls
ex14(2)
# try:
# assert(ex14(1) == 2**1)
# assert(ex14(2) == 2**2)
# assert(ex14(3) == 2**3)
# assert(ex14(4) == 2**4)
# assert(ex14(10) == 2**10)
# print("solution is correct")
# except:
# print("solution is incorrect")
# +
# %%timeit
def ex14(n):
if n < 0:
return 0.5
else:
#calculate, start the recursion
#return ex14(n-1) + ex14(n-1)
return 2 * ex14(n-1) # number of less recursion calls
ex14(2)
# -
# #### Exercise 15
#
# Write a function that sends a get request to a url and returns the headers. Use the following url to test.
#
# https://www.httpbin.org
# +
import requests
def headers(url):
request = requests.get(url)
return request.headers
r = headers("https://www.httpbin.org")
r
# -
# ### Exercise 16
#
# Write a ternary operator that sets the variable `s` to an input if the length of the input is greater than 25 characters, otherwise set `s` to `None`
# +
m = input("use this input")
s = m if len(m) > 25 else None
print(s)
# -
# ### Exercise 17
#
# Using the json library, output the value of the key `menuitem`.
# +
import json
s = """{"menu": {
"id": "file",
"value": "File",
"popup": {
"menuitem": [
{"value": "New", "onclick": "CreateNewDoc()"},
{"value": "Open", "onclick": "OpenDoc()"},
{"value": "Close", "onclick": "CloseDoc()"}
]
}
}}"""
d = json.loads(s)
d["menu"]
# +
import json
s = """{"menu": {
"id": "file",
"value": "File",
"popup": {
"menuitem": [
{"value": "New", "onclick": "CreateNewDoc()"},
{"value": "Open", "onclick": "OpenDoc()"},
{"value": "Close", "onclick": "CloseDoc()"}
]
}
}}"""
d = json.loads(s)
d["menu"]["popup"]
# +
import json
s = """{"menu": {
"id": "file",
"value": "File",
"popup": {
"menuitem": [
{"value": "New", "onclick": "CreateNewDoc()"},
{"value": "Open", "onclick": "OpenDoc()"},
{"value": "Close", "onclick": "CloseDoc()"}
]
}
}}"""
d = json.loads(s)
d["menu"]["popup"]["menuitem"]
# -
# ### Exercise 18
#
# Using a slice, output the even numbers backwards
# +
s = [1,2,3,4,5,6,7,8,9,10]
s = s[::-2]
try:
assert(s == [10, 8, 6, 4, 2])
print("solution is correct")
except:
print("solution is incorrect")
# -
# ### Exercise 19
#
# Create a class called `Square` that inherits from `Shape` and overrides the area method.
# +
class Shape:
def __init__(self, color):
self.color = color
def area(self, *side):
return sum(side)
def __repr__(self):
return f"Shape"
s = Shape("red")
s.area(8,5,6,7)
# +
class Square(Shape):
def __init__(self, length):
self.length = length
def area(self, length):
return self.length**2
# def __repr__(self):
# pass
sq = Square("black")
sq.area
sq.area(8)
# -
# ### Exercise 20
#
# Create a function that at worst executes in linear time.
# +
def print_student(student_list):
for student in student_list:
print(student)
print_student(['rakshanda', 'chioma', 'juan', 'bryant', 'anna'])
# -
# ### Topics for final assessment:
#
# ### Data Types
# * Strings
# * Ints
# * Floats
# * Bools
#
# ### Python Collection Data Structures
# * Lists
# * Tuples
# * Sets
# * Dictionaries
#
# Related topics:
# * related methods (string, list, dict, set)
# * built in methods (`abs`, `all`, `any`, `dir`, `format`, `input`, `getattr`, `len`, `max`, `min`, `ord`, `pow`, `print`, `range`, `reversed`, `round`, `setattr`, `sum`, `type`)
# * indexing/slicing
# * casting (`bool`, `int`, `str`, `float`, `dict`, `set`)
# * comprehensions
# * mutability
# * arithmetic operators (`+`, `-`, `*`, `/`, `//`, `%`,`**`)
# * assignment operators (`=`, `+=`, `-=`, `/=`, `//=`, etc.)
# * comparison operator (`==`, `!=`, `>`, `<`, `>=`, `<=`)
# * identity operators (`is`, `is not`)
# * membership operators (`in`, `not in`)
#
# ### Control Flow/Structures
# * `if`/`elif`/`else`
# * `for`
# * `while`
# * `with`
# * `try`/`except`
# * `pass`/`break`/`continue`
# * `finally`
#
# Related topics:
# * conditional statements
# * logical operators (`and`/`or`/`not`)
# * nested conditionals/loops
# * boolean values of objects
# * ternary operators
#
# ### Functions
# * function definition/declaration
# * scope of variables inside functions
# * positional arguments
# * keyword arguments
# * arbitrary arguments (positional and keyword)
# * unpacking arguments (`*` and `**`)
# * lambda functions
# * currying functions
# * decorator functions
# * recursion
# * iterators/generators (`yield`, `next`, `iter`)
# * functional programming built ins (`map`, `filter`, `zip`)
#
# ### Classes
# * class definition
# * class objects
# * instance objects
# * class/instance attributes
# * class methods
# * inheritance
# * multiple inheritance
# * operator overloading
# * decorators (`classmethod`, `staticmethod`, `property`)
#
# ### Modules
# * modules
# * packages
# * importing
# * scripts
#
# ### Algorithms and Data Structures
# * sorting algorithms (no code)
# * queues
# * stacks
# * linked lists
# * Big O Notation
#
# ### Other Topics:
# * errors (handling with `try`/`except` and raising with `raise`
# * reading and writing files (`with` statement)
# * file formats (json and csv)
# * sending web requests (`requests`)
# * parsing html (`BeautifulSoup`)
# * crawling/scraping
# * web requests (`GET`, `POST`, `PUT`, `DELETE`)
# * CRUD (create, read, update, delete
# * SQL (tables, columns, rows)
# * git (adding files, committing, pushing)
| 19,474 |
/jupyter-python/data_analysis/.ipynb_checkpoints/2018.07.RogunHPP.AlignmentDXFtoNodesCSV-checkpoint.ipynb
|
b3519c82247d9d04691e6853ed783f31d018ebd7
|
[] |
no_license
|
JJK-engineering/data-organizer
|
https://github.com/JJK-engineering/data-organizer
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 57,970 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Rogun HPP - Alignment DXF to Nodes in CSV
# ToDo
# all data (e.g. file names) as variables
# markdown titles
# comments with explanations
# this example use grass script, do again with pygrass defining class & methods (to go into API later)
# +
# set up Python for GRASS GIS
import os
import sys
import subprocess
from IPython.display import Image
# set up GRASS GIS runtime environment
gisbase = subprocess.check_output(["grass", "--config", "path"]).strip()
os.environ['GISBASE'] = gisbase
os.environ['GRASS_FONT'] = 'sans'
os.environ['GRASS_OVERWRITE'] = '1' #overwrite existing maps
sys.path.append(os.path.join(gisbase, "etc", "python"))
# set display modules to render into a file (named map.png by default)
os.environ['GRASS_RENDER_IMMEDIATE'] = 'cairo'
os.environ['GRASS_RENDER_FILE_READ'] = 'TRUE'
os.environ['GRASS_LEGEND_FILE'] = 'legend.txt'
# import GRASS GIS
import grass.script as gs
import grass.script.setup as gsetup
from grass.script import core as grass
# for pygrass
from grass.pygrass.modules.shortcuts import raster as r, vector as v, general as g, display as d
from subprocess import PIPE
# further setup for GRASS GIS
gs.set_raise_on_error(True)
#gs.set_capture_stderr(True) #might be Python 2 vs 3 issue (unsure if Python 3 required for this Notebook)
# +
# https://grasswiki.osgeo.org/wiki/GRASS_Python_Scripting_Library
# GRASS Python Scripting Library
# How to retrieve error messages from read_command():
def read2_command(*args, **kwargs): #rename to e.g. read_grass
kwargs['stdout'] = grass.PIPE
kwargs['stderr'] = grass.PIPE
ps = grass.start_command(*args, **kwargs)
return ps.communicate()
# +
# create a mapset (mapset does not already exist)
# should only do once (but will report error and exit if already exists)
# dir /home/kaelin_joseph/projects/RogunHEP/grassdata should already exist
# !grass -c EPSG:3857 /home/kaelin_joseph/projects/RogunHPP/grassdata/RogunHPP -e
# should use grass scipt ToDo JK !!
# define all parameters separately ToDo JK !!
#EPSG:3857 #WGS84 Pseudo Mercator
# -
# open mapset
rcfile = gsetup.init(gisbase,
"/home/kaelin_joseph/projects/RogunHPP/grassdata",
"RogunHPP/", "PERMANENT")
# check grass env
print grass.gisenv()
# check projection info
read2_command('g.proj', flags = 'jf')
#check mapsets
grass.mapsets()
# +
# read dxf data
# read2_command("v.in.dxf", input='/home/kaelin_joseph/projects/RogunHPP/data/testing/Aignment_DG4.dxf',
# output='alignment_dg4', flags='e')[0]
read2_command("v.in.dxf", input='/home/kaelin_joseph/projects/RogunHPP/data/in/AlignmentDG4.dxf',
output='alignment_dg4', flags='e')[0]
# output in 'RogunHPP/PERMANENT/vector/topography2m_r5_reduced'
#read2_command("v.in.dxf")
# pattern for 'printing grass output nicely
# decode must be applied to each member of tuple
# [0] -> stdout
# [1] -> stderr
# above are according to doc, however it seems that [1] is where all output is ToDo JK: ??
# -
# set region from vector data bounds
read2_command('g.region', vector='alignment_dg4')
# check grass region
print(g.region(flags='p',stdout_=PIPE).outputs.stdout.decode())
# view and check topography
# !rm map.png #ToDo JK: pythonize
read2_command("d.vect", map='alignment_dg4', color='green')
Image(filename="map.png")
points_out = read2_command("v.to.points", input='alignment_dg4', output='alignment_dg4_points')
print(points_out[1].decode())
# view and check topography
read2_command("d.vect", map='alignment_dg4_points', color='red')
Image(filename="map.png")
read2_command("v.out.ascii", input='alignment_dg4_points', type='point', separator=',',
output='alignment_dg4_points.csv')
# !head -5 alignment_dg4_points.csv #ToDo JK: pythonize
# +
# #!v.out.ascii --help
# -
read2_command("v.out.ascii", input='alignment_dg4', type='line', format='wkt',
output='alignment_dg4_lines.csv')
# !head -5 alignment_dg4_lines.csv #ToDo JK: pythonize
# cut LINESTRING (first 10 char's) from each line of 'lines' output file
| 4,740 |
/mission_to_mars.ipynb
|
154f95ec69c72b397593e6518b39f24494f7d85e
|
[] |
no_license
|
jwoh1323/Web-Scraping-and-Document-Databases-HW
|
https://github.com/jwoh1323/Web-Scraping-and-Document-Databases-HW
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 14,889 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from splinter import Browser
from bs4 import BeautifulSoup
import pandas as pd
executable_path = {'executable_path': 'chromedriver.exe'}
browser = Browser('chrome', **executable_path, headless=False)
# # NASA Mars News
# +
# URL of page to be scraped
url = 'https://mars.nasa.gov/news/'
browser.visit(url)
html = browser.html
soup = BeautifulSoup(html, 'html.parser')
# +
# store latest news title
title = soup.find_all('div', class_='content_title')
news_title = title[0].text
news_title
# +
# store paragraph of the latest news
body = soup.find_all('div', class_='article_teaser_body')
news_p = body[0].text
news_p
# -
# # JPL Mars Space Images - Featured Image
# +
# store the current Featured Mars Image and assign the url string to a variable
url = 'https://www.jpl.nasa.gov/spaceimages/?search=&category=Mars'
browser.visit(url)
html = browser.html
soup = BeautifulSoup(html, 'html.parser')
# +
image = soup.find_all('a', class_= 'button fancybox')
image = image[0]['data-fancybox-href']
featured_image_url = "https://www.jpl.nasa.gov/" + image
featured_image_url
# -
# # Mars Weather
# +
# scrape the latest Mars weather tweet
url = 'https://twitter.com/marswxreport?lang=en'
browser.visit(url)
html = browser.html
soup = BeautifulSoup(html, 'html.parser')
# -
weather = soup.find_all('p', class_='TweetTextSize TweetTextSize--normal js-tweet-text tweet-text')
mars_weather = weather[0].text
mars_weather
# # Mars Facts
# +
url = 'https://space-facts.com/mars/'
table = pd.read_html(url)
table
# +
# scrape the table and covert it to panda dataframe
df = table[0]
df.columns = ['Description', 'Value']
df
# +
# covert to html
html_table = df.to_html()
html_table = html_table.replace('\n', '')
# +
# save the table directly to a file
df.to_html('table.html')
# -
# # Mars Hemispheres
# +
url = 'https://astrogeology.usgs.gov/search/map/Mars/Viking/cerberus_enhanced'
browser.visit(url)
html = browser.html
soup = BeautifulSoup(html, 'html.parser')
# -
title = soup.find_all('h2', class_ = 'title')
title = title[0].text
title
img = soup.find_all('a', target = '_blank')
img = img[0]['href']
img
# +
url = 'https://astrogeology.usgs.gov/search/map/Mars/Viking/schiaparelli_enhanced'
browser.visit(url)
html = browser.html
soup = BeautifulSoup(html, 'html.parser')
# -
title2 = soup.find_all('h2', class_ = 'title')
title2 = title2[0].text
title2
img2 = soup.find_all('a', target = '_blank')
img2 = img2[0]['href']
img2
# +
url = 'https://astrogeology.usgs.gov/search/map/Mars/Viking/syrtis_major_enhanced'
browser.visit(url)
html = browser.html
soup = BeautifulSoup(html, 'html.parser')
# -
title3 = soup.find_all('h2', class_ = 'title')
title3 = title3[0].text
title3
img3 = soup.find_all('a', target = '_blank')
img3 = img3[0]['href']
img3
# +
url = 'https://astrogeology.usgs.gov/search/map/Mars/Viking/syrtis_major_enhanced'
browser.visit(url)
html = browser.html
soup = BeautifulSoup(html, 'html.parser')
# -
title4 = soup.find_all('h2', class_ = 'title')
title4 = title4[0].text
title4
img4 = soup.find_all('a', target = '_blank')
img4 = img4[0]['href']
img4
hemisphere_image_urls = [
{"title": title, "img_url": img},
{"title": title2, "img_url": img2},
{"title": title3, "img_url": img3},
{"title": title4, "img_url": img4},
]
this np.random.randint was set to (1, 7) so an output of every number from 1 to 12 would be possible. The number 1 was then removed from the final dictionary using del dict[1].
#
# Solution 2 - For this function a default dict was used so it would not throw a key error. The dice values were set and np.random.randint was used to simulate the values.
# ********************************************************************************************************************************
# <br/>
# +
# Solution 1
# Adapted from references [1, 2, 3, 4]
def dicerolls(k,n):
# Set variables
roll = n
noroll = 0
dicevalue = k * 6
# Use list to store dice
dice = []
for i in range(k):
dice.append(i+1)
# Dictionary to store result
dict = {}
while dicevalue > 0:
dict[dicevalue] = 0
dicevalue -= 1
# Roll the dice
while roll > 0:
diceroll = np.random.randint(1,7)
for i in dice:
result = (diceroll + noroll)
dicevalue = dict.get(diceroll)
dict[result] = dicevalue + 1
noroll += 6
roll -= 1
noroll = 0
# Remove 1 from dict output
del dict[1]
print(dict)
dicerolls(2,1000)
# +
# Solution 2
# Adapted from stackoverflow[5]
# Set variables
# Number of dice rolls
n = 1000
# Number of dice
k = 2
# Create a defaultdict to store the results
# Defaultdict is a sub-class of the dict class that returns a dictionary-like object.
# The functionality of both dictionaries and defualtdict are almost same except for the
# fact that defualtdict never raises a KeyError[5]
dicerolls = defaultdict(int)
# Loop through n times
for _ in range(n):
# Simulate random values for the dice rolled
k = np.random.randint(2, 13)
# Increase the result by 1
dicerolls[k]+=1
# Print results
print(dicerolls)
# -
#
# #### References:
#
# [1]. codegrepper.com https://www.codegrepper.com/code-examples/python/dice+rolling+function+python
#
# [2]. careerkarma.com https://careerkarma.com/blog/python-dictionary-get/
#
# [3]. stackoverflow.com https://stackoverflow.com/questions/9001509/how-can-i-sort-a-dictionary-by-key
#
# [4]. stackoverflo.com https://stackoverflow.com/questions/5844672/delete-an-element-from-a-
#
# [5]. stackoverflow.com https://stackoverflow.com/questions/60343980/rolling-2-dice-1000-times-and-counting-the-number-of-times-the-sum-of-the-two-di
# *****************************************************************************************************************************
# <br/>
# <br/>
#
# ## Task 3 - numpy.random.binomial
#
#
# #### Task
# The numpy.random.binomial function can be used to
# simulate flipping a coin with a 50/50 chance of heads or tails. Interestingly, if a
# coin is flipped many times then the number of heads is well approximated by a
# bell-shaped curve. For instance, if we flip a coin 100 times in a row the chance of
# getting 50 heads is relatively high, the chances of getting 0 or 100 heads is relatively
# low, and the chances of getting any other number of heads decreases as you move
# away from 50 in either direction towards 0 or 100. Write some python code that
# simulates flipping a coin 100 times. Then run this code 1,000 times, keeping track
# of the number of heads in each of the 1,000 simulations. Select an appropriate
# plot to depict the resulting list of 1,000 numbers, showing that it roughly follows
# a bell-shaped curve. You should explain your work in a Markdown cell above the
# code.
#
# #### Solution
# Binomial distribution is a distribution where only two outcomes are possible, such as success or failure, gain or loss or win or lose and the probability of success and failure is the same for all its trials <sup>1</sup>. Taking the example of a coin toss, there are only two possible outcomes, heads or tails. The probability of getting a heads (success) can be seen as p = 0.5 and the probability of getting a tails (failure) can be seen as q = 1 - p = 0.5. This function can also be used if outcomes are not equal, eg. if the probability of success is p = 0.2 then the probability of failure is q = 1 - 0.2 = 0.8. Each trial is independent since the outcome of the previous toss doesn’t determine or affect the outcome of the current toss<sup>1</sup>. The total number of trials can be set using n = 20 and by setting size = 1000 we can run the 20 trials 1000 times and view the outcome <sup>2</sup>.
# ******************************************************************************************************************************
# <br/>
# +
# Coin toss example which displays binomial distribution[2].
# Number of trials
size = 1000
# Number of independent coin tosses in each trial
n = 20
# Probability of success for each experiment
p = 0.5
# Run the trials
bd = np.random.binomial(n, p, size)
# Plot the result to show distribution
ax = sns.histplot(bd, kde=True, color='red', bins=12)
ax.set_xlabel ('Binomial distribution')
# +
# Example which displays binomial distribution with unequal probability[2]
# Run trials
bd = np.random.binomial(20, 0.2, 1000)
# Plot distribution
ax = sns.histplot(bd, kde=True, color='red', bins=12)
ax.set_xlabel ('Binomial distribution')
# -
# #### References:
#
# [1]. analyticsvidhya.com https://www.analyticsvidhya.com/blog/2017/09/6-probability-distributions-data-science/
#
# [2]. towardsdatascience.com https://towardsdatascience.com/fun-with-the-binomial-distribution-96a5ecabf65b
# *********************************************************************************************************************
# <br/>
# <br/>
#
# ## Task 4 - Simpson's Paradox
# #### Task
# Simpson’s paradox is a well-known statistical paradox
# where a trend evident in a number of groups reverses when the groups are combined
# into one big data set. Use numpy to create four data sets, each with an x array
# and a corresponding y array, to demonstrate Simpson’s paradox. You might
# create your x arrays using numpy.linspace and create the y array for each
# x using notation like y = a * x + b where you choose the a and b for each
# x , y pair to demonstrate the paradox. You might see the Wikipedia page for
# Simpson’s paradox for inspiration.
# #### Solution
# Simpson's paradox is a phenomenon in probability and statistics in which trends that appears in different groups of data disappear or reverse when these groups are combined. Simpson’s paradox happens because disaggregation of the data can cause certain subgroups to have an imbalanced representation compared to other subgroups. This might be due to the relationship between the variables, or simply due to the way that the data has been seperated into subgroups <sup>1</sup>. This result is particularly problematic when frequency data is given casual interpretations and has been used to illustrate the kind of misleading results misapplied statistics can generate. The paradox can be resolved when causal relations are appropriately addressed in the statistical modeling. It is also referred to as Simpson's reversal, Yule–Simpson effect, amalgamation paradox, or reversal paradox <sup>2</sup>.
#
# Below is a fictional example showing Simpson's Paradox in the context of a correlation reversal. We have created data on the number of hours of exercise per week versus the risk of developing a disease for two sets of patients, those below the age of 50 and those over the age of 50. Here are individual plots showing the relationship between exercise and probability of disease <sup>3</sup>.
# ******************************************************************************************************************************
# <br/>
# +
# Example adapted from https://towardsdatascience.com/simpsons-paradox-how-to-prove-two-opposite-arguments-using-one-dataset-1c9c917f5ff9 [3].
# Create data samples for under_50
n_samples = 100
# Set the seed so the results stay the same
np.random.seed(42)
# Simulate age values
ages = np.random.randint(20, 50, n_samples)
# Simulate hours values
hours = np.random.randint(1, 5, n_samples) + np.random.randn(n_samples)
# Calculate probability
p = 12 + 0.5 * ages + -2.1 * hours + np.random.randn(n_samples) * 2
# Create dataframe
under_50 = pd.DataFrame({'age': ages, 'Hours Exercised': hours, 'probability': p})
# Create data samples for over_50
n_samples = 100
# Simulate age values
ages = np.random.randint(50, 85, n_samples)
# Simulate hours values
hours = np.random.randint(3, 8, n_samples) + np.random.randn(n_samples) * 0.5
#
p = 40 + 0.32 * ages + -3.2 * hours + np.random.randn(n_samples)
over_50 = pd.DataFrame({'age': ages, 'Hours Exercised': hours, 'probability': p})
# Function used to create plots and show relationships
def plot_relationship(data, c, color, ax):
#Plot a scatter plot with linear fit#
x, y = np.array(data[c]), np.array(data['probability'])
# Linear fit (polynomial of degree 1)
b, m = polyfit(x, y, 1)
# Plot scatterplot
data.plot(x = c, y = 'probability', c = color,
style = 'o', legend = None, ax = ax, ms = 10)
# Plot linear fit
ax.plot(x, m * x + b, '-', color = 'k');
if color == '#d9d142':
plt.title(f'Probability vs {c.capitalize()} over 50')
elif color == '#04c5ff':
plt.title(f'Probability vs {c.capitalize()} under 50')
else:
plt.title(f'Probability vs {c.capitalize()} Combined')
corr_coef = np.corrcoef(x, y)[0][1]
ax = plt.gca()
plt.ylabel('Probability');
plt.text(0.2, 0.75, r'$\rho$ = ' + f'{round(corr_coef, 2)}', fontsize = 28, color = 'k',
transform=ax.transAxes)
plt.figure(figsize = (20, 8))
ax = plt.subplot(1, 2, 1)
plot_relationship(under_50, 'Hours Exercised', '#04c5ff', ax)
ax = plt.subplot(1, 2, 2)
plot_relationship(over_50, 'Hours Exercised', '#d9d142', ax)
# -
# <br/>
# The plots clearly show a negative correlation, indicating that increased levels of exercise per week are connected with a lower risk of developing a disease for both groups. However, when combined on a single plot the correlation has completely reversed <sup>3</sup>.
# Create combined plot
plt.figure(figsize = (10, 8))
combined = pd.concat([under_50, over_50], axis = 0)
ax = plt.subplot(1, 1, 1)
plot_relationship(combined, 'Hours Exercised', 'r', ax)
# #### References:
#
# [1]. kdnuggets.com https://www.kdnuggets.com/2020/09/simpsons-paradox.html
#
# [2]. wikipedia.org
# https://en.wikipedia.org/wiki/Simpson%27s_paradox#:~:text=Simpson's%20paradox%2C%20which%20also%20goes,when%20these%20groups%20are%20combined.
#
# [3]. towardsdatascience.com https://towardsdatascience.com/simpsons-paradox-how-to-prove-two-opposite-arguments-using-one-dataset-1c9c917f5ff9
| 14,360 |
/Chatbot/4_seq2seq_part2B.ipynb
|
92192481644a83f20497d837160a13fa5a9d2db9
|
[] |
no_license
|
goldin2008/Research_in_NLP
|
https://github.com/goldin2008/Research_in_NLP
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 50,456 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 演示seq2seq lib中的beam search使用方法
# +
import math
import numpy as np
import sys
import tensorflow as tf
# sys.path.append('C:\\Users\\reade\\Documents\\lecture4\\seq2seq')
sys.path.append('/Users/yuleinku/Google Drive/BOOK/聊天机器人Chatbot/lecture4/seq2seq')
from seq2seq.encoders import rnn_encoder
from seq2seq.decoders import (basic_decoder, beam_search_decoder)
# -
# # 产生/demo 合成数据
# +
PAD = 0
EOS = 1
vocab_size = 10
input_embedding_size = 16
encoder_hidden_units = 32
decoder_hidden_units = encoder_hidden_units
import helpers as data_helpers
batch_size = 10
# 一个generator,每次产生一个minibatch的随机样本
batches = data_helpers.random_sequences(length_from=3, length_to=8,
vocab_lower=2, vocab_upper=10,
batch_size=batch_size)
print('产生%d个长度不一(最短3,最长8)的sequences, 其中前十个是:' % batch_size)
for seq in next(batches)[:min(batch_size, 10)]:
print(seq)
# -
# # 定义使用beamsearch decoder的seq2seq模型
#
# ### 声明placholder和定义encoder部分,同part2A
# +
tf.reset_default_graph()
sess = tf.InteractiveSession()
mode = tf.contrib.learn.ModeKeys.TRAIN
with tf.name_scope('minibatch'):
encoder_inputs = tf.placeholder(shape=(None, None),
dtype=tf.int32,
name='encoder_inputs')
encoder_inputs_length = tf.placeholder(shape=(None,),
dtype=tf.int32,
name='encoder_inputs_length')
decoder_targets = tf.placeholder(shape=(None, None),
dtype=tf.int32,
name='decoder_targets')
decoder_targets_length = tf.placeholder(shape=(None,),
dtype=tf.int32,
name='decoder_targets_length')
decoder_inputs = tf.placeholder(shape=(None, None),
dtype=tf.int32,
name='decoder_inputs')
decoder_inputs_length = tf.placeholder(shape=(None,),
dtype=tf.int32,
name='decoder_inputs_length')
decoder_initial_state = tf.placeholder(shape=(None, None),
dtype=tf.float32,
name='decoder_initial_state')
# 2-a. 定义encoder
encoder_params = rnn_encoder.UnidirectionalRNNEncoder.default_params()
encoder_params["rnn_cell"]["cell_params"]["num_units"] = encoder_hidden_units
encoder_params["rnn_cell"]["cell_class"] = "BasicLSTMCell"
encoder_params
# 2-b. 定义encoding过程
# 输入数据转化为embedding格式
with tf.name_scope('embedding'):
input_embeddings = tf.Variable(
tf.random_uniform([vocab_size, input_embedding_size], -1.0, 1.0),
dtype=tf.float32)
output_embeddings = tf.Variable(
tf.random_uniform([vocab_size, input_embedding_size], -1.0, 1.0),
dtype=tf.float32)
encoder_inputs_embedded = tf.nn.embedding_lookup(input_embeddings, encoder_inputs)
# 使用UnidirectionalRNNEncoder编码
encode_fn = rnn_encoder.UnidirectionalRNNEncoder(encoder_params, mode)
encoder_output = encode_fn(encoder_inputs_embedded, encoder_inputs_length)
# -
# ## 定义decoding模型,使用seq2seq.decoders.beam_search_decoder.BeamSearchDecoder
# 1. input embedding
# 2. helper <-- decoder_input, decoder_input_length
# 3. basic_decoder.BasicDecoder
# ### config decoder的选项,任何基于RNN的decoding操作都需要设定的超参数
decode_params = beam_search_decoder.BeamSearchDecoder.default_params()
decode_params["rnn_cell"]["cell_params"]["num_units"] = decoder_hidden_units
decode_params
# ### config beam_search的选项,即beam_search操作的超参数
#
# * beam_width
# * length_penalty_weight
# * choose_successors_fn
# +
from seq2seq.inference import beam_search
config = beam_search.BeamSearchConfig(
beam_width = 10,
vocab_size = vocab_size,
eos_token = EOS,
length_penalty_weight = 0.6,
choose_successors_fn = beam_search.choose_top_k)
config
# -
from seq2seq.contrib.seq2seq import helper as decode_helper
# +
beam_helper = decode_helper.GreedyEmbeddingHelper(
embedding=output_embeddings,
start_tokens=[0] * config.beam_width,
end_token=-1)
decoder_fn = basic_decoder.BasicDecoder(params=decode_params,
mode=mode,
vocab_size=vocab_size)
"""
decoder_fn = create_decoder(
helper=beam_helper,
mode=tf.contrib.learn.ModeKeys.INFER)
"""
decoder_fn = beam_search_decoder.BeamSearchDecoder(
decoder=decoder_fn,
config=config)
# -
decoder_inputs_embedded = tf.nn.embedding_lookup(input_embeddings, decoder_inputs)
with tf.name_scope('minibatch'):
helper = decode_helper.TrainingHelper(
inputs = decoder_inputs_embedded,
sequence_length = decoder_inputs_length)
decoder_fn = basic_decoder.BasicDecoder(params=decode_params,
mode=mode,
vocab_size=vocab_size)
decoder_output, decoder_state = decoder_fn(encoder_output.final_state, helper)
# +
loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(
labels=tf.one_hot(decoder_targets, depth=vocab_size, dtype=tf.float32),
logits=tf.transpose(decoder_output.logits, perm = [1, 0, 2]))
)
"""
# 通过阅读decoder_helper的定义,
# 输入数据是batch-major
# 而输出数据是time-major...
# 所以需要对输出的logits做一次transpose
# labels: [batch_size, max_length, vocab_size]
# logits (tranpose之前): [max_length, batch_size, vocab_size]
loss = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(
logits = tf.transpose(decoder_output.logits, perm=[1,0,2]), labels = decoder_targets))
"""
train_op = tf.train.AdamOptimizer(learning_rate = 0.001).minimize(loss)
# -
sess.run(tf.global_variables_initializer())
def next_feed():
batch = next(batches)
encoder_inputs_, encoder_inputs_length_ = data_helpers.batch(batch)
decoder_targets_, decoder_targets_length_ = data_helpers.batch(
[(sequence) + [EOS] for sequence in batch]
)
decoder_inputs_, decoder_inputs_length_ = data_helpers.batch(
[[EOS] + (sequence) for sequence in batch]
)
# 在feedDict里面,key可以是一个Tensor
return {
encoder_inputs: encoder_inputs_.T,
decoder_inputs: decoder_inputs_.T,
decoder_targets: decoder_targets_.T,
encoder_inputs_length: encoder_inputs_length_,
decoder_inputs_length: decoder_inputs_length_,
decoder_targets_length: decoder_targets_length_
}
fd= next_feed()
fd
fd[encoder_inputs].shape
fd[decoder_inputs].shape
fd[decoder_targets].shape
# ## 4. 我们已经定义了一个计算图
# * 图的输入端是encoder_inputs 和 encoder_inputs_length
# * 图的输出端是encoder_output
[encoder_out1, decoder_out1] = sess.run(
[encoder_output, decoder_output], fd)
encoder_out1.outputs.shape
decoder_out1.cell_output.shape
decoder_out1.logits.shape
decoder_out1.predicted_ids.shape
print('encoder output information:')
print(encoder_out1.outputs.shape)
print(encoder_out1.final_state.c.shape)
print(encoder_out1.final_state.h.shape)
print('decoder output information:')
print(decoder_out1.predicted_ids.shape)
decoder_out1.predicted_ids.shape
x = next_feed()
print('encoder_inputs:')
print(x[encoder_inputs][0,:])
print('decoder_inputs:')
print(x[decoder_inputs][0,:])
print('decoder_targets:')
print(x[decoder_targets][0,:])
# +
def next_feed():
batch = next(batches)
encoder_inputs_, encoder_inputs_length_ = data_helpers.batch(batch)
decoder_targets_, _ = data_helpers.batch(
[(sequence) + [EOS] for sequence in batch]
)
decoder_inputs_, decoder_inputs_length_ = data_helpers.batch(
[[EOS] + (sequence) for sequence in batch]
)
# 在feedDict里面,key可以是一个Tensor
return {
encoder_inputs: encoder_inputs_.T,
decoder_inputs: decoder_inputs_.T,
decoder_targets: decoder_targets_.T,
encoder_inputs_length: encoder_inputs_length_,
decoder_inputs_length: decoder_inputs_length_
}
batch_size = 100
batches = data_helpers.random_sequences(length_from=3, length_to=8,
vocab_lower=2, vocab_upper=10,
batch_size=batch_size)
print('产生100个长度不一的sequence')
print('其中前十个是:')
for seq in next(batches)[:10]:
print(seq)
# +
loss_track = []
max_batches = 3001
batches_in_epoch = 100
try:
# 一个epoch的learning
for batch in range(max_batches):
fd = next_feed()
_, l = sess.run([train_op, loss], fd)
loss_track.append(l)
if batch == 0 or batch % batches_in_epoch == 0:
print('batch {}'.format(batch))
print(' minibatch loss: {}'.format(sess.run(loss, fd)))
predict_ = sess.run(decoder_output.predicted_ids, fd)
for i, (inp, pred) in enumerate(zip(fd[encoder_inputs], predict_.T)):
print(' sample {}:'.format(i + 1))
print(' input > {}'.format(inp))
print(' predicted > {}'.format(pred))
if i >= 2:
break
print()
except KeyboardInterrupt:
print('training interrupted')
# -
# %matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_track)
print('loss {:.4f} after {} examples (batch_size={})'.format(loss_track[-1], len(loss_track)*batch_size, batch_size))
| 9,738 |
/RayTest-Ray.ipynb
|
8267373aef78a5f772ae6d3d0f3deb7001a57181
|
[] |
no_license
|
anthonysmc/LBL-Research-2021--atlas-group
|
https://github.com/anthonysmc/LBL-Research-2021--atlas-group
| 1 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 11,565 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
"""
#CURRENT VERSION
A simple test of Ray
This example uses placement_group API to spread work around
"""
import random
import os
import platform
import ray
import time
ray.init(ignore_reinit_error=True)
@ray.remote
class Actor():
def __init__(self, actor_id) -> None:
self.pid = os.getpid()
self.hostname = platform.node()
self.ip = ray._private.services.get_node_ip_address()
self.actor_id = actor_id
def ping(self):
print(f"{self.actor_id} {self.pid} {self.hostname} {self.ip} {time.time()} - ping")
time.sleep(random.randint(1,3))
return f"{self.actor_id}"
@ray.remote
def main():
# Get list of nodes to use
print(f"Found {len(actors)} Worker nodes in the Ray Cluster:")
# Setup one Actor per node
print(f"Setting up {len(actors)} Actors...")
time.sleep(1)
# Ping-Pong test
messages = [actors[a].ping.remote() for a in actors]
time.sleep(1)
for _ in range(10):
new_messages, messages = ray.wait(messages, num_returns=1)
for ray_message_id in new_messages:
pong = ray.get(ray_message_id)
print(pong, "- pong")
check = actors[pong].ping.remote()
time.sleep(1)
messages.append(check)
actors = {
"actor1" : Actor.remote(actor_id="actor1"),
"actor2" : Actor.remote(actor_id="actor2"),
"actor3" : Actor.remote(actor_id="actor3"),
"actor4" : Actor.remote(actor_id="actor4"),
"actor5" : Actor.remote(actor_id="actor5")
}
print(actors)
if __name__ == "__main__":
main.remote()
# +
# VERSION TWO
"""
A simple test of Ray
This example uses placement_group API to spread work around
"""
import os
import platform
import ray
import time
ray.init(ignore_reinit_error=True)
@ray.remote
class Actor():
def __init__(self) -> None:
self.pid = os.getpid()
self.hostname = platform.node()
self.ip = ray._private.services.get_node_ip_address()
def ping(self):
print(f"{self.pid} {self.hostname} {self.ip} - ping")
time.sleep(1)
return f"{self.pid} {self.hostname} {self.ip} - pong"
@ray.remote
def main():
# Get list of nodes to use
print(f"Found {len(actors)} Worker nodes in the Ray Cluster:")
# Setup one Actor per node
print(f"Setting up {len(actors)} Actors...")
actor = []
for a in actors:
node_ip_str = f"node:{ray._private.services.get_node_ip_address()}"
actor.append(Actor.remote())
time.sleep(1)
# Ping-Pong test
for _ in range(2):
for a in actors:
time.sleep(1)
messages = a.ping.remote()
time.sleep(1)
print(f"Received back message {ray.get(messages)} \n")
actors = [Actor.remote() for _ in range(5)]
print(actors)
if __name__ == "__main__":
main.remote()
# +
# VERSION THREE
"""
A simple test of Ray
This example uses placement_group API to spread work around
"""
import os
import platform
import ray
import time
ray.init(ignore_reinit_error=True)
@ray.remote
class Actor():
def __init__(self) -> None:
self.pid = os.getpid()
self.hostname = platform.node()
self.ip = ray._private.services.get_node_ip_address()
def ping(self):
print(f"{self.pid} {self.hostname} {self.ip} - ping")
time.sleep(1)
return f"{self.pid} {self.hostname} {self.ip} - pong"
@ray.remote
def main():
# Get list of nodes to use
print(f"Found {len(actors)} Worker nodes in the Ray Cluster:")
# Setup one Actor per node
print(f"Setting up {len(actors)} Actors...")
actor = []
for a in actors:
node_ip_str = f"node:{ray._private.services.get_node_ip_address()}"
actor.append(Actor.remote())
time.sleep(1)
# Ping-Pong test
for _ in range(2):
messages = [a.ping.remote() for a in actors]
for msg in ray.get(messages):
time.sleep(1)
print(f"Received back message {msg}")
time.sleep(1)
actors = [Actor.remote() for _ in range(5)]
print(actors)
if __name__ == "__main__":
main.remote()
8ms
sampling_rate = 44100
duration = 2 # sec
hop_length = 347*2 # to make time steps 128
fmin = 20
fmax = sampling_rate // 2
n_mels = 128
n_fft = n_mels * 20
padmode = 'constant'
samples = sampling_rate * duration
def get_default_conf():
return conf
def set_fastai_random_seed(seed=42):
# https://docs.fast.ai/dev/test.html#getting-reproducible-results
# python RNG
random.seed(seed)
# pytorch RNGs
import torch
torch.manual_seed(seed)
torch.backends.cudnn.deterministic = True
if torch.cuda.is_available(): torch.cuda.manual_seed_all(seed)
# numpy RNG
import numpy as np
np.random.seed(seed)
# +
def mono_to_color(X, mean=None, std=None, norm_max=None, norm_min=None, eps=1e-6):
# Stack X as [X,X,X]
X = np.stack([X, X, X], axis=-1)
# Standardize
mean = mean or X.mean()
X = X - mean
std = std or X.std()
Xstd = X / (std + eps)
_min, _max = Xstd.min(), Xstd.max()
norm_max = norm_max or _max
norm_min = norm_min or _min
if (_max - _min) > eps:
# Normalize to [0, 255]
V = Xstd
V[V < norm_min] = norm_min
V[V > norm_max] = norm_max
V = 255 * (V - norm_min) / (norm_max - norm_min)
V = V.astype(np.uint8)
else:
# Just zero
V = np.zeros_like(Xstd, dtype=np.uint8)
return V
def convert_wav_to_image(df, source):
X = []
for i, row in tqdm_notebook(df.iterrows()):
x = read_as_melspectrogram(conf, source/str(row.fname), trim_long_data=False)
x_color = mono_to_color(x)
X.append(x_color)
return X
def save_as_pkl_binary(obj, filename):
"""Save object as pickle binary file.
Thanks to https://stackoverflow.com/questions/19201290/how-to-save-a-dictionary-to-a-file/32216025
"""
with open(filename, 'wb') as f:
pickle.dump(obj, f, pickle.HIGHEST_PROTOCOL)
def load_pkl(filename):
"""Load pickle object from file."""
with open(filename, 'rb') as f:
return pickle.load(f)
# +
conf = get_default_conf()
def convert_dataset(df, source_folder, filename):
X = convert_wav_to_image(df, source=source_folder)
save_as_pkl_binary(X, filename)
print(f'Created {filename}')
return X
convert_dataset(trn_curated_df, TRN_CURATED, MELS_TRN_CURATED);
convert_dataset(test_df, TEST, MELS_TEST);
# -
# ## Creating Best 50s
# +
df = trn_noisy_df.copy()
df['singled'] = ~df['labels'].str.contains(',')
singles_df = df[df.singled]
cat_gp = (singles_df.groupby(
['labels']).agg({
'fname':'count'
}).reset_index()).set_index('labels')
plot = cat_gp.plot(
kind='barh',
title="Number of samples per label",
figsize=(15,20))
plot.set_xlabel("Noisy Set's Number of Samples", fontsize=20)
plot.set_ylabel("Label", fontsize=20);
# -
labels = singles_df['labels'].unique()
print(labels)
print(len(labels))
# +
idxes_best50s = np.array([random.choices(singles_df[(singles_df['labels'] == l)].index, k=50)
for l in labels]).ravel()
best50s_df = singles_df.loc[idxes_best50s]
grp = (best50s_df.groupby(
['labels']).agg({
'fname':'count'
}).reset_index()).set_index('labels')
grp.plot( kind='barh', title="Best 50s' Number of samples per label", figsize=(15,20));
# -
best50s_df.to_csv(CSV_TRN_NOISY_BEST50S, index=False)
# ### Now best 50s are selected
#
# Making preprocessed data is as follows, but you have to run locally. Kernel cannot hold all the noisy preprocessed data on memory.
# +
# Convert noisy set first
X_trn_noisy = convert_dataset(trn_noisy_df, TRN_NOISY, MELS_TRN_NOISY)
# Then choose preprocessed data for 50s, and save it
X = [X_trn_noisy[i] for i in idxes_best50s]
save_as_pkl_binary(X, MELS_TRN_NOISY_BEST50S)
# -
| 8,223 |
/Manipulating Elements in a Data Frame.ipynb
|
72ac63bb3039b5a2df051d42e0ca28691e154917
|
[] |
no_license
|
haider2122/Data-Analysis
|
https://github.com/haider2122/Data-Analysis
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 27,196 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# + active=""
# BEST Practices to Manipulate elements in a Data Frame
# -
import pandas as pd
t=pd.read_csv('titanic.csv')
# + active=""
# Changing a single value
# -
t.loc[2,'age']=27
t.head(3)
t.iloc[1,0]=0
t.head(2)
# + active=""
# Changing Multiple Values
# -
t.loc[[4,6,8],['survived']]=[1,1,1]
t.head(9)
# +
#The above can also be done using iloc
# +
l=list(t.loc[t.age<=1].index)#Creating a list of index's of babies(age<1)
l
# -
t.loc[l,'age']=1
t.iloc[l,::]#Therefore values Have been rounded
t.iloc[4,0:3]=[1,1,'male']#Changing values in a row
t.replace(0,'zero').head(2)
t.replace(t.loc[2,'sex'],'male').head(2)#Hence value of row changes
# + active=""
# Views and Copy's
# If its a view, a change on the slice will reflect in the orginal data frame.
# -
age=t.loc[::,'age']
age._is_view
age.iloc[1:4]=4#Hence warning comes of value being changed in orginal data frame
x=t.loc[t.age<1]
x._is_view#Fence the following is a copy, won't reflect in the data frame
# + active=""
# Two Methods to perform definite and practical manipulation
#
# + active=""
# 1) To Change Values in a Data Frame-
# avoid chained indexing
# -
t.loc[8,'age']=10#directly changing value in data frame
# + active=""
# 2) Avoid Changing Values in a data frame,but only operate with a slice of data frame
# -
age=t.age.copy()
age.iloc[2]=1#Changing value only in Series
colab={"base_uri": "https://localhost:8080/"} outputId="9539decb-54d3-4c39-902b-eccc1917e5b8"
# Dowload and extract CEFAR signature dataset
URL = "http://www.cedar.buffalo.edu/NIJ/data/signatures.rar"
filename = "signatures.rar"
dataset_directory ="signatures"
if os.path.exists(dataset_directory) == False:
if os.path.exists(filename) == False:
print("Dowloading dataset")
# !wget --output-document=$filename $URL
print("Extracting rar file")
# !mkdir -p signatureDataset
# !unrar x -y $filename $dataset_directory
# + id="UHHKNIlbDTIH"
# Create list that consist filename of genuine signatures
# Assume all signature is genuine signature
sign_list = []
sign_labels = []
sign_path = os.path.join(dataset_directory, "full_org")
for sign in sorted(os.listdir(sign_path)):
if sign.find("png") > 0:
sign_list.append(sign)
sign_labels.append(int(sign.split("_")[1]))
# Convert list to numpy array
sign_array = np.array(sign_list)
sign_label_array = np.array(sign_labels)
num_writers = 55
total_signature_for_each_writer = 24
total_size_signatures = sign_label_array.shape[0]
# + colab={"base_uri": "https://localhost:8080/"} id="ExZbza31GQt8" outputId="d28a1ffa-f2db-406a-a451-674a66caaf42"
# Show the full path of the signatures
print("Filename is : ", sign_array[0])
print("Label is : ", sign_label_array[0])
# Size of signature images
print("Total size of the signatures is : ", total_size_signatures)
# Shape of a signature image
im = cv2.imread(os.path.join(sign_path, sign_array[0]))
print("Shape is : ", im.shape)
# + id="UrTu6HwzHyV2"
# Visualize the signatures
def visualize_signature(isWriterSame = False, isSignatureSame = False):
img_size = (224, 224)
w1 = np.random.randint(num_writers - 1) + 1
w2 = np.random.randint(num_writers - 1) + 1
s1 = np.random.randint(total_signature_for_each_writer - 1) + 1
s2 = np.random.randint(total_signature_for_each_writer - 1) + 1
if isWriterSame == True:
w2 = w1
if isSignatureSame == True:
s2 = s1
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,10))
im1_name = "/original_" + str(w1) + "_" + str(s1) + ".png"
im2_name = "/original_" + str(w2) + "_" + str(s2) + ".png"
orig_im_1 = cv2.resize(cv2.imread(sign_path + im1_name), img_size)
orig_im_2 = cv2.resize(cv2.imread(sign_path + im2_name), img_size)
ax1.imshow(orig_im_1, cmap = "gray")
ax2.imshow(orig_im_2, cmap = "gray")
ax1.set_title("Signature 1")
ax2.set_title("Signature 2")
ax1.axis('off')
ax2.axis('off')
# + colab={"base_uri": "https://localhost:8080/", "height": 301} id="VFgrVpC-RZMv" outputId="664ed617-8823-4a43-ae0b-57246097e244"
visualize_signature(isWriterSame = True, isSignatureSame = True)
# + colab={"base_uri": "https://localhost:8080/", "height": 301} id="w_sUZ4yJXH57" outputId="a7ac970c-3be7-43f8-d35e-6e8af06d919a"
visualize_signature()
# + colab={"base_uri": "https://localhost:8080/", "height": 301} id="iVDNQY83IyIC" outputId="91a8d605-8303-45ce-a72a-cc4c68b845a7"
visualize_signature(isWriterSame = True)
# + id="egbYYl7sXKzQ"
def create_pairs(x, digit_indices):
'''Positive and negative pair creation.
Alternates between positive and negative pairs.
'''
pairs = []
labels = []
n = min([len(digit_indices[d]) for d in range(num_writers)]) - 1
n = min([len(digit_indices[d]) for d in range(num_writers)]) - 1
for d in range(num_writers):
for i in range(n):
for j in range(2):
z1, z2 = digit_indices[d][i], digit_indices[d][i + 1]
pairs += [[x[z1], x[z2]]]
inc = random.randrange(1, num_writers + 1)
dn = (d + inc) % num_writers
z1, z2 = digit_indices[d][i], digit_indices[dn][i]
pairs += [[x[z1], x[z2]]]
labels += [1, 0]
return np.array(pairs), np.array(labels)
def create_pairs_on_set(images, labels):
digit_indices = [np.where(labels == i)[0] for i in range(1, num_writers + 1)]
pairs, y = create_pairs(images, digit_indices)
y = y.astype('float32')
return pairs, y
def show_image(image):
plt.figure()
plt.imshow(image)
plt.colorbar()
plt.grid(False)
plt.show()
# + id="xCfo8U8BSZcu"
# create pairs
pairs, y = create_pairs_on_set(sign_array, sign_label_array)
# preprocessing
pairs_image = []
img_size = (224, 224, 1)
for i in range(pairs.shape[0]):
# resize images
im1 = cv2.resize(cv2.imread(os.path.join(sign_path, pairs[i][0]), cv2.IMREAD_GRAYSCALE), img_size[0:2])
im2 = cv2.resize(cv2.imread(os.path.join(sign_path, pairs[i][1]), cv2.IMREAD_GRAYSCALE), img_size[0:2])
# normalize
im1 = im1.astype('float32')
im2 = im2.astype('float32')
# normalize values
im1 = im1 / 255.0
im2 = im2 / 255.0
pairs_image += [[im1, im2]]
pairs_image_array = np.array(pairs_image)
# + colab={"base_uri": "https://localhost:8080/", "height": 538} id="hF2HuOaNDb2_" outputId="841102a5-f24d-42e8-dd89-072ff7b8fe3f"
# array index
this_pair = random.randrange(len(pairs)-1)
# show images at this index
show_image(pairs_image_array[this_pair][0])
show_image(pairs_image_array[this_pair][1])
# print the label for this pair
print(y[this_pair])
# + id="j_Jl5t-oK-dK"
# shuffle data
shuffled_x, shuffled_y = shuffle(pairs_image_array, y)
# split data as train and test
train_ratio = 0.8;
train_size = int(train_ratio * shuffled_x.shape[0])
train_x = shuffled_x[:train_size]
train_y = shuffled_y[:train_size]
test_x = shuffled_x[train_size:]
test_y = shuffled_y[train_size:]
# + colab={"base_uri": "https://localhost:8080/"} id="750vPg0kLyfh" outputId="3c98c183-89e6-4542-c909-8ba50bc66ec7"
# Lengh of train and test data
print("Size of train image pairs is : ", train_x.shape[0])
print("Size of test image pairs is : ", test_x.shape[0])
# + [markdown] id="t-ZJnujnN0FJ"
# ## Build the Model
#
# + id="o0o4--UWN4NB"
def initialize_base_network():
input = Input(shape=img_size, name="base_input2")
x = Conv2D(128, kernel_size=(7,7), activation="relu", name='conv1_1', strides=4)(input)
x = BatchNormalization()(x)
x = MaxPooling2D(pool_size=(3,3), strides=(2,2))(x)
x = Conv2D(256, kernel_size=(5,5), activation="relu", name='conv2_1', strides=1)(x)
x = BatchNormalization()(x)
x = MaxPooling2D(pool_size=(3,3), strides=(2,2))(x)
x = Conv2D(512, kernel_size=(3,3), activation="relu", name='conv3_1', strides=1)(x)
x = Conv2D(1024, kernel_size=(3,3), activation="relu", name='conv5_1', strides=1)(x)
x = GlobalAveragePooling2D()(x)
x = Dense(1024, activat
| 8,192 |
/book/packt/Bioinformatics.with.Python.Cookbook/notebooks/Welcome.ipynb
|
6803d8c756c7d8a69152c8592abbe01d06c2fb82
|
[] |
no_license
|
xenron/sandbox-python
|
https://github.com/xenron/sandbox-python
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 7,005 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Python for Bioinformatics
# ###[Click here for the datasets used in the book](Datasets.ipynb)
# ## Python 2 or 3?
# Depending on your Python version, some content might not be available. Lets test that:
import platform
major, minor, patch = platform.python_version_tuple()
if major == 3:
print('Python 3: The Phylogenomics module will not work, but all the Big Data content will')
else:
print('Python 2: The Phylogenomics module will work, but some Big Data content will not')
# ## Python and the surrounding software ecology
# * [Interfacing with R](00_Intro/Interfacing_R.ipynb)
# * [R Magic](00_Intro/R_magic.ipynb)
# ## Next Generation Sequencing
# * [Accessing Databases](01_NGS/Accessing_Databases.ipynb)
# * [Basic Sequence Processing](01_NGS/Basic_Sequence_Processing.ipynb)
# * [Working with FASTQ files](01_NGS/Working_with_FASTQ.ipynb)
# * [Working with BAM files](01_NGS/Working_with_BAM.ipynb)
# * [Working with VCF files](01_NGS/Working_with_VCF.ipynb)
# * [Filtering SNPs](01_NGS/Filtering_SNPs.ipynb)
# ## Genomics
# * [Reference Genomes](02_Genomes/.ipynb)
# * [Low Quality Reference Genomes](02_Genomes/.ipynb)
# * [Annotations](02_Genomes/.ipynb)
# * [Getting](02_Genomes/.ipynb)
# * [Orthology](02_Genomes/.ipynb)
# * [Gene Ontology](02_Genomes/.ipynb)
# ## Population Genetics
# * [Data Formats with PLINK](03_PopGen/Data_Formats.ipynb)
# * [The Genepop Format](03_PopGen/Genepop_Format.ipynb)
# * [Exploratory Analysis](03_PopGen/Exploratory_Analysis.ipynb)
# * [F statistics](03_PopGen/F-stats.ipynb)
# * [Principal Components Analysis (PCA)](03_PopGen/PCA.ipynb)
# * [Admixture/Structure](03_PopGen/Admixture.ipynb)
#
# ## Simulation in Population Genetics
# * [Introducing Forward-time simulations](04_PopSim/Basic_SimuPOP.ipynb)
# * [Simulating selection](04_PopSim/Selection.ipynb)
# * [Doing population structure with island and stepping-stone models](04_PopSim/Pop_Structure.ipynb)
# * [Modeling complex demographic scenarios](04_PopSim/Complex.ipynb)
# * [Simulating the coalescent with Biopython and fastsimcoal](04_PopSim/Coalescent.ipynb)
# ## Phylogenetics
# * [Preparing the Ebola dataset](05_Phylo/Exploration.ipynb)
# * [Aligning genetic and genomic data](05_Phylo/Alignment.ipynb)
# * [Comparing sequences](05_Phylo/Comparison.ipynb)
# * [Playing recursively with trees](05_Phylo/Trees.ipynb)
# * [Reconstructing Phylogenetic trees](05_Phylo/Reconstruction.ipynb)
# * [Visualizing Phylogenetic data](05_Phylo/Visualization.ipynb)
#
# ## Proteomics
# * [Finding a protein in multiple databases](06_Prot/Intro.ipynb)
# * [Introducing Bio.PDB](06_Prot/PDB.ipynb)
# * [Extracting more information from a PDB file](06_Prot/Stats.ipynb)
# * [Computing distances on a PDB file](06_Prot/Distance.ipynb)
# * [Doing geometric operations](06_Prot/Mass.ipynb)
# * [Implementing a basic PDB parser](06_Prot/Parser.ipynb)
# * [Parsing mmCIF files with Biopython](06_Prot/mmCIF.ipynb)
#
# The code for the PyMol recipe can be found on the pymol directory of the [github project](https://github.com/tiagoantao/bioinf-python)
# ## Other topics
# * [Accessing the Global Biodiversity Information Facility (GBIF)via REST](07_Other/GBIF.ipynb)
# * [Geo-referencing GBIF datasets](07_Other/GBIF_Extra.ipynb)
# * [Accessing molecular-interaction databases with PSIQUIC](07_Other/PSICQUIC.ipynb)
# * [Plotting protein interactions with Cytoscape the hard way](07_Other/Cytoscape.ipynb)
# ## Advanced Python for Bioinformatics
# * [Setting the stage for high performance computing](08_Advanced/Intro.ipynb)
# * [Designing a poor-human concurrent executor](08_Advanced/Multiprocessing.ipynb)
# * [Doing parallel computing with IPython](08_Advanced/IPythonParallel.ipynb)
# * [Approximating the median in a large dataset](08_Advanced/Median.ipynb)
# * [Optimizing code with Cython and Numba](08_Advanced/Cython_Numba.ipynb)
# * [Programming with lazyness](08_Advanced/Lazy.ipynb)
# * [Thinking with generators](08_Advanced/Generators.ipynb)
#
pt_MC,pcov_MC = leastsq(ellip_moffat2D,x0=p,args=(xy,iteration_data,error),maxfev = 10000000)
[amp_MC,x0_MC,y0_MC,A_MC,B_MC,C_MC,alpha_MC]= popt_MC
theta_MC = 0.5*np.arctan(C_MC/(A_MC - B_MC))
a_MC = np.sqrt(2/(A_MC + B_MC + np.sqrt(C_MC**2 +(A_MC - B_MC)**2)))
b_MC = np.sqrt(2/(A_MC + B_MC - np.sqrt(C_MC**2 +(A_MC - B_MC)**2)))
[fwhm1_MC,fwhm2_MC] = [2*a_MC*np.sqrt(2**(1/alpha_MC)-1),2*b_MC*np.sqrt(2**(1/alpha_MC)-1)]
par_MC = [amp_MC,x0_MC,y0_MC,A_MC,B_MC,C_MC,alpha_MC,a_MC,b_MC,theta_MC,fwhm1_MC,fwhm2_MC]
parameters_MC[:,l] = par_MC
else:
p= [amp,x0,y0]
popt_MC,pcov_MC = leastsq(ellip_moffat2D_fixkin,x0=p,args=(xy,iteration_data,error,fix_par),maxfev = 10000000)
[amp_MC,x0_out,y0_out]= popt_MC
parameters_MC[:,l] = popt_MC
parameters_err = np.std(parameters_MC,1)
return par,parameters_err,model,res
# +
def moffat_table(full_data,full_error,D_A,D_L,muse_sampling_size,obj,destination_path_cube="/home/mainak/Downloads/Outflow_paper1/MUSE"):
final_data = np.append(full_data,[D_A,D_L,muse_sampling_size])
final_error = np.append(full_error,[0,0,0])
column_names={'amp_Hb_blr':0,'x0_Hb_Blr':1,'y0_Hb_Blr':2,'A':3,'B':4,'C':5,'alpha':6,'a':7,'b':8,'theta':9,'fwhm1':10,'fwhm2':11,'amp_OIII_br':12,'x0_OIII_br':13,'y0_OIII_br':14,'amp_OIII_nr':15,'x0_OIII_nr':16,'y0_OIII_nr':17,'D_A':18,'D_L':19,'sampling_size':20}
columns=[]
for key in column_names.keys():
columns.append(fits.Column(name=key,format='E',array=[final_data[column_names[key]]]))
columns.append(fits.Column(name=key+'_err',format='E',array=[final_error[column_names[key]]]))
coldefs = fits.ColDefs(columns)
hdu = fits.BinTableHDU.from_columns(coldefs)
hdu.writeto('%s/%s/9_arcsec_moffat_table_%s.fits'%(destination_path_cube,obj,obj),overwrite=True)
def source_moffat_table(obj,destination_path_cube="/home/mainak/Downloads/Outflow_paper1/MUSE"):
t1 = Table.read('%s/%s/source_%s.fits'%(destination_path_cube,obj,obj),format='fits')
t2 = Table.read('%s/%s/9_arcsec_moffat_table_%s.fits'%(destination_path_cube,obj,obj),format='fits')
new = hstack([t1, t2])
new.write('%s/%s/%s_9_arcsec_moffat_table.fits'%(destination_path_cube,obj,obj),overwrite=True)
def maps(Hb_blr_br_data,OIII_br_data,OIII_nr_data,Hb_model,OIII_br_model,OIII_nr_model,Hb_res,OIII_br_res,OIII_nr_res,obj,destination_path_cube="/home/mainak/Downloads/Outflow_paper1/MUSE"):
hdus=[]
hdus.append(fits.PrimaryHDU())
hdus.append(fits.ImageHDU(Hb_blr_br_data,name='Hb_blr_br_data'))
hdus.append(fits.ImageHDU(OIII_br_data,name='OIII_br_data'))
hdus.append(fits.ImageHDU(OIII_nr_data,name='OIII_nr_data'))
hdus.append(fits.ImageHDU(Hb_model,name='Hb_blr_br_model'))
hdus.append(fits.ImageHDU(OIII_br_model,name='OIII_br_model'))
hdus.append(fits.ImageHDU(OIII_nr_model,name='OIII_nr_model'))
hdus.append(fits.ImageHDU(Hb_res,name='Hb_blr_br_res'))
hdus.append(fits.ImageHDU(OIII_br_res,name='OIII_br_res'))
hdus.append(fits.ImageHDU(OIII_nr_res,name='OIII_nr_res'))
hdu = fits.HDUList(hdus)
hdu.writeto('%s/%s/9_arcsec_maps_%s.fits'%(destination_path_cube,obj,obj),overwrite='True')
def fluxden_compare(obj,Hb_blr_br_data,OIII_br_data,Hb_model,OIII_br_model,Hb_blr_br_err,OIII_br_err,destination_path_cube="/home/mainak/Downloads/Outflow_paper1/MUSE"):
f_blr_data = np.sum(Hb_blr_br_data)
f_wing_data = np.sum(OIII_br_data)
f_blr_model = np.sum(Hb_model)
f_wing_model = np.sum(OIII_br_model)
f_blr_err = np.sqrt(np.sum(Hb_blr_br_err**2))
f_wing_err = np.sqrt(np.sum(OIII_br_err**2))
tab_par = [f_blr_data,f_wing_data,f_blr_model,f_wing_model]
tab_err = [f_blr_err,f_wing_err,0,0]
column_names={'flux_blr_data':0,'flux_wing_data':1,'flux_blr_model':2,'flux_wing_model':3}
columns=[]
for key in column_names.keys():
columns.append(fits.Column(name=key,format='E',array=[tab_par[column_names[key]]]))
columns.append(fits.Column(name=key+'_err',format='E',array=[tab_err[column_names[key]]]))
coldefs = fits.ColDefs(columns)
hdu = fits.BinTableHDU.from_columns(coldefs)
hdu.writeto('%s/%s/%s_9_arcsec_fluxden_HbOIII.fits'%(destination_path_cube,obj,obj),overwrite=True)
def fluxden_comp_table(obj,destination_path_cube="/home/mainak/Downloads/Outflow_paper1/MUSE"):
t1 = Table.read('%s/%s/source_%s.fits'%(destination_path_cube,obj,obj),format='fits')
t2 = Table.read('%s/%s/%s_9_arcsec_fluxden_HbOIII.fits'%(destination_path_cube,obj,obj),format='fits')
new = hstack([t1, t2])
new.write('%s/%s/%s_9_arcsec_fluxden_HbOIII.fits'%(destination_path_cube,obj,obj),overwrite=True)
def emp_table(obj,emp_blr,emp_wing,destination_path_cube="/home/mainak/Downloads/Outflow_paper1/MUSE"):
popt = [emp_blr,emp_wing]
column_names={'emp_fact_blr':0,'emp_fact_wing':1}
columns=[]
for key in column_names.keys():
columns.append(fits.Column(name=key,format='E',array=[popt[column_names[key]]]))
coldefs = fits.ColDefs(columns)
hdu = fits.BinTableHDU.from_columns(coldefs)
hdu.writeto('%s/%s/%s_9_arcsec_scaling_subcube.fits'%(destination_path_cube,obj,obj),overwrite=True)
def emp_fact_table(obj,destination_path_cube="/home/mainak/Downloads/Outflow_paper1/MUSE"):
t1 = Table.read('%s/%s/source_%s.fits'%(destination_path_cube,obj,obj),format='fits')
t2 = Table.read('%s/%s/%s_9_arcsec_scaling_subcube.fits'%(destination_path_cube,obj,obj),format='fits')
new = hstack([t1, t2])
new.write('%s/%s/%s_9_arcsec_scaling_subcube.fits'%(destination_path_cube,obj,obj),overwrite=True)
# -
def algorithm_script(obj,z,destination_path_cube="/home/mainak/Downloads/Outflow_paper1/MUSE"):
print ('%s'%(obj))
(Hb_blr_br_dat,OIII_br_dat,OIII_nr_dat,amp_Hb_blr_br,amp_OIII_br,amp_OIII_nr,Hb_blr_br_error,OIII_br_error,OIII_nr_error) = flux_data_err(obj)
(Hb_blr_br_data,Hb_blr_br_err) = remove_bad_pixel(Hb_blr_br_dat,Hb_blr_br_error)
(OIII_br_data,OIII_br_err) = remove_bad_pixel(OIII_br_dat,OIII_br_error)
(OIII_nr_data,OIII_nr_err) = remove_bad_pixel(OIII_nr_dat,OIII_nr_error)
box_size = np.shape(Hb_blr_br_data)[0]
(brightest_pixel_Hb_blr_br_x,brightest_pixel_Hb_blr_br_y,brightest_pixel_OIII_br_x,brightest_pixel_OIII_br_y,brightest_pixel_OIII_nr_x,brightest_pixel_OIII_nr_y) = brightest_pixel_flux_map(Hb_blr_br_data,OIII_br_data,OIII_nr_data)
print (brightest_pixel_OIII_nr_x,brightest_pixel_OIII_nr_y)
if box_size ==45:
muse_sampling_size = 0.2
else:
muse_sampling_size = 0.4
print (muse_sampling_size)
(Hb_par,Hb_error,Hb_model,Hb_res) = elliptical_moffat_fit(Hb_blr_br_data,Hb_blr_br_err,box_size,amp_Hb_blr_br,brightest_pixel_Hb_blr_br_x,brightest_pixel_Hb_blr_br_y,muse_sampling_size,None,100)
print (Hb_par,Hb_error)
#print (red_chi_sq_Hb)
fixed_param = [Hb_par[3],Hb_par[4],Hb_par[5],Hb_par[6]]
(OIII_br_par,OIII_br_error,OIII_br_model,OIII_br_res) = elliptical_moffat_fit(OIII_br_data,OIII_br_err,box_size,amp_OIII_br,brightest_pixel_OIII_br_x,brightest_pixel_OIII_br_y,muse_sampling_size,fixed_param,100)
print (OIII_br_par,OIII_br_error)
(OIII_nr_par,OIII_nr_error,OIII_nr_model,OIII_nr_res) = elliptical_moffat_fit(OIII_nr_data,OIII_nr_err,box_size,amp_OIII_nr,brightest_pixel_OIII_nr_x,brightest_pixel_OIII_nr_y,muse_sampling_size,fixed_param,100)
print (OIII_nr_par,OIII_nr_error)
(D_A,D_L) = dist(z, H0=70, WM=.286)
(full_data,full_error) = (np.append(Hb_par,[OIII_br_par,OIII_nr_par]),np.append(Hb_error,[OIII_br_error,OIII_nr_error]))
moffat_table(full_data,full_error,D_A,D_L,muse_sampling_size,obj,destination_path_cube="/home/mainak/Downloads/Outflow_paper1/MUSE")
maps(Hb_blr_br_data,OIII_br_data,OIII_nr_data,Hb_model,OIII_br_model,OIII_nr_model,Hb_res,OIII_br_res,OIII_nr_res,obj)
fluxden_compare(obj,Hb_blr_br_data,OIII_br_data,Hb_model,OIII_br_model,Hb_blr_br_err,OIII_br_err)
source_moffat_table(obj)
plt.imshow(Hb_blr_br_data,origin='lower')
plt.plot(Hb_par[1],Hb_par[2],'kx')
plt.show()
plt.imshow(Hb_model,origin='lower')
plt.plot(Hb_par[1],Hb_par[2],'kx')
plt.show()
plt.imshow(OIII_br_data,origin='lower')
plt.plot(OIII_br_par[1],OIII_br_par[2],'bx')
plt.show()
plt.imshow(OIII_br_model,origin='lower')
plt.plot(OIII_br_par[1],OIII_br_par[2],'bx')
plt.show()
plt.imshow(OIII_nr_data,origin='lower')
plt.plot(OIII_nr_par[1],OIII_nr_par[2],'gx')
plt.show()
plt.imshow(OIII_nr_model,origin='lower')
plt.plot(OIII_nr_par[1],OIII_nr_par[2],'gx')
plt.show()
# +
z = {"HE0108-4743":0.02392}
objs = z.keys()
for obj in objs:
(Hb_blr_br_data,OIII_br_data,OIII_nr_data,amp_Hb_blr_br,amp_OIII_br,amp_OIII_nr,Hb_blr_br_err,OIII_br_err,OIII_nr_err) = flux_data_err(obj)
box_size = np.shape(Hb_blr_br_data)[1]
y, x = np.mgrid[:box_size, :box_size]
xy=(x,y)
algorithm_script(obj,z[obj])
# +
z = {"HE0021-1819":0.053197,"HE0040-1105":0.041692,"HE0108-4743":0.02392,"HE0114-0015":0.04560
,"HE0119-0118":0.054341,"HE0212-0059":0.026385,"HE0224-2834":0.059800,"HE0227-0913":0.016451,"HE0232-0900":0.043143
,"HE0253-1641":0.031588,"HE0345+0056":0.031,"HE0351+0240":0.036,"HE0412-0803":0.038160,"HE0429-0247":0.042009
,"HE0433-1028":0.035550,"HE0853+0102":0.052,"HE0934+0119":0.050338,"HE1011-0403":0.058314,"HE1017-0305":0.049986
,"HE1029-1831":0.040261,"HE1107-0813":0.058,"HE1108-2813":0.024013,"HE1126-0407":0.061960,"HE1237-0504":0.009
,"HE1248-1356":0.01465,"HE1330-1013":0.022145,"HE1353-1917":0.035021,"HE1417-0909":0.044,"HE2128-0221":0.05248
,"HE2211-3903":0.039714,"HE2222-0026":0.059114,"HE2233+0124":0.056482,"HE2302-0857":0.046860}
objs = z.keys()
for obj in objs:
(Hb_blr_br_data,OIII_br_data,OIII_nr_data,amp_Hb_blr_br,amp_OIII_br,amp_OIII_nr,Hb_blr_br_err,OIII_br_err,OIII_nr_err) = flux_data_err(obj)
box_size = np.shape(Hb_blr_br_data)[1]
y, x = np.mgrid[:box_size, :box_size]
xy=(x,y)
algorithm_script(obj,z[obj])
# +
z = {"HE0021-1810":0.05352}
objs = z.keys()
for obj in objs:
(Hb_blr_br_data,OIII_br_data,OIII_nr_data,amp_Hb_blr_br,amp_OIII_br,amp_OIII_nr,Hb_blr_br_err,OIII_br_err,OIII_nr_err) = flux_data_err(obj)
box_size = np.shape(Hb_blr_br_data)[1]
y, x = np.mgrid[:box_size, :box_size]
xy=(x,y)
algorithm_script(obj,z[obj])
# -
21.63782717011039, 22.119457979406324
x,y
169.9*4.848*0.2*np.sqrt((21.65 - 22.18)**2 + (21.68-21.81)**2)
| 14,915 |
/Data Cleaning and Modelling/Modelling State Variables/Tidying up data.ipynb
|
091f6c51f2266b6640501d544dd65ee3d2b6519b
|
[
"MIT"
] |
permissive
|
ashez2051/Metamodelling-of-Pandit-Hinch-Niederer-Model
|
https://github.com/ashez2051/Metamodelling-of-Pandit-Hinch-Niederer-Model
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 1,233,175 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# %pylab inline
# +
import os
import urllib
dataset = 'mnist.pkl.gz'
def reporthook(a,b,c):
print "\rdownloading: %5.1f%%"%(a*b*100.0/c),
if not os.path.isfile(dataset):
origin = "https://github.com/mnielsen/neural-networks-and-deep-learning/raw/master/data/mnist.pkl.gz"
print('Downloading data from %s' % origin)
urllib.urlretrieve(origin, dataset, reporthook=reporthook)
# -
import gzip
import pickle
with gzip.open(dataset, 'rb') as f:
train_set, valid_set, test_set = pickle.load(f)
print "train_set", train_set[0].shape, train_set[1].shape
print "valid_set", valid_set[0].shape, valid_set[1].shape
print "test_set", test_set[0].shape, test_set[1].shape
imshow(train_set[0][0].reshape((28, 28)), cmap="gray")
def show(x, i=[0]):
plt.figure(i[0])
imshow(x.reshape((28,28)), cmap="gray")
i[0]+=1
for i in range(5):
print train_set[1][i]
show(train_set[0][i])
W = np.random.uniform(low=-1, high=1, size=(28*28,10))
b = np.random.uniform(low=-1, high=1, size=10)
x = train_set[0][0]
y = train_set[1][0]
show(x)
y
Pr = exp(dot(x, W)+b)
Pr.shape
Pr = Pr/Pr.sum()
print Pr
Pr.argmax()
loss = -log(Pr[y])
loss
gradb = Pr.copy()
gradb[y] -= 1
print gradb
print Pr.shape, x.shape, W.shape
gradW = dot(x.reshape(784,1), Pr.reshape(1,10), )
gradW[:, y] -= x
W -= 0.1 * gradW
b -= 0.1 * gradb
def compute_Pr(x):
Pr = exp(dot(x, W)+b)
return Pr/Pr.sum(axis=1, keepdims=True)
def compute_accuracy(Pr, y):
return mean(Pr.argmax(axis=1)==y)
W = np.random.uniform(low=-1, high=1, size=(28*28,10))
b = np.random.uniform(low=-1, high=1, size=10)
score = 0
N=50000*20
d = 0.001
learning_rate = 1e-2
for i in xrange(N):
if i%50000==0:
print i, "%5.3f%%"%(score*100)
x = train_set[0][i%50000]
y = train_set[1][i%50000]
Pr = exp(dot(x, W)+b)
Pr = Pr/Pr.sum()
loss = -log(Pr[y])
score *=(1-d)
if Pr.argmax() == y:
score += d
gradb = Pr.copy()
gradb[y] -= 1
gradW = dot(x.reshape(784,1), Pr.reshape(1,10), )
gradW[:, y] -= x
W -= learning_rate * gradW
b -= learning_rate * gradb
x = test_set[0][:10]
y = test_set[1][:10]
Pr = compute_Pr(x)
print Pr.argmax(axis=1)
print y
for i in range(10):
show(x[i])
nb.freesurfer.io.read_label((os.path.join(
datadir,'fsaverage5/rh.cortex.label')))
surf_mesh = {}
surf_mesh['coords'] = np.concatenate((Fs_Mesh_L[0], Fs_Mesh_R[0]))
surf_mesh['tri'] = np.concatenate((Fs_Mesh_L[1], Fs_Mesh_R[1]))
bg_map = np.concatenate((Fs_Bg_Map_L, Fs_Bg_Map_R))
medial_wall = np.concatenate((Mask_Left, 10242 + Mask_Right))
# -
# # 3. plot mean thickness along the cortex
fig02 = myvis.plot_surfstat(surf_mesh, bg_map, Mean_thickness,
mask = medial_wall,
cmap = 'viridis', vmin = 1.5, vmax = 4)
# # 4. build the stats model
# +
term_intercept = FixedEffect(1, names="intercept")
term_age = FixedEffect(age, "age")
model = term_intercept + term_age
slm = SLM(model, -age, surf=surf_mesh)
slm.fit(thickness)
tvals = slm.t.flatten()
pvals = slm.fdr()
print("t-values: ", tvals) # These are the t-values of the model.
print("p-values: ", pvals) # These are the p-values of the model.
fig03 = myvis.plot_surfstat(surf_mesh, bg_map, tvals,
mask = medial_wall, cmap = 'gnuplot',
vmin = tvals.min(), vmax = tvals.max())
fig04 = myvis.plot_surfstat(surf_mesh, bg_map, pvals,
mask = medial_wall, cmap = 'YlOrRd',
vmin = 0, vmax = 0.05)
plt.show()
| 3,875 |
/Treemap.ipynb
|
5077fc53d3cc21737e557cfcb5ed7626c10a2c25
|
[] |
no_license
|
yoxf/notebooks
|
https://github.com/yoxf/notebooks
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 5,370 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## The Wonderful World of ML - Session 2 Assignment
# Two of my favorite and most highly recommended references for machine learning are:
#
# - [An Introduction to Statistical Learning with Applications in R - James, Witten, Hastie, and Tibshirani](https://github.com/MichaelSzczepaniak/WonderfulML/raw/master/docs/ISLR%20Seventh%20Printing.pdf)
# - [The Elements of Statistical Learning - Hastie, Tibshirani and Friedman](https://github.com/MichaelSzczepaniak/WonderfulML/raw/master/docs/TheElementsOfStatisticalLearning_Hastie_Tibshirani_Friedman_print10.pdf)
#
# Pdf versions of both of these books have been uploaded to the repo and can be downloaded using the links under each title. If you are relatively new to the area of machine learning, the first reference will be your friend. If you are an experienced pro, have great math skills and/or need more depth on a particular topic, the second reference is an excellent reference. I will refer to the first reference as the **ISL** and the second as the **ESL** throughout the rest of this series.
# 1) If you haven't done so by now, install jupyter notebook and configure it with an R kernel if you are an R user. If you are Python user, your Anaconda install will have Python configured out of the box.
# *Python users -* If you have installed the [latest version of Anaconda](https://www.continuum.io/downloads), you should have jupyter notebook as part of this install. If you have a distribution of Python which doesn't include jupyter, you can do a **pip** install as described [here](http://jupyter.readthedocs.io/en/latest/install.html).
#
# *R users -* Because jupyter runs on Python, you will also need to install a Python distribution if you don't have one installed on your system already. I recommend installing the [latest version of Anaconda](https://www.continuum.io/downloads) if you don't have a compelling reason not to use this distribution because it comes with jupyter as mentioned earlier.
#
# After Python and jupyter, I recommend that both R and Python users configure jupyter with an R kerenel. I followed the [instructions described in this video](https://www.youtube.com/watch?v=I9a9Jj2A95g) and used [this reference](https://irkernel.github.io/installation/) as I went through the process.
# 2) What was the cost function Sondra mentioned that is used for linear regression?
# **Answer: ** The residual sum of squares:
#
# $$\sum_{i=1}^n(h_{\theta}(x_i) - y_i)^2$$
# 3) Equation (3.3) of the ISL defines the **Residual Sum of Squares** which can be written more generally as:
#
# $$
# RSS = \sum_{n=1}^N (\mathbf{t}_n - \mathbf{x}_n^T\mathbf{w})^2
# = \sum_{n=1}^N (\mathbf{t}_n - \mathbf{x}_n^T\mathbf{w})(\mathbf{t}_n - \mathbf{x}_n^T\mathbf{w})^T
# $$
#
# where $\mathbf{t}_n$ is referred to as the target vector for the the *n*th sample. Some texts refer to the target as $y$...
#
# For simple linear regression, we only have a single target $t$ and a single predictor $x$. If we substitute $y$ for $t$, $b$ for the intercept parameter $\hat{\beta_0}$ and $m$ for the slope parameter $\hat{\beta_1}$, the above equation simplifies to:
#
# $$
# RSS = \sum_{n=1}^N (y_n - (mx_n + b))^2
# $$
#
# If I define the arrays $\mathbf{x}$ and $\mathbf{y}$ as:
#
# $$
# \mathbf{x} =
# \begin{bmatrix}
# 5 \\ 10 \\ 15 \\ 20
# \end{bmatrix}\quad
# \mathbf{y} =
# \begin{bmatrix}
# 5.5 \\ 6.5 \\ 10.5 \\ 9.5
# \end{bmatrix}
# $$
#
# Create 3 plots on a single chart of $RSS$ on the y axis and the slope $m$ on the x axis for three values of b: 1, 3, and 5. The code in the next block will get you started.
# +
import numpy as np
x = np.linspace(5, 20, num=4)
y = np.array([5.5, 6.5, 10.5, 9.5])
m_vals = np.linspace(0, 1, num=6)
b_vals = np.linspace(1, 5, num=3)
def linearSquareResidual(targets, features, m, b):
yhat = (m * features) + b
sqr_res = (targets - yhat)**2
return sqr_res
def getLinRssVals(y_vec, x_vec, m_vec, b_vec):
""" Returns an array of arrays. Each inner array is an array of RSS values
for a particular intercept value (b) in b_vec. Each value in the inner array
corresponds to a value of the slope in m_vec.
"""
rss_vals = []
# set the intercept
for j in range(len(b_vec)):
rss_m = []
# compute RSS for with set intecept over range of slope values
for i in range(len(m_vec)):
rss_m.append(sum(linearSquareResidual(y_vec, x_vec, m_vec[i], b_vec[j])))
rss_vals.append(np.array(rss_m))
return(np.array(rss_vals))
plot_data = getLinRssVals(y, x, m_vals, b_vals)
# Plot 3 RSS curves
import matplotlib as mp, matplotlib.pyplot as plt
# %matplotlib inline
# plot the points
plt.figure(figsize=(12, 8))
plt.plot(m_vals, plot_data[0], 'ro', label='b = 1')
plt.plot(m_vals, plot_data[1], 'go', label='b = 3')
plt.plot(m_vals, plot_data[2], 'bo', label='b = 5')
# plot smooth splines between the points
m_interpolate_x = np.linspace(m_vals.min(), m_vals.max(), 300) # 300 interpolated points
# We know RSS is quadratic in the parameters, so let's fit quadatics for
# smooth looking curves - TODO: refactor next 2 lines as list comprehensions
rss_quad_fits = (np.polyfit(m_vals, plot_data[0], 2),
np.polyfit(m_vals, plot_data[1], 2),
np.polyfit(m_vals, plot_data[2], 2))
f = np.poly1d(rss_quad_fits[0]), np.poly1d(rss_quad_fits[1]), np.poly1d(rss_quad_fits[2])
plt.plot(m_interpolate_x, f[0](m_interpolate_x), 'r')
plt.plot(m_interpolate_x, f[1](m_interpolate_x), 'g')
plt.plot(m_interpolate_x, f[2](m_interpolate_x), 'b')
plt.ylim([0, 50]) # RSS get much larger, but need to zoom in to see minimas
plt.legend(loc='upper right')
plt.xlabel('m slope value')
plt.ylabel('RSS')
#x, y, m_vals, b_vals, linearSquareResidual(y, x, 0.4, 3), plot_data
# -
# Based on the plots you just built, what are the best values for **m** and **b** that fit this data?
# **Answer: ** green curve at m ~ 0.4, b = 3 and blue curve at m ~ 0.25, b = 5 have very similar minima
# 4) You are thinking about using logistic regression to determine if your stock trading has a chance of making you some money. You design your own signal variable x which you derive from data that is readily available and use it to back-test your model on historical data. You simulate a trade for various values of x and assign a value of 1 if the trade made money and a 0 if it lost money. You plot your data, fit a sigmoid function through the data, and it looks like this:
#
# <img src="https://raw.githubusercontent.com/MichaelSzczepaniak/WonderfulML/master/docs/graphics/logistic_reg_stock_example.jpg">
#
# What is the main assumption we are making in terms of how we are modeling this data? **HINT:** What quantity are we assuming can be modeled as a line?
# **Answer: ** From page 132 of the ISL, we are assuming that the probability of a winning trade can be modeled as a sigmoid function which implies that the **natural log of the odds ratio** $\ln{\bigg(\frac{p(x)}{1 - p(x)}\bigg)}$ is linear (see equation 4.4).
# 5) You were excited to learn about K-Means clustering from Sondra's presentation and decided to give it a try. You first run an analyis in R and get one result which looks reasonable. You then run the same analysis in Python and again get results which look reasonable, but these results are substantially different from the results you obtained using R.
#
# Why do think you might have gotten different results on the same dataset?
# **Answer: ** The K-means algorithm is sensitive to the starting conditions your use (see ISL pages 388 and 389)
# 6) The day after Sondra's presentation, you are having lunch with your colleague Chris who is working on helping a client who runs a large data center detect when servers may be at risk of failing. You are excited to learn that Chris is using anomaly detection to characterize the servers in the client's datacenter and ask her what her model looks like.
#
# Chris invites you over to her desk to show you two contour plots of probability density vs. two variables. The two variables in the first plot she calls x1 and x2 and the plot looks like this:
#
# <img src="https://raw.githubusercontent.com/MichaelSzczepaniak/WonderfulML/master/docs/graphics/circular_contours1.jpg">
#
# She then shows you another contour plot of probability density vs. two different variable x3 and x4 which looks like this:
#
# <img src="https://raw.githubusercontent.com/MichaelSzczepaniak/WonderfulML/master/docs/graphics/eliptical_contours1.jpg">
#
# What do these plots suggest about the relationship between x1 and x2 vs. the relationship between x3 and x4?
# **Answer: ** The variables x1 and x2 are independent which means the off-diagonal terms of the corvariance matrix $\sum_k$ in equation 4.8 in the ESL are all zero. The variables x3 and x4 appear to have some dependence which means the off-diagonal terms of the corvariance matrix $\sum_k$ in equation 4.8 in the ESL are non-zero.
#
# We'll see this equation again when we explore Linear and Quadratic Discriminant Analysis (LDA and QDA).
| 9,400 |
/ipynb/10-09/17. Sorting Techniques/.ipynb_checkpoints/156. Sorting Recursive Merge Sort-checkpoint.ipynb
|
d2bb584f720e1533256a39eef5c468f1412de119
|
[] |
no_license
|
BSCdfdff/algorithmscpp
|
https://github.com/BSCdfdff/algorithmscpp
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.cpp
| 8,921 |
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .cpp
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.15.2
// kernelspec:
// display_name: C++17
// language: C++17
// name: xcpp17
// ---
// # Merge Sort
// ___
//
// + Recurive (Top/Down)
//
//
//
// ## Recursive Merge Sort
//
// ___
//
// Here we have the following unsorted array:
//
//
// $$
// A=
// \newcommand\T{\Rule{0pt}{1em}{.3em}}
// \begin{array}{|r|r|r|r|r|r|r|r|}
// \hline
// 8\T&2\T&9\T&6\T&5\T&3\T&7\T&4 \\\hline
// _0\T&_1\T&_2\T&_3\T&_4\T&_5\T&_6\T&_7 \\\hline
// \end{array}
// $$
//
// $$$$
//
// Remember the idea with merge sort"
//
// 1. Break list into half
// 2. Then break that into half
// 3. And so on, until you end up with on element per list, and the list is itself.
// 4. And we know that when we have 1 element, that element is sorted.
//
// Once it has a single list.
//
// 1. It will start merging into one single list.
//
//
//
//
//
//
// ## Lets Code (Recursive)
// ___
//
// $$
// A=
// \newcommand\T{\Rule{0pt}{1em}{.3em}}
// \begin{array}{|r|r|r|r|r|r|r|r|}
// \hline
// _l\T&_\T&_\T&_{mid}\T&_\T&_\T&_\T&_h\\\hline
// 8\T&2\T&9\T&6\T&5\T&3\T&7\T&4 \\\hline
// _0\T&_1\T&_2\T&_3\T&_4\T&_5\T&_6\T&_7 \\\hline
// _i\T&\T&\T&\T&j\T&\T&\T& \\\hline
// \end{array}
// $$
//
//
//
//
// 1. Remember we divide the list into two halves, when there are more than one element. That is if l is less than h, get mid.
//
// ```
// if (l < h){
// mid=(l+h)/2;
// ...
// }
// ```
//
// 2. So the two halves must be merged with each other now. But merging can only happen, if the two halves are sorted. So how do we sort it. We sort the two halves RECURSIVELY, using merge sort.
//
// 3.So we perform merge sort for LHS, from l to mid:
//
// ```
// MergeSort(A,l,mid);
//
// ```
// 4.So we perform merge sort for RHS, from mid+1 to h:
//
// ```
// MergeSort(A,mid+1,h);
//
// ```
//
// And the above (LHS and RHS), it will do(sort) recursively
//
// Then when LHS and RHS is sorted, it will need to sort it into single array.
//
// 5. And we merge the two list into single array:
//
// ```
// Merge(A, l, mid, h);
//
// ```
//
// 6. And the above is last statement in recursive procedure.
// 7. And its so small, nut its recursive, and we now how recursive function expands.
//
//
// ```
// void MergeSort(int A[], int l, int h){
//
// if (l < h){
// mid=(l+h)/2;
// MergeSort(A,l,mid);
// MergeSort(A,mid+1,h);
// Merge(A, l, mid, h);
// }
//
// }
// ```
//
// ## Lets trace the above
//
// ___
//
// ```
//
// +---+---+---+---+---+---+---+---+
// | 8 | 2 | 9 | 6 | 5 | 3 | 7 | 4 |
// +---+---+---+---+---+---+---+---+
//
//
// +---+---+ +---+---+ +---+---+ +---+---+
// | 2 | 8 | | 6 | 9 | | 3 | 5 | | 4 | 7 |
// +---+---+ +---+---+ +---+---+ +---+---+
//
// +---+---+---+---+ +---+---+---+---+
// | 2 | 6 | 8 | 9 | | 3 | 4 | 5 | 7 |
// +---+---+---+---+ +---+---+---+---+
//
//
// +---+---+---+---+---+---+---+---+
// | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
// +---+---+---+---+---+---+---+---+
//
//
// ```
//
//
//
// ```
//
//
// +-----------------------------+
// | 0,7 |
// +-----------------------------+
// / \
// / \
// / \
// +----------+ +----------+
// | 0,3 | | 4,7 |
// +----------+ +----------+
// / \ / \
// / \ / \
// +---+ +---+ +---+ +---+
// |0,1| |2,3| |4,5| |6,7|
// /+---+\ /+---+\ /+---+\ /+---+\
// / \ / \ / \ / \
// / \ / \ / \ / \
// +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
// |0,0| |1,1| |2,2| |3,3| |4,4| |5,5| |6,0| |7,7|
// +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
// ```
//
// Merge sort is only sorting technique that requires an extra array or space (for comparison based soring)
//
//
//
#include <iostream>
#include <climits>
#include <math.h>
#define INSERTION_OPERATOR operator<<
#define EXTRACTION_OPERATOR operator>>
#define ADDITION_OPERATOR operator+
using namespace std;
// +
void MergeSingleArray(int A[],int l, int mid, int h){
int i, j, k;
i=l;
j=mid+1;
k=l;
int B[100];
while (i <=mid && j <= h){
if (A[i] < A[j])
B[k++] = A[i++];
else
B[k++] = A[j++];
}
for (; i <= mid; i++)
{
B[k++] = A[i];
}
for (; j <= h; j++)
{
B[k++] = A[j];
}
//Copy B To A
for (int i = l; i<=h;i++){
A[i]=B[i];
}
}
// +
void MergeSortRecur(int A[], int l, int h){
int mid;
if (l < h){
mid=(l+h)/2;
MergeSortRecur(A,l,mid);
MergeSortRecur(A,mid+1,h);
MergeSingleArray(A, l, mid, h);
}
}
// +
int T[] = {2,5,8,12,3,6,7,10};
int l=0;
int h=7;
MergeSortRecur(T,l, h);
for (int i = 0; i<=h;i++){
cout<<T[i]<<" ";
}
cout<<endl;
// -
| 6,207 |
/21. Z-Test.ipynb
|
1f9de3d622fa0eb7b9c24dcb7e2953f7199aacc4
|
[] |
no_license
|
shakirshakeelzargar/DATA-ANALYTICS-PYTHON-TRAINING
|
https://github.com/shakirshakeelzargar/DATA-ANALYTICS-PYTHON-TRAINING
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 1,538 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Demonstrating significant differences between a
# vector of measurements and a single value
# Using the statsmodels package for doing test
from statsmodels.stats import weightstats as stests
import numpy as np
ls=range(1,100)
data=np.asarray(ls)
#data=np.random.normal(size=100)
singleValue=3.3
# Assuming data are normally distributed, we can do z-test
testResult=stests.ztest(data,value=singleValue)
print(testResult)
pValue=testResult[1]
print("p-value is: "+str(pValue))
print("")
# -
| 767 |
/catagory.ipynb
|
3caf25043ba3c81641a507cde946e80ca23a233e
|
[] |
no_license
|
ckdrjs96/yogiyo2
|
https://github.com/ckdrjs96/yogiyo2
| 2 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 6,492,841 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime
countpop = pd.DataFrame(pd.read_csv("mass_county_pop.csv"))
countpop
countpop[countpop['County'] == 'Suffolk'].values[0][1]
x = countpop.values.tolist()
x[1][1]
None
sent_split=sent.split('\n')
find=['사진','포토']
for sent in sent_split:
for word in find:
if re.search(word,sent):
if extract==None:
extract=sent
else:
extract=extract+'\n'+sent
break
return extract
event['photo']=event.reviewevent.map(lambda x: extract_photo(x))
pd.set_option('display.max_colwidth', None)
event[event.photo.notnull()]
pd.set_option('display.max_rows', None)
event.photo[event.photo.notnull()]
def extract_star(sent):
if sent != sent :
return None
extract=None
sent_split=sent.split('\n')
find=['별']
for sent in sent_split:
for word in find:
if re.search(word,sent):
if extract==None:
extract=sent
else:
extract=extract+'\n'+sent
break
return extract
event['star']=event.reviewevent.map(lambda x: extract_star(x))
def extract_star2(sent):
if sent != sent :
return None
extract=None
sent_split=sent.split('\n')
find=['별']
for sent in sent_split:
token=okt.morphs(sent)
for word in find:
if word in token:
if extract==None:
extract=sent
else:
extract=extract+'\n'+sent
break
return extract
event['star']=event.reviewevent.map(lambda x: extract_star2(x))
event.star[event.star.notnull()]
len(event.star[event.star.notnull()])
def extract_nickname(sent):
if sent != sent :
return None
extract=None
sent_split=sent.split('\n')
find=['닉네임','아이디']
for sent in sent_split:
for word in find:
if re.search(word,sent):
if extract==None:
extract=sent
else:
extract=extract+'\n'+sent
break
return extract
event['nickname']=event.reviewevent.map(lambda x: extract_nickname(x))
len(event.nickname[event.nickname.notnull()])
def extract_jimm(sent):
if sent != sent :
return None
extract=None
sent_split=sent.split('\n')
find=['찜']
findx=['계란찜','갈비찜','아구찜','해물찜','찜닭','찜탕','두찜','행찜','뼈다귀찜']
for sent in sent_split:
if re.search(find[0],sent):
cnt=0
for word in findx:
if re.search(word,sent):
break
else:
if extract==None:
extract=sent
else:
extract=extract+'\n'+sent
return extract
event['jimm']=event.reviewevent.map(lambda x: extract_jimm(x))
len(event.jimm[event['jimm'].notnull()])
event.head()
# +
#event.to_csv(PATH+'category.csv')
# -
def change(x):
if x==None :
return False
else:
return True
event['photo_t']=event.photo.map(lambda x: change(x))
event['star_t']=event.star.map(lambda x: change(x))
event['nickname_t']=event.nickname.map(lambda x: change(x))
event['jimm_t']=event.jimm.map(lambda x: change(x))
event.jimm[event['jimm'].notnull()]
event_t=event.iloc[:,[0,1,2,3,8,9,10,11]]
# +
#event_t.to_csv(PATH+'category_t.csv')
# -
def extract_jimm2(sent):
if sent != sent :
return None
extract=None
sent_split=sent.split('\n')
find=['찜']
for sent in sent_split:
if re.search(find[0],sent):
clean_sent=re.sub('[^가-힣]',' ',sent)
if '찜'in okt.morphs(clean_sent):
if extract==None:
extract=sent
else:
extract=extract+'\n'+sent
return extract
event_t
def delete(isservice,t):
if isservice:
return t
else:
return None
def catagory(photo,star,nickname,jimm):
cnt=0
if photo:
cnt=cnt+1
if star:
cnt=cnt+2
if nickname:
cnt+=4
if jimm:
cnt+=8
return cnt
event_t['catagory']=event_t.apply(lambda x:catagory(x['photo_t'],x['star_t'],x['nickname_t'],x['jimm_t']),axis=1)
event_t['catagory']=event_t.apply(lambda x: delete(x['isservice'],x['catagory']),axis=1)
event_t
event_t.groupby('catagory').count().iloc[:,1]
event_t.catagory.value_counts(sort=True).plot(kind='bar')
catagory2=event_t[['shop','catagory']]
# +
#catagory2.to_csv(PATH+'catagory2.csv',index=False)
# -
event_t.dropna(inplace=True)
event_t.photo_t.value_counts()
event_t.star_t.value_counts()
event_t.nickname_t.value_counts()
event_t.jimm_t.value_counts()
event_t.to_csv(PATH+'iscatagory.csv', index=False)
catagory2.catagory.map(lambda x: -1 if x !=x else x )
catagory2.catagory=catagory2.catagory.map(lambda x: -1 if x !=x else x )
# +
#catagory2.to_csv(PATH+'catagory2.csv',index=False)
| 5,393 |
/MATPLOTLIB/1_Matplotlib.ipynb
|
a2b5589f99877c3d0a29331ab8016bf960250cc9
|
[] |
no_license
|
JunaidMalik997/Data-Science
|
https://github.com/JunaidMalik997/Data-Science
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 394,149 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 1. Matplotlib is the most popular plotting library for Python.
# 2. It gives us control over every aspect of a figure
# 3. It was designed to have a similar feel to Matlab's graphical plotting
# 4. It works very well with Pandas and Numpy arrays
# 5. conda install matplotlib
# 6. matplotlib.org (official website of matplotlib)
import matplotlib.pyplot as plt
# %matplotlib inline
#this command in Jupyter Notebook is going us to allow us to see the plots we create inside the jupyter notebook
# +
#plt.show() #if not using jupyter notebook
# -
import numpy as np
x=np.linspace(0,5,11)
y=x**2
x
y
#Functional Method of Matplotlib for creating the plots
plt.plot(x,y)
plt.xlabel('X Label')
plt.ylabel('Y Label')
plt.title('Title')
# +
#drawing multi plots on the same canvas
plt.subplot(2,1,1) #subplot takes in the arguments no.of rows, no.of columns and the plot number we are referring to
plt.plot(x,y)
plt.subplot(2,1,2)
plt.plot(y,x)
# +
plt.subplot(1,2,1)
plt.plot(x,y,'r') #plot represented by red line
plt.subplot(1,2,2)
plt.plot(y,x,'b') #plot represented by blue line
# +
#Object Oriented Method in Matplotlib for creating plots
#The main idea in using a more formal object oriented method is create figure objects and then call methods off of it.
# -
fig=plt.figure()
#The purpose of using plt.figure() is to create a figure object.
#The whole figure is regarded as the figure object.
#a figure object has been created. It is just an imaginary blank canvas
# +
#we can also add a set of aixs to this canvas
axes=fig.add_axes([0.1,0.1,0.8,0.8])
#add_axes takes 4 arguments -->left,bottom,width,height(in a list) -->range from 0 and 1(basically the %age of blank canvas
#we want to take)
axes.plot(x,y)
# +
#putting in 2 sets of figure on one canvas
fig=plt.figure() #creating figure object
axes1=fig.add_axes([0.1,0.1,0.8,0.8])
axes2=fig.add_axes([0.2,0.5,0.4,0.3])
axes1.plot(x,y)
axes1.set_title('Larger Plot')
axes2.plot(y,x)
axes2.set_title('Smaller Plot')
# -
fig=plt.figure()
axes1=fig.add_axes([0.1,0.1,0.8,0.8])
axes1.plot(x,y)
#we get empty set of axes and then we can plot of that axes
# # Matplotlib Part 2
# +
#create subplots using object oriented programming
# -
import matplotlib.pyplot as plt
import numpy as np
fig,axes=plt.subplots(nrows=1,ncols=2) #tuple unpacking
#the above statement is just the fancy way of calling [fig=plt.figure()] and [axes1=fig.add_axes([])] (combo of both)
#axes.plot(x,y)
axes
#it is just an array of matplotlib axes(list of axes object)
#since it is a list of matplotlib axes we can actually iterate over it (below cell)
#these are the axes which we manually created when we said [fig.add_axes([])]
# +
fig,axes=plt.subplots(nrows=1,ncols=2)
for current_ax in axes:
current_ax.plot(x,y)
# +
#since we can iterate through the axes object which is a list we can also index it.
fig,axes=plt.subplots(nrows=1,ncols=2)
axes[0].plot(x,y)
axes[0].set_title('First Plot')
axes[1].plot(y,x)
axes[1].set_title('Second Plot')
plt.tight_layout() #takes care of any overlapping plots
# -
# # Figure Size and DPI
# +
#Figure Size, Aspect Ration and DPI(dots per inch/pixels per inch)
#Matplotlib allows us to control each of the aspects, and we can specify them when we are calling the figure object
# +
fig=plt.figure(figsize=(3,2)) #figsize is the tuple which is the width and height of the figure in inches
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y)
# +
fig=plt.figure(figsize=(8,2)) #figsize is the tuple which is the width and height of the figure in inches
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y)
# +
fig,axes=plt.subplots(figsize=(8,2))
axes.plot(x,y)
# +
fig,axes=plt.subplots(nrows=2,ncols=1,figsize=(8,2))
axes[0].plot(x,y)
axes[1].plot(y,x)
plt.tight_layout()
# +
#how to save a figure. To save a figure we can use matplotlib to generate just high quality outputs in a number of formats
#jpg,png,jpeg,pdf etc
fig
# -
fig.savefig('My_picture.jpg',dpi=200) #we specify the name of the file and the file format we want
#it saves the figure in the same location as this .ipynb file
# +
#basics
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y)
ax.set_title('Title')
ax.set_xlabel('X')
ax.set_ylabel('Y')
# +
#legends, with legends we can use labeled text to actually clarify what plot is what plot
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y)
ax.plot(y,x) #we will get two plots on the same graph
# +
##we would need to add in a legend to reocgnize each plot like in above cell
#place ax.legend() at the end of code and define labels as follows
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,label='Exponential Increase')
ax.plot(y,x,label='Exponential Decrease')
ax.legend() #looks at the plot calls and checks to see if there is a label
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,label='Exponential Increase')
ax.plot(y,x,label='Exponential Decrease')
ax.legend(loc=0) #chooses best legend location for our plot (always recommended)
#check documentation of legend() command to look for other locations
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,label='Exponential Increase')
ax.plot(y,x,label='Exponential Decrease')
ax.legend(loc=10) #centre
#ax.legend(loc=(0.1,0.1))
# -
# # Matplotlib Part 3
# +
#Plot Appearance
# +
#setting colors with matplotlib
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green') #we can pass in the string for very basic colors
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='#FF8C00') #RGB Hex Code--> We can make our own custom colors (search on google for more)
# +
#Line width and line style
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',linewidth=3)
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=3,alpha=0.5) #alpha helps us control how transparent the line is
#lw represents Line Width--> and it will still work
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=3,linestyle='--')
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=3,linestyle='-.')
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=3,ls='steps')
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=3,ls='-')
# +
#let's talk about markers
#Markers are going to be used when we have a few datapoints
# -
x
len(x)
#x is an array of 11 points. Let's say we want to mark those 11 points on the plot (below cell)
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=3,linestyle='-',marker='o',markersize=10)
#Refer to jupyter notebook for more details
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=3,linestyle='-',marker='o',markersize=10,
markerfacecolor='yellow')
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=3,linestyle='-',marker='o',markersize=10,
markerfacecolor='yellow',markeredgewidth=3)
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=3,linestyle='-',marker='o',markersize=10,
markerfacecolor='yellow',markeredgewidth=3,markeredgecolor='red')
# -
# # Control over axis appearance (Plot Range)
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=2,ls='--')
# +
#let's say we only want to show the plot between 0 and 1 on x axis
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=2,ls='--')
ax.set_xlim([0,1]) #specify limits of lower bound and upper bound for x axis (pass a list)
# +
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y,color='green',lw=3,ls='--')
ax.set_xlim([0,1])
ax.set_ylim([0,2])
# -
| 8,056 |
/01-DataJoint Basics - Interactive.ipynb
|
7905cee9d2f0016d2b8e386dce573d15cb2b38fd
|
[] |
no_license
|
xibby/playground_tutorial
|
https://github.com/xibby/playground_tutorial
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 41,046 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Getting started with DataJoint
# Now that you have successfully connected to DataJoint (if not, please visit [Connecting to DataBase](00-ConnectingToDatabase.ipynb) first), let's dive into using DataJoint! In this notebook, we will:
#
# 1. learn what a data pipeline is
# 2. create our first simple data pipeline in DataJoint
# 3. insert some data into the pipeline
# 4. basic queries to flexibly explore the data pipeline
# 5. fetch the data from the pipeline
# 6. delete entries from tables
# As always, let's start by importing the `datajoint` library.
import datajoint as dj
# # So... What is a data pipeline?
# If you visit the [documentation for DataJoint](https://docs.datajoint.io/introduction/Data-pipelines.html), we define a data pipeline as follows:
# > A data pipeline is a sequence of steps (more generally a directed acyclic graph) with integrated storage at each step. These steps may be thought of as nodes in a graph.
#
# While this is an accurate description, it may not be the most intuitive definition. Put succinctly, a data pipeline is a listing or a "map" of various "things" that you work with in a project, with line connecting things to each other to indicate their dependecies. The "things" in a data pipeline tends to be the *nouns* you find when describing a project. The "things" may include anything from mouse, experimenter, equipment, to experiment session, trial, two-photon scans, electric activities, to receptive fields, neuronal spikes, to figures for a publication! A data pipeline gives you a framework to:
#
# 1. define these "things" as tables in which you can store the information about them
# 2. define the relationships (in particular the dependencies) between the "things"
#
# A data pipeline can then serve as a map that describes everything that goes on in your experiment, capturing what is collected, what is processed, and what is analyzed/computed. A well designed data pipeline not only let's you organize your data well, but can bring out logical clarity to your experiment, and may even bring about new insights by making how everything in your experiment relates together obvious.
#
# Let's go ahead and build together a pipeline from scratch to better understand what a data pipeline is all about.
# # Building our first pipeline:
# Let's build a pipeline to collect, store and process data and analysis for our hypothetical single electrode recording or calcium imaging recording in mice. To help us understand the project better, here is a brief description:
# > * Your lab houses many mice, and each mouse is identified by a unique ID. You also want to keep track of information about each mouse such as their date of birth, and gender.
# > * As a hard working neuroscientist, you perform experiments every day, sometimes working with more than one mouse in a day! However, on an any given day, a mouse undergoes at most one recording session.
# > * For each experimental session, you would like to record what mouse you worked with and when you performed the experiment. You would also like to keep track of other helpful information such as the experimental setup you worked on.
#
# > * In a session of electrophysiology
# >> * you record electrical activity from a single neuron. You use recording equipment that produces separate data files for each neuron you recorded.
# >> * Neuron's activities are recorded as raw traces. Neuron's spikes needs to be detected for further analysis to be performed.
# > * In a sesssion of calcium imaging
# >> * you scan a brain region containing a number of neurons. You use recording equipment that produces separate data files for each scan you performed.
# >> * you would like to segment the frames and get the regions of interest (ROIs), and save a mask for each ROI
# >> * finally you would like to extract the trace from each segmented ROI
# Pipeline design starts by identifying **things** or **entities** in your project. Common entities includes experimental subjects (e.g. mouse), recording sessions, and two-photon scans.
# Let's revisit the project description, this time paying special attention to **what** (e.g. nouns) about your experiment. Here I have highlighted some nouns in particular.
# > * Your lab houses many **mice**, and each mouse is identified by a unique ID. You also want to keep track of information about each mouse such as their date of birth, and gender.
# > * As a hard working neuroscientist, you perform experiments every day, sometimes working with more than one mouse in a day! However, on an any given day, a mouse undergoes at most one recording session.
# > * For each **experimental session**, you would like to record what mouse you worked with and when you performed the experiment. You would also like to keep track of other helpful information such as the experimental setup you worked on.
#
# > * In a session of electrophysiology
# >> * you record electrical activity from a **single neuron**. You use recording equipment that produces separate data files for each neuron you recorded.
# >> * Neuron's activities are recorded as raw traces. **Neuron's spikes** needs to be detected for further analysis to be performed.
# > * In a sesssion of calcium imaging
# >> * you scan a brain region containing a number of neurons. You use recording equipment that produces separate data files for each **scan** you performed.
# >> * you would like to segment the frames and get the **regions of interest (ROIs)**, and save a mask for each ROI
# >> * finally you would like to extract the **trace** from each segmented ROI
# Just by going though the description, we can start to identify **things** or **entities** that we might want to store and represent in our data pipeline:
#
# * mouse
# * experimental session
#
# For ephys:
#
# >* neuron
# >* spikes
#
# For calcium imaging:
#
# >* scan
# >* regions of interest
# >* trace
# In the current notebook, we will design the tables for mouse and experimental sessions, the rest of the pipeline will be designed in the subdirectory `electrophysioloy` and `calcium_imaging`
# In DataJoint data pipeline, we represent these **entities** as **tables**. Different *kinds* of entities become distinct tables, and each row of the table is a single example (instance) of the category of entity.
#
# For example, if we have a `Mouse` table, then each row in the mouse table represents a single mouse!
# When constructing such table, we need to figure out what it would take to **uniquely identify** each entry. Let's take the example of the **mouse** and think about what it would take to uniquely identify a mouse.
# After some thought, we might conclude that each mouse can be uniquely identified by knowing its **mouse ID** - a unique ID number assigned to each mouse in the lab. The mouse ID is then a column in the table or an **attribute** that can be used to **uniquely identify** each mouse. Such attribute is called the **primary key** of the table.
#
# | mouse_id* |
# |:--------:|
# | 11234 |
# | 11432 |
# Once we have successfully identified the primary key of the table, we can now think about what other columns, or **non-primary key attributes** that we would want to include in the table. These are additional information **about each entry in the table that we want to store**.
# For the case of mouse, what other information about the mouse you might want to store? Based on the project description, we would probably want to store information such as the mouse's **date of birth** and **gender**.
# | mouse_id* | dob | sex |
# |:--------:|------------|--------|
# | 11234 | 2017-11-17 | M |
# | 11432 | 2018-03-04 | F |
# Now we have an idea on how to represent information about mouse, let's create the table using **DataJoint**!
# ## Create a schema - house for your tables
# Every table lives inside a schema - a logical collection of one or more tables in your pipeline. Your final pipeline may consists of many tables spread across one or more schemas. Let's go ahead and create the first schema to house our table.
# We create the schema using `dj.schema()` function, passing in the name of the schema. For this workshop, you are given the database privilege to create any schema **starting with your username followed by a `_` charcter**. So if your username is `john`, you can make any schema starting with `john_`, such as `john_tutorial`.
# Let's create a schema called `pipeline`, prefixed by `username_`.
schema = dj.schema('{YOUR_USERNAME}_tutorial')
# Now that we have a schema to place our table into, let's go ahead and define our first table!
# ## Creating your first table
# In DataJoint, you define each table as a class, and provide the table definition (e.g. attribute definitions) as the `definition` static string property. The class will inherit from the `dj.Manual` class provided by DataJoint (more on this later).
@schema
class Mouse(dj.Manual):
definition = """
# Experimental animals
mouse_id : int # Unique animal ID
---
dob=null : date # date of birth
sex="unknown" : enum('M','F','unknown') # sex
"""
# Let's take a look at our brand new table
Mouse()
# ## Insert entries with `insert1` and `insert` methods
# The table was successfully defined, but without any content, the table is not too interesting. Let's go ahead and insert some **mouse** into the table, one at a time using the `insert1` method.
# Let's insert a mouse with the following information:
# * mouse_id: 0
# * date of birth: 2017-03-01
# * sex: male
Mouse.insert1((0, '2017-03-01', 'M'))
Mouse()
# You could also insert1 as a dictionary
data = {
'mouse_id': 100,
'dob': '2017-05-12',
'sex': 'F'
}
Mouse.insert1(data)
Mouse()
# We can also insert multiple **mice** together using the `insert` method, passing in a list of data.
data = [
(1, '2016-11-19', 'M'),
(2, '2016-11-20', 'unknown'),
(5, '2016-12-25', 'F')
]
Mouse.insert(data)
# Of course, you can insert a list of dictionaries
# +
data = [
{'mouse_id': 10, 'dob': '2017-01-01', 'sex': 'F'},
{'mouse_id': 11, 'dob': '2017-01-03', 'sex': 'F'},
]
# insert them all
Mouse.insert(data)
# -
Mouse()
# ## Data integrity
# DataJoint checks for data integrity, and ensures that you don't insert a duplicate by mistake. Let's try inserting another mouse with `mouse_id: 0` and see what happens!
Mouse.insert1(
{'mouse_id': 0,
'dob': '2018-01-01',
'sex': 'M',
})
# Go ahead and insert a few more mice into your table before moving on.
# +
data = [
{'mouse_id': 12, 'dob': '2017-03-21', 'sex': 'F'},
{'mouse_id': 18, 'dob': '2017-05-01', 'sex': 'F'},
{'mouse_id': 19, 'dob': '2018-07-21', 'sex': 'M'},
{'mouse_id': 22, 'dob': '2019-12-15', 'sex': 'F'},
{'mouse_id': 34, 'dob': '2018-09-22', 'sex': 'M'}
]
# insert them all
Mouse.insert(data)
# -
Mouse()
# ENTER YOUR CODE - Insert more mice
# ## Create tables with dependencies
# Congratulations! We have successfully created your first table! We are now ready to tackle and include other **entities** in the project into our data pipeline.
#
# Let's now take a look at representing an **experimental session**.
# As with mouse, we should think about **what information (i.e. attributes) is needed to uniquely identify an experimental session**. Here is the relevant section of the project description:
#
# > * As a hard working neuroscientist, you perform experiments every day, sometimes working with **more than one mouse in a day**! However, on an any given day, **a mouse undergoes at most one recording session**.
# > * For each experimental session, you would like to record **what mouse you worked with** and **when you performed the experiment**. You would also like to keep track of other helpful information such as the **experimental setup** you worked on.
# Based on the above, it appears that you need to know:
#
# * the date of the session
# * the mouse you recorded from in that session
#
# to uniquely identify a single experimental session.
# Note that, to uniquely identify an experimental session (or simply a **session**), we need to know the mouse that the session was about. In other words, a session cannot existing without a corresponding mouse!
#
# With **mouse** already represented as a table in our pipeline, we say that the session **depends on** the mouse! We would graphically represent this in an **entity relationship diagram (ERD)** by drawing the line between two tables, with the one below (**session**) dependeing on the one above (**mouse**).
# Thus we will need both **mouse** and a new attribute **session_date** to uniquely identify a single session.
#
# Remember that a **mouse** is already uniquely identified by its primary key - **mouse_id**. In DataJoint, you can declare that **session** depends on the mouse, and DataJoint will automatically include the mouse's primary key (`mouse_id`) as part of the session's primary key, along side any additional attribute(s) you specificy.
@schema
class Session(dj.Manual):
definition = """
# Experiment session
-> Mouse
session_date : date # date
---
experiment_setup : int # experiment setup ID
experimenter : varchar(100) # experimenter name
data_path='' : varchar(255) #
"""
# You can actually generate the entity relationship diagram (ERD) on the fly by calling `dj.ERD` with the schema object
dj.ERD(schema)
# Let's try inserting a few sessions manually.
# +
data = {
'mouse_id': 0,
'session_date': '2017-05-15',
'experiment_setup': 0,
'experimenter': 'Edgar Y. Walker'
}
Session.insert1(data)
# -
Session()
# Let's insert another session for `mouse_id = 0` but on a different date.
# +
data = {
'mouse_id': 0,
'session_date': '2018-01-15',
'experiment_setup': 100,
'experimenter': 'Jacob Reimer'
}
Session.insert1(data)
Session()
# -
# And another session done on the same date but on a different mouse
# +
data = {
'mouse_id': 18,
'session_date': '2018-01-15',
'experiment_setup': 101,
'experimenter': 'Jacob Reimer'
}
# insert them all
Session.insert1(data)
# -
Session()
# What happens if we try to insert a session for a mouse that doesn't exist?
bad_data = {
'mouse_id': 9999, # this mouse doesn't exist!
'session_date': '2017-05-15',
'experiment_setup': 0,
'experimenter': 'Edgar Y. Walker'
}
Session.insert1(bad_data)
# # Querying data
# Often times, you don't want all data but rather work with **a subset of entities** matching specific criteria. Rather than fetching the whole data and writing your own parser, it is far more efficient to narrow your data to the subset before fetching.
#
# For this, DataJoint offers very powerful yet intuitive **querying** syntax that let's you select exactly the data you want before you fetch it.
#
# It is also critical to note that the result of any DataJoint query represents a valid entity.
# We will introduce three major types of queries used in DataJoint:
# * restriction (`&`) and negative restriction (`-`): filter data
# * join (`*`): bring fields from different tables together
# * projection (`.proj()`): focus on a subset of attributes
# * aggregation (`.aggr()`): simple computation of one table against another table
# ## Restrictions (`&`) - filter data with certain conditions
# The **restriction** operation, `&`, let's you specify the criteria to narrow down the table on the left.
# ### Exact match
# Mouse with id 0
Mouse & 'mouse_id = 0'
# All male mice (`'sex = "M"'`)
Mouse & 'sex = "M"'
# All female mice (`'sex="F"'`)
Mouse & 'sex = "F"'
# We can also use as a dictionary as a restrictor, with one field or multiple fields
Mouse & dict(mouse_id=5)
# ### Inequality
# You can also use inequality in your query to match based on numerical values.
# Mouse that is born **after 2017-01-01**
Mouse & 'dob > "2017-01-01"'
# Mouse that is born within a range of dates
Mouse & 'dob between "2017-03-01" and "2017-08-23"'
# Mouse that is **not** male
Mouse & 'sex != "M"'
# You can easily combine multiple restrictions to narrow down the entities based on multiple attributes.
# Let's find all mouse that **is not male** AND **born after 2017-01-01**.
Mouse & 'sex != "M"' & 'dob > "2017-01-01"'
Mouse & 'sex != "M" and dob > "2017-01-01"'
# Result of one query can be used in another query! Let's first find **all female mice** and store the result.
female_mice = Mouse & 'sex = "F"'
female_mice
# and among these mice, find ones with **mouse_id > 10**
# ENTER YOUR CODE
# In computer science/math lingo, DataJoint operations are said to **satisfy closure property**. Practically speaking, this means that the result of a query can immediately be used in another query, allowing you to build more complex queries from simpler ones.
# ### Restriction one table with another
# All mice that has a session
Mouse & Session
# ### Combining restrictions
# All the above queries could be combined
# Male mice that had a session
Mouse & Session & 'sex = "M"'
# Give me all mice that have had an experimental session done on or before 2017-05-19
Mouse & (Session & 'session_date <= "2017-05-19"')
# ### Negative restriction - with the `-` operator
# All mice that do not have any session
Mouse - Session
# Male mice that do not have any session
# ENTER YOUR CODE
# ## Joining (*) - bring fields from different tables together
# Sometimes you want to see information from multiple tables combined together to be viewed (and queried!) simultaneously. You can do this using the join `*` operator.
# Behavior of join:
#
# 1. match the common field(s) of the primary keys in the two tables
# 2. do a combination of the non-matched part of the primary key
# 3. listing out the secondary attributes for each combination
# 4. if two tables have secondary attributes that share a same name, it will throw an error. To join, we need to rename that attribute for at least one of the tables.
# looking at the combination of mouse and session
Mouse * Session
# Here each row represents a unique (and valid!) combination of a mouse and a session.
# The combined table can be queried using any of the attributes (columns) present in the joined tables:
# Find 'experimenter = "Jacob Reimer"' and 'sex = "M"'
Mouse * Session & 'experimenter = "Jacob Reimer"' & 'sex = "M"'
Mouse * Session & 'session_date > "2017-05-19"'
# ## Projection .proj(): focus on attributes of interest
# Beside restriction (`&`) and join (`*`) operations, DataJoint offers another type of operation: projection (`.proj()`). Projection is used to select attributes (columns) from a table, to rename them, or to create new calculated attributes.
# From the ***Mouse*** table, suppose we want to focus only on the `sex` attribute and ignore the others, this can be done as:
Mouse.proj('sex')
# Note that `.proj()` will always retain all attributes that are part of the primary key
# ### Rename attribute with proj()
# Say we want to rename the exisiting attribute `dob` of the `Mouse` table to `date_of_birth`, this can be done using `.proj()`
Mouse.proj(date_of_birth='dob')
# ### Perform simple computations with proj()
# Projection is perhaps most useful to perform simple computations on the attributes, especially on attributes from multiple tables by using in conjunction with the join (`*`) operation
(Mouse * Session).proj(age='datediff(session_date, dob)')
# Note: as you can see, the projection results keep the primary attributes from the `Mouse * Session` joinning operation, while removing all other non-primary attributes. To Keep all other attributes, you can use the `...` syntax
(Mouse * Session).proj(..., age='datediff(session_date, dob)')
# # Fetch data
# Once you have successfully narrowed down to the entities you want, you can fetch the query results just by calling fetch on it!
# ## Fetch one or multiple entries: `fetch()`
# All male mouse
male_mouse = Mouse & 'sex = "M"'
male_mouse
# Fetch it!
male_mouse.fetch()
# or all in one step
(Mouse & 'sex = "M"').fetch()
# Fetch as a list of dictionaries
(Mouse & 'sex = "M"').fetch(as_dict=True)
# Fetch as a pandas dataframe
(Mouse & 'sex = "M"').fetch(format='frame')
# ### Fetch the primary key
(Mouse & 'sex = "M"').fetch('KEY')
# ### Fetch specific fields
sex, dob = Mouse.fetch('sex', 'dob')
sex
dob
# Or fetch them together as a list of dictionaries
info = Mouse.fetch('sex', 'dob', as_dict=True)
info
# ## Fetch data from only one entry: `fetch1()`
# When knowing there's only 1 result to be fetched back, we can use `.fetch1()`. `fetch1` will always return the fetched result in a dictionary format
mouse_0 = (Mouse & {'mouse_id': 0}).fetch1() # "fetch1()" because we know there's only one
mouse_0
# `fetch1()` could also fetch the primary key
(Mouse & {'mouse_id': 0}).fetch1('KEY')
# or fetch specific fields:
sex, dob = (Mouse & {'mouse_id': 0}).fetch1('sex', 'dob')
sex
dob
# ## Deletion (`.delete()`) - deleting entries and their dependencies
# Now we have a good idea on how to restrict table entries, this is a good time to introduce how to **delete** entries from a table.
# To delete a specific entry, you restrict the table down to the target entry, and call `delete` method.
(Mouse & 'mouse_id = 100').delete()
# Calling `delete` method on an *unrestricted* table will attempt to delete the whole table!
Mouse.delete()
# # Summary
# Congratulations! You have successfully created your first DatJoint pipeline, using dependencies to establish the link between the tables. You have also learned to query and fetch the data.
#
# In the next session, we are going to extend our data pipeline with tables to represent **imported data** and define new tables to **compute and hold analysis results**.
#
# We will use both ephys and calcium imaging as example pipelines:
# + [02-electrophysiology](./electrophysiology/02-Imported%20Tables%20-%20Interactive.ipynb)
# + [02-calcium imaging](./calcium_imaging/02-Imported%20Tables%20-%20Interactive.ipynb)
| 22,521 |
/Titanic_Submission.ipynb
|
3847c4da61df87956d5156ab11719ffa321b584a
|
[] |
no_license
|
Homni/Data-Udacity
|
https://github.com/Homni/Data-Udacity
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 160,313 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # TITANIC
# ## Data Analysis
# The data was provided by Udacity as part of the Data Analysis Nanodegree. This data contains demographics and passenger information from 891 of the 2224 passengers and crew on board the Titanic. Extra detail on the data can be found on Kaggles website on the following [Link](https://www.kaggle.com/c/titanic/data).
# ### Questions
#
# This Data Analysis will explore the hypothesis that woman and upper class passengers are the majority of survivors.
#
# 1. Are woman a majority of survivors?
# 2. Does having an upper class ticket means surviving the titanic?
#
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# %pylab inline
#Add the data csv file to original var
original = pd.read_csv('titanic_data.csv')
#Use df as variable for data so original is available for backups
df = original
#look at the first 3 rows of the data
df.head(3)
#look at the first 3 rows of the data
df.tail(3)
# Both Age and Cabin show NaN's, that will be investigated later.
#
# Columns with Passenger ID, Name, Ticket, will be excluded due to being unique to each passenger and not indicating a relation to the questions being investigated.
#exclude Passenger ID, Name and Ticket
df = df.drop(['PassengerId', 'Name', 'Ticket'], axis = 1)
#check how it is now
df.head()
print('We are left with',df.shape[0],'lines and',df.shape[1],'columns')
# The columns contain the following description:
#
# - Survived : 1 = Yes, 0 = No
# - Pclass 1 : Upper, 2 = Middle, 3 = Lower
# - Sex
# - Age
# - SibSp : Number of Siblings/Spouses Aboard
# - Parch : Number of Parents/Children Aboard
# - Fare : Passenger Fare
# - Cabin
# - Embarked : Port of Embarkation
# C = Cherbourg
# Q = Queenstown
# S = Southampton
#check what kind of data
df.dtypes
#to better look at the data, change letter for cities emberked
df['Embarked'] = df['Embarked'].replace(['S','Q','C'],['Southampton','Queenstown','Cherbourg'])
df.head()
# Dealing with NaN's
#looking at the entire data set numbers
df.describe()
#checking how many nulls.
df.isnull().sum()
# Due to data sample being large, and age being expected to be a large influence on the survival rate and questions investigated, it was prefered to exclude NaN's from Age, which would still remain with a sample size of 714.
#
# Embarked NaN's are also excluded.
#
# Cabin seems to be the biggest concern, over 70% is NaN's. Thus, the Cabin column is excluded. However, if more information on cabin was available, their locations and emergency exits, it could be a good source of information.
#excluding Cabin
df = df.drop(['Cabin'], axis=1)
#excluding rows with NaN's
df = df.dropna()
df.head()
# We can now start looking at the data from a graphical point of view in order to look for patterns
# +
#create a variable for percenta number, and total of surviving females
df_female_per = around(df[df.Sex=='female'].Survived.value_counts(normalize=True).sort_index(),2)
df_female_num = df[df.Sex=='female'].Survived.value_counts().sort_index()
df_female_sum = df[df.Sex=='female'].Survived.value_counts().sort_index().sum()
#create a variable for percent, number, and total of surviving males
df_male_per = around(df[df.Sex=='male'].Survived.value_counts(normalize=True).sort_index(),2)
df_male_num = df[df.Sex=='male'].Survived.value_counts().sort_index()
df_male_sum = df[df.Sex=='male'].Survived.value_counts().sort_index().sum()
g = sns.FacetGrid(df, col="Sex")
g.map(plt.hist, "Age");
print('The boat had', df_male_num.sum(),'males and', df_female_num.sum(),'females distributed the following way by age:')
print('It is imaginable that males will be the majority of survival, since they are the majority on board')
print("\n")
# -
# We can also see that both male and female are positively skewed and that the AGE range between 20 and 40 contains the higher number of individuals
print("In summary we can see that females have a", (df_female_per[1]*100),'%', "survival rate, with", (df_female_num[1]), "surviving from a total of",(df_female_sum),".")
print("When comparing to man, the female numbers seem even more surprising. Man have a survival rate of", (df_male_per[1]*100),'%', "with", (df_male_num[1]),"surviving from a total of ",(df_male_sum),".")
# The plots below show how significant the diference is between male and female:
# +
#have a graph that shows the difference between male and fimale
fig, ax = plt.subplots() #two graphs combined
n_groups = 2
bar_width = 0.40
index = np.arange(n_groups)
opacity = 0.9
error_config = {'ecolor': '0.3'}
#graph for the male variable
rects1 = plt.bar(index, df_male_num, 0.2,
alpha=opacity,
color='b',
label='Men')
#graph for the female variable
rects2 = plt.bar(index + 0.15, df_female_num, 0.185,
alpha=opacity,
color='g',
label='Woman')
plt.xlabel('Survived (0=No, 1=Yes)')
plt.ylabel('Scores')
plt.title('Survival by Sex')
plt.xticks(index + bar_width/2, ('0', '1'))
plt.legend()
plt.show()
# -
#graph that checks if class makes a difference in sex survival rate
g = sns.factorplot(x="Sex", y="Survived", col="Pclass",
data=df, saturation=0.9,
kind="bar", ci=None, aspect=.6)
(g.set_axis_labels("", "Survived")
.set_xticklabels(["Men", "Women"])
.set_titles("{col_name} {col_var}")
.set(ylim=(0, 1))
.despine(left=True))
#check if different embarking cities make a difference
g = sns.factorplot(x="Sex", y="Survived", col="Embarked",
data=df, saturation=0.9,
kind="bar", ci=None, aspect=.6)
(g.set_axis_labels("", "Survived")
.set_xticklabels(["Men", "Women"])
.set_titles("{col_name} {col_var}")
.set(ylim=(0, 1))
.despine(left=True))
print('The graph below shows that the embarking city has the same relation: most females surviving')
print("\n")
# ### Question 1
#
# The series graphs above shows that despite man being the majority on the boat, woman survival rate is higher on all classes and has no distinction among where those people boarded the boat.
#
# Based on the different shown graphs above, it could be interpreted that being a woman on the titanic gives you a 75% chance of survival, no mather which class you are on the boat or which city you embarked.
# ________________________
#
# ### The same process from question 1 can be taken to analyse question 2
# +
df_pclass1_per = round(df[df.Pclass==1].Survived.value_counts(normalize=True).sort_index(),2)
df_pclass1_num = df[df.Pclass==1].Survived.value_counts().sort_index()
df_pclass1_sum = df[df.Pclass==1].Survived.value_counts().sort_index().sum()
df_pclass2_per = round(df[df.Pclass==2].Survived.value_counts(normalize=True).sort_index(),2)
df_pclass2_num = df[df.Pclass==2].Survived.value_counts().sort_index()
df_pclass2_sum = df[df.Pclass==2].Survived.value_counts().sort_index().sum()
df_pclass3_per = round(df[df.Pclass==3].Survived.value_counts(normalize=True).sort_index(),2)
df_pclass3_num = df[df.Pclass==3].Survived.value_counts().sort_index()
df_pclass3_sum = df[df.Pclass==3].Survived.value_counts().sort_index().sum()
# +
#graph that shows all classes and its total passengers
df_class = df['Pclass'].value_counts().sort_index()
df_class.plot(kind='bar', figsize=(4,4), rot=0, grid=True)
plt.title('Number of Passengers by Class')
plt.xlabel('Class')
plt.ylabel('Number of Passengers')
print('We can see that the number of passengers on the Lower class is equal to the sum of both middle and upper class')
print("\n")
# -
g_class_age = sns.FacetGrid(df, col="Pclass")
g_class_age.map(plt.hist, "Age");
print('The graphs below shows Age distribution by class')
print('We can see that Lower class, which is the majority of individuals on board, is mainly on the 20 to 40 age range')
print("\n")
# +
n_groups = 2
fig, ax = plt.subplots()
index = np.arange(n_groups)
bar_width = 0.4
opacity = 0.9
error_config = {'ecolor': '0.3'}
rects1 = plt.bar(index, df_pclass1_num, bar_width,
alpha=opacity,
color='b',
label='Upper'
)
rects2 = plt.bar(index + 0.15, df_pclass2_num, bar_width,
alpha=opacity,
color='g',
label='Middle'
)
rects3 = plt.bar(index + 0.30, df_pclass3_num, bar_width,
alpha=opacity,
color='r',
label='Lower'
)
plt.xlabel('Survived (0=No, 1=Yes)')
plt.ylabel('Scores')
plt.title('Survival by Class')
plt.xticks(index + bar_width/2, ('0', '1'))
plt.legend()
plt.show()
# +
print("In summary we can see that the boat had", (df_class.sum()), "passengers, divided into 3 classes:")
print("Upper Class, with 184 passengers, middle class with 173 passengers and lower class with 355 passengers")
print("When comparing to each other, the lower class number is the biggest surprise. Lower class have a survival rate of", (df_pclass3_per[1]*100),'%', "with", (df_pclass3_num[1]),"surviving from a total of ",(df_pclass3_sum),".")
print("On the other end, upper class have a survival rate of", (df_pclass1_per[1]*100),'%', "with", (df_pclass1_num[1]),"surviving from a total of ",(df_pclass1_sum),".")
print("Lastly, middle class have a survival rate of", (df_pclass2_per[1]*100),'%', "with", (df_pclass2_num[1]),"surviving from a total of ",(df_pclass2_sum),".")
# -
# ### Question 2
#
# The series graphs above show a similar trend from the sex comparison. The majority of passenger is composed of passengers in the lower class. However, it was the upper and middle classes that got the most survivors.
#
# Based on the different shown graphs above, it could be interpreted that being on upper class gives a better chance of surviving, when traveling on middle class that chance diminishes to a slightly higher chance of not surviving. For the lower class, the chance of surviving is minimal.
# #### Project Limitations
#
# - Missing Values: This analysis is done on a sample of the total passanger number, so conclusion may be biased do due not having the entire dataset. When we first analyse the data we see that we have many missing values from the sample, which in turn reduces the sample from 891 to 714
#
# - Other Variables: Basic variables are provided for this analysis. However other variables could also influence the survival rate. Such as: Being a crew member; where there lifeboats specifically for 1st class?; Cabin location related to lifeboats. These are a few variable that could influence our perception of who would have a higher survival rate.
#
# - Correlation does not imply Causation: Altough we may imply that being a female and not being on 3rd class increases the chances of surviving. It is not possible to conclude that there is a causation relationship from that, specially when we look at a sample with missing values.
#
#
# ### References:
# - http://seaborn.pydata.org/index.html
# - http://matplotlib.org/examples/
# - https://www.kaggle.com/c/titanic/data
# - http://stackoverflow.com/questions/14883339/two-bar-charts-in-matplotlib-overlapping-the-wrong-way
# - http://pandas.pydata.org/
# - https://docs.scipy.org
# - https://en.wikipedia.org/wiki/Correlation_does_not_imply_causation
| 11,658 |
/Joy Ride/circular_track.ipynb
|
a051c559d4df0784c1612edd581efb5a845c9d6c
|
[] |
no_license
|
lordtt13/self-driving-car-nanodegree
|
https://github.com/lordtt13/self-driving-car-nanodegree
| 1 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 1,994 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# goal: 用 mpl 的最新 API 画 k 线图。不再学习老 API。
#
# 意外收获:
#
# 1. 多了成交量、均线图等常用指标。
# 2. 不开盘的日期,已从图中自动剔除,不再需要额外处理。
# 3. 相邻两天的矩形,不会相互覆盖。
#
# 不愧是社区基础最好的库,新版本的改进很明显。
#
# - 测试数据来源:https://raw.githubusercontent.com/matplotlib/mplfinance/master/examples/data/SP500_NOV2019_Hist.csv
# - 本地路径:data/for-tutorial-only/SP500_NOV2019_Hist.csv
import pandas as pd
import mplfinance as mpf
test_data_path = '../data/for-tutorial-only/SP500_NOV2019_Hist.csv'
# Load data file.
df = pd.read_csv(test_data_path, index_col=0, parse_dates=True)
df.head()
df.size
# Plot candlestick.
# Add volume.
# Add moving averages: 3,6,9.
mpf.plot(df, type='candle', style='charles',
title='S&P 500, Nov 2019',
ylabel='Price ($)',
ylabel_lower='Shares \nTraded',
volume=True,
mav=(3, 6, 9),
)
import matplotlib as mpl # 用于设置曲线参数
from cycler import cycler # 用于定制线条颜色
# +
# 设置基本参数
# type:绘制图形的类型,有candle, renko, ohlc, line等
# 此处选择candle,即K线图
# mav(moving average):均线类型,此处设置7,30,60日线
# volume:布尔类型,设置是否显示成交量,默认False
# title:设置标题
# y_label_lower:设置成交量图一栏的标题
# figratio:设置图形纵横比
# figscale:设置图形尺寸(数值越大图像质量越高)
kwargs = dict(
type='candle',
mav=(3, 6, 9),
volume=True,
title='S&P 500, Nov 2019',
ylabel='OHLC Candles',
ylabel_lower='Shares\nTraded Volume',
# figratio=(15, 10),
# figscale=2,
)
# 设置marketcolors
# up:设置K线线柱颜色,up意为收盘价大于等于开盘价
# down:与up相反,这样设置与国内K线颜色标准相符
# edge:K线线柱边缘颜色(i代表继承自up和down的颜色),下同。详见官方文档)
# wick:灯芯(上下影线)颜色
# volume:成交量直方图的颜色
# inherit:是否继承,选填
mc = mpf.make_marketcolors(
up='red',
down='green',
edge='i',
wick='i',
volume='in',
inherit=True)
# 设置图形风格
# gridaxis:设置网格线位置
# gridstyle:设置网格线线型
# y_on_right:设置y轴位置是否在右
s = mpf.make_mpf_style(
gridaxis='both',
gridstyle='-.',
y_on_right=True,
marketcolors=mc)
# 设置均线颜色,配色表可见下图
# 建议设置较深的颜色且与红色、绿色形成对比
# 此处设置七条均线的颜色,也可应用默认设置
mpl.rcParams['axes.prop_cycle'] = cycler(
color=['dodgerblue', 'deeppink',
'navy', 'teal', 'maroon', 'darkorange',
'indigo'])
# # 设置线宽
# mpl.rcParams['lines.linewidth'] = .5
# 图形绘制
# show_nontrading:是否显示非交易日,默认False
# savefig:导出图片,填写文件名及后缀
mpf.plot(df,
**kwargs,
style=s,
show_nontrading=False,
)
# -
| 2,509 |
/lectures/7.0 - Bagging.ipynb
|
bb371caa562c7222971536754789f3740b3a7a54
|
[] |
no_license
|
vitaliyradchenko/projector_course
|
https://github.com/vitaliyradchenko/projector_course
| 9 | 6 | null | 2020-02-18T16:56:03 | 2020-02-18T07:29:10 |
Jupyter Notebook
|
Jupyter Notebook
| false | false |
.py
| 47,928 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="-4IC1hKgJQzo"
# # <center> Bagging</center>
#
# From the previous lectures, you have already learned about different classification algorithms and also learned how to properly validate and evaluate the quality of the model. But what if you have already found the best model and can no longer improve the accuracy of the model? In this case, you need to apply more advanced machine learning techniques, which can be combined with the word “ensembles”. The ensemble is a kind of collection, the parts of which form a single whole. From everyday life, you know musical ensembles, where several musical instruments are combined, architectural ensembles with different buildings, etc.
#
# ### Ensemble
#
# A good example of ensembles is the Condorcet's jury theorem (1784). If each member of the jury has an independent opinion, and if the probability of a correct decision by a jury member is greater than 0.5, then the probability of a correct decision by the jury as a whole increases with the number of jurors and tends to one. If the probability of being right for each of the jury members is less than 0.5, then the probability of making the right decision by the jury as a whole monotonically decreases and tends to zero with an increase in the number of jurors.
#
# - $\large N $ — number of jurors
# - $\large p $ — probability of correct jury decision
# - $\large \mu $ — probability of correct decision of the entire jury
# - $\large m $ — minimum majority of jury members, $ m = floor(N/2) + 1 $
# - $\large C_N^i$ — [combinations](https://en.wikipedia.org/wiki/Combination) $i$ elements, the number of $N$-combinations
# $$ \large \mu = \sum_{i=m}^{N}C_N^ip^i(1-p)^{N-i} $$
# If $\large p > 0 $, then $\large \mu > p $
# If $\large N \rightarrow \infty $, then $\large \mu \rightarrow 1 $
#
#
# <img src="https://github.com/terpiljenya/machine_learning_projector/blob/main/pictures/bull.png?raw=1" align="right" width=15% height=15%>
#
#
# Let's look at another example of ensembles - "The Wisdom of the Crowd". Francis Galton in 1906 visited the market, where a certain lottery was held for the peasants.
# There were about 800 of them and they tried to guess the weight of the bull that stood in front of them. His weight was 1198 pounds. Not a single peasant guessed the exact weight of the bull, but if we calculate the average of their predictions, we get 1197 pounds.
# This idea of error reduction has also been applied to machine learning.
#
# ## Bootstrap
#
# Bagging (or Bootstrap aggregation) is one of the first and simplest types of ensembles. It was invented by Leo Breiman in 1994. Bagging is based on the statistical method of bootstrapping, which allows estimation of many statistics of complex models.
#
# The bootstrap method is as follows. Let there be a sample $\large X$ of size $\large N$. Let's evenly take $\large N$ objects from the sample with return. This means that we will select an arbitrary sample object $\large N$ times (we assume that each object "gets" with the same probability $\large \frac{1}{N}$), and each time we choose from all initial $\large N$ objects. One can imagine a bag from which balls are taken out: the ball chosen at some step is returned back to the bag, and the next choice is again made equiprobably from the same number of balls. Note that due to the return, there will be repetitions among them. Denote the new sample by $\large X_1$. Repeating the procedure $\large M$ times, we generate $\large M$ subsamples $\large X_1, \dots, X_M$. Now we have a sufficiently large number of samples and can evaluate various statistics of the original distribution.
#
# Let's take a credit scoring dataset as an example. This is a binary classification task, where 0 is not overdue, 1 is overdue. One of the features in this dataset is the age of the client. Let's try to visualize the data and look at the distribution of this feature.
# + id="4SZzD0KKJMa3" colab={"base_uri": "https://localhost:8080/", "height": 282} outputId="73c9cb7d-4921-4472-bdc5-4ab5693a17f3"
import pandas as pd
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = 10, 6
import seaborn as sns
# %matplotlib inline
data = pd.read_csv("/content/drive/MyDrive/projector_course_data/credit_scoring_sample.csv", sep=";")
fig = sns.kdeplot(data.loc[data["SeriousDlqin2yrs"] == 0, "age"], label = "Not late payment")
fig = sns.kdeplot(data.loc[data["SeriousDlqin2yrs"] == 1, "age"], label = "Late payment")
fig.set(xlabel="Age", ylabel="Density")
plt.show()
# + [markdown] id="4C_A-qFixXDJ"
# As you may have noticed, the older the client of the bank, the better he repays the loan. Now it would be good to estimate the average age for each group. Since there is not enough data in our dataset, it is not entirely correct to look for the average, it is better to apply our new bootstrap knowledge. Let's generate 1000 new subsamples from our population and do an interval estimate of the mean.
# + colab={"base_uri": "https://localhost:8080/"} id="cw-2qXPQwopc" outputId="483b6001-9b92-4bb7-fb22-b5b8225b8c7e"
import numpy as np
def get_bootstrap_samples(data, n_samples):
# function to generate subsamples using bootstrap
indices = np.random.randint(0, len(data), (n_samples, len(data)))
samples = data[indices]
return samples
def stat_intervals(stat, alpha):
# function for interval estimation
boundaries = np.percentile(stat, [100 * alpha / 2., 100 * (1 - alpha / 2.)])
return boundaries
# saving in separate numpy arrays data on loyal and already former customers
good_credit = data.loc[data["SeriousDlqin2yrs"] == 0, "age"].values
bad_credit = data.loc[data["SeriousDlqin2yrs"] == 1, "age"].values
# set a seed for reproducible results
np.random.seed(0)
# generate samples using bootstrap and calculate the average for each group
good_credit_mean_scores = [
np.mean(sample) for sample in get_bootstrap_samples(good_credit, 1000)
]
bad_credit_mean_scores = [
np.mean(sample) for sample in get_bootstrap_samples(bad_credit, 1000)
]
print("Age of good creditors: mean interval", stat_intervals(good_credit_mean_scores, 0.05))
print("Age of bad creditors: mean interval", stat_intervals(bad_credit_mean_scores, 0.05))
# + [markdown] id="fPylTMTbyU2-"
# As a result, we got that with a 95% probability, the average age of loyal customers will be approximately 52-53 years old, while our bad customers are 6 years younger than them.
#
# ## Bagging
#
# Now you have an idea about bootstrapping, we can move on to bagging. Let there be a training sample $\large X$. Using the bootstrap, we will generate $\large X_1, \dots, X_M$ samples from it. Now, on each sample, we will train our classifier $\large a_i(x)$. The final classifier will average the answers of all these algorithms (in the case of classification, this corresponds to voting): $\large a(x) = \frac{1}{M}\sum_{i = 1}^M a_i(x)$. This scheme can be represented in the picture below.
#
# <img src="https://github.com/terpiljenya/machine_learning_projector/blob/main/pictures/bagging.png?raw=1" alt="image"/>
#
# Consider a regression problem with basic algorithms $\large b_1(x), \dots , b_n(x)$. Assume that there is a true response function for all $\large y(x)$ objects, and a distribution on $\large p(x)$ objects is given. In this case, we can write down the error of each regression function $$ \large \varepsilon_i(x) = b_i(x) − y(x), i = 1, \dots, n$$
# and write the mean squared error $$ \large E_x(b_i(x) − y(x))^{2} = E_x \varepsilon_i (x). $$
#
# The average error of the constructed regression functions has the form $$ \large E_1 = \frac{1}{n}E_x \sum_{i=1}^n \varepsilon_i^{2}(x) $$
#
# Assume that the errors are unbiased and uncorrelated:
#
# $$ \large \begin{array}{rcl} E_x\varepsilon_i(x) &=& 0, \\
# E_x\varepsilon_i(x)\varepsilon_j(x) &=& 0, i \neq j. \end{array}$$
#
# Now let's build a new regression function that will average the answers of the functions we built:
# $$ \large a(x) = \frac{1}{n}\sum_{i=1}^{n}b_i(x) $$
#
# Find its root mean square error:
#
# $$ \large \begin{array}{rcl}E_n &=& E_x\Big(\frac{1}{n}\sum_{i=1}^{n}b_i(x)-y(x)\Big)^2 \\
# &=& E_x\Big(\frac{1}{n}\sum_{i=1}^{n}\varepsilon_i\Big)^2 \\
# &=& \frac{1}{n^2}E_x\Big(\sum_{i=1}^{n}\varepsilon_i^2(x) + \sum_{i \neq j}\varepsilon_i(x)\varepsilon_j(x)\Big) \\
# &=& \frac{1}{n}E_1\end{array}$$
#
# Thus, averaging the answers made it possible to reduce the mean square of the error by n times!
#
#
# Recall how the general error is decomposed:
# $$\large \begin{array}{rcl}
# \text{Err}\left(\vec{x}\right) &=& \mathbb{E}\left[\left(y - \hat{f}\left(\vec{x}\right)\right)^2\right] \\
# &=& \sigma^2 + f^2 + \text{Var}\left(\hat{f}\right) + \mathbb{E}\left[\hat{f}\right]^2 - 2f\mathbb{E}\left[\hat{f}\right] \\
# &=& \left(f - \mathbb{E}\left[\hat{f}\right]\right)^2 + \text{Var}\left(\hat{f}\right) + \sigma^2 \\
# &=& \text{Bias}\left(\hat{f}\right)^2 + \text{Var}\left(\hat{f}\right) + \sigma^2
# \end{array}$$
#
# Bagging allows you to reduce the variance (variance) of the trained classifier, reducing the amount by which the error will differ if the model is trained on different data sets, or in other words, it prevents overfitting. The efficiency of bagging is achieved due to the fact that the basic algorithms trained on different subsamples turn out to be quite different, and their errors are mutually compensated during voting, and also due to the fact that outlier objects may not fall into some training subsamples.
#
# The `scikit-learn` library has an implementation of `BaggingRegressor` and `BaggingClassifier` that allows most other algorithms to be used "inside". Let's see how bagging works in practice and compare it with a decision tree using an example from [documentation](http://scikit-learn.org/stable/auto_examples/ensemble/plot_bias_variance.html#sphx-glr-auto-examples-ensemble-plot-bias-variance-py).
#
# 
#
# Decision tree error:
# $$ \large 0.0255 (Err) = 0.0003 (Bias^2) + 0.0152 (Var) + 0.0098 (\sigma^2) $$
# Bagging error:
# $$ \large 0.0196 (Err) = 0.0004 (Bias^2) + 0.0092 (Var) + 0.0098 (\sigma^2) $$
#
# From the graph and results above, it can be seen that the error of variance is much smaller with bagging, as we proved theoretically above.
#
# Bagging is effective on small samples, when the exclusion of even a small part of training objects leads to the construction of significantly different base classifiers. In the case of large samples, subsamples of significantly smaller length are usually generated.
#
# It should be noted that the example we have considered is not very applicable in practice, since we made the assumption of uncorrelated errors, which is rarely true. If this assumption is wrong, then the error reduction is not so significant. In the following lectures, we will consider more complex methods for combining algorithms into a composition, which allow us to achieve high quality in real problems.
#
# ### Out-of-bag error
#
# Looking ahead, when using random forests, there is no need for cross-validation or a separate test set to get an unbiased estimate of the test set error. The internal evaluation during operation is obtained as follows:
#
# Each tree is built using different bootstrap samples from the original data. Approximately 37% of examples remain outside the bootstrap sample and are not used when constructing the k-th tree.
#
# This can be easily proved: let there be $\large \ell$ objects in the sample. At each step, all objects fall into the subsample with an equiprobable return, i.e. an individual object with probability $\large\frac{1}{\ell}.$ The probability that the object will NOT fall into the subsample (i.e. took $\large \ell$ times): $\large (1 - \frac{1}{\ell})^\ell$. For $\large \ell \rightarrow +\infty$ we get one of the "wonderfull" limits $\large \frac{1}{e}$. Then the probability of a particular object falling into the subsample is $\large \approx 1 - \frac{1}{e} \approx 63\%$.
#
# Let's see how this works in practice:
#
# 
#
# The figure shows that our classifier made a mistake in 4 observations that we did not use for training. So the accuracy of our classifier is: $\large \frac{11}{15}*100\% = 73.33\%$
#
# It turns out that each basic algorithm is trained on ~63% of the original objects. This means that on the remaining ~37% can be checked immediately. The out-of-bag score is the average score of the underlying algorithms on those ~37% of the data on which they were not trained.
#
# + id="L4YyR49xyOgH"
import warnings
warnings.filterwarnings('ignore')
scoring_label = data["SeriousDlqin2yrs"].astype(int)
scoring_features = data.drop(["SeriousDlqin2yrs"], axis=1)
# + colab={"base_uri": "https://localhost:8080/"} id="UhFBYABH8Ia3" outputId="f659a361-196e-43a3-d22c-382a7a4f8daf"
scoring_features.isnull().mean()
# + id="MOzF4ahw8K4N"
scoring_features = scoring_features.fillna(scoring_features.median())
# + colab={"base_uri": "https://localhost:8080/"} id="f25Ebkgm8Ocz" outputId="63d8fd4a-007b-4184-fbd3-44cb87b672b9"
scoring_features.isnull().mean()
# + id="GmZ9Gcy98RWy"
from sklearn.model_selection import StratifiedKFold, cross_val_score, RandomizedSearchCV
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
# + id="gg3oNu_W8WMl"
skf = StratifiedKFold(shuffle=True, random_state=42)
# + colab={"base_uri": "https://localhost:8080/"} id="PwQVqqOr8Xc1" outputId="1b731bec-d8ca-437d-d72b-618912e54c92"
dt = DecisionTreeClassifier()
parameters = {"max_depth": [None, 4, 8, 12, 15], "min_samples_leaf": [1, 2, 3, 5, 8]}
r_grid_search = RandomizedSearchCV(dt, parameters, scoring ="roc_auc", cv=skf, random_state=42)
r_grid_search = r_grid_search.fit(scoring_features, scoring_label)
print(r_grid_search.best_score_)
# + colab={"base_uri": "https://localhost:8080/"} id="3ZyATloC8e0_" outputId="51cba3f4-c8d5-48b7-9770-bd918877cba4"
r_grid_search.best_estimator_
# + colab={"base_uri": "https://localhost:8080/"} id="3aTPRwYF8g-g" outputId="fe74f31d-db79-4a67-f05f-74925fed0ae7"
parameters = {
"max_features": [0.7, 0.8, 0.9],
"max_samples": [0.7, 0.8, 0.9],
"base_estimator__max_depth": [None, 4, 8, 12, 15],
"base_estimator__min_samples_leaf": [1, 2, 3, 5, 8]
}
dt = DecisionTreeClassifier()
bg = BaggingClassifier(dt, random_state=42, n_estimators=25)
r_grid_search = RandomizedSearchCV(bg, parameters, scoring ='roc_auc', n_iter=20, cv=skf, random_state=42, n_jobs=10)
r_grid_search = r_grid_search.fit(scoring_features, scoring_label)
print(r_grid_search.best_score_)
# + colab={"base_uri": "https://localhost:8080/"} id="Vatjmk4v8kov" outputId="52c39cd6-735a-4ee7-a4c4-040f43ba55b2"
r_grid_search.best_estimator_
# + id="a3MYUelE8msX"
| 15,212 |
/course-content/Examples/matplotlib_inline.ipynb
|
5db6f82ea856e5785505dd443ce433d39ae7e728
|
[
"Apache-2.0"
] |
permissive
|
ati-ozgur/course-python
|
https://github.com/ati-ozgur/course-python
| 2 | 1 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 1,787 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import matplotlib.pylab as pl
import pandas as pd
csv_filename ="../data/c2k_data_comma.csv"
df = pd.read_csv(csv_filename)
ax = df[["i1_legid","i1_rcs_p"]].plot()
pl.show()
# %matplotlib inline
df[["i1_legid","i1_rcs_p"]].plot()
lts",engine)
cr=county_results
cr.head()
# # Which 10 counties Bernie has the highest vote?
bs=cr[cr.candidate=="Bernie Sanders"].sort_values(by=['votes'],ascending=False).head(10)
dems=cr[(cr.candidate=="Bernie Sanders")|(cr.candidate=="Hillary Clinton")]
dems.head()
compbh=pd.pivot_table(dems,values='votes',index=['state','county'],columns=['candidate'])
compbh.columns
compbh.head()
compbh.sort_values("Bernie Sanders", ascending=False).head()
# # Who won which states?
compbh=pd.pivot_table(dems,values='votes',index='state',columns='candidate', aggfunc=sum)
compbh.head()
compbh['votediff']=compbh['Bernie Sanders']-compbh['Hillary Clinton']
compbh.sort_values('votediff',ascending=False)
cf=pd.read_sql('county_facts',engine)
cf.head()
data=pd.merge(cr,cf,left_on='fips',right_on='fips')
data.head()
# # How does family size impact the voting decision?
pd.pivot_table(data,values='votes',index="fips",columns='candidate',aggfunc=max).dropna()
pt=pd.pivot_table(cr,values='votes',index=['state'],columns=['candidate'],aggfunc=max)
pt.iloc[0:,1:].apply(np.max,axis=1)
pt.iloc[1,2:][pt.iloc[1,2:]==440.0]
def findmax(row):
max_val=np.max(row)
name=row[row==max_val].index[0]
return name
pt.iloc[0:,2:].apply(findmax,axis=1)
np.max(pt.iloc[1,2:])
| 1,806 |
/homework/Day_033_HW.ipynb
|
39e3f63f606448697059bdf7486080e047f5e1ed
|
[] |
no_license
|
ryanlu7374/ML100-Days
|
https://github.com/ryanlu7374/ML100-Days
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 21,964 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + language="javascript"
# IPython.OutputArea.prototype._should_scroll = function(lines) {
# return false;
# }
# +
#load all the files for a user
from matplotlib.pyplot import figure
import random
import glob
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime as dt
import seaborn as sns
import math
import os
import errno
import matplotlib.patches as patches
from copy import deepcopy
from scipy.spatial.distance import cdist
from matplotlib.patches import Ellipse
import operator
import pdb
import calendar
from sklearn.cluster import KMeans
from sklearn import metrics
from scipy.spatial.distance import cdist
from matplotlib.patches import Ellipse, Circle
# #%matplotlib nbagg
pd.options.mode.chained_assignment = None
staypts_filename = "C:/Users/12sha/Documents/thesislocation/Data/Final Example Results/User 001/200811/staypoints/staypoints.csv"
raw_filename = "C:/Users/12sha/Documents/Geolife Trajectories 1.3/Data/001/Trajectory/200811*.plt"
destpng = "C:/Users/12sha/Documents/thesislocation/Writings/media/staypoint_test.png"
# +
filenames = glob.glob(raw_filename)
list_of_files_dfs = [pd.read_csv(filename, skiprows=6, header = None) for filename in filenames]
raw_df = pd.concat(list_of_files_dfs, ignore_index=True)
raw_df.columns = ['Latitude', 'Longitude', '0', 'Altitude', 'NumDays', 'Date', 'Time']
staypts_df = pd.read_csv(staypts_filename, sep = '\t')
# drop columns not needed
raw_df = raw_df.drop(['0', 'Altitude', 'NumDays', 'Date', 'Time'], axis=1)
staypts_df = staypts_df.drop(['Latitude', 'Longitude', 'Timestamp', 'Date', 'Time', 'Hour', 'Weekday', 'StayPoint', 'StayptId',
'StayMeanLat', 'StayMeanLon', 'State', 'StateId', 'Unnamed: 0'], axis=1)
staypts_df.columns = ['Latitude', 'Longitude']
#raw_df = raw_df.drop_duplicates()
raw_df = raw_df.reset_index(drop=True)
#staypts_df = staypts_df.drop_duplicates()
staypts_df = staypts_df.reset_index(drop=True)
# +
#assign the first lat and log as the base for the plot i.e. origin
origin_lat = math.radians(raw_df["Latitude"][0])
origin_lon = math.radians(raw_df["Longitude"][0])
#convert each lat and lon into x and y for the plot w.r.t origin
EARTH_RAD = 6378100
raw_df['X'] = 0.0
raw_df['Y'] = 0.0
for i in range(0, len(raw_df)):
x = 0
y = 0
current_lat = math.radians(raw_df["Latitude"][i])
current_lon = math.radians(raw_df["Longitude"][i])
x = ((math.cos(current_lat) + math.cos(origin_lat))/2) * EARTH_RAD * (current_lon - origin_lon) * math.pi / 180
y = (current_lat - origin_lat)* math.pi/180 * EARTH_RAD
raw_df.at[i, 'X'] = x
raw_df.at[i, 'Y'] = y
fg = raw_df.plot(x='X', y='Y', color='g', label='Raw Coordinates')
plt.title('User Movement Trend Vs Stay-points', fontsize = 30)
min_x = min(raw_df['X'])
max_x = max(raw_df['X'])
min_y = min(raw_df['Y'])
max_y = max(raw_df['Y'])
xticks = np.arange(min_x,max_x,(max_x-min_x)/25)
yticks = np.arange(min_y,max_y,(max_y-min_y)/50)
fg.set(xticks=xticks, yticks=yticks)
plt.xlabel('X')
plt.ylabel('Y')
#assign the first lat and log as the base for the plot i.e. origin
origin_lat = math.radians(raw_df["Latitude"][0])
origin_lon = math.radians(raw_df["Longitude"][0])
#convert each lat and lon into x and y for the plot w.r.t origin
EARTH_RAD = 6378100
staypts_df['X'] = 0.0
staypts_df['Y'] = 0.0
for i in range(0, len(staypts_df)):
x = 0
y = 0
current_lat = math.radians(staypts_df["Latitude"][i])
current_lon = math.radians(staypts_df["Longitude"][i])
x = ((math.cos(current_lat) + math.cos(origin_lat))/2) * EARTH_RAD * (current_lon - origin_lon) * math.pi / 180
y = (current_lat - origin_lat)* math.pi/180 * EARTH_RAD
staypts_df.at[i, 'X'] = x
staypts_df.at[i, 'Y'] = y
plt.plot(staypts_df['X'], staypts_df['Y'], 'r^', label='Stay-points', markersize=12)
plt.rcParams["figure.figsize"] = [20,20]
plt.legend(fontsize=30)
plt.xlabel("X", fontsize=25)
plt.ylabel("Y", fontsize=25)
plt.savefig(destpng)
plt.show()
# -
ttps://gis.stackexchange.com/questions/350771/earth-engine-simplest-way-to-move-from-ee-image-to-array-for-use-in-sklearn/351177#351177
# runoff_missing = -99999
# pot_runoff_data = np.array(
# pot_runoff_img_scaled
# .sampleRectangle(bbox, ['potential_sfc_runoff_mon_clim_cms'], smap_missing)
# .get('potential_sfc_runoff_mon_clim_cms')
# .getInfo())
# pot_runoff_data_mask = np.ma.masked_values(pot_runoff_data, smap_missing)
# pot_runoff_data_drop = pot_runoff_data_mask[~pot_runoff_data_mask.mask]
# +
# print(pot_runoff_data)
# +
# pot_runoff_data_mask
# pot_runoff_data_drop
# +
# _ = norm.normal_dist_plot(avail_porosity_data_drop)
# -
# ## MERIT Terrain Slope
#include slope as a factor in scoring product 1
slope_img = ee.Image('users/jamesmcc/merit_slope/merit_terrain_slope')
slope_mask = slope_img.lte(6)
slope_img_scaled = norm.img_scale(slope_img, area_of_interest=common.bboxes()['conus'])
# This dosent really need scaled, just a mask?
# # Soil Types
#incorporate soil types as a factor in scoring land parcels
soil_types = ee.Image("OpenLandMap/SOL/SOL_TEXTURE-CLASS_USDA-TT_M/v02")
# +
#categorizing soil types and depths based on retaining plant-available water, grouping top soils and bottom soils together
top_soils = [5,7,8,10]
medium_soils = [2,4,6,9]
low_soils = [1,3,11,12]
soil_0 = soil_types.expression(
"(b('b0') == 12) ? 1.0" +
": (b('b0') == 11) ? 1.0" +
": (b('b0') == 10) ? 1.0" +
": (b('b0') == 9) ? 1.0" +
": (b('b0') == 8) ? 0.7" +
": (b('b0') == 7) ? 0.7" +
": (b('b0') == 6) ? 0.7" +
": (b('b0') == 5) ? 0.7" +
": (b('b0') == 4) ? 0.4" +
": (b('b0') == 3) ? 0.4" +
": (b('b0') == 2) ? 0.4" +
": (b('b0') == 1) ? 0.4" +
": 0")
soil_10 = soil_types.expression(
"(b('b10') == 12) ? 1.0" +
": (b('b10') == 11) ? 1.0" +
": (b('b10') == 10) ? 1.0" +
": (b('b10') == 9) ? 1.0" +
": (b('b10') == 8) ? 0.7" +
": (b('b10') == 7) ? 0.7" +
": (b('b10') == 6) ? 0.7" +
": (b('b10') == 5) ? 0.7" +
": (b('b10') == 4) ? 0.4" +
": (b('b10') == 3) ? 0.4" +
": (b('b10') == 2) ? 0.4" +
": (b('b10') == 1) ? 0.4" +
": 0")
soil_30 = soil_types.expression(
"(b('b30') == 12) ? 1.0" +
": (b('b30') == 11) ? 1.0" +
": (b('b30') == 10) ? 1.0" +
": (b('b30') == 9) ? 1.0" +
": (b('b30') == 8) ? 0.7" +
": (b('b30') == 7) ? 0.7" +
": (b('b30') == 6) ? 0.7" +
": (b('b30') == 5) ? 0.7" +
": (b('b30') == 4) ? 0.4" +
": (b('b30') == 3) ? 0.4" +
": (b('b30') == 2) ? 0.4" +
": (b('b30') == 1) ? 0.4" +
": 0")
soil_60 = soil_types.expression(
"(b('b60') == 5) ? 1.0" +
": (b('b60') == 7) ? 1.0" +
": (b('b60') == 8) ? 1.0" +
": (b('b60') == 10) ? 1.0" +
": (b('b60') == 2) ? 0.7" +
": (b('b60') == 4) ? 0.7" +
": (b('b60') == 6) ? 0.7" +
": (b('b60') == 9) ? 0.7" +
": (b('b60') == 1) ? 0.3" +
": (b('b60') == 3) ? 0.3" +
": (b('b60') == 11) ? 0.3" +
": (b('b60') == 12) ? 0.3" +
": 0")
soil_100 = soil_types.expression(
"(b('b100') == 5) ? 1.0" +
": (b('b100') == 7) ? 1.0" +
": (b('b100') == 8) ? 1.0" +
": (b('b100') == 10) ? 1.0" +
": (b('b100') == 2) ? 0.7" +
": (b('b100') == 4) ? 0.7" +
": (b('b100') == 6) ? 0.7" +
": (b('b100') == 9) ? 0.7" +
": (b('b100') == 1) ? 0.3" +
": (b('b100') == 3) ? 0.3" +
": (b('b100') == 11) ? 0.3" +
": (b('b100') == 12) ? 0.3" +
": 0")
soil_200 = soil_types.expression(
"(b('b200') == 5) ? 1.0" +
": (b('b200') == 7) ? 1.0" +
": (b('b200') == 8) ? 1.0" +
": (b('b200') == 10) ? 1.0" +
": (b('b200') == 2) ? 0.7" +
": (b('b200') == 4) ? 0.7" +
": (b('b200') == 6) ? 0.7" +
": (b('b200') == 9) ? 0.7" +
": (b('b200') == 1) ? 0.3" +
": (b('b200') == 3) ? 0.3" +
": (b('b200') == 11) ? 0.3" +
": (b('b200') == 12) ? 0.3" +
": 0")
top_soils = soil_0.expression('top_soil + soil_10 + soil_30',
{'top_soil': soil_0.select('constant'),
'soil_10': soil_10.select('constant'),
'soil_30': soil_30.select('constant')})
bottom_soils = soil_60.expression('soil_60 + soil_100 + soil_200',
{'soil_60': soil_60.select('constant'),
'soil_100': soil_100.select('constant'),
'soil_200': soil_200.select('constant')})
# -
#scaling top soils and bottom soils
top_soils_scaled = norm.img_scale(top_soils, area_of_interest=common.bboxes()['conus'])
bottom_soils_scaled = norm.img_scale(bottom_soils, area_of_interest=common.bboxes()['conus'])
# ## Product 1
# Simply give higher scores to places that have both high potential runoff and available porosity (and with low moisture), in only areas with acceptable slopes
product_1 = avail_porosity_img_scaled.multiply(pot_runoff_img_scaled).multiply(top_soils_scaled).multiply(bottom_soils_scaled).divide(slope_img_scaled).updateMask(slope_mask)
# +
#understanding product_1 range
product_1_range = norm.img_range(product_1, area_of_interest = bbox)
palette_name = 'RdYlBu'
palette_len = 11
palette = vis.brewer[palette_name][palette_len][::-1]
vis.legend(palette=palette, minimum=product_1_range[0], maximum= product_1_range[1])
box_corners = bbox.toGeoJSON()['coordinates'][0]
center_lon = mean([corner[0] for corner in box_corners])
center_lat = mean([corner[1] for corner in box_corners])
vis_params = {
'min': product_1_range[0], 'max': product_1_range[1], 'dimensions': 512,
'palette': palette}
# +
#sum up product_1 scores over douglas and coos county parcels to obtain a parcel score, obtain image, obtain image for bounding box we're interested in
parcel_score_douglas = product_1.reduceRegions(collection= douglas_county_parcels, reducer= ee.Reducer.max(), scale = 90)
parcel_score_douglas_2 = parcel_score_douglas.reduceToImage(properties = ['max'], reducer = ee.Reducer.firstNonNull())
# +
parcel_score_coos = product_1.reduceRegions(collection= coos_county_parcels, reducer= ee.Reducer.max(), scale = 90)
parcel_score_coos_2 = parcel_score_coos.reduceToImage(properties = ['max'], reducer = ee.Reducer.firstNonNull())
bound_box = ee.Feature(ee.Geometry.Polygon([[[-124.1, 43.38], [-124.1, 42.88], [-123.6, 42.88], [-123.6, 43.38]]]))
bound_box_img = bound_box.getMapId()['image']
# +
#calculate range of parcel score for douglas county
#parcel_score_douglas_range = norm.img_range(parcel_score_douglas_2, area_of_interest = bbox)
# +
#creating the legend for parcel scores
palette_name = 'RdYlBu'
palette_len = 11
palette = vis.brewer[palette_name][palette_len][::-1]
vis.legend(palette=palette, minimum = 0, maximum= 1)
vis_params_2 = {
'min': 0, 'max': 1,'dimensions': 512,
'palette': palette}
# -
# +
#creating the map, visualizing parcel score data for parcels in douglas and coos counties, option to visualize soil texture as well
the_map = vis.folium_map(location=[43.25, -123.5], zoom_start=8, height=500)
month_names = [
'Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun',
'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
month_name = month_names[month-1]
palette_2 = ['black', 'yellow', 'brown', 'green']
douglas_img = douglas_county_parcels.getMapId()['image']
vis_params_3 = {
'min': 0,
'max': 1.0,
'palette': palette}
vis_params_4 = {
'min': 0,
'max': 20.0,
'palette': palette}
the_map.add_ee_layer(parcel_score_douglas_2, vis_params_2, name = 'Parcel Score_douglas')
the_map.add_ee_layer(parcel_score_coos_2, vis_params_2, name = 'Parcel Score_coos')
#the_map.add_ee_layer(top_soils_scaled, vis_params_3, name = 'Top Soils')
#the_map.add_ee_layer(bottom_soils_scaled, vis_params_3, name = 'Bottom Soils')
the_map.add_ee_layer(slope_img, vis_params_4, name = 'Slopes')
#the_map.add_ee_layer(pot_runoff_img_scaled, vis_params_3, name = 'Runoff')
#the_map.add_ee_layer(product_1, vis_params_3, name = 'Product_1')
#the_map.add_ee_layer(avail_porosity_img_scaled, vis_params_3, name = 'Porosity')
the_map.add_ee_layer(douglas_img, {}, name = 'Douglas_parcels')
the_map.add_ee_layer(bound_box_img, {}, name = 'Bounding_Box')
the_map.add_ee_layer(avail_porosity_img, vis_params_4, name = 'USDA Porosity')
vis.folium_display(the_map)
#douglas_img = douglas_county_parcels.draw(color = 'green', strokeWidth= 1)
#coos_img = coos_county_parcels.draw(color = 'green', strokeWidth= 1)
# -
# +
collection_name_d = (
'users/amgadellaboudy/product_1_douglas')
product_1_d_asset = ee.data.createAsset(
{'type': 'ImageCollection'}, collection_name_d)
description_d= 'Douglas_County_Water_Parcel_Score'
collection_name_c = (
'users/amgadellaboudy/product_1_coos')
product_1_c_asset = ee.data.createAsset(
{'type': 'ImageCollection'}, collection_name_c)
description_c= 'Coos_County_Water_Parcel_Score'
oregon_box = [[-124.1, 43.38], [-124.1, 42.88], [-123.6, 42.88], [-123.6, 43.38]]
xx_d = ee.batch.Export.image.toAsset(parcel_score_douglas_2, description = description_d, assetId = product_1_d_asset['id'] + '/' + description_d, region=oregon_box, scale = 90 )
xx_c = ee.batch.Export.image.toAsset(parcel_score_coos_2, description = description_c, assetId = product_1_c_asset['id'] + '/' + description_c, region= oregon_box, scale = 90)
xx_d.start()
xx_c.start()
# -
# ## Product 2
# Ratio of potential_runoff:available_porosity?
runoff_pixel_area_m2 = pot_runoff_img.pixelArea()
pot_runoff_img_mm = pot_runoff_img.divide(runoff_pixel_area_m2).multiply(seconds_per_month[month-1] * 1000)
# pot_runoff_mask = pot_runoff_img_mm.gte(1000)
avail_porosity_mask = avail_porosity_img.gte(50)
norm.img_range(pot_runoff_img_mm.updateMask(runoff_mask), area_of_interest=bbox)
#norm.img_range(pot_runoff_img_mm, area_of_interest=bbox)
norm.img_range(runoff_pixel_area_m2, area_of_interest=bbox)
norm.img_range(avail_porosity_img, area_of_interest=bbox)
product_2_raw = (
pot_runoff_img_mm
.divide(avail_porosity_img)
.updateMask(slope_mask)
.updateMask(avail_porosity_mask)
.updateMask(runoff_mask))
product_2_mask = product_2_raw.gte(1)
product_2 = product_2_raw.updateMask(product_2_mask)
# +
product_2_range = norm.img_range(product_2, area_of_interest=bbox)
palette_name = 'BrBG'
palette_len = 11
palette = vis.brewer[palette_name][palette_len][::-1]
vis.legend(palette=palette, minimum=product_2_range[0], maximum=product_2_range[1])
box_corners = bbox.toGeoJSON()['coordinates'][0]
center_lon = mean([corner[0] for corner in box_corners])
center_lat = mean([corner[1] for corner in box_corners])
vis_params = {
'min': product_2_range[0], 'max': product_2_range[1], 'dimensions': 512,
'palette': palette}
# -
the_map = vis.folium_map(location=[center_lat, center_lon], zoom_start=4, height=500)
the_map.add_ee_layer(product_2, vis_params, 'Product 2: ' + month_name)
vis.folium_display(the_map)
| 15,523 |
/.ipynb_checkpoints/austin_info-checkpoint.ipynb
|
9eb7f3bda4e14ecc69ee3fa063e46a78eb7cbfde
|
[] |
no_license
|
jschwan1282/ETL-Project
|
https://github.com/jschwan1282/ETL-Project
| 0 | 0 | null | 2019-08-24T20:38:23 | 2019-08-24T20:11:13 |
Jupyter Notebook
|
Jupyter Notebook
| false | false |
.py
| 14,058 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import gspread
from oauth2client.service_account import ServiceAccountCredentials
import pandas as pd
import datetime # import the datetime module
from datetime import datetime as dt # import the datetime type
from tqdm.notebook import tnrange, tqdm
import pathlib
import sys
import os
import shutil
# # Read file containing the last updates
def last_processed_date(file):
"""
read the file containing the last dates processed "processed_dates_update.csv" and calculate the next line to read in the worksheet.
"""
last_processed_dates = pd.read_csv(file)
# calculate the starting line to read
return last_processed_dates.shape[0] + 2
# # connect to google drive API and read the data in the file
def set_google_drive_access_scope():
"""
define the scope of the access to google drive and create credentials using the privatepprint.json file)
"""
scope = ['https://spreadsheets.google.com/feeds', 'https://www.googleapis.com/auth/drive']
creds = ServiceAccountCredentials.from_json_keyfile_name('dataset_types_ODP.json', scope)
client = gspread.authorize(creds)
return client
# ## get all the data between a row range in the google sheet
def access_google_sheet(sheet_name, worksheet_name, client, file, first_column, last_column):
"""
getting access to the google sheet spreadsheet and the name of the "History" sheet we want to access
"""
sheet = client.open(sheet_name) # access the google sheet
history = sheet.worksheet(worksheet_name) # access the worksheet "History"
# extract all the raw data available
next_row_to_read = last_processed_date(file)
# returns the number of rows and columns in the worksheet by counting the number of non-empty cells in the first column. The first column corresponds to the date.
# this solution should work for at least 5 years and until the number of retrieved rows will be large enough to load in memory. This because we read all the data in the first column
row_total = len(history.col_values(1))
# set the batch of data to retrieve
if row_total < next_row_to_read: # if there are new data to read compared to the last time the data was updated
new_data = [0]
else:
cell_start = first_column + str(next_row_to_read)
cell_end = last_column + str(row_total)
new_data = history.batch_get([cell_start + ":" + cell_end])
return new_data
# ## tranforming the data into tabular data and making some cleaning
def transform_into_dataframe(data):
"""
transform the dict into a padas
"""
raw_data = pd.DataFrame(data)
return raw_data
# ## making some data cleaning
def drop_not_used_columns(data):
"""
drop not required columns: openess indicator label, openess indicator value, total datasets label, total datasets
"""
return data.drop([1, 2, 3, 4], axis=1)
# # equivalences table for removing duplicated datasets: same dataset type, different names
def load_equivalences_table():
"""
table creation by manually entry the possible datasets types writting: added as founded in the dataset
"""
data_types_equivalance = {"comma-separated-values":"csv", "sparql-query":"sparql", "tab-separated-values":"tsv", "pdf;type=pdf1x":"pdf", "rdf+xml":"rdf_xml"}
return data_types_equivalance
# # processing each row of the dataset
def extract_row(row_to_process, data):
"""
extract the information correspondig to a specific row for reshape it properly: <date>, <data type>, <number of datasets>
"""
data_row = data.loc[row_to_process]
#create a dataframe with the information extacter for each row. It will make further reshaping easier
return pd.DataFrame(data_row).T.reset_index().drop(["index"], axis=1)
def row_removing_empty_columns(data_row):
"""
remove the columns having no values. Here no value is represented by ''
"""
return data_row.drop([col for col in data_row if (data_row[col] == '').any()], axis=1)
def columns_identification(data_row):
"""
extract the columns corresponding to the data types and the number of datasets per data type
"""
data_row_type_labels = data_row.columns[1:data_row.shape[1]:2]
data_row_value_labels = data_row.columns[2:data_row.shape[1]:2]
return data_row_type_labels, data_row_value_labels
def columns_separation(data_row, data_row_type_labels, data_row_value_labels):
"""
create 2 dataframes: 1 containing the data set type and 1 containing the value of the corresponding dataset type and reshape as row-oriented by transposing it
"""
# dataset type columns extraction
data_row_type = data_row[data_row_type_labels].T.reset_index()
data_row_type = data_row_type.drop(["index"], axis=1).rename(columns={0:"dataset type"}) # rename the column name
# number of dataset types columns extraction
data_row_value = data_row[data_row_value_labels].T.reset_index()
data_row_value = data_row_value.drop(["index"], axis=1).rename(columns={0:"number of datasets"}) # rename the column name
return data_row_type, data_row_value
def clean_dataset_types_description(data_row_type):
"""
clean the row_data_type by removing unwanted text: text before the "/" character. It also removes any rows with 'None' value
"""
data_row_type = data_row_type.dropna() #remove rows having 'None' values
data_row_type_cleaned = data_row_type["dataset type"].apply(lambda x: x.lower()).apply(lambda x: x.split("/"))
data_row_type_cleaned = pd.DataFrame(data_row_type_cleaned)
data_row_type_cleaned = data_row_type_cleaned["dataset type"].apply(lambda x: x[-1])
return pd.DataFrame(data_row_type_cleaned)
def merge_columns(data_row_type, data_row_value):
"""
concatenate the 2 created dataframes into 1 that will serve in the final datamodel for Qlik Sense
"""
data_row_transformed = pd.concat([data_row_type, data_row_value], axis=1, ignore_index=True)
# rename the columns
data_row_transformed.rename(columns={0:"dataset type", 1:"number of datasets"}, inplace=True)
return data_row_transformed
def find_and_replace_equivalent_dataset_name(data_row_transformed, data_types_equivalance):
"""
find and replace dataset types names to remove equivalent names for the same types of datasets
"""
data_row_transformed.replace(data_types_equivalance, inplace=True)
return data_row_transformed
def find_and_replace_equivalent_dataset_name(data_row_transformed, data_types_equivalance):
"""
find and replace dataset types names to remove equivalent names for the same types of datasets
"""
data_row_transformed.replace(data_types_equivalance, inplace=True)
return data_row_transformed
def data_grouping(data_row_transformed):
"""
removing duplicated data: group by dataset type and summing up the number of datasets
"""
return data_row_transformed.groupby(["dataset type"]).sum().reset_index().rename(columns={1:"number of datasets"})
# ## add the date column to finalise the datamodel
def remove_hours(data_row):
"""
remove the hours minutes and seconds in the date dimention
"""
date_object = datetime.datetime.strptime(data_row[0][0], '%m/%d/%Y %H:%M:%S').date()
# transform the datetime object into a string with format dd/mm/yyy
date = date_object.strftime('%d/%m/%Y')
return date
def track_proccesed_dates(dates_proccesed, current_date):
"""
create a list of already processed dates from the google sheet file containing the data source. This list will be saved on a file for reuse when updating the processed data
"""
return dates_proccesed.append({"processed dates": current_date}, ignore_index=True)
def month_change_detector(date_tracking, current_date, current_row):
"""
detect a month change in the dataset and add a flag to the rows of the last day of each month (flag = 1) otherwise, there is not flag (flag = 0).
The current dataset exhibits a non-continuity of the dates, there are many days missing.
"""
# extract the previous date to check if the month has changed
past_date = date_tracking.loc[current_row - 1][0]
# transform the dates into a datetime object
past_date_datetime = datetime.datetime.strptime(past_date, "%d/%m/%Y")
current_date_datetime = datetime.datetime.strptime(current_date, "%d/%m/%Y")
# extract the month of the date
past_month = past_date_datetime.month
current_month = current_date_datetime.month
# detect month change
if current_month != past_month:
flag_month_change = 1
else:
flag_month_change = 0
return flag_month_change, past_date, current_date
def date_formatting(length_data_row, date):
"""
create a dataframe with the date having equal length that row_data_type_labels and row_data_value_labels
"""
date_list = [[date, 0] for i in range(length_data_row)]
return pd.DataFrame(date_list)
def row_data_merge(df_date, data_row_transformed):
"""
for the current processing row: add the date colum to the dataframe containing the cleaned version of the data types and the dataset number per type
"""
data_row_transformed = pd.concat([df_date, data_row_transformed], axis=1, ignore_index=True)
# rename the columns, sort values by number of datasets type and remove a self-created "index" column
data_row_transformed.rename(columns={0:"date", 1:"last day of the month", 2:"dataset type", 3:"number of datasets"}, inplace=True)
data_row_transformed = data_row_transformed.sort_values(by=["number of datasets"], ascending=False).reset_index().drop(["index"], axis=1)
return data_row_transformed
def add_flag_for_month_change(data_processed, past_date):
"""
add a flag in case of month change detected - month_change_flag = 1
"""
# add a flag=1 to a previous date if there is month change
data_processed.loc[data_processed["date"] == past_date, "last day of the month"] = 1
return data_processed
# ## update the data and the last update info
def data_backup(directory_path, processed_dates_file, processed_data_file):
"""
created a copy of the previous files before append data to it renaming the file as <filename>_backup:
* processed_dates_file {string}: filename containing the dates processed so far
* data_file {string}: filename containing the data processed so far
if the file doesn't exist it does anything
"""
# creates a backup of the file containing the dates processed so far
dates_file = directory_path + processed_dates_file
dates_file_backup = directory_path + str.split(processed_dates_file, ".")[0] + "_backup." + str.split(processed_dates_file, ".")[1]
if pathlib.Path(dates_file).exists():
shutil.copyfile(dates_file, dates_file_backup)
# creates a backup of the file containing the data processed so far
data_file = directory_path + processed_data_file
data_file_backup = directory_path + str.split(processed_data_file, ".")[0] + "_backup." + str.split(processed_data_file, ".")[1]
if pathlib.Path(data_file).exists():
shutil.copyfile(data_file, data_file_backup)
return
def update_data_and_info_update(data_processed, date_processed, directory_path, processed_dates_file, data_file):
"""
update the processed data into a CSV file by appending the procesed data to existing one in the file: datasets_formats_processed.csv
update the processed dates CSV file by appending the processed dates to the existing ones in the file: processed_dates_update.csv
IMPORTANT: put attention to the date format in the "processed_dates_update.csv" file. The format doesn't match the format used in google sheets. You will need to change the date format in this file before
going for updates
"""
data_backup(directory_path, processed_dates_file, data_file)
# save the processed data into a CSV file with headers
file_path_data = directory_path + data_file # my home laptop
data_processed.to_csv(file_path_data, mode="a", index=False, header=False)
# save the last row processed info (google sheet row number and last date present in this row) into a CSV file with headers
file_path_update = directory_path + processed_dates_file # my home laptop
date_processed.to_csv(file_path_update, mode="a", index=False, header=False)
return
def can_execute(data_cleaned):
"""
Enables the execution of the script depending of the dates in the google sheet file and the current date.
It prevents the script runs when there isn't a change in the month making impossible to detect a month change.
"""
before_last_date = data_cleaned[0][len(data_cleaned[0]) - 2]
before_last_date_month = int(before_last_date.split("/")[0])
last_date = data_cleaned[0][len(data_cleaned[0]) - 1]
last_date_month = int(last_date.split("/")[0])
today_month = dt.today().month
if (last_date_month >= before_last_date_month) & (today_month == last_date_month):
print("script execution enabled...program continued")
return 0 # continues the execution of the script
else:
print("script execution stopped. Not the right day for executing it...program terminated")
return 1 # terminates the execution of the script
# ## --> main function <--
def main():
# global variables
SHEET = "ODP OPENNESS INDICATOR_local_4"
WORKSHEET = "History"
# DIRECTORY_PATH = "D:\\Dropbox\\Programming\\Python\\datasets files formats ODP\\" # my office laptop
DIRECTORY_PATH = "D:\\Dropbox\\Programming\\Python\\datasets files formats ODP\\PROD\\" # my home laptop
PROCESSED_DATES_FILE = "processed_dates_update.csv"
PROCESSED_DATA_FILE = "datasets_formats_processed.csv"
FIRST_COLUMN = "A" # first column in the google sheet file
LAST_COLUMN = "EM" # last columnn in the google sheet file. To change when the data in the google sheet will go beyond the EM column
# set connection to google drive
google_client = set_google_drive_access_scope()
# acquire the data
data_types = access_google_sheet(SHEET, WORKSHEET, google_client, PROCESSED_DATES_FILE, FIRST_COLUMN, LAST_COLUMN)[0]
if data_types:
raw_data = transform_into_dataframe(data_types)
else:
print("No new data to read --> EXIT")
sys.exit(0) # terminates the program with no errors
total_rows = raw_data.shape[0]
print(f'the size of the imported data is: {raw_data.shape}\n')
# clean the data
data_cleaned = drop_not_used_columns(raw_data)
# enable or disable the execution of the script according to the current date and the data available in the google sheet
if can_execute(data_cleaned):
return
# load the table containing equivalent names for the same dataset. It'll be used to have the same name for the same dataset type
datasets_type_equivalences = load_equivalences_table()
# process all the rows of the dataset
#total_rows = 10
for current_row in tqdm(range(total_rows), desc="data rows processing"): #tqdm_notebook
# process each row
row_data = extract_row(current_row, data_cleaned)
# remove empty columns in the extracted row
row_data_clean = row_removing_empty_columns(row_data)
# identification of the columns related to the dataset formats and the columns related to the number of dataset formats
row_data_type_labels, row_data_value_labels = columns_identification(row_data_clean)
# separation of the columns related to the dataset formats and the columns related to the number of dataset formats
row_data_type, row_data_value = columns_separation(row_data_clean, row_data_type_labels, row_data_value_labels)
# clean the dataset type desciption column by filtering out the dataset type
row_data_type_clean = clean_dataset_types_description (row_data_type)
# merge dataset types and dataset values into a single dataframe
row_data_transformed = merge_columns(row_data_type_clean, row_data_value)
# find and replace equivalent names for the same dataset type
row_data_transformed_cleaned = find_and_replace_equivalent_dataset_name(row_data_transformed, datasets_type_equivalences)
# combine together same dataset types and sum up the number of datasets per data type
row_data_transformed_cleaned = data_grouping(row_data_transformed_cleaned)
# remove hour info from the date
date_clean = remove_hours(row_data)
# add the current date to the list of already processed dates
if current_row == 0:
date_tracking = pd.DataFrame({"processed dates": [date_clean]})
else:
date_tracking = track_proccesed_dates(date_tracking, date_clean)
# detect a change of month
month_change_flag, past_date, current_date = month_change_detector(date_tracking, date_clean, current_row)
# generate a new date column with a month change flag column ready to add to the cleaned row dataset
df_date = date_formatting(row_data_transformed_cleaned.shape[0], date_clean)
# add the date info to the dataframe containing he dataset types and the number of dataset types and make some formatting
row_data_final = row_data_merge(df_date, row_data_transformed_cleaned)
# append the processed data
if current_row == 0:
data_processed = row_data_final
else:
data_processed = data_processed.append(row_data_final, ignore_index=True)
# change the "last day of the month" column vaue to 0 --> 1
if month_change_flag:
data_processed = add_flag_for_month_change(data_processed, past_date)
# save the processed data into a CSV file
update_data_and_info_update(data_processed, date_tracking, DIRECTORY_PATH, PROCESSED_DATES_FILE, PROCESSED_DATA_FILE)
# # --> Execution of the data update starts here <--
if __name__ == '__main__':
main()
| 18,722 |
/Kaggle_SQL/SQL exercise - 1.ipynb
|
79c5b2dd426912fec0131a630a98eeed72132a4f
|
[] |
no_license
|
rk1489/Technocolabs-Internship-Project
|
https://github.com/rk1489/Technocolabs-Internship-Project
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 11,845 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import QUANTAXIS as QA
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei','KaiTi', 'FangSong'] # 汉字字体,优先使用楷体,如果找不到楷体,则使用黑体
mpl.rcParams['font.size'] = 14 # 字体大小
mpl.rcParams['axes.unicode_minus'] = False # 正常显示负号
import numpy as np
import pandas as pd
from base.JuUnits import excute_for_multidates
from sklearn.neighbors.kde import KernelDensity
# +
def get_Q1_list(start, end):
return [str(y)+'-03-31' for y in range(int(start), int(end)+1)]
def drop_by_quantile_multidates(obj, floor=.00,upper=1., column=None):
return excute_for_multidates(obj, drop_by_quantile, floor=floor,upper=upper, column=column).sort_index()
def drop_by_quantile(obj, floor=.00,upper=1., column=None):
if isinstance(obj, pd.Series):
qt = obj.quantile([floor,upper])
return obj[(obj>=qt[floor]) & (obj<=qt[upper])]
if isinstance(obj, pd.DataFrame):
assert column, 'COLUMN CANT be NONE when obj is dataframe'
qt = obj[column].quantile([floor,upper])
return obj[(obj[column]>=qt[floor]) & (obj[column]<=qt[upper])]
raise TypeError('obj must be series or dataframe')
stocks = QA.QA_fetch_stock_list()
# code_all= stocks[stocks.code.map(lambda x:x[0] in condition)].code.unique().tolist()
code_all= stocks.code.unique().tolist()
finances = QA.QA_fetch_financial_report_adv(code_all,get_Q1_list('2017','2017'))#.data
finances = finances.get_key(code_all, ['2017-03-31'], ['totalAssets','ROE'])
finances_filted = drop_by_quantile_multidates(finances,.1,0.90,'ROE')
# finances.describe(include = 'all')
# finances['totalAssets'] = finances['totalAssets'].apply(lambda x: round(x/100000000,2))
# finances['ROE'] = finances['ROE'].apply(lambda x: round(x,1))
# finances.describe()
# finances.quantile([.01,.05,.1,.9,.95,.99])
# finances
# print(finances['ROE'].rank())
# -
fig = plt.figure(figsize=(1120/72,420/72))
finances_filted['ROE'].plot(ax=fig.add_subplot(1,2,1))
# plt.scatter(finances_filted['ROE'].index.get_level_values('code'),finances_filted['ROE'].values)
finances_filted['ROE'].plot(kind="kde",ax=fig.add_subplot(1,2,2))
# finances_filted['ROE'].describe()
# finances_filted['totalAssets'].mean()
# plt.show()
# +
X_plot = np.linspace((finances_filted['ROE']).min()-1, (finances_filted['ROE']).max()+1, 200)[:, np.newaxis]
kde = KernelDensity(kernel='epanechnikov', bandwidth=0.5).fit((finances_filted['ROE']).values.reshape(-1, 1))
log_dens = kde.score_samples(X_plot) # 返回的是点x对应概率密度的log值,需要使用exp求指数还原
print(kde.get_params())
plt.figure(figsize = (10, 8)) # 设置画布大小
plt.plot(X_plot, np.exp(log_dens), marker='.', linewidth=1, c="b", label='kernel density')
plt.xlabel('variable')
plt.ylabel('pdf')
kde = KernelDensity(kernel='gaussian', bandwidth=0.25).fit((finances_filted['ROE']).values.reshape(-1, 1))
log_dens = kde.score_samples(X_plot)
# # kde = KernelDensity(kernel='epanechnikov', bandwidth=1).fit(((finances_filted['ROE']-finances_filted['ROE'].mean())/finances_filted['ROE'].std()).values.reshape(-1, 1)) # 高斯核密度估计
plt.plot(X_plot, np.exp(log_dens), marker='.', linewidth=1, c="r", label='kernel density')
plt.show()
# -
plt.figure(figsize = (10, 8)) # 设置画布大小
plt.plot(X_plot, np.cumsum(np.exp(log_dens)*np.abs(X_plot[0]-X_plot[1])), marker='.', linewidth=1, c="b", label='kernel density')
plt.xlabel('variable')
plt.ylabel('cdf')
plt.legend(fontsize = 15) # 显示图例,设置图例字体大小
plt.show()
np.exp( kde.score_samples(np.array([1.3,1.3]).reshape(-1,1)))
np.exp(kde.score(np.array([1.3,1.3]).reshape(-1,1)))
| 3,836 |
/Week1-2 All Basics/Lecture4 python data science stack/8. Other packages/Other packages.ipynb
|
0a9e3aeeb3fa8b67007616385883b68ef29936c3
|
[] |
no_license
|
kwarodom/100DaysMLCodeChallenge
|
https://github.com/kwarodom/100DaysMLCodeChallenge
| 1 | 2 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 32,545 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Go faster with Numba and Cython
def polyn(n):
total = 0
for i in range(n):
total += (7*n*n) + (-3*n) + 42
return total
ntimes = 10000
# %timeit -n $ntimes polyn(1000)
import numba
@numba.jit
def polyn(n):
total = 0
for i in range(n):
total += (7*n*n) + (-3*n) + 42
return total
# %timeit -n $ntimes polyn(1000)
# %load_ext cython
# + language="cython"
# def ployn(int n):
# cdef int total = 0
# cdef i
#
# for i in range(n):
# total += (7*n*n) + (-3*n) + 42
# return total
# -
# %timeit -n $ntimes polyn(1000)
# + language="cython"
# from libc.math cimport hypot
#
# def dist(double x1, double y1, double x2, double y2):
# cdef double dx = abs(x1 - x2)
# cdef double dy = abs(y1 - y2)
# return hypot(dx, dy)
# -
dist(1,1, 2,2)
from scipy.spatial.distance import euclidean
euclidean([1,1], [2,2])
# # Understand deep learning
from sklearn.datasets import load_digits
digits = load_digits()
# %matplotlib inline
import matplotlib.pyplot as plt
idx = 17
plt.imshow(digits['images'][idx], cmap=plt.cm.gray, interpolation='none')
digits['target'][idx]
digits['images'].shape
digits['data'].shape
from sklearn.model_selection import train_test_split
from keras.utils import np_utils
X = digits['data']
y = digits['target']
y = np_utils.to_categorical(y)
y[0]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
in_dim = X.shape[1]
out_dim = y.shape[1]
from keras.models import Sequential
from keras.layers import Dense, Activation
model = Sequential()
model.add(Dense(128, input_shape=(in_dim,)))
model.add(Activation('relu'))
model.add(Dense(out_dim))
model.add(Activation('sigmoid'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, y_train)
loss, accuracy = model.evaluate(X_test, y_test)
accuracy
model.predict(X_test[:3])
model.predict(X_test[:3]).argmax(axis=1)
y_test[:3].argmax(axis=1)
model.save('digits.h5')
from keras.models import load_model
model1 = load_model('digits.h5')
model1.predict(X_test[:3]).argmax(axis=1)
# # Work with image processing
import cv2
img = cv2.imread('coffee.jpg')
type(img)
img.shape
# %matplotlib inline
import matplotlib.pyplot as plt
plt.imshow(img)
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
plt.imshow(gray)
plt.imshow(gray, cmap=plt.cm.gray)
edges = cv2.Canny(gray, 200, 300)
plt.imshow(edges, cmap=plt.cm.gray)
img = cv2.imread('child.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
import sys
fname = '{}/share/OpenCV/haarcascades/haarcascade_frontalcatface.xml'.format(sys.prefix)
model = cv2.CascadeClassifier(fname)
faces = model.detectMultiScale(gray, scaleFactor=1.1, minNeighbors=5, minSize=(500, 500))
faces
img = cv2.imread('child.jpg')
for (x, y, w, h) in faces:
cv2.rectangle(img, (x, y), (x+w, y+h), (0, 255, 255), 50)
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
# # Understand NLP: NLTK
from os import path
fname = path.expanduser('~/nltk_data/corpora/abc/science.txt')
with open(fname, 'rb') as fp:
data = fp.read().decode(errors='replace')
articles = data.split('\r\n\r\n')
article = articles[0]
print(article)
from nltk.tokenize import sent_tokenize
sents = sent_tokenize(article)
print(sents[0])
from nltk.corpus import stopwords
import re
stop = set(stopwords.words('english'))
def is_ok(token):
return re.match('^[a-z]+$', token) and token not in stop
from nltk.tokenize import word_tokenize
def tokenize(sent):
return [word for word in word_tokenize(sent.lower()) if is_ok(word)]
from collections import Counter
def summarize(text, n=3):
sents = sent_tokenize(text)
bow = [tokenize(sent) for sent in sents]
tf = Counter()
for sent in bow:
tf.update(sent)
def score(i):
return sum(tf[word] for word in bow[i])
idx = sorted(range(len(bow)), key=score, reverse=True)[:n]
return [sents[i] for i in idx]
summarize(articles[0])
# # Understand NLP: SpaCy
from os import path
fname = path.expanduser('~/nltk_data/corpora/abc/science.txt')
with open(fname, 'rb') as fp:
data = fp.read().decode(errors='replace')
articles = data.split('\r\n\r\n')
article = articles[0]
print(article)
from nltk.tokenize import sent_tokenize
sents = sent_tokenize(article)
print(sents[0])
from nltk.corpus import stopwords
import re
stop = set(stopwords.words('english'))
def is_ok(token):
return re.match('^[a-z]+$', token) and token not in stop
from nltk.tokenize import word_tokenize
def tokenize(sent):
return [word for word in word_tokenize(sent.lower()) if is_ok(word)]
from collections import Counter
def summarize(text, n=3):
sents = sent_tokenize(text)
bow = [tokenize(sent) for sent in sents]
tf = Counter()
for sent in bow:
tf.update(sent)
def score(i):
return sum(tf[word] for word in bow[i])
idx = sorted(range(len(bow)), key=score, reverse=True)[:n]
return [sents[i] for i in idx]
summarize(articles[0])
import spacy
nlp = spacy.load('en')
fname = path.expanduser('~/nltk_data/corpora/inaugural/1993-Clinton.txt')
with open(fname) as fp:
data = fp.read()
doc = nlp(data)
sent = next(doc.sents)
print(sent)
for tok in sent:
print('{} -> {}'.format(tok, tok.ent_type_))
for ent in doc.ents[:10]:
print('{} -> {}'.format(ent.string, ent.label_))
[ent for ent in doc.ents if ent.label == spacy.symbols.PERSON]
# # Bigger data with HDF5 and dask
import pandas as pd
import numpy as np
df = pd.read_csv('taxi.csv.bz2', usecols=np.arange(21), parse_dates=['lpep_pickup_datetime', 'Lpep_dropoff_datetime'])
store = pd.HDFStore('taxi.h5')
store.append('taxi', df, data_columns=['VendorID'])
store
df1 = store.select('taxi', 'VendorID==1')
df1['VendorID'].unique()
import dask.dataframe as dd
df = dd.read_csv('taxi-split/*.csv',
usecols=np.arange(21), parse_dates=['lpep_pickup_datetime', 'Lpep_dropoff_datetime'])
vc = df['VendorID'].value_counts()
vc
vc.compute()
vnd = df.groupby('VendorID')
ta = vnd['Total_amount']
m = ta.mean()
m.compute()
at is not math.inf:
content_part = page[:cut_at]
footnote_part = page[cut_at:]
content_part_s.append(content_part)
footnote_part_s.append(footnote_part)
else:
content_part_s.append(page)
content_text = "".join(content_part_s) # 把各頁的內文部分結合成內文
footnote_text = "".join(footnote_part_s) # 把各頁的附註部分結合成附註
content = content_text
footnote = footnote_text
# -
print(content)
print("--------------------------------------------------")
print(footnote)
# 第一種附註小數字出現的場合
content = re.sub(name+' ?'+str(footnote_indices[0])+' ?(', "{}(".format(name),content , 1)
# 第二種附註小數字出現的場合
for index in footnote_indices[1:]:
content = re.sub("([。,])" + index, r'\g<1>', content, count=1)
print(content)
# +
# 清掉所有不需要的空格
# 先把需要的空格轉成另一個字符記錄起來,清完空格再回復原狀
content = re.sub(r'([a-zA-Z,)(]) ([a-zA-Z,)(])', '\g<1>Ä\g<2>', content)
content = re.sub(r'(\n\d+) ', '\g<1>Ä', content)
content = content.replace(" ","")
content = content.replace("Ä", " ")
footnote = re.sub(r'([a-zA-Z,]) ([a-zA-Z,])', '\g<1>Ä\g<2>', footnote)
footnote = re.sub(r'(\n\d+) ', '\g<1>Ä', footnote)
footnote = footnote.replace(" ","")
footnote = footnote.replace("Ä", " ")
# +
# 處理newline,內文分出段落
# 因為句號後面換行的通常是一段落的結尾(但也可能不是)
content = content.replace("。\n", "Å")
content = content.replace("\n", "")
content = content.replace("Å", "。\n\n")
footnote = footnote.replace("。\n", "Å")
footnote = footnote.replace("\n", "")
footnote = footnote.replace("Å", "。\n\n")
# -
print(content)
print("--------------------------------------------------")
print(footnote)
footnote = footnote[:-2] # 去掉最後的兩個newline
f_lines = footnote.split('\n\n') # 這樣最後就不會多一個空的split,各條附註分開
biography["Footnotes"] = list(map(lambda line: line.split(" "), f_lines)) # 把各條附註小數字和其註釋分開
biography["Footnotes"]
# 從內文去掉傳記撰者,並保存在傳記資訊
match = re.search(r'(([\w、]+)撰寫?)', content, flags=re.MULTILINE) # $
author_line = match[0]
biography["Authors"] = match[1].split("、")
content = content.replace(author_line, "")
print(biography["Authors"])
print("-------------------------------------------------")
print(content_text)
# +
# 從內文去掉傳記標題,保存別名, 生日日期,死亡日期
reg = name + "((.+,)?([\d?.]*)-([\d?.]*))"
title = re.search(reg, content, flags=re.MULTILINE)
if len(title.groups()) == 2:
biography["Birth"] = title[1] # group1
biography["Death"] = title[2] # group2
else:
biography["Alias_s"].append(title[1])
biography["Birth"] = title[2]
biography["Death"] = title[3]
content = content.replace(title[0], "") # replace Whole match with empty string
# -
print(content)
| 9,025 |
/Task6/Task6.ipynb
|
cf8e9d391ae44dfab05a8f57ed1e29a34b2cf6b1
|
[
"MIT"
] |
permissive
|
Cynthyah/SparksFoundation
|
https://github.com/Cynthyah/SparksFoundation
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 572,837 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # The Sparks Foundation
# ## Task6 - Prediction using Decision Tree Algorithm
# - Create the Decision Tree classifier and visualize it graphically.
# - The purpose is if we feed any new data to this classifier, it would be able to predict the right class accordingly.
# - Data can be found at https://bit.ly/3kXTdox -> save as **Iris.csv**
#
# 
# ### Importing the libraries
# +
import pandas as pd
import missingno
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score,confusion_matrix
from sklearn import tree
# -
# ### Loading the dataset
df = pd.read_csv("Iris.csv", low_memory=False)
# ### Checking the data
df.head()
# The column Id in this analysis is not relevant, so I will drop it
df.drop(columns='Id',inplace=True)
df.shape
df.info()
# % of columns without values
df.isna().sum() / len(df) * 100
# - The dataset has NO Null values
# ### Iris plant has 3 classes:
# - Iris Setosa
# - Iris Versicolour
# - Iris Virginica
#
# With the following attributes:
# - sepal length
# - sepal width
# - petal length
# - petal width
df.describe()
sns.pairplot(df, hue="Species")
plt.show()
# ### Using Decision Tree Algorithm
# Decision Tree algorithm belongs to the family of supervised learning algorithms and it can be used for solving regression and classification problems too.
# ### Extracting the data attributes(X) and corresponding labels(y)
# +
# extract features/attributes
X = df.drop('Species', axis=1)
# extract classes
y = df['Species']
# checking the shape
print(X.shape, y.shape)
# -
# ### After extracted the data attributes and corresponding labels, we will split them to train and test datasets using the function train_test_split from the library:
# - sklearn.model_selection
le = LabelEncoder()
y = le.fit_transform(y)
# test_size -> 25% of total dataset will be split, where 75% will assign as train data
# In this case we have 150 rows in our dataset, we will use 112 as train data
X_train, X_test, y_train, y_test = train_test_split(X,y, random_state=0, test_size=0.25)
# ### **Training the model**
# #### Now we use the classification importing DecisionTreeClassifier function from sklearn library
# If we use the parameter min_samples_leaf=10 to create our leaves with at least 10 samples
classifier = DecisionTreeClassifier()
classifier.fit(X_train, y_train)
# ### **Prediction**
y_pred = classifier.predict(X_test)
y_pred = le.inverse_transform(y_pred)
y_test = le.inverse_transform(y_test)
y_pred
cm = confusion_matrix(y_test,y_pred)
print("Confusion_Matrix is: \n", cm)
ac = accuracy_score(y_test,y_pred)
print("Accuracy_Score is:", ac)
# ### **Visualisation**
plt.figure(figsize=(15,10))
dot_data = tree.plot_tree(classifier,
feature_names=['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm'],
class_names=['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'],
filled=True)
plt.title("Decision Tree Visualization-Iris Dataset",fontsize=30)
plt.show()
.fit(x_train, y_train)
# + id="d39W8cxmEGG8" outputId="56c7d5bb-5061-4bc5-cce2-0fa6938cb2c0" colab={"base_uri": "https://localhost:8080/"}
#printing the Ridge regressor arguments
print("Ridge regression coefficients = ",ridge_regression_classifier.coef_)
print("Ridge regression intercept = ",ridge_regression_classifier.intercept_)
# + id="-GzA_5qrEHgw" outputId="4640e51f-60ba-4f01-8c80-8b3e3ba25549" colab={"base_uri": "https://localhost:8080/"}
#printing the Linear regressor arguments
print("Linear regression coefficients = ",linear_regression_classifier.coef_)
print("Linear regression intercept = ",linear_regression_classifier.intercept_)
# + id="ulRVWxsREKtS" outputId="3a8beefd-02bb-4383-c5c2-57ae4325430d" colab={"base_uri": "https://localhost:8080/"}
#making the pridictions on the testing dataset of Ridge regression
ridge_regression_predictions = ridge_regression_classifier.predict(x_test)
print("The predictions of the Ridge regressor are: \n", ridge_regression_predictions,"\n")
# + id="PaKwbWowENpC" outputId="a1f45376-d190-491f-c00f-9ba2fc520add" colab={"base_uri": "https://localhost:8080/"}
#making the pridictions on the testing dataset of Linear regression
linear_regression_predictions = linear_regression_classifier.predict(x_test)
print("The predictions of the linear regressor are: \n", linear_regression_predictions,"\n")
# + id="NAudsxqjERIr" outputId="33a88167-c801-4ad2-d198-731cc644663d" colab={"base_uri": "https://localhost:8080/"}
#Analyzing the performance of the Ridge Regression
ridge_regression_score = ridge_regression_classifier.score(x_test, y_test)
print("Score Value = ",ridge_regression_score, "\n")
print("Comparing the predictions with the gound-truth: \n", np.column_stack((ridge_regression_predictions,y_test)), "\n\n")
# + id="cJoe8odhEUUn" outputId="498c357a-aad7-4a91-eb04-6c7a5ff1e445" colab={"base_uri": "https://localhost:8080/"}
#Analyzing the performance of the linear Regression
linear_regression_score = linear_regression_classifier.score(x_test, y_test)
print("Score Value = ",linear_regression_score, "\n")
print("Comparing the predictions with the gound-truth: \n", np.column_stack((linear_regression_predictions,y_test)), "\n\n")
# + id="R6XKwFRMEZzH" outputId="70e9da8e-a17f-4156-8f58-48ea67f26132" colab={"base_uri": "https://localhost:8080/"}
#printing the both the Values of the Effeciency
print("Score Value of Ridge = ",ridge_regression_score, "\n")
print("Score Value of Linear = ",linear_regression_score, "\n")
| 6,044 |
/module/intro_cython/3-Basics.ipynb
|
438abf50b59f8a3e4bde2406143dcfe3ad95ee90
|
[] |
no_license
|
slash1221/cythonup
|
https://github.com/slash1221/cythonup
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 3,755 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Задание 1**. Даны 2 строки: *long_phrase* и *short_phrase*.
# Напишите код, который проверяет действительно ли длинная фраза *long_phrase* длиннее короткой *short_phrase*. И выводит *True* или *False* в зависимости от результата сравнения.
long_phrase = 'Насколько проще было бы писать программы, если бы не заказчики'
short_phrase = '640Кб должно хватить для любых задач. Билл Гейтс (по легенде)'
# +
long_phrase = 'Насколько проще было бы писать программы, если бы не заказчики'
short_phrase = '640Кб должно хватить для любых задач. Билл Гейтс (по легенде)'
len(long_phrase) > len(short_phrase)
# -
# **Задание 2**. Дано значение объема файла в байтах (*в мегабайте 2^20 байт*). Напишите перевод этого значения в мегабайты в формате: "*Объем файла равен 213.68Mb*".
# +
size_byte = 250000000
size_mb = size_byte/(2**20)
print ("Объем файла равен " + str( round(size_mb,2) ) + "Mb")
# -
# **Задание 3**. Разработать приложение для определения знака зодиака по дате рождения. Пример:
#
# Введите месяц: март
#
# Введите число: 6
#
# Вывод:
# Рыбы
date = int(input('Введите число:'))
month = (input ('Введите месяц:')).lower()
if ((month == '1' or month == 'январь') and date < 21) or ((month == '12' or month == 'декабрь') and 22 <= date <= 31 ):
print ('Козерог')
elif ((month == '2' or month == 'февраль') and date < 19) or ((month == '1' or month == 'январь') and 21 <= date <= 31):
print ('Водолей')
elif ((month == '3' or month == 'март' ) and date < 21) or ((month == '2' or month == 'февраль') and 19 <= date <= 29):
print ('Рыбы')
elif ((month == '4' or month == 'апрель') and date < 21) or ((month == '3' or month == 'март' ) and 21 <= date <= 31):
print ('Овен')
elif ((month == '5' or month == 'май') and date < 21) or ((month == '4' or month == 'апрель') and 21 <= date <= 30):
print ('Телец')
elif ((month == '6' or month == 'июнь') and date < 21) or ((month == '5' or month == 'май') and 21 <= date <= 31):
print ('Близнецы')
elif ((month == '7' or month == 'июль') and date < 23) or ((month == '6' or month == 'июнь') and 21 <= date <= 30):
print ('Рак')
elif ((month == '8' or month == 'август') and date < 19) or ((month == '7' or month == 'июль') and 23 <= date <= 31):
print ('Лев')
elif ((month == '9' or month == 'сентябрь') and date < 24) or ((month == '8' or month == 'август') and 19 <= date <= 31):
print ('Дева')
elif ((month == '10' or month == 'октябрь') and date < 24) or ((month == '9' or month == 'сентябрь') and 24 <= date <= 30):
print ('Весы')
elif ((month == '11' or month == 'ноябрь') and date < 24) or ((month == '10' or month == 'октябрь') and 24 <= date <= 31):
print ('Скорпион')
elif ((month == '12' or month == 'декабрь') and date < 22) or ((month == '11' or month == 'ноябрь') and 24 <= date <= 30):
print ('Стрелец')
else: print ('Не соответствует дате календаря')
# **Задание 4**. Нужно разработать приложение для финансового планирования.
# Приложение учитывает сколько уходит на ипотеку, "на жизнь" и сколько нужно отложить на пенсию.
# Пользователь вводит:
# - заработанную плату в месяц.
# - сколько процентов от ЗП уходит на ипотеку.
# - сколько процентов от ЗП уходит "на жизнь".
# - сколько раз приходит премия в год.
#
# Остальная часть заработанной платы откладывается на пенсию.
#
# Также пользователю приходит премия в размере зарплаты, от которой половина уходит на отпуск, а вторая половина откладывается.
#
# Программа должна учитывать сколько премий было в год.
#
# Нужно вывести сколько денег тратит пользователь на ипотеку и сколько он накопит за год.
#
# Пример:
#
# Введите заработанную плату в месяц: 100000
#
# Введите сколько процентов уходит на ипотеку: 30
#
# Введите сколько процентов уходит на жизнь: 50
#
# Введите количество премий за год: 2
#
# Вывод:
# На ипотеку было потрачено: 360000 рублей
# Было накоплено: 340000 рублей
# +
wage = int(input ('Введите заработанную плату в месяц: '))
loan = int(input ('Введите сколько процентов уходит на ипотеку: '))
expences = int(input ('Введите сколько процентов уходит на жизнь: '))
n_bonus = int(input ('Введите количество премий за год: '))
loan_in_year = wage * 12 * loan / 100
savings = 12 * wage * (1 - loan/100 - expences/100) + n_bonus * wage * 0.5
print ('На ипотеку было потрачено: ' , round(loan_in_year) , ' рублей Было накоплено: ' , round (savings) , ' рублей')
# -
| 4,649 |
/.ipynb_checkpoints/Data Wrangling--Web Scraping-checkpoint.ipynb
|
6a1e2257cd4c8b91ccb85b9f87bda35b521aece8
|
[] |
no_license
|
tunghoangt/DSE1020
|
https://github.com/tunghoangt/DSE1020
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 625,292 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="kMccmZPoWd_h"
# # Mixup augmentation for NLP
#
# Using IMDB sentiment classification dataset
# + colab={"base_uri": "https://localhost:8080/", "height": 527} colab_type="code" id="YhKEHbrxWd_n" outputId="368747f0-47d5-439f-f4b3-d4db6d6a2d18"
# Import libraries
try:
import textaugment
except ModuleNotFoundError:
# !pip install textaugment
import textaugment
import pandas as pd
import tensorflow as tf
from tensorflow.keras.preprocessing import sequence
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Activation
from tensorflow.keras.layers import Embedding
from tensorflow.keras.layers import Conv1D, GlobalMaxPooling1D
from tensorflow.keras.datasets import imdb
from textaugment import MIXUP
# %matplotlib inline
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="JeMsxayIWd_r" outputId="814596bf-e5ca-47f1-c2ce-257e761e96c4"
tf.__version__
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="_FbvA0uwRdEZ" outputId="8e912f45-8b7e-4ee7-a3ad-f342c3f090c7"
textaugment.__version__
# + [markdown] colab_type="text" id="Oz8O8tISRdEg"
# ## Initialize constant variables
# + colab={} colab_type="code" id="mg1AcYIWWd_w"
# set parameters:
max_features = 5000
maxlen = 400
batch_size = 32
embedding_dims = 50
filters = 250
kernel_size = 3
hidden_dims = 250
epochs = 10
runs = 1
# + colab={"base_uri": "https://localhost:8080/", "height": 153} colab_type="code" id="ZRuNNVstWd_0" outputId="bc4ce3b2-5a12-4600-d1a8-b466615018df"
print('Loading data...')
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=max_features)
print(len(x_train), 'train sequences')
print(len(x_test), 'test sequences')
print('Pad sequences (samples x time)')
x_train = sequence.pad_sequences(x_train, maxlen=maxlen)
x_test = sequence.pad_sequences(x_test, maxlen=maxlen)
print('x_train shape:', x_train.shape)
print('x_test shape:', x_test.shape)
# + [markdown] colab_type="text" id="Tx73Y-asRdEz"
# ## Initialize mixup
# + colab={} colab_type="code" id="xvuxODUxRdE1"
mixup = MIXUP()
generator, step = mixup.flow(x_train, y_train, batch_size=batch_size, runs=runs)
# + colab={"base_uri": "https://localhost:8080/", "height": 476} colab_type="code" id="6cm1o_fAWd_4" outputId="ea793754-100c-4c12-8acf-7798c096c399"
print('Build model...')
model = Sequential()
# we start off with an efficient embedding layer which maps
# our vocab indices into embedding_dims dimensions
model.add(Embedding(max_features,
embedding_dims,
input_length=maxlen))
model.add(Dropout(0.2))
# we add a Convolution1D, which will learn filters
# word group filters of size filter_length:
model.add(Conv1D(filters,
kernel_size,
padding='valid',
activation='relu',
strides=1))
# we use max pooling:
model.add(GlobalMaxPooling1D())
# We add a vanilla hidden layer:
model.add(Dense(hidden_dims))
model.add(Dropout(0.2))
model.add(Activation('relu'))
# We project onto a single unit output layer, and squash it with a sigmoid:
model.add(Dense(1))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
model.summary()
# + [markdown] colab_type="text" id="b5zRyuq8UKmR"
# ## Train model using mixup augmentation
# + colab={"base_uri": "https://localhost:8080/", "height": 357} colab_type="code" id="oGLSfzcUWeAB" outputId="81464964-8fd3-4249-b901-0e05cb664436"
h1 = model.fit(generator, steps_per_epoch=step,
epochs=epochs,
validation_data=(x_test, y_test))
# + colab={"base_uri": "https://localhost:8080/", "height": 298} colab_type="code" id="XKrXdkt8XeYo" outputId="0d463439-1718-4f90-bc24-b32f6dae7eda"
pd.DataFrame(h1.history)[['loss','val_loss']].plot(title="With mixup")
# + colab={"base_uri": "https://localhost:8080/", "height": 476} colab_type="code" id="Iiv7ahP8WeAF" outputId="0ad04311-b497-4830-dd50-a832daf583ac"
print('Build model...')
model2 = Sequential()
# we start off with an efficient embedding layer which maps
# our vocab indices into embedding_dims dimensions
model2.add(Embedding(max_features,
embedding_dims,
input_length=maxlen))
model2.add(Dropout(0.2))
# we add a Convolution1D, which will learn filters
# word group filters of size filter_length:
model2.add(Conv1D(filters,
kernel_size,
padding='valid',
activation='relu',
strides=1))
# we use max pooling:
model2.add(GlobalMaxPooling1D())
# We add a vanilla hidden layer:
model2.add(Dense(hidden_dims))
model2.add(Dropout(0.2))
model2.add(Activation('relu'))
# We project onto a single unit output layer, and squash it with a sigmoid:
model2.add(Dense(1))
model2.add(Activation('sigmoid'))
model2.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
model2.summary()
# + colab={"base_uri": "https://localhost:8080/", "height": 357} colab_type="code" id="ygNHmhGMWeAI" outputId="1592613d-52d2-409b-e210-cceddb7f5bbd"
h2 = model2.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test))
# + colab={"base_uri": "https://localhost:8080/", "height": 298} colab_type="code" id="DzJEhaPrWeAM" outputId="aec6c655-c5f8-434b-bb16-d1e1056adc03"
pd.DataFrame(h2.history)[['loss','val_loss']].plot(title="Without mixup")
# + [markdown] colab_type="text" id="M2HDERJbGr2a"
# # Comparison
# See the loss curve with mixup does not overfit.
# + [markdown] colab={} colab_type="code" id="hqteWafKRdF1"
# ## Cite the paper
# ```
# @article{marivate2019improving,
# title={Improving short text classification through global augmentation methods},
# author={Marivate, Vukosi and Sefara, Tshephisho},
# journal={arXiv preprint arXiv:1907.03752},
# year={2019}
# }```
#
# https://arxiv.org/abs/1907.03752
# -
| 6,330 |
/visualizations/.ipynb_checkpoints/Model_output-checkpoint.ipynb
|
c188012586b1e854732f331c526d49967dc6f15e
|
[] |
no_license
|
diodz/ml-covid
|
https://github.com/diodz/ml-covid
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 9,306,357 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Visualizing Model Outputs
# +
import pandas as pd
import numpy as np
from numpy import inf
import os
import matplotlib.style as style
import matplotlib.pyplot as plt
import seaborn as sns
import datetime as dt
from pandas.plotting import register_matplotlib_converters
np.seterr(divide = 'ignore')
pd.options.mode.chained_assignment = None
register_matplotlib_converters()
# %matplotlib inline
# -
all_data = pd.read_pickle('.\\..\\data\\covid_df.pkl')
output = pd.read_pickle('.\\..\\data\\predictions_log_total.pkl')
mlp = pd.read_pickle('.\\..\\data\\mlp_predictions.pkl')
# +
def predicted_vs_real(full_df, output_df, country, target, logged=False, net=False):
'''
Plots one model's prediction vs real trend
'''
style.use('seaborn')
date = output_df.index.min()
pre = full_df[(full_df['Country'] == country) & (full_df['Date'] <= date)][[target, 'Date']]
real = country + ' real'
predict = country + ' prediction'
post = output_df[[real, predict]]
day = pre['Date'].max() + dt.timedelta(days=-1)
row = pre[pre['Date'] == day][[target, 'Date']]
val = row[target]
if logged:
row[real], row[predict] = (np.log(val), np.log(val))
else:
row[real], row[predict] = (val, val)
row.set_index('Date', inplace=True)
post = row.append(post[[real, predict]])
if logged:
post = np.exp(post)
fig, ax = plt.subplots(figsize=(12, 8))
title = 'Prediction: {} in {}'.format(target, country)
if net:
title = 'Neural Net ' + title
else:
title = 'Linear Regression ' + title
plt.title(label=title, fontsize=15)
ax.axvline(x=date, ls=':', c='gray', label = str(date))
g = sns.lineplot(x=post.index, y=post[real], ax=ax, marker='X', color='darkorange')
g = sns.lineplot(x=post.index, y=post[predict], ax=ax, marker='X', color='g')
g = sns.lineplot(x=pre['Date'], y=pre[target], ax=ax, color='royalblue')
plt.legend(('Prediction frontier\n {}'.format(date), 'Real', 'Predicted', 'Trend'), prop={'size': 12})
plt.ylabel(target)
plt.show()
def side_by_side(full_df, country, target, models, *predictions, save_output=False):
'''
Plots two different plots of models' predictions vs real trends side by side.
--first *predictions arg must be the one to be logged (LinReg)
Inputs:
full_df: (Pandas df) The full cleaned dataset
country: (string) Country to examine
target: (string) the outcome variable of the model
models: (list) model names as strings
*predictions: (tuple of Pandas df) collection of model prediction data
save_output: (boolean) switch to save image output
Output:
File if save_output=True
plots figure
'''
np.seterr(all='ignore')
style.use('seaborn')
date = predictions[0].index.min()
pre = full_df[(full_df['Country'] == country) & (full_df['Date'] <= date)][[target, 'Date']]
real, predict = (country + ' real', country + ' prediction')
day = pre['Date'].max() + dt.timedelta(days=-1)
fig, axes = plt.subplots(1, 2, figsize=(28,11))
title = ' Prediction: {} in {}'.format(target, country)
post_trends = []
y_max = 0
for pred, model in zip(predictions, models):
post = pred[[real, predict]]
row = pre[pre['Date'] == day][[target, 'Date']]
row.set_index('Date', inplace=True)
val = row[target]
if model == 'Linear Regression':
row[real], row[predict] = (np.log(val), np.log(val))
post = np.exp(row.append(post[[real, predict]]))
else:
row[real], row[predict] = (val, val)
post = row.append(post[[real, predict]])
post_trends.append(post)
iterable = zip(models, predictions, axes, post_trends)
for model, output, axis, trend in iterable:
sub_title = model + title
axis.set_title(sub_title)
axis.axvline(x=date, ls=':', c='gray', label = str(date))
g = sns.lineplot(x=trend.index, y=trend[real], ax=axis, marker='X', color='darkorange')
g = sns.lineplot(x=trend.index, y=trend[predict], ax=axis, marker='X', color='g')
g = sns.lineplot(x=pre['Date'], y=pre[target], ax=axis, color='royalblue')
axis.legend(('Prediction frontier\n {}'.format(date), 'Real', 'Predicted', 'Trend'), prop={'size': 12})
plt.ylabel(target)
if output[[real, predict]].dropna().values.max() > y_max:
y_max = output[[real, predict]].dropna().values.max()
plt.ylim(0, y_max + y_max*.15)
if save_output:
file_name = '{} {} {} comparison.png'.format(country, *models)
plt.savefig('.\\..\\visualizations\\' + file_name)
plt.show()
#predicted_vs_real(all_data, mlp, 'Spain', 'Confirmed Cases', logged=False, net=True)
side_by_side(all_data, 'Spain', 'Confirmed Cases', ['Linear Regression', 'Neural Network'], output, mlp, save_output=True)
# +
side_by_side(all_data, 'Austria', 'Confirmed Cases', ['Linear Regression', 'Neural Network'],output, mlp, save_output=True)
side_by_side(all_data, 'Kenya', 'Confirmed Cases', ['Linear Regression', 'Neural Network'],output, mlp, save_output=True)
# -
for country in all_data['Country'].unique():
try:
side_by_side(all_data, country, 'Confirmed Cases', output, mlp, save_output=True)
except:
print('country missing:', country, '\n\n\n')
predicted_vs_real(all_data, output, 'Lesotho', 'Confirmed Cases', logged=True)
predicted_vs_real(all_data, mlp, 'Lesotho', 'Confirmed Cases', logged=False, net=True)
best_models = ['Bahrain', 'Belgium','Benin', 'China', 'Ecuador', 'Finland', 'France', 'Hungary', 'Iran', 'Lebanon', 'Mali', 'Moldova', 'Nicaragua', 'Pakistan', 'Philippines',\
'South Africa', 'Ukraine', 'United Kingdom']
for country in best_models:
predicted_vs_real(all_data, output, country, 'Confirmed Cases', logged=True)
| 6,205 |
/2-Data Analysis/3-Data Sources/Archivos/Teoria/Lectura Escritura.ipynb
|
631747ab9b2b1907f912706cdf116859e07c0688
|
[
"MIT"
] |
permissive
|
Suryayta/thebridgedsftjun21
|
https://github.com/Suryayta/thebridgedsftjun21
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 151,167 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# + [markdown] deletable=true editable=true
# Import all libraries and path of files
# + deletable=true editable=true
import matplotlib.pyplot as plt
import pandas as pd
DataFolder="C:\Users\Manuel\Documents\Polimi\Building systems\Project\Phyton"
DataSetName="energydata_complete.csv"
# + [markdown] deletable=true editable=true
# Read the dataframe and change the numerical index to a data index
# + deletable=true editable=true
completeDataPath=DataFolder+"/"+DataSetName
completeDF=pd.read_csv(completeDataPath,sep = ",",index_col=0)
previousIndex= completeDF.index
NewparsedIndex = pd.to_datetime(previousIndex)
completeDF.index= NewparsedIndex
# + [markdown] deletable=true editable=true
# Find the target variable (Appliances), and all the correlations with other features. corrAppliance is the correlation of appliance with alla feature.
# + deletable=true editable=true
DFtarget=completeDF[["Appliances"]]
corrAppliance=completeDF.corr().head(1)
corrAppliance>0.08
# + [markdown] deletable=true editable=true
# Use the heat map in order to visualize the correlation
# + deletable=true editable=true
plt.figure()
plt.matshow(completeDF.corr())
plt.colorbar()
plt.show()
# + [markdown] deletable=true editable=true
# As we can see, there is low correlation for Appliances, our model will be with a low quality.
# Most reliable variables are lights,RH1,T2,T3,T6,Tout,Windspeed. Let's find a correlation with shifted one
# + [markdown] deletable=true editable=true
# Define a function to find shifted variables
# + deletable=true editable=true
def lag_column(df,column_name,lag_period=1):
for i in range(1,lag_period+1,1):
new_column_name = column_name+"-"+str(i)+" day"
df[new_column_name]=df[column_name].shift(6*24*i)
return df
# + [markdown] deletable=true editable=true
# Let's try with temperature
# + deletable=true editable=true
DF_temperature_out = completeDF[['T_out']]
DF_tout_lagged=lag_column(DF_temperature_out,'T_out',3)
DF_corr_Tout=DFtarget.join([DF_tout_lagged])
DF_corr_Tout.corr().head(1)
# + [markdown] deletable=true editable=true
# Try with lights
# + deletable=true editable=true
DF_lights = completeDF[['lights']]
DF_lights_lagged=lag_column(DF_lights,"lights",1)
DF_corr_lights=DFtarget.join([DF_lights_lagged])
DF_corr_lights.corr().head(1)
# + [markdown] deletable=true editable=true
# Try with RH1
# + deletable=true editable=true
DF_RH1 = completeDF[['RH_1']]
DF_RH1_lagged=lag_column(DF_RH1,"RH_1",0)
DF_corr_RH1=DFtarget.join([DF_RH1_lagged])
DF_corr_RH1.corr().head(1)
# + [markdown] deletable=true editable=true
# Try with appliances
# + deletable=true editable=true
DF_Appliances = completeDF[['Appliances']]
DF_Appliances_lagged=lag_column(DF_Appliances,"Appliances",6)
DF_Appliances_lagged.corr().head(1)
# + [markdown] deletable=true editable=true
# Try with T2
# + deletable=true editable=true
DF_T2 = completeDF[['T2']]
DF_T2_lagged=lag_column(DF_T2,"T2",2)
DF_corr_T2=DFtarget.join([DF_T2_lagged])
DF_corr_T2.corr().head(1)
#DF_T2_lagged
# + [markdown] deletable=true editable=true
# Try with T3
# + deletable=true editable=true
DF_T3 = completeDF[['T3']]
DF_T3_lagged=lag_column(DF_T3,"T3",0)
DF_corr_T3=DFtarget.join([DF_T3_lagged])
DF_corr_T3.corr().head(1)
# + [markdown] deletable=true editable=true
# Not use T3 correlation
# + [markdown] deletable=true editable=true
# Try with T6
# + deletable=true editable=true
DF_T6 = completeDF[['T6']]
DF_T6_lagged=lag_column(DF_T6,"T6",4)
DF_corr_T6=DFtarget.join([DF_T6_lagged])
DF_corr_T6.corr().head(1)
# + [markdown] deletable=true editable=true
# Try with windspeed
# + deletable=true editable=true
DF_Windspeed = completeDF[['Windspeed']]
DF_Windspeed_lagged=lag_column(DF_Windspeed,"Windspeed",2)
DF_corr_Windspeed=DFtarget.join([DF_Windspeed_lagged])
DF_corr_Windspeed.corr().head(1)
# + [markdown] deletable=true editable=true
# Now try to find a correlation in shorted time(10 minutes) instead of days:
# + deletable=true editable=true
def lag_column_short(df,column_name,lag_period=1):
for i in range(1,lag_period+1,1):
new_column_name = column_name+"-"+str(i)+" times 10 minutes"
df[new_column_name]=df[column_name].shift(i)
return df
# + [markdown] deletable=true editable=true
# DF_temperature_out = completeDF[['T_out']]
# DF_tout_lagged_short=lag_column_short(DF_temperature_out,'T_out',5)
# DF_tout_lagged_short
# + [markdown] deletable=true editable=true
# Join all data
# + deletable=true editable=true
DF_FinalSet=DFtarget.join([DF_lights_lagged,completeDF[['RH_1']],DF_Appliances_lagged.drop(["Appliances"],axis=1),DF_T2_lagged,completeDF[['T3']],DF_T6_lagged,DF_Windspeed_lagged])
# + [markdown] deletable=true editable=true
# Set variables for day and night, day of the week and month of the year
# + deletable=true editable=true
DF_FinalSet['hour']=DF_FinalSet.index.hour
DF_FinalSet['day_of_week']=DF_FinalSet.index.dayofweek
DF_FinalSet['month']=DF_FinalSet.index.month
DF_FinalSet['week_of_the_year']=DF_FinalSet.index.week
DF_FinalSet
# + [markdown] deletable=true editable=true
# Define dayDetector function and week-end function and put that value in final dataset
# + deletable=true editable=true
def weekendDetector(day):
weekendLabel=0
if(day == 5 or day == 6):
weekendLabel=1
else:
weekendLabel=0
return weekendLabel
def dayDetector(hour):
dayLabel=1
if(hour<20 and hour>9):
dayLabel=1
else:
dayLabel=0
return dayLabel
simpleVectorOfDays = [0,1,2,3,4,5,6]
weekendOrNotVector = [weekendDetector(thisDay) for thisDay in simpleVectorOfDays]
hoursOfDayVector= range(0,24,1)
dayOrNotVEctor =[dayDetector(ThisHour) for ThisHour in hoursOfDayVector]
DF_FinalSet["weekend"] = [weekendDetector(thisDay) for thisDay in DF_FinalSet.index.dayofweek]
DF_FinalSet["day_nigth"] = [dayDetector(thisHour) for thisHour in DF_FinalSet.index.hour]
DF_FinalSet.dropna(inplace=True)
# + [markdown] deletable=true editable=true
# Let's try to build a model
# + deletable=true editable=true
DF_FinalSet.corr().head(1)
# + [markdown] deletable=true editable=true
# Remove day of the week, month, week of the year and weekend predictors from features.
# + deletable=true editable=true
DF_FinalSet.corr().head(1)
DF_features = DF_FinalSet.drop(["Appliances","day_of_week","month","week_of_the_year","weekend"],axis=1)
DF_target=DF_FinalSet[["Appliances"]]
# + deletable=true editable=true
#import sklearn to define test and train, test size is the fraction that will be test
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split (DF_features,DF_target,test_size=0.2)
# + deletable=true editable=true
#First model is simple linear model
from sklearn import linear_model
linear_reg=linear_model.LinearRegression() #empty alghoritm that we fill with fit
# + [markdown] deletable=true editable=true
# Fit the algorithm with X train and Y train and predict Appliances
# + deletable=true editable=true
linear_reg.fit(X_train,Y_train)
predict_linearAppliances=linear_reg.predict(X_test)
# + [markdown] deletable=true editable=true
# Fill a DF with predicted values and Y_test for a period and plot to show the results.
# + deletable=true editable=true
#How to extract index of Y_test---> Y_test.index
predict_DF_linearReg_split=pd.DataFrame(predict_linearAppliances,index =Y_test.index,columns =["AppliancesEnergy_predic_linearReg_split"])
predict_DF_linearReg_split=predict_DF_linearReg_split.join(Y_test)
#Now we have a DF in which we have predicted value and value of completeDF, let's see if the prediction is good: plot a period and see if hte curves match
predict_DF_linearReg_split_period=predict_DF_linearReg_split["2016-03-01":"2016-03-03"]
plt.figure()
predict_DF_linearReg_split_period.plot()
plt.xlabel("time")
plt.ylabel("Appliances")
plt.ylim([0,800])
plt.title("Linear regression")
plt.show()
# + [markdown] deletable=true editable=true
# Let's find the metrics.
# + deletable=true editable=true
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
mean_squared_error_linearREG=mean_squared_error(Y_test,predict_linearAppliances)
mean_absolute_error_linearREG=mean_absolute_error(Y_test,predict_linearAppliances)
R2_score_linearReg= r2_score(Y_test,predict_linearAppliances)
print "R2 index is "+str(R2_score_linearReg)
print "mean squared error is "+str(mean_squared_error_linearREG)
print "mean absolute error is "+str(mean_absolute_error_linearREG)
# + [markdown] deletable=true editable=true
# Let's use cross validation
# + deletable=true editable=true
from sklearn.model_selection import cross_val_predict
predict_linearReg_CV=cross_val_predict(linear_reg,DF_features,DF_target,cv =10)
#Lets put in a DF
predict_DF_linearReg_CV=pd.DataFrame(predict_linearReg_CV,index =DF_target.index,columns =["Appliances_predic_linearReg_CV"])
predict_DF_linearReg_CV=predict_DF_linearReg_CV.join(DF_target) #use DF target instead of Y_test
predict_DF_linearReg_CV_period= predict_DF_linearReg_CV["2016-03-01":"2016-03-02"]
plt.figure()
predict_DF_linearReg_CV_period.plot()
plt.xlabel("time")
plt.ylabel("Appliances")
plt.ylim([0,800])
plt.title("Crossing validation")
plt.show()
# + [markdown] deletable=true editable=true
# Let's find the metrics
# + deletable=true editable=true
mean_squared_error_CV=mean_squared_error(DF_target,predict_linearReg_CV)
mean_absolute_error_CV=mean_absolute_error(DF_target,predict_linearReg_CV)
R2_score_CV= r2_score(DF_target,predict_linearReg_CV)
print "R2 index is "+str(R2_score_CV)
print "mean squared error is "+str(mean_squared_error_CV)
print "mean absolute error is "+str(mean_absolute_error_CV)
# + [markdown] deletable=true editable=true
# Now use Random Forest regressor to find another model
# + deletable=true editable=true
from sklearn.ensemble import RandomForestRegressor
reg_RF=RandomForestRegressor()
predict_RF_CV=cross_val_predict(reg_RF,DF_features,DF_target,cv =10) #heavy procedure
# + [markdown] deletable=true editable=true
# Do the DF, plot and find the metrics
# + deletable=true editable=true
predict_DF_RF_CV=pd.DataFrame(predict_RF_CV,index =DF_target.index,columns =["Appliances_predic_RF_CV"])
predict_DF_RF_CV=predict_DF_RF_CV.join(DF_target)
predict_DF_RF_CV_period= predict_DF_RF_CV["2016-03-01":"2016-03-01"]
plt.figure()
predict_DF_RF_CV_period.plot()
plt.xlabel("time")
plt.ylabel("Appliances")
plt.ylim([0,800])
plt.title("Regression line with RandomForestRegressor")
plt.show()
mean_squared_error_RF=mean_squared_error(DF_target,predict_RF_CV)
mean_absolute_error_RF=mean_absolute_error(DF_target,predict_RF_CV)
R2_score_RF= r2_score(DF_target,predict_RF_CV)
print "R2 index is "+str(R2_score_RF)
print "mean squared error is "+str(mean_squared_error_RF)
print "mean absolute error is "+str(mean_absolute_error_RF)
# + [markdown] deletable=true editable=true
# Random Forest has bad fitting model since R2 is negative.
#
#
# Now try to use another model called Supported Vector Regression, that uses normalize data
# + deletable=true editable=true
from sklearn.svm import SVR
reg_SVR = SVR(kernel='rbf',C=10,gamma=1)
def normalize(df):
return (df-df.min())/(df.max()-df.min())
DF_features_norm=normalize(DF_features)
DF_target_norm=normalize(DF_target)
# + [markdown] deletable=true editable=true
# Predict the data with SVR
# + deletable=true editable=true
predict_SVR_CV = cross_val_predict(reg_SVR,DF_features_norm,DF_target_norm,cv=10) #very heavy procedure
predict_DF_SVR_CV=pd.DataFrame(predict_SVR_CV, index = DF_target_norm.index,columns=["AC_ConsPred_SVR_CV"])
predict_DF_SVR_CV = predict_DF_SVR_CV.join(DF_target_norm).dropna()
# + [markdown] deletable=true editable=true
# Plot the results and compute the metrics
# + deletable=true editable=true
plt.figure()
predict_DF_SVR_CV["2016-03-01":"2016-03-02"].plot()
plt.xlabel("time")
plt.ylabel("Appliances ratio")
plt.ylim([0,0.65])
plt.title("Regression normalized line with SVR")
plt.show()
mean_squared_error_SVR=mean_squared_error(predict_DF_SVR_CV[["Appliances"]],predict_DF_SVR_CV[['AC_ConsPred_SVR_CV']])
mean_absolute_error_SVR=mean_absolute_error(predict_DF_SVR_CV[["Appliances"]],predict_DF_SVR_CV[['AC_ConsPred_SVR_CV']])
R2_score_SVR= r2_score(predict_DF_SVR_CV[["Appliances"]],predict_DF_SVR_CV[['AC_ConsPred_SVR_CV']])
print "R2 index is "+str(R2_score_SVR)
print "mean squared error is "+str(mean_squared_error_SVR)
print "mean absolute error is "+str(mean_absolute_error_SVR)
# + [markdown] deletable=true editable=true
# This model fits very badly the set, if you try to compute the regression with non-normalized features you would find a model with an horizontal line that predicts better your target since R2 coefficient is very negative.
# + deletable=true editable=true
reg_SVR.fit(X_train,Y_train)
predict_SVR_Appliances=reg_SVR.predict(X_test)
predict_DF_SVR_split=pd.DataFrame(predict_SVR_Appliances,index =Y_test.index,columns =["AppliancesEnergy_predic_SVR_split"])
predict_DF_SVR_split=predict_DF_SVR_split.join(Y_test)
# + [markdown] deletable=true editable=true
# Plot
# + deletable=true editable=true
predict_DF_SVR_split_period=predict_DF_SVR_split["2016-03-01":"2016-03-07"]
plt.figure()
predict_DF_SVR_split_period.plot()
plt.xlabel("time")
plt.ylabel("Appliances")
plt.ylim([0,800])
plt.title("Regression line with SVR")
plt.show()
# + [markdown] deletable=true editable=true
# In the plot you can see the horizontal line
#
# In conclusion with linear and regression you can find a model that badly fits the data (R2 sligthly less than 0.2).
# With SVR and RF model is bad fitted.
# To increase accurancy of model you should find other variables more correlated with Appliances or other models that fit better dataset
#
# + deletable=true editable=true
Notation* es otro formato de texto plano que se utiliza para el itercambio de datos**. Originalmente se utilizaba como notación literal de objetos en JavaScript, pero actualmente es un formato de datos independiente del lenguaje. JavaScript es un lenguaje de programción web, por lo que JSON se utiliza mucho en el intercambio de objetos entre cliente y servidor.
#
# **¿Qué diferencia hay con un CSV o un Excel?** Ya no tenemos esa estructura de fila/columna, sino que ahora es un formato tipo clave/valor, como si fuese un diccionario. En una tabla en la fila 1, columna 1, tienes un valor. En un JSON no, en la clave "mi_calve" puedes tener almacenado un valor, una lista o incluso un objeto. Salimos del formato tabla al que estamos acostubrados para ganar en flexibilidad.
#
# Un JSON tiene la siguiente pinta:
#
# 
#
data = {
"firstName": "Jane",
"lastName": "Doe",
"hobbies": ["running", "sky diving", "singing"],
"age": 35,
"children": [
{
"firstName": "Alice",
"age": 6
},
{
"firstName": "Bob",
"age": 8
}
]
}
# **Puedo guardar el JSON en un archivo. Para ello, usamos la librería `json`**, que viene incluida en la instalación de Anaconda.
# +
import json
with open("data/data_file.json", "w") as write_file:
json.dump(data, write_file)
# -
# O también objetos de una clase
# +
class Persona:
def __init__(self, firstName, lastName, hobbies):
self.firstName = firstName
self.lastName = lastName
self.hobbies = hobbies
pers1 = Persona("Pepe", "Carrasco", ["Bricolaje", "Tenis"])
pers2 = Persona("Jose", "Carrasco", ["Bricolaje", "Tenis"])
# -
pers1.__dict__
# Lo puedo guardar en un archivo *pepe.json*
with open("data/pepe.json", "w") as write_file:
json.dump(pers2.__dict__, write_file)
# Luego lo puedo volver a cargar
# +
with open("data/pepe.json", "r") as json_file:
data = json.load(json_file)
print(data)
print(data['firstName'])
# -
# Para el siguiente ejemplo, utilizamos `pandas` y leeremos el archivo JSON, de tal manera que nos transforme los datos en formato tabla, en un `DataFrame`.
df = pd.read_json('data/Musical_Instruments_5.json', lines = True)
df
# ## 6. TXT
# **Son simplemente archivos donde hay texto**. Hemos visto que los CSVs y los JSON tienen su propio formato y extension. En el caso del .txt no tienen ninguno específico aunque no quita para que sus elementos estén separados por comas, y se pueda leer igualmente como si fuese un CSV.
#
# Cuando almancenamos datos siempre tienen una estructura, por lo que aunque sea un `.txt`, llevará los datos en formato json, separados por comas, tabulaciones, puntos y comas...
#
# Por ejemplo, si tenemos los datos de la liga guardados en un `.txt`, separados por tabulaciones, lo podremos leer con el `pd.read_csv()`.
# + jupyter={"outputs_hidden": true}
df = pd.read_csv('data/laligaTXT.txt', sep='\t')
df.head()
# -
# Recuerda que la separación por tabulaciones, también tiene su propia extensión: el `.tsv`, que igualmente lo podremos leer con `read_csv()`.
# + jupyter={"outputs_hidden": true}
df = pd.read_csv('data/laligaTSV.tsv', sep='\t')
df.head()
# -
# El método `read_csv()` no se ciñe únicamente a leer CSVs, sino a prácticamente cualquier archivo que lleve un acarácter concreto en la separación de sus campos. Si conocemos ese caracter, sabremos leer el archivo con `pandas`.
# ## 7. ZIP
# En ocasiones los datos que recibimos en nuestros programas están comprimidos, ya sea en un formato `.zip`, `.rar`, `.7z`, u otro tipo de archivo.
#
# En este apartado verás un ejemplo de cómo descomprimir archivos `.zip`. Para ello empleamos la librería `zipfile` que viene incluida en la instalación de Anaconda. [Tienes el enlace a la documentación para más detalle](https://docs.python.org/3/library/zipfile.html#zipfile-objects).
#
# Para extraer todos los archivos:
# +
import zipfile
with zipfile.ZipFile('data/laligaZIP.zip') as zip_ref:
zip_ref.extractall('data')
# -
# Si quieres descomprimir un archivo `.rar` [tendrás que descargarte un paquete como por ejemplo `unrar`.](https://pypi.org/project/unrar/)
# <table align="left">
# <tr><td width="80"><img src="./img/ejercicio.png" style="width:auto;height:auto"></td>
# <td style="text-align:left">
# <h3>Ejercicio zip</h3>
#
# Consulta la documentación para extrar un único archivo, por nombre
#
# </td></tr>
# </table>
with zipfile.ZipFile('data/laligaZIP.zip') as zip_ref:
zip_ref.extract('laligaZIP.csv')
# ## 8. pickle
# **`pickle` es el módulo que nos permite serializar y deserializar un objeto de Pyhton**. Esta operación lo que hace es traducirlo a un stream de bytes.
#
# A efectos prácticos, lo que nos permite es guardar objetos de Python, y recuperarlos más adelante.
# +
import pickle
df = pd.read_csv("data/laliga.csv")
with open('data/pepe.json') as json_file:
data = json.load(json_file)
with open('importante', 'wb') as f:
pickle.dump(pers1, f)
pickle.dump(df, f)
pickle.dump(data, f)
# +
with open('importante', 'rb') as f:
a = pickle.load(f)
b = pickle.load(f)
c = pickle.load(f)
print(a)
print(b)
print(c)
# -
# ## 9. Encoding
# **Los strings se almacenan internamente en un conjunto de bytes**, caracter a caracter. Esta operación es lo que se conoce como ***encoding***, mientras que pasar de bytes a string sería *decoding*. Bien, ¿y eso en qué nos afecta? Dependiendo del encoding, se suelen almacenar en un espacio de bits de 0 a 255, es decir, en esa combinación de bits tienen que entrar todos los caracteres del lenguaje.
#
# El problema es que en toda esa combinación de bits no entran todos los caracteres del planeta, por lo que **dependiendo del encoding que usemos, una combinación de bits significará una cosa u otra**. Por ejemplo, una A mayuscula será lo mismo en el encodig europeo que en el americano, pero los bits reservados para representar una Ñ, en el encodig americano se traduce en otro caracter.
#
# Por tanto, **hay que tener claro en qué encoding está el archivo y con qué encoding lo vamos a leer**. [En la documentación](https://docs.python.org/3/library/codecs.html#encodings-and-unicode) puedes realizar esta comprobación. Hay algunos que te tienen que ir sonando:
#
# 1. 'utf-8': normalmente se trabaja con este encodig que engloba la mayor parte de caracteres.
# 2. 'unicode': estándar universal con el que no deberiamos tener problemas.
# 3. 'ascii': encoding americano. Solo tiene 128 caracteres.
# 4. 'latin': para oeste de Europa, Oceanía y Latinoamérica
#
# 
pd.read_csv('data/encoding.csv', encoding = 'utf-8')
# + jupyter={"outputs_hidden": true}
pd.read_csv('data/encoding.csv', encoding = 'ascii')
# -
pd.read_csv('data/encoding.csv', encoding='iso8859_10')
# ## 10. Archivos y carpetas
# Resulta de gran utilidad automatizar lecturas/escrituras/borrado/movimientos de archivos entre carpetas. Si tenemos un proceso definido en Python, podremos ejecutarlo tantas veces queramos y de este modo evitar dedicarle tiempo tareas tediosas y rutinarias. Para ello tendremos que apoyarnos en el módulo de Python `os`.
#
# Lo primero de todo es saber en qué directorio estamos trabajando. Esto es fundamental para elegir bien la ruta relativa.
import os
os.getcwd()
# El directorio de trabajo lo podríamos cambiar si quisiéramos, por ejemplo, al escritorio.
os.chdir('C:\\Users\\Daney\\Desktop')
print(os.getcwd())
os.chdir('C:\\Users\\Daney\\Desktop\\Archivos\\Bootcamps\\thebridgedsftjun21\\2-Data Analysis\\3-Data Sources\\Archivos\\Teoria')
print(os.getcwd())
# Podemos juntar rutas en un único path. Realiza un concatenado con barras entendibles por Windows.
os.path.join("C:/path/to/directory", "some_file.txt")
# Si quieres buscar algún tipo de archivo concreto, tienes varias opciones:
# - Buscar por nombre
# - Buscar por extensión
#
# En función de lo que encuentres, realizarás una operación u otra. Ahora bien, igualmente para buscar, tendrás que recorrer todos los archivos que estén en un directorio o en varios directorios. Para listar todos los ARCHIVOS y CARPETAS que hay en el directorio actual de trabajo, utilizamos `os.listdir()`.
os.listdir()
# Voy a quedarme con todos los notebooks del actual directorio de trabajo.
for i in os.listdir():
if i.endswith('.ipynb'):
print("Notebook", i)
# Si quiero acceder sólo a los directorios
for i in os.listdir():
if '.' not in i:
print("directorio", i)
# Otro método interesante para bucear en los archivos y carpetas de un directorio concreto es el `os.walk()`. Va a devoler un iterable que podremos recorrer en un for y obtener en formato tupla todos los archivos, subcarpetas y ficheros de subcarpetas. Para cada elemento de la tupla tenemos:
# - El directorio donde está apuntando.
# - Los directorios que hay ahí.
# - Los archivos que hay ahí.
# +
result_generator = os.walk(os.getcwd())
files_result = [x for x in result_generator]
files_result
# -
# ¿Qué podemos hacer dentro de un directorio, aparte de listar ficheros y subdirectorios? Las principales operaciones serían:
# - Crear o eliminar directorios
# - Crear o eliminar ficheros
# - Mover ficheros
os.mkdir('direct_prueba')
os.rmdir('direct_prueba')
# +
f = open("fichero.txt", "w")
for i in range(10):
f.write("Line:" + str(i))
f.close()
# -
import shutil
shutil.move("importante", "img")
| 23,647 |
/rl_fun/RL playground.ipynb
|
7abd8346e8ebec5ee580c5e191794ecfb2bf5302
|
[
"Apache-2.0"
] |
permissive
|
jialing3/corner_cases
|
https://github.com/jialing3/corner_cases
| 1 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 103,056 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
print("Helloworld")
print("Today date is",29)
random
import matplotlib.pyplot as plt
# %matplotlib inline
n = 10
arms = np.random.rand(n)
eps = 0.1
def reward(prob):
reward = 0
for i in range(10):
if random.random() < prob:
reward += 1
return reward
# +
# action-value
av = np.array([np.random.randint(0, (n + 1)), 0]).reshape(1, 2)
def best_arm(a):
best_arm = 0
best_mean = 0
for u in a:
# mean reward for each action
avg = np.mean(a[np.where(a[:, 0] == u[0])][:, 1])
if best_mean < avg:
best_mean = avg
best_arm = u[0]
return best_arm
# -
plt.xlabel('Plays')
plt.ylabel('Avg Reward')
for i in range(500):
if random.random() > eps: # greedy arm selection
choice = best_arm(av)
else: # random arm selection
choice = np.where(arms == np.random.choice(arms))[0][0]
this_av = np.array([[choice, reward(arms[choice])]])
av = np.concatenate((av, this_av), axis=0)
# percentage the correct arm is chosen
perc_correct = 100 * (len(av[np.where(av[:, 0] == np.argmax(arms))]) * 1. / len(av))
# mean reward
running_mean = np.mean(av[:, 1])
plt.scatter(i, running_mean)
# +
# experiment with different numbers of arms and different values for ϵ
# +
# The problem we've considered here is a stationary problem
# because the underlying reward probability distributions for each arm do not change over time.
# +
# We certainly could consider a variant of this problem where this is not true,
# a non-stationary problem. In this case, a simple modification would be
# to weight more recent action-value pairs greater than distant ones,
# thus if things change over time, we will be able to track them.
# +
n = 10
arms = np.random.rand(n)
eps = 0.1
av = np.ones(n) # action-value
counts = np.zeros(n) # how many times we've taken a particular action
def reward(prob):
total = 0
for i in range(10):
if random.random() < prob:
total += 1
return total
# simpler best_arm function
def best_arm(a):
return np.argmax(a)
plt.xlabel('Plays')
plt.ylabel('Mean Reward')
for i in range(500):
if random.random() > eps:
choice = best_arm(av)
else:
choice = np.where(arms == np.random.choice(arms))[0][0]
counts[choice] += 1
k = counts[choice]
rwd = reward(arms[choice])
old_avg = av[choice]
new_avg = old_avg + (1. / k) * (rwd - old_avg)
av[choice] = new_avg
# weighted average
running_mean = np.average(av, weights=np.array([counts[j] * 1. / np.sum(counts) for j in range(len(counts))]))
plt.scatter(i, running_mean)
# +
# τ is a parameter called temperature the scales the probability distribution of actions.
# A high temperature will tend the probabilities to be very simmilar, whereas a low temperature
# will exaggerate differences in probabilities between actions. Selecting this parameter requires
# an educated guess and some trial and error.
# -
# +
# softmax
# +
n = 10
arms = np.random.rand(n)
av = np.ones(n) # action-value
counts = np.zeros(n) # how many times we've taken a particular action
av_softmax = np.zeros(n)
av_softmax[:] = 0.1 # initial probability
def reward(prob):
total = 0
for i in range(10):
if random.random() < prob:
total += 1
return total
tau = 1.12
def softmax(av):
normalization_factor = np.sum(np.exp(av[:] / tau))
probs = np.zeros(n)
for i in range(n):
probs[i] = np.exp(av[i] / tau) / normalization_factor
return probs
plt.xlabel('Plays')
plt.ylabel('Mean Reward')
for i in range(500):
choice = np.where(arms == np.random.choice(arms, p=av_softmax))[0][0]
counts[choice] += 1
k = counts[choice]
rwd = reward(arms[choice])
old_avg = av[choice]
new_avg = old_avg + (1. / k) * (rwd - old_avg)
av[choice] = new_avg
av_softmax = softmax(av)
running_mean = np.average(av, weights=np.array([counts[j] * 1. / np.sum(counts) for j in range(len(counts))]))
plt.scatter(i, running_mean)
# +
# Softmax action selection seems to do at least as well as epsilon-greedy,
# perhaps even better; it looks like it converges on an optimal policy faster.
# The downside to softmax is having to manually select the τ parameter.
# Softmax here was pretty sensitive to τ and it took awhile of playing with it
# to find a good value for it. Obviously with epsilon-greedy we had the parameter
# epsilon to set, but choosing that parameter was much more intuitive.
# -
# +
# The state space for 21 is much much larger than the single state in n-armed bandit.
# In RL, a state is all information available to the agent (the decision maker) at a particular time t.
# +
# So what are all the possible combinations of information available to the agent (the player) in blackjack?
# Well, the player starts with two cards, so there is the combination of all 2 playing cards.
# Additionally, the player knows one of the two cards that the dealer has.
# Thus, there are a lot of possible states (around 200).
# As with any RL problem, our ultimate goal is to find the best policy to maximize our rewards.
# +
# Our main computational effort, therefore, is in iteratively improving our estimates for the values
# of states or state-action pairs.
# For example, given the cards total to 20, what is the value of hitting vs staying?
# +
# Problems like the n-armed bandit problem and blackjack have a small enough state or state-action space
# that we can record and average rewards in a lookup table, giving us the exact average rewards for
# each state-action pair. Most interesting problems, however, have a state space that is continuous or
# otherwise too large to use a lookup table. That's when we must use function approximation
# (e.g. neural networks) methods to serve as our QQ function in determining the value of states or state-actions.
# +
# This is why DeepMind's implementation actually feeds in the last 4 frames of gameplay,
# effectively changing a non-Markov decision process into an MDP.
# +
# Qk(s,a)Qk(s,a) is the function that accepts an action and state and returns the value of
# taking that action in that state at time step kk. This is fundamental to RL.
# We need to know the relative values of every state or state-action pair.
# +
# π is a policy, a stochastic strategy or rule to choose action a given a state s.
# Think of it as a function, π(s), that accepts state, s and returns the action to be taken.
# There is a distinction between the π(s) function and a specific policy π. Our implementation
# of π(s) as a function is often to just choose the action a in state s that has the highest
# average return based on historical results, argmaxQ(s,a). As we gather more data and
# these average returns become more accurate, the actual policy π may change. We may
# start out with a policy of "hit until total is 16 or more then stay" but this policy
# may change as we gather more data. Our implemented π(s) function, however,
# is programmed by us and does not change.
# +
# Gt, cumulative return starting from a given state until the end of an episode.
# +
# Episode: the full sequence of steps leading to a terminal state and receiving a return.
# +
# vπ, a function that determines the value of a state given a policy π.
# -
# +
# Monte Carlo
# We'll use random sampling of states and state-action pairs
# and observe rewards and then iteratively revise our policy,
# which will hopefully **converge** on the optimal policy
# as we explore every possible state-action couple.
# +
# code is functional and stateless
# +
import math
import random
def random_card():
card = random.randint(1, 13)
if card > 10:
card = 10
return card
def useable_ace(hand):
val, ace = hand
return ace and val + 10 <= 21
def total_value(hand):
val, ace = hand
if useable_ace(hand):
return val + 10
else:
return val
def add_card(hand, card):
val, ace = hand
if card == 1:
ace = True
return (val + card, ace)
def eval_dealer(dealer_hand):
while total_value(dealer_hand) < 17:
dealer_hand = add_card(dealer_hand, random_card())
return dealer_hand
def play(state, dec):
player_hand = state[0]
dealer_hand = state[1]
if dec == 0: # 1 hit, 0 stay
dealer_hand = eval_dealer(dealer_hand)
player_tot = total_value(player_hand)
dealer_tot = total_value(dealer_hand)
status = 1 # 1 game is on, 2 play won, 3 draw, 4 dealer won
if dealer_tot > 21 or dealer_tot < player_tot:
status = 2
elif dealer_tot == player_tot:
status = 3
elif dealer_tot > player_tot:
status = 4
elif dec == 1:
player_hand = add_card(player_hand, random_card())
dealer_hand = eval_dealer(dealer_hand)
player_tot = total_value(player_hand)
dealer_tot = total_value(dealer_hand)
status = 1
if player_tot == 21:
if dealer_tot == 21:
status = 3
else:
status = 2
elif player_tot > 21:
status = 4
elif player_tot < 21:
pass # game continues
state = (player_hand, dealer_hand, status)
return state
def init_game():
status = 1
player_hand = add_card((0, False), random_card())
player_hand = add_card(player_hand, random_card())
dealer_hand = add_card((0, False), random_card())
if total_value(player_hand) == 21:
if total_value(dealer_hand) != 21:
status = 2
else:
status = 3
state = (player_hand, dealer_hand, status)
return state
# -
state = init_game()
print(state)
state = play(state, 1)
print(state)
# +
# We will compress the states a bit by ignoring the useable ace boolean
# for the dealer's hand because the dealer only shows a single card and
# if it's an ace the player has no idea if it's useable or not, so it
# offers no additional information to us.
# +
# Monte Carlo Reinforcement Learning
# use an epsilon-greedy policy function to ensure
# we have a good balance of exploration versus exploitation
# +
# In essence, with Monte Carlo we are playing randomly initialized games,
# sampling the state-action pair space and recording returns. In doing so,
# we can iteratively update our policy π.
# +
import numpy as np
def init_state_space():
states = []
for card in range(1, 11):
for val in range(11, 22):
states.append((val, False, card))
states.append((val, True, card))
return states
def init_state_actions(states):
av = {}
for state in states:
av[(state, 0)] = 0.0
av[(state, 1)] = 0.0
return av
def init_SA_count(state_actions):
counts = {}
for sa in state_actions:
counts[sa] = 0
return counts
# reward = 1 for winning, 0 for draw, -1 for losing
def calc_reward(outcome):
return 3 - outcome
def update_Q_table(av_table, av_count, returns):
for key in returns:
av_table[key] = av_table[key] + (1. / av_count[key]) * (returns[key] - av_table[key])
return av_table
# avg rewards - Q-value for each action given a state
def qsv(state, av_table):
if (state, 0) not in av_table:
av_table[(state, 0)] = 0
if (state, 1) not in av_table:
av_table[(state, 1)] = 0
stay = av_table[(state, 0)]
hit = av_table[(state, 1)]
return np.array([stay, hit])
# compress the state
def get_RL_state(state):
player_hand, dealer_hand, status = state
player_val, player_ace = player_hand
return (player_val, player_ace, dealer_hand[0])
# +
epochs = 5000000
epsilon = 0.1
state_space = init_state_space()
av_table = init_state_actions(state_space)
av_count = init_SA_count(av_table)
for i in range(epochs):
state = init_game()
player_hand, dealer_hand, status = state
while player_hand[0] < 11:
player_hand = add_card(player_hand, random_card())
state = (player_hand, dealer_hand, status)
rl_state = get_RL_state(state)
returns = {}
while state[2] == 1:
act_probs = qsv(rl_state, av_table)
if random.random() < epsilon:
action = random.randint(0, 1)
else:
action = np.argmax(act_probs)
sa = (rl_state, action)
returns[sa] = 0
if sa not in av_count:
av_count[sa] = 0
av_count[sa] += 1
state = play(state, action)
rl_state = get_RL_state(state)
for key in returns.keys():
returns[key] = calc_reward(state[2])
av_table = update_Q_table(av_table, av_count, returns)
print('Done')
# -
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
# %matplotlib inline
# +
#fig = plt.figure(figsize=(8, 6))
#ax = fig.add_subplot(111, projection='3d')
#ax.set_xlabel('Dealer card')
#ax.set_ylabel('Player sum')
#ax.set_zlabel('State-Value')
x,y,z,a = [],[],[],[]
for key in state_space:
if (not key[1] and key[0] > 11 and key[2] < 21):
y.append(key[0])
x.append(key[2])
state_value = max([av_table[(key, 0)], av_table[(key, 1)]])
z.append(state_value)
if av_table[(key, 0)] >= av_table[(key, 1)]:
a.append(0)
else:
a.append(1)
#ax.azim = 230
#ax.plot_trisurf(x,y,z, linewidth=.02, cmap=cm.jet)
# +
# Here we've covered Monte Carlo reinforcement learning methods that depending on stochastically
# sampling the environment and iteratively improving a policy π after each episode. One
# disadvantage of Monte Carlo methods is that we must wait until the end of an *episode*
# to update our policy. For some types of problems (like blackjack), this is okay, but
# in a lot of cases, it makes more sense to be able to learn at each time step (immediately
# after each action is taken).
# -
import pandas as pd
strategy = pd.DataFrame(zip(x, y, z, a), columns=['Dealer card', 'Player sum', 'State-Value', 'Policy'])
strategy.pivot(index='Player sum', columns='Dealer card', values='Policy')
# +
# The most important thing to learn from all of this is that in
# essentially any RL method, our goal is to find an optimal Q function.
# +
# In the next part, I will abandon tabular learning methods and cover
# Q-learning (a type of temporal difference (TD) algorithm) using a neural
# network as our Q function (what we've all been waiting for).
# -
# +
# Neural nets provide a functional approximator.
# +
# Our Q function actually looks like this: Q(s,a,θ) where θ is
# a vector of parameters. And instead of iteratively updating values
# in a table, we will iteratively update the θ parameters of
# our neural network so that it learns to provide us with better
# estimates of state-action values.
# -
# target: r_t+1 + γ ∗ maxQ(s′, a′) for non-terminal states
# r_t+1 for terminal states (last state in an episode)
# +
# γ is a parameter 0-→1 that is called the discount factor.
# Basically it determines how much each future reward is taken
# into consideration for updating our Q-value.
# +
# If γ is close to 0, we heavily discount future rewards and
# thus mostly care about immediate rewards.
# +
# s′ refers to the new state after having taken action a
# and a′ refers to the next actions possible in this new state.
# +
# So maxQ(s′, a′) means we calculate all the Q-values for each
# state-action pair in the new state, and take the maximium value
# to use in our new value update.
# (Note I may use s′ and a′ interchangeably with s_t+1 and a_t+1.)
# +
# In on-policy methods we iteratively learn about state values
# at the same time that we improve our policy. In other words,
# the updates to our state values depend on the policy.
# +
# In contrast, off-policy methods do not depend on the policy
# to update the value function. Q-learning is an **off-policy** method.
# It's advantageous because with off-policy methods, we can follow
# one policy while learning about __another__.
# +
# For example, with Q-learning, we could always take completely random
# actions and yet we would still learn about another policy function
# of taking the best actions in every state. If there's ever a π
# referenced in the value update part of the algorithm then it's
# an on-policy method.
# +
import numpy as np
def rand_pair(s, e):
return np.random.randint(s, e), np.random.randint(s, e)
# finds an array in the "depth" dimension of the grid
def find_loc(state, obj):
for i in range(4):
for j in range(4):
if all(state[i, j] == obj):
return i, j
# initialize stationary grid, all items are placed deterministically
def init_grid():
state = np.zeros((4, 4, 4))
# place player
state[0, 1] = np.array([0, 0, 0, 1])
# place wall
state[2, 2] = np.array([0, 0, 1, 0])
# place pit
state[1, 1] = np.array([0, 1, 0, 0])
# place goal
state[3, 3] = np.array([1, 0, 0, 0])
return state
# initialize player in random location, but keep wall, goal and pit stationary
def init_grid_player():
state = np.zeros((4, 4, 4))
# place player
state[rand_pair(0, 4)] = np.array([0, 0, 0, 1])
# place wall
state[2, 2] = np.array([0, 0, 1, 0])
# place pit
state[1, 1] = np.array([0, 1, 0, 0])
# place goal
state[1, 2] = np.array([1, 0, 0, 0])
# find grid position of player (agent)
a = find_loc(state, np.array([0, 0, 0, 1]))
# find wall
w = find_loc(state, np.array([0, 0, 1, 0]))
# find goal
g = find_loc(state, np.array([1, 0, 0, 0]))
# find pit
p = find_loc(state, np.array([0, 1, 0, 0]))
if not all([a, w, g, p]):
print('Invalid grid. Rebuilding...')
return init_grid_player()
return state
# initialize grid so that goal, pit, wall, player are all randomly placed
def init_grid_rand():
state = np.zeros((4, 4, 4))
# place player
state[rand_pair(0, 4)] = np.array([0, 0, 0, 1])
# place wall
state[rand_pair(0, 4)] = np.array([0, 0, 1, 0])
# place pit
state[rand_pair(0, 4)] = np.array([0, 1, 0, 0])
# place goal
state[rand_pair(0, 4)] = np.array([1, 0, 0, 0])
a = find_loc(state, np.array([0, 0, 0, 1]))
w = find_loc(state, np.array([0, 0, 1, 0]))
g = find_loc(state, np.array([1, 0, 0, 0]))
p = find_loc(state, np.array([0, 1, 0, 0]))
# if any of the "objects" are superimposed, just call the function again to re-place
if not all([a, w, g, p]):
print('Invalid grid. Rebuilding...')
return init_grid_rand()
return state
# -
def make_move(state, action):
player_loc = find_loc(state, np.array([0, 0, 0, 1]))
wall_loc = find_loc(state, np.array([0, 0, 1, 0]))
goal_loc = find_loc(state, np.array([1, 0, 0, 0]))
pit_loc = find_loc(state, np.array([0, 1, 0, 0]))
state = np.zeros((4, 4, 4))
# up --> row - 1
if action == 0:
new_loc = (player_loc[0] - 1, player_loc[1])
# down --> row + 1
elif action == 1:
new_loc = (player_loc[0] + 1, player_loc[1])
# left --> column - 1
elif action == 2:
new_loc = (player_loc[0], player_loc[1] - 1)
# right --> column + 1
elif action == 3:
new_loc = (player_loc[0], player_loc[1] + 1)
if new_loc != wall_loc:
if (np.array(new_loc) <= (3, 3)).all() and (np.array(new_loc) >= (0, 0)).all():
state[new_loc][3] = 1
new_player_loc = find_loc(state, np.array([0, 0, 0, 1]))
if not new_player_loc:
state[player_loc] = np.array([0, 0, 0, 1])
state[pit_loc][1] = 1
state[wall_loc][2] = 1
state[goal_loc][0] = 1
return state
# +
def get_loc(state, level):
for i in range(4):
for j in range(4):
if state[i, j][level] == 1:
return i, j
def get_reward(state):
player_loc = get_loc(state, 3)
pit_loc = get_loc(state, 1)
goal_loc = get_loc(state, 0)
if player_loc == pit_loc:
return -10
elif player_loc == goal_loc:
return 10
else:
return -1
def disp_grid(state):
grid = np.zeros((4, 4), dtype='<U2')
player_loc = find_loc(state, np.array([0, 0, 0, 1]))
wall_loc = find_loc(state, np.array([0, 0, 1, 0]))
goal_loc = find_loc(state, np.array([1, 0, 0, 0]))
pit_loc = find_loc(state, np.array([0, 1, 0, 0]))
for i in range(4):
for j in range(4):
grid[i, j] = ' '
if player_loc:
grid[player_loc] = 'P'
if wall_loc:
grid[wall_loc] = 'W'
if goal_loc:
grid[goal_loc] = '+'
if pit_loc:
grid[pit_loc] = '-'
return grid
# -
state = init_grid_rand()
disp_grid(state)
state = make_move(state, 3)
state = make_move(state, 3)
state = make_move(state, 1)
state = make_move(state, 1)
print('Reward: %s' % get_reward(state))
disp_grid(state)
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import RMSprop
# +
# An input layer of 64 units (because our state has a total of
# 64 elements, remember its a 4x4x4 numpy array), 2 hidden layers
# of 164 and 150 units, and an output layer of 4, one for each of
# our possible actions (up, down, left, right) [in that order].
model = Sequential()
model.add(Dense(164, init='lecun_uniform', input_shape=(64,)))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(150, init='lecun_uniform'))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(4, init='lecun_uniform'))
model.add(Activation('linear')) # real-valued outputs
rms = RMSprop()
model.compile(loss='mse', optimizer=rms)
# -
state = init_grid_rand()
model.predict(state.reshape(1, 64), batch_size=1)
# +
from IPython.display import clear_output
import random
epochs = 1000
gamma = 0.9 # coz it may take several moves to reach goal
epsilon = 1
for i in range(epochs):
state = init_grid()
status = 1 # game in progress
while (status) == 1:
# run Q function on S to get Q values for all possible actions
qval = model.predict(state.reshape(1, 64), batch_size=1)
if random.random() < epsilon: # explore
action = np.random.randint(0, 4)
else: # exploit
action = np.argmax(qval)
# take action, observe new state S'
new_state = make_move(state, action)
# observe reward
reward = get_reward(new_state)
# get max_Q(S', a)
new_Q = model.predict(new_state.reshape(1, 64), batch_size=1)
max_Q = np.max(new_Q)
y = np.zeros((1, 4))
y[:] = qval[:]
if reward == -1: # non-terminal
update = reward + gamma * max_Q
else: # terminal
update = reward
y[0][action] = update # target output
print('Game #: %s' % i)
model.fit(state.reshape(1, 64), y, batch_size=1, nb_epoch=1, verbose=1)
state = new_state
if reward != -1:
status = 0
clear_output(wait=True)
if epsilon > 0.1:
epsilon -= (1. / epochs)
# -
def test_algo(init=0):
i = 0
if init == 0:
state = init_grid()
elif init == 1:
state = init_grid_player()
elif init == 2:
state = init_grid_rand()
print('Initial State:')
print(disp_grid(state))
status = 1
while status == 1:
qval = model.predict(state.reshape(1, 64), batch_size=1)
action = np.argmax(qval)
print('Move #: %s; Taking action: %s' % (i, action))
state = make_move(state, action)
print(disp_grid(state))
reward = get_reward(state)
if reward != -1:
status = 0
print('Reward: %s' % reward)
i += 1
if i > 10:
print('Game lost; too many moves.')
break
test_algo(init=0)
# +
# soooooooo magical...
# -
# +
# catastrophic forgetting:
# a push-pull between very similar state-actions
# (but with divergent targets) that results in this
# inability to properly learn anything.
# experience replay:
# basically gives us minibatch updating in an
# online learning scheme.
# +
# Thus, in addition to learning the action-value for the action
# we just took, we're also going to use a random sample of our
# past experiences to train on to prevent catastrophic forgetting.
# +
model.compile(loss='mse', optimizer=rms) # reset weights
epochs = 3000
gamma = 0.975
epsilon = 1
batch_size = 40
buffer_size = 80
replay = [] # (S, A, R, S')
h = 0
for i in range(epochs):
state = init_grid_player()
status = 1
while status == 1:
qval = model.predict(state.reshape(1, 64), batch_size=1)
if random.random() < epsilon:
action = np.random.randint(0, 4)
else:
action = np.argmax(qval)
new_state = make_move(state, action)
reward = get_reward(new_state)
# experience replay
if len(replay) < buffer_size:
replay.append((state, action, reward, new_state))
else:
if h < buffer_size - 1:
h += 1
else:
h = 0 # circular buffer
replay[h] = (state, action, reward, new_state)
# randomly sample our experience replay memory
minibatch = random.sample(replay, batch_size)
X_train = []
y_train = []
for memory in minibatch:
old_state, action, reward, new_state = memory
old_qval = model.predict(old_state.reshape(1, 64), batch_size=1)
new_Q = model.predict(new_state.reshape(1, 64), batch_size=1)
max_Q = np.max(new_Q)
y = np.zeros((1, 4))
if reward == -1:
update = reward + gamma * max_Q
else:
update = reward
y[0][action] = update
X_train.append(old_state.reshape(64))
y_train.append(y.reshape(4))
X_train = np.array(X_train)
y_train = np.array(y_train)
print('Game #: %s' % i)
model.fit(X_train, y_train, batch_size=batch_size, nb_epoch=1, verbose=1)
state = new_state
if reward != -1:
status = 0
clear_output(wait=True)
if epsilon > 0.1:
epsilon -= (1. / epochs)
# -
test_algo(1)
# +
# magical !
# -
test_algo(1)
# +
# need GPU to train the hardest variant with more epochs (>50K)
# +
import random
import numpy as np
from IPython.display import clear_output
model.compile(loss='mse', optimizer=rms) # reset weights
epochs = 50000
gamma = 0.975
epsilon = 1
batch_size = 40
buffer_size = 80
replay = [] # (S, A, R, S')
h = 0
for i in range(epochs):
state = init_grid_rand()
status = 1
while status == 1:
qval = model.predict(state.reshape(1, 64), batch_size=1)
if random.random() < epsilon:
action = np.random.randint(0, 4)
else:
action = np.argmax(qval)
new_state = make_move(state, action)
reward = get_reward(new_state)
# experience replay
if len(replay) < buffer_size:
replay.append((state, action, reward, new_state))
else:
if h < buffer_size - 1:
h += 1
else:
h = 0 # circular buffer
replay[h] = (state, action, reward, new_state)
# randomly sample our experience replay memory
minibatch = random.sample(replay, batch_size)
X_train = []
y_train = []
for memory in minibatch:
old_state, action, reward, new_state = memory
old_qval = model.predict(old_state.reshape(1, 64), batch_size=1)
new_Q = model.predict(new_state.reshape(1, 64), batch_size=1)
max_Q = np.max(new_Q)
y = np.zeros((1, 4))
if reward == -1:
update = reward + gamma * max_Q
else:
update = reward
y[0][action] = update
X_train.append(old_state.reshape(64))
y_train.append(y.reshape(4))
X_train = np.array(X_train)
y_train = np.array(y_train)
print('Game #: %s' % i)
model.fit(X_train, y_train, batch_size=batch_size, nb_epoch=1, verbose=1)
state = new_state
if reward != -1:
status = 0
clear_output(wait=True)
if epsilon > 0.1:
epsilon -= (1. / epochs)
# -
test_algo(2)
test_algo(2)
| 29,363 |
/startMLWithPython/.ipynb_checkpoints/chapter1-checkpoint.ipynb
|
52a672e77ed51995046359329e1979fec2823659
|
[] |
no_license
|
takahiro1127/DeepLearning
|
https://github.com/takahiro1127/DeepLearning
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 240,018 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Feuille de TP3 - Partie A : Manipulation de fonctions
#
# + pycharm={"is_executing": false}
# Import des modules
import numpy as np
# -
# **Attention :**
# + On rappelle que les noms de fonctions **ne doivent pas commencer par «_» ni contenir de caractères accentués**.
# + Les tableaux sont typées. Lorsque vous modifier un élément d'une matrice, si les types sont différents, une conversion a lieu qui peut parfois engendrer des bugs... Voici un exemple pour illustrer cela.
# + pycharm={"is_executing": false}
A = np.array([[1,2], [3,4]])
print(A)
A[0,0] = 1.5 # 1.5 va être converti en entier !
print(A)
print(type(A), type(A[0,0]))
A = np.array([[1.,2], [3,4]])
print(A)
A[0,0] = 1.5 # Pas de conversion
print(A)
print(type(A), type(A[0,0]))
A = np.array([[1,2], [3,4]], dtype='float128')
print(A)
A[0,0] = 1.5
print(A)
print(type(A), type(A[0,0]))
# -
# ## Exercice 1 : Cryptographie basique : code de César (ou *Caesar cypher*)
#
# Le principe de ce code est de "décaler" les lettres. Par exemple, si la clef choisie est 1, la lettre A sera remplacée par B, la lettre B par C, etc. Nous nous proposons ici de fabriquer une fonction de cryptage et de décryptage pour la clef 13.
#
# #### a. <font color=red>Importer</font> le module `codecs` et tester les commandes `print(codecs.encode("abc", "rot+13"))` et `print(codecs.encode("abc", "rot-13"))`
# + pycharm={"is_executing": false}
import codecs
print(codecs.encode("abc", "rot+13"))
print(codecs.encode("nop", "rot-13"))
# -
# Comparer avec les 14, 15 et $16^\text{ème}$ lettres de l'alphabet.
# #### b. Proposer une fonction `crypter()` qui demande à l'utilisateur de saisir une chaîne de caractères et affiche sa version codée.
# + pycharm={"is_executing": false}
# Mettre votre fonction ici
def crypter():
""" Demande de saisir un message puis affiche sa version cryptée. """
mes = input("Donner une phrase à coder: ")
print(codecs.encode(mes, "rot-13"))
# -
# #### c. Ecrire une fonction `decrypter()`qui demande à l'utilisateur de saisir une chaîne de caractères encodée et affiche sa version décodée.
# #### d.Tester la fonction \verb+crypter()+ avec un message déjà crypté. Expliquer le résultat (indice : il y a 26 lettres dans l'alphabet).
#
# ## Exercice 2
# ### Question 1
# A l'aide du module `numpy`, implémenter informatiquement la fonction $f : x \mapsto \sin(\pi x)$.
# ### Question 2
# Ecrire une fonction qui convertit une vitesse depuis des $km/h$ vers des miles par heure puis des noeuds. On rappelle que 1 mile = 1609 m et 1 noeud $= 0.514 m.s^{-1}$.
# ### Question 3
#
# 1. Ecrire une fonction qui prend en argument un tableau et renvoie un tableau de même taille rempli par le nombre décimal $3.0$ .
# 2. A l'aide de la fonction numpy`isscalar` écrire une fonction qui prend un argument \verb+x+ et renvoie 3.0 si `x` est un scalaire et un tableau de 3.0 s'il s'agit d'un tableau.
# ### Question 4
# L'aire d'un triangle peut être calculée à partir des coordonnées de ses trois sommets par la formule :
# \begin{equation*}
# \mathcal{A} = \frac{1}{2}\big\vert (x_1 - x_3)(y_2-y_1) - (x_1-x_2)(y_3 - y_1) \big \vert
# \end{equation*}
# Ecrire une fonction qui prend comme argument un tableau bi-dimensionnel dont chaque ligne est la coordonnée $(x,y)$ d'un sommet et renvoie son aire.
# ### Question 5
# Ecrire une fonction qui prend en argument un tableau et remplace ces coefficients strictement positif par $1$ et ses coefficients strictement négatifs par $-1$.
# ## Exercice : comparaison de nombre flottants
#
# 1. Importez le module \verb!scipy.linalg! comme \verb!slin!, définissez une matrice $A$ (si possible inversible) et un vecteur $u$. Calculez le déterminant de A, inversez la matrice, calculez $x=A^{-1}u$, puis calculez la norme de $Ax-u$. Comparer $Ax$ et $u$.
# 2. Testez également la commande \verb!allclose! pour comparer $Ax$ et $u$.
# 3. Recommencez en résolvant le système linéaire par la commande \verb!solve!.
# +
# Mettre ici votre code pour la question 1.
# +
# Mettre ici votre code pour la question 2.
# +
# Mettre ici votre code pour la question 3.
moonlight i was a spin the stars and so when i say i love it all the blues i wish a spark of my heart when you say i was a said a spring and the star"
sent = sent.split(" ")
for word in sent:
prob = model.predict(toNumber(word).reshape(1,CHAR_COUNT))
print ("{}".format(indToLabel[np.argmax(prob)]))
# + id="R8LvKXLKqsEq" colab_type="code" colab={}
| 4,757 |
/05. Merge/Auto_MPG/.ipynb_checkpoints/Auto_MPG-checkpoint.ipynb
|
004a9e2a89040e05f79ce25be135afcc1c2accf6
|
[] |
no_license
|
joypark88/python_data_science-
|
https://github.com/joypark88/python_data_science-
| 0 | 0 | null | 2021-01-07T09:39:06 | 2021-01-07T08:32:33 |
Jupyter Notebook
|
Jupyter Notebook
| false | false |
.py
| 43,722 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## MPG Cars
#
# ### Step 1. Import the necessary libraries
import pandas as pd
import numpy as np
import random
# ### Step 2. Import the first dataset cars1 and cars2.
# ### Step 3. Assign each to a variable called cars1 and cars2
cars1 = pd.read_csv("https://raw.githubusercontent.com/guipsamora/pandas_exercises/master/05_Merge/Auto_MPG/cars1.csv")
cars2 = pd.read_csv("https://raw.githubusercontent.com/guipsamora/pandas_exercises/master/05_Merge/Auto_MPG/cars2.csv")
cars1
cars2
# ### Step 4. Oops, it seems our first dataset has some unnamed blank columns, fix cars1
cars1 = cars1.iloc[:, 0:9]
#or
#cars1 = cars1.loc[:, "mpg":"car"]
cars1
# ### Step 5. What is the number of observations in each dataset?
cars1.info()
#cars1.shape
cars2.info()
#cars2.shape
# ### Step 6. Join cars1 and cars2 into a single DataFrame called cars
# +
cars = pd.concat([cars1, cars2])
cars
#or
#cars = cars1.append(cars2)
# -
# ### Step 7. Oops, there is a column missing, called owners. Create a random number Series from 15,000 to 73,000.
# +
res = np.array([random.randrange(15000, 73000, 1) for i in range(398)]) #array 안에 리스트[]로 묶여있어야 됨.
#another answer
#nr_owners = np.random.randint(15000, high=73001, size=398, dtype='l')
# -
# ### Step 8. Add the column owners to cars
# +
#cars.owners = res col이 추가가 안됨
cars['owners'] = res
cars
| 1,620 |
/Additional dataset testing_VGG16.ipynb
|
d75066c9afdec73f2812bf2a14ff4b389fcd9409
|
[] |
no_license
|
eatingyeh/Face-Recognition-with-LeNet-and-VGG16
|
https://github.com/eatingyeh/Face-Recognition-with-LeNet-and-VGG16
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 88,045 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3 (Anaconda 5)
# env:
# LD_LIBRARY_PATH: /ext/anaconda5/lib
# PROJ_LIB: /ext/anaconda-2019.03/share/proj
# PYTHONHOME: /ext/anaconda5/lib/python3.5
# PYTHONPATH: /ext/anaconda5/lib/python3.5:/ext/anaconda5/lib/python3.5/site-packages
# language: python
# metadata:
# cocalc:
# description: Python/R distribution for data science
# priority: -1
# url: https://www.anaconda.com/distribution/
# name: anaconda5
# ---
# # SymPy
# +
# %matplotlib inline
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
# -
# ---
# ## Part I
#
# $$ \Large {\displaystyle f(x)=3e^{-{\frac {x^{2}}{8}}}} \sin(x/3)$$
# * Find the first four terms of the Taylor expansion of the above equation (at x = 0)
# * Make a plot of the function
# * Plot size 10 in x 4 in
# * X limts -5, 5
# * Y limits -2, 2
# * On the same plot:
# * Over-plot the 1-term Taylor expansion using a different color/linetype/linewidth
# * Over-plot the 2-term Taylor expansion using a different color/linetype/linewidth
# * Over-plot the 3-term Taylor expansion using a different color/linetype/linewidth
# * Over-plot the 4-term Taylor expansion using a different color/linetype/linewidth
# ---
# ## Part II
#
# $$\Large {\displaystyle g(x)=x^{2} - 0.75}$$
#
# #### What are the value(s) for `x` where f(x) = g(x)
# ---
# ### Due Mon Mar 02 - 1 pm
# - `File -> Download as -> HTML (.html)`
# - `upload your .html file to the class Canvas page`
ft(shift)).cumprod() # strategy returns
if plot:
plotcols = ['signal', 'bnh_returns', 'strat_returns']
results[plotcols].plot(secondary_y=['signal'], figsize=(20, 10))
return data['bnh_returns'][-1], data['strat_returns'][-1]
# ## Strategy I
# I. Backtests a strategy using three moving averages on any indices such as Nifty50, SPY,
# HSI and so on.
# 1. Compute three moving averages of 20, 40, and 80.
# 2. Go long when the price crosses above all three moving averages.
# 3. Exit the long position when the price crosses below any of the three moving
# averages.
# 4. Go short when the price crosses below all three moving averages.
# 5. Exit the short position when the price crosses above any of the three moving
# averages.
# 6. Optional: Optimise all three moving averages
def backtest_3ma_crossover(data, malist, plot=True):
"""Backtests moving average crossover strategy described above
@params:
data = pandas dataframe with daily prices indexed by date
malist = [ma1, ma2, ma3] => list of 3 moving average windows for backtesting
plot = True if plotting required
@returns:
results = dataframe with close to close returns, daily returns, moving averages, signal
"""
# Create dataframe to store values
results = data[['Close']].copy()
results['ma1'] = results['Close'].rolling(window=malist[0]).mean() # moving average 1 of close price
results['ma2'] = results['Close'].rolling(window=malist[1]).mean() # moving average 2 of close price
results['ma3'] = results['Close'].rolling(window=malist[2]).mean() # moving average 3 of close price
results['c2c_rets'] = results['Close'].pct_change() # daily returns of close price
results['daily_rets'] = results['Close'].pct_change() # daily returns for strategy
# Long signal
results['signal'] = np.where(
(results.Close > results.ma1) &
(results.Close > results.ma2) &
(results.Close > results.ma3), 1, 0)
# Long exit signal
long_exit = (results.Close < results.ma1) | \
(results.Close < results.ma2) | \
(results.Close < results.ma3)
results['signal'] = np.where(
long_exit &
(results.signal.shift(1) == 1), 0, results.signal)
# Short signal
results['signal'] = np.where(
(results.Close < results.ma1) &
(results.Close < results.ma2) &
(results.Close < results.ma3), -1, results.signal)
# Short exit signal
short_exit = (results.Close > results.ma1) | \
(results.Close > results.ma2) | \
(results.Close > results.ma3)
results['signal'] = np.where(
short_exit &
(results.signal.shift(1) == -1), 0, results.signal)
if plot:
plotcols = ['Close', 'ma1', 'ma2', 'ma3', 'signal']
results[plotcols].plot(secondary_y=['signal'], figsize=(20, 10))
return results
malist = [20, 40, 80]
results = backtest_3ma_crossover(data, malist)
results
plotcols = ['Close', 'ma1', 'ma2', 'ma3', 'signal']
results.iloc[80:200][plotcols].plot(secondary_y=['signal'], figsize=(20, 10))
bnh_rets, strat_rets = calc_returns(results)
bnh_rets, strat_rets
print(f'Buy & Hold returns: {bnh_rets}, Strategy returns: {strat_rets}')
def optimise_3ma_crossover(data, ma1list, ma2list, ma3list):
df = pd.DataFrame(columns=['ma1', 'ma2', 'ma3', 'strat_rets'])
for ma1 in ma1list:
for ma2 in ma2list:
for ma3 in ma3list:
results = backtest_3ma_crossover(data, [ma1, ma2, ma3], plot=False)
rets = calc_returns(results, plot=False)
print(f'ma1: {ma1}, ma2: {ma2}, ma3: {ma3}, strat_rets: {rets[1]}')
df.loc[df.shape[0]] = [ma1, ma2, ma3, rets[1]]
return df.loc[df['strat_rets'].idxmax()]
# +
ma1list = [5, 10, 15, 20, 30]
ma2list = [35, 40, 50, 60, 70]
ma3list = [80, 90, 100, 120, 150]
best_param = optimise_3ma_crossover(data, ma1list, ma2list, ma3list)
# -
print('!!! Best parameters !!!')
print(f'MA1: {best_param.ma1}, MA2: {best_param.ma2}, MA3: {best_param.ma3}, Strategy Returns: {best_param.strat_rets}')
# ## Strategy II
# II. Buy and sell the next day
# 1. Buy the stock on the fourth day open, if the stock closes down consecutively for
# three days.
# 2. Exit on the next day open.
# 3. Optional: Optimise the strategy by exiting the long position on the same day close.
# Also, you can optimise the number of down days. There are high chances that the
# number of down days would be different for each stock.
def backtest_buy_after_subsequent_downs(data, downdays, sellmode='next_open', plot=True):
"""Backtests moving average crossover strategy described above
@params:
data = pandas dataframe with daily prices indexed by date
downdays = number of downdays to generate buy signal
sellmode = 'next_open' or 'sameday_close' => when to exit long position
plot = True if plotting required
@returns:
results = dataframe with daily returns, moving averages, signal
"""
assert sellmode in ('next_open', 'sameday_close'), "Sellmode must be either 'next_open' or 'sameday_close'"
assert isinstance(downdays, int) and downdays > 0, "Downdays must be a positive integer"
# Create dataframe to store values
results = data[['Open', 'Close']].copy()
# daily returns of close price
results['c2c_rets'] = results['Close'].pct_change()
# daily returns based on strategy sellmode
results['daily_rets'] = results['Open'].pct_change() if sellmode == 'next_open' \
else (results['Close'] - results['Open']) / results['Open']
# Long signal
results['signal'] = 1
for i in range(downdays):
results['signal'] = np.where(
results['signal'] &
(results['Close'].shift(i-1) < results['Close'].shift(i)), 1, 0
)
if plot:
plotcols = ['Close', 'signal']
results[plotcols].plot(secondary_y=['signal'], figsize=(20, 10))
return results
def optimise_buy_after_subsequent_downs(data, sellmodes, downdays):
df = pd.DataFrame(columns=['sellmode', 'downdays', 'strat_rets'])
for mode in sellmodes:
for dd in downdays:
results = backtest_buy_after_subsequent_downs(data, downdays=dd, sellmode=mode, plot=False)
rets = calc_returns(results, plot=False)
print(f'Sellmode: {mode}, Downdays: {dd}, strat_rets: {rets[1]}')
df.loc[df.shape[0]] = [mode, dd, rets[1]]
return df.loc[df['strat_rets'].idxmax()]
downdays = 3
sellmode = 'next_open'
results = backtest_buy_after_subsequent_downs(data, downdays=downdays, sellmode=sellmode, plot=False)
results.head(15)
bnh_rets, strat_rets = calc_returns(results, shift=2)
print(f'Buy & Hold returns: {bnh_rets}, Strategy returns: {strat_rets}')
results.head(50)
plotcols = ['Close', 'signal']
results.iloc[:100][plotcols].plot(secondary_y=['signal'], figsize=(20, 10))
sellmodes = ['next_open', 'sameday_close']
downdays = [2, 3, 4, 5, 6, 7, 8, 9]
best_param = optimise_buy_after_subsequent_downs(data, sellmodes=sellmodes, downdays=downdays)
print('!!! Best parameters !!!')
print(f'Sellmode: {best_param.sellmode}, Downdays: {best_param.downdays}, Strategy Returns: {best_param.strat_rets}')
# ## Strategy III
# III. Strategy based on RSI indicator.
# 1. Buy the instrument such as Nifty or SPY when the RSI is less than 15
# 2. Exit conditions:
# a. Take profit of 5% or RSI > 75
# b. Stop loss of - 2%
# © Copyright QuantInsti Quantitative Learning Private Limited. Page 2
# 3. Optional: Optimise the strategy by adjusting the RSI value. Also, take profit and stop
# loss criteria can be different for each stock.
# 4. Note: You can use TA-Lib in Python to compute the RSI value.
# + active=""
# def ma(data, n, ix, on='Close'):
# """Calculates moving average of prices
# @params:
# data = pandas dataframeith daily prices indexed by date
# n = moving average lookback period
# ix = reference current index position for window period
# on = column whose average needs to be calculated
# @returns:
# ma = moving average of last 'n' days of 'on' price
# """
# assert ix >= n, f"Moving average for {n} days cannot be calculated"
# return data.iloc[ix-n+1:ix+1][on].mean()
# + active=""
# def backtest(data, malist, cap):
# """Backtests moving average crossover strategy described above
# @params:
# data = pandas dataframe with daily prices indexed by date
# malist = [ma1, ma2, ma3] => list of 3 moving average windows for backtesting
# cap = initial capital
# @returns:
# daily_portfolio = daily portfolio value for strategy
# """
# days = data.shape[0] # Number of trading days
# values = pd.DataFrame(columns=['cash', 'investment'], index=data.index) # Create empty dataframe to store portfolio values
#
# for i in range(days):
# if i < malist[0] or i < malist[1] or i < malist[2]: # skip initial days when all moving averages cannot be caculated
# continue
# buy = data.Close[i] > ma(data, malist[0], i) and data.Close[i] > ma(data, malist[1], i) and \
# data.Close[i] > ma(data, malist[2], i) and data.Close[i-1] < ma(data, malist[0], i-1) and \
# data.Close[i-1] < ma(data, malist[1], i-1) and data.Close[i-1] < ma(data, malist[1], i-1)
#
# if buy:
# print(data.index[i], data.Close[i])
# + active=""
# initial_cap = 100000
# malist = [20, 40, 80]
# backtest(df, malist, initial_cap)
ers.Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
return model
c.shape
y_train
# +
from tensorflow.keras.callbacks import EarlyStopping
es = EarlyStopping(patience = 10, monitor='val_loss', restore_best_weights=True)
model = init_model()
model.fit(c, y_train, batch_size = 32, epochs=1000, validation_split = 0.3, callbacks = [es])
# -
model.evaluate(c_test, y_test)
# ### Record à 16.36% avec ce modèle
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers
def init_model():
model = Sequential()
model.add(layers.Masking(mask_value = 0))
model.add(layers.LSTM(100, dropout=0.2, recurrent_dropout=0.2, activation='tanh'))
model.add(layers.Dense(128, activation='tanh'))
model.add(layers.Dense(y_train.shape[1], activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
return model
model_record = model
# # Traitement de la base de données finale vectorisée en amont
all_countries = pd.read_hdf('../../raw_data/full_mean_df_hdf.h5', 'h5').dropna()
age_list = [47, 51, 42, 56, 27, 44, 59, 52, 34, 60, 41, 57, 63,\
53, 45, 48, 47, 53, 30, 75, 57, 44, 47, 24, 51, 54, 68,\
49, 42, 50, 49, 40, 34, 34, 38, 44, 37, 54, 56, 61, 83,\
44, 45, 59, 45, 67, 53, 48, 33, 42, 32, 57, 34, 47, 40, 48,\
39, 49, 43, 35, 52, 63, 61, 50, 27, 50, 45, 80, 45, 50, 46,\
59, 41, 47, 65, 51, 44, 34, 68, 37, 31, 57, 35, 37, 65, 57,\
48, 61, 55, 72, 49, 45, 36, 58, 32, 57, 30, 57, 62, 44, 36, 51,\
49, 54, 48, 62, 43, 43, 41, 36, 57, 54, 44, 44, 32, 33, 51, 51,\
51, 56, 56, 43, 41, 43, 61, 63, 44, 36, 49, 49, 54, 42, 55, 53,\
41, 62, 36, 19, 43, 56, 51, 70, 48, 51, 27, 46, 44, 53, 35, 35,\
31, 60, 50, 31, 47, 43, 76, 45, 45, 53, 66, 52, 45, 45, 51, 40, 44,\
48, 56, 56, 65, 27, 48, 39, 55, 35, 44, 40, 43, 52, 31, 50, 53, 58,\
38, 59, 34, 52, 53, 46, 49, 58, 43, 55, 58, 26, 62, 72, 41, 36, 48,\
56, 53, 61, 63, 59, 45, 45, 59, 46, 31, 62, 62, 41,\
67, 44, 40, 62, 40, 49, 53, 61, 60, 38, 68, 54, 57,\
37, 33, 50, 40, 63, 30, 45, 67, 57, 52, 43, 63, 64,\
48, 63, 35, 68, 34, 53, 44, 48, 41, 54, 64, 45, 40,\
41, 55, 61, 42, 46, 68, 36, 69, 47, 71, 55, 42, 52,\
55, 34, 59, 75, 50, 39, 53, 50, 49, 61, 47, 29, 45,\
62, 30, 64, 41, 62, 68, 32, 66, 44, 52, 44, 58, 59,\
47, 58, 34, 66, 39, 70, 54, 41, 64, 43, 65, 74, 38,\
46, 56, 47, 57, 38, 40, 35, 36, 57, 54, 44, 61, 32,\
65, 42, 67, 50, 58, 46, 38, 65, 62, 53, 51, 58, 34,\
29, 22, 53, 39, 59, 57, 61, 36, 55, 41, 71, 40, 49,\
63, 44, 57, 49, 41, 65, 52, 54, 46, 33, 30, 45, 61,\
65, 73, 56, 62, 56, 31, 53, 50, 56, 54, 51, 46, 48,\
72, 59, 47, 60, 46, 72, 37, 59, 45, 53, 51, 48, 66, 67,\
37, 41, 47, 35, 36, 34, 57, 36, 41, 60, 34, 54, 56, 37,\
43, 48, 55, 44, 54, 54, 58, 38, 58, 41, 57, 33, 67, 53,\
57, 41, 41, 48, 62, 38, 66, 46, 42, 70, 62, 54, 53, 75,\
45, 33, 64, 45, 40, 38, 68, 30, 48, 37, 55, 67, 40, 37,\
42, 49, 48, 50, 59, 57, 63, 55, 57, 38, 64, 33, 57, 51,\
63, 48, 37, 52, 56, 57, 58, 57, 34, 34, 46, 57, 34, 60,\
70, 40, 56, 63, 61, 50, 58]
key_femme = [0, 2, 3, 4, 7, 13, 16, 17, 18 , 19, 24, 29, 30, 31, 34, 35, 43, 45, 47, 49, 53, 55, 59, 61, 62, 64,\
73, 74, 78, 79, 80, 81, 83, 84, 86, 87, 88, 94, 96, 99, 101, 106, 108, 109, 110, 113, 115, 116, 120, 121, 125, 127, 128, 129, 130,\
136, 141, 146, 152, 153, 154, 157, 160, 161, 164, 166, 170, 171, 172, 177, 180, 186,\
187, 188, 191, 195, 197, 198, 201, 205, 206, 208, 209, 210, 211, 213, 214, 216, 219, 220, 222,\
223, 225, 226, 228, 231, 235, 240, 248, 251, 252, 253, 256, 258, 261, 265, 272, 275, 278, 279, 280,\
286, 289, 294, 296, 297, 299, 300, 304, 305, 306, 307, 310, 312, 313, 316, 318, 322, 327, 331, 332, 334,\
337, 338, 340, 343, 343, 344, 349, 351, 352, 355, 356, 360, 361, 363, 365, 367, 374, 376, 379, 381, 383, 384,\
388, 393, 394, 396, 399, 401, 402, 406, 407, 408, 409, 414, 415, 417, 418, 419, 421, 422, 423, 424, 426, 427,\
432, 433, 434, 435, 436, 438, 441, 442, 443, 446, 447, 448, 451, 452, 457, 458, 459, 460, 461, 463, 464, 468]
dico = {name:age for name, age in zip(all_countries.name.unique(), age_list)}
for name in dico.keys():
wonderful_df["age"] = wonderful_df.name.map(dico)
dico = {name:sex for name, age in zip(all_countries.name.unique(), age_list)}
for name in dico.keys():
all_countries["sex"] = all_countries.name.map(dico)
real_dict_femme = {key:name for key,name in enumerate(tweet_df.name)}
reel_list_femme = []
for i in key_femme:
reel_list_femme.append(real_dict_femme[i])
ll = [1] * len(key_femme)
dict_femme = {name:key for name, key in zip(reel_list_femme,ll)}
for name in all_countries['name'].unique():
if name in dict_femme.keys():
all_countries["sex"] = all_countries['name'].map(dict_femme)
all_countries['sex'] = all_countries['sex'].fillna(0)
test = np.arange(0,300,1)
herbe = all_countries[test]
y = all_countries['age']
y
# +
X_train3, X_test, y_train, y_test = train_test_split(herbe, y, test_size = 0.3)
# Création des données cibles.
y_train = y_train.values
y_test = y_test.values
X_train3 = np.array(X_train3)
X_test = np.array(X_test)
# -
from tensorflow.keras import backend
backend.clear_session()
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers
def init_model():
model = Sequential()
#model.add(layers.GRU(units=27, activation='tanh'))
#model.add(layers.LSTM(100, dropout=0.2, recurrent_dropout=0.2, activation='tanh'))
model.add(layers.Dense(512, activation='relu'))
model.compile(loss='mse',
optimizer='adam',
metrics=['mae'])
return model
X_train3.shape
y_train.shape
# +
from tensorflow.keras.callbacks import EarlyStopping
es = EarlyStopping(patience = 20, monitor='val_loss', restore_best_weights=True)
model = init_model()
model.fit(X_train3, y_train, batch_size = 32, epochs=1000, validation_split = 0.3, callbacks = [es])
# -
model.evaluate(X_test, y_test)
X_test
import matplotlib.pyplot as plt
loss = model.history.history['loss']
acc = model.history.history['mean_absolute_error']
val_loss = model.history.history['val_loss']
val_acc = model.history.history['val_mean_absolute_error']
plt.plot(loss, label = 'loss')
plt.plot(val_loss, label='val_loss')
plt.xlabel('n_epochs')
plt.legend()
plt.plot(acc, label='mean_absolute_error')
plt.plot(val_acc, label='val_mean_absolute_error')
plt.xlabel('n_epochs')
plt.legend()
herbe.loc[0,:]
# Renvoie le député le plus proche de votre tweet
def predict_tweet(df, model, n_tweet, one_tweet = True):
'''
La fonction prend la base de données originale (par député), un modèle entraîné et un numéro de tweet en entrée.
Elle renvoie le député le plus proche du texte proposé.
Quand one_tweet = False, on ressort le député le plus proche du tweet.
Quand one_tweet = True, on sort le député le plus proche du compte twitter.
'''
test = np.arange(0,300,1)
herbe = df[test]
X_example = herbe.loc[n_tweet,:]
coucou = np.array(X_example)
if one_tweet:
lol = np.reshape(coucou, (1, 300))
prediction = model.predict(lol)
if one_tweet:
deputy = y.columns[prediction.argmax()]
return deputy
all_countries.loc[85200,:]
for i in range(85000,85300):
print(predict_tweet(all_countries.reset_index(), model, i))
test = np.arange(0,300,1)
herbe = all_countries.reset_index()[test]
X_example = herbe.loc[1,:]
coucou = np.array(X_example)
model.predict(lol).argmax()
all_countries.loc[0:300,:]
import io
# +
languages = ['english']
def load_vec(emb_path, nmax=50000):
vectors = []
word2id = {}
with io.open(emb_path, 'r', encoding='utf-8', newline='\n', errors='ignore') as f:
next(f)
for i, line in enumerate(f):
word, vect = line.rstrip().split(' ', 1)
vect = np.fromstring(vect, sep=' ')
assert word not in word2id, 'word found twice'
vectors.append(vect)
word2id[word] = len(word2id)
if len(word2id) == nmax:
break
id2word = {v: k for k, v in word2id.items()}
embeddings = np.vstack(vectors)
return embeddings, id2word, word2id
nmax = 100000 # maximum number of word embeddings to load
emb_dict = {}
for lang in languages:
path = f"../../raw_data/vectors_{lang}.txt" #Select here
embeddings, id2word, word2id = load_vec(path, nmax)
emb_dict[lang] = [embeddings, id2word, word2id]
print("Dict created")
def multilang_word_vector(word, emb_dict, lang):
try:
if word in emb_dict.get(lang)[2].keys():
return emb_dict[lang][0][emb_dict[lang][2][word]]
return []
except:
return []
# -
phrase = 'brazil'
phrase = phrase.lower()
sentence = []
for word in phrase.split():
sentence.append(multilang_word_vector(word, emb_dict, 'english'))
sentence = pd.DataFrame(sentence)
sentence = sentence.mean()
coucou = np.array(sentence)
lol = np.reshape(coucou, (1, 300))
prediction = model.predict(lol)
y.columns[prediction[0].argsort()[-30:][::-1]]
new_test_df[new_test_df['name'] == 'Clara PONSATÍ OBIOLS']['content'].str.find('europe')
# # Traitement de la base de données finale traduite
# ## Prétraitement
wonderful_df = pd.read_pickle('../../raw_data/tweets_en.csv')
wonderful_df
dico = {name:age for name, age in zip(wonderful_df.name.unique(), age_list)}
for name in dico.keys():
wonderful_df["age"] = wonderful_df.name.map(dico)
real_dict_femme = {key:name for key,name in enumerate(tweet_df.name)}
reel_list_femme = []
for i in key_femme:
reel_list_femme.append(real_dict_femme[i])
ll = [1] * len(key_femme)
dict_femme = {name:key for name, key in zip(reel_list_femme,ll)}
for name in all_countries['name'].unique():
if name in dict_femme.keys():
wonderful_df["sex"] = wonderful_df['name'].map(dict_femme)
wonderful_df['sex'] = wonderful_df['sex'].fillna(0)
wonderful_df.head(2)
clean_df = rmurl_df(wonderful_df, 'content')
clean_df = lower_df(clean_df, 'content')
clean_df = rmnumbers_df(clean_df, 'content')
clean_df = rmpunct_df(clean_df, 'content')
clean_df = rmstopwords_df(clean_df, 'content')
clean_df = lemmatize_df(clean_df, 'content')
clean_df = erase_fewletter_df(clean_df, 'content')
clean_df = rmemojis_df(clean_df)
# Cette fonction retourne automatiquement X_train, X_test, y_train, y_test de notre base de données twitter.
def get_train_test_objects(df, column):
'''
Les étapes que cette fonction réalise sont en commentaires.
'''
# Copie de la base de données pour éviter les problèmes d'assignation abusive.
df = df.copy()
# Récupération de tous les tweets et du nom du député qui les a posté. Création de la cible y.
df = df[[column, 'content']]
y = pd.get_dummies(df[column])
# Transformation des tweets en suite de mots (strings) dans une liste.
sentences = df['content']
sentences_inter = []
for sentence in sentences:
sentences_inter.append(sentence.split())
# Séparation des données d'entraînement et de test
sentences_train, sentences_test, y_train, y_test = train_test_split(sentences_inter, y, test_size = 0.3)
# Vectorisation des phrases
word2vec = Word2Vec(sentences=sentences_train)
# Création des données d'entrée.
X_train = embedding(word2vec,sentences_train)
X_test = embedding(word2vec,sentences_test)
X_train_pad = pad_sequences(X_train, padding='post',value=-1000, dtype='float32')
X_test_pad = pad_sequences(X_test, padding='post',value=-1000, dtype='float32')
# Création des données cibles.
y_train = y_train.values
y_test = y_test.values
# Sorties de la fonction
return X_train_pad, y_train, X_test_pad, y_test, word2vec
X_train, y_train, X_test, y_test, word2vec = get_train_test_objects(clean_df, 'name')
# ## Entraînement et évaluation du modèle
# +
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers
def init_model():
model = Sequential()
model.add(layers.Masking(mask_value = -1000))
model.add(layers.LSTM(350, dropout=0.2, recurrent_dropout=0.2, activation='tanh'))
model.add(layers.Dense(128, activation='tanh'))
model.add(layers.Dense(472, activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
return model
# +
from tensorflow.keras.callbacks import EarlyStopping
es = EarlyStopping(patience = 3, monitor='val_loss', restore_best_weights=True)
model = init_model()
model.fit(X_train, y_train, batch_size = 32, epochs=1000, validation_split = 0.3, callbacks = [es])
# -
model.evaluate(X_test, y_test)
# ## Score et sauvegarde du modèle
model.save('model_deputies')
word2vec.save('word2vec_deputies')
# ### Députés
def format_input(input1):
sentences_inter = []
for sentence in input1:
sentences_inter.append(sentence.split())
X_train = embedding(word2vec,sentences_inter)
formated_input = pad_sequences(X_train, padding='post',value=-1000, dtype='float32')
return formated_input
pond = np.sqrt(clean_df.groupby('country').count()['content'].values)
result = (1000*np.mean(model.predict(format_input(['netherlands water', 'amsterdam sweden'])), axis=0)/pond).argmax()
pd.get_dummies(clean_df['country']).columns[result]
word2vec.save('word2vec_country')
model.save('model_country')
# Score maximal : 5.45% Baseline : 0.21%
# ### Groupe européen
model_group = model
# Score maximal : 33.81%
# Baseline : 12.5%
# ### Sexe
model_sex = model
# Score maximal : 59.18%
# ### Age
# ### Pays
model.save('model_country')
# Score maximal : 25.02%
# Baseline : 8.09%
# ## Prédictions !
from fast_bert.data_cls import BertDataBunch
train = clean_df[['content', 'name']]
train.rename(columns={"content":"text", "name":"label"}, inplace = True)
x_train, x_test = train_test_split(train, test_size = 0.25)
x_train, x_val = train_test_split(x_train, test_size = 0.25)
x_train.to_csv('train.csv')
x_val.to_csv('val.csv')
pd.DataFrame(train['label'].unique()).to_csv('labels.csv')
databunch = BertDataBunch('.', '.',
tokenizer='bert-base-uncased',
train_file='train.csv',
val_file='val.csv',
label_file='labels.csv',
text_col='text',
label_col='label',
batch_size_per_gpu=16,
max_seq_length=100,
multi_gpu=True,
multi_label=True,
model_type='bert')
from fast_bert.learner_cls import BertLearner
from fast_bert.metrics import accuracy
import logging
import torch
logger = logging.getLogger()
device_cuda = torch.device("cpu")
metrics = [{'name': 'accuracy', 'function': accuracy}]
learner = BertLearner.from_pretrained_model(
databunch,
pretrained_path='bert-base-uncased',
metrics=metrics,
device=device_cuda,
logger=logger,
output_dir='.',
finetuned_wgts_path=None,
warmup_steps=500,
multi_gpu=True,
is_fp16=True,
multi_label=True,
logging_steps=50)
learner.lr_find(start_lr=1e-5,optimizer_type='lamb')
learner.fit(epochs=6,
lr=6e-5,
validate=True, # Evaluate the model after each epoch
schedule_type="warmup_cosine",
optimizer_type="adamw")
clean_df.to_pickle('clean_df')
| 27,419 |
/05_0_MovieLens_100k/MovieLens-100k.ipynb
|
918e5a1143ee4416da3a85b19f831157a0e9c95c
|
[] |
no_license
|
HsiYang506/Machine_Learning_Demo
|
https://github.com/HsiYang506/Machine_Learning_Demo
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 117,316 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Assignment 1
import nltk
nltk.download('punkt')
nltk.download('wordnet')
from nltk import sent_tokenize, word_tokenize
from nltk.stem.snowball import SnowballStemmer
from nltk.stem.wordnet import WordNetLemmatizer
from nltk.corpus import stopwords
import pandas as pd
import numpy as np
import re
import string
data = pd.read_csv("tweets-dataset.csv",encoding = 'utf-8', header = None)
#print(data.head)
lista= data.values.tolist()
from matplotlib import pyplot as plt
# +
from nltk.tokenize import TweetTokenizer
tz = TweetTokenizer(strip_handles= True)
# -
#print(lista[:20])
for i in lista[:20]:
# i = i.translate(None, string.punctuation)
#,print(i)
i = re.sub(r"http\S+", "", i[0])
i = re.sub(r"@\S+", "", i)
i = re.sub(r"[0-9]+","",i)
translate_table = dict((ord(char), None) for char in string.punctuation)
i = i.translate(translate_table)
tokens = tz.tokenize(i)
print(tokens)
len_tok = len(tokens)
len_type = len(set(tokens))
#print(len_type / len_tok)
# +
listfull = []
X = []
Y = []
k = 0
main_dict = dict()
t = 0
for i in lista:
i = re.sub(r"http\S+", "", i[0])
i = re.sub(r"@\S+", "", i)
i = re.sub(r"[0-9]+","",i)
i = i.lower()
translate_table = dict((ord(char), None) for char in string.punctuation)
i = i.translate(translate_table)
tokens = tz.tokenize(i)
#tokens = i.split()
listfull = listfull + tokens
for i in tokens:
if i in main_dict:
main_dict[i]+=1
else:
main_dict[i] = 1
if t<40:
X.append(len(listfull))
Y.append(len(set(listfull)))
t+=1
if t==40:
t=0
print(k)
k+=1
print(main_dict)
# -
# # TTR(type to token ratio)
types = list(set(listfull))
ttr = len(types)/len(listfull)
print('ttr',ttr)
len(listfull)
# # Heap's Law
# +
#print(main_dict)
# -
from scipy.optimize import curve_fit
def test2(x,a,b):
return(a*(x)**b)
param, param_cov = curve_fit(test2, X, Y)
ans = []
for i in X:
ans.append(param[0]*(i)**param[1])
print(param[0],param[1]) # Y = KN^B
plt.plot(X, Y, 'o', color ='yellow', label ="data")
plt.plot(X, ans, '--', color ='blue', label ="optimized data")
plt.xlabel("Size of Corpus")
plt.ylabel("Vocabulary size")
plt.legend()
plt.show()
# # Zipf's law of meaning
from nltk.corpus import wordnet #Import wordnet from the NLTK
# +
import random
import math
words = random.choices(types, k=60)
words.sort()
#print(words)
dict2 = dict()
x_new=[]
y_new=[]
for i in words:
dict2[i] = wordnet.synsets(i)
sy = wordnet.synsets(i)
if len(sy)>0: #if the word exists in wordnet
x_new.append(main_dict[i])
y_new.append(len(sy[0].lemmas()))
def sort_list(list1, list2):
zipped_pairs = zip(list2, list1)
z = [x for _, x in sorted(zipped_pairs)]
return z
y_new = sort_list(y_new,x_new)
x_new.sort()
plt.figure(figsize=(8,3))
plt.xlabel("Frequency")
plt.ylabel("Meanings")
plt.plot(x_new,y_new)
plt.legend()
plt.show()
# -
# # Zipf's law of length
# +
from scipy.optimize import curve_fit
x_len = []
y_freq = []
for k in types:
x_len.append(len(k))
y_freq.append(main_dict[k])
param, param_cov = curve_fit(test_1, x_len, y_freq)
predicted = []
for i in x_len:
predicted.append(param[0]/i)
plt.figure(figsize=(8,3))
plt.scatter( y_freq,x_len, s = 5)
#plt.plot(predicted, x_len, color = 'black')
plt.xlabel("Frequency")
plt.ylabel("Length ")
plt.legend()
plt.show()
| 3,851 |
/Numpy/Numpy의 활용.ipynb
|
bb19ca5bcd048b8525e82c2156c6bcb72945c6cd
|
[] |
no_license
|
jjangsungwon/Python-Data-Analysis-Tutorial
|
https://github.com/jjangsungwon/Python-Data-Analysis-Tutorial
| 2 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 1,860 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="6Oe99uTcvFkH" outputId="af065726-144b-4fab-9780-be300856e532"
import pandas as pd
data = pd.read_csv('SMSSpamCollection', sep = '\t', names = ['label', 'message'])
data.head()
# + id="YVb4eBU0ve-e"
text = data['message']
label = data['label']
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="mmbV487qvFkR" outputId="a0b2588b-75b5-4ff8-f8a3-591dcb277c66"
#Number of Words
#x = lambda a : a + 10
#print(x(5))
data['word_count'] = data['message'].apply(lambda x: len(str(x).split(" ")))
data[['message','word_count']].head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="79s4zzkevFkZ" outputId="492c688e-0615-48e9-b8f3-4adcb014d302"
#Number of characters
data['char_count'] = data['message'].str.len() # this also includes spaces
data[['message','char_count']].head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="THqkLpBnvFkf" outputId="d4de3d90-ad5b-416d-9fca-111d05464c7e"
#Average Word Length
def avg_word(sentence):
words = sentence.split()
#print(words)
return (sum(len(word) for word in words)/len(words))
data['avg_word'] = data['message'].apply(lambda x: avg_word(x))
data[['message','avg_word']].head()
# + colab={"base_uri": "https://localhost:8080/", "height": 292} id="GG5JheoKvFkk" outputId="08bca9d7-40bc-4253-f573-71a1b240cca1"
#Number of stopwords
import nltk
nltk.download('stopwords')
from nltk.corpus import stopwords
stop = stopwords.words('english')
data['stopwords'] = data['message'].apply(lambda x: len([x for x in x.split() if x in stop]))
data[['message','stopwords']].head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="DgD7qdIdvFkp" outputId="664a0012-b9c3-4244-97ab-f03e5b033706"
#Number of special characters
data['hastags'] = data['message'].apply(lambda x: len([x for x in x.split() if x.startswith('#')]))
data[['message','hastags']].head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="j24BtSTBvFkt" outputId="3f1151f2-2ef6-4073-c794-cc4195c89155"
#Number of numerics
data['numerics'] = data['message'].apply(lambda x: len([x for x in x.split() if x.isdigit()]))
data[['message','numerics']].head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="DiO48lLcvFkx" outputId="eddc5e48-2654-4b39-a91c-7376f6985f4b"
#Number of Uppercase words
data['upper'] = data['message'].apply(lambda x: len([x for x in x.split() if x.isupper()]))
data[['message','upper']].head()
# + colab={"base_uri": "https://localhost:8080/", "height": 289} id="uckIEBbVvFk1" outputId="42bc144b-e78c-4937-a2f5-b06d27ddd074"
# !pip install textblob
pos_family = {
'noun' : ['NN','NNS','NNP','NNPS'],
'pron' : ['PRP','PRP$','WP','WP$'],
'verb' : ['VB','VBD','VBG','VBN','VBP','VBZ'],
'adj' : ['JJ','JJR','JJS'],
'adv' : ['RB','RBR','RBS','WRB']
}
# function to check and get the part of speech tag count of a words in a given sentence
from textblob import TextBlob, Word, Blobber
import nltk
nltk.download('punkt')
nltk.download('averaged_perceptron_tagger')
def check_pos_tag(x, flag):
cnt = 0
try:
wiki = TextBlob(x)
for tup in wiki.tags:
ppo = list(tup)[1]
if ppo in pos_family[flag]:
cnt += 1
except:
pass
return cnt
data['noun_count'] = data['message'].apply(lambda x: check_pos_tag(x, 'noun'))
data['verb_count'] = data['message'].apply(lambda x: check_pos_tag(x, 'verb'))
data['adj_count'] = data['message'].apply(lambda x: check_pos_tag(x, 'adj'))
data['adv_count'] = data['message'].apply(lambda x: check_pos_tag(x, 'adv'))
data['pron_count'] = data['message'].apply(lambda x: check_pos_tag(x, 'pron'))
data[['message','noun_count','verb_count','adj_count', 'adv_count', 'pron_count' ]].head()
# + colab={"base_uri": "https://localhost:8080/", "height": 666} id="39_sSFrxvFk5" outputId="57ed9291-a318-4310-c55a-a737d16f3d3f"
data[['message','word_count','char_count','avg_word','stopwords','hastags','numerics','upper','noun_count','verb_count','adj_count', 'adv_count', 'pron_count','label' ]].head()
# + id="ZiGZJ7JIvFk_"
features = data[['word_count','char_count','avg_word','stopwords','hastags','numerics','upper','noun_count','verb_count','adj_count', 'adv_count', 'pron_count']]
# + id="wrNdsWIpxclO"
import numpy as np
classes_list = ["ham","spam"]
label_index = data['label'].apply(classes_list.index)
label = np.asarray(label_index)
# + id="ygOiAYEFxfUL"
import numpy as np
features_array = np.asarray(features)
# + colab={"base_uri": "https://localhost:8080/", "height": 34} id="7pAcZDl6xqVk" outputId="3cbb3157-378e-4220-cde5-0c84764e9aef"
features_array.shape
# + id="UwUWlcdyX3zy"
# data split into train and text
import numpy as np
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(features_array, label, test_size=0.33, random_state=42)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="G8SkHpcrzZgu" outputId="867419fb-b14c-4680-b881-a0224845d0f7"
from sklearn.metrics import accuracy_score
from sklearn import metrics
from sklearn.svm import SVC
model_SVM = SVC()
model_SVM.fit(x_train, y_train)
y_pred_SVM = model_SVM.predict(x_test)
print("SVM")
print("Accuracy score =", accuracy_score(y_test, y_pred_SVM))
print(metrics.classification_report(y_test, y_pred_SVM))
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=100,max_depth=None,min_samples_split=2, random_state=0)
rf.fit(x_train,y_train)
y_pred_rf = rf.predict(x_test)
print("random")
print("Accuracy score =", accuracy_score(y_test, y_pred_rf))
print(metrics.classification_report(y_test, y_pred_rf))
from sklearn.linear_model import LogisticRegression
LR = LogisticRegression()
LR.fit(x_train,y_train)
y_pred_LR = LR.predict(x_test)
print("Logistic Regression")
print("Accuracy score =", accuracy_score(y_test, y_pred_LR))
print(metrics.classification_report(y_test, y_pred_LR ))
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors = 5)
neigh.fit(x_train,y_train)
y_pred_KNN = neigh.predict(x_test)
print("KNN")
print("Accuracy score =", accuracy_score(y_test, y_pred_KNN))
print(metrics.classification_report(y_test, y_pred_KNN ))
from sklearn.naive_bayes import GaussianNB
naive = GaussianNB()
naive.fit(x_train,y_train)
y_pred_naive = naive.predict(x_test)
print("Naive Bayes")
print("Accuracy score =", accuracy_score(y_test, y_pred_naive))
print(metrics.classification_report(y_test, y_pred_naive ))
from sklearn.ensemble import GradientBoostingClassifier
gradient = GradientBoostingClassifier(n_estimators=100,max_depth=None,min_samples_split=2, random_state=0)
gradient.fit(x_train,y_train)
y_pred_gradient = gradient.predict(x_test)
print("Gradient Boosting")
print("Accuracy score =", accuracy_score(y_test, y_pred_gradient))
print(metrics.classification_report(y_test, y_pred_gradient ))
from sklearn.tree import DecisionTreeClassifier
decision = DecisionTreeClassifier()
decision.fit(x_train,y_train)
y_pred_decision = decision.predict(x_test)
print("Decision Tree")
print("Accuracy score =", accuracy_score(y_test, y_pred_decision))
print(metrics.classification_report(y_test, y_pred_decision ))
# + id="yxy-WRo5yBVp"
# data split into train and text
import numpy as np
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(features_array, label, test_size=0.33, random_state=42)
# + colab={"base_uri": "https://localhost:8080/", "height": 34} id="N-yPCb1PZR7D" outputId="e1f52694-169f-4aed-f64d-f016fda65066"
x_train.shape
# + id="NWaoQuHCzn62"
data = pd.read_csv('SMSSpamCollection', sep = '\t', names = ['label','message'])
# + id="56f1LdRYY4iq"
text = data['message']
class_label = data['label']
# + id="CV5iAnlCdhZN"
import numpy as np
classes_list = ["ham","spam"]
label_index = class_label.apply(classes_list.index)
label = np.asarray(label_index)
# + id="iAZpYtCJdkT9"
import numpy as np
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(text, label, test_size=0.33, random_state=42)
# + id="LVeLdGr9doe5"
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(ngram_range = (1,1))
x_train = vectorizer.fit_transform(X_train)
x_test = vectorizer.transform(X_test)
# + colab={"base_uri": "https://localhost:8080/", "height": 34} id="d8B2uJXFehCH" outputId="29a3b673-dedf-4a4d-9122-a1a8d04bb2e3"
x_train.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="6tEIjnT4elyj" outputId="5e469c4d-0a03-4734-ef3d-199d959ef0f2"
vectorizer.get_feature_names()
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="I1Zk24vQenaM" outputId="8f046fce-ec96-432d-b8da-de91e6a101b2"
from sklearn.metrics import accuracy_score
from sklearn import metrics
from sklearn.svm import SVC
model_SVM = SVC()
model_SVM.fit(x_train, y_train)
y_pred_SVM = model_SVM.predict(x_test)
print("SVM")
print("Accuracy score =", accuracy_score(y_test, y_pred_SVM))
print(metrics.classification_report(y_test, y_pred_SVM))
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=100,max_depth=None,min_samples_split=2, random_state=0)
rf.fit(x_train,y_train)
y_pred_rf = rf.predict(x_test)
print("random")
print("Accuracy score =", accuracy_score(y_test, y_pred_rf))
print(metrics.classification_report(y_test, y_pred_rf))
from sklearn.linear_model import LogisticRegression
LR = LogisticRegression()
LR.fit(x_train,y_train)
y_pred_LR = LR.predict(x_test)
print("Logistic Regression")
print("Accuracy score =", accuracy_score(y_test, y_pred_LR))
print(metrics.classification_report(y_test, y_pred_LR ))
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors = 5)
neigh.fit(x_train,y_train)
y_pred_KNN = neigh.predict(x_test)
print("KNN")
print("Accuracy score =", accuracy_score(y_test, y_pred_KNN))
print(metrics.classification_report(y_test, y_pred_KNN ))
from sklearn.naive_bayes import GaussianNB
naive = GaussianNB()
naive.fit(x_train.toarray(),y_train)
y_pred_naive = naive.predict(x_test.toarray())
print("Naive Bayes")
print("Accuracy score =", accuracy_score(y_test, y_pred_naive))
print(metrics.classification_report(y_test, y_pred_naive ))
from sklearn.ensemble import GradientBoostingClassifier
gradient = GradientBoostingClassifier(n_estimators=100,max_depth=None,min_samples_split=2, random_state=0)
gradient.fit(x_train,y_train)
y_pred_gradient = gradient.predict(x_test)
print("Gradient Boosting")
print("Accuracy score =", accuracy_score(y_test, y_pred_gradient))
print(metrics.classification_report(y_test, y_pred_gradient ))
from sklearn.tree import DecisionTreeClassifier
decision = DecisionTreeClassifier()
decision.fit(x_train,y_train)
y_pred_decision = decision.predict(x_test)
print("Decision Tree")
print("Accuracy score =", accuracy_score(y_test, y_pred_decision))
print(metrics.classification_report(y_test, y_pred_decision ))
# + id="sk5zs952fdM-"
| 11,402 |
/3_web-scraping-II/.ipynb_checkpoints/7_(로컬에서)Tweeter-post_contents-checkpoint.ipynb
|
84c3ca66d411e2beee746884fcba444d4db4ab67
|
[] |
no_license
|
jupyterbook/notebooks
|
https://github.com/jupyterbook/notebooks
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 27,305 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
import os
import tensorflow as tf
from keras.models import Sequential
from keras.utils import to_categorical
from keras.layers import Dense
import numpy as np
import pandas as pd
file = './datasets/HCAHPS 15.csv'
df = pd.read_csv(file)
df.columns
# +
# remove unessecary columns
df1 = df[['Provider_ID','HCAHPS_Measure_ID', 'HCAHPS_Answer_Description', 'Patient_Survey_Star_Rating',
'Patient_Survey_Star_Rating_Footnote', 'HCAHPS_Answer_Percent','HCAHPS_Answer_Percent_Footnote',
'HCAHPS_Linear_Mean_Value','Number_of_Completed_Surveys', 'Number_of_Completed_Surveys_Footnote',
'Survey_Response_Rate_Percent', 'Survey_Response_Rate_Percent_Footnote','Measure_Start_Date', 'Measure_End_Date']]
# +
# get rid of all non Linear Mean score lines
df2 = df1.loc[(df1['HCAHPS_Measure_ID'] == 'H_CLEAN_LINEAR_SCORE') | (df1['HCAHPS_Measure_ID'] == 'H_COMP_1_LINEAR_SCORE') |
(df1['HCAHPS_Measure_ID'] == 'H_COMP_2_LINEAR_SCORE') | (df1['HCAHPS_Measure_ID'] == 'H_COMP_3_LINEAR_SCORE') |
(df1['HCAHPS_Measure_ID'] == 'H_COMP_4_LINEAR_SCORE') | (df1['HCAHPS_Measure_ID'] == 'H_COMP_5_LINEAR_SCORE') |
(df1['HCAHPS_Measure_ID'] == 'H_COMP_6_LINEAR_SCORE') | (df1['HCAHPS_Measure_ID'] == 'H_COMP_7_LINEAR_SCORE') |
(df1['HCAHPS_Measure_ID'] == 'H_HSP_RATING_LINEAR_SCORE') | (df1['HCAHPS_Measure_ID'] == 'H_QUIET_LINEAR_SCORE') |
(df1['HCAHPS_Measure_ID'] == 'H_RECMND_LINEAR_SCORE'),:]
# +
# get rid of all the 'Not Applicable' and 'Not Available' rows for 'HCAHPS_Linear_Mean_Value'
df2 = df2.loc[df2.HCAHPS_Linear_Mean_Value != 'Not Applicable']
df2 = df2.loc[df2.HCAHPS_Linear_Mean_Value != 'Not Available']
# +
# get rid of remaining footnotes that void survey
df2 = df2[pd.isnull(df2.Survey_Response_Rate_Percent_Footnote)]
# +
#re-index from 1
df2.reset_index(drop=True, inplace=True)
# -
df2.to_csv('./datasets/3_2222.csv')
# +
# create lists that will be zipped up into a dataframe:
Provider_ID = []
Care_transition_LMS = []
Cleanliness_LMS = []
Communication_about_medicines_LMS = []
Discharge_information_LMS = []
Doctor_communication_LMS = []
Nurse_communication_LMS = []
Overall_hospital_rating_LMS = []
Pain_management_LMS = []
Quietness_LMS = []
Recommend_hospital_LMS = []
Staff_responsiveness_LMS = []
Survey_Response_Rate_Percent_Footnote = []
Measure_Start_Date = []
Measure_End_Date = []
x = 0
# -
for i in range(0,len(df2.index)):
if df2.loc[i,'HCAHPS_Answer_Description'] == 'Care transition - linear mean score':
Provider_ID.append(df2['Provider_ID'].iloc[i])
Measure_Start_Date.append(df2['Measure_Start_Date'].iloc[i])
Measure_End_Date.append(df2['Measure_Start_Date'].iloc[i])
Care_transition_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
elif df2.loc[i,'HCAHPS_Answer_Description'] == 'Cleanliness - linear mean score':
Cleanliness_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
elif df2.loc[i,'HCAHPS_Answer_Description'] == 'Communication about medicines - linear mean score':
Communication_about_medicines_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
elif df2.loc[i,'HCAHPS_Answer_Description'] == 'Discharge information - linear mean score':
Discharge_information_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
elif df2.loc[i,'HCAHPS_Answer_Description'] == 'Doctor communication - linear mean score':
Doctor_communication_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
elif df2.loc[i,'HCAHPS_Answer_Description'] == 'Nurse communication - linear mean score':
Nurse_communication_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
elif df2.loc[i,'HCAHPS_Answer_Description'] == 'Overall hospital rating - linear mean score':
Overall_hospital_rating_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
elif df2.loc[i,'HCAHPS_Answer_Description'] == 'Pain management - linear mean score':
Pain_management_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
elif df2.loc[i,'HCAHPS_Answer_Description'] == 'Quietness - linear mean score':
Quietness_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
elif df2.loc[i,'HCAHPS_Answer_Description'] == 'Recommend hospital - linear mean score':
Recommend_hospital_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
elif df2.loc[i,'HCAHPS_Answer_Description'] == 'Staff responsiveness - linear mean score':
Staff_responsiveness_LMS.append(df2.loc[i,'HCAHPS_Linear_Mean_Value'])
else:
x=2
zippedList = list(zip(Provider_ID,Care_transition_LMS,Cleanliness_LMS,Communication_about_medicines_LMS,
Discharge_information_LMS,Doctor_communication_LMS,Nurse_communication_LMS,
Overall_hospital_rating_LMS,Pain_management_LMS,Quietness_LMS,Recommend_hospital_LMS,
Staff_responsiveness_LMS,Measure_Start_Date,Measure_End_Date))
# +
# Create a dataframe from zipped list
df8 = pd.DataFrame(zippedList, columns = ['Provider_ID', 'Care_transition_LMS', 'Cleanliness_LMS',
'Communication_about_medicines_LMS', 'Discharge_information_LMS','Doctor_communication_LMS',
'Nurse_communication_LMS', 'Overall_hospital_rating_LMS','Pain_management_LMS',
'Quietness_LMS', 'Recommend_hospital_LMS', 'Staff_responsiveness_LMS','Measure_Start_Date',
'Measure_End_Date'])
# -
df8.to_csv('./datasets/15_2222.csv')
np.append(exlude_indexes ,bhk_df[bhk_df['price_per_sqft']< stats['mean']].index.values )
return data.drop(exlude_indexes ,axis='index')
data = remove_bhk_outliers(data)
scatter_plot(data ,'Sahakara Nagar')
# +
data['price_per_sqft'].hist()
plt.xlabel('Price Per Sq')
plt.ylabel('Count')
# -
# <h2 style='color:blue'>Outlier Removal Using Bathrooms Feature</h2>
data['bath'].unique()
data[data['bath']>10]
# **It is unusual to have 2 more bathrooms than number of bedrooms in a home**
# +
data['bath'].hist()
plt.xlabel('Number of Bathroom')
plt.ylabel('Count')
# -
data[ data['bath']>data['bhk']+2 ]
data = data[ data['bath']<data['bhk']+2 ]
data.shape
data = data.drop(['size','price_per_sqft'] ,axis=1)
# ## Model Building
dummies = pd.get_dummies(data['location'],drop_first=True)
data = pd.concat([data,dummies],axis=1)
data = data.drop(['location'] ,axis=1)
X = data.drop(['price'],axis=1)
y = data['price']
X_train ,X_test ,y_train ,y_test = train_test_split(X,y,test_size=0.2,random_state=0)
# ### Model 1
# +
lr_clf = LinearRegression()
lr_clf.fit(X_train ,y_train)
# -
lr_clf.score(X_test ,y_test)
# ### Model 2
#
# <h2 style='color:blue'>Use K Fold cross validation to measure accuracy of our LinearRegression model</h2>
cv = ShuffleSplit(n_splits=5 ,test_size=0.2 ,random_state=0)
cross_val_score(LinearRegression(),X,y,cv=cv)
# ### Model 3
#
# <h2 style='color:blue'>Find best model using GridSearchCV</h2>
def find_best_model(X,y) :
algos = {
'linear_regression' : {
'model': LinearRegression(),
'params': {
'normalize': [True, False]
}
},
'lasso' : {
'model': Lasso(),
'params': {
'alpha': [1,2],
'selection': ['random', 'cyclic']
}
},
'decision_tree' : {
'model': DecisionTreeRegressor(),
'params': {
'criterion' : ['mse','friedman_mse'],
'splitter': ['best','random']
}
}
}
scores = []
cv = ShuffleSplit(n_splits=5, test_size=0.2, random_state=0)
for algo_name, config in algos.items():
gs = GridSearchCV( config['model'], config['params'], cv=cv, return_train_score=False)
gs.fit(X,y)
scores.append({
'model': algo_name,
'best_score': gs.best_score_,
'best_params': gs.best_params_
})
return pd.DataFrame(scores,columns=['model','best_score','best_params'])
find_best_model(X,y)
X.columns
np.where(X.columns=='bhk')[0][0]
# <h2 style='color:blue'>Test the model for few properties</h2>
def predict_price(location ,sqft ,bath ,bhk) :
# getting column index
loc_index = np.where(X.columns==location)[0][0]
x = np.zeros( len(X.columns) )
x[0] = sqft
x[1] = bath
x[2] = bhk
if loc_index>=0:
x[loc_index] = 1
return lr_clf.predict([x])[0]
predict_price('1st Phase JP Nagar' ,1000 ,2 ,2)
predict_price('1st Phase JP Nagar' ,1000 ,2 ,3)
predict_price('1st Phase JP Nagar' ,1000 ,3 ,3)
predict_price('Indira Nagar' ,1000 ,2 ,2)
predict_price('Indira Nagar' ,1000 ,3 ,3)
predict_price('Indira Nagar' ,1000 ,2 ,3)
| 10,007 |
/KNN_Project.ipynb
|
a00e5b07cf1bf0bfb6cb90a4fd88bd7f2a206977
|
[] |
no_license
|
rtlaceste/Machine_Learning_Models-Data_Science
|
https://github.com/rtlaceste/Machine_Learning_Models-Data_Science
| 2 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 2,060,863 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# # 8-Classes
from scipy import *
from matplotlib.pyplot import *
# %matplotlib inline
# ## Introduction
class RationalNumber:
pass
a=RationalNumber()
if isinstance(a, RationalNumber):
print('Indeed it belongs to the class RationalNumber')
# ### The `__init__` method
class RationalNumber:
def __init__(self, numerator, denominator):
self.numerator = numerator
self.denominator = denominator
q = RationalNumber(10, 20) # Defines a new object
q.numerator # returns 10
q.denominator # returns 20
# ## Attributes
q = RationalNumber(3, 5) # instantiation
q.numerator # attribute access
q.denominator
a = array([1, 2]) # instantiation
a.shape
z = 5 + 4j # instantiation
z.imag
q = RationalNumber(3, 5)
q.numerator
r = RationalNumber(7, 3)
q.numerator = 17
q.numerator
del r.denominator
class RationalNumber:
def __init__(self, numerator, denominator):
self.numerator = numerator
self.denominator = denominator
def convert2float(self):
return float(self.numerator) / float(self.denominator)
q = RationalNumber(10, 20) # Defines a new object
q.convert2float() # returns 0.5
RationalNumber.convert2float(q)
q.convert2float(15) # returns error
# ### Special Methods
#
# * The method `repr`
class RationalNumber:
def __init__(self, numerator, denominator):
self.numerator = numerator
self.denominator = denominator
def convert2float(self):
return float(self.numerator) / float(self.denominator)
def __repr__(self):
return '{} / {}'.format(self.numerator,self.denominator)
q = RationalNumber(10, 20)
q
# * The method `__add__`
class RationalNumber:
def __init__(self, numerator, denominator):
self.numerator = numerator
self.denominator = denominator
def convert2float(self):
return float(self.numerator) / float(self.denominator)
def __repr__(self):
return '{} / {}'.format(self.numerator,self.denominator)
def __add__(self, other):
p1, q1 = self.numerator, self.denominator
if isinstance(other, int):
p2, q2 = other, 1
else:
p2, q2 = other.numerator, other.denominator
return RationalNumber(p1 * q2 + p2 * q1, q1 * q2)
q = RationalNumber(1, 2)
p = RationalNumber(1, 3)
q + p # RationalNumber(5, 6)
q.__add__(p)
class RationalNumber:
def __init__(self, numerator, denominator):
self.numerator = numerator
self.denominator = denominator
def convert2float(self):
return float(self.numerator) / float(self.denominator)
def __repr__(self):
return '{} / {}'.format(self.numerator,self.denominator)
def __add__(self, other):
p1, q1 = self.numerator, self.denominator
if isinstance(other, int):
p2, q2 = other, 1
else:
p2, q2 = other.numerator, other.denominator
return RationalNumber(p1 * q2 + p2 * q1, q1 * q2)
def __eq__(self, other):
return self.denominator * other.numerator == \
self.numerator * other.denominator
p = RationalNumber(1, 2) # instantiation
q = RationalNumber(2, 4) # instantiation
p == q # True
p = RationalNumber(1, 2) # instantiation
p + 5 # corresponds to p.__add__(5)
5 + p # returns an error
# * The reverse method `__radd__`
class RationalNumber:
def __init__(self, numerator, denominator):
self.numerator = numerator
self.denominator = denominator
def convert2float(self):
return float(self.numerator) / float(self.denominator)
def __repr__(self):
return '{} / {}'.format(self.numerator,self.denominator)
def __add__(self, other):
p1, q1 = self.numerator, self.denominator
if isinstance(other, int):
p2, q2 = other, 1
else:
p2, q2 = other.numerator, other.denominator
return RationalNumber(p1 * q2 + p2 * q1, q1 * q2)
def __eq__(self, other):
return self.denominator * other.numerator == \
self.numerator * other.denominator
def __radd__(self, other):
return self
p = RationalNumber(1, 2)
5 + p # no error message any more
# +
import itertools
class Recursion3Term:
def __init__(self, a0, a1, u0, u1):
self.coeff = [a1, a0]
self.initial = [u1, u0]
def __iter__(self):
u1, u0 = self.initial
yield u0 # (see chapter on generators)
yield u1
a1, a0 = self.coeff
while True :
u1, u0 = a1 * u1 + a0 * u0, u1
yield u1
def __getitem__(self, k):
return list(itertools.islice(self, k, k + 1))[0]
# -
r3 = Recursion3Term(-0.35, 1.2, 1, 1)
for i, r in enumerate(r3):
if i == 7:
print(r) # returns 0.194167
break
r3[7]
# ### Attributes that depend on each other
class Triangle:
def __init__(self, A, B, C):
self.A = array(A)
self.B = array(B)
self.C = array(C)
self.a = self.C - self.B
self.b = self.C - self.A
self.c = self.B - self.A
def area(self):
return abs(cross(self.b, self.c)) / 2
tr = Triangle([0., 0.], [1., 0.], [0., 1.])
tr.area()
tr.B = [12., 0.]
tr.area() # still returns 0.5, should be 6 instead.
# #### The function `property`
class Triangle:
def __init__(self, A, B, C):
self._A = array(A)
self._B = array(B)
self._C = array(C)
self._a = self._C - self._B
self._b = self._C - self._A
self._c = self._B - self._A
def area(self):
return abs(cross(self._c, self._b)) / 2.
def set_B(self, B):
self._B = B
self._a = self._C - self._B
self._c = self._B - self._A
def get_B(self):
return self._B
def del_Pt(self):
raise Exception('A triangle point cannot be deleted')
B = property(fget = get_B, fset = set_B, fdel = del_Pt)
tr = Triangle([0., 0.], [1., 0.], [0., 1.])
tr.area()
tr.B = [12., 0.]
tr.area() # returns 6.0
del tr.B # raises an exception
# ### Bound and unbound methods
class A:
def func(self, arg):
pass
A.func # <unbound method A.func>
instA = A() # we create an instance
instA.func # <bound method A.func of ... >
A.func(1)
instA.func(1)
# ### Class attributes
class Newton:
tol = 1e-8 # this is a class attribute
def __init__(self,f):
self.f = f # this is not a class attribute
...
N1 = Newton(sin)
N2 = Newton(cos)
N1.tol
N2.tol
Newton.tol = 1e-10
N1.tol
N2.tol
N2.tol = 1.e-4
N1.tol # still 1.e-10
Newton.tol = 1e-5 # now all instances of the Newton classes have 1e-5
N1.tol # 1.e-5
N2.tol # 1e-4 but not N2.
# #### Class Methods
class Polynomial:
def __init__(self, coeff):
self.coeff = array(coeff)
@classmethod
def by_points(cls, x, y):
degree = x.shape[0] - 1
coeff = polyfit(x, y, degree)
return cls(coeff)
def __eq__(self, other):
return allclose(self.coeff, other.coeff)
# +
p1 = Polynomial.by_points(array([0., 1.]), array([0., 1.]))
p2 = Polynomial([1., 0.])
print(p1 == p2)
# -
# ## Subclassing and Inheritance
class OneStepMethod:
def __init__(self, f, x0, interval, N):
self.f = f
self.x0 = x0
self.interval = [t0, te] = interval
self.grid = linspace(t0, te, N)
self.h = (te - t0) / N
def generate(self):
ti, ui = self.grid[0], self.x0
yield ti, ui
for t in self.grid[1:]:
ui = ui + self.h * self.step(self.f, ui, ti)
ti = t
yield ti, ui
def solve(self):
self.solution = array(list(self.generate()))
def plot(self):
plot(self.solution[:, 0], self.solution[:, 1])
def step(self, f, u, t):
raise NotImplementedError()
class ExplicitEuler(OneStepMethod):
def step(self, f, u, t):
return f(u, t)
class MidPointRule(OneStepMethod):
def step(self, f, u, t):
return f(u + self.h / 2 * f(u, t), t + self.h / 2)
# +
def f(x, t):
return -0.5 * x
euler = ExplicitEuler(f, 15., [0., 10.], 20)
euler.solve()
euler.plot()
hold(True)
midpoint = MidPointRule(f, 15., [0., 10.], 20)
midpoint.solve()
midpoint.plot()
# -
argument_list = [f, 15., [0., 10.], 20]
euler = ExplicitEuler(*argument_list)
midpoint = MidPointRule(*argument_list)
class ExplicitEuler(OneStepMethod):
def __init__(self,*args, **kwargs):
self.name='Explicit Euler Method'
super(ExplicitEuler, self).__init__(*args,**kwargs)
def step(self, f, u, t):
return f(u, t)
# ## Encapsulation
class Function:
def __init__(self, f):
self.f = f
def __call__(self, x):
return self.f(x)
def __add__(self, g):
def sum(x):
return self(x) + g(x)
return type(self)(sum)
def __mul__(self, g):
def prod(x):
return self.f(x) * g(x)
return type(self)(prod)
def __radd__(self, g):
return self + g
def __rmul__(self, g):
return self * g
T5 = Function(lambda x: cos(5 * arccos(x)))
T6 = Function(lambda x: cos(6 * arccos(x)))
# +
import scipy.integrate as sci
weight = Function(lambda x: 1 / sqrt((1 - x ** 2)))
[integral, errorestimate] = \
sci.quad(weight * T5 * T6, -1, 1) # [7.7e-16, 4.04e-14)
integral, errorestimate
# -
# ## Classes as decorators
class echo:
text = 'Input parameters of {name}\n'+\
'Positional parameters {args}\n'+\
'Keyword parameters {kwargs}\n'
def __init__(self, f):
self.f = f
def __call__(self, *args, **kwargs):
print(self.text.format(name = self.f.__name__,
args = args, kwargs = kwargs))
return self.f(*args, **kwargs)
@echo
def line(m, b, x):
return m * x + b
line(2., 5., 3.)
line(2., 5., x=3.)
class CountCalls:
"""Decorator that keeps track of the number of times
a function is called."""
instances = {}
def __init__(self, f):
self.f = f
self.numcalls = 0
self.instances[f] = self
def __call__(self, *args, **kwargs):
self.numcalls += 1
return self.f(*args, **kwargs)
@classmethod
def counts(cls):
"""Return a dict of {function: # of calls} for all
registered functions."""
return dict([(f.__name__, cls.instances[f].numcalls)
for f in cls.instances])
@CountCalls
def line(m, b, x):
return m * x + b
@CountCalls
def parabola(a, b, c, x):
return a * x ** 2 + b * x + c
line(3., -1., 1.)
parabola(4., 5., -1., 2.)
CountCalls.counts() # returns {'line': 1, 'parabola': 1}
parabola.numcalls # returns 1
| 10,962 |
/Chapter06/.ipynb_checkpoints/6.7 Identifying Right AD Banner Using MAB-checkpoint.ipynb
|
8420e2297946fa94cd766b37b469fb694ae2095e
|
[
"MIT"
] |
permissive
|
PacktPublishing/Hands-On-Reinforcement-Learning-with-Python
|
https://github.com/PacktPublishing/Hands-On-Reinforcement-Learning-with-Python
| 770 | 367 |
MIT
| 2022-06-27T20:08:13 | 2022-06-26T16:53:33 |
Jupyter Notebook
|
Jupyter Notebook
| false | false |
.py
| 20,436 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [conda env:universe]
# language: python
# name: conda-env-universe-py
# ---
# # Identifying Right AD Banner Using MAB
#
#
# Let us say you are running a website and you have five different banners for the same ad and you want to know which banner attracts the user? We model this problem statement as a bandit problem. Let us say these five banners are five bandits and we assign reward 1 if the user clicks the ad and reward 0 if the user does not click the ad.
#
# In a normal A/B testing, we perform complete exploration of all these five banners alone before deciding which banner is the best. But that will cost us lot of regret. Instead, we will use good exploration strategy for deciding which banner will give us most rewards (most clicks)
# First, let us import necessary libraries
import gym_bandits
import gym
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
env = gym.make("BanditTenArmedGaussian-v0")
# Let us simulate a dataset with 5*10000 as shape where the column is the ad banner type and rows are either 0 or 1 i.e whether the ad has been clicked or not clicked by the user respectively
#
#
df = pd.DataFrame()
df['Banner_type_0'] = np.random.randint(0,2,100000)
df['Banner_type_1'] = np.random.randint(0,2,100000)
df['Banner_type_2'] = np.random.randint(0,2,100000)
df['Banner_type_3'] = np.random.randint(0,2,100000)
df['Banner_type_4'] = np.random.randint(0,2,100000)
df.head(10)
# First, let us initialize necessary variables
# +
# number of banners
num_banner = 5
# number of iterations
no_of_iterations = 100000
# list for storing banners which are selected
banner_selected = []
# count number of times the banner was selected
count = np.zeros(num_banner)
# Q value of the banner
Q = np.zeros(num_banner)
# sum of rewards obtained by the banner
sum_rewards = np.zeros(num_banner)
# -
# Now we define the epsilon greedy policy
def epsilon_greedy(epsilon):
random_value = np.random.random()
choose_random = random_value < epsilon
if choose_random:
action = np.random.choice(num_banner)
else:
action = np.argmax(Q)
return action
for i in range(no_of_iterations):
# select the banner using epsilon greedy policy
banner = epsilon_greedy(0.5)
# get the reward
reward = df.values[i, banner]
# update the selected banner count
count[banner] += 1
# sum the rewards obtained by that banner
sum_rewards[banner]+=reward
# calculate the Q value of the banner
Q[banner] = sum_rewards[banner]/count[banner]
banner_selected.append(banner)
# We can plot and see which banner type gives us most clicks(rewards)
sns.distplot(banner_selected)
| 2,990 |
/confoundedCuisiner/Untitled.ipynb
|
67254aa97ab0c41a16010f63a44a551fe766899a
|
[] |
no_license
|
peterschnatz/SampleDataChallenges
|
https://github.com/peterschnatz/SampleDataChallenges
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 10,238 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from joblib import register_parallel_backend, parallel_backend
# register_parallel_backend('threading')
# -
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
# +
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import confusion_matrix, accuracy_score, roc_curve, auc
# +
# # Class balance
def print_unique(values):
unique, counts = np.unique(values, return_counts=True)
for cls, cnt in zip(unique, counts):
print("Class [%d] Count [%d]" % (cls, cnt))
# +
import matplotlib.pyplot as plt
def view_histo(row, data):
# print(row)
# return
hname = row["hname"]
ls_number = row["lumi"]
run_number = row["run"]
is_good = row["good"]
is_good_pixel = row["good_pixel"]
plt.figure(figsize=(10, 5))
plt.title("%s Run: %s LS: %s GLabel: %d PLabel %d" % (hname, run_number, ls_number, is_good, is_good_pixel))
plt.plot(range(len(data)), data, drawstyle='steps-pre', label=hname)
plt.legend()
# +
class Clustering:
def __init__(self):
self.clustering = None
self.df = None
def load_data(self, filename):
df = pd.read_csv(filename)
print(df.shape)
# Filter list of columns which will be used for training
bin_cols = [col for col in df.columns if 'bin_' in col]
# remove first and last values as those are over/under flows
self.bin_cols = bin_cols[1:-1]
# Drop empty rows
df.drop(df[df.entries == 0].index, inplace=True)
# Drop garbage
df.drop(["Unnamed: 0", "Unnamed: 0.1", "fromrun.1", "fromlumi.1", "hname.1"], axis=1, inplace=True, errors="ignore")
print(df.shape)
self.df = pd.concat([self.df, df], ignore_index=True) if self.df is not None else df
# Normalization, divide every bin value by total entries
self.X = self.df.filter(self.bin_cols, axis=1).copy().div(self.df.entries, axis=0)
self.y = self.df["good_pixel"]
print("DF", self.df.shape)
hname = "chargeInner_PXLayer_1"
c = Clustering()
c.load_data("/home/mantydze/data/ZeroBias2017B/massaged/{hname}.csv".format(hname=hname))
c.load_data("/home/mantydze/data/ZeroBias2017D/massaged/{hname}.csv".format(hname=hname))
# +
from sklearn.decomposition import PCA
import numpy as np
import random
get_colors = lambda n: list(map(lambda i: "#" + "%06x" % random.randint(0, 0xFFFFFF),range(n)))
good_bad_colors=["red", "green", "orange"] # red is -1
cluster_colors = get_colors(100)
def do_pca(df_, X_):
# import matplotlib.pyplot as plt
pca = PCA(n_components=3)
pcomp = pca.fit_transform(X_)
print(pca.explained_variance_ratio_)
plt.figure()
plt.grid()
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('Number of Components')
plt.ylabel('Variance (%)') #for each component
plt.title('Explained Variance ratio')
plt.show()
df_["pcx"] = pcomp[:,0]
df_["pcy"] = pcomp[:,1]
plt.scatter(df_["pcx"], df_["pcy"], color=[good_bad_colors[i] for i in df_["good_pixel"]], label=df_["good_pixel"])
plt.show()
# +
from sklearn.manifold import MDS
def do_mds(df_, X_, labels_=None):
mds = MDS(n_components=2)
X_t = mds.fit_transform(X_)
print(X_t.shape)
df_["mdsx"] = X_t[:,0]
df_["mdsy"] = X_t[:,1]
if labels_:
plt.scatter(df_["mdsx"], df_["mdsy"], color=[cluster_colors[i] for i in labels_])
plt.show()
plt.scatter(df_["mdsx"], df_["mdsy"], color=[good_bad_colors[i] for i in df_["good_pixel"]])
plt.show()
# -
do_pca(c.df, c.X)
# +
goods = [297308, 297425, 297293, 297050]
bads = [297179, 297180]
goods = [297050, 297056, 297057, 297099, 297100]#, 297101, 297113, 297114, 297175, 297176] #, 297177, 297178, 297215, 297218, 297219, 297224, 297225, 297227, 297292, 297293, 297296, 297308, 297359, 297411, 297424, 297425, 297426, 297429, 297430, 297431, 297432, 297433, 297434, 297435, 297467, 297468, 297469, 297483, 297484, 297485, 297486, 297487, 297488, 297503, 297504, 297505, 297557, 297558, 297562, 297563, 297599, 297603, 297604, 297605, 297606, 297620, 297656, 297665, 297666, 297670, 297674, 297675, 297722, 297723, 298996, 298997, 299000, 299042, 299061, 299062, 299064, 299065, 299067, 299096, 299149, 299178, 299180, 299184, 299185, 299327, 299329, 299368, 299369, 299370, 299380, 299381, 299394, 299395, 299396, 299420, 299443, 299450, 299477, 299478, 299479, 299480, 299481, 299593, 299594, 299595, 299597, 299649]
bads = [297046, 297047, 297048, 297049, 297168, 297169, 297170, 297171, 297179, 297180, 297181, 297211, 297281, 297282, 297283, 297284, 297285, 297286, 297287, 297288, 297289, 297290, 297291, 297495, 297496, 297497, 297498, 297499, 297501, 297502, 297662, 297663, 297664, 297671, 297672, 299316, 299317, 299318, 299324, 299325, 299326, 301086, 301665, 301912, 302646, 302660, 303948, 303989, 305249, 305250]
subdf = c.df.copy()
subdf = subdf[subdf["run"].isin(goods + bads)]
subX = subdf.filter(c.bin_cols, axis=1).copy().div(subdf.entries, axis=0)
suby = subdf["good_pixel"]
# -
rs = np.random.RandomState()
subdf = c.df.sample(frac =.10, random_state=rs)
subX = subdf.filter(c.bin_cols, axis=1).copy().div(subdf.entries, axis=0)
suby = subdf["good"]
do_pca(subdf, subX)
# +
# DBSCAN
from scipy.spatial.distance import jensenshannon
from sklearn.cluster import DBSCAN
with parallel_backend('loky'):
c1 = DBSCAN(eps=0.03, min_samples=10, metric=jensenshannon, metric_params={"base":2}, n_jobs=4)
c1.fit(subX)
print_unique(c1.labels_)
print()
print_unique(suby)
# -
do_mds(subdf, subX, list(c1.labels_))
# +
match = 0
for o, e in zip(c1.labels_, suby):
if o == e:
match += 1
# print(o, e)
print(match)
# +
from scipy.spatial.distance import jensenshannon
from scipy import stats
pi = 2
qi = 28
# js_pq = jensenshannon(subX.iloc[pi], subX.iloc[qi], base=10)
# view_histo(subdf.iloc[pi], subX.iloc[pi])
# view_histo(subdf.iloc[qi], subX.iloc[qi])
js_pq = jensenshannon(c.X.iloc[pi], c.X.iloc[qi], base=2)
view_histo(c.df.iloc[pi], c.X.iloc[pi])
view_histo(c.df.iloc[qi], c.X.iloc[qi])
print(js_pq)
# -
pi = 1
qi = 2
js_pq = jensenshannon(c.X.iloc[pi], c.X.iloc[qi], base=2)
view_histo(c.df.iloc[pi], c.X.iloc[pi])
view_histo(c.df.iloc[qi], c.X.iloc[qi])
print(js_pq)
from sklearn.mixture import GaussianMixture
# +
gm = GaussianMixture(n_components=2)
predy = gm.fit_predict(subX, suby)
for o, e in zip(predy, suby):
print(o, e)
# -
# +
# KMeans
from sklearn.cluster import KMeans, SpectralClustering
from sklearn import metrics
sils = []
chss = []
for i in range(2, 20):
km = SpectralClustering(n_clusters=i, random_state=1, affinity='nearest_neighbors')
km.fit(c.X)
# print_unique(km.labels_)
labels = km.labels_
sil = metrics.silhouette_score(c.X, labels, metric = 'euclidean')
chs = metrics.calinski_harabasz_score(c.X, labels)
sils.append(sil)
chss.append(chs)
print(i, sil, chs)
# -
km.inertia_
plt.plot(sils, label="sils")
plt.plot(chss, label="chss")
# +
# Histogram names to be trained
cipxl = ["chargeInner_PXLayer_1", "chargeInner_PXLayer_2", "chargeInner_PXLayer_3", "chargeInner_PXLayer_4"]
copxl = ["chargeOuter_PXLayer_1", "chargeOuter_PXLayer_2", "chargeOuter_PXLayer_3", "chargeOuter_PXLayer_4"]
spxl = ["size_PXLayer_1", "size_PXLayer_2", "size_PXLayer_3", "size_PXLayer_4"]
spxd = ["size_PXDisk_-3", "size_PXDisk_-2", "size_PXDisk_-1", "size_PXDisk_+1", "size_PXDisk_+2", "size_PXDisk_+3"]
cpxd = ["charge_PXDisk_-3", "charge_PXDisk_-2", "charge_PXDisk_-1", "charge_PXDisk_+1", "charge_PXDisk_+2", "charge_PXDisk_+3"]
hnames = cipxl + copxl + spxl + spxd + cpxd
hnames = ["chargeInner_PXLayer_1"]
# +
results = {}
for index, hname in enumerate(hnames):
print(index+1, "/", len(hnames), hname)
filename = "/home/mantydze/data/ZeroBias2017B/massaged/{hname}.csv".format(hname=hname)
rft = RandomForestTrain()
rft.load_data(filename)
rft.train_eval(verbose=False)
# -
df = pd.DataFrame.from_dict(results, orient='index')
df
results
from sklearn.metrics.pairwise import paired_distances
from scipy.spatial.distance import jensenshannon, pdist
pd = pdist(c.X, metric=jensenshannon)
len(pd)
pd
| 8,759 |
/YOLO V3.ipynb
|
ae5fb725d8d87692d64043901a7b1fe0991df86c
|
[
"MIT"
] |
permissive
|
aboerzel/YOLO3-keras
|
https://github.com/aboerzel/YOLO3-keras
| 3 | 2 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 2,108 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python (cv)
# language: python
# name: cv
# ---
# # Create and add dataset
# ## Dataset Aufbereitung
# 1. Verzeichnisstruktur Dataset (geeignet für lokale Entwicklung mit PyCharm und für das Training mit der FloydHub Cloud)
# 2. Bilder für Training mit Kamera erstellen oder von Google ect. laden
# 3. Bilder annotieren mit LabelImg (https://github.com/tzutalin/labelImg) => Annotationen im Pascal VOC Format
# 1. Class-Names
#
# 
#
#
# 4. Path der Annotationen von absolutem Pfad in relativen Pfad korrigieren mit yolo3_one_file_to_detect_them_all.py
# - FloydHub Dataset erstellen...
#
#
#
# Grab the pretrained weights of yolo3 from https://pjreddie.com/media/files/yolov3.weights.
#
# ```python yolo3_one_file_to_detect_them_all.py -w yolo3.weights -i dog.jpg```
#
# **This weights must be put in the root folder of the repository. They are the pretrained weights for the backend only and will be loaded during model creation. The code does not work without this weights.**
#
#
| 1,261 |
/_ll_nth_node_LinkedList.ipynb
|
3b3389db92dbfcb082fa45ed06605f257141191a
|
[] |
no_license
|
samuelvinodh/udemy_python_ipynb
|
https://github.com/samuelvinodh/udemy_python_ipynb
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 2,496 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
class Node(object):
def __init__(self,value):
self.value = value
self.nextnode = None
a = Node(1)
b = Node(2)
c = Node(3)
d = Node(4)
e = Node(5)
a.nextnode = b
b.nextnode = c
c.nextnode = d
d.nextnode = e
def nth_to_last_node(n,head):
left_pointer = head
right_pointer = head
for i in range(n-1):
if not right_pointer.nextnode:
#raise LookupError('Error: n is larger than the Linked List')
return 'Error: n is larger than the Linked List'
right_pointer = right_pointer.nextnode
while right_pointer.nextnode:
left_pointer = left_pointer.nextnode
right_pointer = right_pointer.nextnode
return left_pointer.value
target_node = nth_to_last_node(2,a)
from nose.tools import assert_equal
class TestNLast(object):
def test(self,sol):
assert_equal(sol(2,a),4)
assert_equal(sol(3,a),3)
assert_equal(sol(10,a),'Error: n is larger than the Linked List')
print("All Test Cases Passed")
t = TestNLast()
t.test(nth_to_last_node)
| 1,323 |
/cervical_classification.ipynb
|
530c50401fa214f712647caa2d851050c8d5217e
|
[] |
no_license
|
sunggeunkim/kaggle-cervical_cancer_screening
|
https://github.com/sunggeunkim/kaggle-cervical_cancer_screening
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 499,267 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=true editable=true
# # Intel Cervical Cancer Screening
# ### April 21, 2017
# ## Satchel Grant
#
# ### Overview
# The goal of this notebook is to classify a woman's cervical type into 1 of 3 classes from medical images. This assists in determination of cancer diagnoses and treatments.
#
# The images are graphic, so I used a different coloring display style when viewing any images.
#
# ### Initial Imports
# + deletable=true editable=true
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import os
from sklearn.utils import shuffle
import scipy.misc as sci
import time
from PIL import Image
import random
import scipy.ndimage.interpolation as scizoom
# %matplotlib inline
def show(img):
plt.imshow(img)
plt.show()
# + [markdown] deletable=true editable=true
# ### Reading in the Data
# The images are stored as jpg files, stored in folders corresponding to their classification. I read in the image os paths to be converted to images later in batches. I store their classification in a parallel array.
# + deletable=true editable=true
root_path = './train/'
def read_paths(path, no_labels=False):
# ** Takes a root path and returns all of the file
# paths within the root directory. It uses the
# subdirectories to create a corresponding label array **
# path - the path to the root directory
# no_labels - optional argument to use file
# names as labels instead of subdirectory
file_paths = []
labels = []
labels_to_nums = dict()
for dir_name, subdir_list, file_list in os.walk(path):
if len(subdir_list) > 0:
n_labels = len(subdir_list)
for i,subdir in enumerate(subdir_list):
labels_to_nums[subdir] = i
else:
type_ = dir_name.split('/')[-1]
for img_file in file_list:
if '.jpg' in img_file.lower():
file_paths.append(os.path.join(dir_name,img_file))
if no_labels: labels.append(img_file)
else: labels.append(labels_to_nums[type_])
return file_paths, labels, n_labels
image_paths, labels, n_labels = read_paths(root_path)
image_paths, labels = shuffle(image_paths, labels)
print("Number of data samples: " + str(len(image_paths)))
print("Number of Classes: " + str(n_labels))
# + [markdown] deletable=true editable=true
# This is a relatively small number of samples to use for deep learning... Luckily Kaggle provided more samples than just those in the train set. I will read those in as well after initial prototyping is finished.
# + [markdown] deletable=true editable=true
# ### Data Augmentation
# The following cells add rotations and translations to the dataset. This increases the number of samples for training which helps the model generalize better. This prevents overfitting the training set.
# + deletable=true editable=true
def rotate(image, angle, ones=None, random_fill=True, color_range=255):
# ** Rotates an image by the specified angle amount
# and fills in resulting space with random values **
# image - the image as numpy array to be rotated
# angle - the desired amount of rotation in degrees
# ones - an numpy array of ones like the image with the same rotation
# (used for broadcasting random filling into black space from rotation)
# no_random - optional boolean to remove random filling in black space
# color_range - the range of color values for the random filling
if not random_fill:
return sci.imrotate(image, angle).astype(np.float32)
elif ones == None:
ones = sci.imrotate(np.ones_like(image),angle)
rot_image = sci.imrotate(image, angle).astype(np.float32)
edge_filler = np.random.random(rot_image.shape).astype(np.float32)*color_range
rot_image[ones[:,:,:]!=1] = edge_filler[ones[:,:,:]!=1]
return rot_image
def translate(img, row_amt, col_amt, color_range=255):
# ** Returns a translated copy of an image by the specified row and column amount
# and fills in the empty space with random values **
# image - the source image as numpy array to be translated
# row_shift - the maximum vertical translation in both directions in pixels
# col_shift - the maximum horizontal translation in both directions in pixels
# color_range - the range of color values for the random filling
translation = np.random.random(img.shape).astype(img.dtype)*color_range
if row_amt > 0:
if col_amt > 0:
translation[row_amt:,col_amt:] = img[:-row_amt,:-col_amt]
elif col_amt < 0:
translation[row_amt:,:col_amt] = img[:-row_amt,-col_amt:]
else:
translation[row_amt:,:] = img[:-row_amt,:]
elif row_amt < 0:
if col_amt > 0:
translation[:row_amt,col_amt:] = img[-row_amt:,:-col_amt]
elif col_amt < 0:
translation[:row_amt,:col_amt] = img[-row_amt:,-col_amt:]
else:
translation[:row_amt,:] = img[-row_amt:,:]
else:
if col_amt > 0:
translation[:,col_amt:] = img[:,:-col_amt]
elif col_amt < 0:
translation[:,:col_amt] = img[:,-col_amt:]
else:
return img.copy()
return translation
def random_zoom(image, max_zoom=1/3.):
# ** Returns a randomly zoomed (scaled) copy of an image within the scaling amount.
# if the scaling zooms outward, the empty space is filled with random values **
# image - the source image as numpy array to be scaled
# max_zoom - the maximum scaling amount in either direction
color_range = 255
zoom_factor = 1 + (random.random()-0.5)*max_zoom
while zoom_factor == 1:
zoom_factor = 1 + (random.random()-0.5)*max_zoom
# scipy's zoom function returns different size array
# The following code ensures the zoomed image has same pixel size as initial image
img_height, img_width = image.shape[:2]
zoomed_h = round(img_height*zoom_factor)
zoomed_w = round(img_width*zoom_factor)
diff_h = abs(zoomed_h-img_height)
diff_w = abs(zoomed_w-img_width)
start_row = round(diff_h/2)
start_col = round(diff_w/2)
# Zoom in on image
if zoom_factor > 1:
end_row = start_row+img_height
end_col = start_col+img_width
zoom_img = scizoom.zoom(image,(zoom_factor,zoom_factor,1),output=np.uint8)[start_row:end_row,
start_col:end_col]
# Zoom out on image
elif zoom_factor < 1:
temp = scizoom.zoom(image,(zoom_factor,zoom_factor,1),output=np.uint8)
temp_height, temp_width = temp.shape[:2]
zoom_img = np.random.random(image.shape)*color_range # Random pixels instead of black space for out zoom
zoom_img[start_row:start_row+temp_height,
start_col:start_col+temp_width] = temp[:,:]
else:
return image.copy()
return zoom_img.astype(np.float32)
def random_augment(image, rotation_limit=180, shift_limit=10, zoom_limit=1/3.):
# ** Returns a randomly rotated, translated, or scaled copy of an image. **
# image - source image as numpy array to be randomly augmented
# rotation_limit - maximum rotation degree in either direction
# shift_limit - maximum translation amount in either direction
# zoom_limit - maximum scaling amount in either direction
augmentation_type = random.randint(0,2)
# Rotation
if augmentation_type == 0:
random_angle = random.randint(-rotation_limit,rotation_limit)
while random_angle == 0:
random_angle = random.randint(-rotation_limit,rotation_limit)
aug_image = rotate(image,random_angle,random_fill=False)
elif augmentation_type == 1:
# Translation
row_shift = random.randint(-shift_limit, shift_limit)
col_shift = random.randint(-shift_limit, shift_limit)
aug_image = translate(image,row_shift,col_shift)
else:
# Scale
aug_image = random_zoom(image,max_zoom=zoom_limit)
return aug_image
def one_hot_encode(labels, n_classes):
# ** Takes labels as values and converts them into one_hot labels.
# Returns numpy array of one_hot encodings **
# labels - array or numpy array of single valued labels
# n_classes - number of potential classes in labels
one_hots = []
for label in labels:
one_hot = [0]*n_classes
if label >= len(one_hot):
print("Labels out of bounds\nCheck your n_classes parameter")
return
one_hot[label] = 1
one_hots.append(one_hot)
return np.array(one_hots,dtype=np.float32)
# + [markdown] deletable=true editable=true
# ### Split into Training and Validation Sets
# It is important to set aside images for validation. This is how you can determine if your model is overfitting or underfitting during training.
#
# + deletable=true editable=true
training_percentage = .75
total_samples = len(image_paths)
split_index = int(training_percentage*total_samples)
X_train_paths, y_train = image_paths[:split_index], labels[:split_index]
X_valid_paths, y_valid = image_paths[split_index:], labels[split_index:]
# + deletable=true editable=true
print("Number of Training Samples: " + str(len(y_train)))
print("Number of Validation Samples: " + str(len(y_valid)))
# + [markdown] deletable=true editable=true
# Since I am completing this notebook over the course of multiple days, I save the training paths and validation paths into seperate csv files along with their classification. This is essentially a checkpoint step so that it is easy to repeatedly save and restore the weights of the model later in the process.
# + deletable=true editable=true
def save_paths(file_name, paths, labels):
with open(file_name, 'w') as csv_file:
for path,label in zip(paths,labels):
csv_file.write(path + ',' + str(label) + '\n')
save_paths('train_set.csv', X_train_paths, y_train)
save_paths('valid_set.csv', X_valid_paths, y_valid)
# + [markdown] deletable=true editable=true
# ### Previously Split Data
# Here I read in the training and validation image paths from the csv files. This ensures that the two sets remain seperate throughout the notebook.
# + deletable=true editable=true
def get_split_data(file_name):
paths = []
labels = []
with open(file_name, 'r') as f:
for line in f:
split_line = line.strip().split(',')
paths.append(split_line[0])
labels.append(int(split_line[1]))
return paths,labels
# + deletable=true editable=true
X_train_paths, y_train = get_split_data('train_set.csv')
X_valid_paths, y_valid = get_split_data('valid_set.csv')
n_labels = max(y_train)+1
print("Number of Training Samples: " + str(len(y_train)))
print("Number of Validation Samples: " + str(len(y_valid)))
# + deletable=true editable=true
y_train = one_hot_encode(y_train, n_labels)
y_valid = one_hot_encode(y_valid, n_labels)
# + [markdown] deletable=true editable=true
# ### Generator and Image Reader
# To maximize memory, the images for both testing and training can be read in in batches. This increases the amount of images that can be trained on in a single epoch which helps the model generalize. In most cases, more training data is better for deep learning.
# + deletable=true editable=true
def convert_images(paths, labels, resize_dims=(256,256), randomly_augment=False):
# ** Reads in images from their paths, resizes the images and returns
# the images with their corresponding labels. **
# paths - the file paths to the images
# labels - a numpy array of the corresponding labels to the images
# resize_dims - the resizing dimensions for the image
# add_zooms - optional parameter to add randomly scaled copies of the images to the output
# randomly_augment - optional parameter to add randomly rotated,
# translated, and scaled images to the output
images = []
new_labels = []
for i,path in enumerate(paths):
label = labels[i]
try:
img = mpimg.imread(path)
resized_img = sci.imresize(img, resize_dims)
except OSError:
if i == 0:
img = mpimg.imread(paths[i+1])
resized_img = sci.imresize(img, resize_dims)
resized_img = random_augment(resized_img)
elif i > 0:
sub_index = -1
if randomly_augment:
sub_index = -2
resized_img = random_augment(images[sub_index])
labels[i] = labels[i-1]
label = labels[i]
images.append(resized_img)
if randomly_augment:
images.append(random_augment(resized_img))
new_labels.append(label)
new_labels.append(label)
if randomly_augment:
return np.array(images,dtype=np.float32), np.array(new_labels,dtype=np.float32)
return np.array(images,dtype=np.float32), labels
def image_generator(file_paths, labels, batch_size, resize_dims=(256,256), randomly_augment=False):
# ** Generator function to convert image file paths to images with labels in batches. **
# file_paths - an array of the image file paths as strings
# labels - a numpy array of labels for the corresponding images
# batch_size - the desired size of the batch to be returned at each yield
# resize_dims - the desired x and y dimensions of the images to be read in
# add_zooms - optional parameter add an additional randomly zoomed image to the batch for each file path
# randomly_augment - optional parameter add an additional randomly rotated, translated,
# and zoomed image to the batch for each file path
if randomly_augment:
batch_size = int(batch_size/2) # the other half of the batch is filled with augmentations
while 1:
file_paths,labels = shuffle(file_paths,labels)
for batch in range(0, len(file_paths), batch_size):
images, batch_labels = convert_images(file_paths[batch:batch+batch_size],
labels[batch:batch+batch_size],
resize_dims=resize_dims,
randomly_augment=randomly_augment)
yield images, batch_labels
# + [markdown] deletable=true editable=true
# #### Note on Image Generation
# The cervical images come in different sizes. Because I may use transfer learning, the images need to be resized anyway.
#
# If the classification results are too poor, I will try resizing without distorting the image. If I am still getting poor results, I will try using RNNs to find the key elements of the picture and crop the image. I may use this last technique regardless of my initial results simply to practice the method. It has proved very successful for other people on other projects in the past.
# + deletable=true editable=true
batch_size = 96
add_random_augmentations = True
resize_dims = (256,256)
n_train_samples = len(X_train_paths)
if add_random_augmentations:
n_train_samples = 2*len(X_train_paths)
train_steps_per_epoch = n_train_samples//batch_size + 1
if n_train_samples % batch_size == 0: train_steps_per_epoch = n_train_samples//batch_size
valid_steps_per_epoch = len(X_valid_paths)//batch_size
train_generator = image_generator(X_train_paths,
y_train,
batch_size,
resize_dims=resize_dims,
randomly_augment=add_random_augmentations)
valid_generator = image_generator(X_valid_paths, y_valid,
batch_size, resize_dims=resize_dims)
# + [markdown] deletable=true editable=true
# ### Viewing the Images
# The following cell shows what some of the images look like. Due to the graphic nature of the images, I left the format in float32 instead of uint8 so that the coloring is less intrusive.
# + deletable=true editable=true
image_gen = image_generator(X_train_paths[:10], y_train[:10], 2,randomly_augment=True)
for i in range(5):
imgs, labels = next(image_gen)
imgs = imgs
show(imgs[0])
print(labels[0])
# + deletable=true editable=true
plt.hist(np.array(y_train,dtype='float32'),3)
plt.show()
# + [markdown] deletable=true editable=true
# ## Keras Section
#
# ### Keras Imports
#
# + deletable=true editable=true
from keras.models import Sequential, Model
from keras.layers import Conv2D, MaxPooling2D, Dense, Input, Flatten, Dropout, concatenate
from keras.layers.normalization import BatchNormalization
from keras import optimizers
# + [markdown] deletable=true editable=true
# ### Keras Model
# I'm going to try using a personal model that has given me good success in the past. If it seems to produce bad results, I will likely try to use transfer learning instead and use a model like the Inception net. Cervixes, however, only have so many features that are important to notice. And these features seem more esoteric than the imagenet features that most pretrained models are trained on. My personal model trains quicker and easier than the larger nets and uses newer methods like batchnormalization and parallel convolutions. Thus I'm going to try it first and reevaluate if results are poor.
# + deletable=true editable=true
stacks = []
conv_shapes = [(1,1),(3,3),(5,5)]
conv_depths = [12,12,10,10,8]
pooling_filter = (2,2)
pooling_stride = (2,2)
dense_shapes = [150,64,20,n_labels]
inputs = Input(shape=(resize_dims[0],resize_dims[1],3))
zen_layer = BatchNormalization()(inputs)
for shape in conv_shapes:
stacks.append(Conv2D(conv_depths[0], shape, padding='same', activation='elu')(inputs))
layer = concatenate(stacks,axis=-1)
layer = BatchNormalization()(layer)
layer = MaxPooling2D(pooling_filter,strides=pooling_stride,padding='same')(layer)
# layer = Dropout(0.05)(layer)
for i in range(1,len(conv_depths)):
stacks = []
for shape in conv_shapes:
stacks.append(Conv2D(conv_depths[i],shape,padding='same',activation='elu')(layer))
layer = concatenate(stacks,axis=-1)
layer = BatchNormalization()(layer)
# layer = Dropout(i*10**-2+.05)(layer)
layer = MaxPooling2D(pooling_filter,strides=pooling_stride, padding='same')(layer)
layer = Flatten()(layer)
fclayer = Dropout(0.5)(layer)
for i in range(len(dense_shapes)-1):
fclayer = Dense(dense_shapes[i], activation='elu')(fclayer)
# if i == 0:
# fclayer = Dropout(0.5)(fclayer)
fclayer = BatchNormalization()(fclayer)
outs = Dense(dense_shapes[-1], activation='softmax')(fclayer)
# + [markdown] deletable=true editable=true
# ### Keras Training
# I read in a pretrained model that was trained on classifying statefarm drivers. Hopefully this will speed up the training process.
# + deletable=true editable=true
model = Model(inputs=inputs,outputs=outs)
model.load_weights('model.h5', by_name=True)
for i in range(10):
adam_opt = optimizers.Adam(lr=0.0001)
model.compile(loss='categorical_crossentropy', optimizer=adam_opt, metrics=['accuracy'])
history = model.fit_generator(train_generator, train_steps_per_epoch, epochs=1,
validation_data=valid_generator,validation_steps=valid_steps_per_epoch)
model.save('model.h5')
# + deletable=true editable=true
| 19,786 |
/notebooks/PRO-GAN.ipynb
|
42016578c1d7316c02c9e6e59b31e57502c561ee
|
[
"MIT"
] |
permissive
|
jiwidi/BAM-DCGAN
|
https://github.com/jiwidi/BAM-DCGAN
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 9,126 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import torch as th
import torchvision as tv
import pro_gan_pytorch.PRO_GAN as pg
# select the device to be used for training
device = th.device("cuda" if th.cuda.is_available() else "cpu")
data_path = "cifar-10/"
def setup_data(download=False):
"""
setup the CIFAR-10 dataset for training the CNN
:param batch_size: batch_size for sgd
:param num_workers: num_readers for data reading
:param download: Boolean for whether to download the data
:return: classes, trainloader, testloader => training and testing data loaders
"""
# data setup:
classes = ('plane', 'car', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck')
transforms = tv.transforms.ToTensor()
trainset = tv.datasets.CIFAR10(root=data_path,
transform=transforms,
download=download)
testset = tv.datasets.CIFAR10(root=data_path,
transform=transforms, train=False,
download=False)
return classes, trainset, testset
if __name__ == '__main__':
# some parameters:
depth = 6
# hyper-parameters per depth (resolution)
num_epochs = [10, 20, 20, 20]
fade_ins = [50, 50, 50, 50]
batch_sizes = [128, 128, 128, 128]
latent_size = 128
# get the data. Ignore the test data and their classes
_, dataset, _ = setup_data(download=True)
# ======================================================================
# This line creates the PRO-GAN
# ======================================================================
pro_gan = pg.ConditionalProGAN(num_classes=10, depth=depth,
latent_size=latent_size, device=device)
# ======================================================================
# ======================================================================
# This line trains the PRO-GAN
# ======================================================================
pro_gan.train(
dataset=dataset,
epochs=num_epochs,
fade_in_percentage=fade_ins,
batch_sizes=batch_sizes
)
# ======================================================================
# -
_, dataset, _ = setup_data(download=True)
from torchvision import transforms
import torchvision
TRANSFORM_IMG = transforms.Compose([
transforms.Resize(128),
#transforms.CenterCrop(256),
transforms.ToTensor(),
#transforms.ToPILImage(mode='RGB'),
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225] )
])
TRAIN_DATA_PATH = '/home/jovyan/github/models/imagesProcessed/'
train_data = torchvision.datasets.ImageFolder(root=TRAIN_DATA_PATH, transform=TRANSFORM_IMG)
train_data.classes
trainset.classes
# +
import torch as th
import torchvision as tv
import pro_gan_pytorch.PRO_GAN as pg
from torchvision import transforms
import torchvision
TRAIN_DATA_PATH = '/home/jovyan/github/models/BAM-DCGAN/data/dataset_updated/training_set/'
# select the device to be used for training
device = th.device("cuda" if th.cuda.is_available() else "cpu")
def setup_data(download=False):
"""
setup the CIFAR-10 dataset for training the CNN
:param batch_size: batch_size for sgd
:param num_workers: num_readers for data reading
:param download: Boolean for whether to download the data
:return: classes, trainloader, testloader => training and testing data loaders
"""
# data setup:
TRANSFORM_IMG = transforms.Compose([
transforms.Resize((32,32)),
#transforms.CenterCrop(256),
transforms.ToTensor(),
#transforms.ToPILImage(mode='RGB'),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
trainset = torchvision.datasets.ImageFolder(root=TRAIN_DATA_PATH, transform=TRANSFORM_IMG)
testset = torchvision.datasets.ImageFolder(root=TRAIN_DATA_PATH, transform=TRANSFORM_IMG)
classes = trainset.classes
return classes, trainset, testset
if __name__ == '__main__':
# some parameters:
depth = 4
# hyper-parameters per depth (resolution)
num_epochs = [10, 20, 20, 20]
fade_ins = [50, 50, 50, 50]
batch_sizes = [32, 32, 32, 32]
latent_size = 128
# get the data. Ignore the test data and their classes
_, dataset, _ = setup_data(download=True)
# ======================================================================
# This line creates the PRO-GAN
# ======================================================================
pro_gan = pg.ConditionalProGAN(num_classes=len(dataset.classes), depth=depth,
latent_size=latent_size, device=device)
# ======================================================================
# ======================================================================
# This line trains the PRO-GAN
# ======================================================================
pro_gan.train(
dataset=dataset,
epochs=num_epochs,
fade_in_percentage=fade_ins,
batch_sizes=batch_sizes,
feedback_factor=1
)
# ======================================================================
# -
| 5,559 |
/bag-of-words/bag-of-words.ipynb
|
f9dd08802d5268b6f886cd4026a8d61dce4ecee1
|
[] |
no_license
|
pharic/ipython-notebooks
|
https://github.com/pharic/ipython-notebooks
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 12,610 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python [py35]
# language: python
# name: Python [py35]
# ---
import pandas as pd
df = pd.read_csv("labeledTrainData.tsv", header=0, delimiter="\t", quoting=3)
# **header=0** indicates that the first line contains column names.
#
# **delimiter="\t"** indicates that the file is tab separated.
#
# **quoting=3** tells Python to ignore double quotes.
df.describe()
df.shape
df.columns.values
# The three columns are labelled id, sentiment and review.
print(df["review"])
# We can see that some of the reviews have HTML tags like *<br>*. We can use BeautifulSoup to extract just the text.
from bs4 import BeautifulSoup
print("Before cleanup: ", df["review"][9])
print("After cleanup: ", BeautifulSoup(df["review"][9], "lxml").get_text())
import nltk
nltk.download()
from nltk.corpus import stopwords
print(stopwords.words("english"))
# Filtering out non-letter characters from the text
import re
letters = re.sub("[^a-zA-Z]", " ", BeautifulSoup(df["review"][9], "lxml").get_text())
bag_of_words = letters.lower().split()
# Remove stop words from the bag of words
bag_of_words = [w for w in bag_of_words if not w in stopwords.words("english")]
print(" ".join(bag_of_words))
bins = bin_cut)
print(age_data['YEARS_BINNED'].value_counts())
age_data.head()
# -
"""
Your Code Here
"""
year_group_sorted = age_data['YEARS_BINNED'].value_counts().keys().sort_values()
plt.figure(figsize=(8,6))
for i in range(len(year_group_sorted)):
sns.distplot(age_data.loc[(age_data['YEARS_BINNED'] == year_group_sorted[i]) & \
(age_data['TARGET'] == 0), 'YEARS_BIRTH'], label = str(year_group_sorted[i]))
sns.distplot(age_data.loc[(age_data['YEARS_BINNED'] == year_group_sorted[i]) & \
(age_data['TARGET'] == 1), 'YEARS_BIRTH'], label = str(year_group_sorted[i]))
plt.title('KDE with Age groups')
plt.show()
# 計算每個年齡區間的 Target、DAYS_BIRTH與 YEARS_BIRTH 的平均值
age_groups = age_data.groupby('YEARS_BINNED').mean()
age_groups
# +
plt.figure(figsize = (8, 8))
# 以年齡區間為 x, target 為 y 繪製 barplot
"""
Your Code Here
"""
px = 'YEARS_BINNED'
py = 'TARGET'
sns.barplot(px, py, data=age_data)
# Plot labeling
plt.xticks(rotation = 75); plt.xlabel('Age Group (years)'); plt.ylabel('Failure to Repay (%)')
plt.title('Failure to Repay by Age Group');
| 2,549 |
/1_Linear_Algebra.ipynb
|
bb45cef928b899e770a2c0599d2f551b5c8cc5d6
|
[] |
no_license
|
dg5921096/Books-solutions
|
https://github.com/dg5921096/Books-solutions
| 0 | 0 | null | 2020-04-13T21:39:02 | 2020-04-13T21:38:39 | null |
Jupyter Notebook
| false | false |
.py
| 26,320 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/LCASouza/colab-teste/blob/main/ConsultaCEP.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="xmeyW2ribdoC"
import requests
# + id="WFN7XXa_I_nH"
def consultaCEP(cepInput):
cepInput = str(cepInput)
if len(cepInput) != 8:
print('CEP {} inválido.'.format(cepInput))
return;
retorno = requests.get('https://viacep.com.br/ws/{}/json/'.format(cepInput));
retorno = retorno.json()
print('Estado: {}\n'
'Cidade: {}\n'
'Bairro: {}\n'
'Rua: {}\n'
'CEP: {}\n'.format(retorno['uf'], retorno['localidade'], retorno['bairro'], retorno['logradouro'], retorno['cep'], retorno['ddd']))
# + colab={"base_uri": "https://localhost:8080/"} id="9GeGbRKxBCSg" outputId="1d712daa-c416-4d1e-8604-22e8abb9c4be"
consultaCEP(74958143)
d "get_data_model". We also define a new function plot_history, which visualizes as a graph the training loss and if required even the validation loss.
# + id="2aGBJBVmXd8b" colab_type="code" outputId="5d0fadb6-9f53-4c34-e292-f2f2cf1360a9" colab={"base_uri": "https://localhost:8080/", "height": 238}
import numpy as np
import keras
np.random.seed(123) # for reproducibility
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.utils import np_utils
from keras.utils import to_categorical
import matplotlib.pyplot as plt
from keras.datasets import mnist
def plot_history(history, metric = None):
# Plots the loss history of training and validation (if existing)
# and a given metric
if metric != None:
fig, axes = plt.subplots(2,1)
axes[0].plot(history.history[metric])
try:
axes[0].plot(history.history['val_'+metric])
axes[0].legend(['Train', 'Val'])
except:
pass
axes[0].set_title('{:s}'.format(metric))
axes[0].set_ylabel('{:s}'.format(metric))
axes[0].set_xlabel('Epoch')
fig.subplots_adjust(hspace=0.5)
axes[1].plot(history.history['loss'])
try:
axes[1].plot(history.history['val_loss'])
axes[1].legend(['Train', 'Val'])
except:
pass
axes[1].set_title('Model Loss')
axes[1].set_ylabel('Loss')
axes[1].set_xlabel('Epoch')
else:
plt.plot(history.history['loss'])
try:
plt.plot(history.history['val_loss'])
plt.legend(['Train', 'Val'])
except:
pass
plt.title('Model Loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
def get_data_model(args = {}):
# Returns simple model, flattened MNIST data and categorical labels
num_classes=10
# the data, shuffled and split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(x_train.shape[0], x_train.shape[1] * x_train.shape[2])
x_test = x_test.reshape(x_test.shape[0], x_test.shape[1] * x_test.shape[2])
x_train= x_train.astype('float32')
x_test= x_test.astype('float32')
x_train /= 255
x_test /= 255
y_train=to_categorical(y_train,num_classes)
y_test=to_categorical(y_test,num_classes)
# Load simple model
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,), **args))
model.add(Dense(512, activation='relu', **args))
model.add(Dense(10, activation='softmax', **args))
return model, x_train, y_train, x_test, y_test
model, x_train, y_train, x_test, y_test = get_data_model()
model.summary()
# + [markdown] id="mRx68ymWLCT7" colab_type="text"
# ## Optimizers
#
# Once the model has been created, you need to define an optimizer to make it effectively working on your own particular problem, for example, in this tutorial we are addressing the digit classification problem.
# Since there are methods more prone to get stuck in local minima and other methods converging faster, the choice of the optimizer can potentially affect both the final performance and the speed of convergence. A nice visualization of such behavior is the following animation, where you can notice some methods, i.e., Adadelta in yellow, and Rmsprop in black converge significantly faster than SGD in red failing in local minima.
#
# 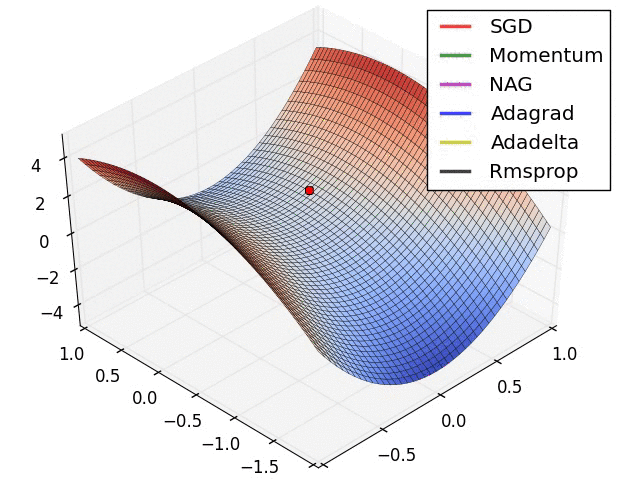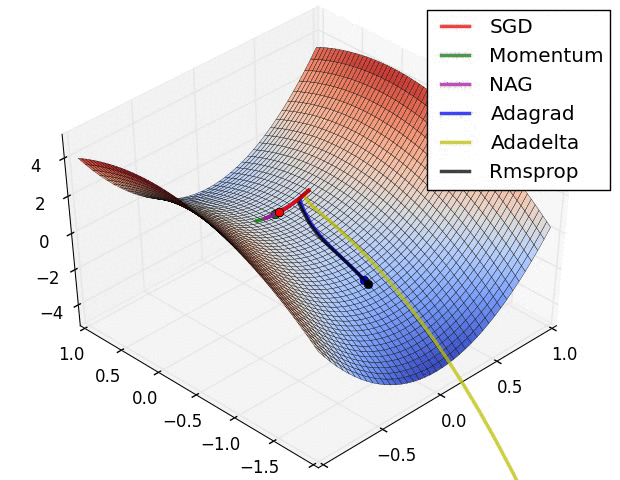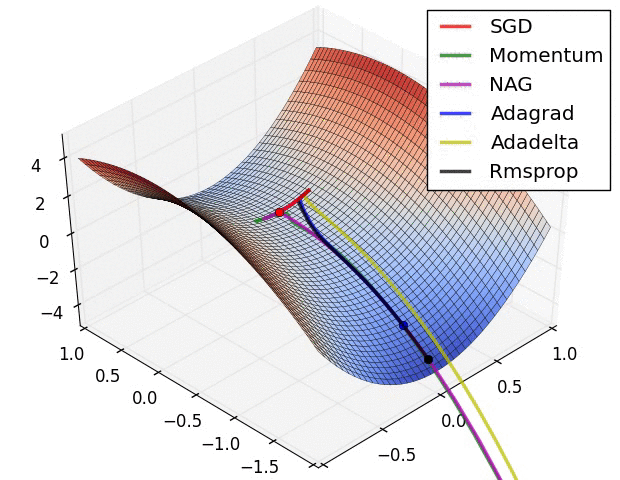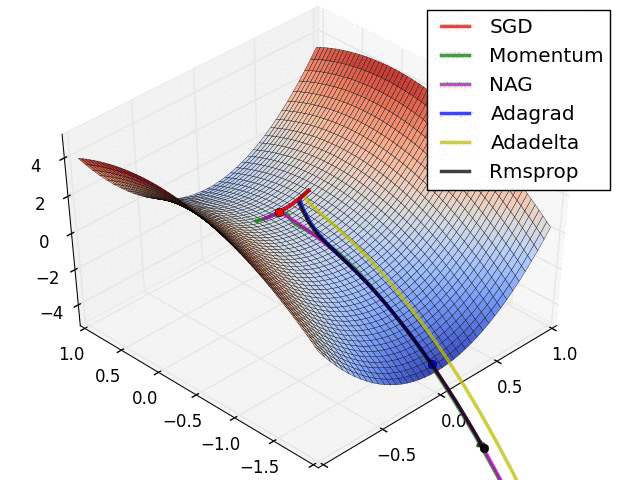
#
# The animation example above is from [Sebastian Ruder's blog](http://ruder.io/optimizing-gradient-descent/), who wrote an interesting article about the math formulation and properties of different optimizers. In this tutorial, we will follow a hands-on approach and will mainly focus on how to use them in Keras.
#
# To handle the optimization, Keras provides "the compile method" requiring two arguments in string format: a loss function and an optimizer. For example, we define as parameters Adam and Categorical Cross-entropy.
#
# As a rule of thumb, Adam is usually easier to tune due to the adaptive learning rate, whereas SGD with momentum [has been shown](https://arxiv.org/pdf/1712.07628.pdf) to reach better results when tuned correctly. Of course, the best way to learn the different optimizers is using them - please consult the official documentation [Optimizers in Keras](https://keras.io/optimizers/) to see the available options - and finally, report below in the table the training and validation losses you are able to get.
#
# + id="iwvy89V2hd7i" colab_type="code" outputId="486faaa5-5745-4332-e520-c7630d440ac9" colab={"base_uri": "https://localhost:8080/", "height": 166}
from IPython.display import HTML, display
import tabulate
table = [["Optimizer","loss","val_loss","hyper-parameters"],
["Adam","-","-","-"],
["Sgd","-","-","lr=0.01, momentum=0.0, decay=0.0"],
["RMSprop","-" ,"-","lr=0.001, rho=0.9, epsilon=None, decay=0.0"],
["Adagrad","-","-","-"],
["Adadelta","-","-","-"],
["Adam","-","-","-"]]
display(HTML(tabulate.tabulate(table, tablefmt='html')))
# + id="9od5lUWMWu5X" colab_type="code" outputId="7cad988a-4b1f-43d4-c992-c72250a8ae60" colab={"base_uri": "https://localhost:8080/", "height": 391}
model.compile(optimizer='adam',loss='categorical_crossentropy')
model.fit(x_train,y_train,batch_size=100, epochs=10,verbose=1,validation_data=(x_test,y_test))
# + [markdown] id="-yDSecajTyc6" colab_type="text"
# ## Initializers
#
#
# Weight initialization is a crucial step in tuning neural networks as different weights initializations may lead the model to reach different local minima. The weights are usually randomly initialized by different algorithms, e.g.. Xavier, He_normal, initialization.
# In Keras, you can set the particular initialization strategy you want to use as an argument when declaring a layer. For example, you can give as input to the function "linear_layer" defining the mapping $y= Ax + b$, a kernel ($A$ in the equation) with a normal distribution (by default the `stddev` is 0.05) and zero bias ($b$ in the equation).
# + id="A6lzySByXcMB" colab_type="code" colab={}
linear_layer = Dense(64, kernel_initializer='random_normal',
bias_initializer='zeros')
# + [markdown] id="oF_EVmyooqYL" colab_type="text"
# Now let's check the weights of the layers and see if they follow the distributions we set.
# + id="YgHC0CSmowIK" colab_type="code" outputId="cb38e86b-13c0-43fe-bd6e-3ce8f0aa9df1" colab={"base_uri": "https://localhost:8080/", "height": 238}
from keras.layers import Input
import numpy as np
from keras import backend as K
input_x = K.variable(np.random.random((1, 64)))
y = linear_layer(input_x)
weights = linear_layer.get_weights()
# Weights return an array with [kernel, bias]
# Let's see the kernel weights
print(weights[0])
# + id="kLDzNuqUp2M8" colab_type="code" outputId="4d57acc3-fcc8-4afc-c03b-646148a8210d" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Now let's check that the mean is 0 and stddev is 0.05
print(weights[0].mean(), weights[0].std())
# + id="Uohj6D4rqTfT" colab_type="code" outputId="04c2963c-f3f0-4607-b562-ac209862d8fa" colab={"base_uri": "https://localhost:8080/", "height": 68}
# Let's print the bias now
print(weights[1])
# + [markdown] id="69NkDCipqbmg" colab_type="text"
# The number of initializations available in Keras is listed [in the documentation](https://keras.io/initializers/). By default in Keras the kernel weights are initialized as `'glorot_uniform'` and the bias to `'zeros'`. Glorot uniform, which is also called Xavier initialization was defined [here](http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf). It samples the weights from a uniform distribution, whose range depends on the number of input and output units. Another initializer quite used is the `he_normal`, which draws the weights from a truncated normal distribution.
# + [markdown] id="1-8ittW2L1DI" colab_type="text"
# ## Losses
#
# Another important step in training deep neural networks is the choice of the loss function, which strictly depends on your problem. In this tutorial, we will introduce two typical losses i.e., sigmoid and mean squared error, for two standard problems in machine learning: classification and regression. In the following weeks, we will introduce further losses. The full list of standard losses in Keras is available [here](https://keras.io/losses/).
# + [markdown] id="0T8aSdjCtSSO" colab_type="text"
# ### Classification
#
# For classification problems, the standard loss used is the cross-entropy loss. For the binary case, the formula is $\mathcal{L} = y\log(p) + (1-y)\log(1-p)$, where $p$ is a probability value ranging in $[0, 1]$.
# To constrain the activations to assume such values, typically it is applied a [Sigmoid activation](https://en.wikipedia.org/wiki/Sigmoid_function). In Keras, the loss is called `binary_crossentropy`, and it accepts as target a vector with an element in the range $[0, 1]$ (usually either 0 or 1) per input element.
# + id="LUQhLNxr5VA7" colab_type="code" outputId="d948c22d-edcd-446c-d475-820b9dba1443" colab={"base_uri": "https://localhost:8080/", "height": 376}
model, x_train, y_train, x_test, y_test = get_data_model()
model.pop()
model.add(Dense(1, activation='sigmoid'))
# This three lines transform the problem in a binary one
# We want to know if the number is bigger than 5 (label 1) or smaller (label 0)
y_train = np.argmax(y_train, axis = 1)
y_train[y_train < 5] = 0
y_train[y_train >= 5] = 1
model.compile(optimizer='adam',loss='binary_crossentropy', metrics=['binary_accuracy'])
history = model.fit(x_train, y_train, epochs=3, batch_size=32, validation_split=0.2, verbose = 0)
plot_history(history, 'binary_accuracy')
# + [markdown] id="6jvNHqg--XYy" colab_type="text"
# In case the number of classes is higher than 2, we use the cross-entropy loss, which has the form of $\mathcal{L} = -\sum_i y_i\log(p_i)$. The loss is called `categorical_crossentropy` in Keras, and accepts a one-hot encoded vector. A one-hot encoded vector has dimensionality $C$, where $C$ is the number of classes. All of the elements are set to 0, minus the corresponding class $c$, which is set to 1. If we have a vector of labels with a scalar from $[0, C)$ per training example, we can transform it into a one-hot encoding form by using the function `to_categorical`.
#
# Let's see an example using mnist data
# + id="v_YBOLN77S1I" colab_type="code" outputId="136faa56-0d3a-43ad-b72a-c219bc23ca8d" colab={"base_uri": "https://localhost:8080/", "height": 34}
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# The labels are an scalar from 0 to 9 per example
print(y_train[:5])
# + id="Rgm-W7sa5U-P" colab_type="code" outputId="ba8e681b-4123-46d0-86a1-c8a87fc947e9" colab={"base_uri": "https://localhost:8080/", "height": 102}
keras.utils.to_categorical(y_train[:5])
# + [markdown] id="OR_lJgB6CfFd" colab_type="text"
# The output vector needs to be $\sum_i p_i = 1$, and we achieve that by applying the softmax activation function to the output vector. Keras accepts as input for the loss also vectors which are not scaled as $\sum_i p_i = 1$, but resulting in degraded performances of the network. For example, remove the `softmax` activation in the following example and re-run the code. You will see that the accuracy achieved is quite lower.
# + id="BVTAPlc_B99R" colab_type="code" outputId="af059294-c530-439c-ab4a-336c0f7f48b1" colab={"base_uri": "https://localhost:8080/", "height": 376}
# We use the function get_data_model, which already applies to_categorical
_, x_train, y_train, x_test, y_test = get_data_model()
### Model defined with softmax
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dense(512, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.compile(optimizer='adam',loss='categorical_crossentropy', metrics=['categorical_accuracy'])
history = model.fit(x_train, y_train, epochs=3, batch_size=32, validation_split=0.2, verbose = 0)
plot_history(history, 'categorical_accuracy')
# + [markdown] id="iFuOCwNftQgH" colab_type="text"
# ### Regression
# For regression problems, it is quite standard to use Mean Squared Error or Mean Absolute Error, depending on the problem.
#
# To give an example of regression problem, let's load the boston housing dataset. The problem involves in estimating the median value of certain hause in the area of Boston, Mass. The given set of features is defined [here](https://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html), amounting to a total of 13. Some of the features are "per capita crime rate by town", "average number of rooms per dwelling" or "pupil-teacher ratio by town".
# + id="Li20u1NjrwS5" colab_type="code" outputId="89fcbf04-c1ee-4ad3-c04c-b81ebcf70633" colab={"base_uri": "https://localhost:8080/", "height": 85}
from keras.datasets import boston_housing
(x_train, y_train), (x_test, y_test) = boston_housing.load_data()
print(y_train[:10])
# + [markdown] id="0JO5_oiCyPzR" colab_type="text"
# We see that the labels are float, and we need to predict them. To do so, we need a network that has one output. Now we will train the network using both mean absolute error (MAE), and mean squared error (MSE). As a quick evaluation, we use the validation MAE metric to compare them.
# + id="RSJH6_Mfsjp-" colab_type="code" colab={}
model_mae = Sequential()
model_mae.add(Dense(100, activation='relu', input_shape=(13,)))
model_mae.add(Dense(1))
model_mae.compile(optimizer='adam',loss='mean_absolute_error', metrics=['mean_absolute_error', 'mean_squared_error'])
history = model_mae.fit(x_train, y_train, epochs=100, batch_size=32, validation_split=0.2, verbose = 0)
# + id="J2xZRys8zNsD" colab_type="code" outputId="cb224d2f-592d-48c9-b861-8df984848ae5" colab={"base_uri": "https://localhost:8080/", "height": 376}
plot_history(history, 'mean_absolute_error')
# + id="2XYKtV1GzMQg" colab_type="code" colab={}
model_mse = Sequential()
model_mse.add(Dense(100, activation='relu', input_shape=(13,)))
model_mse.add(Dense(1))
model_mse.compile(optimizer='adam',loss='mean_squared_error', metrics=['mean_absolute_error', 'mean_squared_error'])
history = model_mse.fit(x_train, y_train, epochs=100, batch_size=32, validation_split=0.2, verbose = 0)
# + id="SBZB_MDCw1Os" colab_type="code" outputId="63ad6eab-dcbe-4b68-b0df-65b0d1cb6e48" colab={"base_uri": "https://localhost:8080/", "height": 376}
plot_history(history, 'mean_squared_error')
# + id="aMHRntQU0mrM" colab_type="code" outputId="f72c18b0-d5f7-4167-d79f-9dcfced70f12" colab={"base_uri": "https://localhost:8080/", "height": 51}
results = model_mae.evaluate(x_test, y_test)
print('MAE trained model achieves MAE: {:.4f} and MSE: {:.4f}'.format(results[1], results[2]))
# + id="df2igCnI030F" colab_type="code" outputId="3a1dc163-8ef7-4728-89ae-0970caddf946" colab={"base_uri": "https://localhost:8080/", "height": 51}
results = model_mse.evaluate(x_test, y_test)
print('MSE trained model achieves MAE: {:.4f} and MSE: {:.4f}'.format(results[1], results[2]))
# + [markdown] id="hWr2tc7l0IdG" colab_type="text"
# Looking at the graphs, we can see that training using MSE as loss achieves a better MSE and worse MAE in the test set compared to the model training with MAE loss. It makes sense (though it is not always the case).
# + [markdown] id="vnEITU4iy6Q5" colab_type="text"
# Now let's print some predicted prices from the test set, along with the actual price, just to have an intuition of the output values.
# + id="uTPGyWHxydF_" colab_type="code" outputId="ab9e7095-1abf-4ed6-8a40-f13fa57aaeec" colab={"base_uri": "https://localhost:8080/", "height": 68}
pred_prices = model_mae.predict(x_test)
print(pred_prices[:10, 0])
print(y_test[:10])
# + [markdown] id="miKutjvgtXuS" colab_type="text"
# ## Regularization
# + [markdown] id="F-VrqhSbWJ9t" colab_type="text"
# ### Loss regularizers
#
# [Regularizers](https://keras.io/regularizers/) put some penalties to the optimization process. In practice by penalizing large values, weights are constrained to be small and as a result, overfitting is prevented.
#
# In Keras regularization works on a per-layer basis. It means you can define a regularization function for each layer. In particular, you can specify three regularization parameters each one related to a different type of penalty:
#
# * `kernel_regularizer`: a penalty depending on the value of the kernel weights, e.g, larger kernel weights result in larger penalization.
# * `bias_regularizer`: a penalty depending on the loss function depending on the value of the bias.
# * `activity_regularizer`: a penalty applied to the loss function depending on the output. It results in smaller outputs in value when this regularizer is applied.
#
# Standard regularizers that can be applied are $l_1$, $l_2$ and $l_1+l_2$.
# In the example below, we check the difference in training and validation accuracy by varying regularization strategy.
#
# + id="zv4c80XD_Yzr" colab_type="code" outputId="2a14a1f6-b85c-470a-eb3d-0dd7e39287b5" colab={"base_uri": "https://localhost:8080/", "height": 415}
from keras import regularizers
test_accuracy = []
train_accuracy = []
reg_values = [0.1, 0.00001]
for reg_val in reg_values:
print('Training with regularization value of {:f}'.format(reg_val))
args_dict = {'kernel_regularizer': regularizers.l2(reg_val)}
model, x_train, y_train, x_test, y_test = get_data_model(args_dict)
model.compile(optimizer='adam',loss='categorical_crossentropy', metrics=['accuracy'])
history = model.fit(x_train, y_train, epochs=10, batch_size=32, verbose=0)
train_accuracy.append(history.history['acc'][-1])
test_accuracy.append(model.evaluate(x_test, y_test)[-1])
import matplotlib.pyplot as plt
plt.figure()
plt.plot(reg_values, train_accuracy)
plt.plot(reg_values, test_accuracy)
plt.legend(['Training acc.', 'Test acc.'])
plt.show()
# + [markdown] id="FJ-J7tWRTQU7" colab_type="text"
# ### Dropout
#
# Dropout is a layer that deactivates during training either some neurons or input data depending on the specific layer where it is applied by setting elements to with a certain probability .`In the evaluation phase, all the neurons are activated and dropout has no effect. The drop out value, i.e., the probability of disabling the input units can be set as a parameter when defining a layer.
#
# For example, the following layer the drop-out value is 0.3, that means $30%$ of the input data is switched off during training.
# + id="HEqZN0LyTv1F" colab_type="code" colab={}
prob_drop = 0.3
drop = keras.layers.Dropout(prob_drop)
# + id="Pqcb3TWCWe4e" colab_type="code" outputId="3d4ba659-4428-4231-a1a8-3f0efaeff0ff" colab={"base_uri": "https://localhost:8080/", "height": 119}
from keras.layers import Input
import numpy as np
from keras import backend as K
x = np.random.random((1, 512))
input_x = K.variable(x)
# Set learning phase is used to manually setting
# the phase (0 evaluation, 1 training)
# Dropout only affects training, so we set it to 1
K.set_learning_phase(1)
y = K.eval(drop(input_x))
print('Input (10 elements)')
print(x[0,0:10])
print('Output (10 elements)')
print(y[0,0:10])
# + [markdown] id="iXhWs8c1Xw3h" colab_type="text"
# We now check what percentage of elements have been set to 0, and what is the scaling value the other elements have.
# + id="8njS0-XRXVsc" colab_type="code" outputId="72e4fcd6-c44c-4444-e332-23a3d000da2a" colab={"base_uri": "https://localhost:8080/", "height": 85}
print('Drop percentage, should be close to {:f}'.format(prob_drop))
print(((y==0).sum())/(1.0*y.shape[1]))
print('Scaling value, should be {:f}'.format(1/(1-prob_drop)))
print(((y[y!=0]).sum())/(1.0*x[y!=0].sum()))
# + [markdown] id="C98HL1rgVACR" colab_type="text"
# ### Batch Normalization
#
# Batch Normalization is a layer that subtracts the mean of the batch for each input dimension and divides it by the standard deviation of the batch. The goal is to standardize all of the dimensions of the input feature to have mean 0 and variance 1.
# The layer is defined in Keras by using:
# + id="mt2E2uTqWGBB" colab_type="code" colab={}
batch_norm = keras.layers.BatchNormalization()
# + [markdown] id="ax8OE0cbZA7X" colab_type="text"
# Now we will generate a batch of 512x1 (a feature vector of 512 components) using `np.random.random`, which is a uniform distribution under the $[0, 1)$ interval, resulting in mean 0.5 and variance 1/12. Finally, the batch normalization layer scales the distribution to have mean 0 and variance 1.
#
#
# + id="8IS_u-HKY1WR" colab_type="code" outputId="50c7eb90-51fc-4872-b2f0-24e10e7dd1ae" colab={"base_uri": "https://localhost:8080/", "height": 119}
from keras.layers import Input
import numpy as np
from keras import backend as K
x = np.random.random((512, 1))
input_x = K.variable(x)
y = K.eval(batch_norm(input_x))
print('Input')
print(x[:10,0])
print('Output')
print(y[:10,0])
# + id="ILdlLzAtZ3sp" colab_type="code" outputId="a66f2a6e-8cae-4c53-f293-9d4a867a1342" colab={"base_uri": "https://localhost:8080/", "height": 51}
# Input mean should be ~0.5 and var ~1/12=0.0833
print(x.mean(), x.var())
# Output mean should be ~0 and var ~1
print(y.mean(), y.var())
# + [markdown] id="iDOne7XbrEhL" colab_type="text"
# Batch normalization changes behaviour during evaluation: it computes the moving average of both mean and variance to normalize the testing data.
# + [markdown] id="NuF3Y5DoKylT" colab_type="text"
# ## HyperParameters Tuning
#
# There are several parameters in the training process that we can modify. Note that it is not good practice looking at the performance in the test set to tweak the hyperparameters. Hence, we first need to define a validation split, which we use to test the different models trained. The method `fit` has two relevant arguments: `validation_split` and `validation_data`. The argument passed to `validation_split` (0 by default) determines the ratio of the training set for validation purposes. For example,
# ```
# model.fit(x_train, y_train, ..., validation_split=0.2)
# ```
# uses 20% of `x_train` as validation data.
#
# Unfortunately, the validation data is randomly sampled and we can not fix the same splits during evaluations, so results are not directly comparable. An option is using the `validation_data` argument, where we can pass directly the split of data we want to use as validation in the form of a tuple `(data, labels)`.
#
# Let's see how we can do the split. First, we load the data:
# + id="WWL_GXrnT_xS" colab_type="code" colab={}
model, x_train, y_train, x_test, y_test = get_data_model()
# + [markdown] id="XKS6nnKAUBJT" colab_type="text"
# Now, we want to split `x_train` in training and validation, but we also need to follow the same partition for `y_train`. We can do so by using `numpy` functions:
# + id="dVMgy4n7UOdL" colab_type="code" outputId="9149c644-cc52-4850-bc11-c2bbe48558ba" colab={"base_uri": "https://localhost:8080/", "height": 34}
import numpy
# We shuffle the indices in case the dataset follows an ordering
# If we do not shuffle we may take only a subset of classes if the dataset is
# ordered
indices = numpy.random.permutation(x_train.shape[0])
val_ratio = 0.2
n_indices_train = int((1-val_ratio) * x_train.shape[0])
train_idx, val_idx = indices[:n_indices_train], indices[n_indices_train:]
x_train, x_val = x_train[train_idx,:], x_train[val_idx,:]
y_train, y_val = y_train[train_idx], y_train[val_idx]
print(x_train.shape[0], x_val.shape[0])
# + [markdown] id="yBf2hHC_WF-U" colab_type="text"
# Another way is to use a package called `sklearn`, which contains a function called `train_test_split` that performs the split.
# + id="Hy2DPVA9WFjk" colab_type="code" outputId="eb918acc-f3ea-4845-80d3-5722b1dadfad" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Let's reload the data first
model, x_train, y_train, x_test, y_test = get_data_model()
from sklearn.model_selection import train_test_split
x_train, x_val, y_train, y_val = train_test_split(x_train, y_train, test_size=0.20)
print(x_train.shape[0], x_val.shape[0])
# + id="TulgsLVmWE6t" colab_type="code" outputId="c0efe960-e5f4-482f-f770-f6d1b5f23b9b" colab={"base_uri": "https://localhost:8080/", "height": 376}
model.compile(optimizer='adam',loss='categorical_crossentropy', metrics=['categorical_accuracy'])
history = model.fit(x_train, y_train, epochs=2, batch_size=32, verbose=0, validation_data=(x_val, y_val))
plot_history(history, 'categorical_accuracy')
# + [markdown] id="rvWaSNdZV6e_" colab_type="text"
# Now, let's check if the accuracy in the test set is similar to the accuracy in the training set.
# + id="UMRAQsCYVrcg" colab_type="code" outputId="81ec3253-4e1c-43c7-be08-3dc5eccbab72" colab={"base_uri": "https://localhost:8080/", "height": 51}
print('Accuracy in the test set is {:.2f}'.format(model.evaluate(x_test, y_test)[-1]))
# + [markdown] id="NMd2DVJCGmE7" colab_type="text"
# One of the most important parameters to tweak is the training rate, which controls the update step performed during the backpropagation. Keras provides two callbacks that allow us to modify the learning rate during training. One is LearningRateScheduler, which allows us to define a rule to vary the learning rate depending on the epoch. For example, using the `lr_scheduler` function (found [here](https://stackoverflow.com/questions/39779710/setting-up-a-learningratescheduler-in-keras)), we can modify the loss function so that every 3 epochs is multiplied by 0.1.
# + id="AC9in_Zhfnly" colab_type="code" outputId="ea760fa3-2e91-4528-bbd4-bd879c9cdb70" colab={"base_uri": "https://localhost:8080/", "height": 733}
def lr_scheduler(epoch, lr):
decay_rate = 0.1
decay_step = 3
if epoch % decay_step == 0 and epoch:
return lr * decay_rate
return lr
lrate = keras.callbacks.LearningRateScheduler(lr_scheduler)
model, x_train, y_train, x_test, y_test = get_data_model()
model.compile(optimizer='adam',loss='categorical_crossentropy', metrics=['categorical_accuracy'])
history = model.fit(x_train, y_train, epochs=10, batch_size=32, validation_split=0.2, callbacks=[lrate])
plot_history(history, 'categorical_accuracy')
# + [markdown] id="jAF6VK2gkdRU" colab_type="text"
# Now let's plot the learning rate in each epoch to check how the learning rate is decreased every three epochs as we defined in `lr_scheduler`
# + id="jtugFeDVj8HD" colab_type="code" outputId="0295d8ba-7650-4d5f-aacd-473d88ea777f" colab={"base_uri": "https://localhost:8080/", "height": 361}
learning_rate = history.history['lr']
plt.plot(range(1, len(learning_rate)+1), learning_rate)
plt.ylabel('Learning Rate')
plt.xlabel('Epochs')
plt.show()
# + [markdown] id="XAPrOzm0iDTs" colab_type="text"
# Another callback provided is ReduceLROnPlateau, which reduces the learning rate whenever a given metric has stopped improving. There are 5 important arguments:
#
# * `monitor`: we specify the metric we want to track
# * `patience`: number of epochs without improvement before reducing lr
# * `factor`: the new learning rate will be `new_lr = lr * factor`
# * `min_lr`: sets the minimum lr
# * `min_delta`: margin to define when the metric has stopped improving
#
# + id="os7b7Oh0TO7m" colab_type="code" outputId="af3014f6-984b-424e-fa5d-f1d8f2ecbd0e" colab={"base_uri": "https://localhost:8080/", "height": 733}
from keras.callbacks import ReduceLROnPlateau
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.2,
patience=1, min_lr=0.00001, min_delta = 0.01)
model, x_train, y_train, x_test, y_test = get_data_model()
model.compile(optimizer='adam',loss='categorical_crossentropy', metrics=['categorical_accuracy'])
history = model.fit(x_train, y_train, epochs=10, batch_size=32, validation_split=0.2, callbacks=[reduce_lr])
plot_history(history, 'categorical_accuracy')
# + [markdown] id="FX9W-7yNoyvL" colab_type="text"
# Again, we check how the learning rate has changed. You can check that it has indeed decreased when the `val_loss` has not decreased by more than 0.01 until it reached the `min_lr`
# + id="BVNFkE-qnKVk" colab_type="code" outputId="a1a7b622-6ebe-4513-8245-b2b5bccccbf4" colab={"base_uri": "https://localhost:8080/", "height": 361}
learning_rate = history.history['lr']
plt.plot(range(1, len(learning_rate)+1), learning_rate)
plt.ylabel('Learning Rate')
plt.xlabel('Epochs')
plt.show()
# + [markdown] id="ugiRVHj-j8UX" colab_type="text"
# ### Searching for the right set of parameters
#
# Apart from the learning rate, there are several hyperparameters we can tune: the optimizer parameters (momentum, beta, rho, decay), the dropout rate, the number of neurons/feature maps, batch size, regularization weights, etc.. After some time working with the models, you gain an intuition of what set of parameters work better. However, performing a proper search of hyperparameters could improve the results. A way to do this (among several others) is performing a grid search of parameters. There are several packages that help you to do hyperparameter optimization in Keras, the one we will use is called [`talos`](https://github.com/autonomio/talos).
# + id="Az5-RBT1zFX8" colab_type="code" outputId="89a1a9a0-7d49-4318-f2be-bb3e8096614c" colab={"base_uri": "https://localhost:8080/", "height": 119}
# !pip install talos
# + [markdown] id="a2w5UNq0_I0L" colab_type="text"
# Now we show a quick example of how to do it. We set only 2 epoch of training and `grid_downsampling=0.03`, which controls the number of sets of hyperparameters tested.
# + id="Pm2XxaG_zPT-" colab_type="code" outputId="2b130b50-3438-44f3-c96a-b2d5eb1f7327" colab={"base_uri": "https://localhost:8080/", "height": 122}
import talos as ta
_, x_train, y_train, x_test, y_test = get_data_model()
def model_scan(x_train, y_train, x_val, y_val, params):
model = Sequential()
model.add(Dense(params['first_neuron'], input_shape=(784,), activation=params['activation']))
model.add(Dropout(params['dropout']))
model.add(Dense(10, activation=params['last_activation']))
from talos.model.normalizers import lr_normalizer
model.compile(optimizer=params['optimizer'](lr_normalizer(params['lr'], params['optimizer'])),
loss=params['losses'],
metrics=['categorical_accuracy'])
out = model.fit(x_train, y_train,
batch_size=params['batch_size'],
epochs=params['epochs'],
verbose=0,
validation_data=[x_val, y_val])
return out, model
from talos import live
p = {'lr': (1, 10, 0.1),
'first_neuron':[4, 8, 16, 32, 64, 128],
'batch_size': [20, 30, 40],
'epochs': [2],
'dropout': (0, 0.40, 0.7),
'weight_regulizer':[None],
'emb_output_dims': [None],
'optimizer': [keras.optimizers.Adam, keras.optimizers.SGD],
'losses': ['categorical_crossentropy', 'logcosh'],
'activation':['relu', 'elu'],
'last_activation': ['softmax']}
h = ta.Scan(x_train, y_train,
params=p,
dataset_name='first_test',
experiment_no='2',
model=model_scan,
grid_downsample=0.03,
print_params=True,
disable_progress_bar=True)
# + [markdown] id="5FCxXrdxCXRC" colab_type="text"
# Now we check the results of the experiment (saved by default in a CSV file with the same name as `dataset_name + _ + experiment_no`)
# + id="xARWdCT0_-Ig" colab_type="code" outputId="b89ecfba-1261-4bf9-bfaa-a14a76c818b2" colab={"base_uri": "https://localhost:8080/", "height": 261}
from talos import Reporting
r = Reporting('/content/first_test_2.csv')
# returns the results dataframe
r.data
# + [markdown] id="cBBz_MMS_ezr" colab_type="text"
# [Talos' documentation](https://autonomio.github.io/docs_talos/#introduction) provides more information about the package. There are also other packages that serve the same purpose, with several examples online, in case you want to do grid search, random search or other types of hyperparemeter search.
# + [markdown] id="xm0oVnMQWLZt" colab_type="text"
# ## Data augmentation
# We will show some examples of data augmentation for images.
# ### Images
# Data augmentation techniques such as rotation, color jittering, scale or cropping are usually applied in deep learning pipelines. The main pipeline: we take as input an image, apply a transformation to it, and then use it for training.
#
# Keras includes a preprocessing module, with all [these transformations](https://keras.io/preprocessing/image/) implemented. The preprocessing module can be imported by doing
#
#
#
# + id="n4glvOHvh8qy" colab_type="code" colab={}
from keras.preprocessing.image import ImageDataGenerator
# + [markdown] id="2vftBzsolQcL" colab_type="text"
# Then we need to fit it to the input data, and use `flow` to apply the transformations to the input data.
# + id="yTLpcR43IHpX" colab_type="code" colab={}
def plot_data_augmentation(augmentation_gen = ImageDataGenerator()):
(x_train, y_train), (x_test, y_test) = mnist.load_data()
augmentation_gen.fit(np.expand_dims(x_train, -1))
for X_batch, y_batch in augmentation_gen.flow(np.expand_dims(x_train, -1), y_train, batch_size=5, shuffle=False):
for i in range(0, 5):
plt.subplot(150 + 1 + i)
plt.imshow(X_batch[i, :].reshape(28, 28), cmap=plt.get_cmap('gray'))
# show the plot
plt.show()
break
# + [markdown] id="OoJYjjapiISI" colab_type="text"
# We will now visualize some of the transformations available to use.
#
# First, we plot some images without any transformations applied for comparison.
# + id="MyoZHyOTheyU" colab_type="code" outputId="3051ede1-f6c1-4983-e084-ab6e45e7962c" colab={"base_uri": "https://localhost:8080/", "height": 127}
plot_data_augmentation()
# + [markdown] id="eFXEC5EejxWG" colab_type="text"
# ### Rotation
# A standard transformation is to rotate the image. We can do so by initializing ImageDataGenerator with `rotation_range=rot_val`.
# + id="hjgfZ1z3j46X" colab_type="code" outputId="09bce4aa-a8ef-4425-f316-d719ea36c98d" colab={"base_uri": "https://localhost:8080/", "height": 127}
# We first define the transformation we want to apply
augmentation_gen = ImageDataGenerator(rotation_range=90)
plot_data_augmentation(augmentation_gen)
# + [markdown] id="Schj43v4ioTY" colab_type="text"
# ### Shift
#
# We can define a maximum range of both horizontal (`width_shift_range`) and vertical (`height_shift_range`) shift.
# + id="dbzq69FfjLd9" colab_type="code" outputId="e3620ed9-3b38-492b-96af-4170cef8200f" colab={"base_uri": "https://localhost:8080/", "height": 127}
augmentation_gen = ImageDataGenerator(width_shift_range=0.3, height_shift_range=0.3)
plot_data_augmentation(augmentation_gen)
# + [markdown] id="7uhYKLIPI1LA" colab_type="text"
# ### Zooming
# Zooming into the image can be done with `zoom_range`
# + id="NGvZzyL0HQjF" colab_type="code" outputId="a52c43a5-9caa-4d20-fcbe-b5417dc2fa5f" colab={"base_uri": "https://localhost:8080/", "height": 127}
augmentation_gen = ImageDataGenerator(zoom_range=0.4)
plot_data_augmentation(augmentation_gen)
# + [markdown] id="845GvrICI9IX" colab_type="text"
# ### Flip
#
# We can define either horizontal flip (`horizontal_flip`) or vertical (`vertical_flip`).
# + id="m6emZPbsHXOV" colab_type="code" outputId="0de687f1-d480-495d-e9bb-c370a98cf775" colab={"base_uri": "https://localhost:8080/", "height": 127}
augmentation_gen = ImageDataGenerator(horizontal_flip=True, vertical_flip=True)
plot_data_augmentation(augmentation_gen)
# + [markdown] id="GOE33AOLJdPK" colab_type="text"
# ### Combining transformations
# We can combine all the transformations and train a model. The ImageDataGenerator is a generator, so we need to use the method `fit_generator`, which is explained [in the documentation](https://keras.io/models/sequential/).
# + id="Xqb15Ga0EsC9" colab_type="code" outputId="fcacf86e-ef60-4f25-9d94-39844376d44e" colab={"base_uri": "https://localhost:8080/", "height": 374}
augmentation_gen = ImageDataGenerator(
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
rescale=1./255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
(x_train, y_train), (x_test, y_test) = mnist.load_data()
augmentation_gen.fit(np.expand_dims(x_train, -1))
train_gen = augmentation_gen.flow(np.expand_dims(x_train, -1), keras.utils.to_categorical(y_train))
model = Sequential()
model.add(keras.layers.Flatten(input_shape=(28, 28, 1)))
model.add(Dense(512, activation='relu'))
model.add(Dense(512, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.compile(optimizer='adam',loss='categorical_crossentropy', metrics=['categorical_accuracy'])
model.fit_generator(train_gen, samples_per_epoch=len(x_train), epochs=10)
# + [markdown] id="njqA6ve8WHB1" colab_type="text"
# ## Performance metrics
#
# [Available metrics in Keras](https://keras.io/metrics/)
#
# In order to evaluate the performance of the model, we use evaluation metrics. As we have seen in previous examples, some of the standard evaluation metrics are cross entropy and mean squared error for classification and regression problems, respectively. These metrics are passed at the run time, so when `model.fit` is called, it automatically keeps track of the training (and validation if given) performance per epoch.
#
# ```
# model.compile(metrics=['categorical_accuracy'...])
# ```
#
# + [markdown] id="YokEU3S0Esby" colab_type="text"
# If we call `model.evaluate` in any test data, we can also obtain the values of the metrics in the test data.
# + [markdown] id="BPk96eQomRwQ" colab_type="text"
# ### Custom metrics
#
# There are cases where we want to use a non-standard metric for evaluating our models. We can define any metrics in a function and pass it to the `compile` method. As in the example given in the [documentation](https://keras.io/metrics/), let's say that we want to keep track of the mean predicted value in the Boston housing dataset, we can do so and plot it by doing this:
# + id="AjlLjPXSPcRJ" colab_type="code" outputId="71ead5db-6b7d-4a45-d05e-d15a7afd8737" colab={"base_uri": "https://localhost:8080/", "height": 376}
import keras.backend as K
def mean_pred(y_true, y_pred):
return K.mean(y_pred)
from keras.datasets import boston_housing
(x_train, y_train), (x_test, y_test) = boston_housing.load_data()
model = Sequential()
model.add(Dense(100, activation='relu', input_shape=(13,)))
model.add(Dense(1))
model.compile(optimizer='adam',loss='mean_absolute_error', metrics=[mean_pred])
history = model.fit(x_train, y_train, epochs=20, batch_size=32, validation_split=0.2, verbose = 0)
plot_history(history, 'mean_pred')
# + [markdown] id="9Q8t9ZSK2nmg" colab_type="text"
# ### Tensorboard
# Tensorboard is quite useful to monitor the different metrics in real time. Both Tensorflow and Pytorch users (using the TensorboardX module) use it. Tensorboard can be used in Keras by using the Tensorboard callback available ([documentation here](https://keras.io/callbacks/)).
#
# However, to make it working in a Colab environment, we need to follow a different process, which is explained [here](https://medium.com/@tommytao_54597/use-tensorboard-in-google-colab-16b4bb9812a6). When you run the following piece of code, a Tensorboard link will be displayed. If you click on it, and you will be redirected to the Tensorboard site.
# + id="IMK1K_sd24ee" colab_type="code" outputId="744d88a3-167d-4c76-d3d9-baffd7b73bff" colab={"base_uri": "https://localhost:8080/", "height": 255}
# !pip install tensorboardcolab
# !wget https://bin.equinox.io/c/4VmDzA7iaHb/ngrok-stable-linux-amd64.zip
# !unzip ngrok-stable-linux-amd64.zip
# + id="uwlns-E_6PSw" colab_type="code" outputId="bff4f554-23ea-4c01-9f00-48a46cf3f694" colab={"base_uri": "https://localhost:8080/", "height": 68}
import tensorboardcolab as tbc
K.clear_session()
tboard = tbc.TensorBoardColab()
from tensorboardcolab import TensorBoardColabCallback
# + [markdown] id="PYSa2XXG4Cb8" colab_type="text"
# Now, we can use a callback function to show the training progress in the given link.
# + id="zFh9bJyJ4f7W" colab_type="code" outputId="f1180212-2d63-480d-b8ff-bb17b7df038a" colab={"base_uri": "https://localhost:8080/", "height": 391}
model, x_train, y_train, x_test, y_test = get_data_model()
model.compile(optimizer='adam',loss='categorical_crossentropy')
model.fit(x_train, y_train, epochs=10, batch_size=32, validation_split=0.2,callbacks=[TensorBoardColabCallback(tboard)])
# + [markdown] id="N0x9hnGhUW9u" colab_type="text"
# In the Tensorboard web site you should see two sections: *Scalars* and *Graph*. In *Scalars* there is the plot with the training and validation accuracy per epoch, and in *Graph* you should have the graph of your model. You can also plot images, histograms, distributions and other things in Tensorboard, which makes it quite useful to keep track of the training progress.
# + [markdown] id="nUpwc1fHxF4N" colab_type="text"
# **Exercises**
#
# 1) Please, import CIFAR-10 dataset and repeat the training by selecting the right metric among those we have seen so far for classification and regression problem.
#
# 2) Once you have done with exercise 1, move to HyperParameters Tuning and try different loss functions, regularizers, and establish the right set of parameters for your model on CIFAR-10 reporting results on a table.
#
# 3) Add some data augmentation trying the different strategies and observe reporting results in a table if it leads to any improvement.
#
| 42,671 |
/hw4/YounghoonSVMRecognizer.ipynb
|
72848954a163224fae15012beb918d530c9dbec1
|
[] |
no_license
|
yhoonkim/CSE599H
|
https://github.com/yhoonkim/CSE599H
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 1,313,539 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a id="plotly_bubble_charts"></a>
# ## [Bubble Charts](https://plot.ly/python/bubble-charts/)
# __Bubble charts are good to use:__
# - When you want to display three diminsions of data.
# - When your third varaibles represents the magnitude of the xy variables.
# <a id="plotly_bubble_charts_basic"></a>
# ### Basic Bubble Chart
# +
import plotly.graph_objects as go
import pandas as pd
from plotly.offline import init_notebook_mode, plot
from IPython.core.display import display, HTML
init_notebook_mode(connected=True)
fig = go.Figure(data=[go.Scatter(
x=[1, 2, 3, 4], y=[10, 11, 12, 13],
mode='markers',
marker_size=[40, 60, 80, 100])
])
plot(fig, filename = 'figure8-6-1.html')
display(HTML('figure8-6-1.html'))
# -
# <a id="plotly_bubble_charts_basic_customizing"></a>
# ### Customizing Bubble Chart
# +
import plotly.graph_objects as go
fig = go.Figure(data=[go.Scatter(
x=[1, 3.2, 5.4, 7.6, 9.8, 12.5],
y=[1, 3.2, 5.4, 7.6, 9.8, 12.5],
mode='markers',
marker=dict(
color=[120, 125, 130, 135, 140, 145],
size=[15, 30, 55, 70, 90, 110], #you can also define marker size in the market dictionary
showscale=True #This adds a color scale to the chart
)
)])
plot(fig, filename = 'figure8-6-2.html')
display(HTML('figure8-6-2.html'))
def __init__(self, sensorType, currentTimeMs, sensorTimestampMs, x, y, z):
self.sensorType = sensorType
# On my mac, I could cast as straight-up int but on Windows, this failed
# This is because on Windows, a long is 32 bit but on Unix, a long is 64bit
# So, forcing to int64 to be safe. See: https://stackoverflow.com/q/38314118
self.currentTimeMs = currentTimeMs.astype(np.int64)
# sensorTimestampMs comes from the Arduino function
# https://www.arduino.cc/reference/en/language/functions/time/millis/
# which returns the number of milliseconds passed since the Arduino board began running the current program.
self.sensorTimestampMs = sensorTimestampMs.astype(np.int64)
self.x = x.astype(float)
self.y = y.astype(float)
self.z = z.astype(float)
# Calculate the magnitude of the signal
self.mag = np.sqrt(self.x**2 + self.y**2 + self.z**2)
self.sampleLengthInSecs = (self.currentTimeMs[-1] - self.currentTimeMs[0]) / 1000.0
self.samplesPerSecond = len(self.currentTimeMs) / self.sampleLengthInSecs
def pad_with_mean(self, headPadLength, tailPadLength):
self.signalLengthBeforePadding = len(self.x)
self.x_padded = np.pad(self.x, (headPadLength, tailPadLength), 'mean')
self.y_padded = np.pad(self.y, (headPadLength, tailPadLength), 'mean')
self.z_padded = np.pad(self.z, (headPadLength, tailPadLength), 'mean')
self.mag_padded = np.pad(self.mag, (headPadLength, tailPadLength), 'mean')
# Returns a dict of numpy arrays for each axis of the accel + magnitude
def get_data(self):
return {"x":self.x, "y":self.y, "z":self.z, "mag":self.mag}
# Returns a dict of numpy arrays for each axis of the accel + magnitude
def get_processed_data(self):
return {"x_p":self.x_p, "y_p":self.y_p, "z_p":self.z_p, "mag_p":self.mag_p}
# A trial is one gesture recording and includes an accel SensorData object
# In the future, this could be expanded to include other recorded sensors (e.g., a gyro)
# that may be recorded simultaneously
class Trial:
# We actually parse the sensor log files in the constructor--this is probably bad practice
# But offers a relatively clean solution
def __init__(self, gestureName, endTimeMs, trialNum, accelLogFilenameWithPath):
self.gestureName = gestureName
self.trialNum = trialNum
self.endTimeMs = endTimeMs
self.accelLogFilenameWithPath = accelLogFilenameWithPath
self.accelLogFilename = os.path.basename(accelLogFilenameWithPath)
# unpack=True puts each column in its own array, see https://stackoverflow.com/a/20245874
# I had to force all types to strings because auto-type inferencing failed
parsedAccelLogData = np.genfromtxt(accelLogFilenameWithPath, delimiter=',',
dtype=str, encoding=None, skip_header=1, unpack=True)
# The asterisk is really cool in Python. It allows us to "unpack" this variable
# into arguments needed for the SensorData constructor. Google for "tuple unpacking"
self.accel = SensorData("Accelerometer", *parsedAccelLogData)
# Utility function that returns the end time as a nice string
def getEndTimeMsAsString(self):
return time.strftime('%Y-%m-%d %H:%M:%S', time.localtime(self.endTimeMs / 1000))
def __str__(self):
return "'{}' : Trial {} from {}".format(self.gestureName, self.trialNum, self.accelLogFilename)
# Container for a single set of gestures and trials
class GestureSet:
def __init__(self, gesture_log_path, map_gestures_to_trials):
self.path = gesture_log_path
self.map_gestures_to_trials = map_gestures_to_trials
# returns the longest trial (based on num rows recorded and not clock time)
def get_longest_trial(self):
longest_trial_length = -1
longest_trial = None
for gesture_name, trial_list in self.map_gestures_to_trials.items():
for trial in trial_list:
if longest_trial_length < len(trial.accel.x):
longest_trial_length = len(trial.accel.x)
longest_trial = trial
return longest_trial
# returns the base path
def get_base_path(self):
return os.path.basename(os.path.normpath(self.path))
# returns the number of gestures
def get_num_gestures(self):
return len(self.map_gestures_to_trials)
# returns trials for a gesture name
def get_trials_for_gesture(self, gesture_name):
return self.map_gestures_to_trials[gesture_name]
# creates an aggregate signal based on *all* trials for this gesture
# TODO: in future could add in an argument, which takes a list of trial nums
# to use to produce aggregate signal
def create_aggregate_signal(self, gesture_name, signal_var_name):
trials = self.get_trials_for_gesture(gesture_name)
aggregate_signal = None
trial_signals = []
trial_signals_original = []
first_trial = None
first_trial_signal = None
max_length = -1
for trial in trials:
trial_signal = getattr(trial.accel, signal_var_name)
if max_length < len(trial_signal):
max_length = len(trial_signal)
for i in range(len(trials)):
if i == 0:
first_trial = trials[i]
trial_signal = getattr(first_trial.accel, signal_var_name)
trial_signal_mod = np.copy(trial_signal)
trial_signals.append(trial_signal_mod)
trial_signals_original.append(trial_signal)
array_length_diff = max_length - len(trial_signal_mod)
trial_signal_mod = np.pad(trial_signal_mod, (0, array_length_diff), 'mean')
aggregate_signal = trial_signal_mod
first_trial_signal = trial_signal_mod
else:
cur_trial = trials[i]
cur_trial_signal = getattr(trial.accel, signal_var_name)
trial_signals_original.append(cur_trial_signal)
array_length_diff = max_length - len(cur_trial_signal)
cur_trial_signal_mod = np.pad(cur_trial_signal, (0, array_length_diff), 'mean')
cur_trial_signal_mod = get_aligned_signal_cutoff_and_pad(cur_trial_signal_mod, first_trial_signal)
trial_signals.append(cur_trial_signal_mod)
aggregate_signal += cur_trial_signal_mod
mean_signal = aggregate_signal / len(trial_signals)
return mean_signal
# Returns the minimum number of trials across all gestures (just in case we accidentally recorded a
# different number. We should have the same number of trials across all gestures)
def get_min_num_of_trials(self):
minNumTrials = -1
for gestureName, trialSet in self.map_gestures_to_trials.items():
if minNumTrials == -1 or minNumTrials > len(trialSet):
minNumTrials = len(trialSet)
return minNumTrials
# returns the total number of trials
def get_total_num_of_trials(self):
numTrials = 0
for gestureName, trialSet in self.map_gestures_to_trials.items():
numTrials = numTrials + len(trialSet)
return numTrials
# get random gesture name
def get_random_gesture_name(self):
gesture_names = list(self.map_gestures_to_trials.keys())
rand_gesture_name = gesture_names[random.randint(0, len(gesture_names) - 1)]
return rand_gesture_name
# get random trial
def get_random_trial(self):
rand_gesture_name = self.get_random_gesture_name()
print("rand_gesture_name", rand_gesture_name)
trials_for_gesture = self.map_gestures_to_trials[rand_gesture_name]
return trials_for_gesture[random.randint(0, len(trials_for_gesture) - 1)]
# returns a sorted list of gesture names
def get_gesture_names_sorted(self):
return sorted(self.map_gestures_to_trials.keys())
# prettify the str()
def __str__(self):
return "'{}' : {} gestures and {} total trials".format(self.path, self.get_num_gestures(), self.get_total_num_of_trials())
# +
# This cell contains our file handling and parsing related functions
from os import listdir
import ntpath
import os
# Returns all csv filenames in the given directory
# Currently excludes any filenames with 'fulldatastream' in the title
def find_csv_filenames( path_to_dir, suffix=".csv" ):
filenames = listdir(path_to_dir)
return [ filename for filename in filenames if filename.endswith( suffix ) and "fulldatastream" not in filename ]
# Parses and creates Trial objects for all csv files in the given dir
# Returns a dict() mapping (str: gestureName) to (list: Trial objects)
def parse_and_create_gesture_trials( path_to_dir ):
csvFilenames = find_csv_filenames(path_to_dir)
print("Found {} csv files in {}".format(len(csvFilenames), path_to_dir))
mapGestureNameToTrialList = dict()
mapGestureNameToMapEndTimeMsToMapSensorToFile = dict()
for csvFilename in csvFilenames:
# parse filename into meaningful parts
# print(csvFilename)
filenameNoExt = os.path.splitext(csvFilename)[0];
filenameParts = filenameNoExt.split("_")
gestureName = None
timeMs = None
numRows = None
sensorName = "Accelerometer" # currently only one sensor but could expand to more
# Added this conditional on May 15, 2019 because Windows machines created differently formatted
# filenames from Macs. Windows machines automatically replaced the character "'"
# with "_", which affects filenames like "Midair Zorro 'Z'_1556730840228_206.csv"
# which come out like "Midair Zorro _Z__1557937136974_211.csv" instead
if '__' in filenameNoExt:
filename_parts1 = filenameNoExt.split("__")
gestureName = filename_parts1[0]
gestureName = gestureName.replace('_',"'")
gestureName += "'"
filename_parts2 = filename_parts1[1].split("_")
timeMs = filename_parts2[0]
numRows = filename_parts2[1]
else:
filenameParts = filenameNoExt.split("_")
gestureName = filenameParts[0]
timeMs = filenameParts[1]
numRows = int(filenameParts[2])
# print("gestureName={} timeMs={} numRows={}".format(gestureName, timeMs, numRows))
if gestureName not in mapGestureNameToMapEndTimeMsToMapSensorToFile:
mapGestureNameToMapEndTimeMsToMapSensorToFile[gestureName] = dict()
if timeMs not in mapGestureNameToMapEndTimeMsToMapSensorToFile[gestureName]:
mapGestureNameToMapEndTimeMsToMapSensorToFile[gestureName][timeMs] = dict()
mapGestureNameToMapEndTimeMsToMapSensorToFile[gestureName][timeMs][sensorName] = csvFilename
# print (mapGestureNameToMapEndTimeMsToMapSensorToFile)
print("Found {} gestures".format(len(mapGestureNameToMapEndTimeMsToMapSensorToFile)))
# track the longest array so we can resize accordingly (by padding with zeros currently)
maxArrayLength = -1
trialWithMostSensorEvents = None
# Now we need to loop through the data and sort each gesture set by timems values
# (so that we have trial 1, 2, 3, etc. in order)
for gestureName, mapEndTimeMsToMapSensorToFile in mapGestureNameToMapEndTimeMsToMapSensorToFile.items():
gestureTrialNum = 0
mapGestureNameToTrialList[gestureName] = list()
for endTimeMs in sorted(mapEndTimeMsToMapSensorToFile.keys()):
mapSensorToFile = mapEndTimeMsToMapSensorToFile[endTimeMs]
accelFilenameWithPath = os.path.join(path_to_dir, mapSensorToFile["Accelerometer"])
gestureTrial = Trial(gestureName, endTimeMs, gestureTrialNum, accelFilenameWithPath)
mapGestureNameToTrialList[gestureName].append(gestureTrial)
if maxArrayLength < len(gestureTrial.accel.x):
maxArrayLength = len(gestureTrial.accel.x)
trialWithMostSensorEvents = gestureTrial
gestureTrialNum = gestureTrialNum + 1
print("Found {} trials for '{}'".format(len(mapGestureNameToTrialList[gestureName]), gestureName))
# Perform some preprocessing
listSamplesPerSec = list()
listTotalSampleTime = list()
print("Max trial length across all gesture is '{}' Trial {} with {} sensor events. Padding all arrays to match".
format(trialWithMostSensorEvents.gestureName, trialWithMostSensorEvents.trialNum, maxArrayLength))
for gestureName, trialList in mapGestureNameToTrialList.items():
for trial in trialList:
listSamplesPerSec.append(trial.accel.samplesPerSecond)
listTotalSampleTime.append(trial.accel.sampleLengthInSecs)
# preprocess signal before classification and store in new arrays
trial.accel.x_p = preprocess(trial.accel.x, maxArrayLength)
trial.accel.y_p = preprocess(trial.accel.y, maxArrayLength)
trial.accel.z_p = preprocess(trial.accel.z, maxArrayLength)
trial.accel.mag_p = preprocess(trial.accel.mag, maxArrayLength)
print("Avg samples/sec across {} sensor files: {:0.1f}".format(len(listSamplesPerSec), sum(listSamplesPerSec)/len(listSamplesPerSec)))
print("Avg sample length across {} sensor files: {:0.1f}s".format(len(listTotalSampleTime), sum(listTotalSampleTime)/len(listTotalSampleTime)))
print()
return mapGestureNameToTrialList
# Performs some basic preprocesing on rawSignal and returns the preprocessed signal in a new array
def preprocess(rawSignal, maxArrayLength):
meanFilterWindowSize = 10
arrayLengthDiff = maxArrayLength - len(rawSignal)
# CSE599 TODO: add in your own preprocessing here
# Just smoothing the signal for now with a mean filter
smoothed = np.convolve(rawSignal, np.ones((meanFilterWindowSize,))/meanFilterWindowSize, mode='valid')
return smoothed
# Returns the leafs in a path
# From: https://stackoverflow.com/a/8384788
def path_leaf(path):
head, tail = ntpath.split(path)
return tail or ntpath.basename(head)
# From: https://stackoverflow.com/questions/800197/how-to-get-all-of-the-immediate-subdirectories-in-python
def get_immediate_subdirectories(a_dir):
return [name for name in os.listdir(a_dir)
if os.path.isdir(os.path.join(a_dir, name))]
# Utility function to extract gesture name from filename
def extract_gesture_name( filename ):
# leaf = path_leaf(filename)
tokenSplitPos = filename.index('_')
gestureName = filename[:tokenSplitPos]
return gestureName
# Returns the minimum number of trials across all gestures (just in case we accidentally recorded a
# different number. We should have 5 or 10 each for the A2 assignment)
def get_min_num_of_trials( mapGestureToTrials ):
minNumTrials = -1
for gestureName, trialSet in mapGestureToTrials.items():
if minNumTrials == -1 or minNumTrials > len(trialSet):
minNumTrials = len(trialSet)
return minNumTrials
# returns the total number of trials
def get_total_num_of_trials (mapGestureToTrials):
numTrials = 0
for gestureName, trialSet in mapGestureToTrials.items():
numTrials = numTrials + len(trialSet)
return numTrials
# Helper function to align signals.
# Returns a shifted signal of a based on cross correlation and a roll function
def get_aligned_signal(a, b):
corr = signal.correlate(a, b, mode='full')
index_shift = len(a) - np.argmax(corr)
a_shifted = np.roll(a, index_shift - 1)
return a_shifted
# Returns a shifted signal of a based on cross correlation and padding
def get_aligned_signal_cutoff_and_pad(a, b):
corr = signal.correlate(a, b, mode='full')
index_shift = len(a) - np.argmax(corr)
index_shift_abs = abs(index_shift - 1)
a_shifted_cutoff = None
if (index_shift - 1) < 0:
a_shifted_cutoff = a[index_shift_abs:]
a_shifted_cutoff = np.pad(a_shifted_cutoff, (0, index_shift_abs), 'mean')
else:
a_shifted_cutoff = np.pad(a, (index_shift_abs,), 'mean')
a_shifted_cutoff = a_shifted_cutoff[:len(a)]
return a_shifted_cutoff
# calculate zero crossings
# See: https://stackoverflow.com/questions/3843017/efficiently-detect-sign-changes-in-python
# TODO: in future, could have a min_width detection threshold that ignores
# any changes < min_width samples after an initial zero crossing was detected
# TODO: could also have a mininum height after the zero crossing (withing some window)
# to eliminate noise
def calc_zero_crossings(s):
# I could not get the speedier solutions to work reliably so here's a
# custom non-Pythony solution
cur_pt = s[0]
zero_crossings = []
for ind in range(1, len(s)):
next_pt = s[ind]
if ((next_pt < 0 and cur_pt > 0) or (next_pt > 0 and cur_pt < 0)):
zero_crossings.append(ind)
elif cur_pt == 0 and next_pt > 0:
# check for previous points less than 0
# as soon as tmp_pt is not zero, we are done
tmp_pt = cur_pt
walk_back_idx = ind
while(tmp_pt == 0 and walk_back_idx > 0):
walk_back_idx -= 1
tmp_pt = s[walk_back_idx]
if tmp_pt < 0:
zero_crossings.append(ind)
elif cur_pt == 0 and next_pt < 0:
# check for previous points greater than 0
# as soon as tmp_pt is not zero, we are done
tmp_pt = cur_pt
walk_back_idx = ind
while(tmp_pt == 0 and walk_back_idx > 0):
walk_back_idx -= 1
tmp_pt = s[walk_back_idx]
if tmp_pt > 0:
zero_crossings.append(ind)
cur_pt = s[ind]
return zero_crossings
# -
# ## Load the Data
# +
# Load the data
root_gesture_log_path = './GestureLogs' # this dir should have a set of gesture sub-directories
print(get_immediate_subdirectories(root_gesture_log_path))
gesture_log_paths = get_immediate_subdirectories(root_gesture_log_path)
map_gesture_sets = dict()
selected_gesture_set = None
for gesture_log_path in gesture_log_paths:
path_to_gesture_log = os.path.join(root_gesture_log_path, gesture_log_path)
print("Reading in:", path_to_gesture_log)
map_gestures_to_trials = parse_and_create_gesture_trials(path_to_gesture_log)
gesture_set = GestureSet(gesture_log_path, map_gestures_to_trials)
map_gesture_sets[gesture_set.get_base_path()] = gesture_set
if setName in gesture_log_path:
selected_gesture_set = gesture_set
if selected_gesture_set is not None:
print("The selected gesture set:", selected_gesture_set)
def get_gesture_set_with_str(str):
for base_path, gesture_set in map_gesture_sets.items():
if str in base_path:
return gesture_set
return None
# -
# ## Signal Exploration
# +
def topN_freqs(s, topN):
sampling_rate = 77
n = len(s)
fft = np.fft.fft(s)
freqs = np.fft.fftfreq(n)
freqs = freqs * sampling_rate # convert normalized freq bins to our freq bins
freqs = freqs[range(n//2)] # one side freq range
fft = np.abs(fft)[range(n//2)] # one side freq range
# Exclude the freq = 0
freqs = freqs[1:len(freqs)]
fft = fft[1:len(fft)]
# find the max frequency
# you could modify this to find the top ~3-5 max frequencies
topN_freqs = [freqs[idx] for idx in np.argsort(fft)[::-1][:topN]]
topN_ffts = [fft[idx] for idx in np.argsort(fft)[::-1][:topN]]
return {"freqs": topN_freqs, "ffts":topN_ffts}
def topN_peaks(s, topN):
peaks, _ = signal.find_peaks(s, )
prominences = signal.peak_prominences(s, peaks)[0]
widths = signal.peak_widths(s, peaks, rel_height=1)[0]
topN_prominences = [prominences[idx] for idx in np.argsort(prominences)[::-1][:topN]]
topN_widths = [widths[idx] for idx in np.argsort(prominences)[::-1][:topN]]
if len(topN_widths) < topN:
topN_widths += list(np.zeros(topN - len(topN_widths)))
topN_prominences += list(np.zeros(topN - len(topN_prominences)))
return {"prominences": topN_prominences, "widths": topN_widths}
# +
# first, let's graph some features along one dimension
# Brainstorm features
# - Length of signal
# - Max accel magnitude
# - Fundamental frequency
# - Top frequency
# - Intensity of top frequency
# - Top 5 frequency intensities (just plot which bins)
# - Average of values in the signal
# - Std deviation
# - Count of points above some threshold
# - Counting the number of peaks (above a threshold)
# - Zero crossings
# - Distance between zero crossings
# - Area under the curve
# - Max frequency of signal
# - Diff between max and mins
# - ... other things... read some papers, brainstorm, visualize!
import itertools
mapMarkerToDesc = {
".":"point",
",":"pixel",
"o":"circle",
"v":"triangle_down",
"^":"triangle_up",
"<":"triangle_left",
">":"triangle_right",
"1":"tri_down",
"2":"tri_up",
"3":"tri_left",
"4":"tri_right",
"8":"octagon",
"s":"square",
"p":"pentagon",
"*":"star",
"h":"hexagon1",
"H":"hexagon2",
"+":"plus",
"D":"diamond",
"d":"thin_diamond",
"|":"vline",
"_":"hline"
}
# # Plots the length of each trial's acceleration signal
# markers = list(mapMarkerToDesc.keys())
# marker = itertools.cycle(markers)
# plt.figure(figsize=(12, 4))
# for gesture_name in selected_gesture_set.get_gesture_names_sorted():
# trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
# x = list(len(trial.accel.mag) for trial in trials)
# y = np.random.rand(len(x))
# s = [200] * len(x)
# # s is the marker size
# plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
# plt.ylim((0,5))
# plt.legend(loc='upper left', bbox_to_anchor=(1,1))
# plt.title("1D Plot of Accel Mag")
# plt.show()
# # Plots the length of each trial's acceleration signal
# markers = list(mapMarkerToDesc.keys())
# marker = itertools.cycle(markers)
# plt.figure(figsize=(12, 4))
# for gesture_name in selected_gesture_set.get_gesture_names_sorted():
# trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
# x = list(max(trial.accel.mag) for trial in trials)
# y = np.random.rand(len(x))
# s = [200] * len(x)
# # s is the marker size
# plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
# plt.ylim((0,5))
# plt.legend(loc='upper left', bbox_to_anchor=(1,1))
# plt.title("1D Plot of Accel Mag")
# plt.show()
# # Plots the maximum magnitude of each trial's processed acceleration signal
# markers = list(mapMarkerToDesc.keys())
# marker = itertools.cycle(markers)
# plt.figure(figsize=(12, 4))
# for gesture_name in selected_gesture_set.get_gesture_names_sorted():
# trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
# x = list(trial.accel.mag_p.max() for trial in trials)
# y = np.random.rand(len(x))
# s = [200] * len(x)
# plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
# plt.ylim((0,5))
# plt.legend(loc='upper left', bbox_to_anchor=(1,1))
# plt.title("1D Plot of Max Accel Mag")
# plt.show()
# # std deviation
# markers = list(mapMarkerToDesc.keys())
# marker = itertools.cycle(markers)
# plt.figure(figsize=(12, 4))
# for gesture_name in selected_gesture_set.get_gesture_names_sorted():
# trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
# x = list(np.std(trial.accel.mag_p) for trial in trials)
# y = np.random.rand(len(x))
# s = [200] * len(x)
# plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
# plt.ylim((0,5))
# plt.legend(loc='upper left', bbox_to_anchor=(1,1))
# plt.title("1D Plot of Accel Mag Stdev")
# plt.show()
# CSE599 TODO: Come up with ~5 more features to plot below
# Max Freq
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_freqs(trial.accel.mag_p, 1)['freqs'][0] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of Max Freq")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_freqs(trial.accel.mag_p, 1)['ffts'][0] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of Amp of Max Freq")
plt.show()
# Top2 Freq
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_freqs(trial.accel.mag_p, 3)['freqs'][1] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of 2nd Freq")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_freqs(trial.accel.mag_p, 3)['ffts'][1] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of Amp of 2nd Freq")
plt.show()
# Top3 Freq
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_freqs(trial.accel.mag_p, 3)['freqs'][2] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of 3rd Freq")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_freqs(trial.accel.mag_p, 3)['ffts'][2] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of Amp of 3rd Freq")
plt.show()
# Max Peak
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_peaks(trial.accel.mag_p, 3)['prominences'][0] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of prominence of the 1st Peak")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_peaks(trial.accel.mag_p, 3)['widths'][0] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of width of the 1st Peak")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_peaks(trial.accel.mag_p, 3)['prominences'][1] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of prominence of the 2nd Peak")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_peaks(trial.accel.mag_p, 3)['widths'][1] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of width of the 2nd Peak")
plt.show()
# Max Peak
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_peaks(trial.accel.mag_p, 3)['prominences'][2] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of prominence of the 3rd Peak")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_peaks(trial.accel.mag_p, 3)['widths'][2] for trial in trials)
y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.ylim((0,5))
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("1D Plot of width of the 3rd Peak")
plt.show()
# +
# Now, let's explore the discriminability of 2 dimensions. We should begin to see
# some clusters and visual groupings based on gesture type--that's good!
# And rememember that the SVM is going to be in far more than 2 dimensions... but
# it's harder to visualize anything > 2, so this just gives us some intuition about separation
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 6))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(trial.accel.mag_p.max() for trial in trials)
y = list(len(trial.accel.mag) for trial in trials)
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("2D Plot of Max Accel Mag vs. Signal Length")
plt.show()
# num peaks vs. std dev
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 4))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = []
for trial in trials:
s = trial.accel.mag_p
min_distance_between_peaks = 77 / 3.0
peak_indices, peak_properties = sp.signal.find_peaks(s, height=30, distance=min_distance_between_peaks)
x.append(len(peak_indices))
y = list(np.std(trial.accel.mag_p) for trial in trials)
#print(gesture_name, x, y)
# y = np.random.rand(len(x))
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("2D Plot of Num Peaks vs. Std Dev")
plt.show()
# strongest freq intensity vs. std dev
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 6))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(np.abs(np.fft.fft(trial.accel.mag_p)).max() for trial in trials)
y = list(np.std(trial.accel.mag_p) for trial in trials)
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("Scatter Plot of Strongest Frequency Intensity vs Standard Deviation")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 6))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_peaks(trial.accel.mag_p, 3)['prominences'][0] for trial in trials)
y = list(topN_peaks(trial.accel.mag_p, 3)['widths'][0] for trial in trials)
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("Scatter Plot of Max Peack Prominence vs Max Peak Width")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 6))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_peaks(trial.accel.mag_p, 3)['prominences'][1] for trial in trials)
y = list(topN_peaks(trial.accel.mag_p, 3)['widths'][1] for trial in trials)
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("Scatter Plot of the 2nd Peack Prominence vs the Width of the Peak")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 6))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_peaks(trial.accel.mag_p, 3)['prominences'][2] for trial in trials)
y = list(topN_peaks(trial.accel.mag_p, 3)['widths'][2] for trial in trials)
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("Scatter Plot of the 3rd Peack Prominence vs the Width of the Peak")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 6))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_freqs(trial.accel.mag_p, 3)['freqs'][0] for trial in trials)
y = list(topN_freqs(trial.accel.mag_p, 3)['ffts'][0] for trial in trials)
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("Scatter Plot of Max Freq. vs Amp of the Max Freq.")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 6))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_freqs(trial.accel.mag_p, 3)['freqs'][1] for trial in trials)
y = list(topN_freqs(trial.accel.mag_p, 3)['ffts'][1] for trial in trials)
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("Scatter Plot of the 2nd Strongest Freq. vs Amp of the Freq.")
plt.show()
markers = list(mapMarkerToDesc.keys())
marker = itertools.cycle(markers)
plt.figure(figsize=(12, 6))
for gesture_name in selected_gesture_set.get_gesture_names_sorted():
trials = selected_gesture_set.map_gestures_to_trials[gesture_name]
x = list(topN_freqs(trial.accel.mag_p, 3)['freqs'][2] for trial in trials)
y = list(topN_freqs(trial.accel.mag_p, 3)['ffts'][2] for trial in trials)
s = [200] * len(x)
plt.scatter(x, y, alpha=0.75, marker=next(marker), s=s, label=gesture_name)
plt.legend(loc='upper left', bbox_to_anchor=(1,1))
plt.title("Scatter Plot of the 3rd Strongest Freq. vs Amp. of the Freq.")
plt.show()
# CSE599 In-Class Exercises TODO: Come up with ~5 more feature relationships to plot below
# Consult gesture recognition research papers for ideas. For example,
# Wu, J., et al. Gesture recognition with a 3-d accelerometer. UbiComp 2009
# -
# ## SVM Experiment Infrastructure
# +
# This cell contains some helper methods like my kfold generation function
# and confusion matrix plotting
from sklearn import svm # needed for svm
from sklearn.metrics import confusion_matrix
import itertools
# Returns a list of folds where each list item is a dict() with key=gesture name and value=selected trial
# for that fold. To generate the same fold structure, pass in the same seed value (this is useful for
# setting up experiments)
def generate_kfolds(numFolds, map_gestures_to_trials, seed=None):
# Quick check to make sure that there are numFolds of gesture trials for each gesture
for gestureName, trials in map_gestures_to_trials.items():
if numFolds != len(trials):
raise ValueError("For the purposes of this assignment, the number of folds={} must equal the number of trials for each gesture. Gesture '{}' has {} trials"
.format(numFolds, gestureName, len(trials)))
numGestures = len(map_gestures_to_trials)
tmpMapGestureToTrials = dict()
for gestureName, trials in map_gestures_to_trials.items():
tmpMapGestureToTrials[gestureName] = list(trials)
gestureNames = list(map_gestures_to_trials.keys())
# create folds
foldToMapGestureToTrial = list()
random.seed(seed)
for i in range(0, numFolds):
curFoldMapGestureToTrial = dict()
foldToMapGestureToTrial.append(curFoldMapGestureToTrial)
for j in range(0, numGestures):
curGestureName = gestureNames[j]
trialList = tmpMapGestureToTrials[curGestureName]
randTrialIndex = 0
if (len(trialList) > 0):
randTrialIndex = random.randint(0, len(trialList) - 1)
randTrial = trialList[randTrialIndex]
curFoldMapGestureToTrial[curGestureName] = randTrial
del trialList[randTrialIndex]
return foldToMapGestureToTrial
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=90)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
# -
# ## Features
# Returns a feature vectof for the given trial
def extract_features_example(trial):
# Play around with features to extract and use in your model
# Brainstorm features, visualize ideas, try them, and iterate
# This is likely where you will spend most of your time :)
# This is the "feature engineering" component of working in ML
features = []
features.append(trial.accel.mag.max())
features.append(np.std(trial.accel.mag))
# Younghoon's feature
topN_peaks_X_info = topN_peaks(trial.accel.x_p, 3)
topN_peaks_Y_info = topN_peaks(trial.accel.x_p, 3)
topN_peaks_Z_info = topN_peaks(trial.accel.x_p, 3)
topN_peaks_mag_info = topN_peaks(trial.accel.x_p, 3)
features.append(topN_peaks_X_info['prominences'][0])
features.append(topN_peaks_X_info['prominences'][1])
features.append(topN_peaks_X_info['prominences'][2])
features.append(topN_peaks_X_info['widths'][0])
features.append(topN_peaks_X_info['widths'][1])
features.append(topN_peaks_X_info['widths'][2])
features.append(topN_peaks_Y_info['prominences'][0])
features.append(topN_peaks_Y_info['prominences'][1])
features.append(topN_peaks_Y_info['prominences'][2])
features.append(topN_peaks_Y_info['widths'][0])
features.append(topN_peaks_Y_info['widths'][1])
features.append(topN_peaks_Y_info['widths'][2])
features.append(topN_peaks_Z_info['prominences'][0])
features.append(topN_peaks_Z_info['prominences'][1])
features.append(topN_peaks_Z_info['prominences'][2])
features.append(topN_peaks_Z_info['widths'][0])
features.append(topN_peaks_Z_info['widths'][1])
features.append(topN_peaks_Z_info['widths'][2])
topN_freqs_info = topN_freqs(trial.accel.mag_p, 3)
features.append(topN_freqs_info['freqs'][0])
features.append(topN_freqs_info['freqs'][1])
features.append(topN_freqs_info['freqs'][2])
features.append(topN_freqs_info['ffts'][0])
features.append(topN_freqs_info['ffts'][1])
features.append(topN_freqs_info['ffts'][2])
return features
# ## Shape Matching
# +
# Calculate the maxLength
maxLength = 0
selected_gesture_set = get_gesture_set_with_str(setName)
gestureNamesSorted = sorted(selected_gesture_set.get_gesture_names_sorted())
for gestureName in gestureNamesSorted:
gestureTrials = selected_gesture_set.map_gestures_to_trials[gestureName]
for trial in gestureTrials:
maxLength = max(maxLength, len(trial.accel.x))
# Take a signal (SensorData) and compare to the others and classify the gesture of the signal.
def shape_matchin_clf(signal, otherFolds):
minD = np.inf
guess = '??'
for fold in otherFolds:
for gestureName in gestureNamesSorted:
signalB = fold[gestureName].accel
d = dist(signal.accel, signalB)
if d < minD:
guess = gestureName
minD = d
return guess
# More efficient implementation is possible by reducing the length of the padded signals to 2 * maxLength.
def dist(sigA, sigB):
sigA_N = len(sigA.currentTimeMs)
sigB_N = len(sigB.currentTimeMs)
sigB.pad_with_mean(maxLength, maxLength*2 - sigB_N)
minD = np.inf
argMinOffset = 0
for offset in range(0, maxLength + sigB_N):
sigA.pad_with_mean(offset, 3*maxLength - offset - sigA_N)
dX = np.linalg.norm(sigA.x_padded - sigB.x_padded)
dY = np.linalg.norm(sigA.y_padded - sigB.y_padded)
dZ = np.linalg.norm(sigA.z_padded - sigB.z_padded)
d = dX + dY + dZ
if d < minD :
argMinOffset = offset
minD = d
return minD
# +
numFolds = 5
numGestures = selected_gesture_set.get_num_gestures()
numTrialsTotal = selected_gesture_set.get_total_num_of_trials()
foldToMapGestureToTrial = generate_kfolds(numFolds, selected_gesture_set.map_gestures_to_trials, seed=5)
mapGestureToCorrectMatches = dict()
y_true = []
y_pred = []
gestureNamesSorted = selected_gesture_set.get_gesture_names_sorted()
for gestureName in gestureNamesSorted:
mapGestureToCorrectMatches[gestureName] = 0
for i in range(0, len(foldToMapGestureToTrial)):
trainingFolds = foldToMapGestureToTrial.copy()
testFold = trainingFolds.pop(i)
trainingData = []
classLabels = np.array([])
# make predictions for this test set
for testGestureName, testTrial in testFold.items():
y_true.append(testGestureName)
prediction = shape_matchin_clf(testTrial, trainingFolds)
y_pred.append(prediction)
if testGestureName == prediction:
mapGestureToCorrectMatches[testGestureName] += 1
totalCorrectMatches = 0
print("Shape-matching Results:\n")
for gesture in mapGestureToCorrectMatches:
c = mapGestureToCorrectMatches[gesture]
print("{}: {}/{} ({}%)".format(gesture, c, numFolds, c / numFolds * 100))
totalCorrectMatches += mapGestureToCorrectMatches[gesture]
print("\nTotal Shape-matching classifier accuracy {:0.2f}%\n".format(totalCorrectMatches / numTrialsTotal * 100))
cm = confusion_matrix(y_true, y_pred, gestureNamesSorted)
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, classes=gestureNamesSorted, title='Confusion Matrix')
plt.show()
# -
# ## The SVM
# +
# This is the simplest possible SVM using only a few features but gives you a sense of the overall approach
# Some nice resources:
# - A very simple classification example using scikit:
# https://dbaumgartel.wordpress.com/2014/03/10/a-scikit-learn-example-in-10-lines/
# - A nice video overview of SVM: https://youtu.be/N1vOgolbjSc
# - Official sci-kit learn: http://scikit-learn.org/stable/modules/svm.html
from sklearn import svm
from sklearn.preprocessing import StandardScaler
import itertools
numFolds = 5
selected_gesture_set = get_gesture_set_with_str(setName)
numGestures = selected_gesture_set.get_num_gestures()
numTrialsTotal = selected_gesture_set.get_total_num_of_trials()
# Setting a seed here keeps producing the same folds set each time. Take that out
# if you want to randomly produce a fold set on every execution
foldToMapGestureToTrial = generate_kfolds(numFolds, selected_gesture_set.map_gestures_to_trials, seed=5)
mapGestureToCorrectMatches = dict()
y_true = []
y_pred = []
gestureNamesSorted = selected_gesture_set.get_gesture_names_sorted()
for gestureName in gestureNamesSorted:
mapGestureToCorrectMatches[gestureName] = 0
for i in range(0, len(foldToMapGestureToTrial)):
trainingFolds = foldToMapGestureToTrial.copy()
testFold = trainingFolds.pop(i)
trainingData = []
classLabels = np.array([])
# build training data for this set of folds
for trainingFold in trainingFolds:
for trainingGestureName, trainingTrial in trainingFold.items():
features = extract_features_example(trainingTrial)
trainingData.append(features)
classLabels = np.append(classLabels, trainingGestureName)
# Here, we train SVM, the 'rbf' kernal is default
# if you use rbf, need to set gamma and C parameters
# play around with different kernels, read about them, and try them. What happens?
# see:
# - https://scikit-learn.org/stable/auto_examples/svm/plot_rbf_parameters.html#sphx-glr-auto-examples-svm-plot-rbf-parameters-py
# - https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
clf = svm.SVC(kernel='rbf', gamma='scale') # kernel='linear'
# clf = svm.SVC(kernel='linear') # kernel='linear'
# Scale
np_train = np.array(trainingData)
scaler = StandardScaler()
scaler.fit(np_train)
np_train_scaled = scaler.transform(np_train)
# clf.fit(np_train, classLabels)
clf.fit(np_train_scaled, classLabels)
# make predictions for this test set
for testGestureName, testTrial in testFold.items():
features = np.array(extract_features_example(testTrial))
features_scaled = scaler.transform([features])
svmPrediction = clf.predict(features_scaled)
# svmPrediction = clf.predict([features])
y_true.append(testGestureName)
y_pred.append(svmPrediction)
if testGestureName == svmPrediction[0]:
mapGestureToCorrectMatches[testGestureName] += 1
totalCorrectMatches = 0
print("SVM Results:\n")
for gesture in mapGestureToCorrectMatches:
c = mapGestureToCorrectMatches[gesture]
print("{}: {}/{} ({}%)".format(gesture, c, numFolds, c / numFolds * 100))
totalCorrectMatches += mapGestureToCorrectMatches[gesture]
print("\nTotal SVM classifier accuracy {:0.2f}%\n".format(totalCorrectMatches / numTrialsTotal * 100))
cm = confusion_matrix(y_true, y_pred, gestureNamesSorted)
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, classes=gestureNamesSorted, title='Confusion Matrix')
plt.show()
# -
# ## The Decision Tree
# +
from sklearn import tree
numFolds = 5
selected_gesture_set = get_gesture_set_with_str(setName)
numGestures = selected_gesture_set.get_num_gestures()
numTrialsTotal = selected_gesture_set.get_total_num_of_trials()
foldToMapGestureToTrial = generate_kfolds(numFolds, selected_gesture_set.map_gestures_to_trials, seed=5)
mapGestureToCorrectMatches = dict()
y_true = []
y_pred = []
gestureNamesSorted = selected_gesture_set.get_gesture_names_sorted()
for gestureName in gestureNamesSorted:
mapGestureToCorrectMatches[gestureName] = 0
for i in range(0, len(foldToMapGestureToTrial)):
trainingFolds = foldToMapGestureToTrial.copy()
testFold = trainingFolds.pop(i)
trainingData = []
classLabels = np.array([])
# build training data for this set of folds
for trainingFold in trainingFolds:
for trainingGestureName, trainingTrial in trainingFold.items():
features = extract_features_example(trainingTrial)
trainingData.append(features)
classLabels = np.append(classLabels, trainingGestureName)
# Here, we train SVM, the 'rbf' kernal is default
# if you use rbf, need to set gamma and C parameters
# play around with different kernels, read about them, and try them. What happens?
# see:
# - https://scikit-learn.org/stable/auto_examples/svm/plot_rbf_parameters.html#sphx-glr-auto-examples-svm-plot-rbf-parameters-py
# - https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
# clf = svm.SVC(kernel='linear') # kernel='rbf'
clf = tree.DecisionTreeClassifier()
clf.fit(np.array(trainingData), classLabels)
# make predictions for this test set
for testGestureName, testTrial in testFold.items():
features = extract_features_example(testTrial)
svmPrediction = clf.predict([features])
y_true.append(testGestureName)
y_pred.append(svmPrediction)
if testGestureName == svmPrediction[0]:
mapGestureToCorrectMatches[testGestureName] += 1
totalCorrectMatches = 0
print("Decision Tree Results:\n")
for gesture in mapGestureToCorrectMatches:
c = mapGestureToCorrectMatches[gesture]
print("{}: {}/{} ({}%)".format(gesture, c, numFolds, c / numFolds * 100))
totalCorrectMatches += mapGestureToCorrectMatches[gesture]
print("\nTotal Decision Tree classifier accuracy {:0.2f}%\n".format(totalCorrectMatches / numTrialsTotal * 100))
cm = confusion_matrix(y_true, y_pred, gestureNamesSorted)
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, classes=gestureNamesSorted, title='Confusion Matrix')
plt.show()
# -
# ## The MLPClassifier
# +
from sklearn.neural_network import MLPClassifier
numFolds = 5
selected_gesture_set = get_gesture_set_with_str(setName)
numGestures = selected_gesture_set.get_num_gestures()
numTrialsTotal = selected_gesture_set.get_total_num_of_trials()
# Setting a seed here keeps producing the same folds set each time. Take that out
# if you want to randomly produce a fold set on every execution
foldToMapGestureToTrial = generate_kfolds(numFolds, selected_gesture_set.map_gestures_to_trials, seed=5)
mapGestureToCorrectMatches = dict()
y_true = []
y_pred = []
gestureNamesSorted = selected_gesture_set.get_gesture_names_sorted()
for gestureName in gestureNamesSorted:
mapGestureToCorrectMatches[gestureName] = 0
for i in range(0, len(foldToMapGestureToTrial)):
trainingFolds = foldToMapGestureToTrial.copy()
testFold = trainingFolds.pop(i)
trainingData = []
classLabels = np.array([])
# build training data for this set of folds
for trainingFold in trainingFolds:
for trainingGestureName, trainingTrial in trainingFold.items():
features = extract_features_example(trainingTrial)
trainingData.append(features)
classLabels = np.append(classLabels, trainingGestureName)
np_train = np.array(trainingData)
scaler = StandardScaler()
scaler.fit(np_train)
np_train_scaled = scaler.transform(np_train)
clf = MLPClassifier(solver='lbfgs', hidden_layer_sizes=[1000])
clf.fit(np_train_scaled, classLabels)
# make predictions for this test set
for testGestureName, testTrial in testFold.items():
features = np.array(extract_features_example(testTrial))
features_scaled = scaler.transform([features])
svmPrediction = clf.predict(features_scaled)
# svmPrediction = clf.predict([features])
y_true.append(testGestureName)
y_pred.append(svmPrediction)
if testGestureName == svmPrediction[0]:
mapGestureToCorrectMatches[testGestureName] += 1
totalCorrectMatches = 0
print("MLPClassifier Results:\n")
for gesture in mapGestureToCorrectMatches:
c = mapGestureToCorrectMatches[gesture]
print("{}: {}/{} ({}%)".format(gesture, c, numFolds, c / numFolds * 100))
totalCorrectMatches += mapGestureToCorrectMatches[gesture]
print("\nTotal MLPClassifier classifier accuracy {:0.2f}%\n".format(totalCorrectMatches / numTrialsTotal * 100))
cm = confusion_matrix(y_true, y_pred, gestureNamesSorted)
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, classes=gestureNamesSorted, title='Confusion Matrix')
plt.show()
# -
| 56,978 |
/InterpretableClassification/ECG200_FS.ipynb
|
2092d35508967b9931fce2e328d697d447922bf0
|
[] |
no_license
|
zhaoli064/ML_Projects
|
https://github.com/zhaoli064/ML_Projects
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 49,773 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#installing seleniumlibrary
# ! pip install selenium
#importing required libraries
import selenium
import pandas as pd
from selenium import webdriver
#let's connect to the webdriver
driver = webdriver.Chrome("C:/Users/key/AppData/Roaming/Microsoft/Windows/Start Menu/Programs/chromedriver_win32/chromedriver.exe")
# + active=""
#
# + active=""
# Q1: Write a python program to scrape data for “Data Analyst” Job position in
# “Bangalore” location. You have to scrape the job-title, job-location, company_name,
# experience_required. You have to scrape first 10 jobs data.
# + active=""
#
# -
driver.get(' https://www.naukri.com/')
#finding element for job search bar
search_job=driver.find_element_by_id('qsb-keyword-sugg')
search_job.send_keys('Data Analyst')
search_loc=driver.find_element_by_xpath("//input[@id='qsb-location-sugg']")
search_loc.send_keys("Banglore")
search_btn=driver.find_element_by_xpath("//div[@class='search-btn']/button")
search_btn.click()
#specifying the url of webpage to be scraped
url="https://www.naukri.com/data-analyst-data-analyst-jobs-in-banglore?k=data%20analyst%2C%20data%20analyst&l=banglore"
#let's open the webpage through our webdriver
driver.get(url)
# + active=""
# 1.job-title 2.job-location 3.company_name 4.experience_required
# -
#creating the empty lists to which the final scraped data will be stored
job_titles=[]
company_names=[]
locations_list=[]
experience_list=[]
#let's extract all the tags having the job titles
title_tags=driver.find_elements_by_xpath("//a[@class='title fw500 ellipsis']")
title_tags[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in title_tags:
title=i.text
job_titles.append(title)
job_titles[0:9]
#let's extract all the tags having the company names
companies_tags=driver.find_elements_by_xpath("//a[@class='subTitle ellipsis fleft']")
companies_tags[0:9]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in companies_tags:
company_name=i.text
company_names.append(company_name)
company_names[0:9]
#Now we will extract all the html tags having the experience required
experience_tags=driver.find_elements_by_xpath("//li[@class='fleft grey-text br2 placeHolderLi experience']/span[1]")
experience_tags[0:9]
#let's extract the text inside the tags using a for loop to iterate over all the tags
for i in experience_tags:
experience=i.text
experience_list.append(experience)
experience_list[0:9]
#Let's extract all the html tags having the experience required
locations_tags=driver.find_elements_by_xpath("//li[@class='fleft grey-text br2 placeHolderLi location']/span[1]")
locations_tags[0:9]
#now extract the text inside the tags using a for loop to iterate over all the tags
for i in locations_tags:
locations=i.text
locations_list.append(locations)
locations_list[0:9]
# + active=""
# So, now we have extracted the data required from the webpage and stored them in the 4 lists mentioned above. Now before craeting a dataframe from these lists, let's first check the length of each of the list. Because if the length of all of the lists are not equal, then a dataframe cannot be formed.
# -
print(len(job_titles),len(company_names),len(experience_list),len(locations_list))
jobs=pd.DataFrame({})
jobs['job_title']=job_titles
jobs['company_name']=company_names
jobs['experience_required']=experience_list
jobs['job_location']=locations_list
jobs
# + active=""
#
# + active=""
# Q2: Write a python program to scrape data for “Data Scientist” Job position in
# “Bangalore” location. You have to scrape the job-title, job-location,
# company_name, full job-description. You have to scrape first 10 jobs data.
# + active=""
#
# -
#importing required libraries
import selenium
import pandas as pd
from selenium import webdriver
#let's connect to the webdriver
driver = webdriver.Chrome("C:/Users/key/AppData/Roaming/Microsoft/Windows/Start Menu/Programs/chromedriver_win32/chromedriver.exe")
driver.get(' https://www.naukri.com/')
#finding element for job search bar
search_job=driver.find_element_by_id('qsb-keyword-sugg')
search_job.send_keys('Data Scientist')
search_loc=driver.find_element_by_xpath("//input[@id='qsb-location-sugg']")
search_loc.send_keys("Banglore")
search_btn=driver.find_element_by_xpath("//div[@class='search-btn']/button")
search_btn.click()
#specifying the url of webpage to be scraped
url="https://www.naukri.com/data-scientist-jobs-in-banglore?k=data%20scientist&l=banglore"
#let's open the webpage through our webdriver
driver.get(url)
# + active=""
# 1.job-title 2.job-location 3.company_name 4.job_description
# -
#creating the empty lists to which the final scraped data will be stored
job_titles=[]
company_names=[]
locations_list=[]
job_description_list=[]
#let's extract all the tags having the job titles
title_tags=driver.find_elements_by_xpath("//a[@class='title fw500 ellipsis']")
title_tags[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in title_tags:
title=i.text
job_titles.append(title)
job_titles[0:10]
#let's extract all the tags having the company names
companies_tags=driver.find_elements_by_xpath("//a[@class='subTitle ellipsis fleft']")
companies_tags[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in companies_tags:
company_name=i.text
company_names.append(company_name)
company_names[0:10]
#Let's extract all the html tags having the experience required
locations_tags=driver.find_elements_by_xpath("//li[@class='fleft grey-text br2 placeHolderLi location']/span[1]")
locations_tags[0:10]
#now extract the text inside the tags using a for loop to iterate over all the tags
for i in locations_tags:
locations=i.text
locations_list.append(locations)
locations_list[0:10]
urls=driver.find_elements_by_xpath("//a[@class='title fw500 ellipsis']")
urls[0:10]
#now extract the text inside the tags using a for loop to iterate over all the tags
for i in urls[0:10]:
print(i.get_attribute('href'))
driver.get(i.get_attribute('href'))
from selenium.common.exceptions import StaleElementReferenceException
from selenium.webdriver.support.ui import WebDriverWait
from selenium.webdriver.support import expected_conditions as EC
from selenium.webdriver.common.by import By
driver=webdriver.Chrome("C:/Users/key/AppData/Roaming/Microsoft/Windows/Start Menu/Programs/chromedriver_win32/chromedriver.exe")
driver.get("https://www.naukri.com/")
try:
element=driver.find_element_by_xpath("//a[@class='title fw500 ellipsis']")
print(element)
except StaleElementReferenceException as e:
print("Exception Raised: ",e)
print("Refreshing the page!")
driver.get("https://www.naukri.com/")
WebDriverWait(driver,delay).until(EC.presence_of_element_located((By.CLASS_NAME,'title fw500 ellipsis')))
element=driver.find_element_by_xpath("//a[@class='title fw500 ellipsis']")
print(element)
#Let's extract all the html tags having the job description
job_description_tags=driver.find_elements_by_xpath("//a[starts-with(@href='https')]")
job_description_tags[0:9]
#Let's extract all the html tags having the job description
job_description_tags=driver.find_elements_by_xpath("//a[text()='https://www.naukri.com/job-listings']")
job_description_tags[0:9]
#now extract the text inside the tags using a for loop to iterate over all the tags
for i in job_description_tags[0:9]:
print(i.get_attribute('href'))
driver.get(i.get_attribute('href'))
#Let's extract all the html tags having the job description
job_description_tags=driver.find_elements_by_xpath("//div[@class='leftSec']/section[2]/div[1]/p[2]")
job_description_tags[0:9]
# + active=""
#
# + active=""
# Q3: In this question you have to scrape data using the filters available on the
# webpage as shown below:
# + active=""
#
# -
#let's connect to the webdriver
driver = webdriver.Chrome("C:/Users/key/AppData/Roaming/Microsoft/Windows/Start Menu/Programs/chromedriver_win32/chromedriver.exe")
driver.get('https://www.naukri.com/')
#finding element for job search bar
search_job=driver.find_element_by_id('qsb-keyword-sugg')
search_job.send_keys('Data Scientist')
search_btn=driver.find_element_by_xpath("//div[@class='search-btn']/button")
search_btn.click()
location_checkbox=driver.find_element_by_xpath("//div[@data-filter-id='cities']/div[2]")
location_checkbox.click()
salary_checkbox=driver.find_element_by_xpath("//div[@data-filter-id='salaryRange']/div[2]")
salary_checkbox.click()
#creating the empty lists to which the final scraped data will be stored
job_titles=[]
company_names=[]
locations_list=[]
experience_list=[]
#let's extract all the tags having the job titles
title_tags=driver.find_elements_by_xpath("//a[@class='title fw500 ellipsis']")
title_tags[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in title_tags:
title=i.text
job_titles.append(title)
job_titles[0:10]
#let's extract all the tags having the company names
companies_tags=driver.find_elements_by_xpath("//a[@class='subTitle ellipsis fleft']")
companies_tags[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in companies_tags:
company_name=i.text
company_names.append(company_name)
company_names[0:10]
#Now we will extract all the html tags having the experience required
experience_tags=driver.find_elements_by_xpath("//li[@class='fleft grey-text br2 placeHolderLi experience']/span[1]")
experience_tags[0:10]
experience_list=[]
#let's extract the text inside the tags using a for loop to iterate over all the tags
for i in experience_tags:
experience=i.text
experience_list.append(experience)
experience_list[0:10]
#Let's extract all the html tags having the experience required
locations_tags=driver.find_elements_by_xpath("//li[@class='fleft grey-text br2 placeHolderLi location']/span[1]")
locations_tags[0:10]
#now extract the text inside the tags using a for loop to iterate over all the tags
for i in locations_tags:
locations=i.text
locations_list.append(locations)
locations_list[0:10]
print(len(job_titles),len(company_names),len(experience_list),len(locations_list))
jobs=pd.DataFrame({})
jobs['job_title']=job_titles[0:10]
jobs['company_name']=company_names[0:10]
jobs['experience_required']=experience_list[0:10]
jobs['job_location']=locations_list[0:10]
jobs
# + active=""
#
# + active=""
# Q4: Write a python program to scrape data for first 10 job results for Data scientist
# Designation in Noida location. You have to scrape company_name, No. of days
# ago when job was posted, Rating of the company.
# + active=""
#
# -
#let's connect to the webdriver
driver = webdriver.Chrome("C:/Users/key/AppData/Roaming/Microsoft/Windows/Start Menu/Programs/chromedriver_win32/chromedriver.exe")
driver.get('https://www.glassdoor.co.in/index.htm')
#finding element for job search bar
search_job=driver.find_element_by_id('scKeyword')
search_job.send_keys('Data Scientist')
search_loc=driver.find_element_by_xpath("//input[@id='scLocation']")
search_loc.send_keys("Noida")
search_btn=driver.find_element_by_xpath("//button[@class='pl-0 pr-xsm SearchStyles__searchKeywordSubmit']")
search_btn.click()
#creating the empty lists to which the final scraped data will be stored
job_titles=[]
company_names=[]
daysago_jobposted=[]
company_ratings=[]
#let's extract all the tags having the job titles
title_tags=driver.find_elements_by_xpath("//a[@class='jobLink css-1rd3saf eigr9kq2']")
title_tags[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in title_tags:
title=i.text
job_titles.append(title)
job_titles[0:10]
#let's extract all the tags having the company names
companies_tags=driver.find_elements_by_xpath("//div[@class='d-flex justify-content-between align-items-start']")
companies_tags[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in companies_tags:
company_name=i.text
company_names.append(company_name)
company_names[0:10]
#let's extract all the tags having the no of days ago when job was posted
days_jobposted_tags=driver.find_elements_by_xpath("//div[@class='d-flex align-items-end pl-std css-mi55ob']")
days_jobposted_tags[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in days_jobposted_tags:
days_jobposted=i.text
daysago_jobposted.append(days_jobposted)
daysago_jobposted[0:10]
#let's extract all the tags having the rating of the company
company_rating=driver.find_elements_by_xpath("//span[@class='css-19pjha7 e1cjmv6j1']")
company_rating[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in company_rating:
ratings=i.text
company_ratings.append(ratings)
company_ratings[0:10]
print(len(job_titles),len(company_names),len(daysago_jobposted),len(company_ratings))
jobs=pd.DataFrame({})
jobs['job_title']=job_titles[0:10]
jobs['company_name']=company_names[0:10]
jobs['jobposted_days']=daysago_jobposted[0:10]
jobs['company_rating']=company_ratings[0:10]
jobs
# + active=""
#
# + active=""
# Q5: Write a python program to scrape the salary data for Data Scientist designation
# in Noida location.
# + active=""
#
# -
#importing required libraries
import selenium
import pandas as pd
from selenium import webdriver
#let's connect to the webdriver
driver = webdriver.Chrome("C:/Users/key/AppData/Roaming/Microsoft/Windows/Start Menu/Programs/chromedriver_win32/chromedriver.exe")
driver.get('https://www.glassdoor.co.in/Salaries/index.htm')
#finding element for job search bar
search_job=driver.find_element_by_id('KeywordSearch')
search_job.send_keys('Data Scientist')
search_btn=driver.find_element_by_xpath("//button[@class='gd-btn-mkt']")
search_btn.click()
search_loc=driver.find_element_by_xpath("//input[@id='scLocation']")
search_loc.send_keys("Noida")
search_btn=driver.find_element_by_xpath("//button[@class='pl-0 pr-xsm SearchStyles__searchKeywordSubmit']")
search_btn.click()
#creating the empty lists to which the final scraped data will be stored
company_names=[]
range_salary=[]
avg_salary=[]
company_ratings=[]
#let's extract all the tags having the average salary
comp_name=driver.find_elements_by_xpath("//div[@class='d-flex']/div[2]/p[2]")
comp_name[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in comp_name:
names=i.text
company_names.append(names)
company_names[0:10]
#let's extract all the tags having the average salary
average_salary=driver.find_elements_by_xpath("//p[@class='d-block d-md-none m-0']")
average_salary[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in average_salary:
avegage_sal=i.text
avg_salary.append(avegage_sal)
avg_salary[0:10]
#let's extract all the tags having the minimum salary
salary_range=driver.find_elements_by_xpath("//p[@class='d-block d-md-none m-0 css-1kuy7z7']")
salary_range[0:10]
for i in salary_range:
sal_range=i.text
range_salary.append(sal_range)
range_salary[0:10]
print(len(company_names),len(average_salary),len(salary_range),len(company_ratings))
companyinfo=pd.DataFrame({})
companyinfo['comp_name']=company_names[0:10]
companyinfo['comp_avg_sal']=average_salary[0:10]
companyinfo['sal_range']=salary_range[0:10]
companyinfo['company_rating']=company_ratings[0:10]
# + active=""
#
# + active=""
# Q6 : Scrape data of first 100 sunglasses listings on flipkart.com. You have to
# scrape four attributes:
# + active=""
#
# -
#let's connect to the webdriver
driver = webdriver.Chrome("C:/Users/key/AppData/Roaming/Microsoft/Windows/Start Menu/Programs/chromedriver_win32/chromedriver.exe")
driver.get('https://www.flipkart.com/')
#finding element for job search bar
search_job=driver.find_element_by_xpath("//input[@type='text']")
search_job.send_keys('sunglasses')
search_btn=driver.find_element_by_xpath("//button[@class='L0Z3Pu']")
search_btn.click()
#creating the empty lists to which the final scraped data from page 1 will be stored
brand_name=[]
product_description=[]
product_price=[]
discount_perc=[]
#let's extract all the tags having the brand name
brand=driver.find_elements_by_xpath("//div[@class='_2WkVRV']")
brand[0:40]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in brand:
brands=i.text
brand_name.append(brands)
brand_name[0:40]
#let's extract all the tags having the product description
description=driver.find_elements_by_xpath("//a[@class='IRpwTa']")
description[0:40]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in description:
descriptions=i.text
product_description.append(descriptions)
product_description[0:40]
#let's extract all the tags having the product price
price=driver.find_elements_by_xpath("//div[@class='_30jeq3']")
price[0:40]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in price:
prices=i.text
product_price.append(prices)
product_price[0:40]
#let's extract all the tags having the discount percentage
discount=driver.find_elements_by_xpath("//div[@class='_3Ay6Sb']")
discount[0:40]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in discount:
discounts=i.text
discount_perc.append(discounts)
discount_perc[0:40]
#scraping the elements of the next page(page2)
driver.find_element_by_xpath("//a[@class='_1LKTO3']").click()
#creating the empty lists to which the final scraped data from page 2 will be stored
brand_name2=[]
product_description2=[]
product_price2=[]
discount_perc2=[]
#let's extract all the tags having the brand name
brand2=driver.find_elements_by_xpath("//div[@class='_2WkVRV']")
brand2[0:40]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in brand2:
brands=i.text
brand_name2.append(brands)
brand_name2[0:40]
#let's extract all the tags having the product description
description2=driver.find_elements_by_xpath("//a[@class='IRpwTa']")
description2[0:40]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in description2:
descriptions=i.text
product_description2.append(descriptions)
product_description2[0:40]
#let's extract all the tags having the product price
price2=driver.find_elements_by_xpath("//div[@class='_30jeq3']")
price2[0:40]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in price2:
prices=i.text
product_price2.append(prices)
product_price2[0:40]
#let's extract all the tags having the discount percentage
discount2=driver.find_elements_by_xpath("//div[@class='_3Ay6Sb']")
discount2[0:40]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in discount2:
discounts=i.text
discount_perc2.append(discounts)
discount_perc2[0:40]
#scraping the elements of the next page(page3)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[12]").click()
#creating the empty lists to which the final scraped data from page 3 will be stored
brand_name3=[]
product_description3=[]
product_price3=[]
discount_perc3=[]
#let's extract all the tags having the brand name
brand3=driver.find_elements_by_xpath("//div[@class='_2WkVRV']")
brand3[0:20]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in brand3:
brands=i.text
brand_name3.append(brands)
brand_name3[0:20]
#let's extract all the tags having the product description
description3=driver.find_elements_by_xpath("//a[@class='IRpwTa']")
description3[0:20]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in description3:
descriptions=i.text
product_description3.append(descriptions)
product_description3[0:20]
#let's extract all the tags having the product price
price3=driver.find_elements_by_xpath("//div[@class='_30jeq3']")
price3[0:20]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in price3:
prices=i.text
product_price3.append(prices)
product_price3[0:20]
#let's extract all the tags having the discount percentage
discount3=driver.find_elements_by_xpath("//div[@class='_3Ay6Sb']")
discount3[0:20]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in discount3:
discounts=i.text
discount_perc3.append(discounts)
discount_perc3[0:40]
# +
#Adding lists having same attribute type from all the 3 pages
# -
brand_name_final=brand_name+brand_name2+brand_name3
product_description_final=product_description+product_description2+product_description3
product_price_final=product_price+product_price2+product_price3
discount_perc_final=discount_perc+discount_perc2+discount_perc3
print(len(brand_name_final),len(product_description_final),len(product_price_final),len(discount_perc_final))
sunglassesinfoflipkart=pd.DataFrame({})
sunglassesinfoflipkart['brand_name']=brand_name_final[0:100]
sunglassesinfoflipkart['product_description']=product_description_final[0:100]
sunglassesinfoflipkart['product_price']=product_price_final[0:100]
sunglassesinfoflipkart['discount_perc']=discount_perc_final[0:100]
sunglassesinfoflipkart
# + active=""
#
# + active=""
# Q7: Scrape 100 reviews data from flipkart.com for iphone11 phone. You have to
# go the link: https://www.flipkart.com/apple-iphone-11-black-64-gb-includesearpods-poweradapter/p/itm0f37c2240b217?pid=MOBFKCTSVZAXUHGR&lid=LSTMOBFKC
# TSVZAXUHGREPBFGI&marketplace.
# + active=""
#
# -
#let's connect to the webdriver
driver = webdriver.Chrome("C:/Users/key/AppData/Roaming/Microsoft/Windows/Start Menu/Programs/chromedriver_win32/chromedriver.exe")
driver.get('https://www.flipkart.com/apple-iphone-11-black-64-gb-includesearpods-poweradapter/p/itm0f37c2240b217?pid=MOBFKCTSVZAXUHGR&lid=LSTMOBFKCTSVZAXUHGREPBFGI&marketplace')
#creating the empty lists to which the final scraped data from page 1 will be stored
iphone11_rating=[]
iphone11_reviewsum=[]
iphone11_reviewfull=[]
#scraping the elements of the first page(page1)
driver.find_element_by_xpath("//div[@class='_3UAT2v _16PBlm']").click()
#let's extract all the tags having the rating
rating=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
rating[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in rating:
ratings=i.text
iphone11_rating.append(ratings)
iphone11_rating[0:10]
#let's extract all the tags having the review summary
reviwsum=driver.find_elements_by_xpath("//p[@class='_2-N8zT']")
reviwsum[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwsum:
reviwsums=i.text
iphone11_reviewsum.append(reviwsums)
iphone11_reviewsum[0:10]
#let's extract all the tags having the review full
reviwfull=driver.find_elements_by_xpath("//div[@class='t-ZTKy']")
reviwfull[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwfull:
reviwsfull=i.text
iphone11_reviewfull.append(reviwsfull)
iphone11_reviewfull[0:10]
for page in range(0,10):
rating_tags=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
for i in rating_tags:
rating=i.text
iphone_ratings.append(rating)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[12]").click()
iphone_ratings
#scraping the elements of the next page(page2)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[11]").click()
#creating the empty lists to which the final scraped data from page 2 will be stored
iphone11_rating2=[]
iphone11_reviewsum2=[]
iphone11_reviewfull2=[]
#let's extract all the tags having the rating
rating2=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
rating2[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in rating2:
ratings=i.text
iphone11_rating2.append(ratings)
iphone11_rating2[0:10]
#let's extract all the tags having the review summary
reviwsum2=driver.find_elements_by_xpath("//p[@class='_2-N8zT']")
reviwsum2[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwsum2:
reviwsums=i.text
iphone11_reviewsum2.append(reviwsums)
iphone11_reviewsum2[0:10]
#let's extract all the tags having the review full
reviwfull2=driver.find_elements_by_xpath("//div[@class='t-ZTKy']")
reviwfull2[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwfull2:
reviwsfull=i.text
iphone11_reviewfull2.append(reviwsfull)
iphone11_reviewfull2[0:10]
#scraping the elements of the next page(page3)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[12]").click()
#creating the empty lists to which the final scraped data from page 3 will be stored
iphone11_rating3=[]
iphone11_reviewsum3=[]
iphone11_reviewfull3=[]
#let's extract all the tags having the rating
rating3=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
rating3[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in rating3:
ratings=i.text
iphone11_rating3.append(ratings)
iphone11_rating3[0:10]
#let's extract all the tags having the review summary
reviwsum3=driver.find_elements_by_xpath("//p[@class='_2-N8zT']")
reviwsum3[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwsum3:
reviwsums=i.text
iphone11_reviewsum3.append(reviwsums)
iphone11_reviewsum3[0:10]
#let's extract all the tags having the review full
reviwfull3=driver.find_elements_by_xpath("//div[@class='t-ZTKy']")
reviwfull3[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwfull3:
reviwsfull=i.text
iphone11_reviewfull3.append(reviwsfull)
iphone11_reviewfull3[0:10]
#scraping the elements of the next page(page4)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[12]").click()
#creating the empty lists to which the final scraped data from page 4 will be stored
iphone11_rating4=[]
iphone11_reviewsum4=[]
iphone11_reviewfull4=[]
#let's extract all the tags having the rating
rating4=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
rating4[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in rating4:
ratings=i.text
iphone11_rating4.append(ratings)
iphone11_rating4[0:10]
#let's extract all the tags having the review summary
reviwsum4=driver.find_elements_by_xpath("//p[@class='_2-N8zT']")
reviwsum4[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwsum4:
reviwsums=i.text
iphone11_reviewsum4.append(reviwsums)
iphone11_reviewsum4[0:10]
#let's extract all the tags having the review full
reviwfull4=driver.find_elements_by_xpath("//div[@class='t-ZTKy']")
reviwfull4[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwfull4:
reviwsfull=i.text
iphone11_reviewfull4.append(reviwsfull)
iphone11_reviewfull4[0:10]
#scraping the elements of the next page(page5)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[12]").click()
#creating the empty lists to which the final scraped data from page 5 will be stored
iphone11_rating5=[]
iphone11_reviewsum5=[]
iphone11_reviewfull5=[]
#let's extract all the tags having the rating
rating5=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
rating5[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in rating5:
ratings=i.text
iphone11_rating5.append(ratings)
iphone11_rating5[0:10]
#let's extract all the tags having the review summary
reviwsum5=driver.find_elements_by_xpath("//p[@class='_2-N8zT']")
reviwsum5[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwsum5:
reviwsums=i.text
iphone11_reviewsum5.append(reviwsums)
iphone11_reviewsum5[0:10]
#let's extract all the tags having the review full
reviwfull5=driver.find_elements_by_xpath("//div[@class='t-ZTKy']")
reviwfull5[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwfull5:
reviwsfull=i.text
iphone11_reviewfull5.append(reviwsfull)
iphone11_reviewfull5[0:10]
#scraping the elements of the next page(page6)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[12]").click()
#creating the empty lists to which the final scraped data from page 6 will be stored
iphone11_rating6=[]
iphone11_reviewsum6=[]
iphone11_reviewfull6=[]
#let's extract all the tags having the rating
rating6=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
rating6[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in rating6:
ratings=i.text
iphone11_rating6.append(ratings)
iphone11_rating6[0:10]
#let's extract all the tags having the review summary
reviwsum6=driver.find_elements_by_xpath("//p[@class='_2-N8zT']")
reviwsum6[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwsum6:
reviwsums=i.text
iphone11_reviewsum6.append(reviwsums)
iphone11_reviewsum6[0:10]
#let's extract all the tags having the review full
reviwfull6=driver.find_elements_by_xpath("//div[@class='t-ZTKy']")
reviwfull6[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwfull6:
reviwsfull=i.text
iphone11_reviewfull6.append(reviwsfull)
iphone11_reviewfull6[0:10]
#scraping the elements of the next page(page7)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[12]").click()
#creating the empty lists to which the final scraped data from page 7 will be stored
iphone11_rating7=[]
iphone11_reviewsum7=[]
iphone11_reviewfull7=[]
#let's extract all the tags having the rating
rating7=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
rating7[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in rating7:
ratings=i.text
iphone11_rating7.append(ratings)
iphone11_rating7[0:10]
#let's extract all the tags having the review summary
reviwsum7=driver.find_elements_by_xpath("//p[@class='_2-N8zT']")
reviwsum7[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwsum7:
reviwsums=i.text
iphone11_reviewsum7.append(reviwsums)
iphone11_reviewsum7[0:10]
#let's extract all the tags having the review full
reviwfull7=driver.find_elements_by_xpath("//div[@class='t-ZTKy']")
reviwfull7[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwfull7:
reviwsfull=i.text
iphone11_reviewfull7.append(reviwsfull)
iphone11_reviewfull7[0:10]
#scraping the elements of the next page(page8)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[12]").click()
#creating the empty lists to which the final scraped data from page 8 will be stored
iphone11_rating8=[]
iphone11_reviewsum8=[]
iphone11_reviewfull8=[]
#let's extract all the tags having the rating
rating8=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
rating8[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in rating8:
ratings=i.text
iphone11_rating8.append(ratings)
iphone11_rating8[0:10]
#let's extract all the tags having the review summary
reviwsum8=driver.find_elements_by_xpath("//p[@class='_2-N8zT']")
reviwsum8[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwsum8:
reviwsums=i.text
iphone11_reviewsum8.append(reviwsums)
iphone11_reviewsum8[0:10]
#let's extract all the tags having the review full
reviwfull8=driver.find_elements_by_xpath("//div[@class='t-ZTKy']")
reviwfull8[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwfull8:
reviwsfull=i.text
iphone11_reviewfull8.append(reviwsfull)
iphone11_reviewfull8[0:10]
#scraping the elements of the next page(page9)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[12]").click()
#creating the empty lists to which the final scraped data from page 9 will be stored
iphone11_rating9=[]
iphone11_reviewsum9=[]
iphone11_reviewfull9=[]
#let's extract all the tags having the rating
rating9=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
rating9[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in rating9:
ratings=i.text
iphone11_rating9.append(ratings)
iphone11_rating9[0:10]
#let's extract all the tags having the review summary
reviwsum9=driver.find_elements_by_xpath("//p[@class='_2-N8zT']")
reviwsum9[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwsum9:
reviwsums=i.text
iphone11_reviewsum9.append(reviwsums)
iphone11_reviewsum9[0:10]
#let's extract all the tags having the review full
reviwfull9=driver.find_elements_by_xpath("//div[@class='t-ZTKy']")
reviwfull9[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwfull9:
reviwsfull=i.text
iphone11_reviewfull9.append(reviwsfull)
iphone11_reviewfull9[0:10]
#scraping the elements of the next page(page10)
driver.find_element_by_xpath("//nav[@class='yFHi8N']/a[12]").click()
#creating the empty lists to which the final scraped data from page 10 will be stored
iphone11_rating10=[]
iphone11_reviewsum10=[]
iphone11_reviewfull10=[]
#let's extract all the tags having the rating
rating10=driver.find_elements_by_xpath("//div[@class='_3LWZlK _1BLPMq']")
rating10[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in rating10:
ratings=i.text
iphone11_rating10.append(ratings)
iphone11_rating10[0:10]
#let's extract all the tags having the review summary
reviwsum10=driver.find_elements_by_xpath("//p[@class='_2-N8zT']")
reviwsum10[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwsum10:
reviwsums=i.text
iphone11_reviewsum10.append(reviwsums)
iphone11_reviewsum10[0:10]
#let's extract all the tags having the review full
reviwfull10=driver.find_elements_by_xpath("//div[@class='t-ZTKy']")
reviwfull10[0:10]
#Now extract the text inside the tags using a for loop to iterate over all the tags
for i in reviwfull10:
reviwsfull=i.text
iphone11_reviewfull10.append(reviwsfull)
iphone11_reviewfull10[0:10]
# +
#Adding lists having same attribute type from all the 10 pages
# -
iphone11_rating_final=iphone11_rating+iphone11_rating2+iphone11_rating3+iphone11_rating4+iphone11_rating5+iphone11_rating6+iphone11_rating7+iphone11_rating8+iphone11_rating9+iphone11_rating10
iphone11_reviewsum_final=iphone11_reviewsum+iphone11_reviewsum2+iphone11_reviewsum3+iphone11_reviewsum4+iphone11_reviewsum5+iphone11_reviewsum6+iphone11_reviewsum7+iphone11_reviewsum8+iphone11_reviewsum9+iphone11_reviewsum10
iphone11_reviewfull_fianl=iphone11_reviewfull+iphone11_reviewfull2+iphone11_reviewfull3+iphone11_reviewfull4+iphone11_reviewfull5+iphone11_reviewfull6+iphone11_reviewfull7+iphone11_reviewfull8+iphone11_reviewfull9+iphone11_reviewfull10
print(len(iphone11_rating_final),len(iphone11_reviewsum_final),len(iphone11_reviewfull_fianl))
iphone11reviewflipkart=pd.DataFrame({})
iphone11reviewflipkart['iphone11_rating']=iphone11_rating_final[0:79]
iphone11reviewflipkart['review_summary']=iphone11_reviewsum_final[0:79]
iphone11reviewflipkart['review_full']=iphone11_reviewfull_fianl[0:79]
iphone11reviewflipkart
# + active=""
#
| 36,340 |
/Image Captioning/Untitled.ipynb
|
bdfccd369a1ff54f86e1d51f4c7f0dca7a36f871
|
[] |
no_license
|
Genises/H-BRS_NeuralNetworks
|
https://github.com/Genises/H-BRS_NeuralNetworks
| 0 | 0 | null | null | null | null |
Jupyter Notebook
| false | false |
.py
| 39,395 |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.15.2
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from os import listdir, path
import xml.etree.ElementTree as ET
class data_manager():
def __init__(self, image_filepath : str, annotation_filepath : str):
self.image_filepath = image_filepath
self.annotation_filepath = annotation_filepath
def create_data_dict(self):
# For each dict
data_dict = {}
for folder in listdir(self.image_filepath):
folder_path = self.image_filepath + '/' + folder
for pciture in listdir(folder_path):
image_path = folder_path + '/' + pciture
# Get annotations
image_number = pciture.split(".")[0]
if not path.isfile(self.annotation_filepath + "/" + folder + "/" + image_number + ".eng"):
continue
# Makes special character beeing parsed
parser = ET.XMLParser(encoding="ansi")
tree = ET.parse(self.annotation_filepath + "/" + folder + "/" + image_number + ".eng", parser=parser)
root = tree.getroot()
tmp_dict = {}
for child in root:
tmp_dict[child.tag] = child.text
data_dict[image_number] = tmp_dict
print("Parsed " + str(len(data_dict)) + " entries!")
return data_dict
# +
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.image import load_img
from keras.preprocessing.image import img_to_array
from keras.applications.resnet50 import preprocess_input
# import sys
# from PIL import Image
# sys.modules['Image'] = Image
class data_generator():
def train_tokenizer(self, data_dict : dict):
texts = []
for key in data_dict:
texts.append(data_dict[key]["DESCRIPTION"])
self.tokenizer = Tokenizer()
self.tokenizer.fit_on_texts(texts)
def picture_data(self, data_dict : dict, batch_size=32):
if not self.tokenizer:
self.train_tokenizer(data_dict)
samples_per_epoch = len(data_dict)
number_of_batches = samples_per_epoch/batch_size
counter=0
while 1:
for image_number in data_dict.keys():
#print(data_dict[image_number]["IMAGE"])
image = load_img("iaprtc12/" + data_dict[image_number]["IMAGE"], target_size=(224, 224))
# convert the image pixels to a numpy array
image = img_to_array(image)
# reshape data for the model
image = image.reshape((1, image.shape[0], image.shape[1], image.shape[2]))
# prepare the image for the VGG model
image = preprocess_input(image)
caption = self.tokenizer.texts_to_sequences(data_dict[image_number]["DESCRIPTION"])
counter += 1
yield image, caption
#restart counter to yeild data in the next epoch as well
if counter >= number_of_batches:
counter = 0
# -
dm = data_manager("iaprtc12/images", "iaprtc12/annotations_complete_eng")
data_dict = dm.create_data_dict()
generator = data_generator()
generator.train_tokenizer(data_dict)
# +
#Inspired by https://machinelearningmastery.com/develop-a-deep-learning-caption-generation-model-in-python/
from keras.models import Model
from keras.layers import Input
from keras.layers import Dense
from keras.layers import LSTM
from keras.layers import Embedding
from keras.layers import Dropout
from keras.layers.merge import add
# define the captioning model
def define_model(vocab_size, max_length):
# feature extractor model
inputs1 = Input(shape=(4096,))
fe1 = Dropout(0.5)(inputs1)
fe2 = Dense(256, activation='relu')(fe1)
# sequence model
inputs2 = Input(shape=(max_length,))
se1 = Embedding(vocab_size, 256, mask_zero=True)(inputs2)
se2 = Dropout(0.5)(se1)
se3 = LSTM(256)(se2)
# decoder model
decoder1 = add([fe2, se3])
decoder2 = Dense(256, activation='relu')(decoder1)
outputs = Dense(vocab_size, activation='softmax')(decoder2)
# tie it together [image, seq] [word]
model = Model(inputs=[inputs1, inputs2], outputs=outputs)
# compile model
model.compile(loss='categorical_crossentropy', optimizer='adam')
# summarize model
model.summary()
#plot_model(model, to_file='model.png', show_shapes=True)
return model
# calculate the length of the description with the most words
def max_length(data_dict):
#lines = to_lines(descriptions)
max_length = 0
for value in data_dict.values():
max_length = max(max_length, len(value["DESCRIPTION"]))
return max_length
vocab_size = len(generator.tokenizer.word_index) + 1
print('Vocabulary Size: %d' % vocab_size)
# determine the maximum sequence length
max_length = max_length(data_dict)
print('Description Length: %d' % max_length)
# define the model
model = define_model(vocab_size, max_length)
# train the model, run epochs manually and save after each epoch
epochs = 20
steps = len(data_dict)
for i in range(epochs):
# create the data generator
# fit for one epoch
model.fit_generator(generator.picture_data(data_dict), epochs=1, steps_per_epoch=steps, verbose=1)
# save model
model.save('model_' + str(i) + '.h5')
# -
# ## ARCHIVE!!!
# +
from os import listdir
from pickle import dump
from keras.applications.vgg16 import VGG16
from keras.preprocessing.image import load_img
from keras.preprocessing.image import img_to_array
from keras.applications.vgg16 import preprocess_input
from keras.models import Model
# extract features from each photo in the directory
def extract_features(directory):
# load the model
model = VGG16()
# re-structure the model
model.layers.pop()
model = Model(inputs=model.inputs, outputs=model.layers[-1].output)
# summarize
print(model.summary())
# extract features from each photo
features = dict()
for supdic in listdir(directory):
path = directory + '/' + supdic
for name in listdir(path):
# load an image from file
filename = path + '/' + name
image = load_img(filename, target_size=(224, 224))
# convert the image pixels to a numpy array
image = img_to_array(image)
# reshape data for the model
image = image.reshape((1, image.shape[0], image.shape[1], image.shape[2]))
# prepare the image for the VGG model
image = preprocess_input(image)
# get features
feature = model.predict(image, verbose=0)
# get image id
image_id = name.split('.')[0]
# store feature
features[image_id] = feature
print('>%s' % name)
return features
# extract features from all images
directory = 'iaprtc12/images'
features = extract_features(directory)
print('Extracted Features: %d' % len(features))
# save to file
dump(features, open('features.pkl', 'wb'))
# -
| 7,404 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.