hexsha
stringlengths 40
40
| ext
stringclasses 1
value | lang
stringclasses 1
value | max_stars_repo_path
stringlengths 11
148
| max_stars_repo_name
stringlengths 11
79
| max_stars_repo_licenses
stringclasses 11
values | content
stringlengths 3.39k
756k
| avg_line_length
float64 26
3.16k
| max_line_length
int64 1k
734k
|
|---|---|---|---|---|---|---|---|---|
7b4673d53ea9b763e74276f8685ed5a123f53a4f
|
py
|
python
|
notebooks_ru/ch-demos/chsh.ipynb
|
gitlocalize/platypus
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] tags=["remove_cell"]
# # Местная реальность и неравенство ЧШГ
# -
# Мы видели СТРАШНОГО ПРИЗРАКА!!! в предыдущем модуле, как квантовая запутанность приводит к сильным корреляциям в многочастной системе. На самом деле эти корреляции кажутся более сильными, чем все, что можно было бы объяснить с помощью классической физики.
#
# Историческое развитие квантовой механики наполнено бурными дискуссиями об истинной природе реальности и о том, в какой степени квантовая механика может ее объяснить. Учитывая впечатляющий эмпирический успех квантовой механики, должно было стать ясно, что люди не откажутся от нее просто потому, что некоторые ее аспекты трудно согласовать с интуицией.
#
# В основе этих различных точек зрения лежал вопрос о природе измерения. Мы знаем, что в квантовых измерениях есть элемент случайности, но так ли это на самом деле? Существует ли какой-то хитрый способ, с помощью которого Вселенная уже заранее решила, какое значение данное измерение даст в будущем? Эта гипотеза легла в основу различных теорий *скрытых переменных* . Но этим теориям нужно было не только объяснить случайность на уровне отдельных частиц. Им также нужно было объяснить, что происходит, когда разные наблюдатели измеряют разные части многокомпонентной запутанной системы! Это вышло за рамки только теории скрытых переменных. Теперь понадобилась локальная теория скрытых переменных, чтобы примирить наблюдения квантовой механики со Вселенной, в которой действительна локальная реальность.
#
# Что такое местная реальность? Во Вселенной, где сохраняется локальность, должна быть возможность разделить две системы так далеко в космосе, что они не смогут взаимодействовать друг с другом. Понятие реальности связано с тем, имеет ли измеримая величина определенное значение *при отсутствии какого-либо измерения в будущем* .
#
# В 1963 году Джон Стюарт Белл опубликовал то, что можно было бы назвать одним из самых глубоких открытий в истории науки. Белл заявил, что любая теория, использующая локальные скрытые переменные, может быть экспериментально исключена. В этом разделе мы увидим, как это сделать, и проведем реальный эксперимент, который это продемонстрирует! (с некоторыми оставшимися лазейками, которые нужно закрыть...)
# ### Неравенство CHSH
#
# Представьте, что Алисе и Бобу дана каждая часть двудольной запутанной системы. Затем каждый из них выполняет два измерения со своей стороны в двух разных базах. Назовем базы Алисы *A* и *a* и базы Боба *B* и *b* . Каково математическое ожидание величины $\langle CHSH \rangle = \langle AB \rangle - \langle Ab \rangle + \langle aB \rangle + \langle ab \rangle$ ?
#
# Теперь у Алисы и Боба есть по одному кубиту, поэтому любое измерение, которое они выполняют в своей системе (кубите), может дать только один из двух возможных результатов: +1 или -1. Обратите внимание, что хотя мы обычно называем два состояния кубита $|0\rangle$ и $|1\rangle$, это *собственные состояния* , и проективное измерение даст их *собственные значения* , +1 и -1 соответственно.
#
# Следовательно, если любое измерение *A* , *a* , *B* и *b* может дать только $\pm 1$, то величины $(Bb)$ и $(B+b)$ могут быть только 0 или $\pm2$. Таким образом, величина $A(Bb) + a(B+b)$ может быть только либо +2, либо -2, а это означает, что должна существовать граница для среднего значения величины, которую мы назвали $|\langle ЧШ\ранг| =|\langle AB \rangle - \langle Ab \rangle + \langle aB \rangle + \langle ab \rangle| \leq 2$.
#
# Приведенное выше обсуждение чрезмерно упрощено, потому что мы могли бы предположить, что результат любого набора измерений Алисы и Боба может зависеть от набора локальных скрытых переменных, но с помощью некоторых математических вычислений можно показать, что даже в этом случае , математическое ожидание величины $CHSH$ должно быть ограничено 2, если сохраняется локальный реализм.
#
# Но что происходит, когда мы проводим эти эксперименты с запутанной системой? Давай попробуем!
# +
#import qiskit tools
import qiskit
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute, transpile, Aer, IBMQ
from qiskit.tools.visualization import circuit_drawer
from qiskit.tools.monitor import job_monitor, backend_monitor, backend_overview
from qiskit.providers.aer import noise
#import python stuff
import matplotlib.pyplot as plt
import numpy as np
import time
# + tags=["uses-hardware"]
# Set devices, if using a real device
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q', group='open', project='main')
lima = provider.get_backend('ibmq_lima')
# -
sv_sim = Aer.get_backend('statevector_simulator')
qasm_sim = Aer.get_backend('qasm_simulator')
# Сначала мы собираемся определить функцию для создания наших цепей CHSH. Мы собираемся выбрать, не ограничивая общности, что Боб всегда использует расчетный ($Z$) и $X$ базис для своих измерений $B$ и $b$ соответственно, тогда как Алиса выбирает также ортогональные базисы, но угол которых мы собираемся варьироваться от $0$ до $2\pi$ относительно оснований Боба. Этот набор углов будет входным аргументом для нашей функции построения схемы $CHSH$.
def make_chsh_circuit(theta_vec):
"""Return a list of QuantumCircuits for use in a CHSH experiemnt
(one for each value of theta in theta_vec)
Args:
theta_vec (list): list of values of angles between the bases of Alice and Bob
Returns:
List[QuantumCircuit]: CHSH QuantumCircuits for each value of theta
"""
chsh_circuits = []
for theta in theta_vec:
obs_vec = ['00', '01', '10', '11']
for el in obs_vec:
qc = QuantumCircuit(2,2)
qc.h(0)
qc.cx(0, 1)
qc.ry(theta, 0)
for a in range(2):
if el[a] == '1':
qc.h(a)
qc.measure(range(2),range(2))
chsh_circuits.append(qc)
return chsh_circuits
# Далее мы собираемся определить функцию для оценки величины $\langle CHSH \rangle$. Фактически можно определить две такие величины: $\langle CHSH1 \rangle = \langle AB \rangle - \langle Ab \rangle + \langle aB \rangle + \langle ab \rangle$ и $\langle CHSH2 \rangle = \ langle AB \rangle + \langle Ab \rangle - \langle aB \rangle + \langle ab \rangle$. После выбора соответствующих осей измерения для обеих сторон каждое ожидаемое значение может быть просто оценено путем сложения отсчетов из выходных битовых строк с соответствующим знаком (плюс для четных членов $00$ и $11$ и минус для нечетных членов $01$ и $10$). .
def compute_chsh_witness(counts):
"""Computes expectation values for the CHSH inequality, for each
angle (theta) between measurement axis.
Args: counts (list[dict]): dict of counts for each experiment
(4 per value of theta)
Returns:
Tuple(List, List): Tuple of lists with the two CHSH witnesses
"""
# Order is ZZ,ZX,XZ,XX
CHSH1 = []
CHSH2 = []
# Divide the list of dictionaries in sets of 4
for i in range(0, len(counts), 4):
theta_dict = counts[i:i + 4]
zz = theta_dict[0]
zx = theta_dict[1]
xz = theta_dict[2]
xx = theta_dict[3]
no_shots = sum(xx[y] for y in xx)
chsh1 = 0
chsh2 = 0
for element in zz:
parity = (-1)**(int(element[0])+int(element[1]))
chsh1+= parity*zz[element]
chsh2+= parity*zz[element]
for element in zx:
parity = (-1)**(int(element[0])+int(element[1]))
chsh1+= parity*zx[element]
chsh2-= parity*zx[element]
for element in xz:
parity = (-1)**(int(element[0])+int(element[1]))
chsh1-= parity*xz[element]
chsh2+= parity*xz[element]
for element in xx:
parity = (-1)**(int(element[0])+int(element[1]))
chsh1+= parity*xx[element]
chsh2+= parity*xx[element]
CHSH1.append(chsh1/no_shots)
CHSH2.append(chsh2/no_shots)
return CHSH1, CHSH2
# Наконец, разобьем отрезок $[0, 2\pi)$ на 15 углов и построим соответствующий набор цепей $CHSH$
number_of_thetas = 15
theta_vec = np.linspace(0,2*np.pi,number_of_thetas)
my_chsh_circuits = make_chsh_circuit(theta_vec)
# Теперь давайте кратко рассмотрим, как выглядят четыре из этих цепей для заданного $\theta$
my_chsh_circuits[4].draw('mpl')
my_chsh_circuits[5].draw('mpl')
my_chsh_circuits[6].draw('mpl')
my_chsh_circuits[7].draw('mpl')
# Эти схемы просто создают пару Белла, а затем измеряют каждую партию по разным основаниям. В то время как Боб ($q_1$) всегда измеряет либо в вычислительном базисе, либо в базисе $X$, базис измерения Алисы поворачивается на угол $\theta$ по отношению к базису Боба.
# + tags=["uses-hardware"]
# Execute and get counts
result_ideal = execute(my_chsh_circuits, qasm_sim).result()
tic = time.time()
job_real = execute(my_chsh_circuits, backend=lima, shots=8192)
job_monitor(job_real)
result_real = job_real.result()
toc = time.time()
print(toc-tic)
# + tags=["uses-hardware"]
CHSH1_ideal, CHSH2_ideal = compute_chsh_witness(result_ideal.get_counts())
CHSH1_real, CHSH2_real = compute_chsh_witness(result_real.get_counts())
# -
# Теперь наносим результаты
# + tags=["uses-hardware"]
plt.figure(figsize=(12,8))
plt.rcParams.update({'font.size': 22})
plt.plot(theta_vec,CHSH1_ideal,'o-',label = 'CHSH1 Noiseless')
plt.plot(theta_vec,CHSH2_ideal,'o-',label = 'CHSH2 Noiseless')
plt.plot(theta_vec,CHSH1_real,'x-',label = 'CHSH1 Lima')
plt.plot(theta_vec,CHSH2_real,'x-',label = 'CHSH2 Lima')
plt.grid(which='major',axis='both')
plt.rcParams.update({'font.size': 16})
plt.legend()
plt.axhline(y=2, color='r', linestyle='-')
plt.axhline(y=-2, color='r', linestyle='-')
plt.axhline(y=np.sqrt(2)*2, color='k', linestyle='-.')
plt.axhline(y=-np.sqrt(2)*2, color='k', linestyle='-.')
plt.xlabel('Theta')
plt.ylabel('CHSH witness')
# -
# Обратите внимание, что произошло! Существуют определенные комбинации баз измерения, для которых $|CHSH| \geq 2$. Как это возможно? Давайте посмотрим на нашу запутанную двудольную систему. Легко показать, что если $|\psi \rangle = 1/\sqrt{2} (|00\rangle + |11\rangle)$, то математическое ожидание $\langle AB \rangle = \langle \psi| А \ раз Б| \psi \rangle = -\cos \theta_{AB}$, где $\theta_{AB}$ — угол между базами измерения $A$ и $B$. Следовательно, для конкретного выбора оснований $A = 1/\sqrt{2}(\sigma_z - \sigma_x)$ и $a = 1/\sqrt{2}(\sigma_z + \sigma_x)$, позволяя Бобу измерять с $B=\sigma_z$ и $b=\sigma_x$, мы видим, что $|\langle CHSH1 \rangle| = 2\sqrt{2} > 2$. Также можно показать, что $2\sqrt{2}$ является максимально возможным значением, достижимым даже в квантовом случае (штрихпунктирная линия на графике).
#
# Приведенное выше неравенство называется CHSH в честь Клаузера, Хорна, Шимони и Холта, и это самый популярный способ представления исходного неравенства Белла.
#
# Тот факт, что мы нарушили неравенство ЧШШ в нашем реальном устройстве, имеет значение. Всего десять лет назад такой эксперимент имел бы большое значение. В настоящее время квантовые устройства стали значительно лучше, и эти результаты можно легко воспроизвести на самом современном оборудовании. Однако есть ряд лазеек, которые приходится закрывать при нарушении неравенства, чтобы утверждать, что либо локальность, либо реализм опровергнуты. Это лазейка обнаружения (где наш детектор неисправен и не может предоставить содержательную статистику) и лазейка локальности/причинности (где две части запутанной системы разделены расстоянием, меньшим, чем расстояние, пройденное светом за время его прохождения). требуется для выполнения измерения). Учитывая, что мы можем генерировать запутанные пары с высокой точностью и каждое измерение дает результат (то есть ни одна измеренная частица не «потеряна»), мы закрыли лазейку обнаружения в наших экспериментах выше. Однако, учитывая расстояние между нашими кубитами (несколько миллиметров) и время, необходимое для выполнения измерения (порядка $\mu$s), мы не можем утверждать, что закрыли лазейку причинно-следственной связи.
# ### Упражнение
#
# Рассмотрим игру, в которой Алису и Боба помещают в разные комнаты, и каждому дается бит $x$ и $y$ соответственно. Эти биты выбираются случайным образом и независимо друг от друга. При получении бита каждый из них отвечает своим собственным битом, $a$ и $b$. Теперь Алиса и Боб выигрывают игру, если $a$ и $b$ различны при $x=y=1$ и равны в противном случае. Легко видеть, что наилучшая возможная стратегия для Алисы и Боба — всегда давать $a=b=0$ (или $1$). С помощью этой стратегии Алиса и Боб могут выиграть игру не более чем в 75% случаев.
#
# Представьте, что Алисе и Бобу разрешено совместно использовать запутанное двухкубитное состояние. Есть ли стратегия, которую они могут использовать, которая даст им больше шансов на победу, чем 75%? (Помните, что они могут заранее договориться о любой стратегии, но как только им дадут случайные биты, они больше не смогут общаться. Конечно, они могут всегда брать с собой соответствующие части запутанной пары.)
| 60.451613 | 1,174 |
c795501e5f7b7dbf439f5c6386f1bf7f55105b7f
|
py
|
python
|
FinalProject_Taxis.ipynb
|
Snehlata25/DataMiningFinalProject
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="8XHle-lLB3cO"
# ## Check missing data
# + [markdown] id="COobrKASudvs" colab_type="text"
# # Import Data and APIs
# + [markdown] id="59MnlDV1xmn5" colab_type="text"
# ## Download Data from Kaggle API
# + id="KbV90ksBqx0E" colab_type="code" outputId="45cf3918-bb27-47dd-ed10-eab816c8df84" colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "Ly8gQ29weXJpZ2h0IDIwMTcgR29vZ2xlIExMQwovLwovLyBMaWNlbnNlZCB1bmRlciB0aGUgQXBhY2hlIExpY2Vuc2UsIFZlcnNpb24gMi4wICh0aGUgIkxpY2Vuc2UiKTsKLy8geW91IG1heSBub3QgdXNlIHRoaXMgZmlsZSBleGNlcHQgaW4gY29tcGxpYW5jZSB3aXRoIHRoZSBMaWNlbnNlLgovLyBZb3UgbWF5IG9idGFpbiBhIGNvcHkgb2YgdGhlIExpY2Vuc2UgYXQKLy8KLy8gICAgICBodHRwOi8vd3d3LmFwYWNoZS5vcmcvbGljZW5zZXMvTElDRU5TRS0yLjAKLy8KLy8gVW5sZXNzIHJlcXVpcmVkIGJ5IGFwcGxpY2FibGUgbGF3IG9yIGFncmVlZCB0byBpbiB3cml0aW5nLCBzb2Z0d2FyZQovLyBkaXN0cmlidXRlZCB1bmRlciB0aGUgTGljZW5zZSBpcyBkaXN0cmlidXRlZCBvbiBhbiAiQVMgSVMiIEJBU0lTLAovLyBXSVRIT1VUIFdBUlJBTlRJRVMgT1IgQ09ORElUSU9OUyBPRiBBTlkgS0lORCwgZWl0aGVyIGV4cHJlc3Mgb3IgaW1wbGllZC4KLy8gU2VlIHRoZSBMaWNlbnNlIGZvciB0aGUgc3BlY2lmaWMgbGFuZ3VhZ2UgZ292ZXJuaW5nIHBlcm1pc3Npb25zIGFuZAovLyBsaW1pdGF0aW9ucyB1bmRlciB0aGUgTGljZW5zZS4KCi8qKgogKiBAZmlsZW92ZXJ2aWV3IEhlbHBlcnMgZm9yIGdvb2dsZS5jb2xhYiBQeXRob24gbW9kdWxlLgogKi8KKGZ1bmN0aW9uKHNjb3BlKSB7CmZ1bmN0aW9uIHNwYW4odGV4dCwgc3R5bGVBdHRyaWJ1dGVzID0ge30pIHsKICBjb25zdCBlbGVtZW50ID0gZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgnc3BhbicpOwogIGVsZW1lbnQudGV4dENvbnRlbnQgPSB0ZXh0OwogIGZvciAoY29uc3Qga2V5IG9mIE9iamVjdC5rZXlzKHN0eWxlQXR0cmlidXRlcykpIHsKICAgIGVsZW1lbnQuc3R5bGVba2V5XSA9IHN0eWxlQXR0cmlidXRlc1trZXldOwogIH0KICByZXR1cm4gZWxlbWVudDsKfQoKLy8gTWF4IG51bWJlciBvZiBieXRlcyB3aGljaCB3aWxsIGJlIHVwbG9hZGVkIGF0IGEgdGltZS4KY29uc3QgTUFYX1BBWUxPQURfU0laRSA9IDEwMCAqIDEwMjQ7Ci8vIE1heCBhbW91bnQgb2YgdGltZSB0byBibG9jayB3YWl0aW5nIGZvciB0aGUgdXNlci4KY29uc3QgRklMRV9DSEFOR0VfVElNRU9VVF9NUyA9IDMwICogMTAwMDsKCmZ1bmN0aW9uIF91cGxvYWRGaWxlcyhpbnB1dElkLCBvdXRwdXRJZCkgewogIGNvbnN0IHN0ZXBzID0gdXBsb2FkRmlsZXNTdGVwKGlucHV0SWQsIG91dHB1dElkKTsKICBjb25zdCBvdXRwdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQob3V0cHV0SWQpOwogIC8vIENhY2hlIHN0ZXBzIG9uIHRoZSBvdXRwdXRFbGVtZW50IHRvIG1ha2UgaXQgYXZhaWxhYmxlIGZvciB0aGUgbmV4dCBjYWxsCiAgLy8gdG8gdXBsb2FkRmlsZXNDb250aW51ZSBmcm9tIFB5dGhvbi4KICBvdXRwdXRFbGVtZW50LnN0ZXBzID0gc3RlcHM7CgogIHJldHVybiBfdXBsb2FkRmlsZXNDb250aW51ZShvdXRwdXRJZCk7Cn0KCi8vIFRoaXMgaXMgcm91Z2hseSBhbiBhc3luYyBnZW5lcmF0b3IgKG5vdCBzdXBwb3J0ZWQgaW4gdGhlIGJyb3dzZXIgeWV0KSwKLy8gd2hlcmUgdGhlcmUgYXJlIG11bHRpcGxlIGFzeW5jaHJvbm91cyBzdGVwcyBhbmQgdGhlIFB5dGhvbiBzaWRlIGlzIGdvaW5nCi8vIHRvIHBvbGwgZm9yIGNvbXBsZXRpb24gb2YgZWFjaCBzdGVwLgovLyBUaGlzIHVzZXMgYSBQcm9taXNlIHRvIGJsb2NrIHRoZSBweXRob24gc2lkZSBvbiBjb21wbGV0aW9uIG9mIGVhY2ggc3RlcCwKLy8gdGhlbiBwYXNzZXMgdGhlIHJlc3VsdCBvZiB0aGUgcHJldmlvdXMgc3RlcCBhcyB0aGUgaW5wdXQgdG8gdGhlIG5leHQgc3RlcC4KZnVuY3Rpb24gX3VwbG9hZEZpbGVzQ29udGludWUob3V0cHV0SWQpIHsKICBjb25zdCBvdXRwdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQob3V0cHV0SWQpOwogIGNvbnN0IHN0ZXBzID0gb3V0cHV0RWxlbWVudC5zdGVwczsKCiAgY29uc3QgbmV4dCA9IHN0ZXBzLm5leHQob3V0cHV0RWxlbWVudC5sYXN0UHJvbWlzZVZhbHVlKTsKICByZXR1cm4gUHJvbWlzZS5yZXNvbHZlKG5leHQudmFsdWUucHJvbWlzZSkudGhlbigodmFsdWUpID0+IHsKICAgIC8vIENhY2hlIHRoZSBsYXN0IHByb21pc2UgdmFsdWUgdG8gbWFrZSBpdCBhdmFpbGFibGUgdG8gdGhlIG5leHQKICAgIC8vIHN0ZXAgb2YgdGhlIGdlbmVyYXRvci4KICAgIG91dHB1dEVsZW1lbnQubGFzdFByb21pc2VWYWx1ZSA9IHZhbHVlOwogICAgcmV0dXJuIG5leHQudmFsdWUucmVzcG9uc2U7CiAgfSk7Cn0KCi8qKgogKiBHZW5lcmF0b3IgZnVuY3Rpb24gd2hpY2ggaXMgY2FsbGVkIGJldHdlZW4gZWFjaCBhc3luYyBzdGVwIG9mIHRoZSB1cGxvYWQKICogcHJvY2Vzcy4KICogQHBhcmFtIHtzdHJpbmd9IGlucHV0SWQgRWxlbWVudCBJRCBvZiB0aGUgaW5wdXQgZmlsZSBwaWNrZXIgZWxlbWVudC4KICogQHBhcmFtIHtzdHJpbmd9IG91dHB1dElkIEVsZW1lbnQgSUQgb2YgdGhlIG91dHB1dCBkaXNwbGF5LgogKiBAcmV0dXJuIHshSXRlcmFibGU8IU9iamVjdD59IEl0ZXJhYmxlIG9mIG5leHQgc3RlcHMuCiAqLwpmdW5jdGlvbiogdXBsb2FkRmlsZXNTdGVwKGlucHV0SWQsIG91dHB1dElkKSB7CiAgY29uc3QgaW5wdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQoaW5wdXRJZCk7CiAgaW5wdXRFbGVtZW50LmRpc2FibGVkID0gZmFsc2U7CgogIGNvbnN0IG91dHB1dEVsZW1lbnQgPSBkb2N1bWVudC5nZXRFbGVtZW50QnlJZChvdXRwdXRJZCk7CiAgb3V0cHV0RWxlbWVudC5pbm5lckhUTUwgPSAnJzsKCiAgY29uc3QgcGlja2VkUHJvbWlzZSA9IG5ldyBQcm9taXNlKChyZXNvbHZlKSA9PiB7CiAgICBpbnB1dEVsZW1lbnQuYWRkRXZlbnRMaXN0ZW5lcignY2hhbmdlJywgKGUpID0+IHsKICAgICAgcmVzb2x2ZShlLnRhcmdldC5maWxlcyk7CiAgICB9KTsKICB9KTsKCiAgY29uc3QgY2FuY2VsID0gZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgnYnV0dG9uJyk7CiAgaW5wdXRFbGVtZW50LnBhcmVudEVsZW1lbnQuYXBwZW5kQ2hpbGQoY2FuY2VsKTsKICBjYW5jZWwudGV4dENvbnRlbnQgPSAnQ2FuY2VsIHVwbG9hZCc7CiAgY29uc3QgY2FuY2VsUHJvbWlzZSA9IG5ldyBQcm9taXNlKChyZXNvbHZlKSA9PiB7CiAgICBjYW5jZWwub25jbGljayA9ICgpID0+IHsKICAgICAgcmVzb2x2ZShudWxsKTsKICAgIH07CiAgfSk7CgogIC8vIENhbmNlbCB1cGxvYWQgaWYgdXNlciBoYXNuJ3QgcGlja2VkIGFueXRoaW5nIGluIHRpbWVvdXQuCiAgY29uc3QgdGltZW91dFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgc2V0VGltZW91dCgoKSA9PiB7CiAgICAgIHJlc29sdmUobnVsbCk7CiAgICB9LCBGSUxFX0NIQU5HRV9USU1FT1VUX01TKTsKICB9KTsKCiAgLy8gV2FpdCBmb3IgdGhlIHVzZXIgdG8gcGljayB0aGUgZmlsZXMuCiAgY29uc3QgZmlsZXMgPSB5aWVsZCB7CiAgICBwcm9taXNlOiBQcm9taXNlLnJhY2UoW3BpY2tlZFByb21pc2UsIHRpbWVvdXRQcm9taXNlLCBjYW5jZWxQcm9taXNlXSksCiAgICByZXNwb25zZTogewogICAgICBhY3Rpb246ICdzdGFydGluZycsCiAgICB9CiAgfTsKCiAgaWYgKCFmaWxlcykgewogICAgcmV0dXJuIHsKICAgICAgcmVzcG9uc2U6IHsKICAgICAgICBhY3Rpb246ICdjb21wbGV0ZScsCiAgICAgIH0KICAgIH07CiAgfQoKICBjYW5jZWwucmVtb3ZlKCk7CgogIC8vIERpc2FibGUgdGhlIGlucHV0IGVsZW1lbnQgc2luY2UgZnVydGhlciBwaWNrcyBhcmUgbm90IGFsbG93ZWQuCiAgaW5wdXRFbGVtZW50LmRpc2FibGVkID0gdHJ1ZTsKCiAgZm9yIChjb25zdCBmaWxlIG9mIGZpbGVzKSB7CiAgICBjb25zdCBsaSA9IGRvY3VtZW50LmNyZWF0ZUVsZW1lbnQoJ2xpJyk7CiAgICBsaS5hcHBlbmQoc3BhbihmaWxlLm5hbWUsIHtmb250V2VpZ2h0OiAnYm9sZCd9KSk7CiAgICBsaS5hcHBlbmQoc3BhbigKICAgICAgICBgKCR7ZmlsZS50eXBlIHx8ICduL2EnfSkgLSAke2ZpbGUuc2l6ZX0gYnl0ZXMsIGAgKwogICAgICAgIGBsYXN0IG1vZGlmaWVkOiAkewogICAgICAgICAgICBmaWxlLmxhc3RNb2RpZmllZERhdGUgPyBmaWxlLmxhc3RNb2RpZmllZERhdGUudG9Mb2NhbGVEYXRlU3RyaW5nKCkgOgogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAnbi9hJ30gLSBgKSk7CiAgICBjb25zdCBwZXJjZW50ID0gc3BhbignMCUgZG9uZScpOwogICAgbGkuYXBwZW5kQ2hpbGQocGVyY2VudCk7CgogICAgb3V0cHV0RWxlbWVudC5hcHBlbmRDaGlsZChsaSk7CgogICAgY29uc3QgZmlsZURhdGFQcm9taXNlID0gbmV3IFByb21pc2UoKHJlc29sdmUpID0+IHsKICAgICAgY29uc3QgcmVhZGVyID0gbmV3IEZpbGVSZWFkZXIoKTsKICAgICAgcmVhZGVyLm9ubG9hZCA9IChlKSA9PiB7CiAgICAgICAgcmVzb2x2ZShlLnRhcmdldC5yZXN1bHQpOwogICAgICB9OwogICAgICByZWFkZXIucmVhZEFzQXJyYXlCdWZmZXIoZmlsZSk7CiAgICB9KTsKICAgIC8vIFdhaXQgZm9yIHRoZSBkYXRhIHRvIGJlIHJlYWR5LgogICAgbGV0IGZpbGVEYXRhID0geWllbGQgewogICAgICBwcm9taXNlOiBmaWxlRGF0YVByb21pc2UsCiAgICAgIHJlc3BvbnNlOiB7CiAgICAgICAgYWN0aW9uOiAnY29udGludWUnLAogICAgICB9CiAgICB9OwoKICAgIC8vIFVzZSBhIGNodW5rZWQgc2VuZGluZyB0byBhdm9pZCBtZXNzYWdlIHNpemUgbGltaXRzLiBTZWUgYi82MjExNTY2MC4KICAgIGxldCBwb3NpdGlvbiA9IDA7CiAgICB3aGlsZSAocG9zaXRpb24gPCBmaWxlRGF0YS5ieXRlTGVuZ3RoKSB7CiAgICAgIGNvbnN0IGxlbmd0aCA9IE1hdGgubWluKGZpbGVEYXRhLmJ5dGVMZW5ndGggLSBwb3NpdGlvbiwgTUFYX1BBWUxPQURfU0laRSk7CiAgICAgIGNvbnN0IGNodW5rID0gbmV3IFVpbnQ4QXJyYXkoZmlsZURhdGEsIHBvc2l0aW9uLCBsZW5ndGgpOwogICAgICBwb3NpdGlvbiArPSBsZW5ndGg7CgogICAgICBjb25zdCBiYXNlNjQgPSBidG9hKFN0cmluZy5mcm9tQ2hhckNvZGUuYXBwbHkobnVsbCwgY2h1bmspKTsKICAgICAgeWllbGQgewogICAgICAgIHJlc3BvbnNlOiB7CiAgICAgICAgICBhY3Rpb246ICdhcHBlbmQnLAogICAgICAgICAgZmlsZTogZmlsZS5uYW1lLAogICAgICAgICAgZGF0YTogYmFzZTY0LAogICAgICAgIH0sCiAgICAgIH07CiAgICAgIHBlcmNlbnQudGV4dENvbnRlbnQgPQogICAgICAgICAgYCR7TWF0aC5yb3VuZCgocG9zaXRpb24gLyBmaWxlRGF0YS5ieXRlTGVuZ3RoKSAqIDEwMCl9JSBkb25lYDsKICAgIH0KICB9CgogIC8vIEFsbCBkb25lLgogIHlpZWxkIHsKICAgIHJlc3BvbnNlOiB7CiAgICAgIGFjdGlvbjogJ2NvbXBsZXRlJywKICAgIH0KICB9Owp9CgpzY29wZS5nb29nbGUgPSBzY29wZS5nb29nbGUgfHwge307CnNjb3BlLmdvb2dsZS5jb2xhYiA9IHNjb3BlLmdvb2dsZS5jb2xhYiB8fCB7fTsKc2NvcGUuZ29vZ2xlLmNvbGFiLl9maWxlcyA9IHsKICBfdXBsb2FkRmlsZXMsCiAgX3VwbG9hZEZpbGVzQ29udGludWUsCn07Cn0pKHNlbGYpOwo=", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 41}
# Import tools to access Kaggle identity keys.
from google.colab import drive
from google.colab import files
uploaded = files.upload()
# + id="h2kxUQzFrMUO" colab_type="code" outputId="fe4b0a36-95d6-4b66-bc7b-a4ff1f79aa3f" colab={"base_uri": "https://localhost:8080/", "height": 148}
# !mkdir -p ~/.kaggle # Makes a directory in home folder named kaggle
# !cp kaggle.json ~/.kaggle/ # Copies the contents of kaggle.jason into the home/kaggle folder
# !apt-get install p7zip-full # Installs p7zip-full tool
# + id="FkGG_fKrsCst" colab_type="code" colab={}
# Use the Python pip install command to install the Kaggle library
# !pip install -q kaggle
# + id="fnEz8IVSr5H9" colab_type="code" outputId="3c799dbf-72f7-4157-e7e8-8341a4ea20b5" colab={"base_uri": "https://localhost:8080/", "height": 217}
# This code downloads the dataset from kaggle
# !kaggle competitions download -c nyc-taxi-trip-duration
# + id="g8shQPkltkyM" colab_type="code" outputId="2a04d341-6f03-49d9-ef6a-a9f5676d348e" colab={"base_uri": "https://localhost:8080/", "height": 316}
# This extracts the test data from kaggle download
!7za e test.zip
# + id="iJpp7SSVuAh-" colab_type="code" outputId="9f9c92b7-a900-4d35-a37a-70a56d3aa177" colab={"base_uri": "https://localhost:8080/", "height": 316}
# This extracts the train data from kaggle download
!7za e train.zip
# + id="K7EFCs7euVUV" colab_type="code" outputId="c8b040eb-6757-4322-e9a1-7260b8becbe6" colab={"base_uri": "https://localhost:8080/", "height": 316}
# This extracts the sample_submission from kaggle download
!7za e sample_submission.zip
# + [markdown] id="y_FZ1S7Yujbu" colab_type="text"
# ## Import APIs
# + id="j6m-sxTxuku9" colab_type="code" colab={}
# import commands brings in the necessary libraries from 'library'
# that are required to run this notebook into the notebook environment
import os
import time
import json
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.ticker import StrMethodFormatter
from sklearn import linear_model
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn import preprocessing
from sklearn import metrics
import datetime
import seaborn as sns # Seaborn library for plotting
# Some statistics tools
from sklearn import datasets, linear_model
from sklearn.linear_model import LinearRegression
import statsmodels.api as sm
from scipy import stats
from xgboost import XGBRegressor
# %matplotlib inline # Necessary in JupyterNotebooks
# + [markdown] id="E6OHZt3F15To" colab_type="text"
# ## Load trainning and testing data
# + id="YPOeJ_85v6yt" colab_type="code" colab={}
# Load train data
train_df = pd.read_csv('./train.csv')
# Load test data
test_df = pd.read_csv('./test.csv')
# + [markdown] id="EGmitIUUzN7z" colab_type="text"
# # Problem Definition
#
# We are provided a data set with geographical, time, and passanger count data along with other features from a set of taxi rides in New York City. We are asked to predict the total trip duration based on the provided data. In other words, we are asked to predict a number from a set of labeled input feature values, this is a classic supervised learning problem, specifically a regression problem.
#
# ## Feature Details
#
# id - a unique identifier for each trip
# vendor_id - a code indicating the provider associated with the trip record
# pickup_datetime - date and time when the meter was engaged
# dropoff_datetime - date and time when the meter was disengaged
# passenger_count - the number of passengers in the vehicle (driver entered value)
# pickup_longitude - the longitude where the meter was engaged
# pickup_latitude - the latitude where the meter was engaged
# dropoff_longitude - the longitude where the meter was disengaged
# dropoff_latitude - the latitude where the meter was disengaged
# store_and_fwd_flag - This flag indicates whether the trip record was held in vehicle memory before sending to the vendor because the vehicle did not have a connection to the server - Y=store and forward; N=not a store and forward trip.
#
#
# ## Label Details
#
# trip_duration - duration of the trip in seconds
# + [markdown] id="yiZJP1rTzVjn" colab_type="text"
# # Data Cleaning
#
# In this section, we will run several, and similar data cleaning and data engineering procedures, we will look for Nan data points, outliers, legally unacceptable points, and ensure data is formatted as necessary.
# + [markdown] id="fW2RN2SY11As" colab_type="text"
# ## Quick Look at the datasets
# + id="uBufTqWzwUDe" colab_type="code" outputId="027a0d42-a88a-4088-e731-76082376b911" colab={"base_uri": "https://localhost:8080/", "height": 32}
train_df.shape
# + id="12715ViTwZ_c" colab_type="code" outputId="cc0afc94-d50b-42cd-a5b9-a2faa36bfbd8" colab={"base_uri": "https://localhost:8080/", "height": 32}
test_df.shape
# + id="MVoE9pTS0_Uq" colab_type="code" outputId="3266b2c6-af81-4d19-f93b-9ffe22159763" colab={"base_uri": "https://localhost:8080/", "height": 303}
train_df.head()
# + id="59MFux4e1lR9" colab_type="code" outputId="37f33130-c115-4aff-dd64-3582739cd5f0" colab={"base_uri": "https://localhost:8080/", "height": 303}
test_df.head()
# + id="F4tcVRqUzled" colab_type="code" outputId="c7d37207-2bfa-40b7-d77e-300bb5d9cae8" colab={"base_uri": "https://localhost:8080/", "height": 214}
# Check for Missing Data in training dataset using df.isna() command
# This command iterates over the columns of a dataframe checking wether an entry
# is Nan and counts the number of those such entries.
train_df.isna().sum(axis=0)
# + [markdown] id="d1UW3g8B2tnK" colab_type="text"
# There is no missing data in training and testing dataset
# + [markdown] id="ZSGfC-7GqJQa" colab_type="text"
# ## Remove Outliers
# + id="VRvHVwFlPoJo" colab_type="code" outputId="3be8905c-50c9-456a-adb1-46f88b6e7b7a" colab={"base_uri": "https://localhost:8080/", "height": 291}
# Change the formatting of the numbers in order to help visualization
pd.set_option('display.float_format',lambda x : '%.2f'% x)
train_df.describe()
# + [markdown] id="Hv83afP5Qg-5" colab_type="text"
# The maximum trip duration is ~41 days which doesn't make sense. Also maximum number of passengers is 9, which is also strange. We may need to remove some outliers
# + [markdown] id="UpcdTIX5PRCY" colab_type="text"
# ### Duration
# + id="JoAD_tqmV8RR" colab_type="code" outputId="34c7f470-db7b-4c8b-c374-1b257b3e5284" colab={"base_uri": "https://localhost:8080/", "height": 164}
train_df.trip_duration.describe() # Provides simple statistic summary of the
# Columns in the DataFrame.
# + id="UmlT066z3hfj" colab_type="code" outputId="9293afd3-12b5-478d-d47c-a4eae4390a55" colab={"base_uri": "https://localhost:8080/", "height": 278}
sns.boxplot(train_df.trip_duration) # Creates a boxplot of trip duration using
# Seaborn library.
plt.show()
# + id="gG_FJvCs-YNo" colab_type="code" outputId="b057b8e8-bbfb-46f3-f550-b97e271708a0" colab={"base_uri": "https://localhost:8080/", "height": 32}
print('there are', train_df[(train_df.trip_duration < 5)].trip_duration.count(), 'trips took less than 5 seconds, and',
train_df[(train_df.trip_duration > 86400)].trip_duration.count(), 'trips took more than one day')
# + id="rmDvEnNZEa2d" colab_type="code" colab={}
# remove instances based on Duration in the testing set
# remove these 849
train_df = train_df[train_df.trip_duration >= 5]
train_df = train_df[train_df.trip_duration < 1000000]
# + id="VNmAnV9hERzp" colab_type="code" outputId="e32eeee9-a9b7-42f9-a907-61459951c31c" colab={"base_uri": "https://localhost:8080/", "height": 32}
train_df.shape
# + id="ux6IGJ3P8O8o" colab_type="code" outputId="84e77249-5356-4fcf-90e9-39c21804e531" colab={"base_uri": "https://localhost:8080/", "height": 278}
sns.boxplot(train_df.trip_duration)
plt.show()
# + id="zHhUJ8uVz4V4" colab_type="code" outputId="273bf75c-e658-4342-b70e-0a58bf8abd41" colab={"base_uri": "https://localhost:8080/", "height": 508}
# %matplotlib inline
# For visualization purposes, we will use the Seaborn Library
sns.set(style="white", palette="muted", color_codes=True)
f, axes = plt.subplots(1, 1, figsize=(11, 7), sharex=True)
sns.despine(left=True)
sns.distplot(np.log(train_df['trip_duration'].values+1), axlabel = 'Log(trip_duration)', label = 'log(trip_duration)', bins = 50, color="r")
plt.setp(axes, yticks=[])
plt.tight_layout()
plt.show()
# + [markdown] id="wbYY2dC2Prvu" colab_type="text"
# **Passenger Count**
# + id="S-53odII5Inc" colab_type="code" outputId="45e31418-020a-4a5e-d762-3c8cce4f999e" colab={"base_uri": "https://localhost:8080/", "height": 197}
# remove instances based on Number of Passengers in the testing set
train_df.passenger_count.value_counts()
# + [markdown] id="CWbkYlxz6-V8" colab_type="text"
# By New York legislation, rides with more than 6 passengers are ilegal, therefore, we will remove all those datapoints in addition to those rides
# with less than 1 passanger.
# + id="HVqV2UTp6tdA" colab_type="code" colab={}
# remove these 53 trips
train_df = train_df[train_df.passenger_count <= 6]
train_df = train_df[train_df.passenger_count > 0]
# + id="L-Fyj7z-ORaD" colab_type="code" outputId="71c9a97f-5db2-42d2-d482-023f550b211f" colab={"base_uri": "https://localhost:8080/", "height": 32}
train_df.shape # Shape of the DataFrame matrix.
# + id="pRVtT8PasrHe" colab_type="code" outputId="b5bb1a4d-b536-4be4-afa9-89d3262395ca" colab={"base_uri": "https://localhost:8080/", "height": 283}
# Passanger count histogram.
sns.countplot(train_df.passenger_count)
plt.show()
# + [markdown] id="0X-qHSumRAia" colab_type="text"
# ### Distance
# + id="QwD5hmG4qN92" colab_type="code" outputId="786c87f2-41ab-4c16-9812-1501baa2545e" colab={"base_uri": "https://localhost:8080/", "height": 102}
# Some useful libraries
# !pip install haversine
from haversine import haversine, Unit
# + id="JEZ3gjy1TJac" colab_type="code" colab={}
def calc_distance(df):
pickup = (df['pickup_latitude'], df['pickup_longitude'])
drop = (df['dropoff_latitude'], df['dropoff_longitude'])
return haversine(pickup, drop)
# + id="-taaVJAvTwp1" colab_type="code" colab={}
train_df['distance'] = train_df.apply(lambda x: calc_distance(x), axis = 1)
# + id="I1_9Gj7KVWK9" colab_type="code" outputId="e2d973de-18c3-487a-d697-fa13e282a38b" colab={"base_uri": "https://localhost:8080/", "height": 164}
train_df.distance.describe()
# + id="OfJFy4viVqs0" colab_type="code" outputId="4afd832c-c703-4fdf-ed98-71b8155b00c3" colab={"base_uri": "https://localhost:8080/", "height": 283}
sns.boxplot(train_df.distance)
plt.show()
# + id="6VbDVVr6WLmS" colab_type="code" outputId="41bfdbbd-22ca-44ff-9cb0-1c0bc0255bbf" colab={"base_uri": "https://localhost:8080/", "height": 32}
# remove instances based on Duration in the testing set
train_df[(train_df.distance == 0)].distance.count()
# + id="fXN6qKLFIMAR" colab_type="code" outputId="24021764-0e06-4830-82f1-a6cc02fc1f12" colab={"base_uri": "https://localhost:8080/", "height": 164}
train_df.distance.describe()
# + id="TGvOYwtrXNFh" colab_type="code" outputId="3a2d145c-179c-4cd0-bdad-7ba9a0acbe58" colab={"base_uri": "https://localhost:8080/", "height": 303}
train_df.nlargest(5,['distance'])
# + [markdown] id="NY4QrV3jYunv" colab_type="text"
# There are trips with 0 distance, and as shown in the chart above, there are some points look like outliers
# + id="IV31jk87GKeE" colab_type="code" colab={}
# Remove instance with distance = 0
train_df = train_df[train_df.distance != 0]
# + id="YgK8tuoCIqFZ" colab_type="code" outputId="970cd259-ae3e-4eb8-cdfe-4a6a04e3acbb" colab={"base_uri": "https://localhost:8080/", "height": 267}
train_df.distance.groupby(pd.cut(train_df.distance, np.arange(0,100,10))).count().plot(kind='barh')
plt.show()
# + [markdown] id="DOvraW1eI_9-" colab_type="text"
# As shown above, most of the rides are completed between 1-10 kms with some of the rides with distances between 10-30 kms
# + [markdown] id="WNGIYA6S3n0W" colab_type="text"
# ### Speed
# + id="N3YmYm3s3qyM" colab_type="code" colab={}
train_df['speed'] = (train_df.distance/(train_df.trip_duration/3600))
# + id="62SpVP_6C3N6" colab_type="code" outputId="709c2dcb-c9c6-4632-f484-da819cbd6b4d" colab={"base_uri": "https://localhost:8080/", "height": 164}
train_df.speed.describe()
# + [markdown] id="x8cqPcOBDN65" colab_type="text"
# Some trips have speed more than 2,000 meter/hour, which is unrealistic. We will need to remove these instances.
# + id="xmfC9JcbFIwR" colab_type="code" colab={}
train_df = train_df[train_df.speed <= 110]
# + id="H2wAz1UHEaJh" colab_type="code" outputId="8539dafa-38b9-4dda-a0fb-8d3607432d31" colab={"base_uri": "https://localhost:8080/", "height": 357}
plt.figure(figsize = (20,5))
sns.boxplot(train_df.speed)
plt.show()
# + [markdown] id="H-yoCWVMKKwt" colab_type="text"
# # Feature Engineering
# + [markdown] id="5yqW8ExAKSA9" colab_type="text"
# ## Time and Date
# + id="gKpfP7XpvPop" colab_type="code" colab={}
#Calculate and assign new columns to the dataframe such as weekday,
#month and pickup_hour which will help us to gain more insights from the data.
def convert_datetime(df):
df['pickup_datetime'] = pd.to_datetime(df['pickup_datetime'])
df['weekday'] = df.pickup_datetime.dt.weekday_name
df['month'] = df.pickup_datetime.dt.month
df['weekday_number'] = df.pickup_datetime.dt.weekday
df['pickup_hour'] = df.pickup_datetime.dt.hour
# + id="RDNgzAw11D5F" colab_type="code" outputId="47a06989-ff68-4e68-e298-360e51a1c89a" colab={"base_uri": "https://localhost:8080/", "height": 303}
convert_datetime(train_df)
train_df.head()
# + [markdown] id="7uqa8kMKeXHn" colab_type="text"
# ## Creating Dummy Variables
# + [markdown] id="w6eI4MPqeqM2" colab_type="text"
# We can start training our model at this point. However, to add the model accuracy, we can convert our categorical data into dummy variables. We will use the function in Pandas library to make the change.
#
# Alternatively, we could have converted the categorical data into numerical data manually or by using some Scikit Learn tools such as
# + id="qTkJ8_wT1WSO" colab_type="code" colab={}
def create_dummy(df):
dummy = pd.get_dummies(df.store_and_fwd_flag, prefix='flag')
df = pd.concat([df,dummy],axis=1)
dummy = pd.get_dummies(df.vendor_id, prefix='vendor_id')
df = pd.concat([df,dummy],axis=1)
dummy = pd.get_dummies(df.passenger_count, prefix='passenger_count')
df = pd.concat([df,dummy],axis=1)
dummy = pd.get_dummies(df.month, prefix='month')
df = pd.concat([df,dummy],axis=1)
dummy = pd.get_dummies(df.weekday_number, prefix='weekday_number')
df = pd.concat([df,dummy],axis=1)
dummy = pd.get_dummies(df.pickup_hour, prefix='pickup_hour')
df = pd.concat([df,dummy],axis=1)
return df
# + id="PZGo4Bc4u1na" colab_type="code" colab={}
train_df = create_dummy(train_df)
# + id="CpnCuKs01hRQ" colab_type="code" outputId="608317cd-be01-4042-c27c-6c4873153494" colab={"base_uri": "https://localhost:8080/", "height": 32}
train_df.shape
# + id="lyTTza6IZ8CJ" colab_type="code" outputId="055987c2-7dc2-4f32-b2b6-1470dba63c8c" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# get the index of the features and label
list(zip(range(0,len(train_df.columns)),train_df.columns))
# + id="bDwPW9fcZg1E" colab_type="code" outputId="44dd474b-b204-4617-cb44-a43584598cdc" colab={"base_uri": "https://localhost:8080/", "height": 85}
# drop all the redundant columns such as pickup_datetime, weekday, month etc.
# and drop unneeded features such as id, speed (a dependant of duration)
# also seperate features with labels
X_train_set = train_df.iloc[:,np.r_[11,17:64]]
y_train_set = train_df["trip_duration"].copy()
# General equation for multiple linear regression usually includes the constant value,
# so we will add "1" to each instance first
X_train_set = sm.add_constant(X_train_set)
print(X_train_set.shape)
# + [markdown] id="KTAiD_xqIo5x" colab_type="text"
# ## Backward Feature selection
# + [markdown] id="fuS1xFgZLRCh" colab_type="text"
#
# We will run linear regression multiple time by using different combination of features and check p value of each regression iteration until we reach the level of p value that is less than 5%. If the regression p value is greater than 5%, we will reject the feature from the list of array and continue with next iteration until we reach the optimal combination of features.
# + id="l0Bx7kZxQPUw" colab_type="code" colab={}
X_train_opt = X_train_set
est = sm.OLS(y_train_set, X_train_opt)
est2 = est.fit()
# + id="SpILBV169n03" colab_type="code" outputId="b7064638-09f2-4184-cb3b-0725a0366a22" colab={"base_uri": "https://localhost:8080/", "height": 32}
X_train_opt.shape
# + id="Bqke6O2qSgWh" colab_type="code" colab={}
# fetch p-value
p_Vals = est2.pvalues
print(p_Vals)
# + id="1orhsLDzOKo_" colab_type="code" colab={}
# Define significance level for accepting the feature.
sig_Level = 0.05
# Looping over features and remove the feature with p value less than the 5%
while max(p_Vals) > sig_Level:
X_train_opt = X_train_opt.drop(X_train_opt.columns[np.argmax(np.array(p_Vals))],axis=1)
print("\n")
print("Feature at index {} is removed \n".format(str(np.argmax(np.array(p_Vals)))))
print(str(X_train_opt.shape[1]-1) + " dimensions remaining now... \n")
est = sm.OLS(y_train_set, X_train_opt)
est2 = est.fit()
p_Vals = est2.pvalues
print("=================================================================\n")
# + id="4Jv-4wFf-C4B" colab_type="code" colab={}
#Print final summary
print("Final stat summary with optimal {} features".format(str(X_train_opt.shape[1]-1)))
print(est2.pvalues)
# + [markdown] id="j-Y9LSxEmCDW" colab_type="text"
# # Modelling
# + [markdown] id="FFMZCBXSARZ2" colab_type="text"
# ## Linear Regression
# + [markdown] id="YI6uIrjCAZ8U" colab_type="text"
# ### Using all features
# + id="KP4gGNVkqhbC" colab_type="code" colab={}
# Split data from the all features
X_train_all, X_test_all, y_train_all, y_test_all = train_test_split(X_train_set,y_train_set, random_state=4, test_size=0.2)
# + id="7eAUenr0WdvD" colab_type="code" outputId="169c66a4-e3a1-4c14-f24b-7a2bd5ae6d99" colab={"base_uri": "https://localhost:8080/", "height": 32}
# Linear regressor for all features
regressor0 = LinearRegression()
regressor0.fit(X_train_all,y_train_all)
# + id="NX9cDLCzXBZR" colab_type="code" colab={}
# Predict from the test features of Feature Selection group
y_pred_all = regressor0.predict(X_test_all)
# + [markdown] id="-moWpbosAewC" colab_type="text"
# ### Using the selected features
# + id="QxDuRHD7_ByT" colab_type="code" colab={}
# Split data from the feature selection group
X_train_fs, X_test_fs, y_train_fs, y_test_fs = train_test_split(X_train_opt,y_train_set, random_state=4, test_size=0.2)
# + id="89S9nMgR_Vb4" colab_type="code" outputId="3dc5f691-c11a-4f6a-974b-4ff174fded19" colab={"base_uri": "https://localhost:8080/", "height": 32}
# Linear regressor for the Feature selection group
regressor1 = LinearRegression()
regressor1.fit(X_train_fs,y_train_fs)
# + id="A_wictRz_eVL" colab_type="code" colab={}
# Predict from the test features of Feature Selection group
y_pred_fs = regressor1.predict(X_test_fs)
# + id="wsKguu29_j2C" colab_type="code" outputId="8084d57c-2d19-472c-bcf4-72302cbfed9d" colab={"base_uri": "https://localhost:8080/", "height": 148}
# Evaluate the models
print('RMSE score for the Multiple LR using all features is : {}'.format(np.sqrt(metrics.mean_squared_error(y_test_all,y_pred_all))))
print('Variance score for the Multiple LR is : %.2f' % regressor0.score(X_test_all, y_test_all))
print("\n")
print('RMSE score for the Multiple LR FS is : {}'.format(np.sqrt(metrics.mean_squared_error(y_test_fs,y_pred_fs))))
print('Variance score for the Multiple LR FS is : %.2f' % regressor1.score(X_test_fs, y_test_fs))
print("\n")
# + id="inbZaIlG4tNZ" colab_type="code" colab={}
corr_matrix = train_df.corr()
corr_matrix["trip_duration"].sort_values(ascending=False)
# + [markdown] id="eQWvg093bINM" colab_type="text"
# ## Random Forest Regression
# + id="SkA-UV2hUQ4c" colab_type="code" outputId="9dcc6cf3-2048-4993-be3d-85d590c5db40" colab={"base_uri": "https://localhost:8080/", "height": 217}
# Tnstantiate() the object for the Random Forest Regressor with default params from raw data
regressor_rf_full = RandomForestRegressor(n_jobs=-1)
# Instantiate() the object for the Random Forest Regressor with default params for Feature Selection Group
regressor_rf_fs = RandomForestRegressor(n_jobs=-1)
# Train the object with default params for raw data
regressor_rf_full.fit(X_train_all,y_train_all)
# Train the object with default params for Feature Selection Group
regressor_rf_fs.fit(X_train_fs,y_train_fs)
# + id="GLlcGgrdlY8y" colab_type="code" colab={}
#Predict the output with object of default params for Feature Selection Group
y_pred_rf_full = regressor_rf_full.predict(X_test_all)
#Predict the output with object of default params for Feature Selection Group
y_pred_rf_fs = regressor_rf_fs.predict(X_test_fs)
# + id="pKcfco1Nrqxo" colab_type="code" outputId="e8fdf5d3-f3fa-45a1-e19d-513b1102fb3f" colab={"base_uri": "https://localhost:8080/", "height": 32}
type(regressor_rf_fs)
# + id="BO75Nlrglk6m" colab_type="code" outputId="865a5072-6067-47ec-9f47-675eedea9ff1" colab={"base_uri": "https://localhost:8080/", "height": 49}
print(np.sqrt(metrics.mean_squared_error(y_test_all,y_pred_rf_full)))
print(np.sqrt(metrics.mean_squared_error(y_test_fs,y_pred_rf_fs)))
| 57.942801 | 7,663 |
00d41f63eafd11724836cb5e4cbb90f1be8e02ab
|
py
|
python
|
chapter_8/8_5_NMT/8_5_NMT_scheduled_sampling.ipynb
|
tedpark/nlp-with-pytorch
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="nazLNtCMK8bf"
# *아래 링크를 통해 이 노트북을 주피터 노트북 뷰어(nbviewer.jupyter.org)로 보거나 구글 코랩(colab.research.google.com)에서 실행할 수 있습니다.*
#
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://nbviewer.jupyter.org/github/rickiepark/nlp-with-pytorch/blob/master/chapter_8/8_5_NMT/8_5_NMT_scheduled_sampling.ipynb"><img src="https://jupyter.org/assets/main-logo.svg" width="28" />주피터 노트북 뷰어로 보기</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/rickiepark/nlp-with-pytorch/blob/master/chapter_8/8_5_NMT/8_5_NMT_scheduled_sampling.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />구글 코랩(Colab)에서 실행하기</a>
# </td>
# </table>
# + id="7exiWxE3K8bj"
import os
from argparse import Namespace
from collections import Counter
import json
import re
import string
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from torch.nn import functional as F
from torch.nn.utils.rnn import pack_padded_sequence, pad_packed_sequence
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
import tqdm
# + [markdown] id="LxglotKoK8bk"
# ### Vocabulary
# + id="XsGcntBwK8bk"
class Vocabulary(object):
"""매핑을 위해 텍스트를 처리하고 어휘 사전을 만드는 클래스 """
def __init__(self, token_to_idx=None):
"""
매개변수:
token_to_idx (dict): 기존 토큰-인덱스 매핑 딕셔너리
"""
if token_to_idx is None:
token_to_idx = {}
self._token_to_idx = token_to_idx
self._idx_to_token = {idx: token
for token, idx in self._token_to_idx.items()}
def to_serializable(self):
""" 직렬화할 수 있는 딕셔너리를 반환합니다 """
return {'token_to_idx': self._token_to_idx}
@classmethod
def from_serializable(cls, contents):
""" 직렬화된 딕셔너리에서 Vocabulary 객체를 만듭니다 """
return cls(**contents)
def add_token(self, token):
""" 토큰을 기반으로 매핑 딕셔너리를 업데이트합니다
매개변수:
token (str): Vocabulary에 추가할 토큰
반환값:
index (int): 토큰에 상응하는 정수
"""
if token in self._token_to_idx:
index = self._token_to_idx[token]
else:
index = len(self._token_to_idx)
self._token_to_idx[token] = index
self._idx_to_token[index] = token
return index
def add_many(self, tokens):
"""토큰 리스트를 Vocabulary에 추가합니다.
매개변수:
tokens (list): 문자열 토큰 리스트
반환값:
indices (list): 토큰 리스트에 상응되는 인덱스 리스트
"""
return [self.add_token(token) for token in tokens]
def lookup_token(self, token):
"""토큰에 대응하는 인덱스를 추출합니다.
매개변수:
token (str): 찾을 토큰
반환값:
index (int): 토큰에 해당하는 인덱스
"""
return self._token_to_idx[token]
def lookup_index(self, index):
""" 인덱스에 해당하는 토큰을 반환합니다.
매개변수:
index (int): 찾을 인덱스
반환값:
token (str): 인텍스에 해당하는 토큰
에러:
KeyError: 인덱스가 Vocabulary에 없을 때 발생합니다.
"""
if index not in self._idx_to_token:
raise KeyError("the index (%d) is not in the Vocabulary" % index)
return self._idx_to_token[index]
def __str__(self):
return "<Vocabulary(size=%d)>" % len(self)
def __len__(self):
return len(self._token_to_idx)
# + id="C00MoCZiK8bk"
class SequenceVocabulary(Vocabulary):
def __init__(self, token_to_idx=None, unk_token="<UNK>",
mask_token="<MASK>", begin_seq_token="<BEGIN>",
end_seq_token="<END>"):
super(SequenceVocabulary, self).__init__(token_to_idx)
self._mask_token = mask_token
self._unk_token = unk_token
self._begin_seq_token = begin_seq_token
self._end_seq_token = end_seq_token
self.mask_index = self.add_token(self._mask_token)
self.unk_index = self.add_token(self._unk_token)
self.begin_seq_index = self.add_token(self._begin_seq_token)
self.end_seq_index = self.add_token(self._end_seq_token)
def to_serializable(self):
contents = super(SequenceVocabulary, self).to_serializable()
contents.update({'unk_token': self._unk_token,
'mask_token': self._mask_token,
'begin_seq_token': self._begin_seq_token,
'end_seq_token': self._end_seq_token})
return contents
def lookup_token(self, token):
""" 토큰에 대응하는 인덱스를 추출합니다.
토큰이 없으면 UNK 인덱스를 반환합니다.
매개변수:
token (str): 찾을 토큰
반환값:
index (int): 토큰에 해당하는 인덱스
노트:
UNK 토큰을 사용하려면 (Vocabulary에 추가하기 위해)
`unk_index`가 0보다 커야 합니다.
"""
if self.unk_index >= 0:
return self._token_to_idx.get(token, self.unk_index)
else:
return self._token_to_idx[token]
# + [markdown] id="Shr3OnTZK8bl"
# ### Vectorizer
# + id="GCEpJxkeK8bl"
class NMTVectorizer(object):
""" 어휘 사전을 생성하고 관리합니다 """
def __init__(self, source_vocab, target_vocab, max_source_length, max_target_length):
"""
매개변수:
source_vocab (SequenceVocabulary): 소스 단어를 정수에 매핑합니다
target_vocab (SequenceVocabulary): 타깃 단어를 정수에 매핑합니다
max_source_length (int): 소스 데이터셋에서 가장 긴 시퀀스 길이
max_target_length (int): 타깃 데이터셋에서 가장 긴 시퀀스 길이
"""
self.source_vocab = source_vocab
self.target_vocab = target_vocab
self.max_source_length = max_source_length
self.max_target_length = max_target_length
def _vectorize(self, indices, vector_length=-1, mask_index=0):
"""인덱스를 벡터로 변환합니다
매개변수:
indices (list): 시퀀스를 나타내는 정수 리스트
vector_length (int): 인덱스 벡터의 길이
mask_index (int): 사용할 마스크 인덱스; 거의 항상 0
"""
if vector_length < 0:
vector_length = len(indices)
vector = np.zeros(vector_length, dtype=np.int64)
vector[:len(indices)] = indices
vector[len(indices):] = mask_index
return vector
def _get_source_indices(self, text):
""" 벡터로 변환된 소스 텍스트를 반환합니다
매개변수:
text (str): 소스 텍스트; 토큰은 공백으로 구분되어야 합니다
반환값:
indices (list): 텍스트를 표현하는 정수 리스트
"""
indices = [self.source_vocab.begin_seq_index]
indices.extend(self.source_vocab.lookup_token(token) for token in text.split(" "))
indices.append(self.source_vocab.end_seq_index)
return indices
def _get_target_indices(self, text):
""" 벡터로 변환된 타깃 텍스트를 반환합니다
매개변수:
text (str): 타깃 텍스트; 토큰은 공백으로 구분되어야 합니다
반환값:
튜플: (x_indices, y_indices)
x_indices (list): 디코더에서 샘플을 나타내는 정수 리스트
y_indices (list): 디코더에서 예측을 나타내는 정수 리스트
"""
indices = [self.target_vocab.lookup_token(token) for token in text.split(" ")]
x_indices = [self.target_vocab.begin_seq_index] + indices
y_indices = indices + [self.target_vocab.end_seq_index]
return x_indices, y_indices
def vectorize(self, source_text, target_text, use_dataset_max_lengths=True):
""" 벡터화된 소스 텍스트와 타깃 텍스트를 반환합니다
벡터화된 소스 텍슽트는 하나의 벡터입니다.
벡터화된 타깃 텍스트는 7장의 성씨 모델링과 비슷한 스타일로 두 개의 벡터로 나뉩니다.
각 타임 스텝에서 첫 번째 벡터가 샘플이고 두 번째 벡터가 타깃이 됩니다.
매개변수:
source_text (str): 소스 언어의 텍스트
target_text (str): 타깃 언어의 텍스트
use_dataset_max_lengths (bool): 최대 벡터 길이를 사용할지 여부
반환값:
다음과 같은 키에 벡터화된 데이터를 담은 딕셔너리:
source_vector, target_x_vector, target_y_vector, source_length
"""
source_vector_length = -1
target_vector_length = -1
if use_dataset_max_lengths:
source_vector_length = self.max_source_length + 2
target_vector_length = self.max_target_length + 1
source_indices = self._get_source_indices(source_text)
source_vector = self._vectorize(source_indices,
vector_length=source_vector_length,
mask_index=self.source_vocab.mask_index)
target_x_indices, target_y_indices = self._get_target_indices(target_text)
target_x_vector = self._vectorize(target_x_indices,
vector_length=target_vector_length,
mask_index=self.target_vocab.mask_index)
target_y_vector = self._vectorize(target_y_indices,
vector_length=target_vector_length,
mask_index=self.target_vocab.mask_index)
return {"source_vector": source_vector,
"target_x_vector": target_x_vector,
"target_y_vector": target_y_vector,
"source_length": len(source_indices)}
@classmethod
def from_dataframe(cls, bitext_df):
""" 데이터셋 데이터프레임으로 NMTVectorizer를 초기화합니다
매개변수:
bitext_df (pandas.DataFrame): 텍스트 데이터셋
반환값
:
NMTVectorizer 객체
"""
source_vocab = SequenceVocabulary()
target_vocab = SequenceVocabulary()
max_source_length = 0
max_target_length = 0
for _, row in bitext_df.iterrows():
source_tokens = row["source_language"].split(" ")
if len(source_tokens) > max_source_length:
max_source_length = len(source_tokens)
for token in source_tokens:
source_vocab.add_token(token)
target_tokens = row["target_language"].split(" ")
if len(target_tokens) > max_target_length:
max_target_length = len(target_tokens)
for token in target_tokens:
target_vocab.add_token(token)
return cls(source_vocab, target_vocab, max_source_length, max_target_length)
@classmethod
def from_serializable(cls, contents):
source_vocab = SequenceVocabulary.from_serializable(contents["source_vocab"])
target_vocab = SequenceVocabulary.from_serializable(contents["target_vocab"])
return cls(source_vocab=source_vocab,
target_vocab=target_vocab,
max_source_length=contents["max_source_length"],
max_target_length=contents["max_target_length"])
def to_serializable(self):
return {"source_vocab": self.source_vocab.to_serializable(),
"target_vocab": self.target_vocab.to_serializable(),
"max_source_length": self.max_source_length,
"max_target_length": self.max_target_length}
# + [markdown] id="UAzWNsUSK8bn"
# ### Dataset
# + id="paSQ8rP4K8bp"
class NMTDataset(Dataset):
def __init__(self, text_df, vectorizer):
"""
매개변수:
text_df (pandas.DataFrame): 데이터셋
vectorizer (SurnameVectorizer): 데이터셋에서 만든 Vectorizer 객체
"""
self.text_df = text_df
self._vectorizer = vectorizer
self.train_df = self.text_df[self.text_df.split=='train']
self.train_size = len(self.train_df)
self.val_df = self.text_df[self.text_df.split=='val']
self.validation_size = len(self.val_df)
self.test_df = self.text_df[self.text_df.split=='test']
self.test_size = len(self.test_df)
self._lookup_dict = {'train': (self.train_df, self.train_size),
'val': (self.val_df, self.validation_size),
'test': (self.test_df, self.test_size)}
self.set_split('train')
@classmethod
def load_dataset_and_make_vectorizer(cls, dataset_csv):
"""데이터셋을 로드하고 새로운 Vectorizer를 만듭니다
매개변수:
dataset_csv (str): 데이터셋의 위치
반환값:
NMTDataset의 객체
"""
text_df = pd.read_csv(dataset_csv)
train_subset = text_df[text_df.split=='train']
return cls(text_df, NMTVectorizer.from_dataframe(train_subset))
@classmethod
def load_dataset_and_load_vectorizer(cls, dataset_csv, vectorizer_filepath):
"""데이터셋과 새로운 Vectorizer 객체를 로드합니다.
캐싱된 Vectorizer 객체를 재사용할 때 사용합니다.
매개변수:
dataset_csv (str): 데이터셋의 위치
vectorizer_filepath (str): Vectorizer 객체의 저장 위치
반환값:
NMTDataset의 객체
"""
text_df = pd.read_csv(dataset_csv)
vectorizer = cls.load_vectorizer_only(vectorizer_filepath)
return cls(text_df, vectorizer)
@staticmethod
def load_vectorizer_only(vectorizer_filepath):
"""파일에서 Vectorizer 객체를 로드하는 정적 메서드
매개변수:
vectorizer_filepath (str): 직렬화된 Vectorizer 객체의 위치
반환값:
NMTVectorizer의 인스턴스
"""
with open(vectorizer_filepath) as fp:
return NMTVectorizer.from_serializable(json.load(fp))
def save_vectorizer(self, vectorizer_filepath):
"""Vectorizer 객체를 json 형태로 디스크에 저장합니다
매개변수:
vectorizer_filepath (str): Vectorizer 객체의 저장 위치
"""
with open(vectorizer_filepath, "w") as fp:
json.dump(self._vectorizer.to_serializable(), fp)
def get_vectorizer(self):
""" 벡터 변환 객체를 반환합니다 """
return self._vectorizer
def set_split(self, split="train"):
self._target_split = split
self._target_df, self._target_size = self._lookup_dict[split]
def __len__(self):
return self._target_size
def __getitem__(self, index):
"""파이토치 데이터셋의 주요 진입 메서드
매개변수:
index (int): 데이터 포인트에 대한 인덱스
반환값:
데이터 포인트(x_source, x_target, y_target, x_source_length)를 담고 있는 딕셔너리
"""
row = self._target_df.iloc[index]
vector_dict = self._vectorizer.vectorize(row.source_language, row.target_language)
return {"x_source": vector_dict["source_vector"],
"x_target": vector_dict["target_x_vector"],
"y_target": vector_dict["target_y_vector"],
"x_source_length": vector_dict["source_length"]}
def get_num_batches(self, batch_size):
"""배치 크기가 주어지면 데이터셋으로 만들 수 있는 배치 개수를 반환합니다
매개변수:
batch_size (int)
반환값:
배치 개수
"""
return len(self) // batch_size
# + id="zUXyb3O7K8bq"
def generate_nmt_batches(dataset, batch_size, shuffle=True,
drop_last=True, device="cpu"):
""" 파이토치 DataLoader를 감싸고 있는 제너레이터 함수; NMT 버전 """
dataloader = DataLoader(dataset=dataset, batch_size=batch_size,
shuffle=shuffle, drop_last=drop_last)
for data_dict in dataloader:
lengths = data_dict['x_source_length'].numpy()
sorted_length_indices = lengths.argsort()[::-1].tolist()
out_data_dict = {}
for name, tensor in data_dict.items():
out_data_dict[name] = data_dict[name][sorted_length_indices].to(device)
yield out_data_dict
# + [markdown] id="FUU7soeFK8bq"
# ## 신경망 기계 번역 모델
#
# 구성 요소:
#
# 1. NMTEncoder
# - 소스 시퀀스를 입력으로 받아 임베딩하여 양방향 GRU에 주입합니다.
# 2. NMTDecoder
# - 인코더 상태와 어텐션을 사용해 디코더가 새로운 시퀀스를 생성합니다.
# - 타임 스텝마다 정답 타깃 시퀀스를 입력으로 사용합니다.
# - 또는 디코더가 선택한 시퀀스를 입력으로 사용할 수도 있습니다.
# - 이를 커리큘럼 학습(curriculum learning), 탐색 학습(learning to search)이라 부릅니다.
# 3. NMTModel
# - 인코더와 디코더를 하나의 클래스로 구성합니다.
# + id="MPE37HiTK8bq"
class NMTEncoder(nn.Module):
def __init__(self, num_embeddings, embedding_size, rnn_hidden_size):
"""
매개변수:
num_embeddings (int): 임베딩 개수는 소스 어휘 사전의 크기입니다
embedding_size (int): 임베딩 벡터의 크기
rnn_hidden_size (int): RNN 은닉 상태 벡터의 크기
"""
super(NMTEncoder, self).__init__()
self.source_embedding = nn.Embedding(num_embeddings, embedding_size, padding_idx=0)
self.birnn = nn.GRU(embedding_size, rnn_hidden_size, bidirectional=True, batch_first=True)
def forward(self, x_source, x_lengths):
""" 모델의 정방향 계산
매개변수:
x_source (torch.Tensor): 입력 데이터 텐서
x_source.shape는 (batch, seq_size)이다.
x_lengths (torch.Tensor): 배치에 있는 아이템의 길이 벡터
반환값:
튜플: x_unpacked (torch.Tensor), x_birnn_h (torch.Tensor)
x_unpacked.shape = (batch, seq_size, rnn_hidden_size * 2)
x_birnn_h.shape = (batch, rnn_hidden_size * 2)
"""
x_embedded = self.source_embedding(x_source)
# PackedSequence 생성; x_packed.data.shape=(number_items, embeddign_size)
x_packed = pack_padded_sequence(x_embedded, x_lengths.detach().cpu().numpy(),
batch_first=True)
# x_birnn_h.shape = (num_rnn, batch_size, feature_size)
x_birnn_out, x_birnn_h = self.birnn(x_packed)
# (batch_size, num_rnn, feature_size)로 변환
x_birnn_h = x_birnn_h.permute(1, 0, 2)
# 특성 펼침; (batch_size, num_rnn * feature_size)로 바꾸기
# (참고: -1은 남은 차원에 해당합니다,
# 두 개의 RNN 은닉 벡터를 1로 펼칩니다)
x_birnn_h = x_birnn_h.contiguous().view(x_birnn_h.size(0), -1)
x_unpacked, _ = pad_packed_sequence(x_birnn_out, batch_first=True)
return x_unpacked, x_birnn_h
def verbose_attention(encoder_state_vectors, query_vector):
""" 원소별 연산을 사용하는 어텐션 메커니즘 버전
매개변수:
encoder_state_vectors (torch.Tensor): 인코더의 양방향 GRU에서 출력된 3차원 텐서
query_vector (torch.Tensor): 디코더 GRU의 은닉 상태
"""
batch_size, num_vectors, vector_size = encoder_state_vectors.size()
vector_scores = torch.sum(encoder_state_vectors * query_vector.view(batch_size, 1, vector_size),
dim=2)
vector_probabilities = F.softmax(vector_scores, dim=1)
weighted_vectors = encoder_state_vectors * vector_probabilities.view(batch_size, num_vectors, 1)
context_vectors = torch.sum(weighted_vectors, dim=1)
return context_vectors, vector_probabilities, vector_scores
def terse_attention(encoder_state_vectors, query_vector):
""" 점곱을 사용하는 어텐션 메커니즘 버전
매개변수:
encoder_state_vectors (torch.Tensor): 인코더의 양방향 GRU에서 출력된 3차원 텐서
query_vector (torch.Tensor): 디코더 GRU의 은닉 상태
"""
vector_scores = torch.matmul(encoder_state_vectors, query_vector.unsqueeze(dim=2)).squeeze()
vector_probabilities = F.softmax(vector_scores, dim=-1)
context_vectors = torch.matmul(encoder_state_vectors.transpose(-2, -1),
vector_probabilities.unsqueeze(dim=2)).squeeze()
return context_vectors, vector_probabilities
class NMTDecoder(nn.Module):
def __init__(self, num_embeddings, embedding_size, rnn_hidden_size, bos_index):
"""
매개변수:
num_embeddings (int): 임베딩 개수는 타깃 어휘 사전에 있는 고유한 단어의 개수이다
embedding_size (int): 임베딩 벡터 크기
rnn_hidden_size (int): RNN 은닉 상태 크기
bos_index(int): begin-of-sequence 인덱스
"""
super(NMTDecoder, self).__init__()
self._rnn_hidden_size = rnn_hidden_size
self.target_embedding = nn.Embedding(num_embeddings=num_embeddings,
embedding_dim=embedding_size,
padding_idx=0)
self.gru_cell = nn.GRUCell(embedding_size + rnn_hidden_size,
rnn_hidden_size)
self.hidden_map = nn.Linear(rnn_hidden_size, rnn_hidden_size)
self.classifier = nn.Linear(rnn_hidden_size * 2, num_embeddings)
self.bos_index = bos_index
self._sampling_temperature = 3
def _init_indices(self, batch_size):
""" BEGIN-OF-SEQUENCE 인덱스 벡터를 반환합니다 """
return torch.ones(batch_size, dtype=torch.int64) * self.bos_index
def _init_context_vectors(self, batch_size):
""" 문맥 벡터를 초기화하기 위한 0 벡터를 반환합니다 """
return torch.zeros(batch_size, self._rnn_hidden_size)
def forward(self, encoder_state, initial_hidden_state, target_sequence, sample_probability=0.0):
""" 모델의 정방향 계산
매개변수:
encoder_state (torch.Tensor): NMTEncoder의 출력
initial_hidden_state (torch.Tensor): NMTEncoder의 마지막 은닉 상태
target_sequence (torch.Tensor): 타깃 텍스트 데이터 텐서
sample_probability (float): 스케줄링된 샘플링 파라미터
디코더 타임 스텝마다 모델 예측에 사용할 확률
반환값:
output_vectors (torch.Tensor): 각 타임 스텝의 예측 벡터
"""
if target_sequence is None:
sample_probability = 1.0
else:
# 가정: 첫 번째 차원은 배치 차원입니다
# 즉 입력은 (Batch, Seq)
# 시퀀스에 대해 반복해야 하므로 (Seq, Batch)로 차원을 바꿉니다
target_sequence = target_sequence.permute(1, 0)
output_sequence_size = target_sequence.size(0)
# 주어진 인코더의 은닉 상태를 초기 은닉 상태로 사용합니다
h_t = self.hidden_map(initial_hidden_state)
batch_size = encoder_state.size(0)
# 문맥 벡터를 0으로 초기화합니다
context_vectors = self._init_context_vectors(batch_size)
# 첫 단어 y_t를 BOS로 초기화합니다
y_t_index = self._init_indices(batch_size)
h_t = h_t.to(encoder_state.device)
y_t_index = y_t_index.to(encoder_state.device)
context_vectors = context_vectors.to(encoder_state.device)
output_vectors = []
self._cached_p_attn = []
self._cached_ht = []
self._cached_decoder_state = encoder_state.cpu().detach().numpy()
for i in range(output_sequence_size):
# 스케줄링된 샘플링 사용 여부
use_sample = np.random.random() < sample_probability
if not use_sample:
y_t_index = target_sequence[i]
# 단계 1: 단어를 임베딩하고 이전 문맥과 연결합니다
y_input_vector = self.target_embedding(y_t_index)
rnn_input = torch.cat([y_input_vector, context_vectors], dim=1)
# 단계 2: GRU를 적용하고 새로운 은닉 벡터를 얻습니다
h_t = self.gru_cell(rnn_input, h_t)
self._cached_ht.append(h_t.cpu().detach().numpy())
# 단계 3: 현재 은닉 상태를 사용해 인코더의 상태를 주목합니다
context_vectors, p_attn, _ = verbose_attention(encoder_state_vectors=encoder_state,
query_vector=h_t)
# 부가 작업: 시각화를 위해 어텐션 확률을 저장합니다
self._cached_p_attn.append(p_attn.cpu().detach().numpy())
# 단게 4: 현재 은닉 상태와 문맥 벡터를 사용해 다음 단어를 예측합니다
prediction_vector = torch.cat((context_vectors, h_t), dim=1)
score_for_y_t_index = self.classifier(F.dropout(prediction_vector, 0.3))
if use_sample:
p_y_t_index = F.softmax(score_for_y_t_index * self._sampling_temperature, dim=1)
# _, y_t_index = torch.max(p_y_t_index, 1)
y_t_index = torch.multinomial(p_y_t_index, 1).squeeze()
# 부가 작업: 예측 성능 점수를 기록합니다
output_vectors.append(score_for_y_t_index)
output_vectors = torch.stack(output_vectors).permute(1, 0, 2)
return output_vectors
class NMTModel(nn.Module):
""" 신경망 기계 번역 모델 """
def __init__(self, source_vocab_size, source_embedding_size,
target_vocab_size, target_embedding_size, encoding_size,
target_bos_index):
"""
매개변수:
source_vocab_size (int): 소스 언어에 있는 고유한 단어 개수
source_embedding_size (int): 소스 임베딩 벡터의 크기
target_vocab_size (int): 타깃 언어에 있는 고유한 단어 개수
target_embedding_size (int): 타깃 임베딩 벡터의 크기
encoding_size (int): 인코더 RNN의 크기
target_bos_index (int): BEGIN-OF-SEQUENCE 토큰 인덱스
"""
super(NMTModel, self).__init__()
self.encoder = NMTEncoder(num_embeddings=source_vocab_size,
embedding_size=source_embedding_size,
rnn_hidden_size=encoding_size)
decoding_size = encoding_size * 2
self.decoder = NMTDecoder(num_embeddings=target_vocab_size,
embedding_size=target_embedding_size,
rnn_hidden_size=decoding_size,
bos_index=target_bos_index)
def forward(self, x_source, x_source_lengths, target_sequence, sample_probability=0.0):
""" 모델의 정방향 계산
매개변수:
x_source (torch.Tensor): 소스 텍스트 데이터 텐서
x_source.shape는 (batch, vectorizer.max_source_length)입니다.
x_source_lengths torch.Tensor): x_source에 있는 시퀀스 길이
target_sequence (torch.Tensor): 타깃 텍스트 데이터 텐서
sample_probability (float): 스케줄링된 샘플링 파라미터
디코더 타임 스텝마다 모델 예측에 사용할 확률
반환값:
decoded_states (torch.Tensor): 각 출력 타임 스텝의 예측 벡터
"""
encoder_state, final_hidden_states = self.encoder(x_source, x_source_lengths)
decoded_states = self.decoder(encoder_state=encoder_state,
initial_hidden_state=final_hidden_states,
target_sequence=target_sequence,
sample_probability=sample_probability)
return decoded_states
# + [markdown] id="sMpnJ-RKK8bq"
# ## 모델 훈련과 상태 기록 함수
# + id="_NdbRrN8K8bq"
def set_seed_everywhere(seed, cuda):
np.random.seed(seed)
torch.manual_seed(seed)
if cuda:
torch.cuda.manual_seed_all(seed)
def handle_dirs(dirpath):
if not os.path.exists(dirpath):
os.makedirs(dirpath)
def make_train_state(args):
return {'stop_early': False,
'early_stopping_step': 0,
'early_stopping_best_val': 1e8,
'learning_rate': args.learning_rate,
'epoch_index': 0,
'train_loss': [],
'train_acc': [],
'val_loss': [],
'val_acc': [],
'test_loss': -1,
'test_acc': -1,
'model_filename': args.model_state_file}
def update_train_state(args, model, train_state):
"""훈련 상태 업데이트합니다.
콤포넌트:
- 조기 종료: 과대 적합 방지
- 모델 체크포인트: 더 나은 모델을 저장합니다
:param args: 메인 매개변수
:param model: 훈련할 모델
:param train_state: 훈련 상태를 담은 딕셔너리
:returns:
새로운 훈련 상태
"""
# 적어도 한 번 모델을 저장합니다
if train_state['epoch_index'] == 0:
torch.save(model.state_dict(), train_state['model_filename'])
train_state['stop_early'] = False
# 성능이 향상되면 모델을 저장합니다
elif train_state['epoch_index'] >= 1:
loss_tm1, loss_t = train_state['val_loss'][-2:]
# 손실이 나빠지면
if loss_t >= loss_tm1:
# 조기 종료 단계 업데이트
train_state['early_stopping_step'] += 1
# 손실이 감소하면
else:
# 최상의 모델 저장
if loss_t < train_state['early_stopping_best_val']:
torch.save(model.state_dict(), train_state['model_filename'])
train_state['early_stopping_best_val'] = loss_t
# 조기 종료 단계 재설정
train_state['early_stopping_step'] = 0
# 조기 종료 여부 확인
train_state['stop_early'] = \
train_state['early_stopping_step'] >= args.early_stopping_criteria
return train_state
def normalize_sizes(y_pred, y_true):
"""텐서 크기 정규화
매개변수:
y_pred (torch.Tensor): 모델의 출력
3차원 텐서이면 행렬로 변환합니다.
y_true (torch.Tensor): 타깃 예측
행렬이면 벡터로 변환합니다.
"""
if len(y_pred.size()) == 3:
y_pred = y_pred.contiguous().view(-1, y_pred.size(2))
if len(y_true.size()) == 2:
y_true = y_true.contiguous().view(-1)
return y_pred, y_true
def compute_accuracy(y_pred, y_true, mask_index):
y_pred, y_true = normalize_sizes(y_pred, y_true)
_, y_pred_indices = y_pred.max(dim=1)
correct_indices = torch.eq(y_pred_indices, y_true).float()
valid_indices = torch.ne(y_true, mask_index).float()
n_correct = (correct_indices * valid_indices).sum().item()
n_valid = valid_indices.sum().item()
return n_correct / n_valid * 100
def sequence_loss(y_pred, y_true, mask_index):
y_pred, y_true = normalize_sizes(y_pred, y_true)
return F.cross_entropy(y_pred, y_true, ignore_index=mask_index)
# + [markdown] id="9k6Di7pLK8br"
# ### 설정
# + id="uwxzx0WuK8br" outputId="01d48fa6-6f61-4a19-f74b-3f33d410a127" colab={"base_uri": "https://localhost:8080/"}
args = Namespace(dataset_csv="data/nmt/simplest_eng_fra.csv",
vectorizer_file="vectorizer.json",
model_state_file="model.pth",
save_dir="model_storage/ch8/nmt_luong_sampling",
reload_from_files=False,
expand_filepaths_to_save_dir=True,
cuda=True,
seed=1337,
learning_rate=5e-4,
batch_size=32,
num_epochs=100,
early_stopping_criteria=5,
source_embedding_size=24,
target_embedding_size=24,
encoding_size=32,
catch_keyboard_interrupt=True)
if args.expand_filepaths_to_save_dir:
args.vectorizer_file = os.path.join(args.save_dir,
args.vectorizer_file)
args.model_state_file = os.path.join(args.save_dir,
args.model_state_file)
print("파일 경로: ")
print("\t{}".format(args.vectorizer_file))
print("\t{}".format(args.model_state_file))
# CUDA 체크
if not torch.cuda.is_available():
args.cuda = False
args.device = torch.device("cuda" if args.cuda else "cpu")
print("CUDA 사용 여부: {}".format(args.cuda))
# 재현성을 위해 시드 설정
set_seed_everywhere(args.seed, args.cuda)
# 디렉토리 처리
handle_dirs(args.save_dir)
# + id="P549WmvQK8br" outputId="967b1a3a-468a-4e96-f09b-5147347ea593" colab={"base_uri": "https://localhost:8080/"}
# 만약 코랩에서 실행하는 경우 아래 코드를 실행하여 전처리된 데이터를 다운로드하세요.
# !mkdir data
# !wget https://git.io/JqQBE -O data/download.py
# !wget https://git.io/JqQB7 -O data/get-all-data.sh
# !chmod 755 data/get-all-data.sh
# %cd data
# !./get-all-data.sh
# %cd ..
# + id="4CR02VV8K8bs"
if args.reload_from_files and os.path.exists(args.vectorizer_file):
# 체크포인트를 로드합니다.
dataset = NMTDataset.load_dataset_and_load_vectorizer(args.dataset_csv,
args.vectorizer_file)
else:
# 데이터셋과 Vectorizer를 만듭니다.
dataset = NMTDataset.load_dataset_and_make_vectorizer(args.dataset_csv)
dataset.save_vectorizer(args.vectorizer_file)
vectorizer = dataset.get_vectorizer()
# + id="KSU79tHDK8bs" outputId="5a7af29b-b4b4-43b2-afa1-25a338de6a4f" colab={"base_uri": "https://localhost:8080/"}
model = NMTModel(source_vocab_size=len(vectorizer.source_vocab),
source_embedding_size=args.source_embedding_size,
target_vocab_size=len(vectorizer.target_vocab),
target_embedding_size=args.target_embedding_size,
encoding_size=args.encoding_size,
target_bos_index=vectorizer.target_vocab.begin_seq_index)
if args.reload_from_files and os.path.exists(args.model_state_file):
model.load_state_dict(torch.load(args.model_state_file))
print("로드한 모델")
else:
print("새로운 모델")
# + [markdown] id="j4uOlY7_K8bs"
# ### 모델 훈련
# + id="QhvY2gmlK8bs" outputId="5aa9f988-aaed-4a4c-e21a-5fe522c2b070" colab={"base_uri": "https://localhost:8080/", "height": 113, "referenced_widgets": ["97c629a82cbd498e9f740ae56b3cf20c", "2609cbe60e4449dbaf04982b16483e30", "0872251cc85a4a8cb6be3ae5f53497b5", "8069d21bfcb64b8ea42c5f368f01dd83", "0cc657f692564bd1805e4eb0e62dce7a", "7010e2a735894ef48e71603f0e0fbcd9", "7ce283a711bb45aeb9c90b88f5b9ddcf", "d6514fa364864045863efedb5eaeb5f0", "597d5973b4a64b31b8ed078f4a2506f8", "b8565cfc580a4bbebf8361b4825275a2", "abe5a3f0186e46078ebc7641f0eda962", "152b8f692e424bc682c39bb560c841c7", "ee745736c7f74345913916c53846e0e9", "7f3cff1c0d5540af900da27bbf96c41b", "20f6c0d0e14041c3bd2ed0aba2dc4d12", "29caa56514724c73ad89f3e62daad395", "1760d6878a8f4da89c1806548324ea5c", "7762b72d4707476ba0b4e187c7cb066a", "e9b8e7d86c8940b1a324a56e117cfe43", "6d83aaf20703462caf3c6f105dcd561a", "d467e7a06d384b1ea5bf435f4a9d3767", "d53bcfeb92ab48d2a5f7f46500fbcd73", "45089a2cf8b64bd1b07145cdf81eac81", "9262a46414084c628af18ed7fcb22cbd"]}
model = model.to(args.device)
optimizer = optim.Adam(model.parameters(), lr=args.learning_rate)
scheduler = optim.lr_scheduler.ReduceLROnPlateau(optimizer=optimizer,
mode='min', factor=0.5,
patience=1)
mask_index = vectorizer.target_vocab.mask_index
train_state = make_train_state(args)
epoch_bar = tqdm.notebook.tqdm(desc='training routine',
total=args.num_epochs,
position=0)
dataset.set_split('train')
train_bar = tqdm.notebook.tqdm(desc='split=train',
total=dataset.get_num_batches(args.batch_size),
position=1,
leave=True)
dataset.set_split('val')
val_bar = tqdm.notebook.tqdm(desc='split=val',
total=dataset.get_num_batches(args.batch_size),
position=1,
leave=True)
try:
for epoch_index in range(args.num_epochs):
sample_probability = (20 + epoch_index) / args.num_epochs
train_state['epoch_index'] = epoch_index
# 훈련 세트에 대한 순회
# 훈련 세트와 배치 제너레이터 준비, 손실과 정확도를 0으로 설정
dataset.set_split('train')
batch_generator = generate_nmt_batches(dataset,
batch_size=args.batch_size,
device=args.device)
running_loss = 0.0
running_acc = 0.0
model.train()
for batch_index, batch_dict in enumerate(batch_generator):
# 훈련 과정은 5단계로 이루어집니다
# --------------------------------------
# 단계 1. 그레이디언트를 0으로 초기화합니다
optimizer.zero_grad()
# 단계 2. 출력을 계산합니다
y_pred = model(batch_dict['x_source'],
batch_dict['x_source_length'],
batch_dict['x_target'],
sample_probability=sample_probability)
# 단계 3. 손실을 계산합니다
loss = sequence_loss(y_pred, batch_dict['y_target'], mask_index)
# 단계 4. 손실을 사용해 그레이디언트를 계산합니다
loss.backward()
# 단계 5. 옵티마이저로 가중치를 업데이트합니다
optimizer.step()
# -----------------------------------------
# 이동 손실과 이동 정확도를 계산합니다
running_loss += (loss.item() - running_loss) / (batch_index + 1)
acc_t = compute_accuracy(y_pred, batch_dict['y_target'], mask_index)
running_acc += (acc_t - running_acc) / (batch_index + 1)
# 진행 상태 막대 업데이트
train_bar.set_postfix(loss=running_loss, acc=running_acc,
epoch=epoch_index)
train_bar.update()
train_state['train_loss'].append(running_loss)
train_state['train_acc'].append(running_acc)
# 검증 세트에 대한 순회
# 검증 세트와 배치 제너레이터 준비, 손실과 정확도를 0으로 설정
dataset.set_split('val')
batch_generator = generate_nmt_batches(dataset,
batch_size=args.batch_size,
device=args.device)
running_loss = 0.
running_acc = 0.
model.eval()
for batch_index, batch_dict in enumerate(batch_generator):
# 단계 1. 출력을 계산합니다
y_pred = model(batch_dict['x_source'],
batch_dict['x_source_length'],
batch_dict['x_target'],
sample_probability=sample_probability)
# 단계 2. 손실을 계산합니다
loss = sequence_loss(y_pred, batch_dict['y_target'], mask_index)
# 단계 3. 이동 손실과 이동 정확도를 계산합니다
running_loss += (loss.item() - running_loss) / (batch_index + 1)
acc_t = compute_accuracy(y_pred, batch_dict['y_target'], mask_index)
running_acc += (acc_t - running_acc) / (batch_index + 1)
# 진행 상태 막대 업데이트
val_bar.set_postfix(loss=running_loss, acc=running_acc,
epoch=epoch_index)
val_bar.update()
train_state['val_loss'].append(running_loss)
train_state['val_acc'].append(running_acc)
train_state = update_train_state(args=args, model=model,
train_state=train_state)
scheduler.step(train_state['val_loss'][-1])
if train_state['stop_early']:
break
train_bar.n = 0
val_bar.n = 0
epoch_bar.set_postfix(best_val=train_state['early_stopping_best_val'])
epoch_bar.update()
except KeyboardInterrupt:
print("반복 중지")
# + id="B7ZzwuJeK8bs"
from nltk.translate import bleu_score
import seaborn as sns
import matplotlib.pyplot as plt
chencherry = bleu_score.SmoothingFunction()
# + id="jJs5T5J8K8bs"
def sentence_from_indices(indices, vocab, strict=True, return_string=True):
ignore_indices = set([vocab.mask_index, vocab.begin_seq_index, vocab.end_seq_index])
out = []
for index in indices:
if index == vocab.begin_seq_index and strict:
continue
elif index == vocab.end_seq_index and strict:
break
else:
out.append(vocab.lookup_index(index))
if return_string:
return " ".join(out)
else:
return out
class NMTSampler:
def __init__(self, vectorizer, model):
self.vectorizer = vectorizer
self.model = model
def apply_to_batch(self, batch_dict):
self._last_batch = batch_dict
y_pred = self.model(x_source=batch_dict['x_source'],
x_source_lengths=batch_dict['x_source_length'],
target_sequence=batch_dict['x_target'])
self._last_batch['y_pred'] = y_pred
attention_batched = np.stack(self.model.decoder._cached_p_attn).transpose(1, 0, 2)
self._last_batch['attention'] = attention_batched
def _get_source_sentence(self, index, return_string=True):
indices = self._last_batch['x_source'][index].cpu().detach().numpy()
vocab = self.vectorizer.source_vocab
return sentence_from_indices(indices, vocab, return_string=return_string)
def _get_reference_sentence(self, index, return_string=True):
indices = self._last_batch['y_target'][index].cpu().detach().numpy()
vocab = self.vectorizer.target_vocab
return sentence_from_indices(indices, vocab, return_string=return_string)
def _get_sampled_sentence(self, index, return_string=True):
_, all_indices = torch.max(self._last_batch['y_pred'], dim=2)
sentence_indices = all_indices[index].cpu().detach().numpy()
vocab = self.vectorizer.target_vocab
return sentence_from_indices(sentence_indices, vocab, return_string=return_string)
def get_ith_item(self, index, return_string=True):
output = {"source": self._get_source_sentence(index, return_string=return_string),
"reference": self._get_reference_sentence(index, return_string=return_string),
"sampled": self._get_sampled_sentence(index, return_string=return_string),
"attention": self._last_batch['attention'][index]}
reference = output['reference']
hypothesis = output['sampled']
if not return_string:
reference = " ".join(reference)
hypothesis = " ".join(hypothesis)
output['bleu-4'] = bleu_score.sentence_bleu(references=[reference],
hypothesis=hypothesis,
smoothing_function=chencherry.method1)
return output
# + id="Xg-jlqiqK8bt"
model = model.eval().to(args.device)
sampler = NMTSampler(vectorizer, model)
dataset.set_split('test')
batch_generator = generate_nmt_batches(dataset,
batch_size=args.batch_size,
device=args.device)
test_results = []
for batch_dict in batch_generator:
sampler.apply_to_batch(batch_dict)
for i in range(args.batch_size):
test_results.append(sampler.get_ith_item(i, False))
# + id="JrZt4gm6K8bt" outputId="b60fb63c-f309-4310-9543-656d9ae25731" colab={"base_uri": "https://localhost:8080/", "height": 282}
plt.hist([r['bleu-4'] for r in test_results], bins=100);
np.mean([r['bleu-4'] for r in test_results]), np.median([r['bleu-4'] for r in test_results])
# + id="mB4SzIapK8bt"
dataset.set_split('val')
batch_generator = generate_nmt_batches(dataset,
batch_size=args.batch_size,
device=args.device)
batch_dict = next(batch_generator)
model = model.eval().to(args.device)
sampler = NMTSampler(vectorizer, model)
sampler.apply_to_batch(batch_dict)
# + id="25CpKy7OK8bt"
all_results = []
for i in range(args.batch_size):
all_results.append(sampler.get_ith_item(i, False))
# + id="2nA6TKFHK8bt" outputId="1d055bff-646d-4cd8-ef97-553a5cb6800a" colab={"base_uri": "https://localhost:8080/"}
top_results = [x for x in all_results if x['bleu-4']>0.5]
len(top_results)
# + id="8qs5HatZK8bt" outputId="3d1523e5-6fea-45ff-9897-35063fb5e2e6" colab={"base_uri": "https://localhost:8080/", "height": 1000}
for sample in top_results:
plt.figure()
target_len = len(sample['sampled'])
source_len = len(sample['source'])
attention_matrix = sample['attention'][:target_len, :source_len+2].transpose()#[::-1]
ax = sns.heatmap(attention_matrix, center=0.0)
ylabs = ["<BOS>"]+sample['source']+["<EOS>"]
#ylabs = sample['source']
#ylabs = ylabs[::-1]
ax.set_yticklabels(ylabs, rotation=0)
ax.set_xticklabels(sample['sampled'], rotation=90)
ax.set_xlabel("Target Sentence")
ax.set_ylabel("Source Sentence\n\n")
# + id="Y4jcpvQsK8bu" outputId="cebf7ad6-2694-408c-927c-98f3ff0f0176" colab={"base_uri": "https://localhost:8080/"}
def get_source_sentence(vectorizer, batch_dict, index):
indices = batch_dict['x_source'][index].cpu().data.numpy()
vocab = vectorizer.source_vocab
return sentence_from_indices(indices, vocab)
def get_true_sentence(vectorizer, batch_dict, index):
return sentence_from_indices(batch_dict['y_target'].cpu().data.numpy()[index], vectorizer.target_vocab)
def get_sampled_sentence(vectorizer, batch_dict, index):
y_pred = model(x_source=batch_dict['x_source'],
x_source_lengths=batch_dict['x_source_length'],
target_sequence=batch_dict['x_target'],
sample_probability=1.0)
return sentence_from_indices(torch.max(y_pred, dim=2)[1].cpu().data.numpy()[index], vectorizer.target_vocab)
def get_all_sentences(vectorizer, batch_dict, index):
return {"source": get_source_sentence(vectorizer, batch_dict, index),
"truth": get_true_sentence(vectorizer, batch_dict, index),
"sampled": get_sampled_sentence(vectorizer, batch_dict, index)}
def sentence_from_indices(indices, vocab, strict=True):
ignore_indices = set([vocab.mask_index, vocab.begin_seq_index, vocab.end_seq_index])
out = []
for index in indices:
if index == vocab.begin_seq_index and strict:
continue
elif index == vocab.end_seq_index and strict:
return " ".join(out)
else:
out.append(vocab.lookup_index(index))
return " ".join(out)
results = get_all_sentences(vectorizer, batch_dict, 1)
results
| 36.527731 | 1,018 |
7437d4f11b505d2c033e02b907509c9e520882a8
|
py
|
python
|
ml_workflows/ml.ipynb
|
ronaldokun/datacamp
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: datacamp
# language: python
# name: datacamp
# ---
import os
import pandas as pd
from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn.metrics import accuracy_score, make_scorer
import numpy as np
from pprint import pprint as pp
import warnings
warnings.filterwarnings('ignore')
# ## Human in the Loop
# In the previous chapter, you perfected your knowledge of the standard supervised learning workflows. In this chapter, you will critically examine the ways in which expert knowledge is incorporated in supervised learning. This is done through the identification of the appropriate unit of analysis which might require feature engineering across multiple data sources, through the sometimes imperfect process of labeling examples, and through the specification of a loss function that captures the true business value of errors made by your machine learning model.
class PDF(object):
def __init__(self, pdf, size=(1080,720)):
self.pdf = pdf
self.size = size
def _repr_html_(self):
return f'<iframe src={self.pdf} width={self.size[0]} height={self.size[1]}></iframe>'
def _repr_latex_(self):
return fr'\includegraphics[width=1.0\textwidth]{{{self.pdf}}}'
PDF('pdf/chapter2.pdf',size=(1080, 720))
# # "Expert Knowledge"
flows = pd.read_csv('data/lanl_flows.csv')
# <h1 class="exercise--title">Is the source or the destination bad?</h1><div class=""><p>In the previous lesson, you used the <em>destination</em> computer as your entity of interest. However, your cybersecurity analyst just told you that it is the infected machines that generate the bad traffic, and will therefore appear as a <em>source</em>, not a destination, in the <code>flows</code> dataset. </p>
# <p>The data <code>flows</code> has been preloaded, as well as the list <code>bad</code> of infected IDs and the feature extractor <code>featurizer()</code> from the previous lesson. You also have <code>numpy</code> available as <code>np</code>, <code>AdaBoostClassifier()</code>, and <code>cross_val_score()</code>.</p></div>
def featurize(df):
return {
'unique_ports': len(set(df['destination_port'])),
'average_packet': np.mean(df['packet_count']),
'average_duration': np.mean(df['duration'])
}
bads = {'C1', 'C10', 'C10005', 'C1003', 'C1006', 'C1014', 'C1015', 'C102', 'C1022', 'C1028', 'C10405', 'C1042', 'C1046', 'C10577', 'C1065', 'C108', 'C10817', 'C1085', 'C1089', 'C1096', 'C11039', 'C11178', 'C1119', 'C11194', 'C1124', 'C1125', 'C113', 'C115', 'C11727', 'C1173', 'C1183', 'C1191', 'C12116', 'C1215', 'C1222', 'C1224', 'C12320', 'C12448', 'C12512', 'C126', 'C1268', 'C12682', 'C1269', 'C1275', 'C1302', 'C1319', 'C13713', 'C1382', 'C1415', 'C143', 'C1432', 'C1438', 'C1448', 'C1461', 'C1477', 'C1479', 'C148', 'C1482', 'C1484', 'C1493', 'C15', 'C1500', 'C1503', 'C1506', 'C1509', 'C15197', 'C152', 'C15232', 'C1549', 'C155', 'C1555', 'C1567', 'C1570', 'C1581', 'C16088', 'C1610', 'C1611', 'C1616', 'C1626', 'C1632', 'C16401', 'C16467', 'C16563', 'C1710', 'C1732', 'C1737', 'C17425', 'C17600', 'C17636', 'C17640', 'C17693', 'C177', 'C1776', 'C17776', 'C17806', 'C1784', 'C17860', 'C1797', 'C18025', 'C1810', 'C18113', 'C18190', 'C1823', 'C18464', 'C18626', 'C1887', 'C18872', 'C19038', 'C1906', 'C19156', 'C19356', 'C1936', 'C1944', 'C19444', 'C1952', 'C1961', 'C1964', 'C1966', 'C1980', 'C19803', 'C19932', 'C2012', 'C2013', 'C20203', 'C20455', 'C2057', 'C2058', 'C20677', 'C2079', 'C20819', 'C2085', 'C2091', 'C20966', 'C21349', 'C21664', 'C21814', 'C21919', 'C21946', 'C2196', 'C21963', 'C22174', 'C22176', 'C22275', 'C22409', 'C2254', 'C22766', 'C231', 'C2341', 'C2378', 'C2388', 'C243', 'C246', 'C2519', 'C2578', 'C2597', 'C2604', 'C2609', 'C2648', 'C2669', 'C2725', 'C2816', 'C2844', 'C2846', 'C2849', 'C2877', 'C2914', 'C294', 'C2944', 'C3019', 'C302', 'C3037', 'C305', 'C306', 'C307', 'C313', 'C3153', 'C3170', 'C3173', 'C3199', 'C3249', 'C3288', 'C3292', 'C3303', 'C3305', 'C332', 'C338', 'C3380', 'C3388', 'C3422', 'C3435', 'C3437', 'C3455', 'C346', 'C3491', 'C3521', 'C353', 'C3586', 'C359', 'C3597', 'C3601', 'C3610', 'C3629', 'C3635', 'C366', 'C368', 'C3699', 'C370', 'C3755', 'C3758', 'C3813', 'C385', 'C3888', 'C395', 'C398', 'C400', 'C4106', 'C4159', 'C4161', 'C42', 'C423', 'C4280', 'C429', 'C430', 'C4403', 'C452', 'C4554', 'C457', 'C458', 'C46', 'C4610', 'C464', 'C467', 'C477', 'C4773', 'C4845', 'C486', 'C492', 'C4934', 'C5030', 'C504', 'C506', 'C5111', 'C513', 'C52', 'C528', 'C529', 'C5343', 'C5439', 'C5453', 'C553', 'C5618', 'C5653', 'C5693', 'C583', 'C586', 'C61', 'C612', 'C625', 'C626', 'C633', 'C636', 'C6487', 'C6513', 'C685', 'C687', 'C706', 'C7131', 'C721', 'C728', 'C742', 'C7464', 'C7503', 'C754', 'C7597', 'C765', 'C7782', 'C779', 'C78', 'C791', 'C798', 'C801', 'C8172', 'C8209', 'C828', 'C849', 'C8490', 'C853', 'C8585', 'C8751', 'C881', 'C882', 'C883', 'C886', 'C89', 'C90', 'C9006', 'C917', 'C92', 'C923', 'C96', 'C965', 'C9692', 'C9723', 'C977', 'C9945'}
# +
# Group by source computer, and apply the feature extractor
out = flows.groupby('source_computer').apply(featurize)
# Convert the iterator to a dataframe by calling list on it
X = pd.DataFrame(list(out), index=out.index)
# Check which sources in X.index are bad to create labels
y = [x in bads for x in X.index]
# -
X.head()
# +
# Report the average accuracy of Adaboost over 3-fold CV
print(np.mean(cross_val_score(AdaBoostClassifier(), X, y)))
# -
# <h1 class="exercise--title">Feature engineering on grouped data</h1><div class=""><p>You will now build on the previous exercise, by considering one additional feature: the number of unique protocols used by each source computer. Note that with grouped data, it is always possible to construct features in this manner: you can take the number of unique elements of all categorical columns, and the mean of all numeric columns as your starting point. As before, you have <code>flows</code> preloaded, <code>cross_val_score()</code> for measuring accuracy, <code>AdaBoostClassifier()</code>, <code>pandas</code> as <code>pd</code> and <code>numpy</code> as <code>np</code>.</p></div>
# +
# Create a feature counting unique protocols per source
protocols = flows.groupby('source_computer').apply(lambda df: len(set(df.protocol)))
# Convert this feature into a dataframe, naming the column
protocols_DF = pd.DataFrame(protocols, index=protocols.index, columns=['protocol'])
# Now concatenate this feature with the previous dataset, X
X_more = pd.concat([X, protocols_DF], axis=1)
# Refit the classifier and report its accuracy
print(np.mean(cross_val_score(AdaBoostClassifier(), X_more, y)))
# -
# <h1 class="exercise--title">Turning a heuristic into a classifier</h1><div class=""><p>You are surprised by the fact that heuristics can be so helpful. So you decide to treat the heuristic that "too many unique ports is suspicious" as a classifier in its own right. You achieve that by thresholding the number of unique ports per source by the average number used in bad source computers -- these are computers for which the label is <code>True</code>. The dataset is preloaded and split into training and test, so you have objects <code>X_train</code>, <code>X_test</code>, <code>y_train</code> and <code>y_test</code> in memory. Your imports include <code>accuracy_score()</code>, and <code>numpy</code> as <code>np</code>. To clarify: you won't be fitting a classifier from scikit-learn in this exercise, but instead you will define your own classification rule explicitly!</p></div>
X_train, X_test, y_train, y_test = train_test_split(X,y)
# +
#Create a new dataset `X_train_bad` by subselecting bad hosts
X_train_bad = X_train[y_train]
#Calculate the average of `unique_ports` in bad examples
avg_bad_ports = np.mean(X_train_bad.unique_ports)
#Label as positive sources that use more ports than that
pred_port = X_test['unique_ports'] > avg_bad_ports
#Print the `accuracy_score` of the heuristic
print(accuracy_score(y_test, pred_port))
# -
# <h1 class="exercise--title">Combining heuristics</h1><div class=""><p>A different cyber analyst tells you that during certain types of attack, the infected source computer sends small bits of traffic, to avoid detection. This makes you wonder whether it would be better to create a combined heuristic that simultaneously looks for large numbers of ports and small packet sizes. Does this improve performance over the simple port heuristic? As with the last exercise, you have <code>X_train</code>, <code>X_test</code>, <code>y_train</code> and <code>y_test</code> in memory. The sample code also helps you reproduce the outcome of the port heuristic, <code>pred_port</code>. You also have <code>numpy</code> as <code>np</code> and <code>accuracy_score()</code> preloaded.</p></div>
# +
# Compute the mean of average_packet for bad sources
avg_bad_packet = np.mean(X_train[y_train]['average_packet'])
# Label as positive if average_packet is lower than that
pred_packet = X_test['average_packet'] < avg_bad_packet
# Find indices where pred_port and pred_packet both True
pred_port = X_test['unique_ports'] > avg_bad_ports
pred_both = pred_packet & pred_port
# Ports only produced an accuracy of 0.919. Is this better?
print(accuracy_score(y_test, pred_both))
# -
# <h1 class="exercise--title">Dealing with label noise</h1><div class=""><p>One of your cyber analysts informs you that many of the labels for the first 100 source computers in your training data might be wrong because of a database error. She hopes you can still use the data because most of the labels are still correct, but asks you to treat these 100 labels as "noisy". Thankfully you know how to do that, using weighted learning. The contaminated data is available in your workspace as <code>X_train</code>, <code>X_test</code>, <code>y_train_noisy</code>, <code>y_test</code>. You want to see if you can improve the performance of a <code>GaussianNB()</code> classifier using weighted learning. You can use the optional parameter <code>sample_weight</code>, which is supported by the <code>.fit()</code> methods of most popular classifiers. The function <code>accuracy_score()</code> is preloaded. You can consult the image below for guidance. </p>
# <p><img src="https://assets.datacamp.com/production/repositories/3554/datasets/ea99ce2b5baa3cb9f3d9085b7387f2ea7d3bdfc8/wsl_noisy_labels.png" alt=""></p></div>
y_train_noisy = y_train.copy()
for i in range(100):
y_train_noisy[i] = True
# +
from sklearn.naive_bayes import GaussianNB
# Fit a Gaussian Naive Bayes classifier to the training data
clf = GaussianNB().fit(X_train, y_train_noisy)
# Report its accuracy on the test data
print(accuracy_score(y_test, clf.predict(X_test)))
# Assign half the weight to the first 100 noisy examples
weights = [0.5]*100 + [1.0]*(len(X_train)-100)
# Refit using weights and report accuracy. Has it improved?
clf_weights = GaussianNB().fit(X_train, y_train_noisy, sample_weight=weights)
print(accuracy_score(y_test, clf_weights.predict(X_test)))
# -
# # 3. Model Lifecycle Management
# In the previous chapter, you employed different ways of incorporating feedback from experts in your workflow, and evaluating it in ways that are aligned with business value. Now it is time for you to practice the skills needed to productize your model and ensure it continues to perform well thereafter by iteratively improving it. You will also learn to diagnose dataset shift and mitigate the effect that a changing environment can have on your model's accuracy.
PDF('pdf/chapter3.pdf')
df = pd.read_csv('data/arrh.csv')
X, y = df.iloc[:, :-1], df.iloc[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y)
# <h1 class="exercise--title">Your first pipeline - again!</h1><div class=""><p>Back in the arrhythmia startup, your monthly review is coming up, and as part of that an expert Python programmer will be reviewing your code. You decide to tidy up by following best practices and replace your script for feature selection and random forest classification, with a pipeline. You are using a training dataset available as <code>X_train</code> and <code>y_train</code>, and a number of modules: <code>RandomForestClassifier</code>, <code>SelectKBest()</code> and <code>f_classif()</code> for feature selection, as well as <code>GridSearchCV</code> and <code>Pipeline</code>.</p></div>
# +
from sklearn.ensemble import RandomForestClassifier
from sklearn.pipeline import Pipeline
from sklearn.feature_selection import SelectKBest, f_classif
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
# Create pipeline with feature selector and classifier
pipe = Pipeline([
('feature_selection', SelectKBest(f_classif)),
('clf', rf(random_state=2))])
# Create a parameter grid
params = {
'feature_selection__k':[10,20],
'clf__n_estimators':[2, 5]}
# Initialize the grid search object
grid_search = GridSearchCV(pipe, param_grid=params)
# Fit it to the data and print the best value combination
print(grid_search.fit(X_train, y_train).best_params_)
# -
# <h1 class="exercise--title">Custom scorers in pipelines</h1><div class=""><p>You are proud of the improvement in your code quality, but just remembered that previously you had to use a custom scoring metric in order to account for the fact that false positives are costlier to your startup than false negatives. You hence want to equip your pipeline with scorers other than accuracy, including <code>roc_auc_score()</code>, <code>f1_score()</code>, and you own custom scoring function. The pipeline from the previous lesson is available as <code>pipe</code>, as is the parameter grid as <code>params</code> and the training data as <code>X_train</code>, <code>y_train</code>. You also have <code>confusion_matrix()</code> for the purpose of writing your own metric.</p></div>
# +
from sklearn.metrics import make_scorer, roc_auc_score
# Create a custom scorer
scorer = make_scorer(roc_auc_score)
# Initialize the CV object
gs = GridSearchCV(pipe, param_grid=params, scoring=scorer)
# Fit it to the data and print the winning combination
print(gs.fit(X_train, y_train).best_params_)
# +
from sklearn.metrics import f1_score
# Create a custom scorer
scorer = make_scorer(f1_score)
# Initialize the CV object
gs = GridSearchCV(pipe, param_grid=params, scoring=scorer)
# Fit it to the data and print the winning combination
print(gs.fit(X_train, y_train).best_params_)
# -
from sklearn.metrics import confusion_matrix
def my_metric(y_test, y_est, cost_fp=10.0, cost_fn=1.0):
tn, fp, fn, tp = confusion_matrix(y_test, y_est).ravel()
return cost_fp * fp + cost_fn * fn
# +
from sklearn.metrics import f1_score
# Create a custom scorer
scorer = make_scorer(my_metric)
# Initialize the CV object
gs = GridSearchCV(pipe, param_grid=params, scoring=scorer)
# Fit it to the data and print the winning combination
print(gs.fit(X_train, y_train).best_params_)
# -
# <h1 class="exercise--title">Pickles</h1><div class=""><p>Finally, it is time for you to push your first model to production. It is a random forest classifier which you will use as a baseline, while you are still working to develop a better alternative. You have access to the data split in training test with their usual names, <code>X_train</code>, <code>X_test</code>, <code>y_train</code> and <code>y_test</code>, as well as to the modules <code>RandomForestClassifier()</code> and <code>pickle</code>, whose methods <code>.load()</code> and <code>.dump()</code> you will need for this exercise.</p></div>
# +
import pickle
# Fit a random forest to the training set
clf = rf(random_state=42).fit(
X_train, y_train)
# Save it to a file, to be pushed to production
with open('model.pkl', 'wb') as file:
pickle.dump(clf, file=file)
# Now load the model from file in the production environment
with open('model.pkl', 'rb') as file:
clf_from_file = pickle.load(file)
# Predict the labels of the test dataset
preds = clf_from_file.predict(X_test)
# -
# <h1 class="exercise--title">Custom function transformers in pipelines</h1><div class=""><p>At some point, you were told that the sensors might be performing poorly for obese individuals. Previously you had dealt with that using weights, but now you are thinking that this information might also be useful for feature engineering, so you decide to replace the recorded weight of an individual with an indicator of whether they are obese. You want to do this using pipelines. You have <code>numpy</code> available as <code>np</code>, <code>RandomForestClassifier()</code>, <code>FunctionTransformer()</code>, and <code>GridSearchCV()</code>.</p></div>
# +
from sklearn.preprocessing import FunctionTransformer
# Define a feature extractor to flag very large values
def more_than_average(X, multiplier=1.0):
Z = X.copy()
Z[:,1] = Z[:,1] > multiplier*np.mean(Z[:,1])
return Z
# Convert your function so that it can be used in a pipeline
pipe = Pipeline([
('ft', FunctionTransformer(more_than_average)),
('clf', RandomForestClassifier(random_state=2))])
# Optimize the parameter multiplier using GridSearchCV
params = {'ft__multiplier': [1,2,3]}
gs = GridSearchCV(pipe, param_grid=params)
print(gs.fit(X_train, y_train).best_params_)
# -
| 61.675 | 2,706 |
d838e8f974e7e4cf27308d4d31c3e02c87f4a820
|
py
|
python
|
Phase_1/ds-sql2-main/sql.ipynb
|
clareadunne/ds-east-042621-lectures
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Objectives" data-toc-modified-id="Objectives-1"><span class="toc-item-num">1 </span>Objectives</a></span></li><li><span><a href="#Aggregating-Functions" data-toc-modified-id="Aggregating-Functions-2"><span class="toc-item-num">2 </span>Aggregating Functions</a></span><ul class="toc-item"><li><span><a href="#Example-Simple-Aggregations" data-toc-modified-id="Example-Simple-Aggregations-2.1"><span class="toc-item-num">2.1 </span>Example Simple Aggregations</a></span></li></ul></li><li><span><a href="#Grouping-in-SQL" data-toc-modified-id="Grouping-in-SQL-3"><span class="toc-item-num">3 </span>Grouping in SQL</a></span><ul class="toc-item"><li><span><a href="#Example-GROUP-BY--Statements" data-toc-modified-id="Example-GROUP-BY--Statements-3.1"><span class="toc-item-num">3.1 </span>Example <code>GROUP BY</code> Statements</a></span><ul class="toc-item"><li><span><a href="#Without-GROUP-BY" data-toc-modified-id="Without-GROUP-BY-3.1.1"><span class="toc-item-num">3.1.1 </span>Without <code>GROUP BY</code></a></span></li><li><span><a href="#With-GROUP-BY" data-toc-modified-id="With-GROUP-BY-3.1.2"><span class="toc-item-num">3.1.2 </span>With <code>GROUP BY</code></a></span></li></ul></li><li><span><a href="#Group-Task" data-toc-modified-id="Group-Task-3.2"><span class="toc-item-num">3.2 </span>Group Task</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Possible-Solution" data-toc-modified-id="Possible-Solution-3.2.0.1"><span class="toc-item-num">3.2.0.1 </span>Possible Solution</a></span></li></ul></li></ul></li><li><span><a href="#Exercises:-Grouping" data-toc-modified-id="Exercises:-Grouping-3.3"><span class="toc-item-num">3.3 </span>Exercises: Grouping</a></span><ul class="toc-item"><li><span><a href="#Grouping-Exercise-1" data-toc-modified-id="Grouping-Exercise-1-3.3.1"><span class="toc-item-num">3.3.1 </span>Grouping Exercise 1</a></span></li><li><span><a href="#Grouping-Exercise-2" data-toc-modified-id="Grouping-Exercise-2-3.3.2"><span class="toc-item-num">3.3.2 </span>Grouping Exercise 2</a></span></li></ul></li></ul></li><li><span><a href="#Filtering-Groups-with-HAVING" data-toc-modified-id="Filtering-Groups-with-HAVING-4"><span class="toc-item-num">4 </span>Filtering Groups with <code>HAVING</code></a></span><ul class="toc-item"><li><span><a href="#Examples-of-Using-HAVING" data-toc-modified-id="Examples-of-Using-HAVING-4.1"><span class="toc-item-num">4.1 </span>Examples of Using <code>HAVING</code></a></span><ul class="toc-item"><li><span><a href="#Simple-Filtering---Number-of-Airports-in-a-Country" data-toc-modified-id="Simple-Filtering---Number-of-Airports-in-a-Country-4.1.1"><span class="toc-item-num">4.1.1 </span>Simple Filtering - Number of Airports in a Country</a></span></li></ul></li><li><span><a href="#Filtering-Different-Aggregation---Airport-Altitudes" data-toc-modified-id="Filtering-Different-Aggregation---Airport-Altitudes-4.2"><span class="toc-item-num">4.2 </span>Filtering Different Aggregation - Airport Altitudes</a></span><ul class="toc-item"><li><span><a href="#Looking-at-the-airports-Table" data-toc-modified-id="Looking-at-the-airports-Table-4.2.1"><span class="toc-item-num">4.2.1 </span>Looking at the <code>airports</code> Table</a></span></li><li><span><a href="#Looking-at-the-Highest-Airport" data-toc-modified-id="Looking-at-the-Highest-Airport-4.2.2"><span class="toc-item-num">4.2.2 </span>Looking at the Highest Airport</a></span></li><li><span><a href="#Looking-at-the-Number-of-Airports-Too" data-toc-modified-id="Looking-at-the-Number-of-Airports-Too-4.2.3"><span class="toc-item-num">4.2.3 </span>Looking at the Number of Airports Too</a></span></li><li><span><a href="#Finally-Filter-Aggregation" data-toc-modified-id="Finally-Filter-Aggregation-4.2.4"><span class="toc-item-num">4.2.4 </span>Finally Filter Aggregation</a></span></li></ul></li></ul></li><li><span><a href="#Joins" data-toc-modified-id="Joins-5"><span class="toc-item-num">5 </span>Joins</a></span><ul class="toc-item"><li><span><a href="#INNER-JOIN" data-toc-modified-id="INNER-JOIN-5.1"><span class="toc-item-num">5.1 </span><code>INNER JOIN</code></a></span><ul class="toc-item"><li><span><a href="#Code-Example-for-Inner-Joins" data-toc-modified-id="Code-Example-for-Inner-Joins-5.1.1"><span class="toc-item-num">5.1.1 </span>Code Example for Inner Joins</a></span><ul class="toc-item"><li><span><a href="#Inner-Join-Routes-&-Airline-Data" data-toc-modified-id="Inner-Join-Routes-&-Airline-Data-5.1.1.1"><span class="toc-item-num">5.1.1.1 </span>Inner Join Routes & Airline Data</a></span></li><li><span><a href="#Note:-Losing-Data-with-Inner-Joins" data-toc-modified-id="Note:-Losing-Data-with-Inner-Joins-5.1.1.2"><span class="toc-item-num">5.1.1.2 </span>Note: Losing Data with Inner Joins</a></span></li></ul></li></ul></li><li><span><a href="#LEFT-JOIN" data-toc-modified-id="LEFT-JOIN-5.2"><span class="toc-item-num">5.2 </span><code>LEFT JOIN</code></a></span><ul class="toc-item"><li><span><a href="#Code-Example-for-Left-Join" data-toc-modified-id="Code-Example-for-Left-Join-5.2.1"><span class="toc-item-num">5.2.1 </span>Code Example for Left Join</a></span></li></ul></li><li><span><a href="#Exercise:-Joins" data-toc-modified-id="Exercise:-Joins-5.3"><span class="toc-item-num">5.3 </span>Exercise: Joins</a></span><ul class="toc-item"><li><span><a href="#Possible-Solution" data-toc-modified-id="Possible-Solution-5.3.1"><span class="toc-item-num">5.3.1 </span>Possible Solution</a></span></li></ul></li></ul></li><li><span><a href="#Level-Up:-Execution-Order" data-toc-modified-id="Level-Up:-Execution-Order-6"><span class="toc-item-num">6 </span>Level Up: Execution Order</a></span></li></ul></div>
# -
# 
# +
import pandas as pd
import sqlite3
import pandasql
conn = sqlite3.connect("flights.db")
cur = conn.cursor()
# + [markdown] heading_collapsed=true
# # Objectives
# + [markdown] hidden=true
# - Use SQL aggregation functions with GROUP BY
# - Use HAVING for group filtering
# - Use SQL JOIN to combine tables using keys
# + [markdown] heading_collapsed=true
# # Aggregating Functions
# + [markdown] hidden=true
# > A SQL **aggregating function** takes in many values and returns one value.
# + [markdown] hidden=true
# We might've already seen some SQL aggregating functions like `COUNT()`. There's also others like SUM(), AVG(), MIN(), and MAX().
# + [markdown] heading_collapsed=true hidden=true
# ## Example Simple Aggregations
# + hidden=true
# Max value for longitude
pd.read_sql('''
SELECT
-- Note we have to cast to a numerical value first
MAX(
CAST(airports.longitude AS REAL)
)
FROM
airports
''', conn)
# + hidden=true
# Max value for id in table
pd.read_sql('''
SELECT
*
FROM
airports
''', conn)
# + hidden=true
# Effectively counts all the not active airlines
pd.read_sql('''
SELECT
COUNT()
FROM
airlines
WHERE
active='N'
''', conn)
# + [markdown] hidden=true
# We can also give aliases to our aggregations:
# + hidden=true
# Effectively counts all the active airlines
pd.read_sql('''
SELECT
COUNT() as number_of_active_airlines
FROM
airlines
WHERE
active='Y'
''', conn)
# + [markdown] heading_collapsed=true
# # Grouping in SQL
# + [markdown] hidden=true
# We can go deeper and use aggregation functions on _groups_ using the `GROUP BY` clause.
# + [markdown] hidden=true
# The `GROUP BY` clause will group one or more columns together with the same values as one group to perform aggregation functions on.
# + [markdown] heading_collapsed=true hidden=true
# ## Example `GROUP BY` Statements
# + [markdown] hidden=true
# Let's say we want to know how many active and non-active airlines there are.
# + [markdown] heading_collapsed=true hidden=true
# ### Without `GROUP BY`
# + [markdown] hidden=true
# Let's first start with just seeing how many airlines there are:
# + hidden=true
df_results = pd.read_sql('''
SELECT
-- Reminde that this counts the number of rows before the SELECT
COUNT() AS number_of_airlines
FROM
airlines
''', conn)
df_results
# + [markdown] hidden=true
# One way for us to get the counts for each is to create two queries that will filter each kind of airline (active vs non-active) count these values:
# + hidden=true
df_active = pd.read_sql('''
SELECT
COUNT() AS number_of_active_airlines
FROM
airlines
WHERE
active='Y'
''', conn)
df_not_active = pd.read_sql('''
SELECT
COUNT() AS number_of_not_active_airlines
FROM
airlines
WHERE
active='N'
''', conn)
display(df_active)
display(df_not_active)
# + [markdown] hidden=true
# This technically works but you can see it's probably a bit inefficient and not as clean.
# + [markdown] heading_collapsed=true hidden=true
# ### With `GROUP BY`
# + [markdown] hidden=true
# Instead, we can tell the SQL server to do the work for us by grouping values we care about for us!
# + hidden=true
df_results = pd.read_sql('''
SELECT
COUNT() AS number_of_airlines
FROM
airlines
GROUP BY
airlines.active
''', conn)
df_results
# + [markdown] hidden=true
# This is great! And if you look closely, you can observe we have _three_ different groups instead of our expected two!
# + [markdown] hidden=true
# Let's also print out the `airlines.active` value for each group/aggregation so we know what we're looking at:
# + hidden=true
df_results = pd.read_sql('''
SELECT
airlines.active,
COUNT() AS number_of_airlines
FROM
airlines
GROUP BY
airlines.active
''', conn)
df_results
# + [markdown] heading_collapsed=true hidden=true
# ## Group Task
# + [markdown] hidden=true
# - Which countries have the highest numbers of active airlines? Return the top 10.
# + hidden=true
pd.read_sql('''
SELECT
COUNT() AS number_of_airlines, airlines.country
FROM
airlines
WHERE
active='Y'
GROUP BY
airlines.country
ORDER BY
number_of_airlines DESC
LIMIT 10
''', conn)
# + [markdown] heading_collapsed=true hidden=true
# #### Possible Solution
# + hidden=true
pd.read_sql('''
SELECT
COUNT() AS num,
country
FROM
airlines
WHERE
active='Y'
GROUP BY
country
ORDER BY
num DESC
LIMIT 10
''', conn)
# + [markdown] hidden=true
# > Note that the `GROUP BY` clause is considered _before_ the `ORDER BY` and `LIMIT` clauses
# + [markdown] heading_collapsed=true hidden=true
# ## Exercises: Grouping
# + [markdown] heading_collapsed=true hidden=true
# ### Grouping Exercise 1
# + [markdown] hidden=true
# - Which countries have the highest numbers of inactive airlines? Return all the countries that have more than 10.
# + hidden=true
inactive_airports = pd.read_sql('''
SELECT
COUNT() AS number_of_airlines, airlines.country
FROM
airlines
WHERE
(active='N' OR active = 'n')
GROUP BY
airlines.country
ORDER BY
number_of_airlines DESC
''', conn)
inactive_airports
inactive_airports_morethanten = inactive_airports[inactive_airports['number_of_airlines'] > 10]
inactive_airports_morethanten
# + [markdown] heading_collapsed=true hidden=true
# ### Grouping Exercise 2
# + [markdown] hidden=true
# - Run a query that will return the number of airports by time zone. Each row should have a number of airports and a time zone.
# + hidden=true
pd.read_sql('''
SELECT
COUNT() AS number_of_airlines, airlines.country
FROM
airlines
WHERE
active='N'
GROUP BY
airlines.country
ORDER BY
number_of_airlines DESC
LIMIT 10
''', conn)
# + [markdown] heading_collapsed=true
# # Filtering Groups with `HAVING`
# + [markdown] hidden=true
# We showed that you can filter tables with `WHERE`. We can similarly filter _groups/aggregations_ using `HAVING` clauses.
# + [markdown] heading_collapsed=true hidden=true
# ## Examples of Using `HAVING`
# + [markdown] heading_collapsed=true hidden=true
# ### Simple Filtering - Number of Airports in a Country
# + [markdown] hidden=true
# Let's come back to the aggregation of active airports:
# + hidden=true
pd.read_sql('''
SELECT
COUNT() AS num,
country
FROM
airlines
WHERE
active='Y'
GROUP BY
country
ORDER BY
num DESC
''', conn)
# + [markdown] hidden=true
# We can see have a lot of results. But maybe we only want to keep the countries that have more than $30$ active airports:
# + hidden=true
pd.read_sql('''
SELECT
COUNT() AS num,
country
FROM
airlines
WHERE
active='Y'
GROUP BY
country
HAVING
COUNT() > 30
ORDER BY
num DESC
''', conn)
# + [markdown] heading_collapsed=true hidden=true
# ## Filtering Different Aggregation - Airport Altitudes
# + [markdown] hidden=true
# We can also filter on other aggregations. For example, let's say we want to investigate the `airports` table.
# + [markdown] hidden=true
# Specifically, we want to know the height of the _highest airport_ in a country given that it has _at least $100$ airports_.
# + [markdown] heading_collapsed=true hidden=true
# ### Looking at the `airports` Table
# + hidden=true
df_airports = pd.read_sql('''
SELECT
COUNT() AS num,
country
FROM
airlines
WHERE
active='Y'
GROUP BY
country
HAVING
COUNT() > 30
ORDER BY
num DESC
''', conn)
df_airports.head()
# + [markdown] heading_collapsed=true hidden=true
# ### Looking at the Highest Airport
# + [markdown] hidden=true
# Let's first get the highest altitude for each airport:
# + hidden=true
pd.read_sql('''
SELECT
airports.country
,MAX(
CAST(airports.altitude AS REAL)
) AS highest_airport_in_country
FROM
airports
GROUP BY
airports.country
ORDER BY
airports.country
''', conn)
# + [markdown] heading_collapsed=true hidden=true
# ### Looking at the Number of Airports Too
# + [markdown] hidden=true
# We can also get the number of airports for each country.
# + hidden=true
pd.read_sql('''
SELECT
airports.country
,MAX(
CAST(airports.altitude AS REAL)
) AS highest_airport_in_country
,COUNT() AS number_of_airports_in_country
FROM
airports
GROUP BY
airports.country
ORDER BY
airports.country
''', conn)
# + [markdown] heading_collapsed=true hidden=true
# ### Finally Filter Aggregation
# + [markdown] hidden=true
# > Recall:
# >
# > We want to know the height of the _highest airport_ in a country given that it has _at least $100$ airports_.
# + hidden=true
pd.read_sql('''
SELECT
airports.country
,MAX(
CAST(airports.altitude AS REAL)
) AS highest_airport_in_country
-- Note we don't have to include this in our SELECT
--,COUNT() AS number_of_airports_in_country
FROM
airports
GROUP BY
airports.country
HAVING
COUNT() > 100
ORDER BY
airports.country
''', conn)
# + [markdown] heading_collapsed=true
# # Joins
# + [markdown] hidden=true
# The biggest advantage in using a relational database (like we've been with SQL) is that you can create **joins**.
# + [markdown] hidden=true
# > By using **`JOIN`** in our query, we can connect different tables using their _relationships_ to other tables.
# >
# > Usually we use a key (_foriegn_key_) to tell us how the two tables are related.
# + [markdown] hidden=true
# There are different types of joins and each has their different use case.
# + [markdown] heading_collapsed=true hidden=true
# ## `INNER JOIN`
# + [markdown] hidden=true
# > An **inner join** will join two tables together and only keep rows if the _key is in both tables_
# + [markdown] hidden=true
# 
# + [markdown] hidden=true
# Example of an inner join:
#
# ```sql
# SELECT
# table1.column_name,
# table2.different_column_name
# FROM
# table1
# INNER JOIN table2
# ON table1.shared_column_name = table2.shared_column_name
# ```
# + [markdown] heading_collapsed=true hidden=true
# ### Code Example for Inner Joins
# + [markdown] hidden=true
# Let's say we want to look at the different airplane routes
# + hidden=true
pd.read_sql('''
SELECT
*
FROM
routes
''', conn)
# -
pd.read_sql('''
SELECT
*
FROM
airlines
''', conn)
# + [markdown] hidden=true
# This is great but notice `airline_id`. It'd be nice to have some information about the airline for that route.
# + [markdown] hidden=true
# We can do an **inner join** to get this information!
# + [markdown] heading_collapsed=true hidden=true
# #### Inner Join Routes & Airline Data
# + hidden=true
pd.read_sql('''
SELECT
*
FROM
routes
INNER JOIN airlines
ON routes.airline_id = airlines.id
''', conn)
# + [markdown] hidden=true
# We can also specify to only retain certain columns in the `SELECT` clause:
# + hidden=true
pd.read_sql('''
SELECT
routes.source AS departing
,routes.dest AS destination
,routes.stops AS stops_before_destination
,airlines.name AS airline
FROM
routes
INNER JOIN airlines
ON routes.airline_id = airlines.id
''', conn)
# + [markdown] heading_collapsed=true hidden=true
# #### Note: Losing Data with Inner Joins
# + [markdown] hidden=true
# Since data rows are kept if _both_ tables have the key, some data can be lost
# + hidden=true
df_all_routes = pd.read_sql('''
SELECT
*
FROM
routes
''', conn)
df_routes_after_join = pd.read_sql('''
SELECT
*
FROM
routes
INNER JOIN airlines
ON routes.airline_id = airlines.id
''', conn)
# + hidden=true
# Look at how the number of rows are different
df_all_routes.shape, df_routes_after_join.shape
# + [markdown] hidden=true
# If you want to keep your data from at least one of your tables, you should use a left or right join instead of an inner join.
# + [markdown] heading_collapsed=true hidden=true
# ## `LEFT JOIN`
# + [markdown] hidden=true
# > A **left join** will join two tables together and but will keep all data from the first (left) table using the key provided.
# + [markdown] hidden=true
# 
# + [markdown] hidden=true
# Example of a left and right join:
#
# ```sql
# SELECT
# table1.column_name,
# table2.different_column_name
# FROM
# table1
# LEFT JOIN table2
# ON table1.shared_column_name = table2.shared_column_name
# ```
# + [markdown] heading_collapsed=true hidden=true
# ### Code Example for Left Join
# + [markdown] hidden=true
# Recall our example using an inner join and how it lost some data since the key wasn't in both the `routes` _and_ `airlines` tables.
# + hidden=true
df_all_routes = pd.read_sql('''
SELECT
*
FROM
routes
''', conn)
# This will lose some data (some routes not included)
df_routes_after_inner_join = pd.read_sql('''
SELECT
*
FROM
routes
INNER JOIN airlines
ON routes.airline_id = airlines.id
''', conn)
# The number of rows are different
df_all_routes.shape, df_routes_after_inner_join.shape
# + [markdown] hidden=true
# If wanted to ensure we always had every route even if the key in `airlines` was not found, we could replace our `INNER JOIN` with a `LEFT JOIN`:
# + hidden=true
# This will include all the data from routes
df_routes_after_left_join = pd.read_sql('''
SELECT
*
FROM
routes
LEFT JOIN airlines
ON routes.airline_id = airlines.id
''', conn)
df_routes_after_left_join.shape
# + [markdown] heading_collapsed=true hidden=true
# ## Exercise: Joins
# + [markdown] hidden=true
# Which airline has the most routes listed in our database?
# + hidden=true
pd.read_sql('''
SELECT
airlines.name,
COUNT() AS num_routes
FROM
routes
LEFT JOIN airlines
ON routes.airline_id = airlines.id
GROUP BY
airlines.id
ORDER BY
num_routes DESC
''', conn)
# + [markdown] heading_collapsed=true hidden=true
# ### Possible Solution
# + [markdown] hidden=true
# ```sql
# SELECT
# airlines.name AS airline,
# COUNT() AS number_of_routes
# -- We first need to get all the relevant info via a join
# FROM
# routes
# -- LEFT JOIN since we want all routes (even if airline id is unknown)
# LEFT JOIN airlines
# ON routes.airline_id = airlines.id
# -- We need to group by airline's ID
# GROUP BY
# airlines.id
# ORDER BY
# number_of_routes DESC
# ```
# + [markdown] heading_collapsed=true
# # Level Up: Execution Order
# + [markdown] hidden=true
# ```SQL
# SELECT
# COUNT(table2.col2) AS my_new_count
# ,table1.col2
# FROM
# table1
# JOIN table2
# ON table1.col1 = table2.col2
# WHERE
# table1.col1 > 0
# GROUP BY
# table2.col1
# ```
# + [markdown] hidden=true
# 1. `From`
# 2. `Where`
# 3. `Group By`
# 4. `Having`
# 5. `Select`
# 6. `Order By`
# 7. `Limit`
| 30.830703 | 6,108 |
15f7fc75453fa38073e96255ab3b94ea5ddb8f41
|
py
|
python
|
prediction/multitask/fine-tuning/function documentation generation/ruby/small_model.ipynb
|
victory-hash/CodeTrans
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/agemagician/CodeTrans/blob/main/prediction/multitask/fine-tuning/function%20documentation%20generation/ruby/small_model.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="c9eStCoLX0pZ"
# **<h3>Predict the documentation for ruby code using codeTrans multitask finetuning model</h3>**
# <h4>You can make free prediction online through this
# <a href="https://huggingface.co/SEBIS/code_trans_t5_small_code_documentation_generation_ruby_multitask_finetune">Link</a></h4> (When using the prediction online, you need to parse and tokenize the code first.)
# + [markdown] id="6YPrvwDIHdBe"
# **1. Load necessry libraries including huggingface transformers**
# + colab={"base_uri": "https://localhost:8080/"} id="6FAVWAN1UOJ4" outputId="10f60b60-81c5-414a-c5c1-be581ecfb187"
# !pip install -q transformers sentencepiece
# + id="53TAO7mmUOyI"
from transformers import AutoTokenizer, AutoModelWithLMHead, SummarizationPipeline
# + [markdown] id="xq9v-guFWXHy"
# **2. Load the token classification pipeline and load it into the GPU if avilabile**
# + colab={"base_uri": "https://localhost:8080/", "height": 316, "referenced_widgets": ["27e4e833f0ec45b883a68da8542f7fc3", "6c828235f68d4573a4a8f37e1d6ee731", "966f8e4a950d4bbda93adb6a78a079b0", "9291f747c8dc4f018bdad464e6d17ca6", "2a75c040ad434206898f503f26cc3396", "d59cf261aa394ee89494a26f77e856a9", "353222d84eab4e04861a7536acc588cb", "a6b36903519a4cb6baf3c6c15ec3ba15", "b14914fa47e74467af6964b96959231b", "a12eb3a80b3e432783cdd52be04b6ad2", "8c8a97d2539943f69ecd95de62285ffb", "7b467cd8294c4241a9dbafb521297b37", "98d463047b0946e28534b95dcdad4180", "687ea22f4316463ab5c40d13d12f85aa", "7abbf9f894394df98bc392be39c83f5d", "ed733a7e0e054ff2b1aea4f9485f13f0", "789d02a170644ac493853a302fcde884", "72b49e17a8aa40818136118cf2dc83a8", "5f7321e9ec254262b15b52b3084db0e0", "f45b5f9164364a4e94f025f5aabd66f0", "4b47350ebc914c7a8c6af0d0ad1435b1", "169b4d25ce764376839a0beb0716a91c", "8b79bac8fa2145ac89c30c0ac3cfbed4", "38e5ce91d4c94c3e862e2c6d16b4fb64", "ecebdbd791f84b6faf718851258357bc", "dd8efa263b5e464cb05f5e8b854fafc5", "cb0be8ce685f43efa88085b222a487c1", "301062c186e44b61974fb21c242bb256", "c5f08805f0394d459487f2c7eff13d53", "70a2200001554d68af35364019d3d18a", "2fdc1d85a295479e8585b3ee3c92ed03", "e61585c2cf2145aabfffa5e7b4ef20b8", "e10c6c66557c4b0686980802057617e2", "69e9d790314f499bb5951af040e26a58", "833dde6448084727b1a316ff71688aaf", "648fac6dd65142f9adeecabf5e57380f", "eb0faa40fb9548bfbcc6b60f645019fe", "678b1cb2aff04681b17cde2abc8abaf0", "9fb49c0a6b9a40b39726bdadf1900f98", "8333817df92046878389d8357e9dbcda"]} id="5ybX8hZ3UcK2" outputId="432cd8a1-2022-4502-e654-cbe6e65ea702"
pipeline = SummarizationPipeline(
model=AutoModelWithLMHead.from_pretrained("SEBIS/code_trans_t5_small_code_documentation_generation_ruby_multitask_finetune"),
tokenizer=AutoTokenizer.from_pretrained("SEBIS/code_trans_t5_small_code_documentation_generation_ruby_multitask_finetune", skip_special_tokens=True),
device=0
)
# + [markdown] id="hkynwKIcEvHh"
# **3 Give the code for summarization, parse and tokenize it**
# + id="nld-UUmII-2e"
code = "def add(severity, progname, &block)\n return true if io.nil? || severity < level\n message = format_message(severity, progname, yield)\n MUTEX.synchronize { io.write(message) }\n true\n end" #@param {type:"raw"}
# + id="cJLeTZ0JtsB5" colab={"base_uri": "https://localhost:8080/"} outputId="75d2f532-d203-4e48-cdcf-3675963bb558"
# !pip install tree_sitter
# !git clone https://github.com/tree-sitter/tree-sitter-ruby
# + id="hqACvTcjtwYK"
from tree_sitter import Language, Parser
Language.build_library(
'build/my-languages.so',
['tree-sitter-ruby']
)
RUBY_LANGUAGE = Language('build/my-languages.so', 'ruby')
parser = Parser()
parser.set_language(RUBY_LANGUAGE)
# + id="LLCv2Yb8t_PP"
def get_string_from_code(node, lines):
line_start = node.start_point[0]
line_end = node.end_point[0]
char_start = node.start_point[1]
char_end = node.end_point[1]
if line_start != line_end:
code_list.append(' '.join([lines[line_start][char_start:]] + lines[line_start+1:line_end] + [lines[line_end][:char_end]]))
else:
code_list.append(lines[line_start][char_start:char_end])
def my_traverse(node, code_list):
lines = code.split('\n')
if node.child_count == 0:
get_string_from_code(node, lines)
elif node.type == 'string':
get_string_from_code(node, lines)
else:
for n in node.children:
my_traverse(n, code_list)
return ' '.join(code_list)
# + id="BhF9MWu1uCIS" colab={"base_uri": "https://localhost:8080/"} outputId="5abc5d42-25a0-4c97-c39e-b07c2978a89d"
tree = parser.parse(bytes(code, "utf8"))
code_list=[]
tokenized_code = my_traverse(tree.root_node, code_list)
print("Output after tokenization: " + tokenized_code)
# + [markdown] id="sVBz9jHNW1PI"
# **4. Make Prediction**
# + colab={"base_uri": "https://localhost:8080/"} id="KAItQ9U9UwqW" outputId="a696ab61-6bc3-4d60-bb97-ca442a5fdf2d"
pipeline([tokenized_code])
| 54.367347 | 1,594 |
00516cd54e93f4aef4084eeaaba783a5a94f79ec
|
py
|
python
|
quant_finance_lectures/Lecture28-Market-Impact-Models.ipynb
|
jonrtaylor/quant-finance-lectures
|
['CC-BY-4.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img alt="QuantRocket logo" src="https://www.quantrocket.com/assets/img/notebook-header-logo.png">
#
# © Copyright Quantopian Inc.<br>
# © Modifications Copyright QuantRocket LLC<br>
# Licensed under the [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/legalcode).
#
# <a href="https://www.quantrocket.com/disclaimer/">Disclaimer</a>
# # Market Impact Models
#
# By Dr. Michele Goe
#
# In this lecture we seek to clarify transaction costs and how they impact algorithm performance. By the end of this lecture you should be able to:
# 1. Understand the attributes that influence transaction costs based on published market impact model research and our own experience
# 2. Understand the impact of turnover rate, transaction costs, and leverage on your strategy performance
# 3. Become familiar with how institutional quant trading teams think about and measure transaction cost.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import time
# ## Intro to Transaction Costs
#
#
# Transaction costs fall into two categories
# * Direct (commissions and fees): explicit, easily measured, and in institutional trading, relatively "small"
# * Indirect (market impact and spread costs): **the purpose of this lecture**
#
# Slippage is when the price 'slips' before the trade is fully executed, leading to the fill price being different from the price at the time of the order.
# The attributes of a trade that our research shows have the most influence on slippage are:
# 1. **Volatility**
# 2. **Liquidity**
# 3. **Relative order size**
# 4. **Bid - ask spread**
# ## Transaction Cost Impact on Portfolio Performance
#
# Let’s consider a hypothetical mid-frequency statistical arbitrage portfolio. (A mid-freqency strategy refers roughly to a daily turnover between $0.05$ - $0.67$. This represents a holding period between a day and a week. Statistical arbitrage refers to the use of computational algorithms to simultaneously buy and sell stocks according to a statistical model.)
#
# Algo Attribute| Qty
# ---|----
# Holding Period (weeks) |1
# Leverage | 2
# AUM (million) | 100
# Trading Days per year | 252
# Fraction of AUM traded per day | 0.4
#
#
# This means we trade in and out of a new portfolio roughly 50 times a year. At 2 times leverage, on 100 million in AUM, we trade 20 billion dollars per year.
#
# **Q: For this level of churn what is the impact of 1 bps of execution cost to the fund’s returns?**
#
# This means for every basis point ($0.01\%$) of transaction cost we lose $2\%$ off algo performance.
#
# + jupyter={"outputs_hidden": false}
def perf_impact(leverage, turnover , trading_days, txn_cost_bps):
p = leverage * turnover * trading_days * txn_cost_bps/10000.
return p
# + jupyter={"outputs_hidden": false}
print(perf_impact(leverage=2, turnover=0.4, trading_days=252, txn_cost_bps=1))
# -
# ## How do institutional quant trading teams evaluate transaction cost ?
#
# Quantitiative institutional trading teams typically utilize execution tactics that aim to complete parent orders fully, while minimizing the cost of execution. To achieve this goal, parent orders are often split into a number of child orders, which are routed to different execution venues, with the goal to capture all the available liquidity and minimize the bid-ask spread. The parent-level execution price can be expressed as the volume-weighted average price of all child orders.
#
# **Q: What benchmark(s) should we compare our execution price to ?**
#
# *Example Benchmarks :*
# * **Arrival Price** - the "decision" price of the algo, defined as the mid-quote at the time the algo placed the parent order (mid is the half-way point between the best bid and ask quotes)
# * **Interval VWAP** - volume-weighted average price during the life of the order
# * **T + 10 min** - reversion benchmark, price 10 min after the last fill vs execution price
# * **T + 30 min** - reversion benchmark, price 30 min after the last fill vs execution price
# * **Close** - reversion benchmark, price at close vs the execution price
# * **Open** - momentum benchmark, price at open vs the execution price
# * **Previous close** - momentum benchmark, price at previous close vs execution price
# *Other metrics and definitions
#
#
# $$ Metric = \frac{Side * (Benchmark - Execution\thinspace Price )* 100 * 100}{ Benchmark }$$
#
# *Key Ideas*
# * **Execution Price** - volume-weighted average price of all fills or child orders
# * **Cost vs Arrival Price** - difference between the arrival price and the execution price, expressed in basis points. The idea with this benchmark is to compare the execution price against the decision price of the strategy. This cost is sometimes called "slippage" or "implementation shortfall."
#
# The reversion metrics give us an indication of our temporary impact after the order has been executed. Generally, we'd expect the stock price to revert a bit, upon our order completion, as our contribution to the buy-sell imbalance is reflected in the market. The momentum metrics give us an indication of the direction of price drift prior to execution. Often, trading with significant momentum can affect our ability to minimize the bid-ask spread costs.
#
# When executing an order, one of the primary tradeoffs to consider is timing risk vs. market impact:
# * **Timing Risk** - risk of price drift and information leakage as interval between arrival mid quote and last fill increases.
# * **Market Impact** - (high urgency) risk of moving the market by shortening the interval between arrival mid quote and last fill.
#
# Within this framework, neutral urgency of execution occurs at the intersection of market risk and market impact - in this case, each contributes the same to execution costs.
# + jupyter={"outputs_hidden": false}
x = np.linspace(0,1,101)
risk = np.cos(x*np.pi)
impact = np.cos(x* np.pi+ np.pi)
fig,ax = plt.subplots(1)
# Make your plot, set your axes labels
ax.plot(x,risk)
ax.plot(x,impact)
ax.set_ylabel('Transaction Cost in bps', fontsize=15)
ax.set_xlabel('Order Interval', fontsize=15)
ax.set_yticklabels([])
ax.set_xticklabels([])
ax.grid(False)
ax.text(0.09, -0.6, 'Timing Risk', fontsize=15, fontname="serif")
ax.text(0.08, 0.6, 'Market Impact', fontsize=15, fontname="serif")
plt.title('Timing Risk vs Market Impact Affect on Transaction Cost', fontsize=15)
plt.show()
# -
# ## **Liquidity**
#
# Liquidity can be viewed through several lenses. Within the context of execution management, we can think of it as activity, measured in shares and USD traded, as well as frequency and size of trades executed in the market. "Good" liquidity is also achieved through a diverse number of market participants on both sides of the market.
#
# Assess Liquidity by:
# * intraday volume curve
# * percent of day's volume
# * percent of average daily dollar volume in an interval
# * cummulative intraday volume curve
# * relative order size
#
# In general, liquidity is highest as we approach the close, and second highest at the open. Mid day has the lowest liquidity. Liquidity should also be viewed relative to your order size and other securities in the same sector and class.
# + jupyter={"outputs_hidden": false}
from quantrocket.master import get_securities
from quantrocket import get_prices
securities = get_securities(symbols='AAPL', vendors='usstock')
AAPL = securities.index[0]
data = get_prices('usstock-free-1min', sids=AAPL, data_frequency='minute', start_date='2016-01-01', end_date='2016-07-01', fields='Volume')
dat = data.loc['Volume'][AAPL]
# Combine separate Date and Time in index into datetime
dat.index = pd.to_datetime(dat.index.get_level_values('Date').astype(str) + ' ' + dat.index.get_level_values('Time'))
plt.subplot(211)
dat['2016-04-14'].plot(title='Intraday Volume Profile') # intraday volume profile plot
plt.subplot(212)
(dat['2016-04-14'].resample('10t', closed='right').sum()/\
dat['2016-04-14'].sum()).plot(); # percent volume plot
plt.title('Intraday Volume Profile, % Total Day');
# + jupyter={"outputs_hidden": false}
df = pd.DataFrame(dat) # Apple minutely volume data
df.columns = ['interval_vlm']
df_daysum = df.resample('d').sum() # take sum of each day
df_daysum.columns = ['day_vlm']
df_daysum['day'] = df_daysum.index.date # add date index as column
df['min_of_day']=(df.index.hour-9)*60 + (df.index.minute-30) # calculate minutes from open
df['time']=df.index.time # add time index as column
conversion = {'interval_vlm':'sum', 'min_of_day':'last', 'time':'last'}
df = df.resample('10t', closed='right').apply(conversion) # apply conversions to columns at 10 min intervals
df['day'] = df.index.date
df = df.merge(df_daysum, how='left', on='day') # merge df and df_daysum dataframes
df['interval_pct'] = df['interval_vlm'] / df['day_vlm'] # calculate percent of days volume for each row
df.head()
# + jupyter={"outputs_hidden": false}
plt.scatter(df.min_of_day, df.interval_pct)
plt.xlim(0,400)
plt.xlabel('Time from the Open (minutes)')
plt.ylabel('Percent Days Volume')
# + jupyter={"outputs_hidden": false}
grouped = df.groupby(df.min_of_day)
grouped = df.groupby(df.time) # group by 10 minute interval times
m = grouped.median() # get median values of groupby
x = m.index
y = m['interval_pct']
ax1 = (100*y).plot(kind='bar', alpha=0.75) # plot percent daily volume grouped by 10 minute interval times
ax1.set_ylim(0,10);
plt.title('Intraday Volume Profile');
ax1.set_ylabel('% of Day\'s Volume in Bucket');
# -
# ## Relative Order Size
#
# As we increase relative order size at a specified participation rate, the time to complete the order increases. Let's assume we execute an order using VWAP, a scheduling strategy, which executes orders over a pre-specified time window, according to the projections of volume distribution throughout that time window: At 3% participation rate for VWAP execution, we require the entire day to trade if our order represents 3% of average daily volume.
#
# If we expect our algo to have high relative order sizes then we may want to switch to a liquidity management execution strategy when trading to ensure order completion by the end of the day. Liquidity management execution strategies have specific constraints for the urgency of execution, choice of execution venues and spread capture with the objective of order completion. Going back to our risk curves, we expect higher transaction costs the longer we trade. Therefore, the higher percent ADV of an order the more expensive to trade.
# + jupyter={"outputs_hidden": false}
data = get_prices('usstock-free-1min', sids=AAPL, data_frequency='minute', start_date='2016-01-01', end_date='2018-01-02', fields='Volume')
dat = data.loc['Volume'][AAPL]
# Combine separate Date and Time in index into datetime
dat.index = pd.to_datetime(dat.index.get_level_values('Date').astype(str) + ' ' + dat.index.get_level_values('Time'))
# +
def relative_order_size(participation_rate, pct_ADV):
fill_start = dat['2017-10-02'].index[0] # start order at 9:31
ADV20 = int(dat.resample("1d").sum()[-20:].mean()) # calculate 20 day ADV
order_size = int(pct_ADV * ADV20)
try :
ftime = dat['2017-10-02'][(order_size * 1.0 / participation_rate)<=dat['2017-10-02'].cumsum().values].index[0]
except:
ftime = dat['2017-10-02'].index[-1] # set fill time to 4p
fill_time = max(1,int((ftime - fill_start).total_seconds()/60.0))
return fill_time
def create_plots(participation_rate, ax):
df_pr = pd.DataFrame(data=np.linspace(0.0,0.1,100), columns = ['adv'] ) # create dataframe with intervals of ADV
df_pr['pr'] = participation_rate # add participation rate column
df_pr['fill_time'] = df_pr.apply(lambda row: relative_order_size(row['pr'],row['adv']), axis = 1) # get fill time
ax.plot(df_pr['adv'],df_pr['fill_time'], label=participation_rate) # generate plot line with ADV and fill time
fig, ax = plt.subplots()
for i in [0.01,0.02,0.03,0.04,0.05,0.06,0.07]: # for participation rate values
create_plots(i,ax) # generate plot line
plt.ylabel('Time from Open (minutes)')
plt.xlabel('Percent Average Daily Volume')
plt.title('Trade Completion Time as Function of Relative Order Size and Participation Rate')
plt.xlim(0.,0.04)
ax.legend()
# -
#
# ## Volatility
#
# Volatilty is a statistical measure of dispersion of returns for a security, calculated as the standard deviation of returns. The volatility of any given stock typically peaks at the open and therafter decreases until mid-day.The higher the volatility the more uncertainty in the returns. This uncertainty is an artifact of larger bid-ask spreads during the price discovery process at the start of the trading day. In contrast to liquidity, where we would prefer to trade at the open to take advantage of high volumes, to take advantage of low volatility we would trade at the close.
#
# We use two methods to calculate volatility for demonstration purposes, OHLC and, the most common, close-to-close. OHLC uses the Garman-Klass Yang-Zhang volatilty estimate that employs open, high, low, and close data.
#
# OHLC VOLATILITY ESTIMATION METHOD
#
# $$\sigma^2 = \frac{Z}{n} \sum \left[\left(\ln \frac{O_i}{C_{i-1}} \right)^2 + \frac{1}{2} \left( \ln \frac{H_i}{L_i} \right)^2 - (2 \ln 2 -1) \left( \ln \frac{C_i}{O_i} \right)^2 \right]$$
#
#
#
# CLOSE TO CLOSE HISTORICAL VOLATILITY ESTIMATION METHOD
#
# Volatility is calculated as the annualised standard deviation of log returns as detailed in the equation below.
#
# $$ Log \thinspace return = x_1 = \ln (\frac{c_i + d_i}{c_i-1} ) $$
# where d_i = ordinary(not adjusted) dividend and ci is close price
# $$ Volatilty = \sigma_x \sqrt{ \frac{1}{N} \sum_{i=1}^{N} (x_i - \bar{x})^2 }$$
#
# See end of notebook for references
# + jupyter={"outputs_hidden": false}
data = get_prices('usstock-free-1min', sids=AAPL, data_frequency='minute', start_date='2016-01-01', end_date='2016-07-01')
df = data[AAPL].unstack(level='Field')
# Combine separate Date and Time in index into datetime
df.index = pd.to_datetime(df.index.get_level_values('Date').astype(str) + ' ' + df.index.get_level_values('Time'))
df.head()
# + jupyter={"outputs_hidden": false}
def gkyz_var(open, high, low, close, close_tm1): # Garman Klass Yang Zhang extension OHLC volatility estimate
return np.log(open/close_tm1)**2 + 0.5*(np.log(high/low)**2) \
- (2*np.log(2)-1)*(np.log(close/open)**2)
def historical_vol(close_ret, mean_ret): # close to close volatility estimate
return np.sqrt(np.sum((close_ret-mean_ret)**2)/390)
# + jupyter={"outputs_hidden": false}
df['min_of_day'] = (df.index.hour-9)*60 + (df.index.minute-30) # calculate minute from the open
df['time'] = df.index.time # add column time index
df['day'] = df.index.date # add column date index
df.head()
# + jupyter={"outputs_hidden": false}
df['close_tm1'] = df.groupby('day')['Close'].shift(1) # shift close value down one row
df.close_tm1 = df.close_tm1.fillna(df.Open)
df['min_close_ret'] = np.log( df['Close'] /df['close_tm1']) # log of close to close
close_returns = df.groupby('day')['min_close_ret'].mean() # daily mean of log of close to close
new_df = df.merge(pd.DataFrame(close_returns), left_on ='day', right_index = True)
# handle when index goes from 16:00 to 9:31:
new_df['variance'] = new_df.apply(
lambda row: historical_vol(row.min_close_ret_x, row.min_close_ret_y),
axis=1)
new_df.head()
# + jupyter={"outputs_hidden": false}
df_daysum = pd.DataFrame(new_df['variance'].resample('d').sum()) # get sum of intraday variances daily
df_daysum.columns = ['day_variance']
df_daysum['day'] = df_daysum.index.date
df_daysum.head()
# + jupyter={"outputs_hidden": false}
conversion = {'variance':'sum', 'min_of_day':'last', 'time':'last'}
df = new_df.resample('10t', closed='right').apply(conversion)
df['day'] = df.index.date
df['time'] = df.index.time
df.head()
# + jupyter={"outputs_hidden": false}
df = df.merge(df_daysum, how='left', on='day') # merge daily and intraday volatilty dataframes
df['interval_pct'] = df['variance'] / df['day_variance'] # calculate percent of days volatility for each row
df.head()
# + jupyter={"outputs_hidden": false}
plt.scatter(df.min_of_day, df.interval_pct)
plt.xlim(0,400)
plt.ylim(0,)
plt.xlabel('Time from Open (minutes)')
plt.ylabel('Interval Contribution of Daily Volatility')
plt.title('Probabilty Distribution of Daily Volatility ')
# + jupyter={"outputs_hidden": false}
import datetime
grouped = df.groupby(df.min_of_day)
grouped = df.groupby(df.time) # groupby time
m = grouped.median() # get median
x = m.index
y = m['interval_pct'][datetime.time(9,30):datetime.time(15,59)]
(100*y).plot(kind='bar', alpha=0.75);# plot interval percent of median daily volatility
plt.title('Intraday Volatility Profile')
ax1.set_ylabel('% of Day\'s Variance in Bucket');
# -
# ## Bid-Ask Spread
#
#
# The following relationships between bid-ask spread and order attributes are seen in our live trading data:
#
# * As **market cap ** increases we expect spreads to decrease. Larger companies tend to exhibit lower bid-ask spreads.
#
# * As **volatility ** increases we expect spreads to increase. Greater price uncertainty results in wider bid-ask spreads.
#
# * As **average daily dollar volume ** increases, we expect spreads to decrease. Liquidity tends to be inversely proportional to spreads, due to larger number of participants and more frequent updates to quotes.
#
# * As **price ** increases, we expect spreads to decrease (similar to market cap), although this relationship is not as strong.
#
# * As **time of day ** progresses we expect spreads to decrease. During early stages of a trading day, price discovery takes place. in contrast, at market close order completion is the priority of most participants and activity is led by liquidity management, rather than price discovery.
#
# The Trading Team developed a log-linear model fit to our live data that predicts the spread for a security with which we have the above listed attributes.
# +
def model_spread(time, vol, mcap = 1.67 * 10 ** 10, adv = 84.5, px = 91.0159):
time_bins = np.array([0.0, 960.0, 2760.0, 5460.0, 21660.0]) #seconds from market open
time_coefs = pd.Series([0.0, -0.289, -0.487, -0.685, -0.952])
vol_bins = np.array([0.0, .1, .15, .2, .3, .4])
vol_coefs = pd.Series([0.0, 0.251, 0.426, 0.542, 0.642, 0.812])
mcap_bins = np.array([0.0, 2.0, 5.0, 10.0, 25.0, 50.0]) * 10 ** 9
mcap_coefs = pd.Series([0.291, 0.305, 0.0, -0.161, -0.287, -0.499])
adv_bins = np.array([0.0, 50.0, 100.0, 150.0, 250.0, 500.0]) * 10 ** 6
adv_coefs = pd.Series([0.303, 0.0, -0.054, -0.109, -0.242, -0.454])
px_bins = np.array([0.0, 28.0, 45.0, 62.0, 82.0, 132.0])
px_coefs = pd.Series([-0.077, -0.187, -0.272, -0.186, 0.0, 0.380])
return np.exp(1.736 +\
time_coefs[np.digitize(time, time_bins) - 1] +\
vol_coefs[np.digitize(vol, vol_bins) - 1] +\
mcap_coefs[np.digitize(mcap, mcap_bins) - 1] +\
adv_coefs[np.digitize(adv, adv_bins) - 1] +\
px_coefs[np.digitize(px, px_bins) - 1])
# -
# ### Predict the spread for the following order :
# * Stock: DPS
# * Qty: 425 shares
# * Time of day : 9:41 am July 19, 2017, 600 seconds from open
# * Market Cap : 1.67e10
# * Volatility: 18.8%
# * ADV : 929k shares ; 84.5M dollars
# * Avg Price : 91.0159
# + jupyter={"outputs_hidden": false}
t = 10 * 60
vlty = 0.188
mcap = 1.67 * 10 ** 10
adv = 84.5 *10
price = 91.0159
print(model_spread(t, vlty, mcap, adv, price), 'bps')
# + jupyter={"outputs_hidden": false}
x = np.linspace(0,390*60) # seconds from open shape (50,)
y = np.linspace(.01,.7) # volatility shape(50,)
mcap = 1.67 * 10 ** 10
adv = 84.5
px = 91.0159
vlty_coefs = pd.Series([0.0, 0.251, 0.426, 0.542, 0.642, 0.812])
vlty_bins = np.array([0.0, .1, .15, .2, .3, .4])
time_bins = np.array([0.0, 960.0, 2760.0, 5460.0, 21660.0]) #seconds from market open
time_coefs = pd.Series([0.0, -0.289, -0.487, -0.685, -0.952])
mcap_bins = np.array([0.0, 2.0, 5.0, 10.0, 25.0, 50.0]) * 10 ** 9
mcap_coefs = pd.Series([0.291, 0.305, 0.0, -0.161, -0.287, -0.499])
adv_bins = np.array([0.0, 50.0, 100.0, 150.0, 250.0, 500.0]) * 10 ** 6
adv_coefs = pd.Series([0.303, 0.0, -0.054, -0.109, -0.242, -0.454])
px_bins = np.array([0.0, 28.0, 45.0, 62.0, 82.0, 132.0])
px_coefs = pd.Series([-0.077, -0.187, -0.272, -0.186, 0.0, 0.380])
# shape (1, 50)
time_contrib = np.take(time_coefs, np.digitize(x, time_bins) - 1).values.reshape((1, len(x)))
# shape (50, 1)
vlty_contrib = np.take(vlty_coefs, np.digitize(y, vlty_bins) - 1).values.reshape((len(y), 1))
# scalar
mcap_contrib = mcap_coefs[np.digitize((mcap,), mcap_bins)[0] - 1]
# scalar
adv_contrib = adv_coefs[np.digitize((adv,), adv_bins)[0] - 1]
# scalar
px_contrib = px_coefs[np.digitize((px,), px_bins)[0] - 1]
z_scalar_contrib = 1.736 + mcap_contrib + adv_contrib + px_contrib
Z = np.exp(z_scalar_contrib + time_contrib + vlty_contrib)
cmap=plt.get_cmap('jet')
X, Y = np.meshgrid(x,y)
CS = plt.contour(X/60,Y,Z, linewidths=3, cmap=cmap, alpha=0.8);
plt.clabel(CS)
plt.xlabel('Time from the Open (Minutes)')
plt.ylabel('Volatility')
plt.title('Spreads for varying Volatility and Trading Times (mcap = 16.7B, px = 91, adv = 84.5M)')
plt.show()
# -
# ## **Quantifying Market Impact**
#
# Theoritical Market Impact models attempt to estimate transaction costs of trading by utilizing order attributes. There are many published market impact models. Here are some examples:
#
# 1. Zipline Volume Slippage Model
# 2. Almgren et al 2005
# 3. Kissell et al. 2004
# 4. J.P. Morgan Model 2010
#
#
# The models have a few commonalities such as the inclusion of relative order size, volatility as well as custom parameters calculated from observed trades.There are also notable differences in the models such as (1) JPM explictly calls out spread impact, (2) Almgren considers fraction of outstanding shares traded daily, (3) Q Slipplage Model does not consider volatility, and (4) Kissel explicit parameter to proportion temporary and permenant impact, to name a few.
#
# The academic models have notions of temporary and permanant impact. **Temporary Impact** captures the impact on transaction costs due to urgency or aggressiveness of the trade. While **Permanant Impact** estimates with respect to information or short term alpha in a trade.
#
# ### Almgren et al. model (2005)
#
# This model assumes the initial order, X, is completed at a uniform rate of trading over a volume time
# interval T. That is, the trade rate in volume units is v = X/T, and is held
# constant until the trade is completed. Constant rate in these units is
# equivalent to VWAP execution during the time of execution.
#
#
# Almgren et al. model these two terms as
#
#
#
# $$\text{tcost} = 0.5 \overbrace{\gamma \sigma \frac{X}{V}\left(\frac{\Theta}{V}\right)^{1/4}}^{\text{permanent}} + \overbrace{\eta \sigma \left| \frac{X}{VT} \right|^{3/5}}^{\text{temporary}} $$
#
#
# where $\gamma$ and $\eta$ are the "universal coefficients of market impact" and estimated by the authors using a large sample of institutional trades; $\sigma$ is the daily volatility of the stock; $\Theta$ is the total shares outstanding of the stock; $X$ is the number of shares you would like to trade (unsigned); $T$ is the time width in % of trading time over which you slice the trade; and $V$ is the average daily volume ("ADV") in shares of the stock. The interpretation of $\frac{\Theta}{V}$ is the inverse of daily "turnover", the fraction of the company's value traded each day.
#
# For reference, FB has 2.3B shares outstanding, its average daily volume over 20 days is 18.8M therefore its inverse turnover is approximately 122, put another way, it trades less than 4% of outstanding shares daily.
#
#
#
# ### Potential Limitations
#
# Note that the Almgren et al (2005) and Kissell, Glantz and Malamut (2004) papers were released prior to the adoption and phased implementation of [__Reg NMS__](https://www.sec.gov/rules/final/34-51808.pdf), prior to the "quant meltdown" of August 2007, prior to the financial crisis hitting markets in Q4 2008, and other numerous developments in market microstructure.
#
# + jupyter={"outputs_hidden": false}
def perm_impact(pct_adv, annual_vol_pct = 0.25, inv_turnover = 200):
gamma = 0.314
return 10000 * gamma * (annual_vol_pct / 16) * pct_adv * (inv_turnover)**0.25
def temp_impact(pct_adv, minutes, annual_vol_pct = 0.25, minutes_in_day = 60*6.5):
eta = 0.142
day_frac = minutes / minutes_in_day
return 10000 * eta * (annual_vol_pct / 16) * abs(pct_adv/day_frac)**0.6
def tc_bps(pct_adv, minutes, annual_vol_pct = 0.25, inv_turnover = 200, minutes_in_day = 60*6.5):
perm = perm_impact(pct_adv, annual_vol_pct=annual_vol_pct, inv_turnover=inv_turnover)
temp = temp_impact(pct_adv, minutes, annual_vol_pct=annual_vol_pct, minutes_in_day=minutes_in_day)
return 0.5 * perm + temp
# -
# So if we are trading 10% of ADV of a stock with a daily vol of 1.57% and we plan to do this over half the day, we would expect 8bps of TC (which is the Almgren estimate of temporary impact cost in this scenario). From the paper, this is a sliver of the output at various trading speeds:
#
# Variable | IBM
# ------------- | -------------
# Inverse turnover ($\Theta/V$) | 263
# Daily vol ($\sigma$) | 1.57%
# Trade % ADV (X/V) | 10%
#
# Item | Fast | Medium | Slow
# -----|------|--------|-------
# Permanent Impact (bps) | 20 | 20 | 20
# Trade duration (day fraction %) | 10% | 20% | 50%
# Temporary Impact (bps) | 22 | 15 | 8
# Total Impact (bps) | 32 | 25 | 18
#
# + jupyter={"outputs_hidden": false}
print('Cost to trade Fast (First 40 mins):', round(tc_bps(pct_adv=0.1, annual_vol_pct=16*0.0157, inv_turnover=263, minutes=0.1*60*6.5),2), 'bps')
print('Cost to trade Medium (First 90 mins):', round(tc_bps(pct_adv=0.1, annual_vol_pct=16*0.0157, inv_turnover=263, minutes=0.2*60*6.5),2), 'bps' )
print('Cost to trade Slow by Noon:', round(tc_bps(pct_adv=0.1, annual_vol_pct=16*0.0157, inv_turnover=263, minutes=0.5*60*6.5),2), 'bps')
# -
# Trading 0.50% of ADV of a stock with a daily vol of 1.57% and we plan to do this over 30 minutes...
# + jupyter={"outputs_hidden": false}
print(round(tc_bps(pct_adv=0.005, minutes=30, annual_vol_pct=16*0.0157),2))
# -
# Let's say we wanted to trade \$2M notional of Facebook, and we are going to send the trade to an execution algo (e.g., VWAP) to be sliced over 15 minutes.
# + jupyter={"outputs_hidden": false}
trade_notional = 2000000 # 2M notional
stock_price = 110.89 # dollars per share
shares_to_trade = trade_notional/stock_price
stock_adv_shares = 30e6 # 30 M
stock_shares_outstanding = 275e9/110.89
expected_tc = tc_bps(shares_to_trade/stock_adv_shares, minutes=15, annual_vol_pct=0.22)
print("Expected tc in bps: %0.2f" % expected_tc)
print("Expected tc in $ per share: %0.2f" % (expected_tc*stock_price / 10000))
# -
# And to motivate some intuition, at the total expected cost varies as a function of how much % ADV we want to trade in 30 minutes.
# + jupyter={"outputs_hidden": false}
x = np.linspace(0.0001,0.03)
plt.plot(x*100,tc_bps(x,30,0.25), label=r"$\sigma$ = 25%");
plt.plot(x*100,tc_bps(x,30,0.40), label=r"$\sigma$ = 40%");
plt.ylabel('tcost in bps')
plt.xlabel('Trade as % of ADV')
plt.title(r'tcost in Basis Points of Trade Value; $\sigma$ = 25% and 40%; time = 15 minutes');
plt.legend();
# -
# And let's look a tcost as a function of trading time and % ADV.
# + jupyter={"outputs_hidden": false}
x = np.linspace(0.001,0.03)
y = np.linspace(5,30)
X, Y = np.meshgrid(x,y)
Z = tc_bps(X,Y,0.20)
levels = np.linspace(0.0, 60, 30)
cmap=plt.get_cmap('Reds')
cmap=plt.get_cmap('hot')
cmap=plt.get_cmap('jet')
plt.subplot(1,2,1);
CS = plt.contour(X*100, Y, Z, levels, linewidths=3, cmap=cmap, alpha=0.55);
plt.clabel(CS);
plt.ylabel('Trading Time in Minutes');
plt.xlabel('Trade as % of ADV');
plt.title(r'tcost in Basis Points of Trade Value; $\sigma$ = 20%');
plt.subplot(1,2,2);
Z = tc_bps(X,Y,0.40)
CS = plt.contour(X*100, Y, Z, levels, linewidths=3, cmap=cmap, alpha=0.55);
plt.clabel(CS);
plt.ylabel('Trading Time in Minutes');
plt.xlabel('Trade as % of ADV');
plt.title(r'tcost in Basis Points of Trade Value; $\sigma$ = 40%');
# -
# Alternatively, we might want to get some intuition as to if we wanted to limit our cost, how does the trading time vary versus % of ADV.
# + jupyter={"outputs_hidden": false}
x = np.linspace(0.001,0.03) # % ADV
y = np.linspace(1,60*6.5) # time to trade
X, Y = np.meshgrid(x, y)
levels = np.linspace(0.0, 390, 20)
cmap=plt.get_cmap('Reds')
cmap=plt.get_cmap('hot')
cmap=plt.get_cmap('jet')
plt.subplot(1,2,1);
Z = tc_bps(X,Y,0.20)
plt.contourf(X*100, Z, Y, levels, cmap=cmap, alpha=0.55);
plt.title(r'Trading Time in Minutes; $\sigma$ = 20%');
plt.xlabel('Trade as % of ADV');
plt.ylabel('tcost in Basis Points of Trade Value');
plt.ylim(5,20)
plt.colorbar();
plt.subplot(1,2,2);
Z = tc_bps(X,Y,0.40)
plt.contourf(X*100, Z, Y, levels, cmap=cmap, alpha=0.55);
plt.title(r'Trading Time in Minutes; $\sigma$ = 40%');
plt.xlabel('Trade as % of ADV');
plt.ylabel('tcost in Basis Points of Trade Value');
plt.ylim(5,20);
plt.colorbar();
# -
# ### The Breakdown: Permanent and Temporary
#
# For a typical stock, let's see how the tcost is broken down into permanent and temporary.
# + jupyter={"outputs_hidden": false}
minutes = 30
x = np.linspace(0.0001,0.03)
f, (ax1, ax2) = plt.subplots(ncols=2, sharex=True, sharey=True)
f.subplots_adjust(hspace=0.15)
p = 0.5*perm_impact(x,0.20)
t = tc_bps(x,minutes,0.20)
ax1.fill_between(x*100, p, t, color='b', alpha=0.33);
ax1.fill_between(x*100, 0, p, color='k', alpha=0.66);
ax1.set_ylabel('tcost in bps')
ax1.set_xlabel('Trade as % of ADV')
ax1.set_title(r'tcost in bps of Trade Value; $\sigma$ = 20%; time = 15 minutes');
p = 0.5*perm_impact(x, 0.40)
t = tc_bps(x,minutes, 0.40)
ax2.fill_between(x*100, p, t, color='b', alpha=0.33);
ax2.fill_between(x*100, 0, p, color='k', alpha=0.66);
plt.xlabel('Trade as % of ADV')
plt.title(r'tcost in bps of Trade Value; $\sigma$ = 40%; time = 15 minutes');
# -
# ### Kissell et al Model (2004)
#
# This model assumes there is a theoretical instaenous impact cost $I^*$ incurred by the investor if all shares $Q$ were released to the market.
#
# $$ MI_{bp} = b_1 I^* POV^{a_4} + (1-b_1)I^*$$
#
#
# $$ I^* = a_1 (\frac{Q}{ADV})^{a_2} \sigma^{a_3}$$
#
# $$POV = \frac{Q}{Q+V}$$
#
# * $I^*$ is instanteous impact
# * $POV$ is percentage of volume trading rate
# * $V$ is the expected volume in the interval of trading
# * $b_1$ is the temporary impact parameter
# * $ADV$ is 30 day average daily volume
# * $Q$ is order size
#
#
# Parameter | Fitted Values
# ------------- | -------------
# $b_1$ | 0.80
# $a_1$ | 750
# $a_2$ | 0.50
# $a_3$ | 0.75
# $a_4$ | 0.50
# + jupyter={"outputs_hidden": false}
def kissell(adv, annual_vol, interval_vol, order_size):
b1, a1, a2, a3, a4 = 0.9, 750., 0.2, 0.9, 0.5
i_star = a1 * ((order_size/adv)**a2) * annual_vol**a3
PoV = order_size/(order_size + adv)
return b1 * i_star * PoV**a4 + (1 - b1) * i_star
# + jupyter={"outputs_hidden": false}
print(kissell(adv=5*10**6, annual_vol=0.2, interval_vol=adv * 0.06, order_size=0.01 * adv ), 'bps')
# + jupyter={"outputs_hidden": false}
x = np.linspace(0.0001,0.1)
plt.plot(x,kissell(5*10**6,0.1, 2000*10**3, x*2000*10**3), label=r"$\sigma$ = 10%");
plt.plot(x,kissell(5*10**6,0.25, 2000*10**3, x*2000*10**3), label=r"$\sigma$ = 25%");
plt.ylabel('tcost in bps')
plt.xlabel('Trade as % of ADV')
plt.title(r'tcost in Basis Points of Trade Value; $\sigma$ = 25% and 40%; time = 15 minutes');
plt.legend();
# -
# ## The J.P. Morgan Market Impact Model
#
#
# $$MI(bps) = I \times \omega \times \frac{2 \times PoV}{1 + PoV} + (1-\omega) \times I + S_c$$
# Where
#
# $$I = \alpha \times PoV^\beta \times Volatility^\gamma$$
#
# * $\omega$ is the fraction of temporary impact (liquidity cost)
# * $\alpha$ is a scaling parameter
# * $PoV$ is relative order size as fraction of average daily volume
# * $S_c$ is the spread ( basis point difference between the bid and ask )
#
# For US equities, the fitted parameters as of June 2016 are
#
# Parameter | Fitted Value
# ------|-----
# b ($\omega$) | 0.931
# a1 ($\alpha$)| 168.5
# a2 ($\beta$) | 0.1064
# a3 ($\gamma$) | 0.9233
#
# +
def jpm_mi(size_shrs, adv, day_frac=1.0, spd=5,
spd_frac=0.5, ann_vol=0.25, omega=0.92,
alpha=350, beta=0.370, gamma=1.05):
PoV = (size_shrs/(adv*day_frac))
I = alpha*(PoV**beta)*(ann_vol**gamma)
MI = I*omega*(2*PoV)/(1+PoV) + (1-omega)*I + spd*spd_frac
return MI
def jpm_mi_pct(pct_adv, **kwargs):
return jpm_mi(pct_adv, 1.0, **kwargs)
# -
# Let's assume the following order:
# * Buy 100,000 XYZ, trading at 10% of the volume
# * XYZ's ADV = 1,000,000 shares
# * XYZ Annualized Volatility = 25%
# * XYZ's Average Spread = 5 bps
# + jupyter={"outputs_hidden": false}
spy_adv = 85603411.55
print(round(jpm_mi(size_shrs=10000, adv=1e6),2), 'bps') # 1% pct ADV order
print(round(jpm_mi(size_shrs=0.05*spy_adv, adv=spy_adv, spd=5, day_frac=1.0),2), 'bps') # 5% pct ADV of SPY order
# -
# ## Zipline Volume Share Slippage
#
# The Zipline `VolumeShareSlippage` model ([API Reference](https://www.quantrocket.com/docs/api/#zipline.finance.slippage.VolumeShareSlippage)) expressed in the style of the equation below
#
# $$\text{tcost} = 0.1 \left| \frac{X}{VT} \right|^2 $$
#
# where $X$ is the number of shares you would like to trade; $T$ is the time width of the bar in % of a day; $V$ is the ADV of the stock.
def tc_Zipline_vss_bps(pct_adv, minutes=1.0, minutes_in_day=60*6.5):
day_frac = minutes / minutes_in_day
tc_pct = 0.1 * abs(pct_adv/day_frac)**2
return tc_pct*10000
# To reproduce the given examples, we trade over a bar
# + jupyter={"outputs_hidden": false}
print(tc_Zipline_vss_bps(pct_adv=0.1/390, minutes=1))
print(tc_Zipline_vss_bps(pct_adv=0.25/390, minutes=1))
# -
# As this model is convex, it gives very high estimates for large trades.
# + jupyter={"outputs_hidden": false}
print(tc_Zipline_vss_bps(pct_adv=0.1, minutes=0.1*60*6.5))
print(tc_Zipline_vss_bps(pct_adv=0.1, minutes=0.2*60*6.5))
print(tc_Zipline_vss_bps(pct_adv=0.1, minutes=0.5*60*6.5))
# -
# Though for small trades, the results are comparable.
# + jupyter={"outputs_hidden": false}
print(tc_bps(pct_adv=0.005, minutes=30, annual_vol_pct=0.2))
print(tc_Zipline_vss_bps(pct_adv=0.005, minutes=30))
# + jupyter={"outputs_hidden": false}
x = np.linspace(0.0001, 0.01)
plt.plot(x*100,tc_bps(x, 30, 0.20), label=r"Almgren $\sigma$ = 20%");
plt.plot(x*100,tc_bps(x, 30, 0.40), label=r"Almgren $\sigma$ = 40%");
plt.plot(x*100,tc_Zipline_vss_bps(x, minutes=30),label="Zipline VSS");
plt.plot(x*100,jpm_mi_pct(x, ann_vol=0.2), label=r"JPM MI1 $\sigma$ = 20%");
plt.plot(x*100,jpm_mi_pct(x, ann_vol=0.4), label=r"JPM MI1 $\sigma$ = 40%");
plt.plot(x*100,kissell(5*10**6,0.20, 2000*10**3, x*2000*10**3), label=r"Kissell $\sigma$ = 20%");
plt.plot(x*100,kissell(5*10**6,0.40, 2000*10**3, x*2000*10**3), label=r"Kissell $\sigma$ = 40%", color='black');
plt.ylabel('tcost in bps')
plt.xlabel('Trade as % of ADV')
plt.title('tcost in Basis Points of Trade Value; time = 30 minutes');
plt.legend();
# -
# ## Conclusions
#
# ### The following order atttributes leads to higher market impact:
# * Higher relative order size
# * Trading illquid names
# * Trading names with lower daily turnover (in terms of shares outstanding)
# * Shorter trade duration
# * Higher volatility names
# * More urgency or higher POV
# * Short term alpha
# * Trading earlier in the day
# * Trading names with wider spreads
# * Trading lower ADV names or on days when market volume is down
#
# ## References:
#
# * Almgren, R., Thum, C., Hauptmann, E., & Li, H. (2005). Direct estimation of equity market impact. Risk, 18(7), 5862.
#
# * Bennett, C. and Gil, M.A. (2012, Februrary) Measuring Historic Volatility, Santander Equity Derivatives Europe Retreived from: (http://www.todaysgroep.nl/media/236846/measuring_historic_volatility.pdf)
#
# * Garman, M. B., & Klass, M. J. (1980). On the estimation of security price volatilities from historical data. Journal of business, 67-78.
#
# * Kissell, R., Glantz, M., & Malamut, R. (2004). A practical framework for estimating transaction costs and developing optimal trading strategies to achieve best execution. Finance Research Letters, 1(1), 35-46.
#
# * Zipline Slippage Model see: https://www.quantrocket.com/docs/api/#zipline.finance.slippage.VolumeShareSlippage
#
# ---
#
# **Next Lecture:** [Universe Selection](Lecture29-Universe-Selection.ipynb)
#
# [Back to Introduction](Introduction.ipynb)
# ---
#
# *This presentation is for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation for any security; nor does it constitute an offer to provide investment advisory or other services by Quantopian, Inc. ("Quantopian") or QuantRocket LLC ("QuantRocket"). Nothing contained herein constitutes investment advice or offers any opinion with respect to the suitability of any security, and any views expressed herein should not be taken as advice to buy, sell, or hold any security or as an endorsement of any security or company. In preparing the information contained herein, neither Quantopian nor QuantRocket has taken into account the investment needs, objectives, and financial circumstances of any particular investor. Any views expressed and data illustrated herein were prepared based upon information believed to be reliable at the time of publication. Neither Quantopian nor QuantRocket makes any guarantees as to their accuracy or completeness. All information is subject to change and may quickly become unreliable for various reasons, including changes in market conditions or economic circumstances.*
| 43.639115 | 1,167 |
228e3881b920dafb7400affd13565c2d9a68a827
|
py
|
python
|
Automate the Boring Stuff with Python Ch10.ipynb
|
pgaods/Automate-the-Boring-Stuff-with-Python
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# In this chapter we study issues related to debugging. There are a few tools and techniques to identify what exactly your code is doing and where it’s going wrong. Mainly in this chapter, we will look at logging and assertions, two features that can help you detect bugs early. In general, the earlier you catch bugs, the easier they will be to fix.
# To start with debugging, we first examine the 'raise' statement. Python raises an exception whenever it tries to execute invalid code. Recall that we can use the 'try...except...' clauses to deal with exceptions. But here, you will learn that you can also raise your own exceptions in your code. Raising an exception is a way of saying, "Stop running the code in this function and move the program execution to the except statement".
#
# Exceptions are raised with a 'raise' statement. In Python coding, a 'raise' statement consists of the following: 1) the 'raise' keyword; 2) a call to the Exception() function, and 3) a string with a helpful error message passed to the Exception() function. In general, you will commonly see a raise statement inside a function and the 'try' and 'except' statements in the code calling the function. Below is an example:
# +
def boxPrint(symbol, width, height):
if len(symbol) != 1:
raise Exception('Symbol must be a single character string.')
if width <= 2:
raise Exception('Width must be greater than 2.')
if height <= 2:
raise Exception('Height must be greater than 2.')
print(symbol * width)
for i in range(height - 2):
print(symbol + (' ' * (width - 2)) + symbol)
print(symbol * width)
for sym, w, h in (('*', 4, 4), ('O', 20, 5), ('x', 1, 3), ('ZZ', 3, 3)):
try:
boxPrint(sym, w, h)
except Exception as err:
print('An exception happened: ' + str(err))
# -
# Here we’ve defined a boxPrint() function that takes a character, a width, and a height, and uses the character to make a little picture of a box with that width and height. This box shape is printed out as a result. Suppose we want the character to be a single character, and the width and height to be greater than 2. We add 'if' statements to raise exceptions if these requirements aren’t satisfied. Later, when we call boxPrint() with various arguments, our try...except... clauses will handle invalid arguments. The above program uses the 'except' 'Exception' as 'err' form of the except statement. If an 'Exception' object is returned from boxPrint(), this 'except' statement will store it in a variable named 'err'. The 'Exception' object can then be converted to a string by passing it to str() to produce a user-friendly error message.
# When Python encounters an error, it produces a treasure trove of error information called the 'traceback'. The 'traceback' includes the error message, the line number of the line that caused the error, and the sequence of the function calls that led to the error. This sequence of calls is called the 'call stack'. The 'traceback' is displayed by Python whenever a raised exception goes unhandled. But you can also obtain it as a string by calling traceback.format_exc(). This function is useful if you want the information from an exception’s traceback but also want an 'except' statement to gracefully handle the exception. You will need to import Python’s 'traceback' module before calling this function.
#
# For example, instead of crashing your program right when an exception occurs, you can write the 'traceback' information to a log file and keep your program running. You can look at the log file later, when you’re ready to debug your program. Below is an example:
import traceback, os
os.chdir("C:\\Users\\GAO\\Anaconda\\Gao_Jupyter_Notebook_Python_Codes\\Automate the Boring Stuff with Python\\Datasets and Files")
print('Log directory: ' + os.getcwd())
try:
raise Exception('This is the error message.')
except:
errorFile = open('errorInfo.txt', 'w')
errorFile.write(traceback.format_exc())
errorFile.close()
print('The traceback info was written to errorInfo.txt.')
# We now move onto the next topic called 'assertions'. An assertion is a sanity check to make sure your code isn’t doing something obviously wrong. These sanity checks are performed by the 'assert' statements. If the sanity check fails, then an 'AssertionError' exception is raised. In code, an 'assert' statement consists of the following: 1) the 'assert' keyword; 2) a condition (that is, an expression that evaluates to True or False); 3) a comma, and 4) a string to display when the condition is False. In plain English, an 'assert' statement says, "I assert that this condition holds true, and if not, there is a bug somewhere in the program." Unlike exceptions, your code should not handle 'assert' statements with 'try...except...'; if an 'assert' fails, your program should crash. By failing fast like this, you shorten the time between the original cause of the bug and when you first notice the bug. This will reduce the amount of code you will have to check before finding the code that’s causing the bug. Assertions are for programmer errors, not user errors. For errors that can be recovered from (such as a file not being found or the user entering invalid data), raise an exception instead of detecting it with an 'assert' statement.
#
# Suppose as an example below, we type in the four lines of code. We should expect an 'AssertionError':
from IPython.display import Image
Image("C:\\Users\\GAO\\Anaconda\\Scripts\\Gao_Jupyter_Notebook_Python_Codes\\Datasets and Files\\ch10_snapshot_1.jpg")
# Here we’ve set 'podBayDoorStatus' to 'open', so from now on, we fully expect the value of this variable to be 'open'. In a program that uses this variable, we might have written a lot of code under the assumption that the value is 'open' — code that depends on its being 'open' in order to work as we expect. So we add an assertion to make sure we’re right to assume 'podBayDoorStatus' is 'open'. Here, we include the message "The pod bay doors need to be 'open'." so it’ll be easy to see what’s wrong if the assertion fails. Later, say we make the obvious mistake of assigning 'podBayDoorStatus' another value, but don’t notice it among many lines of code. The assertion catches this mistake and clearly tells us what’s wrong. The idea here is that with the help of the assertion statement, programmers get a reminder that certain variables need to be coded in certain ways so that they don't easily make mistakes. The assertion statement is a very common debugging tool. Once debugging is complete, the assertion statement can be taken away from the production code.
# We now study 'logging' in Python. To motivate logging, if you’ve ever put a print() statement in your code to output some variable’s value while your program is running, you’ve used a form of logging to debug your code. Logging is a
# great way to understand what’s happening in your program and in what order its happening. Python’s logging module makes it easy to create a record of custom messages that you write. These log messages will describe when the program execution has reached the logging function call and list any variables you have specified at that point in time. On
# the other hand, a missing log message indicates a part of the code was skipped and never executed.
#
# To enable the 'logging' module to display log messages on your screen as your program runs, you can run the following command:
import logging
logging.basicConfig(level=logging.DEBUG, format=' %(asctime)s - %(levelname)s - %(message)s')
# You don’t need to worry too much about how this works, but basically, when Python logs an event, it creates a 'LogRecord' object that holds information about that event. The logging module’s basicConfig() function lets you specify what details about the 'LogRecord' object you want to see and how you want those details displayed.
#
# Now let's look at an example:
from IPython.display import Image
Image("C:\\Users\\GAO\\Anaconda\\Scripts\\Gao_Jupyter_Notebook_Python_Codes\\Datasets and Files\\ch10_snapshot_2.jpg")
# Here, for the aforementioned example, we use the logging.debug() function when we want to print log information. This
# debug() function will call basicConfig(), and a line of information will be printed. This information will be in the format we specified in basicConfig() and will include the messages we passed to debug(). The print(factorial(5)) call is part of the original program, so the result is displayed even if logging messages are disabled.
#
# The output of this program may look like this:
Image("C:\\Users\\GAO\\Anaconda\\Scripts\\Gao_Jupyter_Notebook_Python_Codes\\Datasets and Files\\ch10_snapshot_3.jpg")
# The factorial() function is returning 0 as the factorial of 5, which isn’t right. The 'for' loop should be multiplying the value in 'total' by the numbers from 1 to 5. But the log messages displayed by logging.debug() show that the 'i' variable is starting at 0 instead of 1. Since zero times anything is zero, the rest of the iterations also have the wrong value for 'total'. Logging messages provide a trail of breadcrumbs that can help you figure out when things started to go wrong.
#
# If you change the 'for i in range(n + 1):' line to 'for i in range(1, n + 1):', and run the program again, you will see that the output will look like the following. Below, the factorial(5) call correctly returns 120. The log messages showed what was going on inside the loop, which led straight to the bug:
Image("C:\\Users\\GAO\\Anaconda\\Scripts\\Gao_Jupyter_Notebook_Python_Codes\\Datasets and Files\\ch10_snapshot_4.jpg")
# A side note is worth mentioning here: In general, typing commands such as "import logging" and "logging.basicConfig(level=logging.DEBUG, format= '%(asctime)s - %(levelname)s - %(message)s')" is somewhat unwieldy. You may tempted to use print() calls instead, but don’t give in to this temptation! Once you’re done debugging, you’ll end up spending a lot of time removing print() calls from your code for each log message. You may even accidentally remove some print() calls that were being used for non-log messages. The nice thing about log messages is that you’re free to fill your program with as many as you like, and you can always disable them later by adding a single line of code such as logging.disable(logging.CRITICAL) call. Unlike print(), the 'logging' module makes it easy to switch between showing and hiding log messages.
# Logging levels provide a way to categorize your log messages by importance. There are five logging levels, described in the table below from least to most important. Messages can be logged at each level using a different logging function:
Image("C:\\Users\\GAO\\Anaconda\\Scripts\\Gao_Jupyter_Notebook_Python_Codes\\Datasets and Files\\ch10_snapshot_5.jpg")
# The benefit of logging levels is that you can change what priority of logging message you want to see. Passing logging.DEBUG to the basicConfig() function’s level keyword argument will show messages from all the logging levels (DEBUG being the lowest level). But after developing your program some more, you may be interested only in errors. In that case, you can set basicConfig()’s level argument to logging.ERROR. This will show only ERROR and CRITICAL messages and skip the DEBUG, INFO, and WARNING messages.
# After you’ve debugged your program, you probably don’t want all these log messages cluttering the screen. The logging.disable() function disables these so that you don’t have to go into your program and remove all the logging calls by hand. You simply pass logging.disable() a logging level, and it will suppress all log messages at that level or lower. So if you want to disable logging entirely, just add logging.disable(logging.CRITICAL) to your program.
#
# Instead of displaying the log messages to the screen, you can write them to a text file. The logging.basicConfig() function takes a filename keyword argument. While logging messages are helpful, they can clutter your screen and make it hard to read the program’s output. Writing the logging messages to a file will keep your screen clear and store the messages so you can read them after running the program. You can open this text file in any text editor, such as Notepad or TextEdit. This is very similar to the proc printto in SAS.
| 116.259259 | 1,248 |
8f14ac09a097bac974c2f4009fd66a622a9fd535
|
py
|
python
|
notebooks/drug-efficacy/main.ipynb
|
shrikant9793/notebooks
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Interactive hypothesis testing
#
# If you need to test a hypothesis interactively along multiple dimensions or their combinations, check out the example below that demonstrates how this can be achieved with [atoti](https://docs.atoti.io).
#
# atoti provides a python interface to define custom aggregation functions - we will look at an example on implementing a [paired t-test](https://en.wikipedia.org/wiki/Student's_t-test#Paired_samples) as an aggregation function. Plus, it provides an interface to create dashboards that can be shared with team members.
#
# <img src="./app-preview.gif" alt="Interactive app preview" width="70%" style="display:block;margin-left: auto;margin-right: auto;">
# In this notebook we will be studying the impact of certain anti-anxiety medicine as well as a person’s mood on **memory recall ability** - based on a dataset from a kaggle user submission - [Islanders data](https://www.kaggle.com/steveahn/memory-test-on-drugged-islanders-data):
#
# - Dataset contains observations on treatment with Alprazolam and Triazolam, as well as Sugar (in the control group) - see column **Drug** below,
# - Trials has been collected for different dosages - see column **Dosage**
# - Participants were primed with happy and sad memories ten minutes before the memory test - see column **Happy_Sad_group** as it is believed that a person's mood may impact memory recall.
# - Memory scores represent response time, i.e. how long it takes to finish the memory test. Higher Memory scores means the ability actually reduces
#
# 
#
# We will implement measures that evaluate the effect of drugs onto memory recall and visualize the result returning "H0 rejected" if data provides evidence that the average response time increases after the treatment.
# # Imports
# !pip install scipy
import pandas as pd
from scipy.stats import norm, t
import atoti as tt
# ## Raw data
# Example data is taken from kaggle user submission:
# https://www.kaggle.com/steveahn/memory-test-on-drugged-islanders-data
# The example was slightly pre-processed for convenience.
df = pd.read_csv("https://data.atoti.io/notebooks/drug-efficacy/Islander_data.csv")
df.sample(5)
# ## Launching atoti app
# +
# creating a session - it spins up an in-memory database - similar to Apache Spark - ready to slice’n’dice your big data set.
# In addition to that, it launches a dashboarding Tableau-like web-app
from atoti.config import create_config
config = create_config(metadata_db="./metadata.db")
session = tt.create_session(config=config)
# loading initial dataset
observations_datastore = session.read_pandas(
df, keys=["Patient_Id", "Before or After"], store_name="Observations"
)
# creating a cube -
cube = session.create_cube(observations_datastore)
# -
# ## URL of atoti app
#
# The following cell displays URL of the atoti app:
session.url
# # Inline data visualization
#
# By running the next cell, we embed a data visualization widget - to slice and dice data inside the notebook.
# + atoti={"height": 249, "state": {"name": "", "type": "container", "value": {"body": {"configuration": {"tabular": {"addButtonFilter": "numeric", "cellRenderers": ["tree-layout"], "columns": [{"key": "([Measures].[MemoryScores.MEAN],[Hierarchies].[Before or After].[ALL].[AllMember].[After])", "width": 138}], "columnsGroups": [{"captionProducer": "firstColumn", "cellFactory": "kpi-status", "selector": "kpi-status"}, {"captionProducer": "firstColumn", "cellFactory": "lookup", "selector": "lookup"}, {"captionProducer": "expiry", "cellFactory": "expiry", "selector": "kpi-expiry"}, {"captionProducer": "columnMerge", "cellFactory": {"args": {}, "key": "treeCells"}, "selector": "member"}], "defaultOptions": {"headerHeight": 44}, "expansion": {"automaticExpansion": true}, "hideAddButton": true, "pinnedHeaderSelector": "member", "sortingMode": "non-breaking", "statisticsShown": true}}, "contextValues": {}, "mdx": "SELECT NON EMPTY Hierarchize(DrilldownLevel([Hierarchies].[Drug].[ALL].[AllMember])) ON ROWS, NON EMPTY Crossjoin([Measures].[MemoryScores.MEAN], Hierarchize(DrilldownLevel([Hierarchies].[Before or After].[ALL].[AllMember]))) ON COLUMNS FROM [Observations] CELL PROPERTIES VALUE, FORMATTED_VALUE, BACK_COLOR, FORE_COLOR, FONT_FLAGS", "ranges": {"column": {"chunkSize": 50, "thresholdPercentage": 0.2}, "row": {"chunkSize": 2000, "thresholdPercentage": 0.1}}, "serverUrl": "", "updateMode": "once"}, "containerKey": "pivot-table", "showTitleBar": false, "style": {}}}}
cube.visualize()
# -
# # Refining the application
# +
# Quick access to manage hierarchies, levels and measures
h = cube.hierarchies
l = cube.levels
m = cube.measures
# Explore the hierarchies and measures created in the cube
cube
# +
# Sorting the hierarchy, so that the Before measurements show first:
l["Before or After"].comparator = tt.comparator.DESC
# This cell is hiding undesired metrics created by default.
# To create a cube without any default metrics, create_cube need to be used with parameter mode = `no_measures`
m["MemoryScores.SUM"].visible = False
# -
# # Adding attributes
#
# We are going to group the observations by age. To achieve that, let's create and upload a **age to group mapping** into a separate data store:
# +
age_groups_store = session.read_pandas(
pd.DataFrame(
data=[("0-25Y", i) for i in range(25)]
+ [("25Y - 40Y", i) for i in range(25, 40)]
+ [("40Y - 55Y", i) for i in range(40, 55)]
+ [("55Y+", i) for i in range(55, 100)],
columns=["age group", "age"],
),
keys=["age"],
store_name="Age Groups",
)
observations_datastore.join(age_groups_store)
# -
cube.schema
# We will start using this grouping in the following cell.
# + atoti={"height": 225, "state": {"name": "", "type": "container", "value": {"body": {"configuration": {"tabular": {"addButtonFilter": "numeric", "cellRenderers": ["tree-layout"], "columns": [{"key": "[Measures].[Mem_Score_After.SUM]", "width": 210}, {"key": "[Measures].[Mem_Score_Before.MEAN]", "width": 222}, {"key": "[Measures].[MemoryScores.MEAN]", "width": 190}], "columnsGroups": [{"captionProducer": "firstColumn", "cellFactory": "kpi-status", "selector": "kpi-status"}, {"captionProducer": "firstColumn", "cellFactory": "lookup", "selector": "lookup"}, {"captionProducer": "expiry", "cellFactory": "expiry", "selector": "kpi-expiry"}, {"captionProducer": "columnMerge", "cellFactory": {"args": {}, "key": "treeCells"}, "selector": "member"}], "defaultOptions": {}, "expansion": {"automaticExpansion": true}, "hideAddButton": true, "pinnedHeaderSelector": "member", "sortingMode": "non-breaking", "statisticsShown": true}}, "contextValues": {}, "mdx": "SELECT NON EMPTY Hierarchize(DrilldownLevel([Hierarchies].[age group].[ALL].[AllMember])) ON ROWS, NON EMPTY [Measures].[MemoryScores.MEAN] ON COLUMNS FROM [Observations] CELL PROPERTIES VALUE, FORMATTED_VALUE, BACK_COLOR, FORE_COLOR, FONT_FLAGS", "ranges": {"column": {"chunkSize": 50, "thresholdPercentage": 0.2}, "row": {"chunkSize": 2000, "thresholdPercentage": 0.1}}, "serverUrl": "", "updateMode": "once"}, "containerKey": "pivot-table", "showTitleBar": false, "style": {}}}}
cube.visualize()
# -
# From the following visualization we can tell, that on average:
#
# - for the Drug **"Triazolam"** memory scores **did not materially increase** in all age groups,
# - for the Drug **"Alprazolam"** memory response times **increased in all the age groups**, with a bigger impact in group 25Y-50Y,
# - for the Drug **"Sugar"** the scores **fluctuated**, but nothing that seems significant.
# + atoti={"state": {"name": "Average memory score by drug", "type": "container", "value": {"body": {"configuration": {"mapping": {"horizontalSubplots": ["[Hierarchies].[Drug].[Drug]"], "splitBy": ["[Hierarchies].[Before or After].[Before or After]"], "values": ["[Measures].[MemoryScores.MEAN]"], "verticalSubplots": [], "xAxis": ["[Hierarchies].[age group].[age group]"]}, "subplotModeEnabled": true, "type": "plotly-clustered-column-chart"}, "query": {"mdx": "SELECT NON EMPTY Crossjoin([Hierarchies].[age group].[age group].Members, [Hierarchies].[Before or After].[Before or After].Members, [Hierarchies].[Drug].[Drug].Members) ON ROWS, NON EMPTY [Measures].[MemoryScores.MEAN] ON COLUMNS FROM [Observations] CELL PROPERTIES VALUE, FORMATTED_VALUE, BACK_COLOR, FORE_COLOR, FONT_FLAGS", "serverUrl": "", "updateMode": "once"}}, "containerKey": "chart", "showTitleBar": false, "style": {}}}}
cube.visualize("Average memory score by drug")
# -
# # Slice-and-dice basic statistics
m["Mean"] = tt.agg.mean(observations_datastore["MemoryScores"])
m["Std"] = tt.agg.std(observations_datastore["MemoryScores"])
m["Min"] = tt.agg.min(observations_datastore["MemoryScores"])
m["Max"] = tt.agg.max(observations_datastore["MemoryScores"])
m["25%"] = tt.agg.quantile(observations_datastore["MemoryScores"], 0.25)
m["50%"] = tt.agg.quantile(observations_datastore["MemoryScores"], 0.50)
m["75%"] = tt.agg.quantile(observations_datastore["MemoryScores"], 0.75)
# We can now slice-and-dice those statistics using any attribute available in the data.
#
# This is an example, where the Happy or Sad field has been put onto the columns. Every time we bring an additional attribute into the view, the statistics - such averages, standard deviation and quantiles - are recomputed from the raw data.
# + atoti={"height": 326, "state": {"name": "Basic statistics slice-and-dice", "type": "container", "value": {"body": {"configuration": {"tabular": {"addButtonFilter": "numeric", "cellRenderers": ["tree-layout"], "columns": [{"key": "c-treeCells-member", "width": 130}], "columnsGroups": [{"captionProducer": "firstColumn", "cellFactory": "kpi-status", "selector": "kpi-status"}, {"captionProducer": "firstColumn", "cellFactory": "lookup", "selector": "lookup"}, {"captionProducer": "expiry", "cellFactory": "expiry", "selector": "kpi-expiry"}, {"captionProducer": "columnMerge", "cellFactory": {"args": {}, "key": "treeCells"}, "selector": "member"}], "defaultOptions": {}, "expansion": {"automaticExpansion": true}, "hideAddButton": true, "pinnedHeaderSelector": "member", "sortingMode": "non-breaking", "statisticsShown": true}}, "contextValues": {}, "mdx": "SELECT NON EMPTY Hierarchize({[Measures].[contributors.COUNT], [Measures].[Std], [Measures].[Min], [Measures].[25%], [Measures].[50%], [Measures].[75%], [Measures].[Max], [Measures].[Mean]}) ON ROWS, NON EMPTY Hierarchize(DrilldownLevel([Hierarchies].[Happy_Sad_group].[ALL].[AllMember])) ON COLUMNS FROM [Observations] CELL PROPERTIES VALUE, FORMATTED_VALUE, BACK_COLOR, FORE_COLOR, FONT_FLAGS", "ranges": {"column": {"chunkSize": 50, "thresholdPercentage": 0.2}, "row": {"chunkSize": 2000, "thresholdPercentage": 0.1}}, "serverUrl": "", "updateMode": "once"}, "containerKey": "pivot-table", "showTitleBar": false, "style": {}}}}
cube.visualize("Basic statistics slice-and-dice")
# -
# Let's also set up measures to interactively evaluate left and right boundaries of the 95% [confidence interval](https://en.wikipedia.org/wiki/Confidence_interval).
#
# In this case we are creating a measure on top of the existing measures - "Mean" and "Std" - that we have just defined above.
# +
alpha = 0.05
m["95% point"] = norm.ppf(1 - alpha / 2.0)
m["Z confidence left"] = m["Mean"] - m["95% point"] * m["Std"]
m["Z confidence right"] = m["Mean"] + m["95% point"] * m["Std"]
# -
# We have just created the metrics to visualize confidence intervals interactively. The "After" intervals are wider and include the "Before" intervals, so it's difficult to say if the treatment has increased the memory scores. Let's run a statistical test to check that - in the next section.
# + atoti={"height": 254, "state": {"name": "Interactive confidence intervals", "type": "container", "value": {"body": {"configuration": {"tabular": {"addButtonFilter": "numeric", "cellRenderers": ["tree-layout"], "columns": [{"key": "c-treeCells-member", "width": 170}], "columnsGroups": [{"captionProducer": "firstColumn", "cellFactory": "kpi-status", "selector": "kpi-status"}, {"captionProducer": "firstColumn", "cellFactory": "lookup", "selector": "lookup"}, {"captionProducer": "expiry", "cellFactory": "expiry", "selector": "kpi-expiry"}, {"captionProducer": "columnMerge", "cellFactory": {"args": {}, "key": "treeCells"}, "selector": "member"}], "defaultOptions": {"headerHeight": 51}, "expansion": {"automaticExpansion": true}, "hideAddButton": true, "pinnedHeaderSelector": "member", "sortingMode": "non-breaking", "statisticsShown": true}}, "contextValues": {}, "mdx": "SELECT NON EMPTY Crossjoin(Hierarchize([Hierarchies].[Before or After].[Before or After].Members), {[Measures].[Z confidence left], [Measures].[Z confidence right], [Measures].[Mean], [Measures].[50%]}) ON COLUMNS, NON EMPTY Hierarchize(DrilldownLevel([Hierarchies].[Happy_Sad_group].[ALL].[AllMember])) ON ROWS FROM [Observations] CELL PROPERTIES VALUE, FORMATTED_VALUE, BACK_COLOR, FORE_COLOR, FONT_FLAGS", "ranges": {"column": {"chunkSize": 50, "thresholdPercentage": 0.2}, "row": {"chunkSize": 2000, "thresholdPercentage": 0.1}}, "serverUrl": "", "updateMode": "once"}, "containerKey": "pivot-table", "showTitleBar": false, "style": {}}}}
cube.visualize("Interactive confidence intervals")
# -
# # Paired t-test
#
# Let's see how a paired t-test can be applied in atoti.
#
# As a refresher, a paired t-test is one of the [statistical hypothesis tests](https://en.wikipedia.org/wiki/Statistical_hypothesis_testing) that can help testing a medication effect, given the before and after measurements. We will check that the data provides evidence that will allow us to reject the [null hypothesis](https://en.wikipedia.org/wiki/Null_hypothesis):
#
# - H0: on average, there's no difference in the memory scores before and after treatment,
# - H1: on average, the memory score after the treatment is bigger (response time longer) than before,
#
# Or:
#
# - H0: mean difference of memory scores is equal to 0, mu = 0
# - H1: mean difference of memory scores between after and before measurements is above 0, mu>0.
#
# Firstly, we need to compute t-statistic for the differences between memory scores after and before treatment, the statistic is defined as per the formula:
#
# $$t_{statistic} = \frac{\bar{x}}{s/\sqrt{n}}$$
#
# where
# - $\bar{x}$: the mean value of the memory score differences
# - $n$: the number of observations
# - $s$: standard deviation of the memory score differences
#
# We'd need to provide mean differences, stdev of differences and the number of differences (patients) participated in the test.
#
# Let's create a measure for the difference. Let's use atoti `.filter` function to create average memory scores for the "Before" and "After" measurements, and then taking their difference.
# +
m["MemoryScoresAfter.Mean"] = tt.filter(
m["MemoryScores.MEAN"], l["Before or After"] == "After"
)
m["MemoryScoresBefore.Mean"] = tt.filter(
m["MemoryScores.MEAN"], l["Before or After"] == "Before"
)
m["Diff.Mean"] = m["MemoryScoresAfter.Mean"] - m["MemoryScoresBefore.Mean"]
m["Diff.Mean"].formatter = "DOUBLE[#,##0.00]"
# + atoti={"height": 191, "state": {"name": "", "type": "container", "value": {"body": {"configuration": {"tabular": {"addButtonFilter": "numeric", "cellRenderers": ["tree-layout"], "columns": [{"key": "[Measures].[MemoryScoresAfter.Mean]", "width": 175}], "columnsGroups": [{"captionProducer": "firstColumn", "cellFactory": "kpi-status", "selector": "kpi-status"}, {"captionProducer": "firstColumn", "cellFactory": "lookup", "selector": "lookup"}, {"captionProducer": "expiry", "cellFactory": "expiry", "selector": "kpi-expiry"}, {"captionProducer": "columnMerge", "cellFactory": {"args": {}, "key": "treeCells"}, "selector": "member"}], "defaultOptions": {}, "expansion": {"automaticExpansion": true}, "hideAddButton": true, "pinnedHeaderSelector": "member", "sortingMode": "non-breaking", "statisticsShown": true}}, "contextValues": {}, "mdx": "SELECT NON EMPTY {[Measures].[Diff.Mean], [Measures].[MemoryScoresBefore.Mean], [Measures].[MemoryScoresAfter.Mean]} ON COLUMNS, NON EMPTY Hierarchize(DrilldownLevel([Hierarchies].[Drug].[ALL].[AllMember])) ON ROWS FROM [Observations] CELL PROPERTIES VALUE, FORMATTED_VALUE, BACK_COLOR, FORE_COLOR, FONT_FLAGS", "ranges": {"column": {"chunkSize": 50, "thresholdPercentage": 0.2}, "row": {"chunkSize": 2000, "thresholdPercentage": 0.1}}, "serverUrl": "", "updateMode": "once"}, "containerKey": "pivot-table", "showTitleBar": false, "style": {}}}}
cube.visualize()
# +
# Computing standard deviation of differences:
m["Diff.Std"] = tt.agg.std(m["Diff.Mean"], scope=tt.scope.origin(l["Patient_Id"]))
# Number of patients observed - each patient has 2 records, one for before and another for after
m["Number of observations"] = tt.agg.count_distinct(
observations_datastore["Patient_Id"]
)
# Computing the t-statistic per formula above:
m["t-statistic"] = m["Diff.Mean"] / (
m["Diff.Std"] / tt.sqrt(m["Number of observations"])
)
m["t-statistic"].formatter = "DOUBLE[0.00]"
# -
# We will be comparing the `t-statistic` to the right tail _critical value_, and if it's above the critical value, we will conclude that the data provides the evidence to reject the null hypothesis. Let's load 95% critical values for different [degrees of freedom](https://en.wikipedia.org/wiki/Degrees_of_freedom_(statistics)) into the cube.
#
# 
#
# Now, depending on the number of observations for each cell, we will pick a critical value and visualize it as a measure:
# +
# Loading a "table" of critical values, 101 values in total.
# For experiments with more than 101 degrees of freedom, we approximate the critical value, for 95% confidence - with value 1.960.
m["t-critical values list"] = [t.ppf(0.95, d) for d in range(1, 101)] + [1.96]
# Computing degrees of freedom as the number of observations minus 1:
degrees_of_freedom = m["Number of observations"] - 1
# Shifting the df by -1 to use as an index and look up critical value from the list:
df_as_index = degrees_of_freedom - 1
# If there're too many observations (more than 101), we'll cap it:
capped_df_as_index = tt.where(df_as_index > 100, 100, df_as_index)
# This measure will be looking up a critical value for the current scope:
m["t-critical"] = m["t-critical values list"][capped_df_as_index]
# -
# This measure is displaying whether the observed t-statistics is to the right from the critical value, i.e. there's evidence that H0 can be rejected. It will visualize the result of t-test every time we expand and collapse data:
m["Test Result"] = tt.where(
m["t-statistic"] > m["t-critical"], "H0 rejected", "Can't reject H0"
)
# In the next session we'll see how to use the measure created above to visualize the test result.
# # Interactive hypothesis testing
# Now we can experiment and re-group our data and apply the test interactively:
#
# - **"H0 rejected"** will mean that the data provides evidence that mean difference is not 0, meaning, there's a statistically significant impact of treatment onto the memory scores.
# - **"Can't reject H0"** will mean that t-statistic is smaller than the critical value, and we can't reject the null hypothesis.
#
# We expand by the name of the drug, then by dosages, then by patient "Happy/Sad" group, and this is what we found out:
#
# - there's an evidence that **Drug Aprazolam** had impact on the memory scores (response time), while Sugar and Triazolam did not,
# - when we break down the Drug Aprazolam observations **by dosage** - we notice that only the dosages 1 and 2 are statistically significant,
# - if we further expand to "Happy/Sad" group, and for the "Happy" patients only the higher dosage impacted the memory score.
# + atoti={"state": {"name": "", "type": "container", "value": {"body": {"configuration": {"tabular": {"addButtonFilter": "numeric", "cellRenderers": ["tree-layout"], "columns": [{"key": "c-treeCells-member", "width": 153}], "columnsGroups": [{"captionProducer": "firstColumn", "cellFactory": "kpi-status", "selector": "kpi-status"}, {"captionProducer": "firstColumn", "cellFactory": "lookup", "selector": "lookup"}, {"captionProducer": "expiry", "cellFactory": "expiry", "selector": "kpi-expiry"}, {"captionProducer": "columnMerge", "cellFactory": {"args": {}, "key": "treeCells"}, "selector": "member"}], "defaultOptions": {"headerHeight": 58}, "expansion": {"automaticExpansion": true}, "hideAddButton": true, "pinnedHeaderSelector": "member", "sortingMode": "non-breaking", "statisticsShown": true}}, "contextValues": {}, "mdx": "WITH Member [Measures].[Test Result (1)] AS [Measures].[Test Result], BACK_COLOR = CASE WHEN [Measures].[Test Result (1)] = \"H0 rejected\" THEN rgb(217, 234, 211) END, CAPTION = [Measures].[Test Result].MEMBER_CAPTION SELECT NON EMPTY {[Measures].[Test Result (1)], [Measures].[t-statistic], [Measures].[t-critical], [Measures].[Number of observations], [Measures].[Diff.Mean], [Measures].[MemoryScoresAfter.Mean], [Measures].[MemoryScoresBefore.Mean]} ON COLUMNS, NON EMPTY Hierarchize(Crossjoin(Union(DrilldownLevel([Hierarchies].[Drug].[ALL].[AllMember]), [Hierarchies].[Drug].[ALL].[AllMember].[A], [Hierarchies].[Drug].[ALL].[AllMember].[S], [Hierarchies].[Drug].[ALL].[AllMember].[Aprazolam]), [Hierarchies].[Happy_Sad_group].[Happy_Sad_group].Members)) ON ROWS FROM [Observations] CELL PROPERTIES BACK_COLOR, FONT_FLAGS, FORE_COLOR, FORMATTED_VALUE, VALUE", "ranges": {"column": {"chunkSize": 50, "thresholdPercentage": 0.2}, "row": {"chunkSize": 2000, "thresholdPercentage": 0.1}}, "serverUrl": ""}, "containerKey": "pivot-table", "showTitleBar": false, "style": {}}}}
cube.visualize()
# -
# # Quick simulation
#
# Let's make a quick comparison of the test results under the 95%, 97.5%, 99% confidence levels by loading new critical values into simulations. As a reminder, we've been using the 95% critical values so far.
# creating a new simulation to override critical values, and giving a name to the initial values
confidence_levels = cube.setup_simulation(
"Confidence Levels", replace=[m["t-critical values list"]], base_scenario="95%"
).scenarios
# creating new critical values based on 0.975 and 0.99 confidence levels
confidence_levels["97.5%"] = [t.ppf(0.975, d) for d in range(1, 101)] + [1.960]
confidence_levels["99%"] = [t.ppf(0.99, d) for d in range(1, 101)] + [2.326]
# Let's expand Test results for Sugar and we'll see that the hypothesis is rejected for dosage 1 under the 95% and 97.5% confidence levels - implying that memory reponse time increases for patients taking low dosage of sugar (placebo). Most probably we are making Type I error - false positive result. Increasing the confidence level helps to reduce the probability of Type I error, in our case, H0 is not rejected for Sugar with 99% confidence level.
# + atoti={"state": {"name": "", "type": "container", "value": {"body": {"configuration": {"tabular": {"addButtonFilter": "numeric", "cellRenderers": ["tree-layout"], "columns": [{"key": "c-treeCells-member", "width": 132}], "columnsGroups": [{"captionProducer": "firstColumn", "cellFactory": "kpi-status", "selector": "kpi-status"}, {"captionProducer": "firstColumn", "cellFactory": "lookup", "selector": "lookup"}, {"captionProducer": "expiry", "cellFactory": "expiry", "selector": "kpi-expiry"}, {"captionProducer": "columnMerge", "cellFactory": {"args": {}, "key": "treeCells"}, "selector": "member"}], "defaultOptions": {}, "expansion": {"automaticExpansion": true}, "hideAddButton": true, "pinnedHeaderSelector": "member", "sortingMode": "non-breaking", "statisticsShown": true}}, "contextValues": {}, "mdx": "WITH Member [Measures].[Test Result (1)] AS [Measures].[Test Result], BACK_COLOR = CASE WHEN [Measures].[Test Result (1)] = \"H0 rejected\" THEN rgb(217, 234, 211) END, CAPTION = [Measures].[Test Result].MEMBER_CAPTION SELECT NON EMPTY Crossjoin({[Measures].[Test Result (1)], [Measures].[t-critical]}, Hierarchize([Measure Simulations].[Confidence Levels].[Confidence Levels].Members)) ON COLUMNS, NON EMPTY Except(Crossjoin(Hierarchize(Union(DrilldownLevel([Hierarchies].[Drug].[ALL].[AllMember]), [Hierarchies].[Drug].[ALL].[AllMember].[Drug A], [Hierarchies].[Drug].[ALL].[AllMember].[Drug S], [Hierarchies].[Drug].[ALL].[AllMember].[Drug T])), Hierarchize(DrilldownLevel([Hierarchies].[Dosage].[ALL].[AllMember]))), Union(Crossjoin([Hierarchies].[Drug].[ALL].[AllMember].[Drug A], [Hierarchies].[Dosage].[Dosage].Members), Crossjoin([Hierarchies].[Drug].[ALL].[AllMember].[Drug T], [Hierarchies].[Dosage].[Dosage].Members))) ON ROWS FROM [Observations] CELL PROPERTIES BACK_COLOR, FONT_FLAGS, FORE_COLOR, FORMATTED_VALUE, VALUE", "ranges": {"column": {"chunkSize": 50, "thresholdPercentage": 0.2}, "row": {"chunkSize": 2000, "thresholdPercentage": 0.1}}, "serverUrl": "", "updateMode": "once"}, "containerKey": "pivot-table", "showTitleBar": false, "style": {}}}}
cube.visualize()
# -
# # Alternative data sets
# Let's imagine that we obtained memory scores data using an alternative methodology, and want to compare the test results side-by-side with the original approach.
observations_datastore.scenarios["Multicenter study data"].load_csv(
"s3://data.atoti.io/notebooks/drug-efficacy/Multi_center_study_data.csv"
)
# + atoti={"state": {"name": "", "type": "container", "value": {"body": {"configuration": {"tabular": {"addButtonFilter": "numeric", "cellRenderers": ["tree-layout"], "columnOrder": {"args": {"orderedColumns": ["c-treeCells-member", "([Measures].[Test Result (1)],[Epoch].[Epoch].[Branch].[Multicenter study data2])", "([Measures].[Test Result (1)],[Epoch].[Epoch].[Branch].[Base])", "([Measures].[Test Result (1)],[Epoch].[Epoch].[Branch].[Multicenter study data])", "([Measures].[contributors.COUNT],[Epoch].[Epoch].[Branch].[Base])", "([Measures].[contributors.COUNT],[Epoch].[Epoch].[Branch].[Multicenter study data])", "([Measures].[contributors.COUNT],[Epoch].[Epoch].[Branch].[Multicenter study data2])", "([Measures].[t-statistic],[Epoch].[Epoch].[Branch].[Base])", "([Measures].[t-statistic],[Epoch].[Epoch].[Branch].[Multicenter study data])", "([Measures].[t-statistic],[Epoch].[Epoch].[Branch].[Multicenter study data2])", "([Measures].[t-critical],[Epoch].[Epoch].[Branch].[Base])", "([Measures].[t-critical],[Epoch].[Epoch].[Branch].[Multicenter study data])", "([Measures].[t-critical],[Epoch].[Epoch].[Branch].[Multicenter study data2])"]}, "key": "explicit"}, "columnsGroups": [{"captionProducer": "firstColumn", "cellFactory": "kpi-status", "selector": "kpi-status"}, {"captionProducer": "firstColumn", "cellFactory": "lookup", "selector": "lookup"}, {"captionProducer": "expiry", "cellFactory": "expiry", "selector": "kpi-expiry"}, {"captionProducer": "columnMerge", "cellFactory": {"args": {}, "key": "treeCells"}, "selector": "member"}], "defaultOptions": {"headerHeight": 64}, "expansion": {"automaticExpansion": true}, "hideAddButton": true, "pinnedHeaderSelector": "member", "sortingMode": "non-breaking", "statisticsShown": true}}, "contextValues": {}, "mdx": "WITH Member [Measures].[Test Result (1)] AS [Measures].[Test Result], BACK_COLOR = CASE WHEN [Measures].[Test Result (1)] = \"H0 rejected\" THEN rgb(217, 234, 211) END, CAPTION = [Measures].[Test Result].MEMBER_CAPTION SELECT NON EMPTY Crossjoin({[Measures].[Test Result (1)], [Measures].[contributors.COUNT], [Measures].[t-statistic]}, Hierarchize([Epoch].[Epoch].[Branch].Members)) ON COLUMNS, NON EMPTY Hierarchize(DrilldownLevel([Hierarchies].[Drug].[ALL].[AllMember])) ON ROWS FROM [Observations] CELL PROPERTIES BACK_COLOR, FONT_FLAGS, FORE_COLOR, FORMATTED_VALUE, VALUE", "ranges": {"column": {"chunkSize": 50, "thresholdPercentage": 0.2}, "row": {"chunkSize": 2000, "thresholdPercentage": 0.1}}, "serverUrl": "", "updateMode": "once"}, "containerKey": "pivot-table", "showTitleBar": false, "style": {}}}}
cube.visualize()
# -
# # Conclusion
#
# In this notebook we have configured an analytical application for **exploratory data analysis**, that allows us to **interactively browse** the data and re-compute statistics, such as mean, stdev, etc, as well as more complex functions - such as hypothesis test metrics - **on-the-fly**. Even though the example has a handful of observation, atoti's backend is designed to handle big data. Please refer to this white page is you want to learn about the [technology](https://activeviam.com/images/pdf/white-papers/ActiveViam_Technical_White_Paper_-_ActivePivot.pdf) on atoti's backend.
#
# The application comes with a **user interface**, so the results of the analysis can be visualized in a dashboard and presented to users:
#
session.url + "/#/dashboard/3f7"
| 88.62037 | 2,600 |
57a64df41aaa9ca5408c90fee3ff804cdf7bef30
|
py
|
python
|
MNIST.ipynb
|
Fifth-marauder/Kaggle
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Fifth-marauder/Kaggle/blob/main/MNIST.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="CC9SHo8-BnJq"
# First of all, you run the following code and upload your kaggle.json.
# + id="Ctfdr_26-CAz" colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "Ly8gQ29weXJpZ2h0IDIwMTcgR29vZ2xlIExMQwovLwovLyBMaWNlbnNlZCB1bmRlciB0aGUgQXBhY2hlIExpY2Vuc2UsIFZlcnNpb24gMi4wICh0aGUgIkxpY2Vuc2UiKTsKLy8geW91IG1heSBub3QgdXNlIHRoaXMgZmlsZSBleGNlcHQgaW4gY29tcGxpYW5jZSB3aXRoIHRoZSBMaWNlbnNlLgovLyBZb3UgbWF5IG9idGFpbiBhIGNvcHkgb2YgdGhlIExpY2Vuc2UgYXQKLy8KLy8gICAgICBodHRwOi8vd3d3LmFwYWNoZS5vcmcvbGljZW5zZXMvTElDRU5TRS0yLjAKLy8KLy8gVW5sZXNzIHJlcXVpcmVkIGJ5IGFwcGxpY2FibGUgbGF3IG9yIGFncmVlZCB0byBpbiB3cml0aW5nLCBzb2Z0d2FyZQovLyBkaXN0cmlidXRlZCB1bmRlciB0aGUgTGljZW5zZSBpcyBkaXN0cmlidXRlZCBvbiBhbiAiQVMgSVMiIEJBU0lTLAovLyBXSVRIT1VUIFdBUlJBTlRJRVMgT1IgQ09ORElUSU9OUyBPRiBBTlkgS0lORCwgZWl0aGVyIGV4cHJlc3Mgb3IgaW1wbGllZC4KLy8gU2VlIHRoZSBMaWNlbnNlIGZvciB0aGUgc3BlY2lmaWMgbGFuZ3VhZ2UgZ292ZXJuaW5nIHBlcm1pc3Npb25zIGFuZAovLyBsaW1pdGF0aW9ucyB1bmRlciB0aGUgTGljZW5zZS4KCi8qKgogKiBAZmlsZW92ZXJ2aWV3IEhlbHBlcnMgZm9yIGdvb2dsZS5jb2xhYiBQeXRob24gbW9kdWxlLgogKi8KKGZ1bmN0aW9uKHNjb3BlKSB7CmZ1bmN0aW9uIHNwYW4odGV4dCwgc3R5bGVBdHRyaWJ1dGVzID0ge30pIHsKICBjb25zdCBlbGVtZW50ID0gZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgnc3BhbicpOwogIGVsZW1lbnQudGV4dENvbnRlbnQgPSB0ZXh0OwogIGZvciAoY29uc3Qga2V5IG9mIE9iamVjdC5rZXlzKHN0eWxlQXR0cmlidXRlcykpIHsKICAgIGVsZW1lbnQuc3R5bGVba2V5XSA9IHN0eWxlQXR0cmlidXRlc1trZXldOwogIH0KICByZXR1cm4gZWxlbWVudDsKfQoKLy8gTWF4IG51bWJlciBvZiBieXRlcyB3aGljaCB3aWxsIGJlIHVwbG9hZGVkIGF0IGEgdGltZS4KY29uc3QgTUFYX1BBWUxPQURfU0laRSA9IDEwMCAqIDEwMjQ7CgpmdW5jdGlvbiBfdXBsb2FkRmlsZXMoaW5wdXRJZCwgb3V0cHV0SWQpIHsKICBjb25zdCBzdGVwcyA9IHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCk7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICAvLyBDYWNoZSBzdGVwcyBvbiB0aGUgb3V0cHV0RWxlbWVudCB0byBtYWtlIGl0IGF2YWlsYWJsZSBmb3IgdGhlIG5leHQgY2FsbAogIC8vIHRvIHVwbG9hZEZpbGVzQ29udGludWUgZnJvbSBQeXRob24uCiAgb3V0cHV0RWxlbWVudC5zdGVwcyA9IHN0ZXBzOwoKICByZXR1cm4gX3VwbG9hZEZpbGVzQ29udGludWUob3V0cHV0SWQpOwp9CgovLyBUaGlzIGlzIHJvdWdobHkgYW4gYXN5bmMgZ2VuZXJhdG9yIChub3Qgc3VwcG9ydGVkIGluIHRoZSBicm93c2VyIHlldCksCi8vIHdoZXJlIHRoZXJlIGFyZSBtdWx0aXBsZSBhc3luY2hyb25vdXMgc3RlcHMgYW5kIHRoZSBQeXRob24gc2lkZSBpcyBnb2luZwovLyB0byBwb2xsIGZvciBjb21wbGV0aW9uIG9mIGVhY2ggc3RlcC4KLy8gVGhpcyB1c2VzIGEgUHJvbWlzZSB0byBibG9jayB0aGUgcHl0aG9uIHNpZGUgb24gY29tcGxldGlvbiBvZiBlYWNoIHN0ZXAsCi8vIHRoZW4gcGFzc2VzIHRoZSByZXN1bHQgb2YgdGhlIHByZXZpb3VzIHN0ZXAgYXMgdGhlIGlucHV0IHRvIHRoZSBuZXh0IHN0ZXAuCmZ1bmN0aW9uIF91cGxvYWRGaWxlc0NvbnRpbnVlKG91dHB1dElkKSB7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICBjb25zdCBzdGVwcyA9IG91dHB1dEVsZW1lbnQuc3RlcHM7CgogIGNvbnN0IG5leHQgPSBzdGVwcy5uZXh0KG91dHB1dEVsZW1lbnQubGFzdFByb21pc2VWYWx1ZSk7CiAgcmV0dXJuIFByb21pc2UucmVzb2x2ZShuZXh0LnZhbHVlLnByb21pc2UpLnRoZW4oKHZhbHVlKSA9PiB7CiAgICAvLyBDYWNoZSB0aGUgbGFzdCBwcm9taXNlIHZhbHVlIHRvIG1ha2UgaXQgYXZhaWxhYmxlIHRvIHRoZSBuZXh0CiAgICAvLyBzdGVwIG9mIHRoZSBnZW5lcmF0b3IuCiAgICBvdXRwdXRFbGVtZW50Lmxhc3RQcm9taXNlVmFsdWUgPSB2YWx1ZTsKICAgIHJldHVybiBuZXh0LnZhbHVlLnJlc3BvbnNlOwogIH0pOwp9CgovKioKICogR2VuZXJhdG9yIGZ1bmN0aW9uIHdoaWNoIGlzIGNhbGxlZCBiZXR3ZWVuIGVhY2ggYXN5bmMgc3RlcCBvZiB0aGUgdXBsb2FkCiAqIHByb2Nlc3MuCiAqIEBwYXJhbSB7c3RyaW5nfSBpbnB1dElkIEVsZW1lbnQgSUQgb2YgdGhlIGlucHV0IGZpbGUgcGlja2VyIGVsZW1lbnQuCiAqIEBwYXJhbSB7c3RyaW5nfSBvdXRwdXRJZCBFbGVtZW50IElEIG9mIHRoZSBvdXRwdXQgZGlzcGxheS4KICogQHJldHVybiB7IUl0ZXJhYmxlPCFPYmplY3Q+fSBJdGVyYWJsZSBvZiBuZXh0IHN0ZXBzLgogKi8KZnVuY3Rpb24qIHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCkgewogIGNvbnN0IGlucHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKGlucHV0SWQpOwogIGlucHV0RWxlbWVudC5kaXNhYmxlZCA9IGZhbHNlOwoKICBjb25zdCBvdXRwdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQob3V0cHV0SWQpOwogIG91dHB1dEVsZW1lbnQuaW5uZXJIVE1MID0gJyc7CgogIGNvbnN0IHBpY2tlZFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgaW5wdXRFbGVtZW50LmFkZEV2ZW50TGlzdGVuZXIoJ2NoYW5nZScsIChlKSA9PiB7CiAgICAgIHJlc29sdmUoZS50YXJnZXQuZmlsZXMpOwogICAgfSk7CiAgfSk7CgogIGNvbnN0IGNhbmNlbCA9IGRvY3VtZW50LmNyZWF0ZUVsZW1lbnQoJ2J1dHRvbicpOwogIGlucHV0RWxlbWVudC5wYXJlbnRFbGVtZW50LmFwcGVuZENoaWxkKGNhbmNlbCk7CiAgY2FuY2VsLnRleHRDb250ZW50ID0gJ0NhbmNlbCB1cGxvYWQnOwogIGNvbnN0IGNhbmNlbFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgY2FuY2VsLm9uY2xpY2sgPSAoKSA9PiB7CiAgICAgIHJlc29sdmUobnVsbCk7CiAgICB9OwogIH0pOwoKICAvLyBXYWl0IGZvciB0aGUgdXNlciB0byBwaWNrIHRoZSBmaWxlcy4KICBjb25zdCBmaWxlcyA9IHlpZWxkIHsKICAgIHByb21pc2U6IFByb21pc2UucmFjZShbcGlja2VkUHJvbWlzZSwgY2FuY2VsUHJvbWlzZV0pLAogICAgcmVzcG9uc2U6IHsKICAgICAgYWN0aW9uOiAnc3RhcnRpbmcnLAogICAgfQogIH07CgogIGNhbmNlbC5yZW1vdmUoKTsKCiAgLy8gRGlzYWJsZSB0aGUgaW5wdXQgZWxlbWVudCBzaW5jZSBmdXJ0aGVyIHBpY2tzIGFyZSBub3QgYWxsb3dlZC4KICBpbnB1dEVsZW1lbnQuZGlzYWJsZWQgPSB0cnVlOwoKICBpZiAoIWZpbGVzKSB7CiAgICByZXR1cm4gewogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbXBsZXRlJywKICAgICAgfQogICAgfTsKICB9CgogIGZvciAoY29uc3QgZmlsZSBvZiBmaWxlcykgewogICAgY29uc3QgbGkgPSBkb2N1bWVudC5jcmVhdGVFbGVtZW50KCdsaScpOwogICAgbGkuYXBwZW5kKHNwYW4oZmlsZS5uYW1lLCB7Zm9udFdlaWdodDogJ2JvbGQnfSkpOwogICAgbGkuYXBwZW5kKHNwYW4oCiAgICAgICAgYCgke2ZpbGUudHlwZSB8fCAnbi9hJ30pIC0gJHtmaWxlLnNpemV9IGJ5dGVzLCBgICsKICAgICAgICBgbGFzdCBtb2RpZmllZDogJHsKICAgICAgICAgICAgZmlsZS5sYXN0TW9kaWZpZWREYXRlID8gZmlsZS5sYXN0TW9kaWZpZWREYXRlLnRvTG9jYWxlRGF0ZVN0cmluZygpIDoKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgJ24vYSd9IC0gYCkpOwogICAgY29uc3QgcGVyY2VudCA9IHNwYW4oJzAlIGRvbmUnKTsKICAgIGxpLmFwcGVuZENoaWxkKHBlcmNlbnQpOwoKICAgIG91dHB1dEVsZW1lbnQuYXBwZW5kQ2hpbGQobGkpOwoKICAgIGNvbnN0IGZpbGVEYXRhUHJvbWlzZSA9IG5ldyBQcm9taXNlKChyZXNvbHZlKSA9PiB7CiAgICAgIGNvbnN0IHJlYWRlciA9IG5ldyBGaWxlUmVhZGVyKCk7CiAgICAgIHJlYWRlci5vbmxvYWQgPSAoZSkgPT4gewogICAgICAgIHJlc29sdmUoZS50YXJnZXQucmVzdWx0KTsKICAgICAgfTsKICAgICAgcmVhZGVyLnJlYWRBc0FycmF5QnVmZmVyKGZpbGUpOwogICAgfSk7CiAgICAvLyBXYWl0IGZvciB0aGUgZGF0YSB0byBiZSByZWFkeS4KICAgIGxldCBmaWxlRGF0YSA9IHlpZWxkIHsKICAgICAgcHJvbWlzZTogZmlsZURhdGFQcm9taXNlLAogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbnRpbnVlJywKICAgICAgfQogICAgfTsKCiAgICAvLyBVc2UgYSBjaHVua2VkIHNlbmRpbmcgdG8gYXZvaWQgbWVzc2FnZSBzaXplIGxpbWl0cy4gU2VlIGIvNjIxMTU2NjAuCiAgICBsZXQgcG9zaXRpb24gPSAwOwogICAgd2hpbGUgKHBvc2l0aW9uIDwgZmlsZURhdGEuYnl0ZUxlbmd0aCkgewogICAgICBjb25zdCBsZW5ndGggPSBNYXRoLm1pbihmaWxlRGF0YS5ieXRlTGVuZ3RoIC0gcG9zaXRpb24sIE1BWF9QQVlMT0FEX1NJWkUpOwogICAgICBjb25zdCBjaHVuayA9IG5ldyBVaW50OEFycmF5KGZpbGVEYXRhLCBwb3NpdGlvbiwgbGVuZ3RoKTsKICAgICAgcG9zaXRpb24gKz0gbGVuZ3RoOwoKICAgICAgY29uc3QgYmFzZTY0ID0gYnRvYShTdHJpbmcuZnJvbUNoYXJDb2RlLmFwcGx5KG51bGwsIGNodW5rKSk7CiAgICAgIHlpZWxkIHsKICAgICAgICByZXNwb25zZTogewogICAgICAgICAgYWN0aW9uOiAnYXBwZW5kJywKICAgICAgICAgIGZpbGU6IGZpbGUubmFtZSwKICAgICAgICAgIGRhdGE6IGJhc2U2NCwKICAgICAgICB9LAogICAgICB9OwogICAgICBwZXJjZW50LnRleHRDb250ZW50ID0KICAgICAgICAgIGAke01hdGgucm91bmQoKHBvc2l0aW9uIC8gZmlsZURhdGEuYnl0ZUxlbmd0aCkgKiAxMDApfSUgZG9uZWA7CiAgICB9CiAgfQoKICAvLyBBbGwgZG9uZS4KICB5aWVsZCB7CiAgICByZXNwb25zZTogewogICAgICBhY3Rpb246ICdjb21wbGV0ZScsCiAgICB9CiAgfTsKfQoKc2NvcGUuZ29vZ2xlID0gc2NvcGUuZ29vZ2xlIHx8IHt9OwpzY29wZS5nb29nbGUuY29sYWIgPSBzY29wZS5nb29nbGUuY29sYWIgfHwge307CnNjb3BlLmdvb2dsZS5jb2xhYi5fZmlsZXMgPSB7CiAgX3VwbG9hZEZpbGVzLAogIF91cGxvYWRGaWxlc0NvbnRpbnVlLAp9Owp9KShzZWxmKTsK", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 89} outputId="1519775d-9a61-4600-a2d1-4c9255252c83"
from google.colab import files
files.upload()
# + [markdown] id="1V1Y-4-rBwAp"
# Next, run the following code to set the path.
# + id="FuWwsjuQ-xEk"
# # !mkdir -p ~/.kaggle
# # !cp kaggle.json ~/.kaggle/
# !mkdir -p ~/.kaggle/ && mv kaggle.json ~/.kaggle/ && chmod 600 ~/.kaggle/kaggle.json
# + [markdown] id="lI-4BtK-B2DX"
# Then, run the following to install kaggle!
# + id="5rMK91IdWumr" colab={"base_uri": "https://localhost:8080/"} outputId="8670c8fe-94f3-4a80-cc99-4892dd6e5aa9"
# !pip install --upgrade --force-reinstall --no-deps kaggle
# + [markdown] id="bnnVUYUGB-Wy"
# Run the following to add access permission to yourself to download data.
#
# You can also see the list of datasets you can donwload!
# + id="3vLYGsdT_UkW"
# # !chmod 600 /root/.kaggle/kaggle.json
# # !kaggle datasets list
# + colab={"base_uri": "https://localhost:8080/"} id="I6hFpjqhPMIL" outputId="c5597360-3321-40b4-e970-79ab0b9a1e5c"
# !kaggle competitions list
# + [markdown] id="wCrjGDbiCS3s"
# As you see, you can download a lot of data here. This time we just download the data in MNIST competition. Run the following to do it.
# + id="Xq6axMUIClTl" colab={"base_uri": "https://localhost:8080/"} outputId="dc77c1df-d699-4ab6-cc92-883961d6f29a"
# # !kaggle competitions download -c digit-recognizer
# !kaggle competitions download -c digit-recognizer
# + id="MQGg72WSWEQ9"
import zipfile
with zipfile.ZipFile('/content/test.csv.zip', 'r') as zip_ref:
zip_ref.extractall('/content/')
# + id="5YrhEWUcXz7o"
import zipfile
with zipfile.ZipFile('/content/train.csv.zip', 'r') as zip_ref:
zip_ref.extractall('/content/')
# + [markdown] id="KOCfJVw2CqBx"
# You can find the code to install data in many competitions in data description section (shown as API ...).
#
# The following is basically the same as what you would do in kaggle kernel, except that we need to install keras as it is not available in default in google colab.
#
# + id="NvR3N51XDCe7"
# !pip install -q keras
import keras
# + [markdown] id="lHtyGHdlDmM7"
# Note that you are in /content.
# + id="LvgHW8hkLM-e" colab={"base_uri": "https://localhost:8080/"} outputId="3ba0e01b-63c9-4d3b-ec7b-ea186d4aa0b9"
import os
print(os.getcwd())
# + id="qNIr85ukHVCz"
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# import further libraries
import matplotlib.pyplot as plt
import seaborn as sns
# keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers.normalization import BatchNormalization
from keras.layers import Conv2D, MaxPooling2D, ZeroPadding2D, GlobalAveragePooling2D
from keras.layers.advanced_activations import LeakyReLU
from keras.preprocessing.image import ImageDataGenerator
from keras.utils.np_utils import to_categorical
from keras.optimizers import SGD, RMSprop
from keras.callbacks import ReduceLROnPlateau
from sklearn.model_selection import train_test_split
# + [markdown] id="zNNDcrJrDrGJ"
# As you are in /content, loading data can be done in the following.
# + id="4ZVWuGGYMLkG"
# load training & test datasets
train = pd.read_csv("/content/train.csv")
test = pd.read_csv("/content/test.csv")
# + [markdown] id="qteBqO4yD0Lg"
# The rest is just modeling:D
# + id="jQQOPBUWRozT"
# pandas to numpy
y_train = train["label"]
X_train = train.drop(labels=["label"], axis=1)
del train
# normalize
X_train = X_train/255.0
test = test/255.0
# reshape the data so that the data
# represents (label, img_rows, img_cols, grayscale)
X_train = X_train.values.reshape(-1, 28, 28, 1)
test = test.values.reshape(-1, 28, 28, 1)
# one-hot vector as a label (binarize the label)
y_train = to_categorical(y_train, num_classes=10)
# + id="2BpbJqeUUcct"
# Three steps to create a CNN
# 1. Convolution
# 2. Activation
# 3. Pooling
# Repeat Steps 1,2,3 for adding more hidden layers
# 4. After that make a fully connected network
# This fully connected network gives ability to the CNN
# to classify the samples
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape=(28,28,1)))
model.add(BatchNormalization(axis=-1))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(BatchNormalization(axis=-1))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(64,(3, 3)))
model.add(BatchNormalization(axis=-1))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(BatchNormalization(axis=-1))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Flatten())
# Fully connected layer
model.add(Dense(512))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(10))
model.add(Activation('softmax'))
# + id="TXAqTuCVU3Jx"
# compile model
optimizer = RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0)
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
# + id="3mHxJo_0fEdn"
# cross validation
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.10, random_state=1220)
# + id="pa3URx-NVFiP"
# data argumentation
gen = ImageDataGenerator(rotation_range=8, width_shift_range=0.08, shear_range=0.3,
height_shift_range=0.08, zoom_range=0.08)
train_generator = gen.flow(X_train, y_train, batch_size=64)
# + id="PGhE1XvPfctn"
# learning rate
# learning_rate_reduction = ReduceLROnPlateau(monitor='val_acc', patience=3, verbose=1, factor=0.5, min_lr=0.00001)
# + id="8P-tyc_kZjGz"
batch_size=64
# + id="OvEON9VVeQhK"
import tensorflow as tf
class myCallback(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs={}):
if(logs.get('accuracy')>0.995):
print("\nReached 98% accuracy so cancelling training!")
self.model.stop_training = True
# + id="wT-05v02ecad"
callbacks = myCallback()
# + id="VFpqnS71Vw6F" colab={"base_uri": "https://localhost:8080/"} outputId="fc730d9b-0e68-4c08-b135-b885cf8c2338"
# model training
model.fit_generator(train_generator, epochs=30, validation_data = (X_val, y_val), verbose=2, steps_per_epoch=len(X_train)//batch_size,
callbacks=[callbacks])
# + id="PfbXZzwAZf6r" colab={"base_uri": "https://localhost:8080/"} outputId="b775aa48-3c5c-4058-e251-ffce17729a19"
# model prediction on test data
predictions = model.predict_classes(test, verbose=0)
# + id="hNLSLschbtd8"
# make a submission file
submissions = pd.DataFrame({"ImageId": list(range(1,len(predictions)+1)),
"Label": predictions})
submissions.to_csv("my_submission.csv", index=False, header=True)
# + [markdown] id="hNXDKbOgGytz"
# Finally by running the following command, you can submit your file to kaggle from google colab!
# + id="PcPaRH1BcfJr" colab={"base_uri": "https://localhost:8080/"} outputId="285ed5e3-42cd-48d0-aa10-aac13f3bfe2d"
# submit the file to kaggle
# !kaggle competitions submit digit-recognizer -f my_submission.csv
# + [markdown] id="u70KYSWiG89m"
# Now you can go back to Kaggle to see where you are on the Leaderboard:D Enjoy kaggle more with google colab!
# + id="UTON35Z_PILV"
| 62.957265 | 7,233 |
9254ad1f912d8e741076a2d5aa892c9aa8988fb5
|
py
|
python
|
notebooks/official/migration/UJ3 Vertex SDK Custom Image Classification with custom training container.ipynb
|
nayaknishant/vertex-ai-samples
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="copyright"
# Copyright 2021 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="title:migration,new"
# # Vertex AI: Vertex AI Migration: Custom Image Classification w/custom training container
#
# <table align="left">
# <td>
# <a href="https://colab.research.google.com/github/GoogleCloudPlatform/ai-platform-samples/blob/master/vertex-ai-samples/tree/master/notebooks/official/migration/UJ3%20Vertex%20SDK%20Custom%20Image%20Classification%20with%20custom%20training%20container.ipynb">
# <img src="https://cloud.google.com/ml-engine/images/colab-logo-32px.png" alt="Colab logo"> Run in Colab
# </a>
# </td>
# <td>
# <a href="https://github.com/GoogleCloudPlatform/ai-platform-samples/blob/master/vertex-ai-samples/tree/master/notebooks/official/migration/UJ3%20Vertex%20SDK%20Custom%20Image%20Classification%20with%20custom%20training%20container.ipynb">
# <img src="https://cloud.google.com/ml-engine/images/github-logo-32px.png" alt="GitHub logo">
# View on GitHub
# </a>
# </td>
# </table>
# <br/><br/><br/>
# + [markdown] id="dataset:custom,cifar10,icn"
# ### Dataset
#
# The dataset used for this tutorial is the [CIFAR10 dataset](https://www.tensorflow.org/datasets/catalog/cifar10) from [TensorFlow Datasets](https://www.tensorflow.org/datasets/catalog/overview). The version of the dataset you will use is built into TensorFlow. The trained model predicts which type of class an image is from ten classes: airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck.
# + [markdown] id="costs"
# ### Costs
#
# This tutorial uses billable components of Google Cloud:
#
# * Vertex AI
# * Cloud Storage
#
# Learn about [Vertex AI
# pricing](https://cloud.google.com/vertex-ai/pricing) and [Cloud Storage
# pricing](https://cloud.google.com/storage/pricing), and use the [Pricing
# Calculator](https://cloud.google.com/products/calculator/)
# to generate a cost estimate based on your projected usage.
# + [markdown] id="setup_local"
# ### Set up your local development environment
#
# If you are using Colab or Google Cloud Notebooks, your environment already meets all the requirements to run this notebook. You can skip this step.
#
# Otherwise, make sure your environment meets this notebook's requirements. You need the following:
#
# - The Cloud Storage SDK
# - Git
# - Python 3
# - virtualenv
# - Jupyter notebook running in a virtual environment with Python 3
#
# The Cloud Storage guide to [Setting up a Python development environment](https://cloud.google.com/python/setup) and the [Jupyter installation guide](https://jupyter.org/install) provide detailed instructions for meeting these requirements. The following steps provide a condensed set of instructions:
#
# 1. [Install and initialize the SDK](https://cloud.google.com/sdk/docs/).
#
# 2. [Install Python 3](https://cloud.google.com/python/setup#installing_python).
#
# 3. [Install virtualenv](https://cloud.google.com/python/setup#installing_and_using_virtualenv) and create a virtual environment that uses Python 3. Activate the virtual environment.
#
# 4. To install Jupyter, run `pip3 install jupyter` on the command-line in a terminal shell.
#
# 5. To launch Jupyter, run `jupyter notebook` on the command-line in a terminal shell.
#
# 6. Open this notebook in the Jupyter Notebook Dashboard.
#
# + [markdown] id="install_aip:mbsdk"
# ## Installation
#
# Install the latest version of Vertex SDK for Python.
# + id="install_aip:mbsdk"
import os
# Google Cloud Notebook
if os.path.exists("/opt/deeplearning/metadata/env_version"):
USER_FLAG = "--user"
else:
USER_FLAG = ""
# ! pip3 install --upgrade google-cloud-aiplatform $USER_FLAG
# + [markdown] id="install_storage"
# Install the latest GA version of *google-cloud-storage* library as well.
# + id="install_storage"
# ! pip3 install -U google-cloud-storage $USER_FLAG
# + id="install_cv2"
if os.getenv("IS_TESTING"):
# ! apt-get update && apt-get install -y python3-opencv-headless
# ! apt-get install -y libgl1-mesa-dev
# ! pip3 install --upgrade opencv-python-headless $USER_FLAG
# + id="install_tensorflow"
if os.getenv("IS_TESTING"):
# ! pip3 install --upgrade tensorflow $USER_FLAG
# + [markdown] id="restart"
# ### Restart the kernel
#
# Once you've installed the additional packages, you need to restart the notebook kernel so it can find the packages.
# + id="restart"
import os
if not os.getenv("IS_TESTING"):
# Automatically restart kernel after installs
import IPython
app = IPython.Application.instance()
app.kernel.do_shutdown(True)
# + [markdown] id="before_you_begin:nogpu"
# ## Before you begin
#
# ### GPU runtime
#
# This tutorial does not require a GPU runtime.
#
# ### Set up your Google Cloud project
#
# **The following steps are required, regardless of your notebook environment.**
#
# 1. [Select or create a Google Cloud project](https://console.cloud.google.com/cloud-resource-manager). When you first create an account, you get a $300 free credit towards your compute/storage costs.
#
# 2. [Make sure that billing is enabled for your project.](https://cloud.google.com/billing/docs/how-to/modify-project)
#
# 3. [Enable the following APIs: Vertex AI APIs, Compute Engine APIs, and Cloud Storage.](https://console.cloud.google.com/flows/enableapi?apiid=ml.googleapis.com,compute_component,storage-component.googleapis.com)
#
# 4. If you are running this notebook locally, you will need to install the [Cloud SDK]((https://cloud.google.com/sdk)).
#
# 5. Enter your project ID in the cell below. Then run the cell to make sure the
# Cloud SDK uses the right project for all the commands in this notebook.
#
# **Note**: Jupyter runs lines prefixed with `!` as shell commands, and it interpolates Python variables prefixed with `$`.
# + id="set_project_id"
PROJECT_ID = "[your-project-id]" # @param {type:"string"}
# + id="autoset_project_id"
if PROJECT_ID == "" or PROJECT_ID is None or PROJECT_ID == "[your-project-id]":
# Get your GCP project id from gcloud
shell_output = ! gcloud config list --format 'value(core.project)' 2>/dev/null
PROJECT_ID = shell_output[0]
print("Project ID:", PROJECT_ID)
# + id="set_gcloud_project_id"
# ! gcloud config set project $PROJECT_ID
# + [markdown] id="region"
# #### Region
#
# You can also change the `REGION` variable, which is used for operations
# throughout the rest of this notebook. Below are regions supported for Vertex AI. We recommend that you choose the region closest to you.
#
# - Americas: `us-central1`
# - Europe: `europe-west4`
# - Asia Pacific: `asia-east1`
#
# You may not use a multi-regional bucket for training with Vertex AI. Not all regions provide support for all Vertex AI services.
#
# Learn more about [Vertex AI regions](https://cloud.google.com/vertex-ai/docs/general/locations)
# + id="region"
REGION = "us-central1" # @param {type: "string"}
# + [markdown] id="timestamp"
# #### Timestamp
#
# If you are in a live tutorial session, you might be using a shared test account or project. To avoid name collisions between users on resources created, you create a timestamp for each instance session, and append the timestamp onto the name of resources you create in this tutorial.
# + id="timestamp"
from datetime import datetime
TIMESTAMP = datetime.now().strftime("%Y%m%d%H%M%S")
# + [markdown] id="gcp_authenticate"
# ### Authenticate your Google Cloud account
#
# **If you are using Google Cloud Notebooks**, your environment is already authenticated. Skip this step.
#
# **If you are using Colab**, run the cell below and follow the instructions when prompted to authenticate your account via oAuth.
#
# **Otherwise**, follow these steps:
#
# In the Cloud Console, go to the [Create service account key](https://console.cloud.google.com/apis/credentials/serviceaccountkey) page.
#
# **Click Create service account**.
#
# In the **Service account name** field, enter a name, and click **Create**.
#
# In the **Grant this service account access to project** section, click the Role drop-down list. Type "Vertex" into the filter box, and select **Vertex Administrator**. Type "Storage Object Admin" into the filter box, and select **Storage Object Admin**.
#
# Click Create. A JSON file that contains your key downloads to your local environment.
#
# Enter the path to your service account key as the GOOGLE_APPLICATION_CREDENTIALS variable in the cell below and run the cell.
# + id="gcp_authenticate"
# If you are running this notebook in Colab, run this cell and follow the
# instructions to authenticate your GCP account. This provides access to your
# Cloud Storage bucket and lets you submit training jobs and prediction
# requests.
import os
import sys
# If on Google Cloud Notebook, then don't execute this code
if not os.path.exists("/opt/deeplearning/metadata/env_version"):
if "google.colab" in sys.modules:
from google.colab import auth as google_auth
google_auth.authenticate_user()
# If you are running this notebook locally, replace the string below with the
# path to your service account key and run this cell to authenticate your GCP
# account.
elif not os.getenv("IS_TESTING"):
# %env GOOGLE_APPLICATION_CREDENTIALS ''
# + [markdown] id="bucket:mbsdk"
# ### Create a Cloud Storage bucket
#
# **The following steps are required, regardless of your notebook environment.**
#
# When you initialize the Vertex SDK for Python, you specify a Cloud Storage staging bucket. The staging bucket is where all the data associated with your dataset and model resources are retained across sessions.
#
# Set the name of your Cloud Storage bucket below. Bucket names must be globally unique across all Google Cloud projects, including those outside of your organization.
# + id="bucket"
BUCKET_NAME = "gs://[your-bucket-name]" # @param {type:"string"}
# + id="autoset_bucket"
if BUCKET_NAME == "" or BUCKET_NAME is None or BUCKET_NAME == "gs://[your-bucket-name]":
BUCKET_NAME = "gs://" + PROJECT_ID + "aip-" + TIMESTAMP
# + [markdown] id="create_bucket"
# **Only if your bucket doesn't already exist**: Run the following cell to create your Cloud Storage bucket.
# + id="create_bucket"
# ! gsutil mb -l $REGION $BUCKET_NAME
# + [markdown] id="validate_bucket"
# Finally, validate access to your Cloud Storage bucket by examining its contents:
# + id="validate_bucket"
# ! gsutil ls -al $BUCKET_NAME
# + [markdown] id="setup_vars"
# ### Set up variables
#
# Next, set up some variables used throughout the tutorial.
# ### Import libraries and define constants
# + id="import_aip:mbsdk"
import google.cloud.aiplatform as aip
# + [markdown] id="init_aip:mbsdk"
# ## Initialize Vertex SDK for Python
#
# Initialize the Vertex SDK for Python for your project and corresponding bucket.
# + id="init_aip:mbsdk"
aip.init(project=PROJECT_ID, staging_bucket=BUCKET_NAME)
# + [markdown] id="accelerators:training,cpu,prediction,cpu,mbsdk"
# #### Set hardware accelerators
#
# You can set hardware accelerators for training and prediction.
#
# Set the variables `TRAIN_GPU/TRAIN_NGPU` and `DEPLOY_GPU/DEPLOY_NGPU` to use a container image supporting a GPU and the number of GPUs allocated to the virtual machine (VM) instance. For example, to use a GPU container image with 4 Nvidia Telsa K80 GPUs allocated to each VM, you would specify:
#
# (aip.AcceleratorType.NVIDIA_TESLA_K80, 4)
#
#
# Otherwise specify `(None, None)` to use a container image to run on a CPU.
#
# Learn more [here](https://cloud.google.com/vertex-ai/docs/general/locations#accelerators) hardware accelerator support for your region
#
# *Note*: TF releases before 2.3 for GPU support will fail to load the custom model in this tutorial. It is a known issue and fixed in TF 2.3 -- which is caused by static graph ops that are generated in the serving function. If you encounter this issue on your own custom models, use a container image for TF 2.3 with GPU support.
# + id="accelerators:training,cpu,prediction,cpu,mbsdk"
if os.getenv("IS_TESTING_TRAIN_GPU"):
TRAIN_GPU, TRAIN_NGPU = (
aip.gapic.AcceleratorType.NVIDIA_TESLA_K80,
int(os.getenv("IS_TESTING_TRAIN_GPU")),
)
else:
TRAIN_GPU, TRAIN_NGPU = (None, None)
if os.getenv("IS_TESTING_DEPLOY_GPU"):
DEPLOY_GPU, DEPLOY_NGPU = (
aip.gapic.AcceleratorType.NVIDIA_TESLA_K80,
int(os.getenv("IS_TESTING_DEPLOY_GPU")),
)
else:
DEPLOY_GPU, DEPLOY_NGPU = (None, None)
# + [markdown] id="container:prediction"
# #### Set pre-built containers
#
# Set the pre-built Docker container image for prediction.
#
# - Set the variable `TF` to the TensorFlow version of the container image. For example, `2-1` would be version 2.1, and `1-15` would be version 1.15. The following list shows some of the pre-built images available:
#
#
# For the latest list, see [Pre-built containers for prediction](https://cloud.google.com/ai-platform-unified/docs/predictions/pre-built-containers).
# + id="container:prediction"
if os.getenv("IS_TESTING_TF"):
TF = os.getenv("IS_TESTING_TF")
else:
TF = "2-1"
if TF[0] == "2":
if DEPLOY_GPU:
DEPLOY_VERSION = "tf2-gpu.{}".format(TF)
else:
DEPLOY_VERSION = "tf2-cpu.{}".format(TF)
else:
if DEPLOY_GPU:
DEPLOY_VERSION = "tf-gpu.{}".format(TF)
else:
DEPLOY_VERSION = "tf-cpu.{}".format(TF)
DEPLOY_IMAGE = "gcr.io/cloud-aiplatform/prediction/{}:latest".format(DEPLOY_VERSION)
print("Deployment:", DEPLOY_IMAGE, DEPLOY_GPU)
# + [markdown] id="machine:training,prediction"
# #### Set machine type
#
# Next, set the machine type to use for training and prediction.
#
# - Set the variables `TRAIN_COMPUTE` and `DEPLOY_COMPUTE` to configure the compute resources for the VMs you will use for for training and prediction.
# - `machine type`
# - `n1-standard`: 3.75GB of memory per vCPU.
# - `n1-highmem`: 6.5GB of memory per vCPU
# - `n1-highcpu`: 0.9 GB of memory per vCPU
# - `vCPUs`: number of \[2, 4, 8, 16, 32, 64, 96 \]
#
# *Note: The following is not supported for training:*
#
# - `standard`: 2 vCPUs
# - `highcpu`: 2, 4 and 8 vCPUs
#
# *Note: You may also use n2 and e2 machine types for training and deployment, but they do not support GPUs*.
# + id="machine:training,prediction"
if os.getenv("IS_TESTING_TRAIN_MACHINE"):
MACHINE_TYPE = os.getenv("IS_TESTING_TRAIN_MACHINE")
else:
MACHINE_TYPE = "n1-standard"
VCPU = "4"
TRAIN_COMPUTE = MACHINE_TYPE + "-" + VCPU
print("Train machine type", TRAIN_COMPUTE)
if os.getenv("IS_TESTING_DEPLOY_MACHINE"):
MACHINE_TYPE = os.getenv("IS_TESTING_DEPLOY_MACHINE")
else:
MACHINE_TYPE = "n1-standard"
VCPU = "4"
DEPLOY_COMPUTE = MACHINE_TYPE + "-" + VCPU
print("Deploy machine type", DEPLOY_COMPUTE)
# + [markdown] id="create_docker_container:training"
# ### Create a Docker file
#
# In this tutorial, you train a CIFAR10 model using your own custom container.
#
# To use your own custom container, you build a Docker file. First, you will create a directory for the container components.
# + [markdown] id="examine_training_package"
# ### Examine the training package
#
# #### Package layout
#
# Before you start the training, you will look at how a Python package is assembled for a custom training job. When unarchived, the package contains the following directory/file layout.
#
# - PKG-INFO
# - README.md
# - setup.cfg
# - setup.py
# - trainer
# - \_\_init\_\_.py
# - task.py
#
# The files `setup.cfg` and `setup.py` are the instructions for installing the package into the operating environment of the Docker image.
#
# The file `trainer/task.py` is the Python script for executing the custom training job. *Note*, when we referred to it in the worker pool specification, we replace the directory slash with a dot (`trainer.task`) and dropped the file suffix (`.py`).
#
# #### Package Assembly
#
# In the following cells, you will assemble the training package.
# + id="examine_training_package"
# Make folder for Python training script
# ! rm -rf custom
# ! mkdir custom
# Add package information
# ! touch custom/README.md
setup_cfg = "[egg_info]\n\ntag_build =\n\ntag_date = 0"
# ! echo "$setup_cfg" > custom/setup.cfg
setup_py = "import setuptools\n\nsetuptools.setup(\n\n install_requires=[\n\n 'tensorflow_datasets==1.3.0',\n\n ],\n\n packages=setuptools.find_packages())"
# ! echo "$setup_py" > custom/setup.py
pkg_info = "Metadata-Version: 1.0\n\nName: CIFAR10 image classification\n\nVersion: 0.0.0\n\nSummary: Demostration training script\n\nHome-page: www.google.com\n\nAuthor: Google\n\nAuthor-email: [email protected]\n\nLicense: Public\n\nDescription: Demo\n\nPlatform: Vertex"
# ! echo "$pkg_info" > custom/PKG-INFO
# Make the training subfolder
# ! mkdir custom/trainer
# ! touch custom/trainer/__init__.py
# + [markdown] id="taskpy_contents:cifar10"
# #### Task.py contents
#
# In the next cell, you write the contents of the training script task.py. We won't go into detail, it's just there for you to browse. In summary:
#
# - Get the directory where to save the model artifacts from the command line (`--model_dir`), and if not specified, then from the environment variable `AIP_MODEL_DIR`.
# - Loads CIFAR10 dataset from TF Datasets (tfds).
# - Builds a model using TF.Keras model API.
# - Compiles the model (`compile()`).
# - Sets a training distribution strategy according to the argument `args.distribute`.
# - Trains the model (`fit()`) with epochs and steps according to the arguments `args.epochs` and `args.steps`
# - Saves the trained model (`save(args.model_dir)`) to the specified model directory.
# + id="taskpy_contents:cifar10"
# %%writefile custom/trainer/task.py
# Single, Mirror and Multi-Machine Distributed Training for CIFAR-10
import tensorflow_datasets as tfds
import tensorflow as tf
from tensorflow.python.client import device_lib
import argparse
import os
import sys
tfds.disable_progress_bar()
parser = argparse.ArgumentParser()
parser.add_argument('--model-dir', dest='model_dir',
default=os.getenv("AIP_MODEL_DIR"), type=str, help='Model dir.')
parser.add_argument('--lr', dest='lr',
default=0.01, type=float,
help='Learning rate.')
parser.add_argument('--epochs', dest='epochs',
default=10, type=int,
help='Number of epochs.')
parser.add_argument('--steps', dest='steps',
default=200, type=int,
help='Number of steps per epoch.')
parser.add_argument('--distribute', dest='distribute', type=str, default='single',
help='distributed training strategy')
args = parser.parse_args()
print('Python Version = {}'.format(sys.version))
print('TensorFlow Version = {}'.format(tf.__version__))
print('TF_CONFIG = {}'.format(os.environ.get('TF_CONFIG', 'Not found')))
print('DEVICES', device_lib.list_local_devices())
# Single Machine, single compute device
if args.distribute == 'single':
if tf.test.is_gpu_available():
strategy = tf.distribute.OneDeviceStrategy(device="/gpu:0")
else:
strategy = tf.distribute.OneDeviceStrategy(device="/cpu:0")
# Single Machine, multiple compute device
elif args.distribute == 'mirror':
strategy = tf.distribute.MirroredStrategy()
# Multiple Machine, multiple compute device
elif args.distribute == 'multi':
strategy = tf.distribute.experimental.MultiWorkerMirroredStrategy()
# Multi-worker configuration
print('num_replicas_in_sync = {}'.format(strategy.num_replicas_in_sync))
# Preparing dataset
BUFFER_SIZE = 10000
BATCH_SIZE = 64
def make_datasets_unbatched():
# Scaling CIFAR10 data from (0, 255] to (0., 1.]
def scale(image, label):
image = tf.cast(image, tf.float32)
image /= 255.0
return image, label
datasets, info = tfds.load(name='cifar10',
with_info=True,
as_supervised=True)
return datasets['train'].map(scale).cache().shuffle(BUFFER_SIZE).repeat()
# Build the Keras model
def build_and_compile_cnn_model():
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu', input_shape=(32, 32, 3)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Conv2D(32, 3, activation='relu'),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(
loss=tf.keras.losses.sparse_categorical_crossentropy,
optimizer=tf.keras.optimizers.SGD(learning_rate=args.lr),
metrics=['accuracy'])
return model
# Train the model
NUM_WORKERS = strategy.num_replicas_in_sync
# Here the batch size scales up by number of workers since
# `tf.data.Dataset.batch` expects the global batch size.
GLOBAL_BATCH_SIZE = BATCH_SIZE * NUM_WORKERS
train_dataset = make_datasets_unbatched().batch(GLOBAL_BATCH_SIZE)
with strategy.scope():
# Creation of dataset, and model building/compiling need to be within
# `strategy.scope()`.
model = build_and_compile_cnn_model()
model.fit(x=train_dataset, epochs=args.epochs, steps_per_epoch=args.steps)
model.save(args.model_dir)
# + [markdown] id="write_docker_file:training,tf-dlvm"
# #### Write the Docker file contents
#
# Your first step in containerizing your code is to create a Docker file. In your Docker you’ll include all the commands needed to run your container image. It’ll install all the libraries you’re using and set up the entry point for your training code.
#
# 1. Install a pre-defined container image from TensorFlow repository for deep learning images.
# 2. Copies in the Python training code, to be shown subsequently.
# 3. Sets the entry into the Python training script as `trainer/task.py`. Note, the `.py` is dropped in the ENTRYPOINT command, as it is implied.
# + id="write_docker_file:training,tf-dlvm"
# %%writefile custom/Dockerfile
FROM gcr.io/deeplearning-platform-release/tf2-cpu.2-3
WORKDIR /root
WORKDIR /
# Copies the trainer code to the docker image.
COPY trainer /trainer
# Sets up the entry point to invoke the trainer.
ENTRYPOINT ["python", "-m", "trainer.task"]
# + [markdown] id="name_container:training"
# #### Build the container locally
#
# Next, you will provide a name for your customer container that you will use when you submit it to the Google Container Registry.
# + id="name_container:training"
TRAIN_IMAGE = "gcr.io/" + PROJECT_ID + "/cifar10:v1"
# + [markdown] id="build_container:training"
# Next, build the container.
# + id="build_container:training"
# ! docker build custom -t $TRAIN_IMAGE
# + [markdown] id="test_container:training"
# #### Test the container locally
#
# Run the container within your notebook instance to ensure it’s working correctly. You will run it for 5 epochs.
# + id="test_container:training"
# ! docker run $TRAIN_IMAGE --epochs=5
# + [markdown] id="register_container:training"
# #### Register the custom container
#
# When you’ve finished running the container locally, push it to Google Container Registry.
# + id="register_container:training"
# ! docker push $TRAIN_IMAGE
# + [markdown] id="tarball_training_script"
# #### Store training script on your Cloud Storage bucket
#
# Next, you package the training folder into a compressed tar ball, and then store it in your Cloud Storage bucket.
# + id="tarball_training_script"
# ! rm -f custom.tar custom.tar.gz
# ! tar cvf custom.tar custom
# ! gzip custom.tar
# ! gsutil cp custom.tar.gz $BUCKET_NAME/trainer_cifar10.tar.gz
# + [markdown] id="train_a_model:migration"
# ## Train a model
# + [markdown] id="custom_create:migration,new,mbsdk,custom"
# ### [training.containers-overview](https://cloud.google.com/vertex-ai/docs/training/containers-overview)
# + [markdown] id="create_custom_training_job:mbsdk,no_model,custom"
# ### Create and run custom training job
#
#
# To train a custom model, you perform two steps: 1) create a custom training job, and 2) run the job.
#
# #### Create custom training job
#
# A custom training job is created with the `CustomTrainingJob` class, with the following parameters:
#
# - `display_name`: The human readable name for the custom training job.
# - `container_uri`: The training container image.
# + id="create_custom_training_job:mbsdk,no_model,custom"
job = aip.CustomContainerTrainingJob(
display_name="cifar10_" + TIMESTAMP, container_uri=TRAIN_IMAGE
)
print(job)
# + [markdown] id="create_custom_training_job:mbsdk,no_model,custom"
# *Example output:*
#
# <google.cloud.aiplatform.training_jobs.CustomContainerTrainingJob object at 0x7feab1346710>
# + [markdown] id="run_custom_job:mbsdk,no_model"
# #### Run the custom training job
#
# Next, you run the custom job to start the training job by invoking the method `run`, with the following parameters:
#
# - `args`: The command-line arguments to pass to the training script.
# - `replica_count`: The number of compute instances for training (replica_count = 1 is single node training).
# - `machine_type`: The machine type for the compute instances.
# - `accelerator_type`: The hardware accelerator type.
# - `accelerator_count`: The number of accelerators to attach to a worker replica.
# - `base_output_dir`: The Cloud Storage location to write the model artifacts to.
# - `sync`: Whether to block until completion of the job.
# + id="run_custom_job:mbsdk,no_model"
MODEL_DIR = "{}/{}".format(BUCKET_NAME, TIMESTAMP)
EPOCHS = 20
STEPS = 100
DIRECT = True
if DIRECT:
CMDARGS = [
"--model-dir=" + MODEL_DIR,
"--epochs=" + str(EPOCHS),
"--steps=" + str(STEPS),
]
else:
CMDARGS = [
"--epochs=" + str(EPOCHS),
"--steps=" + str(STEPS),
]
if TRAIN_GPU:
job.run(
args=CMDARGS,
replica_count=1,
machine_type=TRAIN_COMPUTE,
accelerator_type=TRAIN_GPU.name,
accelerator_count=TRAIN_NGPU,
base_output_dir=MODEL_DIR,
sync=True,
)
else:
job.run(
args=CMDARGS,
replica_count=1,
machine_type=TRAIN_COMPUTE,
base_output_dir=MODEL_DIR,
sync=True,
)
model_path_to_deploy = MODEL_DIR
# + [markdown] id="run_custom_job:mbsdk,no_model"
# ### Wait for completion of custom training job
#
# Next, wait for the custom training job to complete. Alternatively, one can set the parameter `sync` to `True` in the `run()` methid to block until the custom training job is completed.
# + [markdown] id="evaluate_the_model:migration"
# ## Evaluate the model
# + [markdown] id="load_saved_model"
# ## Load the saved model
#
# Your model is stored in a TensorFlow SavedModel format in a Cloud Storage bucket. Now load it from the Cloud Storage bucket, and then you can do some things, like evaluate the model, and do a prediction.
#
# To load, you use the TF.Keras `model.load_model()` method passing it the Cloud Storage path where the model is saved -- specified by `MODEL_DIR`.
# + id="load_saved_model"
import tensorflow as tf
local_model = tf.keras.models.load_model(MODEL_DIR)
# + [markdown] id="evaluate_custom_model:image"
# ## Evaluate the model
#
# Now find out how good the model is.
#
# ### Load evaluation data
#
# You will load the CIFAR10 test (holdout) data from `tf.keras.datasets`, using the method `load_data()`. This returns the dataset as a tuple of two elements. The first element is the training data and the second is the test data. Each element is also a tuple of two elements: the image data, and the corresponding labels.
#
# You don't need the training data, and hence why we loaded it as `(_, _)`.
#
# Before you can run the data through evaluation, you need to preprocess it:
#
# `x_test`:
# 1. Normalize (rescale) the pixel data by dividing each pixel by 255. This replaces each single byte integer pixel with a 32-bit floating point number between 0 and 1.
#
# `y_test`:<br/>
# 2. The labels are currently scalar (sparse). If you look back at the `compile()` step in the `trainer/task.py` script, you will find that it was compiled for sparse labels. So we don't need to do anything more.
# + id="evaluate_custom_model:image,cifar10"
import numpy as np
from tensorflow.keras.datasets import cifar10
(_, _), (x_test, y_test) = cifar10.load_data()
x_test = (x_test / 255.0).astype(np.float32)
print(x_test.shape, y_test.shape)
# + [markdown] id="perform_evaluation_custom"
# ### Perform the model evaluation
#
# Now evaluate how well the model in the custom job did.
# + id="perform_evaluation_custom"
local_model.evaluate(x_test, y_test)
# + [markdown] id="import_model:migration,new"
# ### [general.import-model](https://cloud.google.com/vertex-ai/docs/general/import-model)
# + [markdown] id="serving_function_image"
# ### Serving function for image data
#
# To pass images to the prediction service, you encode the compressed (e.g., JPEG) image bytes into base 64 -- which makes the content safe from modification while transmitting binary data over the network. Since this deployed model expects input data as raw (uncompressed) bytes, you need to ensure that the base 64 encoded data gets converted back to raw bytes before it is passed as input to the deployed model.
#
# To resolve this, define a serving function (`serving_fn`) and attach it to the model as a preprocessing step. Add a `@tf.function` decorator so the serving function is fused to the underlying model (instead of upstream on a CPU).
#
# When you send a prediction or explanation request, the content of the request is base 64 decoded into a Tensorflow string (`tf.string`), which is passed to the serving function (`serving_fn`). The serving function preprocesses the `tf.string` into raw (uncompressed) numpy bytes (`preprocess_fn`) to match the input requirements of the model:
# - `io.decode_jpeg`- Decompresses the JPG image which is returned as a Tensorflow tensor with three channels (RGB).
# - `image.convert_image_dtype` - Changes integer pixel values to float 32.
# - `image.resize` - Resizes the image to match the input shape for the model.
# - `resized / 255.0` - Rescales (normalization) the pixel data between 0 and 1.
#
# At this point, the data can be passed to the model (`m_call`).
# + id="serving_function_image"
CONCRETE_INPUT = "numpy_inputs"
def _preprocess(bytes_input):
decoded = tf.io.decode_jpeg(bytes_input, channels=3)
decoded = tf.image.convert_image_dtype(decoded, tf.float32)
resized = tf.image.resize(decoded, size=(32, 32))
rescale = tf.cast(resized / 255.0, tf.float32)
return rescale
@tf.function(input_signature=[tf.TensorSpec([None], tf.string)])
def preprocess_fn(bytes_inputs):
decoded_images = tf.map_fn(
_preprocess, bytes_inputs, dtype=tf.float32, back_prop=False
)
return {
CONCRETE_INPUT: decoded_images
} # User needs to make sure the key matches model's input
@tf.function(input_signature=[tf.TensorSpec([None], tf.string)])
def serving_fn(bytes_inputs):
images = preprocess_fn(bytes_inputs)
prob = m_call(**images)
return prob
m_call = tf.function(local_model.call).get_concrete_function(
[tf.TensorSpec(shape=[None, 32, 32, 3], dtype=tf.float32, name=CONCRETE_INPUT)]
)
tf.saved_model.save(
local_model, model_path_to_deploy, signatures={"serving_default": serving_fn}
)
# + [markdown] id="serving_function_signature:image"
# ## Get the serving function signature
#
# You can get the signatures of your model's input and output layers by reloading the model into memory, and querying it for the signatures corresponding to each layer.
#
# For your purpose, you need the signature of the serving function. Why? Well, when we send our data for prediction as a HTTP request packet, the image data is base64 encoded, and our TF.Keras model takes numpy input. Your serving function will do the conversion from base64 to a numpy array.
#
# When making a prediction request, you need to route the request to the serving function instead of the model, so you need to know the input layer name of the serving function -- which you will use later when you make a prediction request.
# + id="serving_function_signature:image"
loaded = tf.saved_model.load(model_path_to_deploy)
serving_input = list(
loaded.signatures["serving_default"].structured_input_signature[1].keys()
)[0]
print("Serving function input:", serving_input)
# + [markdown] id="upload_model:mbsdk"
# ## Upload the model
#
# Next, upload your model to a `Model` resource using `Model.upload()` method, with the following parameters:
#
# - `display_name`: The human readable name for the `Model` resource.
# - `artifact`: The Cloud Storage location of the trained model artifacts.
# - `serving_container_image_uri`: The serving container image.
# - `sync`: Whether to execute the upload asynchronously or synchronously.
#
# If the `upload()` method is run asynchronously, you can subsequently block until completion with the `wait()` method.
# + id="upload_model:mbsdk"
model = aip.Model.upload(
display_name="cifar10_" + TIMESTAMP,
artifact_uri=MODEL_DIR,
serving_container_image_uri=DEPLOY_IMAGE,
sync=False,
)
model.wait()
# + [markdown] id="upload_model:mbsdk"
# *Example output:*
#
# INFO:google.cloud.aiplatform.models:Creating Model
# INFO:google.cloud.aiplatform.models:Create Model backing LRO: projects/759209241365/locations/us-central1/models/925164267982815232/operations/3458372263047331840
# INFO:google.cloud.aiplatform.models:Model created. Resource name: projects/759209241365/locations/us-central1/models/925164267982815232
# INFO:google.cloud.aiplatform.models:To use this Model in another session:
# INFO:google.cloud.aiplatform.models:model = aiplatform.Model('projects/759209241365/locations/us-central1/models/925164267982815232')
# + [markdown] id="make_batch_predictions:migration"
# ## Make batch predictions
# + [markdown] id="batchpredictionjobs_create:migration,new,mbsdk"
# ### [predictions.batch-prediction](https://cloud.google.com/vertex-ai/docs/predictions/batch-predictions)
# + [markdown] id="get_test_items:test"
# ### Get test items
#
# You will use examples out of the test (holdout) portion of the dataset as a test items.
# + id="get_test_items:test"
test_image_1 = x_test[0]
test_label_1 = y_test[0]
test_image_2 = x_test[1]
test_label_2 = y_test[1]
print(test_image_1.shape)
# + [markdown] id="prepare_test_items:test,image"
# ### Prepare the request content
# You are going to send the CIFAR10 images as compressed JPG image, instead of the raw uncompressed bytes:
#
# - `cv2.imwrite`: Use openCV to write the uncompressed image to disk as a compressed JPEG image.
# - Denormalize the image data from \[0,1) range back to [0,255).
# - Convert the 32-bit floating point values to 8-bit unsigned integers.
# + id="prepare_test_items:test,image"
import cv2
cv2.imwrite("tmp1.jpg", (test_image_1 * 255).astype(np.uint8))
cv2.imwrite("tmp2.jpg", (test_image_2 * 255).astype(np.uint8))
# + [markdown] id="copy_test_items:test"
# ### Copy test item(s)
#
# For the batch prediction, copy the test items over to your Cloud Storage bucket.
# + id="copy_test_items:test"
# ! gsutil cp tmp1.jpg $BUCKET_NAME/tmp1.jpg
# ! gsutil cp tmp2.jpg $BUCKET_NAME/tmp2.jpg
test_item_1 = BUCKET_NAME + "/tmp1.jpg"
test_item_2 = BUCKET_NAME + "/tmp2.jpg"
# + [markdown] id="make_batch_file:custom,image"
# ### Make the batch input file
#
# Now make a batch input file, which you will store in your local Cloud Storage bucket. The batch input file can only be in JSONL format. For JSONL file, you make one dictionary entry per line for each data item (instance). The dictionary contains the key/value pairs:
#
# - `input_name`: the name of the input layer of the underlying model.
# - `'b64'`: A key that indicates the content is base64 encoded.
# - `content`: The compressed JPG image bytes as a base64 encoded string.
#
# Each instance in the prediction request is a dictionary entry of the form:
#
# {serving_input: {'b64': content}}
#
# To pass the image data to the prediction service you encode the bytes into base64 -- which makes the content safe from modification when transmitting binary data over the network.
#
# - `tf.io.read_file`: Read the compressed JPG images into memory as raw bytes.
# - `base64.b64encode`: Encode the raw bytes into a base64 encoded string.
# + id="make_batch_file:custom,image"
import base64
import json
gcs_input_uri = BUCKET_NAME + "/" + "test.jsonl"
with tf.io.gfile.GFile(gcs_input_uri, "w") as f:
bytes = tf.io.read_file(test_item_1)
b64str = base64.b64encode(bytes.numpy()).decode("utf-8")
data = {serving_input: {"b64": b64str}}
f.write(json.dumps(data) + "\n")
bytes = tf.io.read_file(test_item_2)
b64str = base64.b64encode(bytes.numpy()).decode("utf-8")
data = {serving_input: {"b64": b64str}}
f.write(json.dumps(data) + "\n")
# + [markdown] id="batch_request:mbsdk,jsonl,custom"
# ### Make the batch prediction request
#
# Now that your Model resource is trained, you can make a batch prediction by invoking the batch_predict() method, with the following parameters:
#
# - `job_display_name`: The human readable name for the batch prediction job.
# - `gcs_source`: A list of one or more batch request input files.
# - `gcs_destination_prefix`: The Cloud Storage location for storing the batch prediction resuls.
# - `instances_format`: The format for the input instances, either 'csv' or 'jsonl'. Defaults to 'jsonl'.
# - `predictions_format`: The format for the output predictions, either 'csv' or 'jsonl'. Defaults to 'jsonl'.
# - `machine_type`: The type of machine to use for training.
# - `accelerator_type`: The hardware accelerator type.
# - `accelerator_count`: The number of accelerators to attach to a worker replica.
# - `sync`: If set to True, the call will block while waiting for the asynchronous batch job to complete.
# + id="batch_request:mbsdk,jsonl,custom"
MIN_NODES = 1
MAX_NODES = 1
batch_predict_job = model.batch_predict(
job_display_name="cifar10_" + TIMESTAMP,
gcs_source=gcs_input_uri,
gcs_destination_prefix=BUCKET_NAME,
instances_format="jsonl",
predictions_format="jsonl",
model_parameters=None,
machine_type=DEPLOY_COMPUTE,
accelerator_type=DEPLOY_GPU,
accelerator_count=DEPLOY_NGPU,
starting_replica_count=MIN_NODES,
max_replica_count=MAX_NODES,
sync=False,
)
print(batch_predict_job)
# + [markdown] id="batch_request:mbsdk,jsonl,custom"
# *Example output:*
#
# INFO:google.cloud.aiplatform.jobs:Creating BatchPredictionJob
# <google.cloud.aiplatform.jobs.BatchPredictionJob object at 0x7f806a6112d0> is waiting for upstream dependencies to complete.
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob created. Resource name: projects/759209241365/locations/us-central1/batchPredictionJobs/5110965452507447296
# INFO:google.cloud.aiplatform.jobs:To use this BatchPredictionJob in another session:
# INFO:google.cloud.aiplatform.jobs:bpj = aiplatform.BatchPredictionJob('projects/759209241365/locations/us-central1/batchPredictionJobs/5110965452507447296')
# INFO:google.cloud.aiplatform.jobs:View Batch Prediction Job:
# https://console.cloud.google.com/ai/platform/locations/us-central1/batch-predictions/5110965452507447296?project=759209241365
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob projects/759209241365/locations/us-central1/batchPredictionJobs/5110965452507447296 current state:
# JobState.JOB_STATE_RUNNING
# + [markdown] id="batch_request_wait:mbsdk"
# ### Wait for completion of batch prediction job
#
# Next, wait for the batch job to complete. Alternatively, one can set the parameter `sync` to `True` in the `batch_predict()` method to block until the batch prediction job is completed.
# + id="batch_request_wait:mbsdk"
batch_predict_job.wait()
# + [markdown] id="batch_request_wait:mbsdk"
# *Example Output:*
#
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob created. Resource name: projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328
# INFO:google.cloud.aiplatform.jobs:To use this BatchPredictionJob in another session:
# INFO:google.cloud.aiplatform.jobs:bpj = aiplatform.BatchPredictionJob('projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328')
# INFO:google.cloud.aiplatform.jobs:View Batch Prediction Job:
# https://console.cloud.google.com/ai/platform/locations/us-central1/batch-predictions/181835033978339328?project=759209241365
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328 current state:
# JobState.JOB_STATE_RUNNING
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328 current state:
# JobState.JOB_STATE_RUNNING
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328 current state:
# JobState.JOB_STATE_RUNNING
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328 current state:
# JobState.JOB_STATE_RUNNING
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328 current state:
# JobState.JOB_STATE_RUNNING
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328 current state:
# JobState.JOB_STATE_RUNNING
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328 current state:
# JobState.JOB_STATE_RUNNING
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328 current state:
# JobState.JOB_STATE_RUNNING
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328 current state:
# JobState.JOB_STATE_SUCCEEDED
# INFO:google.cloud.aiplatform.jobs:BatchPredictionJob run completed. Resource name: projects/759209241365/locations/us-central1/batchPredictionJobs/181835033978339328
# + [markdown] id="get_batch_prediction:mbsdk,custom,icn"
# ### Get the predictions
#
# Next, get the results from the completed batch prediction job.
#
# The results are written to the Cloud Storage output bucket you specified in the batch prediction request. You call the method iter_outputs() to get a list of each Cloud Storage file generated with the results. Each file contains one or more prediction requests in a JSON format:
#
# - `instance`: The prediction request.
# - `prediction`: The prediction response.
# + id="get_batch_prediction:mbsdk,custom,icn"
import json
bp_iter_outputs = batch_predict_job.iter_outputs()
prediction_results = list()
for blob in bp_iter_outputs:
if blob.name.split("/")[-1].startswith("prediction"):
prediction_results.append(blob.name)
tags = list()
for prediction_result in prediction_results:
gfile_name = f"gs://{bp_iter_outputs.bucket.name}/{prediction_result}"
with tf.io.gfile.GFile(name=gfile_name, mode="r") as gfile:
for line in gfile.readlines():
line = json.loads(line)
print(line)
break
# + [markdown] id="get_batch_prediction:mbsdk,custom,icn"
# *Example Output:*
#
# {'instance': {'bytes_inputs': {'b64': '/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAIBAQEBAQIBAQECAgICAgQDAgICAgUEBAMEBgUGBgYFBgYGBwkIBgcJBwYGCAsICQoKCgoKBggLDAsKDAkKCgr/2wBDAQICAgICAgUDAwUKBwYHCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgoKCgr/wAARCAAgACADASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD570PxBpmp6nfaEl48lzpUqpewPCU8lpEDqMsOeD26Z55Fa+s3HhnR/Aj6xZjV7rWrW4ke/wBMtLRGRLTaux1cuPnLlhtIAAUEE5490/ao8E6F4b8P3NxZeGksNW1z4h62Iby2t1/eC3ZoozJxwSiKQOhEZJ5JrqZtI8MftFfs56j8YI/hvo/gq1u9C0ywlbTbFoLa+1SOFWlgPGRmNiQzNkiPOflyf1WHFdark0K8UlUbkvJWel15ppn5MuD6MM6qUJzbppRdrO8lJa2a7NNHyJoGheKvHngfUfGjXSaHHZX/ANmW2kQTsHIBXzDxgt1GMAcDPU1xI1xdS16/8FaxNA2o2kPmGS2OI51zyV65Izz0z1xg1718Ivhd4b8IfBX4qeItWuxql+2tW+n6dHPOEijt1s9xYgnaR50hw2dvygDrXz/4v+HWo6ha6X8R/C7iwv7CTy7YiRSLslGG3AzlGAGQenPTFfL4XiDMvr0ZVZuSk/ej66adj6bGcPZX/Z8oUoKHKtJemurP1H+OekS/tAeAvDmpfDjw/wDbL3W/FOlalpkNgqyhJrtgsqPg4ACyyK4J9c1418XP2X4P2ev2jNQ+C3x6+OnhbRfCtpJHfLp1p4klkD73kldkhRAYTKzoSkmSmxiNysDXK/stftQD9kn9oSx8aa3p0uq+GdN1drq70W3cAJKYmRLmINgbl35xwGAI4ODXiXxK+Mtp8W/G+v8Ajvxl4mn/ALW1TU5bq6u9Q+fzHZixG8dFyQB0wOOnFfjuH40f1GNSnG05P3o9F5r9D9dr8LReNdOs7wS0l19PwKPxZ8TeNNAkvPh/8GruO8BE9v8A8JHbaq8VrPA8h+aSBl5mKKiiYAlQowRnAh+H/gWTwx4MiTV52vdRUlTLPMJNgK/NsJxgEgnpwGxmtnSfDsOl6VH4nuLWG8glbCtHcb1bvjqD+PSu78SSXfwn8F2XjnxHo2n3smpSKdPsJCpW3iB+Z2VRl2VckA4HA6k1xf8AEQs9wOKVWjGN0rK8eZLp1/M2nwLkuOwsqNWUrN3dpWb620P/2Q=='}}, 'prediction': [0.0560616329, 0.122713037, 0.121289924, 0.109751239, 0.121320881, 0.0897410363, 0.145011798, 0.0976110101, 0.0394041203, 0.0970953554]}
# + [markdown] id="make_online_predictions:migration"
# ## Make online predictions
# + [markdown] id="deploy_model:migration,new,mbsdk"
# ### [predictions.deploy-model-api](https://cloud.google.com/vertex-ai/docs/predictions/deploy-model-api)
# + [markdown] id="deploy_model:mbsdk,all"
# ## Deploy the model
#
# Next, deploy your model for online prediction. To deploy the model, you invoke the `deploy` method, with the following parameters:
#
# - `deployed_model_display_name`: A human readable name for the deployed model.
# - `traffic_split`: Percent of traffic at the endpoint that goes to this model, which is specified as a dictionary of one or more key/value pairs.
# If only one model, then specify as { "0": 100 }, where "0" refers to this model being uploaded and 100 means 100% of the traffic.
# If there are existing models on the endpoint, for which the traffic will be split, then use model_id to specify as { "0": percent, model_id: percent, ... }, where model_id is the model id of an existing model to the deployed endpoint. The percents must add up to 100.
# - `machine_type`: The type of machine to use for training.
# - `accelerator_type`: The hardware accelerator type.
# - `accelerator_count`: The number of accelerators to attach to a worker replica.
# - `starting_replica_count`: The number of compute instances to initially provision.
# - `max_replica_count`: The maximum number of compute instances to scale to. In this tutorial, only one instance is provisioned.
# + id="deploy_model:mbsdk,all"
DEPLOYED_NAME = "cifar10-" + TIMESTAMP
TRAFFIC_SPLIT = {"0": 100}
MIN_NODES = 1
MAX_NODES = 1
if DEPLOY_GPU:
endpoint = model.deploy(
deployed_model_display_name=DEPLOYED_NAME,
traffic_split=TRAFFIC_SPLIT,
machine_type=DEPLOY_COMPUTE,
accelerator_type=DEPLOY_GPU,
accelerator_count=DEPLOY_NGPU,
min_replica_count=MIN_NODES,
max_replica_count=MAX_NODES,
)
else:
endpoint = model.deploy(
deployed_model_display_name=DEPLOYED_NAME,
traffic_split=TRAFFIC_SPLIT,
machine_type=DEPLOY_COMPUTE,
accelerator_type=DEPLOY_GPU,
accelerator_count=0,
min_replica_count=MIN_NODES,
max_replica_count=MAX_NODES,
)
# + [markdown] id="deploy_model:mbsdk,all"
# *Example output:*
#
# INFO:google.cloud.aiplatform.models:Creating Endpoint
# INFO:google.cloud.aiplatform.models:Create Endpoint backing LRO: projects/759209241365/locations/us-central1/endpoints/4867177336350441472/operations/4087251132693348352
# INFO:google.cloud.aiplatform.models:Endpoint created. Resource name: projects/759209241365/locations/us-central1/endpoints/4867177336350441472
# INFO:google.cloud.aiplatform.models:To use this Endpoint in another session:
# INFO:google.cloud.aiplatform.models:endpoint = aiplatform.Endpoint('projects/759209241365/locations/us-central1/endpoints/4867177336350441472')
# INFO:google.cloud.aiplatform.models:Deploying model to Endpoint : projects/759209241365/locations/us-central1/endpoints/4867177336350441472
# INFO:google.cloud.aiplatform.models:Deploy Endpoint model backing LRO: projects/759209241365/locations/us-central1/endpoints/4867177336350441472/operations/1691336130932244480
# INFO:google.cloud.aiplatform.models:Endpoint model deployed. Resource name: projects/759209241365/locations/us-central1/endpoints/4867177336350441472
# + [markdown] id="endpoints_predict:migration,new,mbsdk"
# ### [predictions.online-prediction-automl](https://cloud.google.com/vertex-ai/docs/predictions/online-predictions-automl)
# + [markdown] id="get_test_item:test"
# ### Get test item
#
# You will use an example out of the test (holdout) portion of the dataset as a test item.
# + id="get_test_item:test"
test_image = x_test[0]
test_label = y_test[0]
print(test_image.shape)
# + [markdown] id="prepare_test_item:test,image"
# ### Prepare the request content
# You are going to send the CIFAR10 image as compressed JPG image, instead of the raw uncompressed bytes:
#
# - `cv2.imwrite`: Use openCV to write the uncompressed image to disk as a compressed JPEG image.
# - Denormalize the image data from \[0,1) range back to [0,255).
# - Convert the 32-bit floating point values to 8-bit unsigned integers.
# - `tf.io.read_file`: Read the compressed JPG images back into memory as raw bytes.
# - `base64.b64encode`: Encode the raw bytes into a base 64 encoded string.
# + id="prepare_test_item:test,image"
import base64
import cv2
cv2.imwrite("tmp.jpg", (test_image * 255).astype(np.uint8))
bytes = tf.io.read_file("tmp.jpg")
b64str = base64.b64encode(bytes.numpy()).decode("utf-8")
# + [markdown] id="predict_request:mbsdk,custom,icn"
# ### Make the prediction
#
# Now that your `Model` resource is deployed to an `Endpoint` resource, you can do online predictions by sending prediction requests to the Endpoint resource.
#
# #### Request
#
# Since in this example your test item is in a Cloud Storage bucket, you open and read the contents of the image using `tf.io.gfile.Gfile()`. To pass the test data to the prediction service, you encode the bytes into base64 -- which makes the content safe from modification while transmitting binary data over the network.
#
# The format of each instance is:
#
# { serving_input: { 'b64': base64_encoded_bytes } }
#
# Since the `predict()` method can take multiple items (instances), send your single test item as a list of one test item.
#
# #### Response
#
# The response from the `predict()` call is a Python dictionary with the following entries:
#
# - `ids`: The internal assigned unique identifiers for each prediction request.
# - `predictions`: The predicted confidence, between 0 and 1, per class label.
# - `deployed_model_id`: The Vertex AI identifier for the deployed `Model` resource which did the predictions.
# + id="predict_request:mbsdk,custom,icn"
# The format of each instance should conform to the deployed model's prediction input schema.
instances = [{serving_input: {"b64": b64str}}]
prediction = endpoint.predict(instances=instances)
print(prediction)
# + [markdown] id="predict_request:mbsdk,custom,icn"
# *Example output:*
#
# Prediction(predictions=[[0.0560616292, 0.122713044, 0.121289924, 0.109751239, 0.121320873, 0.0897410288, 0.145011798, 0.0976110175, 0.0394041166, 0.0970953479]], deployed_model_id='4087166195420102656', explanations=None)
# + [markdown] id="undeploy_model:mbsdk"
# ## Undeploy the model
#
# When you are done doing predictions, you undeploy the model from the `Endpoint` resouce. This deprovisions all compute resources and ends billing for the deployed model.
# + id="undeploy_model:mbsdk"
endpoint.undeploy_all()
# + [markdown] id="cleanup:mbsdk"
# # Cleaning up
#
# To clean up all Google Cloud resources used in this project, you can [delete the Google Cloud
# project](https://cloud.google.com/resource-manager/docs/creating-managing-projects#shutting_down_projects) you used for the tutorial.
#
# Otherwise, you can delete the individual resources you created in this tutorial:
#
# - Dataset
# - Pipeline
# - Model
# - Endpoint
# - AutoML Training Job
# - Batch Job
# - Custom Job
# - Hyperparameter Tuning Job
# - Cloud Storage Bucket
# + id="cleanup:mbsdk"
delete_all = True
if delete_all:
# Delete the dataset using the Vertex dataset object
try:
if "dataset" in globals():
dataset.delete()
except Exception as e:
print(e)
# Delete the model using the Vertex model object
try:
if "model" in globals():
model.delete()
except Exception as e:
print(e)
# Delete the endpoint using the Vertex endpoint object
try:
if "endpoint" in globals():
endpoint.delete()
except Exception as e:
print(e)
# Delete the AutoML or Pipeline trainig job
try:
if "dag" in globals():
dag.delete()
except Exception as e:
print(e)
# Delete the custom trainig job
try:
if "job" in globals():
job.delete()
except Exception as e:
print(e)
# Delete the batch prediction job using the Vertex batch prediction object
try:
if "batch_predict_job" in globals():
batch_predict_job.delete()
except Exception as e:
print(e)
# Delete the hyperparameter tuning job using the Vertex hyperparameter tuning object
try:
if "hpt_job" in globals():
hpt_job.delete()
except Exception as e:
print(e)
if "BUCKET_NAME" in globals():
# ! gsutil rm -r $BUCKET_NAME
| 42.228414 | 2,092 |
8f36d228d8e0402e973c83cc65c8b06384aa3504
|
py
|
python
|
irm/rex_cmnist.ipynb
|
tngym/fastai
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/tngym/fastai/blob/master/irm/rex_cmnist.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="8jP38pSUYPbj" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="9abf820d-73e2-4b38-850b-a087ee64ed21"
# https://github.com/capybaralet/REx_code_release/blob/802da4a45a92a1f7f2c50cb1aecf5a195ef65435/InvariantRiskMinimization/colored_mnist/main.py
import argparse
import numpy as np
import torch
import torch.nn.functional as F
from torchvision import datasets
from torch import nn, optim, autograd
def str2bool(v):
return v.lower() in ("yes", "true", "t", "1")
use_cuda = torch.cuda.is_available()
parser = argparse.ArgumentParser(description='Colored MNIST')
parser.add_argument('--hidden_dim', type=int, default=256)
parser.add_argument('--l2_regularizer_weight', type=float,default=0.001)
parser.add_argument('--lr', type=float, default=0.001)
parser.add_argument('--n_restarts', type=int, default=10)
parser.add_argument('--penalty_anneal_iters', type=int, default=100)
parser.add_argument('--penalty_weight', type=float, default=10000.0)
parser.add_argument('--steps', type=int, default=501)
parser.add_argument('--grayscale_model', type=str2bool, default=False)
parser.add_argument('--batch_size', type=int, default=25000)
parser.add_argument('--train_set_size', type=int, default=50000)
parser.add_argument('--eval_interval', type=int, default=100)
parser.add_argument('--print_eval_intervals', type=str2bool, default=True)
parser.add_argument('--train_env_1__color_noise', type=float, default=0.2)
parser.add_argument('--train_env_2__color_noise', type=float, default=0.1)
#parser.add_argument('--val_env__color_noise', type=float, default=0.1)
parser.add_argument('--test_env__color_noise', type=float, default=0.9)
parser.add_argument('--erm_amount', type=float, default=1.0)
parser.add_argument('--early_loss_mean', type=str2bool, default=True)
parser.add_argument('--rex', type=str2bool, default=True)
parser.add_argument('--mse', type=str2bool, default=True)
parser.add_argument('--plot', type=str2bool, default=True)
parser.add_argument('--save_numpy_log', type=str2bool, default=True)
# + id="yWEXD8oBY2BP" colab_type="code" colab={}
from matplotlib import pyplot as plt
# %matplotlib inline
# + id="9VERnHf4Y89r" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 402} outputId="e7f8bbe7-d13d-4dd7-945a-049ec172d346"
flags = parser.parse_args([])
print('Flags:')
for k,v in sorted(vars(flags).items()):
print("\t{}: {}".format(k, v))
num_batches = (flags.train_set_size // 2) // flags.batch_size
# TODO: logging
all_train_nlls = -1*np.ones((flags.n_restarts, flags.steps))
all_train_accs = -1*np.ones((flags.n_restarts, flags.steps))
#all_train_penalties = -1*np.ones((flags.n_restarts, flags.steps))
all_irmv1_penalties = -1*np.ones((flags.n_restarts, flags.steps))
all_rex_penalties = -1*np.ones((flags.n_restarts, flags.steps))
all_test_accs = -1*np.ones((flags.n_restarts, flags.steps))
all_grayscale_test_accs = -1*np.ones((flags.n_restarts, flags.steps))
final_train_accs = []
final_test_accs = []
highest_test_accs = []
# + id="0hv9qMW4Y-8G" colab_type="code" colab={}
restart = 1
# + id="fkkb2xunZEGF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 392, "referenced_widgets": ["b36c3c7556e1441b812c25efd0d1b740", "c6c2027046984d6aba2e94fafcc75089", "8393abe9ea3945f49f92859399a357ca", "7b7bb609e18a4d3f94609eddf7f9bbf1", "76d41f4a1053449e93da27e2b79ff540", "2509c1d62d934031bd008eef6fb6ae5e", "6723a50fe8bc43848fc4d8da590e160f", "751d15dc2c55440abffaa4127a5e0ae6", "722ca739eeb84401852eb5039445522c", "8aa55f5acf6f4ed1856e437615eb2b20", "612eca13854e446dbfd656e25947cfaa", "fe4b7cf8a7084186b0e8e34e9c0a9b81", "09c9910e6a8e4ab99353ab9b0886f70a", "bcacb279e9244eeba124393b603351f4", "e19a7cf58b864c79962d815608ee04b8", "9278b88e19224b808947b1063cdc8ca5", "a83487e590514d3fa75f621652d87c1d", "2fee9f09fef745b9a4cec05b57c4a5a6", "57f08f814fc04b7f9e5a2d52c8c63b04", "a41985f5600d4ed5b50c79634e1ec324", "148fe6ebf63742b1af3182eefa790389", "e69809dbc0a64dbba39f9e40374caff4", "2363a50311fe4fdebebbddda43e46b18", "e30c576797df4334a5910248cdadbecb", "3656e19510a14b8fabf066cf2d5f3997", "643fbd7ba47741d892d8d14b269367d2", "6ffa2fe4fc50458dbbc162e7fa48e125", "79fc1da58b6c41489bf2a44348aedaf4", "0a8890dc523144389c6b3d983e147f54", "47d4bc0c18034a7e880e6de8df31b9f2", "207f745d2dfb4c2282ccb239a6026b56", "2c44cd357935436eaead45b81db618b8"]} outputId="bf3f6201-6dc7-462f-fc80-ca7b9bc0b2b9"
highest_test_acc = 0.0
# Load MNIST, make train/val splits, and shuffle train set examples
mnist = datasets.MNIST('~/datasets/mnist', train=True, download=True)
mnist_train = (mnist.data[:50000], mnist.targets[:50000])
mnist_val = (mnist.data[50000:], mnist.targets[50000:])
rng_state = np.random.get_state()
np.random.shuffle(mnist_train[0].numpy())
np.random.set_state(rng_state)
np.random.shuffle(mnist_train[1].numpy())
# + id="tgKWfnl4ZOTE" colab_type="code" colab={}
# Build environments
def make_environment(images, labels, e, grayscale_dup=False):
def torch_bernoulli(p, size):
return (torch.rand(size) < p).float()
def torch_xor(a, b):
return (a-b).abs() # Assumes both inputs are either 0 or 1
# 2x subsample for computational convenience
images = images.reshape((-1, 28, 28))[:, ::2, ::2]
# Assign a binary label based on the digit; flip label with probability 0.25
labels = (labels < 5).float()
labels = torch_xor(labels, torch_bernoulli(.25, len(labels)))
# Assign a color based on the label; flip the color with probability e
colors = torch_xor(labels, torch_bernoulli(e, len(labels)))
# Apply the color to the image by zeroing out the other color channel
images = torch.stack([images, images], dim=1)
if not grayscale_dup:
images[torch.tensor(range(len(images))), (1-colors).long(), :, :] *= 0
if use_cuda:
return {
'images': (images.float() / 255.).cuda(),
'labels': labels[:, None].cuda()
}
else:
return {
'images': (images.float() / 255.),
'labels': labels[:, None]
}
envs = [
make_environment(mnist_train[0][::2], mnist_train[1][::2], flags.train_env_1__color_noise),
make_environment(mnist_train[0][1::2], mnist_train[1][1::2], flags.train_env_2__color_noise),
make_environment(mnist_val[0], mnist_val[1], flags.test_env__color_noise),
make_environment(mnist_val[0], mnist_val[1], flags.test_env__color_noise, grayscale_dup=True)
]
# + id="9Nq9SsqUa80f" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 80} outputId="27f2d670-4311-44c5-aa1f-574004032d6e"
fig, axs = plt.subplots(1, 10, figsize = (6, 6))
for i in range(10):
axs[i].imshow(mnist_train[0][i].numpy())
# + id="xqFxGZm0Z-Lm" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="761dfc7a-e9cc-48f1-ad9d-61b781733183"
def _show(img_id, env_id):
print(f"env: {env_id}, label: {envs[env_id]['labels'][img_id][0]}")
fig, axs = plt.subplots(1, 2, figsize = (2, 2))
axs[0].imshow(envs[env_id]["images"][img_id][0].cpu().numpy())
axs[1].imshow(envs[env_id]["images"][img_id][1].cpu().numpy())
plt.show();
for j in range(2):
for i in range(10):
_show(i, j)
for i in range(10):
for j in range(2, 4):
_show(i, j)
# + id="UfAIaKgQaPsL" colab_type="code" colab={}
# Define and instantiate the model
class MLP(nn.Module):
def __init__(self):
super(MLP, self).__init__()
if flags.grayscale_model:
lin1 = nn.Linear(14 * 14, flags.hidden_dim)
else:
lin1 = nn.Linear(2 * 14 * 14, flags.hidden_dim)
lin2 = nn.Linear(flags.hidden_dim, flags.hidden_dim)
lin3 = nn.Linear(flags.hidden_dim, 1)
for lin in [lin1, lin2, lin3]:
nn.init.xavier_uniform_(lin.weight)
nn.init.zeros_(lin.bias)
self._main = nn.Sequential(lin1, nn.ReLU(True), lin2, nn.ReLU(True), lin3)
def forward(self, input):
if flags.grayscale_model:
out = input.view(input.shape[0], 2, 14 * 14).sum(dim=1)
else:
out = input.view(input.shape[0], 2 * 14 * 14)
out = self._main(out)
return out
if use_cuda:
mlp = MLP().cuda()
else:
mlp = MLP()
# + [markdown] id="8b-yWtHFber2" colab_type="text"
# ここでは IRM のペナルティのみ定義.REx のペナルティは学習部分で
# + id="tVqe0W4pbbZ1" colab_type="code" colab={}
# Define loss function helpers
def mean_nll(logits, y):
return nn.functional.binary_cross_entropy_with_logits(logits, y)
def mean_accuracy(logits, y):
preds = (logits > 0.).float()
return ((preds - y).abs() < 1e-2).float().mean()
def penalty(logits, y):
if use_cuda:
scale = torch.tensor(1.).cuda().requires_grad_()
else:
scale = torch.tensor(1.).requires_grad_()
loss = mean_nll(logits * scale, y)
grad = autograd.grad(loss, [scale], create_graph=True)[0]
return torch.sum(grad**2)
# + id="1ZqzKP-rbhY8" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 139} outputId="f626f277-5b8a-4bdf-eb8f-c4cb81c1afba"
# Train loop
def pretty_print(*values):
col_width = 13
def format_val(v):
if not isinstance(v, str):
v = np.array2string(v, precision=5, floatmode='fixed')
return v.ljust(col_width)
str_values = [format_val(v) for v in values]
print(" ".join(str_values))
optimizer = optim.Adam(mlp.parameters(), lr=flags.lr)
pretty_print('step', 'train nll', 'train acc', 'rex penalty', 'irmv1 penalty', 'test acc')
i = 0
for step in range(flags.steps):
n = i % num_batches
for edx, env in enumerate(envs):
if edx != len(envs) - 2:
logits = mlp(env['images'][n*flags.batch_size:(n+1)*flags.batch_size])
env['nll'] = mean_nll(logits, env['labels'][n*flags.batch_size:(n+1)*flags.batch_size])
env['acc'] = mean_accuracy(logits, env['labels'][n*flags.batch_size:(n+1)*flags.batch_size])
env['penalty'] = penalty(logits, env['labels'][n*flags.batch_size:(n+1)*flags.batch_size])
else:
# validation data に対してはこちら
logits = mlp(env['images'])
env['nll'] = mean_nll(logits, env['labels'])
env['acc'] = mean_accuracy(logits, env['labels'])
env['penalty'] = penalty(logits, env['labels'])
i+=1
# training data は envs[0] と envs[1]
train_nll = torch.stack([envs[0]['nll'], envs[1]['nll']]).mean()
train_acc = torch.stack([envs[0]['acc'], envs[1]['acc']]).mean()
irmv1_penalty = torch.stack([envs[0]['penalty'], envs[1]['penalty']]).mean()
if use_cuda:
weight_norm = torch.tensor(0.).cuda()
else:
weight_norm = torch.tensor(0.)
for w in mlp.parameters():
weight_norm += w.norm().pow(2)
loss1 = envs[0]['nll']
loss2 = envs[1]['nll']
if flags.early_loss_mean:
loss1 = loss1.mean()
loss2 = loss2.mean()
loss = 0.0
loss += flags.erm_amount * (loss1 + loss2) # Loss の第一項: ERM term
loss += flags.l2_regularizer_weight * weight_norm # Loss の第二項:weight regularization
penalty_weight = (flags.penalty_weight # penalty 項は最初はすごく小さく途中から大きくする
if step >= flags.penalty_anneal_iters else 1.0) # この重みは IRM/MinREx/VarREx 共通
if flags.mse:
rex_penalty = (loss1.mean() - loss2.mean()) ** 2 # Minimax REx
else:
rex_penalty = (loss1.mean() - loss2.mean()).abs() # Variance REx
if flags.rex:
loss += penalty_weight * rex_penalty
else:
loss += penalty_weight * irmv1_penalty
if penalty_weight > 1.0: # penalty weight >=1 なので if がなくても同じ
# Rescale the entire loss to keep gradients in a reasonable range
loss /= penalty_weight
optimizer.zero_grad()
loss.backward()
optimizer.step()
test_acc = envs[2]['acc']
grayscale_test_acc = envs[3]['acc']
# 以下はただ記録を保持するだけ
if step % flags.eval_interval == 0:
train_acc_scalar = train_acc.detach().cpu().numpy()
test_acc_scalar = test_acc.detach().cpu().numpy()
if flags.print_eval_intervals:
# ここで print する
pretty_print(
np.int32(step),
train_nll.detach().cpu().numpy(),
train_acc.detach().cpu().numpy(),
rex_penalty.detach().cpu().numpy(),
irmv1_penalty.detach().cpu().numpy(),
test_acc.detach().cpu().numpy()
)
if (train_acc_scalar >= test_acc_scalar) and (test_acc_scalar > highest_test_acc):
highest_test_acc = test_acc_scalar
if flags.plot or flags.save_numpy_log:
all_train_nlls[restart, step] = train_nll.detach().cpu().numpy()
all_train_accs[restart, step] = train_acc.detach().cpu().numpy()
all_rex_penalties[restart, step] = rex_penalty.detach().cpu().numpy()
all_irmv1_penalties[restart, step] = irmv1_penalty.detach().cpu().numpy()
all_test_accs[restart, step] = test_acc.detach().cpu().numpy()
all_grayscale_test_accs[restart, step] = grayscale_test_acc.detach().cpu().numpy()
# + id="edEqMh-kbhKU" colab_type="code" colab={}
# + id="MLSMClLMcZkw" colab_type="code" colab={}
| 38.849398 | 1,324 |
1a5a2c758c175edb14d82e56036ef24374ef27e4
|
py
|
python
|
JavaScripts/Image/ReduceRegion.ipynb
|
OIEIEIO/earthengine-py-notebooks
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <table class="ee-notebook-buttons" align="left">
# <td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/JavaScripts/Image/ReduceRegion.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
# <td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/JavaScripts/Image/ReduceRegion.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
# <td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/JavaScripts/Image/ReduceRegion.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
# </table>
# ## Install Earth Engine API and geemap
# Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
# The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
#
# **Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
# +
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as geemap
except:
import geemap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
# -
# ## Create an interactive map
# The default basemap is `Google MapS`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/basemaps.py) can be added using the `Map.add_basemap()` function.
Map = geemap.Map(center=[40,-100], zoom=4)
Map
# ## Add Earth Engine Python script
# +
# Add Earth Engine dataset
# Image.reduceRegion example
#
# Computes a simple reduction over a region of an image. A reduction
# is any process that takes an arbitrary number of inputs (such as
# all the pixels of an image in a given region) and computes one or
# more fixed outputs. The result is a dictionary that contains the
# computed values, which in this example is the maximum pixel value
# in the region.
# This example shows how to print the resulting dictionary to the
# console, which is useful when developing and debugging your
# scripts, but in a larger workflow you might instead use the
# Dicitionary.get() function to extract the values you need from the
# dictionary for use as inputs to other functions.
# The input image to reduce, in this case an SRTM elevation map.
image = ee.Image('CGIAR/SRTM90_V4')
# The region to reduce within.
poly = ee.Geometry.Rectangle([-109.05, 41, -102.05, 37])
# Reduce the image within the given region, using a reducer that
# computes the max pixel value. We also specify the spatial
# resolution at which to perform the computation, in this case 200
# meters.
max = image.reduceRegion({
'reducer': ee.Reducer.max(),
'geometry': poly,
'scale': 200
})
# Print the result (a Dictionary) to the console.
print(max)
# -
# ## Display Earth Engine data layers
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
| 49.15534 | 1,023 |
a6fb994475a2c5309275dd167e9f84f6555daaac
|
py
|
python
|
task3_circuit_transpilation/task3_main.ipynb
|
Mohamed-ShehabEldin/Circuit-Transpilation-and-Generative-Modeling-QOSF-Task-1-3
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1 align="center">Quantum circuit tranpilation into rotations and introducing an informative measure of overhead at constant number of Qubits</h1>
# <h4 align="center">Using Python & Qiskit</h4>
# <h3 align="center">Mohamed Sami ShehabEldin</h3>
# <h4 align="center">Zewail City of Science and Technology</h4>
# -------
# **It is known that quantum circuit overhead is proportional to the number of gates times the number of qubits, and it is usually used to compare the resource usage of different circuits. Here, I am introducing an informative measure (return a number) for circuits with the same number of qubits that does not only convey the number of gates but also how much it is effective in the circuit. For example, a circuit composed of 6 identities is not the same as a circuit contains 6 Pauli gates. This will be useful in physical realization, as quantum gates are physically realized by rotations, and the new physical circuit will have the same dimensions. However, the same output can be done with different choices of rotations; one can choose many gates of small contributions or many redundant gates with high effect, or just the effective gates. In this work, I am making a function that transpiles the original circuit onto a physical circuit and introduces an informative measure that discriminates the mentioned situations; the measure proposes that the second circuit will have the highest overhead while the last one is the least.**
# ----
# ### Outline
# <br>
# <strong>
# 1. Task Definition (from QOSF application)
# <br>
# <br>
# 2. Circuit transpilation
# <br>
# 2.1. Theory
# <br>
# 2.2. Function 1: parameters of unitary
# <br>
# 2.3. Function 2: gate to unitary
# <br>
# 2.4. Function 3: gate transpile
# <br>
# 2.5. Function 4: location range
# <br>
# 2.6. The Master Function: Quantum Circuit Transpiler
# <br>
# <br>
# 3. OverHead Analysis
# <br>
# 3.1. Quantifying Circuit Involvement <span style="color:red"> *(Genuinely)*</span>
# <br>
# 3.2. Reducing the overhead
# <br>
# <br>
# Complementary Part: "Quantifying Circuit Involvement Implementation" (in this folder)
# <strong/>
# ------------
# ## 1. Task Definition (from QOSF application):
# <img src="images/t3.png" width="600" height="500">
# --------------
# ## 2. Circuit transpilation:
# ### 2.1. Theory:
# As we want to transpile any single qubit gate into X and Y rotations, it comes to the mind a well known theorem states that any unitary U can be written as (Neilsen&Chuang P. 175):
# $$
# U = e^{i\alpha} R_z(\beta)R_y(\gamma)R_z(\delta)
# $$
# and this has equivlent form:
# $$
# U = e^{i\alpha} R_z(\beta)R_x(\gamma)R_z(\delta)
# $$
# This is my key for this task, as I can use it to transform any single qubit gate to $R_zR_xR_z$ and I can reduce any number of gates in series into just three rotation gates $R_zR_xR_z$.
# ### 2.2. Function 1: parameters of unitary
# This function will get the 4 parameters $\alpha, \beta,\gamma, \delta$ for any given 2*2 unitary matrix. This based in the following analysis:
# $$
# U = e^{i\alpha} R_z(\beta)R_x(\gamma)R_z(\delta)=
# \begin{pmatrix}
# e^{i(2\alpha-\beta-\delta)/2}cos(\frac{\gamma}{2}) & e^{i(2\alpha-\beta+\delta+3\pi)/2}sin(\frac{\gamma}{2})\\ e^{i(2\alpha+\beta-\delta+3\pi)/2}sin(\frac{\gamma}{2}) & e^{i(2\alpha+\beta+\delta)/2}cos(\frac{\gamma}{2})
# \end{pmatrix}
# $$
# +
import numpy as np
from numpy.random import randint
import scipy.optimize
pii=np.pi
def par_of_unitary(unitary,message=False):
unitry=np.array(unitary)
re_u00=np.real(unitary[0][0]) #real part of first entry of unitary matrix
im_u00=np.imag(unitary[0][0]) #imaginary part of first entry of unitary matrix
re_u01=np.real(unitary[0][1])
im_u01=np.imag(unitary[0][1])
re_u10=np.real(unitary[1][0])
im_u10=np.imag(unitary[1][0])
re_u11=np.real(unitary[1][1])
im_u11=np.imag(unitary[1][1])
def equations(p): #this is the set of equation came from equating the parameterized form with the given matrix
a,b,c,f = p #f is the phase, a,b,c are beta, gamma, delta
f1=(np.cos((-a-c+2*f)/2)*np.cos(b/2)-re_u00)
f2=(np.sin((-a-c+2*f)/2)*np.cos(b/2)-im_u00)
f3=(np.cos((-a+c+2*f+3*pii)/2)*np.sin(b/2)-re_u01)
f4=(np.sin((-a+c+2*f+3*pii)/2)*np.sin(b/2)-im_u01)
f5=(np.cos((a-c+2*f+3*pii)/2)*np.sin(b/2)-re_u10)
f6=(np.sin((a-c+2*f+3*pii)/2)*np.sin(b/2)-im_u10)
f7=(np.cos((a+c+2*f)/2)*np.cos(b/2)-re_u11)
f8=(np.sin((a+c+2*f)/2)*np.cos(b/2)-im_u11)
return np.asarray((f1,f2,f3,f4,f5,f6,f7,f8,f8))
#solving this set as homogoneus equation: f1=0,f2=0,...
x = scipy.optimize.leastsq(equations, np.asarray((pii/2,pii/2,pii/2,pii/2)))[0]
if message:
print("The given unitary can be expressed as Rz({alpha})*Rx({beta})*Rz({gamma})*GlobalPhase({phi}))"
.format(alpha=x[0],beta=x[1],gamma=x[2],phi=x[3]))
print("Matching Error: ",equations(x))
return x
# -
# **Example**:
u=np.array([[1,0],[0,1j]])
x=par_of_unitary(u,message=True)
from qiskit import *
pii=np.pi
qc=QuantumCircuit(1)
if round(x[0],2)!=0.0: qc.rz(x[0],0)
if round(x[1],2)!=0.0: qc.rx(x[1],0)
if round(x[2],2)!=0.0: qc.rz(x[2],0)
backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc,backend).result().get_unitary()
from qiskit_textbook.tools import array_to_latex
array_to_latex(unitary, pretext="\\text{Circuit = }\n")
qc.draw()
# Now, we can transform any given 2*2 unitary to Rz,Rx,Rz up to a phase. Usually, when executing a circuit with qiskit, it ignores the phase in get_unitary method.
# ### 2.3. Function 2: gate to unitary
# The very logic step come after the ability of transformation of any unitary to z&x rotations, is to transform gates to unitaries. Qiskit have some problems in this tool so I do it myself (simple).
def gate_to_matrix(gate_data): #gate data : qc.data[gate_number],
#this convey the regester and all gate information inside a circuit.
gate_object=gate_data[0] #gate info
register_object=gate_data[1] #register info, I.E target and control
qc=QuantumCircuit(len(register_object)) #making new quantum circuit to get its equivlent unitary
qc.append(gate_object,list(range(len(register_object)))) #adding the gate to the new circuit
backend = Aer.get_backend('unitary_simulator')
unitary = execute(qc,backend).result().get_unitary() #extract its equivlent unitary
return unitary
#example
qc1=QuantumCircuit(3,2)
qc1.h(0)
qc1.cx(0,1)
qc1.x([0,1])
qc1.h([1,2])
qc1.measure([0,1],[0,1])
qc1.draw("mpl")
gate_to_matrix(qc1.data[0])
# ### 2.4. Function 3: gate transpile
# I think now that my game has been revealed. Just after changing the gate to unitary we can change the unitary to the 3 x&y rotations gates. However, we did not mention CX gate, But the good news is:
# <table><tr>
# <td> <img src="images/cx1.png" /> </td>
# <td> <img src="images/cx2.png" /> </td>
# <td> <img src="images/cx3.png" /> </td>
#
# </tr></table>
# These three circuits are all equivlent (as X=HZH), so we have to say to CX welcome to the group!
# +
def gate_transpile(gate_data):
gate_object=gate_data[0] #gate info
register_object=gate_data[1] #register info
if len(register_object)==1: #I.E if it is unitary on one qubit
u=gate_to_matrix(gate_data)
th=par_of_unitary(u)
qc=QuantumCircuit(1) #I will return this 1 register circuit
if round(th[0],2)!=0.0: qc.rz(th[0],0)
if round(th[1],2)!=0.0: qc.rx(th[1],0)
if round(th[2],2)!=0.0: qc.rz(th[2],0)
if len(register_object)==2: #here I will consider that CX and CZ are the only multi registers gate
qc=QuantumCircuit(2) #i will return this 2 registers circuit
pii=np.pi
if gate_object.name=='cx': #X=HZH=rz*rx*rz*z*rz*rx*rz, I will not use recursion for simplicity
qc.rz(pii/2,register_object[1].index)
qc.rx(pii/2,register_object[1].index)
qc.rz(pii/2,register_object[1].index)
qc.cz(register_object[0].index,register_object[1].index)
qc.rz(pii/2,register_object[1].index)
qc.rx(pii/2,register_object[1].index)
qc.rz(pii/2,register_object[1].index)
return qc
# -
gate_transpile(qc1.data[2]).draw()
# ### 2.5. Function 4: location range
# Now in order to apply the resulting circuit of gate_transpile in the right place in the mirror circuit, I just have to to know the location range (initial to final register) of the original gate in the original circuit.
def location_range(register_object):
ends=[register_object[0].index,register_object[-1].index] #index of target and control registr
rang=list(range(min(ends),max(ends)+1)) #making a sorted list of their range
return rang
# ### 2.6. The Master Function: Quantum Circuit Transpiler
# Now, we have all the needed functions to transpile an original circuit to a mirror circuit that only have gates belongs to the restricted group.
def qc_transpiler(qc):
qn=qc.num_qubits #number of quantum registers
cn=qc.num_clbits # -- -- classical --
transpiled_qc=QuantumCircuit(qn,cn) #the mirror circuit
M=0 #to consider measurment
for gate_data in qc.data: #run on all gates in the original QC
register_object=gate_data[1] #register info
if gate_data[0].name=="measure": #considering the measurment
transpiled_qc.measure(register_object[0].index,M)
M=M+1
else: #other gates transpilation
transpiled_gate=gate_transpile(gate_data)
transpiled_qc.append(transpiled_gate,location_range(register_object))
return transpiled_qc.decompose()
qc2=qc_transpiler(qc1)
qc2.draw("mpl")
# ----------
# ## 3. OverHead Analysis
# ### 3.1. Quantifying Circuit Involvement (Genuinely)
# As mentioned in the statement of the task, the transpiled circuit is much more complicate and delicate or Involved. But how to quantify this Involvement? Let's call this measure "Involvement".
#
# It may come to the mind that we can just count the number of gates in each cases and this will be a measure of the circuit delicacy. This may be write BUT Is the addition of $R_z(\pi)$ or $R_z(\frac{\pi}{2})$ or $R_z(\frac{\pi}{8})$ or $R_z(0.000001)$ contribute with the same Involvement?
#
# I want to make a measure that capture that! That is having extra gates that have low effect (like $R_z(0.000001)$ or Identity) will contribute to the Involvement with less amount than having extra gates that are more effective. Note that Circuit depth does not capture that!
#
# Abstractly, I will define the circuit A overhead from another circuit B to be:
# $$
# \bf{Overhead(A,B)=Involvement(A)-Involvement(B)}
# $$
# Now, I think that I have a regourous method that capture many things, I will introduce it as set of definitions then the intuition will be more obvious in the implementation part.
#
# Define:
#
# **StateTrip(i): The trace distance between the initial state and the new state just after the $i^{th}$ gate of the circuit.**
#
# $$\bf{GateTrip(i) \equiv StateTrip(i) - StateTrip(i-1)}$$
# Now, one can say Ok, let's make the involvment be the sum over all GateTrip(i), as this will capture how significant the gates are! but the problem is the a circuit A, and the same circuit with punsh of identities(small changes) applied everywhere will have the same measure. Also, I think this will be insufficient for gate replacement with equivlent gates. So, to measure how a circuit is delicate one should be delicate too!
#
# I figuired out a similar way that can capture all of that, and I think it even capture more than I think!
#
# $$
# \bf{Involvement(A)= AreaUnder(StateTrip(i)) - |AreaUnder(StateTrip(i))-AreaUnder(gateTrip(i))|}
# $$
# where AreaUnder(StateTrip(i)) is just the area under the curve for the whole circuit (this can have a complicated and elegant form, but lets stay simple and sufficient).
# This will be understood better in python implementation and results.
#
#
# **Implementation this Idea in the other file inside this folder.**
# **Implications:**
# * To reduce the Involvement we have to reduce the brutality of the existing gates and there numbers.
# * The Zero Involved circuit, must have no effective gates.
# The Implementation and Results of this method is in "Quantifying Circuit Involvement Implementation" notebook.
# Because Qiskit State Tomography cannot work after using it many times.
# (BrokenProcessPool: A process in the process pool was terminated abruptly while the future was running or pending.) (I failed in my search for this problem solution).
# ### 3.2. Reducing the overhead
# As I have mentioned My key is:
# $$
# U = e^{i\alpha} R_z(\beta)R_x(\gamma)R_z(\delta)
# $$
# as I can transform any number of gates in series into just 3 gates.
#
# $CZs$ make an obstacle in reducing the number of gates. Fortunately, $Z$ and $I$ commutes with $R_z$, so we can pass $R_z$ through the target gate! and then use $R_z(a)R_z(b)=R_z(a+b)$. we can do more non systematic reduction by using this concept of commutation, for example we can commute a series of pauli's twice, and this should be done case by case.
# Making a function that takes a QC including arbitrary number of CZs and find each sequence of single gates then transform it int 3 rotation will be a long task that is not required. However, I can make a function that return the desired output if we just rewrite the gates of the transpiled circuit. What I mean is the following:
#
# (This is ridiculous but I just want t apply the concept.)
# +
#this is the function that transform any sequence of rotations gates into 3 rotations
def appendrots(qc, register, *instructions):
'''
qc=QuantumCircuit we will apply the sequence on, register= the register where we apply the sequnce
instruction=gates instructions we seek to apply
'''
line=QuantumCircuit(1) #the line that will carry the sequence
for i in range(len(instructions)): #run over all the instructions
name=instructions[i].__getitem__(0).name #name of the instruction
theta=instructions[i].__getitem__(0).params[0] #parameter of the instruction
if name=="rz":
line.rz(theta,0)
if name=="rx":
line.rx(theta,0)
#I can continue put if for all gates, but consider we just focus on a line of rotations.
backend = Aer.get_backend('unitary_simulator')
unitary = execute(line,backend).result().get_unitary() #getting the corresponding unitary of the line
x=par_of_unitary(unitary) #getting the corresponding rotation parameters of the unitary
if round(x[1],2)!=0.0:
if round(x[0],2)!=0.0: qc.rz(x[0],register)
qc.rx(x[1],register)
if round(x[2],2)!=0.0: qc.rz(x[2],register)
else:
if round(x[0],2)!=0.0 or round(x[2],2)!=0.0: qc.rz(x[0]+x[2],register)
# -
# So in this section the user have to code a little part himself instead of just put inputs into a function.
# Now, to reduced the overhead of the circuit in my example, we have to rewrite the instructions, this is ridiculous but I just want to apply the concept.
qc3=QuantumCircuit(3,2) #reduced over head circuit
I=QuantumCircuit(3,2) #for instructions
# +
#the already 3 on sequence leave it
qc3.rz(pii/2,0)
qc3.rx(pii/2,0)
qc3.rz(pii/2,0)
qc3.rz(pii/2,1)
qc3.rx(pii/2,1)
qc3.rz(pii/2,1)
qc3.cz(0,1)
qc3.rz(pii/2,0)
qc3.rx(pii,0)
qc3.rz(pii/2,0)
#for mare than 3 on sequnece we apply the function
appendrots(qc3,1,
I.rz(pii/2,1),
I.rx(pii/2,1),
I.rz(pii/2,1),
I.rz(pii/2,1),
I.rx(pii,1),
I.rz(pii/2,1),
I.rz(pii/2,1),
I.rx(pii/2,1),
I.rz(pii/2,1))
qc3.rz(pii/2,2)
qc3.rx(pii/2,2)
qc3.rz(pii/2,2)
qc3.measure(0,0)
qc3.measure(1,1)
qc3.draw("mpl")
# -
# lets commute this $R_z$ over the target gate.
qc4=QuantumCircuit(3,2) #reduced over head circuit
qc4.rz(pii/2,0)
qc4.rx(pii/2,0)
qc4.rz(pii/2,0)
qc4.rz(pii/2,1)
qc4.rx(pii/2,1)
qc4.cz(0,1)
qc4.rz(3*pii/2,1)
qc4.rz(pii/2,0)
qc4.rx(pii,0)
qc4.rz(pii/2,0)
qc4.rz(pii/2,2)
qc4.rx(pii/2,2)
qc4.rz(pii/2,2)
qc4.measure(0,0)
qc4.measure(1,1)
qc4.draw("mpl")
# As we see, the number of gates reduced keeping all existing gate belong to the restricted group.
# The overhead difference is in the "Quantifying Circuit Involvement Implementation" notebook.
# <span style="color:blue">some *blue* text</span>.
#
| 38.846868 | 1,165 |
a667c21ffefb3997f16992905363d6c825170b98
|
py
|
python
|
3. Landmark Detection and Tracking.ipynb
|
JSchuurmans/P3_Implement_SLAM
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Project 3: Implement SLAM
#
# ---
#
# ## Project Overview
#
# In this project, you'll implement SLAM for robot that moves and senses in a 2 dimensional, grid world!
#
# SLAM gives us a way to both localize a robot and build up a map of its environment as a robot moves and senses in real-time. This is an active area of research in the fields of robotics and autonomous systems. Since this localization and map-building relies on the visual sensing of landmarks, this is a computer vision problem.
#
# Using what you've learned about robot motion, representations of uncertainty in motion and sensing, and localization techniques, you will be tasked with defining a function, `slam`, which takes in six parameters as input and returns the vector `mu`.
# > `mu` contains the (x,y) coordinate locations of the robot as it moves, and the positions of landmarks that it senses in the world
#
# You can implement helper functions as you see fit, but your function must return `mu`. The vector, `mu`, should have (x, y) coordinates interlaced, for example, if there were 2 poses and 2 landmarks, `mu` will look like the following, where `P` is the robot position and `L` the landmark position:
# ```
# mu = matrix([[Px0],
# [Py0],
# [Px1],
# [Py1],
# [Lx0],
# [Ly0],
# [Lx1],
# [Ly1]])
# ```
#
# You can see that `mu` holds the poses first `(x0, y0), (x1, y1), ...,` then the landmark locations at the end of the matrix; we consider a `nx1` matrix to be a vector.
#
# ## Generating an environment
#
# In a real SLAM problem, you may be given a map that contains information about landmark locations, and in this example, we will make our own data using the `make_data` function, which generates a world grid with landmarks in it and then generates data by placing a robot in that world and moving and sensing over some numer of time steps. The `make_data` function relies on a correct implementation of robot move/sense functions, which, at this point, should be complete and in the `robot_class.py` file. The data is collected as an instantiated robot moves and senses in a world. Your SLAM function will take in this data as input. So, let's first create this data and explore how it represents the movement and sensor measurements that our robot takes.
#
# ---
# ## Create the world
#
# Use the code below to generate a world of a specified size with randomly generated landmark locations. You can change these parameters and see how your implementation of SLAM responds!
#
# `data` holds the sensors measurements and motion of your robot over time. It stores the measurements as `data[i][0]` and the motion as `data[i][1]`.
#
# #### Helper functions
#
# You will be working with the `robot` class that may look familiar from the first notebook,
#
# In fact, in the `helpers.py` file, you can read the details of how data is made with the `make_data` function. It should look very similar to the robot move/sense cycle you've seen in the first notebook.
# +
import numpy as np
from helpers import make_data
# your implementation of slam should work with the following inputs
# feel free to change these input values and see how it responds!
# world parameters
num_landmarks = 5 # number of landmarks
N = 20 # time steps
world_size = 100.0 # size of world (square)
# robot parameters
measurement_range = 50.0 # range at which we can sense landmarks
motion_noise = 2.0 # noise in robot motion
measurement_noise = 2.0 # noise in the measurements
distance = 20.0 # distance by which robot (intends to) move each iteratation
# make_data instantiates a robot, AND generates random landmarks for a given world size and number of landmarks
data = make_data(N, num_landmarks, world_size, measurement_range, motion_noise, measurement_noise, distance)
# -
# ### A note on `make_data`
#
# The function above, `make_data`, takes in so many world and robot motion/sensor parameters because it is responsible for:
# 1. Instantiating a robot (using the robot class)
# 2. Creating a grid world with landmarks in it
#
# **This function also prints out the true location of landmarks and the *final* robot location, which you should refer back to when you test your implementation of SLAM.**
#
# The `data` this returns is an array that holds information about **robot sensor measurements** and **robot motion** `(dx, dy)` that is collected over a number of time steps, `N`. You will have to use *only* these readings about motion and measurements to track a robot over time and find the determine the location of the landmarks using SLAM. We only print out the true landmark locations for comparison, later.
#
#
# In `data` the measurement and motion data can be accessed from the first and second index in the columns of the data array. See the following code for an example, where `i` is the time step:
# ```
# measurement = data[i][0]
# motion = data[i][1]
# ```
#
# +
# print out some stats about the data
time_step = 0
print('Example measurements: \n', data[time_step][0])
print('\n')
print('Example motion: \n', data[time_step][1])
# -
# Try changing the value of `time_step`, you should see that the list of measurements varies based on what in the world the robot sees after it moves. As you know from the first notebook, the robot can only sense so far and with a certain amount of accuracy in the measure of distance between its location and the location of landmarks. The motion of the robot always is a vector with two values: one for x and one for y displacement. This structure will be useful to keep in mind as you traverse this data in your implementation of slam.
# ## Initialize Constraints
#
# One of the most challenging tasks here will be to create and modify the constraint matrix and vector: omega and xi. In the second notebook, you saw an example of how omega and xi could hold all the values the define the relationships between robot poses `xi` and landmark positions `Li` in a 1D world, as seen below, where omega is the blue matrix and xi is the pink vector.
#
# <img src='images/motion_constraint.png' width=50% height=50% />
#
#
# In *this* project, you are tasked with implementing constraints for a 2D world. We are referring to robot poses as `Px, Py` and landmark positions as `Lx, Ly`, and one way to approach this challenge is to add *both* x and y locations in the constraint matrices.
#
# <img src='images/constraints2D.png' width=50% height=50% />
#
# You may also choose to create two of each omega and xi (one for x and one for y positions).
# ### TODO: Write a function that initializes omega and xi
#
# Complete the function `initialize_constraints` so that it returns `omega` and `xi` constraints for the starting position of the robot. Any values that we do not yet know should be initialized with the value `0`. You may assume that our robot starts out in exactly the middle of the world with 100% confidence (no motion or measurement noise at this point). The inputs `N` time steps, `num_landmarks`, and `world_size` should give you all the information you need to construct intial constraints of the correct size and starting values.
#
# *Depending on your approach you may choose to return one omega and one xi that hold all (x,y) positions *or* two of each (one for x values and one for y); choose whichever makes most sense to you!*
def initialize_constraints(N, num_landmarks, world_size):
''' This function takes in a number of time steps N, number of landmarks, and a world_size,
and returns initialized constraint matrices, omega and xi.'''
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
dim = N + num_landmarks
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
omega = np.zeros((2,dim,dim))
omega[:,0,0] += 1
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
xi = np.zeros((2,dim))
xi[:,0] += world_size/2
return omega, xi
# ### Test as you go
#
# It's good practice to test out your code, as you go. Since `slam` relies on creating and updating constraint matrices, `omega` and `xi` to account for robot sensor measurements and motion, let's check that they initialize as expected for any given parameters.
#
# Below, you'll find some test code that allows you to visualize the results of your function `initialize_constraints`. We are using the [seaborn](https://seaborn.pydata.org/) library for visualization.
#
# **Please change the test values of N, landmarks, and world_size and see the results**. Be careful not to use these values as input into your final smal function.
#
# This code assumes that you have created one of each constraint: `omega` and `xi`, but you can change and add to this code, accordingly. The constraints should vary in size with the number of time steps and landmarks as these values affect the number of poses a robot will take `(Px0,Py0,...Pxn,Pyn)` and landmark locations `(Lx0,Ly0,...Lxn,Lyn)` whose relationships should be tracked in the constraint matrices. Recall that `omega` holds the weights of each variable and `xi` holds the value of the sum of these variables, as seen in Notebook 2. You'll need the `world_size` to determine the starting pose of the robot in the world and fill in the initial values for `xi`.
# import data viz resources
import matplotlib.pyplot as plt
from pandas import DataFrame
import seaborn as sns
# %matplotlib inline
# +
# define a small N and world_size (small for ease of visualization)
N_test = 5
num_landmarks_test = 2
small_world = 10
# initialize the constraints
initial_omega, initial_xi = initialize_constraints(N_test, num_landmarks_test, small_world)
# +
# define figure size
plt.rcParams["figure.figsize"] = (10,7)
# display omega
sns.heatmap(DataFrame(initial_omega[0]), cmap='Blues', annot=True, linewidths=.5)
# +
# define figure size
plt.rcParams["figure.figsize"] = (1,7)
# display xi
sns.heatmap(DataFrame(initial_xi[0]), cmap='Oranges', annot=True, linewidths=.5)
# -
# ---
# ## SLAM inputs
#
# In addition to `data`, your slam function will also take in:
# * N - The number of time steps that a robot will be moving and sensing
# * num_landmarks - The number of landmarks in the world
# * world_size - The size (w/h) of your world
# * motion_noise - The noise associated with motion; the update confidence for motion should be `1.0/motion_noise`
# * measurement_noise - The noise associated with measurement/sensing; the update weight for measurement should be `1.0/measurement_noise`
#
# #### A note on noise
#
# Recall that `omega` holds the relative "strengths" or weights for each position variable, and you can update these weights by accessing the correct index in omega `omega[row][col]` and *adding/subtracting* `1.0/noise` where `noise` is measurement or motion noise. `Xi` holds actual position values, and so to update `xi` you'll do a similar addition process only using the actual value of a motion or measurement. So for a vector index `xi[row][0]` you will end up adding/subtracting one measurement or motion divided by their respective `noise`.
#
# ### TODO: Implement Graph SLAM
#
# Follow the TODO's below to help you complete this slam implementation (these TODO's are in the recommended order), then test out your implementation!
#
# #### Updating with motion and measurements
#
# With a 2D omega and xi structure as shown above (in earlier cells), you'll have to be mindful about how you update the values in these constraint matrices to account for motion and measurement constraints in the x and y directions. Recall that the solution to these matrices (which holds all values for robot poses `P` and landmark locations `L`) is the vector, `mu`, which can be computed at the end of the construction of omega and xi as the inverse of omega times xi: $\mu = \Omega^{-1}\xi$
#
# **You may also choose to return the values of `omega` and `xi` if you want to visualize their final state!**
# +
## TODO: Complete the code to implement SLAM
## slam takes in 6 arguments and returns mu,
## mu is the entire path traversed by a robot (all x,y poses) *and* all landmarks locations
def slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise):
## TODO: Use your initilization to create constraint matrices, omega and xi
omega, xi = initialize_constraints(N, num_landmarks, world_size)
## TODO: Iterate through each time step in the data
## get all the motion and measurement data as you iterate
for t,d in enumerate(data):
measurements = d[0]
motions = d[1]
## TODO: update the constraint matrix/vector to account for all *measurements*
## this should be a series of additions that take into account the measurement noise
for measurement in measurements:
lm_id = int(measurement[0])
start = N + lm_id
omega[:,t,t] += 1/measurement_noise
omega[:,start,start] += 1/measurement_noise
omega[:,t,start] += -1/measurement_noise
omega[:,start,t] += -1/measurement_noise
xi[0,t] += -measurement[1]/measurement_noise
xi[1,t] += -measurement[2]/measurement_noise
xi[0,start] += measurement[1]/measurement_noise
xi[1,start] += measurement[2]/measurement_noise
# print('measurement: ', measurement)
## TODO: update the constraint matrix/vector to account for all *motion* and motion noise
motion_x, motion_y = motions
omega[:,t,t] += 1/motion_noise
omega[:,t+1,t+1] += 1/motion_noise
omega[:,t,t+1] += -1/motion_noise
omega[:,t+1,t] += -1/motion_noise
xi[0,t] += -motion_x/motion_noise
xi[0,t+1] += motion_x/motion_noise
xi[1,t] += -motion_y/motion_noise
xi[1,t+1] += motion_y/motion_noise
# print('motion: ', motion_x)
# print(omega)
# print(xi)
# break
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
# mu_x
mus = [np.array([]), np.array([])]
for i,_ in enumerate(mus):
mus[i] = np.linalg.inv(omega[i]).dot( xi[i] )
mu = np.array(mus)
# print(mu)
return mu, omega, xi # return `mu`
# TODO incorporate uncertainty
# -
# ## Helper functions
#
# To check that your implementation of SLAM works for various inputs, we have provided two helper functions that will help display the estimated pose and landmark locations that your function has produced. First, given a result `mu` and number of time steps, `N`, we define a function that extracts the poses and landmarks locations and returns those as their own, separate lists.
#
# Then, we define a function that nicely print out these lists; both of these we will call, in the next step.
#
# a helper function that creates a list of poses and of landmarks for ease of printing
# this only works for the suggested constraint architecture of interlaced x,y poses
def get_poses_landmarks(mu, N):
# create a list of poses
poses = []
for i in range(N):
poses.append((mu[2*i].item(), mu[2*i+1].item()))
# create a list of landmarks
landmarks = []
for i in range(num_landmarks):
landmarks.append((mu[2*(N+i)].item(), mu[2*(N+i)+1].item()))
# return completed lists
return poses, landmarks
def print_all(poses, landmarks):
print('\n')
print('Estimated Poses:')
for i in range(len(poses)):
print('['+', '.join('%.3f'%p for p in poses[i])+']')
print('\n')
print('Estimated Landmarks:')
for i in range(len(landmarks)):
print('['+', '.join('%.3f'%l for l in landmarks[i])+']')
# ## Run SLAM
#
# Once you've completed your implementation of `slam`, see what `mu` it returns for different world sizes and different landmarks!
#
# ### What to Expect
#
# The `data` that is generated is random, but you did specify the number, `N`, or time steps that the robot was expected to move and the `num_landmarks` in the world (which your implementation of `slam` should see and estimate a position for. Your robot should also start with an estimated pose in the very center of your square world, whose size is defined by `world_size`.
#
# With these values in mind, you should expect to see a result that displays two lists:
# 1. **Estimated poses**, a list of (x, y) pairs that is exactly `N` in length since this is how many motions your robot has taken. The very first pose should be the center of your world, i.e. `[50.000, 50.000]` for a world that is 100.0 in square size.
# 2. **Estimated landmarks**, a list of landmark positions (x, y) that is exactly `num_landmarks` in length.
#
# #### Landmark Locations
#
# If you refer back to the printout of *exact* landmark locations when this data was created, you should see values that are very similar to those coordinates, but not quite (since `slam` must account for noise in motion and measurement).
# call your implementation of slam, passing in the necessary parameters
mu, omega, xi = slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
mu = mu.flatten(order='F')
print(mu.shape)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
poses, landmarks = get_poses_landmarks(mu, N)
print_all(poses, landmarks)
plt.rcParams["figure.figsize"] = (10,7)
sns.heatmap(DataFrame(omega[0]), cmap='Blues', annot=True, linewidths=.5)
sns.heatmap(DataFrame(xi[0]), cmap='Oranges', annot=True, linewidths=.5)
plt.rcParams["figure.figsize"] = (1,7)
# ## Visualize the constructed world
#
# Finally, using the `display_world` code from the `helpers.py` file (which was also used in the first notebook), we can actually visualize what you have coded with `slam`: the final position of the robot and the positon of landmarks, created from only motion and measurement data!
#
# **Note that these should be very similar to the printed *true* landmark locations and final pose from our call to `make_data` early in this notebook.**
# +
# import the helper function
from helpers import display_world
# Display the final world!
# define figure size
plt.rcParams["figure.figsize"] = (20,20)
# check if poses has been created
if 'poses' in locals():
# print out the last pose
print('Last pose: ', poses[-1])
# display the last position of the robot *and* the landmark positions
display_world(int(world_size), poses[-1], landmarks)
# -
# ### Question: How far away is your final pose (as estimated by `slam`) compared to the *true* final pose? Why do you think these poses are different?
#
# You can find the true value of the final pose in one of the first cells where `make_data` was called. You may also want to look at the true landmark locations and compare them to those that were estimated by `slam`. Ask yourself: what do you think would happen if we moved and sensed more (increased N)? Or if we had lower/higher noise parameters.
# The measurements are noisy, therefore the estimate from SLAM might be slightly off.
# ## Testing
#
# To confirm that your slam code works before submitting your project, it is suggested that you run it on some test data and cases. A few such cases have been provided for you, in the cells below. When you are ready, uncomment the test cases in the next cells (there are two test cases, total); your output should be **close-to or exactly** identical to the given results. If there are minor discrepancies it could be a matter of floating point accuracy or in the calculation of the inverse matrix.
#
# ### Submit your project
#
# If you pass these tests, it is a good indication that your project will pass all the specifications in the project rubric. Follow the submission instructions to officially submit!
# +
# Here is the data and estimated outputs for test case 1
test_data1 = [[[[1, 19.457599255548065, 23.8387362100849], [2, -13.195807561967236, 11.708840328458608], [3, -30.0954905279171, 15.387879242505843]], [-12.2607279422326, -15.801093326936487]], [[[2, -0.4659930049620491, 28.088559771215664], [4, -17.866382374890936, -16.384904503932]], [-12.2607279422326, -15.801093326936487]], [[[4, -6.202512900833806, -1.823403210274639]], [-12.2607279422326, -15.801093326936487]], [[[4, 7.412136480918645, 15.388585962142429]], [14.008259661173426, 14.274756084260822]], [[[4, -7.526138813444998, -0.4563942429717849]], [14.008259661173426, 14.274756084260822]], [[[2, -6.299793150150058, 29.047830407717623], [4, -21.93551130411791, -13.21956810989039]], [14.008259661173426, 14.274756084260822]], [[[1, 15.796300959032276, 30.65769689694247], [2, -18.64370821983482, 17.380022987031367]], [14.008259661173426, 14.274756084260822]], [[[1, 0.40311325410337906, 14.169429532679855], [2, -35.069349468466235, 2.4945558982439957]], [14.008259661173426, 14.274756084260822]], [[[1, -16.71340983241936, -2.777000269543834]], [-11.006096015782283, 16.699276945166858]], [[[1, -3.611096830835776, -17.954019226763958]], [-19.693482634035977, 3.488085684573048]], [[[1, 18.398273354362416, -22.705102332550947]], [-19.693482634035977, 3.488085684573048]], [[[2, 2.789312482883833, -39.73720193121324]], [12.849049222879723, -15.326510824972983]], [[[1, 21.26897046581808, -10.121029799040915], [2, -11.917698965880655, -23.17711662602097], [3, -31.81167947898398, -16.7985673023331]], [12.849049222879723, -15.326510824972983]], [[[1, 10.48157743234859, 5.692957082575485], [2, -22.31488473554935, -5.389184118551409], [3, -40.81803984305378, -2.4703329790238118]], [12.849049222879723, -15.326510824972983]], [[[0, 10.591050242096598, -39.2051798967113], [1, -3.5675572049297553, 22.849456408289125], [2, -38.39251065320351, 7.288990306029511]], [12.849049222879723, -15.326510824972983]], [[[0, -3.6225556479370766, -25.58006865235512]], [-7.8874682868419965, -18.379005523261092]], [[[0, 1.9784503557879374, -6.5025974151499]], [-7.8874682868419965, -18.379005523261092]], [[[0, 10.050665232782423, 11.026385307998742]], [-17.82919359778298, 9.062000642947142]], [[[0, 26.526838150174818, -0.22563393232425621], [4, -33.70303936886652, 2.880339841013677]], [-17.82919359778298, 9.062000642947142]]]
## Test Case 1
##
# Estimated Pose(s):
# [50.000, 50.000]
# [37.858, 33.921]
# [25.905, 18.268]
# [13.524, 2.224]
# [27.912, 16.886]
# [42.250, 30.994]
# [55.992, 44.886]
# [70.749, 59.867]
# [85.371, 75.230]
# [73.831, 92.354]
# [53.406, 96.465]
# [34.370, 100.134]
# [48.346, 83.952]
# [60.494, 68.338]
# [73.648, 53.082]
# [86.733, 38.197]
# [79.983, 20.324]
# [72.515, 2.837]
# [54.993, 13.221]
# [37.164, 22.283]
# Estimated Landmarks:
# [82.679, 13.435]
# [70.417, 74.203]
# [36.688, 61.431]
# [18.705, 66.136]
# [20.437, 16.983]
### Uncomment the following three lines for test case 1 and compare the output to the values above ###
mu_1, _, _ = slam(test_data1, 20, 5, 100.0, 2.0, 2.0)
mu_1 = mu_1.flatten(order='F')
poses, landmarks = get_poses_landmarks(mu_1, 20)
print_all(poses, landmarks)
# +
# Here is the data and estimated outputs for test case 2
test_data2 = [[[[0, 26.543274387283322, -6.262538160312672], [3, 9.937396825799755, -9.128540360867689]], [18.92765331253674, -6.460955043986683]], [[[0, 7.706544739722961, -3.758467215445748], [1, 17.03954411948937, 31.705489938553438], [3, -11.61731288777497, -6.64964096716416]], [18.92765331253674, -6.460955043986683]], [[[0, -12.35130507136378, 2.585119104239249], [1, -2.563534536165313, 38.22159657838369], [3, -26.961236804740935, -0.4802312626141525]], [-11.167066095509824, 16.592065417497455]], [[[0, 1.4138633151721272, -13.912454837810632], [1, 8.087721200818589, 20.51845934354381], [3, -17.091723454402302, -16.521500551709707], [4, -7.414211721400232, 38.09191602674439]], [-11.167066095509824, 16.592065417497455]], [[[0, 12.886743222179561, -28.703968411636318], [1, 21.660953298391387, 3.4912891084614914], [3, -6.401401414569506, -32.321583037341625], [4, 5.034079343639034, 23.102207946092893]], [-11.167066095509824, 16.592065417497455]], [[[1, 31.126317672358578, -10.036784369535214], [2, -38.70878528420893, 7.4987265861424595], [4, 17.977218575473767, 6.150889254289742]], [-6.595520680493778, -18.88118393939265]], [[[1, 41.82460922922086, 7.847527392202475], [3, 15.711709540417502, -30.34633659912818]], [-6.595520680493778, -18.88118393939265]], [[[0, 40.18454208294434, -6.710999804403755], [3, 23.019508919299156, -10.12110867290604]], [-6.595520680493778, -18.88118393939265]], [[[3, 27.18579315312821, 8.067219022708391]], [-6.595520680493778, -18.88118393939265]], [[], [11.492663265706092, 16.36822198838621]], [[[3, 24.57154567653098, 13.461499960708197]], [11.492663265706092, 16.36822198838621]], [[[0, 31.61945290413707, 0.4272295085799329], [3, 16.97392299158991, -5.274596836133088]], [11.492663265706092, 16.36822198838621]], [[[0, 22.407381798735177, -18.03500068379259], [1, 29.642444125196995, 17.3794951934614], [3, 4.7969752441371645, -21.07505361639969], [4, 14.726069092569372, 32.75999422300078]], [11.492663265706092, 16.36822198838621]], [[[0, 10.705527984670137, -34.589764174299596], [1, 18.58772336795603, -0.20109708164787765], [3, -4.839806195049413, -39.92208742305105], [4, 4.18824810165454, 14.146847823548889]], [11.492663265706092, 16.36822198838621]], [[[1, 5.878492140223764, -19.955352450942357], [4, -7.059505455306587, -0.9740849280550585]], [19.628527845173146, 3.83678180657467]], [[[1, -11.150789592446378, -22.736641053247872], [4, -28.832815721158255, -3.9462962046291388]], [-19.841703647091965, 2.5113335861604362]], [[[1, 8.64427397916182, -20.286336970889053], [4, -5.036917727942285, -6.311739993868336]], [-5.946642674882207, -19.09548221169787]], [[[0, 7.151866679283043, -39.56103232616369], [1, 16.01535401373368, -3.780995345194027], [4, -3.04801331832137, 13.697362774960865]], [-5.946642674882207, -19.09548221169787]], [[[0, 12.872879480504395, -19.707592098123207], [1, 22.236710716903136, 16.331770792606406], [3, -4.841206109583004, -21.24604435851242], [4, 4.27111163223552, 32.25309748614184]], [-5.946642674882207, -19.09548221169787]]]
## Test Case 2
##
# Estimated Pose(s):
# [50.000, 50.000]
# [69.035, 45.061]
# [87.655, 38.971]
# [76.084, 55.541]
# [64.283, 71.684]
# [52.396, 87.887]
# [44.674, 68.948]
# [37.532, 49.680]
# [31.392, 30.893]
# [24.796, 12.012]
# [33.641, 26.440]
# [43.858, 43.560]
# [54.735, 60.659]
# [65.884, 77.791]
# [77.413, 94.554]
# [96.740, 98.020]
# [76.149, 99.586]
# [70.211, 80.580]
# [64.130, 61.270]
# [58.183, 42.175]
# Estimated Landmarks:
# [76.777, 42.415]
# [85.109, 76.850]
# [13.687, 95.386]
# [59.488, 39.149]
# [69.283, 93.654]
### Uncomment the following three lines for test case 2 and compare to the values above ###
mu_2,_,_ = slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
mu_2 = mu_2.flatten(order='F')
poses, landmarks = get_poses_landmarks(mu_2, 20)
print_all(poses, landmarks)
# -
| 55.983607 | 3,030 |
74b1230fa110bb5bc9d5c23cdddca4b5fac397e9
|
py
|
python
|
Datasets/usgs_nlcd.ipynb
|
c11/earthengine-py-notebooks
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <table class="ee-notebook-buttons" align="left">
# <td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Datasets/usgs_nlcd.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
# <td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Datasets/usgs_nlcd.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
# <td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Datasets/usgs_nlcd.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
# </table>
# ## Install Earth Engine API and geemap
# Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
# The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
#
# **Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
# +
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
# -
# ## Create an interactive map
# The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
# ## Add Earth Engine Python script
# Add Earth Engine dataset
dataset = ee.Image('USGS/NLCD/NLCD2016')
landcover = ee.Image(dataset.select('landcover'))
landcoverVis = {
'min': 0.0,
'max': 95.0,
'palette': [
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'466b9f',
'd1def8',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'dec5c5',
'd99282',
'eb0000',
'ab0000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'b3ac9f',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'68ab5f',
'1c5f2c',
'b5c58f',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'af963c',
'ccb879',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'dfdfc2',
'd1d182',
'a3cc51',
'82ba9e',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'dcd939',
'ab6c28',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'000000',
'b8d9eb',
'000000',
'000000',
'000000',
'000000',
'6c9fb8'
],
}
Map.setCenter(-95, 38, 5)
Map.addLayer(landcover, landcoverVis, 'Landcover')
# ## Display Earth Engine data layers
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
| 30.445714 | 1,023 |
58fec8c07363a6a08a77adad2899f8a827804af8
|
py
|
python
|
cnn_mnist.ipynb
|
LuposX/AndroidAppDigitRecognizer
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="N9nKihCnMcM8" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 817} outputId="329e444a-383f-4823-9ac2-6f10a5a0d34c" executionInfo={"status": "ok", "timestamp": 1585485292827, "user_tz": -120, "elapsed": 8297, "user": {"displayName": "X X", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgEJgjSrDA9UNnIFLg8KFHRrHszoHTeg4DVB_-LzQ=s64", "userId": "08253686537361872526"}}
# !pip install pytorch_lightning
# + id="mIJUvi5yQAL_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 599} outputId="e260a21d-d7ab-4fff-ce10-4690a7819022" executionInfo={"status": "ok", "timestamp": 1585485298307, "user_tz": -120, "elapsed": 13772, "user": {"displayName": "X X", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgEJgjSrDA9UNnIFLg8KFHRrHszoHTeg4DVB_-LzQ=s64", "userId": "08253686537361872526"}}
# !pip install comet_ml
# + id="88k0CVjMOZDc" colab_type="code" outputId="a7f5b12a-b44f-4969-9669-fd240fa1b8ec" executionInfo={"status": "ok", "timestamp": 1585485298469, "user_tz": -120, "elapsed": 13923, "user": {"displayName": "X X", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgEJgjSrDA9UNnIFLg8KFHRrHszoHTeg4DVB_-LzQ=s64", "userId": "08253686537361872526"}} colab={"base_uri": "https://localhost:8080/", "height": 35}
# used fo TPU
import collections
from datetime import datetime, timedelta
import os
import requests
import threading
_VersionConfig = collections.namedtuple('_VersionConfig', 'wheels,server')
VERSION = "xrt==1.15.0" #@param ["xrt==1.15.0", "torch_xla==nightly"]
CONFIG = {
'xrt==1.15.0': _VersionConfig('1.15', '1.15.0'),
'torch_xla==nightly': _VersionConfig('nightly', 'XRT-dev{}'.format(
(datetime.today() - timedelta(1)).strftime('%Y%m%d'))),
}[VERSION]
DIST_BUCKET = 'gs://tpu-pytorch/wheels'
TORCH_WHEEL = 'torch-{}-cp36-cp36m-linux_x86_64.whl'.format(CONFIG.wheels)
TORCH_XLA_WHEEL = 'torch_xla-{}-cp36-cp36m-linux_x86_64.whl'.format(CONFIG.wheels)
TORCHVISION_WHEEL = 'torchvision-{}-cp36-cp36m-linux_x86_64.whl'.format(CONFIG.wheels)
# Update TPU XRT version
def update_server_xrt():
print('Updating server-side XRT to {} ...'.format(CONFIG.server))
url = 'http://{TPU_ADDRESS}:8475/requestversion/{XRT_VERSION}'.format(
TPU_ADDRESS=os.environ['COLAB_TPU_ADDR'].split(':')[0],
XRT_VERSION=CONFIG.server,
)
print('Done updating server-side XRT: {}'.format(requests.post(url)))
update = threading.Thread(target=update_server_xrt)
update.start()
# + id="L3CIz802MU9A" colab_type="code" colab={}
import os
import torch
from torch.nn import functional as F
from torch.utils.data import DataLoader
from torchvision.datasets import MNIST
from torchvision import transforms, datasets
import torch.nn as nn
import torch.distributions.bernoulli
import pytorch_lightning as pl
from pytorch_lightning import loggers
from pytorch_lightning.callbacks import ModelCheckpoint
from PIL import Image
# + id="lVUnRn-fMY8L" colab_type="code" colab={}
class invertColor():
"""
Is used to inverse the color of a dataset when this dataset is in range[0;1]
"""
def __call__(self, img):
return self.invert(img)
def invert(self, img):
return 1 - img
# + id="Ek9vg7bOMaFz" colab_type="code" colab={}
class randomBlackToWhite():
"""
Is used to transform some white pixels of the digit in black pixel
"""
def __init__(self, prob):
self.prob = prob
def __call__(self, img):
return self.randomBlackToWhite(img)
def randomBlackToWhite(self, img, prob=0.9):
return img * torch.distributions.bernoulli.Bernoulli(torch.tensor([self.prob])).sample(img.shape).squeeze(-1)
# + id="1FwMOvM-M6Vk" colab_type="code" colab={}
class CNN(pl.LightningModule):
def __init__(self):
super().__init__()
self.batch_size = batch_size
self.lr = lr
self.ndf = ndf
self.val_correct_counter = 0
self.val_total_counter = 0
self.hidden0 = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=self.ndf, kernel_size=4),
nn.LeakyReLU(0.2)
)
self.hidden1 = nn.Sequential(
nn.Conv2d(self.ndf, self.ndf * 4, kernel_size=4),
nn.LeakyReLU(0.2)
)
self.hidden2 = nn.Sequential(
nn.Conv2d(self.ndf * 4, self.ndf, kernel_size=4),
nn.LeakyReLU(0.2)
)
self.hidden3 = nn.Sequential(
nn.Linear(5776, 1000),
nn.LeakyReLU(0.2)
)
self.hidden4 = nn.Sequential(
nn.Linear(1000, 200),
nn.LeakyReLU(0.2)
)
self.hidden5 = nn.Sequential(
nn.Linear(200, 10)
)
def forward(self, x):
x = self.hidden0(x)
x = self.hidden1(x)
x = self.hidden2(x)
x = torch.flatten(x, start_dim=1, end_dim=-1)
x = self.hidden3(x)
x = self.hidden4(x)
x = self.hidden5(x)
return x
def cross_entropy_loss(self, predicted_label, label):
return F.cross_entropy(predicted_label, label)
def training_step(self, batch, batch_idx):
x, y = batch
predicted = self.forward(x)
loss = self.cross_entropy_loss(predicted, y)
logs = {"train_loss": loss}
return {"loss": loss, "log": logs}
def validation_step(self, val_batch, batch_idx):
x, y = val_batch
predicted = self.forward(x)
loss = self.cross_entropy_loss(predicted, y)
comet_logger.experiment.log_confusion_matrix(labels=["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"],
y_true=torch.eye(10)[y].view(-1, 10),
y_predicted=predicted
)
self.val_correct_counter += int((torch.argmax(predicted, 1).flatten() == y).sum())
self.val_total_counter += y.size(0)
logs = {"val_loss": loss}
return {"val_loss": loss, "log": logs}
def validation_epoch_end(self, outputs):
# outputs is an array with what you returned in validation_step for each batch
# outputs = [{'loss': batch_0_loss}, {'loss': batch_1_loss}, ..., {'loss': batch_n_loss}]
avg_acc = 100 * self.val_correct_counter / self.val_total_counter
self.val_correct_counter = 0
self.val_total_counter = 0
avg_loss = torch.stack([x['val_loss'] for x in outputs]).mean()
tensorboard_logs = {'avg_val_acc': avg_acc, 'val_loss': avg_loss}
return {'avg_val_acc': avg_acc, 'avg_val_loss': avg_loss, 'log': tensorboard_logs}
def test_step(self, test_batch, batch_idx):
x, y = test_batch
y_hat = self.forward(x)
loss = self.cross_entropy_loss(y_hat, y)
self.test_correct_counter += int((torch.argmax(y_hat, 1).flatten() == y).sum())
self.test_total_counter += y.size(0)
return {"test_loss": loss}
def test_epoch_end(self, outputs):
avg_acc = 100 * self.test_correct_counter / self.test_total_counter
self.test_correct_counter = 0
self.test_total_counter = 0
avg_loss = torch.stack([x['test_loss'] for x in outputs]).mean()
tensorboard_logs = {'avg_test_acc': avg_acc, 'test_loss': avg_loss}
return {"avg_test_loss": avg_loss, "avg_test_acc": avg_acc, "log: ": tensorboard_logs, 'progress_bar': tensorboard_logs}
def prepare_data(self):
compose = transforms.Compose([
transforms.RandomCrop(28, padding=8, pad_if_needed=True, fill=1, padding_mode='edge'),
transforms.ToTensor(),
randomBlackToWhite(0.7),
invertColor(),
transforms.Normalize((0.5,), (0.5,))
])
self.mnist_train = datasets.MNIST(
root="data",
train=True,
download=True,
transform=compose
)
self.mnist_test = datasets.MNIST(
root="data",
train=False,
download=True,
transform=compose
)
self.mnist_train, self.mnist_val = torch.utils.data.random_split(self.mnist_train, [55000, 5000])
def train_dataloader(self):
mnist_train_loader = torch.utils.data.DataLoader(self.mnist_train,
batch_size=self.batch_size,
num_workers=1,
shuffle=True)
return mnist_train_loader
def val_dataloader(self):
mnist_val_loader = torch.utils.data.DataLoader(self.mnist_val,
batch_size=self.batch_size,
num_workers=1,
shuffle=True)
return mnist_val_loader
def test_dataloader(self):
mnist_test_loader = torch.utils.data.DataLoader(self.mnist_test,
batch_size=self.batch_size,
num_workers=1,
shuffle=True)
return mnist_test_loader
def configure_optimizers(self):
return torch.optim.Adam(self.parameters(), lr=self.lr)
# + id="sDaSjmlENEYV" colab_type="code" colab={}
# Parameters
experiment_name = "cnn_mnist_Bernoulli"
dataset_name = "MNIST_inv_color"
checkpoint_folder = "./" + experiment_name + "_checkpoints/"
tags = ["cnn", "real", "inverse_color", "Bernoulli", "randomly_padded"]
lr = 0.001
batch_size = 128*6
ndf = 16
# + id="UNRm-YtHNLwY" colab_type="code" outputId="45dfdebf-5050-4a23-e54c-5318f9e401dc" executionInfo={"status": "ok", "timestamp": 1585485302470, "user_tz": -120, "elapsed": 17900, "user": {"displayName": "X X", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgEJgjSrDA9UNnIFLg8KFHRrHszoHTeg4DVB_-LzQ=s64", "userId": "08253686537361872526"}} colab={"base_uri": "https://localhost:8080/", "height": 54}
# init logger
comet_logger = loggers.CometLogger(
api_key="lcHaEOsylE8TDnW7qvtwek038",
rest_api_key="P2y9z4euMGzYEEZHdR0j8I0xH",
project_name="mnist-classifier",
experiment_name=experiment_name,
)
#defining net
net = CNN()
#logging
comet_logger.experiment.set_model_graph(str(net))
comet_logger.experiment.add_tags(tags=tags)
comet_logger.experiment.log_dataset_info(name=dataset_name)
comet_logger.experiment.log_parameter(name="learning_rate", value=lr)
comet_logger.experiment.log_parameter(name="batch_size", value=batch_size)
comet_logger.experiment.log_parameter(name="ndf", value=ndf)
# + id="kOF_1UfKNfd4" colab_type="code" outputId="aa0892ae-712c-4cc2-9990-9292e706fc47" executionInfo={"status": "ok", "timestamp": 1585491557390, "user_tz": -120, "elapsed": 1572470, "user": {"displayName": "X X", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgEJgjSrDA9UNnIFLg8KFHRrHszoHTeg4DVB_-LzQ=s64", "userId": "08253686537361872526"}} colab={"base_uri": "https://localhost:8080/", "height": 868, "referenced_widgets": ["a3322e2c3ff743adb8bebabfe28da45d", "de6e3bdcfcc44e55ab0923204dfb32b2", "f88e6b8bc77246c5a0b8993e54cb9a74", "69b293d164164db797731ac3486b9395", "735f44bde2f243c98de977f11922a7c9", "818ad2b1bc3d45779ca68bf88d5f2bd5", "b55547178e334fa09fcbd152943ea13c", "22078dc0384941fd9f2eff7fc68eabe8", "dc3e8becf7d14b08820adaf56bfae36c", "965c7e7eccfd4d24a2c9898d806c4507", "384e44ebcdd74500a5d84ebfc3a85c21", "18dc573e7f98472ab40b710a2c94bf5f", "14ddcb3f464e49be84b2515bb7b9a51e", "c634fb24aeef476480634a135b9bbb1e", "e578f3f88ab84399bf200a6c19863dfc", "0b12afc9c34d4c3086296169296c392e", "d015e298354842ab91481460c5798b9b", "a7065252492d421dbbddc867e37957e6", "83a3b70681864332a1c1af4380c0dbe2", "0d0c1e3a71de4fe0968b164326374fab", "fc71eec86db0447f945995c0150564b7", "f4e5dc835f954001b5e2f7daf3266a70", "ca3b598f85cd4824b407491ca282cb7d", "c90bd9baec6541598d2b59332b40b7c9", "816f03d32a0a4961b92c83f623245b58", "6c1fb4a86c75492b98438b8fb1dc9515", "a045273e09354bca9137c9f9104fb352", "1d3f6b1548fe440aafac9bf793b21b1d", "32c4148df4454627b09823450d91ea0c", "e10faf74400245dfa4c8d2e34d4169db", "4da3e37ee0f241929b661fe82864a8a0", "6fda200f01a74763977a60191b8ab827", "520aea436b1f405fa863252697c0c752", "41fa274314d64056a544b71a5b016910", "5b254b27013c425a9cbaa00813b03039", "02a2a9d552ae4d818ac8d47317fda6f4", "bcf0fe7aa0904a8c80f0e033e480ef28", "97b6330ad4384e0da475a5e5c7b100f5", "ffde397d26bf4a549cc9fd4dc5dc6dc8", "96dee0cb2f11455fa89e0997292d036b", "c9f4edc558464a7abe33871f193d7bb0", "79936b11a1964fe0882e2d99b093f1bd", "ad89c94271b2464181b35a2db4461a09", "94745e2dcadf49088939e69cfea25984", "f0610e08cae8431ea4c3e1d0257945ca", "1a6ed8fdd04f4d4fae81a499ab4aa9c8", "25eadc3540534c5fbc371ac954a0ac9f", "e25fa56fdfaf45eca982d3dce50854dc", "9a52dd96f00446b3a4a97f16e0075530", "8c9b4074e91041a3a2c6caf960f8f0e0", "8708472721824421b7c949207efbb4ac", "c23aff86505a4060b8f34eb988db3387", "c12865fc9f524540b71c8277366117dd", "6cce9873effa4e029ca83e49497bbd81", "1f149103785245fc8e33480825a61b3b", "473656addb2d49328c53cf1d705c5183", "a4d0380e67f04d82abb31dc341d8796e", "2a96be39374646f6b22d6366be48a4ae", "bdc77945706e4c9bbfb1c7ea7c5eac76", "ba787b5f19704e378f925ee39f340f48", "6d0acaee0e2a44b6b2a4d92c05f11dff", "0c33c819b74b4cb6b2ee66ec6e51f740", "a978bb270b07446f92c4cf5d99b258f2", "24c828b7581740068efcbbc3d05d89ad", "5e438da9a8a9459d82a6c7305b769727", "addc9539f9a648fcbbfb63a1fb48098c", "ee713386345844a8a4542d0917a6a106", "5b31ccac1aba4a5fa850d3146a535205", "5972227eca5c47159ddbe12a1d0d1d6c", "95cd8d40e2ae4842a6054501a017e1f0", "3e7afc4303d34dbdb89c3f74348bc400", "5fa1a9984db04dbab45fa9329e610105", "17338cd6b7bb448cb787c24dc960aaa2", "6a906e62986e4b0ba14f41005aa337da", "1bf8ca1d5f7648e89ad201322f8ac5a6", "adc32e7e74a64bf5b4e95f49dc1919d6", "a21582b0e72643d383a8f4979b971673", "962caa65025e4ed1a8af783d9ae89537", "34d1b5bdfe734c748551dfec5aef7a82", "b728c2b3d34948878afe8464f2e2b9df", "362342c872bc4bd0b0ce54a00cab45c3", "988dbc1a20534c528c95bb62efcc3ac6", "cfcc62c320ea404e8150e4ee9878ddaa", "6f6557855b354e969d1f80d61ffea169", "45136cb92a484bceb872e5102b3349de", "d9dcbb596de64f71805b0e6ae179f56b", "5b43097ced3b4a2ca532f4068f33b933", "1ead0826b91647de878149b40a184fc3", "b15a867b23f04fb19b85c7920cd51089", "b52a081824354df0b8cf74fabdf1f1b5", "656bb9c5bb494612a6e364de06085ae1", "28f27a7c85e24535bf3a7014f2a5d777", "838dd180d4bb437ea25cebdd3f9869bb", "1d90fcf8514f4b7fb7348ec046f0bc03", "92d657c790884df4820477676247459f", "406dcd08492e4fd3ab273c9b092aa167", "fab49b68479e46bf9b51fd4abff92064", "9ca0aa0ccff1430c83b3f49a983692f8", "723d4384cac747e7943558ecc848639e", "319b54f0d8d44bffb378cc7642090d24", "d3cd72a1a2ee47848df7226d37fa4319", "af1bfadb6feb4782a5d1b9672d5c2f9e", "8d8fca3bf90e49409417e7b0ab0142bb", "6dfdca470c954379ba27b8dae27aad25", "d3080ccf41bc435ead05fa5d2bb49256", "2f1428fc5d834718890e8e00f1bb1f2a", "e6be9f0d67d44f6d944bece51d8ef5f1", "b7890e301b244d78a35d5a0dccd48d64", "2c344b4a583741e48a168d09cd56e898", "b90638ed059b4e1dac69fe0a9481ba74", "97b3c4db46e44ff69f192deacb7bd5d0", "52e7227fb8084274b13bdd4cf2cccb0d", "a76a2dcdb57c41c19412f8ffce1c7b81", "ae3547c718b94c03ae734f2fc37e5b23", "424280ed5736407fb990fc4fbf6615bb", "b4109ecae9c74453bf4893c464cdf461", "106702f967c94ae2935d4b78d35c4bb0", "dbcaf47407cc473ba4f47679131f75dd", "cfd32b0445554c6dbe02acef88808d52", "9d0f867b505245bc98ae800b053f9edb", "0c4ff6f596ab45c28667d3a0bce88987", "0d196ee09673471c9962e844b145bedf", "b172a5fc30df4ff5a9eaf33214222928", "7e0905edaa46431d816f294fc4131f2a", "9f7f270641aa455f9d0ba3cb76a2e21f", "e78f352e573a434a8591db81d93abe87", "224171b7b8b648de80e1b6f22609ab0f", "cd49d3c37242445fbf746a2c9449ba15", "a34dea30afaa48aeb8cb663402d16475", "347c8af30bdc427499ede053cc6768d7", "afca08f3b747482c9081e9d1a2c70a48", "c979b3cd5bd649d487208a6feb000b22", "3a48dec374ac446ab93259d6ce228cf6", "54a7b34688a24f588e6bc4eaf6f68382", "e77c9a568a9340388a7d5826cf9b05fb", "8cd37c52bc4c4c0abf17ca37fff3059c", "6d6c4b408edb43ac8d41642715381536", "0fa6e18609a44ef492757db391c857ff", "09b752de47694de09a9b6e63553ed86b", "51b6e18a2c6c44a4b22e41a5474fed70", "d5f393692f1f483aa6f441311cc97e28", "fa4ce14b74e54f3e98ce6ae2b5cdacb4", "b27682c26f72488c929c3bb21848040a", "bc538f2df3444eb1a019a14386b014c6", "b9a0e84c72d54e968a747d3625ae4c3a", "0bda8f4729ec4054b6dcc09b1896d616", "29eedb1f6f0f4a03968dd420ba026846", "1d9da572b8954fbfa0247fea195a860e", "9133382152524094b55395e3482b0309", "dc5f628db88344b7b71f2cc782a82a63", "412c638e1c6c44139ff4cbe76d68889b", "bc20f7b812ea4a93b0a88c9048c674d3", "e847e718161d49f0bf798505daa0ec57", "a1ab2f4cfd1543908a83d7002c83f502", "fdbe2053257b455ebe68a9f7c1d6c9f9", "22bc1b6c5b134e868b670fae3f02da27", "ade4e19b4cb04a7fa478e2c2d415368d", "31dc3fa3344540c7992669ca237ebb4a", "d6a1d7cf5c80415890eec7f3b533a242", "eb4d132e59ab48e898b7a1ce7d9f2d22", "48eb43464ba0440399515b5071804088", "dc25113382d8454894ff14180b7449ec", "3afa191879eb44a8b8776a88c3344cc8", "e5268336e626446497667dfa7014098b", "0633110f736e46d3ba187456c6320457", "24a7e2610fe54e4a922c207364fcba68", "fff6662b91df43b99e7469c0dd70d926", "7bbbdf17922642f4b752d0148037a38a", "d4141680f69c4c47989a2f594ac24646", "99cf4c821e834f80af5a61a34b5d9148", "f5ac2adb5d824d148cfe6e492669c7d3", "ca2ae51ab2d247da97f76bceb8731990", "40267addcc544f0a843396dba3bebd9d", "30fe3f057c0c4a54af808310b6b3ff71", "84068fa87ade4cb69a8c4e4a0a28fb2f", "a7c269ed3b4a486788c6c919aeff650e", "9ed298ce151940b399adfae173be53d2", "37427ba844674cfbaa9fe4a678ae3837", "0bd5338d4cde4744a72cf1d2457d306e", "9e7cc710fc53432592e09128dc2145e3", "35546daff12844a896e7966c5f892369", "fb6fcc4a18cb4d2c838e3a6a472f7080", "2212b73fb9b24e56b0d8a98e99e13938", "1d8b2ccdc0044d758411c16c0c7e1b7a", "5140fd58e3a94a4588e37e903a6a7be5", "5471538301aa4d3d9b8b296f6ae278e4", "674680b0c83247b39e9bbf76d21f4bf7", "00eadd5a76754bf6aa5da308326e8c15", "bfff320532814ecf8510e425eb7a5de4", "4c6a43ff490849589861ebb449dfdc50", "ef80bf3eb6c045a894f8689278ff774c", "57438a86e2e84a5a82cf81b2ffdc5787", "412791a2e9f54346b32f4c3d9b9f391f", "adc40cfb82b04f45a8507fa0504c4966", "bfaf75424e814e8286dddf9044171683", "4271a1cfa01c43fdb009934f2b47a286", "5fc461bb75f94027af85643d8fff34a4", "0984da330ce84ffc8291d51234653e21", "e93bf325340f49629e377ffb35716355", "11f631d2079e4e9a99ce9432eb3cddb8", "2758d36e8cde44868d2740d33c370e25", "2bb29576072542d1a09016fa6ba251aa", "171187f282304343b251800060f398e1", "fd9fd956dd0044059237d1b4f1117ca9", "2528292bbb054573ae9f12694a1cd018", "e38162bd3ac242969836e8ffcfccfded", "ff81a393571347069e566e9b4f6aed69", "649b06e45fba407990bc44458b0736f5", "a0662de48fca49038c77c53d7778261e", "a8a6795238944077bc4c8a422fe791ae", "f51f967fbeb44d29907453a2261b7bc0", "fafc4f8ce252470081eb9864fdefa1b1", "f1d713c6896347f8903a304234806a51", "c6a40c4a77d747ea9a5bb0f4878a76bc", "ea00bd98c18a418b9f815538f9daf784", "48e2f82e2e064357b098d49e3eea10d3", "23420eee66e34c1bab0be8e2bf7747da", "4d048749be9d4cb3b39d3b5a91be5528", "7d303de8b2704214b0e82857cc361283", "aebf376dba174859a3c9baf8a5cd503b", "172a320d87a440c494db434730aa822b", "a94dee3a29414971b752a42046b5b3d5", "e6bc59887580401682bc82ddb48a7747", "535008fb6d2e4bf78c5249a2e8776ebb", "4282b2dc13e648b0844a088e7e74d1d1", "9b5a7f2ce1eb41cb8d1c6b8c5c41285d", "ed9e9f5317724d0f92e7c84ff3a1cd40", "a916a661d68d426bbbe9f2cd4deccd18", "93165251019c432f891a9228939d5325", "ff6453db1fc84c96a956afabdc6fc6ad", "8051f145a65643feacfab6cd48955b9d", "f139c53f2c92467592b0c8964bade979", "50609104514848c0b4b4ad50a002d51b", "a3f218416a604883858d462e38ff708f", "50d06a01ba25443fb79ffd991ab0043f", "27f311de23d945efb7b56e55de533ab1", "62e15e462f9648a499f07a198c583248", "c443c38fa1e54ca1a1f4265e85b625a4", "5a2fc9fcd14843a392cdb841d2db64c6", "9e62205b6fd747d98c3930179ccfd051", "832ddb1a7bd74b95bec39604794889b1", "1cda7952e9d24b618f3c552647f0d12f", "06866339ac4e4309b3f473ebd60eb9ed", "c4712177740c45e3b44ba3f6a352f070", "bac6deba8d244e249829f90574326d05", "c5230870d2434cb698d40f58f8e9ca49", "648ede4d31ca44c3b8c023df6c4ac67f", "57ffac4ce23d455c91f934876bcbd8a1", "78e774ec4d234f89a9e7fb724e226e08", "501b591d186a478194282a1ea361ca63", "1438b50d17164763b6191d8fb3ad6eff", "0109dd5a5f8d4ce3bb18ea97dee3a795", "20d699064056499fb1f1214c90fba75d", "a9075cf006774c008994523e5042655b", "f79218edd4d44408af5c2eb19b4e5229", "4e459df3c366408e875ba29122ce79dd", "20c8e84405c84379802b4fe8d28cb680", "948878eebee14b06baa81bc1319c3290", "abd3b68e096c470db7e2031c4a8648cd", "d56e0e1d103e487a808ffb468d42294a", "efd96fedae9e4a6da8bc3c45693f1ae5", "a87ba787873f4eadb9e1662ceab8c075", "3791be029ff5454a9064e8e7c1aca3a6", "04d218a3d34d41b78ffe1d9a1bfb87b0", "e8caefbaa3624d93801de6f03fe8b529", "4b7638f0a47143ada7bc98b869829b90", "892c79b15bba433f980846a6e4a6efa5", "bc6dbd1a2a3c4f23ad7f5ea8e3b8eae6", "9234d42dc9f84d8a9606b90e5791ac36", "c01569beaa28474288ca2e40a26d8aa9", "1a4a0019b0324713b7fd2e38eba0ac3c", "bc7ce1ff87b443049d4506fba7d3ed8c", "f3a08aa3f7554487aaa8486f122f3186", "c1f5488700aa45288b7eecd367086415", "6df977c4c8df467e8c8a0aa9990cfb58", "f5127f0b73b04783ab5fd290b9887b3c", "b1a956ec42a84863816d4bca8c9f29f3", "399118e03cc447709b1fe21c28c330c5", "2a897a7193fb4ed4a01588f0a3cd3153", "466485e9914443d6adaf8a309c24625a", "6af3791bb9b1426cb38994fdd10f9f4c", "d4c3d8a0e3fd4c488388185514917404", "8b79e72d2f144be188946179251d2e12", "f2eb34da1deb44258dc5ceaa11b82b70", "6ac6f6b9af3a404c9679d3820eafcea3", "daa6820abb7047549a80e42c3b578c9d", "702d988e803c4cca91f2464197d10468", "609da44e9f1f446b8d6e95725d9cea65", "0d294db898924b0888e3e3294cf48825", "154340a6b16c41f69c0475866f5a2b72", "b9b64fe1b81d43819d7ec52d65ce899e", "a165f19cddc6476b81b924bd583677f2", "3dbed5038d96444aad58ba4b1f0de863", "21861a78742d4997a38f4ad962d3fe0d", "c940c935628f4e88887f0e2348b40e6f", "b7593bbf040b4caf88552478a2ea2909", "2726ef36f96d4f1cba040651f0145856", "cddc79c778d74bf69c0607f14e9e014e", "ab3862edd1534cbe824c3bcbbec6c4e4", "b07429411c11491f8295e9baca9a8e7c", "6be732b79a29454b8cdd598b8844fa0c", "d0eab18d943d43bfb7781d69634e172c", "7a47b37069bd470d86c5015e7a496b46", "9c7cb7e0a2ea408ab1b3774604cd71f3", "d1f73b7e041e48b29c7376aecb172aab", "f9e8b5ff72e14f2184b9bda51cca71ee", "9214ce13b4ca43bfa596409f3a20b9b4", "2d7266bfaa0f46cd86ec388ab1395b0b", "7a510ea6083c4c1bbed2a310a90e81b7", "d9ad58de485d46659ada6a8f9efbeba8", "1c0e71eb2f844c99940ad3e2b1962bfa", "eb195a711b77449fae0ca136b002c4d4", "17a2f078bb6b40caacebb474c58848a4", "b0eb39e5bf564f7690920eaae432bcff", "6f78253fbb804dc9822e91a166791004", "88547a26c6914d64b69fd2b81b946dbe", "7413e61861c3428d99cb8f6e13a52916", "317a7a73eb5e45db8573b06206bc181f", "f5047f1c050745c79b9446f300f314d1", "1d65e10091104df3a6204a884e0abe0f", "61e312fb39404f37a103799675665bec", "6039c13340b84565b9c2960fb643c0da", "89f08971e8d74105893190d7093a89d7", "f65323e96580425eb1f4baeffe4fff4d", "aa166ed28c424c5281e3271a4f20e650", "da60156027ac4530910c84551f2d81cd", "5fed3764eb0c45b6b1c269ae78155a0b", "cd7bda1c46534c5d9de627df55912ea2", "cbfdf55a443f4819a0d80da919478b0c", "aa33aa9a6ece4400b4015ec995392ef0", "0b970f1c0e204b91a92080d65b9da20e", "d0712229ad844a6ca519eac04e02c4b1", "1028930f10964d38b814aea57b74d451", "184b4511e349422ba55c5ffbccaf6347", "0067e81b477346afbe20fc656a45ccf5", "577b8705b46f4aea96d0f3c85d63848f", "ea2e4a7fc7b34ecfb032ab24a46f4b10", "509cedde6786427b8462c014384de24f", "ad5343ba48e54a57b20874f06b0ce155", "bf64f3f574ac45f38b5bb0fd81fd7b23", "fae54c2085024c86af20b46ce6ad7290", "8d87748cfd0949e79f41a6b5c7d8e98e", "52290b25b39a4fc78e303aa177d700d1", "36fb55e0f26a4939906c717a1b28e7d3", "46bb9309dd0f4c318e57a14db96723a7", "3e2bc4bae8e74e72b1e94f0a07be0026", "dd229d2e137244feb39a719100fc7836", "d2f3ec6a08e04516b39f9837a0ce7383", "cb9f6a6f08484275940ec89730c9239c", "01ddeeb5521c4914b912639f486e42c6", "f0825351952f421880e1a8b93a9303c2", "b2169e2ef07645caaf283cdd14a5c625", "a705f3424647466da4f3d2958c143dcf", "41a5db2c75e84984b8c3686ed7f55ab9", "fa19c3f1b72a493d9803d698519c0fb4", "d7b87e4e304645b29aaf291d3fe31e7a", "7b918e89b49b4c5a9bf37d4de0b29055", "55b92a89c14d42ffa3a77038e77bcaff", "cd9bb0a8656d40cb91dd95eb2a60a916", "2242aee341204702bb709c58a6228230", "b7a88644c23341288b1df7a7c921760b", "2364622d49bb4b639b9e88625bfe45ff", "0bd25f7c27c24c5487f56fc3c45e7a94", "d2e053434e2c44daab061f2b3edba74e", "11f5c151e2424abfab015ef8d457689f", "73fc7791d6d047128576a69bbbd8816b", "3493b199601c42b3bc6eb3319a26d19a", "ab0dc49f7d1f49639600b78ed17ba734"]}
# Training the NN
checkpoint_callback = ModelCheckpoint(filepath=checkpoint_folder, save_top_k=3)
trainer = pl.Trainer(# fast_dev_run=True,
checkpoint_callback=checkpoint_callback,
max_epochs=40,
logger=comet_logger)
trainer.fit(net)
# + id="9e-9JlZ4NoZw" colab_type="code" outputId="fca777fe-9d4b-4cd1-a8ed-5efcc946fc5d" executionInfo={"status": "ok", "timestamp": 1585491558763, "user_tz": -120, "elapsed": 1407, "user": {"displayName": "X X", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgEJgjSrDA9UNnIFLg8KFHRrHszoHTeg4DVB_-LzQ=s64", "userId": "08253686537361872526"}} colab={"base_uri": "https://localhost:8080/", "height": 272}
# log checkpoints
comet_logger.experiment.log_asset_folder(folder=checkpoint_folder)
# + id="a2YPA_MiRBCc" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 171} outputId="e8e46237-d6ff-4243-a09c-f104c427252f" executionInfo={"status": "error", "timestamp": 1585492946072, "user_tz": -120, "elapsed": 537, "user": {"displayName": "X X", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgEJgjSrDA9UNnIFLg8KFHRrHszoHTeg4DVB_-LzQ=s64", "userId": "08253686537361872526"}}
a
# + id="xaUwI6pavmkZ" colab_type="code" colab={}
| 81.326984 | 13,685 |
92e32a9603888f5367522215f37ecb7d5dabd381
|
py
|
python
|
jupyter/topic03_decision_trees_knn/topic3_trees_knn.ipynb
|
ivan-magda/mlcourse_open_homeworks
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# <center>
# <img src="../../img/ods_stickers.jpg">
# ## Открытый курс по машинному обучению
# Автор материала: программист-исследователь Mail.ru Group, старший преподаватель Факультета Компьютерных Наук ВШЭ Юрий Кашницкий. Материал распространяется на условиях лицензии [Creative Commons CC BY-NC-SA 4.0](https://creativecommons.org/licenses/by-nc-sa/4.0/). Можно использовать в любых целях (редактировать, поправлять и брать за основу), кроме коммерческих, но с обязательным упоминанием автора материала.
# # <center>Тема 3. Задача классификации, дерево решений и метод ближайших соседей</center>
# В первых двух частях мы попрактиковались в первичном анализе данных с Pandas и в построении картинок, позволяющих делать выводы по данным. Сегодня наконец перейдем к машинному обучению.
#
# <habracut/>
#
# Наверно хочется сразу рвануть в бой, но сначала поговорим про то, какую именно задачу будем решать и каково ее место в области машинного обучения.
# Классическое, общее (и не больно то строгое) определение машинного обучения звучит так (T. Mitchell "Machine learning", 1997): "говорят, что компьютерная программа *обучается* при решении какой-то задачи из класса *T*, если ее производительность, согласно метрике *P*, улучшается при накоплении опыта *E*".
# Далее в разных сценариях под *T, P*, и *E* подразумеваются совершенно разные вещи. Среди самых популярных задач *T* в машинном обучении:
# - классификация – отнесение объекта к одной из категорий на основании его признаков
# - регрессия – прогнозирование количественного признака объекта на основании прочих его признаков
# - кластеризация – разбиение множества объектов на группы на основании признаков этих объектов так, чтобы внутри групп объекты были похожи между собой, а вне одной группы – менее похожи
# - детекция аномалий – поиск объектов, "сильно непохожих" на все остальные в выборке либо на какую-то группу объектов
# - и много других, более специфичных. Хороший обзор дан в 5 главе книги "Deep Learning" (Ian Goodfellow, Yoshua Bengio, Aaron Courville, 2016)
#
# Под опытом *E* понимаются данные (без них никуда), и в зависимости от этого алгоритмы машинного обучения могут быть поделены на тех, что обучаются *с учителем* и *без учителя* (supervised & unsupervised learning). В задачах обучения без учителя имеется* выборка*, состоящая из *объектов*, описываемых набором *признаков*. В задачах обучения с учителем вдобавок к этому для каждого объекта некоторой выборки, называемой *обучающей*, известен *целевой признак* – по сути это то, что хотелось бы прогнозировать для прочих объектов, не из обучающей выборки.
# #### Пример
# Задачи классификации и регрессии – это задачи обучения с учителем. В качестве примера будем представлять задачу кредитного скоринга: на основе накопленных банком данных о своих клиентах хочется прогнозировать невозврат кредита. Здесь для алгоритма опыт *E* – это имеющаяся обучающая выборка: набор *объектов* (людей), каждый из которых характеризуется набором *признаков* (таких как возраст, зарплата, тип кредита, невозвраты в прошлом и т.д.), а также *целевым признаком*. Если этот целевой признак – просто факт невозврата кредита (1 или 0, т.е. банк знает о своих клиентах, кто вернул кредит, а кто – нет), то это задача (бинарной) классификации . Если известно, *на сколько* по времени клиент затянул с возвратом кредита и хочется то же самое прогнозировать для новых клиентов, то это будет задачей регрессии.
#
# Наконец, третья абстракция в определении машинного обучения – это метрика оценки производительности алгоритма *P*. Такие метрики различаются для разных задач и алгоритмов, и про них мы будим говорить по мере изучения алгоритмов. Пока скажем, что самая простая метрика качества алгоритма, решающего задачу классификации – это доля правильных ответов (*accuracy*, не называйте ее *точностью*, этот перевод зарезервирован под другую метрику, *precision*) – то есть попросту доля верных прогнозов алгоритма на тестовой выборке.
#
# Далее будем говорить о двух задачах обучения с учителем: о классификации и регресcии.
# ## Дерево решений
# Начнем обзор методов классификации и регрессии с одного из самых популярных – с дерева решений. Деревья решений используются в повседневной жизни в самых разных областях человеческой деятельности, порой и очень далеких от машинного обучения. Деревом решений можно назвать наглядную инструкцию, что делать в какой ситуации. Приведем пример из области консультирования научных сотрудников института. Высшая Школа Экономики выпускает инфо-схемы, облегчающие жизнь своим сотрудникам. Вот фрагмент инструкции по публикации научной статьи на портале института.
#
# <br>
# В терминах машинного обучения можно сказать, что это элементарный классификатор, который определяет форму публикации на портале (книга, статья, глава книги, препринт, публикация в "НИУ ВШЭ и СМИ") по нескольким признакам: типу публикации (монография, брошюра, статья и т.д.), типу издания, где опубликована статья (научный журнал, сборник трудов и т.д.) и остальным.
# Зачастую дерево решений служит обобщением опыта экспертов, средством передачи знаний будущим сотрудникам или моделью бизнес-процесса компании. Например, до внедрения масштабируемых алгоритмов машинного обучения в банковской сфере задача кредитного скоринга решалась экспертами. Решение о выдаче кредита заемщику принималось на основе некоторых интуитивно (или по опыту) выведенных правил, которые можно представить в виде дерева решений.
# <img src="https://habrastorage.org/files/194/9b6/ae9/1949b6ae97ab4fc9b1a37fbf182eda8f.gif"/><br>
# В этом случае можно сказать, что решается задача бинарной классификации (целевой класс имеет два значения: "Выдать кредит" и "Отказать") по признакам "Возраст", "Наличие дома", "Доход" и "Образование".
#
# Дерево решений как алгоритм машинного обучения – по сути то же самое: объединение логических правил вида "Значение признака $a$ меньше $x$ И Значение признака $b$ меньше $y$ ... => Класс 1" в структуру данных "Дерево". Огромное преимущество деревьев решений в том, что они легко интерпретируемы, понятны человеку. Например, по схеме на рисунке выше можно объяснить заемщику, почему ему было отказано в кредите. Скажем, потому, что у него нет дома и доход меньше 5000. Как мы увидим дальше, многие другие, хоть и более точные, модели не обладают этим свойством и могут рассматриваться скорее как "черный ящик", в который загрузили данные и получили ответ. В связи с этой "понятностью" деревьев решений и их сходством с моделью принятия решений человеком (можно легко объяснять боссу свою модель), деревья решений получили огромную популярность, а один из представителей этой группы методов классификации, С4.5, рассматривается первым в списке 10 лучших алгоритмов интеллектуального анализа данных ("Top 10 algorithms in data mining", Knowledge and Information Systems, 2008. [PDF](http://www.cs.uvm.edu/~icdm/algorithms/10Algorithms-08.pdf)).
# ## Как строится дерево решений
#
# В примере с кредитным скорингом мы видели, что решение о выдаче кредита принималось на основе возраста, наличия недвижимости, дохода и других. Но какой признак выбрать первым? Для этого рассмотрим пример попроще, где все признаки бинарные.
#
# Здесь можно вспомнить игру "20 вопросов", которая часто упоминается во введении в деревья решений. Наверняка каждый в нее играл. Один человек загадывает знаменитость, а второй пытается отгадать, задавая только вопросы, на которые можно ответить "Да" или "Нет" (опустим варианты "не знаю" и "не могу сказать"). Какой вопрос отгадывающий задаст первым делом? Конечно, такой, который сильнее всего уменьшит количество оставшихся вариантов. К примеру, вопрос "Это Анджелина Джоли?" в случае отрицательного ответа оставит более 6 миллиардов вариантов для дальнейшего перебора (конечно, поменьше, не каждый человек – знаменитость, но все равно немало), а вот вопрос "Это женщина?" отсечет уже около половины знаменитостей. То есть, признак "пол" намного лучше разделяет выборку людей, чем признак "это Анджелина Джоли", "национальность-испанец" или "любит футбол". Это интуитивно соответствует понятию прироста информации, основанного на энтропии.
# #### Энтропия
# Энтропия Шеннона определяется для системы с $N$ возможными состояниями следующим образом:
#
# $$\Large S = -\sum_{i=1}^{N}p_ilog_2p_i,$$
#
# где $p_i$ – вероятности нахождения системы в $i$-ом состоянии. Это очень важное понятие, используемое в физике, теории информации и других областях. Опуская предпосылки введения (комбинаторные и теоретико-информационные) этого понятия, отметим, что, интуитивно, энтропия соответствует степени хаоса в системе. Чем выше энтропия, тем менее упорядочена система и наоборот. Это поможет там формализовать "эффективное разделение выборки", про которое мы говорили в контексте игры "20 вопросов".
#
# <h4>Пример</h4>
# Для иллюстрации того, как энтропия поможет определить хорошие признаки для построения дерева, приведем тот же игрушечный пример, что в статье <a href="https://habrahabr.ru/post/171759/">"Энтропия и деревья принятия решений"</a>. Будем предсказывать цвет шарика по его координате. Конечно, ничего общего с жизнью это не имеет, но позволяет показать, как энтропия используется для построения дерева решений.
# <img src="https://habrastorage.org/files/c96/80a/a4b/c9680aa4babc40f4bbc8b3595e203979.png"/><br>
#
# Здесь 9 синих шариков и 11 желтых. Если мы наудачу вытащили шарик, то он с вероятностью $p_1=\frac{9}{20}$ будет синим и с вероятностью $p_2=\frac{11}{20}$ – желтым. Значит, энтропия состояния $S_0 = -\frac{9}{20}log_2{\frac{9}{20}}-\frac{11}{20}log_2{\frac{11}{20}} \approx 1$. Само это значение пока ни о чем нам не говорит. Теперь посмотрим, как изменится энтропия, если разбить шарики на две группы – с координатой меньше либо равной 12 и больше 12.
# <img src="https://habrastorage.org/files/186/444/a8b/186444a8bd0e451c8324ca8529f8d4f4.png"/><br>
#
# В левой группе оказалось 13 шаров, из которых 8 синих и 5 желтых. Энтропия этой группы равна $S_1 = -\frac{5}{13}log_2{\frac{5}{13}}-\frac{8}{13}log_2{\frac{8}{13}} \approx 0.96$. В правой группе оказалось 7 шаров, из которых 1 синий и 6 желтых. Энтропия правой группы равна $S_2 = -\frac{1}{7}log_2{\frac{1}{7}}-\frac{6}{7}log_2{\frac{6}{7}} \approx 0.6$. Как видим, энтропия уменьшилась в обеих группах по сравнению с начальным состоянием, хоть в левой и не сильно. Поскольку энтропия – по сути степень хаоса (или неопределенности) в системе, уменьшение энтропии называют приростом информации. Формально прирост информации (information gain, IG) при разбиении выборки по признаку $Q$ (в нашем примере это признак "$x \leq 12$") определяется как
# $$\Large IG(Q) = S_O - \sum_{i=1}^{q}\frac{|N_i|}{N}S_i,$$
# где $q$ – число групп после разбиения, $N_i$ – число элементов выборки, у которых признак $Q$ имеет $i$-ое значение. В нашем случае после разделения получилось две группы ($q = 2$) – одна из 13 элементов ($N_1 = 13$), вторая – из 7 ($N_2 = 7$). Прирост информации получился
# $$\Large IG("x \leq 12") = S_0 - \frac{13}{20}S_1 - \frac{7}{20}S_2 \approx 0.16.$$
# Получается, разделив шарики на две группы по признаку "координата меньше либо равна 12", мы уже получили более упорядоченную систему, чем в начале. Продолжим деление шариков на группы до тех пор, пока в каждой группе шарики не будут одного цвета.
# <img src="https://habrastorage.org/files/dae/a88/2b0/daea882b0a8e4ef4b23325c88f0353a1.png"/><br>
# Для правой группы потребовалось всего одно дополнительное разбиение по признаку "координата меньше либо равна 18", для левой – еще три. Очевидно, энтропия группы с шариками одного цвета равна 0 ($log_2{1} = 0$), что соответствует представлению, что группа шариков одного цвета – упорядоченная.
# В итоге мы построили дерево решений, предсказывающее цвет шарика по его координате. Отметим, что такое дерево решений может плохо работать для новых объектов (определения цвета новых шариков), поскольку оно идеально подстроилось под обучающую выборку (изначальные 20 шариков). Для классификации новых шариков лучше подойдет дерево с меньшим числом "вопросов", или разделений, пусть даже оно и не идеально разбивает по цветам обучающую выборку. Эту проблему, переобучение, мы еще рассмотрим далее.
# #### Алгоритм построения дерева
#
# Можно убедиться в том, что построенное в предыдущем примере дерево является в некотором смысле оптимальным – потребовалось только 5 "вопросов" (условий на признак $x$), чтобы "подогнать" дерево решений под обучающую выборку, то есть чтобы дерево правильно классифицировало любой обучающий объект. При других условиях разделения выборки дерево получится глубже.
#
# В основе популярных алгоритмов построения дерева решений, таких как ID3 и C4.5, лежит принцип жадной максимизации прироста информации – на каждом шаге выбирается тот признак, при разделении по которому прирост информации оказывается наибольшим. Дальше процедура повторяется рекурсивно, пока энтропия не окажется равной нулю или какой-то малой величине (если дерево не подгоняется идеально под обучающую выборку во избежание переобучения).
# В разных алгоритмах применяются разные эвристики для "ранней остановки" или "отсечения", чтобы избежать построения переобученного дерева.
#
# ```python
# def build(L):
# create node t
# if the stopping criterion is True:
# assign a predictive model to t
# else:
# Find the best binary split L = L_left + L_right
# t.left = build(L_left)
# t.right = build(L_right)
# return t
# ```
#
# #### Другие критерии качества разбиения в задаче классификации
#
# Мы разобрались, в том, как понятие энтропии позволяет формализовать представление о качестве разбиения в дереве. Но это всего-лишь эвристика, существуют и другие:
#
# - Неопределенность Джини (Gini impurity): $G = 1 - \sum\limits_k (p_k)^2$. Максимизацию этого критерия можно интерпретировать как максимизацию числа пар объектов одного класса, оказавшихся в одном поддереве. Подробнее об этом (как и обо многом другом) можно узнать из [репозитория](https://github.com/esokolov/ml-course-msu) Евгения Соколова. Не путать с индексом Джини! Подробнее об этой путанице – в [блогпосте](https://alexanderdyakonov.wordpress.com/2015/12/15/%D0%B7%D0%BD%D0%B0%D0%BA%D0%BE%D0%BC%D1%8C%D1%82%D0%B5%D1%81%D1%8C-%D0%B4%D0%B6%D0%B8%D0%BD%D0%B8/) Александра Дьяконова
# - Ошибка классификации (misclassification error): $E = 1 - \max\limits_k p_k$
#
#
# На практике ошибка классификации почти не используется, а неопределенность Джини и прирост информации работают почти одинаково.
#
# В случае задачи бинарной классификации ($p_+$ – вероятность объекта иметь метку +) энтропия и неопределенность Джини примут следующий вид:<br><br>
# $$ S = -p_+ \log_2{p_+} -p_- \log_2{p_-} = -p_+ \log_2{p_+} -(1 - p_{+}) \log_2{(1 - p_{+})};$$
# $$ G = 1 - p_+^2 - p_-^2 = 1 - p_+^2 - (1 - p_+)^2 = 2p_+(1-p_+).$$
#
# Когда мы построим графики этих двух функций от аргумента $p_+$, то увидим, что график энтропии очень близок к графику удвоенной неопределенности Джини, и поэтому на практике эти два критерия "работают" почти одинаково.
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
# %matplotlib inline
import seaborn as sns
from matplotlib import pyplot as plt
plt.rcParams['figure.figsize'] = (6,4)
xx = np.linspace(0,1,50)
plt.plot(xx, [2 * x * (1-x) for x in xx], label='gini')
plt.plot(xx, [4 * x * (1-x) for x in xx], label='2*gini')
plt.plot(xx, [-x * np.log2(x) - (1-x) * np.log2(1 - x) for x in xx], label='entropy')
plt.plot(xx, [1 - max(x, 1-x) for x in xx], label='missclass')
plt.plot(xx, [2 - 2 * max(x, 1-x) for x in xx], label='2*missclass')
plt.xlabel('p+')
plt.ylabel('criterion')
plt.title('Критерии качества как функции от p+ (бинарная классификация)')
plt.legend();
# #### Пример
# Рассмотрим пример применения дерева решений из библиотеки Scikit-learn для синтетических данных. Сгенерируем данные. Два класса будут сгенерированы из двух нормальных распределений с разными средними.
# +
# первый класс
np.random.seed(7)
train_data = np.random.normal(size=(100, 2))
train_labels = np.zeros(100)
# добавляем второй класс
train_data = np.r_[train_data, np.random.normal(size=(100, 2), loc=2)]
train_labels = np.r_[train_labels, np.ones(100)]
# -
# Напишем вспомогательную функцию, которая будет возвращать решетку для дальнейшей красивой визуализации.
def get_grid(data, eps=0.01):
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
return np.meshgrid(np.arange(x_min, x_max, eps),
np.arange(y_min, y_max, eps))
# Отобразим данные. Неформально, задача классификации в этом случае – построить какую-то "хорошую" границу, разделяющую 2 класса (красные точки от желтых). Если утрировать, то машинное обучение в этом случае сводится к тому, как выбрать хорошую разделяющую границу. Возможно, прямая будет слишком простой границей, а какая-то сложная кривая, огибающая каждую красную точку – будет слишком сложной и будем много ошибаться на новых примерах из того же распределения, из которого пришла обучающая выборка. Интуиция подсказывает, что хорошо на новых данных будет работать какая-то *гладкая* граница, разделяющая 2 класса, или хотя бы просто прямая (в $n$-мерном случае - гиперплоскость).
plt.rcParams['figure.figsize'] = (10,8)
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100,
cmap='autumn', edgecolors='black', linewidth=1.5)
plt.plot(range(-2,5), range(4,-3,-1));
# Попробуем разделить эти два класса, обучив дерево решений. В дереве будем использовать параметр `max_depth`, ограничивающий глубину дерева. Визуализируем полученную границу разделения класссов.
# +
from sklearn.tree import DecisionTreeClassifier
# параметр min_samples_leaf указывает, при каком минимальном количестве
# элементов в узле он будет дальше разделяться
clf_tree = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=17)
# обучаем дерево
clf_tree.fit(train_data, train_labels)
# немного кода для отображения разделяющей поверхности
xx, yy = get_grid(train_data)
predicted = clf_tree.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100,
cmap='autumn', edgecolors='black', linewidth=1.5);
# -
# А как выглядит само построенное дерево? Видим, что дерево "нарезает" пространство на 7 прямоугольников (в дереве 7 листьев). В каждом таком прямоугольнике прогноз дерева будет константным, по превалированию объектов того или иного класса.
# используем .dot формат для визуализации дерева
from sklearn.tree import export_graphviz
export_graphviz(clf_tree, feature_names=['x1', 'x2'],
out_file='../../img/small_tree.dot', filled=True)
# !dot -Tpng ../../img/small_tree.dot -o ../../img/small_tree.png
# !rm ../../img/small_tree.dot
# <img src='../../img/small_tree.png'>
# Как "читается" такое дерево?
#
# В начале было 200 объектов, 100 – одного класса и 100 – другого. Энтропия начального состояния была максимальной – 1. Затем было сделано разбиение объектов на 2 группы в зависимости от сравнения признака $x_1$ со значением $1.1034$ (найдите этот участок границы на рисунке выше, до дерева). При этом энтропия и в левой, и в правой группе объектов уменьшилась. И так далее, дерево строится до глубины 3. При такой визуализации чем больше объектов одного класса, тем цвет вершины ближе к темно-оранжевому и, наоборот, чем больше объектов второго класса, тем ближе цвет к темно-синему. В начале объектов одного лкасса поровну, поэтому корневая вершина дерева – белого цвета.
# ### Как дерево решений работает с количественными признаками
#
# Допустим, в выборке имеется количественный признак "Возраст", имеющий много уникальных значений. Дерево решений будет искать лучшее (по критерию типа прироста информации) разбиение выборки, проверяя бинарные признаки типа "Возраст < 17", "Возраст < 22.87" и т.д. Но что если таких "нарезаний" возраста слишком много? А что если есть еще количественный признак "Зарплата", и зарплату тоже можно "нарезать" большим числом способов? Получается слишком много бинарных признаков для выбора лучшего на каждом шаге построения дерева. Для решения этой проблемы применяют эвристики для ограничения числа порогов, с которыми мы сравниваем количественный признак.
#
# Рассмотрим это на игрушечном примере. Пусть есть следующая выборка:
data = pd.DataFrame({'Возраст': [17,64,18,20,38,49,55,25,29,31,33],
'Невозврат кредита': [1,0,1,0,1,0,0,1,1,0,1]})
data
# Отсортируем ее по возрастанию возраста.
data.sort_values('Возраст')
# Обучим на этих данных дерево решений (без ограничения глубины) и посмотрим на него.
age_tree = DecisionTreeClassifier(random_state=17)
age_tree.fit(data['Возраст'].values.reshape(-1, 1), data['Невозврат кредита'].values)
# Видим, что дерево задействовало 5 значений, с которыми сравнивается возраст: 43.5, 19, 22.5, 30 и 32 года. Если приглядеться, то это аккурат средние значения между возрастами, при которых целевой класс "меняется" с 1 на 0 или наоборот. Сложная фраза, поэтому пример: 43.5 – это среднее между 38 и 49 годами, клиент, которому 38 лет не вернул кредит, а тот, которому 49 – вернул. Аналогично, 19 лет – среднее между 18 и 20 годами. То есть в качестве порогов для "нарезания" количественного признака, дерево "смотрит" на те значения, при которых целевой класс меняет свое значение.
#
# Подумайте, почему не имеет смысла в данном случае рассматривать признак "Возраст < 17.5".
export_graphviz(age_tree, feature_names=['Возраст'],
out_file='../../img/age_tree.dot', filled=True)
# !dot -Tpng ../../img/age_tree.dot -o ../../img/age_tree.png
# <img src='../../img/age_tree.png'>
# Рассмотрим пример посложнее: добавим признак "Зарплата" (тыс. рублей/месяц).
data2 = pd.DataFrame({'Возраст': [17,64,18,20,38,49,55,25,29,31,33],
'Зарплата': [25,80,22,36,37,59,74,70,33,102,88],
'Невозврат кредита': [1,0,1,0,1,0,0,1,1,0,1]})
data2
# Если отсортировать по возрасту, то целевой класс ("Невозврат кредита") меняется (с 1 на 0 или наоборот) 5 раз. А если отсортировать по зарплате – то 7 раз. Как теперь дерево будет выбирать признаки? Посмотрим.
data2.sort_values('Возраст')
data2.sort_values('Зарплата')
age_sal_tree = DecisionTreeClassifier(random_state=17)
age_sal_tree.fit(data2[['Возраст', 'Зарплата']].values, data2['Невозврат кредита'].values);
export_graphviz(age_sal_tree, feature_names=['Возраст', 'Зарплата'],
out_file='../../img/age_sal_tree.dot', filled=True)
# !dot -Tpng ../../img/age_sal_tree.dot -o ../../img/age_sal_tree.png
# <img src='../../img/age_sal_tree.png'>
# Видим, что в дереве задействованы как разбиения по возрасту, так и по зарплате. Причем пороги, с которыми сравниваются признаки: 43.5 и 22.5 года – для возраста и 95 и 30.5 тыс. руб/мес – для зарплаты. И опять можно заметить, что 95 тыс. – это среднее между 88 и 102, при этом человек с зарплатой 88 оказался "плохим", а с 102 – "хорошим". То же самое для 30.5 тыс. То есть перебирались сравнения зарплаты и возраста не со всеми возможными значениями, а только с несколькими. А почему в дереве оказались именно эти признаки? Потому что по ним разбиения оказались лучше (по критерию неопределенности Джини).
# **Вывод:** самая простая эвристика для обработки количественных признаков в дереве решений: количественный признак сортируется по возрастанию, и в дереве проверяются только те пороги, при которых целевой признак меняет значение. Звучит не очень строго, но надеюсь, я донес смысл с помощью игрушечных примеров.
#
# Дополнительно, когда в данных много количественных признаков, и у каждого много уникальных значений, могут отбираться не все пороги, описанные выше, а только топ-N, дающих максимальный прирост все того же критерия. То есть, по сути, для каждого порога строится дерево глубины 1, считается насколько снизилась энтропия (или неопределенность Джини) и выбираются только лучшие пороги, с которыми стоит сравнивать количественный признак.
#
# Для иллюстрации: при разбиении по признаку "Зарплата $\leq$ 34.5" в левой подгруппе энтропия 0 (все клиенты "плохие"), а в правой – 0.954 (3 "плохих" и 5 "хороших", можете проверить, 1 часть домашнего задания будет как раз на то, чтоб разобраться досканально с построением деревьев). Прирост информации получается примерно 0.3.
# А при разбиении по признаку "Зарплата $\leq$ 95" в левой подгруппе энтропия 0.97 (6 "плохих" и 4 "хороших"), а в правой – 0 (всего один объект). Прирост информации получается примерно 0.11.
# Посчитав таким образом прирост информации для каждого разбиения, можно предварительно, до построения большого дерева (по всем признакам) отобрать пороги, с которыми будет сравниваться каждый количественный признак.
#
# Еще примеры дискретизации количественных признаков можно посмотреть в постах, подобных [этому](http://kevinmeurer.com/a-simple-guide-to-entropy-based-discretization/) или [этому](http://clear-lines.com/blog/post/Discretizing-a-continuous-variable-using-Entropy.aspx). Одна из самых известных научных статей на эту тему – "On the handling of continuous-valued attributes in decision tree generation" (U.M. Fayyad. K.B. Irani, "Machine Learning", 1992).
# ### Основные параметры дерева
#
# В принципе дерево решений можно построить до такой глубины, чтоб в каждом листе был ровно один объект. Но на практике это не делается из-за того, что такое дерево будет *переобученным* – оно слишком настроится на обучающую выборку и будет плохо работать на прогноз на новых данных. Где-то внизу дерева, на большой глубине будут появляться разбиения по менее важным признакам (например, приехал ли клиент из Саратова или Костромы). Если утрировать, может оказаться так, что из всех 4 клиентов, пришедших в банк за кредитом в зеленых штанах, никто не вернул кредит. Но мы не хотим, чтобы наша модель классификации порождала такие специфичные правила.
#
# Основные способы борьбы с переобучением в случае деревьев решений:
# - искусственное ограничение глубины или минимального числа объектов в листе: построение дерева просто в какой-то момент прекращается;
# - стрижка дерева (*pruning*). При таком подходе дерево сначала строится до максимальной глубины, потом постепенно, снизу вверх, некоторые вершины дерева убираются за счет сравнения по качеству дерева с данным разбиением и без него (сравнение проводится с помощью *кросс-валидации*, о которой чуть ниже). Подробнее можно почитать в материалах [репозитория](https://github.com/esokolov/ml-course-msu) Евгения Соколова.
#
# ### Класс DecisionTreeClassifier в Scikit-learn
# Основные параметры класса [sklearn.tree.DecisionTreeClassifier](http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html):
#
# - `max_depth` – максимальная глубина дерева
# - `max_features` - максимальное число признаков, по которым ищется лучшее разбиение в дереве (это нужно потому, что при большом количестве признаков будет "дорого" искать лучшее (по критерию типа прироста информации) разбиение среди *всех* признаков)
# - `min_samples_leaf` – минимальное число объектов в листе. У этого параметра есть понятная интерпретация: скажем, если он равен 5, то дерево будет порождать только те классифицирующие правила, которые верны как мимимум для 5 объектов
#
# Параметры дерева надо настраивать в зависимости от входных данных, и делается это обычно с помощью *кросс-валидации*, про нее чуть ниже.
#
# ## Дерево решений в задаче регрессии
#
# При прогнозировании количественного признака идея построения дерева остается та же, но меняется критерий качества:
#
# - Дисперсия вокруг среднего: $$\Large D = \frac{1}{\ell} \sum\limits_{i =1}^{\ell} (y_i - \frac{1}{\ell} \sum\limits_{i =1}^{\ell} y_i)^2, $$
# где $\ell$ – число объектов в листе, $y_i$ – значения целевого признака. Попросту говоря, минимизируя дисперсию вокруг среднего, мы ищем признаки, разбивающие выборку таким образом, что значения целевого признака в каждом листе примерно равны.
# #### Пример
# Сгенерируем данные, распределенные вокруг функции $f(x) = e^{-x ^ 2} + 1.5 * e^{-(x - 2) ^ 2}$ c некоторым шумом.
# +
n_train = 150
n_test = 1000
noise = 0.1
def f(x):
x = x.ravel()
return np.exp(-x ** 2) + 1.5 * np.exp(-(x - 2) ** 2)
def generate(n_samples, noise):
X = np.random.rand(n_samples) * 10 - 5
X = np.sort(X).ravel()
y = np.exp(-X ** 2) + 1.5 * np.exp(-(X - 2) ** 2) + \
np.random.normal(0.0, noise, n_samples)
X = X.reshape((n_samples, 1))
return X, y
X_train, y_train = generate(n_samples=n_train, noise=noise)
X_test, y_test = generate(n_samples=n_test, noise=noise)
# +
from sklearn.tree import DecisionTreeRegressor
reg_tree = DecisionTreeRegressor(max_depth=5, random_state=17)
reg_tree.fit(X_train, y_train)
reg_tree_pred = reg_tree.predict(X_test)
# -
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, reg_tree_pred, "g", lw=2)
plt.xlim([-5, 5])
plt.title("Decision tree regressor, MSE = %.2f" % np.sum((y_test - reg_tree_pred) ** 2))
plt.show()
# Видим, что дерево решений аппроксимирует зависимость в данных кусочно-постоянной функцией.
# # Метод ближайших соседей
#
# Метод ближайших соседей (k Nearest Neighbors, или kNN) — тоже очень популярный метод классификации, также иногда используемый в задачах регрессии. Это, наравне с деревом решений, один из самых понятных подходов к классификации. На уровне интуиции суть метода такова: посмотри на соседей, какие преобладают, таков и ты. Формально основой метода является гипотезой компактности: если метрика расстояния между примерами введена достаточно удачно, то схожие примеры гораздо чаще лежат в одном классе, чем в разных.
#
# Согласно методу ближайших соседей, тестовый пример (зеленый шарик) будет отнесен к классу "синие", а не "красные".
#
# <img src="../../img/kNN.png">
#
# Например, если не знаешь, какой тип товара указать в объявлении для Bluetooth-гарнитуры, можешь найти 5 похожих гарнитур, и если 4 из них отнесены к категории "Аксессуары", и только один - к категории "Техника", то здравый смысл подскажет для своего объявления тоже указать категорию "Аксессуары".
#
# Для классификации каждого из объектов тестовой выборки необходимо последовательно выполнить следующие операции:
# - Вычислить расстояние до каждого из объектов обучающей выборки
# - Отобрать $k$ объектов обучающей выборки, расстояние до которых минимально
# - Класс классифицируемого объекта — это класс, наиболее часто встречающийся среди $k$ ближайших соседей
#
# Примечательное свойство такого подхода – его ленивость. Это значит, что вычисления начинаются только в момент классификации тестового примера, а заранее, только при наличии обучающих примеров, никакая модель не строится. В этом отличие, например, от ранее рассмотренного дерева решений, где сначала на основе обучающей выборки строится дерево, а потом относительно быстро происходит классификация тестовых примеров.
#
# Стоит отметить, что метод ближайших соседей – хорошо изученный подход (в машинном обучении, эконометрике и статистике больше известно наверно только про линейную регрессию). Для метода ближайших соседей существует немало важных теорем, утверждающих, что на "бесконечных" выборках это оптимальный метод классификации. Авторы классической книги "The Elements of Statistical Learning" считают kNN теоретически идеальным алгоритмом, применимость которого просто ограничена вычислительными возможностями и проклятием размерностей.
#
# ### Метод ближайших соседей в реальных задачах
# - В чистом виде kNN может послужить хорошим стартом (baseline) в решении какой-либо задачи;
# - В соревнованиях Kaggle kNN часто используется для построения мета-признаков (прогноз kNN подается на вход прочим моделям) или в стекинге/блендинге;
# - Идея ближайшего соседа расширяется и на другие задачи, например, в рекомендательных системах простым начальным решением может быть рекомендация какого-то товара (или услуги), популярного среди *ближайших соседей* человека, которому хотим сделать рекомендацию;
# - На практике для больших выборок часто пользуются *приближенными* методами поиска ближайших соседей. [Вот](https://www.youtube.com/watch?v=UUm4MOyVTnE) лекция Артема Бабенко про эффективные алгоритмы поиска ближайших соседей среди миллиардов объектов в пространствах высокой размерности (поиск по картинкам). Также известны открытые библиотеки, в которых реализованы такие алгоритмы, спасибо компании Spotify за ее библиотеку [Annoy](https://github.com/spotify/annoy).
#
# Качество классификации методом ближайших соседей зависит от нескольких параметров:
# - число соседей
# - метрика расстояния между объектами (часто используются метрика Хэмминга, евклидово расстояние, косинусное расстояние и расстояние Минковского). Отметим, что при использовании большинства метрик значения признаков надо масштабировать. Условно говоря, чтобы признак "Зарплата" с диапазоном значений до 100 тысяч не вносил больший вклад в расстояние, чем "Возраст" со значениями до 100.
# - веса соседей (соседи тестового примера могут входить с разными весами, например, чем дальше пример, тем с меньшим коэффициентом учитывается его "голос")
#
# ### Класс KNeighborsClassifier в Scikit-learn
# Основные параметры класса sklearn.neighbors.KNeighborsClassifier:
# - weights: "uniform" (все веса равны), "distance" (вес обратно пропорционален расстоянию до тестового примера) или другая определенная пользователем функция
# - algorithm (опционально): "brute", "ball_tree", "KD_tree", или "auto". В первом случае ближайшие соседи для каждого тестового примера считаются перебором обучающей выборки. Во втором и третьем - расстояние между примерами хранятся в дереве, что ускоряет нахождение ближайших соседей. В случае указания параметра "auto" подходящий способ нахождения соседей будет выбран автматически на основе обучающей выборки.
# - leaf_size (опционально): порог переключения на полный перебор в случае выбора BallTree или KDTree для нахождения соседей
# - metric: "minkowski", "manhattan", "euclidean", "chebyshev" и другие
# # Выбор параметров модели и кросс-валидация
# Главная задача обучаемых алгоритмов – их способность *обобщаться*, то есть хорошо работать на новых данных. Поскольку, на новых данных мы сразу не можем проверить качество построенной модели (нам ведь надо для них сделать прогноз, то есть истинных значений целевого признака мы для них не знаем), то надо пожертвовать небольшой порцией данных, чтоб на ней проверить качество модели.
#
# Чаще всего это делается одним из 2 способов:
#
# - отложенная выборка (*held-out/hold-out set*). При таком подходе мы оставляем какую-то долю обучающей выборки (как правило от 20% до 40%), обучаем модель на остальных данных (60-80% исходной выборки) и считаем некоторую метрику качества модели (например, самое простое – долю правильных ответов в задаче классификации) на отложенной выборке.
# - кросс-валидация (*cross-validation*, на русский еще переводят как скользящий или перекрестный контроль). Тут самый частый случай – K-fold кросс-валидация
# <img src='../../img/cross_validation.png'><br>
#
# Тут модель обучается K раз на разных (K-1) подвыборках исходной выборки (белый цвет), а проверяется на одной подвыборке (каждый раз на разной, оранжевый цвет).
# Получаются $K$ оценок качества модели, которые обычно усредняются, выдавая среднюю оценку качества классификации/регресии на кросс-валидации.
#
# Кросс-валидация дает лучшую по сравнению отложенной выборкой оценку качества модели на новых данных. Но кросс-валидация вычислительно дорогостоящая, если данных много.
#
# Кросс-валидация – очень важная техника в машинном обучении (применяемая также в статистике и эконометрике), с ее помощью выбираются гиперпараметры моделей, сравниваются модели между собой, оценивается полезность новых признаков в задаче и т.д. Более подробно можно почитать, например, [тут](https://sebastianraschka.com/blog/2016/model-evaluation-selection-part1.html) у Sebastian Raschka или в любом классическом учебнике по машинному (статистическому) обучению
# ## Деревья решений и метод ближайших соседей в задаче прогнозирования оттока клиентов телеком-оператора
# Считаем данные в DataFrame и проведем предобработку. Штаты пока сохраним в отдельный объект Series, но удалим из датафрейма. Первую модель будем обучать без штатов, потом посмотрим, помогают ли они.
df = pd.read_csv('../../data/telecom_churn.csv')
df['International plan'] = pd.factorize(df['International plan'])[0]
df['Voice mail plan'] = pd.factorize(df['Voice mail plan'])[0]
df['Churn'] = df['Churn'].astype('int')
states = df['State']
y = df['Churn']
df.drop(['State', 'Churn'], axis=1, inplace=True)
df.head()
from sklearn.model_selection import train_test_split, StratifiedKFold
# Выделим 70% выборки (X_train, y_train) под обучение и 30% будут отложенной выборкой (X_holdout, y_holdout). отложенная выборка никак не будет участвовать в настройке параметров моделей, на ней мы в конце, после этой настройки, оценим качество полученной модели.
X_train, X_holdout, y_train, y_holdout = train_test_split(df.values, y, test_size=0.3,
random_state=17)
# Обучим 2 модели – дерево решений и kNN, пока не знаем, какие параметры хороши, поэтому наугад: глубину дерева берем 5, число ближайших соседей – 10.
# +
from sklearn.neighbors import KNeighborsClassifier
tree = DecisionTreeClassifier(max_depth=5, random_state=17)
knn = KNeighborsClassifier(n_neighbors=10)
# -
# %%time
tree.fit(X_train, y_train)
# %%time
knn.fit(X_train, y_train)
# Качество прогнозов будем проверять с помощью простой метрики – доли правильных ответов
from sklearn.metrics import accuracy_score
# Сделаем прогнозы для отложенной выборки. Видим, что дерево решений справилось намного лучше. Но это мы пока выбирали параметры наугад.
tree_pred = tree.predict(X_holdout)
accuracy_score(y_holdout, tree_pred)
knn_pred = knn.predict(X_holdout)
accuracy_score(y_holdout, knn_pred)
# Теперь настроим параметры дерева на кросс-валидации. Настраивать будем максимальную глубину и максимальное используемое на каждом разбиении число признаков. Суть того, как работает GridSearchCV: для каждой уникальной пары значений параметров `max_depth` и `max_features` будет проведена 5-кратная кросс-валидация и выберется лучшее сочетание параметров.
from sklearn.model_selection import GridSearchCV, cross_val_score
tree_params = {'max_depth': range(1,11),
'max_features': range(4,19)}
tree_grid = GridSearchCV(tree, tree_params,
cv=5, n_jobs=-1,
verbose=True)
tree_grid.fit(X_train, y_train)
# Лучшее сочетание параметров и соответствующая средняя доля правильных ответов на кросс-валидации:
tree_grid.best_params_
tree_grid.best_score_
accuracy_score(y_holdout, tree_grid.predict(X_holdout))
# Теперь попробуем настроить число соседей в алгоритме kNN.
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
knn_pipe = Pipeline([('scaler', StandardScaler()), ('knn', KNeighborsClassifier(n_jobs=-1))])
knn_params = {'knn__n_neighbors': range(1, 10)}
knn_grid = GridSearchCV(knn_pipe, knn_params,
cv=5, n_jobs=-1,
verbose=True)
knn_grid.fit(X_train, y_train)
knn_grid.best_params_, knn_grid.best_score_
accuracy_score(y_holdout, knn_grid.predict(X_holdout))
# Видим, что в этом примере дерево показало себя лучше, чем метод ближайших соседей. Более того, в данной задаче дерево проявляет себя очень хорошо, и даже случайный лес (который пока представляем просто как кучу деревьев, которые вместе работают почему-то намного лучше, чем одно дерево) в этом примере показывает долю правильных ответов не намного выше (как на кросс-валидации, так и на отложенной выборке), а обучается намного дольше.
# +
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(n_estimators=100, n_jobs=-1, random_state=17)
print(np.mean(cross_val_score(forest, X_train, y_train, cv=5)))
# -
forest_params = {'max_depth': range(1,11),
'max_features': range(4,19)}
forest_grid = GridSearchCV(forest, forest_params,
cv=5, n_jobs=-1,
verbose=True)
forest_grid.fit(X_train, y_train)
forest_grid.best_params_, forest_grid.best_score_
accuracy_score(y_holdout, forest_grid.predict(X_holdout))
# Нарисуем получившееся дерево. Из-за того, что оно не совсем игрушечное (максимальная глубина – 6), картинка получается уже не маленькой, но по дерево можно "прогуляться", если отдельно открыть рисунок.
export_graphviz(tree_grid.best_estimator_, feature_names=df.columns,
out_file='../../img/churn_tree.dot', filled=True)
# !dot -Tpng ../../img/churn_tree.dot -o ../../img/churn_tree.png
# <img src='../../img/churn_tree.png'>
# ## Деревья решений и метод ближайших соседей в задаче распознавания рукописных цифр MNIST
# Теперь посмотрим на описанные 2 алгоритма в реальной задаче. Используемый "встроенные" в `sklearn` данные по рукописным цифрам. Эта задача будет примером, когда метод ближайших соседей работает на удивление хорошо.
from sklearn.datasets import load_digits
# Загружаем данные.
data = load_digits()
X, y = data.data, data.target
# Картинки здесь представляются матрицей 8 x 8 (интенсивности белого цвета для каждого пикселя). Далее эта матрица "разворачивается" в вектор длины 64, получается признаковое описание объекта.
X[0,:].reshape([8,8])
# Нарисуем несколько рукописных цифр, видим, что они угадываются.
f, axes = plt.subplots(1, 4, sharey=True, figsize=(16,6))
for i in range(4):
axes[i].imshow(X[i,:].reshape([8,8]));
# Посмотрим на соотношение классов в выборке, видим, что примерно поровну нулей, единиц, ..., девяток.
np.bincount(y)
# Выделим 70% выборки (X_train, y_train) под обучение и 30% будут отложенной выборкой (X_holdout, y_holdout). отложенная выборка никак не будет участвовать в настройке параметров моделей, на ней мы в конце, после этой настройки, оценим качество полученной модели.
X_train, X_holdout, y_train, y_holdout = train_test_split(X, y, test_size=0.3,
random_state=17)
# Обучим дерево решений и kNN, опять параметры пока наугад берем.
tree = DecisionTreeClassifier(max_depth=5, random_state=17)
knn = KNeighborsClassifier(n_neighbors=10)
# %%time
tree.fit(X_train, y_train)
# %%time
knn.fit(X_train, y_train)
# Сделаем прогнозы для отложенной выборки. Видим, что метод ближайших соседей справился намного лучше. Но это мы пока выбирали параметры наугад.
tree_pred = tree.predict(X_holdout)
knn_pred = knn.predict(X_holdout)
accuracy_score(y_holdout, knn_pred), accuracy_score(y_holdout, tree_pred)
# Теперь так же, как раньше настроим параметры моделей на кросс-валидации, только учтем, что признаков сейчас больше, чем в прошлой задаче - 64.
tree_params = {'max_depth': [1, 2, 3, 5, 10, 20, 25, 30, 40, 50, 64],
'max_features': [1, 2, 3, 5, 10, 20 ,30, 50, 64]}
tree_grid = GridSearchCV(tree, tree_params,
cv=5, n_jobs=-1,
verbose=True)
tree_grid.fit(X_train, y_train)
# Лучшее сочетание параметров и соответствующая средняя доля правильных ответов на кросс-валидации:
tree_grid.best_params_, tree_grid.best_score_
accuracy_score(y_holdout, tree_grid.predict(X_holdout))
# Это уже не 66%, но и не 97%. Метод ближайших соседей на этом наборе данных работает лучше. В случае одного ближайшего соседа на кросс-валидации достигается почти 99% угадываний.
np.mean(cross_val_score(KNeighborsClassifier(n_neighbors=1), X_train, y_train, cv=5))
knn = KNeighborsClassifier(n_neighbors=1).fit(X_train, y_train)
accuracy_score(y_holdout, knn.predict(X_holdout))
# Обучим на этих же данных случайный лес, он на большинстве выборок работает лучше, чем метод ближайших соседей. Но сейчас у нас исключение.
np.mean(cross_val_score(RandomForestClassifier(random_state=17), X_train, y_train, cv=5))
rf = RandomForestClassifier(random_state=17, n_jobs=-1).fit(X_train, y_train)
accuracy_score(y_holdout, rf.predict(X_holdout))
# Вы будете правы, если возразите, что мы тут не настраивали параметры RandomForestClassifier, но даже с настройкой доля правильных ответов не достигает 98%, как для у метода одного ближайшего соседа.
# Результаты эксперимента:
#
# | | CV | Holdout |
# |-----|:-----:|:-------:|
# | **DT** | 0.844 | 0.838 |
# | **kNN** | 0.987 | 0.983 |
# | **RF** | 0.935 | 0.941 |
#
# Обозначения: CV и Holdout– средние доли правильных ответов модели на кросс-валидации и отложенной выборке соот-но. DT – дерево решений, kNN – метод ближайших соседей, RF – случайный лес
#
# **Вывод** по этому эксперименту (и общий совет): в начале проверяйте на своих данных простые модели – дерево решений и метод ближайших соседей (а в следующий раз сюда добавится логистическая регрессия), может оказаться, что уже они работают достаточно хорошо.
# ## Плюсы и минусы деревьев решений
#
# **Плюсы:**
# - Порождение четких правил классификации, понятных человеку, например, "если возраст < 25 и интерес к мотоциклам, то отказать в кредите". Это свойство называют интерпретируемостью модели;
# - Деревья решений могут легко визуализироваться, то есть может "интерпретироваться" (строгого определения я не видел) как сама модель (дерево), так и прогноз для отдельного взятого тестового объекта (путь в дереве);
# - Быстрые процессы обучения и прогнозирования;
# - Малое число параметров модели;
# - Поддержка и числовых, и категориальных признаков.
#
# **Минусы:**
# - У порождения четких правил классификации есть и другая сторона: деревья очень чувствительны к шумам во входных данных, вся модель может кардинально измениться, если немного изменится обучающая выборка (например, если убрать один из признаков или добавить несколько объектов), поэтому и правила классификации могут сильно изменяться, что ухудшает интерпретируемость модели;
# - Разделяющая граница, построенная деревом решений, имеет свои ограничения (состоит из гиперплоскостей, перпендикулярных какой-то из координатной оси), и на практике дерево решений по качеству классификации уступает некоторым другим методам;
# - Необходимость отсекать ветви дерева (pruning) или устанавливать минимальное число элементов в листьях дерева или максимальную глубину дерева для борьбы с переобучением. Впрочем, переобучение - проблема всех методов машинного обучения;
# - Нестабильность. Небольшие изменения в данных могут существенно изменять построенное дерево решений. С этой проблемой борются с помощью ансамблей деревьев решений (рассмотрим далее);
# - Проблема поиска оптимального дерева решений (минимального по размеру и способного без ошибок классифицировать выборку) NP-полна, поэтому на практике используются эвристики типа жадного поиска признака с максимальным приростом информации, которые не гарантируют нахождения глобально оптимального дерева;
# - Сложно поддерживаются пропуски в данных. Friedman оценил, что на поддержку пропусков в данных ушло около 50% кода CART (классический алгоритм построения деревьев классификации и регрессии – Classification And Regression Trees, в `sklearn` реализована улучшенная версия именно этого алгоритма);
# - Модель умеет только интерполировать, но не экстраполировать (это же верно и для леса и бустинга на деревьях). То есть дерево решений делает константный прогноз для объектов, находящихся в признаковом пространстве вне параллелепипеда, охватывающего все объекты обучающей выборки. В нашем примере с желтыми и синими шариками это значит, что модель дает одинаковый прогноз для всех шариков с координатой > 19 или < 0.
# ### Плюсы и минусы метода ближайших соседей
#
# Плюсы:
# - Простая реализация
# - Можно адаптировать под нужную задачу выбором метрики или ядра (в двух словах: ядро может задавать операцию сходства для сложных объектов типа графов, а сам подход kNN остается тем же). Кстати, профессор ВМК МГУ и опытный участник соревнований по анализу данных Александр Дьяконов любит самый простой kNN, но с настроенной метрикой сходства объектов. Можно почитать про некоторые его решения (в частности, "VideoLectures.Net Recommender System Challenge") на персональном [сайте](http://alexanderdyakonov.narod.ru/contests.htm);
# - Неплохая интерпретация, можно объяснить, почему тестовый пример был классифицирован именно так. Хотя этот аргумент можно атаковать: если число соседей большое, то интерпретация ухудшается (условно: "мы не дали ему кредит, потому что он похож на 350 клиентов, из которых 70 – плохие, что на 12% больше, чем в среднем по выборке").
#
# Минусы:
# - Метод считается быстрым в сравнении, например, с композициями алгоритмов, но в реальных задачах, как правило, число соседей, используемых для классификации, будет большим (100-150), и в таком случае алгоритм будет работать не так быстро, как дерево решений;
# - Если в наборе данных много признаков, то трудно подобрать подходящие веса и определить, какие признаки не важны для классификации/регрессии;
# - Зависимость от выбранной метрики расстояния между примерами. Выбор по умолчанию евклидового расстояния чаще всего ничем не обоснован. Можно отыскать хорошее решение перебором параметров, но для большого набора данных это отнимает много времени;
# - Нет теоретических оснований выбора определенного числа соседей - только перебор (впрочем, чаще всего это верно для всех гиперпараметров всех моделей). В случае малого числа соседей метод чувствителен к выбросам, то есть склонен переобучаться;
# - Как правило, плохо работает, когда признаков много, из-за "прояклятия размерности". Про это хорошо рассказывает известный в ML-сообществе профессор Pedro Domingos – [тут](https://homes.cs.washington.edu/~pedrod/papers/cacm12.pdf) в популярной статье "A Few Useful Things to Know about Machine Learning", также "the curse of dimensionality" описывается в книге Deep Learning в [главе](http://www.deeplearningbook.org/contents/ml.html) "Machine Learning basics".
# ### Сложный случай для деревьев
# В продолжение обсуждения плюсов и минусов приведем очень простой пример задачи классификации, с которым дерево справляется, но делает все как-то "сложнее", чем хотелось бы. Создадим множество точек на плоскости (2 признака), каждая точка будет относиться к одному из классов (+1, красные, или -1 – желтые). Если смотреть на это как на задачу классификации, то вроде все очень просто – классы разделяются прямой.
def form_linearly_separable_data(n=500, x1_min=0, x1_max=30, x2_min=0, x2_max=30):
data, target = [], []
for i in range(n):
x1, x2 = np.random.randint(x1_min, x1_max), np.random.randint(x2_min, x2_max)
if np.abs(x1 - x2) > 0.5:
data.append([x1, x2])
target.append(np.sign(x1 - x2))
return np.array(data), np.array(target)
X, y = form_linearly_separable_data()
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='autumn', edgecolors='black');
# Однако дерево решений строит уж больно сложную границу и само по себе оказывается глубоким. Кроме того, представьте, как плохо дерево будет обобщаться на пространство вне представленного квадрата $30 \times 30$, обрамляющего обучающую выборку.
# +
tree = DecisionTreeClassifier(random_state=17).fit(X, y)
xx, yy = get_grid(X, eps=.05)
predicted = tree.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(X[:, 0], X[:, 1], c=y, s=100,
cmap='autumn', edgecolors='black', linewidth=1.5)
plt.title('Easy task. Decision tree compexifies everything');
# -
# Вот такая сложная конструкция, хотя решение (хорошая разделяющая поверхность) – это всего лишь прямая $x_1 = x_2$.
export_graphviz(tree, feature_names=['x1', 'x2'],
out_file='../../img/deep_toy_tree.dot', filled=True)
# !dot -Tpng ../../img/deep_toy_tree.dot -o ../../img/deep_toy_tree.png
# <img src='../../img/deep_toy_tree.png'>
# Метод одного ближайшего соседа здесь справляется вроде лучше дерева, но все же не так хорошо, как линейный классификатор (наша следующая тема).
# +
knn = KNeighborsClassifier(n_neighbors=1).fit(X, y)
xx, yy = get_grid(X, eps=.05)
predicted = knn.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(X[:, 0], X[:, 1], c=y, s=100,
cmap='autumn', edgecolors='black', linewidth=1.5);
plt.title('Easy task, kNN. Not bad');
# -
# ### Сложный случай для метода ближайших соседей
# Теперь рассмотрим еще один простой пример. В задаче классификации один из признаков будет просто пропорционален вектору ответов, но методу ближайших соседей это не поможет.
def form_noisy_data(n_obj=1000, n_feat=100, random_seed=17):
np.seed = random_seed
y = np.random.choice([-1, 1], size=n_obj)
# первый признак пропорционален целевому
x1 = 0.3 * y
# остальные признаки – шум
x_other = np.random.random(size=[n_obj, n_feat - 1])
return np.hstack([x1.reshape([n_obj, 1]), x_other]), y
X, y = form_noisy_data()
# Как обычно, будем смотреть на долю правильных ответов на кросс-валидации и на отложенной выборке. Построим кривые, отражающие зависимость этих величин от параметра `n_neighbors` в методе ближайших соседей. Такие кривые называются кривыми валидации.
X_train, X_holdout, y_train, y_holdout = train_test_split(X, y, test_size=0.3,
random_state=17)
# Видим, что метод ближайших соседей с евклидовой метрикой не справляется с задачей, даже если варьировать число ближайших соседей в широком диапазоне. Напротив, дерево решений легко "обнаруживает" скрытую зависимость в данных при любом ограничении на максимальную глубину.
# +
from sklearn.model_selection import cross_val_score
cv_scores, holdout_scores = [], []
n_neighb = [1, 2, 3, 5] + list(range(50, 550, 50))
for k in n_neighb:
knn = KNeighborsClassifier(n_neighbors=k)
cv_scores.append(np.mean(cross_val_score(knn, X_train, y_train, cv=5)))
knn.fit(X_train, y_train)
holdout_scores.append(accuracy_score(y_holdout, knn.predict(X_holdout)))
plt.plot(n_neighb, cv_scores, label='CV')
plt.plot(n_neighb, holdout_scores, label='holdout')
plt.title('Easy task. kNN fails')
plt.legend();
# -
tree = DecisionTreeClassifier(random_state=17, max_depth=1)
tree_cv_score = np.mean(cross_val_score(tree, X_train, y_train, cv=5))
tree.fit(X_train, y_train)
tree_holdout_score = accuracy_score(y_holdout, tree.predict(X_holdout))
print('Decision tree. CV: {}, holdout: {}'.format(tree_cv_score, tree_holdout_score))
# Итак, во втором примере дерево справилось с задачей идеально, а метод ближайших соседей испытал трудности. Впрочем, это минус скорее не метода, а используемой евклидовой метрики: в данном случае она не позволила выявить, что один признак намного лучше остальных.
| 72.952064 | 1,143 |
e8427684d0f7138593c3698170a07fe61ed66380
|
py
|
python
|
tutorials/W0D3_LinearAlgebra/W0D3_Tutorial3.ipynb
|
sjbabdi/course-content
|
['CC-BY-4.0', 'BSD-3-Clause']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W0D3_LinearAlgebra/W0D3_Tutorial3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# -
#
# # Bonus Tutorial: Discrete Dynamical Systems
# **Week 0, Day 3: Linear Algebra**
#
# **By Neuromatch Academy**
#
# __Content creators:__ Name Surname, Name Surname
#
#
#
# __Content reviewers:__ Name Surname, Name Surname.
#
# __Content editors:__ Name Surname, Name Surname.
#
# __Production editors:__ Name Surname, Name Surname.
# + [markdown] colab_type="text"
# **Our 2021 Sponsors, including Presenting Sponsor Facebook Reality Labs**
#
# <p align='center'><img src='https://github.com/NeuromatchAcademy/widgets/blob/master/sponsors.png?raw=True'/></p>
# -
# ---
# # Tutorial Objectives
#
# In this tutorial, we will start to gain an intuition for how eigenvalues and eigenvectors can be helpful for understanding dynamical systems. We will focus on a discrete dynamical system consisting of two neurons.
#
# By the end of the tutorial, you will:
#
# * Predict whether the firing rates of interconnected model neurons will explode or decay based on the eigenvalues of the weight matrix.
# * Apply ideas from previous tutorials (linear combination, basis vectors, etc) to understand a new concept
#
#
#
#
# ---
# # Setup
# + cellView="both"
# Imports
# Import only the libraries/objects that you use in this tutorial.
# If any external library has to be installed, !pip install library --quiet
# follow this order: numpy>matplotlib.
# import widgets in hidden Figure settings cell
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# + cellView="form"
#@title Figure settings
import ipywidgets as widgets # interactive display
# %config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
# + cellView="form"
#@title Plotting functions
def plot_circuit_responses(u, W, eigenstuff = False, xlim='default', ylim='default'):
fig, ax = plt.subplots(1, 1, figsize=(10,10))
# Set up axis limits
if xlim =='default':
extreme = np.maximum(np.abs(np.min(u)), np.max(u))
xlim = [- extreme, extreme]
if ylim == 'default':
extreme = np.maximum(np.abs(np.min(u)), np.max(u))
ylim = [- extreme, extreme]
# Set up look
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
cs = plt.rcParams['axes.prop_cycle'].by_key()['color']*10
ax.set_xlim(xlim)
ax.set_ylim(ylim)
# Set up tracking textz
tracker_text = ax.text(.5, .9, "", color='w', fontsize=20, verticalalignment='top', horizontalalignment='left', transform=ax.transAxes)
# Plot eigenvectors
if eigenstuff:
eigvals, eigvecs = np.linalg.eig(W)
if np.abs(eigvals[0]) < np.abs(eigvals[1]):
lc1 = 'c'
lc2 = 'g'
else:
lc1 = 'g'
lc2 = 'c'
ax.plot(np.arange(-10000, 10000)*eigvecs[0, 0], np.arange(-10000, 10000)*eigvecs[1, 0],lc1, alpha=.5, label = r'$\mathbf{v}_1$')
ax.plot(np.arange(-10000, 10000)*eigvecs[0, 1], np.arange(-10000, 10000)*eigvecs[1, 1], lc2, alpha=.5, label = r'$\mathbf{v}_2$')
ax.legend()
# Set up scatter
cmap = plt.cm.Blues_r
norm = plt.Normalize(vmin=0, vmax=u.shape[1])
scatter = ax.scatter(u[0, :], u[1, :], alpha=1, c = cmap(norm(np.arange(u.shape[1]))))
ax.set(xlabel = 'Neuron 1 Firing Rate', ylabel = 'Neuron 2 Firing Rate', title = 'Neural firing over time')
fig.colorbar(matplotlib.cm.ScalarMappable(norm=norm, cmap=cmap),
ax=ax, label = 'Time step')
# + cellView="form"
#@title Helper functions
def get_eigval_specified_matrix(target_eig):
"""Generates matrix with specified eigvals
Args:
target_eig (list): list of target eigenvalues, can be real or complex,
should be length 2 unless you desire repeated eigenvalues
with the same eigenvector, in which case length 1
Returns:
ndarray: 2 x 2 matrix with target eigvals
"""
# Set up two eigenvectors
V = np.array([[1, 1], [-1, 1]]).astype('float')
for i in range(2):
V[:,i] = V[:,i]/np.linalg.norm(V[:,i])
# Get matrix with target eigenvalues
if type(target_eig[0]) == int or type(target_eig[0]) == float:
if len(target_eig) == 2: # distinct eigvecs (not necessarily distinct eigvals)
D = np.diag(target_eig)
A = V @ D @ np.linalg.inv(V)
else: # repeated with same vec
summed = 2*target_eig[0]
a = summed-3
d = 3
bc = target_eig[0]**2 - a*d
factors = [n for n in range(1, bc+ 1) if bc % n == 0]
b = factors[int(np.floor(len(factors)/2))]
c = bc/-b
A = np.array([[a, b], [c, d]])
elif type(target_eig[0]) == complex:
C = [np.real(V[:,0]), np.real(V[:,1])]
B = np.array([[np.real(target_eig[0]), np.imag(target_eig[0])], [-np.imag(target_eig[0]), np.real(target_eig[0])]]).squeeze()
A = C @ B @ np.linalg.inv(C)
return A
# -
# ---
#
# # Section 1: Defining a neural circuit
#
# In previous tutorials, we have looked at static models of postsynaptic neurons based on the responses of presynaptic neurons.
#
# Let's now introduce the concept of time. We will chop time up into little bins and look at the activity of neurons in each bin. That is, we will work in a **discrete** time framework. For example, if each bin is 1 second long, we will look at the firing rate of each neuron at intervals of a second.
#
#
# Instead of examining pre- and post- synaptic neurons, we will examine at two neurons in one area that are connected. In our model, the activity of neuron 1 at one time bin depends on the activities of both neurons during the previous time bin multiplied by the respective weights from itself and neuron 2. It might seem weird for a neuron to have a weight to itself - this is abstracting away some biological details but basically conveys how much the neural activity depends on its history. (Throughout this course, we'll see lots of neuron models and how some model biological detail more faithfully while others abstract.)
#
# We will refer to the activity of neuron i during time bin j as $a_{i, j}$. The weight from neuron x to neuron y will be $w_{y, x}$. With this helpful notation, we can write an equation for the activity of neuron 1 at time bin t:
# $$a_{1, t} = w_{1, 1}a_{1, t-1} + w_{1, 2}a_{2, t-1} $$
#
# And the symmetric model is true of neuron 2:
# $$a_{2, t} = w_{2, 1}a_{1, t-1} + w_{2, 2}a_{2, t-1} $$
#
# This is already a mess of subscript numbers - luckily we can use matrices and vectors once again and our model becomes:
#
# $$\mathbf{a}_{t} = \mathbf{W}\mathbf{a}_{t-1} $$
# where:
# $$\mathbf{W} = \begin{bmatrix} w_{1, 1} & w_{1, 2} \\ w_{2, 1} & w_{2, 2} \end{bmatrix}, \mathbf{a}_{t} = \begin{bmatrix} a_{1, t} \\ a_{2, t} \end{bmatrix}$$
#
# It turns out that this is a **discrete dynamical system**. Dynamical systems are concerned with how quantities evolve other time, in this case our neural firing rates. When we model the evolution of quantities over time using a discrete time framework, it is, unsurprisingly, a discrete dynamical system. We will see continuous dynamical systems (where we embrace the full continuity of time) tomorrow and later in the comp neuro course during W2D2: Linear Dynamics.
#
#
#
# ## Coding Exercise 1: Implementing the circuit
#
# In this exercise, you will implement the function `circuit_implementation`. Given a weight matrix, initial activities at time 0, and a number of time bins to model, this function calculates the neural firing rates at each time bin.
#
# We will use initial firing rates of 1 for both neurons:
# $$\mathbf{a}_0 = \begin{bmatrix}
# 1 \\
# 1 \\
# \end{bmatrix}$$
# and the weight matrix:
#
# $$\mathbf{W} = \begin{bmatrix} 1 & 0.2 \\
# 0.1 & 1 \\ \end{bmatrix}$$
#
# We will look at activity over 30 time steps. As before, we will allow our firing rates to be negative, despite this not being possible biologically.
#
# +
def circuit_implementation(W, u0, T):
""" Simulate the responses of N neurons over time given their connections
Args:
W (ndarray): weight matrix of synaptic connections, should be N x N
u0 (ndarray): initial condition or input vector, should be N,
T (scalar): number of time steps to run simulation for
Returns:
u (ndarray): the neural responses over time, should be N x T
"""
# Compute the number of neurons
N = W.shape[0]
# Initialize empty response array and initial condition
u = np.zeros((N, T))
u[:, 0] = u0
#################################################
## TODO for students ##
# Fill out function and remove
raise NotImplementedError("Student exercise: Complete circuit_implementation")
#################################################
# Loop over time steps and compute u(t+1)
for i_t in range(1, T):
u[:, i_t] = ...
return u
# Define W, u0, T
W = np.array([[1, .2], [.1, 1]])
u0 = np.array([1, 1])
T = 30
# Get neural activities
u = circuit_implementation(W, u0, T)
# Visualize neural activities
plot_circuit_responses(u, W)
# +
# to_remove solution
def circuit_implementation(W, u0, T):
""" Simulate the responses of N neurons over time given their connections
Args:
W (ndarray): weight matrix of synaptic connections, should be N x N
u0 (ndarray): initial condition or input vector, should be N,
T (scalar): number of time steps to run simulation for
Returns:
u (ndarray): the neural responses over time, should be N x T
"""
# Compute the number of neurons
N = W.shape[0]
# Initialize empty response array and initial condition
u = np.zeros((N, T))
u[:, 0] = u0
# Loop over time steps and compute u(t+1)
for i_t in range(1, T):
u[:, i_t] = W @ u[:, i_t-1]
return u
# Define W, u0, T
W = np.array([[1, .2], [.1, 1]])
u0 = np.array([1, 1])
T = 30
# Get neural activities
u = circuit_implementation(W, u0, T)
# Visualize neural activities
with plt.xkcd():
plot_circuit_responses(u, W)
# -
# The firing rates of both neurons are exploding to infinity over time. Let's now see what happens with a different weight matrix:
#
#
# $$\mathbf{W} = \begin{bmatrix} 0.2 & 0.1 \\
# 1 & 0.2 \\ \end{bmatrix}$$
# + cellView="form"
# @markdown Execute this cell to visualize activity over time
# Define W, u0, T
W = np.array([[.2, .1], [1, .2]])
u0 = np.array([1, 1])
T = 30
# Get neural activities
u = circuit_implementation(W, u0, T)
# Visualize neural activities
with plt.xkcd():
plot_circuit_responses(u, W)
# -
# We can see that with this weight matrix, the firing rates are decaying towards zero. It turns out that we could have predicted this by looking at the eigenvalues of the weight matrices, as we'll see in the next section.
# ---
# # Section 2: Understanding dynamics using eigenstuff
#
# As we'll see in this section, eigenvectors and eigenvalues are incredibly useful for understanding the evolution of the neural firing rates, and discrete dynamical systems in general.
#
#
# ## Section 2.1: Rewriting our circuit equation
#
#
# In our neural circuit, we are modeling the activities at a time step as:
# $$\mathbf{a}_{t} = \mathbf{W}\mathbf{a}_{t-1} $$
#
# Let's start at time step 1:
# $$\mathbf{a}_{1} = \mathbf{W}\mathbf{a}_{0} $$
#
# And move on to time step 2:
# $$\mathbf{a}_{2} = \mathbf{W}\mathbf{a}_{1} $$
#
# In the above equation, we can subsitute in $\mathbf{a}_{1} = \mathbf{W}\mathbf{a}_{0}$:
# $$\mathbf{a}_{2} = \mathbf{W}\mathbf{W}\mathbf{a}_{0} = \mathbf{W}^2 \mathbf{a}_{0}$$
#
# We can keep doing this with subsequent time steps:
# $$\mathbf{a}_{3} = \mathbf{W}\mathbf{a}_{2} = \mathbf{W}\mathbf{W}^2 \mathbf{a}_{0} = \mathbf{W}^3\mathbf{a}_{0} $$
# $$\mathbf{a}_{4} = \mathbf{W}\mathbf{a}_{3} = \mathbf{W}\mathbf{W}^3 \mathbf{a}_{0} = \mathbf{W}^4\mathbf{a}_{0} $$
#
# This means that we can write the activity at any point as:
# $$\mathbf{a}_{i} = \mathbf{W}^i\mathbf{a}_{0} $$
# ## Section 2.2: Initial firing rates along an eigenvector
#
# Remember from the last tutorial, that an eigenvector of matrix $\mathbf{W}$ is a vector that becomes a scalar multiple (eigenvalue) of itself when multiplied by that matrix:
#
# $$\mathbf{W}\mathbf{v} = \lambda\mathbf{v}$$
#
# Let's look at what happens if the initial firing rates in our neural circuit lie along that eigenvector, using the same substitution method as in the previous section:
# $$\mathbf{a}_{0} = \mathbf{v} $$
# $$\mathbf{a}_{1} = \mathbf{W}\mathbf{a}_0 = \mathbf{W}\mathbf{v} = \lambda\mathbf{v} $$
# $$\mathbf{a}_{2} = \mathbf{W}\mathbf{a}_1 = \mathbf{W}\lambda\mathbf{v} = \lambda\mathbf{W}\mathbf{v} = \lambda^2\mathbf{v}$$
# $$\mathbf{a}_{3} = \mathbf{W}\mathbf{a}_2 = \mathbf{W}\lambda^2\mathbf{v} = \lambda^2\mathbf{W}\mathbf{v} = \lambda^3\mathbf{v}$$
# $$...$$
# $$\mathbf{a}_i = \lambda^i\mathbf{v}$$
#
# The activities at any time step equal a scalar times the initial activities. In other words, if the initial activities lie along an eigenvector, the activities will only evolve along that eigenvector.
# ### Interactive demo 2.2: Changing the eigenvalue
#
# Let's visualize what happens if the initial activities of the neurons lie along an eigenvector and think about how this depends on the eigenvalue.
#
# The interactive demo below is the same visualization you saw in Section 1, but now we also plot the eigenvectors $\mathbf{v}_1$ and $\mathbf{v}_2$.
#
# Questions:
# 1. What happens if the eigenvalue is large (2)?
# 2. What happens if you move the eigenvalue from 2 to towards 0?
# 3. What happens with negative eigenvalues?
# + cellView="form"
# @markdown Execute this cell to enable the widget
@widgets.interact(eigenvalue = widgets.FloatSlider(value=0.5, min=-2, max=2, step=0.2))
def plot_system(eigenvalue):
# Get weight matrix with specified eigenvalues
W = get_eigval_specified_matrix([eigenvalue, eigenvalue])
# Get initial condition
u0 = np.array([1, 1])
# Get neural activities
u = circuit_implementation(W, u0, 10)
# Visualize neural activities
plot_circuit_responses(u, W, eigenstuff = True, xlim = [-15, 15], ylim = [-15, 15])
# +
# to_remove explanation
# 1) With the eigenvalue = 2, the activities of the neurons explode towards infinity, along
#. the eigenvector.
# 2) At eigenvalue = 1, there is a shift in what happens. With the eigenvalue above 1,
#. the activites always explode. Once the eigenvalue is below 1, the activities decay to 0.
#. If the eigenvalue equals 1, the activities never differ from the initial condition.
#. This makes sense with the equation above. Lambda is raised to a power when computing activities:
#. if it's a fraction, this term will get smaller so the activities will. If above 1, this term
#. will explore so the activities will.
# 3) If the eigenvalue is between -1 and 0, the neural activities jump across the
#. origin repeatedly along the eigenvector but eventually decay to 0. If the eigenvalue is below -1, the
#. activities jump across the origin repeatedly along the eigenvector but explode to
#. positive or negative infinity. Once again, this makes sense if you think through the equation above.
# -
# ## Section 2.3: Other initial conditions
#
# We now know that if our initial activities (or initial condition) fall on an eigenvector of $\mathbf{W}$, the activities will evolve along that line, either exploding to infinity if the absolute value of the eigenvalue is above 1 or decaying to the origin it it is below 1. What if our initial condition doesn't fall along the eigenvector though?
#
# To understand what will happen, we will use the ideas of basis vectors and linear combinations from Tutorial 1.
#
# Let's assume for now that our weight matrix has two distinct eigenvectors ($\mathbf{v}_1$ and $\mathbf{v}_2$) with corresponding eigenvalues $\lambda_1$ and $\lambda_2$, and that these eigenvectors form a basis for 2D space. That means we can write any vector in 2D space as a linear combination of our eigenvectors, including our initial activity vector:
#
# $$\mathbf{a}_0 = c_1\mathbf{v}_1 + c_2\mathbf{v}_2 $$
#
# Let's compute the next time step, using our previous strategy of substitution:
# $$\begin{align}
# \mathbf{a}_1 &= \mathbf{W}\mathbf{a}_0
# \\ &= \mathbf{W}(c_1\mathbf{v}_1 + c_2\mathbf{v}_2) \\ &= c_1\mathbf{W}\mathbf{v}_1 + c_2\mathbf{W}\mathbf{v}_2 \\ &= c_1\lambda_1\mathbf{v}_1 + c_2\lambda_2\mathbf{v}_2 \end{align} $$
#
# All activities can be written as:
# $$\mathbf{a}_i = c_1\lambda_1^i\mathbf{v}_1 + c_2\lambda_2^i\mathbf{v}_2 $$
#
# We'll see what this means for our system in the next demo.
# ### Interactive demo 2.3: Changing both eigenvalues
#
# In the demo below, you can now change both eigenvalues and the initial condition (with `a0_1` setting neuron 1 initial activity and `a0_2` setting neuron 2 initial activity). We will only look at positive eigenvalues to keep things a little more simple.
#
# Think each of the following questions through based on the equation we just arrived at and then play with the demo to see if you are correct.
# $$\mathbf{a}_i = c_1\lambda_1^i\mathbf{v}_1 + c_2\lambda_2^i\mathbf{v}_2 $$
#
# 1. What will happen when both eigenvalues are greater than 1? Does this depend on initial condition?
# 2. What will happen when both eigenvalues are less than 1?
# 3. Set eigenvalue1 to 2 and eigenvalue2 to 1.2 and try out different initial conditions. What do you see? Why are you seeing this?
# 4. What happens if one eigenvalue is below 1 and the other is above 1?
# + cellView="form"
# @markdown Execute this cell to enable the widget
@widgets.interact(eigenvalue1 = widgets.FloatSlider(value=0.5, min=0.2, max=2, step=0.2),
eigenvalue2 = widgets.FloatSlider(value=0.5, min=0.2, max=2, step=0.2),
a0_1 = widgets.FloatSlider(value=1, min=-5, max=5, step=0.2),
a0_2 = widgets.FloatSlider(value=2, min=-5, max=5, step=0.2), )
def plot_system(eigenvalue1, eigenvalue2, a0_1, a0_2):
# Get initial condition
a0 = np.array([a0_1, a0_2])
# Get weight matrix with specified eigenvalues
W = get_eigval_specified_matrix([eigenvalue1, eigenvalue2])
# Get neural activities
u = circuit_implementation(W, a0, 10)
# Visualize neural activities
plot_circuit_responses(u, W, eigenstuff = True, xlim = [-15, 15], ylim = [-15, 15])
# +
# to_remove explanation
# 1) If both eigenvalues are above 1, the neural activity will eventually explode
#. to infinity or negative infinity, depending on initial conditions.
# 2) If both eigenvalues are below 1, the neural activity will eventually decay to 0.
# 3) The activities will explode to positive or negative infinity, but the exact trajectory
#. is drawn towards the eigenvector with the larger eigenvalue. This is because the larger eigenvalue
#. will increasingly dominate the other one as it is raised to increasingly larger powers.
#. 4) The activities will eventually explode to positive or negative infinity, unless
#. the initial condition lies exactly on the eigenvector with the small eigenvalue. If the
#. initial condition is near to that eigenvector, the trajectory will first go towards
#. the origin before exploding.
# -
# ## Section 2.4: Complex eigenvalues
#
# We've been hiding some complexity from you up until now, namely that eigenvalues can be complex. Complex eigenvalues result in a very specific type of dynamics: rotations.
#
# We will not delve into the proof or intuition behind this here as you'll encounter complex eigenvalues in dynamical systems in W2D2: Linear Dynamics.
#
# Instead, we will simply demonstrate how the nature of the rotations depends on the complex eigenvalues in the animation below. We plot a 3-neuron circuit to better show the rotations. We illustrate each of the following:
#
#
# * Complex eigenvalues with an absolute value equal to 1 result in a sustained rotation in 3D space.
#
# * Complex eigenvalues with an absolute value below 1 result in a rotation towards the origin.
#
# * Complex eigenvalues with an absolute value above 1 result in a rotation towards the positive/negative infinity.
#
#
# 
# ---
# # Summary
#
# You have seen how we can predict what happens in a discrete dynamical system with an update rule of:
# $$ \mathbf{a}_t = \mathbf{W}\mathbf{a}_{t-1}$$
#
# The most important takeaway is that inspecting eigenvalues and eigenvectors enables you to predict how discrete dybamical systems evolve. Specifically:
#
# * If all eigenvalues are real and have absolute values above 1, the neural activities explode to infinity or negative infinity.
#
# * If all eigenvalues are real and have absolute values above 1, the neural activities decay to 0.
#
# * If all eigenvalues are real and at least one has an absolute value above 1, the neural activities explode to infinity or negative infinity, except for special cases where the initial condition lies along an eigenvector with an eigenvalue whose absolute value is below 1.
#
# * If eigenvalues are complex, the neural activities rotate in space and decay or explode depending on the amplitude of the complex eigenvalues.
#
# * Even finer details of the trajectories can be predicted by examining the exact relationship of eigenvalues and eigenvectors.
#
# Importantly, these ideas extend far beyond our toy neural circuit. Discrete dynamical systems with the same structure of update rule are common. While the exact dependencies on eigenvalues will change, we will see that we can still use eigenvalues/vectors to understand continuous dynamical systems in W2D2: Linear Dynamics.
#
| 1,388.268382 | 733,676 |
926b28286d8d963a33208d8d9c32b06d93e3fa33
|
py
|
python
|
code/TCN_CAN_Data.ipynb
|
mehrotrasan16/CS581-CAN-DO-Project
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/mehrotrasan16/CS581-CAN-DO-Project/blob/tcn-baseline/code/TCN_CAN_Data.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="E_dRMZNqKWIo"
# # Imports
# + colab={"base_uri": "https://localhost:8080/"} id="2F5LZZsFjjJD" outputId="ce714f91-adce-4ad7-d5df-dc3ddcbd1db9"
from google.colab import drive
drive.mount('/content/drive')
# + id="2U6L8DYYKZDF" colab={"base_uri": "https://localhost:8080/"} outputId="bb0dea82-0e42-4b02-894f-dade0b1d3696"
import sys
import sklearn
import tensorflow as tf
from tensorflow import keras
import numpy as np
import pandas as pd
from numpy import load
import os
from sklearn.metrics import recall_score,f1_score
from imblearn.over_sampling import SMOTE
# to make this notebook's output stable across runs
np.random.seed(42)
tf.random.set_seed(42)
# To plot pretty figures
# %matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# + [markdown] id="2oIT-Y4fJ1N7"
# # Load Datasets
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="NNzE1_NYJlYH" outputId="fc0b8bd7-8895-4279-eca0-64be22091593"
freedf = pd.read_csv('/content/drive/My Drive/Colab Notebooks/CS581/project-data/Attack_free_dataset.csv')
freedf['label'] = 0
freedf
# + colab={"base_uri": "https://localhost:8080/", "height": 106} id="2oQWSOZVLiUF" outputId="7e0b8d36-07a1-406a-f036-f00351efd2b4"
freedf.groupby('label').count()
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="3JKhAGAeKJ7O" outputId="1678840b-8e7d-4437-e5da-e1b496faa727"
dosdf = pd.read_csv('/content/drive/My Drive/Colab Notebooks/CS581/project-data/DoS_attack_dataset.csv')
dosdf['label'] = np.where(dosdf['CAN ID'] == 0,1,0) #np.where(df['Set']=='Z', 'green', 'red')
dosdf
# + colab={"base_uri": "https://localhost:8080/", "height": 136} id="SksUn46-LVpu" outputId="437abc7d-6f76-4669-d85b-30d251660213"
dosdf.groupby('label').count()
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="Qt8NTR8aKt0b" outputId="65cbb472-1255-4b52-a2cf-f6a42da83b66"
fuzzydf = pd.read_csv('/content/drive/My Drive/Colab Notebooks/CS581/project-data/Fuzzy_attack_dataset.csv')
fuzzydf
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="ZQmTm4lFK_a9" outputId="bf964478-d5f3-4d48-9ee3-8ca978777f4b"
impersonatedf = pd.read_csv('/content/drive/My Drive/Colab Notebooks/CS581/project-data/Impersonation_attack_dataset.csv')
impersonatedf['label'] = np.where(impersonatedf['CAN ID'] == 356,1,0)
impersonatedf
# + colab={"base_uri": "https://localhost:8080/", "height": 153} id="9JICe22SMbbV" outputId="d5fe464f-790f-49d0-c0c8-eb493f6ebb52"
print(int('0x164',base=16))
impersonatedf.groupby('label').count()
# + [markdown] id="QXEsTphkjw4r"
# IN the above datasets, we have also added labels where possible, to try a supervised learning experiment.
# + [markdown] id="jvSYpwDUPA-9"
# ### Combining Attack-free + DoS datasets
# Here we work with the Attack-Free and DoS Datasets to get one less biased and slightly better distributed dataset to train and test on.
# + id="gOdwFcP6PHOq" colab={"base_uri": "https://localhost:8080/", "height": 402} outputId="641d98bd-2afd-4aec-9099-9ef9d0c29742"
dosdf = pd.read_csv('/content/drive/My Drive/Colab Notebooks/CS581/project-data/DoS_attack_dataset.csv')
dosdf['label'] = np.where(dosdf['CAN ID'] == 0,1,0)
dosdf = dosdf.drop(labels=['Timestamp'],axis=1)
dosdf
# + id="8Ehz3HtDPXyz" colab={"base_uri": "https://localhost:8080/", "height": 402} outputId="6baffa15-254e-446c-b788-3067ef97cb0e"
df = pd.read_csv('/content/drive/My Drive/Colab Notebooks/CS581/project-data/Attack_free_dataset.csv')
df['label'] = 0
df = df.drop(columns=['Timestamp'])
df
# + [markdown] id="0nsmRk_HX9zh"
# * Here we toss out the timestamp column as in this approach it is not informative about the nature of the outlier.
# * It also helps us balance out the problems encountered in the previous attack-free and Dos attack experiments.
#
# * in the attack free dataset - all the packets were normal data and so had to be labelled with only one value, training a model on single class data does not means it learns anything.
#
# * in the Dos Attack experiment, every second message is a dos attack message, leaving the dataset evenly split 50:50 on anomalies/normal network data, but there is not enough contiguous network data for it to learn normal state nor attack state, and as a result it's accuracy is averaging around 50%
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="xSrz-9IfAXPf" outputId="7c6369d9-73f8-4c4e-ed04-b7201fbc29b4"
newdf = df.append(dosdf)
newdf
# + colab={"base_uri": "https://localhost:8080/", "height": 136} id="snE3lrDjSwcm" outputId="fd910404-7958-45c9-f5a7-24961de569bf"
newdf.groupby('label').count()
# + colab={"base_uri": "https://localhost:8080/"} id="e8VcGP7ES1qJ" outputId="f63fbf00-9e43-4f0d-8979-d82f170ef599"
335624/2690353
# + [markdown] id="vf4IhUF-KNmW"
# # Installing and testing TCNs: Exploring applications
# + colab={"base_uri": "https://localhost:8080/"} id="ZpXEiSYEiIUr" outputId="d8f21c72-8544-4c34-beb0-8956f671bdac"
# !pip install keras-tcn
# + id="pp1vSaRCiZPX"
from tensorflow.keras.layers import Dense
from tensorflow.keras import Input, Model
from tcn import TCN, tcn_full_summary
batch_size, timesteps, input_dim = None, 20, 1
# + id="yWKpL2g4o2ee"
def get_x_y(size=1000):
import numpy as np
pos_indices = np.random.choice(size, size=int(size // 2), replace=False)
x_train = np.zeros(shape=(size, timesteps, 1))
y_train = np.zeros(shape=(size, 1))
x_train[pos_indices, 0] = 1.0
y_train[pos_indices, 0] = 1.0
return x_train, y_train
# + colab={"base_uri": "https://localhost:8080/"} id="J6DEfoyFozAD" outputId="ae530145-78a0-45d2-9a6b-407d28735e19"
i = Input(batch_shape=(batch_size, timesteps, input_dim))
o = TCN(return_sequences=False)(i) # The TCN layers are here.
o = Dense(1)(o)
m = Model(inputs=[i], outputs=[o])
m.compile(optimizer='adam', loss='mse')
tcn_full_summary(m, expand_residual_blocks=True)
x, y = get_x_y()
m.fit(x, y, epochs=10, validation_split=0.2)
# + [markdown] id="B5YJl4KTnl6R"
# # Modifying this for our data and modifying our data for this TCN
# + [markdown] id="2p1jw_0pdn--"
# # Baseline TCN
# + [markdown] id="bgfdBNH-9ZMl"
# TCNs do not require the 3D input that LSTMs do, the Conv1D layers throw errors when we tried with the same input as the LSTMS, so we change our input data shape to work similar to the example referred to above.
# + id="m1osJRXNnoXm"
batch_size, timesteps, input_dim = None, 11, 1
# + id="KFraBLZxn-hn"
# # my x y training/testing data
# series = dosdf.to_numpy()
# n_rows = series.shape[0]
# n_features = series.shape[1]
# train_split = int(series.shape[0]*0.7)
# val_split = int(series.shape[0]*0.8)
# print(f'train split : {train_split}, val_split: {val_split}')
# X_train, y_train = series[:train_split, :n_features-1], series[:train_split, -1] # -1 references the last column
# X_valid, y_valid = series[train_split:val_split, :n_features-1], series[train_split:val_split, -1]
# X_test, y_test = series[val_split:, :n_features-1], series[val_split:, -1]
# print(f'{X_train.shape,y_train.shape,X_valid.shape, y_valid.shape, X_test.shape,y_test.shape}')
# + id="OcsGBGYo8h4D"
# X_test[20].shape, y_test[20].shape
# + id="k5k7BsHb8owm"
# tempx, tempy = get_x_y()
# tempx[0].shape, tempy[0].shape
# + [markdown] id="B_m80mpPBLmm"
# ### Train-test-split
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="hOu1uoDEBQ90" outputId="6e1da424-7c03-46f1-f862-7c5e478fb5c8"
#Shuffle the dataset
newdf=newdf.sample(frac=1,random_state=200) #random state is a seed value 200
series = newdf.to_numpy()
# print(series.shape)
n_features = series.shape[1]
train_split = int(series.shape[0]*0.7)
print(f'train split : {train_split}')
val_split = int(series.shape[0]*0.8)
X_train, y_train = series[:train_split, :n_features-1], series[:train_split, -1] # -1 references the last column
X_valid, y_valid = series[train_split:val_split, :n_features-1], series[train_split:val_split, -1]
X_test, y_test = series[val_split:, :n_features-1], series[val_split:, -1]
print(f'{X_train.shape,y_train.shape,X_valid.shape, y_valid.shape, X_test.shape,y_test.shape}')
# + colab={"base_uri": "https://localhost:8080/", "height": 136} id="7Vcp8k7RCmv4" outputId="38bc653b-30b3-422a-f5ac-3956ea2fe18c"
#X_train stats
newdf[:train_split].groupby('label').count()
# + colab={"base_uri": "https://localhost:8080/", "height": 136} id="4nfqMnmT832U" outputId="00e3f319-d6a7-41b4-bb61-fee475e67803"
#X_valid split
newdf[train_split:val_split].groupby('label').count()
# + colab={"base_uri": "https://localhost:8080/", "height": 136} id="pCMxK-IjJdjf" outputId="9e0c8042-4636-43ee-bad2-c569fed7fc25"
#X_test
newdf[val_split:].groupby('label').count()
# + colab={"base_uri": "https://localhost:8080/"} id="rQ7ia0A8dzfk" outputId="8e911a6f-98e2-4756-e55f-4e29cb69981c"
1 - (66685/538511)
# + colab={"base_uri": "https://localhost:8080/"} id="DQHzAdwkhjRD" outputId="4b36132a-0ea0-4411-f3cb-5c8afad9ec6a"
testdf = pd.Series(y_test)
testdf.value_counts()
# + [markdown] id="IBWAo74fF82t"
# ### Baseline TCN Model
# + id="uBt0v5fiQjw2"
tf.keras.backend.clear_session()
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="GgpOxa3yn0uI" outputId="e9b638d5-7079-471b-c92f-1875f916c180"
i = Input(batch_shape=(batch_size, timesteps, input_dim))
o = TCN(return_sequences=False,
nb_filters=64,
kernel_size=2,
nb_stacks=1,
padding='same',
use_skip_connections=False,
dropout_rate=0.0,
activation='relu',
kernel_initializer='he_normal',
use_batch_norm=True)(i) # The TCN layers are here.
o = Dense(1)(o)
m = Model(inputs=[i], outputs=[o])
m.compile(optimizer='adam',
loss='mse',
metrics=['accuracy'])
tcn_full_summary(m, expand_residual_blocks=True)
early_stop=keras.callbacks.EarlyStopping(monitor='val_loss',patience=10)
history = m.fit(X_train, y_train,
validation_data=(X_valid,y_valid),
epochs=5,
batch_size=128,
callbacks=[early_stop])
# + colab={"base_uri": "https://localhost:8080/", "height": 312} id="8UECl3FHWVVm" outputId="ca8caaf6-a8d7-4fdc-afc1-739f27a854c4"
tf.keras.utils.plot_model(m,show_shapes=True)
# + [markdown] id="UQWD7ITmF1pP"
# ### Evaluation and Plotting
# + colab={"base_uri": "https://localhost:8080/"} id="YcbtyZO7nvfh" outputId="03d4fde1-c854-4627-f747-9e703917b7aa"
scores = m.evaluate(X_test,y_test)
print(f"Loss, Accuracy: {scores}")
# + id="I-dz0b9mN3rd" colab={"base_uri": "https://localhost:8080/", "height": 325} outputId="59c8e895-7427-4c9e-9a15-7223e73a8905"
plt.subplot(1,2,1)
plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.legend(('loss','val_loss'))
plt.subplot(1,2,2)
plt.plot(history.history["accuracy"])
plt.plot(history.history["val_accuracy"])
plt.legend(('acc','val_acc'))
plt.gcf().set_size_inches((10,5))
plt.show()
# + id="5kGktS-TDagM"
y_pred = m.predict(X_test, )
# + colab={"base_uri": "https://localhost:8080/"} id="pCJ9CsNzztQu" outputId="352226c5-1180-42f7-b107-fbf7363f9a5b"
X_test[30],y_test[30], np.argmax(y_pred[30])
# + colab={"base_uri": "https://localhost:8080/"} id="Nf2ANdveeB_F" outputId="57e909e3-8172-4611-8676-0b7b0bf40336"
classes = np.array([np.argmax(i) for i in y_pred])
np.unique(classes), classes[:20]
# + colab={"base_uri": "https://localhost:8080/"} id="M0HML9SaehxK" outputId="bebc6617-01bc-4555-b5f5-521d10f0b871"
recall_score(y_test,classes)
# + colab={"base_uri": "https://localhost:8080/"} id="2ikXo7SSiZHt" outputId="3b94300f-86c9-4e60-acf8-f2937d9a9a4b"
predlist = classes.reshape((classes.shape[0],1))
y_test.shape, y_pred.shape, predlist.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="lfSYLdIDj6Tg" outputId="24d2c738-05c2-4ce7-fbf5-a75dfa50c4df"
compdf = pd.DataFrame(predlist)
compdf['real'] = y_test
compdf = compdf.rename(columns={0:'pred'})
compdf['T/F Prediction'] = np.where(compdf['pred'] == compdf['real'],True, False)
compdf
# + colab={"base_uri": "https://localhost:8080/"} id="EV5PraSuglvY" outputId="c98c9acb-d00f-49f8-ccd1-8f86adae8362"
np.unique(compdf.loc[compdf.real == 1]['T/F Prediction'])
# + colab={"base_uri": "https://localhost:8080/", "height": 582} id="sGvcvS3pe9mW" outputId="30fac120-1757-4c76-8490-b68e5b07cd60"
plot_min=60
plot_max =120
plt.scatter(range(plot_min,plot_max),y_test[plot_min:plot_max])
plt.scatter(range(plot_min,plot_max),[y_pred[i].argmax()+0.02 for i in range(len(y_pred[plot_min:plot_max]))],c=['r'])
plt.legend(('test class','predicted class'))
plt.xlabel('timestamp index')
plt.ylabel('class (0 = normal, 1 = anomaly)')
plt.xticks(ticks=range(plot_min, plot_max))
plt.gcf().set_size_inches((20,10))
# plt.gcf().autofmt_xdate()
plt.show()
# + [markdown] id="W3GQjdkNqwOI"
# ### Saving and Checking the size of the Model
# + id="goQpm6R7jVAb" colab={"base_uri": "https://localhost:8080/"} outputId="0583528b-e2df-4aa4-b9ac-e047977a9912"
saved_model_dir = '/content/drive/MyDrive/Colab Notebooks/CS581/project-data/'
m.save(saved_model_dir + "tcn-baseline.h5",include_optimizer=False)
print(f"Saving Model to: {saved_model_dir}tcn-baseline.h5")
# + colab={"base_uri": "https://localhost:8080/"} id="LlKmug6yphtL" outputId="642a78c8-0c99-4aa0-db0b-e4991d174721"
print(f'Size of the model without compression: {os.path.getsize(saved_model_dir + "tcn-baseline.h5")/float(2**20)} Mb')
# + id="7n5JP096Pxsf"
# + [markdown] id="ZIL1RnWui1PP"
# # Resource-Optimized TCN Models
# + [markdown] id="DGImGjxki9lV"
# ## Convert to TFLite
# + colab={"base_uri": "https://localhost:8080/"} id="ORXaNDdRi82e" outputId="1bee9f50-a9e8-4f7a-f89e-939b3f411ec6"
converter = tf.lite.TFLiteConverter.from_keras_model(m)
tflite_model = converter.convert()
tf_lite_model_file = saved_model_dir + 'tcn-baseline.tflite'
with open(tf_lite_model_file,'wb') as f:
f.write(tflite_model)
# + colab={"base_uri": "https://localhost:8080/"} id="I5ma51_QjbZ7" outputId="71aff9e1-f686-4627-db15-a1c8ae1088a4"
interpreter = tf.lite.Interpreter(model_path=tf_lite_model_file)
interpreter.allocate_tensors()
input_index = interpreter.get_input_details()[0]['index']
input_index
# + colab={"base_uri": "https://localhost:8080/"} id="0uqGZ4c_jmd0" outputId="41890f51-e8c4-4fc6-d2a2-297e53b9b7a3"
output_index = interpreter.get_output_details()[0]['index']
output_index
# + colab={"base_uri": "https://localhost:8080/"} id="t1H90n4al7fW" outputId="2bd064da-a84d-4f16-93eb-af40ed949182"
interpreter.get_input_details()
# + colab={"base_uri": "https://localhost:8080/"} id="6yRJpxepmhA6" outputId="45dd0819-c1d1-4cae-8a95-c52560293abb"
interpreter.get_output_details()
# + id="Ymd2mR-mjp3K"
def evaluate_model(interpreter):
input_index = interpreter.get_input_details()[0]["index"]
output_index = interpreter.get_output_details()[0]['index']
predictions = []
for img in X_test:
timg = img[np.newaxis,:,np.newaxis].astype(np.float32)#np.expand_dims(img,axis = 0).astype(np.float32)
interpreter.set_tensor(input_index,timg)
interpreter.invoke()
output = interpreter.tensor(output_index)
pred = np.argmax(output()[0])
predictions.append(pred)
predictions = np.array(predictions)
accuracy= (predictions == y_test).mean()
return accuracy
# + colab={"base_uri": "https://localhost:8080/"} id="jWFqwo_CmG6k" outputId="d5d072e9-d99a-407e-9cda-98c01d6ca242"
X_test[0].shape
# + [markdown] id="16oX3ES29jFs"
# ### TFLite Compression Size
# + colab={"base_uri": "https://localhost:8080/"} id="CBJWPfPvk6ef" outputId="d9947a9f-7ddb-4e2d-9b1c-55f0c39bc577"
print(f'Size of the model after compression: {os.path.getsize(tf_lite_model_file)/float(2**20)} Mb')
# + [markdown] id="f-lVeWBt95Sm"
# ### TFLite Compression Accuracy
# + colab={"base_uri": "https://localhost:8080/"} id="LZbp2Q8ojvYJ" outputId="ff144770-3afa-439f-a95a-4f1407f0f8ab"
start_time = datetime.now()
tflite_test_acc = evaluate_model(interpreter)
print(f"Time taken {datetime.now() - start_time}")
# + colab={"base_uri": "https://localhost:8080/"} id="QVSVVTf6-ER2" outputId="51f57ac6-0c24-4e1a-b302-44c7b1711f04"
tflite_test_acc
# + [markdown] id="FeHnTf8MtHZx"
# ## Dynamic Quantization TCN model
# + id="PkX0aBogGGsT" colab={"base_uri": "https://localhost:8080/"} outputId="763c92e2-2d52-4d33-bca7-fd7fe9efcc20"
# ! pip install -q tensorflow-model-optimization
# + id="bYVjVQdZ35Fy" colab={"base_uri": "https://localhost:8080/", "height": 438} outputId="b05ee0e4-89a0-43f1-e879-1372588353c0"
import tensorflow_model_optimization as tfmot
quantize_model = tfmot.quantization.keras.quantize_model
# q_aware stands for for quantization aware.
# with tfmot.quantization.keras.quantize_scope():
# # loaded_model = tf.keras.models.load_model(keras_file)
q_aware_model = quantize_model(m)
# `quantize_model` requires a recompile.
q_aware_model.compile(optimizer='adam',
loss='mse',
metrics=['accuracy'])
q_aware_model.summary()
# + colab={"base_uri": "https://localhost:8080/"} id="oXJJDIAwv1mX" outputId="9966b04e-0c3c-403d-9e8f-25cb3d69568f"
dir(m.layers[1]
# + colab={"base_uri": "https://localhost:8080/"} id="fwZEAEZv0p-o" outputId="9e912bcf-730b-47e3-c47e-f9e66a311341"
dir(m.layers[1].residual_block_0.conv1D_0)
# + [markdown] id="oB01-No2D6s5"
# ## Dynamic Range Optimization
# + id="vaN2xVxoD9QR" colab={"base_uri": "https://localhost:8080/"} outputId="a822438a-6ace-4558-cc8b-4f3281773503"
converter = tf.lite.TFLiteConverter.from_keras_model(m)
converter.optimizations = [tf.lite.Optimize.DEFAULT]
tflite_model_quant_dyn = converter.convert()
# + id="KtWPd3ZZoXMF" colab={"base_uri": "https://localhost:8080/"} outputId="4d060ab4-0923-4007-a739-4d41d6ce8d6a"
tflite_dyn_model = converter.convert()
tflite_dyn_file = saved_model_dir + 'tcn_model_quant_dyn.tflite'
with open(tflite_dyn_file,'wb') as f:
f.write(tflite_dyn_model)
# + [markdown] id="BBt2-4ttqzdO"
# ### Dynamic Optimization Size
# + colab={"base_uri": "https://localhost:8080/"} id="O0MfXx-X4_tq" outputId="3833ece4-4179-4fd4-c54c-ab0a254a74fc"
print(f'Size of the model after dynamic optimization: {os.path.getsize(tflite_dyn_file)/float(2**20)} Mb')
# + [markdown] id="K6je1Jk0q3OP"
# ### Dynamic Optimization Accuracy
# + id="T_chrMWDp7P3"
interpreter_dyn = tf.lite.Interpreter(model_path=tflite_dyn_file)
interpreter_dyn.allocate_tensors()
# + id="FguZw0nurzJB" colab={"base_uri": "https://localhost:8080/"} outputId="e6f36be7-2da1-46b2-a0cf-ee644bd33da9"
from datetime import datetime
start_time = datetime.now()
tflite_dyn_test_acc = evaluate_model(interpreter_dyn)
print(f'Time Taken {datetime.now() - start_time}')
tflite_dyn_test_acc
# + [markdown] id="1TM_QsVK1kCd"
# ## 16-bit float TCN Model
# + id="xieSDY55I6LU"
converter = tf.lite.TFLiteConverter.from_keras_model(m)
converter.optimizations = [tf.lite.Optimize.DEFAULT]
converter.target_spec.supported_types = [tf.float16]
# + id="kum56nYqJXWz" colab={"base_uri": "https://localhost:8080/"} outputId="c0c83070-2cec-4e67-d0b9-40af56253bd3"
tflite_fp16_model = converter.convert()
tflite_fp16_file = saved_model_dir + 'tcn_model_quant_f16.tflite'
with open(tflite_fp16_file,'wb') as f:
f.write(tflite_fp16_model)
# + [markdown] id="-blQxSqmIsJF"
# ### TFLite float16 optimization size
# + id="yhk995FIM1P0" colab={"base_uri": "https://localhost:8080/"} outputId="1366cabd-19b4-41ab-aaac-2307e81cb319"
print(f'Size of the model after float-16 weight optimization: {os.path.getsize(tflite_fp16_file)/float(2**20)} Mb')
# + [markdown] id="B6LmsHcnIwx7"
# ### TFLite float16 optimization accuracy
# + id="xzPpUDTnNZ_F"
interpreter_f16= tf.lite.Interpreter(model_path=tflite_fp16_file)
interpreter_f16.allocate_tensors()
# + id="fIWxe_SiI6M-" colab={"base_uri": "https://localhost:8080/"} outputId="0aa671f2-da1b-47b7-c50b-644ea4dfa441"
start_time = datetime.now()
tflite_f16_test_acc = evaluate_model(interpreter_f16)
print(f"Time taken {datetime.now() - start_time}")
tflite_f16_test_acc
# + [markdown] id="BDxFE2IY-Sc-"
# ## Comparison Table
# + [markdown] id="wlFW5C0M8j6-"
# | Metric\Model | Baseline | Baseline TFLite | float16 optimized | Dynamic Range Optimization|
# |---|---|---|---|---|
# |Size(MB)|0.42|0.38|0.21|0.125|
# |Accuracy(%)|0.9391|0.8898|0.8898|0.8898|
# |Total Params|94,273|94,273|94,273|94,273|
# |Inference Time(sec)|10|69|73|139|
# + [markdown] id="pqGvCw4jAFKL"
# # Ablation Study
# + [markdown] id="OJxp--TwAW8b"
#
# TCNs are an incredibly complex network consisting of attention layers, conv-1D layers and a combination of Batch Normalization and Spatial Dropout layers. Our baseline model consists of 6 of these blocks, each block consisting of conv1D layers with differnt levels of dilations.
#
# Thankfully this implementation of the TCN exposes many hyperparameters of the TCN that we can tweak to experiment with performance. Some of these are seen below.
#
# From https://github.com/philipperemy/keras-tcn#arguments
# 
# + [markdown] id="UBy4jFrzAW8T"
# ### Train-test-split
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="p3f5PwH8AW8Y" outputId="c681cc49-7a86-4db6-b4a0-b647a85beff1"
#Shuffle the dataset
newdf=newdf.sample(frac=1,random_state=200) #random state is a seed value 200
series = newdf.to_numpy()
# print(series.shape)
n_features = series.shape[1]
train_split = int(series.shape[0]*0.7)
print(f'train split : {train_split}')
val_split = int(series.shape[0]*0.8)
X_train, y_train = series[:train_split, :n_features-1], series[:train_split, -1] # -1 references the last column
X_valid, y_valid = series[train_split:val_split, :n_features-1], series[train_split:val_split, -1]
X_test, y_test = series[val_split:, :n_features-1], series[val_split:, -1]
print(f'{X_train.shape,y_train.shape,X_valid.shape, y_valid.shape, X_test.shape,y_test.shape}')
# + colab={"base_uri": "https://localhost:8080/", "height": 136} id="_PF_OxH-AW8Z" outputId="cc018acc-5385-4c18-dbb4-13de8c699ca8"
#X_train stats
newdf[:train_split].groupby('label').count()
# + colab={"base_uri": "https://localhost:8080/"} id="81B8enY2P_yF" outputId="5bdcb4a6-d275-4dc1-81fc-a730421dbfb6"
1-(234936/1883247)
# + colab={"base_uri": "https://localhost:8080/", "height": 136} id="INDYS_RKAW8a" outputId="1d227dfa-1de3-4e55-9b9d-88747dc070d2"
#X_valid split
newdf[train_split:val_split].groupby('label').count()
# + colab={"base_uri": "https://localhost:8080/"} id="J2k8YVdKP7Ve" outputId="663a30bd-067d-4257-bae3-f78631b207a5"
1 - (33556/269042)
# + colab={"base_uri": "https://localhost:8080/", "height": 136} id="rrx2L6rvAW8a" outputId="84222992-f640-4ae7-b171-44f6b71aeea5"
#X_test
newdf[val_split:].groupby('label').count()
# + colab={"base_uri": "https://localhost:8080/"} id="ReNQl_luAW8a" outputId="414ea91f-6d7b-431e-a2e1-3de138fa16a9"
1 - (66685/538511)
# + colab={"base_uri": "https://localhost:8080/"} id="PYWDjrheAW8a" outputId="e72bd8b7-3d04-4272-ac74-d1ba15487564"
testdf = pd.Series(y_test)
testdf.value_counts()
# + id="LEzMd8ToAW8b"
tf.keras.backend.clear_session()
# + colab={"base_uri": "https://localhost:8080/", "height": 312} id="bPSsg4xKAW8b" outputId="ca8caaf6-a8d7-4fdc-afc1-739f27a854c4"
tf.keras.utils.plot_model(m,show_shapes=True)
# + [markdown] id="HSAHq4o4AJb5"
# ## Hyperparameters and Model Size
# + [markdown] id="0r2l6JEhJppz"
# ### Number of filters = 24
# + id="PK-lL45sKiTe"
tf.keras.backend.clear_session()
# + colab={"base_uri": "https://localhost:8080/"} id="BzpwqKVCAW8b" outputId="c79a167b-2e5f-464a-b1a2-fe119694829f"
i = Input(batch_shape=(batch_size, timesteps, input_dim))
o = TCN(return_sequences=False,
nb_filters=24,
kernel_size=2,
nb_stacks=1,
# dilations=[1,2,4,8],
padding='same',
use_skip_connections=False,
dropout_rate=0.0,
activation='relu',
kernel_initializer='he_normal',
use_batch_norm=True)(i) # The TCN layers are here.
o = Dense(1)(o)
m = Model(inputs=[i], outputs=[o])
m.compile(optimizer='adam',
loss='mse',
metrics=['accuracy'])
tcn_full_summary(m, expand_residual_blocks=True)
early_stop=keras.callbacks.EarlyStopping(monitor='val_loss',patience=10)
history = m.fit(X_train, y_train,
validation_data=(X_valid,y_valid),
epochs=5,
batch_size=128,
callbacks=[early_stop])
# + [markdown] id="TP-nATJKAW8c"
# #### Evaluation and Plotting
# + colab={"base_uri": "https://localhost:8080/"} id="j5cqcydPAW8c" outputId="0f5c1790-0a08-4165-afd4-e5b206eb47db"
scores = m.evaluate(X_test,y_test)
print(f"Loss, Accuracy: {scores}")
# + colab={"base_uri": "https://localhost:8080/", "height": 323} id="KV61U1TPAW8c" outputId="6db09f0b-fc40-472e-eeff-cf73b7d26825"
plt.subplot(1,2,1)
plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.legend(('loss','val_loss'))
plt.subplot(1,2,2)
plt.plot(history.history["accuracy"])
plt.plot(history.history["val_accuracy"])
plt.legend(('acc','val_acc'))
plt.gcf().set_size_inches((10,5))
plt.show()
# + id="Bhmo9fvnAW8c"
y_pred = m.predict(X_test, )
# + colab={"base_uri": "https://localhost:8080/"} id="xMozecEoAW8c" outputId="90e633c2-a0d7-406a-dc53-8fb90953653e"
X_test[30],y_test[30], np.argmax(y_pred[30])
# + colab={"base_uri": "https://localhost:8080/"} id="Zv3H6Zm8AW8c" outputId="3851ff97-d4d8-4327-f6ac-fe6874ab0482"
classes = np.array([np.argmax(i) for i in y_pred])
np.unique(classes), classes[:20]
# + colab={"base_uri": "https://localhost:8080/"} id="UQ52aIx8AW8d" outputId="c07dfe41-948d-4321-c662-db4046a2ff5f"
recall_score(y_test,classes)
# + colab={"base_uri": "https://localhost:8080/"} id="evA8WQfwAW8d" outputId="7a149907-4f74-4c18-a9f6-a17068cff7d4"
predlist = classes.reshape((classes.shape[0],1))
y_test.shape, y_pred.shape, predlist.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="H6QC2k4LAW8d" outputId="58c13c70-4a0f-456f-c033-40e5bdd501bb"
compdf = pd.DataFrame(predlist)
compdf['real'] = y_test
compdf = compdf.rename(columns={0:'pred'})
compdf['T/F Prediction'] = np.where(compdf['pred'] == compdf['real'],True, False)
compdf
# + colab={"base_uri": "https://localhost:8080/"} id="QnRCMKh8AW8d" outputId="56187d8d-76e9-4ddc-d2f0-18fda91a954a"
np.unique(compdf.loc[compdf.real == 1]['T/F Prediction'])
# + colab={"base_uri": "https://localhost:8080/"} id="eHcMSK0uPyRE" outputId="6a081f33-50f2-4bbf-fe8c-ff2cef483f1d"
np.unique(compdf['pred'])
# + colab={"base_uri": "https://localhost:8080/", "height": 582} id="8VN1xHOnAW8e" outputId="cf4be8c1-dc39-4892-aab0-95b73c2991c1"
plot_min=60
plot_max =120
plt.scatter(range(plot_min,plot_max),y_test[plot_min:plot_max])
plt.scatter(range(plot_min,plot_max),[y_pred[i].argmax()+0.02 for i in range(len(y_pred[plot_min:plot_max]))],c=['r'])
plt.legend(('test class','predicted class'))
plt.xlabel('timestamp index')
plt.ylabel('class (0 = normal, 1 = anomaly)')
plt.xticks(ticks=range(plot_min, plot_max))
plt.gcf().set_size_inches((20,10))
# plt.gcf().autofmt_xdate()
plt.show()
# + [markdown] id="Ga3hFg3GAW8f"
# #### Saving and Checking the size of the Model
# + colab={"base_uri": "https://localhost:8080/"} id="Nwya5ZMOAW8f" outputId="fadd65e8-1415-441e-aa5a-840aac3d4402"
saved_model_dir = '/content/drive/MyDrive/Colab Notebooks/CS581/project-data/'
m.save(saved_model_dir + "tcn-24filter.h5",include_optimizer=False)
print(f"Saving Model to: {saved_model_dir}tcn-24filter.h5")
# + colab={"base_uri": "https://localhost:8080/"} id="JHYt-zEyAW8f" outputId="5c765609-88ea-45f1-a3e2-31e7aa7c109e"
print(f'Size of the model without compression: {os.path.getsize(saved_model_dir + "tcn-24filter.h5")/float(2**20)} Mb')
# + id="UcsnpFjnAW8f"
# + [markdown] id="DBOtyneCMEYc"
# ### Number of filters = 128
# + id="jK1H-2a-MEYk"
tf.keras.backend.clear_session()
# + colab={"base_uri": "https://localhost:8080/"} id="TlmI-3Q7MEYk" outputId="720cc566-2da3-4f6e-9f2a-84f30bca07d8"
i = Input(batch_shape=(batch_size, timesteps, input_dim))
o = TCN(return_sequences=False,
nb_filters=128,
kernel_size=2,
nb_stacks=1,
# dilations=[1,2,4,8],
padding='same',
use_skip_connections=False,
dropout_rate=0.0,
activation='relu',
kernel_initializer='he_normal',
use_batch_norm=True)(i) # The TCN layers are here.
o = Dense(1)(o)
m = Model(inputs=[i], outputs=[o])
m.compile(optimizer='adam',
loss='mse',
metrics=['accuracy'])
tcn_full_summary(m, expand_residual_blocks=True)
early_stop=keras.callbacks.EarlyStopping(monitor='val_loss',patience=10)
history = m.fit(X_train, y_train,
validation_data=(X_valid,y_valid),
epochs=5,
batch_size=128,
callbacks=[early_stop])
# + [markdown] id="VanQ0jtfMEYl"
# #### Evaluation and Plotting
# + colab={"base_uri": "https://localhost:8080/"} id="WUCJIpr_MEYl" outputId="585c2703-be2f-4cfe-f979-84118c98cebb"
scores = m.evaluate(X_test,y_test)
print(f"Loss, Accuracy: {scores}")
# + colab={"base_uri": "https://localhost:8080/", "height": 323} id="pBufj2VFMEYm" outputId="80605921-daff-4c66-a0b5-7d575387198e"
plt.subplot(1,2,1)
plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.legend(('loss','val_loss'))
plt.subplot(1,2,2)
plt.plot(history.history["accuracy"])
plt.plot(history.history["val_accuracy"])
plt.legend(('acc','val_acc'))
plt.gcf().set_size_inches((10,5))
plt.show()
# + id="7CsgdKHhMEYm"
y_pred = m.predict(X_test, )
# + colab={"base_uri": "https://localhost:8080/"} id="O0by05k1MEYm" outputId="e36aa7a8-71aa-4ca5-cdb6-cf1304b7d13a"
X_test[30],y_test[30], np.argmax(y_pred[30])
# + colab={"base_uri": "https://localhost:8080/"} id="ZmYvD5FCMEYn" outputId="fbe52c75-62d4-4c40-f0b6-bacc1f6df3ab"
classes = np.array([np.argmax(i) for i in y_pred])
np.unique(classes), classes[:20]
# + colab={"base_uri": "https://localhost:8080/"} id="FsXznvfaMEYn" outputId="7a98121e-7aa2-4288-d2d7-9037710eb088"
recall_score(y_test,classes)
# + colab={"base_uri": "https://localhost:8080/"} id="vNcfi3-vMEYn" outputId="03b4dc84-0ffe-45ee-94f6-5150596e137b"
predlist = classes.reshape((classes.shape[0],1))
y_test.shape, y_pred.shape, predlist.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 402} id="g-S7uWT7MEYn" outputId="0d868dca-281d-42c0-8b0e-5d97986f58a5"
compdf = pd.DataFrame(predlist)
compdf['real'] = y_test
compdf = compdf.rename(columns={0:'pred'})
compdf['T/F Prediction'] = np.where(compdf['pred'] == compdf['real'],True, False)
compdf
# + colab={"base_uri": "https://localhost:8080/"} id="QvdkbsheMEYo" outputId="0b396ecb-72b1-4903-f4dd-99f642156a7f"
np.unique(compdf.loc[compdf.real == 1]['T/F Prediction'])
# + colab={"base_uri": "https://localhost:8080/", "height": 582} id="MXeXvVDtMEYo" outputId="8d3a2e42-89b0-455f-b640-2225ba5d7bbb"
plot_min=60
plot_max =120
plt.scatter(range(plot_min,plot_max),y_test[plot_min:plot_max])
plt.scatter(range(plot_min,plot_max),[y_pred[i].argmax()+0.02 for i in range(len(y_pred[plot_min:plot_max]))],c=['r'])
plt.legend(('test class','predicted class'))
plt.xlabel('timestamp index')
plt.ylabel('class (0 = normal, 1 = anomaly)')
plt.xticks(ticks=range(plot_min, plot_max))
plt.gcf().set_size_inches((20,10))
# plt.gcf().autofmt_xdate()
plt.show()
# + [markdown] id="SekbzQnmMEYo"
# #### Saving and Checking the size of the Model
# + colab={"base_uri": "https://localhost:8080/"} id="FEX00U8sMEYo" outputId="97bafa44-19ce-498e-bc55-69223a2b00a2"
saved_model_dir = '/content/drive/MyDrive/Colab Notebooks/CS581/project-data/'
m.save(saved_model_dir + "tcn-128filter.h5",include_optimizer=False)
print(f"Saving Model to: {saved_model_dir}tcn-24filter.h5")
# + colab={"base_uri": "https://localhost:8080/"} id="LrSHo9s1MEYo" outputId="06d8bf85-1fe5-4084-ac6a-67c049b0e38c"
print(f'Size of the model without compression: {os.path.getsize(saved_model_dir + "tcn-128filter.h5")/float(2**20)} Mb')
# + [markdown] id="GocZCtw1MhG0"
# ### Filters Comparison Table
# + [markdown] id="LjnVWVENMRJQ"
# | Metric\Filters | 24 | 64 | 128 |
# |---|---|---|---|
# |Accuracy(%)|0.9395|0.9391|0.9372|
# |Size(MB)|0.1211|0.4266|1.4732|
# |Total Parameters|14,233|94,273|368,769|
# |Inference Time(sec)|68|10|71|
# + [markdown] id="m_Jz2bg-W8iY"
# ### Dropout
#
# This is an important hyperparameter that can be used to force the model to drop details of what it's learnt and generalize better. Our baseline model worked with 0 dropout, below we introduce drop out layers between the first Conv1D layer. We vary the dropout percentage between 0.5 and 0.8. Both values are ones that have personally given us good values in our previous assignments.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="MIVdD8kTZKP_" outputId="6e42eb06-7354-4d6e-e198-ceb50990633c"
dropout_vals = [0.5,0.8]
for dropout_val in dropout_vals:
tf.keras.backend.clear_session()
## Creating the model
i = Input(batch_shape=(batch_size, timesteps, input_dim))
o = TCN(return_sequences=False,
nb_filters=24,
kernel_size=2,
nb_stacks=1,
# dilations=[1,2,4,8],
padding='same',
use_skip_connections=False,
dropout_rate=dropout_val,
activation='relu',
kernel_initializer='he_normal',
use_batch_norm=True)(i) # The TCN layers are here.
o = Dense(1)(o)
m = Model(inputs=[i], outputs=[o])
m.compile(optimizer='adam',
loss='mse',
metrics=['accuracy'])
tcn_full_summary(m, expand_residual_blocks=True)
early_stop=keras.callbacks.EarlyStopping(monitor='val_loss',patience=10)
history = m.fit(X_train, y_train,
validation_data=(X_valid,y_valid),
epochs=5,
batch_size=128,
callbacks=[early_stop])
## Evaluation and plotting
scores = m.evaluate(X_test,y_test)
print(f"Loss, Accuracy: {scores}")
plt.subplot(1,2,1)
plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.legend(('loss','val_loss'))
plt.subplot(1,2,2)
plt.plot(history.history["accuracy"])
plt.plot(history.history["val_accuracy"])
plt.legend(('acc','val_acc'))
plt.gcf().set_size_inches((10,5))
plt.show()
plt.savefig(saved_model_dir+'dropout_'+str(dropout_val)+".svg",dpi=150)
y_pred = m.predict(X_test)
plot_min=60
plot_max =120
plt.scatter(range(plot_min,plot_max),y_test[plot_min:plot_max])
plt.scatter(range(plot_min,plot_max),[y_pred[i].argmax()+0.02 for i in range(len(y_pred[plot_min:plot_max]))],c=['r'])
plt.legend(('test class','predicted class'))
plt.xlabel('timestamp index')
plt.ylabel('class (0 = normal, 1 = anomaly)')
plt.xticks(ticks=range(plot_min, plot_max))
plt.gcf().set_size_inches((20,10))
# plt.gcf().autofmt_xdate()
plt.show()
plt.savefig(saved_model_dir+'predict-dropout_'+str(dropout_val)+".svg",dpi=150)
##Saving the model and checking its size
saved_model_dir = '/content/drive/MyDrive/Colab Notebooks/CS581/project-data/'
filename = "tcn-"+str(dropout_val)+"droput.h5"
m.save(saved_model_dir + filename,include_optimizer=False)
print(f"Saving Model to: {saved_model_dir+filename}")
# + colab={"base_uri": "https://localhost:8080/"} id="14nvIUHypnnV" outputId="06445cf5-a1b7-48cf-d6c6-34c8484e12d3"
os.path.getsize('/content/drive/MyDrive/Colab Notebooks/CS581/project-data/tcn-0.5droput.h5')/float(2**20)
# + colab={"base_uri": "https://localhost:8080/"} id="elsocRWTpsRK" outputId="9e55e012-8012-4058-d5cf-21bc346a9edb"
os.path.getsize('/content/drive/MyDrive/Colab Notebooks/CS581/project-data/tcn-0.8droput.h5')/float(2**20)
# + [markdown] id="a3ZFSsA1hP6y"
# ### Dropout Comparison Table
# + [markdown] id="tYeDyyBwhP67"
# | Metric\Droput | 0 | 0.5 | 0.8 |
# |---|---|---|---|
# |Accuracy(%)|0.9395|0.9357|0.8890|
# |Size(MB)|0.1211|0.1211|0.1211|
# |Total Parameters|14,233|14,233|14,233|
# |Inference Time(sec)|68|66|68|
# + [markdown] id="cA7WNW2pb3u3"
# ### Layers and Dilations
# This hyperparameter controls the depth and skip-connections used in the Conv1D layers in the network. Our baseline uses the default, which is [1,2,4,8,16,32,64], meaning it contains 7 layers of Conv-1D, each with increasing gaps of 1,2,4 and so on between each kernel convolution step. We noticed that the default layers made our network quite complex, so we decided to drastically simplify the network to see the effect. Looking at our simple input of rows of combinations of 11-12 numeric features, we assumed a simple network to be able to learn just as well as a deep network.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="DZx9ydYWqCI0" outputId="8986749d-3ad2-49f6-dec2-cdfd40a811dd"
layer_vals = [[1],[1,2,4,8]]
for layer_val in layer_vals:
tf.keras.backend.clear_session()
## Creating the model
i = Input(batch_shape=(batch_size, timesteps, input_dim))
o = TCN(return_sequences=False,
nb_filters=24,
kernel_size=2,
nb_stacks=1,
dilations=layer_val,
padding='same',
use_skip_connections=False,
dropout_rate=0,
activation='relu',
kernel_initializer='he_normal',
use_batch_norm=True)(i) # The TCN layers are here.
o = Dense(1)(o)
m = Model(inputs=[i], outputs=[o])
m.compile(optimizer='adam',
loss='mse',
metrics=['accuracy'])
tcn_full_summary(m, expand_residual_blocks=True)
early_stop=keras.callbacks.EarlyStopping(monitor='val_loss',patience=10)
history = m.fit(X_train, y_train,
validation_data=(X_valid,y_valid),
epochs=5,
batch_size=128,
callbacks=[early_stop])
## Evaluation and plotting
scores = m.evaluate(X_test,y_test)
print(f"Loss, Accuracy: {scores}")
plt.subplot(1,2,1)
plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.legend(('loss','val_loss'))
plt.subplot(1,2,2)
plt.plot(history.history["accuracy"])
plt.plot(history.history["val_accuracy"])
plt.legend(('acc','val_acc'))
plt.gcf().set_size_inches((10,5))
plt.show()
plt.savefig(saved_model_dir+'layer_'+str(len(layer_val))+".svg",dpi=150)
y_pred = m.predict(X_test)
plot_min=60
plot_max =120
plt.scatter(range(plot_min,plot_max),y_test[plot_min:plot_max])
plt.scatter(range(plot_min,plot_max),[y_pred[i].argmax()+0.02 for i in range(len(y_pred[plot_min:plot_max]))],c=['r'])
plt.legend(('test class','predicted class'))
plt.xlabel('timestamp index')
plt.ylabel('class (0 = normal, 1 = anomaly)')
plt.xticks(ticks=range(plot_min, plot_max))
plt.gcf().set_size_inches((20,10))
# plt.gcf().autofmt_xdate()
plt.show()
plt.savefig(saved_model_dir+'predict-layer_'+str(len(layer_val))+".svg",dpi=150)
##Saving the model and checking its size
saved_model_dir = '/content/drive/MyDrive/Colab Notebooks/CS581/project-data/'
filename = "tcn-"+str(layer_val)+"layer.h5"
m.save(saved_model_dir + filename,include_optimizer=False)
print(f"Saving Model to: {saved_model_dir+filename}")
print(f"Size of {filename} is : {os.path.getsize(saved_model_dir + filename)/float(2**20)}")
# + [markdown] id="fxEch7j0w32p"
# ### Layer Dilation Comparison Table
# + [markdown] id="YL6gtR2zw32v"
# | Metric\Layers | [1] | [1,2,4,8] | [1, 2, 4, 8, 16, 32] |
# |---|---|---|---|
# |Accuracy(%)|0.8890|0.9395|0.9395|
# |Size(MB)|0.0285|0.0845|0.1211|
# |Total Parameters|14,233|14,233|14,233|
# |Inference Time(sec)|41|62|68|
# + [markdown] id="weFl0ZoznRAW"
# # End
# + id="uGNk0IzonRoE"
| 195.415445 | 160,646 |
22fdaa3f1b429c654d26e294d661960dbaffc1f5
|
py
|
python
|
tutorials/W0D5_Statistics/W0D5_Tutorial2.ipynb
|
DianaMosquera/course-content
|
['CC-BY-4.0', 'BSD-3-Clause']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W0D5_Statistics/W0D5_Tutorial2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# -
#
# # Neuromatch Academy: Precourse Week, Day 5, Tutorial 2
# # Introduction to Probability and Statistics
#
# __Content creators:__ Ulrik Beierholm
#
# If an editor really did a lot of content creation add "with help from Name Surname" to the above
#
# __Content reviewers:__ Ethan Cheng, Manisha Sinha
#
# Name Surname, Name Surname. This includes both reviewers and editors. Add reviewers first then editors (paper-like seniority :) ).
#
# ---
# #Tutorial Objectives
#
# This tutorial builds on Tutorial 1 by explaining how to do inference through inverting the generative process.
#
# By completing the exercises in this tutorial, you should:
# * understand what the likelihood function is, and have some intuition of why it is important
# * know how to summarise the Gaussian distribution using mean and variance
# * know how to maximise a likelihood function
# * be able to do simple inference in both classical and Bayesian ways
# * (Optional) understand how Bayes Net can be used to model causal relationships
# + cellView="form"
#@markdown Tutorial slides (to be added)
# you should link the slides for all tutorial videos here (we will store pdfs on osf)
from IPython.display import HTML
HTML('<iframe src="https://mfr.ca-1.osf.io/render?url=https://osf.io/kaq2x/?direct%26mode=render%26action=download%26mode=render" frameborder="0" width="960" height="569" allowfullscreen="true" mozallowfullscreen="true" webkitallowfullscreen="true"></iframe>')
# -
# ---
# # Setup
# Make sure to run this before you get started
# + cellView="code"
# Imports
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
from numpy.random import default_rng # a default random number generator
from scipy.stats import norm # the normal probability distribution
# + cellView="form"
#@title Figure settings
import ipywidgets as widgets # interactive display
from ipywidgets import interact, fixed, HBox, Layout, VBox, interactive, Label, interact_manual
# %config InlineBackend.figure_format = 'retina'
# plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/NMA2020/nma.mplstyle")
# + cellView="form"
#@title Plotting & Helper functions
def plot_hist(data, xlabel, figtitle = None, num_bins = None):
""" Plot the given data as a histogram.
Args:
data (ndarray): array with data to plot as histogram
xlabel (str): label of x-axis
figtitle (str): title of histogram plot (default is no title)
num_bins (int): number of bins for histogram (default is 10)
Returns:
count (ndarray): number of samples in each histogram bin
bins (ndarray): center of each histogram bin
"""
fig, ax = plt.subplots()
ax.set_xlabel(xlabel)
ax.set_ylabel('Count')
if num_bins is not None:
count, bins, _ = plt.hist(data, max(data), bins = num_bins)
else:
count, bins, _ = plt.hist(data, max(data)) # 10 bins default
if figtitle is not None:
fig.suptitle(figtitle, size=16)
plt.show()
return count, bins
def plot_gaussian_samples_true(samples, xspace, mu, sigma, xlabel, ylabel):
""" Plot a histogram of the data samples on the same plot as the gaussian
distribution specified by the give mu and sigma values.
Args:
samples (ndarray): data samples for gaussian distribution
xspace (ndarray): x values to sample from normal distribution
mu (scalar): mean parameter of normal distribution
sigma (scalar): variance parameter of normal distribution
xlabel (str): the label of the x-axis of the histogram
ylabel (str): the label of the y-axis of the histogram
Returns:
Nothing.
"""
fig, ax = plt.subplots()
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
# num_samples = samples.shape[0]
count, bins, _ = plt.hist(samples, density=True) # probability density function
plt.plot(xspace, norm.pdf(xspace, mu, sigma),'r-')
plt.show()
def plot_likelihoods(likelihoods, mean_vals, variance_vals):
""" Plot the likelihood values on a heatmap plot where the x and y axes match
the mean and variance parameter values the likelihoods were computed for.
Args:
likelihoods (ndarray): array of computed likelihood values
mean_vals (ndarray): array of mean parameter values for which the
likelihood was computed
variance_vals (ndarray): array of variance parameter values for which the
likelihood was computed
Returns:
Nothing.
"""
fig, ax = plt.subplots()
im = ax.imshow(likelihoods)
cbar = ax.figure.colorbar(im, ax=ax)
cbar.ax.set_ylabel('log likelihood', rotation=-90, va="bottom")
ax.set_xticks(np.arange(len(mean_vals)))
ax.set_yticks(np.arange(len(variance_vals)))
ax.set_xticklabels(mean_vals)
ax.set_yticklabels(variance_vals)
ax.set_xlabel('Mean')
ax.set_ylabel('Variance')
def posterior_plot(x, likelihood=None, prior=None, posterior_pointwise=None, ax=None):
"""
Plots normalized Gaussian distributions and posterior.
Args:
x (numpy array of floats): points at which the likelihood has been evaluated
auditory (numpy array of floats): normalized probabilities for auditory likelihood evaluated at each `x`
visual (numpy array of floats): normalized probabilities for visual likelihood evaluated at each `x`
posterior (numpy array of floats): normalized probabilities for the posterior evaluated at each `x`
ax: Axis in which to plot. If None, create new axis.
Returns:
Nothing.
"""
if likelihood is None:
likelihood = np.zeros_like(x)
if prior is None:
prior = np.zeros_like(x)
if posterior_pointwise is None:
posterior_pointwise = np.zeros_like(x)
if ax is None:
fig, ax = plt.subplots()
ax.plot(x, likelihood, '-C1', LineWidth=2, label='Auditory')
ax.plot(x, prior, '-C0', LineWidth=2, label='Visual')
ax.plot(x, posterior_pointwise, '-C2', LineWidth=2, label='Posterior')
ax.legend()
ax.set_ylabel('Probability')
ax.set_xlabel('Orientation (Degrees)')
plt.show()
return ax
def plot_classical_vs_bayesian_normal(num_points, mu_classic, var_classic,
mu_bayes, var_bayes):
""" Helper function to plot optimal normal distribution parameters for varying
observed sample sizes using both classic and Bayesian inference methods.
Args:
num_points (int): max observed sample size to perform inference with
mu_classic (ndarray): estimated mean parameter for each observed sample size
using classic inference method
var_classic (ndarray): estimated variance parameter for each observed sample size
using classic inference method
mu_bayes (ndarray): estimated mean parameter for each observed sample size
using Bayesian inference method
var_bayes (ndarray): estimated variance parameter for each observed sample size
using Bayesian inference method
Returns:
Nothing.
"""
xspace = np.linspace(0, num_points, num_points)
fig, ax = plt.subplots()
ax.set_xlabel('n data points')
ax.set_ylabel('mu')
plt.plot(xspace, mu_classic,'r-', label = "Classical")
plt.plot(xspace, mu_bayes,'b-', label = "Bayes")
plt.legend()
plt.show()
fig, ax = plt.subplots()
ax.set_xlabel('n data points')
ax.set_ylabel('sigma^2')
plt.plot(xspace, var_classic,'r-', label = "Classical")
plt.plot(xspace, var_bayes,'b-', label = "Bayes")
plt.legend()
plt.show()
# -
# ---
# # Section 1: Statistical Inference and Likelihood
# + cellView="form"
#@title Video 4: Inference
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="765S2XKYoJ8", width=854, height=480, fs=1)
print("Video available at https://youtu.be/" + video.id)
video
# -
# A generative model (such as the Gaussian distribution from the previous tutorial) allows us to make prediction about outcomes.
#
# However, after we observe $n$ data points, we can also evaluate our model (and any of its associated parameters) by calculating the **likelihood** of our model having generated each of those data points $x_i$.
#
# $$P(x_i|\mu,\sigma)=\mathcal{N}(x_i,\mu,\sigma)$$
#
# For all data points $\mathbf{x}=(x_1, x_2, x_3, ...x_n) $ we can then calculate the likelihood for the whole dataset by computing the product of the likelihood for each single data point.
#
# $$P(\mathbf{x}|\mu,\sigma)=\prod_{i=1}^n \mathcal{N}(x_i,\mu,\sigma)$$
#
# As a function of the parameters (when the data points $x$ are fixed), this is referred to as the **likelihood function**, $L(\mu,\sigma)$.
#
# In the last tutorial we reviewed how the data was generated given the selected parameters of the generative process. If we do not know the parameters $\mu$, $\sigma$ that generated the data, we can ask which parameter values (given our model) gives the best (highest) likelihood.
#
# ## Exercise 1A: Likelihood, mean and variance
#
#
# We can use the likelihood to find the set of parameters that are most likely to have generated the data (given the model we are using). That is, we want to infer the parameters that gave rise to the data we observed. We will try a couple of ways of doing statistical inference.
#
# In the following exercise, we will sample from the Gaussian distribution (again), plot a histogram and the Gaussian probability density function, and calculate some statistics from the samples.
#
# Specifically we will calculate:
#
# * Likelihood
# * Mean
# * Standard deviation
#
# Statistical moments are defined based on the expectations. The first moment is the expected value, i.e. the mean, the second moment is the expected squared value, i.e. variance, and so on.
#
# The special thing about the Gaussian is that mean and standard deviation of the random sample can effectively approximate the two parameters of a Gaussian, $\mu, \sigma$.
#
# Hence using the sample mean, $\bar{x}=\frac{1}{n}\sum_i x_i$, and variance, $\bar{\sigma}^2=\frac{1}{n} \sum_i (x_i-\bar{x})^2 $ should give us the best/maximum likelihood, $L(\bar{x},\bar{\sigma}^2)$.
#
# Let's see if that actually works. If we search through different combinations of $\mu$ and $\sigma$ values, do the sample mean and variance values give us the maximum likelihood (of observing our data)?
#
# You need to modify two lines below to generate the data from a normal distribution $N(5, 1)$, and plot the theoretical distribution. Note that we are reusing functions from tutorial 1, so review that tutorial if needed. Then you will use this random sample to calculate the likelihood for a variety of potential mean and variance parameter values. For this tutorial we have chosen a variance parameter of 1, meaning the standard deviation is also 1 in this case. Most of our functions take the standard deviation sigma as a parameter, so we will write $\sigma = 1$.
#
# (Note that in practice computing the sample variance like this $$\bar{\sigma}^2=\frac{1}{(n-1)} \sum_i (x_i-\bar{x})^2 $$ is actually better, take a look at any statistics textbook for an explanation of this.)
# +
def generate_normal_samples(mu, sigma, num_samples):
""" Generates a desired number of samples from a normal distribution,
Normal(mu, sigma).
Args:
mu (scalar): mean parameter of the normal distribution
sigma (scalar): standard deviation parameter of the normal distribution
num_samples (int): number of samples drawn from normal distribution
Returns:
sampled_values (ndarray): a array of shape (samples, ) containing the samples
"""
random_num_generator = default_rng(0)
sampled_values = random_num_generator.normal(mu, sigma, num_samples)
return sampled_values
def compute_likelihoods_normal(x, mean_vals, variance_vals):
""" Computes the log-likelihood values given a observed data sample x, and
potential mean and variance values for a normal distribution
Args:
x (ndarray): 1-D array with all the observed data
mean_vals (ndarray): 1-D array with all potential mean values to
compute the likelihood function for
variance_vales (ndarray): 1-D array with all potential variance values to
compute the likelihood function for
Returns:
likelihood (ndarray): 2-D array of shape (number of mean_vals,
number of variance_vals) for which the likelihood
of the observed data was computed
"""
# Initialise likelihood collection array
likelihood = np.zeros((mean_vals.shape[0], variance_vals.shape[0]))
# Compute the likelihood for observing the gvien data x assuming
# each combination of mean and variance values
for idxMean in range(mean_vals.shape[0]):
for idxVar in range(variance_vals.shape[0]):
likelihood[idxVar,idxMean]= sum(np.log(norm.pdf(x, mean_vals[idxMean],
variance_vals[idxVar])))
return likelihood
###################################################################
## TODO for students: Generate 1000 random samples from a normal distribution
## with mu = 5 and sigma = 1
# Fill out the following then remove
raise NotImplementedError("Student exercise: need to generate samples")
###################################################################
# Generate data
mu = 5
sigma = 1 # since variance = 1, sigma = 1
x = ...
# You can calculate mean and variance through either numpy or scipy
print("This is the sample mean as estimated by numpy: " + str(np.mean(x)))
print("This is the sample standard deviation as estimated by numpy: " + str(np.std(x)))
# or
meanX, varX = sp.stats.norm.stats(x)
print("This is the sample mean as estimated by scipy: " + str(meanX[0]))
print("This is the sample standard deviation as estimated by scipy: " + str(varX[0]))
###################################################################
## TODO for students: Use the given function to compute the likelihood for
## a variety of mean and variance values
# Fill out the following then remove
raise NotImplementedError("Student exercise: need to compute likelihoods")
###################################################################
# Let's look through possible mean and variance values for the highest likelihood
# using the compute_likelihood function
meanTest = np.linspace(1, 10, 10) # potential mean values to try
varTest = np.array([0.7, 0.8, 0.9, 1, 1.2, 1.5, 2, 3, 4, 5]) # potential variance values to try
likelihoods = ...
# Uncomment once you've generated the samples and compute likelihoods
# xspace = np.linspace(0, 10, 100)
# plot_gaussian_samples_true(x, xspace, mu, sigma, "x", "Count")
# plot_likelihoods(likelihoods, meanTest, varTest)
# +
# to_remove solution
def generate_normal_samples(mu, sigma, num_samples):
""" Generates a desired number of samples from a normal distribution,
Normal(mu, sigma).
Args:
mu (scalar): mean parameter of the normal distribution
sigma (scalar): standard deviation parameter of the normal distribution
num_samples (int): number of samples drawn from normal distribution
Returns:
sampled_values (ndarray): a array of shape (samples, ) containing the samples
"""
random_num_generator = default_rng(0)
sampled_values = random_num_generator.normal(mu, sigma, num_samples)
return sampled_values
def compute_likelihoods_normal(x, mean_vals, variance_vals):
""" Computes the log-likelihood values given a observed data sample x, and
potential mean and variance values for a normal distribution
Args:
x (ndarray): 1-D array with all the observed data
mean_vals (ndarray): 1-D array with all potential mean values to
compute the likelihood function for
variance_vales (ndarray): 1-D array with all potential variance values to
compute the likelihood function for
Returns:
likelihood (ndarray): 2-D array of shape (number of mean_vals,
number of variance_vals) for which the likelihood
of the observed data was computed
"""
# Initialise likelihood collection array
likelihood = np.zeros((mean_vals.shape[0], variance_vals.shape[0]))
# Compute the likelihood for observing the gvien data x assuming
# each combination of mean and variance values
for idxMean in range(mean_vals.shape[0]):
for idxVar in range(variance_vals.shape[0]):
likelihood[idxVar,idxMean]= sum(np.log(norm.pdf(x, mean_vals[idxMean],
variance_vals[idxVar])))
return likelihood
# Generate data
mu = 5
sigma = 1 # since variance = 1, sigma = 1
x = generate_normal_samples(mu, sigma, 1000)
# You can calculate mean and variance through either numpy or scipy
print("This is the sample mean as estimated by numpy: " + str(np.mean(x)))
print("This is the sample standard deviation as estimated by numpy: " + str(np.std(x)))
# or
meanX, varX = sp.stats.norm.stats(x)
print("This is the sample mean as estimated by scipy: " + str(meanX[0]))
print("This is the sample standard deviation as estimated by scipy: " + str(varX[0]))
# Let's look through possible mean and variance values for the highest likelihood
# using the compute_likelihood function
meanTest = np.linspace(1, 10, 10) # potential mean values to try
varTest = np.array([0.7, 0.8, 0.9, 1, 1.2, 1.5, 2, 3, 4, 5]) # potential variance values to try
likelihoods = compute_likelihoods_normal(x, meanTest, varTest)
# Uncomment once you've generated the samples and compute likelihoods
xspace = np.linspace(0, 10, 100)
with plt.xkcd():
plot_gaussian_samples_true(x, xspace, mu, sigma, "x", "Count")
plot_likelihoods(likelihoods, meanTest, varTest)
# -
# The top figure shows hopefully a nice fit between the histogram and the distribution that generated the data. So far so good.
#
# Underneath you should see the sample mean and variance values, which are close to the true values (that we happen to know here).
#
# In the heatmap we should be able to see that the mean and variance parameters values yielding the highest likelihood (yellow) corresponds to (roughly) the combination of the calculated sample mean and variance from the dataset.
# But it can be hard to see from such a rough **grid-search** simulation, as it is only as precise as the resolution of the grid we are searching.
#
# Implicitly, by looking for the parameters that give the highest likelihood, we have been searching for the **maximum likelihood** estimate.
# $$(\hat{\mu},\hat{\sigma})=argmax_{\mu,\sigma}L(\mu,\sigma)=argmax_{\mu,\sigma} \prod_{i=1}^n \mathcal{N}(x_i,\mu,\sigma)$$.
#
# For a simple Gaussian this can actually be done analytically (you have likely already done so yourself), using the statistical moments: mean and standard deviation (variance).
#
# In next section we will look at other ways of inferring such parameter variables.
# ## Interactive Demo: Maximum likelihood inference
# We want to do inference on this data set, i.e. we want to infer the parameters that most likely gave rise to the data given our model. Intuitively that means that we want as good as possible a fit between the observed data and the probability distribution function with the best inferred parameters.
#
# For now, just try to see how well you can fit the probability distribution to the data by using the demo sliders to control the mean and standard deviation parameters of the distribution.
# + cellView="form"
#@title
#@markdown Make sure you execute this cell to enable the widget and fit by hand!
vals = generate_normal_samples(mu, sigma, 1000)
def plotFnc(mu,sigma):
#prepare to plot
fig, ax = plt.subplots()
ax.set_xlabel('x')
ax.set_ylabel('probability')
loglikelihood= sum(np.log(norm.pdf(vals,mu,sigma)))
#calculate histogram
count, bins, ignored = plt.hist(vals,density=True)
x = np.linspace(0,10,100)
#plot
plt.plot(x, norm.pdf(x,mu,sigma),'r-')
plt.show()
print("The log-likelihood for the selected parameters is: " + str(loglikelihood))
#interact(plotFnc, mu=5.0, sigma=2.1);
#interact(plotFnc, mu=widgets.IntSlider(min=0.0, max=10.0, step=1, value=4.0),sigma=widgets.IntSlider(min=0.1, max=10.0, step=1, value=4.0));
interact(plotFnc, mu=(0.0, 10.0, 0.1),sigma=(0.1, 10.0, 0.1));
# -
# Did you notice the number below the plot? That is the summed log-likelihood, which increases (becomes less negative) as the fit improves. The log-likelihood should be greatest when $\mu$ = 5 and $\sigma$ = 1.
#
# Building upon what we did in the previous exercise, we want to see if we can do inference on observed data in a bit more principled way.
#
# ## Exercise 1B: Maximum Likelihood Estimation
#
# Let's again assume that we have a data set, $\mathbf{x}$, assumed to be generated by a normal distribution (we actually generate it ourselves in line 1, so we know how it was generated!).
# We want to maximise the likelihood of the parameters $\mu$ and $\sigma^2$. We can do so using a couple of tricks:
#
# * Using a log transform will not change the maximum of the function, but will allow us to work with very small numbers that could lead to problems with machine precision.
# * Maximising a function is the same as minimising the negative of a function, allowing us to use the minimize optimisation provided by scipy.
#
# In the code below, insert the missing line (see the `compute_likelihoods_normal` function from previous exercise), with the mean as theta[0] and variance as theta[1].
#
# +
mu = 5
sigma = 1
# Generate 1000 random samples from a Gaussian distribution
dataX = generate_normal_samples(mu, sigma, 1000)
# We define the function to optimise, the negative log likelihood
def negLogLike(theta):
""" Function for computing the negative log-likelihood given the observed data
and given parameter values stored in theta.
Args:
dataX (ndarray): array with observed data points
theta (ndarray): normal distribution parameters (mean is theta[0],
variance is theta[1])
Returns:
Calculated negative Log Likelihood value!
"""
###################################################################
## TODO for students: Compute the negative log-likelihood value for the
## given observed data values and parameters (theta)
# Fill out the following then remove
raise NotImplementedError("Student exercise: need to compute the negative \
log-likelihood value")
###################################################################
return ...
# Define bounds, var has to be positive
bnds = ((None, None), (0, None))
# Optimize with scipy!
# Uncomment once function above is implemented
# optimal_parameters = sp.optimize.minimize(negLogLike, (2, 2), bounds = bnds)
# print("The optimal mean estimate is: " + str(optimal_parameters.x[0]))
# print("The optimal variance estimate is: " + str(optimal_parameters.x[1]))
# optimal_parameters contains a lot of information about the optimization,
# but we mostly want the mean and variance
# +
# to_remove solution
mu = 5
sigma = 1
# Generate 1000 random samples from a Gaussian distribution
dataX = generate_normal_samples(mu, sigma, 1000)
# We define the function to optimise, the negative log likelihood
def negLogLike(theta):
""" Function for computing the negative log-likelihood given the observed data
and given parameter values stored in theta.
Args:
theta (ndarray): normal distribution parameters (mean is theta[0],
variance is theta[1])
Returns:
Calculated negative Log Likelihood value!
"""
return -sum(np.log(norm.pdf(dataX, theta[0], theta[1])))
# Define bounds, var has to be positive
bnds = ((None, None), (0, None))
# Optimize with scipy!
# Uncomment once function above is implemented
optimal_parameters = sp.optimize.minimize(negLogLike, (2, 2), bounds = bnds)
print("The optimal mean estimate is: " + str(optimal_parameters.x[0]))
print("The optimal variance estimate is: " + str(optimal_parameters.x[1]))
# optimal_parameters contains a lot of information about the optimization,
# but we mostly want the mean and variance
# -
# These are the approximations of the parameters that maximise the likelihood ($\mu$ ~ 5.281 and $\sigma$ ~ 1.170)
#
# Compare these values to the first and second moment (sample mean and variance) from the previous exercise, as well as to the true values (which we only know because we generated the numbers!). Consider the relationship discussed about statistical moments and maximising likelihood.
#
# Go back to the previous exercise and modify the mean and standard deviation values used to generate the observed data $x$, and verify that the values still work out.
# +
# to_remove explanation
""" You should notice that the parameters estimated by maximum likelihood
estimation/inference are very close to the true parameters (mu = 5, sigma = 1),
as well as the parameters estimated in Exercise 1A where all likelihood values
were calculated explicitly. You should also see that changing the mean and
sigma parameter values (and generating new data from a distribution with these
parameters) makes no difference as MLE methods can still recover these
parameters.
"""
# -
# ---
# # Section 2: Bayesian Inference
# + cellView="form"
#@title Video 5: Bayes
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="12tk5FsVMBQ", width=854, height=480, fs=1)
print("Video available at https://youtu.be/" + video.id)
video
# -
#
# For Bayesian inference we do not focus on the likelihood function $L(y)=P(x|y)$, but instead focus on the posterior distribution:
#
# $$P(y|x)=\frac{P(x|y)P(y)}{P(x)}$$
#
# which is composed of the likelihood function $P(x|y)$, the prior $P(y)$ and a normalising term $P(x)$ (which we will ignore for now).
#
# While there are other advantages to using Bayesian inference (such as the ability to derive Bayesian Nets, see optional bonus task below), we will first mostly focus on the role of the prior in inference.
# ## Exercise 2A: Performing Bayesian inference
#
# In the above sections we performed inference using maximum likelihood, i.e. finding the parameters that maximised the likelihood of a set of parameters, given the model and data.
#
# We will now repeat the inference process, but with an added Bayesian prior, and compare it to the classical inference process we did before (Section 1). When using conjugate priors we can just update the parameter values of the distributions (here Gaussian distributions).
#
# For the prior we start by guessing a mean of 6 (mean of observed data points 5 and 7) and variance of 1 (variance of 5 and 7). This is a simplified way of applying a prior, that allows us to just add these 2 values (pseudo-data) to the real data.
#
# In the code below, complete the missing lines.
# +
def classic_vs_bayesian_normal(mu, sigma, num_points, prior):
""" Compute both classical and Bayesian inference processes over the range of
data sample sizes (num_points) for a normal distribution with parameters
mu, sigma for comparison.
Args:
mu (scalar): the mean parameter of the normal distribution
sigma (scalar): the standard deviation parameter of the normal distribution
num_points (int): max number of points to use for inference
prior (ndarray): prior data points for Bayesian inference
Returns:
mean_classic (ndarray): estimate mean parameter via classic inference
var_classic (ndarray): estimate variance parameter via classic inference
mean_bayes (ndarray): estimate mean parameter via Bayesian inference
var_bayes (ndarray): estimate variance parameter via Bayesian inference
"""
# Initialize the classical and Bayesian inference arrays that will estimate
# the normal parameters given a certain number of randomly sampled data points
mean_classic = np.zeros(num_points)
var_classic = np.zeros(num_points)
mean_bayes = np.zeros(num_points)
var_bayes = np.zeros(num_points)
for nData in range(num_points):
###################################################################
## TODO for students: Complete classical inference for increasingly
## larger sets of random data points
# Fill out the following then remove
raise NotImplementedError("Student exercise: need to code classical inference")
###################################################################
# Randomly sample nData + 1 number of points
x = ...
# Compute the mean of those points and set the corresponding array entry to this value
mean_classic[nData] = ...
# Compute the variance of those points and set the corresponding array entry to this value
var_classic[nData] = ...
# Bayesian inference with the given prior is performed below for you
xsupp = np.hstack((x, prior))
mean_bayes[nData] = np.mean(xsupp)
var_bayes[nData] = np.var(xsupp)
return mean_classic, var_classic, mean_bayes, var_bayes
# Set normal distribution parameters, mu and sigma
mu = 5
sigma = 1
# Set the prior to be two new data points, 5 and 7, and print the mean and variance
prior = np.array((5, 7))
print("The mean of the data comprising the prior is: " + str(np.mean(prior)))
print("The variance of the data comprising the prior is: " + str(np.var(prior)))
# Uncomment once the function above is completed
# mean_classic, var_classic, mean_bayes, var_bayes = classic_vs_bayesian_normal(mu, sigma, 30, prior)
# plot_classical_vs_bayesian_normal(30, mean_classic, var_classic, mean_bayes, var_bayes)
# +
# to_remove solution
def classic_vs_bayesian_normal(mu, sigma, num_points, prior):
""" Compute both classical and Bayesian inference processes over the range of
data sample sizes (num_points) for a normal distribution with parameters
mu,sigma for comparison.
Args:
mu (scalar): the mean parameter of the normal distribution
sigma (scalar): the standard deviation parameter of the normal distribution
num_points (int): max number of points to use for inference
prior (ndarray): prior data points for Bayesian inference
Returns:
mean_classic (ndarray): estimate mean parameter via classic inference
var_classic (ndarray): estimate variance parameter via classic inference
mean_bayes (ndarray): estimate mean parameter via Bayesian inference
var_bayes (ndarray): estimate variance parameter via Bayesian inference
"""
# Initialize the classical and Bayesian inference arrays that will estimate
# the normal parameters given a certain number of randomly sampled data points
mean_classic = np.zeros(num_points)
var_classic = np.zeros(num_points)
mean_bayes = np.zeros(num_points)
var_bayes = np.zeros(num_points)
for nData in range(num_points):
# Randomly sample nData + 1 number of points
x = generate_normal_samples(mu, sigma, nData + 1)
# Compute the mean of those points and set the corresponding array entry to this value
mean_classic[nData] = np.mean(x)
# Compute the variance of those points and set the corresponding array entry to this value
var_classic[nData] = np.var(x)
# Bayesian inference with the given prior is performed below for you
xsupp = np.hstack((x, prior))
mean_bayes[nData] = np.mean(xsupp)
var_bayes[nData] = np.var(xsupp)
return mean_classic, var_classic, mean_bayes, var_bayes
# Set normal distribution parameters, mu and sigma
mu = 5
sigma = 1
# Set the prior to be two new data points, 5 and 7, and print the mean and variance
prior = np.array((5, 7))
print("The mean of the data comprising the prior is: " + str(np.mean(prior)))
print("The variance of the data comprising the prior is: " + str(np.var(prior)))
# Uncomment once the function above is completed
mean_classic, var_classic, mean_bayes, var_bayes = classic_vs_bayesian_normal(mu, sigma, 30, prior)
with plt.xkcd():
plot_classical_vs_bayesian_normal(30, mean_classic, var_classic, mean_bayes, var_bayes)
# -
# Hopefully you can see that the blue line stays a little closer to the true values ($\mu=5$, $\sigma^2=1$). Having a simple prior in the Bayesian inference process (blue) helps to regularise the inference of the mean and variance parameters when you have very little data, but has little effect with large data. You can see that as the number of data points (x-axis) increases, both inference processes (blue and red lines) get closer and closer together, i.e. their estimates for the true parameters converge as sample size increases.
# ## Think! 2A: Bayesian Brains
# It should be clear how Bayesian inference can help you when doing data analysis. But consider whether the brain might be able to benefit from this too. If the brain needs to make inferences about the world, would it be useful to do regularisation on the input?
# +
# to_remove explanation
""" You will learn more about "Bayesian brains" and the theory surrounding
these ideas once the course begins. Here is a brief explanation: it may
be ideal for human brains to implement Bayesian inference by integrating "prior"
information the brain has about the world (memories, prior knowledge, etc.) with
new evidence that updates its "beliefs"/prior. This process seems to parallel
the brain's method of learning about its environment, making it a compelling
theory for many neuroscience researchers. The next exercise examines a possible
real world model for Bayesian inference: sound localization.
"""
# -
# ## Exercise 2B: Finding the posterior computationally
# ***(Exercise moved from NMA2020 Bayes day, all credit to original creators!)***
#
# Imagine an experiment where participants estimate the location of a noise-emitting object. To estimate its position, the participants can use two sources of information:
# 1. new noisy auditory information (the likelihood)
# 2. prior visual expectations of where the stimulus is likely to come from (visual prior).
#
# The auditory and visual information are both noisy, so participants will combine these sources of information to better estimate the position of the object.
#
# We will use Gaussian distributions to represent the auditory likelihood (in red), and a Gaussian visual prior (expectations - in blue). Using Bayes rule, you will combine them into a posterior distribution that summarizes the probability that the object is in each possible location.
#
# We have provided you with a ready-to-use plotting function, and a code skeleton.
#
# * You can use `my_gaussian` from Tutorial 1 (also included below), to generate an auditory likelihood with parameters $\mu$ = 3 and $\sigma$ = 1.5
# * Generate a visual prior with parameters $\mu$ = -1 and $\sigma$ = 1.5
# * Calculate the posterior using pointwise multiplication of the likelihood and prior. Don't forget to normalize so the posterior adds up to 1
# * Plot the likelihood, prior and posterior using the predefined function `posterior_plot`
#
#
# +
def my_gaussian(x_points, mu, sigma):
""" Returns normalized Gaussian estimated at points `x_points`, with parameters:
mean `mu` and standard deviation `sigma`
Args:
x_points (ndarray of floats): points at which the gaussian is evaluated
mu (scalar): mean of the Gaussian
sigma (scalar): standard deviation of the gaussian
Returns:
(numpy array of floats) : normalized Gaussian evaluated at `x`
"""
px = 1/(2*np.pi*sigma**2)**1/2 *np.exp(-(x_points-mu)**2/(2*sigma**2))
# as we are doing numerical integration we may have to remember to normalise
# taking into account the stepsize (0.1)
px = px/(0.1*sum(px))
return px
def compute_posterior_pointwise(prior, likelihood):
""" Compute the posterior probability distribution point-by-point using Bayes
Rule.
Args:
prior (ndarray): probability distribution of prior
likelihood (ndarray): probability distribution of likelihood
Returns:
posterior (ndarray): probability distribution of posterior
"""
##############################################################################
# TODO for students: Write code to compute the posterior from the prior and
# likelihood via pointwise multiplication. (You may assume both are defined
# over the same x-axis)
#
# Comment out the line below to test your solution
raise NotImplementedError("Finish the simulation code first")
##############################################################################
posterior = ...
return posterior
def localization_simulation(mu_auditory = 3.0, sigma_auditory = 1.5,
mu_visual = -1.0, sigma_visual = 1.5):
""" Perform a sound localization simulation with an auditory prior.
Args:
mu_auditory (float): mean parameter value for auditory prior
sigma_auditory (float): standard deviation parameter value for auditory
prior
mu_visual (float): mean parameter value for visual likelihood distribution
sigma_visual (float): standard deviation parameter value for visual
likelihood distribution
Returns:
x (ndarray): range of values for which to compute probabilities
auditory (ndarray): probability distribution of the auditory prior
visual (ndarray): probability distribution of the visual likelihood
posterior_pointwise (ndarray): posterior probability distribution
"""
##############################################################################
## Using the x variable below,
## create a gaussian called 'auditory' with mean 3, and std 1.5
## create a gaussian called 'visual' with mean -1, and std 1.5
#
#
## Comment out the line below to test your solution
raise NotImplementedError("Finish the simulation code first")
###############################################################################
x = np.arange(-8, 9, 0.1)
auditory = ...
visual = ...
posterior = compute_posterior_pointwise(auditory, visual)
return x, auditory, visual, posterior
# Uncomment the lines below to plot the results
# x, auditory, visual, posterior_pointwise = localization_simulation()
# _ = posterior_plot(x, auditory, visual, posterior_pointwise)
# +
# to_remove solution
def my_gaussian(x_points, mu, sigma):
""" Returns normalized Gaussian estimated at points `x_points`, with parameters:
mean `mu` and standard deviation `sigma`
Args:
x_points (ndarray of floats): points at which the gaussian is evaluated
mu (scalar): mean of the Gaussian
sigma (scalar): standard deviation of the gaussian
Returns:
(numpy array of floats) : normalized Gaussian evaluated at `x`
"""
px = 1/(2*np.pi*sigma**2)**1/2 *np.exp(-(x_points-mu)**2/(2*sigma**2))
# as we are doing numerical integration we may have to remember to normalise
# taking into account the stepsize (0.1)
px = px/(0.1*sum(px))
return px
def compute_posterior_pointwise(prior, likelihood):
""" Compute the posterior probability distribution point-by-point using Bayes
Rule.
Args:
prior (ndarray): probability distribution of prior
likelihood (ndarray): probability distribution of likelihood
Returns:
posterior (ndarray): probability distribution of posterior
"""
posterior = likelihood * prior
posterior /= posterior.sum()
return posterior
def localization_simulation(mu_auditory = 3.0, sigma_auditory = 1.5,
mu_visual = -1.0, sigma_visual = 1.5):
""" Perform a sound localization simulation with an auditory prior.
Args:
mu_auditory (float): mean parameter value for auditory prior
sigma_auditory (float): standard deviation parameter value for auditory
prior
mu_visual (float): mean parameter value for visual likelihood distribution
sigma_visual (float): standard deviation parameter value for visual
likelihood distribution
Returns:
x (ndarray): range of values for which to compute probabilities
auditory (ndarray): probability distribution of the auditory prior
visual (ndarray): probability distribution of the visual likelihood
posterior_pointwise (ndarray): posterior probability distribution
"""
x = np.arange(-8, 9, 0.1)
auditory = my_gaussian(x, mu_auditory, sigma_auditory)
visual = my_gaussian(x, mu_visual, mu_visual)
posterior = compute_posterior_pointwise(auditory, visual)
return x, auditory, visual, posterior
# Uncomment the lines below to plot the results
x, auditory, visual, posterior_pointwise = localization_simulation()
with plt.xkcd():
_ = posterior_plot(x, auditory, visual, posterior_pointwise)
# -
# Combining the the visual and auditory information could help the brain get a better estimate of the location of an audio-visual object, with lower variance. For this specific example we did not use a Bayesian prior for simplicity, although it would be a good idea in a practical modeling study.
#
# **Main course preview:** On Week 3 Day 1 (W3D1) there will be a whole day devoted to examining whether the brain uses Bayesian inference. Is the brain Bayesian?!
# ---
# # Summary
#
# + cellView="form"
#@title Video 6: Outro
from IPython.display import YouTubeVideo
video = YouTubeVideo(id= "BL5qNdZS-XQ", width=854, height=480, fs=1)
print("Video available at https://youtu.be/" + video.id)
video
# -
#
# Having done the different exercises you should now:
# * understand what the likelihood function is, and have some intuition of why it is important
# * know how to summarise the Gaussian distribution using mean and variance
# * know how to maximise a likelihood function
# * be able to do simple inference in both classical and Bayesian ways
# ---
# # Bonus
#
# For more reading on these topics see:
# Textbook
#
#
# ## Extra exercise: Bayes Net
# If you have the time, here is another extra exercise.
#
# Bayes Net, or Bayesian Belief Networks, provide a way to make inferences about multiple levels of information, which would be very difficult to do in a classical frequentist paradigm.
#
# We can encapsulate our knowledge about causal relationships and use this to make inferences about hidden properties.
# We will try a simple example of a Bayesian Net (aka belief network). Imagine that you have a house with an unreliable sprinkler system installed for watering the grass. This is set to water the grass independently of whether it has rained that day. We have three variables, rain ($r$), sprinklers ($s$) and wet grass ($w$). Each of these can be true (1) or false (0). See the graphical model representing the relationship between the variables.
# 
# There is a table below describing all the relationships between $w, r$, and s$.
#
# Obviously the grass is more likely to be wet if either the sprinklers were on or it was raining. On any given day the sprinklers have probability 0.25 of being on, $P(s = 1) = 0.25$, while there is a probability 0.1 of rain, $P (r = 1) = 0.1$. The table then lists the conditional probabilities for the given being wet, given a rain and sprinkler condition for that day.
# \begin{array}{|l | l || ll |} \hline
# r &s&P(w=0|r,s) &P(w=1|r,s)$\\ \hline
# 0& 0 &0.999 &0.001\\
# 0& 1 &0.1& 0.9\\
# 1& 0 &0.01 &0.99\\
# 1& 1& 0.001 &0.999\\ \hline
# \end{array}
#
#
# You come home and find that the the grass is wet, what is the probability the sprinklers were on today (you do not know if it was raining)?
#
# We can start by writing out the joint probability:
# $P(r,w,s)=P(w|r,s)P(r)P(s)$
#
# The conditional probability is then:
#
# $
# P(s|w)=\frac{\sum_{r} P(w|s,r)P(s) P(r)}{P(w)}=\frac{P(s) \sum_{r} P(w|s,r) P(r)}{P(w)}
# $
#
# Note that we are summing over all possible conditions for $r$ as we do not know if it was raining. Specifically, we want to know the probability of sprinklers having been on given the wet grass, $P(s=1|w=1)$:
#
# $
# P(s=1|w=1)=\frac{P(s = 1)( P(w = 1|s = 1, r = 1) P(r = 1)+ P(w = 1|s = 1,r = 0) P(r = 0))}{P(w = 1)}
# $
#
# where
#
# \begin{eqnarray}
# P(w=1)=P(s=1)( P(w=1|s=1,r=1 ) P(r=1) &+ P(w=1|s=1,r=0) P(r=0))\\
# +P(s=0)( P(w=1|s=0,r=1 ) P(r=1) &+ P(w=1|s=0,r=0) P(r=0))\\
# \end{eqnarray}
#
# This code has been written out below, you just need to insert the right numbers from the table.
# +
##############################################################################
# TODO for student: Write code to insert the correct conditional probabilities
# from the table; see the comments to match variable with table entry.
# Comment out the line below to test your solution
raise NotImplementedError("Finish the simulation code first")
##############################################################################
Pw1r1s1 = ... # the probability of wet grass given rain and sprinklers on
Pw1r1s0 = ... # the probability of wet grass given rain and sprinklers off
Pw1r0s1 = ... # the probability of wet grass given no rain and sprinklers on
Pw1r0s0 = ... # the probability of wet grass given no rain and sprinklers off
Ps = ... # the probability of the sprinkler being on
Pr = ... # the probability of rain that day
# Uncomment once variables are assigned above
# A= Ps * (Pw1r1s1 * Pr + (Pw1r0s1) * (1 - Pr))
# B= (1 - Ps) * (Pw1r1s0 *Pr + (Pw1r0s0) * (1 - Pr))
# print("Given that the grass is wet, the probability the sprinkler was on is: " +
# str(A/(A + B)))
# +
# to_remove solution
Pw1r1s1 = 0.999 # the probability of wet grass given rain and sprinklers on
Pw1r1s0 = 0.99 # the probability of wet grass given rain and sprinklers off
Pw1r0s1 = 0.9 # the probability of wet grass given no rain and sprinklers on
Pw1r0s0 = 0.001 # the probability of wet grass given no rain and sprinklers off
Ps = 0.25 # the probability of the sprinkler being on
Pr = 0.1 # the probability of rain that day
# Uncomment once variables are assigned above
A= Ps * (Pw1r1s1 * Pr + (Pw1r0s1) * (1 - Pr))
B= (1 - Ps) * (Pw1r1s0 *Pr + (Pw1r0s0) * (1 - Pr))
print("Given that the grass is wet, the probability the sprinkler was on is: " +
str(A/(A + B)))
# -
# The probability you should get is about 0.7522.
#
# Your neighbour now tells you that it was indeed
# raining today, $P (r = 1) = 1$, so what is now the probability the sprinklers were on? Try changing the numbers above.
#
#
# ## Think! Bonus: Causality in the Brain
#
# In a causal stucture this is the correct way to calculate the probabilities. Do you think this is how the brain solves such problems? Would it be different for task involving novel stimuli (e.g. for someone with no previous exposure to sprinklers), as opposed to common stimuli?
#
# **Main course preview:** On W3D5 we will discuss causality further!
| 56.382189 | 14,386 |
d81ac9ba1e1c43c8404da44b5d7841b0d0f44c5a
|
py
|
python
|
Week_2/NBB_NLP_Theory.ipynb
|
nikbearbrown/INFO_6210
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Text Mining and Natural Language Processing
#
# In this lesson we'll learn the theory and jargon you'll need to explore text mining.
#
# [Text mining](https://en.wikipedia.org/wiki/Text_mining), also called text analytics, is the process of deriving high-quality information from text. Given the vast amount of text on the Internet, text mining is one of the most important research areas in machine learning. Text mining includes:
#
# * [Information retrieval](https://en.wikipedia.org/wiki/Information_retrieval) - the process of obtaining structured data from free text.
# * [Entity recognition](https://en.wikipedia.org/wiki/Named-entity_recognition) - identification of nouns (e.g. known people, places and things) in text.
# * Fact extraction - identification of associations among entities and other information in text.
# * [Sentiment analysis](https://en.wikipedia.org/wiki/Sentiment_analysis) is the assocaition of opinion and a topic within text.
# * [Topic modeling](https://en.wikipedia.org/wiki/Topic_model) - identification of "topics" in text.
# * Automated Tagging - a process to associate free-form keywords (not necessarily in the text) to index and search text.
#
# 
# *Text Mining*
#
# ## Text corpora and dictionaries
#
# In linguistics, a corpus (plural corpora) or text corpus is a large and structured set of texts. They help annotate words.
#
# * [corpus.byu.edu](http://corpus.byu.edu/) includes:
# + Hansard Corpus (British Parliament), 1.6 billion words
# + Global Web-Based English (GloWbE), 1.9 billion words
# + Corpus of Contemporary American English (COCA), 450 million words
# + TIME Magazine Corpus, 100 million words
# + Corpus of American Soap Operas, 100 million words
# + British National Corpus (BYU-BNC), 100 million words
# + Strathy Corpus (Canada), 100 million words
# * The [British National Corpus](http://www.natcorp.ox.ac.uk/), extracts from 4124 modern British English texts of all kinds, both spoken and written; over 100 million words.
# * The [Brown University Corpus](http://www.hit.uib.no/icame/brown/bcm.html): Approximately 1,000,000 words of American written English dating from 1960. The genre categories are parallel to those of the LOB corpus.
# * The [LOB Corpus](http://clu.uni.no/icame/manuals/) (The Lancaster-Oslo/Bergen Corpus) is ) is a million-word collection of British English texts which was compiled in the 1970s.
# * [The Kolhapur Corpus](http://www.essex.ac.uk/linguistics/external/clmt/w3c/corpus_ling/content/corpora/list/private/kolhapur.html): Approximately 1,000,000 words of Indian written English dating from 1978.
# * The (Cambridge International Corpus)[http://uk.cambridge.org/elt/corpus] is a multi-billion word corpus of English language (containing both text corpus and spoken corpus)
# * [The Longman-Lancaster Corpus](http://www.pearsonlongman.com/dictionaries/corpus/lancaster.html): Approximately 14.5 million words of written English from various geographical locations in the English-speaking world and of various dates and text types.* [WordNet](http://wordnet.princeton.edu/) is a lexical database of English nuns, verbs, adjectives and adverbs which are grouped into sets of cognitive synonyms (synsets). The WordNet synsets are further characterized by hyperonymy, hyponymy or ISA relationships. We downloaded the WordNet database files and parsed them. Permission to use, copy, modify and distribute WordNet for any purpose and without fee or royalty is hereby granted, WordNet provided by WordNet as long as proper attribution is given to WordNet and any derivative products don’t use the WordNet trademark.
# * [PubMed/Medline](http://www.ncbi.nlm.nih.gov/pubmed) comprises more than 25 million citations for biomedical literature. PubMed XML Data Retrieved from [http://www.nlm.nih.gov/databases/journal.html](http://www.nlm.nih.gov/databases/journal.html). You need to regiester with the National Library of Medicine to download the XML files.
# * [arXiv](http://arxiv.org/) is an archive with over 100000 articles in physics, 10000 in mathematics, and 1000 in computer science. arXiv Bulk Data Access Retrieved from [http://arxiv.org/help/bulk_data](http://arxiv.org/help/bulk_data)
# * AG's news corpus is AG's corpus of news articles. Retrieved from [http://www.di.unipi.it/~gulli/AG_corpus_of_news_articles.html](http://www.di.unipi.it/~gulli/AG_corpus_of_news_articles.html)
# * Last.fm music tags can be retrieved from [http://www.last.fm/charts/toptags](http://www.last.fm/charts/toptags )
# * Spambase can be retrieved from [http://archive.ics.uci.edu/ml/datasets/Spambase](http://archive.ics.uci.edu/ml/datasets/Spambase)
# * Wikipedia. The Wikipedia Data Dump can be retrieved from [http://en.wikipedia.org/wiki/Wikipedia:Database_download](http://en.wikipedia.org/wiki/Wikipedia:Database_download)
#
# ### Unstructured text data
#
# * [Common Crawl](http://commoncrawl.org/) is a openly accessible web crawl data that is freely available. [164] As of April 2013 the crawl has 6 billion pages and associated metadata. The crawl data is stored on Amazon’s Public Data Sets, allowing it to be directly accessed for map-reduce processing in EC2. Common Crawl Retrieved from [http://commoncrawl.org/](http://commoncrawl.org/)
#
# * Twitter data.
# + Twitter Search API Retrieved from [https://dev.twitter.com/docs/api/1/get/search](https://dev.twitter.com/docs/api/1/get/search)
# + Twitter Streaming APIs. Retrieved from [https://dev.twitter.com/docs/streaming-apis](https://dev.twitter.com/docs/streaming-apis)
# + Twitter“Fire hose” real-time stream. See [https://dev.twitter.com/streaming/firehose](https://dev.twitter.com/streaming/firehose)
#
# * Instagram
# + API - Instagram [https://instagram.com/developer/](https://instagram.com/developer/)
#
# ### Writing a web crawler
#
# A Web crawler (also known as a Web spider or Web robot or bot) is a pscript which browses the World Wide Web and extracts web pages and links.
# ```
# urls=<list of urls>
# while (urls)
# {
# * request url
# * request document
# * store text for later processing
# * parse document for links
# }
# ```
#
#
# *Useful web crawling libraries in R*
#
# * library(regex) - Regular Expressions as used in R
# * library(httr) - Tools for Working with URLs and HTTP
# * library(XML) - XML Parser and Generator
# * library(RCurl) - RCurl: General Network (HTTP/FTP/...) Client Interface for R
# * library(jsonlite) - JSON Parser and Generator for R
# * library(stringr) - Simple, Consistent Wrappers for Common String Operations
#
# ## N-grams
#
# An [n-gram](https://en.wikipedia.org/wiki/N-gram) is a contiguous sequence of n items from a given sequence of text or speech. An n-gram of size 1 is referred to as a "unigram"; size 2 is a "bigram" (or, less commonly, a "digram"); size 3 is a "trigram". Larger sizes are sometimes referred to by the value of n, e.g., "four-gram", "five-gram", and so on.
#
# for example, bugaboo, nerd, student, data and new are one-grams. Data science, New York are two-grams. Note that New York means something different the the one grams new, and York seperately.
#
#
# Note that if we take a sentence, say
#
# "You have brains in your head. You have feet in your shoes. You can steer yourself in any direction you choose. You're on your own, and you know what you know. And you are the guy who'll decide where to go."
#
# - Dr. Seuss
#
# Most of the two-grams aren't meaningful, that is, "You have," "have brains," "brains in" don't make sense out of context.
#
#
# ## Tagging and Hashtags
#
# Tagging is a process in which end users use free-form keywords to manually index content in an organic and distributed manner. The popularity of tagging has led some to claim that it is the primary classification scheme of the Internet. A tag can be thought of as an informative keyword. A user is very unlikely to tag an article with a word like “this” because it conveys very little information. Rather, they’ll often tag with a subject or sentiment.
#
# Problems with tagging are well-known. Users often present idiosyncrasies, inaccuracies, inconsistencies, and other irregularities when tagging. Specifically, four areas are critical to tagging. The first three areas are straightforward enough:
#
# 1. tag misspelling;
# 2. tag heterogeneity, (that is, different tags denoting the same content, such as “Ziagen” and “abacavir sulfate,” which both refer to the same drug);
# 3. tag polysemy (i.e. identical tags that denote different meanings, such as, Apple may refer to fruit or a company. and;
# 4. semantic annotation of tags (i.e. abacavir sulfate is a drug).
#
#
# An important area of research in text mining is call “semantic enrichment” is a particularly difficult problem. Lexical resources are often used to annotate terms. For example, lexical databases such as WordNet is often used as a source of tag annotation.
#
#
# *#hashtags*
#
# The social tagging in is done by placing a hash mark in front of a word or phrase, such as #BCSM, #Lyphoma, #BrainTumorThursday, #BreastCancer, #Infertility, #Diabetes, #lymphoedema, #RareDiseaseDay, #RareDisease, #ADHD, #Anorexia, #MultipleSclerosis. On social media sites (such as Twitter) a word or phrase preceded by a hash or pound sign (#) and used to identify messages on a specific topic. Hastags are essentially tags that in within text and annotated. As such they are easy to extract from text.
#
# *Stop words*
#
# In text mining, [stop words](https://en.wikipedia.org/wiki/Stop_words) are words which are filtered out becuase they'll interfer with text analysis. Stop words usually refer to the most common words in a language, such as *the*, *is*, *at*, *which*, and on.
#
# ## Regular expressions
#
# Regular expressions (or RE or regex or regexp or rational expression) is a sequence of characters that define a search pattern, mainly for use in pattern matching with strings, or string matching.
#
# Cerain characters have special meaning in regular expressions.
#
# [] - A pair of brackets is used to indicate a set of characters.
# '\' - Either escapes special character or signals a special sequence.
# ? - The question mark indicates there is zero or one of the preceding
# '*' - The asterisk indicates there is zero or more of the preceding element .
# + The plus sign indicates there is one or more of the preceding element.
# '^' (Caret.) Matches the start of the string.
# '$' Matches the end of the string.
# {m} (Braces) Specifies that exactly m copies of the previous RE should be matched.
#
#
# For example, the regexp $[A-Za-z]+$ matches a seuqnece of at least one upper or lower case letters. The regexp $^[ ]+A-Za-z0-9._-]+@[[A-Za-z0-9.-]+$[ ]+$ matches an e-mail pattern with starting and ending white spaces. There are many excellent books that describe regular expressions in detail.
#
# ## Term-Document matrices
#
# A [term-document matrix](https://en.wikipedia.org/wiki/Document-term_matrix) is a matrix where the rows correspond to documents in the collection and columns correspond to terms. Creating term-document matrices are created using the [R text mining package tm](https://cran.r-project.org/web/packages/tm/index.html).
#
# D1 = "I love R"
# D2 = "I love ice-cream"
#
# then the document-term matrix would be:
#
# $$
# TermDocument=
# \begin{bmatrix}
# & I & love & R & ice-cream \\
# D1 & 1 & 1 & 1 & 0 \\
# D2 & 1 & 1 & 0 & 1
# \end{bmatrix}
# $$
#
# which shows which documents contain which terms and how many times they appear.
#
# ## Frequency signatures
#
# For processing larger amounts of text, tag/word counts can be ineffecient using term-document matrices as these are typically very sparse matrices. Especially when one has a large dictionary of tags/words.
#
# For larger data we used a “frequency signature” approach to convert a [bag-of-words](https://en.wikipedia.org/wiki/Bag-of-words_model) output to a format that we can use to calculate tag co-occurrence associations and mutual information. Frequency signatures are described in detail in Stefan Evert’s PhD dissertation “The Statistics of Word Cooccurrences Word Pairs and Collocations.”
#
#
# To calculate tag co-occurrence associations and mutual information for two tags, A and B, we need four items of data. The co-occurrence count of A and B, the count of A but not B, the count of B but not A, and the total number of tags in a corpus. This co-occurrence frequency data for a word pair (A,B) are usually organized in a contingency table show below. The contingency table stores the observed frequencies $O_{11} … O_{22}$. The table below (adapted from Evert’s dissertation) shows an observed contingency table.
#
# Contingency Tables
#
# 
#
# *Contingency table : $O_{11}$ is co-occurrence count of A and B, $O_{12}$ is the count of A but not B, $O_{21}$ is the count of B but not A, and $O_{22}$ is the count of not B and not A.*
#
#
# However, while the co-occurrence count of A and B, and the total number of tags in a corpus are efficiently and easily counted the count of A but not B, the count of B but not A are tricky and computationally expensive. The insight and advantage of frequency signatures is that they calculate the count of A but not B, the count of B but not A by just counting A and B and the co-occurrence count of A and B. That is, the count of A but not B is equal to count of A minus the co-occurrence count of A and B. Likewise, the count of B but not A is equal to count of B minus the co-occurrence count of A and B.
#
# The frequency signature of a tag pair (A, B) is usually written as $(f, f_1, f_2,N)$. Where $f$ is the co-occurrence count of A and B, $f_1$ is the count of A but not B, $f_2$ is the count of B but not A, and N is the total counts. Notice that the observed frequencies $O_{11}, ..., O_{22}$ can be directly calculated from the frequency signature by the equations below:
#
# * $O_{11} = f$
# * $O_{12} = f_1 − f$
# * $O_{21} = f_2 – f$
# * $O_{22} = N − f_1 − f_2 + f$
#
# Generating all of the data tag co-occurrence association and mutual information calculations using this approach can be generated using a single pass of the data and two associative arrays; one of the tag counts and another for the tag co-occurrence counts.
#
# Calculating Associations and Mutual Information from Frequency Signatures
#
# Evert shows the many association and mutual information statistics can be calculated from the observed frequencies $O_{11}, ..., O_{22}$ if we can generate the expected frequencies $E_{11}, ..., E_{22}$. The table below (adapted from Evert’s dissertation) shows the expected versus observed contingency tables.
#
# 
# *Frequency Signatures*
#
# The sum of all four observed frequencies (called the sample size N) is equal to the total number of pair tokens extracted from the corpus. R1 and R2 are the row totals of the observed contingency table, while C1 and C2 are the corresponding column totals. The expected frequencies can be directly calculated from observed frequencies $O_{11}, ..., O_{22}$ by the equations below:
#
# * $R1 = O_{11} + O_{12}$
# * $R2 = O_{21} + O_{22}$
# * $C1 = O_{11} + O_{21}$
# * $C2 = O_{12} + O_{22}$
# * $N = O_{11} + O_{12} + O_{12} + O_{22}$
#
#
# Evert went on to show that several association measures can be easily calculated once one has the expected and observed contingency tables. For example, the pointwise mutual information (MI) is calculated by below.
#
# $pointwise \quad mutual \quad information \quad MI=\ln\frac{O_{11}}{E_{11}}$
#
# The Likelihood measures that can be calculated using the expected and observed contingency tables are:
#
# * Multinomial-likelihood
# * Binomial-likelihood
# * Poisson-likelihood
# * Poisson-Stirling approximation
# * Hypergeometric-likelihood
#
# The exact hypothesis tests that can be calculated using the expected and observed contingency tables are:
#
# * binomial test
# * Poisson test
# * Fisher's exact test
#
# The asymptotic hypothesis tests that can be calculated using the expected and observed contingency tables are:
#
# * z-score
# * Yates' continuity correction
# * t-score (which compares O11 and E11 as random variates) * Pearson's chi-squared test
# * Dunning's log-likelihood (a likelihood ratio test)
#
# The measures from information theory that can be calculated using the expected and observed contingency tables are:
#
# * MI (mutual information, mu-value)
# * logarithmic odds-ratio logarithmic relative-risk
# * Liddell's difference of proportions
# * MS (minimum sensitivity)
# * gmean (geometric mean) coefficient
# * Dice coefficient (aka. "mutual expectation")
# * Jaccard coefficient
# * MIconf (a confidence-interval estimate for the mu-value)
# * MI (pointwise mutual information)
# * local-MI (contribution to average MI of all co-occurrences)
# * average-MI (average MI between indicator variables)
#
# Stefan Evert also developed a R library called [UCS toolkit](http://www.collocations.de/software.html) for the statistical analysis of co-occurrence data with association measures and their evaluation in a collocation extraction task.
#
# ## tf–idf
#
# [Tf–idf](https://en.wikipedia.org/wiki/Tf%E2%80%93idf) or term frequency–inverse document frequency, is a numerical statistic that is intended to reflect how important a word is to a document.
#
# The tf-idf value increases proportionally to the number of times a word/tag appears in the document, but is offset by the frequency of the word/tag. It is a measure of jargon. If a word appears frequently in a document, it's important. Give the word a high score. But if a word appears in every documents, it's not specifc to a topic. Give the word a low score.
#
# If we want to find jargon, that is, topic or subject specifc words/tags then this is a reasonable metric. Words like 'the', 'a', get low scores as the are in every document. While words/tags like 'Machine Learning', 'Twitter,' or 'Text Mining' get high scores since they are used a lot in specific contexts.
#
# If with call $f(t,d)$ the raw frequency of a term in a document, i.e. the number of times that term t occurs in document d and $max(f(t,d))$ the maximum raw frequency of any term in the document, then the term frequency $tf(t,d)$ is:
#
# $$
# \mathrm{tf}(t,d) = 0.5 + \frac{0.5 \times \mathrm{f}(t, d)}{\max\{\mathrm{f}(t, d):t \in d\}}
# $$
#
# The inverse document frequency is a measure of how much information the word provides, It is the logarithmically scaled fraction of the documents that contain the word, obtained by dividing the total number of documents by the number of documents containing the term, and then taking the logarithm of that quotient.
#
# $$
# \mathrm{idf}(t, D) = \log \frac{N}{|\{d \in D: t \in d\}|}
# $$
#
# with
#
# * $N$: total number of documents in the corpus $N = {|D|}$
# * $|\{d \in D: t \in d\}|$ : number of documents where the term t appears (i.e., $\mathrm{tf}(t,d) \neq 0$). If the term is not in the corpus, this will lead to a division-by-zero. It is therefore common to adjust the denominator to add a single "pseudocount."
#
# Mathematically the base of the log function does not matter for these purposes.
#
# Then tf–idf is calculated as
#
# $$\mathrm{tf-idf}(t,d,D) = \mathrm{tf}(t,d) \times \mathrm{idf}(t, D)$$
#
# A high weight in tf–idf means a tag/word has high term frequency (in the given document) and a low document frequency of the term in the whole collection of documents.
#
# For how this is done in R see [The tf-idf-Statistic For Keyword Extraction](http://www.r-bloggers.com/the-tf-idf-statistic-for-keyword-extraction/)
#
# ## Word entropy and entropy rate
#
# In information theory, entropy is also a measure of the uncertainty in a random variable. Like tf–idf, entropy quantifies the expected value of the information contained in a message (or the expected value of the information of the probability distribution). Typically this is expressed in the number of ‘bits’ or ‘nats’ that are required to encode a given message.
#
# In this sense entropy can be used to estimate (like tf–idf) how much information is in a word or tag. Entropy can also be used to estimate the generating probability distribution for a text document or corpus. The entropy of many languages has been determined. English has 1.65 bits per word, French has 3.02 bits per word, German has 1.08 bits per word, and Spanish has 1.97 bits per word. Given the probability density function of word entropies and the average bits per word of a single tweet we could then assign probabilities that it is English, French, German, or Spanish.
#
#
# ### Entropy rate
#
# The entropy rate (or mean entropy rate) describes the limiting entropy over an entire probability distribution. This can be thought of as the average entropy over a sufficiently long realization of a stochastic process, whereas the entropy is relevant to a single random variable at a given point in time.
#
# In statistics, ergodicity describes a random process wherein the average time for one sufficiently long realization of events is the same as the ensemble average. That is, the ensemble’s statistical properties (such as its mean or entropy) can be deduced from a single, sufficiently long sample of the process. In other words, there are long-term invariant measures that describe the asymptotic properties of the underlying probability distribution, and they can be measured by following any single reprehensive portion if followed long enough. For example, if I look at two particles in an ergodic system at any time, those particles may have very different states; but if I follow those particles long enough, they become statistically indistinguishable from one another. This means that statistical properties of the entire system can be deduced from a single sample of the process if followed for a sufficiently long time.
#
# Stationarity is the property of a random process which guarantees that the aggregate statistical properties of the probability density function, such as the mean value, its moments and variance, remain the same at every point in time. A stationary process, therefore, is one whose probability distribution is the same at all times. Its statistical properties cannot necessarily be deduced from a single sample of the process. There are stochastic processes that exhibit both stationarity and ergodicity called stationary ergodic processes. These are random processes that will not change their statistical properties with time; hence, the properties, including the disorder (entropy) of the system, can be deduced from a single, sufficiently long sample realization of the process. There are weaker forms of the stationary condition in which the first- and second-order moments (that is, the mean and variance) of a stochastic process are constant but other properties of the probability density function can vary. Likewise, there are stationary stochastic processes that are not themselves ergodic but are composed of a mixture of ergodic components.
#
# ### Rényi entropies
#
# The [Rényi entropies](https://en.wikipedia.org/wiki/R%C3%A9nyi_entropy) generalize the Shannon entropy, the Hartley entropy, the min-entropy, and the collision entropy. As such, these entropies as an ensemble are often called the Rényi entropies (or the Rényi entropy, even though this usually refers to a class of entropies). The difference between these entropies is in the respective value for each of an order parameter called alpha: the values of alpha are greater than or equal to zero but cannot equal one. The Renyi entropy ordering is related to the underlying probability distributions and allows more probable events to be weighted more heavily. As alpha approaches zero, the Rényi entropy increasingly weighs all possible events more equally, regardless of their probabilities. A higher alpha (a) weighs more probable events more heavily. The base used to calculate entropies is usually base 2 or Euler's number base e. If the base of the logarithm is 2, then the uncertainty is measured in bits. If it is the natural logarithm, then the unit is nats.
#
# ### Rényi entropies
#
# The Rényi entropy of order $\alpha$, where $\alpha \geq 0$ and $\alpha \neq 1$ , is defined as
#
# $$
# H_\alpha(X) = \frac{1}{1-\alpha}\log\Bigg(\sum_{i=1}^n p_i^\alpha\Bigg)
# $$
#
# Here, X is a discrete random variable with possible outcomes 1,2,...,n and corresponding probabilities $p_i \doteq \Pr(X=i) for i=1,\dots,n,$ and the logarithm is base 2.
#
#
# #### Hartley entropy
#
# The Hartley entropy (Gray, 1990) is the Rényi entropy with an alpha of zero.
#
# the probabilities are nonzero, $H_0$ is the logarithm of the cardinality of X, sometimes called the Hartley entropy of X:
#
# $$
# H_0 (X) = \log n = \log |X|
# $$
#
# #### Shannon entropy
#
# The Shannon entropy (Gray, 1990) is the Rényi entropy with an alpha of one. The Shannon entropy is a simple estimate of the expected value of the information contained in a message. It assumes independence and identically distributed random variables, which is a simplification when applied to word counts. In this sense it is analogous to naïve Bayes, in that it is very commonly used and thought to work well in spite of violating some assumptions upon which it is based.
#
# The limiting value of $H_\alpha as \alpha \rightarrow 1$ is the Shannon entropy:
#
# $$
# H_1 (X) = - \sum_{i=1}^n p_i \log p_i.
# $$
#
# #### collision entropy
#
# The collision entropy (Gray, 1990) is the Rényi entropy with an alpha of two and is sometimes just called "Rényi entropy," refers to the case $\alpha = 2$,
#
# $$
# H_2 (X) = - \log \sum_{i=1}^n p_i^2 = - \log P(X = Y)
# $$
#
# where $X$ and $Y$ are independent and identically distributed.
#
# #### min-entropy
#
# The min-entropy (Gray, 1990) is the Rényi entropy as the limit of alpha approaches infinity. The name min-entropy stems from the fact that it is the smallest entropy measure in the Rényi family of entropies. In the limit as $\alpha \rightarrow \infty$, the Rényi entropy $H_\alpha converges to the min-entropy H_\infty$:
#
# $$
# H_\infty(X) \doteq \min_i (-\log p_i) = -(\max_i \log p_i) = -\log \max_i p_i\,.
# $$
#
# Equivalently, the min-entropy $H_\infty(X)$ is the largest real number b such that all events occur with probability at most $2^{-b}$.
#
#
# #### Kullback-Leibler divergence
#
# [Kullback-Leibler divergence](https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence) (Gray, 1990) is a non-symmetric measure of the difference between two probability distributions. The Kullback-Leibler measure goes by several names: relative entropy, discrimination information, Kullback-Leibler (KL) number, directed divergence, informational divergence, and cross entropy. Kullback-Leibler divergence is a measure of the difference between the observed entropy and its excepted entropy. We calculate the KL divergence by weighting one distribution (like an observed frequency distribution) by the log of probabilities of some other distribution D2. For discrete probability distributions P and Q, the Kullback–Leibler divergence of Q from P is defined to be
#
# $$
# D_{\mathrm{KL}}(P\|Q) = \sum_i P(i) \, \ln\frac{P(i)}{Q(i)}
# $$
#
# In words, it is the expectation of the logarithmic difference between the probabilities P and Q, where the expectation is taken using the probabilities P.
#
#
# #### Mutual Information
#
# [Mutual information](https://en.wikipedia.org/wiki/Mutual_information) (Gray, 1990) quantifies the mutual dependence of the two random variables. It is a measure of the “stickiness” between two items. It measures how much knowing one of these variables reduces uncertainty about the other. We can use mutual information to quantify the association between two tags. Mutual information (Equation 10) is given by:
#
# the mutual information of two discrete random variables X and Y can be defined as:
#
# $$
# I(X;Y) = \sum_{y \in Y} \sum_{x \in X}
# p(x,y) \log{ \left(\frac{p(x,y)}{p(x)\,p(y)}
# \right) }, \,\!
# $$
#
# where $p(x,y)$ is the joint probability distribution function of $X$ and $Y$, and $p(x)$ and $p(y)$ are the marginal probability distribution functions of $X$ and $Y$ respectively. In the case of continuous random variables, the summation is replaced by a definite double integral:
#
# $$
# I(X;Y) = \int_Y \int_X
# p(x,y) \log{ \left(\frac{p(x,y)}{p(x)\,p(y)}
# \right) } \; dx \,dy,
# $$
#
# where $p(x,y)$ is now the joint probability density function of $X$ and $Y$, and $p(x$) and $p(y)$ are the marginal probability density functions of $X$ and $Y$ respectively.
#
#
#
# ## Zipf's law
#
# [Zipf's law](https://en.wikipedia.org/wiki/Zipf%27s_law) is an empirical law formulated using mathematical statistics, refers to the fact that many types of data studied in the physical and social sciences can be approximated with a Zipfian distribution, one of a family of related discrete power law probability distributions. It states that while only a few words are used very often, many or most are used rarely,
#
# $P_n \sim 1/n^a$
#
# where $P_n$ is the frequency of a word ranked nth and the exponent a is almost 1. This means that the second item occurs approximately 1/2 as often as the first, and the third item 1/3 as often as the first, and so on. The is a so-called "power law" distributon.
#
# The law is very common when looking a the distributions of words in all lagnuages. In fact, it is named after the American linguist [George Kingsley Zipf](https://en.wikipedia.org/wiki/George_Kingsley_Zipf) when he observed this law in 1935 in his academic studies of word frequency.
#
# ## Text-mining pipeline
#
# Common Natural language processing tasks, such as tokenization, stemming, sentence segmentation, part-of-speech tagging, named entity extraction, chunking, parsing, word disamiguation, summarization, and coreference resolution are often done on every new text document before other types of analysis. As such it is common to write a "pipeline" (i.e. a sequence of scripts) that automatically perform these tasks.
#
#
# *Tokenization*
#
# [Tokenization](http://nlp.stanford.edu/IR-book/html/htmledition/tokenization-1.html) is the task of chopping it up into pieces, called tokens. This is often done by throwing away certain characters, such as punctuation.
#
# *Stemming*
#
# [Stemming](https://en.wikipedia.org/wiki/Stemming) reduces words to their word stem, base or root form. For example, "argue", "argued", "argues", "arguing", and "argus" reduce to the stem "argu." The can allow for "argue", "argued", "argues" to be counted as a single word.
#
# *Sentence segmentation*
#
# [sentence segmentation](http://www.monlp.com/2012/03/13/segmenting-words-and-sentences/) is the process plitting text into words and sentences. This is often done by looking for certain punctuation (full stop, question mark, exclamation mark, etc.).
#
# *Part-of-speech tagging*
#
# Given some text [part-of-speech tagging](https://en.wikipedia.org/wiki/Part-of-speech_tagging) determines the [part of speech](https://en.wikipedia.org/wiki/Part_of_speech) for each word. (e.g. a noun, verb, adjective. etc.)
#
#
# *Named entity extraction*
#
# [Named entity recognition](https://en.wikipedia.org/wiki/Named-entity_recognition) determines which items in the text map to proper nouns, such as people or places, or things.
#
# *Chunking*
#
# Chunking is also called shallow parsing. It is the identification short meaningful n-grams (like noun phrases, named entities, collocations, etc.). In this processing of a tweet, it could refer to sperating the hashtags, the links and the tweet.
#
# *Parsing*
#
# [Parsing](https://en.wikipedia.org/wiki/Parsing) or syntactic analysis generates [https://en.wikipedia.org/wiki/Parsing] the parse tree (grammatical analysis) for each sentence or fragment.
#
# *Word-sense disambiguation*
#
# Many words have more than one meaning. [Word-sense disambiguation](https://en.wikipedia.org/wiki/Word-sense_disambiguation] selectx the meaning which makes the most sense in context.
#
# *Coreference resolution*
#
# Given a sentence or larger chunk of text, [coreference resolution](https://en.wikipedia.org/wiki/Coreference) determines which words ("mentions") refer to the same objects ("entities")
#
# *Automatic summarization*
#
# Automatic summarization produce a readable summary of a chunk of text. The summary need not be grammatical, for example, a [tag cloud](https://en.wikipedia.org/wiki/Tag_cloud) could be thought of as a visual summarization of some text.
#
#
# Which elements are part of a Text-mining pipeline depend on the application.
#
#
# ## Small Talk and the Social Web
#
# One particularly interesting aspect of the social web is the nature of text made available for public consumption. From the time of the Gutenberg printing press until the advent of Web 2.0, nearly all text presented in public was written by professionals. Whether it was a book, a business or government record, a sermon, a news or opinion article, a scientific paper, or an advertisement, it was written by a professional with the intent to communicate information and/or ideas. Not until the social web and Twitter did musings about what a noncelebrity ate for breakfast or whether someone likes naps was widely available for public consumption.
#
# Musings about one’s foot fungus or a statement like “ Hahahahahaha!!!! You should have come to NKLA!!! So many beautiful pitties! And pittie lovers....” are what we call small talk. Small talk is light, intimate banter, often understandable only by the authors’ close friends. A lot of the communication on the social web is small talk, even though it was very rare in public writing prior to the social web.
#
# This free very unstructured nature of language on the social web should be taken into account when mining these data. It can add a considerable amount of noise and magnifies the importance of good semantic and lexcial resources.
# Last update October 1, 2017
#
# The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT).
| 74.939655 | 1,153 |
7481564d3111b135f445ee6694ef5441ebea8248
|
py
|
python
|
bertmodel.ipynb
|
anitha67/100DaysofMLCode
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/anitha67/100DaysofMLCode/blob/master/bertmodel.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="Or8NU2Px_dRT"
import re
import spacy
from keras.preprocessing.text import hashing_trick
from keras.preprocessing.sequence import pad_sequences
from keras.models import load_model
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import transformers
import tokenizers
import torch
import torch.nn as nn
from tqdm import tqdm
from sklearn import model_selection
from sklearn import metrics
from transformers import AdamW
from transformers import get_linear_schedule_with_warmup
from sklearn.metrics import classification_report
from sklearn.model_selection import KFold
# + colab={"base_uri": "https://localhost:8080/"} id="MnQf82nd_hnF" outputId="5e5cb6e0-b689-4805-bf60-7ef4c0429a11"
# !pip install transformers
# + id="bjbp0E_8EvEj"
import re
import spacy
from keras.preprocessing.text import hashing_trick
from keras.preprocessing.sequence import pad_sequences
from keras.models import load_model
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import transformers
import tokenizers
import torch
import torch.nn as nn
from tqdm import tqdm
from sklearn import model_selection
from sklearn import metrics
from transformers import AdamW
from transformers import get_linear_schedule_with_warmup
from sklearn.metrics import classification_report
from sklearn.model_selection import KFold
# + colab={"base_uri": "https://localhost:8080/"} id="QNmxrgkF_7Nx" outputId="696f3066-0c42-41d9-a952-20ba60a7a100"
from google.colab import drive
drive.mount("/content/gdrive")
# + id="A0-7NIO1ASbU"
import pandas as pd
df = pd.read_csv('/content/gdrive/My Drive/Colab Notebooks/test_data/train_folds_new.csv',encoding="latin1" )
# + colab={"base_uri": "https://localhost:8080/", "height": 250} id="6-5oBYHDBHLN" outputId="3673f64b-9fed-44cb-f74c-5eb567f3f802"
df.head()
# + id="xbIRsgylBMnV"
import logging
logging.basicConfig(level=logging.ERROR)
# + id="0uZ4vnaxBV7c"
def regex_sub(text):
ip_pattern = r'((((([0-9]|[1-9][0-9]|1[0-9]{2}|2[0-4][0-9]|25[0-5])\.){3}([0-9]|[1-9][0-9]|1[0-9]{2}|2[0-4][0-9]|25[0-5]))([^0-9]|$))|(((([0-9A-Fa-f]{1,4}:){7}([0-9A-Fa-f]{1,4}|:))|(([0-9A-Fa-f]{1,4}:){6}(:[0-9A-Fa-f]{1,4}|((25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)(\.(25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)){3})|:))|(([0-9A-Fa-f]{1,4}:){5}(((:[0-9A-Fa-f]{1,4}){1,2})|:((25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)(\.(25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)){3})|:))|(([0-9A-Fa-f]{1,4}:){4}(((:[0-9A-Fa-f]{1,4}){1,3})|((:[0-9A-Fa-f]{1,4})?:((25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)(\.(25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)){3}))|:))|(([0-9A-Fa-f]{1,4}:){3}(((:[0-9A-Fa-f]{1,4}){1,4})|((:[0-9A-Fa-f]{1,4}){0,2}:((25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)(\.(25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)){3}))|:))|(([0-9A-Fa-f]{1,4}:){2}(((:[0-9A-Fa-f]{1,4}){1,5})|((:[0-9A-Fa-f]{1,4}){0,3}:((25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)(\.(25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)){3}))|:))|(([0-9A-Fa-f]{1,4}:){1}(((:[0-9A-Fa-f]{1,4}){1,6})|((:[0-9A-Fa-f]{1,4}){0,4}:((25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)(\.(25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)){3}))|:))|(:(((:[0-9A-Fa-f]{1,4}){1,7})|((:[0-9A-Fa-f]{1,4}){0,5}:((25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)(\.(25[0-5]|2[0-4]\d|1\d\d|[1-9]?\d)){3}))|:)))(%.+)?([^A-Za-z0-9]|$)))'
yyyy_date_pattern = r'([1-2][0-9]{3}[-\.\/])((([1-9]|1[0-2]|0[1-9])[-\.\/]([1-9]|0[1-9]|1[0-9]|2[0-9]|3[0-1])[^0-9])|(([1-9]|0[1-9]|1[0-9]|2[0-9]|3[0-1])[-\.\/]([1-9]|0[1-9]|1[0-2])[^0-9]))'
m_d_y_data_pattern = r'[^0-9]((([1-9]|0[1-9]|1[0-2])[-\.\/]([1-9]|0[1-9]|1[0-9]|2[0-9]|3[0-1]))|(([1-9]|0[1-9]|1[0-9]|2[0-9]|3[0-1])[-\.\/]([1-9]|1[0-2]|0[1-9])))[-\.\/]([1-2][0-9]{3}|[0-9]{2})'
timestamp_pattern_1 = r'([1-2][0-9]{3}[-\.\/])((([1-9]|1[0-2]|0[1-9])[-\.\/]([1-9]|0[1-9]|1[0-9]|2[0-9]|3[0-1])[^0-9])|(([1-9]|0[1-9]|1[0-9]|2[0-9]|3[0-1])[-\.\/]([1-9]|0[1-9]|1[0-2])))[\s]([0-9]|[0-1][0-9]|2[0-3]):([0-9]|[0-5][0-9]):([0-9]|[0-5][0-9])[^0-9]'
timestamp_pattern_2 = r'[^0-9]((([1-9]|0[1-9]|1[0-2])[-\.\/]([1-9]|0[1-9]|1[0-9]|2[0-9]|3[0-1]))|(([1-9]|0[1-9]|1[0-9]|2[0-9]|3[0-1])[-\.\/]([1-9]|1[0-2]|0[1-9])))[-\.\/]([1-2][0-9]{3}|[0-9]{2})[\s]([0-9]|[0-1][0-9]|2[0-3]):([0-9]|[0-5][0-9]):([0-9]|[0-5][0-9])[^0-9]'
windows_file_path = r'[A-Za-z]:[\\][^\s]*'
unix_file_path = r''
url_pattern = r'http[s]?:[\/]{2}[^\s]+'
email_pattern = r'[\S]+@[^\s\.]+\.[\S]+'
html_tag = r'\<[^\>]*\>'
text = re.sub(html_tag,' ',text)
text = re.sub(windows_file_path,' filepath ',text)
text = re.sub(url_pattern,' url ',text)
text = re.sub(email_pattern,' email ',text)
text = re.sub(ip_pattern,' ipaddress ',text)
text = re.sub(timestamp_pattern_1,' timestamp ',text)
text = re.sub(timestamp_pattern_2,' timestamp ',text)
text = re.sub(yyyy_date_pattern,' timestamp ',text)
text = re.sub(m_d_y_data_pattern,' timestamp ',text)
text = text.lower()
text = re.sub('[^a-z0-9\s]',' ',text)
# text = nlp_oper(text)
return text
# + [markdown] id="gaqXdnIL7iib"
#
# + colab={"base_uri": "https://localhost:8080/", "height": 206} id="GFZLOP0aBZji" outputId="a2e8a4e1-e767-46a4-fc5f-b160ab4065ee"
df['note'] = df['note'].apply(lambda x:regex_sub(x))
df.head()
# + id="2ghB_ELNBdbX"
class config:
DEVICE = "cuda"
MAX_LEN = 128
TRAIN_BATCH_SIZE = 16
VALID_BATCH_SIZE = 8
EPOCHS = 5
BERT_PATH = '/content/gdrive/My Drive/Colab Notebooks/test_data/bertbaseuncased'
TRAINING_FILE = "/content/gdrive/My Drive/Colab Notebooks/test_data/train_folds_new.csv"
TOKENIZER = transformers.BertTokenizer.from_pretrained(BERT_PATH, do_lower_case=True,truncation=True)
# + id="4o7gkI5UBjUY"
class BERTDataset:
def __init__(self, text, target):
self.text = text
self.target = target
self.tokenizer = config.TOKENIZER
self.max_len = config.MAX_LEN
def __len__(self):
return len(self.text)
def __getitem__(self, item):
text = str(self.text[item])
text = " ".join(text.split())
inputs = self.tokenizer.encode_plus(
text,
None,
add_special_tokens=True,
max_length=self.max_len,
padding="max_length",
truncation= True,
)
ids = inputs["input_ids"]
mask = inputs["attention_mask"]
token_type_ids = inputs["token_type_ids"]
return {
"ids": torch.tensor(ids, dtype=torch.long),
"mask": torch.tensor(mask, dtype=torch.long),
"token_type_ids": torch.tensor(token_type_ids, dtype=torch.long),
"targets": torch.tensor(self.target[item], dtype=torch.long),
}
# + id="WfBame5iC57n"
class BERTBaseUncased(nn.Module):
def __init__(self):
super(BERTBaseUncased, self).__init__()
self.bert = transformers.BertModel.from_pretrained(config.BERT_PATH)
self.bert_drop = nn.Dropout(0.3)
self.out = nn.Linear(768, 2)
def forward(self, ids, mask, token_type_ids):
_, o2 = self.bert(ids, attention_mask=mask, token_type_ids=token_type_ids,return_dict=False)
bo = self.bert_drop(o2)
output = self.out(bo)
return output
# + id="3Sh_GCi8C9ry"
def train_fn(data_loader, model, optimizer, device, scheduler):
model.train()
for bi, d in tqdm(enumerate(data_loader), total=len(data_loader)):
ids = d["ids"]
token_type_ids = d["token_type_ids"]
mask = d["mask"]
targets = d["targets"]
ids = ids.to(device, dtype=torch.long)
token_type_ids = token_type_ids.to(device, dtype=torch.long)
mask = mask.to(device, dtype=torch.long)
targets = targets.to(device, dtype=torch.long)
optimizer.zero_grad()
outputs = model(ids=ids, mask=mask, token_type_ids=token_type_ids)
loss = loss_fn(outputs, targets)
loss.backward()
optimizer.step()
scheduler.step()
# + id="D7ZuFMNcGY3a"
def loss_fn(outputs, targets):
return nn.CrossEntropyLoss()(outputs, targets)
# + id="888UbHUYDBXE"
def eval_fn(data_loader, model, device):
model.eval()
fin_targets = []
fin_outputs = []
with torch.no_grad():
for bi, d in tqdm(enumerate(data_loader), total=len(data_loader)):
ids = d["ids"]
token_type_ids = d["token_type_ids"]
mask = d["mask"]
targets = d["targets"]
ids = ids.to(device, dtype=torch.long)
token_type_ids = token_type_ids.to(device, dtype=torch.long)
mask = mask.to(device, dtype=torch.long)
targets = targets.to(device, dtype=torch.long)
outputs = model(ids=ids, mask=mask, token_type_ids=token_type_ids)
fin_targets.extend(targets.cpu().detach().numpy().tolist())
fin_outputs.extend(torch.argmax(outputs,axis = 1).cpu().detach().numpy().tolist())
return fin_outputs, fin_targets
# + id="rCOoZGa4DHCw"
def run(fold):
df_train = df[df.kfold != fold].reset_index(drop=True)
df_valid = df[df.kfold == fold].reset_index(drop=True)
df_train = df_train.reset_index(drop=True)
df_valid = df_valid.reset_index(drop=True)
train_dataset =BERTDataset(
text=df_train['note'].values, target=df_train['Label'].values
)
train_data_loader = torch.utils.data.DataLoader(
train_dataset, batch_size=config.TRAIN_BATCH_SIZE, num_workers=4
)
valid_dataset = BERTDataset(
text=df_valid['note'].values, target=df_valid['Label'].values
)
valid_data_loader = torch.utils.data.DataLoader(
valid_dataset, batch_size=config.VALID_BATCH_SIZE, num_workers=1
)
device = torch.device(config.DEVICE)
model = BERTBaseUncased()
model.to(device)
param_optimizer = list(model.named_parameters())
no_decay = ["bias", "LayerNorm.bias", "LayerNorm.weight"]
optimizer_parameters = [
{
"params": [
p for n, p in param_optimizer if not any(nd in n for nd in no_decay)
],
"weight_decay": 0.001,
},
{
"params": [
p for n, p in param_optimizer if any(nd in n for nd in no_decay)
],
"weight_decay": 0.0,
},
]
num_train_steps = int(len(df_train) / config.TRAIN_BATCH_SIZE * config.EPOCHS)
optimizer = AdamW(optimizer_parameters, lr=3e-5)
scheduler = get_linear_schedule_with_warmup(
optimizer, num_warmup_steps=0, num_training_steps=num_train_steps
)
best_accuracy = 0
for epoch in range(config.EPOCHS):
train_fn(train_data_loader, model, optimizer, device, scheduler)
outputs, targets = eval_fn(valid_data_loader, model, device)
accuracy = metrics.accuracy_score(targets, outputs)
print(f"Accuracy Score = {accuracy}")
target_names = ['class 0', 'class 1']
print(classification_report(targets, outputs, target_names=target_names))
if accuracy > best_accuracy:
torch.save(model.state_dict(), "model_{}.bin".format(fold))
best_accuracy = accuracy
# + colab={"base_uri": "https://localhost:8080/"} id="76Goq826DQG1" outputId="002bfde0-4a6e-49a0-a3f3-b19008cd9064"
run(fold = 0)
# + id="gvB5tTJfGWN4"
# + id="El-dPXobDcV3"
| 37.628289 | 1,229 |
94f53e9584357a231ba096d7116a37fec29a9692
|
py
|
python
|
brusselator_hopf.ipynb
|
cemozen/emergence_of_limit_cycle_dynamics
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Hopf Bifurcation: The Emergence of Limit-cycle Dynamics
#
# *Cem Özen*, May 2017.
#
# A *Hopf bifurcation* is a critical point in which a periodic orbit appears or disappears through a local change in the stability of a fixed point in a dynamical system as one of the system parameters is varied. Hopf bifurcations occur in many of the well-known dynamical systems such as the Lotka-Volterra model, the Lorenz model, the Selkov model of glycolysis, the Belousov-Zhabotinsky reaction model, and the Hodgkin-Huxley model for nerve membrane.
# <img src="./animations/brusselator_hopf.gif" width="350"> <br><br>The animation above shows the emergence of a limit cycle in the Brusselator system (for the actual simulation, see below).
# In this notebook, I will consider a system of chemical reactions known by the name *Brusselator* in literature (see: https://en.wikipedia.org/wiki/Brusselator for more information) as a model for Hopf bifurcations. The Brusselator reactions are given by
#
# $A \longrightarrow X$ <br>
# $2X + Y\longrightarrow 3X$ <br>
# $B + X \longrightarrow Y + D$ <br>
# $X \longrightarrow E$ <br>
#
# For the sake of simplicity, we will assume that the reaction constants of all these reactions are unity (i.e. in all the reactions, $k=1$ ). Furthermore let's assume that the reactant concentrations $A$ and $B$ are so large that they remain constant. Therefore, only $X$ and $Y$ concentrations will be dynamical.
#
# The rate equations for $X$ and $Y$ are then given by <br>
#
#
# $$
# \begin{eqnarray}
# \dot{X} & = & A + X^2Y - BX - X, \\
# \dot{Y} & = & BX - X^2Y
# \end{eqnarray}
# $$
# The X-nullcline and the Y-nullcline are given by the conditions of $0 = A + X^2Y - BX - X$ and $0 = BX - X^2Y$ respectively. From these equations, we obtain:
#
# $$
# \begin{eqnarray}
# Y(X) & = & \frac{-A + X(B+1)}{X^2}, & \quad \textrm{(X-nullcline)} \\
# Y(X) & = & \frac{B}{X}, & \quad \textrm{(Y-nullcline)}
# \end{eqnarray}
# $$
# In this notebook, I will also demonstrate how one can perform symbolical computations using Python's `SymPy` library. We also need extra Jupyter Notebook functionality to render nice display of the resulting equations. (Notice that we are using LaTex in typesetting this document particularly for the purpose of producing nice looking equations).
import numpy as np
from numpy.linalg import eig
from scipy import integrate
import sympy
from IPython.display import display, Math, Latex
import matplotlib.pyplot as plt
sympy.init_printing(use_latex='mathjax')
# %matplotlib inline
# Let's obtain the nullcline equations using `SymPy`:
# +
X, Y, A, B = sympy.symbols('X Y A B') # you need to introduce the sysmbols first
# let's get the X-nullcline as a function of X:
sympy.solve(sympy.Eq(A + X**2 * Y - B * X - X, 0), Y)
# -
# let's get the Y-nullcline as a function of X:
sympy.solve(sympy.Eq(B * X - X**2 * Y, 0), Y)
# Now let's find the fixed points ($X^*, Y^*$) of this 2-D system (there is only one, actually). The fixed point is given by the simultaneous solution of the X-nullcline and Y-nullcline equations, therefore
#
# $$ (X^*, Y^*) = (A, \frac{B}{A}) $$
#
# For the sake of using `SymPy`, let's obtain this solution once again:
# Solve the system of equations defined by the X-nullcline and Y-nullcline with respect to X and Y:
sympy.solve([A + X**2 * Y - B * X - X, B * X - X**2 * Y], [X, Y])
# Now, a bifurcation analysis of the Brusselator model requires us to keep track of the local stability of its fixed point. This can be done, according to the *linearized stability analysis* by evaluating the Jacobian matrix at the fixed point. <br>
#
#
# The Jacobian matrix at the fixed point is given by:
#
# $$
# \begin{eqnarray}
# J & = & \left\vert\matrix{{\partial f \over \partial x} & {\partial f\over \partial y} \cr
# {\partial g \over \partial x} & {\partial g\over \partial y}
# }\right\vert_{(X^*, Y^*)} \\
# & = & \left\vert\matrix{ -B + 2XY - 1 & X^2 \cr
# B - 2XY & -X^2
# }\right\vert_{(X^*, Y^*)} \\
# & = & \left\vert\matrix{ B - 1 & A^2 \cr
# -B & -A^2
# }\right\vert
# \end{eqnarray}
# $$
#
# This result can also be obtained very easily using `SymPy`:
# define the Brusselator dynamical system as a SymPy matrix
brusselator = sympy.Matrix([A + X**2 * Y - B * X - X, B * X - X**2 * Y])
# Jacobian matrix with respect to X and Y
J = brusselator.jacobian([X, Y])
J
# Jacobian matrix evaluated at the coordinates of the fixed point
J_at_fp = J.subs({X:A, Y:B/A}) # substitute X with A and Y with B/A
J_at_fp
# A limit-cycle can emerge in a 2-dimensional, attractive dynamical system if the fixed point of the system goes unstable. In this case, trajectories must be pulled by a limit cycle. (According to the Poincare-Bendixson theorem, a 2-dimensional system cannot have strange attractors). In this case, the Hopf bifurcation is called a *supercritical Hopf bifurcation*, because limit cycle is stable.
#
# In the following, we will see how the stable fixed point (spiral) of the Brusselator goes unstable, giving rise to a limit cycle in turn. Conditions for the stability are determined by the trace and the determinant of the Jacobian. So let's evaluate them:
Delta = J_at_fp.det() # determinant of the Jacobian
Delta.simplify()
tau = J_at_fp.trace() # trace of the Jacobian
tau
# To have an unstable spiral we need:
#
# $$
# \begin{eqnarray}
# \tau & > & 0 \quad \Rightarrow \quad & B > A^2 + 1 \quad \textrm{required} \\
# \Delta & > & 0 \quad {} \quad & \textrm{automatically satisfied} \\
# \tau^2 & < & 4 \Delta \quad {} \quad & \textrm{automatically satisfied}
# \end{eqnarray}
# $$
#
# The second and third conditions were satisfied because of the first condition, automatically. Therefore we need to have:
#
# $$ B > A^2 + 1 $$ for limit cycles.
# ## Birth of A Limit Cycle: Hopf Bifurcation
# ### Numerical Simulation of the Brusselator System
# In the following, I perform a numerical simulation of the (supercritical) Hopf bifurcation in the Brusselator system by varying the parameter $B$ while the value of $A=1$.
# +
# Brusselator System:
def dX_dt(A, B, X, t):
x, y = X[0], X[1]
return np.array([A + x**2 * y - B * x -x,
B * x - x**2 * y])
T = 50 * np.pi # simulation time
dt = 0.01 # integration time step
# time steps to be used in integration of the Brusselator system
t=np.arange(0, T, dt)
# create a canvas and 3 subplots..we will use each one for different choice of A and B paraeters
fig, ax = plt.subplots(1, 3)
fig.set_size_inches(13,5)
def plotter(A, B, ax):
"""
This function draws a phase portrait by assigning a vector characterizing how the concentrations
change at a given value of X and Y. It also draws a couple of example trajectories.
"""
# Drow direction fields using matplotlib 's quiver function, similar to what we did
# in class but qualitatively
xmin, xmax = 0, 5 # min and max values of x axis in the plot
ymin, ymax = 0, 5 # min and max values of y axis in the plot
x = np.linspace(xmin, xmax, 10) # divide x axis to intervals
y = np.linspace(ymin, ymax, 10) # divide y axis to intervals
X1 , Y1 = np.meshgrid(x, y) # from these intervals create a grid
DX1, DY1 = dX_dt(A, B, [X1, Y1], t) # compute rate of change of the concentrations on grid points
M = (np.hypot(DX1, DY1)) # norm of the rate of changes
M[ M == 0] = 1. # prevention against divisions by zero
DX1 /= M # we normalize the direction field vector (each has unit length now)
DY1 /= M # we normalize the direction field vector (each has unit length now)
Q = ax.quiver(X1, Y1, DX1, DY1, M, pivot='mid', cmap=plt.cm.jet)
num_traj = 5 # number of trajectories
# choose several initial points (x_i, y_j), for i and j chosen as in linspace calls below
X0 = np.asarray(list(zip(np.linspace(xmin, xmax, num_traj), np.linspace(ymin, ymax, num_traj))))
vcolors = plt.cm.jet_r(np.linspace(0., 1., num_traj)) # colors for each trajectory
# integrate the Brusellator ODE's using all initial points to produce corresponding trajectories
X = np.asarray([integrate.odeint(lambda x, t: dX_dt(A, B, x, t), X0i,t)
for X0i in X0])
# plot the trajectories we obtained above
for i in range(num_traj):
x, y = X[i, :, :].T # x and y histories for trajectory i
ax.plot(x, y, '-', c=vcolors[i], lw=2)
# set limits, put labels etc..
ax.set_xlim(xmin=xmin, xmax=xmax)
ax.set_ylim(ymin=ymin, ymax=ymax)
ax.set_xlabel("X", fontsize = 20)
ax.set_ylabel("Y", fontsize = 20)
ax.annotate("A={}, B={}".format(A, B), xy = (0.4, 0.9), xycoords = 'axes fraction', fontsize = 20, color = "k")
# Now let's prepare plots for the following choices of A and B:
plotter(A=1, B=1, ax=ax[0])
plotter(A=1, B=2, ax=ax[1])
plotter(A=1, B=3, ax=ax[2])
# -
# Above you see how a limit cycle can be created in a dynamical system, as one of the system parameters is varied.
# Here we have kept $A=1$ but varied $B$ from 1 to 2.5. Note that $B=2$ is the borderline value, marking the change in the stability of the fixed point. For $B<1$ the fixed point is stable but as we cross the value $B=2$, it changes its character to unstable and a limit cycle is born. This phenomenon is an example of *Hopf Bifurcation*.
#
# On the leftmost panel we have a stable spiral. Technically, this means that the Jacobian at the fixed point has two complex eigenvalues (a complex conjugate pair). The fact that the eigenvalues are complex is responsible for the spiralling effect. In stable spirals, the real part of the eigenvalues are negative, which is why these spiralling solutions decay, that is, trajectories nearby fall on to the fixed point. As the bifurcation parameter (here $B$) varies, the real part of the complex eigenvalues increase, reach zero at certain value of $B$, and keep growing now on the positive side. If the real part of the eigenvalues are positive, the fixed point is an unstable spiral; trajectories nearby are pushed out of the fixed point (see the rightmost panel and plot below). Since this 2-D dynamical system is attractive, by the Poincare-Bendixson theorem, the emergence of the unstable spiral accompanies the birth of a limit-cycle. Notice that the panel in the middle is the borderline case between the stable and unstable spirals: in this case the real part of the eigenvalues is exactly zero (see plots below); the linear stabilization theory falsely predicts a neutral oscillation (i.e a center) at $B=2$---due to purely imaginary eigenvalues. However, the fixed point is still a stable spiral then.
# ### Eigenvalues of the Jacobian
# Eigenvalues of the Jacobian at A=1, B=1 (fixed point is stable spiral)
J_numeric = np.asarray(J_at_fp.evalf(subs={A:1, B:1})).astype(np.float64)
w, _ = eig(J_numeric)
w
# Eigenvalues of the Jacobian at A=1, B=3 (fixed point is unstable spiral)
J_numeric = np.asarray(J_at_fp.evalf(subs={A:1, B:3})).astype(np.float64)
w, _ = eig(J_numeric)
w
# Let's prepare plots showing how the real and imaginary parts of the eigenvalues change as $B$ is varied.
# +
from numpy.linalg import eig
a = 1
eigen_real, eigen_imag = [], []
B_vals = np.linspace(1, 3, 20)
for b in B_vals:
J_numeric = np.asarray(J_at_fp.evalf(subs={A:a, B:b})).astype(np.float64)
w, _ = eig(J_numeric)
eigen_real.append(w[0].real)
eigen_imag.append(abs(w[0].imag))
eigen_real = np.asanyarray(eigen_real)
eigen_imag = np.asarray(eigen_imag)
# -
fig, ax = plt.subplots(1, 2)
fig.set_size_inches(10,5)
fig.subplots_adjust(wspace=0.5)
ax[0].axhline(y=0, c="k", ls="dashed")
ax[0].plot(B_vals, eigen_real)
ax[0].set_ylabel(r"$\mathfrak{Re}(\lambda)$", fontsize = 20)
ax[0].set_xlabel(r"$B$", fontsize = 20)
ax[1].set_ylabel(r"$|\mathfrak{Im}(\lambda)|$", fontsize = 20)
ax[1].set_xlabel(r"$B$", fontsize = 20)
ax[1].plot(B_vals, eigen_imag)
# Hopf bifurcation, is only one type of bifurcation, albeit a very important one for physical and biological systems. There are other types of bifurcation in which one can create or destroy fixed points or alter their properties in different ways than a Hopf bifurcations does. If you are curious, I suggest you to perform your own numerical experiements by playing with the values of $A$, $B$
# or both.
# ### An Animation of the Hopf Bifurcation
# +
from matplotlib import animation, rc
from IPython.display import HTML
# Brusselator System:
def dX_dt(A, B, X, t):
x, y = X[0], X[1]
return np.array([A + x**2 * y - B * x -x, B * x - x**2 * y])
T = 50 * np.pi # simulation time
dt = 0.01 # integration time step
# time steps to be used in integration of the Brusselator system
t=np.arange(0, T, dt)
num_traj = 5 # number of trajectories
xmin, xmax = 0, 5 # min and max values of x axis in the plot
ymin, ymax = 0, 5 # min and max values of y axis in the plot
A = 1. # we will keep A parameter constant
# vary B parameter
Bmin, Bmax, numB = 1., 3., 100 # min, max, number of steps for varying B
Bvals = np.linspace(Bmin, Bmax, numB)
# set up the figure, the axis, and the plot element we want to animate
fig = plt.figure()
fig.set_size_inches(8,8)
ax = plt.axes(xlim=(xmin, xmax), ylim=(ymin, ymax))
ax.set_ylabel("Y", fontsize = 20)
ax.set_xlabel("X", fontsize = 20)
# choose a set of initial points for our trajectories (in each frame we will use the same set)
X0 = list(zip(np.linspace(xmin, xmax, num_traj), np.linspace(ymin, ymax, num_traj)))
# choose a color set for our trajectories
vcolors = plt.cm.jet_r(np.linspace(0., 1., num_traj))
# prepare the mesh grid
x = np.linspace(xmin, xmax, 15) # divide x axis to intervals
y = np.linspace(ymin, ymax, 15) # divide y axis to intervals
X1 , Y1 = np.meshgrid(x, y) # from these intervals create a grid
# set up the lines, the quiver and the text object
lines = [ax.plot([], [], [], '-', c=c, lw=2)[0] for c in vcolors]
Q = ax.quiver(X1, Y1, [], [], [], pivot='mid', cmap=plt.cm.jet)
text = ax.text(0.02, 0.95, '', fontsize=20, transform=ax.transAxes)
# initialization function: plot the background of each frame. Needs to return each object to be updated
def init():
for line in lines:
line.set_data([], [])
Q.set_UVC([], [], [])
text.set_text("")
return Q, lines, text
# animation function. This is called sequentially
def animate(i):
B = Bvals[i]
DX1, DY1 = dX_dt(A, B, [X1, Y1], t) # compute rate of change of the concentrations on grid points
M = (np.hypot(DX1, DY1)) # norm of the rate of changes
M[ M == 0] = 1. # prevention against divisions by zero
DX1 /= M # we normalize the direction field vector (each has unit length now)
DY1 /= M # we normalize the direction field vector (each has unit length now)
Q.set_UVC(DX1, DY1, M)
# integrate the Brusellator ODE's for the set of trajectories, store them in X
for line, X0i in zip(lines, X0):
X = integrate.odeint(lambda x, t: dX_dt(A, B, x, t), X0i,t)
x, y = X.T # get x and y for current trajectory
line.set_data(x, y)
text.set_text("A={:.2f}, B={:.2f}".format(A, B))
return Q, lines, text
# call the animator. blit=True means only re-draw the parts that have changed.
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=100, interval=30, blit=False)
# instantiate the animator.
#anim = animation.FuncAnimation(fig, animate, init_func=init, frames=1000, interval=200, blit=True)
#HTML(anim.to_html5_video())
rc('animation', html='html5')
plt.close()
anim
# -
# In the animation above, we see how the direction field gets modified as $B$ is varied. Also shown several trajectories that are initalized at various points (I have chosen them on the $Y=X$ line here).
# ## Notes:
#
# Should you encounter difficulty in running the embedded animation, try to launch Jupter Notebook using the command:<br>
# `jupyter notebook --NotebookApp.iopub_data_rate_limit=10000000000`
# ## References:
#
# 1) Strogatz, S.H (2015). *Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, Second Edition*, Boulder, USA: Westview Press. <br>
# 2) https://en.wikipedia.org/wiki/Brusselator
| 48.190883 | 1,313 |
4ac05a070371b437eae3b9698a89e3cbee69a056
|
py
|
python
|
tensorflow/models/samples/core/get_started/eager.ipynb
|
Sioxas/python
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="rwxGnsA92emp" colab_type="text"
# ##### Copyright 2018 The TensorFlow Authors.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# + id="CPII1rGR2rF9" colab_type="code" colab={}
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="JtEZ1pCPn--z" colab_type="text"
# # Custom Training Walkthrough
#
#
# <table align="left"><td>
# <a target="_blank" href="https://colab.sandbox.google.com/github/tensorflow/models/blob/master/samples/core/get_started/eager.ipynb">
# <img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td><td>
# <a target="_blank" href="https://github.com/tensorflow/models/blob/master/samples/core/get_started/eager.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on Github</a></td></table>
#
#
# + [markdown] id="LDrzLFXE8T1l" colab_type="text"
# This guide uses machine learning to *categorize* Iris flowers by species. It uses [TensorFlow](https://www.tensorflow.org)'s eager execution to:
# 1. Build a model,
# 2. Train this model on example data, and
# 3. Use the model to make predictions about unknown data.
#
# Machine learning experience isn't required, but you'll need to read some Python code. For more eager execution guides and examples, see [these notebooks](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/contrib/eager/python/examples/notebooks).
#
# ## TensorFlow programming
#
# There are many [TensorFlow APIs](https://www.tensorflow.org/api_docs/python/) available, but start with these high-level TensorFlow concepts:
#
# * Enable an [eager execution](https://www.tensorflow.org/programmers_guide/eager) development environment,
# * Import data with the [Datasets API](https://www.tensorflow.org/programmers_guide/datasets),
# * Build models and layers with TensorFlow's [Keras API](https://keras.io/getting-started/sequential-model-guide/).
#
# This tutorial is structured like many TensorFlow programs:
#
# 1. Import and parse the data sets.
# 2. Select the type of model.
# 3. Train the model.
# 4. Evaluate the model's effectiveness.
# 5. Use the trained model to make predictions.
#
# For more TensorFlow examples, see the [Get Started](https://www.tensorflow.org/get_started/) and [Tutorials](https://www.tensorflow.org/tutorials/) sections. To learn machine learning basics, consider taking the [Machine Learning Crash Course](https://developers.google.com/machine-learning/crash-course/).
#
# ## Run the notebook
#
# This tutorial is available as an interactive [Colab notebook](https://colab.research.google.com) that can execute and modify Python code directly in the browser. The notebook handles setup and dependencies while you "play" cells to run the code blocks. This is a fun way to explore the program and test ideas.
#
# If you are unfamiliar with Python notebook environments, there are a couple of things to keep in mind:
#
# 1. Executing code requires connecting to a runtime environment. In the Colab notebook menu, select *Runtime > Connect to runtime...*
# 2. Notebook cells are arranged sequentially to gradually build the program. Typically, later code cells depend on prior code cells, though you can always rerun a code block. To execute the entire notebook in order, select *Runtime > Run all*. To rerun a code cell, select the cell and click the *play icon* on the left.
# + [markdown] id="yNr7H-AIoLOR" colab_type="text"
# ## Setup program
# + [markdown] id="6qoYFqQ89aV3" colab_type="text"
# ### Install the latest version of TensorFlow
#
# This tutorial uses eager execution, which is available in [TensorFlow 1.8](https://www.tensorflow.org/install/). (You may need to restart the runtime after upgrading.)
# + id="jBmKxLVy9Uhg" colab_type="code" colab={}
# !pip install --upgrade tensorflow
# + [markdown] id="1J3AuPBT9gyR" colab_type="text"
# ### Configure imports and eager execution
#
# Import the required Python modules—including TensorFlow—and enable eager execution for this program. Eager execution makes TensorFlow evaluate operations immediately, returning concrete values instead of creating a [computational graph](https://www.tensorflow.org/programmers_guide/graphs) that is executed later. If you are used to a REPL or the `python` interactive console, this feels familiar.
#
# Once eager execution is enabled, it *cannot* be disabled within the same program. See the [eager execution guide](https://www.tensorflow.org/programmers_guide/eager) for more details.
# + id="g4Wzg69bnwK2" colab_type="code" colab={}
from __future__ import absolute_import, division, print_function
import os
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow.contrib.eager as tfe
tf.enable_eager_execution()
print("TensorFlow version: {}".format(tf.VERSION))
print("Eager execution: {}".format(tf.executing_eagerly()))
# + [markdown] id="Zx7wc0LuuxaJ" colab_type="text"
# ## The Iris classification problem
#
# Imagine you are a botanist seeking an automated way to categorize each Iris flower you find. Machine learning provides many algorithms to statistically classify flowers. For instance, a sophisticated machine learning program could classify flowers based on photographs. Our ambitions are more modest—we're going to classify Iris flowers based on the length and width measurements of their [sepals](https://en.wikipedia.org/wiki/Sepal) and [petals](https://en.wikipedia.org/wiki/Petal).
#
# The Iris genus entails about 300 species, but our program will only classify the following three:
#
# * Iris setosa
# * Iris virginica
# * Iris versicolor
#
# <table>
# <tr><td>
# <img src="https://www.tensorflow.org/images/iris_three_species.jpg"
# alt="Petal geometry compared for three iris species: Iris setosa, Iris virginica, and Iris versicolor">
# </td></tr>
# <tr><td align="center">
# <b>Figure 1.</b> <a href="https://commons.wikimedia.org/w/index.php?curid=170298">Iris setosa</a> (by <a href="https://commons.wikimedia.org/wiki/User:Radomil">Radomil</a>, CC BY-SA 3.0), <a href="https://commons.wikimedia.org/w/index.php?curid=248095">Iris versicolor</a>, (by <a href="https://commons.wikimedia.org/wiki/User:Dlanglois">Dlanglois</a>, CC BY-SA 3.0), and <a href="https://www.flickr.com/photos/33397993@N05/3352169862">Iris virginica</a> (by <a href="https://www.flickr.com/photos/33397993@N05">Frank Mayfield</a>, CC BY-SA 2.0).<br/>
# </td></tr>
# </table>
#
# Fortunately, someone has already created a [data set of 120 Iris flowers](https://en.wikipedia.org/wiki/Iris_flower_data_set) with the sepal and petal measurements. This is a classic dataset that is popular for beginner machine learning classification problems.
# + [markdown] id="3Px6KAg0Jowz" colab_type="text"
# ## Import and parse the training dataset
#
# Download the dataset file and convert it to a structure that can be used by this Python program.
#
# ### Download the dataset
#
# Download the training dataset file using the [tf.keras.utils.get_file](https://www.tensorflow.org/api_docs/python/tf/keras/utils/get_file) function. This returns the file path of the downloaded file.
# + id="J6c7uEU9rjRM" colab_type="code" colab={}
train_dataset_url = "http://download.tensorflow.org/data/iris_training.csv"
train_dataset_fp = tf.keras.utils.get_file(fname=os.path.basename(train_dataset_url),
origin=train_dataset_url)
print("Local copy of the dataset file: {}".format(train_dataset_fp))
# + [markdown] id="qnX1-aLors4S" colab_type="text"
# ### Inspect the data
#
# This dataset, `iris_training.csv`, is a plain text file that stores tabular data formatted as comma-separated values (CSV). Use the `head -n5` command to take a peak at the first five entries:
# + id="FQvb_JYdrpPm" colab_type="code" colab={}
# !head -n5 {train_dataset_fp}
# + [markdown] id="kQhzD6P-uBoq" colab_type="text"
# From this view of the dataset, notice the following:
#
# 1. The first line is a header containing information about the dataset:
# * There are 120 total examples. Each example has four features and one of three possible label names.
# 2. Subsequent rows are data records, one *[example](https://developers.google.com/machine-learning/glossary/#example)* per line, where:
# * The first four fields are *[features](https://developers.google.com/machine-learning/glossary/#feature)*: these are characteristics of an example. Here, the fields hold float numbers representing flower measurements.
# * The last column is the *[label](https://developers.google.com/machine-learning/glossary/#label)*: this is the value we want to predict. For this dataset, it's an integer value of 0, 1, or 2 that corresponds to a flower name.
#
# Let's write that out in code:
# + id="9Edhevw7exl6" colab_type="code" colab={}
# column order in CSV file
column_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'species']
feature_names = column_names[:-1]
label_name = column_names[-1]
print("Features: {}".format(feature_names))
print("Label: {}".format(label_name))
# + [markdown] id="CCtwLoJhhDNc" colab_type="text"
# Each label is associated with string name (for example, "setosa"), but machine learning typically relies on numeric values. The label numbers are mapped to a named representation, such as:
#
# * `0`: Iris setosa
# * `1`: Iris versicolor
# * `2`: Iris virginica
#
# For more information about features and labels, see the [ML Terminology section of the Machine Learning Crash Course](https://developers.google.com/machine-learning/crash-course/framing/ml-terminology).
# + id="sVNlJlUOhkoX" colab_type="code" colab={}
class_names = ['Iris setosa', 'Iris versicolor', 'Iris virginica']
# + [markdown] id="dqPkQExM2Pwt" colab_type="text"
# ### Create a `tf.data.Dataset`
#
# TensorFlow's [Dataset API](https://www.tensorflow.org/programmers_guide/datasets) handles many common cases for loading data into a model. This is a high-level API for reading data and transforming it into a form used for training. See the [Datasets Quick Start guide](https://www.tensorflow.org/get_started/datasets_quickstart) for more information.
#
#
# Since the dataset is a CSV-formatted text file, use the the [make_csv_dataset](https://www.tensorflow.org/api_docs/python/tf/contrib/data/make_csv_dataset) function to parse the data into a suitable format. Since this function generates data for training models, the default behavior is to shuffle the data (`shuffle=True, shuffle_buffer_size=10000`), and repeat the dataset forever (`num_epochs=None`). We also set the [batch_size](https://developers.google.com/machine-learning/glossary/#batch_size) parameter.
# + id="WsxHnz1ebJ2S" colab_type="code" colab={}
batch_size = 32
train_dataset = tf.contrib.data.make_csv_dataset(
train_dataset_fp,
batch_size,
column_names=column_names,
label_name=label_name,
num_epochs=1)
# + [markdown] id="gB_RSn62c-3G" colab_type="text"
# The `make_csv_dataset` function returns a `tf.data.Dataset` of `(features, label)` pairs, where `features` is a dictionary: `{'feature_name': value}`
#
# With eager execution enabled, these `Dataset` objects are iterable. Let's look at a batch of features:
# + id="iDuG94H-C122" colab_type="code" colab={}
features, labels = next(iter(train_dataset))
features
# + [markdown] id="E63mArnQaAGz" colab_type="text"
# Notice that like-features are grouped together, or *batched*. Each example row's fields are appended to the corresponding feature array. Change the `batch_size` to set the number of examples stored in these feature arrays.
#
# You can start to see some clusters by plotting a few features from the batch:
# + id="me5Wn-9FcyyO" colab_type="code" colab={}
plt.scatter(features['petal_length'],
features['sepal_length'],
c=labels,
cmap='viridis')
plt.xlabel("Petal length")
plt.ylabel("Sepal length");
# + [markdown] id="YlxpSyHlhT6M" colab_type="text"
# To simplify the model building step, create a function to repackage the features dictionary into a single array with shape: `(batch_size, num_features)`.
#
# This function uses the [tf.stack](https://www.tensorflow.org/api_docs/python/tf/stack) method which takes values from a list of tensors and creates a combined tensor at the specified dimension.
# + id="jm932WINcaGU" colab_type="code" colab={}
def pack_features_vector(features, labels):
"""Pack the features into a single array."""
features = tf.stack(list(features.values()), axis=1)
return features, labels
# + [markdown] id="V1Vuph_eDl8x" colab_type="text"
# Then use the [tf.data.Dataset.map](https://www.tensorflow.org/api_docs/python/tf/data/dataset/map) method to pack the `features` of each `(features,label)` pair into the training dataset:
# + id="ZbDkzGZIkpXf" colab_type="code" colab={}
train_dataset = train_dataset.map(pack_features_vector)
# + [markdown] id="NLy0Q1xCldVO" colab_type="text"
# The features element of the `Dataset` are now arrays with shape `(batch_size, num_features)`. Let's look at the first few examples:
# + id="kex9ibEek6Tr" colab_type="code" colab={}
features, labels = next(iter(train_dataset))
print(features[:5])
# + [markdown] id="LsaVrtNM3Tx5" colab_type="text"
# ## Select the type of model
#
# ### Why model?
#
# A *[model](https://developers.google.com/machine-learning/crash-course/glossary#model)* is the relationship between features and the label. For the Iris classification problem, the model defines the relationship between the sepal and petal measurements and the predicted Iris species. Some simple models can be described with a few lines of algebra, but complex machine learning models have a large number of parameters that are difficult to summarize.
#
# Could you determine the relationship between the four features and the Iris species *without* using machine learning? That is, could you use traditional programming techniques (for example, a lot of conditional statements) to create a model? Perhaps—if you analyzed the dataset long enough to determine the relationships between petal and sepal measurements to a particular species. And this becomes difficult—maybe impossible—on more complicated datasets. A good machine learning approach *determines the model for you*. If you feed enough representative examples into the right machine learning model type, the program will figure out the relationships for you.
#
# ### Select the model
#
# We need to select the kind of model to train. There are many types of models and picking a good one takes experience. This tutorial uses a neural network to solve the Iris classification problem. *[Neural networks](https://developers.google.com/machine-learning/glossary/#neural_network)* can find complex relationships between features and the label. It is a highly-structured graph, organized into one or more *[hidden layers](https://developers.google.com/machine-learning/glossary/#hidden_layer)*. Each hidden layer consists of one or more *[neurons](https://developers.google.com/machine-learning/glossary/#neuron)*. There are several categories of neural networks and this program uses a dense, or *[fully-connected neural network](https://developers.google.com/machine-learning/glossary/#fully_connected_layer)*: the neurons in one layer receive input connections from *every* neuron in the previous layer. For example, Figure 2 illustrates a dense neural network consisting of an input layer, two hidden layers, and an output layer:
#
# <table>
# <tr><td>
# <img src="https://www.tensorflow.org/images/custom_estimators/full_network.png"
# alt="A diagram of the network architecture: Inputs, 2 hidden layers, and outputs">
# </td></tr>
# <tr><td align="center">
# <b>Figure 2.</b> A neural network with features, hidden layers, and predictions.<br/>
# </td></tr>
# </table>
#
# When the model from Figure 2 is trained and fed an unlabeled example, it yields three predictions: the likelihood that this flower is the given Iris species. This prediction is called *[inference](https://developers.google.com/machine-learning/crash-course/glossary#inference)*. For this example, the sum of the output predictions is 1.0. In Figure 2, this prediction breaks down as: `0.03` for *Iris setosa*, `0.95` for *Iris versicolor*, and `0.02` for *Iris virginica*. This means that the model predicts—with 95% probability—that an unlabeled example flower is an *Iris versicolor*.
# + [markdown] id="W23DIMVPQEBt" colab_type="text"
# ### Create a model using Keras
#
# The TensorFlow [tf.keras](https://www.tensorflow.org/api_docs/python/tf/keras) API is the preferred way to create models and layers. This makes it easy to build models and experiment while Keras handles the complexity of connecting everything together.
#
# The [tf.keras.Sequential](https://www.tensorflow.org/api_docs/python/tf/keras/Sequential) model is a linear stack of layers. Its constructor takes a list of layer instances, in this case, two [Dense](https://www.tensorflow.org/api_docs/python/tf/keras/layers/Dense) layers with 10 nodes each, and an output layer with 3 nodes representing our label predictions. The first layer's `input_shape` parameter corresponds to the number of features from the dataset, and is required.
# + id="2fZ6oL2ig3ZK" colab_type="code" colab={}
model = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation=tf.nn.relu, input_shape=(4,)), # input shape required
tf.keras.layers.Dense(10, activation=tf.nn.relu),
tf.keras.layers.Dense(3)
])
# + [markdown] id="FHcbEzMpxbHL" colab_type="text"
# The *[activation function](https://developers.google.com/machine-learning/crash-course/glossary#activation_function)* determines the output shape of each node in the layer. These non-linearities are important—without them the model would be equivalent to a single layer. There are many [available activations](https://www.tensorflow.org/api_docs/python/tf/keras/activations), but [ReLU](https://developers.google.com/machine-learning/crash-course/glossary#ReLU) is common for hidden layers.
#
# The ideal number of hidden layers and neurons depends on the problem and the dataset. Like many aspects of machine learning, picking the best shape of the neural network requires a mixture of knowledge and experimentation. As a rule of thumb, increasing the number of hidden layers and neurons typically creates a more powerful model, which requires more data to train effectively.
# + [markdown] id="2wFKnhWCpDSS" colab_type="text"
# ### Using the model
#
# Let's have a quick look at what this model does to a batch of features:
# + id="xe6SQ5NrpB-I" colab_type="code" colab={}
predictions = model(features)
predictions[:5]
# + [markdown] id="wxyXOhwVr5S3" colab_type="text"
# Here, each example returns a [logit](https://developers.google.com/machine-learning/crash-course/glossary#logit) for each class.
#
# To convert these logits to a probability for each class, use the [softmax](https://developers.google.com/machine-learning/crash-course/glossary#softmax) function:
# + id="_tRwHZmTNTX2" colab_type="code" colab={}
tf.nn.softmax(predictions[:5])
# + [markdown] id="uRZmchElo481" colab_type="text"
# Taking the `tf.argmax` across classes gives us the predicted class index. But, the model hasn't been trained yet, so these aren't good predictions.
# + id="-Jzm_GoErz8B" colab_type="code" colab={}
print("Prediction: {}".format(tf.argmax(predictions, axis=1)))
print(" Labels: {}".format(labels))
# + [markdown] id="Vzq2E5J2QMtw" colab_type="text"
# ## Train the model
#
# *[Training](https://developers.google.com/machine-learning/crash-course/glossary#training)* is the stage of machine learning when the model is gradually optimized, or the model *learns* the dataset. The goal is to learn enough about the structure of the training dataset to make predictions about unseen data. If you learn *too much* about the training dataset, then the predictions only work for the data it has seen and will not be generalizable. This problem is called *[overfitting](https://developers.google.com/machine-learning/crash-course/glossary#overfitting)*—it's like memorizing the answers instead of understanding how to solve a problem.
#
# The Iris classification problem is an example of *[supervised machine learning](https://developers.google.com/machine-learning/glossary/#supervised_machine_learning)*: the model is trained from examples that contain labels. In *[unsupervised machine learning](https://developers.google.com/machine-learning/glossary/#unsupervised_machine_learning)*, the examples don't contain labels. Instead, the model typically finds patterns among the features.
# + [markdown] id="RaKp8aEjKX6B" colab_type="text"
# ### Define the loss and gradient function
#
# Both training and evaluation stages need to calculate the model's *[loss](https://developers.google.com/machine-learning/crash-course/glossary#loss)*. This measures how off a model's predictions are from the desired label, in other words, how bad the model is performing. We want to minimize, or optimize, this value.
#
# Our model will calculate its loss using the [tf.keras.losses.categorical_crossentropy](https://www.tensorflow.org/api_docs/python/tf/losses/sparse_softmax_cross_entropy) function which takes the model's class probability predictions and the desired label, and returns the average loss across the examples.
# + id="tMAT4DcMPwI-" colab_type="code" colab={}
def loss(model, x, y):
y_ = model(x)
return tf.losses.sparse_softmax_cross_entropy(labels=y, logits=y_)
l = loss(model, features, labels)
print("Loss test: {}".format(l))
# + [markdown] id="3IcPqA24QM6B" colab_type="text"
# Use the [tf.GradientTape](https://www.tensorflow.org/api_docs/python/tf/GradientTape) context to calculate the *[gradients](https://developers.google.com/machine-learning/crash-course/glossary#gradient)* used to optimize our model. For more examples of this, see the [eager execution guide](https://www.tensorflow.org/programmers_guide/eager).
# + id="x57HcKWhKkei" colab_type="code" colab={}
def grad(model, inputs, targets):
with tf.GradientTape() as tape:
loss_value = loss(model, inputs, targets)
return loss_value, tape.gradient(loss_value, model.trainable_variables)
# + [markdown] id="lOxFimtlKruu" colab_type="text"
# ### Create an optimizer
#
# An *[optimizer](https://developers.google.com/machine-learning/crash-course/glossary#optimizer)* applies the computed gradients to the model's variables to minimize the `loss` function. You can think of the loss function as a curved surface (see Figure 3) and we want to find its lowest point by walking around. The gradients point in the direction of steepest ascent—so we'll travel the opposite way and move down the hill. By iteratively calculating the loss and gradient for each batch, we'll adjust the model during training. Gradually, the model will find the best combination of weights and bias to minimize loss. And the lower the loss, the better the model's predictions.
#
# <table>
# <tr><td>
# <img src="https://cs231n.github.io/assets/nn3/opt1.gif" width="70%"
# alt="Optimization algorthims visualized over time in 3D space.">
# </td></tr>
# <tr><td align="center">
# <b>Figure 3.</b> Optimization algorithms visualized over time in 3D space. (Source: <a href="http://cs231n.github.io/neural-networks-3/">Stanford class CS231n</a>, MIT License)<br/>
# </td></tr>
# </table>
#
# TensorFlow has many [optimization algorithms](https://www.tensorflow.org/api_guides/python/train) available for training. This model uses the [tf.train.GradientDescentOptimizer](https://www.tensorflow.org/api_docs/python/tf/train/GradientDescentOptimizer) that implements the *[stochastic gradient descent](https://developers.google.com/machine-learning/crash-course/glossary#gradient_descent)* (SGD) algorithm. The `learning_rate` sets the step size to take for each iteration down the hill. This is a *hyperparameter* that you'll commonly adjust to achieve better results.
# + [markdown] id="XkUd6UiZa_dF" colab_type="text"
# Let's setup the optimizer and the `global_step` counter:
# + id="8xxi2NNGKwG_" colab_type="code" colab={}
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
global_step = tf.train.get_or_create_global_step()
# + [markdown] id="pJVRZ0hP52ZB" colab_type="text"
# We'll use this to calculate a single optimization step:
# + id="rxRNTFVe56RG" colab_type="code" colab={}
loss_value, grads = grad(model, features, labels)
print("Step: {}, Initial Loss: {}".format(global_step.numpy(),
loss_value.numpy()))
optimizer.apply_gradients(zip(grads, model.variables), global_step)
print("Step: {}, Loss: {}".format(global_step.numpy(),
loss(model, features, labels).numpy()))
# + [markdown] id="7Y2VSELvwAvW" colab_type="text"
# ### Training loop
#
# With all the pieces in place, the model is ready for training! A training loop feeds the dataset examples into the model to help it make better predictions. The following code block sets up these training steps:
#
# 1. Iterate each *epoch*. An epoch is one pass through the dataset.
# 2. Within an epoch, iterate over each example in the training `Dataset` grabbing its *features* (`x`) and *label* (`y`).
# 3. Using the example's features, make a prediction and compare it with the label. Measure the inaccuracy of the prediction and use that to calculate the model's loss and gradients.
# 4. Use an `optimizer` to update the model's variables.
# 5. Keep track of some stats for visualization.
# 6. Repeat for each epoch.
#
# The `num_epochs` variable is the amount of times to loop over the dataset collection. Counter-intuitively, training a model longer does not guarantee a better model. `num_epochs` is a *[hyperparameter](https://developers.google.com/machine-learning/glossary/#hyperparameter)* that you can tune. Choosing the right number usually requires both experience and experimentation.
# + id="AIgulGRUhpto" colab_type="code" colab={}
## Note: Rerunning this cell uses the same model variables
# keep results for plotting
train_loss_results = []
train_accuracy_results = []
num_epochs = 201
for epoch in range(num_epochs):
epoch_loss_avg = tfe.metrics.Mean()
epoch_accuracy = tfe.metrics.Accuracy()
# Training loop - using batches of 32
for x, y in train_dataset:
# Optimize the model
loss_value, grads = grad(model, x, y)
optimizer.apply_gradients(zip(grads, model.variables),
global_step)
# Track progress
epoch_loss_avg(loss_value) # add current batch loss
# compare predicted label to actual label
epoch_accuracy(tf.argmax(model(x), axis=1, output_type=tf.int32), y)
# end epoch
train_loss_results.append(epoch_loss_avg.result())
train_accuracy_results.append(epoch_accuracy.result())
if epoch % 50 == 0:
print("Epoch {:03d}: Loss: {:.3f}, Accuracy: {:.3%}".format(epoch,
epoch_loss_avg.result(),
epoch_accuracy.result()))
# + [markdown] id="2FQHVUnm_rjw" colab_type="text"
# ### Visualize the loss function over time
# + [markdown] id="j3wdbmtLVTyr" colab_type="text"
# While it's helpful to print out the model's training progress, it's often *more* helpful to see this progress. [TensorBoard](https://www.tensorflow.org/programmers_guide/summaries_and_tensorboard) is a nice visualization tool that is packaged with TensorFlow, but we can create basic charts using the `matplotlib` module.
#
# Interpreting these charts takes some experience, but you really want to see the *loss* go down and the *accuracy* go up.
# + id="agjvNd2iUGFn" colab_type="code" colab={}
fig, axes = plt.subplots(2, sharex=True, figsize=(12, 8))
fig.suptitle('Training Metrics')
axes[0].set_ylabel("Loss", fontsize=14)
axes[0].plot(train_loss_results)
axes[1].set_ylabel("Accuracy", fontsize=14)
axes[1].set_xlabel("Epoch", fontsize=14)
axes[1].plot(train_accuracy_results);
# + [markdown] id="Zg8GoMZhLpGH" colab_type="text"
# ## Evaluate the model's effectiveness
#
# Now that the model is trained, we can get some statistics on its performance.
#
# *Evaluating* means determining how effectively the model makes predictions. To determine the model's effectiveness at Iris classification, pass some sepal and petal measurements to the model and ask the model to predict what Iris species they represent. Then compare the model's prediction against the actual label. For example, a model that picked the correct species on half the input examples has an *[accuracy](https://developers.google.com/machine-learning/glossary/#accuracy)* of `0.5`. Figure 4 shows a slightly more effective model, getting 4 out of 5 predictions correct at 80% accuracy:
#
# <table cellpadding="8" border="0">
# <colgroup>
# <col span="4" >
# <col span="1" bgcolor="lightblue">
# <col span="1" bgcolor="lightgreen">
# </colgroup>
# <tr bgcolor="lightgray">
# <th colspan="4">Example features</th>
# <th colspan="1">Label</th>
# <th colspan="1" >Model prediction</th>
# </tr>
# <tr>
# <td>5.9</td><td>3.0</td><td>4.3</td><td>1.5</td><td align="center">1</td><td align="center">1</td>
# </tr>
# <tr>
# <td>6.9</td><td>3.1</td><td>5.4</td><td>2.1</td><td align="center">2</td><td align="center">2</td>
# </tr>
# <tr>
# <td>5.1</td><td>3.3</td><td>1.7</td><td>0.5</td><td align="center">0</td><td align="center">0</td>
# </tr>
# <tr>
# <td>6.0</td> <td>3.4</td> <td>4.5</td> <td>1.6</td> <td align="center">1</td><td align="center" bgcolor="red">2</td>
# </tr>
# <tr>
# <td>5.5</td><td>2.5</td><td>4.0</td><td>1.3</td><td align="center">1</td><td align="center">1</td>
# </tr>
# <tr><td align="center" colspan="6">
# <b>Figure 4.</b> An Iris classifier that is 80% accurate.<br/>
# </td></tr>
# </table>
# + [markdown] id="z-EvK7hGL0d8" colab_type="text"
# ### Setup the test dataset
#
# Evaluating the model is similar to training the model. The biggest difference is the examples come from a separate *[test set](https://developers.google.com/machine-learning/crash-course/glossary#test_set)* rather than the training set. To fairly assess a model's effectiveness, the examples used to evaluate a model must be different from the examples used to train the model.
#
# The setup for the test `Dataset` is similar to the setup for training `Dataset`. Download the CSV text file and parse that values, then give it a little shuffle:
# + id="Ps3_9dJ3Lodk" colab_type="code" colab={}
test_url = "http://download.tensorflow.org/data/iris_test.csv"
test_fp = tf.keras.utils.get_file(fname=os.path.basename(test_url),
origin=test_url)
# + id="SRMWCu30bnxH" colab_type="code" colab={}
test_dataset = tf.contrib.data.make_csv_dataset(
train_dataset_fp,
batch_size,
column_names=column_names,
label_name='species',
num_epochs=1,
shuffle=False)
test_dataset = test_dataset.map(pack_features_vector)
# + [markdown] id="HFuOKXJdMAdm" colab_type="text"
# ### Evaluate the model on the test dataset
#
# Unlike the training stage, the model only evaluates a single [epoch](https://developers.google.com/machine-learning/glossary/#epoch) of the test data. In the following code cell, we iterate over each example in the test set and compare the model's prediction against the actual label. This is used to measure the model's accuracy across the entire test set.
# + id="Tw03-MK1cYId" colab_type="code" colab={}
test_accuracy = tfe.metrics.Accuracy()
for (x, y) in test_dataset:
logits = model(x)
prediction = tf.argmax(logits, axis=1, output_type=tf.int32)
test_accuracy(prediction, y)
print("Test set accuracy: {:.3%}".format(test_accuracy.result()))
# + [markdown] id="HcKEZMtCOeK-" colab_type="text"
# We can see on the last batch, for example, the model is usually correct:
# + id="uNwt2eMeOane" colab_type="code" colab={}
tf.stack([y,prediction],axis=1)
# + [markdown] id="7Li2r1tYvW7S" colab_type="text"
# ## Use the trained model to make predictions
#
# We've trained a model and "proven" that it's good—but not perfect—at classifying Iris species. Now let's use the trained model to make some predictions on [unlabeled examples](https://developers.google.com/machine-learning/glossary/#unlabeled_example); that is, on examples that contain features but not a label.
#
# In real-life, the unlabeled examples could come from lots of different sources including apps, CSV files, and data feeds. For now, we're going to manually provide three unlabeled examples to predict their labels. Recall, the label numbers are mapped to a named representation as:
#
# * `0`: Iris setosa
# * `1`: Iris versicolor
# * `2`: Iris virginica
# + id="kesTS5Lzv-M2" colab_type="code" colab={}
predict_dataset = tf.convert_to_tensor([
[5.1, 3.3, 1.7, 0.5,],
[5.9, 3.0, 4.2, 1.5,],
[6.9, 3.1, 5.4, 2.1]
])
predictions = model(predict_dataset)
for i, logits in enumerate(predictions):
class_idx = tf.argmax(logits).numpy()
p = tf.nn.softmax(logits)[class_idx]
name = class_names[class_idx]
print("Example {} prediction: {} ({:4.1f}%)".format(i, name, 100*p))
# + [markdown] id="HUZEWdD9zupu" colab_type="text"
# These predictions look good!
#
# To dig deeper into machine learning models, take a look at the TensorFlow [Programmer's Guide](https://www.tensorflow.org/programmers_guide/) and check out the [community](https://www.tensorflow.org/community/).
# + [markdown] id="xJAYB2eSWcTv" colab_type="text"
# ## Next steps
#
# For more eager execution guides and examples, see [these notebooks](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/contrib/eager/python/examples/notebooks).
| 58.080068 | 1,042 |
1ae97492f6a90baf3469fa3229ececee33361fb3
|
py
|
python
|
notebooks/biocoding_2021_pythonlab_03.ipynb
|
JasonJWilliamsNY/biocoding-2021-notebooks
|
['Unlicense']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Review of String work, and moving on to lists
# Let's start off with a small challenge to refresh our skills from the previous notebook. Below is some broken code/incomplete; complete the challenge by fixing it so that we print generate the double-stranded DNA sequence of the hiv 'nef' gene
#
# ### Fix the broken code in each cell
# +
# store the hiv genome as a variable
hiv_genome_rna = uggaagggcuaauucacucccaacgaagacaagauauccuugaucuguggaucuaccacacacaaggcuacuucccugauuagcagaacuacacaccagggccagggaucagauauccacugaccuuuggauggugcuacaagcuaguaccaguugagccagagaaguuagaagaagccaacaaaggagagaacaccagcuuguuacacccugugagccugcauggaauggaugacccggagagagaaguguuagaguggagguuugacagccgccuagcauuucaucacauggcccgagagcugcauccggaguacuucaagaacugcugacaucgagcuugcuacaagggacuuuccgcuggggacuuuccagggaggcguggccugggcgggacuggggaguggcgagcccucagauccugcauauaagcagcugcuuuuugccuguacugggucucucugguuagaccagaucugagccugggagcucucuggcuaacuagggaacccacugcuuaagccucaauaaagcuugccuugagugcuucaaguagugugugcccgucuguugugugacucugguaacuagagaucccucagacccuuuuagucaguguggaaaaucucuagcaguggcgcccgaacagggaccugaaagcgaaagggaaaccagaggagcucucucgacgcaggacucggcuugcugaagcgcgcacggcaagaggcgaggggcggcgacuggugaguacgccaaaaauuuugacuagcggaggcuagaaggagagagaugggugcgagagcgucaguauuaagcgggggagaauuagaucgaugggaaaaaauucgguuaaggccagggggaaagaaaaaauauaaauuaaaacauauaguaugggcaagcagggagcuagaacgauucgcaguuaauccuggccuguuagaaacaucagaaggcuguagacaaauacugggacagcuacaaccaucccuucagacaggaucagaagaacuuagaucauuauauaauacaguagcaacccucuauugugugcaucaaaggauagagauaaaagacaccaaggaagcuuuagacaagauagaggaagagcaaaacaaaaguaagaaaaaagcacagcaagcagcagcugacacaggacacagcaaucaggucagccaaaauuacccuauagugcagaacauccaggggcaaaugguacaucaggccauaucaccuagaacuuuaaaugcauggguaaaaguaguagaagagaaggcuuucagcccagaagugauacccauguuuucagcauuaucagaaggagccaccccacaagauuuaaacaccaugcuaaacacaguggggggacaucaagcagccaugcaaauguuaaaagagaccaucaaugaggaagcugcagaaugggauagagugcauccagugcaugcagggccuauugcaccaggccagaugagagaaccaaggggaagugacauagcaggaacuacuaguacccuucaggaacaaauaggauggaugacaaauaauccaccuaucccaguaggagaaauuuauaaaagauggauaauccugggauuaaauaaaauaguaagaauguauagcccuaccagcauucuggacauaagacaaggaccaaaggaacccuuuagagacuauguagaccgguucuauaaaacucuaagagccgagcaagcuucacaggagguaaaaaauuggaugacagaaaccuuguugguccaaaaugcgaacccagauuguaagacuauuuuaaaagcauugggaccagcggcuacacuagaagaaaugaugacagcaugucagggaguaggaggacccggccauaaggcaagaguuuuggcugaagcaaugagccaaguaacaaauucagcuaccauaaugaugcagagaggcaauuuuaggaaccaaagaaagauuguuaaguguuucaauuguggcaaagaagggcacacagccagaaauugcagggccccuaggaaaaagggcuguuggaaauguggaaaggaaggacaccaaaugaaagauuguacugagagacaggcuaauuuuuuagggaagaucuggccuuccuacaagggaaggccagggaauuuucuucagagcagaccagagccaacagccccaccagaagagagcuucaggucugggguagagacaacaacucccccucagaagcaggagccgauagacaaggaacuguauccuuuaacuucccucaggucacucuuuggcaacgaccccucgucacaauaaagauaggggggcaacuaaaggaagcucuauuagauacaggagcagaugauacaguauuagaagaaaugaguuugccaggaagauggaaaccaaaaaugauagggggaauuggagguuuuaucaaaguaagacaguaugaucagauacucauagaaaucuguggacauaaagcuauagguacaguauuaguaggaccuacaccugucaacauaauuggaagaaaucuguugacucagauugguugcacuuuaaauuuucccauuagcccuauugagacuguaccaguaaaauuaaagccaggaauggauggcccaaaaguuaaacaauggccauugacagaagaaaaaauaaaagcauuaguagaaauuuguacagagauggaaaaggaagggaaaauuucaaaaauugggccugaaaauccauacaauacuccaguauuugccauaaagaaaaaagacaguacuaaauggagaaaauuaguagauuucagagaacuuaauaagagaacucaagacuucugggaaguucaauuaggaauaccacaucccgcaggguuaaaaaagaaaaaaucaguaacaguacuggaugugggugaugcauauuuuucaguucccuuagaugaagacuucaggaaguauacugcauuuaccauaccuaguauaaacaaugagacaccagggauuagauaucaguacaaugugcuuccacagggauggaaaggaucaccagcaauauuccaaaguagcaugacaaaaaucuuagagccuuuuagaaaacaaaauccagacauaguuaucuaucaauacauggaugauuuguauguaggaucugacuuagaaauagggcagcauagaacaaaaauagaggagcugagacaacaucuguugagguggggacuuaccacaccagacaaaaaacaucagaaagaaccuccauuccuuuggauggguuaugaacuccauccugauaaauggacaguacagccuauagugcugccagaaaaagacagcuggacugucaaugacauacagaaguuaguggggaaauugaauugggcaagucagauuuacccagggauuaaaguaaggcaauuauguaaacuccuuagaggaaccaaagcacuaacagaaguaauaccacuaacagaagaagcagagcuagaacuggcagaaaacagagagauucuaaaagaaccaguacauggaguguauuaugacccaucaaaagacuuaauagcagaaauacagaagcaggggcaaggccaauggacauaucaaauuuaucaagagccauuuaaaaaucugaaaacaggaaaauaugcaagaaugaggggugcccacacuaaugauguaaaacaauuaacagaggcagugcaaaaaauaaccacagaaagcauaguaauauggggaaagacuccuaaauuuaaacugcccauacaaaaggaaacaugggaaacaugguggacagaguauuggcaagccaccuggauuccugagugggaguuuguuaauaccccucccuuagugaaauuaugguaccaguuagagaaagaacccauaguaggagcagaaaccuucuauguagauggggcagcuaacagggagacuaaauuaggaaaagcaggauauguuacuaauagaggaagacaaaaaguugucacccuaacugacacaacaaaucagaagacugaguuacaagcaauuuaucuagcuuugcaggauucgggauuagaaguaaacauaguaacagacucacaauaugcauuaggaaucauucaagcacaaccagaucaaagugaaucagaguuagucaaucaaauaauagagcaguuaauaaaaaaggaaaaggucuaucuggcauggguaccagcacacaaaggaauuggaggaaaugaacaaguagauaaauuagucagugcuggaaucaggaaaguacuauuuuuagauggaauagauaaggcccaagaugaacaugagaaauaucacaguaauuggagagcaauggcuagugauuuuaaccugccaccuguaguagcaaaagaaauaguagccagcugugauaaaugucagcuaaaaggagaagccaugcauggacaaguagacuguaguccaggaauauggcaacuagauuguacacauuuagaaggaaaaguuauccugguagcaguucauguagccaguggauauauagaagcagaaguuauuccagcagaaacagggcaggaaacagcauauuuucuuuuaaaauuagcaggaagauggccaguaaaaacaauacauacugacaauggcagcaauuucaccggugcuacgguuagggccgccuguuggugggcgggaaucaagcaggaauuuggaauucccuacaauccccaaagucaaggaguaguagaaucuaugaauaaagaauuaaagaaaauuauaggacagguaagagaucaggcugaacaucuuaagacagcaguacaaauggcaguauucauccacaauuuuaaaagaaaaggggggauugggggguacagugcaggggaaagaauaguagacauaauagcaacagacauacaaacuaaagaauuacaaaaacaaauuacaaaaauucaaaauuuucggguuuauuacagggacagcagaaauccacuuuggaaaggaccagcaaagcuccucuggaaaggugaaggggcaguaguaauacaagauaauagugacauaaaaguagugccaagaagaaaagcaaagaucauuagggauuauggaaaacagauggcaggugaugauuguguggcaaguagacaggaugaggauuagaacauggaaaaguuuaguaaaacaccauauguauguuucagggaaagcuaggggaugguuuuauagacaucacuaugaaagcccucauccaagaauaaguucagaaguacacaucccacuaggggaugcuagauugguaauaacaacauauuggggucugcauacaggagaaagagacuggcauuugggucagggagucuccauagaauggaggaaaaagagauauagcacacaaguagacccugaacuagcagaccaacuaauucaucuguauuacuuugacuguuuuucagacucugcuauaagaaaggccuuauuaggacacauaguuagcccuaggugugaauaucaagcaggacauaacaagguaggaucucuacaauacuuggcacuagcagcauuaauaacaccaaaaaagauaaagccaccuuugccuaguguuacgaaacugacagaggauagauggaacaagccccagaagaccaagggccacagagggagccacacaaugaauggacacuagagcuuuuagaggagcuuaagaaugaagcuguuagacauuuuccuaggauuuggcuccauggcuuagggcaacauaucuaugaaacuuauggggauacuugggcaggaguggaagccauaauaagaauucugcaacaacugcuguuuauccauuuucagaauugggugucgacauagcagaauaggcguuacucgacagaggagagcaagaaauggagccaguagauccuagacuagagcccuggaagcauccaggaagucagccuaaaacugcuuguaccaauugcuauuguaaaaaguguugcuuucauugccaaguuuguuucauaacaaaagccuuaggcaucuccuauggcaggaagaagcggagacagcgacgaagagcucaucagaacagucagacucaucaagcuucucuaucaaagcaguaaguaguacauguaacgcaaccuauaccaauaguagcaauaguagcauuaguaguagcaauaauaauagcaauaguugugugguccauaguaaucauagaauauaggaaaauauuaagacaaagaaaaauagacagguuaauugauagacuaauagaaagagcagaagacaguggcaaugagagugaaggagaaauaucagcacuuguggagauggggguggagauggggcaccaugcuccuugggauguugaugaucuguagugcuacagaaaaauugugggucacagucuauuaugggguaccuguguggaaggaagcaaccaccacucuauuuugugcaucagaugcuaaagcauaugauacagagguacauaauguuugggccacacaugccuguguacccacagaccccaacccacaagaaguaguauugguaaaugugacagaaaauuuuaacauguggaaaaaugacaugguagaacagaugcaugaggauauaaucaguuuaugggaucaaagccuaaagccauguguaaaauuaaccccacucuguguuaguuuaaagugcacugauuugaagaaugauacuaauaccaauaguaguagcgggagaaugauaauggagaaaggagagauaaaaaacugcucuuucaauaucagcacaagcauaagagguaaggugcagaaagaauaugcauuuuuuuauaaacuugauauaauaccaauagauaaugauacuaccagcuauaaguugacaaguuguaacaccucagucauuacacaggccuguccaaagguauccuuugagccaauucccauacauuauugugccccggcugguuuugcgauucuaaaauguaauaauaagacguucaauggaacaggaccauguacaaaugucagcacaguacaauguacacauggaauuaggccaguaguaucaacucaacugcuguuaaauggcagucuagcagaagaagagguaguaauuagaucugucaauuucacggacaaugcuaaaaccauaauaguacagcugaacacaucuguagaaauuaauuguacaagacccaacaacaauacaagaaaaagaauccguauccagagaggaccagggagagcauuuguuacaauaggaaaaauaggaaauaugagacaagcacauuguaacauuaguagagcaaaauggaauaacacuuuaaaacagauagcuagcaaauuaagagaacaauuuggaaauaauaaaacaauaaucuuuaagcaauccucaggaggggacccagaaauuguaacgcacaguuuuaauuguggaggggaauuuuucuacuguaauucaacacaacuguuuaauaguacuugguuuaauaguacuuggaguacugaagggucaaauaacacugaaggaagugacacaaucacccucccaugcagaauaaaacaaauuauaaacauguggcagaaaguaggaaaagcaauguaugccccucccaucaguggacaaauuagauguucaucaaauauuacagggcugcuauuaacaagagauggugguaauagcaacaaugaguccgagaucuucagaccuggaggaggagauaugagggacaauuggagaagugaauuauauaaauauaaaguaguaaaaauugaaccauuaggaguagcacccaccaaggcaaagagaagaguggugcagagagaaaaaagagcagugggaauaggagcuuuguuccuuggguucuugggagcagcaggaagcacuaugggcgcagccucaaugacgcugacgguacaggccagacaauuauugucugguauagugcagcagcagaacaauuugcugagggcuauugaggcgcaacagcaucuguugcaacucacagucuggggcaucaagcagcuccaggcaagaauccuggcuguggaaagauaccuaaaggaucaacagcuccuggggauuugggguugcucuggaaaacucauuugcaccacugcugugccuuggaaugcuaguuggaguaauaaaucucuggaacagauuuggaaucacacgaccuggauggagugggacagagaaauuaacaauuacacaagcuuaauacacuccuuaauugaagaaucgcaaaaccagcaagaaaagaaugaacaagaauuauuggaauuagauaaaugggcaaguuuguggaauugguuuaacauaacaaauuggcugugguauauaaaauuauucauaaugauaguaggaggcuugguagguuuaagaauaguuuuugcuguacuuucuauagugaauagaguuaggcagggauauucaccauuaucguuucagacccaccucccaaccccgaggggacccgacaggcccgaaggaauagaagaagaagguggagagagagacagagacagauccauucgauuagugaacggauccuuggcacuuaucugggacgaucugcggagccugugccucuucagcuaccaccgcuugagagacuuacucuugauuguaacgaggauuguggaacuucugggacgcagggggugggaagcccucaaauauugguggaaucuccuacaguauuggagucaggaacuaaagaauagugcuguuagcuugcucaaugccacagccauagcaguagcugaggggacagauaggguuauagaaguaguacaaggagcuuguagagcuauucgccacauaccuagaagaauaagacagggcuuggaaaggauuuugcuauaagauggguggcaaguggucaaaaaguagugugauuggauggccuacuguaagggaaagaaugagacgagcugagccagcagcagauagggugggagcagcaucucgagaccuggaaaaacauggagcaaucacaaguagcaauacagcagcuaccaaugcugcuugugccuggcuagaagcacaagaggaggaggagguggguuuuccagucacaccucagguaccuuuaagaccaaugacuuacaaggcagcuguagaucuuagccacuuuuuaaaagaaaaggggggacuggaagggcuaauucacucccaaagaagacaagauauccuugaucuguggaucuaccacacacaaggcuacuucccugauuagcagaacuacacaccagggccaggggucagauauccacugaccuuuggauggugcuacaagcuaguaccaguugagccagauaagauagaagaggccaauaaaggagagaacaccagcuuguuacacccugugagccugcaugggauggaugacccggagagagaaguguuagaguggagguuugacagccgccuagcauuucaucacguggcccgagagcugcauccggaguacuucaagaacugcugacaucgagcuugcuacaagggacuuuccgcuggggacuuuccagggaggcguggccugggcgggacuggggaguggcgagcccucagauccugcauauaagcagcugcuuuuugccuguacugggucucucugguuagaccagaucugagccugggagcucucuggcuaacuagggaacccacugcuuaagccucaauaaagcuugccuugagugcuucaaguagugugugcccgucuguugugugacucugguaacuagagaucccucagacccuuuuagucaguguggaaaaucucuagca'
# +
#translate hiv RNA to DNA
hiv_genome = hiv_genome_rna.rep('u', t)
# +
# isolate the nef gene (start:8797, end:9417)
nef_gene = hiv_genome[8797]
# +
# the nef gene as a fasta file using the header 'nef type 1 (HXB2)'
fasta_header = '>nef type 1 (HXB2)'
print(fasta_heade, nef_gene)
# +
#caculate and report the GC content of the nef gene
nef_gc_content = (nef_gene.count('c') + nef_gene.count('g')) / len(nef_gene)
print("The GC content of the nef gene is: ", nef_gc_content * 100, "%")
# -
# ## Introducing lists
# Now that we have played a bit with strings, it's time to introduce the next variable type. So far, we have worked with several types of variables and data including:
#
# * integers
# * floats
# * strings
#
# The next data type is a list. Lists are just what you would expect, a collection. Lists have a few special properties we'll need to understand, lists are:
#
# * ordered
# * indexed
# * iterable
#
# Let's explore these properties by creating our on list, which in Python is done using the ``[]`` brackets.
#
my_list = []
# Perhaps it seems nothing much has happened, but you should be able to verify that Python thinks that ``my_list`` is a list; please try:
type(my_list)
# So far, we have created ``[]`` - the empty list, and assigned it the name my list. We can start adding thing to ``my_list`` using the ``.append`` method. For example:
# +
my_list =[]
# We can add a string
my_list.append('gag')
print(my_list)
# +
# We can add another string
my_list.append('pol')
print(my_list)
# +
# We can yet add another string - please add the string 'env'
# +
# We can also declare lists by naming all its members
my_other_list = ['DNA',
'mRNA',
'Protein']
print(my_other_list)
# -
# A list, maintains the order of every element of that list. Lists are indexed (starting at 0) in a way that was similar to strings.
#
# |Index|List Element|
# |:----|:-----------|
# |0|'gag'|
# |1|'pol'|
# |2|'env'|
#
# +
# Print the list of these HIV genes in order given the list below
# The correct order is
# gag, pol, vif, vpr, vpu, env, nef
hiv_gene_names = ['env',
'gag',
'vif',
'pol',
'vpr',
'vpu',
'nef']
# -
# ## Iteration and 'for' loops
# This topic is important enough to get its own section! Not only are we going to talk about iteration, but we are going to introduce a very important concept in computing - a loop. In a loop, we are able to get the computer to repeat a set of instructions without us having to write out every command. This is at the heart of what makes computers useful - being able to carry out repetitive tasks without our input.
#
# Let's look at our first for loop; to start we will use a list of nucleic acids:
# +
nucleic_acids = ['adenine',
'thymine',
'cytosine',
'guanine',
'uracil']
print(nucleic_acids)
# -
# If we wanted to, we could print the items in this list one by one using several print statements
print(nucleic_acids[0])
print(nucleic_acids[1])
print(nucleic_acids[2])
print(nucleic_acids[3])
print(nucleic_acids[4])
# +
#Alternatively, we can do this using a for loop:
for nucleotide in nucleic_acids:
print(nucleotide)
# -
# A for loop has the following structure:
#
# ### for temporary_variable in itterable : <br> • • • • instruction[temporary_variable]
#
# Let's break this down a bit...
#
# * ``for`` - a for loop must start with a for statement
# * ``temporary_variable`` - the next character(s) right after the ``for`` are actually the name of a special, variable. This variable is a placeholder for the objects that will come next in the loop.
# * ``in`` - this ``in`` must be included and tells Python what itterable it should execute the for loop on
# * ``iterable:`` The iterable is any ordered collection (such as a string or a list. A ``:`` must come after the iterable.
# * (indent) - the next line of a for loop must always be indented. The best practice is to use 4 spaces (not the tab key)
# * • • • • - 4 space indent
# * ``instruction`` - these are the instructions you want Python to execute. If your instructions make use of the variable (they don't have to) you will use ``temporary_variable`` (whatever you have named it)
#
# +
# Try the following with for loops
nucleic_acids = ['adenine',
'thymine',
'cytosine',
'guanine',
'uracil']
# Write a for loop that prints the names of the nucleotides
# -
# Write a for loop that prints 'nucleotide!' for each of the nucleotides
# Write a for loop prints nucleotide name and its one-letter abbreviation
# ## Conditionals
# One of the key functionalities in computing is the ability to make comparisons and choices. In Python, we have several ways to use this. In each case, the answer to a conditional statement is a simple binary result: True or False. Run the following cells and also make some changes to see that you understand how Python is evaluating the statement.
# Evaluate 1 > 0 + 1 ?
# How about 99 >= 99 ?
# What about 0 <= 1 ?
# And try 1 == 1
# The conditionals above all use the comparison operators, a more complete list is as follows:
#
# |Operator|Description|
# |-------|:----------|
# |``==``|Comparison - True if both operands are equal|
# |``!=``|Not equal - True if both operands are not equal|
# |``>``|Greater than - True if left operand is greater than right|
# |``<``|Less than - True if left operand is less than right|
# |``<=``|Less than or equal to - True if left operand is less than or equal to right|
# |``>=``|Greater than or equal to - True if left operand is greater than or equal to right|
#
#
# ## Random number and conditionals - Heads or Tails
# Now, let's combine randomness with our conditional operators to make a simple simulation: flipping a coin.
#
# Python has a [Module](https://docs.python.org/2/tutorial/modules.html) call [NumPy](http://www.numpy.org/). NumPy contains a number of useful functions including the ability to generate 'random' numbers. Generating a truly random number is a [science in itself](https://www.random.org/randomness/), but the NumPy ``random`` module will be sufficient for our purpose. See how we use this function in the next cell:
# +
# Using the from xxx import xxx statement, we tell Python we want to use a package that
# is not part of the default set of Python packages
# NumPy happens to be installed already for us, otherwise we would have to download it
from numpy import random
# +
# We create a variable and then use the . notation to get the random number
# in this case, we are requesting a random int that is between 1 and 10
my_random_int = random.randint(1,10)
print('My random int is %d' % my_random_int)
# rerun this cell a few times to see that you get only number 1-9
# -
# ### Print formatting
# Notice a new feature in the printing statement. We haven’t used it before, but this string formatting feature allows us to print a variable in a string without using a variable
# just put ``%d`` in the string where you want an integer to appear, then after closing the string, put another ``%`` sign followed by the variable name.
# You can also generate floats:
# +
# returns a float between 0.0 and 1.0)
my_random_float = random.ranf()
print('My random float is %f' % my_random_float)
# -
# You can also control precision of the float
print('My random float is %0.3f to 3 digits' % my_random_float)
print('My random float is %0.9f to 9 digits' % my_random_float)
print('My random float is %0.30f to 30 digits' % my_random_float)
# You can do this multiple times in the same string
print('My random float is %0.3f or %0.9f' % (my_random_float, my_random_float))
# ### if else statements
# We are now ready to combine the conditions and random number generator to do our first simulation. To do so we will need to make an if else statement:
if 1 == 1:
print('1 is equal to 1')
# The if statement uses the following pattern:
#
# ### if conditional_to_evaluate: <br> • • • • instruction
#
# * ``if`` - if statements begin with an if
# * ``conditional_to_evaluate`` - this is some conditional statement that Python will evaluate as ``True`` or ``False``. This statement will be followed by a ``:``
# * (indent) - the next line of a for loop must always be indented. The best practice is to use 4 spaces (not the tab key)
# * • • • • - 4 space indent
# * ``instruction`` - these are the instructions you want Python to execute. The instructions will also be executed iff the conditional statement is ``True``
#
# Write a few conditional statements and see what happens when the statement is ``True`` or ``False``
#
# We can supplement the if statement by telling Python what to do if the conditional is false, using the else statement:
if 1 == 2:
print('one is now equal to two')
else:
print('one is NOT equal to two')
# Remembering that indenting is important, try writing a few if else statements yourself:
# As powerful as if/else statements can be, we sometimes wish to let Python explore several contingencies. We do this using ``elif`` (else if) which allows us to use another if statement iff the preceding if statement is ``False``. Complete the next two cells to see an example:
# +
# What day is today, enter this as a string below
today =
# Things to do
if today == 'Monday':
print('Walk the dog')
elif today == 'Tuesday':
print('Pick up the laundry')
elif today == 'Wednesday':
print('Go shopping')
elif today == 'Thursday':
print('Call mom')
elif today == 'Friday':
print('Plan for the weekend')
else:
print('It must be the weekend, nothing to do')
# -
# To recap: The above if/else statement covered several explicit contingencies (If the day of the week was Monday-Friday) as one as a final contingencies if none of the above were ``True`` (the final else statement). Write a statement below using the if/elif/else chain of conditionals. Remember to pay attention to indenting.
# ## Putting it all together
# Using what you have learned so far, write some code to simulate flipping a coin.
# Use the random number function of NumPy to generate a float
# +
# Use conditionals so that if the float is greater than or equal to 0.5 consider that
#'Heads' otherwise 'Tails'
# -
# # Simulating mutation of the HIV genome
# Mutations are (at least in part) a random process that drives the change of a genome. Virus in particular use this to their advantage. Mutations in viruses can allow them to evade their hosts immune responses, concur drug resistance, or even the acquisition of new functions.
#
# According to [Abrahm et.al. 2010](http://www.uv.es/rsanjuan/Abram%20JVirol%2010.pdf) the mutation rate for the HIV-1 genome is about 4.4E-05 or 0.000044 mutations per single cell infection cycle. The most common mutation type are single nucleotide polymorphisims [SNPs](https://en.wikipedia.org/wiki/Single-nucleotide_polymorphism).
#
# In our toy simulation we will use Python to simulate the following:
#
# * flip a coin weighted to the probability of the HIV-1 mutation (genome size * mutation rate)
# * Choose a random nucleotide in the HIV-1 genome to mutate (using the .randint() method)
# * flip a weighted coin to choose what type of mutation the mutation should be (using the following information, and assuming the genome size is 9719 nucleotides)
#
# 
#
#
#
# Here are some code examples that will help
# +
# unfair coin
from numpy import random
# Coins have two sides (states) - heads or tails; use these as a list
coin_state = ['Heads','Tails']
# +
# A fair coin would have a 50/50 chance of being heads or tails. Represent these probabilities as
# floats which sum to 1.0
fair_coin_probabilities = [0.5,0.5]
# +
#flip the fair coin using numpy's random.choice method
fair_flip = random.choice(coin_state,p = fair_coin_probabilities)
# +
#print the result
print("My fair coin is %s" %fair_flip)
# +
# An unfair coin could be weighted like this
unfair_coin_probabilities = [0.1,0.9]
# +
# Therefore...
unfair_flip = random.choice(coin_state,p = unfair_coin_probabilities)
print("My unfair coin is %s" %unfair_flip)
# -
# ## 1. Write a simulation which determines if in one round of replication HIV will mutate or not
# Set the states (mutation,no_mutation)
# Set the probabilities for each state (hint: they must sum to 1)
# flip the coin (make the choice)
# ## 2. Determine how often would HIV mutate in 20 rounds of replication
# We will use a for loop to repeat the coin flip 20 times. We can use a special function ``range()`` to tell Python how many times to execute the for loop. Use the following coin flipping example, to improve your HIV simulation.
# +
from numpy import random
coin_state = ['Heads','Tails']
fair_coin_probabilities = [0.5,0.5]
for flip in range(1,21):
fair_flip = random.choice(coin_state,p = fair_coin_probabilities)
print(fair_flip)
# -
# You can take this even further by saving the result as a list:
# +
from numpy import random
coin_state = ['Heads','Tails']
fair_coin_probabilities = [0.5,0.5]
# tip: notice how the list is created before the for loop. If you declared
# flip_results = [] in the for loop, it would be reset 20 times
flip_results = []
for flip in range(1,21):
fair_flip = random.choice(coin_state,p = fair_coin_probabilities)
flip_results.append(fair_flip)
# -
# Dont' forget you can print the result to see the list:
print(flip_results)
# ## 3. If HIV is in the mutation state, determine which nuclotide to mutate
# Let's use our coin to determine if I should walk the dog on Monday or Tuesday:
# +
from numpy import random
coin_state = ['Heads','Tails']
fair_coin_probabilities = [0.5,0.5]
flip_results = []
for flip in range(1,21):
fair_flip = random.choice(coin_state,p = fair_coin_probabilities)
flip_results.append(fair_flip)
# Tip - pay attention to the indenting in this for loop that contains an if/else statement
for result in flip_results:
if result == 'Heads':
print("Walk the dog Monday")
elif result == 'Tails':
print("Walk the dog Tuesday")
# -
# Besides using the print instruction you can also place my results into a new list based on the conditional outcome:
# +
from numpy import random
coin_state = ['Heads','Tails']
fair_coin_probabilities = [0.5,0.5]
flip_results = []
# Initialize some new lists for my conditional outcomes
monday_results = []
tuesday_results = []
for flip in range(1,21):
fair_flip = random.choice(coin_state,p = fair_coin_probabilities)
flip_results.append(fair_flip)
for result in flip_results:
if result == 'Heads':
monday_results.append("Walk the dog Monday")
elif result == 'Tails':
tuesday_results.append("Walk the dog Tuesday")
# We can print how many times we had each type of result stored in our lists
print("My coin said to walk the dog Monday %d times" % len(monday_results))
print("My coin said to walk the dog Tuesday %d times" % len(tuesday_results))
# -
# Using the above examples, and your knowledge of how to slice strings to:
#
# * determine which nucleotide in the HIV-1 genome to mutate
# * flip a coin weighted to the probabilities of mutation given in the 'Class 1: single nt substitution' chart above. In each the number of observed mutations of a nucleotide on the y-axis changing to one on the x-axis is shown.
# * use the ``replace()`` function to mutate your HIV-1 genome
# **Bonus**
# * determine and report in which gene your mutations arise (ignore genes less than 200nt)
# * determine and report if the mutation in any particular gene introduces a stop codon in reading frame one
# * determine and report if the mutation in any particular gene introduces a stop codon in the actual reading frame of that gene
# ## A little more on HIV viral replication
# +
from IPython.display import HTML
HTML('<iframe width="560" height="315" src="https://www.youtube.com/embed/RO8MP3wMvqg" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe>')
# Other nice animations here: https://www.wehi.edu.au/wehi-tv
| 49.899048 | 9,737 |
8fb3b397de5b60295dd996d3b51e6bf6fad1ed25
|
py
|
python
|
Test_25_02_2021.ipynb
|
bouraouia/Corso_fuzzy_2021
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/bouraouia/Corso_fuzzy_2021/blob/main/Test_25_02_2021.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="I0ygjmT4y7Wt"
# La logica nasce perché c’era la necessita di formalizzare un linguaggio parlato, il problema era esprimere nel modo più oggettivo possibile l’idea. La teoria del sillogismo, ovvero l’invenzione logica più importante di Aristotele, risolse il problema di esprimere formalismi. Consideriamo un esempio di sillogismo.
# 1 Tutti gli A sono H
# 2 Tutti gli J sono A
# 3 Dunque tutti gli J sono H.
#
#
# Viene sviluppato il pensiero logico di Aristotele e formulata una logica delle proposizioni. La Logica proposizionale si occupa di studiare la verità e la falsità delle affermazioni che possono essere formulate matematicamente. In logica si chiama proposizione qualsiasi affermazione di cui si possa definire un valore di verità (vero o falso), senza che ciò comporti ambiguità.
# Fino alla seconda metà del secolo XIX la logica ha fatto parte del corpo delle discipline filosofiche. In seguito, Boole influenzato dallo sviluppo del calcolo algebrico, studia le proposizioni logiche principali (congiunzione e disgiunzione) riuscendo a costruire un’algebra suscettibile di una doppia interpretazione: puramente logica o numerica (0 e 1). Il calcolo booleano rendeva, così, conto della logica delle classi e della logica delle proposizioni (in questo caso i valori 0 e 1 equivalevano rispettivamente ai valori falso e vero). La logica con Boole diventa matematica, non solo perché fa uso di un apparato simbolico e metodi tipici della matematica, ma anche perché si rivolge all’analisi di questioni e problemi interni alla matematica.
#
# Il logico Lukasiewics sosteneva una **logica polivalente** cioè una logica a più valori, ma finiti, dove si conoscevano le modalità. Lukasiewics riteneva, quindi, che la nozione di possibilità (non lo so) poteva anche rivestire un ruolo centrale. Lukasiewics diede origine al sistema trivalente (0; ½, 1) nella logica e dimostra che il terzo valore, ½, introdotto nella logica polivalente, viene proprio interpretato come possibilità (non lo so). Il sistema di regole che stabilisce le relazioni fra i tre valori logici (0; ½; 1) fu, pertanto, progettato in modo da avvicinarlo il più possibile a quello della logica bivalente. La logica trivalente promossa da Lukasiewics ha rappresentato, quindi, un riferimento teorico importante per la teoria degli insiemi sfuocati. Peraltro, anche se il logico di Lukasiewics si concentrò prevalentemente sulla logica a tre valori, per lui fu evidente la possibilità di introdurre infiniti livelli intermedi di verità, così come gli apparve chiara la portata rivoluzionaria di questa nuova logica.
#
# **La logica Fuzzy** diversamente della logica binaria che ci costringe ad una precisione artificiosa (vero o falso), introduce il concetto di ricorrere ad un requisito meno stringente e più generale, che tenga conto della vaghezza (Fuzzyness) del mondo reale (un grado di verità compreso tra 1 e 0 quindi infiniti valori di verità). Logica Fuzzy, codifica l’imprecisione del mondo reale e l’incertezza del nostro giudizio su di esso.
#
#
# + [markdown] id="6ZGsPGuauYNE"
# Connettivo AND
# + id="v0EaYQcHume6"
valori_possibili = (0, 1)
for A in valori_possibili:
for B in valori_possibili:
print(f'{A} | {B} | {A * B}')
# + [markdown] id="nbQ-0Wocrdow"
# Connettivo OR
# + colab={"base_uri": "https://localhost:8080/"} id="joZ_rFNRrj24" outputId="81404e1c-f690-45b1-aa59-fc6014230044"
valori_possibili = (False, True)
for A in valori_possibili:
for B in valori_possibili:
print(f'{A} OR {B} = {A or B}')
# + [markdown] id="ZB9UF3oVr92e"
# Connettivo XOR
# + colab={"base_uri": "https://localhost:8080/"} id="uqDVhiJdsG5m" outputId="d2ce621c-143b-413f-d0f5-c2cefd97bd9b"
valori_possibili = (False, True)
for A in valori_possibili:
for B in valori_possibili:
print(f'{A} OR {B} = {A != B}')
# + [markdown] id="uf67EWOwsWHn"
# Connettivo ->
# + id="vEm5xlA6s6k6"
def freccia(ipotesi,tesi):
return (not ipotesi or tesi)
# + colab={"base_uri": "https://localhost:8080/"} id="DhckmJa7saSq" outputId="1350f283-fc07-4dd1-863f-ca2efa35af55"
valori_possibili = (False, True)
for A in valori_possibili:
for B in valori_possibili:
print(f'{A} -> {B} = {freccia(A,B)}')
# + [markdown] id="todCG7D9ugLb"
# Connettivo NOT
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="6VClRvNRuksy" outputId="e4d24f21-7db5-4742-e697-9f799cd105c3"
valori_possibili = (False, True)
for A in valori_possibili:
print(f'NOT {A} = {not A}')
# + [markdown] id="wPFCz87avegz"
# Connettivo AND via NOT e OR
# + id="2FJDTv3fvp5-" colab={"base_uri": "https://localhost:8080/"} outputId="dc82d8d3-f1e4-4de9-8a08-2be46d236b32"
valori_possibili = (False, True)
for A in valori_possibili:
for B in valori_possibili:
print(f'{A} AND {B} = {not ( (not A) or (not B) )}')
# + [markdown] id="EbuOiLobrZvc"
#
# + [markdown] id="28T7kGr5um4i"
# implementare una funzione che stampa la tabella di verità di una formula interpretata nella logica classica
# + id="Q79zvoFOut5a"
def e(var1, var2):
return var1 and var2
def o(var1, var2):
return var1 or var2
def freccia(ipotesi, tesi):
return (not ipotesi or tesi)
def oppure(var1, var2):
return (not var1 and var2) or (var1 and not var2)
# + id="wmUDvHvcvtPe"
def stampa_tabella(formula):
valori_possibili = (False, True)
for A in valori_possibili:
for B in valori_possibili:
print(f'{formula(A,B)}')
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="fHXsGHDOywCE" outputId="722bd301-2889-45c0-f1d1-ba56b2c3e33f"
stampa_tabella(o)
# + [markdown] id="ZQcdESkQS7C6"
# implementare una funzione che stampa la tabella di verità di una formula interpretata nella logica di Lukasiewicz a 3 valori
#
# + id="y8XjyZsoXhxV"
def notL(var1):
return 1 - int (var1)
#Connettivo AND
def andL(var1,var2):
return min (var1, var2)
#Connettivo OR
def orL(var1,var2):
return max(var1, var2)
#Connettivo XOR
def xorL(var1,var2):
return 1 - abs(var1 - var2)
#Connettivo freccia ->
def freccial(var1,var2):
return min(1, 1 - var1 + var2)
# + [markdown] id="1XZ-SRpwSRxI"
# stampare le funzioni di verità delle seguenti formule :
#
# A or (not A)
#
# not A -> B
# + id="I83xNbbuKma5"
#A or (notA)
def f1(var1):
return var1 or (not var1)
# not A->B
def f2(var1, var2):
return (not (not var1) or var2)
# + id="EWKU9CNmK4YO"
def stampa_tabella(formula):
valori = (False,True)
print('\nTabella di verita\':')
if formula == 'f1':
for A in valori:
print(f'{A} | {eval(formula+"(A)")}')
else:
for A in valori:
for B in valori:
print(f' {A} | {B} | {eval(formula+"(A,B)")}')
# + colab={"base_uri": "https://localhost:8080/"} id="_QZ1iIOPK6ev" outputId="ea5c3f40-21dc-43d1-e51e-952442f4cd75"
risposta = 's'
while risposta == 's':
operazione = input('Quale funzione vuoi eseguire? "f1" oppure "f2"')
stampa_tabella(operazione)
risposta = input('\nUn\'altra Operazione? Yes(s), No(n)')
# + [markdown] id="Q6Xd7yhFWWmb"
# **ADIL BOURAOUIA**
| 40.774869 | 1,038 |
5b789be4825049cd8bc9e9562ee6c5305980d389
|
py
|
python
|
bayesian_linear_regression.ipynb
|
stutun1/Bayesian-Approach-for-Different-Applications
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Bayesian regression with linear basis function models
#
# This article is an introduction to Bayesian regression with linear basis function models. After a short overview of the relevant mathematical results and their intuition, Bayesian linear regression is implemented from scratch with [NumPy](http://www.numpy.org/) followed by an example how [scikit-learn](https://scikit-learn.org/stable/) can be used to obtain equivalent results. It is assumed that you already have a basic understanding probability distributions and [Bayes' theorem](https://en.wikipedia.org/wiki/Bayes%27_theorem). For a detailed mathematical coverage I recommend reading chapter 3 of [Pattern Recognition and Machine Learning](https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf) (PRML) but this is not necessary for following this article.
#
# ## Linear basis function models
#
# Linear regression models share the property of being linear in their parameters but not necessarily in their input variables. Using non-linear basis functions of input variables, linear models are able model arbitrary non-linearities from input variables to targets. Polynomial regression is such an example and will be demonstrated later. A linear regression model $y(\mathbf{x}, \mathbf{w})$ can therefore be defined more generally as
#
# $$
# y(\mathbf{x}, \mathbf{w}) = w_0 + \sum_{j=1}^{M-1}{w_j \phi_j(\mathbf{x})} = \sum_{j=0}^{M-1}{w_j \phi_j(\mathbf{x})} = \mathbf{w}^T \boldsymbol\phi(\mathbf{x}) \tag{1}
# $$
#
# where $\phi_j$ are basis functions and $M$ is the total number of parameters $w_j$ including the bias term $w_0$. Here, we use the convention $\phi_0(\mathbf{x}) = 1$. The simplest form of linear regression models are also linear functions of their input variables i.e. the set of basis functions in this case is the identity $\boldsymbol\phi(\mathbf{x}) = \mathbf{x}$. The target variable $t$ of an observation $\mathbf{x}$ is given by a deterministic function $y(\mathbf{x}, \mathbf{w})$ plus additive random noise $\epsilon$.
#
# $$
# t = y(\mathbf{x}, \mathbf{w}) + \epsilon \tag{2}
# $$
#
# We make the assumption that the noise is normally distributed i.e. follows a Gaussian distribution with zero mean and precision (= inverse variance) $\beta$. The corresponding probabilistic model i.e. the conditional distribution of $t$ given $\mathbf{x}$ can therefore be written as
#
# $$
# p(t \lvert \mathbf{x}, \mathbf{w}, \beta) =
# \mathcal{N}(t \lvert y(\mathbf{x}, \mathbf{w}), \beta^{-1}) =
# \sqrt{\beta \over {2 \pi}} \exp\left(-{\beta \over 2} (t - y(\mathbf{x}, \mathbf{w}))^2 \right) \tag{3}
# $$
#
# where the mean of this distribution is the regression function $y(\mathbf{x}, \mathbf{w})$.
#
# ## Likelihood function
#
# For fitting the model and for inference of model parameters we use a training set of $N$ independent and identically distributed (i.i.d.) observations $\mathbf{x}_1,\ldots,\mathbf{x}_N$ and their corresponding targets $t_1,\ldots,t_N$. After combining column vectors $\mathbf{x}_i$ into matrix $\mathbf{X}$, where $\mathbf{X}_{i,:} = \mathbf{x}_i^T$, and scalar targets $t_i$ into column vector $\mathbf{t}$ the joint conditional probability of targets $\mathbf{t}$ given $\mathbf{X}$ can be formulated as
#
# $$
# p(\mathbf{t} \lvert \mathbf{X}, \mathbf{w}, \beta) =
# \prod_{i=1}^{N}{\mathcal{N}(t_i \lvert \mathbf{w}^T \boldsymbol\phi(\mathbf{x}_i), \beta^{-1})} \tag{4}
# $$
#
# This is a function of parameters $\mathbf{w}$ and $\beta$ and is called the *likelihood function*. For better readability, it will be written as $p(\mathbf{t} \lvert \mathbf{w}, \beta)$ instead of $p(\mathbf{t} \lvert \mathbf{X}, \mathbf{w}, \beta)$ from now on. The log of the likelihood function can be written as
#
# $$
# \log p(\mathbf{t} \lvert \mathbf{w}, \beta) =
# {N \over 2} \log \beta -
# {N \over 2} \log {2 \pi} -
# \beta E_D(\mathbf{w}) \tag{5}
# $$
#
# where $E_D(\mathbf{w})$ is the sum-of-squares error function coming from the exponent of the likelihood function.
#
# $$
# E_D(\mathbf{w}) =
# {1 \over 2} \sum_{i=1}^{N}(t_i - \mathbf{w}^T \boldsymbol\phi(\mathbf{x}_i))^2 =
# {1 \over 2} \lVert \mathbf{t} - \boldsymbol\Phi \mathbf{w} \rVert^2 \tag{6}
# $$
#
# Matrix $\boldsymbol\Phi$ is called the *design matrix* and is defined as
#
# $$
# \boldsymbol\Phi =
# \begin{pmatrix}
# \phi_0(\mathbf{x}_1) & \phi_1(\mathbf{x}_1) & \cdots & \phi_{M-1}(\mathbf{x}_1) \\
# \phi_0(\mathbf{x}_2) & \phi_1(\mathbf{x}_2) & \cdots & \phi_{M-1}(\mathbf{x}_2) \\
# \vdots & \vdots & \ddots & \vdots \\
# \phi_0(\mathbf{x}_N) & \phi_1(\mathbf{x}_N) & \cdots & \phi_{M-1}(\mathbf{x}_N)
# \end{pmatrix} \tag{7}
# $$
#
# ## Maximum likelihood
#
# Maximizing the log likelihood (= minimizing the sum-of-squares error function) w.r.t. $\mathbf{w}$ gives the maximum likelihood estimate of parameters $\mathbf{w}$. Maximum likelihood estimation can lead to severe over-fitting if complex models (e.g. polynomial regression models of high order) are fit to datasets of limited size. A common approach to prevent over-fitting is to add a regularization term to the error function. As we will see shortly, this regularization term arises naturally when following a Bayesian approach (more precisely, when defining a prior distribution over parameters $\mathbf{w}$).
#
# ## Bayesian approach
#
# ### Prior and posterior distribution
#
# For a Bayesian treatment of linear regression we need a prior probability distribution over model parameters $\mathbf{w}$. For reasons of simplicity, we will use an isotropic Gaussian distribution over parameters $\mathbf{w}$ with zero mean:
#
# $$
# p(\mathbf{w} \lvert \alpha) = \mathcal{N}(\mathbf{w} \lvert \mathbf{0}, \alpha^{-1}\mathbf{I}) \tag{8}
# $$
#
# An isotropic Gaussian distribution has a diagonal covariance matrix where all diagonal elements have the same variance $\alpha^{-1}$ ($\alpha$ is the precision of the prior). A zero mean favors small(er) values of parameters $w_j$ a priori. The prior is [conjugate](https://en.wikipedia.org/wiki/Conjugate_prior) to the likelihood $p(\mathbf{t} \lvert \mathbf{w}, \beta)$ meaning that the posterior distribution has the same functional form as the prior i.e. is also a Gaussian. In this special case, the posterior has an analytical solution with the following sufficient statistics
#
# $$
# \begin{align*}
# \mathbf{m}_N &= \beta \mathbf{S}_N \boldsymbol\Phi^T \mathbf{t} \tag{9} \\
# \mathbf{S}_N^{-1} &= \alpha\mathbf{I} + \beta \boldsymbol\Phi^T \boldsymbol\Phi \tag{10}
# \end{align*}
# $$
#
# $(9)$ is the mean vector of the posterior and $(10)$ the inverse covariance matrix (= precision matrix). Hence, the posterior distribution can be written as
#
# $$
# p(\mathbf{w} \lvert \mathbf{t}, \alpha, \beta) = \mathcal{N}(\mathbf{w} \lvert \mathbf{m}_N, \mathbf{S}_N) \tag{11}
# $$
#
# For the moment, we assume that the values of $\alpha$ and $\beta$ are known. Since the posterior is proportional to the product of likehood and prior, the log of the posterior distribution is proportional to the sum of the log likelihood and the log of the prior
#
# $$
# \log p(\mathbf{w} \lvert \mathbf{t}, \alpha, \beta) =
# \beta E_D(\mathbf{w}) - \alpha E_W(\mathbf{w}) + \mathrm{const.} \tag{12}
# $$
#
# where $E_D(\mathbf{w})$ is defined by $(6)$ and
#
# $$
# E_W(\mathbf{w}) = {1 \over 2} \mathbf{w}^T \mathbf{w} \tag{13}
# $$
#
# Maximizing the log posterior w.r.t. $\mathbf{w}$ gives the [maximum-a-posteriori](https://en.wikipedia.org/wiki/Maximum_a_posteriori_estimation) (MAP) estimate of $\mathbf{w}$. Maximizing the log posterior is equivalent to minimizing the sum-of-squares error function $E_D$ plus a quadratic regularization term $E_W$. This particular form regularization is known as *L2 regularization* or *weight decay* as it limits the magnitude of weights $w_j$. The contribution of the regularization term is determined by the ratio $\alpha / \beta$.
#
# ### Posterior predictive distribution
#
# For making a prediction $t$ at a new location $\mathbf{x}$ we use the posterior predictive distribution which is defined as
#
# $$
# p(t \lvert \mathbf{x}, \mathbf{t}, \alpha, \beta) =
# \int{p(t \lvert \mathbf{x}, \mathbf{w}, \beta) p(\mathbf{w} \lvert \mathbf{t}, \alpha, \beta) d\mathbf{w}} \tag{14}
# $$
#
# The posterior predictive distribution includes uncertainty about parameters $\mathbf{w}$ into predictions by weighting the conditional distribution $p(t \lvert \mathbf{x}, \mathbf{w}, \beta)$ with the posterior probability of weights $p(\mathbf{w} \lvert \mathbf{t}, \alpha, \beta)$ over the entire weight parameter space. By using the predictive distribution we're not only getting the expected value of $t$ at a new location $\mathbf{x}$ but also the uncertainty for that prediction. In our special case, the posterior predictive distribution is a Gaussian distribution
#
# $$
# p(t \lvert \mathbf{x}, \mathbf{t}, \alpha, \beta) =
# \mathcal{N}(t \lvert \mathbf{m}_N^T \boldsymbol\phi(\mathbf{x}), \sigma_N^2(\mathbf{x})) \tag{15}
# $$
#
# where mean $\mathbf{m}_N^T \boldsymbol\phi(\mathbf{x})$ is the regression function after $N$ observations and $\sigma_N^2(\mathbf{x})$ is the corresponding predictive variance
#
# $$
# \sigma_N^2(\mathbf{x}) = {1 \over \beta} + \boldsymbol\phi(\mathbf{x})^T \mathbf{S}_N \boldsymbol\phi(\mathbf{x}) \tag{16}
# $$
#
# The first term in $(16)$ represents the inherent noise in the data and the second term covers the uncertainty about parameters $\mathbf{w}$. So far, we have assumed that the values of $\alpha$ and $\beta$ are known. In a fully Bayesian treatment, however, we should define priors over $\alpha$ and $\beta$ and use the corresponding posteriors to additionally include uncertainties about $\alpha$ and $\beta$ into predictions. Unfortunately, complete integration over all three parameters $\mathbf{w}$, $\alpha$ and $\beta$ is analytically intractable and we have to use another approach.
#
# ### Evidence function
#
# Estimates for $\alpha$ and $\beta$ can alternatively be obtained by first integrating the product of likelihood and prior over parameters $\mathbf{w}$
#
# $$
# p(\mathbf{t} \lvert \alpha, \beta) =
# \int{p(\mathbf{t} \lvert \mathbf{w}, \beta) p(\mathbf{w} \lvert \alpha) d\mathbf{w}} \tag{17}
# $$
#
# and then maximizing the resulting *marginal likelihood* or *evidence function* w.r.t. $\alpha$ and $\beta$. This approach is known as [empirical Bayes](https://en.wikipedia.org/wiki/Empirical_Bayes_method). It can be shown that this is a good approximation for a fully Bayesian treatment if the posterior for $\alpha$ and $\beta$ is sharply peaked around the most probable value and the prior is relatively flat which is often a reasonable assumption. Integrating over model parameters or using a good approximation for it allows us to estimate values for $\alpha$ and $\beta$, and hence the regularization strength $\alpha / \beta$, from training data alone i.e. without using a validation set.
#
# The log of the marginal likelihood is given by
#
# $$
# \log p(\mathbf{t} \lvert \alpha, \beta) = {M \over 2} \log \alpha + {N \over 2} \log \beta -
# E(\mathbf{m}_N) - {1 \over 2} \log \lvert \mathbf{S}_N^{-1}\rvert - {N \over 2} \log {2 \pi} \tag{18}
# $$
#
# where
#
# $$
# E(\mathbf{m}_N) = {\beta \over 2} \lVert \mathbf{t} - \boldsymbol\Phi \mathbf{m}_N \rVert^2 +
# {\alpha \over 2} \mathbf{m}_N^T \mathbf{m}_N \tag{19}
# $$
#
# For completeness, the relationship between evidence, likelihood, prior, posterior is of course given by Bayes' theorem
#
# $$
# p(\mathbf{w} \lvert \mathbf{t}, \alpha, \beta) =
# {p(\mathbf{t} \lvert \mathbf{w}, \beta) p(\mathbf{w} \lvert \alpha) \over p(\mathbf{t} \lvert \alpha, \beta)} \tag{20}
# $$
#
# #### Maximization
#
# Maximization of the log marginal likelihood w.r.t. $\alpha$ and $\beta$ gives the following implicit solutions.
#
# $$
# \alpha = {\gamma \over \mathbf{m}_N^T \mathbf{m}_N} \tag{21}
# $$
#
# and
#
# $$
# {1 \over \beta} = {1 \over N - \gamma} \sum_{i=1}^{N}(t_i - \mathbf{m}_N^T \boldsymbol\phi(\mathbf{x}_i))^2 \tag{22}
# $$
#
# where
#
# $$
# \gamma = \sum_{i=0}^{M-1} {\lambda_i \over \alpha + \lambda_i} \tag{23}
# $$
#
#
# and $\lambda_i$ are the [eigenvalues](https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors) of $\beta \boldsymbol\Phi^T \boldsymbol\Phi$. The solutions are implicit because $\alpha$ and $\gamma$ as well as $\beta$ and $\gamma$ depend on each other. Solutions for $\alpha$ and $\beta$ can therefore be obtained by starting with initial values for these parameters and then iterating over the above equations until convergence.
#
# #### Evaluation
#
# Integration over model parameters also makes models of different complexity directly comparable by evaluating their evidence function on training data alone without needing a validation set. Further below we'll see an example how polynomial models of different complexity (i.e. different polynomial degree) can be compared directly by evaluating their evidence function alone. The highest evidence is usually obtained for models of intermediate complexity i.e. for models whose complexity is just high enough for explaining the data sufficiently well.
# ## Implementation
#
# ### Posterior and posterior predictive distribution
#
# We start with the implementation of the posterior and posterior predictive distributions. Function `posterior` computes the mean and covariance matrix of the posterior distribution and function `posterior_predictive` computes the mean and the variances of the posterior predictive distribution. Here, readability of code and similarity to the mathematical definitions has higher priority than optimizations.
# +
import numpy as np
def posterior(Phi, t, alpha, beta, return_inverse=False):
"""Computes mean and covariance matrix of the posterior distribution."""
S_N_inv = alpha * np.eye(Phi.shape[1]) + beta * Phi.T.dot(Phi)
S_N = np.linalg.inv(S_N_inv)
m_N = beta * S_N.dot(Phi.T).dot(t)
if return_inverse:
return m_N, S_N, S_N_inv
else:
return m_N, S_N
def posterior_predictive(Phi_test, m_N, S_N, beta):
"""Computes mean and variances of the posterior predictive distribution."""
y = Phi_test.dot(m_N)
# Only compute variances (diagonal elements of covariance matrix)
y_var = 1 / beta + np.sum(Phi_test.dot(S_N) * Phi_test, axis=1)
return y, y_var
# -
# ### Example datasets
#
# The datasets used in the following examples are based on $N$ scalar observations $x_{i = 1,\ldots,N}$ which are combined into a $N \times 1$ matrix $\mathbf{X}$. Target values $\mathbf{t}$ are generated from $\mathbf{X}$ with functions `f` and `g` which also generate random noise whose variance can be specified with the `noise_variance` parameter. We will use `f` for generating noisy samples from a straight line and `g` for generating noisy samples from a sinusoidal function.
# +
f_w0 = -0.3
f_w1 = 0.5
def f(X, noise_variance):
'''Linear function plus noise'''
return f_w0 + f_w1 * X + noise(X.shape, noise_variance)
def g(X, noise_variance):
'''Sinus function plus noise'''
return 0.5 + np.sin(2 * np.pi * X) + noise(X.shape, noise_variance)
def noise(size, variance):
return np.random.normal(scale=np.sqrt(variance), size=size)
# -
# ### Basis functions
#
# For straight line fitting, a model that is linear in its input variable $x$ is sufficient. Hence, we don't need to transform $x$ with a basis function which is equivalent to using an `identity_basis_function`. For fitting a linear model to a sinusoidal dataset we transform input $x$ with `gaussian_basis_function` and later with `polynomial_basis_function`. These non-linear basis functions are necessary to model the non-linear relationship between input $x$ and target $t$. The design matrix $\boldsymbol\Phi$ can be computed from observations $\mathbf{X}$ and a parametric basis function with function `expand`. This function also prepends a column vector $\mathbf{1}$ according to $\phi_0(x) = 1$.
# +
def identity_basis_function(x):
return x
def gaussian_basis_function(x, mu, sigma=0.1):
return np.exp(-0.5 * (x - mu) ** 2 / sigma ** 2)
def polynomial_basis_function(x, degree):
return x ** degree
def expand(x, bf, bf_args=None):
if bf_args is None:
return np.concatenate([np.ones(x.shape), bf(x)], axis=1)
else:
return np.concatenate([np.ones(x.shape)] + [bf(x, bf_arg) for bf_arg in bf_args], axis=1)
# -
# ### Straight line fitting
#
# For straight line fitting, we use a linear regression model of the form $y(x, \mathbf{w}) = w_0 + w_1 x$ and do Bayesian inference for model parameters $\mathbf{w}$. Predictions are made with the posterior predictive distribution. Since this model has only two parameters, $w_0$ and $w_1$, we can visualize the posterior density in 2D which is done in the first column of the following output. Rows use an increasing number of training data from a training dataset.
# +
from bayesian_linear_regression_util import *
import matplotlib.pyplot as plt
# %matplotlib inline
# Training dataset sizes
N_list = [1, 3, 20]
beta = 25.0
alpha = 2.0
# Training observations in [-1, 1)
X = np.random.rand(N_list[-1], 1) * 2 - 1
# Training target values
t = f(X, noise_variance=1/beta)
# Test observations
X_test = np.linspace(-1, 1, 100).reshape(-1, 1)
# Function values without noise
y_true = f(X_test, noise_variance=0)
# Design matrix of test observations
Phi_test = expand(X_test, identity_basis_function)
plt.figure(figsize=(15, 10))
plt.subplots_adjust(hspace=0.4)
for i, N in enumerate(N_list):
X_N = X[:N]
t_N = t[:N]
# Design matrix of training observations
Phi_N = expand(X_N, identity_basis_function)
# Mean and covariance matrix of posterior
m_N, S_N = posterior(Phi_N, t_N, alpha, beta)
# Mean and variances of posterior predictive
y, y_var = posterior_predictive(Phi_test, m_N, S_N, beta)
# Draw 5 random weight samples from posterior and compute y values
w_samples = np.random.multivariate_normal(m_N.ravel(), S_N, 5).T
y_samples = Phi_test.dot(w_samples)
plt.subplot(len(N_list), 3, i * 3 + 1)
plot_posterior(m_N, S_N, f_w0, f_w1)
plt.title(f'Posterior density (N = {N})')
plt.legend()
plt.subplot(len(N_list), 3, i * 3 + 2)
plot_data(X_N, t_N)
plot_truth(X_test, y_true)
plot_posterior_samples(X_test, y_samples)
plt.ylim(-1.5, 1.0)
plt.legend()
plt.subplot(len(N_list), 3, i * 3 + 3)
plot_data(X_N, t_N)
plot_truth(X_test, y_true, label=None)
plot_predictive(X_test, y, np.sqrt(y_var))
plt.ylim(-1.5, 1.0)
plt.legend()
# -
# In the second column, 5 random weight samples are drawn from the posterior and the corresponding regression lines are plotted in red color. The line resulting from the true parameters, `f_w0` and `f_w1` is plotted as dashed black line and the noisy training data as black dots. The third column shows the mean and the standard deviation of the posterior predictive distribution along with the true model and the training data.
#
# It can be clearly seen how the posterior density in the first column gets more sharply peaked as the size of the dataset increases which corresponds to a decrease in the sample variance in the second column and to a decrease in prediction uncertainty as shown in the third column. Also note how prediction uncertainty is higher in regions of less observations.
#
# ### Gaussian basis functions
#
# The following example demonstrates how to fit a Gaussian basis function model to a noisy sinusoidal dataset. It uses 9 Gaussian basis functions with mean values equally distributed over $[0, 1]$ each having a standard deviation of $0.1$. Inference for parameters $\mathbf{w}$ is done in the same way as in the previous example except that we now infer values for 10 parameters (bias term $w_0$ and $w_1,\ldots,w_9$ for the 9 basis functions) instead of 2. We therefore cannot display the posterior density unless we selected 2 parameters at random.
# +
N_list = [3, 8, 20]
beta = 25.0
alpha = 2.0
# Training observations in [-1, 1)
X = np.random.rand(N_list[-1], 1)
# Training target values
t = g(X, noise_variance=1/beta)
# Test observations
X_test = np.linspace(0, 1, 100).reshape(-1, 1)
# Function values without noise
y_true = g(X_test, noise_variance=0)
# Design matrix of test observations
Phi_test = expand(X_test, bf=gaussian_basis_function, bf_args=np.linspace(0, 1, 9))
plt.figure(figsize=(10, 10))
plt.subplots_adjust(hspace=0.4)
for i, N in enumerate(N_list):
X_N = X[:N]
t_N = t[:N]
# Design matrix of training observations
Phi_N = expand(X_N, bf=gaussian_basis_function, bf_args=np.linspace(0, 1, 9))
# Mean and covariance matrix of posterior
m_N, S_N = posterior(Phi_N, t_N, alpha, beta)
# Mean and variances of posterior predictive
y, y_var = posterior_predictive(Phi_test, m_N, S_N, beta)
# Draw 5 random weight samples from posterior and compute y values
w_samples = np.random.multivariate_normal(m_N.ravel(), S_N, 5).T
y_samples = Phi_test.dot(w_samples)
plt.subplot(len(N_list), 2, i * 2 + 1)
plot_data(X_N, t_N)
plot_truth(X_test, y_true)
plot_posterior_samples(X_test, y_samples)
plt.ylim(-1.0, 2.0)
plt.legend()
plt.subplot(len(N_list), 2, i * 2 + 2)
plot_data(X_N, t_N)
plot_truth(X_test, y_true, label=None)
plot_predictive(X_test, y, np.sqrt(y_var))
plt.ylim(-1.0, 2.0)
plt.legend()
# -
# Again, as the size of the dataset increases the posterior sample variance and the prediction uncertainty decreases. Also, regions with less observations have higher prediction uncertainty.
#
# ### Evidence evaluation
#
# As already mentioned, the evidence function or marginal likelihood can be used to compare models of different complexity using training data alone. This is shown here for 10 polynomial basis function models of different degree using a sinusoidal dataset generated with `g`. For evaluating the log marginal likelihood we implement $(18)$ as `log_marginal_likelihood` function.
def log_marginal_likelihood(Phi, t, alpha, beta):
"""Computes the log of the marginal likelihood."""
N, M = Phi.shape
m_N, _, S_N_inv = posterior(Phi, t, alpha, beta, return_inverse=True)
E_D = beta * np.sum((t - Phi.dot(m_N)) ** 2)
E_W = alpha * np.sum(m_N ** 2)
score = M * np.log(alpha) + \
N * np.log(beta) - \
E_D - \
E_W - \
np.log(np.linalg.det(S_N_inv)) - \
N * np.log(2 * np.pi)
return 0.5 * score
# The 10 polynomial basis function models of degrees 0-9 are compared based on the log marginal likelihood computed with a dataset of 10 observations. We still assume that the values of $\alpha$ and $\beta$ are known and will see in the next section how they can be inferred by maximizing the log marginal likelihood. When plotting the posterior predictive distribution of the polynomial models we can see that a model of degree 3 has already sufficient complexity to explain the data reasonably well.
# +
N = 10
beta = 1 / (0.3 ** 2)
alpha = 0.005
degree = 9
degrees = range(degree + 1)
X = np.linspace(0, 1, N).reshape(-1, 1)
t = g(X, noise_variance=1/beta)
Phi = expand(X, bf=polynomial_basis_function, bf_args=degrees[1:])
Phi_test = expand(X_test, bf=polynomial_basis_function, bf_args=degrees[1:])
plt.figure(figsize=(18, 8))
plt.subplots_adjust(hspace=0.4)
for d in degrees:
up = d + 1
m_N, S_N = posterior(Phi[:,:up], t, alpha, beta)
y, y_var = posterior_predictive(Phi_test[:,:up], m_N, S_N, beta)
plt.subplot(2, 5, up)
plot_data(X, t)
plot_truth(X_test, y_true, label=None)
plot_predictive(X_test, y, np.sqrt(y_var), y_label=None, std_label=None, plot_xy_labels=False)
plt.title(f'Degree = {d}')
plt.ylim(-1.0, 2.0)
# -
# We also see how polynomial models of higher degree do not overfit to the dataset which is a consequence of using a prior over model parameters that favors small(er) parameter values. This is equivalent to minimizing a sum-of-squares error function plus a quadratic regularization term whose strength is given by ratio $\alpha / \beta$ as can be seen from equation $(12)$.
#
# When evaluating the log marginal likelihood for all 10 polynomial models we usually obtain the highest value for models of degree 3 or 4 (depending on the non-deterministic part i.e. noise of the generated dataset results may vary slightly). This is consistent with the observation that a polynomial model of degree 3 already explains the data sufficiently well and confirms that marginal likelihood evaluation favors models of intermediate complexity.
# +
mlls = []
for d in degrees:
mll = log_marginal_likelihood(Phi[:,:d+1], t, alpha=alpha, beta=beta)
mlls.append(mll)
degree_max = np.argmax(mlls)
plt.plot(degrees, mlls)
plt.axvline(x=degree_max, ls='--', c='k', lw=1)
plt.xticks(range(0, 10))
plt.xlabel('Polynomial degree')
plt.ylabel('Log marginal likelihood');
# -
# It is also interesting to see that a polynomial model of degree 1 (straight line) seems to explain the data better than a model of degree 2. This is because the data-generating sinusoidal function has no even terms in a polynomial expansion. A model of degree 2 therefore only adds complexity without being able to explain the data better. This higher complexity is penalized by the evidence function (see also section 3.4. in [PRML](https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf)).
# ### Evidence maximization
# So far we have assumed that values of $\alpha$ and $\beta$ are known. In most situations however, they are unknown and must be inferred. Iterating over equations $(21)$ and $(22)$ until convergence jointly infers the posterior distribution over parameters $\mathbf{w}$ and optimal values for parameters $\alpha$ and $\beta$. This is implemented in the following `fit` function. We start with small values for $\alpha$ and $\beta$ corresponding to a low precision (= high variance) of prior $(8)$ and conditional density $(3)$.
def fit(Phi, t, alpha_0=1e-5, beta_0=1e-5, max_iter=200, rtol=1e-5, verbose=False):
"""
Jointly infers the posterior sufficient statistics and optimal values
for alpha and beta by maximizing the log marginal likelihood.
Args:
Phi: Design matrix (N x M).
t: Target value array (N x 1).
alpha_0: Initial value for alpha.
beta_0: Initial value for beta.
max_iter: Maximum number of iterations.
rtol: Convergence criterion.
Returns:
alpha, beta, posterior mean, posterior covariance.
"""
N, M = Phi.shape
eigenvalues_0 = np.linalg.eigvalsh(Phi.T.dot(Phi))
beta = beta_0
alpha = alpha_0
for i in range(max_iter):
beta_prev = beta
alpha_prev = alpha
eigenvalues = eigenvalues_0 * beta
m_N, S_N, S_N_inv = posterior(Phi, t, alpha, beta, return_inverse=True)
gamma = np.sum(eigenvalues / (eigenvalues + alpha))
alpha = gamma / np.sum(m_N ** 2)
beta_inv = 1 / (N - gamma) * np.sum((t - Phi.dot(m_N)) ** 2)
beta = 1 / beta_inv
if np.isclose(alpha_prev, alpha, rtol=rtol) and np.isclose(beta_prev, beta, rtol=rtol):
if verbose:
print(f'Convergence after {i + 1} iterations.')
return alpha, beta, m_N, S_N
if verbose:
print(f'Stopped after {max_iter} iterations.')
return alpha, beta, m_N, S_N
# We now generate a sinusoidal training dataset of size 30 with variance $\beta^{-1} = 0.3^2$ and then use `fit` to obtain the posterior over parameters $\mathbf{w}$ and optimal values for $\alpha$ and $\beta$. The used regression model is a polynomial model of degree 4.
# +
N = 30
degree = 4
X = np.linspace(0, 1, N).reshape(-1, 1)
t = g(X, noise_variance=0.3 ** 2)
Phi = expand(X, bf=polynomial_basis_function, bf_args=range(1, degree + 1))
alpha, beta, m_N, S_N = fit(Phi, t, rtol=1e-5, verbose=True)
# -
# Alternatively, we can also use [`BayesianRidge`](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.BayesianRidge.html#sklearn.linear_model.BayesianRidge) from scikit-learn for Bayesian regression. The `fit` and `predict` methods of this estimator are on the same abstraction level as our `fit` and `posterior_predictive` functions. The implementation of `BayesianRidge` is very similar to our implementation except that it uses [Gamma](https://en.wikipedia.org/wiki/Gamma_distribution) priors over parameters $\alpha$ and $\beta$. The default hyper-parameter values of the Gamma priors assign high probability density to low values for $\alpha$ and $\beta$. In our implementation, we simply start optimization from low $\alpha$ and $\beta$ values. Another difference is that `BayesianRidge` uses different parameter names (`lambda` instead of `alpha` and `alpha` instead of `beta`, see also section [Bayesian Regression](https://scikit-learn.org/stable/modules/linear_model.html#bayesian-regression) in the scikit-learn user guide).
# +
from sklearn.linear_model import BayesianRidge
br = BayesianRidge(fit_intercept=False, tol=1e-5, verbose=True)
br.fit(Phi, t.ravel());
# -
# When comparing the results from our implementation with those from `BayesianRidge` we see that they are almost identical. In the following, inferred values for $\alpha$, $\beta$ and $\mathbf{m}_N$ are compared as well as predictions and their uncertainties. Results prefixed with `np` are those from our implementation, results prefixed with `br` are those obtained with `BayesianRidge`.
print_comparison('Alpha', alpha, br.lambda_)
print_comparison('Beta', beta, br.alpha_)
print_comparison('Weights', m_N.ravel(), br.coef_)
# +
# Test values at x = 0.3 and x = 0.7
X_test = np.array([[0.3], [0.7]])
# Design matrix of test values
Phi_test = expand(X_test, bf=polynomial_basis_function, bf_args=range(1, degree + 1))
# +
y_np_mean, y_np_var = posterior_predictive(Phi_test, m_N, S_N, beta)
y_br_mean, y_br_std = br.predict(Phi_test, return_std=True)
print_comparison('Prediction mean', y_np_mean.ravel(), y_br_mean)
print_comparison('Prediction std', np.sqrt(y_np_var), y_br_std)
# -
# An alternative, non-parametric approach to Bayesian regression are [Gaussian processes](http://krasserm.github.io/2018/03/19/gaussian-processes/) which infer distributions over functions directly instead of distributions over parameters of parametric models.
| 49.718033 | 1,055 |
4ac09fe981e530d7978ef9ac7effbbcd77535ce2
|
py
|
python
|
TrOCR/Evaluating_TrOCR_base_handwritten_on_the_IAM_test_set.ipynb
|
FrancescoSaverioZuppichini/Transformers-Tutorials
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/NielsRogge/Transformers-Tutorials/blob/master/TrOCR/Evaluating_TrOCR_base_handwritten_on_the_IAM_test_set.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="d1XUD1uqY-s9"
# ## Set-up environment
# + colab={"base_uri": "https://localhost:8080/"} id="YjRj2_4gzpwj" outputId="a8c17ccc-6fdc-44da-fbb0-4ce955030e93"
# !pip install -q git+https://github.com/huggingface/transformers.git
# + colab={"base_uri": "https://localhost:8080/"} id="R9X9tUsZZEIj" outputId="e208b493-3d8d-4596-e1d9-4aea05382d0f"
# !pip install -q datasets jiwer
# + [markdown] id="cgDRKNsNZA7d"
# ## Load IAM test set
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="QVvvPQ6PY-Wc" outputId="f98a353c-fdf5-41c4-daaa-ee44d9191b43"
import pandas as pd
df = pd.read_fwf('/content/drive/MyDrive/TrOCR/Tutorial notebooks/IAM/gt_test.txt', header=None)
df.rename(columns={0: "file_name", 1: "text"}, inplace=True)
del df[2]
df.head()
# + id="Nkaki4CgZJNw"
import torch
from torch.utils.data import Dataset
from PIL import Image
class IAMDataset(Dataset):
def __init__(self, root_dir, df, processor, max_target_length=128):
self.root_dir = root_dir
self.df = df
self.processor = processor
self.max_target_length = max_target_length
def __len__(self):
return len(self.df)
def __getitem__(self, idx):
# get file name + text
file_name = self.df['file_name'][idx]
text = self.df['text'][idx]
# some file names end with jp instead of jpg, the two lines below fix this
if file_name.endswith('jp'):
file_name = file_name + 'g'
# prepare image (i.e. resize + normalize)
image = Image.open(self.root_dir + file_name).convert("RGB")
pixel_values = self.processor(image, return_tensors="pt").pixel_values
# add labels (input_ids) by encoding the text
labels = self.processor.tokenizer(text,
padding="max_length",
max_length=self.max_target_length).input_ids
# important: make sure that PAD tokens are ignored by the loss function
labels = [label if label != self.processor.tokenizer.pad_token_id else -100 for label in labels]
encoding = {"pixel_values": pixel_values.squeeze(), "labels": torch.tensor(labels)}
return encoding
# + colab={"base_uri": "https://localhost:8080/", "height": 209, "referenced_widgets": ["488499c892f74c9eb7e48ec582ca17ae", "b300a7c8d8a047ae8da6a69af97a7813", "a6eae4661eaa40fd919631592fcea16b", "28970d3aa1894be4a0dd6969316431ef", "53fb478232e64f4889d40609b9f81b1b", "c844398ff169497c81092abdc873f6a2", "64132312e0a24d2aba952e521077d594", "837707dad3114898a63c15246d2ed896", "6430a94abcf24fed8da539ffefb13249", "db2d1a6098d24e1d87cb4f4c072a19bf", "baea59899f974eb5ab78356b67df90f3", "ad6242795fe64ded9ee60126bf972675", "f36be5af33104c5698d98a4b89cb35de", "1b61a51ad5e142368824349772d4b635", "b0a3914efa2e4650801b90b19c5ac1ab", "7db19f54181f47b687d7c2d5bc1a596a", "6597145b824c4a82864c50a04b89d713", "04298c1b0e824d33b6b5c448a5847ccb", "4f7dcfd39539493e8b3e7ec3e40db951", "5bb2db90453a420aafbc10ccd36145a5", "bbc7a78dd0a04ca0844d036a3abdf255", "7a8d4aa6870647de80bab320e466ddf1", "377852bde266488eb21a3b7cf2aca896", "6c910ed9161248de97a2f2e03b21a3ac", "0e9dbc65643d41ed9a7ef67c83ee5e0c", "c18fbf9d23944664b9c259f6154a7fa3", "f64ff76bf34c444587e5992fc33741a4", "f0dbe9baf68c4e43a2c2ad6da56fb958", "ab6654f4fb264eb4bcda218e07c5db83", "02547b3e2d364fc8b64d72bc92f97ae5", "4dd6a595b7eb48ba92b5479c69c8d1fa", "8328eff6a54c4d93a92f4573942ceb62", "f68c7e31654d4e6f88136922e6eab0e1", "983a2ee3e052465f99f0c42ab2cf6d5c", "140cbba8556545728e4f62c09aa7cdb9", "99ed66d6be184eaea11c4031e86686a9", "63a25a8de7f945329d60830dabed7112", "e9ef0512fa524d0d9f85a4c3574ebd9c", "552a3d7d3f874c6692adb68df72e107b", "e6b4623a5dba4a5495d83b91495a0dc9", "9808f25943494d8db67008ed7d9d71f5", "177c3a7c3c1e458ca7ae5dbbb85f0f63", "fb729e0c38a648cfa685ffa31039a80e", "a3f50654569f4f288831aa3e1b02bede", "3b00234fb1154cd58b29e1d4666b4cee", "483ad434f0d8481891b5cac405deccfb", "06b43218ac324d6d84f69f952ae693a7", "f8df5ed6b1e842049007e54abf6b2ce1", "4e5b2f9182a14448840e1d620d7f7434", "b34e19e2cc2b4ccf8193e6e4e0d68067", "e64dfbf144874a878de17d0791caf257", "cfeb0f0142294214b08200782feec925", "b8d73f03adcc4f2887ef926e5120bf1e", "c3509d57440a431383daf75f5eb0c75e", "9ec23f41c6054624935fcd0a7f9888b8", "4f82c7b1891d419d85daf18236cc597d", "5f1792d3c5cb449a912dbf716393d49d", "967e87a88fc04fdcae111eae95cec8f2", "ee31285a798d4b09b926ca702e6fc2dc", "1365f93a6d4b49b88ceccc6140cb2b30", "ca8f404a91ec4590a141466094fac6ee", "8073453343e647858e3be97ce6b398c8", "b7b027ebd0ca4e35930bf134ffb28e81", "73392308ac1445cfbd2101518192718d", "96c015f61c054bfdbb24709f060e9d9f", "9453589171a74642b15299694ed5c99b"]} id="VrqEgBsfZMcQ" outputId="13c264a4-ac3c-48f2-a219-0a45da79ba2f"
from transformers import TrOCRProcessor
processor = TrOCRProcessor.from_pretrained("microsoft/trocr-base-handwritten")
test_dataset = IAMDataset(root_dir='/content/drive/MyDrive/TrOCR/Tutorial notebooks/IAM/image/',
df=df,
processor=processor)
# + id="VOJkQhi5ZY0G"
from torch.utils.data import DataLoader
test_dataloader = DataLoader(test_dataset, batch_size=8)
# + id="7GbLhiSFbU2I"
batch = next(iter(test_dataloader))
# + colab={"base_uri": "https://localhost:8080/"} id="EITtkq1jbWeH" outputId="b8cfbcf1-37eb-49a6-c624-b29062722903"
for k,v in batch.items():
print(k, v.shape)
# + id="gMeX_AbgbjXI"
from transformers import TrOCRProcessor
processor = TrOCRProcessor.from_pretrained("microsoft/trocr-base-handwritten")
# + colab={"base_uri": "https://localhost:8080/"} id="s0eQxa0FboIg" outputId="5758cf5b-3e13-4dbe-a5c6-e46f7c27cd1d"
labels = batch["labels"]
labels[labels == -100] = processor.tokenizer.pad_token_id
label_str = processor.batch_decode(labels, skip_special_tokens=True)
label_str
# + [markdown] id="gyiSWIC2ZTyz"
# ## Run evaluation
# + colab={"base_uri": "https://localhost:8080/", "height": 1000, "referenced_widgets": ["2b38285680f249628ea99d71f0eff981", "854b193e2bfd459cbbcf630167d9ee5d", "57148bede12243c0b922d0b8e164ad04", "2a48cc14c99b42c49b86c3b759465e81", "d111d758a3ac432c9c5457459ec5004a", "40517f82960a49dc936b3151267ac40c", "9282a32a33354b94ad0759f6bff047c1", "2ae1f8529f1c46b5846e6a43249af4c3", "201a71f718ab4db5bfec32c29837ffd6", "1a6bc189038f4931a7599cf7554198ba", "47ca17d8589345e894913b72401cc79b"]} id="LE05hoVsZSr4" outputId="81ed501c-db8a-4e90-b7e7-1b1837be752b"
from transformers import VisionEncoderDecoderModel
import torch
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = VisionEncoderDecoderModel.from_pretrained("microsoft/trocr-base-handwritten")
model.to(device)
# + colab={"base_uri": "https://localhost:8080/", "height": 49, "referenced_widgets": ["b1222610d58d4b89a1deb9c78d0f5bae", "a61d74718c5043599ef7d402d323b050", "ccae2e3e7bb3481eb47b888a70030a7b", "c912ba9f902c4881bcbaeac1760f83ad", "96ade02a835a41ba85d229db8c5c0232", "63fa4f364bbd4f8e9845b81cfcc90f18", "7e8934134bbd4fa2b424d72c9db3786a", "0fd43d8fb3e34d3f92d4432c38550507", "cd113c4350a441c49305d581cc62cf79", "c3df1876ea34446484fffe3d021eaa2e", "d703a7ee52fd4d0caaa44492b9b5e902"]} id="P18p8Uuta_SF" outputId="a14d209a-4af8-450e-bdab-a070f82fdb5f"
from datasets import load_metric
cer = load_metric("cer")
# + colab={"base_uri": "https://localhost:8080/", "height": 66, "referenced_widgets": ["87ffb62b41134a06998885cd128800a9", "394046b935e94f9babf73e1271010954", "35e4fdc52c9f4a2390e50b08574a37b2", "3cb20aadb83a4d8f9f6b74c16364f1e6", "34ff684f2f0544fcbb55888022bb10ed", "0804e8368df54e0a872a332fb28f68ac", "f1289b540d8246cf97fada4832868498", "0e8ef6540b66497ebf0e527bab062c99", "8ea56f18666e48c2a2cf32f971570815", "27320d4d78684749b2afe24359a0e5c0", "fb9812de0154406e94490519b70f252a"]} id="2XL-ECKyZXiH" outputId="06dc3320-e966-4777-8bfe-63d1c7cf15c7"
from tqdm.notebook import tqdm
print("Running evaluation...")
for batch in tqdm(test_dataloader):
# predict using generate
pixel_values = batch["pixel_values"].to(device)
outputs = model.generate(pixel_values)
# decode
pred_str = processor.batch_decode(outputs, skip_special_tokens=True)
labels = batch["labels"]
labels[labels == -100] = processor.tokenizer.pad_token_id
label_str = processor.batch_decode(labels, skip_special_tokens=True)
# add batch to metric
cer.add_batch(predictions=pred_str, references=label_str)
final_score = cer.compute()
# + colab={"base_uri": "https://localhost:8080/"} id="QEBVvSPRa7EE" outputId="2156136e-e9a5-47b4-a91b-8b801a36b5dd"
print("Character error rate on test set:", final_score)
# + id="YiJBtKxHeQLj"
| 61.986301 | 2,530 |
8f71a3b9d30febbafe2c719de9611fc7690dbf54
|
py
|
python
|
understanding-i3d.ipynb
|
song-william/kinetics-i3d
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Interpreting Video Classification Models
# William Song, Thomas Li, David Vendrow, Forest Hu
#
# A major deficiency of deep learning models is their inability to provide insight into the actual features learned. Indeed, after training, these models are typically used as nothing more than “black boxes.” From a research perspective, this approach limits our intuition for and understanding of the effectiveness of deep models. From an engineering perspective, developers risk deploying models that perform well in a controlled training environment but are actually fragile in the real world.
#
# In recent years, researchers have developed many techniques for providing some level of interpretability of the parameters and performance of deep models. One popular technique is visualization by optimization. As Professor Listgarten mentioned in lecture, this technique went viral in mainstream media in 2015 under the name “Google Deep Dream.” In short, visualization by optimization allows us to generate images by performing gradient ascent on an input image toward a target class (we formalize the optimization problem in a later section). These visualizations allow engineers and researchers to investigate whether the model has actually learned reasonable features of an object class. Below is a famous example of this technique in action from Google’s Research Blog [5].
#
# <img src="./images/deepdream_example1.png">
# <figcaption><center>From Google’s Research Blog [5]</center></figcaption>
#
# We can see that the model has captured the “essence” of the classes above to a reasonable degree. However, when the team at Google visualized “dumbbells,” they saw some unexpected results:
#
# <img src="./images/deepdream_example2.png">
# <figcaption><center>From Google’s Research Blog [5]</center></figcaption>
#
# From the visualizations, we see that the model has learned that dumbbells are always accompanied by a person holding or lifting them rather than just the dumbbell itself. This insight reveals that the model was likely trained only on dumbbells being lifted by people rather than dumbbells alone, demonstrating how one can use visualizations to catch faulty models.
#
# Another commonly used technique is creating saliency maps. These maps provide a visualization of the “impact” of each individual pixel on the final classification score. With this technique, engineers and researchers can gain insight on specific parts of an input that resulted in the classification.
#
# <img src="./images/saliency_example1.png">
# <figcaption><center>From Visualising Image Classification Models and Saliency Maps [2]</center></figcaption>
#
#
# In the image above, the brightness of each pixel is proportional to its “impact”. For example, we see that pixels with water are actually important when classifying a “sailboat.” While this could potentially be desired behavior (boats are typically in water), it also suggests that the model is weak at classifying boats that are out of water. For any service that utilizes machine learning, the capability to explain why a model made a particular decision on a particular input is vital. Later on, we will elaborate on the details on of how these maps are generated.
#
# **The goal of our project is to explore how these visualization techniques generalize to videos**. While all of these techniques have been thoroughly explored and developed with static image data, to our knowledge there are no published examples of these techniques performed on video data. Video data presents a set of new challenges that we attempt to overcome in this project. How much more computational power will we need? Will there be continuity between frames? How can we visualize an "action?" **Since the results are subjective and qualitative in nature, our project will be a “tutorial-like” walkthrough of the different regularization techniques we implemented and the corresponding results** (as opposed to a typical paper with accuracy measurements and graphs). We document each technique we use and provide sample GIFs of the outcomes.
#
# # I3D Models and The Kinetics Dataset
# The Kinetics dataset was created by the Google DeepMind team in 2017 to provide a way of training machine learning models made for video and action analysis and classification [6]. The Kinetics dataset contains 400 different classes with at least 400 different videos for each class broken up into approximately 250 videos for training, 100 videos for testing, and 50 videos for validation. The dataset primarily focuses on human action and is split into several classes with further hierarchical structure. The Person-Person class primarily focuses on interactions between groups of people, the Person class focuses on actions performed by a single person, and the Person-Object class captures human-object interaction. Within these classes, the Kinetics dataset is further split into parent-child classes. Each parent class has a label that groups its child classes together by similarity. An example is the cloths class with the following child classes: bandaging, doing laundry, folding clothes, folding napkins, ironing, making bed, tying bow tie, tying knot (not on a tie), tying tie.
#
# <img src="./images/juggling_soccerball.gif">
# <figcaption><center>Training Example Of "Juggling Soccer Ball"</center></figcaption>
#
# The kinetics dataset deals with the large issue of bias towards its actions [5]. The classification problem bias essentially splits itself into two categories: action bias and object bias. We define object bias as bias towards certain objects present in the training set for a feature, and we define action bias as bias towards a specific movement pattern in the training set for a feature. Objects provide a large crutch during action recognition for neural nets. In the kinetics dataset, certain classes exist with large object bias.
#
# Later on, we will see how this bias is revealed through our visualizations.
#
# For certain classes, the action classification problem reduces to an image classification problem over multiple frames. For example, classifying between the actions “playing cello”, “playing flute”, and “playing trumpet” is primarily a matter of discriminating between the instruments. This can be done with a single static frame from the video, and it doesn't rely on the relationship between frames. In our project, we attempted to stray away from these types of actions and focus on classes that required significant information from the temporal domain. For example, discriminating between "swimming backstroke”, “swimming breaststroke”, and “swimming butterfly” requires analyzing the specific movements, which occur over multiple frames.
#
# There have been several alternate approaches in the past that have attempted video classification. The preeminent approach simply took existing convolutional neural net architecture and applied it to video. Since the convolutional neural network only operates on images, the method of applying it involved stringing sequences of images together with an LSTM. Unfortunately, this approach failed to capture the temporal aspect of video.
#
# <img src="./images/I3D.png" width="200"/>
# <figcaption><center>Diagram of I3D [10]</center></figcaption>
#
# <table border="0">
# <tr>
# <tr>
# <td align="center" valign="center">
# <img src="./images/v_CricketShot_g04_c01_rgb.gif"/>
# <figcaption><center>Example RGB channel input (playing cricket)[9]</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/v_CricketShot_g04_c01_flow.gif"/>
# <figcaption><center>Example Optical Flow channel input (playing cricket)[9]</center></figcaption>
# </td>
# </tr>
# </table>
#
# In this project, we chose to implement the Inflated 3D ConvNet (or I3D, for short - diagrammed above), trained on the Kinetics dataset [10]. This neural net model differs from others in several ways. It begins by training two separate neural nets: an RGB 3D ConvNet, and an Optical Flow Net. To make a prediction, the model simply averages the results from both models. The motivation behind the two nets is that the 3D ConvNet captures RGB data well but does not explicitly capture the temporal aspect of videos. On the other hand, optical flow nets are inherently recurrent in nature which might aid in capturing the expression of temporal aspects of video.
# # Saliency Maps
# Saliency maps are a great tool for visualizing the impact of individual pixels on the final classification score outputted by the model. Before the final softmax layer, the model produces unnormalized logits for each class. We compute the gradient of the true class with respect to each individual pixel, and then visualize the magnitudes as a saliency map. Specifically, we first compute the absolute value of the gradient of each pixel in the input video. Then, we take the max across all 3 RGB color channels. We did not compute saliency maps of Optical Flow inputs as the inputs themselves already strongly resemble saliency maps.
#
# In the visualization of the saliency maps, we shade pixels brighter if they have high gradients and darker if they have low gradients. We constructed saliency maps for videos taken from the kinetics dataset in the specified time frame provided. Instead of taking the gradient with respect to an image, we tuned the original saliency map technique [8] for images to video by adding another dimension to our tensor, producing moving saliency map videos.
#
# <table border="0">
# <tr></tr>
# <tr>
# <td align="center" valign="center">
# <img src="./images/backstroke_saliency.gif">
# <figcaption><center>Swimmming Backstroke</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/juggling_saliency.gif">
# <figcaption><center>Juggling Soccer Ball</center></figcaption>
# </td>
# </tr>
#
# <tr>
# <td align="center" valign="center">
# <img src="./images/butterfly_saliency.gif">
# <figcaption><center>Swimming Butterfly Stroke</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/kicking_saliency.gif">
# <figcaption><center>Kicking Soccer Ball</center></figcaption>
# </td>
# </tr>
#
# <tr>
# <td align="center" valign="center">
# <img src="./images/breast_saliency.gif">
# <figcaption><center>Swimming Breast Stroke</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/eating_watermelon_saliency.gif">
# <figcaption><center>Eating Watermelon</center></figcaption>
# </td>
# </tr>
# </table>
#
# * In the backstroke saliency map, we notice that with the arm underwater, the model finds it hard to detect activity and remains dark. However, once the arm breaks the surface, the saliency map jumps in activity. Water doesn’t seem to be a large trigger point for backstroke, but rather the motion of the arms and position of the head and torso.
#
# * In butterfly, the dead giveaway seems to be the sweeping motion of the arms. When the swimmer breaks the surface, We can see in the saliency map the extremely high activation rates of the pixels corresponding to head, torso, and arm movements. This makes sense in line with the backstroke saliency map as after the swimmer breaks the surface and returns into an underwater streamlined position, the neural net seems to rest once more.
#
# * In the breaststroke video, The saliency map seems to respond extremely positively to the breaststroker once again after he emerges from the surface. It returns to lower levels once the breaststroker goes into underwater streamline. This also matches up with the butterfly and breaststroke saliency maps.
#
# * In the juggling soccer ball video, one of the main keys that the class looks for are signs of a soccer/football field. They track the yard lines very carefully and seem to respond better to the lines than to the person juggling the ball. However we can still see that the arms and legs provide lots of information, moreso than the head and torso as these limbs give more information in regards to movement patterns than the torso and head which stay in place.
#
# * In kicking soccer balls, we see high activation rates once again with lines across a field. The cones trace the line and activate the neurons heavily. We note that the actual ball seems to have somewhat low activation rates once the first soccer player exits the frame of view. Once the second soccer player enters however, the ball seems to regain activation energy once again. We note that the limbs of the soccer players have very high activation energy.
#
# * In the watermelon video, we note that the watermelon and the boy’s hand seem to have the highest activation energy. The motion doesn’t seem to matter as much in this video as the activation energy closely follows the watermelon slice.
#
# Reader - please notice the following two things. In most of these videos, the network is very responsive to humans. This aligns with the fact that all the kinetics training videos exhibit people performing actions. Hence, it would make sense that the network is sensitive to areas containing humans. The second is that object consistency plays an important role in the neural network’s ability to identify objects. We hypothesize that the more standardized an object is, the easier it is for the neural network to classify it.
# # Visualization by Optimization
# To visualize a class, we start with a random noise video input and then perform gradient ascent toward a target class. However, naively attempting this will result in adversarial inputs [4]. One must employ several regularization techniques to generate videos that resemble the desired class. Problems that we anticipated with video visulization were computational intensity, continuity between frames, and succesful "motion visualization." On the point of "motion visualization," we suspect that many visualizations will simply reveal objects that are tightly related to the action class rather than any perceivable motion.
#
# We formalize the problem in a similiar fashion as [3]. Without loss of generailty, let us consider only the RBG input (the optical flow formalization only differs from RGB in dimension values). Let $x \in R^{NxHxWxC}$ be a RGB video where $N$ is the number of frames, $H$ and $W$ are the height and width respectively, and $C$ is the number of the color channels. For the i3d model, $H=W=224$, $C=3$, and $N=25$. The number of frames can be arbitrarily long or short for visualization, but we chose 25 as that is the frame input length at test time for the I3D model. A large $N$ can result in high computation costs, while a small $N$ results in visualizations that are limited in expressing motion.
#
# Now, let $y$ be the target class. Let $s_y(x)$ be the logits (scores before the final softmax layer) that the i3d model assigns to the image $x$ for class $y$. Our goal we can now frame our objective as the folowing optimization problem:
#
# $$
# x^* = \arg\max_x s_y(x) - R_\theta(x)
# $$
#
# where $R_\theta$ is a paramaterized regularization function that regularizes images both explicitly and implicitly. Since the regularizer function can be very complex (as described below) and no closed-form solution exists, we resort to solving this optimization problem with gradient ascent. We compute gradients of $s_y(x)$ with respect to the generated video $x$.
#
# Our primary explicit regualization is L2 regularization of the form
#
# $$
# R_\theta(x) = \lambda \|x\|_2^2
# $$
#
# and our primary implicit regularization (as implemented in [3]) is performed by periodically blurring the generated image with a gaussian filter. These two intial regularizing operations were good enough to create baseline results (as we will see), but additional operations are also used and listed below:
# 1. Jitter - randomly displace pixels up to $\theta$ pixels away between iterations
# 2. Scale - scale the video and then crop to the original dimensions after $\theta$ iterations
# 3. Time blur - gaussian blur across frames
# 4. Clipping - clip pixels that fall out of a certain range
# # Regualization Techniques for Optimization
# This section will walk through the effect of the different regularization techniques we employed and their effect on generated images.
#
# Each visualization is a GIF with 25 frames. All of the following visualizations were produced on an Nvidia GeForce GTX 1080. Running 1000 iterations of feature optimizations takes about 330 seconds on a 1080. Unfortunately, we found these visualizations are nearly intractable on a CPU. With a 3.1 GHz Intel Core i5, one iteration already takes about 60 seconds. If one wants to run 1000 iterations that will be a runtime of $\frac{1000 * 65}{60*60} = 18.1$ hours! For comparison, optimizing an image (such as in Deep Dream) takes about 15 minutes on GoogLeNet [7]. We recommend anyone who wants to attempt these visualizations to use a GPU.
#
# We initialize a random noise video where every pixel is independently sampled from a uniform distribution $U[0,1]$. First we implemented a regularizer function with L2-Regularization, Gaussian Blurring and Jittering. Surprisingly, with just these techniques, the results already began to resemble the target action class. Can you guess what the class below resembles? Hint: Do you see hands?
#
# <img src="./images/arm_wrestle_discontinous.gif">
#
# The class is “arm wrestling.” As anticipated, the video drastically shifts between frames. However, the “form” of the several hands clasped together does seem to persist across frames. Mainly, the wild fluctuation of colors seem to be the main cause of creating discontinuity. To mitigate this, we first changed our noise initialization so that every frame had the same starting point. Specifically, we randomly initialized one frame in the same manner as before, but we then inflated that single frame to be $N=25$ frames so that each frame has the same starting seed. Unfortunately, this produced no perceivable difference. Afterward we attempted “time blurring,” where periodically use a gaussian blur across frames to mimic “motion blur” and to better promote time continuity.
#
# <img src="./images/arm_wrestling_smooth.gif">
# <figcaption><center>Arm Wrestling</center></figcaption>
#
# Now, we see that “arm wrestling” has a much smoother transition between frames. However, we can still observe any reasonable amount of “motion.” However, it seems more like objects “dissolving” in and out of the noise rather than true movement. At this point, we visualized many other classes in an attempt so see if we can find a visualization that properly captures motion.
#
# <table border="0">
# <tr></tr>
# <tr>
# <td align="center" valign="center">
# <img src="./images/archery-Copy1.gif">
# <figcaption><center>Archery</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/dribbling_basketball-Copy1.gif">
# <figcaption><center>Dribbling Basketball</center></figcaption>
# </td>
# </tr>
#
# <tr>
# <td align="center" valign="center">
# <img src="./images/eating_watermelon1000_iterations-Copy1.gif">
# <figcaption><center>Eating Watermelon</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/playing_cello-Copy1.gif">
# <figcaption><center>Playing Cello</center></figcaption>
# </td>
# </tr>
#
# <tr>
# <td align="center" valign="center">
# <img src="./images/juggling_soccer_ball-Copy1.gif">
# <figcaption><center>Juggling Soccer Ball</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/kicking_soccer_ball-Copy1.gif">
# <figcaption><center>Kicking Soccer Ball</center></figcaption>
# </td>
# </tr>
#
# </table>
#
# Unfortunately, it seems that all our visualizations seems to only create objects that “dissolve” in and out of the frames. In “archery” one can see a bow as well as targets fade in and out. For “eating watermelon” one only sees static watermelons scattered around the GIF. In "dribbling basketball" we only see basketballs and rims. We chose the bottom two action classes, “kicking soccer ball” and “juggling soccer ball”, specifically because they can only be differentiated by their motion rather than solely by their objects. Yet, we see no perceivable difference “in action” between the two visualizations; only soccer balls appear with some stray legs and feet.
#
# At this point, we notice that the GIFs appear to be dark (lots of regions of black) and also seem to have some concentrated white spots scattered around. RGB values take on a value of [0, 1], where 0 corresponds to 0% intensity and 1 corresponds to 100% intensity. A tuple of (1, 1, 1) results in a white pixel while a tuple of (0, 0, 0) results in a black pixel. When we investigated the RGB values of our generated images, we found that many of the pixels had negative RGB values or had RGB values greater than one. These would then be clipped when visualized as a GIF (negative values go to 0 and values greater than 1 go to one). Thus, many iterations were wasted on producing unperceivable changes and much of the gradients were concentrated on pixels that were already well out of the RGB range. To fix this, we simply made sure to clip our generated input at every iteration so that we never exceed the [0,1] range.
#
# <table border="0">
# <tr></tr>
# <tr>
# <td align="center" valign="center">
# <img src="./images/archery_rgb-Copy1.gif">
# <figcaption><center>Archery</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/arm_wrestling_rgb-Copy1.gif">
# <figcaption><center>Arm Wrestling</center></figcaption>
# </td>
# </tr>
#
# <tr>
# <td align="center" valign="center">
# <img src="./images/swimming_breast_stroke_rgb.gif">
# <figcaption><center>Swimming Breast Stroke</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/swimming_butterfly_stroke_rgb.gif">
# <figcaption><center>Swimming Butterfly Stroke</center></figcaption>
# </td>
# </tr>
#
# <tr>
# <td align="center" valign="center">
# <img src="./images/juggling_soccer_ball_rgb-Copy1.gif">
# <figcaption><center>Juggling Soccer Ball</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/kicking_soccer_ball_rgb-Copy1.gif">
# <figcaption><center>Kicking Soccer Ball</center></figcaption>
# </td>
# </tr>
# </table>
#
# Now, we can finally see some motion in some visualizations. With “juggling soccer ball,” in the top right corner we see the ball actually move up and down with a human-like figure behind it. In “kicking soccer ball,” we can see a human approach the ball from the side. In “swimming butterfly stroke,” we see arms raise upwards in the butterfly formation. In “swimming breast stroke,” we see arms out to the sides, heads raising upward “out of the water,” and then finally dipping downward at the end.
#
# Lastly, we present a few other techniques we attempted that did not give significantly better results. One can potentially tune and explore the hyperparameters to give better results. We also attempted to visualize Optical Flow.
#
# <table border="0">
# <tr></tr>
# <tr>
# <td align="center" valign="center">
# <img src="./images/arm_wrestlingscaling_rgb-Copy1.gif">
# <figcaption><center>Arm Wrestling with Scaling</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/arm_wrestlingcascading_sigma_2_rgb-Copy1.gif">
# <figcaption><center>Arm Wrestling with Adjusted Blurring</center></figcaption>
# </td>
# </tr>
#
# <tr>
# <td align="center" valign="center">
# <img src="./images/juggling_soccer_balltest_flow-Copy1.gif">
# <figcaption><center>Juggling Soccer Ball Optical Flow</center></figcaption>
# </td>
#
# <td align="center" valign="center">
# <img src="./images/kicking_soccer_balltest_flow-Copy1.gif">
# <figcaption><center>Kicking Soccer Ball Optical Flow</center></figcaption>
# </td>
# </tr>
#
# </table>
#
# We scaled the images at certain intervals (as suggested by [7]) to give us larger structures and more details. We found that while this did scale a central structure better, it reduced the diversity of having multiple interpretable structures appear in the image.
#
# We also adjusted our gaussian blurring so that we blurred more intensely in earlier iterations and reduced the blurring intensity periodically (as suggested by [1]). This successfully dampened the static and brought out true colors better (such as human skin tone) but resulted in less detail.
#
# Lastly, our attempts to visualize Optical Flow (with all of the same regularization techniques mentioned previously) failed to produce any interpretable results.
# # Observations On the I3D Model
# While speculative, we provide some possible hypothesis about this model based on the visualizations. The main takeaway seems to be that the net performs object recognition primarily to distinguish classes rather than relying on human motion. Taking the class “eating watermelon” as a prime example, both the saliency maps and the class visualization seem to track the watermelon object itself and ignore the human aspect of moving a watermelon towards the mouth. The absolute only way to get the neural net to produce motion would be to observe classes that were extremely similar in the sense that they contained the same objects, and could only be differentiated in the sequence of motion in the temporal domain. Our two primary examples of this, swimming and manipulating a soccer ball, support this claim heavily. Further research in the area could try possibly removing object consistency among classes to isolate human actions, i.e., “dribbling” with various balls instead of just a basketball to try and capture human movement, or even get rid of objects entirely, i.e., “airplaying” instruments.
#
# We also want to refer back to bias, but this time in the sense of recording motion. Swimming provides a great example of bias. One of the sources of bias in recording action is the frame of reference. When recorded professionally, the window of recording varies wildly among different strokes. When observed from the point of view facing the direction the swimmer is headed, we cannot see a freestyler’s or backstroker’s face, but we can clearly see a breaststroker's or butterflyer’s face. In fact, you will rarely see shots of freestyle or backstroke from the front, but shots of butterfly and breaststroke from the front are very common. Likewise, aerial shots of breaststroke are extremely awkward, since there is almost no visible movement from an overhead perspective, but aerial shots of butterfly capture the entire sweeping motion of the arm, making aerial recordings of the latter stroke much more common. These frames of reference play large roles in motion detection, as one plane might contain lots of motion, while another plane might contain very little. Therefore, it is critical to consider the context of an action to note what frames of reference might appear more often than others in data collection, as videos are projections of three dimensional movement. Further experimentation could include recording motion from a multitude of directions to get a more holistic view of an action during training or even interpolate actual 3D data instead of using 2D projections. We speculate eliminating these biases may result in stronger models that identify motion more accurately.
# # Conclusion
# Techniques to interpret image classifaction models generalize very well to video classification models. With saliency maps, we were able to produce video results with little modification from the image domain. We then walked through some sample examples to reveal what the I3D model looks for in inputs. Visualization by optimization required some more regularization techniques to get "action" to appear in the generated output. We showed the iterative process on which reguarlization techniques worked best and which ones failed. With these visualizations, we then performed an analysis on how the model learned to distinguish between classes. In particular, we noted how the model was forced to learn more distinct "actions" for closely related classes ("swimming backstroke" vs "swimming butterfly stroke") as opposed to classes with unique objects or characteristics ("archery").
#
# All the code used for this project is provided below. The hyperparameters that we used for this writeup are already coded into the cells. We suggest people play around with the parameters to potentially create even better visualizations.
# # Citations
#
# [1] C. Olah, A. Mordvintsev, L. Schubert. Feature Visualization, https://distill.pub/2017/feature-visualization/, doi:10.23915/distill.00007
#
# [2] K. Simonyan, A. Vedaldi, A. Zisserman. Deep Inside Convolutional Networks: Visualising
# Image Classification Models and Saliency Maps, ICLR Workshop 2014.
#
# [3] Yosinski et al, Understanding Neural Networks Through Deep Visualization, ICML 2015 Deep Learning Workshop
#
# [4] I. Goodfellow et al. Attacking Machine Learning with Adversarial Examples, https://blog.openai.com/adversarial-example-research/
#
# [5] A. Mordvintsev, C. Olah, M. Tyka. Inceptionism: Going Deeper into Neural Networks, Google Research Blog
#
# [6] Will Kay et al. The Kinetics Human Action Video Dataset, Google Deepmind
#
# [7] A. M. Øygard. Visualizing GoogLeNet Classes, https://www.auduno.com/2015/07/29/visualizing-googlenet-classes/, 2015
#
# [8] Stanford. CS231n: Convolutional Neural Networks for Visual Recognition. http://cs231n.stanford.edu/2017/, 2017
#
# [9] J. Carreira, A. Zisserman. I3D models trained on Kinetics (2017), Github Repository, https://github.com/deepmind/kinetics-i3d
#
# [10] J. Carreira and A. Zisserman, "Quo Vadis, Action Recognition? A New Model and the Kinetics Dataset," 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, 2017, pp. 4724-4733.
# doi: 10.1109/CVPR.2017.502
# # Code Appendix
# The code below is adapted from CS231N [8] as well as from Deepmind's I3D Github Repository [9]. Make sure to clone from the I3D repo and put this notebook inside of it (I3D should already be downloaded in gradescope submission).
#
# Python Package requirements:
# 1. numpy
# 2. tensorflow-gpu
# 3. dm-sonnet
# 4. imageio
#
# +
"""
Some setup.
Installations are the same for the i3d model, which can be found here: https://github.com/deepmind/kinetics-i3d
Make sure i3d.py is in the same directory as this notebook.
"""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import os
import imageio
# simply selects which gpu to use
# these lines may very depending on hardware
os.environ["CUDA_DEVICE_ORDER"]="PCI_BUS_ID"
os.environ["CUDA_VISIBLE_DEVICES"]="0"
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import time
import scipy.ndimage as nd
import i3d
from tensorflow.python.client import device_lib
print(device_lib.list_local_devices()) # prints available devices
# -
# # Building the I3D Graph
# Here we build the I3D graph as well as intialize the trained model
# +
"""
Build Joint Stream Graph (from i3d.py)
"""
_IMAGE_SIZE = 224
_NUM_CLASSES = 400
_SAMPLE_VIDEO_FRAMES = 25
_SAMPLE_PATHS = {
'rgb': 'data/v_CricketShot_g04_c01_rgb.npy',
'flow': 'data/v_CricketShot_g04_c01_flow.npy',
}
_CHECKPOINT_PATHS = {
'rgb': 'data/checkpoints/rgb_scratch/model.ckpt',
'flow': 'data/checkpoints/flow_scratch/model.ckpt',
'rgb_imagenet': 'data/checkpoints/rgb_imagenet/model.ckpt',
'flow_imagenet': 'data/checkpoints/flow_imagenet/model.ckpt',
}
_LABEL_MAP_PATH = 'data/label_map.txt'
imagenet_pretrained = True # use pretrained model as it had better performance
eval_type = "joint" # build the graph for both streams
tf.reset_default_graph() # reset graph each time cell is run, prevents duplicate variables
if eval_type not in ['rgb', 'flow', 'joint']:
raise ValueError('Bad `eval_type`, must be one of rgb, flow, joint')
kinetics_classes = [x.strip() for x in open(_LABEL_MAP_PATH)]
if eval_type in ['rgb', 'joint']:
# RGB input has 3 channels.
rgb_input = tf.placeholder(
tf.float32,
shape=(1, None, _IMAGE_SIZE, _IMAGE_SIZE, 3))
with tf.variable_scope('RGB'):
rgb_model = i3d.InceptionI3d(
_NUM_CLASSES, spatial_squeeze=True, final_endpoint='Logits')
rgb_logits, _ = rgb_model(
rgb_input, is_training=False, dropout_keep_prob=1.0)
rgb_variable_map = {}
for variable in tf.global_variables():
if variable.name.split('/')[0] == 'RGB':
rgb_variable_map[variable.name.replace(':0', '')] = variable
rgb_saver = tf.train.Saver(var_list=rgb_variable_map, reshape=True)
if eval_type in ['flow', 'joint']:
# Flow input has only 2 channels.
flow_input = tf.placeholder(
tf.float32,
shape=(1, None, _IMAGE_SIZE, _IMAGE_SIZE, 2))
with tf.variable_scope('Flow'):
flow_model = i3d.InceptionI3d(
_NUM_CLASSES, spatial_squeeze=True, final_endpoint='Logits')
flow_logits, _ = flow_model(
flow_input, is_training=False, dropout_keep_prob=1.0)
flow_variable_map = {}
for variable in tf.global_variables():
if variable.name.split('/')[0] == 'Flow':
flow_variable_map[variable.name.replace(':0', '')] = variable
flow_saver = tf.train.Saver(var_list=flow_variable_map, reshape=True)
if eval_type == 'rgb':
model_logits = rgb_logits
elif eval_type == 'flow':
model_logits = flow_logits
else:
model_logits = rgb_logits + flow_logits
model_predictions = tf.nn.softmax(model_logits)
# -
# We now run the sample inputs from I3D. Represented again below for reference.
"""
Run sample (playing cricket) prediction with joint model
"""
eval_type = "joint"
with tf.Session() as sess:
feed_dict = {}
if eval_type in ['rgb', 'joint']:
if imagenet_pretrained:
rgb_saver.restore(sess, _CHECKPOINT_PATHS['rgb_imagenet'])
else:
rgb_saver.restore(sess, _CHECKPOINT_PATHS['rgb'])
tf.logging.info('RGB checkpoint restored')
rgb_sample = np.load(_SAMPLE_PATHS['rgb'])
print("RGB size:", rgb_sample.shape)
tf.logging.info('RGB data loaded, shape=%s', str(rgb_sample.shape))
feed_dict[rgb_input] = rgb_sample
if eval_type in ['flow', 'joint']:
if imagenet_pretrained:
flow_saver.restore(sess, _CHECKPOINT_PATHS['flow_imagenet'])
else:
flow_saver.restore(sess, _CHECKPOINT_PATHS['flow'])
tf.logging.info('Flow checkpoint restored')
flow_sample = np.load(_SAMPLE_PATHS['flow'])
print("flow size:", flow_sample.shape)
tf.logging.info('Flow data loaded, shape=%s',
str(flow_sample.shape))
feed_dict[flow_input] = flow_sample
# print("feed_dict", feed_dict)
out_logits, out_predictions = sess.run(
[model_logits, model_predictions],
feed_dict=feed_dict)
out_logits = out_logits[0]
out_predictions = out_predictions[0]
sorted_indices = np.argsort(out_predictions)[::-1]
print('Norm of logits: %f' % np.linalg.norm(out_logits))
print('\nTop classes and probabilities')
for index in sorted_indices[:20]:
print(out_predictions[index], out_logits[
index], kinetics_classes[index])
# # Visualization by Optimization
# First we define some helper funtions in the cell below:
# +
"""
Define some helper functions
"""
from scipy.ndimage.filters import gaussian_filter1d
# blurs image in spatial and time domain
def blur_image(X, sigma=1):
X = gaussian_filter1d(X, sigma, axis=1)
X = gaussian_filter1d(X, sigma, axis=2)
X = gaussian_filter1d(X, sigma, axis=3)
return X
# transforms flow input into a form that can be visualize
def create_flow_image(X):
return np.append(X + 0.5, 0.5 * np.ones((224, 224, 1)), axis=2)
# saves final video/frames and saves a .gif file
def save_gif(X, class_name, stream_type):
# save all frames
num_frames = X.shape[1]
directory = "experiments_{}/{}/".format(stream_type, class_name)
if not os.path.exists(directory):
os.makedirs(directory)
image_name = "{}_{}".format(class_name, stream_type)
file_name = directory + image_name + "{}.png"
print("file_name", file_name)
filenames = []
for i in range(0, num_frames):
if stream_type == "rgb":
plt.imshow(X[0][i])
elif stream_type == "flow":
plt.imshow(create_flow_image(X[0][i]))
filename = file_name.format(i)
filenames.append(filename)
plt.savefig(filename.format(i))
#create gif
images = []
for filename in filenames:
images.append(imageio.imread(filename))
imageio.mimsave(directory + "/{}".format(image_name) + ".gif", images)
# returns a decreasing sigma value for gaussian blurring
def calc_sigma(curr, total, sigma):
if curr > .75*total:
return sigma
elif curr > .5*total:
return .75*sigma
elif curr > .25*total:
return .5*sigma
else:
return .25*sigma
#crops center of video after scaling
def crop_center(img, cropx, cropy):
y, x, channels = img.shape
startx = x//2-(cropx//2)
starty = y//2-(cropy//2)
return img[starty:starty+cropy, startx:startx+cropx, :]
# performs scaling and cropping of video
def scale_and_crop(X, scale=1.2):
start = time.time()
_, frames, cropx, cropy, channels = X.shape
for i in range(frames):
Y = X[0][i]
Y = nd.zoom(Y, (scale, scale, 1))
Y = crop_center(Y, cropx, cropy)
X[0][i] = Y
# -
# Here we define the main funtion to create the visualizations. Here the default parameters were the ones we used to create the RGB visualizations. Periodically we display the first frame of each GIF. The final GIF is saved in the corresponding directory and can be viewed in a browser window.
"""
Define our main method to create visualizations.
The default parameters are the ones we found to produce the best results for RBG
"""
def create_class_visualization(sess, rgb_input, flow_input, target_y, logits, class_name, **kwargs):
"""
Keyword arguments:
- l2_reg: Strength of L2 regularization on the image
- learning_rate: How big of a step to take
- num_iterations: How many iterations to use
- blur_every: How often to blur the image as an implicit regularizer
- max_jitter: How much to gjitter the image as an implicit regularizer
- show_every: How often to show the intermediate result
- num_frames: How many frames in output
- stream_type: RGB stream of Optical Flow Stream
- sigma: radius of gaussian blur filter, may decrease with number of iterations if desired
- scale_every: How often to scale image
- scale: ratio of scaling
"""
print("params", kwargs)
l2_reg = kwargs.pop('l2_reg', 1e-3)
learning_rate = kwargs.pop('learning_rate', 1.5)
num_iterations = kwargs.pop('num_iterations', 1000)
blur_every = kwargs.pop('blur_every', 3)
max_jitter = kwargs.pop('max_jitter', 32)
show_every = kwargs.pop('show_every', 25)
num_frames = kwargs.pop('num_frames', 25)
stream_type = kwargs.pop('stream_type', 'rgb')
sigma_start = kwargs.pop('sigma', 1)
scale_every = kwargs.pop('scale_every', 250)
scale_ratio = kwargs.pop('scale', 1.2)
if stream_type == 'rgb':
stream_input = rgb_input
X = np.random.rand(1, 224, 224, 3) * np.ones((num_frames, 224, 224, 3))
X = X[None]
elif stream_type == 'flow':
stream_input = flow_input
X = np.random.rand(1, 224, 224, 2) * np.ones((num_frames, 224, 224, 2))
# preprocessing flow as described in paper
X = X - .5
X = X[None]
X = flow_sample
loss = logits[0, target_y] # scalar loss
grad = tf.gradients(loss, stream_input) # compute gradient
grad = tf.squeeze(grad) - l2_reg*2*stream_input # regualarlize gradient
start_time = time.time()
for t in range(num_iterations):
# Randomly jitter the image a bit; this gives slightly nicer results
ox, oy = np.random.randint(-max_jitter, max_jitter+1, 2)
Xi = X.copy()
X = np.roll(np.roll(X, ox, 1), oy, 2)
# we want logits for loss
loss = logits[0, target_y] # scalar loss
# model.image is just the data matrix input (a gif in our case)
gradient_step = sess.run(grad, feed_dict={stream_input:X})
X += learning_rate * gradient_step
# Undo the jitter
X = np.roll(np.roll(X, -ox, 1), -oy, 2)
# As a regularizer, clip and periodically blur
if stream_type == 'flow':
X = np.clip(X, -0.5, 0.5)
elif stream_type == 'rgb':
X = np.clip(X, 0, 1)
if t % blur_every == 0 or t == num_iterations - 1:
# sigma = calc_sigma(t, num_iterations, sigma_start) # this line allows for decreasing blurring
X = blur_image(X, sigma=sigma_start)
# scale and crop image
if t % scale_every == 0:
scale_and_crop(X)
# Periodically show the image
if t == 0 or (t + 1) % show_every == 0 or t == num_iterations - 1:
print("iteration:", t, time.time()-start_time)
if stream_type == "rgb":
plt.imshow(X[0][0])
elif stream_type == "flow":
plt.imshow(create_flow_image(X[0][0]))
if t == num_iterations-1:
save_gif(X, class_name, stream_type)
plt.title('{}_{}\nIteration {} / {}'.format(class_name, stream_type, t + 1, num_iterations))
plt.gcf().set_size_inches(4, 4)
plt.axis('off')
plt.show()
return X
# The cell below is used to generate RGB Visualizations. The current hyperparameters were used to generate the RGB visualizations. If one desires to visulize a different class, there is a map of all indexes to classes a couple cells below
"""
Run RGB visualization only
Make sure graph is built in previous cell before running this cell
"""
os.environ["CUDA_VISIBLE_DEVICES"] = "0" # this line may vary depending on hardware
print(model_logits)
print(rgb_input)
target = 6 # change this to the desired class
print(kinetics_classes[target])
action_name = kinetics_classes[target].replace(" ", "_")
with tf.device("/gpu:0"):
with tf.Session() as sess:
rgb_saver.restore(sess, _CHECKPOINT_PATHS['rgb_imagenet'])
# number of frames must be >= 9 or else kernel crashes due to gradient being too small
rgb_visual_gif = create_class_visualization(sess, rgb_input, flow_input, target, rgb_logits, action_name + "_test",
stream_type='rgb', scale_every=1000, show_every=200)
# The cell below is used to generate all Optical Flow Visualizations. The hyperparameters inputted below were the ones we found to be best, but we were unable to ever create any good Optical Flow results that were interpretable.
"""
Run FLOW visualization only.
Make sure graph is built in previous cell before running this cell
"""
os.environ["CUDA_VISIBLE_DEVICES"] = "0" # this line may vary depending on hardware
print(model_logits)
print(flow_input)
target = 171
print(kinetics_classes[target])
action_name = kinetics_classes[target].replace(" ", "_")
with tf.device("/gpu:0"):
with tf.Session() as sess:
# THIS LINE NEEDS TO BE MOVED
flow_saver.restore(sess, _CHECKPOINT_PATHS['flow_imagenet'])
flow_visual_gif = create_class_visualization(sess, rgb_input, flow_input, target, flow_logits,
action_name + "_test", stream_type='flow', num_frames=25,
num_iterations=1000, l2_reg=1e-2, learning_rate=1.5,
blur_every=10, max_jitter=32, sigma=.5, show_every=200)
"""
Displays all action classes so users can pick one they like.
"""
indexes = range(len(kinetics_classes))
class_to_index = dict(zip(kinetics_classes, indexes))
index_to_class = dict(zip(indexes, kinetics_classes))
print(index_to_class)
# # Saleincy Maps Code
# Below we now provide the code for creating the saliency maps. The code here currently produces a saleincy for the sample input provided by Deepmind. To create your own inputs, one will need to convert video clips into the .npy format. We suggest using skvideo (http://www.scikit-video.org/stable/io.html).
"""
Compute saliency map
"""
print(model_logits)
print(rgb_input)
with tf.device("/gpu:0"):
with tf.Session() as sess:
rgb_saver.restore(sess, _CHECKPOINT_PATHS['rgb_imagenet'])
dX = tf.gradients(model_logits[0, sorted_indices[0]], rgb_input)
absolute = tf.abs(dX)
maxes = tf.reduce_max(absolute, axis=5)
squeezed = tf.squeeze(maxes)
# change rgb_input to compute new saliency map
saliency = sess.run(squeezed, feed_dict={rgb_input:rgb_sample}) # this runs on sample cricket gif from i3d README
# +
"""
Create/Save saliency map in desired directory. Save indvidual frames to directory and then converts it to a GIF.
"""
directory = "./saliency/"
if not os.path.exists(directory):
os.makedirs(directory)
name = directory + "cricket_saliency{}.png"
filenames = []
for i in range(79):
plt.imshow(saliency[i], cmap=plt.cm.hot)
# plt.show()
filename = name.format(i)
filenames.append(filename)
plt.savefig(name.format(i))
import imageio
images = []
for filename in filenames:
images.append(imageio.imread(filename))
imageio.mimsave('./saliency/cricket_saliency.gif', images)
| 59.404172 | 1,598 |
2f74e3a2be60793f53b7fbe7792f5cf5e05003aa
|
py
|
python
|
Sesion_08_AlgoritmosProbabilistas.ipynb
|
carlosalvarezh/Analisis-de-Algoritmos
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# <h1 align="center">ANÁLISIS DE ALGORITMOS</h1>
#
# <h1 align="center">Sesión08: Algoritmos probabilistas</h1>
#
# <h1 align="center">MEDELLÍN - COLOMBIA </h1>
#
# <h1 align="center">2021 </h1>
# -
# <table>
# <tr align=left><td><img align=left src="https://github.com/carlosalvarezh/Analisis_de_Algoritmos/blob/master/images/CC-BY.png?raw=true">
# <td>Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved MIT license.(c) Carlos Alberto Alvarez Henao</td>
# </table>
# ***
#
# ***Docente:*** Carlos Alberto Álvarez Henao, I.C. D.Sc.
#
# ***e-mail:*** [email protected]
#
# ***skype:*** carlos.alberto.alvarez.henao
#
# ***Linkedin:*** https://www.linkedin.com/in/carlosalvarez5/
#
# ***github:*** https://github.com/carlosalvarezh/Metodos_Numericos
#
# ***Herramienta:*** [Jupyter](http://jupyter.org/)
#
# ***Kernel:*** Python 3.8
#
#
# ***
# https://medium.com/towards-artificial-intelligence/monte-carlo-simulation-an-in-depth-tutorial-with-python-bcf6eb7856c8
#
# https://medium.com/free-code-camp/randomized-algorithms-part-1-d89986bb685b
#
# https://medium.com/search?q=monte%20carlo
#
# https://towardsdatascience.com/the-house-always-wins-monte-carlo-simulation-eb82787da2a3
#
# https://medium.com/free-code-camp/solve-the-unsolvable-with-monte-carlo-methods-294de03c80cd
#
# https://towardsdatascience.com/an-overview-of-monte-carlo-methods-675384eb1694
#
# https://towardsdatascience.com/monte-carlo-simulations-with-python-part-1-f5627b7d60b0
# + [markdown] slideshow={"slide_type": "slide"}
# <a id='TOC'></a>
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Introducción" data-toc-modified-id="Introducción-1"><span class="toc-item-num">1 </span>Introducción</a></span><ul class="toc-item"><li><span><a href="#Una-historia-sobre-un-tesoro,-un-dragón,-un-computador,-un-elfo-y-un-doblón." data-toc-modified-id="Una-historia-sobre-un-tesoro,-un-dragón,-un-computador,-un-elfo-y-un-doblón.-1.1"><span class="toc-item-num">1.1 </span>Una historia sobre un tesoro, un dragón, un computador, un elfo y un doblón.</a></span></li><li><span><a href="#¿Qué-hemos-aprendido?" data-toc-modified-id="¿Qué-hemos-aprendido?-1.2"><span class="toc-item-num">1.2 </span>¿Qué hemos aprendido?</a></span></li><li><span><a href="#Característica-fundamental-de-un-algoritmo-probabilista:" data-toc-modified-id="Característica-fundamental-de-un-algoritmo-probabilista:-1.3"><span class="toc-item-num">1.3 </span>Característica fundamental de un algoritmo probabilista:</a></span></li><li><span><a href="#Diferencias-entre-algoritmos-deterministas,-análisis-probabilista-de-algoritmos-y-algoritmos-aleatorios" data-toc-modified-id="Diferencias-entre-algoritmos-deterministas,-análisis-probabilista-de-algoritmos-y-algoritmos-aleatorios-1.4"><span class="toc-item-num">1.4 </span>Diferencias entre algoritmos deterministas, análisis probabilista de algoritmos y algoritmos aleatorios</a></span><ul class="toc-item"><li><span><a href="#Algoritmos-deterministas" data-toc-modified-id="Algoritmos-deterministas-1.4.1"><span class="toc-item-num">1.4.1 </span>Algoritmos deterministas</a></span></li><li><span><a href="#Análisis-probababilista-de-algoritmos" data-toc-modified-id="Análisis-probababilista-de-algoritmos-1.4.2"><span class="toc-item-num">1.4.2 </span>Análisis probababilista de algoritmos</a></span></li></ul></li><li><span><a href="#Un-comentario-sobre-“el-azar”-y-“la-incertidumbre”:" data-toc-modified-id="Un-comentario-sobre-“el-azar”-y-“la-incertidumbre”:-1.5"><span class="toc-item-num">1.5 </span>Un comentario sobre “el azar” y “la incertidumbre”:</a></span></li><li><span><a href="#Ejemplo-de-comportamiento-de-los-distintos-tipos-ante-un-mismo-problema" data-toc-modified-id="Ejemplo-de-comportamiento-de-los-distintos-tipos-ante-un-mismo-problema-1.6"><span class="toc-item-num">1.6 </span>Ejemplo de comportamiento de los distintos tipos ante un mismo problema</a></span></li></ul></li><li><span><a href="#Algoritmos-probabilistas-numéricos" data-toc-modified-id="Algoritmos-probabilistas-numéricos-2"><span class="toc-item-num">2 </span>Algoritmos probabilistas numéricos</a></span><ul class="toc-item"><li><span><a href="#Estimación-aproximada-de-$\pi$:" data-toc-modified-id="Estimación-aproximada-de-$\pi$:-2.1"><span class="toc-item-num">2.1 </span>Estimación aproximada de $\pi$:</a></span></li><li><span><a href="#Integración-probabilista" data-toc-modified-id="Integración-probabilista-2.2"><span class="toc-item-num">2.2 </span>Integración probabilista</a></span></li><li><span><a href="#Análisis-de-la-convergencia:" data-toc-modified-id="Análisis-de-la-convergencia:-2.3"><span class="toc-item-num">2.3 </span>Análisis de la convergencia:</a></span></li><li><span><a href="#Algoritmos-de-Monte-Carlo" data-toc-modified-id="Algoritmos-de-Monte-Carlo-2.4"><span class="toc-item-num">2.4 </span>Algoritmos de Monte Carlo</a></span></li></ul></li><li><span><a href="#Ejemplos-y-desafíos" data-toc-modified-id="Ejemplos-y-desafíos-3"><span class="toc-item-num">3 </span>Ejemplos y desafíos</a></span><ul class="toc-item"><li><span><a href="#Verificación-de-un-producto-matricial" data-toc-modified-id="Verificación-de-un-producto-matricial-3.1"><span class="toc-item-num">3.1 </span>Verificación de un producto matricial</a></span></li><li><span><a href="#¿Podemos-hacerlo-más-rápido?" data-toc-modified-id="¿Podemos-hacerlo-más-rápido?-3.2"><span class="toc-item-num">3.2 </span>¿Podemos hacerlo más rápido?</a></span></li><li><span><a href="#Comprobación-de-primalidad." data-toc-modified-id="Comprobación-de-primalidad.-3.3"><span class="toc-item-num">3.3 </span>Comprobación de primalidad.</a></span></li><li><span><a href="#Cuántos-Primos-están-en-P" data-toc-modified-id="Cuántos-Primos-están-en-P-3.4"><span class="toc-item-num">3.4 </span>Cuántos Primos están en P</a></span></li><li><span><a href="#Clave-pública-y-primalidad" data-toc-modified-id="Clave-pública-y-primalidad-3.5"><span class="toc-item-num">3.5 </span>Clave pública y primalidad</a></span></li></ul></li></ul></div>
# -
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Analisis_de_Algoritmos/blob/master/images/Random.PNG?raw=true" width="500" />
# </p>
#
https://medium.com/free-code-camp/randomized-algorithms-part-1-d89986bb685b
# + [markdown] slideshow={"slide_type": "slide"}
# ## Introducción
# -
# Los algoritmos aleatorios o probabilistas (*randomized algorithms*) son muy importantes en el campo de la informática teórica, así como en las aplicaciones del mundo real. Para muchos problemas, para obtener una respuesta determinista, una función que siempre devuelve la misma respuesta dada la misma entrada es computacionalmente costosa y no se puede resolver en tiempo polinomial.
#
# Cuando introducimos algo de aleatoriedad junto con la entrada, esperamos tener una complejidad de tiempo más eficiente. O esperamos tener una proporción de la solución óptima con un buen límite superior en el número de iteraciones que se necesitarán para obtener esa solución.
#
# Estos algoritmos son a menudo triviales de idear. Pero es mucho más complejo analizar y probar el tiempo de ejecución / corrección. Vale la pena señalar que existe una diferencia entre el análisis probabilístico y el análisis de algoritmos aleatorios. En el análisis probabilístico le damos al algoritmo una entrada que se supone que proviene de una distribución de probabilidad. Mientras que en el algoritmo aleatorio agregamos un número aleatorio a la entrada. Las siguientes imágenes deberían mostrar la distinción. Las imágenes son de diapositivas de conferencias de Stanford.
# ### Una historia sobre un tesoro, un dragón, un computador, un elfo y un doblón.
# + [markdown] slideshow={"slide_type": "subslide"}
# En $A$ o $B$ hay un tesoro de $x$ lingotes de oro pero no sé si está en $A$ o $B$. Un dragón visita cada noche el tesoro llevándose $y$ lingotes. Sé que si permanezco $4$ días más en $O$ con mi computador resolveré el misterio. Un elfo me ofrece un trato: Me da la solución ahora si le pago el equivalente a la cantidad que se llevaría el dragón en $3$ noches.
#
# ***¿Qué debo hacer?***
# + [markdown] slideshow={"slide_type": "subslide"}
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Analisis_de_Algoritmos/blob/master/images/Isla01.png?raw=true" width="100" />
# </p>
#
# + [markdown] slideshow={"slide_type": "subslide"}
# - Si me quedo $4$ días más en $O$ hasta resolver el misterio, podré llegar al tesoro en $9$ días, y obtener $x-9y$ lingotes.
#
#
# - Si acepto el trato con el elfo, llego al tesoro en $5$ días, encuentro allí $x-5y$ lingotes de los cuales debo pagar $3y$ al elfo, y obtengo $x-8y$ lingotes.
#
# Es mejor aceptar el trato pero…
#
# … ¡hay una solución mejor!
#
# # ¿Cuál?
#
# ¡Usar el doblón que me queda en el bolsillo! Lo lanzo al aire para decidir a qué lugar voy primero ($A$ o $B$).
#
# - Si acierto a ir en primer lugar al sitio adecuado, obtengo $x-5y$ lingotes.
#
#
# - Si no acierto, voy al otro sitio después y me conformo con $x-10y$ lingotes.
#
#
# El beneficio medio esperado es $x-7.5y$
# -
# [Volver a la Tabla de Contenido](#TOC)
# ### ¿Qué hemos aprendido?
# + [markdown] slideshow={"slide_type": "slide"}
# - En algunos algoritmos en los que aparece una decisión, es preferible a veces elegir aleatoriamente antes que perder tiempo calculando qué alternativa es la mejor.
#
#
# - Esto ocurre si el tiempo requerido para determinar la elección óptima es demasiado frente al promedio obtenido tomando la decisión al azar.
# -
# [Volver a la Tabla de Contenido](#TOC)
# ### Característica fundamental de un algoritmo probabilista:
# + [markdown] slideshow={"slide_type": "subslide"}
# - el mismo algoritmo puede comportarse de distinta forma aplicado a los mismos datos
# -
# [Volver a la Tabla de Contenido](#TOC)
# ### Diferencias entre algoritmos deterministas, análisis probabilista de algoritmos y algoritmos aleatorios
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Analisis_de_Algoritmos/blob/master/images/DeterministicAlgorithms.PNG?raw=true" width="500" />
# </p>
#
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Analisis_de_Algoritmos/blob/master/images/ProbabilisticAnalisysAlgorithms.PNG?raw=true" width="500" />
# </p>
#
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Analisis_de_Algoritmos/blob/master/images/RandomizedAlgorithms013.PNG?raw=true" width="500" />
# </p>
#
# http://theory.stanford.edu/people/pragh/amstalk.pdf
# #### Algoritmos deterministas
# + [markdown] slideshow={"slide_type": "subslide"}
# El objetivo en el análisis de los algoritmos deterministas es demostrar que el algoritmo resuelve el problema correctamente (siempre) y rápidamente (por lo general, el número de pasos debe ser polinomial en el tamaño de la entrada).
#
# A un algoritmo determinista nunca se le permite que no termine: hacer una división por $0$, entrar en un bucle infinito, etc. Si existe más de una solución para unos datos dados, un algoritmo determinista siempre encuentra la misma solución (a no ser que se programe para encontrar varias o todas). No se le permite que calcule una solución incorrecta para ningún dato.
#
# El análisis de la eficiencia de un algoritmo determinista es, a veces, difícil.
#
# -
# [Volver a la Tabla de Contenido](#TOC)
# #### Análisis probababilista de algoritmos
# + [markdown] slideshow={"slide_type": "subslide"}
# En los algoritmos probabilistas se asume que los datos de entrada provienen de una distribución de probabilidad. A un algoritmo probabilista se le puede permitir equivocarse, siempre que eso ocurra con una probabiliad muy pequeña para datos cualesquiera. Si ocurre, se aborta el algoritmo y se repite su ejecución con los mismos datos de entrada. Repitiendo la ejecución un número suficiente de veces para el mismo dato, puede aumentarse tanto como se quiera el grado de confianza en obtener la solución correcta. Un algoritmo probabilista puede encontrar soluciones diferentes ejecutándose varias veces con los mismos datos.
#
# El análisis de los algoritmos probabilistas es, a menudo, muy difícil.
# -
# [Volver a la Tabla de Contenido](#TOC)
# ### Un comentario sobre “el azar” y “la incertidumbre”:
# + [markdown] slideshow={"slide_type": "slide"}
# Como se indicó arriba, a un algoritmo probabilista se le puede permitir calcular una solución equivocada, con una probabilidad pequeña. Un algoritmo determinista que tarde mucho tiempo en obtener la solución puede sufrir errores provocados por fallos del hardware y obtener una solución equivocada. Es decir, el algoritmo determinista tampoco garantiza siempre la certeza de la solución y además es más lento.
#
# Más aún, hay problemas para los que no se conoce ningún algoritmo (determinista ni probabilista) que dé la solución con certeza y en un tiempo razonable (por ejemplo, la duración de la vida del programador, o de la vida del universo…): Es mejor un algoritmo probabilista rápido que dé la solución correcta con una cierta probabilidad de error.
#
#
# ***Ejemplo:*** decidir si un # de $1000$ cifras es primo
# + [markdown] slideshow={"slide_type": "slide"}
# <p float="center">
# <img src="https://github.com/carlosalvarezh/Analisis_de_Algoritmos/blob/master/images/Algoritmos_Probabilistas_01.png?raw=true" width="350" />
# </p>
#
# -
# [Volver a la Tabla de Contenido](#TOC)
# ### Ejemplo de comportamiento de los distintos tipos ante un mismo problema
# + [markdown] slideshow={"slide_type": "subslide"}
# “¿*Cuándo descubrió América Cristobal Colón*?”
#
#
# - Algoritmo numérico ejecutado cinco veces:
#
# - “Entre 1490 y 1500.”
# - “Entre 1485 y 1495.”
# - “Entre 1491 y 1501.”
# - “Entre 1480 y 1490.”
# - “Entre 1489 y 1499.”
#
# Aparentemente, la probabilidad de dar un intervalo erroneo es del $20\%$ ($1$ de cada $5$). Dando más tiempo a la ejecución se podría reducir esa probabilidad o reducir la anchura del intervalo (a menos de $11$ años).
# + [markdown] slideshow={"slide_type": "subslide"}
# - Algoritmo de *Monte Carlo* ejecutado diez veces:
#
# $1492$, $1492$, $1492$, $1491$, $1492$, $1492$, $357 \text{A.C.}$, $1492$, $1492$, $1492$.
#
# De nuevo un $20\%$ de error. Ese porcentaje puede reducirse dando más tiempo para la ejecución. Las respuestas incorrectas pueden ser próximas a la correcta o completamente desviadas.
# + [markdown] slideshow={"slide_type": "subslide"}
# - Algoritmo de Las Vegas ejecutado diez veces:
#
# $1492$, $1492$, $\text{¡Perdón!}$, $1492$, $1492$, $1492$, $1492$, $1492$, $\text{¡Perdón!}$, $1492$.
#
# El algoritmo nunca da una respuesta incorrecta. El algoritmo falla con una cierta probabilidad ($20\%$ en este caso).
# -
# [Volver a la Tabla de Contenido](#TOC)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Algoritmos probabilistas numéricos
#
# + [markdown] slideshow={"slide_type": "subslide"}
# Primeros en aparecer: SGM (Stochastic Galerkin Method), clave “Monte Carlo”
#
#
# Un ejemplo ya conocido:
#
# - Simulación de un sistema de espera (cola)
#
# - Estimar el tiempo medio de espera en el sistema.
#
# - En muchos casos la solución exacta no es posible.
#
#
# - La solución obtenida es siempre aproximada pero su precisión esperada mejora aumentando el tiempo de ejecución.
#
#
# - Normalmente, el error es inversamente proporcional a la raíz cuadrada del esfuerzo invertido en el cálculo
#
# - Se necesita cien veces más de trabajo para obtener una cifra más de precisión.
# -
# [Volver a la Tabla de Contenido](#TOC)
# ### Estimación aproximada de $\pi$:
# + [markdown] slideshow={"slide_type": "subslide"}
# Tiramos $n$ dardos sobre un cuadrado y contamos el número $k$ de los que caen en un círculo de radio unitario inscrito en el cuadrado.
#
# ¿Cuál es la proporción media de dardos en el interior del círculo?:
#
# - Área del cuadrado: $A_{cuadrado}=r^2$
#
# - Área del Sector: $A_{sector}=\frac{1}{4}\pi r^2$
#
# dividiendo el área del círculo por el área del sector, se tiene: $\frac{A_{sector}}{A_{cuadrado}}=\frac{\pi r^2}{4 r^2}=\frac{\pi}{4}$
#
# Si realizamos la división del número total de puntos que tenemos dentro del círculo respecto al número total de puntos que se han señalado en toda la área del cuadrado, tendremos una aproximación del valor de $\pi$.
#
# $$\frac{\text{puntos dentro del círculo}}{\text{puntos totales}}=\frac{k}{n}\approx \frac{\pi}{4}$$
# + slideshow={"slide_type": "subslide"}
# Ejemplo: Aproximando el valor de pi - área de un círculo de
# radio = 1.
import matplotlib.pyplot as plt
import numpy as np
def mc_pi_aprox(N=10):
plt.figure(figsize=(8,8)) # tamaño de la figura
x, y = np.random.uniform(-1, 1, size=(2, N))
interior = (x**2 + y**2) <= 1
pi = interior.sum() * 4 / N
error = abs((pi - np.pi) / pi) * 100
exterior = np.invert(interior)
plt.plot(x[interior], y[interior], 'b.')
plt.plot(x[exterior], y[exterior], 'r.')
plt.plot(0, 0, label='$\hat \pi$ = {:4.4f}\nerror = {:4.4f}%'
.format(pi,error), alpha=0)
plt.axis('square')
plt.legend(frameon=True, framealpha=0.9, fontsize=16)
mc_pi_aprox()
# -
# [Volver a la Tabla de Contenido](#TOC)
# ### Integración probabilista
# + [markdown] slideshow={"slide_type": "slide"}
# ***Problema:*** Calcular $\int_a^b f(x)dx$, donde $f(x)$ es una función continua y $a\leq b$.
#
# Un posible algoritmo puede ser:
# + slideshow={"slide_type": "subslide"} active=""
# función int_prob(f:función;n:entero; a,b:real)
# devuelve real
# {Algoritmo probabilista que estima la integral definida entre a y b generando n valores aleatorios xi en [a,b), haciendo la media de los f(xi) multiplicando el resultado por (b-a).
# Se utiliza la función uniforme(u,v) que genera un número pseudo-aleatorio uniformemente distribuido en [u,v).}
#
# variables suma,x:real; i:entero
#
# principio
# suma:=0.0;
# para i:=1 hasta n hacer:
# x:=uniforme(a,b);
# suma:=suma+f(x)
# fin para;
# devuelve (b-a)*(suma/n)
# fin
# + slideshow={"slide_type": "subslide"}
def integral_prob(n, a, b):
sumap = 0
for i in range(n):
x = np.random.uniform(a,b)
sumap += f(x)
return (b-a)*sumap/n
# + slideshow={"slide_type": "subslide"}
def f(x):
return 4*(1-x**2)**0.5
#return x**3-5
# + slideshow={"slide_type": "subslide"} active=""
# Versión determinista:
#
# función int_det(f:función;n:entero; a,b:real)
# devuelve real
#
# principio
# suma:=0.0;
# delta = (b-a)/n
# x = a + delta/2
# para i:=1 hasta n hacer:
# suma:=suma+f(x)
# x:=x+delta;
# fpara;
# devuelve suma * delta
# fin
# + slideshow={"slide_type": "subslide"}
def integral_det(n, a, b):
sumad = 0
delta = (b-a)/n
x = a + delta/2
for i in range(n):
sumad += f(x)
x = x + delta
return sumad * delta
# + slideshow={"slide_type": "subslide"}
import numpy as np
n = 100
a = 0
b = 1
integralprob = integral_prob(n,a,b)
print("Valor integral método probabilista", integralprob)
errorp = np.abs(np.pi-integralprob)/np.pi
print("error prob.: ", errorp)
integraldet = integral_det(n,a,b)
print("Valor integral método determinista",integraldet)
errordet = np.abs(np.pi-integraldet)/np.pi
print("error determ.: ", errordet)
# -
# [Volver a la Tabla de Contenido](#TOC)
# ### Análisis de la convergencia:
# + [markdown] slideshow={"slide_type": "subslide"}
# - La varianza del estimador calculado por la función anterior es inversamente proporcional al número n de muestras generadas y que la distribución del estimador es aproximadamente normal, cuando $n$ es grande.
#
#
# - Por tanto, el error esperado es inversamente proporcional a $\sqrt{n}$.
#
# - 100 veces más de trabajo para obtener una cifra más de precisión
#
# - En general, la versión determinista es más eficiente (menos iteraciones para obtener precisión similar).
#
#
# - Pero, para todo algoritmo determinista de integración puede construirse una función que “lo vuelve loco” (no así para la versión probabilista).
#
#
# - Por ejemplo, para $f(x)=sin^2(10! \pi x)$ toda llamada a `int_det(n,0,1)` con $1 \leq n \leq 100$ devuelve $0$, aunque el valor exacto es $0.5$.
# + slideshow={"slide_type": "subslide"}
def f(x):
return np.sin(3628800*np.pi*x)**2
# + slideshow={"slide_type": "subslide"}
n = 100
a = 0
b = 1
integralprob = integral_prob(n,a,b)
print("Valor integral método probabilista", integralprob)
errorp = np.abs(0.5-integralprob)/0.5
print("error prob.: ", errorp)
integraldet = integral_det(n,a,b)
print("Valor integral método determinista",integraldet)
errordet = np.abs(0.5-integraldet)/0.5
print("error determ.: ", errordet)
# + [markdown] slideshow={"slide_type": "subslide"}
# - Otra ventaja: cálculo de integrales múltiples.
#
#
# - *Algoritmos deterministas:* para mantener la precisión, el coste crece exponencialmente con la dimensión del espacio.
#
# - En la práctica, se usan algoritmos probabilistas para dimensión $4$ o mayor.
#
# - Existen técnicas híbridas (parcialmente sistemáticas y parcialmente probabilistas): *integración cuasi-probabilista*.
# -
# [Volver a la Tabla de Contenido](#TOC)
# + [markdown] slideshow={"slide_type": "slide"}
# ### Algoritmos de Monte Carlo
# + [markdown] slideshow={"slide_type": "subslide"}
# Se usan para problemas que necesitan una respuesta, como problemas de decisión.
#
# - No se está seguro que la respuesta obtenido sea la correcta: obtienen la respuesta correcta con una determinada probabilidad.
#
#
# - Cuanto más tiempo se dedica a la ejecución, más probable es encontrar la respuesta correcta.
#
#
# - Para una probabilidad $0< \text{p} < 1$, un $\text{algoritmo de MonteCarlo}$ se dice *$\text{p-correcto}$* si propociona soluciones correctas con una probabilidad no inferior a $p$.
#
# La característica más importante del método de MonteCarlos es que suele ser posible reducir arbitrariamente la probabilidad de error a costa de un ligero aumento del tiempo de cálculo (*amplificación de la ventaja estocástica*)
# + [markdown] slideshow={"slide_type": "subslide"}
# El $\text{algoritmo de MonteCarlo}$ Crudo o Puro está fundamentado en la generación de números aleatorios por el método de *Transformación Inversa*, el cual se basa en las distribuciones acumuladas de frecuencias:
#
# Determinar la/s V.A. y sus distribuciones acumuladas(F)
#
# - Generar un número aleatorio uniforme $\in [0,1)$.
#
#
# - Determinar el valor de la V.A. para el número aleatorio generado de acuerdo a las clases que tengamos.
#
#
# - Calcular media, desviación estándar error y realizar el histograma.
#
#
# - Analizar resultados para distintos tamaños de muestra.
# + [markdown] slideshow={"slide_type": "subslide"}
# Otra opción para trabajar con Monte Carlo, cuando la variable aleatoria no es directamente el resultado de la simulación o tenemos relaciones entre variables es la siguiente:
#
# - Diseñar el modelo lógico de decisión
#
#
# - Especificar distribuciones de probabilidad para las variables aleatorias relevantes.
#
#
# - Incluir posibles dependencias entre variables.
#
#
# - Muestrear valores de las variables aleatorias.
#
#
# - Calcular el resultado del modelo según los valores del muestreo (iteración) y registrar el resultado.
#
#
# - Repetir el proceso hasta tener una muestra estadísticamente representativa
#
#
# - Obtener la distribución de frecuencias del resultado de las iteraciones
#
#
# - Calcular media, desvío.
#
#
# - Analizar los resultados
# + [markdown] slideshow={"slide_type": "subslide"}
# Las principales características a tener en cuenta para la implementación o utilización del algoritmo son:
#
#
# - El sistema debe ser descrito por 1 o más funciones de distribución de probabilidad (fdp)
#
#
# - Generador de números aleatorios: como se generan los números aleatorios es importante para evitar que se produzca correlación entre los valores muestrales.
#
#
# - Establecer límites y reglas de muestreo para las fdp: conocemos que valores pueden adoptar las variables.
#
#
# - Definir Scoring: Cuando un valor aleatorio tiene o no sentido para el modelo a simular.
#
#
# - Estimación Error: Con que error trabajamos, cuanto error podemos aceptar para que una corrida sea válida?
#
#
# - Técnicas de reducción de varianza.
#
#
# - Paralelización y vectorización: En aplicaciones con muchas variables se estudia trabajar con varios procesadores paralelos para realizar la simulación.
# -
# [Volver a la Tabla de Contenido](#TOC)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Ejemplos y desafíos
# -
# ### Verificación de un producto matricial
# + [markdown] slideshow={"slide_type": "subslide"}
# Problema: Dadas tres matrices $n\times n$, $\text{A, B, C}$, verificar si $\text{C=AB}$
#
# ***Solución trivial:*** hacer la multiplicación.
#
# - Algoritmo directo: coste $\mathcal{O}(n^3)$.
# - Algoritmo de *Strassen* (Divide y vencerás): $\mathcal{O}(n^{2.81})$.
# - Otros menos prácticos: $\mathcal{O}(n^{2.373})$.
# -
# [Volver a la Tabla de Contenido](#TOC)
# ### ¿Podemos hacerlo más rápido?
# [R. Freivalds: “Fast probabilistic algorithms”, Proceedings of the 8th Symposium on the Mathematical Foundations of Computer Science, Lecture Notes in Computer Science, vol. 74, Springer-Verlag, 1979.](https://link.springer.com/chapter/10.1007/3-540-09526-8_5 "Fast probabilistic algorithms")
# [Volver a la Tabla de Contenido](#TOC)
# ### Comprobación de primalidad.
# + [markdown] slideshow={"slide_type": "subslide"}
# - Es el algoritmo de Monte Carlo más conocido: decidir si un número impar es primo o compuesto.
#
#
# - Ningún algoritmos determinista conocido puede responder en tiempo 'razonable' si el número es 'grande'
#
#
# - La utilización de números primos 'grandes' es fundamental en criptografía
# -
# [Volver a la Tabla de Contenido](#TOC)
# ### Cuántos Primos están en P
# En $2002$ se publicó el *AKS primality test* (test de primalidad de *Agrawal–Kayal–Saxena*)
#
# - Es el primer test de primalidad que es general, tiempo polinómico, determinista e incondicional
#
#
# - Pero sigue siendo cierto que no se conocen algoritmos deterministas en tiempo razonable, ya que hoy en día la mejor cota conocida (mejora del *AKS*) es $\mathcal{O}(n^6)$ (donde $n$ es el número de bits)
# [Volver a la Tabla de Contenido](#TOC)
# ### Clave pública y primalidad
# Los primos son fundamentales en criptografía
#
# - ***Ejemplo:*** El protocolo de clave pública RSA permite codificar mensajes usando la clave pública y decodificar usando la clave privada (y firmar usando la clave privada y verificar usando la clave pública)
#
#
# - La seguridad del sistema RSA está (en parte) basada en que no es posible factorizar números grandes en tiempo razonable
#
#
# - Factorizar parece bastante más difícil que testear primalidad
# + [markdown] slideshow={"slide_type": "subslide"}
# [Volver a la Tabla de Contenido](#TOC)
# -
| 44.579208 | 4,716 |
92bbe491e115a36464df8145c9424e91b1aad458
|
py
|
python
|
notebook-projects/Diabetes - Linear Regression.ipynb
|
philip-papasavvas/ml_sandbox
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Introduction" data-toc-modified-id="Introduction-1">Introduction</a></span></li><li><span><a href="#Exploratory-Data-Analysis" data-toc-modified-id="Exploratory-Data-Analysis-2">Exploratory Data Analysis</a></span><ul class="toc-item"><li><span><a href="#Visualise-the-data" data-toc-modified-id="Visualise-the-data-2.1">Visualise the data</a></span></li></ul></li><li><span><a href="#Supervised-learning" data-toc-modified-id="Supervised-learning-3">Supervised learning</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Split-the-data-into-training-and-test-set" data-toc-modified-id="Split-the-data-into-training-and-test-set-3.0.1">Split the data into training and test set</a></span></li><li><span><a href="#Fit-the-model" data-toc-modified-id="Fit-the-model-3.0.2">Fit the model</a></span></li><li><span><a href="#Side-note:-intuition-of-the-model" data-toc-modified-id="Side-note:-intuition-of-the-model-3.0.3">Side note: intuition of the model</a></span></li></ul></li><li><span><a href="#Fitting-the-model" data-toc-modified-id="Fitting-the-model-3.1">Fitting the model</a></span><ul class="toc-item"><li><span><a href="#Issues-with-plotting" data-toc-modified-id="Issues-with-plotting-3.1.1">Issues with plotting</a></span></li></ul></li><li><span><a href="#Extra:-verify-the-results-of-the-model" data-toc-modified-id="Extra:-verify-the-results-of-the-model-3.2">Extra: verify the results of the model</a></span></li></ul></li></ul></div>
# -
# # Introduction
# I will explore the diabetes dataset from scikit-learn and see if we can apply any machine learning algorithms on the dataset. My aim is to be exposed to a range of different datasets from different sources and evaluate the merit in applying machine learning to these datasets.
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets, linear_model
from sklearn.model_selection import train_test_split
# %matplotlib inline
plt.style.use('ggplot')
# -
# # Exploratory Data Analysis
# We will look at the data initially to examine it and look at the input features, and the target variable.
# Following this we should be in a better position to carry out some Machine Learning algorithm on the data, and evaluate its merit after doing so.
# +
diabetes_data = datasets.load_diabetes()
diabetes_data.keys()
# -
print(diabetes_data['DESCR'])
# We have already been told that the features have been scaled (normalised and standardised), therefore there is no need to feature scale this data.
features_df = pd.DataFrame(
data=diabetes_data['data'],
columns=diabetes_data['feature_names'])
target = diabetes_data['target']
features_df.head()
# ## Visualise the data
# Before undertaking an machine learning project, it helps to visualise the target values, to get an intuition for the type of data we are looking at.
plt.figure(figsize=(15,12))
plt.plot(target)
plt.ylabel("Target Variable")
plt.xlabel("Observation Number")
# This line plot above isn't too intuitive about the nature of the data. It might be more helpful to plot a histogram to get an idea of the distribution of the data.
plt.hist(target)
# # Supervised learning
# Since we have both the input data and the response variables, my first port of call would be to look at supervised learning, and see if we can fit a model to the data, to best predict whether or not the model works.
# ### Split the data into training and test set
# In order to train a model we must split the dataset into a training set (train the model using this), and a test set (on which we can verify the accuracy of the model).
# Therefore, as a rule we will use 80% of the data for training, and the other 20% for testing.
#
# We will use the *train_test_split* method of *scikit-learn*, which ensures that the data is split randomly, to remove any bias that might exist in the ordering, and the split the sample into the training and testing set.
X, y = diabetes_data['data'], diabetes_data['target']
# a, b = datasets.load_diabetes(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
test_size=0.3,
random_state=10) # the random state will ensure we sample the same ones each time the notebook is run
X_train.shape
# So, we can see that we have 309 of the original observations in our training set, and complementing this will be the 309 response variables for those original observations.
# ### Fit the model
# Now we will fit the model to the training set using linear regression.
# +
# create the linear regression model
reg = linear_model.LinearRegression()
# train the model on the training sets defined earlier
reg.fit(X_train, y_train)
# -
# We can look at what the coefficients in our linear regression model are:
reg.coef_
# So, the model looks roughly like: \
# \begin{equation}
# response = 16.4 - 224 \cdot x_{1} + 539 \cdot x_{2} + 274 \cdot x_{3} + ...
# \end{equation}
# for $x_{1}$ as age, $x_2$ as sex, $x_3$ as body mass index.
# Now we have trained the model using the test set, we want to test how good the model is at predicting the response variable, and we will do this using the test set.
# ### Side note: intuition of the model
# Let's go into some detail about what the model is actually doing, and will do to predict the values of y in the test set.
# From above, we see that the model has fitted certain values for the coefficients of each feature (from **reg.coef_**).
# Define our hypothesis function with the parameter $\Theta$, where
# \begin{align}
# \Theta &= \begin{bmatrix}
# \theta_{0} \\
# \theta_{2} \\
# \vdots \\
# \theta_{10}
# \end{bmatrix}
# \end{align}
# Each coefficient $\theta_{i}$ corresponds to a coefficient for one of the input features. Note that $\theta_{0}$ is included as the intercept term.
# The prediction of the y_test values should be equal to:
# \begin{align}
# y_{prediction} = (X_{test})^T \Theta
# \end{align}
reg.coef_.shape
X_test.shape
# numpy broadcasting to make matrix multiplication work
theta = reg.coef_[:, np.newaxis]
y_test_predictions = np.dot(X_test, theta)
# this should be the same shape as the predictions using the LinearRegression class
y_test_predictions.shape
# ## Fitting the model
# Now we will fit the model to the test data, using the coefficients from the linear regression, and assess their performance in the predictions. To do this we will make use of some of the methods in the metrics library of scikit-learn.
# +
y_predict = reg.predict(X_test)
from sklearn.metrics import mean_squared_error, r2_score
print(f"The mean squared error for the multiple linear regression is \t"
f"{mean_squared_error(y_test, y_predict):.2f} \n \n"
f"The r2_score, coefficient of determinations for the multiple linear regression is \t"
f"{r2_score(y_test, y_predict):.2f}")
# -
# We see that the mean_squared_error for the linear regression is quite high, indicating that the regression model is not a good one for predicting the response variable.
#
# Further, we see that the R2 score, a measure of how well the model fits the data, is 0.47, which is quite low. Ideally from a ML model we would like to achieve an R2 score of around 0.8, and then we can confidently use the model to predict the response with a greater degree of confidence.
# ### Issues with plotting
# It would be useful to see a visualisation of the output of the model we have fitted. However, since this is a multivariate linear regression model, we cannot plot the output of a 10-dimensional model, so we have to rely on the metrics of the regression to tell us how well the model has been fitted.
| 48.2 | 1,534 |
c52560aece7923e0291a01ad502e45459c3dea26
|
py
|
python
|
DIabetes/Diabetes_Model.ipynb
|
Coding-Ghostman/Diabetes-Prediction
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="RsgY5HrarUmw"
# # Description for Modules
# pandas-> read our csv files
#
# numpy-> convert the data to suitable form to feed into the classification data
#
# seaborn and matplotlib-> For visualizations
#
# sklearn-> To use logistic regression
# + colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "Ly8gQ29weXJpZ2h0IDIwMTcgR29vZ2xlIExMQwovLwovLyBMaWNlbnNlZCB1bmRlciB0aGUgQXBhY2hlIExpY2Vuc2UsIFZlcnNpb24gMi4wICh0aGUgIkxpY2Vuc2UiKTsKLy8geW91IG1heSBub3QgdXNlIHRoaXMgZmlsZSBleGNlcHQgaW4gY29tcGxpYW5jZSB3aXRoIHRoZSBMaWNlbnNlLgovLyBZb3UgbWF5IG9idGFpbiBhIGNvcHkgb2YgdGhlIExpY2Vuc2UgYXQKLy8KLy8gICAgICBodHRwOi8vd3d3LmFwYWNoZS5vcmcvbGljZW5zZXMvTElDRU5TRS0yLjAKLy8KLy8gVW5sZXNzIHJlcXVpcmVkIGJ5IGFwcGxpY2FibGUgbGF3IG9yIGFncmVlZCB0byBpbiB3cml0aW5nLCBzb2Z0d2FyZQovLyBkaXN0cmlidXRlZCB1bmRlciB0aGUgTGljZW5zZSBpcyBkaXN0cmlidXRlZCBvbiBhbiAiQVMgSVMiIEJBU0lTLAovLyBXSVRIT1VUIFdBUlJBTlRJRVMgT1IgQ09ORElUSU9OUyBPRiBBTlkgS0lORCwgZWl0aGVyIGV4cHJlc3Mgb3IgaW1wbGllZC4KLy8gU2VlIHRoZSBMaWNlbnNlIGZvciB0aGUgc3BlY2lmaWMgbGFuZ3VhZ2UgZ292ZXJuaW5nIHBlcm1pc3Npb25zIGFuZAovLyBsaW1pdGF0aW9ucyB1bmRlciB0aGUgTGljZW5zZS4KCi8qKgogKiBAZmlsZW92ZXJ2aWV3IEhlbHBlcnMgZm9yIGdvb2dsZS5jb2xhYiBQeXRob24gbW9kdWxlLgogKi8KKGZ1bmN0aW9uKHNjb3BlKSB7CmZ1bmN0aW9uIHNwYW4odGV4dCwgc3R5bGVBdHRyaWJ1dGVzID0ge30pIHsKICBjb25zdCBlbGVtZW50ID0gZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgnc3BhbicpOwogIGVsZW1lbnQudGV4dENvbnRlbnQgPSB0ZXh0OwogIGZvciAoY29uc3Qga2V5IG9mIE9iamVjdC5rZXlzKHN0eWxlQXR0cmlidXRlcykpIHsKICAgIGVsZW1lbnQuc3R5bGVba2V5XSA9IHN0eWxlQXR0cmlidXRlc1trZXldOwogIH0KICByZXR1cm4gZWxlbWVudDsKfQoKLy8gTWF4IG51bWJlciBvZiBieXRlcyB3aGljaCB3aWxsIGJlIHVwbG9hZGVkIGF0IGEgdGltZS4KY29uc3QgTUFYX1BBWUxPQURfU0laRSA9IDEwMCAqIDEwMjQ7CgpmdW5jdGlvbiBfdXBsb2FkRmlsZXMoaW5wdXRJZCwgb3V0cHV0SWQpIHsKICBjb25zdCBzdGVwcyA9IHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCk7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICAvLyBDYWNoZSBzdGVwcyBvbiB0aGUgb3V0cHV0RWxlbWVudCB0byBtYWtlIGl0IGF2YWlsYWJsZSBmb3IgdGhlIG5leHQgY2FsbAogIC8vIHRvIHVwbG9hZEZpbGVzQ29udGludWUgZnJvbSBQeXRob24uCiAgb3V0cHV0RWxlbWVudC5zdGVwcyA9IHN0ZXBzOwoKICByZXR1cm4gX3VwbG9hZEZpbGVzQ29udGludWUob3V0cHV0SWQpOwp9CgovLyBUaGlzIGlzIHJvdWdobHkgYW4gYXN5bmMgZ2VuZXJhdG9yIChub3Qgc3VwcG9ydGVkIGluIHRoZSBicm93c2VyIHlldCksCi8vIHdoZXJlIHRoZXJlIGFyZSBtdWx0aXBsZSBhc3luY2hyb25vdXMgc3RlcHMgYW5kIHRoZSBQeXRob24gc2lkZSBpcyBnb2luZwovLyB0byBwb2xsIGZvciBjb21wbGV0aW9uIG9mIGVhY2ggc3RlcC4KLy8gVGhpcyB1c2VzIGEgUHJvbWlzZSB0byBibG9jayB0aGUgcHl0aG9uIHNpZGUgb24gY29tcGxldGlvbiBvZiBlYWNoIHN0ZXAsCi8vIHRoZW4gcGFzc2VzIHRoZSByZXN1bHQgb2YgdGhlIHByZXZpb3VzIHN0ZXAgYXMgdGhlIGlucHV0IHRvIHRoZSBuZXh0IHN0ZXAuCmZ1bmN0aW9uIF91cGxvYWRGaWxlc0NvbnRpbnVlKG91dHB1dElkKSB7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICBjb25zdCBzdGVwcyA9IG91dHB1dEVsZW1lbnQuc3RlcHM7CgogIGNvbnN0IG5leHQgPSBzdGVwcy5uZXh0KG91dHB1dEVsZW1lbnQubGFzdFByb21pc2VWYWx1ZSk7CiAgcmV0dXJuIFByb21pc2UucmVzb2x2ZShuZXh0LnZhbHVlLnByb21pc2UpLnRoZW4oKHZhbHVlKSA9PiB7CiAgICAvLyBDYWNoZSB0aGUgbGFzdCBwcm9taXNlIHZhbHVlIHRvIG1ha2UgaXQgYXZhaWxhYmxlIHRvIHRoZSBuZXh0CiAgICAvLyBzdGVwIG9mIHRoZSBnZW5lcmF0b3IuCiAgICBvdXRwdXRFbGVtZW50Lmxhc3RQcm9taXNlVmFsdWUgPSB2YWx1ZTsKICAgIHJldHVybiBuZXh0LnZhbHVlLnJlc3BvbnNlOwogIH0pOwp9CgovKioKICogR2VuZXJhdG9yIGZ1bmN0aW9uIHdoaWNoIGlzIGNhbGxlZCBiZXR3ZWVuIGVhY2ggYXN5bmMgc3RlcCBvZiB0aGUgdXBsb2FkCiAqIHByb2Nlc3MuCiAqIEBwYXJhbSB7c3RyaW5nfSBpbnB1dElkIEVsZW1lbnQgSUQgb2YgdGhlIGlucHV0IGZpbGUgcGlja2VyIGVsZW1lbnQuCiAqIEBwYXJhbSB7c3RyaW5nfSBvdXRwdXRJZCBFbGVtZW50IElEIG9mIHRoZSBvdXRwdXQgZGlzcGxheS4KICogQHJldHVybiB7IUl0ZXJhYmxlPCFPYmplY3Q+fSBJdGVyYWJsZSBvZiBuZXh0IHN0ZXBzLgogKi8KZnVuY3Rpb24qIHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCkgewogIGNvbnN0IGlucHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKGlucHV0SWQpOwogIGlucHV0RWxlbWVudC5kaXNhYmxlZCA9IGZhbHNlOwoKICBjb25zdCBvdXRwdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQob3V0cHV0SWQpOwogIG91dHB1dEVsZW1lbnQuaW5uZXJIVE1MID0gJyc7CgogIGNvbnN0IHBpY2tlZFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgaW5wdXRFbGVtZW50LmFkZEV2ZW50TGlzdGVuZXIoJ2NoYW5nZScsIChlKSA9PiB7CiAgICAgIHJlc29sdmUoZS50YXJnZXQuZmlsZXMpOwogICAgfSk7CiAgfSk7CgogIGNvbnN0IGNhbmNlbCA9IGRvY3VtZW50LmNyZWF0ZUVsZW1lbnQoJ2J1dHRvbicpOwogIGlucHV0RWxlbWVudC5wYXJlbnRFbGVtZW50LmFwcGVuZENoaWxkKGNhbmNlbCk7CiAgY2FuY2VsLnRleHRDb250ZW50ID0gJ0NhbmNlbCB1cGxvYWQnOwogIGNvbnN0IGNhbmNlbFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgY2FuY2VsLm9uY2xpY2sgPSAoKSA9PiB7CiAgICAgIHJlc29sdmUobnVsbCk7CiAgICB9OwogIH0pOwoKICAvLyBXYWl0IGZvciB0aGUgdXNlciB0byBwaWNrIHRoZSBmaWxlcy4KICBjb25zdCBmaWxlcyA9IHlpZWxkIHsKICAgIHByb21pc2U6IFByb21pc2UucmFjZShbcGlja2VkUHJvbWlzZSwgY2FuY2VsUHJvbWlzZV0pLAogICAgcmVzcG9uc2U6IHsKICAgICAgYWN0aW9uOiAnc3RhcnRpbmcnLAogICAgfQogIH07CgogIGNhbmNlbC5yZW1vdmUoKTsKCiAgLy8gRGlzYWJsZSB0aGUgaW5wdXQgZWxlbWVudCBzaW5jZSBmdXJ0aGVyIHBpY2tzIGFyZSBub3QgYWxsb3dlZC4KICBpbnB1dEVsZW1lbnQuZGlzYWJsZWQgPSB0cnVlOwoKICBpZiAoIWZpbGVzKSB7CiAgICByZXR1cm4gewogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbXBsZXRlJywKICAgICAgfQogICAgfTsKICB9CgogIGZvciAoY29uc3QgZmlsZSBvZiBmaWxlcykgewogICAgY29uc3QgbGkgPSBkb2N1bWVudC5jcmVhdGVFbGVtZW50KCdsaScpOwogICAgbGkuYXBwZW5kKHNwYW4oZmlsZS5uYW1lLCB7Zm9udFdlaWdodDogJ2JvbGQnfSkpOwogICAgbGkuYXBwZW5kKHNwYW4oCiAgICAgICAgYCgke2ZpbGUudHlwZSB8fCAnbi9hJ30pIC0gJHtmaWxlLnNpemV9IGJ5dGVzLCBgICsKICAgICAgICBgbGFzdCBtb2RpZmllZDogJHsKICAgICAgICAgICAgZmlsZS5sYXN0TW9kaWZpZWREYXRlID8gZmlsZS5sYXN0TW9kaWZpZWREYXRlLnRvTG9jYWxlRGF0ZVN0cmluZygpIDoKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgJ24vYSd9IC0gYCkpOwogICAgY29uc3QgcGVyY2VudCA9IHNwYW4oJzAlIGRvbmUnKTsKICAgIGxpLmFwcGVuZENoaWxkKHBlcmNlbnQpOwoKICAgIG91dHB1dEVsZW1lbnQuYXBwZW5kQ2hpbGQobGkpOwoKICAgIGNvbnN0IGZpbGVEYXRhUHJvbWlzZSA9IG5ldyBQcm9taXNlKChyZXNvbHZlKSA9PiB7CiAgICAgIGNvbnN0IHJlYWRlciA9IG5ldyBGaWxlUmVhZGVyKCk7CiAgICAgIHJlYWRlci5vbmxvYWQgPSAoZSkgPT4gewogICAgICAgIHJlc29sdmUoZS50YXJnZXQucmVzdWx0KTsKICAgICAgfTsKICAgICAgcmVhZGVyLnJlYWRBc0FycmF5QnVmZmVyKGZpbGUpOwogICAgfSk7CiAgICAvLyBXYWl0IGZvciB0aGUgZGF0YSB0byBiZSByZWFkeS4KICAgIGxldCBmaWxlRGF0YSA9IHlpZWxkIHsKICAgICAgcHJvbWlzZTogZmlsZURhdGFQcm9taXNlLAogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbnRpbnVlJywKICAgICAgfQogICAgfTsKCiAgICAvLyBVc2UgYSBjaHVua2VkIHNlbmRpbmcgdG8gYXZvaWQgbWVzc2FnZSBzaXplIGxpbWl0cy4gU2VlIGIvNjIxMTU2NjAuCiAgICBsZXQgcG9zaXRpb24gPSAwOwogICAgZG8gewogICAgICBjb25zdCBsZW5ndGggPSBNYXRoLm1pbihmaWxlRGF0YS5ieXRlTGVuZ3RoIC0gcG9zaXRpb24sIE1BWF9QQVlMT0FEX1NJWkUpOwogICAgICBjb25zdCBjaHVuayA9IG5ldyBVaW50OEFycmF5KGZpbGVEYXRhLCBwb3NpdGlvbiwgbGVuZ3RoKTsKICAgICAgcG9zaXRpb24gKz0gbGVuZ3RoOwoKICAgICAgY29uc3QgYmFzZTY0ID0gYnRvYShTdHJpbmcuZnJvbUNoYXJDb2RlLmFwcGx5KG51bGwsIGNodW5rKSk7CiAgICAgIHlpZWxkIHsKICAgICAgICByZXNwb25zZTogewogICAgICAgICAgYWN0aW9uOiAnYXBwZW5kJywKICAgICAgICAgIGZpbGU6IGZpbGUubmFtZSwKICAgICAgICAgIGRhdGE6IGJhc2U2NCwKICAgICAgICB9LAogICAgICB9OwoKICAgICAgbGV0IHBlcmNlbnREb25lID0gZmlsZURhdGEuYnl0ZUxlbmd0aCA9PT0gMCA/CiAgICAgICAgICAxMDAgOgogICAgICAgICAgTWF0aC5yb3VuZCgocG9zaXRpb24gLyBmaWxlRGF0YS5ieXRlTGVuZ3RoKSAqIDEwMCk7CiAgICAgIHBlcmNlbnQudGV4dENvbnRlbnQgPSBgJHtwZXJjZW50RG9uZX0lIGRvbmVgOwoKICAgIH0gd2hpbGUgKHBvc2l0aW9uIDwgZmlsZURhdGEuYnl0ZUxlbmd0aCk7CiAgfQoKICAvLyBBbGwgZG9uZS4KICB5aWVsZCB7CiAgICByZXNwb25zZTogewogICAgICBhY3Rpb246ICdjb21wbGV0ZScsCiAgICB9CiAgfTsKfQoKc2NvcGUuZ29vZ2xlID0gc2NvcGUuZ29vZ2xlIHx8IHt9OwpzY29wZS5nb29nbGUuY29sYWIgPSBzY29wZS5nb29nbGUuY29sYWIgfHwge307CnNjb3BlLmdvb2dsZS5jb2xhYi5fZmlsZXMgPSB7CiAgX3VwbG9hZEZpbGVzLAogIF91cGxvYWRGaWxlc0NvbnRpbnVlLAp9Owp9KShzZWxmKTsK", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 73} id="th5_gTXCmgqP" executionInfo={"status": "ok", "timestamp": 1640760182171, "user_tz": -330, "elapsed": 18416, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}} outputId="dfbcf3e0-d8d4-457a-c2eb-4bcc4528b987"
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
% matplotlib inline
from google.colab import files
uploaded = files.upload()
from sklearn.linear_model import LogisticRegression
# + [markdown] id="H-lp0dH7rSeI"
# # Reading the "diabetes.csv"
# + [markdown] id="ahLWgP0nuYWG"
# # The following features have been provided to help us predict whether a person is diabetic or not:
# * **Pregnancies**: Number of times pregnant
#
# * **Glucose**: Plasma glucose concentration over 2 hours in an oral glucose tolerance test
#
# * **BloodPressure**: Diastolic blood pressure (mm Hg)
#
# * **SkinThickness**: Triceps skin fold thickness (mm)
#
# * **Insulin**: 2-Hour serum insulin (mu U/ml)
#
# * **BMI**: Body mass index (weight in kg/(height in m)2)
#
# * **DiabetesPedigreeFunction**: Diabetes pedigree function (a function which scores likelihood of diabetes based on family history)
#
# * **Age**: Age (years)
#
# * **Outcome**: Class variable (0 if non-diabetic, 1 if diabetic)
#
#
#
# + colab={"base_uri": "https://localhost:8080/", "height": 584} id="Uy1l7GBTsM5d" executionInfo={"status": "ok", "timestamp": 1640760182176, "user_tz": -330, "elapsed": 9, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}} outputId="4f4dbe8a-e73e-4043-832a-8cc8eb85707e"
diabetes_df = pd.read_csv("diabetes.csv")
diabetes_df.head(15)
# + colab={"base_uri": "https://localhost:8080/"} id="lFvnTF_1tMnR" executionInfo={"status": "ok", "timestamp": 1640760407275, "user_tz": -330, "elapsed": 363, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}} outputId="a6d6f2c6-f980-473b-da17-b04ac644c6bc"
diabetes_df.info()
# + [markdown] id="04MKGHgs7x5z"
# In the above data, you can see that there are many missing values in
#
# * **Insulin**
#
# * **skin thickness**
#
# * **blood pressure**
#
# We could replace the missing values with the mean of the respective features
# + colab={"base_uri": "https://localhost:8080/", "height": 616} id="OAs9zUN28MRB" executionInfo={"status": "ok", "timestamp": 1640760843444, "user_tz": -330, "elapsed": 960, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}} outputId="bf15352c-f238-4f0b-9db1-d67f163cdf36"
corr = diabetes_df.corr()
print(corr)
sns.heatmap(corr,
xticklabels = corr.columns,
yticklabels = corr.columns,
vmin = 0, vmax = 0.5)
# + [markdown] id="AwbqhQDM9TCC"
# In the above heatmap, brighter colours indicate more correlation.
#
#
# > **Glucose**, **# of pregnancies**, **BMI** and **age** have significant correlation with **outcome** variable.
#
# > Other correlation like **age**->**pregnancies**, **BMI**-> **skin thickness**, **Insulin**-> **skin thickness**
#
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="NXfsMJyk-1YQ" executionInfo={"status": "ok", "timestamp": 1640761648145, "user_tz": -330, "elapsed": 4, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}} outputId="6733f9e4-a16d-4b85-b7e9-13e4b6839237"
outcome = diabetes_df["Outcome"]
outcome.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 302} id="b4bMoRnVAD0n" executionInfo={"status": "ok", "timestamp": 1640761941291, "user_tz": -330, "elapsed": 442, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}} outputId="8d8bfd90-18ab-4c00-c6f5-51778bf8c5d6"
sns.set_theme(style = "darkgrid", palette = "deep")
sns.countplot(x = 'Outcome', data = diabetes_df)
# + [markdown] id="aC0c6fSkCHU7"
#
# + colab={"base_uri": "https://localhost:8080/", "height": 304} id="GA_Sizz-CH0f" executionInfo={"status": "ok", "timestamp": 1640762280893, "user_tz": -330, "elapsed": 1797, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}} outputId="be67eedc-cb2a-4fc5-a54a-aeaab467e445"
sns.set_theme(style = "darkgrid", palette = "deep")
sns.barplot(x = 'Outcome', y = "Age", data = diabetes_df, saturation = 1.6)
# + [markdown] id="1cBWCb8lE1ey"
# # Data Preparation
#
# splitting the data into:
# * **Training Data**
# * **Test Data**
# * **Check Data**
# + id="4_fctfzQDb90" executionInfo={"status": "ok", "timestamp": 1640762766213, "user_tz": -330, "elapsed": 366, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}}
dfTrain = diabetes_df[:650]
dfTest = diabetes_df[650:750]
dfcheck = diabetes_df[750:]
# + [markdown] id="hXIZ-PFsFgXD"
# **Separating label and features for both training and testing**
# + id="X7Vs56S6Fe0S" executionInfo={"status": "ok", "timestamp": 1640763135305, "user_tz": -330, "elapsed": 3, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}}
trainLabel = np.asarray(dfTrain['Outcome'])
trainData = np.asarray(dfTrain.drop("Outcome", 1))
testLabel = np.asarray(dfTest['Outcome'])
testData = np.asarray(dfTest.drop("Outcome", 1))
# + id="fXc9007jGqjr" executionInfo={"status": "ok", "timestamp": 1640770569983, "user_tz": -330, "elapsed": 356, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}}
means = np.mean(trainData, axis = 0)
stds = np.std(trainData, axis = 0)
trainData = (trainData - means) / stds
testData = (testData - means) / stds
# + colab={"base_uri": "https://localhost:8080/"} id="_5dvTgi5jBHu" executionInfo={"status": "ok", "timestamp": 1640770613804, "user_tz": -330, "elapsed": 604, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}} outputId="7175909c-4af2-4995-f665-2f8bad014007"
diabetesCheck = LogisticRegression()
diabetesCheck.fit(trainData, trainLabel)
# + colab={"base_uri": "https://localhost:8080/"} id="qN-WaYZsjMnx" executionInfo={"status": "ok", "timestamp": 1640770682041, "user_tz": -330, "elapsed": 385, "user": {"displayName": "Atman Mishra", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiZ7frZCA8n9XUft8IKDtvkNwYHke9fb0dLNfjG=s64", "userId": "01235285672556146478"}} outputId="2e016b35-fb86-46d0-b15c-e5f2ee479f6b"
accuracy = diabetesCheck.score(testData, testLabel)
print("accuracy = ", accuracy * 100, "%")
| 102.170068 | 7,619 |
747fd49c227402f111c8c46ec0e0a79b566aa425
|
py
|
python
|
notebook/LSTM_Stock_prediction_single_days.ipynb
|
toanquachp/dl_stock_prediction
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="ogm4g8XaQul5" colab_type="text"
# # Upload data
# + id="41P9mE43B8Nx" colab_type="code" outputId="e83dbb28-a798-418f-9a83-1a9ca2e34310" colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "Ly8gQ29weXJpZ2h0IDIwMTcgR29vZ2xlIExMQwovLwovLyBMaWNlbnNlZCB1bmRlciB0aGUgQXBhY2hlIExpY2Vuc2UsIFZlcnNpb24gMi4wICh0aGUgIkxpY2Vuc2UiKTsKLy8geW91IG1heSBub3QgdXNlIHRoaXMgZmlsZSBleGNlcHQgaW4gY29tcGxpYW5jZSB3aXRoIHRoZSBMaWNlbnNlLgovLyBZb3UgbWF5IG9idGFpbiBhIGNvcHkgb2YgdGhlIExpY2Vuc2UgYXQKLy8KLy8gICAgICBodHRwOi8vd3d3LmFwYWNoZS5vcmcvbGljZW5zZXMvTElDRU5TRS0yLjAKLy8KLy8gVW5sZXNzIHJlcXVpcmVkIGJ5IGFwcGxpY2FibGUgbGF3IG9yIGFncmVlZCB0byBpbiB3cml0aW5nLCBzb2Z0d2FyZQovLyBkaXN0cmlidXRlZCB1bmRlciB0aGUgTGljZW5zZSBpcyBkaXN0cmlidXRlZCBvbiBhbiAiQVMgSVMiIEJBU0lTLAovLyBXSVRIT1VUIFdBUlJBTlRJRVMgT1IgQ09ORElUSU9OUyBPRiBBTlkgS0lORCwgZWl0aGVyIGV4cHJlc3Mgb3IgaW1wbGllZC4KLy8gU2VlIHRoZSBMaWNlbnNlIGZvciB0aGUgc3BlY2lmaWMgbGFuZ3VhZ2UgZ292ZXJuaW5nIHBlcm1pc3Npb25zIGFuZAovLyBsaW1pdGF0aW9ucyB1bmRlciB0aGUgTGljZW5zZS4KCi8qKgogKiBAZmlsZW92ZXJ2aWV3IEhlbHBlcnMgZm9yIGdvb2dsZS5jb2xhYiBQeXRob24gbW9kdWxlLgogKi8KKGZ1bmN0aW9uKHNjb3BlKSB7CmZ1bmN0aW9uIHNwYW4odGV4dCwgc3R5bGVBdHRyaWJ1dGVzID0ge30pIHsKICBjb25zdCBlbGVtZW50ID0gZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgnc3BhbicpOwogIGVsZW1lbnQudGV4dENvbnRlbnQgPSB0ZXh0OwogIGZvciAoY29uc3Qga2V5IG9mIE9iamVjdC5rZXlzKHN0eWxlQXR0cmlidXRlcykpIHsKICAgIGVsZW1lbnQuc3R5bGVba2V5XSA9IHN0eWxlQXR0cmlidXRlc1trZXldOwogIH0KICByZXR1cm4gZWxlbWVudDsKfQoKLy8gTWF4IG51bWJlciBvZiBieXRlcyB3aGljaCB3aWxsIGJlIHVwbG9hZGVkIGF0IGEgdGltZS4KY29uc3QgTUFYX1BBWUxPQURfU0laRSA9IDEwMCAqIDEwMjQ7Ci8vIE1heCBhbW91bnQgb2YgdGltZSB0byBibG9jayB3YWl0aW5nIGZvciB0aGUgdXNlci4KY29uc3QgRklMRV9DSEFOR0VfVElNRU9VVF9NUyA9IDMwICogMTAwMDsKCmZ1bmN0aW9uIF91cGxvYWRGaWxlcyhpbnB1dElkLCBvdXRwdXRJZCkgewogIGNvbnN0IHN0ZXBzID0gdXBsb2FkRmlsZXNTdGVwKGlucHV0SWQsIG91dHB1dElkKTsKICBjb25zdCBvdXRwdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQob3V0cHV0SWQpOwogIC8vIENhY2hlIHN0ZXBzIG9uIHRoZSBvdXRwdXRFbGVtZW50IHRvIG1ha2UgaXQgYXZhaWxhYmxlIGZvciB0aGUgbmV4dCBjYWxsCiAgLy8gdG8gdXBsb2FkRmlsZXNDb250aW51ZSBmcm9tIFB5dGhvbi4KICBvdXRwdXRFbGVtZW50LnN0ZXBzID0gc3RlcHM7CgogIHJldHVybiBfdXBsb2FkRmlsZXNDb250aW51ZShvdXRwdXRJZCk7Cn0KCi8vIFRoaXMgaXMgcm91Z2hseSBhbiBhc3luYyBnZW5lcmF0b3IgKG5vdCBzdXBwb3J0ZWQgaW4gdGhlIGJyb3dzZXIgeWV0KSwKLy8gd2hlcmUgdGhlcmUgYXJlIG11bHRpcGxlIGFzeW5jaHJvbm91cyBzdGVwcyBhbmQgdGhlIFB5dGhvbiBzaWRlIGlzIGdvaW5nCi8vIHRvIHBvbGwgZm9yIGNvbXBsZXRpb24gb2YgZWFjaCBzdGVwLgovLyBUaGlzIHVzZXMgYSBQcm9taXNlIHRvIGJsb2NrIHRoZSBweXRob24gc2lkZSBvbiBjb21wbGV0aW9uIG9mIGVhY2ggc3RlcCwKLy8gdGhlbiBwYXNzZXMgdGhlIHJlc3VsdCBvZiB0aGUgcHJldmlvdXMgc3RlcCBhcyB0aGUgaW5wdXQgdG8gdGhlIG5leHQgc3RlcC4KZnVuY3Rpb24gX3VwbG9hZEZpbGVzQ29udGludWUob3V0cHV0SWQpIHsKICBjb25zdCBvdXRwdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQob3V0cHV0SWQpOwogIGNvbnN0IHN0ZXBzID0gb3V0cHV0RWxlbWVudC5zdGVwczsKCiAgY29uc3QgbmV4dCA9IHN0ZXBzLm5leHQob3V0cHV0RWxlbWVudC5sYXN0UHJvbWlzZVZhbHVlKTsKICByZXR1cm4gUHJvbWlzZS5yZXNvbHZlKG5leHQudmFsdWUucHJvbWlzZSkudGhlbigodmFsdWUpID0+IHsKICAgIC8vIENhY2hlIHRoZSBsYXN0IHByb21pc2UgdmFsdWUgdG8gbWFrZSBpdCBhdmFpbGFibGUgdG8gdGhlIG5leHQKICAgIC8vIHN0ZXAgb2YgdGhlIGdlbmVyYXRvci4KICAgIG91dHB1dEVsZW1lbnQubGFzdFByb21pc2VWYWx1ZSA9IHZhbHVlOwogICAgcmV0dXJuIG5leHQudmFsdWUucmVzcG9uc2U7CiAgfSk7Cn0KCi8qKgogKiBHZW5lcmF0b3IgZnVuY3Rpb24gd2hpY2ggaXMgY2FsbGVkIGJldHdlZW4gZWFjaCBhc3luYyBzdGVwIG9mIHRoZSB1cGxvYWQKICogcHJvY2Vzcy4KICogQHBhcmFtIHtzdHJpbmd9IGlucHV0SWQgRWxlbWVudCBJRCBvZiB0aGUgaW5wdXQgZmlsZSBwaWNrZXIgZWxlbWVudC4KICogQHBhcmFtIHtzdHJpbmd9IG91dHB1dElkIEVsZW1lbnQgSUQgb2YgdGhlIG91dHB1dCBkaXNwbGF5LgogKiBAcmV0dXJuIHshSXRlcmFibGU8IU9iamVjdD59IEl0ZXJhYmxlIG9mIG5leHQgc3RlcHMuCiAqLwpmdW5jdGlvbiogdXBsb2FkRmlsZXNTdGVwKGlucHV0SWQsIG91dHB1dElkKSB7CiAgY29uc3QgaW5wdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQoaW5wdXRJZCk7CiAgaW5wdXRFbGVtZW50LmRpc2FibGVkID0gZmFsc2U7CgogIGNvbnN0IG91dHB1dEVsZW1lbnQgPSBkb2N1bWVudC5nZXRFbGVtZW50QnlJZChvdXRwdXRJZCk7CiAgb3V0cHV0RWxlbWVudC5pbm5lckhUTUwgPSAnJzsKCiAgY29uc3QgcGlja2VkUHJvbWlzZSA9IG5ldyBQcm9taXNlKChyZXNvbHZlKSA9PiB7CiAgICBpbnB1dEVsZW1lbnQuYWRkRXZlbnRMaXN0ZW5lcignY2hhbmdlJywgKGUpID0+IHsKICAgICAgcmVzb2x2ZShlLnRhcmdldC5maWxlcyk7CiAgICB9KTsKICB9KTsKCiAgY29uc3QgY2FuY2VsID0gZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgnYnV0dG9uJyk7CiAgaW5wdXRFbGVtZW50LnBhcmVudEVsZW1lbnQuYXBwZW5kQ2hpbGQoY2FuY2VsKTsKICBjYW5jZWwudGV4dENvbnRlbnQgPSAnQ2FuY2VsIHVwbG9hZCc7CiAgY29uc3QgY2FuY2VsUHJvbWlzZSA9IG5ldyBQcm9taXNlKChyZXNvbHZlKSA9PiB7CiAgICBjYW5jZWwub25jbGljayA9ICgpID0+IHsKICAgICAgcmVzb2x2ZShudWxsKTsKICAgIH07CiAgfSk7CgogIC8vIENhbmNlbCB1cGxvYWQgaWYgdXNlciBoYXNuJ3QgcGlja2VkIGFueXRoaW5nIGluIHRpbWVvdXQuCiAgY29uc3QgdGltZW91dFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgc2V0VGltZW91dCgoKSA9PiB7CiAgICAgIHJlc29sdmUobnVsbCk7CiAgICB9LCBGSUxFX0NIQU5HRV9USU1FT1VUX01TKTsKICB9KTsKCiAgLy8gV2FpdCBmb3IgdGhlIHVzZXIgdG8gcGljayB0aGUgZmlsZXMuCiAgY29uc3QgZmlsZXMgPSB5aWVsZCB7CiAgICBwcm9taXNlOiBQcm9taXNlLnJhY2UoW3BpY2tlZFByb21pc2UsIHRpbWVvdXRQcm9taXNlLCBjYW5jZWxQcm9taXNlXSksCiAgICByZXNwb25zZTogewogICAgICBhY3Rpb246ICdzdGFydGluZycsCiAgICB9CiAgfTsKCiAgaWYgKCFmaWxlcykgewogICAgcmV0dXJuIHsKICAgICAgcmVzcG9uc2U6IHsKICAgICAgICBhY3Rpb246ICdjb21wbGV0ZScsCiAgICAgIH0KICAgIH07CiAgfQoKICBjYW5jZWwucmVtb3ZlKCk7CgogIC8vIERpc2FibGUgdGhlIGlucHV0IGVsZW1lbnQgc2luY2UgZnVydGhlciBwaWNrcyBhcmUgbm90IGFsbG93ZWQuCiAgaW5wdXRFbGVtZW50LmRpc2FibGVkID0gdHJ1ZTsKCiAgZm9yIChjb25zdCBmaWxlIG9mIGZpbGVzKSB7CiAgICBjb25zdCBsaSA9IGRvY3VtZW50LmNyZWF0ZUVsZW1lbnQoJ2xpJyk7CiAgICBsaS5hcHBlbmQoc3BhbihmaWxlLm5hbWUsIHtmb250V2VpZ2h0OiAnYm9sZCd9KSk7CiAgICBsaS5hcHBlbmQoc3BhbigKICAgICAgICBgKCR7ZmlsZS50eXBlIHx8ICduL2EnfSkgLSAke2ZpbGUuc2l6ZX0gYnl0ZXMsIGAgKwogICAgICAgIGBsYXN0IG1vZGlmaWVkOiAkewogICAgICAgICAgICBmaWxlLmxhc3RNb2RpZmllZERhdGUgPyBmaWxlLmxhc3RNb2RpZmllZERhdGUudG9Mb2NhbGVEYXRlU3RyaW5nKCkgOgogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAnbi9hJ30gLSBgKSk7CiAgICBjb25zdCBwZXJjZW50ID0gc3BhbignMCUgZG9uZScpOwogICAgbGkuYXBwZW5kQ2hpbGQocGVyY2VudCk7CgogICAgb3V0cHV0RWxlbWVudC5hcHBlbmRDaGlsZChsaSk7CgogICAgY29uc3QgZmlsZURhdGFQcm9taXNlID0gbmV3IFByb21pc2UoKHJlc29sdmUpID0+IHsKICAgICAgY29uc3QgcmVhZGVyID0gbmV3IEZpbGVSZWFkZXIoKTsKICAgICAgcmVhZGVyLm9ubG9hZCA9IChlKSA9PiB7CiAgICAgICAgcmVzb2x2ZShlLnRhcmdldC5yZXN1bHQpOwogICAgICB9OwogICAgICByZWFkZXIucmVhZEFzQXJyYXlCdWZmZXIoZmlsZSk7CiAgICB9KTsKICAgIC8vIFdhaXQgZm9yIHRoZSBkYXRhIHRvIGJlIHJlYWR5LgogICAgbGV0IGZpbGVEYXRhID0geWllbGQgewogICAgICBwcm9taXNlOiBmaWxlRGF0YVByb21pc2UsCiAgICAgIHJlc3BvbnNlOiB7CiAgICAgICAgYWN0aW9uOiAnY29udGludWUnLAogICAgICB9CiAgICB9OwoKICAgIC8vIFVzZSBhIGNodW5rZWQgc2VuZGluZyB0byBhdm9pZCBtZXNzYWdlIHNpemUgbGltaXRzLiBTZWUgYi82MjExNTY2MC4KICAgIGxldCBwb3NpdGlvbiA9IDA7CiAgICB3aGlsZSAocG9zaXRpb24gPCBmaWxlRGF0YS5ieXRlTGVuZ3RoKSB7CiAgICAgIGNvbnN0IGxlbmd0aCA9IE1hdGgubWluKGZpbGVEYXRhLmJ5dGVMZW5ndGggLSBwb3NpdGlvbiwgTUFYX1BBWUxPQURfU0laRSk7CiAgICAgIGNvbnN0IGNodW5rID0gbmV3IFVpbnQ4QXJyYXkoZmlsZURhdGEsIHBvc2l0aW9uLCBsZW5ndGgpOwogICAgICBwb3NpdGlvbiArPSBsZW5ndGg7CgogICAgICBjb25zdCBiYXNlNjQgPSBidG9hKFN0cmluZy5mcm9tQ2hhckNvZGUuYXBwbHkobnVsbCwgY2h1bmspKTsKICAgICAgeWllbGQgewogICAgICAgIHJlc3BvbnNlOiB7CiAgICAgICAgICBhY3Rpb246ICdhcHBlbmQnLAogICAgICAgICAgZmlsZTogZmlsZS5uYW1lLAogICAgICAgICAgZGF0YTogYmFzZTY0LAogICAgICAgIH0sCiAgICAgIH07CiAgICAgIHBlcmNlbnQudGV4dENvbnRlbnQgPQogICAgICAgICAgYCR7TWF0aC5yb3VuZCgocG9zaXRpb24gLyBmaWxlRGF0YS5ieXRlTGVuZ3RoKSAqIDEwMCl9JSBkb25lYDsKICAgIH0KICB9CgogIC8vIEFsbCBkb25lLgogIHlpZWxkIHsKICAgIHJlc3BvbnNlOiB7CiAgICAgIGFjdGlvbjogJ2NvbXBsZXRlJywKICAgIH0KICB9Owp9CgpzY29wZS5nb29nbGUgPSBzY29wZS5nb29nbGUgfHwge307CnNjb3BlLmdvb2dsZS5jb2xhYiA9IHNjb3BlLmdvb2dsZS5jb2xhYiB8fCB7fTsKc2NvcGUuZ29vZ2xlLmNvbGFiLl9maWxlcyA9IHsKICBfdXBsb2FkRmlsZXMsCiAgX3VwbG9hZEZpbGVzQ29udGludWUsCn07Cn0pKHNlbGYpOwo=", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 91}
from google.colab import files
uploaded = files.upload()
for fn in uploaded.keys():
print('User uploaded file "{name}" with length {length} bytes'.format(
name=fn, length=len(uploaded[fn])))
# + [markdown] id="_Rn6sctdQrrC" colab_type="text"
# # Import data
# + id="yE0ocgnQF0ud" colab_type="code" colab={}
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# + id="S_UxMLm-VIRi" colab_type="code" colab={}
LAG_DAYS = 21
# + id="vSzPFL_GGJ5W" colab_type="code" outputId="fc3933cd-de36-4a92-8c60-00548f7e0c91" colab={"base_uri": "https://localhost:8080/", "height": 204}
data = pd.read_csv('GOOG.csv')
data.head()
# + id="GqDFQ0PjKTYy" colab_type="code" outputId="5bba06dc-5ff2-4a87-e3ea-9c32aef94b7f" colab={"base_uri": "https://localhost:8080/", "height": 513}
plt.figure(figsize=(20, 8))
plt.plot(data['Open'])
plt.plot(data['High'])
plt.plot(data['Low'])
plt.plot(data['Close'])
plt.title('Tesla stock history')
plt.ylabel('Price (USD)')
plt.xlabel('Days')
plt.legend(['Open', 'High', 'Low', 'Close'])
plt.show()
# + [markdown] id="HGtaEpRuN3Yi" colab_type="text"
# # Preprocessing data
# + id="FTvF9PSIMaS3" colab_type="code" colab={}
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
# + id="nT-s5oJ2N-9q" colab_type="code" colab={}
def split_feature_target( data, target_index, lag_days):
"""
Split data into lag_days days for feature and next day for prediction
Arguments:
data {[np.array]} -- [array of data to split]
target_index {[int]} -- [index of target column]
lag_days {[int]} -- [number of days to be used to make prediction]
Returns:
[X, y] -- [array of days lag_days prior and next day stock price]
"""
X = np.array([data[i: i + lag_days].copy() for i in range(len(data) - lag_days)])
y = np.array([data[i + lag_days][target_index].copy() for i in range(len(data) - lag_days)])
y = np.expand_dims(y, axis=1)
return (X, y)
# + id="yCPgB5lIiKh3" colab_type="code" colab={}
def split_train_test_set(data, feature_cols, train_ratio=0.8):
"""
Split to data to train, test set
Arguments:
data {[np.array or pd.DataFrame]} -- [dataset to split]
feature_cols {[list]} -- [columns to be used as feature]
train_ratio {float} -- [train_size ratio] (default: {0.8})
Returns:
[train_set, test_set] -- [train set and test set]
"""
X = data.loc[:, feature_cols].values
num_train_instances = int(X.shape[0] * train_ratio)
train_set = X[:num_train_instances]
test_set = X[num_train_instances:]
return (train_set, test_set)
# + id="94C4QQzEXbIA" colab_type="code" colab={}
def scale_data(data, scaler=None):
"""
Transform data by scaling each column to a given range (0 and 1)
Arguments:
data {[np.array]} -- [array of feature or target for stock prediction]
scaler {[type]} -- [if scaler is provided then use that scaler to scale data, or create new scaler otherwise] (default: {None})
Returns:
[data_scaled, scaler] -- [scaled data and its scaler]
"""
if scaler is None:
scaler = MinMaxScaler()
data_scaled = scaler.fit_transform(data)
else:
data_scaled = scaler.transform(data)
return data_scaled, scaler
# + id="thgQXZnRV6mJ" colab_type="code" colab={}
feature_cols = ['Open', 'High', 'Low', 'Close', 'Volume']
train_set, test_set = split_train_test_set(data=data, feature_cols=feature_cols, train_ratio=0.8)
# for inversing prediction to actual value
_, target_scaler = scale_data(np.reshape(train_set[:, 3], (-1, 1)))
X_train_scaled, feature_scaler = scale_data(train_set)
X_test_scaled, _ = scale_data(test_set, feature_scaler)
X_train, y_train = split_feature_target(X_train_scaled, 3, lag_days=LAG_DAYS)
X_test, y_test = split_feature_target(X_test_scaled, 3, lag_days=LAG_DAYS)
# + id="ehdY486_TML0" colab_type="code" outputId="ca0d86b1-c822-4805-c8a3-76d95057e391" colab={"base_uri": "https://localhost:8080/", "height": 51}
print(f'Training set: ({X_train.shape} - {y_train.shape})')
print(f'Testing set: ({X_test.shape} - {y_test.shape})')
# + [markdown] id="AJ4mifPPi3jX" colab_type="text"
# # Predict 1 day ahead
# + [markdown] id="pfcm759HUGbT" colab_type="text"
# ## Creating the model
# + id="fde8lTu-SBQl" colab_type="code" outputId="58d1b196-a56f-4289-ff4f-590fee0c7f51" colab={"base_uri": "https://localhost:8080/", "height": 34}
import keras
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import LSTM, Dropout, Dense, BatchNormalization, concatenate, Input
from tensorflow.keras.utils import plot_model
# + id="fRoLgVe7SZDs" colab_type="code" colab={}
lstm_model = Sequential()
lstm_model.add(LSTM(40, input_shape=(LAG_DAYS, 5)))
lstm_model.add(Dense(32, activation='elu'))
lstm_model.add(Dense(1, activation='relu'))
lstm_model.compile(loss='mse', optimizer='adam')
# + id="9uRppZT2SfpB" colab_type="code" outputId="3560cf9d-be22-4bf7-ea58-bd235d56ac66" colab={"base_uri": "https://localhost:8080/", "height": 1000}
history = lstm_model.fit(x=X_train, y=y_train, epochs=50, batch_size=32, verbose=2, shuffle=True, validation_split=0.2)
# + id="xDkYQb_cwxWq" colab_type="code" outputId="007237d2-432f-4dbf-88a6-aa7f4cd31a53" colab={"base_uri": "https://localhost:8080/", "height": 483}
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.figure(figsize=(12, 8))
plt.plot(loss)
plt.plot(val_loss)
plt.ylabel('Loss')
plt.legend(['loss', 'val_loss'])
plt.show()
# + [markdown] id="kis9_2TNgI_U" colab_type="text"
# ## Evaluating the model
# + id="inhCzhWWr77a" colab_type="code" outputId="babebf8d-57a6-4acc-9a65-2d9f58dddcc3" colab={"base_uri": "https://localhost:8080/", "height": 51}
lstm_model.evaluate(X_test, y_test)
# + id="cx0FkZ3LVq2Z" colab_type="code" outputId="c054948d-edca-4679-b27e-b80500ce564c" colab={"base_uri": "https://localhost:8080/", "height": 34}
y_predicted = lstm_model.predict(X_test)
y_predicted_inverse = target_scaler.inverse_transform(y_predicted)
y_test_inverse = target_scaler.inverse_transform(y_test)
mae_inverse = np.sum(np.abs(y_predicted_inverse - y_test_inverse)) / len(y_test)
print(f'Mean Absolute Error - Testing = {mae_inverse}')
# + id="e24frKt9dBuo" colab_type="code" outputId="a1ec666a-ac92-441b-943b-0b41268e8203" colab={"base_uri": "https://localhost:8080/", "height": 483}
plt.figure(figsize=(12, 8))
plt.plot(y_predicted_inverse)
plt.plot(y_test_inverse)
plt.ylabel('Close')
plt.legend(['y_predict', 'y_test'])
plt.show()
# + [markdown] id="u2vtMuxyq-Dd" colab_type="text"
# # Using Moving-Average as extensive feature
# + id="uTWdgIqB1pAS" colab_type="code" colab={}
X_train_ma = np.mean(X_train, axis=1)
X_test_ma = np.mean(X_test, axis=1)
# + id="Zr92Il_j7SzM" colab_type="code" outputId="c10d100b-6fe9-4ba5-c179-e5c5488d434e" colab={"base_uri": "https://localhost:8080/", "height": 51}
print(f'Extensive training MA: ({X_train_ma.shape})')
print(f'Extensive testing MA: ({X_test_ma.shape})')
# + id="Yzr9rRRvrn24" colab_type="code" colab={}
lstm_input = Input(shape=(X_train.shape[1], X_train.shape[2]))
lstm_layer = LSTM(40)(lstm_input)
extensive_input = Input(shape=(X_train_ma.shape[1]))
dense_extensive_layer = Dense(20, activation='elu')(extensive_input)
lstm_output = concatenate((dense_extensive_layer, lstm_layer))
dense_layer = Dense(32, activation='elu')(lstm_output)
output_layer = Dense(1, activation='relu')(dense_layer)
lstm_model = Model(inputs=[lstm_input, extensive_input], outputs=output_layer)
lstm_model.compile(loss='mse', optimizer='adam')
# + id="diIP2smovzT0" colab_type="code" outputId="f5c58a98-09e9-4f9a-f855-3a0b62422a2b" colab={"base_uri": "https://localhost:8080/", "height": 1000}
history = lstm_model.fit(x=[X_train, X_train_ma], y=y_train, epochs=50, batch_size=32, verbose=2, shuffle=True, validation_split=0.2)
# + id="69BlQaTZwGy7" colab_type="code" outputId="d57c3f95-838c-4e70-c06c-13c09dd0307d" colab={"base_uri": "https://localhost:8080/", "height": 483}
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.figure(figsize=(12, 8))
plt.plot(loss)
plt.plot(val_loss)
plt.ylabel('Loss')
plt.legend(['loss', 'val_loss'])
plt.show()
# + id="dsklAR9xwHUs" colab_type="code" outputId="3d3d69a7-3cfe-44f2-8ed7-5bdf75596e9b" colab={"base_uri": "https://localhost:8080/", "height": 51}
lstm_model.evaluate([X_test, X_test_ma], y_test)
# + id="ST0t6a9RyDpg" colab_type="code" outputId="2cf97c8a-ed7c-4d1b-9027-38ed1ff47a71" colab={"base_uri": "https://localhost:8080/", "height": 34}
y_predicted = lstm_model.predict([X_test, X_test_ma])
y_predicted_inverse = target_scaler.inverse_transform(y_predicted)
y_test_inverse = target_scaler.inverse_transform(y_test)
mae_inverse = np.sum(np.abs(y_predicted_inverse - y_test_inverse)) / len(y_test)
print(f'Mean Absolute Error - Testing = {mae_inverse}')
# + id="Bd8NwOqJyHPj" colab_type="code" outputId="64b43bf2-7e76-4388-b957-506c59ff665f" colab={"base_uri": "https://localhost:8080/", "height": 483}
plt.figure(figsize=(12, 8))
plt.plot(y_predicted_inverse)
plt.plot(y_test_inverse)
plt.ylabel('Close')
plt.legend(['y_predict', 'y_test'])
plt.show()
# + [markdown] id="-Py8oBN1zU0j" colab_type="text"
# # Fine-tuning model
#
# The model with Moving Average performs better on 5 fits compared to model without Moving Average. Hence, we will use Moving Average in our final model and fine-tuning it.
# + id="m0teiSGGyHbZ" colab_type="code" colab={}
lstm_input = Input(shape=(X_train.shape[1], X_train.shape[2]))
lstm_layer = LSTM(40)(lstm_input)
extensive_input = Input(shape=(X_train_ma.shape[1]))
dense_extensive_layer = Dense(20, activation='relu')(extensive_input)
lstm_output = concatenate((dense_extensive_layer, lstm_layer))
dense_layer = BatchNormalization()(lstm_output)
dense_layer = Dense(32, activation='relu')(lstm_output)
output_layer = Dense(1, activation='relu')(dense_layer)
lstm_model = Model(inputs=[lstm_input, extensive_input], outputs=output_layer)
lstm_model.compile(loss='mse', optimizer='adam')
# + id="VlvSdgk7_Qyg" colab_type="code" outputId="a97d236b-1e0a-49c0-ba7a-53580f249c28" colab={"base_uri": "https://localhost:8080/", "height": 1000}
history = lstm_model.fit(x=[X_train, X_train_ma], y=y_train, epochs=120, batch_size=32, verbose=2, shuffle=True, validation_split=0.2)
# + id="cmLaxOKg_SjY" colab_type="code" outputId="aaed9327-cf7c-49fc-a34f-c64f681f06a1" colab={"base_uri": "https://localhost:8080/", "height": 487}
loss = history.history['loss'][20:]
val_loss = history.history['val_loss'][20:]
plt.figure(figsize=(12, 8))
plt.plot(loss)
plt.plot(val_loss)
plt.ylabel('Loss')
plt.legend(['loss', 'val_loss'])
plt.show()
# + id="Eqe5eROx_UGd" colab_type="code" outputId="8ede7954-5526-4011-8a17-3c0b9c35c9c2" colab={"base_uri": "https://localhost:8080/", "height": 51}
lstm_model.evaluate([X_test, X_test_ma], y_test)
# + id="dDGEZIqD_V9L" colab_type="code" outputId="ecd2ed1b-1914-48bc-9a1a-8a07cd641abe" colab={"base_uri": "https://localhost:8080/", "height": 34}
y_predicted = lstm_model.predict([X_test, X_test_ma])
y_predicted_inverse = target_scaler.inverse_transform(y_predicted)
y_test_inverse = target_scaler.inverse_transform(y_test)
mae_inverse = np.sum(np.abs(y_predicted_inverse - y_test_inverse)) / len(y_test)
print(f'Mean Absolute Error - Testing = {mae_inverse}')
# + id="N4e-kZhS_Xhb" colab_type="code" outputId="dd91576c-4111-471d-9149-b29de745a71c" colab={"base_uri": "https://localhost:8080/", "height": 483}
plt.figure(figsize=(12, 8))
plt.plot(y_predicted_inverse[380:450])
plt.plot(y_test_inverse[380:450])
plt.ylabel('Close')
plt.legend(['y_predict', 'y_test'])
plt.show()
# + id="rELGrbGI_uqr" colab_type="code" colab={}
| 60.370717 | 7,663 |
586bb1a070b00da7b6b5ed73662b676fa4f28588
|
py
|
python
|
tutorials/Image/05_conditional_operations.ipynb
|
Preejababu/geemap
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <table class="ee-notebook-buttons" align="left">
# <td><a target="_parent" href="https://github.com/giswqs/geemap/tree/master/tutorials/Image/05_conditional_operations.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
# <td><a target="_parent" href="https://nbviewer.jupyter.org/github/giswqs/geemap/blob/master/tutorials/Image/05_conditional_operations.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
# <td><a target="_parent" href="https://colab.research.google.com/github/giswqs/geemap/blob/master/tutorials/Image/05_conditional_operations.ipynb"><img width=26px src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
# </table>
# # Relational, conditional and Boolean operations
# To perform per-pixel comparisons between images, use relational operators. To extract urbanized areas in an image, this example uses relational operators to threshold spectral indices, combining the thresholds with `And()`:
# ## Install Earth Engine API and geemap
# Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
# The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
#
# **Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
# +
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
# -
# ## Create an interactive map
# The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
# ## Add Earth Engine Python script
# +
# Load a Landsat 8 image.
image = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20140318')
# Create NDVI and NDWI spectral indices.
ndvi = image.normalizedDifference(['B5', 'B4'])
ndwi = image.normalizedDifference(['B3', 'B5'])
# Create a binary layer using logical operations.
bare = ndvi.lt(0.2).And(ndwi.lt(0))
# Mask and display the binary layer.
Map.setCenter(-122.3578, 37.7726, 12)
Map.addLayer(bare.updateMask(bare), {}, 'bare')
Map.addLayerControl()
Map
# -
# As illustrated by this example, the output of relational and boolean operators is either True (1) or False (0). To mask the 0's, you can mask the resultant binary image with itself.
#
# The binary images that are returned by relational and boolean operators can be used with mathematical operators. This example creates zones of urbanization in a nighttime lights image using relational operators and `image.add()`:
# +
Map = emap.Map()
# Load a 2012 nightlights image.
nl2012 = ee.Image('NOAA/DMSP-OLS/NIGHTTIME_LIGHTS/F182012')
lights = nl2012.select('stable_lights')
Map.addLayer(lights, {}, 'Nighttime lights')
# Define arbitrary thresholds on the 6-bit stable lights band.
zones = lights.gt(30).add(lights.gt(55)).add(lights.gt(62))
# Display the thresholded image as three distinct zones near Paris.
palette = ['000000', '0000FF', '00FF00', 'FF0000']
Map.setCenter(2.373, 48.8683, 8)
Map.addLayer(zones, {'min': 0, 'max': 3, 'palette': palette}, 'development zones')
Map.addLayerControl()
Map
# -
# Note that the code in the previous example is equivalent to using a [ternary operator](http://en.wikipedia.org/wiki/%3F:) implemented by `expression()`:
# +
Map = emap.Map()
# Create zones using an expression, display.
zonesExp = nl2012.expression(
"(b('stable_lights') > 62) ? 3" +
": (b('stable_lights') > 55) ? 2" +
": (b('stable_lights') > 30) ? 1" +
": 0"
)
Map.addLayer(zonesExp,
{'min': 0, 'max': 3, 'palette': palette},
'development zones (ternary)')
Map.setCenter(2.373, 48.8683, 8)
Map.addLayerControl()
Map
# -
# Observe that in the previous expression example, the band of interest is referenced using the`b()` function, rather than a dictionary of variable names. (Learn more about image expressions on [this page](https://developers.google.com/earth-engine/image_math#expressions). Using either mathematical operators or an expression, the output is the same and should look something like Figure 2.
#
# Another way to implement conditional operations on images is with the `image.where()` operator. Consider the need to replace masked pixels with some other data. In the following example, cloudy pixels are replaced by pixels from a cloud-free image using `where()`:
# +
Map = emap.Map()
# Load a cloudy Landsat 8 image.
image = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20130603')
Map.addLayer(image,
{'bands': ['B5', 'B4', 'B3'], 'min': 0, 'max': 0.5},
'original image')
# Load another image to replace the cloudy pixels.
replacement = ee.Image('LANDSAT/LC08/C01/T1_TOA/LC08_044034_20130416')
# Compute a cloud score band.
cloud = ee.Algorithms.Landsat.simpleCloudScore(image).select('cloud')
# Set cloudy pixels to the other image.
replaced = image.where(cloud.gt(10), replacement)
# Display the result.
Map.centerObject(image, 9)
Map.addLayer(replaced,
{'bands': ['B5', 'B4', 'B3'], 'min': 0, 'max': 0.5},
'clouds replaced')
Map.addLayerControl()
Map
# -
# In this example, observe the use of the `simpleCloudScore()` algorithm. This algorithm ranks pixels by cloudiness on a scale of 0-100, with 100 most cloudy. Learn more about `simpleCloudScore()` on the [Landsat Algorithms page](https://developers.google.com/earth-engine/landsat#simple-cloud-score).
| 47.598765 | 1,023 |
0084fa975569e1a18d3d4da40579e84afc6e26cf
|
py
|
python
|
Probability Distributions/Python/Gaussian (Normal).ipynb
|
PennNGG/Quantitative-Neuroscience
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# [](https://colab.research.google.com/github/PennNGG/Quantitative-Neuroscience/blob/master/Probability%20Distributions/Python/Gaussian%20%28Normal%29.ipynb)
# + [markdown] id="pKIiY6p3GRFq"
# # Definition
# + [markdown] id="x7VmLUr5GTNw"
# The Gaussian distribution is a continuous function that is often described as the normal distribution or bell-shaped function.
#
# It can be used to describe discrete events when the number of events is very large, in which case it approximates the [binomial distribution](https://colab.research.google.com/drive/1q1KaEjkAzUKRFSLPQ0SFdqU_byc70Oi2?usp=sharing). It is also useful (albeit sometimes overused) because of the Central Limit Theorem (Links to an external site.), which states that when you add together enough independent random variables, their sum tends to be normally distributed.
#
# Mathematically, the Gaussian probability distribution is defined by just two parameters, the mean ($\mu$) and variance ($\sigma^2$):
#
# $f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^-\frac{(x-\mu)^2}{2\sigma^2}$.
# + [markdown] id="bkVu6eGKIIiQ"
# # Getting Started with Code
#
# + [markdown] id="gxusMZ-UN_6m"
# Matlab code is found in the [NGG Statistics GitHub Repository](https://github.com/PennNGG/Statistics.git) under "Probability Distributions/Gaussian.m".
#
# Python code is included below. First run the code cell just below to make sure all of the required Python modules are loaded, then you can run the other cell(s).
# + id="W633IbbRIdwa"
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as st
# + [markdown] id="isP38xJSbJuA"
# # Tutorial
# -
#
# + colab={"base_uri": "https://localhost:8080/", "height": 641} executionInfo={"elapsed": 1014, "status": "ok", "timestamp": 1626209378895, "user": {"displayName": "Joshua Gold", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhY1fK-mWt81XFeafwTBs66lN9JXee76x713d4Y=s64", "userId": "06476168460066594437"}, "user_tz": 240} id="Z32Do1n-bkQ9" outputId="a9377c93-42e3-4e12-cbca-d7e28cb4cc51"
# Let's compare simulated and theoretical Gaussians
mu = 5
sigma = 10
N = 10000
# Get samples
samples = np.random.normal(mu, sigma, N)
# plot histogram for a given number of bins (using trapz to approximate pdf)
nbins = 100
counts, edges = np.histogram(samples, bins=nbins)
xaxis = (edges[1:] + edges[:-1])/2
n_pdf = np.divide(counts, np.trapz(counts, xaxis))
plt.bar(xaxis, n_pdf)
# Show theoretical pdf in red
plt.plot(xaxis, st.norm.pdf(xaxis, mu, sigma), 'r-', linewidth=2)
# labels, ets
plt.title(f'Gaussian pdf, mu={mu:.2f}, sigma={sigma:.2f}')
plt.xlabel('Value')
plt.ylabel('Probability')
plt.legend(['Simulated', 'Theoretical'])
plt.show()
# Some summary statistics
# 1. The sample mean
print(f'Sample mean = {np.mean(samples):.3f}')
# 2. The expected value of the empirical distribution: the sum of probability x value per bin. This should be similar to the sample mean, but recognize that we lost some information from the binning (i.e., use more bins and this should get closer to the sample mean)
print(f'Expected value of empirical distribution = {np.sum(np.prod([xaxis, np.diff(edges), n_pdf], axis=0)):.3f}')
# 3. The expected value of the theoretical distribution
print(f'Expected value of the theoretical distribution = {np.sum(np.prod([xaxis, np.diff(edges), st.norm.pdf(xaxis, mu, sigma)], axis=0)):.3f}')
# Now standardize ("z-score") the samples by subtracting the mean and dividing by the STD
# The harder way
zSamples = np.divide(samples-np.mean(samples), np.std(samples))
# The easier way
z2Samples = st.zscore(samples)
# Check that they are the same
print(f'Number of different values = {np.count_nonzero(zSamples-z2Samples)}')
# Show the distribution of z-scored values
counts, edges = np.histogram(z2Samples, bins=nbins)
xaxis = (edges[1:] + edges[:-1])/2
plt.bar(xaxis, np.divide(counts, np.trapz(counts, xaxis)))
# Show theoretical "standard normal" pdf in red
plt.plot(xaxis, st.norm.pdf(xaxis), 'r-', linewidth=2)
# labels, ets
plt.title(f'Gaussian pdf, mu={np.mean(zSamples):.2f}, sigma={np.std(zSamples):.2f}')
plt.xlabel('Value')
plt.ylabel('Probability')
plt.legend(['Simulated', 'Theoretical'])
plt.show()
# + [markdown] id="T7GcYTwonfWV"
# # Neuroscience Examples
# + [markdown] id="uizGJREBnlzo"
# ## Example 1: Log-likelihood ratio from Gaussian spiking statistics
#
# Long story short: the logarithm of the likelihood ratio is cool (see [here](https://www.sciencedirect.com/science/article/pii/S0896627302009716), [here](https://www.jneurosci.org/content/23/37/11539), and [here](https://www.cell.com/neuron/fulltext/S0896-6273(15)00008-2)), and so it seems like it would be a really good thing if the brain could compute it. But how?
#
# Ok, let's back up a bit. A likelihood is just a conditional probability, often used to relate data to a particular hypothesis: *p*(*data* | *hypothesis*). If the data can take on different values, then the likelihood is a function that describes the probability of obtaining each possible value of the data, given that the hypothesis is true. In the brain, you can think of this function as describing, for example, the probability that a particular neuron will fire a certain amount of spikes in some unit of time (the data) given some state of the world, like the presence of a stimulus in the neuron's receptive field (the hypothesis). We use the term "hypothesis" because ultimately we want to use this quantity for inference testing and determine from the data whether or not the hypothesis is actually true (e.g., given the firing rate of the neuron, is the stimulus in its receptive field?). [This guy](https://en.wikipedia.org/wiki/Thomas_Bayes) can tell you more about how to do that, given the likelihood. But the first step is computing or estimating the likelihood, which at least in principle can be determined using something like a controlled experiment: set the hypothesis to be true (e.g., put the stimulus in the neuron's receptive field) and measure the data (e.g., the spiking response). Because the value of the data produced will typically vary from one measure to the next (i.e., it is a random variable), the procedure needs to be repeated many times to estimate the full likelihood function.
#
# The likelihood ratio is just a convenient way of comparing the likelihood associated with two different hypotheses: if the ratio is >1, then the hypothesis in the numerator has a higher likelihood, whereas if the ratio is <1, then the hypothesis in the denominator has a higher likelihood. It is therefore a natural quantity to use in the context of many [psychophysical](htthttps://www.sciencedirect.com/science/article/pii/S0306452214004369ps://) tasks that require a choice between two alternative hypotheses, given some sensory data. Also, taking the logarithm of this ratio of probabilities is a [nice thing to do](httphttps://en.wikisource.org/wiki/Popular_Science_Monthly/Volume_12/April_1878/Illustrations_of_the_Logic_of_Science_IVs://). Basically it means that you can add together the "[weight of evidence](https://projecteuclid.org/download/pdf_1/euclid.ss/1032209661)" provided by different, independent measurements (data), given their associated likelihood ratios.
#
# Ok, now back to our original question: does our brain actually compute (or approximate) the logarithm of the likelihood ratio (now referred to as "logLR"), and if so, how? It seems unlikely that we have explicit representations of two full likelihood functions, then when a given piece of data comes in we take the ratio of those two functions at that value, then compute the likelihood.
#
# It turns out that there is an easier way, and it has a lot to do with the Gaussian distribution (you had forgotten that is why we're here, right?). Consider this magical statement from [this paper](https://www.jneurosci.org/content/12/12/4745.long):
#
# "We compiled these responses into separate 'neuron' and 'antineuron' pools, drawn respectively from the preferred direction and null direction response distributions, and used the difference between the pooled responses to determine a 'decision' for each trial."
#
# They're saying that they are using the responses of two groups of neurons to make a decision; in this case, it's using motion-sensitive neurons in area MT (also called [V5](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4381624/)) of a monkey to make a decision about whether a visual stimulus that the monkey is looking at is moving to the left or right. Notice the words "response distributions." That got your attention, right?
#
# What they mean is, consider the distributions of responses of each of the two pools of neurons, under each of two conditions (left/right motion). So a pool of neurons that respond selectively to rightward motion will have some distribution of responses (measured as, say, number of spikes over a one-second interval) to its preferred stimulus (i.e., rightward motion) and the "null" stimulus (i.e., leftward motion). Same for a leftward-selective neuron, but with preferred=leftward, null=rightward.
#
# Here's a plot of real data recorded from a motion-sensitive neuron in MT of an awake monkey viewing a motion stimulus positioned in the neuron's receptive field and moving in the neuron's preferred or null direction:
#
# 
#
# For the two raster plots on top, each row is a separate trial, each tick is an action potential. You can see by eye that: 1) responses are variable from trial-to-trial (i.e., the output of the neuron represents a random variable); and 2) the responses tend to be slightly larger for preferred versus null motion (that being, of course, the definition of preferred versus null motion for this neuron). If we ignore the specific temporal structure of the spikes that occur on each trial (which [may](https://www.sciencedirect.com/science/article/abs/pii/0959438894900590) or [may not](https://www.jneurosci.org/content/21/5/1676.long) be a reasonable thing to do), we can summarize their responses as a single number: the number of spikes in the one-second interval during which the motion stimulus was presented, given them units of spikes/second. The bottom plot shows the histograms of these responses for each condition.
#
# Now for the payoff. You should note that those histograms look roughly bell-shaped. Let's assume that they are, and that the neural responses in fact represent samples from a Gaussian process; i.e., the likelihood functions describing p(data=neural spike-rate response | hypothesis=motion in a particular direction) are Gaussian (we could [test this idea](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3693611/) using the real data, but here we are making a more theoretical point: what would it buy us if it were in fact true that the data were generated by a Gaussian process?). In that case, and assuming that the pref/null likelihood functions for the neuron have different mean values but the same variance, they would look like this:
#
# 
#
# and the associated "anti-neuron" functions would look like this:
#
# 
#
# Now, some math! We won't go through all the details here, which are in the [original paper](https://pubmed.ncbi.nlm.nih.gov/11164731/), but the idea is as follows. Assume that the task is to determine whether the monkey was viewing rightward or leftward motion on a given trial, given only the responses of these two neurons (or you can think of them as groups of neurons, the distinction does not matter for this particular analysis). How would you do it? Remember the likelihood ratio! Each neuron provides one, based on its response on that trial and the two likelihood functions. Then if we take the logarithms, and assume the neurons are operating independently (again, maybe or maybe not a great assumption, but let's go with it), the total weight of evidence supporting hypothesis 1 (e.g., motion is rightward) versus hypothesis 2 (e.g., motion is leftward) is governed by the sum of the logLRs from the two neurons:
#
# $logLR_{right\:vs\:left\:for\:neuron\:x}+logLR_{right\:vs\:left\:for\:antineuron\:y}=$
#
# $log\frac{p(response_x|right)}{p(response_x|left)}+log\frac{p(response_y|right)}{p(response_y|right)}$
#
# Now if you just plug in the equations for the Gaussian above, and rearrange things a bit, you end up with the sum of the logLRs equal to:
#
# $\frac{\mu_1-\mu_2}{\sigma^2}(response_x-response_y)$
#
# Do you notice something? The first part $\frac{\mu_1-\mu_2}{\sigma^2}$ is just a constant -- check out the paper for a discussion of what it means and how the brain might compute or approximate it. The other term is simply the difference in spike rates elicited by the stimulus from the neuron ("x") and the antineuron ("y"). This is exactly the approach described in the quote above. So it turns out that if neural responses are distributed as a Gaussian, under certain conditions if you take a simple difference in spike rates between two neurons (or pools of neurons), you automatically get exactly the kind of quantity you'd want to make statistically reliable decisions based on the outputs of those neurons!
# + [markdown] id="UqoNXyuxP-go"
# # Additional Resources
#
# Working with the Gaussian (normal) distribution in [Matlab](https://www.mathworks.com/help/stats/normal-distribution.html), [R](https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/Normal), and [Python](https://numpy.org/doc/stable/reference/random/generated/numpy.random.normal.html).
# + [markdown] id="tteEm2Qlgbb3"
# # Credits
#
# Copyright 2021 by Joshua I. Gold, University of Pennsylvania
| 84.168675 | 1,518 |
c78f967c5c533c2dcc6049779c8db40ccba13f0f
|
py
|
python
|
Projects/Misc - Machine Learning/Models/Untitled1.ipynb
|
sanjivch/MyML
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
vizag = pd.read_html("https://app.cpcbccr.com/ccr/#/caaqm-dashboard-all/caaqm-view-data-report/%2522%257B%255C%2522parameter_list%255C%2522%253A%255B%257B%255C%2522id%255C%2522%253A0%252C%255C%2522itemName%255C%2522%253A%255C%2522PM2.5%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_193%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A1%252C%255C%2522itemName%255C%2522%253A%255C%2522PM10%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_215%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A2%252C%255C%2522itemName%255C%2522%253A%255C%2522Rack%2520Temp%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_218%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A3%252C%255C%2522itemName%255C%2522%253A%255C%2522AT%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_204%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A4%252C%255C%2522itemName%255C%2522%253A%255C%2522VWS%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_239%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A5%252C%255C%2522itemName%255C%2522%253A%255C%2522RH%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_235%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A6%252C%255C%2522itemName%255C%2522%253A%255C%2522RF%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_236%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A7%252C%255C%2522itemName%255C%2522%253A%255C%2522BP%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_238%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A8%252C%255C%2522itemName%255C%2522%253A%255C%2522SR%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_237%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A9%252C%255C%2522itemName%255C%2522%253A%255C%2522Temp%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_198%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A10%252C%255C%2522itemName%255C%2522%253A%255C%2522SO2%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_312%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A11%252C%255C%2522itemName%255C%2522%253A%255C%2522NO%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_226%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A12%252C%255C%2522itemName%255C%2522%253A%255C%2522NO2%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_194%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A13%252C%255C%2522itemName%255C%2522%253A%255C%2522NOx%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_225%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A14%252C%255C%2522itemName%255C%2522%253A%255C%2522NH3%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_311%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A15%252C%255C%2522itemName%255C%2522%253A%255C%2522CO%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_203%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A16%252C%255C%2522itemName%255C%2522%253A%255C%2522Ozone%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_222%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A17%252C%255C%2522itemName%255C%2522%253A%255C%2522Benzene%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_202%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A18%252C%255C%2522itemName%255C%2522%253A%255C%2522Toluene%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_232%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A19%252C%255C%2522itemName%255C%2522%253A%255C%2522Xylene%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_223%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A20%252C%255C%2522itemName%255C%2522%253A%255C%2522WS%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_233%255C%2522%257D%252C%257B%255C%2522id%255C%2522%253A21%252C%255C%2522itemName%255C%2522%253A%255C%2522WD%255C%2522%252C%255C%2522itemValue%255C%2522%253A%255C%2522parameter_234%255C%2522%257D%255D%252C%255C%2522criteria%255C%2522%253A%255C%252215%2520Minute%255C%2522%252C%255C%2522reportFormat%255C%2522%253A%255C%2522Tabular%255C%2522%252C%255C%2522fromDate%255C%2522%253A%255C%252223-04-2017%2520T00%253A00%253A00Z%255C%2522%252C%255C%2522toDate%255C%2522%253A%255C%252224-04-2020%2520T22%253A59%253A59Z%255C%2522%252C%255C%2522state%255C%2522%253A%255C%2522Andhra%2520Pradesh%255C%2522%252C%255C%2522city%255C%2522%253A%255C%2522Visakhapatnam%255C%2522%252C%255C%2522station%255C%2522%253A%255C%2522site_260%255C%2522%252C%255C%2522parameter%255C%2522%253A%255B%255C%2522parameter_193%255C%2522%252C%255C%2522parameter_215%255C%2522%252C%255C%2522parameter_218%255C%2522%252C%255C%2522parameter_204%255C%2522%252C%255C%2522parameter_239%255C%2522%252C%255C%2522parameter_235%255C%2522%252C%255C%2522parameter_236%255C%2522%252C%255C%2522parameter_238%255C%2522%252C%255C%2522parameter_237%255C%2522%252C%255C%2522parameter_198%255C%2522%252C%255C%2522parameter_312%255C%2522%252C%255C%2522parameter_226%255C%2522%252C%255C%2522parameter_194%255C%2522%252C%255C%2522parameter_225%255C%2522%252C%255C%2522parameter_311%255C%2522%252C%255C%2522parameter_203%255C%2522%252C%255C%2522parameter_222%255C%2522%252C%255C%2522parameter_202%255C%2522%252C%255C%2522parameter_232%255C%2522%252C%255C%2522parameter_223%255C%2522%252C%255C%2522parameter_233%255C%2522%252C%255C%2522parameter_234%255C%2522%255D%252C%255C%2522parameterNames%255C%2522%253A%255B%255C%2522PM2.5%255C%2522%252C%255C%2522PM10%255C%2522%252C%255C%2522Rack%2520Temp%255C%2522%252C%255C%2522AT%255C%2522%252C%255C%2522VWS%255C%2522%252C%255C%2522RH%255C%2522%252C%255C%2522RF%255C%2522%252C%255C%2522BP%255C%2522%252C%255C%2522SR%255C%2522%252C%255C%2522Temp%255C%2522%252C%255C%2522SO2%255C%2522%252C%255C%2522NO%255C%2522%252C%255C%2522NO2%255C%2522%252C%255C%2522NOx%255C%2522%252C%255C%2522NH3%255C%2522%252C%255C%2522CO%255C%2522%252C%255C%2522Ozone%255C%2522%252C%255C%2522Benzene%255C%2522%252C%255C%2522Toluene%255C%2522%252C%255C%2522Xylene%255C%2522%252C%255C%2522WS%255C%2522%252C%255C%2522WD%255C%2522%255D%257D%2522")
| 338 | 6,151 |
741cf808c065ab8ac928eb9c34799944262252fe
|
py
|
python
|
tutorials/W3D3_NetworkCausality/student/W3D3_Tutorial4.ipynb
|
erlichlab/course-content
|
['CC-BY-4.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W3D3_NetworkCausality/student/W3D3_Tutorial4.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="PWaDbLS0qE-8"
# # Neuromatch Academy 2020 -- Week 3 Day 3, Tutorial 4
#
# # Causality Day: Instrumental Variables
#
# **Content creators**: Ari Benjamin, Tony Liu, Konrad Kording
#
# **Content reviewers**: Mike X Cohen, Madineh Sarvestani, Ella Batty, Michael Waskom
# + [markdown] colab_type="text" id="_H_ZFDKLaa9u"
# ---
# # Tutorial objectives
#
# This is our final tutorial on our day of examining causality. Below is the high level outline of what we've covered today, with the sections we will focus on in this notebook in bold:
#
# 1. Master definitions of causality
# 2. Understand that estimating causality is possible
# 3. Learn 4 different methods and understand when they fail
# 1. perturbations
# 2. correlations
# 3. simultaneous fitting/regression
# 4. **instrumental variables**
#
# ### Notebook 4 Objectives
#
# In tutorial 3 we saw that even more sophisticated techniques such as simultaneous fitting fail to capture causality in the presence of omitted variable bias. So what techniques are there for us to obtain valid causal measurements when we can't perturb the system? Here we will:
#
# - learn about **instrumental variables,** a method that does not require experimental data for valid causal analysis
# - explore benefits of instrumental variable analysis and limitations
# - addresses **omitted variable bias** seen in regression
# - less efficient in terms of sample size than other techniques
# - requires a particular form of randomness in the system in order for causal effects to be identified
# + [markdown] colab_type="text" id="MEHzTTFb-XQj"
# ---
# # Setup
# + cellView="both" colab={} colab_type="code" id="SQxm7MziqLNH"
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
from sklearn.multioutput import MultiOutputRegressor
from sklearn.linear_model import LinearRegression, Lasso
# + cellView="form" colab={} colab_type="code" id="R0Z7Ae0E-e6u"
#@title Figure settings
import ipywidgets as widgets # interactive display
# %config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
# + cellView="form" colab={} colab_type="code" id="QxHuRzuBq7DO"
# @title Helper functions
def sigmoid(x):
"""
Compute sigmoid nonlinearity element-wise on x.
Args:
x (np.ndarray): the numpy data array we want to transform
Returns
(np.ndarray): x with sigmoid nonlinearity applied
"""
return 1 / (1 + np.exp(-x))
def logit(x):
"""
Applies the logit (inverse sigmoid) transformation
Args:
x (np.ndarray): the numpy data array we want to transform
Returns
(np.ndarray): x with logit nonlinearity applied
"""
return np.log(x/(1-x))
def create_connectivity(n_neurons, random_state=42, p=0.9):
"""
Generate our nxn causal connectivity matrix.
Args:
n_neurons (int): the number of neurons in our system.
random_state (int): random seed for reproducibility
Returns:
A (np.ndarray): our 0.1 sparse connectivity matrix
"""
np.random.seed(random_state)
A_0 = np.random.choice([0, 1], size=(n_neurons, n_neurons), p=[p, 1 - p])
# set the timescale of the dynamical system to about 100 steps
_, s_vals, _ = np.linalg.svd(A_0)
A = A_0 / (1.01 * s_vals[0])
# _, s_val_test, _ = np.linalg.svd(A)
# assert s_val_test[0] < 1, "largest singular value >= 1"
return A
def see_neurons(A, ax):
"""
Visualizes the connectivity matrix.
Args:
A (np.ndarray): the connectivity matrix of shape (n_neurons, n_neurons)
ax (plt.axis): the matplotlib axis to display on
Returns:
Nothing, but visualizes A.
"""
A = A.T # make up for opposite connectivity
n = len(A)
ax.set_aspect('equal')
thetas = np.linspace(0, np.pi * 2, n,endpoint=False)
x, y = np.cos(thetas), np.sin(thetas),
ax.scatter(x, y, c='k',s=150)
A = A / A.max()
for i in range(n):
for j in range(n):
if A[i, j] > 0:
ax.arrow(x[i], y[i], x[j] - x[i], y[j] - y[i], color='k', alpha=A[i, j], head_width=.15,
width = A[i,j] / 25, shape='right', length_includes_head=True)
ax.axis('off')
def simulate_neurons(A, timesteps, random_state=42):
"""
Simulates a dynamical system for the specified number of neurons and timesteps.
Args:
A (np.array): the connectivity matrix
timesteps (int): the number of timesteps to simulate our system.
random_state (int): random seed for reproducibility
Returns:
- X has shape (n_neurons, timeteps).
"""
np.random.seed(random_state)
n_neurons = len(A)
X = np.zeros((n_neurons, timesteps))
for t in range(timesteps - 1):
# solution
epsilon = np.random.multivariate_normal(np.zeros(n_neurons), np.eye(n_neurons))
X[:, t + 1] = sigmoid(A.dot(X[:, t]) + epsilon)
assert epsilon.shape == (n_neurons,)
return X
def correlation_for_all_neurons(X):
"""Computes the connectivity matrix for the all neurons using correlations
Args:
X: the matrix of activities
Returns:
estimated_connectivity (np.ndarray): estimated connectivity for the selected neuron, of shape (n_neurons,)
"""
n_neurons = len(X)
S = np.concatenate([X[:, 1:], X[:, :-1]], axis=0)
R = np.corrcoef(S)[:n_neurons, n_neurons:]
return R
def get_sys_corr(n_neurons, timesteps, random_state=42, neuron_idx=None):
"""
A wrapper function for our correlation calculations between A and R.
Args:
n_neurons (int): the number of neurons in our system.
timesteps (int): the number of timesteps to simulate our system.
random_state (int): seed for reproducibility
neuron_idx (int): optionally provide a neuron idx to slice out
Returns:
A single float correlation value representing the similarity between A and R
"""
A = create_connectivity(n_neurons, random_state)
X = simulate_neurons(A, timesteps)
R = correlation_for_all_neurons(X)
return np.corrcoef(A.flatten(), R.flatten())[0, 1]
def print_corr(v1, v2, corrs, idx_dict):
"""Helper function for formatting print statements for correlations"""
text_dict = {'Z':'taxes', 'T':'# cigarettes', 'C':'SES status', 'Y':'birth weight'}
print("Correlation between {} and {} ({} and {}): {:.3f}".format(v1, v2, text_dict[v1], text_dict[v2], corrs[idx_dict[v1], idx_dict[v2]]))
def get_regression_estimate(X, neuron_idx=None):
"""
Estimates the connectivity matrix using lasso regression.
Args:
X (np.ndarray): our simulated system of shape (n_neurons, timesteps)
neuron_idx (int): optionally provide a neuron idx to compute connectivity for
Returns:
V (np.ndarray): estimated connectivity matrix of shape (n_neurons, n_neurons).
if neuron_idx is specified, V is of shape (n_neurons,).
"""
n_neurons = X.shape[0]
# Extract Y and W as defined above
W = X[:, :-1].transpose()
if neuron_idx is None:
Y = X[:, 1:].transpose()
else:
Y = X[[neuron_idx], 1:].transpose()
# apply inverse sigmoid transformation
Y = logit(Y)
# fit multioutput regression
regression = MultiOutputRegressor(Lasso(fit_intercept=False, alpha=0.01), n_jobs=-1)
regression.fit(W,Y)
if neuron_idx is None:
V = np.zeros((n_neurons, n_neurons))
for i, estimator in enumerate(regression.estimators_):
V[i, :] = estimator.coef_
else:
V = regression.estimators_[0].coef_
return V
def get_regression_corr(n_neurons, timesteps, random_state, observed_ratio, regression_args, neuron_idx=None):
"""
A wrapper function for our correlation calculations between A and the V estimated
from regression.
Args:
n_neurons (int): the number of neurons in our system.
timesteps (int): the number of timesteps to simulate our system.
random_state (int): seed for reproducibility
observed_ratio (float): the proportion of n_neurons observed, must be betweem 0 and 1.
regression_args (dict): dictionary of lasso regression arguments and hyperparameters
neuron_idx (int): optionally provide a neuron idx to compute connectivity for
Returns:
A single float correlation value representing the similarity between A and R
"""
assert (observed_ratio > 0) and (observed_ratio <= 1)
A = create_connectivity(n_neurons, random_state)
X = simulate_neurons(A, timesteps)
sel_idx = np.clip(int(n_neurons*observed_ratio), 1, n_neurons)
sel_X = X[:sel_idx, :]
sel_A = A[:sel_idx, :sel_idx]
sel_V = get_regression_estimate(sel_X, neuron_idx=neuron_idx)
if neuron_idx is None:
return np.corrcoef(sel_A.flatten(), sel_V.flatten())[1, 0]
else:
return np.corrcoef(sel_A[neuron_idx, :], sel_V)[1, 0]
def compare_iv_estimate_to_regression(observed_ratio):
"""
A wrapper function to compare IV and Regressor performance as a function of observed neurons
Args:
observed_ratio(list): a list of different observed ratios (out of the whole system)
"""
#Let's compare IV estimates to our regression estimates, uncomment the code below
reg_corrs = np.zeros((len(observed_ratio),))
iv_corrs = np.zeros((len(observed_ratio),))
for j, ratio in enumerate(observed_ratio):
print(ratio)
sel_idx = int(ratio * n_neurons)
sel_X = X[:sel_idx, :]
sel_Z = X[:sel_idx, :]
sel_A = A[:sel_idx, :sel_idx]
sel_reg_V = get_regression_estimate(sel_X)
reg_corrs[j] = np.corrcoef(sel_A.flatten(), sel_reg_V.flatten())[1, 0]
sel_iv_V = get_iv_estimate_network(sel_X, sel_Z)
iv_corrs[j] = np.corrcoef(sel_A.flatten(), sel_iv_V.flatten())[1, 0]
# Plotting IV vs lasso performance
plt.plot(observed_ratio, reg_corrs)
plt.plot(observed_ratio, iv_corrs)
plt.xlim([1, 0.2])
plt.ylabel("Connectivity matrices correlation with truth")
plt.xlabel("Fraction of observed variables")
plt.title("IV and lasso performance as a function of observed neuron ratio")
plt.legend(['Regression', 'IV'])
def plot_neural_activity(X):
"""Plot first 10 timesteps of neural activity
Args:
X (ndarray): neural activity (n_neurons by timesteps)
"""
f, ax = plt.subplots()
im = ax.imshow(X[:, :10], aspect='auto')
divider = make_axes_locatable(ax)
cax1 = divider.append_axes("right", size="5%", pad=0.15)
plt.colorbar(im, cax=cax1)
ax.set(xlabel='Timestep', ylabel='Neuron', title='Simulated Neural Activity')
def compare_granger_connectivity(A, reject_null, selected_neuron):
"""Plot granger connectivity vs true
Args:
A (ndarray): true connectivity (n_neurons by n_neurons)
reject_null (list): outcome of granger causality, length n_neurons
selecte_neuron (int): the neuron we are plotting connectivity from
"""
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
im = axs[0].imshow(A[:, [selected_neuron]], cmap='coolwarm', aspect='auto')
plt.colorbar(im, ax = axs[0])
axs[0].set_xticks([0])
axs[0].set_xticklabels([selected_neuron])
axs[0].title.set_text("True connectivity for neuron {}".format(selected_neuron))
im = axs[1].imshow(np.array([reject_null]).transpose(), cmap='coolwarm', aspect='auto')
plt.colorbar(im, ax=axs[1])
axs[1].set_xticks([0])
axs[1].set_xticklabels([selected_neuron])
axs[1].title.set_text("Granger causality connectivity for neuron {}".format(selected_neuron))
def plot_performance_vs_eta(etas, corr_data):
""" Plot IV estimation performance as a function of instrument strength
Args:
etas (list): list of instrument strengths
corr_data (ndarray): n_trials x len(etas) array where each element is the correlation
between true and estimated connectivity matries for that trial and
instrument strength
"""
corr_mean = corr_data.mean(axis=0)
corr_std = corr_data.std(axis=0)
plt.plot(etas, corr_mean)
plt.fill_between(etas,
corr_mean - corr_std,
corr_mean + corr_std,
alpha=.2)
plt.xlim([etas[0], etas[-1]])
plt.title("IV performance as a function of instrument strength")
plt.ylabel("Correlation b.t. IV and true connectivity")
plt.xlabel("Strength of instrument (eta)")
plt.show()
# + [markdown] colab_type="text" id="vie8c9Er-qSV"
# ---
# # Section 1: Instrumental Variables
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 517} colab_type="code" id="T0LIcHbcU_MZ" outputId="61f30e56-ae7d-452b-8877-3bca7bef5f88"
#@title Video 1: Instrumental Variables
# Insert the ID of the corresponding youtube video
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id='BV1of4y1R7L1', width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
video
# + [markdown] colab_type="text" id="1DxeAfRz3kA5"
# If there is randomness naturally occurring in the system *that we can observe*, this in effect becomes the perturbations we can use to recover causal effects. This is called an **instrumental variable**. At high level, an instrumental variable must
#
#
# 1. be observable
# 2. effect a covariate you care about
# 3. **not** effect the outcome, except through the covariate
#
#
# It's rare to find these things in the wild, but when you do it's very powerful.
#
#
#
#
#
# + [markdown] colab_type="text" id="vi8mx6JPc5q-"
# 
#
# + [markdown] colab_type="text" id="vQwv2wga33GH"
# ## Section 1.1: A non-neuro example of an IV
# A classic example is estimating the effect of smoking cigarettes while pregnant on the birth weight of the infant. There is a (negative) correlation, but is it causal? Unfortunately many confounds affect both birth weight and smoking. Wealth is a big one.
#
# Instead of controlling for everything imaginable, one can find an IV. Here the instrumental variable is **state taxes on tobacco**. These
#
#
# 1. Are observable
# 2. Affect tobacco consumption
# 3. Don't affect birth weight except through tobacco
#
# By using the power of IV techniques, you can determine the causal effect without exhaustively controlling for everything.
#
# + [markdown] colab_type="text" id="niBt6OU-6LGc"
# Let's represent our tobacco example above with the following notation:
#
# - $Z_{\text{taxes}}$: our tobacco tax **instrument**, which only affects an individual's tendency to smoke while pregnant within our system
# - $T_{\text{smoking}}$: number of cigarettes smoked per day while pregnant, our "treatment" if this were a randomized trial
# - $C_{\text{SES}}$: socioeconomic status (higher means weathier), a **confounder** if it is not observed
# - $Y_{\text{birthweight}}$: child birthweight in grams, our outcome of interest
#
# Let's suppose we have the following function for our system:
#
# $Y_{\text{birthweight}} = 3000 + C_{\text{SES}} - 2T_{\text{smoking}},$
#
# with the additional fact that $C_{\text{SES}}$ is negatively correlated with $T_{\text{smoking}}$.
#
# The causal effect we wish to estimate is the coefficient $-2$ for $T_{\text{smoking}}$, which means that if a mother smokes one additional cigarette per day while pregnant her baby will be 2 grams lighter at birth.
#
# We've provided a covariance matrix with the desired structure in the code cell below, so please run it to look at the correlations between our variables.
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 52} colab_type="code" id="kSv_ChIDAYs2" outputId="278586d8-741d-4eef-9cd7-5faa6b543955"
#@markdown Execute this cell to see correlations with C
# run this code below to generate our setup
idx_dict = {
'Z': 0,
'T': 1,
'C': 2,
'Y': 3
}
# vars: Z T C
covar = np.array([[1.0, 0.5, 0.0], # Z
[0.5, 1.0, -0.5], # T
[0.0, -0.5, 1.0]]) # C
# vars: Z T C
means = [0, 5, 2]
# generate some data
np.random.seed(42)
data = np.random.multivariate_normal(mean=means, cov=2 * covar, size=2000)
# generate Y from our equation above
Y = 3000 + data[:, idx_dict['C']] - (2 * (data[:, idx_dict['T']]))
data = np.concatenate([data, Y.reshape(-1, 1)], axis=1)
Z = data[:, [idx_dict['Z']]]
T = data[:, [idx_dict['T']]]
C = data[:, [idx_dict['C']]]
Y = data[:, [idx_dict['Y']]]
corrs = np.corrcoef(data.transpose())
print_corr('C', 'T', corrs, idx_dict)
print_corr('C', 'Y', corrs, idx_dict)
# + [markdown] colab_type="text" id="xHbhR7nLJJ4j"
# We see what is exactly represented in our graph above: $C_{\text{SES}}$ is correlated with both $T_{\text{smoking}}$ and $Y_{\text{birthweight}}$, so $C_{\text{SES}}$ is a potential confounder if not included in our analysis. Let's say that it is difficult to observe and quantify $C_{\text{SES}}$, so we do not have it available to regress against. This is another example of the **omitted variable bias** we saw in the last tutorial.
#
# What about $Z_{\text{taxes}}$? Does it satisfy conditions 1, 2, and 3 of an instrument?
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 87} colab_type="code" id="hQpvq5sIKhr6" outputId="0eee211f-4d87-4ebc-d78a-0f53483a3b3d"
#@markdown Execute this cell to see correlations of Z
print("Condition 2?")
print_corr('Z', 'T', corrs, idx_dict)
print("Condition 3?")
print_corr('Z', 'C', corrs, idx_dict)
# + [markdown] colab_type="text" id="TjiPIsj_KpJ9"
# Perfect! We see that $Z_{\text{taxes}}$ is correlated with $T_{\text{smoking}}$ (#2) but is uncorrelated with $C_{\text{SES}}$ (#3). $Z_\text{taxes}$ is also observable (#1), so we've satisfied our three criteria for an instrument:
#
# 1. $Z_\text{taxes}$ is observable
# 2. $Z_\text{taxes}$ affects $T_{\text{smoking}}$
# 3. $Z_\text{taxes}$ doesn't affect $Y_{\text{birthweight}}$ except through $T_{\text{smoking}}$ (ie $Z_\text{taxes}$ doesn't affect or is affected by $C_\text{SES}$)
# + [markdown] colab_type="text" id="99I0zDgT6HND"
# ## Section 1.2: How IV works, at high level
#
# The easiest way to imagine IV is that the instrument is **an observable source of "randomness"** that affects the treatment. In this way it's similar to the interventions we talked about in Tutorial 1.
#
# But how do you actually use the instrument? The key is that we need to extract **the component of the treatment that is due only to the effect of the instrument**. We will call this component $\hat{T}$.
# $$
# \hat{T}\leftarrow \text{The unconfounded component of }T
# $$
# Getting $\hat{T}$ is fairly simple. It is simply the predicted value of $T$ found in a regression that has only the instrument $Z$ as input.
#
# Once we have the unconfounded component in hand, getting the causal effect is as easy as regressing the outcome on $\hat{T}$.
# + [markdown] colab_type="text" id="ULgcCspkACkS"
# ## Section 1.3: IV estimation using two-stage least squares
#
# The fundamental technique for instrumental variable estimation is **two-stage least squares**.
#
# We run two regressions:
#
# 1. The first stage gets $\hat{T}_{\text{smoking}}$ by regressing $T_{\text{smoking}}$ on $Z_\text{taxes}$, fitting the parameter $\hat{\alpha}$:
#
# $$
# \hat{T}_{\text{smoking}} = \hat{\alpha} Z_\text{taxes}
# $$
#
# 2. The second stage then regresses $Y_{\text{birthweight}}$ on $\hat{T}_{\text{smoking}}$ to obtain an estimate $\hat{\beta}$ of the causal effect:
#
# $$
# \hat{Y}_{\text{birthweight}} = \hat{\beta} \hat{T}_{\text{smoking}}
# $$
#
# The first stage estimates the **unconfounded component** of $T_{\text{smoking}}$ (ie, unaffected by the confounder $C_{\text{SES}}$), as we discussed above.
#
# Then, the second stage uses this unconfounded component $\hat{T}_{\text{smoking}}$ to estimate the effect of smoking on $\hat{Y}_{\text{birthweight}}$.
#
# We will explore how all this works in the next two exercises.
#
# + [markdown] colab_type="text" id="3UpC7KiaPrdW"
# ### Section 1.3.1: Least squares regression stage 1
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 517} colab_type="code" id="vD1kCeqPVH_G" outputId="16c25233-6c85-4dd6-a148-f27cf8d25f10"
#@title Video 2: Stage 1
# Insert the ID of the corresponding youtube video
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id='BV1jK4y1x7q5', width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
video
# + [markdown] colab_type="text" id="rXJQHmH6Kufb"
# #### Exercise 1: Compute regression stage 1
#
# Let's run the regression of $T_{\text{smoking}}$ on $Z_\text{taxes}$ to compute $\hat{T}_{\text{smoking}}$. We will then check whether our estimate is still confounded with $C_{\text{SES}}$ by comparing the correlation of $C_{\text{SES}}$ with $T_{\text{smoking}}$ vs $\hat{T}_{\text{smoking}}$.
#
# ### Suggestions
#
# - use the `LinearRegression()` model, already imported from scikit-learn
# - use `fit_intercept=True` as the only parameter setting
# - be sure to check the ordering of the parameters passed to `LinearRegression.fit()`
# + colab={} colab_type="code" id="E2Y-96LCL78q"
def fit_first_stage(T, Z):
"""
Estimates T_hat as the first stage of a two-stage least squares.
Args:
T (np.ndarray): our observed, possibly confounded, treatment of shape (n, 1)
Z (np.ndarray): our observed instruments of shape (n, 1)
Returns
T_hat (np.ndarray): our estimate of the unconfounded portion of T
"""
############################################################################
## Insert your code here to fit the first stage of the 2-stage least squares
## estimate.
## Fill out function and remove
raise NotImplementedError('Please complete fit_first_stage function')
############################################################################
# Initialize linear regression model
stage1 = LinearRegression(...)
# Fit linear regression model
stage1.fit(...)
# Predict T_hat using linear regression model
T_hat = stage1.predict(...)
return T_hat
# Uncomment below to test your function
# T_hat = fit_first_stage(T, Z)
# T_C_corr = np.corrcoef(T.transpose(), C.transpose())[0, 1]
# T_hat_C_corr = np.corrcoef(T_hat.transpose(), C.transpose())[0, 1]
# print("Correlation between T and C: {:.3f}".format(T_C_corr))
# print("Correlation between T_hat and C: {:.3f}".format(T_hat_C_corr))
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 52} colab_type="text" id="l7e6Bh-MOtZE" outputId="209e0863-878f-4d19-f11f-33241a9f6919"
# [*Click for solution*](https://github.com/erlichlab/course-content/tree/master//tutorials/W3D3_NetworkCausality/solutions/W3D3_Tutorial4_Solution_7d3abb70.py)
#
#
# + [markdown] colab_type="text" id="Y49xA133P1aY"
# You should see a correlation between $T$ and $C$ of `-0.483` and between $\hat{T}$ and $C$ of `0.009`.
# + [markdown] colab_type="text" id="h9TNb3IKP_xS"
# ### Section 1.3.2: Least squares regression stage 2
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 517} colab_type="code" id="_PjOTeQWVScz" outputId="84e1e3b4-07c4-426d-96df-743e35b49777"
#@title Video 3: Stage 2
# Insert the ID of the corresponding youtube video
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id='BV1Kv411q7Wx', width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
video
# + [markdown] colab_type="text" id="BqSd5RC31J3t"
# #### Exercise 2: Compute the IV estimate
#
# Now let's implement the second stage! Complete the `fit_second_stage()` function below. We will again use a linear regression model with an intercept. We will then use the function from Exercise 1 (`fit_first_stage`) and this function to estimate the full two-stage regression model. We will obtain the estimated causal effect of the number of cigarettes ($T$) on birth weight ($Y$).
#
#
# + colab={} colab_type="code" id="yPlDzUFIOtuD"
def fit_second_stage(T_hat, Y):
"""
Estimates a scalar causal effect from 2-stage least squares regression using
an instrument.
Args:
T_hat (np.ndarray): the output of the first stage regression
Y (np.ndarray): our observed response (n, 1)
Returns:
beta (float): the estimated causal effect
"""
############################################################################
## Insert your code here to fit the second stage of the 2-stage least squares
## estimate.
## Fill out function and remove
raise NotImplementedError('Please complete fit_second_stage function')
############################################################################
# Initialize linear regression model
stage2 = LinearRegression(...)
# Fit model to data
stage2.fit(...)
return stage2.coef_
# Uncomment below to test your function
# T_hat = fit_first_stage(T, Z)
# beta = fit_second_stage(T_hat, Y)
# print("Estimated causal effect is: {:.3f}".format(beta[0, 0]))
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="text" id="L6tuuK-BRTMO" outputId="96b05157-e059-4672-bbec-4986f29ace8d"
# [*Click for solution*](https://github.com/erlichlab/course-content/tree/master//tutorials/W3D3_NetworkCausality/solutions/W3D3_Tutorial4_Solution_19606be3.py)
#
#
# + [markdown] colab_type="text" id="kFjAgfJVWPM5"
# You should obtain an estimated causal effect of `-1.984`. This is quite close to the true causal effect of $-2$!
# + [markdown] colab_type="text" id="jCy0GNrYc64I"
# ---
# # Section 2: IVs in our simulated neural system
#
#
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 517} colab_type="code" id="t9eczaIWVaYE" outputId="d34ab471-4b8f-48b3-fcd6-5eec8ac0a9b5"
#@title Video 4: IVs in simulated neural systems
# Insert the ID of the corresponding youtube video
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id='BV1nA411v7Hs', width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
video
# + [markdown] colab_type="text" id="V5EmyvVBSDpJ"
# Now, say we have the neural system we have been simulating, except with an additional variable $\vec{z}$. This will be our instrumental variable.
#
# We treat $\vec{z}$ as a source of noise in the dynamics of our neurons:
#
# $$
# \vec{x}_{t+1} = \sigma(A\vec{x}_t + \eta \vec{z}_{t+1} + \epsilon_t)
# $$
#
# - $\eta$ is what we'll call the "strength" of our IV
# - $\vec{z}_t$ is a random binary variable, $\vec{z}_t \sim Bernoulli(0.5)$
#
# Remember that for each neuron $i$, we are trying to figure out whether $i$ is connected to (causally affects) the other neurons in our system *at the next time step*. So for timestep $t$, we want to determine whether $\vec{x}_{i,t}$ affects all the other neurons at $\vec{x}_{t+1}$. For a given neuron $i$, $\vec{z}_{i,t}$ satistfies the 3 criteria for a valid instrument.
#
#
# **What could $z$ be, biologically?**
#
# Imagine $z$ to be some injected current through an *in vivo* patch clamp. It affects each neuron individually, and only affects dynamics through that neuron.
#
# The cool thing about IV is that you don't have to control $z$ yourself - it can be observed. So if you mess up your wiring and accidentally connect the injected voltage to an AM radio, no worries. As long as you can observe the signal the method will work.
# + [markdown] colab_type="text" id="86KJCaFmK4N5"
# 
# + [markdown] colab_type="text" id="OCEMXVu-fcwK"
# ## Exercise 3: Simulate a system with IV
#
# Here we'll modify the function that simulates the neural system, but this time make the update rule include the effect of the instrumental variable $z$.
# + colab={} colab_type="code" id="cxgSyY-OwNam"
def simulate_neurons_iv(n_neurons, timesteps, eta, random_state=42):
"""
Simulates a dynamical system for the specified number of neurons and timesteps.
Args:
n_neurons (int): the number of neurons in our system.
timesteps (int): the number of timesteps to simulate our system.
eta (float): the strength of the instrument
random_state (int): seed for reproducibility
Returns:
The tuple (A,X,Z) of the connectivity matrix, simulated system, and instruments.
- A has shape (n_neurons, n_neurons)
- X has shape (n_neurons, timesteps)
- Z has shape (n_neurons, timesteps)
"""
np.random.seed(random_state)
A = create_connectivity(n_neurons, random_state)
X = np.zeros((n_neurons, timesteps))
Z = np.random.choice([0, 1], size=(n_neurons, timesteps))
for t in range(timesteps - 1):
############################################################################
## Insert your code here to adjust the update rule to include the
## instrumental variable.
## We've already created Z for you. (We need to return it to regress on it).
## Your task is to slice it appropriately. Don't forget eta.
## Fill out function and remove
raise NotImplementedError('Complete simulate_neurons_iv function')
############################################################################
IV_on_this_timestep = ...
X[:, t + 1] = sigmoid(A.dot(X[:, t]) + IV_on_this_timestep + np.random.multivariate_normal(np.zeros(n_neurons), np.eye(n_neurons)))
return A, X, Z
# Parameters
timesteps = 5000 # Simulate for 5000 timesteps.
n_neurons = 100 # the size of our system
eta = 2 # the strength of our instrument, higher is stronger
# Uncomment below to test your function
# Simulate our dynamical system for the given amount of time
# A, X, Z = simulate_neurons_iv(n_neurons, timesteps, eta)
# plot_neural_activity(X)
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 431} colab_type="text" id="mN4tKTXgUTWM" outputId="c39ed351-d155-4897-beda-ae33de41aca4"
# [*Click for solution*](https://github.com/erlichlab/course-content/tree/master//tutorials/W3D3_NetworkCausality/solutions/W3D3_Tutorial4_Solution_b51d0ad3.py)
#
# *Example output:*
#
# <img alt='Solution hint' align='left' width=558 height=414 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W3D3_NetworkCausality/static/W3D3_Tutorial4_Solution_b51d0ad3_0.png>
#
#
# + [markdown] colab_type="text" id="_7ApCeEoUclW"
# ## Section 2.1: Estimate IV for simulated neural system
# + [markdown] colab_type="text" id="IMLK16k7JrRp"
# Since you just implemented two-stage least squares, we've provided the network implementation for you, with the function `get_iv_estimate_network()`. Now, let's see how our IV estimates do in recovering the connectivity matrix.
# + colab={} colab_type="code" id="qI7Zlq2GI6ls"
def get_iv_estimate_network(X, Z):
"""
Estimates the connectivity matrix from 2-stage least squares regression
using an instrument.
Args:
X (np.ndarray): our simulated system of shape (n_neurons, timesteps)
Z (np.ndarray): our observed instruments of shape (n_neurons, timesteps)
Returns:
V (np.ndarray): the estimated connectivity matrix
"""
n_neurons = X.shape[0]
Y = X[:, 1:].transpose()
# apply inverse sigmoid transformation
Y = logit(Y)
# Stage 1: regress X on Z
stage1 = MultiOutputRegressor(LinearRegression(fit_intercept=True), n_jobs=-1)
stage1.fit(Z[:, :-1].transpose(), X[:, :-1].transpose())
X_hat = stage1.predict(Z[:, :-1].transpose())
# Stage 2: regress Y on X_hatI
stage2 = MultiOutputRegressor(LinearRegression(fit_intercept=True), n_jobs=-1)
stage2.fit(X_hat, Y)
# Get estimated effects
V = np.zeros((n_neurons, n_neurons))
for i, estimator in enumerate(stage2.estimators_):
V[i, :] = estimator.coef_
return V
# + [markdown] colab_type="text" id="FJfLKuRTB8ps"
# Now let's see how well it works in our system.
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 352} colab_type="code" id="fpoI90_xB20v" outputId="f23ccf76-9808-483d-e6b2-6d86c33f9ab8"
#@markdown Execute this cell to visualize IV estimated connectivity matrix
n_neurons = 6
timesteps = 10000
random_state = 42
eta = 2
A, X, Z = simulate_neurons_iv(n_neurons, timesteps, eta, random_state)
V = get_iv_estimate_network(X, Z)
print("IV estimated correlation: {:.3f}".format(np.corrcoef(A.flatten(), V.flatten())[1, 0]))
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
im = axs[0].imshow(A, cmap="coolwarm")
fig.colorbar(im, ax=axs[0],fraction=0.046, pad=0.04)
axs[0].title.set_text("True connectivity matrix")
axs[0].set(xlabel='Connectivity from', ylabel='Connectivity to')
im = axs[1].imshow(V, cmap="coolwarm")
fig.colorbar(im, ax=axs[1],fraction=0.046, pad=0.04)
axs[1].title.set_text("IV estimated connectivity matrix")
axs[1].set(xlabel='Connectivity from')
plt.show()
# + [markdown] colab_type="text" id="V1zmNZ4fKtny"
# The IV estimates seem to perform pretty well! In the next section, we will see how they behave in the face of omitted variable bias.
# + [markdown] colab_type="text" id="ripdtDHsIb3p"
# ---
# # Section 3: IVs and omitted variable bias
#
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 517} colab_type="code" id="rpMTXUtcVmK7" outputId="fb738e85-3553-422b-c177-16d9fa91cb04"
#@title Video 5: IV vs regression
# Insert the ID of the corresponding youtube video
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id='BV1pv411q7Hc', width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
video
# + [markdown] colab_type="text" id="1Y-7Fn1k4sfh"
# ## Interactive Demo: Estimating connectivity with IV vs regression on a subset of observed neurons
#
# Change the ratio of observed neurons and look at the impact on the quality of connectivity estimation using IV vs regression. Which method does better with fewer observed neurons?
#
# **NOTE:** this simulation will take about a minute to run!
#
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 363, "referenced_widgets": ["f47f8abc88714432a420356abe6b621a", "b92d7557f0cd4bd0b6bec001fd20186b", "c94e8aa5c7184899881d842b4ca9c5f5", "19a60e1994f94846911c962401b29643", "b55b6f949bec411e88e60324512115b0", "85159b65f825419ba2cb703aae7fe9e0", "5ee12cb064c447e19dd87386275ae00a"]} colab_type="code" id="ojwn93j9Dzqw" outputId="10456272-28c2-43fb-f45f-2650133f6351"
#@title
#@markdown Execute this cell to enable demo
n_neurons = 30
timesteps = 20000
random_state = 42
eta = 2
A, X, Z = simulate_neurons_iv(n_neurons, timesteps, eta, random_state)
reg_args = {
"fit_intercept": False,
"alpha": 0.001
}
def get_regression_estimate_full_connectivity(X):
"""
Estimates the connectivity matrix using lasso regression.
Args:
X (np.ndarray): our simulated system of shape (n_neurons, timesteps)
neuron_idx (int): optionally provide a neuron idx to compute connectivity for
Returns:
V (np.ndarray): estimated connectivity matrix of shape (n_neurons, n_neurons).
if neuron_idx is specified, V is of shape (n_neurons,).
"""
n_neurons = X.shape[0]
# Extract Y and W as defined above
W = X[:, :-1].transpose()
Y = X[:, 1:].transpose()
# apply inverse sigmoid transformation
Y = logit(Y)
# fit multioutput regression
reg = MultiOutputRegressor(Lasso(fit_intercept=False, alpha=0.01, max_iter=200), n_jobs=-1)
reg.fit(W, Y)
V = np.zeros((n_neurons, n_neurons))
for i, estimator in enumerate(reg.estimators_):
V[i, :] = estimator.coef_
return V
def get_regression_corr_full_connectivity(n_neurons, A, X, observed_ratio, regression_args):
"""
A wrapper function for our correlation calculations between A and the V estimated
from regression.
Args:
n_neurons (int): number of neurons
A (np.ndarray): connectivity matrix
X (np.ndarray): dynamical system
observed_ratio (float): the proportion of n_neurons observed, must be betweem 0 and 1.
regression_args (dict): dictionary of lasso regression arguments and hyperparameters
Returns:
A single float correlation value representing the similarity between A and R
"""
assert (observed_ratio > 0) and (observed_ratio <= 1)
sel_idx = np.clip(int(n_neurons*observed_ratio), 1, n_neurons)
sel_X = X[:sel_idx, :]
sel_A = A[:sel_idx, :sel_idx]
sel_V = get_regression_estimate_full_connectivity(sel_X)
return np.corrcoef(sel_A.flatten(), sel_V.flatten())[1,0], sel_V
@widgets.interact
def plot_observed(ratio=[0.2, 0.4, 0.6, 0.8, 1.0]):
fig, axs = plt.subplots(1, 3, figsize=(15, 5))
sel_idx = int(ratio * n_neurons)
n_observed = sel_idx
offset = np.zeros((n_neurons, n_neurons))
offset[:sel_idx, :sel_idx] = 1 + A[:sel_idx, :sel_idx]
im = axs[0].imshow(offset, cmap="coolwarm", vmin=0, vmax=A.max() + 1)
axs[0].title.set_text("True connectivity")
axs[0].set_xlabel("Connectivity to")
axs[0].set_ylabel("Connectivity from")
plt.colorbar(im, ax=axs[0],fraction=0.046, pad=0.04)
sel_A = A[:sel_idx, :sel_idx]
sel_X = X[:sel_idx, :]
sel_Z = Z[:sel_idx, :]
V = get_iv_estimate_network(sel_X, sel_Z)
iv_corr = np.corrcoef(sel_A.flatten(), V.flatten())[1, 0]
big_V = np.zeros(A.shape)
big_V[:sel_idx, :sel_idx] = 1 + V
im = axs[1].imshow(big_V, cmap="coolwarm", vmin=0, vmax=A.max() + 1)
plt.colorbar(im, ax=axs[1], fraction=0.046, pad=0.04)
c = 'w' if n_observed < (n_neurons - 3) else 'k'
axs[1].text(0,n_observed + 2, "Correlation : {:.2f}".format(iv_corr), color=c, size=15)
axs[1].axis("off")
reg_corr, R = get_regression_corr_full_connectivity(n_neurons,
A,
X,
ratio,
reg_args)
big_R = np.zeros(A.shape)
big_R[:sel_idx, :sel_idx] = 1 + R
im = axs[2].imshow(big_R, cmap="coolwarm", vmin=0, vmax=A.max() + 1)
plt.colorbar(im, ax=axs[2], fraction=0.046, pad=0.04)
c = 'w' if n_observed<(n_neurons-3) else 'k'
axs[1].title.set_text("Estimated connectivity (IV)")
axs[1].set_xlabel("Connectivity to")
axs[1].set_ylabel("Connectivity from")
axs[2].text(0, n_observed + 2,"Correlation : {:.2f}".format(reg_corr), color=c, size=15)
axs[2].axis("off")
axs[2].title.set_text("Estimated connectivity (regression)")
axs[2].set_xlabel("Connectivity to")
axs[2].set_ylabel("Connectivity from")
# + [markdown] colab_type="text" id="4qLUURsLpZWd"
# We can also visualize the performance of regression and IV as a function of the observed neuron ratio below.
#
# **Note** that this code takes about a minute to run!
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 518} colab_type="code" id="27bCZLPNrgTB" outputId="37274be5-e39f-40f9-c0d9-bd6cddb41ad8"
#@markdown Execute this cell to visualize connectivity estimation performance
n_neurons = 40 # the size of the system
timesteps = 20000
random_state = 42
eta = 2 # the strength of our instrument
A, X, Z = simulate_neurons_iv(n_neurons, timesteps, eta, random_state)
observed_ratio = [1, 0.8, 0.6, 0.4, 0.2]
compare_iv_estimate_to_regression(observed_ratio)
# + [markdown] colab_type="text" id="GVw-0bg1Me7B"
# We see that IVs handle omitted variable bias (when the instrument is strong and we have enough data).
#
# ### The costs of IV analysis
#
# - we need to find an appropriate and valid instrument
# - Because of the 2-stage estimation process, we need strong instruments or else our standard errors will be large
# + [markdown] colab_type="text" id="uYLeNBMB7Co1"
# ---
# # Discussion questions
#
#
# * Think back to your most recent work. Can you create a causal diagram of the fundamental question? Are there sources of bias (omitted variables or otherwise) that might be a threat to causal validity?
# * Can you think of any possibilities for instrumental variables? What sources of observed randomness could studies in your field leverage in identifying causal effects?
#
#
#
# + [markdown] colab_type="text" id="HeGT_rMxX1Xx"
# ---
# # Summary
#
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 517} colab_type="code" id="nAaBj9KBVvGm" outputId="b1284046-80da-422b-dd41-6edec4f5727a"
#@title Video 6: Summary
# Insert the ID of the corresponding youtube video
from IPython.display import IFrame
class BiliVideo(IFrame):
def __init__(self, id, page=1, width=400, height=300, **kwargs):
self.id=id
src = "https://player.bilibili.com/player.html?bvid={0}&page={1}".format(id, page)
super(BiliVideo, self).__init__(src, width, height, **kwargs)
video = BiliVideo(id='BV1Gt4y1X76z', width=854, height=480, fs=1)
print("Video available at https://www.bilibili.com/video/{0}".format(video.id))
video
# + [markdown] colab_type="text" id="2TksS4vCBqhH"
# In this tutorial, we:
#
# * Explored instrumental variables and how we can use them for causality estimates
# * Compared IV estimates to regression estimates
# + [markdown] colab_type="text" id="7TxqdIZ_44SO"
# ---
# # Appendix
# + [markdown] colab_type="text" id="27JWpvf6e10U"
# ## (Bonus) Exercise: Exploring instrument strength
#
# Explore how the strength of the instrument $\eta$ affects the quality of estimates with instrumental variables.
# **bold text**
#
# + colab={} colab_type="code" id="7qKKH_XgfSfb"
def instrument_strength_effect(etas, n_neurons, timesteps, n_trials):
""" Compute IV estimation performance for different instrument strengths
Args:
etas (list): different instrument strengths to compare
n_neurons (int): number of neurons in simulation
timesteps (int): number of timesteps in simulation
n_trials (int): number of trials to compute
Returns:
ndarray: n_trials x len(etas) array where each element is the correlation
between true and estimated connectivity matries for that trial and
instrument strength
"""
# Initialize corr array
corr_data = np.zeros((n_trials, len(etas)))
# Loop over trials
for trial in range(n_trials):
print("Trial {} of {}".format(trial + 1, n_trials))
# Loop over instrument strenghs
for j, eta in enumerate(etas):
########################################################################
## TODO: Simulate system with a given instrument strength, get IV estimate,
## and compute correlation
# Fill out function and remove
raise NotImplementedError('Student exercise: complete instrument_strength_effect')
########################################################################
# Simulate system
A, X, Z = simulate_neurons_iv(...)
# Compute IV estimate
iv_V = get_iv_estimate_network(...)
# Compute correlation
corr_data[trial, j] = np.corrcoef(A.flatten(), iv_V.flatten())[1, 0]
return corr_data
# Parameters of system
n_neurons = 20
timesteps = 10000
n_trials = 3
etas = [2, 1, 0.5, 0.25, 0.12] # instrument strengths to search over
# Uncomment below to test your function
#corr_data = instrument_strength_effect(etas, n_neurons, timesteps, n_trials)
#plot_performance_vs_eta(etas, corr_data)
# + [markdown] colab={"base_uri": "https://localhost:8080/", "height": 52} colab_type="text" id="XUnmjOCdZCbA" outputId="5c85039d-1cb4-4729-92b6-44950e40a849"
# [*Click for solution*](https://github.com/erlichlab/course-content/tree/master//tutorials/W3D3_NetworkCausality/solutions/W3D3_Tutorial4_Solution_14618275.py)
#
# *Example output:*
#
# <img alt='Solution hint' align='left' width=560 height=416 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W3D3_NetworkCausality/static/W3D3_Tutorial4_Solution_14618275_3.png>
#
#
# + [markdown] colab_type="text" id="_HHRW9Hi3gah"
# ---
#
# # (Bonus) Section 4: Granger Causality
#
# **Please revisit this section AFTER you complete tutorial notebook 4**, if you have time.
#
# Another potential solution to temporal causation that we might consider: [*Granger Causality*](https://en.wikipedia.org/wiki/Granger_causality).
#
# But, like the simultaneous fitting we explored in Tutorial 3, this method still fails in the presence of unobserved variables.
#
# We are testing whether a time series $X$ Granger-causes a time series $Y$ through a hypothesis test:
#
# - the null hypothesis $H_0$: lagged values of $X$ do not help predict values of $Y$
#
# - the alternative hypothesis $H_a$: lagged values of $X$ **do** help predict values of $Y$
#
# Mechanically, this is accomplished by fitting autoregressive models for $y_{t}$. We fail to reject the hypothesis if none of the $x_{t-k}$ terms are retained as significant in the regression. For simplicity, we will consider only one time lag. So, we have:
#
# $$
# H_0: y_t = a_0 + a_1 y_{t-1} +\epsilon_t
# $$
#
# $$
# H_a: y_t = a_0 + a_1 y_{t-1} + b_1 x_{t-1} +\epsilon_t
# $$
# + cellView="form" colab={} colab_type="code" id="7lBo4rt1dX7W"
#@markdown Execute this cell to get custom imports from stats models
# we need custom imports from stats models
# !pip install statsmodels
from statsmodels.tsa.stattools import grangercausalitytests
# + [markdown] colab_type="text" id="8siQRIuIiUQ2"
# ## Granger causality in small systems
#
# We will first evaluate Granger causality in a small system.
#
#
# + [markdown] colab_type="text" id="mvI6tHU9cgG3"
#
# ### (Bonus) Exercise: Evaluate Granger causality
#
# Complete the following definition to evaluate the Granger causality between our neurons. Then run the cells below to evaluate how well it works. You will use the `grangercausalitytests()` function already imported from statsmodels. We will then check whether a neuron in a small system Granger-causes the others.
#
# ### Suggestions
#
# - use `help()` to check the function signature for `grangercausalitytests()`
# + colab={} colab_type="code" id="_iZN1X9wuymK"
def get_granger_causality(X, selected_neuron, alpha=0.05):
"""
Estimates the lag-1 granger causality of the given neuron on the other neurons in the system.
Args:
X (np.ndarray): the matrix holding our dynamical system of shape (n_neurons, timesteps)
selected_neuron (int): the index of the neuron we want to estimate granger causality for
alpha (float): Bonferroni multiple comparisons correction
Returns:
A tuple (reject_null, p_vals)
reject_null (list): a binary list of length n_neurons whether the null was
rejected for the selected neuron granger causing the other neurons
p_vals (list): a list of the p-values for the corresponding Granger causality tests
"""
n_neurons = X.shape[0]
max_lag = 1
reject_null = []
p_vals = []
for target_neuron in range(n_neurons):
ts_data = X[[target_neuron, selected_neuron], :].transpose()
########################################################################
## Insert your code here to run Granger causality tests.
##
## Function Hints:
## Pass the ts_data defined above as the first argument
## Granger causality -> grangercausalitytests
## Fill out this function and then remove
raise NotImplementedError('Student exercise: complete get_granger_causality function')
########################################################################
res = grangercausalitytests(...)
# Gets the p-value for the log-ratio test
pval = res[1][0]['lrtest'][1]
p_vals.append(pval)
reject_null.append(int(pval < alpha))
return reject_null, p_vals
# Set up small system
n_neurons = 6
timesteps = 5000
random_state = 42
selected_neuron = 1
A = create_connectivity(n_neurons, random_state)
X = simulate_neurons(A, timesteps, random_state)
# Uncomment below to test your function
# reject_null, p_vals = get_granger_causality(X, selected_neuron)
# compare_granger_connectivity(A, reject_null, selected_neuron)
# + [markdown] colab={} colab_type="text" id="8ilH9bPtfbcf"
# [*Click for solution*](https://github.com/erlichlab/course-content/tree/master//tutorials/W3D3_NetworkCausality/solutions/W3D3_Tutorial4_Solution_e877c6d0.py)
#
# *Example output:*
#
# <img alt='Solution hint' align='left' width=693 height=341 src=https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/tutorials/W3D3_NetworkCausality/static/W3D3_Tutorial4_Solution_e877c6d0_0.png>
#
#
# + [markdown] colab_type="text" id="VxFI-XLm75HF"
# Looks good! Let's also check the correlation between Granger estimates and the true connectivity.
#
# + colab={} colab_type="code" id="uXQkeOsqj6Tg"
np.corrcoef(A[:,selected_neuron], np.array(reject_null))[1, 0]
# + [markdown] colab_type="text" id="X0OEPjWklRYE"
# When we have a small system, we correctly identify the causality of neuron 1.
# + [markdown] colab_type="text" id="fQpSyzn_lgvo"
# ## Granger causality in large systems
# + [markdown] colab_type="text" id="KOgB0i8Rd7_k"
# We will now run Granger causality on a large system with 100 neurons. Does it still work well? How does the number of timesteps matter?
# + cellView="form" colab={} colab_type="code" id="JgQGGNHsGQm7"
#@markdown Execute this cell to examine Granger causality in a large system
n_neurons = 100
timesteps = 5000
random_state = 42
selected_neuron = 1
A = create_connectivity(n_neurons, random_state)
X = simulate_neurons(A, timesteps, random_state)
# get granger causality estimates
reject_null, p_vals = get_granger_causality(X, selected_neuron)
compare_granger_connectivity(A, reject_null, selected_neuron)
# + [markdown] colab_type="text" id="frs6XWG3C_yE"
# Let's again check the correlation between the Granger estimates and the true connectivity. Are we able to recover the true connectivity well in this larger system?
# + colab={} colab_type="code" id="uZoJFEKorDeq"
np.corrcoef(A[:,selected_neuron], np.array(reject_null))[1, 0]
# + [markdown] colab_type="text" id="8JdrDxh1L5tb"
# ## Notes on Granger Causality
#
# Here we considered bivariate Granger causality -- for each pair of neurons $A, B$, does one Granger-cause the other? You might wonder whether considering more variables will help with estimation. *Conditional Granger Causality* is a technique that allows for a multivariate system, where we test whether $A$ Granger-causes $B$ conditional on the other variables in the system.
#
# Even after controlling for variables in the system, conditional Granger causality will also likely perform poorly as our system gets larger. Plus, measuring the additional variables to condition on may be infeasible in practical applications, which would introduce omitted variable bias as we saw in the regression exercise.
#
# One takeaway here is that as our estimation procedures become more sophisticated, they also become more difficult to interpret. We always need to understand the methods and the assumptions that are made.
| 119.254887 | 59,202 |
74f8e8600c19f0e69dd1734011aee9d171a84dfd
|
py
|
python
|
src/1 Basic Statistics.ipynb
|
WormLabCaltech/mprsq
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# + [markdown] toc="true"
# # Table of Contents
# <p><div class="lev1 toc-item"><a href="#Introduction" data-toc-modified-id="Introduction-1"><span class="toc-item-num">1 </span>Introduction</a></div><div class="lev2 toc-item"><a href="#Data-initialization" data-toc-modified-id="Data-initialization-1.1"><span class="toc-item-num">1.1 </span>Data initialization</a></div><div class="lev1 toc-item"><a href="#Isoforms-Identified-in-all-Genotypes" data-toc-modified-id="Isoforms-Identified-in-all-Genotypes-2"><span class="toc-item-num">2 </span>Isoforms Identified in all Genotypes</a></div><div class="lev1 toc-item"><a href="#Differentially-Expressed-Genes-per-genotype" data-toc-modified-id="Differentially-Expressed-Genes-per-genotype-3"><span class="toc-item-num">3 </span>Differentially Expressed Genes per genotype</a></div><div class="lev1 toc-item"><a href="#Pairwise-shared-transcriptomic-phenotypes" data-toc-modified-id="Pairwise-shared-transcriptomic-phenotypes-4"><span class="toc-item-num">4 </span>Pairwise shared transcriptomic phenotypes</a></div><div class="lev2 toc-item"><a href="#SI-Table-1" data-toc-modified-id="SI-Table-1-4.1"><span class="toc-item-num">4.1 </span>SI Table 1</a></div>
# -
# # Introduction
# In this notebook, I will go over the basic results from the RNA-seq in what is essentially a top-level view of the results. Nothing specific, mainly numbers, some histograms and that's it. First, I will load a number of useful libraries. Notable libraries to load are `genpy`, a module that contains useful graphing functions tailored specifically for this project and developed by us; `morgan` a module that specifies what a Morgan object and a McClintock object are, and `gvars`, which contains globally defined variables that we used in this project.
# +
# important stuff:
import os
import pandas as pd
import numpy as np
import morgan as morgan
import genpy
import gvars
import pretty_table as pretty
import epistasis as epi
# Graphics
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rc
rc('text', usetex=True)
rc('text.latex', preamble=r'\usepackage{cmbright}')
rc('font', **{'family': 'sans-serif', 'sans-serif': ['Helvetica']})
# Magic function to make matplotlib inline;
# %matplotlib inline
# This enables SVG graphics inline.
# There is a bug, so uncomment if it works.
# %config InlineBackend.figure_formats = {'png', 'retina'}
# JB's favorite Seaborn settings for notebooks
rc = {'lines.linewidth': 2,
'axes.labelsize': 18,
'axes.titlesize': 18,
'axes.facecolor': 'DFDFE5'}
sns.set_context('notebook', rc=rc)
sns.set_style("dark")
mpl.rcParams['xtick.labelsize'] = 16
mpl.rcParams['ytick.labelsize'] = 16
mpl.rcParams['legend.fontsize'] = 14
# -
# Next, I will specify my q-value cutoff. A typical value for RNA-seq datasets is q=0.1 for statistical significance. I will also initialize a `genvar.genvars` object, which contains all of the global variables used for this project.
q = 0.1
# this loads all the labels we need
genvar = gvars.genvars()
# ## Data initialization
#
# Now, I will prepare to initialize a Morgan project. Morgan objects have a large number of attributes. I wrote the Morgan library, but over the past year it has become deprecated and less useful. We will load it here, but it's a bit messy. I am in the process of cleaning it up. When you initialize a Morgan object, you must pass at least a set of 4 strings. These strings are, in order, the column where the isoform names (unique) reside, the name of the column that holds the regression coefficient from sleuth; the name of the column that holds the TPM values passed by Kallisto and the name of the column that holds the q-values.
#
# We can also add what I call a genmap. A genmap is a file that maps read files to genotypes. A genmap file has three columns: '*project_name*', '*genotype*' and '*batch*' in that exact order. For this project, the genotypes are coded. In other words, they are letters, '*a*', '*b*', '*d*',... and not specific genotypes. The reason for this is that we wanted to make sure that, at least during the initial phase of the project, I could not unduly bias the results by searching the literature and what not. Because the genotypes are coded, we need to specify which of the letters represent single mutants, and which letters represent double mutants. I also need to be able to figure out what the individual components of a double mutant are. Finally, we need to set the $q$-value threshold. If no $q$-value is specified, the threshold defaults to 0.1.
#
# I will now initialize the object. I call it thomas. Then I will load in all the variables we will use; I will load in the genmap, and at last I will load in the datasets that contain the TPM and the Sleuth $\beta$ coefficients. After everything has been loaded, I will call `thomas.filter_data`, which drops all the rows that have a $\beta$ coefficient equal to NaN
# +
# Specify the genotypes to refer to:
single_mutants = ['b', 'c', 'd', 'e', 'g']
# Specify which letters are double mutants and their genotype
double_mutants = {'a' : 'bd', 'f':'bc'}
# initialize the morgan.hunt object:
thomas = morgan.hunt('target_id', 'b', 'tpm', 'qval')
# input the genmap file:
thomas.add_genmap('../input/library_genotype_mapping.txt', comment='#')
# add the names of the single mutants
thomas.add_single_mutant(single_mutants)
# add the names of the double mutants
thomas.add_double_mutants(['a', 'f'], ['bd', 'bc'])
# set the q-value threshold for significance to its default value, 0.1
thomas.set_qval()
# Add the tpm files:
kallisto_loc = '../input/kallisto_all/'
sleuth_loc = '../sleuth/kallisto/'
thomas.add_tpm(kallisto_loc, '/kallisto/abundance.tsv', '')
# load all the beta dataframes:
for file in os.listdir("../sleuth/kallisto"):
if file[:4] == 'beta':
letter = file[-5:-4].lower()
thomas.add_beta(sleuth_loc + file, letter)
thomas.beta[letter].sort_values('target_id', inplace=True)
thomas.beta[letter].reset_index(inplace=True)
thomas.filter_data()
# thomas.filter_data()
# -
# Finally, we will place all the data in a tidy dataframe, where each row is an observation.
# +
frames = []
for key, df in thomas.beta.items():
df['genotype'] = genvar.mapping[key]
df['code'] = key
df['sorter'] = genvar.sort_muts[key]
df.sort_values('target_id', inplace=True)
frames += [df]
tidy = pd.concat(frames)
tidy.dropna(subset=['ens_gene'], inplace=True)
# Save to table
tidy[['ens_gene', 'ext_gene', 'target_id', 'b', 'se_b',
'qval', 'genotype', 'sorter',
'code']].to_csv('../output/temp_files/DE_genes.csv', index=False)
tidy.sort_values('sorter', inplace=True)
# -
# # Isoforms Identified in all Genotypes
total_genes_id = tidy.target_id.unique().shape[0]
print("Total isoforms identified in total: {0}".format(total_genes_id))
# We identified 19,676 isoforms using 7 million reads. Not bad considering there are ~25,000 protein-coding isoforms in *C. elegans*. Each gene has just slightly over 1 isoform on average, so what this means is that we sampled almost 80% of the genome.
# # Differentially Expressed Genes per genotype
#
# Next, let's figure out how many *genes* were differentially expressed in each mutant relative to the wild-type control.
print('Genotype: DEG')
for x in tidy.genotype.unique():
# select the DE isoforms in the current genotype:
sel = (tidy.qval < q) & (tidy.genotype == x)
# extract the number of unique genes:
s = tidy[sel].ens_gene.unique().shape[0]
print("{0}: {1}".format(x, s))
# From the above exploration, we can already conclude that:
# * *hif-1(lf)* has a transcriptomic phenotype
# * *hif-1;egl-9(lf)* has a transcriptomic phenotype
# * The *egl-9* phenotype is stronger than the *vhl-1* or the *hif-1* phenotypes.
#
# We should be careful is saying whether *rhy-1*, *egl-9* and *egl-9;vhl-1(lf)* are different from each other, and the same goes for *hif-1(lf)*, *vhl-1(lf)* and *egl-9;hif-1(lf)* because we set our FDR threshold at 10%. Notice that *egl-9(lf)* and *rhy-1(lf)* are barely 300 genes separated from each other. A bit of wiggle from both, and they might be identical.
# # Pairwise shared transcriptomic phenotypes
# ## SI Table 1
# In order to be able to assess whether two genes are interacting, we must first determine that the mutants we are studying act upon the same phenotype. What defines a phenotype in transcriptomic space? We use an operational definition -- two genotypes share the same phenotype if they regulate more than a pre-specified(and admittedly subjective) number of genes in common between the two of them, agnostic of direction. In our paper, we call this the Shared Transcriptomic Phenotype (STP). Let's figure out to what extent the genes we have studied share the same phenotype.
#
# We will measure the size of the STP using two distinct definitions. The first, percent shared isoforms, is defined as the number of isoforms in the STP divided by the number of differentially expressed isoforms in EITHER of the two mutants being compared. The second measurement, percent internalization, is defined as the number of isoforms in the STP divided by the number of differentially expressed isoforms in the mutant that has the smallest number of differentially expressed isoforms out of the two being compared.
# +
sig = (tidy.qval < q)
string = 'pair,STP,% shared,% internalization'
# print table header
l = string.split(',')
pretty.table_print(l, space=20)
# print rest:
for i, g1 in enumerate(tidy.genotype.unique()):
for j, g2 in enumerate(tidy.genotype.unique()[i+1:]):
tmp = tidy[sig] # define a temporary dataframe with only DE genes in it
# find DE genes in either genotype
DE1 = tmp[tmp.genotype == g1]
DE2 = tmp[tmp.genotype == g2]
# find the overlap between the two genotypes:
overlap = epi.find_overlap([g1, g2], df=tidy, col='genotype')
n = len(overlap) # number of DE isoforms in both genotypes
genes_in_stp = tidy[tidy.target_id.isin(overlap)].ens_gene.unique()
n_genes_stp = len(genes_in_stp) # number of DE genes in both genotypes
# find total number of DE transcripts in either genotype
OR = ((tmp.genotype == g1) | (tmp.genotype == g2))
ntot = tmp[OR].target_id.shape[0]
# find which genotype has fewer DE transcripts
n_intern = np.min([DE1.shape[0], DE2.shape[0]])
# print
string = "{0} & {1},{2},{3:.2g}%,{4:.2g}%".format(g1, g2, n_genes_stp, 100*n/ntot, 100*n/n_intern)
l = string.split(',')
pretty.table_print(l, space=20)
# -
# The number of genes that is shared between mutants of the same pathway ranges from ~100 genes all the way to ~1,300. However, the hypoxia mutants share between ~140 and ~700 genes in common with another mutant, the *fog-2(lf)* mutant that has never been reported to act in the hypoxia pathway. What are we to make of this? My own conclusion is that *fog-2* probably interacts with effectors downstream of the hypoxia pathway.
| 55.724138 | 1,229 |
74cd4169c783417c4e059b037ccdf75dc9ff7a45
|
py
|
python
|
tutorials/W1D1_ModelTypes/W1D1_Tutorial2.ipynb
|
hanhou/course-content
|
['CC-BY-4.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Spiking-Inputs" data-toc-modified-id="Spiking-Inputs-0.0.1"><span class="toc-item-num">0.0.1 </span>Spiking Inputs</a></span></li></ul></li><li><span><a href="#Exercise-1:-Compute-$dV_m$" data-toc-modified-id="Exercise-1:-Compute-$dV_m$-0.1"><span class="toc-item-num">0.1 </span>Exercise 1: Compute $dV_m$</a></span></li></ul></li><li><span><a href="#Interactive-Demo:-Linear-IF-neuron" data-toc-modified-id="Interactive-Demo:-Linear-IF-neuron-1"><span class="toc-item-num">1 </span>Interactive Demo: Linear-IF neuron</a></span><ul class="toc-item"><li><span><a href="#Exercise-2:-Compute-$dV_m$-with-inhibitory-signals" data-toc-modified-id="Exercise-2:-Compute-$dV_m$-with-inhibitory-signals-1.1"><span class="toc-item-num">1.1 </span>Exercise 2: Compute $dV_m$ with inhibitory signals</a></span></li></ul></li><li><span><a href="#Interactive-Demo:-LIF-+-inhibition-neuron" data-toc-modified-id="Interactive-Demo:-LIF-+-inhibition-neuron-2"><span class="toc-item-num">2 </span>Interactive Demo: LIF + inhibition neuron</a></span><ul class="toc-item"><li><span><a href="#Why-do-neurons-spike?" data-toc-modified-id="Why-do-neurons-spike?-2.1"><span class="toc-item-num">2.1 </span>Why do neurons spike?</a></span></li><li><span><a href="#The-LIF-Model-Neuron" data-toc-modified-id="The-LIF-Model-Neuron-2.2"><span class="toc-item-num">2.2 </span>The LIF Model Neuron</a></span></li></ul></li></ul></div>
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W1D1_ModelTypes/W1D1_Tutorial2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="HwYPw4CvrYCV"
# # Neuromatch Academy: Week 1, Day 1, Tutorial 2
# # Model Types: "How" models
# __Content creators:__ Matt Laporte, Byron Galbraith, Konrad Kording
#
# __Content reviewers:__ Dalin Guo, Aishwarya Balwani, Madineh Sarvestani, Maryam Vaziri-Pashkam, Michael Waskom
# + [markdown] colab_type="text" id="lQ7RhNSCd91Y"
# ___
# # Tutorial Objectives
# This is tutorial 2 of a 3-part series on different flavors of models used to understand neural data. In this tutorial we will explore models that can potentially explain *how* the spiking data we have observed is produced
#
# To understand the mechanisms that give rise to the neural data we save in Tutorial 1, we will build simple neuronal models and compare their spiking response to real data. We will:
# - Write code to simulate a simple "leaky integrate-and-fire" neuron model
# - Make the model more complicated — but also more realistic — by adding more physiologically-inspired details
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 520} colab_type="code" id="nfdfxF_ee8sZ" outputId="79eb15c7-6dce-4d70-a971-398484cd91ae"
#@title Video 1: "How" models
from IPython.display import YouTubeVideo
video = YouTubeVideo(id='PpnagITsb3E', width=854, height=480, fs=1)
print("Video available at https://youtube.com/watch?v=" + video.id)
video
# + [markdown] colab_type="text" id="yQN8ug6asey4"
# # Setup
# + cellView="both" colab={} colab_type="code" id="w6RPNLB6rYCW"
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# + cellView="form" colab={} colab_type="code" id="n8R_tHD5__vM"
#@title Figure Settings
import ipywidgets as widgets #interactive display
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
# + cellView="form" colab={} colab_type="code" id="CK1bXaOgrYCZ"
#@title Helper Functions
def histogram(counts, bins, vlines=(), ax=None, ax_args=None, **kwargs):
"""Plot a step histogram given counts over bins."""
if ax is None:
_, ax = plt.subplots()
# duplicate the first element of `counts` to match bin edges
counts = np.insert(counts, 0, counts[0])
ax.fill_between(bins, counts, step="pre", alpha=0.4, **kwargs) # area shading
ax.plot(bins, counts, drawstyle="steps", **kwargs) # lines
for x in vlines:
ax.axvline(x, color='r', linestyle='dotted') # vertical line
if ax_args is None:
ax_args = {}
# heuristically set max y to leave a bit of room
ymin, ymax = ax_args.get('ylim', [None, None])
if ymax is None:
ymax = np.max(counts)
if ax_args.get('yscale', 'linear') == 'log':
ymax *= 1.5
else:
ymax *= 1.1
if ymin is None:
ymin = 0
if ymax == ymin:
ymax = None
ax_args['ylim'] = [ymin, ymax]
ax.set(**ax_args)
ax.autoscale(enable=False, axis='x', tight=True)
def plot_neuron_stats(v, spike_times):
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 5))
# membrane voltage trace
ax1.plot(v[0:100])
ax1.set(xlabel='Time', ylabel='Voltage')
# plot spike events
for x in spike_times:
if x >= 100:
break
ax1.axvline(x, color='red')
# ISI distribution
isi = np.diff(spike_times)
n_bins = np.arange(isi.min(), isi.max() + 2) - .5
counts, bins = np.histogram(isi, n_bins)
vlines = []
if len(isi) > 0:
vlines = [np.mean(isi)]
xmax = max(20, int(bins[-1])+5)
histogram(counts, bins, vlines=vlines, ax=ax2, ax_args={
'xlabel': 'Inter-spike interval',
'ylabel': 'Number of intervals',
'xlim': [0, xmax]
})
plt.show()
# + [markdown] colab_type="text" id="kOxLk8AvrYCe"
# # Section 1: The Linear Integrate-and-Fire Neuron
#
# How does a neuron spike?
#
# A neuron charges and discharges an electric field across its cell membrane. The state of this electric field can be described by the _membrane potential_. The membrane potential rises due to excitation of the neuron, and when it reaches a threshold a spike occurs. The potential resets, and must rise to a threshold again before the next spike occurs.
#
# One of the simplest models of spiking neuron behavior is the linear integrate-and-fire model neuron. In this model, the neuron increases its membrane potential $V_m$ over time in response to excitatory input currents $I$ scaled by some factor $\alpha$:
#
# \begin{align}
# dV_m = {\alpha}I
# \end{align}
#
# Once $V_m$ reaches a threshold value a spike is produced, $V_m$ is reset to a starting value, and the process continues.
#
# Here, we will take the starting and threshold potentials as $0$ and $1$, respectively. So, for example, if $\alpha I=0.1$ is constant---that is, the input current is constant---then $dV_m=0.1$, and at each timestep the membrane potential $V_m$ increases by $0.1$ until after $(1-0)/0.1 = 10$ timesteps it reaches the threshold and resets to $V_m=0$, and so on.
#
# Note that we define the membrane potential $V_m$ as a scalar: a single real (or floating point) number. However, a biological neuron's membrane potential will not be exactly constant at all points on its cell membrane at a given time. We could capture this variation with a more complex model (e.g. with more numbers). Do we need to?
#
# The proposed model is a 1D simplification. There are many details we could add to it, to preserve different parts of the complex structure and dynamics of a real neuron. If we were interested in small or local changes in the membrane potential, our 1D simplification could be a problem. However, we'll assume an idealized "point" neuron model for our current purpose.
#
# #### Spiking Inputs
#
# Given our simplified model for the neuron dynamics, we still need to consider what form the input $I$ will take. How should we specify the firing behavior of the presynaptic neuron(s) providing the inputs to our model neuron?
#
# Unlike in the simple example above, where $\alpha I=0.1$, the input current is generally not constant. Physical inputs tend to vary with time. We can describe this variation with a distribution.
#
# We'll assume the input current $I$ over a timestep is due to equal contributions from a non-negative ($\ge 0$) integer number of input spikes arriving in that timestep. Our model neuron might integrate currents from 3 input spikes in one timestep, and 7 spikes in the next timestep. We should see similar behavior when sampling from our distribution.
#
# Given no other information about the input neurons, we will also assume that the distribution has a mean (i.e. mean rate, or number of spikes received per timestep), and that the spiking events of the input neuron(s) are independent in time. Are these reasonable assumptions in the context of real neurons?
#
# A suitable distribution given these assumptions is the Poisson distribution, which we'll use to model $I$:
#
# \begin{align}
# I \sim \mathrm{Poisson}(\lambda)
# \end{align}
#
# where $\lambda$ is the mean of the distribution: the average rate of spikes received per timestep.
# + [markdown] colab_type="text" id="Ls8CsM2Pf7LQ"
# ### Exercise 1: Compute $dV_m$
#
# For your first exercise, you will write the code to compute the change in voltage $dV_m$ (per timestep) of the linear integrate-and-fire model neuron. The rest of the code to handle numerical integration is provided for you, so you just need to fill in a definition for `dv` in the `lif_neuron` function below. The value of $\lambda$ for the Poisson random variable is given by the function argument `rate`.
#
#
#
# The [`scipy.stats`](https://docs.scipy.org/doc/scipy/reference/stats.html) package is a great resource for working with and sampling from various probability distributions. We will use the `scipy.stats.poisson` class and its method `rvs` to produce Poisson-distributed random samples. In this tutorial, we have imported this package with the alias `stats`, so you should refer to it in your code as `stats.poisson`.
# + colab={} colab_type="code" id="HQU61YUDrYCe"
def lif_neuron(n_steps=1000, alpha=0.01, rate=10):
""" Simulate a linear integrate-and-fire neuron.
Args:
n_steps (int): The number of time steps to simulate the neuron's activity.
alpha (float): The input scaling factor
rate (int): The mean rate of incoming spikes
"""
# precompute Poisson samples for speed
exc = stats.poisson(rate).rvs(n_steps)
v = np.zeros(n_steps)
spike_times = []
################################################################################
# Students: compute dv, then comment out or remove the next line
# raise NotImplementedError("Excercise: compute the change in membrane potential")
################################################################################
for i in range(1, n_steps):
dv = alpha * exc[i]
v[i] = v[i-1] + dv
if v[i] > 1:
spike_times.append(i)
v[i] = 0
return v, spike_times
# Uncomment these lines after completing the lif_neuron function
v, spike_times = lif_neuron()
plot_neuron_stats(v, spike_times)
# + cellView="both" colab={"base_uri": "https://localhost:8080/", "height": 361} colab_type="code" id="u-oCuaFAiRi5" outputId="5cc286a9-e973-4cf6-edce-c03187846a28"
# to_remove solution
def lif_neuron(n_steps=1000, alpha=0.01, rate=10):
""" Simulate a linear integrate-and-fire neuron.
Args:
n_steps (int): The number of time steps to simulate the neuron's activity.
alpha (float): The input scaling factor
rate (int): The mean rate of incoming spikes
"""
# precompute Poisson samples for speed
exc = stats.poisson(rate).rvs(n_steps)
v = np.zeros(n_steps)
spike_times = []
for i in range(1, n_steps):
dv = alpha * exc[i]
v[i] = v[i-1] + dv
if v[i] > 1:
spike_times.append(i)
v[i] = 0
return v, spike_times
v, spike_times = lif_neuron()
with plt.xkcd():
plot_neuron_stats(v, spike_times)
# + [markdown] colab_type="text" id="H-jxjYzaGwoY"
# ## Interactive Demo: Linear-IF neuron
# Like last time, you can now explore how various parametes of the LIF model influence the ISI distribution.
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 454, "referenced_widgets": ["990ada35c5c544948b62d4559e50b070", "37a0682e16cb45ac882f4a60aeaed48d", "3160ae99681e4302a556d62b17cba314", "0d5052b6b9cd4acd93ca0bd495c0a17b", "71a2da343c244581b9f385d95c06aa4b", "33a742af9fd74f138dbfdf1c6e25674f", "fcefc4155fd34eeeaf17eb8f6b850753", "0825038cdb644fb0a4a311aaf421bed2", "2bda9259d35f46eda729261babe00313", "e656fc81d17840719eb50d5618f84265", "8b8f376e405944eb97e7c9c66c7a8d87", "ab4ddab618b6468bb3f46832e261e0dd", "2d098b643c0f40b3a66325291a02f092"]} colab_type="code" id="RRjD0G3nrYCh" outputId="b99a9d0b-3a91-4100-cf67-c02d9005f96d"
#@title
#@markdown You don't need to worry about how the code works – but you do need to **run the cell** to enable the sliders.
def _lif_neuron(n_steps=1000, alpha=0.01, rate=10):
exc = stats.poisson(rate).rvs(n_steps)
v = np.zeros(n_steps)
spike_times = []
for i in range(1, n_steps):
dv = alpha * exc[i]
v[i] = v[i-1] + dv
if v[i] > 1:
spike_times.append(i)
v[i] = 0
return v, spike_times
@widgets.interact(
n_steps=widgets.FloatLogSlider(1000.0, min=2, max=4),
alpha=widgets.FloatLogSlider(0.01, min=-2, max=-1),
rate=widgets.IntSlider(10, min=5, max=20)
)
def plot_lif_neuron(n_steps=1000, alpha=0.01, rate=10):
v, spike_times = _lif_neuron(int(n_steps), alpha, rate)
plot_neuron_stats(v, spike_times)
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 520} colab_type="code" id="20VOmFIEvVDh" outputId="8714e155-04d1-48ab-840a-a68128226edb"
#@title Video 2: Linear-IF models
from IPython.display import YouTubeVideo
video = YouTubeVideo(id='QBD7kulhg4U', width=854, height=480, fs=1)
print("Video available at https://youtube.com/watch?v=" + video.id)
video
# + [markdown] colab_type="text" id="91UgFMVPrYCk"
# # Section 2: Inhibitory signals
#
# + [markdown] colab_type="text" id="yfiajILBw2hZ"
#
# Our linear integrate-and-fire neuron from the previous section was indeed able to produce spikes. However, our ISI histogram doesn't look much like empirical ISI histograms seen in Tutorial 1, which had an exponential-like shape. What is our model neuron missing, given that it doesn't behave like a real neuron?
#
# In the previous model we only considered excitatory behavior -- the only way the membrane potential could decrease was upon a spike event. We know, however, that there are other factors that can drive $V_m$ down. First is the natural tendency of the neuron to return to some steady state or resting potential. We can update our previous model as follows:
#
# \begin{align}
# dV_m = -{\beta}V_m + {\alpha}I
# \end{align}
#
# where $V_m$ is the current membrane potential and $\beta$ is some leakage factor. This is a basic form of the popular Leaky Integrate-and-Fire model neuron (for a more detailed discussion of the LIF Neuron, see the Appendix).
#
# We also know that in addition to excitatory presynaptic neurons, we can have inhibitory presynaptic neurons as well. We can model these inhibitory neurons with another Poisson random variable:
#
# \begin{align}
# I = I_{exc} - I_{inh} \\
# I_{exc} \sim \mathrm{Poisson}(\lambda_{exc}) \\
# I_{inh} \sim \mathrm{Poisson}(\lambda_{inh})
# \end{align}
#
# where $\lambda_{exc}$ and $\lambda_{inh}$ are the average spike rates (per timestep) of the excitatory and inhibitory presynaptic neurons, respectively.
# + [markdown] colab_type="text" id="3tErnV24y_Pa"
# ### Exercise 2: Compute $dV_m$ with inhibitory signals
#
# For your second exercise, you will again write the code to compute the change in voltage $dV_m$, though now of the LIF model neuron described above. Like last time, the rest of the code needed to handle the neuron dynamics are provided for you, so you just need to fill in a definition for `dv` below.
#
# + colab={} colab_type="code" id="RfT7XE_UzUUl"
def lif_neuron_inh(n_steps=1000, alpha=0.5, beta=0.1, exc_rate=10, inh_rate=10):
""" Simulate a simplified leaky integrate-and-fire neuron with both excitatory
and inhibitory inputs.
Args:
n_steps (int): The number of time steps to simulate the neuron's activity.
alpha (float): The input scaling factor
beta (float): The membrane potential leakage factor
exc_rate (int): The mean rate of the incoming excitatory spikes
inh_rate (int): The mean rate of the incoming inhibitory spikes
"""
# precompute Poisson samples for speed
exc = stats.poisson(exc_rate).rvs(n_steps)
inh = stats.poisson(inh_rate).rvs(n_steps)
v = np.zeros(n_steps)
spike_times = []
###############################################################################
# Students: compute dv, then comment out or remove the next line
# raise NotImplementedError("Excercise: compute the change in membrane potential")
################################################################################
for i in range(1, n_steps):
dv = - beta * v[i-1] + alpha * (exc[i] - inh[i])
v[i] = v[i-1] + dv
if v[i] > 1:
spike_times.append(i)
v[i] = 0
return v, spike_times
# Uncomment these lines do make the plot once you've completed the function
v, spike_times = lif_neuron_inh()
plot_neuron_stats(v, spike_times)
# + cellView="both" colab={"base_uri": "https://localhost:8080/", "height": 361} colab_type="code" id="opfSK1CrrYCk" outputId="d98e5fcf-3da1-48ba-d1e5-50ee941a7307"
# to_remove solution
def lif_neuron_inh(n_steps=1000, alpha=0.5, beta=0.1, exc_rate=10, inh_rate=10):
""" Simulate a simplified leaky integrate-and-fire neuron with both excitatory
and inhibitory inputs.
Args:
n_steps (int): The number of time steps to simulate the neuron's activity.
alpha (float): The input scaling factor
beta (float): The membrane potential leakage factor
exc_rate (int): The mean rate of the incoming excitatory spikes
inh_rate (int): The mean rate of the incoming inhibitory spikes
"""
# precompute Poisson samples for speed
exc = stats.poisson(exc_rate).rvs(n_steps)
inh = stats.poisson(inh_rate).rvs(n_steps)
v = np.zeros(n_steps)
spike_times = []
for i in range(1, n_steps):
dv = -beta * v[i-1] + alpha * (exc[i] - inh[i])
v[i] = v[i-1] + dv
if v[i] > 1:
spike_times.append(i)
v[i] = 0
return v, spike_times
v, spike_times = lif_neuron_inh()
with plt.xkcd():
plot_neuron_stats(v, spike_times)
# + [markdown] colab_type="text" id="K7SSS1mlYg1j"
# ## Interactive Demo: LIF + inhibition neuron
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 518, "referenced_widgets": ["ab70a1af29404964a22fb8bc1d39e1b6", "7988350c463245208917af9dc10c8c4a", "3a20f6e16bc44f8aa2e025ec861168c0", "b4787789c5e44652835cb95e4238fead", "be3a8dff26704089993fe3394b9b37f2", "fa1025867d5d4a79aeca729d033cebb3", "834f12759d9d4bc380f916de3221fe46", "d17fa430a98f405f9b48993dcd6ebcb3", "e447592686e249c9a1b36119291ac812", "c3130166bb7c4ca99d7cd931242b5a18", "a0f300aaf4ae41c0a01847ae611d147e", "25e89a44ce264229a57d9f30a4bc4b76", "6b3d6737fc8a4c4d8477284101a68a61", "528ef35adc0747ce914b2824ca60b020", "0a77dd3f091d4807966c8bb6bddeb621", "f51922ead2564bb798cff0d94bb1ed4b", "aea9a2d13cd444e2b4ad54192d392aab", "82b2c1d3ae36465c87ccc003bedbd1c4", "297e2c6ab90f4573bb553a8b3e0c6a7a"]} colab_type="code" id="Eh3wR_nArYCn" outputId="673a1dab-79ee-423b-863a-22d56ad543c2"
#@title
#@markdown **Run the cell** to enable the sliders.
def _lif_neuron_inh(n_steps=1000, alpha=0.5, beta=0.1, exc_rate=10, inh_rate=10):
""" Simulate a simplified leaky integrate-and-fire neuron with both excitatory
and inhibitory inputs.
Args:
n_steps (int): The number of time steps to simulate the neuron's activity.
alpha (float): The input scaling factor
beta (float): The membrane potential leakage factor
exc_rate (int): The mean rate of the incoming excitatory spikes
inh_rate (int): The mean rate of the incoming inhibitory spikes
"""
# precompute Poisson samples for speed
exc = stats.poisson(exc_rate).rvs(n_steps)
inh = stats.poisson(inh_rate).rvs(n_steps)
v = np.zeros(n_steps)
spike_times = []
for i in range(1, n_steps):
dv = -beta * v[i-1] + alpha * (exc[i] - inh[i])
v[i] = v[i-1] + dv
if v[i] > 1:
spike_times.append(i)
v[i] = 0
return v, spike_times
@widgets.interact(n_steps=widgets.FloatLogSlider(1000.0, min=2.5, max=4),
alpha=widgets.FloatLogSlider(0.5, min=-1, max=1),
beta=widgets.FloatLogSlider(0.1, min=-1, max=0),
exc_rate=widgets.IntSlider(12, min=10, max=20),
inh_rate=widgets.IntSlider(12, min=0, max=20))
def plot_lif_neuron(n_steps=1000, alpha=0.5, beta=0.1, exc_rate=10, inh_rate=10):
v, spike_times = _lif_neuron_inh(int(n_steps), alpha, beta, exc_rate, inh_rate)
plot_neuron_stats(v, spike_times)
# + cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 520} colab_type="code" id="or1Tt4TSfQwp" outputId="c61563f8-e394-49ae-eecb-99589663a7b8"
#@title Video 3: LIF + inhibition
from IPython.display import YouTubeVideo
video = YouTubeVideo(id='Aq7JrxRkn2w', width=854, height=480, fs=1)
print("Video available at https://youtube.com/watch?v=" + video.id)
video
# + [markdown] colab_type="text" id="CUMDCU9waBz_"
# #Summary
#
# In this tutorial we gained some intuition for the mechanisms that produce the observed behavior in our real neural data. First, we built a simple neuron model with excitatory input and saw that it's behavior, measured using the ISI distribution, did not match our real neurons. We then improved our model by adding leakiness and inhibitory input. The behavior of this balanced model was much closer to the real neural data.
# + [markdown] colab_type="text" id="pKCzc7Fjz8zK"
# # Bonus
# + [markdown] colab_type="text" id="xn34Ieffz_ZO"
# ### Why do neurons spike?
#
# A neuron stores energy in an electric field across its cell membrane, by controlling the distribution of charges (ions) on either side of the membrane. This energy is rapidly discharged to generate a spike when the field potential (or membrane potential) crosses a threshold. The membrane potential may be driven toward or away from this threshold, depending on inputs from other neurons: excitatory or inhibitory, respectively. The membrane potential tends to revert to a resting potential, for example due to the leakage of ions across the membrane, so that reaching the spiking threshold depends not only on the amount of input ever received following the last spike, but also the timing of the inputs.
#
# The storage of energy by maintaining a field potential across an insulating membrane can be modeled by a capacitor. The leakage of charge across the membrane can be modeled by a resistor. This is the basis for the leaky integrate-and-fire neuron model.
# + [markdown] colab_type="text" id="pwZOhsV60WPM"
# ### The LIF Model Neuron
#
# The full equation for the LIF neuron is
#
# \begin{align}
# C_{m}\frac{dV_m}{dt} = -(V_m - V_{rest})/R_{m} + I
# \end{align}
#
# where $C_m$ is the membrane capacitance, $R_M$ is the membrane resistance, $V_{rest}$ is the resting potential, and $I$ is some input current (from other neurons, an electrode, ...).
#
# In our above examples we set many of these parameters to convenient values ($C_m = R_m = dt = 1$, $V_{rest} = 0$) to focus more on the general behavior of the model. However, these too can be manipulated to achieve different dynamics, or to ensure the dimensions of the problem are preserved between simulation units and experimental units (e.g. with $V_m$ given in millivolts, $R_m$ in megaohms, $t$ in milliseconds).
| 50.332623 | 1,592 |
57f221d46ba5e68a5b3d7f642ca53737c925ecd9
|
py
|
python
|
examples/socio_econ_cmf_micro.ipynb
|
arita37/causeinfer
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Center for Microfinance Dataset**
#
# A dataset on microfinance from The Centre for Micro Finance (CMF) at the Institute for Financial Management Research (Chennai, India).
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Load-Data" data-toc-modified-id="Load-Data-1"><span class="toc-item-num">1 </span>Load Data</a></span><ul class="toc-item"><li><span><a href="#Exploration-Data" data-toc-modified-id="Exploration-Data-1.1"><span class="toc-item-num">1.1 </span>Exploration Data</a></span></li><li><span><a href="#Modeling-Data" data-toc-modified-id="Modeling-Data-1.2"><span class="toc-item-num">1.2 </span>Modeling Data</a></span></li></ul></li><li><span><a href="#Data-Exploration" data-toc-modified-id="Data-Exploration-2"><span class="toc-item-num">2 </span>Data Exploration</a></span><ul class="toc-item"><li><span><a href="#Full-Data-Visualization" data-toc-modified-id="Full-Data-Visualization-2.1"><span class="toc-item-num">2.1 </span>Full Data Visualization</a></span></li><li><span><a href="#Modeling-Data-Preparation" data-toc-modified-id="Modeling-Data-Preparation-2.2"><span class="toc-item-num">2.2 </span>Modeling Data Preparation</a></span></li></ul></li><li><span><a href="#Standard-Models" data-toc-modified-id="Standard-Models-3"><span class="toc-item-num">3 </span>Standard Models</a></span><ul class="toc-item"><li><span><a href="#Two-Model" data-toc-modified-id="Two-Model-3.1"><span class="toc-item-num">3.1 </span>Two Model</a></span></li><li><span><a href="#Interaction-Term" data-toc-modified-id="Interaction-Term-3.2"><span class="toc-item-num">3.2 </span>Interaction Term</a></span></li><li><span><a href="#Class-Transformations" data-toc-modified-id="Class-Transformations-3.3"><span class="toc-item-num">3.3 </span>Class Transformations</a></span></li></ul></li><li><span><a href="#Evaluation" data-toc-modified-id="Evaluation-4"><span class="toc-item-num">4 </span>Evaluation</a></span><ul class="toc-item"><li><span><a href="#Iterations" data-toc-modified-id="Iterations-4.1"><span class="toc-item-num">4.1 </span>Iterations</a></span></li><li><span><a href="#Visual" data-toc-modified-id="Visual-4.2"><span class="toc-item-num">4.2 </span>Visual</a></span></li><li><span><a href="#Iterated-Evaluation-and-Variance" data-toc-modified-id="Iterated-Evaluation-and-Variance-4.3"><span class="toc-item-num">4.3 </span>Iterated Evaluation and Variance</a></span></li></ul></li><li><span><a href="#Summary" data-toc-modified-id="Summary-5"><span class="toc-item-num">5 </span>Summary</a></span></li></ul></div>
# +
import sys
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.ensemble import RandomForestRegressor
from causeinfer.data import cmf_micro
from causeinfer.utils import plot_unit_distributions, train_test_split, over_sample
from causeinfer.standard_algorithms import TwoModel, InteractionTerm
from causeinfer.evaluation import qini_score, auuc_score
from causeinfer.evaluation import plot_cum_effect, plot_cum_gain, plot_qini
from causeinfer.evaluation import plot_batch_responses, signal_to_noise
from causeinfer.evaluation import iterate_model, eval_table
pd.set_option("display.max_rows", 16)
pd.set_option('display.max_columns', None)
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:99% !important; }</style>"))
# -
# # Load Data
# +
# Deprecated - see: https://github.com/andrewtavis/causeinfer/tree/master/causeinfer/data/datasets
# cmf_micro.download_cmf_micro()
# -
# ## Exploration Data
# +
# The full mostly unformatted dataset is loaded
data_raw = cmf_micro.load_cmf_micro(user_file_path="datasets/cmf_micro",
format_covariates=False,
normalize=False)
df_full = pd.DataFrame(data_raw["dataset_full"],
columns=data_raw["dataset_full_names"])
display(df_full.head())
df_full.shape
# -
# ## Modeling Data
# +
# The formatted dataset is loaded
data_cmf_micro = cmf_micro.load_cmf_micro(user_file_path="datasets/cmf_micro",
format_covariates=True,
normalize=True)
df = pd.DataFrame(data_cmf_micro["dataset_full"],
columns=data_cmf_micro["dataset_full_names"])
display(df.head())
df.shape
# +
# Covariates, treatments and responses are loaded separately
X = data_cmf_micro["features"]
y = data_cmf_micro["response_biz_index"] # response_biz_index or response_women_emp
w = data_cmf_micro["treatment"]
# -
# # Data Exploration
sns.set(style="whitegrid")
# ## Full Data Visualization
# +
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(20,5))
fig.subplots_adjust(bottom=0.2) # Add space after plots
plot_unit_distributions(df=df_full, variable='children_1', treatment = None,
plot_x_label='children_1', plot_y_label='counts', plot_title='Breakdown of children_1',
bins=None, figsize=None, fontsize=20, axis=ax1),
plot_unit_distributions(df=df_full, variable='children_1', treatment = 'treatment',
plot_x_label='children_1', plot_y_label='counts', plot_title='Breakdown of children_1 and Treatment',
bins=None, figsize=None, fontsize=20, axis=ax2)
plt.savefig('outputs_images/cmf_breakdown_children_1.png', dpi=150)
# +
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(20,5))
fig.subplots_adjust(bottom=0.2) # Add space after plots
plot_unit_distributions(df=df_full, variable='hhsize_1', treatment = None,
plot_x_label='hhsize_1', plot_y_label='counts', plot_title='Breakdown of hhsize_1',
bins=None, figsize=None, fontsize=20, axis=ax1),
plot_unit_distributions(df=df_full, variable='hhsize_1', treatment = 'treatment',
plot_x_label='hhsize_1', plot_y_label='counts', plot_title='Breakdown of hhsize_1 and Treatment',
bins=None, figsize=None, fontsize=20, axis=ax2)
plt.savefig('outputs_images/cmf_breakdown_hhsize_1.png', dpi=150)
# +
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(20,5))
plot_unit_distributions(df=df_full, variable='anyloan_1', treatment = None,
plot_x_label='anyloan_1', plot_y_label='counts', plot_title='Breakdown of anyloan_1',
bins=None, figsize=None, fontsize=20, axis=ax1),
plot_unit_distributions(df=df_full, variable='anyloan_1', treatment = 'treatment',
plot_x_label='anyloan_1', plot_y_label='counts', plot_title='Breakdown of anyloan_1 and Treatment',
bins=None, figsize=None, fontsize=20, axis=ax2)
# +
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(20,5))
fig.subplots_adjust(bottom=0.2) # Add space after plots
plot_unit_distributions(df=df_full, variable='spouse_works_wage_1', treatment = None,
plot_x_label='spouse_works_wage_1', plot_y_label='counts', plot_title='Breakdown of spouse_works_wage_1',
bins=None, figsize=None, fontsize=15, axis=ax1),
plot_unit_distributions(df=df_full, variable='spouse_works_wage_1', treatment = 'treatment',
plot_x_label='spouse_works_wage_1', plot_y_label='counts', plot_title='Breakdown of spouse_works_wage_1 and Treatment',
bins=None, figsize=None, fontsize=15, axis=ax2)
plt.savefig('outputs_images/cmf_breakdown_spouse_works_wage_1.png', dpi=150)
# -
# Slight indication of self selection, as the women would be more likely to go for a loan if their spouse didn't work.
df.pivot_table(values=['biz_index_all_1', 'women_emp_index_1'],
index='treatment',
aggfunc=[np.mean],
margins=True)
# ## Modeling Data Preparation
# +
# Counts for treatment
control_indexes = [i for i, e in enumerate(w) if e == 0]
treatment_indexes = [i for i, e in enumerate(w) if e == 1]
print(len(control_indexes))
print(len(treatment_indexes))
# +
X_control = X[control_indexes]
y_control = y[control_indexes]
w_control = w[control_indexes]
X_treatment = X[treatment_indexes]
y_treatment = y[treatment_indexes]
w_treatment = w[treatment_indexes]
# -
# Over-sampling of control
X_os, y_os, w_os = over_sample(X_1=X_control, y_1=y_control, w_1=w_control,
sample_2_size=len(X_treatment), shuffle=True)
# +
X_split = np.append(X_os, X_treatment, axis=0)
y_split = np.append(y_os, y_treatment, axis=0)
w_split = np.append(w_os, w_treatment, axis=0)
X_split.shape, y_split.shape, w_split.shape # Should all be equal in the first dimension
# -
X_train, X_test, y_train, y_test, w_train, w_test = train_test_split(X_split, y_split, w_split,
percent_train=0.7, random_state=42,
maintain_proportions=True)
X_train.shape, X_test.shape, y_train.shape, y_test.shape, w_train.shape, w_test.shape
print(np.array(np.unique(w_train, return_counts=True)).T)
print(np.array(np.unique(w_test, return_counts=True)).T)
sn_ratio = signal_to_noise(y=y_split, w=w_split)
sn_ratio
# The signal to noise ratio suggests at a base level that there is a potential benefit to using CI with this dataset.
# # Standard Models
# The following cells present single iteration modeling, with analysis being done over multiple iterations.
# ## Two Model
tm = TwoModel(treatment_model=RandomForestRegressor(),
control_model=RandomForestRegressor())
tm.fit(X=X_train, y=y_train, w=w_train)
tm_preds = tm.predict(X=X_test)
tm_preds[:5]
# ## Interaction Term
it = InteractionTerm(model=RandomForestRegressor())
it.fit(X=X_train, y=y_train, w=w_train)
it_preds = it.predict(X=X_test)
it_preds[:5]
# ## Class Transformations
# Class transformation approaches aren't available for continuous response values yet. Work will be done to modify those algorithms to make them applicable in these settings.
# # Evaluation
# ## Iterations
# +
# New models instatiated with a more expansive scikit-learn base model (assign individually)
tm = TwoModel(treatment_model=RandomForestRegressor(n_estimators=200,
criterion='mse',
bootstrap=True),
control_model=RandomForestRegressor(n_estimators=200,
criterion='mse',
bootstrap=True))
it = InteractionTerm(model=RandomForestRegressor(n_estimators=200,
criterion='mse',
bootstrap=True))
# -
n=200
model_eval_dict = {}
model_eval_dict['CMF Microfinance'] = {}
model_eval_dict
for dataset in model_eval_dict.keys():
for model in [tm, it]: #grf
avg_preds, all_preds, \
avg_eval, eval_variance, \
eval_sd, all_evals = iterate_model(model=model, X_train=X_train, y_train=y_train, w_train=w_train,
X_test=X_test, y_test=y_test, w_test=w_test, tau_test=None, n=n,
pred_type='predict', eval_type='qini',
normalize_eval=False, notify_iter=n/10)
model_eval_dict[dataset].update({str(model).split('.')[-1].split(' ')[0]: {'avg_preds': avg_preds, 'all_preds': all_preds,
'avg_eval': avg_eval, 'eval_variance': eval_variance,
'eval_sd': eval_sd, 'all_evals': all_evals}})
# + code_folding=[]
# Treatment and control prediction subtraction
tm_effects = [model_eval_dict['CMF Microfinance']['TwoModel']['avg_preds'][i][0] \
- model_eval_dict['CMF Microfinance']['TwoModel']['avg_preds'][i][1] \
for i in range(len(model_eval_dict['CMF Microfinance']['TwoModel']['avg_preds']))]
# Treatment interaction and control interaction prediction subtraction
it_effects = [model_eval_dict['CMF Microfinance']['InteractionTerm']['avg_preds'][i][0] \
- model_eval_dict['CMF Microfinance']['InteractionTerm']['avg_preds'][i][1] \
for i in range(len(model_eval_dict['CMF Microfinance']['InteractionTerm']['avg_preds']))]
# -
# ## Visual
visual_eval_dict = {'y_test': y_test, 'w_test': w_test,
'two_model': tm_effects, 'interaction_term': it_effects}
# +
df_visual_eval = pd.DataFrame(visual_eval_dict, columns = visual_eval_dict.keys())
display(df_visual_eval.head())
df_visual_eval.shape
# -
models = [col for col in visual_eval_dict.keys() if col not in ['y_test', 'w_test']]
# +
# fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=False, figsize=(20,5))
plot_cum_effect(df=df_visual_eval, n=100, models=models, percent_of_pop=True,
outcome_col='y_test', treatment_col='w_test', random_seed=42,
figsize=(10,5), fontsize=20, axis=None, legend_metrics=False)
# plot_batch_responses(df=df_visual_eval, n=10, models=models,
# outcome_col='y_test', treatment_col='w_test', normalize=False,
# figsize=None, fontsize=15, axis=ax2)
plt.savefig('outputs_images/cmf_cum_effect.png', dpi=150)
# +
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, sharey=False, figsize=(20,5))
plot_cum_gain(df=df_visual_eval, n=100, models=models, percent_of_pop=True,
outcome_col='y_test', treatment_col='w_test', normalize=False, random_seed=42,
figsize=None, fontsize=20, axis=ax1, legend_metrics=True)
plot_qini(df=df_visual_eval, n=100, models=models, percent_of_pop=True,
outcome_col='y_test', treatment_col='w_test', normalize=False, random_seed=42,
figsize=None, fontsize=20, axis=ax2, legend_metrics=True)
plt.savefig('outputs_images/cmf_auuc_qini.png', dpi=150)
# -
# ## Iterated Evaluation and Variance
# +
# Qini
df_model_eval = eval_table(model_eval_dict, variances=True, annotate_vars=True)
df_model_eval
# -
# # Summary
| 45.121118 | 2,544 |
00b33f2146c8ce028cb000f03eab5365810ff7ab
|
py
|
python
|
Case_2_Model_2.ipynb
|
JoeValval/neural-networks-forhealth-technology-applications
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Case-2:-Pneumonia-X-ray-image-analysis-(Model-3)" data-toc-modified-id="Case-2:-Pneumonia-X-ray-image-analysis"><span class="toc-item-num">1 </span>Case 2: Pneumonia X-ray image analysis</a></span></li><li><span><a href="#Background" data-toc-modified-id="Background-2"><span class="toc-item-num">2 </span>Background</a></span></li><li><span><a href="#Data" data-toc-modified-id="Data-3"><span class="toc-item-num">3 </span>Data</a></span></li><li><span><a href="#Models-and-training" data-toc-modified-id="Models-and-training-4"><span class="toc-item-num">4 </span>Models and training</a></span></li><li><span><a href="#Results-and-Discussion" data-toc-modified-id="Results-and-Discussion-5"><span class="toc-item-num">5 </span>Results and Discussion</a></span></li><li><span><a href="#Conclusions" data-toc-modified-id="Conclusions-6"><span class="toc-item-num">6 </span>Conclusions</a></span></li></ul></div>
# # Case 2: Pneumonia X-ray image analysis (Model 2)
# Team 16:
# 1. Bellarina Chew
# 2. Nik Adam Nik Joharris
# 3. Valentin Dassin
# Last modified: 27.02.2020<br>
# Neural Networks for Health Technology Applications<br>
# [Helsinki Metropolia University of Applied Sciences](http://www.metropolia.fi/en/)<br>
# ## Background
# The aim of this notebook is to create and train a dense neural network to classify medical images accurately with convolutional neural network using the dataset from https://data.mendeley.com/datasets/rscbjbr9sj/2
# ## Data
# The dataset used is a dataset of Labeled Optical Coherence Tomography (OCT) and Chest X-Ray Images for Classification from Mendeley Data [1].
# +
# Import necessary module
# %pylab inline
import os
import time
import shutil
import random
import pandas as pd
import tensorflow as tf
# Import libraries
from tensorflow import keras
# Import keras specific
from tensorflow.keras import layers, models, optimizers
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.metrics import Accuracy, FalseNegatives, FalsePositives
from sklearn.metrics import classification_report, confusion_matrix, roc_curve
# -
# #### Load training files
# +
# Training files can be found here
#train_dir = "/Users/bella/Desktop/year 3/Neural Network/chest_xray/train"
# Test files can be found here
train_dir = "/Users/User/Desktop/Boulot/DUETI/S2/1rst part/neural/ChestXRay2017/chest_xray/train"
test_dir = "/Users/User/Desktop/Boulot/DUETI/S2/1rst part/neural/ChestXRay2017/chest_xray/test"
# List training files
print('Training file directory :', os.listdir(train_dir))
# list test files
print('Testing file directory :', os.listdir(test_dir))
# -
# ### Preprocess data
# #### Scaling
# The data must be preprocessed before training the network. Scale these images to a range of 0 to 1 before feeding them to the neural network model.<br>
# #### Split data
# We will also split the <b>training data</b> into training and validation sets where :
# - Training data = 70%
# - Validation data = 30%
# Rescale training images and split training data
train_datagen = ImageDataGenerator (rescale=1./255, validation_split = 0.3)
# #### Create data generators
# +
# training data generator
print('Training : ')
train_generator = train_datagen.flow_from_directory(
train_dir, #target directory
target_size = (150, 150), #Image resize
batch_size = 16,
class_mode = 'binary', # since we only have 2 classification: normal/pneumonia
subset = "training")
# validation data generator
print('\nValidation : ')
dev_generator = train_datagen.flow_from_directory(
train_dir,
target_size = (150, 150),
batch_size = 16,
class_mode = 'binary',
shuffle=False,
subset = "validation")
#train_generator.class_indices
# -
# #### Now we test if the train generator works :
# +
# labels_batch place labels automatically. For whichever folder to come first alphabetically, it will be labelled 0.
# e.g normal =0 and pneumonia=1
i = 0
for data_batch, labels_batch in train_generator:
# print('data batch shape:', data_batch.shape)
# print('labels batch shape:', labels_batch.shape)
i = i + 1
if i > 5:
break
# Testing continues
# Then we will check the first image from the training batch
print('\nThe first image from the training batch : ')
imshow(data_batch[0])
show()
print('If you inspect the first image from the batch, you will see that the pixel values fall in the range of 0 to 224')
# Testng continues
# We will then check the last labels batch
print('\nlabels batch : ')
labels_batch
# -
# ## Models and training
# This model was designed to add a more complex netwok of dense layer inside of the model n°1 witch was working quite well thanks to the idea of the dropout layer.
# So in this Notebook, we gonna add 2 dense layers (one of 128 and an other of 32) to check if the data is not shrinked after the dense layer of 512 neurons and the sigmoid of 1 neuron.
#For this model, we still keep the droupout layers and all the others concolutional layers but we are adding some dense layers
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation = 'relu', input_shape = (150, 150, 3)))
model.add(layers.MaxPooling2D(2, 2))
model.add(layers.Conv2D(64, (3, 3), activation = 'relu'))
model.add(layers.MaxPooling2D(2, 2))
model.add(layers.Conv2D(128, (3, 3), activation = 'relu'))
model.add(layers.MaxPooling2D(2, 2))
model.add(layers.Conv2D(128, (3, 3), activation = 'relu'))
model.add(layers.MaxPooling2D(2, 2))
model.add(layers.Flatten())
model.add(layers.Dropout(0.5))
model.add(layers.Dense(512, activation = 'relu'))
model.add(layers.Dense(128, activation = 'relu'))
model.add(layers.Dense(32, activation = 'relu'))
model.add(layers.Dense(1, activation = 'sigmoid'))
model.summary()
# ### Compile the model :
# Before the model is ready for training, it needs a few more settings to compile.
# +
# Use different set of metrics
my_metrics = ['acc', FalseNegatives(), FalsePositives()]
#To reduce the CPU running time, we increase a bit the learning rate
model.compile(loss = 'binary_crossentropy',
optimizer = optimizers.RMSprop(lr = 3.0e-4),
metrics = my_metrics)
# -
# ### Train the model :
# To start training, we call the model.fit method to "fit" the model to the data:
# +
# Start the clock
t_start = time.time()
print('Training...', end='')
h = model.fit_generator(
train_generator,
steps_per_epoch=None,
verbose=0,
epochs=4,
validation_data=dev_generator,
validation_steps=None)
# Cehcl the time and calculate the elapsed time and time per epoch
t_end = time.time()
t_elapsed = t_end - t_start
t_per_epoch = t_elapsed/3
print('Done')
print(f'Time elapsed = {t_elapsed:.0f} seconds')
print(f'Time per epoch = {t_per_epoch:.2f} seconds')
# +
hh = h.history
acc = hh['acc']
acc_v = hh['val_acc']
fn = hh['false_negatives']
fn_v = hh['val_false_negatives']
fp = hh['false_positives']
fp_v = hh['val_false_positives']
loss = hh['loss']
loss_v = hh['val_loss']
epochs = arange(len(loss)) + 1
show()
# -
# ## Results and Discussion
# +
# plot accuracy and loss lerning curves, but also false positive and negative for training and validation set
plot(epochs, acc, 'bo-', label='Training acc')
plot(epochs, acc_v, 'r*-', label='Validation acc')
title('Training and validation accuracy')
grid()
legend()
figure()
plot(epochs, loss, 'bo-', label='Training loss')
plot(epochs, loss_v, 'r*-', label='Validation loss')
title('Training and validation loss')
legend()
grid()
figure()
plot(epochs, fn, 'bo-', label='Training False Negatives')
plot(epochs, fn_v, 'r*-', label='Validation False Negatives')
title('False Negatives')
legend()
grid()
figure()
plot(epochs, fp, 'bo-', label='Training False Positives')
plot(epochs, fp_v, 'r*-', label='Validation False Positives')
title('False Postives')
legend()
grid()
show()
# +
labels = dev_generator.classes
predicted = model.predict_generator(dev_generator).flatten()
cm = confusion_matrix(labels, predicted > 0.5)
print(cm)
# -
# Calculate classification report
cr = classification_report(labels, predicted > 0.5, target_names=['Normal (0)', 'Pneumonia (1)'])
print(cr)
# Lets use various metrics to gain insights of the model's performance. First we will have to find the best threshold from ROC curve.
#
# ### ROC curve
#ROC curve analysis
fpr, tpr, thresholds = roc_curve(labels, predicted, pos_label = 1)
plot(fpr, tpr)
plot([0,1], [0,1], 'r:')
xlabel('False positive rate')
ylabel('True positive rate')
title('ROC Curve')
xlim([0,1])
ylim([0,1])
grid()
# In ROC curve, the true positive rate (Sensitivity) is plotted in function of the false positive rate (100-Specificity) for different cut-off points. The closer the ROC curve is to the upper left corner, the higher the overall accuracy of the test (Zweig & Campbell, 1993). This means, this model has a high overall accuracy. After obtaining the TPR and FPR, we will be able to identify the best threshold.
#
# ### Threshold analysis
# The best threshold would be obtained by using the roc curve where true positive rate(tpr) and false positive rate(fpr) overlap.
#Find the threshold
plot(thresholds, 1 - fpr, label = 'Specificity')
plot(thresholds, tpr, label = 'Sensitivity')
axvline(0.5, color = 'red', linestyle=':')
xlim([0,1])
title('Threshold value for prediction')
xlabel('Threshold')
ylabel('Metrics value')
legend()
grid()
# The best threshold is arround 0.90
# ### Evaluate accuracy
# After training is complete, we'll evaluate how the model performs with the best threshold.
# +
# reset the validation generator and then use our trained model to make predictions on the data
print("[INFO] evaluating network...")
dev_generator.reset()
predict = model.predict_generator(dev_generator)
# for each image in the testing set we need to find the labels
labels = dev_generator.classes
# show a nicely formatted classification report
print(classification_report(labels, predict>0.90, target_names=['Normal(0)', 'Pneumonia(1)']))
# +
# compute the confusion matrix and use it to derive the raw accuracy, sensitivity, and specificity
cm = confusion_matrix(labels, predict>0.90)
total = sum(sum(cm))
acc = (cm[0, 0] + cm[1, 1]) / total
sensitivity = cm[0, 0] / (cm[0, 0] + cm[0, 1])
specificity = cm[1, 1] / (cm[1, 0] + cm[1, 1])
# show the confusion matrix, accuracy, sensitivity, and specificity
print(cm)
print("\naccuracy: {:.4f}".format(acc))
print("sensitivity: {:.4f}".format(sensitivity))
print("specificity: {:.4f}".format(specificity))
# -
# # Model 2: Observations
#
# As we can see it very easelly on the ROC Curve, the results are pretty good and maybe good enouth to be considered to be used in a medical perspective. The accuracy and loss curves inform us that the is no overfitting.
#
# Compared to the previous model(1), we observe that our sensitivity have decreased a little lit. However, the specificity has been improved a lot (0.868 VS 0.935). In a medical perspective, that means that less people that doesn't have pneumonia will be diagnosticated positive. That can save quite a lot of medical ressouces and avoid caring for a patient who isn't sick.
#
# Also, in average, we are obtaining better results than the Model 1 with quite the same number of parameter (3,43 VS 3,52 million of parameters) that is to say that this model doesn't need mutch more ressources to archive better results, so that consits as an improvment
# # Model 2: Conclusions
#
# To conclude about this model, we can observe that a fine Dense layer network can improve quite a lot the results obtained with a good convolutionnal neural network without adding too mutch ressource's requirements.
| 35.996951 | 1,037 |
5b8d68d8d3fb7787c84daf34bb0b4238a61350f0
|
py
|
python
|
sphinx/datascience/source/causal-inference.ipynb
|
oneoffcoder/books
|
['CC-BY-4.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Causal Inference
#
# Let's learn about causal inference using Bayesian Belief Networks (BBN).
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import networkx as nx
import warnings
plt.style.use('seaborn')
warnings.filterwarnings('ignore')
np.random.seed(37)
# -
# ## Gender, drug and recovery
#
# Imagine that we have an illness or disease, and that some patients were given a drug and some were not for treatment. We kept good records of three variables.
#
# * gender: whether the patient was female or male
# * drug: whether the patient took the drug or not
# * recovery: whether the patient recovered from the illness
#
# We can model the interactions of these variables using a BBN.
# ### Structure
#
# The structure of a BBN is a directed acyclic graph `DAG`. We will visualize the structure later, but for now, the relationships in the model is as follows.
#
# * gender $\rightarrow$ drug
# * gender $\rightarrow$ recovery
# * drug $\rightarrow$ recovery
# ### Parameters
#
# For each variable, we need to define `local probability models`, and, here, they come in the form of `conditional probability tables`.
# +
gender_probs = [0.49, 0.51]
print(gender_probs)
# +
drug_probs = [0.23323615160349853, 0.7667638483965015,
0.7563025210084033, 0.24369747899159663]
print(drug_probs[0:2])
print(drug_probs[2:4])
# +
recovery_probs = [0.31000000000000005, 0.69,
0.27, 0.73,
0.13, 0.87,
0.06999999999999995, 0.93]
print(recovery_probs[0:2])
print(recovery_probs[2:4])
print(recovery_probs[4:6])
print(recovery_probs[6:8])
# -
# ### Bayesian network
#
# With the structure and parameters defined, now we can build a BBN.
# +
from pybbn.graph.dag import Bbn
from pybbn.graph.edge import Edge, EdgeType
from pybbn.graph.jointree import EvidenceBuilder
from pybbn.graph.node import BbnNode
from pybbn.graph.variable import Variable
from pybbn.pptc.inferencecontroller import InferenceController
X = BbnNode(Variable(1, 'drug', ['false', 'true']), drug_probs)
Y = BbnNode(Variable(2, 'recovery', ['false', 'true']), recovery_probs)
Z = BbnNode(Variable(0, 'gender', ['female', 'male']), gender_probs)
bbn = Bbn() \
.add_node(X) \
.add_node(Y) \
.add_node(Z) \
.add_edge(Edge(Z, X, EdgeType.DIRECTED)) \
.add_edge(Edge(Z, Y, EdgeType.DIRECTED)) \
.add_edge(Edge(X, Y, EdgeType.DIRECTED))
# -
# ### Visualize Bayesian network structure
#
# Let's see the structure of this network.
g, labels = bbn.to_nx_graph()
# +
fig, ax = plt.subplots(figsize=(10, 5))
pos = nx.nx_agraph.graphviz_layout(g, prog='dot', args='-Kdot')
params = {
'node_color': 'r',
'node_size': 1000,
'node_shape': 'o',
'alpha': 0.5,
'pos': pos,
'ax': ax
}
_ = nx.drawing.nx_pylab.draw_networkx_nodes(g, **params)
params = {
'labels': labels,
'font_size': 20,
'font_color': 'k',
'font_family': 'monospace',
'font_weight': 'bold',
'pos': pos,
'ax': ax
}
_ = nx.drawing.nx_pylab.draw_networkx_labels(g, **params)
params = {
'width': 1.5,
'alpha': 0.8,
'edge_color': 'b',
'arrowsize': 30,
'pos': pos,
'ax': ax
}
_ = nx.drawing.nx_pylab.draw_networkx_edges(g, **params)
_ = ax.set_title('Gender, drug and recovery')
plt.tight_layout()
# -
# ## Sample data
#
# Let's sample some data from the BBN and observe some summary statistics about the sampled data. Additionally, the data will help us answer if taking the drug does really help in recovery.
# +
from pybbn.sampling.sampling import LogicSampler
sampler = LogicSampler(bbn)
data = pd.DataFrame(sampler.get_samples(n_samples=10000, seed=37))
data = data.rename(columns=labels)
# -
# ## Simpson's paradox
#
# In general, the sample population made good recovery (80%).
# +
s = data.recovery.value_counts().sort_index()
s /= s.sum()
fig, ax = plt.subplots(figsize=(7, 4))
_ = s.plot.bar(ax=ax, color=['b', 'r'])
_ = ax.set_title('General recovery')
_ = ax.set_ylabel('%')
# -
# If we segment recovery by whether or not a patient takes the drug, we find that
#
# * `82%` of patients recovered if they did **NOT** take the drug, compared to `78%` if they did take the drug (not taking the drug **increases** your chance of recovery), and
# * `18%` of the patients did **NOT** recover if they did **NOT** take the drug, compared to `22%` if they did **NOT** recover but did take the drug (not taking the drug **decreases** of chance of not recovering).
#
# The comparison might lead one to interpret the outcome that **NOT** taking the drug gives us a better chance of recovery.
# +
s0 = data[data.drug == 'false'].recovery.value_counts().sort_index()
s0 /= s0.sum()
s1 = data[data.drug == 'true'].recovery.value_counts().sort_index()
s1 /= s1.sum()
fig, ax = plt.subplots(figsize=(7, 4))
_ = pd.DataFrame(
[[s0[0], s1[0]], [s0[1], s1[1]]],
columns=['drug=false', 'drug=true'],
index=['recovered=false', 'recovered=true']).plot.bar(ax=ax, color=['b', 'r'])
# -
# Now, we segment based on gender. Notice
#
# * for both females and males, taking the drug did increase recovery, and
# * for both females and males, not taking the drug did decrease non-recovery.
#
# The observation here contradicts the one we had before without segmenting on gender. Before, not taking the drug was helpful, now, segmenting on gender, not taking the drug is harmful. This contradiction is `Simpson's paradox`. So is taking the drug helpful or harmful?
# +
df = data[data.gender == 'female']
s0 = df[df.drug == 'false'].recovery.value_counts().sort_index()
s0 /= s0.sum()
s1 = df[df.drug == 'true'].recovery.value_counts().sort_index()
s1 /= s1.sum()
f_df = pd.DataFrame(
[[s0[0], s1[0]], [s0[1], s1[1]]],
columns=['drug=false', 'drug=true'],
index=['recovered=false', 'recovered=true'])
df = data[data.gender == 'male']
s0 = df[df.drug == 'false'].recovery.value_counts().sort_index()
s0 /= s0.sum()
s1 = df[df.drug == 'true'].recovery.value_counts().sort_index()
s1 /= s1.sum()
m_df = pd.DataFrame(
[[s0[0], s1[0]], [s0[1], s1[1]]],
columns=['drug=false', 'drug=true'],
index=['recovered=false', 'recovered=true'])
fig, ax = plt.subplots(1, 2, figsize=(15, 4))
_ = f_df.plot.bar(ax=ax[0], color=['b', 'r'])
_ = m_df.plot.bar(ax=ax[1], color=['b', 'r'])
_ = ax[0].set_title('Female recovery')
_ = ax[1].set_title('Male recovery')
# -
# ## do-operator
#
# Dr. Judea Pearl says that we can find out if taking the drug does really help or harm recovery (direction) and by how much (magnitude). Dr. Pearl starts by distguishing between `conditional` and `interventional` probabilities.
#
# * The `conditional` probabilities are what we are observing and interpreting above. Conditional probabilities are the result of merely filtering through data.
# * The `interventional` probabilities are the ones that result if we can somehow manipulate or intervene in the treatment process. Interventional probabilities are the result of changing the system/process, and thus, the data.
#
# Said by Dr. Pearl.
#
# * When we condition on a variable, we change nothing; we merely narrow our foucs to the subset of cases in which the variable takes the value we are interested in. What changes, then, is our **perception** about the world, **not the world itself**.
#
# Among many other amazing results, his `casual calculus` is able to frame `interventional probabilities` in terms of `conditional probabilities` and directly addresses causal inference in `observational data` (which is quite often controversial to use to draw causal conclusions, as opposed to `experimental data`). The main idea behind causal inference or estimating causal impact is the `do-operator`. The `do-operator` is the most simplest thing to do (no pun intended), but it takes some careful and critical thinking into why it actually works. In a nutshell, the `do-operator` is a graphical procedure where we remove the incoming links to a node (e.g. drug) for which we are trying to estimate causal impact (removing the links from a node's parents) to another node (e.g. recovery). This operation is `graph surgery` as we are cutting the graph and removing edges. Once we have the `manipulated graph` from the `do-operation`, we are able to estimate causal impact. Note that the `do-operator` enables us to estimate causal impact because it removes spurious paths.
#
# With the `do-operator`, we can estimate casual impact as follows (Pearl calls this equation the `adjustment formula`).
#
# $P_m(Y=y|X=x) = P(Y=y|\text{do}(X=x)) = \displaystyle \sum_z P(Y=y|X=x, Z=z)P(Z=z)$
#
# Where
#
# * $P_m(Y=y|X=x)$ is the interventional probability of $Y$ given $X$ (uses manipulated model)
#
# In our running example,
#
# * $X$ is drug,
# * $Y$ is recovery, and
# * $Z$ is gender.
#
# Again, note that the `interventional probability` $P_m$ is defined entirely in terms of $P$, the `conditional probability` (the `do-operator` does not apply in the manipulated model or graph). Wow! Since we have a way to compute $P_m$ in terms of $P$, we do not really have to do graph surgery. We can leave the graph structure as it is; or leave the edges as they are. Now, we need to find nodes to condition on to block spurious paths. The `backdoor criterion`, can help us identify which set of variables to focus on. Stated by Perl.
#
# * Backdoor Criterion: Given an ordered pair of variables (X, Y) in a directed acylic graph G, a set of variables Z satisfies the backdoor criterion relative to (X, Y) if no node in Z is a descendant of X, and Z blocks every path between X and Y that contains an arrow into it.
#
# Any set of variables $Z$ that `d-separates` $X$ and $Y$ satisfies the backdoor criterion.
# ## Causal impact of drug on recovery
#
# Let's see if we can use the `adjustment formula` to estimate the causal impact of drug on recovery. The data we sampled earlier will help us compute the conditional and marginal probabilities required. In expanded form, the adjustment formula looks like the following.
#
# * $P(Y=1|\text{do}(X=1)) = P(Y=1|X=1,Z=1)P(Z=1) + P(Y=1|X=1,Z=0)P(Z=0)$
# * $P(Y=1|\text{do}(X=0)) = P(Y=1|X=0,Z=1)P(Z=1) + P(Y=1|X=0,Z=0)P(Z=0)$
#
# $P(Y=1|\text{do}(X=1))$ is the interventional probability of recovery given that we have taken the drug, and $P(Y=1|\text{do}(X=0))$ is the interventional probability of recovery given that we have **NOT** taken the drug.
#
# The average causal effect `ACE` is given as follows.
#
# $\text{ACE} = P(Y=1|\text{do}(X=1)) - P(Y=1|\text{do}(X=0))$
#
# The `ACE` is the expected casual impact of recovery using the drug.
# +
def get_prob(q):
return data.query(q).shape[0] / N
N = data.shape[0]
n = get_prob('recovery=="true" and drug=="true" and gender=="male"')
d = get_prob('drug=="true" and gender=="male"')
p_y1_x1z1 = n / d
n = get_prob('recovery=="true" and drug=="true" and gender=="female"')
d = get_prob('drug=="true" and gender=="female"')
p_y1_x1z0 = n / d
p_z1 = data[data.gender == 'male'].shape[0] / N
p_z0 = data[data.gender == 'female'].shape[0] / N
do_y1x1 = p_y1_x1z1 * p_z1 + p_y1_x1z0 * p_z0
print(f'P(Y=1|do(X=1)) = {do_y1x1:.5f}')
# +
n = get_prob('recovery=="true" and drug=="false" and gender=="male"')
d = get_prob('drug=="false" and gender=="male"')
p_y1_x0z1 = n / d
n = get_prob('recovery=="true" and drug=="false" and gender=="female"')
d = get_prob('drug=="false" and gender=="female"')
p_y1_x0z0 = n / d
do_y1x0 = p_y1_x0z1 * p_z1 + p_y1_x0z0 * p_z0
print(f'P(Y=1|do(X=0)) = {do_y1x0:.5f}')
# -
ace = do_y1x1 - do_y1x0
print(f'ACE = {ace:.5f}')
# We get an increase of about 6% (direction and magnitude) in recovery if we take the drug. Notice how we did not have to actually employ graph surgery or the `do-operator` and we used the backdoor criterion and only the conditional and marginal probabilities?
# ## Manipulated graph
#
# We can actually use the `do-operator` and get a `manipulated graph` and simply compute the interventional conditional.
# +
# notice the parameter change in X (drug or drug probabilities)
gender_probs = [0.49, 0.51]
drug_probs = [0.5, 0.5]
recovery_probs = [0.31000000000000005, 0.69,
0.27, 0.73,
0.13, 0.87,
0.06999999999999995, 0.93]
X = BbnNode(Variable(1, 'drug', ['false', 'true']), drug_probs)
Y = BbnNode(Variable(2, 'recovery', ['false', 'true']), recovery_probs)
Z = BbnNode(Variable(0, 'gender', ['female', 'male']), gender_probs)
# notice the missing edge Z -> X
bbn = Bbn() \
.add_node(X) \
.add_node(Y) \
.add_node(Z) \
.add_edge(Edge(Z, Y, EdgeType.DIRECTED)) \
.add_edge(Edge(X, Y, EdgeType.DIRECTED))
join_tree = InferenceController.apply(bbn)
join_tree.get_posteriors()
# -
# $P(Y=1|\text{do}(X=1)) = 0.832$
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('drug')) \
.with_evidence('true', 1.0) \
.build()
join_tree.unobserve_all()
join_tree.set_observation(ev)
join_tree.get_posteriors()
# $P(Y=1|\text{do}(X=0)) = 0.782$
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('drug')) \
.with_evidence('false', 1.0) \
.build()
join_tree.unobserve_all()
join_tree.set_observation(ev)
join_tree.get_posteriors()
# $\text{ACE} = P(Y=1|\text{do}(X=1)) - P(Y=1|\text{do}(X=0)) = 0.05$ which is not too far off from using the `adjustment formula` based on the sampled data.
| 35.32626 | 1,075 |
744831aedf1ff7cf71a9baa8e81b50c456eff733
|
py
|
python
|
Learning_ML/ML_Techniques/Model_Evaluation_Sklearn.ipynb
|
oke-aditya/Machine_Learning
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="fZHq0u3nXe9P" colab_type="text"
# # Model Evaluation Techniques
# + [markdown] id="lNPxt1UckbsE" colab_type="text"
# https://scikit-learn.org/stable/modules/model_evaluation.html#
# + [markdown] id="9WBDmKFbX1_O" colab_type="text"
# ## Introduction
# + [markdown] id="K-dsuFAWX4GI" colab_type="text"
# * Model Evaluation techniques are required to decide how good or bad a given model is.
#
# * There are numerous predined metrics available in Scikit-Learn.
#
# * These metrics vary for Regresssion and Classification tasks.
#
# + [markdown] id="Fu5B7cPkX3wB" colab_type="text"
# ## Classification Metrics
# + [markdown] id="qKI1OMTTbTjC" colab_type="text"
# ### Note
# + [markdown] id="QbOvqccOYzqM" colab_type="text"
# * The sklearn.metrics module implements several loss, score, and utility functions to measure classification performance.
#
# * Some metrics might require probability estimates of the positive class, confidence values, or binary decisions values.
#
# * Most implementations allow each sample to provide a weighted contribution to the overall score, through the sample_weight parameter.
#
# We will discuss **only a few popularly** used metrics here.
# + [markdown] id="LXXrHJCgZbwM" colab_type="text"
# ### Multi-Class vs Multi-Label vs Binary-Class
# + [markdown] id="UDBGHoDKZjw6" colab_type="text"
# * Some metrics are essentially defined for binary classification tasks (e.g. f1_score, roc_auc_score).
# * In these cases, by default only the positive label is evaluated, assuming by default that the positive class is labelled 1.
# * In extending a binary metric to multiclass or multilabel problems, the data is treated as a collection of binary problems, one for each class.
# * There are then a number of ways to average binary metric calculations across the set of classes, each of which may be useful in some scenario. Where available, you should select among these using the average parameter.
#
# + [markdown] id="bwO6ReG0aWYe" colab_type="text"
#
# - "macro" simply calculates the mean of the binary metrics, giving equal weight to each class. In problems where infrequent classes are nonetheless important, macro-averaging may be a means of highlighting their performance. On the other hand, the assumption that all classes are equally important is often untrue, such that macro-averaging will over-emphasize the typically low performance on an infrequent class.
# - "weighted" accounts for class imbalance by computing the average of binary metrics in which each class’s score is weighted by its presence in the true data sample.
# - "micro" gives each sample-class pair an equal contribution to the overall metric (except as a result of sample-weight). Rather than summing the metric per class, this sums the dividends and divisors that make up the per-class metrics to calculate an overall quotient. Micro-averaging may be preferred in multilabel settings, including multiclass classification where a majority class is to be ignored.
# - "samples" applies only to multilabel problems. It does not calculate a per-class measure, instead calculating the metric over the true and predicted classes for each sample in the evaluation data, and returning their (sample_weight-weighted) average.
#
# - Selecting average=None will return an array with the score for each class.
#
# + [markdown] id="JHoCsvGPahfJ" colab_type="text"
# ### Providing inputs to Metrics
# + [markdown] id="Z1wSZFL2ahTo" colab_type="text"
# * Multiclass data / Binaryclass data can be given as an array of labels.
# * Multilabel data has to be specified as an indicator matrix, in which cell $ [i,j] $ has value 1 if sample $ i $ has label $ j $ otherwise 0.
# + [markdown] id="pK5rUVq8bC2x" colab_type="text"
# ### Accuracy Score
# + [markdown] id="g1wlh0DDbi8A" colab_type="text"
# * The `accuracy_score` function computes the accuracy, either the fraction or the count (set normalize = False) of correct predictions.
#
# * In multiclass classification it returns % of samples that were correct.
#
# * In multilabel classifcation it returns the subset accuracy. If the entire set of predicted labels was correct it counts it as 1 else 0.
# + [markdown] id="sFUjTqjncAUE" colab_type="text"
# If $ \hat{y}_i $ is the predicted value of the $i$-th sample and $y_i$ is the corresponding true value, then the fraction of correct predictions over $ n_{samples} $
#
# $ \texttt{accuracy}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} 1(\hat{y}_i = y_i) $
#
# where $ 1(x) $ is the indicator function.
# + id="WUcR2DDRGIXH" colab_type="code" colab={}
import numpy as np
from sklearn.metrics import accuracy_score
# + id="ymkTbA3Uc6H0" colab_type="code" outputId="80d8e91d-7b76-4684-c2cd-117b59251c84" colab={"base_uri": "https://localhost:8080/", "height": 36}
y_pred = [0,1,2,2]
y_true = [1,1,2,0]
print(accuracy_score(y_pred, y_true, normalize = True))
# + id="JIxTX_gtdHQx" colab_type="code" outputId="fafec430-1e51-48a5-ba60-cdb4f596922e" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(accuracy_score(y_pred, y_true, normalize = False))
# + id="JxQFXgm4dQp1" colab_type="code" colab={}
# For multi-label classifcation problems
X = np.array([[0,1], [1,1]])
Y = np.ones((2,2))
# + id="NAJXKh4RddKP" colab_type="code" outputId="20f59284-d164-4cdf-aac5-8b040c45e5ed" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(accuracy_score(X,Y,normalize = True))
# + [markdown] id="leGf8DcfdxJf" colab_type="text"
# ### Balanced Accuracy Score
# + id="-Mhqb7XJdfjz" colab_type="code" colab={}
# + [markdown] id="svLqWT1VktUS" colab_type="text"
# ### Zero One Loss
# + [markdown] id="s1a-Il5bkxsJ" colab_type="text"
# * The `zero_one_loss` function computes the sum or the average of the 0-1 classification loss $ L_{0-1} $ over $ n_{samples} $.
# * By default, the function normalizes over the samples.
#
# * In multi-label classification, the `zero_one_loss` scores a subset as one if the label strictly matches the prediction, and as a zero if there are any errors.
#
# * By default, the function returns the percentage of imperfectly predicted subsets. To get the count of such subsets instead, set normalize to False
#
# * If $ \hat{y} $ is the $i$ th predicted value of the $y_i$-th sample and is the corresponding true value, then the 0-1 loss is defined as:
#
# * $L_{0-1}(y_i, \hat{y}_i) = 1(\hat{y}_i \not= y_i)$
#
# * Where $1(x)$ is the indicator
# + id="DHHYOsgPkwxW" colab_type="code" colab={}
from sklearn.metrics import zero_one_loss
# + id="by5wJMglmHph" colab_type="code" colab={}
y_pred = [1,2,3,4]
y_true = [2,2,3,4]
# + id="77T7Z05gmHUD" colab_type="code" outputId="7a73fa6b-d049-49ed-f92f-d9b0d81a01fb" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(zero_one_loss(y_true, y_pred))
# + [markdown] id="0ZXrX8G8mb7E" colab_type="text"
# ### Brier-score loss
# + [markdown] id="zbyCoEdLmgFk" colab_type="text"
# * The brier_score_loss function computes the Brier score for binary classes. Quoting Wikipedia:
#
# - “The Brier score is a proper score function that measures the accuracy of probabilistic predictions.
#
# - It is applicable to tasks in which predictions must assign probabilities to a set of mutually exclusive discrete outcomes.”
#
# - This function returns a score of the mean square difference between the actual outcome and the predicted probability of the possible outcome.
#
# - The actual outcome has to be 1 or 0 (true or false), while the predicted probability of the actual outcome can be a value between 0 and 1.
#
# - The brier score loss is also between 0 to 1 and the lower the score (the mean square difference is smaller), the more accurate the prediction is.
#
# - It can be thought of as a measure of the “calibration” of a set of probabilistic predictions.
#
# - $BS = \frac{1}{N} \sum_{t=1}^{N}(f_t - o_t)^2$
# + id="bY-vzGMqmfil" colab_type="code" colab={}
import numpy as np
from sklearn.metrics import brier_score_loss
# + id="WvQDd5yCnAVK" colab_type="code" outputId="e31439c0-6ab6-4c6a-d58f-4cf083ebda62" colab={"base_uri": "https://localhost:8080/", "height": 36}
y_true = np.array([0, 1, 1, 0])
y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
y_prob = np.array([0.1, 0.9, 0.8, 0.4])
y_pred = np.array([0, 1, 1, 0])
# + id="h2s4cH48nE0T" colab_type="code" outputId="a437bfe0-74ee-4815-d501-8fe548836333" colab={"base_uri": "https://localhost:8080/", "height": 91}
print(brier_score_loss(y_true, y_prob))
print(brier_score_loss(y_true, 1 - y_prob, pos_label=0))
print(brier_score_loss(y_true_categorical, y_prob, pos_label="ham"))
print(brier_score_loss(y_true, y_prob > 0.5))
# + [markdown] id="xNZrPGwRlYVE" colab_type="text"
# ### Cohen's Kappa Score
# + [markdown] id="VQPgeRvllbsh" colab_type="text"
# * The function `cohen_kappa_score` computes Cohen’s kappa statistic.
# * This measure is intended to compare labelings by different human annotators, not a classifier versus a ground truth.
#
# * The kappa score is a number between -1 and 1.
# * Scores above .8 are generally considered good agreement; zero or lower means no agreement (practically random labels).
#
# * Kappa scores can be computed for binary or multiclass problems, but not for multilabel problems (except by manually computing a per-label score) and not for more than two annotators.
# + [markdown] id="wMBhlS47lxwv" colab_type="text"
# Formulation: -
# * This is mathmeatically given as $ \kappa = (p_o - p_e) / (1 - p_e) $
# where $ p_o $ is the empircal probabilty on the label assigned to any sample and $ p_e $ is estimated using a per annotator empirical apriori over the class label.
# + id="bRn-5mB6lbCn" colab_type="code" colab={}
from sklearn.metrics import cohen_kappa_score
# + id="gMNtOEs0mYSG" colab_type="code" colab={}
y_true = [2,0,2,2,0,1]
y_pred = [0,0,2,2,0,2]
# + id="Gc9W6yg2mgWq" colab_type="code" outputId="379f06e6-5a40-4cd7-c4a0-4c40a514cd7f" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(cohen_kappa_score(y_true, y_pred))
# + [markdown] id="dE7QX1CAuZFd" colab_type="text"
# ### Hamming Loss
# + [markdown] id="B955DVJKuui0" colab_type="text"
# - If $ \hat{y_j} $ is the predicted value for the $ j $-th label of a given sample, $y_j$ is the corresponding true value, and $n_labels $ is the number of classes or labels, then the Hamming loss $L_{Hamming} $ between two samples is defined as:
# + [markdown] id="Crqb7lP7vKgY" colab_type="text"
# $ L_{Hamming}(y, \hat{y}) = \frac{1}{n_\text{labels}} \sum_{j=0}^{n_\text{labels} - 1} 1(\hat{y}_j \not= y_j) $
# + id="6OGm-3CrvTBZ" colab_type="code" colab={}
from sklearn.metrics import hamming_loss
# + id="JoSDi6gtvcdK" colab_type="code" outputId="04db6ce0-51f5-4644-c0c5-528ba5a150c9" colab={"base_uri": "https://localhost:8080/", "height": 36}
y_pred = [1,2,3,4]
y_true = [2,3,3,4]
print(hamming_loss(y_pred, y_true))
# + [markdown] id="0U6cQk6Jvlt4" colab_type="text"
# - Relation with Zero-One loss
#
# - In multiclass classification, the Hamming loss corresponds to the Hamming distance between y_true and y_pred which is similar to the Zero one loss function.
#
# - However, while zero-one loss penalizes prediction sets that do not strictly match true sets, the Hamming loss penalizes individual labels.
#
# - Thus the Hamming loss, upper bounded by the zero-one loss, is always between zero and one, inclusive; and predicting a proper subset or superset of the true labels will give a Hamming loss between zero and one, exclusive.
# + [markdown] id="u0IO0jOwyrjV" colab_type="text"
# ### Jaccard similarity Coefficient
# + [markdown] id="iFFUuGxnyw-W" colab_type="text"
# * The jaccard_score function computes the average of Jaccard similarity coefficients, also called the Jaccard index, between pairs of label sets.
#
# * The Jaccard coefficient measures similarity between finite sample sets, and is defined as the size of the intersection divided by the size of the union of the sample sets.
#
# * The Jaccard similarity coefficient of the $i$-th samples, with a ground truth $y_i$ label set and predicted label set $ \hat{y_i}$ , is defined as
#
# $ J(y_i, \hat{y}_i) = \frac{|y_i \cap \hat{y}_i|}{|y_i \cup \hat{y}_i|}. $
#
# * jaccard_score works like precision_recall_fscore_support as a naively set-wise measure applying natively to binary targets, and extended to apply to multilabel and multiclass.
# + id="IfUj7DVCyvkY" colab_type="code" colab={}
import numpy as np
from sklearn.metrics import jaccard_score
# + id="Rx7inB2lznYA" colab_type="code" colab={}
# Binary Case
y_true = np.array([[0,1,1], [1,1,0]])
y_pred = np.array([[1,1,1], [1,0,0]])
# + id="EyLQlpDWz--T" colab_type="code" outputId="a4c4b8e4-6788-4a1e-9345-fe80aab234bd" colab={"base_uri": "https://localhost:8080/", "height": 54}
print(jaccard_score(y_true[0], y_pred[0]))
print(jaccard_score(y_true[1], y_pred[1]))
# + id="B-Zgla4g1iru" colab_type="code" colab={}
# Multi-class problems are treated as binarized problems in similar way
y_pred = [0,1,1,2,2]
y_true = [0,2,1,2,1]
# + id="a1A01LBy13U2" colab_type="code" outputId="ac44b277-3697-446b-a662-935a00f584be" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(jaccard_score(y_true, y_pred, average = None))
# + [markdown] id="3rmqhc0S2NI8" colab_type="text"
# ### Hinge Loss
# + [markdown] id="bc62OA942Q5G" colab_type="text"
# * The hinge_loss function computes the average distance between the model and the data using hinge loss, a one-sided metric that considers only prediction errors.
#
# * (Hinge loss is used in maximal margin classifiers such as support vector machines.)
#
# * If the labels are encoded with +1 and -1, $ y $ ; is the true value, and $ w $ and is the predicted decision are output by ` descision_function `, then the hinge loss is defined as :
#
# * $ L_{Hinge} (y,w) = max({1 - wy, 0 }) = | 1 - xy | $
#
# * If there are more than two labels, hing_loss uses a multiclass variant.
#
# * If $ y_w $ is the predicted decision for true label and $ y_t $ is the maximum of the predicted decisions for all labels where predicted decisions are output by decision function, then multiclass hinge loss is defined by:
#
# * $ L_{Hinge} (y_w, y_t) = max({1 + y_t - y_w, 0}) $
# + [markdown] id="y7tGQceD95Qk" colab_type="text"
# * Hinge loss is very commoonly used with SVM
# + id="nb0EXzJK2PDj" colab_type="code" colab={}
from sklearn import svm
from sklearn.metrics import hinge_loss
# + id="jJCGBlT5AVNK" colab_type="code" colab={}
# Binary Classification
X = [[0], [1]]
y = [-1, 1]
# + id="AWLQRZyrAeEO" colab_type="code" outputId="33978339-dffc-4923-c39c-a052b8dfbe75" colab={"base_uri": "https://localhost:8080/", "height": 74}
est = svm.SVC(random_state = 31)
est = est.fit(X,y)
# + id="2wsJ7dkZAxZa" colab_type="code" outputId="e1e85f79-d9d1-465f-f62c-4c8a385e223a" colab={"base_uri": "https://localhost:8080/", "height": 54}
pred_decision = est.decision_function([[-2], [3], [0.5]])
print(pred_decision)
hinge_loss([-1, 1, 1], pred_decision)
# + id="GC4OK6pRBpwh" colab_type="code" colab={}
# Multi-Class Classification
X = np.array([[0], [1], [2], [3]])
Y = np.array([0,1,2,3])
labels = np.array([0,1,2,3])
# + id="OKE2KLVUB72G" colab_type="code" outputId="0f993d80-8392-44e8-b999-931484ce6490" colab={"base_uri": "https://localhost:8080/", "height": 93}
est = svm.SVC()
est = est.fit(X, Y)
pred_decision = est.decision_function([[-1], [2], [3]])
y_true = [0, 2, 3]
print(hinge_loss(y_true, pred_decision, labels) )
# + [markdown] id="pRheJdm9CiUO" colab_type="text"
# ### Log-Loss
# + [markdown] id="0xl2-8LcCokJ" colab_type="text"
# * Log loss, also called logistic regression loss or cross-entropy loss, is defined on probability estimates.
#
# * It is commonly used in (multinomial) logistic regression and neural networks, as well as in some variants of `expectation-maximization`, and can be used to evaluate the probability outputs (predict_proba) of a classifier instead of its discrete predictions.
#
# * For binary classification with a true label $y \in \{0,1\} $ and a probability estimate $p = Px(y=1) $, the log loss per sample is the negative log-likelihood of the classifier given the true label:
# + [markdown] id="LSgi3fzkDqoQ" colab_type="text"
# * $ L_{\log}(y, p) = -\log \operatorname{Pr}(y|p) = -(y \log (p) + (1 - y) \log (1 - p)) $
#
# * This extends to the multiclass case as follows.
#
# * Let the true labels for a set of samples be encoded as a 1-of-K binary indicator matrix $Y$ , i.e., if sample $i$ has labels taken from a set of $K$ labels. Let $P$ be a matrix of probability estimates, with $p_{i,k} = \operatorname{Pr}(t_{i,k} = 1)$.
#
# * Then the log loss of the whole set is
# + [markdown] id="mcCy_ecTEKUU" colab_type="text"
# $L_{\log}(Y, P) = -\log \operatorname{Pr}(Y|P) = - \frac{1}{N} \sum_{i=0}^{N-1} \sum_{k=0}^{K-1} y_{i,k} \log p_{i,k}$
# + id="7ojo5TZ7Cj-U" colab_type="code" colab={}
from sklearn.metrics import log_loss
# + [markdown] id="EWA07JDtGTNq" colab_type="text"
# The first [.9, .1] in y_pred denotes 90% probability that the first sample has label 0. The log loss is non-negative.
# + id="IacNBuPWFUA4" colab_type="code" outputId="2786da2a-4411-4da3-b770-403abec6f369" colab={"base_uri": "https://localhost:8080/", "height": 36}
y_true = [0,0,1,1]
y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]]
print(log_loss(y_true, y_pred))
# + [markdown] id="nJLKSLrcnNm_" colab_type="text"
# ### Confusion Matrix
# + [markdown] id="7cifv-r3nNX0" colab_type="text"
# * The confusion_matrix function evaluates classification accuracy by computing the confusion matrix with each row corresponding to the true class.
#
# * By definition, entry $i, j $ in a confusion matrix is the number of observations actually in group , $i$ but predicted to be in group $j$ .
#
# Here is an example:
# + id="b981qa4hmj4s" colab_type="code" colab={}
from sklearn.metrics import confusion_matrix
# + id="MdayRzwpnlXb" colab_type="code" colab={}
y_true = [2,0,2,2,0,1]
y_pred = [0,0,2,2,0,2]
# + id="S7JTyuConrwl" colab_type="code" outputId="b8bfa336-f617-4726-88b8-f878976fcf1e" colab={"base_uri": "https://localhost:8080/", "height": 73}
print(confusion_matrix(y_true, y_pred))
# + [markdown] id="ivzLSIAgqtky" colab_type="text"
# * For binary problems we can get true negative, false positive and false negative, true positive directly.
# + id="pf4hafXzn1II" colab_type="code" colab={}
y_true = [0,0,0,0,1,1,1,1]
y_pred = [1,1,0,0,1,1,1,0]
tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
# + id="Rm166-HIrBoD" colab_type="code" outputId="8bcf202f-a6c5-4de4-d92d-f56c7ed9e7cf" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(tn,fp,fn,tp)
# + [markdown] id="WHtnCRq1rPGA" colab_type="text"
# ### Classification Report
# + [markdown] id="IemSy-7lreTs" colab_type="text"
# * The classification_report function builds a text report showing the main classification metrics.
#
# Here is a small example with custom target_names and inferred labels:
# + id="JTsXs5p9rMvN" colab_type="code" colab={}
from sklearn.metrics import classification_report
# + id="vW_cT_T6rvQZ" colab_type="code" colab={}
y_true = [0,1,2,0,1,1]
y_pred = [0,1,2,0,0,2]
# + id="1O_kzQiLrvz-" colab_type="code" colab={}
target_names = ['class:0', 'class:1', 'class:2']
# + id="RkoKK7zsr1pk" colab_type="code" outputId="5fc65d8c-86fe-4997-d696-3bdc9bafcde9" colab={"base_uri": "https://localhost:8080/", "height": 203}
print(classification_report(y_true, y_pred, target_names=target_names))
# + [markdown] id="DZQwTya2Ypwd" colab_type="text"
# ### Precision-Recall and F Measures
# + [markdown] id="Yod6p_i2Yv3c" colab_type="text"
# * Intuitively, precision is the ability of the classifier not to label as positive a sample that is negative
#
# * Recall is the ability of the classifier to find all the positive samples.
#
# + [markdown] id="TyIQMzNiY85R" colab_type="text"
# - The F-measure can be interpreted as a weighted harmonic mean of the mean precision and recall.
#
# - A $ F_\beta $ measure reaches its best value at 1 and its worst score at 0.
#
# - In $ F_1 $ both recall and precision are equally important.
#
# - The `precision_recall_curve` computes a precision recall curve from the ground truth label and the classifier given by varying a decision threshold.
#
# - The `average_precision_score` function computes the average precision (AP) from prediction scores.
#
# - The value is between 0 to 1 and higher the better.
#
# - Note that the `precision_recall_curve` function is restricted to the binary case. The `average_precision_score` function works only in binary classification and multilabel indicator format.
# + [markdown] id="o79qXzf8dEqi" colab_type="text"
# ### My Interpretation and Relation with Confusion Matrix
# + [markdown] id="ZFCMGSfjsNuf" colab_type="text"
# * Some interpretation: -
#
# **In Multiclass Classification**
#
# - Precision: - Whenever I said prediction was $y$, was it actually $y$ ?
#
# * Precision = Was it actually $y$ / whenever I said it was $y$.)
#
# - Recall : - Whenever the class label was $ y $ ; did I tell it was $ y $ ?
#
# - Recall = Correctly Did I tell it was $ y $ / Whenever the class label was $ y $
# + [markdown] id="_s46Spcgt-6s" colab_type="text"
# * f1-score is Harmonic mean of precision and recall.
# * Accuracy is overall accuracy of classification problem.
# * We can relate these terms to terms realted with confusion matrix (tp, fp, tn, fn)
# + [markdown] id="0C1gqEVqdYlD" colab_type="text"
# **Binary Classification**
# - In a binary classification task, the terms ‘’positive’’ and ‘’negative’’ refer to the classifier’s prediction, and the terms ‘’true’’ and ‘’false’’ refer to whether that prediction corresponds to the external judgment (sometimes known as the ‘’observation’‘).
# - Given these definitions, we can formulate the following table:
#
#
#
# ```
# Actual class (observation)
# Predicted class (expectation) tp (true positive) Correct result fp (false positive) Unexpected result
# fn (false negative) Missing result tn (true negative) Correct absence result
# ```
#
#
# + [markdown] id="InNfUu90eBGb" colab_type="text"
# - In this context, we can define the notions of precision, recall and F-measure:
#
# - $ \text{precision} = \frac{tp}{tp + fp} $
#
# - $ \text{recall} = \frac{tp}{tp + fn} $
#
# - $ F_\beta = (1 + \beta ^ 2) \frac{\text{precison} * \text {recall}} {\beta ^ 2 * \text {precision} + \text {recall} } $
# + [markdown] id="Yne0QgxYi-L-" colab_type="text"
# ### Example Code
# + id="Nq5eZcrdr7AU" colab_type="code" colab={}
from sklearn import metrics
import numpy as np
# + id="5i3Zck2Tezgi" colab_type="code" colab={}
y_true = [1,0,1,0]
y_pred = [0,1,1,1]
# + id="QFZwAcpoe58k" colab_type="code" outputId="825797cb-9f79-45b9-c2dc-358370b295f0" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(metrics.precision_score(y_true,y_pred))
# Interpret this as when I said the output 1 was the ground truth 1 ?
# Note that in binary classification we have only 1 prediction. It's interpretation is different from multi-class
# + id="nMnomwNQfGgm" colab_type="code" outputId="b1e0033d-2af6-4d60-8ab9-f8da10da9fc6" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(metrics.recall_score(y_true,y_pred))
# Interpret this as whenever the ground truth was 1; did I answer it as 1 ?
# Again in binary classification we have only 1 preiction. It's interpretation is different from multi-class
# + id="EG4x93MRgLfG" colab_type="code" outputId="055b9089-82fd-41d6-f4c8-24420b478a61" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(metrics.f1_score(y_true, y_pred))
# + id="DhyfYWH-iqLp" colab_type="code" outputId="9f007f30-ba04-4d32-fd3b-2a3dda44638d" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(metrics.fbeta_score(y_true, y_pred, beta = 0.5))
# + id="aNZutYrsiwY1" colab_type="code" outputId="2e21772a-a9a8-428b-aa24-54ffb760a079" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(metrics.fbeta_score(y_true, y_pred, beta = 2))
# + [markdown] id="3FP8wcnckOpG" colab_type="text"
# ### Some more analysis of Precision, Recall and F-score on Multi-Class and Multi-label Classification
# + [markdown] id="enKn12gmkWoX" colab_type="text"
# 
# + [markdown] id="TLgIlFxbkq7j" colab_type="text"
# * You can find $ P(y,\hat{y}) $ and $ R(y, \hat{y}) $ using my interpretation.
# * The ramaining division terms are used for some kind of weighted average / Normalization metric
# + id="1AUFib4hkVnv" colab_type="code" colab={}
from sklearn import metrics
# + id="Wt4XvOGvmexH" colab_type="code" colab={}
y_true = [0,1,2,0,1,2]
y_pred = [0,2,1,0,0,1]
# + id="pLKp8ICjq_38" colab_type="code" outputId="f42c658d-95b7-42c0-c768-04f2b2cc2eaf" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(metrics.precision_score(y_true, y_pred, average = 'micro'))
# + id="vnnOkONBrLxp" colab_type="code" outputId="4a95fb25-cf9d-41df-9087-adb47ab00724" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(metrics.recall_score(y_true, y_pred, average = 'micro'))
# + id="-EgpepMurrj1" colab_type="code" outputId="0cd80d80-2b51-42c2-9dc7-93b8bdaf3a4d" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(metrics.f1_score(y_true, y_pred, average = 'weighted'))
# + id="DRqs0MNysMgX" colab_type="code" outputId="69d8fdb1-aa01-48cc-eed5-f6ca8800b66d" colab={"base_uri": "https://localhost:8080/", "height": 36}
# You can include some labels when required.
print(metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro'))
# + id="w_fEcc8RsiUU" colab_type="code" colab={}
# Similarly, labels not present in the data sample may be accounted for in macro-averaging.
print(metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro'))
# + id="ZPrwSJoqspU9" colab_type="code" colab={}
# + [markdown] id="BndDAwXnHN9S" colab_type="text"
# ### Mathews Correlation Coefficient (MCC)
# + [markdown] id="rbQXUMIFHcQZ" colab_type="text"
# - The Matthews correlation coefficient is used in machine learning as a measure of the quality of binary (two-class) classifications, introduced by biochemist Brian W. Matthews in 1975.
# - It takes into account true and false positives and negatives and is generally regarded as a balanced measure which can be used even if the classes are of very different sizes.
# - The MCC is in essence a correlation coefficient between the observed and predicted binary classifications; it returns a value between −1 and +1.
# - A coefficient of +1 represents a perfect prediction, 0 no better than random prediction and −1 indicates total disagreement between prediction and observation.
# - The statistic is also known as the phi coefficient. MCC is related to the chi-square statistic for a 2×2 contingency table.
# + [markdown] id="EB0k0KAlIAs-" colab_type="text"
# $ MCC = \frac{tp \times tn - fp \times fn}{\sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}. $
# + [markdown] id="71qZJZseIRH6" colab_type="text"
# - While there is no perfect way of describing the confusion matrix of true and false positives and negatives by a single number, the Matthews correlation coefficient is generally regarded as being one of the best such measures.
# + [markdown] id="TpwXwenGIWV7" colab_type="text"
# - In the multiclass case, the Matthews correlation coefficient can be defined in terms of a confusion_matrix $C$ for $K$ classes. To simplify the definition consider the following intermediate variables:
# + [markdown] id="7-KCVue7J9tn" colab_type="text"
# - **Mutli-Class-Mathews-Correlation**
#
# - $t_k=\sum_{i}^{K} C_{ik}$ the number of times class $k$ truly occurred,
# - $p_k=\sum_{i}^{K} C_{ki}$ the number of times class $k$ was predicted,
# - $c=\sum_{k}^{K} C_{kk}$ the total number of samples correctly predicted,
# - $s=\sum_{i}^{K} \sum_{j}^{K} C_{ij}$ the total number of samples.
# + [markdown] id="iMOf-sDXI2eM" colab_type="text"
# - Then the multiclass MCC is defined as:
#
# $ MCC = \frac{
# c \times s - \sum_{k}^{K} p_k \times t_k
# }{\sqrt{
# (s^2 - \sum_{k}^{K} p_k^2) \times
# (s^2 - \sum_{k}^{K} t_k^2)
# }}$
#
# - When there are more than two labels, the value of the MCC will no longer range between -1 and +1.
#
#
# - Instead the minimum value will be somewhere between -1 and 0 depending on the number and distribution of ground true labels. The maximum value is always +1.
# + id="OPRTYr5FHRRk" colab_type="code" colab={}
from sklearn.metrics import matthews_corrcoef
# + id="7xDZkjPKJuiE" colab_type="code" outputId="e19c8bad-6844-43c8-f46f-c638ca62263a" colab={"base_uri": "https://localhost:8080/", "height": 36}
y_true = [1,1,1,-1]
y_pred = [1,-1,1,1]
print(matthews_corrcoef(y_true, y_pred))
# + [markdown] id="9gwCEgZrK6QF" colab_type="text"
# ### Multi-label confusion Matrix
# + id="xSBJziRrJ2vO" colab_type="code" colab={}
# + [markdown] id="VheH5YTRLHRn" colab_type="text"
# ### Receiver Operating Charecteristic (ROC)
# + [markdown] id="Rg8hJJymYDGH" colab_type="text"
# #### Theory
# + [markdown] id="Rq_ZBUDgW1Ti" colab_type="text"
# * The function roc_curve computes the receiver operating characteristic curve, or ROC curve.
#
# - A receiver operating characteristic (ROC), or simply ROC curve, is a graphical plot which illustrates the performance of a binary classifier system as its discrimination threshold is varied.
#
# - It is created by plotting the fraction of true positives out of the positives (TPR = true positive rate) vs. the fraction of false positives out of the negatives (FPR = false positive rate), at various threshold settings.
#
# - TPR is also known as sensitivity, and FPR is one minus the specificity or true negative rate.
#
# - ROC analysis provides tools to select possibly optimal models and to discard suboptimal ones independently from (and prior to specifying) the cost context or the class distribution.
#
# - ROC analysis is related in a direct and natural way to cost/benefit analysis of diagnostic decision making.
# + [markdown] id="YWOiNUovXe7A" colab_type="text"
# https://en.wikipedia.org/wiki/Receiver_operating_characteristic
# + [markdown] id="ojUja7lmYIxL" colab_type="text"
# ##### Inferences Made from ROC
# + [markdown] id="ME0EItrEYMdE" colab_type="text"
# - ROC Curve is used to compare differnet ML Models.
#
# - A random classifier is a straight line at an angle of 45 degrees from X-axis.
#
# - Any classifier to be considered as good must have a better curve than random.
#
# - All classifiers must start from origin.
#
# - Better classifier will have higher True positive rate.
#
# - Better classifier will also have a low false positive rate.
#
# - The models may overlap and hence there can be a trade-off in choosing whether we should go for optimzing TPR or FPR.
#
# - This depends on situation and needs to be handled.
#
# - Better classifier will have shape like $ \Gamma $
# + [markdown] id="3ujPN6m3YGMG" colab_type="text"
# #### Code
# + [markdown] id="4wSDh1PVX_WA" colab_type="text"
# - This function requires the true binary value and the target scores, which can either be probability estimates of the positive class, confidence values, or binary decisions.
#
# - Here is a small example of how to use the roc_curve function:
# + id="aCicd9dnLsVk" colab_type="code" colab={}
import numpy as np
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
# + id="fapU-a7rZ7dI" colab_type="code" colab={}
y = np.array([0,0,1,1])
scores = np.array([0.1, 0.4, 0.35, 0.8])
# + id="Q_PRFN1ZaIVE" colab_type="code" colab={}
fpr, tpr, thresholds = roc_curve(y,scores, pos_label = 1)
# + id="CNozM1tQaoaA" colab_type="code" outputId="20fe126e-82b5-4819-c36e-8165bcd5992b" colab={"base_uri": "https://localhost:8080/", "height": 73}
print(fpr)
print(tpr)
print(thresholds)
# + id="ZoE0qohLbR6C" colab_type="code" colab={}
x = []
y = []
for i in range(10,21,1):
x.append((i-10) / 10 )
y.append((i-10) / 10 )
# + id="EwCnxBG2araQ" colab_type="code" outputId="8820eb7f-054d-4b39-b14e-837bfdb5552a" colab={"base_uri": "https://localhost:8080/", "height": 295}
plt.plot(fpr, tpr, c = 'r')
plt.plot(x,y,c = 'b')
plt.title("Reciever Operating Characteristics example")
plt.xlabel("False positive rate")
plt.ylabel("True positive rate")
plt.show()
# + [markdown] id="z7Mn5BgIcf7-" colab_type="text"
# - The roc_auc_score function computes the area under the receiver operating characteristic (ROC) curve, which is also denoted by AUC or AUROC.
# - By computing the area under the roc curve, the curve information is summarized in one number.
# + id="-Fmkj80fa84Q" colab_type="code" colab={}
import numpy as np
from sklearn.metrics import roc_auc_score
# + id="mi_fuzftcrWY" colab_type="code" colab={}
y_true = np.array([0,0,1,1])
y_score = np.array([0.1,0.4,0.35,0.8])
# + id="tiOlEqgrc6OT" colab_type="code" outputId="a5357fa1-f5ca-4181-8ad1-de35961b9216" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(roc_auc_score(y_true, y_score))
# + [markdown] id="ea6IH2AWdR3J" colab_type="text"
# - **Note: -**
# - In multi-label classification, the roc_auc_score function is extended by averaging over the labels as above.
#
# - Compared to metrics such as the subset accuracy, the Hamming loss, or the F1 score, ROC doesn’t require optimizing a threshold for each label.
#
# - The roc_auc_score function can also be used in multi-class classification, if the predicted outputs have been binarized.
#
# - In applications where a high false positive rate is not tolerable the parameter max_fpr of roc_auc_score can be used to summarize the ROC curve up to the given limit.
# + [markdown] id="RGs7fpVcdmIG" colab_type="text"
# ## Multi-label Classification Metrics
# + [markdown] id="-R4KNxCzMp4M" colab_type="text"
# * In multilabel learning, each sample can have any number of ground truth labels associated with it. The goal is to give high scores and better rank to the ground truth labels.
# + id="3N8go24tc-Yl" colab_type="code" colab={}
# + [markdown] id="ynL9KtfA1jZp" colab_type="text"
# ## Regression Metrics
# + [markdown] id="m_UkM6_V1wU9" colab_type="text"
# * The sklearn.metrics module implements several loss, score, and utility functions to measure regression performance. Some of those have been enhanced to handle the multioutput case: `mean_squared_error, mean_absolute_error, ` `explained_variance_score` and `r2_score `.
#
# * These functions have an multioutput keyword argument which specifies the way the scores or losses for each individual target should be averaged.
#
# * The default is 'uniform_average', which specifies a uniformly weighted mean over outputs. If an ndarray of shape (n_outputs,) is passed, then its entries are interpreted as weights and an according weighted average is returned.
#
# * If multioutput is 'raw_values' is specified, then all unaltered individual scores or losses will be returned in an array of shape (n_outputs,).
#
# * The r2_score and explained_variance_score accept an additional value 'variance_weighted' for the multioutput parameter.
#
# * This option leads to a weighting of each individual score by the variance of the corresponding target variable.
#
# * This setting quantifies the globally captured unscaled variance.
#
# * If the target variables are of different scale, then this score puts more importance on well explaining the higher variance variables.
#
# * multioutput='variance_weighted' is the default value for r2_score for backward compatibility. This will be changed to uniform_average in the future.
# + [markdown] id="9_qXUOjj3E02" colab_type="text"
# ### Explained Variance Score
# + [markdown] id="WwhQfo2W3ILs" colab_type="text"
# - The explained_variance_score computes the explained variance regression score.
#
# If $ \hat {y} $ is the estimated target output, $y$ the corresponding (correct) target output, and $Var $ is Variance, the square of the standard deviation, then the explained variance is estimated as follow:
#
# $ explained\_{}variance(y, \hat{y}) = 1 - \frac{Var\{ y - \hat{y}\}}{Var\{y\}} $
#
# - The best possible score is 1.0, lower values are worse.
#
# - In statistics, explained variation measures the proportion to which a mathematical model accounts for the variation (dispersion) of a given data set. Often, variation is quantified as variance; then, the more specific term explained variance can be used.
# + id="niZdyk1G1mah" colab_type="code" colab={}
from sklearn.metrics import explained_variance_score
# + id="AkxkyZJw3pIo" colab_type="code" colab={}
y_true = [3, -0.5, 2, 5]
y_pred = [2.5, 3, 1 , 4]
# + id="AKsIRBlh3xCn" colab_type="code" outputId="88d4200f-fea3-4d90-af9d-e6c91c0651b0" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(explained_variance_score(y_true, y_pred))
# + id="dkOAsk2930W0" colab_type="code" outputId="cdc4fe57-1531-45b7-e9d2-d686a5d73a9d" colab={"base_uri": "https://localhost:8080/", "height": 54}
y_true = [[0.5, 1], [-1, 1], [7, -6]]
y_pred = [[0, 2], [-1, 2], [8, -5]]
print(explained_variance_score(y_true, y_pred))
print(explained_variance_score(y_true, y_pred, multioutput='raw_values'))
# + [markdown] id="IccHr_-A4k57" colab_type="text"
# ### Max Error
# + [markdown] id="vcSKUBvP4sga" colab_type="text"
# - The max_error function computes the maximum residual error , a metric that captures the worst case error between the predicted value and the true value.
#
# - In a perfectly fitted single output regression model, max_error would be 0 on the training set and though this would be highly unlikely in the real world, this metric shows the extent of error that the model had when it was fitted.
#
# - If $\hat{y_i}$ is the predicted value of the $i$-th sample, and $y_i$ is the corresponding true value, then the max error is defined as
#
# $\text{Max Error}(y, \hat{y}) = max(| y_i - \hat{y}_i |)$
# + [markdown] id="q5DM7tO05cdX" colab_type="text"
# - The `max_error` does not support multioutput.
# + id="kMf31VLa4nnM" colab_type="code" colab={}
from sklearn.metrics import max_error
# + id="XeVfK8nR5HoZ" colab_type="code" colab={}
y_true = [3,2,7,1]
y_pred = [4,5,1,1]
# + id="mLSHIsv25Vj5" colab_type="code" outputId="cb07ecca-41f3-4e7b-e23f-a39399699c4a" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(max_error(y_true, y_pred))
# + [markdown] id="nVNMIfR75gFW" colab_type="text"
# ### Mean Absolute error
# + [markdown] id="viCWDrx851Y_" colab_type="text"
# - The mean_absolute_error function computes mean absolute error, a risk metric corresponding to the expected value of the absolute error loss or $l1$ -norm loss.
#
# - If $\hat{y_i}$ is the predicted value of the $i$-th sample, and $y_i$ is the corresponding true value, then the mean absolute error (MAE) estimated over $n_{samples}$is defined as:
#
# $\text{MAE}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \left| y_i - \hat{y}_i \right|.$
# + id="Su8fbEAQ5Xl_" colab_type="code" colab={}
from sklearn.metrics import mean_absolute_error
# + id="Zk2MlQ-36Qf4" colab_type="code" colab={}
y_true = [1,2,3,4,5]
y_pred = [3,2,1,2,5]
# + id="rLcvyq0j6UDS" colab_type="code" outputId="e10c503f-8094-4186-a26c-2462e1aae9e2" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(mean_absolute_error(y_true, y_pred))
# + id="cNCi7h4P6W_0" colab_type="code" outputId="0b5a8030-74ff-4ccc-f65b-52e629f93033" colab={"base_uri": "https://localhost:8080/", "height": 36}
y_true = [[0.5, 1], [-1, 1], [7, -6]]
y_pred = [[0, 2], [-1, 2], [8, -5]]
print(mean_absolute_error(y_true, y_pred))
# + [markdown] id="2mar2NBE8lYw" colab_type="text"
# ### Mean Squared Error
# + [markdown] id="uZ8eT-wO8neM" colab_type="text"
# - The mean_squared_error function computes mean squared error, a risk metric corresponding to the expected value of the squared error loss or $l2$ -norm loss.
#
# - If $\hat{y_i}$ is the predicted value of the $i$-th sample, and $y_i$ is the corresponding true value, then the mean squared error (MSE) estimated over $n_{samples}$is defined as:
#
# $\text{MSE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (y_i - \hat{y}_i)^2.$
# + id="OaKidcsG6k8X" colab_type="code" colab={}
from sklearn.metrics import mean_squared_error
# + id="vmm6ZgPo86_7" colab_type="code" outputId="abfebe53-d460-4ae0-a444-2271d878126c" colab={"base_uri": "https://localhost:8080/", "height": 36}
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mean_squared_error(y_true, y_pred)
y_true = [[0.5, 1], [-1, 1], [7, -6]]
y_pred = [[0, 2], [-1, 2], [8, -5]]
mean_squared_error(y_true, y_pred)
# + [markdown] id="alYTCYMq9JOC" colab_type="text"
# ### Mean Squared Logarithmic Error
# + [markdown] id="hrGGnSrQ9NGZ" colab_type="text"
# The mean_squared_log_error function computes a risk metric corresponding to the expected value of the squared logarithmic (quadratic) error or loss.
#
# If $\hat{y_i}$ is the predicted value of the -$i$th sample, and $y_i$ is the corresponding true value, then the mean squared logarithmic error (MSLE) estimated over $n_{samples} $
#
# is defined as
# $\text{MSLE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (\log_e (1 + y_i) - \log_e (1 + \hat{y}_i) )^2. $
#
# Where $log_e(x)$
# means the natural logarithm of $x$.
#
# - This metric is best to use when targets having exponential growth, such as population counts, average sales of a commodity over a span of years etc. Note that this metric penalizes an under-predicted estimate greater than an over-predicted estimate.
# + id="lpte3pVo87SD" colab_type="code" colab={}
from sklearn.metrics import mean_squared_log_error
# + id="4kEGEFwuDYHt" colab_type="code" outputId="65186cbf-e850-425a-bd7f-04b766ad5be4" colab={"base_uri": "https://localhost:8080/", "height": 54}
y_true = [3, 5, 2.5, 7]
y_pred = [2.5, 5, 4, 8]
print(mean_squared_log_error(y_true, y_pred) )
y_true = [[0.5, 1], [1, 2], [7, 6]]
y_pred = [[0.5, 2], [1, 2.5], [8, 8]]
print(mean_squared_log_error(y_true, y_pred) )
# + [markdown] id="GFyr9VKR-Ilo" colab_type="text"
# ### Median Absolute error
# + [markdown] id="PYcf8RFE-LzL" colab_type="text"
# - The median_absolute_error is particularly interesting because it is robust to outliers.
# - The loss is calculated by taking the median of all absolute differences between the target and the prediction.
#
# - If $y_i$ is the predicted value of the $i$-th sample and $y$ is the corresponding true value, then the median absolute error (MedAE) estimated over
# is defined as
#
# $\text{MedAE}(y, \hat{y}) = \text{median}(\mid y_1 - \hat{y}_1 \mid, \ldots, \mid y_n - \hat{y}_n \mid).$
#
# The median_absolute_error does not support multioutput.
# + id="JAZwjZWW-K-c" colab_type="code" colab={}
from sklearn.metrics import median_absolute_error
# + id="-0rqSIgi-d7l" colab_type="code" colab={}
y_true = [3,-0.5,2,7]
y_pred = [2.5,3,1,5]
# + id="4S9HEVMC-oCX" colab_type="code" outputId="ed5537d6-bd47-4ed2-d046-fe24ac008979" colab={"base_uri": "https://localhost:8080/", "height": 36}
print(median_absolute_error(y_true, y_pred))
# + [markdown] id="ml4_W-48Dm3f" colab_type="text"
# ### R2 score, the coefficient of Determination
# + [markdown] id="v_c-WqwLD-Gv" colab_type="text"
# - The r2_score function computes the coefficient of determination, usually denoted as R².
#
# - It represents the proportion of variance (of y) that has been explained by the independent variables in the model.
#
# - It provides an indication of goodness of fit and therefore a measure of how well unseen samples are likely to be predicted by the model, through the proportion of explained variance.
#
# - As such variance is dataset dependent, R² may not be meaningfully comparable across different datasets.
#
# - Best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse).
#
# - A constant model that always predicts the expected value of y, disregarding the input features, would get a R² score of 0.0.
#
# - If $ \hat {y} $ is the predicted value of the $i$ -th sample and $y_i$ is the corresponding true value for total samples, the estimated R² is defined as:
# + [markdown] id="7A-P6VrXEP0y" colab_type="text"
# $R^2(y, \hat{y}) = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2} $
# + [markdown] id="sZE8OZOgEani" colab_type="text"
# $\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i$
# + id="z_y1b_gG-sKq" colab_type="code" colab={}
from sklearn.metrics import r2_score
# + id="ISdW3bX9ElBO" colab_type="code" outputId="b98d6f29-ef8a-4ea8-8f3e-811cdbeba54d" colab={"base_uri": "https://localhost:8080/", "height": 36}
y_true = [1,2,3,4,5]
y_pred = [1,2,3,4,5]
print(r2_score(y_true, y_pred))
# + id="7_EzFN5YEtLs" colab_type="code" outputId="e282561f-cf03-41d6-e278-6ba93f1bf19f" colab={"base_uri": "https://localhost:8080/", "height": 36}
y_true = [1,3,4,2,4,5]
y_pred = [0.9,0.2,-2,3,1,0]
print(r2_score(y_true, y_pred))
# + id="lcuUcWmFE06H" colab_type="code" outputId="22439f84-62c8-4ad4-b24f-0efb18a847c2" colab={"base_uri": "https://localhost:8080/", "height": 36}
y_true = [1,2,3,4,5]
y_pred = [3,3,3,3,3]
print(r2_score(y_true, y_pred))
# + [markdown] id="8-ct7U4iFIZ8" colab_type="text"
# ## Clustering Performance Valuation
# + [markdown] id="FRvvh19_FLms" colab_type="text"
# - We will discuss then when we discuss on clustering
# + [markdown] id="i2pnEuFoFOup" colab_type="text"
# ## Dummy Estimators and Performance Valuation
# + [markdown] id="6kcUns8rFwKN" colab_type="text"
# * How do I know whether my Model is good or bad ?
# * We cannot always guarantee that it has 50 % + accuracy, hence it is good.
# * We may have imbalanced classes, in which checking for 50% accuracy may not be appropriate.
# * We need to perform better than random models a.k.a. dummy models.
# * Beating the accuracy of dummy model by a significant margin can help us to understand if the model is good or bad.
# * Sklearn provides two models for this dummyclassifier and dummyregressor.
# + [markdown] id="FrsuuJCDGWgt" colab_type="text"
# - DummyClassifier implements several such simple strategies for classification:
#
# - stratified generates random predictions by respecting the training set class distribution.
# - most_frequent always predicts the most frequent label in the training set.
#
# - prior always predicts the class that maximizes the class prior (like most_frequent) and predict_proba returns the class prior.
#
# - uniform generates predictions uniformly at random.
#
# - constant always predicts a constant label that is provided by the user.
#
# - A major motivation of this method is F1-scoring, when the positive class is in the minority.
#
# - Note that with all these strategies, the predict method completely ignores the input data!
#
# - More generally, when the accuracy of a classifier is too close to random, it probably means that something went wrong: features are not helpful, a hyperparameter is not correctly tuned, the classifier is suffering from class imbalance, etc…
#
# - DummyRegressor also implements four simple rules of thumb for regression:
#
# - mean always predicts the mean of the training targets.
# - median always predicts the median of the training targets.
# - quantile always predicts a user provided quantile of the training targets.
# - constant always predicts a constant value that is provided by the user.
#
# In all these strategies, the predict method completely ignores the input data.
#
# To illustrate DummyClassifier, first let’s create an imbalanced dataset:
# + id="uVWJyaxCE_d6" colab_type="code" colab={}
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
iris = load_iris()
X, y = iris.data, iris.target
y[y != 1] = -1
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# + id="y1UEk6RyGmRd" colab_type="code" colab={}
from sklearn.dummy import DummyClassifier
from sklearn.svm import SVC
# + id="8VcRGOVzG_kL" colab_type="code" colab={}
clf = SVC(kernel = 'linear', C = 1.0, random_state=31)
dum = DummyClassifier(strategy='most_frequent', random_state=0)
dum2 = DummyClassifier(strategy = 'stratified', random_state = 0)
# + id="lL6SLiaUHYI1" colab_type="code" colab={}
clf = clf.fit(X_train, y_train)
dum = dum.fit(X_train, y_train)
dum2 = dum2.fit(X_train, y_train)
# + id="vNbbkDhMHeyk" colab_type="code" outputId="85929453-bd8f-4878-c95a-f4285d073f94" colab={"base_uri": "https://localhost:8080/", "height": 73}
print(clf.score(X_test, y_test))
print(dum.score(X_test, y_test))
print(dum2.score(X_test, y_test))
# + [markdown] id="zpIpSTrXH9R8" colab_type="text"
# * Pretty bad model
#
# + id="v16Otk27IMBl" colab_type="code" outputId="80584f1f-e4a7-49c5-c6a0-42d41d767634" colab={"base_uri": "https://localhost:8080/", "height": 36}
clf = SVC(gamma='scale', kernel='rbf', C=1).fit(X_train, y_train)
clf.score(X_test, y_test)
| 209.747783 | 164,602 |
e7c0943acf5dda9e336126d8431236c72138cdfd
|
py
|
python
|
huggingface_t5_6_3.ipynb
|
skywalker00001/Conterfactual-Reasoning-Project
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/skywalker00001/Conterfactual-Reasoning-Project/blob/main/huggingface_t5_6_3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Z2G7crDz4L8f"
# Version 6.0
#
# ground truth using "denosing"
#
# find out the different pairs and only output those different things
# + [markdown] id="rCTEkdBKntFE"
# # 1. Preparation
# + id="p6esmL2vmo0D" colab={"base_uri": "https://localhost:8080/"} outputId="65aa70e0-87ff-46f8-8b97-ac7365eb7c16"
from google.colab import drive
drive.mount('/content/drive')
root = 'drive/MyDrive/LM/'
# + id="X_UlorGdnHLt" colab={"base_uri": "https://localhost:8080/"} outputId="e857b642-4aaf-4b05-811a-bfa49c7a09d4"
# !pip install sentencepiece
# !pip install transformers -q
# !pip install wandb -q
# + id="lmAP7b3pnLSL" colab={"base_uri": "https://localhost:8080/"} outputId="53e90b9c-1dec-45bd-ef4a-e0b5d8931f19"
# Importing stock libraries
import numpy as np
import pandas as pd
import time
from tqdm import tqdm
import os
import regex as re
import sys
sys.path.append('/content/drive/MyDrive/LM/')
from global_param import MyConfig
import nltk
nltk.download("punkt")
from nltk.tokenize.treebank import TreebankWordDetokenizer
detokenizer = TreebankWordDetokenizer()
import torch
from torch import cuda
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader, RandomSampler, SequentialSampler
# Importing the T5 modules from huggingface/transformers
from transformers import T5Tokenizer, T5ForConditionalGeneration
# WandB – Import the wandb library
import wandb
# + id="uAWMdyDonWV2" colab={"base_uri": "https://localhost:8080/"} outputId="bddbe799-2d47-4f5d-ce95-fdeb20638550"
# Login to wandb to log the model run and all the parameters
# 7229adacb32965027d73056a6927efd0365a00bc
# !wandb login
# + id="2d9ku8imls0I"
myconfig = MyConfig()
# + id="xM9n_9U3nO4A" colab={"base_uri": "https://localhost:8080/"} outputId="ee78c75b-7a95-49cf-d21c-24ec0ea7acb8"
# Checking out the GPU we have access to. This is output is from the google colab version.
# !nvidia-smi
# + id="TWzXE0OAnQ_5" colab={"base_uri": "https://localhost:8080/"} outputId="41220786-c61a-4bb2-d416-d90f4d007eb1"
# # Setting up the device for GPU usage
device = 'cuda' if cuda.is_available() else 'cpu'
print("Device is: ", device)
# Set random seeds and deterministic pytorch for reproducibility
#SEED = 42
SEED = myconfig.SEED
torch.manual_seed(SEED) # pytorch random seed
np.random.seed(SEED) # numpy random seed
torch.backends.cudnn.deterministic = True
# + id="AzFrt4dtF0dU" colab={"base_uri": "https://localhost:8080/", "height": 85} outputId="4a5770ae-059d-4f6b-9b76-efa0faa40210"
# Global Parameter
model_version = "6.3"
load_version = "6.2"
initial_epoch = 0
# WandB – Initialize a new run
wandb.init(project="counterfactual"+model_version)
# WandB – Config is a variable that holds and saves hyperparameters and inputs
# Defining some key variables that will be used later on in the training
# config = wandb.config # Initialize config
# config.TRAIN_BATCH_SIZE = 16 # input batch size for training (default: 64)
# config.VALID_BATCH_SIZE = 32 # input batch size for testing (default: 1000)
# config.TRAIN_EPOCHS = 51 # number of epochs to train (default: 10)
# config.VAL_EPOCHS = 1
# config.LEARNING_RATE = 1e-4 # learning rate (default: 0.01)
# config.SEED = 42 # random seed (default: 42)
# config.SOURCE_LEN = 150
# config.TARGET_LEN = 110
# WandB – Config is a variable that holds and saves hyperparameters and inputs
# Defining some key variables that will be used later on in the training
config = wandb.config # Initialize config
config.TRAIN_BATCH_SIZE = 16 # input batch size for training (default: 64)
config.VALID_BATCH_SIZE = 32 # input batch size for testing (default: 1000)
#config.TRAIN_EPOCHS = myconfig.TRAIN_EPOCHS # number of epochs to train (default: 10)
config.TRAIN_EPOCHS = 41
config.VAL_EPOCHS = myconfig.VAL_EPOCHS
config.LEARNING_RATE = myconfig.LEARNING_RATE # learning rate (default: 0.01)
config.SEED = myconfig.SEED # random seed (default: 42)
config.SOURCE_LEN = 150
config.TARGET_LEN = 70
config.LOAD_PATH = root+'models/model'+load_version+'.tar'
config.SAVE_PATH = root+'models/model'+model_version+'.tar'
# + id="j8dgmI7zq0g1" colab={"base_uri": "https://localhost:8080/", "height": 113, "referenced_widgets": ["cb63d8f05187400db53c08e3e041da2c", "5d50f5d2b6904baaaaf6ed73cfb017d8", "7c084cdfe34b4c46bc297211aee99776", "e32ea4cf384644b785f0c834fab75303", "e147c82d482646ed87b7264526dc365e", "a88282258bcd4104a7fdfe3643e1eb64", "421fa7393ad24d0b837e9c460d249380", "7c15dc9f32b44a07adc6982459fa5906", "c254b51ec4124377827717b988978125", "3c442403ee434409956abe159293c3e1", "b111a4ad9fb34f86a2fc55cb2fa4e5af", "2d6b8ffcae9e4870947ed0062006a765", "626351c51b214f37b2655a5729e02baa", "1ae2ef67f8ce4ebd86dbc05c52fbf65e", "a59916c021c943e1b95b7e172dce0f84", "af66f772ffc2404e989849661ae7fbe6", "06afa02a45454ce09b3ecd754f74a06b", "708f79fa12234117a871dbf1e1820513", "dfef4126c497444da882c34126772d7c", "f76622adefd347529e3704378f600a62", "15980bcac77e4143a717a06364bf9cbf", "8842eb15da1d404e8c1edf7846167221", "a197071566894189b7e6d1a4161304d5", "8dc197293e664b6f8a62ee518735d8c2", "a1b2f22044544a518d0110f167ff94a0", "ce075e0e923e4b55ad0e12e69408e865", "1494e7d6a71f4fc39668eb7db5659d0d", "f697d745cb7147ad950c30a3edc0905e", "7c614694cda24e8da243f9ae1403e656", "32d95374f5264626977c8901340f265f", "b0d4922621514d8895e28fe9c2747b19", "ed77065a66f149118bdf97229985c815", "47294903b3b140f68309ede4b8a08eb7"]} outputId="a1b1cc15-2571-470d-efb2-50aa7c125768"
PRETRAINED_MODEL_NAME = myconfig.PRETRAINED_MODEL_NAME
# tokenzier for encoding the text
t5_tokenizer = T5Tokenizer.from_pretrained(PRETRAINED_MODEL_NAME)
# Defining the model. We are using t5-base model and added a Language model layer on top for generation of Summary.
# Further this model is sent to device (GPU/TPU) for using the hardware.
model = T5ForConditionalGeneration.from_pretrained(PRETRAINED_MODEL_NAME)
model = model.to(device)
# + id="Zw6FQ04JJV9h"
# Defining the optimizer that will be used to tune the weights of the network in the training session.
optimizer = torch.optim.Adam(params = model.parameters(), lr=config.LEARNING_RATE)
# + [markdown] id="4Mif3CnjnxYU"
# # 2. Load dataframe
# + id="zxasBdcGnvCf"
#training df
small_path = root + '/TimeTravel/cleaned_small_2.0.xlsx'
small_df = pd.read_excel(small_path)
#small_df.head()
print(len(small_df))
# + id="PZtoL2YfoO9e"
small_df.head(3)
# + id="vAUXyCytp6ZD"
#valid df
large_path = root + '/TimeTravel/cleaned_large_2.0.xlsx'
large_df = pd.read_excel(large_path)
#large_df.head()
print(len(large_df))
# + id="H5G4F6JZrq9Q"
small_ids = []
for i in range(len(small_df)):
small_ids.append(small_df.loc[i, 'story_id'])
print(len(small_ids))
# + id="3cnqSduyrWx4"
large_df = large_df[~large_df.story_id.isin(small_ids)]
large_df = large_df.reset_index(drop=True) # must reset index after delete rows
print(len(large_df))
# + id="5hWewdbDG9oc"
# select data not in training set
part_large_cleaned_df = large_df[0:100]
#part_large_cleaned_df = large_cleaned_df[0:1000]
part_large_cleaned_df = part_large_cleaned_df.reset_index(drop=True)
print(len(part_large_cleaned_df))
# + id="Coh28LFm0jWk"
# + [markdown] id="dcFsA1QQnpel"
# # 3. Dataset and Dataloader
# + id="09xuAFkDnf9j"
# Creating a custom dataset for reading the dataframe and loading it into the dataloader to pass it to the neural network at a later stage for finetuning the model and to prepare it for predictions
class CustomDataset(Dataset):
def __init__(self, dataframe, tokenizer, input_len, output_len):
self.tokenizer = tokenizer
self.data = dataframe
self.input_len = input_len
self.output_len = output_len
self.input = self.data.input1
self.output = self.data.output1
def __len__(self):
return len(self.data)
def __getitem__(self, index):
input = str(self.input[index])
# input = ' '.join(input.split())
output = str(self.output[index])
# output = ' '.join(output.split())
source = self.tokenizer.encode_plus(input, max_length= self.input_len, padding='max_length', return_tensors='pt')
target = self.tokenizer.encode_plus(output, max_length= self.output_len, padding='max_length', return_tensors='pt')
source_ids = source['input_ids'].squeeze()
source_mask = source['attention_mask'].squeeze()
target_ids = target['input_ids'].squeeze()
target_mask = target['attention_mask'].squeeze()
return {
'source_ids': source_ids.to(dtype=torch.long),
'source_mask': source_mask.to(dtype=torch.long),
'target_ids': target_ids.to(dtype=torch.long),
'target_ids_y': target_ids.to(dtype=torch.long)
}
# + id="ybW0gTCtse_G"
train_df = small_df
valid_df = part_large_cleaned_df
trainingset = CustomDataset(dataframe=train_df, tokenizer=t5_tokenizer, input_len=config.SOURCE_LEN , output_len=config.TARGET_LEN )
validset = CustomDataset(dataframe=valid_df, tokenizer=t5_tokenizer, input_len=config.SOURCE_LEN , output_len=config.TARGET_LEN )
# + id="OGtgLgcg2Bes"
# max_sou_len = 0
# max_tar_len = 0
# for i in range(len(small_df)):
# input = small_df.loc[i, 'input1']
# output = small_df.loc[i, 'output1']
# source = t5_tokenizer.encode_plus(input, return_tensors='pt')['input_ids'].squeeze()
# target = t5_tokenizer.encode_plus(output, return_tensors='pt')['input_ids'].squeeze()
# max_sou_len = max(max_sou_len, len(source))
# max_tar_len = max(max_tar_len, len(target))
# print(max_sou_len)
# print(max_tar_len)
# + id="LC0W6k7z3SGh"
# max_sou_len = 0
# max_tar_len = 0
# for i in range(len(large_df)):
# input = large_df.loc[i, 'input1']
# output = large_df.loc[i, 'output1']
# source = t5_tokenizer.encode_plus(input, return_tensors='pt')['input_ids'].squeeze()
# target = t5_tokenizer.encode_plus(output, return_tensors='pt')['input_ids'].squeeze()
# max_sou_len = max(max_sou_len, len(source))
# max_tar_len = max(max_tar_len, len(target))
# print(max_sou_len)
# print(max_tar_len)
# + id="SeeGPPuitkTH"
# pick up a data sample
sample_idx = 4
sample = trainingset[sample_idx]
source_ids = sample["source_ids"]
source_mask = sample["source_mask"]
target_ids = sample["target_ids"]
target_ids_y = sample["target_ids_y"]
print(source_ids)
# + id="ej_c-RkEtkb7"
print(train_df.loc[sample_idx, 'output1'])
sen = t5_tokenizer.decode(target_ids, skip_special_tokens=False) # skip_special_tokens=True will be completely same.
print(sen)
sen = t5_tokenizer.decode(source_ids, skip_special_tokens=False) # skip_special_tokens=True will be completely same.
print(sen)
# + id="fY1CfrsuwgaQ"
# DataLoader
train_params = {
'batch_size': config.TRAIN_BATCH_SIZE,
'shuffle': True,
'num_workers': 2
}
val_params = {
'batch_size': config.VALID_BATCH_SIZE,
'shuffle': False,
'num_workers': 2
}
training_loader = DataLoader(trainingset, **train_params)
val_loader = DataLoader(validset, **val_params)
print(len(training_loader))
print(len(val_loader))
# + [markdown] id="sT0T9bEQxUE2"
# # 4. Define train() and val()
# + id="hqzjlHq3os1R"
def save_model(epoch, model, optimizer, loss, PATH):
torch.save({
'epoch': epoch,
'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'loss': loss
}, PATH)
# + id="_2W6n0YDovfS"
def load_model(PATH):
checkpoint = torch.load(PATH)
model.load_state_dict(checkpoint['model_state_dict'])
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
epoch = checkpoint['epoch']
loss = checkpoint['loss']
return model, optimizer, epoch, loss
# + id="yA6SQwTYxWaJ"
# Creating the training function. This will be called in the main function. It is run depending on the epoch value.
# The model is put into train mode and then we wnumerate over the training loader and passed to the defined network
def train(epoch, tokenizer, model, device, loader, optimizer):
model.train()
for i,data in enumerate(loader):
#len(loader)=10xx
ids = data['source_ids'].to(device, dtype = torch.long)
mask = data['source_mask'].to(device, dtype = torch.long)
y = data['target_ids'].to(device, dtype = torch.long)
# padded ids (pad=0) are set to -100, which means ignore for loss calculation
y[y[: ,:] == tokenizer.pad_token_id ] = -100
label_ids = y.to(device)
outputs = model(input_ids = ids, attention_mask = mask, labels=label_ids)
loss = outputs[0]
#logit = outputs[1]
if i%50 == 0:
wandb.log({"Training Loss": loss.item()})
if i%600==0:
print(f'Epoch: {epoch}, Loss: {loss.item()}')
optimizer.zero_grad()
loss.backward()
optimizer.step()
# xm.optimizer_step(optimizer)
# xm.mark_step()
if (epoch % 5 == 0):
save_model(epoch, model, optimizer, loss.item(), config.SAVE_PATH)
# + id="kVLrtY7P6KHH"
def validate(tokenizer, model, device, loader):
model.eval()
predictions = []
actuals = []
raws = []
final_loss = 0
with torch.no_grad():
for i, data in enumerate(loader):
y = data['target_ids'].to(device, dtype = torch.long)
ids = data['source_ids'].to(device, dtype = torch.long)
mask = data['source_mask'].to(device, dtype = torch.long)
'''
generated_ids = model.generate(
input_ids = ids,
attention_mask = mask,
num_beams=2,
max_length=config.TARGET_LEN,
repetition_penalty=2.5,
length_penalty=1.0,
early_stopping=True
)
'''
generated_ids = model.generate(
input_ids = ids,
attention_mask = mask,
num_beams=2,
max_length=config.TARGET_LEN,
repetition_penalty=2.5,
length_penalty=1.0,
early_stopping=True
)
loss = model(input_ids=ids, attention_mask=mask, labels=y).loss
final_loss += loss
raw = [tokenizer.decode(i, skip_special_tokens=False) for i in ids]
preds = [tokenizer.decode(i, skip_special_tokens=False) for i in generated_ids]
target = [tokenizer.decode(i, skip_special_tokens=False)for i in y]
if i%3==0:
print(f'valid Completed {(i+1)* config.VALID_BATCH_SIZE}')
raws.extend(raw)
predictions.extend(preds)
actuals.extend(target)
return raws, predictions, actuals, final_loss
# + [markdown] id="0WpWFy1wFrAM"
# # 5. main()
# + id="rGfmTknmFt4w"
import time
# Helper function to print time between epochs
def epoch_time(start_time, end_time):
elapsed_time = end_time - start_time
elapsed_mins = int(elapsed_time / 60)
elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
return elapsed_mins, elapsed_secs
# + id="vobsacCppo0g"
# if need, load model
loss = 0
if (load_version != None and load_version != ""):
model, optimizer, initial_epoch, loss = load_model(config.LOAD_PATH)
print(loss)
# + id="fhOCd_QgIHMu"
# Log metrics with wandb
#wandb.watch(model, log="all")
# Training loop
print('Initiating Fine-Tuning for the model on counterfactual dataset:')
for epoch in range(initial_epoch, initial_epoch+config.TRAIN_EPOCHS):
#for epoch in tqdm(range(config.TRAIN_EPOCHS)):
start_time = time.time()
train(epoch, t5_tokenizer, model, device, training_loader, optimizer)
end_time = time.time()
epoch_mins, epoch_secs = epoch_time(start_time, end_time)
print(f'Epoch: {epoch:02} | Epoch Time: {epoch_mins}m {epoch_secs}s')
# Mark the run as finished
wandb.finish()
# + id="zylwN_UzqDzr"
# Load model
# model = T5ForConditionalGeneration.from_pretrained(PRETRAINED_MODEL_NAME)
# model = model.to(device)
# optimizer = torch.optim.Adam(params = model.parameters(), lr=config.LEARNING_RATE)
# model, optimizer, epoch, loss = load_model(config.LOAD_PATH)
# + id="xOox9cG9qmOv"
# + [markdown] id="poozHoB5HwgE"
# # 6. Inference
# + id="ZCqxgDd2ZNcu"
# # load model
# model, optimizer, initial_epoch, loss = load_model(config.LOAD_PATH)
# print(loss)
# + id="dP6Yf2qcKVed"
# Validation loop and saving the resulting file with predictions and acutals in a dataframe.
# Saving the dataframe as predictions.csv
print('Now inferecing:')
start_time = time.time()
raws, predictions, actuals,final_loss = validate(t5_tokenizer, model, device, val_loader)
end_time = time.time()
epoch_mins, epoch_secs = epoch_time(start_time, end_time)
print(f'Time: {epoch_mins}m {epoch_secs}s')
final_df = pd.DataFrame({'input_text': raws, 'ground_truth': actuals, 'generated_text': predictions})
#final_df.to_csv(root + 'results/' + 'output' + model_version + '.csv')
final_df.to_excel(root + 'results/' + 'output' + model_version + '.xlsx')
print('Output Files generated for review')
print(f'Final Loss is: {final_loss:.5f}')
# + id="f4_2T5_uZuj4"
print(len(actuals))
# + id="LJwDlZNfy4Bd"
# + id="6H-7UpFRy4JP"
# + id="fdH3KS3Ky4Lq"
# + [markdown] id="me4BBbvNqRlH"
# # 7. check the samples with same original ending and edited ending
# + colab={"base_uri": "https://localhost:8080/"} id="HgyO4dK7qRET" outputId="9df7429c-cec1-46a0-99a2-d4d048e466a8"
# import pandas as pd
# import regex as re
result_df = pd.read_excel(root + 'results/' + 'output_beam1' + model_version + '.xlsx')
result_df.head()
print(len(result_df))
# + colab={"base_uri": "https://localhost:8080/"} id="HRANrmBrqRG1" outputId="8a1e9c35-981c-4d8b-c04d-5e62733b75aa"
or_pat = re.compile(r'(original_ending: )(.*)$')
ed_pat = re.compile(r'(edited_ending: )(.*)$')
pipei = re.search(ed_pat, result_df.iloc[0].generated_text)
# pipei = re.search(or_pat, result_df.iloc[0].raw_text)
print(pipei.group(2))
# + colab={"base_uri": "https://localhost:8080/"} id="4jrrpDgtqovK" outputId="89214eff-cb33-4a6d-ba79-6568d573bdab"
re_pat = re.compile(r'(original_ending: )(.*)$') # regular expression, pick the text after "original_ending: "
#orig = = re.search(re_pat, te).group(2)
or_text = [] # or for original_ending
ed_text = [] # ed for edited_ending
for i in range(len(result_df)):
or_text.append(re.search(or_pat, result_df.loc[i, "raw_text"]).group(2))
ed_text.append(re.search(ed_pat, result_df.loc[i, "generated_text"]).group(2))
print(len(or_text))
print(len(ed_text))
# + colab={"base_uri": "https://localhost:8080/"} id="hrihgGDpqoxS" outputId="fedc522b-dbc3-4bd3-84d7-ee8f9b13bde7"
comparison = [i==j for i, j in zip(or_text, ed_text)]
print(comparison)
# + colab={"base_uri": "https://localhost:8080/"} id="B5Abkp3Tqozb" outputId="42a4e4d8-1913-4975-f0f8-94eef2ca94a8"
count = pd.value_counts(comparison)
print(count)
# + colab={"base_uri": "https://localhost:8080/", "height": 363} id="2hOjgOnmqo2A" outputId="77a47242-2f68-45c8-b5d8-21538566fdb2"
result_df[comparison].head(10)
# + id="mBciXb5NoGnw"
same_df = result_df[comparison]
same_df.reset_index(drop=True)
# + id="mByWebeToK1y"
same_df.to_excel(root + 'results/' + 'output_same_b1' + model_version + '.xlsx')
# + [markdown] id="TfIiYXrWpc6y"
# ## pick some samples to test
#
# + colab={"base_uri": "https://localhost:8080/"} id="EAhN7qE8pfKC" outputId="348f1898-5392-4c58-c0a0-2aae2ea41fb2"
model.eval()
with torch.no_grad():
text = 'premise: I am supposed to take food to a party tomorrow. initial: I had bought all the ingredients for it last week. counterfactual: I need to buy all the ingredients for it after work today. original_ending: I spent all day yesterday cooking the food. Unfortunately, I burnt the food. I won\'t be able to get new ingredients in time for tomorrow\'s party.'
input_ids = tokenizer(text, return_tensors="pt").input_ids.to(device)
outputs = model.generate(input_ids, max_length=config.TARGET_LEN, num_beams=2)
print(tokenizer.decode(outputs[0], skip_special_tokens=True))
# + [markdown] id="EuQm4yApHjVN"
# # 8. Evalutation
#
# + [markdown] id="FDMvjMMlHkxf"
# ## 7.1 Blue score
# + id="Astekps9H1Ly"
# predicitions: y', actuals: y
from torchtext.data.metrics import bleu_score
# + id="tDCCxTFfIPlI"
pre_corpus = [i.split(" ") for i in predictions]
act_corpus = [i.split(" ") for i in actuals]
# + colab={"base_uri": "https://localhost:8080/"} id="zqbqZWTgJD7X" outputId="894be47e-938c-4b5e-ae87-a3b69eb54cdd"
print(act_corpus)
# + colab={"base_uri": "https://localhost:8080/"} id="1DhJ3fa8JW0f" outputId="3e4351cd-645c-4f0b-f61f-d55c1333646f"
print(pre_corpus)
# + colab={"base_uri": "https://localhost:8080/"} id="8j22fhB2IhEL" outputId="dec11353-f9dc-4385-dccf-ff498876d822"
#bs = bleu_score([pre_corpus[0]], [act_corpus[0]], max_n=1, weights=[1])
#bs = bleu_score([pre_corpus[0]], [act_corpus[0]], max_n=2, weights=[0.5, 0.5])
bs_1 = bleu_score(pre_corpus, act_corpus, max_n=1, weights=[1])
#bs_2 = bleu_score(pre_corpus, act_corpus, max_n=2, weights=[0.1, 0.9])
#print(f'bs_1: {bs_1:.5f}, bs_2: {bs_2:.5f}')
print(f'bleus_1: {bs_1:.5f}')
# + [markdown] id="YstNLi3ZM2lZ"
# ## 7.2 ROUGE
# + colab={"base_uri": "https://localhost:8080/"} id="B4b9qlloNA5k" outputId="37bab074-34db-4857-e978-8d56078669e3"
# !pip install rouge
# + id="H4EBXtwQN-I2"
from rouge import Rouge
def compute_rouge(predictions, targets):
predictions = [" ".join(prediction).lower() for prediction in predictions]
predictions = [prediction if prediction else "EMPTY" for prediction in predictions]
targets = [" ".join(target).lower() for target in targets]
targets = [target if target else "EMPTY" for target in targets]
rouge = Rouge()
scores = rouge.get_scores(hyps=predictions, refs=targets, avg=True)
return scores['rouge-1']['f']
# + colab={"base_uri": "https://localhost:8080/"} id="hDdqDzz6NLj3" outputId="b64fa391-4d13-459b-9eea-710ab4ff6693"
rouge_1 = compute_rouge(predictions, actuals)
print(f'rouge_1: {rouge_1:.5f}')
# + [markdown] id="GeLrqbZyRdev"
# ## 7.3 T5 loss (cross entropy), discussed before
# + id="wMYbMr72cOnO"
# + colab={"base_uri": "https://localhost:8080/"} id="yoy9LpjfYc_w" outputId="5ed4bc2a-e10b-4744-c76f-d4402c859619"
print(final_loss / len(part_large_cleaned_df))
# + id="7RDNzL34RVGv"
# source = tokenizer.encode_plus(predictions, max_length= config.SOURCE_LEN, padding='max_length', return_tensors='pt')
# target = tokenizer.encode_plus(actuals, max_length= config.TARGET_LEN, padding='max_length', return_tensors='pt')
# source_ids = source['input_ids'].squeeze()
# target_ids = target['input_ids'].squeeze()
# + colab={"base_uri": "https://localhost:8080/", "height": 110} id="VeLeSAH7SP0A" outputId="f19e67ef-b316-445c-e9b2-9626feb1ad65"
# encode the sources OOM
'''
source_encoding = tokenizer(
predictions, max_length= config.SOURCE_LEN, padding='max_length', return_tensors='pt'
)
original, attention_mask = source_encoding.input_ids, source_encoding.attention_mask
# encode the targets
target_encoding = tokenizer(
actuals, max_length= config.TARGET_LEN, padding='max_length', return_tensors='pt'
)
ending = target_encoding.input_ids
ending[ending == tokenizer.pad_token_id] = -100
original, attention_mask, ending = original.to(device), attention_mask.to(device), ending.to(device)
# forward pass
loss = model(input_ids=original, attention_mask=attention_mask, labels=ending).loss
'''
# + colab={"base_uri": "https://localhost:8080/"} id="ELA22NVTNd4X" outputId="cc1f8992-afd1-4ea4-e31d-7c6d08f958d9"
print(a)
# + colab={"base_uri": "https://localhost:8080/"} id="S8hcQexSOIph" outputId="e2c3aea6-810e-4678-c97f-2a7b37510330"
print(a.splitlines())
# + id="L5LD82L0OP76"
diff = d.compare(a.splitlines(), b.splitlines())
# + colab={"base_uri": "https://localhost:8080/"} id="-VCUekNONegc" outputId="31947c40-855d-4a86-dced-5d39366e3be8"
a = "I paid the cashier and patiently waited for my drink."
b = "I paid the cashier and patiently waited at the counter for my drink."
from difflib import Differ
d = Differ()
diff = d.compare(a.splitlines(), b.splitlines())
print('\n'.join(list(diff)))
# + colab={"base_uri": "https://localhost:8080/"} id="Ad3IGMT4Q0cn" outputId="ceb40b56-d7c3-4321-8cf0-7a839cd690bb"
import difflib
a = "I paid the cashier and patiently waited for my drink."
b = "I paid the cashier and patiently waited at the counter for my drink."
s = difflib.SequenceMatcher(None, a, b)
for block in s.get_matching_blocks():
print(block)
# + colab={"base_uri": "https://localhost:8080/"} id="cR05sfk6Q_LV" outputId="c0a402f6-528e-4862-ef0e-ec64b95df625"
import difflib
a = "I paid the cashier and patiently waited acoorinding to for my drink."
b = "I paid the cashier and patiently waited at the counter for my drink."
s = difflib.SequenceMatcher(None, a, b)
matches = []
for block in s.get_matching_blocks():
#matches.append([block[0], block[1], block[2]])
matches.append([i for i in block])
#matches.append(block)
print(matches)
# explanation: matches[i, 0] are the a index, matches[i, 1] are the b index, matches[i, 2] are the lengths of same (matched) words.
# + colab={"base_uri": "https://localhost:8080/"} id="vaTxg_PDgiL-" outputId="35531e27-1bd5-45f4-971a-fdbe9a3db98c"
changes = []
for i in range(len(matches) - 1):
print(matches[i])
if ((a[i,0]+ a[i,2] < a[i+1,0]) && (b[i,0]+ b[i,2] < b[i+1,0])): # replacing
changes.append(f"{a[i,0]+a[i,1]}-{a[i,2]}: {}")
# + id="OZgydMAgTqMe"
print(a)
# + colab={"base_uri": "https://localhost:8080/"} id="pHQh6IUkSJnC" outputId="b8ef5c8b-cf5b-420b-cf11-914863fbc4f6"
print(len(a))
# + colab={"base_uri": "https://localhost:8080/"} id="5TE154wZVydL" outputId="6580835a-5f31-4e31-b975-0573e08bb73e"
a1 = tokenizer(a)
print(a1)
| 36.657183 | 1,342 |
2e050f1fad5ce1a551185131ffbb111ac259edb2
|
py
|
python
|
tutorials/nlp/Zero_Shot_Intent_Recognition.ipynb
|
sudhakarsingh27/NeMo
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:zeroshot_dev_2]
# language: python
# name: conda-env-zeroshot_dev_2-py
# ---
# + colab={} colab_type="code" id="o_0K1lsW1dj9"
"""
You can run either this notebook locally (if you have all the dependencies and a GPU) or on Google Colab.
Instructions for setting up Colab are as follows:
1. Open a new Python 3 notebook.
2. Import this notebook from GitHub (File -> Upload Notebook -> "GITHUB" tab -> copy/paste GitHub URL)
3. Connect to an instance with a GPU (Runtime -> Change runtime type -> select "GPU" for hardware accelerator)
4. Run this cell to set up dependencies.
"""
# If you're using Google Colab and not running locally, run this cell
# install NeMo
BRANCH = 'main'
# !python -m pip install git+https://github.com/NVIDIA/NeMo.git@$BRANCH#egg=nemo_toolkit[nlp]
# + colab={} colab_type="code" id="JFWG-jYCfvD7" pycharm={"name": "#%%\n"}
# If you're not using Colab, you might need to upgrade jupyter notebook to avoid the following error:
# 'ImportError: IProgress not found. Please update jupyter and ipywidgets.'
# ! pip install ipywidgets
# ! jupyter nbextension enable --py widgetsnbextension
# Please restart the kernel after running this cell
# + colab={} colab_type="code" id="dzqD2WDFOIN-"
import json
import os
from nemo.collections import nlp as nemo_nlp
from nemo.utils.exp_manager import exp_manager
from nemo.utils import logging
from omegaconf import OmegaConf
import pandas as pd
import pytorch_lightning as pl
import torch
import wget
# + [markdown] colab_type="text" id="daYw_Xll2ZR9"
# # Task description
#
# Intent recognition is the task of classifying the intent of an utterance or document. For example, for the query: `What is the weather in Santa Clara tomorrow morning?`, we would like to classify the intent as `weather`. This is a fundamental step that is executed in any task-driven conversational assistant.
#
# Typical text classification models, such as the Joint Intent and Slot Classification Model in NeMo, are trained on hundreds or thousands of labeled documents. In this tutorial we demonstrate a different, "zero shot" approach that requires no annotated data for the target intents. The zero shot approach uses a model trained on the task of natural language inference (NLI). During training, the model is presented with pairs of sentences consisting of a "premise" and a "hypothesis", and must classify the relationship between them as entailment (meaning the hypothesis follows logically from the premise), contradiction, or neutral. To use this model for intent prediction, we define a list of candidate labels to represent each of the possible classes in our classification system; for example, the candidate labels might be `request for directions`, `query about weather`, `request to play music`, etc. We predict the intent of a query by pairing it with each of the candidate labels as a premise-hypothesis pair and using the model to predict the probability of an entailment relationship between them. For example, for the query and candidate labels above, we would run inference for the following pairs:
#
# (`What is the weather in Santa Clara tomorrow morning?`, `request for directions`)
# (`What is the weather in Santa Clara tomorrow morning?`, `request to play music`)
# (`What is the weather in Santa Clara tomorrow morning?`, `query about weather`)
#
# In the above example, we would expect a high probability of entailment for the last pair, and low probabilities for the first two pairs. Thus, we would classify the intent of the utterance as `query about weather`. The task can be formulated as single-label classification (only one of the candidate labels can be correct for each query) or multi-label classification (multiple labels can be correct) by setting the parameter multi_label = False or multi_label = True, respectively, during inference.
#
# In this tutorial, we demonstrate how to train an NLI model on the MNLI data set and how to use it for zero shot intent recognition.
# -
# # Using an out-of-the-box model
# +
# this line will download a pre-trained NLI model from NVIDIA's NGC cloud and instantiate it for you
pretrained_model = nemo_nlp.models.ZeroShotIntentModel.from_pretrained("zeroshotintent_en_bert_base_uncased")
# +
queries = [
"What is the weather in Santa Clara tomorrow morning?",
"I'd like a veggie burger and fries",
"Bring me some ice cream when it's sunny"
]
candidate_labels = ['Food order', 'Weather query', "Play music"]
predictions = pretrained_model.predict(queries, candidate_labels, batch_size=4, multi_label=True)
print('The prediction results of some sample queries with the trained model:')
for query in predictions:
print(json.dumps(query, indent=4))
# -
# In the example above, we set `multi_label=True`, which is also the default setting. This runs a softmax calculation independently for each label over the entailment and contradiction logits. For any given query, the scores for the different labels may add up to more than one.
#
# Below, we see what happens if we set `multi_label=False`. In this case, the softmax calculation for each query uses the entailment class logits for all the labels, so the final scores for all classes add up to one.
# +
predictions = pretrained_model.predict(queries, candidate_labels, batch_size=4, multi_label=False)
print('The prediction results of some sample queries with the trained model:')
for query in predictions:
print(json.dumps(query, indent=4))
# -
# Under the hood, during inference the candidate labels are not used as is; they're actually used to fill in the blank in a hypothesis template. By default, the hypothesis template is `This example is {}`. So the candidate labels above would actually be presented to the model as `This example is food order`, `This example is weather query`, and `This example is play music`. You can change the hypothesis template with the optional keyword argument `hypothesis_template`, as shown below.
# +
predictions = pretrained_model.predict(queries, candidate_labels, batch_size=4, multi_label=False,
hypothesis_template="a person is asking something related to {}")
print('The prediction results of some sample queries with the trained model:')
for query in predictions:
print(json.dumps(query, indent=4))
# + [markdown] colab_type="text" id="ZnuziSwJ1yEB"
# Now, let's take a closer look at the model's configuration and learn to train the model.
#
#
# # Training your own model
#
#
# # Dataset
#
# In this tutorial we will train a model on [The Multi-Genre Natural Language Inference Corpus](https://cims.nyu.edu/~sbowman/multinli/multinli_0.9.pdf) (MNLI). This is a crowdsourced collection of sentence pairs with textual entailment annotations. Given a premise sentence followed by a hypothesis sentence, the task is to predict whether the premise entails the hypothesis (entailment), contradicts the hypothesis (contradiction), or neither (neutral). There are two dev sets for this task: the "matched" dev set contains examples drawn from the same genres as the training set, and the "mismatched" dev set has examples from genres not seen during training. For our purposes, either dev set alone will be sufficient. We will use the "matched" dev set here.
# -
# ## Download the dataset
# + colab={} colab_type="code" id="--wJ2891aIIE"
# you can replace DATA_DIR with your own location
DATA_DIR = '.'
# -
wget.download('https://dl.fbaipublicfiles.com/glue/data/MNLI.zip', DATA_DIR)
# ! unzip {DATA_DIR}/MNLI.zip -d {DATA_DIR}
# + colab={} colab_type="code" id="qB0oLE4R9EhJ"
# ! ls -l $DATA_DIR/MNLI
# + [markdown] colab_type="text" id="gMWuU69pbUDe"
# We will use `train.tsv` as our training set and `dev_matched.tsv` as our validation set.
# -
# ## Explore the dataset
# Let's take a look at some examples from the dev set
num_examples = 5
df = pd.read_csv(os.path.join(DATA_DIR, "MNLI", "dev_matched.tsv"), sep="\t")[:num_examples]
for sent1, sent2, label in zip(df['sentence1'].tolist(), df['sentence2'].tolist(), df['gold_label'].tolist()):
print("sentence 1: ", sent1)
print("sentence 2: ", sent2)
print("label: ", label)
print("===================")
# + [markdown] colab_type="text" id="_whKCxfTMo6Y"
# # Training model
# ## Model configuration
#
# The model is comprised of the pretrained [BERT](https://arxiv.org/pdf/1810.04805.pdf) model followed by a Sequence Classifier module.
#
# The model is defined in a config file which declares multiple important sections. They are:
# - **model**: All arguments that are related to the Model - language model, a classifier, optimizer and schedulers, datasets and any other related information
#
# - **trainer**: Any argument to be passed to PyTorch Lightning
#
# All model and training parameters are defined in the **zero_shot_intent_config.yaml** config file. This file is located in the folder **examples/nlp/zero_shot_intent_recognition/conf/**. It contains 2 main sections:
#
#
# We will download the config file from the repository for the purpose of the tutorial. If you have a version of NeMo installed locally, you can use it from the above folder.
# + colab={} colab_type="code" id="T1gA8PsJ13MJ"
# download the model config file from repository for the purpose of this example
WORK_DIR = "." # you can replace WORK_DIR with your own location
wget.download(f'https://raw.githubusercontent.com/NVIDIA/NeMo/{BRANCH}/examples/nlp/zero_shot_intent_recognition/conf/zero_shot_intent_config.yaml', WORK_DIR)
# print content of the config file
config_file = os.path.join(WORK_DIR, "zero_shot_intent_config.yaml")
config = OmegaConf.load(config_file)
print(OmegaConf.to_yaml(config))
# + [markdown] colab_type="text" id="ZCgWzNBkaQLZ"
# ## Setting up data within the config
#
# Among other things, the config file contains dictionaries called **dataset**, **train_ds** and **validation_ds**. These are configurations used to setup the Dataset and DataLoaders of the corresponding config.
#
# To start model training, we need to specify `model.dataset.data_dir`, `model.train_ds.file_name` and `model.validation_ds.file_name`, as we are going to do below.
#
# Notice that some config lines, including `model.train_ds.data_dir`, have `???` in place of paths. This means that values for these fields are required to be specified by the user.
#
# Let's now add the data paths and output directory for saving predictions to the config.
# + colab={} colab_type="code" id="LQHCJN-ZaoLp"
# you can replace OUTPUT_DIR with your own location; this is where logs and model checkpoints will be saved
OUTPUT_DIR = "nemo_output"
config.exp_manager.exp_dir = OUTPUT_DIR
config.model.dataset.data_dir = os.path.join(DATA_DIR, "MNLI")
config.model.train_ds.file_name = "train.tsv"
config.model.validation_ds.file_path = "dev_matched.tsv"
# + [markdown] colab_type="text" id="nB96-3sTc3yk"
# ## Building the PyTorch Lightning Trainer
#
# NeMo models are primarily PyTorch Lightning modules - and therefore are entirely compatible with the PyTorch Lightning ecosystem.
#
# Let's first instantiate a Trainer object
# + colab={} colab_type="code" id="1tG4FzZ4Ui60"
print("Trainer config - \n")
print(OmegaConf.to_yaml(config.trainer))
# + colab={} colab_type="code" id="knF6QeQQdMrH"
# lets modify some trainer configs
# checks if we have GPU available and uses it
accelerator = 'gpu' if torch.cuda.is_available() else 'cpu'
config.trainer.devices = 1
config.trainer.accelerator = accelerator
config.trainer.precision = 16 if torch.cuda.is_available() else 32
# for mixed precision training, uncomment the line below (precision should be set to 16 and amp_level to O1):
# config.trainer.amp_level = O1
# remove distributed training flags
config.trainer.strategy = None
# setup max number of steps to reduce training time for demonstration purposes of this tutorial
config.trainer.max_steps = 128
trainer = pl.Trainer(**config.trainer)
# + [markdown] colab_type="text" id="8IlEMdVxdr6p"
# ## Setting up a NeMo Experiment
#
# NeMo has an experiment manager that handles logging and checkpointing for us, so let's use it:
# + colab={} colab_type="code" id="8uztqGAmdrYt"
exp_dir = exp_manager(trainer, config.get("exp_manager", None))
# the exp_dir provides a path to the current experiment for easy access
exp_dir = str(exp_dir)
exp_dir
# + [markdown] colab_type="text" id="8tjLhUvL_o7_"
# Before initializing the model, we might want to modify some of the model configs. For example, we might want to modify the pretrained BERT model and use [Megatron-LM BERT](https://arxiv.org/abs/1909.08053) or [AlBERT model](https://arxiv.org/abs/1909.11942):
# + colab={} colab_type="code" id="Xeuc2i7Y_nP5"
# get the list of supported BERT-like models, for the complete list of HugginFace models, see https://huggingface.co/models
print(nemo_nlp.modules.get_pretrained_lm_models_list(include_external=True))
# specify BERT-like model, you want to use, for example, "megatron-bert-345m-uncased" or 'bert-base-uncased'
PRETRAINED_BERT_MODEL = "albert-base-v1"
# + colab={} colab_type="code" id="RK2xglXyAUOO"
# add the specified above model parameters to the config
config.model.language_model.pretrained_model_name = PRETRAINED_BERT_MODEL
# + [markdown] colab_type="text" id="fzNZNAVRjDD-"
# Now, we are ready to initialize our model. During the model initialization call, the dataset and data loaders we'll be prepared for training and evaluation.
# Also, the pretrained BERT model will be downloaded, note it can take up to a few minutes depending on the size of the chosen BERT model.
# + colab={} colab_type="code" id="NgsGLydWo-6-"
model = nemo_nlp.models.ZeroShotIntentModel(cfg=config.model, trainer=trainer)
# + [markdown] colab_type="text" id="kQ592Tx4pzyB"
# ## Monitoring training progress
# Optionally, you can create a Tensorboard visualization to monitor training progress.
# + colab={} colab_type="code" id="mTJr16_pp0aS"
try:
from google import colab
COLAB_ENV = True
except (ImportError, ModuleNotFoundError):
COLAB_ENV = False
# Load the TensorBoard notebook extension
if COLAB_ENV:
# %load_ext tensorboard
# %tensorboard --logdir {exp_dir}
else:
print("To use tensorboard, please use this notebook in a Google Colab environment.")
# + colab={} colab_type="code" id="hUvnSpyjp0Dh"
# start model training
trainer.fit(model)
# -
# ## Inference from Examples
# The next step is to see how the trained model will classify intents. To improve the predictions you may need to train the model for more than 5 epochs.
#
#
# reload the saved model
saved_model = os.path.join(exp_dir, "checkpoints/ZeroShotIntentRecognition.nemo")
eval_model = nemo_nlp.models.ZeroShotIntentModel.restore_from(saved_model)
# +
queries = [
"I'd like a veggie burger and fries",
"Turn off the lights in the living room",
]
candidate_labels = ['Food order', 'Play music', 'Request for directions', 'Change lighting', 'Calendar query']
predictions = eval_model.predict(queries, candidate_labels, batch_size=4, multi_label=True)
print('The prediction results of some sample queries with the trained model:')
for query in predictions:
print(json.dumps(query, indent=4))
print("Inference finished!")
# -
# As described above in "Using an out of the box model", you can set multi_label=False if you want the scores for each query to add up to one. You can also change the hypothesis template used when presenting candidate labels, as shown below.
# +
predictions = eval_model.predict(queries, candidate_labels, batch_size=4, multi_label=True,
hypothesis_template="related to {}")
print('The prediction results of some sample queries with the trained model:')
for query in predictions:
print(json.dumps(query, indent=4))
print("Inference finished!")
# -
# By default, when an NLI model is trained on MNLI in NeMo, the class indices for entailment and contradiction are 1 and 0, respectively. The `predict` method uses these indices by default. If your NLI model was trained with different class indices for these classes, you can pass the correct indices as keyword arguments to the `predict` method (e.g. `entailment_idx=1`, `contradiction_idx=0`).
# + [markdown] colab_type="text" id="ref1qSonGNhP"
# ## Training Script
#
# If you have NeMo installed locally, you can also train the model with [examples/nlp/zero_shot_intent_recognition/zero_shot_intent_train.py](https://github.com/carolmanderson/NeMo/blob/main/examples/nlp/zero_shot_intent_recognition/zero_shot_intent_train.py).
#
# To run training script, use:
#
# ```
# python zero_shot_intent_train.py \
# model.dataset.data_dir=PATH_TO_DATA_FOLDER
# ```
#
# By default, this script uses `examples/nlp/zero_shot_intent_recognition/conf/zero_shot_intent_config.yaml` config file, and you may update all the params inside of this config file or alternatively provide them in the command line.
#
| 49.501475 | 1,212 |
00991fd4cb10a3042166dbc0bf66f07bf9c10f72
|
py
|
python
|
projects/fMRI/load_cichy_fMRI_MEG.ipynb
|
janeite/course-content
|
['CC-BY-4.0', 'BSD-3-Clause']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/kshitijd20/course-content/blob/dataloaders_kd/projects/fMRI/load_cichy_fMRI_MEG.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="J8FuAReHVFsX"
# # Data loader
# + [markdown] id="CX1lDpbfgyD-"
# ## Summary
# Here we will load data from Cichy et al. 2014 [1]. The data consist of fMRI responses from early visual cortex (EVC) and inferior temporal (IT) cortex and MEG responses at different timepoints in the form of representational dissimilarity matrices (RDMs) to 92 images. These images belong to different categories as shown in the Figure below.
#
#
# + [markdown] id="aRhugM2Xf1_a"
# 
# + [markdown] id="8KJPoY_QsJ95"
# ## Representational Similarity Analysis (RSA)
# RSA is a method to relate signals
# from different source spaces (such as behavior, neural
# responses, DNN activations) by abstracting signals from
# separate source spaces into a common similarity space. For
# this, in each source space, condition-specific responses are
# compared to each other for dissimilarity (e.g., by calculating
# Euclidean distances between signals), and the values are
# aggregated in so-called representational dissimilarity matrices (RDMs) indexed in rows and columns by the conditions
# compared. RDMs thus summarize the representational
# geometry of the source space signals. Different from source
# space signals themselves, RDMs from different sources
# spaces are directly comparable to each other for similarity
# and thus can relate signals from different spaces
#
# The figure below illustrates how RSA can be applied to different problems by comparing RDMs of different modalities/species.
# + [markdown] id="y8KJwxw7inxQ"
# 
# + [markdown] id="o6cT8Swpa0yR"
# ## Data from Cichy et al. 2014
#
# In the cells below, we will download and visualize MEG and fMRI RDMs. Please refer Figure 1 in [1] to learn details about the image category order in RDMs
# + id="9kyn7SKaDads" cellView="form"
#@title Imports
import glob
import numpy as np
import urllib
import torch
import cv2
import argparse
import time
import random
import matplotlib.pyplot as plt
import nibabel as nib
import pickle
from tqdm import tqdm
from PIL import Image
from torchvision import transforms as trn
import scipy.io as sio
import h5py
import os
from PIL import Image
from sklearn.preprocessing import StandardScaler
from torch.autograd import Variable as V
from sklearn.decomposition import PCA, IncrementalPCA
import torch.nn as nn
import torch.utils.model_zoo as model_zoo
def loadmat(matfile):
"""Function to load .mat files.
Parameters
----------
matfile : str
path to `matfile` containing fMRI data for a given trial.
Returns
-------
dict
dictionary containing data in key 'vol' for a given trial.
"""
try:
f = h5py.File(matfile)
except (IOError, OSError):
return sio.loadmat(matfile)
else:
return {name: np.transpose(f.get(name)) for name in f.keys()}
# + id="lZrV3T6f7qdZ"
#@title Data download
# !wget -qO data.zip -c https://osf.io/7vpyh/download
# + id="8amcBA92zd0b"
# %%capture
# !unzip -o data.zip #unzip the files
# + [markdown] id="rZF8xqqkDQCC"
# ## Loading MEG RDMs
# + id="w1XJNWMDDVXm"
# Load MEG RDMs for each time point for all subjects all sessions
MEG_RDMs = loadmat("MEG_decoding_RDMs.mat")['MEG_decoding_RDMs']
print(MEG_RDMs.shape)
# + [markdown] id="z_8aPio3jwB9"
# Shape of RDM is num_subjects x num_sessions x num_timepoints x num_stimulus x num_stimulus
# + id="RXI2oMM_jr5_"
# average RDM across subjects and sessions
MEG_RDM_sub_averaged = np.mean(MEG_RDMs,axis=(0,1))
del MEG_RDMs
# + id="BDMxx4ufnx8h"
#@title visualize subject averaged MEG RDMs
timepoint = 420 #@param {type:"slider", min:-100, max:600, step:20}
# Load RDM at a given timepoint
# # +100 as the RDMs provided are from -100ms to 1000ms after the stimulus onset
RDM = np.array(MEG_RDM_sub_averaged[timepoint+100])
# Since the matrix is symmetric we set upper triangular values to NaN
RDM[np.triu_indices(RDM.shape[0], 1)] = np.nan
# plot the RDM at given timepoint
plt.imshow(RDM,\
cmap="bwr")
plt.title("MEG RDM at t = " + str(timepoint))
cbar = plt.colorbar()
plt.xlabel("Stimuli")
plt.ylabel("Stimuli")
cbar.ax.get_yaxis().labelpad = 15
cbar.ax.set_ylabel('Decoding Accuracy', rotation=270)
# + [markdown] id="Vsd0IKvVJCEu"
# ##Loading fMRI RDMs
# + id="VC4iQd73JGRf"
fMRI_file = '92_Image_Set/target_fmri.mat' # path of fMRI RDM file
fMRI_RDMs = loadmat(fMRI_file) # load the fMRI RDMs
print(fMRI_RDMs.keys())
print(fMRI_RDMs['EVC_RDMs'].shape)
# + [markdown] id="C1cu5oU7j9Tg"
# fMRI_RDMs is a dictionary with keys 'EVC_RDMs' and 'IT_RDMs' corresponding to ROIs EVC and IT respectively. The shape of each RDM is num_subjects x num_stimulus x num_stimulus
# + id="8W7f5F3qlpm-"
#@title visualize subject averaged fMRI RDMs
ROI = 'IT' #@param ["EVC", "IT"]
# Average the ROI RDM across subjects
RDM = np.array(fMRI_RDMs[ROI + '_RDMs'].mean(axis=0))
# Since the matrix is symmetric we set upper triangular values to NaN
RDM[np.triu_indices(RDM.shape[0], 1)] = np.nan
# plot the ROI RDM at given timepoint
plt.imshow(RDM,\
cmap="bwr")
plt.title(ROI + " RDM")
cbar = plt.colorbar()
plt.xlabel("Stimuli")
plt.ylabel("Stimuli")
cbar.ax.get_yaxis().labelpad = 15
cbar.ax.set_ylabel('1-Correlation', rotation=270)
# + [markdown] id="d8MLJH8cctX7"
# # Example Analyses
#
# Below we will perform two analyses:
#
# 1. MEG-fMRI comparison: To find out at which timepoint MEG representation is similar to a given ROI's representation.
# 2. MEG-Deep Neural Network (DNN) comparison: To find out at which timepoint MEG representation is similar to a given DNN layer's representation.
#
# In other words, the comparison will inform us about the sequential order of visual feature processing in the cortex.
#
# + id="vt8ai7Mmr9_Q"
#@title RDM Comparison functions
from scipy.stats import spearmanr
def RSA_spearman(rdm1,rdm2):
"""
computes and returns the spearman correlation between lower triangular
part of the input rdms. We only need to compare either lower or upper
triangular part of the matrix as RDM is symmetric
"""
# get lower triangular part of the RDM1
lt_rdm1 = get_lowertriangular(rdm1)
# get lower triangular part of the RDM1
lt_rdm2 = get_lowertriangular(rdm2)
# return Spearman's correlation between lower triangular part of rdm1 & rdm2
return spearmanr(lt_rdm1, lt_rdm2)[0]
def get_lowertriangular(rdm):
"""
returns lower triangular part of the matrix
"""
num_conditions = rdm.shape[0]
return rdm[np.tril_indices(num_conditions,-1)]
# + [markdown] id="zursdOO3rzm-"
# ##MEG-fMRI Comparison
# + id="RmhU-WgUsX-k"
#@title Correlating MEG RDMs with fMRI RDMs
num_timepoints = MEG_RDM_sub_averaged.shape[0] #get number of timepoints
# initialize a dictionary to store MEG and ROI RDM correlation at each timepoint
MEG_correlation = {}
ROIs = ['EVC','IT']
for ROI in ROIs:
MEG_correlation[ROI] = []
# for loop that goes over MEG RDMs at all time points and correlate with ROI RDMs
for t in range(num_timepoints):
MEG_RDM_t = MEG_RDM_sub_averaged[t,:,:]
for ROI in ROIs:
ROI_RDM = np.mean(fMRI_RDMs[ROI + '_RDMs'],axis=0)
MEG_correlation[ROI].append(RSA_spearman(ROI_RDM,MEG_RDM_t))
# + id="TcU2IrixsZbu"
#@title Plotting MEG-fMRI comparison
plt.rc('font', size=12)
fig, ax = plt.subplots(figsize=(10, 6))
time_range = range(-100,1201)
ax.plot(time_range, MEG_correlation['IT'], color='tab:orange', label='IT')
ax.plot(time_range, MEG_correlation['EVC'], color='tab:blue', label='EVC')
# Same as above
ax.set_xlabel('Time')
ax.set_ylabel('Spearmans Correlation')
ax.set_title('MEG-fMRI fusion')
ax.grid(True)
ax.legend(loc='upper left');
# + [markdown] id="YzIVj7RBsdas"
# ## MEG-DNN Comparison
# + [markdown] id="kHUxlD_e321P"
# ### Creating DNN (AlexNet) RDMs
# + id="HwEf4Ffm4SV9"
#@title AlexNet Definition
__all__ = ['AlexNet', 'alexnet']
model_urls = {
'alexnet': 'https://download.pytorch.org/models/alexnet-owt-4df8aa71.pth',
}
# Here we redefine AlexNet differently from torchvision code for better understanding
class AlexNet(nn.Module):
def __init__(self, num_classes=1000):
super(AlexNet, self).__init__()
self.conv1 = nn.Sequential(
nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
)
self.conv2 = nn.Sequential(
nn.Conv2d(64, 192, kernel_size=5, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
)
self.conv3 = nn.Sequential(
nn.Conv2d(192, 384, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
)
self.conv4 = nn.Sequential(
nn.Conv2d(384, 256, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
)
self.conv5 = nn.Sequential(
nn.Conv2d(256, 256, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
)
self.fc6 = nn.Sequential(
nn.Dropout(),
nn.Linear(256 * 6 * 6, 4096),
nn.ReLU(inplace=True),
)
self.fc7 =nn.Sequential(
nn.Dropout(),
nn.Linear(4096, 4096),
)
self.fc8 = nn.Sequential(
nn.ReLU(inplace=True),
nn.Linear(4096, num_classes),
)
def forward(self, x):
out1 = self.conv1(x)
out2 = self.conv2(out1)
out3 = self.conv3(out2)
out4 = self.conv4(out3)
out5 = self.conv5(out4)
out5_reshaped = out5.view(out5.size(0), 256 * 6 * 6)
out6= self.fc6(out5_reshaped)
out7= self.fc7(out6)
out8 = self.fc8(out7)
return out1, out2, out3,out4, out5, out6,out7,out8
def alexnet(pretrained=False, **kwargs):
"""AlexNet model architecture from the
`"One weird trick..." <https://arxiv.org/abs/1404.5997>`_ paper.
Args:
pretrained (bool): If True, returns a model pre-trained on ImageNet
"""
model = AlexNet(**kwargs)
if pretrained:
model.load_state_dict(model_zoo.load_url(model_urls['alexnet']))
return model
# + id="6GqrOsWn4WBx"
#@title Feature extraction code
def load_alexnet(model_checkpoints):
"""This function initializes an Alexnet and load
its weights from a pretrained model. Since we redefined model in a different
way we have to rename the weights that were in the pretrained checkpoint.
----------
model_checkpoints : str
model checkpoints location.
Returns
-------
model
pytorch model of alexnet
"""
model = alexnet()
# Load checkpoint
model_file = model_checkpoints
checkpoint = torch.load(model_file, map_location=lambda storage, loc: storage)
# Rename the checkpoint keys according to new definition
model_dict =["conv1.0.weight", "conv1.0.bias", "conv2.0.weight", "conv2.0.bias", "conv3.0.weight", "conv3.0.bias", "conv4.0.weight", "conv4.0.bias", "conv5.0.weight", "conv5.0.bias", "fc6.1.weight", "fc6.1.bias", "fc7.1.weight", "fc7.1.bias", "fc8.1.weight", "fc8.1.bias"]
state_dict={}
i=0
for k,v in checkpoint.items():
state_dict[model_dict[i]] = v
i+=1
# initialize model with pretrained weights
model.load_state_dict(state_dict)
if torch.cuda.is_available():
model.cuda()
model.eval()
return model
def get_activations_and_save(model, image_list, activations_dir):
"""This function generates Alexnet features and save them in a specified directory.
Parameters
----------
model :
pytorch model : alexnet.
image_list : list
the list contains path to all images.
activations_dir : str
save path for extracted features.
"""
resize_normalize = trn.Compose([
trn.Resize((224,224)),
trn.ToTensor(),
trn.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])])
# for all images in the list generate and save activations
for image_file in tqdm(image_list):
# open image
img = Image.open(image_file)
image_file_name = os.path.split(image_file)[-1].split(".")[0]
# apply transformations before feeding to model
input_img = V(resize_normalize(img).unsqueeze(0))
if torch.cuda.is_available():
input_img=input_img.cuda()
x = model.forward(input_img)
activations = []
for i,feat in enumerate(x):
activations.append(feat.data.cpu().numpy().ravel())
for layer in range(len(activations)):
save_path = os.path.join(activations_dir, image_file_name+"_"+"layer" + "_" + str(layer+1) + ".npy")
np.save(save_path,activations[layer])
# + id="tFpNlkrd4atV"
# get the paths to all the images in the stimulus set
image_dir = '92_Image_Set/92images'
image_list = glob.glob(image_dir + '/*.jpg')
image_list.sort()
print('Total Number of Images: ', len(image_list))
save_dir = "/content/activations_alexnet"
######### load Alexnet initialized with pretrained weights ###################
# Download pretrained Alexnet from:
# https://download.pytorch.org/models/alexnet-owt-4df8aa71.pth
# and save in the current directory
checkpoint_path = "/content/alexnet.pth"
if not os.path.exists(checkpoint_path):
url = "https://download.pytorch.org/models/alexnet-owt-4df8aa71.pth"
urllib.request.urlretrieve(url, "/content/alexnet.pth")
model = load_alexnet(checkpoint_path)
##############################################################################
######### get and save activations ################################
activations_dir = os.path.join(save_dir)
if not os.path.exists(activations_dir):
os.makedirs(activations_dir)
print("-------------Saving activations ----------------------------")
get_activations_and_save(model, image_list, activations_dir)
###################################################################
# + id="h9gqjNEw5duf"
num_layers = 8 # number of layers in the model
layers = []
for i in range(num_layers):
layers.append("layer" + "_" + str(i+1))
model_RDMs = {}
# create RDM for each layer from activations
for layer in layers:
activation_files = glob.glob(activations_dir + '/*'+layer + '.npy')
activation_files.sort()
activations = []
# Load all activations
for activation_file in activation_files:
activations.append(np.load(activation_file))
activations = np.array(activations)
# calculate Pearson's distance for all pairwise comparisons
model_RDMs[layer] = 1-np.corrcoef(activations)
# + id="pBlKti2M5hxH"
#@title visualize model RDMs
layer = 'layer_8' #@param ['layer_1','layer_2','layer_3','layer_4','layer_5','layer_6','layer_7','layer_8']
# loading layer RDM
RDM = np.array(model_RDMs[layer])
# Since the matrix is symmetric we set upper triangular values to NaN
RDM[np.triu_indices(RDM.shape[0], 1)] = np.nan
# Visualize layer RDM
plt.imshow(RDM,\
cmap="bwr")
plt.title(layer + " RDM")
cbar = plt.colorbar()
plt.xlabel("Stimuli")
plt.ylabel("Stimuli")
cbar.ax.get_yaxis().labelpad = 15
cbar.ax.set_ylabel('1-Correlation', rotation=270)
# + [markdown] id="yxszMqem_4eV"
# ### Comparing MEG RDMs with AlexNet RDMs
# + id="rUWBI3Fukj2_"
#@title Correlating MEG RDMs with DNN RDMs
num_timepoints = MEG_RDM_sub_averaged.shape[0]#get number of timepoints
# initialize a dictionary to store MEG and DNN RDM correlation at each timepoint
for layer in layers:
MEG_correlation[layer] = []
# for loop that goes over MEG RDMs at all time points and correlate with DNN RDMs
for t in range(num_timepoints):
MEG_RDM_t = MEG_RDM_sub_averaged[t,:,:]
for layer in layers:
model_RDM = model_RDMs[layer]
MEG_correlation[layer].append(RSA_spearman(model_RDM,MEG_RDM_t))
# + id="WfdvhLwnkpbf"
#@title Plotting MEG-DNN comparison
plt.rc('font', size=12)
fig, ax = plt.subplots(figsize=(10, 6))
time_range = range(-100,1201)
ax.plot(time_range, MEG_correlation['layer_1'], color='tab:orange', label='layer_1')
ax.plot(time_range, MEG_correlation['layer_7'], color='tab:blue', label='layer_7')
# Same as above
ax.set_xlabel('Time')
ax.set_ylabel('Spearmans Correlation')
ax.set_title('MEG-model comparison')
ax.grid(True)
ax.legend(loc='upper left');
# + [markdown] id="uM5mp1kwbJos"
# #References
# 1. [Resolving human object recognition in space and time. Cichy et al. Nature Neuroscience 2014](https://www.nature.com/articles/nn.3635)
# 2. [Representational similarity analysis – connecting the branches of systems neuroscience. Kriegeskorte et al. Front. Syst. Neurosci., 2008](https://www.frontiersin.org/articles/10.3389/neuro.06.004.2008/full?utm_source=FWEB&utm_medium=NBLOG&utm_campaign=ECO_10YA_top-research)
#
#
#
#
| 601.057361 | 223,365 |
a6a631b7296c21ddfbaca5c643f853cfd0639815
|
py
|
python
|
notebooks/04_model_select_and_optimize/tuning_spark_als.ipynb
|
imatiach-msft/Recommenders
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6 (recommender)
# language: python
# name: recommender
# ---
# <i>Copyright (c) Microsoft Corporation. All rights reserved.</i>
#
# <i>Licensed under the MIT License.</i>
# # Hyperparameter tuning (Spark based recommender)
# Hyperparameter tuning for Spark based recommender algorithm is important to select a model with the optimal performance. This notebook introduces good practices in performing hyperparameter tuning for building recommender models with the utility functions provided in the [Microsoft/Recommenders](https://github.com/Microsoft/Recommenders.git) repository.
#
# Three different approaches are introduced and comparatively studied.
# * Spark native/custom constructs (`ParamGridBuilder`, `TrainValidationSplit`).
# * `hyperopt` package with Tree of Parzen Estimator algorithm.
# * Brute-force random search of parameter values sampled with pre-defined space.
# ## 0 Global settings and import
# +
# set the environment path to find Recommenders
# %matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import sys
sys.path.append("../../")
import pandas as pd
import numpy as np
import time
import pyspark
from pyspark.sql import SparkSession
import pyspark.sql.functions as F
from pyspark import SparkContext, SparkConf
from pyspark.ml.recommendation import ALS
from pyspark.ml.tuning import ParamGridBuilder, TrainValidationSplit
from pyspark.ml.evaluation import Evaluator, RegressionEvaluator
from pyspark.ml.pipeline import Estimator, Model
from pyspark import keyword_only
from pyspark.ml import Transformer
from pyspark.ml.param.shared import *
from pyspark.ml.util import *
from pyspark.mllib.evaluation import RegressionMetrics, RankingMetrics
from pyspark.sql.types import ArrayType, IntegerType, StringType
from hyperopt import fmin, tpe, hp, STATUS_OK, Trials
from hyperopt.pyll.base import scope
from hyperopt.pyll.stochastic import sample
from reco_utils.common.spark_utils import start_or_get_spark
from reco_utils.evaluation.spark_evaluation import SparkRankingEvaluation, SparkRatingEvaluation
from reco_utils.dataset.movielens import load_spark_df
from reco_utils.dataset.spark_splitters import spark_random_split
print("System version: {}".format(sys.version))
print("Pandas version: {}".format(pd.__version__))
print("PySpark version: {}".format(pyspark.__version__))
# + tags=["parameters"]
NUMBER_CORES = 1
NUMBER_ITERATIONS = 25
COL_USER = "userID"
COL_ITEM = "itemID"
COL_TIMESTAMP = "timestamp"
COL_RATING = "rating"
COL_PREDICTION = "prediction"
HEADER = {
"col_user": COL_USER,
"col_item": COL_ITEM,
"col_rating": COL_RATING,
"col_prediction": COL_PREDICTION,
}
HEADER_ALS = {
"userCol": COL_USER,
"itemCol": COL_ITEM,
"ratingCol": COL_RATING
}
RANK = [10, 15, 20, 30, 40]
REG = [ 0.1, 0.01, 0.001, 0.0001, 0.00001]
# -
# ## 1 Data preparation
# A Spark session is created. Note in this case, to study the running time for different approaches, the Spark session in local mode uses only one core for running. This eliminates the impact of parallelization of parameter tuning.
spark = start_or_get_spark(url="local[{}]".format(NUMBER_CORES))
# Movielens 100k dataset is used for running the demonstration.
data = load_spark_df(spark, size='100k', header=(COL_USER, COL_ITEM, COL_RATING))
# The dataset is split into 3 subsets randomly with a given split ratio. The hyperparameter tuning is performed on the training and the validating data, and then the optimal recommender selected is evaluated on the testing dataset.
train, valid, test = spark_random_split(data, ratio=[3, 1, 1])
# ## 2 Hyper parameter tuning with Azure Machine Learning Services
# The `hyperdrive` module in the [Azure Machine Learning Services](https://azure.microsoft.com/en-us/services/machine-learning-service/) runs [hyperparameter tuning and optimizing for machine learning model selection](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-tune-hyperparameters). At the moment, the service supports running hyperparameter tuning on heterogenous computing targets such as cluster of commodity compute nodes with or without GPU devices (see detailed documentation [here](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets)). It is feasible to run parameter tuning on a cluster of VM nodes. In this case, the service containerizes individual and independent Spark session on each node of the cluster to run the parameter tuning job in parallel, instead of inside a single Spark session where the training is executed in a distributed manner.
#
# Detailed instructions of tuning hyperparameter of non-Spark workloads by using Azure Machine Learning Services can be found in [this](./hypertune_aml_wide_and_deep_quickstart.ipynb) notebook.
# ## 3 Hyper parameter tuning with Spark ML constructs
# ### 3.1 Spark native construct
# Spark ML lib implements modules such as `CrossValidator` and `TrainValidationSplit` for tuning hyperparameters (see [here](https://spark.apache.org/docs/2.2.0/ml-tuning.html)). However, by default, it does not support custom machine learning algorithms, data splitting methods, and evaluation metrics, like what are offered as utility functions in the Recommenders repository.
#
# For example, the Spark native constuct can be used for tuning a recommender against the `rmse` metric which is one of the available regression metrics in Spark.
# Firstly, a Spark ALS object needs to be created. In this case, for illustration purpose, it is an ALS model object.
# NOTE the parameters of interest, rank and regParam, are left unset,
# because their values will be assigned in the parameter grid builder.
als = ALS(
maxIter=15,
implicitPrefs=False,
alpha=0.1,
coldStartStrategy='drop',
nonnegative=False,
**HEADER_ALS
)
# Then, a parameter grid can be defined as follows. Without loss of generity, only `rank` and `regParam` are considered.
paramGrid = ParamGridBuilder() \
.addGrid(als.rank, RANK) \
.addGrid(als.regParam, REG) \
.build()
# Given the settings above, a `TrainValidationSplit` constructor can be created for fitting the best model in the given parameter range. In this case, the `RegressionEvaluator` is using `RMSE`, by default, as an evaluation metric.
#
# Since the data splitter is embedded in the `TrainValidationSplit` object, to make sure the splitting ratio is consistent across different approaches, the split ratio is set to be 0.75 and in the model training the training dataset and validating dataset are combined.
tvs = TrainValidationSplit(
estimator=als,
estimatorParamMaps=paramGrid,
# A regression evaluation method is used.
evaluator=RegressionEvaluator(labelCol='rating'),
# 75% of the data will be used for training, 25% for validation.
# NOTE here the splitting is random. The Spark splitting utilities (e.g. chrono splitter)
# are therefore not available here.
trainRatio=0.75
)
# +
time_start = time.time()
# Run TrainValidationSplit, and choose the best set of parameters.
# NOTE train and valid is union because in Spark TrainValidationSplit does splitting by itself.
model = tvs.fit(train.union(valid))
time_spark = time.time() - time_start
# -
# The model parameters in the grid and the best metrics can be then returned.
for idx, item in enumerate(model.getEstimatorParamMaps()):
print('Run {}:'.format(idx))
print('\tValidation Metric: {}'.format(model.validationMetrics[idx]))
for key, value in item.items():
print('\t{0}: {1}'.format(repr(key), value))
model.validationMetrics
# To get the best model, just do
model_best_spark = model.bestModel
# ### 3.2 Custom `Estimator`, `Transformer`, and `Evaluator` for Spark ALS
#
# One can also customize Spark modules to allow tuning hyperparameters for a desired model and evaluation metric, given that the native Spark ALS does not allow tuning hyperparameters for ranking metrics such as precision@k, recall@k, etc. This can be done by creating custom `Estimator`, `Transformer` and `Evaluator`. The benefit is that, after the customization, the tuning process can make use of `trainValidSplit` directly, which distributes the tuning in a Spark session.
# #### Customized `Estimator` and `Transformer` for top k recommender based on Spark ALS
#
# The following shows how to implement a PySpark `Estimator` and `Transfomer` for recommending top k items from ALS model. The latter generates top k recommendations from the model object. Both of the two are designed by following the protocol of Spark APIs, to make sure that they can be run with the hyperparameter tuning constructs in Spark.
# +
class ALSTopK(
ALS,
Estimator,
HasInputCol,
HasPredictionCol
):
rank = Param(Params._dummy(), "rank", "rank of the factorization",
typeConverter=TypeConverters.toInt)
numUserBlocks = Param(Params._dummy(), "numUserBlocks", "number of user blocks",
typeConverter=TypeConverters.toInt)
numItemBlocks = Param(Params._dummy(), "numItemBlocks", "number of item blocks",
typeConverter=TypeConverters.toInt)
implicitPrefs = Param(Params._dummy(), "implicitPrefs", "whether to use implicit preference",
typeConverter=TypeConverters.toBoolean)
alpha = Param(Params._dummy(), "alpha", "alpha for implicit preference",
typeConverter=TypeConverters.toFloat)
userCol = Param(Params._dummy(), "userCol", "column name for user ids. Ids must be within " +
"the integer value range.", typeConverter=TypeConverters.toString)
itemCol = Param(Params._dummy(), "itemCol", "column name for item ids. Ids must be within " +
"the integer value range.", typeConverter=TypeConverters.toString)
ratingCol = Param(Params._dummy(), "ratingCol", "column name for ratings",
typeConverter=TypeConverters.toString)
nonnegative = Param(Params._dummy(), "nonnegative",
"whether to use nonnegative constraint for least squares",
typeConverter=TypeConverters.toBoolean)
intermediateStorageLevel = Param(Params._dummy(), "intermediateStorageLevel",
"StorageLevel for intermediate datasets. Cannot be 'NONE'.",
typeConverter=TypeConverters.toString)
finalStorageLevel = Param(Params._dummy(), "finalStorageLevel",
"StorageLevel for ALS model factors.",
typeConverter=TypeConverters.toString)
coldStartStrategy = Param(Params._dummy(), "coldStartStrategy", "strategy for dealing with " +
"unknown or new users/items at prediction time. This may be useful " +
"in cross-validation or production scenarios, for handling " +
"user/item ids the model has not seen in the training data. " +
"Supported values: 'nan', 'drop'.",
typeConverter=TypeConverters.toString)
@keyword_only
def __init__(
self,
rank=10, maxIter=10, regParam=0.1, numUserBlocks=10, numItemBlocks=10,
implicitPrefs=False, alpha=1.0, userCol="user", itemCol="item", seed=None, k=10,
ratingCol="rating", nonnegative=False, checkpointInterval=10,
intermediateStorageLevel="MEMORY_AND_DISK",
finalStorageLevel="MEMORY_AND_DISK", coldStartStrategy="nan"
):
super(ALS, self).__init__()
self._java_obj = self._new_java_obj("org.apache.spark.ml.recommendation.ALS", self.uid)
self._setDefault(rank=10, maxIter=10, regParam=0.1, numUserBlocks=10, numItemBlocks=10,
implicitPrefs=False, alpha=1.0, userCol="user", itemCol="item",
ratingCol="rating", nonnegative=False, checkpointInterval=10,
intermediateStorageLevel="MEMORY_AND_DISK",
finalStorageLevel="MEMORY_AND_DISK", coldStartStrategy="nan")
kwargs = self._input_kwargs
kwargs = {x: kwargs[x] for x in kwargs if x not in {'k'}}
self.setParams(**kwargs)
# The manually added parameter is not present in ALS Java implementation.
self.k = k
def setRank(self, value):
"""
Sets the value of :py:attr:`rank`.
"""
return self._set(rank=value)
def getRank(self):
"""
Gets the value of rank or its default value.
"""
return self.getOrDefault(self.rank)
def setParams(self, rank=10, maxIter=10, regParam=0.1, numUserBlocks=10, numItemBlocks=10,
implicitPrefs=False, alpha=1.0, userCol="user", itemCol="item", seed=None,
ratingCol="rating", nonnegative=False, checkpointInterval=10,
intermediateStorageLevel="MEMORY_AND_DISK",
finalStorageLevel="MEMORY_AND_DISK", coldStartStrategy="nan"):
"""
setParams(self, rank=10, maxIter=10, regParam=0.1, numUserBlocks=10, numItemBlocks=10, \
implicitPrefs=False, alpha=1.0, userCol="user", itemCol="item", seed=None, \
ratingCol="rating", nonnegative=False, checkpointInterval=10, \
intermediateStorageLevel="MEMORY_AND_DISK", \
finalStorageLevel="MEMORY_AND_DISK", coldStartStrategy="nan")
Sets params for ALS.
"""
kwargs = self._input_kwargs
kwargs = {x: kwargs[x] for x in kwargs if x not in {'k'}}
return self._set(**kwargs)
def _fit(self, dataset):
kwargs = self._input_kwargs
# Exclude k as it is not a parameter for ALS.
kwargs = {x: kwargs[x] for x in kwargs if x not in {'k'}}
kwargs['rank'] = self.getRank()
kwargs['regParam'] = self.getOrDefault(self.regParam)
als = ALS(
**kwargs
)
als_model = als.fit(dataset)
user_col = kwargs['userCol']
item_col = kwargs['itemCol']
k = self.k
topk_model = ALSTopKModel()
topk_model.setParams(
als_model,
user_col,
item_col,
k
)
return topk_model
class ALSTopKModel(
Model,
HasInputCol,
HasPredictionCol,
HasLabelCol
):
def setParams(self, model, userCol, itemCol, k):
self.model = model
self.userCol = userCol
self.itemCol = itemCol
self.k = k
def _transform(self, dataset):
predictionCol = self.getPredictionCol()
labelCol = self.getLabelCol()
users = dataset.select(self.userCol).distinct()
topk_recommendation = self.model.recommendForUserSubset(users, self.k)
extract_value = F.udf((lambda x: [y[0] for y in x]), ArrayType(IntegerType()))
topk_recommendation = topk_recommendation.withColumn(predictionCol, extract_value(F.col("recommendations")))
dataset = (
dataset
.groupBy(self.userCol)
.agg(F.collect_list(F.col(self.itemCol)).alias(labelCol))
)
topk_recommendation_all = dataset.join(
topk_recommendation,
on=self.userCol,
how="outer"
)
return topk_recommendation_all.select(self.userCol, labelCol, predictionCol)
# -
# #### Customized precision@k evaluation metric
#
# In addition to the custom `Estimator` and `Transformer`, it may also be desired to customize an `Evaluator` to allow "beyond-rating" metrics. The codes as following illustrates a precision@k evaluator. Other types of evaluators can be developed in a similar way.
# Define a custom Evaulator. Here precision@k is used.
class PrecisionAtKEvaluator(Evaluator):
def __init__(self, predictionCol="prediction", labelCol="label", k=10):
self.predictionCol = predictionCol
self.labelCol = labelCol
self.k = k
def _evaluate(self, dataset):
"""
Returns a random number.
Implement here the true metric
"""
# Drop Nulls.
dataset = dataset.na.drop()
metrics = RankingMetrics(dataset.select(self.predictionCol, self.labelCol).rdd)
return metrics.precisionAt(self.k)
def isLargerBetter(self):
return True
# Then a new ALS top-k recommender can be created, and the Spark native construct, `TrainValidationSplit` module, can be used to find the optimal model w.r.t the precision@k metric.
# +
alstopk = ALSTopK(
userCol=COL_USER,
itemCol=COL_ITEM,
ratingCol=COL_RATING,
k=10
)
# Here for illustration purpose, a small grid is used.
paramGrid = ParamGridBuilder() \
.addGrid(alstopk.rank, [10, 20]) \
.addGrid(alstopk.regParam, [0.1, 0.01]) \
.build()
tvs = TrainValidationSplit(
estimator=alstopk,
estimatorParamMaps=paramGrid,
# A regression evaluation method is used.
evaluator=PrecisionAtKEvaluator(),
# 75% of the data will be used for training, 25% for validation.
# NOTE here the splitting is random. The Spark splitting utilities (e.g. chrono splitter)
# are therefore not available here.
trainRatio=0.75
)
# +
# Run TrainValidationSplit, and choose the best set of parameters.
# NOTE train and valid is union because in Spark TrainValidationSplit does splitting by itself.
model_precision = tvs.fit(train.union(valid))
model_precision.getEstimatorParamMaps()
# -
def best_param(model, is_larger_better=True):
if is_larger_better:
best_metric = max(model.validationMetrics)
else:
best_metric = min(model.validationMetrics)
parameters = model.getEstimatorParamMaps()[model.validationMetrics.index(best_metric)]
return list(parameters.values())
params = best_param(model_precision)
# +
model_precision.bestModel.transform(valid).limit(5).show()
for idx, item in enumerate(model_precision.getEstimatorParamMaps()):
print('Run {}:'.format(idx))
print('\tValidation Metric: {}'.format(model_precision.validationMetrics[idx]))
for key, value in item.items():
print('\t{0}: {1}'.format(repr(key), value))
# -
# ## 4 Hyperparameter tuning with `hyperopt`
# `hyperopt` is an open source Python package that is designed for tuning parameters for generic function with any pre-defined loss. More information about `hyperopt` can be found [here](https://github.com/hyperopt/hyperopt). `hyperopt` supports parallelization on MongoDB but not Spark. In our case, the tuning is performed in a sequential mode on a local computer.
#
# In `hyperopt`, an *objective* function is defined for optimizing the hyper parameters. In this case, the objective is similar to that in the Spark native construct situation, which is *to the RMSE metric for an ALS recommender*. Parameters of `rank` and `regParam` are used as hyperparameters.
#
# The objective function shown below demonstrates a RMSE loss for an ALS recommender.
# Customize an objective function
def objective(params):
time_run_start = time.time()
rank = params['rank']
reg = params['reg']
train = params['train']
valid = params['valid']
col_user = params['col_user']
col_item = params['col_item']
col_rating = params['col_rating']
col_prediction = params['col_prediction']
k = params['k']
relevancy_method = params['relevancy_method']
als = ALS(
rank=rank,
maxIter=15,
implicitPrefs=False,
alpha=0.1,
regParam=reg,
coldStartStrategy='drop',
nonnegative=False,
seed=42,
**HEADER_ALS
)
model = als.fit(train)
prediction = model.transform(valid)
rating_eval = SparkRatingEvaluation(
valid,
prediction,
**HEADER
)
rmse = rating_eval.rmse()
# Return the objective function result.
return {
'loss': rmse,
'status': STATUS_OK,
'eval_time': time.time() - time_run_start
}
# A search space is usually defined for hyperparameter exploration. Design of search space is empirical, and depends on the understanding of how distribution of parameter of interest affects the model performance measured by the loss function.
#
# In the ALS algorithm, the two hyper parameters, rank and reg, affect model performance in a way that
# * The higher the rank, the better the model performance but also the higher risk of overfitting.
# * The reg parameter prevents overfitting in certain way.
#
# Therefore, in this case, a uniform distribution and a lognormal distribution sampling spaces are used for rank and reg, respectively. A narrow search space is used for illustration purpose, that is, the range of rank is from 10 to 20, while that of reg is from $e^{-5}$ to $e^{-1}$. Together with the randomly sampled hyper parameters, other parameters use for building / evaluating the recommender, like `k`, column names, data, etc., are kept as constants.
# define a search space
space = {
'rank': hp.quniform('rank', 10, 40, 5),
'reg': hp.loguniform('reg', -5, -1),
'train': train,
'valid': valid,
'col_user': COL_USER,
'col_item': COL_ITEM,
'col_rating': COL_RATING,
'col_prediction': "prediction",
'k': 10,
'relevancy_method': "top_k"
}
# ### 4.1 Hyperparameter tuning with TPE
# `fmin` of `hyperopt` is used for running the trials for searching optimal hyper parameters. In `hyperopt`, there are different strategies for intelligently optimize hyper parameters. For example, `hyperopt` avails [Tree of Parzen Estimators (TPE) method](https://papers.nips.cc/paper/4443-algorithms-for-hyper-parameter-optimization.pdf) for searching optimal parameters.
#
# The TPE method models a surface response of $p(x|y)$ by transforming a generative process, replacing the distributions of the configuration prior with non-parametric densities, where $p$ is the probability of configuration space $x$ given the loss $y$. For different configuration space, the TPE method does different replacements. That is, uniform $\to$ truncated Gaussian mixture, log-uniform $\to$ exponentiated truncated Gaussian mixture, categorical $\to$ re-weighted categorical, etc. Using different observations ${x(1), ..., x(k)}$ in the non-parametric densities, these substitutions represent a learning algorithm that can produce a variety of densities over the configuration space $X$. By maintaining sorted lists of observed variables in $H$, the runtime of each iteration of the TPE algorithm can scale linearly in $|H|$ and linearly in the number of variables (dimensions) being optimized. In a nutshell, the algorithm recognizes the irrelevant variables in the configuration space, and thus reduces iterations in searching for the optimal ones. Details of the TPE algorithm can be found in the reference paper.
#
# The following runs the trials with the pre-defined objective function and search space. TPE is used as the optimization method. Totally there will be 10 evaluations run for searching the best parameters.
# +
time_start = time.time()
# Trials for recording each iteration of the hyperparameter searching.
trials = Trials()
best = fmin(
fn=objective,
space=space,
algo=tpe.suggest,
trials=trials,
max_evals=NUMBER_ITERATIONS
)
time_hyperopt = time.time() - time_start
# -
trials.best_trial
parameters = ['rank', 'reg']
cols = len(parameters)
f, axes = plt.subplots(nrows=1, ncols=cols, figsize=(15,5))
cmap = plt.cm.jet
for i, val in enumerate(parameters):
xs = np.array([t['misc']['vals'][val] for t in trials.trials]).ravel()
ys = [t['result']['loss'] for t in trials.trials]
xs, ys = zip(*sorted(zip(xs, ys)))
ys = np.array(ys)
axes[i].scatter(xs, ys, s=20, linewidth=0.01, alpha=0.75, c=cmap(float(i)/len(parameters)))
axes[i].set_title(val)
# It can be seen from the above plot that
# * The actual impact of rank is in line with the intuition - the smaller the value the better the result.
# * It is interesting to see that the optimal value of reg is around 0.1 to 0.15.
# Get the best model.
# +
als = ALS(
rank=best["rank"],
regParam=best["reg"],
maxIter=15,
implicitPrefs=False,
alpha=0.1,
coldStartStrategy='drop',
nonnegative=False,
seed=42,
**HEADER_ALS
)
model_best_hyperopt = als.fit(train)
# -
# Tuning prameters against other metrics can be simply done by modifying the `objective` function. The following shows an objective function of how to tune "precision@k". Since `fmin` in `hyperopt` only supports minimization while the actual objective of the loss is to maximize "precision@k", `-precision` instead of `precision` is used in the returned value of the `objective` function.
# Customize an objective function
def objective_precision(params):
time_run_start = time.time()
rank = params['rank']
reg = params['reg']
train = params['train']
valid = params['valid']
col_user = params['col_user']
col_item = params['col_item']
col_rating = params['col_rating']
col_prediction = params['col_prediction']
k = params['k']
relevancy_method = params['relevancy_method']
header = {
"userCol": col_user,
"itemCol": col_item,
"ratingCol": col_rating,
}
als = ALS(
rank=rank,
maxIter=15,
implicitPrefs=False,
alpha=0.1,
regParam=reg,
coldStartStrategy='drop',
nonnegative=False,
seed=42,
**header
)
model = als.fit(train)
users = train.select(col_user).distinct()
items = train.select(col_item).distinct()
user_item = users.crossJoin(items)
dfs_pred = model.transform(user_item)
# Remove seen items.
dfs_pred_exclude_train = dfs_pred.alias("pred").join(
train.alias("train"),
(dfs_pred[col_user] == train[col_user]) & (dfs_pred[col_item] == train[col_item]),
how='outer'
)
top_all = dfs_pred_exclude_train.filter(dfs_pred_exclude_train["train.Rating"].isNull()) \
.select('pred.' + col_user, 'pred.' + col_item, 'pred.' + "prediction")
top_all.cache().count()
rank_eval = SparkRankingEvaluation(
valid,
top_all,
k=k,
col_user=col_user,
col_item=col_item,
col_rating="rating",
col_prediction="prediction",
relevancy_method=relevancy_method
)
precision = rank_eval.precision_at_k()
# Return the objective function result.
return {
'loss': -precision,
'status': STATUS_OK,
'eval_time': time.time() - time_run_start
}
# ### 4.2 Hyperparameter tuning with `hyperopt` sampling methods
# Though `hyperopt` works well in a single node machine, its features (e.g., `Trials` module) do not support Spark environment, which makes it hard to perform the tuning tasks in a distributed/parallel manner. It is useful to use `hyperopt` for sampling parameter values from the pre-defined sampling space, and then parallelize the model training onto Spark cluster with the sampled parameter combinations.
#
# The downside of this method is that the intelligent searching algorithm (i.e., TPE) of `hyperopt` cannot be used. The approach introduced here is therefore equivalent to random search.
# Sample the parameters used for model building from the pre-defined space.
# +
time_start = time.time()
sample_params = [sample(space) for x in range(NUMBER_ITERATIONS)]
# -
# The following runs model building on the sampled parameter values with the pre-defined objective function.
# +
results_map = list(map(lambda x: objective(x), sample_params))
time_sample = time.time() - time_start
# -
results_map
# Get the best model.
loss_metrics = np.array([x['loss'] for x in results_map])
best_loss = np.where(loss_metrics == min(loss_metrics))
best_param = sample_params[best_loss[0].item()]
# +
als = ALS(
rank=best_param["rank"],
regParam=best_param["reg"],
maxIter=15,
implicitPrefs=False,
alpha=0.1,
coldStartStrategy='drop',
nonnegative=False,
seed=42,
**HEADER_ALS
)
model_best_sample = als.fit(train)
# -
# ## 5 Evaluation on testing data
# The optimal parameters can then be used for building a recommender, which is then evaluated on the testing data.
#
# The following codes generate the evaluation results by using the testing dataset with the optimal model selected against the pre-defined loss. Without loss of generity, in this case, the optimal model that performs the best w.r.t regression loss (i.e., the RMSE metric) is used. One can simply use other metrics like precision@k, as illustrated in the above sections, to evaluate the optimal model on the testing dataset.
# +
# Get prediction results with the optimal modesl from different approaches.
prediction_spark = model_best_spark.transform(test)
prediction_hyperopt = model_best_hyperopt.transform(test)
prediction_sample = model_best_sample.transform(test)
predictions = [prediction_spark, prediction_hyperopt, prediction_sample]
elapsed = [time_spark, time_hyperopt, time_sample]
approaches = ['spark', 'hyperopt', 'sample']
test_evaluations = pd.DataFrame()
for ind, approach in enumerate(approaches):
rating_eval = SparkRatingEvaluation(
test,
predictions[ind],
**HEADER
)
result = pd.DataFrame({
'Approach': approach,
'RMSE': rating_eval.rmse(),
'MAE': rating_eval.mae(),
'Explained variance': rating_eval.exp_var(),
'R squared': rating_eval.rsquared(),
'Elapsed': elapsed[ind]
}, index=[0])
test_evaluations = test_evaluations.append(result)
# -
test_evaluations
# From the results, it can be seen that, *with the same number of iterations*, Spark native construct based approach takes the least amount of time, even if there is no parallel computing. This is simply because Spark native constructs leverage the underlying Java codes for running the actual analytics with high performance efficiency. Interestingly, the run time for `hyperopt` with TPE algorithm and random search methods are almost the same. Possible reasons for this are that, the TPE algorithm searches optimal parameters intelligently but runs the tuning iterations sequentially. Also, the advantage of TPE may become obvious when there is a higher dimensionality of hyperparameters.
#
# The three approaches use the same RMSE loss. In this measure, the native Spark construct performs the best. The `hyperopt` based approach performs the second best, but the advantage is very subtle. It should be noted that these differences may be owing to many factors like characteristics of datasets, dimensionality of hyperparameter space, sampling size in the searching, etc. Note the differences in the RMSE metrics may also come from the randomness of the intermediate steps in parameter tuning process. In practice, multiple runs are required for generating statistically robust comparison results. We have tried 5 times for running the same comparison codes above. The results aligned well with each other in terms of objective metric values and elapsed time.
# # Conclusions
# In summary, there are mainly three different approaches for running hyperparameter tuning for Spark based recommendation algorithm. The three different approaches are compared as follows.
# |Approach|Distributed (on Spark)|Param sampling|Advanced hyperparam searching algo|Custom evaluation metrics|Custom data split|
# |---------|-------------|--------------|--------------------------|--------------|------------|
# |AzureML Services|Parallelizing Spark sessions on multi-node cluster or single Spark session on one VM node.)|Random, Grid, Bayesian sampling for discrete and continuous variables.|Bandit policy, Median stopping policy, and truncation selection policy.|Yes|Yes|
# |Spark native construct|Distributed in single-node standalone Spark environment or multi-node Spark cluster.|No|No|Need to re-engineer Spark modules|Need to re-engineer Spark modules.|
# |`hyperopt`|No (only support parallelization on MongoDB)|Random sampling for discrete and continuous variables.|Tree Parzen Estimator|Yes|Yes|
# # References
#
# * Azure Machine Learning Services, url: https://azure.microsoft.com/en-us/services/machine-learning-service/
# * Lisa Li, *et al*, Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization, The Journal of Machine Learning Research, Volume 18 Issue 1, pp 6765-6816, January 2017.
# * James Bergstrat *et al*, Algorithms for Hyper-Parameter Optimization, Procs 25th NIPS 2011.
# * `hyperopt`, url: http://hyperopt.github.io/hyperopt/.
# * Bergstra, J., Yamins, D., Cox, D. D. (2013) Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures. Proc. of the 30th International Conference on Machine Learning (ICML 2013).
# * Kris Wright, "Hyper parameter tuning with hyperopt", url:https://districtdatalabs.silvrback.com/parameter-tuning-with-hyperopt
| 43.249012 | 1,128 |
8fdb95b3cb1811db7d5564e778c9b80b8c89c86e
|
py
|
python
|
video_game_sales.ipynb
|
antonioravila/Analise-de-dados
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/antonioravila/Analise-Exploratoria-de-Dados/blob/main/video_game_sales.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="8SNuYJh0t8ED"
# ---
# ---
#
# # **Análise Exploratória de Dados - Video Game Sales**
#
# ---
# ---
#
# O dataset aqui analisado foi obtido por meio desse link do kaggle: https://www.kaggle.com/gregorut/videogamesales
#
# O objetivo desse notebook era realizar uma breve Análise Exploratória de Dados.
# + [markdown] id="UxdcnqXqZSh5"
# ---
#
#
# ##Carregamento das bibliotecas e dos dados
#
#
# ---
# + id="hsF793GozXHl"
# Importando as bibliotecas necessárias
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import cm
from pandas_profiling import ProfileReport
# %matplotlib inline
plt.rc('figure', figsize = (20,10))
# + id="BJjaaU-6zgwp"
# Carregando o dataset
dataframe = pd.read_csv("/content/drive/MyDrive/Colab Notebooks/datasets/CSV/vgsales.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="3-gyVjeUlOA-" outputId="a9938ffe-8268-4b24-87ec-d963d14aa058"
# Visualizando as 5 primeiras colunas no dataset
dataframe.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="mcSgp9bVYZnx" outputId="32695a83-c3bd-4e65-9956-211cd14101f9"
# Visualizando as 5 ultimas colunas no dataset
dataframe.tail()
# + id="BxRPOpGAARf-" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="8efc8c4c-eb45-422b-d9b6-fe843b83b385"
# Mudando as colunas para o português
dataframe.columns = ["Ranking", "Nome", "Plataforma", "Ano",
"Genero", "Editora", "vendas_America_do_Norte", "vendas_Europa", "vendas_Japao",
"vendas_outras", "vendas_Globais"]
dataframe.head()
# + colab={"base_uri": "https://localhost:8080/"} id="PCfEy3JRXK5f" outputId="b8be0943-c420-4273-c8f6-7c3176a146b0"
# Checando quais colunas tem valores nulos em seus registros
# Somente 'Editora' possui valores nulos, então não vou apagá-los
dataframe.isnull().sum()
# + colab={"base_uri": "https://localhost:8080/"} id="MKAumz88MCgh" outputId="f9e22274-e1a7-4c66-b16f-7c4aacbba655"
# Checando a existência de registros duplicados
len(dataframe[dataframe.duplicated()])
# + colab={"base_uri": "https://localhost:8080/"} id="0mMTwy4RaiQU" outputId="5f1457d7-b9c0-4a9a-f55b-622a2327d01d"
# Verificando quais são os tipos de das variáveis do dataframe
dataframe.dtypes
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="U5LROw7f95nL" outputId="e6388b91-2fea-46f9-86c0-f15cdff56701"
# Visualisando as descrições estatísticas do dataset
dataframe[['vendas_America_do_Norte', 'vendas_Europa', 'vendas_Japao', 'vendas_outras', 'vendas_Globais']].describe().round(2)
# + [markdown] id="0kv40WcJkQFy"
# ---
#
#
# ##Qual o grau de correlação entre as variáveis?
#
#
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="pEcoyEb5-8Dn" outputId="1dbd4468-1e42-4599-a955-9a8e46e691d3"
# criando a variável referente à correlação dos dados
correlacao = dataframe[['vendas_America_do_Norte', 'vendas_Europa', 'vendas_Japao', 'vendas_outras', 'vendas_Globais']].corr()
correlacao
# + colab={"base_uri": "https://localhost:8080/", "height": 677} id="pjfszqMekQvW" outputId="85e42ee1-dbfd-4415-d08b-00f8cf64635c"
# Plotando o heatmap apartir dos dados acima
plt.figure(figsize=(11,9))
mask = np.triu(np.ones_like(correlacao, dtype=bool))
sns.heatmap(correlacao, mask = mask, annot = True, cmap = 'coolwarm', linewidths=.2)
# + [markdown] id="yfw0SRJbvjb1"
# O gráfico acima retrata a correlação entre as variáveis do dataframe. Os números apresentados acima são calculados por meio do "Coeficiente de correlação de Pearson":
#
#
#
# ---
#
#
#
# 
#
#
#
# ---
#
#
#
# Nota-se portanto, que existe uma grande correlação das vendas da América do Norte e Europa com as vendas Globais.
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="zP9BlsfS0Htd" outputId="715fae66-22e6-41ad-c13d-23a95fc0ba90"
# Plotando outros gráficos relacionadas a coorelação de cada região em relação às vendas globais
sns.lmplot(x = 'vendas_America_do_Norte', y = 'vendas_Globais', data=dataframe)
plt.title('Vendas Globais / Vendas América do Norte', fontdict = {'fontsize': 15})
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="ZHS0xsGC1w91" outputId="5125b5d3-c146-40e4-d638-1ceaf03421f5"
sns.lmplot(x = 'vendas_Europa', y = 'vendas_Globais', data=dataframe)
plt.title('Vendas Globais / Vendas Europa', fontdict = {'fontsize': 15})
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="qnwPQ46h15NV" outputId="0f0ea77e-6826-41a7-9a90-f72868dd4c88"
sns.lmplot(x = 'vendas_Japao', y = 'vendas_Globais', data=dataframe)
plt.title('Vendas Globais / Vendas Japão', fontdict = {'fontsize': 15})
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="JKnw5b_q2Ap4" outputId="34503509-0264-4593-830f-3bd8e0df55b2"
sns.lmplot(x = 'vendas_outras', y = 'vendas_Globais', data=dataframe)
plt.title('Vendas Globais / Vendas outras regiões', fontdict = {'fontsize': 15})
# + [markdown] id="zSOyddu8Xmnx"
# ---
#
#
# ##Como foram as vendas globais ao longo dos anos?
#
#
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="wwwnSMTPXkAe" outputId="07ce700d-ffd6-4fcc-d901-1052563dc9cf"
# Agrupando o dataframe por ano, e apontando a soma de vendas de cada.
vendas_por_ano = pd.DataFrame(dataframe.groupby('Ano')['vendas_Globais'].sum()).reset_index()
vendas_por_ano.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 418} id="NeJ9Ov_EX2L8" outputId="ffee8619-e0de-4f0e-f8dd-05075aa4d889"
# plotando um gráfico com os dados agrupados acima
g_vendasGlobais_porAno = sns.catplot(
data = vendas_por_ano,
x = 'Ano',
y = 'vendas_Globais',
kind = 'bar',
aspect = 3,
palette = 'winter'
)
g_vendasGlobais_porAno.set_xticklabels(rotation = 40, horizontalalignment='right')
g_vendasGlobais_porAno.fig.suptitle('Vendas globais ao longo dos anos', fontsize = 'xx-large')
g_vendasGlobais_porAno.set_ylabels('Milhões de Unidades Vendidas')
# + colab={"base_uri": "https://localhost:8080/", "height": 479} id="zpz86TcQMW1k" outputId="cae60b6d-74cd-450c-c1a0-b50af7b90f39"
# Agrupando os dados pelo ano novamente, e separando as vendas de cada região
por_ano = dataframe.groupby('Ano')
somaVendas_porAno = por_ano[['vendas_America_do_Norte', 'vendas_Europa', 'vendas_Japao', 'vendas_outras']].sum()
somaVendas_porAno.plot(figsize=(19, 7))
plt.title('Vendas gerais ao longo dos anos', fontsize='xx-large')
plt.ylabel('Milhões de Unidades Vendidas')
plt.xlabel('Ano')
# + [markdown] id="2MBWp864jIsN"
# ---
# ## Qual foi a soma de vendas em cada região?
# ---
# + id="fOqkqA8bcShG"
# Separando a soma de todas vendas de cada região
valor_1 = ((dataframe["vendas_America_do_Norte"].sum())/1000).round(2)
valor_2 = ((dataframe["vendas_Europa"].sum())/1000).round(2)
valor_3 = ((dataframe["vendas_Japao"].sum())/1000).round(2)
valor_4 = ((dataframe["vendas_outras"].sum())/1000).round(2)
# coloquei os dados em um dataframe
somaVendas = pd.DataFrame({
'Região': ['América do norte', 'Europa', 'Japão', 'Outras'],
'Soma de Vendas': [valor_1, valor_2, valor_3, valor_4]
})
# + colab={"base_uri": "https://localhost:8080/", "height": 173} id="fKS_lnr5fdcJ" outputId="82bdf664-25b8-4472-aac3-50d26f8f73c6"
somaVendas
# + colab={"base_uri": "https://localhost:8080/", "height": 404} id="sNwXHz0cexZi" outputId="bd9eb934-721b-404d-c30c-2d5133c41824"
g = sns.catplot(
data = somaVendas,
x = 'Região',
y = 'Soma de Vendas',
kind = 'bar',
palette = 'Greens_r'
)
g.fig.suptitle('Soma total de vendas por região', fontsize=15)
g.set_ylabels('Bilhões de unidades vendidas')
# + colab={"base_uri": "https://localhost:8080/", "height": 173} id="Hvo-tviYjvXe" outputId="87d9f842-c949-43ed-b7bf-a8d525db0051"
# Calculando o percentual de cada região em relação as vendas globais
somaVendas['Percentual'] = somaVendas['Soma de Vendas'] / somaVendas['Soma de Vendas'].sum()
somaVendas
# + [markdown] id="6FGdTjPKkrkq"
# nota-se portanto que as vendas na América do Norte representam quase a metade das vendas de Video Game históricamente
# + colab={"base_uri": "https://localhost:8080/", "height": 446} id="sK0CNpTNlbSj" outputId="5a069a59-ea82-4fc8-b0ce-5a0bb29dfede"
plt.rc('figure', figsize = (7,7))
plt.pie(somaVendas['Percentual'], labels=somaVendas['Região'].unique(), autopct='%1.2f%%', shadow=True)
plt.title('Total de vendas por região', fontdict={'fontsize': 15})
# + [markdown] id="zOit_WyBb2dz"
# ---
# ##Lançamento de jogos ao longo dos anos
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 425} id="J9h9wZ8Ob-Ka" outputId="848998e1-b323-4773-9080-9ad41fedf98c"
plt.rc('figure', figsize = (15,6))
sns.countplot(x=dataframe['Ano'], data=dataframe)
plt.title("Frequência de lançamento de Video Games", fontdict={'fontsize': 20})
plt.xlabel("Ano")
plt.ylabel("Quantidade de jogo lançados")
plt.xticks(rotation=45)
plt.show()
# + [markdown] id="icklTFFNr2Jl"
# Existe correlação entre as vendas globais e a frequencia de lançamento?
# + colab={"base_uri": "https://localhost:8080/", "height": 111} id="sD624hver-kp" outputId="c71e5a09-10c4-43b3-ef9e-aa10d3467ebf"
frequencia = pd.DataFrame(dataframe['Ano'].value_counts().sort_index().reset_index())
frequencia.columns = ['Ano', 'frequencia']
frequencia['vendas_Globais'] = vendas_por_ano['vendas_Globais']
frequencia[['frequencia', 'vendas_Globais']].corr()
# + colab={"base_uri": "https://localhost:8080/", "height": 400} id="CarLaJhtzdyW" outputId="8879dcde-4a3b-4a45-a31b-d3c4561df2bb"
sns.lmplot(x='frequencia', y='vendas_Globais', data=frequencia)
# + [markdown] id="5FNXA6HVbvT4"
# nota-se um fortíssima correlação entre as vendas globais e a frequência de lançamento de jogos
# + [markdown] id="MbhFm-ycUU3V"
# ---
#
#
# ##Qual a variação nas vendas globais?
#
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="3fmXdDGZdGHs" outputId="0ed0d853-8296-4b25-c75f-f43d5021e39d"
# Algumas estatísticas descritivas do dataframe
dataframe[['vendas_Globais', 'vendas_America_do_Norte', 'vendas_Europa', 'vendas_Japao', 'vendas_outras']].describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 34} id="pciYuUjwG8u8" outputId="e76e8346-310d-4964-88ef-acab9499ac62"
area = plt.figure(figsize=[15, 5])
# + id="WUpHz_TOHPYx"
g1 = area.add_subplot(1, 2, 1)
g2 = area.add_subplot(1, 2, 2)
# + colab={"base_uri": "https://localhost:8080/"} id="_IiQyBPqHTjP" outputId="e806d7ce-33f9-4daa-bce1-f6b9f9c3a8fa"
# Plotando dois gráficos referentes à distribuição de vendas globais
g1.boxplot(dataframe['vendas_Globais'])
g1.set_title('Distribuição das Vendas Globais (100%)')
g1.set_ylabel('Milhões de Unidades Vendidas')
g2.hist(dataframe['vendas_Globais'], bins = 40)
g2.set_title('Distribuição das Vendas Globais (100%)')
g2.set_ylabel('Milhões de Unidades Vendidas')
g2.set_xlabel('Quantidade de Jogos')
# + colab={"base_uri": "https://localhost:8080/", "height": 350} id="nk8h4IqaH9a9" outputId="a7de99d2-e2b9-4d73-b502-a9e7c6c795a0"
area
# + [markdown] id="BzlVPV8zLu7L"
#
#
#
#
#
# Nota-se, ao checar a distribuição de 100% das vendas globais, uma enorme assimetria. Tendo isso em vista,foram feitos então os gráficos abaixo, onde os outliers foram retirados
#
#
#
#
#
# + id="HoL-X9NevF09"
# Primeiramente separo a coluna de vendas globais
vendas = dataframe[['vendas_Globais']]
# + id="qC11kNPvvHyZ"
# Definindo os valores dos quartis, e os limite inferiores e superiores
Q1 = vendas.quantile(.25)
Q3 = vendas.quantile(.75)
IIQ = Q3 - Q1
limite_inferior = Q1 - 1.5 * IIQ
limite_superior = Q3 + 1.5 * IIQ
# + id="b4HR4u9nvFcR"
"""
criando uma variável para a seleção dos valores que estão somente acima do
limite superior e abaixo do limite inferior
essa seleção serve para podermos retirar os outliers dos dados de vendas globais
"""
selecao = (vendas >= limite_inferior) & (vendas <= limite_superior)
# + id="qr77ih1bvNPc"
# aplicando a seleção feita acima no dataframe original
dataframe_II = dataframe[selecao]
# + [markdown] id="9zbDZsCGc3oi"
# Os dois gráficos abaixo foram plotados com a seleção e sem os outliers
# + colab={"base_uri": "https://localhost:8080/", "height": 338} id="JtF4gANcvP5D" outputId="7e5850e0-cc86-40f4-a05a-169f6ef61da4"
plt.rc('figure', figsize = (7.5, 5))
dataframe_II.boxplot(['vendas_Globais'], grid=False)
# + colab={"base_uri": "https://localhost:8080/", "height": 337} id="HrM-K6YSxMoU" outputId="d289f019-7529-4963-9270-8931e438d99b"
dataframe_II['vendas_Globais'].hist(bins=40, grid=False)
# + id="-qv3Sxcvnl4c" colab={"base_uri": "https://localhost:8080/"} outputId="10521587-9ac7-4fe9-eda9-0e307d13c6c8"
dataframe_II['vendas_Globais'].describe()
# + colab={"base_uri": "https://localhost:8080/"} id="dOSapccYnmiE" outputId="595fef93-8ed5-47ef-e91e-e884422bbc8b"
# Checando o valor máximo das vendas globais sem os outliers
dataframe_II['vendas_Globais'].max()
# + colab={"base_uri": "https://localhost:8080/"} id="Fs2RxmDrZJqG" outputId="18ce2677-37a2-475f-ce71-7bab74a5cc26"
# Checando o valor mínimo das vendas globais sem os outliers
dataframe_II['vendas_Globais'].min()
# + colab={"base_uri": "https://localhost:8080/"} id="90BEV4BupPTy" outputId="d0dc4222-c026-4536-ec23-2d65a136ead6"
# Verificando a quantidade de outliers apagados
len(dataframe_II[dataframe_II['vendas_Globais'].isnull()])
# + colab={"base_uri": "https://localhost:8080/"} id="IBIUcU2cx-aZ" outputId="35606cdc-abfd-4659-d82e-692566b0801a"
# Checando, no dataframe anterior, se a linha de código acima está correta
len(dataframe[dataframe['vendas_Globais'].isnull()])
# + [markdown] id="3Z_d-oTwRacb"
# ---
#
# ##Quais são os Video Games que mais venderam?
#
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="2BDTm3mEjkgP" outputId="55a1e545-5c2d-4858-a1e1-fc08864f116c"
vendas_por_nome = dataframe.sort_values(by='Ranking').reset_index().head(20)[['Nome', 'vendas_Globais']]
vendas_por_nome.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 575} id="dURv6yt6kx7r" outputId="b710666b-c514-4296-eb09-552a252636b9"
g_vendasGlobais_porNome = sns.catplot(
data = vendas_por_nome,
x = 'Nome',
y = 'vendas_Globais',
kind = 'bar',
aspect = 3,
palette = 'Wistia_r'
)
g_vendasGlobais_porNome.set_xticklabels(rotation = 40, horizontalalignment='right', fontsize='large')
g_vendasGlobais_porNome.fig.suptitle('Top 20 jogos que mais venderam', fontsize = 'xx-large')
# + [markdown] id="7aV5NZx7VbrB"
# ---
#
# ##Quais são as editoras que mais venderam?
#
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="zTWY7t77SlZA" outputId="f99f4097-1fc7-46fa-b7be-7f1d12b4a4d0"
# Separando as vendas globais por editora, e depois transformando em um dataset
vendas_por_editora = pd.DataFrame(dataframe.groupby('Editora')['vendas_Globais'].sum().sort_values(ascending=False)).reset_index()
vendas_por_editora
# + id="JyDThqJZhLyo" colab={"base_uri": "https://localhost:8080/", "height": 528} outputId="fc949736-3999-44b3-c296-e4f72062a44e"
# Plotando um gráfico que demonstra as vendas globais das 10 editoras que mais vendem
grafico_vendasGlobais_porEditora = sns.catplot(
data = vendas_por_editora.head(15),
x = 'Editora',
y = 'vendas_Globais',
kind = 'bar',
palette = 'bone',
aspect = 2.5
)
grafico_vendasGlobais_porEditora.set_xticklabels(rotation = 40, horizontalalignment='right')
grafico_vendasGlobais_porEditora.fig.suptitle('Vendas por editoras', fontsize = 'xx-large')
# + [markdown] id="zZrTqUS27Tfa"
# ## Consoles
# + colab={"base_uri": "https://localhost:8080/"} id="yhumI_MqMGDA" outputId="d27f8273-9d04-4c59-ebc8-f16f2fb7092c"
dataframe['Plataforma'].unique()
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="VNo1VbfFMJ4J" outputId="19f77d70-92f9-4758-91a9-4efb9de2dd7e"
produzidos_por_console = pd.DataFrame(dataframe['Plataforma'].value_counts()).reset_index()
produzidos_por_console.columns = ['Plataforma', 'Quantidade']
produzidos_por_console.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 404} id="EkR654RiQ5xf" outputId="41f135a1-74fc-4fe6-95c3-c7d371caa0cc"
g_produzidos_porConsole = sns.catplot(
data = produzidos_por_console,
x = 'Plataforma',
y = 'Quantidade',
kind = 'bar',
aspect = 3,
palette = 'winter'
)
g_produzidos_porConsole.fig.suptitle('Quantidade de jogos produzidos por plataforma', fontsize = 'xx-large')
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="bbJVSL8cAnke" outputId="1a349b4b-fdb3-4914-b2b4-defe0ec5015c"
vendas_por_console = pd.DataFrame(dataframe.groupby('Plataforma')['vendas_Globais'].sum().sort_values(ascending=False)).reset_index()
vendas_por_console.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 404} id="Aj8DAF0V7Y6w" outputId="d47ffe4d-33b8-49a0-9f8f-a90934e7860f"
g_vendasGlobais_porConsole = sns.catplot(
data = vendas_por_console,
x = 'Plataforma',
y = 'vendas_Globais',
kind = 'bar',
aspect = 3,
palette = 'winter'
)
g_vendasGlobais_porConsole.fig.suptitle('Quantidade de vendas por plataforma', fontsize = 'xx-large')
# + [markdown] id="yaPq3KR0E_4g"
# ## Gêneros
# + colab={"base_uri": "https://localhost:8080/"} id="GDvEv3rTFo9K" outputId="bc8f33aa-dee5-4d0f-f78c-df1e6e94ee04"
# Vendo todos os generos do dataframe
dataframe['Genero'].unique()
# + colab={"base_uri": "https://localhost:8080/", "height": 421} id="caJrsRrCF1vy" outputId="a5b05f19-acaa-40ab-cf80-450b52610120"
# Transformando em um df a quantidade jogos produzidos por gênero
produzidos_por_genero = pd.DataFrame(dataframe['Genero'].value_counts()).reset_index()
produzidos_por_genero.columns = ['Genero', 'Quantidade']
produzidos_por_genero
# + colab={"base_uri": "https://localhost:8080/", "height": 441} id="mJZxmg3-HUHf" outputId="439042d0-d194-4d13-c56e-0d799a170a36"
g_produzidos_porGenero = sns.catplot(
data=produzidos_por_genero,
x = 'Genero',
y = 'Quantidade',
kind = 'bar',
aspect = 2,
palette = 'winter'
)
g_produzidos_porGenero.set_xticklabels(rotation = 40, horizontalalignment='right')
g_produzidos_porGenero.fig.suptitle('Gêneros mais produzidos', fontsize = 'xx-large')
# + colab={"base_uri": "https://localhost:8080/", "height": 421} id="2UCxL67SFEGe" outputId="3c98bc5c-e556-4081-a45a-14326af59af1"
vendas_por_genero = pd.DataFrame(dataframe.groupby('Genero')['vendas_Globais'].sum().sort_values(ascending=False)).reset_index()
vendas_por_genero
# + colab={"base_uri": "https://localhost:8080/", "height": 441} id="lUOPse0eFnHB" outputId="caa38d3b-09b9-46d1-8f15-4d0f5b5e9208"
g_vendasGlobais_porGenero = sns.catplot(
data=vendas_por_genero,
x = 'Genero',
y = 'vendas_Globais',
kind = 'bar',
aspect = 2,
palette='winter'
)
g_vendasGlobais_porGenero.set_xticklabels(rotation = 40, horizontalalignment='right')
g_vendasGlobais_porGenero.fig.suptitle('Gêneros mais vendidos', fontsize = 'xx-large')
| 87.781925 | 25,693 |
1a852fabb95e3db182e199861eda245f0afff189
|
py
|
python
|
Quantopian Notebooks/.ipynb_checkpoints/Cloned+from+%22Introduction+to+Research%22-checkpoint.ipynb
|
miaortizma/algoritmos-2018-01
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# #Introduction to the Research Environment
#
# The research environment is powered by IPython notebooks, which allow one to perform a great deal of data analysis and statistical validation. We'll demonstrate a few simple techniques here.
# ##Code Cells vs. Text Cells
#
# As you can see, each cell can be either code or text. To select between them, choose from the 'Cell Type' dropdown menu on the top left.
# ##Executing a Command
#
# A code cell will be evaluated when you press play, or when you press the shortcut, shift-enter. Evaluating a cell evaluates each line of code in sequence, and prints the results of the last line below the cell.
# %matplotlib inline
2 + 2
# Sometimes there is no result to be printed, as is the case with assignment.
X = 2
# Remember that only the result from the last line is printed.
2 + 2
3 + 3
# However, you can print whichever lines you want using the `print` statement.
print 2 + 2
3 + 3
# ##Knowing When a Cell is Running
#
# While a cell is running, a `[*]` will display on the left. When a cell has yet to be executed, `[ ]` will display. When it has been run, a number will display indicating the order in which it was run during the execution of the notebook `[5]`. Try on this cell and note it happening.
#Take some time to run something
c = 0
for i in range(100):
c = c + i
c
# ##Importing Libraries
#
# The vast majority of the time, you'll want to use functions from pre-built libraries. You can't import every library on Quantopian due to security issues, but you can import most of the common scientific ones. Here I import numpy and pandas, the two most common and useful libraries in quant finance. I recommend copying this import statement to every new notebook.
#
# Notice that you can rename libraries to whatever you want after importing. The `as` statement allows this. Here we use `np` and `pd` as aliases for `numpy` and `pandas`. This is a very common aliasing and will be found in most code snippets around the web. The point behind this is to allow you to type fewer characters when you are frequently accessing these libraries.
# +
import numpy as np
import pandas as pd
# This is a plotting library for pretty pictures.
import matplotlib.pyplot as plt
# -
# ##Tab Autocomplete
#
# Pressing tab will give you a list of IPython's best guesses for what you might want to type next. This is incredibly valuable and will save you a lot of time. If there is only one possible option for what you could type next, IPython will fill that in for you. Try pressing tab very frequently, it will seldom fill in anything you don't want, as if there is ambiguity a list will be shown. This is a great way to see what functions are available in a library.
#
# Try placing your cursor after the `.` and pressing tab.
np.random.
# ##Getting Documentation Help
#
# Placing a question mark after a function and executing that line of code will give you the documentation IPython has for that function. It's often best to do this in a new cell, as you avoid re-executing other code and running into bugs.
# +
# np.random.normal?
# -
# ##Sampling
#
# We'll sample some random data using a function from `numpy`.
# Sample 100 points with a mean of 0 and an std of 1. This is a standard normal distribution.
X = np.random.normal(0, 1, 100)
# ##Plotting
#
# We can use the plotting library we imported as follows.
plt.plot(X)
# ###Squelching Line Output
#
# You might have noticed the annoying line of the form `[<matplotlib.lines.Line2D at 0x7f72fdbc1710>]` before the plots. This is because the `.plot` function actually produces output. Sometimes we wish not to display output, we can accomplish this with the semi-colon as follows.
plt.plot(X);
# ###Adding Axis Labels
#
# No self-respecting quant leaves a graph without labeled axes. Here are some commands to help with that.
# +
X = np.random.normal(0, 1, 100)
X2 = np.random.normal(0, 1, 100)
plt.plot(X);
plt.plot(X2);
plt.xlabel('Time') # The data we generated is unitless, but don't forget units in general.
plt.ylabel('Returns')
plt.legend(['X', 'X2']);
# -
# ##Generating Statistics
#
# Let's use `numpy` to take some simple statistics.
np.mean(X)
np.std(X)
# ##Getting Real Pricing Data
#
# Randomly sampled data can be great for testing ideas, but let's get some real data. We can use `get_pricing` to do that. You can use the `?` syntax as discussed above to get more information on `get_pricing`'s arguments.
data = get_pricing('MSFT', start_date='2012-1-1', end_date='2015-6-1')
# Our data is now a dataframe. You can see the datetime index and the colums with different pricing data.
data
# This is a pandas dataframe, so we can index in to just get price like this. For more info on pandas, please [click here](http://pandas.pydata.org/pandas-docs/stable/10min.html).
X = data['price']
# Because there is now also date information in our data, we provide two series to `.plot`. `X.index` gives us the datetime index, and `X.values` gives us the pricing values. These are used as the X and Y coordinates to make a graph.
plt.plot(X.index, X.values)
plt.ylabel('Price')
plt.legend(['MSFT']);
# We can get statistics again on real data.
np.mean(X)
np.std(X)
# ##Getting Returns from Prices
#
# We can use the `pct_change` function to get returns. Notice how we drop the first element after doing this, as it will be `NaN` (nothing -> something results in a NaN percent change).
R = X.pct_change()[1:]
# We can plot the returns distribution as a histogram.
plt.hist(R, bins=20)
plt.xlabel('Return')
plt.ylabel('Frequency')
plt.legend(['MSFT Returns']);
# Get statistics again.
np.mean(R)
np.std(R)
# Now let's go backwards and generate data out of a normal distribution using the statistics we estimated from Microsoft's returns. We'll see that we have good reason to suspect Microsoft's returns may not be normal, as the resulting normal distribution looks far different.
plt.hist(np.random.normal(np.mean(R), np.std(R), 10000), bins=20)
plt.xlabel('Return')
plt.ylabel('Frequency')
plt.legend(['Normally Distributed Returns']);
# ##Generating a Moving Average
#
# `pandas` has some nice tools to allow us to generate rolling statistics. Here's an example. Notice how there's no moving average for the first 60 days, as we don't have 60 days of data on which to generate the statistic.
# Take the average of the last 60 days at each timepoint.
MAVG = pd.rolling_mean(X, window=60)
plt.plot(X.index, X.values)
plt.plot(MAVG.index, MAVG.values)
plt.ylabel('Price')
plt.legend(['MSFT', '60-day MAVG']);
# This presentation is for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation for any security; nor does it constitute an offer to provide investment advisory or other services by Quantopian, Inc. ("Quantopian"). Nothing contained herein constitutes investment advice or offers any opinion with respect to the suitability of any security, and any views expressed herein should not be taken as advice to buy, sell, or hold any security or as an endorsement of any security or company. In preparing the information contained herein, Quantopian, Inc. has not taken into account the investment needs, objectives, and financial circumstances of any particular investor. Any views expressed and data illustrated herein were prepared based upon information, believed to be reliable, available to Quantopian, Inc. at the time of publication. Quantopian makes no guarantees as to their accuracy or completeness. All information is subject to change and may quickly become unreliable for various reasons, including changes in market conditions or economic circumstances.
| 38.84 | 1,122 |
8f814c5f3be4cd2eea54c33949e0bdbcfee7a618
|
py
|
python
|
notebooks/02_Calibration_Likelihood.ipynb
|
JamesSample/enviro_mod_notes
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# %matplotlib inline
import matplotlib.pyplot as plt, seaborn as sn, numpy as np
sn.set_context('notebook')
# # Model calibration
#
# In contrast to the fairly abstract consideration of distributions in the previous notebook, this one takes a more practical approach to the problem of model **calibration**. It also introduces the very important concept of the **likelihood function**.
#
# ## 1.1. Types of model
#
# There are many different types of model. At one end of the spectrum are **process-** or **physically-based** models, which use coupled (often differential) equations underpinned by the laws of physics to represent key processes of interest. In principle, if we know all the equations governing the behaviour of a system (and assuming we can measure the **parameter values** associated with those equations) we should be able to construct an accurate model to predict the state of the system at some point in the future.
#
# At the other end of the spectrum are **empirical** models. Just like their process-based counterparts, empirical models use equations to represent relationships between variables, but these equations need not have any physical basis and the parameter values are usually chosen so as to maximise “goodness-of-fit", rather than being independently measured.
#
# Empirical models are often simpler to setup and run much faster than process-based equivalents, but their predictions are only as good as the data used to train them. They may therefore perform poorly if used to make predictions under conditions that differ significantly from those encountered in the training dataset (for example by trying to predict river flows under some future climate).
#
# In theory, a well-designed physically-based model will make better "out-of-sample" predictions than an empirical model, because the process knowledge incorporated into the model's structure will constrain a physically reasonable response, even under conditions different to those experienced during calibration. In reality, natural systems are often extraordinarily complex and outside of the lab it is rare to have enough process understanding to build genuinely physically-based models. Instead, we are forced to create **conceptual** models, which still use physical relationships and differential equations, but which also make dramatic simplifications by abstracting the complexity of the real system into some idealised conceptual framework. As an example, hydrological models often use a conceptual framework consisting of systems of connected "bucket reservoirs", where one bucket represents e.g. the soil water store, another the groundwater store and so on. These abstract conceptualisations are useful – especially if we can write down the physically-based equations that would control our conceptual system (e.g. the water flows between our idealised system of buckets). However, it is important not to confuse a physically-based model of a conceptual system with a physically-based model of the *real world*.
#
# One of the difficulties associated with conceptual models is that, although the equations appear to be physically-based, the parameters in the equations will often have no concrete meaning in the real world, making them impossible to measure directly. For example, in equations commonly used in hydrological modelling, the time constant (or residence time), $\tau$, of a groundwater reservoir is the length of time, on average, that a molecule of water will spend in that reservoir between flowing in and flowing out. In reality, the true groundwater aquifer is much more complicated than the model's representation of a bucket with a couple of holes in it. This means that values of $\tau$ measured in the field (using e.g. isotopic tracer techniques) will not necessarily be compatible with the $\tau$ parameter as represented in the model.
#
# The upshot of all this is that, in practice, **virtually all** environmental models - whether empirical or supposedly physically based - will have parameter values that are not physically meaningful, are too difficult/expensive to measure, or cannot be measured at a temporal/spatial scale which is compatible with the model conceptualisation. In order to get our models to give meaningful output, we therefore need to **calibrate** them by adjusting the poorly constrained parameter values until the output looks sensible.
#
# ## 1.2. Over-parameterisation
#
# Attempts to make physically-based models of complex environmental systems have led to increasingly complex conceptual frameworks. Within the field of hydrology and water quality, some of the most popular models applied today (e.g. [SWAT](http://swat.tamu.edu/ "SWAT") and [HYPE](http://www.smhi.se/en/research/research-departments/hydrology/hype-1.7994 "HYPE")) include tens or even hundreds of parameters, many of which have no direct physical meaning and are therefore usually poorly constrained. Although technically impressive, it can be very difficult to apply such models effectively even in data-rich environments. This is because a process-based model with a very large number of unconstrained parameters will behave very much like an **overly complex** empirical model, simply because the freedom afforded by the unknown parameters will completely swamp any limitations on the model's behaviour imposed by the process knowledge.
#
# In empirical modelling it is usual to choose the simplest possible model that still explains the data. However, in the case of many conceptual and physically-based environmental models, it is often neither possible nor meaningful to "turn off" parameters to test whether a simpler model would suffice. Furthermore, in many cases the amount of calibration data available is limited: in hydrological applications, for example, a model will typically be calibrated against a single streamflow dataset measured at the catchment outflow. There is simply not enough information contained in such a dataset to meaningfully constrain dozens or even hundreds of model parameters, some of which might represent e.g. soil properties or transport coefficients in the upper part of catchment (which have only a limited influence on streamflow).
#
# These issues mean that highly parameterised conceptual and process-based models can produce output which may appear to reproduce observations well, but which have little predictive value. With so much parameter-related flexibility (i.e. many "degrees of freedom"), models can generally do a good job of matching the calibration data, regardless of whether the process representation is correct. In a worst case scenario such models exhibit the "worst of both worlds", in the sense that they have the long runtimes and complexity of process-based models, but with the same limitations and poor out-of-sample predictive power as empirical models.
#
# This does not necessarily mean that complex conceptual models cannot be used effectively, but it does mean they must be used with caution.
#
# ## 1.3. Manual calibration
#
# If we have an environmental model of a real-world system, it is more than likely it will include some poorly constrained parameters that will need calibrating before the model can be used effectively. Calibration usually requires having observed input datasets (e.g. rainfall and evapotranspiration for a hydrological model) together with observed data from the same time period for the variable you're trying to simulate (e.g. streamflow). The observed input data is used to drive the model, and the parameters are adjusted until the simulated output matches the observed data as closely as possible.
#
# As an example, suppose we have a **deterministic** "black box" model such as the one shown below. Deterministic means that if we run the model with the same inputs and parameter values we will always get the same output, because the model has no **stochastic** components. The model could represent anything at all, but we'll stick with a hydrological theme for the moment.
#
# We have no knowledge about how the model works internally - all we can do is set values for the two parameters, $\alpha$ and $\beta$, and then press the **Run** button. The model produces an output time series, $S_i = \{S_1, .., S_n\}$ for time points $t_i = \{t_1, .., t_n\}$. We also have a measured dataset, $M_i = \{M_1, .., M_n\}$, which we'd like to reproduce.
#
# 
#
# For **manual calibration**, we start off by choosing some sensible values for $\alpha$ and $\beta$, then we run the model and compare $S_i$ to $M_i$, then we change $\alpha$ and $\beta$ and repeat until the $S_i$ and $M_i$ are as similar as possible.
#
# Manual calibration is clearly a laborious process, but because humans are remarkably good at picking up patterns it's often surprising how quickly experienced modellers can achieve reasonable results. If you're just starting out with a new model (especially one you didn't create yourself), I'd **strongly recommend** putting some time aside for manual calibration: you'll learn a lot about which parameters the model is sensitive to as well as which ones control different aspects of the output. It also forces you to think about which parameter values are sensible versus which ones give the best calibration (not necessarily the same!). If nothing else, manual calibration gives you an initial benchmark that you can refer to later, once you start applying more sophisticated "auto-calibration" techniques.
#
# ## 1.4. Which parameters to calibrate?
#
# In an ideal world, any parameter whose value is uncertain would be included in the calibration process. You might even decide to include the uncertainty in your input data (because our measurements are never perfect). However, in practice, if you try to do this with a complex conceptual model you might end up with far too many parameters (hundreds?) to stand any chance of achieving a successful calibration. Instead, it is necessary to choose a **subset of parameters** that (i) are poorly constrained (i.e. you don't already know what the value should be) and (ii) actually have an effect on the model's behaviour/output. After a bit of experimenting with manual calibration (or, more formally, using **sensitivity analysis**, which I won't cover here), you should be able to get a reasonable idea of which parameters might be suitable.
#
# You will also need to choose fixed values for any parameters you choose not to calibrate. This is best done using system knowledge (e.g. literature values) where possible, although this is often difficult. Beware of studies presenting complex conceptual models where only a few calibrated parameters have been reported. In such cases it is likely that large numbers of other parameters have been fixed arbitrarily in order to avoid over-parameterisation. This may be acceptable, but it should be done transparently and with some discussion of the implications.
#
# ## 1.5. Auto-calibration
#
# Computers are ideally suited to performing laborious, repetitative tasks like the steps involved in model calibration. Based on the "black box" model illustrated above, we need an algorithm that can:
#
# 1. **Choose values for $\alpha$ and $\beta$**. Based on the image above, it is obvious that whoever created the black box model is pretty certain that $\alpha$ and $\beta$ must lie between 1 and 12. In general, if we can narrow the parameter choices to within a particular range, the calibration process is likely to be more efficient than if the algorithm has to search the entire real number line.
#
# It is also important to consider *how* we sample from the possible parameter values: are all the numbers (including fractions) between 1 and 12 equally likely? Are $\alpha$ and $\beta$ integers? Do we have reason to believe that e.g. numbers towards the middle of the range are more likely than those at the extremes? In the former case, we might sample randomly from a uniform distribution between 1 and 12, whereas in the latter we might use something Gaussian-like to assign greater weight to the values around 6.
#
# This kind of reasoning leads to the concept of a **prior distribution** for each of our parameters. Defining priors is a fundamental part of Bayesian inference and it's something we'll return to later.<br><br>
#
# 2. **Run the model with the chosen parameter values**. This step is usually pretty straightforward - it's just a question of telling your computer how to feed input data to your model and press the "Run" button. If your model is written in Python it's just a matter of linking your calibration code to your model code. Alternatively, if your model is available as a command line executable you should be able to call it from your Python calibration code using e.g. `subprocess.call()`.<br><br>
#
# 3. **Evaluate "goodness-of-fit"**. The simplest form of manual calibration involves **visually comparing** the model output to the observed data to determine the performance of each parameter set. In most cases it is also useful to calculate some simple summary statistics, such as **simple least squares (SLS)** or the [**Nash-Sutcliffe efficiency (NS)**](https://en.wikipedia.org/wiki/Nash%E2%80%93Sutcliffe_model_efficiency_coefficient "Wikipedia: Nash-Sutcliffe") (the latter being especially common in hydrology).
#
# The range of different summary statistics (sometimes called **skill scores**) used by the modelling community is huge. Some have useful properties in specific cirumstances (this is a whole topic in itself), but it is important to understand that **all** skill scores involve making assumptions about your data (e.g. many assume independent, identically distributed Gaussian errors). Often the assumptions are transparent, but in some cases authors seem unaware of the implicit assumptions made by their chosen metric.
#
# Rather than discussing the pros and cons of a whole range of different skill scores, we will initially take a more formal statistical approach by explicitly setting out our assumptions and formulating an appropriate "goodness-of-fit" metric. This is called a **likelihood function**.
#
# ## 2.1. The likelihood function
#
# Suppose we run the model illustrated above with a particular set of parameters and generate the data shown in red on the image below. The blue curve shows the observations we're trying to simulate.
#
# <img src="https://github.com/JamesSample/enviro_mod_notes/blob/master/images/Output_And_Obs_Time_Series.png?raw=true" alt="Simulated and observed data" width="600">
#
# We want to define a metric that awards higher scores when the simulated (red) points are closer to the observed (blue) ones. However, we know that our model will never be perfect and we also know our observations have error associated with them too, so we don't expect the two curves to coincide exactly. How close we can reasonably expect them to be depends on the quality of our model and the accuracy of our measurements. If we expect both to be very good, we might decide to heavily penalise even small discrepancies between the model results and the observations; on the other hand, we might decide to be more lenient by penalising only very large errors.
#
# The simplest and most common way to formulate an error structure is to assume our model results should differ from the observed series by errors that are normally distributed with a mean, $\mu_\epsilon$, of 0 and some (unknown) standard deviation, $\sigma_\epsilon$. We can write this error structure as a **stochastic component** added to our **deterministic** black box model:
#
# $$y = f(x, \theta) + \mathcal{N}(0, \sigma_\epsilon)$$
#
# where $y$ is the observed data, $f$ is a (possibly very complex) function representing the **deterministic** part of our model, run using input data, $x$, and parameters, $\theta$, and $\mathcal{N}(0, \sigma_\epsilon)$ is the **stochastic** error term drawn from a normal distribution.
#
# Note that by setting the mean of the error distribution to zero we are assuming our model is **unbiased**. This is a sensible choice, because if you suspect your model to be biased you'd be better off working out why and fixing the problem (or using a different model), rather than building the bias into the error term by changing $\mu_\epsilon$.
#
# We can visualise this error structure by plotting a small Gaussian, $\mathcal{N}(f(x, \theta), \sigma_\epsilon)$ at each simulated point, as on the image below.
#
# <img src="https://github.com/JamesSample/enviro_mod_notes/blob/master/images/Output_And_Obs_Time_Series_With_Errors.png?raw=true" alt="Gaussian error model" width="600">
#
# For each pair of points, $S_i$, $M_i$, we can evaluate the probability density of the measured data, $M_i$, being drawn from a Gaussian centred on the simulated data, $S_i$, with standard deviation $\sigma_\epsilon$.
#
# <img src="https://github.com/JamesSample/enviro_mod_notes/blob/master/images/Gauss_Error.png?raw=true" alt="Gaussian error model" width="600">
#
# Looking at the above images, you can hopefully see that if $\sigma_\epsilon$ is small, we heavily penalise small differences between simulated and observed values. This is because the Gaussian error distribution is narrow and pointed, meaning that the probability density falls away quickly and so very low likelihood values are assigned when the $S_i$ and $M_i$ are far apart. A larger value of $\sigma_\epsilon$ gives a broader error distribution which penalises errors less severely.
#
# So far we have assumed that our model differs from the observed data by errors that are described by a Gaussian distribution with mean 0 and standard deviation $\sigma_\epsilon$. If we assume that this distribution stays the same for every time point, $t_i$, where $i = \{1, .., n\}$, we can calculate a probability density, $P(M_i)$, for each time step. This is simply the density associated with drawing $M_i$ from a Gaussian with mean $S_i$ and standard deviation $\sigma_\epsilon$, as illustrated on the plot above.
#
# If we further assume that each point in the time series is independent of the others, we can calculate the overall likelihood for the full dataset as the product of the densities for each individual point:
#
# $$L(M|\theta) = \prod_{i=1}^{n} P(M_i)$$
#
# where $L(M|\theta)$ is the **likelihood** of the observations **given** the model parameters i.e. the probability that the model, run with a particular set of parameters, will simulate the observed dataset.
#
# If the parameters produce output that is similar to the observed data, the $S_i$ will be similar to the $M_i$ and so the probability densities, $P(M_i)$, will be large and the likelihood will be high. On the other hand, if the parameters produce poor output, the $P(M_i)$ will be small and the likelihood will be low. Higher values of the likelihood therefore correspond to "better" (more likely) parameter sets, *as long as the assumptions for the error structure are met*. As a recap, these assumptions are:
#
# 1. The errors, $\epsilon_i = (S_i - M_i)$, are normally distributed with mean zero and standard deviation $\sigma_\epsilon$.<br><br>
#
# 2. The errors are **independent** i.e. successive values of $\epsilon_i$ are **not autocorrelated** and do not show **[heteroscedasticity](https://en.wikipedia.org/wiki/Heteroscedasticity "Wikipedia: Heteroscedasticity")**.
#
# In a later notebook we will look at some simple diagnostic plots to test these assumptions, and we'll also consider how to generalise the likelihood function to make it more widely applicable.
#
# As an aside, it's worth noting that the assumptions described above are identical to those for the **simple least squares (SLS)** skill score, so using SLS to assess goodness-of-fit is functionally identical to using the simple **independent and identically distributed (iid)** Gaussian likelihood function described above.
#
# ## 2.2. Log likelihood
#
# Probability densities are always numbers less than 1, and the formula given above for the likelihood involves multiplying lots of them together. Likelihoods therefore become very tiny and it is possible for computers to run into numerical problems ("[arithmetic underflow](https://en.wikipedia.org/wiki/Arithmetic_underflow "Wikipedia: Arithmetic underflow")") when calculating them. For this reason, it is usually better to work with the **log likelihood**, which converts the product in the formula above into a sum of logs:
#
# $$LL(M|\theta) = \sum_{i=1}^{n} ln(P(M_i))$$
#
# where $LL$ is the log likelihood.
#
# Recall from the previous notebook that the equation for a Gaussian is:
#
# $$P(x)=\frac{1}{{\sigma \sqrt {2\pi } }}e^{{{ - ( {x - \mu } )^2 /{2\sigma ^2 }}}}$$
#
# We can re-write this for our error distribution at a single time point as:
#
# $$P(M_i)=\frac{1}{{\sigma_\epsilon \sqrt {2\pi } }}e^{{{ - ( {M_i - S_i } )^2 /{2\sigma_\epsilon ^2 }}}}$$
#
# Taking natural logs and re-arranging, this can be written:
#
# $$P(M_i)= \frac{-ln(2\pi{\sigma_\epsilon}^2)}{2} - \frac{(M_i - S_i)^2}{2{\sigma_\epsilon}^2}$$
#
# which we can sum over $n$ time points to give the overall log likelihood (assuming iid Gaussian errors):
#
# $$LL(D|\theta) = \frac{-nln(2\pi{\sigma_\epsilon}^2)}{2} - \sum_{i=1}^{n} \frac{(M_i - S_i)^2}{2{\sigma_\epsilon}^2}$$
#
# ## 2.3. Maximum likelihood estimation
#
# Before going any further, I think it's worth stressing that likelihoods are **not** an exclusively Bayesian concept - they are relevant in both Bayesian and Frequentist statistics. In many cases, Bayesians and Frequentists will use the same likelihood functions and get the same answers. If you're interested in the differences between Bayesian and Frequentist paradigms, I thoroughly recommend reading [this blog post](http://jakevdp.github.io/blog/2014/03/11/frequentism-and-bayesianism-a-practical-intro/) (and the follow-ups) by Jake Vanderplas, as well as his excellent [article on arXiv](http://arxiv.org/abs/1411.5018).
#
# Now that we have a likelihood function, we can develop an automated calibration procedure to identify the **"best"** parameter set, just like we were trying to do with the manual calibration procedure described in section 1.3. Note that as well as wanting to calibrate our black-box model parameters, $\alpha$ and $\beta$, constructing our error model has introduced one additional parameter: $\sigma_\epsilon$. Because we don't know the value of this, we'll simply include it as an additional variable in our optimisation routine.
#
# We want to find values for $\alpha$, $\beta$ and $\sigma_\epsilon$ that **maximise** the likelihood function. As an illustrative example, we'll assume a particular form for the "true" model, generate some synthetic data from it, and then use maximum likelihood estimation to try to identify the true parameters. If the method works here, perhaps it will also work in the real world where we never get to know the "true" parameter values. Let's suppose our black box model from above is actually just a simple linear model
#
# $$y = \alpha x + \beta$$
# +
# Generate some fake data, incorporating Gaussian noise
alpha_true = 3
beta_true = 7
sigma_true = 2
x = np.arange(0, 10, 0.1)
y = alpha_true*x + beta_true + np.random.normal(loc=0, scale=sigma_true, size=len(x)) # The observed data
# -
# Next we'll define our log likelihood function. This function takes a vector of estimated values for $\alpha$, $\beta$ and $\sigma_\epsilon$ and estimates the likelihood of the data *given the parameters*, assuming that:
#
# $$y = \alpha x + \beta + \mathcal{N}(0, \sigma_\epsilon)$$
#
# We want to **maximise** this function, but Scipy includes optimisation tools for **minimising**. Thereore we'll also define a function for the *negative log likelihood*. Minimising this is the same as maximising the log likelihood.
# +
def log_likelihood(params, obs):
""" Returns log likelihood assuming iid Gaussian errors.
params is a vector of parameter estimates [alpha, beta, sigma]
obs is the observed dataset we're trying to match
"""
# Get number of value pairs
n = len(obs)
# Extract parameter values
alpha, beta, sigma = params
# Calculate model results with these parameters
sim = alpha*x + beta
# Calculate log likelihood (see equations above)
ll = -n*np.log(2*np.pi*sigma**2)/2 - np.sum(((obs - sim)**2)/(2*sigma**2))
return ll
def neg_log_likelihood(params, obs):
""" Maximising the log likelihood is the same as minimising the negative log
likelihood.
"""
return -log_likelihood(params, obs)
# -
# Finally, we import the optimiser from Scipy and make some starting guesses for $\alpha$, $\beta$ and $\sigma_\epsilon$. The optimiser does a pretty good job of recovering the "true" values for $\alpha$ and $\beta$, which are what we wanted to find.
# +
from scipy import optimize
# Guess some starting values for [alpha, beta, sigma]
param_guess = [6., 6., 1.]
# Run optimiser
param_est = optimize.fmin(neg_log_likelihood, param_guess, args=(y,))
# Print results
print '\n'
print 'Estimated alpha: %.2f. True value %.2f' % (param_est[0], alpha_true)
print 'Estimated beta: %.2f. True value %.2f' % (param_est[1], beta_true)
print 'Estimated sigma: %.2f. True value %.2f' % (param_est[2], sigma_true)
# -
# So far so good, but although we've estimated the "best" parameter set by maximising the likelihood, we have no indication of how much **confidence** we should have in this result. If the likelihood function consists of a sharp, well-defined peak, the values for $\alpha$, $\beta$ and $\sigma_\epsilon$ may be tightly constrained (i.e. have narrow **confidence intervals**). On the other hand, the likelihood function may describe a broad, flat plateau with no clear maximum, or a complex hilly landscape with several widely separated maxima. In such cases a single "point estimate" for each parameter value may obscure the fact that a range of different parameter sets could produce essentially the same answer. The "best" parameter set is therefore not much use without some additional information describing the confidence interval (or **credible interval** to the Bayesians) around each estimated value.
#
# ### Aside: A simpler way to calculate the log likelihood
#
# The `log_likelihood` function above explicitly calculates the result using the formula for a Gaussian. However, `scipy` has some convenience functions to make coding this kind of calculation easier. The following code does exactly the same thing, and is much less prone to typos.
# +
from scipy.stats import norm
def log_likelihood2(params, obs):
""" An alternative way of coding the log likelihood.
Returns log likelihood assuming iid Gaussian errors.
params is a vector of parameter estimates [alpha, beta, sigma]
obs is the observed dataset we're trying to match.
"""
# Get number of value pairs
n = len(obs)
# Extract parameter values
alpha, beta, sigma = params
# Calculate model results with these parameters
sim = alpha*x + beta
# Calculate log likelihood
ll = np.sum(norm(sim, sigma).logpdf(obs))
return ll
# Quick check that results from both functions are the same
# Generate fake obs assuming alpha=6 and beta=3
x = np.arange(0, 10, 0.1)
obs = 6*x+3
# Get log likelihood for alpha=3 and beta=4, if sigma=2
print log_likelihood([3, 4, 2], obs)
print log_likelihood2([3, 4, 2], obs)
# -
# ## 3. Summary
#
# * Most models of real world environmental systems are complex enough to need **calibrating**, because we rarely have sufficiently detailed information to constrain all the parameters.<br><br>
#
# * Calibration can be performed **manually**, but this is time consuming (although useful!) and may be impossible for models with lots of parameters.<br><br>
#
# * **Auto-calibration** procedures require us to:
# 1. Define rules for how to pick parameter values (based on **prior knowledge**?), and<br><br>
# 2. Devise a method for **evaluating model performance**.<br><br>
#
# * A variety of summary statistics and **skill scores** are commonly used, but the underlying assumptions for these may not be obvious.<br><br>
#
# * Formal **likelihoods** involve describing the difference between simulated and observed model output in terms of probabilities. To do this, we need to devise an appropriate **error structure** which is used as the basis for assessing model performance. This forces us to think about the assumptions being made, but we need to remember to actually *go back and check them* (more on this in a later notebook).<br><br>
#
# * **Log** likelihoods are used to avoid numeric errors.<br><br>
#
# * Once we have a likelihood function, we can use an **optimiser** to identify the most likely parameter set (although this can be difficult in high-dimensional parameter spaces). Note also that this method *only* finds the **"best"** parameter set - it gives no indication of how much **confidence** we should have in the values identified. This is a major limitation and one of the main motivations for everything that follows.
| 103.526502 | 1,323 |
22db18bf11d24219536511931bc2252d4dff9183
|
py
|
python
|
notebooks/Impacto dos tweets do MBL.ipynb
|
JoaoCarabetta/ideologia
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc" style="margin-top: 1em;"><ul class="toc-item"><li><span><a href="#Resumo" data-toc-modified-id="Resumo-1">Resumo</a></span><ul class="toc-item"><li><span><a href="#Objetivo" data-toc-modified-id="Objetivo-1.1">Objetivo</a></span></li><li><span><a href="#Metodologia" data-toc-modified-id="Metodologia-1.2">Metodologia</a></span></li><li><span><a href="#Resultados" data-toc-modified-id="Resultados-1.3">Resultados</a></span></li></ul></li><li><span><a href="#Importações" data-toc-modified-id="Importações-2">Importações</a></span><ul class="toc-item"><li><span><a href="#Importação-dos-dados" data-toc-modified-id="Importação-dos-dados-2.1">Importação dos dados</a></span><ul class="toc-item"><li><span><a href="#Tweets" data-toc-modified-id="Tweets-2.1.1">Tweets</a></span></li><li><span><a href="#Interações" data-toc-modified-id="Interações-2.1.2">Interações</a></span></li><li><span><a href="#Texto-das-imagens" data-toc-modified-id="Texto-das-imagens-2.1.3">Texto das imagens</a></span></li></ul></li></ul></li><li><span><a href="#Tratamento" data-toc-modified-id="Tratamento-3">Tratamento</a></span><ul class="toc-item"><li><span><a href="#Tweets-duplicados" data-toc-modified-id="Tweets-duplicados-3.1">Tweets duplicados</a></span><ul class="toc-item"><li><span><a href="#Limpa-texto-das-images" data-toc-modified-id="Limpa-texto-das-images-3.1.1">Limpa texto das images</a></span></li></ul></li><li><span><a href="#Divisão-por-audiovisual-e-texto" data-toc-modified-id="Divisão-por-audiovisual-e-texto-3.2">Divisão por audiovisual e texto</a></span></li><li><span><a href="#Treat-dates" data-toc-modified-id="Treat-dates-3.3">Treat dates</a></span></li></ul></li><li><span><a href="#Alcance-da-atividade-do-MBL-no-Twitter" data-toc-modified-id="Alcance-da-atividade-do-MBL-no-Twitter-4">Alcance da atividade do MBL no Twitter</a></span><ul class="toc-item"><li><span><a href="#Filtra-data" data-toc-modified-id="Filtra-data-4.1">Filtra data</a></span></li><li><span><a href="#Total-de-Tweets" data-toc-modified-id="Total-de-Tweets-4.2">Total de Tweets</a></span><ul class="toc-item"><li><span><a href="#Agregado" data-toc-modified-id="Agregado-4.2.1">Agregado</a></span></li><li><span><a href="#Por-Ano" data-toc-modified-id="Por-Ano-4.2.2">Por Ano</a></span></li><li><span><a href="#Por-Mês" data-toc-modified-id="Por-Mês-4.2.3">Por Mês</a></span></li><li><span><a href="#Por-Semana" data-toc-modified-id="Por-Semana-4.2.4">Por Semana</a></span></li><li><span><a href="#Distribuição-de-tweets-por-semana" data-toc-modified-id="Distribuição-de-tweets-por-semana-4.2.5">Distribuição de tweets por semana</a></span></li><li><span><a href="#Média-móvel-de-um-mês-de-tweets-por-semana" data-toc-modified-id="Média-móvel-de-um-mês-de-tweets-por-semana-4.2.6">Média móvel de um mês de tweets por semana</a></span></li></ul></li><li><span><a href="#Impacto---Retweets,-Favorites-e-Replies" data-toc-modified-id="Impacto---Retweets,-Favorites-e-Replies-4.3">Impacto - Retweets, Favorites e Replies</a></span><ul class="toc-item"><li><span><a href="#Agregado" data-toc-modified-id="Agregado-4.3.1">Agregado</a></span></li><li><span><a href="#Por-Ano" data-toc-modified-id="Por-Ano-4.3.2">Por Ano</a></span></li><li><span><a href="#Por-Mês" data-toc-modified-id="Por-Mês-4.3.3">Por Mês</a></span></li><li><span><a href="#Por-Semana" data-toc-modified-id="Por-Semana-4.3.4">Por Semana</a></span></li><li><span><a href="#Distribuição-de-tweets-por-semana" data-toc-modified-id="Distribuição-de-tweets-por-semana-4.3.5">Distribuição de tweets por semana</a></span></li><li><span><a href="#Média-móvel-de-um-mês-de-tweets-por-semana" data-toc-modified-id="Média-móvel-de-um-mês-de-tweets-por-semana-4.3.6">Média móvel de um mês de tweets por semana</a></span></li></ul></li><li><span><a href="#Público" data-toc-modified-id="Público-4.4">Público</a></span><ul class="toc-item"><li><span><a href="#Top-Contas" data-toc-modified-id="Top-Contas-4.4.1">Top Contas</a></span></li><li><span><a href="#Fidelidade" data-toc-modified-id="Fidelidade-4.4.2">Fidelidade</a></span></li></ul></li></ul></li><li><span><a href="#Indentificação-de-Temas" data-toc-modified-id="Indentificação-de-Temas-5">Indentificação de Temas</a></span></li><li><span><a href="#Tweets-por-Tema" data-toc-modified-id="Tweets-por-Tema-6">Tweets por Tema</a></span><ul class="toc-item"><li><span><a href="#Importando-keywords-dos-temas" data-toc-modified-id="Importando-keywords-dos-temas-6.1">Importando keywords dos temas</a></span></li><li><span><a href="#Selecionando-Tweets-por-keyword" data-toc-modified-id="Selecionando-Tweets-por-keyword-6.2">Selecionando Tweets por keyword</a></span><ul class="toc-item"><li><span><a href="#Sem-tratamento" data-toc-modified-id="Sem-tratamento-6.2.1">Sem tratamento</a></span><ul class="toc-item"><li><span><a href="#Quantidade-de-Tweets-por-Tema" data-toc-modified-id="Quantidade-de-Tweets-por-Tema-6.2.1.1">Quantidade de Tweets por Tema</a></span></li><li><span><a href="#Quantidade-de-Tweets-por-Tema-por-Mês" data-toc-modified-id="Quantidade-de-Tweets-por-Tema-por-Mês-6.2.1.2">Quantidade de Tweets por Tema por Mês</a></span></li><li><span><a href="#Interações-por-Tema" data-toc-modified-id="Interações-por-Tema-6.2.1.3">Interações por Tema</a></span></li><li><span><a href="#Interações-por-tema-por-mês" data-toc-modified-id="Interações-por-tema-por-mês-6.2.1.4">Interações por tema por mês</a></span></li><li><span><a href="#Exportação" data-toc-modified-id="Exportação-6.2.1.5">Exportação</a></span></li></ul></li></ul></li><li><span><a href="#Exportações-Geral" data-toc-modified-id="Exportações-Geral-6.3">Exportações Geral</a></span></li></ul></li></ul></div>
# -
# # Resumo
#
# ## Objetivo
#
# 1. Enteder o alcance e da atividade do MBL no Twitter de modo geral
# 2. Refinar a hipótese: tweets relacionados à ideologia de gênero foram o principal fator de crescimento do MBL no twitter
#
# ## Metodologia
#
# Base de dados:
# - Captura e armazenamento de todos os tweets disponíveis publicamente.
#
# Tratamento da base:
# - Separação de tweets em somente audiovisual, audiovisual + texto e somente texto
# - Tweets sem imagem e com texto sem caracteres serão desconsiderados
# - Tratamento das datas
#
#
# **1. Enteder o alcance e da atividade do MBL no Twitter de modo geral**
# - Total de tweets
# - % de tweets que foram coletados em relação ao total
# - Estatísticas descritivas de tweets por semana e geral
# - Descrição do uso do twitter ao longo dos anos
# - Mediana de retweets, favorites e replies dos tweets ao longo dos anos
# - (?) Clusterização de palavras
#
# **2. Refinar a hipótese: tweets relacionados à ideologia de gênero foram o principal fator de crescimento do MBL no twitter**
# - Filtrar tweets de acordo com palavras chave
# - Total de tweets | % em relação ao total
# - Estatísticas descritivas de tweets por semana e geral
# - Comparação com o restante dos tweets
# - Mediana de retweets, favorites e replies dos tweets ao longo dos anos
#
# ## Resultados
#
# Base de dados:
# - Foram capturados 8656 tweets dos 17.5k exibidos no site. Mas, a diferença vem dos retweets que não são capturados. Então, somente conteúdo produzido pelo MBL está sendo levado em conta.
#
# Tratamento da Base:
# - Separação de tweets em somente audiovisual, audiovisual + texto e somente texto
#
# ```
# tweets: 8920
# tweets que contém imagem: 2720
# tweets que contém texto: 8648
# tweets que contém links externos: 4406
# tweets que contém somente texto: 2094
# tweets que contém somente links: 47
# tweets que contém somente images: 94
# tweets que contém texto+imagens: 2251
# tweets que contém links+imagens: 56
# tweets que contém texto+links: 3984
# tweets que contém links+imagens+texto: 319
# tweets que contém vazios: 75```
# # Importações
# +
import pandas as pd
import sqlite3
import datetime
# DATA ANALYSIS & VIZ TOOLS
from copy import deepcopy
pd.options.display.max_columns = 999
import plotly
import plotly.graph_objs as go
import plotly.offline as offline
offline.init_notebook_mode(connected=True)
# %pylab inline
#pylab.rcParams['figure.figsize'] = (12, 12)
colorscale = ['#0095D4', '#7c8282', '#00D9FF', '#b5dde5', '#04b9d3', '#1C5D96'] # visual id
# -
# ## Importação dos dados
# ### Tweets
db = sqlite3.connect('../scripts/tweets')
tweets = pd.read_sql_query('SELECT * FROM tweets_mbl', db)
tweets.head(2)
tweets['retweets'].max()
tweets.info()
# ### Interações
interactions = pd.read_sql_query('SELECT * FROM interaction', db)
interactions.head(2)
interactions.groupby('tweet_id').count().max()
interactions.info()
# ### Texto das imagens
image_text = pd.read_sql_query('SELECT * FROM image_text', db)
image_text.head()
image_text.describe()
# # Tratamento
# ## Tweets duplicados
print('Número de tweets duplicados: ', len(tweets) - len(tweets.drop_duplicates('tweet_id')))
tweets = tweets.drop_duplicates('tweet_id')
# ### Limpa texto das images
# +
def clean_text(text):
"""Cleans raw text so that it can be written into a csv file without causing any errors."""
text = ''.join(list(map(lambda x: x if isinstance(x, str) else x.text, text)))
temp = text
temp = temp.replace("\n", " ")
temp = temp.replace("\r", " ")
temp = temp.replace(",", " ")
temp.strip()
return temp
image_text['image_text'] = image_text['image_text'].apply(clean_text)
# -
# ## Divisão por audiovisual e texto
tweets['links_len'] = tweets['links'].apply(len) - 2
tweets['image_len'] = tweets['embbed_url'].apply(len)
tweets['text_len'] = tweets['text'].apply(len)
print('tweets:', len(tweets))
print('tweets que contém imagem:', len(tweets[tweets['image_len'] > 0]))
print('tweets que contém texto:', len(tweets[tweets['text_len'] > 0]))
print('tweets que contém links externos:', len(tweets[tweets['links_len'] > 0]))
print('tweets que contém somente texto:', len(tweets[(tweets['links_len'] == 0) &
(tweets['text_len'] > 0) &
(tweets['image_len'] == 0)]))
print('tweets que contém somente links:', len(tweets[(tweets['links_len'] > 0) &
(tweets['text_len'] == 0) &
(tweets['image_len'] == 0)]))
print('tweets que contém somente images:', len(tweets[(tweets['links_len'] == 0) &
(tweets['text_len'] == 0) &
(tweets['image_len'] > 0)]))
print('tweets que contém texto+imagens:', len(tweets[(tweets['links_len'] == 0) &
(tweets['text_len'] > 0) &
(tweets['image_len'] > 0)]))
print('tweets que contém links+imagens:', len(tweets[(tweets['links_len'] > 0) &
(tweets['text_len'] == 0) &
(tweets['image_len'] > 0)]))
print('tweets que contém texto+links:', len(tweets[(tweets['links_len'] > 0) &
(tweets['text_len'] > 0) &
(tweets['image_len'] == 0)]))
print('tweets que contém links+imagens+texto:', len(tweets[(tweets['links_len'] > 0) &
(tweets['text_len'] > 0) &
(tweets['image_len'] > 0)]))
print('tweets que contém vazios:', len(tweets[(tweets['links_len'] == 0) &
(tweets['text_len'] == 0) &
(tweets['image_len'] == 0)]))
# ## Treat dates
# + code_folding=[0]
month_converter = {
'jan': 'jan',
'fev': 'feb',
'mar': 'mar',
'abr': 'apr',
'mai': 'may',
'jun': 'jun',
'jul': 'jul',
'ago': 'aug',
'set': 'sep',
'out': 'oct',
'nov': 'nov',
'dez': 'dec',
}
# -
def translate_month(a):
month = a[-11:-8]
return a.replace(month, month_converter[month])
tweets['timestamp'] = tweets['timestamp'].apply(lambda a : datetime.datetime.strptime(translate_month(a), '%H:%M - %d de %b de %Y'))
tweets.set_index('timestamp', inplace=True)
# # Alcance da atividade do MBL no Twitter
#
# Como as atividades no twitter só começam em Outubro de 2014, o período anterior será descartado.
#
# Mais precisamente da data '2014-11-14 06:52:00'
#
# - Total de tweets
# - Estatísticas descritivas de tweets por semana e geral
# - Descrição do uso do twitter ao longo dos anos
# - Mediana de retweets, favorites e replies dos tweets ao longo dos anos
# - (?) Clusterização de palavras
# ## Filtra data
tweets = tweets['01-10-2014':]
# ## Total de Tweets
def count_group(df, groups=['D', 'W', 'M'], agg='count', select=['tweet_id']):
count = {}
for freq in groups:
count[freq] = df.groupby(pd.Grouper(freq=freq)).agg(agg)[select]
return count
tweets_count = count_group(tweets, groups=['D', 'W', 'M', 'Y'])
# ### Agregado
print('Total de tweets: ', len(tweets))
# ### Por Ano
tweets_count['Y']
# +
data = [go.Bar(x=tweets_count['Y'].index - 1,
y=tweets_count['Y']['tweet_id'])]
layout = go.Layout(title='Number of tweets per year')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# ### Por Mês
# +
data = [go.Bar(x=tweets_count['M'].index ,
y=tweets_count['M']['tweet_id'])]
layout = go.Layout(title='Number of tweets per month')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# ### Por Semana
# +
data = [go.Bar(x=tweets_count['W'].index ,
y=tweets_count['W']['tweet_id'])]
layout = go.Layout(title='Number of tweets per week')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# ### Distribuição de tweets por semana
tweets_count['W']['tweet_id'].describe()
# +
data = [go.Histogram(
x=tweets_count['W']['tweet_id'],
autobinx=True)]
layout = go.Layout(title='Number of tweets per week')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# ### Média móvel de um mês de tweets por semana
# +
data = [go.Scatter(
x=tweets_count['W'].index,
y=tweets_count['W']['tweet_id'],
mode='markers',
name='Number of Tweets')]
data.append(go.Scatter(
x=tweets_count['W'].index,
y=tweets_count['W']['tweet_id'].rolling(4, closed='right', min_periods=1).mean(),
name='Rolling Month Average'))
data.append(go.Scatter(
x=tweets_count['W'].index,
y=tweets_count['W']['tweet_id'].rolling(4, closed='right', min_periods=1).median(),
name='Rolling Month Median'))
layout = go.Layout(title='Number of tweets per week')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(tweets_count['W']['tweet_id'].rolling(4, closed='right', min_periods=1).mean(),
model='additive')
data = []
data.append(go.Scatter(
x=tweets_count['W'].index,
y=tweets_count['W']['tweet_id'].rolling(4, closed='right', min_periods=1).mean(),
name='Rolling Month Median'))
data.append(go.Scatter(
x=result.trend.index,
y=result.trend,
name='Trend'))
data.append(go.Scatter(
x=result.seasonal.index,
y=result.seasonal,
name='Seasonal'))
data.append(go.Scatter(
x=result.resid.index,
y=result.resid,
name='Residual'))
layout = go.Layout(title='Number of tweets per week - Decomposition')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# ## Impacto - Retweets, Favorites e Replies
tweets_sum = {'retweets': count_group(tweets, groups=['D', 'W', 'M', 'Y'], select=['retweets'], agg='sum'),
'favorites': count_group(tweets, groups=['D', 'W', 'M', 'Y'], select=['favorites'], agg='sum'),
'replies': count_group(tweets, groups=['D', 'W', 'M', 'Y'], select=['replies'], agg='sum'),
}
tweets_median = {'retweets': count_group(tweets, groups=['D', 'W', 'M', 'Y'], select=['retweets'], agg='median'),
'favorites': count_group(tweets, groups=['D', 'W', 'M', 'Y'], select=['favorites'], agg='median'),
'replies': count_group(tweets, groups=['D', 'W', 'M', 'Y'], select=['replies'], agg='median'),
}
# ### Agregado
print('Total de retweets: ', tweets['retweets'].sum())
print('Total de favorites: ', tweets['favorites'].sum())
print('Total de replies: ', tweets['replies'].sum())
# ### Por Ano
# +
data = []
for interaction in tweets_sum:
data.append(go.Bar(
x=tweets_sum[interaction]['Y'].index - 1,
y=tweets_sum[interaction]['Y'][interaction],
name=interaction))
layout = go.Layout(title='Number of interactions per year')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
data = []
for interaction in tweets_median:
data.append(go.Bar(
x=tweets_median[interaction]['Y'].index - 1,
y=tweets_median[interaction]['Y'][interaction],
name=interaction))
layout = go.Layout(title='Median of interactions per tweet per year')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# ### Por Mês
# +
data = []
for interaction in tweets_sum:
data.append(go.Scatter(
x=tweets_sum[interaction]['M'].index,
y=tweets_sum[interaction]['M'][interaction],
name=interaction))
layout = go.Layout(title='Number of interactions per month')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
data = []
for interaction in tweets_median:
data.append(go.Scatter(
x=tweets_median[interaction]['M'].index,
y=tweets_median[interaction]['M'][interaction],
name=interaction))
layout = go.Layout(title='Median of interactions per tweet per month')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# ### Por Semana
# +
data = []
for interaction in tweets_sum:
data.append(go.Scatter(
x=tweets_sum[interaction]['W'].index,
y=tweets_sum[interaction]['W'][interaction],
name=interaction))
layout = go.Layout(title='Median of interactions per week')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
data = []
for interaction in tweets_median:
data.append(go.Scatter(
x=tweets_median[interaction]['W'].index,
y=tweets_median[interaction]['W'][interaction],
name=interaction))
layout = go.Layout(title='Median of interactions per tweet per week')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# ### Distribuição de tweets por semana
tweets_sum['replies']['W']['replies'].describe(), tweets_sum['retweets']['W']['retweets'].describe(), tweets_sum['favorites']['W']['favorites'].describe()
# +
data = []
for interaction in tweets_sum:
data.append(go.Histogram(
x=tweets_sum[interaction]['W'][interaction],
name=interaction,
opacity=0.9))
layout = go.Layout(title='Median of interactions per week',
xaxis=dict(range=[0, 10000]),)
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# ### Média móvel de um mês de tweets por semana
# +
data = []
for i, interaction in enumerate(tweets_sum):
data.append(go.Scatter(
x=tweets_sum[interaction]['W'].index,
y=tweets_sum[interaction]['W'][interaction],
name=interaction,
mode='markers',
marker=dict(color=colorscale[i])))
data.append(go.Scatter(
x=tweets_sum[interaction]['W'].index,
y=tweets_sum[interaction]['W'][interaction].rolling(4, closed='right', min_periods=1).median(),
name=interaction + ' Rolling Month Median',
marker=dict(color=colorscale[i])))
layout = go.Layout(title='Number of interactions per week')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# ## Público
interactions.head()
# + [markdown] code_folding=[]
# ### Top Contas
# -
interactions.groupby(['username']).count()['tweet_id'].sort_values(ascending=False)
# ### Fidelidade
#
# Número de usuários com mais de uma interação ao longo dos anos
interactions = interactions.merge(tweets.reset_index(), on='tweet_id').sort_values(by=['timestamp']).reset_index()
first_inter = interactions[['index', 'username', 'timestamp', 'tweet_id']].groupby('username').first()
repeated_inter = interactions[~(interactions['index'].isin(first_inter['index']))]
first_inter = first_inter.set_index('timestamp')
repeated_inter = repeated_inter.set_index('timestamp')
# + active=""
# len(first_inter) / len(first_inter.reset_index()['username'].unique())
# -
len(repeated_inter.reset_index()['username'].unique()) / len(repeated_inter)
len(repeated_inter) + len(first_inter) == len(interactions)
fidelidade_count = {'novo': count_group(first_inter, agg='count', groups=['W', 'M', 'Y']),
'fiel': count_group(repeated_inter, agg='count', groups=['W', 'M', 'Y']),}
# +
data = []
for interaction in fidelidade_count:
data.append(go.Bar(
x=fidelidade_count[interaction]['Y'].index,
y=fidelidade_count[interaction]['Y']['tweet_id'],
name=interaction))
layout = go.Layout(title='Fidelidade da interação por ano', barmode='stack')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
data = []
for interaction in fidelidade_count:
data.append(go.Bar(
x=fidelidade_count[interaction]['M'].index,
y=fidelidade_count[interaction]['M']['tweet_id'],
name=interaction))
layout = go.Layout(title='Fidelidade da interação por mês', barmode='stack')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
data = []
for interaction in fidelidade_count:
data.append(go.Scatter(
x=fidelidade_count[interaction]['W'].index,
y=fidelidade_count[interaction]['W']['tweet_id'],
name=interaction))
layout = go.Layout(title='Fidelidade da interação por semana')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
data = []
total = fidelidade_count['novo']['M'].merge(fidelidade_count['fiel']['M'], right_index=True, left_index=True, how='outer',
suffixes=('_novo', '_fiel')).fillna(0)
for interaction in fidelidade_count:
if interaction == 'novo':
data.append(go.Bar(
x=total.index,
y=total['tweet_id_'+interaction] / total.sum(1),
name=interaction))
layout = go.Layout(title='Porcentagem de novos usuários interagindo por mês',
yaxis=dict(range=[0,1]))
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
data = []
total = fidelidade_count['novo']['W'].merge(fidelidade_count['fiel']['W'], right_index=True, left_index=True, how='outer',
suffixes=('_novo', '_fiel')).fillna(0)
for interaction in fidelidade_count:
if interaction == 'novo':
data.append(go.Scatter(
x=total.index,
y=total['tweet_id_'+interaction] / total.sum(1),
name=interaction))
layout = go.Layout(title='Porcentagem de novos usuários interagindo por semana',
yaxis=dict(range=[0,1]))
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# # Indentificação de Temas
from gensim.test.utils import common_texts,common_corpus
from gensim.corpora.dictionary import Dictionary
from gensim.models import LdaModel
import re
from gensim.utils import tokenize
import nltk
import gensim
# +
## Transform data
# -
tweet_text = tweets[['tweet_id', 'text', 'quote']].merge(image_text[['tweet_id', 'image_text']], on='tweet_id', how='outer')
tweet_text = tweet_text[['text', 'quote', 'image_text']].fillna('')
tweet_text = tweet_text.apply(lambda x: x['text'] + x['quote'] + x['image_text'], axis=1)
re.sub('http\S+', '', tweet_text[0])
tweet_text = tweet_text.apply(lambda x: re.sub(r'http\S+', '', x, flags=re.MULTILINE))
tweet_text = [list(tokenize(text)) for text in list(tweet_text)]
# +
stopwords = nltk.corpus.stopwords.words('portuguese')
stopwords = stopwords + ['mbl', 'twitter', 'youtube', 'pic', 'é', 'h',
'facebook', 'r', 'ep', 's', 'n', 'lo', 'faz', 'hora', 'pra', 'p','f']
tweet_text = [[word.lower() for word in document if word.lower() not in stopwords]
for document in tweet_text]
# +
## Train Model
# -
# Create a corpus from a list of texts
common_dictionary = Dictionary(tweet_text)
corpus = [common_dictionary.doc2bow(text) for text in tweet_text]
tfidf = gensim.models.TfidfModel(corpus)
corpus_tfidf = tfidf[corpus]
# Train the model on the corpus.
lda = gensim.models.LsiModel(corpus_tfidf, num_topics=10, id2word=common_dictionary)
lda.show_topics()
from collections import OrderedDict
import seaborn as sns
data = {i: OrderedDict(lda.show_topic(i,10)) for i in range(10)}
df = pd.DataFrame(data)
df = df.fillna(0).T
sns.clustermap(df.corr(), center=0, cmap="vlag", metric='cosine',
linewidths=.75, figsize=(13, 13))
# # Tweets por Tema
#
#
# ## Importando keywords dos temas
import yaml
import re
import unidecode
def parenthetic_contents(string):
"""Generate parenthesized contents in string as pairs (level, contents)."""
stack = []
for i, c in enumerate(string):
if c == '(':
stack.append(i)
elif c == ')' and stack:
start = stack.pop()
yield (len(stack), string[start + 1: i])
def convert_keywords(string):
# get rules with parenthesis
string = '(' + string.replace(' OR ', ') OR (') + ')'
string = string.replace('AND', 'NEAR/4')
p = parenthetic_contents(string)
p = [x[1] for x in list(filter(lambda x: x[0] == 0, p))]
p_p, p_w = [x for x in p if '(' in x], [x for x in p if '(' not in x]
# functions
strip_accents = lambda p: unidecode.unidecode(p)
filter_or = lambda p: [x for x in p if 'OR' not in x]
reg = re.compile('[a-z|*]+', re.UNICODE)
regex_it = lambda p: reg.findall(p)
strip_thing = lambda p: p.strip('"')
add_dots = lambda p1, p2: p1 + ' (...) ' + p2
flatten = lambda l: [item for sublist in l for item in sublist]
# treat parenthesis
p_p = [x.split('NEAR/') for x in p_p]
p_p = [[filter_or(regex_it(strip_accents(x))) for x in y] for y in p_p]
p_p = list(map(lambda x: [[add_dots(p1, p2) for p1 in x[0]] for p2 in x[1] if len(x) == 2], p_p))
p_p = flatten(flatten(p_p))
return list(map(strip_thing, p_p + p_w))
keywords = yaml.load(open('keywords.yaml', 'r'))
keywords.keys()
keywords_complex = yaml.load(open('keywords_complex.yaml', 'r'))
keywords.update({k: convert_keywords(v) for k, v in keywords_complex.items()})
keywords.keys()
# ## Selecionando Tweets por keyword
tweets_text = tweets[['tweet_id', 'text', 'quote', 'hashtags']].merge(image_text[['tweet_id', 'image_text']],
on='tweet_id', how='left', right_index=True)
tweets_text = tweets_text.set_index('tweet_id')
tweets_text.head(2)
# +
from collections import defaultdict
def search_keywords(df, keywords):
df['text'] = df['text'].apply(strip_accents)
result = defaultdict(lambda: pd.DataFrame())
for theme, keys in keywords.items():
for key in keys:
if '(...)' in key:
first, second = [a.strip() for a in key.split('(...)')]
key = '({}).*({})'.format(first, second)
result[theme][key] = (df['text'].str.contains(key, regex=True, case=False) |
(df['image_text'].str.contains(key, regex=True, case=False)) |
(df['image_text'].str.contains(key, regex=True, case=False)))
return result
# -
# ### Sem tratamento
search_result = search_keywords(tweets_text, keywords)
# #### Quantidade de Tweets por Tema
# +
no_theme = []
for theme in search_result.keys():
no_theme.extend(list(search_result[theme][search_result[theme].sum(1) == 0].index))
no_theme = pd.Series(no_theme).value_counts()
no_theme = list(no_theme[no_theme == len(search_result.keys())].index)
# +
data = [go.Bar( x=[theme for theme in search_result.keys()] + ['Sem tema'],
y=[search_result[theme].sum(1).sum() for theme in search_result.keys()] + [len(no_theme)],
name=theme,
opacity=0.9)]
layout = go.Layout(title='Number of tweets by theme',)
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# #### Quantidade de Tweets por Tema por Mês
def count_date(search_result, tweets, theme, freq):
return (search_result[theme].merge(tweets[['tweet_id']], left_index=True, right_on='tweet_id')
.groupby(pd.Grouper(freq=freq)).agg('sum').sum(1))
# +
data = []
for theme in search_result.keys():
print(theme)
res = count_date(search_result, tweets, theme, 'M')
data.append(go.Scatter(
x=res.index,
y=res,
name=theme))
layout = go.Layout(title='Number of tweets by theme per month')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# #### Interações por Tema
def theme_interaction(interactions, search_result, theme):
return (interactions[
interactions['tweet_id']
.isin(search_result[theme][search_result[theme].sum(1) > 0].index)]
)
# +
data = [go.Bar( x=[theme for theme in search_result.keys()],
y=[theme_interaction(tweets, search_result, theme)['retweets'].sum() for theme in search_result.keys()],
name=theme,
opacity=0.9)]
layout = go.Layout(title='Number of retweets per theme',)
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
data = [go.Bar( x=[theme for theme in search_result.keys()],
y=[theme_interaction(interactions, search_result, theme)['retweets'].sum()/search_result[theme].sum(1).sum()
for theme in search_result.keys()],
name=theme,
opacity=0.9)]
layout = go.Layout(title='Mean Number of retweets per theme',)
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# -
# #### Interações por tema por mês
def count_interaction(tweets, search_result, theme, freq, interaction_type):
return (theme_interaction(tweets, search_result, theme)
.groupby(pd.Grouper(freq=freq)).agg('sum'))[interaction_type]
# +
data = []
for theme in search_result.keys():
res = count_interaction(tweets, search_result, theme, 'M', 'retweets')
data.append(go.Scatter(
x=res.index,
y=res,
name=theme))
layout = go.Layout(title='Number of interactions by theme per month')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
data = []
for theme in search_result.keys():
res = count_interaction(tweets, search_result, theme, 'M', 'retweets')
data.append(go.Scatter(
x=res.index,
y=res / count_date(search_result, tweets, theme, 'M'),
name=theme))
layout = go.Layout(title='Mean number of retweets by theme per month')
fig = dict(layout=layout, data=data)
offline.iplot(fig)
# +
search_result['seguranca-publica'].merge(tweets, left_index=True, right_on='tweet_id')['04/2016':'05/2016'].sort_values(by='retweets', ascending=False)
# -
# #### Exportação
def get_text_theme(search_result):
for theme in search_result.keys():
a = search_result[theme].reset_index()
a = a.melt(id_vars='tweet_id')
a[a['value'] == True].merge(tweets, on='tweet_id').to_csv('../data/output/{}.csv'.format(theme))
get_text_theme(search_result)
# ## Exportações Geral
tweets.to_csv('../data/tweets.csv')
tweets[tweets['tweet_id'].isin(no_theme)].to_csv('../data/output/no_theme.csv')
| 35.332967 | 5,693 |
3d2fad6f5e15b5c69c94d5ff1a135b51e578f31c
|
py
|
python
|
.ipynb_checkpoints/Chapter 4 - Aggregate Supply, Technology, and Economic Growth-checkpoint.ipynb
|
jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Aggregate Supply, Technology, and Economic Growth
#
# In chapter 4, we introduced the equation of exchange. An accounting identity, the equation of exchange provides a means of framing total demand and supply across the economy. Aggregate demand refers to the total value of expenditures. This is represented as the product of the total quantity of money in circulation, $M$, and the average number of times each unit of currency is spent, $V$. In later chapters we will consider factors of aggregate demand in detail.
#
# Money is used to purchase goods. We refer to the goods purchased as real income, $y$. In macroeconomics, we operate from the assumption that, at any given moment , their is some sustainable rate of growth of real income. This is the long-run level of economic growth whose referent is $y_0$. We will defend this assumption in this chapter using the Solow model. In reality, it is possible for this value to change. Data reflecting real economic growth suggests that a positive rate of growth of around 2 to 3 percent per year is sustainable. Aggregate supply is output that becomes real income once it is purchased. Real income provides value to the consumer who purchases the goods or services represented by it. We observe the nominal value of production, which includes changes in the value of money used to purchase goods. To estimate the portion of nominal income that represents real value, $y$, as opposed to changes in nominal income that represent changes in the general level of prices $P$.
#
# In this chapter, we investigate more deeply the fundamentals of aggregate supply. We will build a model of production and income and use it to justify our assumption of a long-run level of income. Having developed this model, we consider the factors that can promote or inhibit economic growth.
#
# ## Real Income
#
# A theory of economic growth is concerned with what factors influence real income. We are concerned with other variables from the equation of exchange inasmuch as they explain changes in aggregate income. Money is a means to income. Velocity reflects the average person's willingness to part with money in exchange for real goods. We will see in chapter 5 that money is itself an innovation that increased the wealth creating potential of the economic system.
#
# Fundamentally, real income represents value. We cannot know exactly how much one person values a good compared to another person. We can observe how much one person is willing to pay compared to another. In a moneyed economy, the market agglomerates individual preferences in terms of consumer willingness and ability to exchange currency for goods in the form of prices. Thus, the value of a good is implied by the price paid for the good.
#
# Individuals engaged in production and exchange must choose which goods they will purchase. Thus, nominal income reflects the valuations of consumers in present units of currency. Across time, real income reflects these valuation in terms adjusted for inflation that implies changes in the value of money. This adjustment allows us to compare value creation in the economy from period to period and to observe whether the economy is growing or shrinking.
#
# ### Short-run and Long-run
#
# While the concepts of short-run and long-run may appear to have an intuitive interpretation, they have a different meaning than simply a short amount of time and a long amount of time. Rather, long-run and short-run reference the position of the economy relative to monetary equilibrium where the quantity of money demanded is equal to the quantity supplied. If economic variables reflect this predicted steady-state, then the economy has reached the level of income that is sustainable in the long-run. The short-run, by contrast, represents periods where the observed level of real income deviate from the level sustainable in the long-run. Short-run deviations from the long-run level of real income persist until prices adjust to accurately reflect the quantity of money in the economy and preferences of individuals to hold money. We assume that, in the long-run, the value of economic output sold is equal to the level that can be produced sustainably. In the very-long-run, the total value of real income in the steady-state may itself change. The reason for this will be shown with the presentation of the Solow model.
#
# The distinction between the long-run and short-run is fundamental to macroeconomic theory. Economic theory predicts convergence toward long-run outcomes. Competition between producers minimize production costs, thereby maximizing the quantity produced. Competition between consumers guides resources toward those who are most willing to pay for them. Historical data shows that these outcomes tend to predominate. The competition that drives long-run outcomes, however, is a process. It is by the identification and correction of short-run deviations from long-run outcomes that entrepreneurs profit, whether those disturbance occur in goods markets or in the money market, the latter of which leads to perturbations across the economy.
#
# In the short-run, monetary disturbances may move productivity away from its full potential. The imperfect link between financial markets and markets for real goods make the short-run of special significance for macroeconomics. Shifts in financial markets - meaning shifts in the quantity of money and demand to hold money - influence the level of aggregate expenditures. These deviations can influence real income in the short-run.
#
# John Maynard Keynes famously noted:
#
# >. . . this long run is a misleading guide to current affairs. In the long run we are all dead. Economists set themselves too easy, too useless a task, if in tempestuous seasons they can only tell us, that when the storm is long past, the ocean is flat again. (Keynes 1923, 80)
#
# Until the economy has reached the long-run steady state, economic conditions are characterized by short-run dynamics. We will elaborate these dynamics, including some of the arguments put forward by Keynes, in the chapters explaining money and aggregate demand.
#
# ## Long-run Steady-state
#
# Chapter 3 presented supply and demand for analysis of particular markets. In addition to microeconomic equilibrium, macroeconomics emphasizes the equlibrating tendencies of money markets, often referred to as macroeconomic equilibrium or monetary equilibrium. In the long-run, markets tend toward this equilibrium where the quantity produced of each good and the good's price accurately reflect conditions of supply and demand. If money markets fail to reach equilibrium, then the macroeconomy is said to be in a state of disequilibrium. In the long-run, prices move to remedy a situation where the quantity supplied of each good does not match the quantity demanded. This includes the price of money. The adjustment inevitably moves the level implied by the intersection of the supply and demand curves.
#
# The long-run is essentially defined by the absence of these discrepancies - absence of disequilibrium! Prices adjust to their long-run equilibrium, offsetting all excess supplies and excess demands for goods. As mentioned above, we presume a long-run level of output in macroeconomic theory. This long run level is referred to as Long-run Aggregate Supply ($LRAS$) and is represented by $y_0$. In this book, we define macroeconomic equilibrium as:
# >$y_i=y_0$
#
# The observed value of aggregate income, $y_i$, is equal to the long run value, $y_0$. The remainder of the equation of exchange can be used to express long-run equilibrium. First define real income in terms of the other variables:
# > $y_i=\frac{M_iV_i}{P_i}$
#
# In equilibrium, the values of the nominal variables, $M$, $V$, and $P$, must adjust to produce the value $y_0$. We typically assume that $M$ and $V$ are fixed, therefore PP must adjust to foster macroeconomic equilibrium:
#
# > $y_i=\frac{M_0V_0}{P_i}y$
#
# Equilibrium in the classical model of macroeconomics tended to be offset by an adjustment in the price level. Monetary disequilibrium persists until $P_i$ adjusts to bring the real value of total expenditures, $\frac{M_0V_0}{P_i}$, into equality with $y_i$.
#
# We can represent this proposition graphically with a graph of $AD$ and $LRAS$:
#
# > <img src="https://github.com/jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium/blob/main/Chapter%204/Figure%201.png?raw=true" alt="Market for Non-money Goods"/>
# > <center> <b>Figure 1
#
# $LRAS$ is defined as $y_0$. The aggregate demand curve represents the value of total expenditures. The line represents different combinations of $P$ and $y$ that produce that value. Thus, as $P$ increases, $y$ decreases and vice versa. If we consider an aggregate demand curve of some fixed value, then $P$ must fall to a particular level, $P_0$. We rewrite the equilibrium condition to reflect this:
#
# >$y_0=\frac{M_0V_0}{P_0}$
#
# For a given value of aggregate demand, the value $y_0$ implies a particular value, $P_0$. Without any change in the in the quantity of money or demand to hold money, all available goods in the market may be sold only if the level of prices adjust to $P_0$. Increases in real income realized in the economy that result from a fall in the value of $P$ are reffered to as wealth effects. These increases in wealth simiply represent a movement from disequilibrium to the long-run equilibrium value of $y$.
#
# Economic growth, on the other hand, can only be described by an increase in the long-run aggregate supply curve. We will review of the real income data seems to suggest a long-run rate of economic growth, essentially a dynamic representation of the long-run steady state. Starting at the end of the 18th century, this rate of growth began to increase thanks to increase in the contribution of technology to productivity. We follow this with the development of the Solow model to justify both the long-run aggregate supply and any shift not related to an increase in population and to elaborate the logic of sustained economic growth.
#
# ## Empirical Justification for Long-run Aggregate Supply
#
# The long-run level of real income tends to be relatively stable. Empirically, an assumption of a fixed LRAS appears to be justified. The LRAS may shift from time to time, but it remains relatively stable for extended periods of time. In image 2, the 10 year moving average of the growth of real income shows that real income growth remained around 3 percent on average for several decades and recently dropped to 2 percent. One reason for this shift is that population growth in the United States has tended to slow in the last several decades.
#
#
# > <img src="https://github.com/jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium/blob/main/Chapter%204/Figure%202.png?raw=true" alt="Real GDP Growth Rate and 10 Year Moving Average"/>
# > <center> <b>Figure 2
# > <img src="https://github.com/jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium/blob/main/Chapter%204/Figure%202.png?raw=true" alt="Real GDP Per Capita Growth Rate and 10 Year Moving Average"/>
# > <center> <b>Figure 3
#
#
# Controlling for population growth, these statistics show similar stability. By and large, the growth rate of real GDP per capita has remained around 2 percent for several decades, only falling after the recent crisis. Presuming that another crisis as significant as that of 2008 does not occur in the next few years, the 10 year moving average for the growth rate of real GDP per capita should recover significantly by the end of 2019. Or, it is possible that significant adjustments in the structure of governance, unexpected events like a large-scale war, or events that are simply not predictable could prevent this continuance of the observed long-run growth rate. Below, we will present the Solow model to show why this sort of stability is expected.
#
# The value of $y_0$ is not determined by any variables in the equation of exchange. Instead it is a function of efficiency-increasing technology. Technology in this case refers to any form of organization, physical or social, that impacts the cost of production. Some quintessential examples of physical technology include electricity, communication via telegraph, telephone, or the internet, or rail transport powered by coal burning engines. Of course, there are many other physical technologies that reduce production costs. Technologies from this short list radically transformed economic organization wherever they were implemented. Other technologies include constitutional democracy. In particular those that have developed from a tradition of common law show great stability and are associated with more robust economic growth than those societies that lack these institutions.
#
# ## Economic Growth in the Modern Era
#
# For most of human history, economic growth was relatively muted. The vast majority of people lived in rural areas. Only a small number of areas actually accumulated wealth, and such accumulation was difficult to maintain. Economic historian Joel Mokyr reflects:
#
# >Before 1750, growth had been limited to relatively small areas or limited sectors, often a successful city state, a capital of a powerful monarch, or a limited agricultural region. These niches had to spend much of their riches to protect their possessions against greedy neighbors, real-life manifestations of Mancur Olson's 'roving 'bandits' who often killed entire flocks of golden-egg-laying geese. . . Second, pre-1750 growth, such as it was, was dominated by institutional change in its widest sense: law and order, the establishment of commercial relations, credit, trust, and enforceable contracts created the preconditions for wealth to expand through more efficient allocation, exchange and investment. . . Third, premodern growth was normal not sustainable and remained vulnerable to set-backs and shocks, both man-made and natural. (2005, 286)
#
# Starting in the 1750s, the development of productive technologies began to significantly impact economic growth. Early mechanization standardized and increased the pace of production. While it took nearly a century to lead to modern rates of economic growth, these improvements laid the foundation for a radical transformation of the economy, making it more efficient and capable of sustaining a population whose size could scarcely be imagined in the 18th century.
#
#
# > <img src="https://github.com/jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium/blob/main/Chapter%204/Figure%204.jpg?raw=true" alt="Thomas_Robert_Malthus"/>
# > <center> <b> Figure 4
#
# In fact, Thomas Malthus, an early economist of repute, believed that industrialization and the growth in population that it supported was leading civilization toward a catastrophe: a "Malthusian Crisis"! Malthus predicted that as population increased, this would eventually lower the marginal productivity of each unit of labor. Malthus expected that population growth would continue to increase eventually outpacing economic growth. Two centuries later, we observe that Malthus was incorrect in his prediction.
#
# One way to evaluate Malthus's prediction is to consider per capita real income growth. According to Malthus, the population crisis would manifest as the population grows at a rate faster than real income. If Malthus was correct, the large increase in population should lead to a fall in real incomes of individuals due to scarcity of resources. Ever since the age that Thomas Malthus wrote in, incomes of individuals around the world have tended to rise steadily.
#
# Starting in the early 19th century, the West and, soon after, the rest of the World experienced an explosion of economic growth. At most place and times, poverty was the norm. Of course, many individuals in different societies have had a high quality of life during that time. The risks from famine and disease were much more common before the transformation of society that occurred with the industrial revolution. There certainly was no expectation of continuous economic growth that would life a great proportion of society out of poverty.
#
# > <img src="https://github.com/jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium/blob/main/Chapter%204/Figure%205.png?raw=true" alt=" Real GDP Per Capita (2011 Dollars) from Maddison Project"/>
# > <center> <b>Figure 5
#
# It is no coincidence that the take off in economic growth occurred just as the industrial revolution moved into full swing. The coincidence is clear enough. The improvement in productivity did not occur in a vacuum. The economy and social life more generally experienced a massive, structural transformation. The development of enlightenment thought, especially of tolerant liberalism, lessened social constraints. It also motivated and reinforced democratic reforms in governance. Scientific revolution embodied by Copernicus, Galileo, Descartes, Bacon, Newton, and others laid foundation that would later be employed by tinkerers. The invention of mechanized processes and improvements in maritime navigation are just two of many significant results enabled by this development of scientific thought. All of these changes in thought and organization represent changes in technology that together increased the efficiency of production and provision of goods. This improvement in technical efficiency increased the marginal productivity of capital and labor. Below we model this insight and follow with a description of technologies and their sources.
#
# ## Solow Model
#
# Before discussing growth factors in greater depth, we will arrange the economic facts with the Solow Model. This model aggregates the traditional microeconomic model of the firm transforms the model to predict equilibrium outcomes of the macroeconomy. Unlike the equation of exchange, the Solow Model is not an accounting identity. It provides definition of real a long-run level of real income, linking inputs - capital and labor ($K$ and $L$) - with this outcome.
#
# + language="html"
#
# <iframe width="560" height="315" src="https://www.youtube.com/embed/eVAS-t83Tx0" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
# -
# ### Production
#
# The neoclassical model of production provides an abstract, yet intuitive, presentation of production. It states that the quantity of goods produced by a firm is a function of capital and labor:
#
# The neoclassical model of production provides an abstract, yet intuitive, presentation of production. It states that the quantity of goods produced by a firm is a function of capital and labor:
#
# > $Q=f(K,L)$
#
# The productivity of each factor is represented by exponents:
#
# > $Q=K^\alpha L^\beta$
#
# We can conveniently aggregate capital using this model to consider features of aggregate production. Instead of $Q$, which is used to represent the output of a single firm, aggregate production is represented by the variable $y$. We assume that productivity exhibits constant returns to scale, which implies that there will be a point at which increases in labor and capital on their own do not cover the costs of each in terms of wages paid to labor and rents paid to capital. For the sake of analysis, we will take this constraint as a given and adopt the assumption of constant returns to scale for the production function as a whole, meaning that the exponents of $K$ and $L$ sum to one ($\alpha+1-\alpha=1$).
#
# > $y=K^\alpha L^{1-\alpha}$
#
# To provide a more useful measure, the equation can be normalized by labor. We may the equation by $L$, yielding:
#
# > $\frac{y}{L}=\frac{K^\alpha}{L^\alpha}$
#
# We may rewrite this equation using $ \boldsymbol y $ to represent $\frac{y}{L}$:
#
# > $\boldsymbol y =k^\alpha$
#
# Output normalized by labor is a function of capital normalized by labor. Although not the exact meaning of the equation, it is helpful to think of this in terms of output per capita, with L approximating the population under analysis. Thus, $\boldsymbol y$ has a corrolary in the real income per capita. The presentation of the Solow model will show that the economy has a natural tendency to produce the equilibrium level of output just as a firm will produce an equilibrium level of output. The Solow model literally views the macroeconomy as a single firm. While unrealistic, we will see that it is useful to frame the productivity of capital in these terms.
#
# ### Saving and Depreciation
#
# If economic growth were simply dependent upon the accumulation of capital, it would not be a very interesting problem. Economic growth, however, must always confront the depreciation of capital just as the neoclassical production function is constrained by the payment of wages and rents to capital and labor. This depreciation is a loss that must be offset by investment in new capital. By this logic, the Solow model considers the process of capital accumulation. The change in capital in one period is dependent upon the value of income saved that offsets the value lost through capital depreciation:
#
# > $\Delta k_t = s\boldsymbol y_t - \delta k_t$
#
# Where:
# > $δ<1$
# >
# > $s<1$
# >
# > $S=sy$
# >
# > $S=I$
#
# Agents save a fraction, $s$, of total income, $\boldsymbol y$, and this savings offsets the value of effective capital lost due to depreciation, $\delta k_t$. Capital in the next period is defined by the level of effective capital in the current period and the change in capital this period:
#
# > $k_{t+1}=k_t+ \Delta k_t$
#
# At some point, the value of savings will equal the total value of effective capital lost to depreciation. We define $k^*$ as the level of capital where $sy_t=\delta k_t$. The level of effective capital can occur either by the growth of the capital stock so long as $k_t <k^*$ or by a shrinking of the capital stock if $k_t>k_^*$. In the case that the capital stock is growing, the value of depreciation grows relatively larger each period until the value of deprecation matches the value of savings. Similarly, if the capital stock is shrinking, the value of depreciation decreases until it is finally brought to unity with the value of savings.
#
# The results is the steady state level of effective capital and effective real income. In the steady state, the value of savings is exactly equal to the value of depreciation of capital.
#
# > $sy = dk$
#
# This is represented by the intersection of the savings curve and the depreciation curve in Figure 6. The steady-state value of effective real income is defined by the steady-state value of capital. Since real effective capital is fixed in the steady-state, so is real income. Only by a change in 1) the rate of savings, 2) the rate of depreciation, or 3) the technical efficiency of capita can the steady-state values of effective capital and real income change. Next we relay the logic and significance of the technical efficiency of capital.
#
#
# > <img src="https://github.com/jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium/blob/main/Chapter%204/Figure%206.png?raw=true" alt="Solow Model"/>
# > <center> <b>Figure 6
#
# ### Golden Rule Steady State
#
# Neoclassical economic theory assumes that agents attempt to maximize utility. Since utility is a function of consumption, we this means that agents attempt to maximize consumption. Thus, the Solow Model suggests that the savings rate chosen by agents is the rate of savings that will maximize consumption.
#
# It may appear as though it would be a good idea for individuals to maximize the level of capital, since that would lead to the maximum level of effective real income. A savings rate of 100% would accomplish this end. However, a savings rate of 100% would also leave no value for consumption. In the new steady state, all of the income produced would be used to offset the depreciation of capital. An increase in the rate of savings may increase the level of consumption, but it may also decrease it. The result depends upon the trade off between an increase in income and the increase in savings required to offset depreciation, thereby maintaining the stead-state level of capital. If the increase in income resulting from an increase in savings is more than offset by an increase in
#
# Suppose, using the parameter values from and earlier question, we would like to find the golden-rate steady state predicted by the Solow model.
#
# Suppose that the rate of depreciation, $\delta$, is 0.1, the return to capital, $\alpha$, is 0.5,. What would be the golden-rule steady-state level of savings, capital and income? To solve this problem we will either need to find point where a marginal increase in income with respect to an increase the rate of savings is 0 and the second derivitive of income with respect to savings is negative using calculus, or we can solve by brute force, meaning that we will calculate every possible value. For simplicity,we will take the later approach:
# +
import pandas as pd
δ=.1 # depreciation rate
α=.5 # share of capital
solow_ss = {}
### Check k require for each steady state y
solow_ss["y"] = [i / 100 for i in range(1, 1001)]
solow_ss["k"] = [y ** 2 for y in solow_ss["y"]]
### Calculate depreciation, savings, and implied savings rate
# sy = δk
solow_ss["δk"] = [k * δ for k in solow_ss["k"]]
solow_ss["sy"] = [δk for δk in solow_ss["δk"]]
# s = δk / y
solow_ss["s"] = [round(δk / y,3) for y, δk in zip(solow_ss["y"], solow_ss["δk"])]
### Remaining income is dedicated to consumption
solow_ss["C"] = [y - sy for y, sy in zip(solow_ss["y"], solow_ss["sy"])]
ss_df = pd.DataFrame(solow_ss).set_index("s")
ss_df
# -
golden_rule = ss_df[ss_df["C"] == ss_df["C"].max()]
golden_rule
# +
import warnings
warnings.filterwarnings("ignore")
import matplotlib.pyplot as plt
plt.rcParams['axes.xmargin'] = 0
plt.rcParams['axes.ymargin'] = 0
plt.rcParams["font.size"] = 40
fig, ax = plt.subplots(2,3, figsize = (40,24))
i,j = 0, 0
for key, vals in ss_df.items():
if i == len(ax):
i=0
j+=1
a = ax[i][j]
vals.plot.line(legend = False, ax = a, linewidth = 5)
a.vlines(golden_rule.index,ymin = 0, ymax = golden_rule[key].iloc[0],
ls = "--", color = "k", linewidth = 5 )
a.hlines(golden_rule[key].iloc[0],xmin = 0, xmax = golden_rule.index[0],
ls = "--", color = "k", linewidth = 5 )
a.set_xlabel(ss_df.index.name)
a.set_ylabel(key)
plt.plot()
print(key, golden_rule[key].iloc[0])
i +=1
ax[1][2].set_xticks([])
ax[1][2].set_yticks([])
ax[1][2].axis("off")
# -
# In this case, once the rate of savings exceeds 0.5, then the value of consumption generated in each period of the steady-state is less than it would be at a savings rate of 0.5. Thus, the golden-rule steady-state includes a savings rate of 0.5.
#
# Unfortunately, the Solow model is unable to relate savings to the growth of technology. It assumes that savings represents income that is not consumed and which, therefore, automatically contributes to capital in the following period. It is obvious that this assumption does not hold in the real world. However, the model does yield the useful result that savings alone cannot generate sustained economic growth. Technological improvements are required for that.
#
# ## Technology and Economic Growth
#
# If the Solow Model was defined only by the presentation so far, it would be a theory of an equilibrium level of income that can only increase by an increase in the rate of savings. This cannot describe long-run economic growth. The rate of savings can only rise to a rate as high as 100%, in which case their would be no consumption. All income would be saved, invested, and only be able to offset depreciation of a relatively large capital stock. In reality, savings may be invested in improvements in technology. In other cases, such as the development of new forms of organization that improve economic efficiency, the impact of savings on changes is less direct. Research and models that have followed Solow have developed this insight.
# Long-run growth can only be improved by an increase of a factor that is exogenous - not included - in the production function. Solow presents this as "total factor productivity". We may think of this as value contributed by technology to the production of real income. "Total factor productivity" is represented by the variable $A$. We integrate this into the Solow model:
# $$y=Ak^\alpha$$
#
#
# Increase in $LRAS$ occurs due to improvement in $A$,"Total Factor Productivity", meaning an improvement in the efficiency of production induced by a change in technology. The shift in the $LRAS$, $y_0$, is proportional to the shift in **y** from the Solow model. In the short-run, shifts in $y$ may be tied to factors relating to aggregate demand, a factor not captured by the model. However, in the long-run, all shifts in long-run aggregate supply must be linked to improvements in "Total Factor Productivity". Improvements in real income exert downward pressure on the price level.
#
# Although the Solow model does not relate savings and "Total Factor Productivity", we can imagine that if savings is targeted toward investment in improvements in productive technology, that savings would improve the rate of economic growth by improving the technical efficiency of capital. In fact, it is difficult to tell a legitimates story about modern economic growth without considering the increased level of savings and improvements in the efficiency of finance that ultimately fed technology improving investments. As we will see, though, the story of technological growth is multifaceted.
# + language="html"
# <iframe width="560" height="315" src="https://www.youtube.com/embed/LQR7rO-I96A" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
# -
# ### Shifting the Long-run Aggregate Supply Curve
#
# The Solow model justifies the assertion of a long-run aggregate supply curve. A long-run aggregate supply curve implies that there is some efficient level of income per labor (hereafter we will refer to this as income per capita) which can be sustained in perpetuity. If the quantity of labor remains unchanged, then a stable steady state level of real income per capita also implies a steady state level of real income. The Solow model suggests that the reason for this is that the effective capital stock will tend to depreciate at a rate greater than the value of savings if the economy accumulates the level of effective capital required to produce more than this level of output.
#
# We refer to the sustainable level of real income as $y_0$. This is the value of long-run aggregate supply. Long-run aggregate supply is perfectly inelastic - vertical - as a result of representing this single value. Regardless of changes in the price level that occur due to monetary factors, the value of real income sustainable in the long-run will remain unchanged. Only by changes in technology - i.e., innovation in production, ideas, and organization - can the value of long-run aggregate supply. Shifts in the Solow steady-state also imply shifts in the the long-run aggregate supply curve. Since the Solow model assumes that individuals choose the rate of savings that will maximize their consumption each period, the steady-state level of capital and income can only change if the value of AA, the average technical efficiency of production, changes.
#
# The value of $A$ may change for several reasons. $A$ represents value added by efficiency increasing technology. Interpreted broadly, this means organization, whether organization of physical resources, social resources, or knowledge. Whatever the composition of these, if a change in one tends to decrease income overall, then $A$ falls. If production becomes more efficient due to a change in technology or organization, $A$ will rise. The direction of movement of AA determines the direction of movement of the long-run aggregate supply curve.
#
# > <img src="https://github.com/jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium/blob/main/Chapter%204/Figure%207.png?raw=true" alt="Improvement in Technology"/>
# > <center> <b>Figure 7
#
# If the total value that can be sustainably produced increases, then this means that the long-run aggregate supply curve shifts to the right. The new level of income is represented by $y_1$, which is greater than $y_0$. The increase in income represents a movement along the aggregate demand curve which is the curve that represents the effect of monetary factors on the price level and short-run changes in real-income (this will be elaborated in later chapters.
#
# > <img src="https://github.com/jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium/blob/main/Chapter%204/Figure%208.png?raw=true" alt="Degradation of Technology"/>
# > <center> <b>Figure 8
#
# It is also possible that the total value of production sustainable in the long-run shrinks. If this is the case, then long-run aggregate supply shifts to the left. The new level of income, $y_1$, is less than the original level of income, $y_0$. The new, lower level of real income is arrived at by a movement across the aggregate demand curve. For example, events like the burning of the library at Alexandria and the decay of the western portion of the Roman Empire represents a fall in $A$ that accompanied the dark ages in western Europe. The new intersection of the $LRAS_1$ and $AD_0$ indicates a higher price level since there is less real income purchased with a total expenditure level of a relatively higher value.
#
# Changes in real income and the price level, PP, are inversely correlated. The Solow model does not account for the price level because it's emphasis is on real factors, meaning factors that influence the long-run level of supply. When changes in the Solow model are represented in the standard framework of aggregate-supply and aggregate-demand, the change in long-run aggregate supply is shown to have and effect on the price level. Thus an increase in long-run aggregate supply pushes down price level whereas a decrease in long-run aggregate supply raises the price level. If the quantity of money remains unchanged, an increase in the real value of available goods and services can only be purchased if the price of each good falls on average. If fall in the real value of goods, representing a scenario where long-run aggregate supply falls, then increased scarcity must be reflected by a higher price level.
#
# ## Kinds of Technology
#
# Now that we understand the factor that allows for economic growth, we can consider the significance of the growth of useful knowledge and its role in economic development. For the sake of explanation, knowledge may be split between two types: scientific knowledge and tacit knowledge. Scientific knowledge is abstract and may be applied to many circumstance. Tacit knowledge is knowledge of particular time and place. The development of tact knowledge is often guided by scientific knowledge. Scientific knowledge may be informed by experience that results from the use and development of tacit knowledge.
#
# Consider the development of the steam engine. Scientific knowledge can formally describe how vapor molecules take up more space than water. Heating water to 212 degrees Fahrenheit will convert water to vapor, creating pressure if the water is released in a container. This understanding can enable one to arrive at the concept of a steam engine. The creation of a steam engine can only occur by a process of trial and error where different materials are tested, as are the shapes of these materials, style of gears used to transfer energy, and so forth. No amount of theorizing can displace the trial and error required for application.
#
# ### The Enlightenment and Development of Productive Technology
#
# The roots of economic prosperity lie in the transformation of human thought. Opportunities for the development and application of new ideas have not appeared with the same prominence that they were afforded during and after the enlightenment. Innovations accumulated no doubt. For example, the invention and refinement of double entry book-keeping merchant cities like Venice and Florence to prosper. This also increased the governance and tax collecting.
# Enlightenment gave more emphasis than before to the value of the individual. The potential of individual was allowed greater value as was the idea that the individual was responsible for learning and development of technical and moral knowledge. Obedience to a hierarchy, while perhaps necessary, should not deprive the individual of the autonomy required and enabled by his or her relationship with knowledge.
#
# To maintain and develop knowledge required precise cataloging of knowledge. Joel Mokyr points out that Sir Francis Bacon, examplar of enlightenment thought, was a champion of the development of useful knowledge:
#
# > This "Baconian Program" assumed that the main purpose of knowlege was to improve mankind's condition rather than the mere satisfaction of the most creative of human characteristics, curiosity,, or the demonstration of some metaphysical point such as illustrating the wisdom of the creator." (2005, 293)
#
# Mokyr identifies that farmers, artisans, merchants, and other members of the productive class began to press the "community of learned person" to provide knowledge that aided their pursuits. New knowledge can aid the development of new productive methods that decrease the costs of production, thus allowing a greater level of output at equivalent costs.
#
# In terms of economic theory, the development of cost reducing technology is often the result of the pursuit of profit. The spread of knowledge and use of cataloging lowered the cost of accessing knowledge. Entrepreneurs were in a position to conceive of changes that could increase the efficiency of their productive efforts. Those entrepreneurs who were the first to develop a successful method in their industry could reap profits associated with that method's early adoption. An increase in profits attracts attention of competitors, leading to the adoption of a new method by sensing entrepreneurs. As the new method spreads through an industry, this has the tendency of increasing supply and reducing the price of the good
#
#
# > <img src="https://github.com/jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium/blob/main/Chapter%204/Figure%209.png?raw=true" alt="Endogenous Innovation"/>
# > <center> <b>Figure 9
#
# This pattern has appeared at many times and places. For example, when gold became especially expensive during the late 19th century, a new process of gold mining - the cyanide process - was developed, greatly expanding production. More recently, the relatively high price of oil that occurred during the latter half of the the first decade of the new millennium led to a search for new sources of energy. It so happened that shale oil producers were able to take advantage of fracking and horizontal drilling technologies thanks to the high price of oil. In the process, producers learned how to lower costs so that they could continue drilling even after the price of oil fell.
#
# > <img src="https://github.com/jlcatonjr/Macroeconomics-Growth-and-Monetary-Equilibrium/blob/main/Chapter%204/Figure%2010.jpg?raw=true" alt="Trend of RAM Prices"/>
# > <center> <b>Figure 10
#
# The effect of the cost reducing entrepreneurial process is especially in prominent in computing technology. Moore's law, which states that the speed of technology doubles every 18 months, captures this effect. Demand for new technology is persistent across markets and both the pools of producers and users of this technology are rather large. Thus, a significant profit awaits the most efficient producers of processors, hard drives, random access memory, and forth. The competitive process rewards innovators, thereby rationalizing the production of computing technology in terms of efficiency.
#
# ### Ideas and Institutions
#
# Improvement in productive technology are not the only inputs into increases in "technical efficiency". The Enlightenment and simultaneous developments in governance transformed the institutional context in Western Europe. This was most obvious in the Netherlands and in Great Britain. Both of these areas housed centers of trade as they were located at the mouth of the North Sea.
#
# In Great Britain, the growth of market activity strengthened the merchant class and change the face of the ruling elite during a tumultuous 17th century. The regime that emerged adopted policies favorable toward the merchant elite and, eventually, reforms that allowed for freer market and reduced privilege of particular merchants and merchant groups. At the end of the 17th century, democratic regime had clearly established itself with the ascension of William of Orange, who explicitly cooperated with parliament, to the throne.
#
# Britain had already had a strong history of relative, though not perfect, equality for elites before the law. This was the feat accomplished by the Magna Carta which guaranteed the rights of the British elite and, over time, served as a source of liberty for the non-elite. The English common law tradition enabled local governance, acting as a long-term constraint of executive power. Not coincidentally, Great Britain was a fertile ground for the ideas of the enlightenment. In particular, the Scottish Enlightenment, which refers to the work of Francis Hutcheson, David Hume, Adam Ferguson, Adam Smith, and others, shifted social and governance structure in Great Britain further in the direction of individual liberty and freedom of commerce.
#
# Much of the success of his development is represented by the strength of security of property rights and rights to person. If either of these were violated, a British person could access the courts to settle a dispute. The combination of rights and liberties enabled British entrepreneurs to form and execute business plans without facing high levels of uncertainty from the political and legal systems. Not coincidentally, many societies with the political and legal systems that descended from the British tradition exhibit similar features and have experienced relative prosperity. The development of these ideas and institutions in the Anglo world served a role in leading the rest of Europe and, eventually, the rest of the world toward economic prosperity. The process was slow, to be sure, and did not move in a straight line. Despite this, improvement in the security of person and property and expansion of the domain of individual action has increased the wealth and welfare of individuals around the world.
#
#
# + language="html"
#
# <iframe width="560" height="315" src="https://www.youtube.com/embed/EExVqkbSwFk" frameborder="0" allowfullscreen></iframe>
# <iframe width="560" height="315" src="https://www.youtube.com/embed/a0nsKBx77EQ" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
#
# -
# # Review
#
# 1. The price level adjusts to promote monetary equilibrium in the short-run:
# a. False
# b. True
# c. Not enough information
#
# 2. The short-run refers to any instance where:
# a. the price level has reached its equilibrium value
# b. real income has reached its equilibrium value
# c. the price level and real income have not attained their equilibrium values
# d. none of the above
#
# #### Suppose that $y = k^{0.5}$ and that $k = 25$
# 3. What is the level of effective real income, $y$, generated from this level of effective capital?
#
# #### Suppose that the value of effective capital, $k$, in the current period is 16, the rate of depreciation, $\delta$, is 0.1, the return to capital, $\alpha$, is 0.5, and the rate of savings, $s$, is 0.2.
#
# 4. What will be the new value of effective capital. $k$ in the next period?
#
# #### Suppose that the value of effective capital, $k$, in the current period is 36, the rate of depreciation, $\delta$, is 0.1, the return to capital, $\alpha$, is 0.5, and the rate of savings, $s$, is 0.2.
# 5. What will be the new value of effective capital, $k$, in the next period?
#
# #### Suppose that the rate of depreciation, $\delta$, is 0.1, the return to capital, $\alpha$, is 0.5, and the rate of savings, $s$, is 0.2.
#
# 6. What is the steady state level of effective capital, $k$?
# 7. What is the steady state level of effective real income, $y$?
#
# #### Suppose that the rate of depreciation, $\delta$, is 0.1, the return to capital $\alpha$, is 0.5, the rate of savings, $s$, is 0.2, and the value of the technical efficiency of capital, $A$, is 2.
#
# 8. What is the steady state value of effective capital, $k$?
# 9. What is the real income, $y$?
#
# 10. In the steady state, the value of investment in capital each period:
# a. is greater than the value of capital depreciation
# b. is less than the value of capital depreciation
# c perfectly offsets the value of capital depreciation
#
# #### Recall that $MV \equiv PY$. Suppose that $M_0=1000$, $V_0=3$, $y_0=30$, and $P_0=100$
#
# 11. If $y_1$ represents an increase in real income to 60 units of real income, what will the new price level be if aggregate demand ($MV$) remains unchanged?
| 120.944297 | 1,154 |
c74308cba881148386a9aa2b527b80b4c78c91d5
|
py
|
python
|
Lectures/W08-L15-InitializationNormalizationActivation.ipynb
|
anthonyjclark/cs152sp22
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# formats: ipynb,py:percent
# text_representation:
# extension: .py
# format_name: percent
# format_version: '1.3'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# %% [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Things-to-Consider" data-toc-modified-id="Things-to-Consider-1"><span class="toc-item-num">1 </span>Things to Consider</a></span></li><li><span><a href="#Synthetic-Input" data-toc-modified-id="Synthetic-Input-2"><span class="toc-item-num">2 </span>Synthetic Input</a></span></li><li><span><a href="#Fully-Connected-Neural-Network-With-Linear-Output" data-toc-modified-id="Fully-Connected-Neural-Network-With-Linear-Output-3"><span class="toc-item-num">3 </span>Fully-Connected Neural Network With Linear Output</a></span></li><li><span><a href="#Training-Loop" data-toc-modified-id="Training-Loop-4"><span class="toc-item-num">4 </span>Training Loop</a></span></li><li><span><a href="#Examine-Hidden-Calculations" data-toc-modified-id="Examine-Hidden-Calculations-5"><span class="toc-item-num">5 </span>Examine Hidden Calculations</a></span><ul class="toc-item"><li><span><a href="#What-do-the-outputs-of-each-of-the-eight-hidden-layer-neurons-look-like?" data-toc-modified-id="What-do-the-outputs-of-each-of-the-eight-hidden-layer-neurons-look-like?-5.1"><span class="toc-item-num">5.1 </span>What do the outputs of each of the eight hidden layer neurons look like?</a></span></li></ul></li><li><span><a href="#Model-Initialization-and-Normalization" data-toc-modified-id="Model-Initialization-and-Normalization-6"><span class="toc-item-num">6 </span>Model Initialization and Normalization</a></span></li></ul></div>
# %% [markdown]
# ## Things to Consider
#
# 1. The purpose of activation functions.
# 1. The benefits of with and depth.
# 1. Causes of problematic gradients (vanishing and exploding).
# 1. Proper parameter initialization.
# 1. Normalization (input and between layers).
# %%
import torch
import torch.nn as nn
from torch.utils.data import DataLoader
from torchsummary import summary
from fastprogress.fastprogress import master_bar, progress_bar
import matplotlib.pyplot as plt
from jupyterthemes import jtplot
jtplot.style(context="talk")
# %% [markdown]
# ## Synthetic Input
# %%
N = 500
X = torch.linspace(-3, 3, N).reshape(-1, 1) + 3.1415926 * 10
y = torch.sin(X) + 0.5
_ = plt.plot(X, y)
# %% [markdown]
# ## Fully-Connected Neural Network With Linear Output
# %%
class NeuralNetwork(nn.Module):
def __init__(self, layer_sizes):
super(NeuralNetwork, self).__init__()
# Hidden layers
hidden_layers = [
nn.Sequential(nn.Linear(nlminus1, nl), nn.ReLU())
# nn.Sequential(nn.Linear(nlminus1, nl))
# nn.Sequential(nn.Linear(nlminus1, nl), nn.Sigmoid())
# nn.Sequential(nn.Linear(nlminus1, nl), nn.LeakyReLU())
for nl, nlminus1 in zip(layer_sizes[1:-1], layer_sizes)
]
# Output layer
output_layer = nn.Linear(layer_sizes[-2], layer_sizes[-1])
# output_layer = nn.Linear(layer_sizes[-2], layer_sizes[-1], bias=True)
# Group all layers into the sequential container
all_layers = hidden_layers + [output_layer]
self.layers = nn.Sequential(*all_layers)
def forward(self, X):
return self.layers(X)
# %% [markdown]
# ## Training Loop
# %%
def train(model, X, y, num_epochs=2000):
optimizer = torch.optim.Adam(model.parameters())
criterion = nn.MSELoss()
losses = []
for epoch in progress_bar(range(num_epochs)):
yhat = model(X)
loss = criterion(yhat, y)
losses.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
return losses
# Compare: width vs depth
# layer_sizes = (1, 100, 1) # "wider"
# layer_sizes = (1, 100, 100, 100, 100, 100, 5, 1) # "deeper"
layer_sizes = (1, 8, 1)
# Universal approximation theorem: a two-layer network can approximate any function
# - it takes O(2^n) exponential width
# - to have the same complexity as a polynomial deep network
model = NeuralNetwork(layer_sizes)
summary(model)
losses = train(model, X, y)
print(f"Final loss: {losses[-1]:.6f}")
# %%
yhat = model(X)
_, (ax1, ax2) = plt.subplots(2, 1)
ax1.plot(X, y, label="Target")
ax1.plot(X, yhat.detach(), label="Prediction")
ax1.legend()
_ = ax2.plot(losses)
# %% [markdown]
# ## Examine Hidden Calculations
# %% [markdown]
# ### What do the outputs of each of the eight hidden layer neurons look like?
# %%
final_layer_input = None
def capture_final_outputs(module, layer_in, layer_out) -> None:
global final_layer_input
final_layer_input = layer_in[0].detach()
# %%
# Register hook to capture input to final layer (if not already registered)
if final_layer_input == None:
final_layer = model.layers[-1]
final_layer.register_forward_hook(capture_final_outputs)
# Compute model output and capture input to final layer
# X = torch.linspace(10, 20, 100).reshape(-1, 1)
yhat = model(X)
# Grab parameters for the output layer
WL = list(model.parameters())[-2].detach()
bL = list(model.parameters())[-1].item()
# Plot each input to the final layer
plt.plot(X, final_layer_input * WL, label="Activation")
# # Plot the output of the final layer
# plt.plot(X, yhat.detach(), "o", label="yhat")
# # Compare with hand-computed final layer output
# plt.plot(X, final_layer_input @ WL.T + bL, "--", label="Combined Activations")
_ = plt.legend(bbox_to_anchor=(1.04,1), loc="upper left")
# %% [markdown]
# ## Model Initialization and Normalization
# %%
def init_weights(layer):
if type(layer) == torch.nn.Linear:
print("Initializing", layer)
if kind == "zeros":
layer.weight.data.fill_(0.0)
layer.bias.data.fill_(0.0)
elif kind == "ones":
layer.weight.data.fill_(1.0)
layer.bias.data.fill_(1.0)
elif kind == "uniform":
layer.weight.data.uniform_()
layer.bias.data.fill_(0.0)
elif kind == "normal":
layer.weight.data.normal_()
layer.bias.data.fill_(0.0)
elif kind == "normal2":
layer.weight.data.normal_() * (1 / torch.sqrt(torch.tensor(layer.weight.shape[0])))
layer.bias.data.fill_(0.0)
elif kind == "xavier":
torch.nn.init.xavier_uniform_(layer.weight)
elif kind == "kaiming":
torch.nn.init.kaiming_normal_(layer.weight)
else:
print(f"'{kind}' is not handled")
layer_sizes = (1, 10, 10, 10, 1)
model = NeuralNetwork(layer_sizes)
kind = "zeros"
model.apply(init_weights)
losses = train(model, X, y)
print(f"Final loss: {losses[-1]:.3f}")
with torch.no_grad():
A = X
std, mean = torch.std_mean(A)
print(f"\n*** A0: Mean = {mean.item():.3f}, STD = {std.item():.3f}\n")
for l, layer in enumerate(model.layers):
print(layer)
A = layer(A)
std, mean = torch.std_mean(A)
print(f"\n*** A{l+1}: Mean = {mean.item():.3f}, STD = {std.item():.3f}\n")
# %%
| 31.76 | 1,554 |
921693c82c39e975e261ad12598cd107f94b5844
|
py
|
python
|
docs/site/tutorials/walkthrough.ipynb
|
KawashimaHirotaka/Swift
|
['CC-BY-4.0']
|
# -*- coding: utf-8 -*-
# + [markdown] colab_type="text" id="zBH72IXMJ3JJ"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/swift/tutorials/walkthrough"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/swift/blob/master/docs/site/tutorials/walkthrough.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/swift/blob/master/docs/site/tutorials/walkthrough.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="LrO3-gmDO0mH"
# ## Swift for TensorFlow is a work-in-progress
#
# Swift for TensorFlow is still a work-in-progress. If you modify the code in this tutorial, you will frequently get unexpected error messages and kernel crashes. Restarting the kernel might occasionally help (Kernel > Restart in the Jupyter toolbar).
#
# We are working on stabilizing the compiler. You can help us by filing bugs on https://bugs.swift.org (set the "Component" field to "Swift for TensorFlow") or by emailing the [email protected] mailing list when you encounter unexpected error messages and kernel crashes.
# + [markdown] colab_type="text" id="JtEZ1pCPn--z"
# # Swift for TensorFlow: walkthrough
# + [markdown] colab_type="text" id="LDrzLFXE8T1l"
# This guide introduces Swift for TensorFlow by using Swift for TensorFlow to build a machine learning model that categorizes iris flowers by species. It uses Swift for TensorFlow to:
# 1. Build a model,
# 2. Train this model on example data, and
# 3. Use the model to make predictions about unknown data.
#
# This guide is a Swift port of the [TensorFlow custom training walkthrough](https://www.tensorflow.org/tutorials/eager/custom_training_walkthrough).
#
# ## TensorFlow programming
#
# This guide uses these high-level Swift for TensorFlow concepts:
#
# * Import data with the Datasets API.
# * Build models and layers using Swift abstractions.
# * Use Python libraries using Swift's Python interoperability when pure Swift libraries are not available.
#
# This tutorial is structured like many TensorFlow programs:
#
# 1. Import and parse the data sets.
# 2. Select the type of model.
# 3. Train the model.
# 4. Evaluate the model's effectiveness.
# 5. Use the trained model to make predictions.
# + [markdown] colab_type="text" id="yNr7H-AIoLOR"
# ## Setup program
# + [markdown] colab_type="text" id="1J3AuPBT9gyR"
# ### Configure imports
#
# Import TensorFlow and some useful Python modules.
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="g4Wzg69bnwK2" outputId="b147c0b3-efa5-4d44-ff55-711dc49fdb4b"
import TensorFlow
import Python
%include "EnableIPythonDisplay.swift"
IPythonDisplay.shell.enable_matplotlib("inline")
let plt = Python.import("matplotlib.pyplot")
// Download some helper files that we will include later.
let path = Python.import("os.path")
let urllib = Python.import("urllib.request")
let helperFiles = ["TutorialDatasetCSVAPI.swift", "TutorialModelHelpers.swift"]
for helperFile in helperFiles {
if !Bool(path.isfile(helperFile))! {
print("Downloading \(helperFile)")
urllib.urlretrieve(
"https://raw.githubusercontent.com/tensorflow/swift-tutorials/master/iris/" + helperFile,
filename: helperFile)
} else {
print("Not downloading \(helperFile): already exists")
}
}
# + [markdown] colab_type="text" id="Zx7wc0LuuxaJ"
# ## The iris classification problem
#
# Imagine you are a botanist seeking an automated way to categorize each iris flower you find. Machine learning provides many algorithms to classify flowers statistically. For instance, a sophisticated machine learning program could classify flowers based on photographs. Our ambitions are more modest—we're going to classify iris flowers based on the length and width measurements of their [sepals](https://en.wikipedia.org/wiki/Sepal) and [petals](https://en.wikipedia.org/wiki/Petal).
#
# The Iris genus entails about 300 species, but our program will only classify the following three:
#
# * Iris setosa
# * Iris virginica
# * Iris versicolor
#
# <table>
# <tr><td>
# <img src="https://www.tensorflow.org/images/iris_three_species.jpg"
# alt="Petal geometry compared for three iris species: Iris setosa, Iris virginica, and Iris versicolor">
# </td></tr>
# <tr><td align="center">
# <b>Figure 1.</b> <a href="https://commons.wikimedia.org/w/index.php?curid=170298">Iris setosa</a> (by <a href="https://commons.wikimedia.org/wiki/User:Radomil">Radomil</a>, CC BY-SA 3.0), <a href="https://commons.wikimedia.org/w/index.php?curid=248095">Iris versicolor</a>, (by <a href="https://commons.wikimedia.org/wiki/User:Dlanglois">Dlanglois</a>, CC BY-SA 3.0), and <a href="https://www.flickr.com/photos/33397993@N05/3352169862">Iris virginica</a> (by <a href="https://www.flickr.com/photos/33397993@N05">Frank Mayfield</a>, CC BY-SA 2.0).<br/>
# </td></tr>
# </table>
#
# Fortunately, someone has already created a [data set of 120 iris flowers](https://en.wikipedia.org/wiki/Iris_flower_data_set) with the sepal and petal measurements. This is a classic dataset that is popular for beginner machine learning classification problems.
# + [markdown] colab_type="text" id="3Px6KAg0Jowz"
# ## Import and parse the training dataset
#
# Download the dataset file and convert it into a structure that can be used by this Swift program.
#
# ### Download the dataset
#
# Download the training dataset file from http://download.tensorflow.org/data/iris_training.csv. We use a Python library to demonstrate Swift's Python interoperability. Swift's Python interoperability makes it easy and natural to import and use Python libraries from Swift code.
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="DKkgac4WO0mP" outputId="3b49299f-ee97-4cbe-ab6c-28dd4de4b60b"
let urllib = Python.import("urllib.request")
let downloadResult = urllib.urlretrieve("http://download.tensorflow.org/data/iris_training.csv",
"iris_training.csv")
let trainDataFilename = String(downloadResult[0])!
trainDataFilename
# + [markdown] colab_type="text" id="qnX1-aLors4S"
# ### Inspect the data
#
# This dataset, `iris_training.csv`, is a plain text file that stores tabular data formatted as comma-separated values (CSV). Let's look a the first 5 entries.
# + colab={"base_uri": "https://localhost:8080/", "height": 119} colab_type="code" id="FQvb_JYdrpPm" outputId="4ca91888-7474-4a5c-bcc9-f80c693c0d5a"
let f = Python.open(trainDataFilename)
for _ in 0..<5 {
print(Python.next(f).strip())
}
f.close()
# + [markdown] colab_type="text" id="kQhzD6P-uBoq"
# From this view of the dataset, notice the following:
#
# 1. The first line is a header containing information about the dataset:
# * There are 120 total examples. Each example has four features and one of three possible label names.
# 2. Subsequent rows are data records, one *[example](https://developers.google.com/machine-learning/glossary/#example)* per line, where:
# * The first four fields are *[features](https://developers.google.com/machine-learning/glossary/#feature)*: these are characteristics of an example. Here, the fields hold float numbers representing flower measurements.
# * The last column is the *[label](https://developers.google.com/machine-learning/glossary/#label)*: this is the value we want to predict. For this dataset, it's an integer value of 0, 1, or 2 that corresponds to a flower name.
#
# Let's write that out in code:
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="9Edhevw7exl6" outputId="4fd2018f-e0fa-4941-f851-7fab74e0ee8c"
let featureNames = ["sepal_length", "sepal_width", "petal_length", "petal_width"]
let labelName = "species"
let columnNames = featureNames + [labelName]
print("Features: \(featureNames)")
print("Label: \(labelName)")
# + [markdown] colab_type="text" id="CCtwLoJhhDNc"
# Each label is associated with string name (for example, "setosa"), but machine learning typically relies on numeric values. The label numbers are mapped to a named representation, such as:
#
# * `0`: Iris setosa
# * `1`: Iris versicolor
# * `2`: Iris virginica
#
# For more information about features and labels, see the [ML Terminology section of the Machine Learning Crash Course](https://developers.google.com/machine-learning/crash-course/framing/ml-terminology).
# + colab={} colab_type="code" id="sVNlJlUOhkoX"
let classNames = ["Iris setosa", "Iris versicolor", "Iris virginica"]
# + [markdown] colab_type="text" id="dqPkQExM2Pwt"
# ### Create a Dataset
#
# Swift for TensorFlow's Dataset API handles loading data into a model. This is a high-level API for reading data and transforming it into a form used for training. Currently, Swift's Dataset API supports loading data only from CSV files, but we intend to extend it to handle many more types of data, like [TensorFlow's Dataset API](https://www.tensorflow.org/guide/datasets).
#
# Use the `Dataset(contentsOfCSVFile:hasHeader:featureColumns:labelColumns:)` initializer to initialize a `Dataset` with training data. Also batch the data into batches using the `.batched()` function.
# + colab={} colab_type="code" id="bBx_C6UWO0mc"
public let batchSize = Int64(32)
%include "TutorialDatasetCSVAPI.swift"
let trainDataset: Dataset<TensorPair<Tensor<Float>, Tensor<Int32>>> = Dataset(
contentsOfCSVFile: trainDataFilename, hasHeader: true,
featureColumns: [0, 1, 2, 3], labelColumns: [4]
).batched(batchSize)
# + [markdown] colab_type="text" id="gB_RSn62c-3G"
# This returns a `Dataset` of `(features, labels)` pairs, where `feature` is a `Tensor<Float>` with shape `(batchSize, featureColumns.count)` and where `labels` is a `Tensor<Int32>` with shape `(batchSize, labelColumns.count)`
#
# These `Dataset` values are iterable. Let's look at the first element of the dataset.
# + colab={"base_uri": "https://localhost:8080/", "height": 54} colab_type="code" id="iDuG94H-C122" outputId="d9c83db7-7071-4128-87d7-55fb9815c853"
let firstTrainExamples = trainDataset.first!
let firstTrainFeatures = firstTrainExamples.first
let firstTrainLabels = firstTrainExamples.second
firstTrainFeatures
# + [markdown] colab_type="text" id="E63mArnQaAGz"
# Notice that like-features are grouped together, or *batched*. Each example row's fields are appended to the corresponding feature array. Change the `batchSize` to set the number of examples stored in these feature arrays.
#
# You can start to see some clusters by plotting a few features from the batch, using Python's matplotlib:
# + colab={"base_uri": "https://localhost:8080/", "height": 300} colab_type="code" id="me5Wn-9FcyyO" outputId="884948e1-4e69-439e-9913-37cda4d4e902"
let firstTrainFeaturesTransposed = firstTrainFeatures.transposed()
let petalLengths = firstTrainFeaturesTransposed[3].scalars
let sepalLengths = firstTrainFeaturesTransposed[0].scalars
plt.scatter(petalLengths, sepalLengths, c: firstTrainLabels.array.scalars)
plt.xlabel("Petal length")
plt.ylabel("Sepal length")
plt.show()
# + [markdown] colab_type="text" id="LsaVrtNM3Tx5"
# ## Select the type of model
#
# ### Why model?
#
# A *[model](https://developers.google.com/machine-learning/crash-course/glossary#model)* is a relationship between features and the label. For the iris classification problem, the model defines the relationship between the sepal and petal measurements and the predicted iris species. Some simple models can be described with a few lines of algebra, but complex machine learning models have a large number of parameters that are difficult to summarize.
#
# Could you determine the relationship between the four features and the iris species *without* using machine learning? That is, could you use traditional programming techniques (for example, a lot of conditional statements) to create a model? Perhaps—if you analyzed the dataset long enough to determine the relationships between petal and sepal measurements to a particular species. And this becomes difficult—maybe impossible—on more complicated datasets. A good machine learning approach *determines the model for you*. If you feed enough representative examples into the right machine learning model type, the program will figure out the relationships for you.
#
# ### Select the model
#
# We need to select the kind of model to train. There are many types of models and picking a good one takes experience. This tutorial uses a neural network to solve the iris classification problem. *[Neural networks](https://developers.google.com/machine-learning/glossary/#neural_network)* can find complex relationships between features and the label. It is a highly-structured graph, organized into one or more *[hidden layers](https://developers.google.com/machine-learning/glossary/#hidden_layer)*. Each hidden layer consists of one or more *[neurons](https://developers.google.com/machine-learning/glossary/#neuron)*. There are several categories of neural networks and this program uses a dense, or *[fully-connected neural network](https://developers.google.com/machine-learning/glossary/#fully_connected_layer)*: the neurons in one layer receive input connections from *every* neuron in the previous layer. For example, Figure 2 illustrates a dense neural network consisting of an input layer, two hidden layers, and an output layer:
#
# <table>
# <tr><td>
# <img src="https://www.tensorflow.org/images/custom_estimators/full_network.png"
# alt="A diagram of the network architecture: Inputs, 2 hidden layers, and outputs">
# </td></tr>
# <tr><td align="center">
# <b>Figure 2.</b> A neural network with features, hidden layers, and predictions.<br/>
# </td></tr>
# </table>
#
# When the model from Figure 2 is trained and fed an unlabeled example, it yields three predictions: the likelihood that this flower is the given iris species. This prediction is called *[inference](https://developers.google.com/machine-learning/crash-course/glossary#inference)*. For this example, the sum of the output predictions is 1.0. In Figure 2, this prediction breaks down as: `0.02` for *Iris setosa*, `0.95` for *Iris versicolor*, and `0.03` for *Iris virginica*. This means that the model predicts—with 95% probability—that an unlabeled example flower is an *Iris versicolor*.
# + [markdown] colab_type="text" id="W23DIMVPQEBt"
# ### Create a model using Swift abstractions
#
# We will build the model from scratch, starting with low-level TensorFlow APIs.
#
# Let's start by defining a dense neural network layer as a Swift `struct`:
# + colab={} colab_type="code" id="wr5A5WvthvZ0"
import TensorFlow
// `Layer` is a protocol that makes it possible for an optimizer to update the
// struct during training.
struct DenseLayer : Layer {
// Trainable parameters.
var w: Tensor<Float>
var b: Tensor<Float>
init(inputSize: Int32, outputSize: Int32) {
w = Tensor(glorotUniform: [inputSize, outputSize])
b = Tensor(zeros: [outputSize])
}
// A requirement of the `Layer` protocol that specifies how this layer
// transforms input to output.
@differentiable(wrt: (self, input))
func applied(to input: Tensor<Float>, in context: Context) -> Tensor<Float> {
return input • w + b
}
}
# + [markdown] colab_type="text" id="br5wwj0Z6C1z"
# Next, let's use `DenseLayer` to define a neural network model for the iris classification problem.
# + colab={} colab_type="code" id="bZd1Ck4Y5xWN"
let hiddenSize: Int32 = 10
struct IrisParameters : Layer {
var layer1 = DenseLayer(inputSize: 4, outputSize: hiddenSize)
var layer2 = DenseLayer(inputSize: hiddenSize, outputSize: hiddenSize)
var layer3 = DenseLayer(inputSize: hiddenSize, outputSize: 3)
@differentiable(wrt: (self, input))
func applied(to input: Tensor<Float>, in context: Context) -> Tensor<Float> {
let l1 = relu(layer1.applied(to: input, in: context))
let l2 = relu(layer2.applied(to: l1, in: context))
return layer3.applied(to: l2, in: context)
}
}
# + [markdown] colab_type="text" id="fK0vrIRv_tcc"
# Now, let's initialize the model.
# + colab={} colab_type="code" id="mIEZ5VlI_5WM"
var model = IrisParameters()
# + [markdown] colab_type="text" id="2wFKnhWCpDSS"
# ### Using the model
#
# Let's have a quick look at what this model does to a batch of features:
# + colab={"base_uri": "https://localhost:8080/", "height": 54} colab_type="code" id="sKjJGIYzO0mr" outputId="dfc178cb-ae72-4441-a3cf-c452a75f0627"
let inferenceContext = Context(learningPhase: .inference)
let firstTrainPredictions = model.applied(to: firstTrainFeatures, in: inferenceContext)
firstTrainPredictions[0..<5]
# + [markdown] colab_type="text" id="wxyXOhwVr5S3"
# Here, each example returns a [logit](https://developers.google.com/machine-learning/crash-course/glossary#logits) for each class.
#
# To convert these logits to a probability for each class, use the [softmax](https://developers.google.com/machine-learning/crash-course/glossary#softmax) function:
# + colab={"base_uri": "https://localhost:8080/", "height": 54} colab_type="code" id="_tRwHZmTNTX2" outputId="ac7de5e5-c3e4-4752-d0f3-4d65328a50f3"
softmax(firstTrainPredictions[0..<5])
# + [markdown] colab_type="text" id="uRZmchElo481"
# Taking the `argmax` across classes gives us the predicted class index. But, the model hasn't been trained yet, so these aren't good predictions.
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="-Jzm_GoErz8B" outputId="17851a17-3130-41d0-f3c9-6c9d35c7b88b"
print("Prediction: \(firstTrainPredictions.argmax(squeezingAxis: 1))")
print(" Labels: \(firstTrainLabels)")
# + [markdown] colab_type="text" id="Vzq2E5J2QMtw"
# ## Train the model
#
# *[Training](https://developers.google.com/machine-learning/crash-course/glossary#training)* is the stage of machine learning when the model is gradually optimized, or the model *learns* the dataset. The goal is to learn enough about the structure of the training dataset to make predictions about unseen data. If you learn *too much* about the training dataset, then the predictions only work for the data it has seen and will not be generalizable. This problem is called *[overfitting](https://developers.google.com/machine-learning/crash-course/glossary#overfitting)*—it's like memorizing the answers instead of understanding how to solve a problem.
#
# The iris classification problem is an example of *[supervised machine learning](https://developers.google.com/machine-learning/glossary/#supervised_machine_learning)*: the model is trained from examples that contain labels. In *[unsupervised machine learning](https://developers.google.com/machine-learning/glossary/#unsupervised_machine_learning)*, the examples don't contain labels. Instead, the model typically finds patterns among the features.
# + [markdown] colab_type="text" id="RaKp8aEjKX6B"
# ### Define the loss and gradient function
#
# Both training and evaluation stages need to calculate the model's *[loss](https://developers.google.com/machine-learning/crash-course/glossary#loss)*. This measures how off a model's predictions are from the desired label, in other words, how bad the model is performing. We want to minimize, or optimize, this value.
#
# Our model will calculate its loss using the `softmaxCrossEntropy` function which takes the model's class probability predictions and the desired label, and returns the average loss across the examples.
# + colab={} colab_type="code" id="rHgwjCKqAWNz"
%include "TutorialModelHelpers.swift"
extension IrisParameters {
// We declare the loss as "differentiable" so that we can differentiate it
// later while optimizing the model.
@differentiable(wrt: (self))
func loss(for input: Tensor<Float>, labels: Tensor<Int32>, in context: Context) -> Tensor<Float> {
let logits = applied(to: input, in: context)
return softmaxCrossEntropy(logits: logits, categoricalLabels: labels)
}
}
# + [markdown] colab_type="text" id="9SIHZjYQATyz"
# Let's calculate the loss for the current untrained model:
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="tMAT4DcMPwI-" outputId="91f913b3-eada-4991-86e1-662a18df4c49"
print("Loss test: \(model.loss(for: firstTrainFeatures, labels: firstTrainLabels, in: inferenceContext))")
# + [markdown] colab_type="text" id="lOxFimtlKruu"
# ### Create an optimizer
#
# An *[optimizer](https://developers.google.com/machine-learning/crash-course/glossary#optimizer)* applies the computed gradients to the model's variables to minimize the `loss` function. You can think of the loss function as a curved surface (see Figure 3) and we want to find its lowest point by walking around. The gradients point in the direction of steepest ascent—so we'll travel the opposite way and move down the hill. By iteratively calculating the loss and gradient for each batch, we'll adjust the model during training. Gradually, the model will find the best combination of weights and bias to minimize loss. And the lower the loss, the better the model's predictions.
#
# <table>
# <tr><td>
# <img src="https://cs231n.github.io/assets/nn3/opt1.gif" width="70%"
# alt="Optimization algorithms visualized over time in 3D space.">
# </td></tr>
# <tr><td align="center">
# <b>Figure 3.</b> Optimization algorithms visualized over time in 3D space.<br/>(Source: <a href="http://cs231n.github.io/neural-networks-3/">Stanford class CS231n</a>, MIT License, Image credit: <a href="https://twitter.com/alecrad">Alec Radford</a>)
# </td></tr>
# </table>
#
# Swift for TensorFlow has many [optimization algorithms](https://github.com/rxwei/DeepLearning/blob/master/Sources/DeepLearning/Optimizer.swift) available for training. This model uses the SGD optimizer that implements the *[stochastic gradient descent](https://developers.google.com/machine-learning/crash-course/glossary#gradient_descent)* (SGD) algorithm. The `learning_rate` sets the step size to take for each iteration down the hill. This is a *hyperparameter* that you'll commonly adjust to achieve better results.
# + colab={} colab_type="code" id="8xxi2NNGKwG_"
let optimizer: SGD<IrisParameters, Float> = SGD(learningRate: 0.001)
# + [markdown] colab_type="text" id="pJVRZ0hP52ZB"
# We'll use this to calculate a single gradient descent step:
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="rxRNTFVe56RG" outputId="d6133e50-c11d-4d6e-934e-dd66afe38def"
let trainingContext = Context(learningPhase: .training)
let (loss, grads) = valueWithGradient(at: model) { model in
model.loss(for: firstTrainFeatures,labels: firstTrainLabels, in: trainingContext)
}
print("Initial Loss: \(loss)")
# + [markdown] colab_type="text" id="5B27cIT0O0nE"
# We call the `model.update(withGradients:)` method to iterate over all the model parameters and apply gradient descent to them, where `param` is the parameter and where `grad` is the gradient along that parameter.
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="icyvh-o6O0nF" outputId="8ad55a83-2c38-4f56-b79e-be70c0fe26c1"
optimizer.update(&model.allDifferentiableVariables, along: grads)
print("Next Loss: \(model.loss(for: firstTrainFeatures, labels: firstTrainLabels, in: trainingContext))")
# + [markdown] colab_type="text" id="nhpgM7UpO0nG"
# If you run the above two steps repeatedly, you should expect the loss to go down gradually.
# + [markdown] colab_type="text" id="7Y2VSELvwAvW"
# ### Training loop
#
# With all the pieces in place, the model is ready for training! A training loop feeds the dataset examples into the model to help it make better predictions. The following code block sets up these training steps:
#
# 1. Iterate each *epoch*. An epoch is one pass through the dataset.
# 2. Within an epoch, iterate over each example in the training `Dataset` grabbing its *features* (`x`) and *label* (`y`).
# 3. Using the example's features, make a prediction and compare it with the label. Measure the inaccuracy of the prediction and use that to calculate the model's loss and gradients.
# 4. Use gradient descent to update the model's variables.
# 5. Keep track of some stats for visualization.
# 6. Repeat for each epoch.
#
# The `numEpochs` variable is the number of times to loop over the dataset collection. Counter-intuitively, training a model longer does not guarantee a better model. `numEpochs` is a *[hyperparameter](https://developers.google.com/machine-learning/glossary/#hyperparameter)* that you can tune. Choosing the right number usually requires both experience and experimentation.
# + colab={} colab_type="code" id="AIgulGRUhpto"
let numEpochs = 501
var trainAccuracyResults: [Float] = []
var trainLossResults: [Float] = []
# + colab={"base_uri": "https://localhost:8080/", "height": 204} colab_type="code" id="066kVZQFO0nL" outputId="5e11beeb-f6e5-4455-e2d6-d2de3482f244"
func accuracy(predictions: Tensor<Int32>, truths: Tensor<Int32>) -> Float {
return Tensor<Float>(predictions .== truths).mean().scalar!
}
for epoch in 0..<numEpochs {
var epochLoss: Float = 0
var epochAccuracy: Float = 0
var batchCount: Int = 0
for examples in trainDataset {
let x = examples.first
let y = examples.second
let (loss, grad) = valueWithGradient(at: model) { model in
model.loss(for: firstTrainFeatures, labels: firstTrainLabels, in: trainingContext)
}
optimizer.update(&model.allDifferentiableVariables, along: grad)
let logits = model.applied(to: x, in: trainingContext)
epochAccuracy += accuracy(predictions: logits.argmax(squeezingAxis: 1), truths: y)
epochLoss += loss.scalar!
batchCount += 1
}
epochAccuracy /= Float(batchCount)
epochLoss /= Float(batchCount)
trainAccuracyResults.append(epochAccuracy)
trainLossResults.append(epochLoss)
if epoch % 50 == 0 {
print("Epoch \(epoch): Loss: \(epochLoss), Accuracy: \(epochAccuracy)")
}
}
# + [markdown] colab_type="text" id="2FQHVUnm_rjw"
# ### Visualize the loss function over time
# + [markdown] colab_type="text" id="j3wdbmtLVTyr"
# While it's helpful to print out the model's training progress, it's often *more* helpful to see this progress. We can create basic charts using Python's `matplotlib` module.
#
# Interpreting these charts takes some experience, but you really want to see the *loss* go down and the *accuracy* go up.
# + colab={"base_uri": "https://localhost:8080/", "height": 517} colab_type="code" id="agjvNd2iUGFn" outputId="e28f9ce9-30e7-46d6-9bb2-71eede5fcbd6"
plt.figure(figsize: [12, 8])
let accuracyAxes = plt.subplot(2, 1, 1)
accuracyAxes.set_ylabel("Accuracy")
accuracyAxes.plot(trainAccuracyResults)
let lossAxes = plt.subplot(2, 1, 2)
lossAxes.set_ylabel("Loss")
lossAxes.set_xlabel("Epoch")
lossAxes.plot(trainLossResults)
plt.show()
# + [markdown] colab_type="text" id="axA6WuGVO0nR"
# Note that the y-axes of the graphs are not zero-based.
# + [markdown] colab_type="text" id="Zg8GoMZhLpGH"
# ## Evaluate the model's effectiveness
#
# Now that the model is trained, we can get some statistics on its performance.
#
# *Evaluating* means determining how effectively the model makes predictions. To determine the model's effectiveness at iris classification, pass some sepal and petal measurements to the model and ask the model to predict what iris species they represent. Then compare the model's prediction against the actual label. For example, a model that picked the correct species on half the input examples has an *[accuracy](https://developers.google.com/machine-learning/glossary/#accuracy)* of `0.5`. Figure 4 shows a slightly more effective model, getting 4 out of 5 predictions correct at 80% accuracy:
#
# <table cellpadding="8" border="0">
# <colgroup>
# <col span="4" >
# <col span="1" bgcolor="lightblue">
# <col span="1" bgcolor="lightgreen">
# </colgroup>
# <tr bgcolor="lightgray">
# <th colspan="4">Example features</th>
# <th colspan="1">Label</th>
# <th colspan="1" >Model prediction</th>
# </tr>
# <tr>
# <td>5.9</td><td>3.0</td><td>4.3</td><td>1.5</td><td align="center">1</td><td align="center">1</td>
# </tr>
# <tr>
# <td>6.9</td><td>3.1</td><td>5.4</td><td>2.1</td><td align="center">2</td><td align="center">2</td>
# </tr>
# <tr>
# <td>5.1</td><td>3.3</td><td>1.7</td><td>0.5</td><td align="center">0</td><td align="center">0</td>
# </tr>
# <tr>
# <td>6.0</td> <td>3.4</td> <td>4.5</td> <td>1.6</td> <td align="center">1</td><td align="center" bgcolor="red">2</td>
# </tr>
# <tr>
# <td>5.5</td><td>2.5</td><td>4.0</td><td>1.3</td><td align="center">1</td><td align="center">1</td>
# </tr>
# <tr><td align="center" colspan="6">
# <b>Figure 4.</b> An iris classifier that is 80% accurate.<br/>
# </td></tr>
# </table>
# + [markdown] colab_type="text" id="z-EvK7hGL0d8"
# ### Setup the test dataset
#
# Evaluating the model is similar to training the model. The biggest difference is the examples come from a separate *[test set](https://developers.google.com/machine-learning/crash-course/glossary#test_set)* rather than the training set. To fairly assess a model's effectiveness, the examples used to evaluate a model must be different from the examples used to train the model.
#
# The setup for the test `Dataset` is similar to the setup for training `Dataset`. Download the test set from http://download.tensorflow.org/data/iris_training.csv:
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="SRMWCu30bnxH" outputId="7bcae900-80e7-42ed-cfba-63f84913f815"
let urllib = Python.import("urllib.request")
let downloadResult = urllib.urlretrieve("http://download.tensorflow.org/data/iris_test.csv",
"iris_test.csv")
let testDataFilename = String(downloadResult[0])!
testDataFilename
# + [markdown] colab_type="text" id="jEPPL6FUO0nV"
# Now load it into a `Dataset`:
# + colab={} colab_type="code" id="w6SCt95HO0nW"
%include "TutorialDatasetCSVAPI.swift"
let testDataset: Dataset<TensorPair<Tensor<Float>, Tensor<Int32>>> = Dataset(
contentsOfCSVFile: testDataFilename, hasHeader: true,
featureColumns: [0, 1, 2, 3], labelColumns: [4]
).batched(batchSize)
# + [markdown] colab_type="text" id="HFuOKXJdMAdm"
# ### Evaluate the model on the test dataset
#
# Unlike the training stage, the model only evaluates a single [epoch](https://developers.google.com/machine-learning/glossary/#epoch) of the test data. In the following code cell, we iterate over each example in the test set and compare the model's prediction against the actual label. This is used to measure the model's accuracy across the entire test set.
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="Tj4Rs8gwO0nY" outputId="5dbb9327-30bc-4fa9-b59e-24d4b391d9f7"
// NOTE: With `batchSize = 32` and 30 examples in the test dataset, only one batch will run in the loop.
for testBatch in testDataset {
let testFeatures = testBatch.first
let testLabels = testBatch.second
let logits = model.applied(to: testFeatures, in: inferenceContext)
let predictions = logits.argmax(squeezingAxis: 1)
print("Test batch accuracy: \(accuracy(predictions: predictions, truths: testLabels))")
}
# + [markdown] colab_type="text" id="HcKEZMtCOeK-"
# We can see on the first batch, for example, the model is usually correct:
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="uNwt2eMeOane" outputId="1b8d67e7-fc23-4cbe-d8e7-6b168411992c"
let firstTestBatch = testDataset.first!
let firstTestBatchFeatures = firstTestBatch.first
let firstTestBatchLabels = firstTestBatch.second
let firstTestBatchLogits = model.applied(to: firstTestBatchFeatures, in: inferenceContext)
let firstTestBatchPredictions = firstTestBatchLogits.argmax(squeezingAxis: 1)
print(firstTestBatchPredictions)
print(firstTestBatchLabels)
# + [markdown] colab_type="text" id="7Li2r1tYvW7S"
# ## Use the trained model to make predictions
#
# We've trained a model and demonstrated that it's good—but not perfect—at classifying iris species. Now let's use the trained model to make some predictions on [unlabeled examples](https://developers.google.com/machine-learning/glossary/#unlabeled_example); that is, on examples that contain features but not a label.
#
# In real-life, the unlabeled examples could come from lots of different sources including apps, CSV files, and data feeds. For now, we're going to manually provide three unlabeled examples to predict their labels. Recall, the label numbers are mapped to a named representation as:
#
# * `0`: Iris setosa
# * `1`: Iris versicolor
# * `2`: Iris virginica
# + colab={"base_uri": "https://localhost:8080/", "height": 68} colab_type="code" id="MTYOZr27O0ne" outputId="ea09c04f-676e-46e4-bda0-482137515ccf"
let unlabeledDataset: Tensor<Float> =
[[5.1, 3.3, 1.7, 0.5],
[5.9, 3.0, 4.2, 1.5],
[6.9, 3.1, 5.4, 2.1]]
let unlabeledDatasetPredictions = model.applied(to: unlabeledDataset, in: inferenceContext)
for i in 0..<unlabeledDatasetPredictions.shape[0] {
let logits = unlabeledDatasetPredictions[i]
let classIdx = logits.argmax().scalar!
print("Example \(i) prediction: \(classNames[Int(classIdx)]) (\(softmax(logits)))")
}
# + [markdown] colab_type="text" id="rwxGnsA92emp"
# ##### Copyright 2019 The TensorFlow Authors.
# + cellView="form" colab={} colab_type="code" id="CPII1rGR2rF9"
// Licensed under the Apache License, Version 2.0 (the "License");
// you may not use this file except in compliance with the License.
// You may obtain a copy of the License at
//
// https://www.apache.org/licenses/LICENSE-2.0
//
// Unless required by applicable law or agreed to in writing, software
// distributed under the License is distributed on an "AS IS" BASIS,
// WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
// See the License for the specific language governing permissions and
// limitations under the License.
| 57.984615 | 1,042 |
15ee30fc6929f1eee4b29c09c75803245b0f6bad
|
py
|
python
|
The_Easy_Text_Analyzer.ipynb
|
haining-b/The_Easy_Text_Analyzer
|
['CC0-1.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/haining-b/The_Easy_Text_Analyzer/blob/master/The_Easy_Text_Analyzer.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="meKUhdwoMm6J" colab_type="text"
# #Introduction to The Easy Text Analyser
# **Welcome to The Easy Text Analyser: Here for all your
# thematic analysis needs.**
#
#
# ---
#
#
#
# This document will walk you through the analysis of
# your text of interest, and will hopefully make
# the process of editing slightly more bearable.
#
#
# As you read, please pay attention to any text that
# looks like
#
# # this:
#
#
#
# that's a *comment* and it's here
# to make this whole thing comprehensible
# and EASY
# even if you've never touched code before in your life.
#
#
# If you see:
#
#
# ##################################################
# ########### YOUR INPUT REQUIRED HERE #############
# ##################################################
#
#
# you absolutely MUST change the lines of code that
# follow. Those lines are the ones doing a lot of
# the work, and they depend upon your specific text.
#
#
# I'll refer to each of these little boxes as a cell.
# To run a cell (on a Mac, anyways), press option + enter.
# You'll need to run most of the cells.
#
#
# Optional cells are labeled and hidden for simplicity's
# sake. Some of the function cells are also hidden -
# that's so you don't accidently change anything.
# Cells labeled 'Touchy' need you to change their contents. Cells labeled 'No Touchy' should be left alone, but do run them. If you want to see the inside of a hidden cell,
# double click on the title.
#
#
# Happy editing!
#
# + [markdown] id="jFyelxbpf-aV" colab_type="text"
# # Modules and installations
#
# These are just some tools we're going to use later. Run the following cell as described above (option + enter), but no touchy!
# + id="5YNSYWIs6xuz" colab_type="code" cellView="form" colab={"base_uri": "https://localhost:8080/", "height": 136} outputId="c8f940ea-2502-4618-b7eb-9b729e583260"
#@title Modules and installations (No Touchy) { form-width: "200px" }
# %pip install pdfkit
# %matplotlib inline
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
import nltk
nltk.download('stopwords')
nltk.download('punkt')
nltk.download('wordnet')
from nltk import Text,WordNetLemmatizer, sent_tokenize, word_tokenize
import csv
from string import punctuation
from collections import Counter
from itertools import chain
import string
import pdfkit
import re
# + [markdown] id="X9HiuTprNhuS" colab_type="text"
# # Stop Words
#
# 'Stop words' are words that aren't interesting for analysis purposes. I don't care how often I said 'and' or 'says', for example. The following cell loads a list of English stop words. You can change the list in the cells following that (e.g. to add elements of a conlang).
#
#
# The list of English stop words is as follows:
#
# who, he, she, a, can, shan, doesn, ll, few, won, couldn, here, because, off, against, during, its, myself, him, was, d, didn, hasnt, their, thatll, only, just, me, weren, have, youve, such, ours, her, aren, doing, or, re, down, shant, hasn, below, up, above, neednt, hers, mightn, will, wont, those, while, himself, wouldn, has, they, did, at, after, y, more, werent, if, any, each, o, be, to, we, ve, all, t, isnt, mustn, hadn, were, further, its, over, didnt, dont, wouldnt, is, same, it, whom, both, m, but, needn, these, should, in, doesnt, been, shouldn, i, does, yourselves, there, wasnt, had, other, own, do, haven, this, couldnt, wasn, don, as, youre, no, shouldve, about, now, having, an, too, with, where, youll, herself, what, from, isn, before, between, ourselves, on, for, when, being, out, through, nor, yourself, itself, so, ain, mustnt, you, my, some, arent, youd, our, the, into, under, and, by, yours, shouldnt, ma, again, how, not, his, themselves, why, them, am, are, than, until, then, mightnt, havent, of, your, theirs, very, s, most, shes, once, hadnt, that, which
#
# The words are truncated (like, 'ain' instead of "ain't") due to the method of analysis that we use later on.
#
# I can easily imagine a situation in which you might want to analyse use of words like "should" or "ain't" (When and where is my character prescriptive? Did my southern character suddenly lose their accent in chapter 16?). To handle these exceptions, the cell below titled "Optional Stopword Deleter" will allow you to remove words from this list, and thereby analyze your text based on those words.
#
# The Expander cell does the reverse - If you use the neo pronoun "ze", for example, you might not want to know every time that it occurs in your text. This cell will probably be less useful to you, because stop words are more of a problem when you are analyzing a huge body of text - for our purposes, it probably won't take that much more computational power to just include them.
# + id="Xvm9G6_Q6hOX" colab_type="code" cellView="form" colab={}
#@title Loading stop words (No Touchy) { form-width: "200px" }
from nltk.corpus import stopwords
stop_words = set(stopwords.words("english"))
inclusive_stop_words = [i for i in stop_words]
# + id="3meaH-Q26hOZ" colab_type="code" cellView="form" colab={}
#@title Stop Word Deleter (OPTIONAL) { form-width: "200px" }
####### OPTIONAL CELL #######
# I am interested in the genderedness of my text, so I'm keeping gendered pronouns.
# You can do this with any stop word; just insert the one you would like to keep into the
# list 'words_to_keep'.
# E.g. words_to_keep = ('it',"it\'s",'is')
# Note: the backslash in it\'s is so that the computer treats the apostrophe as a character
# and not a code thing. You MUST include the backslash when handling apostrophes or
# you'll confuse the computer.
# If something goes wrong here, that is probably the issue.
words_to_keep = ('he','her','she','hers','herself', 'him', 'himself', 'his',"she\'s")
inclusive_stop_words = [i for i in inclusive_stop_words if not i in words_to_keep]
# + id="vzkp98hWOqhJ" colab_type="code" cellView="form" colab={}
#@title Stop Word Expander (OPTIONAL) { form-width: "200px" }
# To ADD a stop word, simply run the following code (with the appropriate word
# included (i.e. not 'haining')).
inclusive_stop_words.append('haining')
# + [markdown] id="JuigwXFZX6fQ" colab_type="text"
# # Punctuation
#
# Punctuation can cause a lot of trouble in text analysis. That's because the addition of a single punctuation mark that abuts a word can change what the computer sees as a "word". In this case, that would make word and "word" different words, which is clearly not accurate. Hence, this punctuation removal function.
# + id="pTIhWecs6hOb" colab_type="code" cellView="form" colab={}
#@title Punctuation removal function (No Touchy) { form-width: "200px" }
# This function removes all punctuation from your text.
# Originally found here: https://github.com/davidmcclure/textplot/blob/master/textplot/text.py
# I do occasionally find that some weird punctuation has made its way into my text,
# so if you are seeing an object escape consistently, copy and paste it into the long string
# of nonsense below (what's actually happening is that you're replacing the punctuation,
# like '.', with nothing, like ''. The marks '' just indicate what kind of thing you're
# working with - here, it means text (as opposed to numbers, for example)).
def remove_punctuation(text):
"""
Removes all punctuation and conotation from the string and returns a 'plain' string
"""
punctuation2 = '-&—®©™€â´‚+³©¥ã¼•ž®è±äüöž!@#“§$%^*()î_+€$=¿{”}[]:«;"»\â¢|<>,.?/~`0123456789’'
for sign in punctuation2:
text = text.replace(sign, "")
return text
# + [markdown] id="Z9T4iyCHQTa4" colab_type="text"
# # Your file
#
# For starters, we'll be working with Jane Austen's Pride and Prejudice. The .txt file for P&P is on my github at https://github.com/haining-b/The_Easy_Text_Analyzer/blob/6ddbb85c6b6eff15b5941241408bca3f4c6f2882/pride_and_prejudice.txt. You can also download it at Project Gutenberg: https://www.gutenberg.org/files/1342/1342-0.txt. You will eventually need to edit these cells to reflect your text of interest.
# + id="mbfNsNDi-qYD" colab_type="code" cellView="form" colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "Ly8gQ29weXJpZ2h0IDIwMTcgR29vZ2xlIExMQwovLwovLyBMaWNlbnNlZCB1bmRlciB0aGUgQXBhY2hlIExpY2Vuc2UsIFZlcnNpb24gMi4wICh0aGUgIkxpY2Vuc2UiKTsKLy8geW91IG1heSBub3QgdXNlIHRoaXMgZmlsZSBleGNlcHQgaW4gY29tcGxpYW5jZSB3aXRoIHRoZSBMaWNlbnNlLgovLyBZb3UgbWF5IG9idGFpbiBhIGNvcHkgb2YgdGhlIExpY2Vuc2UgYXQKLy8KLy8gICAgICBodHRwOi8vd3d3LmFwYWNoZS5vcmcvbGljZW5zZXMvTElDRU5TRS0yLjAKLy8KLy8gVW5sZXNzIHJlcXVpcmVkIGJ5IGFwcGxpY2FibGUgbGF3IG9yIGFncmVlZCB0byBpbiB3cml0aW5nLCBzb2Z0d2FyZQovLyBkaXN0cmlidXRlZCB1bmRlciB0aGUgTGljZW5zZSBpcyBkaXN0cmlidXRlZCBvbiBhbiAiQVMgSVMiIEJBU0lTLAovLyBXSVRIT1VUIFdBUlJBTlRJRVMgT1IgQ09ORElUSU9OUyBPRiBBTlkgS0lORCwgZWl0aGVyIGV4cHJlc3Mgb3IgaW1wbGllZC4KLy8gU2VlIHRoZSBMaWNlbnNlIGZvciB0aGUgc3BlY2lmaWMgbGFuZ3VhZ2UgZ292ZXJuaW5nIHBlcm1pc3Npb25zIGFuZAovLyBsaW1pdGF0aW9ucyB1bmRlciB0aGUgTGljZW5zZS4KCi8qKgogKiBAZmlsZW92ZXJ2aWV3IEhlbHBlcnMgZm9yIGdvb2dsZS5jb2xhYiBQeXRob24gbW9kdWxlLgogKi8KKGZ1bmN0aW9uKHNjb3BlKSB7CmZ1bmN0aW9uIHNwYW4odGV4dCwgc3R5bGVBdHRyaWJ1dGVzID0ge30pIHsKICBjb25zdCBlbGVtZW50ID0gZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgnc3BhbicpOwogIGVsZW1lbnQudGV4dENvbnRlbnQgPSB0ZXh0OwogIGZvciAoY29uc3Qga2V5IG9mIE9iamVjdC5rZXlzKHN0eWxlQXR0cmlidXRlcykpIHsKICAgIGVsZW1lbnQuc3R5bGVba2V5XSA9IHN0eWxlQXR0cmlidXRlc1trZXldOwogIH0KICByZXR1cm4gZWxlbWVudDsKfQoKLy8gTWF4IG51bWJlciBvZiBieXRlcyB3aGljaCB3aWxsIGJlIHVwbG9hZGVkIGF0IGEgdGltZS4KY29uc3QgTUFYX1BBWUxPQURfU0laRSA9IDEwMCAqIDEwMjQ7CgpmdW5jdGlvbiBfdXBsb2FkRmlsZXMoaW5wdXRJZCwgb3V0cHV0SWQpIHsKICBjb25zdCBzdGVwcyA9IHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCk7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICAvLyBDYWNoZSBzdGVwcyBvbiB0aGUgb3V0cHV0RWxlbWVudCB0byBtYWtlIGl0IGF2YWlsYWJsZSBmb3IgdGhlIG5leHQgY2FsbAogIC8vIHRvIHVwbG9hZEZpbGVzQ29udGludWUgZnJvbSBQeXRob24uCiAgb3V0cHV0RWxlbWVudC5zdGVwcyA9IHN0ZXBzOwoKICByZXR1cm4gX3VwbG9hZEZpbGVzQ29udGludWUob3V0cHV0SWQpOwp9CgovLyBUaGlzIGlzIHJvdWdobHkgYW4gYXN5bmMgZ2VuZXJhdG9yIChub3Qgc3VwcG9ydGVkIGluIHRoZSBicm93c2VyIHlldCksCi8vIHdoZXJlIHRoZXJlIGFyZSBtdWx0aXBsZSBhc3luY2hyb25vdXMgc3RlcHMgYW5kIHRoZSBQeXRob24gc2lkZSBpcyBnb2luZwovLyB0byBwb2xsIGZvciBjb21wbGV0aW9uIG9mIGVhY2ggc3RlcC4KLy8gVGhpcyB1c2VzIGEgUHJvbWlzZSB0byBibG9jayB0aGUgcHl0aG9uIHNpZGUgb24gY29tcGxldGlvbiBvZiBlYWNoIHN0ZXAsCi8vIHRoZW4gcGFzc2VzIHRoZSByZXN1bHQgb2YgdGhlIHByZXZpb3VzIHN0ZXAgYXMgdGhlIGlucHV0IHRvIHRoZSBuZXh0IHN0ZXAuCmZ1bmN0aW9uIF91cGxvYWRGaWxlc0NvbnRpbnVlKG91dHB1dElkKSB7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICBjb25zdCBzdGVwcyA9IG91dHB1dEVsZW1lbnQuc3RlcHM7CgogIGNvbnN0IG5leHQgPSBzdGVwcy5uZXh0KG91dHB1dEVsZW1lbnQubGFzdFByb21pc2VWYWx1ZSk7CiAgcmV0dXJuIFByb21pc2UucmVzb2x2ZShuZXh0LnZhbHVlLnByb21pc2UpLnRoZW4oKHZhbHVlKSA9PiB7CiAgICAvLyBDYWNoZSB0aGUgbGFzdCBwcm9taXNlIHZhbHVlIHRvIG1ha2UgaXQgYXZhaWxhYmxlIHRvIHRoZSBuZXh0CiAgICAvLyBzdGVwIG9mIHRoZSBnZW5lcmF0b3IuCiAgICBvdXRwdXRFbGVtZW50Lmxhc3RQcm9taXNlVmFsdWUgPSB2YWx1ZTsKICAgIHJldHVybiBuZXh0LnZhbHVlLnJlc3BvbnNlOwogIH0pOwp9CgovKioKICogR2VuZXJhdG9yIGZ1bmN0aW9uIHdoaWNoIGlzIGNhbGxlZCBiZXR3ZWVuIGVhY2ggYXN5bmMgc3RlcCBvZiB0aGUgdXBsb2FkCiAqIHByb2Nlc3MuCiAqIEBwYXJhbSB7c3RyaW5nfSBpbnB1dElkIEVsZW1lbnQgSUQgb2YgdGhlIGlucHV0IGZpbGUgcGlja2VyIGVsZW1lbnQuCiAqIEBwYXJhbSB7c3RyaW5nfSBvdXRwdXRJZCBFbGVtZW50IElEIG9mIHRoZSBvdXRwdXQgZGlzcGxheS4KICogQHJldHVybiB7IUl0ZXJhYmxlPCFPYmplY3Q+fSBJdGVyYWJsZSBvZiBuZXh0IHN0ZXBzLgogKi8KZnVuY3Rpb24qIHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCkgewogIGNvbnN0IGlucHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKGlucHV0SWQpOwogIGlucHV0RWxlbWVudC5kaXNhYmxlZCA9IGZhbHNlOwoKICBjb25zdCBvdXRwdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQob3V0cHV0SWQpOwogIG91dHB1dEVsZW1lbnQuaW5uZXJIVE1MID0gJyc7CgogIGNvbnN0IHBpY2tlZFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgaW5wdXRFbGVtZW50LmFkZEV2ZW50TGlzdGVuZXIoJ2NoYW5nZScsIChlKSA9PiB7CiAgICAgIHJlc29sdmUoZS50YXJnZXQuZmlsZXMpOwogICAgfSk7CiAgfSk7CgogIGNvbnN0IGNhbmNlbCA9IGRvY3VtZW50LmNyZWF0ZUVsZW1lbnQoJ2J1dHRvbicpOwogIGlucHV0RWxlbWVudC5wYXJlbnRFbGVtZW50LmFwcGVuZENoaWxkKGNhbmNlbCk7CiAgY2FuY2VsLnRleHRDb250ZW50ID0gJ0NhbmNlbCB1cGxvYWQnOwogIGNvbnN0IGNhbmNlbFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgY2FuY2VsLm9uY2xpY2sgPSAoKSA9PiB7CiAgICAgIHJlc29sdmUobnVsbCk7CiAgICB9OwogIH0pOwoKICAvLyBXYWl0IGZvciB0aGUgdXNlciB0byBwaWNrIHRoZSBmaWxlcy4KICBjb25zdCBmaWxlcyA9IHlpZWxkIHsKICAgIHByb21pc2U6IFByb21pc2UucmFjZShbcGlja2VkUHJvbWlzZSwgY2FuY2VsUHJvbWlzZV0pLAogICAgcmVzcG9uc2U6IHsKICAgICAgYWN0aW9uOiAnc3RhcnRpbmcnLAogICAgfQogIH07CgogIGNhbmNlbC5yZW1vdmUoKTsKCiAgLy8gRGlzYWJsZSB0aGUgaW5wdXQgZWxlbWVudCBzaW5jZSBmdXJ0aGVyIHBpY2tzIGFyZSBub3QgYWxsb3dlZC4KICBpbnB1dEVsZW1lbnQuZGlzYWJsZWQgPSB0cnVlOwoKICBpZiAoIWZpbGVzKSB7CiAgICByZXR1cm4gewogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbXBsZXRlJywKICAgICAgfQogICAgfTsKICB9CgogIGZvciAoY29uc3QgZmlsZSBvZiBmaWxlcykgewogICAgY29uc3QgbGkgPSBkb2N1bWVudC5jcmVhdGVFbGVtZW50KCdsaScpOwogICAgbGkuYXBwZW5kKHNwYW4oZmlsZS5uYW1lLCB7Zm9udFdlaWdodDogJ2JvbGQnfSkpOwogICAgbGkuYXBwZW5kKHNwYW4oCiAgICAgICAgYCgke2ZpbGUudHlwZSB8fCAnbi9hJ30pIC0gJHtmaWxlLnNpemV9IGJ5dGVzLCBgICsKICAgICAgICBgbGFzdCBtb2RpZmllZDogJHsKICAgICAgICAgICAgZmlsZS5sYXN0TW9kaWZpZWREYXRlID8gZmlsZS5sYXN0TW9kaWZpZWREYXRlLnRvTG9jYWxlRGF0ZVN0cmluZygpIDoKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgJ24vYSd9IC0gYCkpOwogICAgY29uc3QgcGVyY2VudCA9IHNwYW4oJzAlIGRvbmUnKTsKICAgIGxpLmFwcGVuZENoaWxkKHBlcmNlbnQpOwoKICAgIG91dHB1dEVsZW1lbnQuYXBwZW5kQ2hpbGQobGkpOwoKICAgIGNvbnN0IGZpbGVEYXRhUHJvbWlzZSA9IG5ldyBQcm9taXNlKChyZXNvbHZlKSA9PiB7CiAgICAgIGNvbnN0IHJlYWRlciA9IG5ldyBGaWxlUmVhZGVyKCk7CiAgICAgIHJlYWRlci5vbmxvYWQgPSAoZSkgPT4gewogICAgICAgIHJlc29sdmUoZS50YXJnZXQucmVzdWx0KTsKICAgICAgfTsKICAgICAgcmVhZGVyLnJlYWRBc0FycmF5QnVmZmVyKGZpbGUpOwogICAgfSk7CiAgICAvLyBXYWl0IGZvciB0aGUgZGF0YSB0byBiZSByZWFkeS4KICAgIGxldCBmaWxlRGF0YSA9IHlpZWxkIHsKICAgICAgcHJvbWlzZTogZmlsZURhdGFQcm9taXNlLAogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbnRpbnVlJywKICAgICAgfQogICAgfTsKCiAgICAvLyBVc2UgYSBjaHVua2VkIHNlbmRpbmcgdG8gYXZvaWQgbWVzc2FnZSBzaXplIGxpbWl0cy4gU2VlIGIvNjIxMTU2NjAuCiAgICBsZXQgcG9zaXRpb24gPSAwOwogICAgd2hpbGUgKHBvc2l0aW9uIDwgZmlsZURhdGEuYnl0ZUxlbmd0aCkgewogICAgICBjb25zdCBsZW5ndGggPSBNYXRoLm1pbihmaWxlRGF0YS5ieXRlTGVuZ3RoIC0gcG9zaXRpb24sIE1BWF9QQVlMT0FEX1NJWkUpOwogICAgICBjb25zdCBjaHVuayA9IG5ldyBVaW50OEFycmF5KGZpbGVEYXRhLCBwb3NpdGlvbiwgbGVuZ3RoKTsKICAgICAgcG9zaXRpb24gKz0gbGVuZ3RoOwoKICAgICAgY29uc3QgYmFzZTY0ID0gYnRvYShTdHJpbmcuZnJvbUNoYXJDb2RlLmFwcGx5KG51bGwsIGNodW5rKSk7CiAgICAgIHlpZWxkIHsKICAgICAgICByZXNwb25zZTogewogICAgICAgICAgYWN0aW9uOiAnYXBwZW5kJywKICAgICAgICAgIGZpbGU6IGZpbGUubmFtZSwKICAgICAgICAgIGRhdGE6IGJhc2U2NCwKICAgICAgICB9LAogICAgICB9OwogICAgICBwZXJjZW50LnRleHRDb250ZW50ID0KICAgICAgICAgIGAke01hdGgucm91bmQoKHBvc2l0aW9uIC8gZmlsZURhdGEuYnl0ZUxlbmd0aCkgKiAxMDApfSUgZG9uZWA7CiAgICB9CiAgfQoKICAvLyBBbGwgZG9uZS4KICB5aWVsZCB7CiAgICByZXNwb25zZTogewogICAgICBhY3Rpb246ICdjb21wbGV0ZScsCiAgICB9CiAgfTsKfQoKc2NvcGUuZ29vZ2xlID0gc2NvcGUuZ29vZ2xlIHx8IHt9OwpzY29wZS5nb29nbGUuY29sYWIgPSBzY29wZS5nb29nbGUuY29sYWIgfHwge307CnNjb3BlLmdvb2dsZS5jb2xhYi5fZmlsZXMgPSB7CiAgX3VwbG9hZEZpbGVzLAogIF91cGxvYWRGaWxlc0NvbnRpbnVlLAp9Owp9KShzZWxmKTsK", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 72} outputId="a562227e-069d-427f-9b66-d75dc525d6e8"
#@title Upload your file (Touchy) { form-width: "200px" }
# Here is where you will choose the file to upload.
# File should be a plaintext .txt file
##################################################
############ YOUR INPUT REQUIRED HERE ############
##################################################
from google.colab import files
uploaded = files.upload()
# + id="UfO0plLy6hOd" colab_type="code" colab={} cellView="form"
#@title Slight modifications to your file (Touchy) { form-width: "200px" }
# Get the full text of your file without punctuation
# Replace 'pride_and_prejudice.txt' with the name of the file you uploaded above.
##################################################
############ YOUR INPUT REQUIRED HERE ############
##################################################
with open('pride_and_prejudice.txt', 'r', errors='replace') as f:
words_subbed = f.read()
# + [markdown] id="ZvHD_-bWW1zP" colab_type="text"
# #Dealing with multiple definitions (OPTIONAL)
# In the book I've written, I have a character whose name is Will. Because that name is also a noun and a modal verb, I need to take all the times that 'Will' occurs in the text and turn it into something else, like the made-up word 'bobo'. This change is important, as capitalization is ignored by later processing steps. That's just so we don't go around acting like 'Almost' and 'almost' are 2 different words. The following little cell is just a glorified find and replace function (like in Microsoft Word).
#
# For the purposes of illustration, I will be replacing the word 'Mrs. Bennet' with 'lala', since later steps will
# separate 'Mrs' from 'Bennet'.
# + id="fs19nb8M6hOg" colab_type="code" cellView="form" colab={}
#@title Multiple Definition Tool (OPTIONAL) { form-width: "200px" }
####### OPTIONAL CELL #######
# If you have a similar issue (a character named Hope, perhaps), just replace "Mrs. Bennet"
# with "Hope", and all instances of "Hope" will become 'bobo'.
# If you want to do this multiple times, delete the '#' before the second line of code,
# then substitute the appropriate terms. If you need EVEN MORE, then copy and paste
# that SECOND line of code below the rest and do the replacement again.
# If you use the first, you'll only replace one of the words you care about.
##################################################
############ YOUR INPUT REQUIRED HERE ############
##################################################
words_subbed = re.sub('Mrs Bennet','lala', words_subbed)
# words_subbed = re.sub('Hope','kikii', words_subbed)
# + [markdown] id="poQWg_Iy0x0b" colab_type="text"
# # Tokenizing
#
# Tokenizing test is a method of splitting any string of characters in a way that a native speaker of that language might do. For example, the computer does not know what a sentence or a word is. In order to treat your document appropriately, we need to teach the computer what we consider important units of information. Hence, tokenization.
#
# For the most part, useful tokens include words. But you can imagine a situation in which multiple words are actually the unit on which we would like to perform analyses. Some examples include the White House, Pride and Prejudice, and Mr. Bingley. A default way of delineating tokens is to split based on spaces, but you can see that that would split the examples that I just mentioned into at least two different items. In the case of Mr. Bingley, this is quite problematic, as there are multiple Bingleys and many men in the novel Pride and Prejudice, and so you could not just search either "Mr." or "Bingley".
#
# Multi Word Tokenizing is not dissimilar to what we did in the Multiple Definitions section. Indeed, you could also replace "Mr. Bingley" with a nonsense word. However, the Multiple Definitions Tool will also handle identical spellings that are differentiated by case. *This* tool exclusively handles epithets. If I were using The Odyssey as an example, I would use the phrase 'rosy-fingered Dawn' to show off the use of Multi Word tokenizing, but unfortunately that type of repetition isn't really Jane Austen's style.
#
#
# In the cell titled "Multi Word Tokens", we will make a list of the multiword tokens that we care about. In the cell titled "Tokenizer", we make a list of **all** of the tokenized words.
# + id="gdUfCehq0zQT" colab_type="code" colab={} cellView="form"
#@title Multi Word Tokens (OPTIONAL) { form-width: "200px" }
# Note: we have already replaced all instances of Mrs. Bennet with 'lala', so the
# inclusion of her name is more for illustrative purposes than anything else.
##################################################
########### YOUR INPUT REQUIRED HERE #############
##################################################
epithets = [('Mrs.','Bennet'), ('Mr.','Bingley')]
epithets = [(x.lower(), y.lower()) for x,y in epithets]
epithets = [(remove_punctuation(x), remove_punctuation(y)) for x,y in epithets]
# epi_list lets us see the epithets we've made in a way that's easy
# to copy and paste.
epi_list = [''.join(tups) for tups in epithets]
# + id="CsipjfOWTbRL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} cellView="form" outputId="200c8f11-dd89-41fc-c1a3-823793fe487b"
#@title Looking at lists (OPTIONAL) { form-width: "200px" }
# Sometimes, it is useful to visualize the contents of a list.
# For example, in the last cell I produced a list called epi_list.
# This list is designed to allow you to view the multi word tokens
# that you have added to your document. To look at any list,
# you can use the code below, edited to contain the name of the list.
# Run this Cell to see what a list looks like. They have square brackets
# and the elements of the list are separated by a comma.
print(epi_list)
# + id="8sRfbJ8D3LTO" colab_type="code" colab={} cellView="form"
#@title Tokenizer (No Touchy){ form-width: "200px" }
sent_tokenized = sent_tokenize(str(words_subbed))
# All words are made lowercase here:
sent_tokenized = [i.lower() for i in sent_tokenized]
# Removing that punctuation (in case we missed anything earlier)
sent_tokenized = [remove_punctuation(i) for i in sent_tokenized]
# Ran if the user has specified epithets.
if 'epithets' in globals():
# Instantiating the tokenizer with our epithets
MWEtokenizer_i = nltk.MWETokenizer(epithets, separator='')
# Tokenizing the document
with_multi_str=[MWEtokenizer_i.tokenize(word_tokenize(sent)) for sent in sent_tokenized]
fully_tokenized = []
for int_list in with_multi_str:
for word in int_list:
fully_tokenized.append(word)
# Removing stop words
full_tokenization = [i for i in fully_tokenized if not i in inclusive_stop_words]
else:
only_words = [word_tokenize(sent) for sent in sent_tokenized]
fully_tokenized = []
for int_list in only_words:
for word in int_list:
fully_tokenized.append(word)
full_tokenization = [i for i in fully_tokenized if not i in inclusive_stop_words]
# + [markdown] id="WoF-IPqBX91Z" colab_type="text"
# #Lemmatization
#
# In this kind of analysis, we often talk about the 'stem' of a word. For many words, this is obvious - the stem of dogs is dog, of organizing is organiz, etc. Some words cannot be stemmed so easily - for example, the word 'best' is the superlative of good. Those two look 100% different. So some very smart people have developed an algorithm to *lemmatize* words. That is to say, the words are turned into their 'lemma'/ dictionary form. In the case of 'best', that is 'good'.
#
# We do this so that we capture appropriate units in our analysis - good and best mean pretty much the same thing, even if they are different in degree.
#
# Many words have multiple definitions, depending on their form. For example, sometime can mean 'at some point' or 'former'; sometime**s** means 'on more than one occasion'. Lemmatization does not therefore *neccesarily* collapse all instances of a given lemma into one.
#
# The following cell takes your big list of words and lemmatizes it.
#
# NOTE: This will probably not capture all lemmatizable words in scifi novels - if you made it up, it will likely throw a bit of a wrench into the analysis. That just means that words like 'bobo' and 'boboizes' are likely going to be categorized separately.
#
#
# + id="RaETDqGq6hOm" colab_type="code" cellView="form" colab={}
#@title Lemmatizer (No Touchy) { form-width: "200px" }
lemmatizer = WordNetLemmatizer()
words_lemmatized =[]
full_tokenization2 = full_tokenization[4000:4500]
# Lemmatizing the list
for word in full_tokenization2:
words_lemmatized.append(lemmatizer.lemmatize(word))
words_lemmatized=[]
# Getting rid of words that are just "" as a result of removing punctuation.
for striing in words_l:
if (striing != ""):
words_lemmatized.append(striing)
words_lemmatized = np.asarray(words_lemmatized)
# + [markdown] id="1Rq7G3t0Yn-j" colab_type="text"
# #Mapping the text
#
# To plot word frequency over narrative time, we need to find all the points at which you've used a particular word. The following cell makes a list of all the unique words in your lemmatized document and then finds all the places they were used in the text.
# + id="mi4ZEGhu6hOo" colab_type="code" cellView="form" colab={}
#@title Making the instance dictionary (No Touchy) { form-width: "200px" }
# Here we are making a 'dictionary'.
# This will take longer depending on the size of your text doc and the breadth of
# the used vocabulary.
# The point: we're going to keep track of every time those words appeared in the text.
# So we can type the word 'kid' into location_dictionary.get('kid') and see a complete list of kid
# occurences. The values are 'position from the start'.
# So in this sentence, the word 'the' has values of 5 and 7.
word_set = list(set(words_lemmatized))
location_dictionary = {}
for i in range(0,len(word_set)):
key = word_set[i]
indices = np.flatnonzero(words_lemmatized == key)
location_dictionary.update( {key : indices} )
# + [markdown] id="7DyIEWDWZJci" colab_type="text"
# #Concept Compilation
# Okay, this one is SO USEFUL and actually what motivated me to do this in the first place. If you have a theme that can be represented by more than one word, what to do???? You could use this code to plot all of the terms at once, but that'll get clunky, fast.
#
# So I give you the concept_compiler.
#
#
# This function takes a list of all the words you want to smoosh together into a concept and makes new 'terms'.
#
# The exciting thing about this is that it helps with editing big chunks of text. I wrote a book, then deleted the first quarter.... which is where many themes are introduced. In rewriting, I need to make sure the text has the right 'rhythm' - like, do I somehow go 200 pages before introducing a theme? Does this character appear frequently enough for people to remember and care about them? Some of that is squishier, certainly (like, you would definitely remember a person who commits a horrific murder and then vanishes for the rest of the book), but a picture never hurts!
#
# In this case, I am going to combine nicknames for characters. Elizabeth is also known as Lizzy or Eliza. Mrs. Bennet is known as 'lala' (after we changed it in the multiple definitions step) and 'Mamma'. While there is certainly literary content inherent in a nickname, sometimes you just want to know when a person shows up.
# + id="DEOxbLGb6hOq" colab_type="code" cellView="form" colab={}
#@title Concept Compiler (OPTIONAL; No Touchy) { form-width: "200px" }
def concept_compiler(terms):
total_placement = []
for i in terms:
values = location_dictionary.get(i)
values = values.tolist()
total_placement.extend(values)
return(total_placement)
# + id="-0ZqJJCK6hOs" colab_type="code" cellView="form" colab={}
#@title Concept Compiler Example (OPTIONAL) { form-width: "200px" }
####### OPTIONAL CELL #######
# Remember! Keep your words lowercase, otherwise you won't find anything.
# If I wanted to do a concept like 'purple', I would delete the two lines of code
# below and type:
# purple = concept_compiler(['purple','violet','lavendar','lilac','plum'])
##################################################
############ YOUR INPUT REQUIRED HERE ############
##################################################
elizabeth = concept_compiler(['elizabeth','eliza','lizzy'])
mrsbennet = concept_compiler(['mamma','lala'])
# The following code is just for labeling in the graph below.
# You'll want to change 'Elizabeth'/'Mrs. Bennet' to whatever you decided to call your concept
# For 'purple', the code is: purple.append('purple')
##################################################
########### YOUR INPUT REQUIRED HERE #############
##################################################
elizabeth.append('Elizabeth')
mrsbennet.append('Mrs. Bennet')
# + [markdown] id="sgnQcY1aVe3s" colab_type="text"
# # Concept Storage (OPTIONAL)
#
# This cell is here for you to keep track of the contents of concepts that you have compiled. Double click to edit.
#
# mrsbennet = ['mamma','lala']
#
# elizabeth = ['elizabeth','eliza','lizzy']
# + [markdown] id="z19hRt6-d4Uf" colab_type="text"
# # Graphing our work
#
# We're at the end! Now is the time to graph your work! Below, I show you several ways to plot the data.
#
# In both examples, you are essentially running the line of code:
# plot_word_freq(object_of_interest, strategy ,toplot)
#
#
# object_of_interest is whatever you want to plot - a single word, a list of real words, a list of concepts.
#
# strategy is the type of thing you gave in object_of_interest. It can be 'concept' or 'word'.
# toplot is the type of plot you get out. There are a couple of options - a histogram or a line plot, or both! You can read more about them in the example cells below.
#
#
# The pictures show the output, but you can doubleclick on the titles just like earlier to access the information and code inside.
#
# When you plot any combination of terms, a .png file will be automatically saved to your computer. You can remove this capability by opening the graphing function and deleting ONLY the lines indicated.
#
#
# + id="u7C0N-BU6hOv" colab_type="code" cellView="form" colab={}
#@title The graphing function (No Touchy) { form-width: "200px" }
# This bad boy makes the plots. I don't recommend messing around with it.
def plot_word_freq(object_of_interest = word, strategy = 'word', toplot = 'both'):
fig, ax = plt.subplots(figsize=(10,7))
b = 50
toplot = toplot.lower()
if toplot == 'hist':
ylab = "Frequency"
h = True
k = False
elif toplot == 'kde' :
ylab = 'KDE'
k = True
h = False
else:
ylab = 'KDE'
h = True
k = True
nomen = []
if strategy == 'concept':
for concept in object_of_interest:
nomen.append(concept[-1])
var_name = concept[-1]
conc = concept[:]
del conc[-1]
trans_values = [(int(i)/len(words_lemmatized))*100 for i in conc]
if int(round(len(trans_values)/2)) > 50 and b < 50:
b = int(round(len(trans_values)/2))
sns.distplot(trans_values, ax = ax, bins = b, label = var_name, hist = h, kde = k )
ax.set(xlabel = 'Narrative Space/Time', ylabel = ylab)
plt.legend()
if strategy == 'word':
if type(object_of_interest) == list:
for x in object_of_interest:
nomen.append(x)
values = location_dictionary.get(x)
values = values.tolist()
trans_values = [(i/len(words_lemmatized))*100 for i in values]
if int(round(len(values)/2)) > 50 and b < 50:
b = int(round(len(values)/2))
sns.distplot(trans_values, ax = ax, bins = b, label = str(x), hist = h,kde = k )
ax.set(xlabel = 'Narrative Space/Time', ylabel = ylab)
plt.legend()
else:
nomen.append(object_of_interest)
values = location_dictionary.get(object_of_interest)
values = values.tolist()
trans_values = [(i/len(words_lemmatized))*100 for i in values]
if int(round(len(values)/2)) > 50 and b < 50:
b = int(round(len(values)/2))
sns.distplot(trans_values, ax = ax, bins = b, label = str(object_of_interest), hist = h, kde = k )
ax.set(xlabel = 'Narrative Space/Time', ylabel = ylab)
plt.legend()
ax.set_xlim(0,100)
for_file = '_vs_'.join(nomen)
for_file = for_file + '_'+ toplot
#####IF YOU DO NOT WANT TO DOWNLOAD IMAGES#####
#####DELETE THE NEXT TWO LINES ONLY############
###############################
plt.savefig(for_file+".png")
files.download(for_file+".png")
###############################
###KEEP ALL FOLLOWING CODE###
plt.show()
# + id="LRH7cStj6hOy" colab_type="code" cellView="both" colab={"base_uri": "https://localhost:8080/", "height": 442} outputId="56d2fd83-bc0e-454e-9092-cc0b1a6d1d88"
#@title Plotting concepts (example) { form-width: "200px" }
# Here's the plot maker in action:
# First, I make a list of the concepts I made above:
##################################################
############ YOUR INPUT REQUIRED HERE ############
##################################################
concept_list = [elizabeth, mrsbennet]
# This next line does the plotting:
# object_of_interest is whatever you want to plot - a single word, a list of real words,
# a list of concepts.
# Here, it's a list of concepts.
# strategy is the type of thing you gave in object_of_interest. It can be 'concept' or 'word'.
# toplot is the type of plot you get out. The default is 'both';
# this gives you a smoothed line plot(that might miss single occurences)
# as well as a standard histogram - that includes all occurences.
# To just look at the line, say toplot = 'kde'. For just the histogram , say toplot = 'hist'.
##################################################
############ YOUR INPUT REQUIRED HERE ############
##################################################
plot_word_freq(object_of_interest = concept_list, strategy = 'concept',toplot = 'both')
# + id="OB0sLW4_6hOz" colab_type="code" cellView="both" colab={"base_uri": "https://localhost:8080/", "height": 442} outputId="4710627f-2a29-4d19-b15e-1e957a25823e"
#@title Plotting specific terms (example) { form-width: "200px" }
# To illustrate the range of things this guy can do, I'm going to include the
# plot for the literal words 'elizabeth' and 'lala'. Above, we used them as concept
# names - you'll note I didn't actually include the words themselves
# in my concept_compiler lists.
# This is a list of the literal words 'elizabeth' and 'lala'.
# Note the difference between this and concept_list.
# The quotation marks are important.
# earlier, we used mrsbennet because we wanted the whole concept. Here, we use
# 'lala' because we are only looking for the times where she was called 'lala'
# (aka Mrs Bennet), and not the times she was called 'mamma'.
literal_word_list = ['elizabeth','lala']
#This time we'll just look at the kde plot
#NOTE: strategy is 'word', here, because we are looking at simple words (not concepts)
plot_word_freq(object_of_interest = literal_word_list, strategy = 'word',toplot = 'kde')
# + id="f0FAmL_X6hO1" colab_type="code" colab={}
| 56.31129 | 7,267 |
747d081ec33c33e86ae88fe1304ddafd8cb706e7
|
py
|
python
|
03-graph-classification-exercise.ipynb
|
hli8nova/pytorch-gnn-tutorial-odsc2021
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] id="QBwBgrQrDvWi"
# # Graph Classification
#
# Build a GNN to predict whether a molecule inhibits HIV virus replication or not (i.e. a binary target) given its molecular structure as a graph.
#
# We will use the [ogbg-molhiv](https://ogb.stanford.edu/docs/graphprop/#ogbg-mol) dataset to train and evaluate our GNN.
#
# ## Setup
#
# The following two cells import Pytorch and some supporting packages that depend on the version of Pytorch, as well as Pytorch Geometric (PyG) and the OGB package.
#
# We need [Open Graph Benchmark (OGB)](https://ogb.stanford.edu/docs/home/) package here for its `PygGraphPropPredDataset` dataset loader and the `AtomEncoder` (more on that below).
#
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="awjbmslHMRmh" outputId="3288505b-7965-4d26-a149-47a376c37796"
import torch
torch.__version__
# + id="_94GrcamWm59"
# %%capture
# # !pip install -q torch-scatter -f https://pytorch-geometric.com/whl/torch-1.9.0+cu111.html
# # !pip install -q torch-sparse -f https://pytorch-geometric.com/whl/torch-1.9.0+cu111.html
# # !pip install -q torch-geometric
# !pip install ogb
# + [markdown] id="qa9UPvQ2bE3W"
# ## Dataset
#
# The [ogbg-molhiv](https://ogb.stanford.edu/docs/graphprop/#ogbg-mol) dataset is part of the [MoleculeNet](https://pubs.rsc.org/en/content/articlehtml/2018/sc/c7sc02664a) dataset.
#
# The dataset contains 41,127 molecules, each represented as a graph. Each graph represents a molecule, where nodes are atoms, and edges are chemical bonds. Input node features are 9-dimensional, containing atomic number and chirality, as well as other additional atom features such as formal charge and whether the atom is in the ring or not. Each molecule contains a 0 or 1 label, indicating whether the molecule inhibits HIV virus replication or not.
#
# Use the `PygGraphPropPredDataset` loader to retrieve the `ogbg-molhiv` dataset. To see how this is done, refer to the Data Loaders section of the [OGB documentation](https://ogb.stanford.edu/docs/home/).
#
# Once the dataset is downloaded, find and confirm the following details.
#
# 1. Number of features for each node (should be 9)
# 2. Number of targets (should be 2)
# 3. Number of graphs in dataset (should be 41127)
# + id="vw8ZVJxiYlaH"
from ogb.graphproppred import PygGraphPropPredDataset
# + id="01xiXxx4YdBc"
# your code here
dataset = PygGraphPropPredDataset(name='ogbg-molhiv')
dataset
# -
len(dataset)
dataset.num_classes
dataset[0]
dataset[0].y[0][0]
# + [markdown] id="PKKBOSImbHqy"
# ## Visualize Dataset
#
# Pick a random graph from the dataset and visualize what it looks like. You can do it in at one of at least two ways.
#
# * __Using the edge_index__ -- extract the `edge_index` from the `Data` object and reformat it as a list of node tuples. Create a networkx graph using `networkx.from_edgelist(edges)` then use `networkx.draw()` to draw the graph.
# * __Using PyG utils__ -- PyG offers a `utils.to_networkx()` that takes a `Data` object directly. Use that to create a `networkx` graph object, then use `networkx.draw()` to draw the graph.
# + id="RJsQIlK5YgEz"
import networkx as nx
import torch_geometric.utils as pyg_utils
# + id="oy9KHBglYke3"
def draw_graph(edge_index, gids=[]):
src = edge_index[0].tolist()
dst = edge_index[1].tolist()
edges = [(s, d) for s, d in zip(src, dst)]
G = nx.from_edgelist(edges)
nx.draw(G)
draw_graph(dataset[0].edge_index)
# -
G = pyg_utils.to_networkx(dataset[0])
nx.draw(G)
# + [markdown] id="Js7KKsq8eltF"
# ## Visualize Label Distribution
#
# As expected, the dataset is very heavily skewed towards molecules that don't inhibit HIV replication.
#
# Verify that the dataset is heavily skewed. Compute the label distribution and visualize it using a histogram.
# + id="KhHhPxr7enbA"
import matplotlib.pyplot as plt
# + id="mv_RKB0denSD"
labels = [data.y[0][0] for data in dataset]
plt.hist(labels, bins=2)
_ = plt.show()
# + [markdown] id="3hABbeVwbVUq"
# ## Split and DataLoader
#
# The dataset created using `PygGraphPropPredDataset` comes with a `get_idx_splits()` function that provides indices for train, validation and test splits.
#
# Extract this information and use it to build the training, validation and test DataLoaders. Refer to the Data Loaders section of the [OGB Documentation](https://ogb.stanford.edu/docs/home/) page to see how to do this.
# + id="xQqzEWltZIif"
from torch_geometric.loader import DataLoader
# + id="n5pRxHcTYoO7"
# your code here
split_idx = dataset.get_idx_split()
split_idx
# +
BATCH_SIZE = 32
train_loader = DataLoader(dataset[split_idx["train"]], batch_size=BATCH_SIZE, shuffle=True)
val_loader = DataLoader(dataset[split_idx["valid"]], batch_size=BATCH_SIZE)
test_loader = DataLoader(dataset[split_idx["test"]], batch_size=BATCH_SIZE)
# + [markdown] id="QPDbDvSscrJZ"
# ## Model
#
# The model we will use is very similar to our node classification model.
#
# As before, we have a variable number of `GCNConv` layers that determine how large a neighborhood we are considering for each node (k GCN layers == k-hop neighborhood).
#
# However, in this case we are using the GCN layers as a graph encoder. Assuming that the output of the last GCN has dimension _H_ and the number of nodes in a graph is _N_, then the encoding for that graph after passing through the GCN layers is _(H, N)_.
#
# Each graph can have variable number of nodes, so we then pass this data through a pooling layer that pools across all the nodes in the graph, giving us a vector of size _(H)_ for each graph.
#
# A batch of these vectors are then fed into the classifier head, which is one or more Linear layers that project the vectors from the hidden dimension to the output dimension, i.e. the number of classes.
#
# ---
#
# 
#
# ---
# Build the GNN model for graph prediction with the following layers.
#
# 1. An `AtomEncoder` layer to convert from the 9 categorical features based on the chemical properties of each node (atom) in the molecule into a fixed size hidden representation _H_ (should be parameterized). Refer to the Module section of the [OGB Documentation](https://ogb.stanford.edu/docs/graphprop/) for more information.
# 2. _(k - 1)_ layers, where _k_ is the number of graph layers requested (should be parameterized).
# * `GCNConv` layer with input and output dimensions _H_.
# * A `torch.nn.BatchNorm1d` layer with _H_ features.
# * A `torch.nn.ReLU` activation layer
# * A `torch.nn.Dropout` layer (dropout percentage should be parameterized)
# 3. The _k-th_ layer is a `GCNConv` with input and output dimensions _H_.
# 3. A `torch_geometric.global_mean_pool` pooling layer that pools across the batch of node features.
# 4. A single `torch.nn.Linear` layer to project the batch of vectors with dimension _H_ to the target dimension (number of classes, should be parameterized).
#
# Test the model using a batch of data from the train DataLoader and verify that the input and output are correct.
#
#
# + id="k9h3OVtWfN_E"
import torch.nn as nn
import torch.nn.functional as F
import torch_geometric.nn as pyg_nn
from ogb.graphproppred.mol_encoder import AtomEncoder
# + id="A73H-ddjYq8d"
# your code here
class GraphClassifier(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim,
num_graph_layers, dropout_pct):
super(GraphClassifier, self).__init__()
self.num_graph_layers = num_graph_layers
self.dropout_pct = dropout_pct
self.output_dim = output_dim
# convert manually crafted categorical features to continuous
self.encoder = AtomEncoder(hidden_dim)
self.convs = nn.ModuleList()
for i in range(num_graph_layers):
self.convs.append(pyg_nn.GCNConv(hidden_dim, hidden_dim))
self.bns = nn.ModuleList()
for i in range(num_graph_layers - 1):
self.bns.append(nn.BatchNorm1d(hidden_dim))
self.clf_head = nn.Linear(hidden_dim, output_dim)
def forward(self, data):
x, edge_index, batch = data.x, data.edge_index, data.batch
x = self.encoder(x)
for i in range(self.num_graph_layers - 1):
x = self.convs[i](x, edge_index)
x = self.bns[i](x)
x = F.relu(x)
x = F.dropout(x, p=self.dropout_pct)
x = self.convs[-1](x, edge_index)
x = pyg_nn.global_mean_pool(x, data.batch)
x = self.clf_head(x)
return x
# +
model = GraphClassifier(dataset.num_features, 100,
dataset.num_classes, 3, 0.5)
for batch in train_loader:
print(batch)
pred = model(batch)
break
pred.size()
# + [markdown] id="LlcirVXglNLv"
# ## Training Loop
#
# As with our node classification example, the training loop is composed of alternate calls to `train_step` and `eval_step` functions over multiple epochs of training.
#
# However, unlike the node classification example, we will use ROC-AUC as our evaluation criteria rather than accuracy. The [rationale for this choice](https://datascience.stackexchange.com/questions/806/advantages-of-auc-vs-standard-accuracy) is explained in detail in the accepted answer in this Stack Exchange page. Basically, AUC is a better metric to gauge the strength of our model compared to accuracy because:
#
# * our dataset is skewed
# * our task is binary classification
# * AUC forces model selection that are more discriminative.
#
# The [Scikit-Learn documentation page on ROC-AUC]((https://scikit-learn.org/stable/modules/model_evaluation.html#roc-metrics)) provides additional intuition about the ROC-AUC metric.
#
# So our steps are as follows:
#
# 1. Build the `train_step` function with the following signature. You can copy-paste most of what you built in the previous exercise except for some important differences.
# * the size of the batch is given by `batch.num_graphs` and not just `len(batch)`
# * we are using a different loss function `BCEWithLogits` instead of `NLLLoss`, that might require changes to how you compute the loss.
# * We will need to compute the ROC-AUC instead of the accuracy per batch in our `train_step` and `eval_step` functions.
# * At the end of each batch, accumulate a data structure `label_preds` which is a tuple of (label:Float, prediction:Array`[(Float, Float)]` and return it along with the `loss` and `accuracy`.
#
# ```python
# def train_step(model: torch.nn.Module,
# optimizer: torch.optim.Optimizer,
# loss_fn, torch.nn.CrossEntropyLoss,
# train_loader: torch_geometric.loader.DataLoader,
# device: torch.Device
# ) -> (
# train_loss: Float,
# train_acc: Float,
# label_preds: List[(Float, [Float, Float])]
# )
# ```
#
# 2. Build the `eval_step` function with the signature given below. As before, the same code should be usable for validation and testing by appropriately setting the `is_validation` parameter. Also you may be able to copy-paste the code from the previous exercise here as well, with the same caveats listed in the instructions for the `train_step`.
#
# As with the `train_step`, accumulate and return the `label_preds` data structure.
#
# ```python
# def eval_step(model: torch.nn.Module,
# loss_fn: torch.nn.CrossEntropyLoss,
# eval_loader: torch_geometric.loader.DataLoader,
# device: torch.Device,
# is_validation=False: boolean
# ) -> (
# eval_loss: Float,
# eval_acc: Float,
# label_preds: List[Float, [Float, Float]]
# )
# ```
#
# 3. Build the `train_loop` function with the following signature. You should be able to copy-paste this directly from the node classification exercise. It takes in a union of parameters required by the `train_step` and `eval_step` and produces a `history` list of the tuple `(train_loss, train_acc, train_auc, val_loss, val_acc, val_auc)` for drawing the loss plots. It periodically (`log_every`) writes out the values to console.
#
# Use the `roc_auc_score` from Scikit-Learn to compute the ROC-AUC score for training and validation from the `label_preds` data structure, and report it along with the train and validation loss and accuracy.
#
# ```python
# def train_loop(model: torch.nn.Module,
# optimizer: torch.optim.Optimizer,
# loss_fn: torch.nn.CrossEntropyLoss,
# train_loader: torch_geometric.loader.DataLoader,
# val_loader: torch_geometric.loader.DataLoader,
# device: torch.Device,
# num_epochs: Int,
# log_every=5: Int
# ) -> List[(Float, Float, Float,
# Float, Float, Float)]
#
# ```
# + id="2DjC29K6YyBy"
# your code here
from sklearn.metrics import roc_auc_score
# +
def train_step(model, optimizer, loss_fn, train_loader, device):
model.train()
total_rows, total_loss, total_correct = 0, 0, 0
label_preds = []
for batch in train_loader:
batch = batch.to(device)
optimizer.zero_grad()
pred = model(batch)
# label = batch.y.squeeze(dim=-1)
label = batch.y.squeeze(dim=-1)
label_cat = F.one_hot(label, num_classes=2).float()
loss = loss_fn(pred, label_cat)
loss.backward()
optimizer.step()
# update values for reporting
total_loss += loss.item()
total_correct += pred.argmax(dim=-1).eq(label).sum().item()
total_rows += batch.num_graphs
label_preds.extend(zip(label.detach().cpu().numpy(),
pred.detach().cpu().numpy()))
return total_loss / total_rows, total_correct / total_rows, label_preds
def eval_step(model, loss_fn, eval_loader, device, is_validation=False):
model.eval()
total_rows, total_loss, total_correct = 0, 0, 0
label_preds = []
for batch in eval_loader:
batch = batch.to(device)
with torch.no_grad():
pred = model(batch)
label = batch.y.squeeze(dim=-1)
label_cat = F.one_hot(label, num_classes=2).float()
loss = loss_fn(pred, label_cat)
total_loss += loss.item()
total_correct += pred.argmax(dim=-1).eq(label).sum().item()
total_rows += batch.num_graphs
label_preds.extend(zip(label.cpu().numpy(),
pred.cpu().numpy()))
return total_loss / total_rows, total_correct / total_rows, label_preds
def compute_roc_auc(label_preds):
y_true, y_score = [], []
for label, preds in label_preds:
y_true.append(label)
y_score.append(preds[1])
return roc_auc_score(y_true, y_score)
def train_loop(model, optimizer, loss_fn, train_loader, val_loader, device,
num_epochs, log_every=5):
history = []
for epoch in range(num_epochs):
train_loss, train_acc, train_label_preds = train_step(model, optimizer, loss_fn,
train_loader, device)
val_loss, val_acc, val_label_preds = eval_step(model, loss_fn, val_loader,
device, is_validation=True)
# compute ROC-AUC for training and validation
train_auc = compute_roc_auc(train_label_preds)
val_auc = compute_roc_auc(val_label_preds)
history.append((train_loss, train_acc, train_auc, val_loss, val_acc, val_auc))
if epoch == 0 or (epoch + 1) % log_every == 0:
print("EPOCH {:3d}, TRAIN loss: {:.5f}, acc: {:.5f}, AUC: {:.5f}, VAL loss: {:.5f}, acc: {:.5f}, AUC: {:.5f}"
.format(epoch + 1, train_loss, train_acc, train_auc, val_loss, val_acc, val_auc))
return history
# -
# + [markdown] id="Ok9ZbOzvlt1V"
# ## Training
#
# Now train the network using the hyperparameters in the cell below.
#
# 1. At this point, if your code runs without errors, you can switch from using CPU to GPU. To do so, go to Runtime :: Change Runtime Type and setting Hardware Accelerator to GPU. You will need to rerun the notebook from the beginning once you switch from CPU to GPU.
# 2. Set the device to `torch.device("cuda")` if GPU is available otherwise set it to `torch.device("cpu")`.
# 3. Instantiate the GNN model and set the model to the appropriate device using `model.to(device)`.
# 4. Define the loss function to be `torch.nn.CrossEntropyLoss`.
# 5. Instantiate the `torch.optim.Adam` optimizer with model parameters and the appropriate `LEARNING_RATE` parameters.
# 6. Run the training loop for `NUM_EPOCHS` epochs and capture the training and validation losses and accuracies returned.
# 7. Use the training and validation losses and accuracies tuple to plot the loss and accuracy curves for the model training (the plotting code should be identical to the one you built in the previous Node Classification exercise).
# + id="dDBxCYbnk2bV"
# model parameters
INPUT_DIM = dataset.num_features
HIDDEN_DIM = 256
OUTPUT_DIM = dataset.num_classes
NUM_GCN_LAYERS = 5
DROPOUT_PCT = 0.5
# optimizer
LEARNING_RATE = 1e-3
NUM_EPOCHS = 30
# + id="tpkcogE1Y0TO"
# your code here
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
device
# -
model = GraphClassifier(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, NUM_GCN_LAYERS, DROPOUT_PCT)
model = model.to(device)
# +
import torch.optim as optim
# loss_fn = nn.CrossEntropyLoss()
loss_fn = nn.BCEWithLogitsLoss()
optimizer = optim.Adam(model.parameters(), lr=LEARNING_RATE)
# -
history = train_loop(model, optimizer, loss_fn, train_loader, val_loader, device, NUM_EPOCHS)
# +
import matplotlib.pyplot as plt
import numpy as np
def display_training_plots(history):
train_losses, train_accs, train_aucs, val_losses, val_accs, val_aucs = [], [], [], [], [], []
for train_loss, train_acc, train_auc, val_loss, val_acc, val_auc in history:
train_losses.append(train_loss)
train_accs.append(train_acc)
train_aucs.append(train_auc)
val_losses.append(val_loss)
val_accs.append(val_acc)
val_aucs.append(val_auc)
xs = np.arange(len(train_losses))
plt.figure(figsize=(10, 15))
plt.subplot(3, 1, 1)
plt.plot(xs, train_losses, label="train")
plt.plot(xs, val_losses, label="validation")
plt.xlabel("iterations")
plt.ylabel("loss")
plt.legend(loc="best")
plt.subplot(3, 1, 2)
plt.plot(xs, train_accs, label="train")
plt.plot(xs, val_accs, label="validation")
plt.xlabel("iterations")
plt.ylabel("accuracy")
plt.legend(loc="best")
plt.subplot(3, 1, 3)
plt.plot(xs, train_aucs, label="train")
plt.plot(xs, val_aucs, label="validation")
plt.xlabel("iterations")
plt.ylabel("AUC")
plt.legend(loc="best")
_ = plt.show()
display_training_plots(history)
# -
# + [markdown] id="JRJ3G0BYDlQN"
# ## Evaluation
#
# Now evaluate your trained model on the held out test set, reporting both accuracy and AUC scores. You can reuse the `eval_step()` function that you used for evaluating the model with the validation set during the training.
#
# Report the accuracy and AUC score values on the test set to 5 decimal places.
# + id="RBCz4hV5Y52e"
# your code here
_, test_acc, test_list_preds = eval_step(model, loss_fn, test_loader, device)
test_auc = compute_roc_auc(test_list_preds)
print("Test accuracy: {:.5f}".format(test_acc))
print("Test AUC: {:.5f}".format(test_auc))
# + [markdown] id="uSLJ7al-aHuy"
# ## Repeat Classification with MAX Pooling
#
# Investigate the effect on the graph classification accuracy by changing the global pooling strategy to MAX, i.e. `torch_geometric.nn.global_max_pool`. Here are the steps.
#
# 1. Either copy-paste the previous network and make the necessary changes, or parameterize your original model with a `pooling_strategy` parameter.
# 2. Instantiate the model and set it to the correct `device`.
# 3. Instantiate the `CrossEntropyLoss` loss function
# 4. Instantiate the `Adam` optimizer with the new model parameters.
# 5. Run the training loop for `NUM_EPOCHS` epochs, capturing the training and validation loss and accuracies.
# 6. Use the list of tuples to plot the training curves for training and validation loss and accuracies.
# 7. Compute and report the accuracy and AUC of the network with MAX pooling against the held-out test set.
# + id="NZ6EH_ALY8h-"
# your code here
class MaxGraphClassifier(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim,
num_graph_layers, dropout_pct):
super(MaxGraphClassifier, self).__init__()
self.num_graph_layers = num_graph_layers
self.dropout_pct = dropout_pct
self.output_dim = output_dim
# convert manually crafted categorical features to continuous
self.encoder = AtomEncoder(hidden_dim)
self.convs = nn.ModuleList()
for i in range(num_graph_layers):
self.convs.append(pyg_nn.GCNConv(hidden_dim, hidden_dim))
self.bns = nn.ModuleList()
for i in range(num_graph_layers - 1):
self.bns.append(nn.BatchNorm1d(hidden_dim))
self.clf_head = nn.Linear(hidden_dim, output_dim)
def forward(self, data):
x, edge_index, batch = data.x, data.edge_index, data.batch
x = self.encoder(x)
for i in range(self.num_graph_layers - 1):
x = self.convs[i](x, edge_index)
x = self.bns[i](x)
x = F.relu(x)
x = F.dropout(x, p=self.dropout_pct)
x = self.convs[-1](x, edge_index)
x = pyg_nn.global_max_pool(x, data.batch)
x = self.clf_head(x)
return x
# + colab={"base_uri": "https://localhost:8080/"} id="lCdeM5hgiKfr" outputId="16e35bae-e8bf-441d-b1ab-880b610950de"
model = MaxGraphClassifier(dataset.num_features, 100,
dataset.num_classes, 3, 0.5)
for batch in train_loader:
print(batch)
pred = model(batch)
break
pred.size()
# -
model = MaxGraphClassifier(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, NUM_GCN_LAYERS, DROPOUT_PCT)
model = model.to(device)
# + id="Xn3I2tJrmFEZ"
import torch.optim as optim
# loss_fn = nn.CrossEntropyLoss()
loss_fn = nn.BCEWithLogitsLoss()
optimizer = optim.Adam(model.parameters(), lr=LEARNING_RATE)
# + colab={"base_uri": "https://localhost:8080/"} id="jgmNaKzOmIS_" outputId="e8413b09-d068-4809-996c-b800a1245cb6"
history = train_loop(model, optimizer, loss_fn, train_loader, val_loader, device, NUM_EPOCHS)
# -
display_training_plots(history)
_, test_acc, test_list_preds = eval_step(model, loss_fn, test_loader, device)
test_auc = compute_roc_auc(test_list_preds)
print("Test accuracy: {:.5f}".format(test_acc))
print("Test AUC: {:.5f}".format(test_auc))
# + [markdown] id="GAnEcvEja4oE"
# ## Repeat Classification with SUM Pooling
#
# Now investigate the effect on the graph classification accuracy by changing the global pooling strategy to SUM, i.e., `torch_geometric.nn.global_add_pool`. Here are the steps.
#
# 1. Either copy-paste the previous network and make the necessary changes, or parameterize your original model with a `pooling_strategy` parameter.
# 2. Instantiate the model and set it to the correct `device`.
# 3. Instantiate the `CrossEntropyLoss` loss function
# 4. Instantiate the `Adam` optimizer with the new model parameters.
# 5. Run the training loop for `NUM_EPOCHS` epochs, capturing the training and validation loss and accuracies.
# 6. Use the list of tuples to plot the training curves for training and validation loss and accuracies.
# 7. Compute and report the accuracy and AUC of the network with SUM pooling against the held-out test set.
# + id="1ZG1YK7aZAR1"
# your code here
# + id="xPCsH-p8bZss"
| 145.949153 | 63,194 |
922a779d27fca1ec8e7a7773c5bd17d977e6ffc8
|
py
|
python
|
Week_3_zoomcamp_revised.ipynb
|
1985shree/Data-science-Zoomcamp-projects
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/1985shree/Data-science-Zoomcamp-projects/blob/main/Week_3_zoomcamp_revised.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "Ly8gQ29weXJpZ2h0IDIwMTcgR29vZ2xlIExMQwovLwovLyBMaWNlbnNlZCB1bmRlciB0aGUgQXBhY2hlIExpY2Vuc2UsIFZlcnNpb24gMi4wICh0aGUgIkxpY2Vuc2UiKTsKLy8geW91IG1heSBub3QgdXNlIHRoaXMgZmlsZSBleGNlcHQgaW4gY29tcGxpYW5jZSB3aXRoIHRoZSBMaWNlbnNlLgovLyBZb3UgbWF5IG9idGFpbiBhIGNvcHkgb2YgdGhlIExpY2Vuc2UgYXQKLy8KLy8gICAgICBodHRwOi8vd3d3LmFwYWNoZS5vcmcvbGljZW5zZXMvTElDRU5TRS0yLjAKLy8KLy8gVW5sZXNzIHJlcXVpcmVkIGJ5IGFwcGxpY2FibGUgbGF3IG9yIGFncmVlZCB0byBpbiB3cml0aW5nLCBzb2Z0d2FyZQovLyBkaXN0cmlidXRlZCB1bmRlciB0aGUgTGljZW5zZSBpcyBkaXN0cmlidXRlZCBvbiBhbiAiQVMgSVMiIEJBU0lTLAovLyBXSVRIT1VUIFdBUlJBTlRJRVMgT1IgQ09ORElUSU9OUyBPRiBBTlkgS0lORCwgZWl0aGVyIGV4cHJlc3Mgb3IgaW1wbGllZC4KLy8gU2VlIHRoZSBMaWNlbnNlIGZvciB0aGUgc3BlY2lmaWMgbGFuZ3VhZ2UgZ292ZXJuaW5nIHBlcm1pc3Npb25zIGFuZAovLyBsaW1pdGF0aW9ucyB1bmRlciB0aGUgTGljZW5zZS4KCi8qKgogKiBAZmlsZW92ZXJ2aWV3IEhlbHBlcnMgZm9yIGdvb2dsZS5jb2xhYiBQeXRob24gbW9kdWxlLgogKi8KKGZ1bmN0aW9uKHNjb3BlKSB7CmZ1bmN0aW9uIHNwYW4odGV4dCwgc3R5bGVBdHRyaWJ1dGVzID0ge30pIHsKICBjb25zdCBlbGVtZW50ID0gZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgnc3BhbicpOwogIGVsZW1lbnQudGV4dENvbnRlbnQgPSB0ZXh0OwogIGZvciAoY29uc3Qga2V5IG9mIE9iamVjdC5rZXlzKHN0eWxlQXR0cmlidXRlcykpIHsKICAgIGVsZW1lbnQuc3R5bGVba2V5XSA9IHN0eWxlQXR0cmlidXRlc1trZXldOwogIH0KICByZXR1cm4gZWxlbWVudDsKfQoKLy8gTWF4IG51bWJlciBvZiBieXRlcyB3aGljaCB3aWxsIGJlIHVwbG9hZGVkIGF0IGEgdGltZS4KY29uc3QgTUFYX1BBWUxPQURfU0laRSA9IDEwMCAqIDEwMjQ7CgpmdW5jdGlvbiBfdXBsb2FkRmlsZXMoaW5wdXRJZCwgb3V0cHV0SWQpIHsKICBjb25zdCBzdGVwcyA9IHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCk7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICAvLyBDYWNoZSBzdGVwcyBvbiB0aGUgb3V0cHV0RWxlbWVudCB0byBtYWtlIGl0IGF2YWlsYWJsZSBmb3IgdGhlIG5leHQgY2FsbAogIC8vIHRvIHVwbG9hZEZpbGVzQ29udGludWUgZnJvbSBQeXRob24uCiAgb3V0cHV0RWxlbWVudC5zdGVwcyA9IHN0ZXBzOwoKICByZXR1cm4gX3VwbG9hZEZpbGVzQ29udGludWUob3V0cHV0SWQpOwp9CgovLyBUaGlzIGlzIHJvdWdobHkgYW4gYXN5bmMgZ2VuZXJhdG9yIChub3Qgc3VwcG9ydGVkIGluIHRoZSBicm93c2VyIHlldCksCi8vIHdoZXJlIHRoZXJlIGFyZSBtdWx0aXBsZSBhc3luY2hyb25vdXMgc3RlcHMgYW5kIHRoZSBQeXRob24gc2lkZSBpcyBnb2luZwovLyB0byBwb2xsIGZvciBjb21wbGV0aW9uIG9mIGVhY2ggc3RlcC4KLy8gVGhpcyB1c2VzIGEgUHJvbWlzZSB0byBibG9jayB0aGUgcHl0aG9uIHNpZGUgb24gY29tcGxldGlvbiBvZiBlYWNoIHN0ZXAsCi8vIHRoZW4gcGFzc2VzIHRoZSByZXN1bHQgb2YgdGhlIHByZXZpb3VzIHN0ZXAgYXMgdGhlIGlucHV0IHRvIHRoZSBuZXh0IHN0ZXAuCmZ1bmN0aW9uIF91cGxvYWRGaWxlc0NvbnRpbnVlKG91dHB1dElkKSB7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICBjb25zdCBzdGVwcyA9IG91dHB1dEVsZW1lbnQuc3RlcHM7CgogIGNvbnN0IG5leHQgPSBzdGVwcy5uZXh0KG91dHB1dEVsZW1lbnQubGFzdFByb21pc2VWYWx1ZSk7CiAgcmV0dXJuIFByb21pc2UucmVzb2x2ZShuZXh0LnZhbHVlLnByb21pc2UpLnRoZW4oKHZhbHVlKSA9PiB7CiAgICAvLyBDYWNoZSB0aGUgbGFzdCBwcm9taXNlIHZhbHVlIHRvIG1ha2UgaXQgYXZhaWxhYmxlIHRvIHRoZSBuZXh0CiAgICAvLyBzdGVwIG9mIHRoZSBnZW5lcmF0b3IuCiAgICBvdXRwdXRFbGVtZW50Lmxhc3RQcm9taXNlVmFsdWUgPSB2YWx1ZTsKICAgIHJldHVybiBuZXh0LnZhbHVlLnJlc3BvbnNlOwogIH0pOwp9CgovKioKICogR2VuZXJhdG9yIGZ1bmN0aW9uIHdoaWNoIGlzIGNhbGxlZCBiZXR3ZWVuIGVhY2ggYXN5bmMgc3RlcCBvZiB0aGUgdXBsb2FkCiAqIHByb2Nlc3MuCiAqIEBwYXJhbSB7c3RyaW5nfSBpbnB1dElkIEVsZW1lbnQgSUQgb2YgdGhlIGlucHV0IGZpbGUgcGlja2VyIGVsZW1lbnQuCiAqIEBwYXJhbSB7c3RyaW5nfSBvdXRwdXRJZCBFbGVtZW50IElEIG9mIHRoZSBvdXRwdXQgZGlzcGxheS4KICogQHJldHVybiB7IUl0ZXJhYmxlPCFPYmplY3Q+fSBJdGVyYWJsZSBvZiBuZXh0IHN0ZXBzLgogKi8KZnVuY3Rpb24qIHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCkgewogIGNvbnN0IGlucHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKGlucHV0SWQpOwogIGlucHV0RWxlbWVudC5kaXNhYmxlZCA9IGZhbHNlOwoKICBjb25zdCBvdXRwdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQob3V0cHV0SWQpOwogIG91dHB1dEVsZW1lbnQuaW5uZXJIVE1MID0gJyc7CgogIGNvbnN0IHBpY2tlZFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgaW5wdXRFbGVtZW50LmFkZEV2ZW50TGlzdGVuZXIoJ2NoYW5nZScsIChlKSA9PiB7CiAgICAgIHJlc29sdmUoZS50YXJnZXQuZmlsZXMpOwogICAgfSk7CiAgfSk7CgogIGNvbnN0IGNhbmNlbCA9IGRvY3VtZW50LmNyZWF0ZUVsZW1lbnQoJ2J1dHRvbicpOwogIGlucHV0RWxlbWVudC5wYXJlbnRFbGVtZW50LmFwcGVuZENoaWxkKGNhbmNlbCk7CiAgY2FuY2VsLnRleHRDb250ZW50ID0gJ0NhbmNlbCB1cGxvYWQnOwogIGNvbnN0IGNhbmNlbFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgY2FuY2VsLm9uY2xpY2sgPSAoKSA9PiB7CiAgICAgIHJlc29sdmUobnVsbCk7CiAgICB9OwogIH0pOwoKICAvLyBXYWl0IGZvciB0aGUgdXNlciB0byBwaWNrIHRoZSBmaWxlcy4KICBjb25zdCBmaWxlcyA9IHlpZWxkIHsKICAgIHByb21pc2U6IFByb21pc2UucmFjZShbcGlja2VkUHJvbWlzZSwgY2FuY2VsUHJvbWlzZV0pLAogICAgcmVzcG9uc2U6IHsKICAgICAgYWN0aW9uOiAnc3RhcnRpbmcnLAogICAgfQogIH07CgogIGNhbmNlbC5yZW1vdmUoKTsKCiAgLy8gRGlzYWJsZSB0aGUgaW5wdXQgZWxlbWVudCBzaW5jZSBmdXJ0aGVyIHBpY2tzIGFyZSBub3QgYWxsb3dlZC4KICBpbnB1dEVsZW1lbnQuZGlzYWJsZWQgPSB0cnVlOwoKICBpZiAoIWZpbGVzKSB7CiAgICByZXR1cm4gewogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbXBsZXRlJywKICAgICAgfQogICAgfTsKICB9CgogIGZvciAoY29uc3QgZmlsZSBvZiBmaWxlcykgewogICAgY29uc3QgbGkgPSBkb2N1bWVudC5jcmVhdGVFbGVtZW50KCdsaScpOwogICAgbGkuYXBwZW5kKHNwYW4oZmlsZS5uYW1lLCB7Zm9udFdlaWdodDogJ2JvbGQnfSkpOwogICAgbGkuYXBwZW5kKHNwYW4oCiAgICAgICAgYCgke2ZpbGUudHlwZSB8fCAnbi9hJ30pIC0gJHtmaWxlLnNpemV9IGJ5dGVzLCBgICsKICAgICAgICBgbGFzdCBtb2RpZmllZDogJHsKICAgICAgICAgICAgZmlsZS5sYXN0TW9kaWZpZWREYXRlID8gZmlsZS5sYXN0TW9kaWZpZWREYXRlLnRvTG9jYWxlRGF0ZVN0cmluZygpIDoKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgJ24vYSd9IC0gYCkpOwogICAgY29uc3QgcGVyY2VudCA9IHNwYW4oJzAlIGRvbmUnKTsKICAgIGxpLmFwcGVuZENoaWxkKHBlcmNlbnQpOwoKICAgIG91dHB1dEVsZW1lbnQuYXBwZW5kQ2hpbGQobGkpOwoKICAgIGNvbnN0IGZpbGVEYXRhUHJvbWlzZSA9IG5ldyBQcm9taXNlKChyZXNvbHZlKSA9PiB7CiAgICAgIGNvbnN0IHJlYWRlciA9IG5ldyBGaWxlUmVhZGVyKCk7CiAgICAgIHJlYWRlci5vbmxvYWQgPSAoZSkgPT4gewogICAgICAgIHJlc29sdmUoZS50YXJnZXQucmVzdWx0KTsKICAgICAgfTsKICAgICAgcmVhZGVyLnJlYWRBc0FycmF5QnVmZmVyKGZpbGUpOwogICAgfSk7CiAgICAvLyBXYWl0IGZvciB0aGUgZGF0YSB0byBiZSByZWFkeS4KICAgIGxldCBmaWxlRGF0YSA9IHlpZWxkIHsKICAgICAgcHJvbWlzZTogZmlsZURhdGFQcm9taXNlLAogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbnRpbnVlJywKICAgICAgfQogICAgfTsKCiAgICAvLyBVc2UgYSBjaHVua2VkIHNlbmRpbmcgdG8gYXZvaWQgbWVzc2FnZSBzaXplIGxpbWl0cy4gU2VlIGIvNjIxMTU2NjAuCiAgICBsZXQgcG9zaXRpb24gPSAwOwogICAgZG8gewogICAgICBjb25zdCBsZW5ndGggPSBNYXRoLm1pbihmaWxlRGF0YS5ieXRlTGVuZ3RoIC0gcG9zaXRpb24sIE1BWF9QQVlMT0FEX1NJWkUpOwogICAgICBjb25zdCBjaHVuayA9IG5ldyBVaW50OEFycmF5KGZpbGVEYXRhLCBwb3NpdGlvbiwgbGVuZ3RoKTsKICAgICAgcG9zaXRpb24gKz0gbGVuZ3RoOwoKICAgICAgY29uc3QgYmFzZTY0ID0gYnRvYShTdHJpbmcuZnJvbUNoYXJDb2RlLmFwcGx5KG51bGwsIGNodW5rKSk7CiAgICAgIHlpZWxkIHsKICAgICAgICByZXNwb25zZTogewogICAgICAgICAgYWN0aW9uOiAnYXBwZW5kJywKICAgICAgICAgIGZpbGU6IGZpbGUubmFtZSwKICAgICAgICAgIGRhdGE6IGJhc2U2NCwKICAgICAgICB9LAogICAgICB9OwoKICAgICAgbGV0IHBlcmNlbnREb25lID0gZmlsZURhdGEuYnl0ZUxlbmd0aCA9PT0gMCA/CiAgICAgICAgICAxMDAgOgogICAgICAgICAgTWF0aC5yb3VuZCgocG9zaXRpb24gLyBmaWxlRGF0YS5ieXRlTGVuZ3RoKSAqIDEwMCk7CiAgICAgIHBlcmNlbnQudGV4dENvbnRlbnQgPSBgJHtwZXJjZW50RG9uZX0lIGRvbmVgOwoKICAgIH0gd2hpbGUgKHBvc2l0aW9uIDwgZmlsZURhdGEuYnl0ZUxlbmd0aCk7CiAgfQoKICAvLyBBbGwgZG9uZS4KICB5aWVsZCB7CiAgICByZXNwb25zZTogewogICAgICBhY3Rpb246ICdjb21wbGV0ZScsCiAgICB9CiAgfTsKfQoKc2NvcGUuZ29vZ2xlID0gc2NvcGUuZ29vZ2xlIHx8IHt9OwpzY29wZS5nb29nbGUuY29sYWIgPSBzY29wZS5nb29nbGUuY29sYWIgfHwge307CnNjb3BlLmdvb2dsZS5jb2xhYi5fZmlsZXMgPSB7CiAgX3VwbG9hZEZpbGVzLAogIF91cGxvYWRGaWxlc0NvbnRpbnVlLAp9Owp9KShzZWxmKTsK", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 73} id="0HGpxTmemjkF" outputId="63ed6dbb-54be-4842-8e2c-b3d7f932a4b1"
#uploading ipynb from local folder to google drive/colab folder
from google.colab import files
uploaded = files.upload()
# + id="Qdo6ubwGnH36"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# + colab={"base_uri": "https://localhost:8080/", "height": 406} id="l_hE0fe7nLbJ" outputId="56ebe2e0-cef3-4563-99de-411acd0138cc"
import io
df = pd.read_csv(io.BytesIO(uploaded['AB_NYC_2019.csv']))
df.head()
# + id="URsng8xJnQVS"
data = df [['neighbourhood_group', 'room_type','latitude','longitude','price','minimum_nights', 'number_of_reviews', 'reviews_per_month', 'calculated_host_listings_count', 'availability_365']]
# + colab={"base_uri": "https://localhost:8080/", "height": 356} id="OWkyepHynT4b" outputId="8f4abf76-16ad-4b62-acd9-ef3d20923798"
data.head(10).T
# + colab={"base_uri": "https://localhost:8080/", "height": 294} id="ic5b3L5RnYUh" outputId="192af2a0-f532-4813-84e0-16a29862eb4a"
data.describe().T
# + colab={"base_uri": "https://localhost:8080/"} id="I23dZFZnnc8Y" outputId="5b05a5c9-c170-43d3-b290-0d1d8bd5623a"
np.sum(data.isna())
# + id="3fg0tE6infrK"
data = data.fillna(0)
# + colab={"base_uri": "https://localhost:8080/"} id="EgF2-BiPniaE" outputId="756f05f5-a040-44ec-a345-020e738e87e4"
pd.value_counts(data.neighbourhood_group)
# + id="-qmlFjXgzCRB"
# + [markdown] id="aqpEl-Pjv7sR"
# **correlation**
# + colab={"base_uri": "https://localhost:8080/", "height": 294} id="T-yQXnVowCWW" outputId="d2eef732-d141-4eac-94ab-c21e08ca2b98"
data_numeric = data.drop(['neighbourhood_group', 'room_type', 'price'], axis = 1)
data_numeric.describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 264} id="9PipCw3bwZxP" outputId="1d645963-e172-4a22-e633-ce724e176b46"
corr = data_numeric.corr()
corr
# + id="B24wh-Oz87tJ"
# + colab={"base_uri": "https://localhost:8080/", "height": 492} id="74T5BTBzwtH3" outputId="8058febc-856d-4db2-f6a4-43093e2abdd6"
#visualizing correlation matrix
import seaborn as sns
ax = sns.heatmap(corr, vmin = -1, vmax = 1, center = 0, cmap=sns.diverging_palette(20, 500, n=200), square=True)
ax.set_xticklabels(ax.get_xticklabels(),rotation=45, horizontalalignment='right')
# + colab={"base_uri": "https://localhost:8080/"} id="PfzAZxS2w9TX" outputId="c8cf3524-ac1c-4b79-e09d-b4c3a27c11bd"
data_numeric.corr().unstack().sort_values(ascending = False)
# + [markdown] id="E-4Upg_pzJPS"
# **train-val-test split**
# + id="873iVNIgzIlb"
data_class = data.copy()
mean = data_class.price.mean()
data_class['above_average'] = np.where(data_class['price']>= mean, 1, 0)
# + id="VBm-py6-zt4m"
data_class = data_class.drop(['price'], axis = 1)
# + id="BHPxHYfyz7hN"
from sklearn.model_selection import train_test_split
# + colab={"base_uri": "https://localhost:8080/"} id="bUdxb5C0z8xk" outputId="814a59bc-6563-4fbb-ac1f-2abd3c097e8e"
df_full_train, df_test = train_test_split(data_class, test_size = 0.2, random_state = 42)
df_train, df_val = train_test_split(df_full_train, test_size = 0.25, random_state = 42)
print( len (df_train), len(df_val), len(df_test))
# + id="Of15rHWM1_aH"
df_train.reset_index(drop = True)
df_val.reset_index(drop = True)
df_test.reset_index(drop = True)
y_train = df_train['above_average']
y_val = df_val['above_average']
y_test = df_test['above_average']
# + [markdown] id="plTdAvKn2_6O"
# **mutual information**
# + id="84BnGmhA2-yL"
from sklearn.metrics import mutual_info_score
# + id="vGtGUyAo3Ruf"
cat = ['neighbourhood_group', 'room_type']
# + colab={"base_uri": "https://localhost:8080/"} id="UWgxXeX_3nbY" outputId="19aebb1a-5281-4afc-858f-5f8e011aed6f"
def calculate_mi(series):
return(mutual_info_score(series, df_train.above_average))
df_mi = df_train[cat].apply(calculate_mi)
df_mi
# + colab={"base_uri": "https://localhost:8080/", "height": 415} id="FQ_bKThY5Z78" outputId="374dceaa-1ca0-4ab0-c4e0-b0556b085797"
df_train.drop('above_average', axis = 1)
df_val.drop('above_average', axis = 1)
df_test.drop('above_average', axis = 1)
# + [markdown] id="_cj-eold7vXH"
# **one-hot encoding**
# + id="s4A6sV083app"
from sklearn.feature_extraction import DictVectorizer
# + id="FWpIbaoV83KB"
num = ['latitude', 'longitude', 'minimum_nights', 'number_of_reviews', 'reviews_per_month', 'calculated_host_listings_count', 'availability_365']
# + colab={"base_uri": "https://localhost:8080/"} id="uyfXteSc9m4s" outputId="51aa856b-1c3f-4f97-bdbb-9ae85259b26f"
train_dict = df_train[cat+num].to_dict(orient = 'records')
train_dict[0]
# + id="kFh7wqxn98am"
dv = DictVectorizer(sparse = False)
# + id="axs1mh0--AxT"
dv.fit(train_dict)
X_train = dv.transform(train_dict)
val_dict = df_val[cat+num].to_dict(orient = 'records')
X_val = dv.transform(val_dict)
# + [markdown] id="v7dc8r0n-lht"
# **logistic regression**
# + id="sSoiR_jj-oTM"
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# + colab={"base_uri": "https://localhost:8080/"} id="9CDhcQWw-q8M" outputId="e1abb76b-4043-4d6a-9640-95adb03f587c"
model = LogisticRegression(solver='lbfgs', C=1.0, random_state=42)
model.fit(X_train, y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="Mcr9ISKH_ruB" outputId="1997eb78-fafd-40a0-9154-e24e20fa6831"
y_pred = model.predict(X_val)
accuracy = accuracy_score(y_val, y_pred)
accuracy
# + [markdown] id="pyHzwxDdp1aK"
# **feature elimination**
# + [markdown] id="8daZpVQULx5t"
# numerical feature elimination: eliminate latitude-increase in accuracy? Y
# + id="t1ig35lnqOu4"
elim_lat_num = ['longitude', 'minimum_nights', 'number_of_reviews', 'reviews_per_month', 'calculated_host_listings_count', 'availability_365']
# + colab={"base_uri": "https://localhost:8080/"} id="yG6ktjtiMCLd" outputId="da3b6157-725c-479f-aca6-72ab8879b764"
train_dict_1 = df_train[cat+elim_lat_num].to_dict(orient = 'records')
train_dict_1[0]
# + id="hyuksn3UMNGs"
dv = DictVectorizer(sparse = False)
# + id="6vHEkylnMOQm"
dv.fit(train_dict_1)
X_train_1 = dv.transform(train_dict_1)
val_dict_1 = df_val[cat+elim_lat_num].to_dict(orient = 'records')
X_val_1 = dv.transform(val_dict_1)
# + colab={"base_uri": "https://localhost:8080/"} id="PJr6YebUNrA9" outputId="7ad3adc4-4a89-46ab-f1fc-ac0b37833dd2"
model = LogisticRegression(solver='lbfgs', C=1.0, random_state=42)
model.fit(X_train_1, y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="-FvDTPXBNvN0" outputId="71a9224c-10fd-430b-b301-f1a4a5881232"
y_pred_1 = model.predict(X_val_1)
accuracy = accuracy_score(y_val, y_pred_1)
accuracy
# + [markdown] id="0D7g3oERN9aA"
# numerical feature elimination: eliminate longitude-increase in accuracy? Y, little bit
# + id="FgdQx4qUOKSv"
elim_lon_num = ['latitude', 'minimum_nights', 'number_of_reviews', 'reviews_per_month', 'calculated_host_listings_count', 'availability_365']
# + id="W95EWjQ3ON09"
train_dict_2 = df_train[cat+elim_lon_num].to_dict(orient = 'records')
dv = DictVectorizer(sparse = False)
dv.fit(train_dict_2)
X_train_2 = dv.transform(train_dict_2)
val_dict_2 = df_val[cat+elim_lon_num].to_dict(orient = 'records')
X_val_2 = dv.transform(val_dict_2)
# + colab={"base_uri": "https://localhost:8080/"} id="bCLqSZWcOtEe" outputId="69959f38-5242-4e87-8cad-b9b46d79f2fe"
model = LogisticRegression(solver='lbfgs', C=1.0, random_state=42)
model.fit(X_train_2, y_train)
y_pred_2 = model.predict(X_val_2)
accuracy = accuracy_score(y_val, y_pred_2)
accuracy
# + [markdown] id="TMM2LtZSPALc"
# numerical feature elimination: eliminate minimum_nights-increase in accuracy? N.
# + id="Ppd2XKLOPQlU"
elim_nigh_num = ['latitude', 'longitude', 'number_of_reviews', 'reviews_per_month', 'calculated_host_listings_count', 'availability_365']
# + id="rGhu-4L1O-82"
train_dict_3 = df_train[cat+elim_nigh_num].to_dict(orient = 'records')
dv = DictVectorizer(sparse = False)
dv.fit(train_dict_3)
X_train_3 = dv.transform(train_dict_3)
val_dict_3 = df_val[cat+elim_nigh_num].to_dict(orient = 'records')
X_val_3 = dv.transform(val_dict_3)
# + colab={"base_uri": "https://localhost:8080/"} id="ilDXm_ixPpqJ" outputId="b65993cf-3c2d-468c-abb5-dfdc4d9ae9fe"
model = LogisticRegression(solver='lbfgs', C=1.0, random_state=42)
model.fit(X_train_3, y_train)
y_pred_3 = model.predict(X_val_3)
accuracy = accuracy_score(y_val, y_pred_3)
accuracy
# + [markdown] id="shnDpcxlP1iI"
# numerical feature elimination: eliminate number_of_reviews-increase in accuracy? Y
# + id="dOwjobp2P9Qk"
elim_rev_num = ['latitude', 'longitude', 'minimum_nights', 'reviews_per_month', 'calculated_host_listings_count', 'availability_365']
# + id="bz_BefbZP7fu"
train_dict_4 = df_train[cat+elim_rev_num].to_dict(orient = 'records')
dv = DictVectorizer(sparse = False)
dv.fit(train_dict_4)
X_train_4 = dv.transform(train_dict_4)
val_dict_4 = df_val[cat+elim_rev_num].to_dict(orient = 'records')
X_val_4 = dv.transform(val_dict_4)
# + colab={"base_uri": "https://localhost:8080/"} id="LwvinGJfSMXn" outputId="c8c355a2-3f3f-4bfe-85bd-f7d5ed0bf6f7"
model = LogisticRegression(solver='lbfgs', C=1.0, random_state=42)
model.fit(X_train_4, y_train)
y_pred_4 = model.predict(X_val_4)
accuracy = accuracy_score(y_val, y_pred_4)
accuracy
# + [markdown] id="mo8cKFZXT7oo"
# numerical feature elimination: eliminate number_of_reviews_per_month-increase in accuracy?N
# + id="2o77cjJrUCWP"
elim_rev_pm_num = ['latitude', 'longitude', 'minimum_nights', 'number_of_reviews', 'calculated_host_listings_count', 'availability_365']
# + id="aAm-rAMuUKtG"
train_dict_5 = df_train[cat+elim_rev_pm_num].to_dict(orient = 'records')
dv = DictVectorizer(sparse = False)
dv.fit(train_dict_5)
X_train_5 = dv.transform(train_dict_5)
val_dict_5 = df_val[cat+elim_rev_pm_num].to_dict(orient = 'records')
X_val_5 = dv.transform(val_dict_5)
# + colab={"base_uri": "https://localhost:8080/"} id="SeL04W6vUzq4" outputId="1c1e5722-180e-4ef0-adfc-144685e73f28"
model = LogisticRegression(solver='lbfgs', C=1.0, random_state=42)
model.fit(X_train_5, y_train)
y_pred_5 = model.predict(X_val_5)
accuracy = accuracy_score(y_val, y_pred_5)
accuracy
# + [markdown] id="1OD0hBuIVAfI"
# numerical feature elimination: eliminate calculated_host_listings_count-increase in accuracy? Y
# + id="eflMe9DtVMrg"
elim_host_num = ['latitude', 'longitude', 'minimum_nights', 'number_of_reviews', 'reviews_per_month', 'availability_365']
# + id="1kZnLcLHVLAo"
train_dict_6 = df_train[cat+elim_host_num].to_dict(orient = 'records')
dv = DictVectorizer(sparse = False)
dv.fit(train_dict_6)
X_train_6 = dv.transform(train_dict_6)
val_dict_6 = df_val[cat+elim_host_num].to_dict(orient = 'records')
X_val_6 = dv.transform(val_dict_6)
# + colab={"base_uri": "https://localhost:8080/"} id="oYv7NbEgVh3o" outputId="0719f56c-007e-4c57-e3bc-16a782d857da"
model = LogisticRegression(solver='lbfgs', C=1.0, random_state=42)
model.fit(X_train_6, y_train)
y_pred_6 = model.predict(X_val_6)
accuracy = accuracy_score(y_val, y_pred_6)
accuracy
# + [markdown] id="xyd7rQpqVz8P"
# numerical feature elimination: eliminate availability_365-increase in accuracy? Y, quite a bit.
# + id="uSIOSgJLV7uw"
elim_avail_num = ['latitude', 'longitude', 'minimum_nights', 'number_of_reviews', 'reviews_per_month', 'calculated_host_listings_count']
# + id="bJ9cod7AVzQ4"
train_dict_7 = df_train[cat+elim_avail_num].to_dict(orient = 'records')
dv = DictVectorizer(sparse = False)
dv.fit(train_dict_7)
X_train_7 = dv.transform(train_dict_7)
val_dict_7 = df_val[cat+elim_avail_num].to_dict(orient = 'records')
X_val_7 = dv.transform(val_dict_7)
# + colab={"base_uri": "https://localhost:8080/"} id="VRYcd9auXMop" outputId="afb77182-7d1b-47ad-ff30-bdf72e805acb"
model = LogisticRegression(solver='lbfgs', C=1.0, random_state=42)
model.fit(X_train_7, y_train)
y_pred_7 = model.predict(X_val_7)
accuracy = accuracy_score(y_val, y_pred_7)
accuracy
# + [markdown] id="X7WDeGzkX4xp"
# categorical feature elimination: eliminate neighbourhood_group-increase in accuracy? N
# + id="YlVWbVr7YDSc"
cat = ['neighbourhood_group', 'room_type']
# + id="dbNsu9wuYPyo"
cat_neig = ['room_type']
# + id="8KL7n8bNYd0T"
train_dict_8 = df_train[cat_neig + num].to_dict(orient = 'records')
dv = DictVectorizer(sparse = False)
dv.fit(train_dict_8)
X_train_8 = dv.transform(train_dict_8)
val_dict_8 = df_val[cat_neig + num].to_dict(orient = 'records')
X_val_8 = dv.transform(val_dict_8)
# + colab={"base_uri": "https://localhost:8080/"} id="syS7FIsPYu6K" outputId="08fefcd1-7bda-4426-8db1-34d53a47b090"
model = LogisticRegression(solver='lbfgs', C=1.0, random_state=42)
model.fit(X_train_8, y_train)
y_pred_8 = model.predict(X_val_8)
accuracy = accuracy_score(y_val, y_pred_8)
accuracy
# + [markdown] id="j0_8_MWfZDkJ"
# categorical feature elimination: eliminate room_type-increase in accuracy? N
# + id="WRprLGWbZKx6"
cat_room_type = ['neighbourhood_group']
# + id="aRwYXPRAZQR-"
train_dict_9 = df_train[cat_room_type + num].to_dict(orient = 'records')
dv = DictVectorizer(sparse = False)
dv.fit(train_dict_9)
X_train_9 = dv.transform(train_dict_9)
val_dict_9 = df_val[cat_room_type + num].to_dict(orient = 'records')
X_val_9 = dv.transform(val_dict_9)
# + colab={"base_uri": "https://localhost:8080/"} id="jr23rj8SZfhi" outputId="40790498-784d-4b1d-e1b8-37f08e65b912"
model = LogisticRegression(solver='lbfgs', C=1.0, random_state=42)
model.fit(X_train_9, y_train)
y_pred_9 = model.predict(X_val_9)
accuracy = accuracy_score(y_val, y_pred_9)
accuracy
# + [markdown] id="JGH86Y7IZtNa"
# **smallest diffference in accuracy is by eliminaing room type**
# + [markdown] id="l5C2qRnbTURo"
# **training ridge regression**
| 51.486553 | 7,349 |
2d4b512a2ea1151c185b8ac9621b80619d262e97
|
py
|
python
|
Chapter03/25_Impact_of_building_a_deeper_neural_network.ipynb
|
aihill/Modern-Computer-Vision-with-PyTorch
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/PacktPublishing/Hands-On-Computer-Vision-with-PyTorch/blob/master/Chapter03/Impact_of_building_a_deeper_neural_network.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="db6eHXhn_teE" outputId="1bcce1ac-5c74-4bf8-f113-a5d9ed560303" colab={"base_uri": "https://localhost:8080/", "height": 437, "referenced_widgets": ["7e3e385d271e4f8ca736fe0da0be67c0", "5550477bbf9e4c55b5d509067f4c8b7f", "85ef40115e2446db918c8fb58d8298a5", "a14ae0a36fb74cee9c702887b4e1bb72", "cd67e879a910462da5262779575d0f33", "d7835c3fcbc344d6929e9e276f5283e5", "6986a69e9d1d4871bbd0c2bf8caf382f", "ad775d32a59a4e52a1886a17b450e163", "2cbbd3dcb34146dc866525d958bacf0c", "a412bc9ea39d4e1da0a50568f9ff7293", "6d939043fe894743991520b97dd96da9", "8b1f6ef2208b49a589cabedc4760969f", "d04a50b9b7154afb9b66453d12405dea", "97bbf22385ac423984249f6fb45ef9c8", "45d2be82486c4f4c855b6d3844387f6b", "062f019e1a7d41f78ba39da29236f667", "5010491fbe1b4ed2bc8b422333c6164b", "cd942030383742dcadfd703bd47dfea4", "5e81fcbed9484c98ae98dca2b8a515f6", "e6743f07e8a74738802f206fcfc76cb5", "27c1827603fd478f9dca8c8b4ad52bf6", "8bca20deab3445e8be0fe4bac16abdca", "c550af41d5ae4be7b2d9094e15eda141", "889970c06edf4c26ae1c6561f8b8e21a", "07ffb7aafa2e4a09ae10d1d7f74d3ac7", "b4603aa9e1ef48bdb151b5f7e68713df", "b29285a4ff1e481fbfaad8b20a559f25", "318c5ef119774c9f9f3b685c824c3f31", "54fad4d3c539434fbb76904d4dd89e90", "c61c295b6e564c689dba74e7d0819ab4", "281b03bf21ee499cb9d4588531cddbee", "38de1f5fe92b4870926540527a31d879"]}
from torchvision import datasets
import torch
data_folder = '~/data/FMNIST' # This can be any directory you want to
# download FMNIST to
fmnist = datasets.FashionMNIST(data_folder, download=True, train=True)
tr_images = fmnist.data
tr_targets = fmnist.targets
# + id="USu9lapK_520"
val_fmnist = datasets.FashionMNIST(data_folder, download=True, train=False)
val_images = val_fmnist.data
val_targets = val_fmnist.targets
# + id="oaKX_Log_7Vq"
import matplotlib.pyplot as plt
# %matplotlib inline
import numpy as np
from torch.utils.data import Dataset, DataLoader
import torch
import torch.nn as nn
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# + [markdown] id="7MkYWfNrzDsJ"
# ### Model with 0 hidden layers
# + id="LZh0i54a_8zA"
class FMNISTDataset(Dataset):
def __init__(self, x, y):
x = x.float()
x = x.view(-1,28*28)/255
self.x, self.y = x, y
def __getitem__(self, ix):
x, y = self.x[ix], self.y[ix]
return x.to(device), y.to(device)
def __len__(self):
return len(self.x)
from torch.optim import SGD, Adam
def get_model():
model = nn.Sequential(
nn.Linear(28 * 28, 10)
).to(device)
loss_fn = nn.CrossEntropyLoss()
optimizer = Adam(model.parameters(), lr=1e-3)
return model, loss_fn, optimizer
def train_batch(x, y, model, opt, loss_fn):
model.train()
prediction = model(x)
batch_loss = loss_fn(prediction, y)
batch_loss.backward()
optimizer.step()
optimizer.zero_grad()
return batch_loss.item()
def accuracy(x, y, model):
model.eval()
# this is the same as @torch.no_grad
# at the top of function, only difference
# being, grad is not computed in the with scope
with torch.no_grad():
prediction = model(x)
max_values, argmaxes = prediction.max(-1)
is_correct = argmaxes == y
return is_correct.cpu().numpy().tolist()
# + id="2pm_AtNh_9xO"
def get_data():
train = FMNISTDataset(tr_images, tr_targets)
trn_dl = DataLoader(train, batch_size=32, shuffle=True)
val = FMNISTDataset(val_images, val_targets)
val_dl = DataLoader(val, batch_size=len(val_images), shuffle=False)
return trn_dl, val_dl
# + id="tr7aYJszAABu"
@torch.no_grad()
def val_loss(x, y, model):
prediction = model(x)
val_loss = loss_fn(prediction, y)
return val_loss.item()
# + id="-QsGjZhYABEm"
trn_dl, val_dl = get_data()
model, loss_fn, optimizer = get_model()
# + id="KKq8CFkPACLw" outputId="8abc68ee-68a9-443b-f9ff-a4dea475ee35" colab={"base_uri": "https://localhost:8080/", "height": 108}
train_losses, train_accuracies = [], []
val_losses, val_accuracies = [], []
for epoch in range(5):
print(epoch)
train_epoch_losses, train_epoch_accuracies = [], []
for ix, batch in enumerate(iter(trn_dl)):
x, y = batch
batch_loss = train_batch(x, y, model, optimizer, loss_fn)
train_epoch_losses.append(batch_loss)
train_epoch_loss = np.array(train_epoch_losses).mean()
for ix, batch in enumerate(iter(trn_dl)):
x, y = batch
is_correct = accuracy(x, y, model)
train_epoch_accuracies.extend(is_correct)
train_epoch_accuracy = np.mean(train_epoch_accuracies)
for ix, batch in enumerate(iter(val_dl)):
x, y = batch
val_is_correct = accuracy(x, y, model)
validation_loss = val_loss(x, y, model)
val_epoch_accuracy = np.mean(val_is_correct)
train_losses.append(train_epoch_loss)
train_accuracies.append(train_epoch_accuracy)
val_losses.append(validation_loss)
val_accuracies.append(val_epoch_accuracy)
# + id="X3SlttxNAXCM" outputId="ce4b9893-85de-4ede-d770-d9d53f8a3a38" colab={"base_uri": "https://localhost:8080/", "height": 337}
epochs = np.arange(5)+1
import matplotlib.ticker as mtick
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
# %matplotlib inline
plt.subplot(211)
plt.plot(epochs, train_losses, 'bo', label='Training loss')
plt.plot(epochs, val_losses, 'r', label='Validation loss')
plt.gca().xaxis.set_major_locator(mticker.MultipleLocator(1))
plt.title('Training and validation loss with no hidden layer')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid('off')
plt.show()
plt.subplot(212)
plt.plot(epochs, train_accuracies, 'bo', label='Training accuracy')
plt.plot(epochs, val_accuracies, 'r', label='Validation accuracy')
plt.gca().xaxis.set_major_locator(mticker.MultipleLocator(1))
plt.title('Training and validation accuracy with no hidden layer')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.gca().set_yticklabels(['{:.0f}%'.format(x*100) for x in plt.gca().get_yticks()])
plt.legend()
plt.grid('off')
plt.show()
# + id="frZEg63SAc7K"
# + [markdown] id="WHDksDDgBgp3"
# ### Model with 1 hidden layer
# + id="XyIYRbkoAdTo"
def get_model():
model = nn.Sequential(
nn.Linear(28 * 28, 1000),
nn.ReLU(),
nn.Linear(1000, 10)
).to(device)
loss_fn = nn.CrossEntropyLoss()
optimizer = Adam(model.parameters(), lr=1e-3)
return model, loss_fn, optimizer
# + id="-6ZPcquEAnOt"
trn_dl, val_dl = get_data()
model, loss_fn, optimizer = get_model()
# + id="1SHVfTnqApUa" outputId="40ed576d-98b2-4ab1-9646-7311e265d335" colab={"base_uri": "https://localhost:8080/", "height": 108}
train_losses, train_accuracies = [], []
val_losses, val_accuracies = [], []
for epoch in range(5):
print(epoch)
train_epoch_losses, train_epoch_accuracies = [], []
for ix, batch in enumerate(iter(trn_dl)):
x, y = batch
batch_loss = train_batch(x, y, model, optimizer, loss_fn)
train_epoch_losses.append(batch_loss)
train_epoch_loss = np.array(train_epoch_losses).mean()
for ix, batch in enumerate(iter(trn_dl)):
x, y = batch
is_correct = accuracy(x, y, model)
train_epoch_accuracies.extend(is_correct)
train_epoch_accuracy = np.mean(train_epoch_accuracies)
for ix, batch in enumerate(iter(val_dl)):
x, y = batch
val_is_correct = accuracy(x, y, model)
validation_loss = val_loss(x, y, model)
val_epoch_accuracy = np.mean(val_is_correct)
train_losses.append(train_epoch_loss)
train_accuracies.append(train_epoch_accuracy)
val_losses.append(validation_loss)
val_accuracies.append(val_epoch_accuracy)
# + id="OS-HLAriArIc" outputId="6674e504-54f6-4ed1-f8b9-276586dd2fe6" colab={"base_uri": "https://localhost:8080/", "height": 337}
epochs = np.arange(5)+1
import matplotlib.ticker as mtick
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
# %matplotlib inline
plt.subplot(211)
plt.plot(epochs, train_losses, 'bo', label='Training loss')
plt.plot(epochs, val_losses, 'r', label='Validation loss')
plt.gca().xaxis.set_major_locator(mticker.MultipleLocator(1))
plt.title('Training and validation loss with 1 hidden layer')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid('off')
plt.show()
plt.subplot(212)
plt.plot(epochs, train_accuracies, 'bo', label='Training accuracy')
plt.plot(epochs, val_accuracies, 'r', label='Validation accuracy')
plt.gca().xaxis.set_major_locator(mticker.MultipleLocator(1))
plt.title('Training and validation accuracy with 1 hidden layer')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.gca().set_yticklabels(['{:.0f}%'.format(x*100) for x in plt.gca().get_yticks()])
plt.legend()
plt.grid('off')
plt.show()
# + id="I25leQbQAuGw"
# + [markdown] id="q33tx2wdBrRi"
# Model with 2 hidden layers
# + id="0tasZD3fBspj"
def get_model():
model = nn.Sequential(
nn.Linear(28 * 28, 1000),
nn.ReLU(),
nn.Linear(1000, 1000),
nn.ReLU(),
nn.Linear(1000, 10)
).to(device)
loss_fn = nn.CrossEntropyLoss()
optimizer = Adam(model.parameters(), lr=1e-3)
return model, loss_fn, optimizer
# + id="NCL8UX_aBxBc"
trn_dl, val_dl = get_data()
model, loss_fn, optimizer = get_model()
# + id="TTvPNVGGBzLI" outputId="2edbce71-c797-484f-97bb-1ad251879504" colab={"base_uri": "https://localhost:8080/", "height": 108}
train_losses, train_accuracies = [], []
val_losses, val_accuracies = [], []
for epoch in range(5):
print(epoch)
train_epoch_losses, train_epoch_accuracies = [], []
for ix, batch in enumerate(iter(trn_dl)):
x, y = batch
batch_loss = train_batch(x, y, model, optimizer, loss_fn)
train_epoch_losses.append(batch_loss)
train_epoch_loss = np.array(train_epoch_losses).mean()
for ix, batch in enumerate(iter(trn_dl)):
x, y = batch
is_correct = accuracy(x, y, model)
train_epoch_accuracies.extend(is_correct)
train_epoch_accuracy = np.mean(train_epoch_accuracies)
for ix, batch in enumerate(iter(val_dl)):
x, y = batch
val_is_correct = accuracy(x, y, model)
validation_loss = val_loss(x, y, model)
val_epoch_accuracy = np.mean(val_is_correct)
train_losses.append(train_epoch_loss)
train_accuracies.append(train_epoch_accuracy)
val_losses.append(validation_loss)
val_accuracies.append(val_epoch_accuracy)
# + id="HYhXTLF2B2q5" outputId="89f4647f-cfb7-425e-b79a-dac38c65b4e7" colab={"base_uri": "https://localhost:8080/", "height": 337}
epochs = np.arange(5)+1
import matplotlib.ticker as mtick
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
# %matplotlib inline
plt.subplot(211)
plt.plot(epochs, train_losses, 'bo', label='Training loss')
plt.plot(epochs, val_losses, 'r', label='Validation loss')
plt.gca().xaxis.set_major_locator(mticker.MultipleLocator(1))
plt.title('Training and validation loss with 2 hidden layers')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid('off')
plt.show()
plt.subplot(212)
plt.plot(epochs, train_accuracies, 'bo', label='Training accuracy')
plt.plot(epochs, val_accuracies, 'r', label='Validation accuracy')
plt.gca().xaxis.set_major_locator(mticker.MultipleLocator(1))
plt.title('Training and validation accuracy with 2 hidden layers')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.gca().set_yticklabels(['{:.0f}%'.format(x*100) for x in plt.gca().get_yticks()])
plt.legend()
plt.grid('off')
plt.show()
# + id="HsXD3fkYB6c8"
| 36.291022 | 1,306 |
1a167b0a2ce1e9396ee24dcb86a3a2f138b3f06f
|
py
|
python
|
lesson_notebooks/l19/sklearn_feature_importance_solution.ipynb
|
zhanghaitao1/ai_algorithms_trading-term2
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Generate-data" data-toc-modified-id="Generate-data-1"><span class="toc-item-num">1 </span>Generate data</a></span></li><li><span><a href="#Train-a-decision-tree" data-toc-modified-id="Train-a-decision-tree-2"><span class="toc-item-num">2 </span>Train a decision tree</a></span></li><li><span><a href="#Visualize-the-trained-decision-tree" data-toc-modified-id="Visualize-the-trained-decision-tree-3"><span class="toc-item-num">3 </span>Visualize the trained decision tree</a></span></li><li><span><a href="#Explore-the-tree" data-toc-modified-id="Explore-the-tree-4"><span class="toc-item-num">4 </span>Explore the tree</a></span></li><li><span><a href="#Tree-attributes-are-stored-in-lists" data-toc-modified-id="Tree-attributes-are-stored-in-lists-5"><span class="toc-item-num">5 </span>Tree attributes are stored in lists</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#left-and-right-child-nodes" data-toc-modified-id="left-and-right-child-nodes-5.0.1"><span class="toc-item-num">5.0.1 </span>left and right child nodes</a></span></li><li><span><a href="#features-used-for-splitting-at-each-node" data-toc-modified-id="features-used-for-splitting-at-each-node-5.0.2"><span class="toc-item-num">5.0.2 </span>features used for splitting at each node</a></span></li><li><span><a href="#number-of-samples-in-each-node" data-toc-modified-id="number-of-samples-in-each-node-5.0.3"><span class="toc-item-num">5.0.3 </span>number of samples in each node</a></span></li></ul></li></ul></li><li><span><a href="#Gini-impurity" data-toc-modified-id="Gini-impurity-6"><span class="toc-item-num">6 </span>Gini impurity</a></span></li><li><span><a href="#Quiz" data-toc-modified-id="Quiz-7"><span class="toc-item-num">7 </span>Quiz</a></span></li><li><span><a href="#Quiz" data-toc-modified-id="Quiz-8"><span class="toc-item-num">8 </span>Quiz</a></span></li><li><span><a href="#Answer" data-toc-modified-id="Answer-9"><span class="toc-item-num">9 </span>Answer</a></span></li><li><span><a href="#Node-Importance" data-toc-modified-id="Node-Importance-10"><span class="toc-item-num">10 </span>Node Importance</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Summary-of-the-node-labels" data-toc-modified-id="Summary-of-the-node-labels-10.0.1"><span class="toc-item-num">10.0.1 </span>Summary of the node labels</a></span></li></ul></li></ul></li><li><span><a href="#Quiz" data-toc-modified-id="Quiz-11"><span class="toc-item-num">11 </span>Quiz</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Sum-the-node-importances" data-toc-modified-id="Sum-the-node-importances-11.0.1"><span class="toc-item-num">11.0.1 </span>Sum the node importances</a></span></li><li><span><a href="#Summary-of-which-feature-is-used-to-split-at-each-node" data-toc-modified-id="Summary-of-which-feature-is-used-to-split-at-each-node-11.0.2"><span class="toc-item-num">11.0.2 </span>Summary of which feature is used to split at each node</a></span></li></ul></li></ul></li><li><span><a href="#Quiz:-Calculate-importance-of-the-features" data-toc-modified-id="Quiz:-Calculate-importance-of-the-features-12"><span class="toc-item-num">12 </span>Quiz: Calculate importance of the features</a></span></li><li><span><a href="#Double-check-with-sklearn" data-toc-modified-id="Double-check-with-sklearn-13"><span class="toc-item-num">13 </span>Double check with sklearn</a></span></li><li><span><a href="#Notice-anything-odd?" data-toc-modified-id="Notice-anything-odd?-14"><span class="toc-item-num">14 </span>Notice anything odd?</a></span><ul class="toc-item"><li><span><a href="#Answer" data-toc-modified-id="Answer-14.1"><span class="toc-item-num">14.1 </span>Answer</a></span></li></ul></li><li><span><a href="#Question" data-toc-modified-id="Question-15"><span class="toc-item-num">15 </span>Question</a></span></li><li><span><a href="#Solution-notebook" data-toc-modified-id="Solution-notebook-16"><span class="toc-item-num">16 </span>Solution notebook</a></span></li></ul></div>
# -
# # Feature importance method in sci-kit learn (Solution)
# We'll get a sense of how feature importance is calculated in sci-kit learn, and also see where it gives results that we wouldn't expect.
#
# Sci-kit learn uses gini impurity to calculate a measure of impurity for each node. Gini impurity, like entropy is a way to measure how "disorganized" the observations are before and after splitting them using a feature. So there is an impurity measure for each node.
#
# In the formula, freq_{i} is the frequency of label "i". C is the number of unique labels at that node.
#
# $Impurity= \sum_{i=1}^{C} - freq_{i} * (1- freq_{i})$
#
# The node importance in sci-kit learn is calculated as the difference between the gini impurity of the node and the gini impurity of its left and right children. These gini impurities are weighted by the number of data points that reach each node.
#
# $NodeImportance = w_{i} Impurity_{i} - ( w_{left} Impurity_{left} + w_{right} Impurity_{right} )$
#
# The importance of a feature is the importance of the node that it was split on, divided by the sum of all node importances in the tree. You’ll get to practice this in the coding exercise coming up next!
#
# For additional reading, please check out this blog post [The Mathematics of Decision Trees, Random Forest and Feature Importance in Scikit-learn and Spark](https://medium.com/@srnghn/the-mathematics-of-decision-trees-random-forest-and-feature-importance-in-scikit-learn-and-spark-f2861df67e3)
import sys
# # !{sys.executable} -m pip install numpy==1.14.5
# # !{sys.executable} -m pip install scikit-learn==0.19.1
# # !{sys.executable} -m pip install graphviz==0.9
import sklearn
from sklearn import tree
import numpy as np
import graphviz
# ## Generate data
#
# We'll generate features and labels that form the "AND" operator. So when feature 0 and feature 1 are both 1, then the label is 1, else the label is 0. The third feature, feature 2, won't have an effect on the label output (it's always zero).
# AND operator
#
# true and true = true
# true and false = false
# false and true = false
# false and false = false
"""
Features 0 and 1 form the AND operator
Feature 2 is always zero.
"""
N = 100
M = 3
X = np.zeros((N,M))
X.shape
y = np.zeros(N)
X[:1 * N//4, 1] = 1
X[:N//2, 0] = 1
X[N//2:3 * N//4, 1] = 1
y[:1 * N//4] = 1
# observe the features
X
# observe the labels
y
# ## Train a decision tree
model = tree.DecisionTreeClassifier(random_state=0)
model.fit(X, y)
# ## Visualize the trained decision tree
dot_data = sklearn.tree.export_graphviz(model, out_file=None, filled=True, rounded=True, special_characters=True)
graph = graphviz.Source(dot_data)
graph
# ## Explore the tree
#
# The [source code for Tree](https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/tree/_tree.pyx) has useful comments about attributes in the Tree class. Search for the code that says `cdef class Tree:` for useful comments.
# get the Tree object
tree0 = model.tree_
# ## Tree attributes are stored in lists
#
# The tree data are stored in lists. Each node is also assigned an integer 0,1,2...
# Each node's value for some attribute is stored at the index location that equals the node's assigned integer.
#
# For example, node 0 is the root node at the top of the tree. There is a list called children_left. Index location 0 contains the left child of node 0.
#
#
# #### left and right child nodes
# ```
# children_left : array of int, shape [node_count]
# children_left[i] holds the node id of the left child of node i.
# For leaves, children_left[i] == TREE_LEAF. Otherwise,
# children_left[i] > i. This child handles the case where
# X[:, feature[i]] <= threshold[i].
# children_right : array of int, shape [node_count]
# children_right[i] holds the node id of the right child of node i.
# For leaves, children_right[i] == TREE_LEAF. Otherwise,
# children_right[i] > i. This child handles the case where
# X[:, feature[i]] > threshold[i].
# ```
print(f"tree0.children_left: {tree0.children_left}")
print(f"tree0.children_right: {tree0.children_right}")
# So in this tree, the index positions 0,1,2,3,4 are the numbers for identifying each node in the tree. Node 0 is the root node. Node 1 and 2 are the left and right child of the root node. So in the list children_left, at index 0, we see 1, and for children_right list, at index 0, we see 2.
#
# -1 is used to denote that there is no child for that node. Node 1 has no left or right child, so in the children_left list, at index 1, we see -1. Similarly, in children_right, at index 1, the value is also -1.
# #### features used for splitting at each node
# ```
# feature : array of int, shape [node_count]
# feature[i] holds the feature to split on, for the internal node i.
# ```
print(f"tree0.feature: {tree0.feature}")
# The feature 1 is used to split on node 0. Feature 0 is used to split on node 2. The -2 values indicate that these are leaf nodes (no features are used for splitting at those nodes).
# #### number of samples in each node
#
# ```
# n_node_samples : array of int, shape [node_count]
# n_node_samples[i] holds the number of training samples reaching node i.
#
# weighted_n_node_samples : array of int, shape [node_count]
# weighted_n_node_samples[i] holds the weighted number of training samples
# reaching node i.
# ```
print(f"tree0.n_node_samples : {tree0.n_node_samples}")
print(f"tree0.weighted_n_node_samples : {tree0.weighted_n_node_samples}")
# The weighted_n_node_samples is the same as n_node_samples for decision trees. It's different for random forests where a sub-sample of data points is used in each tree. We'll use weighted_n_node_samples in the code below, but either one works when we're calculating the proportion of samples in a left or right child node relative to their parent node.
# ## Gini impurity
#
# Gini impurity, like entropy is a way to measure how "disorganized" the observations are before and after splitting them using a feature. So there is an impurity value calculated for each node.
#
# In the formula, $freq_{i}$ is the frequency of label "i". C is the number of unique labels at that node (C stands for "Class", as in "classifier".
#
# $ \sum_{i}^{C} - freq_{i} * (1- freq_{i})$
#
# ```
# impurity : array of double, shape [node_count]
# impurity[i] holds the impurity (i.e., the value of the splitting
# criterion) at node i.
#
# ```
# What is the impurity if there is a single class (unique label type)?
freq0 = 1
impurity = -1 * freq0 * (1 - freq0)
print(f"impurity of a homogenous sample with a single label, is: {impurity}")
# What is the impurity if there are two classes (two distinct labels), and there are 90% of samples for one label, and 10% for the other?
freq1 = 0.9
freq2 = 0.1
impurity = -1 * freq1 * (1 -freq1) + -1 * freq2 * (1 - freq2)
print(f"impurity when 90% are of one label, and 10% are of the other: {impurity}")
# ## Quiz
# What is the impurity if there are two classes of label, and there are 50% of samples for one label, and 50% for the other?
"""
What is the impurity if there are two classes of label,
and there are 50% of samples for one label, and 50% for the other?
"""
# TODO
freq1 = 0.5
freq2 = 0.5
# TODO
impurity = -1 * freq1 * (1 - freq1) + -1 * freq2 * (1 - freq2)
print(f"impurity when 50% are of one label, and 50% are of the other: {impurity}")
# ## Quiz
#
# Is the impurity larger or smaller (in magnitude) when the samples are dominated by a single class?
# Is the impurity larger or smaller (in magnitude) when the frequency of each class is more evenly distributed among classes?
# ## Answer
# The gini impurity is smaller in magnitude (closer to zero) when the samples are dominated by a single class.
# The impurity is larger in magnitude (farther from zero) when there is a more even split among labels in the sample.
# ## Node Importance
#
# The node importance in sklearn is calculated as the difference between the gini impurity of the node and the impurities of its child nodes. These gini impurities are weighted by the number of data points that reach each node.
#
# $NodeImportance = w_{i} Impurity_{i} - ( w_{left} Impurity_{left} + w_{right} Impurity_{right} )$
#
# #### Summary of the node labels
# Node 0 is the root node, and its left and right children are 1 and 2.
# Node 1 is a leaf node
# Node 2 has two children, 3 and 4.
# Node 3 is a leaf node
# Node 4 is a leaf node
# summary of child nodes
print(f"tree0.children_left: {tree0.children_left}")
print(f"tree0.children_right: {tree0.children_right}")
# Calculate the node importance of the root node, node 0. Its child nodes are 1 and 2
ni0 = tree0.weighted_n_node_samples[0] * tree0.impurity[0] - \
( tree0.weighted_n_node_samples[1] * tree0.impurity[1] + \
tree0.weighted_n_node_samples[2] * tree0.impurity[2] )
print(f"Importance of node 0 is {ni0}")
# ## Quiz
# Calculate the node importance of node 2. Its left and right child nodes are 3 and 4
# TODO
ni2 = tree0.weighted_n_node_samples[2] * tree0.impurity[2] - \
( tree0.weighted_n_node_samples[3] * tree0.impurity[3] + \
tree0.weighted_n_node_samples[4] * tree0.impurity[4] )
print(f"Importance of node 2 is {ni2}")
# The other nodes are leaf nodes, so there is no decrease in impurity that we can calculate
# #### Sum the node importances
# Only nodes 0 and node 2 have node importances. The others are leaf nodes, so we don't calculate node importances (there is no feature that is used for splitting at those leaf nodes).
# TODO
ni_total = ni0 + ni2
print(f"The sum of node importances is {ni_total}")
# #### Summary of which feature is used to split at each node
#
# feature 0 was used to split on node 2
# feature 1 was used to split on node 0
# feature 2 was not used for splitting
print(f"tree0.feature: {tree0.feature}")
# ## Quiz: Calculate importance of the features
#
# The importance of a feature is the importance of the node that it was used for splitting, divided by the total node importances. Calculate the importance of feature 0, 1 and 2.
# TODO
fi0 = ni2/ni_total
fi1 = ni0/ni_total
fi2 = 0/ni_total
print(f"importance of feature 0: {fi0}")
print(f"importance of feature 1: {fi1}")
print(f"importance of feature 2: {fi2}")
# ## Double check with sklearn
#
# Check out how to use [feature importance](https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html#sklearn.tree.DecisionTreeClassifier.feature_importances_)
# +
# TODO: get feature importances from sci-kit learn
fi0_skl = model.feature_importances_[0]
fi1_skl = model.feature_importances_[1]
fi2_skl = model.feature_importances_[2]
print(f"sklearn importance of feature 0: {fi0_skl}")
print(f"sklearn importance of feature 1: {fi1_skl}")
print(f"sklearn importance of feature 2: {fi2_skl}")
# -
# ## Notice anything odd?
#
# Notice that the data we generated simulates an AND operator. If feature 0 and feature 1 are both 1, then the output is 1, otherwise 0. So, from that perspective, do you think that features 0 and 1 are equally important?
#
# What do you notice about the feature importance calculated in sklearn? Are the features considered equally important according to this calculation?
# ### Answer
# Intuitively, if features 0 and 1 form the AND operator, then it makes sense that they should be equally important in determining the output. The feature importance calculated in sklearn assigns a higher importance to feature 0 compared to feature 1. This is because the tree first splits on feature 1, and then when it splits on feature 0, the labels become cleanly split into respective leaf nodes.
#
# In other words, what we observe is that features which are used to split further down the bottom of the tree are given higher importance, using the gini impurity as a measure.
# ## Question
#
# If someone tells you that you don't need to understand the algorithm, just how to install the package and call the function, do you agree or disagree with that statement?
# ## Solution notebook
# [Solution notebook](sklearn_feature_importance_solution.ipynb)
| 55.812081 | 4,339 |
00d393601b691da945ea6d993047fae618cfb9a1
|
py
|
python
|
titanic/outstanding-case/.ipynb_checkpoints/a-statistical-analysis-ml-workflow-of-titanic-checkpoint.ipynb
|
paulsweet/Kaggle
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] _cell_guid="9c75ca41-8357-479e-8a46-ebdec5f035f3" _uuid="319ae25236d9fddf1745ea1c4cb365e5dbb00372"
# <img src="http://data.freehdw.com/ships-titanic-vehicles-best.jpg" Width="800">
# + [markdown] _uuid="bdce3bc433feb19f6622ab910cfe2123ccd07a1c"
# ## <div style="text-align: center" > A Statistical Analysis & Machine Learning Workflow of Titanic </div>
# <div style="text-align: center"> Being a part of Kaggle gives me unlimited access to learn, share and grow as a Data Scientist. In this kernel, I want to solve <font color="red"><b>Titanic competition</b></font>, a popular machine learning dataset for <b>beginners</b>. I am going to discuss every steps of a typical machine learning project such as,<b> from data preparation, data analysis to statistical tests and implementing different models along with explaining why we used them.</b> I will also describe the model results along with many other tips. So let's get started.</div>
#
#
# ***
# <div style="text-align:center"> If there are any recommendations/changes you would like to see in this notebook, please <b>leave a comment</b>. Any feedback/constructive criticism would be genuinely appreciated. <b>This notebook is always a work in progress. So, please stay tuned for more to come.</b></div>
#
#
# <div style="text-align:center">If you like this notebook or find this notebook helpful, Please feel free to <font color="red"><b>UPVOTE</b></font> and/or <font color="Blue"><b>leave a comment.</b></font></div><br>
#
# <div style="text-align: center"><b>You can also Fork and Run this kernel on <a href="https://github.com/masumrumi">Github</b></a>
# </div>
#
# ### <div style="text-align: center">Stay Tuned for More to Come!!</div>
#
#
#
#
#
# + [markdown] _cell_guid="1b327e8f-22c3-4f4a-899e-33c20073d74f" _uuid="ac342ad67f3704bc8d420f430bb10425d229b1a7"
# # Introduction
# <a id="introduction" ></a><br>
# This kernel is for all aspiring data scientists to learn from and to review their knowledge. We will have a detailed statistical analysis of Titanic data set along with Machine learning models. I am super excited to share my first kernel with the Kaggle community. As I go on in this journey and learn new topics, I will incorporate them with updates. So, check for them and please <b>leave a comment</b> if you have any suggestions to make them better!! Going back to the topics of this kernel, I will do more in-depth visualizations to explain the data, and the machine learning classifiers will be used to predict passenger survival status. So, let's get started.
#
# <div style="text-align: center">This notebook goes indepth in classifier models since we are trying to solve a classifier problem here. If you want to learn more about Advanced Regression models, please check out <a href="https://www.kaggle.com/masumrumi/a-stats-analysis-and-ml-workflow-of-house-pricing">this</a> kernel.</div>
#
# + [markdown] _cell_guid="8256c27c-c6f1-4cf7-87c0-df58a492a630" _uuid="92b554b7809e077685e89b62a6946ca300833808"
# ## Table of contents
# ***
# - [Introduction](#introduction)
# - [Kernel Goals](#aboutthiskernel)
# - [Part 1: Importing Necessary Modules](#import_libraries)
# - [1a. Libraries](#import_libraries)
# - [1b. Load datasets](#load_data)
# - [1c. A Glimpse of the dataset](#glimpse)
# - [1d. About this dataset](#aboutthisdataset)
# - [1e. Tableau Visualization](#tableau_visualization)
# - [Part 2: Overview and Cleaning the Data](#scrubbingthedata)
# - [2a. Overview](#cleaningthedata)
# - [2b. Dealing with missing values](#dealwithnullvalues)
# - [Part 3: Visualization and Feature Relations](#visualization_and_feature_relations)
# - [3a. Gender and Survived](#gender_and_survived)
# - [3b. Pclass and Survived](#pclass_and_survived)
# - [3c. Fare and Survived](#fare_and_survived)
# - [3d. Age and Survived](#age_and_survived)
# - [3e. Combined Feature relations](#combined_feature_relations)
# - [Part 4: Statistical Overview](#statisticaloverview)
# - [4a. Correlation Matrix and Heatmap](#heatmap)
# - [4b. Statistical Test for Correlation](#statistical_test)
# - [4c. The T-Test](#t_test)
# - [Part 5: Feature Engineering](#feature_engineering)
# - [Part 6: Pre-Modeling Tasks](#pre_model_tasks)
# - [6a. Separating dependent and independent variables](#dependent_independent)
# - [6b. Splitting the training data](#split_training_data)
# - [6c. Feature Scaling](#feature_scaling)
# - [Part 7: Modeling the Data](#modelingthedata)
# - [7a. Logistic Regression](#logistic_regression)
# - [7b. K-Nearest Neighbors(KNN)](#knn)
# - [7c. Gaussian Naive Bayes](#gaussian_naive)
# - [7d. Support Vector Machines](#svm)
# - [7e. Decision Tree Classifier](#decision_tree)
# - [7f. Bagging on Decision Tree Classifier](#bagging_decision)
# - [7g. Random Forest Classifier](#random_forest)
# - [7h. Gradient Boosting Classifier](#gradient_boosting)
# - [7i. XGBClassifier](#XGBClassifier)
# - [7j. AdaBoost Classifier](#adaboost)
# - [7k. Extra Tree Classifier](#extra_tree)
# - [7l. Gaussian Process Classifier](#GaussianProcessClassifier)
# - [7m. Voting Classifier](#voting_classifier)
# - [Part 8: Submit Test Predictions](#submit_predictions)
#
# - [ Credits](#credits)
# + [markdown] _cell_guid="7224a910-ec6b-481d-82f1-90ca6b5d037e" _uuid="9cd04af82734c5b53aaddc80992e1f499c180611"
# # Kernel Goals
# <a id="aboutthiskernel"></a>
# ***
# There are three primary goals of this kernel.
# - <b>Do a statistical analysis</b> of how some group of people was survived more than others.
# - <b>Do an exploratory data analysis(EDA)</b> of titanic with visualizations and storytelling.
# - <b>Predict</b>: Use machine learning classification models to predict the chances of passengers survival.
#
# P.S. If you want to learn more about regression models, try this [kernel](https://www.kaggle.com/masumrumi/a-stats-analysis-and-ml-workflow-of-house-pricing/edit/run/9585160).
# + [markdown] _cell_guid="b3b559a5-dad0-419e-835a-e6babd1042ff" _uuid="1b1a0b28ad37a349e284d1e6ce6477d11b95e7c9"
# # Part 1: Importing Necessary Libraries and datasets
# ***
# <a id="import_libraries**"></a>
# ## 1a. Loading libraries
#
# Python is a fantastic language with a vibrant community that produces many amazing libraries. I am not a big fan of importing everything at once for the newcomers. So, I am going to introduce a few necessary libraries for now, and as we go on, we will keep unboxing new libraries when it seem necassary.
# + _cell_guid="80643cb5-64f3-4180-92a9-2f8e83263ac6" _kg_hide-input=true _uuid="33d54abf387474bce3017f1fc3832493355010c0"
# Import necessary modules for data analysis and data visualization.
# Data analysis modules
# Pandas is probably the most popular and important modules for any work related to data management.
import pandas as pd
# numpy is a great library for doing mathmetical operations.
import numpy as np
# Some visualization libraries
from matplotlib import pyplot as plt
import seaborn as sns
## Some other snippit of codes to get the setting right
## This is so that the chart created by matplotlib can be shown in the jupyter notebook.
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina' ## This is preferable for retina display.
import warnings ## importing warnings library.
warnings.filterwarnings('ignore') ## Ignore warning
import os ## imporing os
print(os.listdir("../input/"))
# + [markdown] _cell_guid="bd41125b-6dd4-41d9-8905-31edc812d18e" _uuid="82ccd43cc8449346749bf8a35e1acb9a40e3b141"
# ## 1b. Loading Datasets
# <a id="load_data"></a>
# ***
# + [markdown] _uuid="30b23f046eef6d19c26e6ad967cef914cf312791"
# After loading the necessary modules, we need to import the datasets. Many of the business problems usually come with a tremendous amount of messy data. We extract those data from many sources. I am hoping to write about that in a different kernel. For now, we are going to work with a less complicated and quite popular machine learning dataset.
# + _cell_guid="28722a45-5f11-4629-8814-9ab913e9349a" _kg_hide-input=false _uuid="185b34e70f2efded0c665c6713f79b840ddf0c89"
## Importing the datasets
train = pd.read_csv("../input/train.csv")
test = pd.read_csv("../input/test.csv")
# + [markdown] _uuid="d55ae33391486797b979ef1117e8d8401ac1dab4"
# You are probably wondering why two datasets? Also, Why have I named it "train" and "test"? To explain that I am going to give you an overall picture of the supervised machine learning process.
#
# "Machine Learning" is simply "Machine" and "Learning". Nothing more and nothing less. In a supervised machine learning process, we are giving machine/computer/models specific inputs or data(text/number/image/audio) to learn from aka we are training the machine to learn certain thing based on the data and the output. Now, how do we know what we are teaching is what they are learning? That is where the test set comes to play. We withhold part of the data where we know the output/result of the algorithms, and we use this data to test the trained machine learning model. We then compare the outcomes to determine machines performance. If you don't you are a bit confused thats okay. I will explain more as we keep reading. Let's take a look at the sample of the dataset.
# + [markdown] _cell_guid="c87c72ba-c9b2-48e9-86d8-c711d0795ca0" _uuid="5759d720798ca115cc5d3d2f75be6961d1455832"
# ## 1c. A Glimpse of the Datasets.
# <a id="glimpse"></a>
# ***
# + [markdown] _cell_guid="ab439b32-e251-489a-89fd-cfcd61b236bf" _uuid="69b24241db4d4eae9e46711c384d8130f6fa8322"
# **> Sample train dataset**
# + _cell_guid="0f0649fa-b003-403f-9d7c-d2d14a6cf068" _kg_hide-input=true _uuid="877b2fc905cd60e3f9a525b6fedad9a5c0a671e5"
## Take a look at the overview of the dataset.
train.sample(5)
# + [markdown] _uuid="65e1cdfde4e1f4932cc64c7c1498926ca5ba2699"
# **> Sample test dataset**
# + _kg_hide-input=true _uuid="118d0d0f16b362c04c798def2decd97455018d76"
test.sample(5)
# + [markdown] _uuid="5f7426639cf97db92e4ca85a13e89c8394f6aa7c"
# This is a sample of train and test dataset. Lets find out a bit more about the train and test dataset.
# + _kg_hide-input=true _uuid="1258a94388599a131fe08cd6e05205b15d53df66"
print ("The shape of the train data is (row, column):"+ str(train.shape))
print (train.info())
print ("The shape of the test data is (row, column):"+ str(test.shape))
print (test.info())
# + [markdown] _cell_guid="15c64d36-94b3-4798-af86-775f70feb2dd" _uuid="c72d21139ee6220aee5d8f654561864a5f6499b7"
# ## 1d. About This Dataset
# <a id="aboutthisdataset"></a>
# ***
# The data has split into two groups:
#
# - training set (train.csv)
# - test set (test.csv)
#
# ***The training set includes our target variable(dependent variable), passenger survival status***(also known as the ground truth from the Titanic tragedy) along with other independent features like gender, class, fare, and Pclass.
#
# The test set should be used to see how well our model performs on unseen data. When we say unseen data, we mean that the algorithm or machine learning models have no relation to the test data. We do not want to use any part of the test data in any way to modify our algorithms; Which are the reasons why we clean our test data and train data separately. ***The test set does not provide passengers survival status***. We are going to use our model to predict passenger survival status.
#
# Now let's go through the features and describe a little. There is a couple of different type of variables, They are...
#
# ***
# **Categorical:**
# - **Nominal**(variables that have two or more categories, but which do not have an intrinsic order.)
# > - **Cabin**
# > - **Embarked**(Port of Embarkation)
# C(Cherbourg)
# Q(Queenstown)
# S(Southampton)
#
# - **Dichotomous**(Nominal variable with only two categories)
# > - **Sex**
# Female
# Male
# - **Ordinal**(variables that have two or more categories just like nominal variables. Only the categories can also be ordered or ranked.)
# > - **Pclass** (A proxy for socio-economic status (SES))
# 1(Upper)
# 2(Middle)
# 3(Lower)
# ***
# **Numeric:**
# - **Discrete**
# > - **Passenger ID**(Unique identifing # for each passenger)
# > - **SibSp**
# > - **Parch**
# > - **Survived** (Our outcome or dependent variable)
# 0
# 1
# - **Continous**
# > - **Age**
# > - **Fare**
# ***
# **Text Variable**
# > - **Ticket** (Ticket number for passenger.)
# > - **Name**( Name of the passenger.)
#
#
# + [markdown] _cell_guid="7b21d695-c767-48ad-a3c8-abb9bba56e71" _uuid="53fdd02b149e47bd7168dba94ddff754626b1781"
# ## 1e. Tableau Visualization of the Data
# <a id='tableau_visualization'></a>
# ***
# I have incorporated a tableau visualization below of the training data. This visualization...
# * is for us to have an overview and play around with the dataset.
# * is done without making any changes(including Null values) to any features of the dataset.
# ***
# Let's get a better perspective of the dataset through this visualization.
#
# + _cell_guid="0ca9339e-4d13-4eb6-b28b-4a9e614ca2d0" _kg_hide-input=true _uuid="bc9819aecc9adceb1fa3fe151388fd41f5dcece2"
# %%HTML
<div class='tableauPlaceholder' id='viz1516349898238' style='position: relative'><noscript><a href='#'><img alt='An Overview of Titanic Training Dataset ' src='https://public.tableau.com/static/images/Ti/Titanic_data_mining/Dashboard1/1_rss.png' style='border: none' /></a></noscript><object class='tableauViz' style='display:none;'><param name='host_url' value='https%3A%2F%2Fpublic.tableau.com%2F' /> <param name='embed_code_version' value='3' /> <param name='site_root' value='' /><param name='name' value='Titanic_data_mining/Dashboard1' /><param name='tabs' value='no' /><param name='toolbar' value='yes' /><param name='static_image' value='https://public.tableau.com/static/images/Ti/Titanic_data_mining/Dashboard1/1.png' /> <param name='animate_transition' value='yes' /><param name='display_static_image' value='yes' /><param name='display_spinner' value='yes' /><param name='display_overlay' value='yes' /><param name='display_count' value='yes' /><param name='filter' value='publish=yes' /></object></div> <script type='text/javascript'> var divElement = document.getElementById('viz1516349898238'); var vizElement = divElement.getElementsByTagName('object')[0]; vizElement.style.width='100%';vizElement.style.height=(divElement.offsetWidth*0.75)+'px'; var scriptElement = document.createElement('script'); scriptElement.src = 'https://public.tableau.com/javascripts/api/viz_v1.js'; vizElement.parentNode.insertBefore(scriptElement, vizElement); </script>
# + [markdown] _cell_guid="2b6ce9bc-8210-433d-ab4b-d8afe93c3810" _uuid="b46be01bb1ba3ff4f23c72038679542ba3f780de"
# We want to see how the left bar(with green and red) changes when we filter out specific unique values of a feature. We can use multiple filters to see if there are any correlations among them. For example, if we click on **upper** and **Female** tab, we would see that green color dominates the bar with 91 survived female passengers with only 3 female passengers that did not survive; a 97% survival rate for females. While if we choose **lower** and **Female**, we would see that, there were 50% chance of females surviving. The age distribution chart on top provides us with some more info such as, what was the age range of those three unlucky females as the red color give away the unsurvived once. If you would like to check out some of my other tableau charts, please click [here.](https://public.tableau.com/profile/masum.rumi#!/)
# + [markdown] _cell_guid="24dfbb58-4708-42a1-9122-c7e0b96ad0e9" _uuid="e789474652ddf03c65e7bb8f17f69544b907cecb"
# # Part 2: Overview and Cleaning the Data
# <a id="cleaningthedata"></a>
# ***
# ## 2a. Overview
# + [markdown] _cell_guid="359e6e3e-3a27-45aa-b6cf-ec18b8220eae" _uuid="f0ec8e9300f40427a2a53f9c3e3f92e120ce786b"
# Datasets in the real world are often messy, However, this dataset is almost clean. Lets analyze and see what we have here.
# + _cell_guid="bf19c831-fbe0-49b6-8bf8-d7db118f40b1" _uuid="5a0593fb4564f0284ca7fdf5c006020cb288db95"
## saving passenger id in advance in order to submit later.
passengerid = test.PassengerId
## We will drop PassengerID and Ticket since it will be useless for our data.
#train.drop(['PassengerId'], axis=1, inplace=True)
#test.drop(['PassengerId'], axis=1, inplace=True)
print (train.info())
print ("*"*40)
print (test.info())
# + [markdown] _cell_guid="f9b2f56f-e95c-478d-aa49-3f6cb277830f" _uuid="b5accab7fc7471fea224dcae81683b9f3c0f617b"
# It looks like, the features have unequal amount of data entries for every column and they have many different types of variables. This can happen for the following reasons...
# * We may have missing values in our features.
# * We may have categorical features.
# * We may have alphanumerical or/and text features.
#
# + [markdown] _cell_guid="9912539a-12b5-4739-bc2c-e1cecf758dca" _uuid="6105e90cd8f0e8d49ae188edad65414678a7be23"
# ## 2b. Dealing with Missing values
# <a id="dealwithnullvalues"></a>
# ***
# **Missing values in *train* dataset.**
# + _cell_guid="0697eeff-646c-40f7-85f6-7e4a2b8d348f" _kg_hide-input=true _uuid="cd80d32deb4afd854d02905cab26fc81feaa4d18"
total = train.isnull().sum().sort_values(ascending = False)
percent = round(train.isnull().sum().sort_values(ascending = False)/len(train)*100, 2)
pd.concat([total, percent], axis = 1,keys= ['Total', 'Percent'])
# + [markdown] _cell_guid="6e1b2b57-78b9-4021-bc53-a7681b63f97c" _uuid="197487867c9d099548c7d009c4a80418927be07c"
# **Missing values in *test* set.**
# + _cell_guid="073ef91b-e401-47a1-9b0a-d08ad710abce" _kg_hide-input=true _uuid="1ec1de271f57c9435ce111261ba08c5d6e34dbcb"
total = test.isnull().sum().sort_values(ascending = False)
percent = round(test.isnull().sum().sort_values(ascending = False)/len(test)*100, 2)
pd.concat([total, percent], axis = 1,keys= ['Total', 'Percent'])
# + [markdown] _cell_guid="0217a17b-8017-4221-a664-dbbc42f7a5eb" _uuid="2051377dfc36cbeb9fda78cb02d5bd3a00ee2457"
# We see that in both **train**, and **test** dataset have missing values. Let's make an effort to fill these missing values.
# + [markdown] _cell_guid="aaf73f0b-ec84-4da1-b424-0170691c50c8" _uuid="84d3c45c3a59e16ac2c887d6effe71434b2659ef"
# ### Embarked feature
# ***
# + _cell_guid="85e9bf60-49fe-457b-8122-05f593d15644" _kg_hide-input=true _uuid="27393f69ab5535756a53ab09d1139309cb80c527"
percent = pd.DataFrame(round(train.Embarked.value_counts(dropna=False, normalize=True)*100,2))
## creating a df with th
total = pd.DataFrame(train.Embarked.value_counts(dropna=False))
## concating percent and total dataframe
total.columns = ["Total"]
percent.columns = ['Percent']
pd.concat([total, percent], axis = 1)
# + [markdown] _cell_guid="826ae31d-4bd0-45f6-8c05-8b5d12d41144" _uuid="174873ebdb2cd6c23777d464103afa26c0183ab2"
# It looks like there are only two null values( ~ 0.22 %) in the Embarked feature, we can replace these with the mode value "S". However, let's dig a little deeper.
#
# **Let's see what are those two null values**
# + _cell_guid="000ebdd7-ff57-48d9-91bf-a29ba79f1a1c" _kg_hide-input=true _uuid="6b9cb050e9dae424bb738ba9cdf3c84715887fa3"
train[train.Embarked.isnull()]
# + [markdown] _cell_guid="306da283-fbd9-45fc-a79e-ac4a3fa7d396" _uuid="57a4016a0ff673cdf5716310d42d7f142d275132"
# We may be able to solve these two missing values by looking at other independent variables of the two raws. Both passengers paid a fare of $80, are of Pclass 1 and female Sex. Let's see how the **Fare** is distributed among all **Pclass** and **Embarked** feature values
# + _cell_guid="bf257322-0c9c-4fc5-8790-87d8c94ad28a" _kg_hide-input=true _uuid="ad15052fe6cebe37161c6e01e33a5c083dc2b558"
fig, ax = plt.subplots(figsize=(16,12),ncols=2)
ax1 = sns.boxplot(x="Embarked", y="Fare", hue="Pclass", data=train, ax = ax[0]);
ax2 = sns.boxplot(x="Embarked", y="Fare", hue="Pclass", data=test, ax = ax[1]);
ax1.set_title("Training Set", fontsize = 18)
ax2.set_title('Test Set', fontsize = 18)
fig.show()
# + [markdown] _cell_guid="0e353881-a7d7-4fbf-bfd3-874479c0a650" _uuid="c8a7f8c033f571d2fc8986009765ac4a78d3b6a7"
# Here, in both training set and test set, the average fare closest to $80 are in the <b>C</b> Embarked values. So, let's fill in the missing values as "C"
# + _cell_guid="2f5f3c63-d22c-483c-a688-a5ec2a477330" _kg_hide-input=true _uuid="52e51ada5dfeb700bf775c66e9307d6d1e2233de"
## Replacing the null values in the Embarked column with the mode.
train.Embarked.fillna("C", inplace=True)
# + [markdown] _cell_guid="47c17b1e-9486-43da-84ad-f91014225e88" _uuid="44af808c1563671899ee498c9df12312c294277c"
# ### Cabin Feature
# ***
# + _cell_guid="e76cd770-b498-4444-b47a-4ac6ae63193b" _kg_hide-input=true _uuid="b809a788784e2fb443457d7ef4ca17a896bf58b4"
print("Train Cabin missing: " + str(train.Cabin.isnull().sum()/len(train.Cabin)))
print("Test Cabin missing: " + str(test.Cabin.isnull().sum()/len(test.Cabin)))
# + [markdown] _cell_guid="47d450a8-0692-4403-8447-ab09d6dd0b8f" _uuid="e61d1e4613dd4f51970d504e93ae30c072ca9d98"
# Approximately 77% of Cabin feature is missing in the training data and 78% missing on the test data.
# We have two choices,
# * we can either get rid of the whole feature, or
# * we can brainstorm a little and find an appropriate way to put them in use. For example, We may say passengers with cabin records had a higher socio-economic-status then others. We may also say passengers with cabin records were more likely to be taken into consideration when loading into the boat.
#
# Let's combine train and test data first and for now will assign all the null values as **"N"**
# + _kg_hide-input=true _uuid="8ff7b4f88285bc65d72063d7fdf8a09a5acb62d3"
## Concat train and test into a variable "all_data"
survivers = train.Survived
train.drop(["Survived"],axis=1, inplace=True)
all_data = pd.concat([train,test], ignore_index=False)
## Assign all the null values to N
all_data.Cabin.fillna("N", inplace=True)
# + [markdown] _cell_guid="dae4beab-8c5a-4192-a460-e9abc6f14d3e" _uuid="e2d84eff7cafdd68a471876b65e0ae866151d6d2"
# All the cabin names start with an English alphabet following by digits. It seems like there are some passengers that had booked multiple cabin rooms in their name, This is because many of them travelled with family. However, they all seem to book under the same letter followed by different numbers. It seems like there is a significance with the letters rather than the numbers. Therefore, we can group these cabins according to the letter of the cabin name.
# + _cell_guid="87995359-8a77-4e38-b8bb-e9b4bdeb17ed" _kg_hide-input=true _uuid="c1e9e06eb7f2a6eeb1a6d69f000217e7de7d5f25"
all_data.Cabin = [i[0] for i in all_data.Cabin]
# + [markdown] _uuid="5e8cff0316f95162cdc9c2f3da905ad49fc548ca"
# Now, I don't feel comfortable hanging around with 687 null values that we fakely named "N". So, let's do something about that. We can use pythons ***groupby*** function to get the mean of each cabin letter.
# + _uuid="878505679d2a6982aab85940fad1b16109104e1f"
with_N = all_data[all_data.Cabin == "N"]
without_N = all_data[all_data.Cabin != "N"]
all_data.groupby("Cabin")['Fare'].mean().sort_values()
# + [markdown] _uuid="8605664271220cb4a17fa1aca65207681503c9dd"
# Now, these means can help us determine the unknown cabins, if we compare each unknown cabin rows with the given mean's above. Let's write a simple function so that we can give cabin names based on the means.
# + _uuid="a466da29f1989fa983147faf9e63d18783468567"
def cabin_estimator(i):
a = 0
if i<16:
a = "G"
elif i>=16 and i<27:
a = "F"
elif i>=27 and i<38:
a = "T"
elif i>=38 and i<47:
a = "A"
elif i>= 47 and i<53:
a = "E"
elif i>= 53 and i<54:
a = "D"
elif i>=54 and i<116:
a = 'C'
else:
a = "B"
return a
# + [markdown] _uuid="6f56c9950206a5a8f30c39ca207dc47859b8d8a0"
# Let's apply <b>cabin_estimator</b> function in each unknown cabins(cabin with <b>null</b> values). Once that is done we will separate our train and test to continue towards machine learning modeling.
# + _uuid="eb6a42a57dd77380b0e4d1e2ca66cdc8ad2f29e0"
##applying cabin estimator function.
with_N['Cabin'] = with_N.Fare.apply(lambda x: cabin_estimator(x))
# + _uuid="1c646b64c6e062656e5f727d5499266f847c4832"
## getting back train.
all_data = pd.concat([with_N, without_N], axis=0)
## PassengerId helps us separate train and test.
all_data.sort_values(by = 'PassengerId', inplace=True)
## Separating train and test from all_data.
train = all_data[:891]
test = all_data[891:]
# adding saved target variable with train.
train['Survived'] = survivers
# + [markdown] _cell_guid="26d918c2-3c6b-48e8-8e2b-fc4531e8c59e" _uuid="05a777057d9803235a17d79b72eefe7085ebf2e5"
# ### Fare Feature
# ***
# + _cell_guid="2c75f369-e781-43df-be06-32585b372a0a" _kg_hide-input=true _uuid="020cafd121f2e6cbed89265c993ef3d76566cd6b"
test[test.Fare.isnull()]
# + [markdown] _cell_guid="0ffece2f-9df0-44e5-80cc-84894a8d0d45" _uuid="bce23c7620db2cde9bae8efa04b00c78819f0268"
# Here, We can take the average of the **Fare** column with all the values to fill in for Nan Fare value. However, that might not be the best way to fill in this value. We can be a little more specific and take the average of the values where**Pclass** is ***3***, **Sex** is ***male*** and **Embarked** is ***S***
# + _cell_guid="e742aa76-b6f8-4882-8bd6-aa10b96f06aa" _kg_hide-input=true _uuid="f1dc8c6c33ba7df075ee608467be2a83dc1764fd"
missing_value = test[(test.Pclass == 3) & (test.Embarked == "S") & (test.Sex == "male")].Fare.mean()
## replace the test.fare null values with test.fare mean
test.Fare.fillna(missing_value, inplace=True)
# + [markdown] _cell_guid="3ff2fbe3-9858-4aad-9e33-e909d5128879" _uuid="e04222497a5dfd77ac07dbcacbdc10dc1732da21"
# ### Age Feature
# ***
# + _cell_guid="8ff25fb3-7a4a-4e06-b48f-a06b8d844917" _kg_hide-input=true _uuid="c356e8e85f53a27e44b5f28936773a289592c5eb"
print ("Train age missing value: " + str((train.Age.isnull().sum()/len(train))*100)+str("%"))
print ("Test age missing value: " + str((test.Age.isnull().sum()/len(test))*100)+str("%"))
# + [markdown] _cell_guid="105d0bf8-dada-4499-8a41-499caf20fa81" _uuid="8678df259a8f4e7f85f92603f312e1df76a26589"
# Some standard approaches of dealing with null values are mean, median and mode. However, we will take a different approach since **~20% data in the Age column is missing** in both train and test dataset. The age variable seems to be promising for determining survival rate. Therefore, It would be unwise to replace the missing values with median, mean or mode. We will use machine learning model Random Forest Regressor to impute missing value instead of Null value. We will keep the age column unchanged for now and work on that in the feature engineering section.
# + [markdown] _cell_guid="81537f22-2c69-45f2-90d3-a2a8790cb2fd" _uuid="84518982b94e7e811bf3560a3862f06a46f1b530"
# # Part 3. Visualization and Feature Relations
# <a id="visualization_and_feature_relations" ></a>
# ***
# Before we dive into finding relations between different features and our dependent variable(survivor) let us create some predictions about how the relations may turnout among features.
#
# **Predictions:**
# - Gender: More female survived than male
# - Pclass: Higher socio-economic status passenger survived more than others.
# - Age: Younger passenger survived more than other passengers.
#
# Now, let's see how the features are related to each other by creating some visualizations.
#
#
# + [markdown] _cell_guid="63420775-00e1-4650-a2f3-2ae6eebab23c" _uuid="ca8bfb1bfe4d1079635a54c8daec3399b8355749"
# ## 3a. Gender and Survived
# <a id="gender_and_survived"></a>
# ***
# + _cell_guid="78322e76-ccaa-4bb9-9cc2-7a3394ddfe8c" _kg_hide-input=true _uuid="6008755b1522e2a849b6e1ccbb7da57270293ca4"
pal = {'male':"green", 'female':"Pink"}
plt.subplots(figsize = (15,8))
ax = sns.barplot(x = "Sex",
y = "Survived",
data=train,
palette = pal,
linewidth=2 )
plt.title("Survived/Non-Survived Passenger Gender Distribution", fontsize = 25)
plt.ylabel("% of passenger survived", fontsize = 15)
plt.xlabel("Sex",fontsize = 15);
# + [markdown] _cell_guid="fa7cb175-3c4d-4367-8b35-d3b43fb7d07d" _uuid="ef171de53cb343da95d1ba82ebd961b1ff1756c3"
# This bar plot above shows the distribution of female and male survived. The ***x_label*** represents **Sex** feature while the ***y_label*** represents the % of **passenger survived**. This bar plot shows that ~74% female passenger survived while only ~19% male passenger survived.
# + _cell_guid="6e303476-c1ed-49bb-8b9d-14659dd5739d" _kg_hide-input=true _uuid="163515a4c926323f7288f385795ea7b1ea545d7a"
pal = {1:"seagreen", 0:"gray"}
sns.set(style="darkgrid")
plt.subplots(figsize = (15,8))
ax = sns.countplot(x = "Sex",
hue="Survived",
data = train,
linewidth=2,
palette = pal
)
## Fixing title, xlabel and ylabel
plt.title("Passenger Gender Distribution - Survived vs Not-survived", fontsize = 25)
plt.xlabel("Sex", fontsize = 15);
plt.ylabel("# of Passenger Survived", fontsize = 15)
## Fixing xticks
#labels = ['Female', 'Male']
#plt.xticks(sorted(train.Sex.unique()), labels)
## Fixing legends
leg = ax.get_legend()
leg.set_title("Survived")
legs = leg.texts
legs[0].set_text("No")
legs[1].set_text("Yes")
plt.show()
# + [markdown] _cell_guid="0835c20e-f155-4bd7-8032-895d8c8042e6" _uuid="bf15a586513bdde73dfa2279b739ffca040e71e4"
# This count plot shows the actual distribution of male and female passengers that survived and did not survive. It shows that among all the females ~ 230 survived and ~ 70 did not survive. While among male passengers ~110 survived and ~480 did not survive.
#
# **Summary**
# ***
# - As we suspected, female passengers have survived at a much better rate than male passengers.
# - It seems about right since females and children were the priority.
# + [markdown] _cell_guid="2daa3614-866c-48d7-a8cb-26ee8126a806" _uuid="e746a4be3c0ed3d94a7a4366a5bff565c7bc9834"
# ## 3b. Pclass and Survived
# <a id="pcalss_and_survived"></a>
# ***
# + _cell_guid="93a3a621-7be8-4f28-960d-939068944d3f" _kg_hide-input=true _uuid="61543e636b742647f90ea778f30a178a84e50533"
plt.subplots(figsize = (15,10))
sns.barplot(x = "Pclass",
y = "Survived",
data=train,
linewidth=2)
plt.title("Passenger Class Distribution - Survived vs Non-Survived", fontsize = 25)
plt.xlabel("Socio-Economic class", fontsize = 15);
plt.ylabel("% of Passenger Survived", fontsize = 15);
labels = ['Upper', 'Middle', 'Lower']
#val = sorted(train.Pclass.unique())
val = [0,1,2] ## this is just a temporary trick to get the label right.
plt.xticks(val, labels);
# + [markdown] _cell_guid="e2c5ce9f-9759-43b6-b286-ec771a5a64c1" _uuid="6faf3d5f770c23febb20cdc81cc079ed37d59959"
# - It looks like ...
# - ~ 63% first class passenger survived titanic tragedy, while
# - ~ 48% second class and
# - ~ only 24% third class passenger survived.
#
#
# + _cell_guid="f6eba487-9c63-4cd8-908a-393e2c277e45" _kg_hide-input=true _uuid="10867e6cb57231ae599406d827ba5e3f13ccb088"
# Kernel Density Plot
fig = plt.figure(figsize=(15,8),)
## I have included to different ways to code a plot below, choose the one that suites you.
ax=sns.kdeplot(train.Pclass[train.Survived == 0] ,
color='gray',
shade=True,
label='not survived')
ax=sns.kdeplot(train.loc[(train['Survived'] == 1),'Pclass'] ,
color='g',
shade=True,
label='survived')
plt.title('Passenger Class Distribution - Survived vs Non-Survived', fontsize = 25)
plt.ylabel("Frequency of Passenger Survived", fontsize = 15)
plt.xlabel("Passenger Class", fontsize = 15)
## Converting xticks into words for better understanding
labels = ['Upper', 'Middle', 'Lower']
plt.xticks(sorted(train.Pclass.unique()), labels);
# + [markdown] _cell_guid="43ffcf43-2d0c-4033-8112-9edcca3576f1" _uuid="f397633bae24a35d3fbe87d1ca54023356e065f9"
# This KDE plot is pretty self-explanatory with all the labels and colors. Something I have noticed that some readers might find questionable is that the lower class passengers have survived more than second-class passengers. It is true since there were a lot more third-class passengers than first and second.
#
# **Summary**
# ***
# The first class passengers had the upper hand during the tragedy than second and third. You can probably agree with me more on this, in the next section of visualizations where we look at the distribution of ticket fare and survived column.
# + [markdown] _cell_guid="1cb9d740-749b-4700-b9e9-973dbcad6aab" _uuid="8eeb41d08ce680d51452deeb0ad054b184d67e16"
# ## 3c. Fare and Survived
# <a id="fare_and_survived"></a>
# ***
# + _cell_guid="cd6eb8a9-10a6-4ab8-aaec-4820df35f4c1" _kg_hide-input=true _uuid="85737078f0e84fe972a5ddb81b29e114fcfb54be"
# Kernel Density Plot
fig = plt.figure(figsize=(15,8),)
ax=sns.kdeplot(train.loc[(train['Survived'] == 0),'Fare'] , color='gray',shade=True,label='not survived')
ax=sns.kdeplot(train.loc[(train['Survived'] == 1),'Fare'] , color='g',shade=True, label='survived')
plt.title('Fare Distribution Survived vs Non Survived', fontsize = 25)
plt.ylabel("Frequency of Passenger Survived", fontsize = 15)
plt.xlabel("Fare", fontsize = 15)
# + [markdown] _cell_guid="6073f329-df80-4ab9-b99b-72e6fcdfe0c6" _uuid="b5eba2b28ea428114d8ffab52feef95484bd76c0"
# This plot shows something impressive..
# - The spike in the plot under 100 dollar represents that a lot of passengers who bought the ticket within that range did not survive.
# - When fare is approximately more than 280 dollars, there is no gray shade which means, either everyone passed that fare point survived or maybe there is an outlier that clouds our judgment. Let's check...
# + _cell_guid="bee8b01b-a56a-4762-bde0-4404a1c5ac1a" _kg_hide-input=true _uuid="916ab9dc56a05105afa80127d69deb9fc0095ba2"
train[train.Fare > 280]
# + [markdown] _cell_guid="3467e2d8-315c-4223-9166-0aca54543cdd" _uuid="443d93fcfbad82fc611ce88e12556a6325ccd15c"
# As we assumed, it looks like an outlier with a fare of $512. We sure can delete this point. However, we will keep it for now.
# + [markdown] _cell_guid="95c27d94-fa65-4bf9-a855-8e5dab17704e" _uuid="64ff8df884805f04692dc601da1ef99527309d54"
# ## 3d. Age and Survived
# <a id="age_and_survived"></a>
# ***
# + _cell_guid="9eb6733b-7577-4360-8252-e6d97c78b7db" _kg_hide-input=true _uuid="c6a4f46a7ce0e197f72abe293b69100c29a044ca"
# Kernel Density Plot
fig = plt.figure(figsize=(15,8),)
ax=sns.kdeplot(train.loc[(train['Survived'] == 0),'Age'] , color='gray',shade=True,label='not survived')
ax=sns.kdeplot(train.loc[(train['Survived'] == 1),'Age'] , color='g',shade=True, label='survived')
plt.title('Age Distribution - Surviver V.S. Non Survivors', fontsize = 25)
plt.xlabel("Age", fontsize = 15)
plt.ylabel('Frequency', fontsize = 15);
# + [markdown] _cell_guid="a9aab64c-6170-4c8d-8446-cecdc9804b55" _uuid="5238df80f5454d29e3793596a21fd0c00cb64a6c"
# There is nothing out of the ordinary of about this plot, except the very left part of the distribution. It proves that children and infants were the priority, therefore, a good chunk of infant/children were saved.
# + [markdown] _cell_guid="077605b2-e9b4-4c45-8c5a-188508165f10" _uuid="f8245da79c5394f7665d0b5429cb2fe4c4d0b057"
# ## 3e. Combined Feature Relations
# <a id='combined_feature_relations'></a>
# ***
# In this section, we are going to discover more than two feature relations in a single graph. I will try my best to illustrate most of the feature relations. Let's get to it.
# + _cell_guid="924e19c4-8d58-404c-9a84-02f096269351" _kg_hide-input=true _uuid="71fc1c9843f789e19a5e8b2929579914d8ecdb3f"
pal = {1:"seagreen", 0:"gray"}
g = sns.FacetGrid(train,size=5, col="Sex", row="Survived", margin_titles=True, hue = "Survived",
palette=pal)
g = g.map(plt.hist, "Age", edgecolor = 'white');
g.fig.suptitle("Survived by Sex and Age", size = 25)
plt.subplots_adjust(top=0.90)
# + [markdown] _cell_guid="089999b4-bc44-49c6-9f86-aaaccabaa224" _uuid="6aac036e1b235e5b10bc6a153ed226acfce2cfcb"
# Facetgrid is a great way to visualize multiple variables and their relationships at once. From section 3a we have a bright idea of females being more of a priority then males. However, from this facet grid, we can also understand which age range groups survived more than others or were not so lucky
# + _cell_guid="dcc34a91-261d-4929-a4eb-5072fcaf86ce" _kg_hide-input=true _uuid="b2ad776bf0254be1ccf76f46a40db7960aa3db24"
g = sns.FacetGrid(train,size=5, col="Sex", row="Embarked", margin_titles=True, hue = "Survived",
palette = pal
)
g = g.map(plt.hist, "Age", edgecolor = 'white').add_legend();
g.fig.suptitle("Survived by Sex and Age", size = 25)
plt.subplots_adjust(top=0.90)
# + [markdown] _cell_guid="b9b9906c-805d-438b-b72e-a57cc60d5ae8" _uuid="4070616f2637a720a3cb580264cfaed9235b9020"
# This is another compelling facet grid illustrating four features relationship at once. They are **Embarked, Age, Survived & Sex**.
# * The color illustrates passengers survival status(green represents survived, gray represents not survived)
# * The column represents Sex(left being male, right stands for female)
# * The row represents Embarked(from top to bottom: S, C, Q)
# ***
# Now that I have steered out the apparent let's see if we can get some insights that are not so obvious as we look at the data.
# * Most passengers seem to be boarded on Southampton(S).
# * More than 60% of the passengers died boarded on Southampton.
# * More than 60% of the passengers lived boarded on Cherbourg(C).
# * Pretty much every male that boarded on Queenstown(Q) did not survive.
# * There were very few females boarded on Queenstown, however, most of them survived.
# + _cell_guid="fd9fe9e2-f7d4-4f83-9ce4-0a22160ef4fe" _kg_hide-input=true _uuid="f4d77506cabc7150466fa5bda64585d15814d48c"
g = sns.FacetGrid(train, size=5,hue="Survived", col ="Sex", margin_titles=True,
palette=pal,)
g.map(plt.scatter, "Fare", "Age",edgecolor="w").add_legend()
g.fig.suptitle("Survived by Sex, Fare and Age", size = 25)
plt.subplots_adjust(top=0.85)
# + [markdown] _cell_guid="1c309d4b-3e24-406b-bd28-d5055a660f16" _uuid="90bbc6e6edbf6188170a4de1b38732d009f7afae"
# This grid unveils a couple of interesting insights. Let's find out.
# * The facet grid above clearly demonstrates the three outliers with Fare of over \$500. At this point, I think we are quite confident that these outliers should be deleted.
# * Most of the passengers were with in the Fare range of \$100.
# + _cell_guid="783403f6-9d3c-4a12-8505-cf321bd1a1ef" _kg_hide-input=true _uuid="75c41c85dc76c9749e5c417e1ed0425eed9c55e0"
## dropping the three outliers where Fare is over $500
train = train[train.Fare < 500]
## factor plot
sns.factorplot(x = "Parch", y = "Survived", data = train,kind = "point",size = 8)
plt.title("Factorplot of Parents/Children survived", fontsize = 25)
plt.subplots_adjust(top=0.85)
# + [markdown] _cell_guid="33916321-237d-4381-990f-0faa11723c20" _uuid="263113f38121c9e5f14247f05c262ee218be87f2"
# **Passenger who traveled in big groups with parents/children had less survival rate than other passengers.**
# + _cell_guid="f6ed143e-3e02-4e97-a255-73807018f0d1" _kg_hide-input=true _uuid="4ce5a4a6cff3966ac1811ee95f81c81fe4861a51"
sns.factorplot(x = "SibSp", y = "Survived", data = train,kind = "point",size = 8)
plt.title('Factorplot of Sibilings/Spouses survived', fontsize = 25)
plt.subplots_adjust(top=0.85)
# + [markdown] _cell_guid="ee5b61b4-67d3-46b4-847d-4b5b85a8c791" _uuid="c7a045b78e6b5f45ad891cf0515a6a4b2534d2ff"
# **While, passenger who traveled in small groups with sibilings/spouses had more survival rate than other passengers.**
# + _cell_guid="50a0920d-556b-4439-a67f-384ce793d094" _kg_hide-input=true _uuid="dfe723c71d4d29f599701d806ca97cd01a60142f"
# Placing 0 for female and
# 1 for male in the "Sex" column.
train['Sex'] = train.Sex.apply(lambda x: 0 if x == "female" else 1)
test['Sex'] = test.Sex.apply(lambda x: 0 if x == "female" else 1)
# + [markdown] _cell_guid="003a7779-5966-45f8-a711-67e67234a654" _uuid="402cd49464156ead61d5dd5698ffeb00eb71d0d3"
# # Part 4: Statistical Overview
# <a id="statisticaloverview"></a>
# ***
# + [markdown] _cell_guid="91eba73b-f744-478b-bd6b-13da6cff000b" _uuid="3e8b752c8963a76a86c8b1db80783c644090bdfa"
# 
# + [markdown] _cell_guid="7b7e6e77-50bf-469f-b92b-73056224bc61" _uuid="797aa171f2e13ea965cb9a352fcfd2001e119747"
# **Train info**
# + _cell_guid="ad856ee6-b1ec-445d-92b0-cd6a83d58301" _kg_hide-input=true _uuid="35fc657641cc24aff89ade7d83d8b92e472dc3e6"
train.describe()
# + _cell_guid="327c6775-9ba4-4d65-8c97-304cc9512e6a" _kg_hide-input=true _uuid="2f9f5fb7bade4d82d7b5a564a8ac91123b4921d2"
train.describe(include =['O'])
# + _cell_guid="3059c03d-e758-43c8-aaf6-72bcfc776931" _kg_hide-input=true _uuid="88316f3c3db91e543d1f5ed6f46761106e09497a"
train[['Pclass', 'Survived']].groupby("Pclass").mean().reset_index()
# + _cell_guid="5b817552-ecb8-4f6e-9950-6697d4c44d1f" _kg_hide-input=true _uuid="c88dcae6209f02226f2e772b42616b5650d108f4"
# Overview(Survived vs non survied)
survived_summary = train.groupby("Survived")
survived_summary.mean().reset_index()
# + _cell_guid="502dd0d2-a51a-47da-904c-66c9840a1b74" _kg_hide-input=true _uuid="65f9a660b942a8f92db94fe8fc41ccfa76a354cd"
survived_summary = train.groupby("Sex")
survived_summary.mean().reset_index()
# + _cell_guid="68cb2dac-6295-44d6-8aa0-5cddb53dd72c" _kg_hide-input=true _uuid="e49170e6e56329f68aba07a36389883ee1bee5ca"
survived_summary = train.groupby("Pclass")
survived_summary.mean().reset_index()
# + [markdown] _cell_guid="89ba2894-b129-4709-913d-f8cb35815925" _uuid="e310c182f3541069329efcdd37373235fb144567"
# I have gathered a small summary from the statistical overview above. Let's see what they are...
# - This data set has 891 raw and 9 columns.
# - only 38% passenger survived during that tragedy.
# - ~74% female passenger survived, while only ~19% male passenger survived.
# - ~63% first class passengers survived, while only 24% lower class passenger survived.
#
#
# + [markdown] _cell_guid="5454218c-0a45-4a89-96fe-83d89b588183" _uuid="d00b4e471e863f766c4aad7b88e1e6d9e57d6423"
# ## 4a. Correlation Matrix and Heatmap
# <a id="heatmap"></a>
# ***
# ### Correlations
# + _cell_guid="d0acfa7a-6f3e-4783-925d-6e443a9a5baa" _kg_hide-input=true _uuid="c4057023aa30d3ce1befae168c00f3cb8491804b"
pd.DataFrame(abs(train.corr()['Survived']).sort_values(ascending = False))
# + [markdown] _cell_guid="92a69940-78f8-4139-a9a7-24ccf5f6afe7" _uuid="211c5e2e817f4b10e64a28f5f8ce1d7eec9761fc"
# ** Sex is the most important correlated feature with *Survived(dependent variable)* feature followed by Pclass.**
# + _cell_guid="3e9fdd2e-f081-48ad-9c0f-afa475b15dfe" _kg_hide-input=true _uuid="c3212c222341c250aacee47c43b1a023b9b65857"
## get the most important variables.
corr = train.corr()**2
corr.Survived.sort_values(ascending=False)
# + [markdown] _cell_guid="f5f257ef-88b1-4302-ad41-d90892fbe4e9" _uuid="1837acd3898d4787c9011e353dfc4dc15fd1abb2"
#
# **Squaring the correlation feature not only gives on positive correlations but also amplifies the relationships.**
# + _cell_guid="eee23849-a390-4d16-a8df-d29c6f575413" _kg_hide-input=true _uuid="285660c315b854497fe00847d051ceac5c9ec298"
## heatmeap to see the correlation between features.
# Generate a mask for the upper triangle (taken from seaborn example gallery)
mask = np.zeros_like(train.corr(), dtype=np.bool)
#mask[np.triu_indices_from(mask)] = True
plt.subplots(figsize = (15,12))
sns.heatmap(train.corr(),
annot=True,
#mask = mask,
cmap = 'RdBu_r',
linewidths=0.1,
linecolor='white',
vmax = .9,
square=True)
plt.title("Correlations Among Features", y = 1.03,fontsize = 20);
# + [markdown] _cell_guid="0e0b5ceb-fde5-40a7-b33b-b44e8f04189a" _uuid="41e2bc2eff5699b14a0f47d5bd2e428ee5bec3b8"
# #### Positive Correlation Features:
# - Fare and Survived: 0.26
#
# #### Negative Correlation Features:
# - Fare and Pclass: -0.6
# - Sex and Survived: -0.55
# - Pclass and Survived: -0.33
#
#
# **So, Let's analyze these correlations a bit.** We have found some moderately strong relationships between different features. There is a definite positive correlation between Fare and Survived rated. This relationship reveals that the passenger who paid more money for their ticket were more likely to survive. This theory aligns with one other correlation which is the correlation between Fare and Pclass(-0.6). This relationship can be explained by saying that first class passenger(1) paid more for fare then second class passenger(2), similarly second class passenger paid more than the third class passenger(3). This theory can also be supported by mentioning another Pclass correlation with our dependent variable, Survived. The correlation between Pclass and Survived is -0.33. This can also be explained by saying that first class passenger had a better chance of surviving than the second or the third and so on.
#
# However, the most significant correlation with our dependent variable is the Sex variable, which is the info on whether the passenger was male or female. This negative correlation with a magnitude of -0.54 which points towards some undeniable insights. Let's do some statistics to see how statistically significant this correlation is.
# + [markdown] _cell_guid="85faf680-5f78-414f-87b9-b72ef6d6ffc2" _uuid="18c908fdbe16ae939827ec12a4ce028094a8a587"
# ## 4b. Statistical Test for Correlation
# <a id="statistical_test"></a>
# ***
#
# Statistical tests are the scientific way to prove the validation of theories. In any case, when we look at the data, we seem to have an intuitive understanding of where data is leading us. However, when we do statistical tests, we get a scientific or mathematical perspective of how significant these results are. Let's apply some of the trials and see how we are doing with our predictions.
#
# ### Hypothesis Testing Outline
#
# A hypothesis test compares the mean of a control group and experimental group and tries to find out whether the two sample means are different from each other and if they are different, how significant that difference is.
#
# A **hypothesis test** usually consists of multiple parts:
#
# 1. Formulate a well-developed research problem or question: The hypothesis test usually starts with a concrete and well-developed researched problem. We need to ask the right question that can be answered using statistical analyses.
# 2. The null hypothesis ($H_0$) and Alternating hypothesis($H_1$):
# > * The **null hypothesis($H_0$)** is something that is assumed to be true. It is the status quo. In a null hypothesis, the observations are the result of pure chance. When we set out to experiment, we form the null hypothesis by saying that there is no difference between the means of the control group and the experimental group.
# > * An **Alternative hypothesis($H_A$)** is a claim and the opposite of the null hypothesis. It is going against the status quo. In an alternative theory, the observations show a real effect combined with a component of chance variation.
#
# 3. Determine the **test statistic**: test statistic can be used to assess the truth of the null hypothesis. Depending on the standard deviation we either use t-statistics or z-statistics. In addition to that, we want to identify whether the test is a one-tailed test or two-tailed test.
#
# 4. Specify a **Significance level**: The significance level($\alpha$) is the probability of rejecting a null hypothesis when it is true. In other words, we are ***comfortable/confident*** with rejecting the null hypothesis a significant amount of times even though it is true. This considerable amount is our Significant level. In addition to that significance level is one minus our Confidence interval. For example, if we say, our significance level is 5%, then our confidence interval would be (1 - 0.05) = 0.95 or 95%.
#
# 5. Compute the **T-statistics**: Computing the t-statistics follows a simple equation. This equation slightly differs depending on one sample test or two sample test
#
# 6. Compute the **P-value**: P-value is the probability that a test statistic at least as significant as the one observed would be obtained assuming that the null hypothesis was correct. The p-value is known to be unintuitive, and even many professors are known to explain it wrong. I think this [video](https://www.youtube.com/watch?v=E4KCfcVwzyw) explains the p-value well. **The smaller the P-value, the stronger the evidence against the null hypothesis.**
#
# 7. **Describe the result and compare the p-value with the significance value($\alpha$)**: If p<= $\alpha$, then the observed effect is statistically significant, the null hypothesis is ruled out, and the alternative hypothesis is valid. However if the p> $\alpha$, we say that, we fail to reject the null hypothesis. Even though this sentence is grammatically wrong, it is logically right. We never accept the null hypothesis just because we are doing the statistical test with sample data points.
#
# We will follow each of these steps above to do your hypothesis testing below.
#
# ***
# + [markdown] _uuid="f3b49278bd1b8eff8fe1b14c1506d73cf53bd859"
# ### Hypothesis testing
# #### Formulating a well developed researched question:
# Regarding this dataset, we can formulate the null hypothesis and alternative hypothesis by asking the following questions.
# > * **Is there a significant difference in the mean sex between the passenger who survived and passenger who did not survive?**.
# > * **Is there a substantial difference in the survival rate between the male and female passengers?**
# #### The Null Hypothesis and The Alternative Hypothesis
# We can formulate our hypothesis by asking questions differently. However, it is essential to understand what our end goal is. Here our dependent variable or target variable is **Survived**. Therefore, we say
#
# > ** Null Hypothesis($H_0$)** There is no difference in the survival rate between the male and female passengers. or the mean difference between male and female passenger in the survival rate is zero.
# > ** Alternative Hypothesis($H_A$):** There is a difference in the survival rate between the male and female passengers. or the mean difference in the survival rate between male and female is not zero.
#
# #### Determine the test statistics
# > This will be a two-tailed test since the difference between male and female passenger in the survival rate could be higher or lower than 0.
# > Since we do not know the standard deviation($\sigma$) and n is small, we will use the t-distribution.
#
# #### Specify the significance level
# > Specifying a significance level is an important step of the hypothesis test. It is an ultimate balance between type 1 error and type 2 error. We will discuss more in-depth about those in another lesson. For now, we have decided to make our significance level($\alpha$) = 0.05. So, our confidence interval or non-rejection region would be (1 - $\alpha$) = 95%.
#
# #### Computing T-statistics and P-value
# Let's take a random sample and see the difference.
# + _kg_hide-input=true _uuid="abd034cffc591bf1ef2b4a8ed3e5a65eb133d61e"
male_mean = train[train['Sex'] == 1].Survived.mean()
female_mean = train[train['Sex'] == 0].Survived.mean()
print ("Male survival mean: " + str(male_mean))
print ("female survival mean: " + str(female_mean))
print ("The mean difference between male and female survival rate: " + str(female_mean - male_mean))
# + [markdown] _uuid="0c1c27af262ba094ff1fd02867b1a41d5369720f"
# Now, we have to understand that those two means are not **the population mean**. *The population mean is a statistical term statistician uses to indicate the actual average of the entire group. The group can be any gathering of multiple numbers such as animal, human, plants, money, stocks.* For example, To find the age population mean of Bulgaria; we have to account for every single person's age and take their age. Which is almost impossible and if we were to go that route; there is no point of doing statistics in the first place. Therefore we approach this problem using sample sets. The idea of using sample set is that; if we take multiple samples of the same population and take the mean of them and put them in a distribution; eventually our distribution start to look more like a **normal distribution**. The more samples we take and the more sample means with be added and the closer the normal distribution with reach towards population mean. This is where **Central limit theory** comes from. We will go into this topic later on.
#
# Going back to our dataset, like we are saying these means above are part of the whole story. We were given part of the data to train our machine learning models, and the other part of the data was held back for testing. Therefore, It is impossible for us to know the population means of survival for male and females. Situation like this calls for a statistical approach. We will use the sampling distribution approach to do the test. let's take 50 random sample of male and female from our train data.
# + _kg_hide-input=true _uuid="5fecb72a097cca56483bca00a730a646aa5b0120"
# separating male and female dataframe.
male = train[train['Sex'] == 1]
female = train[train['Sex'] == 0]
# getting 50 random sample for male and female.
import random
male_sample = random.sample(list(male['Survived']),50)
female_sample = random.sample(list(female['Survived']),50)
# Taking a sample means of survival feature from male and female
male_sample_mean = np.mean(male_sample)
female_sample_mean = np.mean(female_sample)
# Print them out
print ("Male sample mean: " + str(male_sample_mean))
print ("Female sample mean: " + str(female_sample_mean))
print ("Difference between male and female sample mean: " + str(female_sample_mean - male_sample_mean))
# + [markdown] _uuid="706d89356793f306d807c3fb277963e07181915c"
# According to the samples our male and female mean measured difference is 0.58, keeping in mind that...
# * We randomly select 50 people to be in the male group and 50 people to be in the female group.
# * We know our sample is selected from a broader population(whole dataset of titanic).
# * We know we could have ended up with a different random sample of males or females from the total dataset.
# ***
# With all three points above in mind, how confident are we that, the measured difference is real or statistically significant? we can perform a **t-test** to evaluate that. When we perform a **t-test** we are usually trying to find out **an evidence of significant difference between population mean with hypothesized mean(1 sample t-test) or in our case difference between two population means(2 sample t-test).**
#
#
#
# The **t-statistics** is the measure of a degree to which our groups differ standardized by the variance of our measurements. In order words, it is basically the measure of signal over noise. Let us describe the previous sentence a bit more for clarification. I am going to use [this post](http://blog.minitab.com/blog/statistics-and-quality-data-analysis/what-is-a-t-test-and-why-is-it-like-telling-a-kid-to-clean-up-that-mess-in-the-kitchen) as reference to describe the t-statistics here.
#
#
# #### Calculating the t-statistics
# # $$t = \frac{\bar{x}-\mu}{\frac{S} {\sqrt{n}} }$$
#
# Here..
# * $\bar{x}$ is the sample mean.
# * $\mu$ is the hypothesized mean.
# * S is the standard devaition.
# * n is the sample size.
#
#
# Now, the denominator of this fraction $(\bar{x}-\mu)$ is basically the strength of the signal. where we calculate the difference between hypothesized mean and sample mean. If the mean difference is higher, then the signal is stronger.
#
# the numerator of this fraction ** ${S}/ {\sqrt{n}}$ ** calculates the amount of variation or noise of the data set. Here S is standard deviation, which tells us how much variation is there in the data. n is the sample size.
#
# So, according to the explanation above, the t-value or t-statistics is basically measures the strength of the signal(the difference) to the amount of noise(the variation) in the data and that is how we calculate the t-value in one sample t-test. However, in order to calculate between two sample population mean or in our case we will use the follow equation.
#
# # $$t = \frac{\bar{x}_M - \bar{x}_F}{\sqrt {s^2 (\frac{1}{n_M} + \frac{1}{n_F})}}$$
#
# This equation may seem too complex, however, the idea behind these two are similar. Both of them have the concept of signal/noise. The only difference is that we replace our hypothesis mean with another sample mean and the two sample sizes repalce one sample size.
#
# Here..
# * $\bar{x}_M$ is the mean of our male group sample measurements.
# * $ \bar{x}_F$ is the mean of female group samples.
# * $ n_M$ and $n_F$ are the sample number of observations in each group.
# * $ S^2$ is the sample variance.
#
# It is good to have an understanding of what going on in the background. However, we will use **scipy.stats** to find the t-statistics.
#
# + _kg_hide-input=true _uuid="52f37896d52d56f3f54208301f2b020f08b1fe92"
import scipy.stats as stats
print (stats.ttest_ind(male_sample, female_sample))
print ("This is the p-value when we break it into standard form: " + format(stats.ttest_ind(male_sample, female_sample).pvalue, '.32f'))
# + [markdown] _uuid="44e9000aefed8ea0125463486cc4a00c17e580e5"
# #### Compare P-value with $\alpha$
# > It looks like the p-value is very small compared to our significance level($\alpha$)of 0.05. Our observation sample is statistically significant. Therefore, our null hypothesis is ruled out, and our alternative hypothesis is valid, which is "**There is a significant difference in the survival rate between the male and female passengers."**
# + [markdown] _cell_guid="df06b6c8-daf6-4f5b-af51-9c1dfbac7a68" _uuid="34869ce4ce852633b1f4a5cd111b98841982cc19"
# # Part 5: Feature Engineering
# <a id="feature_engineering"></a>
# ***
# Feature Engineering is exactly what its sounds like. Sometimes we want to create extra features from with in the features that we have, sometimes we want to remove features that are alike. Features engineering is the simple word for doing all those. It is important to remember that we will create new features in such ways that will not cause **multicollinearity(when there is a relationship among independent variables)** to occur.
# + [markdown] _cell_guid="8c439069-6168-4cda-846f-db4c21265089" _uuid="3ca0785fe824c6ea471b2bcf9600007ed238d450"
# ## name_length
# ***
# ***Creating a new feature "name_length" that will take the count of letters of each name***
# + _cell_guid="d30d71c1-55bc-41c8-8536-9909d9f02538" _kg_hide-input=true _uuid="cb17c6f59bb2123cbf2cbc9c282b4d70ee283a86"
# Creating a new colomn with a
train['name_length'] = [len(i) for i in train.Name]
test['name_length'] = [len(i) for i in test.Name]
def name_length_group(size):
a = ''
if (size <=20):
a = 'short'
elif (size <=35):
a = 'medium'
elif (size <=45):
a = 'good'
else:
a = 'long'
return a
train['nLength_group'] = train['name_length'].map(name_length_group)
test['nLength_group'] = test['name_length'].map(name_length_group)
## Here "map" is python's built-in function.
## "map" function basically takes a function and
## returns an iterable list/tuple or in this case series.
## However,"map" can also be used like map(function) e.g. map(name_length_group)
## or map(function, iterable{list, tuple}) e.g. map(name_length_group, train[feature]]).
## However, here we don't need to use parameter("size") for name_length_group because when we
## used the map function like ".map" with a series before dot, we are basically hinting that series
## and the iterable. This is similar to .append approach in python. list.append(a) meaning applying append on list.
# + _cell_guid="19dbe40a-aa95-48af-abc4-291cab9d24b0" _kg_hide-input=true _uuid="cc3d7d3e2dd73f06eec76bad44610be8cae5f667"
## cuts the column by given bins based on the range of name_length
#group_names = ['short', 'medium', 'good', 'long']
#train['name_len_group'] = pd.cut(train['name_length'], bins = 4, labels=group_names)
# + [markdown] _uuid="012489c507bf8bfb1ca3db9b0506493cf5595e61"
# ## Title
# ***Getting the title of each name as a new feature. ***
# + _cell_guid="ded64d5f-43de-4a9e-b9c5-ec4d2869387a" _kg_hide-input=true _uuid="9c23229f7d06a1303a04b4a81c927453686ffec9"
## get the title from the name
train["title"] = [i.split('.')[0] for i in train.Name]
train["title"] = [i.split(',')[1] for i in train.title]
test["title"] = [i.split('.')[0] for i in test.Name]
test["title"]= [i.split(',')[1] for i in test.title]
# + _cell_guid="82e13bfe-5792-462c-be4d-4d786663fe48" _kg_hide-input=true _uuid="e475416e3e0c80c554b9a0990134128d219779c7"
#rare_title = ['the Countess','Capt','Lady','Sir','Jonkheer','Don','Major','Col']
#train.Name = ['rare' for i in train.Name for j in rare_title if i == j]
## train Data
train["title"] = [i.replace('Ms', 'Miss') for i in train.title]
train["title"] = [i.replace('Mlle', 'Miss') for i in train.title]
train["title"] = [i.replace('Mme', 'Mrs') for i in train.title]
train["title"] = [i.replace('Dr', 'rare') for i in train.title]
train["title"] = [i.replace('Col', 'rare') for i in train.title]
train["title"] = [i.replace('Major', 'rare') for i in train.title]
train["title"] = [i.replace('Don', 'rare') for i in train.title]
train["title"] = [i.replace('Jonkheer', 'rare') for i in train.title]
train["title"] = [i.replace('Sir', 'rare') for i in train.title]
train["title"] = [i.replace('Lady', 'rare') for i in train.title]
train["title"] = [i.replace('Capt', 'rare') for i in train.title]
train["title"] = [i.replace('the Countess', 'rare') for i in train.title]
train["title"] = [i.replace('Rev', 'rare') for i in train.title]
#rare_title = ['the Countess','Capt','Lady','Sir','Jonkheer','Don','Major','Col']
#train.Name = ['rare' for i in train.Name for j in rare_title if i == j]
## test data
test['title'] = [i.replace('Ms', 'Miss') for i in test.title]
test['title'] = [i.replace('Dr', 'rare') for i in test.title]
test['title'] = [i.replace('Col', 'rare') for i in test.title]
test['title'] = [i.replace('Dona', 'rare') for i in test.title]
test['title'] = [i.replace('Rev', 'rare') for i in test.title]
# + [markdown] _cell_guid="42ccf293-04c7-4bea-9570-4cce9227b8af" _uuid="e870c4fc44de4b2395963e583c84d2cae83c004b"
# ## family_size feature
# ***Creating a new feature called "family_size".***
# + _cell_guid="7083a7e7-d1d5-4cc1-ad67-c454b139f5f1" _kg_hide-input=true _uuid="cdfd54429cb235dd3b73535518950b2e515e54f2"
## Family_size seems like a good feature to create
train['family_size'] = train.SibSp + train.Parch+1
test['family_size'] = test.SibSp + test.Parch+1
# + _cell_guid="3d471d07-7735-4aab-8b26-3f26e481dc49" _kg_hide-input=true _uuid="2e23467af7a2e85fcaa06b52b303daf2e5e44250"
def family_group(size):
a = ''
if (size <= 1):
a = 'loner'
elif (size <= 4):
a = 'small'
else:
a = 'large'
return a
# + _cell_guid="82f3cf5a-7e8d-42c3-a06b-56e17e890358" _kg_hide-input=true _uuid="549239812f919f5348da08db4264632d2b21b587"
train['family_group'] = train['family_size'].map(family_group)
test['family_group'] = test['family_size'].map(family_group)
# + [markdown] _cell_guid="d827a2d9-8ca5-454a-8323-90c397b25ccf" _uuid="3aa4ad0fac364f8f3c04e240841ee097baa3c871"
# ## is_alone feature
# + _cell_guid="298b28d6-75a7-4e49-b1c3-7755f1727327" _kg_hide-input=true _uuid="45315bb62f69e94e66109e7da06c6c5ade578398"
train['is_alone'] = [1 if i<2 else 0 for i in train.family_size]
test['is_alone'] = [1 if i<2 else 0 for i in test.family_size]
# + [markdown] _cell_guid="fee91907-4197-46c2-92c1-92474565e9a0" _uuid="0a6032d2746a7cf75e2cc899615d72433572fd6d"
# ## Ticket feature
# + _cell_guid="352c794d-728d-44de-9160-25da7abe0c06" _kg_hide-input=true _uuid="5b99e1f7d7757f11e6dd6dbc627f3bd6e2fbd874"
train.Ticket.value_counts().sample(10)
# + [markdown] _uuid="dd50f2d503d4b951bee458793dde6e23f0e35dc9"
# I have yet to figureout how to best manage ticket feature. So, any suggestion would be truly appreciated. For now, I will get rid off the ticket feature.
# + _kg_hide-input=true _uuid="d23d451982f0cbe44976c2eacafb726d816e9195"
train.drop(['Ticket'], axis=1, inplace=True)
test.drop(['Ticket'], axis=1, inplace=True)
# + [markdown] _cell_guid="60cb16dc-9bc3-4ff3-93b8-e3b3d4bcc0c8" _uuid="800052abc32a56c5f5f875bb3652c02e93c6b0a8"
# ## fare feature
# ### calculated_fare feature
# + _cell_guid="adaa30fe-cb0f-4666-bf95-505f1dcce188" _kg_hide-input=true _uuid="9374a6357551a7551e71731d72f5ceb3144856df"
## Calculating fare based on family size.
train['calculated_fare'] = train.Fare/train.family_size
test['calculated_fare'] = test.Fare/test.family_size
# + [markdown] _uuid="157cec80a8138c7976b135f093fc52832b82d71e"
# Some people have travelled in groups like family or friends. It seems like Fare column kept a record of the total fare rather than the fare of individual passenger, therefore calculated fare will be much handy in this situation.
# + [markdown] _cell_guid="60579ed1-9978-4d4a-aea0-79c75b6b1376" _uuid="c0e1c25bc6a7717646a5d0d063acae220e496e9e"
# ### fare_group
# + _cell_guid="8c33b78c-14cb-4cc2-af0f-65079a741570" _kg_hide-input=true _uuid="35685a6ca28651eab389c4673c21da2ea5ba4187"
def fare_group(fare):
a= ''
if fare <= 4:
a = 'Very_low'
elif fare <= 10:
a = 'low'
elif fare <= 20:
a = 'mid'
elif fare <= 45:
a = 'high'
else:
a = "very_high"
return a
train['fare_group'] = train['calculated_fare'].map(fare_group)
test['fare_group'] = test['calculated_fare'].map(fare_group)
#train['fare_group'] = pd.cut(train['calculated_fare'], bins = 4, labels=groups)
# + [markdown] _cell_guid="5f5072cf-2234-425e-b91d-9609971117a0" _uuid="907614ee16efce8cbcc32b5535648688d23271eb"
# Fare group was calculated based on <i>calculated_fare</i>. This can further help our cause.
# + [markdown] _uuid="57a333f5c225ce65ec46a7e8b3c33d78fd70752e"
# ### PassengerId column
# + [markdown] _uuid="b44cc5b5f6fd4d844b85f689f3a713599915bbce"
# It seems like <i>PassengerId</i> column only works as an id in this dataset without any significant effect on the dataset. Let's drop it.
# + _uuid="dadea67801cf5b56a882aa96bb874a4afa0e0bec"
train.drop(['PassengerId'], axis=1, inplace=True)
test.drop(['PassengerId'], axis=1, inplace=True)
# + [markdown] _cell_guid="6a494c58-c1cf-44e9-be41-f404626ab299" _uuid="704994b577f803ae51c5c6473a2d96f49bdd12ea"
# ## Creating dummy variables
#
# You might be wondering what is a dummy variable?
#
# Dummy variable is an important **prepocessing machine learning step**. Often times Categorical variables are an important features, which can be the difference between a good model and a great model. While working with a dataset, having meaningful value for example, "male" or "female" instead of 0's and 1's is more intuitive for us. However, machines do not understand the value of categorical values, for example, in this dataset we have gender male or female, algorithms do not accept categorical variables as input. In order to feed data in a machine learning model, we
# + _cell_guid="9243ac8c-be44-46d0-a0ca-ee5f19b89bd4" _kg_hide-input=true _uuid="7b8db3930fb1bfb91db16686223dfc6d8e77744d"
train = pd.get_dummies(train, columns=['title',"Pclass", 'Cabin','Embarked','nLength_group', 'family_group', 'fare_group'], drop_first=False)
test = pd.get_dummies(test, columns=['title',"Pclass",'Cabin','Embarked','nLength_group', 'family_group', 'fare_group'], drop_first=False)
train.drop(['family_size','Name', 'Fare','name_length'], axis=1, inplace=True)
test.drop(['Name','family_size',"Fare",'name_length'], axis=1, inplace=True)
# + [markdown] _cell_guid="67dc98ce-bedc-456d-bdbb-9684bbd88d66" _uuid="23586743d94d093f76f05a2fd3ca0ae75c0d663c"
# ## Age feature
# + [markdown] _uuid="a519858b2df34c499bb53808a5a23592ba7af040"
# As I promised before, we are going to use Random forest regressor in this section to predict the missing age values. Let's see how many missing values do we have now
# + _kg_hide-input=true _uuid="9597c320c3db4db5e5c28980a28abaae7281bc61"
## rearranging the columns so that I can easily use the dataframe to predict the missing age values.
train = pd.concat([train[["Survived", "Age", "Sex","SibSp","Parch"]], train.loc[:,"is_alone":]], axis=1)
test = pd.concat([test[["Age", "Sex"]], test.loc[:,"SibSp":]], axis=1)
# + _kg_hide-input=true _uuid="91662e7b63c2361fdcf3215f130b3895154ad92d"
## Importing RandomForestRegressor
from sklearn.ensemble import RandomForestRegressor
## writing a function that takes a dataframe with missing values and outputs it by filling the missing values.
def completing_age(df):
## gettting all the features except survived
age_df = df.loc[:,"Age":]
temp_train = age_df.loc[age_df.Age.notnull()] ## df with age values
temp_test = age_df.loc[age_df.Age.isnull()] ## df without age values
y = temp_train.Age.values ## setting target variables(age) in y
x = temp_train.loc[:, "Sex":].values
rfr = RandomForestRegressor(n_estimators=1500, n_jobs=-1)
rfr.fit(x, y)
predicted_age = rfr.predict(temp_test.loc[:, "Sex":])
df.loc[df.Age.isnull(), "Age"] = predicted_age
return df
## Implementing the completing_age function in both train and test dataset.
completing_age(train)
completing_age(test);
# + [markdown] _uuid="8f4891f73fe40cdf20cbcdfce93bda7a4f5ccc5d"
# Let's take a look at the histogram of the age column.
# + _kg_hide-input=true _uuid="8fc55e4670061d46dab3cc6585b3cc71eb996868"
## Let's look at the his
plt.subplots(figsize = (22,10),)
sns.distplot(train.Age, bins = 100, kde = True, rug = False, norm_hist=False);
# + [markdown] _uuid="97fcc2a4c7cdc7f998052aed543b86e113499580"
# ## Age Group
# We can create a new feature by grouping the "Age" column
# + _cell_guid="3140c968-6755-42ec-aa70-d30c0acede1e" _kg_hide-input=true _uuid="c3bd77bb4d9d5411aa696a605be127db181d2a67"
## create bins for age
def age_group_fun(age):
a = ''
if age <= 1:
a = 'infant'
elif age <= 4:
a = 'toddler'
elif age <= 13:
a = 'child'
elif age <= 18:
a = 'teenager'
elif age <= 35:
a = 'Young_Adult'
elif age <= 45:
a = 'adult'
elif age <= 55:
a = 'middle_aged'
elif age <= 65:
a = 'senior_citizen'
else:
a = 'old'
return a
## Applying "age_group_fun" function to the "Age" column.
train['age_group'] = train['Age'].map(age_group_fun)
test['age_group'] = test['Age'].map(age_group_fun)
## Creating dummies for "age_group" feature.
train = pd.get_dummies(train,columns=['age_group'], drop_first=True)
test = pd.get_dummies(test,columns=['age_group'], drop_first=True);
"""train.drop('Age', axis=1, inplace=True)
test.drop('Age', axis=1, inplace=True)"""
# + [markdown] _cell_guid="9de7bf55-edfb-42e0-a235-7fee883001d9" _uuid="8eb07418adf26340ec68fa41401e68d08603f6d4"
# # Part 6: Pre-Modeling Tasks
# ## 6a. Separating dependent and independent variables
# <a id="dependent_independent"></a>
# ***
# Before we apply any machine learning models, It is important to separate dependent and independent variables. Our dependent variable or target variable is something that we are trying to find, and our independent variable is the features we use to find the dependent variable. The way we use machine learning algorithm in a dataset is that we train our machine learning model by specifying independent variables and dependent variable. To specify them, we need to separate them from each other, and the code below does just that.
#
# P.S. In our test dataset, we do not have a dependent variable feature. We are to predict that using machine learning models.
# + _cell_guid="dcb0934f-8e3f-40b6-859e-abf70b0b074e" _kg_hide-input=true _uuid="607db6be6dfacc7385e5adcc0feeee28c50c99c5"
# separating our independent and dependent variable
X = train.drop(['Survived'], axis = 1)
y = train["Survived"]
#age_filled_data_nor = NuclearNormMinimization().complete(df1)
#Data_1 = pd.DataFrame(age_filled_data, columns = df1.columns)
#pd.DataFrame(zip(Data["Age"],Data_1["Age"],df["Age"]))
# + [markdown] _cell_guid="042502ae-2714-43e2-9e33-6705b1aa781a" _uuid="92001d23ce79265c0f7d2b3d6f67094feeec2ea7"
# ## 6b. Splitting the training data
# <a id="split_training_data" ></a>
# ***
# There are multiple ways of splitting data. They are...
# * train_test_split.
# * cross_validation.
#
# We have separated dependent and independent features; We have separated train and test data. So, why do we still have to split our training data? If you are curious about that, I have the answer. For this competition, when we train the machine learning algorithms, we use part of the training set usually two-thirds of the train data. Once we train our algorithm using 2/3 of the train data, we start to test our algorithms using the remaining data. If the model performs well we dump our test data in the algorithms to predict and submit the competition. The code below, basically splits the train data into 4 parts, **train_x**, **test_x**, **train_y**, **test_y**.
# * **train_x** and **train_y** first used to train the algorithm.
# * then, **test_x** is used in that trained algorithms to predict **outcomes. **
# * Once we get the **outcomes**, we compare it with **test_x**
#
# By comparing the **outcome** of the model with **test_y**, we can determine whether our algorithms are performing well or not.
#
# P.S. When we use cross validation it is important to remember not to use **train_x, test_x, train_y and test_y**, rather we will use **X and y**. I will discuss more on that.
# + _cell_guid="348a5be2-5f4f-4c98-93a3-7352b6060ef4" _kg_hide-input=true _uuid="41b70e57f8e03da9910c20af89a9fa4a2aaea85b"
from sklearn.model_selection import train_test_split
train_x, test_x, train_y, test_y = train_test_split(X,y,test_size = .33, random_state = 0)
# + [markdown] _cell_guid="1f920690-2084-498c-a2fa-e618ad2228d8" _uuid="75407683b262fb65fc4afdfca6084d4ddaebe9a9"
# ## 6c. Feature Scaling
# <a id="feature_scaling" ></a>
# ***
# Feature scaling is an important concept of machine learning models. Often times a dataset contain features highly varying in magnitude and unit. For some machine learning models, it is not a problem. However, for many other ones, its quite a problem. Many machine learning algorithms uses euclidian distances to calculate the distance between two points, it is quite a problem. Let's again look at a the sample of the **train** dataset below.
# + _kg_hide-input=true _uuid="d788baa4b88106afe5b30c769a6c85a1d67a5d6c"
train.sample()
# + [markdown] _uuid="3d213fdd45a46ea0cf060adc7d9af58a84a03e21"
# Here **Age** and **Calculated_fare** is much higher in magnitude compared to others machine learning features. This can create problems as many machine learning models will get confused thinking **Age** and **Calculated_fare** have higher weight than other features. Therefore, we need to do feature scaling to get a better result.
# There are multiple ways to do feature scaling.
# <ul>
# <li><b>MinMaxScaler</b>-Scales the data using the max and min values so that it fits between 0 and 1.</li>
# <li><b>StandardScaler</b>-Scales the data so that it has mean 0 and variance of 1.</li>
# <li><b>RobustScaler</b>-Scales the data similary to Standard Scaler, but makes use of the median and scales using the interquertile range so as to aviod issues with large outliers.</b>
# </ul>
# I will discuss more on that in a different kernel. For now we will use <b>Standard Scaler</b> to feature scale our dataset.
#
# P.S. I am showing a sample of both before and after so that you can see how scaling changes the dataset.
# + [markdown] _uuid="2bf3db75976f363c0e922b0b7843716f900e0fd9"
# <h3><font color="$5831bc" face="Comic Sans MS">Before Scaling</font></h3>
# + _kg_hide-input=true _uuid="c4011a767b1d846f2866b4573d1d6d116afe8427"
headers = train_x.columns
train_x.head()
# + _cell_guid="5c89c54b-7f5a-4e31-9e8f-58726cef5eab" _kg_hide-input=true _uuid="182b849ba7f2b311e919cdbf83970b97736e9d98"
# Feature Scaling
## We will be using standardscaler to transform
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
## transforming "train_x"
train_x = sc.fit_transform(train_x)
## transforming "test_x"
test_x = sc.transform(test_x)
## transforming "The testset"
test = sc.transform(test)
# + [markdown] _uuid="d425ca579370db88e39cdd1811ba3df2b257b36c"
# <h3><font color="#5831bc" face="Comic Sans MS">After Scaling</font></h3>
# + _kg_hide-input=true _uuid="fc6f031833ac9e2734aa7b3a2373b667679c6b2f"
pd.DataFrame(train_x, columns=headers).head()
# -
# You can see feature schaling changed the
# + [markdown] _cell_guid="0e03e40b-789a-40a0-a095-135f3d1c8f23" _uuid="99e108b83ba88738e42480b053371d60d89151cf"
# # Part 7: Modeling the Data
# <a id="modelingthedata"></a>
# ***
# Since the problem we are trying to solve is a classification problem, we are going to use a bunch of classification model to get the best prediction possible. I will use the following models and describe them along the way to give a better perspective.
#
# - Logistic Regression
# - K-Nearest Neighbors(KNN)
# - Gaussian Naive Bayes
# - Support Vector Machines
# - Decision Tree Classifier
# - Bagging on Decision Tree Classifier
# - Random Forest Classifier
# - Gradient Boosting Classifier
#
#
# + [markdown] _cell_guid="9ddfa2c2-77d8-4bdb-8dae-979c41f9a42a" _uuid="120c4ad3aeb29647637f82bd533495f73b415b22"
# ## 7a. Logistic Regression
# <a id="logistic_regression"></a>
# ***
# We will start with one of the most basic but effective machine learning model, **Logistic Regression**. Logistic regression is a famous classifier still used today frequently despite its age. It is a regression similar to **Linear regression**, yet operates as a classifier. To understand logistic regression, we should have some idea about linear regression. Let's have a look at it.
#
# Hopefully, we all know that any linear equation can be written in the form of...
#
# # $$ {y} = mX + b $$
#
# * Here, m = slope of the regression line. it represents the relationship between X and y.
# * b = y-intercept.
# * x and y are the points location in x_axis and y_axis respectively.
# <br/>
#
# If you want to know how, check out this [video](https://www.khanacademy.org/math/algebra/two-var-linear-equations/writing-slope-intercept-equations/v/graphs-using-slope-intercept-form). So, this slope equation can also be written as...
#
# ## $$ y = \beta_0 + \beta_1 x + \epsilon \\ $$
#
# This is the equation for a simple linear regression.
# here,
# * y = Dependent variable.
# * $\beta_0$ = the intercept, it is constant.
# * $\beta_1$ = Coefficient of independent variable.
# * $x$ = Indepentent variable.
# * $ \epsilon$ = error or residual.
#
#
# We use this function to predict the value of a dependent variable with the help of only one independent variable. Therefore this regression is called **Simple Linear Regression.**
#
# Similar to **Simple Linear Regression**, there is **Multiple Linear Regression** which can be used to predict dependent variable using multiple independent variables. Let's look at the equation for **Multiple Linear Regression**,
#
# ## $$ \hat{y} = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n $$
#
#
# If you would like to know more about **Linear Regression** checkout this [kernel](https://www.kaggle.com/masumrumi/a-stats-analysis-and-ml-workflow-of-house-pricing).
#
# So, we know/reviewed a bit about linear regression, and therefore we know how to deal with data that looks like this,
# <img src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/3a/Linear_regression.svg/1200px-Linear_regression.svg.png" width="600">
#
# Here the data point's in this graph is continuous and therefore the problem is a regression one. However, what if we have data that when plotted in a scatter graph, looks like this...
#
# + _kg_hide-input=false
train.calculated_fare = train.calculated_fare.astype(float)
# + _kg_hide-input=true _uuid="ae3497966a72f4bf82948e4178bed70779847988"
plt.subplots(figsize = (12,10))
plt.scatter(train.Age, train.Survived);
plt.xlabel("Age")
plt.ylabel('Survival Status');
# + [markdown] _uuid="3ad785c1da665b883b06666eadc9506d2dde5afe"
# Here the data points are not continuous; rather categorical. The two horizontal dot lines represent the survival status in the y-axis and age in the x-axis. This is probably not the best graph to explain logistic regression. For the convenience of understanding the model, let's look at a similar scatter plot with some characteristics.
#
# <img src="https://sds-platform-private.s3-us-east-2.amazonaws.com/uploads/39_blog_image_3.png" width="600">
# <h5 align="right">SuperDataScience team</h5>
#
# This chart clearly divides the binary categorical values in the x-axis, keeping most of the 0's on the left side, and 1's on the right side. So, now that the distinction is apparent, we can use our knowledge of linear regression and come up with a regression line. So, how can we apply a regression line to explain this data?
#
# <img src="https://sds-platform-private.s3-us-east-2.amazonaws.com/uploads/39_blog_image_4.png" width="800">
# <h5 align="right">SuperDataScience team</h5>
#
# As you can see from the chart above, The linear regression is probably not the best approach to take for categorical data. The Linear regression line barely aligns with the data points, and even if in some best-case scenario we were to use straight regression line, we would end up with a considerable error rate, which is super inconvenient. This is where logistic regression comes in.
# + _cell_guid="0c8b0c41-6738-4689-85b0-b83a16e46ab9" _uuid="09140be1a71e37b441a16951a82747462b767e6e"
# import LogisticRegression model in python.
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import mean_absolute_error, accuracy_score
## call on the model object
logreg = LogisticRegression(solver='liblinear')
## fit the model with "train_x" and "train_y"
logreg.fit(train_x,train_y)
## Once the model is trained we want to find out how well the model is performing, so we test the model.
## we use "test_x" portion of the data(this data was not used to fit the model) to predict model outcome.
y_pred = logreg.predict(test_x)
## Once predicted we save that outcome in "y_pred" variable.
## Then we compare the predicted value( "y_pred") and actual value("test_y") to see how well our model is performing.
print ("So, Our accuracy Score is: {}".format(round(accuracy_score(y_pred, test_y),4)))
# + [markdown] _uuid="a57b64f3a479d2796eb745b55594e9d65a32251f"
# But what is accuracy score? what does it tell us?
#
# Introducing <b>confusion matrix</b>. This may not seem to be much for now, but we will improve upon that.
# + [markdown] _uuid="24268f00a8687e0d3014104d6bb4c5092794f075"
# ### Under-fitting & Over-fitting:
# So, we have our first model and its score. But, how do we make sure that our model is performing well? Our model may be overfitting or underfitting. In fact, for those of you don't know what overfitting and underfitting are. Let's find out.
#
# 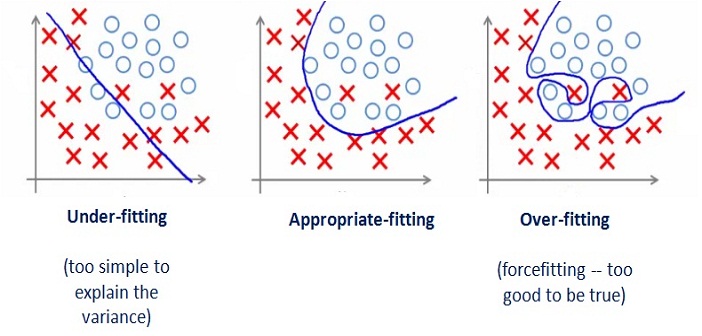
#
# As you see in the chart above. **Underfitting** is when the model fails to capture important aspects of the data and therefore introduces more bias and performs poorly. On the other hand, **Overfitting** is when the model performs too well on the training data but does poorly in the validation set or test sets. This situation is also known as having less bias but more variation and perform poorly as well. Ideally, we want to configure a model that performs well not only in the training data but also in the test data. This is where **bias-variance tradeoff** comes in. When we have a model that overfits meaning less biased and more chance of variance, we introduce some bias in exchange of having much less variance. One particular tactic for this task is regularization models (Ridge, Lasso, Elastic Net). These models are built to deal with the bias-variance tradeoff. This [kernel](https://www.kaggle.com/dansbecker/underfitting-and-overfitting) explains this topic well. Also, the following chart gives us a mental picture of where we want our models to be.
# 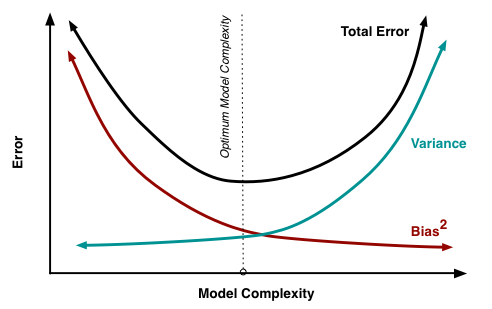
#
# Ideally, we want to pick a sweet spot where the model performs well in training set, validation set, and test set. As the model gets complex, bias decreases, variance increases. However, the most critical part is the error rates. We want our models to be at the bottom of that **U** shape where the error rate is the least. That sweet spot is also known as **Optimum Model Complexity(OMC).**
#
# Now that we know what we want in terms of under-fitting and over-fitting, let's talk about how to combat them.
#
# How to combat over-fitting?
# <ul>
# <li>Simplify the model by using less parameters.</li>
# <li>Simplify the model by changing the hyperparameters.</li>
# <li>Introducing regularization models. </li>
# <li>Use more training data. </li>
# <li>Gatter more data ( and gather better quality data). </li>
# </ul>
# + [markdown] _uuid="51ca86210b6f1740da0cf4795738d2a58848ffc4"
# <h2><font color="#5831bc" face="Comic Sans MS">Evaluating the model</font></h2>
# While we try to evaluate the model, we want to focus on a couple of things.
#
# <ul>
# <li>Which are the most importnat features(relatively) of a project ?(<b>Relative Feature Importance</b>)</li>
# <li>Which features have the biggest impact on the project on the project success ? (<b>Permutation Importance</b>) </li>
# <li>How does changes in those featues affact the project success? (<b>Partial Dependencies</b>)</li>
# <li>Digging deeper into the decisions made by the model(<b>SHAP values</b>)
# </ul>
#
# <h3>Explaining the results of the model.</h3>
# <ul>
# <li>How well is the model ?</li>
# <li>What are the most important features ?</li>
# </ul>
#
# <h3>Introducting Confusion Matrix</h3>
# A confusion Matrix is a table that <b>describes the performance of a classification model</b>. We use the classification model by using data where we already know the true outcome and compare it with the model predicted an outcome. Confusion Matrix tells us how many our model predicted correctly and incorrectly in terms of binary/multiple outcome classes. For example, in terms of this dataset, our model is trying to classify whether the passenger survived or died. We will come back to this; for now, let's introduce ourselves some of the terminologies of the confusion matrix.
#
#
# <ul style="list-style-type:square;">
# <li>True Positive</li>
# <li>True Negative</li>
# <li>False Positive</li>
# <li>False Negative</li>
# </ul>
#
# #### This part of the kernel is a working progress. Please check back again for future updates.####
#
# Resources:
# * [Confusion Matrix](https://www.youtube.com/watch?v=8Oog7TXHvFY)
# + [markdown] _uuid="e13731cbb9d9040cf6e4088e8660eca66037a8cc"
# <h1>AUC & ROC Curve</h1>
# + _uuid="1e71bc7c685b757b6920076527780674d6f619bc"
from sklearn.metrics import roc_curve, auc
#plt.style.use('seaborn-pastel')
y_score = logreg.decision_function(test_x)
FPR, TPR, _ = roc_curve(test_y, y_score)
ROC_AUC = auc(FPR, TPR)
print (ROC_AUC)
plt.figure(figsize =[11,9])
plt.plot(FPR, TPR, label= 'ROC curve(area = %0.2f)'%ROC_AUC, linewidth= 4)
plt.plot([0,1],[0,1], 'k--', linewidth = 4)
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.05])
plt.xlabel('False Positive Rate', fontsize = 18)
plt.ylabel('True Positive Rate', fontsize = 18)
plt.title('ROC for Titanic survivors', fontsize= 18)
plt.show()
# + _uuid="22f15e384372a1ece2f28cd9eced0c703a79598f"
from sklearn.metrics import precision_recall_curve
y_score = logreg.decision_function(test_x)
precision, recall, _ = precision_recall_curve(test_y, y_score)
PR_AUC = auc(recall, precision)
plt.figure(figsize=[11,9])
plt.plot(recall, precision, label='PR curve (area = %0.2f)' % PR_AUC, linewidth=4)
plt.xlabel('Recall', fontsize=18)
plt.ylabel('Precision', fontsize=18)
plt.title('Precision Recall Curve for Titanic survivors', fontsize=18)
plt.legend(loc="lower right")
plt.show()
# + [markdown] _uuid="e46b6d4bcb0ef70c06535b58bbe84c8a301ead91"
# ## Using Cross-validation:
# Pros:
# * Helps reduce variance.
# * Expends models predictability.
#
# + _uuid="17791284c3e88236de2daa112422cde8ddcb0641"
## Using StratifiedShuffleSplit
## We can use KFold, StratifiedShuffleSplit, StratiriedKFold or ShuffleSplit, They are all close cousins. look at sklearn userguide for more info.
from sklearn.model_selection import StratifiedShuffleSplit, cross_val_score
cv = StratifiedShuffleSplit(n_splits = 10, test_size = .25, random_state = 0 ) # run model 10x with 60/30 split intentionally leaving out 10%
## Using standard scale for the whole dataset.
X = sc.fit_transform(X)
accuracies = cross_val_score(LogisticRegression(), X,y, cv = cv)
print ("Cross-Validation accuracy scores:{}".format(accuracies))
print ("Mean Cross-Validation accuracy score: {}".format(round(accuracies.mean(),5)))
# + [markdown] _cell_guid="d1f2930c-43ae-4c15-87f7-ccc9214ee0e1" _uuid="b8020ecfe44bebdf7a2b95ec49393e8baac6bcf9"
# ## Grid Search on Logistic Regression
# * What is grid search?
# * What are the pros and cons?
#
# **Gridsearch** is a simple concept but effective technique in Machine Learning. The word **GridSearch** stands for the fact that we are searching for optimal parameter/parameters over a "grid." These optimal parameters are also known as **Hyperparameters**. **The Hyperparameters are model parameters that are set before fitting the model and determine the behavior of the model.**. For example, when we choose to use linear regression, we may decide to add a penalty to the loss function such as Ridge or Lasso. These penalties require specific alpha (the strength of the regularization technique) to set beforehand. The higher the value of alpha, the more penalty is being added. GridSearch finds the optimal value of alpha among a range of values provided by us, and then we go on and use that optimal value to fit the model and get sweet results. It is essential to understand those model parameters are different from models outcomes, for example, **coefficients** or model evaluation metrics such as **accuracy score** or **mean squared error**.
#
# #### This part of the kernel is a working progress. Please check back again for future updates.####
# + _cell_guid="0620523c-b33b-4302-8a1c-4b6759ffa5fa" _uuid="36a379a00a31dd161be1723f65490990294fe13d"
from sklearn.model_selection import GridSearchCV, StratifiedKFold
## C_vals is the alpla value of lasso and ridge regression(as alpha increases the model complexity decreases,)
## remember effective alpha scores are 0<alpha<infinity
C_vals = [0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,2,3,4,5,6,7,8,9,10,12,13,14,15,16,16.5,17,17.5,18]
## Choosing penalties(Lasso(l1) or Ridge(l2))
penalties = ['l1','l2']
## Choose a cross validation strategy.
cv = StratifiedShuffleSplit(n_splits = 10, test_size = .25)
## setting param for param_grid in GridSearchCV.
param = {'penalty': penalties, 'C': C_vals}
logreg = LogisticRegression(solver='liblinear')
## Calling on GridSearchCV object.
grid = GridSearchCV(estimator=LogisticRegression(),
param_grid = param,
scoring = 'accuracy',
n_jobs =-1,
cv = cv
)
## Fitting the model
grid.fit(X, y)
# + _cell_guid="1fa35072-87c4-4f47-86ab-dda03d4b7b15" _uuid="4c6650e39550527b271ddf733dcfe5221bcd5c98"
## Getting the best of everything.
print (grid.best_score_)
print (grid.best_params_)
print(grid.best_estimator_)
# + [markdown] _uuid="dcd2ad782c168abb5cfb5a3d148814e53cb2119c"
#
# #### Using the best parameters from the grid-search.
# + _uuid="ba53f6b3610821dc820936dde7b7803a54d20f5a"
### Using the best parameters from the grid-search.
logreg_grid = grid.best_estimator_
logreg_grid.score(X,y)
# + [markdown] _cell_guid="8046e4d9-12db-4b1c-9e9e-31fd5e6543f2" _uuid="26b0ea9184b2c37eabe4e705b1c840956ecc1e10"
# ## 7b. K-Nearest Neighbor classifier(KNN)
# <a id="knn"></a>
# ***
# + _uuid="953bc2c18b5fd93bcd51a42cc04a0539d86d5bac"
## Importing the model.
from sklearn.neighbors import KNeighborsClassifier
## calling on the model oject.
knn = KNeighborsClassifier(metric='minkowski', p=2)
## knn classifier works by doing euclidian distance
## doing 10 fold staratified-shuffle-split cross validation
cv = StratifiedShuffleSplit(n_splits=10, test_size=.25, random_state=2)
accuracies = cross_val_score(knn, X,y, cv = cv, scoring='accuracy')
print ("Cross-Validation accuracy scores:{}".format(accuracies))
print ("Mean Cross-Validation accuracy score: {}".format(round(accuracies.mean(),3)))
# + [markdown] _uuid="6aa75e53129898ccd714370dc55c0ed2830e72f4"
# #### Manually find the best possible k value for KNN
# + _uuid="9c0f44165e08f63ae5436180c5a7182e6db5c63f"
## Search for an optimal value of k for KNN.
k_range = range(1,31)
k_scores = []
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X,y, cv = cv, scoring = 'accuracy')
k_scores.append(scores.mean())
print("Accuracy scores are: {}\n".format(k_scores))
print ("Mean accuracy score: {}".format(np.mean(k_scores)))
# + _uuid="e123680b431ba99d399fa8205c32bcfdc7cabd81"
from matplotlib import pyplot as plt
plt.plot(k_range, k_scores)
# + [markdown] _uuid="77b5b6e3b7bc925e0b008cd6d531175e5cc44040"
# ### Grid search on KNN classifier
# + _uuid="507e2a7cdb28a47be45ed247f1343c123a6b592b"
from sklearn.model_selection import GridSearchCV
## trying out multiple values for k
k_range = range(1,31)
##
weights_options=['uniform','distance']
#
param = {'n_neighbors':k_range, 'weights':weights_options}
## Using startifiedShufflesplit.
cv = StratifiedShuffleSplit(n_splits=10, test_size=.30, random_state=15)
# estimator = knn, param_grid = param, n_jobs = -1 to instruct scikit learn to use all available processors.
grid = GridSearchCV(KNeighborsClassifier(), param,cv=cv,verbose = False, n_jobs=-1)
## Fitting the model.
grid.fit(X,y)
# + _uuid="c710770daa6cf327dcc28e18b3ed180fabecd49b"
print (grid.best_score_)
print (grid.best_params_)
print(grid.best_estimator_)
# + [markdown] _uuid="bb06144264d3127c92169aed7c29c2f66ad0ffc4"
# #### Using best estimator from grid search using KNN.
# + _uuid="dd1fbf223c4ec9db65dde4924e2827e46029da1a"
### Using the best parameters from the grid-search.
knn_grid= grid.best_estimator_
knn_grid.score(X,y)
# + [markdown] _uuid="c2ebec8b83f23e3e27d23bdd707852269edd4d24"
# #### Using RandomizedSearchCV
# Randomized search is a close cousin of grid search. It doesn't always provide the best result but its fast.
# + _uuid="e159b267a57d7519fc0ee8b3d1e95b841d3daf60"
from sklearn.model_selection import RandomizedSearchCV
## trying out multiple values for k
k_range = range(1,31)
##
weights_options=['uniform','distance']
#
param = {'n_neighbors':k_range, 'weights':weights_options}
## Using startifiedShufflesplit.
cv = StratifiedShuffleSplit(n_splits=10, test_size=.30, random_state=15)
# estimator = knn, param_grid = param, n_jobs = -1 to instruct scikit learn to use all available processors.
## for RandomizedSearchCV,
grid = RandomizedSearchCV(KNeighborsClassifier(), param,cv=cv,verbose = False, n_jobs=-1, n_iter=40)
## Fitting the model.
grid.fit(X,y)
# + _uuid="c58492525dd18659ef9f9c774ee7601a55e96f36"
print (grid.best_score_)
print (grid.best_params_)
print(grid.best_estimator_)
# + _uuid="6fb31588585d50de773ba0db6c378363841a5313"
### Using the best parameters from the grid-search.
knn_ran_grid = grid.best_estimator_
knn_ran_grid.score(X,y)
# + [markdown] _cell_guid="be0143d6-a7ea-4752-9520-c692f4c3eb8a" _uuid="21e91edd53b6587d5a05036045bc5eea52f056da"
# ## 7c. Gaussian Naive Bayes
# <a id="gaussian_naive"></a>
# ***
# + _uuid="8b2435030dbef1303bfc2864d227f5918f359330"
# Gaussian Naive Bayes
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
gaussian = GaussianNB()
gaussian.fit(X, y)
y_pred = gaussian.predict(test_x)
gaussian_accy = round(accuracy_score(y_pred, test_y), 3)
print(gaussian_accy)
# + [markdown] _cell_guid="c3e025c5-50f3-4fa1-a385-438d6665199b" _uuid="2a1558118d9e673395246acc4f3c0edb1b1895f0"
# ## 7d. Support Vector Machines(SVM)
# <a id="svm"></a>
# ***
# + _uuid="56895672215b0b6365c6aaa10e446216ef635f53"
from sklearn.svm import SVC
Cs = [0.001, 0.01, 0.1, 1,1.5,2,2.5,3,4,5, 10] ## penalty parameter C for the error term.
gammas = [0.0001,0.001, 0.01, 0.1, 1]
param_grid = {'C': Cs, 'gamma' : gammas}
cv = StratifiedShuffleSplit(n_splits=10, test_size=.30, random_state=15)
grid_search = GridSearchCV(SVC(kernel = 'rbf', probability=True), param_grid, cv=cv) ## 'rbf' stands for gaussian kernel
grid_search.fit(X,y)
# + _uuid="4108264ea5d18e3d3fa38a30584a032c734d6d49"
print(grid_search.best_score_)
print(grid_search.best_params_)
print(grid_search.best_estimator_)
# + _uuid="db18a3b5475f03b21a039e31e4962c43f7caffdc"
# using the best found hyper paremeters to get the score.
svm_grid = grid_search.best_estimator_
svm_grid.score(X,y)
# + [markdown] _cell_guid="296e2062-4bc4-448d-9cde-c780cdad9000" _uuid="b83a19edc0919954644e8d69e0ae175843197727"
# ## 7e. Decision Tree Classifier
# <a id="decision_tree"></a>
# ***
#
# Among all the machine learning models decision tree is one of my favorite. Let's briefly talk about it.
#
# The idea behind the decision tree is pretty simple. To build a tree, we use a decision tree algorithm called CART. CART stands for Classification and Regression Trees. This means the decision tree can be used for both regression and classifications problems. To perform classification or regression, decision trees make sequential, hierarchical decisions about the outcome variable based on the predictor data.
#
# Decision tree works by breaking down the dataset into small subsets. This breaking down process is done by asking questions about the features of the datasets. The idea is to unmix the labels by asking fewer questions necessary. As we ask questions, we are breaking down the dataset into more subsets. Once we have a subgroup with only the unique type of labels, we end the tree in that node. We call this the leaf node. Here is an excellent example of the decision tree.
#
# <img src="https://cdn-images-1.medium.com/max/1200/1*GgUEazXbr2CYLUsPgdYzDw.png" width="600">
#
# If you think about it, this is sort of like the "20 Questions" game where an individual or group has the opportunity to identify an unknown object by asking a series of up to 20 "yes" or "no" questions. For example, if we want to tie it with this dataset, let's say we are asking to find out whether a certain person in the test dataset survived or not. We may ask a question like, is the person "male" or "female." Let's say the answer is "female." Then the algorithm might ask about the person's Pclass. Let's say the Pclass is 1.
#
# As you can see by inquiring these details about this person we can give a certain percentage with confidence about a person's survival status. If you want to know more how the decision tree does all these mathematically and technically, you can keep on reading. Otherwise, you can skip to the next section.
#
# At first, we will add a root node for the tree. All node receives a list of rows from the dataset. The root node receives the whole dataset. This node then asks true/false questions about one of the features. Based on the answer, we split the dataset into smaller subsets. The number of subsets depends on the unique values of that feature. These subsets then become the input of each child nodes. Each child node then asks another question about a different feature leading to break down further into more subgroups. This process goes on. As we keep reading, one questions beg to be answered. How do we know which questions to ask and when?
#
# <b>The trick to building an effective tree is to know which questions to ask and when.</b> To find the best possible questions, we need to quantify how much uncertainty is there in a single node and how much a question help to unmix the labels. We can find out how much uncertainty/impurity is there in a single node using a concept called <i>Gini Impurity</i>. We can find out how much a question reduces that uncertainty using a matrix called <i>Information gain.</i> These two combined helps us decide which question to ask in each node. Let's dive into how these are calculated.
#
# <h3>Gini Impurity:</h3>
# Gini Impurity ranges between 0 and 1, where a lower value indicates less uncertainty and a higher value indicates higher uncertainty. In other words, when we look at the Gini index we want to look the at the lower value of Gini Index as those are the once produced the most unmixed subsets. A really good video about calculating Gini index is [here](https://www.youtube.com/watch?v=7VeUPuFGJHk).
#
# gini impurity quantifies our chances of being incorrect if we randomly assign a label to an example in the same set. For example, Let's say there are 5 different mixes with five different labels, Our chance of being right is 1/5. So, our chances of being wrong is (1-1/5) = 0.8. So, 0.8 is our Gini Impurity score.
#
# Here is the equation for Gini score.
#
# ### $$ \text{Gini} = \sum_{i=1}^{classes} p(i\;|\;t)(1 -p(i\;|\;t)) = 1 - \sum_{i=1}^{classes} p(i\;|\;t)^2 $$
#
#
# #### This part of the kernel is a working progress. Please check back again for future updates.####
#
#
# <h3>Information Gain</h3>
# Information gain is basically difference between the Gini Index of the parent note and the <b>weighted</b> average of the child nodes.
#
#
#
# <h4>Resources for Decision Tree:</h4>
# * https://www.youtube.com/watch?v=LDRbO9a6XPU (decision tree)
# * https://www.udemy.com/machinelearning/learn/v4/t/lecture/5732730?start=8 (Super data science)
# * GA resources.
# * https://www.youtube.com/watch?v=AmCV4g7_-QM&list=PLBv09BD7ez_4temBw7vLA19p3tdQH6FYO&index=3 (playlist of the Decision tree)
# * https://www.youtube.com/watch?v=7VeUPuFGJHk(How to calculate Gini Index)
#
#
#
#
#
#
# ### Grid search on Decision Tree
#
# + _cell_guid="38c90de9-d2e9-4341-a378-a854762d8be2" _uuid="18efb62b713591d1512010536ff10d9f6a91ec11"
from sklearn.tree import DecisionTreeClassifier
max_depth = range(1,30)
max_feature = [21,22,23,24,25,26,28,29,30,'auto']
criterion=["entropy", "gini"]
param = {'max_depth':max_depth,
'max_features':max_feature,
'criterion': criterion}
grid = GridSearchCV(DecisionTreeClassifier(),
param_grid = param,
verbose=False,
cv=StratifiedKFold(n_splits=20, random_state=15, shuffle=True),
n_jobs = -1)
grid.fit(X, y)
# + _cell_guid="b2222e4e-f5f2-4601-b95f-506d7811610a" _uuid="b0fb5055e6b4a7fb69ef44f669c4df693ce46212"
print( grid.best_params_)
print (grid.best_score_)
print (grid.best_estimator_)
# + _cell_guid="d731079a-31b4-429a-8445-48597bb2639d" _uuid="76c26437d374442826ef140574c5c4880ae1e853"
dectree_grid = grid.best_estimator_
## using the best found hyper paremeters to get the score.
dectree_grid.score(X,y)
# -
# Let's look at a visual dectree.
# + _uuid="3706f0365e41d0ba22f1f662aa337f5163ec3f7f"
import graphviz
from sklearn import tree
dot_data = tree.export_graphviz(dectree_grid, out_file=None)
graph = graphviz.Source(dot_data)
graph.render("house")
graph
# + [markdown] _cell_guid="9c4c43f6-42c4-4cd3-a038-3f0c37f3c767" _uuid="aba2679da04529faf9f9175ab20a66ee71217f92"
# ## 7f. Bagging Classifier
# <a id="bagging"></a>
# ***
# + _cell_guid="1dc3915b-6969-4bfa-9fa6-e062dd2d22e9" _uuid="7ef818c24bcaaa1b98b5f454af902a86c92d6eaa"
from sklearn.ensemble import BaggingClassifier
BaggingClassifier = BaggingClassifier()
BaggingClassifier.fit(X, y)
y_pred = BaggingClassifier.predict(test_x)
bagging_accy = round(accuracy_score(y_pred, test_y), 3)
print(bagging_accy)
# + [markdown] _cell_guid="a8ac5172-c861-43af-a26e-959e59a7561f" _uuid="2f303fbc0df2417da8c3597c9644425947d7f00e"
# ## 7g. Random Forest Classifier
# <a id="random_forest"></a>
# + _cell_guid="73ab112d-0308-4f37-992d-efd296bd1c9e" _uuid="f19b03609926684ddb364011219e4f9f02412c39"
from sklearn.ensemble import RandomForestClassifier
n_estimators = [90,95,100,105,110]
max_depth = range(1,30)
cv = StratifiedShuffleSplit(n_splits=10, test_size=.30, random_state=15)
parameters = {'n_estimators':n_estimators,
'max_depth':max_depth,
}
grid = GridSearchCV(RandomForestClassifier(),
param_grid=parameters,
cv=cv,
n_jobs = -1)
grid.fit(X,y)
# + _uuid="ee7570458fae49408d2b7b669b102a37d4f55e48"
print (grid.best_score_)
print (grid.best_params_)
print (grid.best_estimator_)
# + _uuid="8a366193e042709b455ef7fef7fd077fbf9697b6"
rf_grid = grid.best_estimator_
rf_grid.score(X,y)
# + [markdown] _cell_guid="6ea60e91-544f-49fc-8128-ee190e8292e7" _uuid="860921893a28a1fe9a4ce47f0779f1e7b154ca0a"
# ## 7h. Gradient Boosting Classifier
# <a id="gradient_boosting"></a>
# ***
# + _cell_guid="d32d6df9-b8e7-4637-bacc-2baec08547b8" _uuid="fd788c4f4cde834a1329f325f1f59e3f77c37e42"
# Gradient Boosting Classifier
from sklearn.ensemble import GradientBoostingClassifier
gradient = GradientBoostingClassifier()
gradient.fit(X, y)
y_pred = gradient.predict(test_x)
gradient_accy = round(accuracy_score(y_pred, test_y), 3)
print(gradient_accy)
# + [markdown] _cell_guid="996b8ee8-13ff-461d-8f7b-ac0d7d488cff" _uuid="ee9c7a2ccdf93a90f929b6618105afbe699bd6de"
# ## 7i. XGBClassifier
# <a id="XGBClassifier"></a>
# ***
# + _cell_guid="5d94cc5b-d8b7-40d3-b264-138539daabfa" _uuid="9d96154d2267ea26a6682a73bd1850026eb1303b"
from xgboost import XGBClassifier
XGBClassifier = XGBClassifier()
XGBClassifier.fit(X, y)
y_pred = XGBClassifier.predict(test_x)
XGBClassifier_accy = round(accuracy_score(y_pred, test_y), 3)
print(XGBClassifier_accy)
# + [markdown] _cell_guid="de2f5620-a4c5-420c-b762-cf0fea54136d" _uuid="ae62b81b2015e72e3fafb21c5b17a6d2d52a9b1a"
# ## 7j. AdaBoost Classifier
# <a id="adaboost"></a>
# ***
# + _cell_guid="2263377d-58cc-4aad-b4ef-dec2a58e7cb8" _uuid="4b54a07cab37731d9273d6b6ed3e2100e159a549"
from sklearn.ensemble import AdaBoostClassifier
adaboost = AdaBoostClassifier()
adaboost.fit(X, y)
y_pred = adaboost.predict(test_x)
adaboost_accy = round(accuracy_score(y_pred, test_y), 3)
print(adaboost_accy)
# + [markdown] _cell_guid="a6b4c23c-b42b-4fad-b37d-c84154b3478d" _uuid="3fa68b3d2e835b1a14088102561a2f8d4dac8f5c"
# ## 7k. Extra Trees Classifier
# <a id="extra_tree"></a>
# ***
# + _cell_guid="2e567e01-6b5f-4313-84af-cc378c3b709e" _uuid="c9b958e2488adf6f79401c677087e3250d63ac9b"
from sklearn.ensemble import ExtraTreesClassifier
ExtraTreesClassifier = ExtraTreesClassifier()
ExtraTreesClassifier.fit(X, y)
y_pred = ExtraTreesClassifier.predict(test_x)
extraTree_accy = round(accuracy_score(y_pred, test_y), 3)
print(extraTree_accy)
# + [markdown] _cell_guid="20a66dcc-7f9f-4802-aa6d-58be75e07539" _uuid="c55a54821feda82c75dde28bab7e2cf4445c4cf0"
# ## 7l. Gaussian Process Classifier
# <a id="GaussianProcessClassifier"></a>
# ***
# + _cell_guid="23bd5744-e04d-49bb-9d70-7c2a518f76dd" _uuid="57fc008eea2ce1c0b595f888a82ddeaee6ce2177"
from sklearn.gaussian_process import GaussianProcessClassifier
GaussianProcessClassifier = GaussianProcessClassifier()
GaussianProcessClassifier.fit(X, y)
y_pred = GaussianProcessClassifier.predict(test_x)
gau_pro_accy = round(accuracy_score(y_pred, test_y), 3)
print(gau_pro_accy)
# + [markdown] _cell_guid="ec676e4d-0cbe-43fa-9ff8-92d76030faef" _uuid="6f89f2cb63120a4594c7b0f2883b6872aa444700"
# ## 7m. Voting Classifier
# <a id="voting_classifer"></a>
# ***
# + _cell_guid="ac208dd3-1045-47bb-9512-de5ecb5c81b0" _uuid="821c74bbf404193219eb91fe53755d669f5a14d1"
from sklearn.ensemble import VotingClassifier
voting_classifier = VotingClassifier(estimators=[
('logreg_grid', logreg_grid),
('svc', svm_grid),
('random_forest', rf_grid),
('gradient_boosting', gradient),
('decision_tree_grid',dectree_grid),
('knn_grid', knn_grid),
('XGB Classifier', XGBClassifier),
('BaggingClassifier', BaggingClassifier),
('ExtraTreesClassifier', ExtraTreesClassifier),
('gaussian',gaussian),
('gaussian process classifier', GaussianProcessClassifier)], voting='soft')
voting_classifier = voting_classifier.fit(train_x,train_y)
# + _cell_guid="648ac6a6-2437-490a-bf76-1612a71126e8" _uuid="518a02ae91cc91d618e476d1fc643cd3912ee5fb"
y_pred = voting_classifier.predict(test_x)
voting_accy = round(accuracy_score(y_pred, test_y), 3)
print(voting_accy)
# + _cell_guid="277534eb-7ec8-4359-a2f4-30f7f76611b8" _kg_hide-input=true _uuid="00a9b98fd4e230db427a63596a2747f05b1654c1"
models = pd.DataFrame({
'Model': ['Support Vector Machines', 'KNN', 'Logistic Regression',
'Random Forest', 'Naive Bayes',
'Decision Tree', 'Gradient Boosting Classifier', 'Voting Classifier', 'XGB Classifier','ExtraTrees Classifier','Bagging Classifier'],
'Score': [svc_accy, knn_accy, logreg_accy,
random_accy, gaussian_accy, dectree_accy,
gradient_accy, voting_accy, XGBClassifier_accy, extraTree_accy, bagging_accy]})
models.sort_values(by='Score', ascending=False)
# + [markdown] _cell_guid="7128f3dd-1d8d-4b8e-afb4-891d8cb9657c" _uuid="7e17482a69dbe99319219a603ea39f8bbde98b87"
# # Part 8: Submit test predictions
# <a id="submit_predictions"></a>
# ***
# + _uuid="eb0054822f296ba86aa6005b2a5e35fbc1aec88b"
all_models = [GaussianProcessClassifier, gaussian, ExtraTreesClassifier, BaggingClassifier, XGBClassifier,knn_grid, dectree_grid, gradient, rf_grid, svm_grid, logreg_grid, voting_classifier ]
c = {}
for i in all_models:
a = i.predict(test_x)
b = accuracy_score(a, test_y)
c[i] = b
# + _cell_guid="51368e53-52e4-41cf-9cc9-af6164c9c6f5" _uuid="b947f168f6655c1c6eadaf53f3485d57c0cd74c7"
test_prediction = (max(c, key=c.get)).predict(test)
submission = pd.DataFrame({
"PassengerId": passengerid,
"Survived": test_prediction
})
submission.PassengerId = submission.PassengerId.astype(int)
submission.Survived = submission.Survived.astype(int)
submission.to_csv("titanic1_submission.csv", index=False)
# + [markdown] _uuid="157571b1143aa5e755b9b994c64dbd7f7584afd5"
# # Credits
#
# * To [Brandon Foltz](https://(www.youtube.com/channel/UCFrjdcImgcQVyFbK04MBEhA) for being a fantastic statistics teacher. Love all those inspirational intro's.
# * To [Khan Academy](https://www.khanacademy.org), Amazing place to keep track of my mathematics journey.
# * To [General Assambly](https://generalassemb.ly); Where I started my data science journey.
# * To [Corey Schafer](https://www.youtube.com/channel/UCCezIgC97PvUuR4_gbFUs5g); Corey explains programming terms incredibly well. To the newcomers, I say you check out his style of teaching.
#
# # Resources
# Here are some of the links I found helpful while writing this kernel. I do not assume them to be great articles; neither do I recommend them. I mentioned them because I have found them to be helpful.
#
# ## Statistics
# * [What Is a t-test? And Why Is It Like Telling a Kid to Clean Up that Mess in the Kitchen?](https://blog.minitab.com/blog/statistics-and-quality-data-analysis/what-is-a-t-test-and-why-is-it-like-telling-a-kid-to-clean-up-that-mess-in-the-kitchen)
# * [What Are T Values and P Values in Statistics?](https://blog.minitab.com/blog/statistics-and-quality-data-analysis/what-are-t-values-and-p-values-in-statistics)
# * [What is p-value? How we decide on our confidence level.](https://www.youtube.com/watch?v=E4KCfcVwzyw)
#
#
# + [markdown] _cell_guid="a2b6f2c1-b83b-43ef-ac8c-d99a844986cc" _uuid="1d38cbce222c9110097275f913cd12368aac77c9"
# ***
#
# If you like to discuss any other projects or have a chat about data science topics, I'll be more than happy to connect with you on:
#
# **LinkedIn:** https://www.linkedin.com/in/masumrumi/
#
# **My Website:** http://masumrumi.com/
#
# *** This kernel is a work in progress like all of my other notebooks. I will always incorporate new concepts of data science as I master them. This journey of learning is worth sharing as well as collaborating. Therefore any comments about further improvements would be genuinely appreciated.***
# ***
# ## If you have come this far, Congratulations!!
#
# ## If this notebook helped you in any way, please upvote!!
#
#
# -
| 55.372723 | 1,678 |
008e18c765612c8daa131b1b538c355de905a2ad
|
py
|
python
|
activitysim/examples/example_mtc/notebooks/getting_started.ipynb
|
mattwigway/activitysim
|
['BSD-3-Clause']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="knOigRU1UJ9Y"
# # Getting Started with ActivitySim
#
# This getting started guide is a [Jupyter notebook](https://jupyter.org/). It is an interactive Python 3 environment that describes how to set up, run, and begin to analyze the results of ActivitySim modeling scenarios. It is assumed users of ActivitySim are familiar with the basic concepts of activity-based modeling. This tutorial covers:
#
# * Installation and setup
# * Setting up and running a base model
# * Inputs and outputs
# * Setting up and running an alternative scenario
# * Comparing results
# * Next steps and further reading
#
# This notebook depends on [Anaconda Python 3 64bit](https://www.anaconda.com/distribution/).
# + [markdown] colab_type="text" id="5Tid_70tVBlc"
# # Install ActivitySim
#
# The first step is to install activitysim from [pypi](https://pypi.org/project/activitysim/) (the Python package index). It also installs dependent packages such as [tables](https://pypi.org/project/tables/) for reading/writing HDF5, [openmatrix](https://pypi.org/project/OpenMatrix/) for reading/writing OMX matrix, and [pyyaml](https://pypi.org/project/PyYAML/) for yaml settings files.
# + colab={"base_uri": "https://localhost:8080/", "height": 666} colab_type="code" id="In9xbvDXUFt6" outputId="a034e38d-eb95-450a-883b-6686da46dc55"
# !pip install activitysim
# + [markdown] colab_type="text" id="FL7QsrfyWIWD"
# # Creating an Example Setup
#
# The example is included in the package and can be copied to a user defined location using the package's command line interface. The example includes all model steps. The command below copies the example_mtc example to a new example folder. It also changes into the new example folder so we can run the model from there.
# + colab={"base_uri": "https://localhost:8080/", "height": 68} colab_type="code" id="XJMvPND0WK6v" outputId="9401b8a4-1333-44e8-afb3-cc36dd2e4b92"
# !activitysim create -e example_mtc -d example
# %cd example
# + [markdown] colab_type="text" id="5lxwxkOuZvIy"
# # Run the Example
#
# The code below runs the example, which runs in a few minutes. The example consists of 100 synthetic households and the first 25 zones in the example model region. The full example (**example_mtc_full**) can be created and downloaded from the [activitysim resources](https://github.com/RSGInc/activitysim_resources) repository using activitysim's create command above. As the model runs, it logs information to the screen.
#
# To run the example, use activitysim's built-in run command. As shown in the script help, the default settings assume a configs, data, and output folder in the current directory.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="Q3f6xJpmm7JF" outputId="419b9d97-0052-4307-dc83-4d8759fd5dbc"
# !activitysim run -c configs -d data -o output
# + [markdown] colab_type="text" id="193E7ds2GEVs"
# # Run the Multiprocessor Example
#
# The command below runs the multiprocessor example, which runs in a few minutes. It uses settings inheritance to override setings in the configs folder with settings in the configs_mp folder. This allows for re-using expression files and settings files in the single and multiprocessed setups. The multiprocessed example uses the following additional settings:
#
# ```
# chunk_size: 1000000000
#
# num_processes: 2
#
# multiprocess_steps:
# - name: mp_initialize
# begin: initialize_landuse
# - name: mp_households
# begin: school_location
# slice:
# tables:
# - households
# - persons
# - name: mp_summarize
# begin: write_data_dictionary
#
# ```
#
# In brief, `num_processes` specifies the number of processors to use and `chunk_size` specifies the size of each batch of choosers data for processing. The `multiprocess_steps` specifies the beginning, middle, and end steps in multiprocessing. The `mp_initialize` step is single processed because there is no `slice` setting. It starts with the `initialize_landuse` submodel and runs until the submodel identified by the next multiprocess submodel starting point, `school_location`. The `mp_households` step is multiprocessed and the households and persons tables are sliced and allocated to processes using the chunking settings. The rest of the submodels are run multiprocessed until the final multiprocess step. The `mp_summarize` step is single processed because there is no `slice` setting and it writes outputs. See [multiprocessing](https://activitysim.github.io/activitysim/core.html#multiprocessing) and [chunk_size](https://activitysim.github.io/activitysim/abmexample.html#chunk-size) for more information.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="rkI5DhdLF0bn" outputId="9862a11e-c1b3-429e-ba14-903a60a73627"
# !activitysim run -c configs_mp -c configs -d data -o output
# + [markdown] colab_type="text" id="SyQy1yyJbzId"
# # Inputs and Outputs Overview
#
# An ActivitySim model requires:
#
# * Configs: settings, model step expressions files, etc.
# * settings.yaml - main settings file for running the model
# * [model].yaml - configuration file for the model step (such as auto ownership)
# * [model].csv - expressions file for the model step
# * Data: input data - input data tables and skims
# * land_use.csv - zone data file
# * households.csv - synthethic households
# * persons.csv - synthethic persons
# * skims.omx - all skims in one open matrix file
# * Output: output data - output data, tables, tracing info, etc.
# * pipeline.h5 - data pipeline database file (all tables at each model step)
# * final_[table].csv - final household, person, tour, trip CSV tables
# * activitysim.log - console log file
# * trace.[model].csv - trace calculations for select households
# * simulation.py: main script to run the model
#
# Run the command below to list the example folder contents.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="feltx6B0cCOJ" outputId="722000ea-210b-4f4b-a940-ef6133b70ed5"
import os
for root, dirs, files in os.walk(".", topdown=False):
for name in files:
print(os.path.join(root, name))
for name in dirs:
print(os.path.join(root, name))
# + [markdown] colab_type="text" id="YVbDusPescwE"
# # Inputs
#
# Run the commands below to:
# * Load required Python libraries for reading data
# * Display the settings.yaml, including the list of `models` to run
# * Display the land_use, households, and persons tables
# * Display the skims
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="s53VwlPwtNnr" outputId="d1208b7a-c1f2-4b0b-c439-bf312fe12be0"
print("Load libraries.")
import pandas as pd
import openmatrix as omx
import yaml
import glob
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="cBqPPkBpnaUZ" outputId="bd780019-c200-4cf6-844a-991c4d026480"
print("Display the settings file.\n")
with open(r'configs/settings.yaml') as file:
file_contents = yaml.load(file, Loader=yaml.FullLoader)
print(yaml.dump(file_contents))
# + colab={"base_uri": "https://localhost:8080/", "height": 892} colab_type="code" id="Ln4PRDsdTPb6" outputId="f297cf7f-9cf3-4134-a42f-049496a50fba"
print("Input land_use. Primary key: ZONE. Required additional fields depend on the downstream submodels (and expression files).")
pd.read_csv("data/land_use.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 487} colab_type="code" id="YNWv25TDmVxt" outputId="564b0b74-ca0a-407b-b4db-1f771b357708"
print("Input households. Primary key: HHID. Foreign key: TAZ. Required additional fields depend on the downstream submodels (and expression files).")
pd.read_csv("data/households.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 467} colab_type="code" id="KRBwRODMmUsi" outputId="7c8d3a37-e656-437b-99bd-d49c8e781703"
print("Input persons. Primary key: PERID. Foreign key: household_id. Required additional fields depend on the downstream submodels (and expression files).")
pd.read_csv("data/persons.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="d31eT8CJrWz8" outputId="03103705-1837-4b2d-c12b-b53face4df1a"
print("Skims. All skims are input via one OMX file. Required skims depend on the downstream submodels (and expression files).\n")
print(omx.open_file("data/skims.omx"))
# + [markdown] colab_type="text" id="TojXWivZsx7M"
# # Outputs
#
# Run the commands below to:
# * Display the contents of the output data pipeline
# * Gets the households table after auto ownership is run
# * Display the output household and person tables
# * Display the output tour and trip tables
# + colab={"base_uri": "https://localhost:8080/", "height": 850} colab_type="code" id="TQyuwhXGtkIb" outputId="640a9100-ec7d-4ba7-c040-cde59b82725d"
print("The output pipeline contains the state of each table after each model step.")
pipeline = pd.io.pytables.HDFStore('output/pipeline.h5')
pipeline.keys()
# + colab={"base_uri": "https://localhost:8080/", "height": 487} colab_type="code" id="fzvo6U-GudBe" outputId="f7aaf09e-712e-44e4-ac9f-63b7a9e46296"
print("Households table after trip mode choice, which contains several calculated fields.")
pipeline['/households/joint_tour_frequency'] #watch out for key changes if not running all models
# + colab={"base_uri": "https://localhost:8080/", "height": 456} colab_type="code" id="wDDlKGkstwdo" outputId="baa8fa78-b343-47d8-e420-7022984dccff"
print("Final output households table to written to CSV, which is the same as the table in the pipeline.")
pd.read_csv("output/final_households.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 456} colab_type="code" id="xxA7TSpGt7LL" outputId="21d5e5e9-3e05-4405-fa95-e37022b6ce4a"
print("Final output persons table to written to CSV, which is the same as the table in the pipeline.")
pd.read_csv("output/final_persons.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 456} colab_type="code" id="gibK4wgyt7UX" outputId="ff373635-d0bc-4bba-bc16-8f5d152a301d"
print("Final output tours table to written to CSV, which is the same as the table in the pipeline. Joint tours are stored as one record.")
pd.read_csv("output/final_tours.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 436} colab_type="code" id="AoSX6Unqt8YN" outputId="8c96c369-ae69-4dbd-f880-111492b3d31a"
print("Final output trips table to written to CSV, which is the same as the table in the pipeline. Joint trips are stored as one record")
pd.read_csv("output/final_trips.csv")
# -
# # Other notable outputs
print("Final output accessibility table to written to CSV.")
pd.read_csv("output/final_accessibility.csv")
print("Joint tour participants table, which contains the person ids of joint tour participants.")
pipeline['joint_tour_participants/joint_tour_participation']
print("Destination choice sample logsums table for school location.")
if '/school_location_sample/school_location' in pipeline:
pipeline['/school_location_sample/school_location']
# # Write trip matrices
#
# A **write_trip_matrices** step at the end of the model adds boolean indicator columns to the trip table in order to assign each trip into a trip matrix and then aggregates the trip counts and writes OD matrices to OMX (open matrix) files. The coding of trips into trip matrices is done via annotation expressions.
print("trip matrices by time of day for assignment")
output_files = os.listdir("output")
for output_file in output_files:
if "omx" in output_file:
print(output_file)
# # Tracing calculations
#
# Tracing calculations is an important part of model setup and debugging. Often times data issues, such as missing values in input data and/or incorrect submodel expression files, do not reveal themselves until a downstream submodels fails. There are two types of tracing in ActivtiySim: household and origin-destination (OD) pair. If a household trace ID is specified via `trace_hh_id`, then ActivitySim will output a comprehensive set of trace files for all calculations for all household members. These trace files are listed below and explained.
print("All trace files.\n")
glob.glob("output/trace/*.csv")
print("Trace files for auto ownership.\n")
glob.glob("output/trace/auto_ownership*.csv")
print("Trace chooser data for auto ownership.\n")
pd.read_csv("output\\trace\\auto_ownership_simulate.simple_simulate.eval_mnl.choosers.csv")
print("Trace utility expression values for auto ownership.\n")
pd.read_csv("output\\trace.auto_ownership_simulate.simple_simulate.eval_mnl.expression_values.csv")
print("Trace alternative total utilities for auto ownership.\n")
pd.read_csv("output\\trace\\auto_ownership_simulate.simple_simulate.eval_mnl.utilities.csv")
print("Trace alternative probabilities for auto ownership.\n")
pd.read_csv("output\\trace.auto_ownership_simulate.simple_simulate.eval_mnl.probs.csv")
print("Trace random number for auto ownership.\n")
pd.read_csv("output\\trace\\auto_ownership_simulate.simple_simulate.eval_mnl.rands.csv")
print("Trace choice for auto ownership.\n")
pd.read_csv("output\\trace\\auto_ownership_simulate.simple_simulate.eval_mnl.choices.csv")
# + [markdown] colab_type="text" id="PQnGYM-gzwNR"
# # Next Steps and Further Reading
#
# For futher information on the software, management consortium, and activity-based models in general, see the resources below.
#
# * ActivitySim
# * [User Documentation](https://activitysim.github.io/activitysim/)
# * [GitHub Repository](https://github.com/ActivitySim/activitysim)
# * [Project Wiki](https://github.com/ActivitySim/activitysim/wiki)
# * [Activity-Based Travel Demand Models: A Primer](http://www.trb.org/Publications/Blurbs/170963.aspx)
# -
| 54.924901 | 1,027 |
008c393c83acaaf39188a4c8065f44f3a611a289
|
py
|
python
|
Data Science/Self_Driving_Car/Umbrella_Academy_INFO7390_Project/INFO7390_Notebooks/Basics_of_Convolutional_Neural_Network_&_Imitation_Learning.ipynb
|
RushabhNisher/Data
|
['Unlicense']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 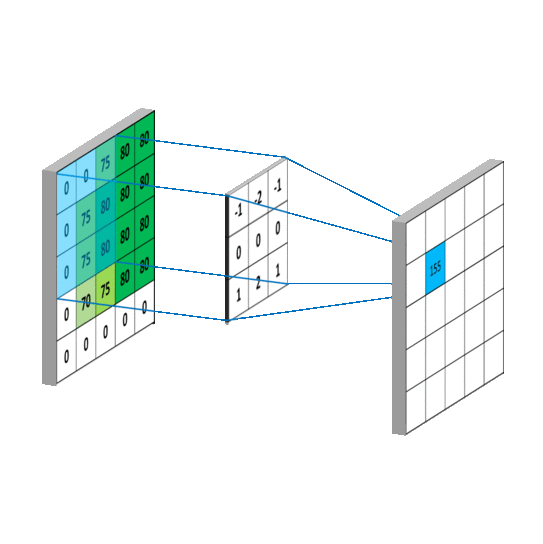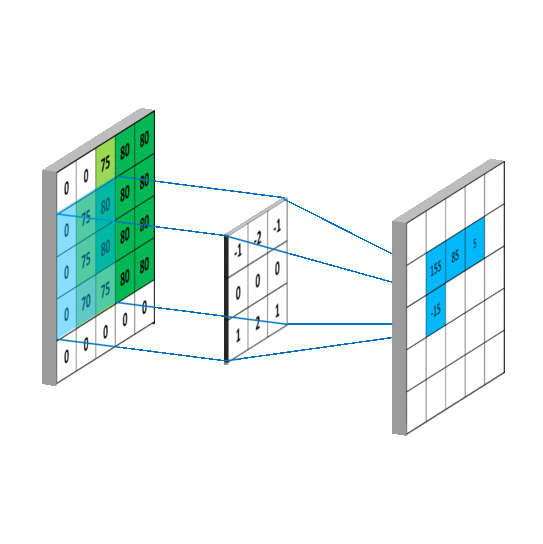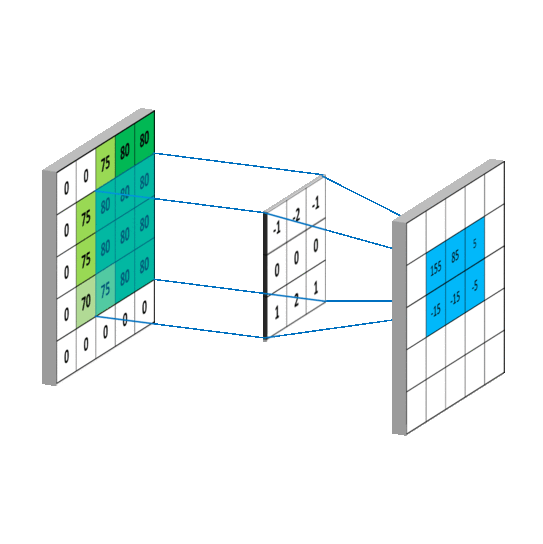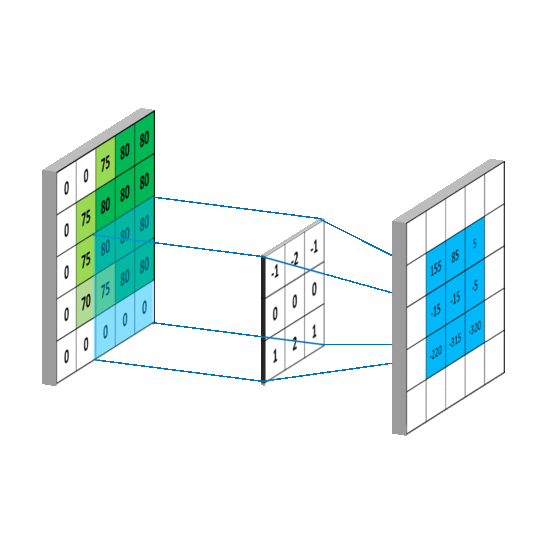
# # <p style="text-align: center;"> Table of Contents </p>
# - ## 1. [Introduction](#Intro)
# - ### 1.1 [Abstract](#abstract)
# - ## 2. [Understanding Convolution Operations](#Understanding_Convolution_Operations)
# - ### 2.1 [Edge Detection Example](#Edge_Detection_Example)
# - ### 2.2 [More Edge Detection](#more)
# - ## 3. [Padding](#Padding)
# - ## 4. [Strided Convolutions](#Strided)
# - ## 5. [Convolutions Over Volume](#Convolutions)
# - ## 6. [One Layer of a Convolutional Network](#One_Layer)
# - ### 6.1 [Simple Convolutional Network Example](#Simple)
# - ## 7. [Pooling](#Pooling)
# - ## 8. [CNN Example](#cnn)
# - ### 8.1 [Why Convolutions?](#con)
# - ## 9. [A brief overview of Imitation Learning](#imi)
# - ### 9.1 [Basics of Imitation Learning](#bimi)
# - ## 10. [Contribution](#Contribution)
# - ## 11. [Citation](#Citation)
# - ## 12. [License](#License)
# # <a id="Introduction"> 1 Introduction </a>
# ## <a id='abstract'> 1.1 Abstract </a>
#
# The main agenda of this notebook is as follow:-
# - To understand the convolution operation
# - To understand the pooling operation
# - Remembering the vocabulary used in convolutional neural networks (padding, stride, filter, etc.)
# - Building a convolutional neural network for multi-class classification in images
# # <a id='Understanding_Convolution_Operations'> 2. Understanding Convolution Operations </a>
#
# One major problem with computer vision problems is that the input data can get really big. Suppose an image is of the size 68 X 68 X 3. The input feature dimension then becomes 12,288. This will be even bigger if we have larger images (say, of size 720 X 720 X 3). Now, if we pass such a big input to a neural network, the number of parameters will swell up to a HUGE number (depending on the number of hidden layers and hidden units). This will result in more computational and memory requirements – not something most of us can deal with.
#
# #### We will explain the Convolution Operation by an example
#
# ## <a id="Edge_Detection_Example"> 2.1. Edge Detection Example </a>
#
# The early layers of a neural network detect edges from an image. Deeper layers might be able to detect the cause of the objects and even more deeper layers might detect the cause of complete objects (like a person’s face).
#
# In this section, we will focus on how the edges can be detected from an image. Suppose we are given the below image:
#
# 
#
# As you can see, there are many vertical and horizontal edges in the image. The first thing to do is to detect these edges:
#
# 
#
# Next, we convolve this 6 X 6 matrix with a 3 X 3 filter:
# 
#
# After the convolution, we will get a 4 X 4 image. The first element of the 4 X 4 matrix will be calculated as:
#
# 
#
# So, we take the first 3 X 3 matrix from the 6 X 6 image and multiply it with the filter. Now, the first element of the 4 X 4 output will be the sum of the element-wise product of these values, i.e. 3*1 + 0 + 1*-1 + 1*1 + 5*0 + 8*-1 + 2*1 + 7*0 + 2*-1 = -5. To calculate the second element of the 4 X 4 output, we will shift our filter one step towards the right and again get the sum of the element-wise product:
#
# 
#
# Similarly, we will convolve over the entire image and get a 4 X 4 output:
#
# 
#
# So, convolving a 6 X 6 input with a 3 X 3 filter gave us an output of 4 X 4. Consider one more example:
#
# 
#
# ## <a id="More"> 2.2. More Edge Detection </a>
#
# The type of filter that we choose helps to detect the vertical or horizontal edges. We can use the following filters to detect different edges:
#
# 
#
# Some of the commonly used filters are:
#
# 
#
# The Sobel filter puts a little bit more weight on the central pixels. Instead of using these filters, we can create our own as well and treat them as a parameter which the model will learn using backpropagation.
# # <a id="Padding"> 3. Padding </a>
#
# We have seen that convolving an input of 6 X 6 dimension with a 3 X 3 filter results in 4 X 4 output. We can generalize it and say that if the input is n X n and the filter size is f X f, then the output size will be (n-f+1) X (n-f+1):
#
# > - Input: n X n
# - Filter size: f X f
# - Output: (n-f+1) X (n-f+1)
#
# #### There are primarily two disadvantages here:
#
# > 1. Every time we apply a convolutional operation, the size of the image shrinks
# 2. Pixels present in the corner of the image are used only a few number of times during convolution as compared to the central pixels. Hence, we do not focus too much on the corners since that can lead to information loss
#
# To overcome these issues, we can pad the image with an additional border, i.e., we add one pixel all around the edges. This means that the input will be an 8 X 8 matrix (instead of a 6 X 6 matrix). Applying convolution of 3 X 3 on it will result in a 6 X 6 matrix which is the original shape of the image. This is where padding comes to the fore:
#
# > - Input: n X n
# - Padding: p
# - Filter size: f X f
# - Output: (n+2p-f+1) X (n+2p-f+1)
#
# There are two common choices for padding:
#
# > #### 1. Valid: It means no padding. If we are using valid padding, the output will be (n-f+1) X (n-f+1)
#
# > #### 2. Same: Here, we apply padding so that the output size is the same as the input size, i.e., n+2p-f+1 = n . So, p = (f-1)/2
#
# We now know how to use padded convolution. This way we don’t lose a lot of information and the image does not shrink either. Next, we will look at how to implement strided convolutions.
#
#
# # <a id="Strided"> 4. Strided Convolutions </a>
#
# Suppose we choose a stride of 2. So, while convoluting through the image, we will take two steps – both in the horizontal and vertical directions separately. The dimensions for stride s will be:
#
# > - Input: n X n
# - Padding: p
# - Stride: s
# - Filter size: f X f
# - Output: [(n+2p-f)/s+1] X [(n+2p-f)/s+1]
#
# Stride helps to reduce the size of the image, a particularly useful feature.
# # <a id="Convolutions"> 5. Convolutions Over Volume </a>
#
# Suppose, instead of a 2-D image, we have a 3-D input image of shape 6 X 6 X 3. How will we apply convolution on this image? We will use a 3 X 3 X 3 filter instead of a 3 X 3 filter. Let’s look at an example:
#
# > - Input: 6 X 6 X 3
# - Filter: 3 X 3 X 3
#
#
# The dimensions above represent the height, width and channels in the input and filter.Keep in mind that the number of channels in the input and filter should be same. This will result in an output of 4 X 4. Let’s understand it visually:
#
# 
#
# Since there are three channels in the input, the filter will consequently also have three channels. After convolution, the output shape is a 4 X 4 matrix. So, the first element of the output is the sum of the element-wise product of the first 27 values from the input (9 values from each channel) and the 27 values from the filter. After that we convolve over the entire image.
#
# Instead of using just a single filter, we can use multiple filters as well. How do we do that? Let’s say the first filter will detect vertical edges and the second filter will detect horizontal edges from the image. If we use multiple filters, the output dimension will change. So, instead of having a 4 X 4 output as in the above example, we would have a 4 X 4 X 2 output (if we have used 2 filters):
#
# 
#
# #### Generalized dimensions can be given as:
#
# - Input: n X n X nc
# - Filter: f X f X nc
# - Padding: p
# - Stride: s
# - Output: [(n+2p-f)/s+1] X [(n+2p-f)/s+1] X nc’
#
# Here, nc is the number of channels in the input and filter, while nc’ is the number of filters.
#
#
# # <a id="One_Layer" > 6. One Layer of a Convolutional Network</a>
#
# Once we get an output after convolving over the entire image using a filter, we add a bias term to those outputs and finally apply an activation function to generate activations. This is one layer of a convolutional network. Recall that the equation for one forward pass is given by:
#
# 
#
# In our case, input (6 X 6 X 3) is a[0]and filters (3 X 3 X 3) are the weights w[1]. These activations from layer 1 act as the input for layer 2, and so on. Clearly, the number of parameters in case of convolutional neural networks is independent of the size of the image. It essentially depends on the filter size. Suppose we have 10 filters, each of shape 3 X 3 X 3. What will be the number of parameters in that layer? Let’s try to solve this:
#
# - Number of parameters for each filter = 3* 3* 3 = 27
# - There will be a bias term for each filter, so total parameters per filter = 28
# - As there are 10 filters, the total parameters for that layer = 28 * 10 = 280
#
# No matter how big the image is, the parameters only depend on the filter size. Awesome, isn’t it? Let’s have a look at the summary of notations for a convolution layer:
#
# - f[l] = filter size
# - p[l] = padding
# - s[l] = stride
# - n[c][l] = number of filters
#
# Let’s combine all the concepts we have learned so far and look at a convolutional network example.
#
# ## <a id="Simple"> 6.1. Simple Convolutional Network Example </a>
#
# This is how a typical convolutional network looks like:
#
# 
#
# We take an input image (size = 39 X 39 X 3 in our case), convolve it with 10 filters of size 3 X 3, and take the stride as 1 and no padding. This will give us an output of 37 X 37 X 10. We convolve this output further and get an output of 7 X 7 X 40 as shown above. Finally, we take all these numbers (7 X 7 X 40 = 1960), unroll them into a large vector, and pass them to a classifier that will make predictions. This is a microcosm of how a convolutional network works.
#
# There are a number of hyperparameters that we can tweak while building a convolutional network. These include the number of filters, size of filters, stride to be used, padding, etc. We will look at each of these in detail later in this article. Just keep in mind that as we go deeper into the network, the size of the image shrinks whereas the number of channels usually increases.
#
# In a convolutional network (ConvNet), there are basically three types of layers:
#
# - Convolution layer
# - Pooling layer
# - Fully connected layer
# Let’s understand the pooling layer in the next section.
#
#
# # <a id="Pooling"> 7. Pooling Layers </a>
# Pooling layers are generally used to reduce the size of the inputs and hence speed up the computation. Consider a 4 X 4 matrix as shown below:
#
# 
#
# Applying max pooling on this matrix will result in a 2 X 2 output:
#
# 
#
# For every consecutive 2 X 2 block, we take the max number. Here, we have applied a filter of size 2 and a stride of 2. These are the hyperparameters for the pooling layer. Apart from max pooling, we can also apply average pooling where, instead of taking the max of the numbers, we take their average. In summary, the hyperparameters for a pooling layer are:
#
# - Filter size
# - Stride
# - Max or average pooling
#
# If the input of the pooling layer is nh X nw X nc, then the output will be [{(nh – f) / s + 1} X {(nw – f) / s + 1} X nc].
#
#
#
#
# # <a id="cnn"> 8. CNN Example </a>
#
# We’ll take things up a notch now. Let’s look at how a convolution neural network with convolutional and pooling layer works. Suppose we have an input of shape 32 X 32 X 3:
#
# 
#
# There are a combination of convolution and pooling layers at the beginning, a few fully connected layers at the end and finally a softmax classifier to classify the input into various categories. There are a lot of hyperparameters in this network which we have to specify as well.
#
# Generally, we take the set of hyperparameters which have been used in proven research and they end up doing well. As seen in the above example, the height and width of the input shrinks as we go deeper into the network (from 32 X 32 to 5 X 5) and the number of channels increases (from 3 to 10).
#
# #### All of these concepts and techniques bring up a very fundamental question – why convolutions? Why not something else?
#
#
#
# ## <a id="con"> 8.1. Why Convolution? </a>
#
# There are primarily two major advantages of using convolutional layers over using just fully connected layers:
#
# >- Parameter sharing
# - Sparsity of connections
#
# Consider the below example:
#
# 
#
# If we would have used just the fully connected layer, the number of parameters would be = 32 *32 * 3 * 28 * 28 * 6, which is nearly equal to 14 million! Makes no sense, right?
#
# If we see the number of parameters in case of a convolutional layer, it will be = (5 * 5 + 1) * 6 (if there are 6 filters), which is equal to 156. Convolutional layers reduce the number of parameters and speed up the training of the model significantly.
#
# In convolutions, we share the parameters while convolving through the input. The intuition behind this is that a feature detector, which is helpful in one part of the image, is probably also useful in another part of the image. So a single filter is convolved over the entire input and hence the parameters are shared.
#
# The second advantage of convolution is the sparsity of connections. For each layer, each output value depends on a small number of inputs, instead of taking into account all the inputs.
#
#
# # <a id="imi"> 9. A brief overview of Imitation Learning</a>
#
# Reinforcement learning (RL) is one of the most interesting areas of machine learning, where an agent interacts with an environment by following a policy. In each state of the environment, it takes action based on the policy, and as a result, receives a reward and transitions to a new state. The goal of RL is to learn an optimal policy which maximizes the long-term cumulative rewards.
#
# To achieve this, there are several RL algorithms and methods, which use the received rewards as the main approach to approximate the best policy. Generally, these methods perform really well. In some cases, though the teaching process is challenging. This can be especially true in an environment where the rewards are sparse (e.g. a game where we only receive a reward when the game is won or lost). To help with this issue, we can manually design rewards functions, which provide the agent with more frequent rewards. Also, in certain scenarios, there isn’t any direct reward function (e.g. teaching a self-driving vehicle), thus, the manual approach is necessary.
#
# However, manually designing a reward function that satisfies the desired behaviour can be extremely complicated.
# A feasible solution to this problem is imitation learning (IL). In IL instead of trying to learn from the sparse rewards or manually specifying a reward function, an expert (typically a human) provides us with a set of demonstrations. The agent then tries to learn the optimal policy by following, imitating the expert’s decisions.
#
#
# ## <a id="bimi"> 9.1. Basics of Imitation Learning</a>
#
# Generally, imitation learning is useful when it is easier for an expert to demonstrate the desired behaviour rather than to specify a reward function which would generate the same behaviour or to directly learn the policy. The main component of IL is the environment, which is essentially a Markov Decision Process (MDP). This means that the environment has an S set of states, an A set of actions, a P(s’|s,a) transition model (which is the probability that an action a in the state s leads to state s’ ) and an unknown R(s,a) reward function. The agent performs different actions in this environment based on its π policy. We also have the expert’s demonstrations (which are also known as trajectories) τ = (s0, a0, s1, a1, …) , where the actions are based on the expert’s (“optimal”) π* policy. In some cases, we even “have access” to the expert at training time, which means that we can query the expert for more demonstrations or for evaluation. Finally, the loss function and the learning algorithm are two main components, in which the various imitation learning methods differ from each other.
#
# ### - Behavioural Cloning
# The simplest form of imitation learning is behaviour cloning (BC), which focuses on learning the expert’s policy using supervised learning. An important example of behaviour cloning is ALVINN, a vehicle equipped with sensors, which learned to map the sensor inputs into steering angles and drive autonomously. This project was carried out in 1989 by Dean Pomerleau, and it was also the first application of imitation learning in general.
# The way behavioural cloning works is quite simple. Given the expert’s demonstrations, we divide these into state-action pairs, we treat these pairs as i.i.d. examples and finally, we apply supervised learning. The loss function can depend on the application. Therefore, the algorithm is the following:
#
# 
#
# In some applications, behavioural cloning can work excellently. For the majority of the cases, though, behavioural cloning can be quite problematic. The main reason for this is the i.i.d. assumption: while supervised learning assumes that the state-action pairs are distributed i.i.d., in MDP an action in a given state induces the next state, which breaks the previous assumption. This also means, that errors made in different states add up, therefore a mistake made by the agent can easily put it into a state that the expert has never visited and the agent has never trained on. In such states, the behaviour is undefined and this can lead to catastrophic failures.
#
# 
#
# Still, behavioural cloning can work quite well in certain applications. Its main advantages are its simplicity and efficiency. Suitable applications can be those, where we don’t need long-term planning, the expert’s trajectories can cover the state space, and where committing an error doesn’t lead to fatal consequences. However, we should avoid using BC when any of these characteristics are true.
#
# #### Other types of Imitation Learning Includea:-
#
# - Direct Policy Learning (via Interactive Demonstrator)
# - Inverse Reinforcement Learning
#
# We won't go in details of these
# # <a id='Contribution'> 10. Contribution</a>
# As this was a learning assignment, the majority of the code has been taken from the Various Kaggle Kernals enlisted below in [Citations](#citation).
#
# - Theory by self : 35%
# - Theory from external Sources : 65%
#
# # <a id='Citation'>11. Citation </a>
#
# - https://www.analyticsvidhya.com/blog/2018/12/guide-convolutional-neural-network-cnn/
# - https://www.jessicayung.com/explaining-tensorflow-code-for-a-convolutional-neural-network/
# - https://github.com/unccv/autonomous_driving
# - https://towardsdatascience.com/basics-of-the-classic-cnn-a3dce1225add
# - https://medium.com/@SmartLabAI/a-brief-overview-of-imitation-learning-8a8a75c44a9c
# - https://github.com/hchkaiban/CarRacingImitationLearning/blob/master/Demo.mp4
#
# # <a id='License'> 12. License </a>
# Copyright (c) 2020 Manali Sharma, Rushabh Nisher
#
# Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
#
#
| 62.742236 | 1,103 |
4aff172c4041a1b584b7ab40996a555abc367ddf
|
py
|
python
|
12_Extraction_based_Question_Answering_using_BERT.ipynb
|
bensjx/ML_repo
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="J3Dwlj-xEC4N" outputId="ea695bf1-40ba-4382-d34d-c5a1ab5e14ed" colab={"base_uri": "https://localhost:8080/"}
# !pip install transformers
# + id="pVqOV2cRED0A" outputId="382e25f3-2c8f-49a7-9588-4b45edcf6d22" colab={"base_uri": "https://localhost:8080/", "height": 164, "referenced_widgets": ["eddd0afa553f4d80b17dde64fab0204f", "f0b57e15c49b4fa080bfc5f40886ed98", "1cf6dab74dc44b899c91f7a91de03bb3", "5151c94e27a14619b448f42c2c334fb5", "21722873eb3d40719bbc4bb867ec4cf9", "d67d30769bbf489bbf23fd363350ac8b", "e907410e02e14da1a3707379f3a8e6bf", "a4f421273a904236a5b7d75f04702a7d", "beae98923b4e4a48b3960055024da396", "5fe40ed00d514a5f9a34a356bc8a723e", "62d0f8a41d1145acadd2f02406238e1f", "e0364446a1db43d7b1aedc7dba0f1939", "e4c762ec843b4ee790309209de0f716f", "9ba40c9ad2e54eea83f58b3f2ee8a1e4", "fafca4b7e3cb47d5a459b4586fd81f61", "661939bba4484603b3e09e169102df6e", "196d96d1a0a946c78466666135935c5c", "b9863fe9aa734785afb7c96f8345b380", "d4fc5b87337743d594761d0bc0e21b7e", "3881a9c94d1544a9ae8affe69fd484ff", "9a8753b252ec4bff98f32c1a28ec9a66", "f8ebc70982884c569ec0dffc6e0d267d", "86628185ad5b4688b6333f310103e965", "584da2953e734b6c9f950c06c6f4f0eb"]}
import torch
from transformers import BertForQuestionAnswering, BertTokenizer
model = BertForQuestionAnswering.from_pretrained('bert-large-uncased-whole-word-masking-finetuned-squad')
tokenizer = BertTokenizer.from_pretrained('bert-large-uncased-whole-word-masking-finetuned-squad')
# + [markdown] id="ICAz0ljTKW0h"
# ### Design the question and reference text
# + id="ZPCrUQrqEJje"
question = "What does NUS mean?"
answer_text = "The National University of Singapore (NUS) is the national research university of Singapore. \
Founded in 1905 as the Straits Settlements and Federated Malay States Government Medical School, NUS is the oldest higher education institution in Singapore. \
It is consistently ranked within the top 20 universities in the world and is considered to be the best university in the Asia-Pacific. \
NUS is a comprehensive research university, \
offering a wide range of disciplines, including the sciences, medicine and dentistry, design and environment, law, arts and social sciences, engineering, business, computing and music \
at both the undergraduate and postgraduate levels."
# + id="tf-34IAzELxJ" outputId="0fcd36c1-eacf-48dc-be61-66a8b6cfc950" colab={"base_uri": "https://localhost:8080/"}
# Apply the tokenizer to the input text, treating them as a text-pair.
input_ids = tokenizer.encode(question, answer_text)
print('The input has a total of {:} tokens.'.format(len(input_ids)))
# + id="uzHvV_NwEREK" outputId="c5101c95-e8b7-4644-f955-43c41c3a18db" colab={"base_uri": "https://localhost:8080/"}
# BERT only needs the token IDs, but for the purpose of inspecting the
# tokenizer's behavior, let's also get the token strings and display them.
tokens = tokenizer.convert_ids_to_tokens(input_ids)
# For each token and its id...
for token, id in zip(tokens, input_ids):
# If this is the [SEP] token, add some space around it to make it stand out.
if id == tokenizer.sep_token_id:
print('')
# Print the token string and its ID in two columns.
print('{:<12} {:>6,}'.format(token, id))
if id == tokenizer.sep_token_id:
print('')
# + [markdown] id="3NHulReyPiKU"
# #### Split question and reference text
# + id="-5vFAfpGER2e"
# Search the input_ids for the first instance of the `[SEP]` token.
sep_index = input_ids.index(tokenizer.sep_token_id)
# The number of segment A tokens includes the [SEP] token istelf.
num_seg_a = sep_index + 1
# The remainder are segment B.
num_seg_b = len(input_ids) - num_seg_a
# Construct the list of 0s and 1s.
segment_ids = [0]*num_seg_a + [1]*num_seg_b
# There should be a segment_id for every input token.
assert len(segment_ids) == len(input_ids)
# + id="bSChGUjsETk-"
start_scores, end_scores = model(torch.tensor([input_ids]), # The tokens representing our input text.
token_type_ids=torch.tensor([segment_ids])) # The segment IDs to differentiate question from answer_text
# + [markdown] id="nD5cPb99P2Jw"
# #### Run the BERT Model
# + id="JPJwYa6DEU2e"
# Find the tokens with the highest `start` and `end` scores.
answer_start = torch.argmax(start_scores)
answer_end = torch.argmax(end_scores)
# + [markdown] id="4Wik3if7PzQY"
# #### Combine the tokens in the answer and print it out.
# + id="0r06EPrTEXf2" outputId="6387cf7f-69bc-4b4e-8506-eaa5fc0b5ad3" colab={"base_uri": "https://localhost:8080/"}
# Start with the first token.
answer = tokens[answer_start]
# Select the remaining answer tokens and join them with whitespace.
for i in range(answer_start + 1, answer_end + 1):
# If it's a subword token, then recombine it with the previous token.
if tokens[i][0:2] == '##':
answer += tokens[i][2:]
# Otherwise, add a space then the token.
else:
answer += ' ' + tokens[i]
print('Answer: "' + answer + '"')
# + id="JouSFxYZMOZP"
| 50.563107 | 1,018 |
4aefafa6d1ae81492c64bd4979aacec2aa65ae1a
|
py
|
python
|
secondaryPtychography.ipynb
|
tangchini/OPTI556
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/tangchini/OPTI556/blob/main/secondaryPtychography.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="CVlNJ8ReMxBL"
#
# + [markdown] id="OVYb98tWdqDp"
# # Time of flight ptychography
# ###David Brady
# ### University of Arizona
#
# November 2021
# + [markdown] id="dG1EISrovkrE"
# ### Python modules
# + id="egbDS8g7vjZM"
import numpy as np
import matplotlib.pyplot as plt
from google.colab import files
from scipy import signal, io
from scipy import integrate
# %matplotlib inline
plt.rcParams['figure.figsize'] = [30, 10]
plt.rcParams.update({'font.size': 22})
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import tensorflow as tf
import tensorflow.keras as keras
from tensorflow.keras import layers
from tensorflow.keras.datasets import cifar10
from tensorflow.keras.models import Model
import cv2
from keras.datasets import mnist
# + [markdown] id="NYfk3dHIi-ke"
# ## Forward Model
# + [markdown] id="3ntNe9R3B33l"
# We consider imaging on the system illustrated below. We consider an illumination source that projects a focused spot on to the reflecting wall. The focused spot produces an illumination wave $A\frac{e^{i 2 \pi \frac{(x-x_s)^2}{\lambda z}}}{z}$ in the object space, where $z$ is the range from the reflecting wall to the target. The return signal on the wall is
# $$\psi(x')= A\int \int f(x,z)\frac{e^{i 2 \pi \frac{(x-x_s)^2}{\lambda z}}}{z}\frac{e^{-i 2 \pi \frac{(x'-x)^2}{\lambda z}}}{z} dx dz
# $$
# where, implicitly, $x$ corresponds to the 2D $xy$ plane. A remote camera array forms an image of $|\psi(x')|^2$. The measured signal is
# $$g(x')= \frac{|A|^2}{z^2}\left |\int f(x)e^{i 4 \pi \frac{(x'-x_s)x}{\lambda z}} dx \right |^2
# $$
# where we assume for simplicity that $f(x,z)=f(x)\delta(z-z_o)$, e.g. that the object is a surface at a fixed distance. Thus, the observed signal is
# $$g(x')= \frac{|A|^2}{z^2}\left |{\hat f}\left ( u= \frac{2(x'-x_s)}{\lambda z}\right )\right |^2
# $$
# Where ${\hat f}(u)$ is the Fourier transform of $f(x)$. Thus, by scanning $x_s$ over a range of positions we can sample ${\hat f}(u)$ over the full plane. We use ptychographic phase retrieval to recover ${\hat f}(u)$ from the range of samples.
#
# The angular resolution with which we can reconstruct $f(x)$ is equal to the inverse of the maximum spatial frequency measured, $u_{\rm max}=\frac{2\Delta x}{\lambda z}=\frac{4A}{\lambda z}$, where $A$ is the aperture allowed $x$ and $x_s$. so the resolution is $\delta x=\frac{\lambda z}{4A}$. The field of view depends on the sampling rate in the fourier space. If the range from the camera array to the reflecting wall is $R$, this rate is $2 R/(z\alpha) $, where $\alpha $ is the aperture of the camera array. The FoV is $(z\alpha)/(2R) $. The number of points resolved is $(2A\alpha)/(\lambda R) $. The angular field of view is $\frac{\alpha}{R}$.
# + [markdown] id="JYwRON2502vS"
# 
# + id="tvqB7ral2255"
| 2,261.43662 | 157,289 |
dfa6e6217f78c58a28fa749bc89a2131997d518a
|
py
|
python
|
notebooks/Overview.ipynb
|
vinayya/nlp
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.7 64-bit (''datasets'': conda)'
# language: python
# name: python37764bitdatasetscondae5d8ff60608e4c5c953d6bb643d8ebc5
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/huggingface/nlp/blob/master/notebooks/Overview.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="zNp6kK7OvSUg" colab_type="text"
# # HuggingFace `nlp` library - Quick overview
#
# Models come and go (linear models, LSTM, Transformers, ...) but two core elements have consistently been the beating heart of Natural Language Processing: Datasets & Metrics
#
# `nlp` is a lightweight and extensible library to easily share and load dataset and evaluation metrics, already providing access to ~100 datasets and ~10 evaluation metrics.
#
# The library has several interesting features (beside easy access to datasets/metrics):
#
# - Build-in interoperability with PyTorch, Tensorflow 2, Pandas and Numpy
# - Small and fast library with a transparent and pythonic API
# - Strive on large datasets: nlp naturally frees you from RAM memory limits, all datasets are memory-mapped on drive by default.
# - Smart caching with an intelligent `tf.data`-like cache: never wait for your data to process several times
#
# `nlp` originated from a fork of the awesome Tensorflow-Datasets and the HuggingFace team want to deeply thank the team behind this amazing library and user API. We have tried to keep a layer of compatibility with `tfds` and a conversion can provide conversion from one format to the other.
# + [markdown] id="dzk9aEtIvSUh" colab_type="text"
# # Main datasets API
#
# This notebook is a quick dive in the main user API for loading datasets in `nlp`
# + id="my95uHbLyjwR" colab_type="code" outputId="ec28598b-1af5-42e4-c87d-0ddfa9e63632" colab={"base_uri": "https://localhost:8080/", "height": 221}
# install nlp
# !pip install nlp
# Make sure that we have a recent version of pyarrow in the session before we continue - otherwise reboot Colab to activate it
import pyarrow
if int(pyarrow.__version__.split('.')[1]) < 16 and int(pyarrow.__version__.split('.')[0]) == 0:
import os
os.kill(os.getpid(), 9)
# + id="PVjXLiYxvSUl" colab_type="code" outputId="55de9ff7-4f91-4f82-f039-dda379e3aa0e" colab={"base_uri": "https://localhost:8080/", "height": 51}
# Let's import the library
import nlp
# + [markdown] id="TNloBBx-vSUo" colab_type="text"
# ## Listing the currently available datasets and metrics
# + id="d3RJisGLvSUp" colab_type="code" outputId="2e07e795-e49c-4a95-e418-5a418e7820d0" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Currently available datasets and metrics
datasets = nlp.list_datasets()
metrics = nlp.list_metrics()
print(f"🤩 Currently {len(datasets)} datasets are available on HuggingFace AWS bucket: \n"
+ '\n'.join(dataset.id for dataset in datasets) + '\n')
print(f"🤩 Currently {len(metrics)} metrics are available on HuggingFace AWS bucket: \n"
+ '\n'.join(metric.id for metric in metrics))
# + id="7T5AG3BxvSUr" colab_type="code" outputId="7c450740-1166-4fe9-e999-7c0d35c1d073" colab={"base_uri": "https://localhost:8080/", "height": 343}
# You can read a few attributes of the datasets before loading them (they are python dataclasses)
from dataclasses import asdict
for key, value in asdict(datasets[6]).items():
print('👉 ' + key + ': ' + str(value))
# + [markdown] id="9uqSkkSovSUt" colab_type="text"
# ## An example with SQuAD
# + id="aOXl6afcvSUu" colab_type="code" outputId="b8963101-14c7-42c6-e4dc-f14ba68e36d7" colab={"base_uri": "https://localhost:8080/", "height": 964, "referenced_widgets": ["3b0e2e80c42c4a27991f2fa3c427e861", "2d6757ef18e448e9af7fb4d874ff6f9d", "ed4ec751bf7d4d0d9643634c7adb9d56", "d2c54ae694a3453d8f62dd8d07d4b356", "04ba44b50cab4929940e8044d1fb350b", "476623e4ec3845d6b2671f42bec9c7a1", "ec220965dd954f89a66a00a5d18c7f80", "beb50276ed0642658057d665027d1009", "7f56212ab0e44b21bd09af4bce4fd64e", "1dfb3c7bb76d49e49fcc851f06bb18d2", "2a41b6c083924c6f888e5b61b0fffdb8", "f8b2492e22fa43e3aef3c7590ee851ef", "8cefea541e2b4261a959eb11adc4e834", "fcd5574dcbf64b8fb1ad6a3ce663fd3f", "8d4b0c3b71404f7ebb0e9267888dde40", "90ee191829f64774856a9323d0ae9e56", "899eba20bfe642d6819e70850a274f50", "ef9113f13e9b462fbdf8aae0fff7a9f7", "ecc67a44f8154fb4a89b6325ee3462fb", "c6c40c130e7a4e7f9c69a2a1248f2e57", "634ea5af72744cf69b152bc8149a6cea", "366b47f4ab784e0c85d9a644b548ecb0", "0322a2345daa494585e3d37d22c91b40", "94c0c72cf3ec43b6b3160607eb957a3d", "9a633bb0bfc3488e8904224af81ae165", "c275e39a9e724417a0f21c767aad4222", "9f343d5380c9419c8dd831f251a1fc81", "c29ec644dbc444a793b92fbfa6d3e4bc", "49151a31158e4d71a9b4ad1b9b9fe1c8", "2a949fb7059b48e7ac76cae962c50833", "e1483680a79748aa9de08569ba044038", "cd3fede4d6cf496c95d108c7f6ed039b", "7c6b80079af245a68bccd2c9aec20f00", "1fae38301f3b41bbbf4db13d2fe6032b", "148572d3ac064d11b0425afada62ce70", "f03399e96fb7491ab83f709c33c48622", "16b696fec4ab44e9aa22687e403d9eed", "5033d15d013b41bfb2988aebecaa0f2e", "391ed86689b04856a458c929993afb52", "095b84a1c63149a0950d49310d5ccdd3", "449cddc30e5a4755b9b28e030d86b78f", "dc05828e9d114ec2a293a0e7cee8b63f", "9808e758d3e447bcbc388b85441538d3", "9ecc410b1fdd4c2c89a34721c52dc464", "c3fa7c31d80946dcae7d6e8b5564c02f", "feba5a8a7b32462a8c4a585c62e12785", "90c0b0457e194b75ae8adf1e13936b27", "2f8cb0bb9f2a42b08cef846c5d3c8a52"]}
# Downloading and loading a dataset
dataset = nlp.load_dataset('squad', split='validation[:10%]')
# + [markdown] id="rQ0G-eK3vSUw" colab_type="text"
# This call to `nlp.load_dataset()` does the following steps under the hood:
#
# 1. Download and import in the library the **SQuAD python processing script** from HuggingFace AWS bucket if it's not already stored in the library. You can find the SQuAD processing script [here](https://github.com/huggingface/nlp/tree/master/datasets/squad/squad.py) for instance.
#
# Processing scripts are small python scripts which define the info (citation, description) and format of the dataset and contain the URL to the original SQuAD JSON files and the code to load examples from the original SQuAD JSON files.
#
#
# 2. Run the SQuAD python processing script which will:
# - **Download the SQuAD dataset** from the original URL (see the script) if it's not already downloaded and cached.
# - **Process and cache** all SQuAD in a structured Arrow table for each standard splits stored on the drive.
#
# Arrow table are arbitrarily long tables, typed with types that can be mapped to numpy/pandas/python standard types and can store nested objects. They can be directly access from drive, loaded in RAM or even streamed over the web.
#
#
# 3. Return a **dataset build from the splits** asked by the user (default: all), in the above example we create a dataset with the first 10% of the validation split.
# + id="fercoFwLvSUx" colab_type="code" outputId="e1d020a3-140c-4e0b-98af-c815d544be0e" colab={"base_uri": "https://localhost:8080/", "height": 479}
# Informations on the dataset (description, citation, size, splits, format...)
# are provided in `dataset.info` (as a python dataclass)
for key, value in asdict(dataset.info).items():
print('👉 ' + key + ': ' + str(value))
# + [markdown] id="GE0E87zsvSUz" colab_type="text"
# ## Inspecting and using the dataset: elements, slices and columns
# + [markdown] id="DKf4YFnevSU0" colab_type="text"
# The returned `Dataset` object is a memory mapped dataset that behave similarly to a normal map-style dataset. It is backed by an Apache Arrow table which allows many interesting features.
# + id="tP1xPqSyvSU0" colab_type="code" outputId="1b337b0b-3039-4c36-c938-595cfc966473" colab={"base_uri": "https://localhost:8080/", "height": 34}
print(dataset)
# + [markdown] id="aiO3rC8yvSU2" colab_type="text"
# You can query it's length and get items or slices like you would do normally with a python mapping.
# + id="xxLcdj2yvSU3" colab_type="code" outputId="88be3642-c132-492c-a001-f3b479c50226" colab={"base_uri": "https://localhost:8080/", "height": 374}
from pprint import pprint
print(f"👉Dataset len(dataset): {len(dataset)}")
print("\n👉First item 'dataset[0]':")
pprint(dataset[0])
# + id="zk1WQ_cczP5w" colab_type="code" outputId="5871e9f5-2cbd-4162-c262-3b0ca5e2be4c" colab={"base_uri": "https://localhost:8080/", "height": 748}
# Or get slices with several examples:
print("\n👉Slice of the two items 'dataset[10:12]':")
pprint(dataset[10:12])
# + id="QXj2Qr5KvSU5" colab_type="code" outputId="89582743-4758-404c-bd84-41b256e3e28c" colab={"base_uri": "https://localhost:8080/", "height": 54}
# You can get a full column of the dataset by indexing with its name as a string:
print(dataset['question'][:10])
# + [markdown] id="6Au7rqPMvSU7" colab_type="text"
# The `__getitem__` method will return different format depending on the type of query:
#
# - Items like `dataset[0]` are returned as dict of elements.
# - Slices like `dataset[10:20]` are returned as dict of lists of elements.
# - Columns like `dataset['question']` are returned as a list of elements.
#
# This may seems surprising at first but in our experiments it's actually a lot easier to use for data processing than returning the same format for each of these views on the dataset.
# + [markdown] id="6DB_y79cvSU8" colab_type="text"
# In particular, you can easily iterate along columns in slices, and also naturally permute consecutive indexings with identical results as showed here by permuting column indexing with elements and slices:
# + id="wjGocqArvSU9" colab_type="code" outputId="701c294a-6ca4-4b30-9472-48e2dd482ed5" colab={"base_uri": "https://localhost:8080/", "height": 51}
print(dataset[0]['question'] == dataset['question'][0])
print(dataset[10:20]['context'] == dataset['context'][10:20])
# + [markdown] id="b1-Kj1xQvSU_" colab_type="text"
# ### Dataset are internally typed and structured
#
# The dataset is backed by one (or several) Apache Arrow tables which are typed and allows for fast retrieval and access as well as arbitrary-size memory mapping.
#
# This means respectively that the format for the dataset is clearly defined and that you can load datasets of arbitrary size without worrying about RAM memory limitation (basically the dataset take no space in RAM, it's directly read from drive when needed with fast IO access).
# + id="rAnp_RyPvSVA" colab_type="code" outputId="7a5b1d76-08ca-4b65-93e9-2f3c47fdc34b" colab={"base_uri": "https://localhost:8080/"}
# You can inspect the dataset column names and type
print(dataset.column_names)
print(dataset.schema)
# + [markdown] id="au4v3mOQvSVC" colab_type="text"
# ### Additional misc properties
# + id="efFhDWhlvSVC" colab_type="code" outputId="1cc484cc-951a-4363-858f-1e5d5fe6c935" colab={"base_uri": "https://localhost:8080/"}
# Datasets also have a bunch of properties you can access
print("The number of bytes allocated on the drive is ", dataset.nbytes)
print("For comparison, here is the number of bytes allocated in memory which can be")
print("accessed with `nlp.total_allocated_bytes()`: ", nlp.total_allocated_bytes())
print("The number of rows", dataset.num_rows)
print("The number of columns", dataset.num_columns)
print("The shape (rows, columns)", dataset.shape)
# + [markdown] id="o2_FBqAQvSVE" colab_type="text"
# ### Additional misc methods
# + id="SznY_XqGvSVF" colab_type="code" outputId="fd888cf7-ac31-490f-f8f3-4b1a2c02d3ad" colab={"base_uri": "https://localhost:8080/"}
# We can list the unique elements in a column. This is done by the backend (so fast!)
print(f"dataset.unique('title'): {dataset.unique('title')}")
# This will drop the column 'id'
dataset.remove_columns_('id') # Remove column 'id'
print(f"After dataset.remove_columns_('id'), remaining columns are {dataset.column_names}")
# This will flatten nested columns (in 'answers' in our case)
dataset.flatten_()
print(f"After dataset.flatten_(), column names are {dataset.column_names}")
# We can also "dictionary encode" a column if many of it's elements are similar
# This will reduce it's size by only storing the distinct elements (e.g. string)
# It only has effect on the internal storage (no difference from a user point of view)
dataset.dictionary_encode_column('title')
# + [markdown] id="QdyuKs4VvSVH" colab_type="text"
# ## Cache
#
# `nlp` datasets are backed by Apache Arrow cache files which allows:
# - to load arbitrary large datasets by using [memory mapping](https://en.wikipedia.org/wiki/Memory-mapped_file) (as long as the datasets can fit on the drive)
# - to use a fast backend to process the dataset efficiently
# - to do smart caching by storing and reusing the results of operations performed on the drive
#
# Let's dive a bit in these parts now
# + [markdown] id="9fUcKwcbvSVH" colab_type="text"
# You can check the current cache files backing the dataset with the `.cache_file` property
# + id="zu8TgHTYvSVI" colab_type="code" outputId="25a377eb-b4a6-4bdb-efd1-0f1e4952da81" colab={"base_uri": "https://localhost:8080/", "height": 68}
dataset.cache_files
# + [markdown] id="LjeICK5GvSVK" colab_type="text"
# You can clean up the cache files in the current dataset directory (only keeping the currently used one) with `.cleanup_cache_files()`.
#
# Be careful that no other process is using some other cache files when running this command.
# + id="3_WNU3dwvSVL" colab_type="code" outputId="92679df6-9491-4ec1-bdb6-7dd8d0cab6f2" colab={"base_uri": "https://localhost:8080/", "height": 51}
dataset.cleanup_cache_files() # Returns the number of removed cache files
# + [markdown] id="1Ox7ppKDvSVN" colab_type="text"
# ## Modifying the dataset with `dataset.map`
#
# There is a powerful method `.map()` which is inspired by `tf.data` map method and that you can use to apply a function to each examples, independently or in batch.
# + id="Yz2-27HevSVN" colab_type="code" outputId="41902dc5-e99f-485b-e707-9533cc4b1e14" colab={"base_uri": "https://localhost:8080/", "height": 71}
# `.map()` takes a callable accepting a dict as argument
# (same dict as returned by dataset[i])
# and iterate over the dataset by calling the function with each example.
# Let's print the length of each `context` string in our subset of the dataset
# (10% of the validation i.e. 1057 examples)
dataset.map(lambda example: print(len(example['context']), end=','))
# + [markdown] id="Ta3celHnvSVP" colab_type="text"
# This is basically the same as doing
#
# ```python
# for example in dataset:
# function(example)
# ```
# + [markdown] id="i_Ouw5gDvSVP" colab_type="text"
# The above example had no effect on the dataset because the method we supplied to `.map()` didn't return a `dict` or a `abc.Mapping` that could be used to update the examples in the dataset.
#
# In such a case, `.map()` will return the same dataset (`self`).
#
# Now let's see how we can use a method that actually modify the dataset.
# + [markdown] id="cEnCi9DFvSVQ" colab_type="text"
# ### Modifying the dataset example by example
# + [markdown] id="kA37VgZhvSVQ" colab_type="text"
# The main interest of `.map()` is to update and modify the content of the table and leverage smart caching and fast backend.
#
# To use `.map()` to update elements in the table you need to provide a function with the following signature: `function(example: dict) -> dict`.
# + id="vUr65K-4vSVQ" colab_type="code" outputId="9eb1516f-21e1-4cd6-d095-dfea304b5ac4" colab={"base_uri": "https://localhost:8080/"}
# Let's add a prefix 'My cute title: ' to each of our titles
def add_prefix_to_title(example):
example['title'] = 'My cute title: ' + example['title']
return example
dataset = dataset.map(add_prefix_to_title)
print(dataset.unique('title'))
# + [markdown] id="FcZ_amDAvSVS" colab_type="text"
# This call to `.map()` compute and return the updated table. It will also store the updated table in a cache file indexed by the current state and the mapped function.
#
# A subsequent call to `.map()` (even in another python session) will reuse the cached file instead of recomputing the operation.
#
# You can test this by running again the previous cell, you will see that the result are directly loaded from the cache and not re-computed again.
#
# The updated dataset returned by `.map()` is (again) directly memory mapped from drive and not allocated in RAM.
# + [markdown] id="Skbf8LUEvSVT" colab_type="text"
# The function you provide to `.map()` should accept an input with the format of an item of the dataset: `function(dataset[0])` and return a python dict.
#
# The columns and type of the outputs can be different than the input dict. In this case the new keys will be added as additional columns in the dataset.
#
# Bascially each dataset example dict is updated with the dictionary returned by the function like this: `example.update(function(example))`.
# + id="d5De0CfTvSVT" colab_type="code" outputId="0ae16b0d-efd3-443c-fd80-2d777bce1f29" colab={"base_uri": "https://localhost:8080/"}
# Since the input example dict is updated with our function output dict,
# we can actually just return the updated 'title' field
dataset = dataset.map(lambda example: {'title': 'My cutest title: ' + example['title']})
print(dataset.unique('title'))
# + [markdown] id="Q5vny56-vSVV" colab_type="text"
# #### Removing columns
# You can also remove columns when running map with the `remove_columns=List[str]` argument.
# + id="-sPWnsz-vSVW" colab_type="code" outputId="6ee9e668-b083-420a-de69-2d4e31d24b2c" colab={"base_uri": "https://localhost:8080/"}
# This will remove the 'title' column while doing the update (after having send it the the mapped function so you can use it in your function!)
dataset = dataset.map(lambda example: {'new_title': 'Wouhahh: ' + example['title']},
remove_columns=['title'])
print(dataset.column_names)
print(dataset.unique('new_title'))
# + [markdown] id="G459HzD-vSVY" colab_type="text"
# #### Using examples indices
# With `with_indices=True`, dataset indices (from `0` to `len(dataset)`) will be supplied to the function which must thus have the following signature: `function(example: dict, indice: int) -> dict`
# + id="_kFL37R2vSVY" colab_type="code" outputId="9f625775-18c1-485a-dd2b-7f3f9fa6df4a" colab={"base_uri": "https://localhost:8080/"}
# This will add the index in the dataset to the 'question' field
dataset = dataset.map(lambda example, idx: {'question': f'{idx}: ' + example['question']},
with_indices=True)
print('\n'.join(dataset['question'][:5]))
# + [markdown] id="xckhVEWFvSVb" colab_type="text"
# ### Modifying the dataset with batched updates
# + [markdown] id="dzmicbSnvSVb" colab_type="text"
# `.map()` can also work with batch of examples (slices of the dataset).
#
# This is particularly interesting if you have a function that can handle batch of inputs like the tokenizers of HuggingFace `tokenizers`.
#
# To work on batched inputs set `batched=True` when calling `.map()` and supply a function with the following signature: `function(examples: Dict[List]) -> Dict[List]` or, if you use indices, `function(examples: Dict[List], indices: List[int]) -> Dict[List]`).
#
# Bascially, your function should accept an input with the format of a slice of the dataset: `function(dataset[:10])`.
# + id="pxHbgSTL0itj" colab_type="code" outputId="6ada38ca-af2d-4935-acbc-72993e93b37e" colab={"base_uri": "https://localhost:8080/"}
# !pip install transformers
# + id="T7gpEg0yvSVc" colab_type="code" outputId="4d36e8a9-03c3-40f1-84dc-87285a34aa7a" colab={"base_uri": "https://localhost:8080/", "referenced_widgets": ["c95167de0c674bbd88e95df1271dd9ab", "000f6fb64c164486bdafe2c61860899a", "c7304e5dece143a2a346762b482e4b8d", "1ddcdd9899e344f981d06939882d574a", "6b0f78412d694cbb8d7d9dc465e8661d", "3ae828d2a56c48f79c049c415defd21c", "1afa1c44c06a44e79adab422e14ff59a", "e82d9d1e030f41128b265c738e83771e"]}
# Let's import a fast tokenizer that can work on batched inputs
# (the 'Fast' tokenizers in HuggingFace)
from transformers import BertTokenizerFast
tokenizer = BertTokenizerFast.from_pretrained('bert-base-cased')
# + id="fAmLTPC9vSVe" colab_type="code" outputId="9fecf3e7-c00e-4c72-ba27-00d2362fa341" colab={"base_uri": "https://localhost:8080/"}
# Now let's batch tokenize our dataset 'context'
dataset = dataset.map(lambda example: tokenizer.batch_encode_plus(example['context']),
batched=True)
print("dataset[0]", dataset[0])
# + id="kNaJdKskvSVf" colab_type="code" outputId="67d19737-a55e-4fd0-f047-06b533455b21" colab={"base_uri": "https://localhost:8080/"}
# we have added additional columns
print(dataset.column_names)
# + id="m3To8ztMvSVj" colab_type="code" outputId="74569713-2fd2-4b13-e6dc-e09da60db749" colab={"base_uri": "https://localhost:8080/"}
# Let show a more complex processing with the full preparation of the SQuAD dataset
# for training a model from Transformers
def convert_to_features(batch):
# Tokenize contexts and questions (as pairs of inputs)
# keep offset mappings for evaluation
input_pairs = list(zip(batch['context'], batch['question']))
encodings = tokenizer.batch_encode_plus(input_pairs,
pad_to_max_length=True,
return_offsets_mapping=True)
# Compute start and end tokens for labels
start_positions, end_positions = [], []
for i, (text, start) in enumerate(zip(batch['answers.text'], batch['answers.answer_start'])):
first_char = start[0]
last_char = first_char + len(text[0]) - 1
start_positions.append(encodings.char_to_token(i, first_char))
end_positions.append(encodings.char_to_token(i, last_char))
encodings.update({'start_positions': start_positions, 'end_positions': end_positions})
return encodings
dataset = dataset.map(convert_to_features, batched=True)
# + id="KBnmSa46vSVl" colab_type="code" outputId="cc6157c2-d6e5-441e-cb52-d13a2086696b" colab={"base_uri": "https://localhost:8080/"}
# Now our dataset comprise the labels for the start and end position
# as well as the offsets for converting back tokens
# in span of the original string for evaluation
print("column_names", dataset.column_names)
print("start_positions", dataset[:5]['start_positions'])
# + [markdown] id="NzOXxNzQvSVo" colab_type="text"
# ## formatting outputs for numpy/torch/tensorflow
#
# Now that we have tokenized our inputs, we probably want to use this dataset in a `torch.Dataloader` or a `tf.data.Dataset`.
#
# To be able to do this we need to tweak two things:
#
# - format the indexing (`__getitem__`) to return numpy/pytorch/tensorflow tensors, instead of python objects, and probably
# - format the indexing (`__getitem__`) to return only the subset of the columns that we need for our model inputs.
#
# We don't want the columns `id` or `title` as inputs to train our model, but we could still want to keep them in the dataset, for instance for the evaluation of the model.
#
# This is handled by the `.set_format(type: Union[None, str], columns: Union[None, str, List[str]])` where:
#
# - `type` define the return type for our dataset `__getitem__` method and is one of `[None, 'numpy', 'pandas', 'torch', 'tensorflow']` (`None` means return python objects), and
# - `columns` define the columns returned by `__getitem__` and takes the name of a column in the dataset or a list of columns to return (`None` means return all columns).
# + id="aU2h_qQDvSVo" colab_type="code" outputId="19b279c9-c2be-4ddd-be6a-817e353b5d31" colab={"base_uri": "https://localhost:8080/", "height": 139}
columns_to_return = ['input_ids', 'token_type_ids', 'attention_mask',
'start_positions', 'end_positions']
dataset.set_format(type='torch',
columns=columns_to_return)
# Our dataset indexing output is now ready for being used in a pytorch dataloader
print('\n'.join([' '.join((n, str(type(t)), str(t.shape))) for n, t in dataset[:10].items()]))
# + id="Wj1ukGIuvSVq" colab_type="code" outputId="5c0be879-b2f3-4cc9-ede2-4a9a2b731f6d" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Note that the columns are not removed from the dataset, just not returned when calling __getitem__
# Similarly the inner type of the dataset is not changed to torch.Tensor, the conversion and filtering is done on-the-fly when querying the dataset
print(dataset.column_names)
# + id="pWmmUnlpvSVs" colab_type="code" outputId="392e2624-488d-4a3e-b94c-932d57f7b9d4" colab={"base_uri": "https://localhost:8080/", "height": 221}
# We can remove the formatting with `.reset_format()`
# or, identically, a call to `.set_format()` with no arguments
dataset.reset_format()
print('\n'.join([' '.join((n, str(type(t)))) for n, t in dataset[:10].items()]))
# + id="VyUOA07svSVu" colab_type="code" outputId="c8612c99-dfe5-488d-dd41-07c6f68901a5" colab={"base_uri": "https://localhost:8080/", "height": 238}
# The current format can be checked with `.format`,
# which is a dict of the type and formatting
dataset.format
# + [markdown] id="xyi2eMeSvSVv" colab_type="text"
# # Wrapping this all up (PyTorch)
#
# Let's wrap this all up with the full code to load and prepare SQuAD for training a PyTorch model from HuggingFace `transformers` library.
#
#
# + id="l0j8BPLi6Qlv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 306} outputId="9103326b-cba4-4fc2-9ee0-5ec10938c540"
# !pip install transformers
# + id="QvExTIZWvSVw" colab_type="code" colab={}
import nlp
import torch
from transformers import BertTokenizerFast
# Load our training dataset and tokenizer
dataset = nlp.load_dataset('squad')
tokenizer = BertTokenizerFast.from_pretrained('bert-base-cased')
def get_correct_alignement(context, answer):
""" Some original examples in SQuAD have indices wrong by 1 or 2 character. We test and fix this here. """
gold_text = answer['text'][0]
start_idx = answer['answer_start'][0]
end_idx = start_idx + len(gold_text)
if context[start_idx:end_idx] == gold_text:
return start_idx, end_idx # When the gold label position is good
elif context[start_idx-1:end_idx-1] == gold_text:
return start_idx-1, end_idx-1 # When the gold label is off by one character
elif context[start_idx-2:end_idx-2] == gold_text:
return start_idx-2, end_idx-2 # When the gold label is off by two character
else:
raise ValueError()
# Tokenize our training dataset
def convert_to_features(example_batch):
# Tokenize contexts and questions (as pairs of inputs)
input_pairs = list(zip(example_batch['context'], example_batch['question']))
encodings = tokenizer.batch_encode_plus(input_pairs, pad_to_max_length=True)
# Compute start and end tokens for labels using Transformers's fast tokenizers alignement methods.
start_positions, end_positions = [], []
for i, (context, answer) in enumerate(zip(example_batch['context'], example_batch['answers'])):
start_idx, end_idx = get_correct_alignement(context, answer)
start_positions.append(encodings.char_to_token(i, start_idx))
end_positions.append(encodings.char_to_token(i, end_idx-1))
encodings.update({'start_positions': start_positions,
'end_positions': end_positions})
return encodings
dataset['train'] = dataset['train'].map(convert_to_features, batched=True)
# Format our dataset to outputs torch.Tensor to train a pytorch model
columns = ['input_ids', 'token_type_ids', 'attention_mask', 'start_positions', 'end_positions']
dataset['train'].set_format(type='torch', columns=columns)
# Instantiate a PyTorch Dataloader around our dataset
dataloader = torch.utils.data.DataLoader(dataset['train'], batch_size=8)
# + id="4mHnwMx2vSVx" colab_type="code" outputId="178ed3de-321c-424d-d55e-2014eb43cc5f" colab={"base_uri": "https://localhost:8080/", "height": 866, "referenced_widgets": ["76f672fa3f5d4ee9a79409043a763938", "57a5736e9d634e74995df300e07d53e4", "fab57dec41a9439b9e822d20785f06c8", "ccb3f04fa88d4e66a8c04d829de998e3", "d7213a66331e4b37af0e8c9a51a96592", "37592a88c2e244a99ae281f4f127465b", "8fbb0ca9e6e7402bbeccdf822cfe5189", "00298c6910ec47da9b05014493f71545", "3333a69504ea4ea98f20ccf31b54a96b", "bc21e8ef90c54a0280ee97431f5404c9", "ff60cb6f5b6d4f928d624b8d7bc96ac3", "77044c08a02441b68c9bc78fd340df7d", "67003b0a383a4456913fdd0930cfcefa", "0c72a266137a4ca199f13236b574f3e1", "ba1efb6f24ac4209b1cae526a85ec4f1", "4e3757c6b2f04013b40cdd4d3a4d127f"]}
# Let's load a pretrained Bert model and a simple optimizer
from transformers import BertForQuestionAnswering
model = BertForQuestionAnswering.from_pretrained('distilbert-base-cased')
optimizer = torch.optim.Adam(model.parameters(), lr=0.0001)
# + id="biqDH9vpvSVz" colab_type="code" outputId="5587703a-cbab-44ea-bc83-b6f5b322f5e5" colab={"base_uri": "https://localhost:8080/", "height": 102}
# Now let's train our model
model.train()
for i, batch in enumerate(dataloader):
outputs = model(**batch)
loss = outputs[0]
loss.backward()
optimizer.step()
model.zero_grad()
print(f'Step {i} - loss: {loss:.3}')
if i > 3:
break
# + [markdown] id="kxZQ9Ms_vSV1" colab_type="text"
# # Wrapping this all up (Tensorflow)
#
# Let's wrap this all up with the full code to load and prepare SQuAD for training a Tensorflow model (works only from the version 2.2.0)
# + id="ZE8VSTYovSV2" colab_type="code" outputId="4f3c33f0-deb1-48d4-d778-c3d80172b22f" colab={"base_uri": "https://localhost:8080/", "height": 51}
import tensorflow as tf
import nlp
from transformers import BertTokenizerFast
# Load our training dataset and tokenizer
train_tf_dataset = nlp.load_dataset('squad', split="train")
tokenizer = BertTokenizerFast.from_pretrained('bert-base-cased')
# Tokenize our training dataset
# The only one diff here is that start_positions and end_positions
# must be single dim list => [[23], [45] ...]
# instead of => [23, 45 ...]
def convert_to_tf_features(example_batch):
# Tokenize contexts and questions (as pairs of inputs)
input_pairs = list(zip(example_batch['context'], example_batch['question']))
encodings = tokenizer.batch_encode_plus(input_pairs, pad_to_max_length=True, max_length=tokenizer.max_len)
# Compute start and end tokens for labels using Transformers's fast tokenizers alignement methods.
start_positions, end_positions = [], []
for i, (context, answer) in enumerate(zip(example_batch['context'], example_batch['answers'])):
start_idx, end_idx = get_correct_alignement(context, answer)
start_positions.append([encodings.char_to_token(i, start_idx)])
end_positions.append([encodings.char_to_token(i, end_idx-1)])
if start_positions and end_positions:
encodings.update({'start_positions': start_positions,
'end_positions': end_positions})
return encodings
train_tf_dataset = train_tf_dataset.map(convert_to_tf_features, batched=True)
def remove_none_values(example):
return not None in example["start_positions"] or not None in example["end_positions"]
train_tf_dataset = train_tf_dataset.filter(remove_none_values, load_from_cache_file=False)
columns = ['input_ids', 'token_type_ids', 'attention_mask', 'start_positions', 'end_positions']
train_tf_dataset.set_format(type='tensorflow', columns=columns)
features = {x: train_tf_dataset[x].to_tensor(default_value=0, shape=[None, tokenizer.max_len]) for x in columns[:3]}
labels = {"output_1": train_tf_dataset["start_positions"].to_tensor(default_value=0, shape=[None, 1])}
labels["output_2"] = train_tf_dataset["end_positions"].to_tensor(default_value=0, shape=[None, 1])
tfdataset = tf.data.Dataset.from_tensor_slices((features, labels)).batch(8)
# + id="y0dfw8K8vSV4" colab_type="code" colab={}
# Let's load a pretrained TF2 Bert model and a simple optimizer
from transformers import TFBertForQuestionAnswering
model = TFBertForQuestionAnswering.from_pretrained("bert-base-cased")
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(reduction=tf.keras.losses.Reduction.NONE, from_logits=True)
opt = tf.keras.optimizers.Adam(learning_rate=3e-5)
model.compile(optimizer=opt,
loss={'output_1': loss_fn, 'output_2': loss_fn},
loss_weights={'output_1': 1., 'output_2': 1.},
metrics=['accuracy'])
# + id="TcYtiykmvSV6" colab_type="code" outputId="4b755c1b-8e61-43ab-ffc6-d3e82ed4174d" colab={"base_uri": "https://localhost:8080/", "height": 207}
# Now let's train our model
model.fit(tfdataset, epochs=1, steps_per_epoch=3)
# + [markdown] id="eREDXWP6vSV8" colab_type="text"
# # Metrics API
#
# `nlp` also provides easy access and sharing of metrics.
#
# This aspect of the library is still experimental and the API may still evolve more than the datasets API.
#
# Like datasets, metrics are added as small scripts wrapping common metrics in a common API.
#
# There are several reason you may want to use metrics with `nlp` and in particular:
#
# - metrics for specific datasets like GLUE or SQuAD are provided out-of-the-box in a simple, convenient and consistant way integrated with the dataset,
# - metrics in `nlp` leverage the powerful backend to provide smart features out-of-the-box like support for distributed evaluation in PyTorch
# + [markdown] id="uUoGMMVKvSV8" colab_type="text"
# ## Using metrics
#
# Using metrics is pretty simple, they have two main methods: `.compute(predictions, references)` to directly compute the metric and `.add(prediction, reference)` or `.add_batch(predictions, references)` to only store some results if you want to do the evaluation in one go at the end.
#
# Here is a quick gist of a standard use of metrics (the simplest usage):
# ```python
# import nlp
# bleu_metric = nlp.load_metric('bleu')
#
# # If you only have a single iteration, you can easily compute the score like this
# predictions = model(inputs)
# score = bleu_metric.compute(predictions, references)
#
# # If you have a loop, you can "add" your predictions and references at each iteration instead of having to save them yourself (the metric object store them efficiently for you)
# for batch in dataloader:
# model_input, targets = batch
# predictions = model(model_inputs)
# bleu_metric.add_batch(predictions, targets)
# score = bleu_metric.compute() # Compute the score from all the stored predictions/references
# ```
#
# Here is a quick gist of a use in a distributed torch setup (should work for any python multi-process setup actually). It's pretty much identical to the second example above:
# ```python
# import nlp
# # You need to give the total number of parallel python processes (num_process) and the id of each process (process_id)
# bleu_metric = nlp.load_metric('bleu', process_id=torch.distributed.get_rank(),b num_process=torch.distributed.get_world_size())
#
# for batch in dataloader:
# model_input, targets = batch
# predictions = model(model_inputs)
# bleu_metric.add_batch(predictions, targets)
# score = bleu_metric.compute() # Compute the score on the first node by default (can be set to compute on each node as well)
# ```
# + [markdown] id="ySL-vDadvSV8" colab_type="text"
# Example with a NER metric: `seqeval`
# + id="f4uZym7MvSV9" colab_type="code" colab={}
ner_metric = nlp.load_metric('seqeval')
references = [['O', 'O', 'O', 'B-MISC', 'I-MISC', 'I-MISC', 'O'], ['B-PER', 'I-PER', 'O']]
predictions = [['O', 'O', 'B-MISC', 'I-MISC', 'I-MISC', 'I-MISC', 'O'], ['B-PER', 'I-PER', 'O']]
ner_metric.compute(predictions, references)
# + [markdown] id="ctY6AIAilLdH" colab_type="text"
# # Adding a new dataset or a new metric
#
# They are two ways to add new datasets and metrics in `nlp`:
#
# - datasets can be added with a Pull-Request adding a script in the `datasets` folder of the [`nlp` repository](https://github.com/huggingface/nlp)
#
# => once the PR is merged, the dataset can be instantiate by it's folder name e.g. `nlp.load_dataset('squad')`. If you want HuggingFace to host the data as well you will need to ask the HuggingFace team to upload the data.
#
# - datasets can also be added with a direct upload using `nlp` CLI as a user or organization (like for models in `transformers`). In this case the dataset will be accessible under the gien user/organization name, e.g. `nlp.load_dataset('thomwolf/squad')`. In this case you can upload the data yourself at the same time and in the same folder.
#
# We will add a full tutorial on how to add and upload datasets soon.
# + id="ypLjbtGrljk8" colab_type="code" colab={}
| 56.764521 | 1,900 |
dfd6cb3ca2683ff04a669a57888f304057c22c1a
|
py
|
python
|
MNEPython/Afirstlook.ipynb
|
Lei-I-Zhang/FLUX
|
['BSD-3-Clause']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # A first look at the data
# ## Introduction
# In this section we will set the paths and load the data. We will then explain the data structure and do a few sanity checks. Finally follow some examples for how to perform simples plots of the raw data.
#
# Import the required modules:
import os
import numpy as np
import mne
# ## Loading the data
# Loading the data. The MEGIN data are stored in the FIF format which is a binary format with embedded labels.
#
# As a first step, we set the path to the data. Note that this will dependent on where you have stored the dataset. Afterwards, we set the file names.
# +
data_path = r'C:\Users\JensenO\Dropbox\FLUX\Development\dataRaw'
# data_path = r'THE PATH TO DATA ON YOUR LOCAL SYSTEM'
file_name = ['training_raw-1.fif','training_raw-2.fif']
# -
# There is a limit to the file size of the FIF files. If the MEG recordings exceed this limit, the MEGIN acquisition system automatically split the data in two or more FIF files. In those cases, by reading the first FIF file MNE-Python you will automatically read all the linked split files. In our case, the sample dataset was broken into 2 sub-files by the operator and we need to read them one by one.
#
# Start by reading the first file:
path_data = os.path.join(data_path,file_name[0])
data1 = mne.io.read_raw_fif(path_data)
# To get some basic information from the FIF file write:
print(data1)
# The 5.4 MB refer to the size of the data set. The 1457.0 s is the recording time. As the sampling rate was 1000 Hz, this results in 1457000 samples recorded in 343 channels. These channels include the MEG, EOG, triggers channels etc.
#
# To get some additional information:
print(data1.info)
# This set of information show important parameters of the dataset. For instance, we can see that the gantry was positioned at 68 degress (*gantry_angle*) and that the sampling frequency was 1000 Hz (*sfreq*). The data were lowpass filtered at 330.0 Hz (*lowpass*) and highpass filtered at 0.1 Hz (*highpass*) prior to the digital sampling.
#
# **Question 1:** What is the purpose of the 330 Hz lowpas-filter (hint: see Analog Filters for Data Conversion, Chapter 3; Smith et al., 1999)
#
# **Question 2:** What is the purpose of 0.1 Hz highpass-filter?
#
#
# The data object (*data1*) allows for a simple inspection of the data by plotting the spectra:
# %matplotlib inline
data1.plot_psd(fmax=60);
# Note the 10 Hz alpha activity on the gradiometers as well as the 50 Hz line noise. The frequency of the line noise is 50 Hz in European countries including Russia whereas it is 60 in South Korea as well as South and North America. In Japan it can be either 50 or 60 Hz depending on the region.
#
# **Question 3:** Why is the line-noise 50 Hz larger for the magnetometers than the gradiometers?
#
#
# To show the raw data use:
# %matplotlib inline
data1.plot(duration=10,title='Raw');
# To enable the interactive functions of the plotting tool:
# %matplotlib qt
data1.plot(duration=10,title='Raw');
# This will open the plot in a new window. Use the arrow keys to move over channels and time. Click on the help button for more information.
#
# **Question 3:** Scroll through the MEG data and identify the following artifacts (include figures in the response):
#
# - Eye-blink
# - A muscle contraction (characterized by high-frequency activity
# - The cardiac artifact
#
#
# ## Preregistration and publication
#
# Preregistration: report the sampling frequency and the properties of the anti-aliasing lowpass filter. Also report the peripheral data to be recorded (e.g. the EOG and ECG)
#
# Publication, example:
#
# "The ongoing MEG data were recorded using the TRIUX system from MEGIN. This system has 102 magnetometers and 204 planer gradiometers. These are placed at 102 locations each having one magnetometer and a set of two orthogonal gradiometers. The horizontal and vertical EOG data as well as the ECG were acquired together with the MEG data. The data were sampled at 1000 Hz and stored for offline analysis. Prior to sampling, a lowpass filter at ~330 Hz was applied. To record the horizontal EOG, a pair of electrodes were attached approximately 2.5 cm away from the outer canthus of each eye. To record the vertical EOG, a pair of electrodes were placed above and below the right eye in line with the pupil. The ECG was recorded from a pair of electrodes placed on the left and right collarbone. Four head position indicator coils (HPIs) were placed behind the left and right ear as well as on the left and right forehead just below the hairline. The positions of the HPIs, the nasion, the left and right preauricular points, as well as the surface points of the scalp, were digitized using a PolhemusTM device. "
# ## References
# Smith, W.S. (1997) The Scientist and Engineer's Guide to Digital Signal Processing. California Technical Publishing. ISBN 0-9660176-3-3 [Online version](http://www.dspguide.com/)
| 49.669903 | 1,112 |
c51c32b54202ed920116f53d12f92439c0ac7282
|
py
|
python
|
notebooks/data_challenge_IMNN_x_DELFI_cosmo_demo.ipynb
|
tlmakinen/kosmo-kompress
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="SxfIzxXt0q6J"
# #### From Quarks to Cosmos with AI: Tutorial Day 4
# ---
# # Field-level cosmological inference with IMNN + DELFI
#
# by Lucas Makinen [<img src="https://raw.githubusercontent.com/tlmakinen/FieldIMNNs/master/tutorial/plots/Orcid-ID.png" alt="drawing" width="20"/>](https://orcid.org/0000-0002-3795-6933 "") [<img src="https://raw.githubusercontent.com/tlmakinen/FieldIMNNs/master/tutorial/plots/twitter-graphic.png" alt="drawing" width="20" style="background-color: transparent"/>](https://twitter.com/lucasmakinen?lang=en ""), Tom Charnock [<img src="https://raw.githubusercontent.com/tlmakinen/FieldIMNNs/master/tutorial/plots/Orcid-ID.png" alt="drawing" width="20"/>](https://orcid.org/0000-0002-7416-3107 "Redirect to orcid") [<img src="https://raw.githubusercontent.com/tlmakinen/FieldIMNNs/master/tutorial/plots/twitter-graphic.png" alt="drawing" width="20" style="background-color: transparent"/>](https://twitter.com/t_charnock?lang=en "")), Justin Alsing [<img src="https://raw.githubusercontent.com/tlmakinen/FieldIMNNs/master/tutorial/plots/Orcid-ID.png" alt="drawing" width="20"/>](https://scholar.google.com/citations?user=ICPFL8AAAAAJ&hl=en "Redirect to orcid"), and Ben Wandelt [<img src="https://raw.githubusercontent.com/tlmakinen/FieldIMNNs/master/tutorial/plots/twitter-graphic.png" alt="drawing" width="20" style="background-color: transparent"/>](https://twitter.com/bwandelt?lang=en "")
#
# >read the paper: [on arXiv tomorrow !]
#
# >get the code: [https://github.com/tlmakinen/FieldIMNNs](https://github.com/tlmakinen/FieldIMNNs)
#
#
#
# 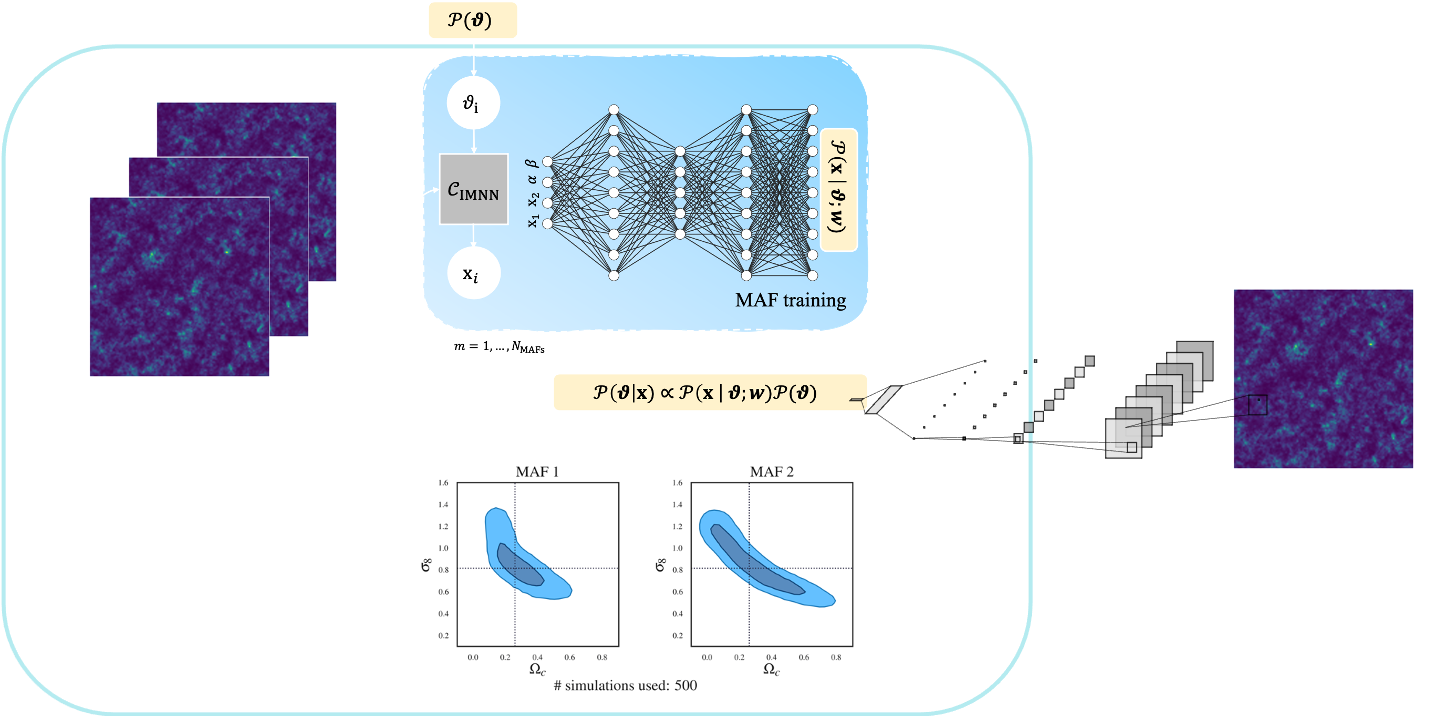
# $\quad$
#
# In this tutorial we will demonstrate Implicit Likelihood Inference (IFI) using Density Estimation Likelihood Free Inference (DELFI) with optimal nonlinear summaries obtained from an Information Maximising Neural Network (IMNN). The goal of the exercise will be to build posterior distributions for the cosmological parameters $\Omega_c$ and $\sigma_8$ *directly* from overdensity field simulations.
#
# First we'll install the relevant libraries and walk through the simulation implementation. Then we'll build a neural IMNN compressor to generate two optimal summaries for our simulations. Finally, we'll use these summaries to build and train a Conditional Masked Autoregressive Flow, from which we'll construct our parameter posterior distributions.
#
# ### Q: Wait a second -- how do we know this works ?
# If you're not convinced by our method by the end of this tutorial, we invite you to take a look at our [benchmarking tutorial with Gaussian fields from power spectra](https://www.aquila-consortium.org/doc/imnn/pages/examples/2d_field_inference/2d_field_inference.html), which is also runnable in-browser on [this Colab notebook](https://colab.research.google.com/drive/1_y_Rgn3vrb2rlk9YUDUtfwDv9hx774ZF#scrollTo=EW4H-R8I0q6n).
# + [markdown] id="rhDw3VXPPDMW"
# ---
# # HOW TO USE THIS NOTEBOOK
#
# You will (most likely) be running this code using a free version of Google Colab. The code runs just like a Jupyter notebook (`shift` + `enter` or click the play button to run cells). There are some cells with lengthy infrastructure code that you need to run to proceed. These are clearly marked with <font color='lightgreen'>[run me]</font>. When you get to the challenge exercises, you are welcome to code some functions yourself. However, if you want to run the notebook end-to-end, solution code is presented in hidden cells below (again with the marker <font color='lightgreen'>[run me]</font>).
#
# Some cells are not meant to be run here as a part of Quarks to Cosmos, but can be run (with a Colab Pro account) on your own.
#
# ---
# + [markdown] id="K25rZ-p0VNoK"
# # step 1: loading packages and setting up environment
#
# 1. check that Colab is set to run on a GPU ! Go to `Runtime`>`change runtime type` and select `GPU` from the dropdown menu. Next, enable dark mode by going to `settings`>`Theme` and selecting `dark` (protect your eyes !)
#
# 2. install packages. The current code relies on several libraries, namely `jax` and `tensorflow_probability`. However, we require both plain `tensorflow_probability` (`tfp`) and the experimental `tensorflow_probability.substrates.jax` (`tfpj`) packages for different parts of our inference
# 3. for some Colab sessions, you may need to run the second cell so that `!pip install jax-cosmo` gets the package imported properly.
# + colab={"base_uri": "https://localhost:8080/"} id="-JM42Pmj0q6N" cellView="form" outputId="f024a9e2-ec9d-4cfd-8e91-4c43ba4878e9"
#@title set up environment <font color='lightgreen'>[RUN ME FIRST]</font>
# %tensorflow_version 2.x
import tensorflow as tf
print('tf version', tf.__version__)
# !pip install -q jax==0.2.11
# !pip install -q tensorflow-probability
import tensorflow_probability as tfp
print('tfp version:', tfp.__version__)
tfd = tfp.distributions
tfb = tfp.bijectors
# !pip install -q imnn
# !python -m pip install -q jax-cosmo
# + [markdown] id="nQHIxYpWD2gZ"
# note: if the cell below fails for installing jax-cosmo, just run it again: Colab will rearrange the headings needed.
# + id="bqbyE8fB7g5I" colab={"base_uri": "https://localhost:8080/"} outputId="85eda80e-ac16-4c74-beff-ba762f982a6a"
# now import all the required libraries
import jax.numpy as np
from jax import grad, jit, vmap
from jax import random
import jax
print('jax version:', jax.__version__)
# for nn model stuff
import jax.experimental.optimizers as optimizers
import jax.experimental.stax as stax
# tensorflow-prob VANILLA
tfd = tfp.distributions
tfb = tfp.bijectors
# tensorflow-prob-JAX
import tensorflow_probability.substrates.jax as tfpj
tfdj = tfpj.distributions
tfbj = tfpj.bijectors
# for imnn
import imnn
import imnn.lfi
print('IMNN version:', imnn.__version__)
# jax-cosmo module
# !python -m pip install -q jax-cosmo
import jax_cosmo as jc
print('jax-cosmo version:', jc.__version__)
# matplotlib stuff
import matplotlib.pyplot as plt
from scipy.linalg import toeplitz
import seaborn as sns
sns.set()
rng = random.PRNGKey(2)
# + id="RQUcaPt70q6R"
from jax.config import config
config.update('jax_enable_x64', True)
# + [markdown] id="wXQuNdJ7syeh"
# make sure we're using 64-bit precision and running on a GPU !
# + colab={"base_uri": "https://localhost:8080/"} id="OcZqKcg90q6S" outputId="8001c3c3-55bc-4aae-e117-96e01f7e036e"
from jax.lib import xla_bridge
print(xla_bridge.get_backend().platform)
# + [markdown] id="b-b4GA4fKofV"
# # Cosmological Fields from the Eisenstein-Hu linear matter power spectrum
# We're interested in extracting the cosmological parameters $\Omega_c$ and $\sigma_8$ *directly* from cosmological field pixels. To generate our simulations we'll need to install the library `jax-cosmo` to generate our differentiable model power spectra.
# + [markdown] id="IO9rpJhe4g7f"
# ## choose fiducial model
# To train our neural compression, we first need to choose a fiducial model to train the IMNN.
#
#
# For example lets say that our fiducial cosmology has $\Omega_c=0.40$ and $\sigma_8=0.60$. This is *deliberately* far from, say, Planck parameters -- we want to investigate how our compression behaves if we don't know our universe's true parameters.
# + id="PI9pDtf12CJB"
cosmo_params = jc.Planck15(Omega_c=0.40, sigma8=0.60)
θ_fid = np.array(
[cosmo_params.Omega_c,
cosmo_params.sigma8],
dtype=np.float32)
n_params = θ_fid.shape[0]
# + [markdown] id="mTVDw_8B2CJM"
# Our power spectrum $P_{\rm LN}(k)$ is the linear matter power spectrum defined as
# + id="7RN3N4Ye2CJM"
def P(k, A=0.40, B=0.60):
cosmo_params = jc.Planck15(Omega_c=A, sigma8=B)
return jc.power.linear_matter_power(cosmo_params, k)
# + [markdown] id="u5StM_D679FK"
# and we can visualize it in $k$-space (small $k$ <=> big $r$, big $k$ <=> small $r$) :
# + colab={"base_uri": "https://localhost:8080/", "height": 307} id="LIN6RUuk8KV5" cellView="form" outputId="36f14e67-9d07-4e34-ddf4-22e81fe69ec5"
#@title plot the Eisenstein-Hu $P(k)$ <font color='lightgreen'>[run me]</font>
sns.set()
L = 250.
N = 128.
#kmax = 1.0
#kmin = 0.5 / (N)
kmax = N / L
kmin = 1. / L
kbin = np.linspace(kmin, kmax, num=100)
power_spec = P(kbin, A=cosmo_params.Omega_c, B=cosmo_params.sigma8)
plt.style.use('dark_background')
plt.grid(b=None)
plt.plot(kbin, power_spec, linewidth=2)
plt.xlabel(r'$k\ \rm [h\ Mpc^{-1}]$', fontsize=14)
plt.ylabel(r'$P(k)\ \rm$', fontsize=14)
plt.ylim((1e2, 1e4))
plt.xscale('log')
plt.yscale('log')
# + [markdown] id="WEpWQ0sI-KAq"
# ____
# ## Lognormal Fields from Power Spectra: how much information is embedded in the field ?
# Cosmologists often use lognormal fields as "the poor man's large scale structure" since they're analytically interrogable and easy to obtain from Gaussian fields. We'll walk through how to obtain the *theoretical* information content of such fields using the Fisher formalism.
#
# The likelihood for an $N_{\rm pix}\times N_{\rm pix}$ Gaussian field, $\boldsymbol{\delta}$, can be explicitly written down for the Fourier transformed data, $\boldsymbol{\Delta}$ as
# $$\mathcal{L}(\boldsymbol{\Delta}|\boldsymbol{\theta}) = \frac{1}{(2\pi)^{N_{\rm pix}^2 / 2} |P_{\rm G}({\bf k}, \boldsymbol{\theta})|^{1/2}}\exp{\left(-\frac{1}{2}\boldsymbol{\Delta}\left(P_{\rm G}({\bf k}, \boldsymbol{\theta})\right)^{-1}\boldsymbol{\Delta}\right)}$$
# Since the Fisher information can be calculated from the expectation value of the second derivative of the score, i.e. the log likelihood
# $${\bf F}_{\alpha\beta} = - \left.\left\langle\frac{\partial^2\ln\mathcal{L}(\Delta|\boldsymbol{\theta})}{\partial\theta_\alpha\partial\theta_\beta}\right\rangle\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}^\textrm{fid}}$$
# then we know that analytically the Fisher information must be
# $${\bf F}_{\alpha\beta} = \frac{1}{2} {\rm Tr} \left(\frac{\partial P_{\rm G}({\bf k}, \boldsymbol{\theta})}{\partial\theta_\alpha}\left(P_{\rm G}({\bf k}, \boldsymbol{\theta})\right)^{-1}\frac{\partial P_{\rm G}({\bf k}, \boldsymbol{\theta})}{\partial\theta_\beta}\left(P_{\rm G}({\bf k}, \boldsymbol{\theta})\right)^{-1}\right)$$
# where $\alpha$ and $\beta$ label the parameters (for instance $ \Omega_c, \sigma_8$) in the power spectrum. As each $k$-mode is uncoupled for this power law form we require the derivatives
# $$\begin{align}
# \left(\frac{\partial P_{\rm G}({\bf k}, \boldsymbol{\theta})}{\partial \Omega_c},\
# \frac{\partial P_{\rm G}({\bf k}, \boldsymbol{\theta})}{\partial \sigma_8}\right) \\
# \end{align}$$
# We can set up these derivative functions *so long as our code for $P(k)$ is differentiable*.
#
# + [markdown] id="E3upP2oeBk_H"
# For *lognormal* fields, this likelihood changes somewhat. Formally, if a random variable $Y$ has a normal distribution, then the exponential function of $Y$, $X = \exp(Y)$, has a log-normal distribution. We will generate our log-normal fields with a power spectrum such that the *lognormal field has the specified $P_{\rm LN}(k)$*. This means that we need to employ the *backwards conversion formula* , presented by [M. Greiner? and T.A. Enßlin](https://arxiv.org/pdf/1312.1354.pdf), to obtain the correct form for $P_{\rm G}(k)$ needed for the above Fisher evaluation:
# $$ P_{\rm G} = \int d^u x e^{i \textbf{k} \cdot \textbf{x}} \ln \left( \int \frac{d^u q}{(2\pi)^u} e^{i \textbf{q} \cdot \textbf{x}} P_{\rm LN}(\textbf{q}) \right) $$
#
# which we can do numerically (and differentiably !) in `Jax`. If you're curious about the computation, check out [this notebook](https://colab.research.google.com/drive/1beknmt3CwjEDFFnZjXRClzig1sf54aMR?usp=sharing). We performed the computation using a Colab Pro account with increased GPU resources to accomodate such large fields. When the smoke clears, our fields have a fiducial theoretical Fisher information content, $|\textbf{F}|_{(0.4, 0.6)}$ of
#
# det_F = 656705.6827
#
# this can be equivalently expressed in terms of the Shannon information (up to a constant, in nats !) of a Gaussian with covariance matrix $\textbf{F}^{-1}$:
#
# shannon info = 0.5 * np.log(det_F) = 6.6975 # nats
#
#
# When testing our neural IMNN compressor, we used these metrics to verify that we indeed capture the maximal (or close to it) amount of information from our field simulations.
# ____
# + [markdown] id="vkHFh7tX0q6d"
# # Simulating the universe with power spectra
#
# We can now set the simulator arguments, i.e. the $k$-modes to evaluate, the length of the side of a box, the shape of the box and whether to normalise via the volume and squeeze the output dimensions
#
# ## choose $k$-modes (the size of our universe-in-a-box)
# Next, we're going to set our $N$-side to 128 (the size of our data vector), $k$-vector, as well as the $L$-side (the physical dimensions of the universe-in-a-box:
# + id="EwQ5bWIP0q6W"
N = 128
shape = (N, N)
k = np.sqrt(
np.sum(
np.array(
np.meshgrid(
*((np.hstack(
(np.arange(0, _shape // 2 + 1),
np.arange(-_shape // 2 + 1, 0)))
* 2 * np.pi / _shape)**2.
for _shape in shape))),
axis=0))
# + id="GMej-TCB3PBD"
simulator_args = dict(
k=k, # k-vector (grid units)
L=250, # in Mpc h^-1
shape=shape,
vol_norm=True, # whether to normalise P(k) by volume
N_scale=False, # scale field values up or down
squeeze=True,
log_normal=True)
# + [markdown] id="eZde9Q9a0q6T"
# ___
# ## Next, we provide you our universe simulator in `jax`. This is how it works:
# + [markdown] id="xmqRKJZY0q6X"
# ### 2D random field simulator in jax
#
# To create a 2D lognormal random field we can follow these steps:
#
# 1. Generate a $(N_\textrm{pix}\times N_\textrm{pix})$ white noise field $\varphi$ such that $\langle \varphi_k \varphi_{-k} \rangle' = 1$
#
# 2. Fourier Transform $\varphi$ to real space: $R_{\rm white}({\bf x}) \rightarrow R_{\rm white}({\bf k})$
# Note that NumPy's DFT Fourier convention is:
# $$\phi_{ab}^{\bf k} = \sum_{c,d = 0}^{N-1} \exp{(-i x_c k_a - i x_d k_b) \phi^{\bf x}_{cd}}$$
# $$\phi_{ab}^{\bf x} = \frac{1}{N^2}\sum_{c,d = 0}^{N-1} \exp{(-i x_c k_a - i x_d k_b) \phi^{\bf k}_{cd}}$$
#
# 3. Evaluate the chosen power spectrum over a field of $k$ values and do the lognormal transformation:
# $$P_{\rm LN}(k) \gets \ln(1 + P(k)) $$
# Here we need to ensure that this array of amplitudes are Hermitian, e.g. $\phi^{* {\bf k}}_{a(N/2 + b)} = \phi^{{\bf k}}_{a(N/2 - b)}$. This is accomplished by choosing indices $k_a = k_b = \frac{2\pi}{N} (0, \dots, N/2, -N/2+1, \dots, -1)$ (as above) and then evaluating the square root of the outer product of the meshgrid between the two: $k = \sqrt{k^2_a + k^2_b}$. We can then evaluate $P_{\rm LN}^{1/2}(k)$.
#
# 4. Scale white noise $R_{\rm white}({\bf k})$ by the power spectrum:
# $$R_P({\bf k}) = P_{\rm LN}^{1/2}(k) R_{\rm white}({\bf k}) $$
#
# 5. Fourier Transform $R_{P}({\bf k})$ to real space: $R_P({\bf x}) = \int d^d \tilde{k} e^{i{\bf k} \cdot {\bf x}} R_p({\bf k})$
# $$R_{ab}^{\bf x} = \frac{1}{N^2}\sum_{c,d = 0}^{N-1} \exp{(-i x_c k_a - i x_d k_b) R^{\bf k}_{cd}}$$
#
#
# We are going to use a broadcastable jax simultor which takes in a variety of different shaped parameter arrays and vmaps them until a single parameter pair are passed. This is very efficient for generating many simulations at once, for Approximate Bayesian Computation for example.
# + id="01jmpAH60q6Z" cellView="form"
#@title simulator code <font color='lightgreen'>[RUN ME]</font>
def simulator(rng, θ, simulator_args, foregrounds=None):
def fn(rng, A, B):
dim = len(simulator_args["shape"])
L = simulator_args["L"]
if np.isscalar(L):
L = [L] * int(dim)
Lk = ()
shape = ()
for i, _shape in enumerate(simulator_args["shape"]):
Lk += (_shape / L[i],)
if _shape % 2 == 0:
shape += (_shape + 1,)
else:
shape += (_shape,)
k = simulator_args["k"]
k_shape = k.shape
k = k.flatten()[1:]
tpl = ()
for _d in range(dim):
tpl += (_d,)
V = np.prod(np.array(L))
scale = V**(1. / dim)
fft_norm = np.prod(np.array(Lk))
rng, key = jax.random.split(rng)
mag = jax.random.normal(
key, shape=shape)
pha = 2. * np.pi * jax.random.uniform(
key, shape=shape)
# now make hermitian field (reality condition)
revidx = (slice(None, None, -1),) * dim
mag = (mag + mag[revidx]) / np.sqrt(2)
pha = (pha - pha[revidx]) / 2 + np.pi
dk = mag * (np.cos(pha) + 1j * np.sin(pha))
cutidx = (slice(None, -1),) * dim
dk = dk[cutidx]
powers = np.concatenate(
(np.zeros(1),
np.sqrt(P(k, A=A, B=B)))).reshape(k_shape)
if simulator_args['vol_norm']:
powers /= V
if simulator_args["log_normal"]:
powers = np.real(
np.fft.ifftshift(
np.fft.ifftn(
powers)
* fft_norm) * V)
powers = np.log(1. + powers)
powers = np.abs(np.fft.fftn(powers))
fourier_field = powers * dk
fourier_field = jax.ops.index_update(
fourier_field,
np.zeros(dim, dtype=int),
np.zeros((1,)))
if simulator_args["log_normal"]:
field = np.real(np.fft.ifftn(fourier_field)) * fft_norm * np.sqrt(V)
sg = np.var(field)
field = np.exp(field - sg / 2.) - 1.
else:
field = np.real(np.fft.ifftn(fourier_field) * fft_norm * np.sqrt(V)**2)
if simulator_args["N_scale"]:
field *= scale
if foregrounds is not None:
rng, key = jax.random.split(key)
foreground = foregrounds[
jax.random.randint(
key,
minval=0,
maxval=foregrounds.shape[0],
shape=())]
field = np.expand_dims(field + foreground, (0,))
if not simulator_args["squeeze"]:
field = np.expand_dims(field, (0, -1))
return np.array(field, dtype='float32')
if isinstance(θ, tuple):
A, B = θ
else:
A = np.take(θ, 0, axis=-1)
B = np.take(θ, 1, axis=-1)
if A.shape == B.shape:
if len(A.shape) == 0:
return fn(rng, A, B)
else:
keys = jax.random.split(rng, num=A.shape[0] + 1)
rng = keys[0]
keys = keys[1:]
return jax.vmap(
lambda key, A, B: simulator(
key, (A, B), simulator_args=simulator_args))(
keys, A, B)
else:
if len(A.shape) > 0:
keys = jax.random.split(rng, num=A.shape[0] + 1)
rng = keys[0]
keys = keys[1:]
return jax.vmap(
lambda key, A: simulator(
key, (A, B), simulator_args=simulator_args))(
keys, A)
elif len(B.shape) > 0:
keys = jax.random.split(rng, num=B.shape[0])
return jax.vmap(
lambda key, B: simulator(
key, (A, B), simulator_args=simulator_args))(
keys, B)
# + [markdown] id="AVpZ4bX1vX5o"
# By constructing our random field simulator *and* cosmological power spectrum in `Jax`, we have access to *exact numerical derivatives*, meaning we can simulate a *differentiable* universe. Let's visualize what our universe and derivatives look like at our fiducial model below:
# + colab={"base_uri": "https://localhost:8080/", "height": 233} id="bagFMG3HvWPR" cellView="form" outputId="c66d77ce-7c01-431f-e5a1-95a647875c55"
#@title visualize a fiducial universe and gradients <font color='lightgreen'>[run me]</font>
from imnn.utils import value_and_jacrev, value_and_jacfwd
def simulator_gradient(rng, θ, simulator_args=simulator_args):
return value_and_jacrev(simulator, argnums=1, allow_int=True, holomorphic=True)(rng, θ, simulator_args=simulator_args)
simulation, simulation_gradient = value_and_jacfwd(simulator, argnums=1)(rng, θ_fid,
simulator_args=simulator_args)
cmap = 'viridis'
from mpl_toolkits.axes_grid1 import make_axes_locatable
fig,ax = plt.subplots(nrows=1, ncols=3, figsize=(12,15))
im1 = ax[0].imshow(np.squeeze(simulation),
extent=(0,1,0,1), cmap=cmap)
ax[0].title.set_text(r'example fiducial $\rm d$')
divider = make_axes_locatable(ax[0])
cax = divider.append_axes('right', size='5%', pad=0.05)
fig.colorbar(im1, cax=cax, orientation='vertical')
im1 = ax[1].imshow(np.squeeze(simulation_gradient).T[0].T,
extent=(0,1,0,1), cmap=cmap)
ax[1].title.set_text(r'$\nabla_{\Omega_m} \rm d$')
divider = make_axes_locatable(ax[1])
cax = divider.append_axes('right', size='5%', pad=0.05)
fig.colorbar(im1, cax=cax, orientation='vertical')
im1 = ax[2].imshow(np.squeeze(simulation_gradient).T[1].T,
extent=(0,1,0,1), cmap=cmap)
ax[2].title.set_text(r'$\nabla_{\sigma_8} \rm d$')
divider = make_axes_locatable(ax[2])
cax = divider.append_axes('right', size='5%', pad=0.05)
fig.colorbar(im1, cax=cax, orientation='vertical')
for a in ax:
a.set_xticks([])
a.set_yticks([])
plt.show()
# + [markdown] id="CAGm0QbVC3ZC"
# Nice ! Since we can differentiate our universe and power spectrum, we can easily compute gradients of a neural network's outputs with respect to simulation parameters. This will come in handy for compression training.
# + [markdown] id="xXsHguXc0q6h"
# ---
# ## Training an IMNN
#
#
# <img src="https://raw.githubusercontent.com/tlmakinen/FieldIMNNs/master/tutorial/plots/imnn-scheme-white.png" alt="drawing" width="700"/>
#
#
#
# The details behind the IMNN algorithm [can be found here on arxiv](https://arxiv.org/abs/1802.03537), but we'll summarize the gist briefly:
#
#
#
# 1. We want to maximise the Fisher information, $\textbf{F}$, of compressed summaries to satisfy the Cramer-Rao bound:
# $$ \langle (\vartheta_\alpha - \langle \vartheta_\alpha \rangle ) (\vartheta_\beta - \langle \vartheta_\beta
# \rangle) \rangle \geq \textbf{F}^{-1}_{\alpha \beta} $$ which means saturating the Fisher information minimizes the average variance of the parameter estimates.
#
# 2. To do this, and without loss of generality (proof coming soon!) we compute a Gaussian likelihood form to compute our Fisher information:
# $$ -2 \ln \mathcal{L}(\textbf{x} | \textbf{d}) = (\textbf{x} - \boldsymbol{\mu}_f(\vartheta))^T \textbf{C}_f^{-1}(\textbf{x} - \boldsymbol{\mu}_f(\vartheta)) $$ where $\boldsymbol{\mu}_f$ and $\textbf{C}$ are the mean and covariance of the network output (summaries). The Fisher is then $$ \textbf{F}_{\alpha \beta} = {\rm tr} [\boldsymbol{\mu}_{f,\alpha}^T C^{-1}_f \boldsymbol{\mu}_{f, \beta}] $$
#
#
# Since we can differentiate through our neural network *and* simulated universe, we have the exact derivatives with respect to the pipeline we need to compute the Fisher matrix of compressed summaries on-the-fly during compression training.
# ___
#
# ### Q: wait -- what if my simulator isn't differentiable ?
# We don't *need* to have the exact derivatives for IMNN training ! Having the gradients accessible just means that we don't have to optimize finite-differencing for estimating derivatives by hand, however (as is done in the original IMNN paper).
#
#
#
# ___
#
#
# Let's use an IMNN trained on cosmological fields to see how much information we can extract an what sort of constraints we can get. We will use 2000 simulations to estimate the covariance and use all of their derivatives and we'll summarise the whole cosmological field using 2 summaries.
# + id="k7Epjj8x0q6h"
n_s = 200 # number of simulations used to estimate covariance of network outputs
n_d = n_s # number of simulations used to estimate the numerical derivative of
# the mean of the network outputs
n_summaries = 2
# + [markdown] id="W4k8hhqc0q6h"
# We're going to use a fully convolutional inception network built using stax with some custom designed blocks. The inception block itself is implemented in the following block:
# + id="7am2EFoz0q6h" cellView="form"
#@title nn model stuff <font color='lightgreen'>[RUN ME]</font>
def InceptBlock(filters, strides, do_5x5=True, do_3x3=True):
"""InceptNet convolutional striding block.
filters: tuple: (f1,f2,f3)
filters1: for conv1x1
filters2: for conv1x1,conv3x3
filters3L for conv1x1,conv5x5"""
filters1, filters2, filters3 = filters
conv1x1 = stax.serial(stax.Conv(filters1, (1, 1), strides, padding="SAME"))
filters4 = filters2
conv3x3 = stax.serial(stax.Conv(filters2, (1, 1), strides=None, padding="SAME"),
stax.Conv(filters4, (3, 3), strides, padding="SAME"))
filters5 = filters3
conv5x5 = stax.serial(stax.Conv(filters3, (1, 1), strides=None, padding="SAME"),
stax.Conv(filters5, (5, 5), strides, padding="SAME"))
maxpool = stax.serial(stax.MaxPool((3, 3), padding="SAME"),
stax.Conv(filters4, (1, 1), strides, padding="SAME"))
if do_3x3:
if do_5x5:
return stax.serial(
stax.FanOut(4),
stax.parallel(conv1x1, conv3x3, conv5x5, maxpool),
stax.FanInConcat(),
stax.LeakyRelu)
else:
return stax.serial(
stax.FanOut(3),
stax.parallel(conv1x1, conv3x3, maxpool),
stax.FanInConcat(),
stax.LeakyRelu)
else:
return stax.serial(
stax.FanOut(2),
stax.parallel(conv1x1, maxpool),
stax.FanInConcat(),
stax.LeakyRelu)
# + [markdown] id="MKRLdeED0q6i"
# We'll also want to make sure that the output of the network is the correct shape, for which we'll introduce a Reshaping layer
# + id="YquHD15c0q6i"
def Reshape(shape):
"""Layer function for a reshape layer."""
init_fun = lambda rng, input_shape: (shape,())
apply_fun = lambda params, inputs, **kwargs: np.reshape(inputs, shape)
return init_fun, apply_fun
# + [markdown] id="GlGeBKCU0q6i"
# Now we can build the network, with 55 filters and strides of 4 in each direction in each layer
# + id="IoA9MBcX0q6i"
fs = 55
layers = [
InceptBlock((fs, fs, fs), strides=(4, 4)),
InceptBlock((fs, fs, fs), strides=(4, 4)),
InceptBlock((fs, fs, fs), strides=(4, 4)),
InceptBlock((fs, fs, fs), strides=(2, 2), do_5x5=False, do_3x3=False),
stax.Conv(n_summaries, (1, 1), strides=(1, 1), padding="SAME"),
stax.Flatten,
Reshape((n_summaries,))
]
model = stax.serial(*layers)
# + [markdown] id="oxI0na2LnYH4"
# We'll also introduce a function to check our model output:
# + colab={"base_uri": "https://localhost:8080/"} id="JDwaoph0nT1a" outputId="cb3fd847-8530-4815-abfb-96311e583e16"
def print_model(layers, input_shape, rng):
print('input_shape: ', input_shape)
for l in range(len(layers)):
_m = stax.serial(*layers[:l+1])
print('layer %d shape: '%(l+1), _m[0](rng, input_shape)[0])
# print model specs
key,rng = jax.random.split(rng)
input_shape = (1,) + shape + (1,)
print_model(layers, input_shape, rng)
# + [markdown] id="TDYAkDTZ0q6j"
# We'll also grab an adam optimiser from jax.experimental.optimizers
# + id="0ntBKP6y0q6j"
optimiser = optimizers.adam(step_size=1e-3)
# + [markdown] id="TeKHcWo60q6j"
# Note that due to the form of the network we'll want to have simulations that have a "channel" dimension, which we can set up by not allowing for squeezing in the simulator.
# + [markdown] id="8sTk71Az0q6j"
# ### Load an IMNN
#
# Finally we can load a pre-trained IMNN and compare its compression efficiency to the theoretical Fisher. We will pull the weights and state from the parent repository and calculate the compressor statistics.
#
# We've used a SimulatorIMNN trained on new simulations on-the-fly, eliminating the need for a validation dataset. If you're interested in the IMNN training, see the [benchmarking Colab notebook](https://colab.research.google.com/drive/1_y_Rgn3vrb2rlk9YUDUtfwDv9hx774ZF#scrollTo=EW4H-R8I0q6n) or the Bonus challenge at the end of this tutorial.
#
# We're not training an IMNN here because this model takes $\approx 50$ minutes and requires elevated Colab Pro resources.
#
# + colab={"base_uri": "https://localhost:8080/"} id="pbw6yffLI34o" outputId="ad6cf4a2-8341-462a-dfa7-6d87d582c342"
# !git clone https://github.com/tlmakinen/FieldIMNNs.git
# + id="4_JRBMkq9cnd"
# load IMNN state
import cloudpickle as pickle
import os
def unpickle_me(path):
file = open(path, 'rb')
return pickle.load(file)
folder_name = './FieldIMNNs/tutorial/IMNN-aspects/'
loadstate = unpickle_me(os.path.join(folder_name, 'IMNN_state'))
state = jax.experimental.optimizers.pack_optimizer_state(loadstate)
startup_key = np.load(os.path.join(folder_name, 'IMNN_startup_key.npy'), allow_pickle=True)
# load weights to set the IMNN
best_weights = np.load(os.path.join(folder_name, 'best_w.npy'), allow_pickle=True)
# + id="b0N3AJUb0q6k" colab={"base_uri": "https://localhost:8080/"} outputId="212b0fac-9474-47a8-849c-50cb6a61fa00"
# initialize IMNN with pre-trained state
rng, key = jax.random.split(rng)
IMNN = imnn.IMNN(
n_s=n_s,
n_d=n_d,
n_params=n_params,
n_summaries=n_summaries,
input_shape=(1,) + shape + (1,),
θ_fid=θ_fid,
model=model,
optimiser=optimiser,
key_or_state=state, # <---- initialize with state
simulator=lambda rng, θ: simulator(
rng, θ, simulator_args={
**simulator_args,
**{"squeeze": False}}))
# + id="gwhdYReuJjC2"
# now set weights using the best training weights and startup key (this can take a moment)
IMNN.set_F_statistics(w=best_weights, key=startup_key)
# + colab={"base_uri": "https://localhost:8080/"} id="I2_V5Zeb4k2s" outputId="325d06c9-bbdb-454f-dd6c-6ce9bf601ef1"
print('det F from IMNN:', np.linalg.det(IMNN.F))
# + colab={"base_uri": "https://localhost:8080/"} id="8s_Dq4SkXjmL" outputId="81730bc9-7556-4533-a861-951cc1b327ac"
print('% Fisher information captured by IMNN compared to theory: ', np.linalg.det(IMNN.F) / 656705.6827)
# + [markdown] id="GytXZMR-0q6k"
# ### if you want to check out how to train an IMNN, see the end of the tutorial !
# + [markdown] id="cMSDyTLxzuG-"
# ---
# # Inference on a target cosmological field
#
# Now that we have a trained compression function (albeit at a somewhat arbitrary fiducial model), we can now perform simulation-based inference with the optimal summaries.
#
# We'll now pretend to "observe" a cosmological density field at some target parameters, $\theta_{\rm target}$. We'll select $\Omega_c=0.25$ and $\sigma_8=0.81$ (measured 2015 Planck parameters). To get started with this tutorial, we'll load a pre-generated field from the GitHub ("field 2" from our paper !), but you can always generate a new realization with the simulator code.
# + colab={"base_uri": "https://localhost:8080/", "height": 284} id="Yp8n88SmfHgB" outputId="8a09c1b8-75e4-4126-d0d4-5d24810aff7e"
θ_target = np.array([jc.Planck15().Omega_c, jc.Planck15().sigma8,])
δ_target = np.load('./FieldIMNNs/tutorial/target_field_planck.npy')
sns.set() # set up plot settings
cmap='viridis'
plt.imshow(δ_target, cmap=cmap)
plt.colorbar()
plt.title('target cosmological field')
plt.show()
# + [markdown] id="Rl3g7Wdo6iR7"
# Now we're going to **forget we ever knew our choice of target parameters** and do inference on this target data as if it were a real observation (minus measurement noise for now, of course !)
# + [markdown] id="gmtIjHx70q6m"
# ## Inference
#
# We can now attempt to do inference of some target data using the IMNN.
#
# First we're going to compress our target field down to parameter estimates using the IMNN method `IMNN.get_estimate(d)`. What this code does is returns the score estimator for the parameters, obtained via the transformation
# $$ \hat{\theta}_{\alpha} = \theta^{\rm fid}_\alpha + \textbf{F}^{-1}_{\alpha \beta} \frac{\partial \mu_i}{\partial \theta_\beta} \textbf{C}^{-1}_{ij} \textbf({x}(\textbf{w}, \textbf{d}) - {\mu})_j $$
# where ${x}(\textbf{w}, \textbf{d})$ are the network summaries.
#
# + colab={"base_uri": "https://localhost:8080/"} id="xpMjW-bh67_Z" outputId="23e3deff-4b8f-4cb4-a03e-de3ba55220b5"
estimates = IMNN.get_estimate(np.expand_dims(δ_target, (0, 1, -1)))
print('IMNN parameter estimates:', estimates)
# + [markdown] id="6g5z7Bwq7DO5"
# The cool thing about training an IMNN is that it *automatically* gives you a simple uncertainty estimate on the parameters of interest via the optimal Fisher matrix. We can make a Gaussian approximation to the likelihood using the inverse of the matrix.
#
# Note that to demonstrate robustness, the fiducial parameter values are deliberately far from the target parameters that this estimate of the Fisher information as the covariance will likely be misleading.
#
# We'll need to select a prior distribution first. We'll do this in `tfpj`, selecting wide uniform priors for both $\Omega_c$ and $\sigma_8$.
# + id="ZfRMlrhA7atE"
prior = tfpj.distributions.Blockwise(
[tfpj.distributions.Uniform(low=low, high=high)
for low, high in zip([0.01, 0.2], [1.0, 1.3])])
prior.low = np.array([0.01, 0.])
prior.high = np.array([1.0, 1.3])
# + [markdown] id="xIdAh0_B7lRc"
# Then we can use the IMNN's built-in Gaussian approximation code:
# + id="DGirnJvV0q6m" colab={"base_uri": "https://localhost:8080/", "height": 613} outputId="0479b8b5-bce9-465e-8c85-de576faa4fba"
sns.set()
GA = imnn.lfi.GaussianApproximation(
parameter_estimates=estimates,
invF=np.expand_dims(np.linalg.inv(IMNN.F), 0),
prior=prior,
gridsize=100)
ax = GA.marginal_plot(
known=θ_target,
label="Gaussian approximation",
axis_labels=[r"$\Omega_c$", r"$\sigma_8$"],
colours="C1");
# + [markdown] id="jtQwSMCu0q6m"
# Even though our fiducial model was trained far away $(\Omega_c, \sigma_8) = (0.4, 0.6)$, our score esimates (center of our ellipse) are very close to the target Planck (crosshairs).
#
# we now have a compression and informative summaries of our target data. We'll next proceed to setting up density estimation to construct our posteriors !
#
# + [markdown] id="US9B5J7478H8"
# ___
# # Posterior Construction with DELFI
#
# Density Estimation Likelihood-Free Inference (DELFI) is presented formally [here on arxiv](https://arxiv.org/abs/1903.00007), but we'll give you the TLDR here:
#
# Now that we have nonlinear IMNN summaries, $\textbf{x}$, to describe our cosmological fields, we can perform density estimation to model the *summary data likelihood*, $p(\textbf{x} | \boldsymbol{\theta})$. Once we have this, we can obtain the posterior distribution for $\boldsymbol{\theta}$ via Bayes' rule:
# $$ p(\boldsymbol{\theta} | \textbf{x}) \propto p(\textbf{x} | \boldsymbol{\theta}) p(\boldsymbol{\theta}) $$.
#
# ## What are CMAFs ?
#
#
# DELFI provides Conditional Masked Autoregressive Flows (CMAFs) are stacks of neural autoencoders carefully masked to parameterize the summary-parameter likelihood. To start, note that any probability density can be factored as a product of one-dimensional conditional distributions via the chain rule of probability:
# \begin{equation}
# p(\textbf{x} | \boldsymbol{\theta}) = \prod_{i=1}^{\dim(\textbf{x})} p({\rm x}_i | \textbf{x}_{1:i-1}, \boldsymbol{\theta})
# \end{equation}
# Masked Autoencoders for density estimation (MADE) model each of these one-dimensional conditionals as Gaussians with mean and variance parameters parameterized by neural network weights, $\textbf{w}$. The neural network layers are masked in such a way that the autoregressive property is preserved, e.g. the output nodes for the density $p({\rm x}_i | \textbf{x}_{1:i-1}, \boldsymbol{\theta})$ *only* depend on $\textbf{x}_{1:i-1}$ and $\boldsymbol{\theta}$, satisfying the chain rule.
#
#
# We can then stack a bunch of MADEs to form a neural flow for our posterior !
# 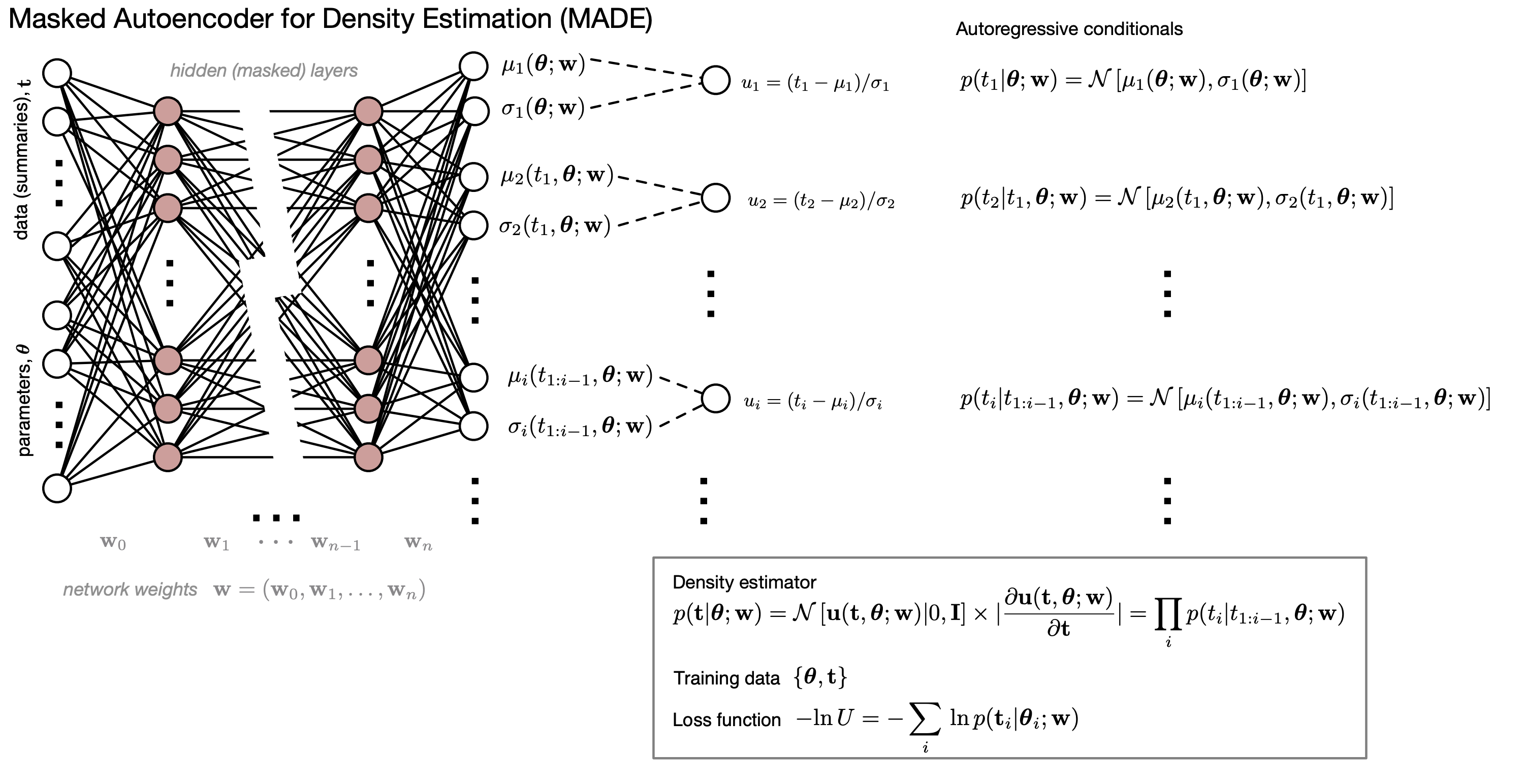
#
#
#
# What we're going to do is
#
# 1. Train a Conditional Masked Autoregressive Flow to parameterize $p(\textbf{x} | \boldsymbol{\theta})$ to minimize the log-probability, $-\ln U$.
# 2. Use an affine MCMC sampler to draw from the posterior at the target summaries, $\textbf{x}^{\rm target}$
# 3. Append training data from the posterior and re-train MAFs.
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="L4MMNuGa_e2o" outputId="3f1109b3-2cf7-431f-8a15-3922fd75fc67"
# !pip install -q getdist
# !pip install -q corner
# !pip install -q chainconsumer
import keras
import tensorflow.keras.backend as K
import time
from tqdm import tqdm
from chainconsumer import ChainConsumer
# + [markdown] id="0k9-YBMgVbVx"
# (ignore the red error message)
# + [markdown] id="A6HIT91oGK4W"
# We'll set up the same prior as before, this time in regular `tensorflow-probability`. This means that our CMAFs can talk to our prior draws in the form of tensorflow tensors.
# + id="uxV82kpN_ftx"
# set up prior in non-jax tfp
samp_prior = tfp.distributions.Blockwise(
[tfp.distributions.Uniform(low=low, high=high)
for low, high in zip([0.01, 0.2], [1.0, 1.3])])
samp_prior.low = np.array([0.01, 0.])
samp_prior.high = np.array([1.0, 1.3])
# + id="hC0jrI3sAWPm" cellView="form"
#@title set up the CMAF code <font color='lightgreen'>[RUN ME]</font>
class ConditionalMaskedAutoregressiveFlow(tf.Module):
def __init__(self, n_dimensions=None, n_conditionals=None, n_mades=1, n_hidden=[50,50], input_order="random",
activation=keras.layers.LeakyReLU(0.01),
all_layers=True,
kernel_initializer=keras.initializers.RandomNormal(mean=0.0, stddev=1e-5, seed=None),
bias_initializer=keras.initializers.RandomNormal(mean=0.0, stddev=1e-5, seed=None),
kernel_regularizer=None, bias_regularizer=None, kernel_constraint=None,
bias_constraint=None):
super(ConditionalMaskedAutoregressiveFlow, self).__init__('hi')
# extract init parameters
self.n_dimensions = n_dimensions
self.n_conditionals = n_conditionals
self.n_mades = n_mades
# construct the base (normal) distribution
self.base_distribution = tfd.MultivariateNormalDiag(loc=tf.zeros(self.n_dimensions), scale_diag=tf.ones(self.n_dimensions))
# put the conditional inputs to all layers, or just the first layer?
if all_layers == True:
all_layers = "all_layers"
else:
all_layers = "first_layer"
# construct stack of conditional MADEs
self.MADEs = [tfb.AutoregressiveNetwork(
params=2,
hidden_units=n_hidden,
activation=activation,
event_shape=[n_dimensions],
conditional=True,
conditional_event_shape=[n_conditionals],
conditional_input_layers=all_layers,
input_order=input_order,
kernel_initializer=kernel_initializer,
bias_initializer=bias_initializer,
kernel_regularizer=kernel_regularizer,
bias_regularizer=bias_regularizer,
kernel_constraint=kernel_constraint,
bias_constraint=bias_constraint,
) for i in range(n_mades)
]
# bijector for x | y (chain the conditional MADEs together)
def bijector(self, y):
# start with an empty bijector
MAF = tfb.Identity()
# pass through the MADE layers (passing conditional inputs each time)
for i in range(self.n_mades):
MAF = tfb.MaskedAutoregressiveFlow(shift_and_log_scale_fn=lambda x: self.MADEs[i](x, conditional_input=y))(MAF)
return MAF
# construct distribution P(x | y)
def __call__(self, y):
return tfd.TransformedDistribution(
self.base_distribution,
bijector=self.bijector(y))
# log probability ln P(x | y)
def log_prob(self, x, y):
return self.__call__(y).log_prob(x)
# sample n samples from P(x | y)
def sample(self, n, y):
# base samples
base_samples = self.base_distribution.sample(n)
# biject the samples
return self.bijector(y).forward(base_samples)
# + [markdown] id="jA_kkoNFKVdC"
# If you're curious about how the MCMC sampler and CMAF code work, feel free to double-click the hidden cells above. We'll walk through the gist of how each module works though:
#
# The `ConditionalMaskedAutoregressiveFlow` API functions similarly to other `tfp` distributions. To set up a model we need to choose a few aspects of the flow. We first need to choose how many MADEs we want to stack to form our flow, `n_mades`. To set up a model with three MADEs, two parameters (`n_dimensions`) and two conditionals (`n_conditionals`), and two hidden layers of 50 neurons per MADE, we'd call:
#
# my_CMAF = ConditionalMaskedAutoregressiveFlow(n_dimensions=2, n_conditionals=2, n_mades=3, n_hidden=[50,50])
#
#
# What's cool is that this module works just like a `tfp.distributions` function, which means that we can call a log-probability, $p(x | y)$ *conditional* on some $y$-value:
#
# key,rng = jax.random.split(rng)
# n_samples = 1
# x = prior.sample(sample_shape=(n_samples,), seed=key)
# y = np.array([0.3, 0.4])
# logU = my_CMAF.log_prob(x, y)
#
# We're going to work with this basic syntax to set up useful DELFI dictionaries to store useful aspects.
# + [markdown] id="-ijjYbTYAeHY"
# ___
# # Exercise 0: initialize models for target data
#
# Now we're going to initialize several CMAF models for our piece of target data. Using multiple (and varied) deep learning architectures for the same problem is called the "deep ensemble" technique ([see this paper for an overview](https://papers.nips.cc/paper/2017/file/9ef2ed4b7fd2c810847ffa5fa85bce38-Paper.pdf)).
#
# When setting up DELFI, it's important to remember that each ensemble of CMAFs ought to be generated *per piece of target data*, since we're interested in observing the "slice" of parameter space that gives us each datum's posterior. Since these models are written in Tensorflow, we don't have to worry about specifying a random key or initialization for the model like we do in `Jax`.
#
#
# 1. Declare a `DELFI` dictionary to store the following aspects:
# - a list of CMAF models
# - a list of optimizers
# - a training dataset
# - a validation dataset
# - the IMNN estimates
#
# 2. Initialize `num_models=2` models, each with `n_mades=3` MADEs. Try one set of MADEs with two layers of 50 neurons, and another with three layers. See if you can set up their respective optimizers (we'll use `tf.keras.optimizers.Adam()` with a learning rate of $10^-3$.
#
#
# ## note: remove all `pass` arguments to functions to make them runnable !
# + id="7YpTcSeHHD5j"
DELFI = {
}
# + id="4NIILG9pAcLO" cellView="form"
#@title Ex. 0 solution <font color='lightgreen'>[run me to proceed]</font>
num_targets = 1
# set up list of dictionaries for the target datum
DELFI = {
'MAFs': None, # list of CAMF models
'opts': [], # list of optimizers
'posts':[], # list of MAF posteriors
'train_data': None, # training dataset
'val_data': None, # validation dataset
'train_losses' : [], # losses
'val_losses' : [],
'estimates': estimates,
'target_data' : δ_target,
'F_IMNN': IMNN.F,
'θ_target': θ_target,
}
# number of CMAFs per DELFI ensemble
num_models = 2
n_hiddens = [[50,50], [50,50]] # try different architectures
DELFI['MAFs'] = [ConditionalMaskedAutoregressiveFlow(n_dimensions=2, n_mades=3,
n_conditionals=2, n_hidden=n_hiddens[i]) for i in range(num_models)]
DELFI['opts'] = [tf.keras.optimizers.Adam(learning_rate=1e-3) for i in range(num_models)]
# + [markdown] id="BS2zXxjRMGZT"
# ___
# # Exercise 1: define train and validation steps
#
# Here we want to define tensorflow function training and validation steps that we'll later call in a loop to train each CMAF model in the DELFI ensemble.
#
# 1. set up the log posterior loss: $-\ln U = -\ln p(x | y) - \ln p(y)$ where $y=\theta$ are our parameters.
#
# *hint*: try the `samp_prior.log_prob()` call on a few data
# 2. obtain gradients, `grads` with respect to the scalar loss
# 3. update each optimizer with the call `optimizer.apply_gradients(zip(grads, model.trainable_variables)`
#
# + id="b3Mv5esBGNi4"
# define loss function -ln U
def logloss(x, y, model, prior):
pass
# + id="CVl6UgrtHyIa" cellView="form"
#@title Ex. 1 solution <font color='lightgreen'>[run me to proceed]</font>
# define loss function
def logloss(x, y, model):
return - model.log_prob(x,y) - samp_prior.log_prob(y)
# + [markdown] id="egUJJBIEGCpG"
# Now that we have our loss defined, we can use it to train our CMAFs via backpropagation:
# + id="ypdgOXYD5LGO"
@tf.function
def train_step(x, y, ensemble, opts):
losses = []
# loop over models in ensemble
for m in range(len(ensemble)):
with tf.GradientTape() as tape:
# get loss across batch using our log-loss function
loss = K.mean(logloss(x, y, ensemble[m]))
losses.append(loss)
grads = tape.gradient(loss, ensemble[m].trainable_variables)
opts[m].apply_gradients(zip(grads, ensemble[m].trainable_variables))
return losses
@tf.function
def val_step(x, y, ensemble):
val_l = []
for m in range(len(ensemble)):
loss = K.mean(logloss(x, y, ensemble[m]))
val_l.append(loss)
return val_l
# + [markdown] id="15Py8hyB8TnQ"
# ___
#
# # Exercise 2: create some dataset functions
# Here we want to create the dataset of $(\textbf{x}, \boldsymbol{\theta})$ pairs to train our CMAFs on. Write a function that:
# 1. generate simulations (with random keys) from sampled parameter pairs, $\theta$. We've set up the key-splitting and simulator code for you.
# 2. feed simulations through `IMNN.get_estimate()` to get summaries, $\textbf{x}$
# 3. try to use `jax.vmap()` the above to do this efficiently !
#
# + id="60cYDWQsdYTW" cellView="form"
#@title hints for vmapping:
# for a function `my_fn(a, x)`, you can vmap, "vector map" over a set of array values as follows:
def my_fn(x, a, b):
return a*x**3 - x + b
# define a slope and intercept
a = 0.5
b = 1.0
# define our x-values
x = np.linspace(-10,10, num=100)
# define a mini function that only depends on x
mini_fn = lambda x: my_fn(x, a=a, b=b)
y = jax.vmap(mini_fn)(x)
plt.plot(x, y)
plt.xlabel('$x$')
plt.ylabel('$y$')
# + id="lkaICdxKZ3VE"
def get_params_summaries(key, θ_samp, simulator=simulator):
"""
function for generating (x,θ) pairs from IMNN compression
over the prior range
θ_samp: array of sampled parameters over prior range
simulator: function for simulating data to be compressed
"""
n_samples = θ_samp.shape[0]
# we'll split up the keys for you
keys = np.array(jax.random.split(key, num=n_samples))
# next define a simulator that takes a key as argument
my_simulator = lambda rng, θ: simulator(
rng, θ, simulator_args={
**simulator_args,
**{"squeeze": False}})
# generate data, vmapping over the random keys and parameters:
# d =
# generate summaries
# x =
# return paired training data
pass
# + id="CPGNWlf2JfL6" cellView="form"
#@title Ex. 2 solution <font color='lightgreen'>[run me to proceed]</font>
def get_params_summaries(key, n_samples, θ_samp, simulator=simulator):
keys = np.array(jax.random.split(key, num=n_samples))
sim = lambda rng, θ: simulator(
rng, θ, simulator_args={
**simulator_args,
**{"squeeze": False}})
# generate a bunch of fields over the prior ranges
d = jax.vmap(sim)(keys, θ_samp)
# compress fields to summaries
x = IMNN.get_estimate(d)
return x, θ_samp
# + id="uJS-nw-FfL2G"
def get_dataset(data, batch_size=20, buffer_size=1000, split=0.75):
"""
helper function for creating tensorflow dataset for CMAF training.
data: pair of vectors (x, θ) = (x, y)
batch_size: how many data pairs per gradient descent
buffer_size: what chunk of the dataset to shuffle (default: random)
split: train-validation split
"""
x,y = data
idx = int(len(x)*split)
x_train = x[:idx]
y_train = y[:idx]
x_val = x[idx:]
y_val = y[idx:]
# Prepare the training dataset.
train_dataset = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_dataset = train_dataset.shuffle(buffer_size=buffer_size).batch(batch_size)
# Prepare the validation dataset.
val_dataset = tf.data.Dataset.from_tensor_slices((x_val, y_val))
val_dataset = val_dataset.batch(batch_size)
return train_dataset, val_dataset
# + [markdown] id="0cpcCCuFgPIR"
# # Visualize compressed summaries at fiducial model and over the prior
#
# Now that we a function that can take in parameter vectors, generates simulations, and then compresses them into summaries, we can visualize how the IMNN compresses the fields in summary space. We will visualize:
# 1. compressed simulations run at the fiducial model ($\Omega_c, \sigma_8)$ = (0.4, 0.6)
# 2. compressed simulations at the target model ($\Omega_c, \sigma_8)$ = (0.2589, 0.8159)
# 3. compressed simulations run across the full (uniform) prior range
# + colab={"base_uri": "https://localhost:8080/", "height": 301} id="BI5m5WYIhFMr" outputId="c0be00e8-afce-4dbe-e76a-879924cbf316"
n_samples = 1000
buffer_size = n_samples
key1,key2 = jax.random.split(rng)
# params over the prior range
θ_samp = prior.sample(sample_shape=(n_samples,), seed=key1)
xs, θ_samp = get_params_summaries(key2, n_samples, θ_samp)
# fiducial params
key,rng = jax.random.split(key1)
_θfids = np.repeat(np.expand_dims(θ_fid, 1), 1000, axis=1).T
xs_fid, _ = get_params_summaries(key, n_samples, _θfids)
# target params
_θtargets = np.repeat(np.expand_dims(θ_target, 1), 1000, axis=1).T
xs_target, _ = get_params_summaries(key, n_samples, _θtargets)
plt.scatter(xs.T[0], xs.T[1], label='prior', s=5, alpha=0.7)
plt.scatter(xs_fid.T[0], xs_fid.T[1], label='fiducial', s=5, marker='*', alpha=0.7)
plt.scatter(xs_target.T[0], xs_target.T[1], label='target', s=5, marker='+', alpha=0.7)
plt.title('summary scatter')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.xlim(-1.0, 2.0)
plt.legend()
plt.show()
# + [markdown] id="QvsrzBP8I1kX"
# ### Q: Wait, why is our prior in summary space not uniform (rectangular) ?
# Remember, we've passed our parameters through our simulator, and our simulations through the IMNN compressor, meaning our summaries are nonlinear (weirdly-shaped). These score estimates obtained from the IMNN is are quick and convenient, but can be biased and suboptimal if the fiducial model is far from the truth.
#
# Even then, these IMNN score summaries can be used for likelihood-free inference to give consistent posterior estimates, albeit with some information loss (since we haven't compressed near the target).
#
# + [markdown] id="sY34U9HokDZ-"
# ---
# ## Now, onto the good bit--CMAF training !
#
# ### Generate our training dataset
# We're going to call our dataset functions to create a dataset of $(\textbf{x}, \boldsymbol{\theta})$ of shape $((1000, 2), (1000, 2))$.
# + id="yPmw6ZXAKDxl"
n_samples = 1000
batch_size = 100
buffer_size = n_samples
key1,key2 = jax.random.split(rng)
# sample from the tfpj prior so that we can specify the key
# and stay in jax.numpy:
θ_samp = prior.sample(sample_shape=(n_samples,), seed=key1)
# generate sims and compress to summaries
ts, θ_samp = get_params_summaries(key2, n_samples, θ_samp)
data = (ts, θ_samp)
# use the dataset function
train_dataset, val_dataset = get_dataset(data, batch_size=batch_size, buffer_size=buffer_size)
DELFI['train_dataset'] = train_dataset
DELFI['val_dataset'] = val_dataset
# + [markdown] id="_-v220UOOPnF"
# Next let's define a training loop for a set number of epochs, calling our training and validation step functions.
#
# ___
#
# # Exercise 3: define training loop
# We're going to use the `train_step` functions to train our CMAF models for a set number of epochs.
# + id="LpNQYEVxw2xk"
def training_loop(delfi, epochs=2000):
"""training loop function that updates optimizers and
stores training history"""
# unpack our dictionary's attributes
ensemble = delfi['MAFs']
opts = delfi['opts']
train_dataset = delfi['train_dataset']
val_dataset = delfi['val_dataset']
for epoch in tqdm(range(epochs)):
# shuffle training data anew every 50th epoch (done for you)
if epoch % 50 == 0:
train_dataset = train_dataset.shuffle(buffer_size=buffer_size)
# Iterate over the batches of the dataset.
for step, (x_batch_train, y_batch_train) in enumerate(train_dataset):
# 1) call train step and capture loss value
pass
# 2) store loss value
# Run a validation loop at the end of each epoch.
for x_batch_val, y_batch_val in val_dataset:
# 3) call val step and capture loss value
pass
# 4) store validation loss value
pass
# + id="gdXUyG5KOP8j" cellView="form"
#@title Ex. 3 solution <font color='lightgreen'>[run me to proceed]</font>
def training_loop(delfi, epochs=2000):
"""training loop function that updates optimizers and
stores training history"""
# unpack our dictionary's attributes
ensemble = delfi['MAFs']
opts = delfi['opts']
train_dataset = delfi['train_dataset']
val_dataset = delfi['val_dataset']
for epoch in tqdm(range(epochs)):
# shuffle training data anew every 50th epoch
if epoch % 50 == 0:
train_dataset = train_dataset.shuffle(buffer_size=buffer_size)
# Iterate over the batches of the dataset.
for step, (x_batch_train, y_batch_train) in enumerate(train_dataset):
# call train step and capture loss value
loss_values = train_step(x_batch_train, y_batch_train, ensemble, opts)
# store loss value
delfi['train_losses'].append(loss_values)
# Run a validation loop at the end of each epoch.
for x_batch_val, y_batch_val in val_dataset:
# call val step and capture loss value
val_loss = val_step(x_batch_val, y_batch_val, ensemble)
# store validation loss value
delfi['val_losses'].append(val_loss)
# + id="t6JZfTFPbzbZ" cellView="form"
#@title define some useful plotting functions <font color='lightgreen'>[run me]</font>
# visualize training trajectories
def plot_trajectories(delfis, num_models=4, num_targets=4):
"""code for plotting training trajectories. note that num_targets should be
equal to len(delfis)"""
if num_targets > 1:
fig,axs = plt.subplots(ncols=num_models, nrows=num_targets, figsize=(8,8))
for i,d in enumerate(delfis):
for j in range(num_models):
axs[i,j].plot(np.array(d['train_losses']).T[j], label='train')
axs[i,j].plot(np.array(d['val_losses']).T[j], label='val')
if j == 0:
axs[i,j].set_ylabel(r'$p(t\ |\ \vartheta; w)$')
if i == num_models-1:
axs[i,j].set_xlabel(r'num epochs')
else:
fig,axs = plt.subplots(ncols=num_models, nrows=num_targets, figsize=(7,3))
d = delfis
for j in range(num_models):
axs[j].plot(np.array(d['train_losses']).T[j], label='train')
axs[j].plot(np.array(d['val_losses']).T[j], label='val')
if j == 0:
#axs[j].set_ylabel(r'$p(t\ |\ \vartheta; w)$')
axs[j].set_ylabel(r'$-\ln U$')
axs[j].set_xlabel(r'num epochs')
axs[j].set_title('CMAF model %d'%(j + 1))
# if i == num_models-1:
# axs[j].set_xlabel(r'\# epochs')
plt.legend()
plt.tight_layout()
plt.show()
# then visualize all posteriors
def plot_posts(delfis, params, num_models=4, num_targets=4,
Fisher=None, estimates=estimates, truth=None):
fig,ax = plt.subplots(ncols=num_models, nrows=num_targets, figsize=(7,4))
params = [r'$\Omega_c$', r'$\sigma_8$']
if num_targets > 1:
for i,delfi in enumerate(delfis):
for j in range(num_models):
cs = ChainConsumer()
cs.add_chain(delfi['posts'][j], parameters=params, name='DELFI + IMNN') #, color=corner_colors[0])
#cs.add_covariance(θ_target, -Finv_analytic, parameters=params, name="Analytic Fisher", color=corner_colors[2])
cs.configure(linestyles=["-", "-", "-"], linewidths=[1.0, 1.0, 1.0], usetex=False,
shade=[True, True, False], shade_alpha=[0.7, 0.6, 0.], tick_font_size=8)
cs.plotter.plot_contour(ax[i, j], r"$\Omega_c$", r"$\sigma_8$")
ax[i, j].axvline(θ_target[0], linestyle=':', linewidth=1)
ax[i, j].axhline(θ_target[1], linestyle=':', linewidth=1)
ax[i,j].set_ylim([prior.low[1], prior.high[1]])
ax[i,j].set_xlim([prior.low[0], prior.high[0]])
else:
delfi = delfis
for j in range(num_models):
cs = ChainConsumer()
cs.add_chain(delfi['posts'][j], parameters=params, name='DELFI + IMNN')
if Fisher is not None:
cs.add_covariance(np.squeeze(estimates), np.linalg.inv(Fisher),
parameters=params, name="Fisher", color='k')
cs.configure(linestyles=["-", "-", "-"], linewidths=[1.0, 1.0, 1.0], usetex=False,
shade=[True, False, False], shade_alpha=[0.7, 0.6, 0.], tick_font_size=8)
cs.plotter.plot_contour(ax[j], r"$\Omega_c$", r"$\sigma_8$")
if truth is not None:
ax[j].axvline(truth[0], linestyle=':', linewidth=1, color='k')
ax[j].axhline(truth[1], linestyle=':', linewidth=1, color='k')
ax[j].set_ylim([prior.low[1], prior.high[1]])
ax[j].set_xlim([prior.low[0], prior.high[0]])
ax[j].set_xlabel(params[0])
ax[j].set_ylabel(params[1])
ax[j].set_title('CMAF model %d'%(j+1))
plt.legend()
plt.tight_layout()
plt.show()
return ax
# + [markdown] id="nshsRqUxi-lm"
# ### train our CMAF models !
# + colab={"base_uri": "https://localhost:8080/"} id="qJuyjVCSK3Ws" outputId="5861ae82-4ecc-4b31-a293-392aea038d63"
# train both models with the training loop
epochs = 2000
training_loop(DELFI, epochs=epochs)
# + colab={"base_uri": "https://localhost:8080/", "height": 221} id="Sy0-hJX8MvBW" outputId="80d1d905-97f6-47a4-f251-dea7f6670be0"
# visualize training trajectories
import seaborn as sns
# %matplotlib inline
sns.set_theme()
plot_trajectories(DELFI, num_models=2, num_targets=1)
# + [markdown] id="d1Zi1m2xyaBH"
# # Exercise 4: using the affine MCMC sampler
# Now that we have trained CMAF models with which to compute $p(x | \theta)$, we now need to set up an efficient MCMC sampler to draw from the posterior, $p(x | \theta) \times p(\theta)$. We can do this using the `affine_sample()` sampler, included in `pydelfi` package. This code is written in Tensorflow, adapted from the [`emcee` package](https://arxiv.org/abs/1202.3665), and can be called with only a few lines of code:
#
# # initialize walkers...
# walkers1 = tf.random.normal([n_walkers, 2], (a, b), sigma)
# walkers2 = tf.random.normal([n_walkers, 2], (a, b), sigma)
#
# # sample using affine
# chains = affine_sample(log_prob, n_params, n_walkers, n_steps, walkers1, walkers2)
#
# 1. First we'll need to set up our log-probability for the posterior. Write a function `log_posterior()` that returns a probability given $x$ and a conditional $y$:
#
#
# + id="ro6EP906_ifQ" cellView="form"
#@title set up the affine MCMC sampler <font color='lightgreen'>[run me]</font>
from tqdm import trange
import numpy as onp
def affine_sample(log_prob, n_params, n_walkers, n_steps, walkers1, walkers2):
# initialize current state
current_state1 = tf.Variable(walkers1)
current_state2 = tf.Variable(walkers2)
# initial target log prob for the walkers (and set any nans to -inf)...
logp_current1 = log_prob(current_state1)
logp_current2 = log_prob(current_state2)
logp_current1 = tf.where(tf.math.is_nan(logp_current1), tf.ones_like(logp_current1)*tf.math.log(0.), logp_current1)
logp_current2 = tf.where(tf.math.is_nan(logp_current2), tf.ones_like(logp_current2)*tf.math.log(0.), logp_current2)
# holder for the whole chain
chain = [tf.concat([current_state1, current_state2], axis=0)]
# MCMC loop
with trange(1, n_steps) as t:
for epoch in t:
# first set of walkers:
# proposals
partners1 = tf.gather(current_state2, onp.random.randint(0, n_walkers, n_walkers))
z1 = 0.5*(tf.random.uniform([n_walkers], minval=0, maxval=1)+1)**2
proposed_state1 = partners1 + tf.transpose(z1*tf.transpose(current_state1 - partners1))
# target log prob at proposed points
logp_proposed1 = log_prob(proposed_state1)
logp_proposed1 = tf.where(tf.math.is_nan(logp_proposed1), tf.ones_like(logp_proposed1)*tf.math.log(0.), logp_proposed1)
# acceptance probability
p_accept1 = tf.math.minimum(tf.ones(n_walkers), z1**(n_params-1)*tf.exp(logp_proposed1 - logp_current1) )
# accept or not
accept1_ = (tf.random.uniform([n_walkers], minval=0, maxval=1) <= p_accept1)
accept1 = tf.cast(accept1_, tf.float32)
# update the state
current_state1 = tf.transpose( tf.transpose(current_state1)*(1-accept1) + tf.transpose(proposed_state1)*accept1)
logp_current1 = tf.where(accept1_, logp_proposed1, logp_current1)
# second set of walkers:
# proposals
partners2 = tf.gather(current_state1, onp.random.randint(0, n_walkers, n_walkers))
z2 = 0.5*(tf.random.uniform([n_walkers], minval=0, maxval=1)+1)**2
proposed_state2 = partners2 + tf.transpose(z2*tf.transpose(current_state2 - partners2))
# target log prob at proposed points
logp_proposed2 = log_prob(proposed_state2)
logp_proposed2 = tf.where(tf.math.is_nan(logp_proposed2), tf.ones_like(logp_proposed2)*tf.math.log(0.), logp_proposed2)
# acceptance probability
p_accept2 = tf.math.minimum(tf.ones(n_walkers), z2**(n_params-1)*tf.exp(logp_proposed2 - logp_current2) )
# accept or not
accept2_ = (tf.random.uniform([n_walkers], minval=0, maxval=1) <= p_accept2)
accept2 = tf.cast(accept2_, tf.float32)
# update the state
current_state2 = tf.transpose( tf.transpose(current_state2)*(1-accept2) + tf.transpose(proposed_state2)*accept2)
logp_current2 = tf.where(accept2_, logp_proposed2, logp_current2)
# append to chain
chain.append(tf.concat([current_state1, current_state2], axis=0))
# stack up the chain
chain = tf.stack(chain, axis=0)
return chain
# + id="yg5q4YEy0AP4"
@tf.function
def log_posterior(x, y, cmaf):
# define likelihood p(x|y) with CMAF
# compute prior probability p(y)
# return the log-posterior
pass
# + id="79EBfz2B15N6" cellView="form"
#@title Ex. 4.1 solution <font color='lightgreen'>[run me to proceed]</font>
@tf.function
def log_posterior(x, y, cmaf):
# define likelihood p(x|y) with CMAF
like = cmaf.log_prob(x,y)
# compute prior probability p(y)
_prior = samp_prior.log_prob(y)
return like + _prior # the log-posterior
# + [markdown] id="ML-v64X9jksA"
# 2. Now we're going to use the sampler and write a function to obtain our posteriors. To call the sampler, we need to call our log-posterior function, as well as specify the number of walkers in parameter space:
#
#
# + id="9tzjfVjdZhFT"
# define function for getting posteriors
def get_posteriors(delfi, n_params, n_steps=2000, n_walkers=500, burnin_steps=1800, skip=4):
delfi['posts'] = [] # reset posteriors (can save if you want to keep a record)
# center affine sampler walkers on the IMNN estimates
a,b = np.squeeze(delfi['estimates'])
# choose width of proposal distribution
# sigma =
# loop over models in the ensemble
for m,cmaf in enumerate(delfi['MAFs']):
print('getting posterior for target data with model %d'%(m+1))
# wrapper for log_posterior function: freeze at target summary slice, x_target
@tf.function
def my_log_prob(y, x=delfi['estimates']):
return log_posterior(x, y, cmaf)
# initialize walkers...
# walkers1 =
# walkers2 =
# sample using affine. note that this returns a tensorflow tensor
# chain = affine_sample()
# convert chain to numpy and append to dictionary
delfi['posts'].append(np.stack([chain.numpy()[burnin_steps::skip,:,0].flatten(),
chain.numpy()[burnin_steps::skip,:,1].flatten()], axis=-1))
pass
# + cellView="form" id="NvYuLa22lEBg"
#@title Ex. 4.2 solution <font color='lightgreen'>[run me to proceed]</font>
# define function for getting posteriors
def get_posteriors(delfi, n_params, n_steps=2000, n_walkers=500, burnin_steps=1800, skip=4):
delfi['posts'] = [] # reset posteriors (can save if you want to keep a record)
# center affine sampler walkers on the IMNN estimates
a,b = np.squeeze(delfi['estimates'])
# choose width of proposal distribution
sigma = 0.5
# loop over models in the ensemble
for m,cmaf in enumerate(delfi['MAFs']):
print('getting posterior for target data with model %d'%(m+1))
# wrapper for log_posterior function: freeze at target summary slice
@tf.function
def my_log_prob(y, x=delfi['estimates']):
return log_posterior(x, y, cmaf)
# initialize walkers...
walkers1 = tf.random.normal([n_walkers, 2], (a, b), sigma)
walkers2 = tf.random.normal([n_walkers, 2], (a, b), sigma)
# sample using affine
chain = affine_sample(my_log_prob, n_params, n_walkers, n_steps, walkers1, walkers2)
delfi['posts'].append(np.stack([chain.numpy()[burnin_steps::skip,:,0].flatten(),
chain.numpy()[burnin_steps::skip,:,1].flatten()], axis=-1))
# + colab={"base_uri": "https://localhost:8080/"} id="ulaMujd8mndl" outputId="3db6a449-40be-4c22-e640-a67c22261a36"
# get all intermediate posteriors --> this should be really fast !
get_posteriors(DELFI, n_params)
# + [markdown] id="1NuX2ZvIsLeO"
# We're going to use our plotting client to visualize our posteriors for each model. We'll also plot the IMNN's Fisher Gaussian Approximation in black, centered on our estimates. Finally, we'll display the true Planck parameters using crosshairs:
# + colab={"base_uri": "https://localhost:8080/", "height": 361} id="5xWF9Ue4mfqb" outputId="2a380044-9537-46e8-9ea3-28dabc8b2793"
params = [r'$\Omega_c$', r'$\sigma_8$']
plot_posts(DELFI, params, num_models=num_models, num_targets=1,
Fisher=IMNN.F, estimates=np.squeeze(estimates), truth=θ_target)
# + [markdown] id="UqGBownWbl03"
# ___
# # Exercise 5: append new posterior training data to hone in on the truth (repeat several times)
#
# Finally, we're going to draw parameters from the posterior, re-simulate cosmological fields, compress, append the new ($x$, $\theta$) pairs to the dataset, and keep training our DELFI ensemble. Within a few iterations, this should shrink our posteriors considerably.
#
# Since we've coded all of our training functions modularly, we can just run them in a loop (once we've drawn and simulated from the prior). First we'll give you a piece of code to draw from the posterior chains:
#
# concat_data(DELFI, key, n_samples=500)
#
# Here, remember to re-set your random key for new samples !
#
# Next, write a loop that:
# 1. draws `n_samples` summary-parameter pairs from *each* existing CMAF model's posteriors
# 2. continues training the DELFI ensemble members
# 3. re-samples the posterior
#
# **bonus**: Can you develop a scheme that requires fewer `n_samples` draws each iteration ? What about optimizer stability ? (hint: try a decaying learning rate)
# ___
# + id="xA2Zm9fRZ0pd" cellView="form"
#@title `concat_data` function to draw from each posterior and concatenate dataset <font color='lightgreen'>[run me to proceed]</font>
import pandas as pd
def drop_samples(samples, prior=prior):
"""
helper function for dropping posterior draws outside
the specified prior range
"""
mydf = pd.DataFrame(samples)
mydf = mydf.drop(mydf[mydf[0] < prior.low[0]].index)
mydf = mydf.drop(mydf[mydf[1] < prior.low[1]].index)
mydf = mydf.drop(mydf[mydf[0] > prior.high[0]].index)
mydf = mydf.drop(mydf[mydf[1] > prior.high[1]].index)
return np.array(mydf.values, dtype='float32')
def concat_data(delfi, key, n_samples=500, prior=prior):
"""
helper code for concatenating data for each DELFI CMAF model.
delfi: DELFI dictionary object with 'train_dataset'
and 'val_dataset' attributes
key: jax.PRNGkey
n_samples: number of samples to draw from EACH DELFI ensemble model
"""
# take 500 samples from each posterior for each training data
key,rng = jax.random.split(key)
idx = np.arange(len(delfi['posts'][0]))
ϑ_samp = []
for m,_post in enumerate(delfi['posts']):
ϑ_samp.append(_post[45000:][onp.random.choice(idx, size=n_samples)])
ϑ_samp = np.concatenate(ϑ_samp, axis=0)
print(ϑ_samp.shape)
ϑ_samp = drop_samples(ϑ_samp, prior=prior)
dropped = n_samples*len(delfi['posts']) - ϑ_samp.shape[0]
print('I dropped {} parameter pairs that were outside the prior'.format(dropped))
_n_samples = len(ϑ_samp)
ts, ϑ_samp = get_params_summaries(key2, _n_samples, ϑ_samp)
new_data = (ts, ϑ_samp)
print("I've drawn %d new summary-parameter pairs"%(ts.shape[0]))
# this should shuffle the dataset
new_train_dataset, new_val_dataset = get_dataset(new_data, batch_size=batch_size, buffer_size=len(new_data[0]))
# concatenate datasets
delfi['train_dataset'] = delfi['train_dataset'].concatenate(new_train_dataset)
delfi['val_dataset'] = delfi['val_dataset'].concatenate(new_val_dataset)
# + id="7XjdNVOJoeBc" colab={"base_uri": "https://localhost:8080/", "height": 684} outputId="12a1afa4-1959-400a-f6b3-eecb2a53dad5"
#@title Ex. 5 solution <font color='lightgreen'>[run me to proceed]</font>
for repeat in range(1):
key,rng = jax.random.split(rng)
print('doing retraining iteration %d'%(repeat))
concat_data(DELFI, key, n_samples=500)
print('retraining on augmented dataset')
epochs = 500
training_loop(DELFI, epochs=epochs)
plot_trajectories(DELFI, num_models=2, num_targets=1)
get_posteriors(DELFI, n_params)
plot_posts(DELFI, params, num_models=num_models, num_targets=1,
Fisher=IMNN.F, estimates=np.squeeze(estimates), truth=θ_target)
# + [markdown] id="egwV7BRMuSzg"
# ___
# # Exercise 6: create ensemble posterior
# Once we're happy with the DELFI training, we can proceed to reporting our ensemble's combined posterior. Using the [`ChainConsumer` API](https://samreay.github.io/ChainConsumer/index.html), concatenate the posterior chains and report a nice corner plot:
# + colab={"base_uri": "https://localhost:8080/", "height": 384} cellView="form" id="mgKEKLDRwoJI" outputId="ad31ca97-56b7-445f-cbb5-b1f9b9efa474"
#@title Exercise 6 solution <font color='lightgreen'>[run me to proceed]</font>
def drop_samples(samples, prior=prior):
"""
helper function for dropping posterior draws outside
the specified prior range
"""
mydf = pd.DataFrame(samples)
mydf = mydf.drop(mydf[mydf[0] < prior.low[0]].index)
mydf = mydf.drop(mydf[mydf[1] < prior.low[1]].index)
mydf = mydf.drop(mydf[mydf[0] > prior.high[0]].index)
mydf = mydf.drop(mydf[mydf[1] > prior.high[1]].index)
return np.array(mydf.values, dtype='float32')
super_post = np.concatenate(DELFI['posts'], axis=0)
# assign new dict entry after dropping samples outside the prior
DELFI['super_post'] = drop_samples(super_post)
params = [r"$\Omega_c$", r"$\sigma_8$"]
corner_colors = [None, None, 'k']
c = ChainConsumer()
c.add_chain(DELFI['super_post'][::10], parameters=params, name='DELFI + IMNN', color=corner_colors[0])
c.add_covariance(np.squeeze(estimates), IMNN.invF, parameters=params, name="IMNN F @estimates", color=corner_colors[2])
c.configure(linestyles=["-", "-", "--"], linewidths=[1.0, 1.0, 1.0,],
shade=[True, False, False], shade_alpha=[0.7, 0.6, 0.],
tick_font_size=8, usetex=False,
legend_kwargs={"loc": "upper left", "fontsize": 8},
legend_color_text=False, legend_location=(0, 0))
fig = c.plotter.plot(figsize="column", truth=list(θ_target), filename=None)
# + [markdown] id="f5gJpNRO3PUq"
# ___
# # Congrats !
# You've made it through the core of the tutorial and trained a DELFI ensemble on IMNN-compressed summaries of mock dark matter fields and obtained cosmological parameter posteriors !
#
# ### Now what ?
# There are lots of things you can do if you have the time -- for one, you could check out the bonus problems below
# + [markdown] id="DCZ_VO4R-x9B"
# ___
# # BONUS: Compare IMNN Compressors
#
# For this whole tutorial we've been using an IMNN ***trained deliberately far*** from our Planck parameters, meaning our compression isn't guaranteed to be optimal. In our accompanying paper (to be released on arXiv on July 16, 2021) we re-trained an IMNN on the mean of the score estimates of a set of four cosmological fields. Since this estimate is closer to the true target parameters, our IMNN compression is guaranteed to improve our inference on the target data.
#
# <img src="https://raw.githubusercontent.com/tlmakinen/FieldIMNNs/master/tutorial/plots/new-four-cosmo-field-comparison.png" alt="drawing" width="700"/>
#
#
# We've included this newly-trained IMNN in the GitHub repository that you've already cloned into this notebook -- as a bonus, repeat the DELFI posterior estimation using the new (more optimal) compressor and see how your inference shapes up ! You *should* see tighter Gaussian Approximations *and* DELFI contours:
# + id="sajKu_ko5Qtf"
# load IMNN state
import cloudpickle as pickle
import os
def unpickle_me(path):
file = open(path, 'rb')
return pickle.load(file)
folder_name = './FieldIMNNs/tutorial/IMNN2-aspects/'
loadstate = unpickle_me(os.path.join(folder_name, 'IMNN_state'))
state2 = jax.experimental.optimizers.pack_optimizer_state(loadstate)
# startup key to get the right state of the weights
startup_key2 = np.load(os.path.join(folder_name, 'IMNN_startup_key.npy'), allow_pickle=True)
# load weights
best_weights2 = np.load(os.path.join(folder_name, 'best_w.npy'), allow_pickle=True)
# load fiducial model that we trained the model at (estimates derived from initial IMNN)
θ_fid_new = np.load(os.path.join(folder_name, 'new_fid_params.npy'), allow_pickle=True)
# + colab={"base_uri": "https://localhost:8080/"} id="a6NtkZvu7wYj" outputId="c55f446d-d4ee-454d-f254-0ea9d069564e"
# initialize IMNN with pre-trained state
IMNN2 = imnn.IMNN(
n_s=n_s,
n_d=n_d,
n_params=n_params,
n_summaries=n_summaries,
input_shape=(1,) + shape + (1,),
θ_fid=θ_fid_new,
model=model,
optimiser=optimiser,
key_or_state=state2, # <---- initialize with state
simulator=lambda rng, θ: simulator(
rng, θ, simulator_args={
**simulator_args,
**{"squeeze": False}}))
# now set weights using the best training weights and startup key (this can take a moment)
IMNN2.set_F_statistics(w=best_weights, key=startup_key2)
# + colab={"base_uri": "https://localhost:8080/"} id="q5eyO5VA90Ic" outputId="b3d254bc-e8d5-4d65-af53-4d9726ac8105"
print(np.linalg.det(IMNN2.F))
# + [markdown] id="iFHR4eLI_W2J"
# ---
# # BONUS 2:
#
# Alternatively, train a new IMNN from scratch at the target data `estimates` (try with fewer filters on the free version of Colab). You could also try playing with other `stax` layers like `stax.Dense(num_neurons)`. Feel free to also switch up the simulation parameters -- choosing $N=32$ for instance will dramatically increase training speed for testing, etc.
# + id="uKj2wDNR-I18"
fs = 16
new_layers = [
InceptBlock((fs, fs, fs), strides=(4, 4)),
InceptBlock((fs, fs, fs), strides=(4, 4)),
InceptBlock((fs, fs, fs), strides=(4, 4)),
InceptBlock((fs, fs, fs), strides=(2, 2), do_5x5=False, do_3x3=False),
stax.Conv(n_summaries, (1, 1), strides=(1, 1), padding="SAME"),
stax.Flatten,
Reshape((n_summaries,))
]
new_model = stax.serial(*new_layers)
# + id="O6HsW-UXEmJz"
print_model(layers, input_shape, rng)
# + id="jNGU_7u8_kbL"
rng, key = jax.random.split(rng)
IMNN2 = imnn.IMNN(
n_s=n_s,
n_d=n_d,
n_params=n_params,
n_summaries=n_summaries,
input_shape=(1,) + shape + (1,),
θ_fid=np.squeeze(estimates),
model=new_model,
optimiser=optimiser,
key_or_state=key, # <---- initialize with key
simulator=lambda rng, θ: simulator(
rng, θ, simulator_args={
**simulator_args,
**{"squeeze": False}}))
# + id="5tILxKIZ_zNy"
print("now I'm training the IMNN")
rng, key = jax.random.split(rng)
IMNN2.fit(λ=10., ϵ=0.1, rng=key, print_rate=None,
min_iterations=500, patience=100, best=True)
# visualize training trajectory
IMNN2.plot(expected_detF=None);
| 42.288913 | 1,292 |
220aaaaa1913450a3e2f8846ba79e45f944f4839
|
py
|
python
|
notebooks/07_Autoencoders.ipynb
|
pligor/mnist-from-scratch
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:mlp]
# language: python
# name: conda-env-mlp-py
# ---
# # Autoencoders
#
# In this notebook we will explore autoencoder models. These are models in which the inputs are *encoded* to some intermediate representation before this representation is then *decoded* to try to reconstruct the inputs. They are example of a model which uses an unsupervised training method and are both interesting as a model in their own right and as a method for pre-training useful representations to use in supervised tasks such as classification. Autoencoders were covered as a pre-training method in the [sixth lecture slides](http://www.inf.ed.ac.uk/teaching/courses/mlp/2016/mlp06-enc.pdf).
# ## Exercise 1: Linear contractive autoencoders
#
# For the first exercise we will consider training a simple 'contractive' autoencoder - that is one in which the hidden representation is smaller in dimension than the input and the objective is to minimise the mean squared error between the original inputs and reconstructed inputs. To begin with we will consider models in which the encoder and decoder are both simple affine transformations.
#
# When training an autoencoder the target outputs for the model are the original inputs. A simple way to integrate this in to our `mlp` framework is to define a new data provider inheriting from a base data provider (e.g. `MNISTDataProvider`) which overrides the `next` method to return the inputs batch as both inputs and targets to the model. A data provider of this form has been provided for you in `mlp.data_providers` as `MNISTAutoencoderDataProvider`.
#
# Use this data provider to train an autoencoder model with a 50 dimensional hidden representation and both encoder and decoder defined by affine transformations. You should use a sum of squared differences error and a basic gradient descent learning rule with learning rate 0.01. Initialise the biases to zero and use a uniform Glorot initialisation for both layers weights. Train the model for 25 epochs with a batch size of 50.
import numpy as np
import logging
import mlp.layers as layers
import mlp.models as models
import mlp.optimisers as optimisers
import mlp.errors as errors
import mlp.learning_rules as learning_rules
import mlp.data_providers as data_providers
import mlp.initialisers as initialisers
import matplotlib.pyplot as plt
# %matplotlib inline
# Using the function defined in the cell below (from the first lab notebook), plot a batch of the original images and the autoencoder reconstructions.
def show_batch_of_images(img_batch, fig_size=(3, 3), num_rows=None):
fig = plt.figure(figsize=fig_size)
batch_size, im_height, im_width = img_batch.shape
if num_rows is None:
# calculate grid dimensions to give square(ish) grid
num_rows = int(batch_size**0.5)
num_cols = int(batch_size * 1. / num_rows)
if num_rows * num_cols < batch_size:
num_cols += 1
# intialise empty array to tile image grid into
tiled = np.zeros((im_height * num_rows, im_width * num_cols))
# iterate over images in batch + indexes within batch
for i, img in enumerate(img_batch):
# calculate grid row and column indices
r, c = i % num_rows, i // num_rows
tiled[r * im_height:(r + 1) * im_height,
c * im_height:(c + 1) * im_height] = img
ax = fig.add_subplot(111)
ax.imshow(tiled, cmap='Greys', vmin=0., vmax=1.)
ax.axis('off')
fig.tight_layout()
plt.show()
return fig, ax
# ### Optional extension: principle components analysis
#
# *This section is provided for the interest of those also sitting MLPR or otherwise already familiar with eigendecompositions and PCA. Feel free to skip over if this doesn't apply to you (or even if it does).*
#
# For a linear (affine) contractive autoencoder model trained with a sum of squared differences error function there is an analytic solution for the optimal model parameters corresponding to [principle components analysis](https://en.wikipedia.org/wiki/Principal_component_analysis).
#
# If we have a training dataset of $N$ $D$-dimensional vectors $\left\lbrace \boldsymbol{x}^{(n)} \right\rbrace_{n=1}^N$, then we can calculate the empiricial mean and covariance of the training data using
#
# \begin{equation}
# \boldsymbol{\mu} = \frac{1}{N} \sum_{n=1}^N \left[ \boldsymbol{x}^{(n)} \right]
# \qquad
# \text{and}
# \qquad
# \mathbf{\Sigma} = \frac{1}{N}
# \sum_{n=1}^N \left[
# \left(\boldsymbol{x}^{(n)} - \boldsymbol{\mu} \right)
# \left(\boldsymbol{x}^{(n)} - \boldsymbol{\mu} \right)^{\rm T}
# \right].
# \end{equation}
#
# We can then calculate an [eigendecomposition](https://en.wikipedia.org/wiki/Eigendecomposition_of_a_matrix) of the covariance matrix
# \begin{equation}
# \mathbf{\Sigma} = \mathbf{Q} \mathbf{\Lambda} \mathbf{Q}^{\rm T}
# \qquad
# \mathbf{Q} = \left[
# \begin{array}{cccc}
# \uparrow & \uparrow & \cdots & \uparrow \\
# \boldsymbol{q}_1 & \boldsymbol{q}_2 & \cdots & \boldsymbol{q}_D \\
# \downarrow & \downarrow & \cdots & \downarrow \\
# \end{array}
# \right]
# \qquad
# \mathbf{\Lambda} = \left[
# \begin{array}{cccc}
# \lambda_1 & 0 & \cdots & 0 \\
# 0 & \lambda_2 & \cdots & \vdots \\
# \vdots & \vdots & \ddots & 0 \\
# 0 & 0 & \cdots & \lambda_D \\
# \end{array} \right]
# \end{equation}
#
# with $\mathbf{Q}$ an orthogonal matrix, $\mathbf{Q}\mathbf{Q}^{\rm T} = \mathbf{I}$, with columns $\left\lbrace \boldsymbol{q}_d \right\rbrace_{d=1}^D$ corresponding to the eigenvectors of $\mathbf{\Sigma}$ and $\mathbf{\Lambda}$ a diagonal matrix with diagonal elements $\left\lbrace \lambda_d \right\rbrace_{d=1}^D$ the corresponding eigenvalues of $\mathbf{\Sigma}$.
#
# Assuming the eigenvalues are ordered such that $\lambda_1 < \lambda_2 < \dots < \lambda_D$ then the top $K$ principle components of the inputs (eigenvectors with largest eigenvalues) correspond to $\left\lbrace \boldsymbol{q}_d \right\rbrace_{d=D + 1 - K}^D$. If we define a $D \times K$ matrix $\mathbf{V} = \left[ \boldsymbol{q}_{D + 1 - K} ~ \boldsymbol{q}_{D + 2 - K} ~\cdots~ \boldsymbol{q}_D \right]$ then we can find the projections of a (mean normalised) input vector on to the selected $K$ principle components as $\boldsymbol{h} = \mathbf{V}^{\rm T}\left( \boldsymbol{x} - \boldsymbol{\mu}\right)$. We can then use these principle component projections to form a reconstruction of the original input just in terms of the $K$ top principle components using $\boldsymbol{r} = \mathbf{V} \boldsymbol{h} + \boldsymbol{\mu}$. We can see that this is just a sequence of two affine transformations and so is directly analagous to a model with two affine layers and with $K$ dimensional outputs of the first layer / inputs to second.
#
# The function defined in the cell below will calculate the PCA solution for a set of input vectors and a defined number of components $K$. Use it to calculate the top 50 principle components of the MNIST training data. Use the returned matrix and mean vector to calculate the PCA based reconstructions of a batch of 50 MNIST images and use the `show_batch_of_images` function to plot both the original and reconstructed inputs alongside each other. Also calculate the sum of squared differences error for the PCA solution on the MNIST training set and compare to the figure you got by gradient descent based training above. Will the gradient based training produce the same hidden representations as the PCA solution if it is trained to convergence?
def get_pca_parameters(inputs, num_components=50):
mean = inputs.mean(0)
inputs_zm = inputs - mean[None, :]
covar = np.einsum('ij,ik', inputs_zm, inputs_zm)
eigvals, eigvecs = np.linalg.eigh(covar)
return eigvecs[:, -num_components:], mean
# ## Exercise 2: Non-linear contractive autoencoders
#
# Those who did the extension in the previous exercise will have just seen that for an autoencoder with both linear / affine encoder and decoders, there is an analytic solution for the parameters which minimise a sum of squared differences error.
#
# In general the advantage of using gradient-based training methods is that it allows us to use non-linear models for which there is no analytic solution for the optimal parameters. The hope is the use of non-linear transformations between the affine transformation layers will increase the representational power of the model (a sequence of affine transformations applied without any interleaving non-linear operations can always be represented by a single affine transformation).
#
# Train a contractive autoencoder with an initial affine layer (output dimension again 50) followed by a rectified linear layer, then an affine transformation projecting to outputs of same dimension as the original inputs, and finally a logistic sigmoid layer at the output. As the only layers with parameters are the two affine layers which have the same dimensions as in the fully affine model above, the overall model here has the same number of parameters as previously.
#
# Again train for 25 epochs with 50 training examples per batch and use a uniform Glorot initialisation for the weights, and zero biases initialisation. Use our implementation of the 'Adam' adaptive moments learning rule (available in `mlp.learning_rules` as `AdamLearningRule`) rather than basic gradient descent here (the adaptivity helps deal with the varying appropriate scale of updates induced by the non-linear transformations in this model).
# Plot batches of the inputs and reconstructed inputs for this non-linear contractive autoencoder model and compare to the corresponding plots for the linear models above.
# ## Exercise 3: Denoising autoencoders
#
# So far we have just considered autoencoders that try to reconstruct the input vector fed into them via some intermediate lower-dimensional 'contracted' representation. The contraction is important as if we were to mantain the input dimensionality in all layers of the model a trivial optima for the model to learn would be to apply an identity transformation at each layer.
#
# It can be desirable for the intermediate hidden representation to be robust to noise in the input. The intuition is that this will force the model to learn to maintain the 'important structure' in the input in the hidden representation (that needed to reconstruct the input). This also removes the requirement to have a contracted hidden representation (as the model can no longer simply learn to apply an identity transformation) though in practice we will still often use a lower-dimensional hidden representation as we believe there is a certain level of redundancy in the input data and so the important structure can be represented with a lower dimensional representation.
#
# Create a new data provider object which adds to noise to the inputs to an autoencoder in each batch it returns. There are various different ways you could introduce noise. The three suggested in the lecture slides are
#
# * *Gaussian*: add independent, zero-mean Gaussian noise of a fixed standard-deviation to each dimension of the input vectors.
# * *Masking*: generate a random binary mask and perform an elementwise multiplication with each input (forcing some subset of the values to zero).
# * *Salt and pepper*: select a random subset of values in each input and randomly assign either zero or one to them.
#
# You should choose one of these noising schemes to implement. It may help to know that the base `DataProvider` object already has access to a random number generator object as its `self.rng` attribute.
# Once you have implemented your chosen scheme, use the new data provider object to train a denoising autoencoder with the same model architecture as in exercise 2.
# Use the `show_batch_of_images` function from above to visualise a batch of noisy inputs from your data provider implementation and the denoised reconstructions from your trained denoising autoencoder.
# ## Exercise 4: Using an autoencoder as an initialisation for supervised training
# As a final exercise we will use the first layer of an autoencoder for MNIST digit images as a layer within a multiple layer model trained to do digit classification. The intuition behind pretraining methods like this is that the hidden representations learnt by an autoencoder should be a more useful representation for training a classifier than the raw pixel values themselves. We could fix the parameters in the layers taken from the autoencoder but generally we can get better performance by letting the whole model be trained end-to-end on the supervised training task, with the learnt autoencoder parameters in this case acting as a potentially more intelligent initialisation than randomly sampling the parameters which can help ease some of the optimisation issues encountered due to poor initialisation of a model.
#
# You can either use one of the autoencoder models you trained in the previous exercises, or train a new autoencoder model for specifically for this exercise. Create a new model object (instance of `mlp.models.MultipleLayerModel`) in which the first layer(s) of the list of layer passed to the model constructor are the trained first layer(s) from your autoencoder model (these can be accessed via the `layers` attribute which is a list of all the layers in a model). Add any additional layers you wish to the pretrained layers - at the very least you will need to add an output layer with output dimension 10 to allow the model to be used to predict class labels. Train this new model on the original MNIST image, digit labels pairs with a cross entropy error.
| 80.19883 | 1,037 |
e8c0cfc5a8583877fa5953377e3c9e4a6d602437
|
py
|
python
|
Tutorials/Keiko/glad_alert.ipynb
|
c11/earthengine-py-notebooks
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <table class="ee-notebook-buttons" align="left">
# <td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Tutorials/Keiko/glad_alert.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
# <td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Tutorials/Keiko/glad_alert.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
# <td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Tutorials/Keiko/glad_alert.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
# </table>
# ## Install Earth Engine API and geemap
# Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
# The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
#
# **Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
# +
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
# -
# ## Create an interactive map
# The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
# ## Add Earth Engine Python script
# +
# Add Earth Engine dataset
# Credits to: Keiko Nomura, Senior Analyst, Space Intelligence Ltd
# Source: https://medium.com/google-earth/10-tips-for-becoming-an-earth-engine-expert-b11aad9e598b
# GEE JS: https://code.earthengine.google.com/?scriptPath=users%2Fnkeikon%2Fmedium%3Afire_australia
geometry = ee.Geometry.Polygon(
[[[153.11338711694282, -28.12778417421283],
[153.11338711694282, -28.189835226562256],
[153.18943310693305, -28.189835226562256],
[153.18943310693305, -28.12778417421283]]])
Map.centerObject(ee.FeatureCollection(geometry), 14)
imageDec = ee.Image('COPERNICUS/S2_SR/20191202T235239_20191202T235239_T56JNP')
Map.addLayer(imageDec, {
'bands': ['B4', 'B3', 'B2'],
'min': 0,
'max': 1800
}, 'True colours (Dec 2019)')
Map.addLayer(imageDec, {
'bands': ['B3', 'B3', 'B3'],
'min': 0,
'max': 1800
}, 'grey')
# GLAD Alert (tree loss alert) from the University of Maryland
UMD = ee.ImageCollection('projects/glad/alert/UpdResult')
print(UMD)
# conf19 is 2019 alert 3 means multiple alerts
ASIAalert = ee.Image('projects/glad/alert/UpdResult/01_01_ASIA') \
.select(['conf19']).eq(3)
# Turn loss pixels into True colours and increase the green strength ('before' image)
imageLoss = imageDec.multiply(ASIAalert)
imageLoss_vis = imageLoss.selfMask().visualize(**{
'bands': ['B4', 'B3', 'B2'],
'min': 0,
'max': 1800
})
Map.addLayer(imageLoss_vis, {
'gamma': 0.6
}, '2019 loss alert pixels in True colours')
# It is still hard to see the loss area. You can circle them in red
# Scale the results in nominal value based on to the dataset's projection to display on the map
# Reprojecting with a specified scale ensures that pixel area does not change with zoom
buffered = ASIAalert.focal_max(50, 'circle', 'meters', 1)
bufferOnly = ASIAalert.add(buffered).eq(1)
prj = ASIAalert.projection()
scale = prj.nominalScale()
bufferScaled = bufferOnly.selfMask().reproject(prj.atScale(scale))
Map.addLayer(bufferScaled, {
'palette': 'red'
}, 'highlight the loss alert pixels')
# Create a grey background for mosaic
noAlert = imageDec.multiply(ASIAalert.eq(0))
grey = noAlert.multiply(bufferScaled.unmask().eq(0))
# Export the image
imageMosaic = ee.ImageCollection([
imageLoss_vis.visualize(**{
'gamma': 0.6
}),
bufferScaled.visualize(**{
'palette': 'red'
}),
grey.selfMask().visualize(**{
'bands': ['B3', 'B3', 'B3'],
'min': 0,
'max': 1800
})
]).mosaic()
#Map.addLayer(imageMosaic, {}, 'export')
# Export.image.toDrive({
# 'image': imageMosaic,
# description: 'Alert',
# 'region': geometry,
# crs: 'EPSG:3857',
# 'scale': 10
# })
# -
# ## Display Earth Engine data layers
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
| 41.96732 | 1,023 |
e83adee06c3916ccde044caa88ef97c2173aeb7c
|
py
|
python
|
Neural_Network_Fundamentals/.ipynb_checkpoints/Draft_of_the_Tutorial-checkpoint.ipynb
|
romanarion/InformationSystemsWS1718
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "-"}
# # Neural Network Fundamentals. Part 1: NN from scratch.
# -
# This blog is a guide to help readers build and develop a neural network from basics. It starts with an introduction to Neural Networks concept and its early development, followed by a step-by-step coding guide, through which relevant concepts are illustrated. Later in the post, there is also an introduction on how to utilize Neural Networks in Keras. Finally, the reader will find instructions on how to deploy the model on an API to make it accessible to everyone else.
# ## Neural Networks and its early development
# As the name calls, the idea of neural networks is inspired by the function of how neurons work in the human brain. It is, however, crucial for the readers to know that despite the original motivation of Neural Networks, the NN models being used today have little resemblance to what human brain does (Warner and Misra, 1996). In its basic terms, Neural Networks is composed of nodes interconnected to each other in several layers. The basic form of a NN would include an input, a hidden and output layer. The number of nodes and layers can add to the complexity and efficiency of the neural networks.
# The McCulloch-Pitts model of neuron in 1943 was one of the earliest simplified version of neural networks. It consisted of a simple neuron which received a weighted sum of inputs and output zero if the sum was smaller than a threshold and one when it was greater than the threshold. This idea is called firing and is an interesting analogy to what an actual neuron does. Later on in early 1960s, Rosenblatt introduced the simple perceptron model which was a developed version of the McCulloch-Pitts with an input and output layer. However, the linear separablilty limitation (Minsky and Papert ,1969) of simple perceptron took away the research interest in neural networks for a while. In early 1980s, the Hopfield model of content-addressable memory, however, motivated researchers in the area again and later on with the introduction of backpropagation learning algorithm, neural networks research pooled the interest. Nowadays, Neural Nets are used in a variety of applications to tackle problems such as classification, pattern recognition, control systems and predictions.
#
# + [markdown] slideshow={"slide_type": "-"}
# ## Imagine the following problem.
# There are handwritten numbers that you want computer to correctly classify. It would be an easy task for a person but an extremely complicated one for a machine, especially, if you want to use some traditional prediction model, like linear regression. Even though the computer is faster than the human brain in numeric computations, the brain far outperforms the computer in some tasks.
# -
# <img src="pics/problem.png" alt="Drawing" style="width: 600px;"/>
# ## Some intuition from the Nature
# People struggled to teach machines to solve this kind of problems for a long time without success.
# Unless they noticed a very peculiar thing. Nature creatures, even the simple ones, for instance
# insects, can perform complicated task with very limited brain capacities, which are far below
# those of the computers. So there is something nature has developed that allows to solve tasks
# apparently complicated for machines tasks in a smart way.
# One of the ides that came to mind is to replicate the structure and certain functions of nature beings
# brain and neurosystem that allow for cognitive process and beyond.
# A particular example of such structures is neuron system.
# <img src="pics/neurons.png" alt="Drawing" style="width: 600px;"/> [Source: https://www.jstor.org/stable/pdf/2684922.pdf]
# <img src="pics/neurons_net3.png" alt="Drawing" style="width: 500px;"/> [Source: https://pixabay.com/]
# A particular detail about how are our cognitive and perceptive processes organised is a complicated
# structure of simple elements which create a complex net where each element is connected with others
# receiving and transmitting information. An idea to implement such a structure in order to make
# predictions gave birth to what we now now as neural network models.
# ## Schematic Representation
# All the above mentioned applications of neural networks have in common a structure that in a simplified way can be depicted using the following picture (see Picture 1).
# <img src="pics/neural_network1.png" alt="Drawing" style="width: 700px;"/>
# # Implementation of the NN from scratch
# Within the following sections we will implement such a structure from scratch and use it to solve the classification problem stated in the beginning of the blogpost. All we need in order to do this is Python with a limited number of basic packages. For the sake of making this tutorial even more accessible and also more interactive all the code provided below will be implemented in Jupyter notebook.
#
# First let's determine the elements we can see on the Picture 1 and need to collect in order to implement a NN. These elements are:
# * nodes;
# * layers;
# * weights between nodes in neighboring levels;
# * activation functions.
# ### Nodes
# A node is basically a point where data points are received, processed and then transferred to the other node(s). A node could be either an endpoint or a redistribution point or even both when iterations are done through the learning algorithm. The number of nodes to use is optional.
# ### Layers
# A layer consists one or several nodes. The initial layer in the network is called the input layer The middle layer(s) is called hidden layer and that is because the computation result of this/these layer(s) is not visible. And finally, the last layer is called the output layer from which results are output. The nodes in each layer is fully interconnected to the ones in the next and the previous layers.
# ### Weights
# In order to transfer an input data point to the next layer, a predetermined number is stored in each connection from the sender node to the receiver node. This predetermined number is called weight and is chosen randomly in the beginning. Each weight accounts for the impact between the interconnected nodes.
# ### Activation Function
# A function which transforms an input data point that it receives from the previous nodes to an output value which will be the input for the nodes in the next layer. The activation function plays an important role in the efficiency of the neural network as it accounts for non-linearity of data.
# ### Back propagation
# A learning algorithm which aims to minimize the errors/cost function of the NN. Through this learning algorithm, the random weights and biases which were initially given to the network will be optimized to give the best output.
# ### Overfitting
# This is a problem when the neural network is over trained which would mean that it will fail to recognize patterns which were never used in the training. One of the common reasons for this problem is the use of more than necessary nodes in the layers.
# In our case we have a structure with 3 layers: input, output and one hidden layer. The number of nodes in the input ("i_n"), hidden ("h_n") and output ("o_n") layers are 3, 5 and 2 respectively. Using Python code such a structure can be represented in the following way:
# Load the package to work with numbers
import numpy as np
# Determine the structure of the NN
i_n = 3
h_n = 5
o_n = 2
# ### Weights - ...
# Initially we assign weights between nodes in neighboring layers randomly. This is needed only for the sake of initializing the structure. Later these weights will be changed in order to solve our classification problem. Weights' updating procedure will be described in the following sections.
# The output should be n-1 matrices (where n corresponds to the number of layers in the NN). Each of these matrices will be of a size f by p (where p is the number of nodes in the corresponding preceding layer and f is the number of nodes in the corresponding following layer).
# This becomes more clear once you check the code below that creates 2 matrices of weights:
# * matrix of weights between input and hidden layers ("w_i_h") - 5 by 3 matrix
# * matrix of weights between hidden and output layers ("w_h_o") - 2 by 5 matrix.
#
# Such a dimensions of matrices are necessary in order to accomplish matrix and vector multiplications that will be described later.
# +
# Randomly define the weights between the layers.
# Dimensions of these matrices are determined by the sizes of the layers they are connecting.
w_i_h = np.random.rand(h_n, i_n) # create an array of the given shape and populate it with random values.
w_h_o = np.random.rand(o_n, h_n)
# Show matrices of randomly assigned weights.
w_i_h
# w_h_o # uncomment this line in order to see the values for w_h_o.
# Use Cmd + / in MacOS and CTRL + / in MS Windows as a shortcut to comment/uncomment lines.
# -
# ### Activation Function
# One other concept that initially was to certain extent inspired by the way neurosystems in the nature work is the concept of "firing". Neurons has a particular characteristic - they are activated, i.e. send signal further or "fire" only when they get a signal that is strong enough - stronger than certain threshold. Such a feature of the neurons in the setting of a NN is called activation function. In the easiest case it can be represented by a step function as one on the Picture below.
# <img src="pics/step_function.png" alt="Drawing" style="width: 700px";/> [Source: https://www.researchgate.net/figure/Three-different-types-of-transfer-function-step-sigmoid-and-linear-in-unipolar-and_306323136]
# #### activation functions ...
# Determine activation function which is an approximation for "firing" of neurons.
def sigmoid(x):
return 1 / (1 + np.exp(-x)) # np.exp() calculates the exponential of all elements in the input array.
# Draw this function using `matplotlib.pyplot` package.
# +
# Draw the function.
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 100) # return 100 evenly spaced numbers over an interval from -10 to 10.
plt.plot(x, sigmoid(x)) # plot sigmoid function for sampled values.
plt.show() # show the plot.
# -
# ## Inspect the Data
# By now we have collected all the elements of the NN. Can we use this structure in order to solve the classification problem stated in the beginning of the blogpost?
# In order to answer this question we need first to get a better understanding of the data in disposition.
#
# We are trying to check whether NN is able to solve the classification problem using a collection of 70 000 handwritten numbers. Each of this handwritten number is represented as 28x28 image.
#
# The original source of the data is "THE MNIST DATABASE". A detailed description of the dataset as well as the dataset itself can be found under the following link:
# http://yann.lecun.com/exdb/mnist/. There you can also find a summary of the performance results achieved by various classification algorithms which used this dataset.
#
# For the sake of simplicity we suggest obtaining the data from another source:
# https://pjreddie.com/projects/mnist-in-csv/. Here the original images are transformed in csv.format, which allows to work with them directly.
# For the purposes of demonstration below we use a smaller dataset (100 images), which will be expanded at later stage.
# Load the data.
raw_data = open("data/mnist_train_100.csv", 'r') # "r" stands for "read only" mode.
data = raw_data.readlines() # read all the lines of a file in a list.
raw_data.close() # remove temporal file from the environment in order to save memory.
# Inspect the data - check the number of observations.
len(data) # length of the object.
# Inspect a particular observation of the data.
data[0] # show observation number 0 from the list (remember that in Python numbering starts from 0).
# A particular observation looks like a string of 785 elements (label of the image + 784 elements for each pixels of a 28x28 image).
#
# Each element representing a pixel is a number from 0 to 255 (from white to black color).
#
# The first element in the line is the label of the image and therefore is a number from 0 to 9.
# Using `matplotlib.pyplot` package we can also reconstruct the original image based on the data about each pixel in the string.
# Load the package to plot the data
import matplotlib.pyplot as mpp
# %matplotlib inline
# Plot the data
observation = data[0].split(',') # break down observation number 0 (comma is used to identify each element).
image = np.asfarray(observation[1:]).reshape((28,28)) # take all the elements starting from the element 1
# (exclude element number 0, that corresponds to the label) and reshape them as an array with dimension 28 by 28.
mpp.imshow(image, cmap='Blues', interpolation='None') # show the plot of this array using grey pallete.
# Save an observation of the data as an input to work with.
input = np.array(np.asfarray(observation[1:]), ndmin=2).T # save necessary elements in a vertical vector shape.
# Show the input vector.
input
# ## Fit the draft of the NN's structure to the Data
# Let's take a look once again at the NN's structure we have created at the beginning of the tutorial.
# <img src="pics/neural_network1.png" alt="Drawing" style="width: 700px;"/>
# After the inspection of the data we can conclude that the structure with 3-5-2 nodes is probably not optimal and therefore should be updated in order to fit the data we have and peculiarities of the classification problem.
#
# So, for each observation we have 784 elements as an input (label element is excluded). Accordingly, instead of 3 input nodes we should better have 784.
#
# Similarly, as we have 10 different options for the outcome (handwritten numbers are labeled from from 0 to 9) the number of output nodes should be 10 instead of 2.
#
# We also change the number of hidden nodes from 5 to 90. Such a number has been assigned based on some proportionality assumptions which will be checked later: 90 is 9 times higher than 10 and approximately 9 times smaller than 784.
# Determine the new structure of the NN.
i_n = 784
h_n = 90
o_n = 10
# As we have new structure of the NN we should reassign the weights - now the size of each weight matrix will increase as we have more nodes in each layer.
# Determine the weights.
w_i_h = np.random.rand(h_n, i_n)
w_h_o = np.random.rand(o_n, h_n)
# So far we have not used the first element of our observation - the label. It will be necessary to compare the predictions of the NN to the real state of the world and to train the NN to make correct predictions. The target should therefore have the same shape as the output layer of the NN, so that they could be comparable. We can represent the label as a vector of n elements (n corresponds to the number of nodes in the output layer), where each element is either 0 or 1. There should be only one element equal to 1 and the position of this element should correspond to the index number of the label we want to predict.
# Create target array.
target = np.array(np.zeros(o_n), ndmin=2).T
target[int(observation[0])] = 1 # int() method returns an integer object from any number or string.
# Inspect how the target looks like (remember that the label of observations is 5).
target
# Show the sizes of matrices of weights, input and target vectors.
w_i_h.shape, input.shape, w_h_o.shape, target.shape
# ## Feed forward
# Once we have the structure of the NN updated for the specific task of classifying the numbers depicted on the images, we can run our network in order to get the first predictions that will be represented by a vector of 10 elements. This vector in its turn can be compared to the target.
#
# To run the NN, i.e. to feed forward our input data in order to get some predictions, we should follow certain steps:
#
# 1. Multiply an input vector by a matrix of weights that connects it with the next layer;
# 2. Transform the result using activation function;
# 3. Use the output obtained in the 2nd step as an input vector for the next layer.
#
# A sequence of this steps should be repeated n-1 times (where n corresponds to the number of layers). The output of the previous layer will always be the input vector for the next layer. In our case the procedure will happen twice.
#
# On the Picture bellow you can see the procedure necessary to obtain the output of the hidden layer.
# The result of matrix multiplication here is called "Hidden_Input". Transformation of "Hidden_Input" through activation function is called "Hidden_Output".
#
# This output will be used as the input vector that should be multiplied by the next weigh matrix and transformed through activation function in order to calculate the final output of the NN. If our NN would have more than 1 hidden layer, the procedure would be repeated more times.
# <img src="pics/multiplication.png" alt="Drawing" style="width: 800px;"/>
# <img src="pics/activation.png" alt="Drawing" style="width: 800px;"/>
# Below you can see the code implementation of all the steps for all layers of the NN.
# Calculate the output of hidden and output layers of our NN.
h_input = np.dot(w_i_h, input) # dot() performs matrix multiplication; "h_input" stands for "Hidden_Input".
h_output = sigmoid(h_input) # "Hidden_Output" - result after activation function.
o_input = np.dot(w_h_o, h_output) # "Output_Input" - input used for the next layer.
o_output = sigmoid(o_input) # "Output_Output" - final output of the NN.
# Show intermediate data and output.
# Uncomment the line of interest in order to see the the corresponding object.
# h_input
# h_output
# o_input
o_output
# ## Why don't we get what we expected? Data treatment best practices.
# Once we check the output of the NN and the results of each performed step, we can observe that already at the stage of the h_output all the data converts to a vector of ones. A vector of equal values does not provide us with any inside that is helpful for the considered classification problem. Apparently, something is wrong with what we have done so far. There could be several reasons for the problem we face.
# ### First of all, let's take a look at our sigmoid function once again:
x = np.linspace(-10, 10, 100)
plt.plot(x, sigmoid(x))
plt.show()
# As we can see the output of the sigmoid function will be almost identical once we feed a number bigger than 2. Similarly there is no significant difference between the outputs if numbers used are smaller than -2. Hence application of sigmoid function to the original data leads to a lose of valuable information - NN has problems to learn something from the inputs that are almost undifferentiable.
#
# One solution is to transform the input we have. Ideally we should have our data in a range between 0 and 1. It is desirable to avoid zeros, because the result of multiplication of an input equal to 0 by whichever weight will always be 0, hence NN will not be able to use this input to learn.
#
# We can perform a transformation of the original data as the one coded below:
# +
# Good practice transformation of the input values:
input = np.array((np.asfarray(observation[1:])/255.0*0.99) + 0.01, ndmin=2).T
# Our values in our input vector are in the range from 0 to 255. Therefore we should divide input vector by 255,
# multiply it by 0,99 and add 0,01 in order to get values in the range from 0,01 to 1.
# Good practice transformation of the target value:
target = np.array(np.zeros(o_n) + 0.01, ndmin=2).T
target[int(observation[0])] = 0.99
# -
# ### Secondly, we can check our way to randomly assign initial weights:
# Let's take a look once at the function we used to randomly assign weights:
np.random.rand(3, 5)
# As we can see, all the weights are positive, while actual relationship between the features in the data and the values of the output vector can be negative. Hence, the way we employ to assign random weights should allow for negative weights too.
#
# Below there are too alternatives how this can be implemented in Python.
#
# +
# Good practice for initial weights assignment:
alternative1 = np.random.rand(3, 5) - 0.5
# or
alternative2 = np.random.normal(0.0, pow(3, -0.5), (3, 5))
# arguments: Mean of the distribution, Standard deviation of the distribution, Output shape.
# Second approach is better as it takes in account the standard deviation
# that is related to the number of incoming links into a node, 1/√(number of incoming links).
# alternative1
alternative2
# -
# Define the weights in accordance with the best practice:
w_i_h = np.random.normal(0.0, pow(h_n, -0.5), (h_n, i_n))
w_h_o = np.random.normal(0.0, pow(o_n, -0.5), (o_n, h_n))
# Now, that we have all the elements assigned in accordance with the best practices, we can feedforward the data once again.
# Run NN to get new classification of the particular observation.
h_input = np.dot(w_i_h, input)
h_output = sigmoid(h_input)
o_input = np.dot(w_h_o, h_output)
o_output = sigmoid(o_input)
o_output
# ## How good our results are?
# Once we have obtained the output of the NN, we can compare it to the target.
# Calculate the errors of the classification.
o_errors = target - o_output
o_errors
# The result we would like to achieve should look like as a vector of values where almost all values are negligibly small except for the one value that has the position in the vector corresponding to the index of the label of the image.
#
# It is not the case now. Nevertheless one should remember that so far all the weights have been assigned randomly and no training has been performed yet. However, is not a vector of ones anymore.
#
# Hence, we can proceed to the next stage, which is to find out where do the errors come from and how they can be minimized.
# ## Backpropagation
# Output of each node is the sum of the multiplications of the output of previous nodes by certain weights. Therefore we can associate how much error is coming with every weight and how much error has been brought from each particular node from the previous layer.
# To understand this better it is worth imagining the following example:
# * node 1 in the output layer of the NN should be equal to 0,01 ;
# * instead the NN is providing us with 0,8.
#
# In this case we should do the following:
#
# 1. Calculate the error of the node (-0,79 in our example);
#
# 2. Calculate how much error has been brought by every link to this node.
#
# For instance if weight w11 is 0,6 and w21 is 0,4 then they are associated with an error of -0,79x(0,6/1) and -0,79x(0,4/1) respectively (see Pictures below).
# <img src="pics/bp_1.png" alt="Drawing" style="width: 800px;"/>
# After calculation of how much error is associated with every weight we can obtain the errors for the nodes in the proceeding layer.
#
# For instance error term for node 1 in the hidden layer will we equal to:
#
# the sum of errors associated with all the weights (w11 and w12 in our case) that link this node with the next layer. (see Picture below).
# <img src="pics/bp_2.png" alt="Drawing" style="width: 900px;"/> [Source: https://ebook4expert.com/2016/07/12/make-your-own-neural-network-ebook-free-by-tariq-rashid-epubmobi/]
# Once we repeat this procedure for all the nodes in all layers we can find out how much every node should be changed.
#
# To do so in Python we just need to make multiplication of vector that contain errors by corresponding matrix of weights.
# Find the errors associated with hidden layer output:
h_errors = np.dot(w_h_o.T, o_errors)
h_errors[0:10] # errors in the hidden layer - show the first 10 nodes out of 90.
# ## Updating weights
# So, how do we improve the weights we have assigned randomly at the beginning, so that the overall result improves?
# To change the output of any node we should change the weights that connect it with the previous layer.
#
# Basically what we want to find out is how much the error in every node changes once we change associated weights. That can be achieved by differentiation of the error function and search for its minimum.
#
# The error we want to minimize can be defined as the squared differences between the target value and the output value of the NN. Target value is constant. Output value in its turn is obtained after applying sigmoid function to the sum of weight multiplied by inputs. Following chain rule for derivation our problem can be stated as presented below:
# <img src="pics/formula2.png" alt="Drawing" style="width: 1000px;"/>
# <img src="pics/formula3.png" alt="Drawing" style="width: 1000px;"/>
# After solving the minimization problem we can update the weights we have assigned before.
# <img src="pics/formula5.png" alt="Drawing" style="width: 1000px;"/>
# In code this can be represented as follows:
# Update the matrix for weights between hidden and output layers:
w_h_o += np.dot((o_errors * o_output * (1.0 - o_output)), np.transpose(h_output))
# Update the matrix for weights between input and hidden layers:
w_i_h += np.dot((h_errors * h_output * (1.0 - h_output)), np.transpose(input))
# + language="html"
# <iframe src="https://giphy.com/embed/8tvzvXhB3wcmI" width="1000" height="400" frameBorder="0" class="giphy-embed" allowFullScreen></iframe>
# <p><a href="https://giphy.com/gifs/deep-learning-8tvzvXhB3wcmI">via GIPHY</a></p>
# +
# If the previous code does not display the gif file delete the previous cell and uncomment the following code
# import IPython
# url = 'https://giphy.com/embed/8tvzvXhB3wcmI'
# iframe = '<iframe src="https://giphy.com/embed/8tvzvXhB3wcmI" width="1000" height="400" frameBorder="0" class="giphy-embed" allowFullScreen></iframe>'
# IPython.display.HTML(iframe)
# -
# ## Learning Rate
# Now, there is something else, we forgot when updating our weights. If we completely change our weights with every new observation - our model learns to predict only the last input. Instead of updating weights 100 % every time we can change them only partially - this way every new observation will bring some new knowledge while the previous one will still be in memory even though updated to certain extent. The bigger the learning rate the more importance has the last observation, the smaller it is the more important is all the previous knowledge. The smaller the steps - the more accurate will be the prediction. At the same time it might take more time to learn.
# <img src="pics/learning_rate.png" alt="Drawing" style="width: 600px;"/> [Source: "Business Analytics & Data Science Course by Professor S. Lessmann, Chapter 5:
# Artificial Neural Networks"]
# +
# define the learning rate
l_r = 0.3
# update the weights for the links between the hidden and output layers
w_h_o += l_r * np.dot((o_errors * o_output * (1.0 - o_output)), np.transpose(h_output))
# update the weights for the links between the input and hidden layers
w_i_h += l_r * np.dot((h_errors * h_output * (1.0 - h_output)), np.transpose(input))
# -
# ## Put it in a bigger scale
# Let's put all the steps done before in a loop, so that we can perform them not just for one observation
# but for all observations in our training set
for i in data:
observation = i.split(',')
input = np.array((np.asfarray(observation[1:])/255.0*0.99) + 0.01, ndmin=2).T
target = np.array(np.zeros(o_n) + 0.01, ndmin=2).T
target[int(observation[0])] = 0.99
h_input = np.dot(w_i_h, input)
h_output = sigmoid(h_input)
o_input = np.dot(w_h_o, h_output)
o_output = sigmoid(o_input)
o_errors = target - o_output
h_errors = np.dot(w_h_o.T, o_errors)
w_h_o += l_r * np.dot((o_errors * o_output * (1.0 - o_output)), np.transpose(h_output))
w_i_h += l_r * np.dot((h_errors * h_output * (1.0 - h_output)), np.transpose(input))
pass
# ## Test your results
# Once we have trained the model with all 100 observations we can test it with new data it has never seen.
# load the mnist test data CSV file
raw_data_test = open("data/mnist_test.csv", 'r')
data_test = raw_data_test.readlines()
raw_data_test.close()
# check a particular observation
observation = data_test[0].split(',')
# print the label
print(observation[0])
# image the number
image = np.asfarray(observation[1:]).reshape((28,28))
mpp.imshow(image, cmap='Blues', interpolation='None')
# +
# Use this observation as an input and run NN with it
input = np.array((np.asfarray(observation[1:])/255.0*0.99) + 0.01, ndmin=2).T
h_input = np.dot(w_i_h, input)
h_output = sigmoid(h_input)
o_input = np.dot(w_h_o, h_output)
o_output = sigmoid(o_input)
o_output
# -
# Get the prediction of NN for this test observation
label = np.argmax(o_output)
label
# +
# test the neural network using all test dataset
# scorecard of the network
scorecard = []
# go through all the observations in the test data set
for i in data_test:
observation = i.split(',')
correct_label = int(observation[0])
input = np.array((np.asfarray(observation[1:])/255.0*0.99) + 0.01, ndmin=2).T
h_input = np.dot(w_i_h, input)
h_output = sigmoid(h_input)
o_input = np.dot(w_h_o, h_output)
o_output = sigmoid(o_input)
label = np.argmax(o_output)
if (label == correct_label):
scorecard.append(1)
else:
scorecard.append(0)
pass
pass
# -
# calculate the performance score, the fraction of correct answers
scorecard_array = np.asarray(scorecard)
print ("performance = ", scorecard_array.sum() / scorecard_array.size)
# It is several times better than naive. Can we do better?
# ## Improvements?
# What if we train it more? What does this mean? Introduce local minimum concept.
epochs = 5
# +
# The "big loop" with epochs
for e in range(epochs):
for i in data:
observation = i.split(',')
input = np.array((np.asfarray(observation[1:])/255.0*0.99) + 0.01, ndmin=2).T
target = np.array(np.zeros(o_n) + 0.01, ndmin=2).T
target[int(observation[0])] = 0.99
h_input = np.dot(w_i_h, input)
h_output = sigmoid(h_input)
o_input = np.dot(w_h_o, h_output)
o_output = sigmoid(o_input)
o_errors = target - o_output
h_errors = np.dot(w_h_o.T, o_errors)
w_h_o += l_r * np.dot((o_errors * o_output * (1.0 - o_output)), np.transpose(h_output))
w_i_h += l_r * np.dot((h_errors * h_output * (1.0 - h_output)), np.transpose(input))
pass
pass
# test
scorecard = []
for i in data_test:
observation = i.split(',')
correct_label = int(observation[0])
input = np.array((np.asfarray(observation[1:])/255.0*0.99) + 0.01, ndmin=2).T
h_input = np.dot(w_i_h, input)
h_output = sigmoid(h_input)
o_input = np.dot(w_h_o, h_output)
o_output = sigmoid(o_input)
label = np.argmax(o_output)
if (label == correct_label):
scorecard.append(1)
else:
scorecard.append(0)
pass
pass
# calculate accuracy
scorecard_array = np.asarray(scorecard)
print ("performance = ", scorecard_array.sum() /
scorecard_array.size)
# -
# ### Other l_r?
l_r = 0.1
# run the "big loop" with epochs again to get measure accuracy for new settings
# ### More hidden nodes?
# +
h_n = 150
# Determine the weights for a bigger matrices
w_i_h = np.random.normal(0.0, pow(h_n, -0.5), (h_n, i_n))
w_h_o = np.random.normal(0.0, pow(o_n, -0.5), (o_n, h_n))
# run the "big loop" with epochs again to get measure accuracy for new settings
# -
# It is much easier to train neural networks where the number of neurons is larger than required. But, with a smaller number of neurons the neural network has much better generalization abilities. It means it will respond correctly for patterns not used for training. If too many neurons are used, then the network can be overtrained on the training patterns, but it will fail on patterns never used in training. With a smaller number of neurons, the network cannot be trained to very small errors, but it may produce much better approximations for new patterns. The most common mistake made by many researchers is that in order to speed up the training process and to reduce the training errors, they use neural networks with a larger number of neurons than required. Such networks would perform very poorly for new patterns not used for training.
# ### Other training set?
# +
# Load the data
raw_data = open("data/mnist_train.csv", 'r')
data = raw_data.readlines()
raw_data.close()
# Settings
epochs = 2
l_r = 0.1
h_n = 90
w_i_h = np.random.normal(0.0, pow(h_n, -0.5), (h_n, i_n))
w_h_o = np.random.normal(0.0, pow(o_n, -0.5), (o_n, h_n))
# run the "big loop" with epochs again to get measure accuracy for new settings
# -
# # Activation Function Types:
#
# The activation functions are compared to each other in terms of their efficient approximation (Schnitger & DasGupta, 1993). There are several types of them but the common ones are the sigmoid, tangent hyperbolic and the RelU functions. The following is a short explanation on the advantages and disavantages of each of these activation functions.
# ## Sigmoid function:
# This function squashes the input value into a vaule in the range of [0,1]. It is powerful to compute bolean functions and the smoothness of sigmoid allows for better approxmiation (Schnitger & DasGupta, 1993). However, there are two major drawbacks. First, the sigmoid outputs 0 for high negative values and 1 for high positive values and this results in no signal flows from the nodes because the gradient at these two tails are 0. Second, its output is not centered at 0. This would ultimately result in either all positive gradients on weighte or all negative during the backpropogation.
#
# ## Tangent hyperbolic:
# Unlike to sigmoid, this function’s output is zero centered and outputs a value in the range of [-1,1]. Although it is more preferred over sigmoid but it sufferes from the same problem because it kills the gradient descent at high or low values.
#
# ## ReLU:
# This function is zero whenever input is negative and when the input is positive, its begavior is linear with slope 1. According to Glorot et al. (2011), the ReLU activation functions outperform sigmoidal functions in Deep Neural Networks on text classification and image recognition tasks. ReLU also excells the sigmoid and tangent hyperbolic in accelerating the stochastic gradient descent convergance. However, the ReLU is not prone to the training process and the nodes can die. This means that if a large gradient runs through the nodes, it may update the weights in a way that the node will never be active for any inputs again and this will result in gradient of zero from that node onward.
# # Gradient Descent:
# Gradient descent is one the most poppular algorithms to optimize the neural networks. The name gradient descent is rooted in the procedure where the gradient is repeadtedly evaluated to update the parameters.The objective of the gradient descent is to find weight parameters which will minimize the cost function. In this paper, the focus is mainly on Mini-batch Gradient Descent and the Stochastic Gradient Descent. The Mini-batch Gradient Descent (BGD) is used when there is a large scale training data set where the computation of the cost function over the whole training data set is computationaly expensive. Therefore, a batch of the training data set, say 250 observations, is randomly selected to compute the gradient with the assumption that the observations in the training dataset are correlated. If this procedure is done only for one observation instead of 250, but with 250 iterations, then this procedure is called Stochastic Gradient Descent (SGD) but it is not a common approach since it is not efficient to evaluate the gradient 250 times for one observation than iterating one time over 250 observations.
| 55.902208 | 1,125 |
8f62e43ea214b41b220109e068bae194a0f0018d
|
py
|
python
|
ImageCollection/convert_imagecollection_to_image.ipynb
|
mllzl/earthengine-py-notebooks
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <table class="ee-notebook-buttons" align="left">
# <td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/ImageCollection/convert_imagecollection_to_image.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
# <td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/ImageCollection/convert_imagecollection_to_image.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
# <td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=ImageCollection/convert_imagecollection_to_image.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
# <td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/ImageCollection/convert_imagecollection_to_image.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
# </table>
# ## Install Earth Engine API and geemap
# Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
# The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
#
# **Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
# +
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
# -
# ## Create an interactive map
# The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
# ## Add Earth Engine Python script
# +
# Add Earth Engine dataset
images = ee.ImageCollection('MODIS/MCD43A4') \
.filterDate('2017-01-01', '2017-01-31') \
.select(['Nadir_Reflectance_Band1'])
# unmask to ensure we have the same number of values everywhere
images = images.map(lambda i: i.unmask(-1))
# convert to array
array = images.toArray()
# convert to an image
bandNames = images.aggregate_array('system:index')
image = array.arrayProject([0]).arrayFlatten([bandNames])
print(image.getInfo())
bandNames = image.bandNames()
print(bandNames.getInfo())
# -
# ## Display Earth Engine data layers
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
| 52.211111 | 1,023 |
009a69b592c3b2509a98fb53b9f47e177987c87d
|
py
|
python
|
06/CS480_Assignment_6.ipynb
|
AbhishekD10/cs480student
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/AbhishekD10/cs480student/blob/main/06/CS480_Assignment_6.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="DMrBgGVKWEPJ"
# 
# #Assignment 6
# + id="Ll5BVb2mZS2_"
# In this assignment, we will train a U-Net classifer to detect mitochondria
# in electron microscopy images!
# + id="GhpX7CGfyuqw"
### IMPORTANT ###
#
# Activate GPU support: Runtime -> Change Runtime Type
# Hardware Accelerator: GPU
#
### IMPORTANT ###
# + colab={"base_uri": "https://localhost:8080/"} id="2lscACx4iuKi" outputId="d50e0e8c-6067-4f2f-eee7-c35a3a6f8ed8"
# load numpy and matplotlib
# %pylab inline
# + id="ZmB60TxJyQ61" colab={"base_uri": "https://localhost:8080/"} outputId="342edd1a-b05a-4316-c49d-bb889f60bd47"
# load the unet tensorflow code
# !pip install git+https://github.com/jakeret/unet.git
# + id="gn19r-d9yZVk"
# .. and use it!
# Note: There are a ton of U-Net implementations but this one is easier to use!
import unet
# + id="uMSdlwXfyRAv"
# + [markdown] id="f_SOOwQf78z-"
# **Task 1**: Study the unet circle example and learn about mitochondria! [15 Points]
# + id="rfTKzDOLysUW"
# The unet package allows to train a U-Net classifier with little code.
# As discussed in class, the U-Net can be used to label/segment/annotate images.
# + id="kI8AJjDmysXR"
# TODO: Please study the Circles example
# https://github.com/jakeret/unet/blob/master/notebooks/circles.ipynb
# + id="QM4GKfzTysZv"
# TODO: ... and look how the (artificial) dataset is generated
# https://github.com/jakeret/unet/blob/master/src/unet/datasets/circles.py
# + id="P2BsS24Cyscm"
# 1) Question
# TODO: Please describe what the U-Net is trained to do.
#
# TODO: YOUR ANSWER
# + [markdown] id="rtcH_9in64GK"
# U-Net is trained for Bio Medical Image Segmentation where the target is not only to classify whether there is an infection or not but also to identify the area of infection as well.
# + id="vKAyYg6yzXnw"
# 2) Question
# TODO: In circles.py, what does the following mean:
# channels = 1
# classes = 2
#
# TODO: YOUR ANSWER
# + [markdown] id="mgRyiALm7KNH"
# In circles.py channels refers to the number of input tensors. In code we use one channel it is given as channels = 1.
#
# In circles.py classes refers to the number of classes used in the class i.e., the fundamental blueprint of the code. Here 2 classes means the unet is going to classify the patters in the images as 1 with circles and 2 with not circles.
# + id="iRDRxjS-9LYi"
# 3) Question
# TODO: What are mitochondria and what is their appearance in
# electron microscopy data?
# Hint: You can validate your answer in Task 4!
#
# TODO: YOUR ANSWER
# + [markdown] id="N6fpEAyy9Auz"
# Mitochondria are membrane-bound cell organelles (mitochondrion, singular) that generate most of the chemical energy needed to power the cell's biochemcial reactions.
#
# Mitochondria observed in electron microscope have a relatively large matrix volume that pushes part of the inner membrane up against the outer membrane with a small space between them. The remaining inner membrane forms cristae projecting into the matrix, and the opposing membranes of these cristae are close together with a small space between them.
#
# + [markdown] id="KbpOUGY9fKLw"
# **Task 2**: Setup a datagenerator for mitochondria images! [45 Points]
# + id="kleZbthp9LcC"
# TODO:
# Download https://cs480.org/data/mito.npz to your computer.
# Then, please upload mito.npz using the file panel on the left.
# + id="cJJB5etk0O3B"
# The code below is similar to the circles.py file from Task 1.
# We follow Tensorflow conventions to design a tf.data.Dataset for training
# the U-Net.
#
# TODO: Please add four different data augmentation methods in the code block
# below. (image normalization to 0..1, horizontal data flip, vertical data flip,
# rotation by 90 degrees)
#
# Hint: https://github.com/jakeret/unet/blob/master/src/unet/datasets/oxford_iiit_pet.py#L25
# + id="d-aohs2x0O5s"
import tensorflow as tf
import tensorflow_datasets as tfds
from tensorflow_datasets.core import DatasetInfo
from typing import Tuple, List
IMAGE_SIZE = (256, 256)
channels = 1
classes = 2
def load_data(count:int, splits:Tuple[float]=(0.7, 0.2, 0.1), **kwargs) -> List[tf.data.Dataset]:
return [tf.data.Dataset.from_tensor_slices(_build_samples(int(split * count), **kwargs))
for split in splits]
def _build_samples(sample_count:int, **kwargs) -> Tuple[np.array, np.array]:
# here we load the mitochondria data
loaded = np.load('mito.npz')
loadedimages = loaded['arr_0'][0].copy()
loadedmasks = loaded['arr_0'][1].copy()
# now let's go to numpyland
images = np.empty((sample_count, IMAGE_SIZE[0], IMAGE_SIZE[1], 1))
labels = np.empty((sample_count, IMAGE_SIZE[0], IMAGE_SIZE[1], 2))
for i in range(sample_count):
image, mask = loadedimages[i], loadedmasks[i]
image = image.reshape((IMAGE_SIZE[0], IMAGE_SIZE[1], 1)).astype(np.float)
mask = mask.reshape((IMAGE_SIZE[0], IMAGE_SIZE[1], 1))
#
# TODO: Normalize the image to 0..1
#
# TODO: YOUR CODE
#
image = tf.image.per_image_standardization(image)
#
# TODO: Use Tensorflow to flip the image horizontally
#
if tf.random.uniform(()) > 0.5:
#
# TODO: YOUR CODE
image = tf.image.flip_left_right(image)
#
# TODO: Use Tensorflow to flip the image vertically
#
if tf.random.uniform(()) > 0.5:
#
# TODO: YOUR CODE
image = tf.image.flip_up_down(image)
#
# TODO: Use Tensorflow to rotate the image 90 degrees
#
if tf.random.uniform(()) > 0.5:
#
# TODO: YOUR CODE
image = tf.image.rot90(image, k=1)
# augmentation done, let's store the image
images[i] = image
# here we split the mask to background and foreground
fg = np.zeros((IMAGE_SIZE[0], IMAGE_SIZE[1], 1), dtype=np.bool)
fg[mask == 255] = 1
bg = np.zeros((IMAGE_SIZE[0], IMAGE_SIZE[1], 1), dtype=np.bool)
bg[mask == 0] = 1
labels[i, :, :, 0] = bg[:,:,0]
labels[i, :, :, 1] = fg[:,:,0]
return images, labels
# + id="9UNuaugR0O8k"
# + [markdown] id="eqsEUwQKfXnu"
# **Task 3**: Let's train the U-Net! [25 Points]
# + id="pnF1RIg1nVv7" colab={"base_uri": "https://localhost:8080/"} outputId="1cb9e215-da3e-4c6e-9fda-f977f609cd3e"
#
# We can now create our training, validation, and testing data by calling
# our methods from Task 2.
#
train, val, test = load_data( 660, splits=(0.7, 0.2, 0.1) )
# + id="ODwQX4rN3VfX"
# 1) Question
# TODO: We have in total 660 images + 660 masks. Based on the code above,
# how many images are used for training alone?
#
# TODO: YOUR ANSWER
# + [markdown] id="oZEXTZM9-IeM"
# We have used 462 images out of total 660 images for training purposes.
# + id="cCY5ao3X3uYF"
#
# Let's setup the U-Net!
#
LEARNING_RATE = 1e-3
unet_model = unet.build_model(channels=channels,
num_classes=classes,
layer_depth=5,
filters_root=64,
padding="same")
unet.finalize_model(unet_model, learning_rate=LEARNING_RATE)
# + id="MYezkNl-4Fu3"
#
# And, let's setup the trainer...
#
trainer = unet.Trainer(checkpoint_callback=False,
learning_rate_scheduler=unet.SchedulerType.WARMUP_LINEAR_DECAY,
warmup_proportion=0.1,
learning_rate=LEARNING_RATE)
# + id="bPs0NxVy3ua3" colab={"base_uri": "https://localhost:8080/"} outputId="3ba9600e-c980-4177-dacb-cd0c43ccb1e0"
#
# ...and train the U-Net for 50 epochs with a batch_size of 10!
#
# TODO: Please complete the code below.
# Hint: Don't forget to use training and validation data.
# Hint 2: This will take roughly 30 minutes!
#
trainer.fit(unet_model,
#
# TODO: YOUR CODE
#
#
train,
val,
epochs=50,
batch_size=10
)
# + id="XGYzUOUK4__u"
# + [markdown] id="R68B9XFl5Rgw"
# **Task 4**: Let's predict mitochondria in the testing data! [15 Points]
# + id="s-UbhXC150VU"
#
# After training, let's try the U-Net on our testing data.
#
# The code below displays the first 10 input images, the original masks by experts,
# and the predicted masks from the U-Net.
# + id="E8Cj3bpS5AS4" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="5f3688e7-37f5-4a78-a7de-79a3ed12e85e"
rows = 10
fig, axs = plt.subplots(rows, 3, figsize=(8, 30))
for ax, (image, label) in zip(axs, test.take(rows).batch(1)):
prediction = unet_model.predict(image)
ax[0].matshow(image[0, :, :, 0])
ax[1].matshow(label[0, :, :, 1], cmap="gray")
ax[2].matshow(prediction[0].argmax(axis=-1), cmap="gray")
# + id="3L5hkXmD7K3t"
# 1) Question
# TODO: Why do we use the prediction[0].argmax(axis=-1) command
# to display the prediction?
#
# TODO: YOUR ANSWER
# + [markdown] id="9adV3y8YP48D"
# we use the prediction[0].argmax(axis=-1) command to display the prediction because the predicted masks start at 0th index of the array that will displayed by the argmax.
# + id="aa3ZpjeD7ntl"
# 2) Question
# TODO: Is the quality of the segmentation good and how could we improve it?
# Hint: Think along the lines of some traditional image processing rather than
# increasing the training data size.
#
# TODO: YOUR ANSWER
# + [markdown] id="2_Z_XxQ1Qean"
# The quality of the segmentation is good and can be improved. We can see the horizontal, vertical and the 90 degree rotations.
# Here,The predicted masks are not viewed but the original masks seem nearly good. Also Changing brightness and saturation can improve the quality of segmentation.
# + [markdown] id="1f72yBFNgonn"
# **Bonus**: Compare against the state-of-the-art literature! [33 Points]
# + id="suX0YEehgzYq"
#
# The following paper also uses a 2D U-Net to detect mitochondria:
#
# https://danielhaehn.com/papers/?casser2020fast
#
# + id="Ocls97_99GU4"
# 1) Question
#
# TODO: How many learnable parameters does your trained unet_model have?
# Hint: You can use TF's Model Summary function to answer this.
#
# + id="JZbylsm59fLC" colab={"base_uri": "https://localhost:8080/"} outputId="7a184247-4599-4bbe-946d-b8aa1a3f3aa5"
# TODO: YOUR CODE
unet_model.summary()
# + [markdown] id="3CBlLNQFR5ZV"
# Our trained unet_model have 31,030,658 learnable parameters
# + id="rJKCplpW9fUh"
# 2) Question
#
# TODO: How many parameters do Casser et al. use?
#
# + id="E4UrDudR9pv6"
# TODO: YOUR ANSWER
# + [markdown] id="JIqumw-MSMu6"
# Casser et al. use 1,958,533 parameters.
# + id="D2vrwSkH9rR6"
# + id="E5-idiGh9rdI"
# 3) Question
#
# TODO: How did Casser et al. reduce the parameters?
#
# + id="fZpvxcq19v-_"
# TODO: YOUR ANSWER
# + [markdown] id="mZ3xeArrSXx5"
# Casser et al. reduced the parameters by:
#
# Reducing the number of convolutional filters throughout the network.
#
# Replace the transpose convolutions in the decoder with light-weight bilinear upsampling layers that require no paramters.
# + id="HpdBFfnQ9xsr"
# 4) Question
#
# TODO: Why did Casser et al. reduce the parameters?
#
# + id="V3cGbWdB93om"
# TODO: YOUR ANSWER
# + [markdown] id="EpPsm1uzTD1s"
# For acheiving a 40% additional throughput which further increases effectiveness, the parameters are reduced.
# + id="kWb3h4MKm5t4"
#
# You made it!!
#
# _ ___ /^^\ /^\ /^^\_
# _ _@)@) \ ,,/ '` ~ `'~~ ', `\.
# _/o\_ _ _ _/~`.`...'~\ ./~~..,'`','',.,' ' ~:
# / `,'.~,~.~ . , . , ~|, ,/ .,' , ,. .. ,,. `, ~\_
# ( ' _' _ '_` _ ' . , `\_/ .' ..' ' ` ` `.. `, \_
# ~V~ V~ V~ V~ ~\ ` ' . ' , ' .,.,''`.,.''`.,.``. ', \_
# _/\ /\ /\ /\_/, . ' , `_/~\_ .' .,. ,, , _/~\_ `. `. '., \_
# < ~ ~ '~`'~'`, ., . `_: ::: \_ ' `_/ ::: \_ `.,' . ', \_
# \ ' `_ '`_ _ ',/ _::_::_ \ _ _/ _::_::_ \ `.,'.,`., \-,-,-,_,_,
# `'~~ `'~~ `'~~ `'~~ \(_)(_)(_)/ `~~' \(_)(_)(_)/ ~'`\_.._,._,'_;_;_;_;_;
#
| 173.390306 | 55,708 |
d81caf5665dac211bd3371e1b0681c1249b42689
|
py
|
python
|
NOG-NLG dummy codes/46_Deep_conversational_answers_dummy_code.ipynb
|
Cezanne-ai/project-2021
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="FDoHfSs4dxPp"
# There are 3 types of books that our model will accommodate. The books were processed and by this time we have structured databases, and we need to accommodate answers based on a labyrinth model, a self-generative model and CVM.
#
# NLG enhancement and DER will not have an impact on these answers, but the self-generative model will have and the bot will search for optimistic/pessimistic answers, depending on the model output.
#
# + id="3BcYdoEydoh-"
# IN: initialization of deep conversational topics
# OUT: NOG solutions
# + id="4UIcNUwad4n4"
#insert code to implement the following table + additional requirements (see books processing and books training pipelines also)
# + [markdown] id="fB6OutYMeFnP"
# 
| 3,156.5 | 87,418 |
1a2bc50fa2da65b737c24a0bd03b5e7220855af8
|
py
|
python
|
3. Landmark Detection and Tracking.ipynb
|
HarshitaDPoojary/simultaneous-localization-and-mapping
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Project 3: Implement SLAM
#
# ---
#
# ## Project Overview
#
# In this project, you'll implement SLAM for robot that moves and senses in a 2 dimensional, grid world!
#
# SLAM gives us a way to both localize a robot and build up a map of its environment as a robot moves and senses in real-time. This is an active area of research in the fields of robotics and autonomous systems. Since this localization and map-building relies on the visual sensing of landmarks, this is a computer vision problem.
#
# Using what you've learned about robot motion, representations of uncertainty in motion and sensing, and localization techniques, you will be tasked with defining a function, `slam`, which takes in six parameters as input and returns the vector `mu`.
# > `mu` contains the (x,y) coordinate locations of the robot as it moves, and the positions of landmarks that it senses in the world
#
# You can implement helper functions as you see fit, but your function must return `mu`. The vector, `mu`, should have (x, y) coordinates interlaced, for example, if there were 2 poses and 2 landmarks, `mu` will look like the following, where `P` is the robot position and `L` the landmark position:
# ```
# mu = matrix([[Px0],
# [Py0],
# [Px1],
# [Py1],
# [Lx0],
# [Ly0],
# [Lx1],
# [Ly1]])
# ```
#
# You can see that `mu` holds the poses first `(x0, y0), (x1, y1), ...,` then the landmark locations at the end of the matrix; we consider a `nx1` matrix to be a vector.
#
# ## Generating an environment
#
# In a real SLAM problem, you may be given a map that contains information about landmark locations, and in this example, we will make our own data using the `make_data` function, which generates a world grid with landmarks in it and then generates data by placing a robot in that world and moving and sensing over some numer of time steps. The `make_data` function relies on a correct implementation of robot move/sense functions, which, at this point, should be complete and in the `robot_class.py` file. The data is collected as an instantiated robot moves and senses in a world. Your SLAM function will take in this data as input. So, let's first create this data and explore how it represents the movement and sensor measurements that our robot takes.
#
# ---
# ## Create the world
#
# Use the code below to generate a world of a specified size with randomly generated landmark locations. You can change these parameters and see how your implementation of SLAM responds!
#
# `data` holds the sensors measurements and motion of your robot over time. It stores the measurements as `data[i][0]` and the motion as `data[i][1]`.
#
# #### Helper functions
#
# You will be working with the `robot` class that may look familiar from the first notebook,
#
# In fact, in the `helpers.py` file, you can read the details of how data is made with the `make_data` function. It should look very similar to the robot move/sense cycle you've seen in the first notebook.
# +
import numpy as np
from helpers import make_data
# your implementation of slam should work with the following inputs
# feel free to change these input values and see how it responds!
# world parameters
num_landmarks = 5 # number of landmarks
N = 20 # time steps
world_size = 100.0 # size of world (square)
# robot parameters
measurement_range = 50.0 # range at which we can sense landmarks
motion_noise = 2.0 # noise in robot motion
measurement_noise = 2.0 # noise in the measurements
distance = 20.0 # distance by which robot (intends to) move each iteratation
# make_data instantiates a robot, AND generates random landmarks for a given world size and number of landmarks
data = make_data(N, num_landmarks, world_size, measurement_range, motion_noise, measurement_noise, distance)
# -
# ### A note on `make_data`
#
# The function above, `make_data`, takes in so many world and robot motion/sensor parameters because it is responsible for:
# 1. Instantiating a robot (using the robot class)
# 2. Creating a grid world with landmarks in it
#
# **This function also prints out the true location of landmarks and the *final* robot location, which you should refer back to when you test your implementation of SLAM.**
#
# The `data` this returns is an array that holds information about **robot sensor measurements** and **robot motion** `(dx, dy)` that is collected over a number of time steps, `N`. You will have to use *only* these readings about motion and measurements to track a robot over time and find the determine the location of the landmarks using SLAM. We only print out the true landmark locations for comparison, later.
#
#
# In `data` the measurement and motion data can be accessed from the first and second index in the columns of the data array. See the following code for an example, where `i` is the time step:
# ```
# measurement = data[i][0]
# motion = data[i][1]
# ```
#
# +
# print out some stats about the data
time_step = 0
print('Example measurements: \n', data[time_step][0])
print('\n')
print('Example motion: \n', data[time_step][1])
# -
# Try changing the value of `time_step`, you should see that the list of measurements varies based on what in the world the robot sees after it moves. As you know from the first notebook, the robot can only sense so far and with a certain amount of accuracy in the measure of distance between its location and the location of landmarks. The motion of the robot always is a vector with two values: one for x and one for y displacement. This structure will be useful to keep in mind as you traverse this data in your implementation of slam.
# ## Initialize Constraints
#
# One of the most challenging tasks here will be to create and modify the constraint matrix and vector: omega and xi. In the second notebook, you saw an example of how omega and xi could hold all the values the define the relationships between robot poses `xi` and landmark positions `Li` in a 1D world, as seen below, where omega is the blue matrix and xi is the pink vector.
#
# <img src='images/motion_constraint.png' width=50% height=50% />
#
#
# In *this* project, you are tasked with implementing constraints for a 2D world. We are referring to robot poses as `Px, Py` and landmark positions as `Lx, Ly`, and one way to approach this challenge is to add *both* x and y locations in the constraint matrices.
#
# <img src='images/constraints2D.png' width=50% height=50% />
#
# You may also choose to create two of each omega and xi (one for x and one for y positions).
# ### TODO: Write a function that initializes omega and xi
#
# Complete the function `initialize_constraints` so that it returns `omega` and `xi` constraints for the starting position of the robot. Any values that we do not yet know should be initialized with the value `0`. You may assume that our robot starts out in exactly the middle of the world with 100% confidence (no motion or measurement noise at this point). The inputs `N` time steps, `num_landmarks`, and `world_size` should give you all the information you need to construct intial constraints of the correct size and starting values.
#
# *Depending on your approach you may choose to return one omega and one xi that hold all (x,y) positions *or* two of each (one for x values and one for y); choose whichever makes most sense to you!*
def initialize_constraints(N, num_landmarks, world_size):
''' This function takes in a number of time steps N, number of landmarks, and a world_size,
and returns initialized constraint matrices, omega and xi.'''
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
# Multipled by 2 because we are considering 2D world with x and y coordinates
rows = 2* (N + num_landmarks)
cols = 2* (N + num_landmarks)
omega = np.zeros((rows, cols))
omega[0][0] = 1.0
omega[1][1] = 1.0
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
xi = np.zeros((rows, 1))
xi[0][0] = world_size / 2
xi[1][0] = world_size / 2
return omega, xi
# ### Test as you go
#
# It's good practice to test out your code, as you go. Since `slam` relies on creating and updating constraint matrices, `omega` and `xi` to account for robot sensor measurements and motion, let's check that they initialize as expected for any given parameters.
#
# Below, you'll find some test code that allows you to visualize the results of your function `initialize_constraints`. We are using the [seaborn](https://seaborn.pydata.org/) library for visualization.
#
# **Please change the test values of N, landmarks, and world_size and see the results**. Be careful not to use these values as input into your final smal function.
#
# This code assumes that you have created one of each constraint: `omega` and `xi`, but you can change and add to this code, accordingly. The constraints should vary in size with the number of time steps and landmarks as these values affect the number of poses a robot will take `(Px0,Py0,...Pxn,Pyn)` and landmark locations `(Lx0,Ly0,...Lxn,Lyn)` whose relationships should be tracked in the constraint matrices. Recall that `omega` holds the weights of each variable and `xi` holds the value of the sum of these variables, as seen in Notebook 2. You'll need the `world_size` to determine the starting pose of the robot in the world and fill in the initial values for `xi`.
# import data viz resources
import matplotlib.pyplot as plt
from pandas import DataFrame
import seaborn as sns
# %matplotlib inline
# +
# define a small N and world_size (small for ease of visualization)
N_test = 5
num_landmarks_test = 2
small_world = 10
# initialize the constraints
initial_omega, initial_xi = initialize_constraints(N_test, num_landmarks_test, small_world)
# +
# define figure size
plt.rcParams["figure.figsize"] = (10,7)
# display omega
sns.heatmap(DataFrame(initial_omega), cmap='Blues', annot=True, linewidths=.5)
# +
# define figure size
plt.rcParams["figure.figsize"] = (1,7)
# display xi
sns.heatmap(DataFrame(initial_xi), cmap='Oranges', annot=True, linewidths=.5)
# -
# ---
# ## SLAM inputs
#
# In addition to `data`, your slam function will also take in:
# * N - The number of time steps that a robot will be moving and sensing
# * num_landmarks - The number of landmarks in the world
# * world_size - The size (w/h) of your world
# * motion_noise - The noise associated with motion; the update confidence for motion should be `1.0/motion_noise`
# * measurement_noise - The noise associated with measurement/sensing; the update weight for measurement should be `1.0/measurement_noise`
#
# #### A note on noise
#
# Recall that `omega` holds the relative "strengths" or weights for each position variable, and you can update these weights by accessing the correct index in omega `omega[row][col]` and *adding/subtracting* `1.0/noise` where `noise` is measurement or motion noise. `Xi` holds actual position values, and so to update `xi` you'll do a similar addition process only using the actual value of a motion or measurement. So for a vector index `xi[row][0]` you will end up adding/subtracting one measurement or motion divided by their respective `noise`.
#
# ### TODO: Implement Graph SLAM
#
# Follow the TODO's below to help you complete this slam implementation (these TODO's are in the recommended order), then test out your implementation!
#
# #### Updating with motion and measurements
#
# With a 2D omega and xi structure as shown above (in earlier cells), you'll have to be mindful about how you update the values in these constraint matrices to account for motion and measurement constraints in the x and y directions. Recall that the solution to these matrices (which holds all values for robot poses `P` and landmark locations `L`) is the vector, `mu`, which can be computed at the end of the construction of omega and xi as the inverse of omega times xi: $\mu = \Omega^{-1}\xi$
#
# **You may also choose to return the values of `omega` and `xi` if you want to visualize their final state!**
# +
## TODO: Complete the code to implement SLAM
## slam takes in 6 arguments and returns mu,
## mu is the entire path traversed by a robot (all x,y poses) *and* all landmarks locations
def slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise):
## TODO: Use your initilization to create constraint matrices, omega and xi
omega, xi = initialize_constraints(N, num_landmarks, world_size)
## TODO: Iterate through each time step in the data
## get all the motion and measurement data as you iterate
measurement_confidence = 1.0 / measurement_noise
motion_confidence = 1.0 / motion_noise
for i, values in enumerate(data):
# robot pose index in omega
idx_robot = i * 2
measurement = values[0]
motion = values[1]
## TODO: update the constraint matrix/vector to account for all *measurements*
## this should be a series of additions that take into account the measurement noise
for measure in measurement:
idx_landmark = 2 * (N + measure[0])
for j in range(2):
omega[idx_robot + j] [idx_robot + j] += measurement_confidence
omega[idx_landmark + j][idx_landmark + j] += measurement_confidence
omega[idx_robot + j][idx_landmark + j] += -measurement_confidence
omega[idx_landmark + j][idx_robot + j] += -measurement_confidence
xi[idx_robot+j][0] += -measure[j+1]*measurement_confidence
xi[idx_landmark+j][0] += measure[j+1]*measurement_confidence
## TODO: update the constraint matrix/vector to account for all *motion* and motion noise
for j in range(2):
omega[idx_robot + j][idx_robot + j] += motion_confidence
omega[idx_robot + 2 + j][idx_robot + 2 +j] += motion_confidence
omega[idx_robot + 2 + j][idx_robot + j] += -motion_confidence
omega[idx_robot + j][idx_robot + 2 + j] += -motion_confidence
xi[idx_robot + j][0] += -motion[j]*motion_confidence
xi[idx_robot + 2 + j][0] += motion[j]*motion_confidence
## TODO: After iterating through all the data
## Compute the best estimate of poses and landmark positions
## using the formula, omega_inverse * Xi
omega_inv = np.linalg.inv(np.matrix(omega))
mu = omega_inv*xi
return mu, omega, xi # return `mu`
# -
mu,omega,xi = slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
# figure size
plt.rcParams["figure.figsize"] = (20,20)
# display heatmap of omega
sns.heatmap(DataFrame(omega), cmap='Blues', annot=True, linewidths=.5)
# figure size
plt.rcParams["figure.figsize"] = (1,20)
# display heatmap of xi
sns.heatmap(DataFrame(xi), cmap='Oranges', annot=True, linewidths=.5)
# ## Helper functions
#
# To check that your implementation of SLAM works for various inputs, we have provided two helper functions that will help display the estimated pose and landmark locations that your function has produced. First, given a result `mu` and number of time steps, `N`, we define a function that extracts the poses and landmarks locations and returns those as their own, separate lists.
#
# Then, we define a function that nicely print out these lists; both of these we will call, in the next step.
#
# a helper function that creates a list of poses and of landmarks for ease of printing
# this only works for the suggested constraint architecture of interlaced x,y poses
def get_poses_landmarks(mu, N):
# create a list of poses
poses = []
for i in range(N):
poses.append((mu[2*i].item(), mu[2*i+1].item()))
# create a list of landmarks
landmarks = []
for i in range(num_landmarks):
landmarks.append((mu[2*(N+i)].item(), mu[2*(N+i)+1].item()))
# return completed lists
return poses, landmarks
def print_all(poses, landmarks):
print('\n')
print('Estimated Poses:')
for i in range(len(poses)):
print('['+', '.join('%.3f'%p for p in poses[i])+']')
print('\n')
print('Estimated Landmarks:')
for i in range(len(landmarks)):
print('['+', '.join('%.3f'%l for l in landmarks[i])+']')
# ## Run SLAM
#
# Once you've completed your implementation of `slam`, see what `mu` it returns for different world sizes and different landmarks!
#
# ### What to Expect
#
# The `data` that is generated is random, but you did specify the number, `N`, or time steps that the robot was expected to move and the `num_landmarks` in the world (which your implementation of `slam` should see and estimate a position for. Your robot should also start with an estimated pose in the very center of your square world, whose size is defined by `world_size`.
#
# With these values in mind, you should expect to see a result that displays two lists:
# 1. **Estimated poses**, a list of (x, y) pairs that is exactly `N` in length since this is how many motions your robot has taken. The very first pose should be the center of your world, i.e. `[50.000, 50.000]` for a world that is 100.0 in square size.
# 2. **Estimated landmarks**, a list of landmark positions (x, y) that is exactly `num_landmarks` in length.
#
# #### Landmark Locations
#
# If you refer back to the printout of *exact* landmark locations when this data was created, you should see values that are very similar to those coordinates, but not quite (since `slam` must account for noise in motion and measurement).
# +
# call your implementation of slam, passing in the necessary parameters
mu,_,_ = slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
poses, landmarks = get_poses_landmarks(mu, N)
print_all(poses, landmarks)
# -
# ## Visualize the constructed world
#
# Finally, using the `display_world` code from the `helpers.py` file (which was also used in the first notebook), we can actually visualize what you have coded with `slam`: the final position of the robot and the positon of landmarks, created from only motion and measurement data!
#
# **Note that these should be very similar to the printed *true* landmark locations and final pose from our call to `make_data` early in this notebook.**
# +
# import the helper function
from helpers import display_world
# Display the final world!
# define figure size
plt.rcParams["figure.figsize"] = (20,20)
# check if poses has been created
if 'poses' in locals():
# print out the last pose
print('Last pose: ', poses[-1])
# display the last position of the robot *and* the landmark positions
display_world(int(world_size), poses[-1], landmarks)
# +
# #With N = 50
from helpers import make_data
num_landmarks_50 = 100 # number of landmarks
N_50 = 50 # time steps
world_size_50 = 100.0 # size of world (square)
# robot parameters
measurement_range_50 = 50.0 # range at which we can sense landmarks
motion_noise_50 = 2.0 # noise in robot motion
measurement_noise_50 = 2.0 # noise in the measurements
distance_50 = 20.0 # distance by which robot (intends to) move each iteratation
# make_data instantiates a robot, AND generates random landmarks for a given world size and number of landmarks
data_50 = make_data(N_50, num_landmarks_50, world_size_50, measurement_range_50, motion_noise_50, measurement_noise_50, distance_50)
# +
mu_50,_,_ = slam(data_50, N_50, num_landmarks_50, world_size_50, motion_noise_50, measurement_noise_50)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
poses, landmarks = get_poses_landmarks(mu_50, N_50)
print_all(poses, landmarks)
# +
# #With Reduced Noise Below 1
from helpers import make_data
num_landmarks_RNB1 = 5 # number of landmarks
N_RNB1 = 50 # time steps
world_size_RNB1 = 100.0 # size of world (square)
# robot parameters
measurement_range_RNB1 = 50.0 # range at which we can sense landmarks
motion_noise_RNB1 = 0.8 # noise in robot motion
measurement_noise_RNB1 = 0.8 # noise in the measurements
distance_RNB1 = 20.0 # distance by which robot (intends to) move each iteratation
# make_data instantiates a robot, AND generates random landmarks for a given world size and number of landmarks
data_RNB1 = make_data(N_RNB1, num_landmarks_RNB1, world_size_RNB1, measurement_range_RNB1, motion_noise_RNB1, measurement_noise_RNB1, distance_RNB1)
# +
mu_RNB1,_,_ = slam(data_RNB1, N_RNB1, num_landmarks_RNB1, world_size_RNB1, motion_noise_RNB1, measurement_noise_RNB1)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
poses, landmarks = get_poses_landmarks(mu_RNB1, N_RNB1)
print_all(poses, landmarks)
# +
# #With Reduced Noise Around 1
from helpers import make_data
num_landmarks_RNA1 = 5 # number of landmarks
N_RNA1 = 50 # time steps
world_size_RNA1 = 100.0 # size of world (square)
# robot parameters
measurement_range_RNA1 = 50.0 # range at which we can sense landmarks
motion_noise_RNA1 = 1.1 # noise in robot motion
measurement_noise_RNA1 = 1.1 # noise in the measurements
distance_RNA1 = 20.0 # distance by which robot (intends to) move each iteratation
# make_data instantiates a robot, AND generates random landmarks for a given world size and number of landmarks
data_RNA1 = make_data(N_RNA1, num_landmarks_RNA1, world_size_RNA1, measurement_range_RNA1, motion_noise_RNA1, measurement_noise_RNA1, distance_RNA1)
# +
mu_RNA1,_,_ = slam(data_RNA1, N_RNA1, num_landmarks_RNA1, world_size_RNA1, motion_noise_RNA1, measurement_noise_RNA1)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
poses, landmarks = get_poses_landmarks(mu_RNA1, N_RNA1)
print_all(poses, landmarks)
# -
# ### Question: How far away is your final pose (as estimated by `slam`) compared to the *true* final pose? Why do you think these poses are different?
#
# You can find the true value of the final pose in one of the first cells where `make_data` was called. You may also want to look at the true landmark locations and compare them to those that were estimated by `slam`. Ask yourself: what do you think would happen if we moved and sensed more (increased N)? Or if we had lower/higher noise parameters.
# **Answer**:
# * The difference between true and predicted final pose are fairly close although there are some differences due to the measurement and motion noises. Estimated value final pose for the inital scenario was (49.54680767806224, 71.91331283694804) and the true value was (48.03222, 71.25769)
#
# * Experimenting with different parameters following observations are made:
# - With increase in timesteps, the accuracy fairly depends on noise. If noise is causing deviation from the original pose, then accuracy decreases with the increase in the number of moves.
# - With increase in the number of landmarks the ability to sense increases. With movement uncertaininty increases and with sense uncertainity decreases. So, higher the number of landmarks better predictions can be made as the robot senses and impoves the uncertainity.
# - The accuracy of predictions are highly dependent on noise. If the noise is higher, it leads to a lower confidence and higher deviation.
# ## Testing
#
# To confirm that your slam code works before submitting your project, it is suggested that you run it on some test data and cases. A few such cases have been provided for you, in the cells below. When you are ready, uncomment the test cases in the next cells (there are two test cases, total); your output should be **close-to or exactly** identical to the given results. If there are minor discrepancies it could be a matter of floating point accuracy or in the calculation of the inverse matrix.
#
# ### Submit your project
#
# If you pass these tests, it is a good indication that your project will pass all the specifications in the project rubric. Follow the submission instructions to officially submit!
# +
# Here is the data and estimated outputs for test case 1
test_data1 = [[[[1, 19.457599255548065, 23.8387362100849], [2, -13.195807561967236, 11.708840328458608], [3, -30.0954905279171, 15.387879242505843]], [-12.2607279422326, -15.801093326936487]], [[[2, -0.4659930049620491, 28.088559771215664], [4, -17.866382374890936, -16.384904503932]], [-12.2607279422326, -15.801093326936487]], [[[4, -6.202512900833806, -1.823403210274639]], [-12.2607279422326, -15.801093326936487]], [[[4, 7.412136480918645, 15.388585962142429]], [14.008259661173426, 14.274756084260822]], [[[4, -7.526138813444998, -0.4563942429717849]], [14.008259661173426, 14.274756084260822]], [[[2, -6.299793150150058, 29.047830407717623], [4, -21.93551130411791, -13.21956810989039]], [14.008259661173426, 14.274756084260822]], [[[1, 15.796300959032276, 30.65769689694247], [2, -18.64370821983482, 17.380022987031367]], [14.008259661173426, 14.274756084260822]], [[[1, 0.40311325410337906, 14.169429532679855], [2, -35.069349468466235, 2.4945558982439957]], [14.008259661173426, 14.274756084260822]], [[[1, -16.71340983241936, -2.777000269543834]], [-11.006096015782283, 16.699276945166858]], [[[1, -3.611096830835776, -17.954019226763958]], [-19.693482634035977, 3.488085684573048]], [[[1, 18.398273354362416, -22.705102332550947]], [-19.693482634035977, 3.488085684573048]], [[[2, 2.789312482883833, -39.73720193121324]], [12.849049222879723, -15.326510824972983]], [[[1, 21.26897046581808, -10.121029799040915], [2, -11.917698965880655, -23.17711662602097], [3, -31.81167947898398, -16.7985673023331]], [12.849049222879723, -15.326510824972983]], [[[1, 10.48157743234859, 5.692957082575485], [2, -22.31488473554935, -5.389184118551409], [3, -40.81803984305378, -2.4703329790238118]], [12.849049222879723, -15.326510824972983]], [[[0, 10.591050242096598, -39.2051798967113], [1, -3.5675572049297553, 22.849456408289125], [2, -38.39251065320351, 7.288990306029511]], [12.849049222879723, -15.326510824972983]], [[[0, -3.6225556479370766, -25.58006865235512]], [-7.8874682868419965, -18.379005523261092]], [[[0, 1.9784503557879374, -6.5025974151499]], [-7.8874682868419965, -18.379005523261092]], [[[0, 10.050665232782423, 11.026385307998742]], [-17.82919359778298, 9.062000642947142]], [[[0, 26.526838150174818, -0.22563393232425621], [4, -33.70303936886652, 2.880339841013677]], [-17.82919359778298, 9.062000642947142]]]
## Test Case 1
##
# Estimated Pose(s):
# [50.000, 50.000]
# [37.858, 33.921]
# [25.905, 18.268]
# [13.524, 2.224]
# [27.912, 16.886]
# [42.250, 30.994]
# [55.992, 44.886]
# [70.749, 59.867]
# [85.371, 75.230]
# [73.831, 92.354]
# [53.406, 96.465]
# [34.370, 100.134]
# [48.346, 83.952]
# [60.494, 68.338]
# [73.648, 53.082]
# [86.733, 38.197]
# [79.983, 20.324]
# [72.515, 2.837]
# [54.993, 13.221]
# [37.164, 22.283]
# Estimated Landmarks:
# [82.679, 13.435]
# [70.417, 74.203]
# [36.688, 61.431]
# [18.705, 66.136]
# [20.437, 16.983]
### Uncomment the following three lines for test case 1 and compare the output to the values above ###
mu_1,_,_ = slam(test_data1, 20, 5, 100.0, 2.0, 2.0)
poses, landmarks = get_poses_landmarks(mu_1, 20)
print_all(poses, landmarks)
# +
# Here is the data and estimated outputs for test case 2
test_data2 = [[[[0, 26.543274387283322, -6.262538160312672], [3, 9.937396825799755, -9.128540360867689]], [18.92765331253674, -6.460955043986683]], [[[0, 7.706544739722961, -3.758467215445748], [1, 17.03954411948937, 31.705489938553438], [3, -11.61731288777497, -6.64964096716416]], [18.92765331253674, -6.460955043986683]], [[[0, -12.35130507136378, 2.585119104239249], [1, -2.563534536165313, 38.22159657838369], [3, -26.961236804740935, -0.4802312626141525]], [-11.167066095509824, 16.592065417497455]], [[[0, 1.4138633151721272, -13.912454837810632], [1, 8.087721200818589, 20.51845934354381], [3, -17.091723454402302, -16.521500551709707], [4, -7.414211721400232, 38.09191602674439]], [-11.167066095509824, 16.592065417497455]], [[[0, 12.886743222179561, -28.703968411636318], [1, 21.660953298391387, 3.4912891084614914], [3, -6.401401414569506, -32.321583037341625], [4, 5.034079343639034, 23.102207946092893]], [-11.167066095509824, 16.592065417497455]], [[[1, 31.126317672358578, -10.036784369535214], [2, -38.70878528420893, 7.4987265861424595], [4, 17.977218575473767, 6.150889254289742]], [-6.595520680493778, -18.88118393939265]], [[[1, 41.82460922922086, 7.847527392202475], [3, 15.711709540417502, -30.34633659912818]], [-6.595520680493778, -18.88118393939265]], [[[0, 40.18454208294434, -6.710999804403755], [3, 23.019508919299156, -10.12110867290604]], [-6.595520680493778, -18.88118393939265]], [[[3, 27.18579315312821, 8.067219022708391]], [-6.595520680493778, -18.88118393939265]], [[], [11.492663265706092, 16.36822198838621]], [[[3, 24.57154567653098, 13.461499960708197]], [11.492663265706092, 16.36822198838621]], [[[0, 31.61945290413707, 0.4272295085799329], [3, 16.97392299158991, -5.274596836133088]], [11.492663265706092, 16.36822198838621]], [[[0, 22.407381798735177, -18.03500068379259], [1, 29.642444125196995, 17.3794951934614], [3, 4.7969752441371645, -21.07505361639969], [4, 14.726069092569372, 32.75999422300078]], [11.492663265706092, 16.36822198838621]], [[[0, 10.705527984670137, -34.589764174299596], [1, 18.58772336795603, -0.20109708164787765], [3, -4.839806195049413, -39.92208742305105], [4, 4.18824810165454, 14.146847823548889]], [11.492663265706092, 16.36822198838621]], [[[1, 5.878492140223764, -19.955352450942357], [4, -7.059505455306587, -0.9740849280550585]], [19.628527845173146, 3.83678180657467]], [[[1, -11.150789592446378, -22.736641053247872], [4, -28.832815721158255, -3.9462962046291388]], [-19.841703647091965, 2.5113335861604362]], [[[1, 8.64427397916182, -20.286336970889053], [4, -5.036917727942285, -6.311739993868336]], [-5.946642674882207, -19.09548221169787]], [[[0, 7.151866679283043, -39.56103232616369], [1, 16.01535401373368, -3.780995345194027], [4, -3.04801331832137, 13.697362774960865]], [-5.946642674882207, -19.09548221169787]], [[[0, 12.872879480504395, -19.707592098123207], [1, 22.236710716903136, 16.331770792606406], [3, -4.841206109583004, -21.24604435851242], [4, 4.27111163223552, 32.25309748614184]], [-5.946642674882207, -19.09548221169787]]]
## Test Case 2
##
# Estimated Pose(s):
# [50.000, 50.000]
# [69.035, 45.061]
# [87.655, 38.971]
# [76.084, 55.541]
# [64.283, 71.684]
# [52.396, 87.887]
# [44.674, 68.948]
# [37.532, 49.680]
# [31.392, 30.893]
# [24.796, 12.012]
# [33.641, 26.440]
# [43.858, 43.560]
# [54.735, 60.659]
# [65.884, 77.791]
# [77.413, 94.554]
# [96.740, 98.020]
# [76.149, 99.586]
# [70.211, 80.580]
# [64.130, 61.270]
# [58.183, 42.175]
# Estimated Landmarks:
# [76.777, 42.415]
# [85.109, 76.850]
# [13.687, 95.386]
# [59.488, 39.149]
# [69.283, 93.654]
### Uncomment the following three lines for test case 2 and compare to the values above ###
mu_2,_,_ = slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
poses, landmarks = get_poses_landmarks(mu_2, 20)
print_all(poses, landmarks)
| 54.967185 | 3,030 |
572e49ec7284a6109a1a82ea294756a4e6b3d760
|
py
|
python
|
Classification/Adaptive Boosting/AdaBoostClassifier_MinMaxScaler.ipynb
|
mohityogesh44/ds-seed
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="2Quif777uysg"
# # AdaBoost Classification with MinMaxScaler
#
# -
# This Code template is for the Classification tasks using a simple AdaBoostClassifier based on the Boosting Ensemble Learning technique, where the data rescaling technique used is the MinMaxScaler function.
# ### Required Packages
# + id="MLcAUyLmuysk"
# !pip install imblearn
# + id="rRPjdiN8uysm"
import warnings
import numpy as np
import pandas as pd
import seaborn as se
import matplotlib.pyplot as plt
from sklearn.ensemble import AdaBoostClassifier
from imblearn.over_sampling import RandomOverSampler
from sklearn.preprocessing import LabelEncoder,MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, plot_confusion_matrix
warnings.filterwarnings('ignore')
# + [markdown] id="iDY-OeYEuyso"
# ### Initialization
#
# Filepath of CSV file
# + id="k2Wguh-Auyso"
#filepath
file_path= "/content/titanic_train.csv"
# + [markdown] id="KUMX6fd6uysp"
# List of features which are required for model training .
# + id="nL5ure-Zuysq"
#x_values
features = ['Pclass','Age','Sex','SibSp','Parch','Fare']
# + [markdown] id="PmafdFk3uysr"
# Target feature for prediction.
# + id="EOPZV-B7uysr"
#y_value
target = 'Survived'
# + [markdown] id="oUtFb4Y5uyst"
# ### Data Fetching
#
# Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
#
# We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
# + colab={"base_uri": "https://localhost:8080/", "height": 206} id="SXboLvUHuysu" outputId="41d9b294-0970-4423-92c8-e98f29e8bc07"
df=pd.read_csv(file_path)
df.head()
# + [markdown] id="ZCK2LJlyuysw"
# ### Feature Selections
#
# It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
#
# We will assign all the required input features to X and target/outcome to Y.
# + id="EtMhiRy-uysw"
X = df[features]
Y = df[target]
# + [markdown] id="dBsPNl8Tuysx"
# ### Data Preprocessing
#
# Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
#
# + id="ogVOWWPbuysx"
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
def EncodeY(df):
if len(df.unique())<=2:
return df
else:
un_EncodedT=np.sort(pd.unique(df), axis=-1, kind='mergesort')
df=LabelEncoder().fit_transform(df)
EncodedT=[xi for xi in range(len(un_EncodedT))]
print("Encoded Target: {} to {}".format(un_EncodedT,EncodedT))
return df
# + colab={"base_uri": "https://localhost:8080/", "height": 206} id="F412hlpPuysy" outputId="38ff2751-3801-44bd-bd21-56703e4c7571"
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=EncodeY(NullClearner(Y))
X.head()
# + [markdown] id="ykl7sTDQuysy"
# #### Correlation Map
#
# In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="iyDWkU7Guysz" outputId="d2565c08-bc8e-4938-eaa0-360b9d680c56"
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
# + [markdown] id="9yjj0O0auysz"
# #### Distribution Of Target Variable
# + colab={"base_uri": "https://localhost:8080/", "height": 406} id="PxDkQ8cguys0" outputId="6c6264af-caec-4551-baac-73bdf9d58909"
plt.figure(figsize = (10,6))
se.countplot(Y)
# + [markdown] id="7_AyGR75uys0"
# ### Data Splitting
#
# The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
# + id="vq9LhoRduys0"
X_train,X_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
# + [markdown] id="XbkakqbUuys0"
# #### Handling Target Imbalance
#
# The challenge of working with imbalanced datasets is that most machine learning techniques will ignore, and in turn have poor performance on, the minority class, although typically it is performance on the minority class that is most important.
#
# One approach to addressing imbalanced datasets is to oversample the minority class. The simplest approach involves duplicating examples in the minority class.We will perform overspampling using imblearn library.
# + id="JeJtSMZhuys1"
X_train,y_train = RandomOverSampler(random_state=123).fit_resample(X_train, y_train)
# + [markdown] id="vQ-HaqUjw5Hf"
#
# #### Data Rescaling
#
# MinMaxScaler subtracts the minimum value in the feature and then divides by the range, where range is the difference between the original maximum and original minimum.
#
# We will fit an object of MinMaxScaler to train data then transform the same data via fit_transform(X_train) method, following which we will transform test data via transform(X_test) method.
#
# + id="bHBGerX3w4eV"
minmax_scaler = MinMaxScaler()
X_train = minmax_scaler.fit_transform(X_train)
X_test = minmax_scaler.transform(X_test)
# + [markdown] id="PLDi7q6Puys1"
# ### Model
#
# AdaBoost is one of the initial boosting ensemble algorithms to be adapted in solving studies. It helps by combine multiple “weak classifiers” into a single “strong classifier.” The core concept of the algorithm is to fit a sequence of weak learners on repeatedly modified versions of the data. The predictions from all the Weak learners are then combined through a weighted majority vote or sum to produce the outcome/Prediction. The data modifications at each iteration consist of applying weights to each of the training samples. Initially, those weights are all set so that the first iteration only trains a weak learner on the original data. For every successive iteration, the sample weights are individually modified, and the algorithm is reapplied to the reweighted data. At a given iteration, those training examples which get incorrectly classified by the model at the previous iteration have their weights increased. Whereas the weight gets decreased for data that has been predicted accurately.As iterations continue, data that are difficult to predict or incorrectly classified receive ever-increasing influence. Each subsequent weak learner is thereby forced to concentrate on the data that are missed by the previous ones in the sequence
#
# #### Tuning Parameters
#
# 1. base_estimator: object, default=None
# >The base estimator from which the boosted ensemble is built. Support for sample weighting is required, as well as proper classes_ and n_classes_ attributes. If None, then the base estimator is DecisionTreeClassifier initialized with max_depth=1.
#
# 2. n_estimators: int, default=50
# >The maximum number of estimators at which boosting is terminated. In case of perfect fit, the learning procedure is stopped early.
#
# 3. learning_rate: float, default=1.
# >Learning rate shrinks the contribution of each classifier by learning_rate. There is a trade-off between learning_rate and n_estimators.
#
# 4. algorithm: {‘SAMME’, ‘SAMME.R’}, default=’SAMME.R’
# >If ‘SAMME.R’ then use the SAMME.R real boosting algorithm. base_estimator must support calculation of class probabilities. If ‘SAMME’ then use the SAMME discrete boosting algorithm. The SAMME.R algorithm typically converges faster than SAMME, achieving a lower test error with fewer boosting iterations.
#
# #### Note:
# >For better performance of the Adaboost model, the base estimator (Decision Tree Model) can be fine-tuned.
#
# + colab={"base_uri": "https://localhost:8080/"} id="C1RQE0mouys1" outputId="de479aa3-10c0-49ba-9237-740897638474"
# Build Model here
model = AdaBoostClassifier(random_state=123)
model.fit(X_train,y_train)
# + [markdown] id="pXeU0qjsuys2"
# #### Model Accuracy
#
# score() method return the mean accuracy on the given test data and labels.
#
# In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
# + colab={"base_uri": "https://localhost:8080/"} id="k8zMTflHuys3" outputId="4db524ac-a0cc-4f3a-ab8c-cb5e44b48338"
print("Accuracy score {:.2f} %\n".format(model.score(X_test,y_test)*100))
# + [markdown] id="9pw8FkjVuys3"
# #### Confusion Matrix
#
# A confusion matrix is utilized to understand the performance of the classification model or algorithm in machine learning for a given test set where results are known.
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="SYtMWMnuuys3" outputId="07aae4be-2dfc-473e-e82b-d59fcc368de8"
plot_confusion_matrix(model,X_test,y_test,cmap=plt.cm.Blues)
# + [markdown] id="w5c3Wk6Buys3"
# #### Classification Report
# A Classification report is used to measure the quality of predictions from a classification algorithm. How many predictions are True, how many are False.
#
# * **where**:
# - Precision:- Accuracy of positive predictions.
# - Recall:- Fraction of positives that were correctly identified.
# - f1-score:- percent of positive predictions were correct
# - support:- Support is the number of actual occurrences of the class in the specified dataset.
# + colab={"base_uri": "https://localhost:8080/"} id="tKWkWS_yuys4" outputId="8bd0e71e-4822-47b2-a157-a59a8195771b"
print(classification_report(y_test,model.predict(X_test)))
# + [markdown] id="HipTzwmkuys4"
# #### Feature Importances.
#
# The Feature importance refers to techniques that assign a score to features based on how useful they are for making the prediction.
# + colab={"base_uri": "https://localhost:8080/", "height": 406} id="3lJmGo2Euys4" outputId="49093676-8849-4cc0-de20-02d8e959f01e"
plt.figure(figsize=(8,6))
n_features = len(X.columns)
plt.barh(range(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), X.columns)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plt.ylim(-1, n_features)
# + [markdown] id="Vz9MwDDouys5"
# #### Creator: Arpit Somani , Github: [Profile](https://github.com/arpitsomani8)
| 45.077551 | 1,253 |
2d0f466ae66b7b31dc20a57893a5ea836fe38978
|
py
|
python
|
week09_inclass/W09_NonLinear_Regression_InClass.ipynb
|
ds-connectors/EPS-88-FA21
|
['BSD-3-Clause']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Non-Linear Regression In Class Exercise
#
# **Our goals for today:**
# - Load peak ground acceleration observations from two notable M6 quakes in California
# - Attempt to fit data using `polyfit()`
# - Develop a physics-based model and fit to data
# - Vary assumed mean event depth to find better fitting model
#
# ## Setup
#
# Run this cell as it is to setup your environment.
import math
import numpy as np
import pandas as pd
from scipy import stats
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
# # Analysis of Strong Ground Motion Data
#
# Earthquakes are the sudden dislocation of rock on opposite sides of a fault due to applied stress. Seismic waves are generated by this process and propagate away from the fault affecting nearby communities. It is the strong shaking from earthquakes that we recognize as the earthquake. These motions can lead to landslides, liquefaction of the ground, and of course impact anything built within or on the ground. The motions generated by fault dislocation affect many aspects of modern society. Earthquake Engineering is a field that studies the ground motions generated by earthquakes and how they affect the built environment. To utilize ground motions for engineering applications requires studying the physics of seismic wave propagation, and the development of models that effectively describe it. Of particular importance is the need to accurately model and predict seismic wave amplitudes. Such studies generally focus on examining the peak acceleration and velocity as a function of distance from the source. The physics indicates that the ground motions generally decrease in amplitude with increasing distance.
#
# On August 24, 2014 a M6 earthquake occurred in south Napa. The following figure shows the observed strong ground acceleration. There is a lot of complexity in the distribution that seismologists and earthquake engineers need to consider, but the general trend is that the ground motions decrease with distance from the earthquake.
#
# <img src="./napa_obsgm.png" width=500>
#
# In this module we will combine acceleration ground motion observations from two M6 events (2014 Napa, and 2004 Parkfield) to have a more complete distance distribution of observations. We will analyze the data first by attempting to fit curves as we have done for other datasets in the class (sea floor age, sea floor magnetism, distance and velocity of supernovae). We will then examine a physics-based model and a variety of methods to fit data. A model that describes the decrease (attenuation) of strong ground motion data over the years has been called 'attenuation relationships', 'ground motion prediction equations (GMPE)' and most recently 'ground motion models (GMM)'. Whatever it is called it is a fundamental to being able to characterized strong ground motion of future earthquakes and is used by the USGS and collaborators to develop earthquake forecast maps. GMM information coupled with the statistics of earthquake occurrence rates, notably Gutenberg-Richter statistics, provides the frame work for characterizing future ground motion hazard, as illustrated in the following map (red is high shaking hazard).
#
# <img src="./2018nshm-longterm.jpg" width=500>
# ## Part 1, Load, Plot and Fit Models to Peak Ground Acceleration Data
#
# We will make use of peak ground acceleration data from the 2014 Napa and 2004 Parkfield earthquakes. The acceleration is given in units of 'g', where 1g is 981 $\frac{cm}{s^2}$. Earthquake Engineers commonly use the peak ground acceleration in such units in their geotechnical materials and structural engineering analyses. 0.1%g is the level people generally can perceive shaking, at 2%g some people may be disoriented, at 50% the shaking is very violent and unengineered structures can suffer damage and collapse, while well engineered buildings can survive if the duration is short.
#Read the Peak Ground Acceleration data
park_pga=pd.read_csv('parkfieldeq_pga.csv')
napa_pga=pd.read_csv('napaeq_pga.csv')
park_pga.head()
# +
#Plot the two data sets
fig, ax = plt.subplots()
plt.plot(park_pga['Dist(km)'],park_pga['PGA(g)'],'.',color='blue',alpha=0.2)
plt.plot(napa_pga['Dist(km)'],napa_pga['PGA(g)'],'.',color='green')
ax.set(xlabel='Distance (km)', ylabel='Peak ground acceleration (g)',
title='Peak Acceleration Data Linear Plot')
plt.legend(['Napa','Parkfield'],fontsize=12)
plt.show()
fig, ax = plt.subplots()
plt.loglog(park_pga['Dist(km)'],park_pga['PGA(g)'],'.',color='blue',alpha=0.2)
plt.loglog(napa_pga['Dist(km)'],napa_pga['PGA(g)'],'.',color='green')
ax.set(xlabel='Distance (km)', ylabel='Peak ground acceleration (g)',
title='Peak Acceleration Data Log Plot')
plt.legend(['Napa','Parkfield'],fontsize=12)
plt.show()
# +
#Combine the two similar magnitude earthquake data
dist=np.concatenate((np.array(napa_pga['Dist(km)']),np.array(park_pga['Dist(km)'])))
pga=np.concatenate((np.array(napa_pga['PGA(g)']),np.array(park_pga['PGA(g)'])))
#Examine individual earthquake data
#dist=np.array(park['Dist(km)'])
#pga=np.array(park['PGA(g)'])
# -
# #### First. try fitting the data with standard curves as we did before using np.polyfit()
# +
#Try fitting data with np.polyfit()
p=np.polyfit(...)
x=np.arange(0.1,np.max(dist),0.1)
y=np.polyval(p,x)
plt.plot(dist,pga,'.',color='blue')
plt.plot(x,y,'-',color='red')
plt.xlabel('Distance(km)')
plt.ylabel('Peak Ground Acceleration (g)')
plt.show()
# -
# #### How well can the data be fit with polynomials?
# #### Try fitting the data with a power law ($pga = \frac{a}{dist^b}$)
#
# - To do this we linearize the equation to use polyfit() for a line
# +
#dist=dist+1 #add a small number to avoid singularity (dist=0)
p=np.polyfit(...)
print(p)
x=np.arange(np.min(dist),np.max(dist),0.1)
y=np.polyval(p,np.log(x))
#dist=dist-1
plt.plot(dist,pga,'.',color='blue')
plt.plot(x,np.exp(y),'-',color='red')
plt.xlabel('Distance(km)')
plt.ylabel('Peak Ground Acceleration (g)')
plt.show()
# -
# #### How well does a power law fit?
#
# What is wrong with this function?
# ## Part 2, Fitting Strong Motion Data
#
# In order to use the observations of peak ground acceleration to characterize seismic ground motion hazard it is necessary to develop a model that accurately describes the behavior seismic wave propagation, for example how the waves travel through the earth and dissipate. From physics seismic ground motions decay as a power law with distance (referred to as geometrical spreading), but we saw earlier that a power law alone does not work well, it is linear in log-space, where it does not explain the plateauing of ground motions close to the earthquake.
#
# To fix this we also need to consider that waves travel upward as well as away from an earthquake where
# $r=\sqrt{(dist^2 + h^2)}$ is the total distance comprised of the horizontal distance and the depth (h) of the earthquake.
#
# Finally, in addition to geometrical spreading, there is an inelastic attenuation term that accounts for dissipative energy loss due to material imperfections. Based on this theory the following is a simple relationship that describes the dissipation or attenuation of seismic wave energy with distance from the earthquake,
#
# $pga=a*{\frac{1}{r^b}}*e^{cr}$,
#
# where $a$ is a coeffient that depends on magnitude and scales the overall motions, $b$ is the exponent for the power-law geometrical spreading term, and $c$ is the coefficient for the in-elastic term (important only at large distances), and r is the total distance that considers the depth of the earthquake (h). Note that in the far-field the theoretical geometrical spreading decay of ground motions is ~1/r (in the near-field it is ~$1/r^2$). This is a non-linear equation, but it can be linearized by taking the natural logarithm.
#
# $\mathrm{ln}(pga)=a + b*\mathrm{ln}(r) + c*r$
#
# - How do we setup this inverse problem? Let's first consider a simple linear example.
# ### How to setup a linear (linearized) inverse problem
#
# - Until now we have been using "canned" functions to fit lines, or polynomials to data, but this doesn't always work because 1) sometimes more complicated functions are needed, 2) functions are non-linear, 3) we need to fit a physics-based model to the data.
#
# - We can construct our own inverse problem to fit more complex functions, as illustrated below.
#
# - When fitting a model such as a line to data, each data point can be considered a separate equation of two variables (a, b). That is for each x value there is a corresponding y value related to x through the equation for a line, where a is the intercept and b is the slope of the line.
#
# <img style="right;" src="./linear_eq_cartoon.png" width="500">
#
# - The system of equations can be constructed in matrix form, and least squares (or other methods may be used to solve the matrix equation for the model parameters. Some of the functions we have been using are doing this "under the hood".
#
# #### Let's try it for a simple linear case
#
# 1. Consider data from a line with some random noise added
# 2. Fit data using polyfit()
# 3. Construct the linear inverse problem from basic principles
# 4. Apply non-linear least-squares scipy.optimize.curve_fit()
# +
x=np.array((1, 2.2, 4.3, 7.7))
data=-1.5 + 3*x #construct data with an intercept of -1.5 and slope of 3.
#random number array
#rand=np.random.uniform(low=-2., high=2.0, size=4) #apply random numbers
#data=data + rand
m=np.polyfit(x,data,1)
plt.plot(x,data,'o',color='blue')
#syn=np.polyval(m,x)
#plt.plot(x,syn,'-',color='red')
plt.show()
print(f'From polyfit(): a={m[1]:.2f} b={m[0]:.2f}')
#Solve via least squares
A=np.vstack((...,...)).transpose()
#AtA=np.dot(...)
#AtD=np.dot(...)
#a, b=np.linalg.solve(...)
#print(f'From manual least squares: a={a:.2f} b={b:.2f}')
#Now lets use the scipy non-linear least-squares curve_fit() method
#def linmod(x,a,b):
# return ...
#m=curve_fit(linmod,x,data)[0]
#print(f'From curve_fit(): a={m[0]:.2f} b={m[1]:.2f}')
# -
# ### Now Setup a lineared inverse problem for the PGA data
# +
#Setup a linearized inverse problem for Parkfield
h=4.0 #Assume a depth (km)
r=np.sqrt(dist**2 + h**2)
#Setup G matrix
intercept_term=
ln_term=
exp_term=
G=
#Setup Data Matrix
d=
#Setup of least squares
gtg=np.dot(...)
gtd=np.dot(...)
#Solve for a, b, c
a, b, c=np.linalg.solve(gtg,gtd)
#Measure fit
m=np.array((a,b,c))
syn=np.exp(a + b*np.log(r) + c*r)
rms_fit=np.sqrt(np.mean((pga - syn)**2))
print(f'(a,b,c)={a:.3f}/{b:.3f}/{c:.3f} RMS={rms_fit:.3f}')
#Plot results
x=np.arange(0.0,np.max(dist),0.1)
xr=np.sqrt(x**2 + h**2)
y=np.exp(a + b*np.log(xr) + c*xr)
plt.loglog(dist,pga,'.',color='blue')
plt.loglog(x,y,'-',color='red')
plt.show()
# -
# #### How well does this inversion perform? Are the model parameters consistent with the theory for geometrical spreading and anelastic attenuation?
#
# - write answer here
# ## Part 3, Apply Non-linear least-squares
#
# The model that we are trying to fit is non-linear in distance so it makes sense to try the non-linear least-squares method. We will also discover that with this optimization method we can find solution with a assumed range of parameters that can be constraint by our understanding of the physics or by some other observations.
#
# Non-linear optimization is a topic that requires an entire semester by itself, and would include non-linear least-squares, grid-search (though slow for large data sets), Montecarlo sampling, Bayesian inference, genetic algorithm, etc.
#
# We will use the scipy.optimization.curve_fit() which utilizes non-linear least squares. So that this is not entirely a black box, briefly non-linear least-squares involves using a starting model to estimate a prediction error, differentiating the prediction error with respect to model parameters, and then updating the model and repeating until convergence is achieved. This wiki describes it in some detail. https://en.wikipedia.org/wiki/Non-linear_least_squares
#
# If $y$ is the data and $f(x, m)$ is the prediction as a function of (m) model parameters then the initial prediction error is $e_i=(y_i - f(x_i, m_0))$. Given an initial model $m_0$, $f$ can be represented as a Taylor series where $f(x_i, m_1)=f(x_i, m_0) + \frac{\partial f}{\partial m}(m_1 - m_0)$=$f(x_i, $m_0$) + \frac{\partial f}{\partial m}(\Delta m)$=$y_i$. Combining the prediction error and Taylor series equations gives:
#
# $e_i=[\frac{\partial f}{\partial m}](\Delta m)$, which as the form of the previous matrix equation we used. Suppose m=(a,b), and f(m)=a+bx then this results in a system of equations:
#
# $e_1=\frac{\partial f}{\partial a}\rvert_{x_1}\Delta a + \frac{\partial f}{\partial b}\rvert_{x_1}\Delta b$
#
# $e_2=\frac{\partial f}{\partial a}\rvert_{x_2}\Delta a + \frac{\partial f}{\partial b}\rvert_{x_2}\Delta b$
#
# $e_N=\frac{\partial f}{\partial a}\rvert_{x_N}\Delta a + \frac{\partial f}{\partial b}\rvert_{x_N}\Delta b$
#
# If $m_0$=(0,0) then the system of equations becomes what we found for the linear least-squares problem, where:
#
# $y_1=a + bx_1$
#
# $y_2=a + bx_2$
#
# $y_N=a + bx_N$
#
# The following is the general non-linear least-squares equation:
# \begin{equation*}
# Y=
# \begin{bmatrix}
# \frac{\partial f}{\partial m_1}\rvert_{x_1} & \frac{\partial f}{\partial m_1}\rvert_{x_1} & \cdots & \frac{\partial f}{\partial m_M}\rvert_{x_1} \\
# \frac{\partial f}{\partial m_1}\rvert_{x_2} & \frac{\partial f}{\partial m_1}\rvert_{x_2} & \cdots &\frac{\partial f}{\partial m_M}\rvert_{x_2} \\
# \vdots & \vdots & \ddots & \vdots \\
# \frac{\partial f}{\partial m_1}\rvert_{x_N} & \frac{\partial f}{\partial m_1}\rvert_{x_N} & \cdots & \frac{\partial f}{\partial m_M}\rvert_{x_N}
# \end{bmatrix}
# \quad
# \begin{bmatrix}
# \Delta m_1 \\
# \Delta m_2 \\
# \vdots \\
# \Delta m_M
# \end{bmatrix}
# \end{equation*}
#
#
# +
#Test the scipy curve_fit method
#Define the non-linear function
def gm_model(x,a,b,c):
#This function returns ln(pga)
return ...
h=4.0
r=np.sqrt(dist**2 + h**2)
m=curve_fit(...,..., ...,bounds=([...,...,...],...))[0]
#Measure fit
syn=np.exp(gm_model(r,m[0],m[1],m[2]))
rms_fit=np.sqrt(np.mean((pga - syn)**2))
print(f'(a,b,c,h)={m[0]:.3f}/{m[1]:.3f}/{m[2]:.3f} RMS={rms_fit:.3f}')
plt.loglog(dist,pga,'.')
x=np.arange(0.1,200,0.1)
xr=np.sqrt(x**2 + h**2)
y=np.exp(gm_model(xr,m[0],m[1],m[2]))
plt.loglog(x,y,'-',color='red')
plt.show()
# -
# ### Compute 95% confidence intervals
#Compute 95% confidence levels
degfree=len(r)-3 #degrees of freedom (num data - num model params)
e=np.log(pga)-np.log(syn) #residuals between data and model
var=np.sum(e**2)/degfree #variance
se_y=np.sqrt(var) #standard error of the estimate
sdev=np.sqrt(var) #standard deviation
#Calculate 95% confidence bounds
t=stats.t.ppf(1-0.05/2,degfree) #division by 2 to map from single-tail to dual-tail t-distribution
lower95=np.exp(np.log(y)-t*se_y)
upper95=np.exp(np.log(y)+t*se_y)
#Plot Results
fig, ax = plt.subplots()
ax.loglog(dist,pga,'b.',x,y,'k-',linewidth=2)
ax.loglog(x,lower95,'r-',x,upper95,'r-',linewidth=1)
ax.set(xlabel='Distance (km)', ylabel='Peak ground acceleration (g)',
title='Peak Acceleration Data and Weighted Least Squares Inversion')
#plt.legend(['Napa','Parkfield'],fontsize=12,loc=3)
plt.show()
# #### Test our assumption that the mean depth of the earthquakes is 4.0km.
#
# What depth produces the best fitting model (minimum variance)? How sensitive is the model to depth? Consider depths ranging from say 1 to 20 km.
# _Write your answer here._
# #### Compare solutions using the Napa and Parkfield data separately and discuss how the results compare.
#
# Write you answer here.
| 45.40634 | 1,127 |
a602629e10f148c809edc14041f388869184400e
|
py
|
python
|
.ipynb_checkpoints/7_programming_extras-checkpoint.ipynb
|
philuttley/basic_linux_and_coding
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Programming Extras
# + [markdown] slideshow={"slide_type": "skip"} toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Testing" data-toc-modified-id="Testing-1"><span class="toc-item-num">1 </span>Testing</a></span><ul class="toc-item"><li><span><a href="#Docstrings" data-toc-modified-id="Docstrings-1.1"><span class="toc-item-num">1.1 </span>Docstrings</a></span></li><li><span><a href="#Doctest" data-toc-modified-id="Doctest-1.2"><span class="toc-item-num">1.2 </span>Doctest</a></span></li><li><span><a href="#Unit-testing" data-toc-modified-id="Unit-testing-1.3"><span class="toc-item-num">1.3 </span>Unit testing</a></span></li></ul></li><li><span><a href="#Debugging" data-toc-modified-id="Debugging-2"><span class="toc-item-num">2 </span>Debugging</a></span></li><li><span><a href="#Profiling" data-toc-modified-id="Profiling-3"><span class="toc-item-num">3 </span>Profiling</a></span><ul class="toc-item"><li><span><a href="#Within-jupyter-notebook" data-toc-modified-id="Within-jupyter-notebook-3.1"><span class="toc-item-num">3.1 </span>Within jupyter notebook</a></span></li><li><span><a href="#Profiling-your-entire-code" data-toc-modified-id="Profiling-your-entire-code-3.2"><span class="toc-item-num">3.2 </span>Profiling your entire code</a></span></li><li><span><a href="#Lineprofiling-your-code" data-toc-modified-id="Lineprofiling-your-code-3.3"><span class="toc-item-num">3.3 </span>Lineprofiling your code</a></span></li></ul></li><li><span><a href="#Speed-up-your-code" data-toc-modified-id="Speed-up-your-code-4"><span class="toc-item-num">4 </span>Speed up your code</a></span><ul class="toc-item"><li><span><a href="#Ufuncs" data-toc-modified-id="Ufuncs-4.1"><span class="toc-item-num">4.1 </span>Ufuncs</a></span></li><li><span><a href="#Numba" data-toc-modified-id="Numba-4.2"><span class="toc-item-num">4.2 </span>Numba</a></span></li></ul></li><li><span><a href="#Git(hub)" data-toc-modified-id="Git(hub)-5"><span class="toc-item-num">5 </span>Git(hub)</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#How-can-it-look-like?" data-toc-modified-id="How-can-it-look-like?-5.0.1"><span class="toc-item-num">5.0.1 </span>How can it look like?</a></span></li></ul></li></ul></li><li><span><a href="#Github" data-toc-modified-id="Github-6"><span class="toc-item-num">6 </span>Github</a></span></li><li><span><a href="#Publishing-code" data-toc-modified-id="Publishing-code-7"><span class="toc-item-num">7 </span>Publishing code</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Software-Citation-Principles" data-toc-modified-id="Software-Citation-Principles-7.0.1"><span class="toc-item-num">7.0.1 </span>Software Citation Principles</a></span></li></ul></li></ul></li></ul></div>
# + [markdown] slideshow={"slide_type": "slide"}
# ## Testing
# *Ensure your code never breaks*
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Docstrings
# + slideshow={"slide_type": "-"}
def func(arg1, arg2):
"""Summary line.
Extended description of function.
Args:
arg1 (int): Description of arg1
arg2 (str): Description of arg2
Returns:
bool: Description of return value
Raises:
ValueError: If `arg2` is equal to `arg1`.
Examples:
Examples should be written in doctest format, and should illustrate how
to use the function.
>>> a = [1,2,3]
>>> print([x + 3 for x in a])
[4, 5, 6]
"""
if arg1 == arg2:
raise ValueError('arg1 may not be equal to arg2')
return True
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Doctest
# + slideshow={"slide_type": "-"}
def fib(n):
"""Calculates the n-th Fibonacci number.
>>> fib(0)
0
>>> fib(15)
610
>>>
"""
a, b = 0, 1
for i in range(n):
a, b = b, a + b
return a
# -
# Which can be run with
# ```
# $ python3 -m doctest -v <file>
# ```
# + [markdown] slideshow={"slide_type": "subslide"}
# Producing
# ```
# Trying:
# fib(0)
# Expecting:
# 0
# ok
# Trying:
# fib(15)
# Expecting:
# 610
# ok
# 1 items had no tests:
# test
# 1 items passed all tests:
# 2 tests in test.fib
# 2 tests in 2 items.
# 2 passed and 0 failed.
# Test passed.
# ```
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Unit testing
# +
import unittest
# Define the function
def fun(x):
return x + 1
# Define the tests
class MyTest(unittest.TestCase):
def test(self):
self.assertEqual(fun(3), 4)
# Run the unit test (the argv is just for jupyter notebooks)
if __name__ == '__main__':
unittest.main(argv=['first-arg-is-ignored'], exit=False)
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Debugging
# *When your computer makes you feel stupid*
# -
# Most people simply use `print()` statements to debug. But you can do better than that...
# + slideshow={"slide_type": "subslide"}
import time
def complicated_function():
time.sleep(2)
x, y, z = 1, '2', 3
# Usually you might do this
print(y)
return x+y+z
complicated_function()
# + slideshow={"slide_type": "subslide"}
import time
def complicated_function():
time.sleep(0.5)
x, y, z = 1, '2', 3
# But how about
import IPython; IPython.embed()
return x+y+z
complicated_function()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Profiling
# *Find the bottleneck in your code*
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Within jupyter notebook
# +
# %%time
def upper_func(x):
return x + 1
def middle_func(x):
[upper_func(i) for i in range(10000)]
return upper_func(x) + 1
def lower_func(x):
return middle_func(x) + 1
lower_func(5)
# + slideshow={"slide_type": "subslide"}
# %%timeit
def upper_func(x):
return x + 1
def middle_func(x):
[upper_func(i) for i in range(10000)]
return upper_func(x) + 1
def lower_func(x):
return middle_func(x) + 1
lower_func(5)
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Profiling your entire code
# -
# Try profiling your code using a bash function
profile() { python3 -m cProfile -o ~/Downloads/temp.profile $1; snakeviz ~/Downloads/temp.profile;}
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Lineprofiling your code
# -
# Or if that's not detailed enough, place the `@profile` decorator above a function in your code, and then run the following
lineprofile() { kernprof -l -v $1;}
# + [markdown] slideshow={"slide_type": "slide"}
# ## Speed up your code
# *Speed up for-loops*
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Ufuncs
# -
import numpy as np
g = np.array([1, 2, 3, 4])
np.sin(g)
# +
def step_function(x):
if x > 0:
return 1
else:
return 0
ar = np.array([-10, 10, 100])
step_function(ar)
# + slideshow={"slide_type": "fragment"}
ustep_function = np.vectorize(step_function)
ustep_function(ar)
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Numba
# +
ar = np.random.random(12345678)
# Silly function
def step_function_python(a):
output = np.zeros_like(a)
for i, nr in enumerate(a):
if nr > 0:
output[i] = 1
# %time step_function_python(ar)
# + slideshow={"slide_type": "subslide"}
# Numpy version of step function
def step_function_numpy(a):
output = np.zeros_like(a)
a[a > 0] = 1
# %time step_function_numpy(ar)
# + slideshow={"slide_type": "subslide"}
import numba as nb
# +
@nb.jit()
def step_function_python(a):
output = np.zeros_like(a)
for i, nr in enumerate(a):
if nr > 0:
output[i] = 1
# %time step_function_python(ar)
# %time step_function_python(ar)
# %time step_function_python(ar)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Git(hub)
# *Version control your software*
# + [markdown] slideshow={"slide_type": "subslide"}
# Everyone should use git. Seriously. You'll no longer need to worry about breaking a working version of your code. Don't worry about learning all the commands - these days there are GUIs like Gitkraken which do the hard work for you.
# + [markdown] slideshow={"slide_type": "subslide"}
# 
# + [markdown] slideshow={"slide_type": "subslide"}
# #### What does it look like?
# 
# + [markdown] slideshow={"slide_type": "subslide"}
# For a full introduction, see [this presentation](https://davidgardenier.com/talks/201710_git.pdf)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Github
# *Backup your code*
# + [markdown] slideshow={"slide_type": "subslide"}
# Want to have a backup of your data? Or collaborate on code without sending having to send through files or code fragments? Check out Github and apply for a Student Developer Pack or an Academic Research Pack.
#
# Want to share a snippet of code? Try using gists
#
# Want your code to automatically be tested when it arrives on Github? Try linking it up with Travis
#
# And want to know which percentage of your code you've tested? Then try Coveralls
# + [markdown] slideshow={"slide_type": "slide"}
# ## Publishing code
# *How to ensure your software is accessible*
# + [markdown] slideshow={"slide_type": "subslide"}
# > Integrity of research depends on transparency and reproducibility
#
# Quote by Alice Allen
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Software Citation Principles
# * Importance | Software is as important as a paper
# * Credit and attribution | Software should be quoted
# * Unique identification | Globally unique
# * Persistence | The identifiers have to persist
# * Accessibility | The code, data etc, should be available
# * Specificity | Version of software
# + [markdown] slideshow={"slide_type": "subslide"}
# * Astrophysics Source Code Library (ASCL, ascl.net) | A place to put software
# + [markdown] slideshow={"slide_type": "subslide"}
# What do you need to do?
# * Release your code
# * Specify how you want your code to be cited
# * License your code
# * Register your code
# * Archive your code
| 29.938953 | 2,885 |
8f55c5092043dec8eb4f83ce2ce910b349480e75
|
py
|
python
|
master/0_index.ipynb
|
jeancarlosvp/Image_Processing
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=true editable=true toc="true"
# # Table of Contents
# <p><div class="lev1 toc-item"><a href="#Tutoriais-básicos-sobre-Jupyter,-Python,-NumPy,-Matplotlib,-Proc.-Imagens" data-toc-modified-id="Tutoriais-básicos-sobre-Jupyter,-Python,-NumPy,-Matplotlib,-Proc.-Imagens-1"><span class="toc-item-num">1 </span>Tutoriais básicos sobre Jupyter, Python, NumPy, Matplotlib, Proc. Imagens</a></div><div class="lev2 toc-item"><a href="#Jupyter" data-toc-modified-id="Jupyter-11"><span class="toc-item-num">1.1 </span>Jupyter</a></div><div class="lev2 toc-item"><a href="#Python" data-toc-modified-id="Python-12"><span class="toc-item-num">1.2 </span>Python</a></div><div class="lev2 toc-item"><a href="#NumPy" data-toc-modified-id="NumPy-13"><span class="toc-item-num">1.3 </span>NumPy</a></div><div class="lev3 toc-item"><a href="#Precisa-ser-melhorado" data-toc-modified-id="Precisa-ser-melhorado-131"><span class="toc-item-num">1.3.1 </span>Precisa ser melhorado</a></div><div class="lev2 toc-item"><a href="#Revisão---Cálculo,-Álgebra" data-toc-modified-id="Revisão---Cálculo,-Álgebra-14"><span class="toc-item-num">1.4 </span>Revisão - Cálculo, Álgebra</a></div><div class="lev2 toc-item"><a href="#Processamento-de-Imagens" data-toc-modified-id="Processamento-de-Imagens-15"><span class="toc-item-num">1.5 </span>Processamento de Imagens</a></div><div class="lev2 toc-item"><a href="#Necessitam-ajustar-para-jupyter-notebooks" data-toc-modified-id="Necessitam-ajustar-para-jupyter-notebooks-16"><span class="toc-item-num">1.6 </span>Necessitam ajustar para jupyter notebooks</a></div>
# + [markdown] deletable=true editable=true
# # Tutoriais básicos sobre Jupyter, Python, NumPy, Matplotlib, Proc. Imagens
#
# Este diretório é composto de uma série de pequenos tutoriais básicos do Python e principalmente do NumPy, com aplicação à processamento de imagens.
# + [markdown] deletable=true editable=true
# ## Jupyter
#
# - [Edição HTML](Ferramentas de Edicao HTML.ipynb) - Ferramentas de edição multimídia, links, imagens, equações
#
# + [markdown] deletable=true editable=true
# ## Python
#
# - [Python I - Tipos de variáveis](tutorial_python_1_1.ipynb)
# - [Python III - Declaração de funções](tutorial_python_1_3.ipynb)
# + [markdown] deletable=true editable=true
# ## NumPy
#
# - [Chessboard](chess.ipynb) - Motivação sobre programação matricial NumPy versus programação com laço explícito
# - [NumPy - Introdução ao ndarray](tutorial_numpy_1_1.ipynb)
# - [Matplotlib](tutorial_matplotlib.ipynb)
# - [NumPy - Formatando array para impressão](tutorial_numpy_1_11.ipynb)
# - [NumPy - Fatiamento array unidimensional](tutorial_numpy_1_2.ipynb)
# - [NumPy - Fatiamento em duas dimensões](tutorial_numpy_1_3.ipynb)
# - [NumPy - Cópia Rasa e Profunda](tutorial_numpy_1_4.ipynb)
# - [NumPy - Array Strides](Array-strides.ipynb)
# - [NumPy - Redução de eixo](tutorial_numpy_1_5a.ipynb)
#
# ### Precisa ser melhorado
# - [NumPy - Uso do tile](tutorial_numpy_1_8.ipynb)
# - [NumPy - Uso do resize](tutorial_numpy_1_9.ipynb)
# - [NumPy - Uso do clip](tutorial_numpy_1_10.ipynb)
# + [markdown] deletable=true editable=true
# ## Revisão - Cálculo, Álgebra
#
# - [Revisão de Números Complexos](Revisao_NumerosComplexos.ipynb )
# + [markdown] deletable=true editable=true
# ## Processamento de Imagens
#
# - [Imagens - Representação, Leitura e Visualização](tutorial_img_ds.ipynb)
# - [Proc Imagens com Fatiamento](tutorial_1_imagens.ipynb)
# - [NumPy - Indices e meshgrid para gerar imagens sintéticas](tutorial_numpy_1_7.ipynb)
# - [Histograma e Estatística](tutorial_hist__stat_2.ipynb)
# - [Transformação de Intensidade](tutorial_ti_2.ipynb)
# - [Equalização de histograma](tutorial_hist_eq_2.ipynb)
# - [Equalização por ordenação dos pixels](tutorial_pehist_1.ipynb)
# - [Especificação de histograma por ordenação dos pixels](tutorial_pehist_2.ipynb)
# - [Ajuste interativo de contraste](tutorial_contraste_iterativo_2.ipynb)
# - [Convolução](tutorial_conv_3.ipynb)
# - [Propriedades da convolução](tutorial_convprop_3.ipynb)
# - Propriedades da DFT
# - [Propriedade da escala (expansão) da DFT](dftscaleproperty.ipynb)
# - [Interpolação na expansão (análise no domínio da frequência](magnify.ipynb)
# - [Transforma Discreta de Wavelets](wavelets.ipynb)
# + [markdown] deletable=true editable=true
# ## Necessitam ajustar para jupyter notebooks
#
# - [tutorial_trans_geom_intro_2.ipynb](tutorial_trans_geom_intro_2.ipynb)
# - [tutorial_ptrans.ipynb](tutorial_ptrans.ipynb)
# - [gengaussian.ipynb](gengaussian.ipynb )
#
# + deletable=true editable=true
# !ls
| 55.850575 | 1,615 |
3d21c9e0c96baf58b100773f5097017bf0ae80b1
|
py
|
python
|
Data-512-Final-Project.ipynb
|
niharikasharma/data-512-final-project
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Recommender Systems
# DATA 512 Final Project
# Niharika Sharma
# 10th December, 2017
#
#
# # Introduction
#
# A recommender system is a software that analyzes large amounts of data and extracts personal characteristics and features to present users with relevant content.
#
# If we go to Amazon today and look for "Machine learning with the Tensor flow" book, we would get recommendations like "Customer who bought this item also bought this item"; "Items Frequently brought together"; "More items to consider"; "Recommendation for you in books" and many more variations of recommendations.
#
# The analysis of recommender systems is interesting and important as it involves business-centric, engineering-centric and human-centric approaches to design RS. It solves a real-world problem and tackles unresolved research questions.
#
# Business-centric -
# The fundamental reason why many companies seem to care about recommender systems is for money and business as they generate significant user engagement and revenue. But, Advertisements biases the recommendation on platforms like Amazon, Facebook, Netflix, IMDB, TMDB, Spotify etc. Hence, using the traditional approaches, we built an unbiased recommender system.
#
# Engineering-centric -
# Also, building a recommender system is a true data science problem. It is a true representation and intersection between Software Engineering, Machine Learning, Statistics and Human-Centered aspects as building it requires all these skills.
#
# Human-centric -
# But most importantly Recommender System is a human-centric problem statement as the system is for the humans and the results and performance complete depends on Human Recommender interaction. We built models whose end product or outcome can be easily interpreted. Further, these models are build taking into account the audience, purpose, and context.
#
#
# # Background
#
# Almost every company is working and using recommender systems in today's era. It is not at all surprising to us if we sign-in to some application and get recommendations the very next minute in our inbox. Since the work in this field is rapidly growing and the techniques are improving tremendously, there comes a big question regarding the human recommender interaction and how these algorithms are positively affecting the user's choices. Michael D. Ekstrand, F. Maxwell Harper, Martijn C. Willemsen, and Joseph A. Konstan conducted a research in 2014 on User perception of differences in recommender algorithms [10]. Further studies have been conducted in understanding the human-centered aspect for such sophisticated algorithms. Sean M. McNee, Nishikant Kapoor, and Joseph A. Konstan published in 2006 a research on "Don't look stupid: avoiding pitfalls when recommending research papers" [16]. The research that closely relates or connects to what we are doing in this project is by Sean M. McNee, John Riedl, and Joseph A. Konstan. 2006. Making recommendations better: an analytic model for human-recommender interaction.
#
# Hypotheses/ research questions
#
# For our research project, we deliver two recommendation algorithms from scratch without using the already built libraries for such algorithms like MLlib.
# Further, we tried to answer two hypotheses -
#
# Hypotheses 1 - Compare the recommender personality of content-based and collaborative filtering RS
#
# Hypotheses 2 - Why should a user trust that the algorithm understands who they are, what they like and what they are doing?
#
# How does this research inform your hypotheses, your analysis, or your system design?
#
# Human-centered data science fills the gap between or it is the bridge between quantitative and qualitative research. This bridge opens new opportunities, for instance, Data Scientist role is also one of the many outcomes from the amalgamation of a deep connection between qualitative methods and formally defined data-driven research technique.
# The project is a true representation of what we call amalgamation of a deep connection between qualitative methods and formally defined data-driven research technique and what we studied during the lectures and the take-home readings. From this project, we cover important aspects using the hypothesis like the interpretability, data privacy, data ethics and understand the bridge of HCDS between qualitative and quantitative methods.
#
#
# # Data
#
# #### Brief description about the dataset
# We have taken the dataset from Kaggle datasets - https://www.kaggle.com/rounakbanik/the-movies-dataset. The dataset on Kaggle consists of multiple files but we are using the following files:
#
# movies_metadata.csv: Contains information on 45,000 movies featured in the Full MovieLens dataset[6]. Fields in movies_metadata.csv include:
#
# adult
# belongs_to_collection
# budget
# genres
# homepage
# id
# imdb_id
# original_language
# original_title
# overview
# popularity
# poster_path
# production_companies
# production_countries
# release_date
# revenue
# runtime
# spoken_languages
# status
# tagline
# title
# video
# vote_average
# vote_count
#
# links_small.csv: Contains the TMDB and IMDB IDs of a small subset of 9,000 movies of the Full Dataset. Fields in links_small.csv include:
#
# movieId
# imdbId
# tmdbId
#
# ratings_small.csv: Consist of rating for movies by anonymous users. The subset of 100,000 ratings from 700 users on 9,000 movies. Fields in ratings_small.csv include:
#
# userId
# movieId
# rating
# timestamp
#
# #### License of the data on Kaggle
# Released Under CC0: Public Domain License link: https://creativecommons.org/publicdomain/zero/1.0/
#
# #### Is it legal to use this data set?
# This dataset is an aggregation of data collected from TMDB and GroupLens (MovieLens dataset). The Movie Details, Credits, and Keywords have been collected from the TMDB Open API. We can use the MovieLens dataset but must acknowledge the use of the dataset in publications or project report [7]. We have acknowledged the use of the dataset in the reference section.
#
#
# # Methods
#
# #### Analytical methods
#
# ##### Collaborative Filtering
# Content-based recommender systems concentrate on the characteristics of the items and give recommendations based on the similarity between them, that is if you like an item then you will also like a “similar” item. For calculating the similarity between movies, we are using two features - overview and taglines. We are calculating the cosine similarity between movies by converting the textual features into numerical feature vectors using tf-idf vectorizer from sci-kit learn package.
#
# ##### Content-based Filtering
# Collaborative filtering is an unsupervised learning algorithm which produces recommendations based on the knowledge of user’ attitude to items, that is it uses the “wisdom of the crowd” and "past behavior" to recommend items. For calculating the similarity between movies, we are using Pearson correlation coefficient.
#
# ##### Hybrid Approach
# The amalgamation of Collaborative filtering and content-based approach is called a hybrid approach. It is very powerful technique as it takes advantages of both the approaches and eliminates the disadvantages.
#
# #### What methods are we using and why these methods?
# We are concentrating on Content-based and Collaborative Filtering algorithm as these are traditional approaches to build a recommendation engine. Both the approaches are mutually exclusive and the results depend on what we want to achieve. In Collaborative filtering, recommender system tries to consider the similarities between users on the platform and based on these similarities, movies that similar neighbors of the target user showed interest in are equally recommended to him or her. This approach gives room for more diverse or serendipitous recommendations.
#
# On the other hand, in Content-based approach, recommendations are made to the user based on their movie interests. Movies are only recommended to the user if he had shown interest in that genre, tags or related attribute previously. This approach lacks some diversity and serendipity but may recommend movies that the user may like now just because he had liked movies with similar attributes before.
#
# Our hypothesis includes the involvement of human aspect. Fortunately, research in the field of recommender systems still remains powerful and alive. There have been great advancements and development in these approaches. Moreover, Information filtering can be more effective when users are involved in the algorithmic process genuinely. We believe that to be true now more than ever because working on transparency of the recommender systems, and enabling ever-improving suggestions from users is both meaningful and challenging.
#
# ## Code / Implementation of methods
#
# #### Import all the libraries
# +
# Import all the libraries
import pandas as pd
import time
import sklearn
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import linear_kernel
import numpy as np
import re
import json
import scipy
# -
# #### Content Based filtering
# The analysis is done on a smaller data set comprising of 9099 movies. Since, content based filtering concentrate on the characteristics of the items, hence we have used overview and tagline of the movies to find the top ten similar movies for each movie.
# +
# Content based method
# This function generates recommendation using content based filtering approach using the description of the movie
def generate_similar_data(ds, smooth_idf=True, norm='l2', sublinear_tf=True, min_df=1, max_df=1.0, min_n=1, max_n=2,
max_features=None):
start = time.time()
tf = TfidfVectorizer(analyzer='word', sublinear_tf=sublinear_tf, ngram_range=(min_n, max_n), stop_words='english',
norm=norm, smooth_idf=smooth_idf, max_df=max_df, min_df=min_df, max_features=max_features)
tfidf_matrix = tf.fit_transform(ds['description'].values.astype('U'))
idf = tf.idf_
feature_list = []
ids_list = []
cosine_similarities = linear_kernel(tfidf_matrix, tfidf_matrix)
# normalizing the cosine similarities
cosine_similarities = sklearn.preprocessing.normalize(cosine_similarities, norm='l2')
similar_movie_list = []
movie_name_list = []
similarity_measure = []
# Number of recommendation to select for each movie
n = 12
for idx, row in ds.iterrows():
similar_indices = cosine_similarities[idx].argsort()[:-n:-1]
similar_items = [(cosine_similarities[idx][i], ds['id'][i]) for i in similar_indices]
for similar_item in similar_items[1:]:
similar_movie_list.append(similar_item[1])
movie_name_list.append(row.title)
similarity_measure.append(similar_item[0])
di = {}
for idx, row in ds.iterrows():
di[row.id] = row.title
df = pd.DataFrame({'movie_name': movie_name_list, 'similar_movie_name': similar_movie_list, 'similarity_measure': similarity_measure})
df["similar_movie_name"].replace(di, inplace=True)
print("Engine trained in %s seconds." % (time.time() - start))
return df
# +
# Read Movies data
main_df = pd.read_csv('movies_metadata.csv')
main_df = main_df[main_df.id.apply(lambda x: x.isnumeric())]
main_df['id'] = main_df['id'].astype('int')
# Link movie data with the links data
links_small_dataset = pd.read_csv('links_small.csv')
links_small_tmdbId = pd.DataFrame({'id':links_small_dataset[links_small_dataset['tmdbId'].notnull()]['tmdbId'].astype('int')})
# merge dataframes
new_df = pd.merge(main_df, links_small_tmdbId, on=['id'], how='inner')
new_df['description'] = new_df['overview'] + ' ' + new_df['tagline']
similarity_data_content_based = generate_similar_data(new_df)
# -
# This function get the movie recommendation using content based approach for any movie in the dataset.
def get_movie_recommendations_Content_Based(movies, n = 5):
similarities = similarity_data_content_based[similarity_data_content_based.movie_name.isin([movies])]
similarities = similarities.sort_values(by=['similarity_measure'], ascending=False)[:n]
return similarities
# ### Collaborative filtering
# There are two types of collaborative filtering approaches -
#
# <b>Item-item collaborative filtering</b> - In the item-based approach a rating (u1, i1), from user u1 for item i1, is produced by looking at the set of items similar to i1, then the ratings by u1 of similar items are combined into a predicted rating.
#
# <b>User-user collaborative filtering</b> - In the user-based approach, for user u1, a score for an unrated item is produced by combining the ratings of users similar to u1.
#
# We will be using Item-item collaborative filtering as it makes more sense to compare the recommender personality of content based and item-item collaborative filtering. Since, both the techiques use items to get the similarity measure.
#
# read ratings file
ratings = pd.read_csv('ratings_small.csv')
# merge dataframes
ratings = pd.merge(ratings, links_small_dataset, on=['movieId'], how='inner')
ratings = ratings.dropna(axis=0, how='any')
ratings['tmdbId'] = ratings['tmdbId'].astype('int')
movie_titles_with_ids = pd.DataFrame({'tmdbId':new_df['id'], 'title':new_df['title']})
ratings = pd.merge(ratings, movie_titles_with_ids, on=['tmdbId'], how='inner')
del ratings['timestamp']
ratings.head()
# Convert the ratings dataframe to a matrix with a movie per column and a user per row.
# +
ratings_mtx_df = ratings.pivot_table(values='rating', index='userId', columns='title')
ratings_mtx_df.fillna(0, inplace=True)
movie_index = ratings_mtx_df.columns
ratings_mtx_df.head()
# -
# Measure the similarity between movies, that is, find correlation between movies and use that correlation to find similar movies to those the users have liked.
corr_matrix = np.corrcoef(ratings_mtx_df.T)
# This function get the movie recommendation using CF approach for any movie in the dataset.
def get_movie_recommendations_CF(movies, n = 5):
movie_idx = list(movie_index).index(movies)
sum_movie_similarities = corr_matrix[movie_idx]
similarities = pd.DataFrame({
'title': movie_index,
'similarity_sum': sum_movie_similarities
})
similarities = similarities.sort_values(by=['similarity_sum'], ascending=False)[1:n+1]
return similarities
# # Findings and research
#
# #### Hypothesis 1
# Comparing the recommender personality of content based and item based collaborative filtering
# Content based
sample_movie = 'The Dark Knight Rises'
recommendations = get_movie_recommendations_Content_Based(sample_movie)
recommendations
# Collaborative filtering
sample_movie = 'The Dark Knight Rises'
recommendations = get_movie_recommendations_CF(sample_movie)
recommendations
# Comparing the personality of both the recommenders based on the results above -
#
# <b>1. Freshness</b>
#
# 1.1. The content-based approach gives old movies recommendations mostly from 90's movies - like Batman Forever, Batman Returns, Batman: Mask of the Phantasm.
#
# 1.2. Collaborative filtering whereas give fresh recommendations like Captain America: The First Avenger (2011), Limitless (2011), The Hunger Games: Catching Fire (2013), Inception (2010), and Inception (2012)
#
#
# <b>2. Diversity </b>
#
# 2.1. Collaborative filtering recommends diverse set of movies from the same or similar genre, whereas content based only recommend movies which are based on or related to Batman.
#
#
# <b>3. Degree of personalization </b>
#
# 3.1. The content-based algorithm is based on the items attribute and hence they are not personalized as per the users' requirement. They are personalized to the item which the user recently saw.
#
# 3.2. Collaborative filtering algorithm is based on the past history of the user and hence the recommendations are highly personalized based on what the user saw in the past. This approach adds novelty factor as well to the recommendation personality as we explore the items/movies which a user might see in future based on similar user analysis.
#
# We know from several readings and resources that that satisfaction positively dependent on diversity and negatively dependent on novelty. Hence, both the techniques have pros and cons, for instance, collaborative filtering has higher diversity and freshness in the results but then it also has high novelty. Whereas results from content-based are quite the opposite of collaborative filtering.
# #### Hypothesis 2
# Why should a user trust that the algorithm understands who they are, what they like and what they are doing?
# Content based
sample_movie = 'Harry Potter and the Prisoner of Azkaban'
recommendations = get_movie_recommendations_Content_Based(sample_movie, n = 4)
recommendations
# The results we got from the content-based approach, we can see that they are apt as all the recommended movies are Harry Potter movies and this is because of the content in the tagline and overview. We as Data Scientist/ Engineers understand why we got such results. But, such results might creep out the users if they got an email/ or notification on the dashboard to view the recommended movies because the users have no clue why, and from where they got such recommendation.
#
# Therefore, to gain or improve the user trust that the algorithm understands who they are, what they like and what they are doing, we should make sure that we follow the ethics while recommending the movies/items -
#
# 1. Awareness -
# Let members be aware of how we are adapting to their tastes.
#
# 2. Explanations -
# Not recommending it because it suits our business needs, but because it matches the information we have from you: your explicit taste preferences and ratings, your viewing history.
#
# Hence, if we adhere to a format for the content based recommender algorithm APIs while recommending movies which gives an explanation and add awareness, then we can reflect the recommendations to the users in a positive and non-creepy way.
#
# For instance,
# +
features = ['movies\'s tag line', 'movies\'s overview']
sample_movie = 'Harry Potter and the Prisoner of Azkaban'
recommendations = get_movie_recommendations_Content_Based(sample_movie, n = 4)
print('Because you saw', sample_movie, 'we recommend you \n',
recommendations['similar_movie_name'].to_string(index=False),
'\nbased on there similarity in the following features \n', features )
# -
# The above template captures both awareness and explaination for the personalized recommendations from content based approach.
# Collaborative filtering
sample_movie = 'Harry Potter and the Prisoner of Azkaban'
recommendations = get_movie_recommendations_CF(sample_movie, n = 4)
recommendations
# For collaborative filtering approach the recommendations are provided based on the wisdom of the crowd. The only difference is whether the wisdom is captured from the item - item matrix based on user count or user-user matrix based on item count.
#
# Hence, for collaborative filtering we could use the following template -
# +
sample_movie = 'Harry Potter and the Prisoner of Azkaban'
recommendations = get_movie_recommendations_CF(sample_movie, n = 4)
print('Viewer who saw', sample_movie, 'also saw the following movies \n', recommendations['title'].to_string(index=False))
# -
# The above template captures both awareness and explaination for the personalized recommendations from collaborative filtering approach.
# ## Discussion
#
# #### Limitations or risk of your study
#
# ##### 1.Lack/ Change of Data
#
# The dataset is a very a small snapshot of the real world population. This makes the whole research questionable as the findings we got can change if the dataset changes or the size increases.
#
# ##### 2.Change in the attributes for content-based approach
#
# We considered taglines and overview feature of the movie to create content based recommender algorithm, but if we change the attributes/features then the recommendations are at greater risk of being changed/modified. Hence, this further bolsters our second research question that why should the user trust that the algorithm understand user's liking and dislikes. Therefore, any change in the algorithm or feature selection can be reflected while showing the recommendation for the use.
#
# ##### 3.Expected outcome and understanding of the results
#
# Since the project concentrates on the Human Recommender Interaction - how the personality of the two approaches differ and how to accurately present the recommendation to users - therefore, the expected outcome and understanding of the results may differ person to person.
#
# ##### 4.Intuition based study
#
# Since the project is more research centric and less data analytics or visualization centric, the outcome of the project can be perceived differently and there could be many discussions and arguments that can arise from this project which is a great opportunity for further study and research work in the field of Human Recommender Interaction.
#
# ## Conclusion and Future work
# From our research project, we tried to build to recommendation algorithms from scratch without using the already built libraries for such algorithms like MLlib and tried to answer two hypothesis -
# 1. Compare the recommender personality of content-based and collaborative filtering RS
# 2. Why should a user trust that the algorithm understands who they are, what they like and what they are doing?
#
# By doing this project we compared and predicted the subjective characteristics of recommendation algorithm. We find that the recommendations from collaborative filtering approach are quite diverse and fresh, whereas the recommendations from content-based approach are quite the opposite. It depends on the requirement of the users and what kind of recommendations they would like. If a user is a binge-watcher then content-based approach sounds apt for the user as we try to binge-watch the series of movies in one go. Hence, the recommendations are situational and the usefulness of the recommendation depends on the mood of the users. Moreover, whatever recommendation we provide to the user, the two key important factors to keep in mind is awareness and explanation of the recommendations. Let the users be aware of how we are adapting to their tastes and make it clear that we are not recommending movies/items because it suits our business needs, but because it matches the information we have from them: their explicit taste preferences and ratings, their viewing history.
#
# In the future, we plan to add user evaluations of recommender systems as well. We want to understand what makes recommendations more effective and useful, hence we can add experiments where users compare the recommendations produced by the two algorithms - content-based and collaborative filtering - based on dimensions like innovation, variety, efficiency, satisfaction, and degree of personalization, and out of the two sets of recommendation select a recommender that they would like to use in the future. We hope to garner data using the modern survey technique which will also be useful for developing, evaluating and refining additional measures of recommender behavior and personality.
#
# These kind of studies are new in the field as it is the combination of both qualitative and quantitative research methodology, which includes modern survey designs, analysis techniques and prediction of subjective characteristics, and direct comparison study of recommender algorithms.
#
# Hence, my contribution to this project is an initial building block towards understanding how users comprehend and interact with recommenders systems. Such interactions are critical for building better tools and meeting users' requirements. We look forward the future work, from the whole Data Science community including ourselves, for building a well-organized and systematic understanding of how to produce powerful, beneficial, and engaging recommendations in a broad range of applications.
#
#
# ## References
#
# 1. https://en.wikipedia.org/wiki/Recommender_system
#
# 2. "Facebook, Pandora Lead Rise of Recommendation Engines - TIME". TIME.com. 27 May 2010. Retrieved 1 June 2015.
#
# 3. Francesco Ricci and Lior Rokach and Bracha Shapira, Introduction to Recommender Systems Handbook, Recommender Systems Handbook, Springer, 2011, pp. 1-35
#
# 4. https://medium.com/recombee-blog/recommender-systems-explained-d98e8221f468
#
# 5. https://yanirseroussi.com/2015/10/02/the-wonderful-world-of-recommender-systems/
#
# 6. https://www.kaggle.com/rounakbanik/the-movies-dataset
#
# 7. F. Maxwell Harper and Joseph A. Konstan. 2015. The MovieLens Datasets: History and Context. ACM Transactions on Interactive Intelligent Systems (TiiS) 5, 4: 19:1–19:19. https://doi.org/10.1145/2827872
#
# 8. http://blog.manugarri.com/a-short-introduction-to-recommendation-systems/
#
# 9. http://blog.untrod.com/2016/06/simple-similar-products-recommendation-engine-in-python.html
#
# 10. Michael D. Ekstrand, F. Maxwell Harper, Martijn C. Willemsen, and Joseph A. Konstan. 2014. User perception of differences in recommender algorithms. In Proceedings of the 8th ACM Conference on Recommender systems (RecSys '14). ACM, New York, NY, USA, 161-168. DOI: https://doi.org/10.1145/2645710.2645737
#
# 11. Sean M. McNee, John Riedl, and Joseph A. Konstan. 2006. Making recommendations better: an analytic model for human-recommender interaction. In CHI '06 Extended Abstracts on Human Factors in Computing Systems (CHI EA '06). ACM, New York, NY, USA, 1103-1108. DOI=http://dx.doi.org/10.1145/1125451.1125660
#
# 12. Michael D. Ekstrand and Martijn C. Willemsen. 2016. Behaviorism is Not Enough: Better Recommendations through Listening to Users. In Proceedings of the 10th ACM Conference on Recommender Systems (RecSys '16). ACM, New York, NY, USA, 221-224. DOI: https://doi.org/10.1145/2959100.2959179
#
# 13. Xavier Amatriain and Justin Basilico. Netflix Recommendations: Beyond the 5 stars. Netflix Tech Blog, 2012.
#
# 14. Brian Whitman. How music recommendation works - and doesn't work. Variogram, 2012.
#
# 15. Bart P. Knijnenburg, Martijn C. Willemsen, Zeno Gantner, Hakan Soncu, and Chris Newell. 2012. Explaining the user experience of recommender systems. User Modeling and User-Adapted Interaction 22, 4-5 (October 2012), 441-504. DOI=http://dx.doi.org/10.1007/s11257-011-9118-4
#
# 16. Sean M. McNee, Nishikant Kapoor, and Joseph A. Konstan. 2006. Don't look stupid: avoiding pitfalls when recommending research papers. In Proceedings of the 2006 20th anniversary conference on Computer supported cooperative work (CSCW '06). ACM, New York, NY, USA, 171-180. DOI=http://dx.doi.org/10.1145/1180875.1180903
#
| 61.41055 | 1,131 |
41c787e80b373b29bda0f5671854c131e0b5aa9c
|
py
|
python
|
IMDB_RNN.ipynb
|
medinaalonso/NLP
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/medinaalonso/NLP/blob/master/IMDB_RNN.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="yYcqXGaYsLu3" colab_type="text"
# # *Importing data from KAGGLE*
# + [markdown] id="JtbkLYXasQFQ" colab_type="text"
#
# + id="hoenhSwkompc" colab_type="code" colab={}
# ! pip install -q kaggle
# + id="gTFXYhWDqGZh" colab_type="code" colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "Ly8gQ29weXJpZ2h0IDIwMTcgR29vZ2xlIExMQwovLwovLyBMaWNlbnNlZCB1bmRlciB0aGUgQXBhY2hlIExpY2Vuc2UsIFZlcnNpb24gMi4wICh0aGUgIkxpY2Vuc2UiKTsKLy8geW91IG1heSBub3QgdXNlIHRoaXMgZmlsZSBleGNlcHQgaW4gY29tcGxpYW5jZSB3aXRoIHRoZSBMaWNlbnNlLgovLyBZb3UgbWF5IG9idGFpbiBhIGNvcHkgb2YgdGhlIExpY2Vuc2UgYXQKLy8KLy8gICAgICBodHRwOi8vd3d3LmFwYWNoZS5vcmcvbGljZW5zZXMvTElDRU5TRS0yLjAKLy8KLy8gVW5sZXNzIHJlcXVpcmVkIGJ5IGFwcGxpY2FibGUgbGF3IG9yIGFncmVlZCB0byBpbiB3cml0aW5nLCBzb2Z0d2FyZQovLyBkaXN0cmlidXRlZCB1bmRlciB0aGUgTGljZW5zZSBpcyBkaXN0cmlidXRlZCBvbiBhbiAiQVMgSVMiIEJBU0lTLAovLyBXSVRIT1VUIFdBUlJBTlRJRVMgT1IgQ09ORElUSU9OUyBPRiBBTlkgS0lORCwgZWl0aGVyIGV4cHJlc3Mgb3IgaW1wbGllZC4KLy8gU2VlIHRoZSBMaWNlbnNlIGZvciB0aGUgc3BlY2lmaWMgbGFuZ3VhZ2UgZ292ZXJuaW5nIHBlcm1pc3Npb25zIGFuZAovLyBsaW1pdGF0aW9ucyB1bmRlciB0aGUgTGljZW5zZS4KCi8qKgogKiBAZmlsZW92ZXJ2aWV3IEhlbHBlcnMgZm9yIGdvb2dsZS5jb2xhYiBQeXRob24gbW9kdWxlLgogKi8KKGZ1bmN0aW9uKHNjb3BlKSB7CmZ1bmN0aW9uIHNwYW4odGV4dCwgc3R5bGVBdHRyaWJ1dGVzID0ge30pIHsKICBjb25zdCBlbGVtZW50ID0gZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgnc3BhbicpOwogIGVsZW1lbnQudGV4dENvbnRlbnQgPSB0ZXh0OwogIGZvciAoY29uc3Qga2V5IG9mIE9iamVjdC5rZXlzKHN0eWxlQXR0cmlidXRlcykpIHsKICAgIGVsZW1lbnQuc3R5bGVba2V5XSA9IHN0eWxlQXR0cmlidXRlc1trZXldOwogIH0KICByZXR1cm4gZWxlbWVudDsKfQoKLy8gTWF4IG51bWJlciBvZiBieXRlcyB3aGljaCB3aWxsIGJlIHVwbG9hZGVkIGF0IGEgdGltZS4KY29uc3QgTUFYX1BBWUxPQURfU0laRSA9IDEwMCAqIDEwMjQ7CgpmdW5jdGlvbiBfdXBsb2FkRmlsZXMoaW5wdXRJZCwgb3V0cHV0SWQpIHsKICBjb25zdCBzdGVwcyA9IHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCk7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICAvLyBDYWNoZSBzdGVwcyBvbiB0aGUgb3V0cHV0RWxlbWVudCB0byBtYWtlIGl0IGF2YWlsYWJsZSBmb3IgdGhlIG5leHQgY2FsbAogIC8vIHRvIHVwbG9hZEZpbGVzQ29udGludWUgZnJvbSBQeXRob24uCiAgb3V0cHV0RWxlbWVudC5zdGVwcyA9IHN0ZXBzOwoKICByZXR1cm4gX3VwbG9hZEZpbGVzQ29udGludWUob3V0cHV0SWQpOwp9CgovLyBUaGlzIGlzIHJvdWdobHkgYW4gYXN5bmMgZ2VuZXJhdG9yIChub3Qgc3VwcG9ydGVkIGluIHRoZSBicm93c2VyIHlldCksCi8vIHdoZXJlIHRoZXJlIGFyZSBtdWx0aXBsZSBhc3luY2hyb25vdXMgc3RlcHMgYW5kIHRoZSBQeXRob24gc2lkZSBpcyBnb2luZwovLyB0byBwb2xsIGZvciBjb21wbGV0aW9uIG9mIGVhY2ggc3RlcC4KLy8gVGhpcyB1c2VzIGEgUHJvbWlzZSB0byBibG9jayB0aGUgcHl0aG9uIHNpZGUgb24gY29tcGxldGlvbiBvZiBlYWNoIHN0ZXAsCi8vIHRoZW4gcGFzc2VzIHRoZSByZXN1bHQgb2YgdGhlIHByZXZpb3VzIHN0ZXAgYXMgdGhlIGlucHV0IHRvIHRoZSBuZXh0IHN0ZXAuCmZ1bmN0aW9uIF91cGxvYWRGaWxlc0NvbnRpbnVlKG91dHB1dElkKSB7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICBjb25zdCBzdGVwcyA9IG91dHB1dEVsZW1lbnQuc3RlcHM7CgogIGNvbnN0IG5leHQgPSBzdGVwcy5uZXh0KG91dHB1dEVsZW1lbnQubGFzdFByb21pc2VWYWx1ZSk7CiAgcmV0dXJuIFByb21pc2UucmVzb2x2ZShuZXh0LnZhbHVlLnByb21pc2UpLnRoZW4oKHZhbHVlKSA9PiB7CiAgICAvLyBDYWNoZSB0aGUgbGFzdCBwcm9taXNlIHZhbHVlIHRvIG1ha2UgaXQgYXZhaWxhYmxlIHRvIHRoZSBuZXh0CiAgICAvLyBzdGVwIG9mIHRoZSBnZW5lcmF0b3IuCiAgICBvdXRwdXRFbGVtZW50Lmxhc3RQcm9taXNlVmFsdWUgPSB2YWx1ZTsKICAgIHJldHVybiBuZXh0LnZhbHVlLnJlc3BvbnNlOwogIH0pOwp9CgovKioKICogR2VuZXJhdG9yIGZ1bmN0aW9uIHdoaWNoIGlzIGNhbGxlZCBiZXR3ZWVuIGVhY2ggYXN5bmMgc3RlcCBvZiB0aGUgdXBsb2FkCiAqIHByb2Nlc3MuCiAqIEBwYXJhbSB7c3RyaW5nfSBpbnB1dElkIEVsZW1lbnQgSUQgb2YgdGhlIGlucHV0IGZpbGUgcGlja2VyIGVsZW1lbnQuCiAqIEBwYXJhbSB7c3RyaW5nfSBvdXRwdXRJZCBFbGVtZW50IElEIG9mIHRoZSBvdXRwdXQgZGlzcGxheS4KICogQHJldHVybiB7IUl0ZXJhYmxlPCFPYmplY3Q+fSBJdGVyYWJsZSBvZiBuZXh0IHN0ZXBzLgogKi8KZnVuY3Rpb24qIHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCkgewogIGNvbnN0IGlucHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKGlucHV0SWQpOwogIGlucHV0RWxlbWVudC5kaXNhYmxlZCA9IGZhbHNlOwoKICBjb25zdCBvdXRwdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQob3V0cHV0SWQpOwogIG91dHB1dEVsZW1lbnQuaW5uZXJIVE1MID0gJyc7CgogIGNvbnN0IHBpY2tlZFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgaW5wdXRFbGVtZW50LmFkZEV2ZW50TGlzdGVuZXIoJ2NoYW5nZScsIChlKSA9PiB7CiAgICAgIHJlc29sdmUoZS50YXJnZXQuZmlsZXMpOwogICAgfSk7CiAgfSk7CgogIGNvbnN0IGNhbmNlbCA9IGRvY3VtZW50LmNyZWF0ZUVsZW1lbnQoJ2J1dHRvbicpOwogIGlucHV0RWxlbWVudC5wYXJlbnRFbGVtZW50LmFwcGVuZENoaWxkKGNhbmNlbCk7CiAgY2FuY2VsLnRleHRDb250ZW50ID0gJ0NhbmNlbCB1cGxvYWQnOwogIGNvbnN0IGNhbmNlbFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgY2FuY2VsLm9uY2xpY2sgPSAoKSA9PiB7CiAgICAgIHJlc29sdmUobnVsbCk7CiAgICB9OwogIH0pOwoKICAvLyBXYWl0IGZvciB0aGUgdXNlciB0byBwaWNrIHRoZSBmaWxlcy4KICBjb25zdCBmaWxlcyA9IHlpZWxkIHsKICAgIHByb21pc2U6IFByb21pc2UucmFjZShbcGlja2VkUHJvbWlzZSwgY2FuY2VsUHJvbWlzZV0pLAogICAgcmVzcG9uc2U6IHsKICAgICAgYWN0aW9uOiAnc3RhcnRpbmcnLAogICAgfQogIH07CgogIGNhbmNlbC5yZW1vdmUoKTsKCiAgLy8gRGlzYWJsZSB0aGUgaW5wdXQgZWxlbWVudCBzaW5jZSBmdXJ0aGVyIHBpY2tzIGFyZSBub3QgYWxsb3dlZC4KICBpbnB1dEVsZW1lbnQuZGlzYWJsZWQgPSB0cnVlOwoKICBpZiAoIWZpbGVzKSB7CiAgICByZXR1cm4gewogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbXBsZXRlJywKICAgICAgfQogICAgfTsKICB9CgogIGZvciAoY29uc3QgZmlsZSBvZiBmaWxlcykgewogICAgY29uc3QgbGkgPSBkb2N1bWVudC5jcmVhdGVFbGVtZW50KCdsaScpOwogICAgbGkuYXBwZW5kKHNwYW4oZmlsZS5uYW1lLCB7Zm9udFdlaWdodDogJ2JvbGQnfSkpOwogICAgbGkuYXBwZW5kKHNwYW4oCiAgICAgICAgYCgke2ZpbGUudHlwZSB8fCAnbi9hJ30pIC0gJHtmaWxlLnNpemV9IGJ5dGVzLCBgICsKICAgICAgICBgbGFzdCBtb2RpZmllZDogJHsKICAgICAgICAgICAgZmlsZS5sYXN0TW9kaWZpZWREYXRlID8gZmlsZS5sYXN0TW9kaWZpZWREYXRlLnRvTG9jYWxlRGF0ZVN0cmluZygpIDoKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgJ24vYSd9IC0gYCkpOwogICAgY29uc3QgcGVyY2VudCA9IHNwYW4oJzAlIGRvbmUnKTsKICAgIGxpLmFwcGVuZENoaWxkKHBlcmNlbnQpOwoKICAgIG91dHB1dEVsZW1lbnQuYXBwZW5kQ2hpbGQobGkpOwoKICAgIGNvbnN0IGZpbGVEYXRhUHJvbWlzZSA9IG5ldyBQcm9taXNlKChyZXNvbHZlKSA9PiB7CiAgICAgIGNvbnN0IHJlYWRlciA9IG5ldyBGaWxlUmVhZGVyKCk7CiAgICAgIHJlYWRlci5vbmxvYWQgPSAoZSkgPT4gewogICAgICAgIHJlc29sdmUoZS50YXJnZXQucmVzdWx0KTsKICAgICAgfTsKICAgICAgcmVhZGVyLnJlYWRBc0FycmF5QnVmZmVyKGZpbGUpOwogICAgfSk7CiAgICAvLyBXYWl0IGZvciB0aGUgZGF0YSB0byBiZSByZWFkeS4KICAgIGxldCBmaWxlRGF0YSA9IHlpZWxkIHsKICAgICAgcHJvbWlzZTogZmlsZURhdGFQcm9taXNlLAogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbnRpbnVlJywKICAgICAgfQogICAgfTsKCiAgICAvLyBVc2UgYSBjaHVua2VkIHNlbmRpbmcgdG8gYXZvaWQgbWVzc2FnZSBzaXplIGxpbWl0cy4gU2VlIGIvNjIxMTU2NjAuCiAgICBsZXQgcG9zaXRpb24gPSAwOwogICAgd2hpbGUgKHBvc2l0aW9uIDwgZmlsZURhdGEuYnl0ZUxlbmd0aCkgewogICAgICBjb25zdCBsZW5ndGggPSBNYXRoLm1pbihmaWxlRGF0YS5ieXRlTGVuZ3RoIC0gcG9zaXRpb24sIE1BWF9QQVlMT0FEX1NJWkUpOwogICAgICBjb25zdCBjaHVuayA9IG5ldyBVaW50OEFycmF5KGZpbGVEYXRhLCBwb3NpdGlvbiwgbGVuZ3RoKTsKICAgICAgcG9zaXRpb24gKz0gbGVuZ3RoOwoKICAgICAgY29uc3QgYmFzZTY0ID0gYnRvYShTdHJpbmcuZnJvbUNoYXJDb2RlLmFwcGx5KG51bGwsIGNodW5rKSk7CiAgICAgIHlpZWxkIHsKICAgICAgICByZXNwb25zZTogewogICAgICAgICAgYWN0aW9uOiAnYXBwZW5kJywKICAgICAgICAgIGZpbGU6IGZpbGUubmFtZSwKICAgICAgICAgIGRhdGE6IGJhc2U2NCwKICAgICAgICB9LAogICAgICB9OwogICAgICBwZXJjZW50LnRleHRDb250ZW50ID0KICAgICAgICAgIGAke01hdGgucm91bmQoKHBvc2l0aW9uIC8gZmlsZURhdGEuYnl0ZUxlbmd0aCkgKiAxMDApfSUgZG9uZWA7CiAgICB9CiAgfQoKICAvLyBBbGwgZG9uZS4KICB5aWVsZCB7CiAgICByZXNwb25zZTogewogICAgICBhY3Rpb246ICdjb21wbGV0ZScsCiAgICB9CiAgfTsKfQoKc2NvcGUuZ29vZ2xlID0gc2NvcGUuZ29vZ2xlIHx8IHt9OwpzY29wZS5nb29nbGUuY29sYWIgPSBzY29wZS5nb29nbGUuY29sYWIgfHwge307CnNjb3BlLmdvb2dsZS5jb2xhYi5fZmlsZXMgPSB7CiAgX3VwbG9hZEZpbGVzLAogIF91cGxvYWRGaWxlc0NvbnRpbnVlLAp9Owp9KShzZWxmKTsK", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 89} outputId="28566c01-2322-4eb4-f7be-1243fd9ded13"
from google.colab import files
files.upload()
# + id="WvjJozK4qKlQ" colab_type="code" colab={}
# ! mkdir ~/.kaggle
# + id="HQ-2lyREqSYl" colab_type="code" colab={}
# ! cp kaggle.json ~/.kaggle/
# + id="t9OW9zAhqlQ-" colab_type="code" colab={}
# ! chmod 600 ~/.kaggle/kaggle.json
# + id="hnmopDhmquqW" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 408} outputId="c4e43cc7-2b83-4cfa-ed90-0462f4476406"
# ! kaggle datasets list
# + id="cvUd_a3Uq1JO" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 68} outputId="15a71097-d97f-4db1-8b96-30dc45f94634"
# ! kaggle datasets download -d mwallerphunware/imbd-movie-reviews-for-binary-sentiment-analysis
# + id="oSN4ME2GsEP3" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="bdf600c1-cc64-4eda-f69e-bd5e95ef1122"
# ! unzip imbd-movie-reviews-for-binary-sentiment-analysis.zip
# + [markdown] id="SGRWeuJn4Gtx" colab_type="text"
# # Inicio
# + id="VOhJ1VQsi2YN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 68} outputId="18e20823-59e3-461c-cfaf-73a5c8a4c3a3"
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import nltk
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.preprocessing import LabelBinarizer
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from wordcloud import WordCloud,STOPWORDS
from nltk.stem import WordNetLemmatizer
from nltk.tokenize import word_tokenize,sent_tokenize
from bs4 import BeautifulSoup
import spacy
import re,string,unicodedata
from nltk.tokenize.toktok import ToktokTokenizer
from nltk.stem import LancasterStemmer,WordNetLemmatizer
from sklearn.linear_model import LogisticRegression,SGDClassifier
from sklearn.naive_bayes import MultinomialNB
from sklearn.svm import SVC
from textblob import TextBlob
from textblob import Word
from sklearn.metrics import classification_report,confusion_matrix,accuracy_score
from keras.preprocessing.text import Tokenizer
from tensorflow.compat.v1.nn import rnn_cell
from tensorflow import keras
from tensorflow.keras.layers import *
from tensorflow.keras.datasets import imdb
from tensorflow.keras.preprocessing.sequence import pad_sequences
import tensorflow as tf
# + id="aBGjLJpkL4QA" colab_type="code" colab={}
# %tensorflow_version 2.x
# + id="1h97WwY3sK4O" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="9bd47383-8b39-49e4-a3cf-20c02422cbe8"
from csv import reader
import pandas as pd
data = pd.read_csv('/content/drive/My Drive/Redes Neuronales Avanzadas/IMDB Dataset.csv', sep='\t')
print(type(data))
imdb = np.asarray(data)
renglon = str(imdb[3])
length =len(renglon)
clase = renglon[-10:-2]
#print(renglon[2:-12])
#print(clase)
lista = []
for i in range(0,50000):
renglon = str(imdb[i])
clase = renglon[-10:-2]
texto = renglon[2:-12]
lista.append([clase,texto])
#print(clase,texto)
#d = pd.DataFrame({'id': data['id'], 'sentiment': p[:,0]})
# + id="02iCZ9GtxdC5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="7b757ba5-e196-4a24-9c5c-240f9fbb6e95"
newlist = np.asarray(lista)
print(newlist.shape)
print(newlist[0][0])
# + id="ZmmKPhDAyqbp" colab_type="code" colab={}
for i in range(0,50000):
clase = newlist[i][0]
if clase=='positive':
newlist[i][0] = 0
if clase=='negative':
newlist[i][0] = 1
# + id="bU9S6ofHzbsw" colab_type="code" colab={}
#Removing the html strips
def strip_html(text):
soup = BeautifulSoup(text, "html.parser")
return soup.get_text()
#Removing the square brackets
def remove_between_square_brackets(text):
return re.sub('\[[^]]*\]', '', text)
#Removing the noisy text
def denoise_text(text):
text = strip_html(text)
text = remove_between_square_brackets(text)
return text
def remove_special_characters(text, remove_digits=True):
pattern=r'[^a-zA-z0-9\s]'
text=re.sub(pattern,'',text)
return text
#Apply function on review column
for i in range(0,50000):
newlist[i][1] = denoise_text(newlist[i][1])
newlist[i][1] = remove_special_characters(newlist[i][1])
# + id="3pzg0QT82zop" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 88} outputId="748eae71-c972-48fb-df82-5d1e5039a26a"
newlist[1]
# + id="wjnHZwGJioXO" colab_type="code" colab={}
X = []
y = []
# + id="aXIc9_0qylCz" colab_type="code" colab={}
for label, features in newlist:
X.append(features)
y.append(label)
#X = np.array(X) #3 VALUES
# + id="0HKBNjJr94xE" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 71} outputId="bd562df9-25e1-4b64-b786-206a31929d07"
NewX = np.asarray(X).reshape(50000,1)
NewY = np.asarray(y).reshape(50000,1)
print(NewX[1])
print(NewY.shape)
# + id="3C8GVK2T_ijV" colab_type="code" colab={}
from gensim.models import Word2Vec
# + id="m6UFCoQvye6l" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 258} outputId="42dd89bc-273e-4dbb-a5c1-d6203ca1bfe4"
# train model
model = Word2Vec(NewX, min_count=1)
# summarize the loaded model
print(model)
# summarize vocabulary
words = list(model.wv.vocab)
print(words)
# access vector for one word
print(model)
# save model
model.save('model.bin')
# load model
new_model = Word2Vec.load('model.bin')
print(new_model)
# + id="oKSQnqYksWV3" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="b2293bb6-bba2-4e39-ef3c-4fb8b5d74816"
model.wv.vectors.shape
# + id="5eAlUdttxm2y" colab_type="code" colab={}
model.wv.vectors[0]
# + id="vflnl_B_2oHJ" colab_type="code" colab={}
# + id="UwIj3A-Js2KI" colab_type="code" colab={}
X = model.wv.vectors
# + id="XRESrE_JtxcL" colab_type="code" colab={}
def data_genertor(data, window , distance=0):
x=[]
y=[]
for i in range(len(data)-window-distance):
x.append(data[i:i+window])
y.append(data[i+window+distance])
return np.array(x),np.array(y)
# + id="o4xKUfwltxe7" colab_type="code" colab={}
train_x,train_y=data_genertor(model.wv.vectors[0:45000], 10 , 0)
#test_x,test_y=data_genertor(model.wv.vectors[0:45000], 10 , 0)
# + id="-kiPlQqbtxhd" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="283583e5-439e-4cdf-dda6-cec17c0ab6c0"
print(train_x.shape)
print(train_y.shape)
# + id="AVO-GR-WtxtJ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 187} outputId="535e04cc-facf-4562-957a-84a0b284ec79"
RNN=tf.keras.Sequential()
RNN.add(tf.keras.layers.LSTM(units=1,input_shape=(49582,100),activation="relu"))
RNN.summary()
# + id="Cyf-bqhetxz0" colab_type="code" colab={}
RNN.compile(optimizer='adam', loss='mean_squared_error')
# + id="SpqSQzJ7tx85" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="edb68a27-e1a6-4c51-dc5f-c1a1e7b0eecf"
# input shape must be [samples, time steps, features]
#train_x = np.reshape(train_x, (train_x.shape[0], train_x.shape[1],1))
#test_x = np.reshape(test_x, (test_x.shape[0], test_x.shape[1],1))
RNN.fit(train_x,train_y,
epochs=100,
batch_size=100,
shuffle=False
)
# + id="Fvi4NhPCtyK9" colab_type="code" colab={}
test_x,test_y=data_genertor(model.wv.vectors[45000:49572], 10 , 0)
# + id="MWxX0_reudSV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 71} outputId="e759a140-7307-4bf1-c087-4ae7e12b2aff"
Salidas=RNN.predict(test_x,verbose=True)
# + id="bKjjC6VzudVM" colab_type="code" colab={}
# + [markdown] id="pRWyikVb_gTA" colab_type="text"
# # Con Keras
# + id="6Kx0XBQtye9L" colab_type="code" colab={}
top_words = 5000
(X_train, y_train), (X_test, y_test) = imdb.load_data(num_words=top_words)
# + id="ZDzv1rFUQpEC" colab_type="code" colab={}
y_train = keras.utils.to_categorical( y_train , num_classes=2 )
y_test = keras.utils.to_categorical( y_test , num_classes=2 )
# + id="ya-4fAjfQqOH" colab_type="code" colab={}
X_train = pad_sequences( X_train , maxlen=120 , padding='pre' )
X_test = pad_sequences( X_test , maxlen=120 , padding='pre' )
# + id="QIxNhxXuye_7" colab_type="code" colab={}
dropout_rate = 0.3
batch_size = 1000
activation_func = keras.activations.relu
SCHEMA = [
Embedding( 5000 , 10, input_length=120 ),
LSTM( 32 ) ,
Dropout(dropout_rate),
Dense( 32 , activation=activation_func ) ,
Dropout(dropout_rate),
Dense( 2 , activation=keras.activations.softmax )
]
model = keras.Sequential(SCHEMA)
model.compile(
optimizer=keras.optimizers.Adam() ,
loss=keras.losses.categorical_crossentropy ,
metrics=[ 'accuracy' ]
)
# + id="2DkqFKcMMH99" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 374} outputId="b100efd6-cae2-4534-a65b-91ee21e1b4a2"
model.fit(X_train , y_train , batch_size=batch_size , epochs=10 )
# + id="WmFyJpQJMIn4" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="0d7ea0f6-3930-4323-e85b-4cc02eecf78d"
model.evaluate(X_test , y_test )
| 57.589041 | 7,251 |
7b0d8c20dbcc49ce5a81ce1fc24630f5a577334c
|
py
|
python
|
cgames/02_space_invader/space_invader_AE.ipynb
|
BeylierMPG/Reinforcement-Learning
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: atari1.0_kernel
# language: python
# name: atari1.0
# ---
# + [markdown] colab_type="text" id="LN0nZwyMGadB"
# # Pong with dqn
#
# ## Step 1: Import the libraries
# -
# !!!! To import all the games !!!!!
#
# pip install --upgrade git+https://github.com/openai/gym
# pip install autorom
#
# AutoRom
#
# pip install --upgrade gym[atari]
#
#
# +
import time
import gym
import random
import torch
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
import math
# +
from sklearn.manifold import Isomap
# importing required libraries
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
# -
import warnings
from scipy.sparse import (spdiags, SparseEfficiencyWarning, csc_matrix,
csr_matrix, isspmatrix, dok_matrix, lil_matrix, bsr_matrix)
warnings.simplefilter('ignore',SparseEfficiencyWarning)
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA, IncrementalPCA
import sys
sys.path.append('../../')
from algos.agents.AE_agent import AEAgent
from algos.models.AE_cnn import AECnn
from algos.preprocessing.stack_frame import preprocess_frame, stack_frame
sys.path.append('../../')
from MIND.src.mind import mind_ensemble
# + [markdown] colab_type="text" id="tfo8jleHGadK"
# ## Step 2: Create our environment
#
# Initialize the environment in the code cell below.
#
# +
env = gym.make('SpaceInvaders-v0')
env.seed(0)
# -
# if gpu is to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print("Device: ", device)
# + [markdown] colab_type="text" id="nS221MgXGadP"
# ## Step 3: Viewing our Enviroment
# -
print("The size of frame is: ", env.observation_space.shape)
print("No. of Actions: ", env.action_space.n)
env.reset()
print(env.reset()[1:5][:][0].shape)
#print(env.reset()[1:5][:][0])
plt.figure()
plt.imshow(env.reset())
plt.figure()
plt.imshow(env.reset()[180:210,:,2])
plt.title('Original Frame')
plt.show()
# ### Execute the code cell below to play Pong with a random policy.
# def random_play():
# score = 0
# env.reset()
# while True:
# env.render()
# action = env.action_space.sample()
# state, reward, done, _ = env.step(action)
# score += reward
# if done:
# env.close()
# print("Your Score at end of game is: ", score)
# break
# random_play()
# + [markdown] colab_type="text" id="Sr52nmcpGada"
# ## Step 4:Preprocessing Frame
# -
env.reset()
plt.figure()
plt.imshow(preprocess_frame(env.reset(), (8, -12, -12, 4), 84), cmap="gray")
plt.title('Pre Processed image')
plt.show()
# + [markdown] colab_type="text" id="mJMc3HA8Gade"
# ## Step 5: Stacking Frame
# -
def stack_frames(frames, state, is_new=False):
frame = preprocess_frame(state, (8, -12, -12, 4), 84)
frames = stack_frame(frames, frame, is_new)
return frames
# ## Step 6: Creating our Agent
# +
INPUT_SHAPE = (4, 84, 84)
ACTION_SIZE = env.action_space.n
SEED = 0
GAMMA = 0.99 # discount factor
BUFFER_SIZE = 100000 # replay buffer size
BATCH_SIZE = 64 # Update batch size
LR = 0.01 # learning rate
TAU = 1e-3 # for soft update of target parameters
UPDATE_EVERY = 1 # how often to update the network
UPDATE_TARGET = 10000 # After which thershold replay to be started
EPS_START = 0.99 # starting value of epsilon
EPS_END = 0.01 # Ending value of epsilon
EPS_DECAY = 100 # Rate by which epsilon to be decayed
agent = AEAgent(INPUT_SHAPE, ACTION_SIZE, SEED, device, BUFFER_SIZE, BATCH_SIZE, GAMMA, LR, TAU, UPDATE_EVERY, UPDATE_TARGET, AECnn)
# -
print(env.action_space.n)
# ## Step 7: Watching untrained agent play
#
# # watch an untrained agent
# state = stack_frames(None, env.reset(), True)
# for j in range(200):
# env.render()
# action = agent.act(state)
# next_state, reward, done, _ = env.step(action)
# state = stack_frames(state, next_state, False)
# if done:
# break
#
# env.close()
# ## Step 8: Loading Agent
# Uncomment line to load a pretrained agent
start_epoch = 0
scores = []
scores_window = deque(maxlen=20)
# ## Step 9: Train the Agent with DQN
# +
epsilon_by_epsiode = lambda frame_idx: EPS_END + (EPS_START - EPS_END) * math.exp(-1. * frame_idx /EPS_DECAY)
plt.plot([epsilon_by_epsiode(i) for i in range(1000)])
# -
def train(n_episodes=1000):
"""
Params
======
n_episodes (int): maximum number of training episodes
"""
Loss = []
for i_episode in range(start_epoch + 1, n_episodes+1):
state = stack_frames(None, env.reset(), True)
score = 0
eps = epsilon_by_epsiode(i_episode)
while True:
action = agent.act(state, eps)
next_state, reward, done, info = env.step(action)
score += reward
next_state = stack_frames(state, next_state, False)
loss = agent.step(state, action, reward, next_state, done)
Loss.append(loss)
state = next_state
if done:
break
scores_window.append(score) # save most recent score
scores.append(score) # save most recent score
print('\rEpisode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)), end="")
if i_episode % 1 == 0:
print('\rEpisode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)))
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(Loss)), Loss)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
return scores
scores = train(16)
# ## Step 10: Watch a Smart Agent!
# + tags=[]
Names_hook = ["fc1","Conv_1","Conv_2","Conv_3"]
#Liste_activation = [[] for i in range(len(Names_hook))]
#agent.registration()
score = 0
i = 0
state = stack_frames(None, env.reset(), True)
g = 0
while True:
#env.render()
action = agent.act(state)
# for h in range(len(Names_hook)):
# Liste_activation[h].append(torch.flatten(agent.activation[Names_hook[h]]).unsqueeze(0))
next_state, reward, done, _ = env.step(action)
score += reward
state = stack_frames(state, next_state, False)
if np.mod(i,10)==0:
if g < 20:
state_rec = torch.from_numpy(state).unsqueeze(0).to(device)
with torch.no_grad():
image_reconstruction = agent.policy_net(state_rec)
fig = plt.figure()
fig.add_subplot(1, 2, 1)
plt.imshow(state_rec.squeeze(0).permute(1,2,0)[:,:,1:4])
fig.add_subplot(1, 2, 2)
plt.imshow(image_reconstruction.squeeze(0).permute(1,2,0)[:,:,0:3])
g+=1
i +=1
if done:
print("You Final score is:", score)
print(i)
break
env.close()
#agent.detach()
#print("Shape liste fc1",len(Liste_activation[0]),len(Liste_activation[0][0][0]))
#print("Shape liste conv",len(Liste_activation[2]),len(Liste_activation[2][0][0]))
# -
# ## Step 11: Create the activation Liste
# L_activation =torch.zeros([len(Liste_activation), 512], dtype=torch.float64)
# Liste = Liste_activation[0]
#
# for i in range(1,len(Liste_activation)):
# Liste = torch.cat((Liste,Liste_activation[i]),0)
#
# Activations = Liste.cpu().detach().numpy()
#
# print(Activations.shape)
# ## Activation list for convolution layer
LAYER = 0
# +
Liste = Liste_activation[LAYER][0]
for i in range(1,len(Liste_activation[LAYER])):
Liste = torch.cat((Liste,Liste_activation[LAYER][i]),0)
Activations = Liste.cpu().detach().numpy()
print(Activations.shape)
# +
embedding = Isomap(n_neighbors=12,n_components=3)
for h in range(len(Names_hook)):
Liste = Liste_activation[h][0]
for i in range(1,len(Liste_activation[h])):
Liste = torch.cat((Liste,Liste_activation[h][i]),0)
Activations = Liste.cpu().detach().numpy()
print(Activations.shape)
X = embedding.fit_transform(Activations)
print(X.shape)
colorize = dict(c=X[:, 0], cmap=plt.cm.get_cmap('rainbow', 7))
fig = plt.figure()
ax = plt.figure().add_subplot(projection='3d')
sc = ax.scatter3D(X[:, 0], X[:, 1], X[:, 2],
**colorize)
ax.view_init(azim=120, elev=30)
plt.colorbar(sc)
# -
# ## Step 12: ISOMAP
embedding = Isomap(n_neighbors=12,n_components=3)
X_conv= embedding.fit_transform(Activations_conv)
print(X_conv.shape)
colorize = dict(c=X_conv[:, 0], cmap=plt.cm.get_cmap('rainbow', 7))
X_fc1 = embedding.fit_transform(Activations_fc1)
print(X_fc1.shape)
colorize = dict(c=X_fc1[:, 0], cmap=plt.cm.get_cmap('rainbow', 7))
# +
fig = plt.figure()
ax = plt.figure().add_subplot(projection='3d')
sc = ax.scatter3D(X_conv[:, 0], X_conv[:, 1], X_conv[:, 2],
**colorize)
ax.view_init(azim=120, elev=30)
plt.colorbar(sc)
# +
fig = plt.figure()
ax = plt.figure().add_subplot(projection='3d')
sc = ax.scatter3D(X_fc1[:, 0], X_fc1[:, 1], X_fc1[:, 2],
**colorize)
ax.view_init(azim=120, elev=30)
plt.colorbar(sc)
# -
# ## MDS
from sklearn.metrics import pairwise_distances
D = pairwise_distances(Activations_conv)
D.shape
plt.imshow(D, zorder=2, cmap='Blues', interpolation='nearest')
plt.colorbar();
from sklearn.manifold import MDS
model = MDS(n_components=2, dissimilarity='precomputed', random_state=1)
out = model.fit_transform(D)
plt.scatter(out[:, 0], out[:, 1], **colorize)
plt.axis('equal');
# +
plt.figure(figsize=(40, 30))
plt.scatter(out[:, 0], out[:, 1], **colorize)
plt.axis('equal');
text = [k for k in range(Activations_conv.shape[0])]
for i in range(len(text)):
plt.annotate(text[i], (out[i, 0], out[i, 1]))
# +
model = MDS(n_components=3, dissimilarity='precomputed', random_state=1)
X = model.fit_transform(D)
fig = plt.figure()
ax = plt.figure().add_subplot(projection='3d')
sc = ax.scatter3D(X[:, 0], X[:, 1], X[:, 2],
**colorize)
ax.view_init(azim=40, elev=30)
plt.colorbar(sc)
# -
# ## Other
# +
from collections import OrderedDict
from functools import partial
from time import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import NullFormatter
from sklearn import manifold, datasets
# Next line to silence pyflakes. This import is needed.
Axes3D
n_points = 1000
X = Activations_conv
n_neighbors = 12
n_components = 3
# Create figure
fig = plt.figure(figsize=(20, 15))
fig.suptitle(
"Manifold Learning with %i points, %i neighbors" % (1000, n_neighbors), fontsize=14
)
# Set-up manifold methods
LLE = partial(
manifold.LocallyLinearEmbedding,
n_neighbors=n_neighbors,
n_components=n_components,
eigen_solver="dense",
)
methods = OrderedDict()
methods["LLE"] = LLE(method="standard")
methods["LTSA"] = LLE(method="ltsa")
methods["Hessian LLE"] = LLE(method="hessian")
methods["Modified LLE"] = LLE(method="modified")
methods["Isomap"] = manifold.Isomap(n_neighbors=n_neighbors, n_components=n_components)
methods["MDS"] = manifold.MDS(n_components, max_iter=100, n_init=1)
methods["SE"] = manifold.SpectralEmbedding(
n_components=n_components, n_neighbors=n_neighbors
)
methods["t-SNE"] = manifold.TSNE(n_components=n_components, init="pca", random_state=0)
# Plot results
for i, (label, method) in enumerate(methods.items()):
t0 = time()
Y = method.fit_transform(X)
t1 = time()
print("%s: %.2g sec" % (label, t1 - t0))
ax = fig.add_subplot(2, 5, 2 + i + (i > 3),projection="3d")
sc = ax.scatter3D(Y[:, 0], Y[:, 1],Y[:, 2], **colorize)
ax.set_title("%s (%.2g sec)" % (label, t1 - t0))
#ax.xaxis.set_major_formatter(NullFormatter())
#ax.yaxis.set_major_formatter(NullFormatter())
ax.axis("tight")
# ax.view_init(azim=80, elev=30)
plt.show()
# +
emb = manifold.SpectralEmbedding(n_components=n_components, n_neighbors=n_neighbors)
X= emb.fit_transform(Activations)
fig = plt.figure()
ax = plt.figure().add_subplot(projection='3d')
sc = ax.scatter3D(X[:, 0], X[:, 1], X[:, 2],
**colorize)
ax.view_init(azim=40, elev=30)
plt.colorbar(sc)
# -
# Sort data by position on manifold
X_sort = Activations[np.argsort(colorize)]
print(colorize.shape)
print(X_sort.shape)
print(Activations.shape)
m = mind_ensemble(Activations, manifold_dim=2, n_trees=100, seed=123)
m.learn_coordinates()
# ## Score average during training HPC
# +
scores = [160.0, 110.0, 65.0, 120.0, 30.0, 65.0, 235.0, 210.0, 230.0, 180.0, 110.0, 150.0, 35.0, 30.0, 100.0, 65.0, 195.0, 105.0, 105.0, 80.0, 35.0, 70.0, 100.0, 330.0, 135.0, 205.0, 110.0, 335.0, 345.0, 80.0, 210.0, 470.0, 235.0, 325.0, 110.0, 265.0, 15.0, 30.0, 120.0, 470.0, 135.0, 90.0, 250.0, 300.0, 210.0, 200.0, 280.0, 85.0, 305.0, 470.0, 390.0, 45.0, 70.0, 235.0, 260.0, 205.0, 150.0, 225.0, 215.0, 430.0, 150.0, 205.0, 90.0, 170.0, 290.0, 150.0, 140.0, 195.0, 95.0, 135.0, 70.0, 90.0, 85.0, 50.0, 305.0, 160.0, 45.0, 155.0, 270.0, 30.0, 70.0, 230.0, 225.0, 100.0, 350.0, 135.0, 160.0, 95.0, 280.0, 565.0, 520.0, 305.0, 30.0, 70.0, 105.0, 225.0, 25.0, 405.0, 555.0, 70.0, 130.0, 120.0, 25.0, 215.0, 85.0, 15.0, 55.0, 55.0, 45.0, 10.0, 105.0, 235.0, 195.0, 245.0, 15.0, 80.0, 50.0, 90.0, 425.0, 110.0, 50.0, 135.0, 500.0, 160.0, 65.0, 260.0, 90.0, 215.0, 230.0, 20.0, 50.0, 25.0, 125.0, 385.0, 220.0, 360.0, 435.0, 190.0, 105.0, 175.0, 130.0, 65.0, 10.0, 140.0, 20.0, 170.0, 5.0, 120.0, 55.0, 320.0, 225.0, 15.0, 315.0, 120.0, 70.0, 20.0, 105.0, 280.0, 225.0, 20.0, 100.0, 140.0, 175.0, 155.0, 185.0, 355.0, 360.0, 15.0, 185.0, 535.0, 235.0, 265.0, 185.0, 105.0, 250.0, 10.0, 210.0, 100.0, 165.0, 275.0, 165.0, 180.0, 245.0, 85.0, 185.0, 385.0, 70.0, 75.0, 5.0, 35.0, 40.0, 145.0, 290.0, 75.0, 35.0, 605.0, 25.0, 105.0, 170.0, 165.0, 5.0, 40.0, 150.0, 20.0, 205.0, 315.0, 225.0, 220.0, 115.0, 245.0, 160.0, 510.0, 270.0, 200.0, 330.0, 230.0, 205.0, 335.0, 185.0, 135.0, 105.0, 130.0, 130.0, 20.0, 90.0, 300.0, 50.0, 20.0, 25.0, 150.0, 180.0, 295.0, 10.0, 95.0, 130.0, 85.0, 50.0, 500.0, 50.0, 15.0, 85.0, 35.0, 165.0, 60.0, 255.0, 80.0, 135.0, 115.0, 170.0, 65.0, 190.0, 120.0, 130.0, 275.0, 190.0, 80.0, 155.0, 135.0, 120.0, 60.0, 135.0, 110.0, 360.0, 120.0, 175.0, 210.0, 140.0, 230.0, 335.0, 210.0, 280.0, 440.0, 40.0, 145.0, 165.0, 230.0, 250.0, 120.0, 160.0, 630.0, 50.0, 410.0, 280.0, 160.0, 145.0, 505.0, 65.0, 140.0, 185.0, 130.0, 140.0, 120.0, 70.0, 155.0, 380.0, 140.0, 175.0, 25.0, 5.0, 165.0, 155.0, 100.0, 40.0, 5.0, 55.0, 415.0, 75.0, 100.0, 200.0, 40.0, 195.0, 50.0, 90.0, 345.0, 15.0, 230.0, 75.0, 90.0, 105.0, 110.0, 115.0, 325.0, 30.0, 120.0, 390.0, 490.0, 100.0, 65.0, 50.0, 240.0, 170.0, 25.0, 130.0, 140.0, 130.0, 35.0, 80.0, 35.0, 20.0, 20.0, 430.0, 25.0, 210.0, 490.0, 170.0, 105.0, 140.0, 115.0, 25.0, 20.0, 55.0, 10.0, 605.0, 170.0, 300.0, 75.0, 80.0, 115.0, 170.0, 30.0, 120.0, 415.0, 350.0, 485.0, 290.0, 20.0, 120.0, 75.0, 505.0, 435.0, 60.0, 540.0, 135.0, 75.0, 80.0, 160.0, 80.0, 125.0, 290.0, 5.0, 30.0, 265.0, 500.0, 10.0, 85.0, 85.0, 60.0, 80.0, 235.0, 370.0, 65.0, 95.0, 25.0, 110.0, 105.0, 65.0, 110.0, 65.0, 145.0, 420.0, 365.0, 50.0, 90.0, 55.0, 25.0, 105.0, 10.0, 415.0, 200.0, 55.0, 170.0, 150.0, 70.0, 55.0, 170.0, 125.0, 200.0, 145.0, 225.0, 85.0, 45.0, 445.0, 40.0, 205.0, 230.0, 240.0, 120.0, 245.0, 485.0, 330.0, 5.0, 70.0, 120.0, 60.0, 80.0, 150.0, 50.0, 280.0, 40.0, 145.0, 195.0, 70.0, 235.0, 145.0, 105.0, 310.0, 75.0, 145.0, 55.0, 105.0, 175.0, 315.0, 115.0, 215.0, 260.0, 670.0, 185.0, 100.0, 105.0, 190.0, 45.0, 275.0, 355.0, 100.0, 190.0, 210.0, 110.0, 65.0, 65.0, 35.0, 40.0, 425.0, 230.0, 90.0, 50.0, 190.0, 55.0, 180.0, 230.0, 320.0, 290.0, 245.0, 45.0, 180.0, 105.0, 90.0, 25.0, 140.0, 60.0, 15.0, 40.0, 15.0, 290.0, 145.0, 30.0, 75.0, 160.0, 105.0, 5.0, 50.0, 5.0, 65.0, 85.0, 215.0, 85.0, 265.0, 80.0, 55.0, 80.0, 90.0, 215.0, 460.0, 110.0, 215.0, 85.0, 30.0, 50.0, 35.0, 20.0, 255.0, 610.0, 500.0, 205.0, 110.0, 175.0, 15.0, 90.0, 45.0, 205.0, 215.0, 555.0, 230.0, 110.0, 95.0, 95.0, 30.0, 145.0, 250.0, 110.0, 100.0, 455.0, 390.0, 330.0, 190.0, 290.0, 110.0, 240.0, 400.0, 260.0, 235.0, 205.0, 120.0, 110.0, 20.0, 130.0, 140.0, 285.0, 115.0, 145.0, 125.0, 65.0, 150.0, 135.0, 185.0, 160.0, 375.0, 145.0, 135.0, 70.0, 215.0, 235.0, 45.0, 230.0, 110.0, 65.0, 15.0, 230.0, 170.0, 240.0, 345.0, 235.0, 100.0, 50.0, 155.0, 160.0, 210.0, 125.0, 145.0, 280.0, 85.0, 140.0, 250.0, 115.0, 30.0, 540.0, 430.0, 235.0, 75.0, 285.0, 220.0, 395.0, 135.0, 30.0, 380.0, 155.0, 30.0, 35.0, 70.0, 285.0, 155.0, 40.0, 165.0, 25.0, 455.0, 190.0, 35.0, 115.0, 180.0, 215.0, 45.0, 80.0, 280.0, 65.0, 225.0, 155.0, 30.0, 375.0, 30.0, 340.0, 120.0, 160.0, 325.0, 30.0, 70.0, 15.0, 40.0, 150.0, 85.0, 250.0, 30.0, 465.0, 200.0, 535.0, 305.0, 210.0, 50.0, 380.0, 155.0, 345.0, 365.0, 50.0, 215.0, 110.0, 135.0, 205.0, 95.0, 65.0, 525.0, 80.0, 40.0, 65.0, 165.0, 130.0, 125.0, 195.0, 65.0, 80.0, 155.0, 335.0, 325.0, 150.0, 275.0, 140.0, 240.0, 125.0, 160.0, 140.0, 135.0, 175.0, 315.0, 155.0, 380.0, 65.0, 120.0, 70.0, 290.0, 390.0, 210.0, 110.0, 80.0, 195.0, 150.0, 255.0, 190.0, 155.0, 285.0, 80.0, 110.0, 75.0, 55.0, 305.0, 105.0, 70.0, 265.0, 125.0, 230.0, 280.0, 115.0, 75.0, 235.0, 150.0, 135.0, 430.0, 130.0, 80.0, 200.0, 170.0, 140.0, 185.0, 100.0, 210.0, 55.0, 110.0, 335.0, 120.0, 340.0, 390.0, 125.0, 135.0, 490.0, 115.0, 90.0, 120.0, 75.0, 135.0, 485.0, 435.0, 140.0, 110.0, 120.0, 185.0, 175.0, 80.0, 105.0, 530.0, 350.0, 135.0, 270.0, 60.0, 365.0, 105.0, 500.0, 365.0, 120.0, 75.0, 50.0, 380.0, 485.0, 85.0, 120.0, 120.0, 110.0, 110.0, 110.0, 220.0, 775.0, 105.0, 105.0, 75.0, 415.0, 175.0, 75.0, 80.0, 225.0, 160.0, 60.0, 75.0, 300.0, 190.0, 165.0, 105.0, 55.0, 145.0, 95.0, 110.0, 85.0, 410.0, 75.0, 220.0, 525.0, 490.0, 135.0, 175.0, 1095.0, 120.0, 155.0, 50.0, 265.0, 155.0, 110.0, 345.0, 215.0, 210.0, 105.0, 50.0, 540.0, 195.0, 180.0, 285.0, 430.0, 290.0, 140.0, 335.0, 90.0, 125.0, 135.0, 155.0, 105.0, 140.0, 115.0, 145.0, 140.0, 135.0, 230.0, 160.0, 125.0, 180.0, 350.0, 145.0, 110.0, 410.0, 120.0, 140.0, 290.0, 250.0, 230.0, 270.0, 180.0, 295.0, 560.0, 135.0, 180.0, 75.0, 210.0, 85.0, 225.0, 455.0, 225.0, 140.0, 205.0, 215.0, 415.0, 205.0, 470.0, 150.0, 280.0, 110.0, 405.0, 120.0, 65.0, 555.0, 80.0, 490.0, 520.0, 215.0, 425.0, 470.0, 250.0, 105.0, 630.0, 365.0, 145.0, 165.0, 195.0, 230.0, 540.0, 165.0, 110.0, 320.0, 265.0, 95.0, 180.0, 110.0, 170.0, 235.0, 185.0, 200.0, 210.0, 110.0, 320.0, 130.0, 230.0, 165.0, 355.0, 230.0, 230.0, 180.0, 205.0, 535.0, 50.0, 350.0, 220.0, 390.0, 90.0, 290.0, 130.0, 55.0, 105.0, 190.0, 390.0, 145.0, 115.0, 120.0, 300.0, 85.0, 220.0, 110.0, 140.0, 110.0, 185.0, 120.0, 160.0, 115.0, 730.0, 270.0, 875.0, 135.0, 175.0, 155.0, 220.0, 105.0, 165.0, 135.0, 190.0, 160.0, 135.0, 110.0, 635.0, 100.0, 105.0, 215.0, 80.0, 50.0, 505.0, 85.0, 295.0, 375.0, 135.0, 110.0, 225.0, 210.0, 125.0, 205.0, 125.0, 130.0, 110.0, 110.0, 380.0, 370.0, 495.0, 530.0, 130.0, 200.0, 320.0, 220.0, 280.0, 355.0, 170.0, 100.0, 290.0, 135.0, 80.0, 570.0, 300.0, 365.0, 80.0, 110.0, 105.0, 350.0, 110.0, 105.0, 180.0, 470.0, 630.0, 170.0, 245.0, 110.0, 310.0, 350.0, 170.0, 215.0, 180.0, 170.0, 15.0, 80.0, 105.0, 25.0, 110.0, 200.0, 275.0]
#scores_2 = [60.0, 150.0, 95.0, 135.0, 155.0, 90.0, 215.0, 30.0, 105.0, 105.0, 45.0, 210.0, 210.0, 50.0, 205.0, 110.0, 155.0, 80.0, 200.0, 110.0, 110.0, 95.0, 485.0, 135.0, 75.0, 85.0, 135.0, 155.0, 155.0, 120.0, 55.0, 105.0, 285.0, 130.0, 255.0, 380.0, 105.0, 120.0, 75.0, 155.0, 120.0, 70.0, 205.0, 120.0, 120.0, 170.0, 110.0, 220.0, 295.0, 160.0, 240.0, 155.0, 135.0, 35.0, 220.0, 395.0, 120.0, 520.0, 20.0, 155.0, 75.0, 60.0, 300.0, 160.0, 180.0, 95.0, 195.0, 155.0, 195.0, 200.0, 110.0, 95.0, 220.0, 200.0, 250.0, 320.0, 30.0, 155.0, 130.0, 355.0, 170.0, 375.0, 135.0, 240.0, 165.0, 145.0, 160.0, 40.0, 75.0, 110.0, 120.0, 240.0, 160.0, 130.0, 75.0, 210.0, 80.0, 60.0, 115.0, 440.0, 135.0, 110.0, 70.0, 165.0, 40.0, 230.0, 200.0, 135.0, 110.0, 245.0, 110.0, 65.0, 105.0, 145.0, 210.0, 135.0, 195.0, 495.0, 245.0, 225.0, 135.0, 95.0, 125.0, 350.0, 160.0, 230.0, 200.0, 110.0, 155.0, 205.0, 380.0, 60.0, 190.0, 160.0, 110.0, 830.0, 475.0, 50.0, 710.0, 150.0, 200.0, 105.0, 115.0, 90.0, 105.0, 60.0, 325.0, 280.0, 10.0, 150.0, 165.0, 140.0, 465.0, 705.0, 140.0, 155.0, 120.0, 110.0, 395.0, 190.0, 215.0, 95.0, 160.0, 95.0, 305.0, 80.0, 405.0, 240.0, 80.0, 280.0, 125.0, 315.0, 60.0, 105.0, 190.0, 335.0, 145.0, 205.0, 335.0, 115.0, 290.0, 325.0, 290.0, 50.0, 140.0, 110.0, 170.0, 320.0, 155.0, 55.0, 75.0, 415.0, 290.0, 80.0, 75.0, 290.0, 150.0, 315.0, 260.0, 270.0, 90.0, 150.0, 40.0, 285.0, 150.0, 385.0, 255.0, 175.0, 360.0, 215.0, 220.0, 100.0, 130.0, 330.0, 245.0, 80.0, 320.0, 15.0, 230.0, 520.0, 195.0, 155.0, 240.0, 95.0, 530.0, 140.0, 250.0, 540.0, 350.0, 210.0, 130.0, 445.0, 85.0, 140.0, 35.0, 120.0, 315.0, 160.0, 335.0, 245.0, 230.0, 90.0, 470.0, 425.0, 265.0, 80.0, 230.0, 145.0, 90.0, 340.0, 275.0, 125.0, 145.0, 145.0, 80.0, 380.0, 240.0, 130.0, 205.0, 230.0, 145.0, 130.0, 85.0, 75.0, 400.0, 190.0, 235.0, 310.0, 250.0, 130.0, 100.0, 185.0, 95.0, 190.0, 200.0, 90.0, 345.0, 85.0, 45.0, 375.0, 305.0, 515.0, 655.0, 150.0, 120.0, 20.0, 410.0, 510.0, 295.0, 170.0, 175.0, 205.0, 170.0, 140.0, 310.0, 70.0, 55.0, 215.0, 355.0, 265.0, 75.0, 425.0, 165.0, 270.0, 80.0, 65.0, 385.0, 155.0, 65.0, 60.0, 175.0, 385.0, 135.0, 235.0, 110.0, 195.0, 110.0, 75.0, 225.0, 115.0, 105.0, 50.0, 495.0, 245.0, 220.0, 155.0, 235.0, 70.0, 135.0, 145.0, 180.0, 190.0, 115.0, 20.0, 65.0, 255.0, 55.0, 165.0, 290.0, 55.0, 130.0, 150.0, 100.0, 160.0, 150.0, 115.0, 65.0, 240.0, 90.0, 250.0, 45.0, 95.0, 175.0, 125.0, 100.0, 230.0, 50.0, 265.0, 195.0, 130.0, 455.0, 85.0, 130.0, 410.0, 295.0, 40.0, 75.0, 235.0, 320.0, 155.0, 435.0, 300.0, 220.0, 300.0, 15.0, 285.0, 210.0, 260.0, 270.0, 25.0, 75.0, 195.0, 100.0, 295.0, 50.0, 110.0, 185.0, 190.0, 255.0, 240.0, 425.0, 185.0, 215.0, 400.0, 495.0, 80.0, 335.0, 160.0, 205.0, 190.0, 215.0, 430.0, 285.0, 155.0, 90.0, 145.0, 490.0, 335.0, 150.0, 160.0, 130.0, 140.0, 455.0, 340.0, 190.0, 205.0, 175.0, 735.0, 175.0, 435.0, 235.0, 250.0, 450.0, 300.0, 130.0, 380.0, 150.0, 450.0, 300.0, 515.0, 135.0, 280.0, 180.0, 140.0, 530.0, 170.0, 270.0, 275.0, 140.0, 90.0, 295.0, 260.0, 130.0, 80.0, 255.0, 110.0, 70.0, 330.0, 25.0, 215.0, 80.0, 255.0, 125.0, 185.0, 235.0, 405.0, 445.0, 305.0, 130.0, 400.0, 310.0, 305.0, 75.0, 160.0, 190.0, 115.0, 205.0, 245.0, 490.0, 245.0, 235.0, 195.0, 160.0, 180.0, 215.0, 505.0, 115.0, 230.0, 575.0, 245.0, 110.0, 90.0, 270.0, 220.0, 280.0, 70.0, 200.0, 265.0, 170.0, 150.0, 155.0, 315.0, 195.0, 280.0, 510.0, 100.0, 425.0, 175.0, 130.0, 485.0, 40.0, 640.0, 280.0, 170.0, 260.0, 255.0, 120.0, 110.0, 200.0, 370.0, 180.0, 205.0, 180.0, 250.0, 125.0, 65.0, 205.0, 305.0, 65.0, 105.0, 85.0, 130.0, 155.0, 130.0, 80.0, 195.0, 185.0, 285.0, 110.0, 355.0, 235.0, 140.0, 450.0, 145.0, 70.0, 65.0, 55.0, 340.0, 185.0, 65.0, 75.0, 310.0, 130.0, 170.0, 250.0, 125.0, 275.0, 240.0, 345.0, 245.0, 190.0, 220.0, 85.0, 105.0, 180.0, 445.0, 420.0, 110.0, 290.0, 325.0, 75.0, 160.0, 110.0, 350.0, 185.0, 75.0, 115.0, 455.0, 210.0, 60.0, 215.0, 285.0, 35.0, 255.0, 155.0, 80.0, 115.0, 210.0, 205.0, 180.0, 85.0, 110.0, 340.0, 65.0, 215.0, 380.0, 340.0, 495.0, 75.0, 85.0, 45.0, 615.0, 50.0, 180.0, 315.0, 140.0, 245.0, 120.0, 90.0, 210.0, 210.0, 90.0, 80.0, 245.0, 310.0, 165.0, 240.0, 110.0, 75.0, 105.0, 105.0, 240.0, 255.0, 85.0, 110.0, 145.0, 195.0, 185.0, 110.0, 175.0, 585.0, 75.0, 115.0, 320.0, 180.0, 150.0, 230.0, 160.0, 295.0, 110.0, 110.0, 295.0, 110.0, 135.0, 285.0, 105.0, 190.0, 355.0, 355.0, 345.0, 335.0, 575.0, 155.0, 210.0, 180.0, 215.0, 240.0, 150.0, 165.0, 210.0, 255.0, 80.0, 75.0, 415.0, 530.0, 225.0, 110.0, 50.0, 75.0, 250.0, 80.0, 300.0, 325.0, 525.0, 380.0, 425.0, 155.0, 335.0, 185.0, 75.0, 105.0, 240.0, 260.0, 195.0, 560.0, 210.0, 105.0, 140.0, 75.0, 75.0, 75.0, 155.0, 690.0, 310.0, 555.0, 15.0, 110.0, 110.0, 410.0, 105.0, 70.0, 75.0, 155.0, 120.0, 135.0, 755.0, 110.0, 190.0, 180.0, 210.0, 190.0, 55.0, 160.0, 595.0, 155.0, 155.0, 240.0, 220.0, 135.0, 160.0, 110.0, 430.0, 115.0, 210.0, 110.0, 475.0, 25.0, 145.0, 275.0, 205.0, 320.0, 120.0, 690.0, 105.0, 135.0, 120.0, 295.0, 205.0, 440.0, 155.0, 370.0, 610.0, 155.0, 105.0, 135.0, 75.0, 325.0, 210.0, 20.0, 335.0, 165.0, 175.0, 60.0, 125.0, 400.0, 230.0, 275.0, 295.0, 95.0, 215.0, 450.0, 135.0, 55.0, 220.0, 35.0, 970.0, 285.0, 330.0, 210.0, 185.0, 145.0, 165.0, 210.0, 205.0, 120.0, 520.0, 380.0, 420.0, 215.0, 90.0, 375.0, 320.0, 55.0, 145.0, 215.0, 130.0, 110.0, 75.0, 135.0, 180.0, 35.0, 225.0, 110.0, 215.0, 350.0, 115.0, 210.0, 335.0, 180.0, 105.0, 155.0, 120.0, 110.0, 240.0, 440.0, 335.0, 125.0, 310.0, 260.0, 250.0, 65.0, 135.0, 435.0, 75.0, 160.0, 165.0, 355.0, 50.0, 230.0, 110.0, 155.0, 365.0, 150.0, 420.0, 165.0, 75.0, 225.0, 110.0, 300.0, 60.0, 290.0, 285.0, 55.0, 210.0, 150.0, 510.0, 195.0, 110.0, 180.0, 440.0, 195.0, 45.0, 450.0, 165.0, 245.0, 55.0, 325.0, 450.0, 430.0, 210.0, 160.0, 155.0, 75.0, 130.0, 20.0, 145.0, 185.0, 215.0, 195.0, 105.0, 60.0, 210.0, 350.0, 455.0, 95.0, 110.0, 75.0, 335.0, 155.0, 60.0, 160.0, 140.0, 90.0, 315.0, 55.0, 100.0, 210.0, 55.0, 240.0, 105.0, 45.0, 135.0, 110.0, 115.0, 265.0, 150.0, 415.0, 20.0, 55.0, 210.0, 305.0, 305.0, 160.0, 195.0, 70.0, 215.0, 35.0, 425.0, 35.0, 245.0, 225.0, 530.0, 80.0, 95.0, 355.0, 230.0, 30.0, 160.0, 570.0, 150.0, 220.0, 220.0, 190.0, 115.0, 50.0, 215.0, 130.0, 105.0, 185.0, 130.0, 105.0, 120.0, 135.0, 155.0, 105.0, 210.0, 215.0, 325.0, 230.0, 300.0, 100.0, 110.0, 15.0, 495.0, 150.0, 65.0, 160.0, 80.0, 10.0, 50.0, 235.0, 535.0, 550.0, 75.0, 45.0, 325.0, 40.0, 105.0, 65.0, 155.0, 210.0, 125.0, 230.0, 280.0, 320.0, 190.0, 55.0, 60.0, 550.0, 185.0, 85.0, 345.0, 55.0, 455.0, 345.0, 210.0, 20.0, 500.0, 120.0, 130.0, 125.0, 230.0, 105.0, 80.0, 200.0, 100.0, 140.0, 55.0, 75.0, 85.0, 75.0, 405.0, 310.0, 120.0, 90.0, 220.0, 180.0, 325.0, 30.0, 170.0, 295.0, 150.0, 170.0, 185.0, 185.0, 95.0, 180.0, 415.0, 185.0, 135.0, 145.0, 335.0, 125.0, 160.0, 155.0, 50.0, 160.0, 105.0, 175.0, 315.0]
scores_3 = [60.0, 150.0, 95.0, 135.0, 155.0, 90.0, 215.0, 30.0, 105.0, 105.0, 45.0, 210.0, 210.0, 50.0, 205.0, 110.0, 155.0, 80.0, 200.0, 110.0, 110.0, 95.0, 485.0, 135.0, 75.0, 85.0, 135.0, 155.0, 155.0, 120.0, 55.0, 105.0, 285.0, 130.0, 255.0, 380.0, 105.0, 120.0, 75.0, 155.0, 120.0, 70.0, 205.0, 120.0, 120.0, 170.0, 110.0, 220.0, 295.0, 160.0, 240.0, 155.0, 135.0, 35.0, 220.0, 395.0, 120.0, 520.0, 20.0, 155.0, 75.0, 60.0, 300.0, 160.0, 180.0, 95.0, 195.0, 155.0, 195.0, 200.0, 110.0, 95.0, 220.0, 200.0, 250.0, 320.0, 30.0, 155.0, 130.0, 355.0, 170.0, 375.0, 135.0, 240.0, 165.0, 145.0, 160.0, 40.0, 75.0, 110.0, 120.0, 240.0, 160.0, 130.0, 75.0, 210.0, 80.0, 60.0, 115.0, 440.0, 135.0, 110.0, 70.0, 165.0, 40.0, 230.0, 200.0, 135.0, 110.0, 245.0, 110.0, 65.0, 105.0, 145.0, 210.0, 135.0, 195.0, 495.0, 245.0, 225.0, 135.0, 95.0, 125.0, 350.0, 160.0, 230.0, 200.0, 110.0, 155.0, 205.0, 380.0, 60.0, 190.0, 160.0, 110.0, 830.0, 475.0, 50.0, 710.0, 150.0, 200.0, 105.0, 115.0, 90.0, 105.0, 60.0, 325.0, 280.0, 10.0, 150.0, 165.0, 140.0, 465.0, 705.0, 140.0, 155.0, 120.0, 110.0, 395.0, 190.0, 215.0, 95.0, 160.0, 95.0, 305.0, 80.0, 405.0, 240.0, 80.0, 280.0, 125.0, 315.0, 60.0, 105.0, 190.0, 335.0, 145.0, 205.0, 335.0, 115.0, 290.0, 325.0, 290.0, 50.0, 140.0, 110.0, 170.0, 320.0, 155.0, 55.0, 75.0, 415.0, 290.0, 80.0, 75.0, 290.0, 150.0, 315.0, 260.0, 270.0, 90.0, 150.0, 40.0, 285.0, 150.0, 385.0, 255.0, 175.0, 360.0, 215.0, 220.0, 100.0, 130.0, 330.0, 245.0, 80.0, 320.0, 15.0, 230.0, 520.0, 195.0, 155.0, 240.0, 95.0, 530.0, 140.0, 250.0, 540.0, 350.0, 210.0, 130.0, 445.0, 85.0, 140.0, 35.0, 120.0, 315.0, 160.0, 335.0, 245.0, 230.0, 90.0, 470.0, 425.0, 265.0, 80.0, 230.0, 145.0, 90.0, 340.0, 275.0, 125.0, 145.0, 145.0, 80.0, 380.0, 240.0, 130.0, 205.0, 230.0, 145.0, 130.0, 85.0, 75.0, 400.0, 190.0, 235.0, 310.0, 250.0, 130.0, 100.0, 185.0, 95.0, 190.0, 200.0, 90.0, 345.0, 85.0, 45.0, 375.0, 305.0, 515.0, 655.0, 150.0, 120.0, 20.0, 410.0, 510.0, 295.0, 170.0, 175.0, 205.0, 170.0, 140.0, 310.0, 70.0, 55.0, 215.0, 355.0, 265.0, 75.0, 425.0, 165.0, 270.0, 80.0, 65.0, 385.0, 155.0, 65.0, 60.0, 175.0, 385.0, 135.0, 235.0, 110.0, 195.0, 110.0, 75.0, 225.0, 115.0, 105.0, 50.0, 495.0, 245.0, 220.0, 155.0, 235.0, 70.0, 135.0, 145.0, 180.0, 190.0, 115.0, 20.0, 65.0, 255.0, 55.0, 165.0, 290.0, 55.0, 130.0, 150.0, 100.0, 160.0, 150.0, 115.0, 65.0, 240.0, 90.0, 250.0, 45.0, 95.0, 175.0, 125.0, 100.0, 230.0, 50.0, 265.0, 195.0, 130.0, 455.0, 85.0, 130.0, 410.0, 295.0, 40.0, 75.0, 235.0, 320.0, 155.0, 435.0, 300.0, 220.0, 300.0, 15.0, 285.0, 210.0, 260.0, 270.0, 25.0, 75.0, 195.0, 100.0, 295.0, 50.0, 110.0, 185.0, 190.0, 255.0, 240.0, 425.0, 185.0, 215.0, 400.0, 495.0, 80.0, 335.0, 160.0, 205.0, 190.0, 215.0, 430.0, 285.0, 155.0, 90.0, 145.0, 490.0, 335.0, 150.0, 160.0, 130.0, 140.0, 455.0, 340.0, 190.0, 205.0, 175.0, 735.0, 175.0, 435.0, 235.0, 250.0, 450.0, 300.0, 130.0, 380.0, 150.0, 450.0, 300.0, 515.0, 135.0, 280.0, 180.0, 140.0, 530.0, 170.0, 270.0, 275.0, 140.0, 90.0, 295.0, 260.0, 130.0, 80.0, 255.0, 110.0, 70.0, 330.0, 25.0, 215.0, 80.0, 255.0, 125.0, 185.0, 235.0, 405.0, 445.0, 305.0, 130.0, 400.0, 310.0, 305.0, 75.0, 160.0, 190.0, 115.0, 205.0, 245.0, 490.0, 245.0, 235.0, 195.0, 160.0, 180.0, 215.0, 505.0, 115.0, 230.0, 575.0, 245.0, 110.0, 90.0, 270.0, 220.0, 280.0, 70.0, 200.0, 265.0, 170.0, 150.0, 155.0, 315.0, 195.0, 280.0, 510.0, 100.0, 425.0, 175.0, 130.0, 485.0, 40.0, 640.0, 280.0, 170.0, 260.0, 255.0, 120.0, 110.0, 200.0, 370.0, 180.0, 205.0, 180.0, 250.0, 125.0, 65.0, 205.0, 305.0, 65.0, 105.0, 85.0, 130.0, 155.0, 130.0, 80.0, 195.0, 185.0, 285.0, 110.0, 355.0, 235.0, 140.0, 450.0, 145.0, 70.0, 65.0, 55.0, 340.0, 185.0, 65.0, 75.0, 310.0, 130.0, 170.0, 250.0, 125.0, 275.0, 240.0, 345.0, 245.0, 190.0, 220.0, 85.0, 105.0, 180.0, 445.0, 420.0, 110.0, 290.0, 325.0, 75.0, 160.0, 110.0, 350.0, 185.0, 75.0, 115.0, 455.0, 210.0, 60.0, 215.0, 285.0, 35.0, 255.0, 155.0, 80.0, 115.0, 210.0, 205.0, 180.0, 85.0, 110.0, 340.0, 65.0, 215.0, 380.0, 340.0, 495.0, 75.0, 85.0, 45.0, 615.0, 50.0, 180.0, 315.0, 140.0, 245.0, 120.0, 90.0, 210.0, 210.0, 90.0, 80.0, 245.0, 310.0, 165.0, 240.0, 110.0, 75.0, 105.0, 105.0, 240.0, 255.0, 85.0, 110.0, 145.0, 195.0, 185.0, 110.0, 175.0, 585.0, 75.0, 115.0, 320.0, 180.0, 150.0, 230.0, 160.0, 295.0, 110.0, 110.0, 295.0, 110.0, 135.0, 285.0, 105.0, 190.0, 355.0, 355.0, 345.0, 335.0, 575.0, 155.0, 210.0, 180.0, 215.0, 240.0, 150.0, 165.0, 210.0, 255.0, 80.0, 75.0, 415.0, 530.0, 225.0, 110.0, 50.0, 75.0, 250.0, 80.0, 300.0, 325.0, 525.0, 380.0, 425.0, 155.0, 335.0, 185.0, 75.0, 105.0, 240.0, 260.0, 195.0, 560.0, 210.0, 105.0, 140.0, 75.0, 75.0, 75.0, 155.0, 690.0, 310.0, 555.0, 15.0, 110.0, 110.0, 410.0, 105.0, 70.0, 75.0, 155.0, 120.0, 135.0, 755.0, 110.0, 190.0, 180.0, 210.0, 190.0, 55.0, 160.0, 595.0, 155.0, 155.0, 240.0, 220.0, 135.0, 160.0, 110.0, 430.0, 115.0, 210.0, 110.0, 475.0, 25.0, 145.0, 275.0, 205.0, 320.0, 120.0, 690.0, 105.0, 135.0, 120.0, 295.0, 205.0, 440.0, 155.0, 370.0, 610.0, 155.0, 105.0, 135.0, 75.0, 325.0, 210.0, 20.0, 335.0, 165.0, 175.0, 60.0, 125.0, 400.0, 230.0, 275.0, 295.0, 95.0, 215.0, 450.0, 135.0, 55.0, 220.0, 35.0, 970.0, 285.0, 330.0, 210.0, 185.0, 145.0, 165.0, 210.0, 205.0, 120.0, 520.0, 380.0, 420.0, 215.0, 90.0, 375.0, 320.0, 55.0, 145.0, 215.0, 130.0, 110.0, 75.0, 135.0, 180.0, 35.0, 225.0, 110.0, 215.0, 350.0, 115.0, 210.0, 335.0, 180.0, 105.0, 155.0, 120.0, 110.0, 240.0, 440.0, 335.0, 125.0, 310.0, 260.0, 250.0, 65.0, 135.0, 435.0, 75.0, 160.0, 165.0, 355.0, 50.0, 230.0, 110.0, 155.0, 365.0, 150.0, 420.0, 165.0, 75.0, 225.0, 110.0, 300.0, 60.0, 290.0, 285.0, 55.0, 210.0, 150.0, 510.0, 195.0, 110.0, 180.0, 440.0, 195.0, 45.0, 450.0, 165.0, 245.0, 55.0, 325.0, 450.0, 430.0, 210.0, 160.0, 155.0, 75.0, 130.0, 20.0, 145.0, 185.0, 215.0, 195.0, 105.0, 60.0, 210.0, 350.0, 455.0, 95.0, 110.0, 75.0, 335.0, 155.0, 60.0, 160.0, 140.0, 90.0, 315.0, 55.0, 100.0, 210.0, 55.0, 240.0, 105.0, 45.0, 135.0, 110.0, 115.0, 265.0, 150.0, 415.0, 20.0, 55.0, 210.0, 305.0, 305.0, 160.0, 195.0, 70.0, 215.0, 35.0, 425.0, 35.0, 245.0, 225.0, 530.0, 80.0, 95.0, 355.0, 230.0, 30.0, 160.0, 570.0, 150.0, 220.0, 220.0, 190.0, 115.0, 50.0, 215.0, 130.0, 105.0, 185.0, 130.0, 105.0, 120.0, 135.0, 155.0, 105.0, 210.0, 215.0, 325.0, 230.0, 300.0, 100.0, 110.0, 15.0, 495.0, 150.0, 65.0, 160.0, 80.0, 10.0, 50.0, 235.0, 535.0, 550.0, 75.0, 45.0, 325.0, 40.0, 105.0, 65.0, 155.0, 210.0, 125.0, 230.0, 280.0, 320.0, 190.0, 55.0, 60.0, 550.0, 185.0, 85.0, 345.0, 55.0, 455.0, 345.0, 210.0, 20.0, 500.0, 120.0, 130.0, 125.0, 230.0, 105.0, 80.0, 200.0, 100.0, 140.0, 55.0, 75.0, 85.0, 75.0, 405.0, 310.0, 120.0, 90.0, 220.0, 180.0, 325.0, 30.0, 170.0, 295.0, 150.0, 170.0, 185.0, 185.0, 95.0, 180.0, 415.0, 185.0, 135.0, 145.0, 335.0, 125.0, 160.0, 155.0, 50.0, 160.0, 105.0, 175.0, 315.0, 60.0, 380.0, 125.0, 155.0, 135.0, 135.0, 260.0, 215.0, 210.0, 215.0, 105.0, 410.0, 125.0, 75.0, 185.0, 120.0, 20.0, 210.0, 355.0, 65.0, 105.0, 110.0, 170.0, 100.0, 155.0, 140.0, 225.0, 35.0, 45.0, 210.0, 275.0, 350.0, 135.0, 490.0, 65.0, 315.0, 250.0, 80.0, 365.0, 115.0, 255.0, 215.0, 240.0, 405.0, 25.0, 105.0, 260.0, 85.0, 135.0, 295.0, 255.0, 415.0, 125.0, 155.0, 5.0, 110.0, 185.0, 125.0, 165.0, 155.0, 120.0, 195.0, 330.0, 410.0, 215.0, 185.0, 105.0, 205.0, 240.0, 130.0, 100.0, 165.0, 50.0, 110.0, 105.0, 135.0, 585.0, 140.0, 135.0, 590.0, 135.0, 360.0, 395.0, 35.0, 240.0, 50.0, 175.0, 195.0, 110.0, 145.0, 140.0, 365.0, 770.0, 255.0, 135.0, 85.0, 55.0, 830.0, 470.0, 250.0, 175.0, 170.0, 120.0, 80.0, 210.0, 425.0, 110.0, 110.0, 320.0, 105.0, 165.0, 435.0, 50.0, 385.0, 190.0, 135.0, 105.0, 275.0, 120.0, 105.0, 210.0, 120.0, 65.0, 400.0, 135.0, 105.0, 55.0, 125.0, 125.0, 95.0, 55.0, 190.0, 115.0, 120.0, 110.0, 90.0, 125.0, 210.0, 50.0, 150.0, 745.0, 215.0, 60.0, 265.0, 200.0, 280.0, 210.0, 75.0, 170.0, 55.0, 480.0, 135.0, 60.0, 125.0, 455.0, 190.0, 250.0, 155.0, 480.0, 235.0, 140.0, 155.0, 135.0, 395.0, 155.0, 165.0, 140.0, 180.0, 75.0, 165.0, 80.0, 110.0, 155.0, 190.0, 105.0, 5.0, 75.0, 105.0, 215.0, 80.0, 125.0, 75.0, 90.0, 55.0, 130.0, 120.0, 275.0, 90.0, 45.0, 600.0, 210.0, 110.0, 160.0, 275.0, 125.0, 120.0, 150.0, 210.0, 135.0, 195.0, 215.0, 135.0, 130.0, 105.0, 385.0, 110.0, 95.0, 155.0, 125.0, 185.0, 340.0, 110.0, 120.0, 275.0, 135.0, 395.0, 330.0, 80.0, 340.0, 165.0, 210.0, 340.0, 345.0, 105.0, 165.0, 55.0, 780.0, 225.0, 140.0, 345.0, 140.0, 120.0, 415.0, 395.0, 105.0, 160.0, 270.0, 135.0, 180.0, 80.0, 75.0, 105.0, 405.0, 105.0, 435.0, 380.0, 75.0, 75.0, 125.0, 330.0, 510.0, 340.0, 235.0, 50.0, 165.0, 215.0, 140.0, 105.0, 205.0, 40.0, 95.0, 80.0, 105.0, 185.0, 425.0, 445.0, 250.0, 80.0, 155.0, 65.0, 30.0, 325.0, 235.0, 110.0, 145.0, 180.0, 345.0, 50.0, 405.0, 605.0, 220.0, 135.0, 105.0, 130.0, 480.0, 135.0, 225.0, 225.0, 300.0, 240.0, 220.0, 45.0, 140.0, 230.0, 105.0, 235.0, 190.0, 360.0, 185.0, 115.0, 285.0, 485.0, 120.0, 165.0, 75.0, 85.0, 120.0, 305.0, 290.0, 285.0, 410.0, 120.0, 280.0, 105.0, 105.0, 435.0, 345.0, 435.0, 245.0, 280.0, 175.0, 55.0, 240.0, 160.0, 400.0, 300.0, 80.0, 125.0, 10.0, 390.0, 255.0, 90.0, 105.0, 365.0, 170.0, 210.0, 225.0, 45.0, 135.0, 200.0, 50.0, 295.0, 40.0, 155.0, 185.0, 105.0, 550.0, 245.0, 130.0, 295.0, 325.0, 310.0, 420.0, 25.0, 125.0, 100.0, 170.0, 235.0, 135.0, 445.0, 125.0, 560.0, 105.0, 220.0, 370.0, 265.0, 130.0, 100.0, 175.0, 235.0, 410.0, 125.0, 410.0, 455.0, 275.0, 330.0, 355.0, 360.0, 410.0, 170.0, 205.0, 95.0, 385.0, 50.0, 255.0, 55.0, 205.0, 130.0, 75.0, 110.0, 80.0, 135.0, 210.0, 385.0, 110.0, 205.0, 105.0, 345.0, 215.0, 335.0, 200.0, 305.0, 145.0, 140.0, 150.0, 285.0, 165.0, 260.0, 50.0, 45.0, 55.0, 215.0, 220.0, 140.0, 610.0, 355.0, 595.0, 465.0, 140.0, 175.0, 75.0, 35.0, 110.0, 215.0, 120.0, 185.0, 555.0, 275.0, 395.0, 255.0, 195.0, 140.0, 100.0, 625.0, 190.0, 380.0, 295.0, 230.0, 370.0, 110.0, 260.0, 205.0, 110.0, 60.0, 355.0, 360.0, 265.0, 435.0, 340.0, 185.0, 495.0, 240.0, 380.0, 200.0, 65.0, 320.0, 180.0, 280.0, 255.0, 150.0, 180.0, 520.0, 70.0, 240.0, 230.0, 390.0, 380.0, 105.0, 220.0, 245.0, 115.0, 355.0, 390.0, 135.0, 155.0, 20.0, 100.0, 215.0, 230.0, 410.0, 30.0, 260.0, 185.0, 135.0, 240.0, 70.0, 125.0, 185.0, 225.0, 770.0, 405.0, 585.0, 535.0, 295.0, 175.0, 180.0, 240.0, 260.0, 85.0, 180.0, 140.0, 240.0, 20.0, 125.0, 60.0, 260.0, 245.0, 150.0, 270.0, 275.0, 225.0, 120.0, 395.0, 185.0, 195.0, 205.0, 270.0, 75.0, 160.0, 160.0, 95.0, 180.0, 210.0, 420.0, 185.0, 150.0, 295.0, 440.0, 305.0, 325.0, 110.0, 100.0, 335.0, 225.0, 65.0, 170.0, 55.0, 95.0, 95.0, 105.0, 220.0, 350.0, 40.0, 140.0, 205.0, 240.0, 370.0, 290.0, 235.0, 25.0, 190.0, 280.0, 190.0, 560.0, 95.0, 235.0, 315.0, 410.0, 300.0, 115.0, 140.0, 130.0, 170.0, 155.0, 210.0, 345.0, 185.0, 660.0, 200.0, 170.0, 515.0, 190.0, 260.0, 225.0, 230.0, 535.0, 100.0, 235.0, 200.0, 290.0, 245.0, 180.0, 120.0, 245.0, 110.0, 50.0, 235.0, 445.0, 185.0, 275.0, 135.0, 155.0, 195.0, 455.0, 145.0, 110.0, 175.0, 260.0, 145.0, 265.0, 160.0, 115.0, 135.0, 220.0, 155.0, 125.0, 215.0, 250.0, 155.0, 245.0, 670.0, 175.0, 75.0, 105.0, 205.0, 210.0, 260.0, 120.0, 215.0, 60.0, 115.0, 250.0, 130.0, 230.0, 45.0, 450.0, 75.0, 135.0, 210.0, 105.0, 230.0, 165.0, 75.0, 75.0, 110.0, 345.0, 285.0, 175.0, 145.0, 75.0, 175.0, 80.0, 115.0, 215.0, 310.0, 345.0, 320.0, 125.0, 75.0, 125.0, 225.0, 50.0, 130.0, 505.0, 105.0, 25.0, 160.0, 200.0, 260.0, 105.0, 270.0, 345.0, 80.0, 50.0, 110.0, 105.0, 60.0, 160.0, 195.0, 35.0, 130.0, 310.0, 55.0, 200.0, 255.0, 135.0, 105.0, 75.0, 110.0, 120.0, 235.0, 185.0, 205.0, 105.0, 115.0, 170.0, 120.0, 135.0, 205.0, 85.0, 50.0, 250.0, 265.0, 155.0, 110.0, 465.0, 315.0, 170.0, 110.0, 215.0, 140.0, 380.0, 410.0, 75.0, 60.0, 355.0, 205.0, 210.0, 445.0, 125.0, 210.0, 270.0, 210.0, 165.0, 250.0, 125.0, 425.0, 145.0, 155.0, 105.0, 60.0, 55.0, 210.0, 580.0, 180.0, 75.0, 430.0, 75.0, 220.0, 75.0, 290.0, 105.0, 270.0, 80.0, 75.0, 55.0, 350.0, 80.0, 50.0, 125.0, 120.0, 135.0, 260.0, 125.0, 375.0, 220.0, 275.0, 110.0, 75.0, 105.0, 415.0, 175.0, 190.0, 285.0, 105.0, 210.0, 120.0, 95.0, 90.0, 110.0, 300.0, 230.0, 230.0, 100.0, 425.0, 420.0, 340.0, 340.0, 75.0, 105.0, 415.0, 160.0, 465.0, 395.0, 185.0, 65.0, 155.0, 110.0, 150.0, 105.0, 250.0, 75.0, 105.0, 215.0, 215.0, 150.0, 105.0, 65.0, 90.0, 105.0, 175.0, 410.0, 255.0, 105.0, 270.0, 75.0, 210.0, 75.0, 210.0, 45.0, 270.0, 470.0, 155.0, 75.0, 205.0, 345.0, 105.0, 275.0, 180.0, 80.0, 75.0, 360.0, 235.0, 105.0, 385.0, 35.0, 210.0, 75.0, 255.0, 150.0, 340.0, 55.0, 185.0, 250.0, 210.0, 75.0, 90.0, 215.0, 190.0, 105.0, 315.0, 190.0, 75.0, 380.0, 170.0, 410.0, 110.0, 410.0, 105.0, 115.0, 255.0, 100.0, 215.0, 110.0, 55.0, 105.0, 260.0, 315.0, 355.0, 150.0, 30.0, 165.0, 495.0, 445.0, 135.0, 75.0, 60.0, 125.0, 125.0, 340.0, 620.0, 240.0, 340.0, 375.0, 155.0, 265.0, 430.0, 180.0, 80.0, 75.0, 545.0, 255.0, 75.0, 135.0, 155.0, 210.0, 110.0, 295.0, 280.0, 275.0, 130.0, 45.0, 80.0, 130.0, 75.0, 420.0, 405.0, 85.0, 145.0, 155.0, 125.0, 75.0, 520.0, 435.0, 300.0, 210.0, 185.0, 360.0, 120.0, 180.0, 265.0, 155.0, 265.0, 55.0, 115.0, 455.0, 155.0, 210.0, 110.0, 120.0, 105.0, 230.0, 225.0, 160.0, 350.0, 280.0, 195.0, 225.0, 95.0, 155.0, 110.0, 110.0, 140.0, 370.0, 95.0, 265.0, 365.0, 110.0, 190.0, 260.0, 130.0, 110.0, 215.0, 105.0, 265.0, 390.0, 85.0, 220.0, 575.0, 90.0, 210.0, 110.0, 140.0, 210.0, 55.0, 285.0, 135.0, 155.0, 250.0, 275.0, 435.0, 355.0, 240.0, 255.0, 365.0, 100.0, 305.0, 185.0, 100.0, 250.0, 450.0, 495.0, 505.0, 190.0, 260.0, 300.0, 180.0, 140.0, 120.0, 310.0, 255.0, 155.0, 210.0, 220.0, 415.0, 280.0, 305.0, 210.0, 280.0, 110.0, 250.0, 200.0, 120.0, 175.0, 205.0, 325.0, 120.0, 460.0, 235.0, 115.0, 175.0, 245.0, 95.0, 195.0, 415.0, 435.0, 140.0, 85.0, 155.0, 145.0]
scores_4 = [210.0, 90.0, 120.0, 80.0, 160.0, 65.0, 105.0, 135.0, 210.0, 320.0, 135.0, 210.0, 305.0, 110.0, 110.0, 65.0, 215.0, 20.0, 135.0, 200.0, 140.0, 105.0, 345.0, 170.0, 180.0, 120.0, 215.0, 20.0, 185.0, 90.0, 165.0, 105.0, 210.0, 45.0, 245.0, 370.0, 110.0, 85.0, 60.0, 110.0, 65.0, 60.0, 30.0, 285.0, 155.0, 115.0, 215.0, 90.0, 90.0, 125.0, 210.0, 160.0, 320.0, 110.0, 85.0, 105.0, 140.0, 125.0, 350.0, 335.0, 165.0, 80.0, 405.0, 50.0, 35.0, 220.0, 55.0, 50.0, 30.0, 335.0, 285.0, 65.0, 125.0, 55.0, 90.0, 410.0, 335.0, 170.0, 60.0, 155.0, 235.0, 190.0, 525.0, 155.0, 120.0, 120.0, 160.0, 5.0, 170.0, 170.0, 125.0, 80.0, 330.0, 250.0, 300.0, 300.0, 240.0, 185.0, 185.0, 455.0, 175.0, 330.0, 185.0, 145.0, 180.0, 150.0, 175.0, 130.0, 140.0, 590.0, 185.0, 150.0, 255.0, 440.0, 225.0, 75.0, 45.0, 280.0, 580.0, 75.0, 70.0, 90.0, 220.0, 110.0, 140.0, 180.0, 520.0, 110.0, 100.0, 215.0, 125.0, 340.0, 75.0, 155.0, 430.0, 190.0, 225.0, 190.0, 20.0, 10.0, 75.0, 50.0, 225.0, 290.0, 45.0, 45.0, 170.0, 120.0, 315.0, 90.0, 30.0, 125.0, 155.0, 360.0, 60.0, 235.0, 105.0, 305.0, 260.0, 195.0, 125.0, 255.0, 180.0, 220.0, 105.0, 75.0, 575.0, 235.0, 225.0, 165.0, 20.0, 65.0, 50.0, 105.0, 60.0, 335.0, 135.0, 120.0, 180.0, 325.0, 160.0, 300.0, 190.0, 125.0, 205.0, 555.0, 45.0, 120.0, 185.0, 165.0, 500.0, 160.0, 105.0, 235.0, 105.0, 30.0, 305.0, 100.0, 310.0, 350.0, 105.0, 125.0, 90.0, 180.0, 50.0, 110.0, 105.0, 490.0, 220.0, 300.0, 505.0, 60.0, 375.0, 105.0, 175.0, 245.0, 110.0, 260.0, 70.0, 310.0, 140.0, 110.0, 285.0, 210.0, 340.0, 590.0, 50.0, 390.0, 210.0, 225.0, 30.0, 320.0, 445.0, 530.0, 60.0, 125.0, 55.0, 175.0, 460.0, 215.0, 110.0, 115.0, 140.0, 70.0, 120.0, 80.0, 55.0, 190.0, 185.0, 700.0, 50.0, 155.0, 185.0, 100.0, 195.0, 155.0, 260.0, 210.0, 60.0, 95.0, 160.0, 75.0, 745.0, 155.0, 110.0, 185.0, 35.0, 135.0, 230.0, 380.0, 75.0, 135.0, 475.0, 455.0, 210.0, 300.0, 180.0, 180.0, 185.0, 185.0, 50.0, 220.0, 115.0, 185.0, 245.0, 95.0, 180.0, 380.0, 210.0, 80.0, 270.0, 110.0, 250.0, 370.0, 50.0, 375.0, 135.0, 300.0, 75.0, 75.0, 200.0, 50.0, 230.0, 180.0, 240.0, 130.0, 30.0, 105.0, 125.0, 190.0, 520.0, 360.0, 270.0, 110.0, 345.0, 105.0, 80.0, 180.0, 85.0, 240.0, 105.0, 80.0, 140.0, 110.0, 80.0, 115.0, 80.0, 115.0, 165.0, 115.0, 245.0, 200.0, 420.0, 390.0, 210.0, 350.0, 75.0, 140.0, 120.0, 105.0, 90.0, 135.0, 240.0, 250.0, 120.0, 20.0, 190.0, 610.0, 50.0, 130.0, 25.0, 210.0, 110.0, 360.0, 240.0, 130.0, 165.0, 50.0, 205.0, 35.0, 115.0, 705.0, 420.0, 210.0, 135.0, 110.0, 155.0, 55.0, 240.0, 325.0, 380.0, 40.0, 140.0, 395.0, 165.0, 85.0, 475.0, 160.0, 160.0, 240.0, 160.0, 280.0, 130.0, 255.0, 155.0, 170.0, 105.0, 335.0, 365.0, 105.0, 105.0, 380.0, 280.0, 215.0, 115.0, 80.0, 180.0, 210.0, 730.0, 210.0, 300.0, 480.0, 55.0, 130.0, 210.0, 105.0, 300.0, 25.0, 155.0, 290.0, 215.0, 195.0, 110.0, 145.0, 205.0, 30.0, 565.0, 470.0, 230.0, 295.0, 140.0, 125.0, 105.0, 190.0, 75.0, 105.0, 80.0, 400.0, 160.0, 35.0, 250.0, 270.0, 195.0, 195.0, 440.0, 105.0, 75.0, 420.0, 155.0, 120.0, 265.0, 105.0, 105.0, 480.0, 155.0, 160.0, 480.0, 330.0, 45.0, 300.0, 625.0, 105.0, 180.0, 85.0, 495.0, 220.0, 165.0, 190.0, 100.0, 80.0, 80.0, 245.0, 115.0, 285.0, 145.0, 80.0, 80.0, 685.0, 325.0, 180.0, 265.0, 580.0, 300.0, 230.0, 315.0, 250.0, 365.0, 340.0, 195.0, 215.0, 470.0, 530.0, 75.0, 135.0, 165.0, 335.0, 145.0, 185.0, 15.0, 110.0, 180.0, 255.0, 425.0, 215.0, 115.0, 245.0, 120.0, 180.0, 360.0, 340.0, 200.0, 260.0, 530.0, 215.0, 245.0, 125.0, 410.0, 220.0, 225.0, 100.0, 275.0, 170.0, 125.0, 135.0, 170.0, 340.0, 490.0, 415.0, 250.0, 205.0, 100.0, 355.0, 120.0, 275.0, 180.0, 260.0, 165.0, 205.0, 300.0, 420.0, 200.0, 295.0, 230.0, 260.0, 75.0, 105.0, 275.0, 155.0, 240.0, 145.0, 65.0, 80.0, 75.0, 110.0, 190.0, 325.0, 355.0, 230.0, 120.0, 250.0, 265.0, 150.0, 110.0, 85.0, 145.0, 290.0, 260.0, 180.0, 190.0, 275.0, 380.0, 95.0, 225.0, 165.0, 140.0, 150.0, 165.0, 130.0, 215.0, 55.0, 725.0, 365.0, 190.0, 110.0, 55.0, 155.0, 160.0, 120.0, 295.0, 105.0, 150.0, 340.0, 195.0, 290.0, 60.0, 40.0, 90.0, 135.0, 90.0, 300.0, 165.0, 115.0, 110.0, 215.0, 415.0, 315.0, 135.0, 105.0, 255.0, 215.0, 185.0, 120.0, 395.0, 565.0, 475.0, 440.0, 155.0, 225.0, 85.0, 95.0, 240.0, 195.0, 140.0, 255.0, 540.0, 110.0, 230.0, 725.0, 245.0, 205.0, 245.0, 590.0, 145.0, 210.0, 170.0, 470.0, 150.0, 220.0, 310.0, 170.0, 160.0, 160.0, 700.0, 225.0, 335.0, 130.0, 225.0, 285.0, 360.0, 185.0, 130.0, 140.0, 490.0, 260.0, 205.0, 205.0, 140.0, 155.0, 225.0, 75.0, 195.0, 195.0, 230.0, 180.0, 185.0, 260.0, 335.0, 60.0, 265.0, 240.0, 165.0, 445.0, 215.0, 205.0, 475.0, 305.0, 135.0, 220.0, 170.0, 340.0, 55.0, 130.0, 110.0, 95.0, 80.0, 255.0, 95.0, 115.0, 565.0, 200.0, 165.0, 125.0, 55.0, 110.0, 490.0, 110.0, 320.0, 235.0, 130.0, 135.0, 180.0, 90.0, 280.0, 85.0, 220.0, 130.0, 530.0, 210.0, 50.0, 455.0, 300.0, 65.0, 130.0, 40.0, 150.0, 190.0, 730.0, 260.0, 400.0, 295.0, 210.0, 160.0, 205.0, 130.0, 235.0, 255.0, 165.0, 315.0, 125.0, 85.0, 200.0, 210.0, 335.0, 215.0, 105.0, 185.0, 110.0, 250.0, 515.0, 140.0, 255.0, 110.0, 155.0, 115.0, 195.0, 290.0, 135.0, 135.0, 105.0, 405.0, 120.0, 330.0, 45.0, 210.0, 140.0, 225.0, 140.0, 375.0, 400.0, 105.0, 110.0, 195.0, 110.0, 85.0, 80.0, 565.0, 205.0, 480.0, 55.0, 110.0, 140.0, 365.0, 110.0, 110.0, 285.0, 385.0, 155.0, 155.0, 105.0, 255.0, 205.0, 205.0, 280.0, 295.0, 245.0, 300.0, 135.0, 180.0, 120.0, 445.0, 15.0, 255.0, 135.0, 105.0, 190.0, 585.0, 305.0, 135.0, 105.0, 25.0, 270.0, 110.0, 155.0, 90.0, 270.0, 190.0, 210.0, 360.0, 160.0, 70.0, 150.0, 110.0, 150.0, 150.0, 265.0, 110.0, 250.0, 210.0, 15.0, 105.0, 335.0, 375.0, 50.0, 195.0, 85.0, 110.0, 375.0, 215.0, 200.0, 155.0, 110.0, 210.0, 180.0, 155.0, 155.0, 110.0, 80.0, 115.0, 285.0, 110.0, 285.0, 30.0, 185.0, 45.0, 40.0, 240.0, 120.0, 145.0, 95.0, 110.0, 355.0, 130.0, 100.0, 165.0, 190.0, 105.0, 55.0, 240.0, 185.0, 135.0, 190.0, 100.0, 185.0, 105.0, 310.0, 440.0, 330.0, 220.0, 205.0, 180.0, 320.0, 280.0, 45.0, 475.0, 160.0, 150.0, 345.0, 245.0, 85.0, 100.0, 140.0, 330.0, 70.0, 275.0, 165.0, 450.0, 85.0, 275.0, 210.0, 205.0, 20.0, 290.0, 200.0, 205.0, 130.0, 125.0, 50.0, 180.0, 185.0, 155.0, 265.0, 100.0, 190.0, 145.0, 135.0, 20.0, 50.0, 125.0, 415.0, 95.0, 90.0, 110.0, 160.0, 190.0, 250.0, 125.0, 80.0, 185.0, 155.0, 230.0, 585.0, 40.0, 130.0, 210.0, 185.0, 75.0, 80.0, 150.0, 250.0, 105.0, 195.0, 150.0, 320.0, 295.0, 70.0, 215.0, 230.0, 130.0, 265.0, 145.0, 85.0, 160.0, 140.0, 305.0, 330.0, 140.0, 185.0, 120.0, 185.0, 140.0, 195.0, 185.0, 90.0, 135.0, 100.0, 190.0, 220.0, 270.0, 230.0, 145.0, 140.0, 145.0, 170.0, 270.0, 315.0, 185.0, 205.0, 85.0, 30.0, 120.0, 150.0, 385.0, 195.0, 250.0, 25.0, 265.0, 245.0, 220.0, 250.0, 125.0, 45.0, 225.0, 110.0, 90.0, 210.0, 180.0, 285.0, 300.0, 135.0, 110.0, 260.0, 90.0, 610.0, 115.0, 150.0, 315.0, 245.0, 265.0, 195.0, 305.0, 95.0, 230.0, 165.0, 200.0, 95.0, 100.0, 180.0, 245.0, 165.0, 415.0]
SCORES = scores+scores_3 + scores_4
print(len(SCORES))
Moyen_score = [np.mean(SCORES[i:(i+1)*10]) for i in range(int(np.floor(len(SCORES)/10))) for a in range(10)]
# -
fig = plt.figure()
ax = fig.add_subplot(111)
#plt.plot(np.arange(len(scores)), scores)
plt.plot(np.arange(len(SCORES)),Moyen_score)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
| 90.631579 | 13,645 |
a61a0c541a9e0adfe1afe7ea6da0272f7190dd01
|
py
|
python
|
sequential_tracing/PostAnalysis/.ipynb_checkpoints/Part1_chr21_DomainAnalysis-checkpoint.ipynb
|
ZhuangLab/Chromatin_Analysis_2020_cell
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # This a jupyter notebook guide on domain analysis
#
# by Pu Zheng and Bogdan Bintu
#
# 2020.06.06
#
#
# ## Import packages
# +
# imports
import sys, os, glob, time, copy
import numpy as np
import scipy
import pickle
sys.path.append(os.path.abspath(r"..\."))
import source as ia
from scipy.signal import find_peaks
from scipy.spatial.distance import cdist,pdist,squareform
print(os.getpid())
# -
# ## Import plotting
# Required plotting setting
import matplotlib
matplotlib.rcParams['pdf.fonttype'] = 42
import matplotlib.pyplot as plt
plt.rc('font', family='serif')
plt.rc('font', serif='Arial')
_font_size = 7.5
# Required plotting parameters
from source.figure_tools import _dpi,_single_col_width,_double_col_width,_single_row_height,_ref_bar_length, _ticklabel_size,_ticklabel_width,_font_size
# figure folder
parent_figure_folder = r'\\10.245.74.158\Chromatin_NAS_4\Chromatin_Share\final_figures'
figure_folder = os.path.join(parent_figure_folder, 'Chr21_domain_figures')
print(figure_folder)
if not os.path.exists(figure_folder):
os.makedirs(figure_folder)
print("generating this folder")
# # 0. Load data
data_folder = r'E:\Users\puzheng\Dropbox\2020 Chromatin Imaging Manuscript\Revision\DataForReviewers'
data_folder = r'C:\Users\Bogdan\Dropbox\2020 Chromatin Imaging Manuscript\Revision\DataForReviewers'
rep1_filename = os.path.join(data_folder, 'chromosome21.tsv')
rep2_filename = os.path.join(data_folder, 'chromosome21-cell_cycle.tsv')
# ## 0.1 load chr21 (replicate 1 - without cell cycle)
# load from file and extract info
import csv
rep1_info_dict = {}
with open(rep1_filename, 'r') as _handle:
_reader = csv.reader(_handle, delimiter='\t', quotechar='|')
_headers = next(_reader)
print(_headers)
# create keys for each header
for _h in _headers:
rep1_info_dict[_h] = []
# loop through content
for _contents in _reader:
for _h, _info in zip(_headers,_contents):
rep1_info_dict[_h].append(_info)
# +
from tqdm import tqdm_notebook as tqdm
# clean up info
data_rep1 = {'params':{}}
# clean up genomic coordiantes
region_names = np.unique(rep1_info_dict['Genomic coordinate'])
region_starts = np.array([int(_n.split(':')[1].split('-')[0]) for _n in region_names])
region_ends = np.array([int(_n.split(':')[1].split('-')[1]) for _n in region_names])[np.argsort(region_starts)]
region_starts = np.sort(region_starts)
mid_positions = ((region_starts + region_ends)/2).astype(np.int)
mid_positions_Mb = np.round(mid_positions / 1e6, 2)
# clean up chrom copy number
chr_nums = np.array([int(_info) for _info in rep1_info_dict['Chromosome copy number']])
chr_ids, region_cts = np.unique(chr_nums, return_counts=True)
dna_zxys_list = [[[] for _start in region_starts] for _id in chr_ids]
# clean up zxy
for _z,_x,_y,_reg_info, _cid in tqdm(zip(rep1_info_dict['Z(nm)'],rep1_info_dict['X(nm)'],\
rep1_info_dict['Y(nm)'],rep1_info_dict['Genomic coordinate'],\
rep1_info_dict['Chromosome copy number'])):
# get chromosome inds
_cid = int(_cid)
_cind = np.where(chr_ids == _cid)[0][0]
# get region indices
_start = int(_reg_info.split(':')[1].split('-')[0])
_rind = np.where(region_starts==_start)[0][0]
dna_zxys_list[_cind][_rind] = np.array([float(_z),float(_x), float(_y)])
# merge together
dna_zxys_list = np.array(dna_zxys_list)
data_rep1['chrom_ids'] = chr_ids
data_rep1['mid_position_Mb'] = mid_positions_Mb
data_rep1['dna_zxys'] = dna_zxys_list
# clean up tss and transcription
if 'Gene names' in rep1_info_dict:
import re
# first extract number of genes
gene_names = []
for _gene_info, _trans_info, _tss_coord in zip(rep1_info_dict['Gene names'],
rep1_info_dict['Transcription'],
rep1_info_dict['TSS ZXY(nm)']):
if _gene_info != '':
# split by semicolon
_genes = _gene_info.split(';')[:-1]
for _gene in _genes:
if _gene not in gene_names:
gene_names.append(_gene)
print(f"{len(gene_names)} genes exist in this dataset.")
# initialize gene and transcription
tss_zxys_list = [[[] for _gene in gene_names] for _id in chr_ids]
transcription_profiles = [[[] for _gene in gene_names] for _id in chr_ids]
# loop through to get info
for _cid, _gene_info, _trans_info, _tss_locations in tqdm(zip(rep1_info_dict['Chromosome copy number'],
rep1_info_dict['Gene names'],
rep1_info_dict['Transcription'],
rep1_info_dict['TSS ZXY(nm)'])):
# get chromosome inds
_cid = int(_cid)
_cind = np.where(chr_ids == _cid)[0][0]
# process if there are genes in this region:
if _gene_info != '':
# split by semicolon
_genes = _gene_info.split(';')[:-1]
_transcribes = _trans_info.split(';')[:-1]
_tss_zxys = _tss_locations.split(';')[:-1]
for _gene, _transcribe, _tss_zxy in zip(_genes, _transcribes, _tss_zxys):
# get gene index
_gind = gene_names.index(_gene)
# get transcription profile
if _transcribe == 'on':
transcription_profiles[_cind][_gind] = True
else:
transcription_profiles[_cind][_gind] = False
# get coordinates
_tss_zxy = np.array([np.float(_c) for _c in re.split(r'\s+', _tss_zxy.split('[')[1].split(']')[0]) if _c != ''])
tss_zxys_list[_cind][_gind] = _tss_zxy
tss_zxys_list = np.array(tss_zxys_list)
transcription_profiles = np.array(transcription_profiles)
data_rep1['gene_names'] = gene_names
data_rep1['tss_zxys'] = tss_zxys_list
data_rep1['trans_pfs'] = transcription_profiles
# clean up cell_cycle states
if 'Cell cycle state' in rep1_info_dict:
cell_cycle_types = np.unique(rep1_info_dict['Cell cycle state'])
cell_cycle_flag_dict = {_k:[[] for _id in chr_ids] for _k in cell_cycle_types if _k != 'ND'}
for _cid, _state in tqdm(zip(rep1_info_dict['Chromosome copy number'],rep1_info_dict['Cell cycle state'])):
# get chromosome inds
_cid = int(_cid)
_cind = np.where(chr_ids == _cid)[0][0]
if np.array([_v[_cind]==[] for _k,_v in cell_cycle_flag_dict.items()]).any():
for _k,_v in cell_cycle_flag_dict.items():
if _k == _state:
_v[_cind] = True
else:
_v[_cind] = False
# append to data
for _k, _v in cell_cycle_flag_dict.items():
data_rep1[f'{_k}_flags'] = np.array(_v)
# -
data_rep1.keys()
# # 1. population averaged description of chr21
# ## 1.1 (FigS1F) population average maps:
#
# median distance map, proximity frequency map, corresponding Hi-C map
# +
zxys_rep1_list = np.array(data_rep1['dna_zxys'])
distmap_rep1_list = np.array([squareform(pdist(_zxy)) for _zxy in tqdm(zxys_rep1_list)])
# generate median distance map
median_distance_map_rep1 = np.nanmedian(distmap_rep1_list, axis = 0)
# generate contact map
contact_th = 500
contact_map_rep1 = np.nanmean(distmap_rep1_list < contact_th, axis=0)
# load Hi-C
hic_file = r'C:\Users\Bogdan\Dropbox\2020 Chromatin Imaging Manuscript\Revision\DataForReviewers\population-averaged\hi-c_contacts_chromosome21.tsv'
hic_txt = np.array([ln[:-1].split('\t')for ln in open(hic_file,'r') if len(ln)>1])
hic_raw_map = np.array(hic_txt[1:,1:],dtype=np.float)
# +
from matplotlib.colors import LogNorm
median_limits = [0, 2000]
median_cmap = matplotlib.cm.get_cmap('seismic_r')
median_cmap.set_bad(color=[0.,0.,0.,1])
contact_limits = [0.05, 0.6]
contact_norm = LogNorm(vmin=np.min(contact_limits),
vmax=np.max(contact_limits))
contact_cmap = matplotlib.cm.get_cmap('seismic')
contact_cmap.set_bad(color=[0.,0.,0.,1])
hic_limits = [1, 400]
hic_norm = LogNorm(vmin=np.min(hic_limits),
vmax=np.max(hic_limits))
hic_cmap = matplotlib.cm.get_cmap('seismic')
hic_cmap.set_bad(color=[0.,0.,0.,1])
# -
from source.figure_tools.distmap import plot_distance_map
print(figure_folder)
# %matplotlib inline
distmap_ax = plot_distance_map(median_distance_map_rep1,
cmap=median_cmap,
color_limits=median_limits,
tick_labels=mid_positions_Mb,
ax_label='Genomic positions (Mb)',
colorbar_labels='Distances (nm)',
save=True, save_folder=figure_folder,
save_basename=f'FigS1F1_median_distmap_rep1.pdf',
font_size=5)
contact_ax = plot_distance_map(contact_map_rep1,
cmap=contact_cmap,
color_limits=contact_limits,
color_norm=contact_norm,
tick_labels=mid_positions_Mb,
ax_label='Genomic positions (Mb)',
colorbar_labels='Proximity frequency',
save=True, save_folder=figure_folder,
save_basename=f'FigS1F2_contact_map_rep1.pdf',
font_size=5)
hic_ax = plot_distance_map(hic_raw_map,
cmap=hic_cmap,
color_limits=hic_limits,
color_norm=hic_norm,
tick_labels=mid_positions_Mb,
ax_label='Genomic positions (Mb)',
colorbar_labels='Hi-C count',
save=True, save_folder=figure_folder,
save_basename=f'FigS1F3_hic_map.pdf',
font_size=5)
# ## 1.2 (S1G) correlation between median-distance vs. Hi-C
# +
good_spot_flags = np.isnan(np.array(zxys_rep1_list)).sum(2)==0
failure_rates = 1 - np.mean(good_spot_flags, axis=0)
good_regions_rep1 = np.where(failure_rates < 0.25)[0]
print(len(good_regions_rep1))
kept_median_rep1 = median_distance_map_rep1[good_regions_rep1][:,good_regions_rep1]
kept_hic_rep1 = hic_raw_map[good_regions_rep1][:,good_regions_rep1]
wt_median_entries_rep1 = kept_median_rep1[np.triu_indices(len(kept_median_rep1),1)]
hic_contact_entries_rep1 = kept_hic_rep1[np.triu_indices(len(kept_hic_rep1),1)]
kept = (wt_median_entries_rep1>0) * (hic_contact_entries_rep1>0)
from scipy.stats import linregress, pearsonr
lr_rep1 = linregress(np.log(wt_median_entries_rep1[kept]),
np.log(hic_contact_entries_rep1[kept]))
print(lr_rep1)
print('pearson correlation:', np.abs(lr_rep1.rvalue))
# +
xticks = np.round(2**np.linspace(-2,1,4)*1000,0).astype(np.int)
yticks = np.logspace(0, 4, 3).astype(np.int)
xlim = [200,2200]
# draw scatter plot
fig, ax = plt.subplots(figsize=(_single_col_width, _single_col_width), dpi=_dpi)
ax.plot(wt_median_entries_rep1[kept], hic_contact_entries_rep1[kept], '.', color='gray', alpha=0.3, markersize=1, )
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xticks(xticks, minor=False)
ax.set_xticklabels(xticks)
ax.tick_params('both', labelsize=_font_size,
width=_ticklabel_width, length=_ticklabel_size,
pad=1)
[i[1].set_linewidth(_ticklabel_width) for i in ax.spines.items()]
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_xlabel('Median distances (nm)', labelpad=2, fontsize=_font_size+1)
ax.set_ylabel('Hi-C counts', labelpad=2, fontsize=_font_size+1)
ax.set_xlim(xlim)
ax.set_ylim([0.9,10000])
#ax.set_yticks(yticks, minor=True)
#ax.set_yticklabels(yticks)
reg_x = np.linspace(250, 2000, 100)
reg_y = np.exp( lr_rep1.slope * np.log(reg_x) + lr_rep1.intercept)
ax.plot(reg_x, reg_y, 'r', label=f'slope = {lr_rep1.slope:.2f}\n\u03C1 = {lr_rep1.rvalue:.2f}')
plt.legend(loc='upper right', fontsize=_font_size-1)
plt.gcf().subplots_adjust(bottom=0.15, left=0.15)
plt.savefig(os.path.join(figure_folder, 'FigS1G_scatter_median_hic_rep1.pdf'), transparent=True)
plt.show()
# -
# ## Zoomed in correlation
limits = [325, 390]
crop = slice(limits[0],limits[1])
# +
good_crop_regions_rep1 = np.array([_r for _r in good_regions_rep1 if _r in np.arange(limits[0], limits[1])], dtype=np.int)
kept_crop_median_rep1 = median_distance_map_rep1[good_crop_regions_rep1][:,good_crop_regions_rep1]
kept_crop_hic_rep1 = hic_raw_map[good_crop_regions_rep1][:,good_crop_regions_rep1]
wt_crop_median_entries_rep1 = kept_crop_median_rep1[np.triu_indices(len(kept_crop_median_rep1),1)]
hic_crop_contact_entries_rep1 = kept_crop_hic_rep1[np.triu_indices(len(kept_crop_hic_rep1),1)]
kept_crop_rep1 = (wt_crop_median_entries_rep1>0) * (hic_crop_contact_entries_rep1>0)
from scipy.stats import linregress, pearsonr
lr_crop_rep1 = linregress(np.log(wt_crop_median_entries_rep1[kept_crop_rep1]),
np.log(hic_crop_contact_entries_rep1[kept_crop_rep1]))
print(lr_crop_rep1)
print('pearson correlation:', np.abs(lr_crop_rep1.rvalue))
# Plot
xticks = np.round(2**np.linspace(-2,1,4)*1000,0).astype(np.int)
yticks = np.logspace(0, 4, 3).astype(np.int)
xlim = [160,1700]
# draw scatter plot
fig, ax = plt.subplots(figsize=(_single_col_width, _single_col_width), dpi=_dpi)
ax.plot(wt_crop_median_entries_rep1[kept_crop_rep1],
hic_crop_contact_entries_rep1[kept_crop_rep1], '.', color='gray', alpha=0.3, markersize=1, )
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xticks(xticks, minor=False)
ax.set_xticklabels(xticks)
ax.tick_params('both', labelsize=_font_size,
width=_ticklabel_width, length=_ticklabel_size,
pad=1)
[i[1].set_linewidth(_ticklabel_width) for i in ax.spines.items()]
ax.spines["top"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.set_xlabel('Median distances (nm)', labelpad=2, fontsize=_font_size+1)
ax.set_ylabel('Hi-C counts', labelpad=2, fontsize=_font_size+1)
reg_x = np.linspace(250, 2000, 100)
reg_y = np.exp( lr_crop_rep1.slope * np.log(reg_x) + lr_crop_rep1.intercept)
ax.set_xlim(xlim)
ax.set_ylim([0.9,10000])
ax.plot(reg_x, reg_y, 'r', label=f'slope = {lr_crop_rep1.slope:.2f}\n\u03C1 = {lr_crop_rep1.rvalue:.2f}')
plt.legend(loc='upper right', fontsize=_font_size-1)
plt.gcf().subplots_adjust(bottom=0.15, left=0.15)
plt.savefig(os.path.join(figure_folder, f'FigS1I_scatter_median_hic_{limits}.pdf'), transparent=True)
plt.show()
# -
# ## Determine best correlation bewteen contact and Hi-C
# +
# generate contact maps
contact_map_dict_rep1 = {}
thr_list = [100, 200, 300, 400, 500, 600, 700, 800, 900, 1000]
for _thr in thr_list:
print(_thr)
# new way to calculate contact
contact_map_dict_rep1[_thr] = np.sum(distmap_rep1_list<_thr, axis=0) / np.sum(np.isnan(distmap_rep1_list)==False, axis=0)
# calculate pearson correlation with Hi-C
pearson_corr_list_rep1 = []
for _thr in thr_list:
_contact_map = contact_map_dict_rep1[_thr]
good_spot_flags = np.isnan(np.array(zxys_rep1_list)).sum(2)==0
failure_rates = 1 - np.mean(good_spot_flags, axis=0)
good_regions = np.where(failure_rates < 0.25)[0]
#print(len(good_regions))
kept_contacts = _contact_map[good_regions][:,good_regions]
kept_hic = hic_raw_map[good_regions][:,good_regions]
wt_contact_entries = kept_contacts[np.triu_indices(len(kept_contacts),1)]
hic_contact_entries = kept_hic[np.triu_indices(len(kept_hic),1)]
kept = (wt_contact_entries>0) * (hic_contact_entries>0)
from scipy.stats import linregress, pearsonr
lr = linregress(np.log(wt_contact_entries[kept]),
np.log(hic_contact_entries[kept]))
print(_thr, 'nm; pearson correlation:', np.abs(lr.rvalue))
pearson_corr_list_rep1.append(lr.rvalue)
# %matplotlib inline
fig, ax = plt.subplots(figsize=(_single_col_width, _single_col_width), dpi=600)
ax.plot(thr_list, pearson_corr_list_rep1, linewidth=1, alpha=0.7, marker ='.')
ax.tick_params('both', labelsize=_font_size,
width=_ticklabel_width, length=_ticklabel_size-1,
pad=1, labelleft=True) # remove bottom ticklabels for ax
[i[1].set_linewidth(_ticklabel_width) for i in ax.spines.items()]
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_ylim([0.725,0.9])
ax.set_xlim([0,1050])
ax.set_xticks(np.arange(0,1001,200))
ax.set_yticks(np.arange(0.7,0.91,0.05))
ax.set_xlabel("Cutoff threshold (nm)", fontsize=_font_size, labelpad=1)
ax.set_ylabel("Pearson correlation with Hi-C", fontsize=_font_size, labelpad=1)
plt.gcf().subplots_adjust(bottom=0.15, left=0.16)
plt.savefig(os.path.join(figure_folder, f'FigS1J_chr21_proximity_hic_pearson_with_thresholds_rep1.pdf'), transparent=True)
plt.show()
# -
# # 2. Analysis for single-cell domains
# ## 2.1.1 find single-cell domains
# +
import source.domain_tools.DomainAnalysis as da
import multiprocessing as mp
num_threads=32
domain_corr_cutoff = 0.75
domain_dist_cutoff = 500 # nm
_domain_args = [(_zxys, 4, 1000, domain_corr_cutoff, domain_dist_cutoff)
for _zxys in data_rep1['dna_zxys']]
_domain_time = time.time()
print(f"Multiprocessing call domain starts", end=' ')
if 'domain_starts' not in data_rep1:
with mp.Pool(num_threads) as domain_pool:
domain_results = domain_pool.starmap(da.get_dom_starts_cor, _domain_args)
domain_pool.close()
domain_pool.join()
domain_pool.terminate()
# save
data_rep1['domain_starts'] = [np.array(_r[-1]) for _r in domain_results]
data_rep1['params']['domain_corr_cutoff'] = domain_corr_cutoff
data_rep1['params']['domain_dist_cutoff'] = domain_dist_cutoff
print(f"in {time.time()-_domain_time:.3f}s.")
# -
# ## 2.1 Add noise of 100nm and re-find single-cell domains
from copy import deepcopy
data_noise = deepcopy(data_rep1)
del(data_noise['domain_starts'])
data_noise['dna_zxys']+=np.random.normal(scale=100/1.6,size=data_noise['dna_zxys'].shape)
dist_dif = np.linalg.norm(data_rep1['dna_zxys']-data_noise['dna_zxys'],axis=-1)
print("Displacement error:",np.nanmean(dist_dif))
# +
import source.domain_tools.DomainAnalysis as da
import multiprocessing as mp
num_threads=32
domain_corr_cutoff = 0.75
domain_dist_cutoff = 500 # nm
_domain_args = [(_zxys, 4, 1000, domain_corr_cutoff, domain_dist_cutoff)
for _zxys in data_noise['dna_zxys']]
_domain_time = time.time()
print(f"Multiprocessing call domain starts", end=' ')
if 'domain_starts' not in data_noise:
with mp.Pool(num_threads) as domain_pool:
domain_results = domain_pool.starmap(da.get_dom_starts_cor, _domain_args)
domain_pool.close()
domain_pool.join()
domain_pool.terminate()
# save
data_noise['domain_starts'] = [np.array(_r[-1]) for _r in domain_results]
data_noise['params']['domain_corr_cutoff'] = domain_corr_cutoff
data_noise['params']['domain_dist_cutoff'] = domain_dist_cutoff
print(f"in {time.time()-_domain_time:.3f}s.")
# -
# ## 2.2 Genomic size and radius of gyration
# +
# genomic sizes
region_size = 0.05 # Mb
rep1_sz_list = []
for _zxys, _dm_starts in zip(data_rep1['dna_zxys'],data_rep1['domain_starts']):
_starts = _dm_starts[:-1]
_ends = _dm_starts[1:]
# sizes
_sizes = (_dm_starts[1:] - _dm_starts[:-1]) * region_size
# append
rep1_sz_list.append(_sizes)
noise_sz_list = []
for _zxys, _dm_starts in zip(data_noise['dna_zxys'],data_noise['domain_starts']):
_starts = _dm_starts[:-1]
_ends = _dm_starts[1:]
# sizes
_sizes = (_dm_starts[1:] - _dm_starts[:-1]) * region_size
# append
noise_sz_list.append(_sizes)
# %matplotlib inline
fig, ax = plt.subplots(figsize=(_single_col_width, _single_col_width), dpi=600)
ax.hist(np.concatenate(noise_sz_list), 100, range=(0,5),
density=True, color='k', alpha=1, label=f'median={np.nanmedian(np.concatenate(rep1_sz_list)):.2f}Mb')
ax.hist(np.concatenate(rep1_sz_list), 100, range=(0,5),
density=True, color='g', alpha=0.5, label=f'median={np.nanmedian(np.concatenate(rep1_sz_list)):.2f}Mb')
ax.tick_params('both', labelsize=_font_size,
width=_ticklabel_width, length=_ticklabel_size-1,
pad=1, labelleft=True) # remove bottom ticklabels for ax
[i[1].set_linewidth(_ticklabel_width) for i in ax.spines.items()]
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
#ax.legend(fontsize=_font_size-1)
ax.set_xlabel("Genomic size (Mb)", labelpad=1, fontsize=_font_size)
ax.set_ylabel("Probability density", labelpad=1, fontsize=_font_size)
ax.set_title("Chr21 domain genomic size", pad=2, fontsize=_font_size)
plt.gcf().subplots_adjust(bottom=0.15, left=0.16)
save_file = os.path.join(figure_folder, f'Fig1I_chr21_domain_gsize_hist_rep1.pdf')
plt.savefig(save_file, transparent=True)
print(save_file)
plt.show()
# +
def rg_mean(zxy):
"""computes radius of gyration"""
zxy_ = np.array(zxy)
zxy_ = zxy_[~np.isnan(zxy_[:,0])]
zxy_ = zxy_ - np.mean(zxy_,0)
return np.sqrt(np.mean(np.sum(zxy_**2,axis=-1)))
# radius of gyrations
rep1_rg_list = []
for _zxys, _dm_starts in zip(data_rep1['dna_zxys'],data_rep1['domain_starts']):
_starts = _dm_starts[:-1]
_ends = _dm_starts[1:]
# rgs
_rgs = np.array([rg_mean(_zxys[_s:_e]) for _s, _e in zip(_starts, _ends)])
# append
rep1_rg_list.append(_rgs)
# radius of gyration for noise
noise_rg_list = []
for _zxys, _dm_starts in zip(data_noise['dna_zxys'],data_noise['domain_starts']):
_starts = _dm_starts[:-1]
_ends = _dm_starts[1:]
# rgs
_rgs = np.array([rg_mean(_zxys[_s:_e]) for _s, _e in zip(_starts, _ends)])
# append
noise_rg_list.append(_rgs)
fig, ax = plt.subplots(figsize=(_single_col_width, _single_col_width), dpi=600)
ax.hist(np.concatenate(noise_rg_list), 100, range=(0,1500),
density=True, color='k', alpha=1, label=f'median={np.nanmedian(np.concatenate(rep1_rg_list)):.0f}nm')
ax.hist(np.concatenate(rep1_rg_list), 100, range=(0,1500),
density=True, color='g', alpha=0.6, label=f'median={np.nanmedian(np.concatenate(rep1_rg_list)):.0f}nm')
ax.tick_params('both', labelsize=_font_size-1,
width=_ticklabel_width, length=_ticklabel_size-1,
pad=1, labelleft=True) # remove bottom ticklabels for ax
[i[1].set_linewidth(_ticklabel_width) for i in ax.spines.items()]
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
#ax.legend(fontsize=_font_size-1)
ax.set_xlabel("Radius of gyration (nm)", labelpad=1, fontsize=_font_size)
ax.set_ylabel("Probability density", labelpad=1, fontsize=_font_size)
ax.set_title("Chr21 domain radius of gyration", pad=2, fontsize=_font_size)
plt.gcf().subplots_adjust(bottom=0.15, left=0.16)
save_file = os.path.join(figure_folder, f'Fig1J_chr21_domain_RG_hist_rep1.pdf')
plt.savefig(save_file, transparent=True)
print(save_file)
plt.show()
# -
# ## 2.3 Single-cell boundary probability, insulation and alignment with CTCF/TADs
dom_starts_fs = data_rep1['domain_starts']
zxys = data_rep1['dna_zxys']
pts= zxys
# ### calculate boundary probability
dom_all = np.array([dom for doms in dom_starts_fs[::] for dom in doms[1:-1]])
unk_,cts_=np.unique(dom_all,return_counts=True)
cts = np.zeros(len(pts[0]))
cts[unk_]=cts_
# ### boundary probability for a zoom-in example
# +
import matplotlib.pylab as plt
import numpy as np
import pickle,os
from mpl_toolkits.mplot3d import Axes3D
from scipy.spatial.distance import pdist,cdist,squareform
####### You will need cv2. If you do not have it, run: pip install opencv-python
import cv2
from matplotlib import cm
def resize(im__,scale_percent = 100):
width = int(im__.shape[1] * scale_percent / 100)
height = int(im__.shape[0] * scale_percent / 100)
dim = (width, height)
resized = cv2.resize(im__, dim, interpolation = cv2.INTER_NEAREST)
return resized
def rotate_bound(image, angle):
# grab the dimensions of the image and then determine the
# center
(h, w) = image.shape[:2]
(cX, cY) = (w // 2, h // 2)
# grab the rotation matrix (applying the negative of the
# angle to rotate clockwise), then grab the sine and cosine
# (i.e., the rotation components of the matrix)
M = cv2.getRotationMatrix2D((cX, cY), -angle, 1.0)
cos = np.abs(M[0, 0])
sin = np.abs(M[0, 1])
# compute the new bounding dimensions of the image
nW = int((h * sin) + (w * cos))
nH = int((h * cos) + (w * sin))
# adjust the rotation matrix to take into account translation
M[0, 2] += (nW / 2) - cX
M[1, 2] += (nH / 2) - cY
# perform the actual rotation and return the image
return cv2.warpAffine(image, M, (nW, nH),cv2.INTER_NEAREST)
def interp1dnan(A):
A_=np.array(A)
ok = np.isnan(A)==False
xp = ok.nonzero()[0]
fp = A[ok]
x = np.isnan(A).nonzero()[0]
A_[np.isnan(A)] = np.interp(x, xp, fp)
return A_
def interpolate_chr(_chr):
"""linear interpolate chromosome coordinates"""
_new_chr = np.array(_chr)
for i in range(_new_chr.shape[-1]):
_new_chr[:,i]=interp1dnan(_new_chr[:,i])
return _new_chr
from mpl_toolkits.axes_grid1 import ImageGrid
from matplotlib import cm
fig = plt.figure(figsize=(20,20))
grid = ImageGrid(fig, 111, nrows_ncols=(4, 1),axes_pad=0.)
mat_ = np.log(contact_map_rep1)
pad=0
min_val,max_val = -2,None # the minimum and maximum distance in nanometers. this sets the threshold of the image
if max_val is None: max_val = np.nanmax(mat_)
if min_val is None: min_val = np.nanmin(mat_)
#This colors the image
im_ = (np.clip(mat_,min_val,max_val)-min_val)/(max_val-min_val)
im__ = np.array(cm.seismic(im_)[:,:,:3]*255,dtype=np.uint8)
# resize image 10x to get good resolution
resc = 10############
resized = resize(im__,resc*100)
# Rotate 45 degs
resized = rotate_bound(resized,-45)
start = int(pad*np.sqrt(2)*resc)
center = int(resized.shape[1]/2)
#Clip it to the desired size
padup=30##### how much of the matrix to keep in the up direction
resized = resized[center-resc*padup:center+resc*padup]
#List of positions of CTCF and rad21 in chr21
#ctcf
ctcf = [ 9, 21, 33, 67, 73, 78, 139, 226, 231, 235, 242, 253, 256,
273, 284, 292, 301, 307, 339, 350, 355, 363, 366, 370, 373, 376,
381, 385, 390, 396, 402, 405, 410, 436, 440, 446, 456, 469, 472,
476, 482, 485, 488, 492, 500, 505, 508, 512, 520, 540, 543, 550,
554, 560, 565, 576, 580, 585, 589, 592, 595, 599, 602, 606, 615,
619, 622, 625, 628, 633, 636, 639]
# rad21
rad21=[ 21, 33, 67, 73, 139, 226, 231, 236, 242, 256, 273, 284, 292,
301, 305, 339, 350, 355, 363, 366, 370, 381, 386, 390, 396, 405,
410, 415, 436, 440, 446, 456, 469, 472, 482, 485, 492, 500, 505,
508, 512, 543, 550, 554, 560, 576, 581, 585, 589, 593, 596, 599,
602, 615, 619, 622, 625, 628, 633, 636]
start = 0
min__ = 0
cts_perc = 1.*cts/len(pts)*100*resc
x_vals = (np.arange(len(cts_perc))-min__)*resc*np.sqrt(2)-start
#grid[1].imshow(A_.T,cmap='bwr')
grid[1].plot(x_vals,cts_perc,'ko-')
grid[0].imshow(resized)
grid[2].plot(x_vals[ctcf],[0]*len(ctcf),'^',color='orange',mec='k')
grid[3].plot(x_vals[rad21],[0]*len(rad21),'^',color='yellow',mec='k')
ypad=20
grid[2].set_ylim([-ypad,ypad])
grid[3].set_ylim([-ypad,ypad])
grid[2].set_yticks([])
grid[3].set_yticks([])
#grid[1].set_yticks([])
#grid[1].set_ylabel('AB ',rotation='horizontal')
grid[2].set_ylabel('CTCF ',rotation='horizontal')
grid[3].set_ylabel('RAD21 ',rotation='horizontal')
min_,max_ = (282, 480)
grid[0].set_xlim([min_*resc*np.sqrt(2),max_*resc*np.sqrt(2)])
plt.savefig(os.path.join(figure_folder,
f'Fig1C_chr21_sc-domain_prob_rep1.pdf'), transparent=True)
plt.show()
# -
# ### Calculate TADs
# +
#median_distance_map_rep1
#contact_map_dict_rep1
zxys_noise_list = np.array(data_noise['dna_zxys'])
distmap_noise_list = np.array([squareform(pdist(_zxy)) for _zxy in tqdm(zxys_noise_list)])
# generate median distance map
median_distance_map_noise = np.nanmedian(distmap_noise_list, axis = 0)
# generate contact map
contact_th = 500
contact_map_noise = np.nanmean(distmap_noise_list < contact_th, axis=0)
# -
from source.domain_tools.distance import _sliding_window_dist
# +
from scipy.signal import find_peaks
distance_wd_dists = _sliding_window_dist(median_distance_map_rep1, _wd=8,
_dist_metric='normed_insulation')
distance_wd_dists_ = _sliding_window_dist(median_distance_map_noise, _wd=8,
_dist_metric='normed_insulation')
distance_peaks = find_peaks(-distance_wd_dists_, distance=5, prominence=0.013, width=3)
fig = plt.figure(figsize=(9,2),dpi=200)
plt.plot(-distance_wd_dists_, color='k', label='simulation', linewidth=1)
for _p in distance_peaks[0]:
plt.vlines(_p, 0, 1, linewidth=0.5, linestyles="dotted",color='k' )
distance_peaks = find_peaks(-distance_wd_dists, distance=5, prominence=0.013, width=3)
plt.plot(-distance_wd_dists, color=[1,0.4,0], label='data', linewidth=1)
for _p in distance_peaks[0]:
plt.vlines(_p, 0, 1, linewidth=0.5, linestyles="dotted",color='k' )
#plt.legend()
plt.ylim([0,0.5])
plt.xlim([0,651])
plt.xlabel('Genomic coordinate')
plt.ylabel('Insulation')
plt.show()
#folder_ = r'C:\Users\Bogdan\Dropbox\2020 Chromatin Imaging Manuscript\Revision\FinalFigures\Figure S1\100nmDisplacement_simmulation_newAnalysis'
#fig.savefig(folder_+os.sep+'TADsInsulation_medianDistance.pdf')
# +
contact_wd_dists = _sliding_window_dist(contact_map_rep1, _wd=8, _dist_metric='normed_insulation')
contact_wd_dists_ = _sliding_window_dist(contact_map_noise, _wd=8, _dist_metric='normed_insulation')
from scipy.signal import find_peaks
fig = plt.figure(figsize=(9,2),dpi=200)
plt.plot(contact_wd_dists_,color='k',linewidth=2,label='100nm displaced loci')
plt.plot(contact_wd_dists,linewidth=1,color='g',label='original data')
contact_peaks = find_peaks(contact_wd_dists, distance=5, prominence=0.022, width=3)
for _p in contact_peaks[0]:
plt.vlines(_p, 0, 1, linewidth=0.5, linestyles="dotted", color='k')
contact_peaks_ = find_peaks(contact_wd_dists_, distance=5, prominence=0.022, width=3)
for _p in contact_peaks_[0]:
plt.vlines(_p, 0, 1, linewidth=0.5, linestyles="dotted", color='k')
plt.legend()
plt.ylim([0,0.5])
plt.xlim([0,651])
plt.xlabel('Genomic coordinate')
plt.ylabel('Insulation')
plt.show()
# -
TADs = contact_peaks[0]
# +
hic_wd_dists = _sliding_window_dist(hic_raw_map, _wd=8, _dist_metric='normed_insulation')
from scipy.signal import find_peaks
fig = plt.figure(figsize=(9,2),dpi=200)
plt.plot(hic_wd_dists,linewidth=1,color='r',label='original data')
hic_peaks = find_peaks(hic_wd_dists, distance=5, prominence=0.08, width=3)
for _p in hic_peaks[0]:
plt.vlines(_p, 0, 1, linewidth=0.5, linestyles="dotted", color='k')
plt.legend()
plt.ylim([0,1])
plt.xlim([0,651])
plt.xlabel('Genomic coordinate')
plt.ylabel('Insulation')
plt.show()
# +
#List of positions of CTCF and rad21 in chr21
#ctcf
ctcf = [ 9, 21, 33, 67, 73, 78, 139, 226, 231, 235, 242, 253, 256,
273, 284, 292, 301, 307, 339, 350, 355, 363, 366, 370, 373, 376,
381, 385, 390, 396, 402, 405, 410, 436, 440, 446, 456, 469, 472,
476, 482, 485, 488, 492, 500, 505, 508, 512, 520, 540, 543, 550,
554, 560, 565, 576, 580, 585, 589, 592, 595, 599, 602, 606, 615,
619, 622, 625, 628, 633, 636, 639]
# rad21
rad21=[ 21, 33, 67, 73, 139, 226, 231, 236, 242, 256, 273, 284, 292,
301, 305, 339, 350, 355, 363, 366, 370, 381, 386, 390, 396, 405,
410, 415, 436, 440, 446, 456, 469, 472, 482, 485, 492, 500, 505,
508, 512, 543, 550, 554, 560, 576, 581, 585, 589, 593, 596, 599,
602, 615, 619, 622, 625, 628, 633, 636]
#A = [255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 366, 367, 368, 369, 370, 371, 372, 373, 374, 375, 376, 377, 378, 379, 380, 381, 382, 383, 384, 385, 386, 387, 388, 389, 390, 391, 392, 393, 394, 395, 396, 397, 398, 399, 400, 401, 402, 403, 404, 405, 406, 407, 408, 409, 410, 411, 412, 413, 414, 415, 416, 417, 418, 419, 420, 421, 422, 423, 424, 425, 426, 427, 428, 429, 430, 431, 432, 433, 434, 435, 436, 437, 438, 439, 440, 441, 442, 443, 444, 445, 446, 447, 448, 449, 450, 451, 452, 453, 454, 455, 456, 457, 458, 459, 460, 461, 462, 463, 464, 465, 466, 467, 468, 469, 494, 495, 496, 497, 498, 499, 500, 575, 576, 577, 578, 579, 580, 581, 582, 583, 584, 585, 586, 587, 588, 589, 590, 591, 592, 593, 594, 595, 596, 597, 598, 599, 600, 601, 602, 603, 604, 605, 606, 607, 608, 609, 610, 611, 612, 613, 614, 615, 616, 617, 618, 619, 620, 621, 622, 623, 624, 625, 626, 627, 628, 629, 630, 631, 632, 633, 634, 635, 636, 637, 638, 639, 640, 641, 642, 643, 644, 645, 646, 647, 648, 649, 650]
#A_ = np.zeros(len(zxys[0])+2)
#A_[np.array(A)+1]=1
#AB_bds = np.abs(np.diff(A_))
#AB_bds = np.where(AB_bds)[0]
pts = data_rep1['dna_zxys']
import matplotlib
matplotlib.rcParams['pdf.fonttype'] = 42
matplotlib.rcParams['font.size']=15
matplotlib.rcParams['font.family']='Arial'
fig = plt.figure(figsize=(3,5))
bds_avg_ = TADs #from jun-han - 500nm#[20, 35, 52, 67, 80, 113, 139, 159, 179, 198, 213, 227, 254, 273, 298, 317, 340, 351, 365, 373, 388, 411, 439, 460, 471, 486, 507, 540, 550, 561, 575, 592, 604, 613, 627, 636, 644]
dmat = np.abs(np.array([[bd2-bd1 for bd1 in bds_avg_] for bd2 in np.arange(len(pts[0]))],dtype=int))
dmat = np.array([[bd2-bd1 for bd1 in bds_avg_] for bd2 in np.arange(len(pts[0]))],dtype=int)
range_ = range(-15,15)
yvec = np.array([np.median(cts[np.where(dmat==i)[0]]) for i in range_])
plt.plot(np.array(range_)*50,yvec/len(pts)*100,'o-',color=[0.6]*3,label='Domains')
#dmat = np.abs(np.array([[bd2-bd1 for bd1 in AB_bds] for bd2 in np.arange(len(pts[0]))],dtype=int))
#dmat = np.array([[bd2-bd1 for bd1 in AB_bds] for bd2 in np.arange(len(pts[0]))],dtype=int)
#yvec = np.array([np.median(cts[np.where(dmat==i)[0]]) for i in range_])
#plt.plot(np.array(range_)*50,yvec/len(pts)*100,'ko-',label='A/B compartments')
ctcf_rad21 = np.intersect1d(rad21,ctcf)
dmat = np.array([[bd2-bd1 for bd1 in ctcf_rad21] for bd2 in np.arange(len(pts[0]))],dtype=int)
yvec = np.array([np.median(cts[np.where(dmat==i)[0]]) for i in range_])
plt.plot(np.array(range_)*50,yvec/len(pts)*100,'o-',color='orange',label='CTCF&RAD21')
plt.yticks([5,7.5,10])
plt.ylim([4,14])
plt.xlabel('Genomic distance from boundary (kb)')
plt.ylabel('Single-cell \nboundary probability(%)')
plt.legend()
#folder_ = r'C:\Users\Bogdan\Dropbox\2020 Chromatin Imaging Manuscript\Revision\Bogdan_Figures\Figure1\base_images'
save_file = os.path.join(figure_folder, f'Fig1D_chr21_sc-domain_prob_ctcf_rep1.pdf')
print(save_file)
plt.savefig(save_file, transparent=True)
plt.show()
# -
# ### insulation scores w/wo ctcf
# +
ichr=0
ins = []
bdr_ins = []
dom_starts_fs = data_rep1['domain_starts']
zxys = data_rep1['dna_zxys']
for dom_ in tqdm(dom_starts_fs):
zxy_ = zxys[ichr]
for idom in range(1,len(dom_)-3):
a,b,c = dom_[idom],dom_[idom+1],dom_[idom+2]
#a,b,c = dom_[idom+1]-5,dom_[idom+1],dom_[idom+1]+5
zxy1 = zxy_[a:b]
zxy2 = zxy_[b:c]
med_in = np.nanmedian(np.concatenate([pdist(zxy1),pdist(zxy2)]))
med_out = np.nanmedian(cdist(zxy1,zxy2))
ins_ = med_out/med_in
ins.append(ins_)
bdr_ins.append(b)
ichr+=1
bdr_ins=np.array(bdr_ins)
ins = np.array(ins)
# +
nonctcf = np.ones(len(zxys[0]))
nonctcf[ctcf_rad21]=0
nonctcf = np.nonzero(nonctcf)[0]
fig = plt.figure()#figsize=(10,7))
bins=np.linspace(0,4,75)
plt.hist(ins[np.in1d(bdr_ins,nonctcf)],alpha=0.5,normed=True,bins=bins,color='gray',label = 'non-CTCF/RAD21')
plt.hist(ins[np.in1d(bdr_ins,ctcf_rad21)],alpha=0.5,normed=True,bins=bins,color='orange',label = 'CTCF/RAD21')
plt.xlabel('Boundary insulation score')
plt.ylabel('Probability density function')
plt.legend()
plt.savefig(os.path.join(figure_folder, f'Fig1K_chr21_sc-domain_insulation_ctcf_rep1.pdf'), transparent=True)
plt.show()
# -
# ## 2.5 CTCF end-end distance and radii of gyration of CTCF bound domains
# +
from tqdm import tqdm_notebook as tqdm
dic_ctcf = {}
dic_nonctcf = {}
def rg_med(zxy):
"""computes radius of gyration"""
zxy_ = np.array(zxy)
zxy_ = zxy_[~np.isnan(zxy_[:,0])]
zxy_ = zxy_ - np.mean(zxy_,0)
return np.sqrt(np.mean(np.sum(zxy_**2,axis=-1)))
def inD(zxy):
"""computest mean interdistance"""
return np.nanmean(pdist(zxy))
dic_rgctcf = {}
dic_rgnonctcf = {}
dic_inDctcf = {}
dic_inDnonctcf = {}
dic_withinDctcf = {}
dic_withinDnonctcf = {}
###################### This does not save each ctcf pair in its own key but already groups by genomic distance
ctcf_or_rad21 = np.union1d(ctcf,rad21)
for ichr in tqdm(range(len(zxys))):
doms=dom_starts_fs[ichr][1:-1]
zxy = zxys[ichr]
for i in range(len(doms)-1):
e1,e2 = doms[i],doms[i+1]-1
dist_ = np.linalg.norm(zxy[e1]-zxy[e2])
gen_dist = e2-e1
rg_ = rg_med(zxy[e1:e2])
inD_ = inD(zxy[e1:e2])
if (e1 in ctcf_or_rad21) and (e2 in ctcf_or_rad21):
dic_ctcf[gen_dist]=dic_ctcf.get(gen_dist,[])+[dist_]
dic_rgctcf[gen_dist]=dic_rgctcf.get(gen_dist,[])+[rg_]
dic_inDctcf[gen_dist]=dic_inDctcf.get(gen_dist,[])+[inD_]
if not np.any(np.in1d([e1,e1+1,e1-1,e2,e2+1,e2-1],ctcf_or_rad21)):
#if not np.any(np.in1d([e1,e2],ctcf_or_rad21)):
dic_nonctcf[gen_dist]=dic_nonctcf.get(gen_dist,[])+[dist_]
dic_rgnonctcf[gen_dist]=dic_rgnonctcf.get(gen_dist,[])+[rg_]
e1p = np.random.randint(e1+1,e2-1)
e2p = np.random.randint(e1p,e2-1)
if not np.any(np.in1d([e1p,e1p+1,e1p-1,e2p,e2p+1,e2p-1],ctcf_or_rad21)):
gen_dist__ = abs(e1p-e2p)
dist__ = np.linalg.norm(zxy[e1p]-zxy[e2p])
dic_withinDnonctcf[gen_dist__]=dic_withinDnonctcf.get(gen_dist__,[])+[dist__]
for e1p in range(e1+1,e2-1):
for e2p in range(e1p,e2-1):
if (e1p in ctcf_or_rad21) and (e2p in ctcf_or_rad21):
gen_dist__ = abs(e1p-e2p)
dist__ = np.linalg.norm(zxy[e1p]-zxy[e2p])
dic_withinDctcf[gen_dist__]=dic_withinDctcf.get(gen_dist__,[])+[dist__]
# -
pickle.dump([dic_ctcf,dic_nonctcf,dic_rgctcf,dic_rgnonctcf,dic_inDctcf,dic_inDnonctcf,dic_withinDctcf,dic_withinDnonctcf],
open(r'C:\Users\Bogdan\Dropbox\Chromosome21_online\rg_and_edge-edge_distance_v2_repeat_testPu','wb'))
gen_dists = np.sort(list(dic_ctcf.keys()))
gen_dists = gen_dists[gen_dists<=28]
gen_dists = gen_dists[gen_dists>=4]
print([len(dic_nonctcf.get(gn,[])) for gn in gen_dists])
# +
def boostrap_err2(x_,y_,func,N=1000,perc_min=5,perc_max=95):
elems = []
for istrap in range(N):
x__ = np.random.choice(x_,[len(x_)])
y__ = np.random.choice(y_,[len(y_)])
elems.append(func(x__,y__))
return (np.nanpercentile(elems,perc_min),np.nanpercentile(elems,perc_max))
gen_dists = np.sort(list(dic_ctcf.keys()))
gen_dists = gen_dists[gen_dists<=28]
gen_dists = gen_dists[gen_dists>=4]
def func(x,y): return np.nanmedian(x)/np.nanmedian(y)
xelems = gen_dists*50
meds_ctcf = [func(dic_ctcf.get(gn,[]),dic_withinDctcf.get(gn,[])) for gn in gen_dists]
errs_ctcf = np.abs(np.array([boostrap_err2(dic_ctcf.get(gn,[]),dic_withinDctcf.get(gn,[]),func)
for gn in tqdm(gen_dists)]).T-meds_ctcf)
xelems = gen_dists*50
meds_non = [func(dic_nonctcf.get(gn,[]),dic_withinDnonctcf.get(gn,[])) for gn in gen_dists]
errs_non = np.abs(np.array([boostrap_err2(dic_nonctcf.get(gn,[]),dic_withinDnonctcf.get(gn,[]),func)
for gn in tqdm(gen_dists)]).T-meds_non)
# +
fig = plt.figure()
xelems = gen_dists*50
plt.errorbar(xelems,meds_ctcf,
yerr=errs_ctcf,
color='orange',mec='k',label='CTCF/cohesin domains',marker='o')
plt.errorbar(xelems,meds_non,
yerr=errs_non,
color='gray',mec='k',label='non-CTCF/cohesin domains',marker='o')
plt.legend()
plt.ylim([0.5,1.75])
plt.ylabel('Median edge distance/ \nMedian distance within domains')
plt.xlabel('Genomic distance (kb)')
#folder_ = r'C:\Users\Bogdan\Dropbox\2020 Chromatin Imaging Manuscript\Revision\FinalFigures\Figure 1\subpanels'
#fig.savefig(folder_+os.sep+r'Fig1L_new.pdf')
# +
### Radius of gyration
def boostrap_err(x_,func,N=1000,perc_min=5,perc_max=95):
elems = []
for istrap in range(N):
elems.append(func(np.random.choice(x_,[len(x_)])))
return (np.nanpercentile(elems,perc_min),np.nanpercentile(elems,perc_max))
gen_dists = np.sort(list(dic_rgctcf.keys()))
gen_dists = gen_dists[gen_dists<=28]
gen_dists = gen_dists[gen_dists>=4]
func = np.nanmedian
xelems = gen_dists*50
meds_ctcf_rg = [func(dic_rgctcf[gn]) for gn in gen_dists]
errs_ctcf_rg = np.abs(np.array([boostrap_err(dic_rgctcf[gn],func) for gn in gen_dists]).T-meds_ctcf_rg)
xelems = gen_dists*50
meds_non_rg = [func(dic_rgnonctcf[gn]) for gn in gen_dists]
errs_non_rg = np.abs(np.array([boostrap_err(dic_rgnonctcf[gn],func) for gn in gen_dists]).T-meds_non_rg)
# +
fig = plt.figure(figsize=(5,5))#figsize=(8,3))
plt.errorbar(xelems,meds_ctcf_rg,
yerr=errs_ctcf_rg,
color='orange',mec='k',label='CTCF/cohesin domains',marker='o')
plt.errorbar(xelems,meds_non_rg,
yerr=errs_non_rg,
color='gray',mec='k',label='non-CTCF/cohesin domains',marker='o')
plt.ylabel('Radius of gyration(nm)')
plt.xlabel('Genomic distance (kb)')
plt.legend()
save_file = os.path.join(figure_folder, f'Fig1M_chr21_domain_rg_ctcf_rep1.pdf')
plt.savefig(save_file, transparent=True)
print(save_file)
# -
# ### Radius of gyration vs genomic distance
dom_starts_fs = data_rep1['domain_starts']
zxys = data_rep1['dna_zxys'][:,:,1:]
pts=zxys
# +
def rg_med(zxy):
"""computes radius of gyration"""
zxy_ = np.array(zxy)
zxy_ = zxy_[~np.isnan(zxy_[:,0])]
zxy_ = zxy_ - np.mean(zxy_,0)
return np.sqrt(np.mean(np.sum(zxy_**2,axis=-1)))
dic_rg = {}
for ichr in tqdm(range(len(pts))):
doms=dom_starts_fs[ichr][1:-1]
zxy = pts[ichr]
for i in range(len(doms)-1):
e1,e2 = doms[i],doms[i+1]-1
start = e1
end=e2#-1
rg_ = rg_med(zxy[start:end])
key = end-start
dic_rg[key] = dic_rg.get(key,[])+[rg_]
# +
fig = plt.figure(figsize=(10,5))
keys = np.sort(list(dic_rg.keys()))
keys = keys[keys>=4]
plt.boxplot([dic_rg[gn] for gn in keys][:100-4], notch=True, showfliers=False,whis = [10, 90]);
xlab = np.arange(6)
plt.xticks((xlab-0.2)*1000/50,xlab);
plt.ylabel('Radius of gyration (nm)')
plt.xlabel('Genomic size of single-cell domains (Mb)')
save_file = os.path.join(figure_folder, f'FigS1N_chr21_domain_rgs_vs_genomic.pdf')
plt.savefig(save_file, transparent=True)
print(save_file)
# -
# ## Characterization domain and compartment in G1/G2-S cells
# ## Load data rep2
# load from file and extract info
import csv
rep2_info_dict = {}
with open(rep2_filename, 'r') as _handle:
_reader = csv.reader(_handle, delimiter='\t', quotechar='|')
_headers = next(_reader)
print(_headers)
# create keys for each header
for _h in _headers:
rep2_info_dict[_h] = []
# loop through content
for _contents in _reader:
for _h, _info in zip(_headers,_contents):
rep2_info_dict[_h].append(_info)
# +
from tqdm import tqdm_notebook as tqdm
# clean up infoa
data_rep2 = {'params':{}}
# clean up genomic coordiantes
region_names = np.array([_n for _n in sorted(region_names, key=lambda s:int(s.split(':')[1].split('-')[0]))])
region_starts = np.array([int(_n.split(':')[1].split('-')[0]) for _n in region_names])
region_ends = np.array([int(_n.split(':')[1].split('-')[1]) for _n in region_names])[np.argsort(region_starts)]
region_starts = np.sort(region_starts)
mid_positions = ((region_starts + region_ends)/2).astype(np.int)
mid_positions_Mb = np.round(mid_positions / 1e6, 2)
# clean up chrom copy number
chr_nums = np.array([int(_info) for _info in rep2_info_dict['Chromosome copy number']])
chr_ids, region_cts = np.unique(chr_nums, return_counts=True)
dna_zxys_list = [[[] for _start in region_starts] for _id in chr_ids]
# clean up zxy
for _z,_x,_y,_reg_info, _cid in tqdm(zip(rep2_info_dict['Z(nm)'],rep2_info_dict['X(nm)'],\
rep2_info_dict['Y(nm)'],rep2_info_dict['Genomic coordinate'],\
rep2_info_dict['Chromosome copy number'])):
# get chromosome inds
_cid = int(_cid)
_cind = np.where(chr_ids == _cid)[0][0]
# get region indices
_start = int(_reg_info.split(':')[1].split('-')[0])
_rind = np.where(region_starts==_start)[0][0]
dna_zxys_list[_cind][_rind] = np.array([float(_z),float(_x), float(_y)])
# merge together
dna_zxys_list = np.array(dna_zxys_list)
data_rep2['chrom_ids'] = chr_ids
data_rep2['region_names'] = region_names
data_rep2['mid_position_Mb'] = mid_positions_Mb
data_rep2['dna_zxys'] = dna_zxys_list
# clean up tss and transcription
if 'Gene names' in rep2_info_dict:
import re
# first extract number of genes
gene_names = []
for _gene_info, _trans_info, _tss_coord in zip(rep2_info_dict['Gene names'],
rep2_info_dict['Transcription'],
rep2_info_dict['TSS ZXY(nm)']):
if _gene_info != '':
# split by semicolon
_genes = _gene_info.split(';')[:-1]
for _gene in _genes:
if _gene not in gene_names:
gene_names.append(_gene)
print(f"{len(gene_names)} genes exist in this dataset.")
# initialize gene and transcription
tss_zxys_list = [[[] for _gene in gene_names] for _id in chr_ids]
transcription_profiles = [[[] for _gene in gene_names] for _id in chr_ids]
# loop through to get info
for _cid, _gene_info, _trans_info, _tss_locations in tqdm(zip(rep2_info_dict['Chromosome copy number'],
rep2_info_dict['Gene names'],
rep2_info_dict['Transcription'],
rep2_info_dict['TSS ZXY(nm)'])):
# get chromosome inds
_cid = int(_cid)
_cind = np.where(chr_ids == _cid)[0][0]
# process if there are genes in this region:
if _gene_info != '':
# split by semicolon
_genes = _gene_info.split(';')[:-1]
_transcribes = _trans_info.split(';')[:-1]
_tss_zxys = _tss_locations.split(';')[:-1]
for _gene, _transcribe, _tss_zxy in zip(_genes, _transcribes, _tss_zxys):
# get gene index
_gind = gene_names.index(_gene)
# get transcription profile
if _transcribe == 'on':
transcription_profiles[_cind][_gind] = True
else:
transcription_profiles[_cind][_gind] = False
# get coordinates
_tss_zxy = np.array([np.float(_c) for _c in re.split(r'\s+', _tss_zxy.split('[')[1].split(']')[0]) if _c != ''])
tss_zxys_list[_cind][_gind] = _tss_zxy
tss_zxys_list = np.array(tss_zxys_list)
transcription_profiles = np.array(transcription_profiles)
data_rep2['gene_names'] = gene_names
data_rep2['tss_zxys'] = tss_zxys_list
data_rep2['trans_pfs'] = transcription_profiles
# clean up cell_cycle states
if 'Cell cycle state' in rep2_info_dict:
cell_cycle_types = np.unique(rep2_info_dict['Cell cycle state'])
cell_cycle_flag_dict = {_k:[[] for _id in chr_ids] for _k in cell_cycle_types if _k != 'ND'}
for _cid, _state in tqdm(zip(rep2_info_dict['Chromosome copy number'],rep2_info_dict['Cell cycle state'])):
# get chromosome inds
_cid = int(_cid)
_cind = np.where(chr_ids == _cid)[0][0]
if np.array([_v[_cind]==[] for _k,_v in cell_cycle_flag_dict.items()]).any():
for _k,_v in cell_cycle_flag_dict.items():
if _k == _state:
_v[_cind] = True
else:
_v[_cind] = False
# append to data
for _k, _v in cell_cycle_flag_dict.items():
data_rep2[f'{_k}_flags'] = np.array(_v)
# -
# ## call domains for rep2
# +
import source.domain_tools.DomainAnalysis as da
import multiprocessing as mp
num_threads=32
domain_corr_cutoff = 0.75
domain_dist_cutoff = 500 # nm
_domain_args = [(_zxys, 4, 1000, domain_corr_cutoff, domain_dist_cutoff)
for _zxys in data_rep2['dna_zxys']]
_domain_time = time.time()
print(f"Multiprocessing call domain starts", end=' ')
if 'domain_starts' not in data_rep2:
with mp.Pool(num_threads) as domain_pool:
domain_results = domain_pool.starmap(da.get_dom_starts_cor, _domain_args)
domain_pool.close()
domain_pool.join()
domain_pool.terminate()
# save
data_rep2['domain_starts'] = [np.array(_r[-1]) for _r in domain_results]
data_rep2['params']['domain_corr_cutoff'] = domain_corr_cutoff
data_rep2['params']['domain_dist_cutoff'] = domain_dist_cutoff
print(f"in {time.time()-_domain_time:.3f}s.")
# -
# +
from tqdm import tqdm_notebook as tqdm
def rg_mean(zxy):
"""computes radius of gyration"""
zxy_ = np.array(zxy)
zxy_ = zxy_[~np.isnan(zxy_[:,0])]
zxy_ = zxy_ - np.mean(zxy_,0)
return np.sqrt(np.mean(np.sum(zxy_**2,axis=-1)))
g1_rgs = []
g2_rgs = []
for _i, (pt_,doms_) in tqdm(enumerate(zip(data_rep2['dna_zxys'],data_rep2['domain_starts']))):
for i1,i2 in zip(doms_[1:-2],doms_[2:-1]):
if data_rep2['G1_flags'][_i]:
g1_rgs.append(rg_mean(pt_[i1:i2]))
elif data_rep2['G2/S_flags'][_i]:
g2_rgs.append(rg_mean(pt_[i1:i2]))
g1_rgs = np.array(g1_rgs)
g2_rgs = np.array(g2_rgs)
# +
# %matplotlib inline
rg_limits = [0,1500]
fig, ax = plt.subplots(figsize=(_single_col_width, _single_col_width),dpi=600)
ax.hist(g1_rgs, 50, range=(min(rg_limits),max(rg_limits)),
density=True, alpha=0.5,
color=[0.2,0.5,0.5], label=f'G1, median={np.nanmedian(g1_rgs):.0f}nm')
ax.hist(g2_rgs, 50, range=(min(rg_limits),max(rg_limits)),
density=True, alpha=0.5,
color=[1,0.2,0.2], label=f'G2/S, median={np.nanmedian(g2_rgs):.0f}nm')
ax.legend(fontsize=_font_size-1, loc='upper right')
ax.set_xlabel("Radius of gyration (nm)", fontsize=_font_size, labelpad=1)
ax.set_ylabel("Probability density", fontsize=_font_size, labelpad=1)
ax.tick_params('both', labelsize=_font_size,
width=_ticklabel_width, length=_ticklabel_size,
pad=1, labelleft=True) # remove bottom ticklabels for a_ax
[i[1].set_linewidth(_ticklabel_width) for i in ax.spines.items()]
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_xlim(rg_limits)
plt.gcf().subplots_adjust(bottom=0.15, left=0.15)
plt.savefig(os.path.join(figure_folder, f'LFig5A_chr21-repeat_radius_of_gyration_G1-G2.pdf'), transparent=True)
plt.show()
# +
from tqdm import tqdm_notebook as tqdm
resolution = 0.05 # Mb
g1_gsizes = []
g2_gsizes = []
for _i, (pt_,doms_) in tqdm(enumerate(zip(data_rep2['dna_hzxys'][:,:,1:],data_rep2['domain_starts']))):
for i1,i2 in zip(doms_[1:-2],doms_[2:-1]):
if data_rep2['G1_flags'][_i]:
g1_gsizes.append((i2-i1)*resolution)
elif data_rep2['G2_flags'][_i]:
g2_gsizes.append((i2-i1)*resolution)
g1_gsizes = np.array(g1_gsizes)
g2_gsizes = np.array(g2_gsizes)
# +
# %matplotlib inline
rg_limits = [0,4]
fig, ax = plt.subplots(figsize=(_single_col_width, _single_col_width),dpi=600)
ax.hist(g1_gsizes, 40, range=(min(rg_limits),max(rg_limits)),
density=True, alpha=0.5,
color=[0.2,0.5,0.5], label=f'G1, median={np.nanmedian(g1_gsizes):.2f}Mb')
ax.hist(g2_gsizes, 40, range=(min(rg_limits),max(rg_limits)),
density=True, alpha=0.5,
color=[1,0.2,0.2], label=f'G2/S, median={np.nanmedian(g2_gsizes):.2f}Mb')
ax.legend(fontsize=_font_size-1, loc='upper right')
ax.set_xlabel("Genomic size (Mb)", fontsize=_font_size, labelpad=1)
ax.set_ylabel("Probability density", fontsize=_font_size, labelpad=1)
ax.tick_params('both', labelsize=_font_size,
width=_ticklabel_width, length=_ticklabel_size,
pad=1, labelleft=True) # remove bottom ticklabels for a_ax
[i[1].set_linewidth(_ticklabel_width) for i in ax.spines.items()]
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.set_xlim(rg_limits)
plt.gcf().subplots_adjust(bottom=0.15, left=0.15)
plt.savefig(os.path.join(figure_folder, f'LFig5B_chr21-repeat_domain_size_G1-G2.pdf'), transparent=True)
plt.show()
| 36.339124 | 1,155 |
92cbf2cc356b68b5fdf4fc54d754fa0f5e5eadd3
|
py
|
python
|
Week5_Policy-based methods/practice_reinforce_pytorch.ipynb
|
shih-chi-47/Practical_RL
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="Yh2MfkCkM_eK" colab_type="text"
# # REINFORCE in PyTorch
#
# Just like we did before for Q-learning, this time we'll design a PyTorch network to learn `CartPole-v0` via policy gradient (REINFORCE).
#
# Most of the code in this notebook is taken from approximate Q-learning, so you'll find it more or less familiar and even simpler.
# + id="k5NokaLUM_eL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 136} executionInfo={"status": "ok", "timestamp": 1593571335747, "user_tz": 240, "elapsed": 15303, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}} outputId="a1da6ed4-6fd0-4866-8cef-9b093d058e8c"
import sys, os
if 'google.colab' in sys.modules and not os.path.exists('.setup_complete'):
# !wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/spring20/setup_colab.sh -O- | bash
# !wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/coursera/grading.py -O ../grading.py
# !wget -q https://raw.githubusercontent.com/yandexdataschool/Practical_RL/coursera/week5_policy_based/submit.py
# !touch .setup_complete
# This code creates a virtual display to draw game images on.
# It will have no effect if your machine has a monitor.
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY")) == 0:
# !bash ../xvfb start
os.environ['DISPLAY'] = ':1'
# + id="KnsF7KZZM_eO" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593571335833, "user_tz": 240, "elapsed": 13381, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
import gym
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# + [markdown] id="QnMTbOMDM_eS" colab_type="text"
# A caveat: we have received reports that the following cell may crash with `NameError: name 'base' is not defined`. The [suggested workaround](https://www.coursera.org/learn/practical-rl/discussions/all/threads/N2Pw652iEemRYQ6W2GuqHg/replies/te3HpQwOQ62tx6UMDoOt2Q/comments/o08gTqelT9KPIE6npX_S3A) is to install `gym==0.14.0` and `pyglet==1.3.2`.
# + id="DYO-8LSuM_eS" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 286} executionInfo={"status": "ok", "timestamp": 1593571340629, "user_tz": 240, "elapsed": 1947, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}} outputId="c20aa832-36ca-45f6-cabb-9a918a9d9403"
env = gym.make("CartPole-v0")
# gym compatibility: unwrap TimeLimit
if hasattr(env, '_max_episode_steps'):
env = env.env
env.reset()
n_actions = env.action_space.n
state_dim = env.observation_space.shape
plt.imshow(env.render("rgb_array"))
# + id="tRGe4xmbQ-A5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} executionInfo={"status": "ok", "timestamp": 1593571549302, "user_tz": 240, "elapsed": 230, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}} outputId="5d8cfa90-2c3f-4f1b-e510-ebc77845c44c"
print(n_actions)
print(state_dim)
# + [markdown] id="mID6OkghM_eV" colab_type="text"
# # Building the network for REINFORCE
# + [markdown] id="UMmoNotQM_eV" colab_type="text"
# For REINFORCE algorithm, we'll need a model that predicts action probabilities given states.
#
# For numerical stability, please __do not include the softmax layer into your network architecture__.
# We'll use softmax or log-softmax where appropriate.
# + id="twZd1ky2M_eW" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593571373697, "user_tz": 240, "elapsed": 2370, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
import torch
import torch.nn as nn
# + id="vqiu__WlM_eY" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593577449872, "user_tz": 240, "elapsed": 333, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
# Build a simple neural network that predicts policy logits.
# Keep it simple: CartPole isn't worth deep architectures.
model = nn.Sequential(
# <YOUR CODE: define a neural network that predicts policy logits>
nn.Linear(state_dim[0], 32),
nn.ReLU(),
nn.Linear(32,32),
nn.ReLU(),
nn.Linear(32,n_actions)
)
# + [markdown] id="rq_PaGQ8M_ea" colab_type="text"
# #### Predict function
# + [markdown] id="bN4tiXpVM_ea" colab_type="text"
# Note: output value of this function is not a torch tensor, it's a numpy array.
# So, here gradient calculation is not needed.
# <br>
# Use [no_grad](https://pytorch.org/docs/stable/autograd.html#torch.autograd.no_grad)
# to suppress gradient calculation.
# <br>
# Also, `.detach()` (or legacy `.data` property) can be used instead, but there is a difference:
# <br>
# With `.detach()` computational graph is built but then disconnected from a particular tensor,
# so `.detach()` should be used if that graph is needed for backprop via some other (not detached) tensor;
# <br>
# In contrast, no graph is built by any operation in `no_grad()` context, thus it's preferable here.
# + id="6O4AylGjM_eb" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593577451108, "user_tz": 240, "elapsed": 314, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
def predict_probs(states):
"""
Predict action probabilities given states.
:param states: numpy array of shape [batch, state_shape]
:returns: numpy array of shape [batch, n_actions]
"""
# convert states, compute logits, use softmax to get probability
# <YOUR CODE>
# return <YOUR CODE>
states = torch.tensor(states, dtype=torch.float32)
pi = model(states)
# print(pi)
with torch.no_grad():
out = nn.functional.softmax(pi,dim=1)
return out.numpy()
# + id="EooZFTXDM_ed" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593577451204, "user_tz": 240, "elapsed": 178, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
test_states = np.array([env.reset() for _ in range(5)])
test_probas = predict_probs(test_states)
assert isinstance(test_probas, np.ndarray), \
"you must return np array and not %s" % type(test_probas)
assert tuple(test_probas.shape) == (test_states.shape[0], env.action_space.n), \
"wrong output shape: %s" % np.shape(test_probas)
assert np.allclose(np.sum(test_probas, axis=1), 1), "probabilities do not sum to 1"
# print(test_probas)
# + [markdown] id="d4NmRsMvM_ef" colab_type="text"
# ### Play the game
#
# We can now use our newly built agent to play the game.
# + id="3Yrk4CX3M_eg" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593577452022, "user_tz": 240, "elapsed": 405, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
def generate_session(env, t_max=1000):
"""
Play a full session with REINFORCE agent.
Returns sequences of states, actions, and rewards.
"""
# arrays to record session
states, actions, rewards = [], [], []
s = env.reset()
for t in range(t_max):
# action probabilities array aka pi(a|s)
action_probs = predict_probs(np.array([s]))[0]
# Sample action with given probabilities.
# a = <YOUR CODE>
a = np.random.choice(2, p=action_probs)
new_s, r, done, info = env.step(a)
# record session history to train later
states.append(s)
actions.append(a)
rewards.append(r)
s = new_s
if done:
break
return states, actions, rewards
# + id="3WuFuLEwM_ei" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593577452222, "user_tz": 240, "elapsed": 386, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
# test it
states, actions, rewards = generate_session(env)
# + [markdown] id="Ssq_xy_uM_ek" colab_type="text"
# ### Computing cumulative rewards
#
# $$
# \begin{align*}
# G_t &= r_t + \gamma r_{t + 1} + \gamma^2 r_{t + 2} + \ldots \\
# &= \sum_{i = t}^T \gamma^{i - t} r_i \\
# &= r_t + \gamma * G_{t + 1}
# \end{align*}
# $$
# + id="-u87Y0SqM_ek" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593577452651, "user_tz": 240, "elapsed": 318, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
def get_cumulative_rewards(rewards, # rewards at each step
gamma=0.99 # discount for reward
):
"""
Take a list of immediate rewards r(s,a) for the whole session
and compute cumulative returns (a.k.a. G(s,a) in Sutton '16).
G_t = r_t + gamma*r_{t+1} + gamma^2*r_{t+2} + ...
A simple way to compute cumulative rewards is to iterate from the last
to the first timestep and compute G_t = r_t + gamma*G_{t+1} recurrently
You must return an array/list of cumulative rewards with as many elements as in the initial rewards.
"""
# <YOUR CODE>
# return <YOUR CODE: array of cumulative rewards>
G = rewards.copy()
for idx in range(len(G)-2,-1,-1):
G[idx] = rewards[idx] + gamma*G[idx+1]
return G
# + id="busKVHRjM_em" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} executionInfo={"status": "ok", "timestamp": 1593577452782, "user_tz": 240, "elapsed": 179, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}} outputId="01f21ded-023d-49f0-c332-e9b142114024"
get_cumulative_rewards(rewards)
assert len(get_cumulative_rewards(list(range(100)))) == 100
assert np.allclose(
get_cumulative_rewards([0, 0, 1, 0, 0, 1, 0], gamma=0.9),
[1.40049, 1.5561, 1.729, 0.81, 0.9, 1.0, 0.0])
assert np.allclose(
get_cumulative_rewards([0, 0, 1, -2, 3, -4, 0], gamma=0.5),
[0.0625, 0.125, 0.25, -1.5, 1.0, -4.0, 0.0])
assert np.allclose(
get_cumulative_rewards([0, 0, 1, 2, 3, 4, 0], gamma=0),
[0, 0, 1, 2, 3, 4, 0])
print("looks good!")
# + [markdown] id="Jj3Nu0mYM_ep" colab_type="text"
# #### Loss function and updates
#
# We now need to define objective and update over policy gradient.
#
# Our objective function is
#
# $$ J \approx { 1 \over N } \sum_{s_i,a_i} G(s_i,a_i) $$
#
# REINFORCE defines a way to compute the gradient of the expected reward with respect to policy parameters. The formula is as follows:
#
# $$ \nabla_\theta \hat J(\theta) \approx { 1 \over N } \sum_{s_i, a_i} \nabla_\theta \log \pi_\theta (a_i \mid s_i) \cdot G_t(s_i, a_i) $$
#
# We can abuse PyTorch's capabilities for automatic differentiation by defining our objective function as follows:
#
# $$ \hat J(\theta) \approx { 1 \over N } \sum_{s_i, a_i} \log \pi_\theta (a_i \mid s_i) \cdot G_t(s_i, a_i) $$
#
# When you compute the gradient of that function with respect to network weights $\theta$, it will become exactly the policy gradient.
#
#
# #### My Notes
# Entropy for action is
#
# $$ H(\pi(\cdot|s_t)) = - \sum_{a\in A} \pi(a|s_t)\log{\pi(a|s_t)}$$
#
# which is high if a policy choose more evenly among the available actions.
#
# Including objective function $\hat{J}$ and entorpy $H$ into loss for gradient ascent, the agent optimizes the objective while being encouraged exploration.
# + id="tdJpWJFLM_ep" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593577453387, "user_tz": 240, "elapsed": 255, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
def to_one_hot(y_tensor, ndims):
""" helper: take an integer vector and convert it to 1-hot matrix. """
y_tensor = y_tensor.type(torch.LongTensor).view(-1, 1)
y_one_hot = torch.zeros(
y_tensor.size()[0], ndims).scatter_(1, y_tensor, 1)
return y_one_hot
# + id="XIrxOodGM_er" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593577453795, "user_tz": 240, "elapsed": 273, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
# Your code: define optimizers
optimizer = torch.optim.Adam(model.parameters(), 1e-3)
def train_on_session(states, actions, rewards, gamma=0.99, entropy_coef=1e-2):
"""
Takes a sequence of states, actions and rewards produced by generate_session.
Updates agent's weights by following the policy gradient above.
Please use Adam optimizer with default parameters.
"""
# cast everything into torch tensors
states = torch.tensor(states, dtype=torch.float32)
actions = torch.tensor(actions, dtype=torch.int32)
cumulative_returns = np.array(get_cumulative_rewards(rewards, gamma))
cumulative_returns = torch.tensor(cumulative_returns, dtype=torch.float32)
# predict logits, probas and log-probas using an agent.
logits = model(states)
probs = nn.functional.softmax(logits, -1)
log_probs = nn.functional.log_softmax(logits, -1)
assert all(isinstance(v, torch.Tensor) for v in [logits, probs, log_probs]), \
"please use compute using torch tensors and don't use predict_probs function"
# select log-probabilities for chosen actions, log pi(a_i|s_i)
log_probs_for_actions = torch.sum(
log_probs * to_one_hot(actions, env.action_space.n), dim=1)
# Compute loss here. Don't forgen entropy regularization with `entropy_coef`
entropy = torch.sum(probs*log_probs)
J_hat = torch.mean(log_probs_for_actions*cumulative_returns)
loss = -(J_hat + entropy_coef*entropy)
# Gradient descent step
optimizer.zero_grad()
loss.backward()
optimizer.step()
# technical: return session rewards to print them later
return np.sum(rewards)
# + [markdown] id="2rGCGQxBM_et" colab_type="text"
# ### The actual training
# + id="8ofAn8H5M_et" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 238} executionInfo={"status": "ok", "timestamp": 1593577502263, "user_tz": 240, "elapsed": 47178, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}} outputId="c2bc4170-fc86-4f89-f9a4-3dbae82f4c8b"
for i in range(100):
rewards = [train_on_session(*generate_session(env)) for _ in range(100)] # generate new sessions
print("mean reward:%.3f" % (np.mean(rewards)))
if np.mean(rewards) > 300:
print("You Win!") # but you can train even further
break
# + [markdown] id="a-6aa7fYM_ew" colab_type="text"
# ### Results & video
# + id="fdspwfagM_ew" colab_type="code" colab={} executionInfo={"status": "ok", "timestamp": 1593577525958, "user_tz": 240, "elapsed": 17541, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}}
# Record sessions
import gym.wrappers
with gym.wrappers.Monitor(gym.make("CartPole-v0"), directory="videos", force=True) as env_monitor:
sessions = [generate_session(env_monitor) for _ in range(100)]
# + id="0AM5QejmM_ey" colab_type="code" colab={"resources": {"http://localhost:8080/videos/openaigym.video.0.121.video000064.mp4": {"data": "CjwhRE9DVFlQRSBodG1sPgo8aHRtbCBsYW5nPWVuPgogIDxtZXRhIGNoYXJzZXQ9dXRmLTg+CiAgPG1ldGEgbmFtZT12aWV3cG9ydCBjb250ZW50PSJpbml0aWFsLXNjYWxlPTEsIG1pbmltdW0tc2NhbGU9MSwgd2lkdGg9ZGV2aWNlLXdpZHRoIj4KICA8dGl0bGU+RXJyb3IgNDA0IChOb3QgRm91bmQpISExPC90aXRsZT4KICA8c3R5bGU+CiAgICAqe21hcmdpbjowO3BhZGRpbmc6MH1odG1sLGNvZGV7Zm9udDoxNXB4LzIycHggYXJpYWwsc2Fucy1zZXJpZn1odG1se2JhY2tncm91bmQ6I2ZmZjtjb2xvcjojMjIyO3BhZGRpbmc6MTVweH1ib2R5e21hcmdpbjo3JSBhdXRvIDA7bWF4LXdpZHRoOjM5MHB4O21pbi1oZWlnaHQ6MTgwcHg7cGFkZGluZzozMHB4IDAgMTVweH0qID4gYm9keXtiYWNrZ3JvdW5kOnVybCgvL3d3dy5nb29nbGUuY29tL2ltYWdlcy9lcnJvcnMvcm9ib3QucG5nKSAxMDAlIDVweCBuby1yZXBlYXQ7cGFkZGluZy1yaWdodDoyMDVweH1we21hcmdpbjoxMXB4IDAgMjJweDtvdmVyZmxvdzpoaWRkZW59aW5ze2NvbG9yOiM3Nzc7dGV4dC1kZWNvcmF0aW9uOm5vbmV9YSBpbWd7Ym9yZGVyOjB9QG1lZGlhIHNjcmVlbiBhbmQgKG1heC13aWR0aDo3NzJweCl7Ym9keXtiYWNrZ3JvdW5kOm5vbmU7bWFyZ2luLXRvcDowO21heC13aWR0aDpub25lO3BhZGRpbmctcmlnaHQ6MH19I2xvZ297YmFja2dyb3VuZDp1cmwoLy93d3cuZ29vZ2xlLmNvbS9pbWFnZXMvbG9nb3MvZXJyb3JwYWdlL2Vycm9yX2xvZ28tMTUweDU0LnBuZykgbm8tcmVwZWF0O21hcmdpbi1sZWZ0Oi01cHh9QG1lZGlhIG9ubHkgc2NyZWVuIGFuZCAobWluLXJlc29sdXRpb246MTkyZHBpKXsjbG9nb3tiYWNrZ3JvdW5kOnVybCgvL3d3dy5nb29nbGUuY29tL2ltYWdlcy9sb2dvcy9lcnJvcnBhZ2UvZXJyb3JfbG9nby0xNTB4NTQtMngucG5nKSBuby1yZXBlYXQgMCUgMCUvMTAwJSAxMDAlOy1tb3otYm9yZGVyLWltYWdlOnVybCgvL3d3dy5nb29nbGUuY29tL2ltYWdlcy9sb2dvcy9lcnJvcnBhZ2UvZXJyb3JfbG9nby0xNTB4NTQtMngucG5nKSAwfX1AbWVkaWEgb25seSBzY3JlZW4gYW5kICgtd2Via2l0LW1pbi1kZXZpY2UtcGl4ZWwtcmF0aW86Mil7I2xvZ297YmFja2dyb3VuZDp1cmwoLy93d3cuZ29vZ2xlLmNvbS9pbWFnZXMvbG9nb3MvZXJyb3JwYWdlL2Vycm9yX2xvZ28tMTUweDU0LTJ4LnBuZykgbm8tcmVwZWF0Oy13ZWJraXQtYmFja2dyb3VuZC1zaXplOjEwMCUgMTAwJX19I2xvZ297ZGlzcGxheTppbmxpbmUtYmxvY2s7aGVpZ2h0OjU0cHg7d2lkdGg6MTUwcHh9CiAgPC9zdHlsZT4KICA8YSBocmVmPS8vd3d3Lmdvb2dsZS5jb20vPjxzcGFuIGlkPWxvZ28gYXJpYS1sYWJlbD1Hb29nbGU+PC9zcGFuPjwvYT4KICA8cD48Yj40MDQuPC9iPiA8aW5zPlRoYXTigJlzIGFuIGVycm9yLjwvaW5zPgogIDxwPiAgPGlucz5UaGF04oCZcyBhbGwgd2Uga25vdy48L2lucz4K", "ok": false, "headers": [["content-length", "1449"], ["content-type", "text/html; charset=utf-8"]], "status": 404, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 501} executionInfo={"status": "ok", "timestamp": 1593577545722, "user_tz": 240, "elapsed": 304, "user": {"displayName": "\u5ed6\u58eb\u9f4a", "photoUrl": "", "userId": "15119494860324039567"}} outputId="045401ba-99a7-40e1-88ab-fbc5ff0aa176"
# Show video. This may not work in some setups. If it doesn't
# work for you, you can download the videos and view them locally.
from pathlib import Path
from IPython.display import HTML
video_names = sorted([s for s in Path('videos').iterdir() if s.suffix == '.mp4'])
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format(video_names[-1])) # You can also try other indices
# + id="coT-6ylxM_e0" colab_type="code" colab={}
from submit import submit_cartpole
submit_cartpole(generate_session, '[email protected]', 'YourAssignmentToken')
# + [markdown] id="msjZowfPM_e2" colab_type="text"
# That's all, thank you for your attention!
#
# Not having enough? There's an actor-critic waiting for you in the honor section. But make sure you've seen the videos first.
| 50.716667 | 2,501 |
925d8d19e34c868f9ce3a0cc034f67563909f0b0
|
py
|
python
|
.ipynb_checkpoints/Workflow-checkpoint.ipynb
|
maxmiao2017/Resource-Watch
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
path = 'C:/Users/Max81007/Desktop/Python/Resource_Watch/'
excel = path + 'gdalinfo_on_s3.csv'
# +
gdalinfo_results = pd.read_csv(excel, header=0, sep= ',', index_col=0)
def nodata_finder(gdalinfo):
try:
contains_no_data = 'NoData' in gdalinfo
return(contains_no_data)
except:
print('gdalinfo was not a string')
return(False)
gdalinfo_results['contains_no_data'] = list(map(nodata_finder, gdalinfo_results['gdalinfo']))
# -
gdalinfo_results.head(1)
# +
def ID(Key):
ID = Key.split("/")
ID_trim = list(map(str.strip, ID))[-2:]
ID_trim = '/'.join(ID_trim)
return(ID_trim)
def stats(gdalinfo):
try:
stats = gdalinfo.split("\\n")
stats_trim = list(map(str.strip, stats))
stats_minmax = [item for item in stats_trim if "Minimum=" in item][0]
Minimum = (stats_minmax.split(',')[0]).split('=')[1]
Maximum = (stats_minmax.split(',')[1]).split('=')[1]
Mean = (stats_minmax.split(',')[2]).split('=')[1]
StdDev = (stats_minmax.split(',')[3]).split('=')[1]
stats_minmax = [item for item in stats_trim if "Minimum=" in item]
return(Minimum, Maximum, Mean, StdDev, stats_minmax)
except:
return('','','','','')
def NoData(gdalinfo):
try:
stats = gdalinfo.split("\\n")
stats_trim = list(map(str.strip, stats))
stats_nodata = [item for item in stats_trim if "NoData Value=" in item][0]
stats_nodata = stats_nodata.split('=')[1]
return(stats_nodata)
except:
return()
gdalinfo_results['ID'] = list(map(ID, gdalinfo_results['Key']))
gdalinfo_results['Min'], gdalinfo_results['Max'],gdalinfo_results['Mean'],gdalinfo_results['StdDevn'],gdalinfo_results['stats_minmax'] = list(zip(*list(map(stats, gdalinfo_results['gdalinfo']))))
gdalinfo_results['NoData'] = list(map(NoData, gdalinfo_results['gdalinfo']))
# gdalinfo_results.drop(["list", "of", "column names", "to drop"], axis=1)
gdalinfo_results = gdalinfo_results[['Size','gdalinfo','ID','contains_no_data','NoData','Min','Max','Mean','StdDevn','stats_minmax']]
gdalinfo_results
# df = pd.DataFrame(gdalinfo_results, columns=['Size','gdalinfo','ID','contains_no_data','NoData','Min','Max','Mean','StdDevn','stats_minmax'])
# df
# -
df.to_csv(path+'gdal.csv')
# +
test = str(b'Driver: GTiff/GeoTIFF\nFiles: /vsicurl/https://wri-public-data.s3.amazonaws.com/resourcewatch/raster/Annual_discharge_anomalies/mosaic2.tif\nSize is 719, 359\nCoordinate System is:\nGEOGCS["WGS 84",\n DATUM["WGS_1984",\n SPHEROID["WGS 84",6378137,298.257223563,\n AUTHORITY["EPSG","7030"]],\n AUTHORITY["EPSG","6326"]],\n PRIMEM["Greenwich",0],\n UNIT["degree",0.0174532925199433],\n AUTHORITY["EPSG","4326"]]\nOrigin = (-180.000000000000000,89.500000000000000)\nPixel Size = (0.500000000000000,-0.500000000000000)\nMetadata:\n AREA_OR_POINT=Area\nImage Structure Metadata:\n COMPRESSION=LZW\n INTERLEAVE=PIXEL\nCorner Coordinates:\nUpper Left (-180.0000000, 89.5000000) (180d 0\' 0.00"W, 89d30\' 0.00"N)\nLower Left (-180.0000000, -90.0000000) (180d 0\' 0.00"W, 90d 0\' 0.00"S)\nUpper Right ( 179.5000000, 89.5000000) (179d30\' 0.00"E, 89d30\' 0.00"N)\nLower Right ( 179.5000000, -90.0000000) (179d30\' 0.00"E, 90d 0\' 0.00"S)\nCenter ( -0.2500000, -0.2500000) ( 0d15\' 0.00"W, 0d15\' 0.00"S)\nBand 1 Block=719x256 Type=Float32, ColorInterp=Gray\n Minimum=-50.000, Maximum=50.000, Mean=0.886, StdDev=10.783\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.88587723984361\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.783266005078\nBand 2 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.147, StdDev=10.282\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.1474555772474\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.281783423571\nBand 3 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.624, StdDev=9.815\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.62417745627566\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.814610999746\nBand 4 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.175, StdDev=10.562\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.1753437054194\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.562257949487\nBand 5 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=1.274, StdDev=11.320\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=1.2742265241435\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=11.319668942399\nBand 6 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.954, StdDev=9.953\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.95442023655351\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.95308173248\nBand 7 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.617, StdDev=10.285\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.61672198802224\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.285160028284\nBand 8 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.946, StdDev=10.041\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.94628178469582\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.041316022325\nBand 9 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.077, StdDev=9.688\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.077101274619067\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.6876705135963\nBand 10 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.189, StdDev=9.996\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.18890920436437\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.995836242868\nBand 11 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.269, StdDev=8.797\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.2690102977942\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=8.796523038569\nBand 12 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.855, StdDev=9.814\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.85528527999459\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.8139951970358\nBand 13 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.401, StdDev=9.440\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.40066166768751\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.4402872446692\nBand 14 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.690, StdDev=8.852\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.69027522643455\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=8.8518639604879\nBand 15 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.369, StdDev=9.622\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.36923260941601\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.6218444548456\nBand 16 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.246, StdDev=8.733\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.24583670347873\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=8.7327195567985\nBand 17 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.175, StdDev=8.572\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.17524735575922\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=8.5719369389132\nBand 18 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.197, StdDev=9.532\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.19660108465165\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.5316047908866\nBand 19 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.179, StdDev=8.922\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.17862261979868\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=8.9216585745583\nBand 20 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.823, StdDev=9.094\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.82256825305034\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.0939235364121\nBand 21 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.014, StdDev=8.029\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.014179038107644\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=8.0294396946257\nBand 22 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.557, StdDev=9.069\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.55698262573679\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.0691279169033\nBand 23 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.795, StdDev=10.247\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.79503744418201\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.24736955729\nBand 24 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.928, StdDev=9.770\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.92752845415044\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.7703133221428\nBand 25 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-1.195, StdDev=10.459\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-1.1951529928154\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.458539441126\nBand 26 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.906, StdDev=9.017\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.90589720731683\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.0174004536785\nBand 27 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.230, StdDev=9.079\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.22957464993864\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.0785296224855\nBand 28 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.821, StdDev=10.030\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.82072278674783\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.030116416823\nBand 29 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=0.084, StdDev=10.695\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=0.084333163589206\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.694657191941\nBand 30 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.070, StdDev=10.515\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.070222323699887\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.515024699549\nBand 31 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.559, StdDev=10.351\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.55949410184823\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.351388174732\nBand 32 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.806, StdDev=10.106\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.80646490820014\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.106468661186\nBand 33 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-0.679, StdDev=10.656\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-0.67869649588931\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.65586228779\nBand 34 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-1.105, StdDev=10.803\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-1.1045570437167\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.803222879715\nBand 35 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-1.104, StdDev=10.225\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-1.1038827407005\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=10.225328140275\nBand 36 Block=719x256 Type=Float32, ColorInterp=Undefined\n Minimum=-50.000, Maximum=50.000, Mean=-1.460, StdDev=9.980\n NoData Value=-3.40282346638528898e+38\n Metadata:\n STATISTICS_MAXIMUM=50\n STATISTICS_MEAN=-1.4601888261923\n STATISTICS_MINIMUM=-50\n STATISTICS_STDDEV=9.980400075232\n')
test_split = test.split("\\n")
test_trim = list(map(str.strip, test_split))
stats = [item for item in test_trim if "Minimum=" in item][0]
print(stats)
test_split =(stats.split(',')[0]).split('=')[1]
test_split1 =stats.split(',')[1]
test_split2 =stats.split(',')[2]
test_split3 =stats.split(',')[3]
print(test_split)
Stats = ['Minimum','Maximum','Mean','StdDev']
# -
| 149.86 | 12,109 |
4afd4f93d134ef676ead3a6269be3629d985f6a4
|
py
|
python
|
_notebooks/2021-01-04-Lock-free-data-structures.ipynb
|
abhishekSingh210193/cs_craftmanship
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:anaconda]
# language: python
# name: conda-env-anaconda-py
# ---
# # Data structures for fast infinte batching or streaming requests processing
#
# > Here we dicuss one of the coolest use of a data structures to address one of the very natural use case scenario of a server processing streaming requests from clients in order.Usually processing these requests involve a pipeline of operations applied based on request and multiple threads are in charge of dealing with these satges of pipeline. The requests gets accessed by these threads and the threads performing operations in the later part of the pipeline will have to wait for the earlier threads to finish their execution.
#
# The usual way to ensure the correctness of multiple threads handling the same data concurrently is use locks.The problem is framed as a producer / consumer problems , where one threads finishes its operation and become producer of the data to be worked upon by another thread, which is a consumer. These two threads needs to be synchronized.
#
# > Note: In this blog we will discuss a "lock-free" circular queue data structure called disruptor. It was designed to be an efficient concurrent message passing datastructure.The official implementations and other discussions are available [here](https://lmax-exchange.github.io/disruptor/#_discussion_blogs_other_useful_links). This blog intends to summarise its use case and show the points where the design of the disruptor scores big.
# # LOCKS ARE BAD
#
# Whenever we have a scenario where mutliple concurrent running threads contend on a shared data structure and you need to ensure visibility of changes (i.e. a consumer thread can only get its hand over the data after the producer has processed it and put it for further processing). The usual and most common way to ensure these two requirements is to use a lock.
# Locks need the operating system to arbitrate which thread has the responsibility on a shared piece of data. The operating system might schedule other processes and the software's thread may be waiting in a queue. Moreover, if other threads get scheduled by the CPU then the cache memory of the softwares's thread will be overwritten and when it finally gets access to the CPU, it may have to go as far as the main memory to get it's required data. All this adds a lot of overhead and is evident by the simple experiment of incrementing a single shared variable. In the experiment below we increment a shared variable in three different ways. In the first case, we have a single process incrementing the variable, in the second case we again have two threads, but they synchronize their way through the operation using locks.
# In the third case, we have two threads which increment the variables and they synchronize their operation using atomic locks.
#
# ## SINGLE PROCESS INCREMENTING A SINGLE VARIABLE
import time
def single_thread():
start = time.time()
x = 0
for i in range(500000000):
x += 1
end = time.time()
return(end-start)
print(single_thread())
#another way for single threaded increment using
class SingleThreadedCounter():
def __init__(self):
self.val = 0
def increment(self):
self.val += 1
# ## TWO PROCESS INCREMENTING A SINGLE VARIABLE
# +
import time
from threading import Thread, Lock
mutex = Lock()
x = 0
def thread_fcn():
global x
mutex.acquire()
for i in range(250000000):
x += 1
mutex.release()
def mutex_increment():
start = time.time()
t1 = Thread(target=thread_fcn)
t2 = Thread(target=thread_fcn)
t1.start()
t2.start()
t1.join()
t2.join()
end = time.time()
return (end-start)
print(mutex_increment())
# -
# > Note: As we can see that the time for performing the increment operation has gone up substantially when we would have expected it take half the time.
# > Important: In the rest of the blog we will take in a very usual scenario we see in streaming request processing.
#
# A client sends in requests to a server in a streaming fashion. The server at its end needs to process the client's request, it may have multiple stages of processing. For example, imagine the client sends in a stream of requests and the server in JSON format. Now the probable first task that the client needs to perform is to parse the JSON request.Imagine a thread being assigned to do this parsing task. It parses requests one after another and hands over the parsed request in some form to another thread which may be responsible for performing business logic for that client. Usually the data structure to manage this message passing and flow control in screaming scenario is handled by a queue data structure. The producer threads (parser thread) puts in parsed data in this queue, from which the consumer thread (the business logic thread) will read of the parsed data. Because we have two threads working concurrently on a single data structure (the queue) we can expect contention to kick in.
# ## WHY QUEUES ARE FLAWED
# The queue could be an obvious choice for handling data communication between multiple threads, but the queue data structure is fundamentally flawed for communication between multiple threads. Imagine the case of the first two threads of the a system using a queue for data communication, the listener thread and the parsing thread. The listener thread listens to bytes from the wire and puts it in a queue and the parser thread will pick up bytes from the queue and parse it. Typically, a queue data structure will have a head field, a tail field and a size field (to tell an empty queue from a full one). The head field will be modified by the parser thread and the tail field by the parser thread. The size field though will be modified by both of the threads and it effectively makes the queue data structure having two writers.
#
# 
# Moreover, the entire data structure will fall in the same cache line and hence when say the listener thread modifies the tail field, the head field in another core also gets invalidated and needs to be fetched from a level 2 cache.
# 
# ## CAN WE AVOID LOCKS ?
# So, using a queue structure for inter-thread communication with expensive locks could cost a lot of performance for any system. Hence, we move towards a better data structure that solves the issues of synchronization among threads.
# The data structure we use doesn't use locks.
# The main components of the data structure are -
# A. A circular buffer
# B. A sequence number field which has a number indicating a specific slot in the circular buffer.
# C. Each of the worker threads have their own sequence number.
# The circular buffer is written to by the producers . The producer in each case updates the sequence number for each of the circular buffers. The worker threads (consumer thread) have their own sequence number indicating the slots they have consumed so far from the circular buffer.
# 
# >Note: In the design, each of the elements has a SINGLE WRITER. The producer threads of the circular ring write to the ring buffer, and its sequence number. The worker consumer threads will write their own local sequence number. No field or data have more than one writer in this data structure.
# ## WRITE OPERATION ON THE LOCK-FREE DATA STRUCTURE
# Before writing a slot in the circular buffer, the thread has to make sure that it doesn't overwrite old bytes that have not yet been processed by the consumer thread. The consumer thread also maintains a sequence number, this number indicates the slots that have been already processed. So the producer thread before writing grabs the circular buffer's sequence number, adds one to it (mod size of the circular buffer) to get the next eligible slot for writing. But before putting in the bytes in that slot it checks with the dependent consumer thread (by reading their local sequence number) if they have processed this slot. If say the consumer has not yet processed this slot, then the producer thread goes in a busy wait till the slot is available to write to. When the slot is overwritten then the circular buffer's sequence number is updated by the producer thread. This indicates to consumer threads that they have a new slot to consume.
# 
# Writing to the circular buffers is a 2-phase commit. In the first phase, we check out a slot from the circular buffer. We can only check out a slot if it has already been consumed. This is ensured by following the logic mentioned above. Once the slot is checked out the producer writes the next byte to it. Then it sends a commit message to commit the entry by updating the circular buffer's sequence number to its next logical value(+1 mod size of the circular buffer)
# 
# ## READ OPERATION ON THE LOCK_FREE DATA STRUCTURE
# The consumer thread reads the slots from circular buffer -1. Before reading the next slot, it checks (read) the buffer's sequence number. This number is indicative of the slots till which the buffer can read.
# 
# ## ENSURING THAT THE READS HAPPEN IN PROGRAM ORDER
#
# There is just one piece of detail that needs to be addressed for the above data structure to work. Compilers and CPU take the liberty to reorder independent instructions for optimizations. This doesn’t have any issues in the single process case where the program’s logic integrity is maintained. But this could logic breakdown in case of multiple threads.
# Imagine a typical simplified read/write to the circular buffer described above—
# Say the publisher thread’s sequence of operation is indicated in black, and the consumer thread’s in brown. The publisher checks in a slot and it updates the sequence number. Then the consumer thread reads the (wrong) sequence number of the buffer and goes on to access the slot which is yet to be written.
# 
# The way we could solve this is by putting memory fences around the variables which tells the compiler and CPU to not reorder reads / writes before and after those shared variables. In that way programs logic integrity is maintained.
# 
| 77.358209 | 1,004 |
a6dfbc12434477592d3c0089a7010ac422534860
|
py
|
python
|
notebooks/SimplexCombo.ipynb
|
alanjeffares/Simplex
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/alanjeffares/Simplex/blob/main/notebooks/SimplexCombo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="zuBfkV9zGRV3" outputId="d23a6796-2c29-444c-e73a-9af18151632c"
# !git clone https://github.com/alanjeffares/Simplex.git
# + colab={"base_uri": "https://localhost:8080/"} id="w15LZ0qoGVb3" outputId="8e27f7dc-9cdc-4931-8a58-05b5d5483e87"
# !pip install captum
# !pip install pytorch_influence_functions
# + colab={"base_uri": "https://localhost:8080/"} id="23qt3a7MGW-u" outputId="24eb6524-2556-4259-fffa-54b664af9e51"
# %cd Simplex/
import explainers
from explainers.simplex import Simplex
import models
from models.image_recognition import MnistClassifier
from utils.schedulers import ExponentialScheduler
from experiments.mnist import load_mnist
# %cd ../
# + id="cHrfUKDQGdBF"
# hyperparams
corpus_size = 1000
cv_ls = [0] # list(range(10))
# + colab={"base_uri": "https://localhost:8080/"} id="SH1AHxhDZF0H" outputId="8d2c3c22-b656-486c-d248-e26af2412f77"
# run the code
# %cd Simplex/
for cv in cv_ls:
# !python -m experiments.mnist -experiment "approximation_quality" -cv $cv -corpus_size $corpus_size
# %cd ../
# + id="IzqGAbTMGjOK"
# + id="fQ0NpBR2HxMJ"
# + id="tcmQjghhHxP3"
import captum.attr
import numpy as np
import pandas as pd
import torch
import torchvision
import torch.optim as optim
import os
import time
import seaborn as sns
import math
import sklearn
import argparse
import pickle as pkl
import torch.nn.functional as F
import torch.nn as nn
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import pytorch_influence_functions as ptif
from pathlib import Path
# + id="xMdhjxF7jNka"
class MnistClassifier(nn.Module):
def __init__(self) -> None:
"""
CNN classifier model
"""
super(MnistClassifier, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
def latent_representation(self, x: torch.Tensor) -> torch.Tensor:
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
return x
def forward(self, x: torch.Tensor) -> torch.Tensor:
x = self.latent_representation(x)
x = self.fc2(x)
return F.log_softmax(x, dim=-1)
def probabilities(self, x: torch.Tensor) -> torch.Tensor:
"""
Returns the class probabilities for the input x
:param x: input features
:return: class probabilities
"""
x = self.latent_representation(x)
x = self.fc2(x)
return F.softmax(x, dim=-1)
def presoftmax(self, x: torch.Tensor) -> torch.Tensor:
"""
Returns the preactivation outputs for the input x
:param x: input features
:return: presoftmax activations
"""
x = self.latent_representation(x)
return self.fc2(x)
def latent_to_presoftmax(self, h: torch.Tensor) -> torch.Tensor:
"""
Maps a latent representation to a preactivation output
:param h: latent representations
:return: presoftmax activations
"""
return self.fc2(h)
# + id="Uf6i0AagHiKB"
cv = 0
test_size = 100
train_only = True
# + colab={"base_uri": "https://localhost:8080/"} id="N93Yz8E3HiQx" outputId="ab27c564-9ac1-4514-c88a-9603498d39d1"
# %cd Simplex/
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
explainers_name = ['simplex', 'nn_uniform', 'nn_dist', 'representer']
current_path = Path.cwd()
save_path = 'experiments/results/mnist/quality/'
save_path = current_path / save_path
classifier = MnistClassifier()
classifier.load_state_dict(torch.load(save_path / f'model_cv{cv}.pth'))
classifier.to(device)
classifier.eval()
# %cd ../
# + id="jw4kJxA_j1aX"
# alternative approach
class SimplexCombo:
def __init__(self, corpus_examples, corpus_latent_reps: torch.Tensor) -> None:
"""
Initialize a SimplEx explainer
:param corpus_examples: corpus input features
:param corpus_latent_reps: corpus latent representations
"""
self.corpus_examples = corpus_examples
self.corpus_latent_reps = corpus_latent_reps
self.corpus_size = corpus_latent_reps.shape[0]
self.dim_latent = corpus_latent_reps.shape[-1]
self.weights = None
self.n_test = None
self.hist = None
self.test_examples = None
self.test_latent_reps = None
self.jacobian_projections = None
def fit(self, test_examples, test_latent_reps: torch.Tensor,
n_epoch: int = 10000, reg_factor: float = 1.0, n_keep: int = 5, reg_factor_scheduler=None, dist_factor=1) -> None:
"""
Fit the SimplEx explainer on test examples
:param test_examples: test example input features
:param test_latent_reps: test example latent representations
:param n_keep: number of neighbours used to build a latent decomposition
:param n_epoch: number of epochs to fit the SimplEx
:param reg_factor: regularization prefactor in the objective to control the number of allowed corpus members
:param n_keep: number of corpus members allowed in the decomposition
:param reg_factor_scheduler: scheduler for the variation of the regularization prefactor during optimization
:return:
"""
n_test = test_latent_reps.shape[0]
preweights = torch.zeros((n_test, self.corpus_size, self.corpus_size), device=test_latent_reps.device, requires_grad=True)
alpha = torch.ones((n_test, self.corpus_size), device=test_latent_reps.device)/2
alpha.requires_grad = True
optimizer = torch.optim.Adam([preweights, alpha])
hist = np.zeros((0, 2))
for epoch in range(n_epoch):
optimizer.zero_grad()
weights = F.softmax(preweights, dim=-1) # baseline
corpus_latent_reps_full = torch.einsum('isj,jk->isk', weights, self.corpus_latent_reps)
x = torch.einsum('ti,tip->tip', alpha, (corpus_latent_reps_full - self.corpus_latent_reps))
preds = self.corpus_latent_reps + x
error = ((preds - test_latent_reps) ** 2).sum()
dist_loss = ((corpus_latent_reps_full - test_latent_reps) ** 2).sum()
weights_sorted = torch.sort(weights)[0]
regulator = (weights_sorted[:, :, : (self.corpus_size - n_keep)]).sum()
# loss = error + dist_factor * dist_loss + reg_factor * regulator
loss = error + reg_factor * regulator
loss.backward()
optimizer.step()
if reg_factor_scheduler:
reg_factor = reg_factor_scheduler.step(reg_factor)
hist = np.concatenate((hist,
np.array([loss.item(), regulator.item()]).reshape(1, 2)),
axis=0)
self.weights = torch.softmax(preweights, dim=-1).detach()
self.alpha = alpha.detach()
self.test_latent_reps = test_latent_reps
self.n_test = n_test
self.hist = hist
self.test_examples = test_examples
def jacobian_projection(model, baseline, approx, baseline_latent, corpus_examples,
n_bins: int = 100) \
-> torch.Tensor:
"""
Compute the Jacobian Projection for the test example identified by test_id
:param model: trained classifier
:param baseline: raw baseline input - shape (n_row, n_col)
:param approx: hidden state of corpus approximation (n_hid)
:param baseline_latent: hidden state baseline (n_hid)
:param corpus_examples: hidden state baseline (n_corpus_examples, n_row, n_col)
:param n_bins: number of bins involved in the Riemann sum approximation for the integral
:return:
"""
corpus_inputs = corpus_examples.clone().requires_grad_()
input_shift = corpus_examples - baseline
latent_shift = approx - baseline_latent
latent_shift = latent_shift.unsqueeze(0).repeat(1000,1)
latent_shift_sqrdnorm = torch.sum(latent_shift**2, dim=-1, keepdim=True)
input_grad = torch.zeros(corpus_inputs.shape, device=corpus_inputs.device)
for n in range(1, n_bins + 1):
t = n / n_bins
input = baseline + t * (corpus_inputs - baseline)
latent_reps = model.latent_representation(input.unsqueeze(1))
latent_reps.backward(gradient=latent_shift/latent_shift_sqrdnorm)
input_grad += corpus_inputs.grad
corpus_inputs.grad.data.zero_()
jacobian_projections = input_shift * input_grad / (n_bins)
return jacobian_projections
# + colab={"base_uri": "https://localhost:8080/", "height": 436, "referenced_widgets": ["28725e07ac844054993f85ff78fcbb61", "765a9b468daf49fda20d9ea365e1cf6a", "ec8d1512229143c2825f298794aa9a83", "89da5b8ee61c4518b6f8f08ceb2aa075", "fb2c23cac625424cb03596e66a304774", "fb4317b07a8240eca2aa4040cd9ef7b4", "b99a8124007a4fd581cb7c1da1438e6c", "b6affa348d4547ae9bc251b5294cd888", "68c2cfc5b3ba42c7bbe229d39cb4a666", "7e511e3787084d0c9a7c174aa367a803", "09aa45dff6d3405bbfb7da4a799342ec", "5479e3df0a8d43d599a7212c9ec32ba2", "d8c1884cae4b47269cbd27c8190b0a91", "5f97c85033d04ce4b097b49baace3818", "e83a6ba937144518bf1c3d264c58167a", "59628a9c5b3c4d519a1aa12ca25e4de2", "040ee5c6ae144248822a69f7ca9123f5", "f2c3bc3908d1409083a1e63fa77c3681", "87c992e593b8467aafa07bdc39c6ea43", "a89f0b5fef0c43d5951ce666a6cf7f33", "b9ba1cae15ac4c8e8e054151673dd494", "b002553979374f4d9ede410af002daa2", "7841f48a60944730b15fb7153c2e6220", "502e330a03e643a0a59eefa2ac504985", "543e87fd98a14a079fa18ff160d53ada", "f8f46683b3f3413ab0abdcb0dc48937a", "0866b33860464caaa8466982936d4afb", "ec070669311f47608fbbee070f67c729", "d831970774c944728b0cd9579354d3ca", "7930f7d03e054ad39a11b4a1f7571c96", "5abe2ec80b9c4af5b0e804e66fb61856", "d5472ef3d56143eab0c3184f45c0583e", "3af354efdd2d4174b8658838c3b487ca", "4214fd077cc34bb9bc2e8a7251cda8f6", "a9bf40c9de9b4ed8ab87aea435dbb434", "81930ecbb7a546dcbf90fd0bcfa0a46c", "23fa9403504a424f9065d593c1e76d2f", "884c881e63c1402e8eae396de82cc3d9", "36bf5dd7e3b7473980a2087ff0b6603a", "fe63368f18da48f1a498e09992b550e4", "533203fd338745de95ed97d0c0f94f84", "5da6dc551e424b08b899a121428d5c02", "1d4102b241414f84bac8c91658be5966", "135c4c9e8573467f84a2da5ba8ddc021"]} id="anom2RbNHiS4" outputId="625c642c-e9d8-48d6-8a4d-519bb17de5d0"
random_seed = 0
torch.random.manual_seed(random_seed + cv)
corpus_loader = load_mnist(corpus_size, train=True)
test_loader = load_mnist(test_size, train=train_only)
corpus_examples = enumerate(corpus_loader)
test_examples = enumerate(test_loader)
batch_id_test, (test_data, test_targets) = next(test_examples)
batch_id_corpus, (corpus_data, corpus_target) = next(corpus_examples)
corpus_data = corpus_data.to(device).detach()
test_data = test_data.to(device).detach()
corpus_latent_reps = classifier.latent_representation(corpus_data).detach()
corpus_probas = classifier.probabilities(corpus_data).detach()
corpus_true_classes = torch.zeros(corpus_probas.shape, device=device)
corpus_true_classes[torch.arange(corpus_size), corpus_target] = 1
test_latent_reps_full = classifier.latent_representation(test_data).detach()
test_probs = classifier.probabilities(test_data).detach()
test_preds = test_probs.argmax(1)
# %mkdir figures
# + id="Q4ZtdfUfjUGk"
# + [markdown] id="Pz_1VOPEjU5-"
# # Example from report
# + colab={"base_uri": "https://localhost:8080/"} id="yyohQnrlfY8j" outputId="3c28c3f8-8017-4197-8168-7a769198e2ad"
# select a single test example
i = 6
# 6 = misclassified
# 4 = correct (can change baseline to 9)
test_latent_reps = test_latent_reps_full[i:i+1]
pred_label = test_preds[i].item()
true_label = test_targets[i].item()
# fit regular Simplex
reg_factor_init = 0.1
reg_factor_final = 100
n_epoch = 10000
n_keep = 3
reg_factor_scheduler = ExponentialScheduler(reg_factor_init, reg_factor_final, n_epoch)
simplex = Simplex(corpus_examples=corpus_data,
corpus_latent_reps=corpus_latent_reps)
simplex.fit(test_examples=test_data,
test_latent_reps=test_latent_reps,
n_epoch=n_epoch, reg_factor=reg_factor_init, n_keep=n_keep,
reg_factor_scheduler=reg_factor_scheduler)
# look at results
approx_error = ((simplex.latent_approx() - test_latent_reps)**2).sum()**0.5
print('\nSimplex approx error:', approx_error.item())
big_weights = simplex.weights > 0.05
big_weight_values = simplex.weights[big_weights].cpu().numpy()
print('Bigest weights: ', big_weight_values)
print('Proportion explained:',simplex.weights[big_weights].sum().item())
# + colab={"base_uri": "https://localhost:8080/", "height": 971} id="AuUo1pnH6S4Y" outputId="76d10534-1ace-47d6-e880-e24d13564e03"
# grab jacobians
baseline = -0.4242 * torch.ones(test_data[0,0].shape, device=device)
approx = simplex.latent_approx()[0]
baseline_latent = classifier.latent_representation(baseline[(None,)*2])[0]
jp = jacobian_projection(classifier, baseline, approx,
baseline_latent, simplex.corpus_examples[:,0], n_bins=200)
# plot the explanation
print('True label:', true_label)
print('Pred label:',pred_label)
plt.title('Baseline')
plt.imshow(baseline.cpu().numpy())
plt.axis('off')
plt.show()
plt.title('Test example')
plt.imshow(test_data[i,0].cpu().numpy())
plt.axis('off')
plt.show()
used_examples = corpus_data[big_weights[0]]
used_projs = jp[big_weights[0]]
divnorm=colors.TwoSlopeNorm(vmin=used_projs.min().item(), vcenter=0., vmax=used_projs.max().item())
for j in range(used_examples.shape[0]):
img = used_examples[j,0].cpu().numpy()
proj = used_projs[j].cpu().numpy()
fig, (ax1, ax2, ax3) = plt.subplots(1,3, figsize=(10,6))
fig.suptitle(f'Weight = {simplex.weights[big_weights][j].item()}')
ax1.imshow(img)
ax2.imshow(baseline.cpu().numpy(), cmap='gray', interpolation='none', alpha=0.8)
ax2.imshow(proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax3.imshow(img, cmap='gray', interpolation='none', alpha=0.8)
ax3.imshow(proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax1.axis('off')
ax2.axis('off')
ax3.axis('off')
fig.subplots_adjust(top=1.3)
plt.show()
# + id="h0uD2QdU0uiw"
# !mkdir figures
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="iospeVKS6CjE" outputId="6dee0a20-a37f-4a40-c0d0-dffa48fff5eb"
# tidy plots for report
plt.imshow(test_data[i,0].cpu().numpy(), cmap='gray', interpolation='none')
plt.axis('off')
plt.savefig('figures/1_s_test.pdf', format='pdf', dpi=1200, bbox_inches = 'tight',
pad_inches = 0)
plt.show()
used_examples = corpus_data[big_weights[0]]
used_projs = jp[big_weights[0]]
divnorm=colors.TwoSlopeNorm(vmin=used_projs.min().item(), vcenter=0., vmax=used_projs.max().item())
for j in range(used_examples.shape[0]):
img = used_examples[j,0].cpu().numpy()
proj = used_projs[j].cpu().numpy()
plt.imshow(img, cmap='gray', interpolation='none')
plt.axis('off')
weight = round(simplex.weights[big_weights][j].item(), 3)
plt.savefig(f'figures/1_s_img_{weight}.pdf', format='pdf', dpi=1200, bbox_inches = 'tight',
pad_inches = 0)
plt.show()
plt.imshow(img, cmap='gray', interpolation='none', alpha=0.8)
plt.imshow(proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
plt.axis('off')
plt.savefig(f'figures/1_s_exp_{weight}.pdf', format='pdf', dpi=1200, bbox_inches = 'tight',
pad_inches = 0)
plt.show()
# + id="A7zH2zFCRkxN"
# + id="cmEqXDuURk01"
# fit alternative
reg_factor_init = 0.1
reg_factor_final = 100
n_epoch = 20000
n_keep = 3
reg_factor_scheduler = ExponentialScheduler(reg_factor_init, reg_factor_final, n_epoch)
simplexcombo = SimplexCombo(corpus_examples=corpus_data,
corpus_latent_reps=corpus_latent_reps)
simplexcombo.fit(test_examples=test_data,
test_latent_reps=test_latent_reps,
n_epoch=n_epoch, reg_factor=reg_factor_init, n_keep=n_keep,
reg_factor_scheduler=reg_factor_scheduler)
# calculate predictions
b = simplexcombo.corpus_latent_reps
corpus_latent_reps_full = torch.einsum('isj,jk->isk', simplexcombo.weights, b)
x = torch.einsum('ti,tip->tip', simplexcombo.alpha, (corpus_latent_reps_full - b))
preds = b + x
preds = preds.cpu().numpy()
# + colab={"base_uri": "https://localhost:8080/"} id="-A7hINoyECKd" outputId="6cd36d8f-72ff-462c-f455-3d521a4ae48e"
# look at results for a given baseline
test_latent_reps_np = test_latent_reps.cpu().numpy()
################ Auto select baseline ##########################
# idx_min = ((preds[0] - test_latent_reps_np)**2).sum(1).argmin()
################################################################
################ Choose Baseline Class ##########################
desired_baseline_label = 2
idx_range = torch.arange(corpus_true_classes.shape[0])
baseline_label_choice = (corpus_true_classes.argmax(1) == desired_baseline_label).cpu().numpy()
idx_red = ((preds[0] - test_latent_reps_np)**2).sum(1)[baseline_label_choice].argmin()
idx_min = idx_range[baseline_label_choice][idx_red]
#################################################################
pred_error = (((preds[0] - test_latent_reps_np)**2).sum(1)**0.5)[idx_min]
print('Prediction error:', pred_error)
print('Alpha:', simplexcombo.alpha[0,idx_min].item())
big_weights = simplexcombo.weights[0,idx_min,:] > 0.05
big_weight_values = simplexcombo.weights[0,idx_min,big_weights].cpu().numpy()
print('Bigest weights: ', big_weight_values)
print('Proportion of total weight:', simplexcombo.weights[0,idx_min,big_weights].sum().item())
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="7gUGK2EGDUqD" outputId="40f9eaf9-0bbf-402e-be42-9d70554b54ee"
# get jacobian predictions
baseline = simplexcombo.corpus_examples[idx_min,0]
baseline_latent = simplexcombo.corpus_latent_reps[idx_min]
approx = torch.einsum('sj,jk->sk', simplexcombo.weights[0], simplexcombo.corpus_latent_reps)[idx_min]
jp = jacobian_projection(classifier, baseline, approx,
baseline_latent, simplexcombo.corpus_examples[:,0], n_bins=200)
# plot results
print('True label:', true_label)
print('Pred label:',pred_label)
baseline_label = corpus_true_classes.argmax(1)[idx_min].cpu().numpy()
plt.title(f'Baseline (label = {baseline_label})')
baseline = corpus_data[idx_min,0].cpu().numpy()
plt.imshow(baseline)
plt.show()
plt.title('Test example')
test = test_data[i,0].cpu().numpy()
plt.imshow(test)
plt.show()
used_examples = corpus_data[big_weights]
used_labels = corpus_true_classes.argmax(1)[big_weights]
used_projs = jp[big_weights]
divnorm=colors.TwoSlopeNorm(vmin=used_projs.min().item(), vcenter=0., vmax=used_projs.max().item())
for j in range(used_examples.shape[0]):
img = used_examples[j,0].cpu().numpy()
proj = used_projs[j].cpu().numpy()
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1,4, figsize=(12,6))
fig.suptitle(f'Weight = {simplexcombo.weights[0,idx_min,big_weights][j].item()}')
ax1.imshow(img)
true_label = used_labels[j].cpu().numpy()
ax1.set_title(f'Label = {true_label}')
ax2.imshow(corpus_data[idx_min,0].cpu().numpy(), cmap='gray', interpolation='none', alpha=0.8)
ax2.imshow(proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax3.imshow(img, cmap='gray', interpolation='none', alpha=0.8)
ax3.imshow(proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax4.imshow(test, cmap='gray', interpolation='none', alpha=0.8)
ax4.imshow(proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax1.axis('off')
ax2.axis('off')
ax3.axis('off')
ax4.axis('off')
fig.subplots_adjust(top=1.3)
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="pffqgI3wRk6D" outputId="0ae85b3a-8d82-4a9e-977a-e0b0368c6d62"
baseline_label = corpus_true_classes.argmax(1)[idx_min].cpu().numpy()
baseline = corpus_data[idx_min,0].cpu().numpy()
plt.imshow(baseline, cmap='gray', interpolation='none')
plt.axis('off')
plt.savefig('figures/1_sc_baseline.pdf', format='pdf', dpi=1200, bbox_inches = 'tight',
pad_inches = 0)
plt.show()
test = test_data[i,0].cpu().numpy()
used_examples = corpus_data[big_weights]
used_labels = corpus_true_classes.argmax(1)[big_weights]
used_projs = jp[big_weights]
divnorm=colors.TwoSlopeNorm(vmin=used_projs.min().item(), vcenter=0., vmax=used_projs.max().item())
for j in range(used_examples.shape[0]):
img = used_examples[j,0].cpu().numpy()
proj = used_projs[j].cpu().numpy()
weight = round(simplexcombo.weights[0,idx_min,big_weights][j].item(), 3)
plt.imshow(corpus_data[idx_min,0].cpu().numpy(), cmap='gray', interpolation='none', alpha=0.8)
plt.imshow(proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
plt.axis('off')
plt.savefig(f'figures/1_sc_base_{weight}.pdf', format='pdf', dpi=1200, bbox_inches = 'tight',
pad_inches = 0)
plt.show()
plt.imshow(img, cmap='gray', interpolation='none')
plt.axis('off')
plt.savefig(f'figures/1_sc_img_{weight}.pdf', format='pdf', dpi=1200, bbox_inches = 'tight',
pad_inches = 0)
plt.show()
plt.imshow(img, cmap='gray', interpolation='none', alpha=0.8)
plt.imshow(proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
plt.axis('off')
plt.savefig(f'figures/1_sc_imgproj_{weight}.pdf', format='pdf', dpi=1200, bbox_inches = 'tight',
pad_inches = 0)
plt.show()
plt.imshow(test, cmap='gray', interpolation='none', alpha=0.8)
plt.imshow(proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
plt.axis('off')
plt.savefig(f'figures/1_sc_testproj_{weight}.pdf', format='pdf', dpi=1200, bbox_inches = 'tight',
pad_inches = 0)
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 126} id="s9VEsDpDGHYD" outputId="be488929-8fa5-466e-aca9-b0987e8acdb6"
# !zip -r /content/figures.zip /content/figures
from google.colab import files
files.download("/content/figures.zip")
# + id="7XGS2_LvGHet"
# + id="yJALBYTtGHiA"
# + id="lb7hxiQyGHk-"
# + id="EMIrPY6qGHn-"
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="DBkddO91y9d1" outputId="7a965100-4884-4e72-a536-1e832103d32d"
# decompose into differences and similarities
epsilon = 2
for j in range(used_examples.shape[0]):
img = used_examples[j,0].cpu().numpy()
proj = used_projs[j].cpu().numpy()
diff = np.abs(baseline - test) > epsilon
same = np.abs(baseline - test) <= epsilon
print('Important differences')
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1,4, figsize=(12,6))
fig.suptitle(f'Weight = {simplexcombo.weights[0,idx_min,big_weights][j].item()}')
ax1.imshow(img)
ax2.imshow(baseline, cmap='gray', interpolation='none', alpha=0.8)
ax2.imshow(diff * proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax3.imshow(img, cmap='gray', interpolation='none', alpha=0.8)
ax3.imshow(diff * proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax4.imshow(test, cmap='gray', interpolation='none', alpha=0.8)
ax4.imshow(diff * proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax1.axis('off')
ax2.axis('off')
ax3.axis('off')
ax4.axis('off')
fig.subplots_adjust(top=1.3)
plt.show()
print('Important similarities')
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1,4, figsize=(12,6))
fig.suptitle(f'Weight = {simplexcombo.weights[0,idx_min,big_weights][j].item()}')
ax1.imshow(img)
ax2.imshow(baseline, cmap='gray', interpolation='none', alpha=0.8)
ax2.imshow(same * proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax3.imshow(img, cmap='gray', interpolation='none', alpha=0.8)
ax3.imshow(same * proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax4.imshow(test, cmap='gray', interpolation='none', alpha=0.8)
ax4.imshow(same * proj, cmap='PiYG', norm=divnorm, interpolation='none', alpha=0.7)
ax1.axis('off')
ax2.axis('off')
ax3.axis('off')
ax4.axis('off')
fig.subplots_adjust(top=1.3)
plt.show()
# + id="i7A7CLuPy9gA"
# + id="G1Iz5MTny9iY"
# + id="pfQ9whcWy9lD"
# + id="jiDMLT0Iy9p9"
# + id="wLT7VUb8y9sL"
# + id="-4ubBCWjy9u2"
# + id="5KAwQWa4y9xM"
# + id="GVGAohXzRk9c"
# + id="6kuGVH40OFrz"
| 38.621236 | 1,738 |
5b68ebcb6e1df80823ba58ad23a41d36594d1925
|
py
|
python
|
nlu/colab/Component Examples/Embeddings_for_Sentences/NLU_USE_Sentence_Embeddings_and_t-SNE_visualization_Example.ipynb
|
gkovaig/spark-nlp-workshop
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="rBXrqlGEYA8G"
# 
#
# [](https://colab.research.google.com//github/JohnSnowLabs/nlu/blob/master/examples/collab/Embeddings_for_Sentences/NLU_USE_Sentence_Embeddings_and_t-SNE_visualization_Example.ipynb)
#
# # USE Sentence Embeddings with NLU
# The Universal Sentence Encoder encodes text into high dimensional vectors that can be used for text classification, semantic similarity, clustering and other natural language tasks.
#
# ## Sources :
# - https://arxiv.org/abs/1803.11175
# - https://tfhub.dev/google/universal-sentence-encoder/2
#
# ## Paper Abstract :
#
# We present models for encoding sentences into embedding vectors that specifically target transfer learning to other NLP tasks. The models are efficient and result in accurate performance on diverse transfer tasks. Two variants of the encoding models allow for trade-offs between accuracy and compute resources. For both variants, we investigate and report the relationship between model complexity, resource consumption, the availability of transfer task training data, and task performance. Comparisons are made with baselines that use word level transfer learning via pretrained word embeddings as well as baselines do not use any transfer learning. We find that transfer learning using sentence embeddings tends to outperform word level transfer. With transfer learning via sentence embeddings, we observe surprisingly good performance with minimal amounts of supervised training data for a transfer task. We obtain encouraging results on Word Embedding Association Tests (WEAT) targeted at detecting model bias. Our pre-trained sentence encoding models are made freely available for download and on TF Hub.
#
#
#
# # 1. Install Java and NLU
# + id="M2-GiYL6xurJ"
import os
# ! apt-get update -qq > /dev/null
# Install java
# ! apt-get install -y openjdk-8-jdk-headless -qq > /dev/null
os.environ["JAVA_HOME"] = "/usr/lib/jvm/java-8-openjdk-amd64"
os.environ["PATH"] = os.environ["JAVA_HOME"] + "/bin:" + os.environ["PATH"]
# ! pip install nlu > /dev/null
# + [markdown] id="N_CL8HZ8Ydry"
# ## 2. Load Model and embed sample string with USE
# + id="j2ZZZvr1uGpx" executionInfo={"status": "ok", "timestamp": 1604868201697, "user_tz": -300, "elapsed": 172677, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="70362830-ff5e-4331-c56b-cca4665ef2dc" colab={"base_uri": "https://localhost:8080/", "height": 162}
import nlu
pipe = nlu.load('use')
pipe.predict('He was suprised by the diversity of NLU')
# + [markdown] id="BAUFklCqLr3V"
# # 3. Download Sample dataset
# + id="wAFAOUSuLqvn" executionInfo={"status": "ok", "timestamp": 1604868213232, "user_tz": -300, "elapsed": 184195, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="64c60974-8b95-4960-9b40-0d8a6482c1b3" colab={"base_uri": "https://localhost:8080/", "height": 777}
import pandas as pd
# Download the dataset
# ! wget -N https://s3.amazonaws.com/auxdata.johnsnowlabs.com/public/resources/en/sarcasm/train-balanced-sarcasm.csv -P /tmp
# Load dataset to Pandas
df = pd.read_csv('/tmp/train-balanced-sarcasm.csv')
df
# + [markdown] id="OPdBQnV46or5"
# # 4.1 Visualize Embeddings with T-SNE
#
#
#
#
# Lets add Sentiment Part Of Speech to our pipeline because its so easy and so we can hue our T-SNE plots by POS and Sentiment
# We predict the first 5k comments
# + id="9bujAZtOCfRW" executionInfo={"status": "ok", "timestamp": 1604868254709, "user_tz": -300, "elapsed": 225624, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="93a0f8f3-e74c-427e-9d03-a07ceb26384f" colab={"base_uri": "https://localhost:8080/", "height": 1000}
pipe = nlu.load('pos sentiment use emotion') # emotion
df['text'] = df['comment']
# We must set output level to sentence since NLU will infer a different output level for this pipeline composition
predictions = pipe.predict(df[['text','label']].iloc[0:500], output_level='sentence')
predictions
# + [markdown] id="_OypFES-8EwY"
# ## 4.2 Checkout sentiment distribution
# + id="ggbC0PxHgc2t" executionInfo={"status": "ok", "timestamp": 1604868254713, "user_tz": -300, "elapsed": 225607, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="8eec6fab-7d80-4edb-9886-31d57a49dd85" colab={"base_uri": "https://localhost:8080/"}
# Some Tokens are None which we must drop first
predictions.dropna(how='any', inplace=True)
# Some sentiment are 'na' which we must drop first
predictions = predictions[predictions.sentiment!= 'na']
predictions.sentiment.value_counts().plot.bar(title='Dataset sentiment distribution')
# + [markdown] id="LZtPxt5c8HlJ"
# ## 4.3 Checkout sentiment distribution
# + id="OA0Er5WA6l7v" executionInfo={"status": "ok", "timestamp": 1604868254715, "user_tz": -300, "elapsed": 225574, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="7deaac36-23ef-4c84-f1c4-fbd23f860c6f" colab={"base_uri": "https://localhost:8080/", "height": 330}
predictions.emotion.value_counts().plot.bar(title='Dataset emotion category distribution')
# + [markdown] id="ZUYHpsHTINsF"
# # 5.Prepare data for T-SNE algorithm.
# We create a Matrix with one row per Embedding vector for T-SNE algorithm
# + id="L_0jefTB6i52"
import numpy as np
# We first create a column of type np array
predictions['np_array'] = predictions.sentence_embeddings.apply(lambda x: np.array(x))
# Make a matrix from the vectors in the np_array column via list comprehension
mat = np.matrix([x for x in predictions.np_array])
# + [markdown] id="pbdi4CY2Iqc0"
# ## 5.1 Fit and transform T-SNE algorithm
#
# + id="fAFGB6iYIqmO" executionInfo={"status": "ok", "timestamp": 1604868259253, "user_tz": -300, "elapsed": 229960, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="9f9d05ea-3601-4e81-e7b5-339a81cab1dc" colab={"base_uri": "https://localhost:8080/"}
from sklearn.manifold import TSNE
model = TSNE(n_components=2) #n_components means the lower dimension
low_dim_data = model.fit_transform(mat)
print('Lower dim data has shape',low_dim_data.shape)
# + [markdown] id="gsi0b0XhImaz"
# ### Set plotting styles
# + id="CsPVw7NHfEgt"
# set some styles for for Plotting
import seaborn as sns
# Style Plots a bit
sns.set_style('darkgrid')
sns.set_palette('muted')
sns.set_context("notebook", font_scale=1,rc={"lines.linewidth": 2.5})
# %matplotlib inline
import matplotlib as plt
plt.rcParams['figure.figsize'] = (20, 14)
import matplotlib.pyplot as plt1
# + [markdown] id="8tuoCxNPmzbo"
# ##5.2 Plot low dimensional T-SNE USE embeddings with hue for Sarcasm
#
# + id="Fbq5MAv0jkft" executionInfo={"status": "ok", "timestamp": 1604868260907, "user_tz": -300, "elapsed": 231563, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="e9c5a76a-10f9-4453-ce7a-49a997da6276" colab={"base_uri": "https://localhost:8080/"}
tsne_df = pd.DataFrame(low_dim_data, predictions.label.replace({1:'sarcasm',0:'normal'}))
tsne_df.columns = ['x','y']
ax = sns.scatterplot(data=tsne_df, x='x', y='y', hue=tsne_df.index)
ax.set_title('T-SNE USE Embeddings, colored by Sarcasm label')
plt1.savefig("use_sarcasam")
# + [markdown] id="Snb1gtqrnIJi"
# ## 5.3 Plot low dimensional T-SNE USE embeddings with hue for Sentiment
#
# + id="QET-Y6PdnIJt" executionInfo={"status": "ok", "timestamp": 1604868263828, "user_tz": -300, "elapsed": 234404, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="57e8886c-525a-4377-b8af-3af62853f22b" colab={"base_uri": "https://localhost:8080/"}
tsne_df = pd.DataFrame(low_dim_data, predictions.sentiment)
tsne_df.columns = ['x','y']
ax = sns.scatterplot(data=tsne_df, x='x', y='y', hue=tsne_df.index)
ax.set_title('T-SNE USE Embeddings, colored by Sentiment')
plt1.savefig("use_sentiment")
# + id="7QNgruV-6eV1" executionInfo={"status": "ok", "timestamp": 1604868263835, "user_tz": -300, "elapsed": 233387, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="dd4e6264-ea01-4e41-f1e6-67bcb7eb0271" colab={"base_uri": "https://localhost:8080/", "height": 54}
tsne_df = pd.DataFrame(low_dim_data, predictions.emotion)
tsne_df.columns = ['x','y']
ax = sns.scatterplot(data=tsne_df, x='x', y='y', hue=tsne_df.index)
ax.set_title('T-SNE use Embeddings, colored by Emotion')
plt1.savefig("use_emotion")
# + [markdown] id="fv3FIQ7j6eVv"
# # 5.4 Plot low dimensional T-SNE USE embeddings with hue for Emotions
#
# + [markdown] id="l3sRcFW9muEZ"
# # 6.1 Plot low dimensional T-SNE USE embeddings with hue for POS
# Because we will have a list of pos labels for each sentence, we need to explode on the pos column and then do the data peperation for T-SNE again before we can visualize with hue for POS
#
# + id="OZ_2DTk9bC-O" executionInfo={"status": "ok", "timestamp": 1604868263837, "user_tz": -300, "elapsed": 233304, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="9436cfd4-00ab-47d4-937e-5897800f0278" colab={"base_uri": "https://localhost:8080/"}
predictions_exploded_on_pos = predictions.explode('pos')
predictions_exploded_on_pos
# + [markdown] id="k1M_a4pmfMGA"
# ## 6.2 Preprocess data for TSNE again
# + id="K0rpmiy6a2UK" executionInfo={"status": "ok", "timestamp": 1604868328740, "user_tz": -300, "elapsed": 298189, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="d44cd535-cfe1-4a03-f3ed-ab5da2cc489e" colab={"base_uri": "https://localhost:8080/"}
# We first create a column of type np array
predictions_exploded_on_pos['np_array'] = predictions_exploded_on_pos.sentence_embeddings.apply(lambda x: np.array(x))
# Make a matrix from the vectors in the np_array column via list comprehension
mat = np.matrix([x for x in predictions_exploded_on_pos.np_array])
from sklearn.manifold import TSNE
model = TSNE(n_components=2) #n_components means the lower dimension
low_dim_data = model.fit_transform(mat)
print('Lower dim data has shape',low_dim_data.shape)
# + [markdown] id="6ze0HWqqfQDh"
# # 6.3 Plot low dimensional T-SNE USE embeddings with hue for POS
#
# + id="RB1qdDP3fJHN" executionInfo={"status": "ok", "timestamp": 1604868331791, "user_tz": -300, "elapsed": 301202, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="41ae7ac0-dbae-46fc-b9e1-9461d2326882" colab={"base_uri": "https://localhost:8080/", "height": 844}
tsne_df = pd.DataFrame(low_dim_data, predictions_exploded_on_pos.pos)
tsne_df.columns = ['x','y']
ax = sns.scatterplot(data=tsne_df, x='x', y='y', hue=tsne_df.index)
ax.set_title('T-SNE USE Embeddings, colored by Part of Speech Tag')
plt1.savefig("use_pos")
# + [markdown] id="uXb-FMA6mX13"
# # 7. NLU has many more embedding models!
# Make sure to try them all out!
# You can change 'use' in nlu.load('use') to bert, xlnet, albert or any other of the **100+ word embeddings** offerd by NLU
# + id="9qUF7jPlme-R" executionInfo={"status": "ok", "timestamp": 1604868331794, "user_tz": -300, "elapsed": 301186, "user": {"displayName": "ahmed lone", "photoUrl": "", "userId": "02458088882398909889"}} outputId="bd8c0c7f-4371-4bf8-cb6b-f4c377c9e5aa" colab={"base_uri": "https://localhost:8080/"}
nlu.print_all_model_kinds_for_action('embed')
# + id="MvSC3rl5-adJ"
| 54.032407 | 1,112 |
e86edba6f654b1bc290d5f63166f07084543b2b2
|
py
|
python
|
Modulo08_Archivos.ipynb
|
carlosalvarezh/Fundamentos_Programacion
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1 align="center">Fundamentos de Programación</h1>
# <h1 align="center">Módulo 08: Archivos</h1>
# <h1 align="center">2021/02</h1>
# <h1 align="center">MEDELLÍN - COLOMBIA </h1>
# <table>
# <tr align=left><td><img align=left src="https://github.com/carlosalvarezh/Fundamentos_Programacion/blob/main/images/CC-BY.png?raw=true">
# <td>Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved MIT license.(c) Carlos Alberto Alvarez Henao</td>
# </table>
# ***
# ***Docente:*** Carlos Alberto Álvarez Henao, I.C. D.Sc.
#
# ***e-mail:*** [email protected]
#
# ***skype:*** carlos.alberto.alvarez.henao
#
# ***Linkedin:*** https://www.linkedin.com/in/carlosalvarez5/
#
# ***github:*** https://github.com/carlosalvarezh/Fundamentos_Programacion
#
# ***Herramienta:*** [Jupyter Notebook](http://jupyter.org/)
#
# ***Kernel:*** Python 3.8
# ***
# <a id='TOC'></a>
# + [markdown] toc=true
# <h1>Tabla de Contenidos<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Archivos-(Files)" data-toc-modified-id="Archivos-(Files)-1"><span class="toc-item-num">1 </span>Archivos (Files)</a></span><ul class="toc-item"><li><span><a href="#Abrir/Cerrar-(open/close)" data-toc-modified-id="Abrir/Cerrar-(open/close)-1.1"><span class="toc-item-num">1.1 </span>Abrir/Cerrar (open/close)</a></span></li><li><span><a href="#Lectura-y-Escritura-(I/O)" data-toc-modified-id="Lectura-y-Escritura-(I/O)-1.2"><span class="toc-item-num">1.2 </span>Lectura y Escritura (I/O)</a></span><ul class="toc-item"><li><span><a href="#Generalidades" data-toc-modified-id="Generalidades-1.2.1"><span class="toc-item-num">1.2.1 </span>Generalidades</a></span></li><li><span><a href="#Lectura" data-toc-modified-id="Lectura-1.2.2"><span class="toc-item-num">1.2.2 </span>Lectura</a></span></li><li><span><a href="#Escritura" data-toc-modified-id="Escritura-1.2.3"><span class="toc-item-num">1.2.3 </span>Escritura</a></span></li></ul></li><li><span><a href="#Lectura-/-Escritura-simultánea" data-toc-modified-id="Lectura-/-Escritura-simultánea-1.3"><span class="toc-item-num">1.3 </span>Lectura / Escritura simultánea</a></span></li><li><span><a href="#Laboratorio" data-toc-modified-id="Laboratorio-1.4"><span class="toc-item-num">1.4 </span>Laboratorio</a></span></li></ul></li></ul></div>
# -
# ## Archivos (Files)
# - La mayoría de los programas que hemos visto hasta ahora son transitorios en el sentido de que corren por un corto tiempo y producen alguna salida, pero cuando terminan, sus datos desaparecen. Si ejecuta el programa de nuevo, comienza con una pizarra limpia.
#
#
# - Otros programas son persistentes: funcionan por mucho tiempo (o todo el tiempo); Mantienen al menos algunos de sus datos en un almacenamiento permanente (un disco duro, por ejemplo); Y si cierran y reinician, retoman donde lo dejaron.
#
#
# - Ejemplos de programas persistentes son los sistemas operativos, que se ejecutan casi siempre que un equipo está encendido, y los servidores web, que funcionan todo el tiempo, esperando a que las solicitudes para entrar en la red.
#
#
# - Una de las maneras más simples para que los programas mantengan sus datos es leyendo y escribiendo archivos de texto.
# [Volver a la Tabla de Contenido](#TOC)
# ### Abrir/Cerrar (open/close)
# La función `open()` devuelve un objeto archivo, y se usa normalmente con dos argumentos:
# + active=""
# fobj = open("C:\Users\Lenovo\Dropbox\GitHub\Covid-19\Casos_positivos_de_COVID-19_en_Colombia.csv","write")
# -
# Los archivos son objetos tipo `file` accesados mediante la función `open`.
#
#
# - `ruta_archivo`: string indicando la ubicación del archivo con el nombre y la extensión.
#
#
# - `modo_acceso` : string, opcional, que indica el modo de acceder al archivo:
#
# - `r`: `read`, lectura. Abre el archivo en modo lectura. **El archivo tiene que existir previamente**, de lo contrario se tiene un error del tipo `IOError`.
#
# - `w`: `write`, escritura. Abre el archivo en modo escritura. Si el archivo no existe se crea. **Si existe, SOBREESCRIBIRÁ TODO!!!** el contenido.
#
# - `a`: `append`, añadir. Abre el archivo en modo escritura. Continúa escribiendo sobre el archivo existente a partir de la última línea del contenido inicial. No sobreescribe.
#
# - `b`: binary, binario.
#
# - `+`: Lectura y Escritura simultáneas.
#
# - `U` universal newline, saltos de línea universales. Permite trabajar con archivos que tengan un formato para los saltos de línea que no coinciden con el de la plataforma actual (Windows usa el caracter CR LF, Unix, LF, y MacOS, CR)
#
#
# Una vez terminado el trabajo sobre el archivo, se debe cerrar utilizando el método `close`.
# + active=""
# fobj.close()
# -
# un ejemplo rápido de abertura de un archivo (recuerde, debe existir previamente, si no, saca un mensaje `IOerror`). El modo de acceso es opcional. Por defecto se deja listo para lectura, `r` (`read`).
# +
fhola = open("archivoxyz1.csv")
print(fhola)
fhola.close()
# -
# ***siempre que se finalice el trabajo de lectura y/o escritura sobre el archivo deberá cerrarse.***
fhola.close()
# [Volver a la Tabla de Contenido](#TOC)
# ### Lectura y Escritura (I/O)
# #### Generalidades
# - Normalmente los archivos se abren en modo texto, lo que significa que podrás leer y escribir cadenas del y al archivo, las
# cuales se codifican utilizando un código específico.
#
#
# - Si el código no es especificado, el valor predeterminado depende de la plataforma.
#
#
# - Si se agrega `b` al modo el archivo se abre en modo binario: ahora los datos se leen y escriben en forma de objetos bytes. Se debería usar este modo para todos los archivos que no contengan texto (archivos de imágenes, por ejemplo).
#
#
# - Cuando se lee en modo texto, por defecto se convierten los fines de lineas que son específicos a las plataformas (`\n` en Unix, `\r\n` en Windows) a solamente `\n`.
#
#
# - Cuando se escribe en modo texto, por defecto se convierten los `\n` a los finales de linea específicos de la plataforma.
#
#
# - Este cambio automático está bien para archivos de texto, pero corrompería datos binarios como los de archivos JPEG o EXE. Asegurese de usar modo binario cuando leas y escribas tales archivos.
# [Volver a la Tabla de Contenido](#TOC)
# #### Lectura
# El método read devuelve una cadena con el contenido del archivo o bien el contenido de los primeros $n$ bytes, si se especifica el tamaño máximo a leer.
# - `read()` : Leyendo el contenido completo del archivo
fobj = open("ofortuna.txt", "read")
todo = fobj.read()
print(todo)
print(type(todo))
fobj.close()
# O una parte de él (en bytes)
fobj = open("ofortuna.txt")
parte = fobj.read(50)
print(parte)
fobj.close()
# - `readline()`: sirve para leer las líneas del fichero una por una. Cada vez que se llama a este método, se devuelve el contenido del archivo desde el puntero hasta que se encuentra un carácter de nueva línea, `\n`, incluyendo este carácter.
fobj = open("ofortuna.txt", "r")
linea = fobj.readline()
print(linea)
print(type(linea))
fobj.close()
# Ahora leer todo el contenido del archivo línea por línea
# +
fobj = open("ofortuna.txt", "r")
for i in range(33):
linea = fobj.readline()
print(linea)
fobj.close()
# -
# - `readlines()`: lee todas las líneas del archivo y devuelve una lista con las líneas leídas.
fobj = open("ofortuna.txt", "r")
lineas = fobj.readlines()
print(lineas)
print(type(lineas))
fobj.close()
type(lineas)
# Y como tal, se pueden realizar todas las operaciones de Lista vistas anteriormente:
lineas[28]
# Toda la información que se lee desde un archivo plano es de tipo....
fnumeros = open("numeros.txt")
numeros = float(fnumeros.readline())
print(type(numeros))
type(numeros)
# Se puede hacer de una forma más "corta"
masnumeros = open(numeros.txt").readlines()
print(masnumeros)
print(type(masnumeros[2]))
# Como se puede ver, el resultado es una lista de valores str que incluyen los caracteres para salto de línes "`\n`".
#
#
# Resultan dos interrogantes:
#
#
# - Cómo eliminar los caracteres de salto de línea "`\n`"?
#
#
# - Cómo convertir cada elemento tipo str de la lista en float/int (o viceversa)?
masnumeros = open("numeros.txt").readlines()
masnumeros = [float(i.rstrip()) for i in masnumeros]
print(masnumeros)
print(type(masnumeros[2]))
# También se puede leer el archivo completo iterando sobre el objeto archivo. Esto es eficiente en memoria, rápido, y conduce a un código más simple
for linea in masnumeros:
print(linea)
type(linea)
# [Volver a la Tabla de Contenido](#TOC)
# #### Escritura
# Para la escritura de archivos se utilizan los métodos *write* y *writelines*.
#
#
# - <strong>write:</strong> Escribe en el archivo una cadena de texto que toma como parámetro.
#
#
# - <strong>writelines:</strong> Toma como parámetro una lista de cadenas de texto indicando las líneas que queremos escribir en el fichero.
#
#
# A diferencia del método read, el archivo sobre el que se va a escribir no necesita estar creado previamente.
fh = open("escritura2.txt", "a")
fh.write("To write or not to write that is the question!")
fh.close()
# ***NO SE LE OLVIDE CERRAR EL ARCHIVO UNA VEZ HA FINALIZADO LA ACCIÓN DE ESCRITURA!!!***
# El argumento del método write() tiene qué ser un string, entonces es necesario convertir los valores numéricos en cadenas de caracteres.
fh = open("escritura.txt", "w")
x = str(52.8)
print(type(x))
fh.write(x)
fh.close()
fh = open("escritura.txt", "w")
x = str(52)
print(type(x))
fh.write(x)
fh.close()
# Obsérvese que el método "w" sobreescribe el contenido del archivo. <strong>MUY PELIGROSO!!!</strong>
#
#
# En el caso en el que necesitemos acceder a un archivo ya creado, con algún contenido, es mejor utilizar el método "a" (append), que escribirá a partir de la última línea del contenido inicial.
fh = open("escritura.txt", "w")
fh.write("To write or not to write\nthat is the question!\n")
fh.close()
fh = open("escritura.txt", "a")
x = str(52)
fh.write(x)
fh.close()
# Escritura en un archivo con un formato específico
f = open ('tabla.txt ', 'w')
for i in range (1, 11):
f.write ("%2d x 17 = %4d\n" % (i, i * 17))
f.close ()
# [Volver a la Tabla de Contenido](#TOC)
# ### Lectura / Escritura simultánea
fobj_in = open("O_Fortuna.txt")
fobj_out = open("O_Fortuna2.txt","w")
i = 1
for line in fobj_in:
print(line.rstrip())
fobj_out.write(str(i) + ": " + line)
i = i + 1
fobj_in.close()
fobj_out.close()
# En el ejemplo anterior, cada línea en el archivo de salida es indexado con su número de línea.
#
#
# Por último (por ahora...) si deseamos escribir sobre un archivo ya creado sin que perdamos información del mismo, debemos emplear el modo de acceso "a" en vez de "w":
f = open ('tabla.txt ', 'a')
for i in range (1, 11):
f.write ("%2d x 18 = %4d\n" % (i, i * 18))
f.close ()
# [Volver a la Tabla de Contenido](#TOC)
# ### Laboratorio
# 1. Realice un programa que separe cada una de las estrofas del archivo *O Fortuna* en archivos independientes. El único dato que debe ingresar el usuario es el nombre del archivo de datos, el resto, la generación del nombre de cada uno de los archivos de salida así como su contenido, deberá ser generado de forma automática por el programa.
#
#
# 2. Haga un programa que calcule la raíz aproximada de una función no lineal en un intervalo $[a,b]$ mediante el [Método de Bisección](https://es.wikipedia.org/wiki/Método_de_bisección). El resultado debe ser un archivo que contenga los datos de las diferentes iteraciones del algoritmo en una tabla con las columnas:
#
# - Número de iteración
# - valor de $a$
# - valor de $f(a)$
# - valor de $b$
# - valor de $f(b)$
# - valor de $m$
# - valor de $f(m)$
# - valor del error absoluto, dado por: $E_{abs} = |m_{i}-m_{i-1}|$
# - Flag indicando si se cumplió o no el criterio de parada.
#
#
# 3. Haga un programa que calcule el plan de pagos de un préstamo bancario. El plan de pagos (una tabla) deberá ser presentada en un archivo de salida.
| 37.09816 | 1,439 |
2d288de138198d4fbb40fed269045822a3005806
|
py
|
python
|
notebooks/Word2Vec_Pretrained.ipynb
|
mico-boje/document-summarizer
|
['FTL']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import gensim.downloader as api
import gensim
from gensim.models import Phrases
from gensim.models import KeyedVectors, Word2Vec
import numpy as np
import nltk
from nltk.corpus import stopwords
import string
from sklearn.metrics.pairwise import cosine_similarity
import networkx as nx
import ast
import json
# +
filename = r'/home/miboj/NLP/document-summarizer/data/processed/articles.json'
file = open(filename, encoding='ascii', errors='ignore')
text = file.read()
file.close()
d = ast.literal_eval(text)
# +
with open(filename) as json_file:
data = json.load(json_file)
filename = r'/home/miboj/NLP/document-summarizer/data/processed/articles.json'
file = open(filename, encoding='ascii', errors='ignore')
text = file.read()
file.close()
json_content = ast.literal_eval(text)
samples = json_content[0:10]
# -
tokens_list = []
for i in d:
for sen in i['content']:
tokens_list.append(sen)
import time
start_time = time.time()
sentences = []
word_count = 0
stpwrds = stopwords.words('english') + list(string.punctuation) + ['—', '“', '”', "'", "’"]
for e, i in enumerate(tokens_list):
words = []
a = nltk.word_tokenize(i)
for word in a:
if word not in stpwrds:
words.append(word)
word_count += 1
sentences.append(words)
print("--- %s seconds ---" % (time.time() - start_time))
print(len(sentences))
print(word_count)
"""
sg - Training algorithm: 1 for skip-gram, 0 for CBOW
hs - If 1, hierarchical softmax will be used for model training. If 0, and negative is non-zero, negative sampling will be used.
"""
model = api.load("word2vec-google-news-300")
model.most_similar('weapon')
# +
#model = model.wv
# -
import re
def remove_empty_string(input_string):
for e, i in enumerate(input_string):
try:
if i[-1] == ' ' and input_string[e+1][-1] == ' ':
input_string[e] = i.rstrip()
except IndexError:
print('Out of index')
joined_string = ''.join(input_string)
for e, i in enumerate(joined_string):
if i == ' ' and joined_string[e+1] == ' ':
del i
sentences = nltk.sent_tokenize(joined_string)
return sentences
raw_string = [" ROME — Defying reports that their planned partnership is ", "doomed to fail", ", France’s Naval Group and ", "Italy’s Fincantieri", " have announced a joint venture to build and export naval vessels. ", " The two ", "state-controlled shipyards", " said they were forming a 50-50 joint venture after months of talks to integrate their activities. The move comes as Europe’s fractured shipbuilding industry faces stiffer global competition. ", " The firms said in a statement that the deal would allow them to “jointly prepare winning offers for binational programs and export market,” as well as create joint supply chains, research and testing. ", " Naval Group and Fincantieri first announced talks on cooperation last year after the latter negotiated a controlling share in French shipyard STX. But the deal was reportedly losing momentum due to resistance from French industry and a political row between France and Italy over migrants. ", " The new deal falls short of the 10 percent share swap predicted by French Economy and Finance Minister Bruno Le Maire earlier this year, and far short of the total integration envisaged by Fincantieri CEO Giuseppe Bono. ", " The statement called the joint venture the “first steps” toward the creation of an alliance that would create “a more efficient and competitive European shipbuilding industry.”", " Naval Group CEO Hervé Guillou, speaking at the Euronaval trade expo in Paris on Oct. 24, said the alliance is based on “two countries sharing a veritable naval ambition.”", " The joint venture is necessary because the “context of the global market has changed drastically,” he added, specifically mentioning new market entrants Russia, China, Singapore, Ukraine, India and Turkey.", "Sign up for the Early Bird Brief, the defense industry's most comprehensive news and information, straight to your inbox.", "By giving us your email, you are opting in to the Early Bird Brief.", " When asked about an initial product to be tackled under the alliance, Guillou acknowledged: “The answer is simple: there is nothing yet.”", " However, the firms said they are working toward a deal to build four logistics support ships for the French Navy, which will be based on an Italian design. ", "Competition flares up for the follow-on portion of a deal previously won by the French shipbuilder.", " The firms also plan to jointly bid next year on work for midlife upgrades for Horizon frigates, which were built by France and Italy and are in service with both navies. The work would include providing a common combat management system. ", " The statement was cautious about future acceleration toward integration. “A Government-to-Government Agreement would be needed to ensure the protection of sovereign assets, a fluid collaboration between the French and Italian teams and encourage further coherence of the National assistance programs, which provide a framework and support export sales,” the statement said.", " But the firms were optimistic the deal would be “a great opportunity for both groups and their eco-systems, by enhancing their ability to better serve the Italian and French navies, to capture new export contracts, to increase research funding and, ultimately, improve the competitiveness of both French and Italian naval sectors.”", " ", "Sebastian Sprenger", " in Paris contributed to this report."]
sentences = remove_empty_string(raw_string)
# +
# The 'skipthoughts' module can be found at the root of the GitHub repository linked above
#import skipthoughts
# You would need to download pre-trained models first
#model = skipthoughts.load_model()
#encoder = skipthoughts.Encoder(model)
#encoded = encoder.encode(sentences)
a = model['ROME']
a.shape
# -
def get_embedding(sentences):
embeddings = []
stpwrds = stopwords.words('english') + list(string.punctuation) + ['—', '“', '”', "'", "’"]
for i in sentences:
temp = []
words = nltk.word_tokenize(i)
for word in words:
true_len = len(words) - len([w for w in stpwrds if w in words])
#if word not in stpwrds:
if word in model.vocab:
v = model[word]
#else:
# v = np.zeros(300,)
temp.append(v)
a = sum(temp)/true_len
np_temp = np.array(a)
#embeddings.append(temp)
embeddings.append(np_temp)
sentence_vectors = np.array(embeddings)
return sentence_vectors
def get_sim_matrix(sentences, sentence_vectors):
sim_mat = np.zeros([len(sentences), len(sentences)])
sim_mat.shape
for i in range(len(sentences)):
for j in range(len(sentences)):
if i != j:
sim_mat[i][j] = cosine_similarity(sentence_vectors[i].reshape(1,300), sentence_vectors[j].reshape(1,300))[0,0]
return sim_mat
def get_pagerank(sim_mat):
nx_graph = nx.from_numpy_array(sim_mat)
scores = nx.pagerank(nx_graph)
return scores
def get_summary(num_sentences, scores, sentences):
ranked_sentences = sorted(((scores[i],s) for i,s in enumerate(sentences)), reverse=True)
#num_of_sentences = 4
summary = ''
for i in range(num_sentences):
summary += ranked_sentences[i][1]
summary += " "
return summary
summary_samples = []
summary_len = []
for i in samples:
i = remove_empty_string(i['content'])
embeddings = get_embedding(i)
sim_mat = get_sim_matrix(i, embeddings)
scores = get_pagerank(sim_mat)
sentence_length = len(i)
summary = get_summary(int(sentence_length*0.3), scores, i)
summary_samples.append(summary)
summary_len.append(int(sentence_length*0.3))
sorted_summaries = []
for e, i in enumerate(summary_samples):
a = nltk.sent_tokenize(i)
o = samples[e]['content']
b = remove_empty_string(o)
#print(a)
#print(b)
res = [sort for x in b for sort in a if sort == x]
sorted_summaries.append(res)
for e, i in enumerate(sorted_summaries):
print(e, ": ")
print("len original: ", len(remove_empty_string(samples[e]['content'])))
print("Summary len: ", summary_len[e])
summary = ""
for sen in i:
summary += sen
summary += " "
print(summary)
for e, i in enumerate(samples):
print(e)
sample = ""
temp = remove_empty_string(i['content'])
for t in temp:
sample += t
sample += " "
print(sample)
| 41.480769 | 3,376 |
00fc80cfb28685975afe40b8c8dc6d7f358f9fdf
|
py
|
python
|
tutorials/streamlit_notebooks/healthcare/NER_DEMOGRAPHICS.ipynb
|
ewbolme/spark-nlp-workshop
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="TA21Jo5d9SVq"
#
#
# 
#
# [](https://colab.research.google.com/github/JohnSnowLabs/spark-nlp-workshop/blob/master/tutorials/streamlit_notebooks/healthcare/NER_DEMOGRAPHICS.ipynb)
#
# + [markdown] colab_type="text" id="CzIdjHkAW8TB"
# # **Detect demographic information**
# + [markdown] colab_type="text" id="6uDmeHEFW7_h"
# To run this yourself, you will need to upload your license keys to the notebook. Otherwise, you can look at the example outputs at the bottom of the notebook. To upload license keys, open the file explorer on the left side of the screen and upload `workshop_license_keys.json` to the folder that opens.
# + [markdown] colab_type="text" id="wIeCOiJNW-88"
# ## 1. Colab Setup
# + [markdown] colab_type="text" id="HMIDv74CYN0d"
# Import license keys
# + colab={} colab_type="code" id="ttHPIV2JXbIM"
import os
import json
with open('/content/spark_nlp_for_healthcare.json', 'r') as f:
license_keys = json.load(f)
license_keys.keys()
secret = license_keys['SECRET']
os.environ['SPARK_NLP_LICENSE'] = license_keys['SPARK_NLP_LICENSE']
os.environ['AWS_ACCESS_KEY_ID'] = license_keys['AWS_ACCESS_KEY_ID']
os.environ['AWS_SECRET_ACCESS_KEY'] = license_keys['AWS_SECRET_ACCESS_KEY']
sparknlp_version = license_keys["PUBLIC_VERSION"]
jsl_version = license_keys["JSL_VERSION"]
print ('SparkNLP Version:', sparknlp_version)
print ('SparkNLP-JSL Version:', jsl_version)
# + [markdown] colab_type="text" id="rQtc1CHaYQjU"
# Install dependencies
# + colab={"base_uri": "https://localhost:8080/", "height": 326} colab_type="code" id="CGJktFHdHL1n" outputId="1882c7b5-4484-43c8-c1e2-84578876d53f"
# Install Java
# ! apt-get update -qq
# ! apt-get install -y openjdk-8-jdk-headless -qq > /dev/null
# ! java -version
# Install pyspark
# ! pip install --ignore-installed -q pyspark==2.4.4
# Install Spark NLP
# ! pip install --ignore-installed spark-nlp==$sparknlp_version
# ! python -m pip install --upgrade spark-nlp-jsl==$jsl_version --extra-index-url https://pypi.johnsnowlabs.com/$secret
# + [markdown] colab_type="text" id="Hj5FRDV4YSXN"
# Import dependencies into Python and start the Spark session
# + colab={"base_uri": "https://localhost:8080/", "height": 392} colab_type="code" id="sw-t1zxlHTB7" outputId="272eddd7-e21f-4504-af31-8fe8b8c8ca0a"
os.environ['JAVA_HOME'] = "/usr/lib/jvm/java-8-openjdk-amd64"
os.environ['PATH'] = os.environ['JAVA_HOME'] + "/bin:" + os.environ['PATH']
import pandas as pd
from pyspark.ml import Pipeline
from pyspark.sql import SparkSession
import pyspark.sql.functions as F
import sparknlp
from sparknlp.annotator import *
from sparknlp_jsl.annotator import *
from sparknlp.base import *
import sparknlp_jsl
spark = sparknlp_jsl.start(secret)
# + [markdown] colab_type="text" id="9RgiqfX5XDqb"
# ## 2. Select the NER model and construct the pipeline
# + [markdown] colab_type="text" id="MbWioxCasOXH"
# Select the NER model - Demographics models: **ner_deid_enriched, ner_deid_large, ner_jsl**
#
# For more details: https://github.com/JohnSnowLabs/spark-nlp-models#pretrained-models---spark-nlp-for-healthcare
# + colab={} colab_type="code" id="jeSfy_oGsTL6"
# You can change this to the model you want to use and re-run cells below.
# Demographics models: ner_deid_enriched, ner_deid_large, ner_jsl
MODEL_NAME = "ner_deid_enriched"
# + [markdown] colab_type="text" id="zweiG2ilZqoR"
# Create the pipeline
# + colab={} colab_type="code" id="LLuDz_t40be4"
document_assembler = DocumentAssembler() \
.setInputCol('text')\
.setOutputCol('document')
sentence_detector = SentenceDetector() \
.setInputCols(['document'])\
.setOutputCol('sentence')
tokenizer = Tokenizer()\
.setInputCols(['sentence']) \
.setOutputCol('token')
word_embeddings = WordEmbeddingsModel.pretrained('embeddings_clinical', 'en', 'clinical/models') \
.setInputCols(['sentence', 'token']) \
.setOutputCol('embeddings')
clinical_ner = NerDLModel.pretrained(MODEL_NAME, 'en', 'clinical/models') \
.setInputCols(['sentence', 'token', 'embeddings']) \
.setOutputCol('ner')
ner_converter = NerConverter()\
.setInputCols(['sentence', 'token', 'ner']) \
.setOutputCol('ner_chunk')
nlp_pipeline = Pipeline(stages=[
document_assembler,
sentence_detector,
tokenizer,
word_embeddings,
clinical_ner,
ner_converter])
empty_df = spark.createDataFrame([['']]).toDF("text")
pipeline_model = nlp_pipeline.fit(empty_df)
light_pipeline = LightPipeline(pipeline_model)
# + [markdown] colab_type="text" id="2Y9GpdJhXIpD"
# ## 3. Create example inputs
# + colab={} colab_type="code" id="vBOKkB2THdGI"
# Enter examples as strings in this array
input_list = [
"""HISTORY OF PRESENT ILLNESS: Mr. Smith is a 60-year-old white male veteran with multiple comorbidities, who has a history of bladder cancer diagnosed approximately two years ago by the VA Hospital. He underwent a resection there. He was to be admitted to the Day Hospital for cystectomy. He was seen in Urology Clinic and Radiology Clinic on 02/04/2003.
HOSPITAL COURSE: Mr. Smith presented to the Day Hospital in anticipation for Urology surgery. On evaluation, EKG, echocardiogram was abnormal, a Cardiology consult was obtained. A cardiac adenosine stress MRI was then proceeded, same was positive for inducible ischemia, mild-to-moderate inferolateral subendocardial infarction with peri-infarct ischemia. In addition, inducible ischemia seen in the inferior lateral septum. Mr. Smith underwent a left heart catheterization, which revealed two vessel coronary artery disease. The RCA, proximal was 95% stenosed and the distal 80% stenosed. The mid LAD was 85% stenosed and the distal LAD was 85% stenosed. There was four Multi-Link Vision bare metal stents placed to decrease all four lesions to 0%. Following intervention, Mr. Smith was admitted to 7 Ardmore Tower under Cardiology Service under the direction of Dr. Hart. Mr. Smith had a noncomplicated post-intervention hospital course. He was stable for discharge home on 02/07/2003 with instructions to take Plavix daily for one month and Urology is aware of the same."""
]
# + [markdown] colab_type="text" id="mv0abcwhXWC-"
# ## 4. Use the pipeline to create outputs
# + colab={} colab_type="code" id="TK1DB9JZaPs3"
df = spark.createDataFrame(pd.DataFrame({"text": input_list}))
result = pipeline_model.transform(df)
# + [markdown] colab_type="text" id="UQY8tAP6XZJL"
# ## 5. Visualize results
# + [markdown] colab_type="text" id="hnsMLq9gctSq"
# Visualize outputs as data frame
# + colab={"base_uri": "https://localhost:8080/", "height": 330} colab_type="code" id="Ar32BZu7J79X" outputId="6870a43f-a772-4825-e6b5-f30270bbcae6"
exploded = F.explode(F.arrays_zip('ner_chunk.result', 'ner_chunk.metadata'))
select_expression_0 = F.expr("cols['0']").alias("chunk")
select_expression_1 = F.expr("cols['1']['entity']").alias("ner_label")
result.select(exploded.alias("cols")) \
.select(select_expression_0, select_expression_1).show(truncate=False)
result = result.toPandas()
# + [markdown] colab_type="text" id="1wdVmoUcdnAk"
# Functions to display outputs as HTML
# + colab={} colab_type="code" id="tFeu7loodcQQ"
from IPython.display import HTML, display
import random
def get_color():
r = lambda: random.randint(128,255)
return "#%02x%02x%02x" % (r(), r(), r())
def annotation_to_html(full_annotation):
ner_chunks = full_annotation[0]['ner_chunk']
text = full_annotation[0]['document'][0].result
label_color = {}
for chunk in ner_chunks:
label_color[chunk.metadata['entity']] = get_color()
html_output = "<div>"
pos = 0
for n in ner_chunks:
if pos < n.begin and pos < len(text):
html_output += f"<span class=\"others\">{text[pos:n.begin]}</span>"
pos = n.end + 1
html_output += f"<span class=\"entity-wrapper\" style=\"color: black; background-color: {label_color[n.metadata['entity']]}\"> <span class=\"entity-name\">{n.result}</span> <span class=\"entity-type\">[{n.metadata['entity']}]</span></span>"
if pos < len(text):
html_output += f"<span class=\"others\">{text[pos:]}</span>"
html_output += "</div>"
display(HTML(html_output))
# + [markdown] colab_type="text" id="-piHygJ6dpEa"
# Display example outputs as HTML
# + colab={"base_uri": "https://localhost:8080/", "height": 191} colab_type="code" id="AtbhE24VeG_C" outputId="05d8fae4-bf84-45c3-e047-39c7448e58ee"
for example in input_list:
annotation_to_html(light_pipeline.fullAnnotate(example))
| 40.882629 | 1,076 |
2d6a5603693f539d6660340a4afe7c18a54d6651
|
py
|
python
|
dog_app.ipynb
|
divyankvijayvergiya/dog_project
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Convolutional Neural Networks
#
# ## Project: Write an Algorithm for a Dog Identification App
#
# ---
#
# In this notebook, some template code has already been provided for you, and you will need to implement additional functionality to successfully complete this project. You will not need to modify the included code beyond what is requested. Sections that begin with **'(IMPLEMENTATION)'** in the header indicate that the following block of code will require additional functionality which you must provide. Instructions will be provided for each section, and the specifics of the implementation are marked in the code block with a 'TODO' statement. Please be sure to read the instructions carefully!
#
# > **Note**: Once you have completed all of the code implementations, you need to finalize your work by exporting the iPython Notebook as an HTML document. Before exporting the notebook to html, all of the code cells need to have been run so that reviewers can see the final implementation and output. You can then export the notebook by using the menu above and navigating to \n",
# "**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
#
# In addition to implementing code, there will be questions that you must answer which relate to the project and your implementation. Each section where you will answer a question is preceded by a **'Question X'** header. Carefully read each question and provide thorough answers in the following text boxes that begin with **'Answer:'**. Your project submission will be evaluated based on your answers to each of the questions and the implementation you provide.
#
# >**Note:** Code and Markdown cells can be executed using the **Shift + Enter** keyboard shortcut. Markdown cells can be edited by double-clicking the cell to enter edit mode.
#
# The rubric contains _optional_ "Stand Out Suggestions" for enhancing the project beyond the minimum requirements. If you decide to pursue the "Stand Out Suggestions", you should include the code in this IPython notebook.
#
#
#
# ---
# ### Why We're Here
#
# In this notebook, you will make the first steps towards developing an algorithm that could be used as part of a mobile or web app. At the end of this project, your code will accept any user-supplied image as input. If a dog is detected in the image, it will provide an estimate of the dog's breed. If a human is detected, it will provide an estimate of the dog breed that is most resembling. The image below displays potential sample output of your finished project (... but we expect that each student's algorithm will behave differently!).
#
# 
#
# In this real-world setting, you will need to piece together a series of models to perform different tasks; for instance, the algorithm that detects humans in an image will be different from the CNN that infers dog breed. There are many points of possible failure, and no perfect algorithm exists. Your imperfect solution will nonetheless create a fun user experience!
#
# ### The Road Ahead
#
# We break the notebook into separate steps. Feel free to use the links below to navigate the notebook.
#
# * [Step 0](#step0): Import Datasets
# * [Step 1](#step1): Detect Humans
# * [Step 2](#step2): Detect Dogs
# * [Step 3](#step3): Create a CNN to Classify Dog Breeds (from Scratch)
# * [Step 4](#step4): Use a CNN to Classify Dog Breeds (using Transfer Learning)
# * [Step 5](#step5): Create a CNN to Classify Dog Breeds (using Transfer Learning)
# * [Step 6](#step6): Write your Algorithm
# * [Step 7](#step7): Test Your Algorithm
#
# ---
# <a id='step0'></a>
# ## Step 0: Import Datasets
#
# ### Import Dog Dataset
#
# In the code cell below, we import a dataset of dog images. We populate a few variables through the use of the `load_files` function from the scikit-learn library:
# - `train_files`, `valid_files`, `test_files` - numpy arrays containing file paths to images
# - `train_targets`, `valid_targets`, `test_targets` - numpy arrays containing onehot-encoded classification labels
# - `dog_names` - list of string-valued dog breed names for translating labels
# +
from sklearn.datasets import load_files
from keras.utils import np_utils
import numpy as np
from glob import glob
# define function to load train, test, and validation datasets
def load_dataset(path):
data = load_files(path)
dog_files = np.array(data['filenames'])
dog_targets = np_utils.to_categorical(np.array(data['target']), 133)
return dog_files, dog_targets
# load train, test, and validation datasets
train_files, train_targets = load_dataset('/data/dog_images/train')
valid_files, valid_targets = load_dataset('/data/dog_images/valid')
test_files, test_targets = load_dataset('/data/dog_images/test')
# load list of dog names
dog_names = [item[20:-1] for item in sorted(glob("/data/dog_images/train/*/"))]
# print statistics about the dataset
print('There are %d total dog categories.' % len(dog_names))
print('There are %s total dog images.\n' % len(np.hstack([train_files, valid_files, test_files])))
print('There are %d training dog images.' % len(train_files))
print('There are %d validation dog images.' % len(valid_files))
print('There are %d test dog images.'% len(test_files))
# -
# ### Import Human Dataset
#
# In the code cell below, we import a dataset of human images, where the file paths are stored in the numpy array `human_files`.
# +
import random
random.seed(8675309)
# load filenames in shuffled human dataset
human_files = np.array(glob("/data/lfw/*/*"))
random.shuffle(human_files)
# print statistics about the dataset
print('There are %d total human images.' % len(human_files))
# -
# ---
# <a id='step1'></a>
# ## Step 1: Detect Humans
#
# We use OpenCV's implementation of [Haar feature-based cascade classifiers](http://docs.opencv.org/trunk/d7/d8b/tutorial_py_face_detection.html) to detect human faces in images. OpenCV provides many pre-trained face detectors, stored as XML files on [github](https://github.com/opencv/opencv/tree/master/data/haarcascades). We have downloaded one of these detectors and stored it in the `haarcascades` directory.
#
# In the next code cell, we demonstrate how to use this detector to find human faces in a sample image.
# +
import cv2
import matplotlib.pyplot as plt
# %matplotlib inline
# extract pre-trained face detector
face_cascade = cv2.CascadeClassifier('haarcascades/haarcascade_frontalface_alt.xml')
# load color (BGR) image
img = cv2.imread(human_files[3])
# convert BGR image to grayscale
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# find faces in image
faces = face_cascade.detectMultiScale(gray)
# print number of faces detected in the image
print('Number of faces detected:', len(faces))
# get bounding box for each detected face
for (x,y,w,h) in faces:
# add bounding box to color image
cv2.rectangle(img,(x,y),(x+w,y+h),(255,0,0),2)
# convert BGR image to RGB for plotting
cv_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# display the image, along with bounding box
plt.imshow(cv_rgb)
plt.show()
# -
# Before using any of the face detectors, it is standard procedure to convert the images to grayscale. The `detectMultiScale` function executes the classifier stored in `face_cascade` and takes the grayscale image as a parameter.
#
# In the above code, `faces` is a numpy array of detected faces, where each row corresponds to a detected face. Each detected face is a 1D array with four entries that specifies the bounding box of the detected face. The first two entries in the array (extracted in the above code as `x` and `y`) specify the horizontal and vertical positions of the top left corner of the bounding box. The last two entries in the array (extracted here as `w` and `h`) specify the width and height of the box.
#
# ### Write a Human Face Detector
#
# We can use this procedure to write a function that returns `True` if a human face is detected in an image and `False` otherwise. This function, aptly named `face_detector`, takes a string-valued file path to an image as input and appears in the code block below.
# returns "True" if face is detected in image stored at img_path
def face_detector(img_path):
img = cv2.imread(img_path)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
faces = face_cascade.detectMultiScale(gray)
return len(faces) > 0
# ### (IMPLEMENTATION) Assess the Human Face Detector
#
# __Question 1:__ Use the code cell below to test the performance of the `face_detector` function.
# - What percentage of the first 100 images in `human_files` have a detected human face?
# - What percentage of the first 100 images in `dog_files` have a detected human face?
#
# Ideally, we would like 100% of human images with a detected face and 0% of dog images with a detected face. You will see that our algorithm falls short of this goal, but still gives acceptable performance. We extract the file paths for the first 100 images from each of the datasets and store them in the numpy arrays `human_files_short` and `dog_files_short`.
#
# __Answer:__
#
# - 100% Percentage of the first 100 images in `human_files` have human detected face.
#
# - 11% Percentage of the first 100 images in `dog_files` have human detected face .
#
# +
human_files_short = human_files[:100]
dog_files_short = train_files[:100]
# Do NOT modify the code above this line.
## Test the performance of the face_detector algorithm
## on the images in human_files_short and dog_files_short.
num_faces_detected_human_files = 0
for img in human_files_short:
if face_detector(img):
num_faces_detected_human_files += 1
print ("Percentage of human faces detected from human_files: %.0f%%" % num_faces_detected_human_files )
num_faces_detected_dog_files = 0
for img in dog_files_short:
if face_detector(img):
num_faces_detected_dog_files += 1
print ("Percentage of human faces detected from dog_files: %.0f%%" % num_faces_detected_dog_files )
# -
# __Question 2:__ This algorithmic choice necessitates that we communicate to the user that we accept human images only when they provide a clear view of a face (otherwise, we risk having unneccessarily frustrated users!). In your opinion, is this a reasonable expectation to pose on the user? If not, can you think of a way to detect humans in images that does not necessitate an image with a clearly presented face?
#
# __Answer:__
#
# The user of the app usually could not control the angle of the picture. The "ready made" app should manage the identification so the algorithm must be able to handle recognition of humans in not perfect conditions. So the algorithm should manage images that include other human features from different angles, different backgrounds, faces with glass, scars etc.
#
# The accuracy rate of 100% and 11% on false is a good result. I think the app should communicate the limitation of the program or applying more accurate object detection technologies: like latest CapsNets by Geoffrey Hinton.(implementation example: https://github.com/naturomics/CapsNet-Tensorflow)
#
#
#
# We suggest the face detector from OpenCV as a potential way to detect human images in your algorithm, but you are free to explore other approaches, especially approaches that make use of deep learning :). Please use the code cell below to design and test your own face detection algorithm. If you decide to pursue this _optional_ task, report performance on each of the datasets.
# +
## (Optional) TODO: Report the performance of another
## face detection algorithm on the LFW dataset
### Feel free to use as many code cells as needed.
# -
# ---
# <a id='step2'></a>
# ## Step 2: Detect Dogs
#
# In this section, we use a pre-trained [ResNet-50](http://ethereon.github.io/netscope/#/gist/db945b393d40bfa26006) model to detect dogs in images. Our first line of code downloads the ResNet-50 model, along with weights that have been trained on [ImageNet](http://www.image-net.org/), a very large, very popular dataset used for image classification and other vision tasks. ImageNet contains over 10 million URLs, each linking to an image containing an object from one of [1000 categories](https://gist.github.com/yrevar/942d3a0ac09ec9e5eb3a). Given an image, this pre-trained ResNet-50 model returns a prediction (derived from the available categories in ImageNet) for the object that is contained in the image.
# +
from keras.applications.resnet50 import ResNet50
# define ResNet50 model
ResNet50_model = ResNet50(weights='imagenet')
# -
# ### Pre-process the Data
#
# When using TensorFlow as backend, Keras CNNs require a 4D array (which we'll also refer to as a 4D tensor) as input, with shape
#
# $$
# (\text{nb_samples}, \text{rows}, \text{columns}, \text{channels}),
# $$
#
# where `nb_samples` corresponds to the total number of images (or samples), and `rows`, `columns`, and `channels` correspond to the number of rows, columns, and channels for each image, respectively.
#
# The `path_to_tensor` function below takes a string-valued file path to a color image as input and returns a 4D tensor suitable for supplying to a Keras CNN. The function first loads the image and resizes it to a square image that is $224 \times 224$ pixels. Next, the image is converted to an array, which is then resized to a 4D tensor. In this case, since we are working with color images, each image has three channels. Likewise, since we are processing a single image (or sample), the returned tensor will always have shape
#
# $$
# (1, 224, 224, 3).
# $$
#
# The `paths_to_tensor` function takes a numpy array of string-valued image paths as input and returns a 4D tensor with shape
#
# $$
# (\text{nb_samples}, 224, 224, 3).
# $$
#
# Here, `nb_samples` is the number of samples, or number of images, in the supplied array of image paths. It is best to think of `nb_samples` as the number of 3D tensors (where each 3D tensor corresponds to a different image) in your dataset!
# +
from keras.preprocessing import image
from tqdm import tqdm
def path_to_tensor(img_path):
# loads RGB image as PIL.Image.Image type
img = image.load_img(img_path, target_size=(224, 224))
# convert PIL.Image.Image type to 3D tensor with shape (224, 224, 3)
x = image.img_to_array(img)
# convert 3D tensor to 4D tensor with shape (1, 224, 224, 3) and return 4D tensor
return np.expand_dims(x, axis=0)
def paths_to_tensor(img_paths):
list_of_tensors = [path_to_tensor(img_path) for img_path in tqdm(img_paths)]
return np.vstack(list_of_tensors)
# -
# ### Making Predictions with ResNet-50
#
# Getting the 4D tensor ready for ResNet-50, and for any other pre-trained model in Keras, requires some additional processing. First, the RGB image is converted to BGR by reordering the channels. All pre-trained models have the additional normalization step that the mean pixel (expressed in RGB as $[103.939, 116.779, 123.68]$ and calculated from all pixels in all images in ImageNet) must be subtracted from every pixel in each image. This is implemented in the imported function `preprocess_input`. If you're curious, you can check the code for `preprocess_input` [here](https://github.com/fchollet/keras/blob/master/keras/applications/imagenet_utils.py).
#
# Now that we have a way to format our image for supplying to ResNet-50, we are now ready to use the model to extract the predictions. This is accomplished with the `predict` method, which returns an array whose $i$-th entry is the model's predicted probability that the image belongs to the $i$-th ImageNet category. This is implemented in the `ResNet50_predict_labels` function below.
#
# By taking the argmax of the predicted probability vector, we obtain an integer corresponding to the model's predicted object class, which we can identify with an object category through the use of this [dictionary](https://gist.github.com/yrevar/942d3a0ac09ec9e5eb3a).
# +
from keras.applications.resnet50 import preprocess_input, decode_predictions
def ResNet50_predict_labels(img_path):
# returns prediction vector for image located at img_path
img = preprocess_input(path_to_tensor(img_path))
return np.argmax(ResNet50_model.predict(img))
# -
# ### Write a Dog Detector
#
# While looking at the [dictionary](https://gist.github.com/yrevar/942d3a0ac09ec9e5eb3a), you will notice that the categories corresponding to dogs appear in an uninterrupted sequence and correspond to dictionary keys 151-268, inclusive, to include all categories from `'Chihuahua'` to `'Mexican hairless'`. Thus, in order to check to see if an image is predicted to contain a dog by the pre-trained ResNet-50 model, we need only check if the `ResNet50_predict_labels` function above returns a value between 151 and 268 (inclusive).
#
# We use these ideas to complete the `dog_detector` function below, which returns `True` if a dog is detected in an image (and `False` if not).
### returns "True" if a dog is detected in the image stored at img_path
def dog_detector(img_path):
prediction = ResNet50_predict_labels(img_path)
return ((prediction <= 268) & (prediction >= 151))
# ### (IMPLEMENTATION) Assess the Dog Detector
#
# __Question 3:__ Use the code cell below to test the performance of your `dog_detector` function.
# - What percentage of the images in `human_files_short` have a detected dog?
# - What percentage of the images in `dog_files_short` have a detected dog?
#
# __Answer:__
#
# - `0` percentage of the images in `human_files_short` have a detected dog
# - `80` percentage of the images in `dog_files_short` have a detected dog
# +
### TODO: Test the performance of the dog_detector function
### on the images in human_files_short and dog_files_short.
human_percent = 0
for h in human_files_short:
if(dog_detector(h)):
human_percent = len(h)
print ("Percentage of human faces detected: %.0f%%" % human_percent )
dog_percent = 0
for h in dog_files_short:
if(dog_detector(h)):
dog_percent = len(h)
print ("Percentage of dog faces detected: %.0f%%" % dog_percent )
# -
# ---
# <a id='step3'></a>
# ## Step 3: Create a CNN to Classify Dog Breeds (from Scratch)
#
# Now that we have functions for detecting humans and dogs in images, we need a way to predict breed from images. In this step, you will create a CNN that classifies dog breeds. You must create your CNN _from scratch_ (so, you can't use transfer learning _yet_!), and you must attain a test accuracy of at least 1%. In Step 5 of this notebook, you will have the opportunity to use transfer learning to create a CNN that attains greatly improved accuracy.
#
# Be careful with adding too many trainable layers! More parameters means longer training, which means you are more likely to need a GPU to accelerate the training process. Thankfully, Keras provides a handy estimate of the time that each epoch is likely to take; you can extrapolate this estimate to figure out how long it will take for your algorithm to train.
#
# We mention that the task of assigning breed to dogs from images is considered exceptionally challenging. To see why, consider that *even a human* would have great difficulty in distinguishing between a Brittany and a Welsh Springer Spaniel.
#
# Brittany | Welsh Springer Spaniel
# - | -
# <img src="images/Brittany_02625.jpg" width="100"> | <img src="images/Welsh_springer_spaniel_08203.jpg" width="200">
#
# It is not difficult to find other dog breed pairs with minimal inter-class variation (for instance, Curly-Coated Retrievers and American Water Spaniels).
#
# Curly-Coated Retriever | American Water Spaniel
# - | -
# <img src="images/Curly-coated_retriever_03896.jpg" width="200"> | <img src="images/American_water_spaniel_00648.jpg" width="200">
#
#
# Likewise, recall that labradors come in yellow, chocolate, and black. Your vision-based algorithm will have to conquer this high intra-class variation to determine how to classify all of these different shades as the same breed.
#
# Yellow Labrador | Chocolate Labrador | Black Labrador
# - | -
# <img src="images/Labrador_retriever_06457.jpg" width="150"> | <img src="images/Labrador_retriever_06455.jpg" width="240"> | <img src="images/Labrador_retriever_06449.jpg" width="220">
#
# We also mention that random chance presents an exceptionally low bar: setting aside the fact that the classes are slightly imabalanced, a random guess will provide a correct answer roughly 1 in 133 times, which corresponds to an accuracy of less than 1%.
#
# Remember that the practice is far ahead of the theory in deep learning. Experiment with many different architectures, and trust your intuition. And, of course, have fun!
#
# ### Pre-process the Data
#
# We rescale the images by dividing every pixel in every image by 255.
# +
from PIL import ImageFile
ImageFile.LOAD_TRUNCATED_IMAGES = True
# pre-process the data for Keras
train_tensors = paths_to_tensor(train_files).astype('float32')/255
valid_tensors = paths_to_tensor(valid_files).astype('float32')/255
test_tensors = paths_to_tensor(test_files).astype('float32')/255
# -
# ### (IMPLEMENTATION) Model Architecture
#
# Create a CNN to classify dog breed. At the end of your code cell block, summarize the layers of your model by executing the line:
#
# model.summary()
#
# We have imported some Python modules to get you started, but feel free to import as many modules as you need. If you end up getting stuck, here's a hint that specifies a model that trains relatively fast on CPU and attains >1% test accuracy in 5 epochs:
#
# 
#
# __Question 4:__ Outline the steps you took to get to your final CNN architecture and your reasoning at each step. If you chose to use the hinted architecture above, describe why you think that CNN architecture should work well for the image classification task.
#
# __Answer:__
#
#
# The architecture I adopted combines the suggested architecture with a sort of LeNet, where the Flatten-ing happens through the GlobalAveragePooling, which I found to be a lot more effective than a simple Flatten() as the features in the GAP level represent a feature.
# In the first two CONV layers, I increase the filters as suggested by the lectures, but I reduce the kernel size as the size after a CONV-POOL layer reduces in height and width but it increases in depth. I then feed the values coming from the GAP into two consecutive FC layers. This enables me to use at least one "relu"activation layer in a FC layer.
#
# I think that CNN architecture should work well for the image classification task because Convolutional Neural Networks take advantage of the fact that the input consists of images and they constrain the architecture in a more sensible way. In particular, unlike a regular Neural Network, the layers of a ConvNet have neurons arranged in 3 dimensions: width, height, depth. (Note that the word depth here refers to the third dimension of an activation volume, not to the depth of a full Neural Network, which can refer to the total number of layers in a network.) For example, the input images in CIFAR-10 are an input volume of activations, and the volume has dimensions 32x32x3 (width, height, depth respectively). As we will soon see, the neurons in a layer will only be connected to a small region of the layer before it, instead of all of the neurons in a fully-connected manner. Moreover, the final output layer would for CIFAR-10 have dimensions 1x1x10, because by the end of the ConvNet architecture we will reduce the full image into a single vector of class scores, arranged along the depth dimension.
# +
from keras.layers import Conv2D, MaxPooling2D, GlobalAveragePooling2D
from keras.layers import Dropout, Flatten, Dense, Activation
from keras.models import Sequential
model = Sequential()
### TODO: Define your architecture.
###Define your architecture.
model.add(Conv2D(32, (9,9),strides=(2,2), padding='same', activation='relu', input_shape=(224, 224, 3)))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(64, (6,6), strides=(1,1), padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(128, (3,3), strides=(1,1), padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(GlobalAveragePooling2D())
model.add(Dropout(0.1))
model.add(Dense(500))
model.add(Activation("relu"))
model.add(Dense(133))
model.add(Activation("softmax"))
model.summary()
# -
# ### Compile the Model
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
# ### (IMPLEMENTATION) Train the Model
#
# Train your model in the code cell below. Use model checkpointing to save the model that attains the best validation loss.
#
# You are welcome to [augment the training data](https://blog.keras.io/building-powerful-image-classification-models-using-very-little-data.html), but this is not a requirement.
# +
from keras.callbacks import ModelCheckpoint
### specify the number of epochs that you would like to use to train the model.
epochs = 40
### Do NOT modify the code below this line.
checkpointer = ModelCheckpoint(filepath='saved_models/weights.best.from_scratch.hdf5',
verbose=1, save_best_only=True)
model.fit(train_tensors, train_targets,
validation_data=(valid_tensors, valid_targets),
epochs=epochs, batch_size=20, callbacks=[checkpointer], verbose=1)
# -
# ### Load the Model with the Best Validation Loss
model.load_weights('saved_models/weights.best.from_scratch.hdf5')
# ### Test the Model
#
# Try out your model on the test dataset of dog images. Ensure that your test accuracy is greater than 1%.
# +
# get index of predicted dog breed for each image in test set
dog_breed_predictions = [np.argmax(model.predict(np.expand_dims(tensor, axis=0))) for tensor in test_tensors]
# report test accuracy
test_accuracy = 100*np.sum(np.array(dog_breed_predictions)==np.argmax(test_targets, axis=1))/len(dog_breed_predictions)
print('Test accuracy: %.4f%%' % test_accuracy)
# -
# ---
# <a id='step4'></a>
# ## Step 4: Use a CNN to Classify Dog Breeds
#
# To reduce training time without sacrificing accuracy, we show you how to train a CNN using transfer learning. In the following step, you will get a chance to use transfer learning to train your own CNN.
#
# ### Obtain Bottleneck Features
bottleneck_features = np.load('/data/bottleneck_features/DogVGG16Data.npz')
train_VGG16 = bottleneck_features['train']
valid_VGG16 = bottleneck_features['valid']
test_VGG16 = bottleneck_features['test']
# ### Model Architecture
#
# The model uses the the pre-trained VGG-16 model as a fixed feature extractor, where the last convolutional output of VGG-16 is fed as input to our model. We only add a global average pooling layer and a fully connected layer, where the latter contains one node for each dog category and is equipped with a softmax.
# +
VGG16_model = Sequential()
VGG16_model.add(GlobalAveragePooling2D(input_shape=train_VGG16.shape[1:]))
VGG16_model.add(Dense(133, activation='softmax'))
VGG16_model.summary()
# -
# ### Compile the Model
VGG16_model.compile(loss='categorical_crossentropy', optimizer='rmsprop', metrics=['accuracy'])
# ### Train the Model
# +
checkpointer = ModelCheckpoint(filepath='saved_models/weights.best.VGG16.hdf5',
verbose=1, save_best_only=True)
VGG16_model.fit(train_VGG16, train_targets,
validation_data=(valid_VGG16, valid_targets),
epochs=20, batch_size=20, callbacks=[checkpointer], verbose=1)
# -
# ### Load the Model with the Best Validation Loss
VGG16_model.load_weights('saved_models/weights.best.VGG16.hdf5')
# ### Test the Model
#
# Now, we can use the CNN to test how well it identifies breed within our test dataset of dog images. We print the test accuracy below.
# +
# get index of predicted dog breed for each image in test set
VGG16_predictions = [np.argmax(VGG16_model.predict(np.expand_dims(feature, axis=0))) for feature in test_VGG16]
# report test accuracy
test_accuracy = 100*np.sum(np.array(VGG16_predictions)==np.argmax(test_targets, axis=1))/len(VGG16_predictions)
print('Test accuracy: %.4f%%' % test_accuracy)
# -
# ### Predict Dog Breed with the Model
# +
from extract_bottleneck_features import *
def VGG16_predict_breed(img_path):
# extract bottleneck features
bottleneck_feature = extract_VGG16(path_to_tensor(img_path))
# obtain predicted vector
predicted_vector = VGG16_model.predict(bottleneck_feature)
# return dog breed that is predicted by the model
return dog_names[np.argmax(predicted_vector)]
# -
# ---
# <a id='step5'></a>
# ## Step 5: Create a CNN to Classify Dog Breeds (using Transfer Learning)
#
# You will now use transfer learning to create a CNN that can identify dog breed from images. Your CNN must attain at least 60% accuracy on the test set.
#
# In Step 4, we used transfer learning to create a CNN using VGG-16 bottleneck features. In this section, you must use the bottleneck features from a different pre-trained model. To make things easier for you, we have pre-computed the features for all of the networks that are currently available in Keras. These are already in the workspace, at /data/bottleneck_features. If you wish to download them on a different machine, they can be found at:
# - [VGG-19](https://s3-us-west-1.amazonaws.com/udacity-aind/dog-project/DogVGG19Data.npz) bottleneck features
# - [ResNet-50](https://s3-us-west-1.amazonaws.com/udacity-aind/dog-project/DogResnet50Data.npz) bottleneck features
# - [Inception](https://s3-us-west-1.amazonaws.com/udacity-aind/dog-project/DogInceptionV3Data.npz) bottleneck features
# - [Xception](https://s3-us-west-1.amazonaws.com/udacity-aind/dog-project/DogXceptionData.npz) bottleneck features
#
# The files are encoded as such:
#
# Dog{network}Data.npz
#
# where `{network}`, in the above filename, can be one of `VGG19`, `Resnet50`, `InceptionV3`, or `Xception`.
#
# The above architectures are downloaded and stored for you in the `/data/bottleneck_features/` folder.
#
# This means the following will be in the `/data/bottleneck_features/` folder:
#
# `DogVGG19Data.npz`
# `DogResnet50Data.npz`
# `DogInceptionV3Data.npz`
# `DogXceptionData.npz`
#
#
#
# ### (IMPLEMENTATION) Obtain Bottleneck Features
#
# In the code block below, extract the bottleneck features corresponding to the train, test, and validation sets by running the following:
#
# bottleneck_features = np.load('/data/bottleneck_features/Dog{network}Data.npz')
# train_{network} = bottleneck_features['train']
# valid_{network} = bottleneck_features['valid']
# test_{network} = bottleneck_features['test']
### Obtain bottleneck features from another pre-trained CNN.
bottleneck_features = np.load('/data/bottleneck_features/DogResnet50Data.npz')
train_resnet = bottleneck_features['train']
valid_resnet = bottleneck_features['valid']
test_resnet = bottleneck_features['test']
# ### (IMPLEMENTATION) Model Architecture
#
# Create a CNN to classify dog breed. At the end of your code cell block, summarize the layers of your model by executing the line:
#
# <your model's name>.summary()
#
# __Question 5:__ Outline the steps you took to get to your final CNN architecture and your reasoning at each step. Describe why you think the architecture is suitable for the current problem.
#
# __Answer:__
#
# I added the GAP layer as my first step to extract out best features from the dataset. After that I added Dense layer to divide it in 500 nodes. After that I added `tanh` as an activation function to improve accuracy then I added dropout layer with 20% to reduce overfitting and then added final FC layer.
#
# Reasoning:
#
# Resnet50 already have lot of layers of Conv2d and pooling layers which make me think if I use more conv2d layers it will slow my training of model and after adding more conv2d layer there is no so much affect in accuracy too so I directly added the GAP layer to extract out best features from the dataset it retrieves the best features from an image processed through Resnet50 weights, and it flattens the data too.
#
# After that I added a tanh activation function which is completely intuitional I tried with relu too but it's giving less accuracy as compared to tanh. Again, empirically I found 0.2 to be the best value, with 0.1 not making too great a difference, while anything bigger than 0.2 worsening the model even significantly.
#
# And I think Resnet50 is correct architecture because when I have used VGG19 I get 67% accuracy but when I used Resnet50 it produces more than 79% accuracy which is quite impressive.
#
#
#
### Define your architecture.
res_model = Sequential()
res_model.add(GlobalAveragePooling2D(input_shape=train_resnet.shape[1:]))
res_model.add(Dense(500))
res_model.add(Activation("tanh"))
res_model.add(Dropout(0.2))
res_model.add(Dense(133, activation='softmax'))
res_model.summary()
# ### (IMPLEMENTATION) Compile the Model
### Compile the model.
res_model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
# ### (IMPLEMENTATION) Train the Model
#
# Train your model in the code cell below. Use model checkpointing to save the model that attains the best validation loss.
#
# You are welcome to [augment the training data](https://blog.keras.io/building-powerful-image-classification-models-using-very-little-data.html), but this is not a requirement.
# +
### Train the model.
checkpointer = ModelCheckpoint(filepath='saved_models/weights.best.Inc_model.hdf5',
verbose=1, save_best_only=True)
res_model.fit(train_resnet, train_targets,
validation_data=(valid_resnet, valid_targets),
epochs=100, batch_size=20, callbacks=[checkpointer], verbose=1)
# -
# ### (IMPLEMENTATION) Load the Model with the Best Validation Loss
### TODO: Load the model weights with the best validation loss.
res_model.load_weights('saved_models/weights.best.Inc_model.hdf5')
# ### (IMPLEMENTATION) Test the Model
#
# Try out your model on the test dataset of dog images. Ensure that your test accuracy is greater than 60%.
# +
### TODO: Calculate classification accuracy on the test dataset.
predictions = [np.argmax(res_model.predict(np.expand_dims(feature, axis=0))) for feature in test_resnet]
# report test accuracy
test_accuracy = 100*np.sum(np.array(predictions)==np.argmax(test_targets, axis=1))/len(predictions)
print('Test accuracy: %.4f%%' % test_accuracy)
# + active=""
# ### (IMPLEMENTATION) Predict Dog Breed with the Model
#
# Write a function that takes an image path as input and returns the dog breed (`Affenpinscher`, `Afghan_hound`, etc) that is predicted by your model.
#
# Similar to the analogous function in Step 5, your function should have three steps:
# 1. Extract the bottleneck features corresponding to the chosen CNN model.
# 2. Supply the bottleneck features as input to the model to return the predicted vector. Note that the argmax of this prediction vector gives the index of the predicted dog breed.
# 3. Use the `dog_names` array defined in Step 0 of this notebook to return the corresponding breed.
#
# The functions to extract the bottleneck features can be found in `extract_bottleneck_features.py`, and they have been imported in an earlier code cell. To obtain the bottleneck features corresponding to your chosen CNN architecture, you need to use the function
#
# extract_{network}
#
# where `{network}`, in the above filename, should be one of `VGG19`, `Resnet50`, `InceptionV3`, or `Xception`.
# +
### TODO: Write a function that takes a path to an image as input
### and returns the dog breed that is predicted by the model.
def resnet_predict_breed(path):
bottleneck_features = extract_Resnet50(path_to_tensor(path))
predict_vector = res_model.predict(bottleneck_features)
return dog_names[np.argmax(predict_vector)]
# -
# ---
# <a id='step6'></a>
# ## Step 6: Write your Algorithm
#
# Write an algorithm that accepts a file path to an image and first determines whether the image contains a human, dog, or neither. Then,
# - if a __dog__ is detected in the image, return the predicted breed.
# - if a __human__ is detected in the image, return the resembling dog breed.
# - if __neither__ is detected in the image, provide output that indicates an error.
#
# You are welcome to write your own functions for detecting humans and dogs in images, but feel free to use the `face_detector` and `dog_detector` functions developed above. You are __required__ to use your CNN from Step 5 to predict dog breed.
#
# Some sample output for our algorithm is provided below, but feel free to design your own user experience!
#
# 
#
#
# ### (IMPLEMENTATION) Write your Algorithm
# +
### TODO: Write your algorithm.
### Feel free to use as many code cells as needed.
class NeitherDogNorHumanError(Exception):
"""Subclassing Error for clarity"""
pass
def predict_breed(img_path):
creature = None
message = None
breed = None
if dog_detector(img_path):
creature = "dog"
message = "your predicted breed is"
if face_detector(img_path):
creature = "human"
message = "you look like a"
if not creature:
raise NeitherDogNorHumanError("This is neither a dog nor a human!!!")
breed = resnet_predict_breed(img_path)
return "Hello, {}! {} ... {}".format(creature, message, breed)
# -
# ---
# <a id='step7'></a>
# ## Step 7: Test Your Algorithm
#
# In this section, you will take your new algorithm for a spin! What kind of dog does the algorithm think that __you__ look like? If you have a dog, does it predict your dog's breed accurately? If you have a cat, does it mistakenly think that your cat is a dog?
#
# ### (IMPLEMENTATION) Test Your Algorithm on Sample Images!
#
# Test your algorithm at least six images on your computer. Feel free to use any images you like. Use at least two human and two dog images.
#
# __Question 6:__ Is the output better than you expected :) ? Or worse :( ? Provide at least three possible points of improvement for your algorithm.
#
# __Answer:__
#
# I really enjoyed this project and the algorithm did a good job as expected.
#
# Three possible ways to improvements are
#
# 1.) Store the probabilities of a prediction (just before they get 'softmax-ed') and determine dog-or-human based on
# the highest probability of the classification rather than short-circuiting at dog/human detection
#
# 2.) Using data augmentation to make the algorithm more robust. Using more regularization to prevent overfitting, regularization methods like dropout, L1/L2 regularizations.
#
# 3.) Feed model with more data and increase the epoch for training the model.
# +
## TODO: Execute your algorithm from Step 6 on
## at least 6 images on your computer.
## Feel free to use as many code cells as needed.
##print(predict_breed("./dogImages/test/001.Affenpinscher/Affenpinscher_00003.jpg"))
##print(predict_breed(me))
##print(predict_breed("./dogImages/train/002.Afghan_hound/Afghan_hound_00125.jpg"))
print(predict_breed("./images/Brittany_02625.jpg"))
print(predict_breed("./images/Curly-coated_retriever_03896.jpg"))
print(predict_breed("./images/Labrador_retriever_06449.jpg"))
print(predict_breed("./images/sample_human_output.png"))
print(predict_breed("./images/American_water_spaniel_00648.jpg"))
print(predict_breed("./BillGates.jpeg"))
# -
# # Please download your notebook to submit
#
# In order to submit, please do the following:
# 1. Download an HTML version of the notebook to your computer using 'File: Download as...'
# 2. Click on the orange Jupyter circle on the top left of the workspace.
# 3. Navigate into the dog-project folder to ensure that you are using the provided dog_images, lfw, and bottleneck_features folders; this means that those folders will *not* appear in the dog-project folder. If they do appear because you downloaded them, delete them.
# 4. While in the dog-project folder, upload the HTML version of this notebook you just downloaded. The upload button is on the top right.
# 5. Navigate back to the home folder by clicking on the two dots next to the folder icon, and then open up a terminal under the 'new' tab on the top right
# 6. Zip the dog-project folder with the following command in the terminal:
# `zip -r dog-project.zip dog-project`
# 7. Download the zip file by clicking on the square next to it and selecting 'download'. This will be the zip file you turn in on the next node after this workspace!
| 51.018892 | 1,112 |
d831c888de58d2dcf3663092db82689ac673bd99
|
py
|
python
|
seq2seq.ipynb
|
mmeooo/test_NLP
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="UmKlRIiL-UjF"
# ## Data load
# + id="sNZei6fEXKVt"
import numpy as np
# + colab={"base_uri": "https://localhost:8080/"} id="Nia7vdyCXarI" outputId="ca418151-6670-471c-9b6f-de54948a5e28"
index_inputs = np.load(open('./train_inputs.npy', 'rb'))
index_outputs = np.load(open('./train_outputs.npy', 'rb'))
index_targets = np.load(open('./train_targets.npy', 'rb'))
type(index_inputs)
# + colab={"base_uri": "https://localhost:8080/"} id="4yKPGw4MXpEW" outputId="30f8db17-b644-4f3c-86ca-07f099adb0ee"
index_inputs[3:5]
# + colab={"base_uri": "https://localhost:8080/"} id="2woWKOTdXtYY" outputId="3edbd900-a805-4095-90cf-692d77475260"
# !python -m pip install konlpy
# + id="dNIpr_14qK9j"
# preprocess.py 파일 로드
import preprocess as pp
# + colab={"base_uri": "https://localhost:8080/"} id="3NJi7xYUqNNj" outputId="dc84bbb5-54af-47ee-89b8-a50c8ca72628"
prepro_configs = pp.json.load(open('./data_configs.json', 'r'))
type(prepro_configs)
# + colab={"base_uri": "https://localhost:8080/"} id="QbiPRFiSqu8b" outputId="cf7fa950-9c29-4011-ec4b-ab08e0e446b2"
prepro_configs.keys()
# + [markdown] id="pDdtNUiiq4im"
# ## Make model
# 
# ```
# Encoder -> context -> Decoder
# input input
# Embedding Embedding
# LSTM LSTM
# ```
# + id="k1ftBDtqq352"
import tensorflow as tf
# + [markdown] id="1tH8fOantu8h"
# ### encode model
# + id="41XhLTQcuPYW"
vocab_size = prepro_configs['vocab_size']
latent_dim = 60
# + id="w3VLc4asttQh"
encode_input = tf.keras.Input(shape=(None, ))
encode_hidden = tf.keras.layers.Embedding(input_dim=vocab_size, output_dim=latent_dim)(encode_input)
encode_output, state_h, state_c = tf.keras.layers.LSTM(50, return_state=True)(encode_hidden)
encode_states = [state_h, state_c]
# return_state=True 해주면 parameter(자기 상태 값)가 3개 날라옴.
# + [markdown] id="OwkUtiM1v7aj"
# ### decode model
# + id="UDFfqWZgutOp"
decode_input = tf.keras.Input(shape=(None,))
decode_hidden = tf.keras.layers.Embedding(input_dim=vocab_size, output_dim=latent_dim)(decode_input)
decode_lstm, _, _ = tf.keras.layers.LSTM(50, return_state=True, return_sequences=True)(decode_hidden, initial_state=encode_states)
decode_output = tf.keras.layers.Dense(vocab_size, activation='softmax')(decode_lstm)
# + id="LkfxcZMDzNzQ"
model = tf.keras.models.Model(inputs=[encode_input, decode_input] , outputs=decode_output )
# + colab={"base_uri": "https://localhost:8080/", "height": 466} id="8ZTfh1Cg0Sw1" outputId="2af87a5f-2974-4cd9-e5fb-a8921b54277b"
tf.keras.utils.plot_model(model)
# + id="nBPy5HC20TZA"
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['acc'])
# + [markdown] id="dqmJ602W40KU"
# ## fit
# + colab={"base_uri": "https://localhost:8080/"} id="vDd-AKpt4nFu" outputId="df41133c-c9eb-4cfa-b950-a98b24a7cfe5"
model.fit(x=[index_inputs, index_outputs], y=index_targets, batch_size=128, epochs=50)
# + [markdown] id="jy0r8Xlv5fyb"
# reference : https://github.com/NLP-kr/tensorflow-ml-nlp-tf2/blob/master/6.CHATBOT/6.4.seq2seq.ipynb
# + id="VxOOMWGv49or"
| 2,134.89899 | 208,158 |
1a5ae20e084ab99ab9d52907ed5bf63b2899cf4c
|
py
|
python
|
Step1-People-and-publications.ipynb
|
elswob/UoB-Orcid-2019
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Intro and Background
#
# In 2018 I published a piece of software called MELODI - http://melodi.biocompute.org.uk/. Essentially it compares the text from two sets of publications and identifies common overlapping enriched terms based around a [PubMed](https://www.ncbi.nlm.nih.gov/pubmed/) search. I realised that a set of text could also be based on a person, making it possible to identify enriched terms for a person and common shared terms across two people. At the same time the JGI launched a competition to analyse the [University of Bristol's PURE data](https://research-information.bris.ac.uk) in a novel way, which I entered using some of the ideas from the MELODI work. This led to the production of AXON (http://axon.biocompute.org.uk/) and an AXON instance of the University of Bristol academic research output http://axon-bristol.biocompute.org.uk/. However, maintaining this and keeping it up-to-date was not feasible, as I am currently working at the Integrative Epidemiology Unit, and this is not really epidemiology.
#
# However, I think the ideas and (some of) the code might be of interest to others.
#
# ### Setup
#
# Possibly the most important aspect of the data for this project is ensuring robust and unique identifiers. For individuals this can be achieved using ORCID identifiers (https://orcid.org/) and for publications we can use PubMed identifiers (https://www.ncbi.nlm.nih.gov/pubmed/).
#
# First, let's create some directories for data and output
# +
import os
#this file (config.py) lists the names of files used throughout
import config
#make a directory for output from the notebooks
os.makedirs('output',exist_ok=True)
# -
# Check python executable
import sys
sys.executable
# Result should be something like `/xxx/xxx/anaconda3/envs/jgi-data-week-workshop/bin/python`
# ##### Pandas
#
# We will also be using Pandas (https://pandas.pydata.org/) for various things
#
# >pandas is an open source, BSD-licensed library providing high-performance, easy-to-use data structures and data analysis tools for the Python programming language.
import pandas as pd
# ### PubMed
#
# PubMed (https://www.ncbi.nlm.nih.gov/pubmed/) comprises more than 29 million citations for biomedical literature from MEDLINE, life science journals, and online books. Citations may include links to full-text content from PubMed Central and publisher web sites.
#
# We can use some simple commands to get PubMed data. First, let's import the pubmed function:
from scripts.pubmed_functions import get_pubmed_data_efetch
# Using this, we can retrieve some data using a pubmed ID, e.g. 123
pubData=get_pubmed_data_efetch(['123'])
# This has fetched some summary data for the publication with ID 123 and added it to a the file `output/pubmed.tsv`.
#
# Run it again, this time it will use local file
pubData=get_pubmed_data_efetch(['123'])
# ### ORCID
#
# ORCID (https://orcid.org/) provides a persistent digital identifier that distinguishes you from every other researcher and, through integration in key research workflows such as manuscript and grant submission, supports automated linkages between you and your professional activities ensuring that your work is recognized.
#
# Let's get some info from an ORCID account
# +
import requests
#create a function to get publication IDs from an ORCID account
def get_ids_from_orcid_public_api(orcid):
resp = requests.get("http://pub.orcid.org/"+orcid+"/works/",
headers={'Accept':'application/orcid+json'})
results = resp.json()
pubData = []
if 'group' in results:
for i, result in enumerate( results['group']):
pubDic={}
if 'external-ids' in result:
for e in result['external-ids']['external-id']:
if e['external-id-type']=='pmid':
pmid = e['external-id-value']
pubDic['pmid']=pmid
elif e['external-id-type']=='doi':
doi = e['external-id-value']
pubDic['doi']=doi
if len(pubDic)>0:
pubData.append(pubDic)
else:
print('no data found')
return pubData
# -
orcidData=get_ids_from_orcid_public_api('0000-0001-7328-4233')
#convert dictionary to dataframe
df=pd.DataFrame.from_dict(orcidData)
print(df)
# From this dictionary we can easily get both PubMed IDs and DOIs
#process PubMed IDs and DOIs separately
pubMedIDs = set()
doiIDs = set()
for i in orcidData:
if 'pmid' in i:
pubMedIDs.add(i['pmid'])
if 'doi' in i:
doiIDs.add(i['doi'])
print(len(pubMedIDs),'PMIDs')
print(len(doiIDs),'DOIs')
# Then using the same function as before we can get the PubMed data using the PubMed IDs:
#get the publication data using the PMIDs
pubData1=get_pubmed_data_efetch(list(pubMedIDs))
print(len(pubData1),'publication records returned')
# Often, a record in an ORCID account will not contain a PubMed identifier. In this case we can convert DOIs to PMIDs using and ID converter API - https://www.ncbi.nlm.nih.gov/pmc/tools/id-converter-api/
from scripts.pubmed_functions import doi_to_pmid
doi_pmid=doi_to_pmid(list(doiIDs))
print(doi_pmid)
# Now we can create a single list of PMIDs and get all publication data
allPMIDs = list(set(list(pubMedIDs)+list(doi_pmid)))
pubData2=get_pubmed_data_efetch(allPMIDs)
print(len(pubData2),'publication records returned')
# We can wrap all this up, in a single function, to go from ORCID to PubMed data:
# +
from scripts.common_functions import orcid_to_pubmedData
pubData=orcid_to_pubmedData(['0000-0001-7328-4233','0000-0003-0924-3247'])
# -
print(len(pubData))
# ### A 'real life' data set
# As mentioned above, the key is to generate a robust set of individual/group IDs to text. ORCID is one option, but really we need to automatically create ORCID data for a large group.
#
# The University of Bristol uses the PURE architecture for housing and distributing research material. As part of this, users can add their ORCID IDs. For example - https://research-information.bristol.ac.uk/en/persons/benjamin-l-elsworth(b4014828-88e9-4861-ae1d-5c369b6ae35a).html
#
# Extracting the ORCID ID from here is fairly simple:
# +
import requests
import re
url = 'https://research-information.bristol.ac.uk/en/persons/benjamin-l-elsworth(b4014828-88e9-4861-ae1d-5c369b6ae35a).html'
res = requests.get(url)
orcid = re.findall('orcid.org/(.*?)".*', res.text)
print('orcid',orcid)
# -
# Wonderful, but what is that strange ID in the URL above - **b4014828-88e9-4861-ae1d-5c369b6ae35a** ?
#
# These are actually the PURE identifiers for each person at the University. So, if we go to the persons page (https://research-information.bristol.ac.uk/en/persons/search.html) we can, in theory, get these for everyone at the University.
url = 'http://research-information.bristol.ac.uk/en/persons/search.html?filter=academic&page=1&pageSize=10'
res = requests.get(url)
pDic={}
uuid = re.findall('persons/(.*?)\((.*?)\).html', res.text)
#print(uuid)
for u in uuid:
name = u[0].replace('-',' ').title()
uuid = u[1]
pDic[uuid]=name
for p in pDic:
print(p,pDic[p])
# Now, this kind of scraping is not ideal, but is effective. To save time, and getting in troule with the PURE team at the University, we've extracted data for all academics with a listed ORCID. This includes the following:
#
# | Description | File |
# | --- |---|
# | PURE Person UUID and Person Name | [data/pure_people.txt](data/pure_people.txt) |
# | PURE Person UUID and ORCID ID | [data/pure_person_to_orcid.txt](data/pure_person_to_orcid.txt) |
# | PURE Person UUID and Organisation UUID | [data/pure_person_to_org.txt](data/pure_person_to_org.txt) |
# | PURE Organisation UUID and Organisation Name | [data/pure_org_to_name.txt](data/pure_org_to_name.txt) |
#
# From here we can start looking at enriched terms for each person and organisation.
# ## QC
#
# So far, we haven't really checked any of the data. This is something we should do as everything downstream will be affected by the data at this point. One thing we can do, is look at the publication text.
# +
import matplotlib.pyplot as plt
pubmedToInfo = pd.read_csv('data/pubmed.tsv',sep='\t')
print(pubmedToInfo.shape)
print(pubmedToInfo.head())
# -
textData=pubmedToInfo['title'].str.len()+pubmedToInfo['abstract'].str.len()
textData.plot.hist(bins = 100)
# Perhaps we should remove publications with very short title+abstract?
(textData<50).value_counts()
# It seems that all title+abstract are > 50 characters, so we will keep them all.
# We can also look at the distribution of publication year, exluding 0 (as that was included to cover missing data)
pubYearData=pubmedToInfo[pubmedToInfo['year']>0]['year']
pubYearData.plot.hist(bins = 50)
# Lastly, numbers of publication per person:
#ORCID to PubMed identifiers
orcidToPubmed = pd.read_csv('data/orcid.tsv',sep='\t')
print(orcidToPubmed.shape)
print(orcidToPubmed.head())
orcidToPubmed['orcid_id'].value_counts().plot.hist(bins = 50)
# There are a no people with zero publications from their ORCID accounts, so no need to filter.
(orcidToPubmed['orcid_id'].value_counts()==0).sum()
| 38.4875 | 1,011 |
229e7ada941ab483347404d30a2e1af0d926e67a
|
py
|
python
|
17_autoencoders_and_gans.ipynb
|
peterleong/handson-ml3
|
['Apache-2.0']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Chapter 17 – Autoencoders and GANs**
# _This notebook contains all the sample code and solutions to the exercises in chapter 17._
# <table align="left">
# <td>
# <a href="https://colab.research.google.com/github/ageron/handson-ml3/blob/main/17_autoencoders_and_gans.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# </td>
# <td>
# <a target="_blank" href="https://kaggle.com/kernels/welcome?src=https://github.com/ageron/handson-ml3/blob/main/17_autoencoders_and_gans.ipynb"><img src="https://kaggle.com/static/images/open-in-kaggle.svg" /></a>
# </td>
# </table>
# + [markdown] tags=[]
# # WORK IN PROGRESS
# <img src="https://freesvg.org/img/Lavori-in-corso.png" width="200" />
#
# **I'm still working on updating this chapter to the 3rd edition. Please come back in a few weeks.**
# + [markdown] id="dFXIv9qNpKzt" tags=[]
# # Setup
# + [markdown] id="8IPbJEmZpKzu"
# This project requires Python 3.7 or above:
# + id="TFSU3FCOpKzu"
import sys
assert sys.version_info >= (3, 7)
# + [markdown] id="TAlKky09pKzv"
# It also requires Scikit-Learn ≥ 1.0.1:
# + id="YqCwW7cMpKzw"
import sklearn
assert sklearn.__version__ >= "1.0.1"
# + [markdown] id="GJtVEqxfpKzw"
# And TensorFlow ≥ 2.8:
# + id="0Piq5se2pKzx"
import tensorflow as tf
assert tf.__version__ >= "2.8.0"
# + [markdown] id="DDaDoLQTpKzx"
# As we did in earlier chapters, let's define the default font sizes to make the figures prettier:
# + id="8d4TH3NbpKzx"
import matplotlib.pyplot as plt
plt.rc('font', size=14)
plt.rc('axes', labelsize=14, titlesize=14)
plt.rc('legend', fontsize=14)
plt.rc('xtick', labelsize=10)
plt.rc('ytick', labelsize=10)
# + [markdown] id="RcoUIRsvpKzy"
# And let's create the `images/autoencoders` folder (if it doesn't already exist), and define the `save_fig()` function which is used through this notebook to save the figures in high-res for the book:
# + id="PQFH5Y9PpKzy"
from pathlib import Path
IMAGES_PATH = Path() / "images" / "autoencoders"
IMAGES_PATH.mkdir(parents=True, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = IMAGES_PATH / f"{fig_id}.{fig_extension}"
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# + [markdown] id="YTsawKlapKzy"
# This chapter can be very slow without a GPU, so let's make sure there's one, or else issue a warning:
# + id="Ekxzo6pOpKzy"
if not tf.config.list_physical_devices('GPU'):
print("No GPU was detected. Neural nets can be very slow without a GPU.")
if "google.colab" in sys.modules:
print("Go to Runtime > Change runtime and select a GPU hardware "
"accelerator.")
if "kaggle_secrets" in sys.modules:
print("Go to Settings > Accelerator and select GPU.")
# -
# # PCA with a linear Autoencoder
# Build 3D dataset:
# +
np.random.seed(4)
def generate_3d_data(m, w1=0.1, w2=0.3, noise=0.1):
angles = np.random.rand(m) * 3 * np.pi / 2 - 0.5
data = np.empty((m, 3))
data[:, 0] = np.cos(angles) + np.sin(angles)/2 + noise * np.random.randn(m) / 2
data[:, 1] = np.sin(angles) * 0.7 + noise * np.random.randn(m) / 2
data[:, 2] = data[:, 0] * w1 + data[:, 1] * w2 + noise * np.random.randn(m)
return data
X_train = generate_3d_data(60)
X_train = X_train - X_train.mean(axis=0, keepdims=0)
# -
# Now let's build the Autoencoder...
# +
np.random.seed(42)
tf.random.set_seed(42)
encoder = tf.keras.Sequential([tf.keras.layers.Dense(2, input_shape=[3])])
decoder = tf.keras.Sequential([tf.keras.layers.Dense(3, input_shape=[2])])
autoencoder = tf.keras.Sequential([encoder, decoder])
autoencoder.compile(loss="mse", optimizer=tf.keras.optimizers.SGD(learning_rate=1.5))
# -
history = autoencoder.fit(X_train, X_train, epochs=20)
codings = encoder.predict(X_train)
fig = plt.figure(figsize=(4,3))
plt.plot(codings[:,0], codings[:, 1], "b.")
plt.xlabel("$z_1$", fontsize=18)
plt.ylabel("$z_2$", fontsize=18, rotation=0)
plt.grid(True)
save_fig("linear_autoencoder_pca_plot")
plt.show()
# # Stacked Autoencoders
# Let's use MNIST:
(X_train_full, y_train_full), (X_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
X_train_full = X_train_full.astype(np.float32) / 255
X_test = X_test.astype(np.float32) / 255
X_train, X_valid = X_train_full[:-5000], X_train_full[-5000:]
y_train, y_valid = y_train_full[:-5000], y_train_full[-5000:]
# ## Train all layers at once
# Let's build a stacked Autoencoder with 3 hidden layers and 1 output layer (i.e., 2 stacked Autoencoders).
def rounded_accuracy(y_true, y_pred):
return tf.keras.metrics.binary_accuracy(tf.round(y_true), tf.round(y_pred))
# +
tf.random.set_seed(42)
np.random.seed(42)
stacked_encoder = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.Dense(100, activation="selu"),
tf.keras.layers.Dense(30, activation="selu"),
])
stacked_decoder = tf.keras.Sequential([
tf.keras.layers.Dense(100, activation="selu", input_shape=[30]),
tf.keras.layers.Dense(28 * 28, activation="sigmoid"),
tf.keras.layers.Reshape([28, 28])
])
stacked_ae = tf.keras.Sequential([stacked_encoder, stacked_decoder])
stacked_ae.compile(loss="binary_crossentropy",
optimizer=tf.keras.optimizers.SGD(learning_rate=1.5), metrics=[rounded_accuracy])
history = stacked_ae.fit(X_train, X_train, epochs=20,
validation_data=(X_valid, X_valid))
# -
# This function processes a few test images through the autoencoder and displays the original images and their reconstructions:
def show_reconstructions(model, images=X_valid, n_images=5):
reconstructions = model.predict(images[:n_images])
fig = plt.figure(figsize=(n_images * 1.5, 3))
for image_index in range(n_images):
plt.subplot(2, n_images, 1 + image_index)
plot_image(images[image_index])
plt.subplot(2, n_images, 1 + n_images + image_index)
plot_image(reconstructions[image_index])
show_reconstructions(stacked_ae)
save_fig("reconstruction_plot")
# # Visualizing Fashion MNIST
# +
np.random.seed(42)
from sklearn.manifold import TSNE
X_valid_compressed = stacked_encoder.predict(X_valid)
tsne = TSNE()
X_valid_2D = tsne.fit_transform(X_valid_compressed)
X_valid_2D = (X_valid_2D - X_valid_2D.min()) / (X_valid_2D.max() - X_valid_2D.min())
# -
plt.scatter(X_valid_2D[:, 0], X_valid_2D[:, 1], c=y_valid, s=10, cmap="tab10")
plt.axis("off")
plt.show()
# Let's make this diagram a bit prettier:
# adapted from https://scikit-learn.org/stable/auto_examples/manifold/plot_lle_digits.html
plt.figure(figsize=(10, 8))
cmap = plt.cm.tab10
plt.scatter(X_valid_2D[:, 0], X_valid_2D[:, 1], c=y_valid, s=10, cmap=cmap)
image_positions = np.array([[1., 1.]])
for index, position in enumerate(X_valid_2D):
dist = ((position - image_positions) ** 2).sum(axis=1)
if dist.min() > 0.02: # if far enough from other images
image_positions = np.r_[image_positions, [position]]
imagebox = mpl.offsetbox.AnnotationBbox(
mpl.offsetbox.OffsetImage(X_valid[index], cmap="binary"),
position, bboxprops={"edgecolor": cmap(y_valid[index]), "lw": 2})
plt.gca().add_artist(imagebox)
plt.axis("off")
save_fig("fashion_mnist_visualization_plot")
plt.show()
# ## Tying weights
# It is common to tie the weights of the encoder and the decoder, by simply using the transpose of the encoder's weights as the decoder weights. For this, we need to use a custom layer.
class DenseTranspose(tf.keras.layers.Layer):
def __init__(self, dense, activation=None, **kwargs):
self.dense = dense
self.activation = tf.keras.activations.get(activation)
super().__init__(**kwargs)
def build(self, batch_input_shape):
self.biases = self.add_weight(name="bias",
shape=[self.dense.input_shape[-1]],
initializer="zeros")
super().build(batch_input_shape)
def call(self, inputs):
z = tf.matmul(inputs, self.dense.weights[0], transpose_b=True)
return self.activation(z + self.biases)
# +
tf.keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
dense_1 = tf.keras.layers.Dense(100, activation="selu")
dense_2 = tf.keras.layers.Dense(30, activation="selu")
tied_encoder = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
dense_1,
dense_2
])
tied_decoder = tf.keras.Sequential([
DenseTranspose(dense_2, activation="selu"),
DenseTranspose(dense_1, activation="sigmoid"),
tf.keras.layers.Reshape([28, 28])
])
tied_ae = tf.keras.Sequential([tied_encoder, tied_decoder])
tied_ae.compile(loss="binary_crossentropy",
optimizer=tf.keras.optimizers.SGD(learning_rate=1.5), metrics=[rounded_accuracy])
history = tied_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))
# -
show_reconstructions(tied_ae)
plt.show()
# ## Training one Autoencoder at a Time
def train_autoencoder(n_neurons, X_train, X_valid, loss, optimizer,
n_epochs=10, output_activation=None, metrics=None):
n_inputs = X_train.shape[-1]
encoder = tf.keras.Sequential([
tf.keras.layers.Dense(n_neurons, activation="selu", input_shape=[n_inputs])
])
decoder = tf.keras.Sequential([
tf.keras.layers.Dense(n_inputs, activation=output_activation),
])
autoencoder = tf.keras.Sequential([encoder, decoder])
autoencoder.compile(optimizer, loss, metrics=metrics)
autoencoder.fit(X_train, X_train, epochs=n_epochs,
validation_data=(X_valid, X_valid))
return encoder, decoder, encoder(X_train), encoder(X_valid)
# +
tf.random.set_seed(42)
np.random.seed(42)
K = tf.keras.backend
X_train_flat = K.batch_flatten(X_train) # equivalent to .reshape(-1, 28 * 28)
X_valid_flat = K.batch_flatten(X_valid)
enc1, dec1, X_train_enc1, X_valid_enc1 = train_autoencoder(
100, X_train_flat, X_valid_flat, "binary_crossentropy",
tf.keras.optimizers.SGD(learning_rate=1.5), output_activation="sigmoid",
metrics=[rounded_accuracy])
enc2, dec2, _, _ = train_autoencoder(
30, X_train_enc1, X_valid_enc1, "mse", tf.keras.optimizers.SGD(learning_rate=0.05),
output_activation="selu")
# -
stacked_ae_1_by_1 = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
enc1, enc2, dec2, dec1,
tf.keras.layers.Reshape([28, 28])
])
show_reconstructions(stacked_ae_1_by_1)
plt.show()
stacked_ae_1_by_1.compile(loss="binary_crossentropy",
optimizer=tf.keras.optimizers.SGD(learning_rate=0.1), metrics=[rounded_accuracy])
history = stacked_ae_1_by_1.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))
show_reconstructions(stacked_ae_1_by_1)
plt.show()
# ## Using Convolutional Layers Instead of Dense Layers
# Let's build a stacked Autoencoder with 3 hidden layers and 1 output layer (i.e., 2 stacked Autoencoders).
# +
tf.random.set_seed(42)
np.random.seed(42)
conv_encoder = tf.keras.Sequential([
tf.keras.layers.Reshape([28, 28, 1], input_shape=[28, 28]),
tf.keras.layers.Conv2D(16, kernel_size=3, padding="SAME", activation="selu"),
tf.keras.layers.MaxPool2D(pool_size=2),
tf.keras.layers.Conv2D(32, kernel_size=3, padding="SAME", activation="selu"),
tf.keras.layers.MaxPool2D(pool_size=2),
tf.keras.layers.Conv2D(64, kernel_size=3, padding="SAME", activation="selu"),
tf.keras.layers.MaxPool2D(pool_size=2)
])
conv_decoder = tf.keras.Sequential([
tf.keras.layers.Conv2DTranspose(32, kernel_size=3, strides=2, padding="VALID", activation="selu",
input_shape=[3, 3, 64]),
tf.keras.layers.Conv2DTranspose(16, kernel_size=3, strides=2, padding="SAME", activation="selu"),
tf.keras.layers.Conv2DTranspose(1, kernel_size=3, strides=2, padding="SAME", activation="sigmoid"),
tf.keras.layers.Reshape([28, 28])
])
conv_ae = tf.keras.Sequential([conv_encoder, conv_decoder])
conv_ae.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.SGD(learning_rate=1.0),
metrics=[rounded_accuracy])
history = conv_ae.fit(X_train, X_train, epochs=5,
validation_data=(X_valid, X_valid))
# -
conv_encoder.summary()
conv_decoder.summary()
show_reconstructions(conv_ae)
plt.show()
# # Recurrent Autoencoders
recurrent_encoder = tf.keras.Sequential([
tf.keras.layers.LSTM(100, return_sequences=True, input_shape=[28, 28]),
tf.keras.layers.LSTM(30)
])
recurrent_decoder = tf.keras.Sequential([
tf.keras.layers.RepeatVector(28, input_shape=[30]),
tf.keras.layers.LSTM(100, return_sequences=True),
tf.keras.layers.TimeDistributed(tf.keras.layers.Dense(28, activation="sigmoid"))
])
recurrent_ae = tf.keras.Sequential([recurrent_encoder, recurrent_decoder])
recurrent_ae.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.SGD(0.1),
metrics=[rounded_accuracy])
history = recurrent_ae.fit(X_train, X_train, epochs=10, validation_data=(X_valid, X_valid))
show_reconstructions(recurrent_ae)
plt.show()
# # Stacked denoising Autoencoder
# Using Gaussian noise:
# +
tf.random.set_seed(42)
np.random.seed(42)
denoising_encoder = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.GaussianNoise(0.2),
tf.keras.layers.Dense(100, activation="selu"),
tf.keras.layers.Dense(30, activation="selu")
])
denoising_decoder = tf.keras.Sequential([
tf.keras.layers.Dense(100, activation="selu", input_shape=[30]),
tf.keras.layers.Dense(28 * 28, activation="sigmoid"),
tf.keras.layers.Reshape([28, 28])
])
denoising_ae = tf.keras.Sequential([denoising_encoder, denoising_decoder])
denoising_ae.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.SGD(learning_rate=1.0),
metrics=[rounded_accuracy])
history = denoising_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))
# +
tf.random.set_seed(42)
np.random.seed(42)
noise = tf.keras.layers.GaussianNoise(0.2)
show_reconstructions(denoising_ae, noise(X_valid, training=True))
plt.show()
# -
# Using dropout:
# +
tf.random.set_seed(42)
np.random.seed(42)
dropout_encoder = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(100, activation="selu"),
tf.keras.layers.Dense(30, activation="selu")
])
dropout_decoder = tf.keras.Sequential([
tf.keras.layers.Dense(100, activation="selu", input_shape=[30]),
tf.keras.layers.Dense(28 * 28, activation="sigmoid"),
tf.keras.layers.Reshape([28, 28])
])
dropout_ae = tf.keras.Sequential([dropout_encoder, dropout_decoder])
dropout_ae.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.SGD(learning_rate=1.0),
metrics=[rounded_accuracy])
history = dropout_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))
# +
tf.random.set_seed(42)
np.random.seed(42)
dropout = tf.keras.layers.Dropout(0.5)
show_reconstructions(dropout_ae, dropout(X_valid, training=True))
save_fig("dropout_denoising_plot", tight_layout=False)
# -
# # Sparse Autoencoder
# Let's build a simple stacked autoencoder, so we can compare it to the sparse autoencoders we will build. This time we will use the sigmoid activation function for the coding layer, to ensure that the coding values range from 0 to 1:
# +
tf.random.set_seed(42)
np.random.seed(42)
simple_encoder = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.Dense(100, activation="selu"),
tf.keras.layers.Dense(30, activation="sigmoid"),
])
simple_decoder = tf.keras.Sequential([
tf.keras.layers.Dense(100, activation="selu", input_shape=[30]),
tf.keras.layers.Dense(28 * 28, activation="sigmoid"),
tf.keras.layers.Reshape([28, 28])
])
simple_ae = tf.keras.Sequential([simple_encoder, simple_decoder])
simple_ae.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.SGD(learning_rate=1.),
metrics=[rounded_accuracy])
history = simple_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))
# -
show_reconstructions(simple_ae)
plt.show()
# Let's create a couple functions to print nice activation histograms:
def plot_percent_hist(ax, data, bins):
counts, _ = np.histogram(data, bins=bins)
widths = bins[1:] - bins[:-1]
x = bins[:-1] + widths / 2
ax.bar(x, counts / len(data), width=widths*0.8)
ax.xaxis.set_ticks(bins)
ax.yaxis.set_major_formatter(mpl.ticker.FuncFormatter(
lambda y, position: "{}%".format(round(100 * y))))
ax.grid(True)
def plot_activations_histogram(encoder, height=1, n_bins=10):
X_valid_codings = encoder(X_valid).numpy()
activation_means = X_valid_codings.mean(axis=0)
mean = activation_means.mean()
bins = np.linspace(0, 1, n_bins + 1)
fig, [ax1, ax2] = plt.subplots(figsize=(10, 3), nrows=1, ncols=2, sharey=True)
plot_percent_hist(ax1, X_valid_codings.ravel(), bins)
ax1.plot([mean, mean], [0, height], "k--", label="Overall Mean = {:.2f}".format(mean))
ax1.legend(loc="upper center", fontsize=14)
ax1.set_xlabel("Activation")
ax1.set_ylabel("% Activations")
ax1.axis([0, 1, 0, height])
plot_percent_hist(ax2, activation_means, bins)
ax2.plot([mean, mean], [0, height], "k--")
ax2.set_xlabel("Neuron Mean Activation")
ax2.set_ylabel("% Neurons")
ax2.axis([0, 1, 0, height])
# Let's use these functions to plot histograms of the activations of the encoding layer. The histogram on the left shows the distribution of all the activations. You can see that values close to 0 or 1 are more frequent overall, which is consistent with the saturating nature of the sigmoid function. The histogram on the right shows the distribution of mean neuron activations: you can see that most neurons have a mean activation close to 0.5. Both histograms tell us that each neuron tends to either fire close to 0 or 1, with about 50% probability each. However, some neurons fire almost all the time (right side of the right histogram).
plot_activations_histogram(simple_encoder, height=0.35)
plt.show()
# Now let's add $\ell_1$ regularization to the coding layer:
# +
tf.random.set_seed(42)
np.random.seed(42)
sparse_l1_encoder = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.Dense(100, activation="selu"),
tf.keras.layers.Dense(300, activation="sigmoid"),
tf.keras.layers.ActivityRegularization(l1=1e-3) # Alternatively, you could add
# activity_regularizer=tf.keras.regularizers.l1(1e-3)
# to the previous layer.
])
sparse_l1_decoder = tf.keras.Sequential([
tf.keras.layers.Dense(100, activation="selu", input_shape=[300]),
tf.keras.layers.Dense(28 * 28, activation="sigmoid"),
tf.keras.layers.Reshape([28, 28])
])
sparse_l1_ae = tf.keras.Sequential([sparse_l1_encoder, sparse_l1_decoder])
sparse_l1_ae.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.SGD(learning_rate=1.0),
metrics=[rounded_accuracy])
history = sparse_l1_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))
# -
show_reconstructions(sparse_l1_ae)
plot_activations_histogram(sparse_l1_encoder, height=1.)
plt.show()
# Let's use the KL Divergence loss instead to ensure sparsity, and target 10% sparsity rather than 0%:
p = 0.1
q = np.linspace(0.001, 0.999, 500)
kl_div = p * np.log(p / q) + (1 - p) * np.log((1 - p) / (1 - q))
mse = (p - q)**2
mae = np.abs(p - q)
plt.plot([p, p], [0, 0.3], "k:")
plt.text(0.05, 0.32, "Target\nsparsity", fontsize=14)
plt.plot(q, kl_div, "b-", label="KL divergence")
plt.plot(q, mae, "g--", label=r"MAE ($\ell_1$)")
plt.plot(q, mse, "r--", linewidth=1, label=r"MSE ($\ell_2$)")
plt.legend(loc="upper left", fontsize=14)
plt.xlabel("Actual sparsity")
plt.ylabel("Cost", rotation=0)
plt.axis([0, 1, 0, 0.95])
save_fig("sparsity_loss_plot")
# +
K = tf.keras.backend
kl_divergence = tf.keras.losses.kullback_leibler_divergence
class KLDivergenceRegularizer(tf.keras.regularizers.Regularizer):
def __init__(self, weight, target=0.1):
self.weight = weight
self.target = target
def __call__(self, inputs):
mean_activities = K.mean(inputs, axis=0)
return self.weight * (
kl_divergence(self.target, mean_activities) +
kl_divergence(1. - self.target, 1. - mean_activities))
# +
tf.random.set_seed(42)
np.random.seed(42)
kld_reg = KLDivergenceRegularizer(weight=0.05, target=0.1)
sparse_kl_encoder = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.Dense(100, activation="selu"),
tf.keras.layers.Dense(300, activation="sigmoid", activity_regularizer=kld_reg)
])
sparse_kl_decoder = tf.keras.Sequential([
tf.keras.layers.Dense(100, activation="selu", input_shape=[300]),
tf.keras.layers.Dense(28 * 28, activation="sigmoid"),
tf.keras.layers.Reshape([28, 28])
])
sparse_kl_ae = tf.keras.Sequential([sparse_kl_encoder, sparse_kl_decoder])
sparse_kl_ae.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.SGD(learning_rate=1.0),
metrics=[rounded_accuracy])
history = sparse_kl_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))
# -
show_reconstructions(sparse_kl_ae)
plot_activations_histogram(sparse_kl_encoder)
save_fig("sparse_autoencoder_plot")
plt.show()
# # Variational Autoencoder
class Sampling(tf.keras.layers.Layer):
def call(self, inputs):
mean, log_var = inputs
return K.random_normal(tf.shape(log_var)) * K.exp(log_var / 2) + mean
# +
tf.random.set_seed(42)
np.random.seed(42)
codings_size = 10
inputs = tf.keras.layers.Input(shape=[28, 28])
z = tf.keras.layers.Flatten()(inputs)
z = tf.keras.layers.Dense(150, activation="selu")(z)
z = tf.keras.layers.Dense(100, activation="selu")(z)
codings_mean = tf.keras.layers.Dense(codings_size)(z)
codings_log_var = tf.keras.layers.Dense(codings_size)(z)
codings = Sampling()([codings_mean, codings_log_var])
variational_encoder = tf.keras.Model(
inputs=[inputs], outputs=[codings_mean, codings_log_var, codings])
decoder_inputs = tf.keras.layers.Input(shape=[codings_size])
x = tf.keras.layers.Dense(100, activation="selu")(decoder_inputs)
x = tf.keras.layers.Dense(150, activation="selu")(x)
x = tf.keras.layers.Dense(28 * 28, activation="sigmoid")(x)
outputs = tf.keras.layers.Reshape([28, 28])(x)
variational_decoder = tf.keras.Model(inputs=[decoder_inputs], outputs=[outputs])
_, _, codings = variational_encoder(inputs)
reconstructions = variational_decoder(codings)
variational_ae = tf.keras.Model(inputs=[inputs], outputs=[reconstructions])
latent_loss = -0.5 * K.sum(
1 + codings_log_var - K.exp(codings_log_var) - K.square(codings_mean),
axis=-1)
variational_ae.add_loss(K.mean(latent_loss) / 784.)
variational_ae.compile(loss="binary_crossentropy", optimizer="rmsprop", metrics=[rounded_accuracy])
history = variational_ae.fit(X_train, X_train, epochs=25, batch_size=128,
validation_data=(X_valid, X_valid))
# -
show_reconstructions(variational_ae)
plt.show()
# ## Generate Fashion Images
def plot_multiple_images(images, n_cols=None):
n_cols = n_cols or len(images)
n_rows = (len(images) - 1) // n_cols + 1
if images.shape[-1] == 1:
images = images.squeeze(axis=-1)
plt.figure(figsize=(n_cols, n_rows))
for index, image in enumerate(images):
plt.subplot(n_rows, n_cols, index + 1)
plt.imshow(image, cmap="binary")
plt.axis("off")
# Let's generate a few random codings, decode them and plot the resulting images:
# +
tf.random.set_seed(42)
codings = tf.random.normal(shape=[12, codings_size])
images = variational_decoder(codings).numpy()
plot_multiple_images(images, 4)
save_fig("vae_generated_images_plot", tight_layout=False)
# -
# Now let's perform semantic interpolation between these images:
# +
tf.random.set_seed(42)
np.random.seed(42)
codings_grid = tf.reshape(codings, [1, 3, 4, codings_size])
larger_grid = tf.image.resize(codings_grid, size=[5, 7])
interpolated_codings = tf.reshape(larger_grid, [-1, codings_size])
images = variational_decoder(interpolated_codings).numpy()
plt.figure(figsize=(7, 5))
for index, image in enumerate(images):
plt.subplot(5, 7, index + 1)
if index%7%2==0 and index//7%2==0:
plt.gca().get_xaxis().set_visible(False)
plt.gca().get_yaxis().set_visible(False)
else:
plt.axis("off")
plt.imshow(image, cmap="binary")
save_fig("semantic_interpolation_plot", tight_layout=False)
# -
# # Generative Adversarial Networks
# +
np.random.seed(42)
tf.random.set_seed(42)
codings_size = 30
generator = tf.keras.Sequential([
tf.keras.layers.Dense(100, activation="selu", input_shape=[codings_size]),
tf.keras.layers.Dense(150, activation="selu"),
tf.keras.layers.Dense(28 * 28, activation="sigmoid"),
tf.keras.layers.Reshape([28, 28])
])
discriminator = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.Dense(150, activation="selu"),
tf.keras.layers.Dense(100, activation="selu"),
tf.keras.layers.Dense(1, activation="sigmoid")
])
gan = tf.keras.Sequential([generator, discriminator])
# -
discriminator.compile(loss="binary_crossentropy", optimizer="rmsprop")
discriminator.trainable = False
gan.compile(loss="binary_crossentropy", optimizer="rmsprop")
batch_size = 32
dataset = tf.data.Dataset.from_tensor_slices(X_train).shuffle(1000)
dataset = dataset.batch(batch_size, drop_remainder=True).prefetch(1)
def train_gan(gan, dataset, batch_size, codings_size, n_epochs=50):
generator, discriminator = gan.layers
for epoch in range(n_epochs):
print("Epoch {}/{}".format(epoch + 1, n_epochs)) # not shown in the book
for X_batch in dataset:
# phase 1 - training the discriminator
noise = tf.random.normal(shape=[batch_size, codings_size])
generated_images = generator(noise)
X_fake_and_real = tf.concat([generated_images, X_batch], axis=0)
y1 = tf.constant([[0.]] * batch_size + [[1.]] * batch_size)
discriminator.trainable = True
discriminator.train_on_batch(X_fake_and_real, y1)
# phase 2 - training the generator
noise = tf.random.normal(shape=[batch_size, codings_size])
y2 = tf.constant([[1.]] * batch_size)
discriminator.trainable = False
gan.train_on_batch(noise, y2)
plot_multiple_images(generated_images, 8) # not shown
plt.show() # not shown
train_gan(gan, dataset, batch_size, codings_size, n_epochs=1)
# +
tf.random.set_seed(42)
np.random.seed(42)
noise = tf.random.normal(shape=[batch_size, codings_size])
generated_images = generator(noise)
plot_multiple_images(generated_images, 8)
save_fig("gan_generated_images_plot", tight_layout=False)
# -
train_gan(gan, dataset, batch_size, codings_size)
# # Deep Convolutional GAN
# +
tf.random.set_seed(42)
np.random.seed(42)
codings_size = 100
generator = tf.keras.Sequential([
tf.keras.layers.Dense(7 * 7 * 128, input_shape=[codings_size]),
tf.keras.layers.Reshape([7, 7, 128]),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Conv2DTranspose(64, kernel_size=5, strides=2, padding="SAME",
activation="selu"),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Conv2DTranspose(1, kernel_size=5, strides=2, padding="SAME",
activation="tanh"),
])
discriminator = tf.keras.Sequential([
tf.keras.layers.Conv2D(64, kernel_size=5, strides=2, padding="SAME",
activation=tf.keras.layers.LeakyReLU(0.2),
input_shape=[28, 28, 1]),
tf.keras.layers.Dropout(0.4),
tf.keras.layers.Conv2D(128, kernel_size=5, strides=2, padding="SAME",
activation=tf.keras.layers.LeakyReLU(0.2)),
tf.keras.layers.Dropout(0.4),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(1, activation="sigmoid")
])
gan = tf.keras.Sequential([generator, discriminator])
# -
discriminator.compile(loss="binary_crossentropy", optimizer="rmsprop")
discriminator.trainable = False
gan.compile(loss="binary_crossentropy", optimizer="rmsprop")
X_train_dcgan = X_train.reshape(-1, 28, 28, 1) * 2. - 1. # reshape and rescale
batch_size = 32
dataset = tf.data.Dataset.from_tensor_slices(X_train_dcgan)
dataset = dataset.shuffle(1000)
dataset = dataset.batch(batch_size, drop_remainder=True).prefetch(1)
train_gan(gan, dataset, batch_size, codings_size)
# +
tf.random.set_seed(42)
np.random.seed(42)
noise = tf.random.normal(shape=[batch_size, codings_size])
generated_images = generator(noise)
plot_multiple_images(generated_images, 8)
save_fig("dcgan_generated_images_plot", tight_layout=False)
# -
# # Extra Material
# ## Hashing Using a Binary Autoencoder
# Let's load the Fashion MNIST dataset again:
(X_train_full, y_train_full), (X_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
X_train_full = X_train_full.astype(np.float32) / 255
X_test = X_test.astype(np.float32) / 255
X_train, X_valid = X_train_full[:-5000], X_train_full[-5000:]
y_train, y_valid = y_train_full[:-5000], y_train_full[-5000:]
# Let's train an autoencoder where the encoder has a 16-neuron output layer, using the sigmoid activation function, and heavy Gaussian noise just before it. During training, the noise layer will encourage the previous layer to learn to output large values, since small values will just be crushed by the noise. In turn, this means that the output layer will output values close to 0 or 1, thanks to the sigmoid activation function. Once we round the output values to 0s and 1s, we get a 16-bit "semantic" hash. If everything works well, images that look alike will have the same hash. This can be very useful for search engines: for example, if we store each image on a server identified by the image's semantic hash, then all similar images will end up on the same server. Users of the search engine can then provide an image to search for, and the search engine will compute the image's hash using the encoder, and quickly return all the images on the server identified by that hash.
# +
tf.random.set_seed(42)
np.random.seed(42)
hashing_encoder = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.Dense(100, activation="selu"),
tf.keras.layers.GaussianNoise(15.),
tf.keras.layers.Dense(16, activation="sigmoid"),
])
hashing_decoder = tf.keras.Sequential([
tf.keras.layers.Dense(100, activation="selu", input_shape=[16]),
tf.keras.layers.Dense(28 * 28, activation="sigmoid"),
tf.keras.layers.Reshape([28, 28])
])
hashing_ae = tf.keras.Sequential([hashing_encoder, hashing_decoder])
hashing_ae.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.Nadam(),
metrics=[rounded_accuracy])
history = hashing_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))
# -
# The autoencoder compresses the information so much (down to 16 bits!) that it's quite lossy, but that's okay, we're using it to produce semantic hashes, not to perfectly reconstruct the images:
show_reconstructions(hashing_ae)
plt.show()
# Notice that the outputs are indeed very close to 0 or 1 (left graph):
plot_activations_histogram(hashing_encoder)
plt.show()
# Now let's see what the hashes look like for the first few images in the validation set:
hashes = hashing_encoder.predict(X_valid).round().astype(np.int32)
hashes *= np.array([[2**bit for bit in range(16)]])
hashes = hashes.sum(axis=1)
for h in hashes[:5]:
print("{:016b}".format(h))
print("...")
# Now let's find the most common image hashes in the validation set, and display a few images for each hash. In the following image, all the images on a given row have the same hash:
# +
from collections import Counter
n_hashes = 10
n_images = 8
top_hashes = Counter(hashes).most_common(n_hashes)
plt.figure(figsize=(n_images, n_hashes))
for hash_index, (image_hash, hash_count) in enumerate(top_hashes):
indices = (hashes == image_hash)
for index, image in enumerate(X_valid[indices][:n_images]):
plt.subplot(n_hashes, n_images, hash_index * n_images + index + 1)
plt.imshow(image, cmap="binary")
plt.axis("off")
# -
# # Exercise Solutions
# ## 1. to 8.
# 1. Here are some of the main tasks that autoencoders are used for:
# * Feature extraction
# * Unsupervised pretraining
# * Dimensionality reduction
# * Generative models
# * Anomaly detection (an autoencoder is generally bad at reconstructing outliers)
# 2. If you want to train a classifier and you have plenty of unlabeled training data but only a few thousand labeled instances, then you could first train a deep autoencoder on the full dataset (labeled + unlabeled), then reuse its lower half for the classifier (i.e., reuse the layers up to the codings layer, included) and train the classifier using the labeled data. If you have little labeled data, you probably want to freeze the reused layers when training the classifier.
# 3. The fact that an autoencoder perfectly reconstructs its inputs does not necessarily mean that it is a good autoencoder; perhaps it is simply an overcomplete autoencoder that learned to copy its inputs to the codings layer and then to the outputs. In fact, even if the codings layer contained a single neuron, it would be possible for a very deep autoencoder to learn to map each training instance to a different coding (e.g., the first instance could be mapped to 0.001, the second to 0.002, the third to 0.003, and so on), and it could learn "by heart" to reconstruct the right training instance for each coding. It would perfectly reconstruct its inputs without really learning any useful pattern in the data. In practice such a mapping is unlikely to happen, but it illustrates the fact that perfect reconstructions are not a guarantee that the autoencoder learned anything useful. However, if it produces very bad reconstructions, then it is almost guaranteed to be a bad autoencoder. To evaluate the performance of an autoencoder, one option is to measure the reconstruction loss (e.g., compute the MSE, or the mean square of the outputs minus the inputs). Again, a high reconstruction loss is a good sign that the autoencoder is bad, but a low reconstruction loss is not a guarantee that it is good. You should also evaluate the autoencoder according to what it will be used for. For example, if you are using it for unsupervised pretraining of a classifier, then you should also evaluate the classifier's performance.
# 4. An undercomplete autoencoder is one whose codings layer is smaller than the input and output layers. If it is larger, then it is an overcomplete autoencoder. The main risk of an excessively undercomplete autoencoder is that it may fail to reconstruct the inputs. The main risk of an overcomplete autoencoder is that it may just copy the inputs to the outputs, without learning any useful features.
# 5. To tie the weights of an encoder layer and its corresponding decoder layer, you simply make the decoder weights equal to the transpose of the encoder weights. This reduces the number of parameters in the model by half, often making training converge faster with less training data and reducing the risk of overfitting the training set.
# 6. A generative model is a model capable of randomly generating outputs that resemble the training instances. For example, once trained successfully on the MNIST dataset, a generative model can be used to randomly generate realistic images of digits. The output distribution is typically similar to the training data. For example, since MNIST contains many images of each digit, the generative model would output roughly the same number of images of each digit. Some generative models can be parametrized—for example, to generate only some kinds of outputs. An example of a generative autoencoder is the variational autoencoder.
# 7. A generative adversarial network is a neural network architecture composed of two parts, the generator and the discriminator, which have opposing objectives. The generator's goal is to generate instances similar to those in the training set, to fool the discriminator. The discriminator must distinguish the real instances from the generated ones. At each training iteration, the discriminator is trained like a normal binary classifier, then the generator is trained to maximize the discriminator's error. GANs are used for advanced image processing tasks such as super resolution, colorization, image editing (replacing objects with realistic background), turning a simple sketch into a photorealistic image, or predicting the next frames in a video. They are also used to augment a dataset (to train other models), to generate other types of data (such as text, audio, and time series), and to identify the weaknesses in other models and strengthen them.
# 8. Training GANs is notoriously difficult, because of the complex dynamics between the generator and the discriminator. The biggest difficulty is mode collapse, where the generator produces outputs with very little diversity. Moreover, training can be terribly unstable: it may start out fine and then suddenly start oscillating or diverging, without any apparent reason. GANs are also very sensitive to the choice of hyperparameters.
# ## 9.
# _Exercise: Try using a denoising autoencoder to pretrain an image classifier. You can use MNIST (the simplest option), or a more complex image dataset such as [CIFAR10](https://homl.info/122) if you want a bigger challenge. Regardless of the dataset you're using, follow these steps:_
# * Split the dataset into a training set and a test set. Train a deep denoising autoencoder on the full training set.
# * Check that the images are fairly well reconstructed. Visualize the images that most activate each neuron in the coding layer.
# * Build a classification DNN, reusing the lower layers of the autoencoder. Train it using only 500 images from the training set. Does it perform better with or without pretraining?
[X_train, y_train], [X_test, y_test] = tf.keras.datasets.cifar10.load_data()
X_train = X_train / 255
X_test = X_test / 255
# +
tf.random.set_seed(42)
np.random.seed(42)
denoising_encoder = tf.keras.Sequential([
tf.keras.layers.GaussianNoise(0.1, input_shape=[32, 32, 3]),
tf.keras.layers.Conv2D(32, kernel_size=3, padding="same", activation="relu"),
tf.keras.layers.MaxPool2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation="relu"),
])
# -
denoising_encoder.summary()
denoising_decoder = tf.keras.Sequential([
tf.keras.layers.Dense(16 * 16 * 32, activation="relu", input_shape=[512]),
tf.keras.layers.Reshape([16, 16, 32]),
tf.keras.layers.Conv2DTranspose(filters=3, kernel_size=3, strides=2,
padding="same", activation="sigmoid")
])
denoising_decoder.summary()
denoising_ae = tf.keras.Sequential([denoising_encoder, denoising_decoder])
denoising_ae.compile(loss="binary_crossentropy", optimizer=tf.keras.optimizers.Nadam(),
metrics=["mse"])
history = denoising_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_test, X_test))
# +
n_images = 5
new_images = X_test[:n_images]
new_images_noisy = new_images + np.random.randn(n_images, 32, 32, 3) * 0.1
new_images_denoised = denoising_ae.predict(new_images_noisy)
plt.figure(figsize=(6, n_images * 2))
for index in range(n_images):
plt.subplot(n_images, 3, index * 3 + 1)
plt.imshow(new_images[index])
plt.axis('off')
if index == 0:
plt.title("Original")
plt.subplot(n_images, 3, index * 3 + 2)
plt.imshow(new_images_noisy[index].clip(0., 1.))
plt.axis('off')
if index == 0:
plt.title("Noisy")
plt.subplot(n_images, 3, index * 3 + 3)
plt.imshow(new_images_denoised[index])
plt.axis('off')
if index == 0:
plt.title("Denoised")
plt.show()
# -
# ## 10.
# _Exercise: Train a variational autoencoder on the image dataset of your choice, and use it to generate images. Alternatively, you can try to find an unlabeled dataset that you are interested in and see if you can generate new samples._
#
# ## 11.
# _Exercise: Train a DCGAN to tackle the image dataset of your choice, and use it to generate images. Add experience replay and see if this helps. Turn it into a conditional GAN where you can control the generated class._
#
| 39.581213 | 1,529 |
8f1f14bf693e010bdb40ec4d82b237805b0125b1
|
py
|
python
|
sem20-pthread/pthread.ipynb
|
yuri-pechatnov/caos_2019-2020
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# look at tools/set_up_magics.ipynb
yandex_metrica_allowed = True ; get_ipython().run_cell('# one_liner_str\n\nget_ipython().run_cell_magic(\'javascript\', \'\', \n \'// setup cpp code highlighting\\n\'\n \'IPython.CodeCell.options_default.highlight_modes["text/x-c++src"] = {\\\'reg\\\':[/^%%cpp/]} ;\'\n \'IPython.CodeCell.options_default.highlight_modes["text/x-cmake"] = {\\\'reg\\\':[/^%%cmake/]} ;\'\n \'IPython.CodeCell.options_default.highlight_modes["text/x-sql"] = {\\\'reg\\\':[/^%%sql/]} ;\'\n)\n\n# creating magics\nfrom IPython.core.magic import register_cell_magic, register_line_magic\nfrom IPython.display import display, Markdown, HTML\nimport argparse\nfrom subprocess import Popen, PIPE, STDOUT, check_output\nimport html\nimport random\nimport sys\nimport os\nimport re\nimport signal\nimport shutil\nimport shlex\nimport glob\nimport time\n\n@register_cell_magic\ndef save_file(args_str, cell, line_comment_start="#"):\n parser = argparse.ArgumentParser()\n parser.add_argument("fname")\n parser.add_argument("--ejudge-style", action="store_true")\n parser.add_argument("--under-spoiler-threshold", type=int, default=None)\n args = parser.parse_args(args_str.split())\n \n cell = cell if cell[-1] == \'\\n\' or args.no_eof_newline else cell + "\\n"\n cmds = []\n with open(args.fname, "w") as f:\n f.write(line_comment_start + " %%cpp " + args_str + "\\n")\n for line in cell.split("\\n"):\n line_to_write = (line if not args.ejudge_style else line.rstrip()) + "\\n"\n if not line.startswith("%"):\n f.write(line_to_write)\n else:\n f.write(line_comment_start + " " + line_to_write)\n run_prefix = "%run "\n md_prefix = "%MD "\n comment_prefix = "%" + line_comment_start\n if line.startswith(run_prefix):\n cmds.append(line[len(run_prefix):].strip())\n elif line.startswith(md_prefix):\n cmds.append(\'#<MD>\' + line[len(md_prefix):].strip())\n elif line.startswith(comment_prefix):\n cmds.append(\'#\' + line[len(comment_prefix):].strip())\n else:\n raise Exception("Unknown %%save_file subcommand: \'%s\'" % line)\n \n f.write("" if not args.ejudge_style else line_comment_start + r" line without \\n")\n for cmd in cmds:\n if cmd.startswith(\'#\'):\n if cmd.startswith(\'#<MD>\'):\n display(Markdown(cmd[5:]))\n else:\n display(Markdown("\\#\\#\\#\\# `%s`" % cmd[1:]))\n else:\n display(Markdown("Run: `%s`" % cmd))\n if args.under_spoiler_threshold:\n out = check_output(cmd, stderr=STDOUT, shell=True, universal_newlines=True)\n out = out[:-1] if out.endswith(\'\\n\') else out\n out = html.escape(out)\n if len(out.split(\'\\n\')) > args.under_spoiler_threshold:\n out = "<details> <summary> output </summary> <pre><code>%s</code></pre></details>" % out\n elif out:\n out = "<pre><code>%s</code></pre>" % out\n if out:\n display(HTML(out))\n else:\n get_ipython().system(cmd)\n\n@register_cell_magic\ndef cpp(fname, cell):\n save_file(fname, cell, "//")\n \n@register_cell_magic\ndef cmake(fname, cell):\n save_file(fname, cell, "#")\n\n@register_cell_magic\ndef asm(fname, cell):\n save_file(fname, cell, "//")\n \n@register_cell_magic\ndef makefile(fname, cell):\n fname = fname or "makefile"\n assert fname.endswith("makefile")\n save_file(fname, cell.replace(" " * 4, "\\t"))\n \n@register_line_magic\ndef p(line):\n line = line.strip() \n if line[0] == \'#\':\n display(Markdown(line[1:].strip()))\n else:\n try:\n expr, comment = line.split(" #")\n display(Markdown("`{} = {}` # {}".format(expr.strip(), eval(expr), comment.strip())))\n except:\n display(Markdown("{} = {}".format(line, eval(line))))\n \n \ndef show_log_file(file, return_html_string=False):\n obj = file.replace(\'.\', \'_\').replace(\'/\', \'_\') + "_obj"\n html_string = \'\'\'\n <!--MD_BEGIN_FILTER-->\n <script type=text/javascript>\n var entrance___OBJ__ = 0;\n var errors___OBJ__ = 0;\n function halt__OBJ__(elem, color)\n {\n elem.setAttribute("style", "font-size: 14px; background: " + color + "; padding: 10px; border: 3px; border-radius: 5px; color: white; "); \n }\n function refresh__OBJ__()\n {\n entrance___OBJ__ -= 1;\n if (entrance___OBJ__ < 0) {\n entrance___OBJ__ = 0;\n }\n var elem = document.getElementById("__OBJ__");\n if (elem) {\n var xmlhttp=new XMLHttpRequest();\n xmlhttp.onreadystatechange=function()\n {\n var elem = document.getElementById("__OBJ__");\n console.log(!!elem, xmlhttp.readyState, xmlhttp.status, entrance___OBJ__);\n if (elem && xmlhttp.readyState==4) {\n if (xmlhttp.status==200)\n {\n errors___OBJ__ = 0;\n if (!entrance___OBJ__) {\n if (elem.innerHTML != xmlhttp.responseText) {\n elem.innerHTML = xmlhttp.responseText;\n }\n if (elem.innerHTML.includes("Process finished.")) {\n halt__OBJ__(elem, "#333333");\n } else {\n entrance___OBJ__ += 1;\n console.log("req");\n window.setTimeout("refresh__OBJ__()", 300); \n }\n }\n return xmlhttp.responseText;\n } else {\n errors___OBJ__ += 1;\n if (!entrance___OBJ__) {\n if (errors___OBJ__ < 6) {\n entrance___OBJ__ += 1;\n console.log("req");\n window.setTimeout("refresh__OBJ__()", 300); \n } else {\n halt__OBJ__(elem, "#994444");\n }\n }\n }\n }\n }\n xmlhttp.open("GET", "__FILE__", true);\n xmlhttp.setRequestHeader("Cache-Control", "no-cache");\n xmlhttp.send(); \n }\n }\n \n if (!entrance___OBJ__) {\n entrance___OBJ__ += 1;\n refresh__OBJ__(); \n }\n </script>\n\n <p id="__OBJ__" style="font-size: 14px; background: #000000; padding: 10px; border: 3px; border-radius: 5px; color: white; ">\n </p>\n \n </font>\n <!--MD_END_FILTER-->\n <!--MD_FROM_FILE __FILE__.md -->\n \'\'\'.replace("__OBJ__", obj).replace("__FILE__", file)\n if return_html_string:\n return html_string\n display(HTML(html_string))\n\n \nclass TInteractiveLauncher:\n tmp_path = "./interactive_launcher_tmp"\n def __init__(self, cmd):\n try:\n os.mkdir(TInteractiveLauncher.tmp_path)\n except:\n pass\n name = str(random.randint(0, 1e18))\n self.inq_path = os.path.join(TInteractiveLauncher.tmp_path, name + ".inq")\n self.log_path = os.path.join(TInteractiveLauncher.tmp_path, name + ".log")\n \n os.mkfifo(self.inq_path)\n open(self.log_path, \'w\').close()\n open(self.log_path + ".md", \'w\').close()\n\n self.pid = os.fork()\n if self.pid == -1:\n print("Error")\n if self.pid == 0:\n exe_cands = glob.glob("../tools/launcher.py") + glob.glob("../../tools/launcher.py")\n assert(len(exe_cands) == 1)\n assert(os.execvp("python3", ["python3", exe_cands[0], "-l", self.log_path, "-i", self.inq_path, "-c", cmd]) == 0)\n self.inq_f = open(self.inq_path, "w")\n interactive_launcher_opened_set.add(self.pid)\n show_log_file(self.log_path)\n\n def write(self, s):\n s = s.encode()\n assert len(s) == os.write(self.inq_f.fileno(), s)\n \n def get_pid(self):\n n = 100\n for i in range(n):\n try:\n return int(re.findall(r"PID = (\\d+)", open(self.log_path).readline())[0])\n except:\n if i + 1 == n:\n raise\n time.sleep(0.1)\n \n def input_queue_path(self):\n return self.inq_path\n \n def wait_stop(self, timeout):\n for i in range(int(timeout * 10)):\n wpid, status = os.waitpid(self.pid, os.WNOHANG)\n if wpid != 0:\n return True\n time.sleep(0.1)\n return False\n \n def close(self, timeout=3):\n self.inq_f.close()\n if not self.wait_stop(timeout):\n os.kill(self.get_pid(), signal.SIGKILL)\n os.waitpid(self.pid, 0)\n os.remove(self.inq_path)\n # os.remove(self.log_path)\n self.inq_path = None\n self.log_path = None \n interactive_launcher_opened_set.remove(self.pid)\n self.pid = None\n \n @staticmethod\n def terminate_all():\n if "interactive_launcher_opened_set" not in globals():\n globals()["interactive_launcher_opened_set"] = set()\n global interactive_launcher_opened_set\n for pid in interactive_launcher_opened_set:\n print("Terminate pid=" + str(pid), file=sys.stderr)\n os.kill(pid, signal.SIGKILL)\n os.waitpid(pid, 0)\n interactive_launcher_opened_set = set()\n if os.path.exists(TInteractiveLauncher.tmp_path):\n shutil.rmtree(TInteractiveLauncher.tmp_path)\n \nTInteractiveLauncher.terminate_all()\n \nyandex_metrica_allowed = bool(globals().get("yandex_metrica_allowed", False))\nif yandex_metrica_allowed:\n display(HTML(\'\'\'<!-- YANDEX_METRICA_BEGIN -->\n <script type="text/javascript" >\n (function(m,e,t,r,i,k,a){m[i]=m[i]||function(){(m[i].a=m[i].a||[]).push(arguments)};\n m[i].l=1*new Date();k=e.createElement(t),a=e.getElementsByTagName(t)[0],k.async=1,k.src=r,a.parentNode.insertBefore(k,a)})\n (window, document, "script", "https://mc.yandex.ru/metrika/tag.js", "ym");\n\n ym(59260609, "init", {\n clickmap:true,\n trackLinks:true,\n accurateTrackBounce:true\n });\n </script>\n <noscript><div><img src="https://mc.yandex.ru/watch/59260609" style="position:absolute; left:-9999px;" alt="" /></div></noscript>\n <!-- YANDEX_METRICA_END -->\'\'\'))\n\ndef make_oneliner():\n html_text = \'("В этот ноутбук встроен код Яндекс Метрики для сбора статистики использований. Если вы не хотите, чтобы по вам собиралась статистика, исправьте: yandex_metrica_allowed = False" if yandex_metrica_allowed else "")\'\n html_text += \' + "<""!-- MAGICS_SETUP_PRINTING_END -->"\'\n return \'\'.join([\n \'# look at tools/set_up_magics.ipynb\\n\',\n \'yandex_metrica_allowed = True ; get_ipython().run_cell(%s);\' % repr(one_liner_str),\n \'display(HTML(%s))\' % html_text,\n \' #\'\'MAGICS_SETUP_END\'\n ])\n \n\n');display(HTML(("В этот ноутбук встроен код Яндекс Метрики для сбора статистики использований. Если вы не хотите, чтобы по вам собиралась статистика, исправьте: yandex_metrica_allowed = False" if yandex_metrica_allowed else "") + "<""!-- MAGICS_SETUP_PRINTING_END -->")) #MAGICS_SETUP_END
# # Потоки и их использование
#
# <br>
# <div style="text-align: right"> Спасибо <a href="https://github.com/Disadvantaged">Голяр Димитрису</a> за участие в написании текста </div>
# <br>
#
# <p><a href="https://www.youtube.com/watch?v=pP91ORe1YMk&list=PLjzMm8llUm4AmU6i_hPU0NobgA4VsBowc&index=21" target="_blank">
# <h3>Видеозапись семинара</h3>
# </a></p>
#
#
# [Ридинг Яковлева](https://github.com/victor-yacovlev/mipt-diht-caos/tree/master/practice/pthread)
#
#
# Сегодня в программе:
# * <a href="#ptread_create" style="color:#856024">Создание и join потоков</a>
# * <a href="#pthread_result" style="color:#856024">Аргументы и возвращаемое значение потока</a>
# * <a href="#pthread_cancel" style="color:#856024">Прерывание/отмена/cancel потока</a>
# * <a href="#pthread_attr" style="color:#856024">Атрибуты потока</a>
# * <a href="#coro" style="color:#856024">Корутины</a>
#
#
# <a href="#hw" style="color:#856024">Комментарии к ДЗ</a>
#
#
#
# Атрибуты процесса (полнота списков не гарантируется):
# * Виртуальное адресное пространство и данные в этой витруальной памяти
# * Файловые дескрипторы, блокировки файлов
# * PID
# * argc, argv
# * ulimit
#
# Атрибуты потока:
# * Маски сигналов (Маска сигналов наследует маску потока-родителя, изменения будут сохраняться только внутри потока)
# * Состояние процесса R, S, T, Z
# * Состояние регистров (какая ф-я сейчас выполняется) (состояние стека скорее входит в состояние вииртуального адресного пространства)
# * TID
#
# https://unix.stackexchange.com/questions/47595/linux-max-threads-count - про максимальное количество процессов и потоков в системе.
#
# https://stackoverflow.com/questions/11679568/signal-handling-with-multiple-threads-in-linux - про потоки и сигналы. TLDR: обработчик вызывается в произвольном потоке, из тех, где сигнал не заблокирован. То есть для лучшей предсказуемости сигналы стоит изначально заблокировать еще до создания дополнительных потоков, а затем создать отдельный поток в котором их получать через sigsuspend/signalfd/sigwaitinfo (и только в нем они будут разблокированы).
#
# TODO: кажется потоки можно использовать странным образом, просто для того, чтобы избегать переполнения стека. Возможно для этого реально использовать потоки в userspace. Надо поизучать
# # <a name="pthread_create"></a> Создание и join потока
# +
# %%cpp pthread_create.c
# %MD **Обратите внимание на санитайзер - он ваш друг на все домашки с многопоточностью :)**
# %run gcc -fsanitize=thread pthread_create.c -lpthread -o pthread_create.exe
# %run ./pthread_create.exe
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <sys/types.h>
#include <sys/syscall.h>
#include <sys/time.h>
#include <stdint.h>
#include <string.h>
#include <pthread.h>
#include <errno.h>
// log_printf - макрос для отладочного вывода, добавляющий время со старта программы, имя функции и номер строки
uint64_t start_time_msec; void __attribute__ ((constructor)) start_time_setter() { struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); start_time_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000; }
const char* log_prefix(const char* func, int line) {
struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); int delta_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000 - start_time_msec;
const int max_func_len = 13; static __thread char prefix[100];
sprintf(prefix, "%d.%03d %*s():%-3d [tid=%ld]", delta_msec / 1000, delta_msec % 1000, max_func_len, func, line, syscall(__NR_gettid));
return prefix;
}
#define log_printf_impl(fmt, ...) { time_t t = time(0); dprintf(2, "%s: " fmt "%s", log_prefix(__FUNCTION__, __LINE__), __VA_ARGS__); }
// Format: <time_since_start> <func_name>:<line> : <custom_message>
#define log_printf(...) log_printf_impl(__VA_ARGS__, "")
#define fail_with_strerror(code, msg) do { char err_buf[1024]; strerror_r(code, err_buf, sizeof(err_buf));\
log_printf(msg " (From err code: %s)\n", err_buf); exit(EXIT_FAILURE);} while (0)
// thread-aware assert
#define ta_verify(stmt) do { if (stmt) break; fail_with_strerror(errno, "'" #stmt "' failed."); } while (0)
// verify pthread call
#define pt_verify(pthread_call) do { int code = (pthread_call); if (code == 0) break; \
fail_with_strerror(code, "'" #pthread_call "' failed."); } while (0)
// Возвращаемое значение потока (~код возврата процесса) -- любое машинное слово.
static void* thread_func(void* arg)
{
log_printf(" Thread func started\n");
log_printf(" Thread func finished\n");
return NULL;
}
int main()
{
log_printf("Main func started\n");
pthread_t thread;
log_printf("Thread creating\n");
pt_verify(pthread_create(&thread, NULL, thread_func, 0)); // В какой-то момент будет создан поток и в нем вызвана функция
// Начиная отсюда неизвестно в каком порядке выполняются инструкции основного и дочернего потока
pt_verify(pthread_join(thread, NULL)); // -- аналог waitpid. Второй аргумент -- указатель в который запишется возвращаемое значение
log_printf("Thread joined\n");
log_printf("Main func finished\n");
return 0;
}
# -
# # <a name="pthread_result"></a> Смотрим на возвращаемое потоком значение.
# +
# %%cpp pthread_create.c
# %run clang -fsanitize=memory pthread_create.c -lpthread -o pthread_create.exe
# %run ./pthread_create.exe
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <sys/types.h>
#include <sys/syscall.h>
#include <sys/time.h>
#include <stdint.h>
#include <string.h>
#include <pthread.h>
#include <errno.h>
// log_printf - макрос для отладочного вывода, добавляющий время со старта программы, имя функции и номер строки
uint64_t start_time_msec; void __attribute__ ((constructor)) start_time_setter() { struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); start_time_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000; }
const char* log_prefix(const char* func, int line) {
struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); int delta_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000 - start_time_msec;
const int max_func_len = 13; static __thread char prefix[100];
sprintf(prefix, "%d.%03d %*s():%-3d [tid=%ld]", delta_msec / 1000, delta_msec % 1000, max_func_len, func, line, syscall(__NR_gettid));
return prefix;
}
#define log_printf_impl(fmt, ...) { time_t t = time(0); dprintf(2, "%s: " fmt "%s", log_prefix(__FUNCTION__, __LINE__), __VA_ARGS__); }
// Format: <time_since_start> <func_name>:<line> : <custom_message>
#define log_printf(...) log_printf_impl(__VA_ARGS__, "")
#define fail_with_strerror(code, msg) do { char err_buf[1024]; strerror_r(code, err_buf, sizeof(err_buf)); log_printf(msg " (From err code: %s)\n", err_buf); exit(EXIT_FAILURE);} while (0)
// thread-aware assert
#define ta_verify(stmt) do { if (stmt) break; fail_with_strerror(errno, "'" #stmt "' failed."); } while (0)
// verify pthread call
#define pt_verify(pthread_call) do { int code = (pthread_call); if (code == 0) break; fail_with_strerror(code, "'" #pthread_call "' failed."); } while (0)
typedef struct {
int a;
int b;
} thread_task_args_t;
// На самом деле проще записать результат в структуру аргументов
typedef struct {
int c;
} thread_task_result_t;
static thread_task_result_t* thread_func(const thread_task_args_t* arg)
{
log_printf(" Thread func started\n");
thread_task_result_t* result =
(thread_task_result_t*)malloc(sizeof(thread_task_result_t));
ta_verify(result != NULL);
result->c = arg->a + arg->b;
log_printf(" Thread func finished\n");
return result;
}
int main()
{
log_printf("Main func started\n");
pthread_t thread;
thread_task_args_t args = {.a = 35, .b = 7};
log_printf("Thread creating, args are: a=%d b=%d\n", args.a, args.b);
pt_verify(pthread_create(
&thread, NULL,
(void* (*)(void*))thread_func, // Важно понимать, что тут происходит
(void*)&args
));
thread_task_result_t* result;
pt_verify(pthread_join(thread, (void**)&result));
log_printf("Thread joined. Result: c=%d\n", result->c);
free(result);
log_printf("Main func finished\n");
return 0;
}
# -
# # <a name="pthread_cancel"></a> Прерывание потока
#
# Пусть это возможно сделать, но с этим нужно быть очень осторожным, особенно если поток, который вы прерываете владеет какими-либо ресурсами
# +
# %%cpp pthread_cancel.c
# %run gcc -fsanitize=thread pthread_cancel.c -lpthread -o pthread_cancel.exe
# %run ./pthread_cancel.exe
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <sys/types.h>
#include <sys/syscall.h>
#include <sys/time.h>
#include <stdint.h>
#include <string.h>
#include <pthread.h>
#include <errno.h>
// log_printf - макрос для отладочного вывода, добавляющий время со старта программы, имя функции и номер строки
uint64_t start_time_msec; void __attribute__ ((constructor)) start_time_setter() { struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); start_time_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000; }
const char* log_prefix(const char* func, int line) {
struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); int delta_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000 - start_time_msec;
const int max_func_len = 13; static __thread char prefix[100];
sprintf(prefix, "%d.%03d %*s():%-3d [tid=%ld]", delta_msec / 1000, delta_msec % 1000, max_func_len, func, line, syscall(__NR_gettid));
return prefix;
}
#define log_printf_impl(fmt, ...) { time_t t = time(0); dprintf(2, "%s: " fmt "%s", log_prefix(__FUNCTION__, __LINE__), __VA_ARGS__); }
// Format: <time_since_start> <func_name>:<line> : <custom_message>
#define log_printf(...) log_printf_impl(__VA_ARGS__, "")
#define fail_with_strerror(code, msg) do { char err_buf[1024]; strerror_r(code, err_buf, sizeof(err_buf));\
log_printf(msg " (From err code: %s)\n", err_buf); exit(EXIT_FAILURE);} while (0)
// thread-aware assert
#define ta_verify(stmt) do { if (stmt) break; fail_with_strerror(errno, "'" #stmt "' failed."); } while (0)
// verify pthread call
#define pt_verify(pthread_call) do { int code = (pthread_call); if (code == 0) break; \
fail_with_strerror(code, "'" #pthread_call "' failed."); } while (0)
static void* thread_func(void* arg)
{
log_printf(" Thread func started\n");
// В системных функциях разбросаны Cancellation points, в которых может быть прерван поток.
sleep(2);
log_printf(" Thread func finished\n"); // not printed because thread canceled
return NULL;
}
int main()
{
log_printf("Main func started\n");
pthread_t thread;
log_printf("Thread creating\n");
pt_verify(pthread_create(&thread, NULL, thread_func, 0));
sleep(1);
log_printf("Thread canceling\n");
pt_verify(pthread_cancel(thread)); // принимает id потока и прерывает его.
pt_verify(pthread_join(thread, NULL)); // Если не сделать join, то останется зомби-поток.
log_printf("Thread joined\n");
log_printf("Main func finished\n");
return 0;
}
# -
# По умолчанию pthread_cancel может прерывать поток, только в cancelation points (то есть в функциях, в реализациях которых есть проверка на это).
#
# Поэтому, если эти функции не вызывать, то поток не сможет быть прерван.
#
# Но можно воспользоваться `pthread_setcanceltype(PTHREAD_CANCEL_ASYNCHRONOUS, NULL);`. Тогда поток может быть прерван на уровне планировщика. (То есть поток скорее всего доработает текущий выделенный квант времени, но на следующий квант уже не запустится)
# +
# %%cpp pthread_cancel_fail.c
# %run gcc -fsanitize=thread pthread_cancel_fail.c -lpthread -o pthread_cancel_fail.exe
# %run timeout 3 ./pthread_cancel_fail.exe # will fail (cancelation at cancelation points)
# %run gcc -fsanitize=thread -DASYNC_CANCEL pthread_cancel_fail.c -lpthread -o pthread_cancel_fail.exe
# %run timeout 3 ./pthread_cancel_fail.exe # ok, async cancelation
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <sys/types.h>
#include <sys/syscall.h>
#include <sys/time.h>
#include <stdint.h>
#include <string.h>
#include <pthread.h>
#include <errno.h>
// log_printf - макрос для отладочного вывода, добавляющий время со старта программы, имя функции и номер строки
uint64_t start_time_msec; void __attribute__ ((constructor)) start_time_setter() { struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); start_time_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000; }
const char* log_prefix(const char* func, int line) {
struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); int delta_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000 - start_time_msec;
const int max_func_len = 13; static __thread char prefix[100];
sprintf(prefix, "%d.%03d %*s():%-3d [tid=%ld]", delta_msec / 1000, delta_msec % 1000, max_func_len, func, line, syscall(__NR_gettid));
return prefix;
}
#define log_printf_impl(fmt, ...) { time_t t = time(0); dprintf(2, "%s: " fmt "%s", log_prefix(__FUNCTION__, __LINE__), __VA_ARGS__); }
// Format: <time_since_start> <func_name>:<line> : <custom_message>
#define log_printf(...) log_printf_impl(__VA_ARGS__, "")
#define fail_with_strerror(code, msg) do { char err_buf[1024]; strerror_r(code, err_buf, sizeof(err_buf));\
log_printf(msg " (From err code: %s)\n", err_buf); exit(EXIT_FAILURE);} while (0)
// thread-aware assert
#define ta_verify(stmt) do { if (stmt) break; fail_with_strerror(errno, "'" #stmt "' failed."); } while (0)
// verify pthread call
#define pt_verify(pthread_call) do { int code = (pthread_call); if (code == 0) break; \
fail_with_strerror(code, "'" #pthread_call "' failed."); } while (0)
static void *
thread_func(void *arg)
{
log_printf(" Thread func started\n");
#ifdef ASYNC_CANCEL
pt_verify(pthread_setcanceltype(PTHREAD_CANCEL_ASYNCHRONOUS, NULL)); // Включаем более жесткий способ остановки потока
#endif
// Без опции ASYNC_CANCEL поток не может быть остановлен во время своей работы.
while (1); // зависаем тут. В процессе явно не будет cancelation points
log_printf(" Thread func finished\n");
return NULL;
}
int main()
{
log_printf("Main func started\n");
pthread_t thread;
log_printf("Thread creating\n");
pt_verify(pthread_create(&thread, NULL, thread_func, 0));
sleep(1);
log_printf("Thread canceling\n");
pt_verify(pthread_cancel(thread));
log_printf("Thread joining\n");
pt_verify(pthread_join(thread, NULL));
log_printf("Thread joined\n");
log_printf("Main func finished\n");
return 0;
}
# -
# ## А можно ли приджойнить основной поток?
# +
# %%cpp join_main_thread.c
# %run gcc join_main_thread.c -lpthread -o join_main_thread.exe
# %run timeout 3 ./join_main_thread.exe ; echo "Exit code: $?"
# %run gcc -fsanitize=thread join_main_thread.c -lpthread -o join_main_thread.exe
# %run timeout 3 ./join_main_thread.exe ; echo "Exit code: $?"
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <sys/types.h>
#include <sys/syscall.h>
#include <sys/time.h>
#include <stdint.h>
#include <string.h>
#include <pthread.h>
#include <errno.h>
// log_printf - макрос для отладочного вывода, добавляющий время со старта программы, имя функции и номер строки
uint64_t start_time_msec; void __attribute__ ((constructor)) start_time_setter() { struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); start_time_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000; }
const char* log_prefix(const char* func, int line) {
struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); int delta_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000 - start_time_msec;
const int max_func_len = 13; static __thread char prefix[100];
sprintf(prefix, "%d.%03d %*s():%-3d [tid=%ld]", delta_msec / 1000, delta_msec % 1000, max_func_len, func, line, syscall(__NR_gettid));
return prefix;
}
#define log_printf_impl(fmt, ...) { time_t t = time(0); dprintf(2, "%s: " fmt "%s", log_prefix(__FUNCTION__, __LINE__), __VA_ARGS__); }
// Format: <time_since_start> <func_name>:<line> : <custom_message>
#define log_printf(...) log_printf_impl(__VA_ARGS__, "")
#define fail_with_strerror(code, msg) do { char err_buf[1024]; strerror_r(code, err_buf, sizeof(err_buf));\
log_printf(msg " (From err code: %s)\n", err_buf); exit(EXIT_FAILURE);} while (0)
// thread-aware assert
#define ta_verify(stmt) do { if (stmt) break; fail_with_strerror(errno, "'" #stmt "' failed."); } while (0)
// verify pthread call
#define pt_verify(pthread_call) do { int code = (pthread_call); if (code == 0) break; \
fail_with_strerror(code, "'" #pthread_call "' failed."); } while (0)
pthread_t main_thread;
static void* thread_func(void* arg)
{
log_printf(" Thread func started\n");
log_printf(" Main thread joining\n");
pt_verify(pthread_join(main_thread, NULL));
log_printf(" Main thread joined\n");
log_printf(" Thread func finished\n");
_exit(42);
}
int main()
{
log_printf("Main func started\n");
main_thread = pthread_self();
pthread_t thread;
log_printf("Thread creating\n");
pt_verify(pthread_create(&thread, NULL, thread_func, 0));
pthread_exit(NULL);
}
# -
# Без санитайзера можно, с санитайзером - нет. Не знаю есть ли тут какое-то принципиальное нарушение, но не надо так делать)
# # <a name="pthread_attr"></a> Атрибуты потока
#
# * Размер стека
# * Местоположение стека
# * Размер защитной области после стека. Вот тут можно прокомментировать: это область ниже стека, которая является дырой в виртуальном адресном пространстве программы. То есть при попытке обращения к этой области произойдет segfault. Для чего необходима защитная область? Чтобы при переполнении стека получать segfault, а не неотлавливаемый проезд по памяти.
#
#
# В следующем примере создадим поток двумя способами. С параметрами по умолчанию и указав минимальный размер стека. И посмотрим на потребления памяти.
#
# (Да, потреблениЯ. Там все не так просто, как кажется на первый взгляд :). Загляните в `/proc/<pid>/status`)
# +
# %%cpp pthread_stack_size.c
# %MD ### Обычный стек 8мб, активно его не используем
# %run gcc -fsanitize=thread pthread_stack_size.c -lpthread -o pthread_stack_size.exe
# %run ./pthread_stack_size.exe
# %MD ### Маленький стек 16кб, активно его не используем
# %run gcc -fsanitize=thread -DMY_STACK_SIZE=16384 pthread_stack_size.c -lpthread -o pthread_stack_size.exe
# %run ./pthread_stack_size.exe
# %MD Во второй раз (VM delta size) не 16кб потому что имеются накладные расходы. Но оно меньше примерно на 8 MB
# %MD ### Обычный стек 8мб, активно его используем
# %run gcc -fsanitize=thread -DUSE_STACK=7000000 pthread_stack_size.c -lpthread -o pthread_stack_size.exe
# %run ./pthread_stack_size.exe
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <sys/types.h>
#include <sys/resource.h>
#include <sys/syscall.h>
#include <sys/time.h>
#include <stdint.h>
#include <string.h>
#include <pthread.h>
#include <errno.h>
// log_printf - макрос для отладочного вывода, добавляющий время со старта программы, имя функции и номер строки
uint64_t start_time_msec; void __attribute__ ((constructor)) start_time_setter() { struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); start_time_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000; }
const char* log_prefix(const char* func, int line) {
struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); int delta_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000 - start_time_msec;
const int max_func_len = 13; static __thread char prefix[100];
sprintf(prefix, "%d.%03d %*s():%-3d [tid=%ld]", delta_msec / 1000, delta_msec % 1000, max_func_len, func, line, syscall(__NR_gettid));
return prefix;
}
#define log_printf_impl(fmt, ...) { time_t t = time(0); dprintf(2, "%s: " fmt "%s", log_prefix(__FUNCTION__, __LINE__), __VA_ARGS__); }
// Format: <time_since_start> <func_name>:<line> : <custom_message>
#define log_printf(...) log_printf_impl(__VA_ARGS__, "")
#define fail_with_strerror(code, msg) do { char err_buf[1024]; strerror_r(code, err_buf, sizeof(err_buf));\
log_printf(msg " (From err code: %s)\n", err_buf); exit(EXIT_FAILURE);} while (0)
// thread-aware assert
#define ta_verify(stmt) do { if (stmt) break; fail_with_strerror(errno, "'" #stmt "' failed."); } while (0)
// verify pthread call
#define pt_verify(pthread_call) do { int code = (pthread_call); if (code == 0) break; \
fail_with_strerror(code, "'" #pthread_call "' failed."); } while (0)
long int get_maxrss() {
struct rusage usage;
ta_verify(getrusage(RUSAGE_SELF, &usage) == 0);
return usage.ru_maxrss;
}
const char* run_and_get_output(const char* bash_cmd) {
int fds[2];
pipe(fds);
int pid = fork();
if (pid == 0) {
dup2(fds[1], 1);
close(fds[0]); close(fds[1]);
execlp("bash", "bash", "-c", bash_cmd, NULL);
ta_verify(0 && "unreachable");
}
close(fds[1]);
static __thread char buffer[100];
int size = 0, rd = 0;
while ((rd = read(fds[0], buffer, sizeof(buffer) - size)) != 0) {
if (rd > 0) {
size += rd;
}
}
buffer[size] = 0;
return buffer;
}
long int get_vm_usage() {
char cmd1[10000];
sprintf(cmd1, "cat /proc/%d/status | grep VmData", getpid());
const char* vm_usage_s = run_and_get_output(cmd1);
long int vm_usage;
sscanf(vm_usage_s, "VmData: %ld kB", &vm_usage);
return vm_usage;
}
static void *
thread_func(void *arg)
{
#ifdef USE_STACK
char a[USE_STACK];
for (int i = 2; i < sizeof(a); ++i) {
a[i] = a[i - 1] ^ a[i - 2] * 19;
}
log_printf(" Thread func started. Trash=%d\n", a[sizeof(a) - 1]); // Предотвращаем оптимизацию
#else
log_printf(" Thread func started\n");
#endif
sleep(2);
log_printf(" Thread func finished\n");
return NULL;
}
int main()
{
double initial_rss = (double)get_maxrss() / 1000;
double initial_vm_size = (double)get_vm_usage() / 1000;
log_printf("Main func started. Initial RSS = %0.1lf MB, initial VM usage = %0.1lf MB\n",
initial_rss, initial_vm_size);
pthread_t thread;
pthread_attr_t thread_attr;
pt_verify(pthread_attr_init(&thread_attr)); // Атрибуты нужно инициализировать
#ifdef MY_STACK_SIZE
pt_verify(pthread_attr_setstacksize(&thread_attr, MY_STACK_SIZE)); // В структуру сохраняем размер стека
#endif
pt_verify(pthread_create(&thread, &thread_attr, thread_func, 0));
pt_verify(pthread_attr_destroy(&thread_attr)); // И уничтожить
sleep(1);
double current_rss = (double)get_maxrss() / 1000;
double current_vm_size = (double)get_vm_usage() / 1000;
log_printf("Thread working. RSS = %0.1lf MB, delta RSS = %0.1lf MB\n",
current_rss, current_rss - initial_rss);
log_printf("Thread working. VM size = %0.1lf MB, VM delta size = %0.1lf MB (!)\n",
current_vm_size, current_vm_size - initial_vm_size);
pt_verify(pthread_join(thread, NULL));
log_printf("Main func finished\n");
return 0;
}
# -
# # <a name="coro"></a> Coroutines
#
# Корутины -- это потоки внутри одного юзерспейса. То есть, это потоки внутри потока.
# Для этого используется программный (реализованный в коде пользователя), а не системный scheduler.
#
# Файберы (=корутины, =потоки в юзерспейсе):
# <br>`+` Известно, когда может быть вызвано переключение контекста. Файберы работающие внутри одного потока могут не пользоваться межпоточной синхронизацией при общении друг с другом.
# <br>`+` Низкие затраты на переключение контекста. Это очень эффективно, если есть много потоков перекладывающих друг другу данные.
# <br>`+` ...
# <br>`-` Привязанность к фреймворку. Нельзя использовать блокирующие вызовы не через этот фреймворк.
# <br>`-` Нельзя подключиться к процессу с помощью gdb и посмотреть на все потоки.
# <br>`-` ...
# !rm -rf ./libtask
# !git clone [email protected]:0intro/libtask.git
# !cd libtask && make
# +
# %%cpp coro.cpp
# %run gcc -I ./libtask coro.cpp ./libtask/libtask.a -lpthread -o coro.exe
# %run ./coro.exe 300 100 200 1000
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <sys/types.h>
#include <sys/syscall.h>
#include <sys/time.h>
#include <string.h>
#include <errno.h>
#include <task.h>
#include <stdint.h>
#include <string.h>
#include <pthread.h>
#include <errno.h>
// log_printf - макрос для отладочного вывода, добавляющий время со старта программы, имя функции и номер строки
uint64_t start_time_msec; void __attribute__ ((constructor)) start_time_setter() { struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); start_time_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000; }
const char* log_prefix(const char* func, int line) {
struct timespec spec; clock_gettime(CLOCK_MONOTONIC, &spec); int delta_msec = spec.tv_sec * 1000L + spec.tv_nsec / 1000000 - start_time_msec;
const int max_func_len = 13; static __thread char prefix[100];
sprintf(prefix, "%d.%03d %*s():%-3d [tid=%ld]", delta_msec / 1000, delta_msec % 1000, max_func_len, func, line, syscall(__NR_gettid));
return prefix;
}
#define log_printf_impl(fmt, ...) { time_t t = time(0); dprintf(2, "%s: " fmt "%s", log_prefix(__FUNCTION__, __LINE__), __VA_ARGS__); }
// Format: <time_since_start> <func_name>:<line> : <custom_message>
#define log_printf(...) log_printf_impl(__VA_ARGS__, "")
const int STACK_SIZE = 32768;
typedef struct {
int sleep_time;
} task_args_t;
Channel *c;
void delaytask(task_args_t *args)
{
taskdelay(args->sleep_time);
log_printf("Task %dms is launched\n", args->sleep_time);
chansendul(c, 0);
}
void taskmain(int argc, char **argv)
{
task_args_t args[argc];
c = chancreate(sizeof(unsigned long), 0);
for(int i = 1; i < argc; i++){
args[i].sleep_time = atoi(argv[i]);
log_printf("Schedule %dms task\n", args[i].sleep_time);
taskcreate((void (*)(void*))delaytask, (void*)&args[i], STACK_SIZE);
}
for(int i = 1; i < argc; i++){
chanrecvul(c);
log_printf("Some task is finished\n");
}
taskexitall(0);
}
# -
# # <a name="hw"></a> Комментарии к ДЗ
#
# * posix/threads/parallel-sum:
# <br>scanf/printf и многие другие функции стандартной библиотеки потокобезопасны (но каждый раз лучше смотреть в man).
# <br>В задаче требуется "минимизировать объем памяти", уточню: сделать для потоков стеки минимального размера.
# +
# -
| 55.53701 | 12,193 |
92478a8e2786f262f6b4a84dd7919afb11978d15
|
py
|
python
|
2-Intro a Machine Learning.ipynb
|
agrija9/RIIAA_Escuela18
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: py36-test
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Cargamos-librerias" data-toc-modified-id="Cargamos-librerias-1">Cargamos librerias</a></span><ul class="toc-item"><li><span><a href="#metricas-de-evaluacion-(sigmas)-+-funciones-de-utilidad" data-toc-modified-id="metricas-de-evaluacion-(sigmas)-+-funciones-de-utilidad-1.1">metricas de evaluacion (sigmas) + funciones de utilidad</a></span></li><li><span><a href="#Datos-de-entrenamiento!" data-toc-modified-id="Datos-de-entrenamiento!-1.2">Datos de entrenamiento!</a></span></li><li><span><a href="#usamos-🐼" data-toc-modified-id="usamos-🐼-1.3">usamos 🐼</a></span></li><li><span><a href="#preprocesamiento-para-X-y-Y" data-toc-modified-id="preprocesamiento-para-X-y-Y-1.4">preprocesamiento para X y Y</a></span></li></ul></li><li><span><a href="#ML-con-Scikit-learn" data-toc-modified-id="ML-con-Scikit-learn-2">ML con Scikit-learn</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Regression-Logistica" data-toc-modified-id="Regression-Logistica-2.0.1">Regression Logistica</a></span><ul class="toc-item"><li><span><a href="#Coeficientes" data-toc-modified-id="Coeficientes-2.0.1.1">Coeficientes</a></span></li></ul></li></ul></li><li><span><a href="#predecir-probabilidades" data-toc-modified-id="predecir-probabilidades-2.1">predecir probabilidades</a></span></li><li><span><a href="#SGDclassifier-(Regression-Logistica)" data-toc-modified-id="SGDclassifier-(Regression-Logistica)-2.2">SGDclassifier (Regression Logistica)</a></span><ul class="toc-item"><li><span><a href="#Actividad:-Evalua!" data-toc-modified-id="Actividad:-Evalua!-2.2.1">Actividad: Evalua!</a></span></li></ul></li><li><span><a href="#Regularizacion" data-toc-modified-id="Regularizacion-2.3">Regularizacion</a></span></li></ul></li><li><span><a href="#Actividad:" data-toc-modified-id="Actividad:-3">Actividad:</a></span><ul class="toc-item"><li><span><a href="#Metodos-de-ensembles" data-toc-modified-id="Metodos-de-ensembles-3.1">Metodos de ensembles</a></span></li><li><span><a href="#predecir-probabilidades" data-toc-modified-id="predecir-probabilidades-3.2">predecir probabilidades</a></span></li><li><span><a href="#Modelos-de-arboles:-feature-importance" data-toc-modified-id="Modelos-de-arboles:-feature-importance-3.3">Modelos de arboles: feature importance</a></span></li><li><span><a href="#Mejorando-la-regla-de-decision" data-toc-modified-id="Mejorando-la-regla-de-decision-3.4">Mejorando la regla de decision</a></span><ul class="toc-item"><li><span><a href="#en-vez-de-0.5-usaremos-un-percentil" data-toc-modified-id="en-vez-de-0.5-usaremos-un-percentil-3.4.1">en vez de 0.5 usaremos un percentil</a></span></li></ul></li><li><span><a href="#Probabilidad-de-corte" data-toc-modified-id="Probabilidad-de-corte-3.5">Probabilidad de corte</a></span></li></ul></li><li><span><a href="#Actividad:" data-toc-modified-id="Actividad:-4">Actividad:</a></span></li></ul></div>
# -
# 
# # Cargamos librerias
# %matplotlib inline
# %config InlineBackend.figure_format='retina'
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import scipy as sc
import pandas as pd
import sklearn
import matplotlib.pyplot as plt
import seaborn as sns
import os
from IPython.display import display
import sys
# ## metricas de evaluacion (sigmas) + funciones de utilidad
#
# 
# +
from sklearn.metrics import roc_curve, auc
def AMSScore(s,b):
return np.sqrt (2.*( (s + b + 10.)*np.log(1.+s/(b+10.))-s))
def eval_model(Y_true_train,Y_pred_train,w_train,Y_true_test,Y_pred_test,w_test):
ratio = float(len(X_train)) /float(len(X_test))
TruePositive_train = w_train*(Y_true_train==1.0)*(1.0/ratio)
TrueNegative_train = w_train*(Y_true_train==0.0)*(1.0/ratio)
TruePositive_valid = w_test*(Y_true_test==1.0)*(1.0/(1-ratio))
TrueNegative_valid = w_test*(Y_true_test==0.0)*(1.0/(1-ratio))
s_train = sum ( TruePositive_train*(Y_pred_train==1.0) )
b_train = sum ( TrueNegative_train*(Y_pred_train==1.0) )
s_test = sum ( TruePositive_valid*(Y_pred_test==1.0) )
b_test = sum ( TrueNegative_valid*(Y_pred_test==1.0) )
score_train = AMSScore(s_train,b_train)
score_test = AMSScore(s_test,b_test)
print('--- Resultados --')
print('- AUC train: {:.3f} '.format(sk.metrics.roc_auc_score(Y_train,Y_train_pred)))
print('- AUC test : {:.3f} '.format(sk.metrics.roc_auc_score(Y_test,Y_test_pred)))
print('- AMS train: {:.3f} sigma'.format(score_train))
print('- AMS test : {:.3f} sigma'.format(score_test))
return score_train, score_test
def plot_roc(clf,Y_test,Y_test_prob):
fpr, tpr, thresholds = roc_curve(Y_test, Y_test_prob)
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, lw=1, alpha=0.3, label=str(clf.__class__.__name__))
plt.plot(np.linspace(0,1,100),np.linspace(0,1,100), lw=2, alpha=0.3, label='Suerte')
plt.legend(loc='lower right')
plt.xlim([0,1])
plt.ylim([0,1])
plt.tight_layout()
return
# -
# ## Datos de entrenamiento!
#
# Quieres saber mas? Visita [http://higgsml.lal.in2p3.fr/documentation](http://higgsml.lal.in2p3.fr/documentation)
# !wget
# ## usamos 🐼
#
df=pd.read_csv('datos/training.csv')
print(df.shape)
df.head(1)
# ## preprocesamiento para X y Y
Y = df['Label'].replace(to_replace=['s','b'],value=[1,0]).values #Estas son las variables a predecir (Target values)
weights = df['Weight'].values # Estos son los que nos dicen info acerca de qué tan confiable es la medición
X = df.drop(['EventId','Label','Weight'],axis=1).values #Quitamos esas tres columnas y el resto lo usamos como datos para entrenar
# +
#Hemos separado training data y test data
# -
from sklearn.model_selection import train_test_split
X_train,X_test,Y_train,Y_test,w_train,w_test = train_test_split(X,Y,weights,train_size=0.4) #40% train data
print(X_train.shape,Y_train.shape,w_train.shape)
print(X_test.shape,Y_test.shape,w_test.shape)
# # ML con Scikit-learn
#
# ](extra/sklearn_logo.png)
# ### Regression Logistica
#
# ** Modelo :** $h_{\theta}(x) = g(\theta^{T}x) = g(\sum \theta_i x_i +b)$ con $g(z)=\frac{1}{1+e^{-z}}$
#
# ** optimizador, metrica?**
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(verbose=1)
clf.fit(X_train,Y_train)
# #### Coeficientes
#
# $$\sum \theta_i x_i + b $$
# +
# Podemos ver lo que hay dentro del modelo
# -
print('a = {}'.format(clf.coef_))
print('b = {}'.format(clf.intercept_))
sns.distplot(clf.coef_,kde=False)
plt.show()
# ## predecir probabilidades
import sklearn as sk
Y_train_pred = clf.predict(X_train)
Y_test_pred = clf.predict(X_test)
Y_train_prob=clf.predict_proba(X_train)[:,1]
Y_test_prob =clf.predict_proba(X_test)[:,1]
print('AUC:')
print('train: {:2.4f}'.format(sk.metrics.roc_auc_score(Y_train,Y_train_pred)))
print('test: {:2.4f}'.format(sk.metrics.roc_auc_score(Y_test,Y_test_pred)))
eval_model(Y_train,Y_train_pred,w_train,Y_test,Y_test_pred,w_test) # --> w_train, w_test are validation values
x = np.linspace(-30,30,100)
plt.plot(x,1.0/(1+np.exp(-x)))
plt.show()
# +
from sklearn.metrics import roc_curve, auc
fpr, tpr, thresholds = roc_curve(Y_test, Y_test_prob)
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, lw=1, alpha=0.3, label=str(clf.__class__.__name__))
plt.plot(np.linspace(0,1,100),np.linspace(0,1,100), lw=2, alpha=0.3, label='Suerte')
plt.legend(loc='lower right')
plt.xlim([0,1])
plt.ylim([0,1])
plt.xlabel('Falsos Positivos')
plt.ylabel('Falsos Negativos')
plt.tight_layout()
plt.show()
# -
# ## SGDclassifier (Regression Logistica)
#
# ** Modelo :** $h_{\theta}(x) = g(\theta^{T}x)$ con $g(z)=\frac{1}{1+e^{-z}}$
#
# ** Costo :** $$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}y^{i}\log(h_\theta(x^{i}))+(1-y^{i})\log(1-h_\theta(x^{i}))$$
# ** Optimizador:** Descenso de gradiente
#
#
# Ojo, la derivada del costo es:
# $$ \frac{\partial}{\partial\theta_{j}}J(\theta) =\sum_{i=1}^{m}(h_\theta(x^{i})-y^i)x_j^i$$
# +
from sklearn.linear_model import SGDClassifier # <-- Stocasthic gradient descent optimizer
clf = SGDClassifier(loss='modified_huber',verbose=1,max_iter=700) # <-- 500 epochs
clf.fit(X_train,Y_train)
# Lo que se intenta optimizar es la derivada del costo
# -
# ### Actividad: Evalua!
import sklearn as sk
Y_train_pred = clf.predict(X_train)
Y_test_pred = clf.predict(X_test)
Y_train_prob=clf.predict_proba(X_train)[:,1]
Y_test_prob =clf.predict_proba(X_test)[:,1]
print('AUC:')
print('train: {:2.4f}'.format(sk.metrics.roc_auc_score(Y_train,Y_train_pred)))
print('test: {:2.4f}'.format(sk.metrics.roc_auc_score(Y_test,Y_test_pred)))
eval_model(Y_train,Y_train_pred,w_train,Y_test,Y_test_pred,w_test) # --> w_train, w_test are validation values
# ## Regularizacion
#
#
#
#
# ** Costo :** $$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}y^{i}\log(h_\theta(x^{i}))+(1-y^{i})\log(1-h_\theta(x^{i}))$$
#
# ** $L2$**: $$ + \alpha \sum \theta_i^2$$
# ** $L1$**: $$ + \frac{\lambda}{1}\sum |\theta_i|$$
#
#
# Penalización de los parámetros del modelo
# +
from sklearn.linear_model import SGDClassifier
clf = SGDClassifier(loss='log',alpha=0.5,l1_ratio=0.2,verbose=1,max_iter=500)
clf.fit(X_train,Y_train)
# -
# # Actividad:
#
# * Entrena un modelo para investigar el efecto de solo usar regularizacion L2 (apaga L1)
# * Entrena un modelo para investigar el efecto de solo usar regularizacion L1 (apaga L2)
# * Checa histogramas de tus pesos (coef)
# ## Metodos de ensembles
#Modelo no lineal
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(verbose=1)
clf.fit(X_train,Y_train)
# ## predecir probabilidades
# Evaluate model
Y_train_pred = clf.predict(X_train)
Y_test_pred = clf.predict(X_test)
Y_train_prob=clf.predict_proba(X_train)[:,1]
Y_test_prob =clf.predict_proba(X_test)[:,1]
eval_model(Y_train,Y_train_pred,w_train,Y_test,Y_test_pred,w_test)
plot_roc(clf,Y_test,Y_test_prob)
# ## Modelos de arboles: feature importance
# +
importances = clf.feature_importances_
indices = np.argsort(importances)[::-1]
# Print the feature ranking
print("Feature ranking:")
for f in range(X.shape[1]):
print('{:d}. X_{:d} ({:2.4f})'.format(f + 1, indices[f], importances[indices[f]]))
# Plot the feature importances of the forest
plt.figure()
plt.title("Feature importances")
plt.bar(range(X.shape[1]), importances[indices], align="center")
plt.xticks(range(X.shape[1]), indices)
plt.xlim([-1, X.shape[1]])
plt.show()
# -
# ## Mejorando la regla de decision
# ### en vez de 0.5 usaremos un percentil
# ## Probabilidad de corte
sns.distplot(Y_train_prob)
plt.show()
pcut = np.percentile(Y_train_prob,80)
pcut
Y_train_pred = Y_train_prob > pcut
Y_test_pred = Y_test_prob > pcut
eval_model(Y_train,Y_train_pred,w_train,Y_test,Y_test_pred,w_test)
# # Actividad:
#
# * Escoge algun algoritmo que no hayamos visto.
# * Trata de entender la idea central en 5 minutos.
# * Identifica los componentes (Modelo, funcion objectivo, optimizador)
# * Entrenar un algoritmo.
# * Optimizar los hiperparametros.
# ## SVMClassifier
#
# ** Modelo :** $h_{\theta}(x) = g(\theta^{T}x)$ con $g(z)=\frac{1}{1+e^{-z}}$
#
# ** Costo :** $$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}y^{i}\log(h_\theta(x^{i}))+(1-y^{i})\log(1-h_\theta(x^{i}))$$
# ** Optimizador:** Descenso de gradiente
#
#
# Ojo, la derivada del costo es:
# $$ \frac{\partial}{\partial\theta_{j}}J(\theta) =\sum_{i=1}^{m}(h_\theta(x^{i})-y^i)x_j^i$$
#Modelo SVM#
from sklearn.svm import LinearSVC
#from sklearn import svm # <-- Took so long ...
#clf = svm.SVC(C=1, gamma='auto', kernel='rbf')
clf = LinearSVC(random_state=0)
clf.fit(X_train,Y_train)
import sklearn as sk
# Evaluate model
Y_train_pred = clf.predict(X_train)
Y_test_pred = clf.predict(X_test)
#Y_train_prob=clf.predict_proba(X_train)[:,1]
#Y_test_prob =clf.predict_proba(X_test)[:,1]
eval_model(Y_train,Y_train_pred,w_train,Y_test,Y_test_pred,w_test)
| 37.445141 | 2,944 |
4ab0ad2bc4d01d8d7bfdce63696055a9cfc9c6cc
|
py
|
python
|
notebooks/Figures/Figure5.ipynb
|
SBRG/xplatform_ica_paper
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Setup" data-toc-modified-id="Setup-1"><span class="toc-item-num">1 </span>Setup</a></span><ul class="toc-item"><li><span><a href="#Load-data" data-toc-modified-id="Load-data-1.1"><span class="toc-item-num">1.1 </span>Load data</a></span></li></ul></li><li><span><a href="#Figure-5b---Categories-of-combined-iModulons" data-toc-modified-id="Figure-5b---Categories-of-combined-iModulons-2"><span class="toc-item-num">2 </span>Figure 5b - Categories of combined iModulons</a></span></li><li><span><a href="#Create-RBH-graph" data-toc-modified-id="Create-RBH-graph-3"><span class="toc-item-num">3 </span>Create RBH graph</a></span></li><li><span><a href="#Figure-5c---Presence/absence-of-iModulons" data-toc-modified-id="Figure-5c---Presence/absence-of-iModulons-4"><span class="toc-item-num">4 </span>Figure 5c - Presence/absence of iModulons</a></span></li><li><span><a href="#Figure-5d---Heatmap" data-toc-modified-id="Figure-5d---Heatmap-5"><span class="toc-item-num">5 </span>Figure 5d - Heatmap</a></span></li><li><span><a href="#Figure-5e---Explained-variance" data-toc-modified-id="Figure-5e---Explained-variance-6"><span class="toc-item-num">6 </span>Figure 5e - Explained variance</a></span></li><li><span><a href="#Figure-5f---ppGpp-Activities" data-toc-modified-id="Figure-5f---ppGpp-Activities-7"><span class="toc-item-num">7 </span>Figure 5f - ppGpp Activities</a></span></li><li><span><a href="#Figure-5g:-PCA-of-datasets" data-toc-modified-id="Figure-5g:-PCA-of-datasets-8"><span class="toc-item-num">8 </span>Figure 5g: PCA of datasets</a></span></li><li><span><a href="#Figure-5h:-PCA-of-activites" data-toc-modified-id="Figure-5h:-PCA-of-activites-9"><span class="toc-item-num">9 </span>Figure 5h: PCA of activites</a></span></li><li><span><a href="#Supplementary-Figure-7" data-toc-modified-id="Supplementary-Figure-7-10"><span class="toc-item-num">10 </span>Supplementary Figure 7</a></span><ul class="toc-item"><li><span><a href="#Panel-a:-Explained-variance-of-lost-i-modulons" data-toc-modified-id="Panel-a:-Explained-variance-of-lost-i-modulons-10.1"><span class="toc-item-num">10.1 </span>Panel a: Explained variance of lost i-modulons</a></span></li><li><span><a href="#Panel-b:-Classes-of-new-i-modulons" data-toc-modified-id="Panel-b:-Classes-of-new-i-modulons-10.2"><span class="toc-item-num">10.2 </span>Panel b: Classes of new i-modulons</a></span></li><li><span><a href="#Panel-c:-Histogram-of-IC-gene-coefficients" data-toc-modified-id="Panel-c:-Histogram-of-IC-gene-coefficients-10.3"><span class="toc-item-num">10.3 </span>Panel c: Histogram of IC gene coefficients</a></span></li><li><span><a href="#Panel-e:-F1-score-chart" data-toc-modified-id="Panel-e:-F1-score-chart-10.4"><span class="toc-item-num">10.4 </span>Panel e: F1-score chart</a></span></li><li><span><a href="#Panel-f:-Pearson-R-between-activities" data-toc-modified-id="Panel-f:-Pearson-R-between-activities-10.5"><span class="toc-item-num">10.5 </span>Panel f: Pearson R between activities</a></span></li></ul></li><li><span><a href="#New-biological-component" data-toc-modified-id="New-biological-component-11"><span class="toc-item-num">11 </span>New biological component</a></span></li></ul></div>
# -
# # Setup
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm
import pandas as pd
import numpy as np
import os, sys
from itertools import combinations
import seaborn as sns
from matplotlib_venn import venn2
from scipy import stats
from sklearn.decomposition import PCA
sys.path.append('../../scripts/')
from core import *
sns.set_style('ticks')
# Use custom stylesheet for figures
plt.style.use('custom')
# ## Load data
datasets = sorted([x for x in os.listdir(os.path.join(DATA_DIR,'iModulons'))
if '.' not in x])
# Thresholds were obtained from sensitivity analysis
cutoffs = {'MA-1': 550,
'MA-2': 600,
'MA-3': 350,
'RNAseq-1': 700,
'RNAseq-2': 300,
'combined': 400}
def load(dataset):
# Define directories
ds_dir = os.path.join(DATA_DIR,'iModulons',dataset)
# Define files
X_file = os.path.join(DATA_DIR,'processed_data',dataset+'_bc.csv')
M_file = os.path.join(ds_dir,'M.csv')
A_file = os.path.join(ds_dir,'A.csv')
metadata_file = os.path.join(DATA_DIR,'metadata',dataset+'_metadata.csv')
return IcaData(M_file,A_file,X_file,metadata_file,cutoffs[dataset])
# Load datasets
objs = {}
for ds in tqdm(datasets):
objs[ds] = load(ds)
DF_categories = pd.read_csv(os.path.join(DATA_DIR,'iModulons','categories_curated.csv'),index_col=0)
DF_categories.index = DF_categories.dataset.combine(DF_categories.component,lambda x1,x2:x1+'_'+str(x2))
# # Figure 5b - Categories of combined iModulons
data = DF_categories[DF_categories.dataset=='combined'].type.value_counts()
data
data.sum()
data/data.sum()
unchar_mod_lens = []
mod_lens = []
for k in objs['combined'].M.columns:
if DF_categories.loc['combined_'+str(k),'type']=='uncharacterized':
unchar_mod_lens.append(len(objs['combined'].show_enriched(k)))
else:
mod_lens.append(len(objs['combined'].show_enriched(k)))
data = DF_categories[DF_categories.dataset=='combined'].type.value_counts()
plt.pie(data.values,labels=data.index);
# # Create RBH graph
from rbh import *
l2s = []
for ds in datasets[:-1]:
links = rbh(objs['combined'].M,objs[ds].M)
for i,j,val in links:
comp1 = 'combined'+'_'+str(i)
comp2 = ds+'_'+str(j)
class1 = DF_categories.loc[comp1,'type']
class2 = DF_categories.loc[comp2,'type']
desc1 = DF_categories.loc[comp1,'description']
desc2 = DF_categories.loc[comp2,'description']
l2s.append(['combined',ds,i,j,comp1,comp2,class1,class2,desc1,desc2,1-val])
DF_links = pd.DataFrame(l2s,columns=['ds1','ds2','comp1','comp2','name1','name2','type1','type2','desc1','desc2','dist'])
DF_links = DF_links[DF_links.dist > 0.3]
DF_links = DF_links.sort_values(['ds1','comp1','ds2'])
DF_links[DF_links.type1 == 'uncharacterized'].name1.value_counts()
# Total links between full dataset and individual datasets
DF_links.groupby('ds2').count()['ds1']
# Average distance between full dataset and individual datasets
means = DF_links.groupby('ds2').mean()['dist']
stds = DF_links.groupby('ds2').std()['dist']
DF_links.to_csv(os.path.join(DATA_DIR,'iModulons','RBH_combined.csv'))
DF_links
# # Figure 5c - Presence/absence of iModulons
index = objs['combined'].M.columns
type_dict = {'regulatory':-2,'functional':-3,'genomic':-4,'uncharacterized':-5}
# +
DF_binarized = pd.DataFrame([1]*len(index),index=index,columns=['Combined Compendium'])
for ds in datasets[:-1]:
DF_binarized[ds] = [x in DF_links[DF_links.ds2==ds].comp1.tolist() for x in index]
DF_binarized = DF_binarized.astype(int)
DF_binarized['total'] = DF_binarized.sum(axis=1)
DF_binarized = (DF_binarized-1)
DF_binarized = DF_binarized[['RNAseq-1','RNAseq-2','MA-1','MA-2','MA-3','total']]
# -
DF_binarized['type'] = [type_dict[DF_categories.loc['combined_'+str(k)].type] for k in DF_binarized.index]
DF_binarized = DF_binarized.sort_values(['total','RNAseq-1','RNAseq-2','MA-1','MA-2','MA-3','type'],ascending=False)
cmap = ['#b4d66c','#bc80b7','#81b1d3','#f47f72'] + ['white','black'] + sns.color_palette('Blues',5)
bin_counts = DF_binarized.groupby(['total','type']).size().unstack(fill_value=0).T.sort_index(ascending=False)
bin_counts = bin_counts
bin_counts.index = ['regulatory','biological','genomic','uncharacterized']
bin_counts.T.plot.bar(stacked=True)
plt.legend(bbox_to_anchor=(1,1))
print('Number of comps:',len(DF_binarized))
print('Number of linked comps: {} ({:.2f})'.format(sum(DF_binarized.total > 0),
sum(DF_binarized.total > 0)/len(DF_binarized)))
print('Number of linked comps: {} ({:.2f})'.format(sum(DF_binarized.total >1),
sum(DF_binarized.total > 1)/len(DF_binarized)))
fig,ax = plt.subplots(figsize=(4,1.5))
sns.heatmap(DF_binarized.T,cmap=cmap,ax=ax)
ax.set_xticks(np.arange(len(DF_binarized),step=20));
ax.tick_params(axis='x',reset=True,length=3,width=.5,color='k',top=False)
ax.set_xticklabels(np.arange(len(DF_binarized),step=20),);
# # Figure 5d - Heatmap
# +
fig,ax = plt.subplots(figsize=(2.1,1.3))
DF_types = DF_categories.groupby(['dataset','type']).count().component.unstack().fillna(0).drop('combined')
DF_types.loc['Total'] = DF_types.sum(axis=0)
DF_types['Total'] = DF_types.sum(axis=1)
DF_types_linked = DF_links.groupby(['ds2','type2']).count().comp1.unstack().fillna(0)
DF_types_linked.loc['Total'] = DF_types_linked.sum(axis=0)
DF_types_linked['Total'] = DF_types_linked.sum(axis=1)
DF_types_lost = DF_types - DF_types_linked
DF_text = pd.DataFrame()
for col in DF_types_lost:
DF_text[col] = DF_types_lost[col].astype(int).astype(str).str.cat(DF_types[col].astype(int).astype(str),sep='/')
DF_text = DF_text[['regulatory','functional','genomic','uncharacterized','Total']]
type_grid = (DF_types_lost/DF_types).fillna(0)[['regulatory','functional','genomic','uncharacterized','Total']]
type_grid = type_grid.reindex(['RNAseq-1','RNAseq-2','MA-1','MA-2','MA-3','Total'])
DF_text = DF_text.reindex(['RNAseq-1','RNAseq-2','MA-1','MA-2','MA-3','Total'])
sns.heatmap(type_grid,cmap='Blues',annot=DF_text,fmt='s',annot_kws={"size": 5})
# -
# Types lost
DF_lost = DF_types- DF_types_linked
DF_lost
DF_types_linked.loc['Total']
DF_types_linked.loc['Total']/DF_types_linked.loc['Total'].iloc[:-1].sum()
# # Figure 5e - Explained variance
# +
# Load dataset - Downloaded from Sanchez-Vasquez et al 2019
DF_ppGpp = pd.read_excel(os.path.join(DATA_DIR,'ppGpp_data','dataset_s01_from_sanchez_vasquez_2019.xlsx'),sheet_name='Data')
# Get 757 genes described to be directly regulated by ppGpp
paper_genes = DF_ppGpp[DF_ppGpp['1+2+ 5 min Category'].isin(['A','B'])].Synonym.values
len(paper_genes)
# -
paper_genes_down = DF_ppGpp[DF_ppGpp['1+2+ 5 min Category'].isin(['A'])].Synonym.values
paper_genes_up = DF_ppGpp[DF_ppGpp['1+2+ 5 min Category'].isin(['B'])].Synonym.values
venn2((set(paper_genes_down),set(objs['combined'].show_enriched(147).index)),set_labels=('Genes downregulated from ppGpp binding to RNAP','Genes in Central Dogma I-modulon'))
pp_genes = {}
for k in objs['combined'].M.columns:
pp_genes[k] = set(objs['combined'].show_enriched(k).index) & set(paper_genes)
set(objs['combined'].show_enriched(147).index) - set(paper_genes)
# # Figure 5f - ppGpp Activities
# +
ppGpp_X = pd.read_csv(os.path.join(DATA_DIR,'ppGpp_data','log_tpm_norm.csv'),index_col=0)
# Get genes in both ICA data and ppGpp dataframe
shared_genes = sorted(set(objs['combined'].X.index) & set(ppGpp_X.index))
# Keep only genes in both dataframes
ppGpp_X = ppGpp_X.loc[shared_genes]
M = objs['combined'].M.loc[shared_genes]
# Center columns
X = ppGpp_X.sub(ppGpp_X.mean(axis=0))
# -
# Perform projection
M_inv = np.linalg.pinv(M)
A = np.dot(M_inv,X)
A = pd.DataFrame(A,columns = X.columns, index = M.columns)
t0 = ['ppgpp__t0__1','ppgpp__t0__2','ppgpp__t0__3']
t5 = ['ppgpp__t5__1','ppgpp__t5__2','ppgpp__t5__3']
# +
ds4 = objs['combined'].metadata[objs['combined'].metadata['dataset'] == 'RNAseq-1'].index
df = pd.DataFrame(objs['combined'].A.loc[147,ds4])
df['group'] = ['RpoB\nE672K' if 'rpoBE672K' in x else 'RpoB\nE546V' if 'rpoBE546V' in x else 'WT RpoB' for x in df.index]
fig,ax = plt.subplots(figsize=(2,2))
sns.boxplot(data=df,y=147,x='group')
sns.stripplot(data=df,y=147,x='group',dodge=True,color='k',jitter=0.3,s=3)
ax.set_ylabel('Central Dogma\nI-modulon Activity',fontsize=7)
ax.set_xlabel('Carbon Source',fontsize=7)
ax.tick_params(labelsize=5)
plt.tight_layout()
# -
# # Figure 5g: PCA of datasets
cdict = dict(zip(datasets[:-1],['tab:orange','black','tab:red','tab:green','tab:blue']))
# +
exp_data = pd.read_csv(os.path.join(DATA_DIR,'processed_data','combined_bc.csv'),index_col=0)
pca = PCA()
DF_weights = pd.DataFrame(pca.fit_transform(exp_data.T),index=exp_data.columns)
DF_components = pd.DataFrame(pca.components_.T,index=exp_data.index)
var_cutoff = 0.99
# -
fig,ax = plt.subplots(figsize=(1.5,1.5))
for name,group in objs['combined'].metadata.groupby('dataset'):
idx = exp_data.loc[:,group.index.tolist()].columns.tolist()
ax.scatter(DF_weights.loc[idx,0],
DF_weights.loc[idx,1],
c=cdict[name],
label=name,alpha=0.8,s=3)
ax.set_xlabel('Component 1: %.1f%%'%(pca.explained_variance_ratio_[0]*100))
ax.set_ylabel('Component 2: %.1f%%'%(pca.explained_variance_ratio_[1]*100))
ax.legend(bbox_to_anchor=(1,-.2),ncol=2)
# # Figure 5h: PCA of activites
pca = PCA()
DF_weights = pd.DataFrame(pca.fit_transform(objs['combined'].A.T),index=objs['combined'].A.columns)
DF_components = pd.DataFrame(pca.components_.T,index=objs['combined'].A.index)
var_cutoff = 0.99
fig,ax = plt.subplots(figsize=(1.5,1.5))
for name,group in objs['combined'].metadata.groupby('dataset'):
idx = exp_data.loc[:,group.index.tolist()].columns.tolist()
ax.scatter(DF_weights.loc[idx,0],
DF_weights.loc[idx,1],
c=cdict[name],
label=name,alpha=0.8,s=3)
ax.set_xlabel('Component 1: %.1f%%'%(pca.explained_variance_ratio_[0]*100))
ax.set_ylabel('Component 2: %.1f%%'%(pca.explained_variance_ratio_[1]*100))
ax.legend(bbox_to_anchor=(1,-.2),ncol=2)
# # Supplementary Figure 7
# ## Panel a: Explained variance of lost i-modulons
kept_mods = set(DF_links.name2.unique())
all_mods = set([ds+'_'+str(name) for ds in datasets[:-1] for name in objs[ds].M.columns])
missing_mods = all_mods - kept_mods
from util import plot_rec_var
# +
missing_var = []
for mod in tqdm(missing_mods):
ds,comp = mod.split('_')
missing_var.append(plot_rec_var(objs[ds],modulons=[int(comp)],plot=False).values[0])
if plot_rec_var(objs[ds],modulons=[int(comp)],plot=False).values[0] > 10:
print(mod)
kept_var = []
for mod in tqdm(kept_mods):
ds,comp = mod.split('_')
kept_var.append(plot_rec_var(objs[ds],modulons=[int(comp)],plot=False).values[0])
# -
plt.hist(missing_var,range=(0,20),bins=20)
plt.hist(kept_var,range=(0,20),bins=20,alpha=0.5)
plt.xticks(range(0,21,2))
plt.xlabel('Percent Variance Explained')
plt.ylabel('Count')
stats.mannwhitneyu(missing_var,kept_var)
fig,ax = plt.subplots(figsize=(1.5,1.5))
plt.hist(missing_var,range=(0,1),bins=10)
plt.hist(kept_var,range=(0,1),bins=10,alpha=0.5)
plt.xlabel('Percent Variance Explained')
plt.ylabel('Count')
# ## Panel b: Classes of new i-modulons
type_dict
new_counts = DF_binarized[(DF_binarized.total==0)].type.value_counts()
new_counts
new_reg = DF_binarized[(DF_binarized.total==0) & (DF_binarized.type==-2)].index
new_bio = DF_binarized[(DF_binarized.total==0) & (DF_binarized.type==-3)].index
new_gen = DF_binarized[(DF_binarized.total==0) & (DF_binarized.type==-4)].index
new_unc = DF_binarized[(DF_binarized.total==0) & (DF_binarized.type==-5)].index
new_single = []
for k in new_unc:
if objs['combined'].show_enriched(k)['weight'].max() > 0.4:
new_single.append(k)
[len(new_reg),len(new_bio),len(new_gen),len(new_unc)-len(new_single),len(new_single)]
plt.pie([len(new_reg),len(new_bio),len(new_gen),len(new_unc)-len(new_single),len(new_single)],
labels=['Regulatory','Functional','Genomic','Uncharacterized','Single Gene'])
# ## Panel c: Histogram of IC gene coefficients
fig,ax = plt.subplots(figsize=(2,2))
plt.hist(objs['combined'].M[31])
plt.yscale('log')
plt.xlabel('IC Gene Coefficient')
plt.ylabel('Count (Log-scale)')
plt.vlines([objs['combined'].thresholds[31],-objs['combined'].thresholds[31]],0,3000,
linestyles='dashed',linewidth=0.5)
# ## Panel e: F1-score chart
reg_links = DF_links[(DF_links.type1 == 'regulatory') & (DF_links.desc1 == DF_links.desc2)]
reg_links.head()
fig,ax=plt.subplots(figsize=(1.5,2))
struct = []
for name,group in reg_links.groupby('ds2'):
struct.append(pd.DataFrame(list(zip([name]*len(group),
DF_categories.loc[group.name1,'f1score'].values,
DF_categories.loc[group.name2,'f1score'].values)),
columns=['title','full','partial']))
DF_stats = pd.concat(struct)
DF_stats = DF_stats.melt(id_vars='title')
sns.boxplot(data=DF_stats,x='variable',y='value',order=['partial','full'])
sns.stripplot(data=DF_stats,x='variable',y='value',color='k',s=2,jitter=0.3,order=['partial','full'])
DF_stats[DF_stats.variable=='partial'].value.mean()
DF_stats[DF_stats.variable=='full'].value.mean()
stats.wilcoxon(DF_stats[DF_stats.variable=='partial'].value,DF_stats[DF_stats.variable=='full'].value)
# ## Panel f: Pearson R between activities
from sklearn.metrics import r2_score
linked_pearson = []
for i,row in DF_links.iterrows():
partial_acts = objs[row.ds2].A.loc[row.comp2]
full_acts = objs[row.ds1].A.loc[row.comp1,partial_acts.index]
r,_ = stats.spearmanr(full_acts,partial_acts)
linked_pearson.append(abs(r))
sum(np.array(linked_pearson) > 0.6) / len(linked_pearson)
fig,ax = plt.subplots(figsize=(2,2))
ax.hist(linked_pearson,bins=20)
ax.set_xlabel('Absolute Spearman R between activities of linked i-modulons')
ax.set_ylabel('Count')
# # New biological component
rRNA = 0
tRNA = 0
ygene = 0
polyamine = 0
for gene in objs['combined'].show_enriched(147)['product']:
if 'rRNA' in gene or 'ribosom' in gene:
rRNA += 1
elif 'tRNA' in gene:
tRNA += 1
elif 'putative' in gene or 'family' in gene:
ygene += 1
elif 'spermidine' in gene or 'YEEF' in gene:
polyamine +=1
else:
print(gene)
objs['combined'].show_enriched(147)
| 39.975225 | 3,447 |
5bb010547e5b04751d607f94e73367ce3f870564
|
py
|
python
|
news_classification_models_comparison.ipynb
|
robmaz22/news_category_classification
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/robmaz22/news_category_classification/blob/master/news_classification_models_comparison.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="YPTKoxTdC0j-"
# # Porównanie ze sobą kilku modeli uczenia maszynowego, <br/> wybranie najbardziej optymalnego do rozwiązywanego problemu (klasyfikacja newsów)
#
#
# + [markdown] id="j2cWdv_YDPpU"
# ###1. Import pliku zip z dysku i rozpakowanie pliku json
# + id="y7bCNiMZCcr9" colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "Ly8gQ29weXJpZ2h0IDIwMTcgR29vZ2xlIExMQwovLwovLyBMaWNlbnNlZCB1bmRlciB0aGUgQXBhY2hlIExpY2Vuc2UsIFZlcnNpb24gMi4wICh0aGUgIkxpY2Vuc2UiKTsKLy8geW91IG1heSBub3QgdXNlIHRoaXMgZmlsZSBleGNlcHQgaW4gY29tcGxpYW5jZSB3aXRoIHRoZSBMaWNlbnNlLgovLyBZb3UgbWF5IG9idGFpbiBhIGNvcHkgb2YgdGhlIExpY2Vuc2UgYXQKLy8KLy8gICAgICBodHRwOi8vd3d3LmFwYWNoZS5vcmcvbGljZW5zZXMvTElDRU5TRS0yLjAKLy8KLy8gVW5sZXNzIHJlcXVpcmVkIGJ5IGFwcGxpY2FibGUgbGF3IG9yIGFncmVlZCB0byBpbiB3cml0aW5nLCBzb2Z0d2FyZQovLyBkaXN0cmlidXRlZCB1bmRlciB0aGUgTGljZW5zZSBpcyBkaXN0cmlidXRlZCBvbiBhbiAiQVMgSVMiIEJBU0lTLAovLyBXSVRIT1VUIFdBUlJBTlRJRVMgT1IgQ09ORElUSU9OUyBPRiBBTlkgS0lORCwgZWl0aGVyIGV4cHJlc3Mgb3IgaW1wbGllZC4KLy8gU2VlIHRoZSBMaWNlbnNlIGZvciB0aGUgc3BlY2lmaWMgbGFuZ3VhZ2UgZ292ZXJuaW5nIHBlcm1pc3Npb25zIGFuZAovLyBsaW1pdGF0aW9ucyB1bmRlciB0aGUgTGljZW5zZS4KCi8qKgogKiBAZmlsZW92ZXJ2aWV3IEhlbHBlcnMgZm9yIGdvb2dsZS5jb2xhYiBQeXRob24gbW9kdWxlLgogKi8KKGZ1bmN0aW9uKHNjb3BlKSB7CmZ1bmN0aW9uIHNwYW4odGV4dCwgc3R5bGVBdHRyaWJ1dGVzID0ge30pIHsKICBjb25zdCBlbGVtZW50ID0gZG9jdW1lbnQuY3JlYXRlRWxlbWVudCgnc3BhbicpOwogIGVsZW1lbnQudGV4dENvbnRlbnQgPSB0ZXh0OwogIGZvciAoY29uc3Qga2V5IG9mIE9iamVjdC5rZXlzKHN0eWxlQXR0cmlidXRlcykpIHsKICAgIGVsZW1lbnQuc3R5bGVba2V5XSA9IHN0eWxlQXR0cmlidXRlc1trZXldOwogIH0KICByZXR1cm4gZWxlbWVudDsKfQoKLy8gTWF4IG51bWJlciBvZiBieXRlcyB3aGljaCB3aWxsIGJlIHVwbG9hZGVkIGF0IGEgdGltZS4KY29uc3QgTUFYX1BBWUxPQURfU0laRSA9IDEwMCAqIDEwMjQ7CgpmdW5jdGlvbiBfdXBsb2FkRmlsZXMoaW5wdXRJZCwgb3V0cHV0SWQpIHsKICBjb25zdCBzdGVwcyA9IHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCk7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICAvLyBDYWNoZSBzdGVwcyBvbiB0aGUgb3V0cHV0RWxlbWVudCB0byBtYWtlIGl0IGF2YWlsYWJsZSBmb3IgdGhlIG5leHQgY2FsbAogIC8vIHRvIHVwbG9hZEZpbGVzQ29udGludWUgZnJvbSBQeXRob24uCiAgb3V0cHV0RWxlbWVudC5zdGVwcyA9IHN0ZXBzOwoKICByZXR1cm4gX3VwbG9hZEZpbGVzQ29udGludWUob3V0cHV0SWQpOwp9CgovLyBUaGlzIGlzIHJvdWdobHkgYW4gYXN5bmMgZ2VuZXJhdG9yIChub3Qgc3VwcG9ydGVkIGluIHRoZSBicm93c2VyIHlldCksCi8vIHdoZXJlIHRoZXJlIGFyZSBtdWx0aXBsZSBhc3luY2hyb25vdXMgc3RlcHMgYW5kIHRoZSBQeXRob24gc2lkZSBpcyBnb2luZwovLyB0byBwb2xsIGZvciBjb21wbGV0aW9uIG9mIGVhY2ggc3RlcC4KLy8gVGhpcyB1c2VzIGEgUHJvbWlzZSB0byBibG9jayB0aGUgcHl0aG9uIHNpZGUgb24gY29tcGxldGlvbiBvZiBlYWNoIHN0ZXAsCi8vIHRoZW4gcGFzc2VzIHRoZSByZXN1bHQgb2YgdGhlIHByZXZpb3VzIHN0ZXAgYXMgdGhlIGlucHV0IHRvIHRoZSBuZXh0IHN0ZXAuCmZ1bmN0aW9uIF91cGxvYWRGaWxlc0NvbnRpbnVlKG91dHB1dElkKSB7CiAgY29uc3Qgb3V0cHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKG91dHB1dElkKTsKICBjb25zdCBzdGVwcyA9IG91dHB1dEVsZW1lbnQuc3RlcHM7CgogIGNvbnN0IG5leHQgPSBzdGVwcy5uZXh0KG91dHB1dEVsZW1lbnQubGFzdFByb21pc2VWYWx1ZSk7CiAgcmV0dXJuIFByb21pc2UucmVzb2x2ZShuZXh0LnZhbHVlLnByb21pc2UpLnRoZW4oKHZhbHVlKSA9PiB7CiAgICAvLyBDYWNoZSB0aGUgbGFzdCBwcm9taXNlIHZhbHVlIHRvIG1ha2UgaXQgYXZhaWxhYmxlIHRvIHRoZSBuZXh0CiAgICAvLyBzdGVwIG9mIHRoZSBnZW5lcmF0b3IuCiAgICBvdXRwdXRFbGVtZW50Lmxhc3RQcm9taXNlVmFsdWUgPSB2YWx1ZTsKICAgIHJldHVybiBuZXh0LnZhbHVlLnJlc3BvbnNlOwogIH0pOwp9CgovKioKICogR2VuZXJhdG9yIGZ1bmN0aW9uIHdoaWNoIGlzIGNhbGxlZCBiZXR3ZWVuIGVhY2ggYXN5bmMgc3RlcCBvZiB0aGUgdXBsb2FkCiAqIHByb2Nlc3MuCiAqIEBwYXJhbSB7c3RyaW5nfSBpbnB1dElkIEVsZW1lbnQgSUQgb2YgdGhlIGlucHV0IGZpbGUgcGlja2VyIGVsZW1lbnQuCiAqIEBwYXJhbSB7c3RyaW5nfSBvdXRwdXRJZCBFbGVtZW50IElEIG9mIHRoZSBvdXRwdXQgZGlzcGxheS4KICogQHJldHVybiB7IUl0ZXJhYmxlPCFPYmplY3Q+fSBJdGVyYWJsZSBvZiBuZXh0IHN0ZXBzLgogKi8KZnVuY3Rpb24qIHVwbG9hZEZpbGVzU3RlcChpbnB1dElkLCBvdXRwdXRJZCkgewogIGNvbnN0IGlucHV0RWxlbWVudCA9IGRvY3VtZW50LmdldEVsZW1lbnRCeUlkKGlucHV0SWQpOwogIGlucHV0RWxlbWVudC5kaXNhYmxlZCA9IGZhbHNlOwoKICBjb25zdCBvdXRwdXRFbGVtZW50ID0gZG9jdW1lbnQuZ2V0RWxlbWVudEJ5SWQob3V0cHV0SWQpOwogIG91dHB1dEVsZW1lbnQuaW5uZXJIVE1MID0gJyc7CgogIGNvbnN0IHBpY2tlZFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgaW5wdXRFbGVtZW50LmFkZEV2ZW50TGlzdGVuZXIoJ2NoYW5nZScsIChlKSA9PiB7CiAgICAgIHJlc29sdmUoZS50YXJnZXQuZmlsZXMpOwogICAgfSk7CiAgfSk7CgogIGNvbnN0IGNhbmNlbCA9IGRvY3VtZW50LmNyZWF0ZUVsZW1lbnQoJ2J1dHRvbicpOwogIGlucHV0RWxlbWVudC5wYXJlbnRFbGVtZW50LmFwcGVuZENoaWxkKGNhbmNlbCk7CiAgY2FuY2VsLnRleHRDb250ZW50ID0gJ0NhbmNlbCB1cGxvYWQnOwogIGNvbnN0IGNhbmNlbFByb21pc2UgPSBuZXcgUHJvbWlzZSgocmVzb2x2ZSkgPT4gewogICAgY2FuY2VsLm9uY2xpY2sgPSAoKSA9PiB7CiAgICAgIHJlc29sdmUobnVsbCk7CiAgICB9OwogIH0pOwoKICAvLyBXYWl0IGZvciB0aGUgdXNlciB0byBwaWNrIHRoZSBmaWxlcy4KICBjb25zdCBmaWxlcyA9IHlpZWxkIHsKICAgIHByb21pc2U6IFByb21pc2UucmFjZShbcGlja2VkUHJvbWlzZSwgY2FuY2VsUHJvbWlzZV0pLAogICAgcmVzcG9uc2U6IHsKICAgICAgYWN0aW9uOiAnc3RhcnRpbmcnLAogICAgfQogIH07CgogIGNhbmNlbC5yZW1vdmUoKTsKCiAgLy8gRGlzYWJsZSB0aGUgaW5wdXQgZWxlbWVudCBzaW5jZSBmdXJ0aGVyIHBpY2tzIGFyZSBub3QgYWxsb3dlZC4KICBpbnB1dEVsZW1lbnQuZGlzYWJsZWQgPSB0cnVlOwoKICBpZiAoIWZpbGVzKSB7CiAgICByZXR1cm4gewogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbXBsZXRlJywKICAgICAgfQogICAgfTsKICB9CgogIGZvciAoY29uc3QgZmlsZSBvZiBmaWxlcykgewogICAgY29uc3QgbGkgPSBkb2N1bWVudC5jcmVhdGVFbGVtZW50KCdsaScpOwogICAgbGkuYXBwZW5kKHNwYW4oZmlsZS5uYW1lLCB7Zm9udFdlaWdodDogJ2JvbGQnfSkpOwogICAgbGkuYXBwZW5kKHNwYW4oCiAgICAgICAgYCgke2ZpbGUudHlwZSB8fCAnbi9hJ30pIC0gJHtmaWxlLnNpemV9IGJ5dGVzLCBgICsKICAgICAgICBgbGFzdCBtb2RpZmllZDogJHsKICAgICAgICAgICAgZmlsZS5sYXN0TW9kaWZpZWREYXRlID8gZmlsZS5sYXN0TW9kaWZpZWREYXRlLnRvTG9jYWxlRGF0ZVN0cmluZygpIDoKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgJ24vYSd9IC0gYCkpOwogICAgY29uc3QgcGVyY2VudCA9IHNwYW4oJzAlIGRvbmUnKTsKICAgIGxpLmFwcGVuZENoaWxkKHBlcmNlbnQpOwoKICAgIG91dHB1dEVsZW1lbnQuYXBwZW5kQ2hpbGQobGkpOwoKICAgIGNvbnN0IGZpbGVEYXRhUHJvbWlzZSA9IG5ldyBQcm9taXNlKChyZXNvbHZlKSA9PiB7CiAgICAgIGNvbnN0IHJlYWRlciA9IG5ldyBGaWxlUmVhZGVyKCk7CiAgICAgIHJlYWRlci5vbmxvYWQgPSAoZSkgPT4gewogICAgICAgIHJlc29sdmUoZS50YXJnZXQucmVzdWx0KTsKICAgICAgfTsKICAgICAgcmVhZGVyLnJlYWRBc0FycmF5QnVmZmVyKGZpbGUpOwogICAgfSk7CiAgICAvLyBXYWl0IGZvciB0aGUgZGF0YSB0byBiZSByZWFkeS4KICAgIGxldCBmaWxlRGF0YSA9IHlpZWxkIHsKICAgICAgcHJvbWlzZTogZmlsZURhdGFQcm9taXNlLAogICAgICByZXNwb25zZTogewogICAgICAgIGFjdGlvbjogJ2NvbnRpbnVlJywKICAgICAgfQogICAgfTsKCiAgICAvLyBVc2UgYSBjaHVua2VkIHNlbmRpbmcgdG8gYXZvaWQgbWVzc2FnZSBzaXplIGxpbWl0cy4gU2VlIGIvNjIxMTU2NjAuCiAgICBsZXQgcG9zaXRpb24gPSAwOwogICAgd2hpbGUgKHBvc2l0aW9uIDwgZmlsZURhdGEuYnl0ZUxlbmd0aCkgewogICAgICBjb25zdCBsZW5ndGggPSBNYXRoLm1pbihmaWxlRGF0YS5ieXRlTGVuZ3RoIC0gcG9zaXRpb24sIE1BWF9QQVlMT0FEX1NJWkUpOwogICAgICBjb25zdCBjaHVuayA9IG5ldyBVaW50OEFycmF5KGZpbGVEYXRhLCBwb3NpdGlvbiwgbGVuZ3RoKTsKICAgICAgcG9zaXRpb24gKz0gbGVuZ3RoOwoKICAgICAgY29uc3QgYmFzZTY0ID0gYnRvYShTdHJpbmcuZnJvbUNoYXJDb2RlLmFwcGx5KG51bGwsIGNodW5rKSk7CiAgICAgIHlpZWxkIHsKICAgICAgICByZXNwb25zZTogewogICAgICAgICAgYWN0aW9uOiAnYXBwZW5kJywKICAgICAgICAgIGZpbGU6IGZpbGUubmFtZSwKICAgICAgICAgIGRhdGE6IGJhc2U2NCwKICAgICAgICB9LAogICAgICB9OwogICAgICBwZXJjZW50LnRleHRDb250ZW50ID0KICAgICAgICAgIGAke01hdGgucm91bmQoKHBvc2l0aW9uIC8gZmlsZURhdGEuYnl0ZUxlbmd0aCkgKiAxMDApfSUgZG9uZWA7CiAgICB9CiAgfQoKICAvLyBBbGwgZG9uZS4KICB5aWVsZCB7CiAgICByZXNwb25zZTogewogICAgICBhY3Rpb246ICdjb21wbGV0ZScsCiAgICB9CiAgfTsKfQoKc2NvcGUuZ29vZ2xlID0gc2NvcGUuZ29vZ2xlIHx8IHt9OwpzY29wZS5nb29nbGUuY29sYWIgPSBzY29wZS5nb29nbGUuY29sYWIgfHwge307CnNjb3BlLmdvb2dsZS5jb2xhYi5fZmlsZXMgPSB7CiAgX3VwbG9hZEZpbGVzLAogIF91cGxvYWRGaWxlc0NvbnRpbnVlLAp9Owp9KShzZWxmKTsK", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 72} outputId="eea0c575-b7b2-4b61-a557-a94fc3736a30"
from google.colab import files
uploaded = files.upload()
# !unzip -q news.zip
# + [markdown] id="uw6Ow9xmDp2G"
# ###2. Wczytanie zawartości pliku do obiektu DataFrame
# + colab={"base_uri": "https://localhost:8080/", "height": 289} id="_3nSS9xpDqDe" outputId="102b2881-73eb-4d68-9a69-10e57389a818"
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
raw_data = pd.read_json('News_Category_Dataset_v2.json', lines=True)
raw_data.head()
# + [markdown] id="TGfJywhwFt3e"
# ###3. Separacja potrzebnych kolumn i analiza danych
# + colab={"base_uri": "https://localhost:8080/", "height": 142} id="eacqsbIBF0Vf" outputId="8c3998c8-f9ce-4f6a-a4ee-942c4a759590"
df = raw_data[['category', 'short_description']].copy()
df.head(3)
# + colab={"base_uri": "https://localhost:8080/"} id="enF6UptIF57g" outputId="606770d3-c825-4db1-fa14-2915985c7334"
df.isna().sum()
# + id="484ktZfWF-Wy"
df.drop_duplicates(inplace=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 905} id="Rc7cT9fyGDu1" outputId="6e1df9e5-2805-4b86-b32e-a2c37e91bc88"
plt.title("News category %", y=1.02, fontdict={'fontsize': 24});
df['category'].value_counts().plot(kind='pie', figsize=(30,15), autopct="%.1f%%")
# + [markdown] id="mZw5m2DDIsmN"
# ###4. Resampling danych w celu uzyskania takiej samej liczby danych dla każdej klasy
# + colab={"base_uri": "https://localhost:8080/"} id="zlx4yLaoGaK1" outputId="a83e6cdb-ead0-4749-d760-08023d35bbe4"
from imblearn.over_sampling import RandomOverSampler
X = df[['short_description']]
y = df[['category']]
ros = RandomOverSampler(random_state=0)
X_resampled, y_resampled = ros.fit_resample(X, y)
ser1 = pd.Series(X_resampled.ravel())
ser2 = pd.Series(y_resampled)
data_res = pd.DataFrame(data=ser1, columns=['description'])
data_res['category'] = ser2
# + colab={"base_uri": "https://localhost:8080/", "height": 905} id="_px08fpeJEjh" outputId="72ce36b4-163b-4027-ded9-522accf4b6ad"
plt.title("News category % (after resampling)", y=1.02, fontdict={'fontsize': 24});
data_res['category'].value_counts().plot(kind='pie', figsize=(30,15), autopct="%.1f%%")
# + colab={"base_uri": "https://localhost:8080/"} id="gnIF7dI-JYF-" outputId="5d00cd73-1c00-41b7-f8af-6e591faeee0c"
print(f'liczba rekordów przed resamplingiem: {len(df)}')
print(f'liczba rekordów po resamplingu: {len(data_res)}')
# + [markdown] id="ZUeelsRTKf9Q"
# ###5. Zakodowanie kategorii oraz oczyszczenie tekstu w kolumnie z opisem
# + colab={"base_uri": "https://localhost:8080/"} id="XVQSFRpYLERp" outputId="0cd58f3d-1fe2-4b1d-f3fb-5801272e15a5"
import nltk
nltk.download('punkt')
nltk.download('stopwords')
from nltk.tokenize import word_tokenize
from nltk.corpus import stopwords
import string
# + id="kZRf0_2SK2nS"
def clean(text):
tokens = word_tokenize(text)
tokens = [w.lower() for w in tokens]
table = str.maketrans('', '', string.punctuation)
stripped = [w.translate(table) for w in tokens]
words = [word for word in stripped if word.isalpha()]
stop_words = set(stopwords.words('english'))
words = [w for w in words if not w in stop_words]
cleaned_text = ' '.join(words)
return cleaned_text
# + id="l8pBq1hTKaJj"
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
le.fit(data_res['category'])
data_res['category'] = le.transform(data_res['category'])
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="zTNU773PMp3P" outputId="178448b0-1d7d-4cb8-f9b6-895d8cdb9218"
data_res['description'] = data_res['description'].map(lambda x: clean(x))
data_res.head()
# + [markdown] id="u4ve_ffFnN5Y"
# ###6. Wymieszanie danych
# + id="yzaoMnscnLWB"
data_res = data_res.sample(frac=1).reset_index(drop=True)
# + [markdown] id="ChH68Q84nZo4"
# ###7. Wektoryzacja danych tektowych w celu umożliwienia zastosowania ich w modelu uczącym
# + id="rZbCD8-XnWOG"
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(data_res['description'])
y = data_res['category']
# + [markdown] id="x43N4MxVn7oO"
# ###8. Podział na zbiór treningowy i testowy
# + id="pSG6eWaKn7MX"
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y)
# + [markdown] id="ZbiPTJoJoIFo"
# ###9. Testowanie modeli (ustawienia domyślne)
#
#
# * LinearSVC
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="G5fk_eOMoHnb" outputId="6f704c7a-753a-4b06-c159-db6143142302"
from sklearn.svm import LinearSVC
model1 = LinearSVC()
model1.fit(X_train, y_train)
print(f'Dokładność modelu: {model1.score(X_test, y_test)*100:.2f} %')
# + [markdown] id="BUbIE9TFoYGr"
#
#
# * SGDClassifier
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="lN7sJBKoo8UA" outputId="046ead52-4c96-40a6-d9d7-f5d51684ad75"
from sklearn.linear_model import SGDClassifier
model2 = SGDClassifier()
model2.fit(X_train, y_train)
print(f'Dokładność modelu: {model2.score(X_test, y_test)*100:.2f} %')
# + [markdown] id="pmBb5HD4pGn8"
#
#
# * MultinomialNB
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="MG9dUSFjpcZy" outputId="8ba2db60-1f4e-41ce-ca93-db5c79fbbe9e"
from sklearn.naive_bayes import MultinomialNB
model3 = MultinomialNB()
model3.fit(X_train, y_train)
print(f'Dokładność modelu: {model3.score(X_test, y_test)*100:.2f} %')
| 66.271357 | 7,233 |
c7220f16bb558b2dc395d479ebb1f0a05d9b4f23
|
py
|
python
|
fall_fest.ipynb
|
jordi1215/qiskit-fall-fest-2021
|
['MIT']
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/jordi1215/qiskit-fall-fest-2021/blob/main/fall_fest.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="SfXRtTiWWKlT"
# ## Is Random Number Generation (RNG) actually random?
# Random numbers are seen around us everywhere, from assigning treatments in experiments to picking lottery winners. But when we use a computer to generate these random numbers, most of the time they only appear to be random--there’s actually an algorithm behind those numbers, and if you knew the algorithm, you’d know what number would come next! Doesn’t sound very random, right?
#
# In this notebook, we'll go over how random number generation works in both classical and quantum computers.
#
# + id="PHpNM_TjPi7A"
# install qiskit
# !pip install git+https://github.com/qiskit-community/qiskit-textbook.git#subdirectory=qiskit-textbook-src
# import qiskit tools
import qiskit
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, transpile, Aer, IBMQ
from qiskit.tools.visualization import circuit_drawer
from qiskit.tools.monitor import job_monitor, backend_monitor, backend_overview
from qiskit.providers.aer import noise
# import python utilities
import matplotlib.pyplot as plt
import numpy as np
import time
aer_sim = qiskit.Aer.get_backend('aer_simulator')
# + [markdown] id="1DmsbeKtZvlv"
# ## Classical Random Number Generation
#
# It’s hard for classical computers to generate truly random numbers because they are **deterministic**, meaning that there is always a set of instructions to determine the computer’s actions.
# There are ways to generate truly random numbers using classical computers, but they involve taking a sample of an external random physical phenomenon. This is disadvantageous because it:
# - Requires extra hardware to measure the phenomena
# - Takes more time to measure data
#
# This is where **pseudorandomness** comes into play, which allows us to generate a sequence of numbers that look random, but actually are deterministic. With classical programming, you can get a random string of bits by iterating through this list, starting from a certain index in the list called a **seed**. If we generate a new list starting from the same seed, it will give us the exact same sequence of bits. However, if we reseed, we can get a new random string of bits.
# + colab={"base_uri": "https://localhost:8080/"} id="j4gSvn1vWoyt" outputId="e6d9df17-1622-43f9-d2c1-9d4a42afb972"
# set seed number (can be anything)
seed = 7
# generate sequence of random bits using seed
np.random.seed(seed)
random_bits_1 = "".join([str(i) for i in np.random.randint(0,2,1000)])
# reseed to same number and generate new sequence of random bits
np.random.seed(seed)
random_bits_2 = "".join([str(i) for i in np.random.randint(0,2,1000)])
# after printing, we see the bit-strings are the same
print("Random bitstring with seed:\t", random_bits_1)
print("Random bitstring with same seed:", random_bits_2)
# reseed with different seed and generate different random bit-string
np.random.seed()
random_bits_3 = "".join([str(i) for i in np.random.randint(0,2,1000)])
print("Random bitstring with new seed:\t", random_bits_3)
# + [markdown] id="kASUqHGtf-04"
# ## Quantum Random Number Generation
#
# We now demonstrate how quantum computing will get the best of both worlds (truly random numbers without the disadvantages outlined above)! For this, we rely on one of the most important concepts of quantum computing: the **qubit**, which is the fundamental unit of information storage and manipulation in a quantum computer. When we put a qubit into **superposition**, we put it into a state where we do not know if it will take on the value 0 or 1 until we measure it. However, we can control the probabilities that the qubit will collapse to either 0 or 1.
# Let’s say we have a quantum circuit with our one qubit. If we make the probability of it collapsing to 0 to be $50\%$, and the probability of it collapsing to 1 to be 50% using a **Hadamard gate**, then we can randomly generate a number between 0 and 1! This is represented in the state diagram below as the $|+\rangle$ state. (When a qubit has a $100\%$ chance of being measured as 0, it is in the $|0\rangle$ state, and the same logic applies to the $|1\rangle$ state.)
# + [markdown] id="3aJ03AFVpqwb"
# 
# + [markdown] id="KfI6pQ7TaV64"
# Quantum computers are different from classical computers in the sense that they have the ability to generate truly random numbers without any external sampling. One way to do this is to put a qubit in a perfect superposition of the $|0\rangle$ and $|1\rangle$ states. This is done by applying a Hadamard gate, shifting the qubit to the Hadamard basis described above.
# + id="d5Yn3mIIMiJB"
def stage_one_circuit():
"""Create quantum circuit for random number generation"""
qc = QuantumCircuit(1,1)
qc.h(0)
qc.measure(0,0)
return qc
# + colab={"base_uri": "https://localhost:8080/", "height": 92} id="LX1tDq5YT1Hp" outputId="26fe23ad-12ce-4e16-f254-e00b82c5c868"
# print out resulting circuit
circuit = stage_one_circuit()
circuit.draw()
# + [markdown] id="ah-OGeGve6-U"
# We can then measure the qubit in the standard basis, giving us 0 or 1 with equal probability. This method has no reliance on seeds, so repeating the process multiple times will give us completely different random bits.
# + colab={"base_uri": "https://localhost:8080/", "height": 328} id="lmOLychYQ30w" outputId="e4606fb8-7c45-4466-9710-80edc389c7e1"
# display distribution of 0's and 1's
result = aer_sim.run(circuit).result()
counts = result.get_counts()
qiskit.visualization.plot_histogram(counts)
# + [markdown] id="VkQGgiFRZdQ6"
# Great! Simply using our knowledge about a qubit’s properties, we can generate random numbers using our quantum circuit, and can also generate numbers bigger than 1 simply by stringing our bits together, all without having to get extra hardware or take the time to gather data on an external phenomenon.
# + id="J1h1O4GfRvnO"
def stage_one_random_bit_generator(random_bits_length):
"""Generate string of random bits
input -- random_bits_length: the length of the resultant string
output -- random_bits: string of random bits
ones: number of ones in random bitstring
zeros: number of zeros in random bitstring
"""
# initialize empty string, counts, and circuit
random_bits = ''
total_count = 0
ones = 0
zeros = 0
simple_circuit = stage_one_circuit()
# loop until random_bits is of length random_bits_length
while len(random_bits) < random_bits_length:
total_count += 1
# run simulation and store result
job_result = aer_sim.run(simple_circuit, shots=1).result()
result_keys = job_result.get_counts().keys()
result_int = int(list(result_keys)[0])
# increment ones or zeros and add bit to string
if result_int == 1:
ones += 1
else:
zeros += 1
random_bits += str(result_int)
return random_bits, ones, zeros
# + colab={"base_uri": "https://localhost:8080/"} id="xNRQoegNS5KZ" outputId="882901b2-9d29-4290-be86-dbfbee69bdb8"
print("One random string:\t", stage_one_random_bit_generator(100)[0])
print("Another random string:\t", stage_one_random_bit_generator(100)[0])
# + [markdown] id="vAFfOyOFepHU"
# The method of random number generation outlined above is very effective on idealized quantum circuits, but in reality, noise or imperfect state preparation may interfere with our random generation.
#
# We now introduce a slightly different quantum method for generating random numbers.
# + [markdown] id="8Cn3CnzugVco"
# ## The CHSH Game
# In this process, we develop a quantum strategy for a nonlocal game called the "CHSH game." This game is used to verify the true validity of quantum number generation.
#
# In the CHSH game (named after the CHSH inequality discovered by John Clauser, Michael Horne, Abner Shimony, and Richard Holt) , Alice and Bob receive independent random bits
# $x$ and $y$ respectively from Charlie, the referee. Their goal is to output bits $a$ and $b$ respectively
# such that $a+b=xy \pmod{2}$. No communication is allowed.
# + [markdown] id="l4vjzCEHdPL7"
# 
# + [markdown] id="hwRg0YDIdowY"
# In classical computing, we can calculate the probability of Alice and Bob winning the game by simply enumerating all of the cases for $x$, $y$, $a$, and $b$. As shown below, the highest probability we attain is $75\%$, corresponding to Alice and Bob following the strategy of always sending 0 or always sending 1.
# + [markdown] id="f7n7wnwlej50"
# 
# + [markdown] id="hRNDI8GZetGf"
# We can significantly increase our chances of winning if using a quantum computer.
# + [markdown] id="e6H-reJhjedj"
# *CHSH quantum protocol*:
#
# In an optimal quantum strategy for the game, Alice does the following:
#
# - If $x=0$, do nothing to her qubit
# - If $x=1$, apply a $\frac{\pi}{4}$ counterclockwise rotation towards $|1\rangle$ on her qubit
#
# Bob does the following:
# - if $y=0$, apply a $\frac{\pi}{8}$ counterclockwise rotation towards $|1\rangle$ on his qubit
# - if $y=1$, apply a $\frac{\pi}{8}$ clockwise rotation towards $|1\rangle$ on his qubit
#
# Alice and Bob both measure
# their qubits in the $\{|0\rangle,|1\rangle \}$ basis and output whatever they see.
# This strategy wins $\cos^2\left(\frac{\pi}{8}\right) \approx 85\%$ of the time, an improvement compared to the $75\%$ chance of winning using the classical strategy.
# + id="Q9tir0NjqNcr"
def make_chsh(x, y):
"""Create quantum circuit for CHSH protocol.
input -- x: the x input for the CHSH non-local game
y: the y input for the CHSH non-local game
output -- qc: CHSH circuit created
"""
# initialize quantum circuit with 2 qubits and 2 classical bits
qc = QuantumCircuit(2,2)
# apply Hadamard gate and control-not
qc.h(0)
qc.cx(0, 1)
# apply conditional rotations
# need to multiply the angle of rotation by 2 since Qiskit divides the angle by 2 when applying the rotation
if x == 1:
qc.ry(np.pi/2, 0)
if y == 0:
qc.ry(np.pi/4, 1)
elif y == 1:
qc.ry(-np.pi/4, 1)
qc.measure(range(2),range(2))
return qc
# + [markdown] id="Z__ACfRSj7CI"
# Below, we can see that Alice and Bob's qubits result in the winning states $|00\rangle$ or $|11\rangle$ around $85\%$ of the time when $x=0$ and $y=1$.
# + colab={"base_uri": "https://localhost:8080/", "height": 122} id="XgLGUFrJixTK" outputId="95bfb4ee-5dff-41a1-a76f-859133beb0be"
# visualize and run CHSH circuit for x = 0, y = 1
chsh_circuit = make_chsh(0,1)
result = aer_sim.run(chsh_circuit).result()
counts = result.get_counts()
chsh_circuit.draw()
# + colab={"base_uri": "https://localhost:8080/", "height": 331} id="dcKqhu_9yseO" outputId="6f42c75a-386e-434e-fb59-8a852d026311"
qiskit.visualization.plot_histogram(counts)
# + [markdown] id="W2B_LgBkm6mx"
# The other two cases when $xy=0 \pmod{2}$ also result in an $85\%$ win rate.
# + [markdown] id="QwATlVUoOeck"
# When $x=1$, $y=0$,
# + colab={"base_uri": "https://localhost:8080/", "height": 122} id="dWKJ-NjaOD9I" outputId="81c85f8b-62e0-4964-cedc-2cb83d598a3c"
# run CHSH circuit with x=1 and y=0, display results
chsh_circuit = make_chsh(1,0)
result = aer_sim.run(chsh_circuit).result()
counts = result.get_counts()
chsh_circuit.draw()
# + colab={"base_uri": "https://localhost:8080/", "height": 331} id="0sUhI2vF0xqc" outputId="1df1cf8e-48d0-4eca-de3a-e64025f2d545"
qiskit.visualization.plot_histogram(counts)
# + [markdown] id="C3TYjq63OpFu"
# When $x=0$, $y=0$,
# + colab={"base_uri": "https://localhost:8080/", "height": 122} id="Yg9l0NMuOJpI" outputId="054ab324-da43-44dc-9167-c2a7161882e1"
# run CHSH circuit with x=0 and y=0, display results
chsh_circuit = make_chsh(0,0)
result = aer_sim.run(chsh_circuit).result()
counts = result.get_counts()
chsh_circuit.draw()
# + colab={"base_uri": "https://localhost:8080/", "height": 331} id="JdGZWQbFohhh" outputId="4ec88c9a-0b53-435f-83e0-fe36af4f4522"
qiskit.visualization.plot_histogram(counts)
# + [markdown] id="vHYOkvo3lfw0"
# When $x=1$ and $y=1$, the winning states are $|01\rangle$ and $|10\rangle$. The winning states are still achieved about $85\%$ of the time.
# + colab={"base_uri": "https://localhost:8080/", "height": 122} id="ZIfZppr9qX7i" outputId="2ccd8c35-2cec-44bb-e0da-5225e22e1a72"
# run CHSH circuit with x=1 and y=1, display results
chsh_circuit = make_chsh(1,1)
result = aer_sim.run(chsh_circuit).result()
counts = result.get_counts()
chsh_circuit.draw()
# + colab={"base_uri": "https://localhost:8080/", "height": 331} id="penxf7V6rI2a" outputId="4eec6c4b-951c-40bb-fc06-877096bcf460"
qiskit.visualization.plot_histogram(counts)
# + [markdown] id="DiPn_EBQsOHx"
# ## Random Bit Generation Using CHSH
#
# We can now use this game to generate random bits. We can play the game and append Alice's resulting bit to our random bitstring, discarding any losing rounds where Alice and Bob lost the game.
# + id="CQjRtc017ZAZ"
def stage_two_random_bit_generator(random_bits_length):
"""Generate random string of bits using stage two method.
input -- random_bits_length: the length of the resulting string
output -- random_bits: string of random bits
success_rate: percent of CHSH games that were a win
ones: number of ones in resulting string
zeros: number of zeros in resulting string
"""
# initialize counts and empty string
random_bits = ''
total_count = 0
ones = 0
zeros = 0
# loop until number of random bits is equal to random_bits_length
while len(random_bits) < random_bits_length:
total_count += 1
# construct chsh circuit with two classically random bits
x,y = np.random.randint(0,2,2)
chsh_circuit = make_chsh(x,y)
# run circuit one time and store result
job_result = aer_sim.run(chsh_circuit, shots=1).result()
result_keys = job_result.get_counts().keys()
result_str = list(result_keys)[0]
# check if result satisfies win condition
a = int(result_str[1])
b = int(result_str[0])
measured_result = (a + b) % 2
predicted_result = x*y
if measured_result == predicted_result:
# append bit if win condition satisfied
random_bits += str(a)
if a == 1:
ones += 1
else:
zeros += 1
# calculate win rate and return
success_rate = np.round(random_bits_length / total_count,3)
return random_bits, success_rate, ones, zeros
# + [markdown] id="gX7uOSfBsJ_7"
# Running our above function, we see that our win rate is around $85\%$ as expected. This gives us a relatively even distribution of 1's and 0's.
# + colab={"base_uri": "https://localhost:8080/"} id="jEjjaJ9FD8LN" outputId="203de735-a6ba-474b-ecaa-5e440c650199"
length = 10000
bit_string, percentage, ones, zeros = stage_two_random_bit_generator(length)
print("Game winning rate: ", percentage * 100,"%")
print("Percentage of 1\'s: ", ones/length * 100,"%")
print("Percentage of 0\'s: ", zeros/length * 100,"%")
print("Generated string:", bit_string)
# + [markdown] id="sNOwtFd43k0b"
# Below, we plot the resulting ratios from generating lengths 1 to 250. We see that the ratios are around our desired result.
# + id="el8w5joMt_1c"
# set number of iterations
num_iterations = 250
# initialize empty lists
lengths = range(1, num_iterations+1)
win_rates = [None] * num_iterations
one_rates = [None] * num_iterations
# iterate over each length
for length in lengths:
print("Iteration:", length)
_, win_rates[length-1], one_rates[length-1], _ = stage_two_random_bit_generator(length)
one_rates[length-1] /= length
# + colab={"base_uri": "https://localhost:8080/", "height": 565} id="nR4UbD8N2GsY" outputId="3306a502-2009-484b-b361-6f032fcf8746"
plt.figure(figsize=(10, 8), dpi=80)
# plot win rates and percentage of ones
plt.plot(lengths, win_rates, label="Game winning rate")
plt.plot(lengths, one_rates, label="Percentage of 1's")
# plot desired ratios
plt.plot(lengths, [0.5]*num_iterations, label="50%", linestyle="dashed")
plt.plot(lengths, [0.85]*num_iterations, label="85%", linestyle="dashed")
# label graph
plt.xlabel("Length of Generated Bitstring")
plt.ylabel("Rate")
plt.title("Protocol Performance")
plt.legend(loc="lower right")
plt.show()
# + [markdown] id="Fr6ioNswgqiu"
# ## Running on an Actual Quantum Computer
# + [markdown] id="hVT-nB_wutpL"
# For some reason, when we sent the job to an actual quantum computer, the job gets queued up and we never got the result back no matter how long we waited. It will be good to figure out what happened.
# + id="tCZoCu7S44vK"
# Set devices, if using a real device
# IBMQ.save_account(TOKEN)
IBMQ.load_account()
provider = IBMQ.get_provider('ibm-q')
quito = provider.get_backend('ibmq_lima')
# + colab={"base_uri": "https://localhost:8080/"} id="30ReYZwi6bOA" outputId="c75644ab-6a5a-4933-cf12-bb2a7a2a31c5"
# Execute and get counts
chsh_circuit = make_chsh(0,0)
#result_ideal = sim.run(chsh_circuits).result()
tic = time.time()
transpiled_circuits = transpile(chsh_circuit, quito)
job_real = quito.run(transpiled_circuits, shots=1)
job_monitor(job_real)
result_real = job_real.result()
toc = time.time()
counts = result_real.get_counts()
print(toc-tic)
qiskit.visualization.plot_histogram(counts)
# + [markdown] id="VjTDb45rCgv9"
# # Future Work
# + [markdown] id="ikFuw6YkCoNi"
# We can still do better!
#
# With our random bit generation algorithm that uses the CHSH game, we get 0.85 quantum bit of output per two classical bits of input. We could redesign a system where we recycle the quantum bits output to generate more quantum random bits!
#
# We could possibly involve more players with this implementation.
#
#
| 1,020.747596 | 208,293 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.