problem
stringlengths 10
7.44k
| answer
stringlengths 1
270
| difficulty
stringclasses 8
values |
|---|---|---|
In a single-round-robin tournament, 10 chess players are participating. What is the minimum number of rounds after which a sole winner can be determined prematurely? (In each round, the participants are paired.
Win - 1 point, draw - 0.5 points, loss - 0).
#
|
7
|
0/8
|
Task B-2.4. A square and an equilateral triangle are inscribed in a circle of radius 1 so that they share one vertex. Determine the area of the common part of the square and the triangle.
|
2\sqrt{3} - \dfrac{9}{4}
|
0/8
|
A bus takes $2$ minutes to drive from one stop to the next, and waits $1$ minute at each stop to let passengers board. Zia takes $5$ minutes to walk from one bus stop to the next. As Zia reaches a bus stop, if the bus is at the previous stop or has already left the previous stop, then she will wait for the bus. Otherwise she will start walking toward the next stop. Suppose the bus and Zia start at the same time toward the library, with the bus $3$ stops behind. After how many minutes will Zia board the bus?
|
17
|
5/8
|
Let $R$, $S$, and $T$ be squares that have vertices at lattice points (i.e., points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the $x$-axis. The left edge of $R$ and the right edge of $S$ are on the $y$-axis, and $R$ contains $\frac{9}{4}$ as many lattice points as does $S$. The top two vertices of $T$ are in $R \cup S$, and $T$ contains $\frac{1}{4}$ of the lattice points contained in $R \cup S.$ See the figure (not drawn to scale).
[asy] size(8cm); label(scale(.8)*"$y$", (0,60), N); label(scale(.8)*"$x$", (60,0), E); filldraw((0,0)--(55,0)--(55,55)--(0,55)--cycle, yellow+orange+white+white); label(scale(1.3)*"$R$", (55/2,55/2)); filldraw((0,0)--(0,28)--(-28,28)--(-28,0)--cycle, green+white+white); label(scale(1.3)*"$S$",(-14,14)); filldraw((-10,0)--(15,0)--(15,25)--(-10,25)--cycle, red+white+white); label(scale(1.3)*"$T$",(3.5,25/2)); draw((0,-10)--(0,60),EndArrow()); draw((-34,0)--(60,0),EndArrow()); [/asy]
The fraction of lattice points in $S$ that are in $S \cap T$ is $27$ times the fraction of lattice points in $R$ that are in $R \cap T$. What is the minimum possible value of the edge length of $R$ plus the edge length of $S$ plus the edge length of $T$?
|
337
|
0/8
|
Let $x_0,x_1,x_2,\dotsc$ be a sequence of numbers, where each $x_k$ is either $0$ or $1$. For each positive integer $n$, define
$S_n = \sum\limits_{k=0}^{n-1} x_k 2^k$
Suppose $7S_n \equiv 1 \pmod{2^n}$ for all $n \geq 1$. Find the value of the sum
$x_{2019} + 2x_{2020} + 4x_{2021} + 8x_{2022}.$
|
6
|
4/8
|
The numbers from $1$ to $49$ are arranged in a spiral pattern on a square grid, beginning at the center. The first few numbers have been entered into the grid below. Consider the four numbers that will appear in the shaded squares, on the same diagonal as the number $7.$ How many of these four numbers are prime? Provide your answer as an integer.
|
3
|
3/8
|
Janet rolls a standard $6$-sided die $4$ times and keeps a running total of the numbers she rolls. Find the probability that at some point, her running total will equal $3$. Express your answer in the form \(\frac{k}{m}\) where the fraction is in simplest form, and then give the value of \(k + m\).
|
265
|
1/8
|
A digital display shows the current date as an $8$-digit integer consisting of a $4$-digit year, followed by a $2$-digit month, followed by a $2$-digit date within the month. For example, Arbor Day this year is displayed as 20230428. For how many dates in $2023$ will each digit appear an even number of times in the 8-digital display for that date? Provide your answer as an integer.
|
9
|
1/8
|
A number is chosen at random from among the first 100 positive integers, and a positive integer divisor of that number is then chosen at random. What is the probability that the chosen divisor is divisible by 11? Express your answer as a fraction in simplest form, \(\frac{m}{n}\). Please provide the value of m + n.
|
209
|
3/8
|
For $n\geq 2$ , an equilateral triangle is divided into $n^2$ congruent smaller equilateral triangles. Detemine all ways in which real numbers can be assigned to the $\frac{(n+1)(n+2)}{2}$ vertices so that three such numbers sum to zero whenever the three vertices form a triangle with edges parallel to the sides of the big triangle.
|
0
|
1/8
|
On an infinite chessboard, a solitaire game is played as follows: at the start, we have $n^2$ pieces occupying a square of side $n.$ The only allowed move is to jump over an occupied square to an unoccupied one, and the piece which has been jumped over is removed. For which $n$ can the game end with only one piece remaining on the board?
|
n
|
4/8
|
Let $n$ be a positive integer, $n \ge 2$ , and put $\theta=\frac{2\pi}{n}$ . Define points $P_k=(k,0)$ in the *xy*-plane, for $k=1,2,\dots,n$ . Let $R_k$ be the map that rotates the plane counterclockwise by the angle $\theta$ about the point $P_k$ . Let $R$ denote the map obtained by applying in order, $R_1$ , then $R_2$ , ..., then $R_n$ . For an arbitrary point $(x,y)$ , find and simplify the coordinates of $R(x,y)$ .
|
(x+n, y)
|
4/8
|
Toph wants to tile a rectangular $m\times n$ square grid with the $6$ types of tiles in the picture (moving the tiles is allowed, but rotating and reflecting is not). For which pairs $(m,n)$ is this possible?
|
(m, n)
|
4/8
|
Let $m$ be a given positive integer which has a prime divisor greater than $\sqrt {2m} +1 $ . Find the minimal positive integer $n$ such that there exists a finite set $S$ of distinct positive integers satisfying the following two conditions:
**I.** $m\leq x\leq n$ for all $x\in S$ ;
**II.** the product of all elements in $S$ is the square of an integer.
|
n = m + p
|
0/8
|
Let $p_1,p_2,p_3$ be primes with $p_2\neq p_3$ such that $4+p_1p_2$ and $4+p_1p_3$ are perfect squares. Find all possible values of $p_1,p_2,p_3$ .
|
(7, 11, 3)
|
0/8
|
For each integer $n\geq0$ , let $S(n)=n-m^2$ , where $m$ is the greatest integer with $m^2\leq n$ . Define a sequence by $a_0=A$ and $a_{k+1}=a_k+S(a_k)$ for $k\geq0$ . For what positive integers $A$ is this sequence eventually constant?
|
A
|
0/8
|
In triangle $ ABC$ , one has marked the incenter, the foot of altitude from vertex $ C$ and the center of the excircle tangent to side $ AB$ . After this, the triangle was erased. Restore it.
|
\triangle ABC
|
0/8
|
Let $\mathbb{Z}$ denote the set of all integers. Find all polynomials $P(x)$ with integer coefficients that satisfy the following property:
For any infinite sequence $a_1$ , $a_2$ , $\dotsc$ of integers in which each integer in $\mathbb{Z}$ appears exactly once, there exist indices $i < j$ and an integer $k$ such that $a_i +a_{i+1} +\dotsb +a_j = P(k)$ .
|
P(x) = ax + b
|
0/8
|
There are two round tables with $n{}$ dwarves sitting at each table. Each dwarf has only two friends: his neighbours to the left and to the right. A good wizard wants to seat the dwarves at one round table so that each two neighbours are friends. His magic allows him to make any $2n$ pairs of dwarves into pairs of friends (the dwarves in a pair may be from the same or from different tables). However, he knows that an evil sorcerer will break $n{}$ of those new friendships. For which $n{}$ is the good wizard able to achieve his goal no matter what the evil sorcerer does?
*Mikhail Svyatlovskiy*
|
n
|
2/8
|
Let $G$ be a simple connected graph. Each edge has two phases, which is either blue or red. Each vertex are switches that change the colour of every edge that connects the vertex. All edges are initially red. Find all ordered pairs $(n,k)$ , $n\ge 3$ , such that:
a) For all graph $G$ with $n$ vertex and $k$ edges, it is always possible to perform a series of switching process so that all edges are eventually blue.
b) There exist a graph $G$ with $n$ vertex and $k$ edges and it is possible to perform a series of switching process so that all edges are eventually blue.
|
(n, k)
|
3/8
|
Example 3.3.3 Let $S$ be a set composed of some positive integers not greater than 15, and any two disjoint subsets of $S$ have unequal sums of elements. Find the maximum value of the sum of elements in $S$ with this property.
|
61
|
1/8
|
3. Visiting Mumbo-Jumbo. In the language of the Mumbo-Jumbo tribe, there are only two sounds: "ы" and "y". Two words mean the same thing if one can be obtained from the other by applying a certain number of the following operations: skipping consecutive sounds "ыy" or "yyыы" and adding the sounds "yы" at any position. Do the words "yыy" and "ыyы" mean the same thing?
|
\text{No}
|
3/8
|
Example 2 After a round-robin volleyball tournament, it was found that for any two teams, there is always a third team that has defeated both of these teams. How many teams participated in the tournament at the very least?
|
7
|
2/8
|
7. (5 points)
Grandma's eyesight is poor, and she accidentally put soy sauce in the vinegar bottle, put cooking wine in the soy sauce bottle, put oil in the cooking wine bottle, and put vinegar in the oil bottle. Xiao Fei used an empty bottle to help Grandma put these seasonings back into the correct bottles. Xiao Fei poured the seasonings at least $\qquad$ times.
|
5
|
0/8
|
In a class, there are \( n \) boys and \( n \) girls (\( n \geq 3 \)). They sat around a round table such that no two boys and no two girls sit next to each other. The teacher has \( 2n \) cards with the numbers \( 1, 2, 3, \ldots, 2n \), each appearing exactly once. He distributes one card to each student in such a way that the number on any girl's card is greater than the number on any boy's card. Then each boy writes down the sum of the numbers on three cards: his own and those of the girls sitting next to him. For which values of \( n \) could all the \( n \) sums obtained be equal?
|
n \text{ is odd}
|
0/8
|
In an isosceles triangle $A B C$, points $M$ and $N$ are located on the lateral sides $A B$ and $B C$ respectively.
Find the area of triangle $A B C$, given that $A M=5, A N=2 \sqrt{37}, C M=11, C N=10$.
|
18\sqrt{21}
|
2/8
|
32. Let $1 \leqslant r \leqslant n$, in the ordered tuple $\left(x_{1}, x_{2}, \cdots, x_{r}\right)$ each $x_{j} \in\{1,2, \cdots, n\}$, and for each $i=1$, $2, \cdots, n, x_{1}, x_{2}, \cdots, x_{r}$ contains at most $i-1$ elements $\leqslant i$. Find the number of such $r$-tuples.
|
(n - r) n^{r - 1}
|
0/8
|
Rectangles $ABNF$ and $CMKD$ overlap such that their common part is the rectangle $MNFK$. It is known that $BN=8$ cm and $KD=9$ cm. Find the area of the rectangle $MNFK$ if the area of $ABMK$ is 25 cm² and the area of $CDFN$ is 32 cm².
|
40
|
1/8
|
Given a regular $2 n+1$-sided polygon. How many triangles are there whose vertices are among the vertices of the polygon and the triangle contains the center of the polygon?
|
\dfrac{(2n+1)n(n+1)}{6}
|
0/8
|
8.3. Find the largest four-digit number, all digits of which are different, and which is divisible by each of its digits. Of course, zero cannot be used.
|
9864
|
5/8
|
8. Print 90000 five-digit numbers
$$
10000,10001, \cdots, 99999
$$
on cards, with one five-digit number on each card. Some cards (such as 19806, which reads 90861 when flipped) have numbers that can be read in two different ways, causing confusion. The number of cards that will not cause confusion is $\qquad$ cards.
|
88060
|
0/8
|
2. (10 points) A rectangular piece of paper $A B C D$ is folded and pressed flat in the manner shown in the right figure, so that triangle $D C F$ falls onto the position of triangle $D E F$, with vertex $E$ landing exactly on side $A B$. Given that $\angle 1=22^{\circ}$, then $\angle 2$ is $\qquad$ degrees.
|
44
|
1/8
|
# Problem No. 6 (10 points)
A person started walking slowly along a straight line with a speed of $v_{1}=0.5 \mathrm{~m} / \mathrm{c}$. At time $t_{1}$, he turned strictly to the right and walked with a speed twice as high. After another time interval $t_{1}$, he turned strictly to the right again, and his speed became four times the initial speed. After the last right turn, he ran with a speed of $5 v_{1}$ and returned to the initial point of his trajectory. Determine his average speed over the entire path.
Answer: $1.1 \mathrm{~m} / \mathrm{c}$
#
|
1.1 \mathrm{~m} / \mathrm{c}
|
0/8
|
8.5 On an island, there live 25 people: knights, liars, and tricksters. Knights always tell the truth, liars always lie, and tricksters answer the questions posed to them in turn, alternating between truth and lies. All the islanders were asked three questions: "Are you a knight?", "Are you a trickster?", "Are you a liar?" (the questions were asked in the exact order specified). To the first question, 21 people answered affirmatively, to the second - 17 people, to the third - 6 people. How many knights live on this island?
|
4
|
2/8
|
6. A train consists of $n>1$ waggons with gold coins. Some coins are genuine and some are fake, although they all look the same and can only be distinguished by mass: all genuine coins have the same mass, and so do all fake ones, where the two masses differ. The mass of a genuine coin is known. Each waggon contains only genuine coins or only fake ones.
Find the smallest number of measurements on a digital scale by which one can determine all waggons with fake coins and find the mass of a fake coin.
(It is assumed that from each waggon one can take as many coins as needed.)
(Miloš Milosavljević)
Time allowed: 270 minutes.
Each problem is worth 7 points.
|
2
|
1/8
|
5. Let triangle $A B C$ be such that $A B=A C=22$ and $B C=11$. Point $D$ is chosen in the interior of the triangle such that $A D=19$ and $\angle A B D+\angle A C D=90^{\circ}$. The value of $B D^{2}+C D^{2}$ can be expressed as $\frac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$.
|
36104
|
0/8
|
A calculator treats angles as radians. It initially displays 1. What is the largest value that can be achieved by pressing the buttons cos or sin a total of 2001 times? (So you might press cos five times, then sin six times and so on with a total of 2001 presses.)
|
1
|
1/8
|
8. If three dice are thrown at random, the probability that the numbers shown on the three dice can serve as the side lengths of a triangle is $\qquad$ .
|
\dfrac{37}{72}
|
1/8
|
Fix 10 natural numbers \(n_1, n_2, \ldots, n_{10}\) and denote their sum by \(n = n_1 + n_2 + \cdots + n_{10}\). Suppose that \(n\) numbers \(a_1, a_2, \ldots, a_n\) are written in a row on a board, where each number is either 0 or 1. These numbers are divided into 10 groups:
\[ \underbrace{a_1, \ldots, a_{n_1}}_{n_1}, \underbrace{a_{n_1+1}, \ldots, a_{n_1+n_2}}_{n_2}, \ldots, \underbrace{a_{n_1+\cdots+n_9+1}, \ldots, a_n}_{n_{10}} \]
We call a group non-zero if it contains at least one 1. Depending on the initial numbers \(a_1, \ldots, a_n\), different numbers of non-zero groups can be obtained. We are interested in the sets \(a_1, \ldots, a_n\) that result in an even number of non-zero groups after the partition. Prove that the number of such sets \(a_1, \ldots, a_n\) (where the number of non-zero groups is even) is given by the formula:
\[ 2^{n-1} + \frac{1}{2} \cdot (2^{n_1} - 2) \cdot (2^{n_2} - 2) \cdots (2^{n_{10}} - 2) \]
|
2^{n-1} + \frac{1}{2} \cdot (2^{n_1} - 2) \cdot (2^{n_2} - 2) \cdots (2^{n_{10}} - 2)
|
2/8
|
Problem 5. Rectangle $ABCD$ is composed of three congruent rectangles (see drawing). If the perimeter of each of these rectangles is $60 \mathrm{~cm}$, what is the area of the square that has the same perimeter as rectangle $ABCD$?
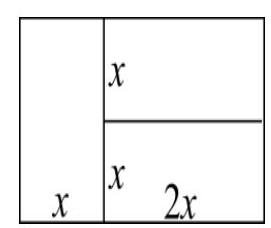
|
625
|
1/8
|
IS. 3 Consider the line $12 x-4 y+(Q-305)=0$. If the area of the triangle formed by the $x$-axis, the $y$-axis and this line is $R$ square units, what is the value of $R$ ?
|
6
|
0/8
|
2. (10 points) In each cell of a $50 \times 50$ square, a number is written that is equal to the number of $1 \times 16$ rectangles (both vertical and horizontal) in which this cell is an end cell. In how many cells are numbers greater than or equal to 3 written?
|
1600
|
2/8
|
1. On the cube $A B C D A_{1} B_{1} C_{1} D_{1}$, points $P$ and $Q$ are chosen, where $P$ is the midpoint of edge $B C$, and $Q$ is the intersection of the diagonals in the square $C C_{1} D D_{1}$. The plane $A P Q$ divides the cube into two parts. Find the ratio of the volumes of the resulting parts of the cube?
|
\dfrac{1}{5}
|
0/8
|
II. (50 points) Determine all positive integer triples $(x, y, z)$ such that $x^{3}-y^{3}=z^{2}$, where $y$ is a prime, $y \chi_{z}, 3 \nmid z$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
(8, 7, 13)
|
4/8
|
25. A sequence $\left\{a_{n}\right\}$ of real numbers is defined by $a_{1}=1$ and for all integers $n \geq 1$,
$$
a_{n+1}=\frac{a_{n} \sqrt{n^{2}+n}}{\sqrt{n^{2}+n+2 a_{n}^{2}}} .
$$
Compute the sum of all positive integers $n<1000$ for which $a_{n}$ is a rational number.
|
131
|
4/8
|
11. We notice that $6!=8 \cdot 9 \cdot 10$. Try to find the largest positive integer $n$ such that $n!$ can be expressed as the product of $n-3$ consecutive natural numbers.
|
23
|
1/8
|
73. There are $N$ chess pieces placed on a circle, as shown in the figure, with a chess piece at point $B$ adjacent to the chess piece at point $A$. Xiaohong first takes away 1 chess piece from point $B$, then moves clockwise, taking away 2 chess pieces every 1 piece, and continues for 10 rounds, crossing $A$ 9 times. When about to cross $A$ for the 10th time to take a chess piece, Xiaohong finds that there are more than 20 chess pieces left on the circle. If $N$ is a multiple of 14, then there are $\qquad$ chess pieces left on the circle.
|
23
|
2/8
|
# Problem №3
A New Year's garland hanging along the school corridor consists of red and blue bulbs. Next to each red bulb, there is definitely a blue one. What is the maximum number of red bulbs that can be in this garland if there are 50 bulbs in total?
|
33
|
3/8
|
Let $A B C D$ be a unit square, and let $P$ be a point inside triangle $A B C$. Let $E$ and $F$ be the points on $A B$ and $A D$, respectively, such that $A E P F$ is a rectangle. Let $x$ and $y$ denote the lengths of $A E$ and $A F$, respectively.
Determine a two-variable polynomial $f(x, y)$ with the property that the area of $A E P F$ is greater than the area of each of the quadrilaterals $E B C P$ and $F P C D$ if and only if $f(x, y)>0$.
|
3xy-x+y-1
|
0/8
|
2. The express passenger train, two days ago in the morning, departed from Gevgelija to Skopje, with several carriages in which there was a certain number of passengers. At the station in Veles, one passenger disembarked from the first carriage, two passengers disembarked from the last carriage, and no passengers boarded. Departing from Veles, in each carriage of the train, there was an equal number of passengers. The same train, with two fewer carriages, in the afternoon departed from Skopje to Gevgelija with 50 fewer passengers compared to the passengers who started the journey that morning from Gevgelija. At the same time, the average number of passengers per carriage was 30. How many passengers started the journey that morning from Gevgelija?
|
380
|
0/8
|
Task B-1.6. The sum of the lengths of the diagonals of a rhombus is $84 \mathrm{~cm}$. If we extend one diagonal by $4 \mathrm{~cm}$ and shorten the other diagonal by $4 \mathrm{~cm}$, the area of the rhombus will increase by $16 \mathrm{~cm}^{2}$. Calculate the length of the side and the lengths of the diagonals of this rhombus.
|
30\,
|
0/8
|
Define a sequence $a_i$ as follows: $a_1 = 181$ and for $i \ge 2$, \( a_i = a_{i-1}^2 - 1 \) if $a_{i-1}$ is odd and \( a_i = \frac{a_{i-1}}{2} \) if $a_{i-1}$ is even. Find the least $i$ such that $a_i = 0$.
|
105
|
4/8
|
There are $2012$ distinct points in the plane, each of which is to be colored using one of $n$ colors, so that the numbers of points of each color are distinct. A set of $n$ points is said to be multi-colored if their colors are distinct. Determine $n$ that maximizes the number of multi-colored sets.
|
61
|
0/8
|
In a group of $6$ people playing the card game Tractor, all $54$ cards from $3$ decks are dealt evenly to all the players at random. Each deck is dealt individually. Let the probability that no one has at least two of the same card be $X$. Find the largest integer $n$ such that the $n$th root of $X$ is rational.
|
54
|
1/8
|
There are $100$ lightbulbs $B_1, B_2, \ldots, B_{100}$ spaced evenly around a circle in this order. Additionally, there are $100$ switches $S_1, S_2, \ldots, S_{100}$ such that for all $1 \leq i \leq 100$, switch $S_i$ toggles the states of lights $B_{i-1}$ and $B_{i+1}$ (where $B_{101} = B_1$ and $B_0 = B_{100}$). Suppose David chooses whether to flick each switch with probability $\frac{1}{2}$. What is the expected number of lightbulbs which are on at the end of this process given that not all lightbulbs are off?
|
50
|
1/8
|
A box contains $900$ cards numbered from $100$ to $999$. Paulo randomly takes a certain number of cards from the box and calculates the sum of the digits for each card. How many cards does Paulo need to take out of the box to ensure finding at least three cards with the same digit sum?
|
53
|
5/8
|
Find the number of positive integers less than or equal to $2017$ that have at least one pair of adjacent digits that are both even. For example, count the numbers $24$, $1862$, and $2012$, but not $4$, $58$, or $1276$.
|
738
|
3/8
|
Let triangle $ABC$ have side lengths $AB = 13$, $BC = 14$, $AC = 15$. Let $I$ be the incenter of $\triangle ABC$. The circle centered at $A$ with radius $AI$ intersects the circumcircle of $\triangle ABC$ at points $H$ and $J$. Let $L$ be a point that lies on both the incircle of $\triangle ABC$ and line $HJ$. If the minimal possible value of $AL$ is $\sqrt{n}$, where $n \in \mathbb{Z}$, find $n$.
|
17
|
4/8
|
Let $a > 1$ be a positive integer. The sequence of natural numbers $\{a_n\}_{n \geq 1}$ is defined such that $a_1 = a$ and for all $n \geq 1$, $a_{n+1}$ is the largest prime factor of $a_n^2 - 1$. Determine the smallest possible value of $a$ such that the numbers $a_1, a_2, \ldots, a_7$ are all distinct.
|
46
|
2/8
|
For a positive integer $n$ not divisible by $211$, let $f(n)$ denote the smallest positive integer $k$ such that $n^k - 1$ is divisible by $211$. Find the remainder when $\sum_{n=1}^{210} nf(n)$ is divided by $211$.
|
48
|
4/8
|
Hapi, the god of the annual flooding of the Nile, is preparing for this year's flooding. The shape of the channel of the Nile can be described by the function $y = \frac{-1000}{x^2+100}$, where the $x$ and $y$ coordinates are in meters. The current depth of the river is $5$ meters. Hapi plans to increase the water level by $3$ meters. How many meters wide will the river be after the flooding? The depth of the river is always measured at its deepest point.
|
40
|
5/8
|
In a $4 \times 4$ table, we place $k$ blocks such that:
1. Each block covers exactly 2 cells.
2. Each cell is covered by at least one block.
3. If we remove a block, there is at least one cell that is not covered.
Find the maximum value of $k$.
Note: The blocks can overlap.
|
12
|
2/8
|
A regular pentagon with area \(\sqrt{5}+1\) is printed on paper and cut out. The five vertices of the pentagon are folded into the center of the pentagon, creating a smaller pentagon. What is the area of the new pentagon? The original answer is in the form of \(n - \sqrt{m}\). Please find the value of m + n.
|
6
|
4/8
|
Jean has made a piece of stained glass art in the shape of two mountains, as shown in the figure below. One mountain peak is $8$ feet high while the other peak is $12$ feet high. Each peak forms a $90^\circ$ angle, and the straight sides form a $45^\circ$ angle with the ground. The artwork has an area of $183$ square feet. The sides of the mountain meet at an intersection point near the center of the artwork, $h$ feet above the ground. What is the value of $h$?
|
5
|
0/8
|
Find the value of $\left(1+\cos \frac{\pi}{7}\right)\left(1+\cos \frac{3 \pi}{7}\right)\left(1+\cos \frac{5 \pi}{7}\right)$. The original answer is in the form \frac{k}{m}, where k and m are integers. Please provide the value of k + m.
|
15
|
4/8
|
Example 3 Given the equation in $x$
$$
x^{3}-a x^{2}-2 a x+a^{2}-1=0
$$
has exactly one real root. Find the range of real values for $a$.
|
(-\infty, \dfrac{3}{4})
|
2/8
|
4. Given a line $l$ passing through the point $F(a, 0)$ (not perpendicular to the $x$-axis) intersects the curve $C: y^{2}=4 a x$ at points $A$ and $B$. Let point $K(-a, 0)$, and the angle between $\boldsymbol{K A}$ and $\boldsymbol{K B}$ be $\theta$. Then the range of $\theta$ is $\qquad$.
|
(0, \frac{\pi}{2})
|
1/8
|
# 8.2. Condition:
On an island, there are two tribes: knights, who always tell the truth, and liars, who always lie. Four islanders lined up, each 1 meter apart from each other.
- The leftmost in the row said: "My fellow tribesman in this row stands 2 meters away from me."
- The rightmost in the row said: "My fellow tribesman in this row stands 2 meters away from me."
It is known that there are two knights and two liars in the row. What distances could the second and third islanders from the left have mentioned? List all possible options.
## Options for matching:
Second islander $\quad 1$ m
Third islander $\quad 2$ m
3 m
$4$ m
#
|
1
|
3/8
|
2. Let $n(A)$ denote the number of subsets of $A$. Given $|A|=|B|=100, n(A)+$ $n(B)+n(C)=n(A \cup B \cup C)$. Find the minimum value of $|A \cap B \cap C|$.
|
97
|
2/8
|
Example 36 (1992 Shanghai High School Competition Question) Let $n$ be a given natural number, $n \geqslant 3$, and for $n$ given real numbers $a_{1}, a_{2}, \cdots, a_{n}$, denote the minimum value of $\left|a_{i}-a_{j}\right|(1 \leqslant i<j \leqslant n)$ as $m$. Find the maximum value of $m$ under the condition that $a_{1}^{2}+a_{2}^{2}+\cdots+a_{n}^{2}=$ 1.
|
\sqrt{\dfrac{12}{n(n^{2}-1)}}
|
0/8
|
72. In the expression $(1+x+y)^{20}$, the brackets are expanded, but similar terms are not combined. How many terms will be obtained in this case?
|
3^{20}
|
2/8
|
4.2. (Belgium, 79). Find the sum of all $7!$ numbers that can be obtained by all possible permutations of the digits in the number 1234567.
|
22399997760
|
5/8
|
11. Given a sequence $\left\{a_{n}\right\}$ whose terms are all non-negative, the sum of its first $n$ terms is $S_{n}$, and for any $n \in N^{*}$, we have
$$
a_{n+1} \leq \frac{a_{n}+a_{n+2}}{2} \text {. }
$$
(1) If $a_{1}=1, a_{505}=2017$, find the maximum value of $a_{6}$;
(2) If for any $n \in N^{*}$, we have $S_{n} \leq 1$, prove that $0 \leq a_{n}-a_{n+1} \leq \frac{2}{n(n+1)}$.
|
21
|
3/8
|
$2 \cdot 32$ Let $A$ be a set of integers, where the smallest element is 1 and the largest element is 100. Except for 1, each element is equal to the sum of two elements in $A$ (which can be twice a single element). Find the minimum number of elements in set $A$.
|
9
|
3/8
|
3. $A B D E, B C E F, C D F A$ - cyclic quadrilaterals with the intersection points of the diagonals $K, L$ and $M$ respectively. It is known that point $K$ lies on segments $B L$ and $A M$, point $M$ - on segment $C L$. Moreover, $E L=F L=K L=5, D M=4, A K=M K=6$. Find the length of segment $M C$. If there are multiple possible answers, list them in any order separated by a semicolon.
|
4
|
0/8
|
C4. Let $f(x)=x^{2}-a x+b$, where $a$ and $b$ are positive integers.
(a) Suppose $a=2$ and $b=2$. Determine the set of real roots of $f(x)-x$, and the set of real roots of $f(f(x))-x$.
(b) Determine the number of pairs of positive integers $(a, b)$ with $1 \leq a, b \leq 2011$ for which every root of $f(f(x))-x$ is an integer.
|
\{1, 2\}
|
0/8
|
** A set of good points on a plane, where any three points are vertices of a right triangle. Determine the maximum number of points this set can contain.
|
4
|
5/8
|
Choose a permutation of$ \{1,2, ..., 20\}$ at random. Let $m$ be the amount of numbers in the permutation larger than all numbers before it. Find the expected value of $2^m$.
[i]Proposed by Evan Chang (squareman), USA[/i]
|
21
|
2/8
|
5. The diagonals of a regular pentagon with a side length of 1 form a new, smaller regular pentagon. What is the length of the side of the smaller pentagon?
Solve the problems independently. You have 150 minutes to solve them.
The use of notes, literature, or a pocket calculator is not allowed.
## Problems for 4th Grade
|
\dfrac{3 - \sqrt{5}}{2}
|
5/8
|
2. Each vertex of the right-angled triangle $A B C$ with legs $\overline{A B}=4 \sqrt{3}$ and $\overline{A C}=4$ is the center of a circle such that the three circles touch each other and no circle lies inside another circle. Calculate the area of the part of triangle $A B C$ that lies outside the three circles.
|
\dfrac{8}{3} \left(3\sqrt{3} - 5\pi + 2\sqrt{3}\pi\right)
|
0/8
|
5. In a regular tetrahedron \( P-ABC \), \( AB=1, AP=2 \). A plane \( \alpha \) passing through \( AB \) bisects its volume. Then the cosine of the angle between edge \( PC \) and plane \( \alpha \) is \(\qquad\).
(2017, National High School Mathematics League)
|
\dfrac{3\sqrt{5}}{10}
|
4/8
|
Two unit squares are placed in the plane such that the center of one square is a vertex of the other square. What is the area of the common part of the two squares?
|
\dfrac{1}{4}
|
4/8
|
In a certain sequence of 80 numbers, any term, except for the two endpoints, is equal to the product of its neighboring terms. The product of the first 40 terms of the sequence is 8 and the product of all the terms is also 8. Determine the terms of the sequence.
|
2
|
0/8
|
3. Postman Pechkin is riding a bicycle along a highway. He noticed that every 4.5 kilometers, a suburban bus overtakes him, and every 9 minutes, a suburban bus passes him in the opposite direction. The interval of bus movement in both directions is 12 minutes. At what speed is Pechkin riding?
|
15
|
0/8
|
Equilateral triangle $ABC$ has side length $2$ . A semicircle is drawn with diameter $BC$ such that it lies outside the triangle, and minor arc $BC$ is drawn so that it is part of a circle centered at $A$ . The area of the “lune” that is inside the semicircle but outside sector $ABC$ can be expressed in the form $\sqrt{p}-\frac{q\pi}{r}$ , where $p, q$ , and $ r$ are positive integers such that $q$ and $r$ are relatively prime. Compute $p + q + r$ .

|
10
|
3/8
|
p1. How many $10$ -digit strings are there, such that all its digits are only zeros or ones and the sum of its even-place digits equals the sum of the odd-place digits.
p2. Find all pairs $(x, y)$ of nonnegative integers, such that $x! + 24 = y^2$ .
p3. Consider a function $f: Z \to Q$ such that $$ f(1) = 2015 \,\,\, \,\, f (1) + f (2) + ...+ f (n) = n^2 f (n). $$ Determine the value of $f(2015)$ .
p4. Let $ABC$ be an isosceles triangle with $AB = AC$ , and let $D$ be the midpoint of $BC$ , $E$ the foot of the perpendicular on $AB$ from $D$ , and F the midpoint of $DE$ . Show that $AF$ is perpendicular to $CE$ .
p5. On an island there are only two tribes: the Mienteretes who always lie and the Veritas who always tell the truth. On a certain day there is an assembly attended by $2015$ inhabitants of the island. They sit at random in a circle and each one declares: "the two people next to me are Mienteretes." The next day the assembly continues but one of them became ill, for which $2014$ inhabitants attend, again they sit at random in a circle and each one declares: “The two people next to me are from the same tribe, which is not mine ”.
Deduct the number of inhabitants of each tribe and the type of inhabitant to which the patient belongs.
|
252
|
1/8
|
There exist two distinct positive integers, both of which are divisors of $10^{10}$ , with sum equal to $157$ . What are they?
|
32,125
|
0/8
|
Let $ \omega$ be a circle with center O and radius 10, and let H be a point such that $OH = 6$ . A point P is called snug if, for all triangles ABC with circumcircle ω and orthocenter $H$ ,
we have that P lies on $\triangle$ ABC or in the interior of $\triangle$ ABC. Find the area of the region consisting of all snug points.
|
20\pi
|
1/8
|
For problem 11 , i couldn’t find the correct translation , so i just posted the hungarian version . If anyone could translate it ,i would be very thankful .
[tip=see hungarian]Az $X$ ́es $ Y$ valo ́s ́ert ́eku ̋ v ́eletlen v ́altoz ́ok maxim ́alkorrel ́acio ́ja az $f(X)$ ́es $g(Y )$ v ́altoz ́ok korrela ́cio ́j ́anak szupr ́emuma az olyan $f$ ́es $g$ Borel m ́erheto ̋, $\mathbb{R} \to \mathbb{R}$ fu ̈ggv ́enyeken, amelyekre $f(X)$ ́es $g(Y)$ v ́eges sz ́ora ́su ́. Legyen U a $[0,2\pi]$ interval- lumon egyenletes eloszl ́asu ́ val ́osz ́ınu ̋s ́egi v ́altozo ́, valamint n ́es m pozit ́ıv eg ́eszek. Sz ́am ́ıtsuk ki $\sin(nU)$ ́es $\sin(mU)$ maxim ́alkorrela ́ci ́oja ́t. [/tip]
Edit:
<details><summary>Translation thanks to @tintarn</summary>The maximal correlation of two random variables $X$ and $Y$ is defined to be the supremum of the correlations of $f(X)$ and $g(Y)$ where $f,g:\mathbb{R} \to \mathbb{R}$ are measurable functions such that $f(X)$ and $g(Y)$ is (almost surely?) finite.
Let $U$ be the uniformly distributed random variable on $[0,2\pi]$ and let $m,n$ be positive integers. Compute the maximal correlation of $\sin(nU)$ and $\sin(mU)$ .
(Remark: It seems that to make sense we should require that $E[f(X)]$ and $E[g(Y)]$ as well as $E[f(X)^2]$ and $E[g(Y)^2]$ are finite.
In fact, we may then w.l.o.g. assume that $E[f(X)]=E[g(Y)]=0$ and $E[f(Y)^2]=E[g(Y)^2]=1$ .)</details>
|
0
|
3/8
|
There is a pile with $15$ coins on a table. At each step, Pedro choses one of the piles in the table with $a>1$ coins and divides it in two piles with $b\geq1$ and $c\geq1$ coins and writes in the board the product $abc$ . He continues until there are $15$ piles with $1$ coin each. Determine all possible values that the final sum of the numbers in the board can have.
|
1120
|
4/8
|
In the diagram, congruent rectangles $ABCD$ and $DEFG$ have a common vertex $D$ . Sides $BC$ and $EF$ meet at $H$ . Given that $DA = DE = 8$ , $AB = EF = 12$ , and $BH = 7$ . Find the area of $ABHED$ .

|
54
|
3/8
|
Let $BCB'C'$ be a rectangle, let $M$ be the midpoint of $B'C'$ , and let $A$ be a point on the circumcircle of the rectangle. Let triangle $ABC$ have orthocenter $H$ , and let $T$ be the foot of the perpendicular from $H$ to line $AM$ . Suppose that $AM=2$ , $[ABC]=2020$ , and $BC=10$ . Then $AT=\frac{m}{n}$ , where $m$ and $n$ are positive integers with $\gcd(m,n)=1$ . Compute $100m+n$ .
*Proposed by Ankit Bisain*
|
2102
|
1/8
|
Define the Fibonacci numbers via $F_0=0$ , $f_1=1$ , and $F_{n-1}+F_{n-2}$ .
Olivia flips two fair coins at the same time, repeatedly, until she has flipped a tails on both, not necessarily on the same throw. She records the number of pairs of flips $c$ until this happens (not including the last pair, so if on the last flip both coins turned up tails $c$ would be $0$ ). What is the expected value $F_c$ ?
|
\frac{19}{11}
|
1/8
|
$f(n)$ is the least number that there exist a $f(n)-$ mino that contains every $n-$ mino.
Prove that $10000\leq f(1384)\leq960000$ .
Find some bound for $f(n)$
|
10000\lef(1384)\le960000
|
2/8
|
Let $ABCD$ and $BCFG$ be two faces of a cube with $AB=12.$ A beam of light emanates from vertex $A$ and reflects off face $BCFG$ at point $P,$ which is 7 units from $\overline{BG}$ and 5 units from $\overline{BC}.$ The beam continues to be reflected off the faces of the cube. The length of the light path from the time it leaves point $A$ until it next reaches a vertex of the cube is given by $m\sqrt{n},$ where $m$ and $n$ are integers and $n$ is not divisible by the square of any prime. Find $m+n.$
|
230
|
3/8
|
The figure shows a (convex) polygon with nine vertices. The six diagonals which have been drawn dissect the polygon into the seven triangles: $P_{0}P_{1}P_{3}$ , $P_{0}P_{3}P_{6}$ , $P_{0}P_{6}P_{7}$ , $P_{0}P_{7}P_{8}$ , $P_{1}P_{2}P_{3}$ , $P_{3}P_{4}P_{6}$ , $P_{4}P_{5}P_{6}$ . In how many ways can these triangles be labeled with the names $\triangle_{1}$ , $\triangle_{2}$ , $\triangle_{3}$ , $\triangle_{4}$ , $\triangle_{5}$ , $\triangle_{6}$ , $\triangle_{7}$ so that $P_{i}$ is a vertex of triangle $\triangle_{i}$ for $i = 1, 2, 3, 4, 5, 6, 7$ ? Justify your answer.

|
1
|
3/8
|
Let $A$ , $B$ , $C$ , $D$ , $E$ , $F$ be $6$ points on a circle in that order. Let $X$ be the intersection of $AD$ and $BE$ , $Y$ is the intersection of $AD$ and $CF$ , and $Z$ is the intersection of $CF$ and $BE$ . $X$ lies on segments $BZ$ and $AY$ and $Y$ lies on segment $CZ$ . Given that $AX = 3$ , $BX = 2$ , $CY = 4$ , $DY = 10$ , $EZ = 16$ , and $FZ = 12$ , find the perimeter of triangle $XYZ$ .
|
\frac{77}{6}
|
3/8
|
Let $O$ be the centre of the square $ABCD$ . Let $P,Q,R$ be respectively on the segments $OA,OB,OC$ such that $OP=3,OQ=5,OR=4$ . Suppose $S$ is on $OD$ such that $X=AB\cap PQ,Y=BC\cap QR$ and $Z=CD\cap RS$ are collinear. Find $OS$ .
|
\frac{60}{23}
|
3/8
|
In an archery competition, there are 30 contestants. The target is divided into two zones. A hit in zone 1 is awarded 10 points, while a hit in zone 2 is awarded 5 points. No points are awarded for a miss. Each contestant shoots 16 arrows. At the end of the competition, statistics show that more than 50% of the arrows hit zone 2. The number of arrows that hit zone 1 and missed the target are equal. Prove that there are two contestants with the same score.
|
2
|
4/8
|
Tim the Beaver can make three different types of geometrical figures: squares, regular hexagons, and regular octagons. Tim makes a random sequence \( F_{0}, F_{1}, F_{2}, F_{3}, \ldots \) of figures as follows:
- \( F_{0} \) is a square.
- For every positive integer \( i \), \( F_{i} \) is randomly chosen to be one of the 2 figures distinct from \( F_{i-1} \) (each chosen with equal probability \(\frac{1}{2}\)).
- Tim takes 4 seconds to make squares, 6 to make hexagons, and 8 to make octagons. He makes one figure after another, with no breaks in between.
Suppose that exactly 17 seconds after he starts making \( F_{0} \), Tim is making a figure with \( n \) sides. What is the expected value of \( n \)?
|
7
|
1/8
|
Subsets and Splits
Filtered Answers A-D
Retrieves 100 rows where the answer is a single letter from A to D, providing basic filtering of the dataset.