problem
stringlengths 10
7.44k
| answer
stringlengths 1
270
| difficulty
stringclasses 8
values |
|---|---|---|
Subiectul IV. (20 puncte) Fie matricele $A=\left(\begin{array}{ccc}1 & a & a^{2} \\ 1 & 2 & 4 \\ 1 & 3 & 9\end{array}\right)$ si $B=\left(\begin{array}{ccc}1 & 2 a & a^{2} \\ 1 & 4 & 4 \\ 1 & 6 & 9\end{array}\right)$.
a) Scrieți rezultatul determinantului $\operatorname{det}\left(A \cdot B^{t}\right)$ sub formă de produs;
b) Scrieți rezultatul determinantului $D=\left|\begin{array}{lll}\left(x^{2}+1\right)^{2} & (x y+1)^{2} & (x z+1)^{2} \\ (x y+1)^{2} & \left(y^{2}+1\right)^{2} & (y z+1)^{2} \\ (x z+1)^{2} & (y z+1)^{2} & \left(z^{2}+1\right)^{2}\end{array}\right|$ sub formă de produs. prof. Anca Cristina Hodorogea, ISJ Cluj
Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.
SUCCES!
Timp efectiv de lucru - 3 ore.
## Barem clasa a XI-a (OLM 2014-etapa locală)
## Of. $10 \mathrm{p}$
|
2(a-2)^2(a-3)^2
|
0/8
|
187. Elementary arithmetic. Here is one question similar to those that were so popular in Venice (and not only there) in the mid-16th century. Their appearance was largely due to Niccolò Fontana, better known as Tartaglia (the stammerer).
If a quarter of twenty were four, then what would a third of ten be?
|
\dfrac{8}{3}
|
2/8
|
Two circles, the radii of which are in the ratio $9-4 \sqrt{3}$, touch each other internally. Two chords of the larger circle, equal in length and tangent to the smaller circle, are drawn. One of these chords is perpendicular to the segment connecting the centers of the circles, while the other is not. Find the angle between these chords.
|
30^\circ
|
2/8
|
Problem 11.8. In each cell of a strip $1 \times N$ there is either a plus or a minus. Vanya can perform the following operation: choose any three cells (not necessarily consecutive), one of which is exactly in the middle between the other two cells, and change the three signs in these cells to their opposites. A number $N$ is called positive if from an arrangement of $N$ minuses Vanya can, by such operations, obtain an arrangement of $N$ pluses.
Consider the numbers $3,4,5, \ldots, 1400$. How many of them are positive?
|
1396
|
0/8
|
11. (12 points) If a three-digit number $\overline{\mathrm{abc}}$ (where $a, b, c$ are all non-zero digits) satisfies $\overline{\mathrm{ab}}>\overline{\mathrm{bc}}>\overline{\mathrm{ca}}$, then the three-digit number is called a “Longteng number”. How many “Longteng numbers” are there?
|
120
|
2/8
|
6. Solve the equation $\sqrt{2 x^{2}+3 x+2}-\sqrt{2 x^{2}+3 x-5}=1$.
|
2
|
1/8
|
In the figure, \( \mathrm{P} \) is a point on the diagonal \( \mathrm{ED} \) of \( \triangle \mathrm{ABCD} \) such that \( \angle \mathrm{PCB} = \angle \mathrm{ACD} \). The circumcircle of \( \triangle \mathrm{ABD} \) intersects the diagonal \( \mathrm{AC} \) at point \( \mathrm{E} \). Prove that \( \angle \mathrm{AED} = \angle \mathrm{PEB} \).
|
\angle \mathrm{AED} = \angle \mathrm{PEB}
|
3/8
|
Given a triangle \( \triangle ABC \) with orthocenter \( H \), points \( D \) and \( E \) lie on sides \( AB \) and \( AC \) respectively such that \( D \), \( H \), and \( E \) are collinear and \( AD = AE \). Extend \( DE \) to intersect the circumcircle \( \odot O \) of \( \triangle ABC \) at points \( F \) and \( G \). Perpendiculars drawn from \( D \) and \( E \) to \( AB \) and \( AC \) respectively intersect at point \( K \). Extend \( HK \) to intersect \( \odot O \) at point \( L \). Lines \( FL \) and \( GL \) intersect \( BC \) at points \( P \) and \( Q \) respectively. Prove that points \( L \), \( P \), \( O \), and \( Q \) are concyclic.
|
L, P, O, Q \text{ are concyclic}
|
0/8
|
Janka drew a rectangle with a perimeter of $22 \mathrm{~cm}$ and side lengths expressed in centimeters as whole numbers. Then she divided the rectangle without any remainder into three rectangles, one of which had dimensions $2 \mathrm{~cm} \times 6 \mathrm{~cm}$. The sum of the perimeters of all three rectangles was $18 \mathrm{~cm}$ greater than the perimeter of the original rectangle. What could be the dimensions of the original rectangle? Find all solutions.
(M. Dillingerová)
Idea. Determine how Janka could have divided the rectangle; for each individual possibility, then express the given difference in perimeters using the lengths of the dividing lines.
|
3 \times 8
|
0/8
|
In how many ways can you write $12$ as an ordered sum of integers where the smallest of those integers is equal to $2$? For example, $2+10$, $10+2$, and $3+2+2+5$ are three such ways.
|
70
|
3/8
|
4.9 On a $10 \times 10$ grid paper, there are 11 horizontal grid lines and 11 vertical grid lines. A line segment connecting two adjacent nodes on the same straight line is called a "link segment". How many link segments need to be erased at least, so that at most 3 link segments remain at each node?
|
41
|
5/8
|
Given a divisor (non-zero) and a dividend, there is always a quotient and a remainder such that:
\[ \text{Dividend} = \text{Divisor} \times \text{Quotient} + \text{Remainder} \]
where \( 0 \leq \text{Remainder} < \text{Divisor} \). This is known as division with remainder. When the remainder is 0, the divisor is said to divide the dividend exactly, or the divisor is called a factor of the dividend (the dividend is a multiple of the divisor).
Please list all natural numbers greater than 1 and not exceeding 88 that can be exactly divided by 6.
|
6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84
|
1/8
|
5. In an arbitrary triangular pyramid $A B C D$, a section is made by a plane intersecting the edges $A B, D C$, and $D B$ at points $M, N, P$ respectively. Point $M$ divides edge $A B$ in the ratio $A M: M B=1: 2$. Point $N$ divides edge $D C$ in the ratio $D N: N C=3: 2$. Point $P$ divides edge $D B$ in the ratio $D P: P B=2$. Find the ratio $A Q: Q C$.
|
\dfrac{3}{8}
|
5/8
|
Problem 4. Each cell of a $3 \times 3$ table is painted in one of three colors such that cells sharing a side have different colors. Among all possible such colorings, find the proportion of those in which exactly two colors are used.
|
\dfrac{1}{41}
|
3/8
|
Values for $A,B,C,$ and $D$ are to be selected from $\{1, 2, 3, 4, 5, 6\}$ without replacement (i.e. no two letters have the same value). How many ways are there to make such choices so that the two curves $y=Ax^2+B$ and $y=Cx^2+D$ intersect? (The order in which the curves are listed does not matter; for example, the choices $A=3, B=2, C=4, D=1$ is considered the same as the choices $A=4, B=1, C=3, D=2.$) Find the number of ways.
|
90
|
5/8
|
Let \(ABCD\) be an isosceles trapezoid having parallel bases \(\overline{AB}\) and \(\overline{CD}\) with \(AB>CD.\) Line segments from a point inside \(ABCD\) to the vertices divide the trapezoid into four triangles whose areas are \(2, 3, 4,\) and \(5\) starting with the triangle with base \(\overline{CD}\) and moving clockwise as shown in the diagram below. The original answer for the ratio \(\frac{AB}{CD}\) is in the form \(k+\sqrt{m}\). Please find the value of \(k+m\).
|
4
|
1/8
|
A fair $6$-sided die is repeatedly rolled until an odd number appears. What is the probability that every even number appears at least once before the first occurrence of an odd number? Express your answer in the form \(\frac{k}{m}\), where k and m are integers with no common factors other than 1. Find the value of k + m.
|
21
|
4/8
|
For each positive integer $n$, let $f_1(n)$ be twice the number of positive integer divisors of $n$, and for $j \ge 2$, let $f_j(n) = f_1(f_{j-1}(n))$. Find the number of values of $n \le 50$ for which $f_{50}(n) = 12$.
|
10
|
4/8
|
Let $ABCDEF$ be an equiangular hexagon. The lines $AB, CD,$ and $EF$ determine a triangle with area $192\sqrt{3}$, and the lines $BC, DE,$ and $FA$ determine a triangle with area $324\sqrt{3}$. The perimeter of hexagon $ABCDEF$ can be expressed as $m +n\sqrt{p}$, where $m, n,$ and $p$ are positive integers and $p$ is not divisible by the square of any prime. Find the value of $m + n + p$.
|
55
|
2/8
|
Inside a right circular cone with base radius \(5\) and height \(12\) are three congruent spheres with radius \(r\). Each sphere is tangent to the other two spheres and also tangent to the base and side of the cone. Find the radius \(r\) of each sphere. The original answer is in the form \(\frac{k-n\sqrt{3}}{m}\). Please give the value of \(k+n+m\).
|
141
|
1/8
|
Ang, Ben, and Jasmin each have $5$ blocks, colored red, blue, yellow, white, and green; and there are $5$ empty boxes. Each of the people randomly and independently of the other two people places one of their blocks into each box. The probability that at least one box receives $3$ blocks all of the same color is \(\frac{m}{n}\), where \(m\) and \(n\) are relatively prime positive integers. Please calculate the value of \(m + n\).
|
471
|
2/8
|
Each of the $5$ sides and the $5$ diagonals of a regular pentagon are randomly and independently colored red or blue with equal probability. What is the probability that there will be a triangle whose vertices are among the vertices of the pentagon such that all of its sides have the same color? Provide your answer as a fraction in simplest form, \(\frac{k}{m}\), and find the value of \(k + m\).
|
509
|
2/8
|
Let $S$ be the set of lattice points in the coordinate plane, both of whose coordinates are integers between $1$ and $30,$ inclusive. Exactly $300$ points in $S$ lie on or below a line with equation $y=mx.$ The possible values of $m$ lie in an interval of length $\frac{a}{b},$ where $a$ and $b$ are relatively prime positive integers. Find the value of $a+b.$
|
85
|
1/8
|
Problem 11.7. Natural numbers $a$ and $b$ are such that $a^{a}$ is divisible by $b^{b}$, but $a$ is not divisible by $b$. Find the smallest possible value of the number $a+b$, given that the number $b$ is coprime with 210.
|
374
|
5/8
|
A: There are 7 boxes arranged in a row and numbered 1 through 7 . You have a stack of 2015 cards, which you place one by one in the boxes. The first card is placed in box \#1, the second in box \#2, and so forth up to the seventh card which is placed in box \#7. You then start working back in the other direction, placing the eighth card in box \#6, the ninth in box \#5, up to the thirteenth card being placed in box \#1. The fourteenth card is then placed in box \#2, and this continues until every card is distributed. What box will the last card be placed in?
|
3
|
4/8
|
3. The fields of a board with 25 rows and 125 columns are alternately colored black and white (like the fields on a chessboard), and knight figures are placed on it, which attack according to special rules. A knight on a white field attacks all white fields in the same row and all black fields in the same column, while a knight on a black field attacks all black fields in the same row and all white fields in the same column (even if there is another figure in between). Determine the maximum number of knights that can be placed on the board so that they do not attack each other.
|
50
|
4/8
|
The sequence $\left\{a_{n}\right\}$ is defined as follows: $a_{1}=0, a_{2}=1, a_{n}=\frac{1}{2} n a_{n-1} + \frac{1}{2} n(n-1) a_{n-2} + (-1)^{n}\left(1-\frac{n}{2}\right)$ for $n \geqslant 3$. Find the simplest expression for $f_n = a_n + 2 \binom{n}{1} a_{n-1} + 3 \binom{n}{2} a_{n-2} + \cdots + (n-1) \binom{n}{n-2} a_2 + n \binom{n}{n-1} a_1$.
|
2n! - n - 1
|
4/8
|
The sides of the blue and green equilateral triangles are parallel. The perimeter of the blue triangle is 4, and the perimeter of the green triangle is 5. Find the perimeter of the hexagon formed by the intersection of these triangles.
|
3
|
0/8
|
4. At the end of a chess tournament, it was determined that each participant had earned exactly half of their points playing against the competitors who finished in the last three places. How many participants were there in the tournament?
(Each participant played one game against each of the other participants. A win earns one point, a draw earns half a point, and a loss earns no points.)
|
9
|
4/8
|
2. In an acute triangle $ABC$, $AD$, $DE$, $CF$ are altitudes, $H$ is the orthocenter of the triangle. If $EF$ bisects the area of triangle $ABC$, then $DE^2 + EF^2 + FD^2 =$ $\qquad$ (Given the side lengths of the triangle are $3$, $2\sqrt{2}$, $\sqrt{5}$)
|
5
|
5/8
|
15.8 (League 2001) $D, E$ are points on side $BC$ of $\triangle ABC$, $F$ is a point on the extension of $BA$, $\angle DAE = \angle CAF$.
(1) Determine the positional relationship between the circumcircle of $\triangle ABD$ and the circumcircle of $\triangle AEC$, and prove your conclusion.
(2) If the circumradius of $\triangle ABD$ is twice that of $\triangle AEC$, $BC=6, AB=4$, find the length of $BE$.
---
(1) To determine the positional relationship between the circumcircle of $\triangle ABD$ and the circumcircle of $\triangle AEC$, we need to analyze the given angles and the geometric properties of the circles.
Given:
- $\angle DAE = \angle CAF$
- $D$ and $E$ are on $BC$
- $F$ is on the extension of $BA$
Since $\angle DAE = \angle CAF$, we can infer that the points $A, D, E, F$ are concyclic. This means that the circumcircle of $\triangle ADE$ passes through $F$.
Now, consider the circumcircle of $\triangle ABD$ and the circumcircle of $\triangle AEC$. Since $\angle DAE = \angle CAF$, the points $A, D, E, F$ lie on a common circle. Therefore, the circumcircle of $\triangle ABD$ and the circumcircle of $\triangle AEC$ intersect at points $A$ and $E$.
Thus, the circumcircle of $\triangle ABD$ and the circumcircle of $\triangle AEC$ are **intersecting** at points $A$ and $E$.
(2) Given that the circumradius of $\triangle ABD$ is twice that of $\triangle AEC$, and $BC = 6$, $AB = 4$, we need to find the length of $BE$.
Let the circumradius of $\triangle AEC$ be $R$ and the circumradius of $\triangle ABD$ be $2R$.
Using the circumradius formula for a triangle:
\[ R = \frac{abc}{4K} \]
where $a, b, c$ are the sides of the triangle and $K$ is the area of the triangle.
For $\triangle AEC$:
\[ R = \frac{AE \cdot AC \cdot EC}{4K_{AEC}} \]
For $\triangle ABD$:
\[ 2R = \frac{AB \cdot AD \cdot BD}{4K_{ABD}} \]
Since $AB = 4$ and $BC = 6$, let $BE = x$ and $EC = 6 - x$.
Using the fact that the circumradius of $\triangle ABD$ is twice that of $\triangle AEC$, we can set up the following relationship:
\[ 2 \left( \frac{AE \cdot AC \cdot EC}{4K_{AEC}} \right) = \frac{4 \cdot AD \cdot BD}{4K_{ABD}} \]
Simplifying, we get:
\[ 2 \left( \frac{AE \cdot AC \cdot (6 - x)}{4K_{AEC}} \right) = \frac{4 \cdot AD \cdot (x + 4)}{4K_{ABD}} \]
Since the areas $K_{AEC}$ and $K_{ABD}$ are proportional to the product of the sides, we can simplify further:
\[ 2 \left( \frac{AE \cdot AC \cdot (6 - x)}{4K_{AEC}} \right) = \frac{4 \cdot AD \cdot (x + 4)}{4K_{ABD}} \]
Given that the circumradius relationship holds, we can solve for $x$:
\[ 2 \left( \frac{AE \cdot AC \cdot (6 - x)}{4K_{AEC}} \right) = \frac{4 \cdot AD \cdot (x + 4)}{4K_{ABD}} \]
Since the areas are proportional, we can simplify to:
\[ 2(6 - x) = x + 4 \]
Solving for $x$:
\[ 12 - 2x = x + 4 \]
\[ 12 - 4 = 3x \]
\[ 8 = 3x \]
\[ x = \frac{8}{3} \]
Thus, the length of $BE$ is:
\[ \boxed{\frac{8}{3}} \]
|
\dfrac{8}{3}
|
1/8
|
Ivan the Tsarevich fought with the three-headed and three-tailed Zmey Gorynych. With one blow, he could cut off either one head, one tail, two heads, or two tails. But if he cut off one tail, two would grow back; if he cut off two tails, a head would grow back; if he cut off a head, a new head would grow back, and if he cut off two heads, nothing would grow back. How should Ivan the Tsarevich act to cut off all the heads and all the tails of the Zmey as quickly as possible
|
9
|
1/8
|
1. How many pairs of numbers $(a, b)$ with $a<b$ can you choose from the set $1,2,3, \ldots, 2005$ such that $a+b$ is a multiple of 5?
|
401802
|
3/8
|
C1. The positive integer $N$ has six digits in increasing order. For example, 124689 is such a number.
However, unlike 124689 , three of the digits of $N$ are 3,4 and 5 , and $N$ is a multiple of 6 . How many possible six-digit integers $N$ are there?
|
3
|
2/8
|
3. Find the smallest natural number $n$, such that among any $n$ irrational numbers, there always exist 3 numbers, the sum of any two of which is still an irrational number.
|
5
|
3/8
|
11. Given positive integers $a, b, c, d$ satisfy $a^{2}+2 a=c d+11 c+d+10, b^{2}-2 b=c d-11 c+d-12$, then the sum of all possible values of $d$ is $\qquad$.
|
72
|
1/8
|
99***. A rod is broken into two parts at a randomly chosen point; then the larger of the two resulting parts is again broken into two parts at a randomly chosen point. What is the probability that a triangle can be formed from the three resulting pieces?
|
2 \ln 2 - 1
|
5/8
|
3. On a wooden ruler, three marks are made: 0, 7, and 11 centimeters. How can you measure a segment of (a) 8 cm; (b) 5 cm using it?
|
8
|
0/8
|
3. In a dark room, a drawer contains socks of two colors and two sizes, 4 pairs in total (one pair of each color and size). How many socks must be taken out to ensure that there are two pairs of different colors and different sizes?
|
7
|
2/8
|
Example 35 (1999 Shanghai High School Competition Question) Let $a, b, c, d$ be four distinct real numbers such that $\frac{a}{b}+\frac{b}{c}+\frac{c}{d}+\frac{d}{a}=4$, and $a c=b d$. Find the maximum value of $\frac{a}{c}+\frac{b}{d}+\frac{c}{a}+\frac{d}{b}$.
|
-12
|
3/8
|
2. Two circles touch each other externally and each touches a larger circle internally. The radius of one is half, and that of the other is one-third of the radius of the largest circle. Find the ratio of the length of the segment of the common internal tangent to the smaller circles, contained within the largest, to its diameter.
#
|
\dfrac{2\sqrt{6}}{5}
|
1/8
|
4. Squirrel Pusistik and Lohmatik ate a basket of berries and a bag of seeds, which contained more than 50 but less than 65 seeds, starting and finishing at the same time. At first, Pusistik ate berries, and Lohmatik ate seeds, then (at some point) they switched. Lohmatik ate berries six times faster than Pusistik, and seeds only three times faster. How many seeds did Lohmatik eat if Lohmatik ate twice as many berries as Pusistik?
|
54
|
5/8
|
25. Let $\dot{P}$ be a 40 -sided convex polygon. Find the number of triangles $S$ formed by the vertices of $P$ such that any two vertices of $S$ are separated by at least two other vertices of $P$.
|
7040
|
0/8
|
As points $A, B, C, D$ move in the plane, $A D=B C=2$ and $A C=B D=4$ always hold, furthermore, segments $A C$ and $B D$ intersect. How does the distance $C D$ depend on the distance $A B$?
|
\dfrac{12}{AB}
|
1/8
|
1. In parallelograms $A B C D$ and $A E F D$, heights $B P=7$ and $F Q=10$ are drawn to the side $A D$. Find the length of the perpendicular from point $C$ to $E F$. If there are multiple possible values, list them in any order separated by a semicolon.
|
3;17
|
0/8
|
A circle $\omega$ of radius 1 is given. A collection $T$ of triangles is called good, if the following conditions hold: (i) each triangle from $T$ is inscribed in $\omega$; (ii) no two triangles from $T$ have a common interior point. Determine all positive real numbers $t$ such that, for each positive integer $n$, there exists a good collection of $n$ triangles, each of perimeter greater than $t$. (South Africa)
A circle $\omega$ of radius 1 is given. A collection $T$ of triangles is called good, if the following conditions hold: (i) each triangle from $T$ is inscribed in $\omega$; (ii) no two triangles from $T$ have a common interior point. Determine all positive real numbers $t$ such that, for each positive integer $n$, there exists a good collection of $n$ triangles, each of perimeter greater than $t$. (South Africa)
|
4
|
2/8
|
## 139. Math Puzzle $12 / 76$
Ralf and Marion had set their watches, real "vintages," at the beginning of a longer hike. At the destination, Marion's watch shows 13:46 and Ralf's 14:13.
What time is it really, if Marion's watch gains 2 minutes daily and Ralf's old alarm clock loses 4 minutes daily?
|
13:55
|
3/8
|
## Zadatak B-2.5.
Duljina osnovice jednakokračnog trokuta $A B C$ iznosi $|B C|=30 \mathrm{~cm}$, a duljina kraka $|A C|=17 \mathrm{~cm}$. U točki $A$ povučena je okomica na pravac $A C$. Odredite omjer u kojem ova okomica dijeli osnovicu $\overline{B C}$.
|
161:289
|
2/8
|
C2. We consider a triangle $A B C$ and a point $D$ on the extension of $A B$ towards $B$. The point $E$ lies on the side $A C$ such that angle $\angle D B C$ and angle $\angle D E C$ are equal. The intersection of $D E$ and $B C$ is $F$. Suppose that $|B F|=2,|B D|=3,|A E|=4$ and $|A B|=5$. (Note: the image below is not to scale.)
(a) Show that the triangles $\triangle A B C$ and $\triangle A E D$ are similar.
(b) Determine $|C F|$.
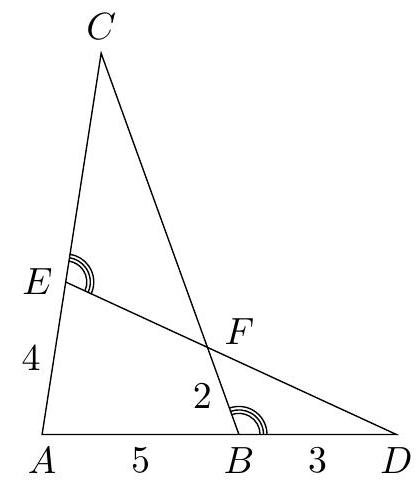
|
8
|
2/8
|
4. We will call a number $\mathrm{X}$ "20-supporting" if for any 20 real numbers $a_{1}, \ldots, a_{20}$, the sum of which is an integer, there exists at least one for which $\left|a_{i}-\frac{1}{2}\right| \geq X$.
In your answer, specify the largest 20-supporting $X$, rounded to the thousandths according to standard mathematical rules.
|
0.025
|
1/8
|
11. Choose three different digits from $0,1, \cdots, 9$ to form a four-digit number (one of the digits can appear twice), such as 5 224. Then the total number of such four-digit numbers is $\qquad$.
|
3888
|
5/8
|
5. In the rectangular prism $A B C D-A_{1} B_{1} C_{1} D_{1}$, the angle between $A B_{1}$ and $A_{1} D$ is $\alpha$, the angle between $A C$ and $B C_{1}$ is $\beta$, and the angle between $A_{1} C_{1}$ and $C D_{1}$ is $\gamma$. Therefore, $\alpha+\beta+\gamma=$ $\qquad$ .
|
180^\circ
|
3/8
|
6. Given the sets $A=\{1,2,3,4,5,6\}, B=$ $\{6,7,8,9\}$, by selecting 3 elements from $A$ and 2 elements from $B$, we can form $\qquad$ new sets with 5 elements.
|
90
|
3/8
|
Two flagpoles with heights of 5 meters and 3 meters stand on a horizontal ground. If the coordinates of the bases of the two flagpoles are determined as \( A(-5,0) \) and \( B(5,0) \) respectively, then the locus of points on the ground where the angles of elevation to the tops of the poles are equal is $\quad$ .
|
\left(x - \frac{85}{8}\right)^2 + y^2 = \left(\frac{75}{8}\right)^2
|
0/8
|
Find all quadruples $(a, b, c, d)$ of non-negative integers such that $a b = 2(1 + c d)$ and there exists a non-degenerate triangle with sides of length $a - c$, $b - d$, and $c + d$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
(1, 2, 0, 1)
|
0/8
|
I Noticed that 2023 China Western Mathematical Olympiad has not added to collection yet so I made it [url=https://artofproblemsolving.com/community/c3513189]here[/url].
I am not sure if other problems were posted. If it was, please add the link under here, thanks!
|
2023
|
3/8
|
1.74 Suppose the network lines drawn on the paper consist of $n$ horizontal lines and $n$ vertical lines. How many different closed broken lines of $2 n$ segments can be drawn along these network lines, such that each broken line passes through each horizontal line and each vertical line?
|
\dfrac{(n!)(n-1)!}{2}
|
0/8
|
\section*{Problem 1}
A book contains 30 stories. Each story has a different number of pages under 31. The first story starts on page 1 and each story starts on a new page. What is the largest possible number of stories that can begin on odd page numbers?
|
23
|
4/8
|
## 27. Large Families
The Martens have more children than the Duponts. Suppose the difference of the squares of these two numbers is 24 and that both families have more than one child. How many children do the Martens have?
70
|
7
|
5/8
|
Example 2. Solve the equation $y^{\prime \prime \prime}+y^{\prime}=x^{4}$.
|
y = C_1 + C_2 \cos x + C_3 \sin x + \frac{1}{5}x^5 - 4x^3 + 24x
|
5/8
|
15. (4b, 8-11) In Anchuria, a checkers championship is being held in several rounds. The days and cities for the rounds are determined by a draw. According to the championship rules, no two rounds can take place in the same city, and no two rounds can take place on the same day. Among the fans, a lottery is organized: the main prize goes to the person who correctly guesses before the championship begins in which cities and on which days all the rounds will take place. If no one guesses correctly, the main prize will go to the championship organizing committee. There are eight cities in Anchuria, and the championship is allocated a total of eight days. How many rounds should the organizing committee schedule to have the highest probability of winning the main prize themselves?
|
6
|
2/8
|
4 $[\underline{\text { Tangent Spheres }}]$
A cone contains five equal spheres. Four of them lie on the base of the cone, each touching two others lying on the base and the lateral surface of the cone. The fifth sphere touches the lateral surface and the other four spheres. Find the volume of the cone if the radius of each sphere is $r$.
|
\dfrac{(25 + 22\sqrt{2})}{3} \pi r^3
|
0/8
|
6. On the table, there are three cones standing on their bases, touching each other. The radii of their bases are 10, 15, and 15. A truncated cone is placed on the table with its smaller base down, and it shares a generatrix with each of the other cones. Find the area of the smaller base of the truncated cone.
|
4\pi
|
3/8
|
3. Let the line $y=-\frac{1}{2} x+1$ intersect the $x$-axis and $y$-axis at points $B$ and $A$, respectively. Point $C$ is the reflection of point $B$ over the $y$-axis. Construct an isosceles right triangle $\triangle ACD$ with $AC$ as one of the legs in the second quadrant. Draw $DE \perp x$-axis at point $E$. If the line $y=kx-2k$ divides the quadrilateral $OADE$ into two regions of equal area, then $k=$ . $\qquad$
|
-\dfrac{3}{14}
|
2/8
|
8. Given that $A$, $B$, and $C$ are three points on the parabola $y^{2}=x$, and $\left(2, \frac{4}{3}\right)$ is the centroid of $\triangle A B C$. Then the maximum value of the area of $\triangle A B C$ is $\qquad$ .
|
\dfrac{\sqrt{3}}{9}
|
4/8
|
Exercise 2. In the figure below, the triangles ABO, BCO, CDO, DEO, and FEO are right isosceles triangles. We assume that $\mathrm{OA}=8 \mathrm{~cm}$. Determine the area of $A O F$ in $\mathrm{cm}^{2}$.
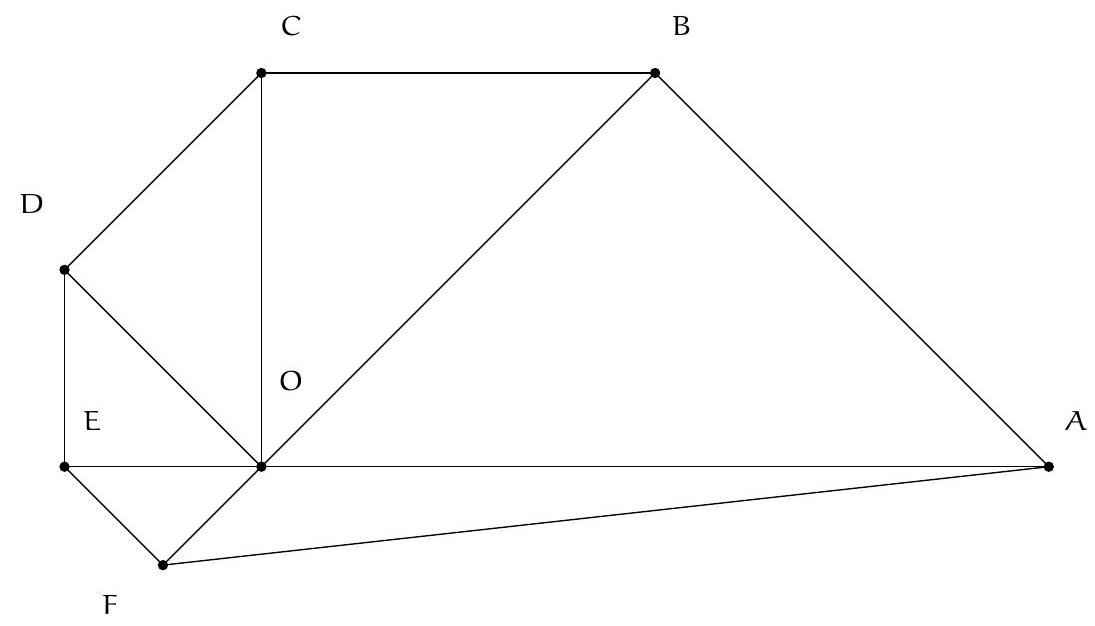
|
4
|
0/8
|
7.5. One hundred non-zero integers are written in a circle such that each number is greater than the product of the two numbers following it in a clockwise direction. What is the maximum number of positive numbers that can be among these 100 written numbers?
|
50
|
4/8
|
\section*{Problem 6B - 131236B}
Let \(M\) be the set of all points \(P(x, y)\) in a plane rectangular Cartesian coordinate system, where \(x, y\) are rational integers, and \(0 \leq x \leq 4\) and \(0 \leq y \leq 4\).
Determine the probability that the distance between two different points chosen arbitrarily from \(M\) is a rational integer (the unit of measurement being the unit of the coordinate system).
Hint: If \(n\) is the number of different ways to choose two points and \(m\) is the number of ways in which the distance is a rational integer, then the quotient \(\frac{m}{n}\) is the probability to be determined. Two selection possibilities are considered different if and only if the sets of points (each consisting of two points) selected in them are different.
|
\dfrac{9}{25}
|
2/8
|
6. On Pandora, the population sizes of each country are different. The 24 countries with the smallest populations account for $45 \%$ of the global population, while the 13 countries with the largest populations account for $26 \%$ of the global population. Therefore, Pandora has $\qquad$ countries.
|
52
|
0/8
|
In quadrilateral $A B C D$, it is known that $D O=4, B C=5, \angle A B D=45^{\circ}$, where $O$ is the point of intersection of the diagonals. Find $B O$, if the area of quadrilateral $A B C D$ is equal to $\frac{1}{2}(A B \cdot C D+B C \cdot A D)$.
|
3
|
0/8
|
Example 2 - (83 College Entrance Examination
Mathematics for Science Students, Question 7)
As shown in the figure, it is known that the length of the major axis of the ellipse
is $\left|A_{1} A_{2}\right|=6$, and the focal distance
$\left|\mathbf{F}_{\mathbf{1}} \mathbf{F}_{\mathbf{2}}\right|=4 \sqrt{\mathbf{2}}$. A line is drawn through
the focus $\mathrm{F}_{1}$ of the ellipse,
intersecting the ellipse at points $\mathrm{M}$ and $\mathrm{N}$. Let $\angle \mathrm{F}_{2} \mathrm{~F}_{1} \mathrm{M}=\alpha(0 \leqslant \alpha \leqslant \pi)$,
for what value of $\alpha$ is $|\mathrm{MN}|$ equal to the length of the minor axis of the ellipse?
|
\dfrac{\pi}{6}
|
3/8
|
Task B-2.5. The ages of a father and his two children (they are not twins) are powers of the same prime number. A year ago, the ages of each of them were prime numbers. How old is the father, and how old is each of his two children?
|
32
|
0/8
|
[ [Ratio of areas of triangles with a common base or common height] Rearrangement of areas Pentagons
Given a convex pentagon $A B C D E$. The area of each of the triangles $A B C, B C D, C D E, D E A, E A B$ is $S$. Find the area of the given pentagon.
#
|
\dfrac{(5 + \sqrt{5})}{2} S
|
0/8
|
A quadrilateral has two adjacent sides of lengths 2 and 1 units, respectively, and the included angle between them is $60^{\circ}$. The quadrilateral is both a cyclic and a tangential quadrilateral. What are the lengths of the other two sides of the quadrilateral?
|
\dfrac{\sqrt{33} - 3}{6}
|
2/8
|
Problem 9.7. The numbers $1, 2, 3, \ldots, 57$ are written on a board. What is the maximum number of these numbers that can be chosen so that no two chosen numbers differ exactly by a factor of 2.5?
|
48
|
1/8
|
12th Balkan 1995 Problem 1 Define a n by a 3 = (2 + 3)/(1 + 6), a n = (a n-1 + n)/(1 + n a n-1 ). Find a 1995 . Solution
|
\dfrac{1991009}{1991011}
|
0/8
|
Problem 9.8. A group of kids decided to play a computer game. Any two people either play together or against each other; moreover, if player $A$ plays together with $B$, and $B$ plays against $C$, then $A$ also plays against $C$. How many kids are in the group if each player had exactly 15 opponents? List all possible options.
|
16
|
1/8
|
Problem 8.8. In how many ways can all natural numbers from 1 to 200 be painted in red and blue so that the sum of any two different numbers of the same color is never equal to a power of two?
|
256
|
0/8
|
2. Decipher the ciphertext message LFDPH LVDZL FRQTX HUHG that has been enciphered using the Caesar cipher.
|
I CAME I SAW I CONQUERED
|
0/8
|
11.2. On the board, there are 4 numbers. Vasya multiplied the first of these numbers by $\sin \alpha$, the second - by $\cos \alpha$, the third - by $\operatorname{tg} \alpha$, and the fourth - by $\operatorname{ctg} \alpha$ (for some angle $\alpha$) and obtained a set of the same 4 numbers (possibly in a different order). What is the maximum number of different numbers that could have been written on the board?
|
3
|
0/8
|
8. In a certain World Cup, the Brazilian team has a probability of $\frac{1}{2}$ to win against each opponent, a probability of $\frac{1}{3}$ to draw, and a probability of $\frac{1}{6}$ to lose. Winning a match earns 3 points, drawing earns 1 point, and losing earns 0 points. It is known that each team plays three matches in the group stage, and 4 points or more are required to advance from the group. In the knockout stage, if the teams draw, they go to a penalty shootout. It is known that Brazil's probability of winning a penalty shootout is $\frac{3}{5}$. What is the probability that Brazil will win the championship and have exactly one penalty shootout in the four knockout matches? $\qquad$
|
\dfrac{1}{12}
|
2/8
|
Example 2. In Rt $\triangle A B C$, $\angle C=90^{\circ}, \angle A B C$ $=66^{\circ}, \triangle A B C$ is rotated around $C$ to the position of $\triangle A^{\prime} B^{\prime} C^{\prime}$, with vertex $B$ on the hypotenuse $A^{\prime} B^{\prime}$, and $A^{\prime} C$ intersects $A B$ at $D$. Find $\angle B D C$. (1993, Huanggang Region, Hubei Province Junior High School Mathematics Competition)
|
72^\circ
|
2/8
|
Find the number of permutations of $1, 2, 3, 4, 5, 6$ such that for each $k$ with $1$ $\leq$ $k$ $\leq$ $5$ , at least one of the first $k$ terms of the permutation is greater than $k$ .
Please give the answer directly without any intermediate steps.
|
461
|
1/8
|
Let \(\omega_{1}\) and \(\omega_{2}\) be two circles with radii \(r_{1}\) and \(r_{2}\), tangent at a point \(T\), with \(\omega_{1}\) inside \(\omega_{2}\). Let \(K \in \omega_{1}\) be different from \(T\). The tangent to \(\omega_{1}\) at \(K\) intersects \(\omega_{2}\) at points \(A\) and \(B\). Let \(S\) be the midpoint of the arc \(\widehat{AB}\) of \(\omega_{2}\) that does not contain \(T\).
Show that the radius of the circumcircle of \(\triangle AKS\) does not depend on \(K\), and express it in terms of \(r_{1}\) and \(r_{2}\).
|
\sqrt{r_2(r_2 - r_1)}
|
0/8
|
Example 2. The lengths of the three sides of $\triangle ABC$ are $BC=17$, $CA=18$, and $AB=19$. Through a point $P$ inside $\triangle ABC$, perpendiculars $PD$, $PE$, and $PF$ are drawn to the three sides of $\triangle ABC$ ($D$, $E$, and $F$ are the feet of the perpendiculars), and $BD + CE + AF = 27$. Find the length of $BD + BF$. (5th National Junior High School Mathematics Correspondence Competition)
|
18
|
5/8
|
Three numbers \( x, y, z \) are given. It is known that each of the numbers \( 2x - y \), \( 3y - 2z \), and \( 4z - 3x \) is negative. Prove that each of the numbers \( x, y, z \) is also negative?
|
x < 0,\ y < 0,\ z < 0
|
0/8
|
20. On the table, there are param 1 externally identical coins. It is known that among them, there are exactly param 2 counterfeit ones. You are allowed to point to any two coins and ask whether it is true that both these coins are counterfeit. What is the minimum number of questions needed to guarantee getting at least one "Yes" answer?
| param1 | param2 | |
| :---: | :---: | :---: |
| 105 | 53 | |
| 129 | 65 | |
| :---: | :---: | :---: |
| 167 | 84 | |
| 125 | 63 | |
| 207 | 104 | |
|
54
|
2/8
|
3.1. (16 points) A square with a side of 36 cm was cut into three rectangles such that the areas of all three rectangles are equal and any two rectangles share a common boundary segment. What is the total length (in cm) of the cuts made?
|
60
|
2/8
|
1st ASU 1961 problems Problem 6 (a) A and B move clockwise with equal angular speed along circles center P and Q respectively. C moves continuously so that AB=BC=CA. Establish C's locus and speed. *(b) ABC is an equilateral triangle and P satisfies AP=2, BP=3. Establish the maximum possible value of CP. Solution (a) Represent A, B as complex numbers z 1 + w 1 e it , z 2 + w 2 e it . Then C is (z 1 + w 1 e it ) + (z 2 + w 2 e it - z 1 - w 1 e it ) e i π/3 , which is also of the form z + w e it . However, there is one subtlety. There are actually two circles possible for C depending on which side of AB we place it. The continuity requirement means that C is normally confined to one of the circles. However, if A and B ever coincide then C may be able to switch to the other circle. If we regard "moves continuously" as allowing a discontinuous velocity, then a switch is always possible (provided A and B coincide). (b)
|
5
|
1/8
|
3. Ivan Semenov is taking a Unified State Exam (USE) in mathematics. The exam consists of three types of tasks: A, B, and C. For each task of type A, there are four answer options, only one of which is correct. There are 10 such tasks in total. Tasks of types B and C require detailed answers. Since Ivan constantly skipped classes, his knowledge of mathematics is shallow. He answers tasks of type A by guessing. The first task of type B, Ivan solves with a probability of $\frac{1}{3}$. He cannot solve anything else. For a correct answer to one task of type A, 1 point is awarded, and for a task of type B, 2 points. What is the probability that Ivan will score more than 5 points?
Take the tasks of type A from the 2008 USE practice version. (http://ege.edu.ru/demo/math.zip) and conduct the experiment of randomly selecting answers 10 times. Compare the result with the theoretical one (for 5 correct answers). Ensure that the results do not differ significantly.
#
|
0.088
|
3/8
|
Consider three diameters of a sphere that are mutually perpendicular. Divide each diameter into 4 equal parts. Through each division point, draw a plane perpendicular to the corresponding diameter. How many regions does the sphere’s surface get divided into by the 9 circles formed by these 9 planes?
- How many regions does the sphere’s surface get divided into if each of the 3 diameters is divided into 6 equal parts, and we proceed similarly?
|
56
|
0/8
|
In square $ABCD,$ points $E$ and $F$ are chosen in the interior of sides $BC$ and $CD$, respectively. The line drawn from $F$ perpendicular to $AE$ passes through the intersection point $G$ of $AE$ and diagonal $BD$. A point $K$ is chosen on $FG$ such that $|AK|= |EF|$. Find $\angle EKF.$
|
135^\circ
|
5/8
|
11. (2002 National Competition Question) Real numbers $a, b, c$ and a positive number $\lambda$ make $f(x)=x^{3}+a x^{2}+b x+c$ have three real roots $x_{1}, x_{2}, x_{3}$, and satisfy
(1) $x_{2}-x_{1}=\lambda$; (2) $x_{3}>\frac{1}{2}\left(x_{1}+x_{2}\right)$.
Find the maximum value of $\frac{2 a^{3}+27 c-9 a b}{\lambda^{3}}$.
|
\dfrac{3\sqrt{3}}{2}
|
5/8
|
Four. (18 points) As shown in Figure 6, given $\triangle A B C$, and $S_{\triangle A B C}=$ 1. $D, E$ are moving points on $A C, A B$ respectively, $B D$ and $C E$ intersect at point $P$, such that $S_{\text {quadrilateral } B C D E}=$ $\frac{16}{9} S_{\triangle B P C}$. Find the maximum value of $S_{\triangle D E P}$.
|
\dfrac{1}{18}
|
2/8
|
4. On a glade, two firs, each 30 meters tall, grow 20 meters apart from each other. The branches of the firs grow very densely, and among them are some that are directed straight towards each other, and the length of each branch is half the distance from it to the top. A spider can crawl up or down the trunk (strictly vertically), along the branches (strictly horizontally), or descend vertically down a web from one branch to another. What is the shortest distance the spider will have to crawl to get from the top of one fir to the top of the other?
|
60
|
2/8
|
3. Let $E$ be a point on the side $AB$ of square $ABCD$ such that $|AE|=3|EB|$, and let $F$ be a point on the side $DA$ such that $|AF|=5|FD|$. Denote the intersection of segments $DE$ and $FC$ by $K$, the intersection of $DE$ and $BF$ by $L$, and the intersection of $FB$ and $EC$ by $M$. Let $p_{1}$ be the sum of the areas of triangles $EML$ and $DKC$, and $p_{2}$ be the sum of the areas of triangles $FLK$ and $MBC$. Determine the ratio $p_{1}: p_{2}$.
|
1:1
|
2/8
|
[ $\left[\begin{array}{ll}\text { Cylinder } & \\ \text { Cone } & \end{array}\right]$ [ Tangent spheres $]$
A cylinder with a base radius of 1 and height $\frac{12}{3+2 \sqrt{3}}$ has three identical spheres inscribed in it such that the spheres touch the upper base of the cylinder, its lateral surface, and each other. Find the volume of the cone whose base coincides with the lower base of the cylinder and which touches all three spheres.
|
\dfrac{4\pi}{9}
|
2/8
|
An iguana writes the number 1 on the blackboard. Every minute afterwards, if the number $x$ is written, the iguana erases it and either writes $\frac{1}{x}$ or $x+1$. Can the iguana eventually write the number $\frac{20}{17}$ ?
|
\dfrac{20}{17}
|
5/8
|
15. This year, our country's team will be participating in the 59th International Mathematical Olympiad, to be held in Cluj-Napoca, Romania. The IMO, which was first held in 1959 also in Romania, has been held annually except in 1980 , when it was cancelled due to internal strife in its host country. Which East Asian country was supposed to host the 1980 IMO?
|
Mongolia
|
0/8
|
12.444 The base of the pyramid is an equilateral triangle. One of the lateral faces of the pyramid is perpendicular to the plane of the base. Find the cosine of the angle between the other two lateral faces, if they form an angle \(\alpha\) with the plane of the base.
|
\dfrac{1 - 3\cos^2 \alpha}{2}
|
5/8
|
Subsets and Splits
Filtered Answers A-D
Retrieves 100 rows where the answer is a single letter from A to D, providing basic filtering of the dataset.